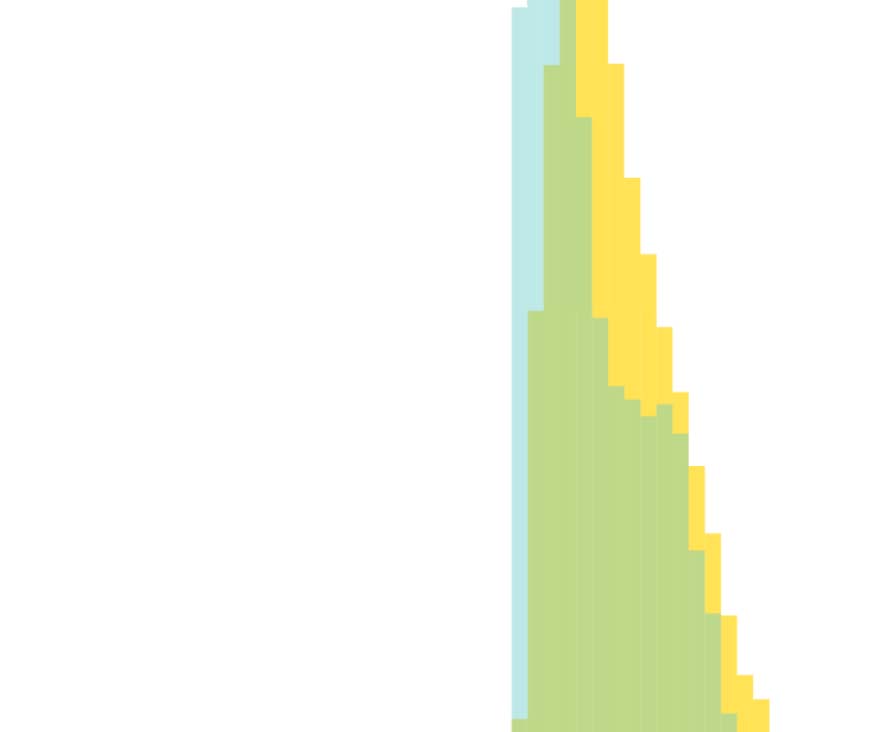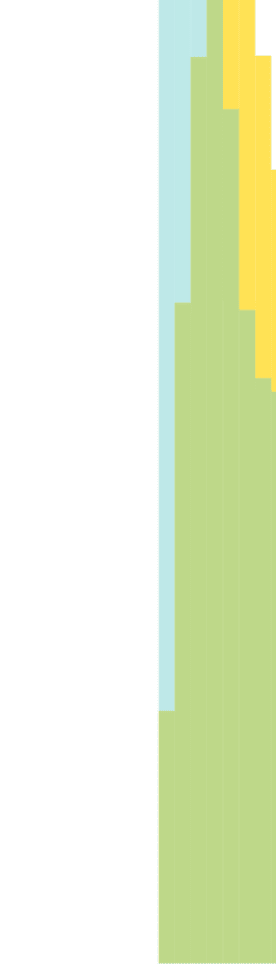INVESTIGACIÓN
Circuit analysis of the Drosophila brain using
connectivity-based neuronal classification reveals
organization of key communication pathways
Ketan Mehta1
, Rebecca F. Goldin2
, and Giorgio A. Ascoli1
1Department of Bioengineering and Center for Neural Informatics, Structures, and Plasticity,
George Mason University, Fairfax, Virginia, EE.UU
2Department of Mathematical Sciences and Center for Neural Informatics, Structures, and Plasticity,
George Mason University, Fairfax, Virginia, EE.UU
un acceso abierto
diario
Palabras clave: Fruit fly connectome, Neural circuits, Dopaminergic hub, Cell type classification,
Functional pathways, Multisensory integration
ABSTRACTO
We present a functionally relevant, quantitative characterization of the neural circuitry of
Drosophila melanogaster at the mesoscopic level of neuron types as classified exclusively
based on potential network connectivity. Starting from a large neuron-to-neuron brain-wide
connectome of the fruit fly, we use stochastic block modeling and spectral graph clustering to
group neurons together into a common “cell class” if they connect to neurons of other classes
according to the same probability distributions. We then characterize the connectivity-based
cell classes with standard neuronal biomarkers, including neurotransmitters, developmental
birthtimes, morphological features, spatial embedding, and functional anatomy. Mutual
information indicates that connectivity-based classification reveals aspects of neurons that are
not adequately captured by traditional classification schemes. Próximo, using graph theoretic and
random walk analyses to identify neuron classes as hubs, sources, or destinations, we detect
pathways and patterns of directional connectivity that potentially underpin specific functional
interactions in the Drosophila brain. We uncover a core of highly interconnected dopaminergic
cell classes functioning as the backbone communication pathway for multisensory integration.
Additional predicted pathways pertain to the facilitation of circadian rhythmic activity, spatial
orientación, fight-or-flight response, and olfactory learning. Our analysis provides experimentally
testable hypotheses critically deconstructing complex brain function from organized connectomic
architecture.
RESUMEN DEL AUTOR
The potential synaptic circuitry of a neural system constitutes the fundamental architectural
underpinning of its in vivo dynamics, plasticity, y funciones. The fruit fly neural circuit
presented here captures the latent stochastic patterns of network connectivity and provides a
fundamental parts list for reverse engineering brain computation. Mapping the interactions
among connectivity-based neuronal classes to development, morfología, physiology, y
transcriptomics result in testable hypotheses on the relationship between whole-brain neural
architecture and behavior.
Citación: Mehta, K., Goldin, R. F., &
Ascoli, GRAMO. A. (2023). Circuit analysis
of the Drosophila brain using
connectivity-based neuronal
classification reveals organization of
key communication pathways. Red
Neurociencia, 7(1), 269–298. https://doi
.org/10.1162/netn_a_00283
DOI:
https://doi.org/10.1162/netn_a_00283
Supporting Information:
https://doi.org/10.1162/netn_a_00283
https://github.com/ k3t3n/ FlyConn
Recibió: 19 Junio 2022
Aceptado: 6 Octubre 2022
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Giorgio A. Ascoli
ascoli@gmu.edu
Editor de manejo:
Jason MacLean
Derechos de autor: © 2022
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
Connectome:
A brain-wide map of neural
connectivity established either at the
level of individual neurons
(microscale), subpopulation of
neuronas (mesoscale), or parcellated
anatomical regions (macroscale).
Cell type or cell class:
A grouping used to identify cells by
subsets of multifarious properties
including but not limited to anatomy,
morfología, physiology, y
biochemistry.
estocástico:
Described by a random probability
distribución.
Graph:
A formalization of a network in
which the nodes and their
interactions are represented as
vertices and edges, respectivamente.
INTRODUCCIÓN
While it is well established that the brain is composed of distinct cell types, the extent of this
cellular diversity remains a long-standing open question in neuroscience (Zeng & Que no es,
2017). A popular approach to studying brain computation is to model the nervous system
as a giant interconnected network of these distinct cell types, each playing a specific role.
The underlying assumption is that the intricate connectivity patterns of the neural network
constitute the fundamental architectural underpinning of its in vivo dynamics and functions
(Abbott et al., 2020; Jonas & cordón, 2015). Desde esta perspectiva, quantitatively character-
izing the distinct cell types and their relation to synaptic circuitry is paramount to deconstruct-
ing brain computation.
Recent advancements in data acquisition and imaging techniques have enhanced our
ability to construct very large scale maps of the neural circuitry in the form of connectomes.
Macroscale connectomes are well suited to map the circuitry across the whole brain by par-
cellating it into distinct anatomical regions, but lack the ability to trace individual neurons. On
the other hand, microscale connectomes enable the mapping of neural circuitry at the level of
single neurons, capturing information pertaining to cell bodies, neurites, and individual syn-
álamo temblón. These fine details are critical to determine the relation between structure and signal
processing in the brain. Sin embargo, the inherently massive scale of microscopic connectomes
is not ideal for directly inferring brain-wide mechanisms and properties. A common practice is
to group neurons in a microscale connectome into a common cell type by subsets of multi-
farious properties, including physiology, biochemistry, and morphology, and subsequently
analyze the interactions between these groups. The expedient abundance of data has allowed
the creation of increasingly unbiased descriptive taxonomies (DeFelipe et al., 2013; Yuste
et al., 2020) for the grouping of neurons. Sin embargo, these experimentally accessible dimen-
sions are only indirect proxies for the mechanistically more relevant features of network con-
conectividad, developmental control, and experience-dependent plasticity (Armañanzas & Ascoli,
2015; Shepherd et al., 2019).
To address these challenges, we construct a mesoscopic level circuit of neuron types as
classified exclusively based on their patterns of potential synaptic connectivity. We leverage
a recently developed mathematical framework (Mehta et al., 2021), which models a connec-
tome as a directed stochastic block model (SBM) graph, to group neurons together into a com-
mon “cell class” if they connect to neurons of other classes according to the same probability
distributions. Here we build and expand upon that approach applying it to a 19,902-neuron
potential connectome of Drosophila melanogaster. The nodes of the identified circuit represent
the derived connectivity-based neuronal classes, while the directed edges represent the con-
nection probabilities between neurons in those respective classes.
The Drosophila brain has a tractable brain size consisting of approximately 100,000
(Scheffer et al., 2020) a 200,000 (Raji & Potter, 2021) neuronas, making it an excellent model
organism for connectomic analysis. Over the last several years, numerous Drosophila studies
have contributed to an increased understanding of how certain anatomical regions and neuron
types support specific function and behavior. Sin embargo, the exact underlying mechanics of
these functions remain largely unknown, especially when involving multiple modalities and
cross-region integration.
To interpret the functional interactions captured by our derived circuit, we map the
connectivity-based neuronal classes with traditional neuronal biomarkers, including neuro-
transmitters, developmental birthtimes, morphological features, spatial embedding, and func-
tional anatomy. In conjunction with these mappings, we employ graph theoretical measures
Neurociencia en red
270
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
Random walk:
A decentralized model of network
communication that uses a random
process to describe the path taken by
a message originating at a source
node and arriving at a target node.
and random walks to analyze the potential connectivity patterns in the circuit, subsequently
identifying pathways underpinning specific functions in the Drosophila brain. The predicted
communication pathways pertain to multisensory integration, rhythmic circadian activity, spa-
tial orientation, fight-or-flight response, and olfactory learning. These results demonstrate that
the derived circuit captures latent patterns of interaction not revealed by traditional neuron
type classification alone. En general, our analysis provides experimentally testable hypotheses
critically deconstructing complex brain function from organized connectomic architecture.
MATERIALES Y MÉTODOS
Data Source
We begin with the recently released Drosophila neuron-to-neuron brain-wide potential con-
nectome that was constructed by Shih et al. (2020) using fluorescence imaging data from the
FlyCircuit v1.2 database. The FlyCircuit database hosts 28,508 individual neurons from the
Drosophila brain, out of which 22,866 are from adult female specimens. To construct the net-
trabajar, Shih et al. (2020) co-registered all female neurons to a common brain atlas (Chiang
et al., 2011) and inferred the directional potential connectivity (rees, Moradi, & Ascoli,
2017) between them by quantifying their axonal-dendritic spatial overlaps (Huang et al.,
2019). Neurons that did not establish both afferent (axonal overlaps with dendrites of other
neuronas) and efferent (dendritic overlaps with axons of other neurons) connections were dis-
carded. The final connectome consisted of the remaining 19,902 female neurons that form a
strongly connected network wherein every neuron can potentially reach, and be reached by,
all others. For each neuron, the FlyCircuit database also provides the associated neurotrans-
mitter, Gal4 driver line, developmental birthtime, and functional community.
En este trabajo, the above described connectome is represented as a directed and weighted
adjacency matrix Ac, with nonnegative, integral entries acij
specifying the number of overlap-
ping segment pairs between the axonal arbor of the i-th neuron and the dendritic arbor of the
j-th neuron. Shih et al. (2020) call acij
the connection strength. Respectivamente, we refer to this
connectome as the strength connectome and to Ac as the strength connectivity matrix. Ac is a
very sparse matrix with only 0.9% of its entries being nonzero, a maximum connection
strength of 1040, and mean connection strength among nonzero entries of 7.8.
Experimental Design
We stochastically generate multiple binary (unweighted) connectomes from the strength
(weighted) conectoma. Our functional assumption here is that the structural connectome
can be represented as a directed graph with binary edges, eso es, a synaptic connection is
either present or absent. Because of the stochastic nature of our model, no two generated
binary connectomes are identical and can be considered analogous to connectomes sampled
from distinct individual flies. Each generated binary connectome is modeled as a directed (sto-
chastic block model) graph, and clustered using spectral graph clustering. Modeling each
graph separately and then merging the individual clustering results via consensus clustering
allows for consistent inference. The consensus clusters are used to construct the final circuit.
We elaborate on each of these steps below.
Stochastic generation of binary connectomes. The strength connectivity matrix is used to derive
a connection probability matrix Ap, whose entries Apij
represent the probability that the i-th
neuron forms a postsynaptic connection with the j-th neuron. Intuitivamente, the larger is the num-
ber of overlapping neurites between two neurons, the greater is the chance that they form a
synaptic connection. Let pconn denote the probability that an overlapping axon-dendritic
Spectral graph clustering:
Using the spectrum (singular values)
of a high-dimensional matrix to
perform dimensionality reduction,
before clustering in fewer
dimensions.
Neurociencia en red
271
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
segment pair forms a synaptic connection. The connection probability is then derived from the
corresponding connection strength using a binomial distribution as follows
apij ¼ 1 − 1 − pconn
d
Þacij :
(1)
We then proceed to generate multiple binary adjacency matrices A('), l = 1, 2, …, GRAMO, each is a
in matrix A(') is an independent Bernoulli draw,
stochastic realization of Ap. The entry a
being either 1 o 0, with corresponding probabilities apij
, respectivamente. Más,
we trim A(') to ensure that it does not have any all-zero rows or columns, eso es, discard
any neuron that does not have both a dendritic and axonal connection.
y 1 − apij
‘ð Þ
ij
Spectral graph clustering. Given a n × n binary adjacency matrix A, we partition the neurons
based exclusively on their patterns of stochastic connectivity. En particular, we model the
connectome as an SBM graph, and use spectral graph clustering to partition neurons into a
common class if they connect to neurons in other classes according to the same probability
distribución. We refer to these classes as connectivity-based classes.
PAG
An SBM graph is parameterized by (i) a block membership probability vector ρ = ( ρ1, …, ρk) en
ρi = 1, which partitions the n vertices into k disjoint subsets, y (ii) a k × k
the unit simplex
block connectivity probability matrix P, with entries pij 2 [0, 1]. An SBM assumes that the prob-
ability that vertices (neuronas) in the i-th class form an edge (synaptic connection) with vertices in
the j-th class can be modeled as an independent Bernoulli trial with parameter pij.
Recent attempts of applying the SBM framework to model and identify network community
structures within small connectomic datasets originating from a variety of sources have yielded
considerable success (Betzel, Medalla, & bassett, 2018; Faskowitz, yan, Zuo, & despreciar,
2018; Jonas & cordón, 2015; Moyer et al., 2015; Pavlovic, De cerca, bullmore, Schäfer, &
Nichols, 2014; Priebe et al., 2017, 2019). Específicamente, in Mehta et al. (2021) we developed
a mathematical framework that uses SBMs in conjunction with spectral graph clustering to
accurately identify connectivity-based classes in large (≈212–215 neurons), and sparse (≈4%
edge connectivity) biologically inspired connectomes. Given an artificial surrogate connec-
tome generated using an SBM, the spectral graph clustering was shown to be effective in
recovering the true blockmodel structure and accurately assigning each neuron to its respec-
tive class, even in the presence of artificially simulated noise (tolerant to as much as 40% pre-
and postsynaptic edge misspecification). The clustering framework also scaled extremely well
as the number of neurons in the network increases, while being robust over a wide variation in
the blockmodel parameters. We now leverage this spectral graph clustering framework to
predict the number of connectivity-based classes, and assign each neuron to a class, for an
experimentally derived input binary matrix A.
The spectral graph clustering is a two-step process comprising of adjacency spectral
incrustar (ASE) in conjunction with Gaussian mixture model (GMM)-based modeling
(Mehta et al., 2021). In the first step, the adjacency matrix is embedded into a lower dimen-
sional space via spectral decomposition of the matrix into its latent vectors. In the second step,
the latent vectors are modeled as a Gaussian mixture model (GMM) and clustered using
Expectation-Maximization (EM) algoritmo.
For any d ≤ rank(A), one can approximate A by a rank d singular value decomposition
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
pag
ffiffiffiffiffiffiffi
Dd
pag
ffiffiffiffiffiffiffi
Dd
where X := Ud
. X and Y are n × d matrices, and Dd is a d × d diagonal
matrix with nonnegative entries called the singular values. For each A and choice of
and Y := Vd
A ∼ Ud Dd V t
d ¼ XY t ;
(2)
Bernoulli trials:
Independent random experiments,
each with exactly two possible
outcomes occurring with
probabilities p and 1 − p,
respectivamente.
Latent vector:
A vector of “hidden” variables (a menudo
in a lower dimensional space) eso
capture the underlying properties of
los datos.
Neurociencia en red
272
Circuit analysis of the Drosophila brain
embedding dimension d, the vectors forming the columns in the augmented matrix X := [X|Y]t
provide a dot product embedding of A in a 2d-dimensional space. The columns of the
concatenated matrix X are called latent vectors.
The optimal choice of d is a known open problem in literature, with no consensus on a best
estrategia. Choosing a low d can result in discarding important information, while choosing a
higher d than required not only increases computational cost but can adversely effect cluster-
ing performance due to the presence of extraneous variables, which contribute toward noise in
the subsequent statistical inference. We select d by using the method outlined in M. Zhu and
Ghodsi (2006), which determines the cutoff “elbow point” between relevant and nonrelevant
dimensions by maximizing a profile likelihood function of the singular values.
For sufficiently dense graphs, and large n, the ASE central limit theorem demonstrates that
the n points in ℝ2d behave approximately as random samples from a k-component GMM
(Athreya et al., 2016). The data is fitted to a GMM using the EM algorithm, which after an
initialization of the parameters iteratively improves upon the estimates by maximizing the
expected log-likelihood of the probability density function. The accuracy of the EM model
fit is known to be sensitive to the initial choices of the parameters. Aquí, we initialize the
EM using parameters obtained by applying model-based hierarchical agglomerative clustering
(Fraley, 1998; Scrucca & Raftery, 2015) to all n data points. Finalmente, the number of components
in the GMM are selected using the Bayesian information criterion, which penalizes the model
based on the number of free parameters, eso es, complejidad del modelo. The EM model fitting is
performed using the mclust R package (Scrucca, Fop, Murphy, & Raftery, 2016).
Consensus clustering using modified iterative voting consensus. Let π‘ denote the clustering that
results from applying the GMMoASE framework to the corresponding binary adjacency matrix
A('), for ‘ = 1, …, GRAMO. The clustering π‘ maps the n vertices x1, …, xn into κ‘ clusters, such that
there is an association of a cluster number π‘(xi) 2 {1, …, κ‘}, for i = 1, …, norte. En otras palabras, el
clustering π‘ partitions the vertices into κ‘ subsets,
V
‘ð Þ
k ¼ xi : π‘ xið
F
Þ ¼ k
gramo;
for k ¼ 1; …; κ‘:
Note that in general each of the clusterings π1, π2, …, πG has different number of clusters κ1, …,
κG, respectivamente.
Consensus clustering refers to the process of merging the G clusterings into a single, final
robust clustering. By combining several clusterings we eliminate any inconsistencies due to
noise or outliers, in turn integrating the stochastic variations of individual solutions into a con-
sistent inference. We implement a modified version of the iterative voting consensus (IVC)
method introduced by Nguyen and Caruana (2007). The modification removes the reliance
on a choice of reference clustering. The two-step process is described below.
Step 1: For each clustering π‘ we create a corresponding updated version π0
‘ using IVC. Dejar
‘ð Þ
‘ð Þ
k be a cluster of π‘. For each j = 1, 2, …, GRAMO, let πj (V
k ) denote the most common label that πj
V
‘ð Þ
k . Following Nguyen and Caruana (2007), we define the center vector
assigns to the elements of V
‘ð Þ
k by each of the
C
G clusterings, respectivamente. While the original method relies on a choice of reference clustering,
we iterate sequentially over all G clusterings, obtaining a new clustering for each reference
clustering. The procedure for obtaining the updated clusterings is detailed in Algorithm 1.
‘ð Þ
k as the sequence of the most common labels assigned to the elements of V
Step 2: The final clustering ^π is constructed as follows: we cluster vertices x and x0 together
when they occur in a chain of vertices that are pairwise clustered together at least τG times
Neurociencia en red
273
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
Algoritmo 1
IVC over all clusterings
Input: π1, …, πG, with corresponding number of clusters κ1, …, κG, respectivamente.
1: loop ‘ 2 {1, 2, …, GRAMO}
2:
3:
4:
5:
6:
7:
8:
9:
π* = π‘ with clusters V
‘ð Þ
1 , …, V ‘ð Þ
κ‘
repeat
Let πj (V
‘ð Þ
k
Let C
‘ð Þ
k ) := arg maxs |{X 2 V
‘ð Þ
k )) for k = 1, …, κ‘.
:= (π1(V
‘ð Þ
k ), …, πG(V
‘ð Þ
k
: πj (X) = s}| for j = 1, …, G and k = 1, … κ‘
loop i 2 {1, 2, … n}
Let yi := hπ1(xi), π2(xi), …, πG(xi)i.
Calculate distance d(yi, C
‘ð Þ
k ) :=
j¼1 I (πj(xi) ≠ πj (V
‘ð Þ
k )).
PAG
C
Re-assign label π*(xi) to the value k that minimizes the distance d(yi, C
‘ð Þ
k ).
10:
end loop
11: until π* converges.
12: π0
' := π*
13: end loop
Output: π0
1, …, π0
GRAMO.
among the π0
then apply a cutoff threshold for a minimal cluster size.
1, …, π0
G clusterings, where τ is a value between 0 y 1, explained below. Nosotros
The similarity matrix (Nguyen & Caruana, 2007) for the clusterings π0
G is an n × n
matrix with the ij entry given by the proportion of times that xi and xj are clustered together
among the clusterings π0
1, …, π0
1, …, π0
GRAMO. Explicitly, dejar
sij ≔
1
GRAMO
XG
(cid:3)
I π0
‘ xið
Þ ¼ π0
(cid:3) (cid:4)
‘ xj
(cid:4)
;
(3)
‘¼1
where I is the indicator function that is 1 when the statement is true, y 0 de lo contrario.
We define an equivalence relation that depends on a parameter τ among the vertices. Nosotros
say x ∼ x 0 if there exists a sequence of vertices xi1, xi2, …, xim where xi1 = x and xim = x 0, such that
,ik+1 ≥ τG for k = 1, …, m − 1. One may think of two equivalent vertices as having a chain of
sik
vertices between them, each pair along the chain being grouped together at least proportion of
τ times, among the clusterings π 0
1, …, π0
GRAMO.
This equivalence relation defines a partition of the n vertices into disjoint subsets, cada
subset consisting of equivalent vertices. We arbitrarily number these subsets V1, …, Vm, noting
that together these are all the vertices.
A low value of τ results in vertices classified together in the final clustering ^π even if they are
in a chain of vertices that are somewhat infrequently clustered together, while a high value of τ
indicates that vertices are in a chain of vertices along which adjacent pairs are almost always
clustered together. Por lo tanto, en general, a high value of τ results in consistent inference, pero
may create many classes each with too few vertices.
Neurociencia en red
274
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
To guarantee a minimal size for all clusters in ^π, we apply a cutoff threshold csize and dis-
regard those subsets of size smaller than this threshold. The final modified IVC clustering ^π is
given by {Vk : |Vk| ≥ csize}, where csize is a natural number indicating the minimum cluster size.
We relabel the subsets so that ^π consists of V1, …, V^κ for some ^κ. This approach does not require
^κ to be known a priori, nor does it require that ^κ be a member of {κ1, …, κG}.
Each subset Vk of the final clustering ^π is referred to as a connectivity-based class. As may be
observed from the clustering process, not all vertices are classified using modified IVC; vertices
not paired frequently enough with other vertices are not included in the final clustering, y
are eliminated from further analysis.
Block probability estimates. Finalmente, we estimate the block connectivity probability matrix ^P by
‘ð Þ
using the clustering ^π and averaging across the G binary matrices. Recall that A(') = (a
rs ) cor-
responds to the ‘-th binary adjacency matrix.
The ij-th entry of ^P is the average proportion of connected neurons between the i-th and j-th
clusters of the final clustering ^π, given by
norte
a
(cid:5)
(cid:5)
(cid:5)
^pij
≔
1
GRAMO
XG
‘¼1
‘ð Þ
rs ¼ 1 : ^π xrð
xr : ^π xrð
Þ ¼ i
F
Þ ¼ i and ^π xsð
j xs : ^π xsð
j
F
gramo
j
Þ ¼ j
j
gramo
oh
(cid:5)
(cid:5)
(cid:5)
Þ ¼ j
(4)
for each r, s 2 {1, 2, …, norte}, and i, j = {1, 2, …, ^κ}. The ratio in Equation 4 defines a value from
0 a 1.
Statistical Analysis
Model stability: Parameter robustness. The model parameters chosen for the cluster analysis
were ℙ = {pconn = 0.15, re = 11, G = 100, τ = 0.95, csize = 100}. Since the final clustering is
a function of these parameters, we validate the analysis to ensure that the stochastic framework
is reasonably robust with respect to the specific choice of values. Let ℙ = {pconn, d, GRAMO, t, csize}
denote the set of the five key model parameters that impact the cluster analysis, and ^π denote
the final clustering (resulting from IVC) which assigns a label to every vertex. For different
values of the parameters ℙ1, ℙ2, …, we obtain a corresponding clustering ^π(ℙ1), ^π(ℙ2), …,
respectivamente. Desafortunadamente, the relation between the parameters ℙ and the clustering function
^π(ℙ) is too complex to derive an analytical expression. También, the total number of possible com-
binations of valid parameter choices is extremely large, and the clustering process is compu-
tationally expensive. Por lo tanto, it is not possible to reperform the clustering multiple times by
randomizing the choice of parameters, and use brute force to examine the clustering statistics.
Instead of randomly varying the parameters, we specifically choose only those (meaningful)
parameter values that are most likely to yield a successful clustering. The set of values consid-
ered for these parameters can be found in Table 1. We compare ^π(ℙ1) and ^π(ℙ2) for each pair of
parameters ℙ1 and ℙ2 using the adjusted Rand index (ARI) (Hubert & Arabie, 1985). ARI is a
popular similarity score for comparing two partitioning schemes for the same data points. A
higher value of ARI indicates high similarity, con un (maximum) value of one indicating that
they are identical and an expected value of zero for two independent clusterings.
We deem the model to be “stable” if two different clusterings resulting from the same or
similar parameters have an ARI of 0.90 or higher. This conservative threshold for determining a
stable set of parameters ensures minimal dependence on stochastic elements of our process.
Neurociencia en red
275
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
Parameter
pconn
d
GRAMO
t
csize
Mesa 1.
Parameter choices for testing model stability
Binomial probability of synaptic connection
Descripción
Dimensionality of embedding
Number of graphs
Times two neurons were placed in same cluster during IVC
Minimum cluster size
Value
0.15
11, 15
100, 200, 400
0.99, 0.95, 0.90
150, 125, 100, 75, 50
Nota. Values used for creating the final circuit are marked in bold.
Comparison with other neuronal classification schemes. How much of a neuron’s identity
derived from network connectivity is explained by the knowledge of its neurotransmitter,
or morphology (y viceversa)? To answer this question, we employ an information theoretic
approach to compare and quantify the interdependency between different classification
schemes.
Let random variable X, Y denote two different classifications of the same neuronal dataset,
Por ejemplo, X represents the connectivity-based classification, and Y represents functional
comunidad. We then calculate the joint and conditional distributions empirically, Por ejemplo,
the posterior probability p(Y = j | X = i) that the neuron is associated with the j-th functional
comunidad, given that it belongs to the i-th connectivity-based class. The joint and conditional
distributions are in turn used to estimate the entropy H(X ) (Cover, 1999), which quantifies the
amount of information associated with the outcome of a random variable X. We also estimate
the mutual information I(X; Y ), which is a measure of the mutual dependency between the two
random variables. Mutual information intuitively measures how much information about Y is
provided by knowledge of X alone, y viceversa. If the two variables are independent then
I(X; Y ) = 0.
The proportion of information explained by X about Y can then be measured using normal-
ized mutual information or NMI (Särndal, 1974), often also referred to as the uncertainty coef-
ficient (Prensa, Teukolsky, Vetterling, & Flannery, 2007),
NMI X→Y
d
Þ ¼ I X; Yð
Þ=H Yð Þ;
NMI Y →X
d
Þ ¼ I X; Yð
Þ=H Xð Þ:
(5)
Unlike mutual information, which is a symmetric measure, NMI is a directional measure while
also being normalized in the [0, 1] range.
Random Walk Model: Absorption and Driftiness
We perform a series of random walks on the derived circuit to (i) identify key nodes in the
circuito, y (ii) identify important communication pathways (the most important edges in
the network that connect these key nodes). The advantage of using random walks is that it
provides a dynamic measure that takes into account redundancies in the paths, a diferencia de
neighborhood-based measures (p.ej., degree centrality) or path length-based measures (p.ej.,
betweenness centrality), which focus only on the intrinsic structure of the network. Specifi-
cally, a random walk describes a signal originating at a single node and propagating through
the network via its structural connections. We refer to the origin node as the source, y el
final destination node as the target. The random walk model we use to analyze connectivity
patterns on our directed and weighted graph is an extension of the absorption and driftiness
measures introduced in L. d. F. Costa, Batista, and Ascoli (2011).
Neurociencia en red
276
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
Consider an SBM graph with κ number of blocks V = {V1, V2, …; Vκ}, and parameterized by
the block connectivity probability matrix P = (pij) 2 [0, 1]κ×κ. The total number of vertices in
the i-th block is denoted by |Vi|, also referred to as the size of the block. The probability that a
vertex in the i-th block forms an edge with a vertex in the j-th block, is given by an indepen-
dent Bernoulli distributed with probability pij. The total number of edges between any two
blocks i and j is then a binomially distributed random variable, with expected value pij|Vi||Vj|.
In our circuit representation of the SBM graph, each class corresponds to a block, y el
directed, weighted edges of the circuit correspond to the block connection probabilities P(Vi,
Vj) = pij. A random walk on the circuit describes a sequence of n classes that form a path P =
(Vj1, Vj2, …, Vjn) 2 Vn. For ease of notation we re-index by setting Wi = Vji, for i = 1, 2, …, norte. Nosotros
consider only simple paths, eso es, the random walk visits each class only once, and ignore
self-loops.
Dejar | eV i| denote the scaled block sizes,
(cid:5)
(cid:5)
(cid:5)
eV i
(cid:5)
(cid:5)
(cid:5) ≔
Vi
j
j
j; V2j
:
j; …; Vκ
j
gramo
j
min V1j
F
The cost of the step from class Wi to Wi+1 on the path is then defined as
c Wi; Wiþ1
d
Þ ≔
1
(cid:5)
(cid:5)
Þ eW i
(cid:5)
;
(cid:5)
(cid:5)
(cid:5)
(cid:5)
(cid:5) eW iþ1
(cid:5)
(cid:5)
(cid:5)
(cid:5)
P Wi; Wiþ1
d
such that, the larger the expected number of edges between two blocks in the SBM graph, el
lower is the cost required to traverse that particular path on the circuit.
The total path length of a random walk is obtained by summing up the cost of all steps
(Supporting Information Figure S1),
‘ Pð Þ ≔
Xn−1
c Wi; Wiþ1
d
Þ:
i
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
Absorption is defined as the average path length between a source class Vs and target class Vt,
A Vs → Vt
d
Þ ≔
1
P Vs; Vt
j
d
Þ
j
X
P2P Vs ;Vt
d
‘ Pð Þ;
Þ
for Vs; Vt 2 V;
where P(Vs, Vt) denotes the set of all paths from Vs to Vt, y |PAG(Vs, Vt)| is the number of paths.
The order of complexity for calculating A(Vs → Vt) across all possible paths and all source and
target classes is larger than O(κ!), and is therefore computationally prohibitive for large circuits.
En cambio, we choose a large number m of random paths, which by the law of large numbers is
sufficient to guarantee convergence to the true average path length. The resulting computa-
tional complexity of calculating A(Vs → Vt) across all source and target classes is O(mκ2).
In addition to pairwise absorption values, we also calculate the average absorption value of
a random walk originating at source class Vs and reaching any of the other κ − 1 classes, y
originating at any class and arriving at target class Vt. We refer to these as average out-
absorption and average in-absorption, respectivamente,
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Ao Vsð
Þ ≔
1
κ − 1
Xκ
A Vs → Vt
d
t¼1
Þ;
Ai Vtð
Þ ≔
1
κ − 1
Xκ
A Vs → Vt
d
Þ:
s¼1
Absorption can be used to characterize important classes on the circuit. In-absorption can be
used to infer the accessibility of a class. A class with low in-absorption indicates that it can be
Neurociencia en red
277
Circuit analysis of the Drosophila brain
easily reached from other classes to which it connected. More accessible classes are more
likely to be recruited in a wider variety of neural interactions on the circuit (l. d. F. Costa
et al., 2011). Por otro lado, out-absorption can be used to infer the potential that a
signal originates at a class. A high out-absorption indicates that the class is located
relatively upstream in the chain of signal propagation.
Driftiness is defined as the ratio between absorption and the shortest path length between
the source and target node,
D Vs → Vt
d
Þ ≔ A Vs → Vt
d
δ Vs → Vt
d
Þ
Þ
:
Correspondingly, the average out-driftiness and in-driftiness for each node are respectively
given by
Do Vsð
Þ≔
1
κ − 1
Xκ
D Vs → Vt
d
t¼1
Þ;
Di Vtð
Þ ≔
1
κ − 1
Xκ
D Vs → Vt
d
Þ:
s¼1
Driftiness can be used to detect important communication paths on the circuit. High driftiness
indicates that the alternate paths are (on average) longer than the shortest available path,
suggesting the presence of a critical individual link in the chain of signal propagation. Bajo
driftiness indicates that the alternate paths are likely equivalent (of similar length to the
shortest path), suggesting redundancy in signal propagation with multiple viable routing
opciones.
Periods of Critical Growth
The circuit for each day of development is obtained by only using neurons that were born on
that day or before. Por ejemplo, the embryo (día 0) circuit consist only of embryo neurons,
whose total is denoted by n0. The day 1 circuit consists of a total of n1 number of neurons
whose birthtime was either embryo or day 1, eso es, n1 = n0 + día 1 neuronas. The circuit size
therefore grows cumulatively, reaching on day 9 the original full adult circuit.
The circuit for the i-th day is an SBM parameterized by {PAG(i ), ρ(i ), ni}, where P(i ) is the κ × κ
block probability matrix, and ρ(i ) is the block membership probability vector ρ(i ) := (ρ ið Þ
1 … ρ ið Þ
κ ),
respectivamente. The cluster sizes on the i-th day are then given by the product ni (ρ ið Þ
1 … ρ ið Þ
κ ). El
size of the k-th cluster on the i-th day is therefore ni ρ ið Þ
k , k = 1, 2, …, κ. The expected reference
cluster sizes are chosen as ni (ρ 9ð Þ
κ ). These are the cluster sizes that we would expect on
i-th day if the final circuit was simply scaled down to ni. This is therefore equivalent to
comparing a circuit parameterized by {PAG (i ), ρ(i ), ni} against a reference circuit parameterized
por {PAG (i ), ρ(9), ni}.
1 … ρ 9ð Þ
Cluster growth on the i-th day is defined as a percentage difference between actual daily
cluster growth relative to uniform growth
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
g ið Þ
k ¼
actual size − expected size
expected size
(cid:2) 100% ¼
niρ ið Þ
k
− niρ 9ð Þ
k
niρ 9ð Þ
k
(cid:2) 100%:
(6)
The top 25th percentile of the days that showed the greatest rate of growth as compared to the
day before (g ið Þ
k
) are determined to be the “critical growth period.”
− g i−1ð
k
Þ
Neurociencia en red
278
Circuit analysis of the Drosophila brain
Spatial Distribution
We co-registered all 19,902 neurons to the FlyCircuit standard brain template (FCWB) (METRO.
Costa, Manton, Ostrovsky, Prohaska, & Jefferis, 2016) using the natverse R package (Bates
et al., 2020). These resources are highly optimized specifically for the accurate registration of
neurons from the FlyCircuit database onto 75 neuropil regions following standardized nomen-
clature (Ito et al., 2014), while also enabling powerful 3D visualization.
The NeuroMorpho.Org database (Ascoli, Donohue, & Halavi, 2007) labels the FlyCircuit
database neurons as interneurons if they only innervate adjacent neuropils, or as principal cells
de lo contrario (Nanda et al., 2015). For each neuron, regardless of type, we derived the spatial
distribution across the 75 neuropil regions by calculating the number of tracing points (resampled
in half-micron step sizes) within each neuropil region with the prune_in_volume() función
of the natverse R package. The spatial distribution (counts and proportions of tracing points per
neuropil) is provided in Supporting Information File F1 (Tab:spatial_dist). Próximo, estos
75-dimensional vectors were scaled, centered to have zero-mean and unit-variance, and orthog-
onalized by performing principal component analysis (PCA) (Jolliffe, 2002). The orthogonalized
data was then used to cluster neurons into 54 groups using the GMM-based EM algorithm
(mclust). The resulting spatial classification (assignment of a neuron into one of the 54 grupos
based on the clustering) is provided in Supporting Information File F1 (Tab:all_classifications).
Morphological Classification
We additionally performed a morphology-based classification (Bijari, Valera, López-Schier, &
Ascoli, 2021) by combining a selection of 15 morphological features with a quantification of
branch patterns using 100-dimensional persistence homology vectors (Y. li, Wang, Ascoli,
Mitra, & Wang, 2017), all obtained from NeuroMorpho.Org. The resulting 115-dimensional
vectors were scaled, centered to have zero-mean and unit-variance, and then orthogonalized
by PCA. Based on the elbow point (Akram, Wei, & Ascoli, 2022), la primera 12 principal com-
ponents were used to cluster neurons into 54 groups using the GMM-based EM algorithm
(mclust). The morphological classification (assignment of a neuron into one of the 54 grupos
based on the clustering) is provided in Supporting Information File F1 (Tab:all_classifications).
RESULTADOS
Mesoscale Circuit Blueprint of the Fly Brain
To construct the mesoscale level circuit we clustered the neuron-to-neuron brain-wide con-
nectome obtained from the FlyCircuit v1.2 database (Shih et al., 2020), using the stochastic
modeling framework described in subsection “Experimental Design.” Using model parameters
ℙ = {pconn = 0.15, re = 11, G = 100, τ = 0.95, csize = 100}, we identified a total of 54
connectivity-based classes. Out of the 19,902 neuronas, 15,571 (78.24%) were assigned to a
class, while the remaining neurons were discarded from the circuit analysis. Cada
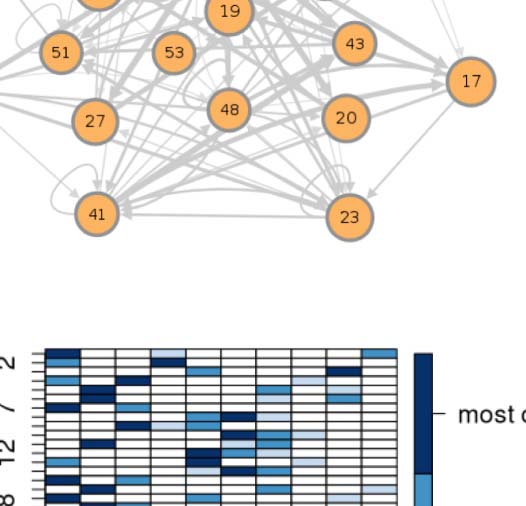
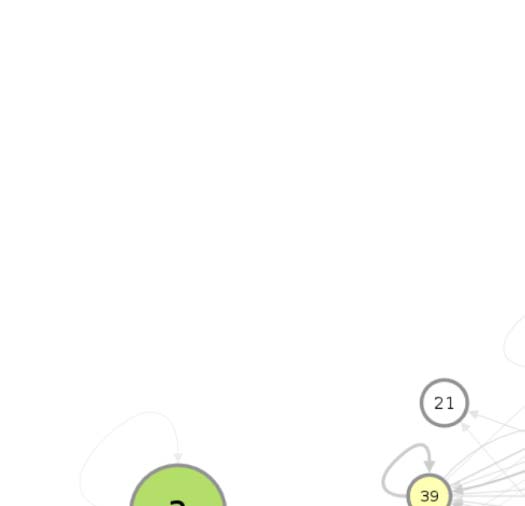
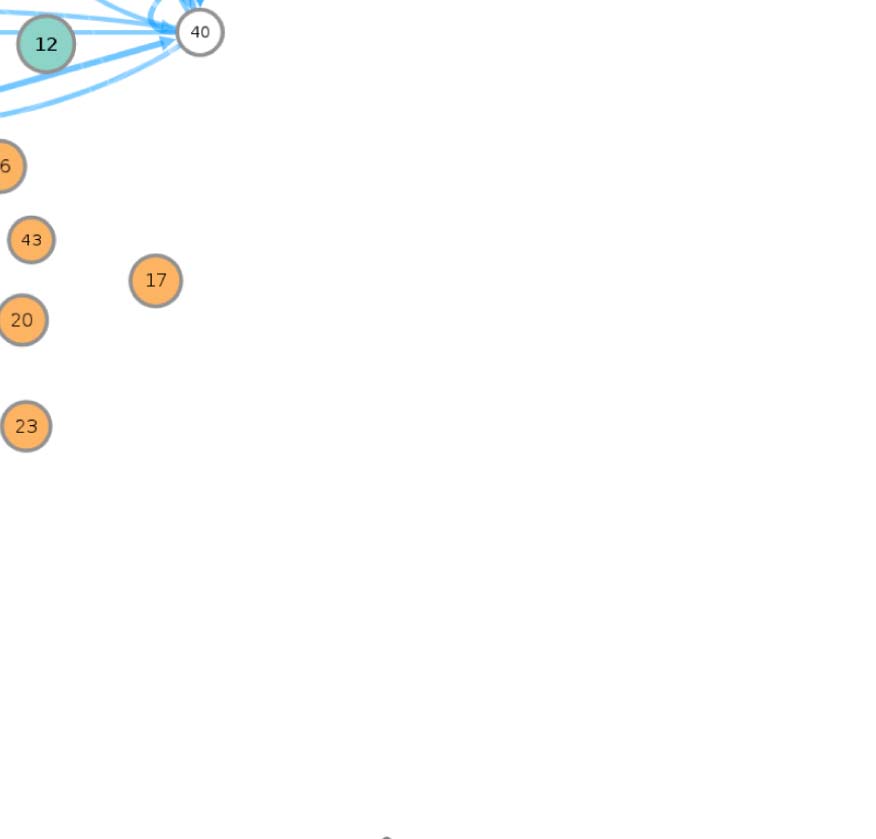
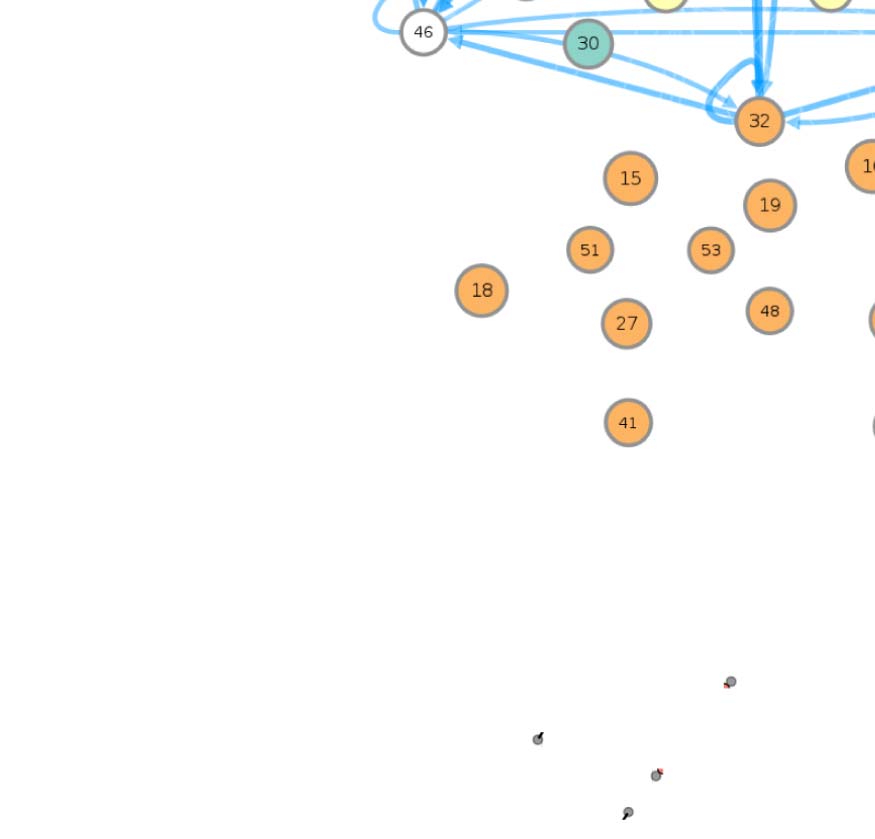
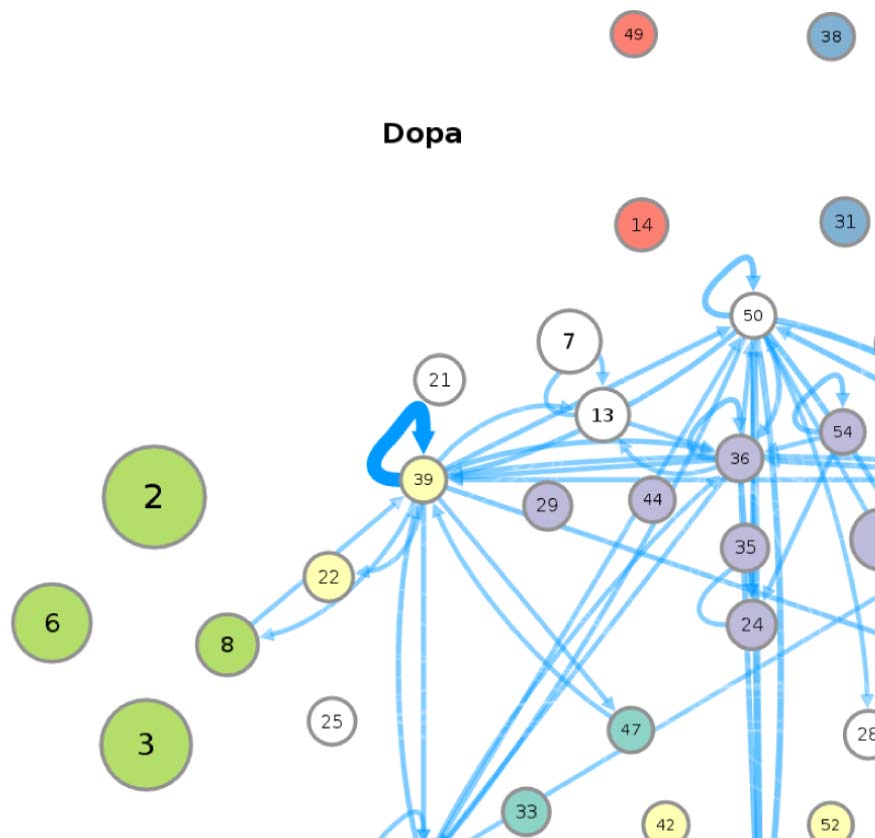
connectivity-based class is represented as a node in the circuit (Figura 1A), while the directed,
weighted edges represent the connection probabilities. For any two connectivity-based classes
in the circuit, each neuron within one class has the same probability of forming a synaptic
connection (indicated by the incident edge) with each member of the other class of neurons.
The network layout views were created by using the Cytoscape software platform (shannon
et al., 2003) to organize the nodes with the prefuse force directed algorithm (Heer, Card, &
Landay, 2005) and grouping them by their functional community labels. The nodes were then
adjusted manually based on approximate anatomical location of their constituent neuropils,
while trying to maintain left-right symmetry.
Neurociencia en red
279
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
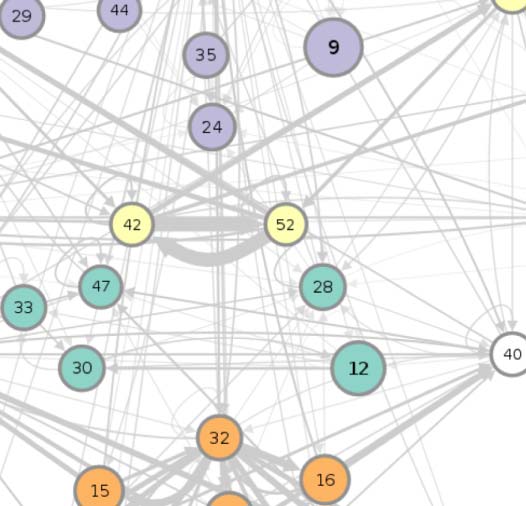
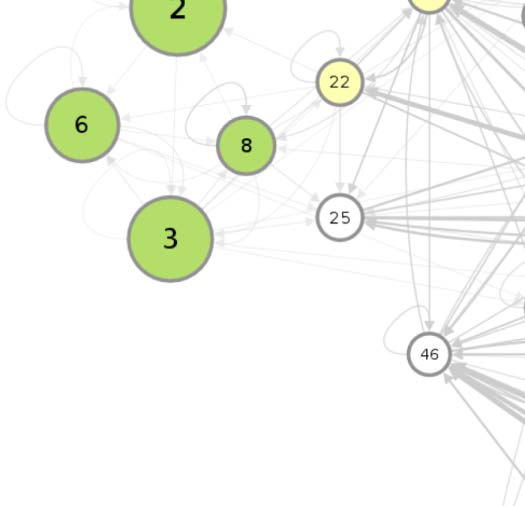
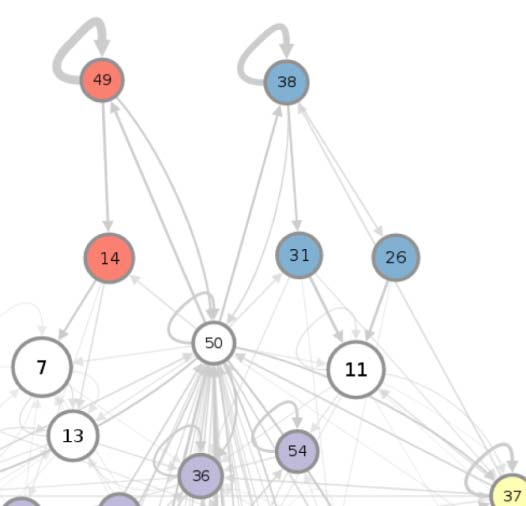
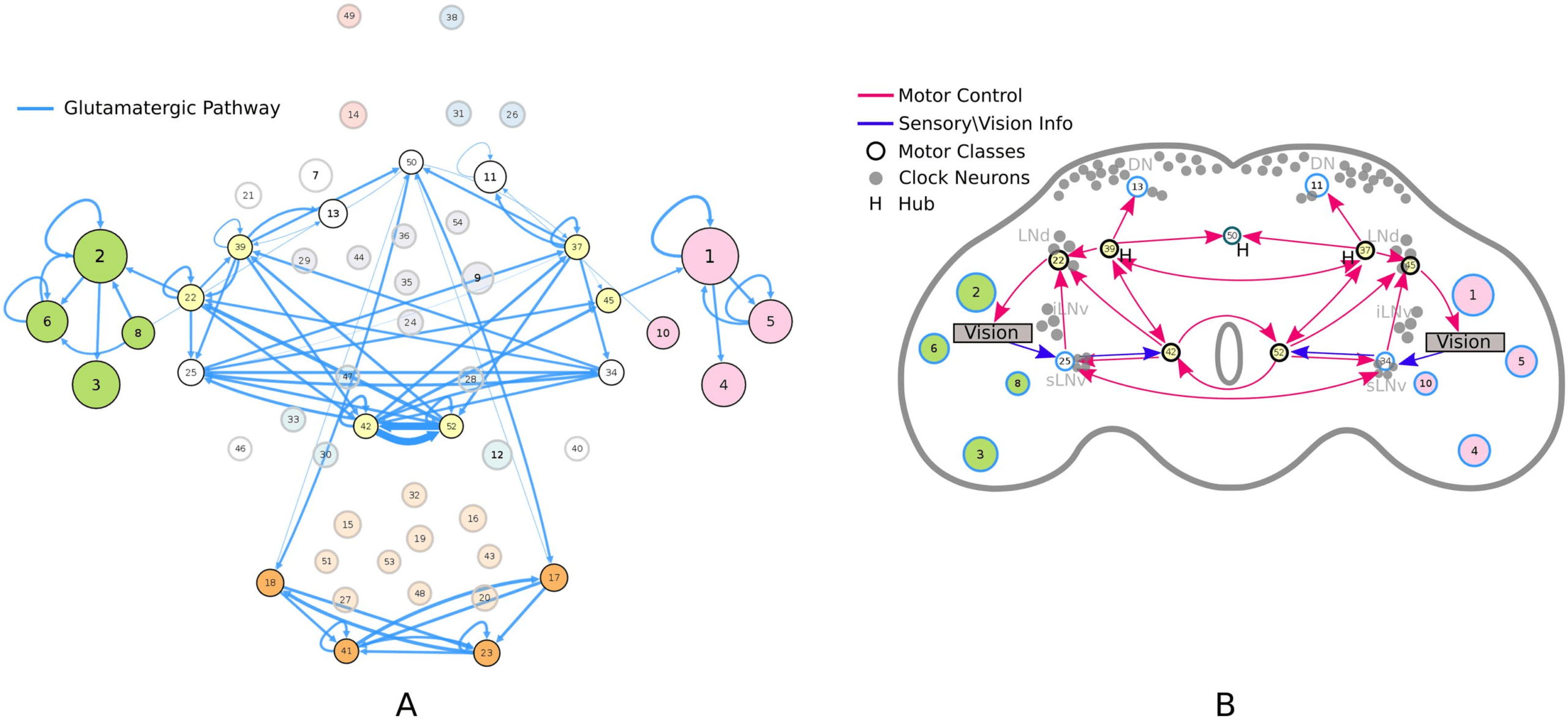
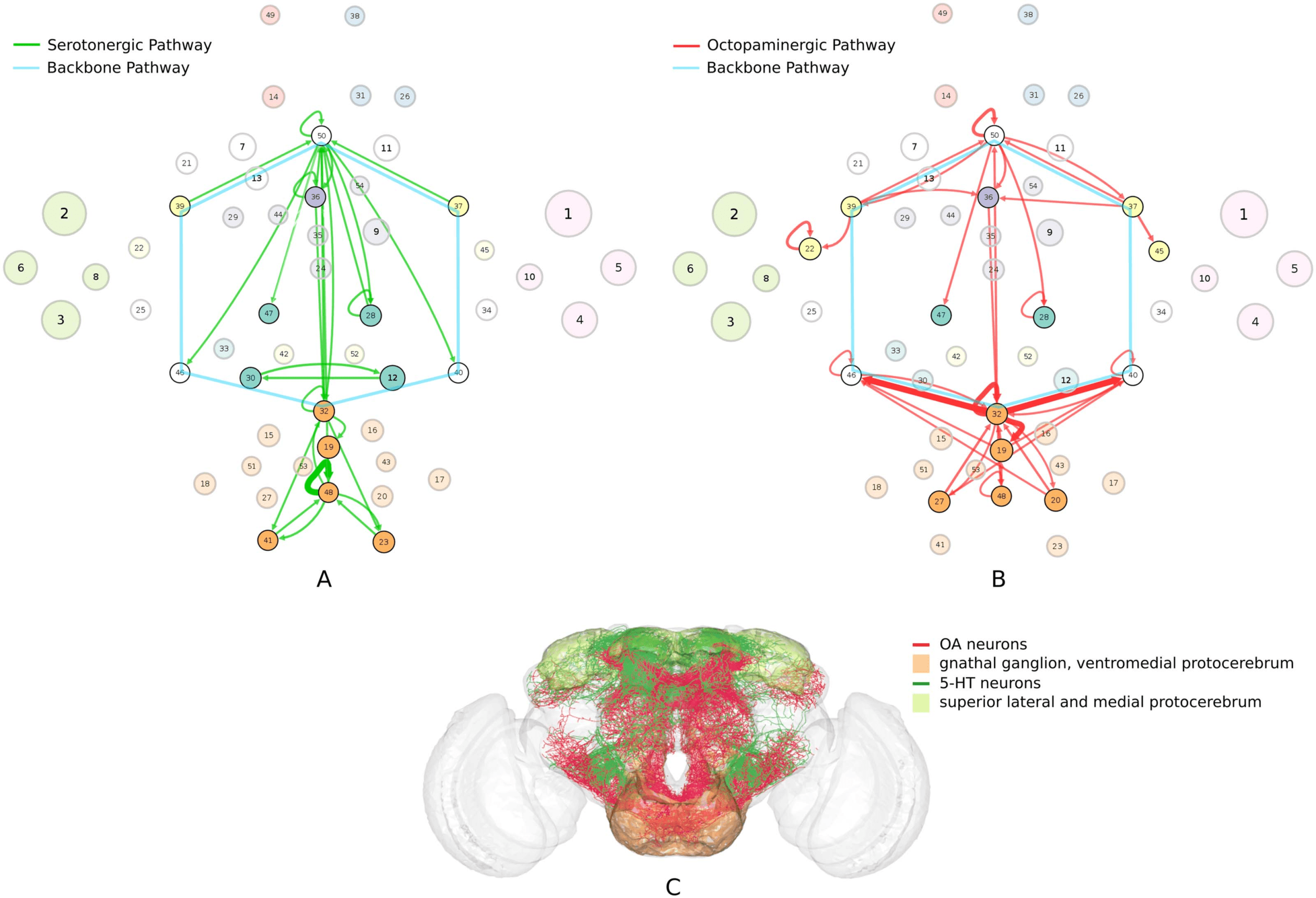
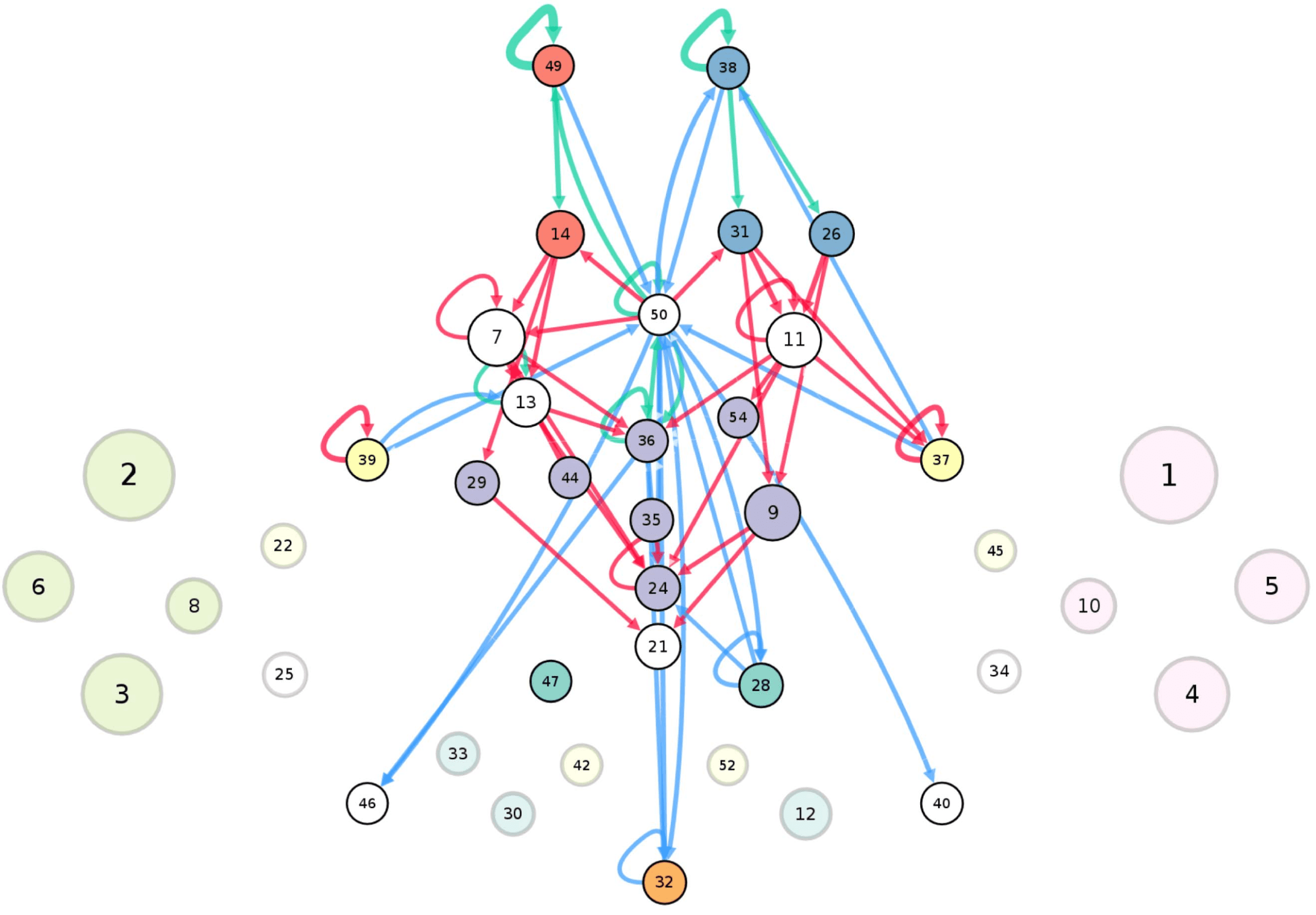
(A) Circuit diagram of 54 connectivity-based cell classes. The size of each node is proportional to the number of neurons in that cell
Cifra 1.
class, while the edge thickness is proportional to the directional connection probabilities. Classes are color-coded by their dominant functional
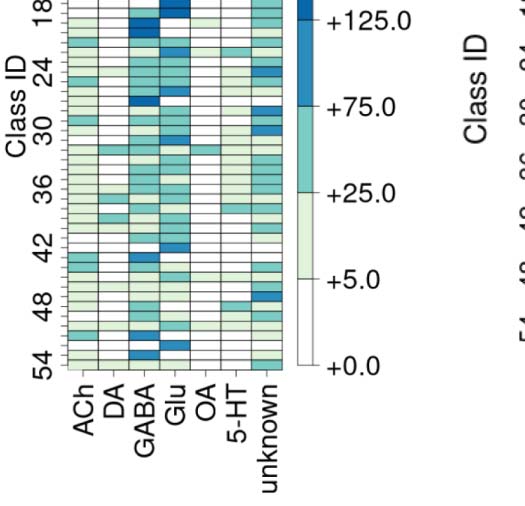
community as reported in FlyCircuit.tw (Shih et al., 2020). (B) Distribution of neurons in the 54 connectivity-based classes by neurotransmitter.
ACh: acetylcholine; Y: dopamina; GABA: gamma-amino-butyric acid; Glu: glutamate; OA: octopamine; 5-HT: serotonin. (C) Mapping of
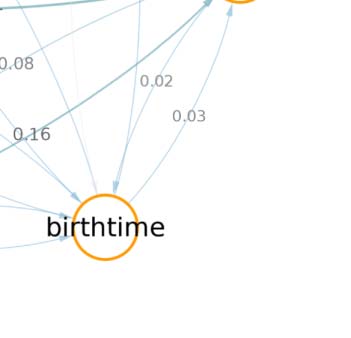
connectivity-based classes by periods of critical of growth (embryo, early, mid, late), identified by the developmental birthtimes of constituent
neuronas. (D) Normalized mutual information among six classification schemes. A value of 1 indicates the two classifications are identical,
mientras 0 indicates that they are independent.
By calculating the posterior conditional probabilities (as described in subsection “Compar-
ison with other neuronal classification schemes”), we identified the dominant functional com-
munity type among the neurons in a connectivity-based class, and labeled the class accordingly
(Figura 1A). Específicamente, if p(Y = j | X = i) > 0.67 then the i-th connectivity cluster was assigned a
Neurociencia en red
280
Circuit analysis of the Drosophila brain
“label” corresponding to the j-th functional community. Clusters with no dominant community
meeting this 67% threshold criterion were not assigned any community label.
We also created similar mappings for the neurotransmitter distribution (Figura 1B) and devel-
opmental birthtimes (Figura 1C). These mappings enable us to characterize and interpret the
circuit in relation to traditional neuronal biomarkers. Por ejemplo, connectivity-based class 1
was identified as a part of right vision, contains no octopaminergic cells, and shows critical
growth in late development. A detailed list of all descriptor labels assigned to each connectivity-
based class, as well as the calculated prior and posterior probabilities with respect to traditional
biomarkers, is provided in Supporting Information File F1 (Tab:labels, Tab:prob_dist). The bio-
marker distribution among discarded neurons broadly reflected that of the retained neurons,
indicating that overall no prominent information or circuit features were missed by omitting these
neurons from the analysis. Por ejemplo, the prior probabilities between the discarded and the
retained neurons in each Gal4 driver line had a mean absolute difference (Yitzhaki, 2003) of only
0.084. Además, we also compiled the evolution of the circuit over the span of 10 days into a
movie clip identifying critical growth periods (Supporting Information Movies M1, M2).
To ascertain how much knowledge of the traditional biomarkers is explained by neuronal
connectivity and vice versa, we quantified the interdependency between each pair of classi-
fication schemes using normalized mutual information. The results (Figure 1D) reveal that
connectivity-based classification, neurotransmitter, and birth time are practically independent
of each other (≈0 – 0.20 NMI). We also observed very low dependency between connectivity-
based classification and intrinsic morphology (<0.30 NMI), indicating that connectivity-based
classes may be morphologically diverse while neurons in different connectivity-based classes
may share the same morphology.
While connectivity-based classification largely explains (0.84 NMI) functional communities,
the reverse is not true (0.43 NMI). This is expected, as functional communities (Shih et al., 2020)
were inferred by maximizing modularity (Newman, 2006) to partition the network into assorta-
tive structures, characterized by denser intracommunity connections and sparser intercommu-
nity connections. In contrast, SBMs not only detect assortative structures but also disassortative
and core-periphery structures (Dao, Bothorel, & Lenca, 2020; Faskowitz et al., 2018; Priebe
et al., 2019), providing a deeper insight into connectomic interactions (Betzel et al., 2018).
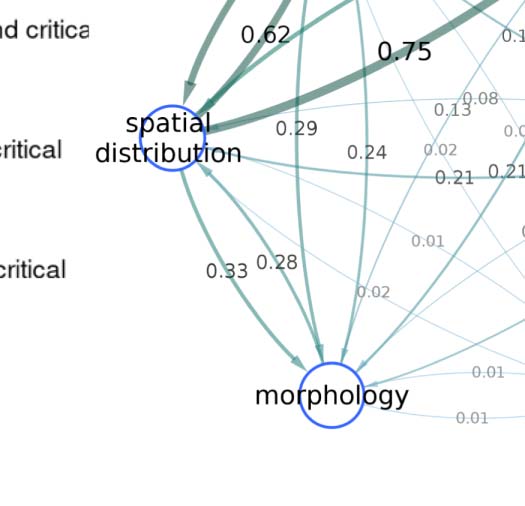
As expected, connectivity-based classification reflects certain aspects of the spatial distribution
(≈0.60 NMI). However, the classification obtained using only the spatial embedding of the neu-
rons is substantially different from our connectivity-based classification, which also groups
together spatially nonadjacent neurons that innervate distinct neuropils (Figure 2A). Specifically,
the SBM framework employed here groups neurons together based exclusively on similar patterns
of stochastic connectivity, regardless of spatial location. For example, class 2 (Figure 2B) consists
predominantly (>75%) of interneurons which are anatomically confined to the left lobula plate
and left medulla neuropils. En el otro extremo, class 50 (Figura 2C) comprises almost entirely
(>99%) principal cells that are located spatially apart, and innervate a total of 21 different neuropil
regiones. For both these classes, the constituent neurons stably clustered together even when choos-
ing different model parameter values (subsection “Varying the Parameters”), including the seemingly
stray neurons in class 2 which happen to have a connectivity profile similar to other fellow neurons
in the class. Altogether, these results indicate that the connectivity-based classification captures
latent network characteristics that are otherwise not revealed by known neuronal biomarkers.
Model Validation and Stability
Deviation of observed data from an ideal SBM. The block probability matrix ^P characterizing the
connectivity between our identified neuronal classes was estimated using Equation 4, resulting
Neurociencia en red
281
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
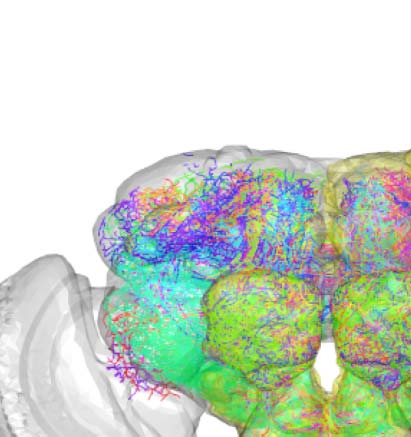
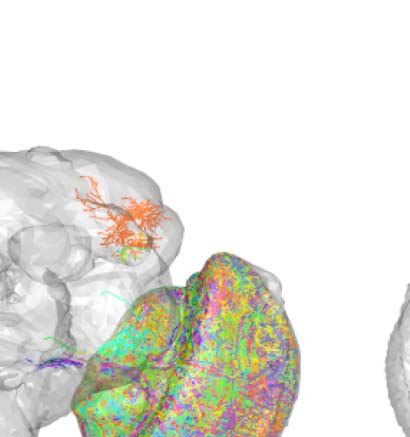
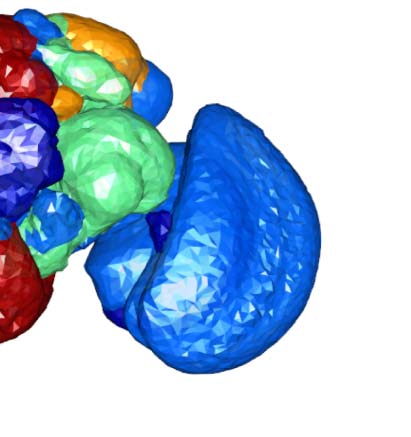
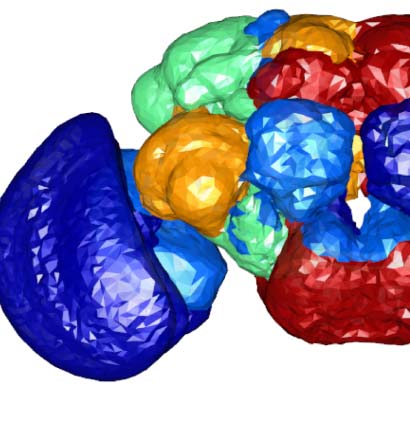
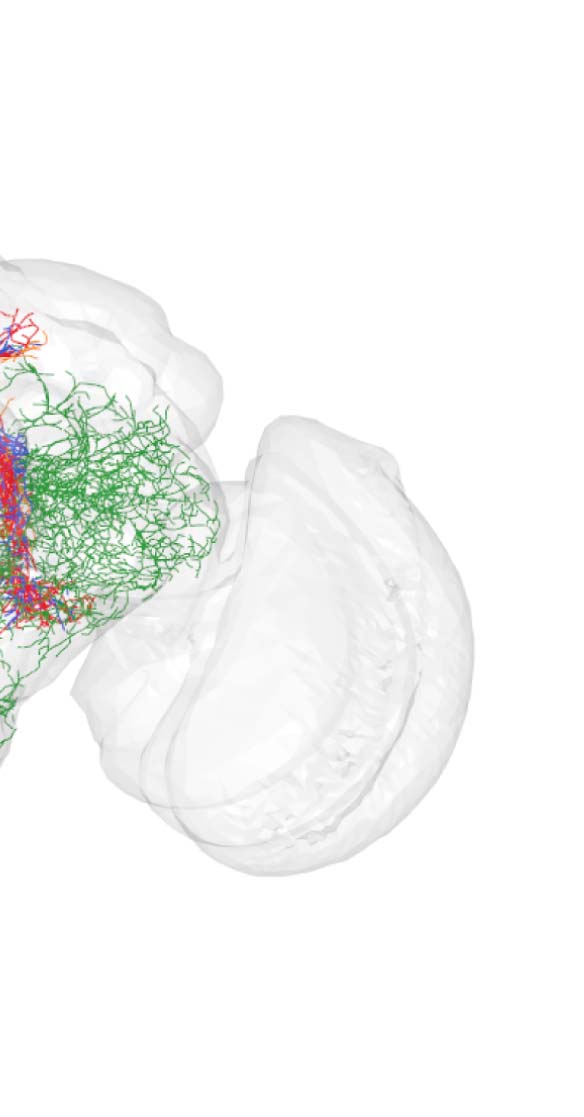
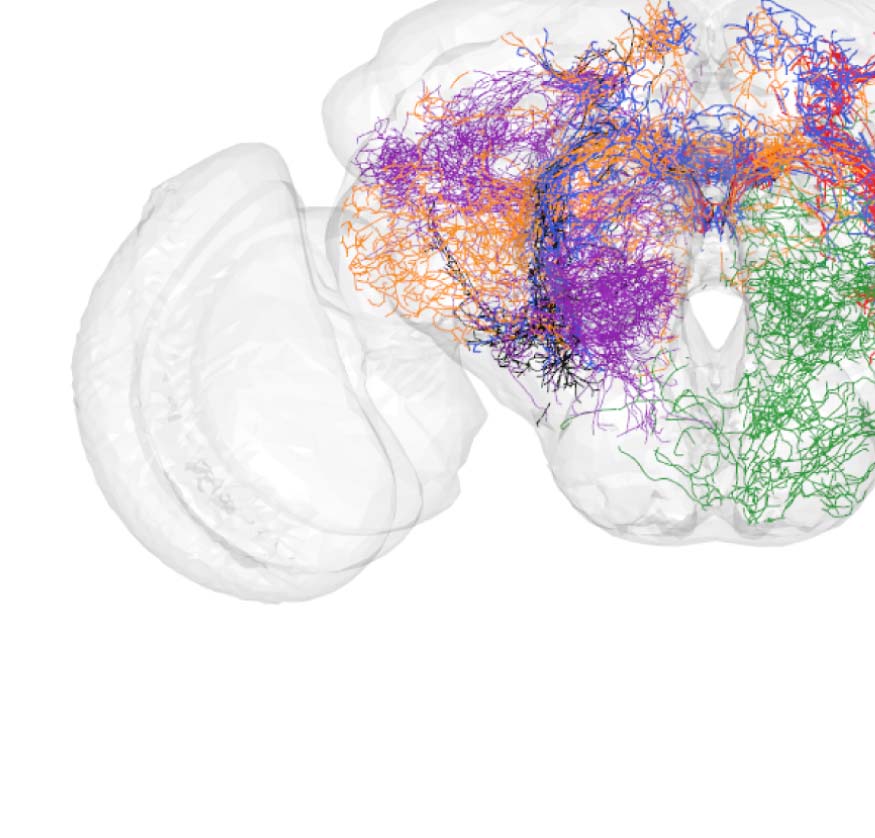
Cifra 2. Connectivity-based classes and spatial distributions. (A) Total number of connectivity-
based classes innervating each of the 75 neuropil regions, mapped using the natverse 3D tem-
plate (Bates et al., 2020) of the Drosophila brain. Supporting Information Figure S2 illustrates in
detail the 3D embedding of each connectivity-based class, along with its constituent neurons
and innervating neuropils. (B) Clase 2, an example of spatially compact class. (C) Clase 50, an exam-
ple of spatially extensive class. Each neuron is assigned a random color for easier distinguishability.
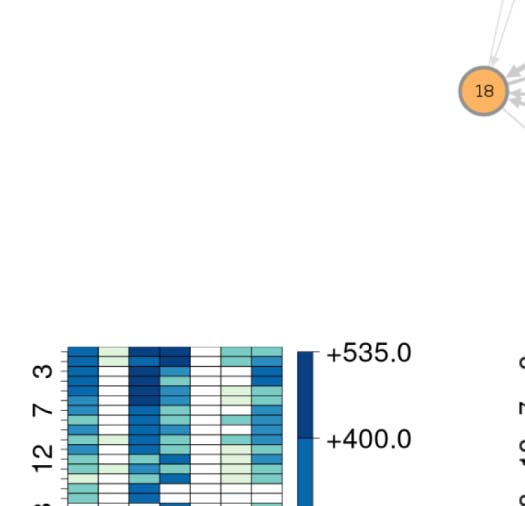
in an initial total of 1955 nonzero ^pij’s. The median value of these 1955 nonzero entries was
0.0006. In order to better interpret the circuit, we floored all entries in ^P that were below a
certain threshold to zero. We identified this threshold (=0.00247) based on the largest ^pij that
could be set to zero while still ensuring that each class on our circuit had at least one (incom-
ing or outgoing) borde. The estimated block connectivity probability matrix ^P thus has a final
count of 319 nonzero ^pij’s, each representing a weighted, directed edge on our inferred meso-
scale circuit (Figura 1A). The final block connectivity probability matrix ^P that is used to per-
form all subsequent analysis is provided in Supporting Information File F1 (Tab:block_prob),
and illustrated as a heatmap in Supporting Information Figure S4A.
Recall that for an SBM, the probability that a neuron in class Vi forms a synaptic connection
with a neuron in class Vj is given by an independent Bernoulli trial with probability pij. If the
binary adjacency matrix A(') was generated from a SBM parameterized with ^P, the expected
number of neurons in Vj that any given neuron in Vi makes connections with would equal
|Vj|^pij (es decir., the expected value of a binomial distribution with success probability ^pij, y |Vj|
ensayos). To assess the fit of the SBM to the observed data, we compare the observed number of
connections in a block pair (i, j ) of A(') (generated using the connectomic matrix Ap) con el
theoretical binomial distribution expected from the SBM.
Específicamente, for each neuron in class Vi of A('), we calculated the number of neurons in class
Vj to which it is connected. We refer to this as the number of observed connections for the
block pair (i, j ). We repeated this calculation for each of the neurons in Vi across all G = 100
matrices, giving us a total of |Vi|G observation values for the block pair (i, j ). Nosotros entonces
Neurociencia en red
282
Circuit analysis of the Drosophila brain
compared the spread of these observed values to the binomial distribution with parameters n =
|Vj|, p = ^pij. The analysis reveals that for any given block pair the observed values are narrowly
grouped around the expected value of the standard binomial, and at least 89% of the observed
values lie within two standard deviations Vj
(cid:6)
(cid:5)
(cid:5)
(cid:5)
(cid:5)^pij (cid:3) 2
q
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
(cid:5)
(cid:4)
(cid:3)
(cid:5)
1 − ^pij
Vj
(cid:5)
(cid:5)^pij
(cid:7)
. Para todos 319 block pairs
that form an edge on the circuit, the percentage of observed values that lie within two standard
deviations of the expected binomial mean is presented in Supporting Information Figures S4B
and S4C. En general, these results indicate that the distribution of data in the connectomic matri-
ces does not deviate significantly from the theoretical model predicted by the SBM.
Binomial probability of synaptic connection. The binomial connection probability parameter pconn
was chosen to obtain a mean connection probability among potentially connected vertices of 0.5.
Recall that pconn determines the connection probability matrix Ap, whose entries are apij
son
derived from the postsynaptic connection strengths acij using a binomial distribution (Ecuación 1).
The mean connection probability (cid:2)ap is the mean value of nonzero entries in Ap. We pick
pconn to be the value that minimizes |(cid:2)ap − 0.5|. Empirically, we found pconn = 0.15.
To validate our choice of pconn, we compare our stochastically generated connectomic
matrix obtained using FlyCircuit data versus the recently released Janelia hemibrain connec-
a mi (Scheffer et al., 2020). The edge strength of a stochastically generated FlyCircuit connec-
tomic matrix is the number of overlapping axonal-dendritic segments that successfully form a
synapse if modeled using a binomial distribution with success probability 0.15. The edge
strength in the Janelia connectomic matrix is the synapse count between two neurons, experto-
imentally determined using electron microscopy. The vertex degree is the number of incoming
and outgoing synapses of a neuron in the connectome (Mesa 2).
Since the FlyCircuit dataset has neurons sampled from the entire brain, we appropriately
truncate the stochastically generated connectome by discarding all vertices that correspond to
neurons that were not embedded in the neuropil regions investigated in the Janelia hemibrain
conjunto de datos. We then also truncated the Janelia hemibrain connectome to match the size of the
truncated FlyCircuit connectome, by randomly (uniformly) sampling neurons from the entire
Janelia dataset. The sparsity and degree statistics of the resized connectomes are almost iden-
tical (Mesa 2), supporting our choice for pconn = 0.15.
We also plot and compare the normalized histograms distributions (probability density
funciones) of the edge strength (Figura 3A), and vertex degree (Figura 3B) of the two truncated
hemibrain connectomes. sea f (X) and g(X) denote the probability density function (PDF) del
edge strengths (or vertex degree) for the Janelia hemibrain connectome and the stochastically
Mesa 2. Comparing the experimentally determined Janelia hemibrain connectome (Scheffer et al., 2020) against our stochastically generated
connectome using pconn = 0.15
Connectome
Electron microscopy experimental data ( Janelia)
# Neuronas
21,739
Sparsity
0.75%
Avg. vertex deg
326.64
Avg. edge str
4.04
Stochastically generated from FlyCircuit data
19,902
0.46% ± 0.01
181.79 ± 0.07
2.32 ± 0.01
Truncated connectomes: Hemibrain only
Electron microscopy experimental data ( Janelia)
Stochastically Generated from FlyCircuit Data
11,461
11,461
0.75% ± 0.01
172.73 ± 2.23
4.01 ± 0.09
0.76% ± 0.01
173.36 ± 0.09
2.58 ± 0.02
Nota. Both connectomic datasets were appropriately resized so that they span the same neuropils in the Drosophila hemibrain. The mean (± standard deviation)
values for the sparsity, degree, and strength, were calculated using a total of 100 randomly sampled connectomes.
Neurociencia en red
283
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
generated FlyCircuit connectome, respectivamente. To measure the similarity between the two dis-
tributions we calculate the area over which the two PDFs intersect (Cha, 2007):
z
Int f; gð
Þ ¼
min f xð Þ; g xð Þ
d
Þdx;
where an intersection value Int(F, gramo) = 1 indicates perfect overlap.
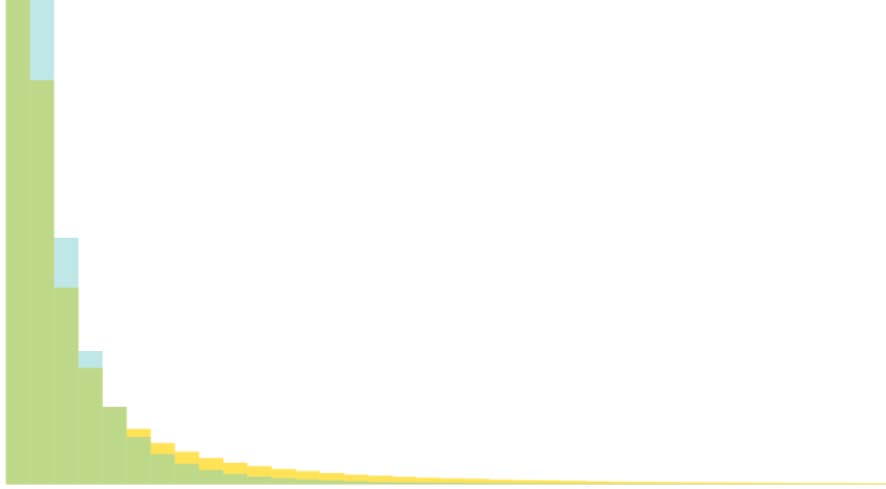
The intersection between the histogram distributions of edge strengths (Cifra 3) es 0.964,
revealing that despite a difference in average edge strength due to long-tail effects, the two
distributions are nearly identical. Further inspection of the Janelia experimental dataset also
indicated that neurons with high- and low-edge strength in the Janelia experimental dataset
appear to be evenly distributed across the neuropil regions. Además, the influence of very
high edge strengths on our model is (exponentially) constrained as per Equation 1, and for
pconn = 0.15 all edge strengths greater than 30 have >0.99 probability of forming an edge
in the stochastically generated binary connectome. The intersection between the histogram
distributions of the vertex degree is also high with an overlap of 0.810 (Figura 3B). Mientras
the two distributions (Figura 3B) have slightly different peaks and spread, the substantial over-
lap along with a nearly identical average vertex degree (Mesa 2) indicates that for pconn = 0.15
the average number of edges across our multiple stochastically generated binary connectomes
is comparable to the experimental dataset. The high measures of similarity between the graph
theoretical statistics of the stochastically generated connectome when compared to the elec-
tron microscopy experimental data further corroborate our choice of pconn.
Varying the parameters. To validate the model stability relative to the values of all parameters
in our framework (Mesa 1), we kept pconn = 0.15 constant and reperformed the clustering for
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. Normalized histogram distributions (probability density functions) del (A) edge strength, y (B) vertex degree, comparing the
experimentally determined Janelia hemibrain connectome (Scheffer et al., 2020) against our stochastically generated connectome using pconn =
0.15. Both connectomic datasets were appropriately resized so that they span the exact same neuropils in the Drosophila hemibrain.
Neurociencia en red
284
Circuit analysis of the Drosophila brain
Mesa 3.
all other parameters constant {pconn = 0.15, re = 11, τ = 0.95, csize = 100}
Pairwise ARI values for varying the number of graphs G 2 {100, 200, 400} while keeping
100
200
400
100
0.9514 (71.94%)
200
0.9818 (72.93%)
400
0.9692 (72.97%)
–
–
0.9649 (71.92%)
0.9737 (73.35%)
–
0.9878 (74.89%)
Nota. The value in parenthesis indicates the percentage (out of all 19,902) neurons classified by both clusterings.
alternative parameter values. The possible choices for the embedding dimensionality d 2
{11, 15} were determined by identifying the first and second elbow point (METRO. Zhu & Ghodsi,
2006), respectivamente, on the scree plot (Supporting Information Figure S3) of singular values. El
values for the other parameters were similarly picked to yield optimal clustering (Mesa 1).
Por ejemplo, to investigate whether increasing the number of the stochastically generated
binary graphs impacted connectivity-based classification, we successively doubled only the
parameter G while keeping all other parameters constant (bold values in Table 1). The very
high pairwise adjusted rand index (ARI) valores (Mesa 3) indicate that the resulting clusterings
are all extremely similar, and that the model is stable over G 2 {100, 200, 400}. The percent-
age of neurons that are assigned a class by our framework (and not discarded by the consensus
clustering and threshold parameters τ, csize) also remain similar over the range of G. Por lo tanto,
increasing the number of graphs beyond 100 does not substantially alter the class assignment
of neurons, but only raises computational complexity. The ARI values along the diagonal
entries of Table 3 were obtained by using identical parameters and number of graphs for each
clustering, but repeating the stochastic generation process with different random seeds. El
diagonal ARI values are therefore an indication of the dependency of the clusterings on the
stochastic elements of our process, and how well we can replicate the results.
Similar ARI results for other different combinations of the parameters in Table 1 are detailed
in the Supporting Information File F2. En general, the ARI remained high (≳0.90) across several
different combinations, demonstrating model stability over a wide range of parameter values.
A limitation of the our inference model is the high computational cost associated with gen-
erating and then consensus clustering multiple large-scale graphs. The provided software code
allows for a relatively easy parallel-processing implementation to significantly reduce the anal-
ysis time needed, but at the cost of requiring increased computational resources. el promedio
CPU time needed for generating and clustering G = 100 graphs, for an embedding dimension
re = 11, was approximately 23 horas. Doubling the number of graphs to G = 200 doubled the
computation time, while increasing the embedding dimension to d = 15 only marginally
increased the computation time (≈24 hours). Varying τ and csize had no noticeable effect on
computation time. All computations were performed on a 20 core CPU cluster with Intel
Haswell architecture, 64 GB of RAM, and using mclust version 5.4.2.
Robustness to sample size. The connectomic dataset used in our analysis consists of 19,902
neuronas, a sample corresponding to approximately 12% of the total number of neurons in a
Drosophila brain. To investigate the robustness of our inferred circuit to the proportion of sam-
pled neurons, we reperformed the clustering on a random subsample from the original dataset
of n = 19,902 neuronas. Each subsample consisted of a subset of ns ≤ n neurons selected using
simple random sampling (without replacement). Each connectomic adjacency matrix A('), para
‘ = 1, …, GRAMO, was accordingly downsized to a size ns × ns matrix, by removing all neurons (y
Neurociencia en red
285
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
Mesa 4.
Pairwise ARI values comparing robustness of the clustering framework to the proportion of sampled neurons, (100ns/n)%
100%
95%
90%
85%
80%
100%
1.00 (78.24%)
95%
0.9657 (72.18%)
90%
0.9424 (71.74%)
85%
0.9105 (72.50%)
80%
0.8596 (70.21%)
–
–
–
–
0.9624 (73.67%)
0.9516 (75.27%)
0.9226 (74.59%)
0.8668 (72.82%)
–
–
–
0.9403 (75.38%)
0.9239 (75.96%)
0.873 (73.75%)
–
–
0.9084 (76.00%)
0.8779 (75.11%)
–
0.8519 (73.08%)
Nota. The value in parenthesis indicates the percentage of neurons classified by both clusterings. All percentage values are expressed in relation to all 19,902
neuronas.
corresponding synaptic connections) that were not included in the subsample. The subsam-
pled (downsized) connectomic matrices were clustered using the model parameters {G = 100,
pconn = 0.15, re = 11, τ = 0.95, csize = 100ns/n}, where the threshold for minimum cluster size
was adjusted to account for the reduced number of neurons in the subsample.
Mesa 4 shows pairwise ARI values obtained using different proportions of the original data-
colocar, when clustering the same G = 100 stochastically generated connectomic matrices used to
construct the circuit (Figura 1A). The entries along the diagonal in Table 4 were obtained by
comparing the clustering results for two (diferente) randomly selected subsamples of ns neu-
ron. The results reveal that the same analysis using 95%, o 90% of the neurons had a neg-
ligible impact on class assignment compared to using all the neurons, as the variability was
comparable to repeating the stochastic generation process with different random seeds (ARI =
0.9514 for ns = n and G = 100 from Table 3). Más, we observe that the number of neurons
that were assigned a class by our framework (and not discarded by the consensus clustering
and threshold parameters τ, csize) did not decrease even as ns decreased. The classification
remained fairly consistent even when using only 85% (ARI > 0.90) y 80% (ARI > 0.85)
of the neurons. The fact that the class assignment of the neurons did not vary significantly
for smaller proportions of the connectomic dataset makes it unlikely that our inferred brain-
wide neural circuit is constricted by the sample size of the considered dataset.
Dopaminergic Hubs Form a Backbone Communication Pathway for Multisensory Integration
To investigate the dopaminergic pathway (Figura 4A), we specifically consider only those neu-
rons in each connectivity-based class whose neurotransmitter is dopamine. Recordar, as per
Ecuación 4 the connection probability ^pij is the average proportion of connected neurons
between classes i and j of the final clustering across the matrices A(') for ‘ = 1, 2, …, 100.
To identify the pathway, we used the same final clustering, but recalculated the connection
probability using only the proportion of connected dopaminergic neurons in the two classes.
Six out of 54 classes (32, 50, 37, 39, 40, 46) alone account for 57% (143/252) of dopami-
nergic neurons. These same classes also show the highest weighted degree and betweenness
centrality among all classes (Figura 4B), characterizing them as graph theoretical hubs in the
circuito. We subsequently refer to these six classes as hub classes. The weighted degree was
defined as the sum of the incoming and outgoing connection probabilities of a class, weighted
(multiplied) by the number of neurons in that class. The betweenness centrality of the class was
defined by the fraction of shortest paths passing through it, where the shortest paths were cal-
culated on a simplified circuit with unweighted edges (Brandes, 2001).
Hub:
A node that exhibits a large number
of connections with other nodes and
is central to the communication
between modules of a network.
Neurociencia en red
286
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
(A) Dopaminergic pathway. (B) Six classes (32, 50, 37, 39, 40, 46) have both high weighted degree and betweenness centrality,
Cifra 4.
characterizing them as graph theoretical hubs in the circuit. (C) The inferred directional connectivity patterns of the identified hub classes
reveal a backbone pathway for multisensory integration. The arrows represent the interpreted connectivity of the hub classes, based on impor-
tant incoming and outgoing communication paths detected by analyzing the absorption and driftiness measurements for these classes (como
detailed in Supporting Information Table T1). (D) Twenty-five representative dopaminergic neurons from the six hub classes that form a single
camino, looping over all 30 edges of the backbone communication pathway.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
The connectivity patterns on the circuit (Figura 4C) were identified by performing a series of
random walk on the entire circuit and calculating the pairwise and average absorption and
driftiness values (Supporting Information File F1 (Tab:abs_drift)). En general, low absorption
values were used to investigate the accessibility of hub classes, while high driftiness values
were used to detect the presence of important communication paths between pairs of classes
(Supporting Information Table T1). Por ejemplo, class 50 is the only one among all classes that
is in the bottom twentieth percentile for both average in-absorption (seventh lowest) así como
average out-absorption (sixth lowest). These extremely low absorption values indicate that class
50 is easily accessible from other nodes on the circuit, and serves as an intermediary connector
for signal propagation; thus reaffirming its role as a hub in the circuit. The connectivity arrows
Neurociencia en red
287
Circuit analysis of the Drosophila brain
depicted for class 50 in Figure 4C indicate high in-driftiness from the olfactory community, y
high in- and out-driftiness from class 32, respectivamente. Específicamente, only class 50 is in the top
tenth percentile of pairwise out-driftiness values for both classes 49 y 38. The very high drifti-
ness values between class 49 → 50 y 38 → 50 indicates that any signal originating in the
antennal lobe of olfactory community is likely to arrive at class 50. Similarmente, class 32 is also the
only class in the top tenth percentile for both in- and out-pairwise driftiness values from class
50. We repeated this process for all six hub classes. A detailed list of all connectivity interpre-
tations made on the circuit using absorption and driftiness measurements, along with a quan-
titative summary of these measurements, is provided in Supporting Information Table T1.
el circuito
The graph theoretic analysis (Figure 4A and 4B) and inferred connectivity patterns
(Figura 4C, Supporting Information Table T1) indicate that these six interconnected classes
work together to form a backbone pathway that facilitate s integration across the sensory
and motor communities. The tightly interconnected loop between the hub classes observed
en
individual dopaminergic neurons
(Figura 4D). Tenga en cuenta que, although these six classes are enriched in dopaminergic neurons, dopa-
mine is still not their dominant neurotransmitter; sin embargo, it is only the dopaminergic neurons
that make these dense interconnections between the six classes. The nondopaminergic neu-
rons in these classes predominantly connect to sensory and motor regions. The identified path-
ways for all the different neurotransmitters are detailed in Supporting Information Figure S5.
level was also identified at
the level of
Curiosamente, these hub classes also exhibit the most extensive neuronal morphologies
among all classes, as characterized by highest total length and number of bifurcations. Devel-
opmental birth times reveal that the backbone communication pathway is one of the earliest
formed pathways in the entire circuit, con 90% of its connections (27/30 bordes) established in
embryo. The three sensory-innervated hub classes show critical growth during the embryo
período, while the three premotor-innervated hub classes show critical growth on day 1.
En general, the analysis suggests that the identified backbone pathway is critical for cross-
modal integration of stimuli. The mechanics of how a fly combines input from multiple sensory
modalities to guide behavior in its natural environment are not fully understood, Por ejemplo,
when combining mechanosensory signals about wind direction along with visual cues to track
an odor. We predict that selectively suppressing activity of neurons in the identified hub clas-
ses using the TH-Gal4 driver line will disrupt the fly’s ability to perform such complex integra-
tive tasks.
Glutamate-Dominant Pathway Bridges the Motor System Interlaterally and Interlinks It with Vision to
Facilitate Rhythmic Activity
To identify the glutamate-dominant pathway, we recalculated the connection probabilities
(Ecuación 4) by using only the proportion of connected glutamatergic neurons in between
classes. Más, since glutamate is a common neurotransmitter in the Drosophila brain, nosotros
restricted our attention to the top 20% of the edges by weight (Figure 5A), eliminating any edges
below this threshold. The resultant graph theoretical pathway shows critical growth during
early development, with classes 42 y 52 especially populated in embryo. These two classes
also have extremely high weighted degree (but low betweenness centrality; Figure 5B) y
appear to act as a central bridge for coordinating motor activity between hemispheres.
Pacemaker neurons are glutamatergic in Drosophila, implicating this neurotransmitter in
behavioral rhythmicity, such as generation of locomotion and modulation of circadian photo-
reception (Azevedo, Hansen, Chen, Rosato, & Kyriacou, 2020; Guo et al., 2016; Zimmerman
et al., 2017). Although the anatomical locations of clock neurons in the Drosophila brain are
Neurociencia en red
288
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
(A) Dominant glutamatergic pathway. (B) Inferred directional connectivity patterns associated with rhythmic motor activity, super-
Cifra 5.
imposed on a schematic of the fly brain illustrating the approximate location of the identified dominant glutamatergic classes in relation to
clock neurons. The arrows represent the interpreted connectivity of the dominant glutamatergic classes, based on important incoming and
outgoing communication paths detected by analyzing the absorption and driftiness measurements for these classes (as detailed in Supporting
Information Table T1).
conocido, their connectivity pathways remain largely unexplored (Dubnau, 2014). Circadian
properties may be an emergent function of the underlying circuitry and not the property of
clock neurons alone (Azevedo et al., 2020; Dissel et al., 2014).
Random walk analysis over the circuit (Figure 5B) revealed that classes 22 y 25 in the left
hemisferio, y 34 y 45 in the right hemisphere, serve as the primary gateways between
the vision and motor systems (Supporting Information Table T1). Específicamente, these classes
receive signals from the visual system and pass on this information to the downstream motor
regiones, while also transmitting motor signals back to vision—possibly control signals to mod-
ulate input. Más, the inferred graph theoretical pathway features multiple interconnecting
loops in the motor region, resembling feedback control, with strong interaction between left
and right hemispheres. We predict that suppressing the activity of glutamatergic neurons in
these identified classes, but not elsewhere, by VGlut-GAL4 driver line targeting will disrupt
motor patterning and circadian rhythms.
Mechanosensory Pathways Rely on Parallel Serotonergic and Octopaminergic Neurotransmission
We identified connectivity-based classes associated with sensory-motor processing through
mappings to functional communities and spatial distribution. Específicamente, we examined those
classes whose neurons heavily innervate the central complex and are identified to be part of
the premotor, auditory, or motor communities. The central complex has been linked to spatial
representación, spatial orientation, visual place learning, and navigation (Turner-Evans &
Jayaraman, 2016). These combined pathways are also believed to be associated with other
mechanosensory functions such as gravity sensation, wind sensation, and air current feedback
during flight (Boekhoff-Falk & Eberl, 2014).
Neurociencia en red
289
Circuit analysis of the Drosophila brain
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
(A) Serotonergic pathway associated with spatial orientation. (B) Octopaminergic pathway associated with fight-or-flight response.
Cifra 6.
(C) The mechanosensory pathways diverge along the dorsal-ventral axis with serotonergic and octopaminergic neurons innervating distinct
neuropils.
The serotonergic pathway (Figure 6A) was identified by restricting attention to only the clas-
ses identified above, and recalculating the connection probabilities (Ecuación 4) using only the
proportion of connected serotonergic neurons in these classes. The serotonergic system is a
critical component of place learning (Zars, 2009). The octopaminergic pathway was similarly
identified by considering only the octopaminergic neurons in the same classes as above
(Figure 6B). While there are only 140 octopaminergic neurons in our connectome, octopamine
is critical for essentially all sensory inputs and is known to play a role in fight-or-flight response
(Sotnikova & Gainetdinov, 2009), stress-related enhancement of motor activity (Sujkowski,
Ramesh, Brockmann, & Wessells, 2017), and aggression (Hoyer et al., 2008). Compared to
the premotor region, which shows critical growth in the early period, the auditory classes grow
predominantly during mid-development, with the octopaminergic classes (19, 20, y 27)
showing continued growth even in the latest stages. Curiosamente, while running in parallel
throughout most of the mechanosensory system, the two graph theoretical pathways diverge
along the dorsal-ventral axis (Figure 6C), with octopaminergic neurons predominantly
innervating the gnathal ganglion and ventromedial protocerebrum, and serotonergic neurons
innervating the superior lateral protocerebrum and superior medial protocerebrum.
Neurociencia en red
290
Circuit analysis of the Drosophila brain
The analysis suggests that these parallel pathways aid in navigation and place learning by
working in conjunction with the hub classes on the backbone pathway to gather information
using sensory cues during flight. We predict that inhibiting the serotonergic neurons in this
pathway using the Trh-Gal4 driver would interfere with the fly’s ability to orient itself in rela-
tion to its surrounding. Además, we hypothesize that selectively inhibiting octopaminergic
neurons in this pathway using the Tdc2-Gal4 driver would prevent the fly from responding
appropriately to potential threats such as moving away from a predator.
Olfactory Learning Depends on Nonredundant GABAergic and Glutamatergic Signaling, While Odor
Tracking Relies on Fast Serotonergic Pathways
To identify the circuit pathways involved in olfaction, we restricted our attention to those clas-
ses that are associated with the olfactory communities, and whose neurons heavily innervate
the antennal lobes, lateral horn, and mushroom body. The mushroom body plays a central role
in associative learning and memory, particularly of olfactory information (Busto, Cervantes-
Sandoval, & davis, 2010). Within the above identified classes, we considered the neurons
associated with the three neurotransmitters involved in olfactory processing, namely GABA
(Busto et al., 2010), glutamate (Liu & wilson, 2013), and serotonin (Johnson, Becnel, &
Nichols, 2011). The olfactory pathways (Cifra 7) were identified by recalculating the
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 7. Predicted olfactory pathways. GABA and glutamate function in parallel to enable olfactory learning, while serotonergic connec-
tions enable cross-modal integration to drive odor tracking.
Neurociencia en red
291
Circuit analysis of the Drosophila brain
connection probabilities using only the proportion of connected GABA (or glutamatergic, o
serotonergic neurons) in these specific classes. The identified graph theoretical pathways are
consistent with findings that GABA and glutamate function in parallel to gate olfactory input
from the antennal lobe to the mushroom body (Liu & wilson, 2013).
Random walk analysis revealed that these pathways have predominantly short local con-
nections with important individual information paths and uncharacteristically few alternative
communication routes. De este modo, we predict that selectively suppressing glutamatergic (a través de
VGlut-Gal4 driver) and GABAergic (via Gad1-Gal4) transmission in this pathway would
impact olfactory learning tasks such as discriminating among similar odors or varying odor
concentrations. Since VGluT-Gal4 and Gad1-Gal4 cover thousands of glutamatergic and
GABAergic neurons, respectivamente, throughout the fly brain, selectively blocking neurotransmis-
sion in this circuit could harness split Gal4 lines (Luan, Diao, Scott, & Blanco, 2020) or other
approaches to spatially target neurons specifically in the olfactory system (Zanon, Zanini, &
Haase, 2022).
Flies are known to track odor by integrating cross-modal mechanosensory and visual input
in flight (Duistermars & Frye, 2010), yet little is known about these descending neural path-
maneras. While the inferred graph theoretical pathways reveal strong olfaction-premotor and
olfaction-vision link via the hub classes, we discovered that there are very few serotonergic
connections to or from the mushroom body (olfactory core) classes themselves. Birthtime anal-
ysis shows that the critical growth period of the olfaction-vision connections occurs in early
desarrollo, while the olfaction-premotor connections are already present in embryo. Nosotros
hypothesize that this pathway enables fast connections from a stimulus (antennal lobe) to a
behavioral response (premotor), and that selective blockage of those serotonergic neurons
via Trh-Gal4 driver line targeting would interfere with odor localization.
DISCUSIÓN
Over the last two decades, Drosophila has been a popular model organism for studying how
structural connections in the brain give rise to functional interactions. Numerous studies have
previously focused on the functional dissection of regional neural circuitry in Drosophila,
including that of vision (Borst, Haag, & Mauss, 2020; Y. Zhu, 2013), olfaction (Busto et al.,
2010), mushroom body (F. Le et al., 2020), and central complex (Turner-Evans & Jayaraman,
2016), to name a few. With advancements in data acquisition and processing, recent large-
scale projects (Scheffer et al., 2020; Shih et al., 2015) have been successful in generating
detailed connectomes of the brain-wide neural circuitry, that go well beyond a single region.
While a complete brain-wide wiring diagram is a necessary prerequisite, unraveling the under-
lying mechanistic pathways to interpolate function and behavior is a problem that cannot be
solved by gathering more data alone (Scheffer & Meinertzhagen, 2021). One of the fundamen-
tal obstacles is the absence of a quantitative specification of neuron types and how they relate
to neural circuitry.
The prevalent approach to analyzing brain-wide microscopic connectomes is to group
neurons into spatially compact regions, Por ejemplo, local processing units (Shih et al.,
2015) or compartments (Scheffer et al., 2020), and then attempt to characterize the connec-
tivity between these groups. While there is undoubtedly a strong spatial component to
synaptic connectivity, anatomical division is by itself insufficient to deconstruct brain com-
putation. Modeling connectomes as a network comprising solely of assortative, anatomically
segregated regions interacting with each other (Shih et al., 2020) may crucially miss many
Neurociencia en red
292
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
functionally relevant characteristics pertaining to the complex mesoscale organization of
the brain.
A diferencia de, our SBM framework groups neurons by their patterns of potential synaptic con-
nectivity to capture assortative and nonassortative features in the underlying neuron-to-neuron
brain-wide network. The information captured by connectivity-based classification is comple-
mentary, yet synergistic, to that provided by traditional neuronal classification—together
enabling functional interpretation not previously possible. By inferring the directed connectiv-
ity patterns on the derived circuit and simultaneously characterizing the circuit with respect to
multiple biomarkers, we have identified functional pathways supporting multiple sensory
modalities and cross-region integration.
A key pathway identified by our circuit is the backbone communication pathway compris-
ing of six interconnected dopaminergic-centric hubs working together to facilitate integration
of the sensory and motor pathways. The neural circuitry for vision, olfaction, and hearing are
well characterized, but the pathways for how these modalities combine to guide behavior
(Currier & Nagel, 2020), Por ejemplo, during navigation, remain elusive. Curiosamente, two
out of these six hubs are the only classes overall that consist of all three neuromodulators—
Y, OA, and 5-HT. Más, since the hubs innervated multiple neuropils, this pathway would
not have been revealed by a classification purely based on anatomy, neurotransmitter, o
morfología. Dopamine is a known neuromodulator central to reinforcement signaling
(Felsenberg, Barnstedt, Cognigni, lin, & Waddell, 2017; Waddell, 2013), and responding to
salient stimuli related to olfaction and vision (Kasture, Hummel, Sucic, & Freissmuth, 2018).
También, while dopamine affects visual tracking (Riemensperger et al., 2011), its role in place
learning or spatial memory remains to be elucidated (Zars, 2009).
Another prominent pathway revealed in our analysis is the glutamate-dominant pathway for
circadian activity. The clock neuron subsets in the Drosophila brain are well described including
their spatial location, morfología, neurotransmitter, and role in behavioral rhythmicity
(Azevedo et al., 2020; Guo et al., 2016; Zimmerman et al., 2017). Sin embargo, the inputs from
other neurons onto clock neurons, and the exact neuronal pathways underlying the entrainment
of the clock for synchronization with the environment are poorly known (Azevedo et al., 2020;
Dubnau, 2014; Hamasaka, Wegener, & Nässel, 2005). The identified pathways link the motor
and vision regions interlaterally, suggesting involvement in coordination of rhythmic activity.
Desafortunadamente, sin embargo, it is unknown which, if any, of the neurons in the 19,902-neuron
FlyCircuit dataset are actually clock neurons.
Over the last several years, optogenetics (Kohsaka & Nose, 2021) have been invaluable in
studying how dynamical interactions on the neural circuit give rise to specific Drosophila
comportamiento. These include circuits relating to rhythmic motor function (Ravbar, zhang, &
Simpson, 2021), olfaction (Bellmann et al., 2010; Hige, Aso, Modi, Frotar, & Tornero, 2015;
Owald et al., 2015), central complex function (Franconville, Beron, & Jayaraman, 2018),
and learning and memory (Simpson & Looger, 2018). Our derived circuit is amenable to
optogenetic manipulation, thus allowing for experimental verification of the predicted func-
tional behavior of the identified pathways. Específicamente, for each of the characterized circuit
pathways, we identify GAL4-UAS driver lines (Brand & Perrimon, 1993) that could potentially
be used for selective neuronal targeting. We also predict the associated loss (or gain) de
function that would accompany the selective deactivation (or activation) of the corresponding
neurons in these pathways.
The connectomic dataset used in our analysis consists of 19,902 neurons reconstructed
from multiple specimen using light microscopy, corresponding to a sample size of
Neurociencia en red
293
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
norte
mi
norte
_
a
_
0
0
2
8
3
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Circuit analysis of the Drosophila brain
aproximadamente 12% of the total number of neurons in a Drosophila brain. As with all research
based on sampled data, we cannot exclude the possibility that our analysis may miss some
essential features of the brain-wide circuitry, due to important neural classes being absent
or not represented with enough neurons in the considered dataset. Our derived mesoscale
circuit does, sin embargo, demonstrate robustness to the proportion of neurons sampled, sugerir-
ing that small variations in the size of the dataset are unlikely to change conclusions signifi-
cantly. The constructed circuit additionally shows excellent left-right symmetry, indicando
bilaterally uniform sampling of the neurons.
A practical limitation of applying the spectral graph clustering framework is that it requires
the size of the dataset (number of vertices in the network) to be much larger than the number of
blocks/classes κ. En particular, κ << n may not hold for connectomic datasets with a limited
number of sampled neurons, or with a large number of classes in relation to total neurons. On
the other hand, the SBM inference model scales extremely well as n increases (Mehta et al.,
2021; Yang, Priebe, Park, & Marchette, 2020); thus, this analysis can be progressively refined
as more neurons continue to be morphologically reconstructed, registered to a common atlas,
and shared with the community (Ascoli, Maraver, Nanda, Polavaram, & Armañanzas, 2017).
Our model could also be applied to dense connectomic reconstructions from electron
microscopy, which is considered the gold standard in the field. However, we view the knowl-
edge derived from sparse light microscopy collected from multiple brains valuable in its own
merit, as it provides complementary information on the shared circuit elements across individ-
uals (Ascoli, 2015). In this regard, it is useful to note that our probabilistic model, currently
restricted to Bernoulli adjacency matrices, can be generalized to cluster nonbinary connec-
tomes using a weighted SBM (Aicher, Jacobs, & Clauset, 2015; Ng & Murphy, 2021), which
would allow accounting for the number of synapses between connected neuron pairs (Tecuatl,
Wheeler, & Ascoli, 2021) in the identification of connectivity-based classes.
ACKNOWLEDGMENTS
We thank our colleagues at the Center for Neural Informatics, Structures, and Plasticity (CN3)
for many insightful discussions. We are especially grateful to Dr. Sumit Nanda for feedback on
the neuropil distribution of the FlyCircuit reconstructions and to Dr. Carolina Tecuatl for help
with the Janelia hemibrain connectome tracing files.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00283.
Supporting information for this article (also available at https://github.com/k3t3n/FlyConn)
includes the following supplementary material. Figure S1: Random walk path length. Figure
S2: Scree plot. Figure S3: 3D spatial embedding of each class. Figure S4: Block connectivity
probability matrix. Figure S5: Neurotransmitter pathways. Table T1: Absorption and driftiness.
File F1: Class labels and data. File F2: ARI results. Movie M1: Critical growth per day. Movie
M2: Critical growth time periods.
AUTHOR CONTRIBUTIONS
Ketan Mehta: Conceptualization; Data curation; Formal analysis; Investigation; Methodology;
Software; Validation; Visualization; Writing – original draft; Writing – review & editing.
Rebecca F. Goldin: Conceptualization; Formal analysis; Investigation; Methodology; Supervi-
sion; Validation; Writing – original draft; Writing – review & editing. Giorgio A. Ascoli:
Network Neuroscience
294
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
n
e
n
_
a
_
0
0
2
8
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circuit analysis of the Drosophila brain
Conceptualization; Data curation; Formal analysis; Funding acquisition; Investigation;
Methodology; Project administration; Resources; Supervision; Validation; Visualization;
Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Giorgio A. Ascoli, National Institutes of Health (https://dx.doi.org/10.13039/100000002),
Award ID: R01NS39600. Giorgio A. Ascoli, National Institutes of Health (https://dx.doi.org
/10.13039/100000002), Award ID: R01NS86082. Giorgio A. Ascoli, National Institutes of
Health (https://dx.doi.org/10.13039/100000002), Award ID: U01MH114829. Giorgio A.
Ascoli, National Institutes of Health (https://dx.doi.org/10.13039/100000002), Award ID:
RF1MH128693. Rebecca F. Goldin, National Science Foundation (https://dx.doi.org/10
.13039/100000001), Award ID: 2152312.
REFERENCES
Abbott, L. F., Bock, D. D., Callaway, E. M., Denk, W., Dulac, C.,
Fairhall, A. L., … Van Essen, D. C. (2020). The mind of a mouse.
Cell, 182(6), 1372–1376. https://doi.org/10.1016/j.cell.2020.08
.010, PubMed: 32946777
Aicher, C., Jacobs, A. Z., & Clauset, A. (2015). Learning latent block
structure in weighted networks. Journal of Complex Networks,
3(2), 221–248. https://doi.org/10.1093/comnet/cnu026
Akram, M. A., Wei, Q., & Ascoli, G. (2022). Machine learning classi-
fication reveals robust morphometric biomarker of glial and neuro-
nal arbors. bioRxiv. https://doi.org/10.1101/2022.04.02.486839
Armañanzas, R., & Ascoli, G. A. (2015). Towards the automatic clas-
sification of neurons. Trends in Neurosciences, 38(5), 307–318.
https://doi.org/10.1016/j.tins.2015.02.004, PubMed: 25765323
Ascoli, G. A. (2015). Trees of the brain, roots of the mind. Cambridge,
MA: MIT Press. https://doi.org/10.7551/mitpress/10292.001.0001
Ascoli, G. A., Donohue, D. E., & Halavi, M. (2007). NeuroMorpho.
Org: A central resource for neuronal morphologies. Journal of
Neuroscience, 27(35), 9247–9251. https://doi.org/10.1523
/JNEUROSCI.2055-07.2007, PubMed: 17728438
Ascoli, G. A., Maraver, P., Nanda, S., Polavaram, S., & Armañanzas,
R. (2017). Win–win data sharing in neuroscience. Nature
Methods, 14(2), 112–116. https://doi.org/10.1038/nmeth.4152,
PubMed: 28139675
Athreya, A., Priebe, C. E., Tang, M., Lyzinski, V., Marchette, D. J., &
Sussman, D. L. (2016). A limit theorem for scaled eigenvectors of
random dot product graphs. Sankhya A, 78(1), 1–18. https://doi
.org/10.1007/s13171-015-0071-x
Azevedo, R. V. D. M. d., Hansen, C., Chen, K.-F., Rosato, E., &
Kyriacou, C. P. (2020). Disrupted glutamate signaling in Dro-
sophila generates locomotor rhythms in constant light. Frontiers
in Physiology, 11, 145. https://doi.org/10.3389/fphys.2020
.00145, PubMed: 32210832
Bates, A. S., Manton, J. D., Jagannathan, S. R., Costa, M., Schlegel, P.,
Rohlfing, T., & Jefferis, G. S. (2020). The natverse, a versatile toolbox
for combining and analysing neuroanatomical data. eLife, 9,
e53350. https://doi.org/10.7554/eLife.53350, PubMed: 32286229
Bellmann, D., Richardt, A., Freyberger, R., Nuwal, N., Schwärzel,
M., Fiala, A., & Störtkuhl, K. F. (2010). Optogenetically induced
olfactory stimulation in Drosophila larvae reveales the neuronal
basis of odor-aversion behavior. Frontiers in Behavioral Neurosci-
ence, 4, 27. https://doi.org/10.3389/fnbeh.2010.00027, PubMed:
20577637
Betzel, R. F., Medaglia, J. D., & Bassett, D. S. (2018). Diversity of
meso-scale architecture in human and non-human connectomes.
Nature Communications, 9(1), 346. https://doi.org/10.1038
/s41467-017-02681-z, PubMed: 29367627
Bijari, K., Valera, G., López-Schier, H., & Ascoli, G. A. (2021).
Quantitative neuronal morphometry by supervised and unsuper-
vised learning. STAR Protocols, 2(4), 100867. https://doi.org/10
.1016/j.xpro.2021.100867, PubMed: 34647039
Boekhoff-Falk, G., & Eberl, D. F. (2014). The Drosophila auditory
system. WIREs Developmental Biology, 3(2), 179–191. https://
doi.org/10.1002/wdev.128, PubMed: 24719289
Borst, A., Haag, J., & Mauss, A. S. (2020). How fly neurons compute
the direction of visual motion. Journal of Comparative Physiology
A, 206(2), 109–124. https://doi.org/10.1007/s00359-019-01375-9,
PubMed: 31691093
Brand, A. H., & Perrimon, N. (1993). Targeted gene expression as a
means of altering cell fates and generating dominant phenotypes.
Development, 118(2), 401–415. https://doi.org/10.1242/dev.118
.2.401, PubMed: 8223268
Brandes, U. (2001). A faster algorithm for betweenness centrality.
Journal of Mathematical Sociology, 25(2), 163–177. https://doi
.org/10.1080/0022250X.2001.9990249
Busto, G. U., Cervantes-Sandoval, I., & Davis, R. L. (2010). Olfac-
tory learning in Drosophila. Physiology, 25(6), 338–346. https://
doi.org/10.1152/physiol.00026.2010, PubMed: 21186278
Cha, S.-H. (2007). Comprehensive survey on distance/similarity
measures between probability density functions. International
Journal of Mathematical Models and Methods in Applied
Sciences, 1(4), 300–307.
Chiang, A.-S., Lin, C.-Y., Chuang, C.-C., Chang, H.-M., Hsieh,
C.-H., Yeh, C.-W., … Hwang, J.-K. (2011). Three-dimensional
reconstruction of brain-wide wiring networks in Drosophila at
single-cell resolution. Current Biology, 21(1), 1–11. https://doi
.org/10.1016/j.cub.2010.11.056, PubMed: 21129968
Costa, L. d. F., Batista, J. L., & Ascoli, G. A. (2011). Communication
structure of cortical networks. Frontiers in Computational
Network Neuroscience
295
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
n
e
n
_
a
_
0
0
2
8
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circuit analysis of the Drosophila brain
Neuroscience, 5, 6. https://doi.org/10.3389/fncom.2011.00006,
PubMed: 21427794
Costa, M., Manton, J. D., Ostrovsky, A. D., Prohaska, S., & Jefferis,
G. S. (2016). NBLAST: Rapid, sensitive comparison of neuronal
structure and construction of neuron family databases. Neuron,
91(2), 293–311. https://doi.org/10.1016/j.neuron.2016.06.012,
PubMed: 27373836
Cover, T. M. (1999). Elements of information theory. New York, NY:
John Wiley & Sons.
Currier, T. A., & Nagel, K. I. (2020). Multisensory control of nav-
igation in the fruit fly. Current Opinion in Neurobiology, 64,
10–16. https://doi.org/10.1016/j.conb.2019.11.017, PubMed:
31841944
Dao, V. L., Bothorel, C., & Lenca, P. (2020). Community structure: A
comparative evaluation of community detection methods. Net-
work Science, 8(1), 1–41. https://doi.org/10.1017/nws.2019.59
DeFelipe, J., López-Cruz, P. L., Benavides-Piccione, R., Bielza, C.,
Larrañaga, P., Anderson, S., … Ascoli, G. A. (2013). New insights
into the classification and nomenclature of cortical GABAergic
interneurons. Nature Reviews Neuroscience, 14(3), 202–216.
https://doi.org/10.1038/nrn3444, PubMed: 23385869
Dissel, S., Hansen, C. N., Özkaya, Ö., Hemsley, M., Kyriacou, C. P.,
& Rosato, E. (2014). The logic of circadian organization in
Drosophila. Current Biology, 24(19), 2257–2266. https://doi.org
/10.1016/j.cub.2014.08.023, PubMed: 25220056
Dubnau, J. (2014). Behavioral genetics of the fly (Drosophila mela-
nogaster). Cambridge, UK: Cambridge University Press. https://
doi.org/10.1017/CBO9780511920585
Duistermars, B. J., & Frye, M. A. (2010). Multisensory integration for
odor tracking by flying Drosophila. Communicative & Integrative
Biology, 3, 60–63. https://doi.org/10.4161/cib.3.1.10076,
PubMed: 20539786
Faskowitz, J., Yan, X., Zuo, X.-N., & Sporns, O. (2018). Weighted
stochastic block models of the human connectome across the life
span. Scientific Reports, 8(1), 12997. https://doi.org/10.1038
/s41598-018-31202-1, PubMed: 30158553
Felsenberg, J., Barnstedt, O., Cognigni, P., Lin, S., & Waddell, S.
(2017). Re-evaluation of learned information in Drosophila.
Nature, 544(7649), 240–244. https://doi.org/10.1038
/nature21716, PubMed: 28379939
Fraley, C. (1998). Algorithms for model-based Gaussian hierarchi-
cal clustering. SIAM Journal on Scientific Computing, 20(1),
270–281. https://doi.org/10.1137/S1064827596311451
Franconville, R., Beron, C., & Jayaraman, V. (2018). Building a func-
tional connectome of the Drosophila central complex. eLife, 7,
e37017. https://doi.org/10.7554/eLife.37017, PubMed: 30124430
Guo, F., Yu, J., Jung, H. J., Abruzzi, K. C., Luo, W., Griffith, L. C., &
Rosbash, M. (2016). Circadian neuron feedback controls the
Drosophila sleep–activity profile. Nature, 536(7616), 292–297.
https://doi.org/10.1038/nature19097, PubMed: 27479324
Hamasaka, Y., Wegener, C., & Nässel, D. R. (2005). GABA modu-
lates Drosophila circadian clock neurons via GABAB receptors
and decreases in calcium. Journal of Neurobiology, 65(3), 225–240.
https://doi.org/10.1002/neu.20184, PubMed: 16118795
Heer, J., Card, S. K., & Landay, J. A. (2005). Prefuse: A toolkit for
interactive information visualization. In Proceedings of the
SIGCHI Conference on Human Factors in Computing Systems
(pp. 421–430). https://doi.org/10.1145/1054972.1055031
Hige, T., Aso, Y., Modi, M. N., Rubin, G. M., & Turner, G. C. (2015).
Heterosynaptic plasticity underlies aversive olfactory learning in
Drosophila. Neuron, 88(5), 985–998. https://doi.org/10.1016/j
.neuron.2015.11.003, PubMed: 26637800
Hoyer, S. C., Eckart, A., Herrel, A., Zars, T., Fischer, S. A., Hardie,
S. L., & Heisenberg, M. (2008). Octopamine in male aggression
of Drosophila. Current Biology, 18(3), 159–167. https://doi.org
/10.1016/j.cub.2007.12.052, PubMed: 18249112
Huang, Y.-C., Wang, C.-T., Su, T.-S., Kao, K.-W., Lin, Y.-J., Chuang,
C.-C., … Lo, C.-C. (2019). A single-cell level and connectome-
derived computational model of the Drosophila brain. Frontiers
in Neuroinformatics, 12, 99. https://doi.org/10.3389/fninf.2018
.00099, PubMed: 30687056
Hubert, L., & Arabie, P. (1985). Comparing partitions. Journal of
Classification, 2(1), 193–218. https://doi.org/10.1007/BF01908075
Ito, K., Shinomiya, K., Ito, M., Armstrong, J. D., Boyan, G.,
Hartenstein, V., … Vosshall, L. B. (2014). A systematic nomencla-
ture for the insect brain. Neuron, 81(4), 755–765. https://doi.org
/10.1016/j.neuron.2013.12.017, PubMed: 24559671
Johnson, O., Becnel, J., & Nichols, C. D. (2011). Serotonin receptor
activity is necessary for olfactory learning and memory in Dro-
sophila melanogaster. Neuroscience, 192, 372–381. https://doi
.org/10.1016/j.neuroscience.2011.06.058, PubMed: 21749913
Jolliffe, I. T. (2002). Principal component analysis. New York, NY:
Springer.
Jonas, E., & Kording, K. (2015). Automatic discovery of cell types
and microcircuitry from neural connectomics. eLife, 4, e04250.
https://doi.org/10.7554/eLife.04250, PubMed: 25928186
Kasture, A. S., Hummel, T., Sucic, S., & Freissmuth, M. (2018). Big
lessons from tiny flies: Drosophila melanogaster as a model to
explore dysfunction of dopaminergic and serotonergic neuro-
transmitter systems. International Journal of Molecular Sciences,
19(6), 1788. https://doi.org/10.3390/ijms19061788, PubMed:
29914172
Kohsaka, H., & Nose, A. (2021). Optogenetics in Drosophila. In H.
Yawo, H. Kandori, A. Koizumi, & R. Kageyama (Eds.), Optoge-
netics: Light-sensing proteins and their applications in neurosci-
ence and beyond (pp. 309–320). New York, NY: Springer.
https://doi.org/10.1007/978-981-15-8763-4_19, PubMed:
33398822
Li, F., Lindsey, J. W., Marin, E. C., Otto, N., Dreher, M., Dempsey,
G., … Rubin, G. M. (2020). The connectome of the adult
Drosophila mushroom body provides insights into function.
eLife, 9, e62576. https://doi.org/10.7554/eLife.62576, PubMed:
33315010
Li, Y., Wang, D., Ascoli, G. A., Mitra, P., & Wang, Y. (2017). Metrics
for comparing neuronal tree shapes based on persistent homol-
ogy. PLoS One, 12(8), e0182184. https://doi.org/10.1371/journal
.pone.0182184, PubMed: 28809960
Liu, W. W., & Wilson, R. I. (2013). Glutamate is an inhibitory neu-
rotransmitter in the Drosophila olfactory system. Proceedings of
the National Academy of Sciences of the United States of Amer-
ica, 110(25), 10294–10299. https://doi.org/10.1073/pnas
.1220560110, PubMed: 23729809
Luan, H., Diao, F., Scott, R. L., & White, B. H. (2020). The Drosophila
split Gal4 system for neural circuit mapping. Frontiers in Neural
Circuits, 14, 603397. https://doi.org/10.3389/fncir.2020.603397,
PubMed: 33240047
Network Neuroscience
296
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
n
e
n
_
a
_
0
0
2
8
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circuit analysis of the Drosophila brain
Mehta, K., Goldin, R. F., Marchette, D., Vogelstein, J. T., Priebe,
C. E., & Ascoli, G. A. (2021). Neuronal classification from net-
work connectivity via adjacency spectral embedding. Network
Neuroscience, 5(3), 689–710. https://doi.org/10.1162/netn_a
_00195, PubMed: 34746623
Moyer, D., Gutman, B., Prasad, G., Faskowitz, J., Steeg, G. V., &
Thompson, P. (2015). Blockmodels for connectome analysis. In
11th International Symposium on Medical Information Processing
and Analysis (Vol. 9681, pp. 62–70). Cuenca, Ecuador: SPIE.
https://doi.org/10.1117/12.2211519
Nanda, S., Allaham, M. M., Bergamino, M., Polavaram, S., Armañanzas,
R., Ascoli, G. A., & Parekh, R. (2015). Doubling up on the fly:
NeuroMorpho.Org meets big data. Neuroinformatics, 13(1),
127–129. https://doi.org/10.1007/s12021-014-9257-y, PubMed:
25576225
Newman, M. E. J. (2006). Modularity and community structure in
networks. Proceedings of the National Academy of Sciences of
the United States of America, 103(23), 8577–8582. https://doi
.org/10.1073/pnas.0601602103, PubMed: 16723398
Ng, T. L. J., & Murphy, T. B. (2021). Weighted stochastic block
model. Statistical Methods & Applications, 30(5), 1365–1398.
https://doi.org/10.1007/s10260-021-00590-6, PubMed:
34840548
Nguyen, N., & Caruana, R. (2007). Consensus clusterings. In
Seventh IEEE International Conference on Data Mining (ICDM
2007 ) (pp. 607–612). Omaha, NE. https://doi.org/10.1109
/ICDM.2007.73
Owald, D., Felsenberg, J., Talbot, C. B., Das, G., Perisse, E.,
Huetteroth, W., & Waddell, S. (2015). Activity of defined mush-
room body output neurons underlies learned olfactory behavior
in Drosophila. Neuron, 86(2), 417–427. https://doi.org/10.1016/j
.neuron.2015.03.025, PubMed: 25864636
Pavlovic, D. M., Vértes, P. E., Bullmore, E. T., Schafer, W. R., &
Nichols, T. E. (2014). Stochastic blockmodeling of the modules
and core of the Caenorhabditis elegans connectome. PLoS
One, 9(7), e97584. https://doi.org/10.1371/journal.pone
.0097584, PubMed: 24988196
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P.
(2007). Numerical recipes: The art of scientific computing
(3rd ed.). Cambridge, UK: Cambridge University Press.
Priebe, C. E., Park, Y., Tang, M., Athreya, A., Lyzinski, V.,
Vogelstein, J. T., … Cardona, A. (2017). Semiparametric spectral
modeling of the Drosophila connectome. arXiv:1705.03297.
https://doi.org/10.48550/arXiv.1705.03297
Priebe, C. E., Park, Y., Vogelstein, J. T., Conroy, J. M., Lyzinski, V.,
Tang, M., … Bridgeford, E. (2019). On a two-truths phenomenon in
spectral graph clustering. Proceedings of the National Academy of
Sciences of the United States of America, 116(13), 5995–6000.
https://doi.org/10.1073/pnas.1814462116, PubMed: 30850525
Raji, J. I., & Potter, C. J. (2021). The number of neurons in Drosoph-
ila and mosquito brains. PLoS One, 16(5), e0250381. https://doi
.org/10.1371/journal.pone.0250381, PubMed: 33989293
Ravbar, P., Zhang, N., & Simpson, J. H. (2021). Behavioral evidence
for nested central pattern generator control of Drosophila groom-
ing. eLife, 10, e71508. https://doi.org/10.7554/eLife.71508,
PubMed: 34936550
Rees, C. L., Moradi, K., & Ascoli, G. A. (2017). Weighing the
evidence in Peters’ rule: Does neuronal morphology predict
connectivity? Trends in Neurosciences, 40(2), 63–71. https://doi
.org/10.1016/j.tins.2016.11.007, PubMed: 28041634
Riemensperger, T., Isabel, G., Coulom, H., Neuser, K., Seugnet, L.,
Kume, K., … Birman, S. (2011). Behavioral consequences of
dopamine deficiency in the Drosophila central nervous system.
Proceedings of the National Academy of Sciences of the United
States of America, 108(2), 834–839. https://doi.org/10.1073/pnas
.1010930108, PubMed: 21187381
Särndal, C. E. (1974). A comparative study of association measures.
Psychometrika, 39(2), 165–187. https://doi.org/10.1007
/BF02291467
Scheffer, L. K., & Meinertzhagen, I. A. (2021). A connectome is not
enough—What is still needed to understand the brain of Dro-
sophila? Journal of Experimental Biology, 224(21), jeb242740.
https://doi.org/10.1242/jeb.242740, PubMed: 34695211
Scheffer, L. K., Xu, C. S., Januszewski, M., Lu, Z., Takemura, S.-Y.,
Hayworth, K. J., … Plaza, S. M. (2020). A connectome and anal-
ysis of the adult Drosophila central brain. eLife, 9, e57443.
https://doi.org/10.7554/eLife.57443, PubMed: 32880371
Scrucca, L., Fop, M., Murphy, T. B., & Raftery, A. E. (2016). mclust
5: Clustering, classification and density estimation using Gauss-
ian finite mixture models. The R Journal, 8(1), 289–317. https://
doi.org/10.32614/RJ-2016-021, PubMed: 27818791
Scrucca, L., & Raftery, A. E. (2015). Improved initialisation of
model-based clustering using Gaussian hierarchical partitions.
Advances in Data Analysis and Classification, 9(4), 447–460.
https://doi.org/10.1007/s11634-015-0220-z, PubMed: 26949421
Shannon, P., Markiel, A., Ozier, O., Baliga, N. S., Wang, J. T.,
Ramage, D., … Ideker, T. (2003). Cytoscape: A software environ-
ment for integrated models of biomolecular interaction networks.
Genome Research, 13(11), 2498–2504. https://doi.org/10.1101
/gr.1239303, PubMed: 14597658
Shepherd, G. M., Marenco, L., Hines, M. L., Migliore, M.,
McDougal, R. A., Carnevale, N. T., … Ascoli, G. A. (2019). Neuron
names: A gene- and property-based name format, with special ref-
erence to cortical neurons. Frontiers in Neuroanatomy, 13, 25.
https://doi.org/10.3389/fnana.2019.00025, PubMed: 30949034
Shih, C.-T., Lin, Y.-J., Wang, C.-T., Wang, T.-Y., Chen, C.-C., Su,
T.-S., … Chiang, A.-S. (2020). Diverse community structures in
the neuronal-level connectome of the Drosophila brain. Neu-
roinformatics, 18(2), 267–281. https://doi.org/10.1007/s12021
-019-09443-w, PubMed: 31797265
Shih, C.-T., Sporns, O., Yuan, S.-L., Su, T.-S., Lin, Y.-J., Chuang,
C.-C., … Chiang, A.-S. (2015). Connectomics-based analysis of
information flow in the Drosophila brain. Current Biology,
25(10), 1249–1258. https://doi.org/10.1016/j.cub.2015.03.021,
PubMed: 25866397
Simpson, J. H., & Looger, L. L. (2018). Functional imaging and opto-
genetics in Drosophila. Genetics, 208(4), 1291–1309. https://doi
.org/10.1534/genetics.117.300228, PubMed: 29618589
Sotnikova, T. D., & Gainetdinov, R. R. (2009). Octopamine and
other monoamines in invertebrates. In L. R. Squire (Ed.), Encyclo-
pedia of neuroscience (pp. 9–15). Cambridge, MA: Academic
Press. https://doi.org/10.1016/B978-008045046-9.01158-X
Sujkowski, A., Ramesh, D., Brockmann, A., & Wessells, R. (2017).
Octopamine drives endurance exercise adaptations in Drosophila.
Cell Reports, 21(7), 1809–1823. https://doi.org/10.1016/j.celrep
.2017.10.065, PubMed: 29141215
Network Neuroscience
297
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
n
e
n
_
a
_
0
0
2
8
3
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Circuit analysis of the Drosophila brain
Tecuatl, C., Wheeler, D. W., & Ascoli, G. A. (2021). A method for
estimating the potential synaptic connections between axons
and dendrites from 2D neuronal images. Bio-protocol, 11(13),
e4073. https://doi.org/10.21769/ BioProtoc.4073, PubMed:
34327270
Turner-Evans, D. B., & Jayaraman, V. (2016). The insect central
complex. Current Biology, 26(11), R453–R457. https://doi.org
/10.1016/j.cub.2016.04.006, PubMed: 27269718
Waddell, S. (2013). Reinforcement signaling in Drosophila; dopa-
mine does it all after all. Current Opinion in Neurobiology,
23(3), 324–329. https://doi.org/10.1016/j.conb.2013.01.005,
PubMed: 23391527
Yang, C., Priebe, C. E., Park, Y., & Marchette, D. J. (2020). Simulta-
neous dimensionality and complexity model selection for spec-
tral graph clustering. Journal of Computational and Graphical
Statistics, 30(2), 422–441. https://doi.org/10.1080/10618600
.2020.1824870
Yitzhaki, S. (2003). Gini’s mean difference: A superior measure of
variability for non-normal distributions. Metron, 61(2), 285–316.
https://doi.org/10.2139/ssrn.301740
Yuste, R., Hawrylycz, M., Aalling, N., Aguilar-Valles, A., Arendt, D.,
Armañanzas, R., … Lein, E. (2020). A community-based tran-
scriptomics classification and nomenclature of neocortical cell
types. Nature Neuroscience, 23(12), 1456–1468. https://doi.org
/10.1038/s41593-020-0685-8, PubMed: 32839617
Zanon, M., Zanini, D., & Haase, A. (2022). All-optical manipulation of
the Drosophila olfactory system. Scientific Reports, 12(1), 8506.
https://doi.org/10.1038/s41598-022-12237-x, PubMed: 35595846
Zars, T. (2009). Spatial orientation in Drosophila. Journal of Neuro-
g e n e t i c s , 2 3 ( 1 – 2 ) , 1 0 4 – 11 0 . h t t p s : / / d o i . o rg / 1 0 . 1 0 8 0
/01677060802441364, PubMed: 19052956
Zeng, H., & Sanes, J. R. (2017). Neuronal cell-type classification:
Challenges, opportunities and the path forward. Nature Reviews
Neuroscience, 18(9), 530–546. https://doi.org/10.1038/nrn.2017
.85, PubMed: 28775344
Zhu, M., & Ghodsi, A. (2006). Automatic dimensionality selection
from the scree plot via the use of profile likelihood. Computa-
tional Statistics & Data Analysis, 51(2), 918–930. https://doi.org
/10.1016/j.csda.2005.09.010
Zhu, Y. (2013). The Drosophila visual system: From neural circuits
to behavior. Cell Adhesion & Migration, 7(4), 333–344. https://
doi.org/10.4161/cam.25521, PubMed: 23880926
Zimmerman, J. E., Chan, M. T., Lenz, O. T., Keenan, B. T., Maislin,
G., & Pack, A. I. (2017). Glutamate is a wake-active neurotrans-
mitter in Drosophila melanogaster. Sleep, 40(2), zsw046. https://
doi.org/10.1093/sleep/zsw046, PubMed: 28364503
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
6
9
2
0
7
2
0
1
8
n
e
n
_
a
_
0
0
2
8
3
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
298