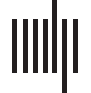INVESTIGACIÓN
Multimodal multilayer network centrality
relates to executive functioning
Lucas C. Breedt1
, Fernando A. norte. Santos1,2, Arjan Hillebrand3, Liesbeth Reneman4,
Anne-Fleur van Rootselaar5, Menno M. Schoonheim1, Cornelis J. Stam3,6, Anouk Ticheler1,
Betty M. Tijms7, Dick J. Veltman8, Chris Vriend1,8, Margot J. Wagenmakers8,9,
Guido A. van Wingen10, Jeroen J. GRAMO. Geurts1, Anouk Schrantee4, and Linda Douw1
1Department of Anatomy and Neurosciences, Amsterdam UMC, Vrije Universiteit Amsterdam,
Amsterdam Neuroscience, Los países bajos
2Institute of Advanced Studies, University of Amsterdam, Los países bajos
3Department of Clinical Neurophysiology and MEG Center, Amsterdam UMC, Vrije Universiteit Amsterdam,
Amsterdam Neuroscience, Los países bajos
4Department of Radiology and Nuclear Medicine, Amsterdam UMC, University of Amsterdam,
Amsterdam Neuroscience, Los países bajos
5Department of Neurology and Clinical Neurophysiology, Amsterdam UMC, University of Amsterdam,
Amsterdam Neuroscience, Los países bajos
6Department of Neurology, Amsterdam UMC, Vrije Universiteit Amsterdam, Amsterdam Neuroscience, Los países bajos
7Alzheimer Center Amsterdam, Department of Neurology, Amsterdam Neuroscience, Amsterdam UMC,
Vrije Universiteit Amsterdam, Los países bajos
8Department of Psychiatry, Amsterdam UMC, Vrije Universiteit Amsterdam, Amsterdam Neuroscience, Los países bajos
9GGZ in Geest Specialized Mental Health Care, Ámsterdam, Los países bajos
10Department of Psychiatry, Amsterdam UMC, University of Amsterdam, Amsterdam Neuroscience, Los países bajos
Palabras clave: Cognición, Graph theory, Conectividad funcional, Structural connectivity, Multiplex
redes, Minimum spanning tree
ABSTRACTO
Executive functioning (EF) is a higher order cognitive process that is thought to depend on a
network organization facilitating integration across subnetworks, in the context of which the
central role of the fronto-parietal network (FPN) has been described across imaging and
neurophysiological modalities. Sin embargo, the potentially complementary unimodal information
on the relevance of the FPN for EF has not yet been integrated. We employ a multilayer framework
to allow for integration of different modalities into one ‘network of networks.’ We used diffusion
resonancia magnética, resting-state functional MRI, MEG, and neuropsychological data obtained from 33 saludable
adults to construct modality-specific single-layer networks as well as a single multilayer network
per participant. We computed single-layer and multilayer eigenvector centrality of the FPN as a
measure of integration in this network and examined their associations with EF. We found that
higher multilayer FPN centrality, but not single-layer FPN centrality, was related to better EF. Nosotros
did not find a statistically significant change in explained variance in EF when using the multilayer
approach as compared to the single-layer measures. En general, our results show the importance of
FPN integration for EF and underline the promise of the multilayer framework toward better
understanding cognitive functioning.
RESUMEN DEL AUTOR
Until now, the relationship between brain network topology and cognition has mostly been
studied using isolated modal information (p.ej., functional MRI or magnetoencephalography).
Such isolated analyses ignore potentially complementary information. Aquí, we use
un acceso abierto
diario
Citación: Breedt, l. C., Santos, F. A. NORTE.,
Hillebrand, A., Reneman, l., camioneta
Rootselaar, A.-F., Schoonheim, METRO. METRO.,
estampar, C. J., Ticheler, A., Tijms, B. METRO.,
Veltman, D. J., Vriend, C., carpinteros,
METRO. J., van Wingen, GRAMO. A., Geurts, j. j. GRAMO.,
Schrantee, A., & Douw, l. (2023).
Multimodal multilayer network centrality
relates to executive functioning. Red
Neurociencia, 7(1), 299–321. https://doi
.org/10.1162/netn_a_00284
DOI:
https://doi.org/10.1162/netn_a_00284
Supporting Information:
https://doi.org/10.1162/netn_a_00284;
https://github.com/nkoub/multinetx;
https://github.com/networkx; https://
github.com/multinetlab-amsterdam
/projects/tree/master/mumo_paper_2021
Recibió: 9 Marzo 2022
Aceptado: 7 Octubre 2022
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Lucas C. Breedt
l.breedt@amsterdamumc.nl
Editor de manejo:
Olaf Sporns
Derechos de autor: © 2022
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
multimodal imaging and neuropsychological data collected from healthy adults to demonstrate
that increased centrality of the fronto-parietal network in a multilayer network is related to better
executive functioning. We find no such relation for single-layer networks. These results show
the importance of fronto-parietal network integration for executive functioning, así como el
value of a multilayer framework in network analyses of the brain.
INTRODUCCIÓN
A thread of network thinking runs through the history of cognition research. En 1983, Fodor
introduced the ‘modularity of mind’ theory of cognition and behavior (Fodor, 1983). Él
posited that lower order processes of the mind are modular, with domain-specific modules
operating independently without interacting with other modules. Contrastingly, he argued that
higher order cognitive processes such as executive functioning (EF), which is thought to be the
most complex and evolutionarily special cognitive domain (Ardila, 2008), are global rather
than modular. Asimismo, the evolution of neuroscience has led to a data-driven approach
toward understanding how the brain governs such higher order cognition by studying the brain
as a complex network through the framework of graph theory (Barrabás, 2016; bullmore &
despreciar, 2009). Brain regions are thus represented as nodes, and the interactions between them
as links.
Different modalities can be used to obtain these brain networks. Anatomically, difusión
magnetic resonance imaging (resonancia magnética nuclear) maps the physical connections (es decir., white matter bun-
dles) between the neural elements of the brain, yielding a structural network. Functionally,
multiple imaging techniques can be used to observe brain activity. Resting-state functional
magnetic resonance imaging (rsfMRI) detects variations in blood oxygenation as an indirect
measure of neuronal activity at a high spatial resolution, and magnetoencephalography
(MEG) provides a direct measure of the summed electromagnetic activity generated by groups
of neurons. In both rsfMRI and MEG, statistical interdependencies between levels of activity in
different areas of the brain are used as a measure for functional connectivity (Aertsen et al.,
1989; Friston et al., 1993), yielding functional networks.
The organization of these structural and functional networks appears to be crucial for EF.
Although the exact mechanisms underlying this cognitive function remain unknown (Jurado &
Rosselli, 2007), EF appears to be highly reliant on network integration, eso es, the interplay
between specialized modules (bullmore & despreciar, 2012). Key in facilitating this integration
is the fronto-parietal network (FPN), a module that plays a crucial central role as a ‘connector’
within the brain network, having diverse connections to other modules of the brain (Bertolero
et al., 2017). The network integration that is hypothetically happening in the individual brain
regions that form the FPN can be characterized through network measures of centrality. Nodal
centrality reflects the relative importance of a node within the network. Highly central regions
are typically connected to many other regions, implying a pivotal role in the facilitation of
network integration (Bertolero et al., 2017; van den heuvel & despreciar, 2011). En efecto, a more
central role of the FPN has been related to better EF in unimodal network studies that utilized
resonancia magnética nuclear (Caeyenberghs et al., 2016), rsfMRI (Cole y col., 2012; Takeuchi et al., 2015), or MEG
(van Dellen et al., 2013).
Sin embargo, in such unimodal network studies the different aspects of the brain network, para
ejemplo, structural and functional, are only studied in isolation, while we know from other
types of complex networks that network structure and different types of functional dynamics
Unimodal:
Consisting of a single form of
imaging, p.ej., only MRI or only MEG.
Neurociencia en red
300
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
Multimodal:
Consisting of more than one form of
imaging, p.ej., MRI as well as MEG.
Multilayer network:
Network comprised of multiple
layers whose nodes interact. Cada
layer contains different information.
occurring on top of it jointly and synergistically determine system behavior (Boccaletti et al.,
2006, 2014; Cardillo et al., 2013; Zanin, 2015). In the brain, it remains unclear exactly how
the integration between these network aspects relates to EF. Sin embargo, the interplay
between structural and functional connectivity has been shown to be nontrivial, sugerencia
both should be considered simultaneously (Damoiseaux & Greicius, 2009; Parque & Friston,
2013; Stam et al., 2016). Además, in the case of networks based on MEG data, the broad-
band signal is often filtered into canonical frequency bands, and network analysis is performed
for each frequency band separately, but the different imaging modalities and frequency bands
each yield unique and even complementary information that should perhaps not be consid-
ered in isolation. Unimodal networks are thus limited representations of the essentially multi-
modal brain network (Garcés et al., 2016; Mandke et al., 2018; Zanin, 2015), but until recently
we lacked the appropriate tools to integrate multiple modalities into a single network
representación.
Multilayer network analysis is a newly developed mathematical framework that enables this
integration and allows for analysis of multimodal data (Boccaletti et al., 2014; De Domenico
et al., 2013; Kivelä et al., 2014). A multilayer network is a ‘network of networks,’ comprised of
multiple interconnected layers, each characterizing a different aspect of the same system.
Cifra 1 illustrates the concept of multilayer networks using the analogy of a commuter net-
trabajar. Although the framework of multilayer networks is relatively new in the field of neuro-
ciencia, promising results have already been reported. Multilayer analysis of dMRI and fMRI
networks of healthy participants confirmed the synergistic nature of the structure and function
of the brain network (Battiston et al., 2017). Further relevance of multilayer analysis has been
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Example of a multilayer transport network, encoding information about train, subway,
Cifra 1.
and road connectivity, and the interlayer links between them. Suppose there is a sudden increase in
commuters in the subway network in the absence of any delayed or cancelled subway cars or sus-
pended subway stations. Considering the single-layer subway network in isolation, the observed
spike in commuters would seem inexplicable, as the properties of the subway network (es decir., el
links and nodes) are unaltered. Sin embargo, observing the entire transport system might reveal severe
delays in the train network, forcing people who usually commute by train to now use the subway,
thus leading to an increase in commuters in the subway network. Asimismo, consider the red node in
the train network. From a single-layer perspective, this is a peripheral station that is of little impor-
tance to the transport system. Sin embargo, the multilayer perspective reveals this to be the only loca-
tion where all three modes of transport connect, and the seemingly peripheral station thus plays a
significant integrative role in the transportation network—a property that would have remained
unnoticed without incorporating all the layers of the system.
Neurociencia en red
301
Multilayer network centrality relates to executive functioning
shown in clinical studies: multilayer connectivity differences were reported between patients
with schizophrenia and healthy controls, and these differences were related to symptom sever-
idad (Brookes et al., 2016). Además, a study in schizophrenia and another study in Alzheimer’s
disease suggested that multilayer centrality could outperform single-layer measures to distin-
guish cases from healthy controls (De Domenico et al., 2016; Guillon et al., 2017). Addition-
ally, an MEG study used nodal centrality metrics to identify brain regions that were vulnerable
in patients with Alzheimer’s disease compared to healthy controls and found that such regions
could only be detected using a multilayer approach. Even more relevant to our work, este
vulnerability of central regions in the multilayer network was related to cognitive dysfunction
(Yu et al., 2017). Multilayer network analysis can thus contribute to a better understanding of
the relation between the FPN and EF.
Aquí, we used multimodal data to assess the association between FPN centrality and EF in
healthy participants and statistically explored the potential added value of a multilayer frame-
work over a single-layer framework. Nosotros (a) hypothesized a positive association between FPN
centrality of both the single- and multilayer networks, which could already indicate that the
multilayer approach is useful to integrate multimodal data toward investigating executive func-
cionando. Además, nosotros (b) aimed to test whether multilayer centrality supersedes its single-layer
equivalents in explaining individual differences in EF statistically, through a significant change
in explained variance.
MÉTODOS
Participantes
This study was preregistered in the International Clinical Trials Registry Platform under trial ID
NTR7510. Thirty-nine (39) healthy participants were prospectively recruited for this specific
study through an online platform, Hersenonderzoek.nl (www.hersenonderzoek.nl), where vol-
unteers can register for participation in neuroscience studies. Participants were selected based
on the following inclusion criteria: (a) age between 20 y 70 years old, (b) native Dutch
speaker, y (C) able to provide written informed consent. The following exclusion criteria
were used: (a) history of neurological or psychiatric disease, (b) current and regular use of
centrally acting drugs, y (C) presence of contra-indications for MRI or MEG. Participantes
were asked not to ingest any caffeine or alcohol on the testing days. Approval was obtained
from the VU University Medical Center Medical Ethical Committee, and all subjects provided
written informed consent prior to participation.
Neuropsychological Evaluation
Participants underwent an extensive customized neuropsychological test battery, consisting of
the Dutch version of Rey’s Auditory Verbal Learning Test (van den Burg et al., 1985), the Con-
cept Shifting Test (CST; van der Elst et al., 2006a), the Memory Comparison Test (van der Elst
et al., 2007), the Stroop Color-Word Test (SCWT; Hammes, 1978), the Location Learning Test
(LLT; Bucks & Willison, 1997), the Categorical Word Fluency Test (Mulder et al., 2006), y
the Letter-Digit Modalities Test (van der Elst et al., 2006b). We used (subscores on) three of
these tests to assess EF. The first test we used was the CST, where the participant was shown
16 small circles, grouped in a large circle, containing either digits (CST part A), letters (CST part
B), or both digits and letters (CST part C). These circles needed to be crossed out in ascending
order in part A, in alphabetical order in part B, and in alternating order (digit-letter) in part C.
The participant was asked to perform the test as quickly as possible without making mistakes.
Además, to correct for motor speed, a null-condition with empty circles (CST zero) era
Neurociencia en red
302
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
carried out three times. The second test we used was the SCWT, where the participant was
asked to read four different cards. On the first card, names of colors—red, verde, yellow,
and blue—were printed in black ink. On the second card, rectangles were printed in these
same colors. On the third card, the names of the colors were printed in an incongruent color
ink; Por ejemplo, the word ‘red’ was printed in yellow ink, and the participant was asked to
read the color of the ink and ignore the word. The fourth card was identical to the third card,
but several words were circled. For these circled words, the participant was asked to read the
word itself instead of the color of the ink. The third test we used was the Word Fluency Test,
where the participant was asked to name as many words in the category ‘animals’ as possible
dentro 60 artículos de segunda clase.
We used validated norms of the CST, SCWT, and Word Fluency Test to transform raw scores
into z-scores relative to a comparable healthy population. Brevemente, raw CST scores were
adjusted for age only, as no effects of gender or age squared were present in the normative
sample of 1,794 Dutch adults (van der Elst et al., 2006a). Raw SCWT scores were corrected for
edad, age squared, and education (classified according to the Dutch Verhage system (Verhage,
1964), which ranges from level 1 [less than 6 years of primary education] a nivel 7 [university
degree]) (Schmand et al., 2012). Raw scores on the Word Fluency Test were corrected for age
and education, as there were no effects of age squared in the normative sample (Schmand
et al., 2012). EF was defined as the average of z-scores for Word Fluency, Stroop-interference
(time to complete card 3 corrected for the time to complete card 2), and CST-shift (time to
complete card C minus the average time to complete cards A and B, adjusted for time to
complete CST zero).
Imagen de resonancia magnética
MRI data were obtained using a 3T MRI system (Philips Ingenia CX) con 32 canales
receive-only head coil at the Spinoza Centre for Neuroimaging in Amsterdam, The Nether-
lands. A high-resolution 3D T1-weighted image was collected with a magnetization-prepared
rapid acquisition with gradient echo (MPRAGE; TR = 8.1 EM, TE = 3.7 EM, flip angle = 8°,
voxel dimensions = 1 mm3 isotropic). This anatomical scan was registered to MNI space
through linear registration with nearest-neighbor interpolation, and was used for
co-registration and normalization of all other modalities (resonancia magnética nuclear, resonancia magnética funcional, and MEG) to the same
espacio.
Diffusion MRI. Diffusion MRI was collected with diffusion weightings of b = 1,000 y
2,000 s/mm2 applied in 29 y 59 directions, respectivamente, junto con 9 nondiffusion weighted
(b = 0 s/mm2) volumes using a multiband sequence (MultiBand SENSE factor = 2, TR = 4.7 s,
TE = 95 EM, flip angle = 90°, voxel dimensions = 2 mm3 isotropic, no interslice gap). In addi-
ción, two scans with opposite phase encoding directions were collected for blip-up blip-down
distortion correction using FSL topup (Andersson et al., 2003). Structural connectomes were
constructed by performing probabilistic anatomically-constrained tractography (ACT) (Herrero
et al., 2012) in MRtrix3 (Tournier et al., 2019). A tissue response function was estimated from
the preprocessed and bias field corrected dMRI data using the multishell multitissue five-
tissue-type algorithm (msmt_5tt). Después, the fiber orientation distribution for each voxel
was determined by performing multishell multitissue constrained spherical deconvolution
(MSMT-CSD) (Jeurissen et al., 2014). ACT was performed by randomly seeding 100 millón
fibers within the white matter to construct a tractogram, and spherical-deconvolution informed
filtering of tractograms (SIFT, SIFT2 method in MRtrix3) (Smith et al., 2015) was then performed
to improve the accuracy of the reconstructed streamlines and reduce false positives. For every
Neurociencia en red
303
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
partícipe, their respective 3D T1-weighted image was used to parcellate the brain into 210
cortical Brainnetome atlas (BNA) (Fan et al., 2016) regiones. We then used this parcellation to
convert the tractogram to a structural network, where weighted edges represented the sum of
all streamlines leading to and from all voxels within two brain regions.
Resting-state functional MRI. Resting-state fMRI was collected using a multiband sequence
(MultiBand SENSE factor = 2, TR = 1.52 s, TE = 30 EM, flip angle = 70°, voxel size = 2.5 ×
2.5 × 2.75 mm3, interslice gap = 0.25 mm, 310 volumes, 12-min acquisition). Participantes
were instructed to remain awake with their eyes open. Preprocessing was done using FSL 5
(FMRIB 2012, Oxford, Reino Unido, https://www.fmrib.ox.ac.uk/fsl) and included brain
extraction, removal of the first four volumes, motion correction by regressing out six motion
parámetros, and spatial smoothing at 5-mm full width half maximum. An independent com-
ponent analysis was performed for automatic removal of motion artifacts (ICA-AROMA) (Pruim
et al., 2015), followed by regressing out white matter and cerebrospinal fluid signals and high-
pass filtering (100 s cutoff ). Mean absolute motion did not exceed 0.6 mm for any participant;
the median was 0.27 mm (0.08–0.59 mm). The rsfMRI data were registered to native 3D T1
space using boundary-based registration. The BNA atlas was then reverse-registered to each
participant’s functional data using nearest-neighbor interpolation. For every participant, a
mask containing only gray matter voxels with reliable rsfMRI signal was constructed by com-
bining a gray matter mask and an rsfMRI mask, excluding all voxels with a signal intensity in
the lowest quartile of the robust range (for more details, see Eijlers et al., 2017). Time series
were extracted from all atlas regions by averaging time series across all voxels within each
región. Thirteen regions with signal loss (es decir., regions with zeros in the functional connectivity
matrices) due to magnetic field inhomogeneities in these echo-planar imaging sequences were
removed from further analyses across all participants and modalities. De este modo, 197 atlas regions
remained for all further analyses. Finalmente, for every participant, Pearson correlation coefficients
between all pairs of time series were calculated to obtain a functional connectivity matrix.
Correlation coefficients were absolutized, as most network metrics do not take into account
negative values, but inverse correlations may carry relevant information (Chai et al., 2012;
Zhan et al., 2017).
Magnetoencephalography
MEG data were recorded in a magnetically shielded room ( Vacuumschmelze GmbH, Hanau,
Alemania) using a 306-channel (102 magnetometers and 204 gradiometers) whole-head MEG
sistema (Elekta Neuromag Oy, Helsinki, Finland) with a sampling frequency of 1250 Hz during
a no-task, eyes-closed condition for 5 minutos, an eyes-open condition for 2 minutos, y un
final eyes-closed condition for another 5 minutos, with the participant in supine position.
Aquí, we used only the first eyes-closed recording for all further analyses. An anti-aliasing filter
de 410 Hz and a high-pass filter of 0.1 Hz were applied online. The cross-validation signal
space separation (xSSS) (van Klink et al., 2017) was applied to aid visual inspection of the data.
We removed channels containing no signal or noisy signal, with a maximum of 12 canales
removed per participant. Further noise removal was performed offline using the temporal
extension of signal space separation (tSSS) (Taulu & Simola, 2006) in MaxFilter (versión
2.2.15). The head position relative to the MEG sensors was recorded continuously using the
signals from five head-localization coils. Coil positions and the scalp outline were digitized
using a 3D digitizer (Fastrak, Polhemus, Colchester, VT). A surface-matching procedure was
used to achieve co-registration of the participant’s digitized scalp surface and their anatomical
resonancia magnética, with an estimated resulting accuracy of 4 mm (Whalen et al., 2008). A single best fitting
sphere was fitted to the outline of the scalp as obtained from the co-registered MRI, which was
Neurociencia en red
304
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
Phase lag index:
Measure of connectivity in MEG
(or EEG) based on the asymmetry of
the distribution of phase differences
between two signals.
used as a volume conductor model for the beamformer approach described below. The co-
registered MRI was spatially normalized to a template MRI, and the voxels in the normalized
co-registered MRI were again labeled according to the same atlas. We then used a scalar beam-
forming approach (Hillebrand et al., 2012) to reconstruct the source of neurophysiological
activity from the sensor signal. The beamformer weights were based on the lead fields, el
broadband (0.5–48 Hz) data covariance, and noise covariance. The data covariance was based
en, on average, 298 s of data (range 293–314 s). A unity matrix was used noise covariance.
Broadband data were then projected through the normalized beamformer weights to obtain
time series for each atlas region. Out of all the voxels that constitute an atlas region, the centroid
(Hillebrand et al., 2016) was selected to reconstruct localized MEG activity, resulting in time
series for each of the 197 included cortical regions. For all participants, we included the first
88 epochs of 4,096 muestras (3.28 s) of the obtained time series (total length 4 min and ∼48 s).
Fast Fourier transforms were applied to filter the time series into six frequency bands: delta (0.5–
4 Hz), theta (4–8 Hz), lower alpha (8–10 Hz), upper alpha (10–13 Hz), beta (13–30 Hz), y
gamma (30–48 Hz). We then computed the phase lag index (PLI) (Stam et al., 2007) entre
the frequency-filtered time series of all pairs of regions using custom-made scripts in MATLAB
(R2018b, Matemáticas, Natick, MAMÁ) to obtain weighted functional connectivity matrices.
Single-Layer Network Construction and Analysis
Primero, we constructed minimum spanning trees (MST) for the six frequency band–specific MEG
networks by applying Kruskal’s algorithm (Kruskal, 1956) to the functional connectivity matri-
ces. The MST is a binarized subgraph of the original graph that connects all the nodes in the
network without forming loops. This represents the backbone of the network (Stam et al.,
2014; Tewarie et al., 2015), cual, importantly, is not hindered by common methodological
issues such as effects of connection strength or link density on the estimated topological char-
acteristics of networks, while measures calculated on this sparse network are closely related to
measures computed on the original underlying network (Tewarie et al., 2015). Edge weights
were defined as the inverted PLI values (1/PLI) when constructing the minimum spanning tree,
since we were interested in the strongest connections (Tewarie et al., 2014).
While the usage of the MST is ubiquitous in MEG studies (Blomsma et al., 2022), it is only
rarely used in dMRI and rsfMRI studies, where weighted networks are more commonly ana-
lyzed. As we here aimed to compare a relatively new multilayer network approach to the now
often-used single-layer methodology, we primarily opted to remain as close as possible to the
existing literature on single-layer networks. We therefore calculated nodal eigenvector central-
idad (EC) individually for each of the six MEG MSTs, and for the fully connected weighted dMRI
and rsfMRI connectivity matrices, using the brain connectivity toolbox (https://sites.google
.com/site/bctnet/) in MATLAB. EC is a measure of nodal centrality that assumes that a node
is more influential if it is connected to nodes that are highly central themselves, and thus con-
siders both the connections of a node itself as well as the connections of its neighbors. Este
makes it an interesting measure of centrality that takes the entire network into account. adi-
cionalmente, EC is a spectral measure, and may therefore be less sensitive to noise than other
measures of centrality (Kardos et al., 2020), particularly when applied to the backbone of
the network. Además, EC has been shown to be highly relevant for cognition in studies
using dMRI (Fagerholm et al., 2015), rsfMRI (Eijlers et al., 2017), and MEG (Hardmeier et al.,
2012). For a more detailed explanation of the EC and its mathematical definition, see Fornito
et al. (2016).
Finalmente, we extracted and subsequently averaged the ECs of all nodes belonging to the FPN
to obtain one value per single-layer network per participant (for a total of eight values per
Neurociencia en red
305
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
Multiplex network:
Special case of multilayer networks,
with interlayer connections present
only between a node’s counterparts
across layers.
Interlayer links:
Connections between two different
layers of a multilayer network.
Intralayer links:
Connections within one layer
(of a multilayer network).
Supra-adjacency matrix:
Matrix representation of a multilayer
network. Diagonal blocks contain
connectivity within a layer; apagado-
diagonal blocks contain connectivity
between layers.
partícipe), allowing us to assess interindividual differences in the integration of the FPN in
the context of the entire brain network. Regions belonging to the FPN were defined based on
an earlier categorization (Vriend et al., 2018) of the regions of the BNA according to the clas-
sical seven-network parcellation by Yeo et al. (2011).
Multilayer Network Construction and Analysis
A multiplex network is a multilayer network used to describe different interactions between the
same set of nodes (Bianconi, 2018). In this context, each layer is characterized by a different
modality of interaction. Por lo tanto, this mathematical framework is useful to encode informa-
tion from brain networks created using different edge weights or imaging modalities as long as
all layers are built using the same atlas. In such a multiplex network, links between different
capas, also known as interlayer links, exclusively connect the same node or brain region
across layers.
There is, as of yet, no established method for determining biologically meaningful weighted
interlayer links between different modalities. Además, network metrics can potentially be
biased by differences in link density (especially when comparing dMRI networks, cuales son
inherently sparse, and functional networks) and average connectivity across layers and
between participants (Mandke et al., 2018). Aquí, we therefore decided to construct binary
multiplex networks. Como consecuencia, in addition to the MEG MSTs described in the section
Single-Layer Network Construction and Analysis, we used Kruskal’s algorithm to construct MSTs
for the dMRI and rsfMRI data. We then integrated these eight MSTs to obtain an interconnected
multiplex network for every participant. Each participant’s multiplex thus consisted of L = 8
capas (one for dMRI, one for rsfMRI, and one for each of the six MEG frequency bands), con
each layer containing the same set of N = 197 nodos (atlas regions), and each spanning tree
and thus layer having M = N − 1 = 196 intralayer links. The weights of the interlayer connec-
tions were set to 1, identical to the intralayer connections. The resulting multilayer network
was represented as an LxN by LxN supra-adjacency matrix with diagonal blocks encoding
intralayer connectivity for each modality and off-diagonal blocks encoding interlayer connec-
actividad. Supra-adjacency matrices were then exported to Python (versión 3.6, Python Software
Base, disponible en https://www.python.org), and multilayer nodal EC was computed
according to earlier work. Brevemente, we first computed the leading eigenvector of the supra-
matriz de adyacencia, and we then aggregated the corresponding eigenvector of size LxN into a
vector of size N, by averaging the entries corresponding to the same nodes, as described in De
Domenico et al. (2013). para hacerlo, we used custom-made scripts that integrate the Python
libraries multiNetX (Solé-Ribalta et al., 2013) and NetworkX (versión 2.3) (Hagberg et al.,
2008), which can be found on GitHub (https://github.com/nkoub/multinetx and https://
github.com/networkx, respectivamente). To validate our code, we compared, for a subset of our
datos, the EC values obtained through the use of our scripts to those obtained using muxViz, a
well-known tool for multilayer analysis (De Domenico et al., 2015b). We then again extracted
and averaged ECs of the FPN nodes, yielding one value for multilayer EC per participant. A
schematic overview of the methods can be found in Figure 2, and a 3D plot of a multilayer
network can be found in the Supporting Information. All of the custom-made scripts, así como
the data that we used in this study, can be found on this project’s GitHub page (https://github
.com/multinetlab-amsterdam/projects/tree/master/mumo_paper_2021).
Statistical Analyses
Frequentist statistics were used, with a significance threshold of 0.05 set before starting the
analiza, through SPSS (versión 26, IBM Corp., Armonk, Nueva York). To assess the relation between
Neurociencia en red
306
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
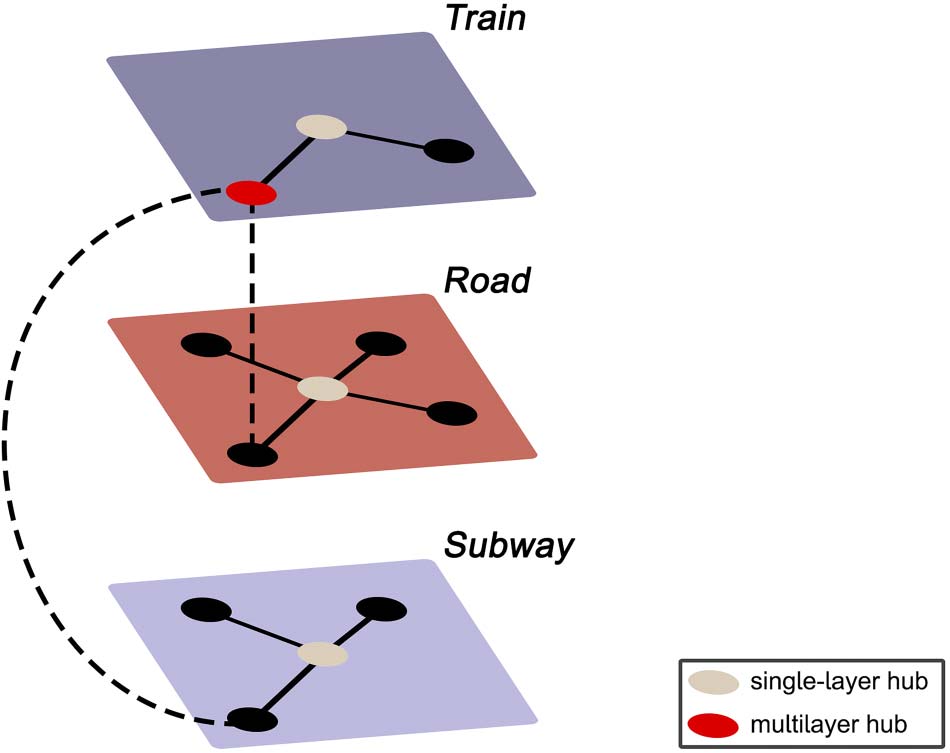
Cifra 2. Schematic overview of the analysis pipeline. For every participant, neuropsychological data was used to compute cognition scores;
raw imaging data obtained from diffusion MRI, resting-state functional MRI, and magnetoencephalography was preprocessed; the brain was
parcellated according to the Brainnetome Atlas; connectivity was calculated to construct weighted connectivity matrices; minimum spanning
trees of the weighted matrices were constructed using Kruskal’s algorithm; and finally a supra-adjacency matrix representing a multilayer
network was constructed. Note that single-layer network measures were computed on the minimum spanning trees of the magnetoenceph-
alography frequency bands, but weighted data was used for diffusion MRI and resting-state functional MRI. NPA = neuropsychological assess-
mento; MEG = magnetoencephalography; rsfMRI = resting-state functional MRI; dMRI = diffusion MRI; BNA = Brainnetome Atlas; MST =
minimum spanning tree.
single- or multilayer EC of the FPN and age, sexo, and education-corrected EF scores, we per-
formed a multiple regression analysis. With EF as the dependent variable, average EC values of
the FPN of each of the eight single-layer networks described in section Single-Layer Network
Construction and Analysis were added in a first block using a backward stepwise procedure
(F probability for removal 0.10), and the average EC of the FPN of the multilayer network was
entered in a second block. To assess whether these data met the assumption of collinearity, nosotros
ran multicollinearity diagnostics based on the variance inflating factor ( VIF). The VIF of a pre-
dictor is calculated by doing a linear regression of that predictor on all other predictors, después
which the VIF is defined by 1/(1 − R2). A high VIF is thus indicative of the presence of mul-
ticollinearity. Tolerance is the inverse of the VIF, and it is suggested that it should not be below
0.2 (Menard, 1995), which we used as a threshold in our manuscript. Regression models were
checked for normality of residuals using a Q-Q plot.
Post Hoc Analyses
To ensure the validity of our main result, we performed several additional post hoc analyses.
En primer lugar, we repeated the multiple regression analysis described above with a forward selection
procedimiento (F probability for entry 0.05). Además, to explore whether the results were
affected by our decision to compute single-layer network metrics on the MSTs for the MEG
redes, but on the fully connected weighted networks for the fMRI and dMRI networks,
we re-ran the same regression using ECs of the FPN calculated on the MSTs of all the
single-layer networks. También, to confirm the relevance of the multilayer framework, nosotros
Neurociencia en red
307
Multilayer network centrality relates to executive functioning
performed a multiple regression relating the average FPN centrality of all single-layer networks
to executive functioning. As before, we added the average FPN centrality values of each of the
eight single-layer networks in a first block by using a backward stepwise procedure; we then
entered the average EC of the FPN across the single-layer networks in a second block. In order
to assess whether EC was, as hypothesized, most sensitive to individual differences in EF, nosotros
also computed the degree centrality of the multilayer network and performed a linear regres-
sion relating the average multilayer degree centrality of the FPN to executive functioning.
Además, we performed a leave-one-out cross-validation for the final regression model
of multilayer EC of the FPN and EF to assess whether regression results were not driven by
any single subject, and computed the cross-validated coefficient of determination (R2) usando
the following equation:
R2 ¼ 100 (cid:2) 1 −
PAG
norte
i¼1 yi − (cid:1)y i
d
PAG
Þ2
norte
i¼1 yið
Þ2
!
;
with n being the number of measurements, y the vector of measurements, and ý the vector of
model predictions, as described previously (Yeatman et al., 2014). Además, we repeated
our analysis using a different parcellation, namely the automated anatomical labeling (AAL)
atlas (Tzourio-Mazoyer et al., 2002), and re-ran the regression model, to compare to the results
that were found using the BNA. Finalmente, as a post hoc analysis, we explored the relationship
between multilayer centrality of the FPN and several other cognitive domains, a saber, verbal
memory ( VM), information processing speed (IPS), working memory ( W.M.), and attention. A
this end, we performed four separate linear regression analyses with multilayer EC of the FPN
as the independent variable and the cognitive domains as the dependent variables. See the
Supporting Information for a detailed specification of the cognitive domains.
Además, we performed a post hoc analysis to validate the methodology we used for
network thresholding within each layer, by comparing our chosen method of the MST to a
preliminary analysis inspired by recent developments on network inference (Nakamura
et al., 2016). Brevemente, in the latter, surrogate data is used to assign each edge in a network a
value reflecting its statistical significance, eso es, edges with significance below a chosen level
are more likely to be “true” edges. Aquí, we leveraged this methodology as follows: nosotros (a)
create an ensemble of 100 null models for each single-layer matrix for every subject in our
grupo, by shuffling the edge weights in the original weighted matrix while preserving the
degree, weight, and strength distributions (using the function null_model_und_sign.m of the
Brain Connectivity Toolbox); (b) perform a nonparametric Kolmogorov–Smirnov test to assess
the significance of each original edge in comparison with the correspondent edges in the ran-
domized matrices (using a significance threshold of 0.05); (C) create a new, thresholded matrix,
containing only those edges that were significantly different from their randomized counter-
partes; y (d) compare the edges of the MST matrix with the significance matrix to establish the
fraction of significant edges in the MST matrix.
RESULTADOS
Participant Characteristics
Del 39 included participants, two participants dropped out before completion of the study,
two were excluded during the study because of contra-indications for MRI, and another two
were excluded after visual inspection of their MRI data revealed artifacts. This resulted in a
total of 33 included participants with complete structural MRI, resonancia magnética nuclear, rsfMRI, MEG, and neu-
ropsychological data that were used in the analyses. Of these participants, 18 were female and
Neurociencia en red
308
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Multilayer network centrality relates to executive functioning
15 were male. They were well spread out in terms of age, ranging between 22 y 70 años
viejo, with a mean age of 46 ± 17 años. Participants were mainly higher educated.
Network Correlates of Cognition
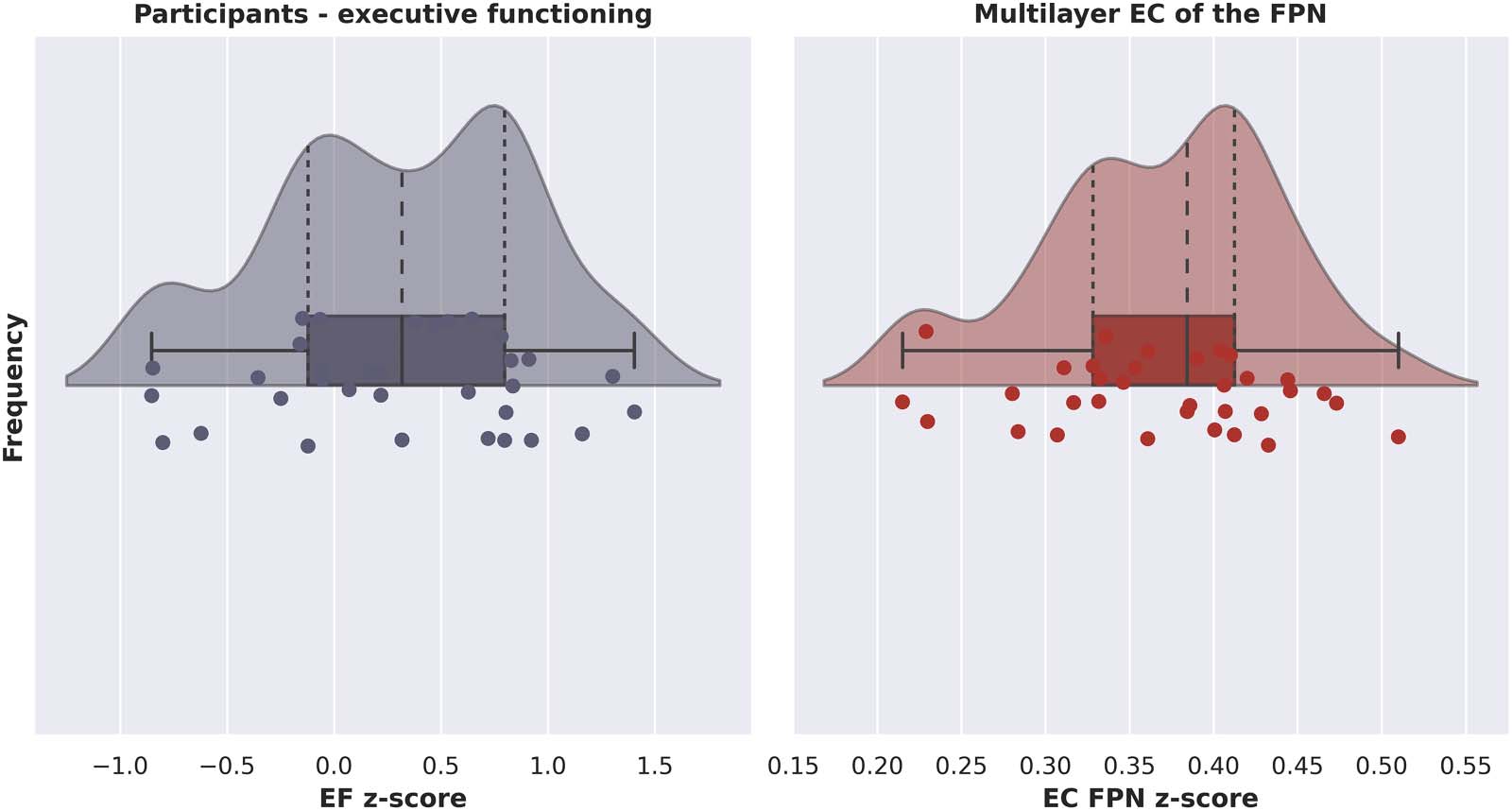
Cifra 3 shows a raincloud plot with the distribution of EF z-scores for all participants. Impor-
tantly, as indicated by the wide range of normed z-scores, our sample was diverse in terms of
EF performance. There was no evidence of problematic multicollinearity between network
variables as indicated by their tolerance values, which were all greater than 0.2 (Menard,
1995). Cifra 4 shows exemplar values of EC for the multilayer network as well as all the
single-layer networks, averaged over all subjects.
Testing our hypotheses, none of the single-layer network eigenvector centralities survived
the backward stepwise selection, ver tabla 1 for the coefficients of the included and excluded
variables. The final regression model, containing only multilayer EC of the FPN as a predictor
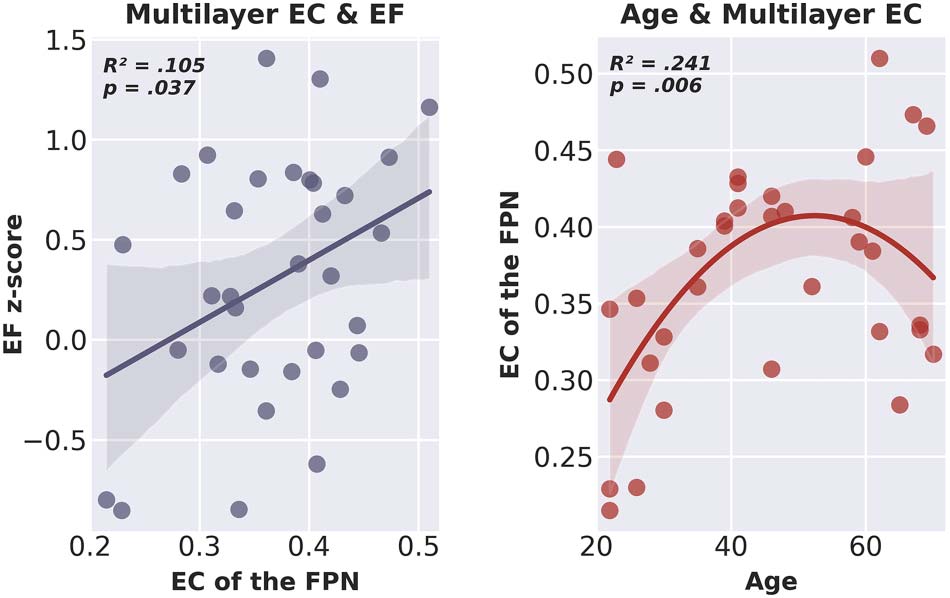
of EF, was statistically significant (R2 = .133, adjusted R2 = .105, F[1, 31] = 4.753, pag = .037).
There was no significant increase in R2 from the second-to-last model, containing two predic-
tores (single-layer EC in the lower alpha band and multilayer EC), to this final significant model.
These results suggest that only EC of the FPN of the multilayer network was a significant pre-
dictor of EF, and that a higher multilayer EC of the FPN was related to better EF (ver figura 5).
Post hoc testing confirmed these results. Repeating the analyses using a forward stepwise
procedure resulted in an identical, significant final model, containing only multilayer EC as a
predictor of EF (R2 = .133, adjusted R2 = .105, F[1, 31] = 4.753, pag = .037). The regression using
the ECs of the FPN calculated on the MSTs of all single-layer networks (instead of the full
matrix for dMRI and rsfMRI) likewise yielded comparable results to the regression model
implemented initially, as the final model contained only the multilayer EC of the FPN. El
multiple regression using the average EC of the single-layer networks instead of the multilayer
EC did not reach significance (pag = .328 for the final model containing only the average EC of
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. Raincloud plots showing probability density, summary statistics, and individual datapoints of the z-score per participant of exec-
utive functioning (izquierda) and multilayer eigenvector centrality of the fronto-parietal network (bien). EF = executive functioning; EC = eigenvector
centrality; FPN = fronto-parietal network.
Neurociencia en red
309
Multilayer network centrality relates to executive functioning
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
norte
mi
norte
_
a
_
0
0
2
8
4
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
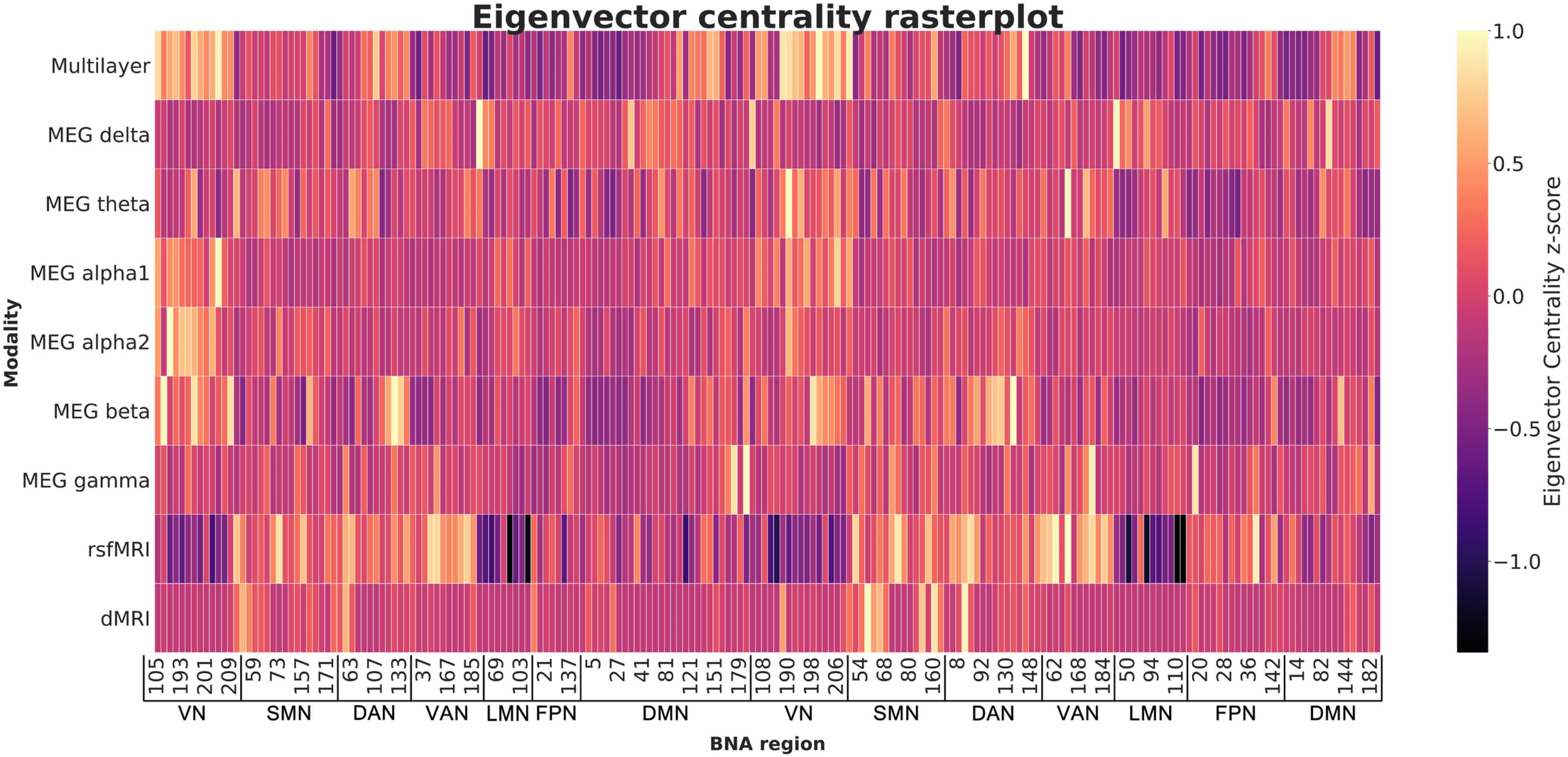
Cifra 4. Raster plot showing eigenvector centrality in the eight single-layer networks and the multilayer network averaged over all subjects,
ordered by subnetwork (all left-hemisphere regions followed by all right-hemisphere regions). Yellow indicates regions with high EC. This shows
the differences in ‘centrality profiles’ across modalities. BNA region numbers refer to the labels as given in Supporting Information Table S1.
MEG = magnetoencephalography. rsfMRI = resting-state functional MRI; dMRI = diffusion MRI; BNA = Brainnetome Atlas; VN = visual network;
SMN = somatomotor network; DAN = dorsal attention network; VAN = ventral attention network; LMN = limbic network; FPN = fronto-parietal
network; DMN = default mode network.
all single-layer networks), indicating that multilayer EC does not simply represent the average
of all single-layer ECs. Multilayer degree centrality of the FPN did not relate significantly to EF
(pag = .091), suggesting that, in the context of a multilayer framework, EC is a more sensitive
correlate of EF than degree centrality. The leave-one-out cross-validation resulted in a cross-
validated coefficient of determination of 20.75 Opuesto a 30.22 for the full, non-cross-
validated, modelo. Repeating the analysis using a different atlas resulted in a nonsignificant final
modelo, albeit with comparable explanatory value to the model based on BNA data (R2 = .177,
adjusted R2 = .122, F[2, 32] = 3.220, pag = .054); sin embargo, single-layer dMRI EC of the FPN was
a significant individual predictor in the final model (pag = .021). Finalmente, additional post hoc
analyses revealed associations between multilayer EC of the FPN and other cognitive domains.
There were no significant associations between multilayer EC of the FPN and VM (pag = .227)
and attention (pag = .565); sin embargo, there were significant associations between multilayer EC
of the FPN and IPS and WM. Higher multilayer EC of the FPN was related to better IPS, R2 =
.395, adjusted R2 = .129, F[1, 31] = 5.744, pag = .023; β = .395. Similarmente, higher multilayer
EC of the FPN was related to better WM, R2 = .171, adjusted R2 = .144, F[1, 31] = 6.402,
pag = .017; β = .414.
Multilayer Network Correlates of Age
To further validate the relevance of multilayer FPN centrality, we tested its relationship with
edad. Single-layer network studies have revealed that the brain network tends to become more
Neurociencia en red
310
Multilayer network centrality relates to executive functioning
Mesa 1.
modelos de regresión
Standardized beta coefficients and p values of included and excluded variables of the
Multilayer EC of the FPN and EF
Final model (R2
adj = .105)
Multilayer EC
Excluded variables
EC MEG delta
EC MEG upper alpha
EC dMRI
EC MEG theta
EC rsfMRI
EC MEG beta
EC MEG gamma
EC MEG lower alpha
Age & multilayer EC of the FPN
Final model (R2
adj = .241)
Age
Age squared
b
.365
.047
.056
.074
−.065
.097
.144
−.204
−.238
b
.014
.00013
PAG
.037*
.798
.752
.669
.716
.587
.407
.234
.163
PAG
.010*
.021*
Nota. Top: multilayer eigenvector centrality of the fronto-parietal network and executive functioning. Bottom:
age and multilayer eigenvector centrality of the fronto-parietal network. EC = eigenvector centrality; FPN =
fronto-parietal network; EF = executive functioning; MEG = magnetoencephalography; dMRI = diffusion
resonancia magnética; rsfMRI = resting-state functional MRI. Asterisk (*) indicates significance at the p < 0.05 level.
Scatter plot including line of best fit of multilayer eigenvector centrality of the fronto-
Figure 5.
parietal network and executive functioning (left) and age and multilayer eigenvector centrality of
the fronto-parietal network (right). EC = eigenvector centrality; EF = executive functioning; FPN =
fronto-parietal network.
Network Neuroscience
311
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
efficiently integrated in early life (Hwang et al., 2013), after which its development plateaus
during middle age (Cao et al., 2014) and subsequently regresses to a less integrative topology
with older age (Onoda & Yamaguchi, 2013). This relation is also reflected in changes in for
example whole-brain (Hedman et al., 2012) and white matter volume (Ge et al., 2002;
Walhovd et al., 2005) across the life-span, indicating that the quadratic relationship
between brain measures and age may be a general developmental principle. We therefore
hypothesized an inverted-U relation between age and multilayer EC of the FPN. We
employed a hierarchical multiple regression model with multilayer centrality as the depen-
dent variable. Age was entered in a first block, and the square of age was added to the
model in a second block.
See Figure 3 for a raincloud plot of multilayer centrality, showing the distribution of mul-
tilayer network EC of the FPN for all participants. The final model with both age and age
squared indicated a statistically significant quadratic relation between age and multilayer
EC of the FPN (R2 = .289, adjusted R2 = .241, F[2, 30] = 6.082, p = .006). The square of
age added significantly to the model, leading to an increase in R2 of .140 (F[1, 30] = 5.915,
p = .021), suggesting that the quadratic model indeed more accurately explained age varia-
tions than the simple linear model. The coefficients of the included variables are reported in
Table 1; Figure 5 shows the relation between age and multilayer EC of the FPN.
Post Hoc: Edge Inference
The results of the comparison between the individual edges in the MST networks used in
our analyses with its correspondent edges in an ensemble of 100 randomized matrices are
detailed in Table 2. On average, over all modalities and all subjects, 74.2% of the edges in
the MSTs are statistically significant. In contrast, on average only 3.9% of edges in the fully
weighted networks are significant. This preliminary analysis provides evidence that most links
in our multilayer network are in fact statistically “true” edges.
Table 2.
the MST network
Edge inference: Comparison between the mean accuracy of the complete network versus
Modality
MEG delta
MEG theta
MEG lower alpha
MEG upper alpha
MEG beta
MEG gamma
rsfMRI
dMRI
Average
Weighted network
3.8%
MST network
73.5%
3.8%
3.8%
3.8%
3.7%
3.9%
4.9%
3.6%
3.9%
73.7%
69.7%
74.1%
68.0%
75.1%
73.5%
85.7%
74.2%
Note. Accuracy represents percentage of edges where p < 0.05. For the full weighted network, the mean accu-
racy is lower than 5% for all modalities; for the MSTs, the mean accuracy is greater than 67% for all modalities.
MST = minimum spanning tree; MEG = magnetoencephalography; rsfMRI = resting-state functional MRI;
dMRI = diffusion MRI.
Network Neuroscience
312
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
DISCUSSION
We studied how multilayer centrality of the FPN was related to individual differences in EF,
and whether this provided additional information to modality- and frequency-specific single-
layer FPN centrality. We found that higher multilayer FPN centrality related to better EF,
whereas FPN centrality of single-layer networks did not significantly explain differences in
EF between healthy adults. Finally, post hoc analyses established an inverted-U relationship
between age and multilayer centrality of the FPN.
Firstly, at least for the multilayer network, these results are in line with other studies display-
ing the importance of FPN network centrality for EF. The relation between FPN centrality and,
by extension, network integration and cognition has been well-established in single-layer net-
works, using different neuroimaging and neurophysiological modalities. Increased integration
of the FPN within the entire brain network specifically has been related to better EF in studies
utilizing dMRI (Caeyenberghs et al., 2016), rsfMRI (Cole et al., 2012; Takeuchi et al., 2015),
and MEG (van Dellen et al., 2013). While network segregation is thought to enable fast pro-
cessing of lower order information (e.g., analysis of visual inputs) (Clune et al., 2013), highly
central nodes like those within the FPN facilitate global communication between these segre-
gated communities, presumably enabling higher order cognitive processes and specifically EF
(see, e.g., Bertolero et al., 2017; Sporns, 2013). Our significant results for EC, but not degree
centrality, may indicate that EC, which is a spectral measure, may be optimally sensitive to
individual differences in EF. Moreover, the associations we found between multilayer central-
ity of the FPN and several other cognitive domains, namely, IPS and WM, suggest that the
importance of FPN integration is not exclusive to EF as defined in this study. IPS, WM, and
EF are closely related constructs (see, e.g., McCabe et al., 2010), and the FPN may play a
similar integrative role in these aspects of cognition.
Secondly, our results demonstrate the relevance of multimodal network analysis through a
multilayer network approach in explaining cognitive variance. While FPN centrality of the
unimodal networks did not relate significantly to EF, higher FPN centrality of the multilayer
networks was indeed associated with better EF. Visual exploration of our data confirmed that
the level of integration per node depends on the modality on which the network is based, and
that this is again different for the multilayer network. Central nodes (i.e., nodes with high EC) in
the multilayer network are thus not the same as central nodes in the single-layer networks (see
Figure 4). Other multilayer studies have similarly reported that the precise node that can be
considered most central in a single-layer network may not serve as the most central node in
a multilayer network, and vice versa (De Domenico et al., 2016; Yu et al., 2017). We build
upon these studies by demonstrating that multimodal information captures variance in EF that
networks obtained from a single modality do not.
Finally, the quadratic relation between age and multilayer centrality possibly reflects the
rise and decline of brain network efficiency across the life-span and is in line with findings
from studies reporting on other brain-related processes as well as unimodal network data.
Whole-brain volume has been shown to increase up to about 35 years of age, and then
decline at a slow but steady rate (Hedman et al., 2012). Another study reported that the per-
centage of white matter volume (relative to intracranial volume) slowly increases until approx-
imately 40 years of age, after which it decreases quickly (Ge et al., 2002). Network measures
have likewise been shown to be sensitive to age effects. Single-layer brain networks become
more segregated or modular during development (He et al., 2019), and connectivity of highly
central regions increases from childhood to adulthood (Hwang et al., 2013), suggesting that
the brain network becomes increasingly efficient (i.e., a better balance between segregation
Network Neuroscience
313
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
and integration emerges) with maturation. However, after a certain age, modularity of the
network seems to decrease (Onoda & Yamaguchi, 2013), indicating a degradation of the effi-
ciency of the brain network. In our study, a similar plateauing seems to occur at middle age.
Together with the literature, these findings indicate that brain characteristics have a universal
tendency to develop in a particular manner across the life-span. As such, FPN centrality of the
multilayer network may be considered an age-relevant metric in future studies. Note that we
corrected EF scores for age, such that the association we find between EF and multilayer cen-
trality cannot be ascribed to age effects alone. However, future work is needed to disentangle
the exact relationship between age, network centrality, and EF: it is possible that age impacts
both EF and network measures, necessitating future studies either investigating the relationship
between EF and network centrality in a homogeneously aged sample, or much larger studies
able to regress age effects from both EF and network measures.
The biological interpretation of the multilayer network used in this work deserves further
consideration. Importantly, the spatial definition of nodes is identical across layers: the nodes
in each modality represented the same brain regions. The use of the Brainnetome Atlas, which
is based on both structural and functional connectivity pattern similarity within and across
brain regions, supports the assumption that these nodes can indeed be seen as canonical units
across layers. This is further evidenced by the results of repeating the analysis using a different
atlas: the final model did not reach statistical significance, although the explanatory value was
comparable to the results based on the Brainnetome Atlas, and FPN centrality of the single-
layer dMRI network was a significant individual predictor. Indeed, single-layer reviews have
shown that network metrics are not necessarily robust across parcellations, especially when
the number of regions differs (Arslan et al., 2018; de Reus & van den Heuvel, 2013). The AAL
atlas is a purely anatomically driven parcellation that comprises 78 cortical regions as opposed
to 210 regions in the Brainnetome Atlas and is based on the single-subject MNI image
(Tzourio-Mazoyer et al., 2002), which may thus be less suited to multilayer analyses, espe-
cially when using multimodal connectivity data as was the case here. We then used interlayer
links between the same brain regions (nodes) across layers to integrate different modalities.
The biological assumption here is that structure and function conflate maximally within the
same brain region. There is ample evidence that this assumption holds across macroscopic
modalities when correlating, for instance, structural and rsfMRI connectivity patterns across
the whole brain (Garcés et al., 2016; Honey et al., 2010; Park & Friston, 2013). The spatial
variation that exists in nodal correlations between structural and functional connectivity
(Honey et al., 2009; Vázquez-Rodríguez et al., 2019), however, may indicate that although
this connectivity is highest within the same region instead of between regions, the linkage
between layers varies per region. Such variations were not taken into account in the current
work, where we used MSTs of the individual layers for the construction of multiplex networks
and set the weights of all interlayer connections in the multilayer networks to one.
It should be noted that using the MST results in networks of very low density (∼1% for
typical brain network sizes). Results may not be the same at different densities, and the effect
of thresholding at different densities perhaps warrants future exploration. Nevertheless, our
decision to use the MST as the foundation for building the multilayer networks in the present
study was well considered. Network thresholding, although well explored in isolated modal-
ities, has not yet been studied extensively in multilayer networks. What we do know, however,
is that the same methodological issues that apply to single-layer networks (i.e., network
measures are influenced by differences in link density and average connectivity) also apply
to multilayer networks, and that constructing MSTs of the individual layers of a multilayer net-
work can adequately correct for these biases (Mandke et al., 2018). Furthermore, replicability
Network Neuroscience
314
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
of results across thresholding densities is an inherent issue of all methodologies for network
thresholding (e.g., Buchanan et al., 2020; Garrison et al., 2015). The MST has not only been
amply used in studies investigating the cognitive relevance of particularly MEG single-layer
network topology for cognition, thus providing a logical springboard for more complicated
analyses such as the multilayer framework we employed here; it is also considered the
backbone of the network (Stam et al., 2014; Tewarie et al., 2015), using mainly the original
network’s strongest connections, which are unlikely to be purely driven by noise. Indeed, the
initial post hoc analyses we performed give a strong indication that most of the edges included
in each network by the MST algorithm are statistically significant. Future work, though, may
benefit from a more data-driven approach for network reconstruction based on statistical
sampling of network ensembles, to ensure that networks comprise statistically significant edges
(Raimondo & De Domenico, 2021).
Next, future studies may attempt to incorporate weighted interlayer links to represent the
spatial variation in within-region correlations across modalities. Additionally, even when
choosing to assign the same weight to all interlayer links, other multilayer work has suggested
that an optimal value for the interlayer weight exists (De Domenico et al., 2016), and future
implementations of the multilayer framework could benefit from optimization of the interlayer
weights. Another potential shortcoming of the binarization of link weights is that it eliminates
layer dominance (Sahneh & Scoglio, 2014): some layers may have a stronger influence on
multilayer network characteristics than others, but when all layers carry the same importance,
this information is lost. However, just as some layers may drive the properties of the multilayer
more strongly than other layers, other layers may play a negligible role. This raises the question
whether all possible layers should be included, or whether an a priori selection should be
made, and, if so, how this selection should be made. A few papers have begun to probe this
issue, for example, in brain networks (De Domenico et al., 2015a) and in a dataset of social
contacts (Casiraghi, 2017), but the layer selection problem in multimodal brain networks
warrants further exploration. Furthermore, although interlayer connectivity may be maximal
within brain regions, there is potential connectivity between different regions across different
modalities, that is, cross-talk between node A in modality X and node B in modality Y may be
relevant to overall functioning of the network. A general multilayer network formulation
allows interlayer links between all nodes in all layers (see, e.g., Bianconi, 2018). However,
multimodal datasets present considerable challenges when constructing a full multilayer
network. Chief among them is determining biologically meaningful interlayer links between
different modalities at the individual participant level. Additionally, a recent modeling study
revealed that interlayer connectivity is driven mostly by one-to-one (i.e., multiplex) connec-
tions (Tewarie et al., 2021), and as evidenced by previous empirical studies (De Domenico
et al., 2016; Yu et al., 2017), a multiplex approach is therefore a logical and intuitive first step
for analyzing multidimensional data. Lastly, we defined the FPN based on a predefined
classification. As such, the FPN was comprised of the same regions across the different
single-layers as well as in the multilayer network. However, subnetworks like the FPN and
the hubs within them have been found to vary depending on the modality used (Brookes
et al., 2011; Garcés et al., 2016), and have also been shown to be different in a multiplex
compared to a single-layer network (De Domenico et al., 2016). Additionally, there is a large
individual variability in the functional topography of the FPN (Marek & Dosenbach, 2018). A
more data-driven approach to the formulation of the FPN may therefore further increase the
explanatory power of the multilayer approach.
Some additional limitations need to be taken into consideration. In this study, we chose to
absolutize negative correlations in the fMRI networks, but it should be noted that there is an
Network Neuroscience
315
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
ongoing debate on what negative correlations indicate and how to best deal with them
(Hallquist & Hillary, 2018). However, the relative magnitude of such negative edge weights
is low and the MST only incorporates the strongest links, and as such it is unlikely that this
decision has impacted our results. Furthermore, there are some inherent drawbacks to the
stepwise regression models we employed to answer our research question. Although this
approach was the one best suited to answer our research question, it is imperative that our
work is replicated in larger samples using our work to establish more straightforward
regression models. Indeed, the relatively small sample size of the present study is particularly
important to take into account: the absence of any single-layer effects could be due to a lack
of statistical power, rather than the true absence of any correlations between single-layer
network metrics and cognition. Our sample was powered using previous studies correlating
cognition with single-layer network properties (Douw et al., 2016; Hassan et al., 2017; Lord
et al., 2017; Ystad et al., 2011), but these may have overestimated the size of the actual
effect: there is significant discussion on the minimal sample size needed to establish reliable
brain-behavior associations (Marek et al., 2022). Moreover, since the multilayer approach has
not been used to explain cognitive variance before, we could not power for significance of
change going from single-layer to multilayer correlates of EF. There was no significant
increase in R2 from the model containing a nonsignificant single-layer plus the multilayer
predictor and the model containing only the significant multilayer predictor. We therefore
cannot claim, statistically, that the multilayer network approach is a better predictor of EF
than the single-layer network approach. However, the fact that the final model containing
only the multilayer predictor was significant, whereas the single-layer predictors were not,
suggests that (a) sample size may have contributed to a lack of statistical power to find
evidence of significant change between these models and (b) a multilayer approach may
require less data points in order to observe significant correlates of EF in the brain. We
therefore conclude that the multilayer methodology is a potentially valuable framework for
explaining EF, although its statistical superiority over single-layer approaches must be
assessed in adequately powered, larger, samples.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
t
.
CONCLUSIONS
Integration of multimodal brain networks through a multilayer framework relates to EF in
healthy adults, and corroborates known brain associations with aging. These findings under-
line the relevance of a multimodal view on integration of the brain network as a correlate of EF.
Furthermore, the multilayer approach may be of particular interest in populations where net-
work alterations differ across modalities. For instance, early neurodegeneration and structural
network deterioration of particularly the most central regions in the brain are initially associ-
ated with increases in functional communication, after which the functional brain networks
seems to collapse (Hillary et al., 2015; Schoonheim et al., 2015). Multilayer network analysis
may advance our understanding of the interplay between structural and different functional
network aspects in such clinical populations.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
ACKNOWLEDGMENTS
The authors would like to thank the Amsterdam Neuroscience research institute for supporting
this study. We would also like to thank Hersenonderzoek.nl, a Dutch online registry that
facilitates participant recruitment for neuroscience studies (www.hersenonderzoek.nl).
Hersenonderzoek.nl is funded by ZonMw-Memorabel (project no. 73305095003), a project
in the context of the Dutch Deltaplan Dementie, Gieskes-Strijbis Foundation, the Alzheimer’s
Network Neuroscience
316
Multilayer network centrality relates to executive functioning
Society in the Netherlands and Brain Foundation Netherlands. We thank the laboratory tech-
nicians of the Amsterdam UMC, Department of Clinical Neurophysiology and MEG Center, as
well as the scan assistants of the Spinoza Centre for Neuroimaging, for their help with the data
acquisition. Finally, we thank all participants for their participation.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00284 and
https://github.com/multinetlab-amsterdam/projects/tree/master/mumo_paper_2021. Addition-
ally, this article made use of scripts available at https://github.com/nkoub/multinetx and
https://github.com/networkx.
AUTHOR CONTRIBUTIONS
Lucas C. Breedt: Data curation; Formal analysis; Investigation; Methodology; Project
administration; Software; Visualization; Writing – original draft; Writing – review & editing.
Fernando A. N. Santos: Data curation; Formal analysis; Methodology; Software; Supervision;
Visualization; Writing – original draft; Writing – review & editing. Arjan Hillebrand: Concep-
tualization; Formal analysis; Funding acquisition; Software; Writing – review & editing.
Liesbeth Reneman: Conceptualization; Funding acquisition; Writing – review & editing.
Anne-Fleur van Rootselaar: Conceptualization; Funding acquisition; Writing – review &
editing. Menno M. Schoonheim: Conceptualization; Funding acquisition; Writing – review
& editing. Cornelis J. Stam: Conceptualization; Funding acquisition; Writing – review &
editing. Anouk Ticheler: Investigation; Project administration; Writing – review & editing.
Betty M. Tijms: Conceptualization; Funding acquisition; Writing – review & editing. Dick J.
Veltman: Conceptualization; Funding acquisition; Writing – review & editing. Chris Vriend:
Conceptualization; Formal analysis; Funding acquisition; Methodology; Writing – review &
editing. Margot J. Wagenmakers: Investigation; Project administration; Writing – review &
editing. Guido A. van Wingen: Conceptualization; Funding acquisition; Writing – review
& editing. Jeroen J. G. Geurts: Conceptualization; Funding acquisition; Supervision; Writing –
review & editing. Anouk Schrantee: Conceptualization; Funding acquisition; Methodology;
Project administration; Supervision; Writing – review & editing. Linda Douw: Conceptuali-
zation; Funding acquisition; Methodology; Project administration; Supervision; Writing –
original draft; Writing – review & editing.
FUNDING INFORMATION
Linda Douw, Amsterdam Neuroscience Alliance Grant. Linda Douw, Netherlands Organiza-
tion for Scientific Research (NWO) Vidi grant, Award ID: 198.015.
REFERENCES
Aertsen, A. M., Gerstein, G. L., Habib, M. K., & Palm, G. (1989).
Dynamics of neuronal firing correlation: Modulation of “effective
connectivity.” Journal of Neurophysiology, 61(5), 900–917.
https://doi.org/10.1152/jn.1989.61.5.900, PubMed: 2723733
Andersson, J. L., Skare, S., & Ashburner, J. (2003). How to correct sus-
ceptibility distortions in spin-echo echo-planar images: Application
to diffusion tensor imaging. NeuroImage, 20(2), 870–888. https://doi
.org/10.1016/S1053-8119(03)00336-7, PubMed: 14568458
Ardila, A. (2008). On the evolutionary origins of executive func-
tions. Brain and Cognition, 68(1), 92–99. https://doi.org/10
.1016/j.bandc.2008.03.003, PubMed: 18397818
Arslan, S., Ktena, S. I., Makropoulos, A., Robinson, E. C., Rueckert,
D., & Parisot, S. (2018). Human brain mapping: A systematic
comparison of parcellation methods for the human cerebral cortex.
NeuroImage, 170, 5–30. https://doi.org/10.1016/j.neuroimage
.2017.04.014, PubMed: 28412442
Network Neuroscience
317
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
Barabási, A.-L. (2016). Network science. Cambridge, UK:
Cambridge University Press.
Battiston, F., Nicosia, V., Chavez, M., & Latora, V. (2017). Multi-
layer motif analysis of brain networks. Chaos: An Interdisciplin-
ary Journal of Nonlinear Science, 27(4), 047404. https://doi.org
/10.1063/1.4979282, PubMed: 28456158
Bertolero, M. A., Yeo, B. T. T., & D’Esposito, M. (2017). The diverse
club. Nature Communications, 8(1), 1277. https://doi.org/10
.1038/s41467-017-01189-w, PubMed: 29097714
Bianconi, G. (2018). Multilayer networks: Structure and function.
Oxford, UK: Oxford University Press. https://doi.org/10.1093
/oso/9780198753919.001.0001
Blomsma, N., de Rooy, B., Gerritse, F., van der Spek, R., Tewarie,
P., Hillebrand, A., Otte, W. M., Stam, C. J., & van Dellen, E.
(2022). Minimum spanning tree analysis of brain networks: A
systematic review of network size effects, sensitivity for neuro-
psychiatric pathology and disorder specificity. Network Neuro-
science, 6(2), 301–319. https://doi.org/10.1162/netn_a_00245,
PubMed: 35733422
Boccaletti, S., Bianconi, G., Criado, R., Del Genio, C. I., Gómez-
Gardeñes, J., Romance, M., Sendiña-Nadal, I., Wang, Z., &
Zanin, M. (2014). The structure and dynamics of multilayer net-
works. Physics Reports, 544(1), 1–122. https://doi.org/10.1016/j
.physrep.2014.07.001, PubMed: 32834429
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., & Hwang, D.-U.
(2006). Complex networks: Structure and dynamics. Physics Reports,
424(4–5), 175–308. https://doi.org/10.1016/j.physrep.2005.10.009
Brookes, M. J., Tewarie, P. K., Hunt, B. A., Robson, S. E., Gascoyne,
L. E., Liddle, E. B., Liddle, P. F., & Morris, P. G. (2016). A
multi-layer network approach to MEG connectivity analysis.
NeuroImage, 132, 425–438. https://doi.org/10.1016/j
.neuroimage.2016.02.045, PubMed: 26908313
Brookes, M. J., Woolrich, M., Luckhoo, H., Price, D., Hale, J. R.,
Stephenson, M. C., Barnes, G. R., Smith, S. M., & Morris, P. G.
(2011). Investigating the electrophysiological basis of resting
state networks using magnetoencephalography. Proceedings of
the National Academy of Sciences, 108(40), 16783–16788.
https://doi.org/10.1073/pnas.1112685108, PubMed: 21930901
Buchanan, C. R., Bastin, M. E., Ritchie, S. J., Liewald, D. C., Madole,
J. W., Tucker-Drob, E. M., Deary, I. J., & Cox, S. R. (2020). The effect
of network thresholding and weighting on structural brain networks
in the UK Biobank. NeuroImage, 211, 116443. https://doi.org/10
.1016/j.neuroimage.2019.116443, PubMed: 31927129
Bucks, R., & Willison, J. R. (1997). Development and validation of
the Location Learning Test (LLT): A test of visuo-spatial learning
designed for use with older adults and in dementia. The Clinical
Neuropsychologist, 11(3), 273–286. https://doi.org/10.1080
/13854049708400456
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897
Caeyenberghs, K., Metzler-Baddeley, C., Foley, S., & Jones, D. K.
(2016). Dynamics of the human structural connectome underly-
ing working memory training. Journal of Neuroscience, 36(14),
4056–4066. https://doi.org/10.1523/JNEUROSCI.1973-15.2016,
PubMed: 27053212
Cao, M., Wang, J.-H., Dai, Z.-J., Cao, X.-Y., Jiang, L.-L., Fan, F.-M.,
Song, X.-W., Xia, M.-R., Shu, N., & Dong, Q. (2014). Topological
organization of the human brain functional connectome across
the lifespan. Developmental Cognitive Neuroscience, 7, 76–93.
https://doi.org/10.1016/j.dcn.2013.11.004, PubMed: 24333927
Cardillo, A., Gómez-Gardeñes, J., Zanin, M., Romance, M., Papo,
D., del Pozo, F., & Boccaletti, S. (2013). Emergence of network
features from multiplexity. Scientific Reports, 3(1), 1344. https://
doi.org/10.1038/srep01344, PubMed: 23446838
Casiraghi, G. (2017). Multiplex network regression: How do rela-
tions drive interactions? arXiv preprint arXiv:1702.02048. https://
doi.org/10.48550/arXiv.1702.02048
Chai, X. J., Castañón, A. N., Öngür, D., & Whitfield-Gabrieli, S.
(2012). Anticorrelations in resting state networks without global
signal regression. NeuroImage, 59(2), 1420–1428. https://doi.org
/10.1016/j.neuroimage.2011.08.048, PubMed: 21889994
Clune, J., Mouret, J.-B., & Lipson, H. (2013). The evolutionary ori-
gins of modularity. Proceedings of the Royal Society B: Biological
Sciences, 280(1755), 20122863. https://doi.org/10.1098/rspb
.2012.2863, PubMed: 23363632
Cole, M. W., Yarkoni, T., Repovš, G., Anticevic, A., & Braver, T. S. (2012).
Global connectivity of prefrontal cortex predicts cognitive control
and intelligence. Journal of Neuroscience, 32(26), 8988–8999. https://
doi.org/10.1523/JNEUROSCI.0536-12.2012, PubMed: 22745498
Damoiseaux, J. S., & Greicius, M. D. (2009). Greater than the sum
of its parts: A review of studies combining structural connectivity
and resting-state functional connectivity. Brain Structure and
Function, 213(6), 525–533. https://doi.org/10.1007/s00429-009
-0208-6, PubMed: 19565262
De Domenico, M., Nicosia, V., Arenas, A., & Latora, V. (2015a).
Structural reducibility of multilayer networks. Nature Communi-
cations, 6(1), 6864. https://doi.org/10.1038/ncomms7864,
PubMed: 25904309
De Domenico, M., Porter, M. A., & Arenas, A. (2015b). MuxViz: A
tool for multilayer analysis and visualization of networks. Journal
of Complex Networks, 3(2), 159–176. https://doi.org/10.1093
/comnet/cnu038
De Domenico, M., Sasai, S., & Arenas, A. (2016). Mapping multi-
plex hubs in human functional brain networks. Frontiers in Neu-
roscience, 10, 326. https://doi.org/10.3389/fnins.2016.00326,
PubMed: 27471443
De Domenico, M., Solé-Ribalta, A., Cozzo, E., Kivelä, M., Moreno,
Y., Porter, M. A., Gómez, S., & Arenas, A. (2013). Mathematical
formulation of multilayer networks. Physical Review X, 3(4),
041022. https://doi.org/10.1103/PhysRevX.3.041022
de Reus, M. A., & van den Heuvel, M. P. (2013). The parcellation-
based connectome: Limitations and extensions. NeuroImage, 80,
397–404. https://doi.org/10.1016/j.neuroimage.2013.03.053,
PubMed: 23558097
Douw, L., Wakeman, D. G., Tanaka, N., Liu, H., & Stufflebeam,
S. M. (2016). State-dependent variability of dynamic functional
connectivity between frontoparietal and default networks relates
to cognitive flexibility. Neuroscience, 339, 12–21. https://doi.org
/10.1016/j.neuroscience.2016.09.034, PubMed: 27687802
Eijlers, A. J. C., Meijer, K. A., Wassenaar, T. M., Steenwijk, M. D.,
Uitdehaag, B. M. J., Barkhof, F., Wink, A. M., Geurts, J. J. G., &
Network Neuroscience
318
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
Schoonheim, M. M. (2017). Increased default-mode network
centrality in cognitively impaired multiple sclerosis patients.
Neurology, 88(10), 952–960. https://doi.org/10.1212/ WNL
.0000000000003689, PubMed: 28179464
Fagerholm, E. D., Hellyer, P. J., Scott, G., Leech, R., & Sharp, D. J.
(2015). Disconnection of network hubs and cognitive impair-
ment after traumatic brain injury. Brain, 138(6), 1696–1709.
https://doi.org/10.1093/brain/awv075, PubMed: 25808370
Fan, L., Li, H., Zhuo, J., Zhang, Y., Wang, J., Chen, L., Yang, Z., Chu,
C., Xie, S., & Laird, A. R. (2016). The human brainnetome atlas:
A new brain atlas based on connectional architecture. Cerebral
Cortex, 26(8), 3508–3526. https://doi.org/10.1093/cercor
/bhw157, PubMed: 27230218
Fodor, J. A. (1983). The modularity of mind. Cambridge, MA: MIT
Press. https://doi.org/10.7551/mitpress/4737.001.0001
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of brain
network analysis. Amsterdam, The Netherlands: Academic Press.
Friston, K. J., Frith, C. D., Liddle, P. F., & Frackowiak, R. S. (1993).
Functional connectivity: The principal-component analysis of
large (PET) data sets. Journal of Cerebral Blood Flow & Metabo-
lism, 13(1), 5–14. https://doi.org/10.1038/jcbfm.1993.4, PubMed:
8417010
Garcés, P., Pereda, E., Hernández-Tamames, J. A., Del-Pozo, F.,
Maestú, F., & Ángel Pineda-Pardo, J. (2016). Multimodal descrip-
tion of whole brain connectivity: A comparison of resting state
MEG, fMRI, and DWI. Human Brain Mapping, 37(1), 20–34.
https://doi.org/10.1002/hbm.22995, PubMed: 26503502
Garrison, K. A., Scheinost, D., Finn, E. S., Shen, X., & Constable,
R. T. (2015). The (in)stability of functional brain network mea-
sures across thresholds. NeuroImage, 118, 651–661. https://doi
.org/10.1016/j.neuroimage.2015.05.046, PubMed: 26021218
Ge, Y., Grossman, R. I., Babb, J. S., Rabin, M. L., Mannon, L. J., &
Kolson, D. L. (2002). Age-related total gray matter and white
matter changes in normal adult brain. Part I: Volumetric MR
imaging analysis. American Journal of Neuroradiology, 23(8),
1327–1333. PubMed: 12223373
Guillon, J., Attal, Y., Colliot, O., La Corte, V., Dubois, B., Schwartz,
D., Chavez, M., & Fallani, F. D. V. (2017). Loss of brain
inter-frequency hubs in Alzheimerʼs disease. Scientific Reports,
7(1), 10879. https://doi.org/10.1038/s41598-017-07846-w,
PubMed: 28883408
Hagberg, A., Swart, P., & S Chult, D. (2008). Exploring network
structure, dynamics, and function using NetworkX. https://www
.osti.gov/biblio/960616
Hallquist, M. N., & Hillary, F. G. (2018). Graph theory approaches
to functional network organization in brain disorders: A critique
for a brave new small-world. Network Neuroscience, 3(1), 1–26.
https://doi.org/10.1162/netn_a_00054, PubMed: 30793071
Hammes, J. G. W. (1978). De Stroop kleur-woord test. San Diego,
CA: Harcourt Test Publishing.
Hardmeier, M., Schoonheim, M. M., Geurts, J. J., Hillebrand, A.,
Polman, C. H., Barkhof, F., & Stam, C. J. (2012). Cognitive dys-
function in early multiple sclerosis: Altered centrality derived
from resting-state functional connectivity using magneto-
encephalography. PLoS One, 7(7), e42087. https://doi.org/10
.1371/journal.pone.0042087, PubMed: 22848712
Hassan, M., Chaton, L., Benquet, P., Delval, A., Leroy, C., Plomhause,
L., Moonen, A. J. H., Duits, A. A., Leentjens, A. F. G., & van Kranen-
Mastenbroek, V. (2017). Functional connectivity disruptions
correlate with cognitive phenotypes in Parkinsonʼs disease.
NeuroImage: Clinical, 14, 591–601. https://doi.org/10.1016/j
.nicl.2017.03.002, PubMed: 28367403
He, W., Sowman, P. F., Brock, J., Etchell, A. C., Stam, C. J., &
Hillebrand, A. (2019). Increased segregation of functional networks
in developing brains. NeuroImage, 200, 607–620. https://doi.org
/10.1016/j.neuroimage.2019.06.055, PubMed: 31271847
Hedman, A. M., van Haren, N. E. M., Schnack, H. G., Kahn, R. S., &
Hulshoff Pol, H. E. (2012). Human brain changes across the life
span: A review of 56 longitudinal magnetic resonance imaging
studies. Human Brain Mapping, 33(8), 1987–2002. https://doi
.org/10.1002/hbm.21334, PubMed: 21915942
Hillary, F. G., Roman, C. A., Venkatesan, U., Rajtmajer, S. M., Bajo,
R., & Castellanos, N. D. (2015). Hyperconnectivity is a funda-
mental response to neurological disruption. Neuropsychology,
29(1), 59–75. https://doi.org/10.1037/neu0000110, PubMed:
24933491
Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., &
Stam, C. J. (2012). Frequency-dependent functional connectivity
within resting-state networks: An atlas-based MEG beamformer
solution. NeuroImage, 59(4), 3909–3921. https://doi.org/10
.1016/j.neuroimage.2011.11.005, PubMed: 22122866
Hillebrand, A., Tewarie, P., van Dellen, E., Yu, M., Carbo, E. W. S.,
Douw, L., Gouw, A. A., van Straaten, E. C. W., & Stam, C. J.
(2016). Direction of information flow in large-scale resting-state
networks is frequency-dependent. Proceedings of the National
Academy of Sciences, 113(14), 3867–3872. https://doi.org/10
.1073/pnas.1515657113, PubMed: 27001844
Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J.-P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106, PubMed: 19188601
Honey, C. J., Thivierge, J.-P., & Sporns, O. (2010). Can structure pre-
dict function in the human brain? NeuroImage, 52(3), 766–776.
https://doi.org/10.1016/j.neuroimage.2010.01.071, PubMed:
20116438
Hwang, K., Hallquist, M. N., & Luna, B. (2013). The development
of hub architecture in the human functional brain network. Cere-
bral Cortex, 23(10), 2380–2393. https://doi.org/10.1093/cercor
/bhs227, PubMed: 22875861
Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A., & Sijbers,
J. (2014). Multi-tissue constrained spherical deconvolution for
improved analysis of multi-shell diffusion MRI data. NeuroImage,
103, 411–426. https://doi.org/10.1016/j.neuroimage.2014.07
.061, PubMed: 25109526
Jurado, M. B., & Rosselli, M. (2007). The elusive nature of executive
functions: A review of our current understanding. Neuropsychol-
ogy Review, 17(3), 213–233. https://doi.org/10.1007/s11065-007
-9040-z, PubMed: 17786559
Kardos, O., London, A., & Vinkó, T. (2020). Stability of network
centrality measures: A numerical study. Social Network Analysis
and Mining, 10(1), 1–17. https://doi.org/10.1007/s13278-020
-00693-0
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., &
Porter, M. A. (2014). Multilayer networks. Journal of Complex Net-
works, 2(3), 203–271. https://doi.org/10.1093/comnet/cnu016
Network Neuroscience
319
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
Kruskal, J. B. (1956). On the shortest spanning subtree of a graph
and the traveling salesman problem. Proceedings of the Ameri-
can Mathematical Society, 7(1), 48–50. https://doi.org/10.1090
/S0002-9939-1956-0078686-7
Lord, A. R., Li, M., Demenescu, L. R., van den Meer, J., Borchardt,
V., Krause, A. L., Heinze, H.-J., Breakspear, M., & Walter, M.
(2017). Richness in functional connectivity depends on the neu-
ronal integrity within the posterior cingulate cortex. Frontiers in
Neuroscience, 11, 184. https://doi.org/10.3389/fnins.2017
.00184, PubMed: 28439224
Mandke, K., Meier, J., Brookes, M. J., O’Dea, R. D., Van Mieghem, P.,
Stam, C. J., Hillebrand, A., & Tewarie, P. (2018). Comparing
multilayer brain networks between groups: Introducing graph
metrics and recommendations. NeuroImage, 166, 371–384.
https://doi.org/10.1016/j.neuroimage.2017.11.016, PubMed:
29138088
Marek, S., & Dosenbach, N. U. F. (2018). The frontoparietal net-
work: Function, electrophysiology, and importance of individual
precision mapping. Dialogues in Clinical Neuroscience, 20(2),
133–140. https://doi.org/10.31887/ DCNS.2018.20.2/smarek,
PubMed: 30250390
Marek, S., Tervo-Clemmens, B., Calabro, F. J., Montez, D. F., Kay,
B. P., Hatoum, A. S., Donohue, M. R., Foran, W., Miller, R. L., &
Hendrickson, T. J. (2022). Reproducible brain-wide association
studies require thousands of individuals. Nature, 603(7902),
654–660. https://doi.org/10.1038/s41586-022-04492-9,
PubMed: 35296861
McCabe, D. P., Roediger III, H. L., McDaniel, M. A., Balota, D. A., &
Hambrick, D. Z. (2010). The relationship between working mem-
ory capacity and executive functioning: Evidence for a common
executive attention construct. Neuropsychology, 24(2), 222–243.
https://doi.org/10.1037/a0017619, PubMed: 20230116
Menard, S. (1995). An introduction to logistic regression diagnostics.
In Applied logistic regression analysis (pp. 58–79). Thousand Oaks,
CA: Sage.
Mulder, J., Dekker, P., & Dekker, R. (2006). Woord-fluency test/
figuur-fluency test, handleiding. Leiden, The Netherlands: PITS.
Nakamura, T., Tanizawa, T., & Small, M. (2016). Constructing net-
works from a dynamical system perspective for multivariate non-
linear time series. Physical Review E, 93(3), 032323. https://doi
.org/10.1103/PhysRevE.93.032323, PubMed: 27078382
Onoda, K., & Yamaguchi, S. (2013). Small-worldness and modular-
ity of the resting-state functional brain network decrease with
aging. Neuroscience Letters, 556, 104–108. https://doi.org/10
.1016/j.neulet.2013.10.023, PubMed: 24157850
Park, H.-J., & Friston, K. (2013). Structural and functional brain
networks: From connections to cognition. Science, 342(6158),
1238411. https://doi.org/10.1126/science.1238411, PubMed:
24179229
Pruim, R. H. R., Mennes, M., van Rooij, D., Llera, A., Buitelaar, J. K.,
& Beckmann, C. F. (2015). ICA-AROMA: A robust ICA-based
strategy for removing motion artifacts from fMRI data. Neuro-
Image, 112, 267–277. https://doi.org/10.1016/j.neuroimage
.2015.02.064, PubMed: 25770991
Raimondo, S., & De Domenico, M. (2021). Measuring topological
descriptors of complex networks under uncertainty. Physical
Review E, 103(2), 022311. https://doi.org/10.1103/ PhysRevE
.103.022311, PubMed: 33735966
Sahneh, F. D., & Scoglio, C. (2014). Competitive epidemic spread-
ing over arbitrary multilayer networks. Physical Review E, 89(6),
062817. https://doi.org/10.1103/PhysRevE.89.062817, PubMed:
25019843
Schmand, B., Houx, P., & De Koning, I. (2012). Normen van psy-
chologische tests voor gebruik in de klinische neuropsychologie.
Sectie Neuropsychologie Nederlands Instituut van Psychologen.
Schoonheim, M. M., Meijer, K. A., & Geurts, J. J. (2015). Network
collapse and cognitive impairment in multiple sclerosis. Frontiers
in Neurology, 6, 82. https://doi.org/10.3389/fneur.2015.00082,
PubMed: 25926813
Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, A. (2012).
Anatomically-constrained tractography: Improved diffusion MRI
streamlines tractography through effective use of anatomical
information. NeuroImage, 62(3), 1924–1938. https://doi.org/10
.1016/j.neuroimage.2012.06.005, PubMed: 22705374
Smith, R. E., Tournier, J.-D., Calamante, F., & Connelly, A. (2015).
SIFT2: Enabling dense quantitative assessment of brain white
matter connectivity using streamlines tractography. NeuroImage,
119, 338–351. https://doi.org/10.1016/j.neuroimage.2015.06
.092, PubMed: 26163802
Solé-Ribalta, A., De Domenico, M., Kouvaris, N. E., Díaz-Guilera,
A., Gómez, S., & Arenas, A. (2013). Spectral properties of the
Laplacian of multiplex networks. Physical Review E, 88(3), 032807.
https://doi.org/10.1103/PhysRevE.88.032807, PubMed: 24125312
Sporns, O. (2013). Network attributes for segregation and integra-
tion in the human brain. Current Opinion in Neurobiology, 23(2),
162–171. https://doi.org/10.1016/j.conb.2012.11.015, PubMed:
23294553
Stam, C. J., Nolte, G., & Daffertshofer, A. (2007). Phase lag index:
Assessment of functional connectivity from multi channel EEG
and MEG with diminished bias from common sources. Human
Brain Mapping, 28(11), 1178–1193. https://doi.org/10.1002
/hbm.20346, PubMed: 17266107
Stam, C. J., Tewarie, P., Van Dellen, E., van Straaten, E. C. W.,
Hillebrand, A., & Van Mieghem, P. (2014). The trees and the for-
est: Characterization of complex brain networks with minimum
spanning trees. International Journal of Psychophysiology, 92(3),
129–138. https://doi.org/10.1016/j.ijpsycho.2014.04.001,
PubMed: 24726900
Stam, C. J., van Straaten, E. C. W., Van Dellen, E., Tewarie, P., Gong,
G., Hillebrand, A., Meier, J., & Van Mieghem, P. (2016). The
relation between structural and functional connectivity patterns
in complex brain networks. International Journal of Psychophys-
iology, 103, 149–160. https://doi.org/10.1016/j.ijpsycho.2015.02
.011, PubMed: 25678023
Takeuchi, H., Taki, Y., Nouchi, R., Sekiguchi, A., Hashizume, H.,
Sassa, Y., Kotozaki, Y., Miyauchi, C. M., Yokoyama, R., & Iizuka,
K. (2015). Degree centrality and fractional amplitude of
low-frequency oscillations associated with Stroop interference.
NeuroImage, 119, 197–209. https://doi.org/10.1016/j
.neuroimage.2015.06.058, PubMed: 26123381
Taulu, S., & Simola, J. (2006). Spatiotemporal signal space separa-
tion method for rejecting nearby interference in MEG measure-
ments. Physics in Medicine & Biology, 51(7), 1759–1768. https://
doi.org/10.1088/0031-9155/51/7/008, PubMed: 16552102
Tewarie, P., Hillebrand, A., Schoonheim, M. M., van Dijk, B. W.,
Geurts, J. J. G., Barkhof, F., Polman, C. H., & Stam, C. J. (2014).
Network Neuroscience
320
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Multilayer network centrality relates to executive functioning
Functional brain network analysis using minimum spanning trees
in multiple sclerosis: An MEG source-space study. NeuroImage,
88, 308–318. https://doi.org/10.1016/j.neuroimage.2013.10
.022, PubMed: 24161625
Tewarie, P., Prasse, B., Meier, J., Byrne, Á., De Domenico, M., Stam,
C. J., Brookes, M. J., Hillebrand, A., Daffertshofer, A., & Coombes,
S. (2021). Interlayer connectivity reconstruction for multilayer
brain networks using phase oscillator models. New Journal of
Physics, 23, 063065. https://doi.org/10.1088/1367-2630/ac066d
Tewarie, P., van Dellen, E., Hillebrand, A., & Stam, C. J. (2015). The
minimum spanning tree: An unbiased method for brain network
analysis. NeuroImage, 104, 177–188. https://doi.org/10.1016/j
.neuroimage.2014.10.015, PubMed: 25451472
Tournier, J.-D., Smith, R., Raffelt, D., Tabbara, R., Dhollander, T.,
Pietsch, M., Christiaens, D., Jeurissen, B., Yeh, C.-H., & Connelly,
A. (2019). MRtrix3: A fast, flexible and open software framework
for medical image processing and visualisation. NeuroImage,
202, 116137. https://doi.org/10.1016/j.neuroimage.2019
.116137, PubMed: 31473352
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello, F.,
Etard, O., Delcroix, N., Mazoyer, B., & Joliot, M. (2002). Auto-
mated anatomical labeling of activations in SPM using a macro-
scopic anatomical parcellation of the MNI MRI single-subject
brain. NeuroImage, 15(1), 273–289. https://doi.org/10.1006
/nimg.2001.0978, PubMed: 11771995
van Dellen, E., de Witt Hamer, P. C., Douw, L., Klein, M., Heimans,
J. J., Stam, C. J., Reijneveld, J. C., & Hillebrand, A. (2013). Con-
nectivity in MEG resting-state networks increases after resective
surgery for low-grade glioma and correlates with improved cog-
nitive performance. NeuroImage: Clinical, 2, 1–7. https://doi.org
/10.1016/j.nicl.2012.10.007, PubMed: 24179752
van den Burg, W., Saan, R. J., & Dellman, B. G. (1985). 15-
woordentest: Provisional manual. Groningen, The Netherlands:
University Hospital, Department of Neuropsychology.
van den Heuvel, M. P., & Sporns, O. (2011). Rich-club organization
of the human connectome. Journal of Neuroscience, 31(44),
15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11
.2011, PubMed: 22049421
van der Elst, W., van Boxtel, M. P. J., van Breukelen, G. J. P., &
Jolles, J. (2006a). The concept shifting test: Adult normative data.
Psychological Assessment, 18(4), 424–432. https://doi.org/10
.1037/1040-3590.18.4.424, PubMed: 17154763
van der Elst, W., van Boxtel, M. P. J., van Breukelen, G. J. P., & Jolles,
J. (2006b). The Letter Digit Substitution Test: Normative data for
1,858 healthy participants aged 24–81 from the Maastricht Aging
Study (MAAS): Influence of age, education, and sex. Journal of
Clinical and Experimental Neuropsychology, 28(6), 998–1009.
https://doi.org/10.1080/13803390591004428, PubMed: 16822738
van der Elst, W., van Boxtel, M. P. J., van Breukelen, G. J. P., &
Jolles, J. (2007). Assessment of information processing in working
memory in applied settings: The paper and pencil memory scan-
ning test. Psychological Medicine, 37(9), 1335–1344. https://doi
.org/10.1017/S0033291707000360, PubMed: 17376260
van Klink, N., van Rosmalen, F., Nenonen, J., Burnos, S., Helle, L.,
Taulu, S., Furlong, P. L., Zijlmans, M., & Hillebrand, A. (2017).
Automatic detection and visualisation of MEG ripple oscillations
in epilepsy. NeuroImage: Clinical, 15, 689–701. https://doi.org
/10.1016/j.nicl.2017.06.024, PubMed: 28702346
Vázquez-Rodríguez, B., Suárez, L. E., Markello, R. D., Shafiei, G.,
Paquola, C., Hagmann, P., van den Heuvel, M. P., Bernhardt,
B. C., Spreng, R. N., & Misic, B. (2019). Gradients of structure–
function tethering across neocortex. Proceedings of the National
Academy of Sciences, 116(42), 21219–21227. https://doi.org/10
.1073/pnas.1903403116, PubMed: 31570622
Verhage, F. (1964). Intelligentie en leeftijd bij volwassenen en
bejaarden. Assen, The Netherlands: Van Gorcum.
Vriend, C., van den Heuvel, O. A., Berendse, H. W., van der Werf,
Y. D., & Douw, L. (2018). Global and subnetwork changes of the
structural connectome in de novo Parkinson’s disease. Neurosci-
ence, 386, 295–308. https://doi.org/10.1016/j.neuroscience
.2018.06.050, PubMed: 30004009
Walhovd, K. B., Fjell, A. M., Reinvang, I., Lundervold, A., Dale,
A. M., Eilertsen, D. E., Quinn, B. T., Salat, D., Makris, N., &
Fischl, B. (2005). Effects of age on volumes of cortex, white mat-
ter and subcortical structures. Neurobiology of Aging, 26(9),
1261–1270. https://doi.org/10.1016/j.neurobiolaging.2005.05
.020, PubMed: 16005549
Whalen, C., Maclin, E. L., Fabiani, M., & Gratton, G. (2008). Valida-
tion of a method for coregistering scalp recording locations with 3D
structural MR images. Human Brain Mapping, 29(11), 1288–1301.
https://doi.org/10.1002/hbm.20465, PubMed: 17894391
Yeatman, J. D., Wandell, B. A., & Mezer, A. A. (2014). Lifespan
maturation and degeneration of human brain white matter.
Nature Communications, 5(1), 4932. https://doi.org/10.1038
/ncomms5932, PubMed: 25230200
Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari,
D., Hollinshead, M., Roffman, J. L., Smoller, J. W., Zöllei, L., &
Polimeni, J. R. (2011). The organization of the human cerebral
cortex estimated by intrinsic functional connectivity. Journal of
Neurophysiology, 106(3), 1125–1165. https://doi.org/10.1152/jn
.00338.2011, PubMed: 21653723
Ystad, M., Hodneland, E., Adolfsdottir, S., Haász, J., Lundervold,
A. J., Eichele, T., & Lundervold, A. (2011). Cortico-striatal con-
nectivity and cognition in normal aging: A combined DTI and
resting state fMRI study. NeuroImage, 55(1), 24–31. https://doi
.org/10.1016/j.neuroimage.2010.11.016, PubMed: 21073962
Yu, M., Engels, M. M. A., Hillebrand, A., van Straaten, E. C. W.,
Gouw, A. A., Teunissen, C., van der Flier, W. M., Scheltens, P.,
& Stam, C. J. (2017). Selective impairment of hippocampus and
posterior hub areas in Alzheimer’s disease: An MEG–based mul-
tiplex network study. Brain, 140(5), 1466–1485. https://doi.org
/10.1093/brain/awx050, PubMed: 28334883
Zanin, M. (2015). Can we neglect the multi-layer structure of func-
tional networks? Physica A: Statistical Mechanics and its Applica-
tions, 430, 184–192. https://doi.org/10.1016/j.physa.2015.02.099
Zhan, L., Jenkins, L. M., Wolfson, O. E., GadElkarim, J. J., Nocito,
K., Thompson, P. M., Ajilore, O. A., Chung, M. K., & Leow, A. D.
(2017). The significance of negative correlations in brain connec-
tivity. Journal of Comparative Neurology, 525(15), 3251–3265.
https://doi.org/10.1002/cne.24274, PubMed: 28675490
Network Neuroscience
321
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
1
2
9
9
2
0
7
2
1
0
2
n
e
n
_
a
_
0
0
2
8
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3