RESEARCH - IA de Investigación especializada en el MIT

INVESTIGACIÓN

Quantifying brain state transition cost via
Schrödinger Bridge

Genji Kawakita1, Shunsuke Kamiya1, Shuntaro Sasai2,3, Jun Kitazono1, and Masafumi Oizumi1

1Graduate School of Arts and Sciences, University of Tokyo, Tokio, Japón
2Araya Inc., Tokio, Japón
3University of Wisconsin–Madison, Madison, Wisconsin, EE.UU

Palabras clave: Brain state transition, Network control theory, Functional MRI, Information theory,
Schrödinger Bridge

un acceso abierto

diario

ABSTRACTO

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

Quantifying brain state transition cost is a fundamental problem in systems neuroscience.
Previous studies utilized network control theory to measure the cost by considering a neural
system as a deterministic dynamical system. Sin embargo, this approach does not capture the
stochasticity of neural systems, which is important for accurately quantifying brain state
transition cost. Aquí, we propose a novel framework based on optimal control in stochastic
sistemas. In our framework, we quantify the transition cost as the Kullback-Leibler divergence
from an uncontrolled transition path to the optimally controlled path, which is known as
Schrödinger Bridge. To test its utility, we applied this framework to functional magnetic
resonance imaging data from the Human Connectome Project and computed the brain state
transition cost in cognitive tasks. We demonstrate correspondence between brain state transition
cost and the difficulty of tasks. The results suggest that our framework provides a general
theoretical tool for investigating cognitive functions from the viewpoint of transition cost.

RESUMEN DEL AUTOR

In our daily lives, we perform numerous tasks with different kinds and levels of cognitive
demand. To successfully perform these tasks, the brain needs to modulate its spontaneous
activity to reach an appropriate state for each task. Previous studies utilized optimal control in
deterministic systems to measure the cost for the brain state transition. Sin embargo, no unified
framework for quantifying brain state transition cost that takes account of the stochasticity of
neural activities has been proposed. Aquí, we describe a novel framework for measuring brain
state transition cost, utilizing the idea of optimal control in stochastic systems. We assessed the
utility of our framework for quantifying the cost of transitioning between various cognitive
tareas. Our framework can be applied to very diverse settings because of its generality.

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

INTRODUCCIÓN

The brain is considered a dynamical system that flexibly transitions through various states
(romper la lanza, 2017; McKenna, McMullen, & Shlesinger, 1994; Vyas, Golub, Susillo, & shenoy,
2020). Depending on the properties of a dynamical system (p.ej., the biophysical properties of
neurons and the connectivity between neurons), some transitions are difficult to realize. De este modo,

Citación: Kawakita, GRAMO., Kamiya, S.,
Sasai, S., Kitazono, J., & Oizumi, METRO.
(2022). Quantifying brain state
transition cost via Schrödinger Bridge.
Neurociencia en red, 6(1), 118–134.
https://doi.org/10.1162/netn_a_00213

DOI:
https://doi.org/10.1162/netn_a_00213

Supporting Information:
https://doi.org/10.1162/netn_a_00213
https://github.com/oizumi-lab/SB
_toolbox

Recibió: 10 Junio 2021
Aceptado: 18 Octubre 2021

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Masafumi Oizumi
c-oizumi@g.ecc.u-tokyo.ac.jp

Editor de manejo:
Andrew Zalesky

Derechos de autor: © 2021
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

Quantifying brain state transition cost via Schrödinger Bridge

Dynamical system:
A system whose state changes over
time following a certain rule.

Network control theory:
A field of study that examines the
control strategies of dynamic
networked systems.

Structural connectivity:
Anatomical connections between
regiones del cerebro.

Control óptimo:
The control law for a dynamical
system that optimizes a certain cost
función.

Kullback-Leibler divergence:
An information-theoretic measure
that quantifies the difference
between two probability
distributions.

Schrödinger Bridge:
The most likely time evolution of a
system from an initial to a target
probability distribution given the
transition probability distribution of
the system, which is mathematically
equivalent to the optimally
controlled path linking the initial and
target distribution.

characterizing the dynamical properties of brain state transition would be important for under-
standing various brain functions (Kringelbach & decoración, 2020), including decision-making
(Taghia et al., 2018), motor control (shenoy, Sahani, & Iglesia, 2013), y trabajando
memory (Simmering & Perone, 2012), with potential applications in the diagnosis and clin-
ical treatment of disease (Adhikari et al., 2017; Aerts et al., 2020; decoración & Kringelbach,
2014). Hasta la fecha, sin embargo, no unified framework for quantifying brain state transition cost from
brain activity data has been available.

One promising framework for quantifying brain state transition cost is the network control–
theoretic framework (Medalla, Pasqualetti, hamilton, Thompson-Schill, & bassett, 2017; ver
also Suweis et al., 2019; Tu et al., 2018, for some limitations). Control theory provides useful
perspectives for measuring the cost required for controlling a dynamical system to reach a
desirable state. Considering the brain as a dynamical system, control-theoretic approaches
enable us to quantify the cost of transitioning to a brain state that produces desirable behavior.
Recientemente, the network control-theoretic framework was proposed for study of the control prop-
erty of the brain by viewing the brain as a networked dynamical system (bassett & despreciar,
2017; Cornblath et al., 2020; Gu et al., 2017; Gu et al., 2015). Although the framework pro-
vides an important new perspective for fundamentally understanding brain state transition, él
has two major limitations. Primero, it does not capture the stochasticity of brain activity, cual es
ubiquitous in brain activity and is essential for accurately describing brain dynamics (decoración,
Rolls, & Romo, 2009; Rieke, 1999; Shadlen & nuevosome, 1998). Disregarding stochasticity
may result in an inaccurate estimation of transition cost. Segundo, the model obtained from
structural connectivity, which is static over time, may not be able to capture change in the
functional dynamics of the brain (Kringelbach & decoración, 2020), such as while performing
tareas, por ejemplo. Además, it is difficult to model even the resting-state dynamics from
structural connectivity (Honey et al., 2009). Recientemente, alternative models using functional
and effective connectivity have been proposed (Deng & Gu, 2020; Szymula, Pasqualetti,
Graybiel, Rocas, & bassett, 2020), but these models still do not capture stochasticity.
De este modo, no unified framework able to take account of the key properties of brain dynamics is
disponible.

Aquí, by employing control-theoretic approaches, we propose a novel framework for mea-
suring brain state transition cost that can account for stochasticity. In our framework, nosotros estafamos-
sider transition from a probability distribution of brain states to another distribution, en vez de
a transition from one brain state to another brain state (es decir., a point-to-point transition in a state-
espacio) in contrast to a previous work (Cornblath et al., 2020) utilizing network control theory.
To transition from an initial distribution to a target distribution, the brain needs to modulate
(control) its baseline transition probability. Although there are many possible ways to reach
the target distribution, in this study we consider the optimally controlled path only and esti-
mate the lower bound of brain state transition cost. We propose defining the minimum brain
state transition cost as the Kullback-Leibler (KL) divergence from the baseline uncontrolled
path to the optimally controlled path, eso es, the closest path to the original path, with the fixed
initial and target distributions. The problem of finding the closest path to the original path con-
necting the initial and target distribution is known as Schrödinger Bridge problem (Schrödinger,
1931), which has been studied in the fields of stochastic process and optimal transport (Beghi,
1996; Chen, Georgiou, & Pavon, 2016a, 2016b; Dai Pra, 1991; Léonard, 2013).

Aquí, as proof of concept, we apply the proposed framework based on the Schrödinger
Bridge problem to evaluate the cost of task switching (monsell, 2003), an executive function
for moving from one task to another. Específicamente, we address two questions. Primero, is the cost of
transitioning to a more difficult task larger? A previous study (Kitzbichler, Henson, Herrero,

Neurociencia en red

119

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

Brain parcellation:
Partitioning the brain into spatially or
functionally distinct regions.

Nathan, & bullmore, 2011) reported that performing effortful tasks drives larger reconfiguration
of functional brain networks. We therefore hypothesized that transitioning to a more difficult
task required a larger cost. Segundo, is the brain state transition cost asymmetric? Específicamente, es
the transition cost from an easier task to a more difficult task larger than the cost accompanying
the reverse transition?

To address these questions, we apply our framework to functional magnetic resonance
imaging (resonancia magnética funcional) data from the Human Connectome Project (HCP; Van Essen et al., 2013).
We use fMRI data of n = 937 subjects in the resting state and in seven cognitive tasks. Después
preprocessing and parcellation, we computed the probability distributions of coarse-grain
brain activity patterns for the rest and cognitive tasks (Cornblath et al., 2020; Lynn, Cornblath,
Papadopoulos, Bertolero, & bassett, 2020). We then calculated the brain state transition cost
by finding the Schrödinger Bridge, eso es, the optimally controlled path (Pavlichin, Quek, &
Weissman, 2019) between the initial and target distributions of brain states. We found that the
transition cost to a more difficult task carried a larger transition cost. We also observed that the
transition cost between an easy and a difficult task is asymmetric. En general, our findings provide
a new perspective on the investigation of brain state transition, which may facilitate our under-
standing of cognitive functions.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

RESULTADOS

Quantification of Brain State Transition Cost From the Schrödinger Bridge Problem

en este estudio, we propose a novel framework to quantify state transition cost in a stochastic
neural system, building on the formulation of the Schrödinger Bridge problem (Beghi,
1996). We consider brain state transition to be the transition from an initial probability distri-
bution of brain states to a target probability distribution. In order to reach the target probability
distribución, the brain is assumed to follow some controlled paths. Although there are many
possible paths that bridge the initial and target probability distributions, we look for the opti-
mally controlled path that minimizes the Kullback-Leibler (KL) divergence from an uncontrolled
to a controlled path. Aquí, we define brain state transition cost as the minimum KL divergence
from an uncontrolled to a controlled path that bridges the initial and target probability distribu-
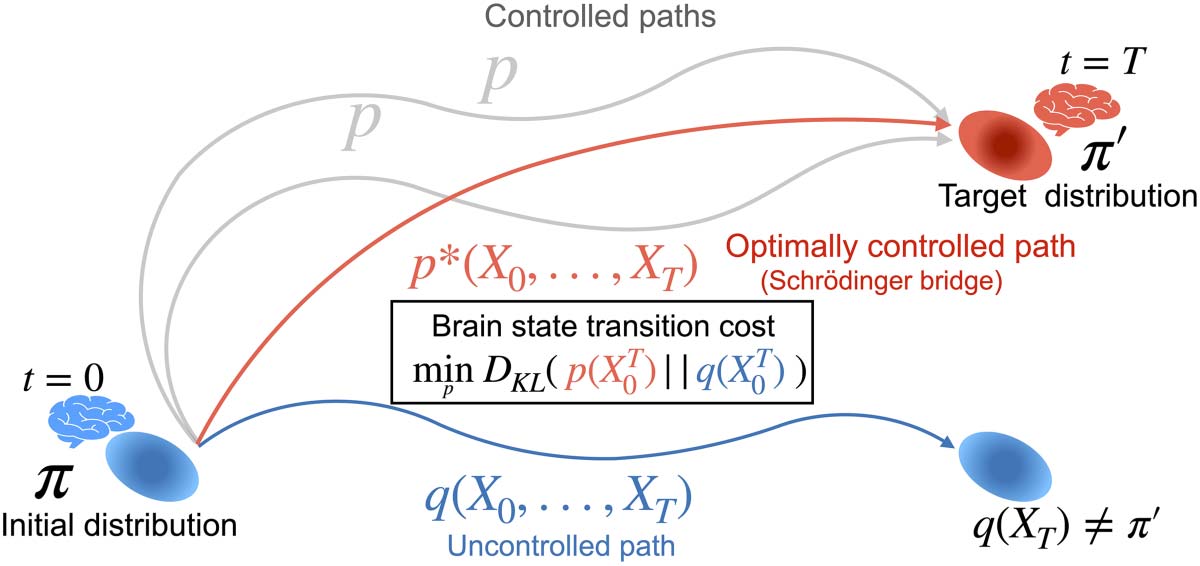
ciones (Cifra 1).

We can mathematically formulate brain state transition as follows. Let Xt be a random var-
iable corresponding to a coarse-grained brain state at time t. We consider each brain state to
be a discrete number included in the finite set S = {1, …, k}, where k is the number of brain
estados. Por ejemplo, Xt = i means that the brain is at the state i at time t. en este estudio, we used
the k-means clustering algorithm to obtain these coarse-grained brain states from high-
dimensional brain activity data as described later. Entonces, dejar (X0, …, XT) be a time series of brain
states that form a first-order Markov chain. We introduce a simplified notation for expressing
0 = (X0, …, XT), where subscript 0 represents the starting time point and
the time series as X T
superscript T represents the ending time point. We denote the joint probability distribution of
0 ) = q(X0, …, XT), which can be expressed using the Markov
the random variables by q(X T
property as follows:

(cid:3)

(cid:1)
q X T
0

¼ q X0ð

YT −1
Þ

d
q Xtþ1jXt

Þ:

t¼0

(1)

Aquí, we consider a problem of controlling the distribution of brain states to a target dis-
tribution, π0, at t = T starting from an initial distribution, Pi, at t = 0. The initial distribution, Pi, es

Neurociencia en red

120

Quantifying brain state transition cost via Schrödinger Bridge

Schematic of brain state transition reframed as the Schrödinger Bridge problem. Nosotros estafamos-
Cifra 1.
sider brain state transition as transition from an initial probability distribution of brain states, Pi, to a
target probability distribution, π0. The brain follows an uncontrolled baseline path, q(X T
0 ), cual
does not lead to the target distribution but to q(XT) ≠ π0, where q(XT) represents the probability dis-
tribution at t = 0, following the uncontrolled path. In order to reach the target distribution, the brain
needs to follow a controlled path, pag(X T
0 ). The brain state transition cost is defined as the minimum
Kullback-Leibler divergence between the controlled and uncontrolled paths p(X T
0 ),
respectivamente. Optimally controlled path, p*(X T

0 ) is equivalent to Schrödinger Bridge.

0 ) and q(X T

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

the same as q(X0), but the target distribution π0 is different from q(XT), eso es, the target distri-
bution, π0, cannot be reached by the original dynamics, q(X T
0 ). De este modo, the transition probability
of the brain needs to be modulated by some control input to the system. Although we do not
explicitly model control input in this study because we do not model the dynamics of the sys-
tema (see Chen et al., 2016a, for the model of linear systems with control input), we assume that
some control input is implicitly applied to modulate the original dynamics. In this context of
0 ), the “uncontrolled path.” In
controlling the dynamics, we call the original dynamics, q(X T
0 ) = p(X0, …,
contrast with the uncontrolled path, q(X T
XT), a “controlled path,” which satisfies the end point constraints, pag(X0) = π and p(XT) = π0.
While there are many possible controlled paths that satisfy the marginal conditions, nosotros estafamos-
sider the problem of finding the optimally controlled path that minimizes some control cost. En
este estudio, we define the control cost as the Kullback-Leibler (KL) divergence between the
uncontrolled path and a controlled path (Beghi, 1996; Chen et al., 2016a),

0 ), we call a controlled dynamics, pag(X T

(cid:1)

(cid:1)
DKL p X T
0

(cid:3)

(cid:1)
‖q X T
0

(cid:3)

X0;X1;…;XT 2S

(cid:3)

(cid:1)
p X T
0

registro

(cid:1)
p X T
0
d
q X T
0

(cid:3)

(2)

0 ) and q(X T

Intuitivamente, KL divergence measures the difference between two probability distributions. If KL
divergence between p(X T
0 ) es 0, then we can tell that two paths are equivalent, eso es,
the system does not change but stays the same. If the KL divergence takes nonzero values, él
indicates that the system follows a different path from the uncontrolled path. Using the KL
divergence as a transition cost is reasonable since the degree of KL divergence should reflect
how different a controlled path is from the uncontrolled path. Aquí, we define the optimally
controlled path, p*(X T

0 ), as the minimizer of KL divergence, as shown below:

Neurociencia en red

(cid:3)

(cid:1)
p* X T
0

¼ arg min
pag

(cid:1)

(cid:1)
DKL p X T
0

(cid:1)
(cid:3)
‖q X T
0

(cid:3)

(3)

121

Quantifying brain state transition cost via Schrödinger Bridge

0 ), is the “closest” to the uncontrolled path,
0 ), in terms of KL divergence. Entonces, using the optimally controlled path, we define the

En otras palabras, the optimally controlled path, p*(X T
q(X T
minimum control cost C as

(cid:1)

(cid:1)
DKL p X T
0

(cid:3)

(cid:1)
‖q X T
0

(cid:3)

(cid:1)
¼ DKL p* X T
0

(cid:1)

(cid:3)

(cid:1)
‖q X T
0

(cid:3)

(4)

C ≡ min
Þ
d
p X T
0

en este estudio, we propose to use the minimum control cost for quantifying the brain state transi-
tion cost. The problem of finding the optimally controlled path from an initial to a target distri-
bution is known to be mathematically equivalent to the Schrödinger Bridge problem, el
problem of finding the most likely path linking the initial and target distribution given the
transition probability distribution of the system (Beghi, 1996; Chen et al., 2016a).

To solve the minimization problem, we first decompose the KL divergence into two terms,

both of which are also KL divergences.
(cid:3)

(cid:3)

(cid:1)

(cid:1)
DKL p X T
0

(cid:1)
‖q X T
0

d
p X0; …; XT

Þ log

Þ
Þ

d
p X0; …; XT
d
q X0; …; XT
Þ
Þ

d
p X0; XT
q X0; XT
d
X

X0;…;XT
X

d
p X0; XT

Þ log

X0;XT

d
p X0; XT

Þ
X1;…;XT −1

d
¼ DKL p X0; XT
d

d
Þ‖q X0; XT

d
p X1; …; XT −1

Þ log

(cid:1)
Þ þ DKL p X T −1

(cid:1)

(5)

Þ
Þ

d
p X1; …; XT −1jX0; XT
q X1; …; XT −1jX0; XT
d
(cid:1)
‖q X T −1
1

jX0; XT

(cid:3)

;

jX0; XT

where X T −1
= (X1, …, XT−1). The two terms are both nonnegative and we can separately min-
imize the two terms. The minimum of the second term is obviously 0 when p*(X T −1
|X0, XT) =
q(X T −1
|X0, XT). Entonces, the minimization problem of finding the whole controlled path is
1
reduced to the problem of finding the optimally controlled joint distribution of the end points,
pag(X0, XT) (Beghi, 1996),

(cid:1)

(cid:1)
DKL p X T
0

(cid:1)
(cid:3)
‖q X T
0

(cid:3)

mín.
Þ
d
p X T
0

¼ min
d
p X0;XT

d
DKL p X0; XT

d
Þ‖q X0; XT

Þ:
Þ

(6)

By introducing the useful notation p(X0, XT) =P, and q(X0, XT) = Q, where Pij = p(X0 = i, XT = j )
and Qij = q(X0 = i, XT = j ) for ease of computation, we can rewrite the KL divergence as

d
DKL p X0; XT

d
Þ‖q X0; XT

Þ ¼ DKL P‖Qð
Þ

Þ ¼

Pij log

i¼1

j¼1

Pij
Qij

(7)

With these new notations, we can restate the original minimization problem (Ecuación 3) como

PAG * ¼ arg min

DKL P‖Qð

PAG

with the following constraints,

Pij ¼ πi;

Pij ¼ π0

Pij ¼ 1:

;

i¼1

j¼1

i¼1

(8)

(9)

To further clarify the mathematical property of the optimization problem, we rewrite the

control cost as follows:

DKL P‖Qð

Þ ¼ −

Pij logQij þ

Pij logPij

i¼1

j¼1

i¼1
Xk

j¼1
Xk

CijPij − H Pð Þ;

Neurociencia en red

i¼1

j¼1

(10)

122

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

where H(PAG) is the entropy of the joint end point distribution, PAG. By rewriting the cost in this way,
we can regard the problem of minimizing KL divergence as the entropy regularized optimal
transport problem with the transportation cost matrix, Cij = −log Qij (Amari, Karakida, &
Oizumi, 2018; Cuturi, 2013; see e.g., Chen, Georgiou, & Pavon, 2021; De Bortoli, Thornton,
Heng, & Doucet, 2021; Léonard, 2013, for the connection between the Schrödinger Bridge
problem and optimal transport problem). The existence and uniqueness of the optimal
solución, PAG *, is guaranteed because this is a strongly convex optimization problem (Amari
et al., 2018; Cuturi, 2013).

Aquí, we explicitly find the solution of the optimization problem using the method of
Lagrange multipliers. Let L(PAG, a, b) be the Lagrangian of Equation 10 with Lagrange multipliers,
αi and βj.

L P; a; b

Þ ¼ −

Pij logQij þ

Pij logPij −

Xk
(cid:1)

αi þ βj

(cid:3)

Pij :

i¼1

j¼1

i¼1

j¼1

i¼1

j¼1

Differentiating Equation 11 with respect to Pij yields

¼ − logQij þ logPij þ 1 − αi þ βj

(cid:1)

(cid:3)

∂L
∂Pij

By setting the partial derivative to 0, we obtain the following optimal solution

where c is the normalization constant,

PAG (cid:2)
ij

¼ ceαi þβj Qij ;

c ¼

PAG

1
j¼1 eαi þβj Qij

k
i¼1

We determine the Lagrange multipliers, αi and βj, by the constraints in Equation 9,

j¼1

PAG (cid:2)
ij

i¼1

PAG (cid:2)
ij

ceαi þβj Qij ¼ πi;

j¼1

i¼1

ceαi þβj Qij ¼ π0

With some manipulation of the above equations, we obtain

αi ¼ log πið

Þ − log

(cid:4) (cid:5)
βj ¼ log π0

− log

eβj Qij

j¼1

− logc;

eαi Qij

i¼1

− logc:

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

These Lagrange multipliers can be numerically determined by iteratively updating αi and βj
according to the above equations starting from arbitrary initial values. This algorithm is known
as the Sinkhorn algorithm (Cuturi, 2013; Sinkhorn, 1967). The implementation of the algorithm
is available at https://github.com/oizumi-lab/SB_toolbox (Kawakita & Oizumi, 2021).

Neurociencia en red

123

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

Quantification of Brain State Transition Cost in fMRI Data
To test the utility of our proposed method, we applied the Schrödinger Bridge–based framework
to real fMRI data. We used resting-state fMRI and task-fMRI (emotion, gambling, idioma,
motor, relational, social, and working memory) from the Human Connectome Project (HCP;
Van Essen et al., 2013). We first performed preprocessing of the BOLD signals and parceled them
en 100 cortical regions (Schaefer et al., 2018). As shown in Figure 2, we concatenated the pre-
processed data of all subjects for all the tasks to obtain M × N time series data, where M is the
number of cortical parcels (100) and N is the total time frames of the concatenated data. Nosotros
consider a point in M = 100 dimensional space as the activity of the whole brain at a particular
time frame. In total, there are N points in this high-dimensional space. We applied the k-means
clustering algorithm to classify N points into k coarse-grained states. En esta sección, we show
only the results when we set the number of coarse-grained states to k = 8 (see Supporting Infor-
mation for the results with different numbers of coarse-grained states).

To compute the brain state transition cost (Ecuación 4), we need to obtain initial and target
distributions as well as the joint probability distribution for the uncontrolled path. Aquí, nosotros
assume that an uncontrolled path in the brain is the resting-state transition probability. To deter-
mine the joint probability distribution for the uncontrolled path, we need to set the value of T,
the time steps to reach the target distribution. We computed brain state transition cost with var-
ious T and observed that the results did not change qualitatively. De este modo, we show here the results
with T = 1, eso es, the next time frame (see Supporting Information S6 for results when T > 1). A
probability distribution for each task was computed as an empirical probability distribution by
counting the number of the occurrences of the coarse-grained states in each task time series
datos. We estimated the joint probability distribution of the resting state for two consecutive
frames by counting transition pairs of the coarse-grained brain states with trajectory bootstrap-
ping (see Methods for more details). From the joint probability distribution, we obtained the
transition probability matrix of the resting state. Using these probability distributions and the
transition probability matrix of the resting state, we calculated brain state transition cost

Empirical probability distribution:
A probability distribution estimated
from empirical data.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2. Clustering fMRI data. After preprocessing raw fMRI data, we concatenated the preprocessed data of all subjects for all the tasks. Nosotros
then used k-means clustering to group similar brain activity patterns into eight coarse-grained brain states. Each point in the 100-dimensional
state space corresponds to the activity of the whole brain at a particular time frame (see S5 in the Supporting Information for brain maps of the
centroids of the eight clusters).

Neurociencia en red

124

Quantifying brain state transition cost via Schrödinger Bridge

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

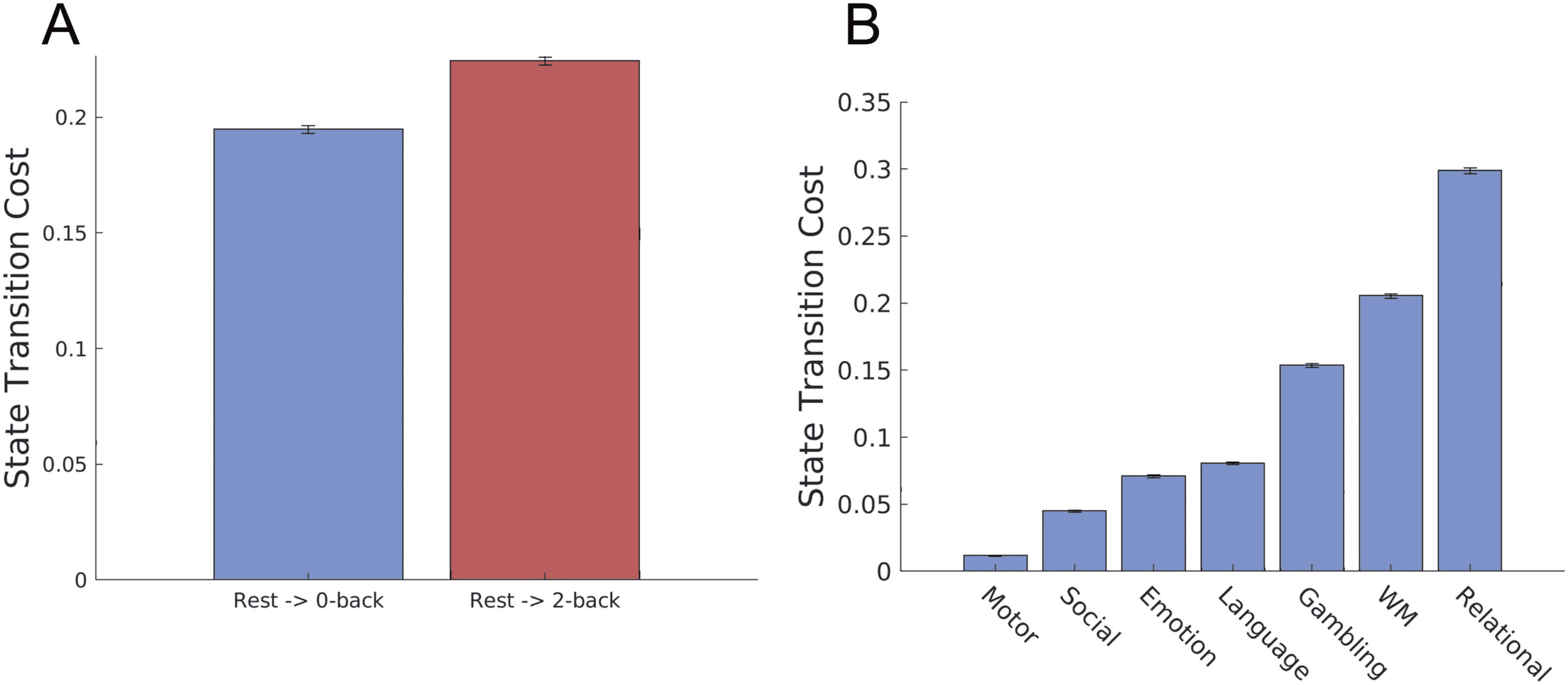
Cifra 3. Brain state transition cost from the resting state to tasks. We computed the transition cost from the rest to cognitive tasks in the HCP
datos, as the minimum Kullback-Leibler divergence from the optimally controlled path to the baseline uncontrolled path. (A) The transition cost
to the 2-back task (mas dificil) is larger than the transition cost to 0-back task (easier) (one-sided t test, p ≪ 0.001, t > 60, df = 198). (B)
Transition cost from the rest to the seven cognitive tasks in the HCP dataset. Values are averaged over 100 bootstrapping trajectories and error
bars indicate one standard deviation estimated with trajectory bootstrapping.

represented by the minimized KL divergence (Ecuación 4). Por ejemplo, when we computed
the transition cost from the gambling task to the motor task, we set the initial distribution, Pi,
to be the empirical probability distribution obtained from the gambling task data and the tar-
get distribution, π0, to be the empirical probability distribution obtained from motor task data.
Aquí, the probability distribution of the uncontrolled path, Qij = q(X0 = i, XT = j ), is computed
by the product of the initial probability distribution πi and the transition probability distribu-
tion of the resting state Qj|i = q(XT = j|X0 = i), Qij = Qj|i πi. With π, π0, and Q, we can determine
the optimally controlled path, PAG *, and then compute the transition cost as C = DKL(PAG *||q).

We began by testing whether transition cost from rest to a more difficult task is larger. Para esto
purpose, we quantified the transition cost from the distribution at rest to those during 0-back
(easier) and 2-back (mas dificil) tasks in the working memory ( W.M.) task data. We chose the
WM task because the WM task data are the only task data in HCP, wherein subjects perform
tasks with objectively different levels of task difficulty. As shown in Figure 3, we found that the
transition cost to a 2-back task is larger than that to a 0-back task. This result suggests that our
cost metric may capture the level of task difficulty from fMRI data.

Brain State Transition Cost to Multiple Tasks

To further check the behavior of the proposed metric for transition cost, we then computed
brain state transition cost to multiple task distributions in the HCP dataset (emotion, gambling,
idioma, motor, relational, social, and working memory). Tenga en cuenta que, unlike the working mem-
ory tasks, we cannot objectively compare their task difficulties since these tasks are qualita-
tively different. De este modo, the analysis here is exploratory without any prior hypothesis.

We found that the degree of transition cost to the seven cognitive tasks is significantly dif-
ferent. Figure 3B shows the rank order of transition costs in the seven cognitive tasks. Notablemente,

N-back task:
A type of working memory task in
which a subject reports whether a
presented stimulus matches a
stimulus shown n times ago.

Neurociencia en red

125

Quantifying brain state transition cost via Schrödinger Bridge

transition cost to a motor task was smallest among the seven tasks, whereas the transition cost
to a relational task was the largest (see Discussion).

Asymmetry of Brain State Transition Cost

We then investigated whether state transition cost between tasks with different task difficulty
was asymmetric. We hypothesized that it would require a larger transition cost to switch from
an easier task to a more difficult task. To test this hypothesis, we computed the transition cost
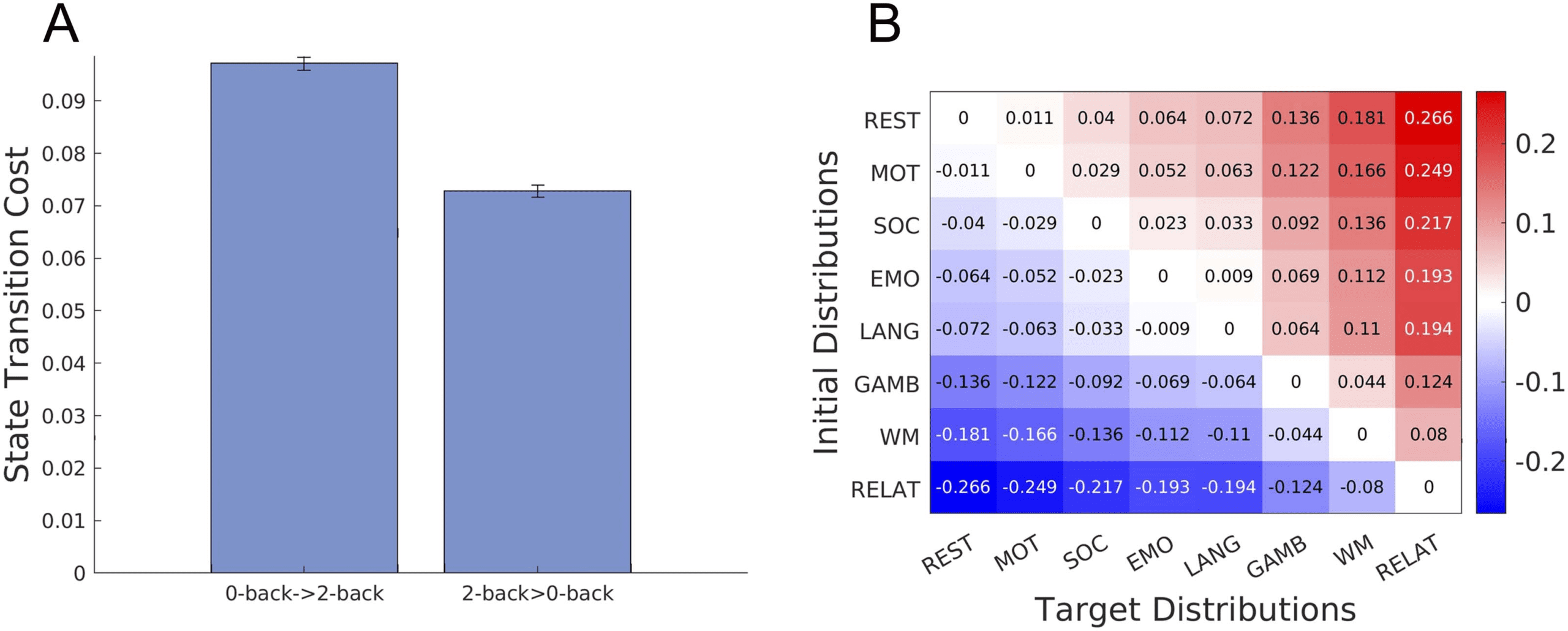
between 0-back and 2-back tasks in the working memory task. As shown in Figure 4A, nosotros
found that the transition cost from a 0-back task to a 2-back task was larger than the cost
accompanying the reverse direction, which agreed with our hypothesis (one-sided t test,
p ≪ 0.001, t > 80, df = 198). Note that the asymmetry of the brain state transition cost
does not result from the asymmetry of KL divergence, because the cost is not solely com-
puted from the end point distributions but with underlying transition probability.

Finalmente, we examined whether the asymmetric property of brain state transition cost would
be observed in other tasks whose task difficulties cannot be objectively compared. Aquí, nosotros
checked whether the following relationship would hold for all the pairs of tasks (note that here
we regarded the rest as a task):

If the transition cost from rest to task A is larger than that from rest to task B, then the tran-

sition cost from task B to task A is larger than that in the reverse direction,

C task B → task A
d
if C rest → task A

Þ > C task A → task B
Þ;
Þ > C rest → task B

d
d

Þ;

(19)

where C(X → Y ) represents the brain state transition cost from X to Y, which is quantified by the
KL divergence. To evaluate the relationship, we calculated the difference in transition cost
between every pair of tasks, which is obtained as follows.

Diff A; Bð

Þ ¼ C task A → task B

Þ − C task B → task A

Þ:

(20)

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 4. Brain state transition cost between task states. (A) Brain state transition cost between the 0-back and 2-back tasks in the working
memory task. Values are averaged over 100 bootstrapping trajectories and error bars indicate one standard deviation estimated using trajectory
bootstrapping. (B) Asymmetry of brain state transition costs for the rest and seven cognitive tasks. Each element in the matrix represents a
difference in transition cost between tasks.

Neurociencia en red

126

Quantifying brain state transition cost via Schrödinger Bridge

The result is summarized in the matrix in Figure 4B, wherein entries (tareas) are arranged in
ascending order by transition cost from rest, eso es, the first row (columna) corresponds to
the task with the smallest transition cost from rest and the last row (columna) corresponds to
the task with the largest transition cost from rest. El (i, j ) entry of the matrix represents Diff
(taski, taskj) = C(task i → task j) − C(task j → task i). We observed that every entry in the upper
(más bajo) triangular parts was positive (negative). This means that the relationship represented in
Ecuación 19 holds for every pair of tasks in the dataset. Eso es, the transition cost is asymmetric
between tasks with different degrees of transition cost.

DISCUSIÓN

en este estudio, we propose a novel framework for quantifying brain state transition cost in stochas-
tic neural systems by framing brain state transition as the Schrödinger Bridge problem (SBP). Este
framework resolves the problem of previous methods that cannot take account of the inherent
stochastisity of neural systems (Daunizeau, Esteban, & Friston, 2012; Deco et al., 2009) mientras
still utilizing principled control-theoretic approaches. Bajo este marco, we assumed that
the brain follows the resting-state activity as the baseline uncontrolled dynamics, and transitions
to other distributions of brain state by modulating the baseline dynamics. Transition cost is
measured as the minimum KL divergence from the uncontrolled path to the controlled path
with the fixed end point probability distributions. We tested the utility of our framework by
applying it to fMRI data from the Human Connectome Project release. The results indicated
that the transition cost metric proposed in our framework may be useful for elucidating the
characteristics of transition cost between tasks with different task difficulties.

Correspondence Between Transition Cost and Cognitive Demands

En el presente estudio, we aimed to examine the relationship between the degree of brain state
transition cost and task difficulty as proof of concept. We refer to task difficulty as objectively
quantifiable task difficulty (p.ej., 0-back and 2-back) solo, not as a subjectively experienced
task difficulty, which could vary among subjects. As for the objective task difficulty, nosotros
observed that the transition cost to a 2-back task (a more difficult task) is larger than that to
a 0-back task (an easier task). Further studies using different types of tasks with various levels of
difficulty are needed to determine the generality of this result.

Por otro lado, we did not deal with subjectively experienced task difficulty or cognitive
demandas, as the dataset does not contain subjective reporting on the cognitive demand of each
tarea. Sin embargo, we quantified the transition cost to the seven qualitatively different tasks,
whose task difficulty or cognitive demand cannot be objectively quantified. Although it is
unclear whether the observed order of transition cost correlates with subjective cognitive
demand (Figura 3B), one may at least consider it reasonable that transition cost to a motor task
is substantially smaller than that to a relational task. This is because performing a motor task only
requires subjects to move a part of their body (p.ej., right hand or tongue), whereas performing a
relational task requires processing multiple visual stimuli and reasoning their relationships,
which appears significantly more demanding than performing a motor task. Although we could
not further examine whether the degree of transition cost correlates with the degree of cognitive
demand, investigating this relation in more detail would be an interesting future work. We expect
that while there may be a rough correlation between transition cost and cognitive demand, allá
can never be one-to-one correspondence, as many factors affect subjective evaluation of cog-
nitive demand (Semillas, lin, decano lobo, Inzlicht, & Shenhav, 2021; Kool, McGuire, rosa, &
Botvinick, 2010; McGuire & Botvinick, 2010; Rosenbaum & Bui, 2019). It would be intriguing

Neurociencia en red

127

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

to investigate the difference in transition cost and cognitive demand and in what cases these
behave similarly or differently. The direction of study proposed in the present study might be
an important step toward bridging cognitive demand and brain activity.

Relation to Previous Theoretical Work

En el presente estudio, we considered the brain dynamics as a discrete stochastic process by coarse-
graining brain activity patterns, which reduced the computational cost. Por otro lado, previ-
ous studies using network control-theoretic framework (Gu et al., 2015) employed a linear
continuous process. Our framework can also be extended to a linear continuous stochastic pro-
cess because the Schrödinger Bridge problem is not limited to a discrete process but has also been
studied in continuous settings as well (Chen et al., 2016b; Dai Pra, 1991; Léonard, 2013). Nosotros
therefore expected that we could directly fit the high-dimensional neural recording data with a
continuous model (p.ej., stochastic differential equations) as recently implemented (Nozari et al.,
2020) and carry out a similar analysis as the present study. Developing a continuous version of
the present framework may allow us to gain more insights into brain state transition cost.

Both the discrete stochastic process (model-free dynamics) utilized in the present study and
linear dynamical models (Chen et al., 2016a; Gu et al., 2015) possess pros and cons for the
application in the analysis of neural activity. In linear dynamical models, because the control
input is explicitly modeled, the biophysical meaning of the control input is clear. By taking
advantage of the high interpretability of the control input, linear dynamical models, for exam-
por ejemplo, can provide insights into the contribution of each brain region to the control of the whole
sistema (Gu et al., 2015). Sin embargo, linear dynamical models are not suitable for the analysis of
neural activity that is highly nonlinear. The discrete stochastic process used in the present
study can be applied to nonlinear neural activity although the biophysical interpretation of
control input is unclear. It is imperative to select an approach that fits the purpose of the study
and the property of the data. By choosing appropriate models, we can compute brain state
transition cost in various types of data (p.ej., resonancia magnética funcional, EEG, ECoG).

Similarly to our framework, some recent works have utilized information theoretic mea-
sures to quantify cognitive costs (Zenón, Solopchuk, & pezzulo, 2019) and connectivity
changes between brain states (Amico, Arenas, & Goñi, 2019). While these studies compute
only distance or divergence between the two distributions of brain state, our framework takes
account of the underlying baseline activity of the brain. We employ this approach because
including this baseline spontaneous activity provides a more accurate transition cost measure
from the viewpoint of dynamical system theory.

Physical Interpretation of the Brain State Transition Cost
The KL divergence–based control cost proposed in this study may seem to be a distant concept
from the conventional control cost, namely the time integral of squared input (Gu et al., 2017),
in a linear deterministic model. Sin embargo, it was shown in a previous study that the KL diver-
gence cost in a stochastic linear model is analytically computed as the expectation of the time
integral of squared input (Beghi, 1996; Chen et al., 2016a). En este sentido, the KL divergence
cost is tightly connected to the conventional control cost in a linear system.

The brain state transition cost proposed in the present study has a clear information theoretic
significado, eso es, the KL divergence between the optimally controlled path and the uncontrolled
camino. Sin embargo, an explicit physical interpretation has yet to be elucidated. A natural choice of
control cost from the viewpoint of physics would be the work needed to realize a controlled path
from an initial distribution to a target distribution (Chen, Georgiou, & Tannenbaum, 2020;

Neurociencia en red

128

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

Conectividad funcional:
Statistical dependencies (a menudo
simply referred to as correlation)
between brain regions estimated
from brain activity data.

Horowitz, zhou, & Inglaterra, 2017). Minimizing the work is equivalent to minimizing entropy
producción (work dissipation; Chen et al., 2020; Horowitz et al., 2017). Previous works inves-
tigated the optimal control that minimized entropy production (or equivalently the work) y
showed that the entropy production is lower bounded by the square of the Wasserstein distance
(Chen et al., 2020; Nakazato & Ito, 2021). Curiosamente, entropy production is given by the
Kullback-Leibler divergence between two probabilities of forward and backward processes
(Kawai, Parrondo, & Van den Broeck, 2007). De este modo, one may consider that there should be some
connection between the Schrödinger Bridge–type information theoretic control cost proposed in
this study and the physical cost, trabajar, or entropy production. It would be interesting to clarify the
relationship between these different types of control cost.

Brain State Transition and Reconfiguration of Functional Connectivity

The brain state transition cost computed in our framework may be related to the reconfigura-
tion of functional connectivity between tasks. Numerous functional neuroimaging studies have
reported the alterations in functional connectivity from the resting-state connectivity during
task performance (Col, bassett, Fuerza, Más valiente, & Petersen, 2014; Col, Ito, Cocuzza, &
Sanchez-Romero, 2021; Davison et al., 2015; Spadone et al., 2015; Stitt et al., 2017). En
our present study, we showed that transitioning to more difficult tasks carries a larger transition
costo. This seems to be consistent with Kitzbichler’s work, which demonstrated that larger cog-
nitive demand induces a more global alteration in brain activity (Kitzbichler et al., 2011). Él
may be the case that our framework captures the cost associated with the degree of reorgani-
zation of functional connectivity between different tasks.

Implications to Task Switching
The Schrödinger Bridge–based framework we proposed in this study may provide a new perspec-
tive for studying task switching from brain activity data. One of the most important and replicated
findings in the task-switching paradigm is the observation of switch cost (monsell, 2003):
Switching to a new task takes a higher reaction time and error rate than repeating the same task.
Various hypotheses have been proposed to explain the source of switch cost (Jersild, 1927; Koch,
Gade, Schuch, & Philipp, 2010), including reconfiguration of the mental set for performing tasks.
Sin embargo, few studies have quantified the switch cost from brain activity. A recent work suggests
that task switching involves the reconfiguration of brain-wide functional connectivity (Daws
et al., 2020). Our framework may be used as a quantitative method for measuring switch cost.
Subsequent investigations should study the relationship between switch cost and brain state tran-
sition cost by measuring brain activity while a subject is performing a task-switching experiment.

Comparison Between the Optimally Controlled Path and the Empirical Path

We investigated only the optimally controlled path, not an empirical path because of the limitation
of fMRI recording. To quantify the efficiency of brain state transition, it would be interesting to
compare empirical and optimal paths. This may provide insight into individual differences in
the performance of task switching. Sin embargo, the fMRI data from the Human Connectome Project
does not include recordings in which subjects perform and switch between multiple tasks, and we
were therefore unable to compute an empirical transition path between initial and target distribu-
tions of brain states. Even if the dataset contained such data, fMRI would not capture rapid
transitions between tasks because the time resolution of the fMRI data is not sufficiently high
(TR = 0.72 s in the HCP dataset). Computing empirical transition paths will require the use of
recording data with better temporal resolution, such as EEG, MEG, or ECoG. A este respecto, nuestro
theoretical framework is applicable to other types of recording data besides fMRI.

Neurociencia en red

129

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

MÉTODOS

fMRI Data Acquisition and Preprocessing

The 3T functional magnetic resonance imaging (resonancia magnética funcional) data of 937 subjects were obtained from
the Washington University–Minnesota Consortium Human Connectome Project (HCP; Van
Essen et al., 2013). Every subject provided a written informed consent to the Human Connec-
tome Project consortium, following the HCP protocol. We used minimally preprocessed fMRI
data at resting state and seven cognitive task states (emotion, gambling, idioma, motor, rela-
tional, social, and working memory). We selected these 937 subjects as they contain complete
data for all the tasks. We then performed denoising by estimating nuisance regressors and sub-
tracting them from the signal at every vertex (Satterthwaite et al., 2013). Para esto, we used 36
nuisance regressors and spike regressors introduced in a previous study, consisting of (1–6) six
motion parameters, (7) a white matter time series, (8) a cerebrospinal fluid time series, (9) a
global signal time series, (10–18) temporal derivatives of (1–9), y (19–36) quadratic terms for
(1–18). Following a previous study (Satterthwaite et al., 2013), the spike regressors were com-
puted with 1.5-mm movement as a spike identification threshold. After regressing these nui-
sance time courses, we also applied a band-pass filter (0.01–0.69 Hz) to the data, in which the
upper bound of the filter corresponds to the Nyquist frequency of the time series. Nosotros entonces
applied a parcellation proposed in (Schaefer et al., 2018) to divide the cortex into 100 cerebro
regiones, which reduced the complexity of the following analysis.

Clustering BOLD Signals

In order to model brain dynamics as a discrete stochastic process, we coarse-grained brain
activity patterns using the k-means clustering algorithm. While there are numerous unsuper-
vised clustering algorithms, we chose the k-means clustering because of its effective fit with the
dynamics of neural activities (Cornblath et al., 2020). We used cosine similarity as a distance
measure between centroids of clusters, which is commonly used in high-dimensional data. Como
described in the previous studies (Cornblath et al., 2020; Lynn et al., 2020), we concatenated
preprocessed BOLD signals of all the subjects during the resting state and seven cognitive
tareas. We obtained an M × N matrix, X, where M is the number of cortical parcels (100),
and N is the number of task types times the number of time frames times the number of sub-
jects. In order to prevent the variability in data size across tasks from affecting the clustering
resultados, we used the same number of time frames for each task data. We used a different
number of time frames depending on whether we divided the working memory task data into
0-back and 2-back tasks. When we divided the working memory task data (Figures 3A and 4A),
we obtain 148 time frames that included either 0-back or 2-back task blocks. Respectivamente, nosotros
used only the first 148 time frames in the other tasks. When we did not divide the working
memory task data (Figures 3B and 4B), we used only the first 176 discrete measurements in
each task since the emotion task—the task with the shortest measurement—was recorded for
176 time frames.

We determined the number of clusters using a similar procedure to that in previous studies
(Cornblath et al., 2020; Lynn et al., 2020). We first computed the percentage variance explained
by the number of clusters varying from k = 2 to k = 12. We observed that the explained variance
plateaued around 75% after k = 5 (S4a in Supporting Information). We then examined whether
all the coarse-grained states would appear in every subject during each task session (S4b in
Supporting Information). We found that when we set the number of clusters to be greater than
k = 8, some coarse-grained states did not appear in the data of some subjects. For these two
razones, we selected the number of clusters to be 8. While we chose k = 8, we were able to

Neurociencia en red

130

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

reproduce the major results with k > 4 (S1–S3 in Supporting Information), which indicates the
robustness of our results regardless of the number of clusters.

Estimating Transition Probabilities and Probability Distributions of Coarse-Grained States Using

Trajectory Bootstrapping

We are limited by the finite length of the time series data for estimating brain state transition
costo, which is calculated using probability distributions and transition probabilities. To ensure
the accuracy of estimated quantities, we applied trajectory bootstrapping (Battle et al., 2016;
Lynn et al., 2020) to calculate error bars on the estimated quantities. After we classified brain
activity data with k-means clustering, we estimated the joint probability distribution matrix,
Mij = q(Xτ = i, Xτ+1 = j ), of coarse-grained states at time t = τ and t = τ + 1 for the resting state.
To obtain the matrix, we first created a list of transitions in concatenated time series data of the
resting state, in accordance with previous work (Lynn et al., 2020):

B
B
B
B
B
B
@

i1
i2
⋅
⋅
⋅
iL−1

C
C
C
C
;
C
C
A

i2
i3
⋅
⋅
⋅
iL

I ¼

(21)

where il is the coarse-grained state at l th frame of the time series, and L is the length of the
concatenated time series (L = the number of time frames × the number of subjects). We sam-
pled a pair of transitions from the list for L times to fill in the matrix, METRO, and normalized it to be
a joint probability matrix. Although the transition list is a concatenated time series across sub-
jects, we excluded pairs of transitions that took place across subjects; we only sampled pairs
within the same subject. By normalizing each row of the matrix, METRO, ser 1, we constructed a
transition probability matrix for the resting state. Similarmente, we computed the probability dis-
tributions of coarse-grained brain state using trajectory bootstrapping. From the concatenated
time series data of each task, we sampled a coarse-grained brain state L times. We counted the
number of occurrences of each coarse-grained brain state and normalized it to 1 to obtain the
probability distribution for each task. While we calculated a probability distribution for each
task including the rest, we computed transition probability only for the resting state for obtain-
ing the uncontrolled path, q. We followed this process 100 times and computed the error bars
on the estimated quantities in this study using the 100 bootstrap trajectories.

CODE AVAILABILITY

The code for computing the transition cost based on optimal control for stochastic systems is
disponible en https://github.com/oizumi-lab/SB_toolbox.

SUPPORTING INFORMATION

Supporting Information (disponible en https://doi.org/10.1162/netn_a_00213) includes the fol-
lowing supplementary figures. S1: Robustness with different numbers of clusters. S2: Orden
of the degrees of transition costs from the resting state. S3: Asymmetry of brain transition cost.
S4: Criteria for determining the number of clusters for k-means clustering algorithm. S5: Figures
of brain maps. S6: Brain state transition cost when the time horizon, t, is set T > 1.

Neurociencia en red

131

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

CONTRIBUCIONES DE AUTOR

Genji Kawakita: Conceptualización; Curación de datos; Análisis formal; Investigación; Methodol-
ogia; Software; Validación; Visualización; Escritura – borrador original; Escritura – revisión & edición.
Shunsuke Kamiya: Curación de datos; Metodología; Software. Shuntaro Sasai: Curación de datos; Soft-
mercancía; Supervisión. Jun Kitazono: Conceptualización; Supervisión. Masafumi Oizumi: Concep-
tualization; Adquisición de financiación; Investigación; Metodología; Administración de proyecto;
Recursos; Supervisión; Software; Validación; Visualización; Escritura – revisión & edición.

INFORMACIÓN DE FINANCIACIÓN

Masafumi Oizumi, Japan Science and Technology Agency (https://dx.doi.org/10.13039
/501100002241), Award ID: JPMJMS2012. Masafumi Oizumi, Japan Science and Technology
Agencia (https://dx.doi.org/10.13039/501100002241), Award ID: JPMJCR1864. Masafumi
Oizumi, Japan Society for the Promotion of Science, Award ID: 18H02713. Masafumi Oizumi,
Japan Society for the Promotion of Science, Award ID: 20H05712.

REFERENCIAS

Adhikari, METRO. h., hacker, C. D., Siegel, j. S., Griffa, A., Hagmann, PAG.,
decoración, GRAMO., & Corbetta, METRO. (2017). Decreased integration and
information capacity in stroke measured by whole brain models
of resting state activity. Cerebro, 140(4), 1068–1085. https://doi.org
/10.1093/brain/awx021, PubMed: 28334882

Aerts, h., Schirner, METRO., Dhollander, T., Jeurissen, B., Achten, MI., Van
Roost, D., … Marinazzo, D. (2020). Modeling brain dynamics
after tumor resection using the virtual brain. NeuroImagen, 213,
116738. https://doi.org/10.1016/j.neuroimage.2020.116738,
PubMed: 32194282

Amari, S.-I., Karakida, r., & Oizumi, METRO. (2018). Information geom-
etry connecting Wasserstein distance and Kullback–Leibler
divergence via the entropy-relaxed transportation problem.
Information Geometry, 1(1), 13–37. https://doi.org/10.1007
/s41884-018-0002-8

Amico, MI., Arenas, A., & Goñi, j. (2019). Centralized and distributed
cognitive task processing in the human connectome. Red
Neurociencia, 3(2), 455–474. https://doi.org/10.1162/netn_a
_00072, PubMed: 30793091

bassett, D. S., & despreciar, oh. (2017). Network neuroscience. Naturaleza
Neurociencia, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844

Battle, C., Broedersz, C. PAG., Fakhri, NORTE., Geyer, V. F., Howard, J.,
Schmidt, C. F., & MacKintosh, F. C. (2016). Broken detailed bal-
ance at mesoscopic scales in active biological systems. Ciencia,
352(6285), 604–607. https://doi.org/10.1126/science.aac8167,
PubMed: 27126047

Beghi, A. (1996). On the relative entropy of discrete-time markov
processes with given end-point densities. IEEE Transactions on
Information Theory, 42(5), 1529–1535. https://doi.org/10.1109
/18.532893

romper la lanza, METRO. (2017). Dynamic models of large-scale brain activ-
idad. Neurociencia de la naturaleza, 20(3), 340–352. https://doi.org/10
.1038/nn.4497, PubMed: 28230845

Chen, y., Georgiou, t. T., & Pavon, METRO. (2016a). On the relation
between optimal transport and Schrödinger bridges: A stochastic

control viewpoint. Journal of Optimization Theory and Applica-
ciones, 169(2), 671–691. https://doi.org/10.1007/s10957-015
-0803-z

Chen, y., Georgiou, t. T., & Pavon, METRO. (2016b). Optimal steering of
a linear stochastic system to a final probability distribution, part I.
IEEE Transactions on Automatic Control, 61(5), 1158–1169.
https://doi.org/10.1109/TAC.2015.2457784

Chen, y., Georgiou, t. T., & Pavon, METRO. (2021). Stochastic control
liaisons: Richard Sinkhorn meets Gaspard Monge on a
Schrödinger Bridge. SIAM Review, 63(2), 249–313. https://doi
.org/10.1137/20M1339982

Chen, y., Georgiou, t. T., & Tannenbaum, A. (2020). estocástico
control and nonequilibrium thermodynamics: Fundamental
limits. IEEE Transactions on Automatic Control, 65(7),
2979–2991. https://doi.org/10.1109/ TAC.2019.2939625,
PubMed: 33746240

Col, METRO. w., bassett, D. S., Fuerza, j. D., Más valiente, t. S., & Petersen,
S. mi. (2014). Intrinsic and task-evoked network architectures of
el cerebro humano. Neurona, 83(1), 238–251. https://doi.org/10
.1016/j.neuron.2014.05.014, PubMed: 24991964

Col, METRO. w., Ito, T., Cocuzza, C., & Sanchez-Romero, R. (2021).
The functional relevance of task-state functional connectivity.
Revista de neurociencia, 41(12), 2684–2702. https://doi.org/10
.1523/JNEUROSCI.1713-20.2021, PubMed: 33542083

Cornblath, mi. J., Ashourvan, A., kim, j. Z., Betzel, R. F., círico, r.,
Adebimpe, A., … Bassett, D. S. (2020). Temporal sequences of
brain activity at rest are constrained by white matter structure
and modulated by cognitive demands. Communications Biology,
3(1), 261. https://doi.org/10.1038/s42003-020-0961-x, PubMed:
32444827

Cuturi, METRO. (2013). Sinkhorn distances: Lightspeed computation of
optimal transport. Avances en el procesamiento de información neuronal
Sistemas, 26, 2292–2300.

Dai Pra, PAG. (1991). A stochastic control approach to reciprocal dif-
fusion processes. Applied Mathematics and Optimization, 23(1),
313–329. https://doi.org/10.1007/BF01442404

Neurociencia en red

132

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

Daunizeau, J., Esteban, k. MI., & Friston, k. j. (2012). estocástico
dynamic causal modelling of fMRI data: Should we care about
neural noise? NeuroImagen, 62(1), 464–481. https://doi.org/10
.1016/j.neuroimage.2012.04.061, PubMed: 22579726

Davison, mi. NORTE., Schlesinger, k. J., bassett, D. S., Lynall, M.-E.,
Molinero, METRO. B., Grafton, S. T., & Carlson, j. METRO. (2015). Brain net-
work adaptability across task states. Biología Computacional PLoS,
11(1), e1004029. https://doi.org/10.1371/journal.pcbi.1004029,
PubMed: 25569227

Daws, R. MI., Scott, GRAMO., Soreq, MI., Sanguijuela, r., Hellyer, PAG. J., &
Hampshire, A. (2020). Optimisation of brain states and behav-
ioural strategies when learning complex tasks.

De Bortoli, v., Thornton, J., Heng, J., & Doucet, A. (2021). Diffusion
Schrödinger bridge with applications to score-based generative
modelado.

decoración, GRAMO., & Kringelbach, METRO. l.

(2014). Great expectations:
Using whole-brain computational connectomics for under-
standing neuropsychiatric disorders. Neurona, 84(5), 892–905.
https://doi.org/10.1016/j.neuron.2014.08.034, PubMed:
25475184

decoración, GRAMO., Rolls, mi. T., & Romo, R. (2009). Stochastic dynamics as
a principle of brain function. Progress in Neurobiology, 88(1),
1-dieciséis. https://doi.org/10.1016/j.pneurobio.2009.01.006,
PubMed: 19428958

Deng, S., & Gu, S. (2020). Controllability analysis of functional

redes cerebrales.

Semillas, r., lin, h., decano lobo, C. K., Inzlicht, METRO., & Shenhav, A.
(2021). Expectations of reward and efficacy guide cognitive con-
trol allocation. Comunicaciones de la naturaleza, 12(1), 1030. https://doi
.org/10.1038/s41467-021-21315-z, PubMed: 33589626

Gu, S., Betzel, R. F., Mattar, METRO. GRAMO., Cieslak, METRO., Delio, PAG. r.,
Grafton, S. T., … Bassett, D. S. (2017). Optimal trajectories of
brain state transitions. NeuroImagen, 148, 305–317. https://doi
.org/10.1016/j.neuroimage.2017.01.003, PubMed: 28088484
Gu, S., Pasqualetti, F., Cieslak, METRO., telesford, q. K., Yu, A. B., Kahn,
A. MI., … Bassett, D. S. (2015). Controllability of structural brain
redes. Comunicaciones de la naturaleza, 6, 8414. https://doi.org/10
.1038/ncomms9414, PubMed: 26423222

Honey, C. J., despreciar, o., Cammoun, l., Gigandet, X., Thiran, j. PAG.,
Meuli, r., & Hagmann, PAG. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Actas
of the National Academy of Sciences, 106(6), 2035–2040. https://
doi.org/10.1073/pnas.0811168106, PubMed: 19188601

Horowitz, j. METRO., zhou, K., & Inglaterra, j. l. (2017). Minimum ener-
getic cost to maintain a target nonequilibrium state. Físico
Review E, 95(4–1), 042102. https://doi.org/10.1103/ PhysRevE
.95.042102, PubMed: 28505816

Jersild, A. t. (1927). Mental set and shift. Archives of Psychology,

14, 89.

Kawai, r., Parrondo, j. METRO. r., & Van den Broeck, C. (2007). Dissi-
pation: The phase-space perspective. Physical Review Letters,
98(8), 080602. https://doi.org/10.1103/PhysRevLett.98.080602,
PubMed: 17359081

Kawakita, GRAMO., & Oizumi, METRO. (2021). Schrödinger’s Bridge toolbox,

GitHub, https://github.com/oizumi-lab/SB_toolbox

Kitzbichler, METRO. GRAMO., Henson, R. norte. A., Herrero, METRO. l., Nathan, PAG. J., &
bullmore, mi. t. (2011). Cognitive effort drives workspace config-
uration of human brain functional networks. Diario de

Neurociencia, 31(22), 8259–8270. https://doi.org/10.1523
/JNEUROSCI.0440-11.2011, PubMed: 21632947

Koch, I., Gade, METRO., Schuch, S., & Philipp, A. METRO. (2010). El rol de
inhibition in task switching: A review. Psychonomic Bulletin and
Revisar, 17(1), 1–14. https://doi.org/10.3758/ PBR.17.1.1,
PubMed: 20081154

Kool, w., McGuire, j. T., rosa, z. B., & Botvinick, METRO. METRO. (2010).
Decision making and the avoidance of cognitive demand. Jour-
nal of Experimental Psychology: General, 139(4), 665–682.
https://doi.org/10.1037/a0020198, PubMed: 20853993

Kringelbach, METRO. l., & decoración, GRAMO. (2020). Brain states and transitions:
Insights from computational neuroscience. Informes celulares, 32(10),
108128. https://doi.org/10.1016/j.celrep.2020.108128, PubMed:
32905760

Léonard, C. (2013). A survey of the Schrödinger problem and some

of its connections with optimal transport.

Lynn, C. w., Cornblath, mi. J., Papadopoulos, l., Bertolero, METRO. A., &
bassett, D. S. (2020). Non-equilibrium dynamics and entropy
production in the human brain.

McGuire, j. T., & Botvinick, METRO. METRO. (2010). Corteza prefrontal, saber-
tive control, y el registro de los costos de decisión. Actas de
the National Academy of Sciences, 107(17), 7922–7926. https://
doi.org/10.1073/pnas.0910662107, PubMed: 20385798

McKenna, t. METRO., McMullen, t. A., & Shlesinger, METRO. F. (1994).
The brain as a dynamic physical system. Neurociencia, 60(3),
587–605. https://doi.org/10.1016/0306-4522(94)90489-8

Medalla, j. D., Pasqualetti, F., hamilton, R. h., Thompson-Schill,
S. l., & bassett, D. S. (2017). Brain and cognitive reserve: Trans-
lation via network control theory. Neuroscience and Biobehav-
ioral Reviews, 75, 53–64. https://doi.org/10.1016/j.neubiorev
.2017.01.016, PubMed: 28104411

monsell, S. (2003). Cambiar de tarea. Tendencias en Ciencias Cognitivas,
7(3), 134–140. https://doi.org/10.1016/S1364-6613(03)00028-7
Nakazato, METRO., & Ito, S. (2021). Geometrical aspects of entropy produc-
tion in stochastic thermodynamics based on Wasserstein distance.
Nozari, MI., stiso, J., Caciagli, l., Cornblath, mi. J., Él, X., Bertolero,
METRO. A., … Bassett, D. S. (2020). Is the brain macroscopically lin-
ear? A system identification of resting state dynamics.

Pavlichin, D. S., Quek, y., & Weissman, t. (2019). Minimum power
to maintain a nonequilibrium distribution of a Markov chain.

Rieke, F. (1999). Spikes: Exploring the neural code. CON prensa.
Rosenbaum, D. A., & Bui, B. V. (2019). Does task sustainability pro-
vide a unified measure of subjective task difficulty? psiconomico
Bulletin Review, 26(6), 1980–1987. https://doi.org/10.3758
/s13423-019-01631-8, PubMed: 31240614

Satterthwaite, t. D., eliot, METRO. A., Gerraty, R. T., Ruparel, K.,
Loughead, J., Calkins, METRO. MI., … Wolf, D. h. (2013). An improved
framework for confound regression and filtering for control of
motion artifact in the preprocessing of resting-state functional
connectivity data. NeuroImagen, 64, 240–256. https://doi.org/10
.1016/j.neuroimage.2012.08.052, PubMed: 22926292

Schaefer, A., kong, r., gordon, mi. METRO., Laumann, t. o., Zuo, X.-N.,
holmes, A. J., … Yeo, B. t. t. (2018). Local-global parcellation of
the human cerebral cortex from intrinsic functional connectivity
resonancia magnética. Corteza cerebral, 28(9), 3095–3114. https://doi.org/10.1093
/cercor/bhx179, PubMed: 28981612

Schrödinger, mi. (1931). Uber die umkehrung der naturgesetze. sitz.

ber. der preuss. Akad. Wissen, Berlin Phys. Matemáticas, 144.

Neurociencia en red

133

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Quantifying brain state transition cost via Schrödinger Bridge

Shadlen, METRO. NORTE., & nuevosome, W.. t. (1998). The variable discharge
of cortical neurons: Implications for connectivity, computation,
and information coding. Revista de neurociencia, 18(10),
3870–3896. https://doi.org/10.1523/JNEUROSCI.18-10-03870
.1998, PubMed: 9570816

shenoy, k. v., Sahani, METRO., & Iglesia, METRO. METRO. (2013). Cortical
control of arm movements: A dynamical systems perspective.
Revisión anual de neurociencia, 36, 337–359. https://doi.org/10
.1146/annurev-neuro-062111-150509, PubMed: 23725001

Simmering, V. r., & Perone, S. (2012). Working memory capacity as
a dynamic process. Fronteras en psicología, 3, 567. https://doi
.org/10.3389/fpsyg.2012.00567, PubMed: 23335902

Sinkhorn, R. (1967). Diagonal equivalence to matrices with pre-
scribed row and column sums. The American Mathematical
Monthly, 74(4), 402–405. https://doi.org/10.2307/2314570

Spadone, S., Della Penna, S., Sestieri, C., Betti, v., Tosoni, A., Perrucci,
METRO. GRAMO., … Corbetta, METRO. (2015). Dynamic reorganization of human
resting-state networks during visuospatial attention. Actas
of the National Academy of Sciences, 112(26), 8112–8117.
https://doi.org/10.1073/pnas.1415439112, PubMed: 26080395
Stitt, I., Hollensteiner, k. J., Galindo-Leon, MI., Pieper, F., Fiedler, MI.,
Stieglitz, T., … Engel, A. k. (2017). Dynamic reconfiguration of
cortical functional connectivity across brain states. Científico
Informes, 7(1), 8797. https://doi.org/10.1038/s41598-017-08050-6,
PubMed: 28821753

Suweis, S., Tu, C., Rocha, R. PAG., Zampieri, S., Zorzi, METRO., & Corbetta,
METRO. (2019). Brain controllability: Not a slam dunk yet. NeuroImagen,

200, 552–555. https://doi.org/10.1016/j.neuroimage.2019.07
.012, PubMed: 31291605

Szymula, k. PAG., Pasqualetti, F., Graybiel, A. METRO., Rocas, t. METRO., &
bassett, D. S. (2020). Habit learning supported by efficiently con-
trolled network dynamics in naive macaque monkeys.

Taghia, J., Cai, w., Ryali, S., Kochalka, J., Nicholas, J., Chen, T., &
menón, V. (2018). Uncovering hidden brain state dynamics that
regulate performance and decision-making during cognition.
Comunicaciones de la naturaleza, 9(1), 2505. https://doi.org/10.1038
/s41467-018-04723-6, PubMed: 29950686

Tu, C., Rocha, R. PAG., Corbetta, METRO., Zampieri, S., Zorzi, METRO., &
Suweis, S. (2018). Warnings and caveats in brain controllability.
NeuroImagen, 176, 83–91. https://doi.org/10.1016/j.neuroimage
.2018.04.010, PubMed: 29654874

VanEssen, D. C., Herrero, S. METRO., Respeto, D. METRO., Behrens, t. mi. J.,
Yacoub, MI., Ugurbil, K., & WU-Minn HCP Consortium. (2013).
The WU-Minn Human Connectome Project: An overview. nuevo-
roImage, 80, 62–79. https://doi.org/10.1016/j.neuroimage.2013
.05.041, PubMed: 23684880

Vyas, S., Golub, METRO. D., Susillo, D., & shenoy, k. V. (2020). Com-
putation through neural population dynamics. Annual Review
Neurociencia, 43, 249–275. https://doi.org/10.1146/annurev
-neuro-092619-094115, PubMed: 32640928

Zenón, A., Solopchuk, o., & pezzulo, GRAMO. (2019). An information-
theoretic perspective on the costs of cognition. Neuropsicología,
123, 5–18. https://doi.org/10.1016/j.neuropsychologia.2018.09
.013, PubMed: 30268880

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

6
1
1
1
8
1
9
8
4
2
1
1
norte
mi
norte
_
a
_
0
0
2
1
3
pag
d