RESEARCH - IA de Investigación especializada en el MIT

INVESTIGACIÓN

Functional coupling networks inferred from
prefrontal cortex activity show experience-related
effective plasticity

Gaia Tavoni1,2, Ulisse Ferrari1,2, Francesco P. Battaglia3, Simona Cocco1, and Rémi Monasson2

1Laboratoire de Physique Statistique, Ecole Normale Supérieure, PSL Research and CNRS – UMR 8550,
Paris Sorbonne UPMC, París, Francia
2Laboratoire de Physique Théorique, Ecole Normale Supérieure, PSL Research and CNRS- UMR 8549,
Paris Sorbonne UPMC, París, Francia
3Donders Institute for Brain, Cognition and Behaviour, Radboud Universiteit, Nimega, Los países bajos

un acceso abierto

diario

Palabras clave: Cell assemblies,
consolidation

Ising model, Statistical

inferencia, Effective plasticity, Memoria

ABSTRACTO

Functional coupling networks are widely used to characterize collective patterns of activity
in neural populations. Aquí, we ask whether functional couplings reﬂect the subtle changes,
such as in physiological interactions, believed to take place during learning. We infer
functional network models reproducing the spiking activity of simultaneously recorded
neurons in prefrontal cortex (PFC) of rats, during the performance of a cross-modal rule shift
tarea (task epoch), and during preceding and following sleep epochs. A large-scale study of
el 96 recorded sessions allows us to detect, en aproximadamente 20% of sessions, effective plasticity
between the sleep epochs. These coupling modiﬁcations are correlated with the coupling
values in the task epoch, and are supported by a small subset of the recorded neurons, cual
we identify by means of an automatized procedure. These potentiated groups increase their
coativation frequency in the spiking data between the two sleep epochs, y, hence,
participate to putative experience-related cell assemblies. Study of the reactivation dynamics
of the potentiated groups suggests a possible connection with behavioral learning.
Reactivation is largely driven by hippocampal ripple events when the rule is not yet learned,
and may be much more autonomous, and presumably sustained by the potentiated PFC
network, when learning is consolidated.

RESUMEN DEL AUTOR

Cell assemblies coding for memories are widely believed to emerge through synaptic
modiﬁcation resulting from learning, yet their identiﬁcation from activity is very arduous.
We propose a functional-connectivity-based approach to identify experience-related cell
assemblies from multielectrode recordings in vivo, and apply it to the prefrontal cortex
activity of rats recorded during a task epoch and the preceding and following sleep epochs.
We infer functional couplings between the recorded cells in each epoch. Comparisons of the
functional coupling networks across the epochs allow us to identify effective potentiation
between the two sleep epochs. The neurons supporting these potentiated interactions
strongly coactivate during the task and subsequent sleep epochs, but not in the preceding
sleep, y, hence, presumably belong to an experience-related cell assembly. Study of the
reactivation of this assembly in response to hippocampal ripple inputs suggests possible
relations between the stage of behavorial learning and memory consolidation mechanisms.

Citación: Tavoni, GRAMO., Ferrari U.,
battaglia, F. PAG., Cocco, S., & Monasson,
R. (2017). Functional coupling
networks inferred from prefrontal
cortex activity show experience-related
effective plasticity. Red
Neurociencia, 1(3), 275–301.
https://doi.org/10.1162/netn_a_00014

DOI:
https://doi.org/10.1162/netn_a_00014

Supporting Information:
https://doi.org/10.1162/netn_a_00014

Recibió: 25 Octubre 2016
Aceptado: 24 Abril 2017

Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.

Autor correspondiente:
Simona Cocco
cocco@lps.ens.fr

Editor de manejo:
Olaf Sporns

Derechos de autor: © 2017
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

En años recientes, many techniques have been developed to monitor brain activity in a de-
tailed way and provide a multichannel, multidimensional picture. Different channels may
represent coarse-grained activity of neurons in ∼ 1 mm3 volumes like in functional mag-
netic resonance imaging (resonancia magnética funcional) (Friston, 2011), or give access to the activity of single neurons,
such as with multielectrode electrophysiological recording (McNaughton, O’Keefe, & Barnes,
1983; Meister, Pino, & Baylor, 1994; Nicolelis, 2007) or calcium imaging (Chhetri et al., 2015;
Nguyen et al., 2016; Wolf et al., 2015). The development of these techniques was motivated
by the need to characterize the brain state at the network level, and to understand how con-
nections between neurons determine the dynamics and the information processing of neural
ensembles. While much progress has been made in characterizing the connectome, eso es,
the exact pattern of connections between neurons in a brain circuit (Seung, 2011), the link
between this anatomical architecture and neural network function remains elusive, at least for
large-scale circuits.

A useful notion in this context is that of functional couplings. Functional couplings are gen-
erally derived by a reverse inference procedure (stevenson, Rebesco, Molinero, & Körding, 2008):
Connections between neurons are assumed to determine neural activity, by way of a statistical
or dynamical model, and the coupling values are calculated as those most likely to produce
the observed activity data. Compared with earlier estimates of functional interactions based
on activity correlations (Aertsen, Gerstein, Habib, & Palm, 1989; Fujisawa, Amarasingham,
harrison, & Buzsáki, 2008; Gerstein & Perkel, 1969; Schwindel, Alí, McNaughton, & Tatsuno,
2014), reverse inference techniques have the advantage of discounting correlations due to
interaction paths going through third-party neurons between the recorded cells, therefore pro-
viding a much sharper picture of the underlying interactions. While functional couplings are
not likely to match one-on-one structural couplings, the ﬁngerprint of neural interactions they
provide could be used to track changes in the underlying connectivity. A central paradigm
in neuroscience is that couplings are plastic: Learning and memory consolidation happen
through changes in neural synaptic couplings following repeated coincident pre- and post-
synaptic activations, as was postulated by D. Hebb and proven by in vitro experiments show-
ing long-term potentiation (LTP) and long-term depression (LIMITADO) after repeated coincident and
non–coincident stimulations (Bliss & Collingridge, 1993; Castillo, 2012).

Hebb further postulated that cell assemblies (Buzsáki, 2010; harris, Csicsvari, Hirase,
Dragoi, & Buzsáki, 2003; Hebb, 1949), closely connected, synchronously activating groups
of cells, are the main constituents of memory and information representations. The activation
and reactivation (“replay”) of cell assemblies is thought to be critical for consolidation and
re-elaboration of memories, working memory, and decision-making (Carr, Jadhav, & Franco,
2011; O’Neill, Pleydell-Bouverie, Dupret, & Csicsvari, 2010; wilson & McNaughton, 1994).
The precise characterization of cell assemblies from experimental data remains, sin embargo, muy
difﬁcult. Current available methods for cell assembly detection and replay estimation often rely
on the identiﬁcation and the matching of templates (Johnson & Redish, 2007; Pfeiffer & Foster,
2013; Cantante, Carr, Karlsson, & Franco, 2013). In the hippocampus, por ejemplo, such templates
are provided by the temporal sequence of ﬁring events of place cells during the awake phase.
The pairwise cross-correlation matrix can also be used to search for clusters of neurons with re-
lated ﬁring patterns (Billeh, Schaub, Anastassiou, Barahona, & Koch, 2014; Lopes-dos-Santos,
Ribeiro, & Tort, 2013), or to approximate templates from principal component analysis
(Peyrache, Benchenane, Khamassi, Wiener, & battaglia, 2010; Peyrache, Khamassi,
(PCA)
Benchenane, Wiener, & battaglia, 2009).

The latter approach was used in particular to analyze the prefrontal cortex activity of be-
having rats, recorded during the awake epoch and during the preceding and subsequent sleep

276

Functional couplings:
Effective interactions between
recorded units explaining the
observed pattern of correlations in
the recorded population neural
actividad.

Replay:
Reactivation of task-associated cell
assemblies during sleep following
aprendiendo.

Cell assembly:
A group of coactivating cells, cual
have been postulated by D. Hebb as
the basis for neural computation and
memory.

Principal component analysis (PCA):
Statistical procedure that explains a
large fraction of the variability in the
data from the top eigenvalues/
eigenvectors of the Pearson
correlation matrix.

Neurociencia en red

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

phases by Peyrache et al. (Peyrache et al., 2009). During the awake epoch the animal faced a
tarea de aprendizaje, where it had to ﬁnd the rewarded arm in a Y-shaped maze; this arm was chosen
according to a rule (left or right arm, or where the light is on or off) set by the operator. Como
soon as the rule was consistently learned it was changed. PCA-based analysis of the recorded
activity showed that the activity of the learning phase was replayed during the subsequent
sleep in some experimental sessions; this replay is at the basis of memory consolidation. Aquí,
we reanalyze the same recordings, with a more sophisticated statistical approach than PCA,
based on the inference of functional connectivity between the recorded cells. Our motivation
is twofold. Primero, the use of functional couplings allows us to characterize task-related changes
in the activity of the sleep epochs in a more quantitative way than with PCA, y, in addi-
ción, to identify more sessions showing replay. Segundo, we expect that our more precise and
extended characterization of replay could make more precise the possible connection with
behavioral learning sketched in the study by Peyrache et al.

Our statistical approach relies on the inference of graphical models expressing the con-
ditional dependencies between the spiking events of the recorded cells through functional
couplings. We make use of the maximum-entropy Ising model from statistical mechanics,
whose parameters are tuned to reproduce the recorded ﬁring frequencies and pairwise cross-
correlations (Schneidman, Berry, Segev, & Bialek, 2006). This inference approach has been
tested on several multielectrode recordings of both in vitro (Barton & Cocco, 2013; Cocco,
Leibler, & Monasson, 2009; Ferrari, Obuchi, & Mora, 2017; Schneidman et al., 2006) and in
vivo (Barton & Cocco, 2013; Posani, Cocco, Jezek, & Monasson, 2017) neural activity. Work-
ing with the inferred couplings rather than considering directly the correlations in the data
allows us to reﬁne the analysis of the recording and to unveil modiﬁcations in the functional
couplings between the two sleep epochs (effective positive or negative potentiation), cuales son
consistent with the functional network derived from the learning epoch. Effective potentiation
is supported by a subset of the recorded cells, which we identify by means of an automatized
procedimiento. Our ﬁndings are supported by a large-scale study of about 100 experimental ses-
siones. Despite the variations from session to session, presumably because of the partial and ran-
dom sampling of cells, we are able to identify in about 20% of sessions a potentiated group. Nosotros
then investigate in the data the change in the collective ﬁring properties of the identiﬁed poten-
tiated groups and ﬁnd a strong increase in coactivation for such groups between the two sleep
epochs. Por eso, these identiﬁed potentiated groups are likely to belong to task-related cell as-
semblies. We then analyze how much the reactivation over time of the potentiated group is re-
lated to hippocampal inputs (ripple events), known to be important for memory consolidation.
In sessions where the rule has not been learned yet, reactivation can be essentially explained
as a fast response to hippocampal ripples. In some of the sessions where the rule was learned,
reactivation shows a strong slow dynamical component, often unrelated to ripples, which pre-
sumably reﬂects the existence of a potentiated prefrontal cortex (PFC) synaptic network.

RESULTADOS

We have reanalyzed recordings of the activity of tens of neurons in the prefrontal cortex of ﬁve
behaving rats (Peyrache et al., 2009); see Materials and Methods for more details. Each one
del 96 recording sessions is divided into three (cid:3) 30-minute epochs: a Task epoch in which
the rat had to learn a cross-modal rule (go left, bien, where the light is on, or off, in a Y-shaped
laberinto), which was changed as soon as the rat had learned it, and two Sleep epochs, one before
(Sleep Pre) and one after (Sleep Post) the Task epoch. Through spike sorting one can identify
the same neurons recorded in the different epochs (Sleep Pre, Tarea, Sleep Post) of a session;
the number N of neurons reliably mapped in all three epochs varies from 3 a 56 depending
on the session. No mapping could be established between different sessions.

Graphical models:
Probabilistic models of interacting
variables, in which the distribution of
each variable generally depends on a
restricted number of other variables.

Ising model:
Mathematical model to describe
systems of binary interacting
components in statistical physics.

Effective potentiation:
A quantity that sums up, over all the
pairs of neurons, the increases of the
coupling, between the sleep after
the task and the sleep before the task,
only if there is a correlated coupling
increase between the task and the
sleep before the task.

Potentiated group:
A group of cells that sustain most
of the potentiated couplings. Este
group is identiﬁed from the largest
components of the top eigenvector of
the potentiation matrix.

Cross-modal rule shift:
An introduction of new rules that can
be based on spatial (go to the left or
to the right) or visual (go where the
light is on or off) señales.

Neurociencia en red

277

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

Inference of Functional Coupling Networks

We brieﬂy present the approach to model the distribution of activity of the N recorded neurons;
see Methods section. The spiking times are binned within small time bins of duration Δt =
10 EM, as illustrated in Figure 1A; see Supporting Information (SI), Section II and Figure S2,
for a discussion of the time-bin choice (Tavoni, Ferrari, battaglia, Cocco, & Monasson, 2017).
The activity conﬁguration (pag
i takes
values one or zero depending on whether the i-th neuron is, respectivamente, active or inactive in
the time bin. We deﬁne fi and fij as the average values over time bins of, respectivamente, pag
i and
pag
pag
j: fi represents the probability that neuron i is active in a time bin, and fij denotes the joint
i

) is a snapshot of the neural activity, where σ

2, …, pag
norte

1, pag

probability that both cells i and j are active in a time bin.

We model the probability distribution of activity conﬁgurations as

PAG(pag

1, pag

2, …, pag
norte

(cid:2)

(cid:3)

) =

1
z[{hi, Jij

}] exp.

Jij

pag
i

pag
j

∑
i 1,
J > 0 and to CI < 1, J < 0; the widths are proportional to the absolute values. Links corresponding to CI or J smaller than one tenth of the maximal correlation index or coupling are not shown. (B) Average values and standard deviations of log CIij over intervals of couplings 0.5 n − 0.25 ≤ < 0.5 n + 0.25, with integer n, for all epochs and sessions. Note the large error bar in J = 0, Jij corresponding to the very large number of pairs i, j carrying vanishing couplings; see Figure 1A. Network Neuroscience 278 Experience-related potentiation of functional connectivity in PFC Adaptive cluster expansion: Technique of inference of the Ising model parameters based on an iterative construction of clusters of strongly interacting variables. reproducing these low-order spiking statistics (Schneidman et al., 2006). We look for the Ising } such that fi and fij match, respectively, the average values of σ model parameters {hi, Jij i (for all neurons i) and σ σ j (for all pairs of neurons i, j) over P. To do so we use the adaptive i inference algorithm (Barton and Cocco, 2013; Cocco & Monasson, cluster expansion (ACE) 2011, 2012), which also gives access to the statistical uncertainties {δhi, δJij } over the inferred parameters (Methods). Parameters hi deﬁne effective local inputs that tune neuronal frequen- cies. Parameters Jij deﬁne the effective pairwise couplings between the cells (Figure 1A): Jij different from zero expresses the presence of a conditional dependence between neurons i and j, not mediated by other neurons in the recorded population. The conditional average activity of neuron i given the other neuron activities {σ j }, with j (cid:5)= i, reads (cid:7) = (cid:6)σ i P(σ 1,...,σ i P(σ =0,...,σ 1,...,σ i )+P(σ N =1,...,σ ) N 1,...,σ i =1,...,σ ) N = eVi 1 + eVi , with Vi ≡ ∑ j((cid:5)=i) Jij σ j + hi . (2) Correlation index (CI): Ratio of the joint probability that a pair of neurons are active in a time bin, and of the product of their individual spiking probabilities. For independent neurons, CI = 1. It is a logistic function of its total input, Vi, equal to the sum of the other neuron activities σ j weighted by the couplings Jij, and of the local input hi. = fij/( fi f j Though effective couplings Jij are abstract quantities deﬁned through Equations 1 and 2 ). As they can be approximated by the logarithms of the correlation indices, CIij shown in Methods, in the simple case of N = 2 recorded neurons only, J12 and log CI12 are equal. For N ≥ 3, log CIij is only an approximation to Jij, and their difference quantiﬁes the indirect contributions to pairwise correlations, mediated by other cells and not due to direct interactions; see Methods. Figure 1B shows that this approximation is good for most couplings in the recorded sessions, but deviations can be observed in particular for large and positive correlation indices; see Barton and Cocco (2013) for a discussion of the differences between log CIij and Jij across various neural datasets. Note that the functional networks are sparse: A large fraction (about 75% over all epochs and sessions) of the couplings are regularized to zero by the inference procedure. Once the coupling and local input parameters are inferred, we may sample the model distribution P through Monte Carlo simulations to check how the statistics of the data are reproduced by the model. The quality of the reproduction of the single-neuron and pairwise spiking probabilities in a time bin is shown in Figure 2A for the Task epoch of one particular session, which we call A. We can then use P to make predictions for higher-order moments, such as triplet ﬁring probabilities and the probability of multiple-neuron ﬁring in a time bin. Results are compared with the same quantities computed from the spiking data in Figure 2B. The quality of the inferred distribution P is then assessed through a cross-validation procedure: We divide the dataset into a train set (three fourths of the time bins) and a test set (one fourth of the bins). The good agreement between the values of observables in the train and test sets in Figures 2A and B conﬁrms the absence of overﬁtting in our inference (see Figure S3 in Tavoni et al., 2017, for results on the other three out of four possible ways to deﬁne training and testing sets). We show in Figure 2C the probabilities of the 210 conﬁgurations of ﬁring of one subset of 10 cells. The Ising model predictions are in much better agreement with the data than the independent-cell model, which reproduces the single-neuron spiking probabilities fi only. Taking into account pairwise correlations through the effective couplings Jij is therefore crucial to better ﬁt the neural activity distribution. Comparison of Functional Couplings Across Epochs Shows Learning-Related Potentiation The distributions (over all sessions) of inferred coupling parameters are similar across epochs; see Figure 3A. In addition, little variation over the magnitudes of couplings is observed from Network Neuroscience 279 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 7 5 1 0 9 2 0 2 3 n e n _ a _ 0 0 0 1 4 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Experience-related potentiation of functional connectivity in PFC l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 7 5 1 0 9 2 0 2 3 n e n _ a _ 0 0 0 1 4 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Figure 2. Quality and validation of the inferred model. Reproduction of the statistics of the spiking data for the Task epoch of session A. All panels compare the values of the observables computed from the spiking data with their counterparts computed from the inferred model distribution P, Equation 1. (A) Firing probabilities of single ( fi, left panel) and pairs of ( fij, right panel) neurons. The agreement between the spiking probabilities computed from the data and from the inferred Ising distribution shows that the inference procedure is accurate. Model distribution P was inferred from three fourths of the recorded data and tested on the same data (blue cross) and on the remaining one fourth of the recording (cross-validation, red squares). (B) Probabilities of ﬁring for triplets ( fijk, left panel) of neurons, and of k neurons to be simultaneously active in a time bin of duration Δt = 10 ms (right panel). The agreement between the data and model multiple-neuron ﬁring probabilities (p(k)) is very good as long as p(k) times the number of time bins in the recording is > 1, eso es, provided
the recording time is sufﬁcient to sample rare conﬁgurations of multiple neuron ﬁring. Same cross-
validation procedure and symbols as in Figure 2A. (C) Probabilities of the 210 = 1, 024 actividad
conﬁgurations over a subset of 10 cells in the Task epoch of session A. Blue symbols show the scatter
plot for the Ising distribution P (inferred from all recorded data), while cyan symbols correspond
= 0, and local inputs hi ﬁtted to reproduce
to the independent-cell model (with all couplings Jij
the single-neuron probabilities fi). Similar plots are found for other subsets of 10 cells among the
norte = 37 recorded cells.

Neurociencia en red

280

Experience-related potentiation of functional connectivity in PFC

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

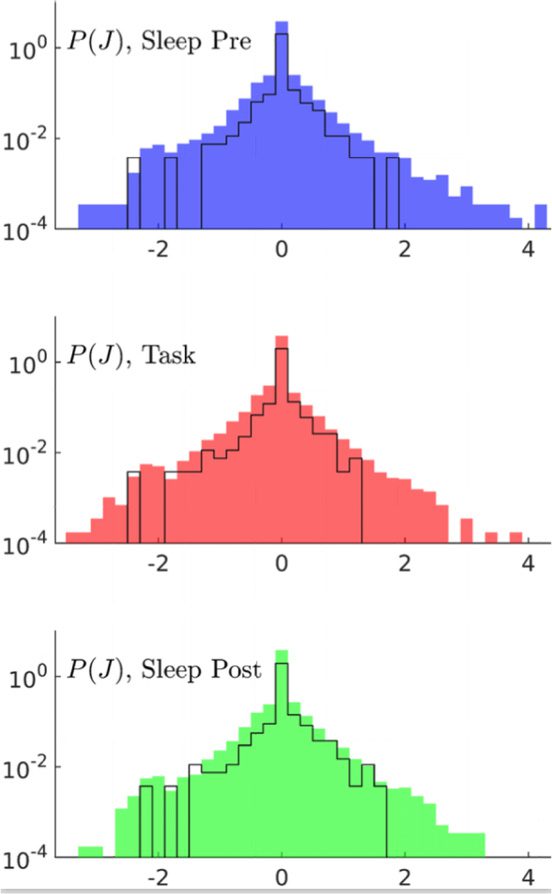
Cifra 3. Comparison of couplings across epochs shows task-related effective potentiation.
(A) Distributions of the inferred couplings J across the recording sessions for the three epochs (de
top to down, Sleep Pre, tarea, and Sleep Post). The black lines show the histograms for session A only.
The sharp peaks in J = 0 in the coupling distributions show that the inferred coupling networks are
sparse. The average fractions of vanishing couplings are close to 0.75 in all three epochs. The part
of the J distributions corresponding to the minimal value of couplings ((cid:3) −2) permitted by the
= 0); see Methods. (B) Fractions
regularization is due to pairs of cells that never spike together ( fij
of pairs of neurons (i, j) en el 27 classes [xyz], where x, y, and z = −, 0, + are the signs of the
inferred couplings Jij in, respectivamente, Sleep Pre, Tarea, and Sleep Post. Fractions are computed from
all epochs in the 96 recorded sessions. Rightmost column: null model for the fractions correspond-
ing to classes x, z in the Sleep epochs, irrespective of the y class in Task. Circle and star symbols
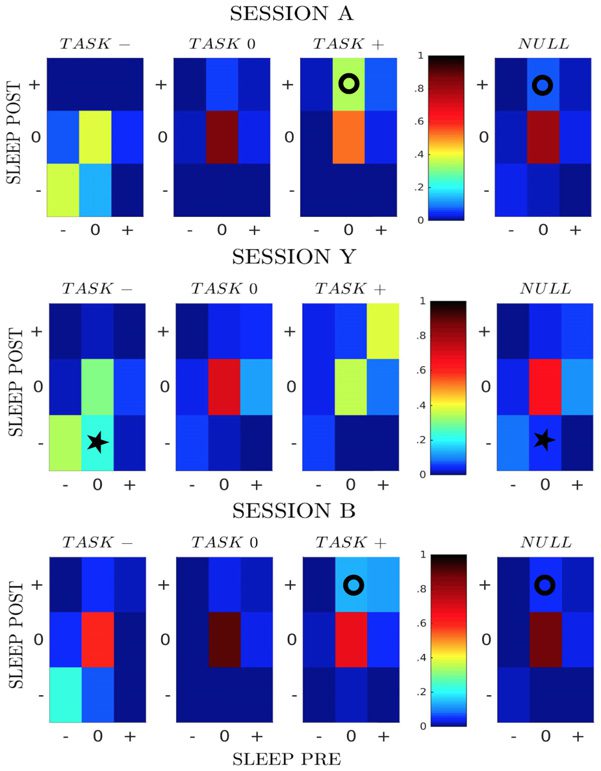
identify classes referred to in main text. (C) Same as panel B, but for sessions A (arriba), Y (middle),
y B (abajo). (D) Effective potentiation Pot (Ecuación 3) is shown for the 96 experimental sessions
as a function of the number of recorded neurons identiﬁed in all three epochs. Colors identify the
ﬁve recorded rats. Sessions A, B, Y are shown with their labels. Red lines show the effective po-
tentiation (promedio: full line, ±1 standard deviation: dashed lines) expected from the null model as
a function of the number of recorded neural cells; see Methods. (mi) Right: control case, where we
have exchanged the Sleep Pre and Sleep Post inferred couplings.

Neurociencia en red

281

Experience-related potentiation of functional connectivity in PFC

session to session. As an illustration we report in Figure 3 the histograms of coupling parameters
for session A. Because of the smaller number of data, the histograms are less smooth than the
average distribution over all sessions, but span the same ranges of values for J. Similar results
hold for local inputs; see SI, Figure S4 (Tavoni et al., 2017).

Despite the overall similarities between the coupling distributions across epochs, subtle
patterns can be observed when tracking the changes in the couplings corresponding to the
same pairs of cells across the different epochs of the same session. We partition the set of cou-
plings in each epoch into three classes, according to their values J and statistical uncertainty
δJ: Couplings reliably inferred as positive, eso es, such that J/δJ > 3, deﬁne the [+] class;
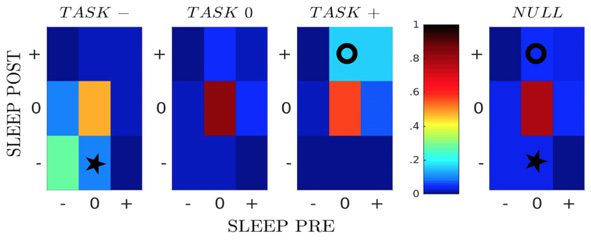
couplings reliably inferred as negative (J/δJ < −3) form the [−] class; and the remaining couplings are gathered into class [0]. Each pair of neurons (i, j) belongs to one of the resulting 27 classes; for example, [− + 0] if Jij is reliably negative in Sleep Pre, positive in Task, and statistically undetermined in Sleep Post. The fractions of pairs of neural cells in the 27 classes, averaged over all sessions, are shown in Figure 3B; see SI, Figure S6 (Tavoni et al., 2017). Because of the sparsity of the inferred functional couplings, classes with vanishing couplings, such as [000], contain most of the cell pairs. We observe the presence of conserved couplings across the three epochs, corresponding to the large fractions of pairs in classes [− − −] and in [+ + +], compared with a simple null model, in which we pull together all couplings according to their classes in Sleep Pre and Post, irrespective of the class in Task (rightmost panel in Figure 3B). An important feature emerging from Figure 3B is the presence of task-related effective (posi- tive) potentiation in the functional couplings. This effect is visible from the relative enrichment of [0 + +] (marked with a circle symbol) with respect to the null model (two-tail binomial test, −5; see Methods), while no such enrichment is found for classes [0 − +] and [00+]. p (cid:10) 10 In other words, we ﬁnd that the fraction of pairs of neurons with close-to-zero couplings in Sleep Pre and positive couplings in both Task and Sleep Post is larger than what would be expected from the knowledge of the coupling classes in the Sleep epochs only. Task-related effective negative potentiation, corresponding to the enrichment of [0 − −] (star symbol), is also found, but with a weaker magnitude (p < 10 −5). While the results above were obtained through averaging over all sessions, there are sub- stantial variations in the fractions of pairs in the classes from session to session. We show in Figure 3C three examples, referred to as sessions A, Y, and B. For sessions A and B effec- tive potentiation, represented in particular by class [0 + +] (circle symbols), is clearly visible −5 and p = 0.002). Session Y shows a strong effective negative (with, respectively, p < 10 potentiation, represented in particular by class [0 − −] (star symbol, p < 10 −5). To characterize quantitatively experience-related changes in the functional couplings in each session, we introduce the following session-wide effective potentiation, measuring the amount of potentiation in the couplings from Sleep Pre to Sleep Post, coherently with their values in Task: Pot = ∑ pairs i, j not in [0] classes in Task and Sleep Post (cid:4) θ JTask ij Sleep Pre − J ij (cid:5) (cid:4) × Sleep Post J ij Sleep Pre − J ij (cid:5) . (3) Summation is restricted to pairs i, j of neurons, whose couplings are signiﬁcantly different from zero in both Task and Sleep Post (same criterion |Jij > 3 as for the classes above).
The presence of the θ function, i(tu) = 1 if the argument u > 0 y 0 if u ≤ 0, restricts

|/δJij

Neurociencia en red

282

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

contributions to pairs, whose effective couplings increase from Sleep Pre to Task. En la práctica
positivo, respectivamente, negative contributions to Pot come mostly from classes [0 + +], respetar-
activamente, [0 + −].

The effective potentiations Pot of all 96 recorded experimental sessions are shown in
Figura 3D. In comparison we show in Figure 3E the same quantity Pot computed after swap-
ping, in each session, the Sleep Pre and Sleep Post couplings in Equation 3. No session is
found to have a large effective potentiation after the swap, ver Figura 3E. This simple control
provides clear evidence for the fact that large values of Pot capture experience-related changes
in the Sleep Post couplings. This empirical observation can be made more precise through the
introduction of a null model, in which the correspondence between pairs of neurons across
the epochs is removed by reshufﬂing the neuron indices, and the values of the couplings are
randomly drawn from the distributions of Figure 3A. Red curves in Figure 3D show the aver-
age value of the effective potentiation within this null model, together with ± one standard
desviación (Métodos). In the control analysis of Figure 3E, where the Sleep Pre and Post data
have been swapped, the effective potentiation is compatible with the expectations of the null
modelo. En cambio, in Figure 3D, where the causal ordering Sleep Pre–Task–Sleep Post has
been maintained, some sessions have large and positive Pot more than one standard deviation
above the null model average.

A major source of variability in the data is the limited number of randomly sampled neurons.
To assess the inﬂuence of sampling on Pot, we focus on one particular session (A) with large
effective potentiation, and remove cells, one at a time, from the recording. Results are shown
in Figure 4A. In most cases removal of one cell does not signiﬁcantly affect the value of Pot. A
substantial decrease is, sin embargo, observed for a small number of cells, indicated by the labels
in Figure 4A. This result clearly shows that most contributions to Pot come from a restricted
subset of the recorded neurons. How many of those relevant cells are or are not well sampled
may explain, at least in part, the variability in potentiation values observed across sessions.

Groups of Neurons Supporting Effective Potentiation Are Replayed in the Sleep Epoch After Learning

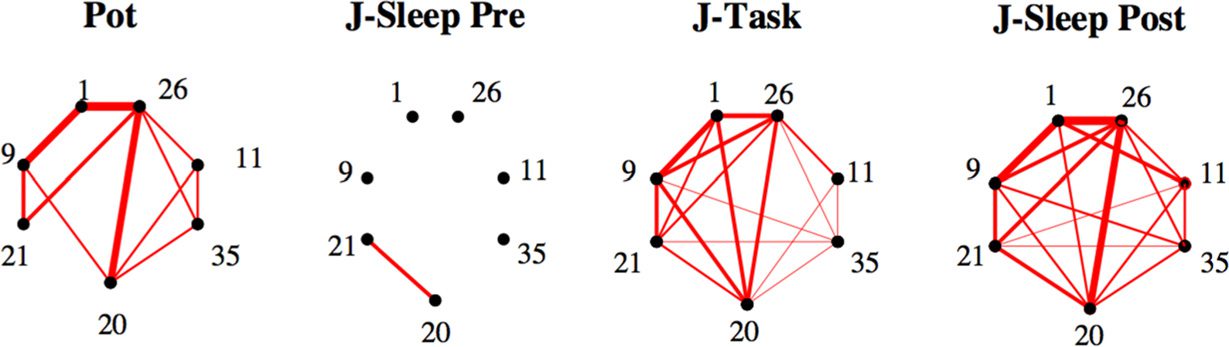
The network of couplings supported by the group of neurons identiﬁed in Figure 4A are shown
for the three epochs of session A in Figure 4B. The effective potentiation from Sleep Pre to
Sleep Post and the strong similarity between the densely interconnected networks in Task and
Sleep Post are clearly visible. For this session the potentiated couplings are not supported by
independiente, nonoverlapping pairs of neurons, but are densely interconnecting a restricted
group of neurons (see Figure SI in Tavoni et al., 2017, for statistical validation). We emphasize
that experience-related change in the correlational structure of Sleep Post is better seen with
effective couplings than with pairwise correlations. For session A again, we show in Figure 4C
(izquierda) the variations of the couplings between the Sleep epochs, JSleep Post
, versus
their values in the Task epoch, JTask
. Most contributions to Pot, located in the top right quad-
rant, are supported by the 7 cells identiﬁed in Figure 4A (red circles in Figure 4C). This shows
again that the changes experienced by the couplings Jij between the Sleep epochs are posi-
tively correlated to their values in Task. En cambio, the same comparison with the CI instead
of the couplings J shows a much blurrier picture; see Figure 4C: The changes in CI between
the Sleep epochs do not seem correlated with their values in Task.

− JSleep Pre
ij

While removing one cell at a time is an effective procedure to determine which neurons
contribute most to Pot, it is computationally demanding. We have therefore developed a
fast and fully automatized spectral procedure to directly identify in each session the group of

Neurociencia en red

283

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

Cifra 4. Group of neural cells supporting effectively potentiated couplings in session A.
(A) Effective potentiation Pot after removal of one cell (index along the x-axis) from the spiking
data of session A. For most cells the removal has no signiﬁcative impact. A substantial decrease is
observed for a few cells, indicated with their indices. (B) Left: main pairwise contributions Potij
to the effective potentiation (Métodos). Right: Networks of couplings supported by the seven-cell
group identiﬁed in panel A, in the three epochs of session A. Line thickness is proportional to Potij
(left panel) and Jij (right panels). (C) Left: Scatter plot of the differences between the couplings in
the Sleep epochs, ΔJij
. Right: same as left panel for
the correlation indices CIij; see text for deﬁnition. A group of seven neurons supports most of the
couplings that are large and positive in Task and in Sleep Post, but not in Sleep Pre; red circles
identify the 21 couplings between those seven neurons.

, vs. their values in Task, JTask

= JPost
ij

− JPre
ij

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

neurons supporting the densest core of strongly potentiated couplings. Our procedure is based
on taking the neurons with largest entries in the top eigenvector of the Pot matrix, whose ele-
ments are the contributions to Pot (Ecuación 3) of the pairs (i, j); see Methods for details. El
top eigenvectors are shown in SI, Figure S9 (Tavoni et al., 2017), for a few sessions. We gener-
ally observe a few large entries, and many small ones. We have set a conservative value for the

Neurociencia en red

284

Experience-related potentiation of functional connectivity in PFC

Coactivation ratio (CoA) of a group
of neurons:
Ratio of the probability that all the
neurons in a group are active within
a time scale, and of the product of
the individual spiking probabilities.
CoA is a multineuron generalization
of CI.

Non-REM sleep:
Stages 1–3 of sleep characterized by
absence of dreams and absence of
rapid eye movements.

threshold to retain only large entries, see Methods and SI (Tavoni et al., 2017). For session A,
our automatized procedure ﬁnds the ﬁve cells (the seven neurons identiﬁed in Figure 4A, pero
neuronas 11 y 35) that support the couplings contributing most to Pot. This result extends
to other sessions: We ﬁnd a high correlation (0.76 ± 0.26 across all sessions) between the
top eigenvectors of the Pot matrices and the “leave-one-out” potentiation vectors (shown in
Figure 4A for session A), which require much more computational efforts.

We now show that the groups of neurons identifed with our automatized procedure across
el 96 sessions really coactivate in the spiking data. To this aim we consider an extension of the
pairwise correlation index CIij to groups of more than two neurons. We deﬁne the assembly
coactivation ratio (CoA) of a group G of neurons over the time scale τ through

CoA(GRAMO, t) = f (GRAMO)
∏i∈G fi

(4)

where f (GRAMO) is the probability that all the neurons in the group are active within the time scale
t, and the denominator is the product of the individual spiking probabilities. For a group of
independent cells the CoA is on average equal to unity. CoA is a very stringent measure of
coactivation, as it takes into account only events in which all the neurons in the potentiated
group are active. A less restrictive measure of the activity of the potentiated group will be
studied in the next section.

We ﬁrst show in Figure 5A the CoA of the ﬁve-cell potentiated group of session A above.
This ﬁve-cell group is found to strongly coactivate in Task on a τ (cid:3) 20 − 40 ms time scale, y
in Sleep Post on a similar time scale, t (cid:3) 30 − 50 EM. The ﬁve-cell group does not coactivate
more than expected by chance in Sleep Pre, which is compatible with the independent-cell
hypothesis due to the low ﬁring frequencies (Métodos). This result shows that the potentiated
group is replayed in Sleep Post. Curiosamente, the coactivation of the potentiated group in Sleep
Post is much stronger during non-REM-Sleep periods (non-REM), in which hippocampal sharp
waves are known to be important for memory consolidation (Figure 5A , bien). Además, el
large CoAs of the potentiated group found in Task and Sleep Post are signiﬁcantly higher than
CoAs for random groups of ﬁve neurons (SI, Figure S15; Tavoni et al., 2017). Those ﬁndings
suggest that the ﬁve-cell group is (part of) a cell assembly that is reinforced by experience.

For each recorded session we then measure the maximal values (over the time scale τ)
reached by the CoA of the group supporting the effectively potentiated couplings in the Sleep
Pre and Sleep Post epochs. The ratio of the maximal CoA in Sleep Post over the maximal CoA
in Sleep Pre is a measure of the reinforcement of the coactivation between the neurons in the
group across the two sleep epochs in a session. Figure 5B shows the scatter plot of the loga-
rithms of the ratios of those two maximal CoA versus the values of the effective potentiations
Pot of the groups (deﬁned as the sums of contributions to Pot over the pairs of neurons in the
grupos) across the recorded sessions. A clear monotonic trend is observed, showing that our
estimate of coupling potentiation is a good estimator of the existence of neural groups in the
spiking data, which reinforce their coactivation in the sleep epoch following task-learning. Nosotros
retain all the sessions in which the increase in the logarithms of maximal CoA across the Sleep
epochs is larger than 1.5, and label them with letters A to Q; see Figure S7 (Tavoni et al., 2017)
for locating sessions A–Q in the potentiation results of Figure 3D . The sizes of the potentiated
groups in sessions A–Q range from two to seven cells. It is important to notice that variants of
the identiﬁed potentiated groups with, decir, one more or less cells, can also have large CoAs.
Varying the threshold used in the spectral procedure allows us to explore these alternative
groups in each session. Examples are provided in SI, Figures S13–S14 (Tavoni et al., 2017).

Neurociencia en red

285

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 5. Neurons supporting effectively potentiated couplings show strong increase in coac-
tivación.
(A) Assembly coactivation ratio (CoA) for groups supporting the effectively potentiated
networks of sessions A, Y, y B. Light and dark blue curves show the CoA for, respectivamente, el
REM and non-REM periods of the Sleep epochs. CoAs are shown for time scales τ ranging from
5 ms to n × 20 EM, where n is the number of neurons in each group considered. Note the varia-
tions in the CoA and temporal scales along the y- and x-axis between the panels. See Methods for
the computation of error bars. Note that values of CoA smaller or equal to unity can be compat-
ible with the independent-cell hypothesis when neurons have very low ﬁring rates; see Methods.
The potentiated groups of sessions A, B, and Y include, respectivamente, ﬁve, ﬁve, and four neurons.
(B) Logarithmic change in the peak CoA of the identiﬁed potentiated group between Sleep Pre and
Sleep Post vs. potentiation Pot for all experimental sessions with at least two cells in the poten-
tiated group. The sessions labeled A–Q have a large group potentiation and a large logarithmic
change in their peak CoA (Δ log Max (CoA) > 1.5). The straight line shows a linear ﬁt of the results
−32), proving that large Pot correspond to strong differences
(slope = 0.85, R2 = 0.8, p value = 10
in coactivation in the spiking data between the Sleep Pre and the Sleep Post epochs.

Neurociencia en red

286

Experience-related potentiation of functional connectivity in PFC

While we have focused above on effective potentiation corresponding to an increase of the
couplings across the Sleep epochs, effective negative potentiation, in which couplings get more
negative in Sleep Post than in Sleep Pre, may be found in some sessions, such as Y (Figura 3C),
despite being weak on average (Figura 3B). An analysis of the [0 − −] coupling class in session
Y has permitted us to identify a cluster of three cells. We show in Figure 5A that this three-cell
group is associated with a decrease of the CoA from Sleep Pre to Sleep Post in non-REM and at
short time scales τ ∼ 20 − 40 EM. Ecuación 3 for Pot can be straightforwardly modiﬁed to deﬁne
the effective negative potentiation; see SI, Section VIII and Figure S16 (Tavoni et al., 2017).
In addition to Y we have identiﬁed another strongly negatively potentiated session, z, y
dos sesiones, C and I, showing both positive and negative potentiations across their coupling
redes. As it is statistically hard to reliably estimate low CoA values, a systematic study of
negative potentiation across all sessions is difﬁcult, and would require longer recordings.

Dynamics of Reactivation: Effects of Hippocampal Ripples and Connection With Behavioral Learning

Sharp-wave ripple complexes:
Large activity bursts in the
hippocampus composed of large
amplitude local ﬁeld potential
deﬂections (sharp waves) associated
with high-frequency ﬁeld
oscilaciones, called ripples, generated
particularly during immobility and
non-REM sleep.

Ripple-conditioned reactivation (RR):
Average reactivation of the
potentiated group following a ripple
evento.

Autocorrelation of the reactivation
(AR):
Autocorrelation of the reactivation of
the potentiated group.

The previous analysis allowed us to identify effective potentiated groups that are strongly coac-
tivated in Sleep Post in sessions A–Q. A fundamental issue is whether the reactivation of those
potentiated groups is mostly triggered by hippocampal inputs (sharp-wave ripples, monitored
in the experiments; see Methods) or reﬂects the internal dynamics of the PFC network, modificación-
iﬁed upon learning. Para abordar esta pregunta, for each of the above sessions, we deﬁne the
Reactivation of the potentiated group in time bin t, R(t) = 1
)
(t), dónde (i1, i2, …, iK
k
are the indices of the K neurons in the group, and the average value of the reactivations over
all time bins, (cid:6)R(cid:7). Reactivation R(t) is less restrictive than CoA in Equation 4 as it does not
require the synchronous coactivation of all the neurons in the group.

pag
i(cid:2)

(cid:2)=1

∑K

We ﬁrst compute the ripple-conditioned reactivation, RR(t), deﬁned as the average value
of the reactivation following a ripple event by a delay τ, normalized by the average reactivation,

RR(t) =

1
Nr (cid:6)R(cid:7)

Nr∑
m=1

R(t + tm),

(5)

where the tms are the times of the Nr ripple events. Figure 6A shows the ripple-conditioned
reactivations RR(t) for the Sleep Post epochs of sessions A, B, C, which are representative of
the variety of RR patterns found across all sessions. In sessions A and B, a marked reactivation
peak is found at short time scales of tens of milliseconds. Además, this “fast” peak is followed
in session B by a long-lasting reactivation, decaying over a few seconds. We stress that fast
versus slow reponses to ripples were not studied session by session in Peyrache et al. (2009),
which reports only the average response over all sessions. No clear response of the reactivation
to ripple events is found in session C on any time scale.

A complementary characterization of the reactivation dynamics, not directly related to

ripples, is provided by the following normalized autocorrelation of the reactivation:

AR(t) =

(cid:6)R(t) R(t + t)(cid:7)
(cid:6)R(cid:7)2

(6)

where the brackets (cid:6)·(cid:7) denote the average over all time bins t. AR captures dynamical scales,
irrespective of their origins (inputs from the hippocampus or internal dynamics of the PFC
network). The behaviors of AR(t) are reported for sessions A, B, C again in Figure 6A. Para
all three sessions we observe a large peak in the autocorrelation at τ = 0, expressing the
tendency of neurons in the potentiated group to ﬁre together and decaying over a few tens of

Neurociencia en red

287

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 6. Ripple-reactivation and auto-reactivation of potentiated groups and learning behaviors.
(A) Sliding average over a 50 ms time window of the ripple-conditioned reactivation (RR(t) en
Ecuación 5, left panels) and auto-reactivation (AR(t) en la ecuación 6, right panels) of the potentiated
groups for sessions A, B, and C. Orange and magenta lines show, respectivamente, exponential ﬁts of
the fast (over the 20 < τ < 100 ms range) and slow (over the 1 < τ < 4 s range) components to RR and AR. Fast decay times are so ﬁtted to τ = 85 ms and τ = 400 ms for, respectively, sessions A and B, and the slow decay time for session B is τ = 3.5 s. Left: blue lines represent the null model for RR (full line: average value of RR, dotted lines: ±1 standard deviation); see Methods. Right: blue lines show for comparison the AR curve of the groups of the same size as the potentiated groups and containing the most active neurons in each session. (B) Z scores Z(τ), Equation 11 in Methods, of the amplitude of the fast (τ = 0) and the slow (averaged over 0.5 s < τ < 1.5 s) components to the ripple-conditioned reactivation for sessions A to Q. Each session is represented by one, two, or three circles of increasing diameters, depending on the number of rules. For each rule the color of the corresponding circle indicates whether the learning-point and rule-changing criteria were reached. Session K is not shown because of the very small number of detected ripples. In session D, both learning-point and rule-changing criteria were met but the rule was not changed in the experiment as it should have been; see SI, Section IX (Tavoni et al., 2017). Average and standard deviation of the fast decay times over the eight sessions with largest fast responses to ripples are τRR− f ast = 230 ± 180 ms. Average value and standard deviation of the slow decay time over the three sessions (I, B, Q) with a signiﬁcant slow response to ripples are τRR−slow = 4 ± 3 s. (C) Amplitudes of the fast (in τ = 0) and the slow (average over 0.5 s < τ < 1.5 s) components in AR(τ) for sessions A to Q. Same color code for learning behavior as in panel B. Fast and slow decay time constants, ﬁtted over all sessions are, respectively, τ AR− f ast = 56 ± 24 ms and τ AR−slow = 3 ± 1.5 s. milliseconds. This “fast” peak is followed by a slow component decaying over few seconds. Remarkably, in session C, for which no reactivation following ripples was detected, AR is stronger than for sessions A and B. The results above were extended through a systematic analysis of sessions A–Q showing strong effective potentiation. The magnitudes of the fast (0 < τ < 50 ms) and slow (0.5 s < τ < 1.5 s) components of the ripple-conditioned reactivation are reported in Figure 6B; results are expressed in terms of Z scores with respect to a null model deﬁned from the behavior Network Neuroscience 288 Experience-related potentiation of functional connectivity in PFC of RR(τ) at negative delays τ < 0; see Methods. In Figure 6C we plot the amplitudes of the fast and slow components to the autocorrelation AR(τ). We now attempt to relate the characterization of sessions in terms of RR and AR to the learning behavior of the rat during the Task epoch. The experimental protocol is described in Methods and in SI, Section IX (Tavoni et al., 2017); see also Peyrache et al. (2009). The rule was changed during the session if the rat had done 10 consecutive correct trials, or made only one error out of 12 successive trials. In most of the selected sessions A–Q, this rule-changing criterion was never reached. In some of the selected sessions, the rule-changing criterion was reached once, and a second rule was introduced; in one session (L), the criterion was met again after the second rule was set, and a third rule was introduced; see SI, Section IX (Tavoni et al., 2017). In addition, during ofﬂine data analysis (Peyrache et al., 2009), a learning point was de- ﬁned, based again on the success rate of the rat but according to a less stringent criterion: the rule was said to be learned if the rat had done three consecutive correct trials, and afterwards had a success rate larger than 80% over the remaining trials (up to the end of the session end or up to the change of the rule). Whether the learning-point and the rule-changing criteria were reached deﬁned different learning scenarios, which are illustrated by sessions A, B, C studied above (Figure 6A). In session A, a new rule was introduced at the beginning of the session, and was neither changed nor learned (learning point not reached) throughout the session. In session B, the rule was the same as in the previous session, and the learning point was reached by the end of the session but the rule was not changed. In session C, the rule was also the same as in the previous session and was changed in the middle of the session since the rat had fulﬁlled the rule-changing criterion; the learning point was not reached for the second rule by the end of session C. These three sessions can be informally seen as three successive levels of behavioral learning: rule not yet learned in session A (none of the two criteria is reached), intermediary learning stage (success rate has reached intermediary values between the learning and rule-changing points) in session B, and ﬁrst rule deﬁnitively learned (both criteria met) for session C. Despite the limited number (16) of selected sessions, these three learning scenarios seem to be in correspondence with general features of RR and AR presented in Figures 6B and 6C (the complete list of sessions with detailed results can be found in SI, Section IX, Tavoni et al., 2017): Nine sessions (E, I, A, Q, B, N, F, M, G) have signiﬁcant fast responses to ripples (RR, Z score > 2).

– The four sessions E, A, F, GRAMO (out of those nine sessions) in which the learning point

was not reached show no slow component to RR.

– In the remaining ﬁve sessions (I, q, B, norte, METRO), the learning point was reached: four
out of those ﬁve sessions show a signiﬁcant slow component to RR (Z score > 1.5);
session M is an exception (Z score for slow component close to zero).

For eight of those nine sessions the rule-changing criterion was never reached; for session
q, the criterion was reached for the ﬁrst rule, but not for the second rule.

Seven sessions (oh, C, PAG, D, k, j, l) show no signiﬁcant response to ripples, neither on
the fast nor on the slow time scales; see Figure 6B. Five out of those seven sessions
(oh, C, PAG, D, k) show both large fast and slow components in the autocorrelation of the
reactivation (AR); see Figure 6C (J and L show neither large RR nor large AR). In four

Neurociencia en red

289

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

of those sessions (C, PAG, D, k) the rule-changing criterion was reached. The exception is
session O, cual, sin embargo, presents some atypical features of long-lasting learning; ver
SI, Section IX (Tavoni et al., 2017).

En resumen, these observations point to the following possible connection between behav-
ioral learning and the features of the ripple-conditioned reactivation and the auto-reactivation
of the neural group identiﬁed from the spiking data: (a) When neither the learning-point nor
the rule-changing criteria are met, RR shows a fast component, and no slow component, mientras
AR is weak, suggesting that the reactivation of the potentiated group is only due to the ripple
inputs; (b) When the learning point is reached but the rule-changing criterion is not met, RR
shows both fast and slow components while AR is weak, suggesting the presence of weak,
underlying synaptic potentiations able to sustain the activity of the group after its initiation
by ripples; (C) When both learning-point and rule-changing criteria are reached, there is no
signiﬁcant RR, but AR is strong; this is compatible with the fact that those sessions have been
recorded at a stage of advanced learning, when reactivation of consolidated task-related cell
assemblies might have become independent of hippocampal inputs. We emphasize that these
observations are highly empirical and speculative. More statistics would deﬁnitively be needed
to ﬁrmly establish and conﬁrm those rules.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

DISCUSIÓN

In the present work we have focused on experience-related modiﬁcations to the functional
connectivity matrix (between tens of recorded neurons) in the prefrontal cortex (PFC) of rats
(Peyrache et al., 2009, 2010). Functional connectivity was deﬁned through the introduction of
a graphical (Ising) modelo, accounting for the statistical dependencies betweens spiking events
of the neurons in the recorded population. Comparing the functional networks in the two
Sleep epochs before and after learning we found, in a substantial fraction of the sessions under
investigación, some changes correlated to the functional connectivity during the learning epoch
sí mismo. In most of these sessions, we found that a fraction of the couplings became effectively
potentiated, and that those couplings were supported by a limited subset of the neuronal cells
(the so-called potentiated group). En otras palabras, a group of cells became much more strongly
interconnected in the Sleep epoch after learning than before. We have directly veriﬁed on the
spiking data that neurons in the identiﬁed potentiated groups coactivated much more in the
Sleep epoch after than before the learning epoch, which is reminiscent of the notion of cell
assembly introduced by Hebb (1949) as the basic unit of neural computation and memory.
Study of the reactivation dynamics of the potentiated groups allowed us to separate effects due
to hippocampal inputs (ripples) or to a putative PFC network, in connection with learning.

Patterns of Changes in Functional Couplings Between Epochs and Potentiated Groups

As a general result we have found that functional couplings deﬁne sparse interaction network
in each single epoch, the class [000] concentrating most of the pairs. In addition there is an
overall correlation between the amplitude of couplings across the different epochs, incluido
Tarea, which can be seen from the relatively large fractions of pairs in classes [− − −] y
[+ + +] compared with other nonsparse classes. Classes [0 + +] y, en un grado menor [0 − −],
contain on average signiﬁcantly more pairs of neurons than, respectivamente, [+ + 0], [0 − +],
y [− − 0], [0 + −], leading to the general conclusion that some effective couplings undergo
substantial Task-related changes from Sleep Pre to Sleep Post. Notice that the classes [+ + +]
y [− − −] corresponding to modulations in the amplitudes of the couplings (keeping a

Neurociencia en red

290

Experience-related potentiation of functional connectivity in PFC

REM sleep:
Phase of sleep characterized by rapid
eye movements and the propensity of
the sleeper to dream.

ﬁxed sign) across the epochs also contribute to, respectivamente, effective positive and negative
potentiation. These effects can be analyzed in detail, session by session.

While most of our analysis was focused on experience-related modiﬁcations to the func-
conectividad nacional, other mechanisms may take place. Tonni and Cirelli (2006) have suggested
eso, during speciﬁc phases of sleep (Genzel, Kroes, Dresler, & battaglia, 2014), small synap-
tic interactions are erased, a phenomenon called homeostasis. The overall similarity between
the distribution of inferred couplings in the two Sleep epochs, with many zero couplings, es
somewhat in agreement with this hypothesis. Sin embargo, it is difﬁcult to distinguish between
small couplings and couplings strictly equal to zero; homeostatic changes, if any, would likely
fall in the most populated [000] class.

A potential bias in our analysis is that neither the non-REM nor the REM periods have equal
durations in the Sleep Pre and Post epochs of the same session (Figure S1, Tavoni et al., 2017).
We have checked the robustness of our estimates for the session-wide effective potentiation,
Figura 3D, and for the group potentiation, Figure 5B, under random uniform subsampling of the
recorded data in which the duration of the non-REM and REM periods were matched between
the two Sleep epochs; see SI, Figure S11 (Tavoni et al., 2017).

The changes in the inferred networks of functional couplings between the Sleep epochs, cor-
related with the coupling network in the Task epoch, are supported by a subset of the recorded
neuronas. The identiﬁcation of these potentiated groups of neurons was done through an au-
tomatized spectral analysis of the Pot matrix. We have shown that the groups of potentiated
neurons strongly coactivate in the Sleep epoch posterior to learning, and are therefore part of
a replayed experience-related cell assembly. It is clear, sin embargo, that the notion of potenti-
ated group should be intended in a statistical sense. Slight variations in the composition of the
grupo, such as adding or removing one speciﬁc neuron, are associated with large coactivation,
as shown in SI, Figures S12 and S14 (Tavoni et al., 2017).

It is a remarkable and somewhat counterintuitive fact that the network of couplings inferred
from pairwise coactivation on short time scales, Δt = 10 EM, sufﬁces to predict coactivation
patterns between n neurons on longer time scales, t (cid:3) n × Δt ms. Sin embargo, even in the case
of coactivation events, the repeated spiking of neurons in short bursts generates a sequence of
pairwise coactivation events (Figura 1A), and the coactivated groups appear as strongly inter-
conectado. Robustness of predictions against the global temporal scale of the cell assembly
and the activation ordering is an important advantage of the Ising model, because cell assembly
can be played and replayed at different time scales (and in direct and reverse orderings).

Functional Couplings: Consequence of Common Inputs or Real Interactions?

As ﬁrst discussed in the works of Gerstein and collaborators (Aertsen et al., 1989; Gerstein &
Perkel, 1969), functional couplings can reﬂect either synaptic connections or the presence of
a transient common input coactivating two or more neurons. Within the Hebbian paradigm,
coactivation is a prerequisite to learning, favoring synaptic potentiation, such as through LTP
(Buzsáki, 2015). en nuestros datos, common inputs could be identiﬁed in the transient sharp waves
from hippocampus to the prefrontal cortex, occurring preferentially during non-REM sleep.
Sharp-wave ripples have been experimentally demonstrated to be essential for memory con-
solidation (Buzsáki, 2015; Genzel et al., 2014; Girardeau, Benchenane, Wiener, Buzsáki, &
Zugaro, 2009). Synaptic potentiation in the cortex has been suggested to take place in the im-
mediately following stage, thanks to spindle oscillations contributing to the shutdown of the
transmission from the hippocampus to the prefrontal cortex. The calcium inﬂux taking place

Neurociencia en red

291

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

during spindle oscillation could facilitate synaptic potentiation between cells in the replayed
assemblies (Genzel et al., 2014; Siapas & wilson, 1998).

An important issue is whether changes in the functional couplings between the Sleep epochs
reﬂect such common inputs, necessary for learning, or “real” plasticity in the synaptic interac-
ciones. In their earlier work Peyrache and collaborators estimated, based on principal compo-
nent analysis, the average reactivation over all sessions, and showed that it occurred within a
2-second time window centered around the sharp-wave event (see Figure 5B in Peyrache et al.,
2009). In our study we computed the reactivation of the more precise potentiated groups de-
ﬁned by the Ising model, for each one of the 16 selected sessions. In sessions with a clear
response to ripple this response starts within 250 ms from the ripple event, and thus shows
a ﬁner temporal resolution. Además, despite the difﬁculty in identifying experience-related
cell assemblies, the complexity of rule-changing scenarios, and the experimental limitations
in the recordings, different scenarios seem to emerge, depending on the learning stage.

For the four sessions in which the rat has not learned the rule, the ripple-conditioned re-
activation RR(t) of the identiﬁed cell assembly decays after a short delay of the order of
τ ∼ 200 EM, comparable to the typical duration of sharp-wave ripples. Por eso, the strongly
interconnected effective network we identiﬁed in Sleep Post (Figura 4D) seemingly mostly ac-
counts for correlations produced by neural coactivation under common hippocampal inputs.

Además, in several sessions with strong effective potentiation and in which the rule (o
two rules in session Q) es (son) learned, towards the session end hippocampal ripples evoke a
persistent reactivation, lasting several seconds after the ripple event. This effect may signal the
existence of an established synaptic potentiation, able to reverberate the activity seconds after
the input is over.
In other sessions in which the rule was deﬁnitively learned and changed,
no signiﬁcant reactivation of the potentiated group following the ripple events was found;
sin embargo, reactivation in those sessions showed a large autocorrelation, decaying over seconds.

A tentative interpretation of these ﬁndings is the following. For sessions in which the rule
has not yet been learned, the large coactivation of the experience-related group, as evidenced
in Figure 5A, seems to be largely supported by the inputs coming from the hippocampus dur-
ing the sharp wave ripples, known to be crucial for memory consolidation. En cambio, nuestro
ﬁnding suggests that when the rule has been learned, reactivation occurs over long time scales
with two possible mechanisms: slowly decaying persistence of ripple-induced activity, cual
is found in sessions where the rule has “just” been learned, or second-long replay periods, y-
related to ripple events, which takes mostly place in sessions where the rule has been learned
and changed (more stringent criterion). The presence of long-lasting reactivation suggests the
existence of a potentiated synaptic network connecting the PFC neurons. This putative net-
work could be either evoked by ripples or subject to spontaneous excitations, depending on
its maturity. A possible interpretation of the absence of ripple-induced activity for sessions in
which the rule has been deﬁnitively learned is that memory has been consolidated, so ripples
are not needed for the passage from short to long-term memory any longer. As stressed in the
Results section, these interpretations are highly speculative, as the limited number of selected
sessions and the variety of behaviors of animals during those sessions did not allow us to draw
any solid statistics.

The above results are also consistent with the ﬁnding that when the rule has not been
learned, the CoA of the potentiated group is often substantially larger in non-REM than in REM;
see for example CoA of session A in Figure 5A. In sessions in which the rule has been learned,
there is a still smaller but signiﬁcative coactivation of the potentiated
on the contrary,

Neurociencia en red

292

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

group also in REM periods, as happens in session B on the time scale of τ ∼ 50 EM (ver
also Figure S13 in Tavoni et al., 2017, for other sessions). Ripple events are indeed more fre-
quent in non-REM sleep. Finally the presence of a CoA larger than one in Sleep Pre, cual
further increases in Sleep Post, is also often present when the rule is not new (see Figure S13,
Tavoni et al., 2017). New experiments and more data for the different learning and rule shift
protocols would be important to conﬁrm these ﬁndings.

Note that in a related work (Tavoni, Cocco, & Monasson, 2016), we have shown how the
simulation of the inferred Ising model in the presence of an external stimulation allowed us to
reveal groups of coactivating cells and to characterize their statistical variations. This external
aporte, introduced as a mathematical tool to scan rare coactivation events in the Ising model
of the population activity, mimicks, in a very crude way, hippocampal inputs to the PFC and
allows for the investigation of collective activation on time scales larger than the elementary
time bin used for inference. The groups of neurons in the experience-related cell assemblies
identiﬁed by our method and the one in Tavoni et al. (2016) coincide for the two sessions
(A and D) common to our set of 16 selected sessions and to our previous work.

Comparison Between Inference Procedures for Ising Model

The couplings deﬁning the graphical model considered in this paper are an extension of the
correlation indices ﬁrst used to quantify functional connectivity (Aertsen et al., 1989; Fujisawa
et al., 2008; Schwindel et al., 2014). Informally speaking, couplings can be viewed as a sparse
set of “direct” correlations among the population of recorded cells. Even for sessions with few
recorded cells, the network of couplings is much sparser than its correlation counterpart (ver
Figura 1A). We have resorted here to the graphical Ising model, which is the maximum en-
tropy model reproducing the one- and two-cell ﬁring statistics. In this probabilistic framework,
different methods exist to infer the couplings parameters.

A competitive inference technique is the standard Boltzmann machine learning algorithm
(Hinton & Sejnowski, 1986), broadly used in the analysis of retinal (Schneidman et al., 2006)
and cortical (Marre, El Boustani, Frégnac, & Destexhe, 2009) multielectrode recordings. Este
inference procedure is slow in its naive version but can become efﬁcient with good initial
guess of the coupling parameters (Barton and Cocco, 2013), upon replacement of the gra-
dient descent for the minimization of the cross-entropy with an approximate version of the
Newton method (Ferrari, 2016), or thanks to improvement speciﬁc to the sparse activity of
neural population (Broderick, Dudik, Tkacik, Schapire, & Bialek, 2007). Two other promising
methods to ﬁt Ising models from data are the pseudolikelihood approach (Aurell & Ekeberg,
2012) and minimal probability ﬂow (Sohl-Dickstein, Battaglino, & DeWeese, 2011). Both ap-
proaches use all the data, and not only the ﬁrst and second moments of the neural activity,
to avoid computing the normalization constant Z in the distribution P; see Equation 1.
En
particular, the minimal probability ﬂow method has been recently applied to multilayer re-
stricted Boltzmann machine to model explicitly the different columns in cortical data (Köster,
Sohl-Dickstein, Gray, & Olshausen, 2014).

Here we have used the adaptive cluster expansion (ACE; see Methods and Barton & Cocco,
2013; Cocco & Monasson, 2011), which has been shown to accurately reproduce interaction
parameters for synthetic data. The Ising distribution inferred with ACE also reproduces the
statistics of retinal or hippocampal recordings of the activity of tens to hundreds of recorded
neuronas, including high-order moments (Barton & Cocco, 2013; Posani et al., 2017). Más
recently this technique was generalized to the case of nonbinary but multiple-categorial

Neurociencia en red

293

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

variable, or Potts model, to model coevolution in protein sequences (Barton, De Leonardis,
Coucke, & Cocco, 2016). Our inference approach is very fast on these neural data, tomando
some seconds on a personal computer to infer the input and functional connectivity param-
eters. It would be possible to use it to identify cell assemblies online. Combined with opto-
genetics techniques (Reutsky-Gefen et al., 2013) this would open exciting perspectives on the
manipulation of cortical cell assemblies in a controlled way.

= Jji.

The Ising model captures the statistics of snapshots of the activities, y, tal como, deﬁnes
symmetric functional couplings Jij
It can therefore not be used to study the order-
ing in the dynamical activation of the neurons. Other functional-connectivity-based infer-
ence approaches, such as the generalized linear (Pillow et al., 2008; Truccolo, Eden, Fellows,
Donoghue, & Marrón, 2005), kinetic Ising (Roudi & Hertz, 2011), and integrate and ﬁre
(Koyama & paninski, 2010; Monasson & Cocco, 2011) models are designed to infer nonsym-
metric connectivity matrices from the temporal sequence of spiking events in the neuronal
población. In Tavoni et al. (2016), we have inferred the couplings on the same cortical dataset
with the generalized linear model and found that they are essentially symmetric, and strongly
correlated with their Ising counterparts. One possible explanation is that cell assemblies in the
prefrontal cortex may also code for instrinsically nontemporal aspects of the task to be learned,
in agreement with the ﬁndings of Peyrache et al. (2010).

Comparison With Existing Procedures to Identify Cell Assemblies

Many of the currently available methods to detect and characterize the replay of neural groups
or cell assemblies rely on the knowledge of how the neural activity correlates with sensory
or internal inputs. Por ejemplo, place cells in the hippocampus are known to encode loca-
tion in space, and replay of place-cell assemblies representing behaviorally meaningful tra-
jectories can be determined with template-matching techniques. Más precisamente, the ordered
activation sequences of place cells observed during salient moments, such as sharp-wave rip-
ple events, during sleep or wakefulness, is matched with the sequences of place cells deter-
mined by the templates observed during locomotion (Marrón, Franco, Espiga, Capricho, & wilson,
1998; Carr et al., 2011; Diba & Buzsáki, 2007; Foster & wilson, 2006; Sotavento & wilson, 2002;
Pfeiffer & Foster, 2013). Similarmente, in sensory systems cell assemblies can be detected and
characterized by studying the neuronal population response to speciﬁc stimuli, easily repro-
ducible in experimental settings. An example is provided by the analysis of neural activity pat-
terns following speciﬁc sounds in the auditory cortex (Bathellier, Ushakova, & Rumpel, 2012).
Sin embargo, those approaches are not easily applicable to all the regions of the brain.
En el
corteza prefrontal, por ejemplo, neurons may not be activated in a well-deﬁned temporal order,
predictable from the knowledge of external stimuli. Cell assemblies might respond to internal
cognitive states, or to a combination of extrinsic covariates and internal states, which are very
difﬁcult to determine and control experimentally.

In this context, principal component analysis (PCA) has been used as a way to build ap-
proximate templates from the correlational structure of data (top principal components), y
to detect reactivation, or replay, of those templates. Though PCA was applied successfully to
detect replay (Benchenane et al., 2010; Peyrache et al., 2009, 2010), it lacks any probabilistic
framework and the interpretation of the large entries of the top components is difﬁcult, incluso
with the use of clustering procedures, such as the assembly vector estimation Lopes-dos-Santos
et al., 2013. Our analysis signiﬁcantly extends the PCA of Peyrache et al. (2009, 2010), as it
identiﬁes the neurons participating to replay-related assemblies in a detailed way. Let us stress
that the whole approach for computing functional connectivity and identifying cell assemblies

Neurociencia en red

294

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

is fully automatized, and requires spiking data only. While our approach identiﬁes a single cell
assembly that contributes the most to functional coupling potentiation, it could be easily ex-
tended to the case of more assemblies; see Methods and Fortunato (2010). Such an extension
could be useful for analyzing bigger recordings in the future.

A community detection technique for cell assembly identiﬁcation, exploiting the Markov
stability method, was recently introduced in (Billeh et al., 2014). The method consists of ﬁnd-
ing a stable partition on a correlation graph and was tested on hippocampal and retinal data.
This graph, unlike the coupling networks we infer here, is deﬁned heuristically and does not
disentangle direct (giving rise to coupling) from indirect (mediated through other neurons) cor-
relaciones.

MATERIALES Y MÉTODOS

Description of Experiments

Experimental methods were described in detail in Benchenane et al. (2010) and Peyrache et al.
(2009) and are summarized in the following. Five Long-Evans male rats weighing 250–300 g at
arrival were implanted with tetrodes in the prelimbic (PL) subdivision of
the medial
corteza prefrontal, and in the intermediate-ventral hippocampus. PL tetrodes were used for
recording of single units: signals were band-pass ﬁltered between 600 y 6,000 Hz, y
spikes were detected whenever the ﬁltered signal exceeded a manually set threshold. The re-
sulting waveform (1.3 ms long) was fed into an automated spike sorting algorithm
(KlustaKwik; Kadir, Buen hombre, & harris, 2014). Hippocampal tetrodes were only used for
local ﬁeld potentials, for the detection of theta rhythms and sharp waves. Non-REM was au-
tomatically detected, based on power in the cortical delta band (1–4 Hz), hippocampal theta
(5–10 Hz), cortical spindles (10–20 Hz), and speed of head motion, by means of a clustering
algoritmo. A quality check on sleep epochs ensures the absence of systematic biases in Sleep
Pre with respect to Sleep Post; see Figure S1 (Tavoni et al., 2017).

The rats performed an attentional set shift task on a Y-maze, which is known to require the
function of the medial prefrontal cortex (mPFC) in rats (Birrell & Marrón, 2000). Each recording
session consisted of a 20- to 30-minute sleep or rest epoch (Sleep Pre epoch) in which the rat
remained undisturbed in a padded ﬂowerpot placed on the central platform of the maze, a
Task epoch, in which the rat performed the behavioral task described below for 20–40 min,
and by a second sleep or rest epoch (Sleep Post epoch; same situation as in Sleep Pre) de
20–30 min. The whole recordings in the Task epoch and in the Sleep phases (both during REM
and non-REM periods) were used for our inference.

Rats started each trial in the same arm (the departure arm). One of the two other (choice)
arms was illuminated at random (pseudorandom schedule: runs of more than four consecutive
trials with the same illuminated arm were avoided, as were repeated bouts of imposed alter-
nation between the two arms). Después, the central platform was lowered, allowing the rat to
access the choice arms. Only one of the choice arms was rewarded, according to one of four
contingency rules. Two contingency rules were spatially guided (always go to the right arm, o
to the left arm); the other two were cue guided (go to the illuminated arm, or to the dark arm).
The rule that was employed at any given moment in time was not signaled to the rat in any
way, so that the animal had to learn the rule by trial and error. Once the rat reached a criterion
de 10 consecutive correct trials, or only one error out of 12 ensayos, the rule was changed with
no further cue warning to the rat. Rule changes were extradimensional, eso es, from a spatially
guided rule to a cue-guided rule, y viceversa. All ﬁve rats learned in a consolidated way

Neurociencia en red

295

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

the right and light rules (al menos 10 consecutive correct trials), whereas only two learned in a
consolidated way the left task and one to go where the light is off.

Inference of Ising Model Parameters

Inference procedure. We have inferred the Ising model parameters with the adaptive cluster
expansion (ACE) algoritmo (Barton & Cocco, 2013; Barton et al., 2016; Cocco & Monasson,
2011), available from https://github.com/johnbarton/ACE. ACE computes an approximation
para el (cross-)entropy of the Ising model reproducing the following data:
(cid:7)

(cid:6)

SIsing

= min
h,j

− ∑
i

hi fi

− ∑
i JSleep Pre
kl

|JSleep Post
|
mn
δJSleep Post

> 3 y

|JTask
ij
δJTask
ij

> 3 ,

(9)

= 0 de lo contrario. Note that the effective potentiation in Equation 3 is obtained by
and pij,kl,mn
summing all three-coupling potentiations pij,ij,ij with the same pairs of neurons in the three
epochs of the sessions. In our null model, the coincidence between the three pairs of neurons
is removed by picking up the three couplings in Equation 9 above uniformly at random among
the set of couplings obtained from all sessions of all rats. The mean and the standard deviation
of the reshufﬂed (mismatched) three-coupling potentiations p among all the sessions are (cid:6)pag(cid:7) (cid:3)
0.0018 and Δp (cid:3) 0.066. Tenga en cuenta que, as the distributions of couplings are similar from one session
a otro (Figura 2A), the distribution of potentiations obtained by reshufﬂing the couplings
within each session only, without pooling all sessions together, gives similar results.

For a session with N recorded neurons, the null model distribution for Pot is obtained by
2 norte(N − 1) randomly drawn reshufﬂed potentiations p. The null model average and

summing 1
its standard deviations are thus given by the following:

(cid:6)Pot(cid:7) = N(N − 1)

(cid:6)pag(cid:7) , Δ Pot =

(cid:10)

norte(N − 1)
2

Δp ,

(10)

which deﬁne the red lines of Figure 3C (izquierda). The null models for the controls in Figure 3C (bien)
are obtained with the same procedure after swapping the Sleep Pre and Sleep Post epochs in
all sessions.

Identiﬁcation of the Group of Neurons Supporting the Most Effectively Potentiated Couplings

In order to identify the subgroup of neurons that supports the couplings with strongest effective
potentiation in a session, we consider the contribution to Pot (Ecuación 3) coming from the pair

Neurociencia en red

297

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

1
3
2
7
5
1
0
9
2
0
2
3
norte
mi
norte
_
a
_
0
0
0
1
4
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Experience-related potentiation of functional connectivity in PFC

(i, j) of neurons, Potij
≡ pij,ij,ij, cf. Ecuación 9. This contribution can be seen as an entry of
an N × N–dimensional matrix. This matrix is sparse, square symmetric, and has large entries
for neurons (i, j) supporting strongly potentiated couplings. The top eigenvector, v = {vi
},
of the matrix is localized over few neurons i, which strongly contribute to Pot (SI, Figure S9,
Tavoni et al., 2017). We deﬁne the potentiated group as the set of neurons i with components
vi larger than a threshold value c (ranging between zero and one for normalized v). In all the
experimental sessions considered here, this simple spectral analysis gives at most one large and
connected neural group. Spectral graph theory offers efﬁcient methods for dealing with more
complex data structures on larger datasets, including more than one largely interconnected
grupo (Fortunato, 2010).

The correlation between the changes in log CoA from Sleep Pre to Post, Δ logCoA, y
the potentiation of the group across all sessions (shown in Figure 5B for c = 0.22) varies with
C. The best correlations are found in practice in the range 0.15 < c < 0.35, with p values −35 (SI, Figure S10, Tavoni et al., 2017). We have arbitrarily set ranging between 10 c = 0.22 in between these two limits. This value is also adequate if one imposes in addition that potentiated groups should include at least three cells (SI, Figure S10, Tavoni et al., 2017). −30 and 10 Statistical Signiﬁcance of the Coactivation Ratio (CoA) To assess the statistical validity of the CoA deﬁned in Equation 4 for a group G of neurons, we compute the error bar on CoA, shown in Figure 5A. Assuming a Poisson distribution for the (τ), coactivation events, the standard deviation of the CoA is estimated to be CoA(τ)/ where NG NG (τ) is the number of coactivation events for the cells in G over the time scale τ. (cid:11) Note that simultaneous-ﬁring events (contributing to f (G)) are unlikely to be found, and the CoA is likely to be zero, if the duration of the recording is small, for example, compared (τ). This happens for the ﬁve-cell potentiated group of session A for with Tmin time scales τ ≤ 40 ms in the Task epoch, and for all the values of τ considered in Sleep Pre and Post in Figure 5A. = τ/ ∏i∈G fi l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 1 3 2 7 5 1 0 9 2 0 2 3 n e n _ a _ 0 0 0 1 4 p d . t Analysis of Ripple-Conditioned Reactivation We deﬁne a null model for the average response to ripples after a delay τ, RR(τ) in Equation 5, as follows. For each session, we compute the average value, RR0, and the standard deviation, δRR0, of RR(τ) over the −3 s < τ < −0.5 s range. The range of delays is sufﬁciently negative to exclude any inaccuracy in the determination of the ripple times tm. The values of RR0 and ± δRR0 are shown in Figure 6A (left panels) for sessions A, B, and C. The Z score of RR0 ripple-conditioned reactivation for positive delay τ is deﬁned through f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Z(τ) = RR(τ) − RR0 δRR0 . (11) The value of the Z score in τ = 0 and its average over the 0.5 s < τ < 1.5 s interval are used to estimate the amplitudes of the, respectively, fast and slow components in RR; see Figure 6B. ACKNOWLEDGMENTS We thank Georges Debregeas for useful comments about the manuscript. This work was funded by the [EU-]FP7 FET OPEN project Enlightenment 284801. Network Neuroscience 298 Experience-related potentiation of functional connectivity in PFC AUTHOR CONTRIBUTIONS Gaia Tavoni: Formal analysis; Investigation; Methodology; Validation; Writing – original draft, ﬁrst, equal; Writing – review & editing. Ulisse Ferrari: Formal analysis; Methodology; Vali- dation; Writing – original draft; Writing – review & editing. Francesco Battaglia: Conceptual- ization; Investigation; Project administration; Supervision; Writing – original draft, ﬁrst, equal; Writing – review & editing. Simona Cocco: Conceptualization; Investigation; Methodology; Project administration; Supervision; Validation; Writing – original draft, last, equal; Writing – review & editing. Rémi Monasson: Conceptualization; Investigation; Methodology; Project administration; Supervision; Validation; Writing – original draft, last, equal; Writing – review & editing. REFERENCES Aertsen, A., Gerstein, G., Habib, M., & Palm, G. (1989). Dynamics of neuronal ﬁring correlation: Modulation of effective connectiv- ity. Journal of Neurophysiology, 61(5), 900–917. Aurell, E., & Ekeberg, M. (2012). Inverse Ising inference using all the data. Physical Review Letters, 108(9), 090201. Barton, J. P., & Cocco, S. Ising models for neural activ- ity inferred via selective cluster expansion: Structural and coding properties. Journal of Statistical Mechanics: Theory and Experi- ment, 2013(03), P03002. (2013). Barton, J. P., De Leonardis, E., Coucke, A., & Cocco, S. (2016). Ace: Adaptive cluster expansion for maximum entropy graph- ical model inference. Bioinformatics, 32(20), 3089. https://doi. org/10.1093/bioinformatics/btw328 Bathellier, B., Ushakova, L., & Rumpel, S. (2012). Discrete neo- cortical dynamics predict behavioral categorization of sounds. Neuron, 76(2), 435–449. Benchenane, K., Peyrache, A., Khamassi, M., Tierney, P. L., Gioanni, Y., Battaglia, F. P., & Weiner, S. I. (2010). Coherent theta oscil- lations and reorganization of spike timing in the hippocampal- prefrontal network upon learning. Neuron, 66(6), 921–936. Billeh, Y. N., Schaub, M. T., Anastassiou, C. A., Barahona, M., & Koch, C. (2014). Revealing cell assemblies at multiple levels of granularity. Journal of Neuroscience Methods, 236, 92–106. Birrell, J. M., & Brown, V. J. (2000). Medial frontal cortex mediates Journal of Neuro- perceptual attentional set shifting in the rat. science, 20(11), 4320–4324. Bliss, T. V., & Collingridge, G. L. (1993). A synaptic model of memory: Long-term potentiation in the hippocampus. Nature, 361(6407), 31–39. Broderick, T., Dudik, M., Tkacik, G., Schapire, R. E., & Bialek, W. (2007). Faster solutions of the inverse pairwise Ising problem. arXiv:0712.2437. Brown, E. N., Frank, L. M., Tang, D., Quirk, M. C., & Wilson, M. A. (1998). A statistical paradigm for neural spike train decoding applied to position prediction from ensemble ﬁring patterns of Journal of Neuroscience, 18(18), rat hippocampal place cells. 7411–7425. Buzsáki, G. (2010). Neural syntax: Cell assemblies, synapsembles, and readers. Neuron, 68(3), 362–385. Buzsáki, G. (2015). Hippocampal sharp wave-ripple: A cognitive biomarker for episodic memory and planning. Hippocampus, 25(10), 1073–1188. Carr, M. F., Jadhav, S. P., & Frank, L. M. (2011). Hippocampal replay in the awake state: A potential substrate for memory consolida- tion and retrieval. Nature Neuroscience, 14(2), 147–153. Castillo, P. E. (2012). Presynaptic LTP and LTD of excitatory and inhibitory synapses. Cold Spring Harbor Perspectives in Biology, 4(2), a005728. Chhetri, R. K., Amat, F., Wan, Y., Höckendorf, B., Lemon, W. C., & Keller, P. J. (2015). Whole-animal functional and developmen- tal imaging with isotropic spatial resolution. Nature Methods, 12(12), 1171–1178. Cocco, S., Leibler, S., & Monasson, R. (2009). Neuronal couplings between retinal ganglion cells inferred by efﬁcient inverse statis- tical physics methods. Proceedings of the National Academy of Sciences, 106(33), 14058–14062. Cocco, S., & Monasson, R. (2011). Adaptive cluster expansion for inferring Boltzmann machines with noisy data. Physical Review Letters, 106(9), 090601. Cocco, S., & Monasson, R. (2012). Adaptive cluster expansion for the inverse Ising problem: convergence, algorithm and tests. Journal of Statistical Physics, 147(2), 252–314. Diba, K., & Buzsáki, G. (2007). Forward and reverse hippocam- pal place-cell sequences during ripples. Nature Neuroscience, 10(10), 1241–1242. Ferrari, U. (2016). Learning maximum entropy models from ﬁnite- size data sets: A fast data-driven algorithm allows sampling from the posterior distribution. Physical Review E, 94(2), 023301. Ferrari, U., Obuchi, T., & Mora, T. (2017). Random versus maximum entropy models of neural population activity. Physical Review E, 95, 042321. Fortunato, S. (2010). Community detection in graphs. Physics Reports, 486(3), 75–174. Foster, D. J., & Wilson, M. A. (2006). Reverse replay of behavioural sequences in hippocampal place cells during the awake state. Nature, 440(7084), 680–683. Friston, K. J. (2011). Functional and effective connectivity: A review. Brain Connectivity, 1(1), 13–36. Fujisawa, S., Amarasingham, A., Harrison, M. T., & Buzsáki, (2008). Behavior-dependent short-term assembly dynamics G. in the medial prefrontal cortex. Nature Neuroscience, 11(7), 823–833. Genzel, L., Kroes, M. C., Dresler, M., & Battaglia, F. P. (2014). Light sleep versus slow wave sleep in memory consolidation: A Network Neuroscience 299 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 7 5 1 0 9 2 0 2 3 n e n _ a _ 0 0 0 1 4 p d t . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Experience-related potentiation of functional connectivity in PFC question of global versus local processes? Trends in Neuro- sciences, 37(1), 10–19. Gerstein, G. L., & Perkel, D. H. (1969). Simultaneously recorded trains of action potentials: Analysis and functional interpretation. Science, 164(3881), 828–830. Girardeau, G., Benchenane, K., Wiener, S. I., Buzsáki, G., & Zugaro, M. B. (2009). Selective suppression of hippocampal ripples im- pairs spatial memory. Nature Neuroscience, 12(10), 1222–1223. Harris, K. D., Csicsvari, J., Hirase, H., Dragoi, G., & Buzsáki, G. (2003). Organization of cell assemblies in the hippocampus. Nature, 424(6948), 552–556. Hebb, D. O. (1949). The organization of behavior: A neuropsycho- logical theory. New York: John Wiley & Sons. Hinton, G. E., & Sejnowski, T. J. (1986). Learning and relearning in Boltzmann machines. Parallel distributed processing (Vol. 1, pp. 282–317). Cambridge, MA: MIT Press. Johnson, A., & Redish, A. D. (2007). Neural ensembles in CA3 tran- siently encode paths forward of the animal at a decision point. Journal of Neuroscience, 27(45), 12176–12189. Kadir, S. N., Goodman, D. F., & Harris, K. D. (2014). High- dimensional cluster analysis with the masked em algorithm. Neu- ral Computation, 26, 2379–2394. Köster, U., Sohl-Dickstein, J., Gray, C. M., & Olshausen, B. A. (2014). Modeling higher-order correlations within cortical mi- crocolumns. PLoS Comput Biol, 10(7), e1003684. Koyama, S., & Paninski, L. (2010). Efﬁcient computation of the maximum a posteriori path and parameter estimation in integrate-and-ﬁre and more general state-space models. Journal of Computational Neuroscience, 29(1–2), 89–105. Lee, A. K., & Wilson, M. A. (2002). Memory of sequential experi- ence in the hippocampus during slow wave sleep. Neuron, 36(6), 1183–1194. Lopes-dos-Santos, V., Ribeiro, S., & Tort, A. B. (2013). Detecting cell assemblies in large neuronal populations. Journal of Neuro- science Methods, 220(2), 149–166. Marre, O., El Boustani, S., Frégnac, Y., & Destexhe, A. (2009). Pre- diction of spatiotemporal patterns of neural activity from pairwise correlations. Physical Review Letters, 102(13), 138101. McNaughton, B. L., O’Keefe, J., & Barnes, C. A. (1983). The stereotrode: A new technique for simultaneous isolation of sev- eral single units in the central nervous system from multiple unit records. Journal of Neuroscience Methods, 8(4), 391–397. Meister, M., Pine, J., & Baylor, D. A. (1994). Multi-neuronal sig- nals from the retina: Acquisition and analysis. Journal of Neuro- science Methods, 51(1), 95–106. Monasson, R., & Cocco, S. (2011). Fast inference of interactions in assemblies of stochastic integrate-and-ﬁre neurons from spike recordings. Journal of Computational Neuroscience, 31(2), 199–227. Nguyen, J. P., Shipley, F. B., Linder, A. N., Plummer, G. S., Liu, M., Setru, S. U., . . . Leifer, A. M. (2016). Whole-brain calcium imaging with cellular resolution in freely behaving caenorhabdi- tis elegans. Proceedings of the National Academy of Sciences, 113(8), E1074–E1081. Nicolelis, M. A. (2007). Methods for neural ensemble recordings. Boca Raton, FL: CRC Press. O’Neill, J., Pleydell-Bouverie, B., Dupret, D., & Csicsvari, J. (2010). Play it again: Reactivation of waking experience and memory. Trends in Neurosciences, 33(5), 220–229. Peyrache, A., Benchenane, K., Khamassi, M., Wiener, S. I., & Battaglia, F. P. (2010). Principal component analysis of ensemble recordings reveals cell assemblies at high temporal resolution. Journal of Computational Neuroscience, 29(1–2), 309–325. Peyrache, A., Khamassi, M., Benchenane, K., Wiener, S. I., & Battaglia, F. P. (2009). Replay of rule-learning related neural pat- terns in the prefrontal cortex during sleep. Nature Neuroscience, 12(7), 919–926. Pfeiffer, B. E., & Foster, D. J. (2013). Hippocampal place-cell sequences depict future paths to remembered goals. Nature, 497(7447), 74–79. Pillow, J. W., Shlens, J., Paninski, L., Sher, A., Litke, A. M., Chichilnisky, E., & Simoncelli, E. P. (2008). Spatio-temporal correlations and visual signalling in a complete neuronal pop- ulation. Nature, 454(7207), 995–999. Posani, L., Cocco, S., Jezek, K., & Monasson, R. (2017). Functional connectivity models for decoding of spatial representations from hippocampal ca1 recordings. Journal of Computational Neuro- science, 43, 17–33. Reutsky-Gefen, I., Golan, L., Farah, N., Schejter, A., Tsur, L., Brosh, I., & Shoham, S. (2013). Holographic optogenetic stimulation of patterned neuronal activity for vision restoration. Nature Com- munications, 4, 1509. Roudi, Y., & Hertz, J. (2011). Mean ﬁeld theory for nonequilib- rium network reconstruction. Physical Review Letters, 106(4), 048702. Schneidman, E., Berry, M. J., Segev, R., & Bialek, W. (2006). Weak pairwise correlations imply strongly correlated network states in a neural population. Nature, 440(7087), 1007–1012. Schwindel, C. D., Ali, K., McNaughton, B. L., & Tatsuno, M. (2014). Long-term recordings improve the detection of weak excitatory– excitatory connections in rat prefrontal cortex. Journal of Neuro- science, 34(16), 5454–5467. Seung, H. S. (2011). Neuroscience: Towards functional connec- tomics. Nature, 471(7337), 170–172. Siapas, A. G., & Wilson, M. A. (1998). Coordinated interactions between hippocampal ripples and cortical spindles during slow- wave sleep. Neuron, 21(5), 1123–1128. Singer, A. C., Carr, M. F., Karlsson, M. P., & Frank, L. M. (2013). Hippocampal SWR activity predicts correct decisions during the initial learning of an alternation task. Neuron, 77(6), 1163– 1173. Sohl-Dickstein, J., Battaglino, P. B., & DeWeese, M. R. (2011). New method for parameter estimation in probabilistic models: Minimum probability ﬂow. Physical Review Letters, 107(22), 220601. Stevenson, I. H., Rebesco, J. M., Miller, L. E., & Körding, K. P. (2008). Inferring functional connections between neurons. Cur- rent Opinion in Neurobiology, 18(6), 582–588. Tavoni, G., Cocco, S., & Monasson, R. (2016). Neural assemblies revealed by inferred connectivity-based models of prefrontal cor- Journal of Computational Neuroscience, 41(3), tex recordings. 269–293. Network Neuroscience 300 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 7 5 1 0 9 2 0 2 3 n e n _ a _ 0 0 0 1 4 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Experience-related potentiation of functional connectivity in PFC Tavoni, G., Ferrari, U., Battaglia, F., Cocco, S., & Monasson, R. (2017). Supplemental material for “Functional coupling networks inferred from perfrontal cortex activity show experience-related effective plasticity.” Network Neuroscience, 1(3), 275–301. https://doi.org/10.1162/netn_a_00014 Tononi, G., & Cirelli, C. (2006). Sleep function and synaptic home- ostasis. Sleep medicine reviews, 10(1), 49–62. Truccolo, W., Eden, U. T., Fellows, M. R., Donoghue, J. P., & Brown, E. N. (2005). A point process framework for relating neural spik- ing activity to spiking history, neural ensemble, and extrinsic co- variate effects. Journal of Neurophysiology, 93(2), 1074–1089. Wilson, M. A. & McNaughton, B. L. (1994). Reactivation of hip- pocampal ensemble memories during sleep. Science, 265(5172), 676–679. Wolf, S., Supatto, W., Debrégeas, G., Mahou, P., Kruglik, S. G., Sintes, J.-M., . . . Candelier, R. (2015). Whole-brain functional imaging with two-photon light-sheet microscopy. Nature Meth- ods, 12(5), 379–380. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 1 3 2 7 5 1 0 9 2 0 2 3 n e n _ a _ 0 0 0 1 4 p d . t f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Network Neuroscience 301 imagen de INVESTIGACIÓN

Descargar PDF