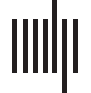INFORME
Competition Between Object Topology and
Surface Features in Children’s Extension
of Novel Nouns
Praveen Kenderla1, Sung-Ho Kim2, and Melissa M. Kibbe1
1Department of Psychological & Brain Sciences, Boston University, Bostón, MAMÁ
2Department of Psychology, Ewha Womans University, Seoul, South Korea
un acceso abierto
diario
Palabras clave: topología, inferencia, word learning, object cognition, categorization
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
oh
pag
metro
i
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
d
oh
i
/
i
/
/
.
1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
oh
pag
metro
_
a
_
0
0
0
7
3
pag
d
.
/
i
ABSTRACTO
Objects’ topological properties play a central role in object perception, superseding objects’
surface features in object representation and tracking from early in development. We asked
about the role of objects’ topological properties in children’s generalization of novel labels to
objects. We adapted the classic name generalization task of Landau et al. (1988, 1992). In three
experimentos, we showed children (norte = 151; 3–8-year-olds) a novel object (the standard) y
gave the object a novel label. We then showed children three potential target objects and asked
children which of the objects shared the same label as the standard. In Experiment 1, el
standard object either did or did not contain a hole, and we asked whether children would
extend the standard’s label to a target object that shared either metric shape or topology with the
standard. Experimento 2 served as a control condition for Experiment 1. In Experiment 3, nosotros
pitted topology against another surface feature, color. We found that objects’ topology competed
with objects’ surface features (both shape and color) in children’s extension of labels to novel
objects. We discuss possible implications for our understanding of the inductive potential of
objects’ topologies for making inferences about objects’ categories across early development.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
INTRODUCCIÓN
The ability to rapidly categorize objects allows us to efficiently store and retrieve large amounts of
information and to make inferences about objects that we have never seen before (Gelman &
Meyer, 2011). Por ejemplo, a toddler learning that “ball” refers to “a round toy that can be thrown,
rolled, and caught” can immediately refer to other ball-like objects that they never encountered
before as “ball” and can infer those objects’ categories and functions. Object categorization is thus
a powerful means for children to efficiently learn about and interact with the world around them.
To categorize objects, children must treat objects of a category as similar in some way, and an
object’s shape can be an important cue in forming categories and learning new words. Evidencia
for this comes from studies that show that children extend labels of objects to other objects that
are similar in shape over other surface features like color, texture, or size, a phenomenon known
as “shape bias” (Diesendruck & Bloom, 2003; Landau et al., 1988, 1992; Smith et al., 1996).
Shape bias is often examined using the name generalization task (Booth & Waxman, 2008;
Diesendruck & Bloom, 2003; Landau et al., 1988, 1992, 1998; see Colunga & Herrero, 2008;
elman, 2008; Kucker et al., 2019; Markson et al., 2008, for reviews). A single trial of the name
generalization task proceeds as follows. An experimenter presents an object (the standard) y
Citación: Kenderla, PAG., kim, S.-H., &
Kibbe, METRO. METRO. (2023). Competition
Between Object Topology and Surface
Features in Children’s Extension of
Novel Nouns. Mente abierta: Descubrimientos
en Ciencias Cognitivas, 7, 93–110.
https://doi.org/10.1162/opmi_a_00073
DOI:
https://doi.org/10.1162/opmi_a_00073
Recibió: 15 Julio 2022
Aceptado: 1 Marzo 2023
Conflicto de intereses: Los autores
declare no conflict of interests.
Autor correspondiente:
Melissa M. Kibbe
kibbe@bu.edu
Derechos de autor: © 2023
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
Topology in children’s noun extension
Kenderla et al.
gives the object a novel label (p.ej., “Look, this is a toma!"). The experimenter then presents three
test objects that each share one feature with the standard object (but differ from the standard in
their other features): Por ejemplo, one is the same shape, one is the same texture, and one is the
same color as the standard object. The experimenter asks children to point to the object that they
think would have the same label as the standard (p.ej., “Which one of these is also a toma?").
Children are more likely to select the object that shares the same shape as the standard over
objects that share other surface features (like color or texture), suggesting that an object’s shape
is rapidly associated with a count noun, and the extension of the noun is taken to refer to objects
with similar shape (Diesendruck & Bloom, 2003; Landau et al., 1988, 1992).
There have been a number of controversies about the interpretations of the shape bias:
Whether this bias results from the perceptual or conceptual salience of shape; whether it is
specific to this name extension task; whether it is a consequence of learning object names;
and how it is associated with knowledge of object function (p.ej., Booth & Waxman, 2002;
Booth et al., 2005; Diesendruck & Bloom, 2003; Landau et al., 1998; Herrero, 1995, 1999; Soja
et al., 1991; Zuniga-Montanez et al., 2021; see the General Discussion section below for our
discussion of these in the context of the current research). Despite these controversies, the idea
that shape plays a critical role in object categorization is widely accepted. Object kinds, par-
ticularly those at the basic level, tend to have similar shapes (p.ej., Rosch, 1978; Rosch et al.,
1976), and thus sensitivity to shape may help children make ecologically valid generalizations
of new labels. Related to this, shape can further provide strong inductive potential to the cat-
egories of artifacts, which children may use as a proxy for the object’s function (Nelson et al.,
2000; Ware & Booth, 2010; but see also Landau et al., 1998). Más importante, the shape of
rigid objects is relatively stable across different contexts while other surface features may vary
depending on lighting conditions. If a caregiver holds up and moves a rigid object in different
ways during naming, an infant will be able to able to abstract invariant shape across different
views of the same object undergoing different transformations, and this invariant shape could
be useful for children learning to name objects, as they could more easily extend the labels
they learn to similar objects they encounter (Gogate & Hollich, 2010).
Despite its importance in object categorization, sin embargo, shape is a complex concept and
what aspect of shape is invariant can depend on the level of description in both perception and
geometric theories (es decir., what is invariant in one level of description can be not invariant in a
different level). en este estudio, we questioned what geometric properties (invariances) can influ-
ence children’s judgments of which objects have the “same shape”, which can therefore be
referred to with the same label. To answer to this question, we were interested in two different
geometrical approaches to shape, Euclidean geometry and topology, in the context of the name
generalization task. According to the mathematician Klein’s transformational geometry frame-
trabajar, theories of geometry and their associated shape properties can be classified into a hier-
archy with increasing levels of abstraction (es decir., Klein hierarchy), in terms of their geometrical
transformations (es decir., invariant transformations) under which certain geometric properties
remain unaltered (Klein, 1893). De este modo, the notion of shape can be defined by the properties that
are stable under different geometrical transformations (see Todd & Petrov, 2022 para una revisión).
In classical Euclidean geometry, there are four types of invariant transformations, called
similarity transformations: traducción, rotation, reflection, and uniform dilation (resizing).1
1 The former three transformations, called Euclidean (or rigid) transformations, preserve both shape (es decir., angle
and length ratios) and size, but the latter one, uniform dilation, preserves shape alone (but not size). According
to a more conservative view, Euclidean geometry is characterized by rigid transformations alone, y por lo tanto,
figures are defined by both size and shape. See Izard et al. (2022) for discussion on different characterizations
of Euclidean geometry in Psychology.
MENTE ABIERTA: Descubrimientos en ciencia cognitiva
94
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
oh
pag
metro
i
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
d
oh
i
/
i
/
/
.
1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
oh
pag
metro
_
a
_
0
0
0
7
3
pag
d
.
/
i
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
These transformations alter an object’s position, orientación, handedness, and size, respetar-
activamente, but preserve its angle and length ratios (which are properties associated with people’s
intuitive notion of shape); de este modo, differences in objects’ location, orientación, handedness, y
size are irrelevant, but variability in properties of angle and length ratio are relevant in char-
acterizing objects for Euclidean geometry. En otras palabras, a large square and a small square in
different orientations and locations are considered equivalent, es decir., having the same Euclidean
(or metric) forma.
If people represent forms according to their Euclidean properties, or people’s intuitive sense
of geometry corresponds to Euclidean geometry, they would be sensitive to transformations
which alter metric shape, but not sensitive to transformations of the properties that are irrele-
vant to defining objects in Euclidean geometry, such as position, orientación, and size. El
notion of Euclidean shape indeed seems consistent with the findings of the shape bias in
literature such as Landau et al.’s original study and many others, which showed that children
extend object labels despite size changes of the same Euclidean shape, but not to changes in
angular properties of the objects (p.ej., from a “U”- to a “L”-shaped object) (p.ej., Landau et al.,
1988; Landau & Leyton, 1999).
In spite of metric shape’s stability under various geometric transformations, there are more
abstract shape properties like structural properties describing relations between object parts
(Hoffman & Richards, 1984; Hummel & Biederman, 1992; Marr & Nishihara, 1978), cual
survive changes in viewpoints and can provide stability to perceptual representations in the
face of changes in the environment. When making perceptual judgments about forms, estos
abstract cues tend to take priority over variations in metric shape (Amir et al., 2014; Lazareva
et al., 2008; Lowet et al., 2018). In the Klein hierarchy of geometry, the most abstract level is
topología. Topology can be conceptualized by its invariant transformations, often called
“rubber-sheet” transformations, which include continuous deformation of objects such as
twisting, stretching, and bending; sin embargo, they do not include tearing an object in two, pok-
ing holes in an object, or gluing two objects together. Topological properties—the number of
holes, connectedness, and inside/outside relationship of an object—remain invariant under
rubber-sheet deformations, and these invariants remain unaltered under the transformations
of all lower-level geometries (es decir., projective, affine, and Euclidean geometries) también, pero
not vice versa, making it the most abstract form of geometry (Todd & Petrov, 2022, for review).
Owing to the generality of topological transformations, two objects are topologically equiva-
lent if they contain the same number of holes, even if they have distinct shapes. Por ejemplo, a
cup with a handle and a donut are topologically equivalent because they each contain a single
agujero, and a solid sphere and a solid triangle are topologically equivalent because they each
contain no holes; but a donut is not equivalent to a sphere because it is not possible to con-
tinuously deform a sphere into a donut.
Visual perception research has revealed that objects’ topological properties, as stable struc-
tural properties, can supersede objects’ surface features (including metric shape) in various
visual tasks involving object representations in adults, such as the perception of apparent
movimiento (Chen, 1985; Zhuo et al., 2003), numerosity perception (He et al., 2015), visual work-
ing memory ( Wei et al., 2019), and multiple object tracking (Zhou y cols., 2010). Por ejemplo,
adults can discriminate topologically distinct objects significantly faster than objects that differ
in metric shape (Chen, 1985). And in a multiple object tracking task, adults’ accuracy to track
items decreased significantly when they tracked objects that changed in topological properties
as they moved (p.ej., a target object with one hole changed to have two holes or no holes), pero
their performance was not hampered when they tracked objects that morphed in shape as they
emocionado (p.ej., a target object changed from triangle to square; Zhou y cols., 2010). Compared to
MENTE ABIERTA: Descubrimientos en ciencia cognitiva
95
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
oh
pag
metro
i
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
d
oh
i
/
i
.
/
/
1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
oh
pag
metro
_
a
_
0
0
0
7
3
pag
d
.
/
i
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
changes in metric shape, topological changes to objects are highly salient and more readily
detected (Todd et al., 2014). Each of these studies provides evidence that the visual system is
able to abstract invariant topological features from objects that have very different metric prop-
erties, such as size and shape, and this information is then used by the visual system in various
object-related processing, such as forming persistent object representations and computing
motion correspondence.
Objects’ topological properties also are fundamental to object perception and cognition
early in development (Chien et al., 2012; Turati et al., 2003). Chien et al. (2012) showed that
infants by around 1 month of age discriminate objects based on topological properties, pero no
until 3.5 months do infants discriminate different shapes, suggesting that infants process topo-
logical properties earlier in development than surface features. Infants’ expectations about
how objects should interact is constrained by topological properties (Por ejemplo, infants have
different expectations about what can happen to an object that hides inside a tube compared
to behind an occluder; Baillargeon et al., 2012; Hespos & Baillargeon, 2001a, 2001b, 2006;
Wang y cols., 2005), y, like adults, infants’ object tracking is impacted by changes in objects’
topologies (Kibbe & Leslie, 2016). By at least 3 años, children also can explicitly identify and
count holes in objects (Giralt & Bloom, 2000), suggesting a role for objects’ topology in higher-
level processing early in childhood.
Given the primacy of topology over surface features like metric shape for object represen-
tation, and given that previous work showed that children have a strong bias toward object
shape when categorizing objects, here we asked what role topology might play in children’s
inferences about the extension of novel nouns. Because topological properties are fundamen-
tal to the invariant structure of an object, these properties could carry different information
about objects than shape or other surface features. Like shape, topological properties can
be diagnostic of an artifact’s category or function (p.ej., despite their similar shapes, a needle
can be threaded while a pin cannot). Topological properties may also be associated with labels
in the real world. Por ejemplo, despite changes in shape, the label ‘ball’ can be used to an
inflated ball and a deflated ball. Topological properties of objects also impact the way humans
interact with objects even when those objects have similar functions. Por ejemplo, to take a
drink we may grip the (topologically open) handle of a mug, pero el (topologically closed)
outside of a cup. De este modo, topological properties of objects may play a different role in inferences
about objects’ categories than shape does. And because topological properties play a more
primary role in object representation than surface featural properties such as shape, ellos
may compete with or even supersede surface features as the relevant object properties in chil-
dren’s inferences about the relevant perceptual dimensions to which a novel label refers.
en este estudio, we examined the role of topological properties in 3–7-year-old children’s
extension of novel labels to objects. In three experiments, we used the classic name general-
ization task that has consistently revealed children’s shape bias (Diesendruck & Bloom, 2003;
Landau et al., 1988, 1992). In Experiment 1, we manipulated the topology of the standard
object (by manipulating whether or not the object had a hole), gave it a novel label, y luego
asked children to choose from three test objects which object shared the same label: an object
with the same metric shape but different topology than the standard, an object with the same
topology but different metric shape than the standard, or a distractor object. Experimento 2
served as a perceptual control for Experiment 1. Finalmente, in Experiment 3, we pitted topology
against another surface feature that is not typically diagnostic of object category in children’s
extension of novel count nouns—color.
We considered three potential hypotheses for the role of topology in children’s extension of
novel labels to objects. One possibility is that, just as topology supersedes surface features like
MENTE ABIERTA: Descubrimientos en ciencia cognitiva
96
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
oh
pag
metro
i
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
d
oh
i
/
i
.
/
/
1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
oh
pag
metro
_
a
_
0
0
0
7
3
pag
d
/
.
i
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
shape and color in object representation and object-based attention, topology supersedes sur-
face features in children’s label extension. Under this possibility, we would observe a strong
“topology bias” when children are asked to extend novel count nouns to novel objects.
Another possibility is that topology does not play a significant role in children’s label extension.
Despite the primacy of topology in vision and its potential inductive role for objects’ categories
or affordances, objects’ topologies may not always be a reliable cue to objects’ categories or
funciones (as in the example of the cup and the mug), and changes to objects’ topologies do not
necessarily change an object’s category, even if they change the object’s structure (Por ejemplo, a
T-shirt with a hole in it can still be worn). Under this possibility, shape should supersede topology,
and we should observe the classic “shape bias” when they are pitted against each other. A third
possibility is that, because topology and surface features play different roles in object represen-
tation and can provide somewhat different information about objects’ categories, we may
observe competition between topology and shape (or color) in children’s label extensions. Eso
es, we may observe that children view both topology and surface features as relevant dimensions
along which to extend a novel label to other objects, and when faced with a forced choice
between topology and surface features, may choose topology on some trials and surface features
on other trials. Under this possibility, we should not observe a strong bias toward either topology
or surface features in children’s extension of novel nouns.
EXPERIMENT 1: TOPOLOGY VERSUS METRIC SHAPE
Métodos
Participantes. Los participantes fueron 66 2–7-year-old children (edad media = 5.0 años, range = 2.39–
7.55). Parents reported their children to be female (34), masculino (25), or declined to report (7).
Four additional children participated but were not included in analyses due to experimenter
error (1), inability to speak English (1), or choosing to terminate the experiment early (2). Datos
were collected in the Museum of Science, Bostón. All participants’ parents gave written con-
sent for their children to participate in the study. Demographic information was not collected
from participants. The Institutional Review Boards of the Boston University Charles River
Campus and the Museum of Science, Boston approved all study procedures.
Our sample size was 4-5 times larger than samples obtained in previous studies using a similar
método (p.ej., Diesendruck & Bloom, 2003, norte = 16; Landau et al., 1988, norte = 12). This was because
we were not certain how topology would impact children’s responses. We reasoned that a larger
sample size would allow us to detect subtle effects of topology (p.ej., competition between shape
and topological class, which would yield similar response rates for these objects).
We also reasoned that the larger sample size would also allow us to potentially detect any
effects of age on children’s responses. Previous work had revealed somewhat contradictory
evidence about the extent to which shape bias develops in early childhood, with some work
showing increases in shape bias between the ages of 2 y 3 años (p.ej., Landau et al., 1988),
and other work showing similar shape bias effects across 2- and 3-year-olds (p.ej., Diesendruck
& Bloom, 2003). Our age range encompassed these younger years, but also older children,
because we wanted to examine the potential influence of topology in children in whom the
shape bias is relatively well established, and because we were not certain whether and when
such an influence would emerge in development.
Materials. On each of the four trials, children viewed a set of four cardboard cutouts (cada
aproximadamente 5 cm × 6 cm). Each set included a standard object, and three targets: an object
of the same shape as the standard but with different topology (hole or no hole), an object with the
MENTE ABIERTA: Descubrimientos en ciencia cognitiva
97
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
oh
pag
metro
i
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
d
oh
i
/
i
.
/
/
1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
oh
pag
metro
_
a
_
0
0
0
7
3
pag
d
/
.
i
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
same topology as the standard but with a different (métrico) forma, and a distractor object of a
different shape from the standard with “bite” taken out of its contour. The “bite” served to roughly
equate the contour complexity of the object with the hole. We created shapes that were not likely
to be nameable by children. The holes in the open objects (aproximadamente 1.5 cm × 2 cm) eran
all differently shaped to prevent children from responding based on shared shape of the holes.
We chose to construct flat cardboard cut-outs to remove the depth of the hole as an added
dimension of the stimuli, which diverges somewhat from previous studies that used real-world
artifacts that were unfamiliar to children. Although the stimuli were flat, children could see that
the objects were three-dimensional since the objects were manipulated by human hands, emocionado
through 3D space, and were placed on a surface such that the surface could be viewed surround-
ing the stimuli and through the holes in the stimuli.
In each of the four trials, children viewed a standard object and three target objects. In two
of those four trials, the standard object had a hole, and in the other two trials the standard
object did not have a hole. Each child saw one of two possible sets of four trials. Across the
two sets, we varied which of the objects contained the hole. Cifra 1, left panel, shows one of
these two sets of stimuli. Templates that can be used to construct both sets of stimuli can be
accessed at https://osf.io/k3hzn/?view_only=e046ab287e6343ac9549269387748e90.
Procedimiento. Children were tested individually in a dedicated research area in the museum.
Children sat across a table from the experimenter. The experimenter told children that they
were going to play a “name game”. On the first trial, the experimenter showed the standard
object from the first set, and gave the object a novel name, p.ej., “Look at this. It’s a toma. Ver,
it’s a toma. This is a toma”. He next placed the three target objects on the table below the
standard (the order of the objects was randomized across children). The experimenter then
prompted children to select one of the three potential target objects, saying, “Ok, see these?
Which one is also a toma?” After children chose, the experimenter noted their choice in a
notebook, cleared the table, and then proceeded with the next three trials in the same way.
Children always chose between a shape-matched object (different in topology from the tar-
conseguir), a topology-matched object (different in shape from the target), and a distractor object with
a conspicuous divot in its outer contour. Including a distractor object on each trial allowed us
to distinguish guessing from competition between the shape- and topology-matched objects. Si
children select the test objects at random, they should choose the distractor object in about a
third of the trials. If children show competition between topology and shape, they should
choose roughly equally between the shape- and topology-matched objects, and choose the
distractor object only rarely.
The standard object on each of the four trials was given a unique label (toma, ziff, wug, o
blicket). Whether a given label was associated with a standard object with a hole or without a
hole was counterbalanced across children. All the objects were placed with random rotations
(eso es, there was no canonical “upright” position for any of the objects). If children attempted
to touch the objects, we discouraged them from doing so (very few children attempted to
touch the objects). The order of the trials was counterbalanced across participants.
Resultados
D a t a f o r E x p e r i m e n t s 1 – 3 a r e a v a i l a b l e a t h t t p s : / / o s f . i o / k 3 h z n / ? v i e w _ o n l y
=e046ab287e6343ac9549269387748e90.
We first asked whether children’s responses were different than what would be expected
if children were simply choosing randomly among the three objects in each trial. Children
MENTE ABIERTA: Descubrimientos en ciencia cognitiva
98
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
oh
pag
metro
i
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
d
oh
i
/
i
/
/
.
1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
oh
pag
metro
_
a
_
0
0
0
7
3
pag
d
/
.
i
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
oh
pag
metro
i
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
d
oh
i
/
i
/
.
/
1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
oh
pag
metro
_
a
_
0
0
0
7
3
pag
d
.
/
i
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 1.
Examples of stimuli from Experiment 1 (top panel), Experimento 2 (middle panel), y
Experimento 3 (bottom panel). Each row represents a trial from one of the possible orders. Children
saw the objects placed with random orientations.
chose the shape matched object on 126/264 ensayos (46.3%), the topology match on 102/264
ensayos (37.5%), and the distractor object on 36/264 ensayos (13.3%). The distribution of children’s
responses was different than would be expected if children were choosing randomly (chance =
33.33%, Chi2(2) = 49.41, pag < .0001). The majority of children’s choices consisted of the
shape- or topology-matched object, with children choosing the distractor only infrequently.
To examine whether shape and topology competed with each other in children’s responses,
we computed a “Bias Score” for each child, taken as the proportion of trials on which they
chose the shape match minus the proportion of trials on which they chose the topology match.
For example, if a child chose the shape-matched object on one trial and the topology-matched
object on three trials, they would receive a Bias Score of (.25 − .75 = −.5). If a child chose the
shape-matched object on two trials and the topology-matched object on two trials, they would
receive a Bias Score of (.5 − .5 = 0). A positive score thus indicates a tendency to choose
shape, a negative score indicates a tendency to choose topology, and a score close to 0 indi-
cates no bias (maximum score = 1, minimum score = −1). Computing Bias Scores for each
child allowed us to test the directional hypothesis that children prefer either shape (scores sig-
nificantly above 0) or topology (scores significantly below 0), or show no strong preference
OPEN MIND: Discoveries in Cognitive Science
99
Topology in children’s noun extension
Kenderla et al.
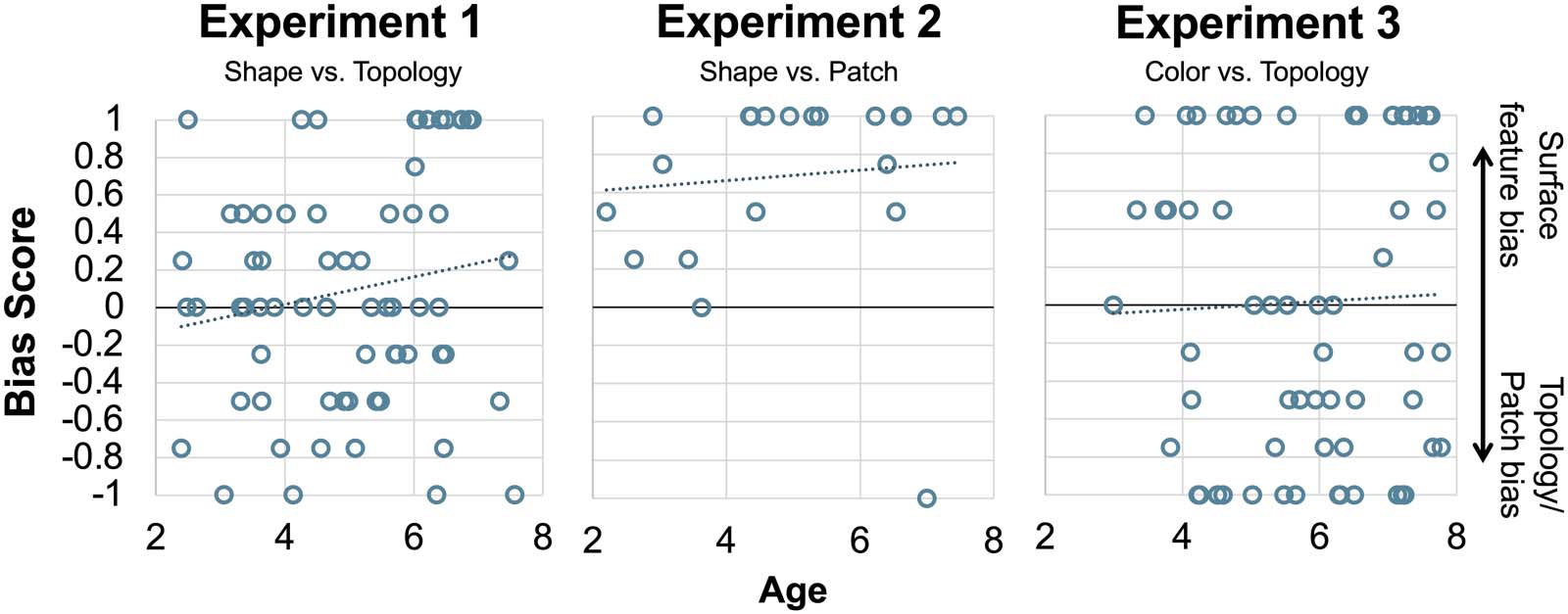
Figure 2. Mean bias scores for Experiments 1, 2, and 3. Error bars indicate ±1 standard error of
the mean.
(scores not significantly different from 0). To do so, we compared these Bias Scores to 0 using a
one-sample t test and Bayes factor analysis. We found that children’s Bias Scores were not
significantly different from 0 (M = .09; t(65) = 1.20, p = .235, 95% CI [−.06 .24]), with Bayes
factor analysis offering support for the null hypothesis (BF01 = 5.13). Children’s Bias Scores
were not correlated with their age in years (continuous) (r(65) = .167, p = .180). Figure 2 shows
children’s mean Bias Scores. Figure 3 shows individual children’s Bias Scores as a function of
age in years (continuous).
Inspection of Figure 3 provides some insights into how individual children respond across
trials. Recall that a score of 1 means that a child consistently selected shape across the four trials,
while a score of −1 means that a child consistently selected topology across the four trials. We
found that around a quarter of the children (17/66, 26%) were “consistent choosers”. The
remaining 74% of children chose topology on some trials and shape on some trials. These
results suggest that, within individual children, topology competed with shape in children’s
extension of novel nouns.
We next asked whether children’s responses differed when the standard had a hole versus
when the standard had no hole. We separately computed Bias Scores across the two trials in
which the standard had a hole and the two trials in which the standard did not have a hole and
Figure 3.
Individual children’s mean Bias Scores as a function of age for Experiments 1, 2, and 3.
OPEN MIND: Discoveries in Cognitive Science
100
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
compared these using a paired samples t test and Bayes factor analysis. Children’s patterns of
responses did not differ significantly between the two trial types (t(65) = −1.82, p = .073, 95%
CI [−.38 .02]), although Bayes factor analysis offered only anecdotal support for the null
hypothesis (BF01 = 2.10). When the standard had a hole, children’s Bias Scores were not sig-
nificantly different from 0 (M = 0; t(65) = 0, p = 1, 95% CI [−.19 .19]) with Bayes factor offering
strong support for the null (BF01 = 10.33). When the standard did not have a hole, children’s
Bias Scores were significantly different from 0 (M = .18, t(65) = 2.11, p = .039, 95% CI [.01
.35]), although Bayes factor offered only anecdotal support for the alternative (BF01 = .81).
Discussion
Previous work pitting shape against other surface features like color and texture found that
children had a strong bias to extend novel nouns to objects that share shape over objects that
share other surface features. In Experiment 1, when we pitted shape against a structural object
property—topological class—we observed competition between shape and topology when
children are tasked with extending novel labels to novel objects. These results suggest that
topology and shape both may contribute to children’s generalization of object labels.
However, before accepting this conclusion, it is important to rule out a potential alternative
explanation for children’s selections that do not exclusively rely on topology. Despite the fact
that the objects visibly moved through 3D space and the texture of the table was clearly visible
around the objects as well as through the objects’ holes, children may not have viewed the
holes as holes, but instead as “patches” on the objects’ surfaces—essentially a figure on top of
a background shape. If so, children may have matched objects based on whether or not they
had this surface feature when deciding which of the objects was in the extension of the novel
label. We tested this hypothesis in Experiment 2.
EXPERIMENT 2: PERCEPTUAL CONTROL
To examine the alternative possibility that the holes in the objects in Experiment 1 were per-
ceived as a material surface in front of a surrounding object, in Experiment 2 we replaced the
holes in the stimuli from Experiment 1 with grey patches. If children’s responses in Experiment 1
were driven by perceiving the holes as figures on top of a background shape, we expected to
observe similar results as in Experiment 1. However, if children in Experiment 1 were attending
to topology (hole vs. no hole) as a structural property of an object, we should observe the classic
shape bias effect in Experiment 2 in which the topological differences of Experiment 1 were
turned into featural differences (patch vs. no patch).
Methods
Participants. Participants were 21 2–7-year-old children (mean age = 5.01 years, range =
2.21–7.46). Parents reported their children to be female (15), male (5), or declined to report
(1). One additional child participated but was not included in the analyses because their par-
ent did not provide their exact date of birth and we were therefore unable to determine their
exact age. All participants’ parents gave written consent for their children to participate in the
study. Children were tested in the Museum of Science, Boston, as in Experiment 1.
We anticipated collecting data from 24 children, but before we reached our planned sam-
ple size, we were forced to terminate data collection at the museum due to the ongoing
COVID-19 pandemic. Our planned sample size was informed by previous work with young
children demonstrating a shape bias using a similar procedure. For example, Diesendruck and
Bloom (2003) included n = 16 children in a similar procedure and observed very large effects
OPEN MIND: Discoveries in Cognitive Science
101
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
comparing children’s selection of the shape-matched object to chance using a one-sample
t test (d > 1.5). A power analysis using the more conservative estimate of the size of the effect
re = 1 suggested a total sample size of n = 10 (alfa = .05, 1-beta = .9). Diesendruck and
Bloom (2003) also compared children’s responses in a condition in which the standard was
labeled with a novel noun (as in the present study) with children’s responses in another con-
dition in which their choices were expected to be evenly distributed across the three objects.
They again observed a large effect size for this between-subjects comparison. A power analysis
for an independent samples t test with effect size d = 1, alfa = .05, and 1-beta = .8 suggested
a sample size of n = 17 per group. Given the novelty of our stimuli, we had opted for a target
sample size of n = 24. Sin embargo, our final sample of n = 21 is sufficiently powered to detect
effects of interest.
Materials and Procedure. Materials were identical to Experiment 1, except that the holes (y
bites of distractor objects) were replaced (or filled) by gray patches in the same position
and of the same shape as the holes/bites in Experiment 1 (ver figura 1, middle panel).
Te m p l a t e s o f
t h e s t i m u l i a r e a v a i l a b l e a t h t t p s : / / o s f . i o / k 3 h zn / ? v i e w _ o n l y
=e046ab287e6343ac9549269387748e90.
The procedure was otherwise identical to Experiment 1.
Resultados
The distribution of children’s responses was different than would be expected by chance
(chance = 33.33%, Chi2(2) = 86.08, pag < .0001) and reflected the shape bias observed in pre-
vious studies (e.g., Diesendruck & Bloom, 2003; Landau et al., 1988, 1992). Children chose
the shape-matched object on the majority of trials (68/84 trials, 70.8%). Of the remaining tri-
als, children chose the patch-matched object on 10/84 trials (10.4%) and the distractor object
on 6/84 trials (6.3%).
As in Experiment 1, we computed Bias Scores for each child by subtracting the mean num-
ber of trials on which they chose the patch-matched object from the mean number of trials on
which they chose the shape-matched object. We found that children’s Bias Scores were sig-
nificantly greater than 0 (M = .69; t(20) = 6.34, p < .001, 95% CI [.46 .92]), with Bayes factor
offering decisive support in favor of the alternative hypothesis that children’s Bias Scores are
reliably different from 0 (BF10 = 6493.5) (see Figure 2). Children’s Bias Scores were not cor-
related with their age in years (continuous) (r(20) = .09, p = .699; see Figure 3). A little over half
of the children were consistent choosers (13/23, 57%), with 12 of those 13 children choosing
shape on all four trials, and the majority of the remaining children biased toward shape (see
Figure 3 for distribution of children’s bias scores). There was no significant difference in chil-
dren’s Bias Scores on trials in which the standard had a patch versus when the standard had no
patch (t(20) = −1.00, p = .329, 95% CI [−.44 .16]), with Bayes factor offering modest support
for the null hypothesis (BF01 = 3.74). Bias Scores were significantly different from 0 both
when the standard had a patch (M = .62; t(20) = 4.24, p < .001, 95% CI [.31 .92], BF10 =
80.02) and when the standard did not have a patch (M = .76; t(20) = 6.78, p < .001, 95%
CI [.53 .99], BF10 = 15,625).
Experiments 1 and 2 Compared. Children’s Bias Scores in Experiment 2 were significantly higher
than in Experiment 1 (t (85) = 4.05, p < .001, 95% CI [.31 .89]), with Bayes factor analysis
offering decisive support for the alternative hypothesis (BF10 = 199.12). Children’s Bias Scores
were not correlated with their age in days, controlling for Experiment (r(89) = .09, p = .414).
OPEN MIND: Discoveries in Cognitive Science
102
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
Discussion
In Experiment 2, when the interior region enclosed by the object changed from an empty hole
into a material surface attached on it, children showed the classic shape bias—children
extended novel labels to objects that shared the same shape as the standard object. These
results suggest that results of Experiment 1 were not due to children perceiving the objects’
holes as figures on top of a background object, but instead suggest competition between
objects’ structural properties (hole or no hole) and surface featural properties (shape) in chil-
dren’s extension of novel nouns.
Most previous research on topological perception reviewed above has (implicitly) treated a
hole as a 2D image region—a uniformly connected region surrounded by another region of a
2D image (e.g., 2D concentric discs forming a doughnut), and thus did not consider whether
the interior region enclosed by the surrounding object was indeed seen as a background sur-
face (a hole). A comparison between Experiments 1 and 2, however, suggests that the percep-
tion of topological properties is not based on image-level representations, but mediated by
surface-level representations (i.e., surface depth order), much as motion perception, texture
segregation, and object recognition are based on surface-level representations (Nakayama
et al., 1995).
Experiment 2 also addressed an additional potential alternative explanation for the results
of Experiment 1. In Experiment 1, because we placed the objects with random rotations,
children could have been less likely to match the objects based on shape, since doing so
required a bit of mental rotation (in order to match the rotated target shape to the standard).
However, in Experiment 2 in which objects also were placed with random rotations, children
generalized a novel name to orientation changes of the same Euclidean shape (i.e., a standard
shape bias), suggesting that the rotations of the objects did not drive the diminished shape
bias we observed in Experiment 1. Further, in line with the notion of Euclidean shape, this
suggests that orientation is not a relevant property characterizing objects in the name gener-
alization task.
EXPERIMENT 3: TOPOLOGY VERSUS COLOR
In Experiment 3, we asked whether topology competes with other surface features more gen-
erally, or whether the effect is limited to metric shape, by pitting objects’ topologies against
objects’ colors. Children viewed a standard object, and then were shown three target objects:
one with the same color as the standard but different topology, one with the same topology as
the standard but different color, and a distractor object. We considered two possible outcomes
for this experiment. On the one hand, both topology and shape can provide cues to the cat-
egories or functions of artifacts, and therefore the competition observed in Experiment 1 may
be specific to the case in which these two object properties are pitted against each other.
On the other hand, children may focus either on structural properties or surface features
when extending labels to novel objects, in which case we may observe competition between
color and topology, similar to the competition between shape and topology observed in
Experiment 1.
Methods
Participants. Participants were 64 3–7-year-olds (mean age = 5.83 years; range = 2.99–7.77).
Parents reported their children to be female (27), male (26), or declined to report their child’s
sex (11). Sample size for this experiment was chosen using the same criteria as in Experiment 1.
Three additional children participated in the study but were excluded from the analysis due
OPEN MIND: Discoveries in Cognitive Science
103
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
.
/
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
to unwillingness to finish the experiment (1), developmental disability (1), or inability to
speak English and therefore to understand the task instructions (1). Children were tested at
the Museum of Science, Boston, as in Experiments 1 and 2.
Materials and Procedure. The materials and procedure were similar to Experiments 1 and 2,
with the following exception. Each trial included one standard object and three target objects:
an object with same color but different topology than the standard, an object with same topol-
ogy but different color than the standard, and a distractor object with bite taken out of its con-
tour, different in color from all the other objects in that trial (see Figure 1). As in Experiment 1,
the shape of each hole varied across all of the objects to prevent children from responding
based on hole shape.
As in Experiment 1, we created two sets of trials, varying which objects had the hole across
the two sets. In each of the sets, there were two trials in which the standard object had a hole
and two trials in which the standard object did not have a hole (see Figure 1 for an example of
one of these sets). The order of the trials was counterbalanced between the participants. Stim-
uli were constructed from different colored carboard using the templates for Experiment 1. The
colors used are shown in Figure 1.
Results
Children’s responses were different than would be expected if they were choosing randomly
between the three target objects (chance = 33.33%, Chi2(2) = 65.299, p < .0001): children
selected the topology-matched object in 113/254 trials (44.48%), the color-matched object
in 117/254 trials (46.06%), and the distractor object in 24/254 trials (9.44%).
As in Experiments 1 and 2, we computed a Bias Score for each child by subtracting the
proportion of trials in which children selected the topology match from the proportion of trials
in which children selected the color match. A positive bias score here indicates a tendency
towards color, a negative bias score indicates a tendency towards topology, and a bias score
closer to 0 indicates competition. Bias Scores were not significantly different from 0 (M = .02,
t(63) = .16, p = .874, 95% CI [−.18 .21]) and Bayes factor analysis resulted in strong support for
the null hypothesis over alternative hypothesis (BF01 = 1.499 × 10−12), see Figure 2. Children’s
Bias Scores were not correlated with age in years (continuous) (r(64) = .037, p = .773; see
Figure 3). Around half of the children consistently chose either color or topology across the
four trials (31/64, 48%), with the remaining children choosing color on some trials and topol-
ogy on other trials suggesting competition between color and topology (see Figure 3 for bias
score distributions).
There was a small but significant difference in children’s responses on trials in which the
standard had a hole compared to trials in which the standard had no hole (t(63), p = .047,
95% CI [−.501, −.003]) although Bayes factor analysis yielded only anecdotal support for
the alternative hypothesis (BF10 = 1.441). Bias Scores across trials in which the standard
object had a hole were not significantly different from 0 (M = −.07, t(63) = −.629, p =
.532, 95% CI [−.293, .153]) and Bayes factor analysis showed moderate support for null
hypothesis (BF01 = 8.381). For trials in which the standard object did not have a hole, Bias
Scores also were not significantly different from 0 (M = .101, t(63) = .994, p = .324, 95% CI
[−.102, .305]) and Bayes factor analysis again showed moderate support for null hypothesis
(BF01 = 6.276).
Experiments 1 and 3 Compared. We compared the distribution of children’s Bias Scores in
Experiments 1 and 3 using a Kolmogorov-Smirnov Test. We found children’s response
OPEN MIND: Discoveries in Cognitive Science
104
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
distributions did not vary between Experiments 1 and 3 ( p = .372) suggesting that shape and
color compete with topology in a similar manner.
Children in Experiment 3 were slightly older on average than in Experiment 1. To examine
whether children’s ages impacted their responses across the two experiments, we ran an
ANOVA on children’s Bias Scores with Experiment (1 and 3) as a between-participants factor
and Age (in years, continuous) as a covariate. This revealed no significant effects of Experiment
(F(1, 127) = .80, p = .374) or Age (F(1, 127) = 1.16, p = .284).
GENERAL DISCUSSION
Past work has shown that objects’ surface features—particularly metric shape—play an
important role in children’s extension of labels to novel artifacts (Dewar & Xu, 2007, 2009;
Diesendruck & Bloom, 2003, Graham & Diesendruck, 2010; Landau et al., 1988, 1992). In a
series of three experiments, we asked whether objects’ structural properties—specifically
topology—also play a role in children’s extension of labels to novel objects. Topological
properties of objects are processed earlier in perception than surface features like shape
(Chen, 1985, 2005), have inductive potential for object categories, and can be associated with
count nouns in the real world (Giralt & Bloom, 2000). Our goal was to examine whether and to
what extent topological properties drive 3-8-year-old children’s extension of count nouns to
novel objects.
In Experiment 1, when topological class was pitted against shape in a name generalization
task, 3–8-year-old children’s extension of novel labels to novel objects suggested competition
between shape and topology: children chose the shape- and topology-matched target objects
at similar rates when asked which target object had the same label as a standard object. These
results were not due to children choosing randomly—children very rarely chose the distractor
object, instead selecting between the shape- or topology-matched objects. The results also
were not driven by children using the shape of the hole to generalize the label, since the shape
of the holes in the test and standard objects varied across all objects. We did not find any
statistical differences in children’s responses when the standard object had a hole compared
to when the standard object did not have a hole, suggesting that children in our sample were
extending labels based on objects’ topology (with or without a hole) and not simply treating
the hole as a salient feature. In Experiment 2, we further confirmed that children’s responses in
Experiment 1 were driven by objects’ topologies by replacing the objects’ holes with gray
patches, reversing the figural status of an interior region enclosed by the surrounding object,
from an empty hole (background) to a material surface (foreground). We observed the classic
shape bias effect in Experiment 2, and children’s responses in Experiment 2 were significantly
different from those in Experiment 1, suggesting that in Experiment 1 topology indeed com-
peted with shape when extending labels to novel objects. This between-experiments contrast
also suggests that unlike a patch on an object, which is not an intrinsic property of the object
(and thus potentially detachable), a hole is an intrinsic and ontologically parasitic property of
its host object (Casati & Varzi, 1994; Kim, 2020), which is stable over changes in viewpoints,
and thus counted for name extension. Finally, in Experiment 3, we pit another surface feature,
color, against topology in the name generalization task, and found competition between color
and topology in children’s extension of novel nouns to novel objects. Together with the results
of Experiments 1 and 2, these results suggest that objects’ structural properties complete with
objects’ surface featural properties in children’s extension of labels to novel objects.
Previous work has shown the primacy of topology for object perception and attention, lead-
ing to the suggestion that topological invariance is a core of object representation (e.g., Chen,
OPEN MIND: Discoveries in Cognitive Science
105
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
2005; Zhou et al., 2010). Nevertheless, we did not observe that topology also superseded sur-
face features in children’s label extensions. One possibility is that the competition we
observed between objects’ topologies and surface features in our name generalization task
is driven by subtle differences in the inductive potential of these properties. Topological class
and surface featural properties both have inductive potential for making inferences about
objects’ functions, but each may provide different types of information about object category.
Consider two objects with similar topologies: a coffee mug and a handbag. These two objects
vary substantially in their surface features and in their basic functions (one is for holding a
beverage which is then consumed, one is for carrying your personal items), but their similar
topologies dictate how the objects can be interacted with by humans (e.g., both are grasped by
the handle). Now consider two objects with different topologies: a needle and a pin. These two
objects are very similar in shape, but their different topologies dictate how the objects can be
interacted with by humans (a needle can be threaded and used for sewing, a pin cannot be
threaded and is used for fastening). Both topological and shape properties of objects map onto
objects’ affordances, but do not necessarily map consistently onto objects’ functions. That is,
while the different functions of a pin and needle solely depend on the difference in the topol-
ogy (and not shape) of these objects, the different functions of a mug and a handbag depend on
surface featural and material properties, such as size and texture, and not topology. In everyday
situations, we likely use both topology and surface features to make these different types of
inferences about object categories. In our experiments, we set up a situation where children
needed to use one or the other, but could not use both, and we therefore speculate that this
therefore drove the competition we observed in our experiments—at least in the context of a
name generalization task.
We admit that this line of argument is speculative and requires further investigation. How-
ever, it not only provides a plausible explanation of our results, but also does not conflict with
extant accounts of the shape bias in the literature. The attention learning account proposes that
children extract statistical associations between the linguistic input (e.g., ‘This’), labels (e.g.,
‘toma’), and perceptual categories (e.g., solid, nonsolid) that exist in the real world and use
these associations to guide their attention to historically relevant perceptual features for the
object or artifact in question to inform about the object category (Colunga & Smith, 2008;
Landau et al., 1998). According to this account, children associate metric shape with artifacts
because objects that belong to same category often share shape in the real world, and there-
fore shape can act as a default bootstrapping mechanism for children to generalize count
nouns in the absence of a prior category knowledge (Colunga & Smith, 2008; Landau et al.,
1998). Like shape, count nouns also may be associated with structural features like topology in
the real world and may therefore drive attention to topological properties. For example, the
label “straw” is associated with elongated objects with holes through their center that can vary
in color, size, and texture. Children may therefore use these past associations between labels
and topology to generalize in a novel situation in which topology is a potentially relevant
feature.
Another account (e.g., Diesendruck & Bloom, 2003; Markson et al., 2008) proposes that
shape acts as a cue to kind membership; children generalize count nouns to objects that share
the same shape because they understand that count nouns are used to refer to object kinds,
and shape provides reliable information about objects’ kinds. Similarly, children also may
have an expectation that topology can provide reliable information about object kinds, even
when overall shape does not. For example, a straw can be used to drink from, while a chop-
stick cannot; a needle can be threaded, while a pin cannot; a colander can be used to drain
pasta, while a bowl cannot; a tank-top can be worn comfortably, while a pillowcase cannot.
OPEN MIND: Discoveries in Cognitive Science
106
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
Children may recognize the inductive potential of topology as they do shape, and may also
expect count nouns to refer to topological properties of objects, at least under some
circumstances.
Indeed, there also are plenty of cases in which objects’ topologies do not impact their func-
tion. It is possible that unless topological differences result in obvious functional differences,
holes may not necessarily play a critical role in categorization. For example, both ring dough-
nuts and filled doughnuts are called doughnuts in spite of their topological differences. And
accidentally generated holes (which are not originally the feature of the objects) usually do not
influence the identity or function of objects. For example, worms can create little holes in
leaves and friction can cause pinholes in T-shirts, but the introduction of these holes does
not change the objects’ categorical identities. In our task, we did not provide children with
explanations for the causal origin of the holes (or lack thereof ) in the objects, which may have
reduced the inferential potential of topology in our task. We also used flat objects whose “arti-
factness” might not have been as readily apparent to children (that is, children may not have
readily inferred that the objects could be used for some purpose). This was by design, since we
wanted to carefully control the perceptual dimensions of the stimuli. However, the structure of
the stimuli may also have reduced the inductive potential of topology in the task. Future work
would investigate whether providing information on specific functions of holes and/or the
causal origins of holes would impact the inferential role of object topologies versus surface
features in children’s object categorization.
Previous work using the name generalization task to understand children’s extension of
labels to novel objects focused on very young children, with some studies finding that shape
bias increases between 2 and 3 years of age (e.g., Landau et al., 1988) and other studies show-
ing no change in shape bias in this age range (Diesendruck & Bloom, 2003). Our experiments,
by contrast, included participants from a wider age range (3–8-year-olds) in order to investi-
gate whether children’s use of objects’ structural properties versus surface featural properties
for noun generalization changed over development. We investigated a wide age range
because our goal was not to find the emergence of a bias, but instead to test whether topology
competes with shape in children for whom the shape bias is relatively well established, and
whether the extent of this competition may change over the course of development. We did
not find significant developmental change in children’s bias towards topology or surface
features across our sample. These results suggest that, even with extensive experience with
language and object categorization, topology may play a fairly consistent role in children’s
generalization of novel nouns across the lifespan. It is possible that a finer-grained examination
into the younger end of our age range, or in children older than 8, could reveal subtle devel-
opmental affects that were not revealed in our study. Future work could examine this
possibility.
Our results provide some potential insights into the role of topology in object representa-
tion. Previous work showed that topological class is processed earlier in vision (e.g., Chen,
1985), earlier in development (e.g., Chen et al., 2003; Chien et al., 2012; but see also Tang
et al., 2021), and plays a significant role in the way objects are represented, tracked, and
attended to across the lifespan (e.g., Baillargeon et al., 2012; He et al., 2015; Hespos &
Baillargeon, 2001a, 2001b, 2006; Kibbe & Leslie, 2016; Rips, 2020; Wang et al., 2005;
Wei et al., 2019; Wolfe & Horowitz, 2017; Zhou et al., 2010; Zhuo et al., 2003). Our results
suggest that objects’ topological properties may also play a role in the formation of object
categories, but topology does not necessarily take precedence over surface features in the
extension of labels. More work is needed to investigate the generalizability of this finding to
contexts outside of label extension in which children are asked to make inferences about
OPEN MIND: Discoveries in Cognitive Science
107
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
.
/
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
objects’ categories or kinds. It is possible that the phenomenon we observed is limited to label
extension in general, or to the label extension task more specifically. For example, by asking
children to choose among alternatives with narrowly-defined parameters, we artificially nar-
rowed the hypothesis space of the possible extensions of the novel nouns (see Fodor, 1972, for
broader discussion). In other, more real-world scenarios, topological properties of objects may
play a different role in children’s inferences about object kinds. Or, our results could reflect a
more general predisposition to attend to topology as a category- or kind-relevant feature.
Future work would examine these possibilities.
In this study we only tested one aspect of topology (holes). However, there are a range of
other topological properties of objects, including inside/outside relationships and connected-
ness between objects, which may play different roles in children’s label extension. It is possi-
ble that holes may provide stronger cues to object category membership than other topological
properties, perhaps because holes may be predictive of objects’ functions. Also, our manipu-
lation of topology (presence versus absence of a hole) may have elicited a more dichotomous
representation than surface featural properties of objects like shape or color, making matching
on topology easier than matching on shape or color. Future research should study the role of
different topological properties in children’s extension of novel objects, including examining
the inductive potential of these features for object categorization, under what circumstances
children may (or may not) use these features in their extension of new nouns, to what extent
topological features compete with each other during label extension, and the factors that may
influence competition between topology and surface features (including the relative salience
of these different object dimensions).
ACKNOWLEDGMENTS
The authors wish to thank the staff at the Museum of Science, Boston, where the data were
collected.
AUTHOR CONTRIBUTIONS
Praveen Kenderla: Conceptualization; Formal analysis; Investigation; Methodology; Resources;
Visualization; Writing – Original draft; Writing – Review & editing. Sung-Ho Kim: Conceptu-
alization; Methodology; Writing – Review & editing. Melissa M. Kibbe: Conceptualization;
Formal analysis; Methodology; Project administration; Visualization; Writing – Review & editing.
DATA AVAILABILITY STATEMENT
D a t a a n d s t i m u l i t e m p l a t e s a r e a v a i l a b l e a t h t t p s : / / o s f . i o / k 3 h z n / ? v i e w _ o n l y
=e046ab287e6343ac9549269387748e90.
REFERENCES
Amir, O., Biederman, I., Herald, S. B., Shah, M. P., & Mintz, T. H.
(2014). Greater sensitivity to nonaccidental than metric shape
properties in preschool children. Vision Research, 97, 83–88.
https://doi.org/10.1016/j.visres.2014.02.006, PubMed:
24582797
Baillargeon, R., Stavans, M., Wu, D., Gertner, Y., Setoh, P.,
Kittredge, A. K., & Bernard, A. (2012). Object individuation
and physical reasoning in infancy: An integrative account. Lan-
guage Learning and Development, 8(1), 4–46. https://doi.org/10
.1080/15475441.2012.630610, PubMed: 23204946
Booth, A. E., & Waxman, S. R. (2002). Word learning is ‘smart’:
Evidence that conceptual information affects preschoolers’
extension of novel words. Cognition, 84(1), B11–B22. https://
doi.org/10.1016/S0010-0277(02)00015-X, PubMed: 12062150
Booth, A. E., & Waxman, S. R. (2008). Taking stock as theories of
word learning take shape. Developmental Science, 11(2),
185–194. https://doi.org/10.1111/j.1467-7687.2007.00664.x,
PubMed: 18333973
Booth, A. E., Waxman, S. R., & Huang, Y. T. (2005). Conceptual
information permeates word learning in infancy. Developmental
OPEN MIND: Discoveries in Cognitive Science
108
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
Psychology, 41(3), 491–505. https://doi.org/10.1037/0012-1649
.41.3.491, PubMed: 15910157
Casati, R., & Varzi, A. C. (1994). Holes and other superficialities.
MIT Press. https://doi.org/10.7551/mitpress/3555.001.0001
Chen, L. (1985). Topological structure in the perception of apparent
motion. Perception, 14(2), 197–208. https://doi.org/10.1068
/p140197, PubMed: 4069950
Chen, L. (2005). The topological approach to perceptual organiza-
tion. Visual Cognition, 12(4), 553–637. https://doi.org/10.1080
/13506280444000256
Chen, L., Zhang, S., & Srinivasan, M. V. (2003). Global perception
in small brains: Topological pattern recognition in honey bees.
Proceedings of the National Academy of Sciences, 100(11),
6884–6889. https://doi.org/10.1073/pnas.0732090100,
PubMed: 12750474
Chien, S. H.-L., Lin, Y.-L., Qian, W., Zhou, K., Lin, M.-K., & Hsu,
H.-Y. (2012). With or without a hole: Young infants’ sensitivity for
topological versus geometric property. Perception, 41(3),
305–318. https://doi.org/10.1068/p7031, PubMed: 22808584
Colunga, E., & Smith, L. B. (2008). Knowledge embedded in
process: The self-organization of skilled noun learning. Develop-
mental Science, 11(2), 195–203. https://doi.org/10.1111/j.1467
-7687.2007.00665.x, PubMed: 18333974
Dewar, K., & Xu, F. (2007). Do 9-month-old infants expect distinct
words to refer to kinds? Developmental Psychology, 43(5),
1227–1238. https://doi.org/10.1037/0012-1649.43.5.1227,
PubMed: 17723047
Dewar, K., & Xu, F. (2009). Do early nouns refer to kinds or distinct
shapes? Evidence from 10-month-old infants. Psychological
Science, 20(2), 252–257. https://doi.org/10.1111/j.1467-9280
.2009.02278.x, PubMed: 19175526
Diesendruck, G., & Bloom, P. (2003). How specific is the shape
bias? Child Development, 74(1), 168–178. https://doi.org/10
.1111/1467-8624.00528, PubMed: 12625443
Elman, J. L. (2008). The shape bias: An important piece in a bigger
puzzle. Developmental Science, 11(2), 219–222. https://doi.org
/10.1111/j.1467-7687.2007.00669.x, PubMed: 18333978
Fodor, J. (1972). Some reflections on L. S. Vygotsky’s thought and
language. Cognition, 1(1), 83–95. https://doi.org/10.1016/0010
-0277(72)90046-7
Gelman, S. A., & Meyer, M. (2011). Child categorization. Wiley
Interdisciplinary Reviews: Cognitive Science, 2(1), 95–105.
https://doi.org/10.1002/wcs.96, PubMed: 23440312
Giralt, N., & Bloom, P. (2000). How special are objects? Children’s
reasoning about objects, parts, and holes. Psychological Science,
11(6), 497–501. https://doi.org/10.1111/1467-9280.00295,
PubMed: 11202496
Gogate, L. J., & Hollich, G. (2010). Invariance detection within an
interactive system: A perceptual gateway to language develop-
ment. Psychological Review, 117(2), 496–516. https://doi.org/10
.1037/a0019049, PubMed: 20438235
Graham, S. A., & Diesendruck, G. (2010). Fifteen-month-old infants
attend to shape over other perceptual properties in an induction
task. Cognitive Development, 25(2), 111–123. https://doi.org/10
.1016/j.cogdev.2009.06.002
He, L., Zhou, K., Zhou, T., He, S., & Chen, L. (2015). Topology-
defined units in numerosity perception. Proceedings of the
National Academy of Sciences, 112(41), E5647–E5655. https://
doi.org/10.1073/pnas.1512408112, PubMed: 26417075
Hespos, S. J., & Baillargeon, R. (2001a). Infants’ knowledge about
occlusion and containment events: A surprising discrepancy.
Psychological Science, 12(2), 141–147. https://doi.org/10.1111
/1467-9280.00324, PubMed: 11340923
Hespos, S. J., & Baillargeon, R. (2001b). Reasoning about contain-
ment events in very young infants. Cognition, 78(3), 207–245.
https://doi.org/10.1016/S0010-0277(00)00118-9, PubMed:
11124350
Hespos, S. J., & Baillargeon, R. (2006). Décalage in infants’ knowl-
edge about occlusion and containment events: Converging evi-
dence from action tasks. Cognition, 99(2), B31–B41. https://doi
.org/10.1016/j.cognition.2005.01.010, PubMed: 15939414
Hoffman, D. D., & Richards, W. A. (1984). Parts of recognition.
Cognition, 18(1–3), 65–96. https://doi.org/10.1016/0010-0277
(84)90022-2, PubMed: 6543164
Hummel, J. E., & Biederman, I. (1992). Dynamic binding in a neural
network for shape recognition. Psychological Review, 99(3),
480–517. https://doi.org/10.1037/0033-295X.99.3.480,
PubMed: 1502274
Izard, V., Pica, P., & Spelke, E. S. (2022). Visual foundations of
Euclidean geometry. Cognitive Psychology, 136, 101494.
https://doi.org/10.1016/j.cogpsych.2022.101494, PubMed:
35751917
Kibbe, M. M., & Leslie, A. M. (2016). The ring that does not bind:
Topological class in infants’ working memory for objects. Cogni-
tive Development, 38, 1–9. https://doi.org/10.1016/j.cogdev
.2015.12.001
Klein, F. (1893). A comparative review of recent researches in
geometry. Bulletin of the New York Mathematical Society,
2(10), 215–249. https://doi.org/10.1090/S0002-9904-1893
-00147-X
Kim, S.-H. (2020). Bouba and Kiki inside objects: Sound-shape cor-
respondence for objects with a hole. Cognition, 195, 104132.
https://doi.org/10.1016/j.cognition.2019.104132, PubMed:
31726323
Kucker, S. C., Samuelson, L. K., Perry, L. K., Yoshida, H., Colunga,
E., Lorenz, M. G., & Smith, L. B. (2019). Reproducibility and
a unifying explanation: Lessons from the shape bias. Infant
Behavior and Development, 54, 156–165. https://doi.org/10
.1016/j.infbeh.2018.09.011, PubMed: 30343894
Landau, B., Smith, L. B., & Jones, S. (1988). The importance of
shape in early lexical learning. Cognitive Development, 3(3),
299–321. https://doi.org/10.1016/0885-2014(88)90014-7
Landau, B., Smith, L. B., & Jones, S. (1992). Syntactic context and
the shape bias in children’s and adults’ lexical learning. Journal
of Memory and Language, 31(6), 807–825. https://doi.org/10
.1016/0749-596X(92)90040-5
Landau, B., Smith, L. B., & Jones, S. (1998). Object perception and
object naming in early development. Trends in Cognitive Sci-
ences, 2(1), 19–24. https://doi.org/10.1016/S1364-6613(97)
01111-X, PubMed: 21244958
Landau, B., & Leyton, M. (1999). Perception, object kind, and
object naming. Spatial Cognition and Computation, 1(1), 1–29.
https://doi.org/10.1023/A:1010073227203
Lazareva, O. F., Wasserman, E. A., & Biederman, I. (2008). Pigeons
and humans are more sensitive to nonaccidental than to metric
changes in visual objects. Behavioural Processes, 77(2), 199–209.
https://doi.org/10.1016/j.beproc.2007.11.009, PubMed: 18248918
Lowet, A. S., Firestone, C., & Scholl, B. J. (2018). Seeing structure:
Shape skeletons modulate perceived similarity. Attention,
Perception, & Psychophysics, 80(5), 1278–1289. https://doi.org
/10.3758/s13414-017-1457-8, PubMed: 29546555
Markson, L., Diesendruck, G., & Bloom, P. (2008). The shape of
thought. Developmental Science, 11(2), 204–208. https://doi
.org/10.1111/j.1467-7687.2007.00666.x, PubMed: 18333975
Marr, D., & Nishihara, H. K. (1978). Representation and recognition
three-dimensional shapes.
the spatial organization of
of
OPEN MIND: Discoveries in Cognitive Science
109
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
/
.
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Topology in children’s noun extension
Kenderla et al.
Proceedings of the Royal Society of London, Series B: Biological
Sciences, 200(1140), 269–294. https://doi.org/10.1098/rspb
.1978.0020, PubMed: 24223
Nakayama, K., He, Z. J., & Shimojo, S. (1995). Visual surface rep-
l i n k b e t w e e n l o we r - l e v e l a n d
r e s e n t a t i o n : A c r i t i c a l
higher-level vision. In S. M. Kosslyn & D. N. Osherson
(Eds.), Visual cognition: An invitation to cognitive science
(pp. 1–70). MIT Press.
Nelson, D. G. K., Frankenfield, A., Morris, C., & Blair, E. (2000).
Young children’s use of functional information to categorize arti-
facts: Three factors that matter. Cognition, 77(2), 133–168.
https://doi.org/10.1016/S0010-0277(00)00097-4, PubMed:
10986365
Rips, L. J. (2020). Possible objects: Topological approaches to indi-
viduation. Cognitive Science, 44(11), e12916. https://doi.org/10
.1111/cogs.12916, PubMed: 33164272
Rosch, E. (1978). Principles of categorization. In E. Rosch & B. B.
Lloyd (Eds.), Cognition and categorization (pp. 27–48). Lawrence
Erlbaum Associates.
Rosch, E., Mervis, C. B., Gray, W. D., Johnson, D. M., & Boyes-
Braem, P. (1976). Basic objects in natural categories. Cognitive
Psychology, 8(3), 382–439. https://doi.org/10.1016/0010-0285
(76)90013-X
Soja, N. N., Carey, S., & Spelke, E. S. (1991). Ontological categories
guide young children’s inductions of word meaning: Object
terms and substance terms. Cognition, 38(2), 179–211. https://
doi.org/10.1016/0010-0277(91)90051-5, PubMed: 2049905
Smith, L. B. (1995). Self-organizing processes in learning to learn
words: Development is not induction. In C. A. Nelson (Ed.), Basic
and applied perspectives on learning, cognition, and develop-
ment (pp. 1–32). Lawrence Erlbaum Associates.
Smith, L. B. (1999). Children’s noun learning: How general learning
processes make specialized learning mechanisms. In B. Mac-
Whinney (Ed.), The emergence of language (pp. 277–303).
Lawrence Erlbaum Associates.
Smith, L. B., Jones, S. S., & Landau, B. (1996). Naming in young
children: A dumb attentional mechanism? Cognition, 60(2),
143–171. https://doi.org/10.1016/0010-0277(96)00709-3,
PubMed: 8811743
Tang, H., Song, R., Hu, Y., Tian, Y., Lu, Z., Chen, L., & Huang, Y.
(2021). Late development of early visual perception: No
topology-priority in peripheral vision until age 10. Child
Development, 92(5), 1906–1918. https://doi.org/10.1111/cdev
.13629, PubMed: 34569057
Todd, J. T., & Petrov, A. A. (2022). The many facets of shape. Jour-
nal of Vision, 22(1), Article 1. https://doi.org/10.1167/jov.22.1.1,
PubMed: 34982105
Todd, J. T., Weismantel, E., & Kallie, C. S. (2014). On the relative
detectability of configural properties. Journal of Vision, 14(1),
Article 18. https://doi.org/10.1167/14.1.18, PubMed: 24453344
Turati, C., Simion, F., & Zanon, L. (2003). Newborns’ perceptual
categorization for closed and open geometric forms. Infancy,
4(3), 309–325. https://doi.org/10.1207/S15327078IN0403_01
Wang, S.-H., Baillargeon, R., & Paterson, S. (2005). Detecting con-
tinuity violations in infancy: A new account and new evidence
from covering and tube events. Cognition, 95(2), 129–173.
https://doi.org/10.1016/j.cognition.2002.11.001, PubMed:
15694644
Ware, E. A., & Booth, A. E. (2010). Form follows function: Learning
about function helps children learn about shape. Cognitive
Development, 25(2), 124–137. https://doi.org/10.1016/j.cogdev
.2009.10.003
Wei, N., Zhou, T., Zhang, Z., Zhuo, Y., & Chen, L. (2019). Visual
working memory representation as a topological defined percep-
tual object. Journal of Vision, 19(7), Article 12. https://doi.org/10
.1167/19.7.12, PubMed: 31323098
Wolfe, J. M., & Horowitz, T. S. (2017). Five factors that guide atten-
tion in visual search. Nature Human Behaviour, 1(3), Article
0058. https://doi.org/10.1038/s41562-017-0058, PubMed:
36711068
Zhou, K., Luo, H., Zhou, T., Zhuo, Y., & Chen, L. (2010). Topolog-
ical change disturbs object continuity in attentive tracking.
Proceedings of the National Academy of Sciences, 107(50),
21920–21924. https://doi.org/10.1073/pnas.1010919108,
PubMed: 21115830
Zhuo, Y., Zhou, T. G., Rao, H. Y., Wang, J. J., Meng, M., Chen, M.,
Zhou, C., & Chen, L. (2003). Contributions of the visual ventral
pathway to long-range motion. Science, 299(5605), 417–420.
https://doi.org/10.1126/science.1077091, PubMed: 12532023
Zuniga-Montanez, C., Kita, S., Aussems, S., & Krott, A. (2021).
Beyond the shape of things: Infants can be taught to generalize
nouns by objects’ functions. Psychological Science, 32(7),
1073–1085. https://doi.org/10.1177/0956797621993107,
PubMed: 34111370
OPEN MIND: Discoveries in Cognitive Science
110
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
o
p
m
i
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
i
/
.
/
1
0
1
1
6
2
o
p
m
_
a
_
0
0
0
7
3
2
0
7
8
8
9
2
o
p
m
_
a
_
0
0
0
7
3
p
d
/
.
i
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3