REPORT - IA de Investigación especializada en el MIT

INFORME

Communicating Compositional Patterns

Eric Schulz1, Francisco Quiroga2, and Samuel J. Gershman3

1Max Planck Institute for Biological Cybernetics

2University College London

3Harvard University

un acceso abierto

diario

Palabras clave: communication games, cultural transmission, composicionalidad, function learning

ABSTRACTO

How do people perceive and communicate structure? We investigate this question by letting
participants play a communication game, where one player describes a pattern, and another
player redraws it based on the description alone. We use this paradigm to compare two
models of pattern description, one compositional (complex structures built out of simpler
unos) and one noncompositional. We ﬁnd that compositional patterns are communicated
more effectively than noncompositional patterns, that a compositional model of pattern
description predicts which patterns are harder to describe, and that this model can be used to
evaluar los dibujos de los participantes, producir calificaciones de calidad humanas. Nuestros resultados sugieren que
El lenguaje natural puede aprovechar un lenguaje de descripción de patrones estructurado composicionalmente..

INTRODUCCIÓN

Los humanos ven patrones en todas partes, y comunicarlos con entusiasmo unos a otros. Sin embargo,
Se sabe poco formalmente sobre cómo comunicamos patrones., ¿Qué tipo de patrones son fáciles?-
Más o más difícil de comunicar., y cómo reconstruimos patrones a partir del lenguaje natural. Este
El artículo busca cerrar esta brecha combinando un juego de comunicación de patrones con una matemática.-
modelo ical de descripción de patrones (Quiroga, Schulz, al borde del discurso, & harvey, 2018; Schulz,
Tenenbaum, Duvenaud, al borde del discurso, & Gershman, 2017).

Considere los gráficos que se muestran en la Figura. 1, que trazan series temporales de emisiones de CO2, aire-
volumen de pasajeros de línea, y frecuencia de búsqueda del término "membresía de gimnasio". experimentos
sugieren que los humanos perciben estos gráficos como composiciones de patrones más simples, como líneas,
oscilaciones, y curvas que cambian suavemente (Quiroga et al., 2018; Schulz, Tenenbaum, et al.,
2017). Por ejemplo, hay variación estacional en el volumen de pasajeros (un componente periódico
con amplitud dependiente del tiempo), superpuesto a un aumento lineal en el tiempo.

Como se describe con más detalle en la siguiente sección, Podemos formalizar esta idea usando un patrón.
Lenguaje de descripción que consta de primitivas funcionales y operaciones algebraicas que se combinan.-
posarlos juntos. Al definir una distribución de probabilidad sobre este lenguaje de descripción, nosotros
puede expresar un sesgo inductivo para ciertos tipos de funciones, en particular, funciones que pueden
ser descrito con un pequeño número de composiciones (Duvenaud, lloyd, Grosse, Tenenbaum,
& Ghahramani, 2013; lloyd, Duvenaud, Grosse, Tenenbaum, & Ghahramani, 2014; Schulz,
Tenenbaum, et al., 2017). En otras palabras, La longitud de la descripción “mental” de una función se relaciona
a la complejidad de su codificación en el lenguaje de descripción de patrones compositivos.

Citación: Schulz, MI., Quiroga, F., &
Gershman, S. j. (2020).
Comunicando composicionalmente
Patrones. Mente abierta: Descubrimientos
en Ciencias Cognitivas, 4, 25–39.
https://doi.org/10.1162/opmi_a_00032

DOI:
https://doi.org/10.1162/opmi_a_00032

Materiales suplementarios:
https://www.mitpressjournals.org/doi/
suppl/10.1162/opmi_a_00032

Recibió: 25 Octubre 2018
Aceptado: 11 Puede 2020

Conflicto de intereses: Los autores
declaran no tener ningún conflicto de
interés.

Autor correspondiente:
Eric Schultz
eric.schulz@tuebingen.mpg.de

Derechos de autor: © 2020
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia

La prensa del MIT

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

Cifra 1. Ejemplos de patrones compositivos. (a) Concentración media mensual de CO2 atmosférico-
ciones recopiladas en el Observatorio Mauna Loa en Hawaii de 1960 a 2010. (b) Número de aerolínea
(2015). (C) consultas de Google para
pasajeros de 1960 a 2010, recopilado originalmente por Box et al..
“Membresía de gimnasio” de 2002 a 2012 en la ciudad de londres.

Es importante tener en cuenta que existen otras formas de reducir la longitud de la descripción además de en-
funciones de codificación con un pequeño conjunto de composiciones (lo que llamaremos “composicional”.
funciones”). Por ejemplo, Una suposición estándar en el aprendizaje automático es que las funciones son
liso (Rasmussen & williams, 2006). Si definimos una distribución de probabilidad sobre func-
ciones que prefieren la suavidad, entonces las funciones fluidas tendrían longitudes de descripción cortas, en
la sensación de que el número de bits necesarios para codificarlos sería menor que el no suave
funciones. Sin embargo, una preferencia por la suavidad no parece ser una explicación adecuada de
cómo los humanos codifican funciones: Funciones que son fluidas pero que no se pueden describir de forma compacta.
por composiciones se codifican con menos facilidad, como lo indica una peor memoria y detección de cambios
rendimiento para estas funciones en comparación con las funciones de composición (Schulz, Tenenbaum,
et al., 2017; ver análisis adicional en los Materiales complementarios).

Aquí ampliamos esta idea un paso más allá., preguntando si hay correspondencia
entre el lenguaje de descripción de patrones y las descripciones de funciones en lenguaje natural. Nosotros
proceder en tres pasos. Primero, Pedimos a los participantes que describan funciones muestreadas de compo.-
distribuciones sicionales o no compositivas. Segundo, Le pedimos a un grupo separado de participantes que
volver a dibujar la función original usando solo la descripción. Tercero, le preguntamos a otro grupo de par-
Los participantes calificarán en qué medida cada dibujo corresponde al original.. Nosotros planteamos la hipótesis de que
Las funciones compositivas serían más fáciles de reconstruir en comparación con las funciones no compositivas.-
ciones, bajo el supuesto de que los primeros permiten una descripción mental que puede ser más
codificado fácilmente en lenguaje natural y decodificado nuevamente en el espacio funcional. nosotros también gobernamos
varias explicaciones alternativas y asigna descripciones específicas de patrones a composiciones
componentes con la ayuda de un experimento adicional.

UN LENGUAJE DE DESCRIPCIÓN DE PATRONES COMPOSICIONALES

Nuestro modelo de descripción de patrones se basa en un proceso gaussiano. (médico de cabecera) enfoque de regresión para
function learning (Rasmussen & williams, 2006; Schulz, al borde del discurso, & Krause, 2017). A
GP es una colección de variables aleatorias., cualquier subconjunto finito del cual es conjuntamente gaussiano. Un médico de cabecera
define una distribución sobre funciones. sea f : X → R denota una función sobre un espacio de entrada X
que se asigna a salidas escalares de valor real. Esta función se puede modelar como un sorteo aleatorio de
un médico de cabecera:

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

f ∼ GP (metro, k).

(1)

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

La función media m especifica la salida esperada de la función dada la entrada x, y el núcleo
La función k especifica la covarianza entre salidas.:

metro(X) = mi [ F (X)]

k(X, incógnita') = mi

(cid:2)

( F (X) − metro(X))( F (incógnita') − metro(incógnita'))

(cid:3)

(2)

(3)

Seguimos la convención estándar al suponer una media previa de 0 (Rasmussen & williams, 2006).

Todos los núcleos semidefinidos positivos son cerrados bajo suma y multiplicación., permitiendo
Nos permite crear núcleos ricamente estructurados e interpretables a partir de componentes básicos bien comprendidos..
Usamos esta propiedad para construir una clase de núcleos compositivos. (Duvenaud et al., 2013;
Lloyd et al., 2014; Schulz, Tenenbaum, et al., 2017). Para dar alguna intuición para este enfoque.,
considere nuevamente los datos de CO2 en la Figura 1. Esta función se descompone naturalmente en una suma
de un componente linealmente creciente y un componente estacionalmente periódico. La composición
kernel captura esta estructura sumando un kernel lineal y periódico.

Los GP composicionales se han utilizado para modelar datos complejos de series de tiempo. (Duvenaud et al.,
2013), así como generar descripciones automatizadas en lenguaje natural a partir de datos (Lloyd et al.,
2014), un enfoque acuñado el "estadístico automatizado" (Ghahramani, 2015). aunque
Con frecuencia se supone que las personas comprenderán fácilmente la descripción generada del
“estadístico automatizado,"No se sabe si los patrones compositivos son realmente más
comunicable.

Seguimos el enfoque desarrollado en Schulz, Tenenbaum, et al. (2017), usando tres bases
Núcleos que definen patrones estructurales básicos.: un núcleo lineal que puede codificar tendencias, una ba radial-
kernel de función sis que puede codificar funciones fluidas, y un núcleo periódico que puede codificar
patrones repetidos (ver tabla 1). Estos núcleos se pueden combinar multiplicando o sumando
ellos juntos. En investigaciones anteriores, encontramos que esta gramática compositiva puede dar cuenta
para el comportamiento de los participantes a través de una variedad de paradigmas experimentales, incluyendo patrón com-
pleciones, detección de cambios, y trabajando, tareas de memoria (Schulz, Tenenbaum, et al., 2017). Nosotros
Fije el número máximo de granos combinados en tres y no permita la repetición de
núcleos para restringir la complejidad de la inferencia (ver la siguiente sección).

Comparamos el modelo compositivo con un modelo no compositivo basado en una especificación.-
mezcla central de granos (ver materiales complementarios, para más detalles). Este modelo se deriva
del hecho de que cualquier núcleo estacionario se puede expresar como una integral utilizando la fórmula de Bochner.-
orem. Este modelo aproxima funciones haciendo coincidir su densidad espectral con una mezcla
de gaussianos. Tiene una expresividad similar al modelo compositivo, pero lo hace

Mesa 1. Núcleos básicos en la gramática compositiva..

Nombre

Definición

Lineal

k(X, incógnita') = (x − θ1)(x′ − θ1)

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

base radial

Periódico

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

k(X, incógnita') = θ2

2 exp. (cid:16)− (x-x′)2

2i2
3

(cid:17)

k(X, incógnita') = θ2

4 exp. (cid:16)− 2 pecado2(Pi|x-x′|i5)

i2
6

(cid:17)

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

no codificar la estructura compositiva explícitamente. Esto significa que ambos modelos serán similares.-
predicciones largas dadas datos ilimitados; sin embargo, dado un régimen de datos finito, la composicional
El núcleo tendrá fuertes sesgos inductivos para las funciones de composición., mientras que el espectral
El núcleo no mostrará tales sesgos inductivos.. wilson, Entonces, lucas, y xing (2015) he usado
este modelo para realizar ingeniería inversa en “núcleos humanos” en tareas estándar de aprendizaje de funciones. Usamos
este núcleo para evaluar si la comunicación de patrones puede describirse bien mediante un núcleo que sea
igualmente expresivo que el núcleo compositivo pero no opera sobre la construcción estructural
bloques. En lugar de optimizar sus parámetros para encontrar núcleos similares a los humanos en la función tradicional-
tareas de aprendizaje, Lo optimizaremos en función de la estructura que los participantes tuvieron que describir.1

APRENDIZAJE DE FUNCIONES DE MODELADO

Modelamos la descripción de patrones humanos usando inferencia bayesiana sobre funciones con un GP previo.,
un enfoque que se ha aplicado con éxito a una variedad de experimentos y observaciones.
datos (Griffiths, lucas, williams, & kalish, 2009; lucas, Griffiths, williams, & kalish, 2015;
Schultz y cols., 2019; Wu, Schulz, al borde del discurso, nelson, & Cama, 2018). Dado un observado
patrón, re = {xn, en}norte
norte=1, donde en ∼ N ( F (xn), p2) es un sorteo de la función latente, el
La distribución predictiva posterior para una nueva entrada x∗ también se distribuye normalmente., dónde

mi[ F (x∗)|D] =k⊤
V[ F (x∗)|D] =k(x∗, x∗) −k⊤

∗ (k + p2I)−1y

⋆ (k + p2I)−1k∗,

(4)

(5)

son la media y la varianza, respectivamente. El término y = [y1, . . . , entonces]⊤, K es la matriz N × N
de covarianzas evaluadas en cada par de entradas observadas, y k∗ = [k(x1, x∗), . . . , k(xN, x∗)]
es la covarianza entre cada entrada observada y la nueva entrada x∗.

Utilizamos un enfoque de comparación de modelos bayesianos para evaluar qué tan bien un ker en particular-
nel captura los datos, teniendo en cuenta la complejidad del modelo. Asumiendo un uniforme previo sobre
granos, la probabilidad posterior a favor de un núcleo particular es proporcional a la marginal
probabilidad de los datos bajo ese modelo. La probabilidad logarítmica marginal para un médico de cabecera con hiperpa-
los parámetros θ están dados por:

iniciar sesión p(y|X, i) := -

1
2

y⊤(k + p2

yo)−1y −

1
2

registro |k + p2

yo| −

norte
2

iniciar sesión 2π,

(6)

donde la dependencia de K de θ queda implícita. Los hiperparámetros se eligen para maximizar
la probabilidad log-marginal, usando optimización basada en gradiente (Rasmussen & Nickish, 2010).

GENERANDO PATRONES

Usamos los mismos patrones que en Schulz., Tenenbaum, et al. (2017). Estos patrones fueron gener-
a partir de elementos compositivos y no compositivos. (mezcla espectral) granos. el compo-
Los patrones posicionales fueron muestreados aleatoriamente de una gramática composicional primero al azar.
muestrear una composición del núcleo y luego muestrear una función de ese núcleo, mientras que el
Los patrones no composicionales se tomaron muestras del núcleo de la mezcla espectral., donde el numero

1 Tenga en cuenta que, aunque el núcleo espectral podría capturarse a priori mediante sumas de funciones de base radial (FBR) y
núcleos periódicos, el extraído (es decir., equipado) “núcleo humano” informado por Wilson et al..
(2015) era más parecido
a una mezcla de una función de base radial y un núcleo lineal. Comparamos ambos tipos de granos de mezcla con
nuestro núcleo compositivo completo en nuestra comparación de modelos lesionados en los Materiales complementarios.

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

de componentes se varió entre dos y seis uniformemente. Un subconjunto de estos pat muestreados-
Luego se eligieron términos de modo que las funciones compositivas y no compositivas coincidieran.
basado en su entropía espectral y distancia de ondas (Görg, 2013), conduciendo a un conjunto final de
40 patrones.

JUEGO DE COMUNICACIÓN DE PATRONES

Nuestro estudio evaluó qué tan bien se pueden comunicar diferentes patrones en una comunidad de forma libre.-
juego de cationes (es decir., sin restricciones en la longitud de las descripciones de los participantes o el uso de palabras).
El estudio constó de tres partes: descripción, dibujo, y calificación de calidad. Los participantes fueron
reclutado de Amazon Mechanical Turk, y a ningún participante se le permitió participar en
más de una parte. El estudio fue aprobado por la junta de revisión institucional de Harvard..

Parte 1: Obtener descripciones

Treinta y un participantes (6 femenino, edad media = 34.91, DE = 10.25) participó en la descripción
estudiar. Los participantes vieron secuencialmente seis patrones diferentes., representados como gráficos que tenían
para describir después. Tres de los patrones fueron muestreados aleatoriamente del 20 componer-
patrones opcionales sin reemplazo, y tres fueron muestreados del grupo no composicional
de patrones. El orden de los patrones presentados se determinó al azar.. En cada prueba,
Los participantes vieron por primera vez un patrón para 10 s, después de lo cual el patrón desapareció. El patrón era
se les muestra como 100 puntos equidistantes que indican una función en un lienzo (ver figura 2). Después
el patrón desapareció, Los participantes tuvieron que describirlo usando tantas palabras como quisieran..
A los participantes se les dijo que pasaríamos sus descripciones a otra persona que
Luego tienes que volver a dibujar los patrones sin haberlos visto nunca..

Dos jueces calificaron de forma independiente las descripciones2 en una escala de 1 (malas descripciones)
a 5 (grandes descripciones). El acuerdo entre los dos jueces fue lo suficientemente alto, con un
correlación entre evaluadores de r(29) = 0.46, t= 2.45, pag = .02, novio = 3.8, y validamos su
Juicios tanto estadísticos como utilizando evaluadores adicionales. (ver los materiales complementarios). Nosotros
Luego retuvo las descripciones con una calificación promedio superior a 3, donación 7 “descriptores” y
un conjunto total de 31 diferentes patrones. Dieciséis de estos patrones eran compositivos., y quince
eran no composicionales. Todos los participantes recibieron su pago. $2 por su participación. l D o w n o a d e desde h t t p : / / directo . mi t . / e d u o p m i / lartice – pdf / ¿yo? / i / / . 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 pd / . yo parte 2: Dibujando los patrones que reclutamos 49 Participantes (21 hembras, edad media = 33.6, DE = 9.6) para la parte de dibujo del experimento. en esta parte, Los participantes solo vieron las descripciones de los patrones y tuvieron que volver a dibujarlos colocando puntos en un lienzo vacío.. Debajo del lienzo, Los participantes vieron las descripciones de los patrones., que sabían que había sido escrito por un participante anterior. Participe- A los pantalones se les dijo que podían colocar cualquier número de puntos en el lienzo., pero tuvieron que colocar al menos cinco puntos para dibujar un patrón antes de poder enviar sus dibujos.. Cada participante recibió las seis descripciones escritas por un participante emparejado al azar de la parte de descripción., eso es, fueron emparejados con uno de los siete "descriptores" principales de la primera parte del estudio. A los participantes se les pagó $2 por su participación.

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Parte 3: Calificar la calidad de los dibujos

Nosotros reclutamos 104 Participantes (35 hembras, edad media = 37.7, DE = 8.6) para calificar la calidad de
Desempeño de los participantes en las partes anteriores.. A los participantes se les explicaron las reglas del juego.

2 Todas las descripciones se pueden encontrar en línea.: https://ericschulz.github.io/comcompresps.pdf.

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

los participantes anteriores habían jugado. Luego tuvieron que calificar 30 dibujos muestreados al azar, dónde
los dibujos siempre se presentaban justo al lado del patrón original. Los participantes no vieron el
Descripciones que condujeron a los eventuales dibujos., sino que sólo tuvo que evaluar en qué medida
el dibujo se parecía al original, eso es, qué tan bien pensaron que se desempeñaron dos participantes en
una ronda del juego. Hicieron esto ingresando valores en un control deslizante desde 0 (mal desempeño)
a 100 (gran rendimiento). Pagamos a los participantes $1 por su participación.

RESULTADOS

Cifra 2 muestra tres ejemplos de descripciones y dibujos de los participantes para ambas composiciones.-
Patrones funcionales y no compositivos.. Primero evaluamos si los participantes en la descripción

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

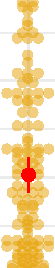
Cifra 2. Ejemplos de descripciones y dibujos.. Las cifras muestran los tres mejores. (basado en las calificaciones de calidad) dibujos únicos para ambos
compositivo (panel superior en naranja) y no composicional (panel inferior en azul) patrones. Las filas superiores siempre muestran el patrón original.,
las filas del medio muestran las descripciones, y las filas inferiores muestran los patrones redibujados.

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

parte del estudio ingresó descripciones más largas para el compositivo que para el no compositivo.
patrones. Este análisis no reveló diferencias significativas entre los dos tipos de patrones.,
t(30) = 0.15, pag = .88, re = 0.03, novio = 0.2. Próximo, Evaluamos si los participantes en el
La parte de dibujo del estudio utilizó más puntos para volver a dibujar los patrones compositivos que los no compositivos.-
charranes. Esto tampoco mostró diferencias entre los dos tipos de patrones., t(49) = 1.00, pag = .32,
re = 0.14, novio = 0.2.

Aunque se podría concluir de estos análisis que las descripciones y redibujos
fueron relativamente similares en las dos clases de patrones, inspección de qué palabras aparecen con frecuencia-
aparecieron en las descripciones compositivas pero no en las no compositivas (y viceversa)
reveló que las descripciones compositivas a menudo incluían palabras más abstractas como “montaña-
manchar," "repetir,” o “valle” (Figura 3a), mientras que las descripciones no compositivas usaban palabras
como "comienza," "abajo,” o “arriba,"probablemente describiendo exactamente cómo dibujar una forma particular
(Figura 3b). Además, evaluamos la diversidad léxica de las descripciones, definido como la suma de
las palabras únicas utilizadas divididas por todas las palabras utilizadas en una descripción (McCarthy & jarvis, 2010).
Las descripciones compositivas mostraron una mayor diversidad léxica que las descripciones no compositivas.-
ciones, t(30) = 4.22, pag < .001, d = 0.76, BF > 100, Figura 3c.

A continuación analizamos la calidad de los dibujos de los participantes.. Para comparar los dos, nosotros
Usé splines de suavizado polinómico para conectar los puntos.. Los splines se vieron obligados a pasar
cada punto del lienzo de modo que los patrones originales y redibujados tengan la misma longitud.
Nuestros resultados también son válidos incluso si solo usamos los puntos sin procesar u otros métodos para extraer los
patrones como modelos aditivos generalizados (ver los materiales complementarios). Luego llamamos-
calculó la diferencia absoluta (error absoluto) entre los patrones originales y los redibujados.
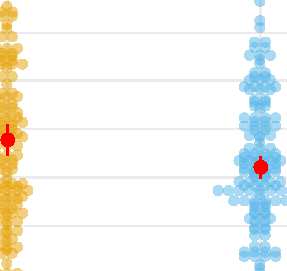
Esta diferencia fue mayor para los patrones no compositivos que para los compositivos. (Figura 4a;
t(49) = 2.43, pag = .01, re = 0.34, novio = 4.1), indicando que los participantes fueron más precisos en
Redibujar patrones compositivos.

La distancia absoluta entre dos patrones podría no ser el mejor indicador del rendimiento.-
mance, porque dos patrones pueden parecerse pero aun así mostrar una gran diferencia absoluta (p.ej.,
si el patrón redibujado es más pequeño que el original, o si un patrón se desplaza ligeramente hacia
cualquier lado). Por lo tanto, también aplicamos una medida de distancia que tiene en cuenta estas posiciones.-
posibles desviaciones al evaluar la similitud de dos patrones en función de sus diferencias después
realizando una transformada wavelet de Haar. La idea detrás de esta medida de similitud es reemplazar

Cifra 3. Características lingüísticas de las descripciones de funciones.. (a) Frecuencia de palabras que fueron
utilizado más de dos veces en las descripciones compositivas pero no en las no compositivas. (b) fre-
frecuencia de palabras que se usaron más de dos veces en el grupo no compositivo pero no en el compositivo
descripciones. (C) Diversidad léxica de descripciones compositivas y no compositivas..

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

Cifra 4. Diferencia entre funciones compositivas y no compositivas. Los colores indican
el tipo de patrón. Los puntos rojos muestran la media., junto con el 95% intervalo de confianza. (a) Absoluto
error entre patrones originales y redibujados. (b) Distancia wavelet entre el original y el redibujado
patrones. (C) La calidad nominal se muestra como calificación 100 para transformarla en una medida de distancia (es decir., más bajo
los valores son mejores).

el patrón original por sus coeficientes de aproximación wavelet, y luego medir la similitud
entre estos coeficientes (montero & vilar, 2014; ver los materiales complementarios). técnico-
cualidades a un lado, Esta medida es robusta ante la ampliación y el cambio de los patrones.. hemos previamente
verificó que se corresponde bien con los juicios de similitud de los participantes al comparar dos
patrones (Schulz, Tenenbaum, et al., 2017). Analizar el desempeño de los participantes usando este
medición (distancia de ondas) mostró una ventaja aún mayor para la palmadita composicional-
charranes (Figura 4b; t(49) = 3.02, pag = .004, re = 0.43, novio = 11.7).

Próximo, Analizamos las calificaciones de calidad recopiladas en la tercera parte de nuestro estudio.. nosotros somos tu-
combinó un modelo lineal de efectos mixtos con efectos aleatorios para una composición vs.. no compuesto-
contraste posicional para los evaluadores, pares descriptor-cajón, y para los artículos (patrones). comparamos
este modelo a otro modelo que también incluía una composición vs.. contraste no composicional
como un efecto fijo (siguiendo la lógica de Barr, Exacción, Transportistas, & Teja, 2013). Los resultados de este
El análisis mostró que agregar el contraste compositivo como un efecto fijo mejoró moderadamente
el modelo general se ajusta (novio = 4.6). Los patrones compositivos recibieron calificaciones más altas que los no-
patrones compositivos (Figura 4c), resultando en una estimación posterior de 39.61 (95% IDH [alto
intervalo de densidad]: 39.03, 40.19) para los patrones compositivos y una estimación posterior de 33.31
(95% IDH: 32.69, 33.93). Curiosamente, La calidad nominal no se vio influida por la duración del
las descripciones (novio = 0.01).

También evaluamos qué tan bien ambos modelos capturaron la dificultad de comunicar el
diferentes patrones, así como las calificaciones de calidad de los participantes.. Primero, evaluamos si la probabilidad-
capota de cada modelo, cuando se ajusta a los patrones originales, fue predictivo de cuán comunicable
ese patrón era. La idea detrás de este análisis era que, si los participantes realmente estuvieran usando uno
de los dos modelos para extraer y comprimir patrones, Entonces, ¿qué tan bien se puede comprimir este modelo?
los patrones (medido por la probabilidad dados los datos) debe estar relacionado con qué tan bien
la gente puede comunicarlo. Por lo tanto, ajustamos un conjunto de modelos de regresión multinivel con el
medidas de error utilizadas previamente como variables dependientes, y la probabilidad logarítmica para cada
patrón estimado por modelos compositivos y no composicionales como el independiente-
variables de abolladuras. También incluimos una intersección aleatoria y una pendiente aleatoria para cada uno de los dos
probabilidades de los modelos, ya que los participantes pueden variar en su capacidad para volver a dibujar el patrón descrito
y qué tan bien los predicen los diferentes modelos. La regresión de efectos fijos resultante
coeficientes (Mesa 2) mostró el mismo patrón para ambas mediciones de error: hubo una señal-
efecto significativo para las probabilidades logarítmicas composicionales, pero no para las no composicionales.. Además,

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

Mesa 2. Resultados de los análisis de regresión..

Error absoluto Wavelet Distancia Clasificaciones de calidad

Interceptar

composicional

No composicional

27.59∗∗
(0.63)
−1,39∗
(0.54)
−0,83
(0.53)

3.26∗∗
(0.07)
−0,19∗∗
(0.06)
−0,08
(0.06)

35.83∗∗
(2.38)
6.73∗∗
(2.12)
−4,03
(3.15)

Nota. Las columnas muestran las estimaciones de regresión de efectos fijos estandarizadas para
modelando el error absoluto, el error de distancia de la ondícula, o la calificación de los participantes-
calificaciones de calidad como variable dependiente. Los errores estándar de los coeficientes son
se muestra debajo de cada coeficiente entre paréntesis.
** pag < .001, * p < .01 we directly compared two mixed-effects regressions solely using either the compositional or the noncompositional log-likelihoods as the independent variable. This comparison strongly favored the compositional log-likelihoods for modeling both the absolute error (BF > 100) y
la distancia de las ondas (BF > 100). Esto significa que los patrones que eran más fáciles de comprimir por el
El modelo compositivo también fue más fácil de comunicar para los participantes.. Esto no fue cierto para
el modelo no composicional.

Finalmente, aplicamos el mismo enfoque de regresión, utilizando la probabilidad logarítmica como índice-
variable pendiente (como efecto fijo y aleatorio), para predecir las calificaciones de calidad recopiladas
en la tercera parte del estudio. La idea detrás de este análisis es que si los participantes fueran realmente
utilizando uno de los dos modelos para evaluar la calidad de los dibujos, entonces deberían evaluar
la probabilidad de que el dibujo haya sido producido por el mismo proceso generativo que el
dibujo original. Sólo el modelo compositivo predijo significativamente las calificaciones de los participantes.
en parte 3 (Mesa 2 y Figura 4c) y la comparación directa entre las características compositivas y
el modelo no compositivo favoreció fuertemente al modelo compositivo (BF > 100). Esta sugerencia-
sugiere que los participantes evaluaron la calidad de los dibujos en función de qué tan bien podrían ser
descrito por composiciones similares a los patrones originales.

Control de componentes individuales

Dado que tanto el núcleo composicional como el no composicional pueden (en el límite de infi-
datos finitos: captura cualquier función, pero, difieren en sus sesgos inductivos dados datos finitos, nosotros también
analizado si alguna estructura individual (Por ejemplo, periodicidad o linealidad) podría haber conducido
las diferencias entre la comunicabilidad de los patrones compositivos y no compositivos. Nosotros
Por lo tanto, analizó las diferencias entre patrones compositivos y no compositivos.
distancias wavelet mientras se controla qué tan bien se describen los diferentes núcleos de un solo componente
los patrones, medido por las probabilidades logarítmicas producidas por un análisis periódico, un lineal, o un
Kernel RBF tomado solo. Hicimos una regresión de las probabilidades logarítmicas de los componentes individuales como
efecto fijo y aleatorio sobre las distancias de las ondas primero. Además, agregamos un muñeco
indicar si un patrón era o no compositivo para esa regresión como un efecto aleatorio.
Después, agregamos la misma variable ficticia como un efecto fijo para evaluar si la composicionalidad
agregó algo a la comunicabilidad más allá de los componentes simples. este análisis
demostró que agregar el factor ficticio mejoraba una regresión que solo contenía el factor periódico

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

(novio = 20.7), el RBF (novio = 28.9), o el lineal (novio = 15.6) probabilidades logarítmicas. De este modo, el anuncio-
La ventaja de la comunicabilidad de los patrones compositivos no surgió únicamente de estructuras únicas.,
persistiendo incluso cuando se controla cada uno de los componentes individuales de la composición
gramática.

Control de la memorabilidad del patrón

Una preocupación con nuestro análisis actual es que los participantes vieron los patrones y luego tuvieron que
describirlos de memoria. De este modo, Las diferencias en la calidad final también podrían haber surgido de
diferencias en la capacidad de memoria de los participantes para diferentes patrones. Para descartar esta alternativa
explicación, También evaluamos cuánto, en todo caso, Las predicciones del modelo composicional.
Capturó la calidad de la comunicación mejor que la simple memorización del patrón.. Por lo tanto ejecutamos un
experimento adicional en el que 51 Participantes (37 masculino, edad media = 31.91, DE = 11.8)
vio patrones secuencialmente para 10 s (como en parte 1 de nuestro experimento principal) y luego tuvo
para volver a dibujarlo inmediatamente (usando la misma configuración de lienzo que en parte 2 de nuestro experimento principal).
Dejamos que los participantes hicieran esto durante seis patrones en total.. Tres de estos patrones eran compositivos.
y tres no eran compositivos. Luego medimos qué tan bien podrían los diferentes patrones
ser recordado calculando las diferencias de wavelets entre el original y el redibujado
patrones y promediarlos para cada patrón individualmente, conduciendo a una medida específica del artículo
de memorabilidad. Próximo, evaluamos cuánto mejoraron nuestras regresiones anteriores agregando-
ingresar opcionalmente las probabilidades logarítmicas del modelo compositivo como un efecto fijo mientras se controla
para la puntuación de memorabilidad específica del ítem (como efecto aleatorio y fijo) y la composición-
Las probabilidades logarítmicas del modelo nacional como efecto aleatorio. Esto reveló que el modelo compositivo
la probabilidad mejoró sustancialmente el modelo de regresión para el error absoluto (novio = 8.9), el
medida de distancia de ondas (novio = 8.3), y las calificaciones de calidad (BF > 100). De este modo, hay
fuertes razones para creer que las diferencias en las cualidades comunicativas no surgieron únicamente
de la memorabilidad del patrón.

Relacionar palabras específicas de la composición con descripciones de composición

También estábamos interesados en cómo las características específicas del lenguaje de los participantes se asignan a las especies.-
composiciones específicas en los patrones. Por lo tanto, llevamos a cabo otro experimento en el que
mostró a un grupo adicional de participantes componentes únicos del modelo compositivo. En
este experimento, 50 Participantes (24 machos, edad media = 34.25, DE = 11.96) vi seis diferentes
patrones secuencialmente. Cada patrón les fue presentado para 10 s después de lo cual desapareció
y tuvieron que describirlo, exactamente como en parte 1 de nuestros experimentos anteriores. Sin embargo, esta vez
Tomamos muestras de patrones de núcleos individuales del modelo compositivo.. De este modo, cada participante
Tuve que describir dos patrones que fueron muestreados de un núcleo periódico., dos patrones muestreados
desde un núcleo RBF, y dos patrones muestreados de un núcleo lineal, presentado a ellos en corrió-
orden dominante. Luego extrajimos la parte superior 10 palabras para cada componente, eso es, las palabras
que se utilizaron con más frecuencia para describir patrones de un componente particular en comparación con
los otros dos componentes. Las palabras resultantes eran intuitivamente plausibles.; Por ejemplo, com-
Las palabras comunes para patrones periódicos eran “pico," "tiempo," y " saludar,”mientras que las palabras frecuentes
para los patrones lineales eran "lineales," "derecho,” y “estable”. Luego evaluamos la frecuencia con la que
extraído, palabras específicas de la composición aparecieron en las descripciones obtenidas en parte 1 de nuestro
experimento anterior. La Figura 5a muestra con cuánta más frecuencia aparecieron las palabras extraídas en
las descripciones de composición en comparación con las descripciones no compositivas en nuestro primer
experimento (calculado restando la frecuencia de ocurrencias en el no composicional
descripciones a partir de la frecuencia de apariciones en las descripciones compositivas). Esta re-
reveló que muchas de las palabras compositivas aparecían con mayor frecuencia en las descripciones de

MENTE ABIERTA: Descubrimientos en ciencia cognitiva

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Communicating Compositional Patterns

Schulz, Quiroga, Gershman

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
oh
pag
metro

i
/

a
r
t
i
C
mi
–
pag
d

F
/

d
oh

i
/

1
0
1
1
6
2
oh
pag
metro
_
a
_
0
0
0
3
2
1
8
6
8
4
0
8
oh
pag
metro
_
a
_
0
0
0
3
2
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 5. Palabras específicas de la composición. Los colores indican el tipo de patrón.. Las barras de error muestran el
error estándar de la media. (a) Recuentos de frecuencia de aparición de palabras.. Las palabras fueron extraídas de
un experimento adicional que pide a los participantes que describan patrones únicos. Los recuentos muestran con qué frecuencia
las palabras extraídas aparecieron en composición vs.. patrones no compositivos en nuestro experimento principal.
Por ejemplo, Los números positivos muestran que apareció una palabra extraída para un componente en particular.
más frecuentemente en las descripciones de patrones compositivos que en las descripciones de patrones no-
patrones compositivos. (b) Probabilidad de que una palabra extraída de las descripciones de un solo componente
Se utilizaría en una descripción de una función compositiva o no compositiva..

patrones compositivos que en las descripciones de patrones no compositivos. Esto también puede ser
Esto se ve al calcular, para cada conjunto de palabras, la probabilidad de que al menos una de las palabras
apareció en la descripción (Figura 5b). Esta probabilidad fue mayor para los patrones de composición.
en general, t(30) = 2.65, pag = .005, re = 0.54, novio = 7.47. Además, ambas palabras que describen pe-
riodico, t(30) = 4.14, pag < .001, d = 0.74, BF > 100, y lineal, t(30) = 3.92, pag < .001, d = 0.70, BF = 63.3, patterns were more frequently used to described compositional than noncompositional patterns. This difference was not present for words describing RBF patterns, t(30) = −0.96, p = .34, d = 0.17, BF = 0.3. This is intuitive because noncompositional patterns might also contain smooth parts. Indeed, the compositional model more frequently interprets patterns sampled from the noncompositional kernel as having RBF components than linear or periodic components (cf. Schulz, Tenenbaum, et al., 2017). Finally, we calculated for each component the probability of being present in each of the described functions. This can be approximated by dividing the summed log-likelihood of kernels containing a particular component by the sum of all log-likelihoods. We then regressed the resulting values onto a binary variable that indicated whether or not a composition-speciﬁc OPEN MIND: Discoveries in Cognitive Science 35 Communicating Compositional Patterns Schulz, Quiroga, Gershman description was present for each description, including a random intercept over participants.3 For example, one would expect that participants might be more likely to use RBF-speciﬁc words the more likely it actually was that an RBF component was part of the seen pattern. This showed that linear words were somewhat more likely to be used the more likely linear patterns were to be present in the data, β = 0.13, z = 2.71, p = .007, BF = 3.8, 95% HDI: 0.04, 0.22, and that the same was also true for RBF-speciﬁc, β = 0.13, z = 2.64, p = .008, BF = 5.2, 95% HDI: 0.01, 0.26, and periodic-speciﬁc words, β = 0.12, z = 2.32, p = 0.02, BF = 4.1, 95% HDI: 0.02, 0.23. DISCUSSION We investigated how people perceive and communicate patterns in a pattern communication game where one participant described a pattern and another participant used this descrip- tion to redraw the pattern. Our results provide evidence that compositional patterns are more communicable, that a compositional model better captures participants’ difﬁculty in commu- nicating patterns, and that participants’ quality ratings when evaluating the performance of other participants are also best captured by a compositional model. Taken together, these re- sults suggest that there is an interface between natural language and the compositional pattern description language uncovered by our earlier work (Schulz, Tenenbaum, et al., 2017). We are not the ﬁrst to study how patterns are transmitted from one person to another. Kalish, Grifﬁths, and Lewandowsky (2007) let participants learn and reproduce functional patterns in an “iterated learning” paradigm. In this paradigm, participants drew functions that were then passed on to the next person, who then had to redraw them, and so forth. The re- sults of this study showed that participants converged to linear functions with a positive slope, even if they started out from linear functions with a negative slope or just random dots. A (2007) did not ask participants to gener- key difference from our study is that Kalish et al. ate natural language descriptions. Another difference is that in iterated-learning studies, the object of interest is typically the stationary distribution, which reveals the learner’s inductive biases (Grifﬁths & Kalish, 2007; Kirby & Hurford, 2002). We have not attempted to simu- late a Markov chain to convergence, so our study does not say anything about the stationary distribution. Here we ask whether particular pattern classes are more or less communicable. Schulz, Tenenbaum, et al. (2017) provide a systematic investigation into the nature of inductive biases in function learning, supporting the claim that these inductive biases are compositional in nature. Our approach ties together neatly with past attempts to model compositional structure in other cognitive domains. Language (Chomsky, 1965) and object perception (Biederman, 1987) have long traditions of emphasizing compositionality. More recently, these ideas have been extended to other domains such as concept (Feldman, 2000) and rule learning (Goodman, Tenenbaum, Feldman, & Grifﬁths, 2008). Our results add to these attempts by linking compo- sitional function representation to linguistic communication. There are four important limitations of the current work, which point the way toward fu- ture research. First, we do not have a computational account of how patterns are encoded into natural language. Based on work in machine learning (Lloyd et al., 2014), one starting point is 3 We did not include a random slope over participants into this model comparison, because there was no evidence for a random slope improving model ﬁts for the regression focusing on RBF-speciﬁc words, BF = 0.02, the regression focusing on linear-speciﬁc words, BF = 0.08, as well as the regression focusing on periodic- speciﬁc words, BF = 0.02. OPEN MIND: Discoveries in Cognitive Science 36 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i . / / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d / . i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Communicating Compositional Patterns Schulz, Quiroga, Gershman to assume that people ﬁrst infer a structural description of the pattern, and then “translate” this structural description into natural language. Although the work of Lloyd et al. (2014) shows how to do this for the compositional GP model, the natural language descriptions are highly technical, and therefore a rather poor match for lay descriptions of patterns. As the word fre- quencies in Figure 3a–b illustrate, people seem to make use of more metaphorical language when describing compositional functions—a property not captured by the austere statistical descriptions of Lloyd and colleagues. What we need is a kind of pattern “vernacular” that maps coherently (though perhaps approximately) to the structural description. The second limitation of our work is that we do not have a computational account of how descriptions are decoded into patterns for redrawing. One natural hypothesis is that this is essentially a reverse of the process described above: natural language descriptions are ﬁrst translated into structural descriptions, which can then be plugged into the GP model to gen- erate the mean function or sample from the posterior. Both of these limitations might be addressed in a data-driven way by using machine learning tools to ﬁnd invertible mappings from structural descriptions to natural language. In particular, we could treat this as a form of structured output prediction, a supervised learning problem in which the inputs and outputs are both multidimensional. Modern structured output prediction algorithms have developed a variety of ways to exploit the structured nature of linguistic data (e.g., Daumé, Langford, & Marcu, 2009; Tsochantaridis, Joachims, Hofmann, & Altun, 2005). These algorithms have not yet been applied to human pattern description. The third limitation of our work is that we have investigated a fairly small set of functions. This set was chosen based on our past work (Schulz, Tenenbaum, et al., 2017) so as to minimize low-level perceptual confounds. However, further work will be required to verify that our results generalize to a broader range of functions. The ﬁnal limitation is that it is currently hard to draw a clear distinction between com- positional and noncompositional patterns. Given that both the compositional and the non- compositional model can capture almost any pattern given enough data, the main differences between the two models can be derived from their predictions under a ﬁnite data regime. The two models’ inductive biases differ substantially given the number of data points we have applied here. Take as an example patterns that exhibited a linear trend. Even though the non- compositional kernel could eventually capture a linear trend, it would require a large number of noncompositional parts to interpolate trends and yet would still struggle to extrapolate be- yond the encountered data; this is because it lacks the required inductive biases to express trends efﬁciently. CONCLUSION The idea that concepts are represented in a “language of thought” is pervasive in cognitive science (Fodor, 1975; Piantadosi, Tenenbaum, & Goodman, 2016), and we have previously shown that human function learning also appears to be governed by a structured “language” of functions (Gershman, Malmaud, & Tenenbaum, 2017; Schulz, Tenenbaum, et al., 2017). Speciﬁcally, people decompose complex patterns into compositions of simpler ones, ulti- mately producing a structural description of patterns that allows them to effectively perform a variety of tasks, such as extrapolation, interpolation, compression, and decision making. The results in this article suggest that the availability of a structural description can also be used to communicate patterns in natural language. Because noncompositional functions are less effectively encoded into a structural description, they are disadvantaged in terms of accurate OPEN MIND: Discoveries in Cognitive Science 37 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i . / / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d / . i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Communicating Compositional Patterns Schulz, Quiroga, Gershman pattern communication. This ﬁnding provides new insight into how a language of thought might mediate translation between vision, language, and action. ACKNOWLEDGMENTS The authors thank Matthias Hofer for helpful discussions. FUNDING INFORMATION ES received funding from the Harvard Data Science Initiative. AUTHOR CONTRIBUTIONS ES: Conceptualization: Equal; Formal analysis: Lead; Investigation: Equal; Visualization: Lead; Writing - Original Draft: Equal. FQ: Conceptualization: Equal; Data curation: Supporting; Software: Lead; Visualization: Supporting; Writing - Original Draft: Supporting. SJG: Conceptu- alization: Equal; Data curation: Supporting; Supervision: Lead; Writing - Original Draft: Equal. REFERENCES Barr, D. J., Levy, R., Scheepers, C., & Tily, H. J. (2013). Random effects structure for conﬁrmatory hypothesis testing: Keep it max- imal. Journal of Memory and Language, 68(3), 255–278. Biederman, I. (1987). Recognition-by-components: A theory of hu- man image understanding. Psychological Review, 94, 115–147. (2015). Time series analysis: Forecasting and control. Hoboken, NJ: Wiley. Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. Chomsky, N. (1965). Aspects of the theory of syntax. Cambridge, MA: MIT Press. Daumé, H., Langford, J., & Marcu, D. (2009). Search-based struc- tured prediction. Machine Learning, 75, 297–325. J. R., Grosse, R., Tenenbaum, J. B., & Duvenaud, D., Lloyd, Ghahramani, Z. (2013). Structure discovery in nonparametric regression through compositional kernel search. In S. Dasgupta & D. McAllester (Eds.), Proceedings of the 30th International Conference on Machine Learning (ICML-13) (pp. 1166–1174). New York, NY: ACM. Feldman, J. (2000). Minimization of boolean complexity in human concept learning. Nature, 407, 630. Fodor, J. A. (1975). The language of thought (Vol. 5). Cambridge, MA: Harvard University Press. Gershman, S. J., Malmaud, J., & Tenenbaum, J. B. (2017). Structured representations of utility in combinatorial domains. Decision, 4, 67–86. Ghahramani, Z. (2015). Probabilistic machine learning and artiﬁcial intelligence. Nature, 521, 452–459. Goerg, G. (2013). Forecastable component analysis. In S. Dasgupta & D. McAllester (Eds.), Proceedings of the 30th International Con- ference on Machine Learning (ICML-13) (pp. 64–72). New York, NY: ACM. Goodman, N. D., Tenenbaum, J. B., Feldman, J., & Grifﬁths, T. L. (2008). A rational analysis of rule-based concept learning. Cog- nitive Science, 32, 108–154. Grifﬁths, T. L., & Kalish, M. L. (2007). Language evolution by iterated learning with Bayesian agents. Cognitive Science, 31, 441–480. Grifﬁths, T. L., Lucas, C., Williams, J., & Kalish, M. L. (2009). Mod- eling human function learning with gaussian processes. In D. Koller, D. Schuurmans, Y. Bengio, & L. Bottou (Eds.), Advances in neural information processing systems 21 (pp. 553–560). Red Hook, NY: Curran Associates. Kalish, M. L., Griffiths, T. L., & Lewandowsky, S. (2007). Iterated learning: Intergenerational knowledge transmission reveals in- ductive biases. Psychonomic Bulletin & Review, 14, 288–294. Kirby, S., & Hurford, J. R. (2002). The emergence of linguistic struc- ture: An overview of the iterated learning model. In A. Cangelosi language & D. Parisi (pp. 121–147). London, UK: Springer. (Eds.), Simulating the evolution of Lloyd, J. R., Duvenaud, D. K., Grosse, R. B., Tenenbaum, J. B., & Ghahramani, Z. (2014). Automatic construction and natural- language description of nonparametric regression models. In Pro- ceedings of the Twenty-Eighth AAAI Conference on Artiﬁcial Intelligence (pp. 1242–1250). Québec City, Canada: Association for the Advancement of Artiﬁcial Intelligence. Lucas, C. G., Grifﬁths, T. L., Williams, J. J., & Kalish, M. L. (2015). A rational model of function learning. Psychonomic Bulletin & Review, 22, 1193–1215. McCarthy, P. M., & Jarvis, S. (2010). Mtld, vocd-d, and hd-d: A validation study of sophisticated approaches to lexical diversity assessment. Behavior Research Methods, 42, 381–392. Montero, P., & Vilar, J. A. (2014). Tsclust: An r package for time series clustering. Journal of Statistical Software, 62, 1–43. Piantadosi, S. T., Tenenbaum, J. B., & Goodman, N. D. (2016). The logical primitives of thought: Empirical foundations for composi- tional cognitive models. Psychological Review, 123, 392–424. Quiroga, F., Schulz, E., Speekenbrink, M., & Harvey, N. (2018). Struc- tured priors in human forecasting. bioRxiv. https://doi.org/10. 1101/285668 OPEN MIND: Discoveries in Cognitive Science 38 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i / . / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d . / i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Communicating Compositional Patterns Schulz, Quiroga, Gershman Rasmussen, C., & Nickisch, H. (2010). Gaussian processes for ma- chine learning (GPML) toolbox. Journal of Machine Learning Re- search, 11, 3011–3015. Rasmussen, C., & Williams, C. (2006). Gaussian processes for ma- chine learning. Cambridge, MA: MIT Press. Schulz, E., Bhui, R., Love, B. C., Brier, B., Todd, M. T., & Gershman, S. J. (2019). Structured, uncertainty-driven exploration in real- world consumer choice. Proceedings of the National Academy of Sciences, 116, 13903–13908. Schulz, E., Speekenbrink, M., & Krause, A. (2017). A tutorial on gaussian process regression: Modelling, exploring, and exploit- ing functions. bioRxiv. https://doi.org/10.1101/095190 Schulz, E., Tenenbaum, J. B., Duvenaud, D., Speekenbrink, M., & Gershman, S. J. (2017). Compositional inductive biases in func- tion learning. Cognitive Psychology, 99, 44–79. Tsochantaridis, I., Joachims, T., Hofmann, T., & Altun, Y. (2005). Large margin methods for structured and interdependent output variables. Journal of Machine Learning Research, 6, 1453–1484. Wilson, A. G., Dann, C., Lucas, C., & Xing, E. P. (2015). The human kernel. In C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, & R. Garnett (Eds.), Advances in neural information processing systems (pp. 2836–2844). Red Hook, NY: Curran Associates. Wu, C. M., Schulz, E., Speekenbrink, M., Nelson, J. D., & Meder, B. (2018). Generalization guides human exploration in vast deci- sion spaces. Nature Human Behaviour, 2, 915–924. https://doi. org/10.1038/s41562-018-0467-4 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / e d u o p m i / l a r t i c e - p d f / d o i / i / . / 1 0 1 1 6 2 o p m _ a _ 0 0 0 3 2 1 8 6 8 4 0 8 o p m _ a _ 0 0 0 3 2 p d . / i f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 OPEN MIND: Discoveries in Cognitive Science 39 INFORME imagen

Descargar PDF