La anestesia propofol altera las ondas de viaje cortical
Sayak Bhattacharya1, Jacob A. Donoghue1, Meredith Mahnke1,
Scott L. Brincat1, Emery N. Brown1,2,3, y Earl K. Miller1
Abstracto
■ Oscillatory dynamics in cortex seem to organize into travel-
ing waves that serve a variety of functions. Recent studies show
that propofol, a widely used anesthetic, dramatically alters corti-
cal oscillations by increasing slow-delta oscillatory power and
coherencia. It is not known how this affects traveling waves.
We compared traveling waves across the cortex of non-human
primates before, durante, and after propofol-induced loss of con-
sciousness (LOC). After LOC, traveling waves in the slow-delta
(∼1 Hz) range increased, grew more organized, and traveled
in different directions relative to the awake state. Higher fre-
quency (8–30 Hz) traveling waves, por el contrario, decreased, perdido
estructura, and switched to directions where the slow-delta waves
were less frequent. The results suggest that LOC may be due, en
part, to increases in the strength and direction of slow-delta trav-
eling waves that, Sucesivamente, alter and disrupt traveling waves in the
higher frequencies associated with cognition. ■
INTRODUCCIÓN
Traveling waves are spatially organized patterns of activity
whose peaks and troughs move sequentially across the
cerebro. They have been observed in a variety of brain
áreas, including the cortex, and across a wide range of fre-
cicaciones (de 1 to ∼40 Hz; Muller, Chavane, Reynolds, &
Sejniano, 2018; Muller, Reynaud, Chavane, & Destexhe,
2014; Muller & Destexhe, 2012; Takahashi, Salado, Penn,
& Hatsopoulos, 2011; Ermentrout & Kleinfeld, 2001).
Traveling waves were first observed under anesthesia in
the visual cortex (Ebersole & Kaplan, 1981; Cowey,
1964) and later in the auditory (Reimer, Hubka, ángel, &
Kral, 2011) and somatosensory cortices (Ferezou, Bolea,
& Petersen, 2006). Their prominence under anesthesia
(Liang et al., 2021; Townsend & Gong, 2018; Sato,
Nauhaus, & Carandini, 2012; Nauhaus, Busse, Carandini,
& Ringach, 2009; Benucci, Frazor, & Carandini, 2007)
may be because of lower background noise (Muller et al,
2018). Traveling waves are also evident in cortex during
sleep (Muller et al., 2016; Massimini, Huber, Ferrarelli, Colina,
& Tononi, 2004) and early development (Watt et al., 2009;
Wong, Meistrón, & Shatz, 1993). Sin embargo, they are also
present in the awake adult cortex (Sreekumar, Wittig,
Chapeton, Inati, & Zaghloul, 2020; Alamia & VanRullen,
2019; Takahashi et al., 2011; Prechtl, cohen, Pesaran,
Mitra, & Kleinfeld, 1997) and hippocampus (zhang,
Watrous, patel, & Jacobs, 2018; Lubenov & Siapas, 2009).
1The Picower Institute for Learning and Memory and Depart-
ment of Brain and Cognitive Sciences, Massachusetts Institute
of Technology, Cambridge, MAMÁ, 2The Department of Anesthe-
es, Critical Care and Pain Medicine, Massachusetts General
Hospital/Harvard Medical School, Bostón, MAMÁ, 3The Institute
for Medical Engineering and Science, Massachusetts Institute
of Technology, Cambridge, MAMÁ
© 2022 Instituto de Tecnología de Massachusetts
De hecho, there is a growing realization that traveling waves
show properties that have functional advantages. They can
be planar or rotational (Bhattacharya, Brincat, Lundqvist,
& Molinero, 2022; Muller et al., 2016; Ermentrout & Kleinfeld,
2001). They tend to flow in certain (no al azar) instrucciones,
vary in different degrees of organization and scale (Muller
et al., 2018). They travel in speeds that are correlated with
their frequency (Bhattacharya et al., 2022; zhang & Jacobs,
2015). Faster waves are purported to travel further than
slower waves (Bhattacharya & Iglesias, 2019). En otra
palabras, traveling waves can have precise properties that,
Sucesivamente, can induce timing relationships into networks.
This can (and seems to) serve a variety of cortical func-
ciones. Traveling waves can foster memory consolidation.
During sleep spindles, rotating waves reliably repeat the
precise timing offsets needed for spike-time-dependent
plasticidad (Muller et al., 2016). Traveling waves may help
“read out” information. A correlation between traveling
wave phase and reaction time suggests their role in mem-
ory retrieval (Mohan, zhang, & Jacobs, 2022). Waves travel
in different directions depending on whether sensory pro-
cessing or memory retrieval is being performed (Mohan
et al., 2022; Alamia & VanRullen, 2019). Traveling waves
also seem to play a role in perception. The timing and posi-
tion of traveling waves in visual cortex regulates spiking to,
and the animal’s ability to detect, visual targets (davis,
Muller, Martinez-Trujillo, Sejniano, & Reynolds, 2020).
Finalmente, traveling waves may also serve fundamental net-
work functions like retaining recent history of network
activations, keeping track of time, and they may even
perform computation (Heitmann & Ermentrout, 2020;
Muller et al., 2018; Muller & Destexhe, 2012; Ermentrout
& Kleinfeld, 2001).
Although traveling waves have been studied in both
anesthetized and awake animals, they have not been
Revista de neurociencia cognitiva 34:7, páginas. 1274–1286
https://doi.org/10.1162/jocn_a_01856
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
/
oh
C
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
oh
C
norte
_
a
_
0
1
8
5
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
directly compared between anesthetized and awake states.
This is relevant because of their potential roles in cortical
function and, por eso, normal consciousness. Sin embargo, es
particularly relevant because of recent studies showing that
propofol, a widely used anesthetic, profoundly affects oscil-
latory dynamics in cortex (Bastos et al., 2021; Redinbaugh
et al., 2020; Purdon, sansón, Pavo real, & Marrón, 2015;
Purdon et al., 2013; Lewis et al., 2012). Following loss of con-
sciousness (LOC), the cortex of nonhuman primates (NHPs)
showed strong increases in low-frequency slow-delta (∼1 Hz)
local field potential (LFP) power and coherence. Este
reversed when propofol was ceased and the NHPs regained
consciousness. En otras palabras, propofol does not merely
“turn off” cortex. It profoundly changes cortical rhythms. Él
is thus likely to affect traveling waves as well.
De este modo, we re-examined data from our previous study of
the effects of propofol on cortical oscillatory power and
coherencia (Bastos et al., 2021). We used methods recently
employed to identify and document traveling wave prop-
erties in cortex (Bhattacharya et al., 2022). Recordings
were made from electrode arrays in three cortical areas:
the ventrolateral prefrontal cortex (vlPFC), FEFs, y el
auditory parabelt cortex of macaque monkeys. The NHPs
transitioned from awake to LOC upon propofol adminis-
tration, and then back to awake state upon propofol
cessation. Propofol-induced LOC increased slow-delta
traveling waves, strengthened their organization, y
caused them to travel in different directions relative to
the awake state. There was a corresponding decrease in
higher-frequency (8–30 Hz) traveling waves. De hecho, el
slow-delta traveling waves seemed to “crowd out” high-
frequency traveling waves, causing them to flow in direc-
tions where the slow-delta waves were less frequent.
MÉTODOS
Sujetos, LFP Recordings, y
Propofol Administration
Experimental data were used from our earlier article
(Bastos et al., 2021). Two rhesus macaques (Macaca
mulatta) aged 14 años (Sujeto 1, masculino, ∼13.0 kg), y
8 años (Sujeto 2, femenino, ∼6.6 kg) participated in these
experimentos. Detailed surgical and housing protocols
can be found in the work of Bastos et al. (2021).
Experimental sessions were carried out in two phases.
In the first phase, a period of 15–90 min of awake baseline
activity was recorded. Próximo, propofol was intravenously
infused via a computer-controlled syringe pump (PHD
ULTRA 4400, Harvard Apparatus). The infusion protocol
was stepped such that unconsciousness was induced via
a higher rate infusion (285 μg/ kg/min for Subject 1;
580 μg/kg/min for Subject 2) para 20 min before dropping
to a maintenance dose (142.5 μg/kg/min for Subject 1;
320 μg/kg/min for Subject 2) for an additional 40 mín..
Facial movements and pupil size were tracked by infra-
rojo (Eyelink 1000 Más, SR-Research) throughout the
sesiones. The instant of eyes-closing that persisted for
the remainder of the infusion was marked as LOC. Recov-
ery of consciousness (ROC) was marked by the instant of
the first to occur between eyes reopening or regaining of
motor activity following propofol infusion cessation. Pelo-
ther details can be found in the work of Bastos et al.
(2021). All procedures followed the guidelines of the
MIT Animal Care and Use Committee (protocol number
0619-035-22) and the US National Institutes of Health.
The subjects were chronically implanted with 8 × 8
iridium-oxide Utah microelectrode arrays (1.0 mm
longitud, 400 μm spacing; Blackrock Microsystems) en el
vlPFC, FEFs, and the auditory parabelt cortex (caudal
parabelt). Signals were recorded on a Blackrock Cerebus.
LFPs were recorded at 30 kHz and filtered on-line via a
low-pass 250-Hz software filter and downsampled to
1 khz. All preprocessing and analysis were performed in
Python or MATLAB (The MathWorks, Cª). Quality control
during recording assured that any electrodes with poor
impedance or a lack of signal were marked as missing.
For the power analysis, the resulting signals were con-
volved with a set of complex Morlet wavelets.
LFP Spatial Phase Maps
The raw LFP traces were filtered in the desired frequency
rango, using a fourth-order Butterworth filter for alpha
(8–12 Hz) and beta (12–30 Hz) rangos, and a third-order
Butterworth filter for slow-delta (0.5–3 Hz) oscilaciones,
forward-reverse in time to prevent phase distortion (ver
MATLAB function filtfilt). A Hilbert transform was used to
obtain the analytical signal for each electrode. The phase
of each electrode for the 8 × 8 array is called the “phase
map” for that time instant. These phase maps (unsmoothed)
were checked for gradients to identify traveling waves.
Shuffling Procedure
To ensure that the probability of detecting traveling waves
exceeded that expected by chance, we performed a ran-
dom shuffling procedure to establish a threshold for the
correlation coefficient—beyond which a traveling wave
was counted. This was done by shuffling the phase values
on the array randomly (con 25 different types of random
permutations) and calculating the correlation coefficient.
The 99th percentile of the resulting distribution of coeffi-
cient values determined a threshold (0.3) above which the
correlation exceeded chance.
Traveling Wave Identification and Classification
We used circular statistics to identify wave patterns.
Methods followed our previous investigation of traveling
waves in the prefrontal cortex (Bhattacharya et al., 2022).
The circular–circular correlation coefficient reports the
spatial gradient similarity between two phase maps that
are adjusted to account for circular phase values. Para el
Bhattacharya et al.
1275
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
j
/
oh
C
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
oh
C
norte
_
a
_
0
1
8
5
6
pag
d
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
waves into four directions (Figure 7A): ρc14 > 0, ρc41 > 0
(red direction), ρc14 > 0, ρc41 < 0 (green direction), ρc14 <
0, ρc41 > 0 (blue direction), and ρc14 < 0, ρc41 < 0 (black
direction). As this was an 8 × 8 array (even numbers), it is
understandable that the bisecting axis was not perfectly
horizontal for ρc14 or perfectly vertical for ρc41. In addi-
tion, it is important to note that our methods were not
dependent upon the exact choice of points (Bhattacharya
et al., 2022).
Using this algorithm, we identified time instants where
traveling waves existed. This did not differentiate between
short-lived waves and continuous wave cycles. This also
ensured that we identified continuous phase gradients
on the array and not just phase-jumps (corresponding to
a pulse).
To distinguish between planar and rotating waves, sim-
ilar to our earlier study (Bhattacharya et al., 2022), we used
a third rotation map around (4, 4) along with the (1, 4) and
(4, 1) maps. Each wave instant thus had its associated three
coefficient values: ρc14, ρc41, and ρc44. Using simulations,
we obtained similar coefficient values for different types
of planar and rotating waves. Waves were simulated using
the following equations (Muller et al., 2016):
g t; φð
ð
Þ ¼ Aei wt−kφ
Þ þ σγ tð Þ
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
signal phase (φ at each array coordinate [a, b]) and the
rotation angle (θ) around the chosen point, the circular–
circular correlation coefficient thus was as follows:
ρ
c
¼
p
ð
ð
− φ
Þ sin θab − θm
Σab sin φ
Þ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
m
ab
Þ
ð
Þ sin2 θab − θm
ð
− φ
Σab sin2 φ
X
ab
!
m
θm ¼ Arg
eiθab
ab
As we showed in our previous study (Bhattacharya et al.,
2022), the choice of point around which the coefficient
was calculated split the array into two regions (Figure 1E).
A traveling wave toward the positive half (red arrows,
Figure 1E) would result in positive values, whereas the
opposite direction would result in negative values. Each
chosen point had a “chance zone” around which the
coefficient values would be too low (less than the thresh-
old determined by the shuffling permutation procedure)
to make a conclusion regarding wave existence. Hence,
two points, (1, 4) and (4, 1), chosen such that their
chance zones did not overlap, were used to determine
wave existence (Figure 1E). If either point reported a
coefficient value greater than the permutation threshold,
a wave was counted. Furthermore, a combination of
the two coefficient values could thus be used to bin the
Figure 1. (A) The
experimental setup, consisting
of periodic sensory stimulation
using a tone followed by an
airpuff. Propofol (yellow)
administered in two phases.
The first phase was a higher
dose to induce LOC, followed
by a lower dose for LOC
maintenance. After propofol
cessation ROC occurred. (B)
LFP amplitudes (slow-delta)
observed across the 8 × 8
recording array during the
awake state of Animal 2. Arrow
indicates direction of wave
propagation. (C) Voltage traces
from one row of the array
(dashed line in B), with peaks
marked. Dashed line indicates
sequential shifts in peak. (D)
Phase maps corresponding to
amplitude maps in (B). (E)
Wave quantification method
based on choice point (yellow).
Red region (red arrows)
indicates positive coefficient
waves, whereas blue denotes
negative. Gray region denotes
areas for which wave existence
could not be conclusively
concluded for that choice point,
that is, the coefficient value
was less than the shuffling
permutation threshold
(see Methods section).
1276
Journal of Cognitive Neuroscience
Volume 34, Number 7
where φ was the input phase map, w was the temporal
frequency, and k was the spatial wavenumber (1/wave-
length). The second term was a Gaussian white noise
term, with zero mean and standard deviation σ.
In this way, we obtained the three coefficient values for
simulated waves, to go with our experimental coefficient
data set. We compared these values to automatically
classify the type of wave observed, based on the Euclidean
distance between a wave type and the observed phase
map. Coefficient matching with three different maps
allowed for greater accuracy with lesser chances of
misclassification. It is important to note that owing to
the size and placement of the recording array, it was
possible, if not likely, that only a part of the rotating waves
was being captured on the array. Our algorithms were able
to capture these “wavelets.”
Wave speed at a time instant was calculated from the
phases ( p) by dividing the temporal frequency (∂p/∂t) at
that time with the spatial frequency (∂p/∂x; Zhang & Jacobs,
2015). The gradients obtained were averaged across elec-
trodes to get the net wave speed for that time instant.
Wave Spatial Coherence
The amplitude envelope obtained from the Hilbert trans-
form of the LFP signal was used to determine the spatial
coherence of the traveling wave. A wave was deemed to
be spatially coherent when it showed similar amplitudes
across the array at a particular instant. A broken wave
would show a larger amplitude variance across elec-
trodes on the same array. We demonstrated this using
two simulations: (1) where the array elements had uni-
form oscillation amplitude ranges, and (2) where the
amplitude ranges were randomly distributed (analogous
to a fragmented cortex). When the same phase gradient
(traveling wave, left to right; Figure 3A) was imposed in
both cases, the first showed a smooth, organized wave
structure (Figure 3A, top), whereas the other showed a
broken traveling wave with heterogeneous amplitudes
across the wave band. For the broken wave, the amplitude
envelope showed larger variance when compared with
the more solid wave. The coefficient of variation was
defined as the standard deviation divided by the mean.
Wave Similarity Analysis
Two phase maps were checked for similarity by computing
the circular–circular correlation between them (Muller
et al., 2016). A high positive coefficient value indicated
similar waves, that is, waves with the same phase organiza-
tion on the array. A high negative coefficient value indi-
cated antisimilar mirror-image type waves. A coefficient
around zero (shaded region, Figure 6, with the threshold
determined by the shuffling permutation procedure)
indicated no conclusive similarity between the phase
maps. This analysis was done across all time instants in
each session.
Statistical Tests
All of our statistical tests were based on the one-sample
t test (two-tailed), between two groups of data where each
group composed of 20 data points (corresponding to the
number of experimental sessions). We report if the
changes observed in a particular time period are signifi-
cantly different ( p < .01) from the awake baseline average
(marked on the plot). If the difference for the time period
is significantly different, a dot (colored corresponding to
the frequency range being assessed) was added below that
time period. No cross-frequency comparison was done.
The goodness of fit for the similarity data in Figure 6 was
measured by calculating the root means square error for
a curve-fitting between the data shown and a sum of
two Gaussian functions with opposite signed means (0.5
and −0.5). The root means square error values for the fit
were as follows:
Slow-delta waves: 0.027 (baseline), 0.009 (post-LOC) –
error reduced threefold.
Alpha waves: 0.028 (baseline), 0.024 (post-LOC).
Beta waves: 0.026 (baseline), 0.024 (post-LOC).
RESULTS
Here, we re-examined data from our study of the neural
effects of propofol (Bastos et al., 2021). Two macaque
monkeys were used. Throughout each experimental
session, they were exposed to sensory stimulation. A tone
was presented every 5–7 sec followed by, after a 0.5 sec gap,
a puff of air that was blown toward the eyes (Figure 1A).
This was used to test their responsiveness to external
stimulation (the airpuff ). It, along with other metrics (see
below), was used to assess state of consciousness.
Propofol was administered (see Methods section)
in two phases (Figure 1A). First, a higher dose (280–
580 μg/kg/min) of propofol was administered to induce
LOC. LOC was deemed at the timestamp where the sub-
ject’s eyes closed and did not reopen for the remainder
of the infusion. Soon afterward, the propofol infusion rate
was reduced to a lower level (140–320 μg/kg/min) that
could still maintain LOC. Later, propofol infusion was
ceased. After a brief period, there was ROC.
We used the same markers for LOC and ROC as our pre-
vious study (for details and analysis, see the work of Bastos
et al., 2021; Figure 1). They included behavioral respon-
siveness to the air puff, heart-rate, blood oxygenation
levels, EMG variance and tone, and so forth. Sensory stim-
ulation was held constant throughout the entire experi-
mental session to ensure that the awake and unconscious
states were identical, other than the anesthesia.
LFPs were recorded from a total of 6 Utah arrays, three
in each animal, placed in the vlPFC, the FEFs, and the
caudal parabelt. Each array consisted of 64 electrodes
(8 × 8 pattern) with a 400-micron spacing (for exact
placement and other details, see the work of Bastos
et al., 2021). We analyzed LFPs for spatiotemporal
Bhattacharya et al.
1277
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
signatures of traveling waves, using the same analytical
methods as Bhattacharya et al. (2022).
Detecting and Quantifying Traveling Waves
A traveling wave is a sequential activation of adjoining neu-
ral groups that gives the appearance of a traveling front of
activity. An example is shown in Figure 1B for an array in
the vlPFC. It plots LFP amplitudes band-pass filtered to
show the slow-delta band (0.5–3 Hz) only. This was
recorded during a “baseline” interval before administra-
tion of propofol, while the animal was awake. Each tile rep-
resents an electrode. Red (blue) indicates higher (lower)
LFP amplitudes. Across time, higher amplitudes move
sequentially across the array. For example, the first panel
(0 msec) shows a high-amplitude peak near the right of
the array. With each time step, the peak amplitudes
“move” toward and through the middle of the array and
then toward the left.
Traveling waves could be detected by observing the gra-
dient in oscillation phase values across the recording array
(Bhattacharya et al., 2022). Figure 1C shows oscillatory
phases (demodulated using the Hilbert transform) across
time on one row of the array (dashed black line in first
panel of Figure 1B). The sequential shift in phase across
adjacent electrodes and time is indicative of a traveling
wave. The phase plots for the whole array are shown in
Figure 1D. Note the progressive increase in phase from
the right to the left. The wave was not just a “pulse” (a sin-
gle front or edge of activity moving across the array). A
phase gradient could be seen in front of and behind the
peak amplitudes, indicating a traveling wave rather than
a traveling “pulse.”
We quantified traveling waves using circular–circular
correlation coefficients to measure the phase gradient
(adjusted for circularity in phase values, see Methods sec-
tion). The coefficient value (ρc) indicates the spatial corre-
lation between the observed phase map at a given time
instant and an idealized rotational phase map around a
particular “choice point” on the array. If this correlation
was greater than a threshold (determined through a shuf-
fling permutation process; see Methods section), a wave
was counted for that time instant. A positive versus nega-
tive ρc indicates wave movement in two opposite direc-
tions across the electrode array (Figure 1E).
To accurately assess wave movement, however, we
needed two choice points. This is because the classifica-
tion of wave directions depended on the choice point.
For example, consider the array shown in Figure 1E.
Two different choice points on the array are shown in
Figure 1E, left and right. With one choice point (circle,
Figure 1E, left), waves directed toward the red region
in Figure 1E (left) showed positive correlation (ρc > 0)
whereas the blue waves showed negative correlation.
With a different choice point (Figure 1E, bien), the waves
also binned into positive and negative directions but the
directions that corresponded to positive versus negative
were different. En ambos casos, some of the waves for one
choice point would be directed toward the gray zone (es decir.,
below threshold for classification as a wave) for the other
choice point. De este modo, to accurately classify all waves, nosotros
needed two points that binned waves in orthogonal
instrucciones. This captured all waves with none errone-
ously falling into the gray zone. If the coefficient for
either choice point showed a value greater than the
threshold value, a wave was counted. This rendered
results independent of any one choice point (Bhattacharya
et al., 2022).
Changes in the Number and Speed of Traveling
Waves after Propofol-induced LOC
We observed traveling waves in three frequency bands
(slow-delta = 0.5–3 Hz, alpha = 8–12 Hz, and beta =
12–30 Hz). After propofol-induced LOC, Había
changes in the number of traveling waves. Figure 2A shows
Cifra 2. (A) Probability of wave detection in three frequency ranges across time, averaged across sessions and arrays. The dots denote statistical
significance from baseline (marked). (B) Fold change in LFP power compared with baseline (marked) a través del tiempo, averaged across sessions and
matrices. The dots denote statistical significance compared with baseline (t test, pag < .01).
1278
Journal of Cognitive Neuroscience
Volume 34, Number 7
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
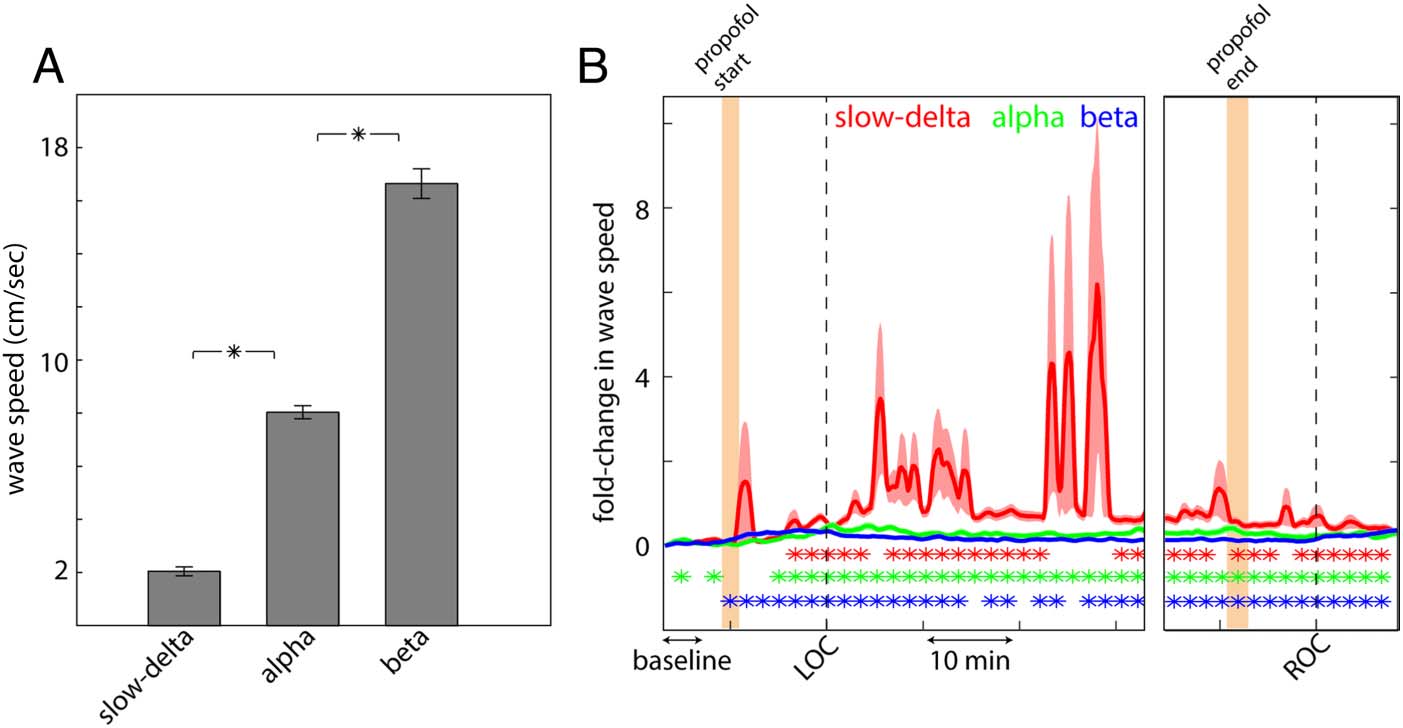
Figure 3. (A) Wave speeds
observed in the three frequency
ranges, averaged across all time
(irrespective of propofol),
sessions, and arrays. An asterisk
denotes statistically significant
differences from baseline for
each frequency band (t test,
p < .01). (B) Fold change in
wave speeds compared with
baseline (marked) across time,
averaged across sessions and
arrays. The colored asterisks
denote statistical significance
(blue for beta, green for
alpha, and red for slow-delta
compared with baseline) from
baseline.
the wave counts in each of three frequency bands, aver-
aged across sessions and arrays, from the awake state
through LOC and then from LOC through ROC. Wave
counts in all bands increased shortly after propofol infu-
sion began (before LOC, orange-shaded area). The num-
ber of alpha (in green) and beta (in blue) waves peaked
around the time of LOC. Slow-delta waves (in red) peaked
shortly after LOC. Throughout LOC, slow-delta waves
showed a large and significant increase in wave counts
relative to the baseline period before infusion of propofol
(Figure 2A, baseline marked). There was a good degree of
variance in slow-delta wave speeds across the population.
By contrast, beta waves decreased after LOC, relative to
baseline. Alpha waves (8–12 Hz) showed an intermediate
response, that is, were more similar to the prepropofol
baseline state than slow-delta and beta. After propofol
administration ceased (shown in orange, Figure 2A, right),
the wave counts started to move toward prepropofol
baseline values.
Plots of LFP power (independent of waves; Figure 2B)
showed correspondingly large increases in slow-delta
oscillations after LOC relative to alpha and beta. This con-
verged back to baseline levels after propofol cessation.
Spectrograms showing details of these power changes
can be found in the work of Bastos et al. (2021).
Propofol also increased traveling wave speed, especially
in the slow-delta band. Oscillation frequency and wave
speeds, as expected, were positively correlated (Zhang &
Jacobs, 2015). They were around the 1- to 20-cm/sec
range throughout the sessions (Figure 3A), consistent
with other LFP traveling wave studies (Takahashi et al.,
2011). The change in traveling wave speeds compared
with baseline across time in the session are shown
Figure 3B. Note the large increase in slow-delta wave
speed after LOC. Alpha and beta waves also significantly
increased in speed but much less so than slow-delta waves.
After ROC, wave speeds reduced. They remained signifi-
cantly higher than the awake state but more similar to
their prepropofol baseline state.
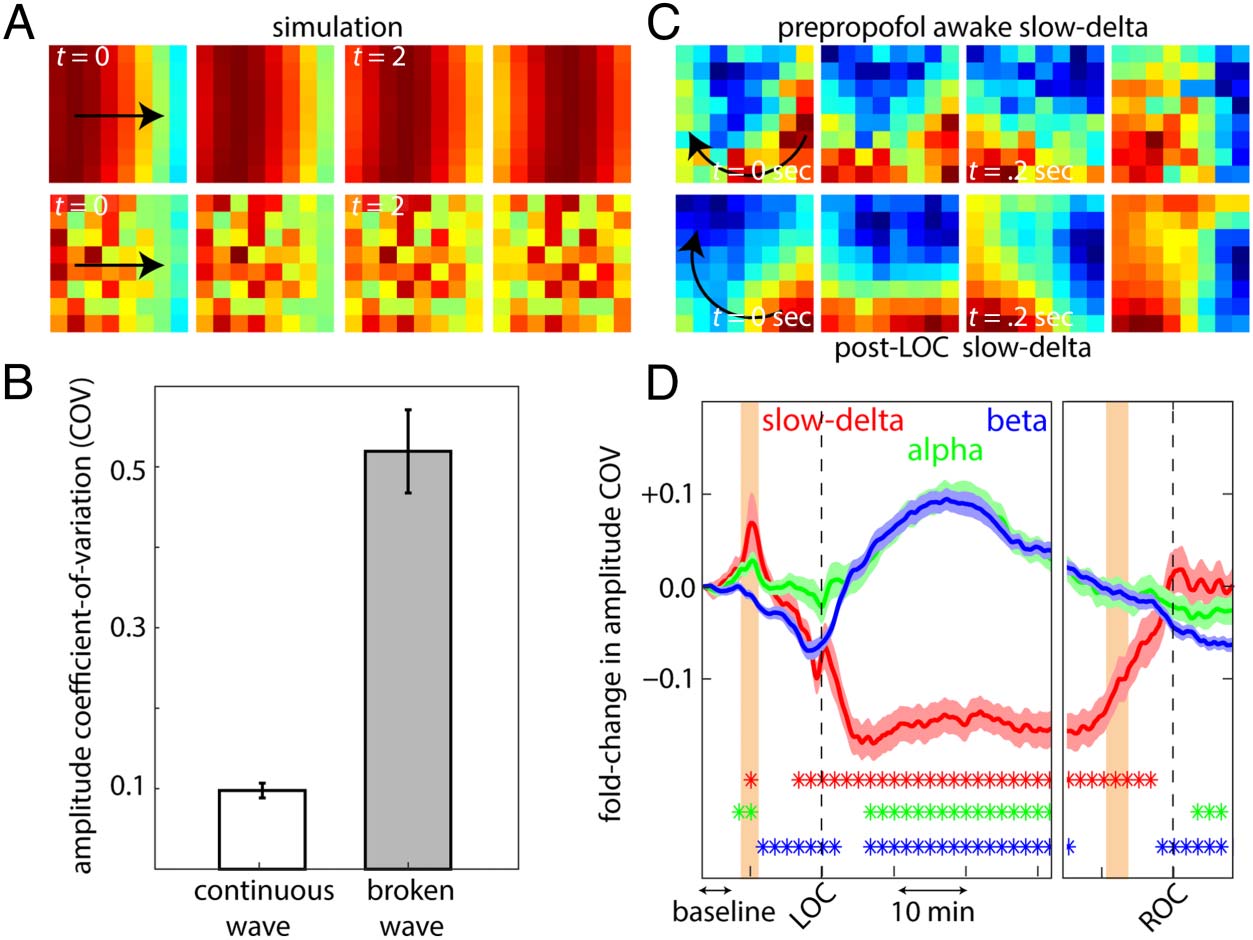
Changes in the Spatial Structure of Traveling Waves
Propofol also changed the spatial organization of the
waves. Specifically, one noticeable change was in their
spatial coherence, that is, whether they were more “solid”
waves or “broken” waves. A solid wave would show similar
amplitudes across adjacent electrodes, and smooth con-
tinuous changes across progressively further electrodes.
In other words, they had a uniformly organized structure
(simulated solid wave Figure 4A, top). A broken wave
would, by contrast, show a larger range of amplitude
values on the array. As the name suggests, this wave would
appear discontinuous on the array (simulated broken
wave Figure 4A, bottom). We quantified this using the
coefficient of variation (COV: standard deviation divided
by the mean) of the amplitude envelope of the traveling
wave. Simulated broken waves showed a significantly
higher amplitude COV when compared with the more
spatially coherent wave (Figure 4B).
We found that slow-delta traveling waves increased
their spatial coherence (became more solid) after LOC,
whereas alpha and beta waves did the opposite.
Figure 4C shows examples of slow-delta waves (moving
in the direction of the black arrow) on the vlPFC recording
array of Subject 1, in the prepropofol baseline state (top)
and after LOC (bottom). The post-LOC slow-delta wave
had more amplitude homogeneity than its baseline coun-
terpart, indicating that it was more solid. The change in
COV (compared with prepropofol baseline) for slow-delta
and beta waves averaged across all arrays, and sessions is
shown in Figure 4D. Slow-delta waves showed significantly
lower amplitude COV after LOC, indicating more spatial
coherence. By contrast, alpha and beta waves became
more broken and less structured after LOC, that is, they
showed a significant increase in COV relative to the base-
line. After ROC, slow-delta waves returned to their base-
line coherence. Beta (and to some extent alpha) waves
not only regained their structure post-ROC but showed a
“rebound.” They showed even stronger spatial coherence
Bhattacharya et al.
1279
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4. (A) Simulations of
traveling waves with different
levels of spatial couplings across
adjacent elements. Top, solid
wave with homogenous
amplitude map, and bottom,
broken wave with heterogenous
amplitude map across the array.
(B) Quantification of the COV of
amplitudes observed across the
array for the simulated solid and
broken waves. (C) Example of
slow-delta waves observed in
the prepropofol state (top) and
unconscious state (bottom) for
Animal 1. (D) Quantification of
the fold change in amplitude
COV for slow-delta, alpha, and
beta waves compared with
baseline (marked) averaged
across sessions and arrays.
The dots denote statistical
significance (blue for beta,
green for alpha, and red
for slow-delta compared
with baseline).
(lower amplitude COV) compared with their prepropofol
baseline state.
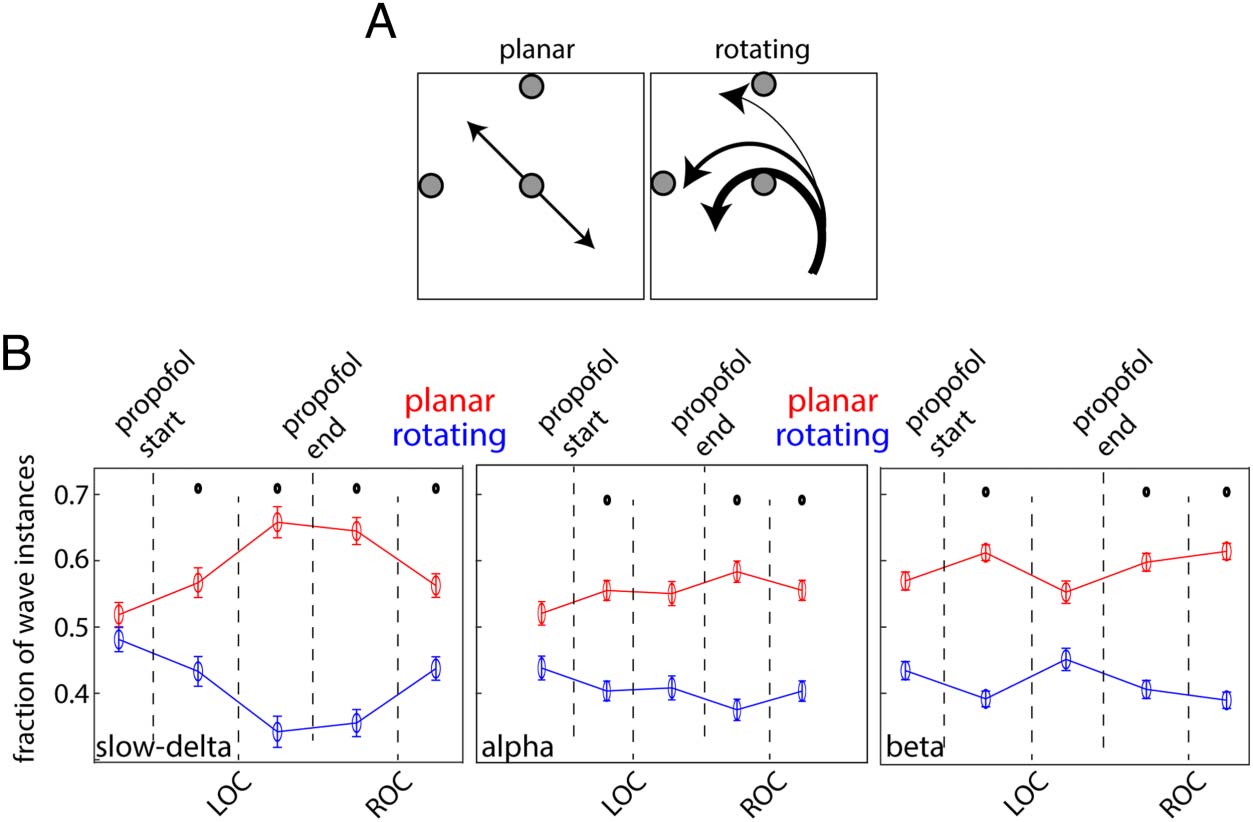
Propofol Changed Traveling Wave Patterns
In a previous study (Bhattacharya et al., 2022), we demon-
strated how one can leverage the properties of three
circular–circular correlation coefficients to distinguish
between rotating and planar waves (Figure 5A). We
applied the same methods here (see Methods section).
Both rotating and planar waves were observed in all the
recording arrays. On average, during the prepropofol
baseline, planar and rotating slow-delta waves had similar
incidence on the arrays (Figure 5B).
After LOC, there was a significant decrease in slow-delta
rotating waves and increase in slow-delta planar waves
(Figure 5B) relative to the slow-delta baseline. This dis-
tinction was evident after propofol induction and per-
sisted through LOC. After ROC, slow-delta planar and
rotating waves started to converge to their baseline
values. By contrast, the changes in alpha and beta wave
patterns were more modest. In the alpha-band, planar
waves increased and rotating waves decreased. Upon
propofol induction, there was a decrease in beta rotating
waves and a modest but significant increase in planar
waves (Figure 5B). The incidence of beta planar versus
rotating waves post LOC was similar to that during base-
line. The changes reappeared after propofol cessation
Figure 5. (A) Planar and
rotating wave examples,
detected with three choice
points on the array (gray
circles). (B) Fraction of planar
and rotating waves noted at
different stages of anesthesia for
slow-delta (left), alpha (middle),
and beta (right) waves averaged
across sessions and arrays. Dots
denote statistical significance
from baseline for each
frequency band.
1280
Journal of Cognitive Neuroscience
Volume 34, Number 7
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Similarity indices noted for slow-delta (A), alpha (B), and beta (C) waves at different stages of anesthesia, averaged across sessions and
arrays. Pre-LOC denotes the period where propofol administration has started but the subject is conscious. Shaded region denotes low similarity
values (threshold determined by shuffling permutation procedure; see Methods section).
and in ROC but were modest as well. It is worthwhile to
note that the arrays likely captured only part of a larger
rotating waves (Bhattacharya et al., 2022). Thus, rotating
waves could appear to become more planar if the rotat-
ing waves shifted in anatomical location. Nonetheless,
these results show that propofol induced changes in
wave patterns, especially in the slow-delta band.
Propofol Made Slow-Delta Traveling Waves
More Stereotyped
Two waves are similar when they not only have the same
direction, but also have similar speed, spatial coherence,
and overall organization. They can also be “antisimilar,”
that is, they are similar in other properties but flow in
opposite directions (like a mirror image). We found that
after propofol-induced LOC, there was an increase in
slow-delta wave antisimilarity.
To quantify this, we performed a similarity analysis on
the wave patterns on each array. We calculated, for each
array separately, the spatial correlation between each wave
at a given snapshot in time with all other waves at other
snapshots in time. A positive correlation indicates repeti-
tion of a particular wave pattern (i.e., high similarity across
time). A negative correlation indicates “antisimilarity,” that
is, repetition of waves that had high similarity across time
but moved in opposite directions. Correlations around
zero indicate randomness in wave properties.
Propofol caused an increase in slow-delta wave antisimi-
larity, relative to baseline. In other words, slow-delta waves
became more stereotyped. Figure 6A shows the wave
similarity values averaged across arrays and sessions. The
distribution for slow-delta traveling waves changed from
a more unimodal histogram centered around zero simi-
larity during baseline to a bimodal histogram after LOC.
This was verified by fitting a sum of two Gaussian func-
tions with means of opposite signs to the data. The good-
ness of fit measure improved during unconsciousness
(Methods section) suggesting increased bimodality. This
meant that slow-delta wave properties were relatively
random during baseline but, after LOC, shifted to a
repetitive pattern of mirror-image similar waves flowing
in opposite directions. This was evident in both early
and late periods of unconsciousness (post-LOC;
Figure 6A). Then, after ROC, slow-delta waves returned
to a unimodal random organization similar to baseline.
By contrast, alpha and beta waves (Figure 6B–6C) did
not show any shift in the distribution of wave similarity.
They were relatively random during baseline and
remained so after LOC.
Bhattacharya et al.
1281
Propofol Caused Slow-Delta and Higher-Frequency
Waves to Flow in Mutually Exclusive Directions
Traveling wave directions were also altered after LOC. To
quantify this, we classified traveling waves into four differ-
ent directions. As before, we used two circular–circular
correlation coefficients from two choice points in order
to capture all wave directions. They were then binned into
four directions—toward the four quadrants shown in
Figure 7A. The exact wave directions for each recording
array depend on the exact placement of the array relative
to the waves (Bhattacharya et al., 2022) and preferred
direction axes in specific regions (Zhang et al., 2018;
Takahashi et al., 2011). Thus, we focus our analyses on the
changes in direction after LOC, relative to the awake state.
An example of wave-direction analyses is shown in
Figure 7B. It plots the probability of detecting waves in
the four binned directions for slow-delta and beta waves
during baseline for the vlPFC array of Subject 1 (array loca-
tion relative to brain sulci is shown on the left). Both slow-
delta and beta waves flowed more frequently toward the
“red” and “black” zones (see Figure 7A), that is, toward
“upper right” and “lower left” of the array. Note that waves
from different frequency bands did not necessarily flow in
the same directions, as seen here. On other arrays, waves
from different frequency bands could have different pre-
ferred directions.
Figure 7C shows the change in wave direction on the
vlPFC array of Subject 1 post-LOC. Fold change was calcu-
lated by dividing the probability of wave detection in each
of the four directions with the probability of wave detec-
tion in the same direction during baseline. Figure 7C
shows this plotted across time averaged across sessions.
Slow-delta waves increased toward the directions pre-
ferred during baseline (i.e., the red and black directions).
By contrast, beta waves reduced in these directions.
Instead, they increased toward the green section (“upper
left”). Notably, the green direction was least preferred for
beta waves during baseline (Figure 7B right). Post-ROC,
the wave directions returned to their baseline preferences.
This segregation of slow-delta and beta waves into dif-
ferent directions post-LOC was seen across all arrays.
The six arrays were each oriented differently with respect
to brain sulci. Plus, the waves were oriented differently
with respect to the arrays (Bhattacharya et al., 2022). Thus,
we could not simply combine the same directions across
arrays (e.g., red to red, black to black). Instead, we rank-
ordered the directions based on which directions changed
the most from baseline to LOC for beta (black arrow
Figure 7C). Rank was assigned based on the signed
change. If all directions decreased—Rank 1 would be the
direction that decreased the least, whereas Rank 4 would
be the direction that decreased the most. If all directions
increased, Rank 1 would be the direction that increased
the most and so on. That is, the direction that saw the most
increase in beta waves after LOC was Rank 1, and the direc-
tion that saw the least increase (or most decrease) was
Rank 4. We applied the same rank ordering from beta to
alpha and slow-delta in order to compare how the direc-
tions changed relative to one another. Directions with
the same rank were combined across arrays (color coded:
red: 1, green: 2, blue: 3, black: 4). We performed the
rank-ordering using the beta band because only one
direction was enhanced for the beta waves after LOC
Figure 7. (A) Four direction bins (red, green, blue, and black) along which waves were categorized. (B) Location of vlPFC array of Animal 1 relative
to brain sulci (left) and baseline levels of wave direction probabilities (right) for the same array. (C) Fold change in wave detection probabilities in
each of the four directions compared with baseline, across time for the same array in B. Black arrow in the beta panel indicates how wave directions
were ranked in this particular case (green got Rank 1, whereas red got Rank 4).
1282
Journal of Cognitive Neuroscience
Volume 34, Number 7
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
waves flowed in after LOC, they dominated. Higher-
frequency waves decreased and lost structure after LOC,
despite showing increased LFP power, and flowed prefer-
entially in directions where slow-delta waves were less
frequent.
Our results are in line with previous reports of the
effects of propofol and of the properties of traveling
waves. The large increase in slow-delta waves after LOC
is consistent with prior work showing increases in slow fre-
quency power and coherence in cortex following
propofol-induced LOC (Bastos et al., 2021; Redinbaugh
et al., 2020, 2021). Our results are also consistent with
prior observations that traveling waves (under anesthesia)
have preferred directions and mirror-reflective properties
(Mitra et al., 2018; Xu, Huang, Takagaki, & Wu, 2007;
Sanchez-Vives & McCormick, 2000). They also support a
hypothesis by Muller et al. (2018). They posited that
decreased spiking activity, as seen under propofol in our
earlier work (Bastos et al., 2021), can lead to a greater
recruitment of neuron groups into a traveling wave. The
result of anesthesia would be more “solid,” organized,
waves than sparse, “broken” waves. That is what we
observed.
Traveling waves under anesthesia seem to cross ana-
tomical boundaries in the visual cortex whereas those in
awake state do not (Muller et al., 2014; Xu et al., 2007).
This could be explained by our observation of increased
slow-delta wave speed and organization after LOC. It could
allow waves to travel longer distances without loss of struc-
ture (Bhattacharya & Iglesias, 2019). Plus, we observed a
decrease in rotating, and an increase in planar, slow-delta
waves after LOC. Planar waves can traverse larger dis-
tances, as rotating waves tend to lose structure away from
their core (Bhattacharya et al., 2022). However, a study in
the somatosensory cortex of freely moving mice showed
traveling waves spread farther compared with those in
mice anesthetized with urethane (Ferezou et al., 2006).
The differences between this study and ours could be
because of use of a different anesthetic, different species,
or a different cortical area (somatosensory cortex). Reimer
et al. (2011) reported that traveling waves in rat cortex did
not change significantly under different anesthetics
(nitrous oxide, isoflurane, or ketamine) but they did not
test propofol. We hypothesize that our results may extend
to other anesthetics that have similar mechanisms of
action through GABAergic circuits (Franks & Lieb, 1994).
The change in slow-delta waves from rotating to planar
after LOC could explain differences between sleep and
anesthesia. Rotating waves during sleep spindles are
associated with memory consolidation by generating
spike timing differences that induce spike-time-
dependent plasticity (Muller et al., 2016). The “unrotating”
of traveling waves by propofol may disrupt those timing
relationships and thus potentially explain anesthesia-
induced retrograde amnesia.
Unlike slow-delta waves, beta and alpha waves
decreased in number and lost structure. It was as if the
Bhattacharya et al.
1283
Figure 8. Fold change in wave detection probabilities averaged
across all arrays—combined through a rank-ordering system (ranked
according to beta wave-change post-LOC as shown in Figure 7). Each
color indicates a particular wave direction. Dots denote statistical
significance for each direction compared with baseline (t test, p < .01).
(slow-delta showed increases in more than one direction).
Thus, beta waves provided a straightforward metric to
standardize and rank-order changes in direction in
other bands.
Figure 8 shows this analysis averaged across all arrays.
Post-LOC slow-delta and beta (and alpha) waves increased
in mutually exclusive directions. Beta waves increased in
one direction (Rank 1, red, by definition) after LOC. By
contrast, there was a decrease in beta waves in the other
directions (green, blue, and black). Alpha waves behaved
similarly as beta waves. Slow-delta waves showed opposite
trends to that of beta waves. They increased in the green
direction especially but also in the black and blue direc-
tions. The red direction, which increased in beta waves,
showed a decrease in slow-delta waves. After ROC, wave
direction preferences converged (or started to converge)
to their prepropofol baseline levels (Figure 8).
DISCUSSION
We found that after propofol-induced LOC, cortical travel-
ing waves were altered. Slow-frequency delta (∼1 Hz)
waves increased while higher-frequency (8–30 Hz) waves
decreased. The slow-delta waves sped up and became
more spatially organized. They became more planar (and
less rotating) and increased mirror-image waves traveling
in opposite directions. Whatever directions slow-delta
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
slow-delta waves were “swamping” cortex and crowding
out the higher-frequency traveling waves and “pushing”
them in different directions. Beta and alpha waves did
not disappear. They seemed to be redirected by the
slow-delta waves. After LOC, higher-frequency (8–30 Hz)
waves reoriented to a direction not being used by
slow-delta waves. We can perhaps think of wave directions
as specific neural pathways/channels. Slow-delta waves
after LOC became stronger, more frequent, and more
directional—showing a drastic pattern shift from random
to mirror-image-like waves. In contrast, higher-frequency
waves did not show any pattern shift and deteriorated in
structure. We hypothesize that this slow-delta wave dom-
inance caused some pathways to become “crowded” but
freed up other pathways to which the higher-frequency
waves “retreated,” often using channels that were
low-preference directions in the awake state.
Beta rhythms are thought to support cognitive func-
tions in NHPs (Bastos, Loonis, Kornblith, Lundqvist, &
Miller, 2018; Lundqvist, Herman, Warden, Brincat, &
Miller, 2018). Our results indicate that the spatial structure
of these rhythms may be important markers of cognition
as well. Beta LFP power increased after LOC (albeit less
than slow-delta). Beta LFP spatial organization, by con-
trast, showed different trends. Beta traveling waves
decreased, lost structure, and seemed to be forced to
change directions by slow-delta waves. Thus, the disrup-
tion of traveling waves in the higher frequencies associ-
ated with cognition may contribute to LOC under propofol
anesthesia.
Acknowledgments
We thank Jesus Ballesteros, Andre Bastos, Alex Major, Dimitris
Pinotsis, and Jefferson Roy for helpful comments.
Reprint requests should be sent to Earl K. Miller, The Picower
Institute for Learning and Memory, Massachusetts Institute of
Technology, 77 Massachusetts Ave, Cambridge, MA 02139,
USA, or via e-mail: mekmiller@mit.eduail.
Author Contributions
Sayak Bhattacharya: Formal analysis; Writing—Original
draft; Writing—Review & editing. Jacob A. Donoghue:
Investigation. Meredith Mahnke: Investigation. Scott L.
Brincat: Data curation; Investigation; Methodology. Emery
N. Brown: Conceptualization; Supervision; Writing—
Review & editing. Earl K. Miller: Conceptualization;
Funding acquisition; Project administration; Supervision;
Writing—Original draft; Writing—Review & editing.
Funding Information
These studies were supported by ONR MURI N00014-16-1-
2832, NIGMS P01GM118269, and The JPB Foundation.
Earl K. Miller, JPB Foundation (https://dx.doi.org/10
.13039/100007457), grant number: MIT-PIIF; Office of
Naval Research (https://dx.doi.org/10.13039/100000006),
grant number: MURI N00014-16-1-2832; National Institute
of General Medical Sciences (https://dx.doi.org/10.13039
/100000057), grant number: P01GM118269; National Insti-
tute of Mental Health (https://dx.doi.org/10.13039
/100000025), grant number: R01MH11559.
Diversity in Citation Practices
Retrospective analysis of the citations in every article pub-
lished in this journal from 2010 to 2021 reveals a persistent
pattern of gender imbalance: Although the proportions of
authorship teams (categorized by estimated gender
identification of first author/ last author) publishing in
the Journal of Cognitive Neuroscience ( JoCN ) during this
period were M(an)/M = .407, W(oman)/M = .32, M/ W =
.115, and W/ W = .159, the comparable proportions for the
articles that these authorship teams cited were M/M =
.549, W/M = .257, M/ W = .109, and W/ W = .085 (Postle
and Fulvio, JoCN, 34:1, pp. 1–3). Consequently, JoCN
encourages all authors to consider gender balance explic-
itly when selecting which articles to cite and gives them
the opportunity to report their article’s gender citation
balance.
REFERENCES
Alamia, A., & VanRullen, R. (2019). Alpha oscillations and traveling
waves: Signatures of predictive coding? PLoS Biology, 17,
e3000487. https://doi.org/10.1371/journal.pbio.3000487,
PubMed: 31581198
Bastos, A. M., Donoghue, J. A., Brincat, S. L., Mahnke, M.,
Yanar, J., Correa, J., et al. (2021). Neural effects of
propofol-induced unconsciousness and its reversal using
thalamic stimulation. eLife, 10, e60824. https://doi.org/10
.7554/eLife.60824, PubMed: 33904411
Bastos, A. M., Loonis, R., Kornblith, S., Lundqvist, M., & Miller,
E. K. (2018). Laminar recordings in frontal cortex suggest
distinct layers for maintenance and control of working
memory. Proceedings of the National Academy of Sciences,
U.S.A., 115, 1117–1122. https://doi.org/10.1073/pnas
.1710323115, PubMed: 29339471
Benucci, A., Frazor, R. A., & Carandini, M. (2007). Standing
waves and traveling waves distinguish two circuits in visual
cortex. Neuron, 55, 103–117. https://doi.org/10.1016/j.neuron
.2007.06.017, PubMed: 17610820
Bhattacharya, S., Brincat, S. L., Lundqvist, M., & Miller, E. K.
(2022). Traveling waves in the prefrontal cortex during
working memory. PLoS Computational Biology, 18,
e1009827. https://doi.org/10.1371/journal.pcbi.1009827,
PubMed: 35089915
Bhattacharya, S., & Iglesias, P. A. (2019). Controlling excitable
wave behaviors through the tuning of three parameters.
Biological Cybernetics, 113, 61–70. https://doi.org/10.1007
/s00422-018-0771-0, PubMed: 30056608
Cowey, A. (1964). Projection of the retina on to striate and
prestriate cortex in the squirrel monkey, Saimiri sciureus.
Journal of Neurophysiology, 27, 366–393. https://doi.org/10
.1152/jn.1964.27.3.366, PubMed: 14168198
Davis, Z. W., Muller, L., Martinez-Trujillo, J., Sejnowski, T., &
Reynolds, J. H. (2020). Spontaneous travelling cortical
waves gate perception in behaving primates. Nature, 587,
1284
Journal of Cognitive Neuroscience
Volume 34, Number 7
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
432–436. https://doi.org/10.1038/s41586-020-2802-y, PubMed:
33029013
Ebersole, J. S., & Kaplan, B. J. (1981). Intracortical evoked
potentials of cats elicited by punctate visual stimuli in
receptive field peripheries. Brain Research, 224, 160–164.
https://doi.org/10.1016/0006-8993(81)91126-4, PubMed:
7284831
Ermentrout, G. B., & Kleinfeld, D. (2001). Traveling electrical
waves in cortex: Insights from phase dynamics and
speculation on a computational role. Neuron, 29, 33–44.
https://doi.org/10.1016/s0896-6273(01)00178-7, PubMed:
11182079
Ferezou, I., Bolea, S., & Petersen, C. C. (2006). Visualizing the
cortical representation of whisker touch: Voltage-sensitive
dye imaging in freely moving mice. Neuron, 50, 617–629.
https://doi.org/10.1016/j.neuron.2006.03.043, PubMed:
16701211
Franks, N. P., & Lieb, W. R. (1994). Molecular and cellular
mechanisms of general anaesthesia. Nature, 367, 607–614.
https://doi.org/10.1038/367607a0
Heitmann, S., & Ermentrout, G. B. (2020). Direction-selective
motion discrimination by traveling waves in visual cortex.
PLoS Computational Biology, 16, e1008164. https://doi.org
/10.1371/journal.pcbi.1008164, PubMed: 32877405
Lewis, L. D., Weiner, V. S., Mukamel, E. A., Donoghue, J. A.,
Eskandar, E. N., Madsen, J. R., et al. (2012). Rapid
fragmentation of neuronal networks at the onset of
propofol-induced unconsciousness. Proceedings of
the National Academy of Sciences, U.S.A., 109,
E3377–E3386. https://doi.org/10.1073/pnas.1210907109,
PubMed: 23129622
Liang, Y., Song, C., Liu, M., Gong, P., Zhou, C., & Knöpfel, T.
(2021). Cortex-wide dynamics of intrinsic electrical activities:
Propagating waves and their interactions. Journal of
Neuroscience, 41, 3665–3678. https://doi.org/10.1523
/JNEUROSCI.0623-20.2021, PubMed: 33727333
Lubenov, E. V., & Siapas, A. G. (2009). Hippocampal theta
oscillations are travelling waves. Nature, 459, 534–539.
https://doi.org/10.1038/nature08010, PubMed: 19489117
Lundqvist, M., Herman, P., Warden, M. R., Brincat, S. L., &
Miller, E. K. (2018). Gamma and beta bursts during working
memory readout suggest roles in its volitional control.
Nature Communications, 9, 394. https://doi.org/10.1038
/s41467-017-02791-8, PubMed: 29374153
Massimini, M., Huber, R., Ferrarelli, F., Hill, S., & Tononi, G.
(2004). The sleep slow oscillation as a traveling wave. Journal
of Neuroscience, 24, 6862–6870. https://doi.org/10.1523
/JNEUROSCI.1318-04.2004, PubMed: 15295020
Mitra, A., Kraft, A., Wright, P., Acland, B., Snyder, A. Z.,
Rosenthal, Z., et al. (2018). Spontaneous infra-slow brain
activity has unique spatiotemporal dynamics and laminar
structure. Neuron, 98, 297–305. https://doi.org/10.1016/j
.neuron.2018.03.015, PubMed: 29606579
Mohan, U. R., Zhang, H., & Jacobs, J. (2022). The direction
and timing of theta and alpha traveling waves modulate
human memory processing. bioRxiv. https://doi.org/10.1101
/2022.02.07.479466
Muller, L., Chavane, F., Reynolds, J., & Sejnowski, T. J. (2018).
Cortical travelling waves: mechanisms and computational
principles. Nature reviews. Neuroscience, 19, 255–268.
https://doi.org/10.1038/nrn.2018.20, PubMed: 29563572
Muller, L., & Destexhe, A. (2012). Propagating waves in
thalamus, cortex and the thalamocortical system:
Experiments and models. Journal of Physiology, Paris, 106,
222–238. https://doi.org/10.1016/j.jphysparis.2012.06.005,
PubMed: 22863604
Muller, L., Piantoni, G., Koller, D., Cash, S. S., Halgren, E., &
Sejnowski, T. J. (2016). Rotating waves during human sleep
spindles organize global patterns of activity that repeat
precisely through the night. eLife, 5, e17267. https://doi.org
/10.7554/eLife.17267, PubMed: 27855061
Muller, L., Reynaud, A., Chavane, F., & Destexhe, A. (2014).
The stimulus-evoked population response in visual cortex
of awake monkey is a propagating wave. Nature
Communications, 5, 3675. https://doi.org/10.1038
/ncomms4675, PubMed: 24770473
Nauhaus, I., Busse, L., Carandini, M., & Ringach, D. L. (2009).
Stimulus contrast modulates functional connectivity in visual
cortex. Nature Neuroscience, 12, 70–76. https://doi.org/10
.1038/nn.2232, PubMed: 19029885
Prechtl, J. C., Cohen, L. B., Pesaran, B., Mitra, P. P., & Kleinfeld,
D. (1997). Visual stimuli induce waves of electrical activity
in turtle cortex. Proceedings of the National Academy of
Sciences, U.S.A., 94, 7621–7626. https://doi.org/10.1073/pnas
.94.14.7621, PubMed: 9207142
Purdon, P. L., Pierce, E. T., Mukamel, E. A., Prerau, M. J., Walsh,
J. L., Wong, K. F. K., et al. (2013). Electroencephalogram
signatures of loss and recovery of consciousness from
propofol. Proceedings of the National Academy of Sciences,
U.S.A., 110, E1142–E1151. https://doi.org/10.1073/pnas
.1221180110, PubMed: 23487781
Purdon, P. L., Sampson, A., Pavone, K. J., & Brown, E. N. (2015).
Clinical electroencephalography for anesthesiologists: Part I:
Background and Basic Signatures. Anesthesiology, 123,
937–960. https://doi.org/10.1097/ALN.0000000000000841,
PubMed: 26275092
Redinbaugh, M. J., Afrasiabi, M., Phillips, J. M., Kambi, N. A.,
Mohanta, S., & Saalmann, Y. B. (2021). Thalamic deep
brain stimulation as a paradigm to reduce consciousness:
Implications for cortico-striatal dynamics, absence epilepsy
and consciousness studies. bioRxiv. https://doi.org/10.1101
/2021.07.27.453855
Redinbaugh, M. J., Phillips, J. M., Kambi, N. A., Mohanta, S.,
Andryk, S., Dooley, G. L., et al. (2020). Thalamus modulates
consciousness via layer-specific control of cortex. Neuron,
106, 66–75. https://doi.org/10.1016/j.neuron.2020.01.005,
PubMed: 32053769
Reimer, A., Hubka, P., Engel, A. K., & Kral, A. (2011). Fast
propagating waves within the rodent auditory cortex.
Cerebral Cortex, 21, 166–177. https://doi.org/10.1093/cercor
/bhq073, PubMed: 20444841
Sanchez-Vives, M. V., & McCormick, D. A. (2000). Cellular and
network mechanisms of rhythmic recurrent activity in
neocortex. Nature Neuroscience, 3, 1027–1034. https://doi
.org/10.1038/79848, PubMed: 11017176
Sato, T. K., Nauhaus, I., & Carandini, M. (2012). Traveling waves
in visual cortex. Neuron, 75, 218–229. https://doi.org/10.1016
/j.neuron.2012.06.029, PubMed: 22841308
Sreekumar, V., Wittig, J. H., Chapeton, J., Inati, S. K., &
Zaghloul, K. A. (2020). Low frequency traveling
waves in the human cortex coordinate neural activity
across spatial scales. bioRxiv. https://doi.org/10.1101/2020.03
.04.977173
Takahashi, K., Saleh, M., Penn, R. D., & Hatsopoulos, N. G.
(2011). Propagating waves in human motor cortex. Frontiers
in Human Neuroscience, 5, 40. https://doi.org/10.3389
/fnhum.2011.00040, PubMed: 21629859
Townsend, R. G., & Gong, P. (2018). Detection and analysis
of spatiotemporal patterns in brain activity. PLoS
Computational Biology, 14, e1006643. https://doi.org/10
.1371/journal.pcbi.1006643, PubMed: 30507937
Watt, A. J., Cuntz, H., Mori, M., Nusser, Z., Sjöström, P. J., &
Häusser, M. (2009). Traveling waves in developing cerebellar
cortex mediated by asymmetrical Purkinje cell connectivity.
Nature Neuroscience, 12, 463–473. https://doi.org/10.1038
/nn.2285, PubMed: 19287389
Bhattacharya et al.
1285
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Wong, R. O., Meister, M., & Shatz, C. J. (1993). Transient period
of correlated bursting activity during development of the
mammalian retina. Neuron, 11, 923–938. https://doi.org/10
.1016/0896-6273(93)90122-8, PubMed: 8240814
Xu, W., Huang, X., Takagaki, K., & Wu, J. Y. (2007).
Compression and reflection of visually evoked cortical waves.
Neuron, 55, 119–129. https://doi.org/10.1016/j.neuron.2007
.06.016, PubMed: 17610821
Zhang, H., & Jacobs, J. (2015). Traveling theta waves in the
human hippocampus. Journal of Neuroscience, 35,
12477–12487. https://doi.org/10.1523/JNEUROSCI.5102-14
.2015, PubMed: 26354915
Zhang, H., Watrous, A. J., Patel, A., & Jacobs, J. (2018). Theta
and alpha oscillations are traveling waves in the human
neocortex. Neuron, 98, 1269–1281. https://doi.org/10.1016/j
.neuron.2018.05.019, PubMed: 29887341
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
j
/
o
c
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
3
4
7
1
2
7
4
2
0
2
8
4
9
3
/
/
j
o
c
n
_
a
_
0
1
8
5
6
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
1286
Journal of Cognitive Neuroscience
Volume 34, Number 7