MÉTODOS
Visibility graphs for fMRI data: Multiplex temporal
graphs and their modulations across
redes en estado de reposo
Speranza Sannino1,4, Sebastiano Stramaglia2, Lucas Lacasa3, and Daniele Marinazzo1
1Department of Data Analysis, Faculty of Psychology and Educational Sciences, University of Ghent, Bélgica
2Department of Physics, University of Bari and INFN Section of Bari, Italia
3School of Mathematical Sciences, Queen Mary University of London, Reino Unido
4Department of Electric and Electronic Engineering, University of Cagliari, Italia
un acceso abierto
diario
Palabras clave: Multivariate visibility graphs, Multiplex networks, Resting state fMRI
ABSTRACTO
Visibility algorithms are a family of methods that map time series into graphs, such that the
tools of graph theory and network science can be used for the characterization of time series.
This approach has proved a convenient tool, and visibility graphs have found applications
across several disciplines. Recientemente, an approach has been proposed to extend this
framework to multivariate time series, allowing a novel way to describe collective dynamics.
Here we test their application to fMRI time series, following two main motivations, a saber
eso (a) this approach allows vs to simultaneously capture and process relevant aspects of
both local and global dynamics in an easy and intuitive way, y (b) this provides a
suggestive bridge between time series and network theory that nicely fits the consolidating
field of network neuroscience. Our application to a large open dataset reveals differences in
the similarities of temporal networks (and thus in correlated dynamics) across resting-state
redes, and gives indications that some differences in brain activity connected to
psychiatric disorders could be picked up by this approach.
RESUMEN DEL AUTOR
Here we present the first application of multivariate visibility graphs to fMRI data. Visibility
graphs are a way to represent a time series as a temporal network, evidencing specific
aspects of its dynamics, such as extreme events. Multivariate time series, as those
encountered in neuroscience, and in fMRI in particular, can be seen as a multiplex network,
in which each layer represents a time series (a region of interest in the brain in our case).
Here we report the method, we describe some relevant aspects of its application to BOLD
time series, and we discuss the analogies and differences with existing methods. Finalmente, nosotros
present an application to a high-quality, publicly available dataset, containing healthy
subjects and psychotic patients, and we discuss our findings. All the code to reproduce the
analyses and the figures is publicly available.
Visibility graphs were recently introduced as a method to map time series into
redes (Lacasa, Luque, Ballesteros, Luque, & Nuño, 2008; Luque, Lacasa, Ballesteros, &
Luque, 2009), with the aims of using the tools of network science (Boccaletti et al., 2014;
Hombre nuevo, 2010) to describe the structure of time series and their underlying dynamics. Este
strategy of transforming time series into graphs has been exploited in recent years by some
authors and several alternative methods have been put forward, contributing to the nascent
Citación: Sannino, S., Stramaglia, S.,
Lacasa L., & Marinazzo, D. (2017).
Visibility graphs for fMRI data:
Multiplex temporal graphs and their
modulations across resting-state
redes. Neurociencia en red,
1(3), 208–221. https://doi.org/10.1162/
netn_a_00012
DOI:
https://doi.org/10.1162/netn_a_00012
Supporting Information:
https://github.com/danielemarinazzo/
Visibility_LA5C_data
https://github.com/danielemarinazzo/
Visibility
Recibió: 15 Febrero 2017
Aceptado: 6 Abril 2017
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
Daniele Marinazzo
daniele.marinazzo@ugent.be
Editor de manejo:
Olaf Sporns
Derechos de autor: © 2017
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
norte
mi
norte
_
a
_
0
0
0
1
2
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Visibility graphs for fMRI data
Visibility graph:
A visibility graph is a network in
which the nodes are time points,
and the links are defined according
to the visibility criteria described
in the text.
Multilayer networks:
Multilayer networks incorporate
multiple types of interactions
between the same nodes. Este
means that multivariate time series
can be represented in a multilayer
visibility graph.
Luque, Ballesteros, Núñez, & Robledo, 2013;
field of performing graph theoretical time series analysis (see Donner, Zou, Donges, Marwan, &
Kurths, 2010; Xu, zhang, & Pequeño, 2008; zhang & Pequeño, 2006, for a few seminal examples
and Gao, Pequeño, & Kurths, 2016 and references therein for a recent overview). Research on
visibility graphs has since then focused essentially on two separated avenues. Primero, analytic
studies have primarily explored the foundations of this mapping (Gutin, Mansour, & Severini,
2011; Iacovacci & Lacasa, 2016; Lacasa, 2016; Luque & Lacasa, n.d.) and elaborated on
mathematical methods (Lacasa, 2014) to extract rigorous results on the topology of visibility
graphs associated to canonical dynamics such as stochastic or chaotic processes (Brú, Gómez-
Castro, & Nuño, 2017; Gonçalves, Carpi, Rosso, & Ravetti, 2016; Lacasa, Luque, Luque, &
Nuño, 2009;
Luque, Lacasa, Ballesteros &
Robledo, 2011) and to obtain combinatoric analogues of different dynamical quantities
(Lacasa, Nuñez, Roldán, Parrondo, & Luque, 2012). The second avenue deals with applica-
tions of this machinery, primarily by using this method as a feature extraction procedure
with which to build feature vectors that can properly characterize time series with the pur-
pose of making statistical learning (see Bhaduri & Ghosh, 2016; Hou, li, Wang, & yan, 2016;
Largo, Fonseca, Aarts, Haakma, & Foussier, 2014; shao, 2010, for a few examples in the life
sciences). A visibility graph is a network in which the nodes are time points, and the links
are defined according to the visibility criteria described in the text.
In this latter context,
the application to neuroscience is in its infancy and has been essentially limited so far to
the analysis of electroencephalogram (EEG) datos (see Ahmadlou, Adeli, & Adeli, 2010, 2012;
Ahmadlou, Ahmadi, Rezazade, & Azad-Marzabadi, 2013; Bhaduri & Ghosh, 2016; Mira-
Iglesias, Conejero, & Navarro-Pardo, 2016 for a few examples). The study of fMRI recordings
under this lens has been scarce, and in this work we would like to motivate and justify why we
think this is a promising enterprise, both from a univariate and—perhaps more interestingly—
from a multivariate time series perspective (Lacasa, Nicosia, & latora, 2015). Multilayer net-
works incorporate multiple types of interactions between the same nodes. This means that
multivariate time series can be represented in a multilayer visibility graph. Among other strate-
gies to map time series intro graphs, using the repertoire of visibility graphs is particularly
interesante, not just because its current application is scarce, but also because these meth-
ods are well suited to handle the specificities of fMRI data. More concretely, these methods
have been shown to be efficient in extracting information and dealing with (a) data polluted
with noise (Lacasa et al., 2009), (b) multivariate (Nicosia & latora, 2015), y (C) non station-
ary time series (Luque et al., 2009). In order to showcase the usefulness of visibility graphs in
neuroscience we will choose a biggish, high-quality public dataset of resting-state fMRI data
(Poldrack et al., 2016), and will make use of the family of visibility algorithms to build a mul-
tilevel graph of temporal networks, where each node represents a time point, and two nodes
are connected if they are visible to each other, according to the algorithm explained below.
In the case of multivariate time series—as the ones acquired in neuroimaging—each of these
networks is actually the layer of a multiplex network (usually associated with a recording in a
different region of interest (ROI). Being able to integrate all the data in a single structure en-
ables both the intralayer (univariate) and the interlayer (multivariate) analysis simultaneously.
We will show that a direct analysis of this network provides genuine and nontrivial information
on fMRI data, potentially including the description and possible noninvasive classification of
some brain diseases.
MATERIALES Y MÉTODOS
fMRI data
We used the public dataset described in Poldrack et al. (2016). These data were obtained from
the OpenfMRI database, with accession number ds000030. We use resting-state fMRI data
Neurociencia en red
209
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
norte
mi
norte
_
a
_
0
0
0
1
2
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Visibility graphs for fMRI data
de 121 healthy controls, 50 individuals diagnosed with schizophrenia, 49 individuals
diagnosed with bipolar disorder, y 40 individuals diagnosed with ADHD (attention-deficit/
hyperactivity disorder). The demographics are reported in the original paper, and they can
additionally be found in the GitHub page containing the results of this study (Marinazzo,
2017a).
The fMRI data were preprocessed with FSL (FMRIB Software Library v5.0). The volumes
were corrected for motion, after which slice timing correction was applied to correct for
temporal alignment. All voxels were spatially smoothed with a 6 mm FWHM (full width at
half maximum) isotropic Gaussian kernel and after intensity normalization, a band pass fil-
ter was applied between 0.01 y 0.08 Hz.
Además, linear and quadratic trends were
removed. We next regressed out the motion time courses, the average cerebrospinal fluid sig-
nal, and the average white matter signal. Global signal regression was not performed. Datos
were transformed to the MNI152 template, such that a given voxel had a volume of 3 mm ×
3 mm × 3mm. Finalmente, we averaged the signal in 278 ROIs using the template described in
shen, Tokoglu, Papademetris, & Constable (2013). In order to localize the results within the
intrinsic connectivity network of the resting brain, we assigned each of these ROIs to one of the
nine resting-state networks (seven cortical networks, plus subcortical regions and cerebellum)
as described in Yeo et al. (2011).
Construction of the visibility graphs
The procedure to build up a visibility graph is extensively and clearly described in Lacasa et al.
(2008, 2009, 2012) for univariate and Lacasa et al. (2015) for multivariate time series. Aquí
we will recall the basic steps and provide a visualization of the application of the methodology
to BOLD data.
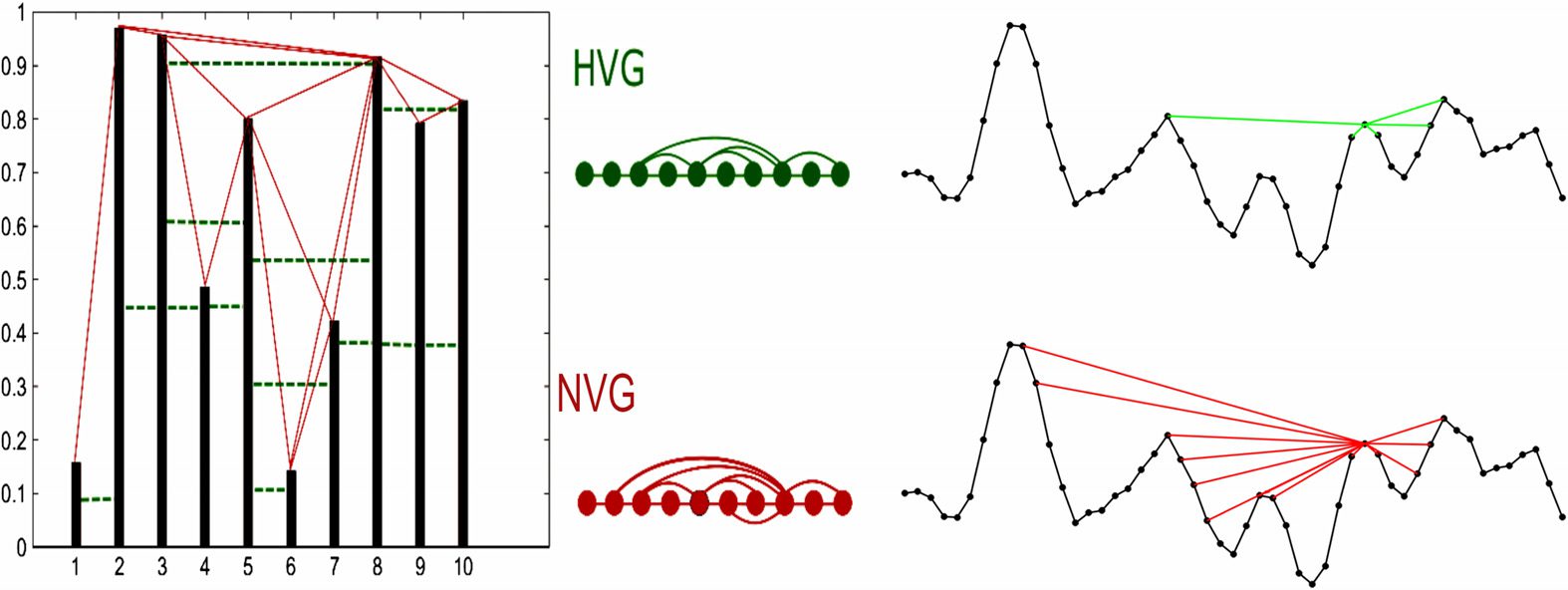
Given a time series of N data, any two time points i and j in which the measured quantity
takes the values yi and yj, respectivamente, will have visibility and consequently will become two
connected nodes in the associated natural visibility graph if any other data point yk placed
between them fulfills the following condition:
yk < yi + (yj − yi)
k − i
j − i .
Together with this convexity criterion, named natural visibility, an ordering criterion, named
horizontal visibility, has also been defined (Lacasa et al., 2009). According to the latter,
two time points i and j, in which the measured quantity takes the values yi and yj, respec-
tively, will now have horizontal visibility if any other data point yk placed between them is
smaller; that is,
yk < inf{yi, yj}, ∀k : i < k < j.
In either case, the resulting graphs have N nodes, are connected by a trivial Hamiltonian
path that induces a natural ordering in the degree sequence, and are undirected (see Figure 1
for an illustration). In the event that the time arrow turns out to be a relevant aspect, directed
graphs can be easily constructed, as detailed in Lacasa et al. (2012). Note that the resulting
horizontal visibility graph (HVG) is simply a core subgraph of the natural visibility graphs
(NVG), the former being analytically tractable (Lacasa, 2014). As a matter of fact, HVG can
Network Neuroscience
210
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
Figure 1. Examples of natural visibility graph (NVG, bottom) and horizontal visibility graph (HVG,
top) algorithms applied to the same sample time series. In each case, a time series of N data map
into a graph of N nodes, where two nodes are linked according to either natural or horizontal
visibility criteria (i.e., convexity and ordering criteria, respectively; see the text). On the right side,
an illustration of the points connected according to either criterion to a given time point from a
typical fMRI region of interest time series.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
be understood as an order statistic (Lacasa & Flanagan, 2015) and therefore filters out any
dependency on the series marginal distributions (this is not true for NVG, so in applications
where marginal distributions are relevant, one should use NVG rather than HVG).
Both algorithms are fast: naive implementations of NVGs have a runtime complexity O(N2);
however, a divide-and-conquer strategy already reduces it to O(N log N) (Lan, Mo, Chen,
Liu, & Deng, 2015). Naive implementation of HVG is already O(N log N) in most of the
cases of practical interest. Finally, these methods are well suited to handle several degrees
of nonstationarity in the associated time series (Lacasa & Flanagan, 2015).
In this work we will be analyzing BOLD data, and for that task we decided to choose NVG
over HVG. This is because NVGs are in principle better suited to handle and extract long-range
correlations than HVGs, as the former naturally allow for the development of hubs, which will
be typically associated with extreme events in the data and can correlate with data at all scales.
Correlations in time series are actually inherited in graph space in the degree distribution. It
is somewhat easier to find fat-tailed degree distributions in NVGs (which account for hubs
with extremely large degrees). On the other hand, HVGs (which have shown to work fine
with processes evidencing short-range correlations) typically display exponentially decaying
degree distributions; this feature is linked to short-scale visibility, making this method more
local.
For illustration, Figure 1 depicts how the links are established in the visibility graph accord-
ing to both visibility criteria. The code used to compute the visibility graphs is available on
GitHub (Marinazzo, 2017b) and it is basically a translation to Matlab of the original visibility
scripts in Fortran 90 (see http://www.maths.qmul.ac.uk/∼lacasa/VG.f90).
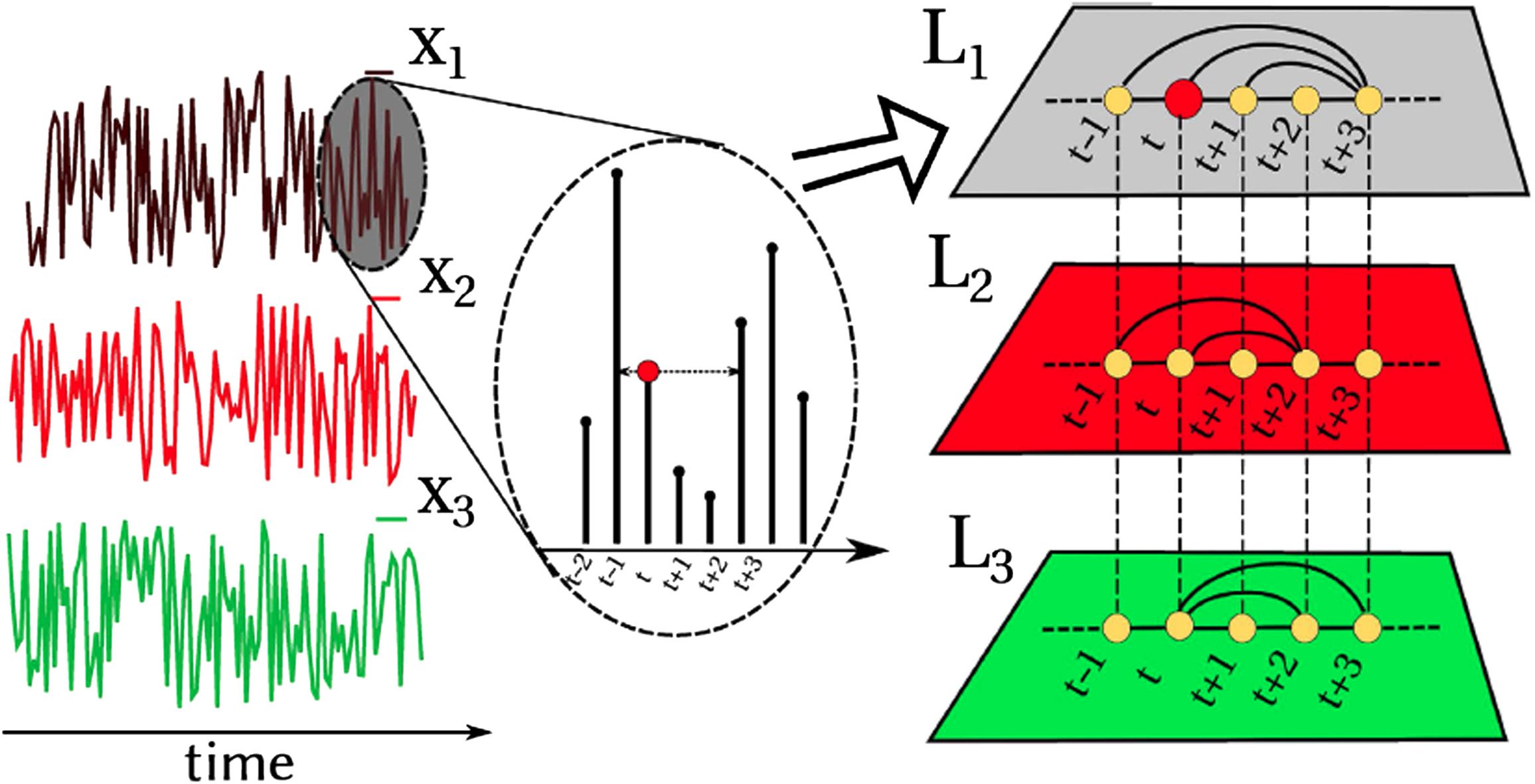
When it comes to the application to multivariate time series formed by M series, note that
each of the M time series yields a different visibility graph to begin with, so in principle the
multivariate series can always be mapped into a multilayer graph with M layers (Lacasa et al.,
2015). Moreover, since for every node i there is a natural correspondence across layers (node
i corresponds to time stamp i, and this is the same time stamp for all components), there exist
a natural alignment between every node of each layer, so the multilayer graph is effectively
Network Neuroscience
211
Visibility graphs for fMRI data
Figure 2.
Example of the construction of a multiplex visibility graph from a multivariate time series
with M = 3 components. In this figure, each layer builds the HVG associated with each variable,
therefore, all layers are well aligned according to the time arrow, making interlayer comparison
straightforward. Adapted from Lacasa et al. (2015).
a so-called multiplex network (Boccaletti et al., 2014; Lacasa et al., 2015, see Figure 2 for an
illustration). Of course, other smarter alignments between graphs could be investigated (for
instance, one could try to find the alignment that minimizes some sort of Hamming distance
between ordered node sets), but in this work we keep it simple and consider the natural align-
ment induced by the time arrow.
Interestingly, this multiplex visibility graph encodes the complex structure of each time
series in the topology of each layer. One can therefore extract in each layer any desired topo-
logical feature (say for instance, the entropy over the degree distribution, which would provide
a different number for each layer), with which one could build a feature vector that provides
a compact representation of the multivariate time series complexity. A similar procedure was
followed, for instance, in Ahmadlou et al. (2010) to extract markers of Alzheimer’s disease
from a graph theoretical characterization of the Hurst index of EEG data.
Second, the complex interdependencies and correlations that might emerge in a multivari-
ate series across variables could in turn be extracted using similarity measures across layers.
There exist a large variety of network measures that one can use for this task (Nicosia & Latora,
2015). A simple example of such a measure is the so-called interlayer mutual information, re-
cently explored in the context of multiplex visibility graphs of coupled chaotic maps Lacasa
et al., 2015. This quantity measures the information shared by every two layers based on the
similarity of the degree distributions. Given the degree distributions P(kα) and P(kβ) of two
arbitrary layers α and β, it is defined as
MIα,β = ∑
k[α]
∑
k[β]
P(k[α]
, k[β]) log
, k[β])
P(k[α]
P(k[α])P(k[β]) .
As the degree distribution captures the structure of each layer, this measure is in turn captur-
ing the information shared between the two layers, that is, the information shared across each
time series component of the multivariate time series. Now, since this is an M × M matrix
whose ij entry provides the mutual information between layers (ROIs) i and j, one can then,
Network Neuroscience
212
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
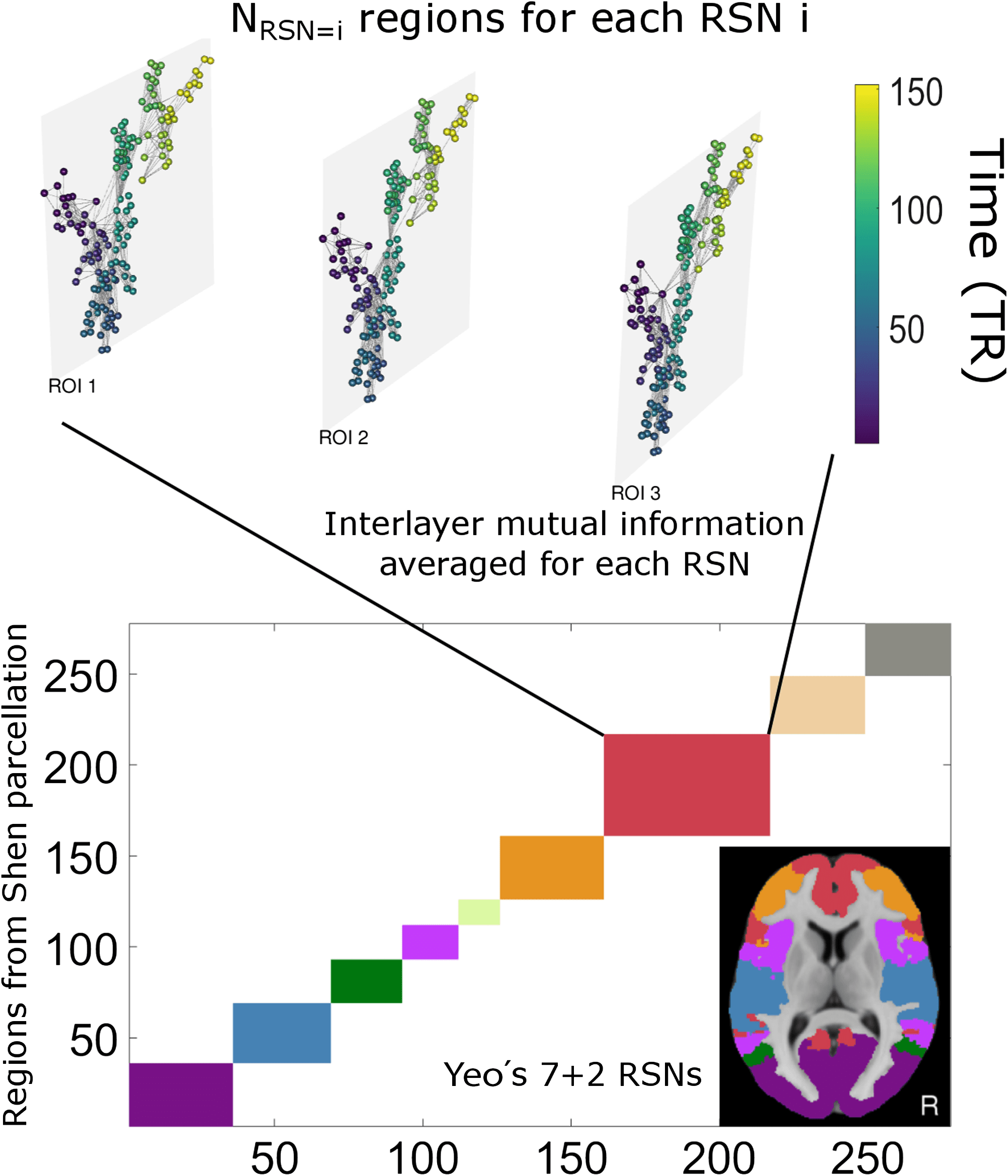
Figure 3.
Scheme of the procedure: Within a given region that aggregates a certain number
of ROIs, one constructs a visibility graph per ROI and builds accordingly a multiplex visibility
graph. We then compute the pairwise mutual information between degree distributions across the
multiplex layers (ROIs) and finally average to obtain a value for each RSN (resting-state network).
The multilayer network is visualized with MuxViz (De Domenico, Porter, & Arenas, 2015).
for instance, average across pairs (that is, across ROIs) to find a scalar quantity (cid:4)MI(cid:5): the mean
value of the mutual information for each intrinsic connectivity network. This methodology
is depicted in Figure 3. Note that other informational or similarity measures between layers
could be used instead (e.g., edge overlap, conditional or partial mutual information, transfer
entropy). Here for the sake of exposition, we consider only mutual information.
The visibility algorithms produce networks whose nodes are time points. As one can observe
in Figure 3, these networks have a modular structure, in which subnetworks are constituted by
time points that are mainly adjacent. A network has a modular structure if it can be divided into
Network Neuroscience
213
Visibility graphs for fMRI data
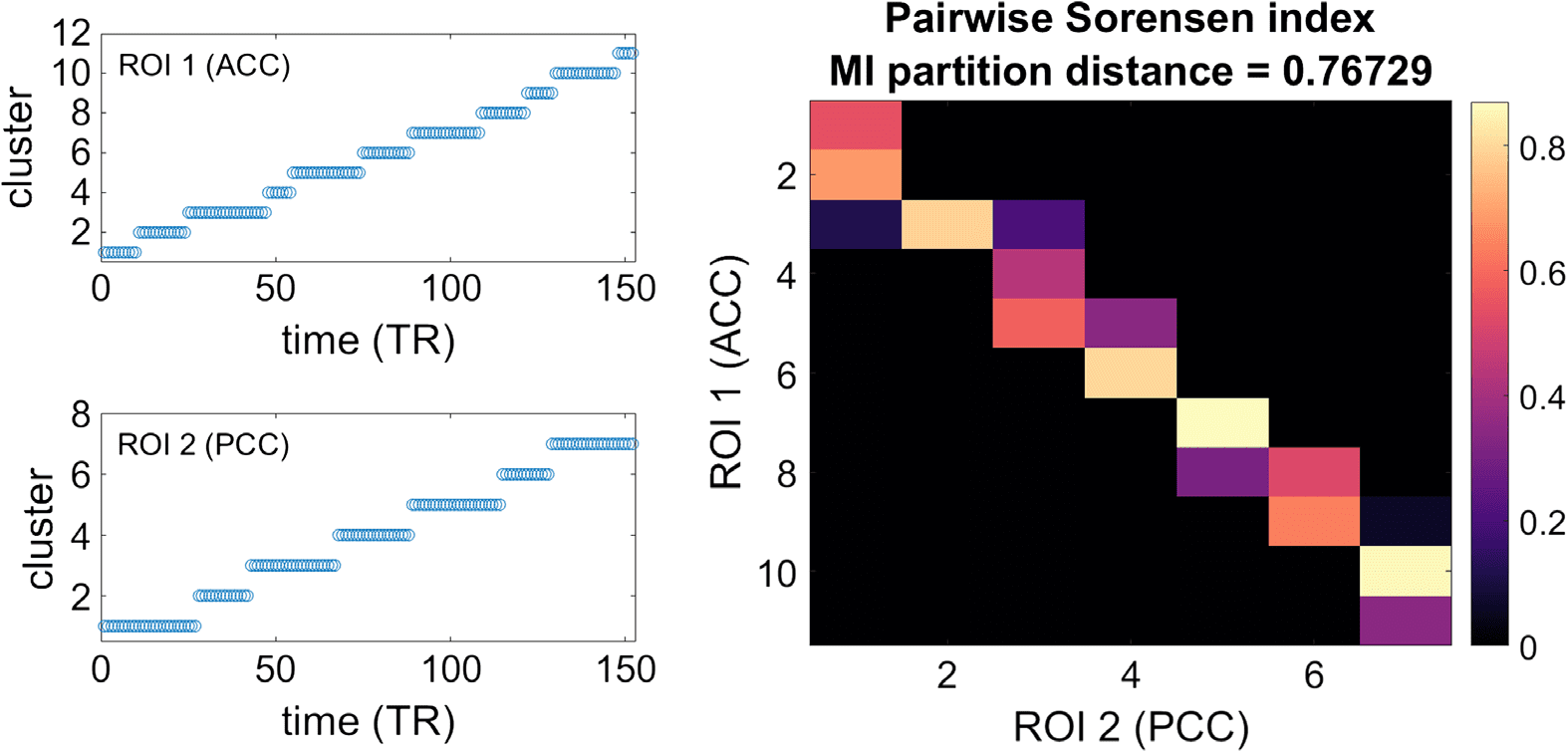
Left: The clusters in which the visibility adjacency matrices from two example ROIs
Figure 4.
are partitioned according to the Louvain algorithm. Right: Sorensen index quantifying the similarity
between pairs of clusters. The value of the distance among the partitioned networks considered as
a whole is also reported, in terms of normalized mutual information.
subnetworks (modules) characterized by a higher probability of connections within each model
than across models. A modular structure in a temporal network is thus an indication of dif-
ferent temporal regimes. The existence of these temporal regimes is what motivated the study of
dynamical functional connectivity (see,
for example, Hansen, Battaglia, Speigler, Deco, &
Jirsa, 2013; Hutchison et al., 2013). Dynamic functional connectivity can be seen in the vis-
ibility framework as the comparison of the temporal networks, taking their modular structure
into account. This comparison can be done in the first place considering the modular network
as a whole. In our case we partitioned the visibility graphs for each ROI using 100 runs of the
Louvain algorithm. We then quantified the distance between the two partitions by means of the
mutual information, using the function in the Brain Connectivity Toolbox (Rubinov & Sporns,
2010). The results of the partition of two ROIs, one in the anterior cingulate cortex (ACC) and
one in the precuneus (PCC), are shown in Figure 4. The modules of the graphs correspond to
consecutive time points (left panels); that is partitioning the visibility graph provides a natural
decomposition of the time series in time intervals. Turning to the interdependency between
the two time series, the right panel of Figure 4 represents the Sorensen similarity between each
pair of modules in the two time series. It shows that there are segments with high Sorensen
indexes, and it is likely that during these segments the two ROIs reflect similar neural events.
RESULTS
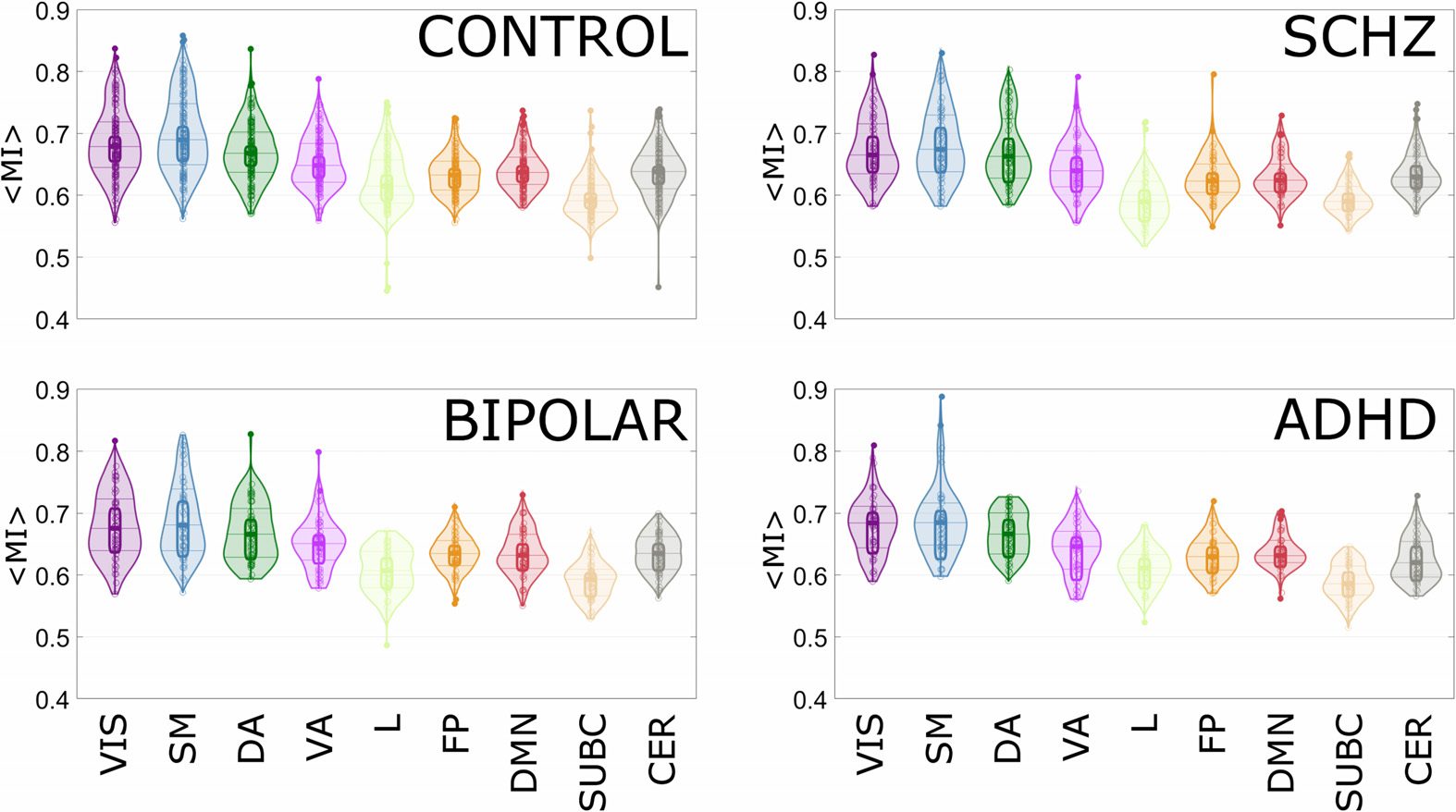
We start by reporting in Figure 5 the results of (cid:4)MI(cid:5) within each of the intrinsic connectivity
networks, for the four groups of subjects considered. For each group of subjects, each circle
corresponds to (cid:4)MI(cid:5) of a given subject, and random average shifted histograms are also pro-
vided. This representation is not parametric, and it is bounded. The plots report the median
of the Harrell-Davis estimator, and the 95% high density intervals using a Bayesian bootstrap.
The Harrell-Davis estimator doe is independent of the distribution (nonparametric) and is a
weighted linear combination of order statistics.
The outliers are detected based on the distance between each pair of data points without
assuming symmetry of distributions.
Harrell-Davis estimator:
The Harrell-Davis estimator does
is independent of the distribution
(nonparametric) and is a weighted
linear combination of order statistics.
Network Neuroscience
214
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
Figure 5.
subjects of the averaged interlayer mutual information.
For each group and each intrinsic connectivity network, we plot the distribution across
Kolmogorov-Smirnov statistic:
The Kolmogorov-Smirnov statistic
is a nonparametric test of the equality
of continuous, one-dimensional
probability distributions.
In order to account for departure from normality of these distributions, we used a graphi-
cal approach and computed the Kolmogorov-Smirnov distance (Rousselet, Pernet, & Wilcox,
2017), obtaining values up to 0.7 (a value of 0.39 would correspond to rejecting the
null hypothesis at a level α < 0.001 for the smallest population). The Kolmogorov-Smirnov
statistic is a nonparametric test of the equality of continuous, one-dimensional probability
distributions.
The number of ROIs constituting each intrinsic state network (thus a proxy for the network
size, given that Shen’s parcellation has ROIs of similar size) is not correlated with the average
value of the mutual information. In particular, it is interesting to observe that the intrinsic con-
nectivity network called limbic in Yeo’s parcellation is the smallest one, but nonetheless it has a
low interlayer mutual information compared with the other networks for all the clinical groups.
The network that showed the clearest differentiation in terms of the average interlayer mutual
information among the four clinical groups is indeed the Limbic one (Figure 6). This evidence
was assessed by means of a multivariate response test with age of the subjects and framewise
displacement as covariates. The p value of 0.005 was corrected for multiple comparisons
using the Bonferroni-Holm criterion with α = 0.05. The Kolmogorov-Smirnov statistics of the
pairwise comparison between the distributions of average interlayer mutual information values
for these particular networks ranged from 0.15 to 0.3. The null hypothesis of values for controls
and schizophrenics drawn from the same distribution would be rejected with an α < 0.005.
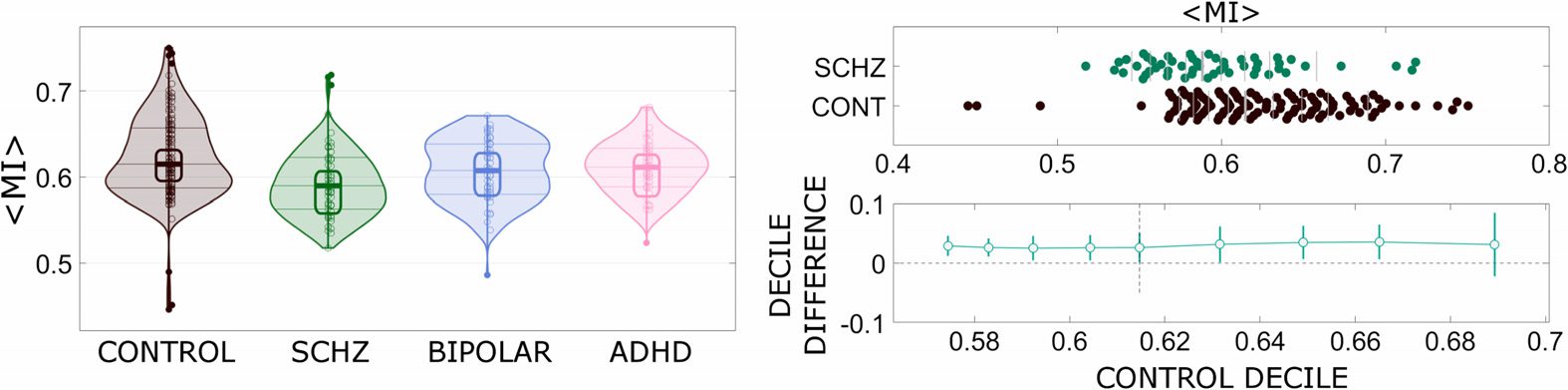
Figure 6 also reports the shift functions to visualize the difference between two distributions, in
this case controls and schizophrenics. The shift function can help us understand and quantify
how the two distributions differ. The shift function describes how one distribution should be
rearranged to match the other one: it estimates how and by how much one distribution must
be shifted.
This function (Wilcox, 1995) does not assume (as t tests do) that two distributions differ only
in the location of the bulk of the observations, and it enables determination of how, and by how
much, two distributions differ. Here the Harrell-Davis quantile estimator is used. Confidence
Shift function:
The shift function can help us
understand and quantify how the
two distributions differ. The shift
function describes how one
distribution should be rearranged to
match the other one: it estimates
how and by how much one
distribution must be shifted.
Network Neuroscience
215
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
Figure 6.
Left: The average interlayer mutual information for the intrinsic connectivity network
denoted as limbic, for the four groups of subjects. Right: Shift function to visually and statistically
compare the distributions for controls and schizoprenics, at different quantiles.
intervals of the decile differences with a bootstrap estimation of the standard error of the deciles
are computed, and one controls for multiple comparisons so that the type I error rate remains
around 0.05 across the nine confidence intervals (Rousselet et al., 2017). In this specific case
we can observe a clear separation for all the quantiles but the ninth one.
To complement this analysis, in Figure 1 we further report two additional ways in which
results of this kind are often represented (mean and standard errors). According to this plot, it
is already evident to the naked eye that the method easily distinguishes controls from patients
with any mental disorder, suggesting that visibility graphs do indeed extract informative fea-
tures that can be used for noninvasive diagnosis. Visualizing results in such a way is indeed
suboptimal and sometimes problematic (nicely explained in Rousselet, Foxe, & Bolam, 2016);
for this reason we initially chose the visualizations provided in Figures 5 and 6 (Rousselet et al.,
2017).
DISCUSSION
Why the (Multivariate) Visibility Graph?
All in all, there are several reasons why we think that visibility graphs are a convenient tool.
We discuss some of these reasons below.
Visibility graphs have been shown to inherit in their topology the essence of the
Usefulness:
associated dynamics, including nontrivial fingerprints that are both descriptive and informative
for statistical learning purposes.
These methods can be used directly in both stationary and nonstationary
Fit for purpose:
signals (i.e., nonstationarity is not required to be removed). Also, series do not require ad hoc
phase partitioning or symbolization. Also, visibility graphs naturally filter out linear trends,
so they do not require such detrending (Lacasa et al., 2008). Furthermore, since HVG is an
order statistic, it is also invariant under monotonic (order-preserving) rescaling on the data
(Lacasa & Flanagan, 2015). The NVG is not invariant under this latter transformation however,
so nonlinear rescaling to make data more “peaky” will necessarily modify the associated NVG
in a nontrivial way.
The method is numerically straightforward to implement
Computationally easy and efficient:
and the runtime algorithms are quite decent, varying from O(N) for so-called visibility sequen-
tial motifs (Iacovacci & Lacasa, 2016) to O(N log N) for the full adjacency matrices using a
divide-and-conquer strategy.
Network Neuroscience
216
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
Amenable to analytical insight: Unlike other strategies for graph theoretical time series analy-
sis, visibility graphs are not computational black boxes. More particularly for HVG ( but not
only Iacovacci & Lacasa, 2016; Luque et al., 2009), there exist several theorems available and
methods to build rigorous results of HVG properties (Lacasa, 2014, 2016; Lacasa et al., 2009,
2012; Luque et al., 2013). The latter is an area of intense research activity at the interface
between combinatorics and dynamical systems.
The methods are not context dependent but are generally applicable to both
Versatile:
univariate and multivariate time series across the disciplines. A drawback of this property
is that the topological features one can extract from these graphs are themselves not context
dependent.
It builds a bridge between time series and networks and thus opens the exciting
Novel:
possibility of exploring the usefulness of a large set of new tools in the endeavor to describe
and classify complex signals.
Coming back to the specific reason why we think that natural visibility graphs are partic-
ularly suited for BOLD data, it has been shown that relevant information on the time course
of the BOLD signal and on correlated activity can be extracted by looking at single frames,
corresponding to peaks in the signal (Liu & Duyn, 2013; Tagliazucchi, Balenzuela, Fraiman, &
Chialvo, 2012), and that these events could be the proxy for an innovation signal at the neural
level (Karahanoglu & Van De Ville, 2015; Wu et al., 2013). In this framework, the degree of
the nodes corresponding to the BOLD peaks in the adjacency matrix constructed according
to natural visibility emphasizes the functional relevance of the neural events and of the cor-
responding patterns of coactivation across the brain. However, both NVG and HVG have been
shown to be useful in different contexts, so there is no general rule of thumb on what method
should we use: this choice shall be addressed on a case-by-case basis.
Finally, what is important and informative when describing the properties of a certain cog-
nitive state? Is it the complex pattern underlying the structure of individual time series (that
is, local activity of ROIs) of different regions? Or are the correlations and interdependencies
(understood in a broad sense) between these regions the key aspect to look at? When the
latter is the case, a functional network analysis approach (Bullmore & Sporns, 2009) seems
appropriate. In the former case where the nature of local activity across regions already cap-
tures information (He, 2011; Zang, Jiang, Lu, He, & Tian, 2004), one does not need to resort
to functional dependencies and local analysis is the correct thing to do. This is obviously an
open question that should be addressed, from a biological point of view, on a case-by-case
basis. A recent study suggests that both conceptual frameworks can indeed be connected
(Sethi, Zerbi, Wenderoth, Fornito, & Fulcher, 2017).
In general, both aspects likely play a
relevant role, and some studies have already successfully merged the two (Ciuciu, Abry, & He,
2014; Tagliazucchi et al., 2016). Nevertheless, the multiplex visibility framework offers a
compact way of extracting at once both the local temporal structure (via the network intra-
layer properties) and the global interconnection pattern (via multiplex interlayer similarities).
Similarity with other measures
We discussed at the end of the Methods section that the modular temporal graphs resulting from
the visibility algorithm are a natural way to describe different dynamical regimes of individual
time series, and their interdependence, without arbitrary and possibly problematic choices
Network Neuroscience
217
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
Modularity in networks:
A network has a modular structure if
it can be divided into subnetworks
(modules) characterized by a higher
density of connections within each
module than across modules.
such as a sliding window and its length (Hindriks et al., 2016; Kudela, Harezlak, & Lindquist,
2017).
Features of the visibility graph, such as the modularity, the clustering coefficient, or the node
degree, could be used as features in classification algorithms aimed to detect modulations of
the local and correlated dynamical regime of BOLD signals.
Furthermore, using the excellent resource NeuroVault (http://neurovault.org/), we
also looked at the maps depicting the results of other measures and noticed that the areas
belonging to the limbic Yeo network are associated with lower levels of regional homogeneity
(Zang et al., 2004), higher coefficient of variation of the BOLD signal (Wu & Marinazzo, 2016),
and lower value of the fractional amplitude of low-frequency fluctuations (fALFF) (Zou et al.,
2008). This evidence speaks to the fact that interlayer mutual information in multiplex visibility
networks is associated with decreased predictability and increased independence between the
degrees of freedom of the measured time series.
Classification of neural disorders
The main focus of this paper is methodological, and a thorough discussion of the implica-
tions of our results on neuroimaging studies of psychiatric disorders is beyond its scope; more-
over, we would not want to hypothesize after the results are known (HARKing) (Poldrack et al.,
2017). However, it is interesting to highlight that the limbic network has been previously asso-
ciated with mental disorders (Kiehl, 2006; Liston, Cohen, Teslovich, Levenson, & Casey, 2011;
Potvin, Lungu, Tikàsz, & Mendrek, 2017; Rdulescu & Mujica-Parodi, 2009; Roberts et al.,
2016; Whalley et al., 2012).
In the same way, we refer the reader to recent studies specifi-
cally aimed at using advanced neuroimaging data analysis tools to map and classify neural
disorders (Cetin et al., 2016; Demirci et al., 2008; Miller, Vergara, Keator, & Calhoun, 2016),
and Fornito, Zalesky, & Breakspear (2015) for a review. Our results shown here using visibility
graphs confirm some of this previous work and further showcase that visibility graphs ex-
tract informative features with which we can find statistically significant signatures of different
neural disorders.
To conclude, given the exposition and results reported in this study, we hope to have
motivated our colleagues to consider visibility graphs as a valuable tool for both exploratory
and focused studies.
ACKNOWLEDGMENTS
We thank Matteo Fraschini (University of Cagliari) for setting up the Erasmus mobility for
Speranza. We thank Caroline Garcia Forlim for consulting on the mutual information code.
We thank Enzo Nicosia (Queen Mary University of London) for stimulating discussions on
visibility graphs.
AUTHOR CONTRIBUTIONS
Speranza Sannino: Formal analysis; Software; Writing – original draft. Sebastiano Stramaglia:
Conceptualization; Methodology; Software; Writing – review & editing.
Lucas Lacasa:
Conceptualization; Software; Writing – original draft; Writing – review & editing. Daniele
Marinazzo: Conceptualization; Investigation; Methodology; Project administration; Software;
Supervision; Validation; Visualization; Writing – original draft; Writing – review & editing.
Network Neuroscience
218
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
REFERENCES
Ahmadlou, M., Adeli, H., & Adeli, A. (2010). New diagnostic EEG
markers of the Alzheimer’s disease using visibility graph. Journal
of Neural Transmission, 117(9), 1099–1109. https://doi.org/10.
1007/s00702-010-0450-3
Ahmadlou, M., Adeli, H., & Adeli, A. (2012). Improved visibility
graph fractality with application for the diagnosis of autism spec-
trum disorder. Physica A: Statistical Mechanics and its Appli-
cations, 391(20), 4720–4726. https://doi.org/10.1016/j.physa.
2012.04.025
Ahmadlou, M., Ahmadi, K., Rezazade, M., & Azad-Marzabadi,
E. (2013). Global organization of functional brain connectivity
in methamphetamine abusers. Clinical Neurophysiology, 124(6),
1122–1131. https://doi.org/10.1016/j.clinph.2012.12.003
Bhaduri, A., & Ghosh, D. (2016). Quantitative assessment of heart
rate dynamics during meditation: An ECG based study with
multi-fractality and visibility graph. Frontiers in Physiology, 7,
44. https://doi.org/10.3389/fphys.2016.00044
Boccaletti, S., Bianconi, G., Criado, R., del Genio, C., Gómez-
Gardeñes, J., Romance, M., . . . Zanin, M. (2014). The structure
and dynamics of multilayer networks. Physics Reports, 544(1),
1–122. https://doi.org/10.1016/j.physrep.2014.07.001
Brú, A., Gómez-Castro, D., & Nuño, J. (2017). Visibility to discern
local from nonlocal dynamic processes. Physica A: Statistical
Mechanics and its Applications, 471, 718–723. https://doi.org/
10.1016/j.physa.2016.12.078
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038/
nrn2575
Cetin, M. S., Houck, J. M., Rashid, B., Agacoglu, O., Stephen, J. M.,
Sui, J., . . . Calhoun, V. D. (2016). Multimodal classification of
schizophrenia patients with MEG and fMRI data using static and
dynamic connectivity measures. Frontiers in Neuroscience, 10,
466. https://doi.org/10.3389/fnins.2016.00466
Ciuciu, P., Abry, P., & He, B. J.
Interplay between func-
tional connectivity and scale-free dynamics in intrinsic fMRI
networks. NeuroImage, 95, 248–263. https://doi.org/10.1016/j.
neuroimage.2014.03.047
(2014).
De Domenico, M., Porter, M. A., & Arenas, A.
(2015). MuxViz:
A tool for multilayer analysis and visualization of networks.
Journal of Complex Networks, 3(2), 159–176. https://doi.org/10.
1093/comnet/cnu038
Demirci, O., Clark, V. P., Magnotta, V. A., Andreasen, N. C.,
Lauriello, J., Kiehl, K. A., . . . Calhoun, V. D.
(2008). A
review of challenges in the use of fMRI for disease classification /
characterization and a projection pursuit application from
Brain Imaging and
a multi-site fMRI schizophrenia study.
Behavior, 2(3), 207–226. https://doi.org/10.1007/s11682-008-
9028-1
Donner, R. V., Zou, Y., Donges, J. F., Marwan, N., & Kurths, J.
(2010). Recurrence networks—A novel paradigm for nonlinear
time series analysis. New Journal of Physics, 12(3), 033025.
Fornito, A., Zalesky, A., & Breakspear, M.
(2015). The connec-
tomics of brain disorders. Nature Reviews Neuroscience, 16(3),
159–172. https://doi.org/10.1038/nrn3901
Gao, Z.-K., Small, M., & Kurths, J.
(2016). Complex network
EPL (Europhysics Letters), 116(5),
analysis of
50001. Retrieved from http://stacks.iop.org/0295-5075/116/i=5/
a=50001
time series.
Gutin, G., Mansour, T., & Severini, S. (2011). A characterization of
horizontal visibility graphs and combinatorics on words. Physica
A, 390(12), 2421–2428.
Gonçalves, B. A., Carpi, L., Rosso, O. A., & Ravetti, M. G. (2016).
Time series characterization via horizontal visibility graph and
Physica A: Statistical Mechanics and its
information theory.
Applications, 464,93–102. https://doi.org/10.1016/j.physa.2016.
07.063
Hansen, E. C. A., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K.
(2015). Functional connectivity dynamics: Modeling the switch-
ing behavior of the resting state. NeuroImage, 105, 525–535.
https://doi.org/10.1016/j.neuroimage.2014.11.001
He, B. J.
(2011). Scale-free properties of the functional magnetic
resonance imaging signal during rest and task. The Journal of
Neuroscience, 31(39), 13786–13795. https://doi.org/10.1523/
JNEUROSCI.2111-11.2011
Hindriks, R., Adhikari, M., Murayama, Y., Ganzetti, M., Mantini, D.,
Logothetis, N., et al. (2016). Can sliding-window correlations re-
veal dynamic functional connectivity in resting-state fMRI? Neu-
roImage, 127, 242–256. https://doi.org/10.1016/j.neuroimage.
2015.11.055
Hou, F., Li, F., Wang, J., & Yan, F. (2016). Visibility graph analysis
of very short-term heart rate variability during sleep. Physica A:
Statistical Mechanics and its Applications, 458, 140–145. https://
doi.org/10.1016/j.physa.2016.03.086
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A.,
Calhoun, V. D., Corbetta, M., . . . Chang, C.
(2013). Dy-
namic functional connectivity: Promise, issues, and interpre-
tations. NeuroImage, 80, 360–378. https://doi.org/10.1016/j.
neuroimage.2013.05.079
Iacovacci, J., & Lacasa, L.
natural visibility graphs.
https://doi.org/10.1103/PhysRevE.94.052309
(2016). Sequential motif profile of
Physical Review E, 94(5), 052309.
Karahanoglu, F. I., & Van De Ville, D. (2015). Transient brain activ-
ity disentangles fMRI resting-state dynamics in terms of spatially
and temporally overlapping networks. Nature Communications,
6, 7751. https://doi.org/10.1038/ncomms8751
Kiehl, K. A.
(2006). A cognitive neuroscience perspective on
psychopathy: Evidence for paralimbic system dysfunction. Psy-
chiatry Research, 142(2–3), 107–128. https://doi.org/10.1016/j.
psychres.2005.09.013
Kudela, M., Harezlak, J., & Lindquist, M. A. (2017). Assessing un-
certainty in dynamic functional connectivity. NeuroImage, 149,
165–177. https://doi.org/10.1016/j.neuroimage.2017.01.056
Lacasa, L.
(2014). On the degree distribution of horizontal vis-
ibility graphs associated with markov processes and dynamical
systems: diagrammatic and variational approaches. Nonlinear-
ity, 27(9), 2063. Retrieved from http://stacks.iop.org/0951-7715/
27/i=9/a=2063
Lacasa, L.
quences.
(2016). Horizontal visibility graphs from integer se-
Journal of Physics A: Mathematical and Theoretical,
Network Neuroscience
219
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Visibility graphs for fMRI data
49(35), 35LT01. Retrieved from http://stacks.iop.org/1751-8121/
49/i=35/a=35LT01
Lacasa, L., & Flanagan, R.
(2015). Time reversibility from visibil-
ity graphs of nonstationary processes. Phys. Rev. E, 92, 022817.
https://doi.org/10.1103/PhysRevE.92.022817
Lacasa, L., Luque, B., Ballesteros, F., Luque, J., & Nuño, J. C. (2008).
From time series to complex networks: The visibility graph. Pro-
ceedings of the National Academy of Sciences of the United
States of America, 105(13), 4972–4975. https://doi.org/10.1073/
pnas.0709247105
Lacasa, L., Luque, B., Luque, J., & Nuño, J. C.
(2009). The vis-
ibility graph: A new method for estimating the hurst exponent
of fractional Brownian motion. EPL (Europhysics Letters), 86(3),
30001. Retrieved from http://stacks.iop.org/0295-5075/86/i=3/
a=30001
Lacasa, L., Nicosia, V., & Latora, V.
(2015). Network structure of
multivariate time series. Scientific Reports, 5, 15508. https://doi.
org/10.1038/srep15508
Lacasa, L., Nuñez, A., Roldán, É., Parrondo, J. M. R., & Luque, B.
(2012). Time series irreversibility: A visibility graph approach.
European Physical Journal B, 85(6), 217. https://doi.org/10.1140/
epjb/e2012-20809-8
Lan, X., Mo, H., Chen, S., Liu, Q., & Deng, Y. (2015). Fast trans-
formation from time series to visibility graphs. Chaos: An Inter-
disciplinary Journal of Nonlinear Science, 25(8), 083105. https://
doi.org/10.1063/1.4927835
Liston, C., Cohen, M. M., Teslovich, T., Levenson, D., & Casey,
B.
(2011). Atypical prefrontal connectivity in attention-deficit/
hyperactivity disorder: Pathway to disease or pathological end
point? Biological Psychiatry, 69(12), 1168–1177. https://doi.org/
10.1016/j.biopsych.2011.03.022
Liu, X., & Duyn, J. H.
(2013). Time-varying functional network
information extracted from brief instances of spontaneous brain
activity. Proceedings of the National Academy of Sciences of the
United States of America, 110(11), 4392–4397. https://doi.org/
10.1073/pnas.1216856110
Long, X., Fonseca, P., Aarts, R. M., Haakma, R., & Foussier, J. (2014).
Modeling cardiorespiratory interaction during human sleep with
complex networks. Applied Physics Letters, 105(20), 203701.
https://doi.org/10.1063/1.4902026
Luque, B., Ballesteros, F. J., Núñez, A. M., & Robledo, A. (2013).
Quasiperiodic graphs: Structural design, scaling and entropic
properties. Journal of Nonlinear Science, 23(2), 335–342. https://
doi.org/10.1007/s00332-012-9153-2
Luque, B., & Lacasa, L.
(n.d.). Canonical horizontal visibility
graphs are uniquely determined by their degree sequence. arXiv:
1605.05222.
Luque, B., Lacasa, L., Ballesteros, F., & Luque, J. (2009). Horizontal
visibility graphs: Exact results for random time series. Phys. Rev.
E, 80, 046103. https://doi.org/10.1103/PhysRevE.80.046103
Luque, B., Lacasa, L., Ballesteros, F. J., & Robledo, A.
(2011).
Feigenbaum graphs: A complex network perspective of chaos.
PLoS ONE, 6(9), 1–8.
https://doi.org/10.1371/journal.pone.
0022411
Marinazzo, D.
(2017a). Visibility_LA5C_data. GitHub reposi-
tory. Retrieved from https://github.com/danielemarinazzo/
Visibility_LA5C_data
Marinazzo, D. (2017b). Visibility. GitHub repository. Retrieved from
https://github.com/danielemarinazzo/Visibility
intertemporal
Miller, R. L., Vergara, V. M., Keator, D. B., & Calhoun, V. D. (2016).
functional-domain connectivity
A method for
analysis: Application to schizophrenia reveals distorted direc-
IEEE Transactions on Biomedical En-
tional information flow.
gineering, 63(12), 2525–2539. https://doi.org/10.1109/TBME.
2016.2600637
Mira-Iglesias, A., Conejero, J. A., & Navarro-Pardo, E. (2016). Nat-
ural visibility graphs for diagnosing attention deficit hyperactivity
disorder (ADHD). Electronic Notes in Discrete Mathematics, 54,
337–342. https://doi.org/10.1016/j.endm.2016.09.058
Newman, M. (2010). Networks: An introduction. Oxford: Oxford
University Press.
Nicosia, V., & Latora, V.
relations in multiplex networks.
https://doi.org/10.1103/PhysRevE.92.032805
(2015). Measuring and modeling cor-
Phys. Rev. E, 92, 032805.
Poldrack, R., Congdon, E., Triplett, W., Gorgolewski, K., Karlsgodt,
K., Mumford, J., . . . Bilder, R. (2016). A phenome-wide examina-
tion of neural and cognitive function. Scientific Data, 3, 160110.
https://doi.org/10.1038/sdata.2016.110
J.,
I., Durnez,
Matthews, P. M., Munafò, M. R., . . . Yarkoni, T. (2017). Scanning
the horizon: Towards transparent and reproducible neuroimag-
ing research. Nature Reviews Neuroscience, 18(2), 115–126.
https://doi.org/10.1038/nrn.2016.167
Poldrack, R. A., Baker, C.
J., Gorgolewski, K.
Potvin, S., Lungu, O., Tikàsz, A., & Mendrek, A. (2017). Abnormal
effective fronto-limbic connectivity during emotion processing
in schizophrenia. Progress in Neuro-Psychopharmacology and
Biological Psychiatry, 72, 1–8. https://doi.org/10.1016/j.pnpbp.
2016.08.004
Rdulescu, A. R., & Mujica-Parodi, L. R. (2009). A principal compo-
nent network analysis of prefrontal-limbic functional magnetic
resonance imaging time series in schizophrenia patients and
healthy controls. Psychiatry Research: Neuro imaging, 174(3),
184–194. https://doi.org/10.1016/j.pscychresns.2009.04.017
Roberts, G., Perry, A., Lord, A., Frankland, A., Leung, V., Holmes-
Preston, E., . . . Breakspear, M. (2016). Structural dysconnectiv-
ity of key cognitive and emotional hubs in young people at high
genetic risk for bipolar disorder. Molecular Psychiatry. Advance
online publication. https://doi.org/10.1038/mp.2016.216
Rousselet, G. A., Foxe, J. J., & Bolam, J. P.
(2016). A few simple
steps to improve the description of group results in neuroscience.
European Journal of Neuroscience, 44(9), 2647–2651. https://
doi.org/10.1111/ejn.13400
Rousselet, G. A., Pernet, C. R., & Wilcox, R. R.
(2017). Beyond
differences in means: Robust graphical methods to compare two
groups in neuroscience. bioRxiv. Retrieved from https://doi.org/
10.1111/ejn.13610
Rubinov, M., & Sporns, O.
(2010). Complex network measures
of brain connectivity: Uses and interpretations. NeuroImage,
52(3), 1059–1069. https://doi.org/10.1016/j.neuroimage.2009.
10.003
Sethi, S. S., Zerbi, V., Wenderoth, N., Fornito, A., & Fulcher,
B. D.
Structural connectome topology relates to
regional BOLD signal dynamics in the mouse brain. Chaos, 27,
047405.
(2017).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
220
Visibility graphs for fMRI data
Shao, Z.-G. (2010). Network analysis of human heartbeat dynam-
ics. Applied Physics Letters, 96(7), 073703. https://doi.org/10.
1063/1.3308505
Shen, X., Tokoglu, F., Papademetris, X., & Constable, R. T. (2013).
Groupwise whole-brain parcellation from resting-state fMRI
data for network node identification. NeuroImage, 82, 403–15.
https://doi.org/10.1016/j.neuroimage.2013.05.081
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3, 15.
https://doi.org/10.3389/fphys.2012.00015
Tagliazucchi, E., Chialvo, D. R., Siniatchkin, M., Amico, E.,
(2016). Large-
Brichant, J.-F., Bonhomme, V., . . . Laureys, S.
scale signatures of unconsciousness are consistent with a depar-
ture from critical dynamics. Journal of the Royal Society Interface,
13(114). https://doi.org/10.1089/rsif.2015.1027
Whalley, H. C., Papmeyer, M., Sprooten, E., Lawrie, S. M.,
Sussmann, J. E., & McIntosh, A. M. (2012). Review of functional
magnetic resonance imaging studies comparing bipolar disorder
and schizophrenia. Bipolar Disorders, 14(4), 411–431. https://
doi.org/10.1111/j.1399-5618.2012.01016.x
Wilcox, R. R.
(1995). Comparing two independent groups via
multiple quantiles. The Statistician, 44(1), 91. https://doi.org/
10.2307/2348620
Wu, G.-R., Liao, W., Stramaglia, S., Ding,
J.-R., Chen, H., &
Marinazzo, D.
(2013). A blind deconvolution approach to
recover effective connectivity brain networks from resting state
fMRI data. Medical Image Analysis, 17(3), 365–374. https://doi.
org/10.1016/j.media.2013.01.003
Wu, G.-R., & Marinazzo, D.
(2016). Sensitivity of the resting-
state haemodynamic response function estimation to autonomic
nervous system fluctuations. Philosophical Transactions of the
Royal Society of London A: Mathematical, Physical and Engineer-
ing Sciences, 374(2067).
Xu, X., Zhang, J., & Small, M. (2008). Superfamily phenomena and
motifs of networks induced from time series. Proceedings of the
National Academy of Sciences, 105(50), 19601–19605.
Yeo, B. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D.,
Hollinshead, M., et al.
(2011). The organization of the human
cerebral cortex estimated by intrinsic functional connectivity.
Journal of Neurophysiology, 106(3), 1125–1165. https://doi.org/
10.1152/jn.00338.2011
Zang, Y., Jiang, T., Lu, Y., He, Y., & Tian, L.
(2004). Regional ho-
mogeneity approach to fMRI data analysis. NeuroImage, 22(1),
394–400. https://doi.org/10.1016/j.neuroimage.2003.12.030
Zhang, J., & Small, M.
(2006). Complex network from pseudo-
periodic time series: Topology versus dynamics. Physical Review
Letters, 96(23), 238701.
Zou, Q.-H., Zhu, C.-Z., Yang, Y., Zuo, X.-N., Long, X.-Y., Cao,
Q.-J., . . . Zang, Y.–F. (2008). An improved approach to detection
of amplitude of low-frequency fluctuation (ALFF) for resting-state
fMRI: Fractional ALFF. Journal of Neuroscience Methods, 172(1),
137–141. https://doi.org/10.1016/j.jneumeth.2008.04.012
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
3
2
0
8
1
0
9
2
0
3
2
n
e
n
_
a
_
0
0
0
1
2
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
221