METHODS - IA de Investigación especializada en el MIT

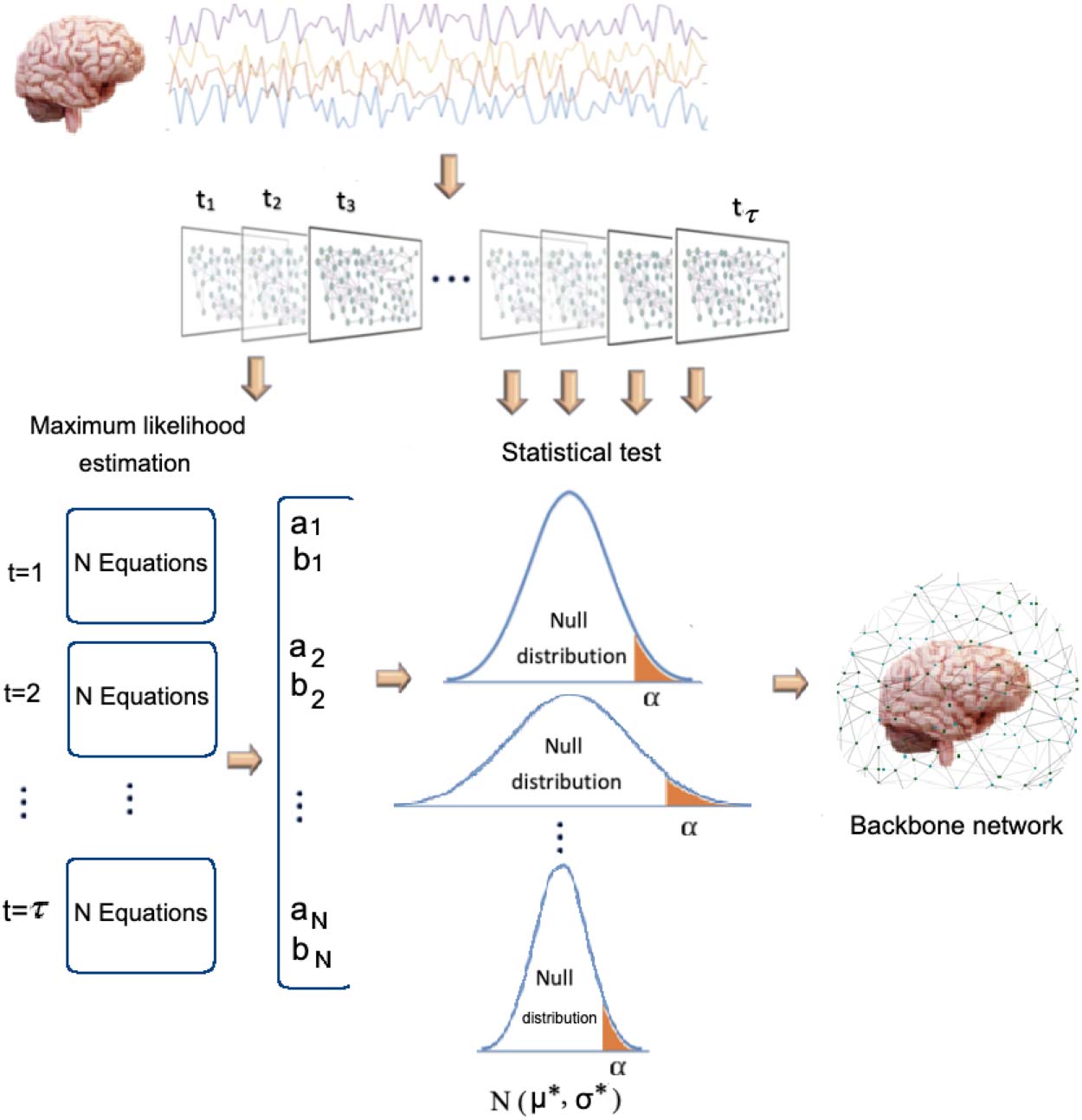
MÉTODOS

The backbone network of dynamic
conectividad funcional

Nima Asadi1

, Ingrid R. Olson2,3, and Zoran Obradovic1

1Department of Computer and Information Sciences, College of Science and Technology,
Temple University, Filadelfia, Pensilvania, EE.UU
2Department of Psychology, College of Liberal Arts, Temple University, Filadelfia, Pensilvania, EE.UU
3Decision Neuroscience, College of Liberal Arts, Temple University, Filadelfia, Pensilvania, EE.UU

Palabras clave: Dynamic functional connectivity, Backbone network, Null model, Optimization,
Autism spectrum disorder

un acceso abierto

diario

ABSTRACTO

Temporal networks have become increasingly pervasive in many real-world applications,
including the functional connectivity analysis of spatially separated regions of the brain. A
major challenge in analysis of such networks is the identification of noise confounds, cual
introduce temporal ties that are nonessential, or links that are formed by chance due to local
properties of the nodes. Several approaches have been suggested in the past for static networks
or temporal networks with binary weights for extracting significant ties whose likelihood
cannot be reduced to the local properties of the nodes. En este trabajo, we propose a data-driven
procedure to reveal the irreducible ties in dynamic functional connectivity of resting-state fMRI
data with continuous weights. This framework includes a null model that estimates the latent
characteristics of the distributions of temporal links through optimization, followed by a
statistical test to filter the links whose formation can be reduced to the activities and local
properties of their interacting nodes. We demonstrate the benefits of this approach by applying
it to a resting-state fMRI dataset, and provide further discussion on various aspects and
advantages of it.

RESUMEN DEL AUTOR

In this work we propose an optimization-based null model to infer the significant ties, significado
the links that cannot be reduced to the local strengths and properties of the nodes, desde el
dynamic functional connectivity network. We asses multiple aspects of this approach and
demonstrate that it is adaptable to most temporal segmentation methods. We demonstrate that
this approach provides several advantages such as taking into account the global information
of the network. We also compare the proposed model with several commonly applied null
models empirically and theoretically.

INTRODUCCIÓN

Dynamic functional connectivity (dFC) has been widely used to analyze temporal associations
among separate regions of the brain as well as the correlation between functional patterns of
connectivity and cognitive abilities (Allen et al., 2014; Jones et al., 2012; Van Dijk et al., 2010;

Citación: Asadi, NORTE., Olson, I. r., &
Obradovic, z. (2021). The backbone
network of dynamic functional
conectividad. Neurociencia en red,
5(4), 851–873. https://doi.org/10.1162
/netn_a_00209

DOI:
https://doi.org/10.1162/netn_a_00209

Supporting Information:
https://doi.org/10.1162/netn_a_00209
https://github.com/ ThisIsNima
/ Weighted-Backbone-Network

Recibió: 21 Abril 2021
Aceptado: 7 Septiembre 2021

Conflicto de intereses:
The authors have declared that
no competing interests exist.

Autor correspondiente:
Nima Asadi
nima.asadi@temple.edu

Editor de manejo:
Álex Amueblado

Derechos de autor: © 2021
Instituto de Tecnología de Massachusetts.
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia.

La prensa del MIT

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

Temporal segmentation:
The process of slicing the fMRI time
courses into consecutive temporal
windows within which connectivity
matrices are formed based on the
correlation between the fMRI time
series. A common temporal
segmentation is the sliding-window
approach that computes a succession
of pairwise correlation matrices using
the time courses from a given
parcellation of brain regions.

Temporal ties:
The link between a pair of nodes
whose weight might vary across the
time of experiment.

von der Malsburg, Phillps, & Cantante, 2010). In order to identify coactivation patterns of dFC
over the period of experiment, a temporal segmentation (such as sliding window) is commonly
applied on the time courses of BOLD activation of brain regions to divide them into consec-
utive temporal windows (Allen et al., 2014; Hutchison et al., 2013; Smith et al., 2012). Entonces,
the connectivity between separate regions is measured to generate one graph adjacency ma-
trix per each temporal window (Damaraju et al., 2014). Building on this core framework, sev-
eral enhancements have been proposed in the past years, such as different temporal
segmentation approaches, to increase the power and precision of dFC analysis (Chang &
guantero, 2010; Heitmann & romper la lanza, 2018; Hindriks et al., 2016; Kiviniemi et al., 2011).

Sin embargo, a major challenge in analysis of dynamic functional connectivity is to distinguish
and address the existing noise confounds in the data, which influence the brain connectivity
measures and the structure of the dFC network (Hijo, Herrero, jones, & Bandettini, 2008; Chang
& guantero, 2009; Kalthoff, Seehafer, Po, Wiedermann, & Hoehn, 2011; Shmueli et al., 2007).
This issue especially intensifies with the increase in spatial resolution of the analysis as well as
in resting-state fMRI data (Hijo, 2012; Hallquist, Hwang, & luna, 2013; Kalthoff et al., 2011).
There are several possible sources of noise in resting-state fMRI data, including displacements,
even as small as a millimeter or less, which could add random noise to the generated time
series, and therefore decrease the statistical power in resting-state functional connectivity
(rsFC) análisis (Van Dijk, Jabonoso, & Buckner, 2012). Even more challenging, it can result
in false positive or negative activation if the displacements are correlated with the stimuli
(Lydon-Staley, círico, Satterthwaite, & bassett, 2019; Patanaik et al., 2018; Savva,
Kassinopoulos, Smyrnis, Matsopoulos, & Mitsis, 2020). Cardiovascular and respiratory signals
are also widely identified as a source of noise, causing synchronized fluctuations in MRI signal
(guantero & Sotavento, 1995).

Because of these challenges, neuroscientists often face the concern of analytical models
being noise-induced (Choe et al., 2017; Gorgolewski, Storkey, Bastin, Whittle, & Pernet,
2013; Murphy, Hijo, & Bandettini, 2013). A number of correction techniques have been sug-
gested in the past to reduce the influence of these confounds, including modeling fMRI signal
variations using independent measures of the cardiac and respiratory signal variations
(Behzadi, Restom, Liau, & Liu, 2007; Bollmann et al., 2017; Bright & Murphy, 2017;
Murphy et al., 2013). Sin embargo, the effect of various sources of noise on the dynamic connec-
tivity of fMRI data is yet to be addressed through a data-driven and systematic framework
(Beall & Lowe, 2007; Kundu, Inati, evans, Luh, & Bandettini, 2012).

Además, temporal ties that can be reduced to node properties can exist between nodes
because of the nature of the data itself. Highly active regions could in principle form a larger
number of trivial ties with other regions, and reciprocally, the information of ties that regions
with lower activity form can be lost in common analytical procedures (Gemmetto, Cardillo, &
Garlaschelli, 2017; Kobayashi, Takaguchi, & Barrat, 2019). En general, if the network repre-
sentation of a real-world system can be inferred based on local properties of the nodes, como
their activity level or degree, the true interaction and functional homologies between the
nodes can not be detected (Gemmetto et al., 2017).

Por lo tanto, the objective of this work is to put forward a data-driven approach to distinguish
the significant ties that construct the functional connectivity of the brain from ties that are the
result of random observational errors or chance. The latter group of temporal links are known
as reducible ties, whereby they can be fully attributed to intrinsic node-specific features such
as degree or strength of their link weights. Por otro lado, the temporal ties that are in-
compatible with the null hypothesis of links being produced at random are known as

Neurociencia en red

852

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

Backbone network:
The network that is formed by the
significant ties between nodes by
filtering out randomly generated
edges or noise-induced links.

Null model:
Null models are formulated as a
baseline for comparison with the
system to verify whether the system
displays properties that would not be
expected on a random basis or as a
consequence of certain constraints.

Latent model variables:
Model variables that are not directly
observed or assigned, but are inferred
from other measurements from the
data or from variables that are
observado.

irreducible or significant ties, and the network of such significant ties is known as the back-
bone network. Por lo tanto, the goal of this study is to develop a data-driven framework to infer
the two-dimensional backbone network from the multilayer network of dynamic functional
conectividad.

Multiple approaches have been proposed to extract the significant ties in a network through
statistical means, most of which target static networks (Alvarez-Hamelin, Dall’Asta, Barrat, &
Vespignani, 2005; Casiraghi, Nanumyan, Scholtes, & Schweitzer, 2017; Gemmetto et al.,
2017; Kobayashi et al., 2019; Mamá, Mamá, zhang, & Wang, 2016; Nadini, Bongiorno, Rizzo, &
Porfiri, 2020; serrano, Boguná, & Vespignani, 2009; Tumminello, Micciche, Lillo, Piilo, &
Mantegna, 2011; yan, Jeub, Llamas, Radicchi, & Fortunato, 2018). Across these ap-
se acerca, a key step towards inferring the backbone network is the formulation of a reliable
null model to characterize the reducible fraction of the temporal interactions, and to steer the
process of filtering that fraction of network links. Several null models have been suggested in
the literature whose focus is on static networks, spanning from basic weight thresholding of
multilayer networks to more advanced techniques (Cimini et al., 2019; Kobayashi et al., 2019;
Le et al., 2014; Tumminello et al., 2011).

One of the main disadvantages with weight thresholding approaches is that they commonly
fail to control for the difference in intrinsic attributes of the nodes, thus they favor highly active
nodes or nodes with other strong local properties, which can potentially have a large number
of reducible links. A number of null models have been used to evaluate the statistical signif-
icance of dFC based on generating null data using randomization frameworks. Two main ap-
proaches of this type include autoregressive randomization (ARR) and phase randomization
(PR) (Allen et al., 2014; Chang & guantero, 2010; Handwerker, Roopchansingh, González-
Castillo, & Bandettini, 2012; Brilla, Proporcionó, cocineros, Perdido, & romper la lanza, 2014). In this cat-
egory of time series–based approaches, null hypothesis testing is then applied by comparing
statistics from the original data against those from the generated null data. A backbone ap-
proach named significant tie filtering (ST filter) for dynamic networks was proposed by
Kobayashi et al. (2019), based on a network modeling concept named activity-driven network
(ADN) where the individual propensity of generating connections over time is determined by a
latent nodal parameter commonly known as activity, and the probability of creating a link at a
specific time instant between two nodes is the product of the individual latent activities of
interacting nodes (Perra, Gonçalves, Pastor-Satorras, & Vespignani, 2012; Starnini & Pastor-
Satorras, 2014; Zino, Rizzo, & Porfiri, 2017). Because of their analytical flexibility and inter-
pretability, activity-driven network models have gained popularity in explaining features of
real networks in various areas of research (Liu, Perra, Karsai, & Vespignani, 2014; Rizzo,
Frasca, & Porfiri, 2014; Zino et al., 2017). Sin embargo, in the mentioned studies, a binomial
or Poisson distribution is considered for the temporal connections over time, which limits
the approach to unweighted networks (Kobayashi et al., 2019; Nadini et al., 2020), mientras
many relational networks based on real data, including various types of fMRI-based networks,
have continuous weights containing significant information regarding the interactions between
the nodes as well as the local and global properties of the network. Por lo tanto, inspired by the
work of Kobayashi et al. (2019), we propose an approach for extracting the significant ties for
temporal networks with continuous weights that meet the characteristics of normality and in-
dependence of temporal ties, which are discussed in the Methodology section. We demon-
strate that this methodology controls for intrinsic local node attributes, with a null model that
takes into account not only the global structure of the network, but also the temporal variations
of the dynamic connectivity links. In the next section we explain the proposed approach in
detail, followed by the experimental results on a real dataset of resting-state fMRI. Nosotros entonces

Neurociencia en red

853

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

present an analysis of the results and discuss the advantages and shortcomings of our
acercarse.

METODOLOGÍA

En esta sección, we outline the methodological framework for identifying the significant links
from the networks of dynamic resting-state functional connectivity. A key step towards extract-
ing the backbone network is the formulation of a valid and robust null model. For the sake of
simplicity, we name our proposed approach the weighted backbone network ( WBN). A null
model assumes that all connections are formed randomly, meaning that the probability of an
interaction between two nodes at a specific time window and the weight of interactions be-
tween them could be explained by chance (Gemmetto et al., 2017; Kobayashi et al., 2019;
Nadini et al., 2020). The objective of inferring the backbone network is thus to detect links that
are not compatible with the null hypothesis, meaning that their formation or strength is not
driven by chance.

The null model that we present can be interpreted as a temporal fitness model, cual es
characterized by latent parameters that shape its distribution. In this vein, the first step is to
estimate these parameters that are not directly observed from the data. For this purpose, nosotros
use a maximum likelihood estimation (MLE) approach that exploits the global and temporal
information of the network of dynamic connectivity. We discuss the details of this methodol-
ogy in the next section.

Estimation of Latent Distribution Variables
We consider a dynamic network of N nodes with links evolving over τ observation windows of
size Δ such that t = 1, …, t. At each time step t, a weighted undirected network is formed
whose adjacency matrix At stochastically varies in time, and the weights of temporal links
(links that are formed at time step t) between each pair of nodes i and j form a Gaussian dis-
tribution over the τ time steps. Normality of the distribution of weights between each pair of
nodes over time τ is concluded based on the central limit theorem and the assumption that the
distribution of temporal weights has a finite variance (Dudley, 1978, 2014; Haller & Bartsch,
2009; Herrero, 2012). Además, an empirical assessment of normality of the distribution of
temporal weights on a real dataset of resting-state fMRI is provided in the Results section.

We define a temporal null model in which each node i is assigned two intrinsic variables ai,
2 (0, 1], that rule the probability of mean μ and standard deviation σ of the temporal dis-

bi
tribution of its interactions with other nodes over (cid:1) time steps, such that

μ
¼ ai (cid:2) aj;
i; j
σi; j ¼ bi (cid:2) bj:

(1)

Por lo tanto, each parameter of the distributions of temporal ties between each pair of node i
and j is the realization of a Bernoulli variable. The null model thus lays out a baseline for the
expected mean and standard deviation of the distribution of interactions between two nodes
encima (cid:1) time given their intrinsic variables, if interacting nodes are selected at random at each
time step.

To uncover significant links with regards to the null model described above, we proceed in
two steps. Primero, given a set of weighted undirected temporal networks with N nodes, nosotros
estimate the intrinsic variables a* = (a1* , …, aN* ) and b* = (b1* , …, bN*) by calculating the
maximum likelihood estimation of the set of parameters for each node. For this purpose, nosotros

Neurociencia en red

854

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

consider the joint probability function over τ time intervals and edge weights w 2 (peso
i;j; i, j 2 1,
…, norte; t 2 1, …, (cid:1)) for the entire temporal connections of the network. Therefore we have the
following:

(cid:1)
f wt
i;j

(cid:3)

jμ

i;j

; σi;j

Y(cid:1)

i;j;i≠j

t¼1

1
pag

ﬃﬃﬃﬃﬃ
2Pi

σi;j

(cid:6)

(cid:5)
− wt
i;j

−μ

i;j

=2σ2

i;j ;

(2)

i,j and σ

where μ
between nodes i and j observed over (cid:1) time steps in the null model.

i,j denote the mean and standard deviation of the distribution of temporal edges

The log-likelihood function for the empirical data wt

i;j (weight of the link between i and j at

time interval t) with replacing the values of μ

i,j = ai.aj and σ

i,j = bi.bj will lead to:

(cid:1)

(cid:1)
log f wt
i;j

(cid:3)

jμ

; σi;j

i;j

i;j;i≠j

(cid:5)
−n log bibj

(cid:6)

− n
2

log2π −

X(cid:1)

t¼1

(cid:5)
2 bibj

(cid:1)
2 peso
i;j

(cid:6)

− aiaj

(cid:3)

(3)

By differentiating the log-likelihood function with respect to the first parameter, ai, and set-

ting it to zero we have

j;j≠i

ai* aj* −

X(cid:1)

t¼1

wo
i;j
(cid:1)

h
X

j;j≠i

ai* aj* − wo
i;j

¼ 0; 8yo ¼ 1; …; norte:

(4)

Similarmente, by differentiating the log-likelihood function with respect to bi and setting it to 0

tenemos

6
4

j;j≠i

(cid:1)
− bi* bj*

(cid:3)
2

(cid:1)

X(cid:1)

wo
i;j

t¼1

− ai* aj*
(cid:1)

(cid:3)
2

7
5 ¼ 0; 8yo ¼ 1; …; norte;

(5)

in which the the maximum likelihood estimation of ai* for every node i was calculated from
Ecuación 4. Por lo tanto, for a temporal network with N nodes, the pair of latent variables ai, bi
for each node i can be estimated by solving the system of N nonlinear Equations 4 y 5. El
system of nonlinear equations can be solved through a standard numerical algorithm such as
the Newton method. The initial values of ai and bi are calculated by dividing the temporal
degree of node i averaged over (cid:1) time steps by the doubled number of total temporal edges
como sigue:

X(cid:1)

Wisconsin;j=(cid:1)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
Wisconsin;j=(cid:1)

(6)

ai ¼

j;j≠i

t¼1

i t
2, the link wij is retained in the backbone network.
Note that the final backbone network is a binary network, meaning that the weight of links is 1

Neurociencia en red

856

The backbone network of dynamic functional connectivity

if the link between two nodes is determined to be significant, y 0 de lo contrario. Sin embargo, a
weighted network of significant ties can be easily created through various error measures such
as averaging the difference between the weights of the temporal links wt
ij and the cth percentile
weight wc

ij of the distribution.

t can be significant even if the weight of temporal link wt

An important property of the proposed null model is that the tie between two nodes at time
i;j is small, with the condition that their
individual latent variables a, b, and in turn the mean and standard deviation of their temporal
distribución, are sufficiently low. On the contrary, ties with large weights might not be deemed
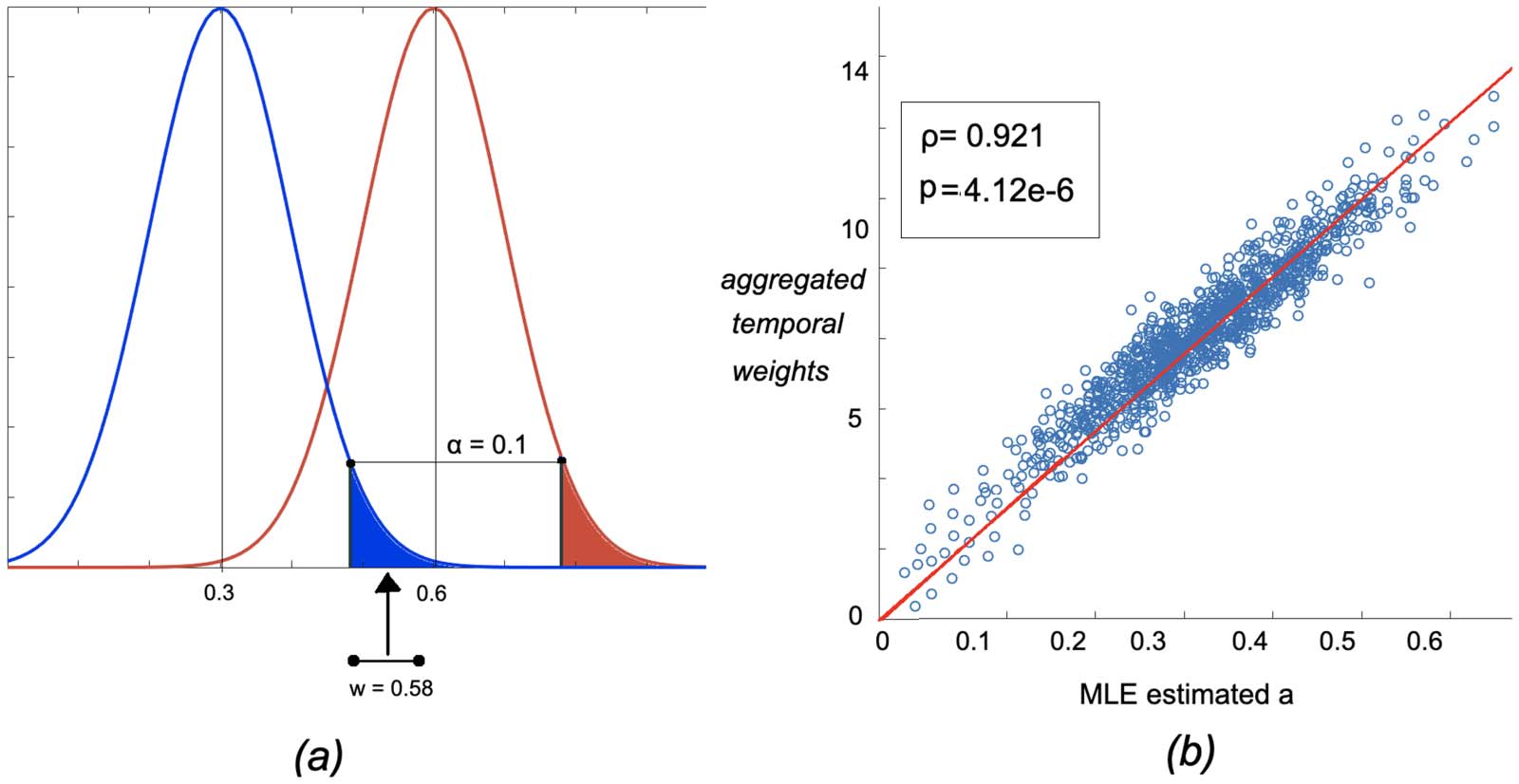
significant by WBN if their estimated a, b are large. This property is illustrated in Figure 2,
where large estimated μ = ai.aj shifts the cth percentile threshold to the right side of the distri-
bution such that it becomes increasingly difficult for temporal links to meet the threshold.

Además, strong correlation exists between the MLE-based estimated values of distribution
medio (ai.aj) and the degree of the nodes, calculated as the sum of weights of the edges over τ
time intervals. An example of such correlation is shown in Figure 2 for left hippocampus (283
vóxeles; further empirical results are provided in the Supporting Information), where the aggre-
gated node degree-estimated latent variable a were averaged across all subjects of the study
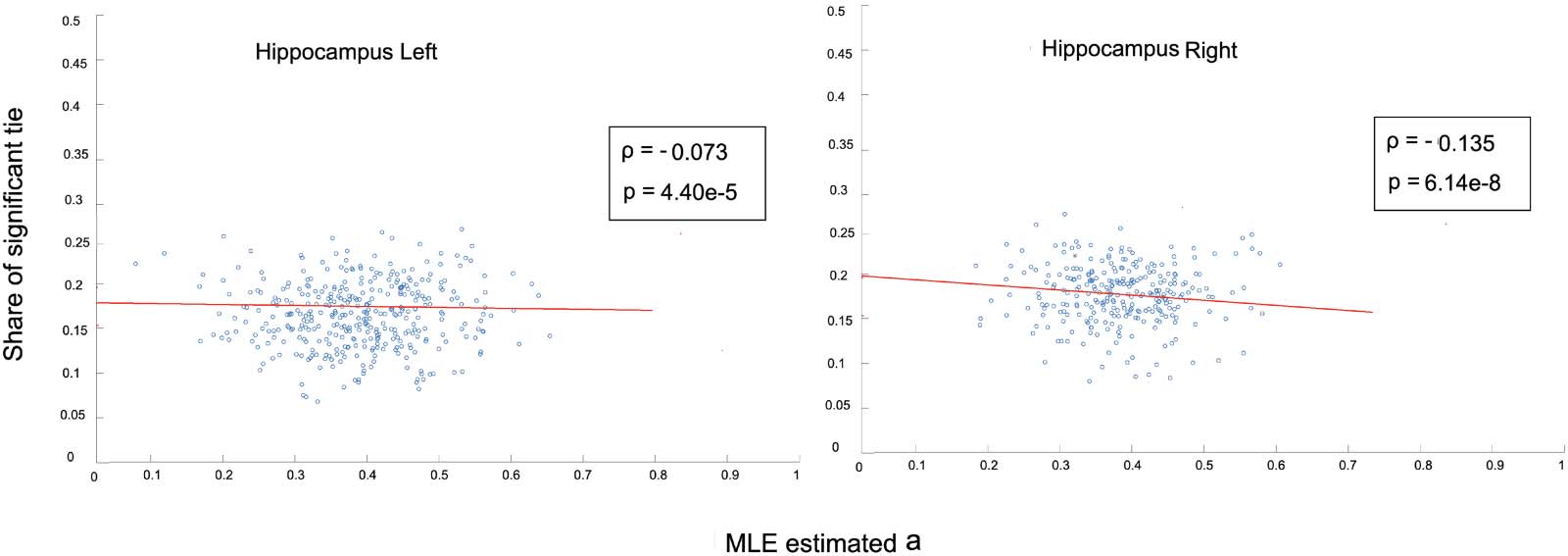
datos. También, as Figure 3 muestra, there exists a weak negative correlation between the share of
significant ties that is connected to each node i, and the MLE-estimated variables ai corre-
sponding to it. The share of significant ties is calculated as the number of ties connected to
node i that are admitted to the final backbone network divided by the total edges connected to
él (N − 1). These results establish the property that, based on the WBN model, the admissibility
of an edge wi,j to the irreducible network is not attributed merely to its degree, therefore con-
trolling for the effect of local strengths of nodes.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 2. Controlling the effect of local strenghts of node and edge weight on admissibility of the link to the backbone network. (A) Un
example of the effect of estimated a (distribution mean parameter) on admissibility of an empirical temporal link w, where the threshold (cid:3)
es 0.1 (90th percentile). A link with a low weight can be admitted to the backbone network as long as its estimated mean is sufficiently low (el
blue distribution), therefore controlling for the effect of high intrinsic distribution weights on acceptance to the backbone network. (B)
Correlation between estimated latent distribution mean variable for each node i (ai) and the aggregated dFC weights corresponding to the
node over τ time steps for the left hippocampus. The weighted degree-estimated a pair values are averaged across all subjects within the study
conjunto de datos.

Neurociencia en red

857

The backbone network of dynamic functional connectivity

Cifra 3. Correlation between share of significant ties connected to each node and the MLE-estimated latent variable a for right and left
hippocamous regions.

In the next section, we assess and compare the backbone networks detected based on
WBN with autoregressive randomization (ARR) as well as phase randomization (PR). ARR
and PR are different from ST filter and WBN in the sense that they are applied to the fMRI time
series of each temporal window before drawing the connectivity maps of the brain regions,
and they are used to explain the fluctuation in generated FC links. ARR assumes that the fMRI
data at time t is a linear combination of the fMRI data from the previous p time points:

xt ¼

Alxt−l

l¼1

þ (cid:4)t;

(9)

where p ≥ 1, xt is the N × 1 vector of fMRI data at time t, y (cid:4) corresponds to zero-mean
Gaussian noise, and Al is an N × N matrix of model parameters that contains the linear de-
pendencies between each time t and its previous time point. ARR first estimates the model
parameters for each time point (A1, …, AP) from the fMRI data. Each null fMRI time series is
generated by randomly selecting p successive time points from the original data, y luego
applying the ARR model to generate Tp new time points until time series of length T are gen-
erated. Naturalmente, significant deviation of the original data from ARR null data means the null
hypothesis is rejected.

The PR procedure initiates the null time series generation by performing discrete Fourier
transform (DFT) of each time course and adds a uniformly distributed random phase for each
frequency, and then same random phase is added across all variables. Finalmente, an inverse DFT
is performed to obtain the null time series. PR generates data with linear, weak-sense stationarity
( WSS), and Gaussian properties whose auto-covariance sequence R0, …, RT−1 is similar to those
of the original time series. A rejection of the null hypothesis based on the two mentioned null
models could be due to the fMRI time series not possessing either one of the three properties
of the null data or a combination of them. The experimental results for WBN as well as the
mentioned baseline approaches are provided in more detail in the next section.

EXPERIMENTAL RESULTS

In order to assess the proposed methodological framework, we apply it to a resting-state fMRI
dataset of 300 subjects from the Autism Brain Imaging Data Exchange (ABIDE) database, en-
cluding 150 subjects diagnosed with autism spectrum disorder (ASD; Di Martino et al., 2014).
This dataset was selected from the C-PAC preprocessing pipeline and was slice time and mo-
tion corrected, and the voxel intensity was normalized using global signal regression. El

Weak-sense stationarity:
A random process whose mean
function and its autocovariance
function do not fluctuate by
variations in time.

Neurociencia en red

858

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

automated anatomical labeling (AAL) atlas was then used for parcellation of regions of interest
(Tzourio-Mazoyer et al., 2002). Entonces, the temporal links between each pair of nodes were
extracted based on the Pearson correlation between their BOLD activation time series within
each temporal window t, and were then rescaled based on min-max feature scaling to have
continuous values within the range [0, 1]. The implementation code for the methodology in
this work is available at https://github.com/ThisIsNima/ Weighted-Backbone-Network (Asadi,
Olson, & Obradovic, 2021).

After extracting the backbone networks, we probed several aspects and measures of them
that will be discussed in this section. En particular, we provide a closer assessment of backbone
networks on four brain regions, namely the left and right hippocampus and the left and right
amygdalas. We also provide part of the experimental results for the cerebellar regions in the
main manuscript and the rest in the Supporting Information. The reason for choosing these
regions is the extensive focus of prior literature related to diagnosis and pattern discovery in
functional connectivity among ASD patients on them and the fact that several types of abnor-
mality have been discovered related to these regions among this group of patients (Cooper
et al., 2017; Guo et al., 2016; Ramos, Balardin, Sato, & Fujita, 2019; Rausch et al., 2016;
Shen et al., 2016).

As the first step of our analysis, we examined the normality of the distribution of temporal
links between each pair of nodes i, j across the experiment time τ. For this purpose, we used
the Kolmogorov-Smirnov test on temporal ties between each pair of nodes for four different
window sizes Δ 2 {5, 10, 15, 20}. Mesa 1 demonstrates the average p values of the normality
tests for the distribution of temporal ties between every pair of voxels across 300 subjects for
four separate regions. These results demonstrate that the p values are below the 0.005 com-
mon threshold for rejecting the null hypothesis. Además, the p value tends to increase as
the size of temporal windows decreases, which can be attributed to the increase in the total
number of temporal windows τ. Beyond the theoretical basis of the central limit theorem, estos
results further highlight that the assumption of normality for the distribution of temporal edges
in our resting-state fMRI data is reasonable.

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

The backbone networks of the right hippocampus (región 38 per the AAL atlas) for one
control subject based on four different threhsolds (c = 1 − α) are provided as heatmaps in
Cifra 4, where each cell represents a voxel, and white cells represent the significant ties.
Note that self links are removed from these networks, thus the value of the diagonals of the
heatmaps are set to 0. For this analysis, time courses were segmented into 20 temporal win-
dows through the sliding-window approach, with an overlap of 5 time points between con-
secutive windows. (This is the default setup for the other parts of the experiments. De lo contrario,
we denote the temporal window size setup.) The visualizations in Figure 4 indicate that the
number of admitted links decreases by increasing the threshold c. Además, the links between

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Mesa 1.
averaged across all links ((norte(N − 1))/2 edges for N nodes) of the network.

P values of Kolmogorov-Smirnov test for normality of the distribution of temporal links. The p values presented in the table are

Brain region
L hippocampus

R hippocampus

L amygdala

R amygdala

Δ = 5
2.1004e−11

8.1161e−13

6.3835e−14

3.3875e−10

Δ = 10
2.4801e−9

2.5102e−10

1.3560e−9

5.0045e−7

Δ = 15
1.1422e−22

1.1084e−9

1.1609e−9

1.4108e−7

Neurociencia en red

Δ = 20
2.5488e−32

1.1100e−9

1.1102e−9

3.0545e−7

859

The backbone network of dynamic functional connectivity

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 4. Derived backbone networks of the right hippocampus from one control subject given
four threshold values.

voxels in the vicinity of the diagonal line tend to endure the increase in threshold c, cual
highlights the strength of links between spatially close voxels.

The relation between the threshold c and the number of significant ties is further inspected
in Figure 8-c in the Supporting Information, where the threshold increases from 0.5 a 1 con un
−2. The number of significant ties for the network within each time
fixed step resolution of 10
window t = 1, …, τ is also provided in Figures 8-a and 8-b, where the red bars show the num-
ber of edges admitted to the final backbone network. As noted earlier, only the ties that meet
the significance threshold in over 50% of the time steps τ qualify to be included in the final
backbone network (red bar), thus the number of admitted links is usually smaller than the sig-
nificant ties within various temporal windows. Sin embargo, as Figure 8 in the Supporting
Information demonstrates, the number of significant ties does not demonstrate a large variation
across different temporal windows.

For the next step of the analysis, we examined and compared the backbone networks of the
two cohorts (control and ASD) within our experimental dataset with similar temporal segmen-
tation as the previous step. For this analysis, the value of α was set to 0.2, eso es, cth percentile =
0.80. Figures 1 y 2 in the Supporting Information present the networks of significant ties
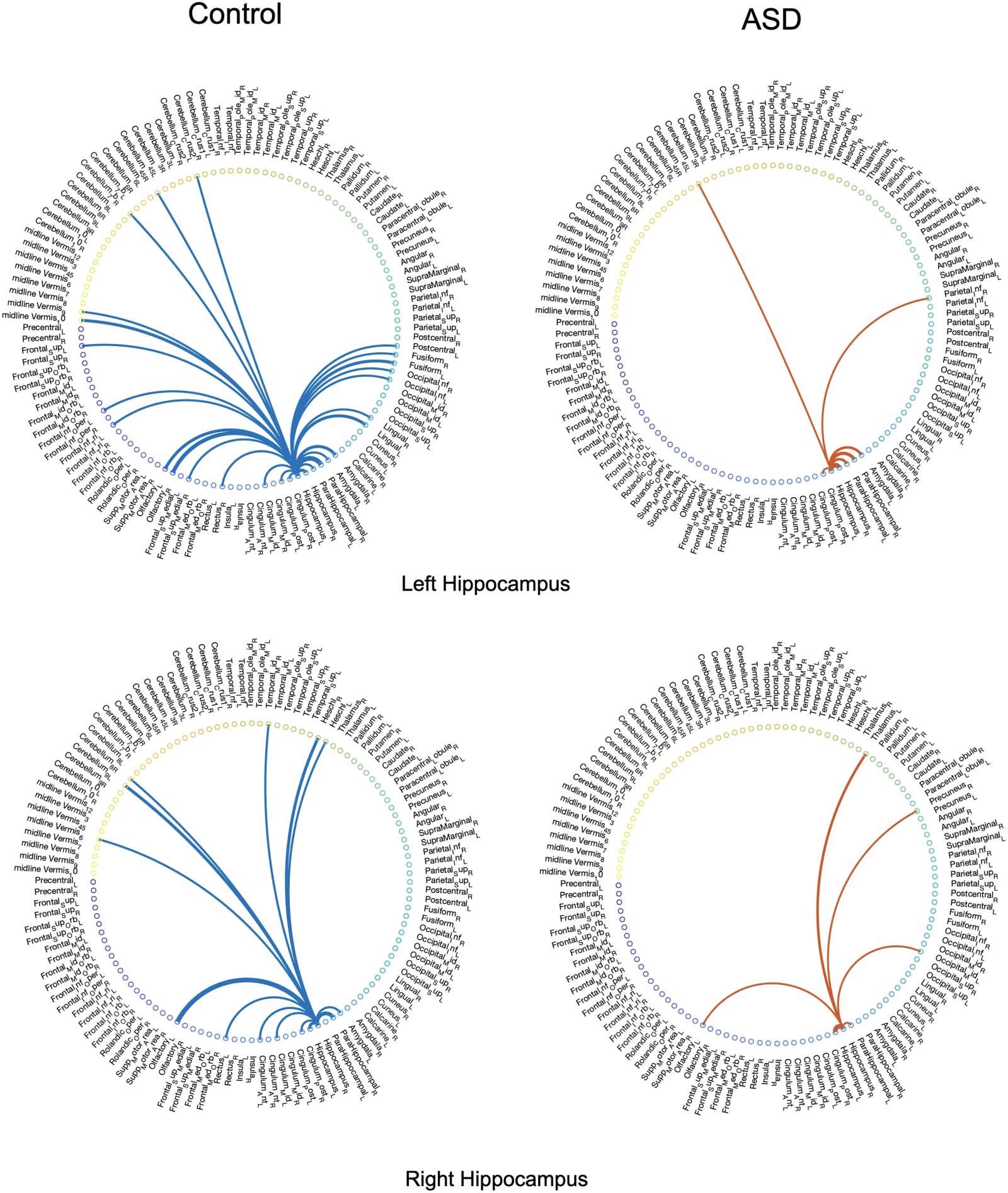
extracted from the dynamic connectivity of the left and right hippocampus from four subjects,
including two subjects diagnosed with ASD, and Figures 3 y 4 in the Supporting Information
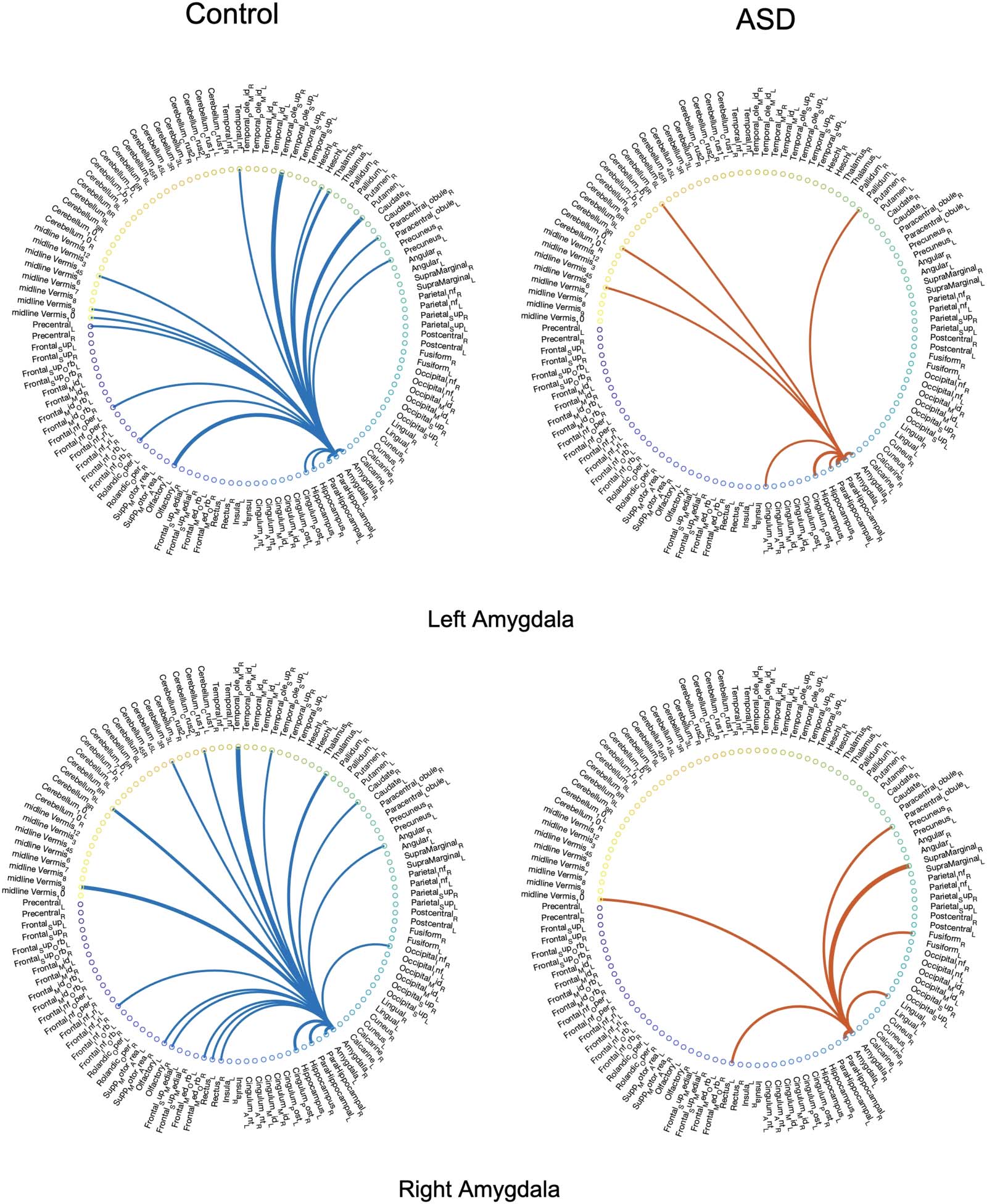
show the extracted significant ties from the left and right amygdalas for eight subjects, four of
whom were diagnosed with ASD. Además, in order to provide a more comprehensive perspec-
tive of the irreducible networks of the mentioned regions, the averaged backbone networks of
the two cohorts (control and ASD) across the entire dataset are presented in Figure 5 y 6 en el
Supporting Information.

As mentioned in the Introduction, several null models have been applied to fMRI connec-
tivity data in the past based on null time series generation. Among these models, autoregressive

Neurociencia en red

860

The backbone network of dynamic functional connectivity

randomization (ARR) and phase randomization (PR) have been two of the most widely focused
approaches. Por lo tanto, we compare the backbone networks based on those two methods with
WBN (Handwerker et al., 2012; Liegeois, Laumann, Snyder, zhou, & yo, 2017; Liegeois, yo,
& Van De Ville, 2021). A comparison of the backbone network extracted through the WBN
approach with ARR and PR null models is provided in Figure 7 in the Supporting
Información, where the averaged backbone networks of the two cohorts for the right hippocam-
pus are provided based on each null model. We can see that compared with the backbone
networks in Figure 5, despite the fact that the backbone networks based on ARR and PR dem-
onstrate a higher density of weights around the diagonals, their averaged values are dispersed
across the regions with lower average values. This means that ARR and PR demonstrate a lower
consistency of null hypothesis rejection across the subjects in this study compared with WBN.
Además, WBN demonstrates higher accuracy in detection of randomly injected edges, cual
will be discussed in the next sections. An explanation for these results can be the fact that in
WBN the global and spatial information of the network are considered in latent parameters of
each node because of their dependency on the parameters of every other node in the network,
which can result in a more stable null model. Another reason can be the fact that the resting-
state time courses of different regions can demonstrate variations in statistical properties (Guan
et al., 2020; Gultepe & Él, 2013). Además, stationary linear Gaussian (SLG) models might
lack the ability to explain more complex aspects of fMRI dynamics. These issue can particularly
intensify in case studies with higher spatial resolution such as voxel-level analysis.

Además, we assessed the effect of the length of temporal windows on the extracted
significant ties. For this purpose, we measured the difference between backbone networks
of dFC based on four different window sizes: Δ 2 {5, 10, 15, 20}, where the overlap between
consecutive windows was 2 time points for the smallest window (Δ = 5), y 5 time points for
the other three window sizes. As the measurement of dissimilarity, we used the mean percent-
age error (MPE) of the voxel-wise difference (between the values of corresponding matrix cells)
between the backbone networks averaged across 300 subjects. The results of this analysis are
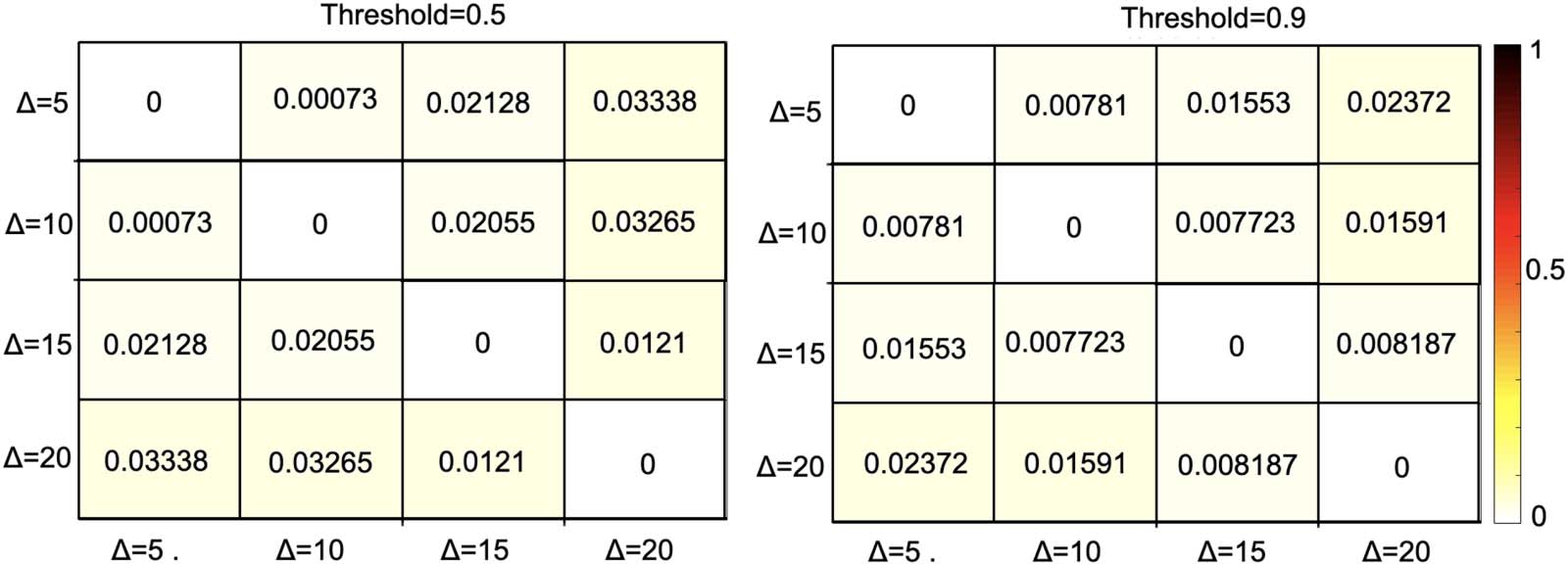
provided in Figure 5 for two threshold values of 0.5 y 0.9. As this analysis demonstrates, el
dissimilarity between the extracted backbone networks calculated as MPE is negligibly small
for both temporal resolutions, which indicates the consistency of the backbone network
against variations of the temporal window size.

In order to evaluate the effect of the choice of temporal segmentation criteria on the back-
bone networks, we compare the networks based on sliding-window criteria as well as a

Cifra 5. A comparison based on different window sizes using mean percentage error (MPE) of the voxel-wise difference between the back-
bone networks of dFC averaged across 300 subjects.

Neurociencia en red

861

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

change point detection (DCR) approach for single-subject data (Cribben, Apostar, & Lindquist,
2013). The DCR approach proposed by Cribben et al. detects the data partitions with the smal-
lest combined Bayesian information criterion (BIC) score to obtain the candidate change points
(Cribben et al., 2013). For this analysis, we assigned the value of Δ (the minimum possible
number of time points between adjacent change points) ser 10 time points. By comparing
Figures 5 (based on sliding window) y 9 (based on DCR) in the Supporting Information, nosotros
can note an overall similar backbone structure between the networks based on the two seg-
mentation approaches.

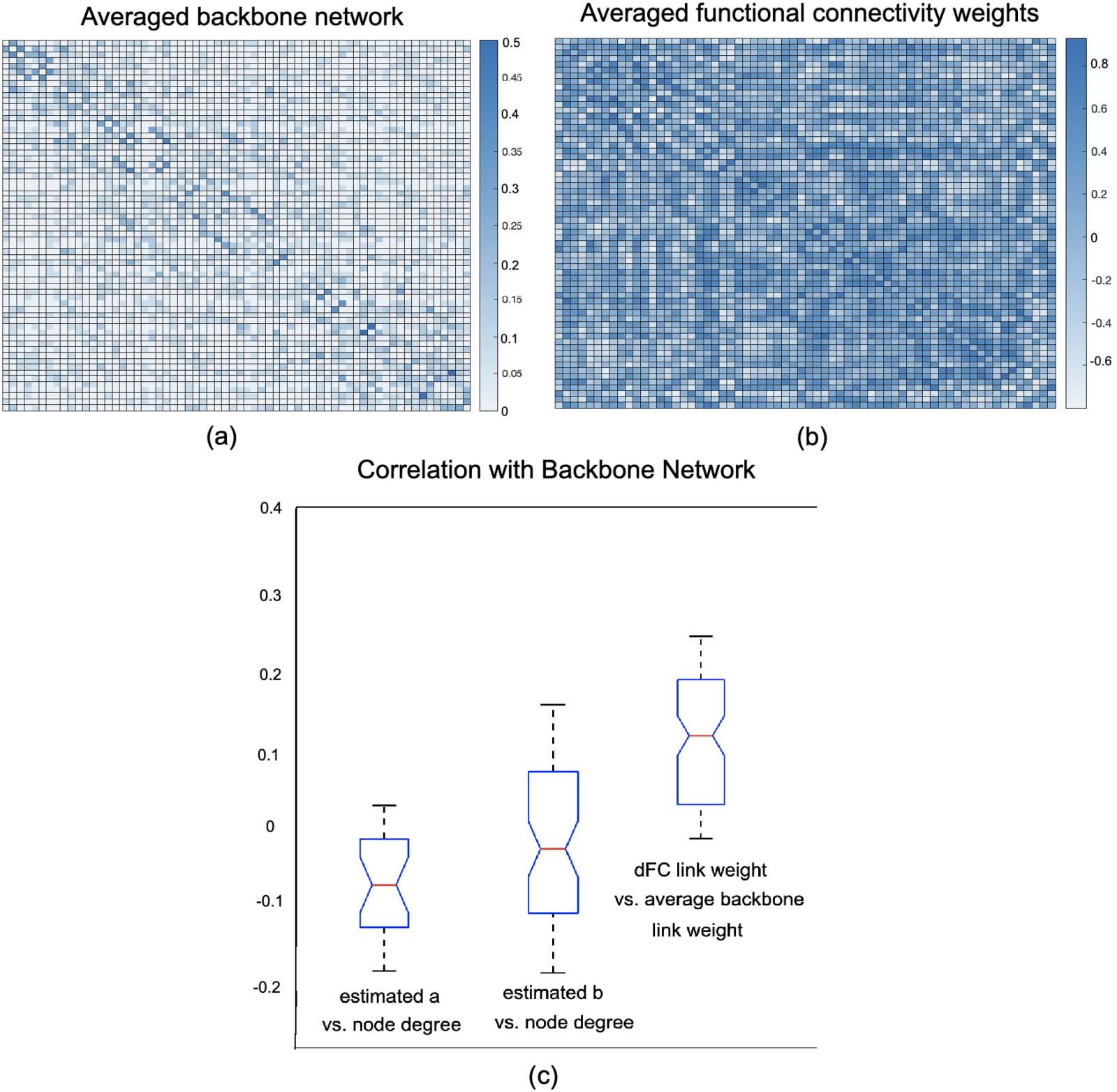
As the last part of the voxel-level experiments, we examined the correlation between the
empirical weight of the links and degree of the nodes in the dynamic functional connectivity
network with the backbone link wights and estimated latent variables a, b. In Figures 6A and
6B, the average backbone network of the right amygdala of 300 subjects as well as their

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 6. Comparison between the average backbone network and average dynamic functional connectivity weights. (A) Average backbone
network of the right amygdala for 300 subjects. (B) Average dFC network of the same region for the same subjects across τ = 20 time intervals.
(C) Correlations between node degree of the backbone network and estimated a, b as well as the correlation between the backbone network
weight and averaged dFC link weight over τ = 20 intervals for 300 subjects.

Neurociencia en red

862

The backbone network of dynamic functional connectivity

average dFC over τ windows are presented. Además, the correlations between node de-
grees of the backbone network, calculated as the sum of the link weights for each node, y
their estimated a, b as well as the correlation between the average backbone link weights of
300 subjects and the average weight of their corresponding dFC links over τ windows are pro-
vided in Figure 6C. Results for additional regions are provided in the Supporting Information.
As these results demonstrate, there is a weak correlation between the weight of the dFC links
and the average weight of backbone links (note that averaging binary backbone links results in
continuous weights). Además, there is a relatively small negative correlation between
node degree of dynamic functional connectivity and estimated distribution latent variables
a, b. In line with the argument provided in the Methodology section, these empirical results
further illustrate that WBN considers global and temporal information of the network beyond
the local node degree and the weight of the links in the dFC.

Full-Brain Analysis

Just like the voxel-level analysis, a full-brain backbone network of rsFC can be extracted where
each node is a region of interest (ROI). For this purpose, the time courses within each region
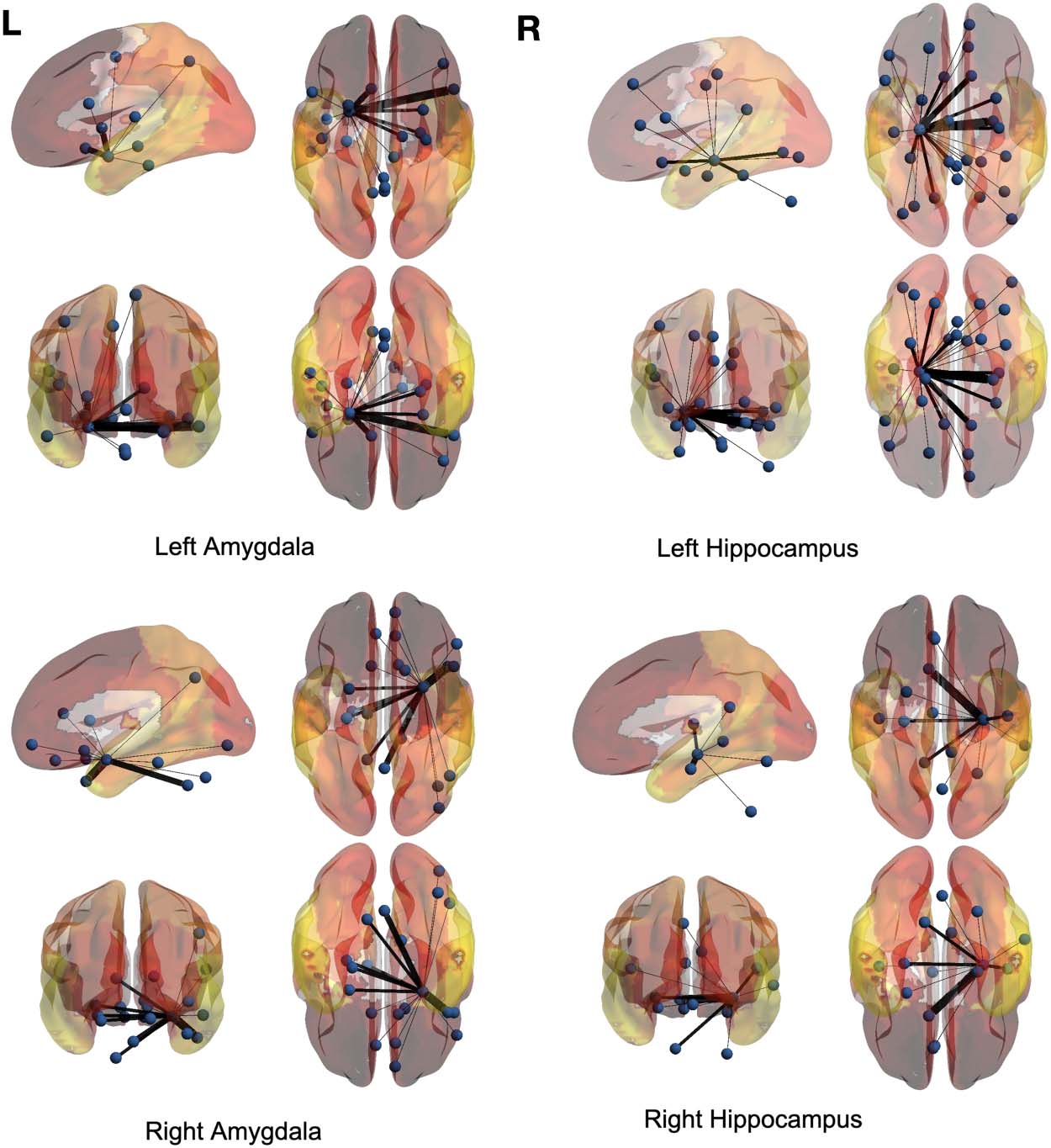
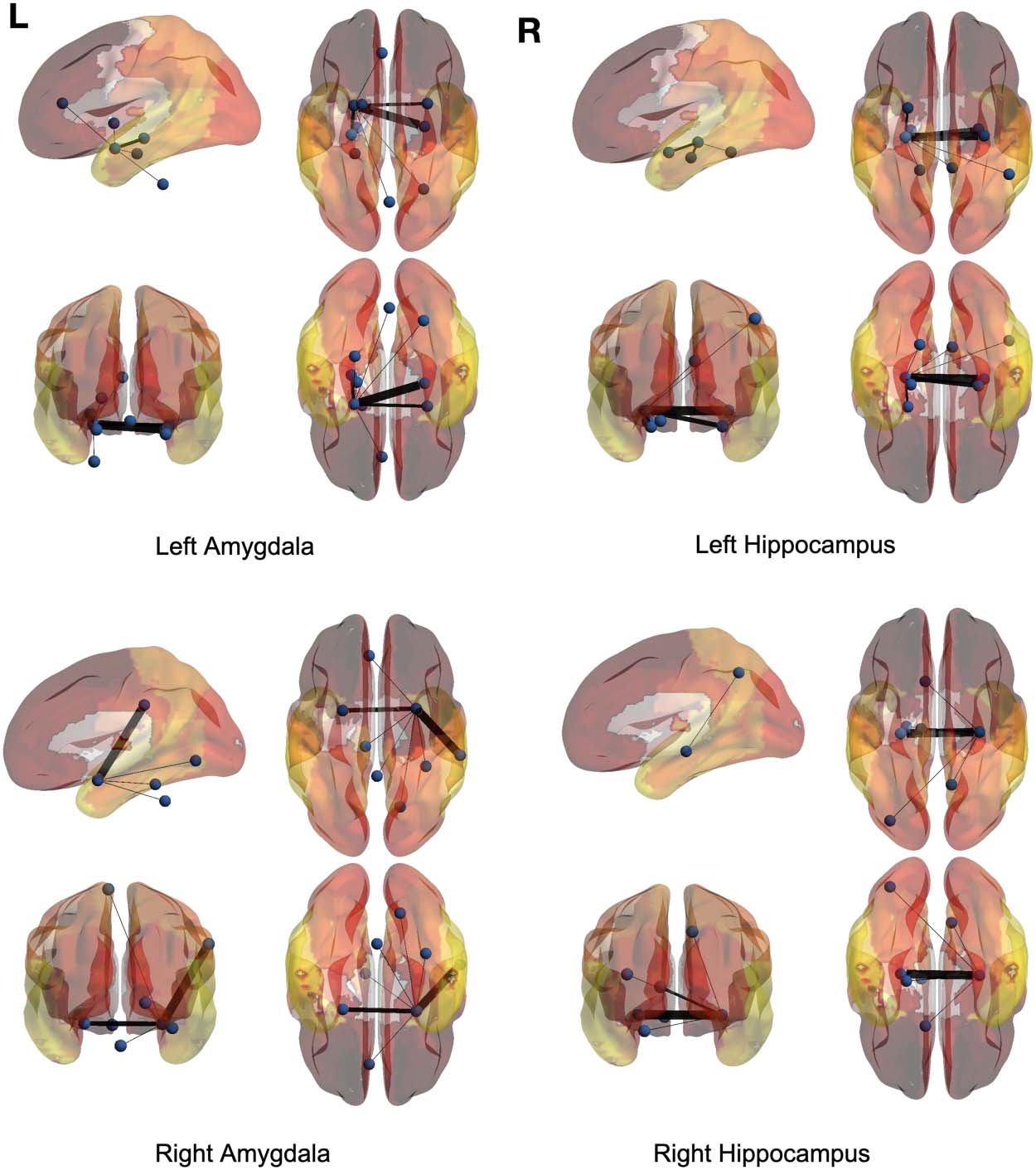
based on the AAL atlas were averaged. The averaged full-brain networks of significant ties for
150 control and 150 ASD subjects are demonstrated in Figures 7, 8, 9, y 10, where the seed

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 7. The averaged full-brain backbone networks of 150 control subjects based on four seed
regiones.

Neurociencia en red

863

The backbone network of dynamic functional connectivity

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 8. The averaged full-brain backbone networks of 150 ASD subjects based on four seed
regiones.

regions are the left and right amygdalas and hippocampus, and the average backbone links
with weights below 0.05 were filtered out to facilitate easier presentation. In these figures, el
link weights (illustrated by thickness in the figure) correspond to the count of their correspond-
ing links appearing in the binary backbone networks across each cohort. We can observe from
Figures 9 y 10 that the amygdalas and hippocmapus develop a larger number of significant
ties with other regions among the control group compared with the ASD cohort, as the net-
work of the latter cohort is more sparse. The width of links in Figures 7 y 8 also represent the
strength of the average correlations. We can therefore also observe a relatively high averaged
backbone link between the right and left hippocampus among both the control and the ASD
grupo. Sin embargo, certain differences can be detected between the two cohorts, including a
stronger average backbone tie between the hippocampus and the cerbellums as well as right
and left olfactories among control subjects compared with the ASD cohort. Además, a higher
average backbone tie can be noticed between the left and right amygdalas and the superior
and the middle temporal gyrus among control subjects. Further related experimental results are
provided in the Supporting Information; these results include the average backbone connec-
tivity with several cerebellar regions being the seed area. These results demonstrate the benefit
of the weighted temporal backbone network in revealing the differences in irreducible ties
between different regions of interest.

Neurociencia en red

864

The backbone network of dynamic functional connectivity

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 9. Averaged full-brain backbone networks of 150 ASD and 150 control subjects with the left and right amygdalas as the seed regions.

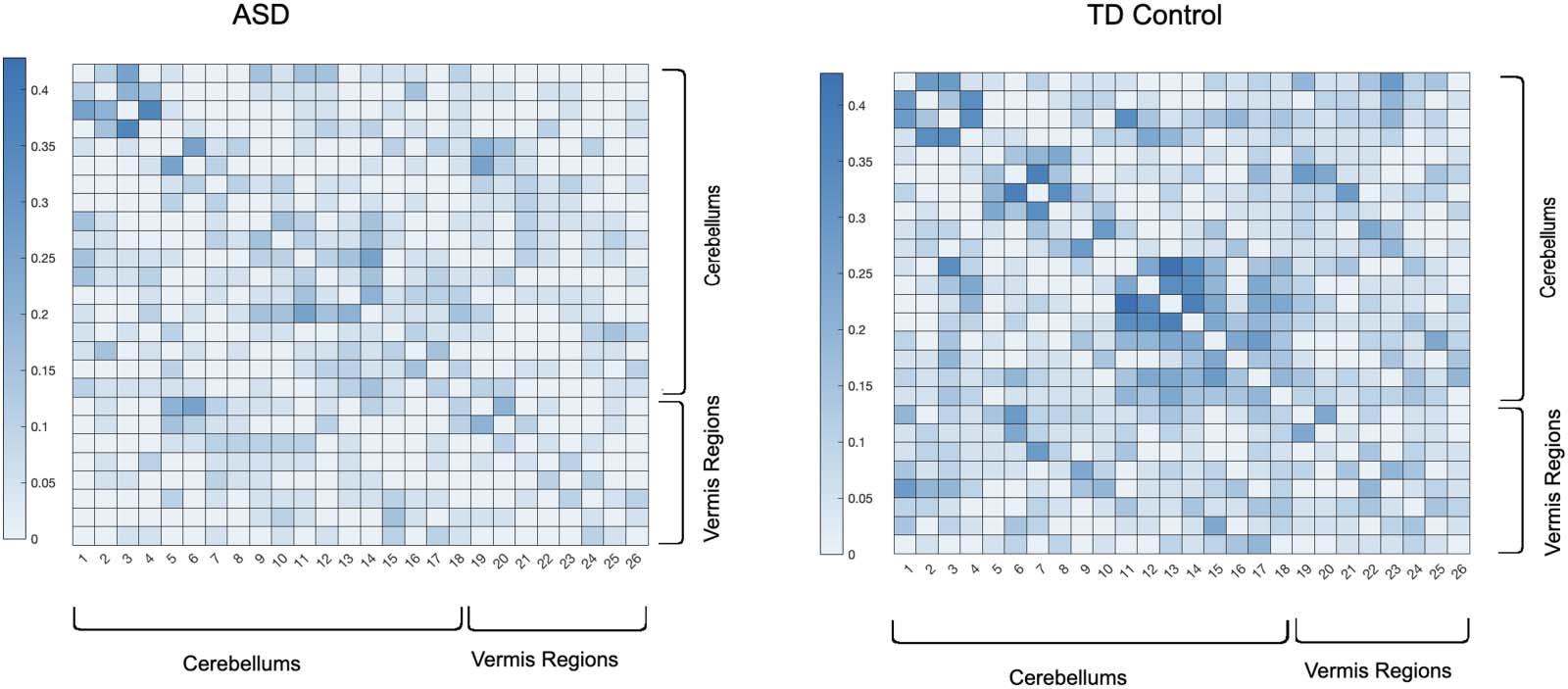
Cifra 11 depicts the averaged backbone connectivity of the cerebellums (18 regions per
AAL) and the vermis (8 regions per AAL) of the two cohorts in this study, which indicates higher
connectivity level among the control group compared with the ASD group. Estos resultados,
along with the experimental results provided in Supporting Information (Figures 5–10), poder
indicate that the increased cerebro-cerebellar functional connectivity detected in some studies
can be driven by a large number of links that fail to be incompatible with the null hypothesis of
links being produced at random. En otras palabras, despite the lower connectivity detected in
cerebro-cerebellar subnetwork among the control group in terms of number of links or their
weights, the number of meaningful and irreducible links in that subnetwork among the healthy

Neurociencia en red

865

The backbone network of dynamic functional connectivity

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 10. Averaged full-brain backbone networks of 150 ASD and 150 control subjects with the left and right hippocampus as the seed
regiones.

cohort tends to be larger compared with the ASD cohort (Khan et al., 2015; Mostofsky et al.,
2009; Ramos et al., 2019).

Detection of Random Links

To compare the performance of the proposed approach with other proposed null models, nosotros
considered three different models, namely binary ST filter, ARR, and PR.

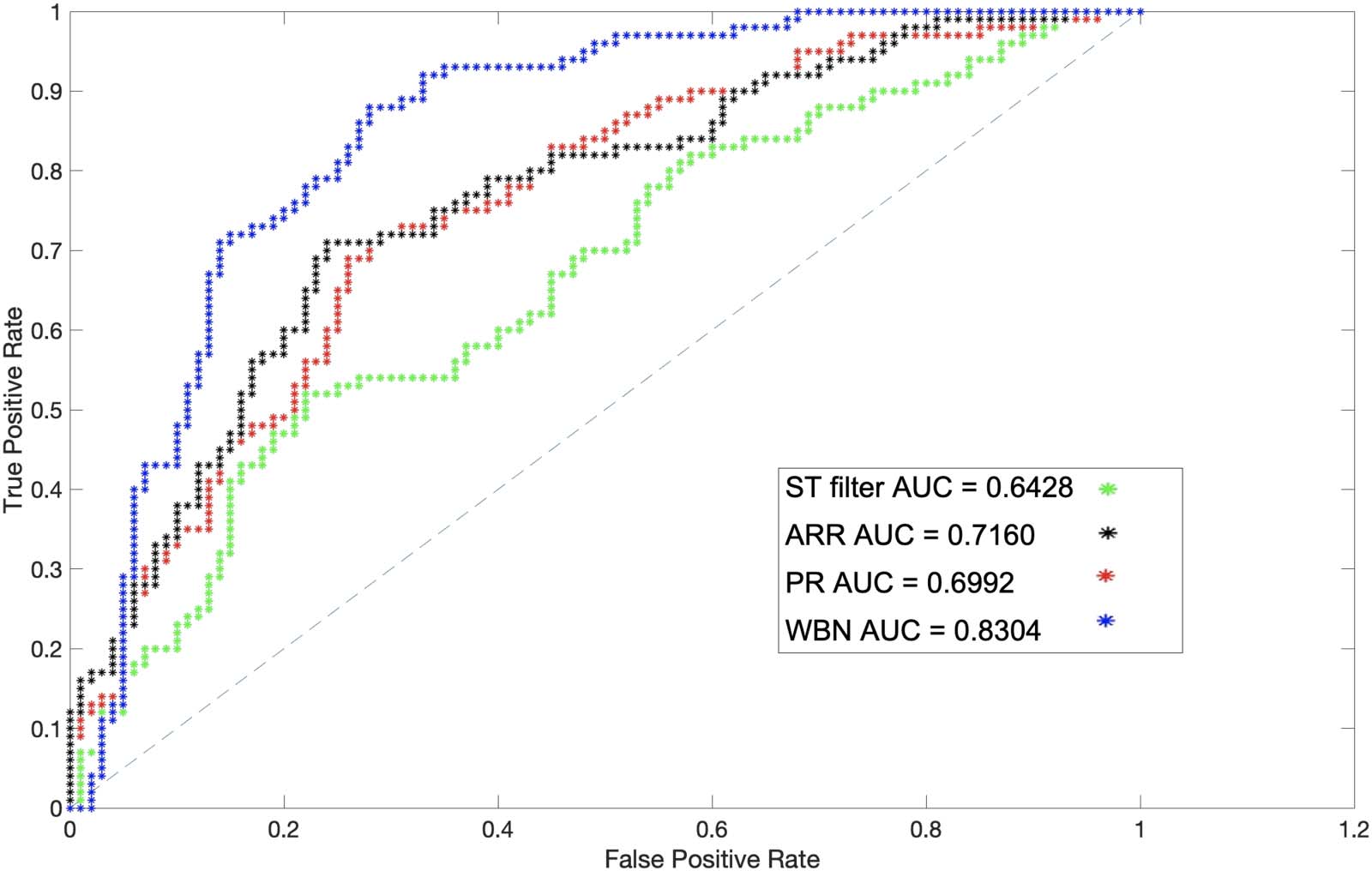
We created a simulated dataset by injecting random weights to a subset of edges of the real
rsFC networks of our dataset. For this purpose, 100 random weights were injected into 100
links of rsFC of the left hippocampus, and the precision of WBN as well as the ST filter

Neurociencia en red

866

The backbone network of dynamic functional connectivity

Cifra 11. Averaged full-brain backbone networks of cerebro-cerebellar and vermis regions across 150 ASD and 150 control subjects.

acercarse, proposed by Kobayashi et al., in excluding them from the final network were cal-
culated (Kobayashi et al., 2019). Because the ST filter operates on temporal binary weight net-
obras, in order to evaluate it we converted the rsFC link weights as well as the randomly
injected weights into binary links by drawing a temporal link between each pair of nodes
whose weight in the original rsFC network was above the entire network’s average. El resultado
of this experiment is provided in Figure 12, where WBN demonstrates an advantage over the
ST filter in random link detection precision. A similar experiment with other regions of interest
was conducted; these results are provided in the Supporting Information (Cifra 20). The eval-
uation measure for this analysis was calculated by comparing the detection of injected random
link weights with the ground truth. Part of the superior performance of WBN can be attributed
to the fact that the process of conversion to a binary network for the ST filter setup results in

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

Cifra 12. The AUC of detection of injected random weights based on the ST filtering, ARR, PR, and WBN in the left hippocampus.

Neurociencia en red

867

The backbone network of dynamic functional connectivity

loss of information and precision, which is an inherent disadvantage of backbone network
detection approaches that are designed for binary networks.

DISCUSIÓN

En este trabajo, we proposed a new approach for detecting the significant ties between nodes on
voxel- and ROI-level networks of resting-state dFC. The proposed framework entails two com-
putational steps: Primero, a maximum likelihood optimization is performed to calculate the latent
variables that characterize the optimal Gaussian distribution of the temporal links between
each pair of nodes across τ time steps. Entonces, the empirical link weights between each pair
of nodes within each temporal window are compared with the cth percentile of the
Gaussian distribution to detect the significant links that form the backbone network. este profesional-
cess is performed for every pair of nodes in the temporal network of dFC. Aside from providing
a systematic filtering framework for weighted temporal networks such as resting-state dFC, este
approach has several analytical advantages over other prior filtering approaches that we dis-
cuss in this section. We also discuss the limitations of the proposed methodology along with
possible suggestions for improvement and future plans.

As mentioned previously, inclusion of a temporal link in the backbone network is deter-
mined by testing the hypothesis that the link can be explained by the null model that links
are created uniformly at random. This comparison is applied to every link in the dFC individ-
ually, eso es, between every pair of nodes and within every temporal window. Por lo tanto, tema-
poral properties and variations of the network structure over time are taken into account in
backbone network inference. This property is an advantage of the proposed methodology over
some of the prior approaches that consider a constant intrinsic activity value for the nodes over
tiempo. It also offers the power of determining a cutoff percentage of ties having a larger weight
over the cth percentile, which was decided to be 50% in this study.

Another advantage of the suggested approach is the fact that it considers the interplay of
global and local information of the network in estimating the latent variables a and b. En otra
palabras, the significance of temporal ties cannot be attributed merely to node properties such as
degree or centrality measures, because each equation in the system of N equations of
Ecuaciones 4 y 5 takes into account the combination of weights over time for each link for
node i as well as their combination with other links between i and every other node in the
network. This property has been discussed in more detail in the Methodology section and eval-
uated in the Results section.

The refinement of parameters of the distribution through maximum likelihood optimization
requires solving the system of N equations for N nodes (one set of N equations for each of the
two parameters), which can be solved through several optimization approaches such as
gradient-based optimization, search methods, or the Newton method. Solving these equations
does not require any hyperparameter tuning, as the only parameters that need to be selected as
input are the threshold value (cid:3) and the percentage of times that the weight of the link meets
the c = 1 − (cid:3) percentile of the distribution, which offer the flexibility for a comprehensive
assessment of the temporal ties in the dynamic connectivity network.

Unlike some of the null models suggested in the past for binary networks based on binomial
or Poisson distributions, the methodology put forward in this work does not assume a strictly
positive weight between interacting nodes. This property provides the flexibility for ties that are
generated through various approaches such as correlation measures to be considered in the
null model, as negative correlation is a possibility between interacting nodes.

Neurociencia en red

868

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

Another advantage of the proposed approach is the fact that the backbone networks are
learned for each subject individually. As explained in the Methodology section, the input
for WBN is the weighted dynamic connectivity network of a subject, and its output is the net-
work of irreducible ties corresponding to the subject. This property has the benefit of taking
into account the individual differences when inferring the backbone network in an isolated
moda.

The suggested methodological framework can be used in studies with various scales and
resolution of dFC networks, meaning that instead of voxel-level analysis, dFC networks con-
sisting of regions of various scales as nodes can benefit from this approach as well. Además,
this approach is independent of a temporal segmentation step, as long as the statistical prop-
erties of independence and normality are met.

Limitaciones

Despite the mentioned advantages, the proposed approach bears certain limitations that we
highlight in this section.

As discussed in the Methodology section, the first step of the suggested framework entails
estimation of latent variables a and b, which rule the propensities to generate a distribution of
links with a certain average and standard deviation. Sin embargo, these variables are estimated
and compared across the experiment time τ, eso es, the length of the fMRI signals. En otra
palabras, the mean and standard deviation of the distributions, and in turn the backbone network
cálculos, can vary depending on the length of the experiment.

The structural characteristics of dFC can be influenced by temporal fluctuations in the data
throughout the course of the experiment. En otras palabras, reducible links might not have the
same statistical features at any time during the observation, as node properties might not be
constant over time. Por lo tanto, more improvements need to be applied to WBN to take such
variations into account.

Despite its adaptability with regards to different temporal segmentation approaches such as
sliding window or DCR, WBN requires an equal number of temporal windows across the en-
tire region of interest for calculating the latent distribution variables for each node because of
the number of optimization equations that it solves.

Another limitation of the suggested approach is the assumption of normality for larger tem-
poral window sizes. As the empirical tests demonstrated, an increase in size of the temporal
windows could in principle weaken the normality assumption of the distribution of the tem-
poral links. Despite the evidence of normality for reasonable and common window sizes in the
literature, this assumption needs to be further explored for different datasets.

The MLE optimization for estimating the intrinsic variables a, b plays the largest role in the
computational complexity of the methodology presented in this work. The computation time
depends on the number of nodes (es decir., spatial resolution) and the number of time intervals that
the signal is segmented to. By definition of the approach, the spatial resolution plays a more
significant role in the computational complexity (refer to Equations 4 y 5). en este estudio, a
system of N equations were solved through the trust-region-dogleg method, whose computa-
tion time for regions below 1,000 voxels was 10 min for 8 GB of RAM. Sin embargo, more effi-
cient approaches can be employed for this purpose.

Alleviating the mentioned limitations requires further methodological explorations and an-
alytical studies on various datasets. As future work, our objective will include assessing the
backbone network of resting-state dFC of other cohorts and data from various neurological

Neurociencia en red

869

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

conditions and studying different group differences. Además, assessing significant temporal
structures and graph communities and motifs as well as exploring the effect of different prepro-
cessing pipelines and temporal sample size on the outcome of the proposed approach can be
fruitful paths for further experiments in the area of dynamic functional connectivity.

SUPPORTING INFORMATION

Supporting information for this article is available at https://doi.org/10.1162/netn_a_00209.
The implementation code for the methodology in this work is available at https://github
.com/ThisIsNima/ Weighted-Backbone-Network.

CONTRIBUCIONES DE AUTOR

Nima Asadi: Conceptualización; Curación de datos; Análisis formal; Investigación; Metodología;
Software; Visualización; Escritura – borrador original; Escritura – revisión & edición. Ingrid R. Olson:
Análisis formal; Investigación; Supervisión; Validación. Zoran Obradovic: Análisis formal;
Administración de proyecto; Supervisión; Validación.

INFORMACIÓN DE FINANCIACIÓN

Ingrid R. Olson, Institutos Nacionales de Salud (https://dx.doi.org/10.13039/100000002), Award
ID: R01HD099165. Ingrid R. Olson, Institutos Nacionales de Salud (https://dx.doi.org/10.13039
/100000002), Award ID: RO1 MH091113. Ingrid R. Olson, Institutos Nacionales de Salud
(https://dx.doi.org/10.13039/100000002), Award ID: R21 HD098509. Ingrid R. Olson,
National
Institutes of Health (https://dx.doi.org/10.13039/100000002), Award ID:
2R56MH091113-11.

REFERENCIAS

allen, mi. A., Damaraju, MI., Plis, S. METRO., Erhardt, mi. B., Eichele, T., &
Calhoun, V. D. (2014). Tracking whole-brain connectivity dy-
namics in the resting state. Corteza cerebral, 24(3), 663–676.
https://doi.org/10.1093/cercor/bhs352, PubMed: 23146964
Alvarez-Hamelin, j. I., Dall’Asta, l., Barrat, A., & Vespignani, A.
(2005). K-core decomposition of internet graphs: Hierarchies,
self-similarity and measurement biases. arXiv:cs/0511007.

Asadi, NORTE., Olson, I. r., & Obradovic, z. (2021). Weighted back-
bone network, GitHub, https://github.com/ThisIsNima
/ Weighted-Backbone-Network

Beall, mi. B., & Lowe, METRO. j. (2007). Isolating physiologic noise
sources with independently determined spatial measures.
NeuroImagen, 37(4), 1286–1300. https://doi.org/10.1016/j
.neuroimage.2007.07.004, PubMed: 17689982

Behzadi, y., Restom, K., Liau, J., & Liu, t. t. (2007). A component
based noise correction method (CompCor) for BOLD and perfu-
sion based fMRI. NeuroImagen, 37(1), 90–101. https://doi.org/10
.1016/j.neuroimage.2007.04.042, PubMed: 17560126

Hijo, R. METRO. (2012). The role of physiological noise in resting-state
conectividad funcional. NeuroImagen, 62(2), 864–870. https://doi
.org/10.1016/j.neuroimage.2012.01.016, PubMed: 22245341
Hijo, R. METRO., Herrero, METRO. A., jones, t. B., & Bandettini, PAG. A. (2008).
The respiration response function: The temporal dynamics of
fMRI signal fluctuations related to changes in respiration.

NeuroImagen, 40(2), 644–654. https://doi.org/10.1016/j
.neuroimage.2007.11.059, PubMed: 18234517

Bollmann, S., Kasper, l., Vannesjo, S. J., Diaconescu, A. o.,
Dietrich, B. MI., Bruto, S., … Pruessmann, k. PAG. (2017). Análisis
and correction of field fluctuations in fMRI data using field mon-
itoring. NeuroImagen, 154, 92–105. https://doi.org/10.1016/j
.neuroimage.2017.01.014, PubMed: 28077303

Bright, METRO., & Murphy, k. (2017). Cleaning up the fMRI time series:
Mitigating noise with advanced acquisition and correction strat-
egies. NeuroImagen, 154, 1–3. https://doi.org/10.1016/j
.neuroimage.2017.03.056, PubMed: 28365420

Casiraghi, GRAMO., Nanumyan, v., Scholtes, I., & Schweitzer, F. (2017).
From relational data to graphs: Inferring significant links using
generalized hypergeometric ensembles. In International confer-
ence on social informatics (páginas. 111–120). https://doi.org/10
.1007/978-3-319-67256-4_11

Chang, C., & guantero, GRAMO. h. (2009). Relationship between respira-
ción, end-tidal CO2, and BOLD signals in resting-state fMRI.
NeuroImagen, 47(4), 1381–1393. https://doi.org/10.1016/j
.neuroimage.2009.04.048, PubMed: 19393322

Chang, C., & guantero, GRAMO. h. (2010). Time-frequency dynamics of
r es t i n g – s t at e b ra i n c o n ne c t i v i t y m e a s u r e d w i t h f M R I .
NeuroImagen, 50(1), 81–98. https://doi.org/10.1016/j.neuroimage
.2009.12.011, PubMed: 20006716

Neurociencia en red

870

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

Choe, A. S., Nebel, METRO. B., Barber, A. D., cohen, j. r., Xu, y., Pekar,
j. J., … Lindquist, METRO. A. (2017). Comparing test-retest reliability
of dynamic functional connectivity methods. NeuroImagen, 158,
155–175. https://doi.org/10.1016/j.neuroimage.2017.07.005,
PubMed: 28687517

Cimini, GRAMO., Squartini, T., Saracco, F., Garlaschelli, D., Gabrielli, A.,
& Caldarelli, GRAMO. (2019). The statistical physics of real-world net-
obras. Nature Reviews Physics, 1(1), 58–71. https://doi.org/10
.1038/s42254-018-0002-6

Cooper, R. A., Richter, F. r., Laureles, PAG. METRO., Plaisted-Grant, k. C.,
Baron-Cohen, S., & simons, j. S. (2017). Reduced hippocampal
functional connectivity during episodic memory retrieval in
autism. Corteza cerebral, 27(2), 888–902. https://doi.org/10
.1093/cercor/bhw417, PubMed: 28057726

Cribben, I., Apostar, T., & Lindquist, METRO. (2013). Detecting functional
connectivity change points for single-subject fMRI data. Frontiers
in Computational Neuroscience, 7, 143. https://doi.org/10.3389
/fncom.2013.00143, PubMed: 24198781

Damaraju, MI., allen, mi. A., Belger, A., Vado, j. METRO., McEwen, S.,
Mathalon, D., … Calhoun, V. D. (2014). Dynamic functional
connectivity analysis reveals transient states of dysconnectivity
in schizophrenia. NeuroImagen: Clinical, 5, 298–308. https://doi
.org/10.1016/j.nicl.2014.07.003, PubMed: 25161896

Di Martino, A., yan, C.-G., li, P., Denio, MI., Castellanos, F. X.,
Alaerts, K., … Milham, METRO. PAG. (2014). The Autism Brain Imaging
Data Exchange: Towards a large-scale evaluation of the intrinsic
brain architecture in autism. Molecular Psychiatry, 19(6), 659–667.
https://doi.org/10.1038/mp.2013.78, PubMed: 23774715

Dudley, R. METRO. (1978). Central limit theorems for empirical mea-
sures. Annals of Probability, 6(6), 899–929. https://doi.org/10
.1214/aop/1176995384

Dudley, R. METRO. (2014). Uniform central limit theorems (volumen. 142).

Prensa de la Universidad de Cambridge.

Gemmetto, v., Cardillo, A., & Garlaschelli, D. (2017). Irreducible
network backbones: Unbiased graph filtering via maximum en-
tropy. arXiv:1706.00230.

guantero, GRAMO. h., & Sotavento, A. t. (1995). Motion artifacts in fMRI:
Comparison of 2DFT with PR and spiral scan methods.
Resonancia Magnética en Medicina, 33(5), 624–635. https://doi
.org/10.1002/mrm.1910330507, PubMed: 7596266

Gorgolewski, k. J., Storkey, A. J., Bastin, METRO. MI., Whittle, I., & Pernet,
C. (2013). Single subject fMRI test–retest reliability metrics and
confounding factors. NeuroImagen, 69, 231–243. https://doi.org
/10.1016/j.neuroimage.2012.10.085, PubMed: 23153967

Guan, S., Jiang, r., Bian, h., Yuan, J., Xu, PAG., Meng, C., & Biswal, B.
(2020). The profiles of non-stationarity and non-linearity in the
time series of resting-state brain networks. Fronteras en
Neurociencia, 14, 493. https://doi.org/10.3389/fnins.2020
.00493, PubMed: 32595440

Gultepe, MI., & Él, B. (2013). A linear/nonlinear characterization of
resting state brain networks in fMRI time series. Cerebro
Topography, 26(1), 39–49. https://doi.org/10.1007/s10548-012
-0249-7, PubMed: 22941499

guo, X., Duan, X., Largo, Z., Chen, h., Wang, y., Zheng, J., …
Chen, h. (2016). Decreased amygdala functional connectivity
in adolescents with autism: A resting-state fMRI study.
Psychiatry Research: NeuroImaging, 257, 47–56. https://doi.org
/10.1016/j.pscychresns.2016.10.005, PubMed: 27969061

Haller, S., & Bartsch, A. j. (2009). Pitfalls in fMRI. European
Radiology, 19(11), 2689–2706. https://doi.org/10.1007/s00330
-009-1456-9, PubMed: 19504107

Hallquist, METRO. NORTE., Hwang, K., & luna, B. (2013). The nuisance of
nuisance regression: Spectral misspecification in a common
approach to resting-state fMRI preprocessing reintroduces noise
and obscures functional connectivity. NeuroImagen, 82, 208–225.
https://doi.org/10.1016/j.neuroimage.2013.05.116, PubMed:
23747457

Handwerker, D. A., Roopchansingh, v., Gonzalez-Castillo, J., &
Bandettini, PAG. A. (2012). Periodic changes in fMRI connectivity.
NeuroImagen, 63(3), 1712–1719. https://doi.org/10.1016/j
.neuroimage.2012.06.078, PubMed: 22796990

Heitmann, S., & romper la lanza, METRO. (2018). Putting the “dynamic” back
into dynamic functional connectivity. Neurociencia en red,
2(2), 150–174. https://doi.org/10.1162/netn_a_00041,
PubMed: 30215031

Hindriks, r., Adhikari, METRO. h., Murayama, y., Ganzetti, METRO., Mantini,
D., Logothetis, norte. K., & decoración, GRAMO. (2016). Can sliding-window
correlations reveal dynamic functional connectivity in resting-
state fMRI? NeuroImagen, 127, 242–256. https://doi.org/10.1016
/j.neuroimage.2015.11.055, PubMed: 26631813

hutchison, R. METRO., Womelsdorf, T., allen, mi. A., Bandettini, PAG. A.,
Calhoun, V. D., Corbetta, METRO., … Chang, C. (2013). Dynamic
conectividad funcional: Promise, asuntos, and interpretations.
N e u r o I m a g e , 8 0 , 3 6 0 – 3 7 8 . h t t p s : / / d o i . o r g / 1 0 . 1 0 1 6 / j
.neuroimage.2013.05.079, PubMed: 23707587

jones, D. T., Vemuri, PAG., Murphy, METRO. C., Gunter, j. l., Senjem, METRO. l.,
Machulda, METRO. METRO., … Clifford, R. J., Jr. (2012). Non-stationarity in
the “resting brain’s” modular architecture. PLoS ONE, 7(6),
e39731. https://doi.org/10.1371/journal.pone.0039731,
PubMed: 22761880

Kalthoff, D., Seehafer, j. Ud., Po, C., Wiedermann, D., & Hoehn, METRO.
(2011). Functional connectivity in the rat at 11.7T: Impact of
physiological noise in resting state fMRI. NeuroImagen, 54(4),
2828–2839. https://doi.org/10.1016/j.neuroimage.2010.10.053,
PubMed: 20974263

Kan, A. J., Nair, A., Keown, C. l., Datko, METRO. C., Lincoln, A. J., &
Müller, R.-A. (2015). Cerebro-cerebellar resting-state functional
connectivity in children and adolescents with autism spectrum
disorder. Biological Psychiatry, 78(9), 625–634. https://doi.org
/10.1016/j.biopsych.2015.03.024, PubMed: 25959247

Kiviniemi, v., Vire, T., Remes, J., Elseoud, A. A., Starck, T.,
Tervonen, o., & Nikkinen, j. (2011). A sliding time-window
ICA reveals spatial variability of the default mode network in
tiempo. Brain Connectivity, 1(4), 339–347. https://doi.org/10.1089
/brain.2011.0036, PubMed: 22432423

Kobayashi, T., Takaguchi, T., & Barrat, A. (2019). The structured
backbone of temporal social ties. Comunicaciones de la naturaleza, 10(1),
1–11. https://doi.org/10.1038/s41467-018-08160-3, PubMed:
30644392

Kundu, PAG., Inati, S. J., evans, j. w., Luh, W.-M., & Bandettini, PAG. A.
(2012). Differentiating BOLD and non-BOLD signals in fMRI time
series using multi-echo EPI. NeuroImagen, 60(3), 1759–1770.
https://doi.org/10.1016/j.neuroimage.2011.12.028, PubMed:
22209809

li, M.-X., Palchykov, v., Jiang, Z.-Q., Kaski, K., Kertész, J.,
Miccichè, S., … Mantegna, R. norte. (2014). Statistically validated

Neurociencia en red

871

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

mobile communication networks: The evolution of motifs in
European and Chinese data. New Journal of Physics, 16(8),
083038. https://doi.org/10.1088/1367-2630/16/8/083038

Liegeois, r., Laumann, t. o., Snyder, A. Z., zhou, J., & yo, B. t.
(2017). Interpreting temporal fluctuations in resting-state func-
tional connectivity MRI. NeuroImagen, 163, 437–455. https://doi
.org/10.1016/j.neuroimage.2017.09.012, PubMed: 28916180
Liegeois, r., yo, t. B., & Van De Ville, D. (2021). Interpreting null
models of resting-state functional MRI. bioRxiv. https://doi.org/10
.1101/2021.03.30.437514

Liu, S., Perra, NORTE., Karsai, METRO., & Vespignani, A. (2014). Controlling
contagion processes in activity driven networks. Physical Review
Letras, 112(11), 118702. https://doi.org/10.1103/ PhysRevLett
.112.118702, PubMed: 24702426

Lydon-Staley, D. METRO., círico, r., Satterthwaite, t. D., & bassett, D. S.
(2019). Evaluation of confound regression strategies for the miti-
gation of micromovement artifact in studies of dynamic resting-
state functional connectivity and multilayer network modularity.
Neurociencia en red, 3(2), 427–454. https://doi.org/10.1162
/netn_a_00071, PubMed: 30793090

Mamá, L.-L., Mamá, C., zhang, H.-F., & Wang, B.-H. (2016). Identifying
influential spreaders in complex networks based on gravity for-
mula. Physica A: Statistical Mechanics and Its Applications, 451,
205–212. https://doi.org/10.1016/j.physa.2015.12.162

Mostofsky, S. h., Powell, S. K., Simmonds, D. J., Goldberg, METRO. C.,
Caffo, B., & Pekar, j. j. (2009). Decreased connectivity and cer-
ebellar activity in autism during motor task performance. Cerebro,
132(9), 2413–2425. https://doi.org/10.1093/ brain/awp088,
PubMed: 19389870

Murphy, K., Hijo, R. METRO., & Bandettini, PAG. A. (2013). Resting-state
fMRI confounds and cleanup. NeuroImagen, 80, 349–359.
https://doi.org/10.1016/j.neuroimage.2013.04.001, PubMed:
23571418

Nadini, METRO., Bongiorno, C., Rizzo, A., & Porfiri, METRO. (2020).
Detecting network backbones against time variations in node
propiedades. Nonlinear Dynamics, 99(1), 855–878. https://doi.org
/10.1007/s11071-019-05134-y

Patanaik, A., Tandi, J., Ong, j. l., Wang, C., zhou, J., & che,
METRO. W.. (2018). Dynamic functional connectivity and its behav-
ioral correlates beyond vigilance. NeuroImagen, 177, 1–10.
https://doi.org/10.1016/j.neuroimage.2018.04.049, PubMed:
29704612

Perra, NORTE., Gonçalves, B., Pastor-Satorras, r., & Vespignani, A.
(2012). Activity driven modeling of time varying networks.
Informes Científicos, 2, 469. https://doi.org/10.1038/srep00469,
PubMed: 22741058

Ramos, t. C., Balardin, j. B., Sato, j. r., & Fujita, A. (2019).
Abnormal cortico-cerebellar functional connectivity in autism
spectrum disorder. Frontiers in Systems Neuroscience, 12, 74.
https://doi.org/10.3389/fnsys.2018.00074, PubMed: 30697151
Rausch, A., zhang, w., Haak, k. v., Mennes, METRO., Hermans, mi. J.,
van Oort, MI., … Groen, W.. B. (2016). Altered functional connec-
tivity of the amygdaloid input nuclei in adolescents and young
adults with autism spectrum disorder: A resting state fMRI study.
Molecular Autism, 7(1), 1–13. https://doi.org/10.1186/s13229
-015-0060-X, PubMed: 26823966

Rizzo, A., Frasca, METRO., & Porfiri, METRO. (2014). Effect of individual be-
havior on epidemic spreading in activity-driven networks.

Physical Review E, 90(4), 042801. https://doi.org/10.1103
/PhysRevE.90.042801, PubMed: 25375543

Savva, A. D., Kassinopoulos, METRO., Smyrnis, NORTE., Matsopoulos, GRAMO. K.,
& Mitsis, GRAMO. D. (2020). Effects of motion related outliers in dy-
namic functional connectivity using the sliding window method.
Journal of Neuroscience Methods, 330, 108519. https://doi.org
/10.1016/j.jneumeth.2019.108519, PubMed: 31730872

serrano, METRO. Á., Boguná, METRO., & Vespignani, A. (2009). Extracting the
multiscale backbone of complex weighted networks. Actas
of the National Academy of Sciences, 106(16), 6483–6488.
https://doi.org/10.1073/pnas.0808904106, PubMed: 19357301
shen, METRO. D., li, D. D., Keown, C. l., Sotavento, A., Johnson, R. T.,
Angkustsiri, K., … Nordahl, C. W.. (2016). Functional connectiv-
ity of the amygdala is disrupted in preschool-aged children with
autism spectrum disorder. Journal of the American Academy of
Child and Adolescent Psychiatry, 55(9), 817–824. https://doi
.org/10.1016/j.jaac.2016.05.020, PubMed: 27566123

Shmueli, K., van Gelderen, PAG., de Zwart, j. A., Horovitz, S. GRAMO.,
Fukunaga, METRO., Jansma, j. METRO., & duyn, j. h. (2007). Low-frequency
fluctuations in the cardiac rate as a source of variance in the
resting-state fMRI BOLD signal. NeuroImagen, 38(2), 306–320.
https://doi.org/10.1016/j.neuroimage.2007.07.037, PubMed:
17869543

Herrero, S. METRO. (2012). The future of fMRI connectivity. NeuroImagen,
62(2), 1257–1266. https://doi.org/10.1016/j.neuroimage.2012
.01.022, PubMed: 22248579

Herrero, S. METRO., Molinero, k. l., Moeller, S., Xu, J., Auerbach, mi. J.,
lana rica, METRO. w., … Ugurbil, k. (2012). Temporally independent
functional modes of spontaneous brain activity. Actas de
the National Academy of Sciences, 109(8), 3131–3136. https://
doi.org/10.1073/pnas.1121329109, PubMed: 22323591

Starnini, METRO., & Pastor-Satorras, R. (2014). Temporal percolation in
activity-driven networks. Physical Review E, 89(3), 032807.
https://doi.org/10.1103/ PhysRevE.89.032807, PubMed:
24730899

Tumminello, METRO., Micciche, S., Lillo, F., Piilo, J., & Mantegna, R. norte.
(2011). Statistically validated networks in bipartite complex sys-
tems. PLoS ONE, 6(3), e17994. https://doi.org/10.1371/journal
.pone.0017994, PubMed: 21483858

Tzourio-Mazoyer, NORTE., Landeau, B., Papathanassiou, D., Crivello, F.,
Etard, o., Delcroix, NORTE., … Joliot, METRO. (2002). Automated anatom-
ical labeling of activations in SPM using a macroscopic anatom-
ical parcellation of the MNI MRI single-subject brain.
NeuroImagen, 15(1), 273–289. https://doi.org/10.1006/nimg
.2001.0978, PubMed: 11771995

Van Dijk, k. r., Hedden, T., Venkataraman, A., evans, k. C., Lázaro,
S. w., & Buckner, R. l. (2010). Intrinsic functional connectivity
as a tool for human connectomics: Teoría, propiedades, and opti-
mization. Revista de neurofisiología, 103(1), 297–321. https://
doi.org/10.1152/jn.00783.2009, PubMed: 19889849

Van Dijk, k. r., Jabonoso, METRO. r., & Buckner, R. l. (2012). The in-
fluence of head motion on intrinsic functional connectivity MRI.
NeuroImagen, 59(1), 431–438. https://doi.org/10.1016/j
.neuroimage.2011.07.044, PubMed: 21810475

von der Malsburg, C. MI., Phillps, W.. A., & Cantante, W.. mi. (2010).
Dynamic coordination in the brain: From neurons to mind.
CON prensa. https://doi.org/10.7551/mitpress/9780262014717
.001.0001

Neurociencia en red

872

D
oh
w
norte
oh
a
d
mi
d

F
r
oh
metro
h

t
t

pag

:
/
/

d
i
r
mi
C
t
.

metro

i
t
.

mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d

F
/

5
4
8
5
1
1
9
7
5
1
9
8
norte
mi
norte
_
a
_
0
0
2
0
9
pag
d

b
y
gramo
tu
mi
s
t

oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3

The backbone network of dynamic functional connectivity

yan, X., Jeub, l. GRAMO., Llamas, A., Radicchi, F., & Fortunato, S.
(2018). Weight thresholding on complex networks. Físico
Review E, 98(4), 042304. https://doi.org/10.1103/PhysRevE.98
.042304

Brilla, A., Proporcionó, A., cocineros, l., Perdido, l. l., & romper la lanza, METRO.
(2014). Time-resolved resting-state brain networks. Actas

of the National Academy of Sciences, 111(28), 10341–10346.
https://doi.org/10.1073/pnas.1400181111, PubMed: 24982140
Zino, l., Rizzo, A., & Porfiri, METRO. (2017). An analytical framework
for the study of epidemic models on activity driven networks.
Journal of Complex Networks, 5(6), 924–952. https://doi.org/10
.1093/comnet/cnx056