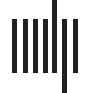MÉTODOS
From static to temporal network theory:
Applications to functional brain connectivity
William Hedley Thompson1, Per Brantefors1, and Peter Fransson1
1Department of Clinical Neuroscience, Karolinska Institutet, Stockholm, Suecia
Palabras clave: Resting-state, Temporal network theory, Temporal networks, Functional connectome,
Dynamic functional connectivity
ABSTRACTO
Network neuroscience has become an established paradigm to tackle questions related to the
functional and structural connectome of the brain. Recientemente, interest has been growing in
examining the temporal dynamics of the brain’s network activity. Although different
approaches to capturing fluctuations in brain connectivity have been proposed, there have
been few attempts to quantify these fluctuations using temporal network theory. This theory is
an extension of network theory that has been successfully applied to the modeling of dynamic
processes in economics, Ciencias Sociales, and engineering article but it has not been adopted
to a great extent within network neuroscience. The objective of this article is twofold:
(i) to present a detailed description of the central tenets of temporal network theory and
describe its measures, y; (ii) to apply these measures to a resting-state fMRI dataset to
illustrate their utility. Además, we discuss the interpretation of temporal network theory
in the context of the dynamic functional brain connectome. All the temporal network
measures and plotting functions described in this article are freely available as the Python
package Teneto.
RESUMEN DEL AUTOR
Temporal network theory is a subfield of network theory that has had limited application to
date within network neuroscience. The aims of this work are to introduce temporal network
theory, define the metrics relevant to the context of network neuroscience, and illustrate their
potential by analyzing a resting-state fMRI dataset. We found both between-subjects and
between-task differences that illustrate the potential for these tools to be applied in a wider
contexto. Our tools for analyzing temporal networks have been released in a Python package
called Teneto.
It is well known that the brain’s large-scale activity is organized into networks. The under-
lying organization of the brain’s infrastructure into networks, at different spatial levels, tiene
been dubbed the brain’s functional and structural connectome (despreciar, 2009; despreciar, Tononi,
& Kotter, 2005). Conectividad funcional, derived by correlating the brain’s activity over a pe-
riod of time, has been successfully applied in both functional magnetic resonance imaging
(resonancia magnética funcional; Greicius, Krasnow, Reiss, & menón, 2003; Fransson, 2005; Fox et al., 2005; Smith et al.,
2009) and magnetoencephalography (MEG; de Pasquale et al., 2010; Brookes et al., 2011;
Hipp, Hawellek, Corbetta, Siegel, & ángel, 2012), yielding knowledge about functional net-
work properties (Buckner et al., 2009; Power et al., 2011; Fuerza, Schlaggar, Lessov-Schlaggar,
un acceso abierto
diario
Citación: Thompson, W.. h., Brantefors,
PAG., & Fransson, PAG. (2017). From static to
temporal network theory: Aplicaciones
to functional brain connectivity.
Neurociencia en red, 1(2), 69–99.
https://doi.org/10.1162/netn_a_00011
DOI:
https://doi.org/10.1162/netn_a_00011
Supporting Information:
Recibió: 23 December 2016
Aceptado: 29 Marzo 2017
Conflicto de intereses: Los autores tienen
declaró que no hay intereses en competencia
existir.
Autor correspondiente:
William Hedley Thompson
hedley@startmail.com
Editor de manejo:
Marcus Kaiser
Derechos de autor: © 2017
Instituto de Tecnología de Massachusetts
Publicado bajo Creative Commons
Atribución 4.0 Internacional
(CC POR 4.0) licencia
La prensa del MIT
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
& Petersen, 2013; Nijhuis, van Cappellen van Walsum, & Norris, 2013) that has been applied
to clinical populations (Fox & Greicius, 2010; zhang & Raichle, 2010).
In parallel to research on the brain’s connectome, there has been a focus on studying the
dynamics of brain activity. When the brain is modeled as a dynamic system, a diverse range
of properties can be explored. Prominent examples of this are metastability (Bressler & Kelso,
2001; decoración, Jirsa, & McIntosh, 2011; Kelso, 1995; Tognoli & Kelso, 2009, 2014) and oscilla-
ciones (Buzsáki, 2006; Buzsáki & Draguhn, 2004; Siegel, Donner, & ángel, 2012). Brain oscil-
laciones, inherently dynamic, have become a vital ingredient in proposed mechanisms ranging
from psychological processes such as memory (Buzsáki, 2005; Friese et al., 2013; Montgomery
& Buzsaki, 2007), and attention (Fries, 2005; Bosman et al., 2012), to basic neural communi-
cation in top-down or bottom-up information transfer (Bressler, Richter, Chen, & Ding, 2007;
Buschman & Molinero, 2007; Bastos et al., 2012; Bastos et al., 2015; Richter, Thompson,
Bosman, & Fries, 2016;
Richter, Coppola, & Bressler, 2016; Michalareas et al., 2016;
van Kerkoerle et al., 2014).
Recientemente, approaches to study brain connectomics and the dynamics of neuronal commu-
nication have started to merge. A significant amount of work has recently been carried out that
aims to quantify dynamic fluctuations of network activity in the brain using fMRI (Allen et al.,
2014; Hutchison et al., 2013; Brilla, Proporcionó, cocineros, Perdido, & romper la lanza, 2014; Brillar
et al., 2015; Thompson & Fransson, 2015a, 2016a; Brillar, Koyejo, & Poldrack, 2016) también
as MEG (de Pasquale et al., 2010; de Pasquale et al., 2012; Hipp, Hawellek, Corbetta, Siegel
& ángel, 2012; Baker et al., 2014; Michalareas et al., 2016). This research area which aims to
unify brain connectommics with the dynamic properties of neuronal communication, ha sido
called the “dynome” (Kopell, Gritton, Whittington, & Kramer, 2014) and the “chronnectome”
(Calhoun, Molinero, Pearlson, & Adalı, 2014). Since the brain can quickly fluctuate between dif-
ferent tasks, the overarching aim of this area of research is to understand the dynamic interplay
of the brain’s networks. The intent of this research is that it will yield insight into the complex
and dynamic nature of cognitive human abilities.
Although temporal network theory has been successfully applied in others fields (p.ej., el
Ciencias Sociales), its implementation in network neuroscience has been limited. In the Theory
and Methods section, we provide an introduction to temporal network theory, by extending
the definitions and logic of static network theory, and define a selection of temporal network
measures. In the Results section, we apply these measures to a resting-state fMRI dataset ac-
quired during eyes-open and eyes-closed conditions, revealing differences in dynamic brain
connectivity between subjects and conditions. Together this material illustrates the potential
and varying information available from applying temporal network theory to network neuro-
ciencia.
THEORY AND METHODS
From Static Networks to Temporal Networks
We begin by defining temporal networks, by expanding upon the basic definitions of network
theory. In network theory, a graph (GRAMO) is defined as a set of nodes and edges:
G = (V, mi ),
(1)
where V is a set containing N nodes. E is a set of tuples that represent the edges or connections
between pairs of nodes (i, j) : i, j ∈ V. The graph may have binary edges (es decir., an edge is either
Temporal network:
A multigraph whose edges contain
temporal information
Neurociencia en red
70
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
present or absent), or E may be weighted, often normalized between 0 y 1, to represent the
magnitude of connectivity. When each edge has a weight, the definition of E is extended to a
3-tuple (i, j, w), where w denotes the weight of the edge between i and j. E is often represented
as a matrix of the tuples, which is called a connectivity matrix, A (sometimes the term adjacency
matrix is used). An element of the connectivity matrix Ai,j represents the degree of connectivity
= w. En el
for a given edge. When G is binary, Ai,j
= Aj,i, for all i and j, the matrix is considered undirected; when this is not the case,
case of Ai,j
the matrix is directed. With static networks, many different properties regarding the patterns
of connectivity between nodes can be quantified, for example through centrality measures,
hub detection, small-world properties, clustering, and efficiency (see Newman, 2010; despreciar,
2009; bullmore & despreciar, 2009, for detailed discussion).
= {0, 1}, and in the weighted version, Ai,j
A graph is only a representation of some state of the world being modeled. The correspon-
dence between the graph model and the state of the world may decrease due to aggregations,
simplifications, and generalizations. Adding more information to the way that nodes are con-
nected can entail that G provides a better representation, thus increasing the likelihood that
subsequently derived properties of the graph will correspond with the state of the world be-
ing modeled. One simplification in Eq. 1 is that two nodes can be connected by one edge
solo.
To capture such additional information in the graph, edges need to be expressed along
adicional, nonnodal dimensions. We can modify Eq. 1 a
G = (V, mi, D),
(2)
where D is a set of the additional, nonnodal dimensions. In the case of multiple additional di-
mensions, D is a class of disjoint sets where each dimension is a set. Ecuación 2 is sometimes
referred to in mathematics as a multigraph network, and in network theory as a multilayer
network (Kivelä et al., 2014). Por ejemplo, D could be a set containing three experimental
indices in seconds
paradigms {“n back,” “go/no go,” “Stroop task”} and/or temporal
{0,1,2, … T}. A graph is said to be a temporal network when D contains an ordered set of
temporal indices that represents time. This type of multilayer network is sometimes called a
multiplex (Kivelä et al., 2014).
In a static graph, the edges E are elements that contain indices (2-tuples) for the nodes that
are connected. In a multilayer network, E consists of (|D| + 2)-tuples for binary graphs, dónde
|D| expresses the number of sets in D. If time is the only dimension in D, then an element in
E is a triplet (i, j, t) : i, j ∈ V, t ∈ D. When G is weighted, E contains ((2 × |D|) + 2)-tuples
as w becomes the size of D, representing one weight per edge.
While shorter definitions of temporal graphs are often used without using general definitions
of multigraph/multilayer networks instead starting directly with the multiplex (see e.g., Holme
& Saramäki, 2012; Masuda & Lambiotte, 2016), these formulations are mathematically equiv-
alent when D only contains temporal information in Eq. 2. We have chosen to define a tem-
poral network in terms of a multilayer network because this is appropriate when considering
what a detailed network description of the human connectome will require. A multilayer net-
work representation of the connectome could include many dimensions of information about
an edge—for example, (i) actividad 100 ms after stimulus onset (tiempo), (ii) activity in the gamma
frequency band, y (iii) activity associated with an n-back trial (task context). Thus we have
introduced temporal networks by extending static network definitions to the broader concept
Multigraph:
A network whose nodes can be
connected by multiple edges
Neurociencia en red
71
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
Graphlet:
A discrete connectivity matrix that
expresses part of a larger network
of multilayer networks. Sin embargo, in more complex multilayer networks with additional,
nontemporal dimensions, the temporal-network measures presented in this article can be used
to examine relationships across time, but either fixation or aggregation over the other dimen-
sions will be required. Sin embargo, more complex measures that consider all dimensions in D
have been proposed elsewhere (p.ej., Berlingerio, Coscia, Giannotti, Monreale, & Pedreschi,
2011).
For the remainder of this article we will consider only the case in which D contains only
En este caso, each edge is indexed by i,j and t. To fa-
an ordered set of temporal indexes.
cilitate readability, connectivity matrix elements are written as At
i,j—that is, with the tem-
poral index of D in the superscript.
Instead of referring to “At” as the “connectivity matrix
at time point t”, some refer to this as a graphlet (Basu, Bar-noy, Johnson, & Ramanathan, 2010;
Thompson & Fransson, 2015a, 2016a); others prefer to call this a snapshot representation
(Masuda & Lambiotte, 2016), and still others call it a supra-adjacency matrix (Kivelä et al.,
It should be noted that some dislike the term graphlet due to possible confusion
2014).
with the static network theory conception of a graphlet. Here a graphlet is a complete, en-
dependent two-dimensional connectivity matrix, but each graphlet is only a part of the en-
tire network. Because graphlets do not need to be snapshots of temporal information under
this definition, it is useful to describe what type of graphlet is being used. Por ejemplo,
a graphlet that expresses temporal information can be called a time-graphlet or t-graphlet
(Thompson & Fransson, 2016a), and a graphlet carrying frequency information, an f-graphlet
(Thompson & Fransson, 2015a).
Instead of representing the data with multiple graphlets, E can be used to derive the contact
sequence or event-based representation containing the nodes and temporal index (Holme &
Saramaäki, 2012; Masuda & Lambiotte, 2016). Unlike the graphlet representations, cual
must be discrete, contact sequences can also be used on continuous data and, when connec-
tions are sparse, can be a more memory-efficient way to store the data.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
MEASURES FOR TEMPORAL NETWORKS
Once the t-graphlets have been derived, various measures can be implemented in order to
quantify the degree and characteristics of the temporal flow of information through the net-
trabajar. We begin by introducing two concepts that are used in several of the temporal network
measures that will be defined later. The focus is on measures that derive temporal properties at
a local level (es decir., per node or edge) or a global level (see Discussion for other approaches). Nosotros
have limited our scope to describe only the case of binary, undirected, and discrete t-graphlets,
although many measures can be extended to continuous time, directed edges, and nonbinary
datos.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Concept: Shortest Temporal Path
In static networks, the shortest path is the minimum number of edges (or sum of edge weights)
that it takes for a node to communicate with another node. In temporal networks, a similar
measure can be derived. Within temporal networks, we can quantify the time taken for one
node to communicate with another node. This is sometimes called the “shortest temporal
distance” or “waiting time.” Temporal paths can be measured differently by calculating either
how many edges are traveled or how many time steps are taken (see Masuda & Lambiotte,
2016); here we quantify the time steps taken.
Shortest temporal path:
The shortest path by which a node
communicates with another node
across multiple intermediate nodes
Neurociencia en red
72
Temporal network theory applied to brain connectivity
Consider the temporal network shown in Figure 1A. Starting at Time Point 1, the shortest
temporal path for Node 1 to reach Node 5 is five time units (Figura 1B, red line). Shortest
temporal paths can never travel edges from a previous time point (es decir., backward in time), pero
it is possible for multiple edges to be visited at each time step. It is thus necessary to determine
how many edges can be traveled at each time point. Por ejemplo, Node 5 at Time Point 2 poder
reach Node 3 in one time step if we allow multiple edges to be traveled (Figura 1C, red line). Si
multiple edges cannot be traveled, then the shortest path for Node 5 to reach Node 2, starting
at Time Point 2, is five time units (Figura 1C, blue line). De este modo, a parameter must be set that
restrains how many edges per time point can be traveled. This parameter should depend on
the temporal resolution of the data and is best chosen given previously established knowledge
of the dynamics of the data. For fMRI, where the temporal resolution is in seconds, it makes
sense to assume that several edges can be traveled per unit of time. Contrarily, in MEG, dónde
the resolution is in the range of milliseconds, it is more reasonable to place a limit on the
number of edges that can be traveled per time unit.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 1.
Illustration of the concept of the shortest temporal path. (A) The basic layout of a tempo-
ral network, viewed in a slice graph representation. (B) The red line indicates the shortest temporal
path possible for Node 1 to reach Node 5. (C) The difference in shortest paths that arises when a
single (blue line) or multiple (red line) edges can be traveled at a single time point.
Neurociencia en red
73
Temporal network theory applied to brain connectivity
Intercontact time:
The time taken between two nodes
with a direct connection
Regarding the shortest temporal path, it is useful to keep in mind that the path is rarely
symmetric, not even when the t-graphlets themselves are symmetric. This is illustrated by
considering the network shown in Figure 1A, in which it takes five units of time for Node 1
to reach Node 5 when starting at t = 1. Sin embargo, for the reversed path, it takes only three
units of time for Node 5 to reach Node 1 (allowing for multiple edges to be traveled per time
punto).
Some consideration is needed of whether thinking about shortest temporal paths makes
sense in all neuroimaging contexts. Shortest temporal paths represent information being trans-
ferred in a network. De este modo, the concept of the shortest temporal path is appropriate in the situ-
ation in which one can assume that the transfer of information is continued across subsequent
time points. When the time scale is in the range of milliseconds (p.ej., EEG and MEG), el corto-
est temporal path should be unproblematic to interpret. A diferencia de, for a longitudinal study in
which the temporal resolution is in years, the concept of the shortest temporal path makes no
sense. Less clear-cut situations are neuroimaging techniques with sluggish temporal resolution
(p.ej., resonancia magnética funcional). Sin embargo, the shortest temporal path seems to be a reasonable measure for ongo-
ing BOLD signals that allow for considering previously observed temporal dynamics, incluir-
ing avalanche behavior (Tagliazucchi, Balenzuela, Fraiman, & Chialvo, 2012), bursty behavior
(Thompson & Fransson, 2016a), and metastability (decoración & Kringelbach, 2016).
Concept: Intercontact Time
The intercontact time between two nodes is defined as the temporal difference distinguishing
two consecutive nonzero edges between those nodes. This definition differs from the shortest
temporal path in so far as it only considers direct connections between two nodes. Considering
Figura 1A, the intercontact times between Nodes 4 y 5 become a list [2,2], since there are
edges present at Time Points 2, 4, y 6. Each edge will have a list of intercontact times. El
number of intercontact times in each list will be the number of nonzero edges between the
nodes minus one. Unlike with shortest temporal paths, graphs that contain intercontact times
will always be symmetric.
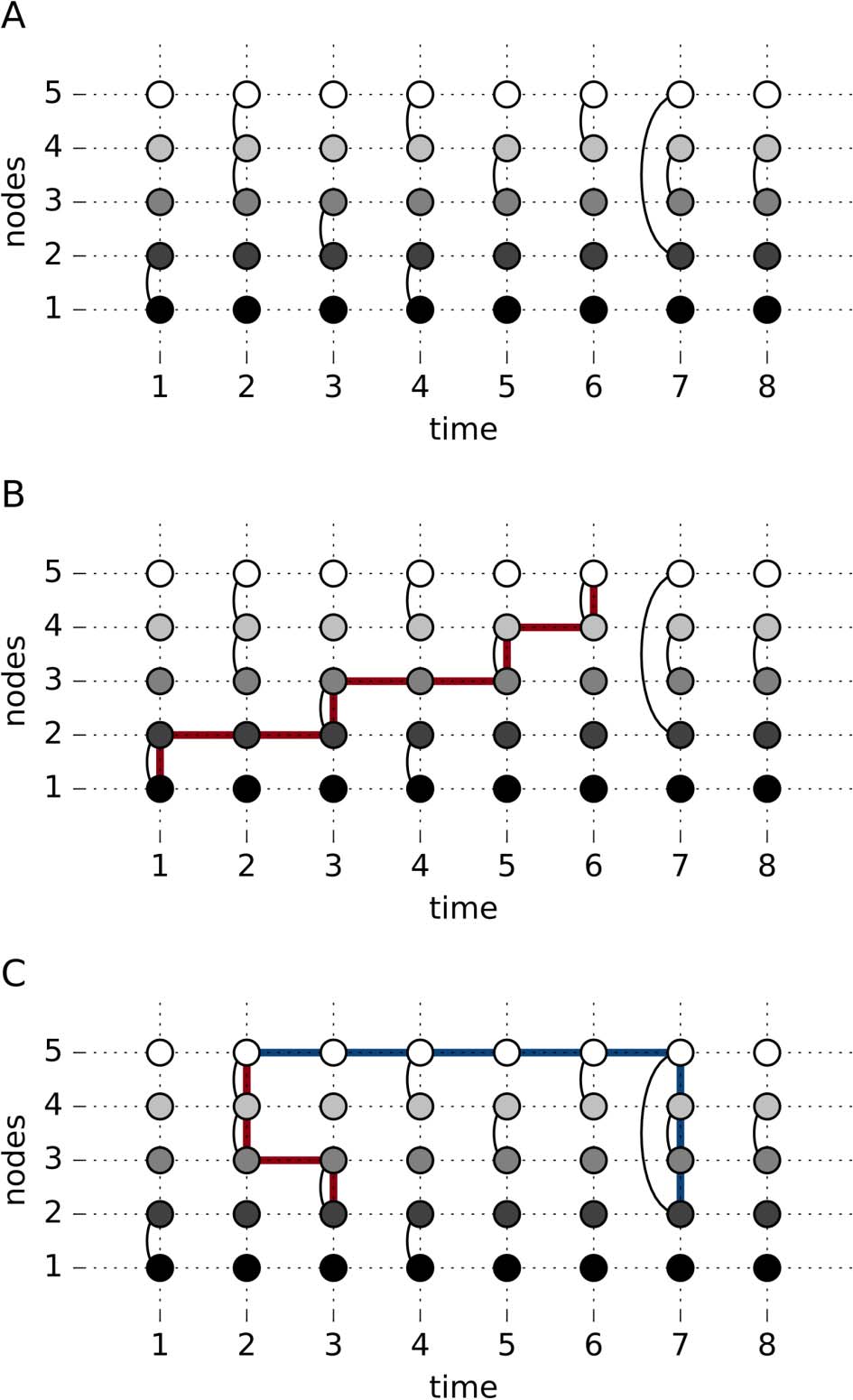
Nodal Measure: Temporal Centrality
A node’s influence in a temporal network can be calculated in a way akin to degree centrality
in the static case, where the sum of the edges for a node is calculated. The difference from its
static counterpart is that we also sum the number of edges across time. Formalmente, the temporal
degree centrality, DT, for a node i is computed as
=
DT
i
norte
∑
j=1
t
∑
t=1
En
i,j,
(3)
where T is the number of time points, N is the number of nodes, and At
i,j is a graphlet.
While it provides an estimate of how active or central a node is in a temporal network,
temporal degree centrality does not quantify the temporal order of the edges. This is illustrated
En figura 2, where Node 3 and Node 2 have identical temporal degree centralities, a pesar de
having very different temporal ordering of their edges.
Neurociencia en red
74
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
Cifra 2. A slice graph representation of a simple example of a temporal network that illustrates
the conceptual difference between temporal degree centrality and temporal closeness centrality.
Nodal Measure: Temporal Closeness Centrality
A centrality measure that does consider the temporal order is temporal closeness centrality
(Cacerola & Saramäki, 2011). This is an extension of the static closeness centrality, which is the
inverse sum of the shortest paths. Temporal closeness centrality is calculated as
CT
i,t
= 1
N − 1
norte
∑
j=1
1
t
d
i,j
,
(4)
t
where d
i,j is the average shortest path between nodes i and j across all time points for which
a shortest path exists. As in the static counterpart, if a node has shorter temporal paths than
other nodes, it will have a larger temporal closeness centrality.
Consider the example given in Figure 2, which shows a temporal sequence of connectivity
among three nodes over 20 time points. Note that the temporal degree centralities are identical
for both Node 2 and Node 3, while the degree centrality for Node 1 is twice as large. Node 2
has the largest temporal closeness centrality, since the time between edges is longer for Node
2 than for Node 3, which has the lowest value of temporal closeness centrality.
Edge Measure: Bursts
By using temporal network theory, bursts have been identified as an important property of
many processes in nature (Barrabás, 2005, 2010; Vázquez et al., 2006; Vazquez, Rácz,
Lukács, & Barrabás, 2007; mín., Goh, & Vazquez, 2011). A hallmark of a bursty edge is the
presence of multiple edges with short intercontact times, followed by longer and varying inter-
contact times. In statistical terms, such a process is characterized by a heavy-tailed distribution
of intercontact time probabilities. Numerous patterns of social communication and behavior
have been successfully modeled as bursty in temporal network theory, including email com-
munication (Barrabás, 2005; Eckmann, Moses, & Sergi, 2004), mobile phone communication
(Jo, Karsai, Kertész, & Kaski, 2012), spreading of sexually transmitted diseases (Vazquez, 2013),
soliciting online prostitution (Rocha, Liljeros, & Holme, 2010), and epidemics Takaguchi,
Masuda, & Holme, 2013. With regard to network neuroscience, we have recently shown that
bursts of brain connectivity can be detected in resting-state fMRI data (Thompson & Fransson,
2016a). Además, bursty temporal patterns have also been identified in the amplitudes
Neurociencia en red
75
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
of the EEG alpha signal (Freyer, Aquino, robinson, Ritter, & romper la lanza, 2009; Freyer, Roberts,
Ritter, & romper la lanza, 2012; Roberts, Boonstra, & romper la lanza, 2015).
There are several strategies to quantify bursts. A first way to check whether a time series of
brain connectivity between two nodes is bursty is simply to plot the distribution of intercontact
veces. De este modo, the complete distribution of τ for a given edge contains information about the tem-
poral evolution of brain connectivity. Sin embargo, other methods are available to quantify bursts.
One example is the burstiness coefficient (B), first presented in Goh and Barabási (2008) y
formulated for discrete graphs, Holme and Saramäki (2012):
=
Bij
pag(t
ij
pag(t
ij
) − μ(t
)
i,j
) ,
) + μ(t
ij
(5)
where τ
ij is a vector of the intercontact times between nodes i and j through time. Cuando
B > 0, it is an indication that the temporal connectivity is bursty. This occurs when the
standard deviation σ(t) is greater than the mean μ(t).
In Eq. 5, bursts are calculated per
borde, which can be problematic when only a limited number of data are available. Funcional
imaging sessions must be long enough to accurately establish whether or not a given temporal
distribution is bursty (too few intercontact times will entail too poor an estimation of σ to
accurately estimate B). Typically, for resting-state fMRI datasets acquired over rather short
time spans (5–6 minutes) with low temporal resolution (typically 2–3 seconds), it might be
difficult to quantify B in a single subject. A potential remedy in some situations is to compute
B after concatenating intercontact times across subjects.
Ecuación 5 calculates the number of bursts per edge. This can easily be extended to a
nodal measure by summing over the bursty coefficients across all edges for a given node.
Alternativamente, a nodal form of B can be calculated by using the intercontact times for all j instead
of averaging over j in Bij. Finalmente, if a process is known to be bursty, instead of quantifying B,
it is possible simply to count the number of bursts present in a time series.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
.
t
Global Measure: Fluctuability
Although centrality measures provide information about the degree of temporal connectivity,
and bursts describe the distribution of the temporal patterns of connectivity at a nodal level,
one might also want to retrieve information about the global state of a temporal network. A
this end, fluctuability aims to quantify the temporal variability of connectivity. We define the
fluctuability F as the ratio of the number of edges present in A over the grand sum of At:
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
F =
)
∑i ∑j U(Ai,j
∑i ∑j ∑t At
i,j
,
(6)
where U is a function that delivers a binary output. Ud.(Ai,j
occurs between nodes i and j across times t = 1, 2, …, t. If not, Ud.(Ai,j
expressed as
)is set to 1 if at least one of an edge
)is set to 0. This can be
Ud.(Aij
) =
⎧
⎨
⎩
1 if ∑T
0 if ∑T
t At
ij
t At
ij
> 0,
= 0,
(7)
76
Neurociencia en red
Temporal network theory applied to brain connectivity
where T is the total number of time points and A has at least one nonzero edge. Desde
definition given in Eq. 6, it follows that the maximum value of F is 1 and that this value only
occurs when every edge is unique and occurs only once in time.
While the above definition of fluctuability may seem counterintuitive, it is an adequate
measure to quantify the temporal diversity of edges. F reveals how connectivity patterns within
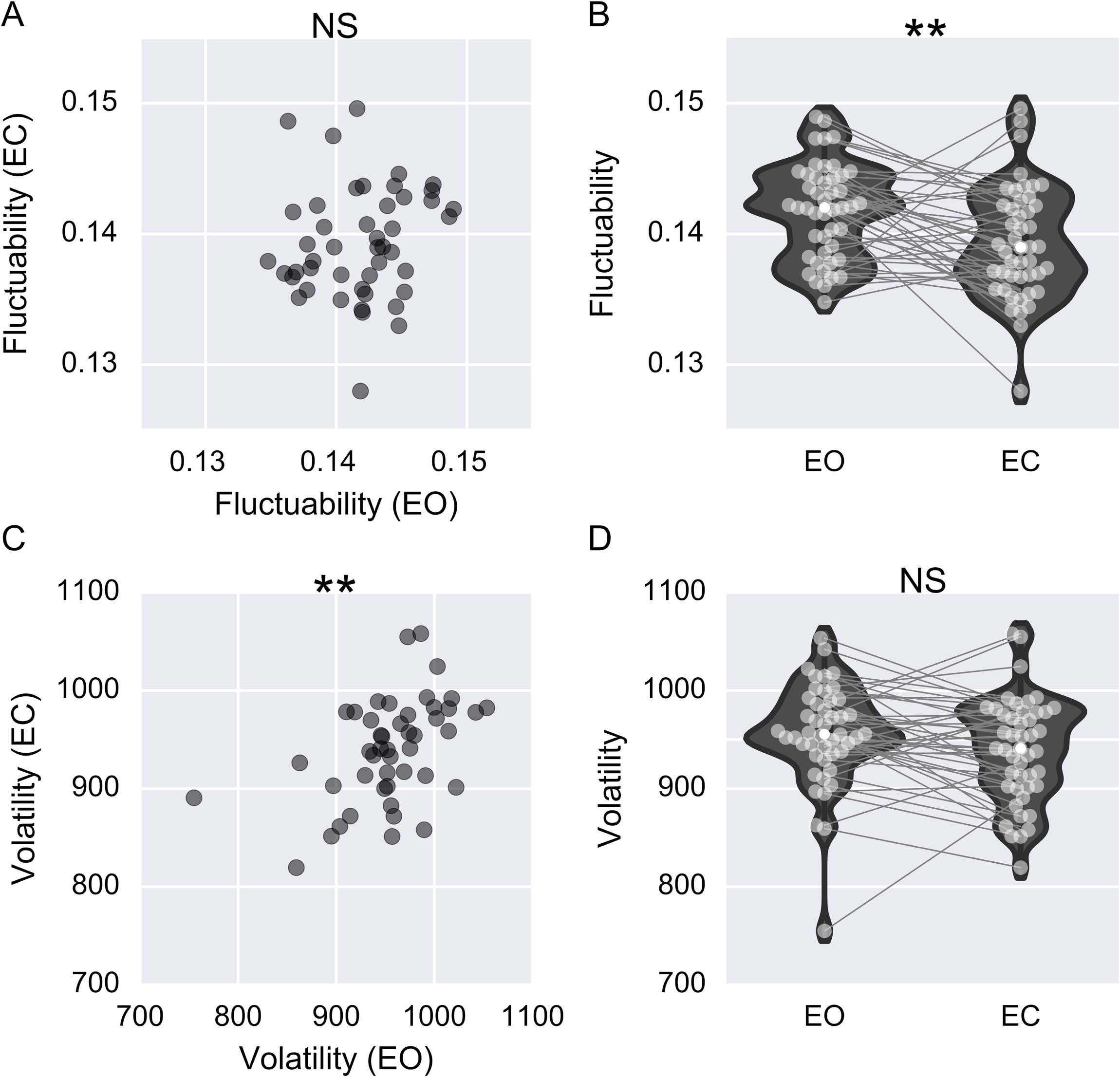
the network fluctuate across time. To see this, consider the networks shown in Figures 3A and
3B, for which two edges are present at each time point. There are only three unique edges
in Figure 3A, meaning that the sum of U is 3 for the network shown in Figure 3A. Sin embargo,
there is greater fluctuation in edge configuration for the network shown in Figure 3B, and all six
possible edges are present (entailing that the sum of U is equal to 6). Since both networks have
en total 24 connections over time, it becomes easy to see that the network shown in Figure 3B
has twice as large a value of F as the network shown in Figure 3A.
Notablemente, fluctuability is insensitive to the temporal order of connectivity. Por ejemplo, el
networks depicted in Figures 3B and 3C have the same fluctuability, despite having consid-
erably different temporal orders of edge connectivity. De este modo, fluctuability can be used as an
indicator of the overall degree of spatial diversity of connectivity over time.
The definition of fluctuability can be changed to work at a nodal level. To achieve this, el
summation in Eq. 6 is applied over only one of the nodal dimensions. Note that for nodes with
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Illustration of the fluctuability and volatility measures. The temporal networks shown
Cifra 3.
in panels A, B, and C all have the same numbers of nodes and edges, but they differ in fluctuability
and volatility. (A) This network has low fluctuability (F = 0.125) and volatility (V = 0.73). (B) Este
network has the highest volatility (V = 2.55) of all three networks and a fluctuability (F = 0.25) igual
to that of the network in panel C. (C) This network has lower volatility than B (V = 1.27) but equal
fluctuability (F = 0.25).
Neurociencia en red
77
Temporal network theory applied to brain connectivity
no connections at all, the denominator will be 0, and to circumvent this hindrance, the nodal
fluctuability FN
i
is defined as
⎧
⎨
⎩
)
∑j U(Ai,j
∑j ∑t At
i,j
0
=
FN
i
if U(Ai,j
if U(Ai,j
) > 0,
) = 0.
(8)
Global Measure: Volatility
One possible global measure of temporal order is how much, on average, the connectivity
between consecutive t-graphlets changes. This indicates how volatile the temporal network is
con el tiempo. De este modo, volatility (V) can be defined as
V = 1
T − 1
T−1
∑
t=1
D(En, At+1),
(9)
where D is a distance function and T is the total number of time points. The distance function
quantifies the difference between a graphlet at t and the graphlet at t + 1. In all the following
examples in this article, for volatility we use the Hamming distance, because it is appropriate
for binary data.
Whereas there was no difference in fluctuability between the networks shown in Figures 3B
and 3C, there is a difference in volatility, since the network in Figure 3B has more abrupt
changes in connectivity than the network shown in Figure 3C.
Extensions of the volatility measure are possible. Like fluctuability, volatility can be defined
at a local level. A per-edge version of volatility can be formulated as
V L
i,j
= 1
T − 1
T−1
∑
t=1
D(En
i,j, At+1
i,j
).
(10)
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
Además, taking the mean V L
i,j over j would give an estimate of volatility centrality.
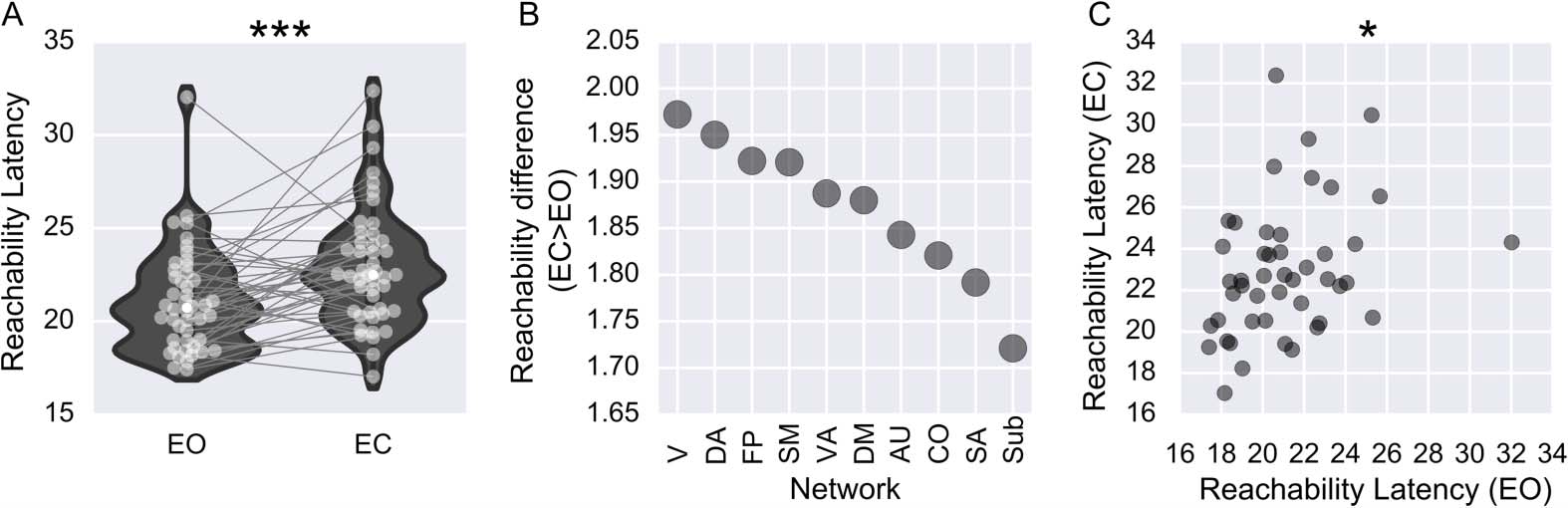
Global Measure: Reachability Latency
Measures of reachability focus on estimating the time taken to “reach” the nodes in a temporal
In Holme (2005), both the reachability ratio and reachability time are used. El
network.
reachability ratio is the percentage of edges that have a temporal path connecting them. El
reachability time is the average length of all temporal paths. Sin embargo, when applying reach-
ability to the brain, the two aforementioned measures are not ideal, given the noncontroversial
assumption that any region in the brain, given sufficient time, can reach all other regions.
With this assumption in mind, we define a measure of reachability, reachability latency,
that quantifies the average time it takes for a temporal network to reach an a-priori-defined
reachability ratio. This is defined as
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Rr = 1
TN
∑
t
∑
i
dt
i,k,
(11)
where dt
i is an ordered vector of length N of the shortest temporal paths for node i at time point
t. The value k represents the (cid:3)rN(cid:4)th element in the vector, which is the rounded product of the
fraction of nodes that can be reached, r, with N being the total number of nodes in the network.
Neurociencia en red
78
Temporal network theory applied to brain connectivity
In the case of r = 1, (es decir., 100% of nodes are reachable), ecuación. 11 can be rewritten as
R1
= 1
TN
∑
t
∑
i
maxj dt
i,j.
(12)
Ecuación 12 has been referred to as the temporal diameter of the network (Nicosia et al., 2013).
If Eq. 12 were modified and calculated per node instead of averaging over nodes, it would be
a temporal extension of node eccentricity.
Unless all nodes are reached at the last time point in the sequence of recorded data, allá
will be a percentage of time points from which all nodes can not be reached. This effectively
reduces their value of R, because dt
i,j cannot always be calculated, but R is still normalized
by T. If this penalization is considered too unfair, it is possible to normalize R by replacing T
with T∗, which is the number of time points where dT
i,j has a real value.
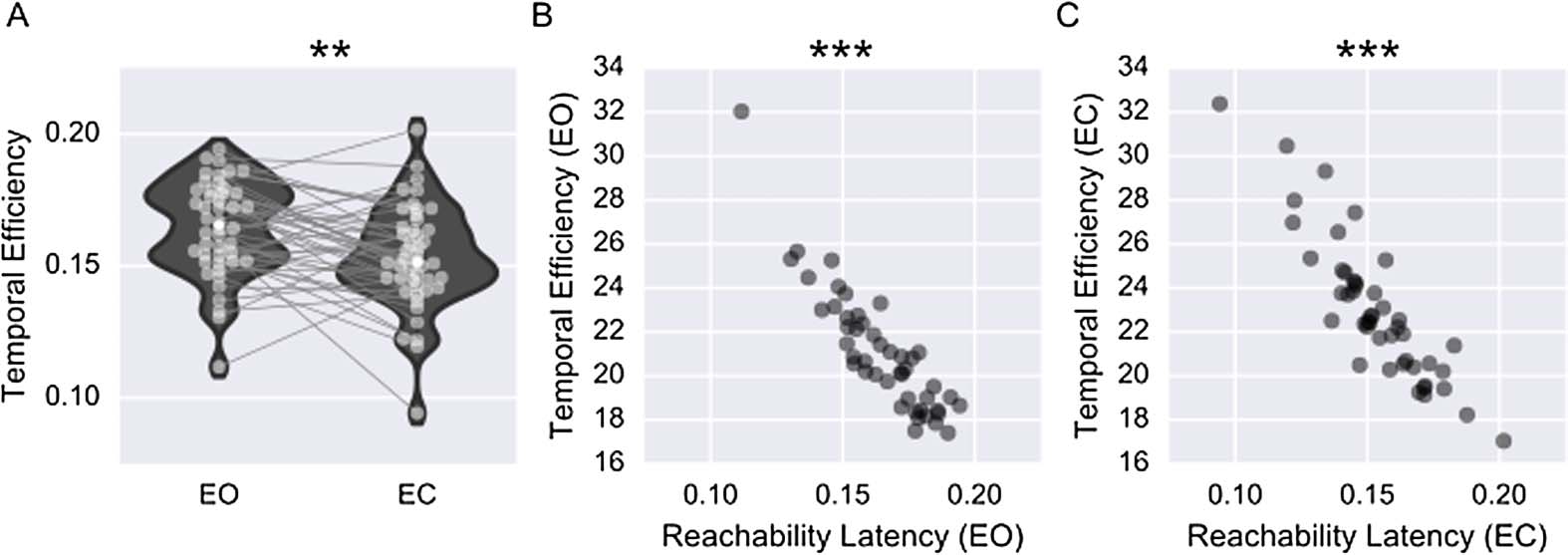
Global Measure: Temporal Efficiency
A similar concept is the idea of temporal efficiency. In the static case, efficiency is computed as
the inverse of the average shortest path for all nodes. Temporal efficiency is first calculated at
each time point as the inverse of the average shortest path length for all nodes. Después,
the inverse average shortest path lengths are averaged across time points to obtain an estimate
of global temporal efficiency, which is defined as
mi =
1
t(N2 − N) ∑
i,j,t
, i (cid:6)= j.
1
dt
i,j
(13)
Although reachability and efficiency estimate similar temporal properties, since both are
based on the shortest temporal paths, the global temporal efficiency may result in different
results than the reachability latency. This is because efficiency is proportional to the average
shortest temporal path, whereas reachability is proportional to the longest shortest temporal
path to reach r percent of the network. Similar to the case of static graphs, temporal efficiency
could be calculated at a nodal level as well, and this would equal the closeness centrality.
Summary of Temporal Network Measures
En mesa 1 we provide a brief summary of the temporal network measures outlined here, accom-
panied by short descriptions. We also signify which measures are sensitive to temporal order.
Mesa 1. Summary of the temporal network measures outlined in this article
Measure
Descripción
Order Dependent?
Temporal centrality
Closeness centrality
Number of overall connections in time
Time between connections
Burstiness
Fluctuability
Volatility
Distribution of subsequent connections
Ratio of unique edges vs. all edges
Rate of change of graphlets per time point
Reachability latency
Time taken for all nodes to be able to reach each other
Temporal efficiency
Inverse average shortest temporal path
norte
Y
Y
norte
Y
Y
Y
Neurociencia en red
Variable
DT
CT
Bij
F
V
Rr
mi
79
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
Statistical Considerations of Temporal Network Measures
When implementing temporal graph measures, it is important to perform adequate statistical
tests to infer differences between the subject groups, task conditions, or chance levels. Para
group comparisons, nonparametric permutation methods are advantageous where the group
assignment of the calculated measure can be shuffled between the groups and a null distri-
bution can be created. Alternativamente, to justify that a measure is significantly present above
chance levels, the construction of null graphs is required. There are multiple ways to create
temporal null graphs, and they each have their own benefits and drawbacks. One method
is to permute the temporal order of entire time series, but this will destroy any autocorrela-
tion present in the data. Another alternative is to permute the phase of the time series prior to
thresholding the t-graphlets. A third option would be to permute blocks of time series data, pero
this may not be appropriate for all network measures (p.ej., volatility). A fourth option would
be to use vector autoregressive null models (Chang & guantero, 2010; Zalesky et al., 2014). Nosotros
refer the reader to Holme & Saramäki (2012) for a full account of approaches to performing
statistical tests on measures derived from temporal network theory.
MÉTODOS
fMRI data
Two resting-state fMRI sessions (3-tesla, TR = 2,000 EM, TE = 30 EM) de 48 healthy subjects
were used in the analysis (19–31 years, 24 femenino). The fMRI data were downloaded from
an online repository: the Beijing Eyes-Open/Eyes-Closed dataset, available at www.nitrc.org
(Liu & duyn, 2013). Each functional volume comprised 33 axial slices (thickness/gap = 3.5/
0.7 mm, in-plane resolution = 64 × 64, field of view = 200 × 200 mm). The dataset contained
three resting-state sessions per subject, and each session lasted 480 s (200 image volumes,
two eyes-closed sessions and one eyes-open session). We used data only from the 2nd or 3rd
session, which were the eyes-open (EO) and second eyes-closed (EC) sessions, where the order
was counterbalanced across subjects. Two subjects were excluded due to incomplete data.
Further details regarding the scanning procedure are given in Liu & duyn (2013).
All resting-state fMRI data was preprocessed using Matlab (Version 2014b, Matemáticas,
Cª) with the CONN (Whitfield-Gabrieli & Nieto-Castanon, 2012) and SPM8 (Friston et al.,
1995) toolboxes. The functional imaging data were realigned and normalized to the EPI MNI
template as implemented in SPM. Spatial smoothing was applied using a Gaussian filter
kernel (FWHM = 8 mm). Additional image artifact regressors attributed to head movement
(Dijk, Jabonoso, & Buckner, 2012; Fuerza, Barnes, Snyder, Schlaggar, & Petersen, 2012) eran
derived by using the ART toolbox for scrubbing (www.nitrc.org). Signal contributions from
white brain matter, cerebrospinal fluid (CSF), and head movement (six parameters), también
as the ART micromovement regressors for scrubbing, were regressed from the data using
the CompCor algorithm (Behzadi, Restom, Liau, & Liu, 2007; the first five principal compo-
nents were removed for both white matter and CSF). After regression, the data were band-
passed between 0.008 y 0.1 Hz, as well as linearly detrended and despiked. Time series
of fMRI brain activity were extracted from 264 regiones de interés (ROI; spherical with a
5-mm radius) using the parcellation scheme for cortex and subcortical structures described
in Power et al. (2011). Each ROI was normalized by demeaning and scaling the standard de-
viation to 1. Estos 264 ROIs were further divided into ten brain networks, as described in
Cole et al. (2013) (technically subgraphs, in network theory terminology). Automatic anatom-
ical labeling (AAL) regions associated with specific ROIs, shown in the Supplementary Tables
(Thompson, Brantefors, & Fransson, 2017), were determined by taking the AAL region at (o
Neurociencia en red
80
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
t
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
Weighted Pearson correlation:
A correlation coefficient for which
the significance of each observation
is determined by a weight
closest to) the center of the ROI. Note that this offers only an approximate anatomical labeling
of the positions of ROIs.
Creating Time-Graphlets (t-Graphlets)
While there are many proposed methods for dynamic functional connectivity (Smith et al.,
2012; Allen et al., 2014; Liu & duyn, 2013; Lindquist, Xu, Nebel, & Caffo, 2014; Brillo y col.,
2015; Thompson & Fransson, 2016a), we chose a weighted correlation strategy (described be-
bajo) because it does not require optimizing any parameters or clustering. The method is based
on our previous work (Thompson & Fransson, 2016a), using the same fundamental assump-
ciones, which results in high temporal sensitivity to fluctuating connectivity. Sin embargo, we here
extended the method presented in Thompson & Fransson (2016a) so that it would compute
unique connectivity estimates for each time point, and thereby avoid the necessity to cluster
the data using a clustering technique such as k-means.
Our logic was to calculate dynamic functional brain connectivity estimates based on a
weighted Pearson correlation. To calculate the conventional Pearson correlation coefficient,
all points are weighted equally. In the weighted version, data points contribute differently to the
correlation coefficient, depending on what weight they have been assigned. These weights are
then used to calculate the weighted mean and weighted covariance to estimate the weighted
correlation coefficient. By using a unique weighting vector per time point, we were able to
get unique connectivity estimates for each time point.
The weighted Pearson correlation between the signals x and y is defined as
r(X, y; w) =
Σx,y;w
Σx,X;wΣy,y;w
,
(14)
where Σ is the weighted covariance matrix and w is a vector of weights that is equal in length
to x and y. The weighted covariance matrix is defined as
Σx,y;w =
∑n
i wi
(x − μx;w)(y − μy;w)
∑n
i wi
,
(15)
where n is the length of the time series. Note that Σ is the covariance matrix and ∑n
over time points. The variables μx;w and μy;w are the weighted means, defined as
i is a sum
μx;w =
∑n
i wixi
∑n
i wi
, μy;w =
∑n
i wiyi
∑n
i wi
.
(16)
Equations 14–16 define the weighted Pearson coefficient with the exception of the weight
vector w. If every element in w is identical, we can easily observe that the unweighted (conven-
tional) Pearson coefficient will be calculated. Aquí, we instead wished to calculate a unique
w for each time point, providing a connectivity estimate based on the weighted mean and
weighted covariance.
Different weighting schemes could be applied. De hecho, many of the different dynamic con-
nectivity methods proposed in the literature are merely different weighting schemes (p.ej., a
nontapered sliding window approach is just a binary weight vector).
We decided upon a global weighting of the spatial dimensions by calculating the distance
between the nodes at a specific time point with all other nodes for every other time point.
Neurociencia en red
81
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
This entails that the weights for the covariance estimates at t are larger for other time points
that display a global spatial pattern across all nodes similar to that of the nodes at t. A new
weight vector is calculated for each time point. The unique weight vector per time point pro-
duces a unique weighted Pearson correlation at each time point. This reflects the weighted
covariance, where time points with similar global spatial brain activation are weighted higher.
This produces, for each edge, a connectivity time series with fluctuating covariance.
Más formalmente, the weights for estimating the connectivity at time t are derived by taking
the distance between the activation of the ROIs at t and at each other time point (indexed
by v):
=
peso
v
1
D(yt, yv) ,
(17)
where D is a distance function and y is the multivariate time series of the ROIs. For the distance
(cid:5)
función, we used Euclidean distance (es decir., D(a, b) =
[∑n
i
(ai
− bi
)2]).
The weight vector of t is created by applying Eq. 17 for all v ∈ T, v (cid:6)=t. This implies that at
the time point of interest, t, we calculate a vector of weights (indexed by v) that reflects how
much the global spatial pattern of brain activity (es decir., all ROIs) differs from the brain activity
at t. Each collection of weight vectors wt can form a t by t matrix w for each subject and
each condition. The values of each matrix are scaled to range between 0 y 1. Finalmente, el
diagonal of w is set to 1. The collection of weight vectors for a single subject is shown for both
EO and EC sessions in Figures 4A–4C. Although this is not explicitly assumed in our method,
neighboring time points have the highest weights (Figura 4C).
After the derivation of the connectivity time series, a Fisher transform and a Box–Cox trans-
form were applied. For the Box–Cox transform, the λ parameter was fit by taking the maximum
likelihood after a grid-search procedure from -5 a 5 in increments of 0.1 for each edge. Previo
to the Box–Cox transformation, the smallest value was scaled to 1 to make sure the Box–Cox
transform performed similarly throughout the time series (Thompson & Fransson, 2016b). Cada
connectivity time series was then standardized by subtracting the mean and dividing by the
standard deviation. Snapshots of the weighted graphlets can be seen in Figure 4D. The entire
connectivity time series for three different ROI pairings are shown in Figures 4E– 4G. Binary
t-graphlets were created by setting edges exceeding two standard deviations to 1, or otherwise
0, for each time series.
Our thresholding approach to create binary connectivity matrices is suboptimal and could
be improved upon in future work (see Discussion). The need to formulate more robust thresh-
olding practices has been an ongoing area of research in static network theory in the neuro-
sciences (Drakesmith et al., 2015). Similar work needs to be carried out for temporal networks,
because a limitation of the current approach is a heightened risk of false positive connections.
Tools for Temporal Network Theory
We have implemented all temporal network measures described in the present work in a
Python package of temporal network tools called Teneto (www.github.com/wiheto/teneto)
for Python 3.x, although the package itself is still under development. The package currently
contains code for all the measures mentioned above and plotting functions for slice plots (p.ej.,
Figure 4F) and for stacking graphlets (p.ej., Figura 4D). Data formats for both the graphlet/
snapshot and event/contact sequence data representations are available.
Neurociencia en red
82
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
t
/
/
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
t
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Temporal network theory applied to brain connectivity
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
/
t
mi
d
tu
norte
mi
norte
a
r
t
i
C
mi
–
pag
d
yo
F
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
norte
mi
norte
_
a
_
0
0
0
1
1
pag
d
.
t
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
7
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
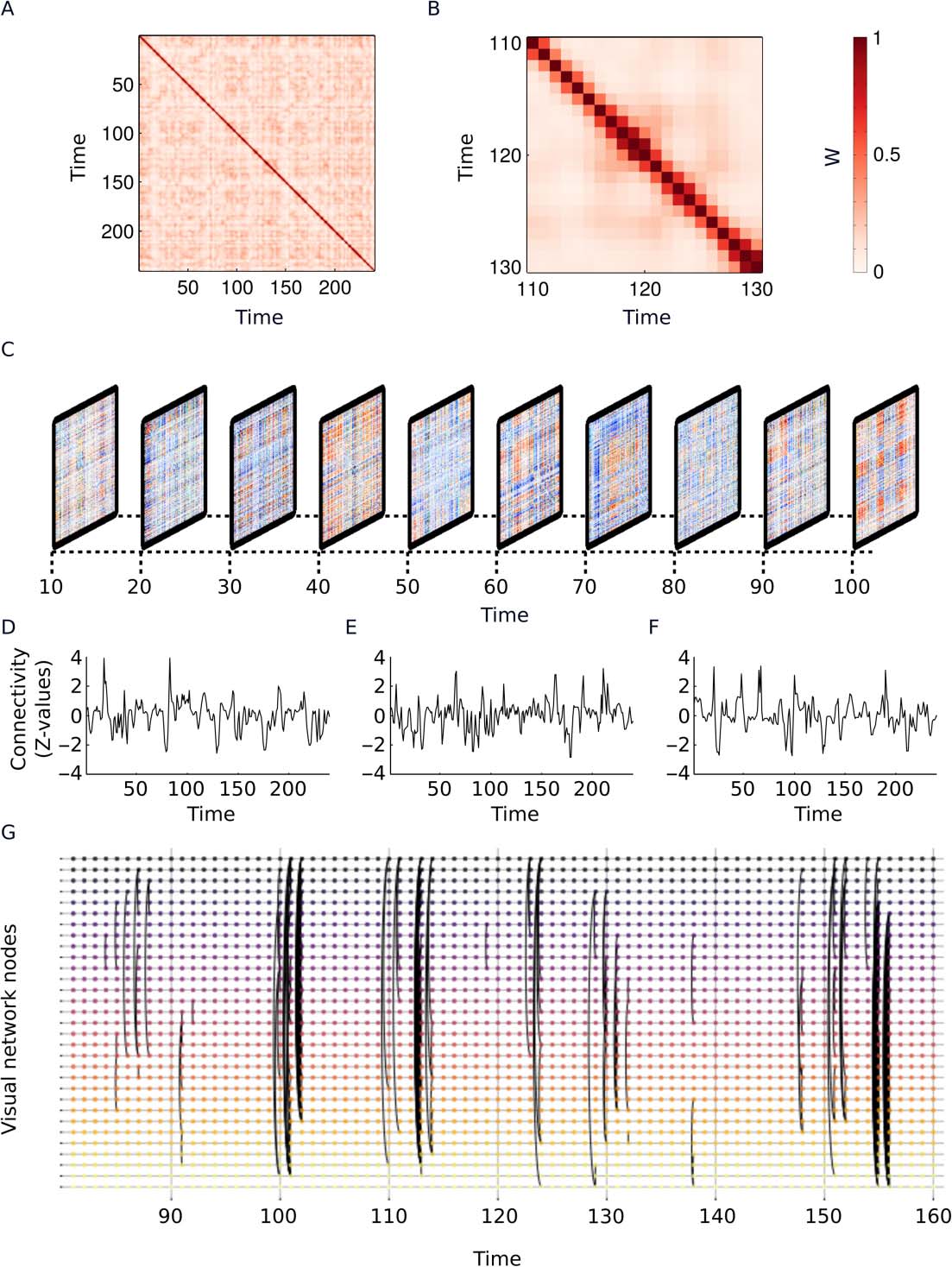
Cifra 4. Outline of the weighted correlation method to estimate dynamic connectivity. (A) Columna-
lection of weight vectors for a single subject in the eyes-open condition. (B) Collection of weight
vectors for a single subject in the eyes-closed condition. (C) A magnified portion of the image shown
(D) Stack of
in panel A that highlights that neighboring time points have the highest weights.
graphlets showing the weighted connectivity for a selection of the resting-state session.
(E–G)
Example connectivity time series for the entire session for a single edge. The edges are (mi) two
nodes from the default mode network, (F) two nodes in the visual network, y (GRAMO) one node in the
visual network and one node in the default mode network. (h) Example of the slice graph represen-
tation of temporal brain connectivity for all nodes in the visual subnetwork with binary connections.
All panels in this figure show data taken from the same subject and, with the exception of panel B,
show the EO condition. All time units in the figure are given in volumes (TR) (es decir., each time step
es 2 s).
Estadísticas
All between-group comparisons in the next section use the between-group permutation method
outlined previously. Null distributions were created with 100,000 permutations of shuffling
which group each subject’s EO/EC results belonged to, and all comparisons were two tailed.
For between-subjects comparisons, Spearman rank correlations were used. To determine
which nodes had a higher-than-chance level of centrality, 1,000 permutations were performed
in which the nodal order for each subject was shuffled. This resulted in 264 null distributions
in which the centrality was averaged over subjects. The distribution with the largest 950th
value was selected to signify p = 0.05.
Neurociencia en red
83
Temporal network theory applied to brain connectivity
RESULTADOS
Applying Temporal Degree Centrality and Temporal Closeness Centrality
With temporal centrality measures we can formulate research questions along the following
líneas: (i) which nodes have the most connections through time (temporal degree centrality), o
(ii) which nodes have short temporal paths to all other nodes (temporal closeness centrality).
For the shortest-paths calculations, we allowed all possible steps at a single time point to be
used in this example.
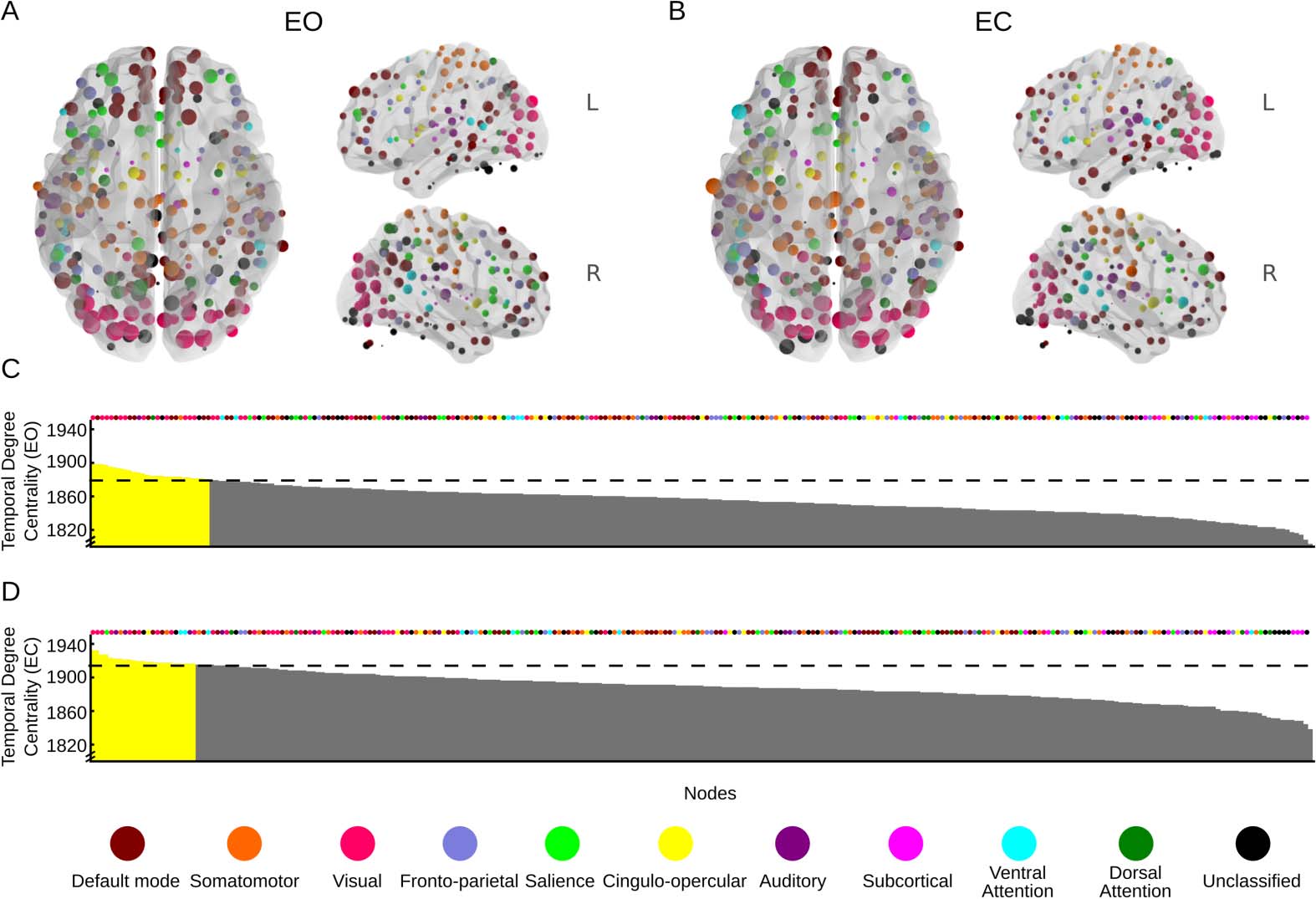
First we illustrate the spatial distribution of both centrality measures in the brain. Temporal
degree centrality, averaged over all subjects, is displayed on the brain for all 264 ROIs for both
the EO (Figure 5A) and EC (Figure 5B) condiciones, respectivamente. Nodes with a higher-than-
expected temporal centrality degree (pag < 0.05) are shown for both conditions in Figures 5C
and 5D, respectively. Tables of all nodes/brain regions that passed the significance threshold
are presented in Supplementary Tables 1 and 2 (Thompson et al., 2017). Of the 25 nodes in
the EO condition that were above the threshold, the majority were located in either the visual
network (12 nodes) or the default mode network (eight nodes). In the EC condition, 26 nodes
passed the statistical threshold. Somewhat surprisingly, many of these nodes still came from
the visual network, but relatively fewer than in the EO condition (nine nodes). Speculatively,
the relatively high centrality of nodes in the visual network might be related to the notion that
many subjects may have performed mental imagery or other activity known to activate areas
of visual cortex during the EC condition (Ganis, Thompson, & Kosslyn, 2004).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5. Spatial patterns of temporal degree centrality displayed on the surface of the brain for
(A) the eyes-open (EO) condition and (B) the eyes-closed (EC) condition. (C) Spatial distribution of
temporal degree centrality across all nodes for the EO condition. Yellow color indicates p < 0.05.
The assigned network of each node is marked by colored dots above the plot. (D) As in panel C, but
for the EC condition. Anatomically detailed information about the nodes that had the largest degrees
of temporal centrality in panels C and D can be found in Supplementary Tables 1 and 2 Thompson
et al., 2017. Nodes located outside the rendered brain images are part of the cerebellum.
Network Neuroscience
84
Temporal network theory applied to brain connectivity
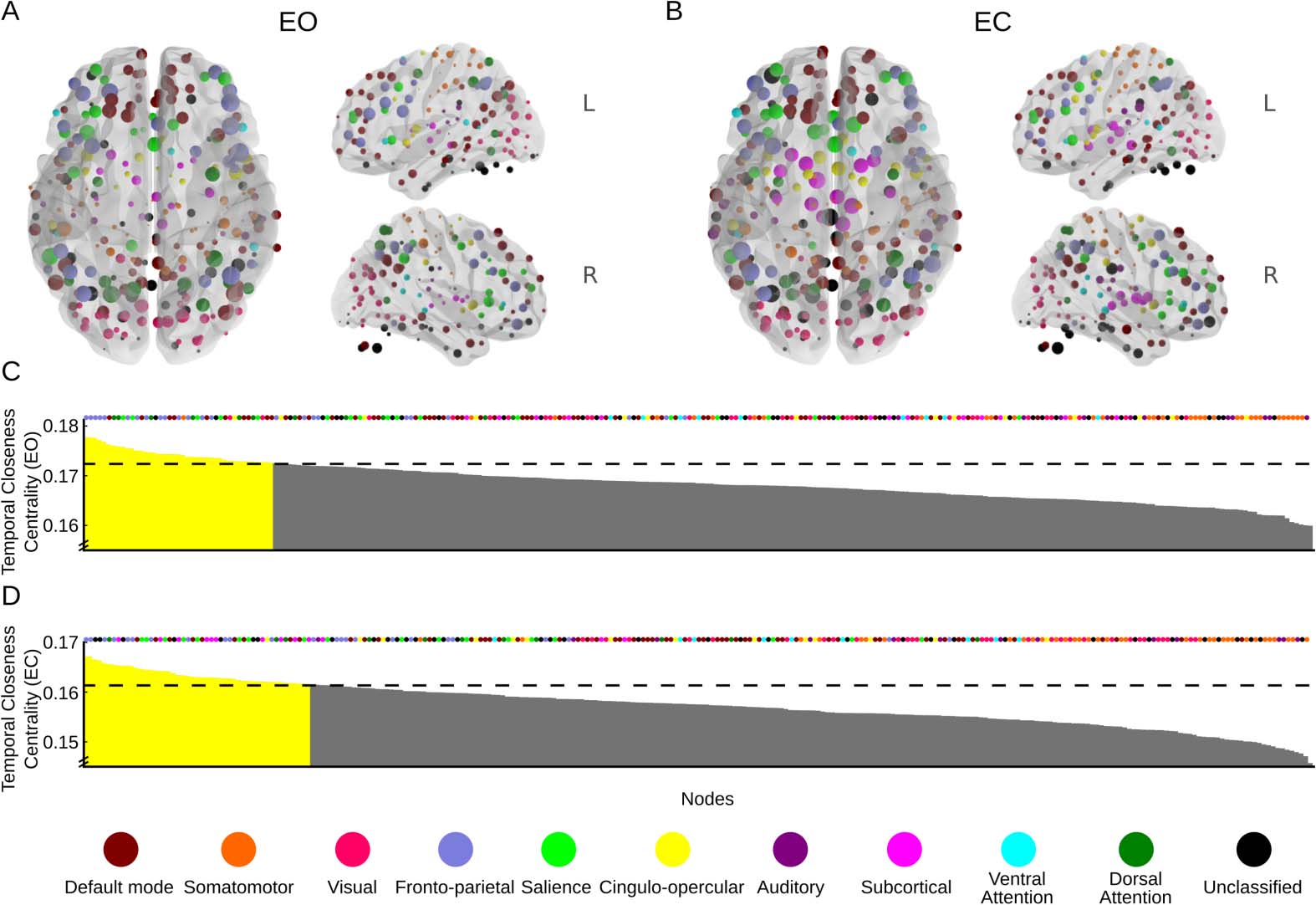
For closeness centrality, we observed that in both the EO condition (Figure 6A) and the
EC condition (Figure 6B), nodes with higher-than-expected temporal closeness centrality (p <
0.05) were located in the frontoparietal, dorsal attention, and default mode networks (Figures 6C
and 6D) (see also Thompson et al., 2017, Supplementary Tables 3 and 4). Notably, for the EO
condition only three nodes in the visual network had a closeness centrality above the threshold,
whereas the EC condition had none. On the other hand, nodes in the saliency and subcortical
networks scored higher in the EC than in the EO condition.
In sum, both centrality measures returned reasonable spatial distributions of high-scoring
nodes across the brain for both conditions, implying that they quantified relevant and inter-
esting information about the dynamics of the BOLD signal. Obviously, this demonstration
is exploratory, and thus we are unable to infer the underlying cognitive processes from the
given centrality measures alone. This task is also made more difficult by the cognitively un-
restrained behavioral conditions in a resting state. For example, the high closeness centrality
of the saliency network in the EC condition might depend on a number of factors, ranging
from focus on the task at hand to the presence of emotional processes. However, the results
allow us to consider how the different centrality measures can provide novel insights into the
network dynamics. That the visual network has the highest centrality in the EO condition for
both measures is reasonable. The observation that the default mode and attentional networks
also score high on both centrality measures also seems reasonable. If, on the other hand, the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Spatial patterns of temporal closeness centrality displayed on the brain surface for the
eyes-open (EO) condition (A) and the eyes-closed (EC) condition (B). (C) Distribution of temporal
closeness degrees over all nodes for the EO condition. Yellow color indicates p < 0.05. The assigned
network of each node is marked by colored dots above the plot. (D) As in panel C, but for the EC
condition. Anatomically detailed information about the largest nodes in panels C and D with the
greatest temporal closeness centrality can be found in Supplementary Tables 3 and 4 Thompson
et al., 2017. Nodes outside the rendered brain images are part of the cerebellum.
Network Neuroscience
85
Temporal network theory applied to brain connectivity
somato-motor network had scored high in both EC and EO, or if the centrality of nodes in
the visual network had been higher during EC than EO, such results would call into question
whether our temporal centrality measures were actually quantifying anything meaningful.
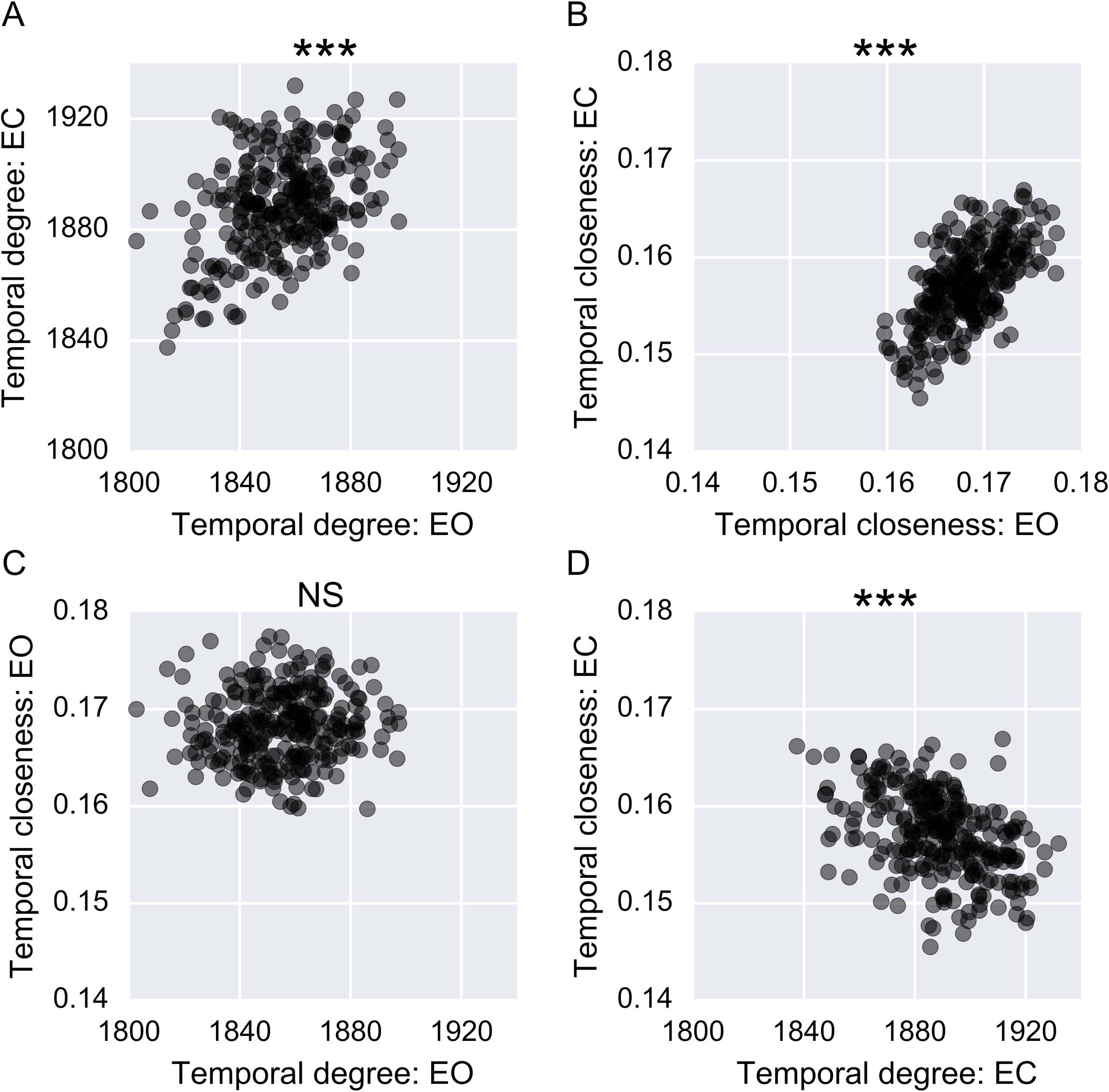
The centrality estimates for nodes were compared across imaging sessions to evaluate
whether the temporal patterns were similar across subjects. Despite differences in the highest-
scoring nodes for each condition, temporal degree centrality correlated significantly between
the EO and EC conditions (Figure 7A, ρ = 0.35, p < 0.0001). A similar trend was observed for
temporal closeness centrality (Figure 7B, ρ = 0.62, p < 0.0001). This entails that nodes ap-
pear to have similar centrality properties in the EO and EC resting-state conditions. Although
both centrality measures showed between-session correlations, there was no consistent re-
lationship between the two measures. No significant relation was observed in the EO ses-
sion (Figure 7C, ρ = 0.09, p = 0.15), and a negative correlation emerged for the EC session
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Applying temporal degree centrality and temporal closeness centrality for the eyes-open
(EO) and eyes-closed (EC) conditions. Each dot represents the centrality of a node. (A) Temporal
degree centrality for the EO versus the EC condition. (B) Temporal closeness centrality for the EO
versus the EC condition.
(C) Temporal degree centrality versus temporal closeness centrality in
the EO condition. (D) Temporal degree versus temporal closeness centrality in the EC condition.
*** signifies p < 0.001.
Network Neuroscience
86
Temporal network theory applied to brain connectivity
(Figure 7D; ρ = 0.45, p < 0.0001). This result is not surprising, since the measures are quite
different by definition, but it is still useful to demonstrate that these different centrality measures
quantify different aspects of the temporal dynamics of the brain.
Applying Burstiness
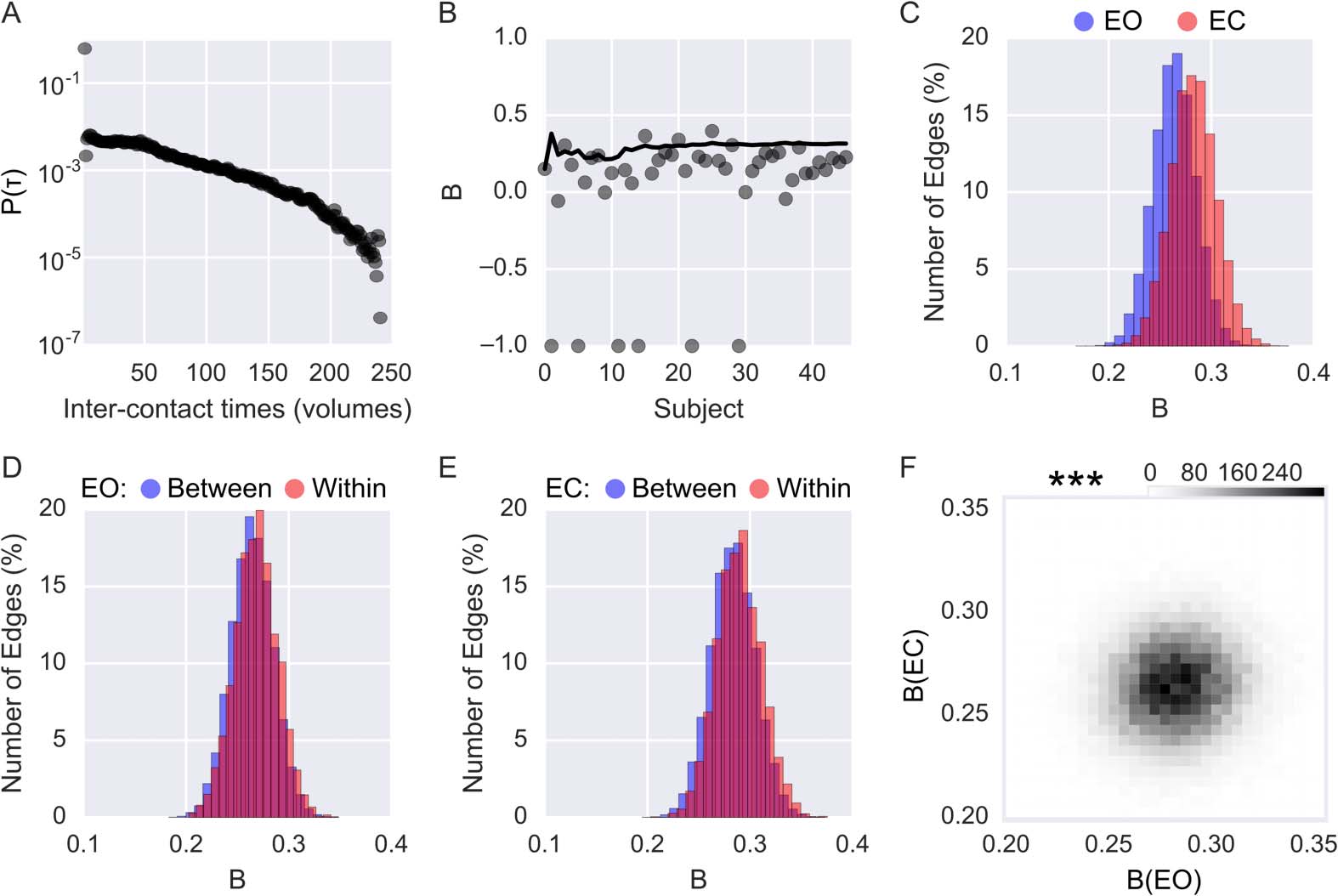
By applying the burstiness measure (B) to an fMRI dataset, we can ask questions related to the
temporal distribution of brain connectivity. To illustrate that there is indeed a bursty pattern
of brain connectivity, we first plotted the distribution of all intercontact times taken from all
subjects and edges for the EO session and observed a heavy-tailed distribution (Figure 8A).
We then considered the question of the most robust way to calculate B, given that our
example fMRI dataset had a rather low temporal resolution and only spanned a limited time
period. It was possible that not enough edges might be present in each subject to allow a stable
estimate of B for a single subject. To test this concern, we evaluated whether there was a differ-
ence in B for a single subject versus the concatenated intercontact times of multiple subjects.
This was done for a single edge that connected right posterior cingulate cortex and right medial
prefrontal cortex in the EO session. As is shown in Figure 8B, there is a considerable variance
in the individual subject estimates of burstiness.
If we cumulatively add subjects, however,
the estimate of burstiness stabilizes after approximately 12 subjects. This illustrates the impor-
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 8. Quantifying bursty connectivity. (A) Distribution of all intercontact probabilities, com-
bining all edges and subjects in the eyes-open (EO) condition. (B) The bursty coefficient (B) for one
edge in the EO condition. Each dot represents B calculated per subject, while the solid line shows
the bursty coefficient when cumulatively adding subjects. Values of −1 indicate that all intercontact
times are identical (i.e., one burst, tonic connectivity, or oscillations in connectivity). (C) Distribu-
tions of B for the different conditions (blue: EO; red: eyes-closed, EC). (D) Distributions of B as a
function of EO within-network connectivity (red) and between-network connectivity (blue). (E) As
in panel D, but for the EC condition. (F) Bursty coefficients for each edge across the two sessions,
displayed as a heat map. *** signifies p < 0.001.
Network Neuroscience
87
Temporal network theory applied to brain connectivity
tance of having enough data to calculate reliable B estimates. Henceforth, all B estimates are
calculated by pooling intercontact times over subjects.
We then wished to contrast EO versus EC in terms of burstiness. Both conditions showed
bursty distributions across all edges (see Figure 8C), and slightly more so for the EC than for the
EO condition. Both within- and between-network connectivity showed bursty distributions of
connectivity patterns in both conditions (Figures 8D and 8E).
Given that both EO and EC showed bursty correlations, we tested whether the values of
B correlated between conditions (Figure 8F). We found a weak, but significant, correlation
between conditions (ρ = 0.066, p < 0.0001). This weak between-condition correlation (ac-
counting for less than one percent of the variance, and probably driven by the number of data
points) suggests that much of the variance of burstiness may have been task-specific. However,
more research on this topic will be needed.
Applying Fluctuability
Using the fluctuability measure, researchers may ask questions regarding how many unique
edges exist in a temporal network model of the dynamic functional brain connectome, indicat-
ing whether more resources (i.e., diversity of connections) are required during a given task.
The fluctuability measure was applied to contrast the EO and EC conditions both between
(Figure 9A) and within (Figure 9B) subjects. We observed no significant between-subjects cor-
relation in F (ρ = 0.18 , p = 0.23) but did find a difference between the average values of
F between conditions (p = 0.0020), with the EO condition having a higher degree of fluctua-
bility. Thus, the EO condition had a more varying configuration of connections through time
than did the EC condition.
Applying Volatility
With volatility, we can ask whether the connectivity changes faster or slower through time.
Some tasks might require the subject to switch between different cognitive faculties or brain
states, while other tasks may require the brain to be more stable and to switch states less.
As with fluctuability, we computed volatility both between subjects (Figure 9C) and between
conditions (Figure 9D). We observed a significant correlation for between-subject volatility
over the two conditions (ρ = 0.46, p = 0.0012; Figure 9C). Additionally, no significant differ-
ence in volatility was observed between EO and EC (p = 0.051; Figure 9D).
Applying Reachability Latency
The measure of reachability latency addresses the following question regarding the overall
connectivity pattern along the temporal axis: how long does it take to travel to every single node
in the temporal network? For example, the reachability latency may be useful for evaluating the
dynamics when either functional or structural connectomes differ substantially. We computed
the reachability latency by setting r = 1 (i.e., all nodes must be reached).
The results are shown in Figure 10, where a significant difference in the average reachability
latencies between conditions is visible (Figure 10A; EO: 21.07, EC: 22.96, p = 0.0005). Given
that there was an overall increase in reachability latencies during EC as compared to EO, we
decided to unpack this finding post hoc and check whether the discovered global difference
in reachability could be localized to brain networks that should differ between the EC and EO
conditions. So, rather than calculating the reachability latency for the entire brain, we averaged
Network Neuroscience
88
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 9. Applying fluctuability and volatility measures for the eyes-closed (EC) and eyes-open
(EO) conditions. (A) Between-subjects correlation for fluctuability. (B) Violin plot showing fluctua-
bility between the EO and EC conditions. Each light gray dot designates a subject, and a line binds
together data obtained from the same subjects during the EO and EC conditions. For clarity, each
line connecting subjects terminates at the centers of the violin plots. The mean value of fluctuability
for each condition is shown with a white dot. (C) As in panel A, but for volatility. (D) As in panel B,
but for volatility. ** signifies p < 0.01.
the measures of reachability latency (to reach all nodes) for ten preassigned brain networks. In
this post hoc analysis, we see that the brain networks with the highest differences in reachability
latency were the visual, dorsal attention, and frontoparietal brain networks (Figure 9B). Thus,
the results show a longer reachability latency for the visual and attention networks when there
is no visual input, a result that appears biologically plausible.
In addition to these between-condition differences in reachability, we observed that there
was also a significant between-subjects relationship (ρ = 0.36, p = 0.015; Figure 9C). Taken
together with the previous finding, our results show that measures of reachability latency reflect
both between-task and between-subjects differences.
Applying Temporal Efficiency
Finally, we computed the global temporal efficiencies for both the EO and EC conditions.
Where reachability latency employs the shortest temporal path to calculate how long it takes
Network Neuroscience
89
Temporal network theory applied to brain connectivity
Figure 10. Applying reachability latency. (A) Violin plots of reachability latency for the eyes-open
(EO) and eyes-closed (EC) conditions. Light gray dots correspond to single subjects, and lines con-
nect each subject’s values between conditions. For clarity, each line connecting subjects terminates
at the centers of the violin plots. White dots mark the mean reachability latencies.
(B) Post hoc
decomposition of the reachability latency difference (EC−EO) across subnetworks. (C) Between-
subjects correlation of reachability between EO and EC. * signifies p < 0.05; *** signifies p < 0.001
to reach a certain percentage of nodes, temporal efficiency relates to the average inverse of all
shortest temporal paths.
We found that temporal efficiency was significantly greater during EO than during EC (p =
0.0011; Figure 11A). This finding means that, on average, the temporal paths are shorter in the
EO than in to the EC condition. We observed strong negative correlations between temporal
efficiency and reachability latency during both conditions (EO: ρ = −0.88, p < 0.0001; EC:
ρ = −0.88, p < 0.0001; see Figures 11B and 11C).
DISCUSSION
Our overarching aim in this work was to provide an overview of the key concepts of temporal
networks, for which we have introduced and defined temporal network measures that can be
used in studies of dynamic functional brain connectivity. Additionally, we have shown the
Figure 11. Applying global temporal efficiency and its relation with reachability latency. (A) Violin
plots of global temporal efficiency for the eyes-open (EO) and eyes-closed (EC) conditions. Light gray
dots correspond to single subjects, and lines connect single subjects, values between conditions.
For clarity, each line connecting subjects terminates at the centers of the violin plots. White dots
indicate the mean global temporal efficiencies. (B) Scatterplot showing each subject’s reachability
latency versus temporal efficiency for the EO condition. (C) As in panel B, but for the EC condition.
** signifies p < 0.01; *** signifies p < 0.001.
Network Neuroscience
90
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
applicability of temporal metrics in network neuroscience by applying them fMRI resting-state
datasets, and then shown that resting-state networks differ in their dynamical properties.
Summary of Applying Temporal Network Measures to fMRI Data
Both temporal degree centrality and closeness centrality were correlated across conditions,
whereas no correlation between the two centrality measures was observed. This entails that
the two centrality measures quantify different dynamic properties of the brain.
At a global network level, we examined the temporal uniqueness of edges (fluctuability) as
well as the rate of change of connectivity (volatility). We could identify a significant condition-
dependent difference in fluctuability, but no difference was observed in volatility between con-
ditions. Conversely, a significant between-subjects correlation was found for temporal network
volatility, but the between-subjects correlation in fluctuability was not significant. The ob-
served differences in volatility—that is, the differences in brain connectivity at different points
in time—were driven to a relatively larger extent by intersubject differences in connectivity
dynamics than by differences related to the tasks (EO/EC) per se.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Our results regarding reachability latencies during the EO and EC conditions indicate task-
driven changes in latencies, especially since the connectivity of the visual and attention brain
networks is known to reconfigure between EO and EC conditions (Zhang et al., 2015). Thus,
the observed difference in reachability latencies might be a reflection of a putative network
reconfiguration. Furthermore, reachability also showed a between-subjects correlation across
conditions.
The distribution of intercontact time points of connectivity between brain nodes was bursty,
in agreement with our previous findings (Thompson & Fransson, 2016a). Notably, our previ-
ous findings were obtained at a high temporal resolution (TR = 0.72 s), and it is therefore
reassuring that we were able to detect similar properties of burstiness in brain connectivity at
a lower temporal resolution (TR = 2 s). Of note, the between-network versus within-network
connectivity difference here varied from that obtained in a previous study that had shown
between-network connectivity to be significantly more bursty than within-network connectiv-
ity (Thompson & Fransson, 2016a). This difference is probably due to the different kinds of
thresholding being applied. Here a variance-based thresholding was applied, instead of the
magnitude-based form used in the previous study. We have discussed previously that these
different strategies will prioritize different edges (Thompson & Fransson, 2015b, 2016b).
In sum, we have shown that measures founded in temporal network theory can be applied
to fMRI data and are sensitive to the dynamical properties of fMRI BOLD connectivity. While
attempting to interpret temporal network measures in a psychological and biological context
has an intuitive appeal, such interpretations remain speculative at this point. Our intention here
was to explore the dynamic connectivity across subjects and across a simple task difference
to demonstrate that temporal network measures are appropriate measures given the signal.
We showned that certain properties may be subject-specific, while others are task-specific.
Furthermore, temporal network measures lead to rankings of network properties that are in
agreement in a resting state during eyes-open and eyes-closed conditions. However, to infer
psychological properties from a specific measure, hypothesis-driven work will be necessary
in which the a priori hypothesis can be explicitly tested. We believe that the present work
demonstrates that such future studies are possible using temporal network theory.
Network Neuroscience
91
Temporal network theory applied to brain connectivity
A final note regarding the interpretation of measures that are dependent on the shortest
paths. In cases in which the temporal resolution is sluggish, as in fMRI, and the spatial res-
olution is coarse in relation to the size of neurons, it would be incorrect to assume that the
shortest path reflects the shortest period of time for a neuron in node i to reach and communi-
cate with another neuron residing in node j. What can the shortest paths reveal, then? When
the temporal paths decrease during performance of a given task between nodes located in two
different brain networks, it tells us that those two networks are interacting. Thus, shortest paths
computed on the basis of fMRI data should be viewed in the context of how nodes in different
brain networks are interacting with each other.
Other Approaches to Remporal Network Theory
The list of measures for temporal networks described here is far from exhaustive. Although we
have focused primarily on temporal properties that can be defined at a nodal and/or global
level, detecting changes in network modularity over time is an active part of network theory
research (Mucha, Richardson, Macon, Porter, & Onnela, 2010; Rosvall & Bergstrom, 2010).
This approach has recently been applied to the brain connectome (Mantzaris et al., 2013;
Bassett et al., 2013) and in the context of learning (Bassett et al., 2011; Basset, Yang, Wymbs,
& Grafton, 2015). In a similar vein, the presence of hyperedges allows us to explore and iden-
tify groups of edges that have similar temporal evolutions (Davison et al., 2015; Davison et al.,
2016). Similarly, investigating how different tasks evoke different network configurations
(Ekman, Derrfuss, Tittgemeyer, & Fiebach, 2012; Cole et al., 2013; Matter, Cole, & Sharon,
2015) is also an active research area. Another recent exciting development is to consider
a control-theory-based approach to network neuroscience (Gu et al., 2015), which can be
applied to networks embedded in time (Gu et al., 2016).
Yet another avenue of temporal network research is to apply static network measures to
each t-graphlet and then derive time series of fluctuating static measures (Bola & Sabel, 2015;
Chiang et al., 2016).
It is also possible is to quantify the properties of dynamic fluctuations
in brain connectivity through time and then to correlate them with the underlying static net-
work. Using such a strategy, between-subjects differences for both the dynamic and the static
networks can be revealed (e.g., Betzel, Fukushima, He, Zuo, & Sporns, 2016).
Finally, considerably more measures within the temporal network literature can be put to
use within the field of network neuroscience. For example, the list of centrality measures
provided here is not complete. A temporal extension of betweenness centrality, which is often
used for static networks, can be adopted in the temporal domain (Tang, Musolesi, Mascolo,
Latora, & Nicosai, 2010). In the same vein, spectral centrality can also be computed in the
temporal domain (see Nicosia et al., 2013, for further details).
When Is Temporal Network Theory Useful?
As we stated in the introduction, graphs are an abstract representation corresponding to some
state in the world. The properties quantified in these representations try to reflect corresponding
properties of the world. Not every representation of brain function will require time, which
would make temporal network measures unsuitable. Under what conditions will temporal
network theory be of use? Networks of neurons are known to reconfigure during different
behavioral states and tasks. This reconfiguration occurs at all levels of brain connectivity:
from microcircuits controlling the digestive system in lobsters (Meyrand, Simmers, & Moulins,
1994) to the differential involvement of large-scale brain networks in cognitive tasks in hu-
mans (Ekman et al., 2012; Cole et al., 2013; Mattar, Cole, & Sharon, 2014). Temporal network
Network Neuroscience
92
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
theory allows us to track and study these reconfigurations, which has the potential to offer more
detailed information about fluctuations in brain network configuration than can be achieved
by aggregating over tasks or behavioral states.
The potential fields of application for the methods described in this work are vast. Obvi-
ous examples range from real-time neuroimaging to tracking ongoing cognitive processes. To
be able to isolate and identify the dynamics of networks may indeed be necessary when the
same networks are involved in multiple cognitive processes. Furthermore, the increased tem-
poral sensitivity provided by temporal networks offers greater systematic discriminative power
between healthy and patient cohorts. To give an example, alterations in static default mode net-
work connectivity have been implicated in depression (Sheline et al., 2009; Hamilton et al.,
2012), schizophrenia (Garrity et al., 2007; Pomarol-Clotet et al., 2008), traumatic brain in-
jury (Bonnelle et al., 2011; Sharp et al., 2011; Thompson, Thelin, Lilja, Bellander, & Fransson,
2016), obsessive–compulsive disorder (Stern, Fitzgerald, Welsh, Abelson, & Taylor, 2012),
autism (Cherkassky, Kana, Keller, & Just, 2006; Weng et al., 2010), fibromyalgia (Nadapow
et al, 2010; Flodin et al., 2014), posttraumatic stress (Sripada et al., 2012), and Alzheimer’s
disease (Greicius, Srivastava, Reiss, & Menon, 2004). This is not an exhaustive list, but it list
suggests that it is very difficult to make inferences regarding static differences in connectivity in
the default network that are specific to a particular patient cohort. We hope that, by adding a
temporal dimension and thus reducing the aggregations and simplifications of a static network
analysis, unique connectivity markers may become viable for different patient cohorts.
A couple of additional Factors should be considered when applying temporal network the-
ory. Interpreting what a measure means can only be done in relation to the temporal resolution
of the data. For example, volatility will obviously entail a different interpretation when it is ap-
plied to a dataset obtained with a temporal resolution of years versus a dataset acquired with a
temporal resolution of milliseconds. Furthermore, measures using shortest temporal paths can
be altogether inappropriate in certain situations (e.g., longtitudinal studies).
Finally, consideration is also needed about which temporal network measure(s) should be
applied to a research question. Although temporal network theory puts a wide array of mea-
sures at the user’s disposal, we advise against applying the entire battery of measures to a given
dataset. Given a hypothesis about some state of the world (S), this should first be translated
into a hypothesis about which network measure will quantify the network representation of S.
A more exploratory analysis showing significant (and multiple-comparison-corrected) correla-
tions in five out of ten measures, when these measures were not first formulated in relation to
S, may become hard, if not impossible, to translate into something meaningful.
Limitations and Extensions for Temporal Network Measures
Our scope was limited to temporal measures that operate on binary time series of brain con-
nectivity (i.e., binary t-graphlets). Most of the measures discussed here can be extended and
defined for series of weighted connectivity matrices. However, certain temporal measures are
not straightforward to convert to the weighted case. Pertinent examples are burstiness and
reachability for which no simple strategy has been identified to apply them in a weighted-
connectivity context.
Regardless of the method used to derive the brain connectivity time series, it is impor-
tant that adequate preprocessing steps be performed on the data to avoid potential bias in
the analysis. Our method of deriving t-graphlets with weighted Pearson correlation coeffi-
cients to compute time series of brain connectivity is not exempted from this concern. In a
Network Neuroscience
93
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
connectivity analysis based on sequences of binary t-graphlets, the absence or presence of
an edge might potentially be influenced by the user’s selection of thresholding. Hence, the
strategy regarding how to optimally threshold the t-graphles into binary graphlets is of vital
importance. We believe that it is important to keep in mind that comparisons of the vari-
ances as well as the means of connectivity time series might be biased by the underlying
mean–variance relationship (Thompson & Fransson, 2015b, 2016b). This further emphasizes
the need for adequate thresholding strategies for connectivity time series. Moreover, subject
head motion, known to be a large problem for fMRI connectivity studies (Dijk et al., 2012;
Power et al., 2012, Power, Schlaggar, & Petersen, 2015), can also lead to spurious dynamic
properties (Laumann et al., 2016).
By providing a survey of the theory of temporal networks and showing their applicability
and usefulness in network neuroscience, we hope that we have stirred the reader’s interest
in using models based on temporal networks when studying the dynamics of functional brain
connectivity. To this end, we have implemented all temporal network measures described in
the present article in a software package that is freely available (Teneto, which is written in
Python and can be downloaded at http://github.com/wiheto/teneto). We plan to extend the
Teneto package to include additional temporal network measures, plotting routines, wrappers
for other programming languages, and dynamic connectivity estimation.
ACKNOWLEDGMENTS
We thank Pontus Plavén-Sigray, Bjärn Schiffler, Granville Matheson, Simon Skau, and Lieke de
Boer for helpful comments and discussions about the manuscript. This work was supported
by the Swedish Research Council (Grant Nos. 621-2012-4911 and 013-61X-08276-26-4) and
the Swedish e-Science Research Center.
AUTHOR CONTRIBUTIONS
William Hedley Thompson: Conceptualization; Formal analysis; Investigation; Methodology;
Software; Visualization; Writing – original draft; Writing – review & editing Per Brantefors:
Conceptualization; Methodology; Writing – review & editing Peter Fransson: Conceptualiza-
tion; Funding acquisition; Investigation; Methodology; Supervision; Writing – original draft;
Writing – review & editing.
REFERENCES
Allen, E. A., Damaraju, E., Plis, S. M., Erhardt, E. B., Eichele, T.,
& Calhoun, V. D.
(2014). Tracking whole-brain connectivity
dynamics in the resting state. Cerebral Cortex, 24, 663–676.
https://doi.org/10.1093/cercor/bhs352
Baker, A. P., Brookes, M. J., Rezek, I. A., Smith, S. M., Behrens, T.,
Smith, P. J. P., & Woolrich, M. (2014). Fast transient networks in
spontaneous human brain activity. ELife, 2014(3), 1–18. https://
doi.org/10.7554/eLife.01867
Barabási, A.-L. (2005). The origin of bursts and heavy tails in hu-
man dynamics. Nature, 435, 207–211. Retrieved from http://
arxiv.org/abs/cond-mat/0505371
Barabási, A.-L.
(2010). Bursts: The hidden pattern behind every-
thing we do. New York, NY: Dutton.
Bassett, D. S., Porter, M. A., Wymbs, N. F., Grafton, S. T., Carlson,
J. M., & Mucha, P. J. (2013). Robust detection of dynamic com-
munity structure in networks. Chaos, 23(1). https://doi.org/10.
1063/1.4790830
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
J. M., & Grafton, S. T.
(2011). Dynamic reconfiguration of hu-
man brain networks during learning. Proceedings of the National
Academy of Sciences, 108(18), 7641–7646. https://doi.org/10.
1073/pnas.1018985108
Bassett, D. S., Yang, M., Wymbs, N. F., & Grafton, S. T.
(2015).
Learning-induced autonomy of sensorimotor systems. Nature
Neuroscience, 18(5), 744–751. https://doi.org/10.1038/nn.3993
Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries,
P., & Friston, K. J.
(2012). Canonical microcircuits for pre-
dictive coding. Neuron, 76(4), 695–711. https://doi.org/10.
1016/j.neuron.2012.10.038
Network Neuroscience
94
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
Bastos, A. M., Vezoli,
J., Bosman, C. A., Schoffelen,
J. M.,
Oostenveld, R., Dowdall, J. R., . . . Fries, P.
(2015). Visual
areas exert feedforward and feedback influences through distinct
frequency channels. Neuron, 85(2), 390–401. https://doi.org/10.
1016/j.neuron.2014.12.018
Basu, P., Bar-noy, A., Johnson, M. P., & Ramanathan, R.
(2010).
Modeling and analysis of time-varying graphs. ArXiv:1012.0260
Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component
based noise correction method (CompCor) for BOLD and perfu-
sion based fMRI. NeuroImage, 37(1), 90–101. https://doi.org/
10.1016/j.neuroimage.2007.04.042
Berlingerio, M., Coscia, M., Giannotti, F., Monreale, A., &
Pedreschi, D. (2011). Foundations of multidimensional network
analysis. In Proceedings of the 2011 International Conference
on Advances in Social Networks Analysis and Mining, ASONAM
2011 (pp. 485–487). Piscataway, NJ: IEEE Press. https://doi.org/
10.1109/ASONAM.2011.103
Betzel, R. F., Fukushima, M., He, Y., Zuo, X. N., & Sporns, O.
(2016). Dynamic fluctuations coincide with periods of high and
low modularity in resting-state functional brain networks. Neu-
roImage, 127, 287–297. https://doi.org/10.1016/j.neuroimage.
2015.12.001
Bola, M., & Sabel, B. A. (2015). Dynamic reorganization of brain
functional networks during cognition. NeuroImage, 114, 398–
413. https://doi.org/10.1016/j.neuroimage.2015.03.057
Bonnelle, V., Leech, R., Kinnunen, K. M., Ham, T. E., Beckmann,
C. F., De Boissezon, X., . . . Sharp, D. J. (2011). Default mode
network connectivity predicts sustained attention deficits after
traumatic brain injury. Journal of Neuroscience, 31(38), 13442–
13451. https://doi.org/10.1523/JNEUROSCI.1163-11.2011
Bosman, C. A., Schoffelen,
J.-M., Brunet, N., Oostenveld, R.,
Bastos, A. M., Womelsdorf, T., . . . Fries, P.
(2012). Atten-
tional stimulus selection through selective synchronization be-
tween monkey visual areas. Neuron, 75(5), 875–888. https://
doi.org/10.1016/j.neuron.2012.06.037
Bressler, S. L., & Kelso, J. A. S.
(2001). Cortical coordination dy-
namics and cognition. Trends in Cognitive Sciences, 5(1), 26–36.
Retrieved from http://doi.org/10.1016/51364-6613(00)01564-3
Bressler, S. L., Richter, C. G., Chen, Y., & Ding, M. (2007). Cortical
functional network organization from autoregressive modeling of
local field potential oscillations. Statistics in Medicine, 26(21),
3875–3885. https://doi.org/10.1002/sim.2935
Brookes, M. J., Woolrich, M., Luckhoo, H., Price, D., Hale, J. R.,
Investigating the
Stephenson, M. C., . . . Morris, P. G.
electrophysiological basis of resting state networks using mag-
netoencephalography. Proceedings of the National Academy of
Sciences, 108(40), 16783–16788. https://doi.org/10.1073/pnas.
1112685108
(2011).
Buckner, R. L., Sepulcre, J., Talukdar, T., Krienen, F. M., Liu, H.,
Hedden, T., . . . Johnson, K. A. (2009). Cortical hubs revealed by
intrinsic functional connectivity: Mapping, assessment of stabil-
ity, and relation to Alzheimer’s disease. Journal of Neuroscience,
29(6), 1860–1873. https://doi.org/10.1523/JNEUROSCI.5062-
08.2009
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038/
nrn2575
Buschman, T. J., & Miller, E. K. (2007). Top-down versus bottom-up
control of attention in the prefrontal and posterior parietal cor-
tices. Science, 315(5820), 1860–1862. https://doi.org/10.1126/
science.1138071
Buzsáki, G.
(2005). Theta rhythm of navigation: Link between
path integration and landmark navigation, episodic and seman-
tic memory. Hippocampus, 15(7), 827–840. https://doi.org/10.
1002/hipo.20113
Buzsáki, G.
(2006). Rhythms of the brain. Oxford, UK: Oxford
University Press. https://doi.org/10.1093/acprof:oso/97801953
01069.001.0001
Buzsáki, G., & Draguhn, A.
(2004). Neuronal oscillations in cor-
tical networks. Science, 304(5679), 1926–1929. https://doi.org/
10.1126/science.1099745
Calhoun, V. D., Miller, R., Pearlson, G., & Adalı, T.
(2014). The
chronnectome: Time-varying connectivity networks as the next
frontier in fMRI data discovery. Neuron, 84(2), 262–274. https://
doi.org/10.1016/j.neuron.2014.10.015
Chang, C., & Glover, G. H.
(2010). Time-frequency dynamics
of resting-state brain connectivity measured with fMRI. Neuro-
Image, 50(1), 81–98.
https://doi.org/10.1016/j.neuroimage.
2009.12.011
Cherkassky, V. L., Kana, R. K., Keller, T. A., & Just, M. A.
(2006).
Functional connectivity in a baseline resting-state network in
autism. NeuroReport, 17(16), 1687–1690. https://doi.org/10.
1097/01.wnr.0000239956.45448.4c
Chiang, S., Cassese, A., Guindani, M., Vannucci, M., Yeh, H. J.,
Haneef, Z., & Stern, J. M.
(2016). Time-dependence of graph
theory metrics in functional connectivity analysis. NeuroImage,
125, 601–615. https://doi.org/10.1016/j.neuroimage.2015.10.
070
Cole, M. W., Reynolds, J. R., Power, J. D., Repovs, G., Anticevic,
A., & Braver, T. S. (2013). Multi-task connectivity reveals flexi-
ble hubs for adaptive task control. Nature Neuroscience, 16(9),
1348–1355. https://doi.org/10.1038/nn.3470
Davison, E. N., Schlesinger, K. J., Bassett, D. S., Lynall, M.-E.,
Miller, M. B., Grafton, S. T., & Carlson, J. M. (2015). Brain net-
work adaptability across task states. PLoS Computational Biology,
11(1). https://doi.org/10.1371/journal.pcbi.1004029
Davison, E. N., Turner, B. O., Schlesinger, K. J., Miller, M. B.,
Grafton, T., Bassett, D. S.
Individual differences in
(2016).
dynamic functional brain connectivity across the human life-
span. ArXiv Preprint, 1–26. https://doi.org/10.1371/journal.pcbi.
1005178
Deco, G., Jirsa, V. K., & McIntosh, A. R.
(2011). Emerging con-
cepts for the dynamical organization of resting-state activity in
the brain. Nature Reviews Neuroscience, 12(1), 43–56. https://
doi.org/10.1038/nrn2961
Deco, G., & Kringelbach, M. L.
(2016). Metastability and coher-
ence: Extending the communication through coherence hypoth-
esis using a Whole-Brain computational perspective. Trends in
Neurosciences, 39(3), 125–135. https://doi.org/10.1016/j.tins.
2016.01.001
de Pasquale, F., Della Penna, S., Snyder, A. Z., Lewis, C.,
(2010). Temporal
Mantini, D., Marzetti, L., . . . Corbetta, M.
Network Neuroscience
95
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
dynamics of spontaneous MEG activity in brain networks.
Proceedings of the National Academy of Sciences, 107(13),
6040–6045. https://doi.org/10.1073/pnas.0913863107
de Pasquale, F., Della Penna, S., Snyder, A. Z., Marzetti, L., Pizzella,
V., Romani, G. L., & Corbetta, M.
(2012). A cortical core for
dynamic integration of functional networks in the resting hu-
man brain. Neuron, 74(4), 753–764. https://doi.org/10.1016/
j.neuron.2012.03.031
Dijk, K. R. A., Sabuncu, M. R., & Buckner, R. L.
(2012). The
influence of head motion on intrinsic functional connectivity
MRI. NeuroImage, 59(1), 431–438. https://doi.org/10.1016/
j.neuroimage.2011.07.044
Drakesmith, M., Caeyenberghs, K., Dutt, a., Lewis, G., David, &
Jones, D.
(2015). Overcoming the effects of false positives
and threshold bias in graph theoretical analyses of neuroimag-
ing data. NeuroImage, 118, 313–333. https://doi.org/10.1016/
j.neuroimage.2015.05.011
Eckmann, J. P., Moses, E., & Sergi, D.
(2004). Entropy of di-
alogues creates coherent structures in e-mail traffic. Proceed-
ings of the National Academy of Sciences of the United States of
America, 101(7), 14333–14337. https://doi.org/10.1073/pnas.
0405728101
Ekman, M., Derrfuss,
J., Tittgemeyer, M., & Fiebach, C.
J.
(2012). Predicting errors from reconfiguration patterns in hu-
man brain networks. Proceedings of the National Academy of
Sciences, 109(41), 16714–16719. https://doi.org/10.1073/pnas.
1207523109
Flodin, P. D., Martinsen, S., Löfgren, M., Bileviciute-Ljungar, I.,
Kosek, E., & Fransson, P. (2014). Fibromyalgia is associated with
decreased connectivity between pain- and sensorimotor brain
areas. Brain Connectivity, 62(2010), 2545. https://doi.org/10.
1089/brain.2014.0274
Fox, M. D., & Greicius, M. D. (2010). Clinical applications of resting
state functional connectivity. Frontiers in Systems Neuroscience,
4, 19. https://doi.org/10.3389/fnsys.2010.00019
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen,
D. C., & Raichle, M. E. (2005). The human brain is intrinsically
organized into dynamic, anticorrelated functional networks.
Proceedings of the National Academy of Sciences, 102(27),
9673–9678. https://doi.org/10.1073/pnas.0504136102
Fransson, P.
(2005). Spontaneous low-frequency BOLD signal
fluctuations: An fMRI investigation of the resting-state default
mode of brain function hypothesis. Human Brain Mapping,
26(1), 15–29. https://doi.org/10.1002/hbm.20113
Freyer, F., Aquino, K., Robinson, P. A., Ritter, P., & Breakspear, M.
(2009). Bistability and non-Gaussian fluctuations in spontaneous
Journal of Neuroscience, 29(26), 8512–8524.
cortical activity.
https://doi.org/10.1523/JNEUROSCI.0754-09.2009
Freyer, F., Roberts, J. A., Ritter, P., & Breakspear, M.
(2012). A
canonical model of multistability and scale-invariance in biolog-
ical systems. PLoS Computational Biology, 8(8). https://doi.org/
10.1371/journal.pcbi.1002634
Fries, P.
(2005). A mechanism for cognitive dynamics: Neuronal
communication through neuronal coherence. Trends in Cog-
nitive Sciences, 9(10), 474–480. https://doi.org/10.1016/j.tics.
2005.08.011
Friese, U., Köster, M., Hassler, U., Martens, U., Trujillo-Barreto, N.,
& Gruber, T. (2013). Successful memory encoding is associated
with increased cross-frequency coupling between frontal theta
and posterior gamma oscillations in human scalp-recorded
EEG. NeuroImage, 66, 642–647.
https://doi.org/10.1016/j.
neuroimage.2012.11.002
Friston, K. J., Holmes, A. P., Worsley, K. J., Poline, J.-P., Frith, C. D.,
& Frackowiak, R. S. J. (1995). Statistical parametric maps in func-
tional imaging: A general linear approach. Human Brain Map-
ping, 2(4), 189–210. https://doi.org/10.1002/hbm.460020402
Ganis, G., Thompson, W. L., & Kosslyn, S. M.
(2004). Brain ar-
eas underlying visual mental imagery and visual perception: An
fMRI study. Cognitive Brain Research, 20(2), 226–241. https://
doi.org/10.1016/j.cogbrainres.2004.02.012
Garrity, A. G., Pearlson, G. D., McKiernan, K., Lloyd, D., Kiehl,
K. A., & Calhoun, V. D.
(2007). Aberrant “default mode”
functional connectivity in schizophrenia. American Journal of
Psychiatry, 164(3), 450–457. https://doi.org/10.1176/ajp.2007.
164.3.450
Goh, K.-I., & Barabási, A.-L. (2008). Burstiness and memory in com-
plex systems. EPL (Europhysics Letters), 81(4), 48002. https://doi.
org/10.1209/0295-5075/81/48002
Greicius, M. D., Krasnow, B., Reiss, A. L., & Menon, V.
(2003).
Functional connectivity in the resting brain: A network analy-
sis of the default mode hypothesis. Proceedings of the National
Academy of Sciences, 100, 253–258. https://doi.org/10.1073/
pnas.0135058100
Greicius, M. D., Srivastava, G., Reiss, A. L., & Menon, V.
(2004).
Default-mode network activity distinguishes Alzheimer’s disease
from healthy aging: Evidence from functional MRI. Proceed-
ings of the National Academy of Sciences, 101(13), 4637–4642.
https://doi.org/10.1073/pnas.0308627101
Gu, S., Betzel, R. F., Cieslak, M., Delio, P. R., Grafton, S. T.,
(2016). Optimal trajectories of
Pasqualetti, F., & Bassett, D. S.
brain state transitions, 1–10. http://arxiv.org/abs/1607.01706
Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, A. B., Kahn,
A. E., . . . Bassett, D. S. (2015). Controllability of structural brain
networks. Nature Communications, 6, 8414. https://doi.org/10.
1038/ncomms9414
Hamilton, J., Furman, D., Chang, C., Thomason, M., Dennis, E., &
Gotlib, I. (2012). Default-mode and task-positive network activ-
ity in Major Depressive Disorder: Implications for adaptive and
maladaptive rumination. Biological Psychiatry, 70(4), 327–333.
https://doi.org/10.1016/j.biopsych.2011.02.003.Default-mode
Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel,
A. K. (2012). Large-scale cortical correlation structure of sponta-
neous oscillatory activity. Nature Neuroscience, 15(6), 884–890.
https://doi.org/10.1038/nn.3101
Holme, P.
(2005). Network reachability of real-world contact se-
quences. Physical Review E, 71(4), 1–8. https://doi.org/10.1103/
PhysRevE.71.046119
Holme, P., & Saramäki, J. (2012). Temporal networks. Physics Re-
ports, 519(3), 97–125. https://doi.org/10.1016/j.physrep.2012.
03.001
Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini,
(2013).
P. A., Calhoun, V. D., Corbetta, M., . . . Chang, C.
Network Neuroscience
96
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
Dynamic functional connectivity: Promise, issues, and inter-
pretations. NeuroImage, 80, 360–378. https://doi.org/10.1016/
j.neuroimage.2013.05.079
Jo, H. H., Karsai, M., Kertész, J., & Kaski, K.
(2012). Circadian
pattern and burstiness in human communication activity. New
Journal of Physics, 14, 013055. https://doi.org/10.1088/1367-
2630/14/1/013055
Kelso, J. A. S. (1995). Dynamic patterns: The self-organization of
brain and behavior. Cambridge, MA: MIT Press. https://doi.org/
10.1016/S0925-2312(00)00221-6
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno,
Y., & Porter, M. A. (2014). Multilayer networks. Journal of Com-
plex Networks, 2(3), 203–271. https://doi.org/10.1093/comnet/
cnu016
Kopell, N. J., Gritton, H. J., Whittington, M. A., & Kramer, M. A.
(2014). Beyond the connectome: The dynome. Neuron, 83(6),
1319–1328. https://doi.org/10.1016/j.neuron.2014.08.016
Laumann, T. O., Snyder, A. Z., Mitra, A., Gordon, E. M., Gratton,
C., Adeyemo, B., . . . Petersen, S. E. (2016). On the stability of
BOLD fMRI correlations. Cerebral Cortex, Advance online pub-
lication. https://doi.org/10.1093/cercor/bhw265
Lindquist, M. A., Xu, Y., Nebel, M. B., & Caffo, B. S. (2014). Evalu-
ating dynamic bivariate correlations in resting-state fMRI: A com-
parison study and a new approach. NeuroImage, 101, 531–546.
https://doi.org/10.1016/j.neuroimage.2014.06.052
Liu, X., & Duyn, J. H.
(2013). Time-varying functional network
information extracted from brief
instances of spontaneous
brain activity. Proceedings of the National Academy of Sciences,
110(11), 4392–4397. https://doi.org/10.1073/pnas.1216856110
Mantzaris, A. V., Bassett, D. S., Wymbs, N. F., Estrada, E., Porter,
(2013). Dynamic net-
M. A., Mucha, P. J., . . . Higham, D. J.
Jour-
work centrality summarizes learning in the human brain.
nal of Complex Networks, 1(1), 83–92. https://doi.org/10.1093/
comnet/cnt001
Masuda, N., & Lambiotte, R. (2016). A guide to temporal networks
(1st ed.). London, UK: World Scientific.
Mattar, M. G., Cole, M. W., & Sharon, L.
(2014). A functional
PLoS Computational Biol-
cartography of cognitive systems.
ogy, 11, e10045331:1–36, https://doi.org/10.1371/journal.pcbi.
1004533
Meyrand, P., Simmers, J., & Moulins, M. (1994). Dynamic construc-
tion of a neural network from multiple pattern generators in the
lobster stomatogastric nervous system. Journal of Neuroscience,
14(2), 630–644.
Michalareas, G., Vezoli, J., van Pelt, S., Schoffelen, J. M., Kennedy,
H., & Fries, P. (2016). Alpha-beta and gamma rhythms subserve
feedback and feedforward influences among human visual cor-
tical areas. Neuron, 89(2), 384–397. https://doi.org/10.1016/
j.neuron.2015.12.018
Min, B., Goh, K.-I., & Vazquez, A. (2011). Spreading dynamics fol-
lowing bursty human activity patterns. Physical Review E, 83(3),
036102. https://doi.org/10.1103/PhysRevE.83.036102
Montgomery, S. M., & Buzsáki, G.
(2007). Gamma oscillations
dynamically couple hippocampal CA3 and CA1 regions during
memory task performance. Proceedings of the National Academy
of Sciences, 104(36), 14495–14500. https://doi.org/10.1073/
pnas.0701826104
Mucha, P. J., Richardson, T., Macon, K., Porter, M. A., & Onnela,
J.-P. (2010). Community structure in time-dependent, multiscale,
and multiplex networks. Science, 328(5980), 876–878. https://
doi.org/10.1126/science.1184819
Napadow, V., LaCount, L., Park, K., As-Sanie, S., Clauw, D. J., &
Harris, R. E. (2010). Intrinsic brain connectivity in fibromyalgia
is associated with chronic pain intensity. Arthritis and Rheuma-
tism, 62(8), 2545–2555. https://doi.org/10.1002/art.27497
Newman, M.
(2010). Networks: An introduction. Oxford, UK:
Oxford University Press.
Nicosia, V., Tang, J., Mascolo, C., Musolesi, M., Russo, G., &
Latora, V. (2013). Graph metrics for temporal networks. In Tem-
poral networks (pp. 15–40). Berlin, Germany: Springer. Re-
trieved from http://arxiv.org/abs/1306.0493v1
Nijhuis, E. H. J., van Cappellen van Walsum, A.-M., & Norris, D. G.
(2013). Topographic hub maps of the human structural neocor-
tical network. PLoS ONE, 8(6), e65511. https://doi.org/10.1371/
journal.pone.0065511
Pan, R. K., & Saramäki, J.
(2011). Path lengths, correlations, and
centrality in temporal networks. Physical Review E, 84(1). https://
doi.org/10.1103/PhysRevE.84.016105
Pomarol-Clotet, E., Salvador, R., Sarró, S., Gomar,
J., Vila, F.,
Martínez, A., . . . McKenna, P. J.
(2008). Failure to deactivate
in the prefrontal cortex in schizophrenia: Dysfunction of the de-
fault mode network? Psychological Medicine, 38(8), 1185–1193.
https://doi.org/10.1017/S0033291708003565
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L., &
Petersen, S. E.
(2012). Spurious but systematic correlations
in functional connectivity MRI networks arise from subject mo-
tion. NeuroImage, 59(3), 2142–2154. https://doi.org/10.1016/j.
neuroimage.2011.10.018
Power, J. D., Cohen, A. L., Nelson, S. M., Wig, G. S., Barnes, K. A.,
Church, J. A., . . . Petersen, S. E. (2011). Functional network or-
ganization of the human brain. Neuron, 72(4), 665–678. https://
doi.org/10.1016/j.neuron.2011.09.006
Power, J. D., Schlaggar, B. L., Lessov-Schlaggar, C. N., & Petersen,
S. E.
Evidence for hubs in human functional brain
networks. Neuron, 79(4), 798–813. https://doi.org/10.1016/
j.neuron.2013.07.035
(2013).
Power, J. D., Schlaggar, B. L., & Petersen, S. E.
(2015). Recent
progress and outstanding issues in motion correction in resting
state fMRI. NeuroImage, 105, 536–551. https://doi.org/10.1016/
j.neuroimage.2014.10.044
Richter, C. G., Coppola, R., & Bressler, S. L.
(2016). Top-down
beta oscillatory signaling conveys behavioral context to primary
visual cortex. BioRxiv, 074609. https://doi.org/10.1101/074609
Richter, C. G., Thompson, W. H., Bosman, C. A., & Fries, P. (2016).
Top-down beta enhances bottom-up gamma [Preprint article],
1–40. https://doi.org/10.1101/054288
Roberts, J. A., Boonstra, T. W., & Breakspear, M. (2015). The heavy
tail of the human brain. Current Opinion in Neurobiology, 31,
164–172. https://doi.org/10.1016/j.conb.2014.10.014
Rocha, L. E. C., Liljeros, F., & Holme, P.
Information dy-
namics shape the sexual networks of Internet-mediated prostitu-
tion. Proceedings of the National Academy of Sciences, 107(13),
5706–5711. https://doi.org/10.1073/pnas.0914080107
(2010).
Network Neuroscience
97
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
Rosvall, M., & Bergstrom, C. T. (2010). Mapping change in large
networks. PLoS ONE, 5(1), e8694. https://doi.org/10.1371/
journal.pone.0008694
Sharp, D. J., Beckmann, C. F., Greenwood, R., Kinnunen, K. M.,
Bonnelle, V., De Boissezon, X., . . . Leech, R.
(2011). Default
mode network functional and structural connectivity after trau-
matic brain injury. Brain, 134(Pt 8), 2233–2247. https://doi.org/
10.1093/brain/awr175
Sheline, Y. I., Barch, D. M., Price, J. L., Rundle, M. M., Vaishnavi,
S. N., Snyder, A. Z., . . . Raichle, M. E. (2009). The default mode
network and self-referential processes in depression. Proceed-
ings of the National Academy of Sciences, 106(6), 1942–1947.
https://doi.org/10.1073/pnas.0812686106
Shine, J. M., Koyejo, O., Bell, P. T., Gorgolewski, K. J., Gilat, M.,
& Poldrack, R. A. (2015). Estimation of dynamic functional con-
nectivity using multiplication of temporal derivatives. Neuro-
Image, 122, 399–407.
https://doi.org/10.1016/j.neuroimage.
2015.07.064
Shine, J. M., Koyejo, O., & Poldrack, R. A. (2016). Temporal meta-
states are associated with differential patterns of dynamic con-
nectivity, network topology and attention. Proceedings of the
National Academy of Sciences, 113, 9888–9891. https://doi.org/
10.1073/pnas.1604898113
Siegel, M., Donner, T. H., & Engel, A. K.
(2012). Spectral finger-
prints of large-scale neuronal interactions. Nature Reviews Neu-
roscience, 13(2), 121–134. https://doi.org/10.1038/nrn3137
Smith, S. M., Fox, P. T., Miller, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. E., . . . Beckmann, C. F.
(2009). Correspondence
of the brain’s functional architecture during activation and rest.
Proceedings of the National Academy of Sciences, 106(31),
13040–13045. https://doi.org/10.1073/pnas.0905267106
Smith, S. M., Miller, K. L., Moeller, S., Xu, J., Auerbach, E. J.,
Woolrich, M. W.,
Temporally-
. Ugurbil, K.
independent functional modes of spontaneous brain activity.
Proceedings of the National Academy of Sciences, 109(8), 3131–
3136. https://doi.org/10.1073/pnas.1121329109
(2012).
.
.
Sporns, O.
Press.
(2009). Networks of the brain. Cambridge, MA: MIT
Sporns, O., Tononi, G., & Kötter, R.
(2005). The human connec-
tome: A structural description of the human brain. PLoS Com-
putational Biology, 1(4), 0245–0251. https://doi.org/10.1371/
journal.pcbi.0010042
Sripada, R. K., King, A. P., Welsh, R. C., Garfinkel, S. N., Wang,
X., Sripada, C. S., & Liberzon, I. (2012). Neural dysregulation in
posttraumatic stress disorder: Evidence for disrupted equilibrium
between salience and default mode brain networks. Psychoso-
matic Medicine, 911(35), 904–911. https://doi.org/10.1097/PSY.
0b013e318273bf33
Stern, E. R., Fitzgerald, K. D., Welsh, R. C., Abelson, J. L., & Taylor,
S. F. (2012). Resting-state functional connectivity between fronto-
parietal and default mode networks in obsessive–compulsive dis-
order. PLoS ONE, 7(5), e36356. https://doi.org/10.1371/journal.
pone.0036356
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology, 3, 15.
https://doi.org/10.3389/fphys.2012.00015
Takaguchi, T., Masuda, N., & Holme, P. (2013). Bursty communica-
tion patterns facilitate spreading in a threshold-based epidemic
dynamics. PLoS ONE, 8(7), e68629. https://doi.org/doi:10.1371/
journal.pone.0068629
Tang, J., Musolesi, M., Mascolo, C., Latora, V., & Nicosia, V. (2010).
Analysing information flows and key mediators through temporal
centrality metrics categories and subject descriptors. In Proceed-
ings of the 3rd Workshop on Social Network Systems (Article 3).
New York,NY: ACM. https://doi.org/10.1145/1852658.1852661
Thompson, W. H., Brantefors, P., & Fransson, P. (2017). Supplemen-
tal material to “From static to temporal network theory: Applica-
tions to functional brain connectivity.” Network Neuroscience,
1(2). https://doi.org/10.1162/netn_a_00011
Thompson, W. H., & Fransson, P. (2015a). The frequency dimension
of fMRI dynamic connectivity: Network connectivity, functional
hubs and integration in the resting brain. NeuroImage, 121,
227–242. https://doi.org/10.1016/j.neuroimage.2015.07.022
Thompson, W. H., & Fransson, P. (2015b). The mean–variance re-
lationship reveals two possible strategies for dynamic brain con-
nectivity analysis in fMRI. Frontiers in Human Neuroscience, 9,
398:1–7. https://doi.org/10.3389/fnhum.2015.00398
Thompson, W. H., & Fransson, P.
(2016a). Bursty properties re-
vealed in large-scale brain networks with a point-based method
for dynamic functional connectivity. Scientific Reports, 6, 39156.
https://doi.org/10.1038/srep39156
Thompson, W. H., & Fransson, P.
(2016b). On stabilizing the
variance of dynamic functional brain connectivity time series.
Brain Connectivity, 6(10), 735–746. https://doi.org/10.1089/
brain.2016.0454
Thompson, W. H., Thelin, E. P., Lilja, A., Bellander, B.-M., &
(2016). Functional resting-state fMRI connectivity
Fransson, P.
correlates with serum levels of the S100B protein in the acute
phase of traumatic brain injury. NeuroImage: Clinical, 12, 1004–
1012. https://doi.org/10.1016/j.nicl.2016.05.005
Tognoli, E., & Kelso, J. A. S.
(2009). Brain coordination dynam-
ics: True and false faces of phase synchrony and metastability.
Progress in Neurobiology, 87(1), 31–40. https://doi.org/10.1016/
j.pneurobio.2008.09.014
Tognoli, E., & Kelso, J. A. S. (2014). The metastable brain. Neuron,
81(1), 35–48. https://doi.org/10.1016/j.neuron.2013.12.022
van Kerkoerle, T., Self, M. W., Dagnino, B., Gariel-Mathis, M.-A.,
Poort, J., van der Togt, C., & Roelfsma, P. R. (2014). Alpha and
gamma oscillations characterize feedback and feedforward pro-
cessing in monkey visual cortex. Proceedings of the National
Academy of Sciences, 111(40), 14332–14341. https://doi.org/
10.1073/pnas.1402773111
Vazquez, A. (2013). Spreading dynamics following bursty activity
patterns. In Temporal networks (pp. 161–174). Berlin, Germany:
Springer. https://doi.org/10.1007/978-3-642-36461-7_8
Vázquez, A., Oliveira, J. G., Dezsö, Z., Goh, K. I., Kondor, I., &
Barabási, A. L.
(2006). Modeling bursts and heavy tails in hu-
man dynamics. Physical Review E, 73(3), 1–19. https://doi.org/
10.1103/PhysRevE.73.036127
Vazquez, A., Rácz, B., Lukács, A., & Barabási, A. L.
Im-
pact of non-poissonian activity patterns on spreading processes.
Physical Review Letters, 98(15), 1–4. https://doi.org/10.1103/
PhysRevLett.98.158702
(2007).
Network Neuroscience
98
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Temporal network theory applied to brain connectivity
Weng, S.-J., Wiggins, J. L., Peltier, S. J., Carrasco, M., Risi, S., Lord,
C., & Monk, C. S. (2010). Alterations of resting state functional
connectivity in the default network in adolescents with autism
spectrum disorders. Brain, 1313, 202–214. https://doi.org/10.
1016/j.brainres.2009.11.057
Whitfield-Gabrieli, S., & Nieto-Castanon, A.
(2012). Conn: A
functional connectivity toolbox for correlated and anticorrelated
brain networks. Brain Connectivity, 2(3), 125–141. https://doi.
org/10.1089/brain.2012.0073
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L., & Breakspear, M.
(2014). Time-resolved resting-state brain networks. Proceedings
the National Academy of Sciences, 111, 10341–10346.
of
https://doi.org/10.1073/pnas.1400181111
Zhang, D., Liang, B., Wu, X., Wang, Z., Xu, P., Chang, S., . . .
Huang, R. (2015). Directionality of large-scale resting-state brain
networks during eyes open and eyes closed conditions. Frontiers
in Human Neuroscience, 9, 81. https://doi.org/10.3389/fnhum.
2015.00081
Zhang, D., & Raichle, M. E.
(2010). Disease and the brain’s dark
energy. Nature Reviews Neurology, 6(1), 15–28. https://doi.org/
10.1038/nrneurol.2009.198
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
1
2
6
9
1
0
9
1
9
4
7
n
e
n
_
a
_
0
0
0
1
1
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
99