CARTA
Communicated by Harel Shouval
Two-Trace Model for Spike-Timing-Dependent
Synaptic Plasticity
Rodrigo Echeveste
echeveste@itp.uni-frankfurt.de
Claudius Gros
gros07@itp.uni-frankfurt.de
Institute for Theoretical Physics, Goethe University Frankfurt,
Hessen 60438, Alemania
We present an effective model for timing-dependent synaptic plasticity
(STDP) in terms of two interacting traces, corresponding to the fraction
of activated NMDA receptors and the Ca2+
concentration in the den-
dritic spine of the postsynaptic neuron. This model intends to bridge
the worlds of existing simplistic phenomenological rules and highly
detailed models, thus constituting a practical tool for the study of the
interplay of neural activity and synaptic plasticity in extended spiking
neural networks. For isolated pairs of pre- and postsynaptic spikes, el
standard pairwise STDP rule is reproduced, with appropriate parameters
determining the respective weights and timescales for the causal and the
anticausal contributions. The model contains otherwise only three free
parámetros, which can be adjusted to reproduce triplet nonlinearities in
hippocampal culture and cortical slices. We also investigate the transi-
tion from time-dependent to rate-dependent plasticity occurring for both
correlated and uncorrelated spike patterns.
1 Introducción
The fact that synaptic plasticity can depend on the precise timing of pre-
and postsynaptic spikes (Bi & Frotar, 2005; Frotar, Gerkin, Bi, & Perro chino, 2005)
indicates that time has to be coded somehow in individual neurons. If the
concentration of a certain ion or molecule, which we will refer to as a trace,
decays in time after a given event in a regular fashion, then the level of that
trace could serve as a time coder, in the same way as the concentration of a
radioactive isotope can be used to date a fossil.
A range of models has been proposed that formulate long-term po-
tentiation (LTP) and long-term depression (LIMITADO) in terms of traces in the
postsynaptic neurons (Karmarkar & Buonomano, 2002; Badoual et al., 2006;
Shouval, Bear, & Cooper, 2002; Rubin et al., 2005; Graupner & Brunel, 2012;
Uramoto & Torikai, 2013). Several of these models successfully reproduce
a wide range of experimental results, including pairwise STDP, triplet, y
Neural Computation 27, 672–698 (2015)
doi:10.1162/NECO_a_00707
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
norte
mi
C
oh
_
a
_
0
0
7
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
2015 Instituto de Tecnología de Massachusetts. Published under a Creative Commons Attribution 3.0 no portado (CC POR 3.0) licencia.
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
673
even quadruplet nonlinearities. Most models, sin embargo, require fitting of a
large number of parameters individually for each experimental setup and
involve heavily nonlinear functions of the trace concentrations. While pos-
sibly realistic in nature, the study of neural systems modeled under these
rules from a dynamical point of view becomes a highly nontrivial task. En
el otro extremo, the connection between predictions of simplified models,
constructed as phenomenological rules (Badoual et al., 2006; Froemke &
Dan, 2002), and the biological underpinnings is normally hard to establish,
as they usually aim to reproduce only the synaptic change and do away
with the information stored in the the traces themselves.
In this letter, we propose a straightforward model formulating synaptic
potentiation and depression in terms of two interacting traces representing
the fraction of activated N-methyl-D-aspartate (NMDA) receptors and the
concentration of intracellular Ca2+ at the postsynaptic spine, with the in-
tention of bridging these two worlds. Having a low number of parameters
and being composed of only polynomial differential equations, el modelo
is able nonetheless to reproduce key features of LTP and LTD. Además,
since the parameters of the model are easily related to the dynamical prop-
erties of the system, it permits making a connection between the observed
synaptic weight change and the behavior of the underlying traces.
2 The Model
Plasticity in our model will be expressed in terms of two interacting traces
on the postsynaptic site, which we denote x and y, representing the fraction
of open-state NMDA receptors (or NMDARs) and the Ca2+ concentration
in the dendritic spine of the postsynaptic neuron, respectivamente. For clarifica-
ción, we recall the overall mechanism of the synaptic transmission process
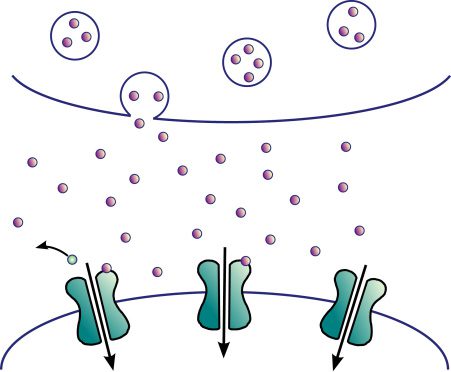
in a glutamatergic synapse, as illustrated in Figure 1.
A presynaptic spike results in the release of glutamate molecules across
the synaptic cleft, which will activate a series of receptors on the postsy-
naptic spine, including the NMDA receptors and α-amino-3-hydroxy-5-
methyl-4-isoxazolepropionic acid (AMPA) receptors (AMPAR) (Meldrum,
2000). Na+ ions will then flow through the AMPAR channels into the den-
dritic spine of the postsynaptic cell, triggering a cascade of events that may
eventually lead to the activation of an axonal spike at the soma of the post-
synaptic cell and of an action potential backpropagating down the dendritic
árbol. This action potential has two effects captured within our model: el
first is the activation of voltage-gated Ca2+ channels (VGCC), allowing an
influx of Ca2+ ions, resulting in an increase of the Ca2+ concentration y;
the second is the unblocking of NMDAR channels, as we detail in what
follows.
Ca2+ ions may flow into the postsynaptic spine also through the NMDAR
canales (Meldrum, 2000), but for this to happen, two conditions need to
be fulfilled. NMDARs are activated when glutamate binds to them, cual
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
norte
mi
C
oh
_
a
_
0
0
7
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
674
R. Echeveste and C. Gros
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
Cifra 1: Illustration of a glutamatergic synapse. Primary AMPA receptors
(AMPAR) are directly activated by glutamate and voltage-gated calcium
canales (VGCC) by the backpropagating action potential. NMDA receptors
(NMDAR) are also activated by glutamate and allow the influx of calcium if
they additionally unblock, which occurs when the backpropagating action po-
tential removes the blocking Mg2+ ion.
opens the receptor’s Ca2+ permeable channel. The channels are said to be
open when the protein’s conformational state permits ions to flow through
a ellos, and closed otherwise. At resting membrane potential, sin embargo, Mg2+
ions are present in the channel’s pore, blocking the channel and prevent-
ing Ca2+ ions from permeating the neuron (Mayer, Westbrook, & Guthrie,
1984). This block is temporarily removed by a backpropagating action po-
tential. For Ca2+ to flow into the postsynaptic spine, two conditions need
to be fulfilled: the presence of glutamate in the synaptic cleft, triggered
by a presynaptic spike, and a back propagating action potential, signaling
a postsynaptic spike. The NMDA receptors are hence the primary agents
within our model for the interaction of pre- and postsynaptic neural activi-
ties in terms of axonal spikes. They are also the primary agents for causality
within the STDP rule.
2.1 Trace Dynamics. We denote with {tσ
pre
} the trains of pre-
and postsynaptic spikes, respectivamente. The update rules for the fraction x of
} y {tσ
post
F
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
norte
mi
C
oh
_
a
_
0
0
7
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
675
open but blocked NMDA receptors and the concentration y of postsynaptic
Ca2+ ions are then given by
(cid:6)
˙x = − x
t
X
+ Ex
(X)
δ(t − t
)
pag
pre
pag
˙y = − y
t
y
+ (X + yc
)Ey
(y)
,
(cid:6)
pag
δ(t − t
pag
post
)
(2.1)
⎧
⎪⎪⎪⎨
⎪⎪⎪⎩
x and τ
where τ
y represent the time constants for the decay of x and y, re-
spectively. In the absence of presynaptic spikes, glutamate in the synaptic
cleft is cleared by passive diffusion and glutamate transporters (Huang &
Bergles, 2004). Ca2+ concentration in the postsynaptic site will decay, en
doblar, in the absence of postsynaptic spikes (Carafoli, 1987). In our model,
each incoming presynaptic spike produces an increase in the number x of
open NMDA channels due to glutamate release, and the Ca2+ concentration
y increases only when a postsynaptic spike is present, as when a backprop-
agating action potential reaches the postsynaptic spine. Calcium increase
in equation 2.1 is composed of two terms: a constant value yc, representing
the contribution of VGCCs, and a term proportional to the fraction of open
NMDA receptors. In this simplified approach, every NMDAR channel still
open from the presynaptic spike is then unblocked by the backpropagating
action potential. Por lo tanto, the transient calcium current through NMDA
receptors is modeled as proportional to x.
The efficacy factors Ex and Ey included in equation 2.1 are defined as
Ez
(z) = θ (zb
− z)
(cid:8)
,
(cid:7)
1 − z
zb
i (z) =
(cid:9)
0
1
z ≤ 0
z > 0
,
(2.2)
where z is either x or y, and determine the efficacy of spikes in increasing
trace concentrations. For trace levels above the respective reference values
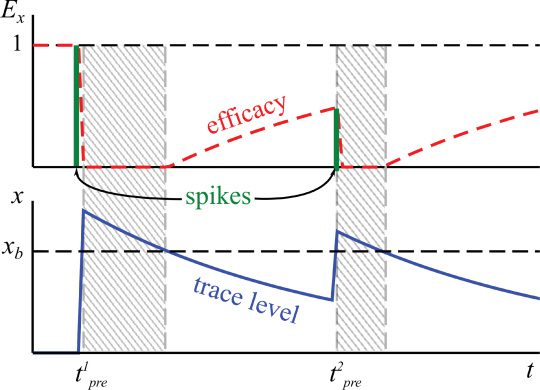
xb and yb, no further increase is possible (ver Figura 2a) and the trace concen-
tration can only decay exponentially. This determines a refractory period,
as shown in Figure 3. The duration of this period is in this case a function of
the decay constant of the trace and the magnitude of the overshoot above
the reference value. Below this level, E will tend asymptotically to unity
as the trace concentration decays. In this way, previous spikes decrease the
efficacy of future spikes. Similar mechanisms of reduced spike efficacy have
been proposed in the past in models of STDP (Froemke & Dan, 2002).
Two forces therefore compete to drive nonlinear plasticity in our model:
trace accumulation and spike suppression, the latter formulated in the
present effective model via a saturation term.
The update rules, equation 2.1, for the traces are reduced in the sense
that all superfluous constants have been rescaled away, as discussed in the
appendix.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
norte
mi
C
oh
_
a
_
0
0
7
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
676
R. Echeveste and C. Gros
Cifra 2: (a) Plot of the limiting factor Ex, as defined by equation 2.2, as a
function of the trace concentration, here exemplified by x (the same applies to
y). (b) Plot of the LTP threshold (y − b)i (y − b) present in equation 2.3.
2.2 Update Rules for the Synaptic Weight. We now formulate the up-
dating rules for the synaptic weight, or synaptic strength, in terms of the
trace concentrations. To this end we consider the contribution of two path-
ways mediated by distinct enzymes (Colbran, 2004), which for simplicity
we denote as LTP and LTD pathways. Calcium is involved in both the LTP
and the LTD pathways (Cormier, madera verde, & Connor, 2001; Neveu &
Zucker, 1996; Cual, Espiga, & Zucker, 1999), with high levels of calcium re-
sulting in LTP and moderate and low levels resulting in LTD. We propose
the following rule for the plasticity of the synaptic weight w,
˙w = αx(y − b)i (y − b)
(cid:6)
pag
δ(t − t
pag
post
) − βxy
(cid:6)
pag
δ(t − t
),
pag
pre
(2.3)
with θ being the same previously defined step function, cual, en este caso,
serves as a lower bound. The first term in equation 2.3 leads to an increase
of the synaptic weight; it is triggered in the presence of a postsynaptic spike
and by the calcium concentration y, but only if y is larger than a given
threshold b (see Figure 2b). A threshold in the calcium concentration Ca2+
for LTP has been experimentally observed (Cormier et al., 2001), and its
dependence with the previous synaptic activity has been studied (Huang,
Colino, Selig, & Malenka, 1992). En este trabajo, we consider a constant b = yc
and will show in the next section that the standard STDP curve is obtained
with this choice.
The second term in equation 2.3 leads to a decrease of the synaptic
weight and needs a finite level for both the calcium concentration y and
the fraction of open NMDA receptors x (which can be taken as a measure
of the glutamate concentration in the synaptic cleft), in addition to the
presence of a presynaptic spike, which acts as a second coincidence detector
as proposed by Karmarkar and Buonomano (2002). The parameters α > 0
and β > 0 represent the relative strengths of these two contributions.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
/
mi
d
tu
norte
mi
C
oh
a
r
t
i
C
mi
–
pag
d
/
yo
F
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
norte
mi
C
oh
_
a
_
0
0
7
0
7
pag
d
.
/
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
677
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
Cifra 3: Illustration of the effect of the limiting factor Ex (dashed red line,
upper panel); compare Figure 2 and equation 2.2, on the trace dynamics (solid
blue line, lower panel; compare equation 2.1). Here for the x-trace (the behavior
is qualitatively the same for y). Two spikes t1
pre are present and indicated
as solid green vertical bars, with the height being proportional to Ex. The sys-
tem ignores further incoming spikes whenever x > xb, resulting in respective
refractory periods (shaded grey areas). For finite values of x < xb, the efficacy
of incoming spikes is reduced proportionally to xb
pre and t2
− x.
The pre- and postsynaptic spikes tσ
pre/post mark the timing of the synaptic
update in our model, equation 2.3, for the synaptic plasticity. Here we
considered δ-like spikes, and one needs, for numerical simulations using
small but finite time steps, to update the traces using equation 2.1 before
updating the weights using equation 2.3.
2.3 The Pairwise STDP Rule. In the limit of low frequencies, the traces
decay to zero in between the occurrence of two pairs of spikes, which may
hence be considered as isolated.
We denote with (cid:8)t the time between the pre- and the postsynaptic spike,
with a positive value corresponding to a causal pre-post order and a neg-
ative (cid:8)t to an anticausal post-pre ordering. For an isolated pair of spikes,
one can easily integrate equations 2.1 and 2.3, obtaining
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
(cid:10)
(cid:8)w =
(cid:11)
−|(cid:8)t|/τ
−|(cid:8)t|/τ
αe
−βyce
x
e
−|(cid:8)t|/τ
y
(cid:12)
− b
x + yc
(cid:8)t > 0
(cid:8)t < 0
.
(2.4)
678
R. Echeveste and C. Gros
The synaptic weight is always depressed for an anticausal time ordering of
the spikes with (cid:8)t < 0 and potentiated for yc
≥ b and a causal time ordering
corresponding to (cid:8)t > 0. The LTP term becomes a simple exponential decay
for b = yc. We have chosen in our model a fully decoupled formulation for
LTP and LTD. While the LTD term is always negative, the restriction on
the LTP term to be always positive could be relaxed by removing the step
function in equation 2.3. Entonces, with the choice b > yc, a depression window
would arise after the peak of potentiation. This window has indeed been
observed in the past in CA1 cells from rat hippocampal slices (Nishiyama,
hong, Mikoshiba, Poo, & Kato, 2000). By setting b < yc, on the other hand,
the decay would be composed of two exponentials. In the LTD term, we have
not included a threshold. Alternatively, one could replace the calcium level
y by an expression (y − bLTD
), analogous to the LTP term, which
= 0 since y is always positive. It
is identical to the case we present for bLTD
(cid:5)= 0. Apart from the step
is, however, worth discussing the cases where bLTD
function θ , the LTD threshold represents only a vertical shift of the negative
portion of the STDP window by a factor βbLTD. If bLTD
< 0, the plot is shifted
downward, which means depression occurs even for isolated presynaptic
spikes ((cid:8)t → −∞). This is usually not the case, as seen in Bi and Poo (1998)
< 0, on the other hand, the plot is
and Froemke and Dan (2002). If bLTD
shifted upward, but because of the step function, the LTD term is always
negative and then the tail of the exponential would be cut off. By looking at
the experimental results in Figures 4 and 6, one observes that the data seem
in fact quite noisy to determine the exact shape of the decay functions. In the
absence of further detail, we have chosen to keep b = yc and no threshold (or
a threshold at 0) for LTD, therefore respecting the exponential fits proposed
in the original papers (Bi, 2002; Froemke & Dan, 2002).
)θ (y − bLTD
Rewriting the constants α, β, τ
= 2τ+,
= τ− where A+, A−, τ+ and τ− represent the maximal intensities and
and τ
y
timescales of LTP and LTD for isolated spike pairs, we obtain with
y as α = A+, β = A−/yc, τ
x, and τ
x
(cid:10)
(cid:8)w =
+A+e
−A−e
−|(cid:8)t|/τ
−|(cid:8)t|/τ
+ (cid:8)t > 0
− (cid:8)t < 0
(2.5)
the classical fit for pairwise STDP proposed in both hippocampal and cor-
tical neurons (Bi, 2002; Froemke & Dan, 2002). This result is independent
of yc, xb, and yb, and these three parameters can be hence be used to repro-
duce additional experimental observations. In what follows, we will use
the amplitudes A± as primary parameters instead of α and β and rewrite
the plasticity rule, equation 2.3, as
+
˙w = A
x(y − yc
)θ (y − yc
)
(cid:6)
σ
δ(t − t
σ
post
) − A−
yc
xy
(cid:6)
σ
δ(t − t
).
σ
pre
(2.6)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
679
This is the final shape of the equation for the evolution of the synaptic
strength that we will use throughout this work; it allows us to interpret
the results for a variety of spike pattern situations in terms of the known
spike pair STDP parameters. The representations 2.6 and 2.3 are, in any
case, equivalent.
2.4 Spike Triplets. The effect of a pair of pre- and postsynaptic spikes
has been experimentally shown to depend, in a nonlinear fashion, not only
on its interspike interval but also on the presence of additional spikes tem-
porally proximal to the pair. The contribution of spike triplets, the simplest
case of spike-pair interactions, cannot be described as a linear sum of two in-
dividual contributions of spike pairs (Froemke & Dan, 2002; Wang, Gerkin,
Nauen, & Bi, 2005).
In the following sections, we will study the model’s results for either two
pre- and one postsynaptic spike in a pre-post-pre order, or one pre- and two
postsynaptic spikes in a post-pre-post ordering. For example, with 15Post5,
we denote a pre-post-pre ordering,
15Post5,
(cid:14)
(cid:13)
t
σ
pre
= {−15, 5},
(cid:14)
(cid:13)
t
σ
post
= {0},
and with 10Pre20 a post-pre-post ordering,
10Pre20,
(cid:14)
(cid:13)
t
σ
pre
= {0},
(cid:14)
(cid:13)
t
σ
post
= {−10, 20},
(2.7)
(2.8)
where the times tσ
pre/post of the spikes are given in milliseconds.
As for spike pairs, the weight change induced by low-frequency triplets
can be computed analytically, obtaining
(cid:7)
+
(cid:8)w = +A
exp
−
(cid:8)
|
|(cid:8)t1
τ+
(cid:7)
−
− A
exp
−
⎡
(cid:8)
⎣1 +
|
|(cid:8)t2
τ−
(cid:17)
− |(cid:8)t1
τ
x
(cid:18)
⎤
|
⎦
exp
yc
(cid:7)
(cid:21)
1 + exp
×
|(cid:8)t1
−
|
| + |(cid:8)t2
τ
x
(cid:8) (cid:7)
1 − 1
xb
(cid:8)(cid:22)
.
for pre-post-pre triplets, and
(cid:7)
−
(cid:8)w = −A
exp
−
(cid:8)
|
(cid:7)
+
+ A
exp
−
|(cid:8)t1
τ−
(cid:23)
×
(cid:21)
1 + ycexp
(cid:23)
(cid:11)
×
1 − exp
|(cid:8)t1
−
| + |(cid:8)t2
τ
y
(cid:12)
|/τ
x
+ yc
|
+
(cid:24) (cid:22)
.
−|(cid:8)t2
yb
(cid:8)
(cid:24)
|
|(cid:8)t2
τ+
|
|(cid:8)t2
τ
x
(2.9)
(2.10)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
680
R. Echeveste and C. Gros
for post-pre-post triplets, where we have assumed that the traces are below
their respective reference levels, xb and yb, respectively, by the time a second
spike arrives (the case of the second spike arriving while the trace is above
the reference level is discussed later in this section). The saturation effect
can reduce the effect of a new spike to zero but not reverse the sign, as seen
in expression 2.2.
We see that the first term in equations 2.9 and 2.10 corresponding to the
first pair remains in both cases unchanged, by construction, with nonlinear-
ities appearing in the second contribution. In the second term of equation
2.9, we find a first factor (the first parenthesis) corresponding to a correc-
tion produced by the interaction between the two traces (the calcium inflow
through NMDAR channels), and a second factor corresponding to the bal-
ance between trace accumulation and spike suppression. In equation 2.10,
we also find a term balancing trace accumulation and spike suppression.
The multiplicative factor exp(|(cid:8)t2
) inside the brackets comes from the
way we have decided to factorize the equation, since τ
x
= 2τ+.
|/τ
x
If the third spike would instead come within the respective refractory
period (see Figure 3), the expressions 2.9 and 2.10 would reduce to
(cid:7)
+
(cid:8)w = +A
exp
−
⎛
exp
×
⎝1 +
(cid:8)
|
|(cid:8)t1
τ+
(cid:17)
− |(cid:8)t1
τ
x
−
− A
(cid:18)
⎞
|
⎠ exp
yc
(cid:7)
exp
−
(cid:8)
|
|(cid:8)t2
τ−
for pre-post-pre triplets, and
(cid:7)
−
(cid:8)w = −A
exp
−
(cid:8)
|
|(cid:8)t1
τ−
(cid:7)
|(cid:8)t1
−
(cid:8)
|
| + |(cid:8)t2
τ
x
(2.11)
(2.12)
for post-pre-post triplets, where in equation 2.12, the second pair is directly
inhibited by the LTP threshold. While this last situation is not encountered
for the low-frequency triplet configurations presented in this work, it be-
comes relevant in high-frequency scenarios. This condition could be relaxed
by replacing the strict threshold by a smooth sigmoidal.
2.5 Interpretation of the Variables and Parameters in the Model.
Our proposed model contains a relatively small number of variables and
parameters and can be considered an effective approach with the biological
underpinnings of STDP being governed by a substantially larger number of
variables and parameters whose functional interdependences are naturally
far more complex than the polynomial description here proposed. Any
effective model will, however, pool together within each effective variable
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
681
or parameter several effects that might depend on a variety of different
factors in the biological neuron.
In section 2.1, we defined x as the fraction of open but unblocked
NMDAR channels. When paired with a postsynaptic spike and under the
simplifications assumed in the model, the value of x can be then associ-
ated with a transient calcium current, and a comparison with experimental
results of the parameters related to x would reflect this role. The time win-
dow for LTP, for instance, results in our model from the value of τ
= 2τ+
x
(as we showed in section 2.3). τ
x can then be interpreted in this context as
the decay time of the transient calcium current. Hao and Oertner (2012)
have argued that the narrow window for LTP results from AMPA-EPSP in
the postsynaptic spine. In fact, as reviewed in the same article, the whole
spine seems to work as an electrical amplifier, locally prolonging the depo-
larization time at the spine. It is therefore not surprising to find different
values of the time constants in different neurons or even within different
synapses within the same neuron. In our model, we do not compute AMPA
currents directly and reduce the overall effect of the spine to the effective
value of τ
x. Similarly, τ
y represents the timescale for decay of the effective
calcium concentration at the spine.
We have included in this work saturation terms for both variables x
and y. As it has been proposed in the past (Froemke & Dan, 2002), triplet
nonlinearities in visual cortical neurons indicate strong suppression effects
on future spikes by previous spikes of the train. The saturation terms in-
cluded in the model provide one possible effective way of dealing with spike
suppression, reducing a biological complex phenomenon further down the
cascade of processes, leading eventually to LTP and to LTD, respectively.
3 Results for the Hippocampus
Our model, as defined by equations 2.1 and 2.6, contains overall seven
adjustable parameters. Four of these parameters—A+ = α, A− = β/yc, τ+,
and τ−—enter explicitly the isolated spike pair STDP rule, equation 2.5,
and are determined directly by experiment. For cultured rat hippocampal
neurons,
+ = 0.86/60, A
− = 0.25/60,
A
τ+ = 19 ms,
τ− = 34 ms
(3.1)
have been measured (Bi, 2002) and we will use these experimental values
throughout the hippocampus part of this study. In Figure 4 we present,
as an illustration, both the experimental and the theory results, with the
latter reproducing, by construction, the experimental fit. For the model
simulation, the experimental protocol of 60 repetitions spaced by 1 second
has been used. However, the 1 Hz frequency of spike pairs is so low that
equation 2.5 could be directly used without any discernible difference.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
682
R. Echeveste and C. Gros
Figure 4: Weight change after a train of 60 pairs at a constant frequency of
1 Hz as a function of the time delay (cid:8)t between pre- and postsynaptic spikes.
The red open circles are the experimental data for hippocampal neurons (Bi
& Poo, 1998). The continuous blue line represents the model’s results when
the parameters are set to A+ = 0.86/60, A− = 0.25/60, τ+ = 19 ms, τ− = 34 ms,
which correspond to a fit of the experimental data, as presented in Bi (2002).
Three parameters entering equations 2.1 and 2.6, namely, yc, xb, and
yb, are to be selected. In a continuous time evolution scenario, xb and yb
determine strict maximal concentrations for the traces. In the discrete time
scenario, overshoots are, however, possible due to the finite increase in the
traces after every spike. In this context and in a low-frequency situation,
the first spike in the stimulation pattern is unaffected by the limiting factor,
and only the efficacy of the following spike is reduced. Since xb and yb then
do not affect pairwise STDP, they need to be selected from higher-order
contributions to the weight change. In this case, we selected the values of
yc, xb, and yb from triplet results, as presented in what follows.
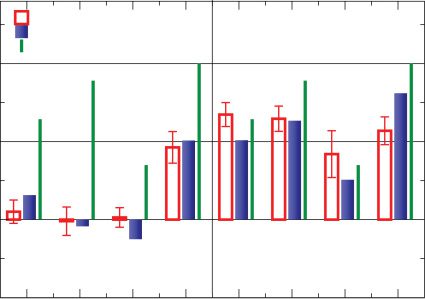
In Figure 5 we now compare our results for triplets, as described in
section 2.4, with experiments for cultured rat hippocampal neurons (Wang
et al., 2005). The triplet stimulation experimental protocol consists of a
regular train of 60 triplets with a repetition frequency of 1 Hz, and we use
the identical protocol for the theory simulations. We also keep the pairwise
STDP parameters, equation 3.1, valid for cultured rat hippocampal neurons
and adjust the remaining three free parameters yc, xb, and yb by minimizing
the standard deviation (SD) between the numerical and the experimental
= 0.66, and xb
results, obtaining yc
We found that the SD varies smoothly, and relatively weakly, with the
exact choice of the three free parameters, as can be expected from the ana-
lytical expressions, and that this freedom can be used to obtain a range of
= 0.62 (with an SD of 6.76).
= 0.28, yb
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
683
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 5: Synaptic strength change in hippocampal neurons induced by triplets
composed of either two pre- and one postsynaptic spike, left side of the diagram
(compare equation 2.7), or one pre- and two postsynaptic spikes, right side of
the diagram (see equation 2.8). We present 60 triplets with a repetition frequency
of 1 Hz. Full blue boxes correspond to the model’s results and empty red bars
to experimental data (Wang et al., 2005), and the green lines represent the linear
addition of the PostPre and PrePost pairs each triplet contains via equation 2.6.
Simulation parameters: A+ = 0.86/60, A− = 0.25/60, τ+ = 19 ms, τ− = 34 ms,
yc
= 0.62, and yb
= 0.28, xb
= 0.66.
functional dependencies of the synaptic plasticity on spiking frequencies,
as discussed in section 5.
We have also included in Figure 5 the expected synaptic weight changes
for the case of a linear superposition of the two respective interspike con-
tributions via equation 2.5. One observes that the discrepancy between the
nonlinear and the linear interactions is much stronger for pre-post-pre than
for post-pre-post triplets, with the former leading to an overall reduced
synaptic weight change and the latter configuration to a substantial poten-
tiation. It is interesting to observe here that spike suppression, as proposed
in Froemke and Dan (2002), from cortical neurons cannot explain nonlin-
earities in hippocampus. Suppression of the second presynaptic spike in the
triplet would reduce depression, and the overall result would be supralinear
potentiation, contrary to the experimental observation. Trace accumulation
is the dominant effect driving nonlinearities in hippocampal neurons.
4 Results for the Cortex
We now repeat the procedure presented previously for the hippocampus,
comparing the results of the proposed plasticity rule to experimental data
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
684
R. Echeveste and C. Gros
Figure 6: As in Figure 4, now for visual cortical neurons. The stimulation fre-
quency is now 0.2 Hz, as in the experiment (Froemke & Dan, 2002). The red
open circles are the experimental data (courtesy of Robert C. Froemke and Yang
Dan), and the continuous blue line represents the model’s results when the
parameters are set to A+ = 1.03/60, A− = 0.51/60, τ+ = 13.3 ms, τ− = 34.5 ms,
corresponding to the fit of the experimental data presented in Froemke and Dan
(2002).
obtained from slices of the visual cortex. As in the previous section, the val-
ues of A+ = α, A− = β/yc, τ+, and τ− are determined directly by experiment.
We use
+ = 1.03/60, A
− = 0.51/60,
A
τ+ = 13.3 ms,
τ− = 34.5 ms
(4.1)
as obtained by Froemke and Dan (2002) for pyramidal neurons in layer
2/3 (L2/3) of rat visual cortical slices. Both the experiment and the STDP
curve are shown in Figure 6, where we have reproduced, for the simulation,
the experimental protocol, using 60 repetitions at 0.2 Hz. Once again, the
frequency of spike pairs is so low that equation 2.5 could be directly used
without any discernible difference.
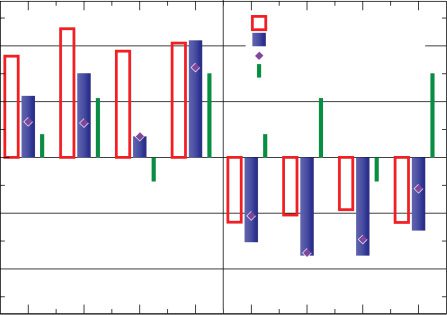
To select yc, xb, and yb we once again resort to triplet results. In Froemke
and Dan (2002), the change produced by triplets of either two pre- and
one postsynaptic spikes or one pre- and two postsynaptic spikes was also
measured. The data consist in this case, however, of a large set of specific
triplet timing configurations, with every individual triplet configuration
measured once. We decided to treat all measurements on an equal foot-
ing, fitting the complete set by minimizing the mean square error without
introducing any further bias.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
685
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
Figure 7: As in Figure 5, now for visual cortical neurons. The stimulation
frequency is now 0.2 Hz as in the experiment (Froemke & Dan, 2002). Full
blue boxes correspond to the model’s results for the best fit of the parameters
and empty red bars to experimental data; the green lines represent the lin-
ear addition of the two PostPre and PrePost pairs each triplet contains. With
diamonds, the model’s results for an alternative set of parameters are pre-
sented. While the quantitative differences are larger with this parameter choice,
the model still qualitatively reproduces cortical triplet nonlinearities. Simula-
tion parameters: A+ = 1.03/60, A− = 0.51/60, τ+ = 13.3 ms, τ− = 34.5 ms, Best
= 0.9, and
fit: yc
xb
= 0.4.Experimental data courtesy of Robert C. Froemke and Yang Dan.
= 0.5. Diamond points: yc
= 10.9, and xb
= 11.6, yb
= 1.0, yb
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
= 11.6, yb
= 10.9, and xb
We obtain in this case yc
= 0.5. The obtained
SD of 37.4 is, in this case, much larger than the one found for hippocam-
pus, though that is partly due to the variance in the experimental data
themselves, corresponding to individual data points and not to averaged
results. Another consequence of the large variance in the data is that the
minimum in the SD is relatively broad. We discuss these points in detail in
what follows.
In order to compare the results for cortical neurons with the previous
section on hippocampal neurons, as presented in Figure 5, we have per-
formed a smooth interpolation of the set of individual experimental results
for cortical triplets by means of gaussian filters. In Figure 7 we compare the
theory results with the interpolated experimental data.
Contrary to the hippocampal triplet results presented in Figure 5, ex-
periments in cortical slices show that post-pre-post triplets lead to strong
depression and pre-post-pre triplets to potentiation. Post-pre-post triplets
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
686
R. Echeveste and C. Gros
deviate, in addition, somewhat more from a linear superposition of the
contribution of the two inherent spike pairs than the pre-post-pre configu-
ration. While the predictions of the model presented in Figure 7 are clearly
not as good as the ones obtained for hippocampal culture, they are still qual-
itatively in agreement with the experimental results, successfully capturing
the asymmetry between post-pre-post and pre-post-pre triplets. While there
is still room for improvement in this regard, we believe it is important that
the model can switch from the hippocampal to the cortical regime in terms
of triplet nonlinearities.
As we previously mentioned, the data have a much larger variance in
this case. To have an idea of of the variability of the data, we computed
the standard deviation of the data to the smooth gaussian interpolation
of width 5 ms that we used for the visual comparison of Figure 7, which
yields an SD of 32.5 (as compared to the SD of 37.4 between model and
experiment). For this reason, we believe that a reasonable goal in this case
is to reproduce the distinct qualitative feature of the triplet nonlinearities
more than an accurate quantitative approximation.
The optimal value of yc
= 11.6 obtained when fitting the experimen-
tal triplet results (see Figure 7), seems to be too large, in particular when
compared to the one obtained for hippocampal neurons. This result can be
traced back to the occurrence of a broad minimum for the least-square fit
together with a relative high variability of the experimental data. We have
hence also examined parameter configurations with lower values for yc.
= 1.0, also representing the
Also included in Figure 7 is an example with yc
observed experimental features qualitatively. We find that the particular
cortical structure of triplets arises from strong saturation, being a conse-
quence of yb
< yc.
5 Frequency Dependence
So far we have considered only pairs or triplets of pre- and postsynaptic
spikes coming at low frequencies and with very precise timings. This will
not necessarily be the case in a natural train of spikes. It is therefore in-
teresting to examine the model’s prediction for spike trains with different
degrees of correlation between pre- and postsynaptic spikes. A neuron usu-
ally receives input from about 10,000 other neurons. While the correlation
of the postsynaptic neuron will be higher for a strong synapse driving the
neuron, the postsynaptic neuron in general will not be correlated with all
of its inputs. We therefore study both types of connections.
We begin in section 5.1 by studying the case of uncorrelated trains of
pre- and postsynaptic spikes and then analyze in section 5.2 the case of a
driving synapse with different degrees of correlation. In these sections, we
numerically evaluate the synaptic strength change as a function of the pre-
and postsynaptic neuronal firing rates.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
687
Figure 8: Average weight change for hippocampal neurons produced by 1 s
trains of uncorrelated Poisson-distributed pre- and postsynaptic spikes, as a
function of the postsynaptic firing frequency fpost and for various constant presy-
naptic firing rates fpre (full lines). Also included is the case for identical pre- and
postsynaptic firing rates (dashed line). The pair-STDP values, equation 3.1,
have been used and two sets of values for the remaining three free parameters,
= 0.28,
both yielding otherwise very similar results for the spike triplets. (a) yc
= 0.8, yb
yb
= 1.34, and xb
= 0.66, and xb
= 0.62. (b) yc
= 1.82.
5.1 Plasticity Induced by Uncorrelated Spikes. We begin by evaluating
the synaptic change produced by uncorrelated trains of Poisson pre- and
postsynaptic spikes. In these simulations, we use the same parameters as
fitted from pairwise and triplet experiments in hippocampus and cortex,
referring to hippocampal and cortical neurons, respectively.
The results of the simulations for hippocampal neurons are shown in
Figure 8. We present two kinds of plots in the diagram: a plot where the
pre- and postsynaptic firing rates are equal and plots of constant presy-
naptic frequency for varying postsynaptic firing rates. We observe in this
last type that the sign of the weight changes as a function of the postsy-
naptic activity for a constant presynaptic frequency, generically switching
from negative to positive at a certain threshold θ
H. This threshold increases
with rising presynaptic frequency, resulting in a sliding threshold. In other
rate-based learning rules like BCM (Bienenstock, Cooper, & Munro, 1982),
similar thresholds for potentiation are determined by appropriate long-
term averages of the postsynaptic activity. In our model, θ
H is set by the
level of the presynaptic activity, as measured on timescales of the respective
traces. This feature would allow the neuron to adjust the threshold of each
synapse independently, setting in each case the level of what constitutes
significant activity.
The overall synaptic change becomes Hebbian for large pre- and post-
firing rates fpre and fpost, in the sense that it is then proportional to the product
). This weight change is influenced in a substantial way by
f pre
the value of yc, and we have presented in Figure 8 two sets of parameters,
· ( f post
− θ
H
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
688
R. Echeveste and C. Gros
= 0.28 (left panel) and one with yc
= 0.8 (right panel), yielding
one with yc
otherwise similar SDs when fitting the experimental triplet data (6.76 and
7.37, respectively).
Potentiation dominates for larger values of yc, as seen in Figure 8(b).
These results seem, at first sight, counterintuitive given the role of yc as a
threshold for LTP. Note, however, that yc contributes to the increase in y
through equation 2.1, and both LTP and LTD are dependent on y in the
plasticity rule, equation 2.6, with the LTD contribution being proportional
to 1/yc.
Comparing Figures 8a and 8b, we observe that yc can be used to regulate
the threshold for potentiation in the rate-encoding limit without changing
the behavior of isolated spike triplets substantially. yc is hence a vehicle
for also adapting the overall postsynaptic activity level, and it would be
interesting, for future research, to study how this regulative mechanism
would interact with other known ways to regulate the overall level of the
postsynaptic neural activity, such as intrinsic plasticity rules (Triesch, 2007;
Markovi´c & Gros, 2012; Linkerhand & Gros, 2013).
It has to be remarked that the solid lines in Figure 8, representing weight
changes as a function of the postsynaptic frequency for a constant presynap-
tic firing rate, while of theoretical interest to understand the behavior of θ
H,
will not correspond to a usual physiological functional relationship between
the rates, at least for a driving synapse. If the presynaptic synapse drives
the postsynaptic neuron, the postsynaptic activity will in general be an in-
= f post
creasing function of the presynaptic rate. Here we have chosen f pre
(the dashed lines in Figures 8 and 9) as an illustration, but a more detailed
transfer function should be selected for accurate and quantitative compar-
isons with experimental results. In this sense, the parameter configuration
of Figure 8(b) shows better agreement with experimental procedures, such
as that of Sj ¨ostr ¨om, Turrigiano, and Nelson (2001), where potentiation is
shown to become stronger with higher frequencies.
No complete set of experimental results has hitherto been published, un-
fortunately, where all pairwise, triplet, and frequency-dependent plasticity
have been measured for the same type of synapse and with the same ex-
perimental stimulation procedure. A full consistency check between model
and experiment is hence not possible to date.
In Figure 9 the results of numerical simulations for L2/3 cortical neurons
for the same protocol of Figure 8 are presented. In this case, depression is
found for all combinations of pre- and postsynaptic frequencies, a robust
prediction of the model. Different values of yc were selected to test this
behavior, and in each case the rest of the parameters were fitted to the
triplet results. In each case, the value of yb obtained by this fitting turned
out to be lower than yc. The y-trace has hence a hard time overcoming the
threshold yc for LTP as calcium increase by further spikes is prevented.
As a test, if yb was artificially set to values larger than yc, potentiation for
larger frequencies was recovered, but the fit of the experimental triplet data
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
689
Figure 9: As in Figure 8, now for visual cortical neurons. Solid lines show the
weight change for specific constant presynaptic frequencies fpre, as a function of
the postsynaptic rate fpost. For the dashed line, pre- and postsynaptic firing rates
are equal. The pair-STDP values, equation 4.1, have been used and two sets of
values for the remaining three free parameters, both yielding otherwise similar
= 1.0,
= 11.6, yb
results for the spike triplets. (a) yc
yb
= 10.9, and xb
= 0.9, and xb
= 0.5. (b) yc
= 0.4.
deteriorated substantially, obtaining potentiation for PostPrePost triplets,
contrary to the experimental results. This indicates that triplet nonlinearities
found in L2/3 cortical neurons result from spike suppression, contrary to
the predominant trace accumulation effect present in hippocampal neurons.
These results, predicted for L2/3 neurons as fitted from Froemke and
Dan (2002), would then be in stark contrast to those of Sj ¨ostr ¨om et al. (2001)
for L5 neurons in visual cortex where LTP dominates for large frequencies.
It should be pointed out, however, that the pairwise STDP plot presented in
Sj ¨ostr ¨om et al. (2001) is already different from that of L2/3 neurons, raising
the question of to what extent results coming from different neurons or
obtained using different stimulation procedures, should be alike.
On the other hand, the prediction of overall depression dominating for
uncorrelated spike trains in certain cortical neurons seems to be in line
with, or at least does not contradict, experimental findings for deprivation
experiments. In cortical areas, where topological maps are usually found,
deprivation of sensory input has been shown to result in depression of
the respective synaptic connections (Trachtenberg, Trepel, & Stryker, 2000;
Feldman, 2000). At the same time, correlation has been found to substan-
tially decrease after these procedures in areas projecting to cortex (Linden,
Heynen, Haslinger, & Bear, 2009), suggesting that decorrelation of spike
trains could be responsible for the observed depression in cortical neurons.
A possible reason behind the observed differences in these studies might
be the stimulation protocol employed. While in Bi and Poo (1998) and
Wang et al. (2005), plasticity is triggered by eliciting the firing of the pre-
and postsynaptic neurons by dual whole-cell clamp, in the cortical results
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
690
R. Echeveste and C. Gros
from Froemke and Dan (2002), extracellular presynaptic stimulation is per-
formed, clamping only the postsynaptic neurons. This creates an asym-
metry between pre-post-pre and post-pre-post triplets. Moreover, in the
case of extracellular stimulation, the question remains to what extent other
synapses are being affected, potentially triggering, in turn, other forms of
plasticity such as local synaptic scaling.
It is important to stress that the robust depression found here for higher
frequencies is a direct consequence of the triplet results, and indeed it
vanishes if one uses hippocampal-like triplet results. The same suppression
effect present for triplets also affects higher-frequency trains, resulting in
depression.
For lower frequencies, the pairwise contribution dominates when deter-
mining the balance between potentiation and depression. Izhikevich and
Desai (2003) show how a straightforward application of the pairwise rule to
Poisson uncorrelated spike trains (as in our simulation), adding up linearly
the effect of every pair in the train according to the pairwise STDP rule
with cortical parameters, always leads to depression, since the pairs simply
sample the STDP curve, which has an overall negative area (the opposite
is true in hippocampal neurons, as we show below). Our model is, by con-
struction, equivalent in the low-frequency limit to the linear pairwise model
since isolated spikes produce no synaptic change in our model and triplets
and higher-order configurations become very infrequent if the frequency is
low. For low pre- and postsynaptic frequencies, the trains of Poisson spikes
can be considered as pairs of random duration that sample the pairwise
STDP curve.
The overall integrated area of the pairwise STDP curve for L2/3 cortical
neurons is negative, while it is positive for hippocampal neurons. One can
easily integrate the exponentials and obtain a relation A for the areas:
A = A+τ+
A−τ−
.
(5.1)
While for hippocampal neurons A = 1.92, we find in cortex A = 0.77.
This means that in the absence of higher-order contributions (which is true if
both the pre- and the postsynaptic frequencies are low), uncorrelated spikes
will on average lead to depression in cortical neurons and to potentiation in
hippocampal neurons. If the frequencies tend to zero, the average interspike
interval will be long compared to the STDP window duration, and the net
amount of synaptic change, whether positive or negative, will be low. In
the following section, this fact will become clear when the synaptic changes
of correlated and uncorrelated spikes are compared.
As the frequencies of pre- and postsynaptic spikes increase, the interspike
period decreases, and when this becomes comparable to the timescale of
the STDP window (which is related to the trace timescale), the pairwise ap-
proximation will break down since interactions can no longer be neglected.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
691
When both the pre- and postsynaptic frequencies are on the order of 10 Hz,
the average time between a pre- and a postsynaptic spike is on the order
of 50 ms and interactions are to be expected. This is where the particular
models for the underlying dynamics will differ. Izhikevich and Desai (2003)
also show with their nearest-neighbor implementation that synaptic change
goes from general depression (in the all-to-all implementation) to BCM-like
when they consider only the closest previous and posterior postsynaptic
spike to each presynaptic spike to compute the linear sum of pairs.
This choice, which at first glance would seem an approximation indepen-
dent of any underlying dynamics, has strong implications for the biolog-
ical underpinnings that could implement this algorithm. A first-neighbor
approximation requires hard resetting any traces possibly present, forget-
ting completely anything that happened outside that window. The nearest-
neighor implementation does not aim to explain triplet nonlinearities such
as those evidenced by the PrePostPre protocol.
The interspike interaction in our model is driven by the undelying traces.
We have chosen in our simulation to use for the frequency-dependence pro-
tocol the same parameters obtained from pairwise and triplet fits. As ob-
served in cortical PostPrePost triplets, strong suppression severely limits the
potentiation of further spikes (compare PostPrePost to linear superposition
results). At high frequencies, triplet interactions become relevant, and the
same suppression should then be evidenced for frequency-dependent plas-
ticity. We believe, then, that any model aiming to reproduce time-dependent
plasticity up to triplet order as measured by Froemke and Dan (2002) should
show depression also for high frequencies in cortical neurons.
5.2 Plasticity Induced by Correlated Spikes. So far we have analyzed
the effect of uncorrelated spikes on the synaptic weight change in both
hippocampal and cortical neurons (see Figures 8 and 9). It is, however,
interesting to see the predictions of the model for a strong synapse driving
the postsynaptic neuron. In this case, pre- and postsynaptic spikes should
be correlated, at least partially, together with a certain positive delay.
To reproduce this effect with our model, we simulated trains of correlated
spikes where, with each presynaptic spike, a postsynaptic spike can occur
with probability p after a certain delay d. As an example, if every presynaptic
spike triggers a postsynaptic spike, then p = 1. This would mean, however,
= p fpre). In order
that the postsynaptic frequency fpost changes with p ( f post
to compare our results for different values of p and keep fpost independent
of p, we complete the train of postsynaptic spikes with Poisson spikes
of frequency (1 − p) f pre. In this way, fpost is independent of p, which now
regulates the degree of correlation between pre- and postsynaptic spikes:
p = 0 represents the fully decorrelated case, since all the postsynaptic spikes
are drawn from the Poisson distribution, and p = 1 represents the fully
correlated case already mentioned.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
692
R. Echeveste and C. Gros
Figure 10: Simulation results of the synaptic weight change induced by a 1
second train of spikes with different degrees of correlation as a function of the
= f post. The fraction p of correlated spikes takes the values 0,
frequency f = f pre
0.5, and 1 in these plots. The delay between pre- and postsynaptic spikes was
taken to be 5 ms in these simulations. The case p = 0 corresponds to the dashed
lines in Figures 8 and 9. (a) The pairwise hippocampal parameters, equation 3.1,
= 0.62, corresponding to
were used, together with yc
the triplet fit. (b) Here the pairwise cortical parameters, equation 4.1, were used,
= 0.5, corresponding to the triplet fit.
together with yc
= 0.66, and xb
= 10.9, and xb
= 0.28, yb
= 11.6, yb
In Figure 10 we present the synaptic changes produced by spike trains
for different values of p. In this case, results for a delay of 5 ms are presented.
The same tests were performed with delays from 2 ms to 10 ms with only
quantitative, not qualitative, differences.
We observe in Figure 10, for both hippocampal and cortical neurons,
that correlated spike trains induce an increasing amount of potentiation for
low to intermediate frequencies (∼ 1 to 10 Hz). In the correlated scenario,
and since in this case we are simulating a driving synapse, postsynaptic
spikes follow presynaptic spikes in a causal order. When the frequency is
higher than 10 Hz, the interspike period becomes comparable to the STDP
time window, and each postsynaptic spike will also “see” the following
presynaptic spike, thus triggering the LTD term. Depending on the trace
saturation constants, LTD or LTP will eventually dominate for large fre-
quencies. If LTD dominates, depression results, and after a certain reversal
frequency, the behavior is switched from Hebbian to anti-Hebbian. This is
the case for the triplet fitted values presented in Figure 10.
It is important to note that the model is also able to produce Hebbian
behavior within the entire physiological range of activities by changing
yc. The smaller the saturation effects are, the larger this reversal frequency
becomes. In fact, with the second set of parameters used in Figure 8b, no
such reversal is found within physiological frequencies (not shown here).
If observed, such a reversal, yet another side of the suppression effect,
would have the benefit of being self-stabilizing, tuning synaptic strength to
help keep neural activities bound.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
693
The kink observable for the fully correlated curve (p = 1.0) of Figure 10b
results from the particularly strong suppression effects in cortical neurons,
< yc. For frequencies above a certain threshold
captured in our model by yb
(about 28 Hz) the trace concentration y is always below the yc and LTP never
triggers.
A fundamental difference between plots a and b in Figure 10 is the differ-
ent qualitative behavior between correlated and uncorrelated spikes. While
in hippocampal neurons, increasing Hebbian, potentiation is always present
for low to intermediate frequencies (whether the spikes are correlated or
not), in cortical neurons, our model predicts that uncorrelated spikes always
produce depression, and therefore Hebbian learning requires the neurons
to be at least partially correlated.
6 Comparison to Other Models
The problem of formulating plasticity in terms of the specific timing of pre-
and postsynaptic spikes can be approached at different levels of detail and
accuracy, ranging from simplistic phenomenological rules to detailed and
complex models describing the different steps of the biological machinery
responsible for STDP. In sections 3 and 4, the comparison of our model
to simple forms of phenomenological rules has already been established,
noting that linear combinations of spike pairs are generically not sufficient
to explain the experimentally observed triplet nonlinearities.
We have also shown that while linear combinations of pairs, plus ad-
ditional suppression, are enough to explain the triplet nonlinearities of
cortical neurons, as shown in Froemke and Dan (2002), hippocampal triplet
nonlinearities cannot be explained by suppression and a trace accumula-
tion mechanism seems to be taking place in these synapses. In any case,
these kinds of phenomenological rules are not likely to generalize well to
arbitrary spike patterns since no information of the underlying plasticity
mechanism is present in the formulation.
Other models, like Albers, Schmiedt, and Pawelzik (2013) and Pfister
and Gerstner (2006), present interesting dynamical formulations of plastic-
ity in terms of generic decaying markers or traces, but they do not attempt
to establish a link to the biological underpinnings of STDP. Calcium con-
centration and NMDA receptors have been shown to play a central role in
time-dependent LTP and LTD, and we therefore believe it is important to
formulate plasticity in those terms. Our model, though simplified, is for-
mulated in terms of these key ingredients and may therefore help to bridge
the worlds of functional and realistic models.
An alternative approach has been proposed by Appleby and Elliott
(2007), where plasticity is described in an ensemble-based formulation.
The authors argue that the observed synaptic changes produced by stan-
dard protocols cannot be explained at a single synapse level, but rather
state that the observed results arise at a population level. They then show
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
694
R. Echeveste and C. Gros
how the pairwise STDP curve can be recovered at the ensemble level from
all-or-nothing potentiation or depression at the single synapse level. The
dependency of the model to the specific timing of triplets is, however, in
this case not computed.
The model we present in this work belongs to the family of calcium-based
spiking neuron models. Within this family, models formulating synaptic
plasticity exclusively in terms of the calcium levels (Uramoto & Torikai,
2013; Graupner & Brunel, 2012), while tuned to reproduce a variety of ex-
perimental results, tend to show paradoxical results when tested in other
setups. The model presented by Uramoto and Torikai (2013), for example,
predicts synaptic changes even when only postsynaptic spikes are present.
The model in Graupner and Brunel (2012) shows plasticity also when either
pre- or postsynaptic spikes are absent, since both pre- and postsynaptic
spikes contribute directly to the calcium level in this model, without the
need of coincidence. To avoid this, in our model we demand the simulta-
neous presence of both pre- and postsynaptic spikes for plasticity to arise,
being proportional to the products of traces x and y in our rule. We believe
this to be an important feature for simulations in situations of complex
spike patterns where the pre- and postsynaptic firing rates do not necessar-
ily match.
7 Discussion
We propose a basic trace model for timing-dependent plasticity that in-
corporates, in a first-order approximation, the fundamental mechanisms
acknowledged to be taking place in STDP. We show that the model success-
fully captures several main features of time-dependent plasticity, including
the standard shape for low-frequency pairing, experimentally observed
triplet nonlinearities, and large frequency effects.
The decay constants for the two traces and the relative intensities of
LTP and LTD can be extracted directly from the standard STDP curves,
as measured for isolated pairs. The model is left hereafter with only three
further parameters, which can be used to fit higher-order contributions to
plasticity. The model successfully reproduces the distinct and contrasting
nonlinearities found in both hippocampal cultures and cortical slices.
While the model predicts a similar frequency dependence for correlated
(or partially correlated) pre- and postsynaptic spikes for both hippocampal
and cortical neurons, the effect of uncorrelated spikes (although smaller)
differs qualitatively in these two types of neurons. In this case, the sign of
the resulting plasticity depends for lower frequencies on the overall area of
the pairwise STDP curve, resulting in potentiation for hippocampal neurons
and depression in cortical ones and for higher frequencies on the balance
between spike suppression and trace accumulation.
We show that the model is able to reproduce typical frequency dependen-
cies for uncorrelated spikes, while fitting pairwise and triplet hippocampal
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
695
parameters. We also find that fitting triplet results for L2/3 cortical neurons
invariably leads to depression, for higher frequencies and of uncorrelated
spikes, contrary to observations in L5 neurons. The question then arises
is to what extent plasticity results for different neurons, or performed un-
der different stimulation conditions, can be expected to match. It seems
essential to have available a consistent set of experiments where pairwise,
triplet, and frequency results are measured for the same type of neuron
and with the same stimulation protocol. Otherwise one runs the risk of
possibly trying to build a complete picture out of mismatching parts. In
this sense, we hope that our predictions serve as a motivation to revisit and
complete triplet and frequency-dependent studies for different types of
neurons.
In order to compare our results with rate-encoding plasticity models,
we have also shown, by setting the presynaptic frequency to a constant
value, that the amount of synaptic change is proportional for hippocampal
neurons to the product of the activities, with a threshold that depends on
the presynaptic firing rate. While the system lacks a longer-term average
threshold, as the one present in BCM, the presynaptic activity acts as a value
of reference for the significant level of activity. If the postsynaptic activity
exceeds this level, then potentiation occurs; otherwise, depression arises.
For correlated spikes, we have shown that the model leads to similar
results for hippocampal and cortical neurons, with an initial Hebbian be-
havior for small to medium frequencies and, depending on choice for the
parameters, a reversal to anti-Hebbian behavior for large frequencies, which
could have the virtue of being self-limiting, avoiding runaway growth of
synaptic connections. It has been shown recently (Echeveste & Gros, 2014),
that this self-limitation results naturally for rate-encoding neurons from the
stationarity principle for Hebbian learning. By tuning the value of yc, the
reversal frequency can be made larger, to the point of producing Hebbian
behavior within the entire physiological range of activities.
The simplicity of our proposed model makes it a useful tool for simula-
tions and studies of the dynamical properties of networks adapted via these
rules. First, the calculations required are straightforward, making comput-
ing time efficient. The relative small number of free parameters and their
direct link to both the biophysical properties of the postsynaptic complex
and the dynamical features of the trace dynamics makes it suitable when
studying the interplay between neural and synaptic dynamics in neural
systems.
Appendix: Dimensionality Analysis
In section 2 we could have started by initially denoting by x(cid:9) and y(cid:9) the
fraction of NMDA receptors and the Ca2+ concentration, respectively, where
the time evolution of these traces is written as
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
696
R. Echeveste and C. Gros
⎧
⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
˙x
(cid:9) = − x(cid:9)
τ
x
˙y
(cid:9) = − y(cid:9)
τ
y
+ c1Ex
(cid:6)
σ
δ(t − t
)
σ
pre
+ (c2x
(cid:9) + y
(cid:9)
c
)Ey
(cid:6)
σ
δ(t − t
σ
post
)
,
(A.1)
y and τ
x represent the time constants in the decay of x(cid:9) and y(cid:9), and
where τ
now two additional parameters c1 and c2 are included. c1 represents the
increase in x(cid:9) caused by a single presynaptic spike (which in this simplified
model we assume constant) and c2 represents the increase, per unit of x(cid:9), in
y(cid:9) concentration. y(cid:9)
c is the constant contribution per postsynaptic spike to
y(cid:9) of the voltage-gated Ca2+ channels. Again, a spike efficacy E is included
that limits trace concentrations, where E is still calculated as in equation 2.2.
Now, by a change of variables,
x = x
(cid:9)/c1
,
= x
(cid:9)
b
/c1
,
xb
y = y
(cid:9)/c1c2
,
= y
(cid:9)
c
/c1c2
,
yc
= y
(cid:9)
b
/c1c2
yb
(A.2)
we rewrite equation A.1 as
⎧
⎪⎪⎪⎨
⎪⎪⎪⎩
˙x = − x
τ
x
˙y = − y
τ
y
+ Ex
(cid:6)
σ
δ(t − t
)
σ
pre
+ (x + yc
)Ey
(cid:6)
σ
δ(t − t
σ
post
)
,
which is exactly the expression presented in section 2. By this procedure,
we have reduced the number of parameters for the trace evolution to five.
Acknowledgments
We acknowledge Robert C. Froemke and Yang Dan for the experimental
data from cortical visual neurons. The support of the German Academic
Exchange Service (DAAD) is acknowledged.
References
Albers, C., Schmiedt, J. T., & Pawelzik, K. R. (2013). Theta-specific susceptibility in a
model of adaptive synaptic plasticity. Frontiers in Computational Neuroscience, 7.
Appleby, P. A., & Elliott, T. (2007). Multispike interactions in a stochastic model of
spike-timing-dependent plasticity. Neural Computation, 19(5), 1362–1399.
Badoual, M., Zou, Q., Davison, A. P., Rudolph, M., Bal, T., Fr´egnac, Y., & Destexhe, A.
(2006). Biophysical and phenomenological models of multiple spike interactions
in spike-timing dependent plasticity. Int. J. Neural Systems, 16 (2), 79–97.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Two-Trace Model for Spike-Timing-Dependent Synaptic Plasticity
697
Bi, G. Q. (2002). Spatiotemporal specificity of synaptic plasticity: Cellular rules and
mechanisms. Biol. Cybern., 87, 319–332.
Bi, G. Q., & Poo, M. M. (1998). Synaptic modifications in cultured hippocampal
neurons: Dependence on spike timing, synaptic strength, and postsynaptic cell
type. J. Neurosci., 18, 10464–10472.
Bi, G. Q., & Rubin, J. (2005). Timing in synaptic plasticity: From detection to integra-
tion. Trends Neurosci., 28, 222–228.
Bienenstock, E. L., Cooper, L. N., & Munro, P. W. (1982). Theory for the development
of neuron selectivity: Orientation specificity and binocular interaction in visual
cortex. Journal of Neuroscience, 2, 32–48.
Carafoli, E. (1987). Intracellular calcium homeostasis. Annual Review of Biochemistry,
56, 395–433.
Colbran, R. J. (2004). Protein phosphatase and calcium/calmodulin-dependent pro-
tein kinase II-dependent synaptic plasticity. J. Neurosci., 24, 8404–8409.
Cormier, R. J., Greenwood, A. C., & Connor, J. A. (2001). Bidirectional synaptic
plasticity correlated with the magnitude of dendritic calcium transients above a
threshold. J. Neurophysiol., 85, 399–406.
Echeveste, G., & Gros, C. (2014). Generating functionals for computational intelli-
gence: The Fisher information as an objective function for self-limiting Hebbian
learning rules. Frontiers in Robotics and AI, 1, 1.
Feldman, D. E. (2000). Timing-based LTP and LTD at vertical inputs to layer II/III
pyramidal cells in rat barrel cortex. Neuron, 27, 45–56.
Froemke, R. C., & Dan, Y. (2002). Spike-timing-dependent synaptic modification
induced by natural spike trains. Nature, 146, 433–438.
Graupner, M., & Brunel, N. (2012). Calcium-based plasticity model explains sensi-
tivity of synaptic changes to spike pattern, rate, and dendritic location. PNAS,
109, 3991–3996.
Hao, J., & Oertner, T. G. (2012) Depolarization gates spine calcium transients and
spike-timing-dependent potentiation Current Opinion in Neurobiology, 22, 509–
515.
Huang, Y. H., & Bergles, D. E. (2004). Glutamate transporters bring competition to
the synapse. Current Opinion in Neurobiology, 14, 346–352.
Huang, Y., Colino, A., Selig, D. K., & Malenka, R. C. (1992). The influence of prior
synaptic activity on the induction of long-term potentiation. Science, 225, 730–
733.
Izhikevich, E. M., & Desai, N. S. (2003). Relating STDP to BCM. Neural Computation,
15(7), 1511–1523.
Karmarkar, U. R., & Buonomano, D. V. (2002). A model of spike-timing dependent
plasticity: One or two coincidence detectors? J. Neurophysiol., 88, 507–513.
Linden, M. L., Heynen, A. J., Haslinger, R. H., & Bear, M. F. (2009). Thalamic activity
that drives visual cortical plasticity. Nature Neuroscience, 12, 390–392.
Linkerhand, C., & Gros, C. (2013). Self-organized stochastic tipping in slow-fast
dynamical systems. Mathematics and Mechanics of Complex Systems, 1, 129–147.
Markovi´c, D., & Gros, C. (2012). Intrinsic adaptation in autonomous recurrent neural
networks. Neural Comput., 24, 523–540.
Mayer, M. L., Westbrook, G. L., & Guthrie, P. B. (1984). Voltage-dependent block by
Mg2+ of NMDA responses in spinal cord neurones. Nature, 309, 261–263.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
698
R. Echeveste and C. Gros
Meldrum, B. S. (2000). Glutamate as a neurotransmitter in the brain: Review of
physiology and pathology. Journal of Nutrition, 130, 1007S–1015S.
Neveu, D., & Zucker, R. S. (1996). Postsynaptic levels of [Ca2+]i needed to trigger
LTD and LTP., Neuron, 16, 619–629.
Nishiyama, M., Hong, K., Mikoshiba, K., Poo, M. M., & Kato, K. (2000). Calcium
stores regulate the polarity and input specificity of synaptic modification. Nature,
408(6812), 584–588.
Pfister, J. P., & Gerstner, W. (2006). Triplets of spikes in a model of spike timing-
dependent plasticity. Journal of Neuroscience, 26, 9673–9682.
Rubin, J. E., Gerkin, R. C., Bi, G. Q., & Chow, C. C. (2005). Calcium time course as a
signal for spike-timing-dependent plasticity. J. Neurophysiol., 96, 2600–2613.
Shouval, H. Z., Bear, M. F., & Cooper, L. N. (2002). A unified model of NMDA
receptor-dependent bidirectional synaptic plasticity. PNAS, 99, 10831–10836.
Sj ¨ostr ¨om, P. J., Turrigiano, G. G., & Nelson, S. B. (2001). Rate, timing, and cooperativity
jointly determine cortical synaptic plasticity. Neuron, 32, 1149–1164.
Trachtenberg, J. T., Trepel, C., & Stryker, M. P. (2000). Rapid extragranular plasticity
in the absence of thalamocortical plasticity in the developing primary visual
cortex. Science, 287, 2029–2032.
Triesch, J. (2007). Synergies between intrinsic and synaptic plasticity mechanisms.
Neural Comput., 19, 885–909.
Uramoto, T., & Torikai, H. (2013). A calcium-based simple model of multiple spike
interactions in spike-timing-dependent plasticity. Neural Computation, 25, 1853–
1869.
Wang, H. X., Gerkin, R. C., Nauen, D. W, & Bi, G. Q. (2005). Coactivation and timing-
dependent integration of synaptic potentiation and depression. Nat. Neurosci., 8,
87–193.
Yang, S. N., Tang, Y. G., & Zucker, R. S. (1999). Selective induction of LTP and LTD
by postsynaptic [Ca2+]i elevation. J. Neurophysiol., 81, 781–787.
Received March 11, 2014; accepted October 1, 2014.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
2
7
3
6
7
2
2
0
1
6
3
2
2
n
e
c
o
_
a
_
0
0
7
0
7
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3