Jean-Franc¸ ois Charles
1 Route de Plamp ´ery
74470 Vailly, Francia
jfc@jeanfrancoischarles.com
A Tutorial on Spectral
Sound Processing Using
Max/MSP and Jitter
For computer musicians, sound processing in the
frequency domain is an important and widely used
técnica. Two particular frequency-domain tools
of great importance for the composer are the phase
vocoder and the sonogram. The phase vocoder, un
analysis-resynthesis tool based on a sequence of
overlapping short-time Fourier transforms, helps
perform a variety of sound modifications, from time
stretching to arbitrary control of energy distribution
through frequency space. The sonogram, a graphical
representation of a sound’s spectrum, offers com-
posers more readable frequency information than a
time-domain waveform.
Such tools make graphical sound synthesis
convenient. A history of graphical sound synthesis is
beyond the scope of this article, but a few important
figures include Evgeny Murzin, Percy Grainger, y
Iannis Xenakis. En 1938, Evgeny Murzin invented a
system to generate sound from a visible image; el
diseño, based on the photo-optic sound technique
used in cinematography, was implemented as the
ANS synthesizer in 1958 (Kreichi 1995). Percy
Grainger was also a pioneer with the “Free Music
Machine” that he designed and built with Burnett
Cross in 1952 (Luis 1991); the device was able
to generate sound from a drawing of an evolving
pitch and amplitude. En 1977, Iannis Xenakis and
associates built on these ideas when they created
the famous UPIC (Unit ´e Polyagogique Informatique
du CEMAMu; Marino, Serra, and Raczinski 1993).
In this article, I explore the domain of graphical
spectral analysis and synthesis in real-time situa-
ciones. The technology has evolved so that now, no
only can the phase vocoder perform analysis and
synthesis in real time, but composers have access to
a new conceptual approach: spectrum modifications
considered as graphical processing. Sin embargo, el
underlying matrix representation is still intimidat-
ing to many musicians. Como consecuencia, the musical
potential of this technique is as yet unfulfilled.
Computer Music Journal, 32:3, páginas. 87–102, Caer 2008
C(cid:1) 2008 Instituto de Tecnología de Massachusetts.
This article is intended as both a presentation of
the potential of manipulating spectral sound data
as matrices and a tutorial for musicians who want
to implement such effects in the Max/MSP/Jitter
ambiente. Throughout the article, I consider
spectral analysis and synthesis as realized by the
Fast Fourier Transform (FFT) and Inverse-FFT
algoritmos. I assume a familiarity with the FFT
(Roads 1995) and the phase vocoder (Dolson 1986).
To make the most of the examples, a familiarity
with the Max/MSP environment is necessary, y
a basic knowledge of the Jitter extension may be
helpful.
I begin with a survey of the software currently
available for working in this domain. I then show
some improvements to the traditional phase vocoder
used in both real time and performance time.
(Whereas real-time treatments are applied on a live
sound stream, performance-time treatments are
transformations of sound files that are generated
during a performance.) Finalmente, I present extensions
to the popular real-time spectral processing method
known as the freeze, to demonstrate that matrix
processing can be useful in the context of real-time
efectos.
Spectral Sound Processing with Graphical
Interaction
Several dedicated software products enable graphic
rendering and/or editing of sounds through their
sonogram. They generally do not work in real time,
because a few years ago, real-time processing of com-
plete spectral data was not possible on computers
accessible to individual musicians. This calculation
limitation led to the development of objects like
IRCAM’s Max/MSP external iana∼, which reduces
spectral data to a set of useful descriptors (Todoroff,
Daubresse, and Fineberg 1995). After a quick
survey of the current limitations of non-real-time
software, we review the environments allowing FFT
processing and visualization in real time.
Charles
87
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 1. FFT data
recorded in a stereo buffer.
Non-Real-Time Tools
AudioSculpt, a program developed by IRCAM, es
characterized by the high precision it offers as well
as the possibility to customize advanced parameters
for the FFT analysis (Bogaards, R ¨obel, and Rodet
2004). Por ejemplo, the user can adjust the analysis
window size to a different value than the FFT size.
Three automatic segmentation methods are pro-
vided and enable high-quality time stretching with
transient preservation. Other important functions
are frequency-bin independent dynamics process-
En g (to be used for noise removal, por ejemplo)
and application of filters drawn on the sonogram.
Advanced algorithms are available, including funda-
mental frequency estimation, calculation of spectral
envelopes, and partial tracking. Synthesis may be
realized in real time with sequenced values of pa-
rameters; these can, sin embargo, not be altered “on the
fly.” The application with graphical user interface
runs on Mac OS X.
MetaSynth (Wenger and Spiegel 2005) aplica
graphical effects to FFT representations of sounds
before resynthesis. The user can apply graphical
filters to sonograms, including displacement maps,
zooming, and blurring. A set of operations involv-
ing two sonograms is also available: blend, fade
in/out, multiply, and bin-wise cross synthesis. Él
is also possible to use formant filters. The pitfall
is that MetaSynth does not give control of the
phase information given by the FFT: phases are
randomized, and the user is given the choice among
several modes of randomization. Although this
might produce interesting sounds, it does not offer
the most comprehensive range of possibilities for
resynthesis.
There are too many other programs in this vein
to list them all, and more are being developed
each year. Por ejemplo, Spear (Klingbeil 2005) para-
cuses on partial analysis, SoundHack (Polansky
and Erbe 1996) has interesting algorithms for spec-
tral mutation, and Praat (Boersma and Weenink
2006) is dedicated to speech processing. el lat-
ter two offer no interactive graphical control,
aunque.
Real-Time Environments
PureData and Max/MSP are two environments
widely used by artists, composers, and researchers
to process sound in real time. Both enable work in
the spectral domain via FFT analysis/resynthesis. I
focus on Max/MSP in this article, primarily because
the MSP object pfft∼ simplifies the developer’s
task by clearly separating the time domain (afuera
the pfft∼ patcher) from the frequency domain
(inside the patcher). When teaching, I find that the
graphical border between the time and frequency
domains facilitates the general understanding of
spectral processing.
Using FFT inside Max/MSP may be seen as
difficult because the FFT representation is two-
dimensional (es decir., values belong to a time/frequency
grid), whereas the audio stream and buffers are
one-dimensional. Cifra 1 shows how data can be
stored when recording a spectrum into a stereo
buffer.
The tension between the two-dimensional nature
of the data and the one-dimensional framework
makes coding of advanced processing patterns (p.ej.,
visualization of a sonogram, evaluation of transients,
and non-random modifications of spatial energy in
the time/frequency grid) somewhat difficult. Un
example of treatment in this context is found in the
work of Young and Lexer (2003), in which the energy
in graphically selected frequency regions is mapped
onto synthesis control parameters.
The lack of multidimensional data within
Max/MSP led IRCAM to develop FTM (Schnell
et al. 2005), an extension dedicated to multidimen-
sional data and initially part of the jMax project.
More specifically, the FTM Gabor objects (Schnell
and Schwarz 2005) enable a “generalized granular
synthesis,” including spectral manipulations. FTM
attempts to operate “Faster Than Music” in that
the operations are not linked to the audio rate but
88
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 2. Phase vocoder
diseño.
are done as fast as possible. FTM is intended to be
cross-platform and is still under active development.
Sin embargo, the environment is not widely used at the
moment, and it is not as easy to learn and use as
Max/MSP.
En 2002, Cycling ’74 introduced its own mul-
tidimensional data extension to Max/MSP: Jitter.
This package is primarily used to generate graphics
(including video and OpenGL rendering), but it en-
ables more generally the manipulation of matrices
inside Max/MSP. Like FTM, it performs operations
on matrices as fast as possible. The seamless in-
tegration with Max/MSP makes implementation
of audio/video links very simple (Jones and Nevile
2005).
Jitter is widely used by video artists. The learning
curve for Max users is reasonable, thanks to the
number of high-quality tutorials available. El
ability to program in Javascript and Java within Max
is also fully available to Jitter objects. De este modo, I chose
Jitter as a future-proof choice for implementing this
proyecto.
An Extended Phase Vocoder
Implementing a phase vocoder in Max/MSP/Jitter
unlocks a variety of musical treatments that would
remain impossible with more traditional approaches.
Previous work using Jitter to process sound in the
frequency domain include two sources: primero, Luke
Dubois’s patch jitter pvoc 2D.pat, distributed
with Jitter, which shows a way to record FFT
data in a matrix, to transform it (via zoom and
rotation), and to play it back via the IFFT; segundo,
an extension of this first work, where the authors
introduce graphical transformations using a transfer
matrix (Sedes, Courribet, and Thiebaut 2004).
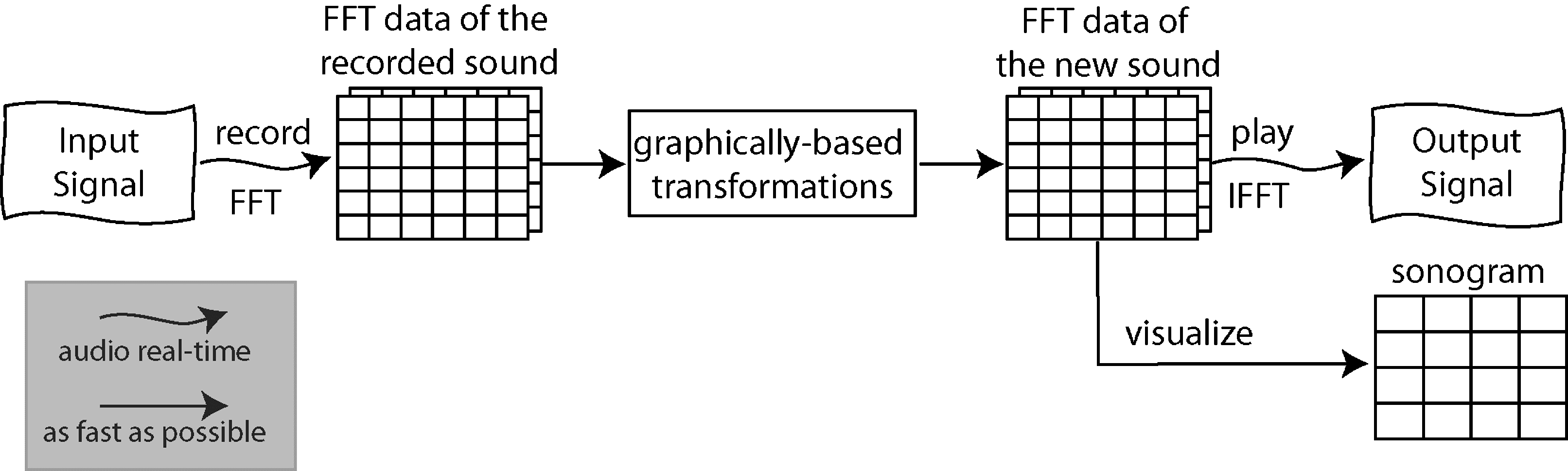
Both use a design similar to the one presented in
Cifra 2.
This section endeavors to make the phase-vocoder
technique accessible, and it presents improvements
in the resynthesis and introduces other approaches
to graphically based transformations.
FFT Data in Matrices
An FFT yields Cartesian values, usually translated
to their equivalent polar representation. Working
with Cartesian coordinates is sometimes useful for
minimizing CPU usage. Sin embargo, to easily achieve
the widest and most perceptively meaningful range
of transformations before resynthesis, we will work
with magnitudes and phase differences (es decir., the bin-
by-bin differences between phase values in adjacent
marcos).
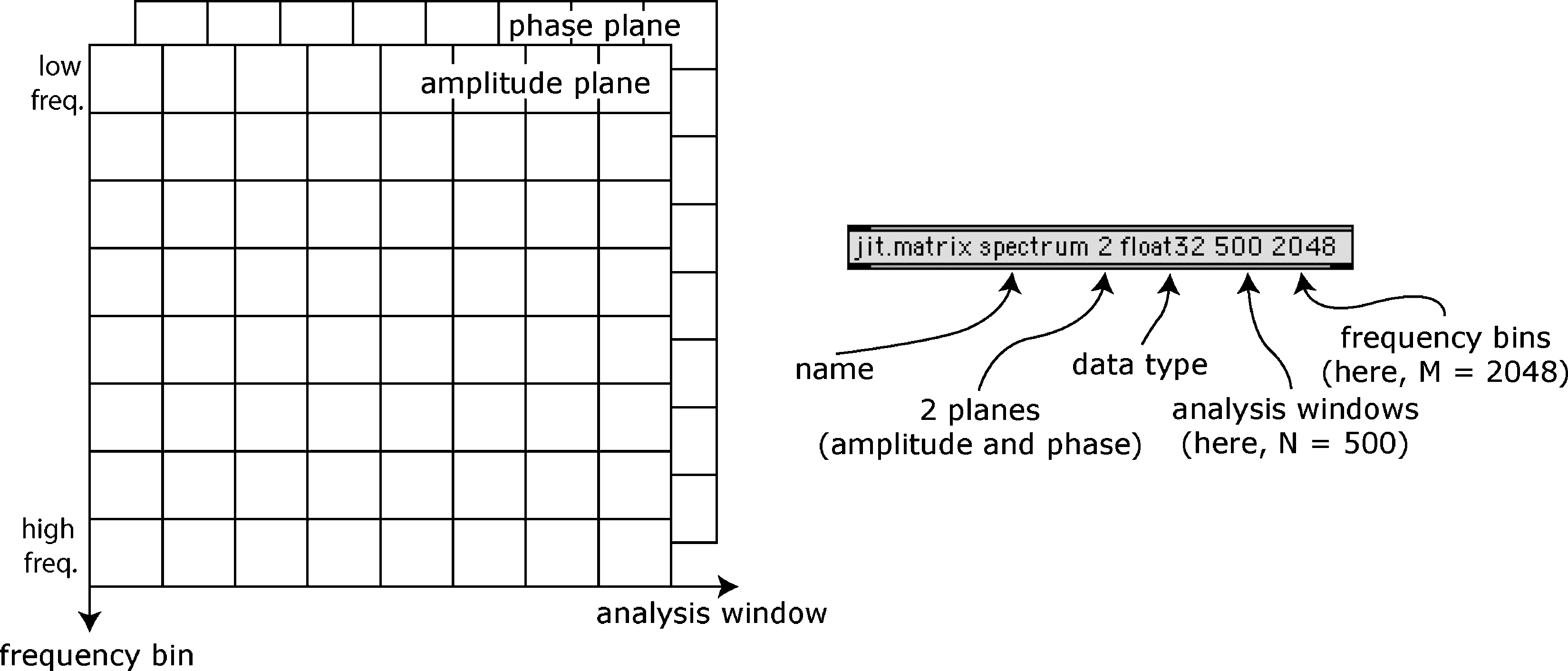
Cifra 3 shows how I store FFT data in a Jitter
matrix throughout this article. We use 32-bit
floating-point numbers here, the same data type
that MSP uses. The grid height is the number of
contenedores de frecuencia, a saber, half the FFT size, and its
length is the number of analysis windows (also called
frames in the FFT literature). It is logical to use a
two-plane matrix: the first is used for magnitudes,
the second for phase differences.
Charles
89
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 3. FFT
representation of a sound
stored in a matrix.
Interacting with a Sonogram
The sonogram represents the distribution of energy
at different frequencies over time. To interact with
this representation of the spectrum, we must scale
the dimension of the picture to the dimension of the
matrix holding the FFT data. To map the matrix
cell coordinates to frequency and time domains, nosotros
use the following relations. Primero, time position t (en
artículos de segunda clase) is given by
t = n × WindowSize
OverlapFactor
× 1
sr
(1)
where n is the number of frames, sr is the sampling
tasa (Hz), and WindowSize is given in samples.
Segundo, the center frequency fc (Hz) of the frequency
bin m is
fc = m×
sr
FFTSize
(2)
Tercero, assuming no more than one frequency is
present in each frequency bin in the analyzed signal,
its value in Hz can be expressed as
f = fc + (cid:1)φ ×
sr
2π × WindowSize
(3)
dónde (cid:1)φ is the phase difference, wrapped within
the range [–π , Pi ] (moore 1990). Note that with the
pfft∼ object, the window size (es decir., frame size) es
the same as the FFT size. (En otras palabras, hay
no zero-padding.)
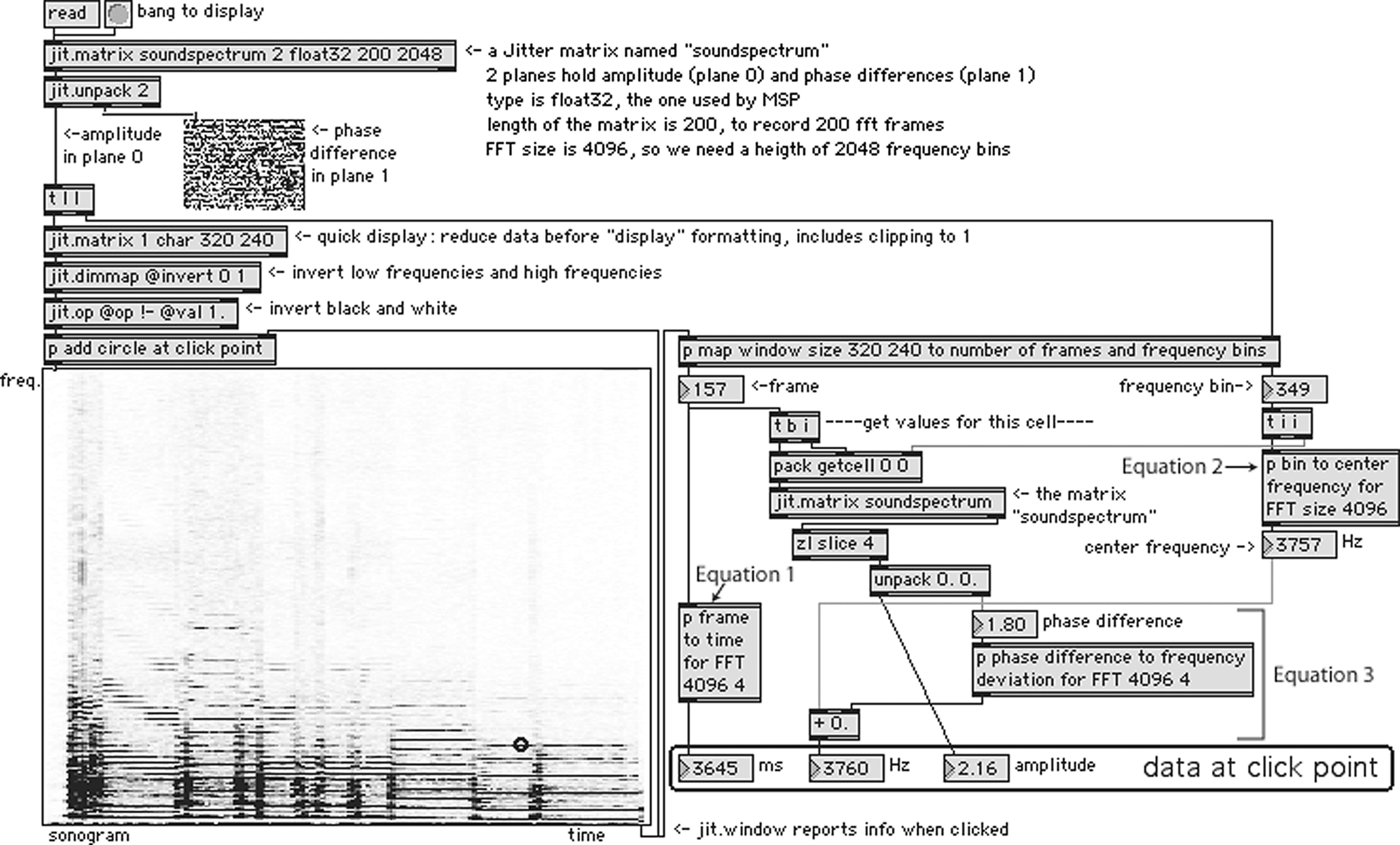
The patch in Figure 4 shows a simple architecture
for interacting with the sonogram. Ecuaciones 1
y 2 and part of Equation 3 are implemented inside
patcher (or p) objects. To reduce computational
costo, the amplitude plane of the matrix holding
the FFT data is converted to a low-resolution
matrix before the display adjustments (es decir., el
inversion of low/high frequencies and inversion of
black and white, because by default, 0 corresponds
to black and 1 to white in Jitter). The OpenGL
implementation of the display is more efficient
and flexible, but it is beyond the scope of this
artículo.
Recording
When implementing the recording of FFT data into
a matrix, we must synchronize the frame iteration
with the FFT bin index. The frame iteration must
happen precisely when the bin index leaps back to
0 at the beginning of a new analysis window. Luke
Dubois’s patch jitter pvoc 2D.pat contains
one implementation of a solution. (See the object
count∼ in [pfft∼ jit.recordfft∼.pat].)
Playback
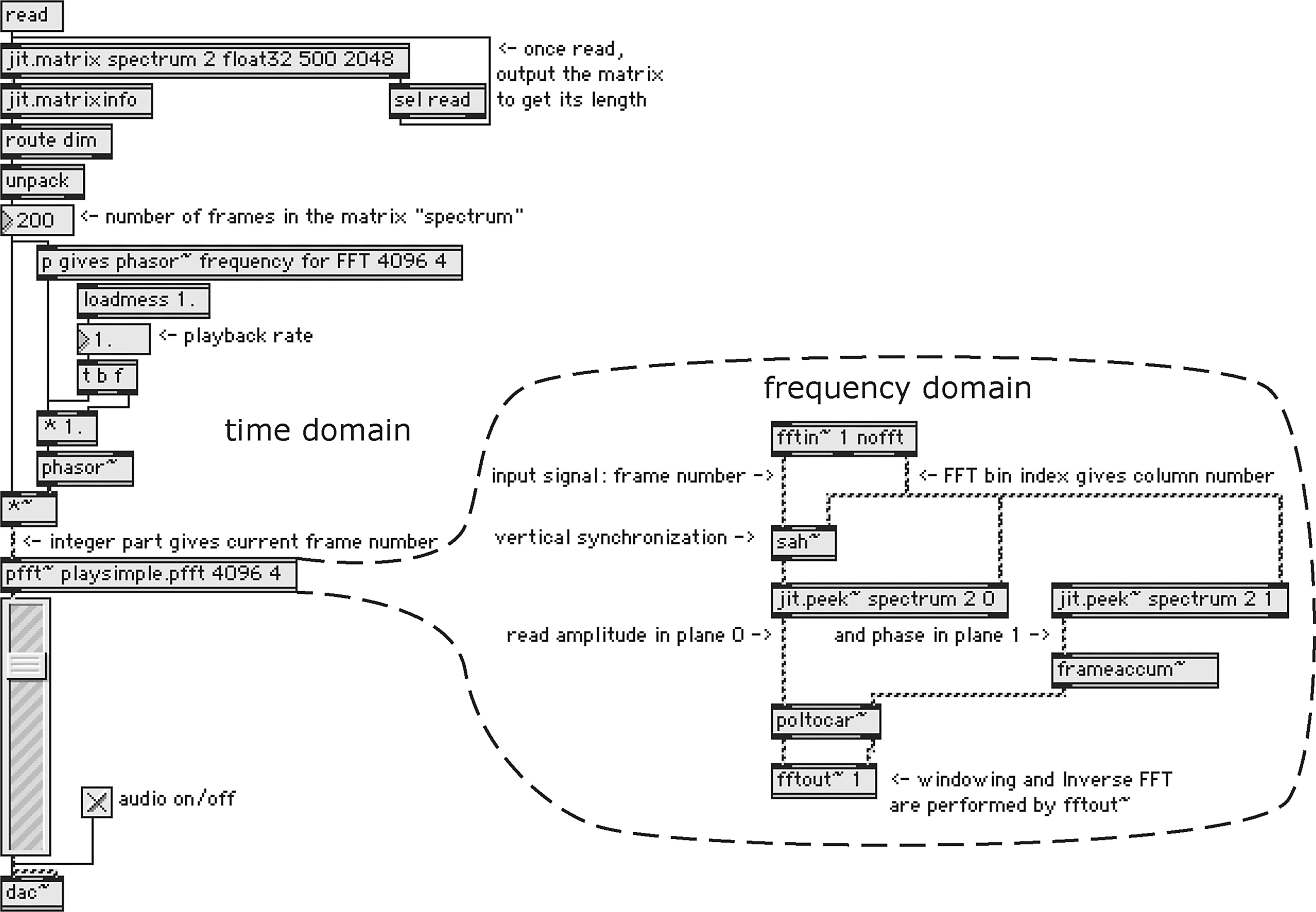
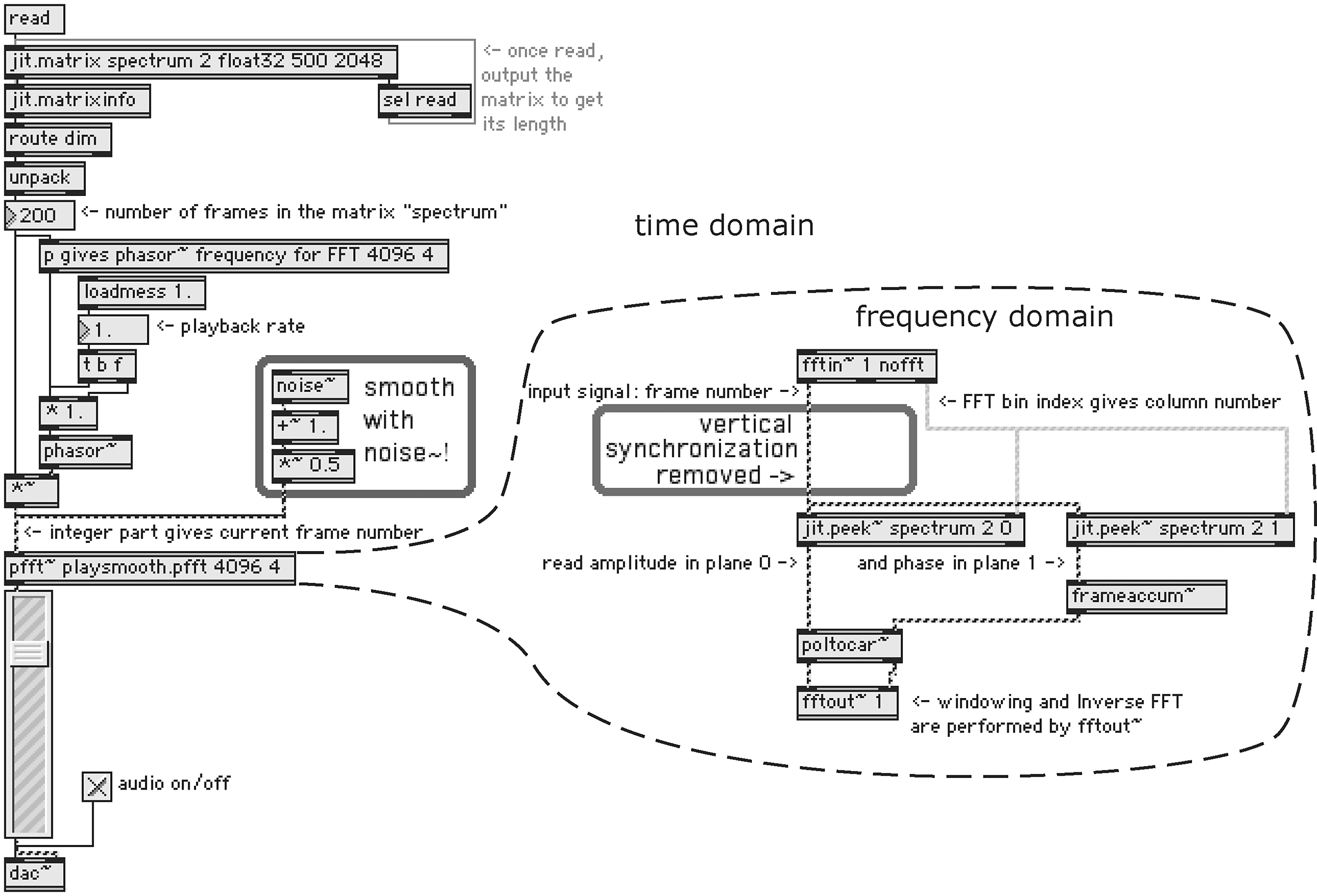
Cifra 5 shows a simple playback algorithm using an
IFFT. A control signal sets the current frame to read.
90
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 4. Interaction with
a sonogram.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
To play back the sound at the original speed, el
control signal must be incremented by one frame at
a period equal to the hop size. Por eso, the frequency
F (in Hz) of the phasor∼ object driving the frame
number is
f =
sr
N × HopSize
× PlaybackRate
(4)
where N is the total number of analysis windows.
Aquí, PlaybackRate sets the apparent speed of the
sound: 1 is normal, 2 is twice as fast, 0 freezes one
marco, and –1 plays the sound backwards.
Advanced Playback
In extreme time stretching, the two main artifacts
of the phase vocoder are the “frame effect” and the
time-stretching of transients. In my composition
Plex for solo instrument and live electronics, ten
seconds are recorded at the beginning of the piece
and played back 36 times more slowly, spread over
6 minutos. Considering an FFT with a hop size of
1,024 samples and a sampling rate of 44,100 Hz,
each analysis window with an original duration of 23
msec is stretched out to 836 mseg. During synthesis
with the traditional phase-vocoder method, the leap
from one frame to the following one is audible with
a low playback speed. This particular artifact, el
“frame effect,” has not received much attention
in the literature. I will describe two methods to
interpolate spectra between two recorded FFT
marcos, one of which can easily be extended to a
real-time “blurring” effect.
When humans slow down the pacing of a spoken
oración, they are bound to slow down vowels
more than consonants, some of which are physically
impossible to slow down. Similarmente, musicians can
naturally slow down the tempo of a phrase without
slowing down the attacks. That is why time-
stretching a sound uniformly, including transients,
does not sound natural. Transient preservation in the
phase vocoder has been studied, and several efficient
algorithms have been presented (Laroche and Dolson
1999; R ¨obel 2003). Sin embargo, these propositions
have not been created in a form adapted to real-time
entornos. I present a simple, more straightfor-
ward approach that computes a transient value for
Charles
91
Cifra 5. A simple player.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
each frame and uses it during resynthesis. That will
naturally lead to an algorithm for segmentation,
designed for performance time as well.
Removing the “Frame Effect”
This section shows two algorithms interpolating
intermediary spectra between two “regular” FFT
marcos, thus smoothing transitions and diminishing
the frame effect. In both cases, a floating-point
number describes the frame to be resynthesized: para
instancia, 4.5 for an interpolation halfway between
marcos 4 y 5.
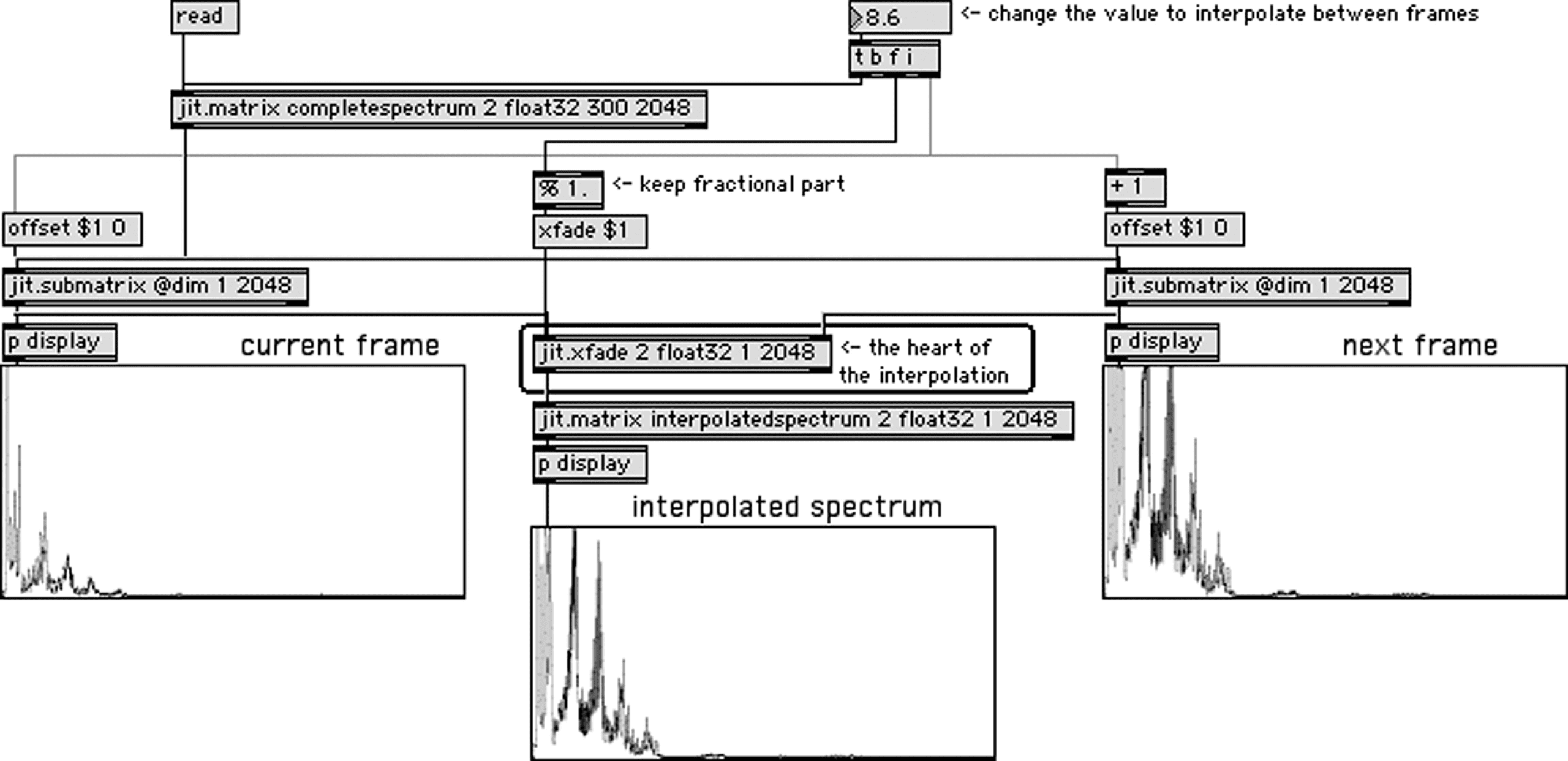
In the first method, the synthesis module con-
tinuously plays a one-frame spectrum stored in a
one-column matrix. As illustrated in Figure 6, este
matrix is fed with linear interpolations between two
frames from the recorded spectrum, computed with
the jit.xfade object. Values from both amplitude
and phase difference planes are interpolated. Con
a frame number of 4.6, the value in a cell of the
interpolated matrix is the sum of 40 por ciento de la
value in the corresponding cell in frame 4 y 60
percent of the value in frame 5.
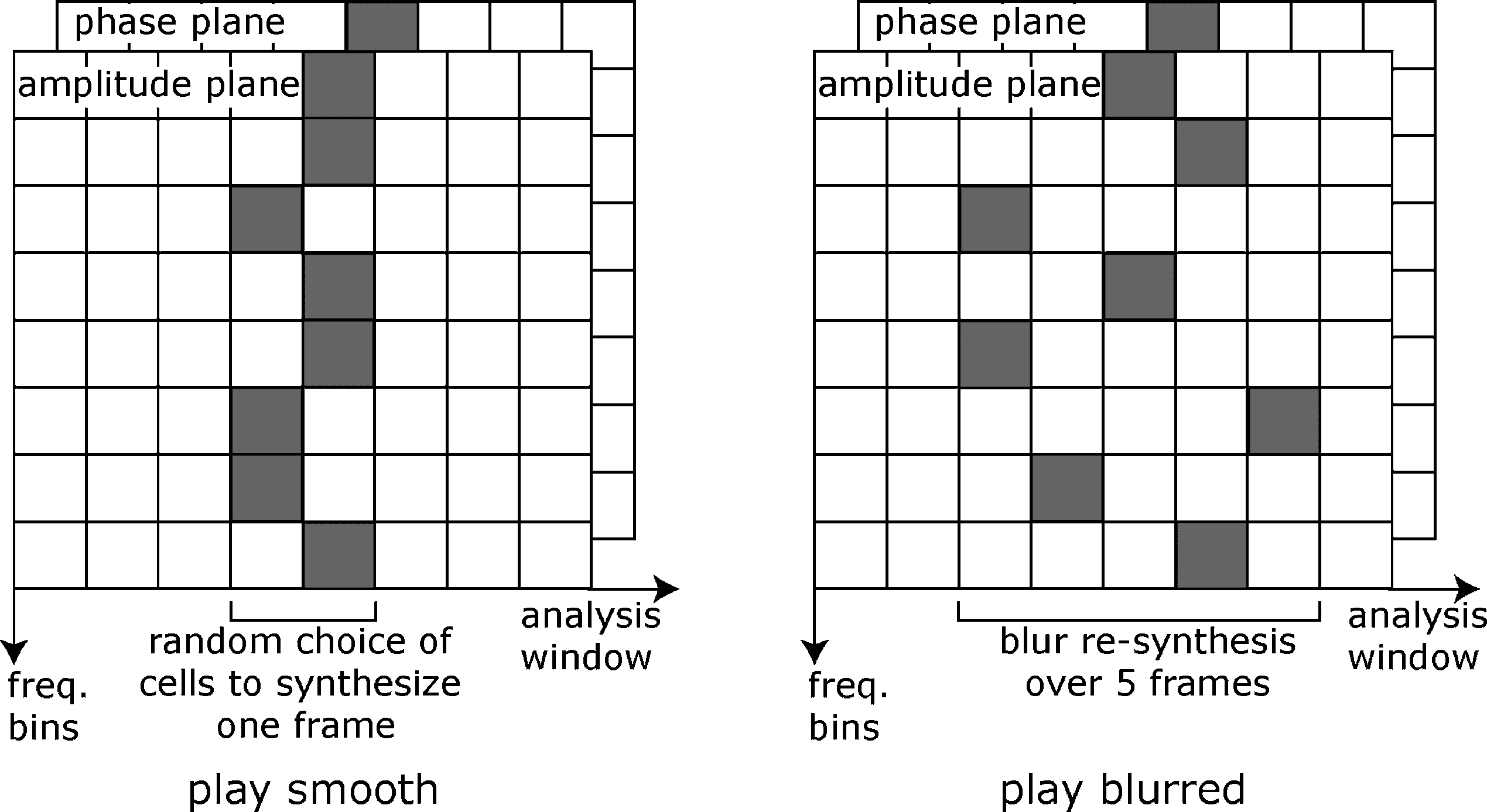
My second approach is a controlled stochastic
spectral synthesis. For each frame to be synthesized,
each amplitude/phase-difference pair is copied from
the recorded FFT data, either from the corresponding
frame or from the next frame. The probability of
picking up values in the next frame instead of the
current frame is the fractional value given by the
user. Por ejemplo, a frame number of 4.6 results in
a probability of 0.4 that values are copied from the
original frame 4 and a probability of 0.6 that values
are copied from the original frame 5. This random
choice is made for each frequency bin within
each synthesis frame, such that two successive
synthesized frames do not have the same spectral
contenido, even if the specification is the same. El
implementation shown in Figure 7 shows a small
92
Computer Music Journal
Cifra 6. Interpolated
spectrum between two
analysis windows.
Cifra 7. A smooth player.
Cifra 6
Cifra 7
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Charles
93
Cifra 8. estocástico
synthesis between two
marcos, blur over several
marcos.
modification to the engine presented Figure 5. A
signal-rate noise with amplitude from 0 a 1 is added
to the frame number. While reading the FFT data
matrix, jit.peek∼ truncates the floating-point
value to an integer giving the frame number. El
vertical synchronization is removed to enable the
frame number to change at any time. Increasing the
floating-point value in the control signal creates an
increased probability of reading the next frame.
This method can be readily extrapolated to blur
any number of frames over time with negligible
additional cost in CPU power. Instead of adding a
noise between 0 y 1, we scale it to [0, R], dónde
R is the blur width in frames. If C is the index of
the current frame, each pair of values is then copied
from a frame randomly chosen between frames C
and C + R, as shown in Figure 8. The musical result
is an ever-moving blur of the sound, improving the
quality of frozen sounds in many cases. The blur
width can be controlled at the audio rate.
Both the interpolated frame and the stochastic
playback methods produce high-quality results
during extremely slow playback, but they are
useful in different contexts. The interpolated frames
often sound more natural. Because it lacks vertical
coherencia, the stochastic method may sound less
natural, but it presents other advantages. Primero,
it is completely implemented in the “perform”
thread of Max/MSP; como resultado, CPU use is constant
regardless of the parameters, including playback
tasa. Sin embargo, the interpolated spectrum must be
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
computed in the low-priority thread, meaning that
the CPU load increases with the number of frames
to calculate. Segundo, the stochastic method offers a
built-in blurring effect, whereas achieving this effect
with matrix interpolation would require additional
programming and be less responsive. In what
follows, I continue to develop this second method,
because it adheres to the original phase-vocoder
architecture and is more flexible.
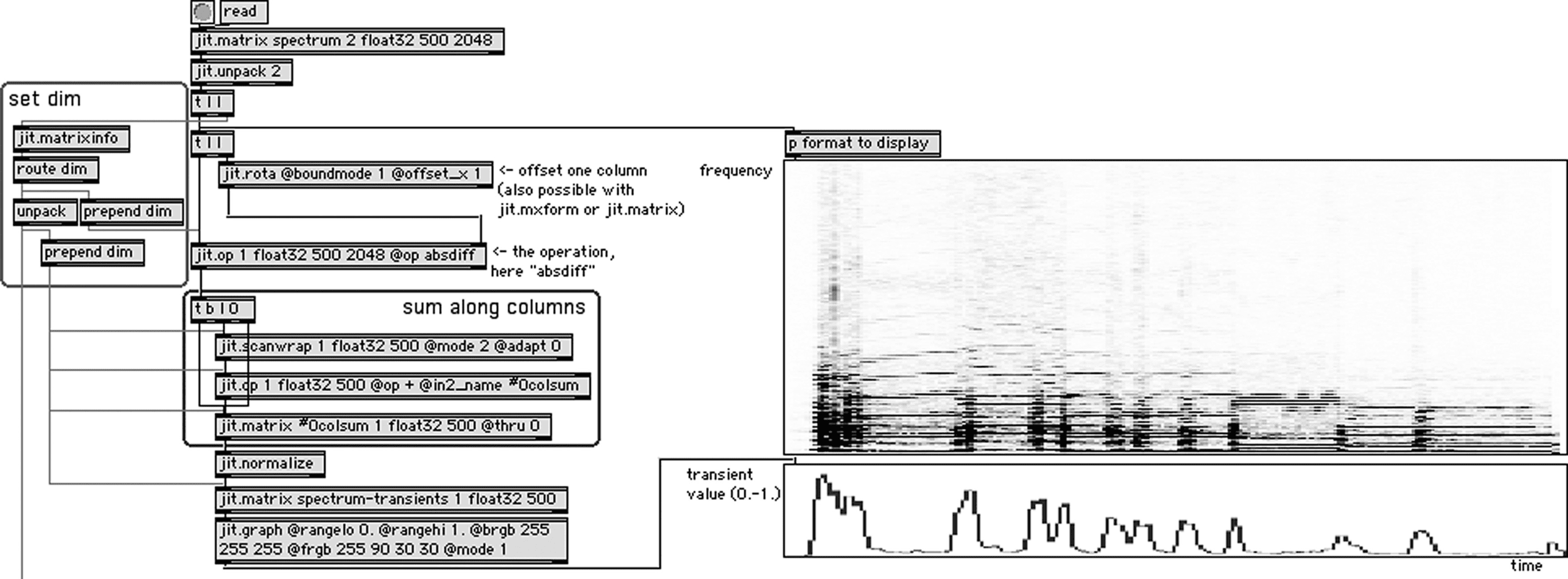
Transient Preservation
I propose a simple algorithm for performance-time
transient evaluation, along with a complementary
algorithm to play a sound at a speed proportional
to the transient value. My approach consists in
assigning to each frame a transient value, defined
as the spectral distance between this frame and the
preceding frame, normalized to [0, 1] over the set of
marcos.
Several choices are possible for the measure of
the spectral distance between two frames. El
Euclidean distance is the most obvious choice.
Given M frequency bins, with am,n the amplitude in
bin m of frame n, the Euclidean distance between
frames n and n – 1 es
(cid:1)
(cid:2)
(cid:2)
(cid:3)
M−1(cid:4)
tn =
(am,n − am,n−1)2
(5)
m= 0
94
Computer Music Journal
Cifra 9. A transient value
for each frame.
In this basic formula, we can modify two parameters
that influence quality and efficiency: primero, the set of
descriptors out of which we calculate the distance,
y segundo, the distance measure itself. The set
of descriptors used in Equation 5 is the complete
set of frequency bins: applying Euclidean distance
weights high frequencies as much as low ones,
which is not perceptually accurate. For a result
closer to human perception, we would weight the
different frequencies according to the ear’s physi-
ology, for instance by using a logarithmic scale for
the amplitudes and by mapping the frequency bins
non-linearly to a set of relevant descriptors like
el 24 Bark or Mel-frequency coefficients. In terms
of CPU load, distance is easier to calculate over
24 coefficients than over the whole range of fre-
quency bins, but the calculation of the coefficients
makes the overall process more computationally
expensive. Although using the Euclidean distance
makes mathematical sense, the square root is a rela-
tively expensive calculation. To reduce computation
load, En figura 9 I use in a rough approximation of
the Euclidean distance:
tn =
M−1(cid:4)
m= 0
(cid:5)
(cid:5)am,n − am,n−1
(cid:5)
(cid:5)
(6)
The playback part of the vocoder can use the
transient value to drive the playback rate. En el
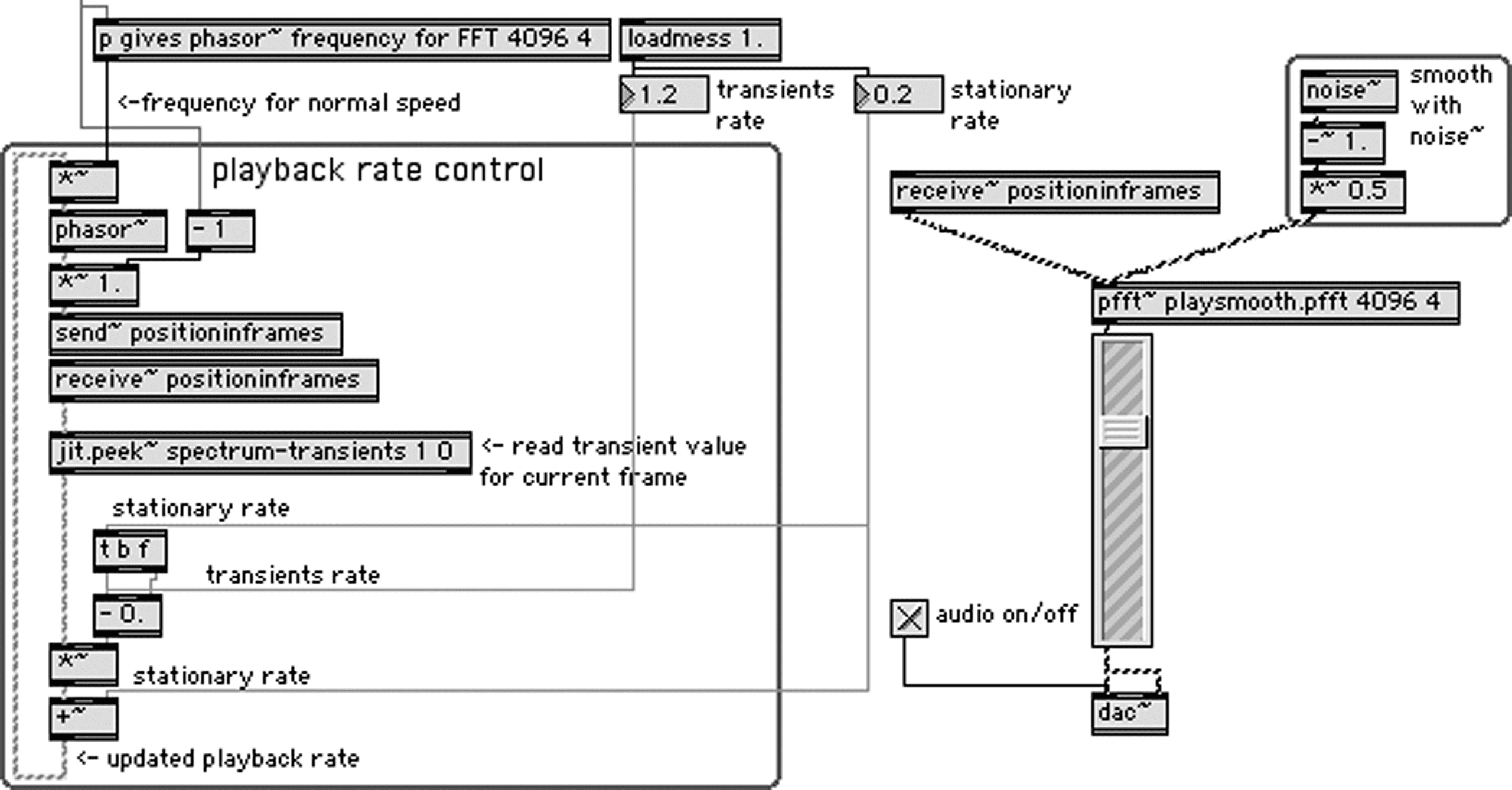
patch presented Figure 10, the user specifies the
playback rate as a transient rate rtrans (the playback
rate for the greatest transient value) and a stationary
rate rstat (the playback rate for the most stationary
part of the sound). Given the current frame’s
transient value tr, the instantaneous playback rate
rinst is given by
rinst = rstat + tr × (rtrans − rstat)
(7)
The musical result of a continuous transient value
entre 0 y 1 is interesting, because it offers a
built-in protection against errors of classification
as transient or stationary. This is especially useful
in a performance-time context. A binary transient
value could, por supuesto, be readily implemented by a
comparison to a threshold applied to all the values
of the transient matrix with a jit.op object.
Controlling the blur width (ver figura 8) con el
transient value may be musically useful as well. El
most basic idea is to make the blur width inversely
proportional to the transient value, as presented
En figura 11. Similarly to the playback rate, el
instantaneous blur width binst is given by
binst = bstat + tr × (btrans − bstat)
(8)
where tr is the current frame transient value, bstat is
the stationary blur width, and btransis the transient
blur width.
Segmentation
This section describes a performance-time method of
segmentation based on transient values of successive
marcos. I place a marker where the spectral changes
Charles
95
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 10. Re-synthesizing
at self-adapting speed.
Cifra 11. Blur width
controlled by transient
valor. durante el
playback of stationary
parts of the sound (izquierda),
the blurred region is wider
than during the playback
of transients (bien).
Cifra 10
Cifra 11
from frame to frame are greater than a given
límite. Como figura 12 muestra, frame n is marked
if and only if its transient value is greater than or
equal to the transient value in the preceding frame
plus a threshold h, eso es, whenever
tn ≥ tn−1 + h
(9)
The formula used to calculate transient values ap-
pears to have a great influence on the segmentation
resultado. In the preceding section, we used Euclidean
distance or an approximation by absolute difference
(Ecuaciones 5 y 6). Both expressions yield a useful
auto-adaptive playback rate, but my experience
is that the following expression is preferable for
ulterior segmentation with Equation 9:
tn =
M−1(cid:4)
m= 0
am,norte
am,n−1
(10)
96
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 12. Automatic
performance-time
segmentation.
En efecto, whereas Euclidean distance or absolute
difference give spectrum changes a lower weight
at locally low amplitudes than at high amplitudes,
the division in Equation 10 enables a scaling of the
degree of spectrum modification to the local level of
amplitude. Musical applications include real-time
leaps from one segmentation marker to another,
resulting in a meaningful shuffling of the sound.
An important point to retain from this section is
eso, whereas ideas may materialize first as iterative
expresiones (p.ej., see the summations in Equations
5, 6, y 10), the implementation in Jitter is reduced
to a small set of operations on matrices. To take
full advantage of Jitter, we implement parallel
equivalents to iterative formulas.
Graphically Based Transformations
Ahora, we explore several ways of transforming a
sound through its FFT representation stored in two-
dimensional matrices. The four categories I examine
are direct transformations, use of masks, interacción
between sounds, and “mosaicing.”
Direct Transformations
The most straightforward transformation consists
of the application of a matrix operation to an FFT
data matrix. In Jitter, we can use all the objects that
work with 32-bit floating-point numbers. A flexible
implementation of such direct transformations is
possible thanks to jit.expr, an object that parses
and evaluates expressions to an output matrix.
Además, all Jitter operators compatible with 32-bit
floating-point numbers are available in jit.expr.
Phase information is important for the quality
of resynthesized sounds. The choice to apply a
treatment to amplitude and phase difference or only
to amplitude, or to apply a different treatment to
the phase-difference plane, is easily implemented
whether in jit.expr or with jit.pack and
jit.unpack objects. This choice depends on the
particular situation and must generally be made
after experimenting.
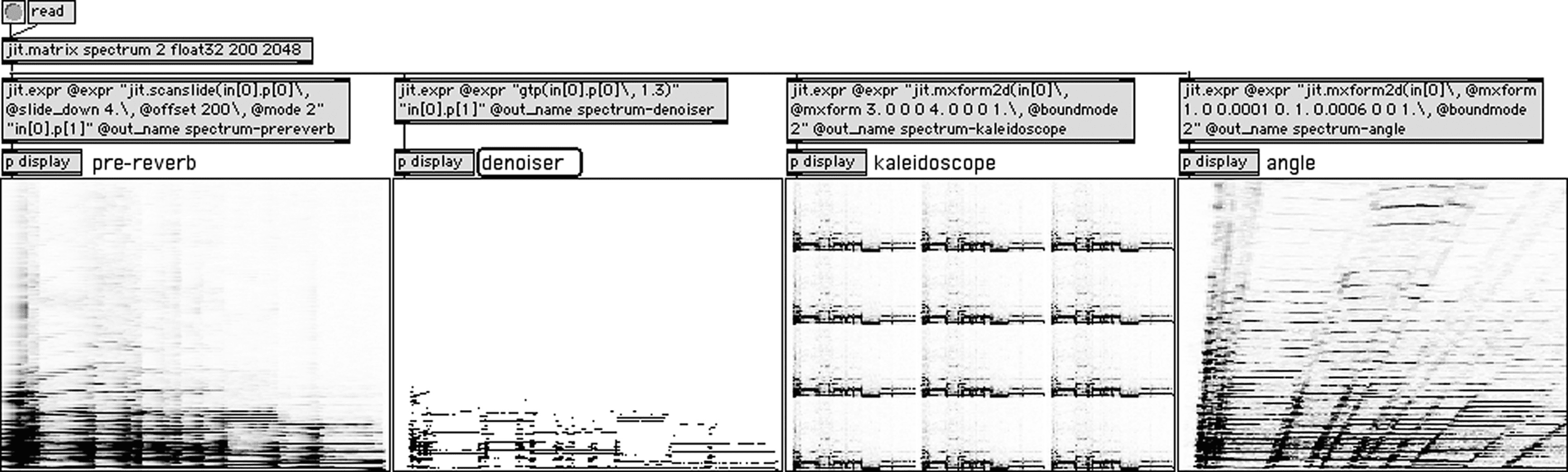
En figura 13, the expression attribute of the
second jit.expr object is [‘‘gtp(en[0].pag[0]\,
1.3)’’ ‘‘in[0].pag[1]'']. The first part of the
expression is evaluated onto plane 0 of the output
matrix; it yields the amplitude of the new sound. Él
applies the operator gtp (which passes its argument
if its value is greater than the threshold, de lo contrario,
it yields 0) to the amplitude plane of the incoming
matrix with the threshold 1.3. It is a rough denoiser.
(In the previous expression, en[0].pag[0] is plane 0
of the matrix in input 0.) The second part of the
expression produces on plane one the first plane of
the incoming matrix (es decir., en[0].pag[1]); the phase
is kept unchanged.
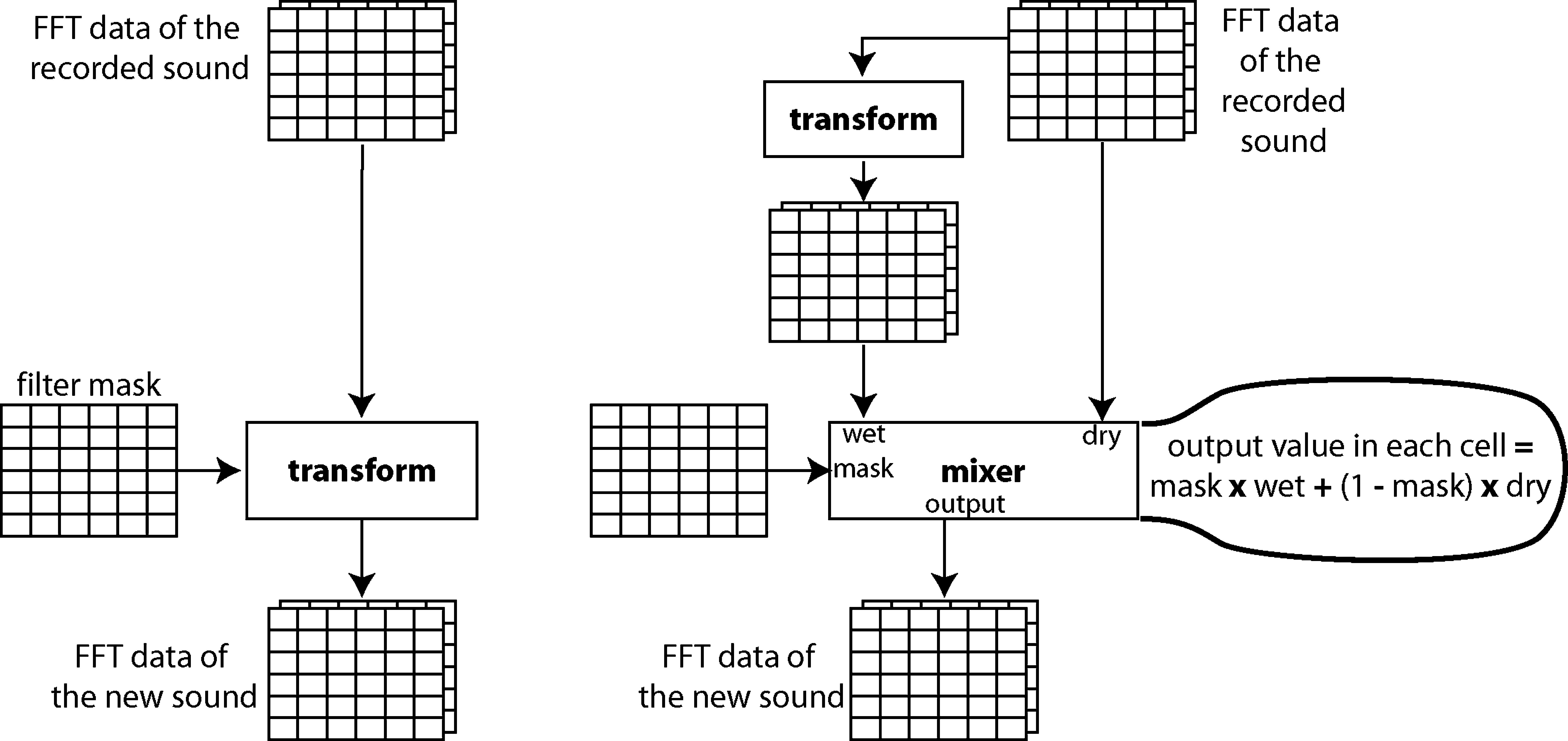
Masks
Masks enable the gradual application of an effect
to a sound, thus refining the sound quality. A
different percentage of the effect can be used in
every frequency bin and every frame. In this article,
Charles
97
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 13. Graphical
transformations.
Cifra 14. Two designs to
use masks.
Cifra 13
Cifra 14
I limit the definition of a mask to a grid of the
same resolution as the FFT analysis of the sound,
with values between 0 y 1. In Jitter, that means
a one-dimensional, 32-bit floating-point matrix, de
the same dimension as the sound matrix.
A mask can be arbitrarily generated, interpolated
from a graphical file, drawn by the user on top of the
sound sonogram, or computed from another sound
or the sound itself. Por ejemplo, let us consider
a mask made of the amplitudes (or the spectral
envelope) of one sound, mapped to [0, 1]. Multiplying
the amplitudes of a source sound with this mask is
equivalent to applying a source-filter cross synthesis.
Cifra 14 presents two possible designs. En el
left version, the processing uses the mask to produce
the final result; this is memory-efficient. En el
right version, the original sound is mixed with the
processed one; this allows a responsive control on
the mix that can be adjusted without re-calculation
of the sound transformation.
Interaction of Sounds
Generalized cross synthesis needs both amplitude
and phase difference from both sounds. Similarmente,
98
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Cifra 15. Context-free
mosaicing algorithm.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
interpolating and morphing sounds typically re-
quires amplitude and phase information from both
sounds.
It is easy to implement interpolation between
sounds with jit.xfade, in the same way as
interpolation between frames in Figure 6. Un
interesting musical effect results from blurring the
cross-faded sound with filters such as jit.streak,
jit.sprinkle , and jit.plur.
As opposed to an interpolated sound, a morphing
between two sounds evolves from the first to the
second within the duration of the synthesized sound
sí mismo. Such a morphing can be implemented as an
interpolation combined with three masks: one for
the disappearance of the first source sound, a second
for the appearance of the second sound, and a third
one to apply a variable amount of blurring.
Mosaicing
Mosaicing is a subset of concatenative synthesis,
where a target sound is imitated as a sequence of
best-matching elements from a database (Schwarz
2006). In the context of the phase vocoder, I provide
a simple mosaicing by spectral frame similarity,
similar to the Spectral Reanimation technique (Lyon
2003). Before resynthesis, each FFT frame in the
target sound is replaced by the closest frame in the
database irrespective of the context. The algorithm
is illustrated in Figure 15.
Three factors influence the speed and quality of
the resulting sound. Primero, the amplitude scale might
be linear (less CPU intensive) or logarithmic (closer
to perception). Segundo, the descriptors for each
frame can take variable sizes. The set of amplitudes
in each frequency bin is directly available, but it is
a large vector. A linear interpolation to a reduced
number of bands, a set of analyzed features (pitch,
centroid, etc.), and a nonlinear interpolation to the
24 Bark or Mel-frequency coefficients are other
possible vectors. The third factor is the distance
used to find the closest vector (Euclidean dis-
tance, or an approximation sparing the square-root
calculation).
My choice has been to use a logarithmic am-
plitude scale, a vector of Bark coefficients, y
Euclidean distance or an approximation similar to
Ecuación 6. The Bark coefficients, reflecting ear
physiology, are well suited to this task.
Charles
99
Cifra 16. Real-time
stochastic freeze
implementación.
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
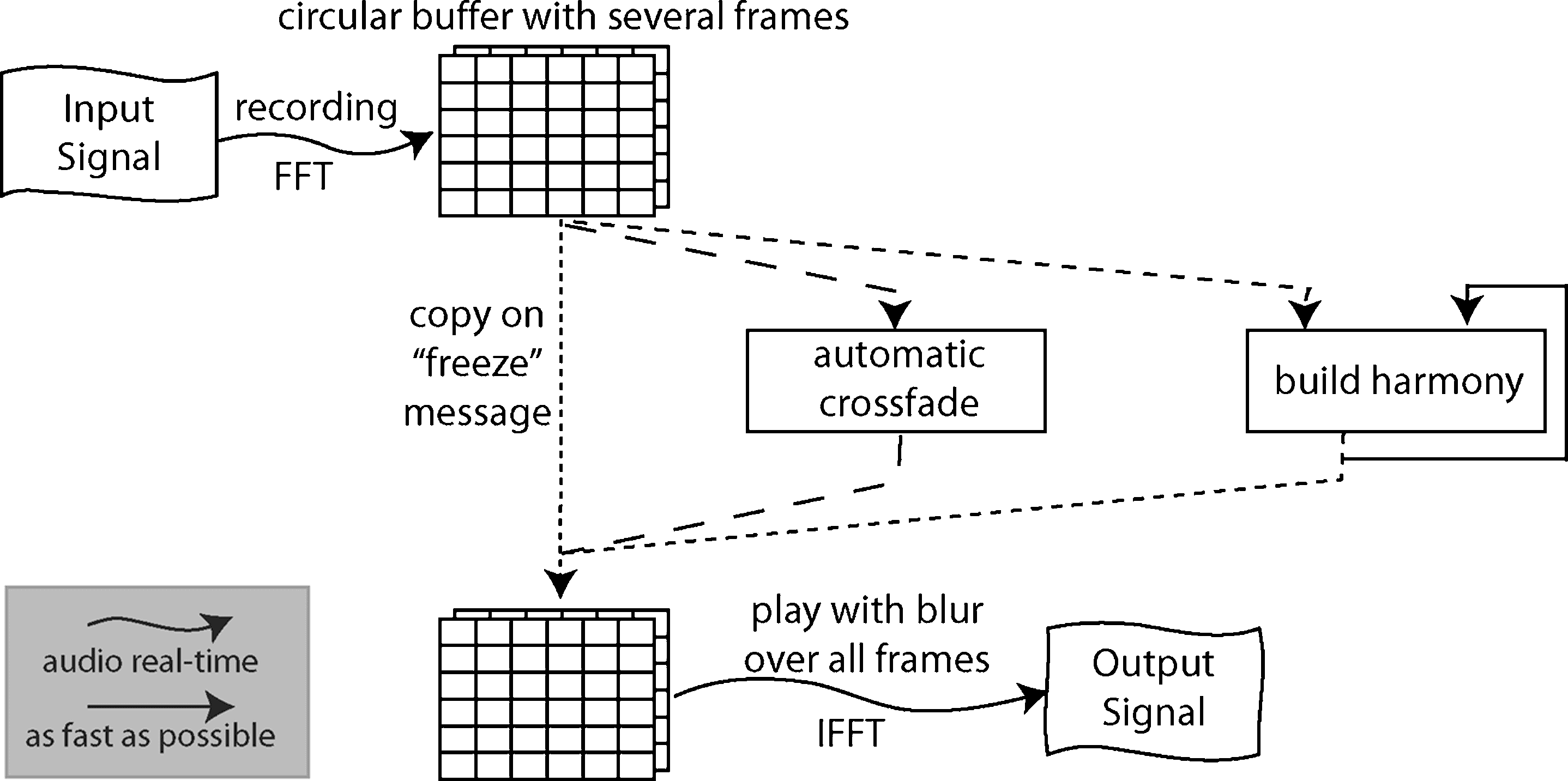
Real-Time Freeze and Beyond
The matrix approach to spectral treatments allows
not only a variety of performance-time extensions
to the phase vocoder but also improvements in
real-time processing, such as freezing a sound and
transforming a melody into a chord.
transition sub-patch between the matrix to freeze
(freeze8-record) and the matrix currently playing
(freeze8-play) can be used to cross-fade when a
new sound is frozen. Such sub-patches incorporate
first a counter to generate a number of transition
matrices, and second a cross-fading object such
as jit.xfade controlled by a user-drawn graph
specifying the cross-fade curve.
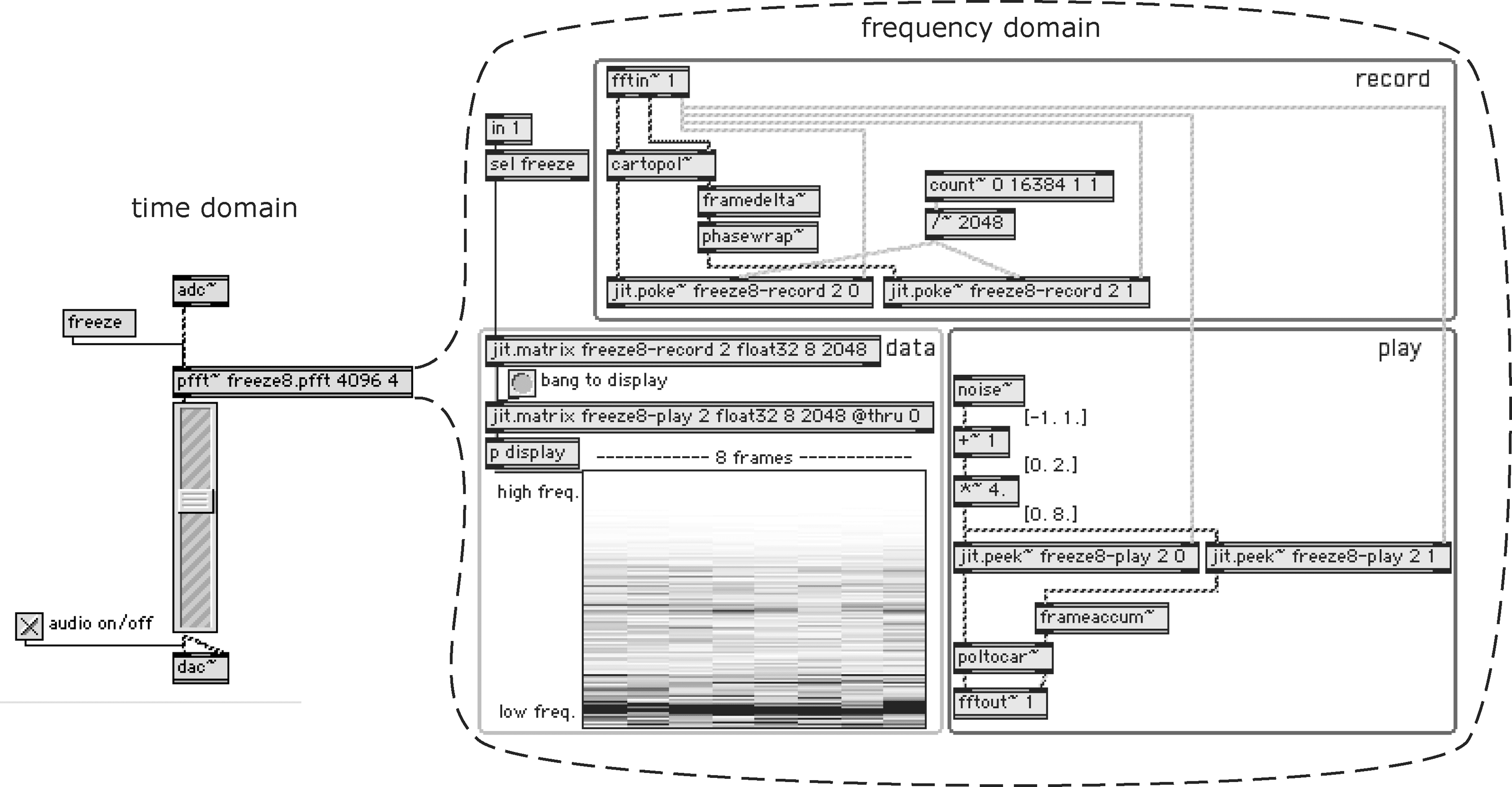
Real-Time Freeze
A simple way to freeze a sound in real time is
to resynthesize one spectral frame continuously. I
improve the sound quality by freezing several frames
at once and then resynthesizing the complete set
of frames with the stochastic blurring technique
described previously (Cifra 8).
My implementation features a continuous spec-
tral recording of the input sound into a circular
buffer of eight frames (an eight-column matrix).
This matrix is copied into the playback matrix upon
receipt of the freeze message.
Automatic Cross-Fade
Melody to Harmony
In my composition Aqua for solo double bass,
aquaphon, clarinet, and live electronics, arpeggios
are transformed in real time into chords with a
modified freeze tool. As shown in Figure 17, el
currently synthesized spectrum is added to the
incoming one via a feedback loop. The “build
harmony” block uses the current output synthesis
data and the new window analysis to calculate a
matrix reflecting the addition of the new note. El
first solution for this computation is to average
the energy in each frequency bin over all frozen
spectra:
The stochastic freeze presented in Figure 16 interruptores
abruptly from one frozen sound to the next. A
an =
(11)
(cid:6)
norte
i = 1 ai
norte
100
Computer Music Journal
Cifra 17. Real-time freeze
design with extensions.
where n is the number of frames to average, an is the
average amplitude, and ai is the amplitude in frame i.
The same formula can be used for phase differences.
The implementation requires a recursive equivalent
to Equation 11:
un + 1 = n × an + ai + 1
norte + 1
(12)
Note that in the case of stochastic blurred resyn-
thesis over eight frames, this operation is done
independently for each frame.
Sin embargo, the solution I ended up using in concert
a paradigm for extensions of the phase vocoder in
which advanced graphical processing is possible
in performance time. The “composition of sound
treatments” described by Hans Tutschku (Nez
2003) is now available not only in the studio,
but also during a concert. I have also described an
improvement to the real-time effect known as freeze.
I hope that these musical tools will help create not
only new sounds, but also new compositional
approaches. Some patches described in this article,
complementary patches, and sound examples are
available online at www.jeanfrancoischarles.com.
is given by
an =
(cid:6)
norte
i = 1 ai√
norte
Expresiones de gratitud
(13)
which is written and implemented recursively as
un + 1 =
√
√
n × an + ai + 1
norte + 1
(14)
En efecto, the latter formula produces a more powerful
sound, compensating for the low-amplitude frames
that may be recorded.
Thanks to Jacopo Baboni Schilingi and Hans
Tutschku for their invitation to present this material
within the Prisma group; the exchanges with the
group have been the source of important develop-
mentos. Thanks to Joshua Fineberg for helping me
through the writing of the article. Thanks to ¨Orjan
Sandred for his useful comments after his attentive
reading of my draft. Thanks to Andrew Bentley for
his invitation to teach this material.
Conclusión
Referencias
This article provides an overview of techniques to
perform spectral audio treatments using matrices in
the environment Max/MSP/Jitter. I have presented
campesinos, PAG., y D. Weenink. 2006. “Praat: Doing Phonet-
ics by Computer.” Available online at www.praat.org.
Accedido 11 Octubre 2006.
Charles
101
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3
Bogaards, NORTE., A. R ¨obel, and X. Rodet. 2004. “Sound Anal-
ysis and Processing with Audiosculpt 2.” Proceedings
del 2004 International Computer Music Conference.
San Francisco, California: International Computer
Music Association, páginas. 462–465.
R ¨obel, A. 2003. “Transient Detection and Preservation
in the Phase Vocoder.” Proceedings of the 2003 Enterrar-
national Computer Music Conference. San Francisco,
California: International Computer Music Association,
páginas. 247–250.
Dolson, METRO. 1986. “The Phase Vocoder: A Tutorial.”
Schnell, NORTE., et al. 2005. “FTM—Complex Data Structures
Computer Music Journal 10(4):14–27.
jones, r., y B. Nevile. 2005. “Creating Visual Music in
Jitter: Approaches and Techniques.” Computer Music
Diario 29(4):55–70.
Klingbeil, METRO. 2005. “Software for Spectral Analysis,
Editing, and Synthesis.” Proceedings of the 2005 Enterrar-
national Computer Music Conference. San Francisco,
California: International Computer Music Association,
páginas. 107–110.
Kreichi, S. 1995. “The ANS Synthesizer: Composing on
a Photoelectronic Instrument.” Leonardo 28(1):59–
62.
Laroche, J., y M. Dolson. 1999. “Improved Phase Vocoder
Time-Scale Modification of Audio.” IEEE Transactions
on Speech and Audio Processing 7(3):323–332.
Luis, t. PAG. 1991. “Free Music.” In T. PAG. Luis, ed. A Source
Guide to the Music of Percy Grainger. White Plains,
Nueva York: Pro-Am Music Resources, páginas. 153–162.
Lyon, mi. 2003. “Spectral Reanimation.” Proceedings of the
Ninth Biennial Symposium on Arts and Technology.
New London, Connecticut: Connecticut College, páginas.
103–105.
Marino, GRAMO., M.-H. Serra, and J.-M. Raczinski. 1993. "El
UPIC System: Origins and Innovations.” Perspectives
of New Music 31(1):258–269.
moore, F. R. 1990. Elements of Computer Music. Engle-
wood Cliffs, New Jersey: Prentice Hall.
Nez, k. 2003. “An Interview with Hans Tutschku.”
Computer Music Journal 27(4):14–26.
Polansky, l., and T. Erbe. 1996. “Spectral Mutation in
SoundHack.” Computer Music Journal 20(1):92–101.
Roads, C. 1995. The Computer Music Tutorial. Cambridge,
Massachusetts: CON prensa.
for Max.” Proceedings of the 2005 Internacional
Computer Music Conference. San Francisco, California:
International Computer Music Association, páginas. 9–12.
Schnell, NORTE., y D. Schwarz. 2005. “Gabor: Multi-
Representation Real-Time Analysis/Synthesis.” Pro-
ceedings of the 8th International Conference on
Digital Audio Effects (DAFx-05). Madrid: Universidad
Polit ´ecnica de Madrid, páginas. 122–126.
Schwarz, D. 2006. “Concatenative Sound Synthesis: El
Early Years.” Journal of New Music Research 35(1):3–22.
Sedes, A., B. Courribet, y j. B. Thiebaut. 2004. “From the
Visualization of Sound to Real-Time Sonification: Dif-
ferent Prototypes in the Max/MSP/Jitter Environment.”
Actas de la 2004 International Computer Music
Conferencia. San Francisco, California: Internacional
Computer Music Association, páginas. 371–374.
Todoroff, T., mi. Daubresse, y j. Fineberg. 1995. “Iana∼
(A Real-Time Environment for Analysis and Extraction
of Frequency Components of Complex Orchestral
Sounds and Its Application within a Musical Context)."
Actas de la 1995 International Computer Music
Conferencia. San Francisco, California: Internacional
Computer Music Association, páginas. 292–293.
Wenger, MI., and E. Spiegel. 2005. MetaSynth 4.0 User
Guide and Reference. San Francisco, California: Ud.&I
Software.
Joven, METRO., and S. Lexer. 2003. “FFT Analysis as
a Creative Tool in Live Performance.” Proceed-
ings of the 6th International Conference on Dig-
ital Audio Effects (DAFX-03). Londres: Queen
Mary, University of London. Available online at
www.elec.qmul.ac.uk/dafx03/proceedings/pdfs/dafx29.
pdf.
102
Computer Music Journal
yo
D
oh
w
norte
oh
a
d
mi
d
F
r
oh
metro
h
t
t
pag
:
/
/
d
i
r
mi
C
t
.
metro
i
t
.
mi
d
tu
/
C
oh
metro
j
/
yo
a
r
t
i
C
mi
–
pag
d
F
/
/
/
/
3
2
3
8
7
1
8
5
5
2
1
5
/
C
oh
metro
j
.
.
2
0
0
8
3
2
3
8
7
pag
d
.
.
.
F
b
y
gramo
tu
mi
s
t
t
oh
norte
0
8
S
mi
pag
mi
metro
b
mi
r
2
0
2
3