Victor Lazzarini, Joseph Timoney, E
Thomas Lysaght
An Grúpa Theicneolaíocht Fuaime agus Ceoil
Dhigitigh
(Sound and Digital Music Technology Group)
National University of Ireland, Maynooth
Maynooth, Co. Kildare, Ireland
Victor.Lazzarini@nuim.ie
{JTimoney, TLysaght}@cs.nuim.ie
The Generation of Natural-
Synthetic Spectra by
Means of Adaptive
Frequency Modulation
Frequency- modulation (FM) synthesis is widely
known as a computationally effi cient method for
synthesizing musically interesting timbres. How-
ever, it has suffered from neglect owing to the
diffi culty in creating natural- sounding spectra and
mapping gestural input to synthesis parameters.
Recentemente, a revival has occurred with the advent of
adaptive audio- processing methods, and this work
proposes a technique called adaptive FM synthesis.
This article derives two novel ways by which an
arbitrary input signal can be used to modulate a
carrier. We show how phase modulation (PM) can
be achieved fi rst by using delay lines and then by
heterodyning. By applying these techniques to
real- world signals, it is possible to generate transi-
tions between natural- sounding and synthesizer-
like sounds. Examples are provided of the spectral
consequences of adaptive FM synthesis using inputs
of various acoustic instruments and a voice. An
assessment of the timbral quality of synthesized
sounds demonstrates its effectiveness.
Background
Frequency modulation (FM), introduced by John
Chowning in his seminal article on the technique
(Chowning 1973), is one of the most important
classic methods of synthesis. It has proved very
useful as an economical means of generating time-
varying complex spectra. For this reason, it was
widely adopted at a time when computational speed
was a determining factor in the choice of signal-
processing algorithms. Tuttavia, the method always
made it diffi cult for composers to produce natural-
sounding spectral evolutions. This in some cases
was caused by the lack of fi ne gestural control over
Computer Music Journal, 32:2, pag. 9–22, Estate 2008
© 2008 Istituto di Tecnologia del Massachussetts.
the sound and in others by the synthetic- sounding
quality of the generated spectra. These shortcom-
ings spurred software and hardware designers to
come up with new solutions for instrument control
and improvements to the basic FM method (Pala-
min, Palamin, and Ronveaux 1988; Tan and Gan
1993; Horner 1996). Nevertheless, these develop-
ments failed to stem the decline in the technique’s
use as increasingly more powerful hardware became
available.
Some of the limitations of gestural controllers
and of synthetic sound in FM can be addressed
together by the use of adaptive techniques, Quale
form an important subset of musical signal-
processing techniques (Verfaille and Arfi b 2002;
Verfaille, Zölzer, and Arfi b 2006). A key aspect of
their usefulness in music composition and perfor-
mance is that they provide a means to retain signifi –
cant gestural information contained in the original
signal. Therefore, these techniques seem to be well
suited to help develop more natural- sounding forms
of FM synthesis. With them, it might be possible to
obtain results that share much of the liveliness
perceived in musical signals of instrumental origin.
The traditional approach has been to treat synthe-
sis and control parameters separately, using some
means of mapping to control the process (Miranda
and Wanderley 2006; Wanderley and Depalle 2004).
This ultimately can lead to a split between gesture
and sonic result, especially in the case of FM, Dove
the mapping is often not clear or too coarsely de-
fi ned. Alternatively, one can approach the problem
from an adaptive point of view, whereby a signal is
both the source of control information (extracted
from it through different analysis processes) and the
input to the synthesis algorithm. Some pioneering
works in the area have proposed interesting appli-
cations of this principle in what has been called
audio- signal driven sound synthesis (Poepel 2004;
Poepel and Dannenberg 2005).
Lazzarini et al.
9
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
In the specifi c case of FM synthesis, it is possible
to use an arbitrary input signal in two ways, either
as a modulator or as a carrier. In the former case,
this signal is used to modulate the frequency of one
or more oscillators. When the input is anything but
a sinusoidal wave, this arrangement produces what
we normally describe as complex FM (Schottstaedt
1977). Although this setup, proposed by Poepel and
Dannenberg (2005), provides a richer means of
gestural control over the process, it does not seem
to capture well the original spectral characteristics
of interesting input sounds (such as the ones origi-
nating from instrumental sources). The spectral
evolutions allowed by the method still resemble the
more synthetic results typical of standard FM
synthesis, because the carrier is still a sine wave
oscillator. If we want to allow as much of the tim-
bral qualities of the input sound to affect the gener-
ated sound, we will get better results using the
input as a carrier signal.
Considering non- sinusoidal inputs, this case is
similar to multiple- carrier FM (Dodge and Jerse
1985). The techniques described in this article
implement this arrangement. Standard multiple-
carrier FM is defi ned by a single modulator being
used to vary the frequency of several sinusoidal
carriers. It has proved useful in a variety of applica-
zioni, including vocal synthesis (Chowning 1989)
and instrumental emulation via spectral matching
(Horner, Beauchamp, and Hakken 1993). By applying
the technique to real- world signals, it is possible to
generate transitions between natural- sounding and
synthesizer- like sounds. Depending on the levels of
modulation, we are able to reveal more or less of the
original timbral qualities of the input. This is the
basis for our technique of adaptive FM synthesis, O
AdFM (Lazzarini, Timoney, and Lysaght 2007).
To use an arbitrary input as a carrier, we must
develop some means of modulating the frequency
(O, to be more precise, the phase) of that signal.
This is required because we no longer use an oscilla-
tor to produce the sound, so we have no implicit
frequency control of the arbitrary signal. IL
following section addresses two different methods
of achieving this. We then discuss the implications
of using complex signals as carriers and details of
parameter extraction.
The Technique
The synthesis technique discussed here is based on
two elements: some means of phase modulation of
an input signal; and the use of an arbitrary, mono-
phonic, pitched or quasi- pitched input to which
parameter estimation will be applied. The phase
modulation effect can be achieved by two basic
metodi: through the use of a variable delay line or
by heterodyning.
Delay- Line Based Phase Modulation
A well- known side- effect of variable delays is the
phase modulation of the delay- line input (Dilsch
and Zölzer 1999). This is the basis for all classic
variable- delay effects such as fl anging, chorusing,
pitch shifting, and vibrato. The principle has also
been used in audio- rate modulation of waveguide
models (Van Duyne and Smith 1992). It is thus
possible to model simple (sinusoidal) audio- rate
phase modulation using a delay- line with a suitable
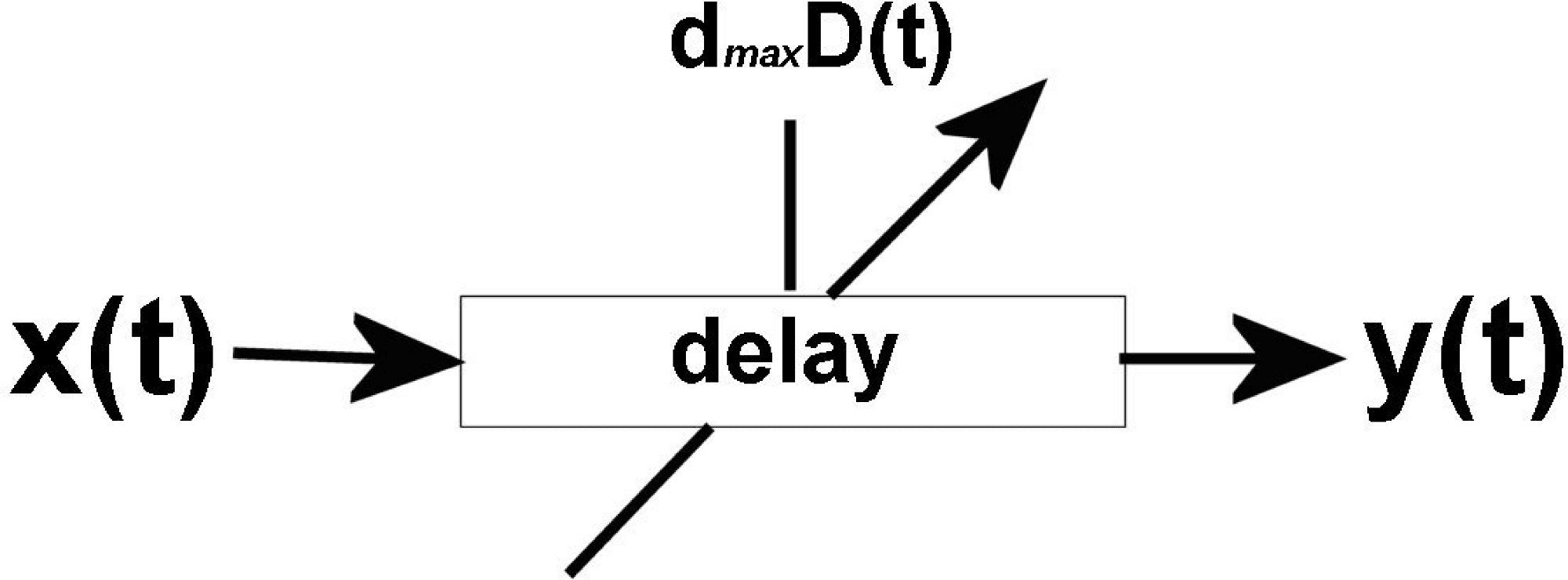
modulating function (Guarda la figura 1).
We now consider the case where the input to the
delay line is a sinusoidal signal of frequency fc:
(1)
X(T) = sin(2(cid:2)fct)
When the modulating source is s(T) = dmaxD(T),
where D(T) ∈{0 . . . 1} is an arbitrary function, and dmax
is the maximum delay, the delay- line phase modu-
lation of Equation 1 can be defi ned (with ω = 2πfc) COME
sì(T) = sin((cid:3)[t − dmaxD(T)])
(2)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
The instantaneous radian frequency ω
io(T) of such a
phase- modulated signal can be estimated from the
derivative of the phase angle θ(T):
(cid:3)
io(T) =
∂(cid:4)(T)
∂t
=
∂(cid:3)[t − dmaxD(T)]
∂t
= (cid:3) −
∂D(T)
∂t
dmax
(cid:3)
(3)
and the instantaneous frequency IF(T) in Hz can be
defi ned as
I F(T) = fc
−
∂D(T)
∂t
dmax
(4)
10
Computer Music Journal
Figura 1. Delay- line based
phase modulation.
Considering the case where the modulating signal
is a scaled raised cosine (cioè., a periodically repeating
Hanning window), we have
D(T) = 0.5cos(2(cid:2)fmt) + 0.5
(5)
E, by substituting D(T) in Equation 4, IF(T) is now
IF(T) = (cid:2)fm sin(2(cid:2)fmt)dmaxfc
+ fc
(6)
which characterizes the instantaneous frequency in
sinusoidal phase modulation. In such an arrange-
ment, the sinusoidal term in Equation 6 is known
as the frequency deviation, whose maximum
absolute value DEVmax is
DEVmax
= (cid:5)d × (cid:2)fmfc
(7)
with Δ d = dmax – dmin.
Now, turning to FM theory, we characterize the
index of modulation I as the ratio of the maximum
deviation and the modulation frequency:
I = DEVmax
fm
=
(cid:5)D(cid:2)fmfc
fm
= (cid:5)D(cid:2)fc
(8)
The Δ d that should apply as the amplitude of our
sinusoidal modulating signal can now be put in
terms of the index of modulation
sì(T) = J 0(IO)sin((cid:3)
ct)+
IO +1
∑
k =1
J k(IO)sin((cid:3)
ct + k(cid:3)
mt)+ J − k(IO)sin((cid:3)
ct − k(cid:3)
mt)
(11)
where ω
of the fi rst kind of order k, E
c = 2πfc, ω
m = 2πfm, Jk(IO) are Bessel functions
J − k(IO) = (−1)kJ k(IO)
(12)
Note that to match the phases as closely as pos-
sible to Equation 11, we require an offset of π / 2 + 2IO
in the input sinusoid and π / 2 in the modulator (both
in relation to cosine phase). Because the carrier
phase depends on the index of modulation in gen-
eral, we only rarely achieve an exact match. Così,
in delay- line phase modulation, we need not be too
concerned with phase offsets.
Interestingly enough, in the delay- line formula-
tion of FM / PM, the index of modulation for a given
variable delay- width is proportional to the carrier-
signal frequency (as seen in Equation 9). Questo
situation does not arise in classic FM. Also, Quando
considering the width of variable delay for a given
value of I, we see that it gets smaller as the frequency
rises. In a digital system, for I = 1, the width will be
less than one sample at the Nyquist frequency.
Phase Modulation Through Heterodyning
The second method proposed here is based on a
simple re- working of the PM formula. We begin by
proposing the following synthetic signal, where I is
the index of modulation and ω
m is the radian modu-
lation frequency (ω
m = 2πfm):
sì(T) = x(T)cos(I sin((cid:3)
mt))
(13)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
(cid:5)d = I
(cid:2)fc
and the modulating signal is now
(9)
Using a sinusoid described in Equation 1 as our input
signal x(T), we obtain, by manipulating the expres-
sion, the following combination of PM signals:
D(T) = I
(cid:2)fc
0.5cos(2(cid:2)fmt) + 0.5
⎦
(10)
The resulting spectrum according to FM theory is
dependent on the values of both I and the carrier- A-
modulator (C:M) frequency ratio:
sì(T) = sin((cid:3)
ct)cos(I sin((cid:3)
ct + I sin((cid:3)
C,(cid:3)
mt))
mt)) + sin((cid:3)
C,−(cid:3)
M, IO,T) + PM((cid:3)
= 0.5[sin((cid:3)
= 0.5[PM((cid:3)
ct − I sin((cid:3)
M, IO,T)]
mt))]
(14)
where the PM signal is defi ned as
Lazzarini et al.
11
⎡
⎣
⎤
PM(C,M,IO,T) = sin(ct + I sin(mt))
(15)
By inspecting Equation 11 , it is clear that this
formulation, based on the mixing of two PM sig-
nals, will lead to the cancellation of certain compo-
nents in the output signal, namely the ones where k
is odd (called in FM theory the odd sidebands).
The signifi cance of this and the previous imple-
mentations of PM can be fully appreciated only
once we move from using sinusoidal inputs to
arbitrary signals. This will allow us to develop the
synthesis designs we propose in this work.
Using Arbitrary Input Signals
We will now examine the results of applying
arbitrary input signals to both formulations just
described, beginning with the delay- line based PM.
In Equation 11, we see the ordinary spectrum of
simple FM. Tuttavia, for our present purposes, we
will assume the input x(T) to be a complex arbitrary
signal made up of N sinusoidal partials of ampli-
tudes an , radian frequencies ω
N,
originating, for instance, from instrumental sources:
N, and phase offsets φ
X(T) =
N −1
∑
n= 0
an sin((cid:3)
nt + (cid:6)
N)
(16)
The resulting phase- modulated output is equiva-
lent to what is normally called multiple- carrier FM
synthesis, because the carrier signal is now com-
plex. This output y(T) can be described as
sì(T) =
N −1
∑
n= 0
an sin((cid:3)
nt + In sin((cid:3)
mt) + (cid:6)
N)
(17)
where ω
m is the modulation frequency and In is the
index of modulation for each partial. According to
Equazione 11, this would be equivalent to the follow-
ing signal:
In
= (cid:5)D(cid:2)fn
= I
(cid:2)fc
(cid:2)fn
= I
fn
fc
(19)
Again, we see here that the effect of the relation-
ship between the index of modulation and the carrier
frequency is that higher- frequency partials will be
modulated more intensely than lower ones. Depend-
ing on the bandwidth and richness of the input sig-
nal, it is quite easy to generate very complex spectra,
which might be objectionable in some cases. Questo
increase in brightness has also been observed in
other applications of audio- rate mod ulation of delay
lines (Välimäki, Tolonen, and Karjalainen 1998;
Tolonen, Välimäki, and Karjalainen 2000).
Turning now to the second technique introduced
herein, we will have a signifi cantly different output,
described by
sì(T) = 0.5
N −1
∑
n= 0
an sin((cid:3)
nt + I sin((cid:3)
mt) + (cid:6)
N)
+
N −1
∑
n= 0
an sin((cid:3)
nt + I sin(−(cid:3)
mt) + (cid:6)
N)
(20)
The most important differences between the spec-
trum of this signal and that described by Equation
18 are that odd sidebands are now canceled, and the
index of modulation I is now constant across the
modulated carrier components. Whereas the former
is responsible for an overall timbral difference
between the two spectra, the latter is responsible for
a more controlled and subtle handling of high
frequencies.
Another key aspect of the proposed methods is
that the c:m ratio parameter can also be taken
advantage of by estimating the fundamental fre-
quency of the input signal (assumed to be mono-
phonic). In questo caso, a variety of different spectral
combinations can be produced, from inharmonic to
harmonic and quasi- harmonic.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
sì(T) =
N −1
∑
n= 0
an
IO +1
∑
k =1
J 0(In)sin((cid:3)
J k(In)sin((cid:3)
J − k(In)sin((cid:3)
nt + (cid:6)
nt + k(cid:3)
nt − k(cid:3)
N) +
mt + (cid:6)
mt + (cid:6)
N) +
N)
The different indices of modulation for each compo-
nent of the carrier signal can be estimated by the
following relationship, derived from Equation 9:
Fundamental Frequency Estimation
(18)
To allow for a full control of c:m ratio and modula-
tion index, it is necessary to estimate the funda-
mental frequency of the carrier signal. That will
allow the modulator signal frequency and ampli-
tude to be set according to Equation 10. This can be
12
Computer Music Journal
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
achieved with the use of a pitch tracker, which is a
standard component of many modern music
signal- processing systems. For the current imple-
mentation, a spectral- analysis pitch- tracking
method was devised, based on an algorithm by
Puckette, Apel, and Ziccarelli (1998) and Puckette
and Brown (1998), that provides fi ne accuracy of
fundamental- frequency estimation. In addition to
tracking the pitch, it is also useful (but not essen-
tial) to obtain the amplitude of the input signal,
which can be used in certain applications to scale
the index of modulation. This is also provided by
our parameter- estimation method.
Signal Bandwidth
Although the spectrum of FM is, in practical terms,
band- limited, it is capable of producing very high
frequencies, as seen in Equations 11 E 18. Con
digital signals, this can lead to aliasing problems if
the bandwidth of the signal exceeds the Nyquist
frequency. The fact that in the delay- based formula-
tion the index of modulation increases with fre-
quency for a given Δ d (Equazione 19) is obviously
problematic. Tuttavia, in practice, the kind of input
signals we will be employing generally exhibit a
spectral envelope that decays with frequency. In
this case, objectionable aliasing problems might be
greatly minimized, given that an in Equation 18 for
higher values of n will be close to zero. Ovviamente, if
our input contains much energy in the higher end of
the spectrum, such as for instance an impulse train,
then aliasing will surely occur.
The simplest solution for such problematic signals
is to impose a decaying spectral envelope using a
fi l ter. This will have the obvious side- effect of modi-
fying the timbre of the input signal. Another, more
computationally costly, solution is to oversample
the input signal. This would either remove the
aliased signals or place them at an inaudible range.
Implementation
We now present a reference implementation of
AdFM using both methods of phase modulation
Figura 2. Delay- line based
AdFM design: (UN) original;
(B) with the optional low-
pass fi lter.
(UN)
(B)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
described herein. These two instrument designs can
serve as the basis for further software- or hardware-
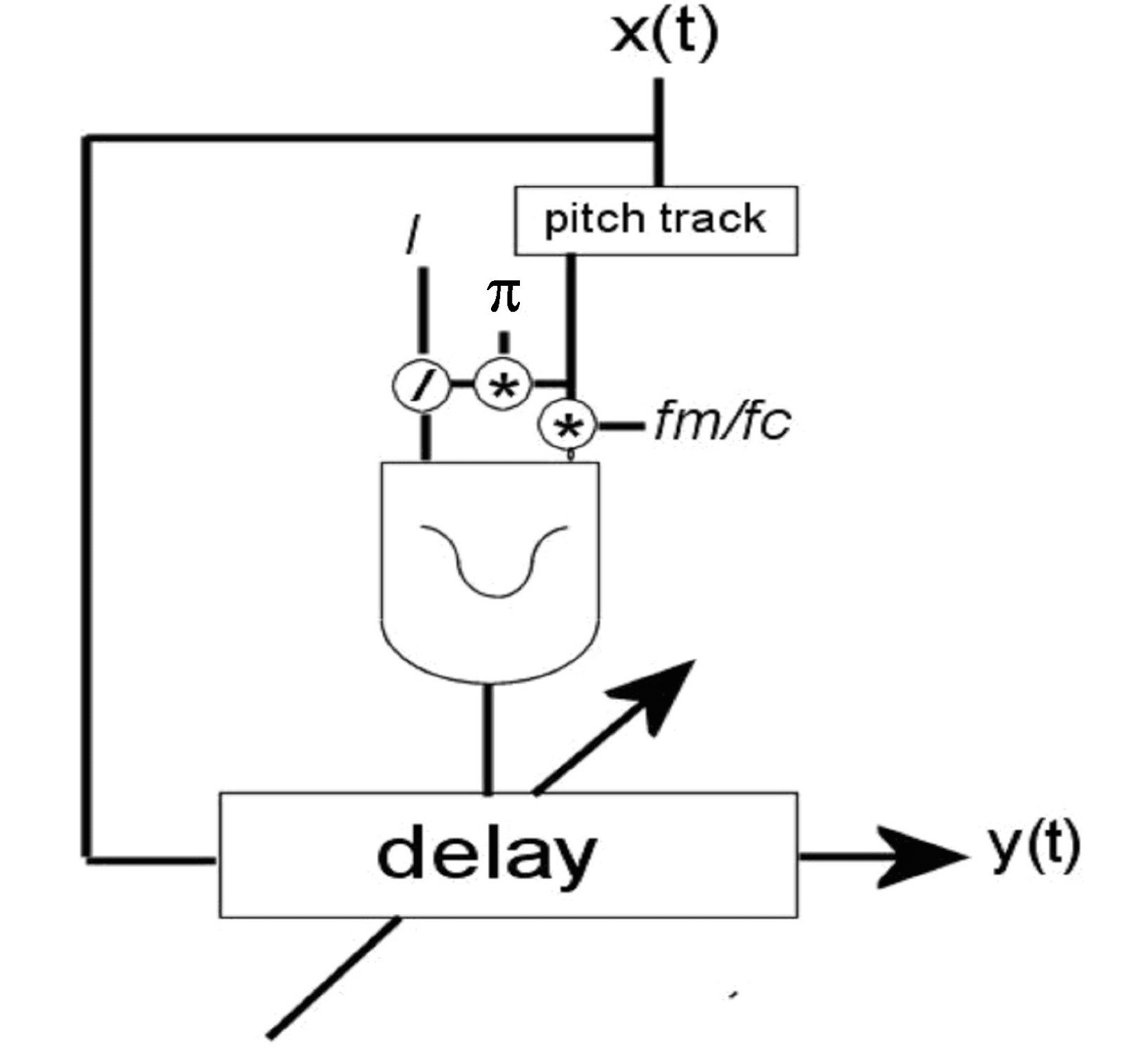
based implementations. The basic fl ow chart of the
delay- based PM instrument is shown in Figure 2a.
There are three basic components: a pitch tracker, UN
modulating source (a table- lookup oscillator), and a
variable delay line with interpolated readout. Each
of these components is found in modern music
signal- processing systems, so the technique is
highly portable. The implementation discussed here
uses Csound 5 (ffi tch 2005) as the synthesis engine,
but similar instruments can be developed under
other musical signal- processing environments,
Lazzarini et al.
13
Figura 3. Delay- based
AdFM code.
Figura 4. The heterodyning
AdFM design.
Figura 5. Heterodyning
AdFM Csound code.
Figura 4
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
such as the SndObj library and PySndObj (Lazza-
rini 2000, 2007). It is important to note that this
design can be used either for real- time or off- line
applications. Inoltre, plug- ins can be easily
developed from it using csLadspa (Lazzarini and
Walsh 2007).
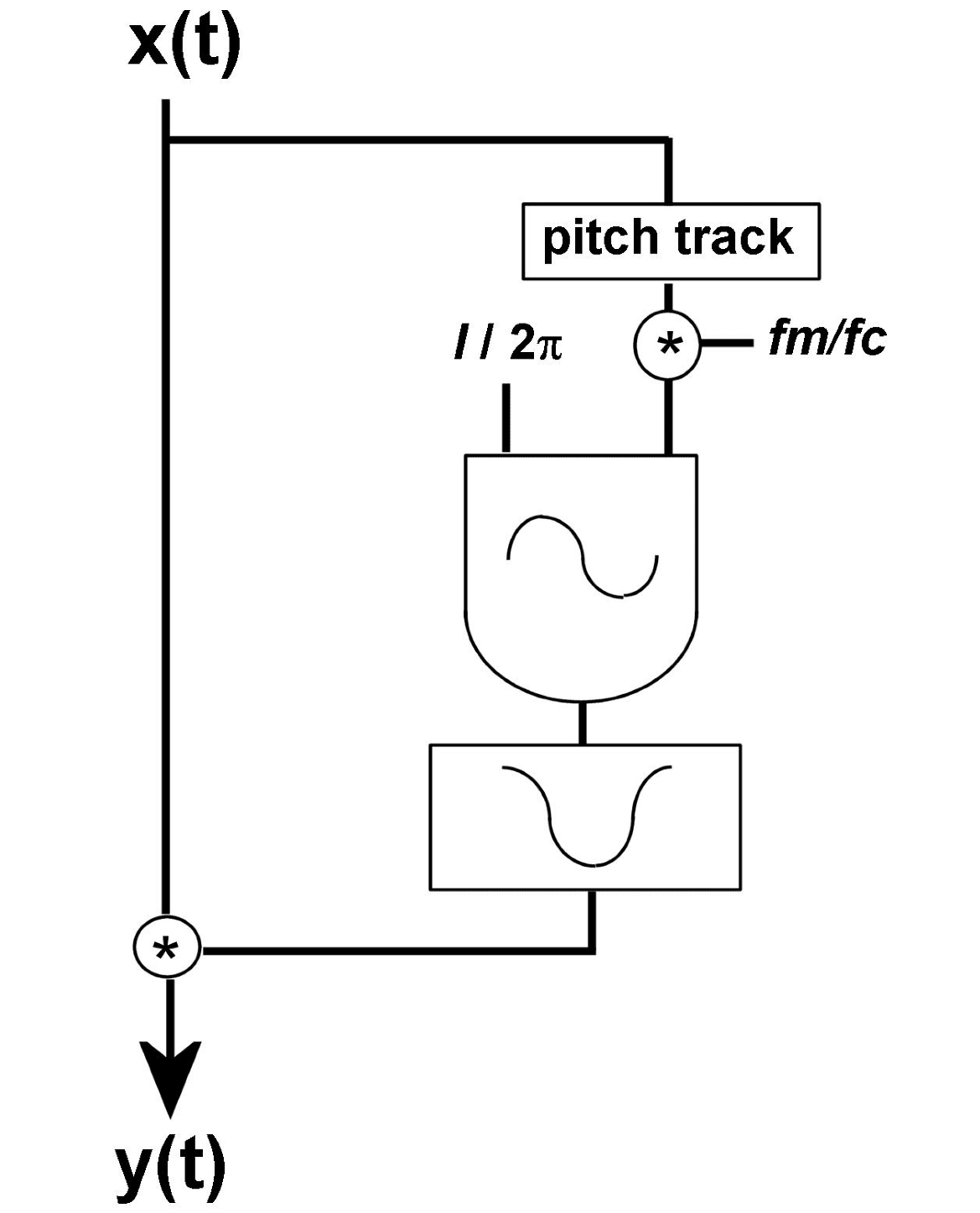
The equivalent Csound 5 code for the fl owchart
design in Figure 2, which implements the delay-
based version, is shown in Figure 3. The heterodyn-
ing PM design is simpler, based on a more or less
straight translation of the formula in Equation 13.
Its fl owchart is shown in Figure 4 and the corre-
sponding Csound code in Figure 5.
Both implementations use a spectral- analysis
pitch- tracking opcode (ptrack) written by the
authors and linear interpolation oscillators to
generate the modulation signal. The DFM opcode
uses a cubic- interpolation variable delay line
(Laakso et al. 1996). Owing to the use of cubic
interpolation, the minimum delay is set to two
Figura 5
samples to avoid errors in the circular- buffer
readout.
A number of variations can be made to the basic
progetto. For instance, the amplitude of the signal,
which is produced together with the pitch- tracking
informazione, can be used to scale the index of
modulation. This can be used to generate typical
14
Computer Music Journal
Figura 6. Steady- state spec-
trum of a fl ute playing C4.
brass- like synthesizer tones (Risset 1969), dove il
brightness of the synthetic output is linked to the
amplitude evolution of the input sound. Alterna-
tively, it can be used to determine the c:m ratio.
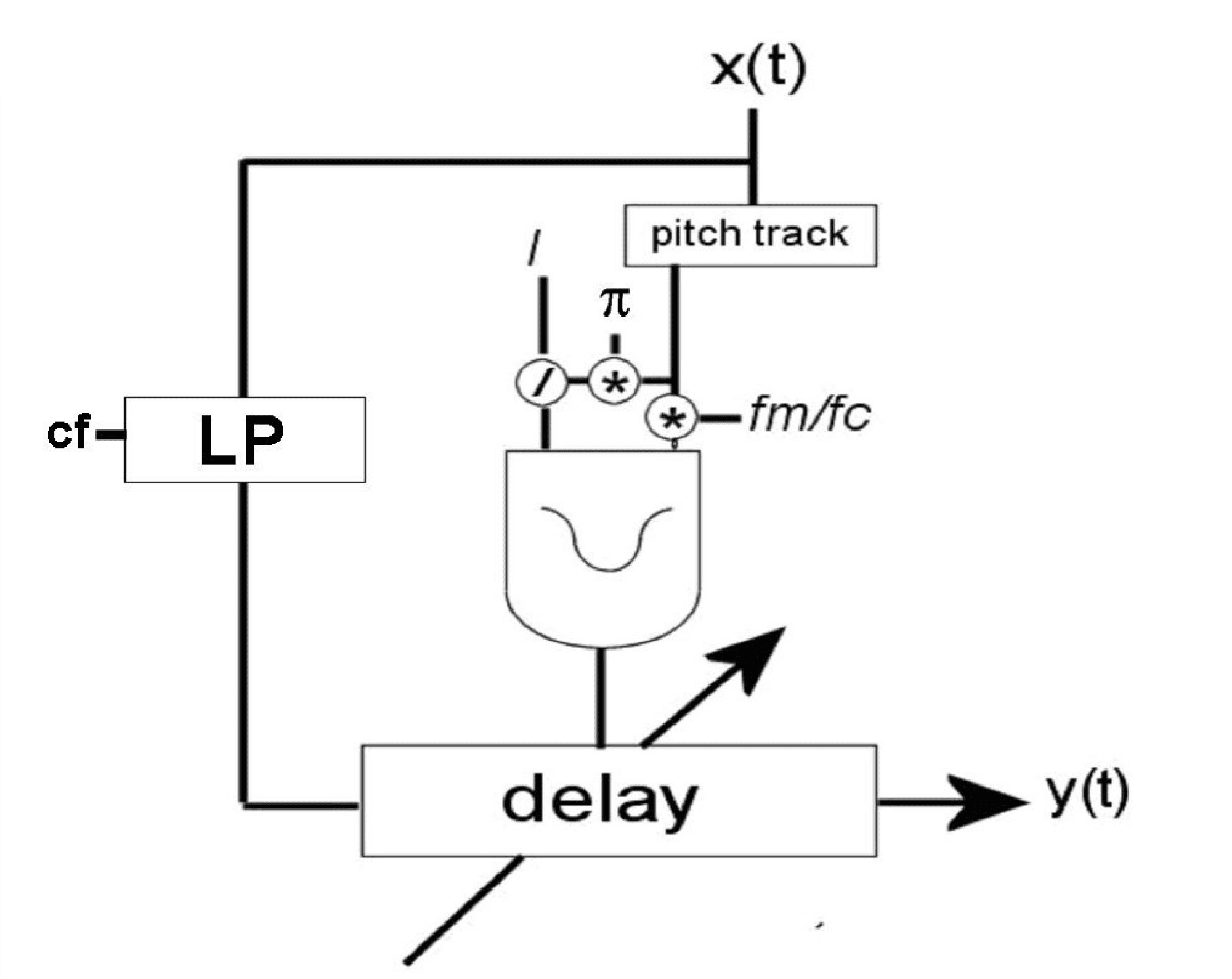
Depending on the characteristics of the input
signal, it might be useful to include a low- pass fi lter
before the signal is sent to the AdFM processors,
especially in the delay- based- version, as shown in
Figure 2b. The cutoff frequency of the low- pass
fi lter can also be controlled by the estimated input
amplitude. As discussed earlier, this will reduce
aliasing as well as overall brightness, both of which
are sometimes a downside of FM synthesis.
Examples and Discussion
Four different types of carrier signals were chosen as
a way of examining the qualities of the AdFM
synthetic signal using both methods described in
Questo articolo. A fl ute input with its spectral energy
concentrated in the lower harmonics is a prime
candidate for experimentation. The clarinet was
chosen for its basic quality of having more promi-
nent odd harmonics. Finalmente, the piano and voice
were used as a means of exploring the possibilities
of synthesizing different types of harmonic and
inharmonic spectra by the use of various c:m ratios.
The sound examples discussed here will be found
on the annual Computer Music Journal DVD (to be
released with the Winter 2008 issue).
Flute Input
The original steady- state fl ute spectrum, effettivamente
with I = 0, is shown in Figure 6. As clearly seen in
that fi gure, it features quite prominent lower har-
monics. Using delay- line AdFM and applying an
index of modulation of 0.3 on a 1:1 C:m confi gura-
zione, we can start enriching the spectrum with
higher harmonics (Guarda la figura 7). At these low values
of I, there is already a considerable addition of com-
ponents between 5 E 10 kHz. The overall spectral
envelope still preserves its original decaying shape.
Using the delay line method with higher values of
IO, we can see a dramatic change in the timbral
characteristics of the original fl ute sound. Figura 8
shows the resulting spectrum, now with I = 1.5.
Here, we can see that components are now spread to
the entire frequency range. The original decaying
spectral envelope is distorted into a much more
gradual shape, and the difference between the
loudest and the softest harmonic is only about 30
dB. The resulting sound can been described as
“string- like,” and the transition between the fl ute
Lazzarini et al.
15
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 7. AdFM spectrum
using a fl ute C4 signal as
carrier with c:m = 1 E
I = 0.3.
Figura 8. AdFM spectrum
using same input as Figure
3, but now with I = 1.5.
Figura 7
Figura 8
and AdFM spectra is capable of providing interest-
ing possibilities for musical expression. Also, it is
important to note that important gestural charac-
teristics of the original sound, such as pitch fl uctua-
zioni, vibrato, and articulation, are preserved in the
synthetic output.
As I gets higher, the spectrum gets even brighter,
but the problems with aliasing start to become
signifi cant. To prevent this and also to allow for a
different spectral envelope, an optional low- pass
fi ltering of the input signal is suggested. In that
case, the fi lter is inserted in the signal path at the
16
Computer Music Journal
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 9. Heterodyning
AdFM synthesis using a
fl ute input with I = 5 E
C:m = 1.
delay- line input. A Butterworth low- pass fi lter with
a cutoff frequency between 1,000 E 5,000 Hz has
proven useful. It is possible to couple the cutoff
frequency with I, so that for higher values of that
parameter, more fi ltering is applied.
The addition of higher harmonics is signifi cantly
reduced in the heterodyning AdFM method. We can
see in Figure 9 how much more attenuated the top
end of the spectrum is in comparison to the pre-
vious technique. This in some cases might be
advantageous; Tuttavia, the effect of the technique
is subtler, resulting in a transition between natural-
sounding and synthesizer- like spectra that is less
dramatic.
tially. In delay- line AdFM with I = 1.5, it is possible
to see that there is very little difference between the
strengths of odd and even components (Guarda la figura 11).
Inoltre, higher- order harmonics become more
present, and the spectral envelope levels out, owing
to the well- known spread of energy that is charac-
teristic of FM synthesis.
The heterodyning method also provides similar
transformations, although again with more subtle
high- frequency results, and still retaining some of
the odd / even balance of the input. Figura 12 demon-
strates that the resulting spectrum features a decay-
ing envelope, in contrast to the previous example
(Guarda la figura 11), which is much fl atter.
Clarinet Input
Piano Input
Our second experiment used a clarinet signal as a
carrier wave for AdFM. The clarinet exhibits a
steady- state spectrum in which the lower- order
even harmonics are signifi cantly less energetic than
their odd neighbors (Guarda la figura 10). Di conseguenza, IL
multiple- carrier- like characteristic of AdFM helps
generate quite a change in the spectra of that
instrument.
As the index of modulation increases, the balance
between odd an even harmonics changes substan-
In the previous examples, we have kept the ratio
between the modulating frequency and carrier fun-
damental at unity. Tuttavia, as we know from FM
theory, a range of different spectra is possible if we
use different ratios. It is possible to create a range of
effects that range from changing the fundamental of
the sound to transforming a harmonic spectrum
into an inharmonic one. We took a piano C2 signal
as our carrier and then tuned our modulator to 1.41
times that frequency. The original piano spectrum
Lazzarini et al.
17
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 10. Detail of
steady- state spectrum of
clarinet C3. Note the
higher relative strength of
inferiore- order odd harmonics
versus even ones.
Figura 11. Detail of AdFM
spectrum using a clarinet
C3 signal as carrier with
C:m = 1 and I = 1.5. Odd
and even harmonics now
have comparable strengths.
Figura 10
Figura 11
is shown in Figure 13, where we can clearly see its
harmonics.
The resulting delay- line AdFM spectrum with
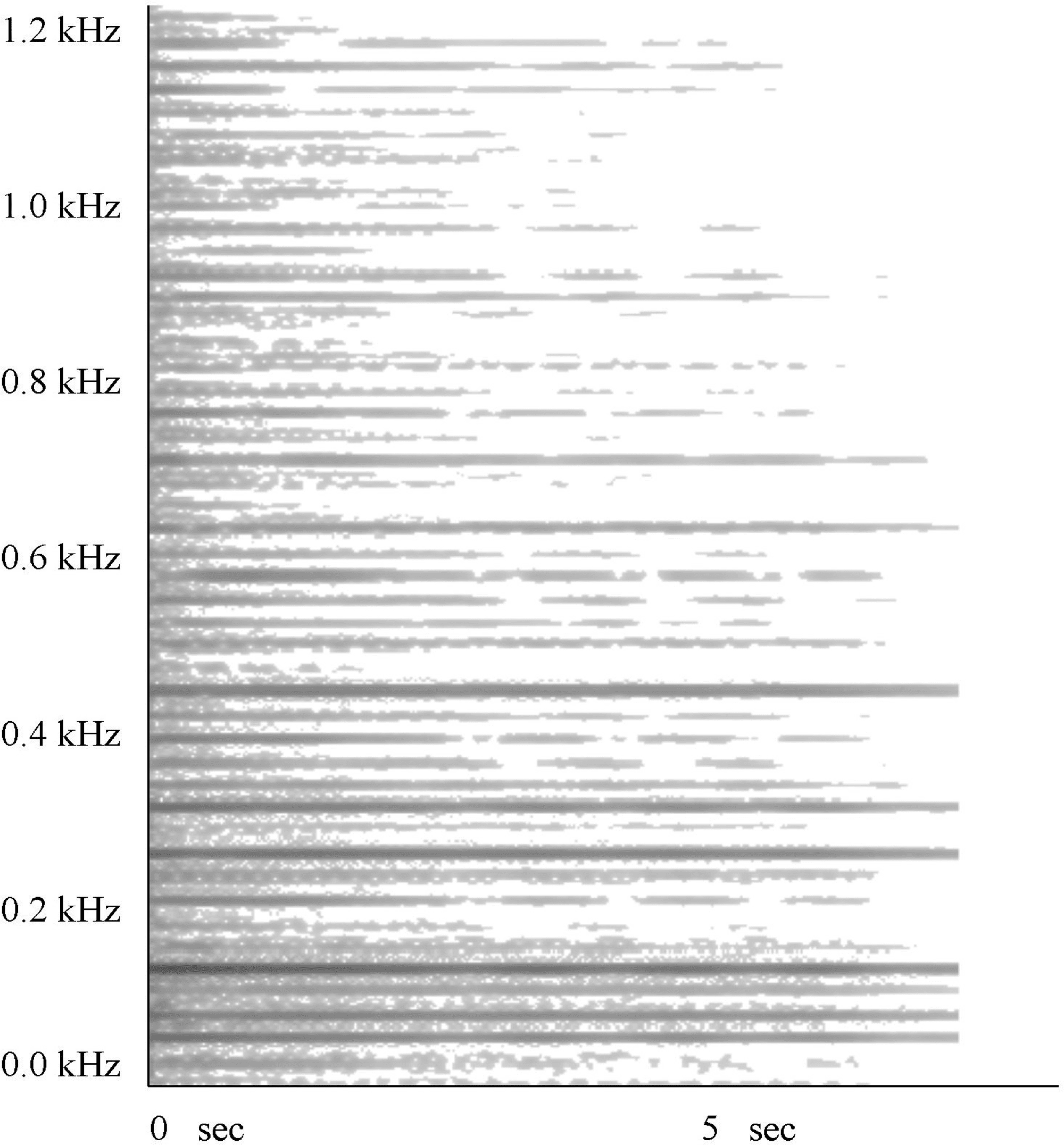
I = 0.15 is shown in Figure 14. This particular ratio
creates a great number of components whose rela-
tionship implies a very low fundamental, così
generating what is perceived as an inharmonic
spectrum. With the 1:1 ratio, the sums and differ-
ences between fc and fm created components whose
frequencies were mostly coincident. Here, a variety
of discrete components will be generated, creating
the denser spectrum seen in Figure 14. The AdFM
18
Computer Music Journal
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 12. Steady- state
spectrum of clarinet- input
heterodyning AdFM, con
I = 5 and c:m = 1.
Figura 13. Spectrogram of a
piano C2 tone, showing its
fi rst harmonics in the
0–1.2 kHz range.
Figura 14. Spectrogram of
an AdFM sound using a
piano C2 signal as carrier,
with c:m = 1:1.41 and I =
0.15, showing the 0–1.2
kHz range. The resulting
inharmonic spectrum,
with a large number of
components, is clearly
seen in comparison with
Figura 13.
Figura 12
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 13
Figura 14
Lazzarini et al.
19
Figura 15. Comparison of
spectral snapshots of a
vocal and an AdFM vocal
sounds, with I = 0.1 E
C:m = 2.
sound resulting from this arrangement has been
described as “bell- like.” Transitions between piano
and bell sounds can be effected by changing I from 0
to the desired value. The application of a low- pass
fi lter at the delay- line input will also allow for some
variety and control over the brightness of the result.
Again, if we apply the heterodyning technique
instead to this input using a similar ratio, we will
obtain a bell- like output that is better behaved in
the higher end of the spectrum. Here the second
method might in fact be more useful, as it can
control the quality of the output more effectively.
Voice Input
A vocal input was used as the fourth different
source examined in this work, demonstrating a
pitch- shift effect. Setting the fc:fm ratio to 2, we are
able to obtain a sound that is now half the pitch of
the original. This is due to the introduction of a
component at half the fundamental frequency
corresponding to fc – fm in Equation 18.
With the index of modulation at low values
(around 0.15), it is possible to preserve some of the
spectral shape of the original sound, a crucial step in
keeping the intelligibility of the vocal phonemes.
Although there is some addition of high- frequency
components and a fl attening of spectral peaks, IL
AdFM voice is still perfectly intelligible.
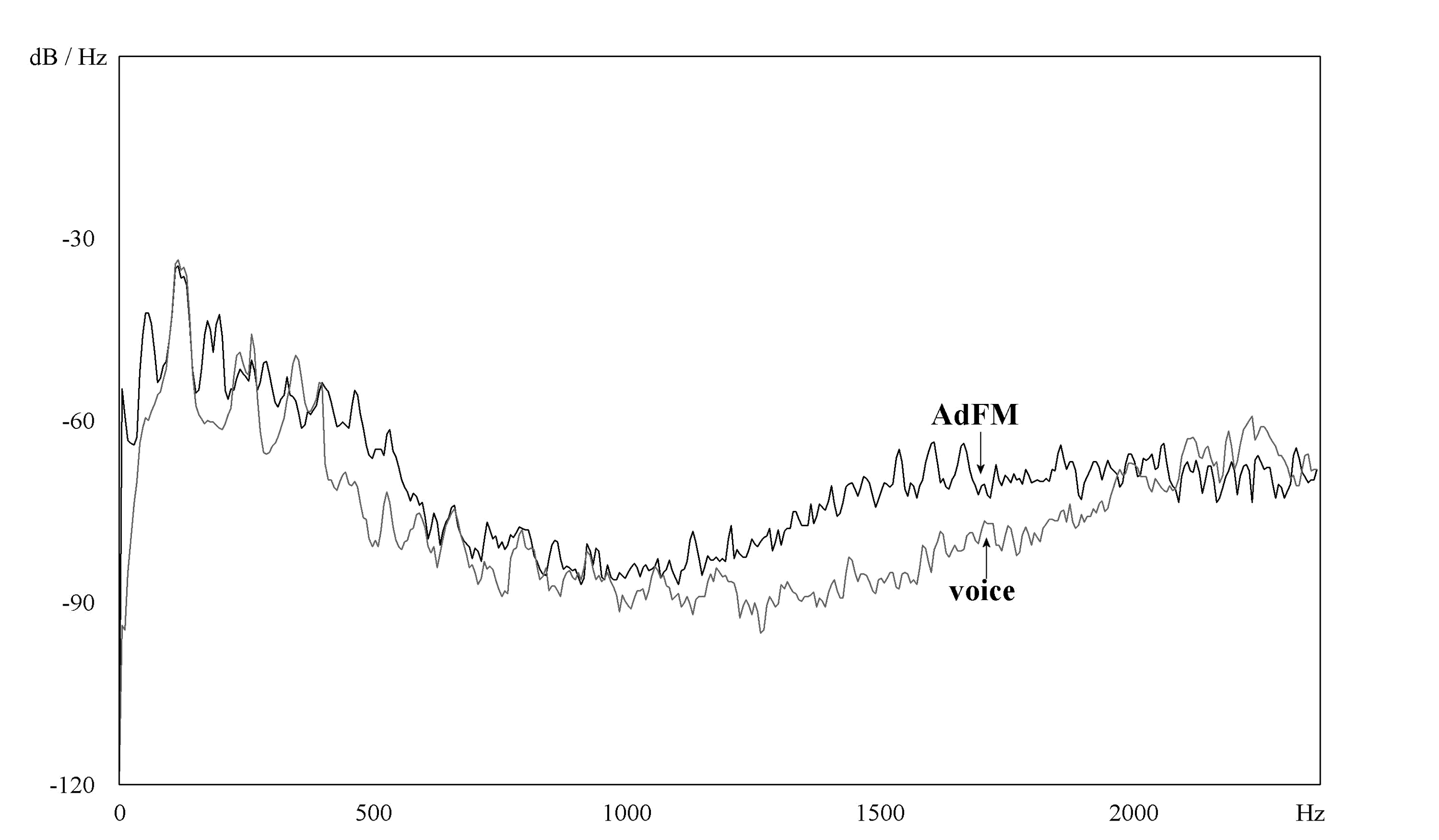
Figura 15 shows a comparison between a vowel
steady- state spectrum and its AdFM- processed
counterpart. The sub- harmonic peak can be seen
at the left of the picture below the original funda-
mental. (A peak at 0 Hz is also present, owing to the
fc – 2fm component.) The recording of the phrase,
“This is AdFM Synthesis,” is shown as a spectro-
gram in Figure 16, both as the original signal (left)
and the AdFM output (right), using the same param-
eters as in the previous example. Again, the octave
change is clearly seen, as well as the increase in the
number of signifi cant components in the signal.
Generalmente, we achieved better results using the
delay- line method with vocal inputs. The hetero-
dyning process seems to be too prone to artifacts
generated by unvoiced phonemes, resulting in
chirps and glitches. Although these are originally
caused by the pitch- tracking mechanism, Essi
are emphasized by certain characteristics of the
method’s implementation.
Conclusione
We presented an alternative approach to the classic
technique of FM synthesis, based on an adaptive
20
Computer Music Journal
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 16. Detail of spectro-
gram of a recording of the
phrase, “This is AdFM
synthesis,” with the origi-
nal vocal sound on the left
and the AdFM vocal on the
right
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
progetto, which we call AdFM. Two different methods
were proposed as a means of modulating an arbi-
trary carrier signal. As the FM synthesis theory is
well known, it was possible to adapt it to determine
the precise characteristics of the output signal. Con
this technique, it is possible to achieve fi ne control
over the synthetic result, which also preserves a
substantial amount of the gestural information in
the original signal. Four different types of carrier
signals were used in this work to demonstrate the
wide range of spectra that the technique can gener-
ate. We are confi dent this is a simple yet effective
way of creating hybrid natural- synthetic sounds for
musical applications.
Future prospects for research into AdFM involve
the development of alternative implementations of
the technique, both in terms of time- domain
variations of the methods discussed here and new
frequency- domain processes. The latter have been
facilitated by the development of the Sliding Phase
Vocoder (SPV; Bradford, Dobson, and ffi tch 2007),
which allows for audio- rate modulation of its
parameters. It is our plan to develop a spectral
version of AdFM in Csound, as SPV analysis / syn-
thesis and audio- rate frequency scaling have been
added to the language in version 5.07.
Riferimenti
Bradford, R., R. Dobson, and J. ffi tch. 2007. "IL
Sliding Phase Vocoder.” Proceedings of the 2007
International Computer Music Conference. San
Francesco: International Computer Music Association,
pag. 449–452.
Chowning, J. 1973. “The Synthesis of Complex Audio
Spectra by Means of Frequency Modulation.” Journal of
the Audio Engineering Society 21:526–534.
Chowning, J. 1989. “Frequency Modulation Synthesis
of the Singing Voice.” In M. Mathews and J. R. Pierce,
eds., Current Directions in Computer Music Research.
Cambridge, Massachusetts: CON Premere, pag. 57–63.
Dilsch, S., and U. Zölzer. 1999. “Modulation And Delay
Line Based Digital Audio Effects.” Proceedings of the
2nd Conference on Digital Audio Effects. Trondheim:
Lazzarini et al.
21
Norwegian University of Science and Technology,
pag. 5–8.
Dodge, C., and T. Jerse. 1985. Computer Music. Nuovo
York: Schirmer Books.
ffi tch, J. 2005. “On the Design of Csound5.” Proceed-
Puckette, M., T. Apel, and D. Ziccarelli. 1998. “Real-
Time Audio Analysis Tools for PD and MSP.” Pro-
ceedings of the 1998 International Computer Music
Conferenza. San Francisco: International Computer
Music Association, pag. 109–112.
ings of the 3rd International Linux Audio Conference.
Karlsruhe: Zentrum für Künst und Medientechnologie,
pag. 37–42.
Puckette, M., and J. Brown. 1998. “Accuracy of Frequency
Estimates from the Phase Vocoder.” IEEE Transactions
on Speech and Audio Processing 6(2):116–172.
Horner, UN. 1996. “Double- Modulator FM Matching
of Instrument Tones.” Computer Music Journal
20(2):57–71.
Risset, J. C. 1969. An Introductory Catalogue of Com-
puter Synthesized Sounds. Murray Hill, New Jersey:
AT&T Bell Laboratories.
Horner, A., J. Beauchamp, and L. Hakken. 1993. “Ma-
Schottstaedt, W. 1977. “The Simulation of Natural Instru-
chine Tongues XVI: Genetic Algorithm and Their Ap-
plication to FM Synthesis.” Computer Music Journal
17(4):17–29.
Laakso, T. I., et al. 1996. “Splitting the Unit Delay: Tools
for Fractional Delay Filter Design.” IEEE Signal Pro-
cessing Magazine 13(1):30–60.
ment Tones Using a Complex Modulating Wave.”
Computer Music Journal 1(4):46–50.
Tan, B. J. , and S. l. Gan. 1993. “Real- Time Implementa-
tion of Asymmetrical Frequency- Modulation Syn-
thesis.” Journal of the Audio Engineering Society
41(5):357–363.
Lazzarini, V. 2000. “The Sound Object Library.” Or-
Tolonen, T., V. Välimäki, and M. Karjalainen. 2000.
ganised Sound 5(1):35–49.
Lazzarini, V. 2007. “Musical Signal Scripting with
PySndObj.” Proceedings of the 5th International Linux
Audio Conference. Berlin: Technische Universität
Berlin, pag. 18–23.
Lazzarini, V., J. Timoney, and T. Lysaght. 2007. “Adaptive
FM Synthesis.” Proceedings of the 10th International
Conference on Digital Audio Effects. Bordeaux: Univer-
sity of Bordeaux, pag. 21–26.
Lazzarini, V., and R. Walsh. 2007. “Developing LADSPA
Plugins with Csound.” Proceedings of the 5th Inter-
national Linux Audio Conference. Berlin: Technische
Universität Berlin, pag. 30–36.
Miranda, E., and M. Wanderley. 2006. New Digital Musi-
cal Instruments. Middleton, Wisconsin: UN- R Editions.
Palamin, J.P., P. Palamin, e A. Ronveaux. 1988. "UN
Method of Generating and Controlling Musical Asym-
metric Spectra.” Journal of the Audio Engineering
Società 36(9):671–685.
Poepel, C. 2004. “Synthesized Strings for String Players.”
Proceedings of 2004 Conference on New Instruments
for Musical Expression. New York: Associazione per
Computing Machinery, pag. 150–153.
Poepel, C., and R. Dannenberg. 2005. “Audio Signal
Driven Sound Synthesis.” Proceedings of the 2005
International Computer Music Conference. Barce-
lona: International Computer Music Association,
pag. 391–394.
“Modeling of Tension Modulation Nonlinearity in
Plucked Strings.” IEEE Transactions on Speech and
Audio Processing 8(3):300–310.
Välimäki, V., T. Tolonen, and M. Karjalainen. 1998.
“Signal- Dependent Nonlinearities for Physical Models
Using Time- Varying Fractional Delay Filters.” Proceed-
ings of the 1998 International Computer Music Confer-
ence. San Francisco: International Computer Music
Association, pag. 264–267.
Van Duyne, S. A., and J. O. Smith. 1992. “Implementa-
tion of a Variable Pick- Up Point on a Waveguide String
Model with FM / AM applications.” Proceedings of the
1992 International Computer Music Conference. San
Francesco: International Computer Music Association,
pag. 154–157.
Verfaille, V., and D. Arfi b. 2002. “Implementation Strate-
gies for Adaptive Digital Effects.” Proceedings of the
5th Conference on Digital Audio Effects. Hamburg:
University of the Federal Armed Forces, pag. 21–26.
Verfaille, V., U. Zölzer, and D. Arfi b. 2006. “Adaptive
Digital Audio Effects (UN- DAFx): A New Class of Sound
Transformations.” IEEE Transactions on Audio, Speech
and Language Processing 14(5):1817–1831.
Wanderley, M. M., and P. Depalle. 2004. “Gestural
Control of Sound Synthesis.” Proceedings of the IEEE
92(4):632–644.
22
Computer Music Journal
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
C
o
M
j
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
3
2
2
9
1
8
5
5
1
3
1
/
C
o
M
j
.
.
2
0
0
8
3
2
2
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3