Using the XCS Classifier System
for Multi-objective Reinforcement
Learning Problems
Abstract We investigate the performance of a learning classifier
system in some simple multi-objective, multi-step maze problems,
using both random and biased action-selection policies for
exploration. Results show that the choice of action-selection
policy can significantly affect the performance of the system in
such environments. Further, this effect is directly related to
population size, and we relate this finding to recent theoretical
studies of learning classifier systems in single-step problems.
Matthew Studley
Larry Bull
Faculty of Computing, Engineering
and Mathematics
University of the West of England
Bristol BS16 1QY, UK
matthew2.studley@uwe.ac.uk
larry.bull@uwe.ac.uk
Keywords
Action selection, autonomous agents,
genetic algorithm, population size
1 introduzione
All living organisms exhibit homeostasis. While the external environment changes constantly, Essi
are able to maintain a relatively constant internal environment; when their ability to do so is
compromised, death may swiftly follow. In order to maintain this stability, they must balance many
conflicting goals or desires, and dynamically change their actions according to their circumstances.
The needs of the moment may override longer-term objectives: the need for food is less than the
need to avoid being eaten, the need for shelter may overcome the drive to mate, and so on. Balancing
these conflicting drives is the difference between success and failure — between life and death — and
the optimization of balancing behaviors is therefore subject to great evolutionary pressure.
For any autonomous artificial entity to perform useful work, it will need to operate in complex
problem domains, and also will need to adapt its behavior to optimize the balance of tasks it must
perform. In this article we consider the use of an adaptive system—here, a learning classifier system
(LCS) [10]—to control an agent that has to solve multi-objective problems. Per esempio, in a simple
case, the agent has to seek the shortest path to a goal state while it also needs to maintain its energy
levels, in similar fashion to a mobile robot that must perform tasks while maintaining its battery power.
The optimal course of action can change dynamically during the course of performing a trial, for its
energy levels may be depleted by its actions: the learner is operating in a changing environment.
In particular, we use Wilson’s XCS [18] as detailed in [2]. The ability of XCS to cope with an
increased number of objectives and larger maze environments is investigated, paying attention to the
choice of action-selection policy.
This article is organized thus: In Section 2 we briefly introduce some related work, and in
Sezione 3 we give an overview of the XCS classifier system. In Sections 4 E 5 we present some
results on multi-step problems of increasing complexity. Throughout, the effects of using two
different methods of selecting an action from the actions suggested by the system are considered. In
most delayed-reward multi-step problems using XCS that have been described in the literature, UN
balance has been enforced between exploration and exploitation by simply performing half the trials
N 2006 Istituto di Tecnologia del Massachussetts
Artificial Life 13: 69 – 86 (2007)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
using a random action-selection policy, and half using a deterministic policy. Since it is our intention
in these investigations to aim always at the use of XCS for multi-objective problems performed by
physical agents in the real world, we first investigate the performance of XCS using the traditional
50/50 random exploration, and then investigate its performance using roulette-wheel action
selection during the exploration trials. The roulette-wheel algorithm is a common implementation
of a selection mechanism in which the selection probability depends upon an individual’s value of
some scalar (usually the fitness) compared with the values of this scalar associated with the rest of
the population. Results show that the two action-selection schemes can have significant conse-
quences for XCS in such domains. In Section 6 we relate these findings to recent theoretical studies
of XCS, and in Section 7 we present our conclusions.
2 Related Work
Most complex real-world problems involve multiple objectives that may conflict. There has been a
considerable amount of work on multi-objective optimization problems, and numerous researchers
have reported success through the application of evolutionary techniques such as genetic algorithms
(GAs) [9] —for example, Vedere [6] for an overview.
The first implementation of an LCS, Holland and Reitman’s CS-1 system [11], was a form of
multi-objective reinforcement learner, since it included resource reservoirs, which ‘‘reflect simple
biological needs’’ and ‘‘deplete regularly in time.’’ Note that the resource reservoirs are not presented
to the condition part of the classifiers as the internal environment, but instead influence the choice of
which classifier’s action is taken by the learner. A rule’s chance of being chosen is proportional to the
specificity of its match to the environment, both internal and external, ‘‘multiplied by the amount of
the current needs fulfilled by this classifier’s predicted payoff.’’ The authors outline a simple maze
environment where the system starts in the middle and can receive at one end a reward that partially
fills the first internal resource reservoir, and at the other end a reward that partially fills the second.
The system learns to perform the task and balance its internal needs.
Dorigo and Colombetti [7] used a novel LCS, Alecsys, to control a robot. The main thrust of
their work was to evolve simple behaviors, and then combine these to produce more complicated
behaviors through a hierarchical system of LCSs. A hierarchy is imposed on a problem, and an LCS
coordinator is introduced to select an action from the LCS lower in the hierarchy. The lower-level LCSs
are trained, or shaped, on their task in isolation, and once an acceptable level of performance is
obtained for each lower-level module, the rules that it contains are fixed. When this happens, IL
shaping of the higher coordinating module takes place. Results were obtained for various following/
avoiding tasks in simple environments in which the coordinator switches between different
behavioral modules as appropriate; the coordinator switched between behaviors, each attempting
to satisfy its own objectives as the global situation required.
Llora and Goldberg [13] present an approach to Pittsburgh-style LCSs [14] — that is, those in
which the GA works with complete sets of rules — which is in itself multi-objective, since they con-
sider at the same time the following objectives: accuracy of the rules, number of rules, and gener-
ality of the solution. In contrast with the work presented in this article, their multiple objectives
describe a balancing of desirable characteristics of the learning system by maintaining a Pareto
front of nondominated solutions — a balance that is implicit in classifier systems where generality
and accuracy are concerned — rather than learning systems solving problems that have multiple
objectives.
There has also been some work related to multi-objective problems within the field of
in the case where an agent
reinforcement learning (RL) [15]. Crabbe [5] makes the point that,
has multiple objectives to satisfy simultaneously, this cannot be optimally achieved through having
separate RL systems (Q-learners [16]) for each objective, with the one with the highest activation
determining the agent’s action. He considers the example of a robot that has two objectives, Quale
can be satisfied in any order: getting power, and getting a building block. If the environment is
70
Artificial Life Volume 13, Numero 1
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
dynamic, there is a chance that conditions will change while seeking one goal in such a way that the
other goal can no longer be achieved — another robot might consume the battery, Per esempio.
Using utility theory, Crabbe shows that the best course of action is not only dependent on the
expected value of the outcome, but is also dependent on the probability of success. Simply stated, In
order to maximize the overall utility, sometimes one should pick the low-hanging fruit, although they
may be less juicy. In order to solve such problems, Crabbe suggests that one could either combine
the output of a number of Q-learners, or have one Q-learner that can manage multiple simultaneous
goals; he examines the latter case. We investigate a similar scenario here.
Gabor et al. [8] have considered similar multi-criteria sequential tasks. Examples of such tasks would
include situations where a robot has to perform a number of tasks, but the way in which it per-
forms task A can lower the value it will receive from performing task B. The example they give is of
‘‘Buridan’s ass’’: placed between two dishes of food, its hunger drives it to one or the other, but in doing
so it raises the possibility that the food on the other dish will be stolen. Since the ass tries to optimize his
overall utility, he guards both dishes, thereby eating nothing. He therefore has two different conflicting
objectives. We present and examine versions of such sequential multi-objective tasks.
3 XCS: A Brief Description
A population [P] of classifiers is created, each classifier having a condition and an associated action.
Classifier conditions use a ternary encoding with a # (‘‘don’t care’’), allowing generalization. On each
discrete time step, a match set [M] is created, consisting of those rules whose conditions match the
current binary input vector from the environment. A system prediction is then formed for each
action in [M] according to a fitness-weighted average of the predictions of rules in each action set [UN],
questo è, the classifiers in [M] advocating the same action. The system action is then selected either
deterministically or randomly (usually with probability 0.5 per trial). If [M] is empty, covering is used to
make a rule whose condition matches the current input, with an equal chance ( p#) that each 1 O 0 In
the input vector will be replaced in the new classifier’s condition by a #. Fitness reinforcement in
XCS consists of updating three parameters via the Widrow-Hoff delta rule: the predicted payoff ( P),
the error in that prediction (q), and the fitness (F ) for each appropriate rule. The fitness is updated
according to the error relative to those of the other rules within the set. The maximum value of the
system’s prediction array is discounted by a factor g and used to update rules from the previous time
step. Thus XCS exploits a form of Q-learning [16] in its reinforcement procedure.
The GA acts in [UN], questo è, niches. Two rules are selected, based on fitness from within the chosen
[UN]. Rule replacement is global and based on the estimated size of each action set a rule participates
In, with the aim of balancing resources across niches. The GA is triggered within a given action set
according to the average time since the members of the niche last participated in a GA. The intention
is to form a complete and accurate mapping of the problem space through efficient generalizations.
In this way, XCS represents a way of using reinforcement learning on complex problems where the
number of possible state-action combinations is very large, by discovering efficient generalizations over
an underlying Q function. The reader is referred to [2] for a full description of XCS.
We now examine the performance of XCS on a number of simple multi-objective tasks. Questo
takes place in adaptations of the familiar Woods1 grid world [17]. In these and all following
esperimenti, results are the average of 10 esperimenti, presented as the running average of the last
50 deterministic exploit trials, as in [18].
4 Sequential Multi-objective Maze Problems
The Woods1 virtual environment is a toroid composed of 25 piazze. A virtual agent, or animat [17],
moves between the squares under the control of the learning algorithm. Movement is possible from
a square to any of the eight adjoining squares, except where one contains a rock. A trial starts in an
empty square chosen at random, and finishes when the animat reaches the goal state, here marked
Artificial Life Volume 13, Numero 1
71
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
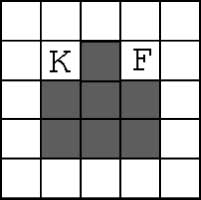
Figura 1. Woods1k.
with F for ‘‘food.’’ In the experiments described here, three characters are used to encode each state
in the environment (to enable future extensions), and the environment is presented to the classifier
system as a binary string representing the states of the eight cells that surround the animat’s current
position, from north clockwise to northwest. The condition of a classifier has an equal number of
characters to the environmental representation. Three characters, allowing the eight possible
directions to be represented, again encode the action. The environment is toroidal; every cell has
eight neighbors. In the Woods1 environment, the reward given upon reaching the goal is 1,000, E
the optimum average path from start to finish is 1.7 steps.
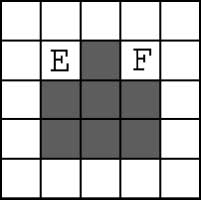
In order to use this, we first present an alteration of the Woods1 environment — Woods1k
(Figura 1) —that not only has a food goal, but also has another goal that we call the key. Each trial
starts with the animat not having visited the key state. The reward function gives a payoff of 1,000
in the case that the animat arrives at the goal state when it has visited the key state; the idea being
that the key is needed to unlock a door to obtain the reward. In order to allow XCS to know whether
the animat has previously visited the key state, an extra character is added to the representation
of the environment, this character being set from its initial state of zero to one when the animat visits
the key. This can be matched by a concomitant extra character in a classifier’s condition. In Figure 2
the key is shown as K. The optimal average number of steps to the goal state is 3.7. A trial cannot
terminate until the key state has been visited before the goal state. Throughout, apart from rule base
size N, the parameters used are h ¼ 0.2, g ¼ 0.71, uGA ¼ 25, q0 ¼ 0.01, a ¼ 0.1, r ¼ 5, m ¼ 0.8,
A ¼ 0.01, udel ¼ 20, y ¼ 0.1, p# ¼ 0.33, pI ¼ 10, qI ¼ 0, FI ¼ 10, usub ¼ 20, umna ¼ 8 (Vedere [2]).
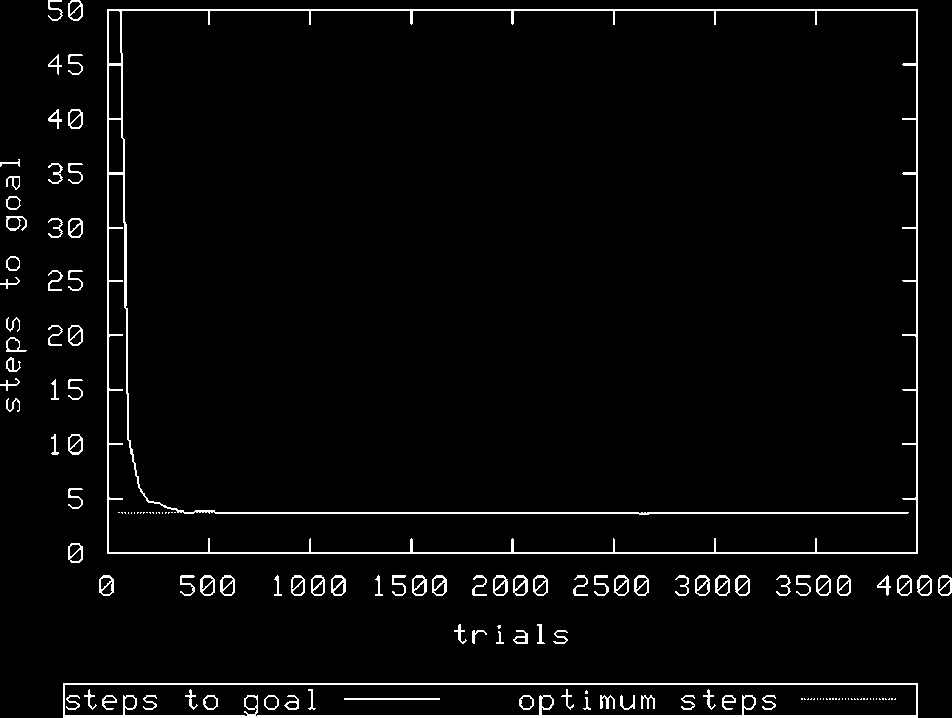
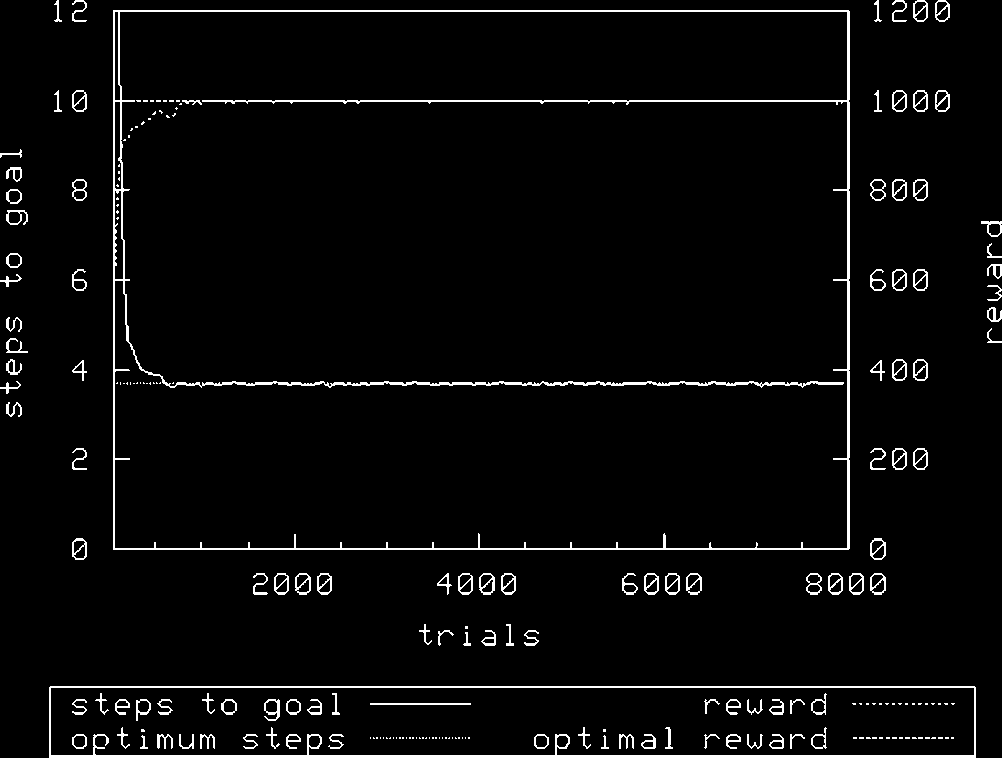
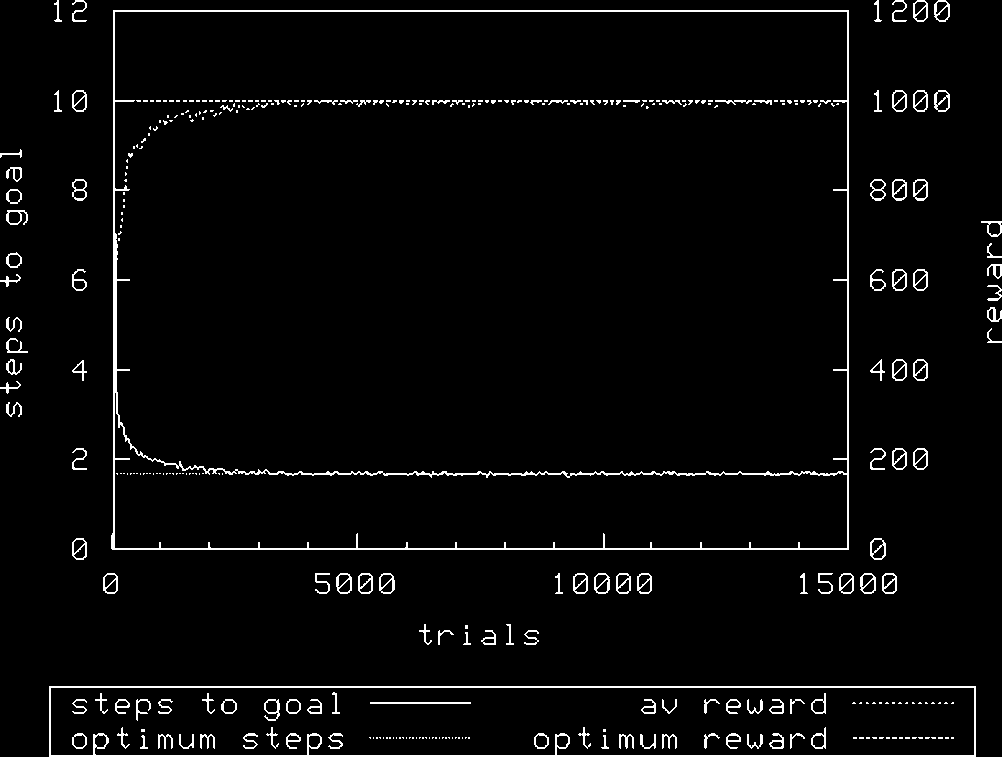
Figura 2 shows the performance of XCS with a population size N of 1,600 and random exploration.
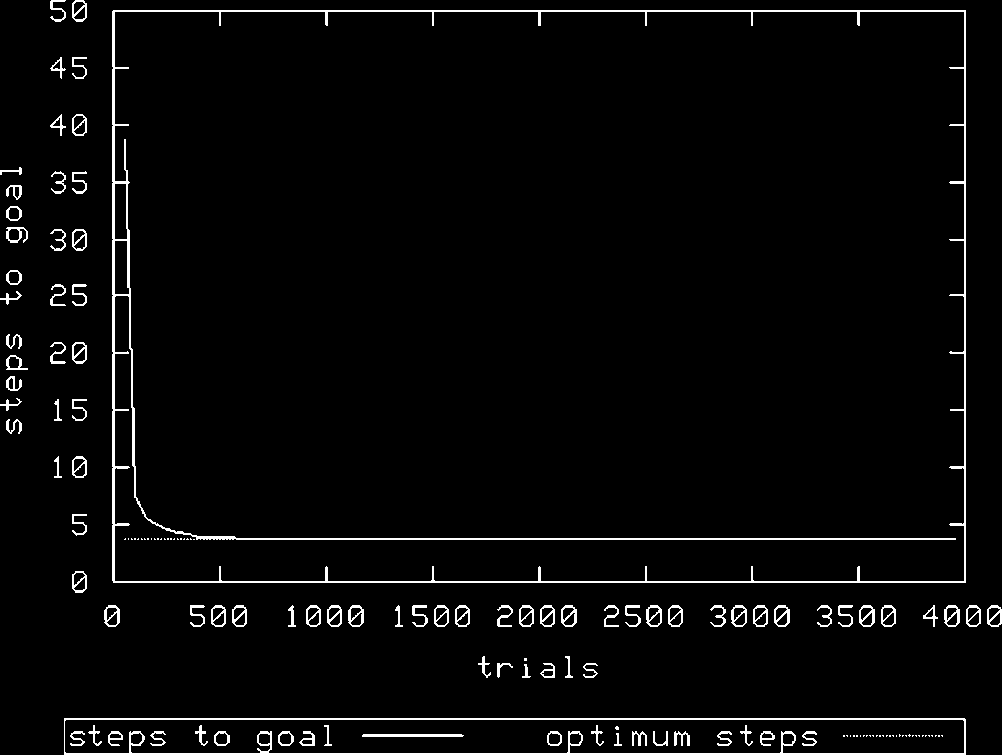
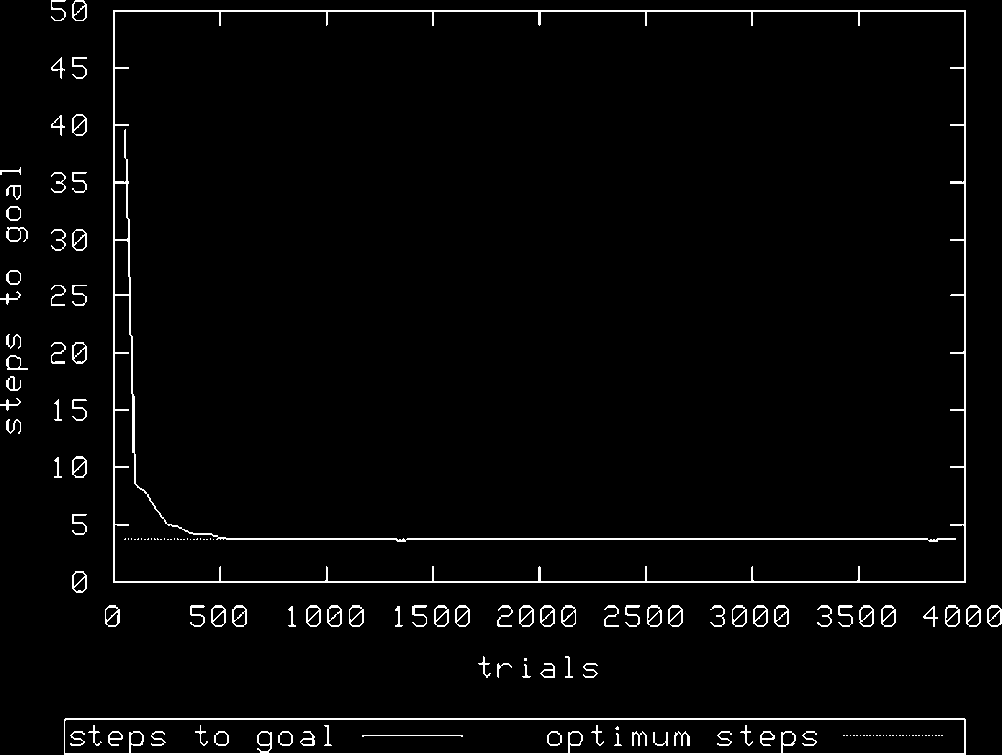
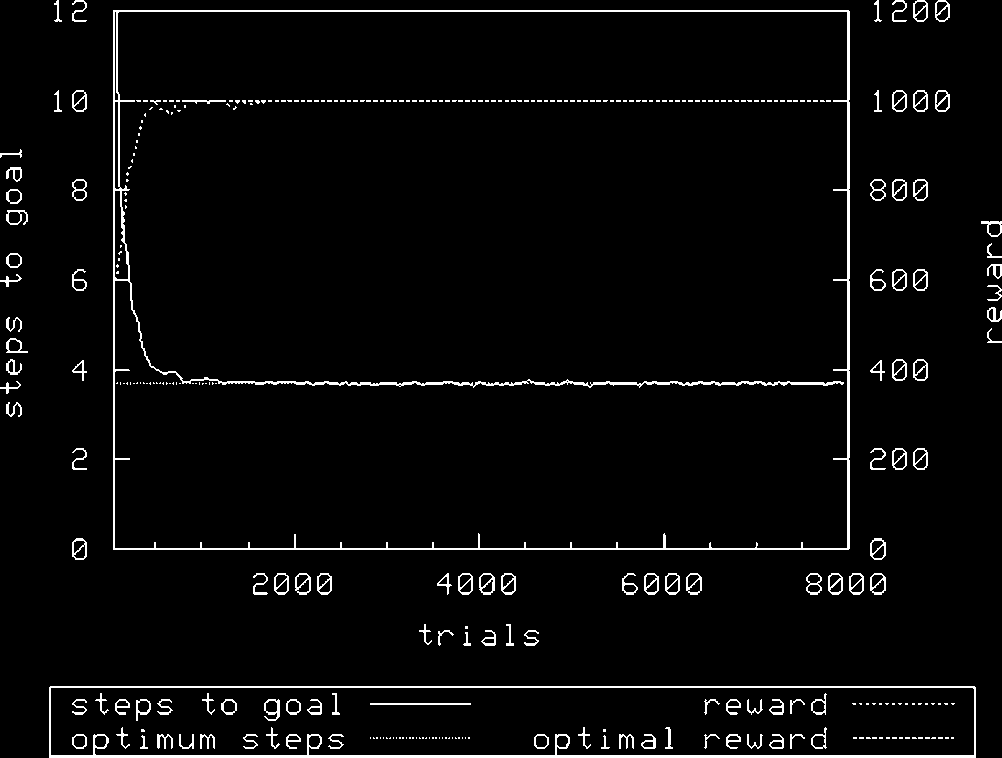
Figura 3 (N ¼ 1,600) and Figure 4 (N ¼ 3,200) show the same treatment using roulette-wheel selection.
Figura 2. Woods1k, N ¼ 1600, random exploration.
72
Artificial Life Volume 13, Numero 1
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figura 3. Woods1k, N ¼ 1600, roulette exploration.
As can be seen, in all treatments XCS achieves optimal performance. Tuttavia, it would appear that
it takes longer to converge to an optimal solution with the roulette action selection mechanism; con
N ¼ 1,600 and using random exploration, XCS achieves optimality after about 500 exploit trials,
whereas using roulette exploration requires almost double this number of trials with the same value of
N. Increasing N is required to allow roulette selection to perform as well—here, a doubling of N.
Ovviamente, the above is a rather trivial problem. The animat can only achieve its reward and
terminate the trial if it has first visited the key state. A slightly more complicated variant is provided
by the same environment, in which the door is always open — Woods1kd. Tuttavia, the reward
gained is dependent on whether the animat has previously visited the key state, being 1,000 if it has,
and otherwise 1. Once again, an extra character in both environment and classifier condition allows
XCS to know whether the animat has previously visited the key state.
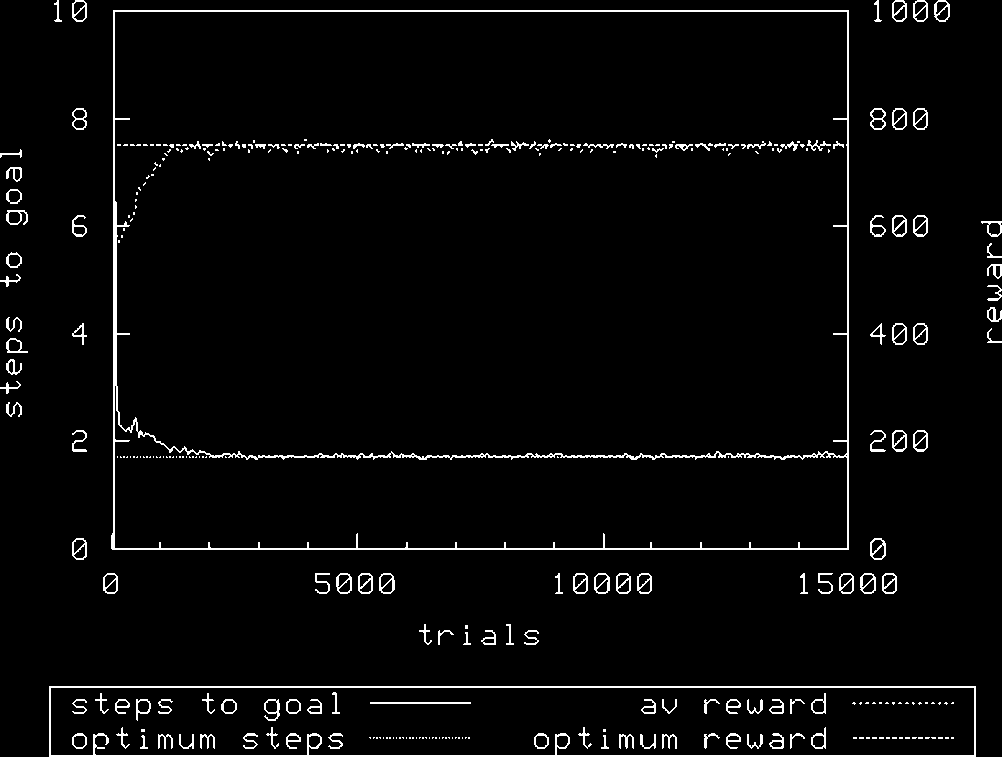
Figura 5 and Figure 6 show the performance of XCS on this second sequential multi-objective
task. With both roulette-wheel exploration and random exploration, there is a reduction in the time
needed to achieve optimal steps to goal as the population size is increased from 1,600 A 3,200. Once
Figura 4. Woods1k, N ¼ 3200, roulette exploration.
Artificial Life Volume 13, Numero 1
73
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figura 5. Woods1kd, N ¼ 1600, random exploration.
Ancora, we also see that random exploration achieves optimal performance faster than with roulette-
wheel exploration for the same population size. When N ¼ 1600, the treatment with random
exploration clearly achieves a better average reward [1000 F 0.0 (mean F SD)] than the treatment
using roulette-wheel exploration [986 F 9.51 (mean F SD)], implying that the map of predicted
payoffs is less accurate in the latter. We now examine another class of multi-objective learning
problems with XCS, finding a similar pattern emerges.
5 Concurrent Multi-objective Maze Problems
Having seen that XCS is capable of optimal performance on simple, sequential, two-objective
problems using both random and roulette-wheel exploration policies, we also considered the more
interesting problems where the learner has to juggle multiple simultaneous objectives.
Figura 6. Woods1kd, N ¼ 3200, roulette exploration.
74
Artificial Life Volume 13, Numero 1
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figura 7. The Woods1e environment.
5.1 Two Objectives
We have used an alteration of the previous Woods1k environment (Figura 7) that not only has a goal
state, but also has another goal that we label energy (E). In a similar fashion to the sequential multi-
objective task, the environment is presented to the classifiers with an additional character, che è
set to one if the animat’s internal energy level is higher than 0.5, and otherwise set to zero. IL
internal energy level varies uniformly, randomly between 0 E 1, and is set at the start of each trial.
The classifiers once again have an additional character in the condition that allows them to match
this extension of the environment. A trial is terminated and reward is given when the animat reaches
either of the goal states.
Each trial starts with the animat’s internal energy level initialized uniformly randomly in the range
[0, 1]. The reward function is stepwise, giving an external reward of 1,000 in the case that the animat
arrives at the energy goal when its energy level is lower than or equal to 0.5, the reward being
otherwise 1. Likewise, the animat receives a reward of 1,000 if it arrives at the food goal when its
energy level is higher than 0.5, the reward being otherwise 1. The optimal average reward that can be
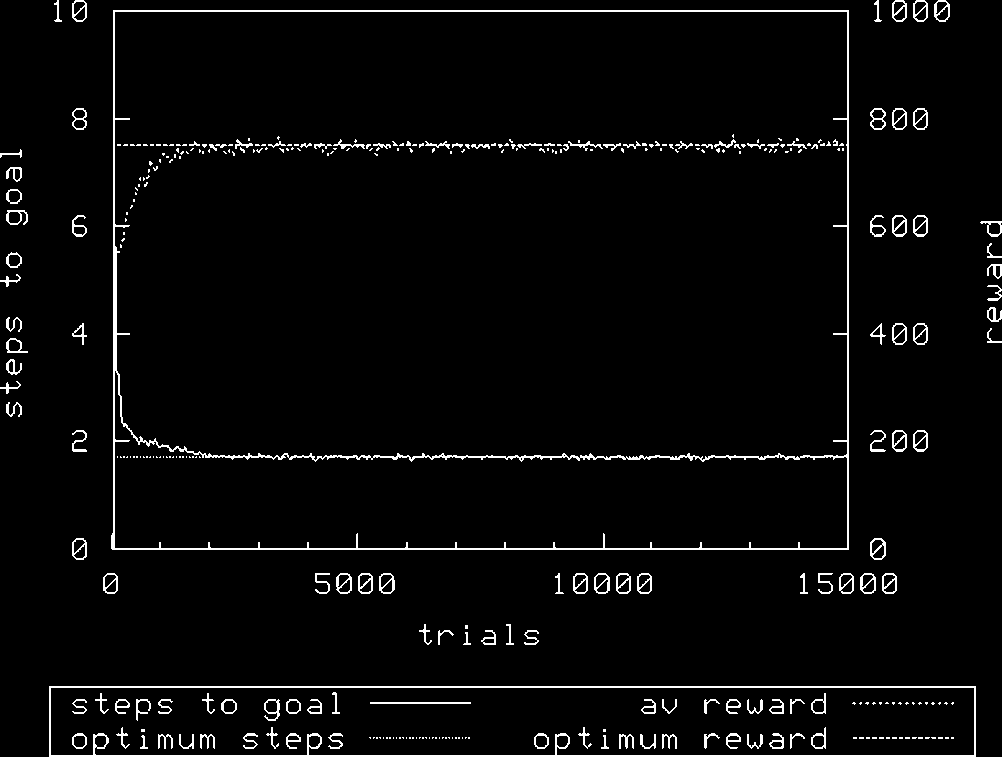
attained is 1,000, and the optimal average number of steps to either goal is 1.7.
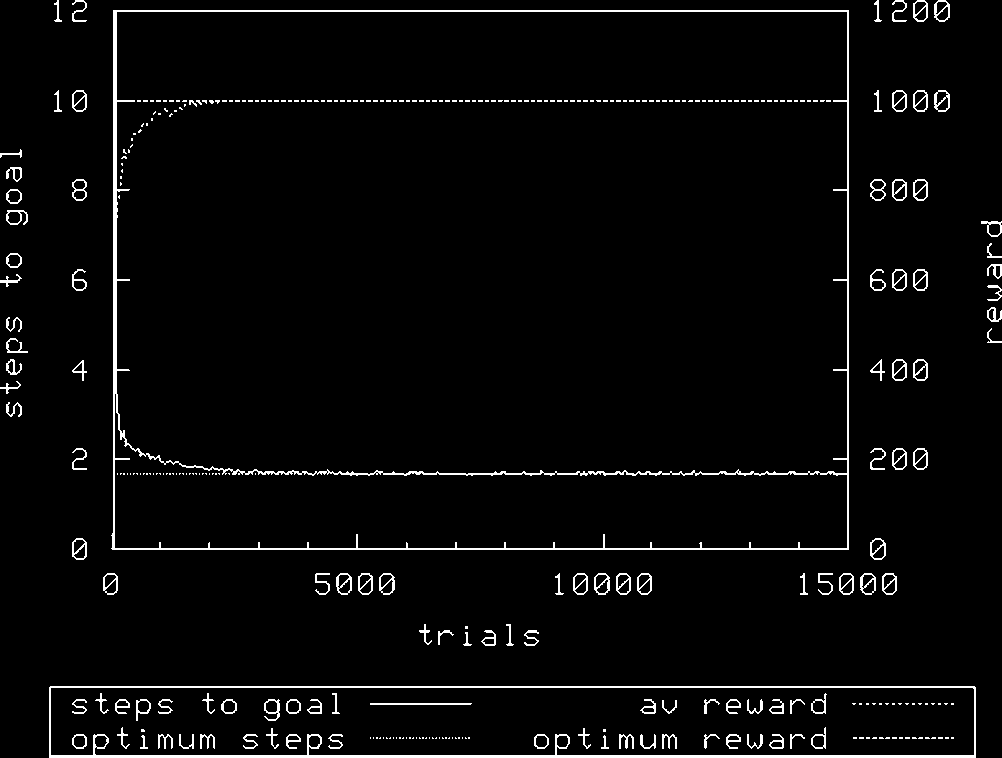
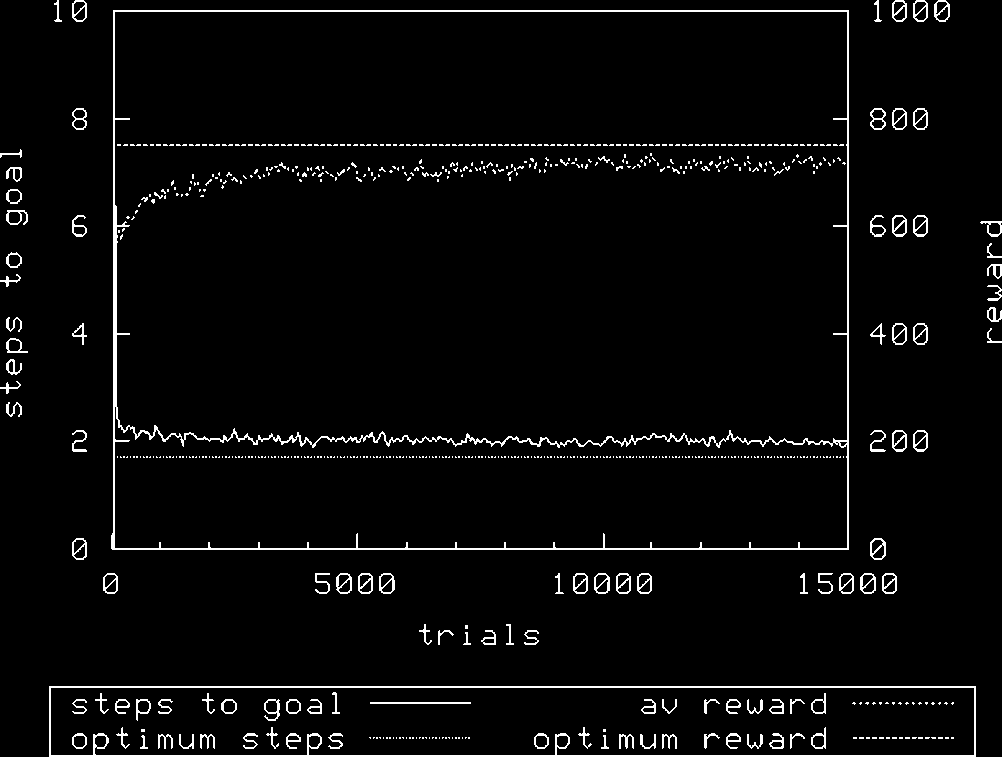
Figura 8 shows XCS achieving optimal performance with N ¼ 1,600 using random exploration.
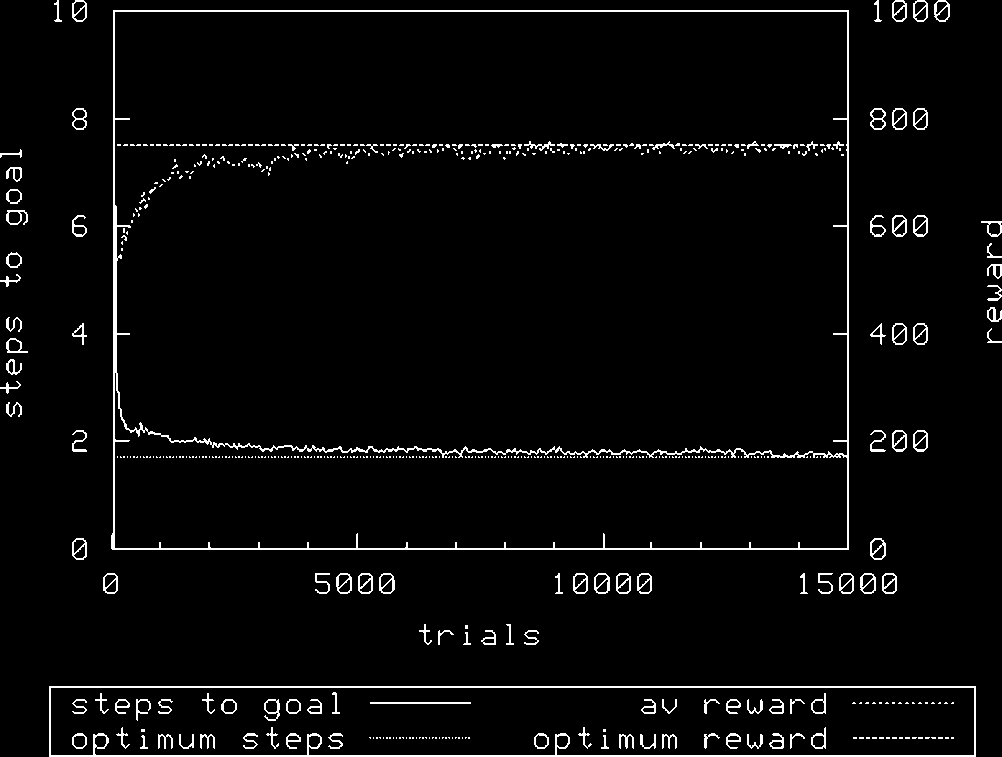
In Figure 9 it will be seen that using roulette exploration, performance is slightly worse in terms of
the average reward achieved [random 1000 F 0, roulette 993 F 3.69 (mean F SD)]. Increasing the
population size allows XCS to address this problem using roulette exploration (not shown), Ancora
indicating the significance of N as seen in the sequential problems above.
Figura 8. Woods1e, N ¼ 1600, random exploration.
Artificial Life Volume 13, Numero 1
75
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figura 9. Woods1e, N ¼ 1600, roulette exploration.
Previously, we have presented a version of the Woods1e environment in which the reward
received for reaching either goal state is a function of its internal energy level [1]. Questo è, the re-
ward received upon arriving at one or other goal state is directly proportional to the energy
level, rather than varying in a stepwise fashion according to the energy level as has hitherto been
the case:
at the energy goal;
reward ¼ 1000e;
at the food goal;
reward ¼ 1000ð1 (cid:3) eÞ;
where e is the animat’s internal energy level, which varies between zero and one. As before, Questo
internal energy level is set randomly at the start of each trial, so that half the trials will start with e <
0.5. A cost of 0.01 energy points is deducted for each move made by the animat in the grid world, in
the same way that a physical robot’s movement has an energetic cost. The animat’s energy level is not
allowed to go below zero. The real value of the internal energy level is hidden from XCS and
presented as an extra environmental character set to one if the energy level is above 0.5, otherwise
zero. While the optimum number of steps to goal remains 1.7 as in the other parallel multi-objective
tasks in the Woods1e environment, the optimum average reward is no longer 1,000, due to the
dynamic reward. If the energy level at the goal state is above 0.5, achieving the correct food goal will
gain a reward in the range [1000, 500]. The same is true when the animat correctly reaches the
energy goal with its energy below 0.5. Assuming an equal random distribution of initial energy levels
for trials, the average reward for success is 750. This problem is here called Woods1ef. Since there is
a cost of movement, the external reward received by the learner is not only dependent upon initial
conditions but also upon its actions.
Figure 10 and Figure 11 show the results using random exploration with N ¼ 1,600 and N ¼
3,200, and Figure 12 and Figure 13 show results with roulette-wheel exploration at these values of
N. Using both methods of exploration, XCS was able to solve this problem with a minimum of
adjustment, achieving optimal performance simultaneously in terms of both reward achieved and
steps taken.
We have so far observed that using roulette-wheel exploration is generally less optimal with
smaller populations, compared with random exploration. As can be seen, this is not the case with
this problem. Interestingly, with N ¼ 1,600, the treatment using roulette exploration outperforms
76
Artificial Life Volume 13, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figure 10. Woods1ef, N ¼ 1600, random exploration.
the equivalent treatment using random exploration, both in reducing to an optimum the average
number of steps taken to the goal state (roulette 1.76 F 0.03, random 1.98 F 0.04), and also with
respect to the average reward gained (roulette 743 F 7.34, random 714 F 9.97). This result is
returned to in Section 6.
5.2 Three Objectives
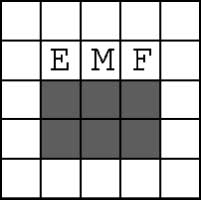
We have also increased the complexity of the Woods1e task by adding a third goal. The new
goal, maintenance, takes priority over the other two goals. We call the resulting task Woods1em
(Figure 14). If the animat reaches the maintenance goal and its need for maintenance is higher than
or equal to 0.5, it is rewarded 1,000, otherwise 1, irrespective of the internal energy level. If the
animat reaches the food goal when the need for maintenance is lower than 0.5 and the energy level is
higher than 0.5, it receives a high reward of 1,000, otherwise a low of 1. Likewise, if the animat
Figure 11. Woods1ef, N ¼ 3200, random exploration.
Artificial Life Volume 13, Number 1
77
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figure 12. Woods1ef, N ¼ 1600, roulette exploration.
reaches the energy goal when the need for maintenance is lower than 0.5 and the energy level is
lower than or equal to 0.5, it receives a high reward, otherwise low.
All other experimental details remain as before, except that the condition part of the classifier
is extended by a further character, which is set to zero if the animat’s maintenance level is lower
than 0.5, and otherwise set to one. As is the case with the internal energy level, the animat’s need
for maintenance is set randomly between 0 and 1 at the start of each trial, so that all combinations
of high and low maintenance need and high and low energy need are represented in equal numbers of
trials. The optimum number of steps to goal increases to around 1.8, and the optimum average reward
that can be achieved is once again 1,000. XCS achieves an optimal average reward using N ¼ 3,200
and random exploration (Figure 15). With an equivalent population size, roulette-wheel exploration
takes longer to achieve similar performance, and the system shows more variability in the average
reward achieved (Figure 16). Again, doubling the population size allowed XCS with roulette-wheel
exploration to achieve results that match those with random exploration (not shown).
Figure 13. Woods1ef, N ¼ 3,200, roulette exploration.
78
Artificial Life Volume 13, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figure 14. Woods1em.
5.3 Three Objectives in a Larger Maze
We then further increased the complexity of the task by increasing the size of the environment with a
version of the well-known Maze5 [12], which we term Maze5em.
Figure 17 shows Maze5em — a bounded environment containing obstacles (O) and three goal
states: food (F), energy (E), and maintenance (M). As before, all environmental states are encoded in
three characters, and eight actions are possible. The payoff matrix remains the same as for the three-
objective Woods1em problem.
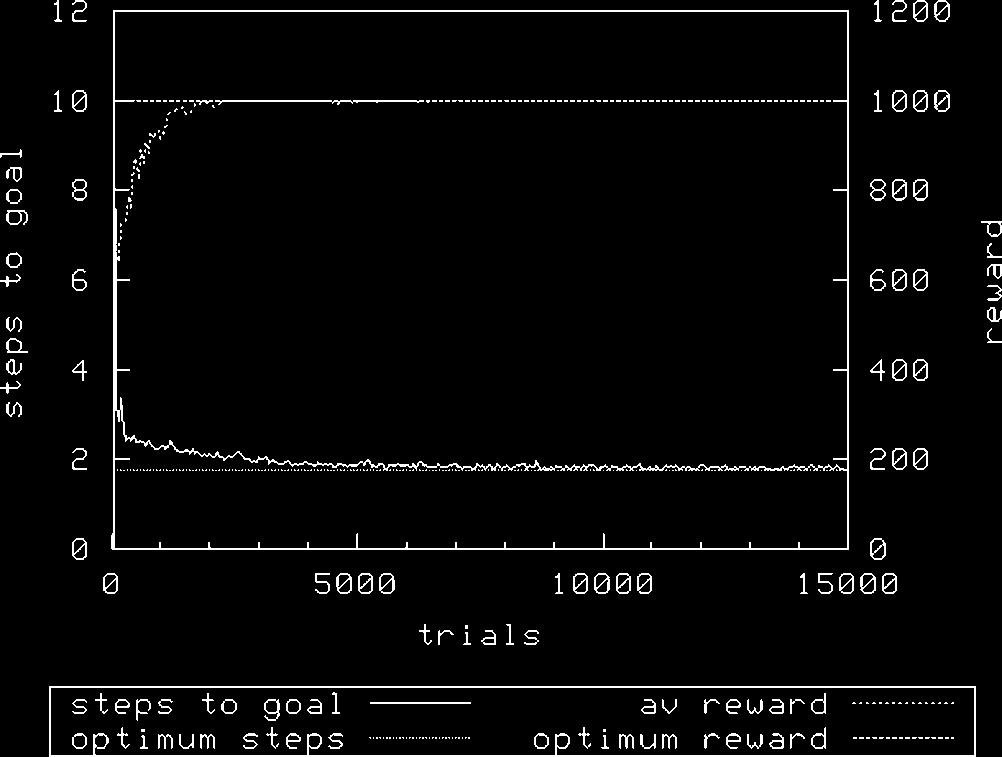
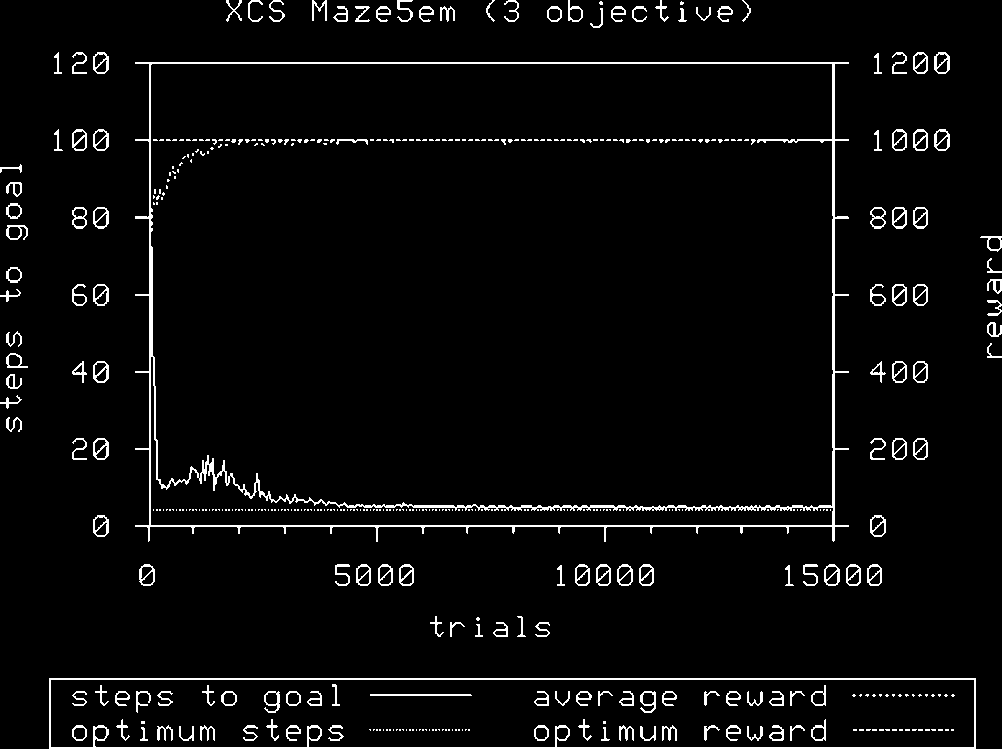
XCS achieves optimality (Figure 18) in the Maze5em environment using random exploration
when the probability of having a don’t-care character at each position in the condition is p# ¼ 0.1
and with N ¼ 6,400. When p# ¼ 0.33, some runs are optimal, but some are not, leading to an
it was less easy to achieve similar
average suboptimal performance (not shown). However,
performance using a roulette-wheel exploration policy. Once again,
it was found necessary to
increase N when using roulette-wheel selection; equivalent performance was achieved with roulette-
wheel action selection using the same value of p# (0.1), and a larger value of N (8,000). Trials using
p# ¼ 0.33 were never found to perform the task optimally.
This last result is interesting. In all other cases, we have found that roulette-wheel exploration can
produce comparable results to that achieved using a random action selection policy at the expense of
increasing N. We now see that in this latter, more complex case it is not enough to increase N; we
must also decrease p#. Here p# controls the probability with which alleles in the condition of the
rules will have the don’t-care symbol, #. It would appear that XCS is suffering from a greater
Figure 15. Woods1em, N ¼ 3200, random exploration.
Artificial Life Volume 13, Number 1
79
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figure 16. Woods1em, N ¼ 3200, roulette exploration.
tendency to produce overgeneral classifiers in Maze5em. This tendency seems to be exacerbated
when using the roulette-wheel action selection policy on explore trials.
We have observed that lowering p# improves XCS’s performance in the three-objective Maze5em
problem in the same way it does in Maze5 [12]. Further, roulette-wheel action selection is in effect
causing XCS to anneal too fast. That is, the best actions in any particular environmental state are
not explored sufficiently, and overgeneral classifiers are allowed to direct the system into suboptimal
actions.
6 Roulette-wheel Exploration — Discussion
We now test the hypothesis that increasing N with roulette action selection improves performance by
decreasing the tendency towards excessive generalization. For each experimental treatment of
Figure 17. Maze5em.
80
Artificial Life Volume 13, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figure 18. Maze5em, random exploration, N ¼ 6400, p# ¼ 0.1.
increasing values of N, with p# ¼ 0.33 or p# ¼ 0.1 and with roulette-wheel action exploration, we
examine the average specificity for all classifiers that match in each environmental state for
Maze5em. The resulting figures are based on 15,000 exploit trials, and are the average of ten runs
(Table 1). With increasing values of N there is a tendency for the amount of specificity to increase.
Bracketed values indicate that optimal performance was not achieved.
The following can be concluded from these results:
(cid:5) We have seen that as N increases, performance is more likely to be optimal.
(cid:5) It is interesting to note that although the two treatments that used random exploration at
N ¼ 6400 had the same overall specificity (fraction of non-# characters), it was only by
using a low value of p# that consistently optimal performance was produced.
(cid:5) There is a general tendency for specificity to increase with increasing N.
(cid:5) There is a dramatic difference between the results with roulette selection and p# ¼ 0.33,
and those of all other treatments.
It would therefore appear that increasing N reduces the speed at which the roulette-wheel action
selection anneals the search within XCS; a larger population size allows more diversity to be
maintained for longer, giving the GA more time to weed out the overgeneral rules.
Table 1. Percentage of non-general characters in all matching classifiers’ conditions.
Random exploration
Roulette exploration
p# ¼ 0.33
p# ¼ 0.1
p# ¼ 0.33
p# ¼ 0.1
[82]
[87]
[80]
87
90
[10]
[18]
[75]
[88]
90
N
1,600
6,400
8,000
Artificial Life Volume 13, Number 1
81
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Considering single-step tasks, Butz et al. [3] have recently identified the reproductive opportunity bound
(ROP bound) under which, given no effects of action-set size or fitness influences in the deletion process,
N > n 2kd þðl (cid:3)kd Þs½ p(cid:8)þ1;
where s[ P] is the value to which the specificity of the population would converge if no fitness
influence were present, n is the number of actions, and kd is the difficulty of the problem —
determined by the length of the minimum order schema that provides guidance on whether one
solution is better than another. This last aspect is illustrated with the extreme case of the parity
problem, in which all characters must be specified to correctly predict the outcome; in such a case, any
partial solution is as little use as a completely general classifier.
It can be seen from the above equation that N must grow with bigger values of both the order of
difficulty kd and the necessary specificity s[ P] in the population. This is based upon the assumption
that binary input strings are encountered that are uniformly distributed over the whole problem
instance space {0, 1}l.
As noted above, the Maze5 environment is one in which little generalization is possible, and thus is
difficult for XCS. To achieve optimal performance with either action selection mechanism required
more specificity (cioè., a lower value of p#). This is as predicted by the ROP bound above. Tuttavia,
the assumption that ‘‘binary input strings are encountered . . . uniformly’’ [3] is satisfied neither in
multi-step problems (states further from the goal are less frequently visited), nor when the action-
selection scheme is other than random. The necessity to further increase N when using roulette-wheel
exploration must therefore be due to the effects of bias in sampling frequency on the ROP bound.
Questo è, when using roulette-wheel action selection, higher-payoff action rules will be picked more often
than lower-payoff ones. Note that this bias will actually increase as more trials are performed and the
payoff values are better approximated by the system. Therefore, new candidate solutions in lower-
payoff niches will be much slower to show their accuracy than those in the more frequently visited
high-payoff niches. We believe that this explains the necessity to increase N in order to get equivalent
optimality to that achieved with random exploration—the dilution effect reduces the probability of
deletion. The differences between individuals are less obvious in a crowd.
Generally then, we have seen that random exploration gives better results for a given value of N
than roulette-wheel exploration. Tuttavia, it will be recalled that when we examined the behavior of
XCS using random and roulette action selection on the Woods1ef problem with a continuous reward
function and associated cost of movement (Sezione 5.2), we noticed that with lower values of N,
roulette selection outperformed random selection. This contradicts all other results, and requires
further explanation.
This problem ( Woods1ef ) in which the seemingly anomalous results occur is a difficult one for
XCS to solve, since the reward varies in direct proportion to the animat’s internal energy level when
it is at a goal state. There will thus be a high degree of error in all predictions of absolute payoff.
Perhaps the results observed in this continuous-reward problem reveal an effect of low values of N
that have been masked in the other, less challenging problems?
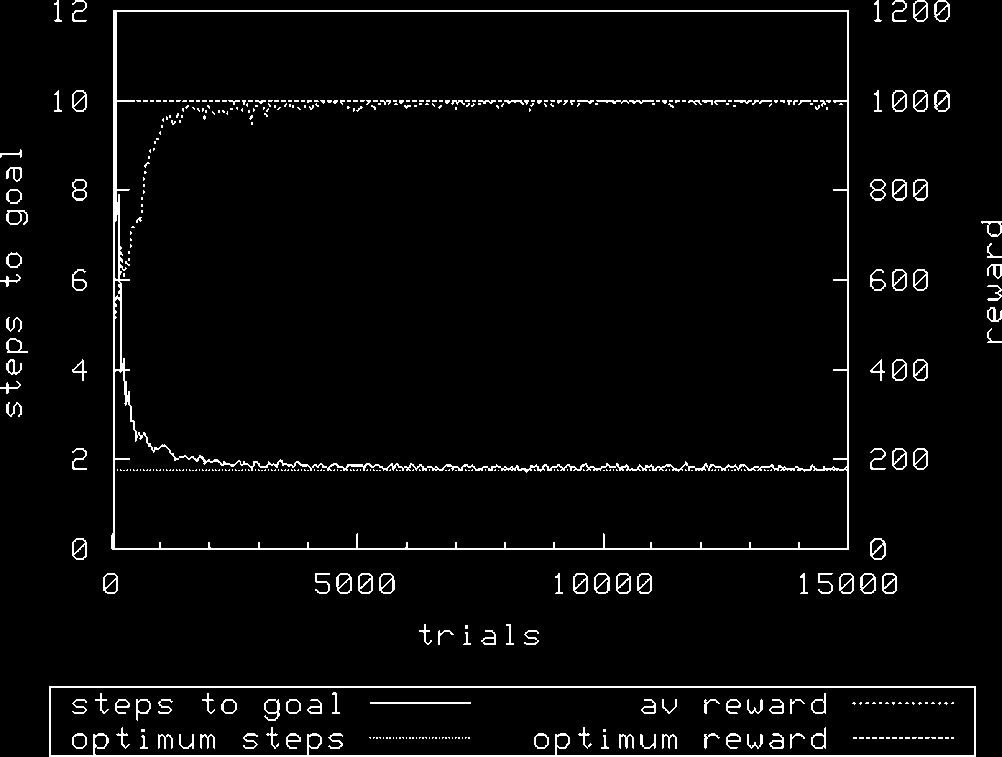
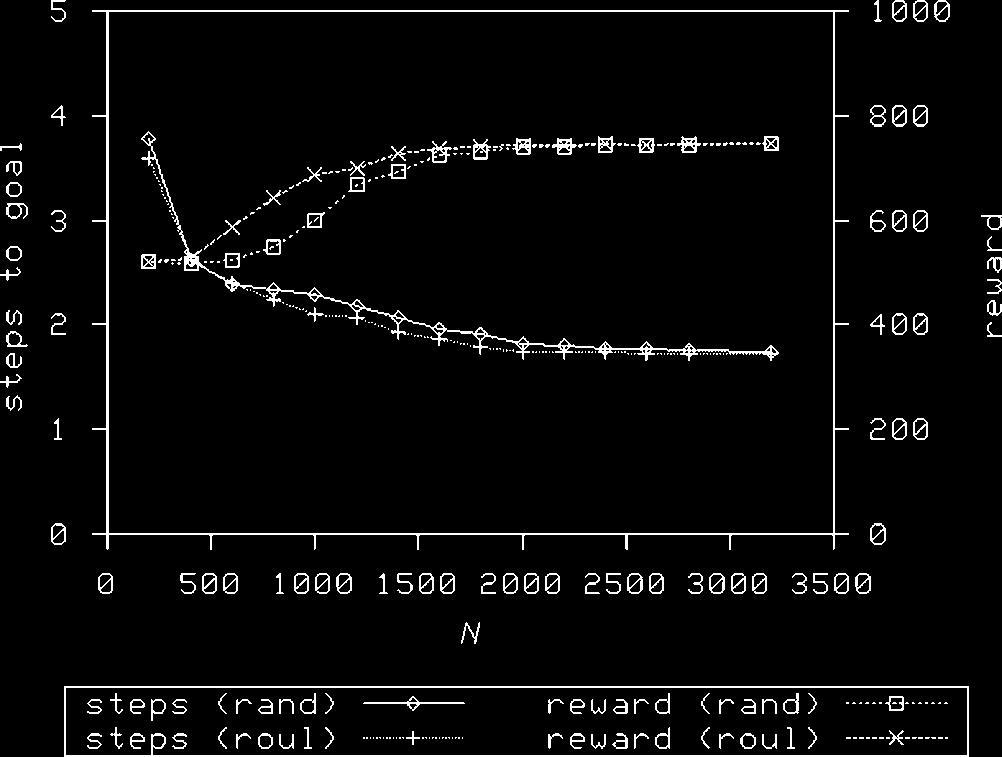
In Figure 19 we see the effect of N on the performance of XCS in the Woods1ef problem, using
the two exploration action-selection strategies. It will be seen that at low values of N, roulette
selection strongly outperforms random exploration. A two-tailed t-test demonstrates that there is a
statistically significant difference between the treatments in the reward gained at values of N between
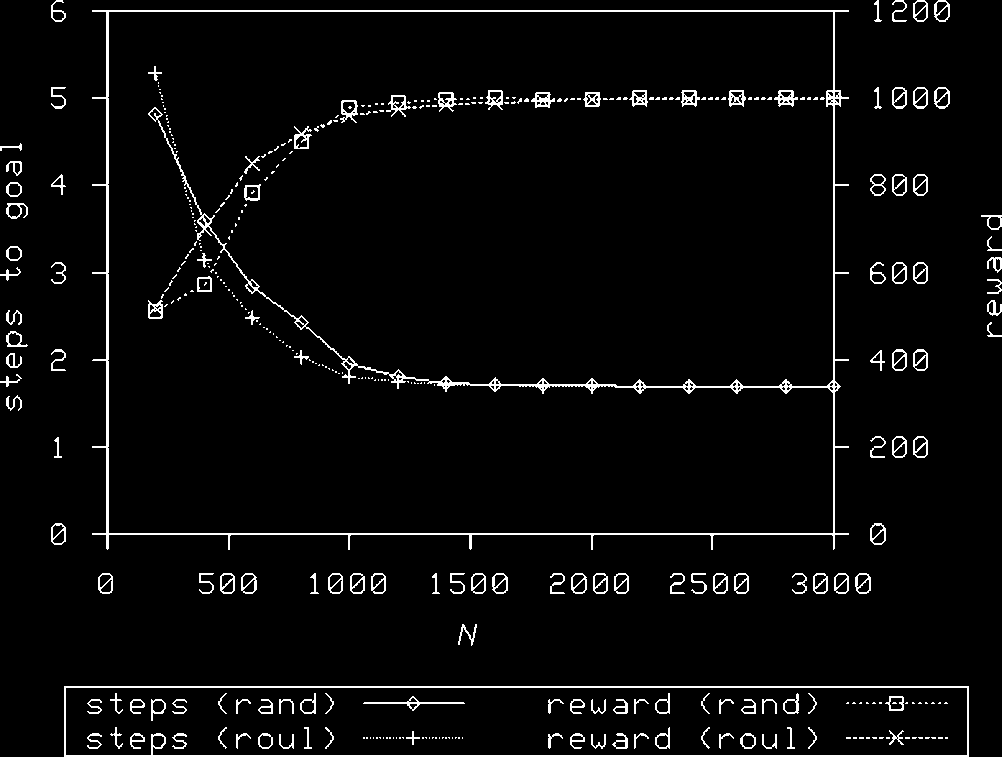
600 E 1,400 inclusive. The same is true in the simpler Woods1e problem, as shown in Figure 20.
Note that the advantages of roulette action selection are reduced as N rises.
In Figure 19, Figura 20, Figura 21, and Figure 22, ‘‘steps to goal’’ is the average of the last
100 windowed average figures for each run, averaged over ten runs. The ‘‘reward’’ measure is
similarly averaged so that it represents the behavior at the end of learning.
How then can we explain the advantages shown by roulette selection at low values of N? È
suggested that using roulette selection, XCS is able to concentrate scarce resources on the high-value
82
Artificial Life Volume 13, Numero 1
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
UN
R
T
l
/
/
l
UN
R
T
io
C
e
–
P
D
F
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
UN
R
T
l
.
/
.
2
0
0
7
1
3
1
6
9
P
D
.
.
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figura 19. Woods1ef, increasing N with roulette and random exploration.
areas of the problem space, thus maximizing its overall returns; if resources are scarce, roulette selec-
tion can only give this performance advantage if classifiers that predict a lower payoff can be deleted.
In XCS there is typically a 90% reduction in fitness from the parents’ values levied on the
offspring of classifiers newly produced by the GA. Figura 21 shows how, when this fitness reduction
does not occur, roulette-wheel exploration ceases to give such a marked advantage at lower values of
N for the Woods1e problem. This supports the hypothesis that roulette-wheel exploration provides a
performance advantage by allowing the system to appropriate resources from lower-payoff niches. In
less visited niches, offspring would normally have their fitness reduced (as indeed would offspring in
all niches). Because the niche is less often visited, they have little chance to boost their fitness by
participation in [UN] (in the current version of XCS, as used here, and in contrast to Wilson’s original
description, fitness increases slowly, since MAM1 does not operate on fitness updates, as it is claimed
that this ‘‘results in a stronger robustness against inaccurate classifiers’’ [2]). These lower-fitness
classifiers then become candidates for deletion when the GA is triggered in a more frequently visited
state; the age threshold on deletion is insufficient here. In this way resources are ‘‘stolen’’ from low-
payoff state-action niches, since the roulette-wheel exploration strategy increases the bias towards
visiting the higher-payoff niches.
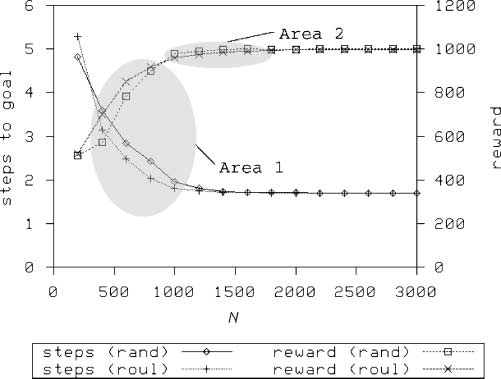
Figura 22 shows two areas where XCS experiences the ROP bound. In area 1, at values of N in-
sufficient to satisfy the bound, the roulette-wheel exploration strategy benefits performance through
‘‘resource theft,’’ as described above. Analysis indicates that the suboptimal performance of XCS is not
due to the cover challenge [4]—that is, to the population being too small and/or specific to avoid cover
firing throughout learning—since for all values of N, cover occurs infrequently and has stopped after
trial 2,000 of a total of 15,000 exploit trials in each experiment (not shown).
In area 2, we suggest that the suboptimal behavior using roulette-wheel exploration is evidence of the
effect of the bias on the ROP. As previously stated, the ROP bound is derived on the assumption that all
possible states in the space {0, 1}l will be uniformly presented to the system. All other things being
equal, this will be true if the exploration policy does not introduce any bias. There is a bias in exploration
when using roulette-wheel action selection; higher-payoff classifiers will be picked more often than
lower-payoff ones, and this bias will increase as more trials are performed. Therefore, new candidate
solutions in lower-payoff niches will be more likely to be deleted before their true accuracy can be
1 MAM (moyenne adaptive modife´e) is a procedure by which a parameter is adjusted using the Widrow-Hoff procedure with the learning
rate parameter h (0 < h V 1) only after a classifier has been adjusted at least 1/h times; otherwise the new value is simply the average of
the previous value and the current one.
Artificial Life Volume 13, Number 1
83
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figure 20. Woods1e, increasing N with roulette and random exploration.
determined when using roulette exploration. We believe that this explains the necessity to increase N in
order to get equivalent optimality to that achieved with random exploration—the dilution effect reduces
the probability of deletion. The ROP bound is dependent upon the exploration policy.
7 Conclusions
In this article we have shown that XCS can optimally solve a variety of simple multi-objective tasks.
It can do so using different action-selection policies in the exploration phase. In the results presented
here, we have seen that:
(cid:5) XCS can be used successfully with roulette-wheel exploration replacing random action
selection, suggesting that it may be used for online control where random actions would
be inappropriate.
Figure 21. Without fitness reduction in offspring, roulette’s advantage at lower N is reduced.
84
Artificial Life Volume 13, Number 1
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
Figure 22. At different values of N, XCS exhibits different behavior due to the ROP bound.
(cid:5) Roulette-wheel action selection functions less well than random action selection at
population sizes sufficient for optimal performance using random action selection.
This appears to be due to overgenerality resulting from a lack of exploration.
(cid:5) When population sizes are too small for random action selection to perform optimally,
roulette-wheel action selection may give a performance benefit. This appears to be
due to the advantages of concentrating resources on high-payoff niches where there
are insufficient resources to form a complete and accurate map of state-action pairs. This
may be of value in a robotic environment; smaller populations are less computationally
expensive.
(cid:5) There is clear evidence for the ROP bound of Butz et al. [3] in multi-step environments,
but it is critically dependent upon the action-selection policy.
We are now exploiting these findings to use XCS to control a real mobile robot that must solve such
multi-objective problems. Investigations of how XCS performs in other types of multi-objective
learning tasks are also being undertaken, along with comparisons with other approaches [1].
References
1. Bull, L., & Studley, M. (2002). Consideration of multiple objectives in neural learning classifier systems.
In Parallel Problem Solving from Nature — PPSN VII (pp. 549 – 557). New York: Springer-Verlag.
2. Butz, M., & Wilson, S. W. (2001). An algorithmic description of XCS. In Advances in Learning Classifier
Systems: Proceedings of the Fourth International Workshop on Learning Classifier Systems (pp. 253 – 272).
New York: Springer-Verlag.
3. Butz, M. V., & Goldberg, D. E. (2003). Bounding the population size in XCS to ensure reproductive
opportunities. Evolutionary Computation, 11(3), 239 – 278.
4. Butz, M., Kovacs, T., Lanzi, P., & Wilson, S. W. (2004). Toward a theory of generalization and learning
in XCS. IEEE Transactions on Evolutionary Computation, 8(1), 28 – 46.
5. Crabbe, F. L. (2001). Multiple goal Q-learning: Issues and functions. In Proceedings of the International
Conference on Computational Intelligence for Modelling Control and Automation (CIMCA). San Mateo, CA:
Morgan Kaufmann.
6. Deb, K. (2001). Multi-objective optimization using evolutionary algorithms. New York: Wiley.
7. Dorigo, M., & Colombetti, M. (1998). Robot shaping: An experiment in behavior engineering. Cambridge, MA:
MIT Press.
Artificial Life Volume 13, Number 1
85
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
M. Studley and L. Bull
XCS Classifier System for Multi-objective Reinforcement Learning Problems
8. Gabor, Z., Kalmar, Z., & Szepesvari, C. (1998). Multi-criteria reinforcement learning. In Proceedings of
the International Conference on Machine Learning. San Mateo, CA: Morgan Kaufmann.
9. Holland, J. H. (1975). Adaptation in natural and artificial systems. Ann Arbor: University of Michigan Press.
10. Holland, J. H. (1976). Adaptation. In R. Rosen & F. M. Snell (Eds.), Progress in theoretical biology
(pp. 263 – 293). San Diego, CA: Academic Press.
11. Holland, J. H., & Reitman, J. S. (1978). Cognitive systems based on adaptive algorithms. In D. A. Waterman
& F. Hayes-Roth (Eds.), Pattern-directed inference systems (pp. 313 – 319). San Diego, CA: Academic Press.
12. Lanzi, P. L. (2000). An analysis of generalization in the XCS classifier system. Evolutionary Computation,
7(2), 125 – 149.
13. Llora, X., & Goldberg, D. E. (2003). Bounding the effect of noise in multiobjective learning classifier
systems. Evolutionary Computation, 11(3), 278 – 297.
14. Smith, S. F. (1980). A learning system based on genetic adaptive algorithms. Ph.D. thesis. University of Pittsburgh,
Pittsburgh, Pennsylvania.
15. Sutton, R. A., & Barto, A. G. (1998). Reinforcement learning: An introduction. Cambridge, MA: MIT Press.
16. Watkins, C. J. C. H. (1989). Learning from delayed rewards. Ph.D. thesis. University of Cambridge,
Cambridge, UK.
17. Wilson, S. W. (1994). ZCS: A zeroth level classifier system. Evolutionary Computation, 2(1), 1 – 18.
18. Wilson, S. W. (1995). Classifier fitness based on accuracy. Evolutionary Computation, 3(2), 149 – 175.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
a
r
t
l
/
/
l
a
r
t
i
c
e
-
p
d
f
/
/
/
/
1
3
1
6
9
1
6
6
2
3
7
6
a
r
t
l
.
/
.
2
0
0
7
1
3
1
6
9
p
d
.
.
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
86
Artificial Life Volume 13, Number 1