Operazioni dell'Associazione per la Linguistica Computazionale, vol. 6, pag. 543–555, 2018. Redattore di azioni: Mark Steedman.
Lotto di invio: 1/2018; Lotto di revisione: 5/2018; 5/2018; Pubblicato 8/2018.
2018 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
C
(cid:13)
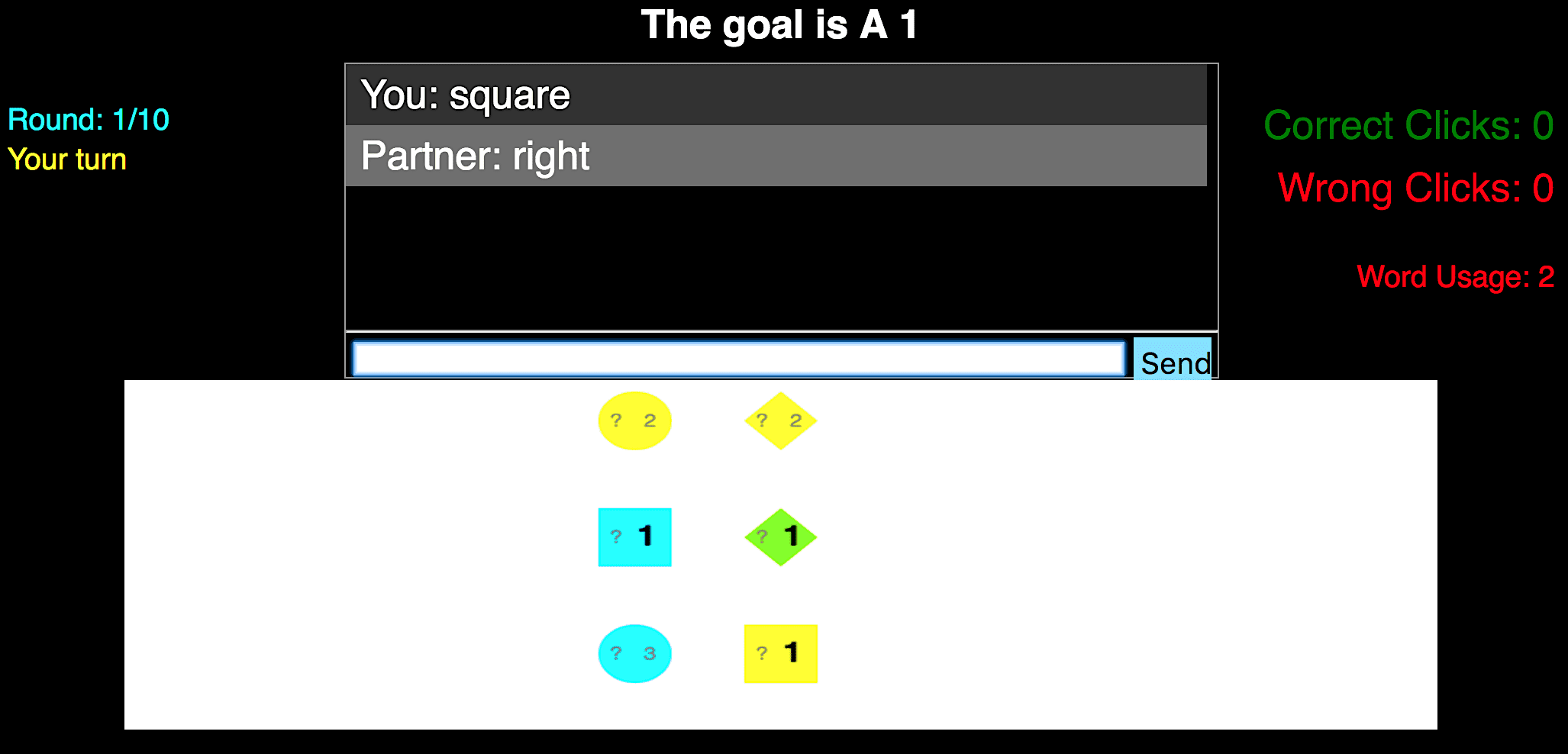
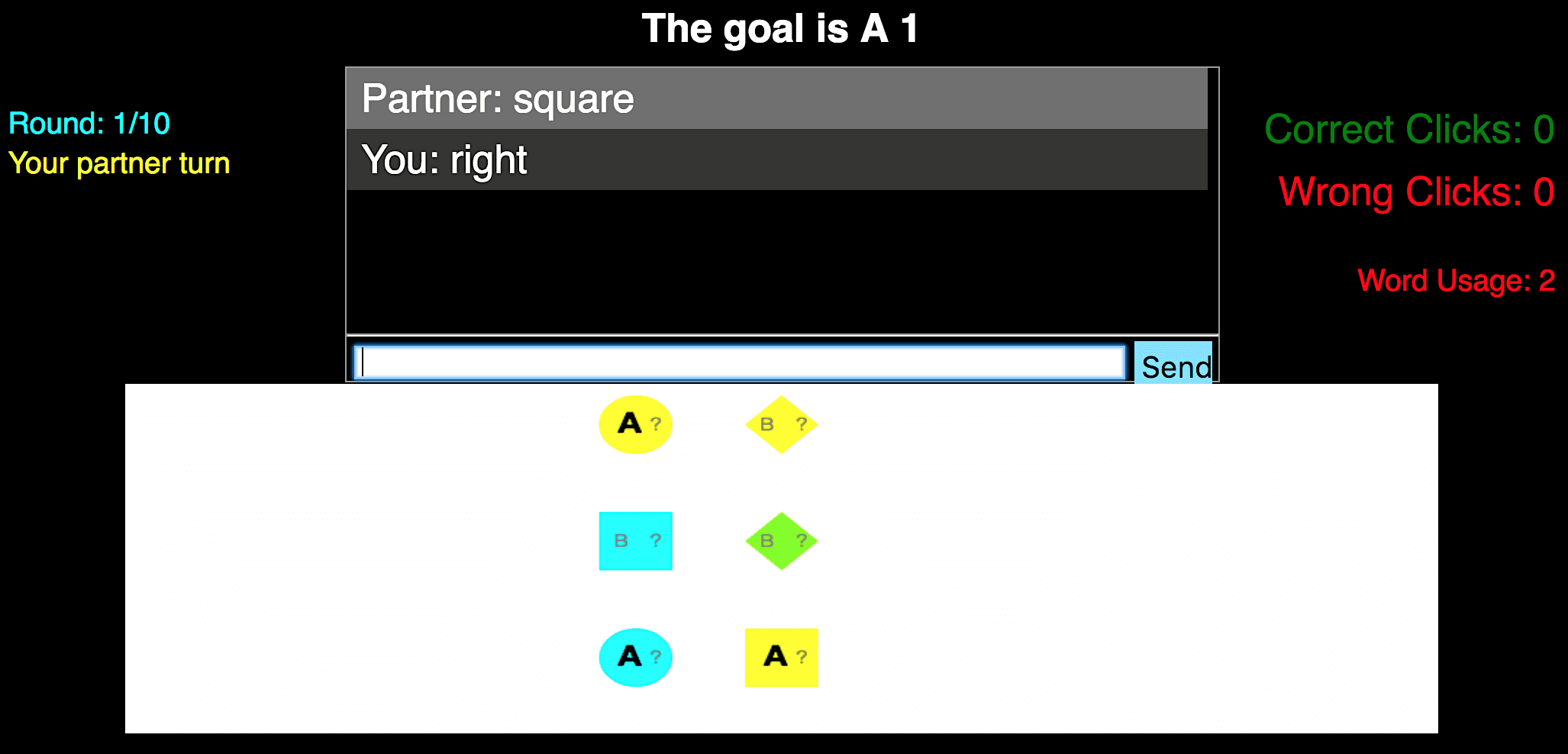
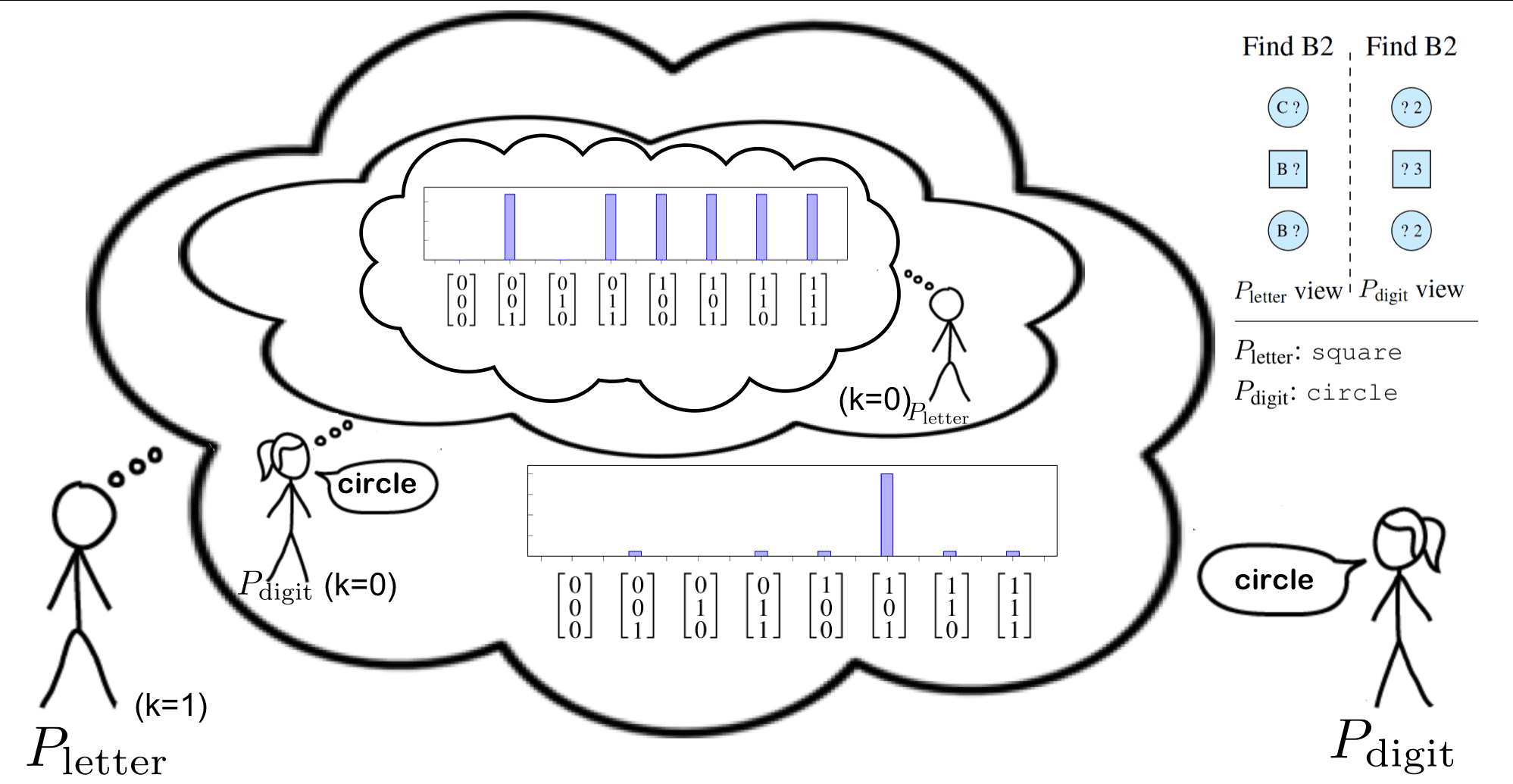
Planning,InferenceandPragmaticsinSequentialLanguageGamesFereshteKhaniStanfordUniversityfereshte@stanford.eduNoahD.GoodmanStanfordUniversityngoodman@stanford.eduPercyLiangStanfordUniversitypliang@cs.stanford.eduAbstractWestudysequentiallanguagegamesinwhichtwoplayers,eachwithprivateinformation,communicatetoachieveacommongoal.Insuchgames,asuccessfulplayermust(io)in-ferthepartner’sprivateinformationfromthepartner’smessages,(ii)generatemessagesthataremostlikelytohelpwiththegoal,E(iii)reasonpragmaticallyaboutthepartner’sstrat-egy.Weproposeamodelthatcapturesallthreecharacteristicsanddemonstratetheirim-portanceincapturinghumanbehavioronanewgoal-orienteddatasetwecollectedusingcrowdsourcing.1IntroductionHumancommunicationisextraordinarilyrich.Peo-pleroutinelychoosewhattosaybasedontheirgoals(planning),figureoutthestateoftheworldbasedonwhatotherssay(inference),allwhiletak-ingintoaccountthatothersarestrategizingagentstoo(pragmatics).Allthreeaspectshavebeenstud-iedinboththelinguisticsandAIcommunities.Forplanning,MarkovDecisionProcessesandtheirex-tensionscanbeusedtocomputeutility-maximizingactionsviaforward-lookingrecurrences(e.g.,Vo-geletal.(2013UN)).Forinference,model-theoreticsemantics(Montague,1973)providesamechanismforutterancestoconstrainpossibleworlds,andthishasbeenimplementedrecentlyinsemanticparsing(Matuszeketal.,2012;KrishnamurthyandKollar,2013).Finalmente,forpragmatics,thecooperativeprin-cipleofGrice(1975)canberealizedbymodelsinwhichaspeakersimulatesalistener—e.g.,Franke(2009)andFrankandGoodman(2012).FindB2FindB2B?B?C?Pletterview?2?3?2PdigitviewPletter:squarePdigit:circlePletter:click(1,3)Planning:Letmefirsttrysquare,whichisjustonepossibility.Inference:Thesquare’slettermustbeB.Pragmatics:Thesquare’sdigitcan-notbe2.Figure1:AgameofInfoJigsawplayedbytwohu-manplayers.Oneoftheplayers(Pletter)onlyseestheletters,whiletheotherone(Pdigit)onlyseesthedigits.Theirgoalistoidentifythegoalobject,B2,byexchangingafewwords.Thecloudsshowthehypothesizedroleofplanning,inference,andprag-maticsintheplayers’choiceofutterances.Inthisgame,thebottomobjectisthegoal(position(1,3)).Therehavebeenafewpreviouseffortsinthelan-guagegamesliteraturetocombinethethreeaspects.Hawkinsetal.(2015)proposedamodelofcommu-nicationbetweenaquestionerandananswererbasedononlyoneroundofquestionanswering.Vogeletal.(2013B)proposedamodeloftwoagentsplayingarestrictedversionofthegamefromtheCardsCor-pus(Potts,2012),wheretheagentsonlycommuni-cateonce.1Inthiswork,weseektocaptureallthreeaspectsinasingle,unifiedframeworkwhichallows1Specifically,twoagentsmustbothco-locatewithaspecificcard.Theagentwhichfindsthecardsoonersharesthecardlocationinformationwiththeotheragent.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
544
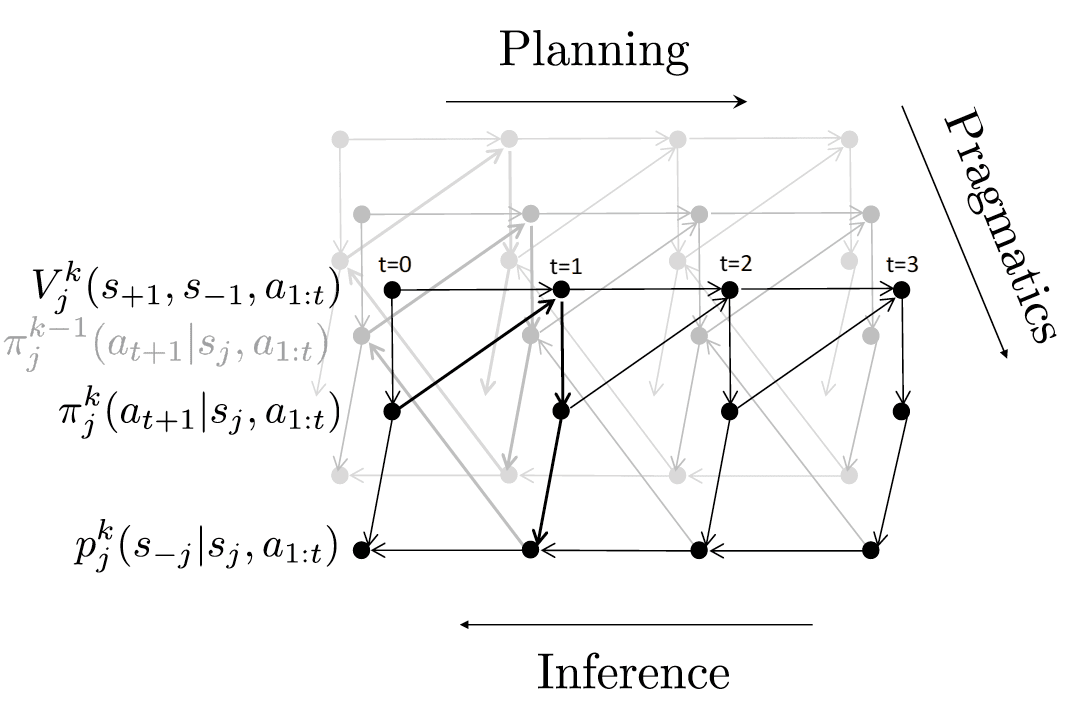
formultipleroundsofcommunication.Specifically,westudyhumancommunicationinasequentiallanguagegameinwhichtwoplayers,eachwithprivateknowledge,trytoachieveacom-mongoalbytalking.Wecreatedaparticularsequen-tiallanguagegamecalledInfoJigsaw(Figure1).InInfoJigsaw,thereisasetofobjectswithpublicprop-erties(shape,colore,position)andprivateproperties(digit,letter).Oneplayer(Pletter)canonlyseetheletters,whiletheotherplayer(Pdigit)canonlyseethedigits.Thetwoplayerswishtoidentifythegoalob-ject,whichisuniquelydefinedbyaletteranddigit.Todothis,theplayerstaketurnstalking;toencour-agestrategiclanguage,weallowatmosttwoEnglishwordsatatime.Atanypoint,aplayercanendthegamebychoosinganobject.Eveninthisrelativelyconstrainedgame,wecanseethethreeaspectsofcommunicationatwork.AsFigure1shows,inthefirstturn,sincePletterknowsthatthegameismulti-turn,shesimplysayssquare;iftheotherplayerdoesnotclickonthesquare,shecantrythebottomcircleinthenextturn(planning).Inthesecondturn,Pdigitinfersfromsquarethatthesquare’sletterisprobablyB(in-ference).Asthedigitonthesquareisnota2,shesayscircle.Finally,Pletterinfersthatdigitsofcir-clesare2,andinadditionsheinfersfromcirclethatthedigitonthesquareisnota2asotherwise,Pdigitwouldhaveclickedonit(pragmatics).There-fore,shecorrectlyclickson(1,3).Inthispaper,weproposeamodelthatcapturesplanning,inference,andpragmaticsforsequentiallanguagegames,whichwecallPIP.Planningre-currenceslookforward,inferencerecurrenceslookback,andpragmaticsrecurrenceslooktosimplerin-terlocutors’model.Theprincipalchallengeistoin-tegrateallthreetypesinacoherentway;wepresenta“two-dimensional”systemofrecurrencestocap-turethis.Ourrecurrencesbottomoutinverysimple,literalsemantics,(e.g.,context-independentmean-ingofcircle),andwerelyonthestructureofre-currencestoendowwordswiththeirrichcontext-dependentmeaning.Asaresult,ourmodelisveryparsimoniousandonlyhasfour(hyper)parameters.Asourinterestisinmodelinghumancommuni-cationinsequentiallanguagegames,weevaluatePIPonitsabilitytopredicthowhumansplayIn-foJigsaw.2WepairedupworkersonAmazonMe-chanicalTurktoplayInfoJigsaw,andcollectedatotalof1680games.Ourfindingsareasfollows:(io)PIPobtainshigherlog-likelihoodthanabase-linethatchoosesactionstoconveymaximuminfor-mationineachround;(ii)PIPobtainshigherlog-likelihoodthanablationsthatremovethepragmaticortheplanningcomponents,supportingtheirim-portanceincommunication;(iii)PIPisbetterthananablationwithatruncatedinferencecomponentthatforgetsthedistantpastonlyforlongergames,butworseforshortergames.Theoverallconclu-sionisthatbycombiningaverysimple,context-independentliteralsemanticswithanexplicitmodelofplanning,inference,andpragmatics,PIPobtainsrichcontext-dependentmeaningsthatcorrelatewithhumanbehavior.2SequentialLanguageGamesInasequentiallanguagegame,therearetwoplay-erswhohaveasharedworldstatew.Inaddition,eachplayerj∈{+1,−1}hasaprivatestatesj.Ateachtimestept=1,2,…,theactiveplayerj(T)=2(tmod2)−1(whichalternates)choosesanaction(includingspeaking)atbasedonitspolicyπj(T)(at|w,sj(T),A1:t−1).Importantlythatplayerj(T)canseeherownprivatestatesj(T),butnotthepartner’ss−j(T).Attheendofthegame(definedbyaterminatingaction),bothplayersreceiveutilityU(w,s+1,s−1,a1:T)∈R.Theutilityconsistsofapenaltyifplayersdidnotreachthegoalandare-wardiftheyreachedthegoalalongwithapenaltyforeachaction.Becausetheplayershaveacommonutilityfunctionthatdependsonprivateinformation,theymustcommunicatethepartoftheirprivatein-formationthatisrelevantformaximizingutility.Inordertosimplifynotation,weusejtorepresentj(T)intherestofthepaper.InfoJigsaw.InInfoJigsaw(seeFigure1foranex-ample),twoplayerstrytoidentifyagoalobject,buteachonlyhaspartialinformationaboutitsidentity.Thus,inordertosolvethetask,theymustcommuni-cate,piecingtheirinformationtogetherlikeajigsaw2OnecouldinprinciplesolveforanoptimalcommunicationstrategyforInfoJigsaw,butthiswouldlikelyresultinasolutionfarfromhumancommunication.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
545
(UN)Pdigitview(B)PletterviewFigure2:ChatinterfacethatAmazonMechanicalTurk(AMT)workersusetoplayInfoJigsaw(forread-ability,objectswiththegoaldigit/letterarebolded).puzzle.Figure2showstheinterfacethathumansusetoplaythegame.Moreformally,thesharedworldstatewincludesthepublicpropertiesofasetofobjects:positiononam×ngrid,colore(blue,yellow,green),andshape(square,diamond,circle).Inaddition,wcontainstheletteranddigitofthegoalobject(e.g.,B2).TheprivatestateofplayerPdigitisadigit(e.g.,1,2,3)foreachobject,andtheprivatestateofplayerPletterisaletter(e.g.,A,B,C)foreachobject.Thesestatesares+1,s−1dependingonwhichplayergoesfirst.Oneachturnt,aplayerj(T)’sactionatcanbeeither(io)amessagecontainingoneortwoEnglishwords3(e.g.,circle),O(ii)aclickonanobject,specifiedbyitsposition(per esempio.,(1,3)).Aclickactionterminatesthegame.Iftheclickedobjectisthegoal,agreensquarewillappeararounditwhichisvisibletobothplayers;iftheclickedobjectisnotthegoal,aredsquareappearsinstead.Todiscouragerandomguessing,wepreventplayersfromclickinginthefirsttimestep.Playersdonotseeanexplicitutil-ity(U);Tuttavia,theyareinstructedtothinkstrate-gicallytochoosemessagesthatleadtoclickingonthecorrectobjectwhileusingaminimumnumberofmessages.Playerscanseethenumberofcorrectclicks,wrongclicks,andnumberofthewordstheyhavesenttoeachothersofaratthetoprightofthescreen.Wewouldliketostudyhowcontext-dependentmeaningarisesoutoftheinterplaybetweena3IfthewordsarenotinsidetheEnglishdictionary,thesenderreceivesanerrorandthemessageisrejected.Thispre-ventsplayersfromcircumventingthegamerulesbyconnectingmultiplewordswithoutspaces.#games#messagesaveragescoreAll168049677.50Kept125933587.48Table1:Statisticsforall1680gamesandthe1259gamesinwhicheachmessagecontainsatleastoneofthe12mostfrequentwordsor“yes”,or“no”.context-independentliteralsemanticswithcontext-sensitiveplanning,inference,andpragmatics.ThesimplicityoftheInfoJigsawgameensuresthatthisinterplayisnotobscuredbyotherchallenges.2.1DatacollectionWegenerated10InfoJigsawscenariosasfollows:Foreachone,werandomlychoosem,ntobeei-ther2×3or3×2(whichresultsin64possiblepri-vatestates).Werandomlychoosethepropertiesofallobjectsandrandomlydesignatedoneasthegoal.WerandomlychooseeitherPletterorPdigittostartthegamefirst.Finally,tomakethescenariosinteresting,wekeepascenarioifitsatisfies:(io)Onlythegoalobject(andnootherobjects)hasthegoalcombina-tionoftheletteranddigit;(ii)Thereexistatleasttwogoal-consistentobjectsforeachplayerandtheirsumofgoal-consistentobjectsisatleastm×n;E(iii)allthegoalconsistentobjectsforeachplayerdonotsharethesamecolor,shape,orposition(whichmeansallthegoal-consistentobjectsarenotinleft,right,top,bottom,ormiddle).WecollectedadatasetofInfoJigsawgamesonAmazonMechanicalTurkusingtheframeworkinHawkins(2015)asfollows:200pairsofplayers
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
546
23456780200400600800#messages#games(UN)Numberofexchangedmes-sagespergame.0123456789100100200300score#games(B)Distributionoffinalgamescores.012345678900.20.40.60.81roundaveragescore(C)Averagescoreovermultipleroundsofgameplay,whichinter-estinglyremainsconstant.lefttopsquareyellowbottombluegreenrightdiamondcirclemiddlenot200400frequency(D)12mostfrequentwords,whichmakeup73%ofalltokens.topleftbottomlefttoprightyellowsquarebluesquarebottomrightyellowdiamondbluegreendiamondbluecirclesquarediamondgreenleftcolumntopmiddlenosquareleftcirclediamondgreensquareyellowtoprowcircletopgreencirclecolortopbottombluegreenyellowgreenblueyellowbottom50100150frequency(e)30mostfrequentmessages,whichmakeup49%ofallmessages.Figure3:Statisticsofthecollectedcorpus.eachplayedall10scenariosinarandomorder.Outof200pairs,32pairsleftthegameprematurelywhichresultsin168pairsplayingthetotalof1680games.Playersperformed4967actions(messagesandclicks)totalandobtainedanaveragescore(cor-rectclicks)of7.5pergame.Theaveragescoreperscenariovariedfrom6.4to8.2.Interestingly,thereisnosignificantdifferenceinscoresacrossthe10scenarios,suggestingthatplayersdonotadaptandbecomemoreproficientwithmoregameplay(Fig-ure3c).Figure3showsthestatisticsofthecollectedcorpus.Figure4showsoneofthegames,alongwiththedistributionofmessagesinthefirsttimestepofallgamesplayedonthisscenario.TofocusonthestrategicaspectsofInfoJigsaw,wefilteredthedatasettoreducethewordsinthetail.Specifically,wekeepagameifallitsmes-sagescontainatleastoneofthe12mostfrequentwords(showninFigure3d)or“yes”or“no”.Forexample,inFigure4,thegamescontainingmes-sagessuchaswhatcolor,midrow,colorarefilteredbecausetheydon’tcontainanyfre-quentwords.Messagessuchasmiddle,eithermiddle,middlemaybe,middleobjectsaremappedtomiddle.1259of1680gamessur-vived.Table1comparesthestatisticsbetweenallgamesandtheonesthatwerekept.Mostgamesthatwerefilteredoutcontainedlessfrequentsynonyms(e.g.roundinsteadofcircle).Somequestionswerefilteredouttoo(e.g.,whatcolor).Filteredgamesare1.15timeslongeronaverage.3LiteralSemanticsInordertounderstandtheprinciplesbehindhowhumansperformplanning,inference,andpragmat-ics,weaimtodevelopaparsimonious,interpretablemodelwithfewparametersratherthanahighlyex-pressive,data-drivenmodel.Therefore,followingthetraditionofRationalSpeechActs(RSA)(FrankandGoodman,2012;GoodmanandFrank,2016),wewilldefineinthissectionamappingfromeachwordtoitsliteralsemantics,andrelyonthePIPre-
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
547
bluesquaremiddlerowsquarediamondbottomrightnottopcolormiddleyellowsquaremiddleleftsquarenotcirclesquaresmiddletwowhatcoloryellowcirclediamondsquareeithermiddlemaybemiddlemidrowmiddleobjects5101520frequencyFindA1FindA1A?UN?B?B?UN?B?Pletterview?3?1?1?1?2?2PdigitviewPdigit:middlePletter:yellowcirclePdigit:bottomrightPletter:click(1,2)Figure4:Bottom:oneofthegamesplayedbyTurkers.Top:thedistributionofutterancesonthefirstmessage.Playerschoosetoexplaintheirpri-vatestateindifferentways.Someusemoregeneralmessages(e.g.,squarediamond),whilesomeusemorespecificones(e.g.,bluesquare).Topdiagramshowsthefirst20mostfrequentmessagesonthefirstround(72%ofallthemessages).currences(whichwewilldescribeinSection4)toprovidecontext-dependence.Onecouldalsolearntheliteralsemanticsbybackpropagatingthroughtheserecurrences,whichhasbeendoneforsimplerRSAmodels(MonroeandPotts,2015);orlearntheliteralsemanticsfromdataandthenputRSAontop(Andreasetal.,2016);weleavethistofuturework.Supposeaplayeruttersasinglewordcircle.Therearemultiplepossiblecontext-dependentinter-pretations:•Areanycirclesgoal-consistent?•Allthecirclesaregoal-consistent.•Somecirclesbutnootherobjectsaregoal-s−1011″#s+1101″#FindB2FindB2B?B?C?Pletterview?2?3?2Pdigitview(cid:74)square(cid:75)=ns:s∧h010i6=h000io(cid:74)topbottom(cid:75)=ns:s∧(cid:16)h100i∨h001i(cid:17)6=h000io(cid:74)topblue(cid:75)=ns:s∧(cid:16)h100i∧h111i(cid:17)6=h000ioFigure5:Privatestateoftheplayersandmeaningoftwoactionsequences.consistent.•Mostofthecirclesaregoal-consistent.•Atleastonecircleisgoal-consistent.Wewillshowthatmostoftheseinterpretationscanarisefromasimplefixedsemantics:roughly“somecirclesaregoalconsistent”.Wewillnowdefineasimpleliteralsemanticsofmessageactionssuchascircle,whichformsthebasecaseofPIP.Recallthatthesharedworldstatewcontainsthegoal(e.g.,B2)E,assumingPlettergoesfirst,theprivatestates−1(s+1)ofplayerPletter(Pdigit)containsthelet-ter(digit)ofeachobject.Fornotationalsimplicity,letusdefines−1(s+1)tobeamatrixcorrespond-ingtothespatiallocationsoftheobjects,whereanentryis1ifthecorrespondingobjecthasthegoallet-ter(digit)and0otherwise.Thussjalsorepresentsthesetofgoal-consistentobjectsgiventheprivateknowledgeofthatplayer.Figure5showstheprivatestatesoftheplayers.Wedefinetwotypesofmessageactions:infor-mative(e.g.,blue,top)andverifying(e.g.,yes,NO).Informativemessageshaveimmediatemean-ing,whileverifyingmessagesdependontheprevi-ousutterance.Informativemessages.Informativemessagesde-scribeconstraintsonthespeaker’sprivatestate(whichthepartnerdoesnotknow).Foramessagea,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
548
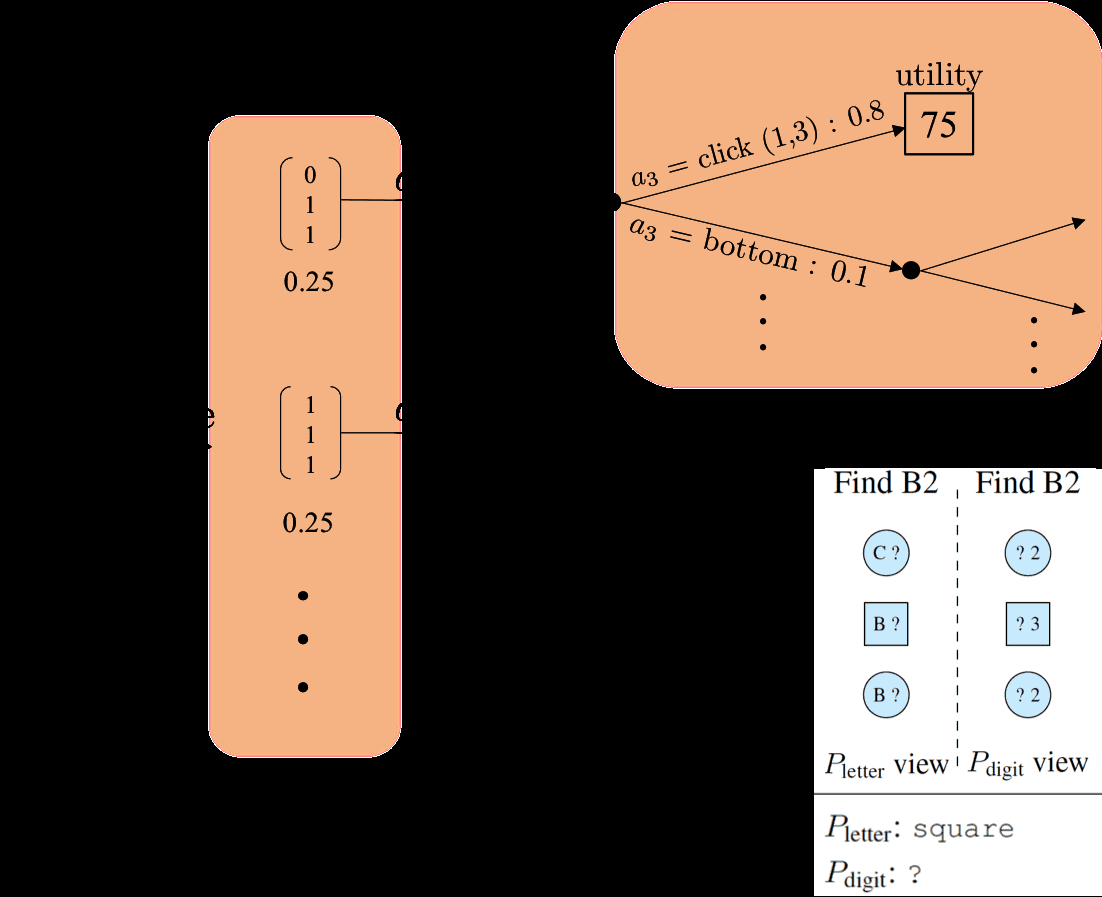
define(cid:74)UN(cid:75)tobethesetofconsistentprivatestates.Forexample,(cid:74)bottom(cid:75)isallprivatestateswheretherearegoal-consistentobjectsinthebottomrow.Formally,foreachwordxthatspecifiessomeob-jectproperty(e.g.,blue,top),definevxtobeann×mmatrixwhereanentryis1ifthecorrespondingobjecthasthepropertyx,and0otherwise.Then,de-finetheliteralsemanticsofasingle-wordmessagextobe(cid:74)X(cid:75)def={S:s∧vx6=0},where∧denoteselement-wiseandand0denotesthezeromatrix.Thatis,single-propertymessagescanbeglossedas“somegoal-consistentobjecthaspropertyx”.Foratwo-wordmessagexy,wedefinetheliteralsemanticsdependingontherelationshipbetweenxandy.Ifxandyaremutuallyexclusive,thenweinterpretxyasxory(e.g.,squarecircle);otherwise,weinterpretxyasxandy(e.g.,bluetop).Formalmente,(cid:74)xy(cid:75)def={S:s∧(vx∧vy)6=0}ifvx∧vy6=0and{S:s∧(vx∨vy)6=0}otherwise.SeeFigure5forsomeexamples.Actionsequences.Wenowdefinetheliteralse-manticsofanentireactionsequence(cid:74)A1:T(cid:75)jwithre-specttoplayerj,whichisthesetofpossiblepart-nerprivatestatess−j.Intuitively,wewanttosim-plyintersectthesetofconsistentprivatestatesoftheinformativemessages,butweneedtoalsohan-dleverifyingmessages(yesandno),whicharecontext-dependent.Formally,wesaythatprivatestates−j∈(cid:74)A1:T(cid:75)jifthefollowingholds:forallinformativemessagesaiutteredby−j,s−j∈(cid:74)AI(cid:75);andforallverifyingmessagesaiutteredby−jifai=yesthen,s−j∈(cid:74)ai−1(cid:75);andifai=nothen,s−j6∈(cid:74)ai−1(cid:75).4ThePlanning-Inference-Pragmatics(PIP)ModelWhydoesPdigitinFigure1choosecircleratherthantoporclick(1,2)?Intuitively,whenaplayerchoosesanaction,sheshouldtakeintoac-countherpreviousactions,herpartner’sactions,andtheeffectofheractionsonfutureturns.Sheshoulddoallthesewhilereasoningpragmaticallythatherpartnerisalsoastrategicplayer.Atahigh-level,PIPdefinesasystemofrecur-rencesrevolvingaroundthreeconcepts,depictedinFigure6:playerj’sbeliefsoverthepartner’spri-Figure6:PIPisdefinedviaasystemofrecur-rencesthatsimultaneouslycapturesplanning,infer-ence,andpragmatics.Thearrowsshowthedepen-denciesbetweenbeliefsp,expectedutilitiesV,andpolicyπ.vatestatepkj(s−j|sj,A1:T),herexpectedutilityofthegameVkj(s+1,s−1,a1:T),andherpolicyπkj(at|sj,A1:t−1).Here,tindexesthecurrenttimeandkindexesthedepthofpragmaticrecursion,whichwillbeexplainedlaterinSection4.3.Tosimplifytheno-tation,wehavedroppedw(sharedworldstate)fromthenotation,sinceeverythingconditionsonit.4.1InferenceFromplayerj’spointofview,thepurposeofinfer-enceistocomputeadistributionoverthepartner’sprivatestates−jgivenallactionsthusfara1:t.Wefirstconsidera“level0”player,whichsimplyas-signsauniformdistributionoverallstatesconsistentwiththeliteralsemanticsofa1:T,whichwedefinedinSection3:p0j(s−j|sj,A1:T)∝(1s−j∈(cid:74)A1:T(cid:75)J,0otherwise.(1)Forexample,Figure7,showsthePletter’sbeliefaboutPdigit’sprivatestateafterobservingcircle.Rememberweshowtheprivatestateoftheplayersasamatrixwhereanentryis1ifthecorrespondingobjecthasthegoalletter(digit)and0otherwise.Aplayer’sownprivatestatesjcanalsoconstrainherbeliefsaboutherpartner’sprivatestates−j.Forexample,inInfoJigsaw,theactiveplayerknowsthereisagoal,andsowesetpkj(s−j|sj,A1:T)=0ifs−j∧sj=0.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
549
00.050.10.15000(cid:20)(cid:21)001(cid:20)(cid:21)010(cid:20)(cid:21)011(cid:20)(cid:21)100(cid:20)(cid:21)101(cid:20)(cid:21)110(cid:20)(cid:21)111(cid:20)(cid:21)Figure7:Pletter’sprobabilitydistributionoverPdigit’sprivatestateafterPdigitsayscircleinthegameshowninFigure5.4.2PlanningThepurposeofplanningistocomputeapolicyπkj,whichspecifiesadistributionoverplayerj’sactionsatgivenallpastactionsa1:t−1.Toconstructthepol-icy,wefirstdefineanexpectedutilityVkjviathefol-lowingforward-lookingrecurrence:Whenthegameisover(e.g.,inInfoJigsaw,oneplayerclicksonanobject),theexpectedutilityofthedialogueissimplyitsutilityasdefinedbythegame:Vkj(s+1,s−1,a1:T)=U(s+1,s−1,a1:T).(2)Otherwise,wecomputetheexpectedutilityassum-ingthatinthenextturn,playerjchoosesactionat+1withprobabilitygovernedbyherpolicyπkj(at+1|sj,A1:T):Vkj(s+1,s−1,a1:T)=Xat+1πkj(at+1|sj,A1:T)Vk−j(s−1,s+1,a1:t+1).(3)Havingdefinedtheexpectedutility,wenowde-finethepolicy.First,letDkjbethegaininexpectedutilityVk−j(s+1,s−1,a1:T)overasimplebaselinepolicythatendsthegameimmediately,yieldingutil-ityU(s+1,s−1,a1:t−1)(whichissimplyapenaltyfornotfindingthecorrectgoalandapenaltyforeachaction).Ofcourse,thepartner’sprivatestates−jisunknownandmustbemarginalizedoutbasedonplayerj’sbeliefs;letEkjbetheexpectedgain.Lettheprobabilityofanactionatbeproportionaltomax(0,Ekj)α,whereα∈[0,∞)isahyperparame-terthatcontrolstherationalityoftheagent(alargerαmeansthattheplayerchoosesutility-maximizingactionsmoreaggressively).Formalmente:Dkj=Vk−j(s+1,s−1,a1:T)−U(s+1,s−1,a1:t−1),Ekj=Xs−jpkj(s−j|sj,A1:t−1)Dkj,πkj(at|sj,A1:t−1)∝max(cid:16)0,Ekj(cid:17)α.(4)Inpractice,weuseadepth-limitedrecurrence,wheretheexpectedutilityiscomputedassumingthatthegamewillendinfturnsandthelastactionisaclickaction(meaningthatweonlyconsidertheactionsequenceswithsize≤fandaclickingactionasthelastaction).Figure8showshowPdigitcom-putestheexpectedgain(Eqn.4)ofsayingcircle.Figure8:PlanningreasoningforthegameinFig-ure1(reproducedhereinthebottomright).(UN)Inordertocalculatetheexpectedgain(E)ofgenerat-ingcircle,foreverystates,PdigitcomputestheprobabilityofsbeingthePletter’sprivatestate.(B)Shethencomputestheexpectedutility(V)ifshegeneratescircleassumingPletter’sprivatestateiss.4.3PragmaticsThepurposeofpragmaticsistotakeintoaccountthepartner’sstrategizing.Wedothisbyconstruct-ingalevel-kplayerthatinfersthepartner’spri-vatestate,followingthetraditionofRationalSpeechActs(RSA)(FrankandGoodman,2012;GoodmanandFrank,2016).Recallthatalevel-0playerp0j(Section4.1)putsauniformdistributionoverallthe
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
550
Figure9:PragmaticreasoningforthegameinFigure1(reproducedhereintheupperright)attimestep3.Playersreasonrecursivelyabouteachothersbeliefs:thelevel-0playerputsauniformdistributionp0joverallthestatesinwhichatleastonecircleisgoal-consistentindependentofthesharedworldstateandpreviousactions.Thelevel-1playerassignsprobabilityoverthepartner’sprivatestatess−jproportionaltotheprobabilitythatshewouldhaveperformedthelastactiongiventhatstates−j.Forexample,ifh001iwerePdigit’sprivatestate,thensayingbottomwouldbemoreprobable(giventhesharedworldstate);ifh111iwerePdigit’sstate,thenclickingonthesquarewouldbeabetteroption(giventhepreviousactions).ButgiventhatPdigitutteredcircle,h101iismostlikely,asreflectedbyp1j.semanticallyvalidprivatestatesofthepartner.Alevel-kplayerassignsprobabilityoverthepartner’sprivatestateproportionaltotheprobabilitythatalevel-(k−1)playerwouldhaveperformedthelastactionat:pkj(s−j|sj,A1:T)∝πk−1−j(at|s−j,A1:t−1)pkj(s−j|sj,A1:t−2).(5)Figure9showsanexampleofthepragmaticrea-soning.4.4AcloserlookatthemeaningofactionsIntheSection4.2,wemodeledtheplayersasra-tionalagentsthatchooseactionsthatleadtohighergainutility.Inthepragmaticssection(Section4.3),wedescribedhowaplayerinfersthepartner’spri-vatestatetakingintoaccountthatherpartnerisactingcooperatively.Thephenomenathatemergesfromthecombinationofthetwoisthetopicofthissection.WefirstdefinethebeliefmarginalsBjofaplayerjtobethemarginalprobabilitiesthateachobjectisgoal-consistentunderthehypothesizedpartner’sprivatestates−j∈Rm×n,conditionedonactionsa1:T:Bj(sj,A1:T)=Xs−jpkj(s−j|sj,A1:T)s−j.(6)Attimet=0(beforeanyactions),thebeliefmarginalsofbothplayersarem×nmatriceswith0.5inallentries.Thechangeinabeliefmarginalafterobservinganactionatgivesasenseoftheef-fective(context-dependent)meaningofthataction.Wefirstexplainhowpragmatics(k>0in(Eqn.5))leadstorichactionmeanings.Whenaplayerobservesherpartner’sactionat,sheassumesthisac-
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
551
FindA2?3?2?1?2Pdigitview(UN)Pdigit:bottomPletter:right(k=0)Pdigit:bottomPletter:right(k=1)PdigitestimationofPletterstate(B)0.5000.6670.5000.667″#0.4240.7690.4230.940″#Figure10:BeliefmarginalsofPdigit(Eqn.6)afterobservingsequencesofactionsfordifferentprag-maticdepthsk.(B)Withoutpragmatics(k=0),Pdigitthinksbothobjectsontherighthasthesameprobabilitytobegoal-consistent.Withpragmatics(k=1),Pdigitthinksthattheobjectinthebottomrightismorelikelytobegoal-consistent.tionwaschosenbecauseitresultsinahigherutilitythanthealternatives.Inotherwords,sheinfersthatherpartner’sprivatestatecannotbeoneinwhichatdoesnotleadtohighutility.Asanexample,say-ingcircleinsteadoftopcircleorbottomcircleimpliesthatthereismorethanonegoal-consistentcircle.Thepragmaticdepthkgovernstheextenttowhichthistypeofreasoningisapplied.RecallinSection4.2,aplayerchoosesanactionconditionedonallpreviousactions,andtheotherplayerassumedthiscontext-dependence.Asanex-ample,Figure10(D)showshowrightchangesitsmeaningwhenitfollowsbottom.5Experiments5.1SetupWeapriorisettherewardofclickingonthegoaltobe+100andclickingonthewrongobjecttobe−100.Wesetthesmoothingα=10andtheactioncosttobe−50basedonthedata.Thelargertheactioncost,thefewermessageswillbeusedbeforeselectinganobject.Formally,afterkactions:Utility=−50k+(+100thegoalobjectisclicked,−100otherwise.(7)Wesmoothedallpolicesbyadding0.01totheprobabilityofeachactionandre-normalizing.Bydefault,wesetk=1(pragmaticdepth(Eqn.4)).Whencomputingtheexpectedutility(Eqn.3)ofthegame,weusealookaheadoff=2.Inferencelooksbackbtimesteps(cioè.,(Eqn.1)E(Eqn.5)arebasedonat−b+1:tratherthana1:T);wesetb=∞bydefault.Weimplementedtwobaselinepolicies:Randompolicy:forplayerj,therandompol-icyrandomlychoosesoneofthesemanticallyvalid(Section3)actionswithrespecttosjorclicksonagoal-consistentobject.Formally,therandompolicyplacesauniformdistributionover:{UN:sj∈(cid:74)UN(cid:75)}∪{click(tu,v):(sj)tu,v=1}.(8)GreedyPolicy:assignshigherprobabilitytotheactionsthatconveymoreinformationabouttheplayer’sprivatestate.Weheuristicallysettheprob-abilityofgeneratinganactionproportionaltohowmuchitshrinksthesetofsemanticallyvalidstates.Formally,forthemessageactions:πmsgj(at|A1:t−1,sj)∝|(cid:74)A1:t−1(cid:75)−j|-|(cid:74)A1:T(cid:75)−j|(9)Fortheclickingactions,wecomputethebeliefstateasexplainedinSection4.4.RememberBu,visthemarginalprobabilityoftheobjectintherowuandcolumnvbeinggoal-consistentinthepartner’spri-vatestate.Formally,forclickingactions:πclickj(click(tu,v)|A1:T,sj)∝min((sj)tu,v,Bj(sj,A1:T)tu,v).(10)Finalmente,thegreedypolicychoosesaclickactionwithprobabilityγandamessageactionwithprobability1−γ.Sothatγincreasesastheplayergetsmoreconfidentaboutthepositionofthegoal,wesetγtobetheprobabilityofthemostprobablepositionofthegoal:γ=maxu,vπclickj(click(tu,v)|A1:T,sj).5.2ResultsFigure11comparesthetwobaselineswithPIPonthetaskofpredictinghumanbehaviorasmeasuredbylog-likelihood.4Toestimatethebestpossible4Webootstrapthedata1000timesandweshow90%confi-denceintervals.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
552
−4.5−4−3.5−3−2.5ceilingPIPgreedyrandomlog-likelihoodAllroundsFirstroundFigure11:Averagelog-likelihoodacrossmessages.(UN)PerformanceofPIPandbaselinesonalltimesteps.(B)PerformanceofPIPandbaselinesononlythefirsttimestepalongwiththeceilinggivenbytheentropyofthehumandata.Theerrorbarsshow90%confidenceintervals.(i.e.,ceiling)performance,wecomputetheentropyoftheactionsonthefirsttimestepbasedonapproxi-mately100datapointsperscenario.Foreachpolicy,weranktheactionsbytheirprobabilityindecreas-ingorder(actionswiththesameprobabilityareran-domlyordered),andthencomputetheaveragerank-ingacrossactionsaccordingtothedifferentpolicies;seeFigure13fortheresults.Toassessthedifferentcomponents(planning,in-ference,pragmatics)ofPIP,werunPIP,ablatingonecomponentatatimefromthedefaultsettingofk=1,f=2,andb=∞(seeFigure12).Pragmatics.LetPIP-pragbePIPbutwithaprag-maticdepth(Eqn.4)ofk=0ratherthank=1,whichmeansthatPIP-pragonlydrawsinferencesbasedontheliteralsemanticsofmessages.PIP-pragloses0.21inaveragelog-likelihoodperaction,high-lightingtheimportanceofpragmaticsinmodelinghumanbehavior.Planning.LetPIP-planbePIP,butlookingaheadonlyf=1stepwhencomputingtheexpectedutil-ity(Eqn.3)ratherthanf=2.Withashorterfu-turehorizon,PIP-plantriestogiveasmuchinforma-tionaspossibleateachturn,whereashumanplayerstendtogiveinformationabouttheirstateincremen-tally.PIP-plancannotcapturethisbehaviorandal-locateslowprobabilitytothesekindsofdialogue.PIP-planhasanaveragelog-likelihoodwhichis0.05lowerthanthatofPIP,highlightingtheimportanceofplanning.Inference.LetPIP-inferbePIP,butonlylookingatthelastutterance(b=1)ratherthanthefullhistory(b=∞).Theresultsherearemorenuanced.Al-thoughPIP-inferactuallyperformsbetterthanPIPonallgames,wefindthatPIP-inferisworsethanPIPbyanaveragelog-likelihoodof0.15inpredictingmes-sagesaftertimestep3,highlightingtheimportanceofinference,butonlyinlonggames.Itislikelythatadditionalnoiseinvolvedintheinferencepro-cessleadstothedecreasedperformancewhenback-wardlookinginferenceisnotactuallyneeded.6RelatedWorkandDiscussionOurworktouchesonideasingametheory,prag-maticmodeling,dialoguemodeling,andlearningcommunicativeagents,whichwehighlightbelow.Gametheory.Accordingtogametheorytermi-nology(ShohamandLeyton-Brown,2008),Info-Jigsawisanon-cooperative(thereisnoofflineop-timizationoftheplayer’spolicybeforethegamestarts),common-payoff(theplayershavethesameutility),incompleteinformation(theplayershaveprivatestate)gamewiththesequentialactions.Onerelatedconceptingametheoryrelatedtoourmodelisrationalizability(Bernheim,1984;Pearce,1984).Astrategyisrationalizableifitisjustifiabletoplayagainstacompletelyrationalplayer.Anotherrelatedconceptisepistemicgames(DekelandSiniscalchi,2015;Perea,2012).Epistemicgametheorystudiesthebehavioralimplicationsofrationalityandmutualbeliefsingames.Itisimportanttonotethatwearenotinterestedinnotionsofglobaloptimaorequilibria;Piuttosto,weareinterestedinmodelinghumanbehavior.Re-strictingwordstoaveryrestrictednaturallanguagehasbeenstudiedinthecontextoflanguagegames(Wittgenstein,1953;Lewis,2008;Nowaketal.,1999;Franke,2009;Hutteggeretal.,2010).Rationalspeechacts.ThepragmaticcomponentofPIPisbasedonRationalSpeechActframework(FrankandGoodman,2012;Gollandetal.,2010),
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
553
PIPPIP-pragPIP-planPIP-infer−3.5−3.4−3.3−3.2log-likelihood(UN)Performanceoverallgamesandallrounds.PIPPIP-pragPIP-planPIP-infer−2.7−2.6−2.5−2.4−2.3−2.2log-likelihood(B)Performanceovermessagesafterround3.PIPPIP-pragPIP-planPIP-inferk(pragmatics)1011F(planning)2212B(inference)∞∞∞1rankall17.119.317.216.9rank≥310.410.811.613.1(C)Top:parametersetup.Bot-tom:expectedrankingofhumanmessagesaccordingtothediffer-entablationsFigure12:PerformanceonablationsofPIP.Averagelog-likelihoodpermessage,thewhiskersshow90%confidenceintervals.PIPhasbetterperformanceofablationofplanningandpragmaticsoverallrounds.Lookingonlyonestepbackwardhasabetterperformanceinthefirstfewroundsbutitisworseafterround3.randomgreedyPIPceiling010203040expectedrankingAllroundsFirstroundFigure13:Expectedrankingofthehumanmes-sagesaccordingtodifferentpolicies.Errorbarsshow90%confidenceintervals.whichdefinesrecurrencescapturinghowoneagentreasonsaboutanother.SimilarideaswereexploredintheprecursorworkofGollandetal.(2010),andmuchworkhasensued(Smithetal.,2013;QingandFranke,2014;MonroeandPotts,2015;Ullmanetal.,2016;AndreasandKlein,2016).Mostofthisworkisrestrictedtoproductionandcomprehensionofasingleutterance.Hawkinsetal.(2015)extendtheseideastotwoutterances(aquestionandananswer).Vogeletal.(2013B)in-tegratesplanningwithpragmaticsusingdecentral-izedpartiallyobservableMarkovprocesses(DEC-POMDPs).Intheirtask,twobotsshouldfindandco-locatewithaspecificcard.IncontrasttoInfo-Jigsaw,theirtaskcanbecompletedwithoutcommu-nication;theiragentsonlycommunicateonceshar-ingthecardlocation.Theyalsoonlystudyartifi-cialagentsplayingtogetherandwerenotconcernedaboutmodelinghumanbehavior.Learningtocommunicate.Thereisarichliter-atureonmulti-agentreinforcementlearning(Buso-niuetal.,2008).Someworksassumefullvisibil-ityandcooperatewithoutcommunication,assumingtheworldiscompletelyvisibletoallagents(LauerandRiedmiller,2000;Littman,2001);othersas-sumeapredefinedconventionforcommunication(ZhangandLesser,2013;Tan,1993).Thereisalsosomeworkthatlearnstheconventionitself(Foersteretal.,2016;Sukhbaataretal.,2016;Lazaridouetal.,2017;MordatchandAbbeel,2018).Lazaridouetal.(2017)putshumansinthelooptomakethecommu-nicationmorehuman-interpretable.Incomparisontotheseworks,weseektopredicthumanbehaviorinsteadofmodelingartificialagentsthatcommuni-catewitheachother.Dialogue.Thereisalsoalotofworkincompu-tationallinguisticsandNLPonmodelingdialogue.AllenandPerrault(1980)providesamodelthatin-
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
554
ferstheintention/planoftheotheragentandusesthisplantogeneratearesponse.ClarkandBrennan(1991)explainshowtwoplayersupdatetheircom-monground(mutualknowledge,mutualbeliefs,andmutualassumptions)inordertocoordinate.Recentworkintask-orienteddialogueusesPOMDPsandend-to-endneuralnetworks(Young,2000;Youngetal.,2013;Wenetal.,2017;Heetal.,2017).Inthiswork,insteadoflearningfromalargecorpus,wepredicthumanbehaviorwithoutlearning,albeitinamuchmorestrategic,stylizedsetting(twowordsperutterance).7ConclusionInthispaper,westartedwiththeobservationthathu-mansuselanguageinaverycontextualwaydrivenbytheirgoals.Weidentifiedthreesalientaspects—planning,inference,pragmatics—andproposedaunifiedmodel,PIP,thatcapturesallthreeaspectssi-multaneously.Ourmainresultisthataverysimple,context-independentliteralsemanticscangiveriseviatherecurrencestorichphenomena.Westudythesephenomenainanewgame,InfoJigsaw,andshowthatPIPisabletocapturehumanbehavior.ReproducibilityAllcode,dati,andexperimentsforthispaperareavailableontheCodaLabplatformathttps://worksheets.codalab.org/worksheets/0x052129c7afa9498481185b553d23f0f9/.AcknowledgmentsWewouldliketothanktheanonymousreviewersandtheactioneditorfortheirhelpfulcomments.WealsothankWillMonroeforprovidingvaluablefeed-backonearlydrafts.ReferencesJamesF.AllenandC.RaymondPerrault.1980.Ana-lyzingintentioninutterances.ArtificialIntelligence,15(3):143–178.JacobAndreasandDanKlein.2016.Reasoningaboutpragmaticswithneurallistenersandspeakers.InEmpiricalMethodsinNaturalLanguageProcessing(EMNLP),pages1173–1182.JacobAndreas,MarcusRohrbach,TrevorDarrell,andDanKlein.2016.Learningtocomposeneuralnet-worksforquestionanswering.InAssociationforComputationalLinguistics(ACL),pages1545–1554.B.DouglasBernheim.1984.Rationalizablestrategicbe-havior.Econometrica:JournaloftheEconometricSo-ciety,pages1007–1028.LucianBusoniu,RobertBabuska,andBartDeSchutter.2008.Acomprehensivesurveyofmultiagentrein-forcementlearning.IEEETrans.Systems,Man,andCybernetics,PartC,38(2):156–172.HerbertH.ClarkandSusanE.Brennan.1991.Ground-inginCommunication.PerspectivesonSociallySharedCognition.EddieDekelandMarcianoSiniscalchi.2015.Epistemicgametheory,volume4.HandbookofGameTheorywithEconomicApplications.JakobFoerster,YannisM.Assael,NandodeFreitas,andShimonWhiteson.2016.Learningtocommuni-catewithdeepmulti-agentreinforcementlearning.InAdvancesinNeuralInformationProcessingSystems(NIPS),pages2137–2145.MichaelC.FrankandNoahD.Goodman.2012.Predict-ingpragmaticreasoninginlanguagegames.Science,336:998–998.MichaelFranke.2009.Signaltoact:Gametheoryinpragmatics.InstituteforLogic,LanguageandCom-putation.DaveGolland,PercyLiang,andDanKlein.2010.Agame-theoreticapproachtogeneratingspatialdescrip-tions.InEmpiricalMethodsinNaturalLanguagePro-cessing(EMNLP),pages410–419.NoahD.GoodmanandMichaelC.Frank.2016.Prag-maticlanguageinterpretationasprobabilisticinfer-ence.TrendsinCognitiveSciences,20(11):818–829.HerbertP.Grice.1975.Logicandconversation.SyntaxandSemantics,3:41–58.RobertX.D.Hawkins,AndreasStuhlm¨uller,JudithDe-gen,andNoahD.Goodman.2015.Whydoyouask?Goodquestionsprovokeinformativeanswers.InPro-ceedingsoftheThirty-SeventhAnnualConferenceoftheCognitiveScienceSociety.RobertX.D.Hawkins.2015.Conductingreal-timemul-tiplayerexperimentsontheweb.BehaviorResearchMethods,47(4):966–976.HeHe,AnushaBalakrishnan,MihailEric,andPercyLiang.2017.Learningsymmetriccollaborativedia-logueagentswithdynamicknowledgegraphembed-dings.InAssociationforComputationalLinguistics(ACL),pages1766–1776.SimonM.Huttegger,BrianSkyrms,RorySmead,andKevin J.S. Zollman. 2010. Evolutionary dynamics of Lewis signaling games: Signaling systems vs. partial pooling. Synthese, 172(1):177–191.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
555
JayantKrishnamurthyandThomasKollar.2013.Jointlylearningtoparseandperceive:Connectingnaturallan-guagetothephysicalworld.TransactionsoftheAsso-ciationforComputationalLinguistics(TACL),1:193–206.MartinLauerandMartinRiedmiller.2000.Analgorithmfordistributedreinforcementlearningincooperativemulti-agentsystems.InInternationalConferenceonMachineLearning(ICML),pages535–542.AngelikiLazaridou,AlexanderPeysakhovich,andMarcoBaroni.2017.Multi-agentcooperationandtheemer-genceof(natural)language.InInternationalConfer-enceonLearningRepresentations(ICLR).DavidLewis.2008.Convention:Aphilosophicalstudy.JohnWiley&Sons.MichaelL.Littman.2001.Value-functionreinforce-mentlearninginMarkovgames.CognitiveSystemsResearch,2(1):55–66.CynthiaMatuszek,NicholasFitzGerald,LukeZettle-moyer,LiefengBo,andDieterFox.2012.Ajointmodeloflanguageandperceptionforgroundedat-tributelearning.InInternationalConferenceonMa-chineLearning(ICML),pages1671–1678.WillMonroeandChristopherPotts.2015.LearningintheRationalSpeechActsmodel.InProceedingsof20thAmsterdamColloquium.RichardMontague.1973.Thepropertreatmentofquan-tificationinordinaryEnglish.InApproachestoNatu-ralLanguage,pages221–242.IgorMordatchandPieterAbbeel.2018.Emergenceofgroundedcompositionallanguageinmulti-agentpop-ulations.InAssociationfortheAdvancementofArtifi-cialIntelligence(Aai).MartinA.Nowak,JoshuaB.Plotkin,andDavidC.Krakauer.1999.Theevolutionarylanguagegame.JournalofTheoreticalBiology,200(2):147–162.DavidG.Pearce.1984.Rationalizablestrategicbehaviorandtheproblemofperfection.Econometrica:JournaloftheEconometricSociety,pages1029–1050.Andr’esPerea.2012.Epistemicgametheory:reasoningandchoice.CambridgeUniversityPress.ChristopherPotts.2012.Goal-drivenanswersintheCardsdialoguecorpus.InProceedingsofthe30thWestCoastConferenceonFormalLinguistics,pages1–20.CiyangQingandMichaelFranke.2014.Gradableadjectives,vagueness,andoptimallanguageuse:Aspeaker-orientedmodel.InSemanticsandLinguisticTheory,volume24,pages23–41.Yoav Shoham and Kevin Leyton-Brown. 2008. Multi-agent Systems: Algorithmic, Game-Theoretic, and Logical Foundations. Cambridge University Press.NathanielJ.Smith,NoahD.Goodman,andMichaelC.Frank.2013.Learningandusinglanguageviare-cursivepragmaticreasoningaboutotheragents.InAdvancesinNeuralInformationProcessingSystems(NIPS),pages3039–3047.SainbayarSukhbaatar,RobFergus,etal.2016.Learningmultiagentcommunicationwithbackpropagation.InAdvancesinNeuralInformationProcessingSystems(NIPS),pages2244–2252.MingTan.1993.Multi-agentreinforcementlearning:Independentvs.cooperativeagents.InInternationalConferenceonMachineLearning(ICML),pages330–337.TomerD.Ullman,YangXu,andNoahD.Goodman.2016.Thepragmaticsofspatiallanguage.InPro-ceedingsofthe38thAnnualConferenceoftheCogni-tiveScienceSociety.AdamVogel,MaxBodoia,ChristopherPotts,andDanielJurafsky.2013a.EmergenceofGriceanmaximsfrommulti-agentdecisiontheory.InNorthAmericanAsso-ciationforComputationalLinguistics(Naacl),pages1072–1081.AdamVogel,ChristopherPotts,andDanJurafsky.2013b.Implicaturesandnestedbeliefsinapproximatedecentralized-POMDPs.InAssociationforComputa-tionalLinguistics(ACL),pages74–80.Tsung-HsienWen,MilicaGasic,NikolaMrksic,LinaM.Rojas-Barahona,Pei-HaoSu,StefanUltes,DavidVandyke,andSteveYoung.2017.Anetwork-basedend-to-endtrainabletask-orienteddialoguesystem.InEuropeanAssociationforComputationalLinguistics(EACL),pages438–449.LudwigWittgenstein.1953.PhilosophicalInvestiga-tions.Blackwell,Oxford.SteveYoung,MilicaGaˇsi´c,BlaiseThomson,andJa-sonD.Williams.2013.POMDP-basedstatisticalspo-kendialogsystems:Areview.InProceedingsoftheIEEE,number5,pages1160–1179.SteveJ.Young.2000.Probabilisticmethodsinspoken-dialoguesystems.PhilosophicalTransactionsoftheRoyalSocietyofLondonA:Mathematical,PhysicalandEngineeringSciences,358(1769):1389–1402.ChongjieZhangandVictorLesser.2013.Coordinatingmulti-agentreinforcementlearningwithlimitedcom-munication.InProceedingsofthe2013InternationalConferenceonAutonomousAgentsandMulti-agentSystems,pages1101–1108.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
0
3
7
1
5
6
7
6
3
8
/
/
T
l
UN
C
_
UN
_
0
0
0
3
7
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
556