Operazioni dell'Associazione per la Linguistica Computazionale, vol. 3, pag. 585–597, 2015. Redattore di azioni: Regina Barzilay.
Lotto di invio: 7/2015; Lotto di revisione: 10/2015; Pubblicato 12/2015.
2015 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
C
(cid:13)
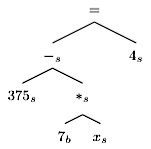
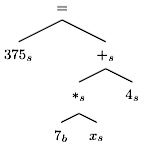
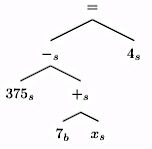
ParsingAlgebraicWordProblemsintoEquationsRikKoncel-Kedziorski,HannanehHajishirzi,AshishSabharwal†,OrenEtzioni†,andSienaDumasAngUniversityofWashington,†AllenInstituteforAI{kedzior,hannaneh,sienaang}@uw.edu,{ashishs,orene}@allenai.orgAbstractThispaperformalizestheproblemofsolv-ingmulti-sentencealgebraicwordproblemsasthatofgeneratingandscoringequationtrees.Weuseintegerlinearprogrammingtogener-ateequationtreesandscoretheirlikelihoodbylearninglocalandglobaldiscriminativemod-els.Thesemodelsaretrainedonasmallsetofwordproblemsandtheiranswers,withoutanymanualannotation,inordertochoosetheequationthatbestmatchestheproblemtext.WerefertotheoverallsystemasALGES.WecompareALGESwithpreviousworkandshowthatitcoversthefullgamutofarithmeticoperationswhereasHosseinietal.(2014)onlyhandleadditionandsubtraction.Inaddition,ALGESovercomesthebrittlenessoftheKush-manetal.(2014)approachonsingle-equationproblems,yieldinga15%to50%reductioninerror.1IntroductionGrade-schoolalgebrawordproblemsarebriefnar-ratives(seeFigure1).Atypicalproblemfirstde-scribesapartialworldstateconsistingofcharacters,entities,andquantities.Nextitupdatestheconditionofanentityorexplicatestherelationshipbetweenentities.Finally,itposesaquestionaboutaquantityinthenarrative.Anordinarychildhastolearntherequiredalge-bra,butwilleasilygraspthenarrativeutilizingex-tensiveworldknowledge,largevocabulary,word-sensedisambiguation,coreferenceresolution,mas-teryofsyntax,andtheabilitytocombineindividualOceansideBikeRentalShopcharges17dollarsplus7dollarsanhourforrentingabike.Tompaid80dollarstorentabike.Howmanyhoursdidhepaytohavethebikecheckedout?=+$17$∗$7$xh80$solution:917+(7∗x)=80Figure1:Exampleproblemandsolutionsentencesintoacoherentmentalmodel.Incontrast,thechallengeforanNLPsystemisto“makesense”ofthenarrative,whichmayrefertoarbitraryactiv-itieslikerentingbikes,collectingcoins,oreatingcookies.Previousworkcopedwiththeopen-domainas-pectofalgebraicwordproblemsbyrelyingondeter-ministicstatetransitionsbasedonverbcategoriza-tion(Hosseinietal.,2014)orbylearningtemplatesthatcoverequationsofparticularforms(Kushmanetal.,2014).Wehavediscovered,Tuttavia,thatbothapproachesarebrittle,particularlyastrainingdataisscarceinthisdomain,andthespaceofequationsgrowsexponentiallywiththenumberofquantitiesmentionedinthemathproblem.WeintroduceALGES,1whichmapsanunseenmulti-sentencealgebraicwordproblemintoasetofpossibleequationtrees.Figure1showsanequationtreealongsidethewordproblemitrepresents.ALGESgeneratesthespaceoftreesviaIntegerLinearProgramming(ILP),whichallowsittocon-1Thecodeanddataispubliclyavailableathttps://gitlab.cs.washington.edu/ALGES/TACL2015. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e – p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 1 6 0 1 5 6 6 8 1 4 / / t l a c _ a _ 0 0 1 6 0 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 586 strainthespaceoftreestorepresenttype-consistentalgebraicequationssatisfyingasmanydesirablepropertiesaspossible.ALGESlearnstomapspansoftexttoarithmeticoperators,tocombinethemgiventheglobalcontextoftheproblem,andtochoosethe“best”treecorrespondingtotheproblem.ThetrainingsetforALGESconsistsofunannotatedalgebraicwordproblemsandtheirsolution.Solv-ingtheequationrepresentedbysuchatreeistrivial.ALGESisdescribedindetailinSection4.ALGESisabletosolvewordproblemswithsingle-variableequationsliketheonesinFigure1.IncontrasttoHosseinietal.(2014),ALGEScovers+,−,∗,and/.TheworkofKushmanetal.(2014)hasbroaderscopebutweshowthatitreliesheav-ilyonoverlapbetweentrainingandtestdata.Whenthatoverlapisreduced,ALGESis15%to50%moreaccuratethanthissystem.Ourcontributionsareasfollows:(1)Weformal-izetheproblemofsolvingmulti-sentencealgebraicwordproblemsasthatofgeneratingandrankingequationtrees;(2)Weshowhowtoscorethelike-lihoodofequationtreesbylearningdiscriminativemodelstrainedfromasmallnumberofwordprob-lemsandtheirsolutions–withoutanymanualan-notation;E(3)WedemonstrateempiricallythatALGEShasbroaderscopethanthesystemofHos-seinietal.(2014),andovercomesthebrittlenessofthemethodofKushmanetal.(2014).2PreviousWorkOurworkisrelatedtosituatedsemanticinterpre-tation,whichaimstomapnaturallanguagesen-tencestoformalmeaningrepresentations(ZelleandMooney,1996;ZettlemoyerandCollins,2005;GeandMooney,2006;Kwiatkowskietal.,2010).Morecloselyrelatedisworkonlanguageground-ing,whosegoalistheinterpretationofasentenceinthecontextofaworldrepresentation(Branavanetal.,2009;Liangetal.,2009;Chenetal.,2010;Bordesetal.,2010;FengandLapata,2010;Ha-jishirzietal.,2011;Matuszeketal.,2012;Hajishirzietal.,2012;ArtziandZettlemoyer,2013;Koncel-Kedziorskietal.,2014;Yatskaretal.,2014;Seoetal.,2014;Hixonetal.,2015).Tuttavia,whilemostpreviousworkconsideredindividualsentencesinisolation,solvingwordproblemsoftenrequiresreasoningacrossthemulti-sentencediscourseoftheproblemtext.Recenteffortsinthemathdo-mainhavestudiednumberwordproblems(Shietal.,2015),logicpuzzleproblems(MitraandBaral,2015),arithmeticwordproblems(Hosseinietal.,2014;RoyandRoth,2015),algebrawordprob-lems(Kushmanetal.,2014;Zhouetal.,2015),andgeometrywordproblems(Seoetal.,2015).Wediscussinmoredetailbelowtwopioneeringworkscloselyrelatedtoourown.Hosseinietal.(2014)solveelementaryadditionandsubtractionproblemsbylearningverbcate-gories.Theygroundtheproblemtexttoaseman-ticsofentitiesandcontainers,anddecideifquanti-tiesareincreasingordecreasinginacontainerbaseduponthelearnedverbcategories.Whilerelyingonlyonverbcategoriesworkswellfor+and−,model-ing∗or/requiresgoingbeyondverbs.Forinstance,“Tinahas2cats.Johnhas3morecatsthanTina.Howmanycatsdotheyhavetogether?”and“Tinahas2cats.Johnhas3timesasmanycatsasTina.Howmanycatsdotheyhavetogether?”haveidenti-calverbs,buttheindicatedoperation(+and*resp.)isdifferent.ALGESmakesuseofaricherseman-ticrepresentationwhichfacilitatesdeeperlearningandawiderscopeofapplication,solvingproblemsinvolvingthe+,−,/,and∗operators(seeTable6).Kushmanetal.(2014)introduceageneralmethodforsolvingalgebraproblems.Thisworkcanalignawordproblemtoasystemofequationswithoneortwounknowns.Theylearnamappingfromwordproblemstoequationtemplatesusingglobalandlo-calfeaturesfromtheproblemtext.However,thelargespaceofequationtemplatesmakesitchalleng-ingforthismodeltolearntofindthebestequationdirectly,asasufficientlysimilartemplatemaynothavebeenobservedduringtraining.Instead,ourmethodmapswordproblemstoequationtrees,tak-ingadvantageofaricherrepresentationofquanti-fiednounsandtheirproperties,aswellastherecur-sivenatureofequationtrees.TheseallowALGEStouseabottom-upapproachtolearnthecorrespon-dencebetweenspansoftextsandarithmeticoper-ators(correspondingtointermediatenodesinthetree).ALGESthenscoresequationsusingglobalstructureoftheproblemtoproducethefinalresult.OurworkisalsorelatedtoresearchinusingILPtoenforceglobalconstraintsinNLPappli- l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e – p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 1 6 0 1 5 6 6 8 1 4 / / t l a c _ a _ 0 0 1 6 0 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 587 cations(RothandYih,2004).Mostpreviouswork(SrikumarandRoth,2011;GoldwasserandRoth,2011;Berantetal.,2014;Liuetal.,2015)uti-lizesILPasaninferenceproceduretofindthebestglobalpredictionoverinitiallytrainedlocalclassi-fiers.Similarly,weuseILPtoenforceglobalanddomainspecificconstraints.We,Tuttavia,useILPtoformcandidateequationswhicharethenusedtogeneratetrainingdataforourclassifiers.Ourworkisalsorelatedtoparserre-ranking(Collins,2005;GeandMooney,2005),whereare-rankermodelat-temptstoimprovetheoutputofanexistingproba-bilisticparser.Similarly,theglobalequationmodeldesignedinALGESattemptstore-rankequationsbasedonglobalproblemstructure.3SetupandProblemDefinitionGivennumericquantitiesVandanunknownxwhosevalueistheanswerweseek,anequationoverVandxisanyvalidmathematicalexpressionformedbycombiningelementsofV∪{X}usingbi-naryoperatorsfromO={+,−,∗,/,=}suchthatxappearsexactlyonce.WheneachelementofVappearsatmostonceintheequation,itmaynatu-rallyberepresentedasanequationtreewhereeachoperatorisanodewithedgestoitstwooperands.2TdenotesthesetofallequationtreesoverVandx.ProblemFormulation.Weaddresstheproblemofsolvinggrade-schoolalgebrawordproblemsthatmaptosingleequations.Solvingsuchawordprob-lemwamountstoselectinganequationtreetrepre-sentingthemathematicalcomputationimplicitinw.Figure1showsanexampleofwwithquantitiesun-derlined,andthecorrespondingtreet.Formally,weuseajointprobabilitydistributionp(T,w)thatde-fineshow“well”anequationtreet∈Tcapturesthemathematicalcomputationexpressedinw.Givenawordproblemwasinput,ourgoalistocompute˜t=argmaxt∈Tp(T|w).AnexhaustiveenumerationoverTquicklybe-comesimpracticalasproblemcomplexityincreasesandn=|V∪{X}|grows.Specifically,|T|>h(N)=n!(n−1)!(n−1)2n−4,h(4)=432,h(6)>1.7M,H(8)>22B,etc.Thisvastsearchspacemakesitchallengingforadiscriminativemodelto2Problemsinvolvingsimultaneousequationsrequirecom-biningmultipleequationtrees,oneperequation.375−(7*X)=4375=(7*X)+4375=(x*7)+4
3.
Train
local
modello
(sec(SU
7.1)
On
Monday,
375
students
went
SU
UN
trip
A
IL
zoo.
Tutto
7
buses
were
filled
E
4
students
had
A
travel
In
cars.
How
many
students
were
In
each
bus
?
Qnt: 375
Ent: Student
Qnt: 7
Ent: Bus
Qnt: 4
Ent: Student
Qnt: X
Ent: Student
Ctr: Bus
1.
Ground
testo
w
into
base
Qsets
(sec(SU
5)
:
subset
Di
T(w)
yielding
correct
solu(SU
375S
*S
-S
4S
7B
xs
=
375S
=
+S
*S
4S
7B
xs
375S
+S
-S
4S
=
7B
xs
(7B,xs)(375S,combine(7B,xs))(7B,xs)(combine(7B,xs),4S)2.
Use
ILP
A
creare
M
equa(SU
trees
T(w)
(Sez(SU
6)
4.
Train
global
modello
(sec(SU
7.2)
:
problem-‐tree
pairs
375+(7*X)=4375=(7/X)+4375−(x+7)=4TrlocalTrglobalTl(w):
operator
nodes
In
Tl(w)T(w)\Tl(w)Training
esempio
Label
*−*+Posi>ve
examples
(from
)
Nega>ve
examples
(from
)
Tl(w)T(w)\Tl(w)Figure2:AnoverviewoftheprocessoflearningforawordproblemanditsQsets.learntofind˜tdirectly,asasufficientlysimilartreemaynothavebeenobservedduringtraining.In-stead,ourmethodfirstgeneratessyntacticallyvalidequationtrees,andthenusesabottom-upapproachtoscoreequationswithalocalmodeltrainedtomapspansoftexttomathoperators,andaglobalmodeltrainedforcoherenceoftheentireequationw.r.t.globalproblemtextstructure.4OverviewoftheApproachFigure2givesanoverviewofourmethod,alsodetailedinFigure3.Inordertobuildequationtrees,weuseacompactrepresentationforeachnodecalledaQuantifiedSetorQsettomodelnaturallan-guagetextquantitiesandtheirproperties(e.g.,‘375students’in‘7buses’).Qsetsareusedfortrackingandcombiningquantitieswhenlearningthecorre-spondencebetweenequationtreesandtext.Definition1.Givenamathwordproblemw,letSbethesetofallpossiblespansoftextinw,φdenotetheemptyspan,andSφ=S∪{φ}.AQsetforwiseitherabaseQsetoracompoundQset.AbaseQsetisatuple(ent,qnt,adj,loc,vrb,syn,ctr)con:•ent∈S:entityorquantitynoun(e.g.,‘student’);•qnt∈R∪{X}:numberorquantity(e.g.,4orx); l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e – p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 1 6 0 1 5 6 6 8 1 4 / / t l a c _ a _ 0 0 1 6 0 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 588 Apprendimento(wordproblemsW,correspondingsolutionsL):1.Foreveryproblem-solutionpair(wi,‘i)withwi∈W,‘i∈L(UN)S←BaseQsetsobtainedbyGroundingtextwiandReorderingtheresultingQsets(Section5)(B)Ti←TopMtype-consistentequationtreecandidatesgeneratedbyILP(wi)(Section6)(C)T‘i←SubsetofTithatyieldsthecorrectnumericalsolution‘i(D)AddtoTrlocalfeatureshs1,s2iwithlabelopforeachoperatoropcombiningQsetss1,s2intreesinT‘i(e)AddtoTrglobalfeatureshw,tilabeledpositiveforeacht∈T‘iandlabelednegativeforeacht∈T\T‘i2.Llocal←TrainalocalQsetrelationshipmodelonTrlocal(Section7.1)3.Gglobal←TrainaglobalequationmodelonTrglobal(Section7.2)4.Outputlocalandglobalmodels(Llocal,Gglobal)Inference(wordproblemw,localsetrelationmodelLlocal,globalequationmodelGglobal):1.S←BaseQsetsobtainedbyGroundingtextwiandReorderingtheresultingQsets(Section5)2.T←TopMtype-consistentequationtreecandidatesgeneratedbyILP(w)(Section6)3.t∗←argmaxti∈T(cid:16)Qtj∈tLlocal(tj|w)(cid:17)×Gglobal(T|w),scoringeachtreeti∈TbasedonEquation14.‘←Numericsolutiontowobtainedbysolvingequationtreet∗fortheunknown5.Output(t∗,‘)Figure3:Overviewofourmethodforsolvingalgebraicwordproblems.•adj⊆Sφ:adjectivesforentinw;•loc∈Sφ:locationofent(e.g.,‘inthedrawer’);•vrb∈Sφ:governingverbforent(e.g.,‘fill’);•syn:syntacticandpositionalinformationforent(e.g.,‘buses’isinsubjectposition);•ctr⊆Sφ:containersofent(e.g.,‘Bus’isacon-tainerforthe‘students’Qset).Propertiesbeingφindicatestheseoptionalproper-tiesareunspecified.AcompoundQsetisformedbycombiningtwoQsetswithanon-equalitybinaryop-eratorasdiscussedinsection5.Qsetscanbefurthercombinedwiththeequalityoperatortoyieldasemanticallyaugmentedequationtree.3TheexampleinFigure2hasfourbaseQsetsextractedfromproblemtext.EachpossibleequationtreecorrespondstoadifferentrecursivecombinationofthesefourQsets.Givenw,ALGESfirstextractsalistofnbaseQsetsS={s1,…,sn}(Section5).ItthenusesanILP-basedoptimizationmethodtocombineex-tractedQsetsintoalistoftype-consistentcandidateequationtrees(Section6).Finalmente,ALGESusesdis-criminativemodelstoscoreeachcandidateequation,usingbothlocalandglobalfeatures(Section7).Specifically,therecursivenatureofourrepresen-tationallowsustodecomposethelikelihoodfunc-tionp(T,w)intolocalscoringfunctionsforeachin-3InspiredbySemanticallyAugmentedParseTrees(GeandMooney,2005)adaptedtoequationallogic.ternalnodeoftfollowedbyscoringtherootnode:P(T|w)∝Ytj∈tLlocal(tj|w)×Gglobal(T|w)(1)wherethelocalfunctionLlocal(tj|w)scoresthelike-lihoodofthesubtreetj,modelingpairwiseQsetre-lationships,whiletheglobalfunctionGglobal(T|w)scoresthelikelihoodoftherootoft,modelingtheequationinitsentirety.Learning.ALGESlearnsinaweaklysupervisedfashion,usingwordproblemswiandonlytheircor-rectanswer‘i(notthecorrespondingequationtree)astrainingdata{(wi,‘i)}i∈{1,…,N}.WegroundeachwiintoorderedQsetsandgeneratealistoftype-consistentcandidatetrainingequationsT‘ithatyieldthecorrectanswer‘i.WebuildalocaldiscriminativemodelLlocaltoscorethelikelihoodthatamathoperatorop∈OcancorrectlycombinetwoQsetss1ands2basedontheirsemanticsandintertextualrelationships.Forexample,inFigure2thismodellearnsthat∗hasahighlikelihoodscorefor‘7buses’and‘xstudents’.Thetrainingdataconsistsoffeaturevectorshs1,s2ilabeledwithop,derivedfromtheequationtreesthatyieldthecorrectsolution.Wealsobuildaglobaldiscriminativemodelthatscoresequationtreesbasedontheglobalproblemstructure:Gglobal=ψ|fglobal(w,T)wherefglobal l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e – p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 1 6 0 1 5 6 6 8 1 4 / / t l a c _ a _ 0 0 1 6 0 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 589 representsglobalfeaturesofwandt,andφarepa-rameterstobelearned.Thetrainingdataconsistsoffeaturevectorshw,tiforequationtreesthatyieldthecorrectsolutionaspositiveexamples,andtherestasnegatives(Figure2).Thedetailsoflearningandin-ferencestepsaredescribedinSection7.5GroundingandCombiningQsetsWediscusshowwordproblemtextisgroundedintoanorderedlistofQsets.AQsetisacompactrep-resentationofthepropertiesofaquantityasde-scribedinasinglesentence.TheuseofQsetsfacil-itatesthebuildingofsemanticallyaugmentedequa-tiontrees.Additionally,bytrackingcertainproper-tiesoftextquantities,ALGEScanresolvepronomi-nalreferencesorelidednounstopropertiesofprevi-ousQsets.Itcanalsocombineinformationaboutquantitiesreferencedindifferentsentencesintoasinglesemanticstructureforfurtheruse.Grounding.ALGEStranslatesthetextoftheprob-lemwintointerrelatedbaseQsets{s1,…,sn},eachassociatedwithaquantityintheproblemtextw.ThepropertiesofeachQset(Definition1)areex-tractedfromthedependencyparserelationspresentinthesentencewherethequantityisreferredtoac-cordingtotherulesdescribedinTable1.Additionally,ALGESassignsasingletargetQsetsxcorrespondingtothequestionsentence.ThepropertiesofthetargetQsetarealsoextractedac-cordingtotherulesoftheTable1.Inparticular,theqntpropertyissettounknown,theentissettothenounappearingafterthewordswhat,manyormuchinthetargetsentence,andtheotherpropertiesareextractedaslistedinTable1.Reordering.Inordertoreducethespaceofpossibleequationtrees,ALGESreordersQsets{s1,…,sn}accordingtosemanticandtextualinformationandenforcesaconstraintthatQsetscanonlycombinewithadjacentQsetsintheequationtree.InFig-ure2,thetargetQsetcorrespondingtotheunknown(x‘students’)ismovedfromitstextuallocationattheendoftheproblemandplacedadjacenttotheQsetwithentity‘buses’.Thismoveistriggeredbytherelationshipbetweenthetargetentity‘student’anditscontainer‘bus’thatisquantifiedbyeachinthelastsentence.Inadditiontothecontainermatchrule,weemploythreeotherrulestomovethetargetForeachquantitymentionedinthetext,properties(qnt,ent,ctr,adj,vrb,loc)ofthecorrespondingQsetareextractedasfollows:1.qnt(quantity)isanumericalvalueordeterminerfoundintheproblemtext,oravariable.2.ent(entity)isanounrelatedtotheqntinthedepen-dencyparsetree.Ifqntisanumericalvalue,entisthenounrelatedbythenum,number,orprepofrela-tions.Ifqntisadeterminer,entisthenounrelatedviathedetrelation.Whensuchanoundoesnotexistduetoparsefailureorpragmaticrecoverability,entisthenounthatisclosesttoqntinthesamesentenceortheentassociatedwiththemostrecentQset.3.ctr(container)isthesubjectoftheverbgovern-ingent,exceptintwocases:whenthissubjectisapronominalreference,thectrissettothectroftheclosestpreviousQset;ifentisrelatedtoanotherQsetwhoseqntisoneofeach,every,UN,an,per,orone,ctrissettotheentofthatQset.4.adj(adjectives)isalistofadjectivesrelatedtoentbytheamodrelation.5.vrb(verb)isagoverningverb,eitherrelatedtoentbynsubjordobj6.loc(location)isanounrelatedtoentbyprepon,prepin,orprepatrelations.Table1:TheprocessofformingasingleQset.QsetasdescribedinTable2.4Combining.TwoQsetsandanarithmeticoperatorcanbecombinedviathecombinefunctiontoformathirdQset,alternatelyreferredtoasacompound.Becauseofthis,wecanrepresentintermediatenodesintheequationtreeasQsetsthemselves.Therecur-sivecombinationofQsetsallowsustoeffectivelydecomposeequationtreesintoacollectionoflocaloperationsoveridenticalabstractions.ThisenableslearningfeaturesofQsetsandtextthatindicatepar-ticularoperationsfrombothleafandintermediatenodes.Themechanicsofc←combine(UN,B,op)aredetailedbelow.Forop=+,thepropertiesofeitherQsetaorbsufficetodefinec.ALGESalwaysformscusingthepropertiesofbinthesesituations.Forop=−,thepropertiesoftheleftoperandadefinetheresul-tantset,asevidencedbythesubtractionoperationspresentinthefirstprobleminTable9.Todetermine4Thesereorderingrulesareintentionallyminimal,butdoprovidesomegainoverbothpreservingthetextorderingofquantitiesorsettingorderingasasoftconstraint.SeeTable7. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e – p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 1 6 0 1 5 6 6 8 1 4 / / t l a c _ a _ 0 0 1 6 0 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 590 1.MoveQsetsitoimmediatelyafterQsetsjifthecon-tainerofsiistheentityofsjandisquantifiedbyeach.2.MovetargetQsettothefrontofthelistiftheques-tionstatementincludeskeywordsstartorbegin.3.MovetargetQsettotheendofthelistifthequestionstatementincludeskeywordsleft,remain,andfinish.4.MovetargetQsettothetextuallocationofaninter-mediatereferencewiththesameentifitsnumprop-ertyisthedeterminersome.Table2:RulesforreorderingQsets.thestickersinLuke’spossession,weneedtotrackstickersrelatedtotheleftQsetwiththeverb‘got’.Forop=∗,theQsetrelationshipiscapturedbythecontainerandentityproperties:theonewhosepropertiespreserveaftermultiplicationhastheother’sentityasitscontainer.InFigure2,the‘bus’Qsetisthecontainerof‘students’.Whenthesearecombinedwiththe∗operator,theresultisofen-titytype‘student’.Forop=/,weusetheprop-ertiesoftheleftoperandtoencourageadistinctionbetweendivisionandmultiplication.6GeneratingEquationTreeswithILPWeuseanILPoptimizationmodeltogenerateequa-tiontreesinvolvingnbaseQsets.Theseequationtreesareusedforbothlearningandinferencesteps.ALGESgeneratesanorderedlistofMofthemostdesirablecandidateequationsforagivenwordprob-lemwusinganILP,whichmodelsglobalconsider-ationssuchastypeconsistencyandappropriatelowexpressioncomplexity.Tofacilitategenerationofequationtrees,werepresenttheminparenthesis-freepostfixorreversePolishnotation,whereabinaryop-eratorimmediatelyfollowsthetwooperandsitop-erateson(e.g.,abc+∗x=).GivenawordproblemwwithnbaseQsets(cf.Table3fornotation),webuildanoptimizationmodelILP(w)overthespaceofpostfixequationsE=e1e2…eLoflengthLinvolvingknumericconstants,k0=n−kunknowns,rpossiblebinaryoperators,andq“types”ofQsets,wheretypecor-respondstotheentitypropertyofQsetsanddeter-mineswhichbinaryrelationshipsarepermittedbe-tweentwogivenQsets.ForsinglevariableequationsoverbinaryoperatorsO,k0=1,r=|O|=5,andL=2n−1.Forbrevity,definem=n+randlet[j]denote{1,…,j}.ExpressionEcanbeevalu-atedbyconsideringe1,e2,…,eLinorder,pushingnon-operatorsymbolsontoastackσ,E,forop-eratorsymbols,poppingthetoptwoelementsofσ,applyingtheoperatortothem,andpushingtheresultbackontoσ.Thestackdepthoftheeiisthestacksizeaftereihasbeenprocessedthisway.INPUTwinputmathwordproblemnnumberofbaseQsetsknumberofnumericconstantsk0numberofunknowns(1forsingle-var.eqns.)rnumberofbinaryoperators(r=|O|=5)mnumberofpossiblesymbols(n+r)typejtypeofj-thbaseQsetMdesirednumberofcandidateequationtreesLdesiredlengthofpostfixequations(2n−1)OUTPUTEpostfixequationtobegeneratedeii-thelementofE;i∈[l]VARIABLESfori∈[l]ximainILPvariablefori-thsymbolofEciindicatorvariable:eiisanumericconstantuiindicatorvariable:eiisanunknownoiindicatorvariable:eiisanoperatordipostfixstackdepthofei;di∈[l]titypeofei(correspondstoQsetentity);ti∈[q]Table3:ILPnotationforcandidateequationsmodelVariables.Integervariablesx1,x2,…,xLencodewhichsymboleacheirefersto.Theirdomain,[M],representstheknumericconstantsinthesameorderastheirrespectiveQsets,followedbythek0unknowns,andfinallyoperatorsintheorder+,−,∗,/,=.Binaryvariablesci,ui,andoiindicatewhethereiisanumericconstant,unknown,oroper-ator,resp.Variablesdiwithdomain[l]equalthepostfixstackdepthofei.Finally,variablestiwithdomain[q]indicatethetypeofei.Forj∈[N],i.e.,forthekconstantsandk0unknowns,typej∈[q]denotestherespectiveQsetentity.Uncertaintyinobjecttypesmaybeincorporatedeasilybytreatingtypejasa(potentiallyweighted)subsetof[q].ConstraintsandObjectiveFunction.ConstraintsinILP(w)includesyntacticvalidity,typeconsis-tency,anddomainspecificsimplicityconsidera-tions.Wedescribethembrieflyhere,leavingdetailstotheAppendix.Theobjectivefunctionminimizesthesumoftheweightsofviolatedsoftconstraints. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / t a c l / l a r t i c e – p d f / d o i / . 1 0 1 1 6 2 / t l a c _ a _ 0 0 1 6 0 1 5 6 6 8 1 4 / / t l a c _ a _ 0 0 1 6 0 p d . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 591 Below,(H)denoteshardconstraints,(W)weightedsoftconstraints,E(P)post-processingsteps.DefinitionalConstraints(H):Constraintsoverin-dicatorvariablesci,ui,andoiensuretheyrepre-senttheirintendedmeaning,includingtheinvariantci+ui+oi=1.Forstackdepthvariables,weaddd1=1anddi=di−1−2oi+1fori>1.SyntacticValidity(H):Validityofthepostfixex-pressionisenforcedeasilythroughconstraintso1=0anddL=1.Inaddition,weaddxL=mandxi