Stefan Riedel - Ricerca sull'intelligenza artificiale specializzata al MIT

Stefan Riedel
and Franz Zotter
Institute of Electronic Music and Acoustics
University of Music and Performing Arts
Inffeldgasse 10/3, 8010 Graz, Austria
{riedel, zotter}@iem.at

Design, Control, E
Evaluation of Mixed-Order,
Compact Spherical
Loudspeaker Arrays

Astratto: Beamforming on the icosahedral loudspeaker (IKO), a compact, spherical loudspeaker array, was recently
established and investigated as an instrument to produce auditory sculptures (cioè., 3-D sonic imagery) in electroacoustic
music. Sound beams in the horizontal plane most effectively and expressively produce auditory objects via lateral
reflections on sufficiently close walls and baffles. Can there be 3-D-printable arrays at drastically reduced cost and
transducer count, but with similarly strong directivity in the horizontal plane? To find out, we adopt mixed-order
Ambisonics schemes to control fewer, and predominantly horizontal, beam patterns, and we propose the 3|9|3 array
as a suitable design, with beamforming crossing over to Ambisonics panning at high frequencies. Analytic models and
measurements on hardware prototypes permit a comparison between the new design and the IKO regarding beamform-
ing capacity. Inoltre, we evaluate our 15-channel 3|9|3 prototype in listening experiments to find out whether the
sculptural qualities and auditory object trajectories it produces are comparable to those of the 20-channel IKO.

Early work on compact, spherical loudspeaker ar-
rays with controllable directivity was described by
Warusfel, Derogis, and Causse (1997) and by Pollow
and Behler (2009). Platonic solids (regular convex
polyhedra, such as dodecahedra or icosahedra) Di-
fer practical housings because of their symmetries
and their small number of faces, each of which
can contain a loudspeaker pointing outward in a
unique direction. Conventional spherical beam-
forming on the 12 transducers of a dodecahedron
uses spherical harmonics up to the second order,
while on the 20 transducers of the icosahedron, it is
limited to third order. To overcome the limitation,
array-specific acoustic radiation modes have been
proposed by Pasqual et al. (2010), but those modes
would require a frequency-dependent beam encod-
ing. Alternatively, the number of transducers per
surface has been increased beyond one, per esempio., to six
per each of the 20 icosahedral facets by Avizienis
et al. (2006), Quale, Tuttavia, is only practical with
high-frequency tweeters because of their small size.
Recentemente, Zotter et al. (2017) presented the icosa-

hedral loudspeaker (IKO) as an instrument for
electroacoustic music in an article in this journal
that outlines the theoretical principles of spherical

Computer Music Journal, 44:4, pag. 60–76, Inverno 2020
doi:10.1162/COMJ_a_00581
© 2021 Istituto di Tecnologia del Massachussetts. Published under
a Creative Commons Attribution 4.0 Internazionale (CC BY 4.0)
licenza.

beamforming and exemplary practical tools required
for its use (ambix and mcfx VST plugins). Wendt
et al. (2017B) and Sharma, Frank, and Zotter (2019)
investigated auditory sculptures and their attributes
that emerge for exemplary static and time-varying
beam compositions, and hereby provide a descrip-
tive framework for the artistic practice. In these
beam compositions, sound is projected onto walls
and baffles to produce auditory objects via acous-
tic reflections, essentially via horizontal beams,
that are most effective. This article investigates
an alternative, 3-D-printable, compact spherical
loudspeaker array design customized to producing
horizontal beams.

Figura 1 shows the IKO and the proposed compact

spherical loudspeaker array design that features a
horizontal ring of transducers but also supplemen-
tary ones above and below. A single horizontal ring
might appear sufficient, but the directional defi-
nition of the resulting beam shape can be of poor
vertical resolution. For compact spherical micro-
phone arrays, Márton Marschall (2014) describes
mixed-order schemes that effectively reduce the
number of transducers by neglecting certain vertical
spherical harmonic modes to maintain a high hor-
izontal resolution. As the gap between horizontal
and overall resolution cannot be overly stretched for
robust beamforming, Chang and Marschall (2018)
present alternative lattice schemes. We present
here the use of a mixed-order scheme to efficiently
increase the horizontal resolution of compact,

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1. The icosahedral
array (IKO) on the left and
IL 3|9|3 array on the right
are typically staged in
front of reflective baffles.
As a nomenclature we

define ne|nh|ne to refer to a
layout with nh transducers
in the horizontal ring, E
ne transducers in the upper
and lower ring (at non-zero
elevation).

Figura 2. Spherical
harmonics control scheme
for the 3|9|3 array (UN), E
the corresponding
mixed-order directivity

pattern (B), dove il
black line indicates a
horizontal cut and the gray
line indicates a vertical
cut.

Figura 1.

Figura 2.

spherical loudspeaker arrays. Figure 2a shows the
spherical harmonics as basis patterns that are
superimposed in spherical beamforming to cre-
ate narrow sound beams with variable direction.
The concept is the same as in Ambisonics, how-
ever, radiating outwards from the compact array.
A fourth-order horizontal and second-order vertical
mixed-order control omits some of the spherical
harmonics (translucent in Figure 2), and hereby

produces a beam pattern that is more focused hori-
zontally than vertically (cf. Figure 2b).

The article begins with a presentation of the
proposed mixed-order schemes to increase the hor-
izontal resolution of, Per esempio, dodecahedral
arrays from second to third order and icosahedral
arrays from third to fourth order. Its main tar-
gets are new three-ring layouts and their scheme
to effectively reduce the number of transducers.

Riedel and Zotter

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

The Array Simulation section numerically simu-
lates the mixed-order layouts and compares their
beamforming capacity based on 2-D and 3-D metrics
of effective beamforming order. Modal beamforming
on common-enclosure loudspeaker arrays requires
decoupling of the transducer movements and radial
filtering, which is not productive at high frequen-
cies. The Control Filter Design section introduces a
measurement-based, low-latency, two-band process
with regularization at low frequencies to minimize
filter lengths and All-Round Ambisonics Decoding
(AllRAD) panning at high frequencies for mini-
mal grating lobes. The Directivity Measurements
section verifies the gain in beamforming capacity
of the new processing scheme and the 3|9|3 loud-
speaker, as depicted in Figure 1, based on openly
accessible measurement data. The final Listening
Experiments section assesses auditory sculpture
attributes and auditory trajectories obtained with
IL 3|9|3 loudspeaker, comparing them to those of
the IKO.

Normalized Mixed-Order Directivity Patterns

Directivity functions for spherical beamform-
ing or Ambisonics panning use a finite-order
(cioè., resolution-limited) representation of a Dirac
delta δ(θT
ated in the variable direction θ,

θ − 1) directed towards θbeam and evalu-

beam

Defining the vectors

yN(θ) = [Y m

N (θ)]n=0…N,m=−n…N,

wN = [wn]n=0…N,m=−n…N,

Equazione 1 can be rewritten as

G(θ) = yN(θ)Tdiag{wN} yN(θbeam),

(3)

(4)

which defines a rotationally symmetric directivity
pattern. The directivity function of mixed order
differs from this by a mask M that selects a subset of
fewer spherical harmonics; see Figures 2 E 3. IL
mask M has (N + 1)2 columns, each representing a
spherical harmonic, and fewer rows, of which each
selects one of the harmonics to be a mixed-order
component:

gM(θ) = yN(θ)TMTdiag{ ˜wM}M yN(θbeam)
= yM(θ)Tdiag{ ˜wM} yM(θbeam).

(5)

The redefined weights ˜wM restore the balance
of the horizontal circular-harmonic content that is
represented by fewer max-rE-weighted components
in every degree m for mixed order. To get ˜wM = [ ˜w(M)
nm ]
we choose the unit vector ux = [1, 0, 0]T to the x
direction

G(θ) =

N(cid:2)

n=0

m=−n

wnm Y m

N (θ)Y m

N (θbeam),

(1)

˜w(M)
nm

= wn

(cid:7)

|M|
N
N(cid:2)=|M|[Y
N(cid:2)
|M|
N
N(cid:2)=|M|[Y
N(cid:2)

(ux)]2wn(cid:2)
(ux)]2wn(cid:2) Mn(cid:2)|M|

(6)

where both of the direction unit vectors
θ and θbeam are Cartesian unit vectors θ =
[cos ϕ sin ϑ, sin ϕ sin ϑ, cos ϑ]T depending on the
azimuth angle ϕ and zenith angle ϑ; or ϕbeam and
ϑbeam in case of θbeam. Y m
ics, and typically, to avoid side lobes, the weights
wnm = wn are the max-rE weights approximated by
Zotter and Frank (2012):

n are the spherical harmon-

wn = Pn

(cid:3)

(cid:4)

cos

π
180

137.9
N+1.51

(cid:5)(cid:6)
,

(2)

where Pn are the Legendre polynomials.

Mixed-Order Transducer Layouts

The mixed-order schemes in Figure 3 and the asso-
ciated spherical harmonic subsets can be controlled
using either Platonic layouts or the new three-ring
layouts consisting of an upper, a horizontal, and a
lower ring. The nomenclature ne|nh|ne refers to a
specific layout, Per esempio, IL 3|9|3 layout with
nh = 9 transducers in the horizontal ring and ne = 3
transducers in the two other rings. The Platonic
arrays can also be seen as three-ring layouts, con
the middle ring being a zigzag ring of loudspeakers

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 3. Control schemes
for the third-order
dodecahedron (UN),
fourth-order IKO (B), E
the new mixed-order
layouts 1|7|1 (C), 3|9|3 (D),
4|8|4 (e), E 5|10|5 (F).
Rows indicate the

spherical harmonics order
n = 0 . . . 4 and columns
indicate the degrees m =
−n . . . N. Gray squares
indicate controlled
spherical harmonics, white
squares indicate
uncontrolled ones. IL

third-order dodecahedral
scheme (UN) also holds for
IL 3|7|3 layout. For
brevity, the second-order
dodecahedral and
third-order icosahedral
schemes are not shown.

Tavolo 1. Coordinates of Mixed-Order Layouts

5|10|5

4|8|4

3|9|3

3|7|3

ϕ, at ϑ = 90◦
ϕ, at ϑ = 45◦
ϕ, at ϑ = 135◦

0:36:324
18:72:306
54:72:342

0:45:315
0:90:270
45:90:315

20:40:340
0:120:240
60:120:300

0:51.4:308.6
20:120:26
80:120:320

Coordinates are denoted as [start:step:stop] degrees of azimuthal coordinates of
the horizontal, superiore, and lower ring of a layout. Zenith coordinates are ϑ =
[90◦, 45◦, 135◦] for horizontal, superiore, and lower ring respectively. IL 1|7|1-layout (non
shown) is an exception: The nonhorizontal positions are the poles ϑ = [0◦, 180◦].

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

oriented at positive and negative elevation angles in
alternation. Questo è, the dodecahedron as a 1| ˜10|1
layout and the icosahedron as a 5| ˜10|5 layout, Quale
yields extended mixed-order control schemes for
those Platonic arrays. The coordinates of the new
three-ring layouts are given in Table 1.

According to Jérôme Daniel (2001), the number
of transducers nh in the horizontal ring determines
the maximum achievable 2-D order N2D,

nh ≥ 2 N2D + 1.

(7)

The ne transducers in the upper and lower rings are
added to stabilize beamforming vertically.

We regard the condition number κ of the mixed-

order spherical harmonics matrix Y M evaluated
at the transducer coordinates θl, to ensure a well-
conditioned pseudoinverse that is required to control
the array,

Y M = MY N,

(8)

N (θl )]l=1…l

with Y N = [Y m

n=0…N,m=−n…N.
Tavolo 2 shows that all Y M matrices (subsets see
Figura 3) are sufficiently well-conditioned as κ (Y M)
is finite and close to unity.

Tavolo 2. Transducer Counts and
Condition Numbers

Dodecahedron
Icosahedron
1|7|1
3|7|3
3|9|3
4|8|4
5|10|5

12
20
9
13
15
16
20

1.6
2.4
1.6
2.0
1.9
1.7
1.8

Number of transducers L and the condi-
tion number κ of Y M used in the speaker
configurations.

Array Simulation

In the following we numerically simulate the mixed-
order layouts by means of the spherical cap model
and compare their beamforming capacity based on
2-D and 3-D metrics of effective beamforming order.

Spherical Cap Model for Sound Radiation

To acoustically simulate the beamforming per-
formance of various array layouts, a reasonably

Riedel and Zotter

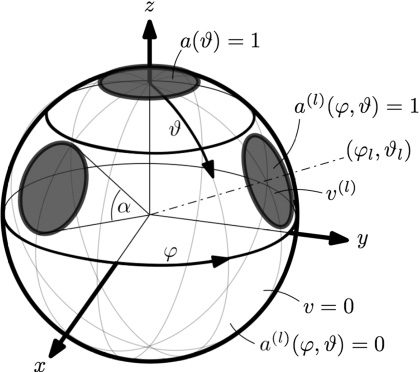
Figura 4. Spherical-cap
modello: UN(l)(ϕ, ϑ ) denotes
the aperture function of
the lth loudspeaker cap, v(l)
the lth cap velocity.

high-order model, with ˆN = 35, was applied by Zot-
ter and Höldrich (2007), assuming moving spherical
caps at the loudspeaker positions on an otherwise
rigid sphere, Guarda la figura 4. Cap-shaped surface veloc-
ity distributions can be expressed in the spherical
harmonics domain as coefficients νnm(R) at a radius
R that can be extrapolated to a far-field sound pres-
sure at the frequency ω in radians (Zotter and Frank
2019, ch. 7.3):

P(θ) =

(cid:8)N(cid:2)

n=0

In
N(kR)

k h(cid:2)

N(cid:2)

(cid:9)
(cid:9)

νnm

m=−n

RY m

N (θ),

(9)

with real-valued spherical harmonics Y m
N , and the
frequency dependency via the derivative h(cid:2)
n of the
spherical Hankel function of the second kind hn,
evaluated at the wave number k = ω/c times array
radius R, with the frequency ω = 2π f in radians per
second and the imaginary unit i. In our case, IL
velocity coefficient νnm is computed as a sum over
the L cap apertures a(l)
nm weighted by the velocities
v(l)

The coefficients of the cap al
transducer’s direction θl are obtained by spherical
convolution of a polar cap an of the aperture α
around z = 1 using

nm around the l-th

UN(l)
nm

= an Y m

N (θl ),

(11)

with an = 2π

(cid:10)
1
cos(α/2) Pn(z) dz,

Dove

Pn is the Legendre polynomial

(see Zotter and Frank 2019),
α

a0 = 2π (1 − cos

), E

2
2 Pn(cos α

cos α

an = 2π

2 ) − Pn+1(cos α
2 )
N

for n > 0.

The model can be written in matrix form

P(θ) = y(θ)Tdiag{H(ω)}diag{UN}Y v.

(12)

The matrices and vectors used are defined as
(cid:12)

(cid:11)

H(ω) =

In
N(kR)
a = [an]n=0…(cid:8)N,m=−n,…,N

k h(cid:2)

n=0,…,(cid:8)N,m=−n,…,N

sì(θ) = [Y m

N (θ)]n=0,…,(cid:8)N,m=−n,…,N

Y = [sì(θ1)…sì(θL)].

(13)

Modal beamforming yields the cap velocities
v in Equation 12 for a desired beam pattern in
the controllable mixed-order subspace. It is de-
scribed by running the weighted beam steering
diag{ ˜wM}yM(θbeam) through the inverse propagator
and aperture, and pseudoinverse rectangular matrix
Y +
M of the cap positions, all in the mixed-order
subspace

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

(cid:9)
(cid:9)

νnm

l(cid:2)

l=1

nm v(l).
UN(l)

(10)

v = Y +

M diag{aM}−1 diag{hM(ω)}−1 diag{ ˜wM}

yM(θbeam).

(14)

Computer Music Journal

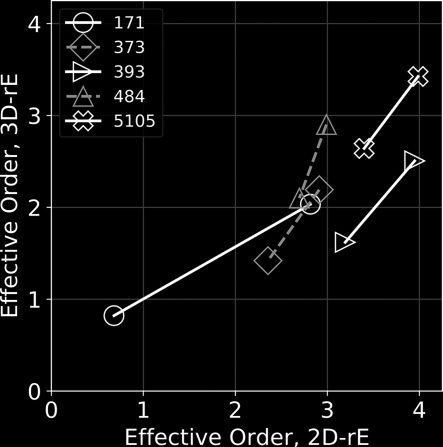
Figura 5. The 2-D and 3-D
effective orders of a
simulated horizontal
beam. Two markers per
layout indicate results at
400 Hz in the operation
range kR < N and 800 Hz where spatial aliasing becomes noticeable kR ≈ N; with N = 3 and radius R = 0.21 m. Platonic arrays gain a full order (in 2-D) with mixed-order control (a). The 3|9|3-array achieves fourth order in the 2-D rating with five transducers fewer than the IKO (b). Longer lines indicate poor robustness against spatial aliasing. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . e d u / c o m j / l a r t i c e - p d f / / / / 4 4 4 6 0 2 0 0 5 9 0 0 / c o m _ a _ 0 0 5 8 1 p d . j f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Simulation Results The results of the simulations are analyzed over frequency by means of a scalar measure of the beam focus. For the analysis of the focus in three dimen- sions, the simulated beam pattern was spherically sampled by the set of directions {θ j} of a J = 5,100- point t-design (Chebyshev-type quadrature; cf. Gräf 2013) to compute the energy vector rE measure r(3D) E = (cid:7) J j=1 (cid:7) J j=1 |p(θ j )|2 θ j |p(θ j )|2 . (15) To exclusively evaluate the beam focus in the hori- zontal plane, equiangular sampling of the azimuth was used (J = 72, i.e., 5◦ steps, φ j = 2π ( j − 1)/J) with the measure (cid:7) J j=1 (cid:7) r(2D) E = |p(φ j + ϕbeam)|2| sin φ j| J j=1 |p(φ j + ϕbeam)|2| sin φ j| (cid:5) (cid:4) cos φ j sin φ j . (16) It involves surface weights | sin φ j| representing the share of each sample of a spherical surface. The weights imply the optimistic interpretation of the 2-D pattern p(φ j + ϕbeam) centered at the beam- forming azimuth ϕbeam as rotationally symmetric in 3-D. The 2-D and 3-D measures hereby match, (cid:6)r(2D) (cid:6), whenever a measured pattern is E more or less isotropic, and there is a mismatch (cid:6)r(2D) (cid:6) whenever the horizontal focus is E stronger than the global one, as targeted by the proposed mixed-order designs. (cid:6) > (cid:6)R(3D)

(cid:6) = (cid:6)R(3D)

The effective order Neﬀ,3D of the 3-D pattern or
the effective order Neﬀ,2D of its 2-D horizontal cut
is evaluated as inverse of the order-dependent maxi-
mum max (cid:6)rE(cid:6) = cos

(π /180)(137.9/(N + 1.51))

(cid:5)
,

(cid:4)

Neﬀ =

180

137.9
arccos (cid:6)rE(cid:6)

− 1.51,

(17)

from the respective r(3D)
Equations 15 O 16.

or r(2D)
E

values estimated by

The simulation results for a cap aperture angle
α = 36◦ and a radius R = 0.21 m in Figure 5a indicate
improvement of the 2-D focus with Platonic arrays
(dodecahedral and icosahedral) by one order when

Riedel and Zotter

Figura 6. Control block
diagram, for the example
of a 3|9|3-array with
L = 15, (N + 1)2 = 36 E
13 controlled harmonics

(MIMO: multiple-input,
multiple-output; SISO:
single-input,
single-output).

using the proposed mixed-order control, at some
loss in the 3-D focus metric for the dodecahedral
array. As seen in Figure 5b, the specific mixed-
order layouts 4|8|4 E 3|9|3, rispettivamente, reach or
exceed the 2-D beam focus of the icosahedral layout,
but with four to five fewer transducers, validating
the mixed-order concept for compact loudspeaker
arrays.

An OpenSCAD model of the 3|9|3 array was
created to 3-D-print the necessary spherical hous-
ing (open access at https://git.iem.at/s1330219/
cmj_mocsla.git). The housing has been printed with
a radius of R = 0.12 m and is mounted with fifteen
2.5-In. wide-band transducers from SB Acoustics.
The odd number of transducers and their low-
frequency roll-off at about 100 Hz suggest adding
a subwoofer, yielding a 15.1-channel layout (beam-
former plus subwoofer) that proved effective in
listening sessions.

Control Filter Design

This section discusses the design of control filters
and its practical implementation as multiple-input,
multiple-output (MIMO) finite impulse response
(FIR) filter matrices.

Overview

As shown in the control overview, Figura 6, a two-
band approach is proposed. The discrete transducers

only control the modal sound field up to a frequency
limit, above which spatial aliasing will cause ripple
in the frequency-specific beampatterns and fre-
quency responses. At this spatial aliasing frequency,
the system uses a crossover from modal beam-
forming to Ambisonics panning. To accomplish
panning using the same Ambisonics input format
as the modal beamformer, the AllRAD approach
is adopted from Zotter and Frank (2012). Encoding
into a sufficiently high order (per esempio., fifth or seventh
order) reduces the number of activated loudspeakers
by means of a narrow directional mapping, E
thus helps to reduce spatial aliasing in the upper
frequency band.

Linkwitz-Riley Band Splitting

A Linkwitz-Riley crossover is composed of two
cascaded low-pass Butterworth filters for the low
band and two cascaded high-pass Butterworth
filters for the high band (cf. D’Appolito 1987). IL
correspondingly squared Butterworth frequency
high- and low-pass responses exhibit −6 dB at
the crossover frequency fc, and their phase is
either strictly opposite or strictly matching at
every frequency. Summing the bands with the
suitable sign ensures a flat response when gains are
equal, or a well-behaved interference when gains
differ. We utilized cascaded third-order Butterworth
filters for a sixth-order crossover between the two
bands.

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

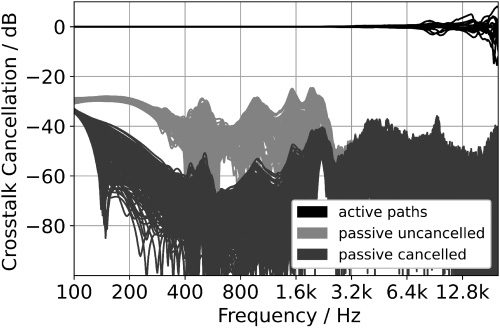
Figura 7. Crosstalk
cancellation performance
for the 3|9|3-array with
cutoff frequencies fbeam1 =
100 Hz and fbeam2 =
2.9 kHz. Loudspeaker

crosstalk is reduced to
levels below −40 dB,
which allows independent
transducer control
necessary for
beamforming.

MIMO Crosstalk Canceler

The reduced stiffness of the air enclosed when
mounting the loudspeakers in a common enclosure
can support beamforming by reducing the acoustic
load on the loudspeakers, in particular at low fre-
quencies. But it also introduces acoustic crosstalk
that needs to be dealt with for beamforming
(Zotter et al. 2017). If one transducer is moved
by a signal, the others will start to move passively,
but beamforming requires independent control of
the transducers.

Formalmente, our L × L MIMO system T can be

described as

v(ω) = T (ω) tu(ω).

(18)

For brevity and to support readability, the fol-

lowing discussion keeps all filter formalism in
the frequency domain, with the notation of the
frequency dependency omitted. System inversion
yields the voltage signals u for a decoupled control
of cone velocities.

and below certain cutoff frequencies by means of a
zero-phase bandpass filter on the passive off-diagonal
responses

˜T eqd = HmeanI + T eqd,passive HBP.

(22)

u = T −1 v.

(19)

Altogether, inversion times the mean active re-
sponse yields a matching and crosstalk-canceling
system X c

A full system inversion would result in both
flat magnitude responses of the direct paths and
crosstalk cancellation over the whole frequency
range, but it can lead to acausal filters and infeasibly
long impulse responses in the time domain. Focusing
on crosstalk cancellation, we reduce the effort
by equalizing the MIMO system so that all its
diagonal entries assume the bandpass-shaped mean
transducer response Hmean, with the minimum-
phase equalizers Heq,l,

TllHeq,l = Hmean,

for l = 1, . . . , l,

heq = [Heq,l]l=1,…,l .

(20)

yielding the correspondingly equalized MIMO
system

T eqd = T diag{heq} = HmeanI + T eqd,passive.

(21)

Inoltre, the inversion effort is regularized by
discarding crosstalk responses at frequencies above

X c = diag{heq} ˜T −1

eqd Hmean.

(23)

In the frequency range of the bandpass
(HBP = 1, so ˜T eqd = T eqd) this equalization
yields the crosstalk-canceled system T X c. As
a proof, the components of X c can be inserted,
T diag{heq} ˜T −1
tion and active response matching

eqd Hmean, to verify crosstalk cancella-

T diag{heq}diag{heq}−1 T −1 Hmean = I Hmean

(24)

within the bandpass range. Figura 7 shows the
crosstalk-cancellation performance for the 3|9|3
array with the response Hmean removed. Within
the bandpass range ( fbeam1 = 125 Hz to fbeam2 =
2.9 kHz) we have little deviation among active
responses (curves at 0 dB) and cancellation by up to
20 dB.

Riedel and Zotter

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Tavolo 3. Cutoff Frequencies for Filter Banks

82
38

146
77

250
141

318
209

450
253

3|9|3
ico-o4

Frequencies fb in Hz.

Low-Frequency Beamforming below Aliasing

Zotter and Frank (2019, ch. 7.3.1, Equazione 7.14)
describe filters Bb(ω) of an equal-phase filter-bank
progetto (D’Appolito 1987) to regularize the theoreti-
cal inverse propagator diag{hM(ω)}−1 in Equation 14
with practically limited loudspeaker excursion, E
we include band-dependent order weights w(B)
nm and
inverse aperture a−1
n to define the radiation control
(cid:11)

(cid:12)

F (ω) =

i−n k h(cid:2)

N(kR) a−1

N(cid:2)

b=n

Bb(ω) w(B)

nmeik R

N,m∈M

and Frank 2012) to approximate vector-base am-
plitude panning (VBAP, see Pulkki 1997) from the
Ambisonically steered input signals. The spherical
harmonics are first evaluated at J = 5,100 virtual t-
design points, which can be interpreted as a decoder
to many virtual transducers,

Y N,J = [yN(θ1), . . . , yN(θJ)]T,

(27)

and the resulting J = 5,100 gains are then mapped by
an L × J VBAP matrix G to the L array transducers

G = [g1, . . . , gJ].

(28)

Note that only one, two, O (in most cases) three
values of g j are nonzero, depending on the direction
θ j, with j = 1, . . . , J. As a source beam we choose
a max-rE weighted fifth-order beam and therefore
need to apply order-dependent weights wN. We arrive
at the precomputed L × (N + 1)2 panning decoder
matrix D

(25)

D = 4π
J

G Y N,J diag{wN}.

(29)

The weights w(B)
nm are obtained from Equation 6 Ma
with summation in the numerator and denominator
limited to the band-specific order b instead of N.
Combined with the frequency-independent decoder
Y +
M (shown in Table 2), radiation control yields the
target velocities

v = Y +

M diag{ F (ω)} yM(θbeam).

(26)

The cutoff frequencies of the filter bank Bb(ω)
were chosen to ensure a limited loudspeaker excur-
sion across the frequency bands, and their array-
specific values are found in Table 3.

High-Frequency AllRAD Panning

In the high-frequency band, the only filtering oper-
ation should be on-axis equalization of the trans-
ducers. Beamforming is replaced by directional
amplitude panning, which is accomplished by en-
coding the source direction yN(θbeam) of sufficiently
high order, e.g. N = 5 or higher, and AllRAD (Zotter

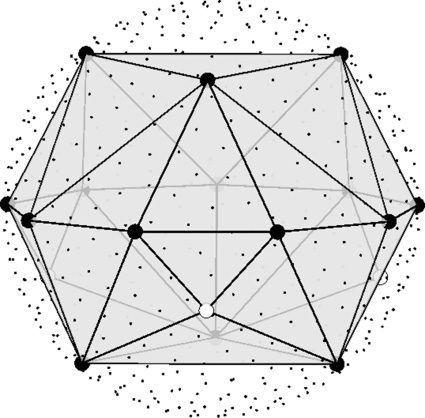
Figura 8 shows the triangulation of the 3|9|3
layout that requires the insertion of imaginary loud-
speakers, (cf. Zotter and Frank 2012). Allo stesso modo, IL
icosahedral layout requires imaginary loudspeakers
at the array vertices to enable proper symmetric
triangulation. The crossover frequency to AllRAD
panning was set to fc,393 = 2.9 kHz for the 3|9|3-
array (R = 0.12 M) and fc,ico = 1.5 kHz for the larger
IKO array (R = 0.21 M).

Band Summation and On-Axis Equalization

With the linear phase delay d(ω) = e−iω τ modeling
the processing delay of the low-frequency band,
we obtain the following expressions for the high-
and low-frequency bands of the processing chain in
Figura 6 and their final combination:

H 1(ω) = HHP(ω) D d(ω),
H 2(ω) = HLP X c(ω) Y +
H (ω) = [H 1(ω) + H 2(ω)] e(ω).

M diag{ F (ω)},

(30)

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 8. Triangulation of
IL 3|9|3-layout. Small
black dots indicate the
virtual AllRAD decoding
layout (J = 540 points in
this visualization). IL

larger black dots mark
physical loudspeaker
positions and white dots
imaginary loudspeakers
inserted to improve the
triangulation geometry.

The last block in the processing chain is the timbral
equalization e(ω) of the loudspeaker array. It flattens
the frequency response of the mean of all on-
axis beams (beams directed towards one of the
loudspeakers), but does not influence the beam
pattern. The magnitude response of the equalizer
(typically a high-shelf response) is reconstructed as a
minimum-phase filter and applied in the frequency
domain (for a detailed description, including figures,
cf. Riedel 2018, sec. 5.6).

The MIMO FIR time-domain response of
H (ω) is obtained by equidistant sampling in the
frequency domain, using ω = 2π k/NFFT with
k = 0, . . . , NFFT/2, and NFFT = 16,384 points,
followed by an inverse FFT to the time domain.
Windowing the impulse responses to 1,024 samples
is possible due to the low-latency designs, enabling
real-time and live-performance applications. IL
real-time FIR matrix convolution can use the jcon-
volver or mcfx_convolver plug-ins, for instance.

Directivity Measurements

As a verification method, acoustic MIMO measure-
ments with a surrounding semicircular microphone
array were taken, similar to the measurements

taken by Schultz et al. (2018). By placing the loud-
speaker array on a remotely controllable turntable,
a sampling grid with a resolution of 10◦ × 10◦ is
achieved.

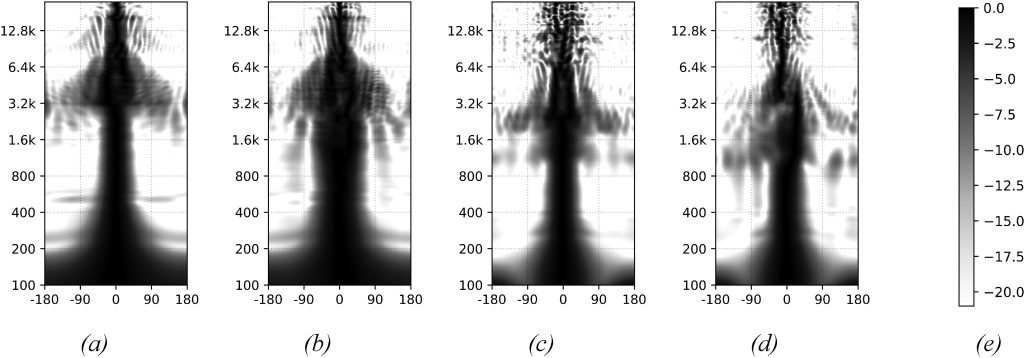
Horizontal and Vertical Cross Sections
of Beam Patterns

Figura 9 shows the directivity patterns of horizontal
beams of the 3|9|3 and IKO arrays. Both arrays
are driven by the mixed-order plus high-frequency
AllRAD control. The crossover to AllRAD panning
reduces side-lobes for high frequencies (crossover set
at fc,393 = 2.9 kHz and fc,ico = 1.5 kHz). Due to its
smaller diameter, the most effective beamforming
range of the 3|9|3-array lies one octave higher than
that of the IKO. Apart from this aspect, it generally
achieves similar or increased directivity compared
to the icosahedral array, regarding the horizontal
cross section of horizontal beams. IL 3|9|3 array
achieves a better control of grating lobes at high
frequencies, presumably due to its horizontal ring,
and a similar beam focus as the icosahedral array
below spatial aliasing.

Effective Orders of Directivity across Frequency

A detailed evaluation of the effectively achieved
orders of directivity Neﬀ (Equazione 17) regarding
the different control systems and different beam
directions is depicted in Figures 10, 11, E 12
(rE-measure-based analysis of the directivity). Obvi-
ously in Figure 10a, the mixed-order ico-o4 control
approach effectively increases horizontal 2-D direc-
tivity by about 0.7 in the region from 400 A 800 Hz
for the IKO array. Each of the two measurement-
based curves stays below the predictions of the
corresponding theoretical cap model (dashed
lines).

The effect of the various subsystems in the
control filter design is analyzed in Figure 11 for
IL 3|9|3 array. A frequency-independent spherical
harmonics decoder Y +
N alone hardly accomplishes
beamforming of a first-order directivity below
1.6 kHz (light gray curve). Applying the limited
radial filters boosts the effective beamforming order

Riedel and Zotter

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 9. Measurement-
based plots of the
horizontal and vertical
cross-sections of horizontal
travi: 3|9|3 horizontal
(UN), 3|9|3 vertical (B),

ico-o4 horizontal (C), E
ico-o4 vertical (D). Relative
dB, normalized to 0 dB for
every frequency, È
indicated by levels of
gray (e).

Figura 10. Effective 2-D (UN)
and 3-D (B) orders of a
horizontal beam based on
directivity measurements
of the IKO array showing
mixed-order (ico-o4)
versus third-order (ico-o3)

control filters. Dashed
lines indicate model
curves simulated with the
spherical-cap radiation
modello, applying the same
radial filters as in the real
filter design.

Figura 9.

Figura 10.

(gray curve, “radfilt”) most distinctively and reaches
horizontal orders of three and global 3-D orders of
two. Finalmente, the directivity increases by up to half
an order below 1.6 kHz by applying the crosstalk
canceler, and above 2.9 kHz the fifth-order AllRAD
Ambisonics panning provides a boost by up to one
order in the 3-D map of the highest frequencies (dark
curve “allrad_ctc_radfilt”). As before, the curves do
not quite reach the theoretical predictions (dashed
curve, “model”) in the modal beamforming range.

Figura 12 analyzes variation induced by beam-

forming direction. The IKO array—built with
high-quality and, hence, more costly parts—
maintains a similarly effective beamforming order
for different beamforming directions, whereas the
3-D-printed 3|9|3 prototype varies with a peak
in directivity for beams in the direction of one
of its loudspeakers (20◦ azimuth). The measure-
ment data is available in the Spatially Oriented
Format for Acoustics, AES69-2015, and can be

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 11. Effective 2-D (UN)
and 3-D (B) orders of a
horizontal beam based on
directivity measurements
del 3|9|3-array showing
different control-filter
designs. As in Figure 10,

dashed lines indicate
model curves simulated
with the spherical-cap
radiation model, applying
the same radial filters as
in the real filter design.

Figura 12. Effective 2-D
orders of horizontal beams
(0◦ to 40◦ azimuth) based
on directivity
measurements of the
3|9|3-array (UN) and IKO (B),

showing the variation
across the azimuth beam
directions. IL
3|9|3-prototype shows
more variation than the
IKO array.

Figura 11.

Figura 12.

downloaded from https://phaidra.kug.ac.at/o:91326
and https://phaidra.kug.ac.at/o:67609.

Listening Experiments

Above, IL 3|9|3 prototype was shown to have
beamforming performance similar to the more
powerful and larger 20-channel IKO. Naturally,

the frequency range for beamforming is higher
because of its smaller size. Although the vertical
beamforming capacity is weaker compared with
the IKO, the fourth-order horizontal beamforming
design effectively exceeds the conventional third-
order beamforming of the IKO, as used in previous
tests and concerts. Because the analysis above is
limited to technical beamforming measurements
and metrics, this section addresses in greater detail

Riedel and Zotter

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 13. Auditory
sculptural attributes of the
IKO and the new 3|9|3
prototype for the musical
signals composed by
Sharma, Frank, and Zotter
(2019). Mean values are

marked by dots, the gray
ellipsoidal region marks
IL 95% confidence ellipse
(Hotelling’s T-squared
distribution, in gray)
around each condition.

the question of whether the auditory impressions
achievable with the 3|9|3 are comparable to those of
the IKO. We adopt some of the perceptual analysis
methods established in previous studies on the IKO
to clarify the 3|9|3-prototype’s potential to be used
as an affordable, personal electroacoustic musical
instrument.

Work by Wendt et al. (2017UN) and by Laitinen
et al. (2015) discusses the option of pointing beams
towards or away from the listener as means of
positioning auditory objects in terms of distance.
Inoltre, Wendt et al. (2017B) and Zotter et al.
(2017) show that time-varying beamforming is
capable of moving auditory objects through the
interior of the playback environment. Sharma,
Frank, and Zotter (2019) establish and evaluate three
auditory sculptural attributes produced by a small
set of signals laid out in static and time-varying
beam compositions.

Listening Experiment 1: Auditory
Sculpture Attributes

The listening experiment was based on comparative
characterization of miniature electroacoustic com-
positions using a limited number of well-described
sounds and their beamforming trajectories, COME

defined by Sharma, Frank, and Zotter (2019, Exper-
iment 3). The goal of the comparative rating is to
evaluate the perceptual discernibility of the three
sculptural qualities directionality, contour, E
plasticity:

1. Directionality describes the potential of

auditory objects in the auditory sculpture
to dynamically guide the listeners attention
through a room;

2. Contour describes the degree of dependency

of the auditory sculpture’s outline (silhouette)
on the listening position, taken and imagined
from temporal evolution; E

3. Plasticity describes the degree of depth grading
of the spatially layered auditory objects of the
auditory sculpture in the room.

The participants could switch between the looped
playback of the compositions S1 . . . S5 (conditions),
and for each of the conditions under comparison,
the task was to find a relative position or rank
within a triangular graphical interface with the
corners directionality, contour, and plasticity (Vedere
Figura 13). Conditions were randomly permuted
regarding the indices, playback buttons, and the
movable markers shown on the interface, as in
Sharma and colleagues’ Experiment 3. In the present

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

experiment, IL 3|9|3 loudspeaker was set up at the
same position and in the same environment as the
2019 experiment. Twelve listeners took part, E,
except for one participant, the comparison task was
done twice. One comparative rating task took the
participants an average time of about 4 minutes. In
total, there were 21 ratings per condition.

Figura 13 compares the results obtained for the

3|9|3 prototype with the results obtained in the
2019 experiment for the IKO array (whose statistics
used 29 data points per condition). The rating of the
conditions in the sculptural quality space is quite
similar, and the mostly contoured, unidirectional
condition S2 can be considered identical between
both experiments. Condition S4, which used a
horizontally circular beam trajectory of pink noise,
was rated less directional for the 3|9|3 prototype
than for the IKO. Informal reports by the listeners
suggest that the contour of the auditory object is
not compact and smooth in space but rather jumps
and occasionally exhibits two separate high- E
low-frequency auditory objects. Our hypothesis
is that the increase of the directivity and higher
operational beamforming frequency range of the
3|9|3 prototype might isolate the wall reflections
better, but this also causes an inconsistent auditory
object trajectory, with low frequencies dispersed.
Inoltre, the horizontal loudspeakers of the IKO
aim, in alternation, at the elevations ±11◦ and so
might never excite the wall reflections as targeted
at high frequencies. A similar consideration could
be used to argue that the conditions S1 and S5 have
been rated less directional and as having a higher
plasticity.

Listening Experiment 2: Auditory
Object Trajectories

The second listening experiment is aligned with
the test design and conditions tested by Wendt
et al. (2017B) and Zotter et al. (2017) using the
IKO, but here the experiment is instead tested with
IL 3|9|3 loudspeaker, set up at the same position
and in the same environment. Six conditions were
used that represented three different trajectories,
each presented with two different sound stimuli

(continuous pink noise and a grain sequence). IL
three investigated trajectories are:

1. a beam towards the listener, fading the Am-
bisonics order from five to zero (omnidirec-
tional) and back (using the size knob in the
VST plugin ambix_encoder),

2. a circular rotation starting left and moving its

horizontal beam clockwise, E

3. a cross-fade from a sound beam toward the
left wall to one pointing to the right wall.

As in the prior experiments with the IKO, the ex-
perimental task used a GUI implemented with Pure
Data to position ten markers that each represented
the auditory event location at half a second within
the looped playback time (each of the conditions
was five seconds long).

There were 13 participants, and it took them
on average 24 minutes to complete the task. Each
participant was tested with the six stimuli in a
random permutation, each test performed twice to
permit checking for consistency of ratings. Data
from the first, ninth, and tenth participants were
discarded because their standard deviation for
repeated ratings exceeded 2 M.

Figura 14 shows the statistical analysis of the
two-dimensional results. Outliers outside the Ma-
halanobis distance of three standard deviations have
been removed (cross symbols, only occurring in the
two front-to-back tests), and the plot shows the 95%
confidence regions of the mean and the mean for
each the time index (13 responses were analyzed
per time index). For comparison, the dark gray dots
show the results taken from the IKO studies (Wendt
et al. 2017B; Zotter et al. 2017).

Although auditory front-to-back trajectories of
the grain signals (Figure 14b) yield a slightly larger
spatial span for the 3|9|3 array (ellipses in light
gray) than for the IKO (dark gray dots), we see an
opposite tendency for the front-to-back movement
of the noise signal in Figure 14a, in which the
IKO condition spans a larger range. In any case,
the monotonic mapping is qualitatively matching.
The full rotation of noise in Figure 14c shows
that beamforming on the 3|9|3 array appears to be
superior, or at least equally capable, in projecting
stationary broadband sound to lateral walls. IL

Riedel and Zotter

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 14. Half-second
localization ratings for
three time-variant beam
layouts with noise and
grain signals: front-to-back
noise (UN), front-to-back
grains (B), full-rotation
noise (C), full-rotation

grains (D), left-to-right
noise (e), and left-to-right
grains (F). The numerals
0–9 are the time indices for
IL 3|9|3-array. IL
numeral positions mark
the mean of 13 responses,
and the gray filled ellipse

around each shows the
95% confidence region.
The dark gray dots are the
results for the IKO, taken
from previous studies
(Wendt et al. 2017B; Zotter
et al. 2017).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Computer Music Journal

3|9|3 auditory trajectories in Figures 14c and 14d
cover a greater area and, although they are similar
to those of the IKO, their details differ and the
trajectory in the latter is offset. A comparable, if
not superior, control seems to be confirmed by
the dedicated left-to-right movement of noise in
Figure 14e. In contrasto, the transient grain stimuli
in Figures 14d and 14f are not fully lateralized to the
right wall as with the IKO. Perhaps as in Experiment
1, the difference in the details can be explained by
the loudspeaker directions of the IKO, which imply
a ±11◦ deflection of high-frequency content from
the horizontal plane.

Despite the fact that there are noticeable differ-
ences in the precise shapes of the ratings, we assume
that the results match sufficiently well for practical
applications.

Conclusione

We have presented a mixed-order control theory
that extends beamforming technology with compact
spherical loudspeaker arrays. To evaluate the design
goal of an improved horizontal beam control, we
used a radiation model and introduced the effective
horizontal (2-D) and global (3-D) order measures, first
to prove the concept on Platonic-solid loudspeaker
arrays. Mixed-order control increases the effective
horizontal beamforming order from second to third
order for the dodecahedral loudspeaker array, E
from third to fourth order for the icosahedral array,
with negligible impact on the effective 3-D order.
New mixed-order layouts were introduced that
are composed of three loudspeaker rings. The ded-
icated mixed-order layouts save transducers while
achieving equal or higher beam orders in the hor-
izontal plane. They are especially suited for the
proposed high-frequency AllRAD panning as many
on-axis loudspeaker directions are aligned with the
horizontal plane to support horizontal amplitude
panning directions for a better directivity focus of
high frequencies.

Based on directivity measurements of the IKO
and the proposed 3-D-printable and inexpensive
prototype of the 3|9|3 loudspeaker, we could prove
the practical feasibility and effectiveness of the

proposed control-filter design based on beamforming
with radial filters and crosstalk cancellation at
low frequencies, and AllRAD panning at high
frequencies.

Two listening experiments that were introduced

and tested with the IKO loudspeaker in previous
publications were repeated with the new 3|9|3
prototype. They confirm the practical applicability
of the new loudspeaker as it achieves results in
terms of auditory-sculpture qualities and auditory-
object trajectories that are similar to those of the
IKO, which is more powerful but more expensive.
This makes the 3|9|3 loudspeaker an alternative,
potentially a personal, electroacoustic musical
instrument.

We point readers to a repository at https:
//git.iem.at/s1330219/cmj_mocsla.git, which con-
tains open-source code for filter design and direc-
tivity plots as well as CAD files for 3-D-printing.
We also refer the reader to the open measure-
ment data at https://phaidra.kug.ac.at/o:91326 E
https://phaidra.kug.ac.at/o:67609.

Ringraziamenti

We thank Gerriet K. Sharma for setting up the
conditions of the listening experiments with the
3|9|3 loudspeaker, Sharma and Valerian Drack for
conducting the listening experiments, the voluntary
participants of these experiments, and the Aus-
trian Knowledge Transfer Centre South (WTZ-Süd,
PI at KUG/IEM: Robert Höldrich) for enabling a
substantial part of our work.

This article is a revised and extended version
of the paper “Design and Control of Mixed-Order
Spherical Loudspeaker Arrays” (Riedel, Zotter,
and Höldrich 2019), presented at the International
Computer Music Conference.

Riferimenti

Avizienis, R., et al. 2006. “A Compact 120 Independent El-
ement Spherical Loudspeaker Array with Programmable
Radiation Patterns.” In Proceedings of the 120th Con-
vention of the Audio Engineering Society, paper 6783.

Riedel and Zotter

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Chang, J., and M. Marschall. 2018. “Periphony-Lattice
Mixed-Order Ambisonic Scheme for Spherical Mi-
crophone Arrays.” IEEE/ACM Transactions on Au-
dio, Speech, and Language Processing 26(5):924–936.
10.1109/TASLP.2018.2800290

Daniel, J. 2001. “Représentation de champs acoustiques,
application à la transmission et à la reproduction de
scènes sonores complexes dans un contexte multimé-
dia.” PhD dissertation, University of Paris VI.

D’Appolito, J. 1987. “Active Realization of Multiway
All-Pass Crossover Systems.” Journal of the Audio
Engineering Society 35(4):239–245.

Gräf, M. 2013. “Efficient Algorithms for the Computa-
tion of Optimal Quadrature Points on Riemannian
Manifolds.” PhD dissertation, Chemnitz University of
Tecnologia, Faculty of Mathematics.

Laitinen, M.-V., et al. 2015. “Controlling the Perceived
Distance of an Auditory Object by Manipulation of
Loudspeaker Directivity.” Journal of the Acoustical
Society of America 137(6):EL462–EL468. 10.1121/
1.4921678

Marschall, M. 2014. “Capturing and Reproducing Realistic
Acoustic Scenes for Hearing Research.” PhD disserta-
zione, Technical University of Denmark, Department of
Electrical Engineering, Lyngby, Denmark.

Pasqual, UN. M., et al. 2010. “Application of Acous-
tic Radiation Modes in the Directivity Control
by a Spherical Loudspeaker Array.” Acta Acustica
united with Acustica 96(1):32–42. 10.3813/AAA
.918253

Pollow, M., and G. K. Behler. 2009. “Variable Directivity
for Platonic Sound Sources Based on Spherical Harmon-
ics Optimization.” Acta Acustica united with Acustica
95(6):1082–1092. 10.3813/AAA.918240

Pulkki, V. 1997. “Virtual Sound Source Positioning Using
Vector Base Amplitude Panning.” Journal of the Audio
Engineering Society 45(6):456–466.

Riedel, S. 2018. “Compact Spherical Loudspeaker Arrays:
New Filter and Layout Ideas.” Master’s thesis, Univer-

sity of Music and Performing Arts Graz, Institute of
Electronic Music and Acoustics.

Riedel, S., F. Zotter, and R. Höldrich. 2019. “Design and

Control of Mixed-Order Spherical Loudspeaker Arrays.”
In Proceedings of the International Computer Music
Conferenza.

Schultz, F., M. Zaunschirm, and F. Zotter. 2018. “Direc-

tivity and Electro-Acoustic Measurements of the IKO.”
In Proceedings of the 144th Convention of the Audio
Engineering Society, e-Brief 444.

Sharma, G. K., M. Frank, and F. Zotter. 2019. “Evaluation
of Three Auditory-Sculptural Qualities Created by an
Icosahedral Loudspeaker.” Applied Sciences 9(13):Arte.
2698. 10.3390/app9132698

Warusfel, O., P. Derogis, and R. Causse. 1997. “Radiation
Synthesis with Digitally Controlled Loudspeakers.”
In Proceedings of the 103rd Convention of the Audio
Engineering Society, paper 4577.

Wendt, F., et al. 2017UN. “Auditory Distance Control Using
a Variable-Directivity Loudspeaker.” MDPI Applied
Scienza 7(7):Arte. 666.

Wendt, F., et al. 2017B. “Perception of Spatial Sound

Phenomena Created by the Icosahedral Loudspeaker.”
Computer Music Journal 41(1):76–88. 10.1162/COMJ_
a_00396

Zotter, F., and M. Frank. 2012. “All-Round Ambisonic

Panning and Decoding.” Journal of the Audio Engineer-
ing Society 60(10):807–820.

Zotter, F., and M. Frank. 2019. Ambisonics: A Practical
3D Audio Theory for Recording, Studio Production,
Sound Reinforcement, and Virtual Reality. Berlin:
Springer.

Zotter, F., and R. Höldrich. 2007. “Modeling Radiation
Synthesis with Spherical Loudspeaker Arrays.” In
Proceedings of the International Congress on Acoustics,
pag. 508–513.

Zotter, F., et al. 2017. “A Beamformer to Play with Wall
Reflections: The Icosahedral Loudspeaker.” Computer
Music Journal 41(3):50–68. 10.1162/comj_a_00429

Computer Music Journal

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
/
C
o
M

j
/

UN
R
T
io
C
e
–
P
D

F
/

4
4
4
6
0
2
0
0
5
9
0
0
/
C
o
M
_
UN
_
0
0
5
8
1
P
D