Revisiting Few-shot Relation Classification:
Evaluation Data and Classification Schemes
Ofer Sabo1 Yanai Elazar1,2 Yoav Goldberg1,2 Ido Dagan1
1Computer Science Department, Bar Ilan University, Israel
2Allen Institute for Artificial Intelligence
{ofersabo,yanaiela,yoav.goldberg,ido.k.dagan}@gmail.com
Astratto
We explore few-shot learning (FSL) for re-
lation classification (RC). Focusing on the
realistic scenario of FSL,
in which a test
instance might not belong to any of the target
categorie (none-of-the-above, [NOTA]), we
first revisit the recent popular dataset struc-
ture for FSL, pointing out its unrealistic data
distribution. To remedy this, we propose a
novel methodology for deriving more realistic
few-shot test data from available datasets for
supervised RC, and apply it to the TACRED
dataset. This yields a new challenging bench-
mark for FSL-RC, on which state of the art
models show poor performance. Prossimo, we ana-
lyze classification schemes within the popular
embedding-based nearest-neighbor approach
for FSL, with respect to constraints they im-
pose on the embedding space. Triggered by
this analysis, we propose a novel classifica-
tion scheme in which the NOTA category is
represented as learned vectors, shown empiri-
cally to be an appealing option for FSL.
1
introduzione
We consider relation classification—an important
sub-task of relation extraction—in which one is
interested in determining, given a text with two
marked entities, whether the entities conform to
one of pre-determined relations, or not. While
supervised methods for this task exist and work
relatively well (Baldini Soares et al., 2019; Zhang
et al., 2018; Wang et al., 2016; Miwa and Bansal,
2016), they require large amounts of training data,
which is hard to obtain in practice.
We are therefore interested in a data-lean sce-
nario in which users provide only a handful of
training examples for each relation they are in-
terested in. This has been formalized in the ma-
chine learning community as few-shot learning
(FSL) (§2).
691
FSL for RC has been recently addressed by the
work of Han et al. (2018) and Gao et al. (2019),
who introduced the FewRel 1.0 and shortly after
the FewRel 2.0 challenges, in which researchers
are provided with a large labeled dataset of back-
ground relations, and are tasked with producing
strong few-shot classifiers: classifiers that will
work well given a few labeled examples of rela-
tions not seen in the training set. The task became
popular, with scores on FewRel 1.0 achieving
an accuracy of 93.9% (Baldini Soares et al.,
2019), surpassing the human level performance of
92.2%. Results on FewRel 2.0 are lower, at 80.3%
for the best system (Gao et al., 2019), but are still
very high considering the difficulty of the task.
Is few-shot relation classification solved? Noi
show that this is far from being the case. We argue
that the evaluation protocol in FewRel 1.0 is based
on highly unrealistic assumptions on how the mod-
els will be used in practice, and while FewRel
2.0 tried to amend it, its evaluation setup remains
highly unrealistic (§3.1). Therefore, we propose a
methodology to transform supervised datasets into
corresponding realistic few-shot evaluation sce-
narios (§3.2). We then apply our transformation
on the supervised TACRED dataset (Zhang et al.,
2017) to create such a new few-shot evaluation set
(§3.3). Our experiments (§6.2) reveal that indeed,
moving to this realistic setup, the performance
of existing state-of-the-art (SOTA) models drop
considerably, from scores of around 80 F1 (COME
well as accuracy) to around 30.
A core factor in a realistic few-shot setup is
the NOTA (none-of-the-above) option; allowing
a case where a particular test instance does not
conform to any of the predefined target relations.
Triggered by presenting an analysis of possible
decision rules for handling the NOTA category
(§5), we propose a novel enhancement that mod-
els NOTA by an explicit set of vectors in the
embedding space (§5.2). This explicit ‘‘NOTA
as vectors’’ approach achieves new SOTA
Operazioni dell'Associazione per la Linguistica Computazionale, vol. 9, pag. 691–706, 2021. https://doi.org/10.1162/tacl a 00392
Redattore di azioni: Radu Florian. Lotto di invio: 9/2020; Lotto di revisione: 1/2021; Pubblicato 8/2021.
C(cid:2) 2021 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
performance for the FewRel 2.0 dataset, E
outperforms other models on our new dataset
(§6). Yet, the realistic scenario of our TACRED-
derived dataset remains far from being solved,
calling for substantial future research. We release
our models, dati, E, more importantly, our data
conversion procedure, to encourage such future
lavoro.
2 Task Setup and Formulation
2.1 Relation Classification
The relation extraction (RE) task takes as input
a set of documents and a list of pre-specified
relations, and aims to extract tuples of the form
(e1, e2, R) where e1 and e2 are entities, r is a
relation that holds between them (r belongs to a
pre-specified list of relations of interest). This task
is often approached by a pipeline that generates
candidate (e1, e2, S) triplets, classifies each one
to a relation (or indicates there is no relation).
The classification task from such triplets to an
expressed relation is called relation classification
(RC). It is often isolated and addressed on its own,
and is also the focus of the current work. Zhang
et al. (2017) demonstrate that improvements in
RC carry over to improvements in RE.
In the RC task each input xi = (e1, e2, S)io
consists of a sentence s with a (ordered) pair of
marked entities (each entity is a span over s), E
the output is one of |R| + 1 classes, indicating
that the entities in s conform to one of the rela-
tions in a set R of target relations, or to none
of them. We refer to a triplet xi as a relation
instance. Per esempio, if the target relations are
R = {Owns, WorksFor}, the relation instance
‘‘Wired reports that in a surprising reshuffle at
Microsofte2, Satya Nadellae1 has taken over as the
managing director of the company.’’ should be
classified as WorksFor. The same sentence with
the entity pair e1 =Satya Nadella and e2 =Wired
should be classified as ‘‘NoRelation’’ (NOTA).
2.2 The Few-Shot N-Way K-Shot Setup
As supervised datasets are often hard and expen-
sive to obtain, there is a growing interest in the
few-shot scenario, where the user is interested in
|R| target-relations, but can provide only a few
labeled instances for each relation. In this work,
we follow the increasingly popular N-Way K-Shot
setup of FSL, proposed by Vinyals et al. (2016)
and Snell et al. (2017). This setup was adapted
The N-Way K-Shot
to relation classification, resulting in the FewRel
and FewRel 2.0 datasets (Han et al., 2018; Gao
et al., 2019). We further discuss the datasets in §3.
Quello
is interested in N target
relations
the user
(Rtarget = {c1, . . . , cN }), and has access to
K instances (typically few) of each one, called
the support set for class cj, denoted by σ:
setup assumes
σ = {σc1, . . . , σcN
σcj = {x1, . . . , xk} s.t. R(xi) = cj
cj ∈ Rtarget
}
where r(X) is the gold relation of instance x; σcj
is the support set for relation cj; and σ is the
support set for all N relations in Rtarget.
A set of target relations and the corresponding
support sets is called a scenario. Given a scenario
S = (Rtarget, P), our goal is to create a decision
function fS(X) : x → Rtarget ∪ { ⊥ }, Dove
⊥ indicates ‘‘none of the relations in Rtarget’’.
Let X = x1, . . . , xm be a set of instances with
corresponding true labels r(x1), . . . , R(xm), our
aim is to minimize the average cumulative eval-
M
uation loss 1
i=1 (cid:3)(fS(xi), R(xi)), Dove (cid:3) is a
M
per-instance loss function, usually zero-one loss.
When treating FSL as a transfer learning prob-
lem, as we do here, there is also a background set
of relations Rbackground, disjoint from the target
relation set, for which there is plenty of labeled
data available. This data can also be used for
constructing the decision function.
(cid:2)
The performance of an N-Way K-Shot FSL
algorithm on a dataset X is highly dependent on
the specific scenario S: Both the choice of the
the N relations that needs to be distinguished as
well as the choice of the specific K examples
for each relation can greatly influence the results.
In a real-life scenario, the user is interested in a
specific set of relations and examples, but when
developing and evaluating FSL algorithms, we
are concerned with the expected performance of
a method given an arbitrary set of categories and
M
examples: ES[ 1
i=1 (cid:3)(fS(xi), R(xi))] Quale
M
can be approximated by averaging the losses for
several random scenarios Sj, each varying the
relation set and the example set. In a practical
evaluation, the number of N-Way K-Shot scenar-
ios that can be considered is limited, relative to
the combinatorial number of possible scenarios.
To maximize the number of considered scenarios,
we re-write the loss to consider expectations also
over the data points: ESE(X)∼X [(cid:3)(fS(X), R(X))].
(cid:2)
692
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
This gives rise to an evaluation protocol that
considers the loss over many episodes, Dove
each episode is composed of: (1) a random choice
Rtarget of N distinct target relations Rtarget =
{c1, . . . , cN }, ci (cid:8)= cj; (2) a corresponding ran-
} of N ∗ K
dom support set σ = {σc1, . . . , σcN
instances (K instances in each σcj ); E (3) UN
single randomly chosen labeled example consid-
ered as a query, (X, R(X)), which does not appear
in the support set. To summarize, an evaluation set
for N-Way K-Shot FSL is a set of episodes, each
consisting of a N target relations, K supporting
examples for each relation, and a query. For each
episode, the algorithm should classify the query
instance to one of the relations in the support set,
or none of them.
In practice, the episodes in an evaluation set
are obtained by sampling episodes from a labeled
dataset. As we discuss in the following section, IL
specifics of the labeled dataset and the sampling
procedure can greatly influence the realism of the
evaluation, and the difficulty of the task.
2.3 Low-resource Relation Classification —
Related Work
Other than FSL, several setups for investigat-
ing RC under low resource setting have been
proposed.
Obamuyide and Vlachos (2019) experimented
with limited supervision settings on TACRED.
Their setting is different than the transfer-based
few-shot setting addressed in our paper, Tuttavia.
In most of their experiments the amount of train-
ing instances per relations is much higher, non
fitting the ad hoc nature of the few-shot setting.
Further, they train a model on all classes, not add-
ressing inference on new class types at test time.
Distant supervision is another approach for
handling low-resource RC (Mintz et al., 2009).
This approach leverages noisy labels for training
a model, produced by aligning relation instances
to a knowledge-base. Particularly, it considers
sentences containing a pair of entities holding
a known relation as instances of that relation.
Per esempio, a sentence containing the entities
‘Barack Obama’, and ‘Hawaii’ will be labeled as
an instance of the born in relation between these
entities, even though that sentence might describe,
Per esempio, a later visit of Obama to Hawaii.
Finalmente, another line of work is the Zero-Shot
setup, where the RC task is reduced to another
inference task, leveraging trained models for that
task. Specifically, Levy et al. (2017) proposed
a method that leverages reading comprehension
models, while Obamuyide and Vlachos (2018)
suggest using textual entailment models.
3 Desired Versus Existing Few-Shot
Relation Classification Datasets
A FSL system is intended to be used in a real-life
scenario. Così, evaluation procedures for FSL
should attempt to mimic the conditions under
which the FSL system will be applied in practice.
In a realistic FSL scenario, the user has a set of
relations of interest (‘‘target relations’’), and can
come up with a handful of examples for each.
The relations in the set are often related to each
other. The user may potentially have access to
a labeled dataset of a different set of relations
(‘‘background relations’’), which they may want
to use to train, or to improve, their FSL system.
The resulting classifier will then be applied
to unlabeled data aiming to detect new target
relations, in which, realistically:
(UN) some relations are rarer than others.
(B) most instances do not correspond to a target
relation.
(C) many instances may not correspond also to a
background relation.
(D) relation instances may include named
entities, as well as pronouns and common
noun entities.
Ideally, the episodes in an FSL evaluation should
be chosen in a way that reflects (UN)–(D) above.1
The first characteristic (UN) naturally follows the
non-uniform distribution of relation types in a
(non-artificial) text collection. The second point
(B) stems from the fact that a natural text refers
to a broad, inherently unbound, range of relation
types, while in an RC setting, particularly for FSL,
there is typically a restricted set of target rela-
zioni. Allo stesso modo, while available RC training sets
(for the supervised setting) may annotate more
relation types than in a typical few-shot setting,
they still contain a limited number of relation
types in comparison to the full range of relations
expressed in the corpus. This is prototypically
evidenced in the naturally distributed RC dataset
1Additional concern of a realistic setup, which we do not
consider in this work, is the accuracy of the entity-extractor
that marks entity boundaries and assigns entity types, prior
to the RC setup.
693
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Dataset
TACRED
Train
Dev
13,012 5,436
Test
3,325 (78.56%)
FS TACRED 8,163
633
804 (94.81%)
Tavolo 1: Number of relation instances in the
original TACRED dataset and in our derived Few-
Shot TACRED. The corresponding test set NOTA
rates appear in parenthesis.
TACRED (§3.3), Dove 78.56% of the labels
are NOTA (Tavolo 1). Finalmente, naturally occurring
textual relations may be used to relate named
entities as well as common nouns or pronouns
(D); Perciò, we expect the annotated RC dataset
entities to include all such entity types.
As we show below, existing FSL-RC datasets
do not conform to these properties, resulting in
artificial—and substantially easier—classifica-
tion tasks. This in turn leads to inflated accuracy
numbers that are not reflective of the real potential
performance of a system. We propose a refined
sampling procedure that adheres to the realis-
tic setting, and results in a substantially more
realistic evaluation set, while conforming to the
same N-Way K-Shot protocol. As we show in
the experiments section (§6), this setup proves
to be substantially more challenging for existing
algorithms. We propose to use this procedure
for future evaluation of FSL-RC algorithms, E
release the corresponding code and data.
3.1 Existing FSL-RC Datasets
An N-Way K-Shot RC dataset was introduced by
Han et al. (2018), called FewRel 1.0. The dataset
became popular, yet proved to be rather easy: IL
current best leaderboard entry by Baldini Soares
et al. (2019) obtains results of over 93.86% accu-
racy for 5-way 1-shot, above the 92% accuracy
of human performance. The dataset was then
updated to FewRel 2.0 (Gao et al., 2019), using an
updated episode sampling procedure (see below),
with the current best system obtaining a 5-way
1-shot score of 80.31 (Gao et al., 2019).
Underlying Labeled Data Both FewRel ver-
sions are based on the same underlying labeled
dataset containing 100 distinct relations, con
700 instances per relation, totalling in 70,000
labeled instances. The sentences are based on
Wikipedia and the entities and relation labels are
assigned automatically using Wikidata, followed
by a human verification step.
Note that while extensive, each relation type
contains the same number of instances, regardless
of any real truthful distribution in a corpus, Rif-
sulting in a highly synthetic dataset, contradict-
ing the realistic assumption (UN) above. In contrasto,
instances in supervised RC datasets such as
TACRED and DocRED (Zhang et al., 2017; Yao
et al., 2019) do respect the relation distribution in
a real corpus.
target entities are mostly
Finalmente, FewRel
including important entity
named entities, non
types such as pronouns and common nouns, Quale
are present in supervised RC datasets (including
TACRED), thus contradicting assumption (D).
Train/Dev/Test Splits The 100 relations are
split into three disjoint sets, Rtrain, Rdev, E
Rtest, consisting of 64, 16, E 20 relations,
rispettivamente. The relations in Rtrain and their
corresponding instances are used as the labeled
corpus of background relations, while evaluation
episodes consist of relations in either Rdev or
Rtest. We refer to this set (either test or dev) COME
Reval. Each episode consists of random subset
Rtarget ⊂ Reval.
Sampling Procedures The episode sampling
procedure of FewRel 1.0 works by sampling
N relations from Reval resulting in a target set
Rtarget, sampling a corresponding size k support
set σcj for each cj ∈ Rtarget, and then sampling
a query example in which r(q) ∈ Rtarget. Quello
È, the query in each episode is guaranteed to
be in Rtarget. This setup is artificial, negating
realistic condition (B) above. This explains the
high performance on FewRel 1.0.
NOTA Following the aforementioned observa-
zione, the FewRel 2.0 work introduced a NOTA
scenario. Here, after sampling the target relation
set Rtarget ⊂ Reval, the query class r is sam-
pled from Rtarget with probability p and from
Reval \ Rtarget with probability 1 − p. Questo è,
1 − p of the episodes contain a query for which
the answer does not correspond to any support
set, in which case the answer is NOTA.
Although a step in the right direction (Infatti,
results in this setup drop from over 90% to around
80%), this setup is still highly unrealistic: not only
all the NOTA instances are guaranteed to be valid
relations, they also always come from the same
694
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
small set, contradicting assumption (C). In a real-
istic setup, we would expect the vast majority of
test instances to be NOTA, but the set of NOTA
instances is expected to vary greatly: some of
them will correspond to relations from the back-
ground relations, some of them will correspond
to unseen relations, and many will not correspond
to any concrete relation. Inoltre, some of
the NOTA cases will appear in sentences that do
contain a target relation, but between different
entities. Supervised relation extraction and rela-
tion classification datasets reflect this situation,
and we argue that the FSL evaluation sets should
also do so.
3.2 Better FSL-RC Evaluation Sets
We propose a methodology for transforming
a supervised RC dataset
into a few-shot RC
dataset, while attempting to maintain properties
(UN)–(D) of the realistic evaluation scenario. Questo
methodology can be applied to existing and future
supervised datasets, thus reducing the need of
collecting new dedicated FSL datasets.
3.2.1 Realistic Underlying Labeled Data
We assume a given supervised dataset, with C cat-
egories, divided into train and test sections, Dove
each section contains all C categories, with dis-
tinct instances in each section (the typical setting
for supervised multi-class classification). Some
instances (in all sections) may be labeled with
‘‘None-of-the-above’’ (also known as ‘‘other’’ in
the classic supervised setting, or ‘‘no relation’’ in
TACRED terminology), hereafter NOTA, mean-
ing these instances do not belong to any of the C
categorie.
Transformation We transform the supervised
dataset
into an FSL dataset containing (as in
FewRel) a set of background relations for training
and a disjoint set of relations for evaluation. A
perform this transformation, we begin by choosing
M categories as Reval.2 The remaining C − M
categories are designated as background relations
Rtrain.3 We now keep the same instance-level
train/dev/test splits of the original supervised
dataset, but relabel the instances in each section:
train set instances whose labels are in Rtrain
2In practice we have MT categories for test and MD for
dev, we refer to both as eval for brevity.
3To preform the N-Way K-Shot setup, M is required to
be larger than N ; in case the original data has a NOTA label,
M may be equal to N .
retain their original labels, while all other training
instances are labeled as NOTA. Similarly for the
test and dev splits. This results in sets where each
set has distinct labels, but some of the NOTA
instances in one set correspond to labels in other
sets.
Multiple Splits The choice of relations for each
set influences the resulting dataset: Some rela-
tions are more similar to each other than others,
and splits that put several similar relations in an
eval set are harder than splits in which similar
relations are split between the train an eval sets.
Inoltre, as the number of labeled instances for
each relation differ, splitting by relation results in
different number of train/dev/test instances. Noi
thus repeat the process several times, each time
with a distinct set of eval relations.
3.2.2 Realistic Episode Sampling
To create an episode, we first sample the N ∗ K
instances, which constitute the N support set as in
previous episodic sampling: Sample N out of M
relations, and then sample K instances for each
relation from the underlying eval set. Tuttavia,
the query for the episode is then sampled uni-
formly from all remaining instances in the eval
set. If the label of the instance chosen as query
differs from the N target relations in the episode,
it is labeled as NOTA. This query sampling pro-
cedure maintains both the label distribution and
NOTA rate of the underlying supervised dataset.
3.3 Few-Shot TACRED: Realistic Few-Shot
Relation Classification
We apply our transformation methodology to
the TACRED RC dataset (Zhang et al., 2017).
The TACRED dataset was collected from a news
corpus, purposing extracting relations involving
100 target entities. Accordingly, each sentence
containing a mention of one of these target en-
tities was used to generate candidate relation
instances for the RC task. The relation label was
annotated as one of 41 pre-defined relation cat-
egories, when appropriate, or into an additional
‘‘no relation’’ category. The ‘‘no relation’’ cat-
egory corresponds to cases where some other
relation type holds between the two arguments, COME
well as cases in which no relation holds between
them, where we consider both types of cases as
falling under our NOTA category.
695
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
4 Background: Prior Few-Shot
RC Models
As mentioned earlier, only a handful of examples
are provided for the target classes in the Few-
Shot setting. It is therefore quite challenging to
utilize these examples effectively for learning or
updating model parameters. Consequently, abbastanza
a few existing few-shot models, in the machine
learning literature as well as in NLP (Vinyals et al.,
2016; Ravi and Larochelle, 2017; Baldini Soares
et al., 2019), perform a representation learning
phase (typically known as embedding learning or
metric learning), followed by nearest neighbor
classificazione. Here, model parameters are first
learned over the background classes, for which
substantial training is available. Then, classifica-
tion of test instances is based on the trained model,
with the hope that this model would generalize
reasonably well for the target classes.4
In the nearest neighbor approach, classificazione
is done via a scoring function score(q, ci), Quale
assigns a score for a query instance, q, and a
target class, ci. Because the class is represented
by its Support Set, σci, the scoring function can
be a similarity function between the query and the
class’s support set:
score(q, ci) (cid:2) sim(q, σci)
Most often, an embedding-based approach is taken
to compute similarity, decomposing the process
into two separate components (Snell et al., 2017;
Baldini Soares et al., 2019; Li et al., 2019). Primo,
instances are embedded into an explicit, typically
dense, vector space, by an embedding function.
Then, query-support similarity is measured over
embedded vectors. Specifically, the prototypical
network of Snell et al. (2017) represents a target
class ci by a class prototype vector μi, che è
the average embedding of the K instances in the
support set of the class. The similarity between
the query and each support set, sim(q, σci), È
then measured as the similarity between the query
4While in the remainder of this paper we focus on this
similarity-based approach, it is worth noting that there exist
other approaches for FSL, which further utilize the few
labeled support examples. These include data augmentation
metodi, which generate additional examples based on the
few initial ones, as well as optimization-based methods
(Ravi and Larochelle, 2017; Finn et al., 2017), dove il
model does utilize the small support sets of the target classes
for parameter learning. Integrating our contributions with
these approaches is left for future work.
Figura 1: Relation distribution across episodes in our
newly derived Few-Shot TACRED and the existing
FewRel 2.0 RC task. On the left side we demonstrate the
relations distribution in Few-Shot TACRED episodes,
which follows a real-world distribution. On the right,
we present the relations distribution in FewRel 2.0,
which is synthetic. The y-axis for both figures is in
log scale. Few-Shot TACRED NOTA’s proportion is
97.5% while in FewRel 2.0 it is 50%.
We choose M = 10 del 41 relations for the
test set, and divide the remaining 31 relations into
25 E 6 for training and development, respec-
tively, and release this split for future research.
Tavolo 1 lists the respective number of train/dev/
test instances in our Few-Shot TACRED, along
with the resulting NOTA rate in the test instances,
as well as the corresponding numbers for the
original TACRED dataset. As we expected, In
a typical few-shot setting over natural text (COME
in Few-Shot TACRED, unlike FewRel), Dove
the number of the targeted classes (N-way) È
piccolo, most instances would correspond to the
NOTA case. This is indeed illustrated in Table 1,
where the original TACRED dataset includes 41
target classes, vs. 10 in Few-Shot TACRED, E
hence have a lower NOTA rate (conversely, in un
5-way setting, the NOTA rate is even higher, Vedere
Figura 2).
Evaluation Sets For evaluation, we consider
sets of 150,000 episodes, sampled according to
the procedure above. For robustness, we create 5
evaluation sets of 30,000 episodes each, and report
the mean and STD scores over the 5 sets. Figura 1
(shown in §1) presents the distribution differences
between Few-Shot TACRED and FewRel 2.0
episodes. As we show in Section 6, the Few-Shot
TACRED evaluation set proves to be a substantial
challenge for Few-Shot algorithms.
696
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
and the corresponding prototype vector, assuming
some similarity function between vectors in the
embedding space:
sim(q, σci) (cid:2) sim(q, μi)
This approach was adopted in the state-of-the-art
method (Baldini Soares et al., 2019) for few-shot
RC (FewRel 1.0, excluding the NOTA category),
as well as by several other works for FSL in NLP
(Bao et al., 2020UN; Yu et al., 2018).
Nearest-neighbor Classification Rule Simi-
larity is computed between a test instance and
each support set, selecting the nearest class:
fS(q) = arg max
cj
sim(q, σcj )
Instance Representation Baldini Soares et al.
(2019) further conducted an empirical analysis
of embedding functions for few-shot RC. Their
most effective embedding method augments the
sentence with special tokens at the beginning and
at the end of each of the two entities of the rela-
tion instance. The instance representation is then
obtained by concatenating the two correspond-
ing start tokens from BERT’s last layer (Devlin
et al., 2019). In our experiments, we adopt this
embedding function, denoted BERTEM (BERT-
based Entity Marking), as well as the use of dot
product as the vector similarity function (after we
reassessed its effectiveness as well).
4.1 FewRel 2.0 BERT Sentence-pair Model
The FewRel 2.0 work presented a model for the
NOTA setting, which skips the embedding learn-
ing phase (Gao et al., 2019). Invece, it utilizes
the embeddings-based next sentence prediction
score of BERT (Devlin et al., 2019), as the simi-
larity score between a query and each support set
instance. Then, similarly to the approach described
above, a nearest-neighbor criterion is applied over
the average similarity score between the query
and all support instances of each class. A paral-
lel scoring mechanism is implemented to decide
whether the NOTA category should be chosen.
4.2 Related FSL Classification Models
In this section we first review some prominent
FSL work addressing other machine-learning
compiti. Additionally, we compare between the no-
tions of Out-Of-Domain (OOD) detection and
NOTA detection.
In a recent work on FSL, Tseng et al. (2020) aim
to improve generalization abilities by providing
supervision for the category transfer phase. In
their learning setting, the classes of each training
episode are divided into two subsets, the first acts
as the ‘‘typical’’ training set while the second sim-
ulates the test set. To improve generalization they
add an additional encoding layer that is optimized
to maximaize performance on the simulated test
categorie.
Another recent FSL work, addressing text
classificazione, suggests weighing words by their
frequency over the training set (Bao et al., 2020B).
The model uses two components to classify the
given text into one of the episode’s categories. IL
first component computes the inverse frequency
of each support set token over the training set. IL
second component estimates the inductive level of
support set tokens with respect to classification.
Finalmente, the output of these two components is
used to train a linear classifier, by which the query
is classified.
Out-Of-Domain Detection The essence of the
NOTA category resembles OOD detection, COME
in both cases the goal is to detect instances not
falling under the known categories. Tan et al.
(2019) define the OOD classes as the set of all
classes that were not part of the training classes
(vs. NOTA, which means that none of the given
support classes in an episode is present). In their
lavoro, the authors suggest a representation learning
approach for OOD detection in text classifica-
zione. Their method combines hinge loss with the
classic cross-entropy loss function. The former is
used to push away the representation of the OOD
instances, while the latter is used to learn correct
classification within the in-domain classes.
5 Classification Rules: Analysis
and Extension
In this section, we provide an analytic perspective
on the bias that different nearest-neighbor classi-
fication rules impose on the learned embedding
spazio. We start with an analysis of the classifica-
tion rule for the basic few-shot RC setting, without
the NOTA category, as was applied in prior work
(Sezione 4). This analysis follows directly the
constraint presented in the influential work of
Weinberger and Saul (2009), and utilized in
subsequent work (per esempio., Shen et al., 2010; Dhillon
et al., 2010). We then extend this analysis to the
697
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
setting that does include the NOTA category.
Primo, we analyze the straightforward threshold-
based approach for this setting. Then, inspired by
this analysis, we propose an alternative approach,
with a corresponding constraint, which represents
the NOTA category by one or more explicit
learned vectors. As shown in subsequent sections,
this new approach performs consistently better
than other methods on both the FewRel 2.0 E
our new Few-Shot TACRED benchmarks, E
is thus suggested as an appealing approach for
few-shot Relation Classification.
5.1 Constraints Imposed by
Nearest-neighbor Classification
Classification without NOTA As described
earlier, the nearest neighbor approach assigns a
query instance to the class of its nearest support
set. We start our analysis by adapting inequality
(10) from Weinberger and Saul (2009), Quale
was introduced to formulate the training goal for
metric learning in k-nearest neighbor classifica-
tion.To this end, we adapt the original inequality
to our nearest-neighbor few-shot classification
setting (Sezione 4). The obtained inequality below
specifies the necessary and sufficient constraints
that the embedding space, along with the sim-
ilarity function over it, should satisfy in order
to reach perfect classification, over all possible
episodes in a given dataset.5 For every possible
query instance q, a support set σr(q) from the same
class as q and a support set σ¬r(q) for a different
class, the following constraint should hold:
∀ q, σr(q), σ¬r(q)
sim(q, σr(q)) > sim(q, σ¬r(q))
(1)
Questo è, to achieve perfect classification, each pos-
sible relation instance q imposes that support sets
of different classes should be positioned further
away from it (being less similar) than the most
distant support set it might have from its own
class. Generally speaking, the nearest neighbor
classification rule implies that instances that are
rather close to their class mates may also be rather
close to other classes, while instances that are far
from their class mates should also be positioned
at least as far from other classes.
5Notice that we drop the margin element in the adapted
inequality, as it is not needed for the analytic purpose of our
constraint.
In the few-shot setting, the embedding function
is learned during training, over the training cate-
sanguinose. As the learning process tries to optimize
classification on the training set, it effectively
attempts to learn an embedding function that
would satisfy the above constraint as much as
possible. Infatti, we often observed almost per-
fect performance over the training data, indicating
Quello, for the training instances, this constraint is
mostly satisfied by the learned embedding func-
zione. Yet, while it is hoped that the embedding
function would separate properly also instances of
new, previously unseen, classes, in practice this
holds to a lesser degree, as indicated by lower test
performance.
Thresholded Classification with NOTA When
the NOTA option is present, the nearest neighbor
classification rule can be naturally augmented
by assigning the NOTA category to test queries
whose similarity to all of the target classes does
not surpass a predetermined (possibly learned)
threshold, θ. Extending our analysis to such clas-
sification rule, to achieve perfect classification,
the embedding space must fulfil the following,
necessary and sufficient constraint, whose left-
hand-side is relevant only for episodes that include
a support set for the query’s class:
∀ q, σr(q), σ¬r(q)
sim(q, σr(q)) > θ > sim(q, σ¬r(q))
(2)
Since the same threshold is applied to all queries,
to achieve perfect classification in this setting θ
should be smaller than all within-class similari-
ties, for any possible pair of query q and a support
set of its class σr(q). Concurrently, it should be
larger than all cross-class similarities, for any
possible query q and a support set of a different
class σ¬r(q).6
We observe that Inequality (2) imposes a global
constraint over the embedding space. It implies
that the degree to which all classes should be
separated from each other is imposed, globally,
by those queries in the entire space which are the
furthest away from their own class support sets.
Accordingly, it requires all classes to be positioned
equally far from each other, regardless of their own
‘‘compactness’’. This makes a much harsher con-
straint, and challenge for the embedding learning,
than Inequality (1), which allows certain classes to
be nearer if their within-class similarities are high.
6Proof provided in the Appendix.
698
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
5.2 NOTA As a Vector (NAV)
Motivated by the last observation, we propose an
alternative classification approach for few-shot
classification with the NOTA category. In this
approach, we represent the NOTA category by an
explicit vector in the embedding space, denoted
VN , which is learned during training. At test time,
the similarity between the query q and this vector,
sim(q, VN ), is computed and regarded as the sim-
ilarity between the query and the NOTA category:
sim(q, NOTA) (cid:2) sim(q, VN )
Then, q is assigned to its nearest class, by the
usual nearest-neighbor classification rule. Così,
the NOTA class is selected if sim(q, VN ) is higher
than q’s similarity to all target classes. Effectively,
this mechanism considers an individual NOTA
classification threshold for each query, namely
sim(q, VN ), which depends on q’s position in the
embedding space relative to VN . We term this
approach ‘‘NOTA As a Vector’’ (NAV).
Classification under the NAV scheme implies
the following constraint on the embedding space,
considering perfect classification:7
∀ q, σr(q), σ¬r(q)
sim(q, σr(q)) > sim(q, VN ) > sim(q, σ¬r(q))
(3)
This constraint implies that, to achieve perfect
classificazione, the similarity between a query and
the NOTA vector VN should be smaller than q’s
similarity to all possible support sets of its own
class, while being larger than its similarity to all
support sets of other classes. In comparison to the
prior classification rules, this approach does allow
instances that are rather close to their class mates
to be closer to other classes than instances that are
positioned further from some of their class mates,
similarly to the lighter constraint in Inequality (1).
Yet, to enable such ‘‘geometry’’ of the embedding
spazio, it is also required that instances would be
positioned appropriately relative to the NOTA
vector, in a way that satisfies the two constraints
in Inequality (3). Using the NAV approach, it is
hoped that the learning process would position the
NOTA vector, and adjust the embedding parame-
ters, such that these constraints would be mostly
7Notice the analogous structure of Inequalities 2 E
3, where sim(q, VN ) replaces the role of θ. A similar
correctness proof applies.
satisfied. Overall, the NAV approach imposes
different constraints on the similarity space than
using a single global classification threshold for
the NOTA category (as in Inequality (2)), and it is
not clear apriori which approach would be more
effective to learn. This question is investigated
empirically in Section 6.
5.3 Multiple NOTA Vectors
A natural extension of the NAV approach, denoted
as MNAV, is to represent the NOTA category by
multiple vectors, whose number is an empirically
tuned hyper-parameter. During classification, IL
model picks the closest vector to the query as
VN , which accordingly defines sim(q, NOTA).
Then, classification is determined as in the NAV
method, where adding multiple NOTA vectors is
expected to effectively ease the embedding space
constraints. In practice, we treat the number of
NOTA vectors as a hyperparameter.
5.4 Training Procedure
For training, we use the same episode sampling
procedure that generated the dev/test sets, Ma
where the target relations are sampled from a set of
train relations, disjoint from the dev/test relations.
We define an epoch to include a fixed number
of episodes, considered a tuned hyper-parameter,
independently sampling episodes for each epoch.
We measure dev set performance after each epoch,
and use early stopping. For each episode E =
(Rtarget, {σc1, . . . , σcN }, q), we encode the query
using BERTEM encoding function (Baldini Soares
et al., 2019), described in §4, (cid:5)q = BERTEM (q)
and similarly for each item x in each support set,
obtaining for each σcj the corresponding average
prototype vector (cid:5)μj = 1
K
BERTEM (X).
(cid:2)
x∈σcj
We define the prototype of the NOTA class to
be the learned NAV vector: (cid:5)μ⊥ = (cid:5)vN . Our loss
term for each episode considers (cid:5)q and the proto-
type vectors (cid:5)μi and tries to optimize Inequality
(3): dot((cid:5)q, (cid:5)μr(q)) > dot((cid:5)q, (cid:5)μ⊥) > dot((cid:5)q, σ¬r(q)).
Concretely we use cross-entropy loss, as used in
previous work (Baldini Soares et al., 2019):
− log
(cid:2)
edot((cid:3)q,(cid:3)μr(q))
i∈Rtarget∪ { ⊥ } edot((cid:3)q, (cid:3)μi)
Note that this works towards satisfying the condi-
tions in Inequality (3): in episodes where r(q) (cid:8)=⊥,
the loss attempts to increase the first term in
Inequality (3) (the similarity between the query
699
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
and the prototypical vector of its class), while
decreasing the similarity of the two other terms
(the similarity between q and all other prototypical
vettori,
including the NAV one). In particu-
lar, it drives towards satisfying sim(q, σr(q)) >
sim(q, VN ). In episodes where r(q) =⊥, the loss
increases the second term, decreasing the similar-
ity in the third term, driving towards satisfying
sim(q, VN ) > sim(q, σ¬r(q)). Analogously, IL
same dynamics apply when the learned (scalar)
threshold value determines the NOTA score.
Following Weinberger and Saul (2009), who
derived a triplet loss objective, and similar to
subsequent lines of work (per esempio., Schroff et al.,
2015; Hoffer and Ailon, 2015; Ming et al., 2017),
we experimented also with adapted versions of
triplet loss. Under this objective, instances not
belonging to the same class are pushed away while
same-class instances are pulled together, aiming
to reach the desired ordering as in Inequalities
(2) E (3). We tried multiple variants of this
objective for FSL training, including objective
versions with a margin element, but these exper-
iments resulted in consistently lower results than
the methods described above.
NOTA Vector Initialization For
the NAV
method, we straightforwardly initialized the sin-
gle NOTA vector randomly. Random initialization
of the multiple NOTA vectors in MNAV evolved
to a single vector being dominantly picked as
the NAV vector by the MNAV decision process.
Consequently, results were very similar to the
(single vector) NAV model. Presumably, this hap-
pened because a single random vector turned out
to be closest to the sub-space initially populated
by the pre-trained BERTEM embedding function.
To avoid this, we wish to scatter all the initial
vectors within the initially populated subspace. A
this end, we initialize a NOTA vector by sampling
a relation and then averaging 10 random instances
from that relation. We repeat this process for each
NOTA vector.
6 Experiments and Results
In this section, we assess our two main contri-
butions. With respect to our Few-Shot TACRED
dataset, we show that models that perform well
on FewRel 2.0 perform poorly on this much
more realistic setting, leaving a huge gap for
improvement by future research. With respect to
our proposed NAV modeling approach, we show
that it is a viable, and advantageous, alternative to
the threshold approach.
Implemented Models We conduct our investi-
gation in the framework of the common embed-
ding based approach to FSL, with respect to the
MNAV, NAV, and threshold-based methods
described in §5. These methods are implemented
following the best-performing embedding and
similarity methods identified for the state-of-
the-art method on FewRel 1.0 (Baldini Soares
et al., 2019), namely, BERTEM applied using
BERTBASE, and dot product similarity (§4).
Inoltre, we train and evaluate the baseline
Sentence-Pair model, described in §4.1.
To select the number of NOTA vectors in the
MNAV model, we experimented with 5 differ-
ent values, ranging from 1 A 20. In practice,
the choice of the number of vectors had rather
little impact on the results (less than one F1
point). We use the best performing value for this
hyperparameter, which was 20.
In terms of memory utilization, as 5-way 5-shot
episodes require feeding the 25 instances of the
support set in addition to the query instances into
BERT simultaneously, they often occupy nearly
the entire 32GB of GPU memory. To leverage
the memory taken by the support set instances,
we include as many queries as we can fit into
the GPU’s memory. In our experiments, we con-
struct 3 episodes for each sampled support set (by
sampling 3 different queries for it), which fully
utilizes the GPU capacity. Since these episodes
occupy the entire GPU memory, we use a single
episode per batch.
We further note that it may be possible to
perform the N-way classification by transforming
it into a pair-wise classification, repeated N times
(both in training and evaluation). This technique
would allow to reduce the memory usage but
would increases the run-time. As we managed to
fit the entire episode to our GPU memory, we
followed the standard N-way approach, for faster
computation, as was previously done by Gao
et al. (2019).
Test Methodology and Metrics Like prior
lavoro, evaluation is conducted over randomly
sampled episodes from the test data, as described
in §2. Prior results for FewRel 2.0 (and FewRel
1.0) were reported in terms of Accuracy. Tuttavia,
700
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Model
NOTA Rate
5-way 1-shot
5-way 5-shot
15% 50% 15% 50%
Sentence-Pair
Threshold
NAV
MNAV
77.67
63.41
77.17
79.06
80.31
76.48
81.47
81.69
84.19
65.43
82.97
85.52
86.06
78.95
87.08
87.74
Tavolo 2: Accuracy results on FewRel2.0 test set,
for the four available settings for this benchmark.
Results are reported for the FewRel2.0 sentence-
pair baseline model and our investigated models.
in realistic, highly imbalanced, relation classifi-
cation datasets,
like our Few-Shot TACRED,
accuracy becomes meaningless. Hence, noi professionisti-
pose micro F1 over the target relations as a more
appropriate measure for future research. Accord-
ingly, we report micro F1 for both datasets, COME
well as accuracy for FewRel experiments, for
compatibility. For both measures we report aver-
age values and standard deviation over 5 different
random samples of episodes (Zhang et al., 2018,
2017). In all experiments, we train and evaluate
five models and report the results of the median
performing model. Unless otherwise mentioned,
reported result differences are significant under
one-tailed t-test at 0.05 confidence.
6.1 FewRel 2.0 Result
We first confirm the appropriateness of our inves-
tigation by comparing performance on the prior
FewRel 2.0 test data. Tavolo 2 presents the figures
on the two official (synthetic) test NOTA rates for
this benchmark. We use 50% NOTA rate to train
all our models, con 6,000 episodes per epoch. As
shown, the MNAV model performs best across all
FewRel settings, obtaining a new SOTA for this
task.8
We next turn to a more comprehensive com-
the investigated embedding-based
parison of
few-shot models, namely, threshold-based, NAV,
and MNAV, over the publicly available FewRel
development set, con 50% NOTA rate. IL
results in Table 3 show that, here as well, IL
8Our MNAV results are also reported at the official
FewRel 2.0 leader-board, as Anonymous Cat, at https://
thunlp.github.io/2/fewrel2 nota.html. Noi
note that the FewRel test set is kept hidden, where models
are submitted to the FewRel authors, who produce (only)
accuracy scores.
Model
Metric
5-way 1-shot
5-way 5-shot
Sentence-Pair
Threshold
NAV
MNAV
Precisione
F1
Precisione
F1
Precisione
F1
Precisione
F1
75.48 ± 0.33%
71.85 ± 0.44%
76.32 ± 0.12%
73.34 ± 0.25%
78.54 ± 0.08%
75.00 ± 0.22%
78.23 ± 0.13%
75.22 ± 0.19%
78.43 ± 0.25%
75.43 ± 0.31%
80.30 ± 0.09%
78.89 ± 0.11%
80.44 ± 0.11%
79.20 ± 0.14%
81.25 ± 0.18%
80.06 ± 0.11%
Tavolo 3: FewRel2.0 development set
accuracy and micro F1.
risultati,
modello
Sentence-Pair
Threshold
NAV
MNAV
5-way 1-shot
10.19 ± 0.81%
6.87 ± 0.48%
8.38 ± 0.80%
5-way 5-shot
−
13.57 ± 0.46%
18.38 ± 2.01%
12.39 ± 1.01% 30.04 ± 1.92%
Tavolo 4: Micro F1 results on Few-Shot TACRED.
For computational memory limitations, we could
not evaluate the Sentence-Pair model in the 5-shot
setting, see Appendix for explanation.
MNAV model outperforms the others in both set-
tings. The gap between MNAV and the threshold
model is significant for the two settings, while the
gap relative to the NAV model is significant only
in the 5-shot setting.
6.2 Few-Shot TACRED Results
We compare the MNAV, NAV, Sentence-Pair,
and threshold-based models over our more realis-
tic Few-Shot TACRED test set (here, epoch size
È 2,000). As seen in Table 4, the MNAV model
outperforms the others, as was the case over
FewRel 2.0.
Notably, performance is drastically lower over
Few-Shot TACRED. We suggest that this indi-
cates the much more challenging nature of a re-
alistic setting, relative to the FewRel 2.0 setting,
while indicating the limitation of all current mod-
els. We further analyze this performance gap in
the next section.
7 Analysis
7.1 Differentiating Characteristics of FewRel
vs. Few-Shot TACRED
As seen in Tables 3 vs. 4, the results on Few-
Shot TACRED are drastically lower than those
obtained for FewRel 2.0, by at least 50 points. Yet,
the performance figures are difficult to compare
due to several differences between the datasets,
including training size, NOTA rate, and different
701
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
tions of relation types in the two subsets, making
them equal, since, as discussed in Section 3, Questo
distribution impacts performance in RC datasets.
Apparently, the impact of entity composition
was different in the 1-shot and 5-shot settings. For
1-shot, the named entities subset yielded slightly
lower performance (6.65 vs. 9.03 micro F1), Quale
is hard to interpret. For 5-shot, performance on
the named entities subset was substantially higher
than when including all entity types (33.48 vs.
18.74), possibly suggesting that a larger diversity
of entity types is more challenging for the model.
In any case, we argue that RC datasets should
include all entity types,
to reflect real-world
corpora.
Summary Overall, the differences we analyzed
account for much of the large performance gap
between the two datasets, particularly in the more
promising 5-shot setting. As argued earlier, we
suggest that Few-Shot TACRED represents more
realistic properties of few-shot RC,
including
realistic non-uniform distribution, ‘‘no relation’’
instances and inclusion of all entity types, E
hence should be utilized in future evaluations.
7.2 Few-Shot versus Supervised TACRED
We next analyze the impact of category transfer
in Few-Shot TACRED. A tal fine, we apply our
same MNAV model in a supervised (non-transfer)
setting, termed Supervised MNAV, and compare
it to the few-shot MNAV (FSL MNAV). Contro-
cretely, we trained the supervised MNAV model
on the training instances of the same categories
as those in the Few-Shot TACRED test data (vs.
training on different background relations in the
transfer-based FSL setting). The supervised model
was then tested for 5-way 5-shot classification
on Few-Shot TACRED, identically to the FSL
MNAV 5-way 5-shot testing in Table 4. IL
results showed a 31 point gap, with the Super-
vised MNAV yielding 61.19 micro F1 while FSL
MNAV scored 30.04, indicating the substantial
challenge when moving from the supervised to
the category transfer setting.
7.3 Qualitative Error Analysis
To obtain some insight on current performance,
we manually analyzed 50 episodes for which the
model predicted an incorrect support class (preci-
sion error) E 50 in which it missed identifying
the right support class (recall error). We sampled
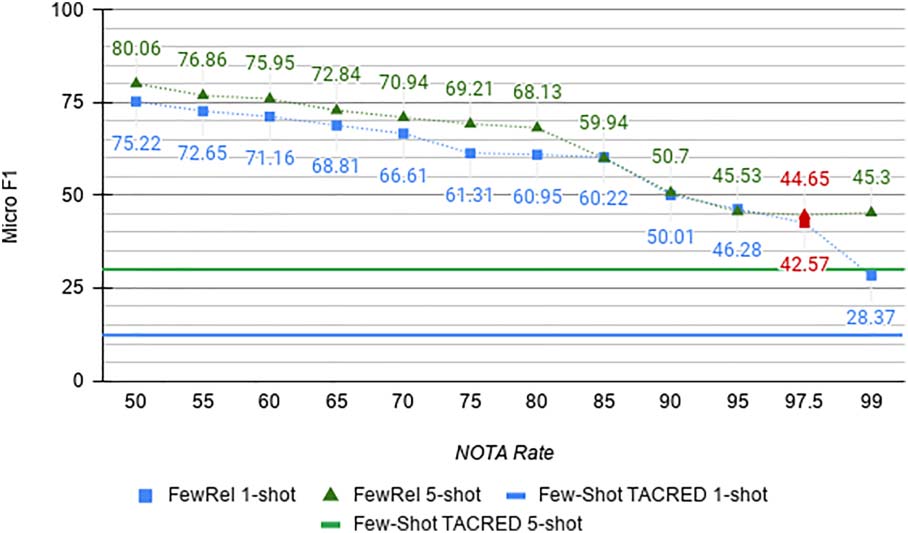
Figura 2: MNAV results on the FewRel 2.0 dev data-
set at different NOTA rates. The red points represent
performances at 97.5% NOTA rate which is the
Few-Shot TACRED NOTA rate. The blue and
green horizontal lines denote the Few-Shot TACRED
performance in the 1 E 5 shot settings, rispettivamente.
entity types. To analyze the possible impact of
these differences, we control for each of them and
observe performance differences. For brevity, we
focus on the MNAV model (1-shot and 5-shot).
Training Size We train the model on FewRel
2.0, taking the same amount of training instances
as in Few-Shot TACRED. Compared to full train-
ing, results dropped by five micro F1 points in
the 1-shot setting and by 1.5 points for 5-shot,
suggesting that the training size explains only a
small portion of the performance gap between the
two datasets.
NOTA Rates We control for the unrealistic
NOTA rate in FewRel 2.0 by training and evaluat-
ing our model on higher NOTA rates. The results
in Figure 2 indicate that realistic higher NOTA
rates are indeed much more challenging: Moving
from the original FewRel 50% NOTA rate to the
97.5% rate as in Few-Shot TACRED shrank the
performance gap by 33 points in the 1-shot setting
e da 35 for 5-shot.
Entity Types
In this experiment, we evalu-
ate performance differences when including all
entity types (named entities, common nouns,
and pronouns), as in Few-Shot TACRED, versus
including only named entities, as in FewRel. A
this end, we sampled two corresponding subsets
of relation instances from Few-Shot TACRED, Di
the same size, with either all entity types or named
entities only.9 Further, we control for the distribu-
9Entity types were automatically identified by the SpaCy
NER model (Honnibal and Montani, 2017), as well as certain
fixed types included in FewRel, such as ranks and titles.
702
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
1-shot episodes since these can be more easily
interpreted, examining a single support instance
per class.
For the precision errors, we found a sin-
gle prominent characteristic. Across all sampled
episodes, both the query and the falsely selected
support instance shared the same (ordered) pair of
entity types. For instance, they may both share the
entity types of person and location, albeit having
different relations, such as city of death vs. state of
residence, or having no meaningful relation for the
query (no relation case). This behavior suggests
that pre-training, together with fine tuning on the
background relations, allowed the BERT-based
model to learn to distinguish entity types, to realize
their criticality for the RC task, and to successfully
match entity types between a query and a support
instance. D'altra parte, the low overall perfor-
mance suggests that the model does not recognize
well the patterns indicating a target relation based
on a small support set. Additional evidence for this
conjecture is obtained when examining confused
class pairs in the predictions’ confusion matrices
(1-shot and 5-shot settings). Out of 10 confused
class pairs, 8 pairs have matching entity types;
in the other two pairs, the location type is con-
fused with organization in the context of school
attended, which often carries a sense of location.
For the recall errors, manual inspection of the
50 episodes did not reveal any prominent insights.
Therefore, we sampled 100,000 1-shot episodes
over which we analyzed various statistics which
may be related to recall errors. Of these, we
present two analyses that seem to explain aspects
of recall misses, in a statistically significant man-
ner (one-tailed t-test at 0.01 significance level),
though only to a partial extent.
The first analysis examines the impact of
whether the relative order of the two marked argu-
ment entities flips between the query and support
instance sentences. To that end, we examined
the about 2,600 episodes in our sample in which
the query belongs to one of the support classes.
We found that for episodes in which argument
order is consistent across the query and support
instance, the model identified the correct class
In 15.68% of the cases, while when the order is
flipped only 10.95% of the episodes are classified
correctly. This suggests that a flipped order makes
it more challenging for the model to match the
relation patterns across the query and support sen-
tences. The second analysis examines the impact
of lexical overlap between the query and support
instance. To that end, we compared 300 episodes
in which the correct support class was success-
fully identified (true positive) E 300 in which
it was missed (false negative). In each episode,
we measured Intersection over Union (IoU) (aka
Jaccard Index) for the two sets of lemmas in
the query and support instance. As expected, IL
IoU value was significantly higher for the true
positive set (0.17) than for the false negative set
(0.12), suggesting that higher lexical match eases
recognizing the correct support instance.
8 Conclusions
In this work, we offer several required criteria for
realistic FSL datasets, while proposing a method-
ology to derive such benchmarks from available
datasets designed for supervised learning. We then
applied our methodology on the TACRED rela-
tion classification dataset, creating a challenging
benchmark for future research. Infatti, previ-
ous models that achieved impressive results on
FewRel, a synthetic dataset for FSL, failed mis-
erably on our naturally distributed dataset. These
results call for better models and loss functions for
FSL, and indicate that we are far from having satis-
fying results on this setup. Our methodology may
be further applied to additional datasets, enriching
the availability of realistic datasets for FSL.
Prossimo, we analyzed the constraints imposed
embedding functions by nearest-neighbor classi-
fication schemes, common for FSL. This analysis
led us to derive a new method for representing the
NOTA category as one or more explicit learned
vettori, yielding a novel classification scheme,
which achieves new state-of-the-art performance.
We suggest that our analysis may further inspire
additional innovations in few-shot learning.
Riferimenti
Livio Baldini Soares, Nicholas FitzGerald, Jeffrey
Ling, and Tom Kwiatkowski. 2019. Matching
the blanks: Distributional similarity for relation
apprendimento. In Proceedings of the 57th Annual
Riunione dell'Associazione per il Computazionale
Linguistica, pages 2895–2905, Florence, Italy.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/P19
-1279
703
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Yujia Bao, Menghua Wu, Shiyu Chang,
testo
and Regina Barzilay. 2020UN. Few-shot
classification with distributional signatures.
In International Conference on Learning
Representations.
Yujia Bao, Menghua Wu, Shiyu Chang,
and Regina Barzilay. 2020B. Few-shot
testo
classification with distributional signatures.
In International Conference on Learning
Representations.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, E
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. Negli Atti di
IL 2019
Conference of the North American Chapter of
the Association for Computational Linguistics:
Tecnologie del linguaggio umano, Volume 1
(Long and Short Papers), pages 4171–4186,
Minneapolis, Minnesota. Association for Com-
Linguistica putazionale.
Paramveer S. Dhillon, Partha Pratim Talukdar,
and Koby Crammer. 2010. Learning better data
representation using inference-driven metric
apprendimento. Negli Atti di
the ACL 2010
Conference Short Papers, pages 377–381,
Uppsala, Sweden. Associazione per il calcolo-
linguistica nazionale.
Chelsea Finn, Pieter Abbeel, and Sergey Levine.
2017. Model-agnostic meta-learning for fast
adaptation of deep networks. Negli Atti di
the 34th International Conference on Machine
Apprendimento, volume 70 of Proceedings of Ma-
chine Learning Research, pages 1126–1135,
International Convention Centre, Sydney,
Australia. PMLR.
Tianyu Gao, Xu Han, Hao Zhu, Zhiyuan Liu,
Peng Li, Maosong Sun, and Jie Zhou. 2019.
FewRel 2.0: Towards more challenging few-
shot relation classification. Negli Atti di
IL 2019 Conferenza sui metodi empirici
in Natural Language Processing and the 9th
International Joint Conference on Natural
(EMNLP-IJCNLP),
Language
pages 6250–6255, Hong Kong, China. Asso-
ciation for Computational Linguistics.
in lavorazione
Xu Han, Hao Zhu, Pengfei Yu, Ziyun Wang, Yuan
Yao, Zhiyuan Liu, and Maosong Sun. 2018.
FewRel: A large-scale supervised few-shot
704
relation classification dataset with state-of-the-
IL 2018
art evaluation. Negli Atti di
Conference on Empirical Methods in Natu-
ral Language Processing, pages 4803–4809,
Brussels, Belgium. Associazione per il calcolo-
linguistica nazionale. https://doi.org/10
.18653/v1/D18-1514
Elad Hoffer and Nir Ailon. 2015. Deep metric
learning using triplet network. In 3rd Inter-
national Conference on Learning Representa-
zioni, ICLR 2015, San Diego, CA, USA, May
7–9, 2015, Workshop Track Proceedings.
Matthew Honnibal and Ines Montani. 2017. Spacy
2: Natural language understanding with bloom
embeddings. Convolutional Neural Networks
and Incremental Parsing, 7(1).
Omer Levy, Minjoon Seo, Eunsol Choi, E
Luke Zettlemoyer. 2017. Zero-shot relation
In
extraction via reading comprehension.
Proceedings of the 21st Conference on Compu-
tational Natural Language Learning (CoNLL
2017), pages 333–342, Vancouver, Canada.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/K17
-1034
Wenbin Li, Lei Wang, Jinglin Xu, Jing Huo, Yang
Gao, and Jiebo Luo. 2019. Revisiting local
descriptor based image-to-class measure for
few-shot learning. In CVPR, pages 7260–7268.
Computer Vision Foundation / IEEE.
Zuheng Ming,
Joseph Chazalon, Muham-
mad Muzzamil Luqman, Muriel Visani, E
Jean-Christophe Burie. 2017. Simple triplet loss
based on intra/inter-class metric learning for
face verification. In 2017 IEEE International
Conference on Computer Vision Workshops,
ICCV Workshops 2017, Venice, Italy, ottobre
22–29, 2017, pages 1656–1664. IEEE Com-
puter Society. https://doi.org/10.1109
/ICCVW.2017.194
Mike Mintz, Steven Bills, Rion Snow, E
Daniel Jurafsky. 2009. Distant supervision for
labeled data. In
relation extraction without
Joint Conference of
Proceedings of
the 47th Annual Meeting of
the ACL and
Joint Conference
IL
on Natural Language Processing of
IL
AFNLP, pages 1003–1011, Suntec, Singapore.
Internazionale
4th
IL
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Associazione per la Linguistica Computazionale.
https://doi.org/10.3115/1690219
.1690287
Makoto Miwa and Mohit Bansal. 2016. End-
to-end relation extraction using LSTMs on
sequences and tree structures. Negli Atti
of the 54th Annual Meeting of the Association
for Computational Linguistics (Volume 1: Lungo
Carte), pages 1105–1116, Berlin, Germany.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/P16
-1105
Abiola Obamuyide and Andreas Vlachos. 2018.
relation classification as textual
Zero-shot
the First
Negli Atti di
entailment.
Workshop on Fact Extraction and VERification
(FEVER), pages 72–78, Brussels, Belgium.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/W18
-5511
Abiola Obamuyide and Andreas Vlachos. 2019.
Model-agnostic meta-learning for relation clas-
sification with
In
limited
Proceedings of the 57th Annual Meeting of the
Associazione per la Linguistica Computazionale,
pages 5873–5879, Florence, Italy. Association
for Computational Linguistics. https://
doi.org/10.18653/v1/P19-1589
supervisione.
Sachin Ravi
and Hugo Larochelle. 2017.
Optimization as a model for few-shot learn-
ing. In 5th International Conference on Learn-
ing Representations,
ICLR 2017, Toulon,
France, April 24–26, 2017, Conference Track
Proceedings. OpenReview.net.
Florian Schroff, Dmitry Kalenichenko, and James
Philbin. 2015. FaceNet: A unified embedding
for face recognition and clustering. In IEEE
Conference on Computer Vision and Pattern
Recognition, CVPR 2015, Boston, MA, USA,
June 7–12, 2015, pages 815–823.
IEEE
Computer Society. https://doi.org/10
.1109/CVPR.2015.7298682
Chunhua Shen, Junae Kim, and Lei Wang. 2010.
Scalable large-margin mahalanobis distance
metric learning. IEEE Transactions on Neural
Networks 21(9):1524–1530. https://doi
.org/10.1109/TNN.2010.2052630,
PubMed: 20709641
Jake Snell, Kevin Swersky,
2017. Prototypical
apprendimento.
and Richard
for
networks
Zemel.
In Advances in Neural
few-shot
Information Processing Systems, volume 30,
pages 4077–4087. Curran Associates, Inc.
Negli Atti di
Ming Tan, Yang Yu, Haoyu Wang, Dakuo Wang,
Saloni Potdar, Shiyu Chang, and Mo Yu. 2019.
Out-of-domain detection for low-resource text
IL
classification tasks.
2019 Conference on Empirical Methods in
Natural Language Processing and the 9th
International Joint Conference on Natural
(EMNLP-IJCNLP),
Language
pagine
3566–3572, Hong Kong, China.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/D19
-1364
in lavorazione
Hung-Yu Tseng, Hsin-Ying Lee, Jia-Bin Huang,
and Ming-Hsuan Yang. 2020. Cross-domain
few-shot classification via learned feature-wise
transformation. In International Conference on
Learning Representations.
Oriol Vinyals, Charles Blundell, Timothy
Lillicrap, Koray Kavukcuoglu, and Daan
Wierstra. 2016. Matching networks for one
In-
shot
formation Processing Systems, volume 29,
pages 3630–3638. Curran Associates, Inc.
In Advances in Neural
apprendimento.
Linlin Wang, Zhu Cao, Gerard de Melo, E
Zhiyuan Liu. 2016. Relation classification via
multi-level attention CNNs. Negli Atti di
the 54th Annual Meeting of the Association for
Linguistica computazionale (Volume 1: Lungo
Carte), pages 1298–1307, Berlin, Germany.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/P16
-1123
Kilian Q. Weinberger and Lawrence K. Saul.
2009. Distance metric learning for large margin
nearest neighbor classification. Journal of
Machine Learning Research, 10(2):207–244.
Yuan Yao, Deming Ye, Peng Li, Xu Han, Yankai
Lin, Zhenghao Liu, Zhiyuan Liu, Lixin Huang,
Jie Zhou, and Maosong Sun. 2019. DocRED: UN
large-scale document-level relation extraction
dataset. In Proceedings of the 57th Annual
Riunione dell'Associazione per il Computazionale
Linguistica, pages 764–777, Florence, Italy.
705
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
T
l
UN
C
_
UN
_
0
0
3
9
2
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/P19
-1074
Mo Yu, Xiaoxiao Guo, Jinfeng Yi, Shiyu Chang,
Saloni Potdar, Yu Cheng, Gerald Tesauro,
Haoyu Wang, and Bowen Zhou. 2018. Diverse
few-shot text classification with multiple met-
rics. Negli Atti del 2018 Conference of
the North American Chapter of the Association
for Computational Linguistics: Human Lan-
guage Technologies, Volume 1 (Documenti lunghi),
pages 1206–1215, New Orleans, Louisiana.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/N18
-1109
Yuhao Zhang, Peng Qi, e Christopher D.
Equipaggio. 2018. Graph convolution over pruned
dependency trees improves relation extraction.
IL 2018 Conference on
Negli Atti di
Empirical Methods in Natural Language Pro-
cessazione, pages 2205–2215, Brussels, Belgium.
Associazione per la Linguistica Computazionale.
https://doi.org/10.18653/v1/D18
-1244
Yuhao Zhang, Victor Zhong, Danqi Chen, Gabor
Angeli, e Christopher D. Equipaggio. 2017.
Position-aware attention and supervised data
improve slot filling. Negli Atti di
IL
2017 Conference on Empirical Methods in
Elaborazione del linguaggio naturale, pages 35–45,
Copenhagen, Denmark. Association for Com-
Linguistica putazionale. https://doi.org
/10.18653/v1/D17-1004
A Appendix
A.1 Proof of Inequality 2
We prove that the two sides of the inequality
are necessary and sufficient to guarantee perfect
classification by the threshold-based classification
rule, over all possible episodes in a given dataset.
We first prove necessity. As the LHS refers
to σr(q), it is relevant only for episodes where
q belongs to one of the support classes. If it
is violated for some episode, then that episode
cannot be classified to r(q) (the correct class)
by the threshold-based classification rule. Quanto a
RHS necessity, consider an episode in which
sim(q, σ¬r(q)) > θ, violating the RHS. Without
loss of generality, we can construct a possible
episode with the same q and σ¬r(q), whose correct
classification is NOTA (making sure to exclude
R(q) from the support classes). This episode cannot
be correctly classified by the classification rule to
NOTA, since q’s similarity to at least one class,
¬r(q), surpasses θ.
To prove sufficiency, we consider the two
cases where an episode’s correct classification
is either NOTA or one of the support classes.
If the correct classification is NOTA, then r(q)
is not within the Support Set. The RHS then
guarantees that sim(q, σ¬r(q)) < θ for all support
classes, implying a correct NOTA classification.
Otherwise, the correct classification is r(q), being
one of the support classes. In this case,
the
LHS guarantees excluding a NOTA classification,
while the RHS excludes classification to any other
category different than r(q). QED.
A.2 Sentence-Pair High GPU Demand
The Sentence-Pair model (Gao et al., 2019)
requires at least twice more GPU memory than a
standard embedding learning model, such as the
threshold model (described in Sec 5). The higher
memory demand arises from feeding BERT with
the concatenation of each support instance to each
query instance. This concatenation effectively
doubles the average input sentence length. Due
to the Transformer architecture, doubling the
input sentence length requires higher GPU RAM
memory. In particular, a fully connected layer
requires four times more memory when fed with
a double-length sequence. Hence, representation
learning models, which embed a single instance
into an embedded vector space, are more memory
efficient than the sentence-pair model.
for
As mentioned in Section 6.2, we could not
the Few-
train the sentence-pair model
Shot TACRED 5-shot setting, due to memory
limitations, even though we used NVIDIA TESLA
V100-32GB GPU. This stems from the fact that
the average sentence length in Few-Shot TACRED
is higher than in FewRel, which did not fit
into our server memory with the higher memory
consumption of the sentence-pair model.
706
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
9
2
1
9
5
5
1
5
5
/
/
t
l
a
c
_
a
_
0
0
3
9
2
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3