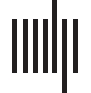REVIEW
Graph theory approaches to functional network
organization in brain disorders: A critique
for a brave new small-world
Michael N. Hallquist
1,2
and Frank G. Hillary
1,2,3
1Department of Psychology, Pennsylvania State University, University Park, PAPÀ, USA
2Social Life and Engineering Sciences Imaging Center, University Park, PAPÀ, USA
Department of Neurology, Hershey Medical Center, Hershey, PAPÀ, USA
3
a n o p e n a c c e s s
j o u r n a l
Keywords: Graph theory, Brain disorders, Network neuroscience, Proportional thresholding
ABSTRACT
Over the past two decades, resting-state functional connectivity (RSFC) methods have
provided new insights into the network organization of the human brain. Studies of brain
disorders such as Alzheimer’s disease or depression have adapted tools from graph theory
to characterize differences between healthy and patient populations. Here, we conducted
a review of clinical network neuroscience, summarizing methodological details from 106
RSFC studies. Although this approach is prevalent and promising, our review identified
four challenges. Primo, the composition of networks varied remarkably in terms of region
parcellation and edge definition, which are fundamental to graph analyses. Secondo,
many studies equated the number of connections across graphs, but this is conceptually
problematic in clinical populations and may induce spurious group differences. Third, few
graph metrics were reported in common, precluding meta-analyses. Fourth, some studies
tested hypotheses at one level of the graph without a clear neurobiological rationale or
considering how findings at one level (per esempio., global topology) are contextualized by another
(per esempio., modular structure). Based on these themes, we conducted network simulations to
demonstrate the impact of specific methodological decisions on case-control comparisons.
Finalmente, we offer suggestions for promoting convergence across clinical studies in order to
facilitate progress in this important field.
INTRODUCTION
Efforts to characterize a “human connectome” have brought sweeping changes to functional
neuroimaging research, with many investigators transitioning from indices of local brain ac-
tivity to measures of interregional communication (Friston, 2011). The broad goal of this con-
ceptual revolution is to understand the brain as a functional network whose coordination is
responsible for complex behaviors (Biswal et al., 2010). The prevailing approach to studying
functional connectomes involves quantifying coupling of the intrinsic brain activity among
regions.
In particular, resting-state functional connectivity (RSFC) metodi (Biswal, Yetkin,
Haughton, & Hyde, 1995) focus on interregional correspondence in low-frequency oscilla-
tions of the BOLD signal (approximately 0.01–0.12 Hz).
Work over the past two decades has demonstrated the value of RSFC approaches for
mapping functional network organization, including the identification of separable brain
Citation: Hallquist, M. N., & Hillary,
F. G. (2019). Graph theory approaches
to functional network organization
in brain disorders: A critique for a
brave new small-world. Network
Neuroscience, 3(1), 1–26.
https://doi.org/10.1162/netn_a_00054
DOI:
https://doi.org/10.1162/netn_a_00054
Supporting Information:
https://doi.org/10.1162/netn_a_00054
Received: 5 Gennaio 2018
Accepted: 3 April 2018
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Frank G. Hillary
fhillary@psu.edu
Handling Editor:
Martijn van den Heuvel
Copyright: © 2018
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
subnetworks (Biswal et al., 2010; Laird et al., 2009; Power et al., 2011; Smith et al., 2009;
van den Heuvel & Hulshoff Pol, 2010). Because RSFC methods do not require the study-specific
designs and cognitive burden associated with task-based fMRI studies, RSFC data are simple
to acquire and have been used in hundreds of studies of human brain function. Neverthe-
less, there are numerous methodological challenges, including concerns about the quality of
RSFC data (Power et al., 2014) and the effect of data processing on substantive conclusions
(Ciric et al., 2017; Hallquist, Hwang, & Luna, 2013; Shirer, Jiang, Price, Di, & Greicius, 2015).
RSFC studies of brain injury or disease typically examine differences in the functional con-
nectomes of a clinical group (per esempio., Parkinson’s disease) compared with a matched control
group. There are specific methodological and substantive considerations that apply to RSFC
studies of brain disorders. Per esempio, differences in the overall level of functional connec-
tivity between patient and control groups could lead to differences in the number of spuri-
ous connections in network analyses, potentially obscuring meaningful group comparisons
(van den Heuvel et al., 2017). Likewise, there is increasing concern in the clinical neuro-
sciences that an unacceptably small percentage of findings are replicable (Müller et al., 2017).
Such concerns echo the growing emphasis on open, reproducible practices in neuroimaging
more generally (Poldrack et al., 2017).
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory:
A subdomain of discrete
mathematics focused on the study
of graphs, mathematical structures
used to model pairwise interactions
(edges/links) among objects
(vertices/nodes). Graphs are
ubiquitous models of both natural
and artificial systems, and have been
used extensively in the physical,
biologico, and social sciences.
Parcellation (brain):
Investigator decision regarding
segregation of the acquired brain
space into distinct functional units
(nodes), representing a pivotal
firststep in creating a brain network.
in questo documento, we review the current state of graph theory approaches to RSFC in the clinical
neurosciences. Based on key themes in this literature, we conducted two network simula-
tions to demonstrate the pitfalls of specific analysis decisions that have particular relevance
to case-control studies. Finalmente, we provide recommendations for best practices to promote
comparability across studies.
Our review does not directly address many important methodological issues that are active
areas of investigation. Per esempio, detecting and correcting motion-related artifacts remains
a central challenge in RSFC studies (Ciric et al., 2017; Dosenbach et al., 2017) that is espe-
cially problematic in clinical and developmental samples (Greene, Black, & Schlaggar, 2016;
Van Dijk, Sabuncu, & Buckner, 2012). The length of resting-state scans (in terms of time, num-
ber of measurements, and number of sessions) also influences the reliability of functional con-
nectivity estimates (Birn et al., 2013; Gonzalez-Castillo, Chen, Nichols, & Bandettini, 2017)
and likely has downstream consequences on network analyses (Abrol et al., 2017; Yang et al.,
2012). Finalmente, brain parcellation—defining the number and form of brain regions—is one of
the most important influences on the composition of RSFC networks. There are numerous par-
cellation approaches, including anatomical atlases, functional boundary mapping, and data-
driven algorithms based on voxelwise BOLD time series (Goñi et al., 2014; Honnorat et al.,
2015). To focus on RSFC graph theory research in the clinical literature, where relevant, we
refer readers to more focused treatments of important issues that are beyond the scope of this
paper.
A Literature Review of Clinical Network Neuroscience Studies
Graph theory is a branch of discrete mathematics that has been applied in numerous studies
of brain networks, both structural and functional. A graph is a collection of objects, called
vertices or nodes; the pairwise relationships among nodes are called edges or links (Newman,
2010). Graphs composed of RSFC estimates among regions provide a window into the in-
trinsic connectivity patterns in the human brain. Figura 1 provides a simple schematic of the
most common graph theory constructs and metrics reported in RSFC studies. For more
Network Neuroscience
2
Graph theory as a tool to understand brain disorders
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 1. A toy graph and related graph theory terminology. Adapted with permission from Hillary
and Grafman (2017).
comprehensive reviews of graph theory applications in network neuroscience, see Bullmore
and Sporns (2009; 2012), or Fornito, Zalesky, and Bullmore (2016).
The goal of our literature search was to obtain a representative cross-section of graph-
theoretic RSFC studies spanning neurological and mental disorders. We focused on functional
connectivity (FC) as opposed to structural connectivity, where a distinct set of methodological
critiques are likely relevant. Also, we reviewed fMRI studies only, excluding electroencepha-
lography (EEG) and magnetoencephalography (MEG). Although there are important advan-
tages of EEG/MEG in some respects (Papanicolaou et al., 2017), we focused on fMRI in part
because the vast majority of clinical RSFC studies have used this modality. Inoltre, there are
fMRI-specific considerations for network definition and spatial parcellation in RSFC studies.
We conducted two related searches of the PubMed database (http://www.ncbi.nlm.nih.gov/
pubmed) to identify articles focusing on graph-theoretic approaches to RSFC in mental and
neurological disorders (for details on the queries, see Methods).
These searches were run in April 2016 and resulted in 626 potential papers for review (281
from neurological query, 345 from mental disorder query). Studies were excluded if they were
recensioni, case studies, animal studies, methodological papers, used electrophysiological meth-
ods (per esempio., EEG or MEG), reported only structural imaging, or did not focus on brain disorders
(per esempio., healthy brain functioning, normal aging). After exclusions, these two searches yielded
distinct 106 studies included in the review (Vedi la tabella 1). A full listing of all studies reviewed
is provided in the Supporting Information (Hallquist & Hillary, 2019).
Below, we outline important general themes from the literature review (our major con-
cerns are summarized in Box 1), including the heterogeneity of data analytic approaches
across graph theoretical studies. We then turn our focus to two critical issues with important
Network Neuroscience
3
Graph theory as a tool to understand brain disorders
Tavolo 1. Clinical disorders represented in the review of 106 clinical network neuroscience studies
Clinical phenotype
Alzheimer’s disease/MCI
Epilepsy/seizure disorder
Depression/affective
Schizophrenia
Alcohol/substance abuse
Parkinson’s disease/subcortical
Traumatic brain injury
Anxiety disorders
ADHD
Stroke
Cancer
Multiple sclerosis
Autism spectrum disorder
Disorders of consciousness
Somatization disorder
Dual Diagnosis
Other neurological disorder
Other psychiatric disorder
N (frequency)
19 (17.9%)
13 (12.3%)
12 (11.3%)
11 (10.4%)
7 (6.6%)
6 (5.7%)
6 (5.7%)
5 (4.7%)
5 (4.7%)
4 (2.8%)
3 (2.8%)
2 (1.9%)
2 (1.9%)
2 (1.9%)
2 (1.9%)
2 (1.9%)
3 (2.8%)
2 (1.9%)
Note. ADHD = attention deficit hyperactivity disorder; MCI = mild cognitive impairment.
implications for interpreting network analyses in case-control studies: (UN) network threshold-
ing (cioè., determining how to define a “connection” from a continuous measure of FC) E (B)
matching the hypothesis to the level of inquiry in the graph. For each of these issues, we offer
network simulations to illustrate the importance of these issues for case-control comparisons.
Box 1. Major challenges in graph-theoretic studies of functional connectivity in brain
disorders
1) There is substantial heterogeneity in defining the nodes and edges of graphs across resting-
state studies that largely precludes quantitative comparisons and formal meta-analyses. Key
sources of heterogeneity include brain parcellations, functional connectivity metrics (per esempio.,
full versus partial correlation), handling of negative FC estimates, and preprocessing
decisions (per esempio., global signal regression).
Inoltre, few graph metrics were reported in common, further undermining an exam-
ination of similarities across studies and disorders.
2) Many studies use proportional thresholding to convert a continuous functional connectivity
metric (per esempio., Pearson correlation) to a binary edge in the graph while controlling for the
total number of edges. This approach may obscure the effects of brain pathology in case-
control designs, where clinical groups may have changes in the number and strength of
functional connections. Proportional thresholding may also identify spurious group differ-
ences when groups differ in the connectivity strength of selected brain regions.
3) The link between many graph metrics and neurobiology has been more commonly
presumed than established (per esempio., neural efficiency).
4) The alignment between study hypotheses and specific graph analyses was often unclear.
Inoltre, many studies have not considered how findings at one level (per esempio., global topol-
ogy) are contextualized by another (per esempio., modular structure).
Proportional thresholding:
A constraint imposed on the network
so that the number of edges for all
subjects is maintained constant
irrespective of the relative network
strength.
Network Neuroscience
4
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
Creating Comparable Networks in Clinical Samples
Defining nodes in functional brain networks. Graph theory analyses of RSFC data fundamen-
tally depend on the definition of nodes (cioè., brain regions) and edges (cioè., the quantification
of functional connectivity). For network analyses to reveal new insights into clinical phenom-
ena, investigators must choose a parcellation scheme that robustly samples the regions and
networks of interest. Our literature review revealed that 76% of studies defined graphs based
on comprehensive parcellations (cioè., sampling most or all of the brain), whereas 24% ana-
lyzed connectivity in targeted subnetworks (per esempio., motor regions only; Table 2a). Inoltre,
we found substantial heterogeneity in parcellations, ranging from 10 A 67,632 nodes (Mode =
90; M = 1,129.2; SD = 7,035.9). Infatti, whereas 25% of studies had 90 nodes (most of these
used the AAL atlas; Tzourio-Mazoyer et al., 2002), the frequency of all other parcellations fell
below 5%, resulting in at least 50 distinct parcellations in 106 studies.
Although it may seem self-evident, it bears mentioning that several popular parcellation
schemes provide a broad, but not complete, sampling of functional brain regions. Per esempio,
recent parcellations based on the cortical surface of the brain (per esempio., Glasser et al., 2016; Gordon
et al., 2016) have provided a new level of detail on functional boundaries in the cortex. Yet if
a researcher is interested in cortical-subcortical connectivity, it is crucial that the parcellation
be extended to include all relevant regions.
There are advantages and challenges to every parcellation approach (per esempio., Honnorat et al.,
2015; Power et al., 2011); here, we focus on two specific concerns. Primo, a goal of most clinical
Tavolo 2. Network construction and edge definition
UN. Network construction
Comprehensive region sampling
Targeted region sampling
B. Edge definition
Weighted network
Binary network
Both
Unknown/unclear
C. Edge FC statistic
Correlation (typically, Pearson’s r)
Partial correlation
Wavelet correlation
Causal modeling (per esempio., SEM)
Other/unclear
D. Treatment of negative edges
Not reported/unclear
Discard negative values
Absolute value
Maintained/analyzed
Other transformation
N (frequency)
80 (75.5%)
26 (24.5%)
N (frequency)
48 (45.3%)
42 (39.6%)
13 (12.3%)
3 (2.8%)
N (frequency)
82 (77.3%)
11 (10.4%)
6 (5.7%)
3 (2.8%)
4 (3.7%)
N (frequency)
61 (57.5%)
23 (21.7%)
10 (9.4%)
9 (8.5%)
3 (2.8%)
Note. FC = functional connectivity; SEM = structural equation modeling.
Network Neuroscience
5
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
network neuroscience studies is to describe group differences in whole-brain connectivity pat-
terns that are reasonably robust to the graph definition. Così, investigators may wish to use at
least two parcellations in the same dataset to determine if the findings are parcellation depen-
dent. Because of the fundamental difficulty in comparing unequal networks (van Wijk, Stam,
& Daffertshofer, 2010), one would not expect identical findings.
In particular, global topo-
logical features such as efficiency or characteristic path length may vary by parcellation, Ma
other features such as modularity and hub architecture are likely to be more robust. Applying
multiple parcellations to the same dataset increases the number of analyses multiplicatively, COME
well as the need to reconcile inconsistent findings. Cassidy et al. (2018) recently demonstrated
that persistent homology, a technique from topological analysis, has the potential to quantify
the similarity of individual functional connectomes across different parcellations. We believe
that such directions hold promise for supporting reproducible findings in clinical RSFC stud-
ies (Craddock, James, Holtzheimer, Eh, & Mayberg, 2012; Roy et al., 2017; Schaefer et al.,
in press).
Secondo, differences in parcellation fundamentally limit the ability to compare studies, both
descriptively and quantitatively. As noted above, our review revealed substantial heterogeneity
in parcellation schemes across studies of brain disorders. Extending our concern about parcel-
lation dependence, such heterogeneity makes it impossible to ascertain whether differences
between two studies of the same clinical population are an artifact of the graph definition
or a meaningful finding. Inoltre, whereas meta-analyses of structural MRI and task-based
fMRI studies have become increasingly popular (per esempio., Goodkind et al., 2015; Müller et al.,
2017), such analyses are not currently possible in graph-theoretic studies in part because of
differences in parcellation. To resolve this issue, we encourage scientists to report results for a
field-standard parcellation, a point we elaborate in our recommendations below. We also be-
lieve there is value in investigators having freedom to test and compare additional parcellations
that may highlight specific findings.
Parcellation defines the nodes comprising a
Defining edges in functional brain networks.
graph, but an equally important decision is how to define functional connections among nodes
(cioè., the edges). The vast majority (77%) of the studies reviewed used bivariate correlation,
especially Pearson or Spearman, as the measure of FC. In Critical Issue 1 below, we consider
how FC estimates are thresholded in order to defines edges as present or absent in binary
graphs.
The statistical measure of FC has important implica-
Quantifying functional connectivity.
tions for network density and the interpretation of relationships among brain regions. IL
prevailing application of marginal association (typically, bivariate correlation) does not sepa-
rate the (statistically) direct connectivity between two regions from indirect effects attributable
to additional regions. By contrast, most conditional association methods (per esempio., partial cor-
relation) rely on inverting the covariance matrix among all regions, thereby removing com-
mon variance and defining edges based on unique connectivity between two regions (Smith
et al., 2011).
At the present time, there is no clear resolution on whether FC should be based on marginal
or conditional association (for useful reviews, see Fallani, Richiardi, Chavez, & Achard, 2014;
Varoquaux & Craddock, 2013). Nevertheless, we wish to highlight that as the average full
correlation increases within a network, partial correlation values, on average, must decrease.
Inoltre, partial and full correlations reveal fundamentally different graph topologies in
Network Neuroscience
6
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
resting-state data (Cassidy et al., 2018) and may yield different conclusions about the same
scientific question (per esempio., identifying functional hubs; see Liang et al., 2012). In cases of neuro-
pathology where one might expect distinct gains or losses of functional connections, the use
of partial correlation should be interpreted based on the relative edge density and mean FC.
Of the studies reviewed here, 10% used partial correlation, but virtually no study accounted
for possible differences in edge density (see Table 2c).
Another important aspect of defining edges is how to handle negative FC
Negative edges.
estimates. Full correlations of RSFC data typically yield an FC distribution in which most edges
are positive, but an appreciable fraction are negative. By contrast, partial correlation methods
often yield a relative balance between positive and negative FC estimates (per esempio., Y. Wang, Kang,
Kemmer, & Guo, 2016). There remains little consensus for handling or interpreting negative
edge weights in RSFC graph analyses (cf. Murphy & Fox, 2017). In our review, 57% del
studies reported insufficient or no information about how negative edges were handled in graph
analyses (Table 2d). Twenty-one percent of studies deleted negative edges prior to analysis,
E 9% included the negative weights as positive weights (cioè., using the absolute value of FC).
As detailed elsewhere, some graph metrics are either not defined or need to be adapted when
negative edges are present (Rubinov & Sporns, 2011).
Importantly, the mean of the marginal association RSFC distribution depends on whether
global signal regression (GSR)
is included in the preprocessing pipeline (Murphy, Birn,
Handwerker, Jones, & Bandettini, 2009). When GSR is included, there is often a balance
between positive and negative correlations. If GSR is included as a nuisance regressor, a large
fraction of FC estimates may simply be discarded as irrelevant to case-control comparisons,
which is a major, untested assumption. The meaning of negative FC, Tuttavia, remains un-
clear, with several investigators attributing negative correlations to statistical artifacts and GSR
(Murphy et al., 2009; Murphy & Fox, 2017; Saad et al., 2012).
Given that negative correlations are observable in the absence of GSR, Tuttavia, others
have examined whether negative weights contribute differentially to information processing
within the network (Parente et al., 2017). Negative correlations may also reflect NMDA ac-
tion in cortical inhibition (Anticevic et al., 2012). These connections bear consideration given
that brain networks composed of only negative connections do not retain a small-world topol-
ogy, but do have properties distinct from random networks (Parente et al., 2017; Schwarz &
McGonigle, 2011). Altogether, the omission of methodological details about negative FC in
empirical reports severely hampers the resolution of this important choice point in defining
graphs.
After resolving the questions of node and
Degree distribution as a fundamental graph metric.
edge definition, we also believe it is crucial for studies to report information about global net-
work metrics such as characteristic path length, clustering coefficient (aka transitivity), E
degree distribution. As noted in Table 3, local and global efficiency were commonly reported
(71% E 74%, rispettivamente) and typically across multiple FC thresholds. Tuttavia, our review
revealed that only 27% of studies provided clear descriptive statistics for mean degree, E
16% plotted the degree distribution. In binary graphs, the degree distribution describes the
relative frequency of edges for each node in the network. A similar property can be quantified
by examining the strength (also known as cost) distribution in weighted graphs. We argue that
presentation of the degree (strength) distribution in published reports is vital to understanding
any RSFC network for a few reasons. Primo, it provides a sanity check on the data. One current
Network Neuroscience
7
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
Functional connectivity thresholding:
The process of determining the
meaningfulness of any edge based on
a continuous measure of FC (per esempio.,
Pearson r value).
Tavolo 3. Graph metrics commonly reported in clinical RSFC studies
Graph metrics
Degree distribution (plotted)
Mean degree (weighted or binary)
Clustering/local efficiency
Path length/global efficiency
Small-worldness
Modularity (per esempio., Q-value)
N (frequency)
17 (16.0%)
29 (27.4%)
76 (71.7%)
79 (74.5%)
33(31.1%)
21 (19.8%)
Note. Total frequency is greater than 100% because some studies reported more than one of
these metrics.
perspective is that human brains are organized to maximize communication while minimiz-
ing wiring and metabolic cost (Bassett et al., 2009; Betzel et al., 2017; Chen, Wang, Hilgetag,
& Zhou, 2013; Tomasi, Wang, & Volkow, 2013), Così, when examining whole-brain RSFC
dati, the most highly connected regions are rare and should be evident in the tail of the de-
gree/strength distribution (Achard, Salvador, Whitcher, Suckling, & Bullmore, 2006). Secondo,
reporting details of the degree distribution facilitates comparisons of graph topology across
studies, as well as the impact of preprocessing and analytic decisions such as FC thresholding.
Finalmente, examining the degree distribution as a first step in data analysis may offer otherwise
unavailable information about the network topology in healthy and clinical samples. For ex-
ample, in prior work, we isolated edges from the tail of the degree distribution to understand
the impact of the most highly connected, and rare, nodes on the network (Hillary et al., 2014).
Critical Issue 1: Edge Thresholding and Comparing Unequal Networks
We now focus on edge thresholding—that is, how to transform a continuous measure of FC
into an edge in the graph. In our review, 39% of studies binarized FC values such that edges
were either present or absent in the graph, whereas 45% of studies retained FC as edge weights
(see Table 2b). Regardless of whether investigators analyze binary or weighted networks, there
are fundamental challenges to comparing networks that differ either in terms of average degree
(k) or the number of nodes (N) (Fornito et al., 2016). In particular, comparing groups on graph
metrics such as path length and clustering coefficient can be ambiguous because these metrics
have mathematical dependencies on both k and N (van Wijk et al., 2010).
Most brain parcellation approaches define graphs with an equivalent number of nodes (N)
in each group. D'altra parte, connection density is often a variable of interest in clinical
studies where the pathology may alter not only connection strength, but also the number of
connections. If N is constant, variation in k between groups constrains the boundaries of local
and global efficiency. If two groups differ systematically in edge density, this almost guarantees
between-group differences in metrics such as clustering coefficient and path length. Determin-
ing where to intervene in this circular problem has great importance in clinical network neu-
roscience, where hypotheses often focus on the number and strength of network connections.
To address this issue, several investigators have recommended proportional thresholding
(PT) in which the edge density is equated across networks (Achard & Bullmore, 2007; Bassett
et al., 2009; Energia, Fair, Schlaggar, & Petersen, 2010). Inoltre, to reduce the possibility
that findings are not specific to the chosen density threshold, 29% of studies have tested for
group differences across a range (per esempio., 5–25%; Tavolo 4). Tuttavia, we argue that defining edges
based on PT may not be ideal for clinical studies, where there are often regional differences in
functional coupling or pathology-induced alterations in the number of functional connections
Network Neuroscience
8
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
Tavolo 4. Thresholding method for defining edges in graphs
Nature of thresholding
All connections retained
Single by value
Multiple by value
Single by density
Multiple by density
Both by value and density
Other (connections lost)
Unknown/unclear
N (frequency)
6 (5.7%)
25 (23.6%)
28 (26.4%)
5 (4.7%)
31 (29.2%)
7 (6.6%)
3 (2.8%)
1 (0.9%)
Note. Value: thresholding determined by FC strength, including statistically corrected and uncor-
rected values; Single: analyses reported at a single threshold value; Multiple: network examined
across multiple thresholds.
(Hillary & Grafman, 2017). Per esempio, in depression, the dorsomedial prefrontal cortex
exhibits enhanced connectivity with default mode, cognitive control, and affective networks
(Sheline, Price, Yan, & Mintun, 2010). As demonstrated below, when FC differs in selected
regions between groups, PT is vulnerable to identifying spurious differences in nodal statistics
(per esempio., degree). The concerns expressed here extend from van den Heuvel et al. (2017), who
demonstrated that PT increases the likelihood of including spurious connections in the network
when groups differ in mean FC.
In the first
Simulation to demonstrate a problem with PT in group comparisons: Whack-a-node.
simulation—“whack-a-node ”—we examined the consequences of PT on regional inferences
when groups differ in FC for selected regions. Unlike empirical resting-state fMRI data, Dove
the underlying causal processes remain relatively unknown, simulations allow one to test the
effect of biologically plausible alterations (per esempio., hyperconnectivity of certain nodes) on network
analyses. Simulations can also clarify the effects of alternative analytic decisions on substan-
tive conclusions in empirical studies. For the details of our simulation approach, see Methods.
Briefly, we used a network bootstrapping approach to simulate resting-state network data for a
case-control study with 50 patients and 50 controls. We repeated this simulation 100 times, In-
creasing connectivity for patients in three randomly targeted nodes (hereafter called “Positive”)
and decreasing connectivity slightly, but nonsignficantly, in three random nodes (“Negative”).
Our simulations captured both between- and within-person variation in FC changes for tar-
geted nodes (see Methods, Equations 5–7). We compared changes in Positive and Negative
nodes to three Comparator nodes that did not differ between groups.
Results of Whack-a-Node Simulation
In a multilevel regression of group difference t statistics (patient–
Proportional thresholding.
controllo) on density threshold, we found that PT was sensitive to hyperconnectivity of Positive
nodes, reliably detecting group differences, average t = 12.4 (SD = 1.15), average p < .0001
(Figure 2A). Importantly, however, degree was significantly lower in patients than controls for
Negative nodes, average t = −6.52 (SD = 1.15), average p < .001. We did not find any
systematic difference between groups in Comparator nodes, average t = −.22 (SD = .65),
average p = .47.
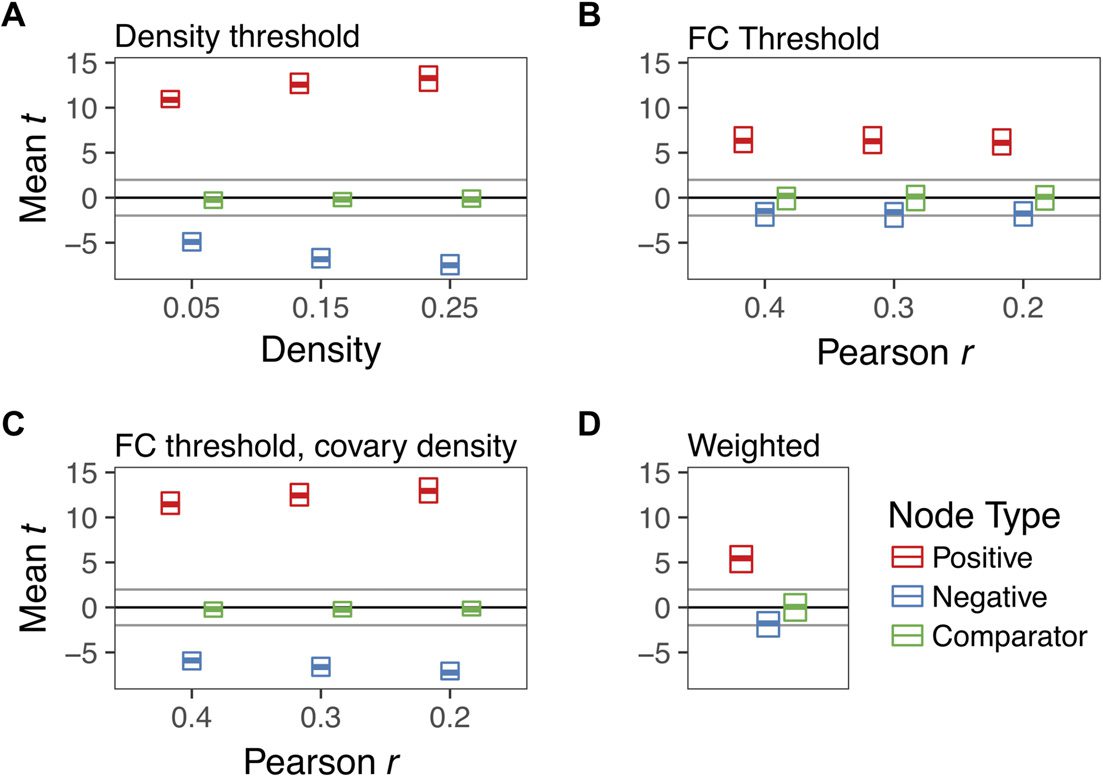
These group differences were qualified by a significant density x node type interaction (p <
.0001) such that group differences for Positive nodes were larger at higher densities (Figure 3,
Whack-a-node:
A simulation used within this
report to test the consequences of
proportional thresholding given
local changes in connectivity
(e.g., enhanced or diminished
connectivity).
Hyperconnectivity:
Common network response observed
in clinical samples when the brain
structure has been altered, resulting
in enhanced functional response
locally.
Network Neuroscience
9
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
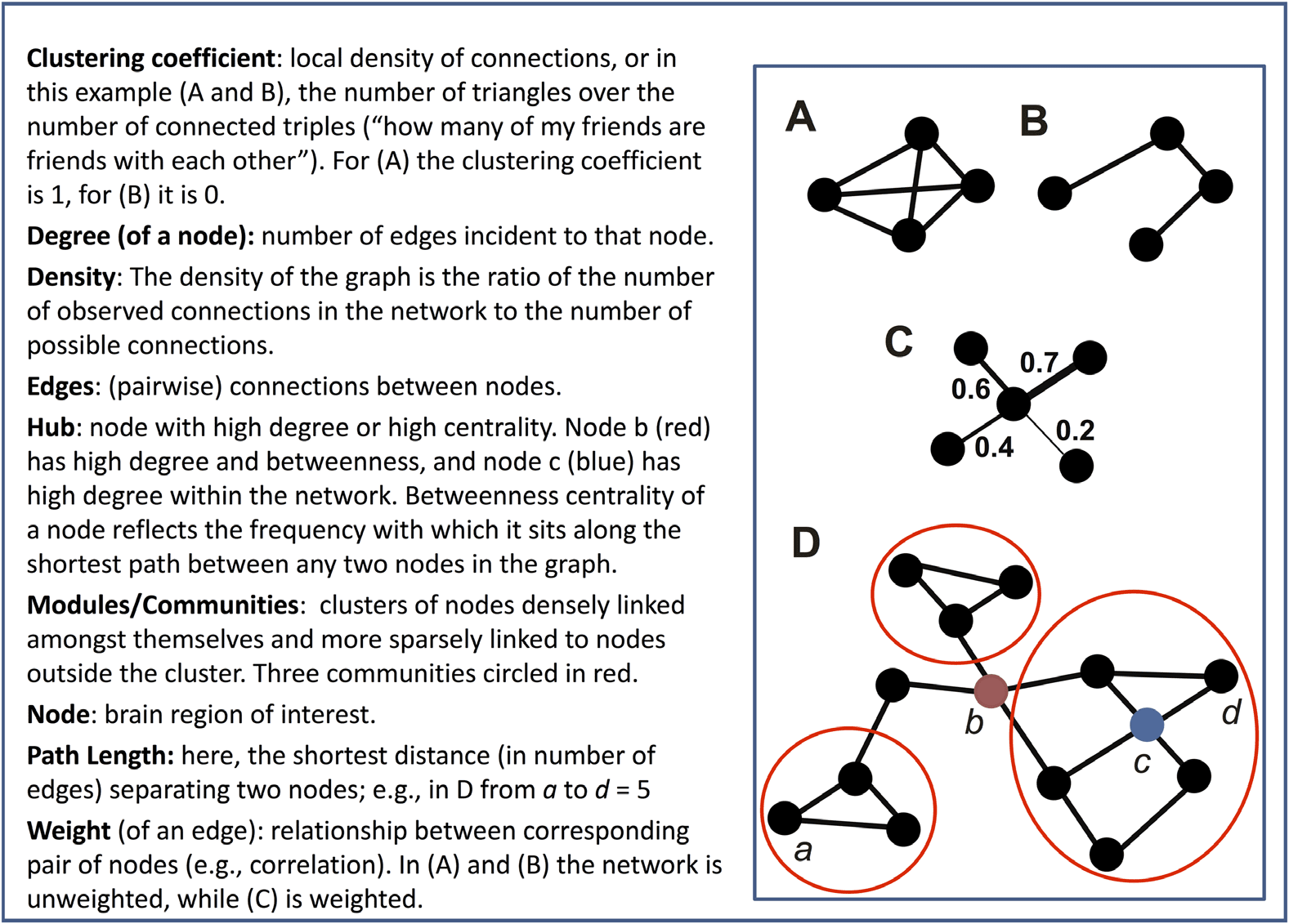
Figure 2. The effect of thresholding method on group differences in degree centrality when there
is strong hyperconnectivity in three randomly selected nodes (Positive) and weak hypoconnectivity
in three nodes (Negative). Three unaffected nodes are depicted for comparison (Comparator). For
parameters of this simulation, see Supporting Information Table S1 (Hallquist & Hillary, 2019),
Whack-a-node hyperconnectivity. The central bar of each rectangle denotes the median t statistic
(patient–control) across 100 replication datasets (patient n = 50, control n = 50), whereas the upper
and lower boundaries denote the 90th and 10th percentiles, respectively. The dark line at t = 0
reflects no mean difference between groups, whereas the light gray lines at t = −1.99 and 1.99
reflect group differences that would be significant at p = .05. (A) Graphs binarized at 5%, 15%, and
25% density. (B) Graphs binarized at r = {.2, .3, .4}. (C) Graphs binarized at r = {.2, .3, .4}, with
density included as a between-subjects covariate. (D) Strength centrality (weighted graphs).
top panel), B = 11.32 (95% CI = 10.59 – 12.04), t = 30.72, p < .0001. Conversely, we
found equal, but opposite, shifts in Negative nodes (Figure 3, middle panel): group differences
became increasingly negative at higher densities, B = −11.93, (95% CI = −12.65 – −11.2),
t = −32.74, p < .0001. However, we did not observe an association between density and
group differences in Comparator nodes, B = .31, p = .40 (Figure 3, bottom panel).
In graphs thresholded at differing levels of FC (rs ranging between .2 and
FC thresholding.
.5), we found reliable increases in Positive nodes in patients, average t = 6.37, average p <
.0001 (Figure 2B). Negative nodes, however, were not significantly different between groups,
average t = −1.75, average p = .23. Neither did Comparator nodes differ by group, average
t = .05, p =.50. Unlike PT, for FC-thresholded graphs, we did not find a significant threshold
x node type interaction, x
(16) = 13.38, p = .65.
2
By definition, FC thresholding
Functional connectivity thresholding with density as covariate.
cannot handle the problem of group differences in mean FC. Thus, the risk of FC thresholding
alone is that nodal statistics may reflect group differences in mean FC that affect interpretation
of topological metrics (e.g., small-worldness). To mitigate this concern, one could threshold
at a target FC value, then include graph density for each subject as a covariate (as suggested
by van den Heuvel et al., 2017). As depicted in Figure 2C, however, although this statistically
controls for density, it also reintroduces the constraint that the groups must be equal in average
degree. As a result, the pattern of effects mirrors the PT graphs (Figures 2A and 3). More specif-
ically, group differences in Positive nodes were reliably detected, average t = 12.39, average
Network Neuroscience
10
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
Figure 3. The effect of density threshold on group differences in degree centrality. Dots denote
the mean t statistic at a given density, whereas vertical lines denote the 95% confidence interval.
All statistics reflect group differences in degree centrality computed on graphs binarized at different
densities.
p < .0001. But patients appeared to be significantly more hypoconnected in Negative nodes
compared with controls, average t = −6.59, average p < .001.
In analyses of strength centrality, we observed significantly greater degree
Weighted analysis.
in Positive nodes, average t = 5.5, average p = .0003 (Figure 2D). As expected, given our
simulation design, Negative and Comparator nodes were not significantly different between
groups, average ps = .19 and .49, respectively.
In our whack-a-node simulation, three nodes were ro-
Discussion of whack-a-node simulation.
bustly hyperconnected in “patients,” while three nodes were weakly hypoconnected. The prin-
cipal finding of this simulation was that enforcing equal average degree using PT can spuriously
magnify changes in group comparisons of nodal statistics. When the groups were otherwise
equal, hyperconnectivity in selected nodes was accurately detected using PT across different
graph densities. However, nodes that were weakly hypoconnected tended to be identified as
statistically significant. The inclusion of low-magnitude, spurious connections into the network
inheres from the way in which PT handles the tails of the FC distribution.
By retaining only edges at the high end of the FC distribution, edges that are on the cusp of
that criterion are most vulnerable to being removed. For example, at a density of 25%, small
variation in FC strength near the 75th percentile could lead to inclusion or omission of an edge.
As a result, if FC for edges incident to a given node tends to be weaker in one group than the
other, then binary graphs generated using PT will magnify the statistical significance of differ-
ences in degree centrality. To the extent that nodal differences in FC strength represent a shift in
the central tendency of the distribution, this problem is not solved by applying multiple density
thresholds (Figure 3). We observed the same problem if the direction of FC changes was flipped
in the simulation: under PT, group comparisons were significant for weakly hyperconnected
Network Neuroscience
11
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
nodes if some nodes were robustly hypoconnected (see Supporting Information Figure S1,
Hallquist & Hillary, 2019). Moreover, our findings were qualitatively unchanged when simu-
lated changes in FC were applied proportionate to the original connection strength, rather than
shifting connectivity in correlational units (see Supporting Information Figure S2, Hallquist &
Hillary, 2019). This additional simulation respected biologically plausible variation in FC (e.g.,
greater average connectivity in functional hubs).
We examined FC-based thresholding (here, using Pearson r as the metric) and weighted
analyses as comparisons to PT. These methods do not suffer from the spurious detection of
nodal differences evident under PT. Rather, FC thresholding accurately detected hypercon-
nected nodes across different thresholds while not magnifying significance of the weakly hypo-
connected nodes. However, as noted elsewhere (van den Heuvel et al., 2017; van Wijk et al.,
2010), if two groups differ in mean FC, thresholding at a given level (e.g., r = .3) in both groups
will lead to differences in graph density. This could manifest as widespread differences in nodal
statistics due to global differences in the number of edges. We considered whether including
per subject graph density as a covariate in group difference analyses could retain the desirable
aspects of FC thresholding while accounting for the possibility of global differences in FC. We
found, however, that statistically covarying for density was qualitatively similar in its effects to
PT because it constrains the sum of degree changes across the network to be zero between
groups (i.e., equal average degree).
The goal of our simulation was to provide a proof of concept that PT may negatively affect
nodal statistics in case-control graph studies by enforcing equal average degree. We did not,
however, test a range of parameters to identify the conditions under which this concern holds
true. The simulation focused specifically on degree centrality in the binary case and strength
in the weighted case. While untested, we anticipate that these effects likely generalize to other
nodal measures such as eigenvector centrality. Importantly, the problems with PT highlighted
above occur regardless of edge density (Figure 3), so the use of multiple edge densities does
not adequately address the whack-a-node issue.
Critical Issue 2: Matching Theory to Scale: Telescoping Levels of Analysis in Graphs
The second major methodological theme from our literature review concerns the alignment
between neurobiological hypotheses and graph analyses. We refer to this as theory-to-scale
matching. RSFC graphs offer telescoping levels of information about intrinsic connectivity
patterns, from global information such as average path length to details such as connectivity
differences in a specific edge. For example, in major depression, resting-state studies have
focused analyses on specific subnetworks composed of the dorsal medial prefrontal cortex,
anterior cingulate cortex (ACC), amygdala, and medial thalamus (for a review, see L. Wang,
Hermens, Hickie, & Lagopoulos, 2012).
We propose that graph analyses should be conceptualized and reported in terms of telescop-
ing levels of analysis from global to specific: global topology, modular structure, nodal effects,
edge effects. Our review of the clinical network neuroscience literature revealed that the ma-
jority of studies (69%; see Table 5) tested whether groups differed on global metrics such as
small-worldness. Importantly, however, many studies provided limited theoretical justification
for why the pathophysiology of a given brain disorder should alter the global topology of the
network.
In the following, we provide more specific comments on path length and small-
worldness, and how investigators might ideally match hypotheses to levels of analysis.
Telescoping:
Graphs provide the opportunity
to examine distinct dimensions
(e.g., local vs. global patterns of
connectivity), and telescoping refers
to movement between these
dimensions to understand distinct
patterns within the network.
Network Neuroscience
12
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
Table 5. Level of group difference hypotheses in graph analyses (i.e., telescoping)
Hypothesis level
Global
Module (subnetwork)
Nodal (region)
Edge
n (frequency)
73 (68.9%)
41 (38.7%)
52 (49.1%)
1 (0.9%)
Note. Global: examining whole-graph network features (e.g., small-worldness); Module: exam-
ining subnetworks/modules (e.g., default mode network). Total frequency is greater than 100%
because some studies tested hypotheses at multiple levels.
In a defining study for network neuroscience,
The clinical meaningfulness of small-worldness.
Watts and Strogatz (1998) demonstrated that the organization of the central nervous system in
C. elegans reflected a “small-world” topology (cf. Muldoon, Bridgeford, & Bassett, 2016). The
impact of this finding continues to resonate in the network neuroscience literature 20 years
later (Hilgetag & Kaiser, 2004; Sporns & Zwi, 2004), with many studies focusing on “dis-
connection” and the loss of network efficiency as quantified by small-worldness (31% of the
studies reviewed here). Although small-world topologies have been observed in most studies
of brain function (Bassett & Bullmore, 2016), the relevance of this organization for facilitating
human information processing remains unclear. Other features of human neural networks,
such as modularity, may have more important implications for network functioning (Hilgetag
& Goulas, 2015). Higher network modularity reflects a graph in which the connections among
nodes tend to form more densely connected communities, which tend to be robust to random
network disruption (Shekhtman, Shai, & Havlin, 2015).
It remains uncertain that, as a general rule, brain pathology should be reflected in a measure
of small-worldness. For example, a small-world topology is preserved even in experiments that
dramatically reduce sensory processing via anesthesia in primates (Vincent et al., 2007) and
in disorders of consciousness in humans (Crone et al., 2014 ). Recognizing that conventional
measures of small-worldness (e.g., Humphries & Gurney, 2008) depend on density and do
not handle variation in connection strength, recent research has recast this concept and its
quantification in terms of the “small world propensity” of a network (Muldoon et al., 2016).
Although we do not dispute the value of global graph metrics such as small-worldness as
important descriptors of a network organization, by definition, they provide information at
only the most macroscopic level. Group differences in global metrics may largely reflect more
specific effects at finer levels of the graph. For example, removing connections in functional
hub regions selectively tends to reduce global efficiency and clustering (Hwang, Hallquist, &
Luna, 2013). Likewise, failing to identify group differences in global structure does not imply
equivalence at other levels of the graph (e.g., nodes or modules). To demonstrate the point that
substantial group differences in finer levels of the graph may not be evident in global metrics,
we conducted a simulation in which the groups differed substantially in modular connectivity.
Simulation to demonstrate the importance of understanding graphs at multiple levels: Global insen-
Extending the basic approach of our whack-a-node simulation,
sitivity to modular effects.
we used a 13-module parcellation of the 264-node groundtruth graph in a simulation of 50
“controls” and 50 “patients” (modular structure from Power et al., 2011). More specifically, we
increased FC in the fronto-parietal network (FPN) and dorsal attention network (DAN) in
controls, and increased FC in the default mode network (DMN) in patients. The simulation
primarily examined group differences in small-worldness (global metric) and within- and
between-module degree (nodal metrics). Additional details are provided in the Methods.
Network Neuroscience
13
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
Consistent with common methods in the field, we
Results of global insensitivity simulation.
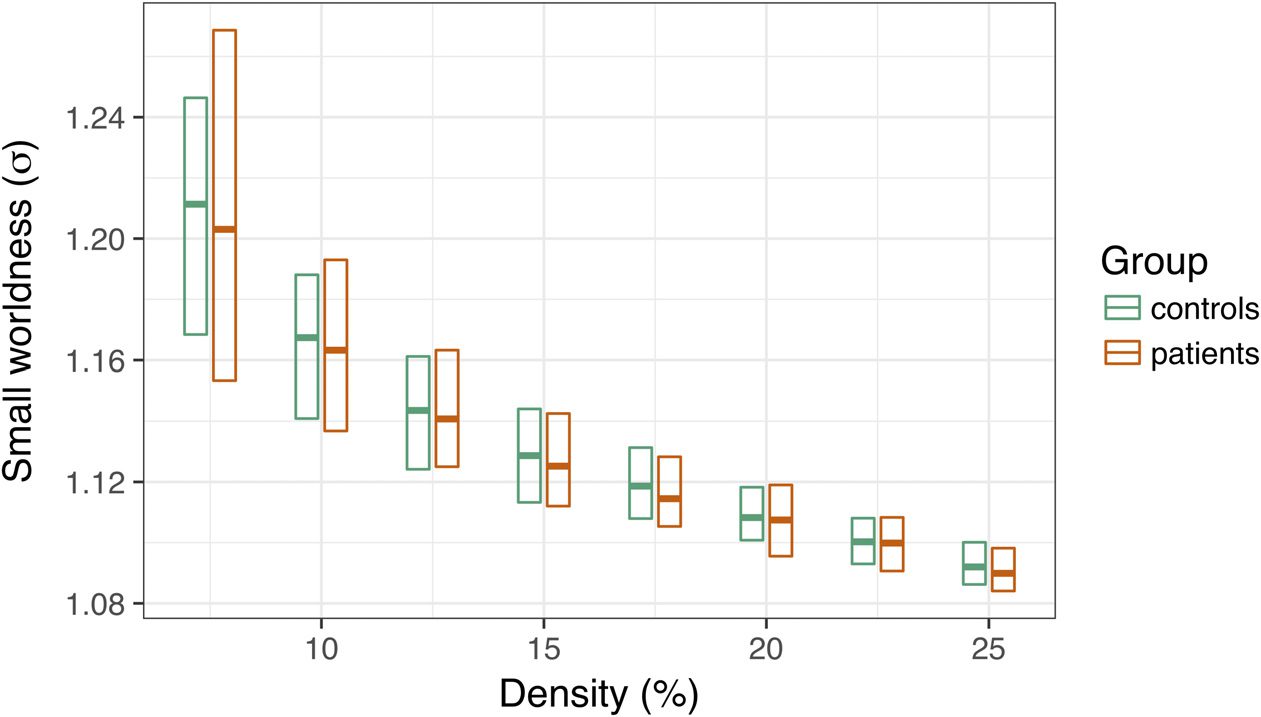
applied PT between 7.5% and 25% to each graph. We computed small-worldness, σ, at each
threshold (see Methods), then tested for group differences in this coefficient. As depicted in
Figure 4, we did not observe any significant group differences in small-worldness at any edge
density, average t = .36, ps > .3.
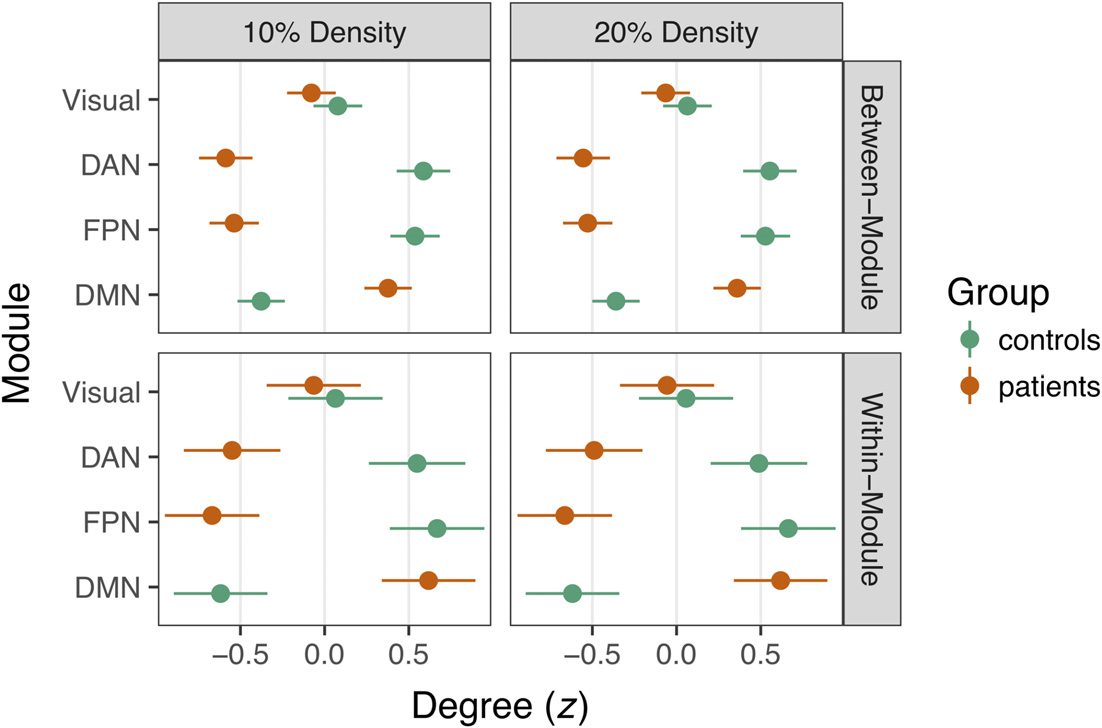
Tuttavia, consistent with the structure of our simulations, we found large group differences
in within- and between-module degree (Figura 5). In a multilevel regression of within-network
degree on group, density, and module, we found a significant DMN increase in patients irre-
spective of density, B = 1.37, t = 33.25, P < .0001. Likewise, controls had significantly higher
within-network degree in the FPN and DAN, ts = 21.67 and 13.52, respectively, ps < .0001.
These findings were mirrored in group analyses of between-network degree in the DMN, FPN,
and DAN, ps < .0001 (see Figure 5).
In the global insensitivity simulation, we induced
Discussion of global insensitivity simulation.
large group changes in FC at the level of functional modules that represent canonical resting-
state networks (e.g., the DMN). The simulation differentially modulated FC within and between
regions of the DAN, FPN, and DMN. In group analyses of within- and between-module degree
centrality, we detected these large shifts in FC. However, despite robust differences in network
structure, the two groups were very similar in the small-world properties of their graphs.
As with the whack-a-node simulation, we did not seek to test the range of conditions under
which these findings would hold. Rather, the global insensitivity simulation provides a proof of
concept that researchers should be aware that the absence of group differences at a higher level
of the graph (here, global topology) does not suggest that the networks are otherwise similar
at lower levels (here, modular connectivity). As we have noted above, in graph analyses of
case-control resting-state networks, we encourage researchers to state their study goals in terms
that clearly match the hypotheses to the scale of the graph.
In the global insensitivity simulation, failing to detect differences in small-worldness should
not be seen as an omnibus test of modular or nodal structure. Likewise, if group differences are
detected at the global level, there may be substantial value in interrogating finer differences in
the networks, even if these were not hypothesized a priori.
Figure 4. Group differences in small-worldness (σ) as a function of edge density. The central bar
of each rectangle denotes the median σ statistic (patient–control), whereas the upper and lower
boundaries denote the 90th and 10th percentiles, respectively.
Network Neuroscience
14
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
Figure 5. Group differences in z-scored degree statistics at 10% and 20% density. Degree dif-
ferences for connections between modules are depicted in the top row, whereas within-module
differences are in the bottom row. Dots denote the mean z statistic across nodes, whereas the lines
represent the 95% confidence interval around the mean. Nonsignificant group differences in the
Visual network are depicted for comparison, whereas connectivity in the DAN, FPN, and DMN was
focally manipulated in the simulation.
General Summary
The overarching goal of this review was to promote shared standards for reporting findings in
clinical network neuroscience. Our survey of the resting-state functional connectivity litera-
ture revealed the popularity and promise of graph theory approaches to network organization
in brain disorders. This potential is evident in large-scale initiatives for acquiring and shar-
ing resting-state data in different populations (e.g., the Human Connectome Project; Barch
et al., 2013). Publicly available resting-state data can also support reproducibility efforts by
serving as replication datasets to corroborate specific findings in an independent sample (e.g.,
Jalbrzikowski et al., 2017). We share the field’s enthusiasm for such work and anticipate that
with further methodological refinement and standardization, the coupling of network science
and brain imaging can provide novel insights into the neurobiological basis of brain disorders.
Our review, however, suggested that the heterogeneity of methods is preventing the field
from realizing its potential. Graph analyses across clinical studies varied substantially in terms
of brain parcellation, FC quantification, and the use of thresholding methods to define edges
in graphs. These decisions are fundamental to graph theory and precede analyses at specific
levels such as global topology. In addition, although it was not a focus of our review, there
was substantial variation in what network metrics were reported across studies. The lack of
standardization in methods at multiple decision points has multiplicative consequences: The
likelihood that any two studies used the same parcellation scheme, FC definition, threshold-
ing strategy, and network metric was remarkably low. This makes formal meta-analyses of
the clinical network neuroscience literature virtually impossible at the present time, detracting
from efforts to distinguish distinct pathophysiological mechanisms or to identify transdiagnostic
commonalities.
In addition, methodological heterogeneity in graph analyses undercuts the
value of data sharing efforts that have made massive datasets available to the network neuro-
science community. For the immense potential of data sharing to be realized, standardization
must occur not only in data acquisition, but also in data analysis, with a shared framework to
guide hypothesis-to-scale matching in graphs.
Network Neuroscience
15
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
As summarized in Box 2, we believe that the field should work toward a principled, com-
mon approach to graph analyses of RSFC data. This is a challenging proposition because of the
rapid and exciting developments in functional brain parcellation (e.g., Schaefer et al., in press),
FC definition (e.g., Cassidy, Rae, & Solo, 2015), edge thresholding (van den Heuvel et al.,
2017), and network metrics (e.g., Vargas & Wahl, 2014). Such developments highlight both
the enthusiasm for, and relative infancy of, network neuroscience as a field. Although we are
sensitive to the importance of continuing to refine functional parcellations of the brain, we also
see great value in developing field-standard parcellations to promote comparability. Indeed,
many aspects of network structure (e.g., homogeneity of functional connectivity patterns within
a region) are largely convergent above a certain level of detail (likely 200–400 nodes) in the
functional parcellation (Craddock et al., 2012; Schaefer et al., in press). Likewise, the optimal
approach for quantifying functional connectivity is an open question (Smith et al., 2011), yet in
the absence of methodological convergence, graphs were often not comparable across studies.
A related dilemma was that in 57% of studies, little or no detail was provided about how
negative FC values were incorporated into graph analyses. This was especially troubling insofar
as global signal regression tends to yield an FC distribution in which approximately half of
edges are negative (Murphy et al., 2009). Furthermore, FC estimates at the low end of the
distribution may have different topological properties such as reduced modularity (Schwarz &
McGonigle, 2011). Even among the 21% of studies in which negative edges were explicitly
dropped, it remains unclear what consequences this decision has on substantive conclusions
about graph structure.
In recent years, there have been advances in quantifying common
graph metrics such as modularity in weighted networks that include negative edges (Rubinov
& Sporns, 2011), as well as increasing calls for weighted, not binary, graph analyses (Bassett
& Bullmore, 2016). Regardless, we believe that greater clarity in reporting of negative FC will
promote comparisons among clinical studies.
Methodological heterogeneity also resulted in very few graph statistics that were reported in
common across studies, an essential ingredient for examining the reproducibility of findings.
Networks that are resilient to the deletion of specific edges often have a highly skewed de-
gree distribution (Callaway, Newman, Strogatz, & Watts, 2000) that may relate to small-world
network properties (Achard et al., 2006). We propose that studies should routinely depict this
distribution. Likewise, broad metrics such as edge density, mean FC, transitivity, and character-
istic path length provide important information about the basic properties of graphs that con-
textualize more detailed inferential analyses. The challenge of developing reporting standards
in clinical network neuroscience echoes the broader conversation in neuroimaging about re-
producibility, especially the importance of detail and transparency in the analytic approach
(Nichols et al., 2017).
In addition to the general issues of standardizing graph analyses and reporting procedures,
our review examined two critical issues in greater detail. First, we considered the potential
benefits and risks of using PT, a common procedure for equating the number of edges between
graphs. Second, we articulated the value of considering the telescoping levels of graph struc-
tures in order to match a hypothesis to the corresponding scale of the graph.
Roughly one-third of the studies included in our review applied PT, thresholding graphs
at single or multiple edge densities. Although this approach is aligned with prior work high-
lighting concerns about comparing unequal networks (van Wijk et al., 2010), its application
in clinical studies is often conceptually problematic. Many brain pathologies appear to affect
targeted regions or networks, while leaving the connectivity of other regions largely undis-
turbed. For example, although frontolimbic circuitry is heavily implicated in mood disorders
Network Neuroscience
16
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
(Price & Drevets, 2010), visual networks largely appear unaffected. There is growing evi-
dence that brain disorders alter the strength of functional coupling and potentially the num-
ber of functional connections (Hillary & Grafman, 2017). Consequently, if some regions are
affected by the pathology, but others are similar to a matched control population, PT may
erroneously remove or add connections to graphs in one group in order to maintain equal
average degree between groups. Furthermore, if a brain pathology alters the density of func-
tional connections—for example, neurological disruption is associated with hyperconnectivity
(Hillary et al., 2015)—PT will preclude the investigator detecting density differences between
groups. If, in truth, the groups differ in edge density, artificially equating density also detracts
from the interpretability of graph analyses (cf. van den Heuvel et al., 2017).
In addition to these conceptual problems, our whack-a-node simulation demonstrated that
PT may result in the detection of spurious group differences (Figure 2A). Altogether, applying
PT in clinical studies may be a methodological double jeopardy, characterized by reduced
sensitivity to pathology-related differences in connection density and the risk of identifying
nodal differences between groups that are a statistical artifact. These risks make PT especially
unappealing when one considers that FC-based thresholding and weighted analyses accurately
detected group differences (Figure 2B and 2D) while also allowing edge density to vary. We
acknowledge, however, that a previous empirical study found that group differences were more
consistent across multiple thresholds using proportional, as opposed to FC-based, thresholding
(Garrison, Scheinost, Finn, Shen, & Constable, 2015).
We therefore have two recommendations for edge thresholding in case-control compar-
isons. First, weighted analyses or FC thresholding should typically be preferred to PT if one
is interested in nodal statistics. Second, to rule out the possibility that nodal findings reflect
global differences in mean FC, one could include mean FC as a covariate in weighted analy-
ses or per subject density in analyses of FC-thresholded binary graphs. Crucially, we propose
that these be treated as sensitivity analyses conducted only after establishing a nodal group
difference. That is, if one identifies group differences in FC-thresholded graphs (e.g., greater
degree in anterior cingulate cortex among patients), does including edge density as a covari-
ate abolish this finding? If so, it suggests that differences in global topology may account for
the nodal finding. However, one should not include density as a covariate in FC-thresholded
graphs as a first step to identify which nodes differ between groups, as this could fall prey to
the whack-a-node problem (i.e., spurious nodal effects).
The second critical issue was that many studies provided limited theoretical justification for
the alignment between a given hypothesis and the corresponding graph analysis. A majority
of studies (69%) tested whether groups differed in global metrics such as small-worldness, but
most pathologies (e.g., brain injury, Alzheimer’s disease) primarily affect regional hubs within
networks (Crossley et al., 2014). Our global insensitivity simulation focused on the importance
of matching hypotheses to graph analyses, or telescoping. We demonstrated that global graph
metrics, specifically small-worldness, may not be sensitive to group differences in module or
node centrality. Metrics such as modularity and nodal centrality offer vital information about
regional brain organization that can be interpreted in the context of alterations in average
degree. The general point is that one cannot generalize findings from one level of a graph to
another, nor should null effects at one level be viewed as suggesting that the groups are similar
at other levels. By conceptualizing a data analysis plan in terms of the telescoping structure
of graphs, researchers can clearly delineate confirmatory from exploratory analyses, which is
consistent with the spirit of reproducible science in neuroimaging (Poldrack et al., 2017).
Network Neuroscience
17
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
Box 2.
neuroscience
Recommendations for best practices and convergence in clinical network
Challenge
Recommendation
Brain parcellations vary substantially
across studies
In the absence of a field standard, we recommend that brain parcellations
should meet the following minimum requirements:
1) Provide comprehensive coverage of functional regions throughout the
brain, including cortical and subcortical structures, as well as cerebellum
2) Divide the brain into at least 200 functional regions (Craddock et al., 2012)
3) Delineate regions based on functional connectivity (as opposed to a
structural atlas; Gordon et al., 2016), potentially combined with multimodal
imaging (e.g., Glasser et al., 2016)
4) Ensure that regions exhibit high functional connectivity homogeneity
(Gordon et al., 2016; Schaefer et al., in press)
5) Provide clear guidance on the modular structure of regions comprising the
parcellation (Yeo et al., 2011). In general, we discourage clinical researchers
from attempting to identify functional modules in their data (e.g., using
community detection algorithms) when a published modular structure exists.
Longer resting-state acquisitions help to improve the stability of FC estimates
and, therefore, their test-retest reliability (Birn et al., 2013). We encourage
clinical researchers to acquire resting-state data for at least 9 minutes and to
use faster temporal sampling (e.g., 1s TR, potentially using multiband imaging;
Demetriou et al., 2016) when possible.
Quantifying functional connectivity: The reliability of functional connectomes
based on conditional association (e.g., partial correlation) diminishes as the
number nodes increases or the number of measurements decreases
(Cassidy et al., 2018), requiring substantially longer scans, both in terms of
time and measurements. The stability of bivariate correlations, however, is not
dependent on the number of nodes and values typically stabilize around 250
measurements (Schönbrodt & Perugini, 2013). For conventional resting-state
data (e.g., 180 volumes with TR = 2 s) and comprehensive parcellations, we
recommend a shrinkage estimator of marginal correlation (Varoquaux &
Craddock, 2013), rather than a conditional association measure.
Proportional thresholding: We caution against using proportional thresholding
to create binary graphs in case-control studies (for more detailed
recommendations, see Simulation 1).
Negative edge weights: Studies should provide details about how negative FC
estimates are handled when constructing graphs, whether weighted or binary.
The deletion of negative edges is a largely untested assumption in network
neuroscience that deserves greater attention. If researchers have many negative
edges (e.g., if global signal regression or partial correlation are used), we
encourage analyzing and reporting them, perhaps using a separate graph.
To promote formal comparisons across studies, we encourage researchers to
report a standard set of graph metrics, even if these are in the form of
descriptive tables or supplementary material. As a minimal set, we propose:
(a) global clustering coefficient, (b) average path length, (c) modularity,
(d) degree, (e) eigenvector centrality, and (f) summary statistics of edge strength.
We encourage researchers to conceptualize and report graph analyses in
terms of telescoping levels of analysis, from global to specific. As demonstrated
in Simulation 2, global metrics may be insensitive to regional effects of
pathology or neurodevelopment. We also advocate articulating the alignment
between the level of the graph and the biological account of neuropathology.
The relevance of some graph metrics (e.g., small-worldness) to understanding
brain disorders remains unclear.
The quality of RSFC data varies as a
function of acquisition length and
time
Edge definition
Graph metrics varied across studies
Need to align neurobiology and
the network representation
Network Neuroscience
18
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
In summary, there is a need for a common framework to inform graph theory analyses of
RSFC data in the clinical neurosciences. Any recommendations should emerge organically
from a scientific community whose investigators voluntarily adopt procedures that maximize
sensitivity to hypothesized effects and simultaneously permit graph comparisons among studies
(cf. the COBIDAS effort in neuroimaging more broadly; Nichols et al., 2017). The implemen-
tation of best practices in task-based fMRI (e.g., handling autocorrelation; Woolrich, Ripley,
Brady, & Smith, 2001) has been supported by powerful, usable, and free software. Although
similar software is increasingly available for resting-state studies (e.g., Chao-Gan & Zang Yu-
Feng, 2010; Whitfield-Gabrieli & Nieto-Castanon, 2012), best practices are still emerging, and
we believe that software developers will be crucial to promoting a standardized graph the-
ory analysis pipeline. We anticipate that a common methodological framework will promote
hypothesis-driven research, alignment between theory and graph analysis, reproducibility, data
sharing, meta-analyses, and ultimately more rapid progress of clinical network neuroscience.
METHODS
PubMed Search Syntax
(graph OR graphical OR graph-theor* OR topology) AND (brain
Neurological disorders query.
OR fMRI OR connectivity OR intrinsic) AND (resting-state OR resting OR rest) AND (neurological OR
brain injury OR multiple sclerosis OR epilepsy OR stroke OR CVA OR aneurysm OR Parkinson’s
OR MCI OR Alzheimer’s OR dementia OR HIV OR SCI OR spinal cord OR autism OR ADHD
OR intellectual disability OR Down syndrome OR Tourette) AND “humans”[MeSH Terms]
(graph OR graphical OR graph-theor* OR topology) AND (brain OR fmri
Mental disorders query.
OR connectivity OR intrinsic) AND (resting-state OR resting OR rest) AND (clinical OR psycho-
pathology OR mental disorder OR psychiatric OR neuropsychiatric OR depression OR mood
OR anxiety OR addiction OR psychosis OR bipolar OR borderline OR autism) AND
“humans”[MeSH Terms]
General Approach to Network Simulations
To approximate the structure of functional brain networks, we identified a young adult female
subject who completed a 5-min resting-state scan in a Siemens 3T Trio Scanner (TR = 1.5 s,
TE = 29 ms, 3.1 × 3.1 × 4.0 mm voxels) with essentially no head movement (mean frame-
wise displacement [FD] = .08 mm; max FD = .17 mm). We preprocessed the data using a
conventional pipeline, including (a) motion correction (FSL mcflirt); (b) slice timing correc-
tion (FSL slicetimer); (c) nonlinear deformation to the MNI template using the concatenation
of functional → structural (FSL flirt) and structural → MNI152 (FSL flirt + fnirt) transforma-
tions; (d) spatial smoothing with a 6-mm full width at half maximum filter (FSL susan); and
(e) and voxelwise intensity normalization to a mean of 100. After these steps, we also simul-
taneously applied nuisance regression and band-pass filtering, where the regressors were six
motion parameters, average cerebrospinal fluid, average white matter, and the derivatives of
these (16 total regressors). The spectral filter retained fluctuations between .009 and .08 Hz
(AFNI 3dBandpass). We then estimated FC of 264 functional regions of interest (ROIs) from
the Power et al. (2011) parcellation, where each region was defined by a 5-mm radius sphere
centered on a specific coordinate. The activity of a region over time was estimated by the first
principal component of voxels in each ROI, and the functional connectivity matrix (264 ×
264) was estimated by the pairwise Pearson correlations of time series.
This 264 × 264 adjacency matrix, W, served as the groundtruth for all simulations, with
specific within-person, between-person, and between-group alterations applied according to
Network Neuroscience
19
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
n
e
n
_
a
_
0
0
0
5
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Graph theory as a tool to understand brain disorders
a multilevel simulation of variation across individuals (details of simulation parameters pro-
vided in Supporting Information Table S1, Hallquist & Hillary, 2019). More specifically, to
approximate population-level variability in a case-control design, we simulated resting-state
adjacency matrices for 50 “patients” and 50 “controls” by introducing systematic and unsys-
tematic sources of variability for each simulated participant. Systematic sources were intended
to test substantive hypotheses about proportional thresholding (whack-a-node simulation)
and insensitivity to global versus modular differences (global insensitivity simulation), whereas
unsystematic sources reflected within- and between-person variation in edge strength.
In this model, the simulated edge strength between two nodes, i and j, for a given subject,
s, is:
(1)
where wij is the edge strength from the groundtruth adjacency matrix W. Global variation
in mean FC is represented by gijs, which reflects contributions of both between- and within-
person variation:
rijs
= wij
+ gijs
+ aijs
+ eijs
where bs represents normally distributed between-person variation in mean FC:
gijs
= bs + uijs
b ∼ N(0, σ
b
)
(2)
(3)
while σ
b controls the level of between-person variation in the sample. The term uijs represents
within-person variation of this edge relative to the person mean FC, bs. Within-person variation
in FC across all edges is assumed to be normally distributed:
u..s ∼ N(0, σw)
(4)
with σw scaling the degree of within-person FC variation across all edges.
Node-specific shifts in FC are represented by α
ijs, which includes both between-person and
within-node components. More specifically, the modulation of FC between nodes i and j is
given by:
where between-person variation in FC for node i is:
α
ijs
= ais
+ vijs
a
i. ∼ N(μai
, σai
)
(5)
(6)
with μai and σa i capturing the mean and standard deviation in FC shifts for node i across
subjects, respectively. Edgewise FC variation of a node i across its neighbors, j, is given by:
vi.s ∼ N(0, σvi
)
(7)
where σvi represents the standard deviation of FC shifts across neighbors of i. When nodes i
and j were both manipulated, the shifts were applied sequentially such that FC for the edge
= 0 for
between i and j was not allowed to have compounding changes. That is, we set α
i > j.
ijs
Finalmente, eijs represents the random variation in FC for the edge between i and j for subject s.
This variation was assumed to be normally distributed across all edges for a subject:
where σe controls the standard deviation of edge noise across subjects.
e..s ∼ N(0, σe)
(8)
20
Network Neuroscience
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
Whack-a-Note Simulation Methods
As mentioned above, PT is often applied in case-control studies to rule out the possibility that
network differences between groups reflect differences in the total number of edges. Impor-
tantly, in graphs of equal order N (cioè., the same number of nodes), proportional thresholding
equates both the density, D, and average degree, (cid:4)k(cid:5) between subjects:
D =
2E
N(N − 1)
, (cid:4)k(cid:5) =
2E
N
=⇒ (cid:4)k(cid:5) = D(N − 1)
(9)
where E denotes the number of unique edges in an undirected graph with no self-loops. As
noted by van den Heuvel et al. (2017), when one applies PT, differences in average connectivity
strength can lead to the inclusion of weaker edges in more sparsely connected groups. Further-
more, weak edges estimated by correlation are more likely to reflect an unreliable relationship
between nodes. Così, if one group has lower mean functional connectivity, PT could introduce
spurious connections, potentially undermining group comparisons of network topology.
Questo è, when groups are otherwise equivalent, the sum of increases in degree in hyper-
connected nodes for a group must be offset by equal, but opposite, decreases in degree for
other nodes in that group. This phenomenon holds because of the mathematical relationship
between average degree and graph density (Equazione 9). For simplicity, our first simulation
represents the scenario where there are meaningful FC increases in patients for selected nodes
and unreliable FC decreases in other nodes. This unreliability is intended to represent sampling
variability that could lead to erroneous false positives.
As described above, we simulated 50 patients and 50
Structure of whack-a-node simulation.
controls based on a groundtruth FC matrix. We estimated 100 replication samples with equal
levels of noise in both groups (see Supporting Information Table S1, Hallquist & Hillary, 2019).
In each replication sample, we increased the mean FC in three nodes, selected at random, by
r = 0.14. We also applied smaller decreases of r = −.04 to three other randomly targeted
nodes1. This level of decrease was chosen such that group differences in analyses of nodal
strength (cioè., computed on weighted graphs) were nonsignificant on average (Mp = .19,
SDp = .02). We applied PT to binarize graphs in each group, varying density between 5%
E 25% In 1% increments. Likewise, for FC thresholding, we binarized graphs at r threshold
between r = .2 E .5 In .02 increments. Finalmente, we retained weighted graphs for all sim-
ulated samples to estimate group differences in nodal strength. To ensure that effects were
not attributable to particular nodes, we averaged group statistics across the 100 replication
samples, where the targeted nodes varied randomly across samples.
In each replication sample, we estimated degree centrality for the Positive (hyperconnected),
Negative (weakly hypoconnected), and Comparator nodes. Comparators were three randomly
selected nodes in each sample that were not specifically modulated by the simulation. These
served as a benchmark to ensure that simulations did not induce group differences in centrality
for nodes not specifically targeted. To quantify the effect of PT versus FC thresholding in binary
graphs, we estimated group differences (patient–control) on degree centrality using two-sample
t tests for each Positive, Negative, and Comparator node. For weighted analyses, we estimated
group differences in strength centrality.
1 Results are qualitatively similar using other values for group shifts in FC.
Network Neuroscience
21
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
Global Insensitivity Simulation Methods: Hypothesis-to-Scale Matching
We simulated a dataset of 50 “controls” and 50 “patients” in which the FPN and DAN were
modulated in controls compared with the groundtruth matrix, W. In this simulation, the patient
group had increased FC in the DMN, a common finding in neurological disorders (Hillary et al.,
2015). In controls, we increased FC strength for edges between FPN/DAN regions and other
networks, M r = 0.2, SD = 0.1. Per module variation in between-network FC changes was
assumed to be normally distributed within each subject, SD = 0.1. We also increased controls’
FC on edges within the FPN and DAN, M r = 0.1, between-subjects SD = 0.05, within-subjects
SD = .05. In patients, between-network FC for DMN nodes was increased, M r = 0.2, between-
subjects SD = 0.1, within-subjects SD = 0.1. Likewise, within-network FC in the DMN was
increased, M r = 0.1, between-subjects SD = .05, within-subjects SD = .05. Questo è, we
applied similar levels of FC modulation to the FPN/DAN in controls and the DMN in patients,
although these changes largely affected different edges in the networks between groups.
We computed the small-worldness coefficient, S, according to the approach of Humphries
and Gurney (2008):
σ = Cg/Crand
Lg/Lrand
Here, Cg represents the transitivity of the graph, whereas Crand denotes the transitivity of a
random graph with an equivalent degree distribution. Likewise, Lg and Lrand represent the
characteristic path length of the target graph and randomly rewired graph, rispettivamente. Values
of σ much larger than 1.0 correspond to a network with small-world properties. To generate
statistics for equivalent random graphs, we applied a rewiring algorithm that retained the de-
gree distribution of the graph while permuting 347,160 edges (10 permutations per edge, SU
average). This algorithm was applied to the target graph 100 times to generate a set of equiv-
alent random networks. Transitivity and characteristic path length were calculated for each
of these, and their averages were used in computing the small-worldness coefficient, P. Noi
also analyzed within- and between-network degree centrality for each node, z-scoring values
within each module and density to allow for comparisons.
ACKNOWLEDGMENTS
We thank Zach Ceneviva, Allen Csuk, Richard Garcia, Melanie Glatz, and Riddhi Patel for their
work collecting, organizing, and coding references for the literature review and manuscript.
AUTHOR CONTRIBUTIONS
Michael Hallquist: Frank G Hillary: Conceptualization; Data curation; Formal analysis; Project
administration; Supervision; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
Michael Hallquist, National Institute of Mental Health (http://dx.doi.org/10.13039/100000025),
Award ID: K01 MH097091. Frank G Hillary, National Center for Advancing Translational
Scienze (http://dx.doi.org/10.13039/100006108), Award ID: UL Tr000127.
Network Neuroscience
22
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
REFERENCES
Abrol, A., Damaraju, E., Mugnaio, R. L., Stephen, J. M., Claus, E. D.,
Mayer, UN. R., & Calhoun, V. D. (2017). Replicability of time-
varying connectivity patterns in large resting state fMRI samples.
NeuroImage, 163, 160–176. https://doi.org/10.1016/j.neuroimage.
2017.09.020
Achard, S., & Bullmore, E. (2007). Efficiency and cost of economi-
cal brain functional networks. PLoS Computational Biology, 3(2),
0174–0183. https://doi.org/10.1371/journal.pcbi.0030017
Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore,
E. (2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hub. The Journal of Neuroscience: The Official Journal of the
Society for Neuroscience, 26(1), 63–72. https://doi.org/10.1523/
JNEUROSCI.3874-05.2006
Anticevic, A., Cole, M. W., Murray, J. D., Corlett, P. R., Wang, X.-J.,
& Krystal, J. H. (2012). The role of default network deactivation
in cognition and disease. Trends in Cognitive Sciences, 16(12),
584–592.
Barch, D. M., Burgess, G. C., Harms, M. P., Petersen, S. E., Schlaggar,
B. L., Corbetta, M., . . . WU-Minn HCP Consortium. (2013). Func-
tion in the human connectome: Task-fMRI and individual dif-
ferences in behavior. NeuroImage, 80, 169–189. https://doi.org/
10.1016/j.neuroimage.2013.05.033
Bassett, D. S., & Bullmore, E. T. (2016). Small-world brain networks
revisited. The Neuroscientist. https://doi.org/1073858416667720
Bassett, D. S., Bullmore, E. T., Meyer-Lindenberg, A., Apud, J. A.,
Weinberger, D. R., & Coppola, R. (2009). Cognitive fitness of
cost-efficient brain functional networks. Proceedings of the National
Academy of Sciences of the United States of America, 106(28),
11747–11752. https://doi.org/10.1073/pnas.0903641106
Betzel, R. F., Medaglia, J. D., Papadopoulos, L., Baum, G. L., Gur,
R., Gur, R., . . . Bassett, D. S. (2017). The modular organization
of human anatomical brain networks: Accounting for the cost
of wiring. Network Neuroscience, 1(1), 42–68. https://doi.org/
10.1162/NETN_a_00002
Birn, R. M., Molloy, E. K., Patriat, R., Parker, T., Meier, T. B., Kirk,
G. R., . . . Prabhakaran, V. (2013). The effect of scan length on
the reliability of resting-state fMRI connectivity estimates. Neuro-
Image, 83, 550–558. https://doi.org/10.1016/j.neuroimage.2013.
05.099
Biswal, B. B., Mennes, M., Zuo, X.-N., Gohel, S., Kelly, C., Smith,
(2010). Toward discovery science of
S. M., . . . Colcombe, S.
human brain function. Proceedings of the National Academy of
Sciences of the United States of America, 107(10), 4734–4739.
Biswal, B. B., Yetkin, F. Z., Haughton, V. M., & Hyde, J. S. (1995).
Functional connectivity in the motor cortex of resting human
brain using echo-planar MRI. Magnetic Resonance in Medicine,
34(4), 537–541. https://doi.org/10.1002/mrm.1910340409
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038/
nrn2575
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214
Callaway, D. S., Newman, M. E., Strogatz, S. H., & Watts, D. J.
(2000). Network robustness and fragility: Percolation on random
graphs. Physical Review Letters, 85(25), 5468–5471. https://doi.
org/10.1103/PhysRevLett.85.5468
Cassidy, B., Bowman, D. B., Rae, C., & Solo, V. (2018). On the reli-
ability of individual brain activity networks. IEEE Transactions on
Medical Imaging, 37(2), 649–662. https://doi.org/10.1109/TMI.
2017.2774364
Cassidy, B., Rae, C., & Solo, V.
(2015). Brain activity: Connectiv-
ità, sparsity, and mutual information. IEEE Transactions on Medi-
cal Imaging, 34(4), 846–860. https://doi.org/10.1109/TMI.2014.
2358681
Chao-Gan, Y., & Zang, Yu-Feng. (2010). DPARSF: A MATLAB tool-
box for “pipeline” data analysis of resting-state fMRI. Frontiers
in Systems Neuroscience, 4. https://doi.org/10.3389/fnsys.2010.
00013
Chen, Y., Wang, S., Hilgetag, C. C., & Zhou, C. (2013). Trade-off
between multiple constraints enables simultaneous formation
of modules and hubs in neural systems. PLoS Computational
Biology, 9(3), e1002937. https://doi.org/10.1371/journal.pcbi.
1002937
Ciric, R., Wolf, D. H., Energia, J. D., Roalf, D. R., Baum, G. L.,
Ruparel, K., . . . Satterthwaite, T. D. (2017). Benchmarking of
participant-level confound regression strategies for the control
of motion artifact in studies of functional connectivity. Neuro-
Image, 154(Supplement C), 174–187. https://doi.org/10.1016/j.
neuroimage.2017.03.020
Craddock, R. C., James, G. A., Holtzheimer, P. E., Eh, X. P., &
Mayberg, H. S. (2012). A whole brain fMRI atlas generated via
spatially constrained spectral clustering. Human Brain Mapping,
33(8), 1914–1928. https://doi.org/10.1002/hbm.21333
Crone, J. S., Soddu, A., Höller, Y., Vanhaudenhuyse, A., Schurz,
M., Bergmann, J., . . . Kronbichler, M. (2014). Altered network
properties of the fronto-parietal network and the thalamus in
impaired consciousness. NeuroImage. Clinical, 4, 240–248.
https://doi.org/10.1016/j.nicl.2013.12.005
Crossley, N. A., Mechelli, A., Scott, J., Carletti, F., Fox, P. T.,
McGuire, P., & Bullmore, E. T. (2014). The hubs of the human
connectome are generally implicated in the anatomy of brain
disorders. Brain, 137(8), 2382–2395.
Demetriou, L., Kowalczyk, O. S., Tyson, G., Bello, T., Newbould,
R. D., & Wall, M. B. (2016). A comprehensive evaluation of
multiband-accelerated sequences and their effects on statistical
outcome measures in fMRI. BioRxiv, 076307. https://doi.org/
10.1101/076307
Dosenbach, N. U. F., Koller, J. M., Earl, E. A., Miranda-Dominguez,
O., Klein, R. L., Van, UN. N., . . . Nguyen, UN. l. (2017). Real-time
motion analytics during brain MRI improve data quality and re-
duce costs. NeuroImage, 161, 80–93.
Fallani, F. D. V., Richiardi, J., Chavez, M., & Achard, S. (2014).
Graph analysis of functional brain networks: Practical issues in
translational neuroscience. Philosophical Transactions of the
Royal Society B: Biological Sciences, 369(1653), 20130521–
20130521. https://doi.org/10.1098/rstb.2013.0521
Network Neuroscience
23
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of
Brain Network Analysis. Amsterdam: Academic Press.
Friston, K. J.
(2011). Functional and effective connectivity: A re-
view. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089/
brain.2011.0008
Garrison, K. A., Scheinost, D., Finn, E. S., Shen, X., & Constable,
R. T. (2015). IL (In)stability of functional brain network mea-
sures across thresholds. NeuroImage, 118, 651–661. https://doi.
org/10.1016/j.neuroimage.2015.05.046
Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D.,
Harwell, J., Yacoub, E., . . . Van Essen, D. C.
(2016). A multi-
modal parcellation of human cerebral cortex. Nature, 536(7615),
171–178. https://doi.org/10.1038/nature18933
Goñi,
J., van den Heuvel, M. P., Avena-Koenigsberger, A.,
de Mendizabal, N. V., Betzel, R. F., Griffa, A., . . . Sporns, O.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Atti del
National Academy of Sciences of the United States of America,
111(2), 833–838.
Gonzalez-Castillo, J., Chen, G., Nichols, T. E., & Bandettini, P. UN.
(2017). Variance decomposition for single-subject task-based
fMRI activity estimates across many sessions. NeuroImage, 154,
206–218. https://doi.org/10.1016/j.neuroimage.2016.10.024
Goodkind, M., Eickhoff, S. B., Oathes, D. J., Jiang, Y., Chang, A.,
Jones-Hagata, l. B., . . . Etkin, UN. (2015). Identification of a
common neurobiological substrate for mental illness. JAMA Psy-
chiatry, 72(4), 305–315. https://doi.org/10.1001/jamapsychiatry.
2014.2206
Gordon, E. M., Laumann, T. O., Adeyemo, B., Huckins, J. F., Kelley,
W. M., & Petersen, S. E. (2016). Generation and evaluation of a
cortical area parcellation from resting-state correlations. Cerebral
Cortex, 26(1), 288–303. https://doi.org/10.1093/cercor/bhu239
Greene, D. J., Black, K. J., & Schlaggar, B. l. (2016). Considerations
for MRI study design and implementation in pediatric and
clinical populations. Developmental Cognitive Neuroscience,
18, 101–112. https://doi.org/10.1016/j.dcn.2015.12.005
Hallquist, M. N., & Hillary, F. G. (2019). Supporting information
for “Graph theory approaches to functional network organiza-
tion in brain disorders: A critique for a brave new small-world.”
Network Neuroscience, 3(1), 1–26. https://doi.org/10.1162/netn_
a_00054
Hallquist, M. N., Hwang, K., & Luna, B. (2013). The nuisance
of nuisance regression: Spectral misspecification in a common
approach to resting-state fMRI preprocessing reintroduces noise
and obscures functional connectivity. NeuroImage, 82, 208–225.
https://doi.org/10.1016/j.neuroimage.2013.05.116
Hilgetag, C. C., & Goulas, UN.
(2015).
Is the brain really a small-
world network? Brain Structure and Function, 221(4), 1–6.
Hilgetag, C. C., & Kaiser, M.
(2004). Clustered organization of
cortical connectivity. Neuroinformatics, 2(3), 353–360. https://
doi.org/10.1385/NI:2:3:353
Hillary, F. G., & Grafman, J. H. (2017). Injured brains and adaptive
networks: The benefits and costs of hyperconnectivity. Trends in
Cognitive Sciences. https://doi.org/10.1016/j.tics.2017.03.003
Hillary, F. G., Rajtmajer, S. M., Roman, C. A., Medaglia, J. D.,
Slocomb-Dluzen, J. E., Calhoun, V. D., . . . Wylie, G. R. (2014).
The rich get richer: Brain injury elicits hyperconnectivity in core
subnetworks. PLoS ONE, 9(8), e104021–e104021. https://doi.
org/10.1371/journal.pone.0104021
Hillary, F. G., Roman, C. A., Venkatesan, U., Rajtmajer, S. M., Bajo,
R., & Castellanos, N. D. (2015). Hyperconnectivity is a funda-
mental response to neurological disruption. Neuropsychology,
29(1), 59–75. https://doi.org/10.1037/neu0000110
Honnorat, N., Eavani, H., Satterthwaite, T. D., Gur, R. E., Gur, R. C.,
& Davatzikos, C.
(2015). GraSP: Geodesic graph-based seg-
mentation with shape priors for the functional parcellation of
the cortex. NeuroImage, 106, 207–221.
Humphries, M. D., & Gurney, K.
(2008). Network ‘small-world-
ness’: A quantitative method for determining canonical network
equivalence. PLoS ONE, 3(4), e0002051–e0002051. https://doi.
org/10.1371/journal.pone.0002051
Hwang, K., Hallquist, M. N., & Luna, B. (2013). The development
of hub architecture in the human functional brain network. Cere-
bral Cortex, 23(10), 2380–2393. https://doi.org/10.1093/cercor/
bhs227
Jalbrzikowski, M., Larsen, B., Hallquist, M. N., Foran, W., Calabro,
F., & Luna, B. (2017). Development of white matter microstruc-
ture and intrinsic functional connectivity between the amygdala
and ventromedial prefrontal cortex: Associations with anxiety
and depression. Biological Psychiatry, 82(7), 511–521. https://
doi.org/10.1016/j.biopsych.2017.01.008
(2009).
Laird, UN. R., Eickhoff, S. B., Li, K., Robin, D. A., Glahn, D. C., &
Fox, P. T.
Investigating the functional heterogeneity of
the default mode network using coordinate-based meta-analytic
modeling. Journal of Neuroscience, 29(46), 14496–14505.
Liang, X., Wang, J., Yan, C., Shu, N., Xu, K., Gong, G., & Lui, Y.
(2012). Effects of different correlation metrics and preprocessing
factors on small-world brain functional networks: A resting-state
functional MRI study. PLoS ONE, 7(3), e32766. https://doi.org/
10.1371/journal.pone.0032766
Muldoon, S. F., Bridgeford, E. W., & Bassett, D. S. (2016). Small-world
propensity and weighted brain networks. Scientific Reports, 6,
22057–22057.
Müller, V. I., Cieslik, E. C., Serbanescu, I., Laird, UN. R., Fox, P. T.,
(2017). Altered brain activity in unipolar de-
& Eickhoff, S. B.
pression revisited: Meta-analyses of neuroimaging studies. JAMA
Psychiatry, 74(1), 47–55.
Murphy, K., Birn, R. M., Handwerker, D. A.,
Jones, T. B., &
Bandettini, P. UN. (2009). The impact of global signal regression
on resting state correlations: Are anti-correlated networks intro-
duced? NeuroImage, 44(3), 893–905. https://doi.org/10.1016/
j.neuroimage.2008.09.036
Murphy, K., & Fox, M. D. (2017). Towards a consensus regarding
global signal regression for resting state functional connectivity
mri. NeuroImage, 154(Supplement C), 169–173. https://doi.org/
10.1016/j.neuroimage.2016.11.052
Newman, M. (2010). Networks: An Introduction (1st ed.). New York:
Oxford University Press.
Nichols, T. E., Das, S., Eickhoff, S. B., Evans, UN. C., Glatard, T.,
Hanke, M., . . . Sì, B. T. T. (2017). Best practices in data analysis
and sharing in neuroimaging using MRI. Nature Neuroscience,
20(3), 299–303. https://doi.org/10.1038/nn.4500
Network Neuroscience
24
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
Papanicolaou, UN. C., Rezaie, R., Narayana, S., Choudhri, UN. F.,
Wheless, J. W., Castillo, E. M., . . . Boop, F. UN. (2017). Clinical
applications of functional neuroimaging: Presurgical functional
In The Oxford Handbook of Functional Brain Imag-
mapping.
ing in Neuropsychology and Cognitive Neurosciences (P. 371).
New York: Oxford University Press.
Parente, F., Frascarelli, M., Mirigliani, A., Di Fabio, F., Biondi,
M., & Colosimo, UN. (2017). Negative functional brain networks.
Brain Imaging and Behavior. https://doi.org/10.1007/s11682-
017-9715-X
Poldrack, R. A., Baker, C.
J.,
I., Durnez,
Matthews, P. M., Munaf `o, M. R., . . . Yarkoni, T. (2017). Scanning
the horizon: Towards transparent and reproducible neuroimag-
ing research. Nature Reviews Neuroscience, 18(2), 115–126. https://
doi.org/10.1038/nrn.2016.167
J., Gorgolewski, K.
Energia, J. D., Cohen, UN. L., Nelson, S. M., Wig, G. S., Barnes, K. A.,
Church, J. A., . . . Petersen, S. E. (2011). Functional network or-
ganization of the human brain. Neuron, 72(4), 665–678. https://
doi.org/10.1016/j.neuron.2011.09.006
Energia, J. D., Fair, D. A., Schlaggar, B. L., & Petersen, S. E. (2010).
The development of human functional brain networks. Neuron,
67(5), 735–748. https://doi.org/10.1016/j.neuron.2010.08.017
Energia, J. D., Mitra, A., Laumann, T. O., Snyder, UN. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84, 320–341. https://doi.org/10.1016/j.neuroimage.2013.08.048
Price, J. L., & Drevets, W. C. (2010). Neurocircuitry of mood dis-
orders. Neuropsychopharmacology, 35(1), 192–216.
Roy, A., Bernier, R. A., Wang, J., Benson, M., French Jr, J. J., Good,
D. C., & Hillary, F. G.
(2017). The evolution of cost-efficiency
in neural networks during recovery from traumatic brain injury.
PloS One, 12(4), e0170541–e0170541.
Rubinov, M., & Sporns, O. (2011). Weight-conserving characteriza-
tion of complex functional brain networks. NeuroImage, 56(4),
2068–2079. https://doi.org/10.1016/j.neuroimage.2011.03.069
Saad, Z. S., Gotts, S. J., Murphy, K., Chen, G., Jo, H. J., Martin,
A., & Cox, R. W. (2012). Trouble at rest: How correlation pat-
terns and group differences become distorted after global signal
regression. Brain Connectivity, 2(1), 25–32. https://doi.org/10.
1089/brain.2012.0080
Schaefer, A., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N.,
Holmes, UN. J., . . . Sì, B. T. T. (in press). Local-global parcellation
of the human cerebral cortex from intrinsic functional connectiv-
ity MRI. Cerebral Cortex. https://doi.org/10.1093/cercor/bhx179
Schönbrodt, F. D., & Perugini, M. (2013). At what sample size do
correlations stabilize? Journal of Research in Personality, 47(5),
609–612. https://doi.org/10.1016/j.jrp.2013.05.009
Schwarz, UN. J., & McGonigle, J.
(2011). Negative edges and soft
thresholding in complex network analysis of resting state func-
tional connectivity data. NeuroImage, 55(3), 1132–1146. https://
doi.org/10.1016/j.neuroimage.2010.12.047
Shekhtman, l. M., Shai, S., & Havlin, S. (2015). Resilience of net-
works formed of interdependent modular networks. New Journal
of Physics, 17(12), 123007. https://doi.org/10.1088/1367-2630/
17/12/123007
tivity between networks via the dorsal nexus. Atti del
National Academy of Sciences of the United States of America,
107(24), 11020–11025.
Shirer, W. R., Jiang, H., Price, C. M., Di, B., & Greicius, M. D.
(2015). Optimization of rs-fMRI pre-processing for enhanced
signal-noise separation,
test-retest reliability, and group dis-
crimination. NeuroImage, 117, 67–79. https://doi.org/10.1016/
j.neuroimage.2015.05.015
. . . Beckmann, C. F.
Smith, S. M., Fox, P. T., Mugnaio, K. L., Glahn, D. C., Fox, P. M.,
Mackay, C. E.,
(2009). Correspon-
dence of the brain’s functional architecture during activation and
riposo. Proceedings of the National Academy of Sciences of the
United States of America, 106(31), 13040–13045. https://doi.
org/10.1073/pnas.0905267106
Smith, S. M., Mugnaio, K. L., Salimi-Khorshidi, G., Webster, M.,
Beckmann, C. F., Nichols, T. E., . . . Woolrich, M. W. (2011).
Network modelling methods for FMRI. NeuroImage, 54(2),
875–891. https://doi.org/10.1016/j.neuroimage.2010.08.063
Sporns, O., & Zwi, J. D. (2004). The small world of the cerebral cor-
tex. Neuroinformatics, 2(2), 145–162. https://doi.org/10.1385/
NI:2:2:145
Tomasi, D., Wang, G. J., & Volkow, N. D.
(2013). Energetic cost
of brain functional connectivity. Proceedings of the National
Academy of Sciences of the United States of America, 110(33),
13642–13647. https://doi.org/10.1073/pnas.1303346110
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., . . . Joliot, M. (2002). Automated
anatomical
labeling of activations in SPM using a macro-
scopic anatomical parcellation of the MNI MRI single-subject
brain. NeuroImage, 15(1), 273–289. https://doi.org/10.1006/
nimg.2001.0978
van den Heuvel, M. P., de Lange, S., Zalesky, A., Seguin, C., Sì,
T., & Schmidt, R.
(2017). Proportional thresholding in resting-
state fMRI functional connectivity networks and consequences
for patient-control connectome studies: Issues and recommen-
dations. NeuroImage, 152, 437–449. https://doi.org/10.1016/
j.neuroimage.2017.02.005
van den Heuvel, M. P., & Hulshoff Pol, H. E. (2010). Exploring the
brain network: A review on resting-state fMRI functional connec-
attività. European Neuropsychopharmacology: The Journal of the
European College of Neuropsychopharmacology, 20(8), 519–534.
https://doi.org/10.1016/j.euroneuro.2010.03.008
Stam, C.
van den Heuvel, M. P.,
J., Boersma, M., &
Hulshoff Pol, H. E. (2008). Small-world and scale-free organ-
ization of voxel-based resting-state functional connectivity in
the human brain. NeuroImage, 43(3), 528–539. https://doi.org/
10.1016/j.neuroimage.2008.08.010
Van Dijk, K. R. A., Sabuncu, M. R., & Buckner, R. l. (2012).
The influence of head motion on intrinsic functional connectiv-
ity MRI. NeuroImage, 59(1), 431–438. https://doi.org/10.1016/
j.neuroimage.2011.07.044
van Wijk, B. C. M., Stam, C. J., & Daffertshofer, UN. (2010). Com-
paring brain networks of different size and connectivity density
using graph theory. PLoS ONE, 5(10), e13701–e13701. https://
doi.org/10.1371/journal.pone.0013701
Sheline, Y. I., Price, J. L., Yan, Z., & Mintun, M. UN. (2010). Resting-
state functional MRI in depression unmasks increased connec-
Vargas, E. R., & Wahl, l. M. (2014). The gateway coefficient:
A novel metric for identifying critical connections in modular
Network Neuroscience
25
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Graph theory as a tool to understand brain disorders
networks. The European Physical Journal B, 87(7), 161. https://
doi.org/10.1140/epjb/e2014-40800-7
Varoquaux, G., & Craddock, R. C. (2013). Learning and compar-
ing functional connectomes across subjects. NeuroImage, 80,
405–415. https://doi.org/10.1016/j.neuroimage.2013.04.007
Vincent, J. L., Patel, G. H., Fox, M. D., Snyder, UN. Z., Baker, J. T.,
Essen, D. C. V.,
. . . Raichle, M. E. (2007). Intrinsic func-
tional architecture in the anaesthetized monkey brain. Nature,
447(7140), 83. https://doi.org/10.1038/nature05758
Wang, L., Hermens, D. F., Hickie, IO. B., & Lagopoulos, J. (2012). UN
systematic review of resting-state functional-MRI studies in major
depression. Journal of Affective Disorders, 142(1), 6–12.
Wang, Y., Kang, J., Kemmer, P. B., & Guo, Y. (2016). An efficient and
reliable statistical method for estimating functional connectivity
in large scale brain networks using partial correlation. Frontiers
in Neuroscience, 10. https://doi.org/10.3389/fnins.2016.00123
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of “small-
world” networks. Nature, 393(6684), 440–442. https://doi.org/
10.1038/30918
Whitfield-Gabrieli, S., & Nieto-Castanon, UN. (2012). Conn: A func-
tional connectivity toolbox for correlated and anticorrelated
brain networks. Brain Connectivity, 2(3), 125–141. https://doi.
org/10.1089/brain.2012.0073
Woolrich, M. W., Ripley, B. D., Brady, M., & Smith, S. M. (2001).
Temporal autocorrelation in univariate linear modeling of FMRI
dati. NeuroImage, 14(6), 1370–1386. https://doi.org/10.1006/
nimg.2001.0931
Yang, Z., Zuo, X.-N., Wang, P., Li, Z., LaConte, S. M., Bandettini,
P. A., & Eh, X. P. (2012). Generalized RAICAR: Discover homo-
geneous subject (sub)groups by reproducibility of their intrinsic
connectivity networks. NeuroImage, 63(1), 403–414. https://doi.
org/10.1016/j.neuroimage.2012.06.060
Sì, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari,
D., Hollinshead, M., . . . Buckner, R. l. (2011). The organization
of the human cerebral cortex estimated by intrinsic functional
Journal of Neurophysiology, 106(3), 1125–1165.
connectivity.
https://doi.org/10.1152/jn.00338.2011
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
3
1
1
1
0
9
2
2
9
8
N
e
N
_
UN
_
0
0
0
5
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Network Neuroscience
26