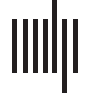REVIEW
From calcium imaging to graph topology
Ann S. Blevins1, Dani S. Bassett1,2,3,4,5,6, Ethan K. Scott7,8, and Gilles C. Vanwalleghem9,10
1Department of Bioengineering, School of Engineering and Applied Science, University of Pennsylvania, Philadelphia, PAPÀ, USA
2Department of Psychiatry, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PAPÀ, USA
3Department of Neurology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PAPÀ, USA
4Department of Electrical and Systems Engineering, School of Engineering and Applied Science, University of Pennsylvania,
Philadelphia, PAPÀ, USA
5Department of Physics and Astronomy, College of Arts and Sciences, University of Pennsylvania, Philadelphia, PAPÀ, USA
6Santa Fe Institute, Santa Fe, NM, USA
7Queensland Brain Institute, University of Queensland, Brisbane, Australia
8Department of Anatomy and Physiology, School of Biomedical Sciences, University of Melbourne, Parkville, Australia
9Danish Research Institute of Translational Neuroscience (DANDRITE), Nordic EMBL Partnership for Molecular Medicine,
Aarhus University, Aarhus, Denmark
10Department of Molecular Biology and Genetics, Aarhus University, Aarhus, Denmark
Keywords: Zebrafish, Topology, Calcium imaging, Graph theory, Systems neuroscience
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
ABSTRACT
Systems neuroscience is facing an ever-growing mountain of data. Recent advances in protein
engineering and microscopy have together led to a paradigm shift in neuroscience; using
fluorescence, we can now image the activity of every neuron through the whole brain of
behaving animals. Even in larger organisms, the number of neurons that we can record
simultaneously is increasing exponentially with time. This increase in the dimensionality of the
data is being met with an explosion of computational and mathematical methods, each using
disparate terminology, distinct approaches, and diverse mathematical concepts. Here we
collect, organize, and explain multiple data analysis techniques that have been, or could be,
applied to whole-brain imaging, using larval zebrafish as an example model. We begin with
methods such as linear regression that are designed to detect relations between two variables.
Prossimo, we progress through network science and applied topological methods, which focus on
the patterns of relations among many variables. Finalmente, we highlight the potential of
generative models that could provide testable hypotheses on wiring rules and network
progression through time, or disease progression. While we use examples of imaging from
larval zebrafish, these approaches are suitable for any population-scale neural network
modeling, and indeed, to applications beyond systems neuroscience. Computational
approaches from network science and applied topology are not limited to larval zebrafish, O
even to systems neuroscience, and we therefore conclude with a discussion of how such
methods can be applied to diverse problems across the biological sciences.
INTRODUCTION
How can we make sense of the brain? Researchers can now record the activity of thousands of
individual neurons across the whole brain (Figure 1A) thanks to methodological improvements
in multielectrode arrays (Branner & Normann, 2000; Paulk et al., 2022; Steinmetz et al., 2019),
and calcium indicators combined with fast microscopy (Aimon et al., 2019; T.-W. Chen et al.,
2013; Hastings et al., 1969; Kim et al., 2017; Miyawaki et al., 1997; Nakai et al., 2001;
a n o p e n a c c e s s
j o u r n a l
Citation: Blevins, UN. S., Bassett, D. S.,
Scott, E. K., & Vanwalleghem, G. C.
(2022). From calcium imaging to graph
topology. Network Neuroscience, 6(4),
1125–1147. https://doi.org/10.1162/netn
_a_00262
DOI:
https://doi.org/10.1162/netn_a_00262
Received: 17 Marzo 2022
Accepted: 13 Giugno 2022
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Gilles C. Vanwalleghem
gilles.vanwalleghem@mbg.au.dk
Handling Editor:
Alex Fornito
Copyright: © 2022
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
From calcium imaging to graph topology
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
/
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 1. Rapid progress of systems neuroscience and the encoding of stimuli. (UN) Across animal models of increasing complexity, we are now
able to record the activity of many neurons. Per esempio, we can record all of the neurons of C. elegans, Di 2,000 neurons of D. melanogaster
(Tainton-Heap et al., 2021), and about 80% of neurons in the larval zebrafish (D. rerio; X. Chen et al., 2018). High-density electrophysiological
probes allow the recording of hundreds of units per session in mice, including deep structures within the brain (Steinmetz et al., 2019); Infatti,
researchers have recorded up to 10,000 neurons in a 0.3 mm3 portion of the brain using two-photon imaging (Stringer et al., 2019). (B). Stimulus
encoding can occur at the single neuron level, Dove, Per esempio, it could encode the direction of a stimulus. Stimulus encoding can also occur
at the population level, where multiple units together can provide a better representation of the stimulus, including its direction and color.
(C) Example of populations of neurons responding to the direction of water flow along the fish’s tail (Vanwalleghem et al., 2020). These
neuronal populations show a tonic activity for the duration (10 S) of a water flow stimulus from the tail to the head (green arrow), or from
the head to the tail (magenta arrow). The neurons were clustered in three categories: bidirectional response (blue), head to tail (pink), or tail
to head (gold). Here we represent their spatial coordinates in the zebrafish brain (left). Telen = telencephalon, OT = optic tectum, TS = torus
semicircularis (small dotted lines), ON = octavolateralis nucleus. (D) It is possible to predict neuronal activity from behavior, which in this
example is the facial movement of a mouse. (Top) Motion energy was computed from consecutive frames (t and t + 1). (Middle) IL
principal components could then be used to predict the neuronal activity of 1,000 neurons. (Bottom) The predicted activity was remarkably
similar (Di 30%) to the real neuronal activity (sorted with an embedding for visualization). Adapted from Stringer et al. (2019).
Calcium indicators:
Fluorescent proteins or dyes whose
fluorescence changes with the
calcium concentration, typically
used as a proxy for neuronal activity.
Nguyen et al., 2016; Stringer et al., 2019; Tsien et al., 1982; Vanwalleghem et al., 2018). Con
these new tools in hand, the number of recorded neurons has doubled every seven years since
1960 E, as a consequence, neuroscience is relying increasingly on “big data” approaches
(IO. H. Stevenson & Kording, 2011). While the methodological advances that allow researchers
to fill the space between individual neurons and the whole brain are exhilarating, the moun-
tains of data behind them present new conceptual challenges to understand them fully.
Systems neuroscience is less interested in the activity, either spontaneous or elicited, Di
each individual neuron, but more in how ensembles, or populations, of neurons form and
interact (Figure 1B). Population coding complements the single neuron encoding approach
(Barlow, 1972; Theunissen & Mugnaio, 1995), with a population-level encoding of information
by ensembles of neurons (Knight, 1972). This population level of encoding can combine mul-
tiple features of a stimulus and ensure the robustness of a behavior despite individual neurons’
Network Neuroscience
1126
From calcium imaging to graph topology
stochasticity and noise (Quian Quiroga & Panzeri, 2009). Ovviamente, population-level encod-
ing can only be described and analyzed if one can record from multiple neurons
simultaneously.
A number of approaches have been developed or adapted for the analysis of population-
level data. These approaches include dimensionality reduction (Mu et al., 2019; UN. W. Thompson
et al., 2016), linear regression (X. Chen et al., 2018; Vladimirov et al., 2018), clustering (Mölter
et al., 2018; Vanwalleghem et al., 2020), nonlinear analyses (Ponce-Alvarez et al., 2018), E
topological approaches (Gracia-Tabuenca et al., 2020; UN. E. Sizemore et al., 2019), to name a
few. For many of these methods, the dimensionality and size of population-level datasets can
be a limiting factor and require either the use of distributed computing (Freeman et al., 2014),
dimensionality reduction (Betzel, 2020), or new mathematical tools (Haesemeyer et al., 2019;
Tajima et al., 2015; Triplett et al., 2020; Watanakeesuntorn et al., 2020). Another challenge is
the fabled needle in a haystack: identifying a potential sparse population that would drive the
animal’s response (Ince et al., 2013; Tajima et al., 2017). In definitiva, all of these tools aim to
understand how the brain encodes stimuli and transforms the sensory input into meaningful
information and behavior.
Neuronal ensembles encoding sensory stimuli have been observed in zebrafish for all sen-
sory modalities from visual, to auditory and vestibular (Avitan et al., 2020; X. Chen et al., 2018;
Favre-Bulle et al., 2020; Favre-Bulle et al., 2018; Friedrich et al., 2004; Migault et al., 2018;
Poulsen et al., 2021; UN. W. Thompson et al., 2016; Vanwalleghem et al., 2017; Vanwalleghem
et al., 2020). Per esempio, the lateral line is a specialized apparatus that senses water flow in
fish and amphibians. We showed the existence of neuronal representations of the direction
and speed of the water flow (Figure 1C), as well as of the simulated distance traveled by
the animal (Vanwalleghem et al., 2020). For visual processing, X. Chen et al. (2018) showed
how the transformation of visual stimuli into motor commands was distributed across the
brain, before converging onto small clusters of neurons in the hindbrain that output the motor
commands. A systems-wide approach was needed to observe the distributed nature of neuro-
nal representations in the above studies and has shown a similar distribution across the brain
in mice using Neuropixels probes (Steinmetz et al., 2019) and across the visual cortex using
two-photon imaging (Figure 1D; Stringer et al., 2019).
The key limitation of most whole-brain work is its descriptive nature. Studies have linked
neuronal responses to stimuli, but few offer testable models or hypotheses on how the sensory
processing can drive behavior. Testing the causal link between neuronal responses and behav-
ior is particularly complex when the responses are spatially distributed, as described above.
Promising approaches for surmounting this challenge include light-shaping and optogenetics,
or ablation, which could allow neuroscientists to interrogate distributed neuronal circuits and
identify the necessary parts underlying a specific behavior (Dal Maschio et al., 2017; Dunn
et al., 2016; Fernandes et al., 2021; Marshel et al., 2019; Naumann et al., 2016; Vladimirov
et al., 2018). Per esempio, Helmbrecht et al. (2018) showed that optogenetic activation of
specific regions within the optic tectum could trigger different behavioral programs: an
approach program or an escape attempt. The investigators further identified multiple classes
of projection neurons from the optic tectum to the hindbrain. These projections could convey
the relevant information to the motor centers, including the position of the stimulus. Such a
combination of structural and functional data provides a more comprehensive picture of, COME
well as testable hypotheses regarding, how information flows between brain regions and how
that information could be transformed to drive specific behaviors.
Our goal is for this review to be accessible to biologists with little or no mathematical training,
since understanding the basis of the most common approaches will empower neuroscientists to
Lateral line:
Sensory organ found in fish and
amphibians; it is composed of
neuromasts, specialized bundles of
hair cells that can detect waterflow.
Optogenetics:
Genetic tools that allow the
manipulation of cells by light,
typically to activate or silence
neurons.
Optic tectum:
Midbrain region that serves as the
main visual processing center in
several vertebrates, homologue to the
superior colliculus of mammals.
Network Neuroscience
1127
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
/
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
choose the most suitable method to answer their specific research question. As most of the
methods we discuss involve relations between units, we will begin with approaches for quan-
tifying simple relations between two variables, and from there build up to approaches involving
multiple variables such as network science. Finalmente, we will examine the potential of generative
models, and discuss avenues for future research, and how these tools can be used in other con-
texts. We direct the readers who want to deepen their understanding of a specific topic to these
excellent reviews on linear models for encoding (Marinescu et al., 2018; Paninski et al., 2007)
and graph theory (Bassett & Sporns, 2017; Sporns, 2018).
EVALUATING RELATIONS BETWEEN TWO UNITS
Systems neuroscience offers the perspective that no one neuron functions alone, visual stimuli
influence future motor sequences, a triggered memory may evoke an emotional reaction, E
sudden sounds shift attention. All of these examples can be simplified into one unit, for exam-
ple a neuron or population (see Figure 2A), that influences, connects to, or relates to another
unit. Determining whether two units are related may seem to be simple at first glance. For
esempio, in which periods of time (Figura 2, x-axis) is the activity time series of one unit track-
ing the activity of the other unit? Despite the simple question statement, the path to an answer
is not immediately obvious, as there are many types of computational methods available from
which we must choose. We will highlight a few classical examples, including linear regression
and causal inferences, but invite interested readers to peruse Cliff et al. (2022) for a deeper
comparison.
Is the Activity of Two Units Pairwise Similar?
The precise definition of pairwise similar has resulted in a multitude of mathematical descrip-
tions that we will not explore here (Bobadilla-Suarez et al., 2020; Miri et al., 2011). At a basic
level, the activity of two units being similar might mean that changes in the activity of unit x
coincide with changes in the activity of unit y (Figure 2B). Per esempio, the correlation between
spinal neurons drastically increases during the development of larval zebrafish (Figure 2C, left;
Warp et al., 2012). The central pattern generator is dependent on this correlated, and contral-
aterally anticorrelated, activity to generate the rhythmic movements mediating swimming in
zebrafish. Importantly there are myriad additional approaches to the problem of evaluating a
relationship between two units (Cutts & Eglen, 2014). While no one method is error-free, sup-
porting conclusions with multiple types of pairwise similarity measures from different domains
can reduce the effects of bias on the overall outcome.
How Is the Activity of Two Units Related?
Given the activity of two neurons, we might want to understand how they are related. Linear
regression can be used to answer this question, by expressing the activity of the second neuron
as a linear function of the activity of the first neuron (Figure 2B, middle). When additional
variables are present that might affect the results, such as neuron type or location, we can also
incorporate these variables into our model to understand or mitigate the influence of such var-
iables on the relationship in question (Smith, 2018). Linear regression is a common but pow-
erful tool that sets the stage for more general approaches such as general linear models and
machine learning. In systems neuroscience specifically, these techniques have been used to
assess learning (Luchiari & Chacon, 2013; Tompson et al., 2020) and to determine neurons
associated with a behavior (Marques et al., 2020; Miri et al., 2011). Linear regression has also
been used to assess the response to auditory stimuli in larval zebrafish (Figure 2C, middle).
Network Neuroscience
1128
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
/
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
T
/
Figura 2. Calculating relationships between two units. (UN) In systems neuroscience, a single unit may correspond to a neuron or a pop-
ulation of neurons. Two units may potentially interact in a variety of ways. Per esempio, one can either activate or inhibit the other; IL
strength of these interactions can also vary, and feedback between units can also exist. As an example, units x (blue) and y (orange) Avere
activities that change over time. At time i, unit x has activity xi and unit y has activity yi. (B) Multiple methods exist for quantifying relations
between two variables. (Left) Pairwise similarity measures often see the leftmost portion of the activity traces as having high similarity and
the middle portion as having low similarity; these measures may vary on their interpretation of the rightmost portion. (Middle) Linear regres-
sion calculates a line of best fit (darker gold) given the points (xi, yi) for each time i. This line of best fit minimizes the error between the
predicted values of yi, using xi, and the true values yi (lighter gold). (Right) Causal inference methods ask whether information about the
activity of unit x between time i − k and the current time i improves the prediction accuracy of the future activity of unit y, above and
beyond the prediction accuracy obtained by using the previous activity of unit y alone. (C) Applications of each method to larval zebrafish
dati. (Left) The pairwise similarity (correlation) between spinal neurons increases dramatically between 18 E 20 hours post fertilization
(hpf ), as can be seen by the blue and red activity traces moving in synchrony. Adapted from Warp et al. (2012). (Middle) Linear regression
was used to quantify the responses to auditory stimuli; the coefficient is mapped to the color of each neuron in the brain, while the coefficient
of determination R2 is mapped to the size of the sphere. Adapted from Poulsen et al. (2021). (Right) The Granger causality approach was used
to identify the flow of information between auditory brain regions in Vanwalleghem et al. (2017). Th = thalamus, TS = torus semicircularis,
ON = octavolateralis nucleus, Hb = hindbrain.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Network Neuroscience
1129
From calcium imaging to graph topology
Poulsen et al. (2021) showed that the auditory responses were more widespread than previ-
ously observed, but also confirmed previous observations of the primary auditory regions in
larval zebrafish (Privat et al., 2019; Vanwalleghem et al., 2017).
Causal Inference
Knowledge of an association does not necessarily help us with designing intervention strate-
gies, mapping out novel circuits, or determining mechanisms (Nienborg & Cumming, 2010). In
order to reach these goals, we need to start with an understanding of causal relationships
between neuronal units. For this review, we will say a cause of an effect must both precede
the effect and provide predictive information about the effect (Cekic et al., 2018; Granger,
1969; Wiener, 1956). This notion of a cause is commonly referred to as Granger causality
or G-causality. If unit x activity causes a change in unit y activity, then given our perspective
on causality, we would expect to see that past and present activity of unit x can predict the
activity of unit y, or that unit x activity Granger-causes unit y activity. These ideas support the
way many expect the brain to function, and so have been used frequently in neuroscience. For
esempio, G-causality has been used to understand information flow in auditory processing,
which confirmed previous results of neuroanatomical studies and aligned with evidence
in the mammalian literature (Figure 2C, right; Vanwalleghem et al., 2017) and prey capture
(Oldfield et al., 2020) in larval zebrafish. G-causality is one among many causal inference
approcci; Per esempio, a method was specifically designed to infer causality using opto-
genetics by compensating for the inherent confounds (Lepperød et al., 2018). Other
metodi, such as empirical dynamic modeling, are more appropriate for nonlinear dynam-
ical systems and have been applied to neuronal data (Watanakeesuntorn et al., 2020).
In summary, there are many ways to test for the presence of a relationship between two
interacting units, and while the methods we discussed have been useful for systems neurosci-
ence, it is important to choose the approach based on the data, the system, and the specific
question at hand (Torres et al., 2020).
EVALUATING PATTERNS OF MANY INTERACTING UNITS
Instead of focusing on only one pair of variables, we can expand our scope to include many
interacting units such as thousands of neurons or hundreds of neuronal populations (Figure 3A).
Approaches under the umbrella of complexity, or network, science mathematically aim to
encode the data as units and parts (interactions, relations) of a quantitative object, such as a
rete, then use computational methods to evaluate the representation and make predictions
about how that structure influences biological function. Below we draw mainly from the two
subfields of network neuroscience and topological data analysis, but we invite the interested
reader to peruse Battiston et al. (2020), Spivak (2009), and Torres et al. (2020) for deeper
discussions.
Encoding Data
The first step is to decide what the units, or nodes, will be, either individual neuronal units, O
nodes representing multiple neuronal units, such as those that respond to the same stimulus
(Figure 3A; Crossley et al., 2013). The choice of encoding method, which takes data and cre-
ates from it a quantitative object (Figure 3B), is crucial to the success of the entire analysis. If
chosen incorrectly, it can cause unexpected results, bias the computations, and prevent the
analysis from answering the initial question (Torres et al., 2020). Finalmente, we must decide what
will constitute a relation between units. As discussed above, one could use pairwise similarity,
Network Neuroscience
1130
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
/
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
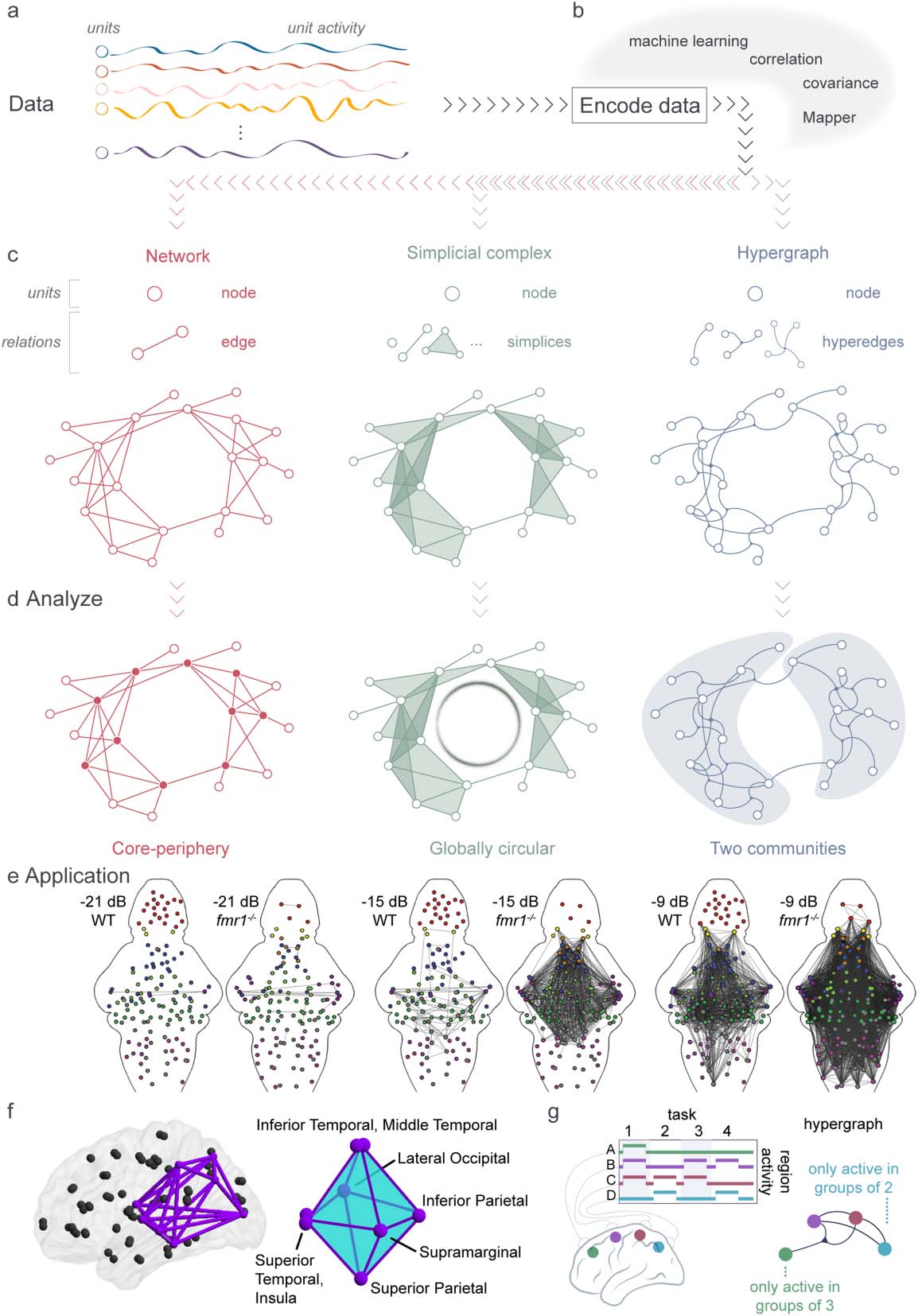
Figura 3. Systems neuroscience uses multiple methods to encode, represent, and analyze data. (UN) Data consists of many units with recorded
activity over time. (B) There are many options for encoding data into a mathematical representation. (C) Examples of representations. (Left) UN
network is composed of nodes and edges that connect exactly two nodes. (Middle) A simplicial complex is constructed from nodes and sim-
plices that connect any number of nodes, and any subset of connected nodes. (Right) A hypergraph is built from nodes and hyperedges that
connect any number of nodes. (D) Based on the type of representation used (rete, simplicial complex, hypergraph), different analysis
approaches become available. Per esempio, representing data as a network allows one to detect many types of structure, and more recently
very specific patterns such as core-periphery organization. Representing data as a simplicial complex permits the use of homology, Quale
perceives the circular nature of the complex. Finalmente, a hypergraph representation enables a unique perspective on the community structure
of the system. While one could use any of these representations to calculate, Per esempio, community structure, we stress that each repre-
sentation will provide a unique perspective on community structure, and furthermore that some representations are more amenable to par-
ticular analyses, Per esempio, finding loops, than others (Torres et al., 2020). (E) Application of network theory to larval zebrafish data. WT and
fmr1-/- larval zebrafish were presented with increasing intensity of sound, from −21 dB to −9 dB, and their neuronal activity was recorded.
Circle plots of the edges between brain region nodes in WT and fmr1-/- zebrafish; an edge was placed if the correlation between their response
to auditory stimuli is above 0.85. Node color indicates brain regions, in order: telencephalon, red; torus semicircularis, dark magenta; cere-
bellum, dark green; thalamus, orange; hindbrain without the Cb and ON, gray; octavolateralis nucleus, magenta; pretectum, light blue; optic
tectum, blue; habenulae, yellow; tegmentum, light green. Adapted from Constantin et al. (2020). (F) Application of topological data analysis
to the structural connectome. Example conserved cavity connecting visual processing regions shown in the brain (left) and abstracted for
ease of interpretation (right). For visual simplicity, the cavity depiction in the brain does not include shading for 2-simplices, only edges.
Adapted from A. E. Sizemore et al. (2018). (G) A hypergraph created from recordings of the on/off activity of brain regions during four tasks
reveals that the green node A is only active in groups of three regions, whereas the blue node D is only active in groups of two regions. As
such the green, magenta, and red nodes are all linked by a hyperedge. Adapted from Torres et al. (2020).
Network Neuroscience
1131
From calcium imaging to graph topology
or causal inference to identify relations between any pair of nodes (Fallani et al., 2015;
Watanakeesuntorn et al., 2020). Using these ideas, one can construct a graphical model
in which a relation between two units indicates a pairwise dependence. Such models are
common in neuroscience (Belilovsky et al., 2015; Chang et al., 2019). Additionally, tech-
niques from machine learning can provide a whole-brain approach to creating networks
(Murugesan et al., 2020). Finalmente, one can use probabilistic graphical models to represent
neuronal ensembles and identify neurons that can activate the whole ensembles (Carrillo-
Reid et al., 2021).
Many of the above discussed methods use data only from the two units in question, Ma
when encoding data involving many units, we can use methods that incorporate all of these
dati. Per esempio, Bayesian networks (Bielza & Larrañaga, 2014; Javidian et al., 2020) provide
a representation of the joint probability distributions across all the units within the system, so
that a relation indicates dependence of the target on the source. Finalmente, a method called Map-
per creates a representation from high-dimensional data by forming nodes from (overlapping)
clusters of data points and relations between nodes with corresponding clusters that share data
points (Cámara, 2017; Singh et al., 2007). Mapper’s representation not only offers a new way
to visualize high-dimensional data, but additionally creates a computational object (rete)
upon which one can perform downstream analyses such as assessing community structure of a
Mapper representation created from fMRI data (Saggar et al., 2018).
Importantly, the type of object constructed from the data-encoding process can be con-
strained by the method of encoding. Let us consider three mathematical frameworks with
which we could represent our data (Figure 3C). The first is a network, which has units (nodes)
and exclusively pairwise relations between nodes. The second and third, simplicial complexes
and hypergraphs, rispettivamente, allow for polyadic relations among nodes, meaning that any
number of nodes can be related. Taken together, in choosing the encoding strategy it is crucial
to consider (UN) how to define nodes, (B) what a relation between nodes should capture, E
(C) the frameworks that can be created with the approach. It is then important to ensure that
all of these fit within the larger research question and biological system.
Network Science
By representing data as a network composed of nodes interconnected by edges, the investi-
gator can answer new questions outside the reach of analytical techniques that focus on pair-
wise interactions (Bassett et al., 2018). Specifically, one can ask questions about how the full
pattern of relations—the network—might relate to the system’s dynamics, the associated pro-
cesses of perception, action, and cognition, and the resultant behavior (Fornito et al., 2016).
Across many networks, the values of related measures are correlated; notably, Tuttavia, IL
converse is not necessarily true (da Fontoura Costa et al., 2007). The values of mathematically
unrelated measures can still be correlated across a network ensemble if they are being simul-
taneously driven by a single mechanism (Onnela et al., 2012; UN. Sizemore et al., 2016). Relat-
edly, some statistical measures might vary across an ensemble in a way that tracks variation in
health, severity of disease, type of computation, and accuracy, complexity, or form of
behavior.
One dimension along which network measures range is the dimension of scale, from local,
as typically thought to be reflected in the clustering coefficient, to global, as typically thought
to be reflected in the shortest path length (Bullmore & Sporns, 2009). Networks that have both
high clustering (similar to a lattice) and low shortest path length (similar to a random network)
are said to have small-world organization (Bassett & Bullmore, 2006, 2017; Muldoon et al.,
Edge:
Connection between two nodes; Esso
indicates they are related, and it can
be weighted (measuring the strength
of that relation) or unweighted (NO
information on the strength). It can
also have direction or not, depending
on the relation metric used.
Network Neuroscience
1132
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
T
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
Degree:
Number of connections (edges) from
a node to other nodes (and itself ).
Fragile X syndrome:
Genetic condition caused by the
silencing of the FMR1 gene on the X
chromosome (hence the name). IL
syndrome is linked to intellectual
disability in humans.
2016). Evidence suggests that the network of neurons in zebrafish larvae has a small-world
organization (Stobb et al., 2012), suggesting its capacity for both local information processing
and global information transmission. This organization is also seen in C. elegans and other
species across diverse evolutionary lineages (Kaiser & Varier, 2011). Tuttavia, it may be that
this small-world organization only holds at certain scales (synapses, circuits, brain areas, eccetera.),
or depends on the empirical approach taken to gather and analyze the data (Hilgetag &
Goulas, 2016; Muller et al., 2014). Per esempio, scale-free networks, where the degree dis-
tribution follows a power law, have also been observed in the optic tectum of larval zebra-
pescare (Avitan et al., 2017), and biological networks as a whole have been found to exhibit
strong to strongest evidence of scale-free structure in 12% of the networks studied (Broido
& Clauset, 2019). It will be important for future generative models to incorporate additional
factors beyond small-worldness, such as the importance of long-term connections to the
functional diversity of distant brain areas, and not only topological considerations (Betzel
& Bassett, 2018).
In the middle of the continuum from local to global structure in networks is the mesoscale
(Figure 3D); Per esempio, a network is said to have core-periphery structure if it contains (UN) UN
core, which is a set of densely interconnected nodes, E (B) a periphery, which is a set of
nodes that connect to the core, but do not tend to connect to other nodes in the periphery
(Rombach et al., 2014). It is important to note that the local and global measures discussed
above are independent of the structure. Notably, mesoscale structure has been shown to vary
across cognitive states (Pedersen et al., 2018) and stages of learning (Bassett & Mattar, 2017),
and to be altered by genetic risk for psychiatric disease (Dimitriadis et al., 2021). These
mesoscale structures have been observed in Drosophila (Shih et al., 2015; Shih et al.,
2020); functional connectomes display hierarchical modularity that reconfigures appreciably
in response to a stimulus in larval zebrafish (Betzel, 2020). Constantin et al. (2020) showed
that the zebrafish model of fragile X syndrome had increased sensitivity to sound, particolarmente
apparent in the higher connectivity across brain regions at lower sound intensity (Figure 3E,
−15 dB). Such an increased connectivity is consistent with one of the theories developed to
explain the basis of the sensory phenotype in fragile X syndrome (Testa-Silva et al., 2012). For
a deeper dive in the use of networks with calcium imaging data, we invite readers to con-
sider Nelson and Bonner (2021).
Topological Data Analysis
Methods from topological data analysis (TDA) aim to provide a quantitative and qualitative
description of how the pieces of the system combine to form the larger whole (Blevins & Bassett,
2020; Geniesse et al., 2019; Ghrist, 2007; Munch, 2017). This topological perspective devi-
ates from many familiar frameworks, such as principal component analysis, by requiring no
a priori assumption about the space of the data (Per esempio, that the data are linear). Similar
to network science, TDA can represent systems with a simplicial complex, which contains
nodes (units) and simplices (parts or interaction representations, see Figure 3C). While the
edge of a graph can connect only two nodes, a simplex can connect any number of nodes.
Per esempio, three nodes can be all together connected by a simplex (illustrated as a filled
triangle in Figure 3C); specifically, a k-simplex connects k + 1 nodes in a simplicial complex.
In Figure 3C, we see that the simplicial complex has simplices drawn as links (1-simplices),
shaded triangles (2-simplices), and shaded tetrahedra (4-simplices), and thus can represent
many more types of multi-node interactions than the network. Encoding such polyadic rela-
tions between nodes provides TDA with distinct advantages, such as the ability to represent
many-unit neuronal interactions and the means to detect system features not perceived in
Network Neuroscience
1133
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
/
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
other domains. If we examine three neurons responding to different stimuli, the simplicial
complex lets us represent the difference between a system in which every pair of neurons
co-fires in response to different stimuli, and a system in which all three neurons fire in
response to the same stimulus. Though we here have presented only a brief introduction to
these TDA ideas, we direct the interested reader to Ahissar and Kleinfeld (2003), Blevins and
Bassett (2020), Lisman and Grace (2005), Ma’ayan et al. (2008), Munch (2017), UN. E. Sizemore
et al. (2019), and Tallon-Baudry et al. (2001).
Loops within a neuronal system can support memories (Lisman & Grace, 2005; Tallon-
Baudry et al., 2001), permit computations (Ahissar & Kleinfeld, 2003), and affect dynamics
(Ma’ayan et al., 2008). We can detect such looped motifs by using homology to detect loops
that surround topological cavities or voids within the simplicial complex representation of
the system (Per esempio, the large looped nature of the simplicial complex in Figure 3D).
Specifically, loops that surround a cavity would intuitively allow for two routes of informa-
tion to travel from one side of the loop to another, or could allow a signal to cyclically
continue around the loop and thus repeat periodically. Inoltre, homology, and its
weighted counterpart, persistent homology, can detect cavities, and thus loops, of any
dimension within the system. Per esempio, Reimann et al. (2017) identify high-dimensional
loops within the correlated activity of neurons, and find that in general such topological
complexity depends upon neuron morphology. Additionally, UN. E. Sizemore et al. (2018)
found loops connecting cortical to subcortical regions in the structural connectome to be
a consistent feature across healthy adults. Shown in Figure 3F, one of these conserved loops
connects higher order visual processing regions and mimics portions of the dorsal and ven-
tral visual streams. The conserved nature of these loops found across individuals, but not in
null models, suggests their importance in computation (UN. E. Sizemore et al., 2018). Addi-
tionally, these homological ideas have improved our understanding of neuronal dynamics
(Bardin et al., 2019; Curto, 2016; Curto et al., 2012), stimulus encoding (Basso et al.,
2016; Giusti et al., 2015; Rubin et al., 2019), and the time-evolving brain (Yoo et al., 2016).
Although we introduced Mapper as a method for encoding data, it has also been used as a
stand-alone tool to understand neural systems as it allows one to represent large datasets in a
reduced form. Simply having the ability to visualize high-dimensional data using the Mapper
algorithm has led to the discovery of a new breast cancer subgroup (Nicolau et al., 2011) E
has been used to predict drug effects in traumatic brain injury (Nielson et al., 2015). Addition-
alleato, Saggar et al. (2018) paired Mapper with functional imaging data to investigate features of
an individual’s brain state space. Their work led to the creation of DyNeuSR (Geniesse et al.,
2019), a Python implementation of Mapper designed specifically for neuroimaging. With these
implementations of Mapper, researchers can get a graphical representation of brain states, for
esempio, observe how individuals traverse across the graph (brain states), and from this
sequence better understand state transitions between different cognitive tasks (Geniesse
et al., 2022).
Traumatic brain injury:
Damage to the brain from physical
trauma, typically from a blow or
impact to the head.
Alternative Representations
Multilayer networks:
These networks allow the
interactions of nodes between
different layers, each representing
different node types, potentially
representing different data types.
Not all neural systems are most faithfully represented by networks or simplicial complexes.
Many other representations exist, including but not limited to hypergraphs, higher order net-
works, multilayer networks, and sheaves, which we will all briefly describe below. Similar to
simplicial complexes, hypergraphs can encode polyadic relationships among nodes (In
Figure 3C, comparing simplices to hyperedges). Tuttavia, whereas a 2-simplex (a shaded tri-
angle) implies that all pairs of nodes are pairwise related, a hyperedge connecting three nodes
Network Neuroscience
1134
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
does not imply that any pair of the three nodes is pairwise related. This feature allows the
hypergraph to represent a wide variety of systems, such as functional (Davison et al., 2015;
Davison et al., 2016) and structural neural systems. Per esempio, after recording neural
responses across different tasks, we could create a hypergraph in which brain regions are con-
nected by a hyperedge if they are coactive in a task (Figure 3G). Per esempio, the three regions
UN, B, C are all coactive in a task (Figure 3G, task 1), but regions A and B are never coactive in
any other task without C. Detecting many large hyperedges (hyperedges that connect many
nodes) indicates that often many populations act in unison in the tasks. Inoltre, if we find
many large hyperedges but few small hyperedges, then we could conclude that generally
these populations function only alongside others, and rarely by themselves or in small groups.
Such a phenomenon can be quantified by the hypergraph-specific measurement called the fill
coefficient (Torres et al., 2020).
Higher order networks (Xu et al., 2016) are designed to handle data from paths, dove il
activity of a node could depend on multiple previous events, such as from a sequence of vis-
ited brain states where the current brain state does not depend on only the one immediately
preceding it. Per esempio, in Figure 3G one could imagine a situation in which the response of
region B to task 4 would depend on the responses of region D not only in task 2, but also in
task 1. Such a situation would show a second-order dependency of B as it depends on the state
of D two steps back. Multilayer networks represent systems that might (UN) have different types
of edges such as correlations in different frequency bands (Buldú & Porter, 2018), or different
data types entirely; (B) evolve with time (W. H. Thompson et al., 2017); O (C) include multiple
subjects (Muldoon & Bassett, 2016). Per esempio, one could imagine a multilayer network
where each node is a neuron and the edges in each layer would represent (UN) structural con-
nectivity, (B) functional connectivity, O (C) synapse types and numbers. These multilayer net-
works offer an attractive option to integrate multiple types of data, as reviewed in Boccaletti
et al. (2014) and discussed later. Additionally, sheaves are a mathematical framework that
allows one to represent not only the connections between nodes (as in the networks above),
but also the specific relationship, such as linear maps, between node activities or properties
that these connections represent. Thus far sheaves have been used for network coding prob-
lems (Ghrist & Hiraoka, 2011), signal processing (Robinson, 2013), and other applications
(Phan-Luong, 2008), but they have great potential for use in biological research (Blevins &
Bassett, 2020; Hansen & Ghrist, 2020). Though certainly not complete, we offer the above
examples to show the seemingly limitless possibilities of mathematical system representations
(Battiston et al., 2020; Torres et al., 2020).
EVALUATING MECHANISMS USING GENERATIVE MODELS
By encoding data as a set of pairwise interactions, a network, or a simplicial complex, inves-
tigators can use statistical and computational techniques to describe the patterns they see.
Tuttavia, description does not amount to explanation, and nor does a measurement automat-
ically produce an understanding. To move beyond description and measurement, and toward
explanation and understanding, it can often be useful to define generative models (Betzel &
Bassett, 2017UN). With what ingredients and assumptions could one generate the observed pair-
wise interactions? Or the network? Or the simplicial complex? If one were able to devise a set
of rules that produced data similar to those observed, then one would have identified a can-
didate mechanism for the observations (Bertolero & Bassett, 2020). Generative models do just
Quello. A generative model is a set of interaction rules that produces an outcome; and hence,
generative modeling as an approach can be used to determine what candidate mechanisms
may have produced the observed data. Although generative models exist at all scales of
Network Neuroscience
1135
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
T
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
analysis, here we will focus on generative models for networks. For those readers interested in
other scales, see Kanashiro et al. (2017) for a cellular-scale generative model of interactions
and Sizemore Blevins and Bassett (2020) for generative models of simplicial complexes.
Generative network models are defined by the specification of a wiring rule. Typically, wir-
ing rules are defined probabilistically. Per esempio, a node has a probability of connecting to
other nodes with certain features. In brain networks, two features are commonly evaluated:
(UN) a geometric feature such as the physical distance between two nodes, E (B) a topological
feature such as the degree or clustering coefficient of a node. Per esempio, one might generate a
network in which the probability of connecting node i to node j is negatively associated with the
distance between them and positively associated with the product of the degree of node i and the
degree of node j. The geometric and topological factors formally encode the two competing
drivers of connectivity: wiring minimization and topological efficiency (Bullmore & Sporns,
2012). A minimally wired network, in which only the shortest possible links are present, would
contain only edges between nearby nodes, requiring inefficient long relays to get information
from one part of the network to another. Conversely, a maximally efficient topology, one in
which topological path lengths are short, would contain edges between randomly chosen pairs
of nodes, requiring costly long-distance tracts. By balancing these two competing pressures, IL
two-feature generative models are able to produce networks with topologies that are notably
similar to those observed in real neural systems.
Generative network models are fairly young, and therefore a relatively small literature exists
applying them to open questions in systems neuroscience. Yet despite their youth, generative
network models have already been considered across species from C. elegans (Nicosia et al.,
2013) to humans (Betzel et al., 2016), from cellular connectomes (Vértes et al., 2014) to mac-
roscale connectomes (Betzel et al., 2016), and from healthy states to diseases states (Vértes
et al., 2012; X. Zhang et al., 2021). Efforts have begun extending generative network models
from the probabilistic so-called single-shot models that we have just described to growth
models; these extensions pose the question of what growth rule (rather than what static wiring
rule) might explain the observed trajectories of development, aging, or disease progression. UN
particularly exciting endeavor along these lines is the examination of a network morpho-
space constructed by the differential or combined expression of N network features (Avena-
Koenigsberger et al., 2014; Avena-Koenigsberger et al., 2015). The approach allows the
investigator to define a given network starting point (per esempio., an infant connectome, or a healthy
connectome) and rewire it to maximize or minimize a predefined set of network features, using
a multi-objective evolutionary algorithm. The goal is to ask whether that rewiring rule can take
the network to a final target point (per esempio., a young adult connectome, or a connectome character-
istic of a decade or more of neurodegeneration), precisely along the trajectory shown by devel-
opment or by disease progression (Tang et al., 2017). Such efforts offer the exciting potential to
test network hypotheses in a much more formal way than was hitherto possible, and to either
validate or disprove posited mechanisms.
DISCUSSION
The methods described above focus on the functional (in the sense of the inferred function of
the neurons) and temporal data from calcium imaging, but an additional challenge will be to
integrate those analyses with the multimodal information that can be collected in parallel with
calcium imaging. The additional modalities can be the physical position of the neurons (Betzel,
2020; X. Chen et al., 2018; Chiang et al., 2011), their ultrastructure (Hildebrand et al., 2017;
Vishwanathan et al., 2022; Zheng et al., 2018), molecular subtype (Lovett-Barron et al., 2017;
Network Neuroscience
1136
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
Shainer et al., 2022), morphology (Kunst et al., 2019), or even other cell-signaling reporters
(Linghu et al., 2020). The data from these various modalities can be categorical (subtypes of
neurons, morphology), time series (other cell signaling reporters), or numerical values (position
and projection trajectory), each potentially coming with their own metrics and specific ques-
zioni. The Euclidean distance between neurons’ spatial locations is easy to quantify, for exam-
ple, but it is less easy to know how to integrate these types of data, alongside functional data,
in the networks, or hypergraphs, and how to weight each modality to construct the model.
Despite the difficulty of the question of how to integrate multimodal datasets, researchers
from many disciplines have pushed forward in this direction. Primo, multilayer frameworks offer
one solution to incorporating multimodal data into one quantitative object. Per esempio, mul-
tilayer networks can combine multiple types of neuron connectivity (Schroeder et al., 2022),
activity from multiple frequency bands (Yu et al., 2017), or even data across individuals
(Vaiana & Muldoon, 2020) within one object. Notably, the multilayer approach is not
restricted to networks. Infatti, one could encode data as a multilayer simplicial complex or
hypergraph following a similar procedure. Alternatively, we can incorporate data about each
node using a node-annotated version of the above frameworks. In an annotated or attributed
rete, each node is also associated with a category (Bothorel et al., 2015; Yang et al., 2013)
or a continuous value. These extra data are then incorporated into analytical methods, for
example in performing community detection using task-based fMRI data (Murphy et al.,
2016). Extending these ideas naturally leads one to matrix-valued graphs (Trinh et al., 2018)
and sheaves (Robinson, 2017), which incorporate additional quantitative information on the
relations between nodes and node activity. Ancora, as we previously discussed, no one frame-
work fits every biological system and experiment, so we leave the finding of the perfect frame-
work as an open question, as there is still incredible space for creative solutions.
Though much of this work has focused on systems composed of individual neurons, an
additional future direction might consider how complex systems of neurons connect to that
of the entire brain (Betzel & Bassett, 2017B). Per esempio, networks could be created from
data collected at the neuron level, population level, and the whole-brain level. In order to
handle these multiple scales, one approach would create one network including all data,
and use hierarchical methods or community detection to find subnetwork structures and deter-
mine how they fit together (Fortunato, 2010; Meunier et al., 2009). Alternatively, one could
create a multilayer network with layers corresponding to the different neural scales (Betzel &
Bassett, 2017B). Such a multilayer approach could even incorporate multiscale temporal data
anche (Betzel & Bassett, 2017B). Networks of networks are even possible and often studied
under the name of interdependent networks using a multilayer network framework (Gao et al.,
2011). In TDA, the mathematics behind the methods allow for simple deconstruction of topo-
logical motifs of small complexes that are sub-complexes of a larger simplicial complex, così
allowing these tools to naturally incorporate multiscale data (Yoon & Ghrist, 2020). Finalmente, at a
more fundamental level one can control the resolution using the definition of nodes. For exam-
ple, one might define a node based on one neuron, a group of neurons, or even similarly clus-
tered data (Betzel, 2020; van Veen et al., 2019).
As described above, graphs and network science may provide a common framework in
which to integrate multiple information modalities (function, position, and neuronal identity,
among others), and multiple scales of information. Notably, graphs can incorporate changes
across time and represent the changing dynamics of the brain in different circumstances. IL
visualization and analytical tools offered by network science can look beyond pairwise inter-
actions and reveal larger patterns of interactions or dynamics. As such, graphs provide a pow-
erful basis on which to generate models of information processing and flow. Based on the
Network Neuroscience
1137
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
/
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
observed network statistics, one can test a set of wiring rules and evaluate whether it generates
a model similar to the observed network. Growth rules can be added to modify the wiring of
the model across various trajectories such as development or disease. These rules can pro-
vide testable hypotheses on the mechanism underlying the observed dynamics of the net-
lavoro. Overall, the best test of any model is in its prediction accuracy, combined with
advances in causal inferences, and circuit disruption technologies. One can imagine a sce-
nario where you can predict how your model would react to a given perturbation of its
wiring, and test it in vivo.
Finalmente, while this review focuses on systems neuroscience, these methods can be used in
any quantitative biological context. In ecology, one can use causal inference to identify how
species affect each other (Sugihara et al., 2012; D. D. Zhang et al., 2011) or network theory
approaches to model food webs or spatial interactions (Casselberry et al., 2020; Krause et al.,
2003). The same applies to cell biology, which benefited immensely from network approaches
for characterizing regulatory gene networks and protein-protein interactions, among other
interactions (Aittokallio & Schwikowski, 2006; Horvath & Dong, 2008; Martin et al., 2010).
With the expansion of calcium imaging into nonneural tissues, the tools discussed here will
also provide additional opportunities to better quantify, modello, and ultimately understand the
role calcium and intercell communication may play in diverse developmental and physiolog-
ical processes (Balaji et al., 2017; UN. J. Stevenson et al., 2020).
The availability of these types of data and their compatibility and searchability, anche
as innovative visualization techniques, will all influence how easily the integration can
occur (Akil et al., 2011). Efforts such as those led by the International Neuroinformatics
Coordinating Facility (BRAINS Expert Working Group et al., 2017; Eglen et al., 2017) exist
to standardize and unify neuroscience datasets, but they have not yet been embraced by
the community at large, and we still need to ensure the code can be reusable (Riquelme &
Gjorgjieva, 2021). Such commitments and infrastructural resources could serve to increase
the power of the analysis of such data, and help to ensure the reproducibility of the
research.
CONCLUSION
We have compiled and explained several of the most common data analysis approaches
available to systems neuroscientists. As we show, no single method is superior to all the
others and several are complimentary; researchers need to understand each method’s lim-
itations to choose the most appropriate one for their specific question. Knowing which
analysis will be used, and its limitations, can also guide experimental design to ensure that
the chosen method can be used to its full potential on the dataset. Per esempio, tools that
can uncover high-dimensional links, such as hypergraphs, would allow for more complex
stimuli or behaviors to be tested. On the contrary, they may require more parameter tuning,
or have more built-in assumptions, which may generate spurious results with low-
dimensional experiments. We also suggest that the complex systems field may provide
robust frameworks with which to integrate multiple streams of information. Per esempio,
multilayer networks, or networks of networks, could represent different information modal-
ities (functional imaging, molecular identity, physical location, or others) or different scales
(subcellular, single cell, populations, or whole brain). These frameworks also benefit from
the numerous tools that the wider mathematics community has developed. In conclusion,
we propose that multilayer networks are our best tool to integrate multimodal information
into a single framework.
Network Neuroscience
1138
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
/
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
CITATION DIVERSITY STATEMENT
Recent work in several fields of science has identified a bias in citation practices such that papers
from women and other minority scholars are under-cited relative to the number of such papers in
the field (Caplar et al., 2017; Dion et al., 2018; Dworkin et al., 2020; Maliniak et al., 2013;
Mitchell et al., 2013). Here we sought to proactively consider choosing references that reflect
the diversity of the field in thought, form of contribution, genere, race, ethnicity, and other fac-
tori. Primo, we obtained the predicted gender of the first and last author of each reference by using
databases that store the probability of a first name being carried by a woman (Dworkin et al.,
2020; Zhou et al., 2020). By this measure (and excluding self-citations to the first and last authors
of our current paper), our references contain 7.05% woman (first) / woman (last), 7.68%
man/woman, 15.18% woman/man, E 70.1% man/man. This method is limited in that (UN)
names, pronouns, and social media profiles used to construct the databases may not, in every
case, be indicative of gender identity and (B) it cannot account for intersex, nonbinary, or trans-
gender people. Secondo, we obtained the predicted racial/ethnic category of the first and last
author of each reference by databases that store the probability of a first and last name being
carried by an author of color (Ambekar et al., 2009; Sood & Laohaprapanon, 2018). By this mea-
sure (and excluding self-citations), our references contain 12.61% author of color (first) / author
of color (last), 16.13% white author / author of color, 22.15% author of color / white author, E
49.11% white author / white author. This method is limited in that (UN) names and Florida Voter
Data to make the predictions may not be indicative of racial/ethnic identity, E (B) it cannot
account for Indigenous and mixed-race authors, or those who may face differential biases due
to the ambiguous racialization or ethnicization of their names. We look forward to future work
that could help us to better understand how to support equitable practices in science.
AUTHOR CONTRIBUTIONS
Ann S. Blevins: Conceptualization; Visualization; Writing – original draft; Writing – review &
editing. Dani S. Bassett: Conceptualization; Supervision; Writing – review & editing. Ethan K.
Scott: Supervision; Writing – review & editing. Gilles Claude Vanwalleghem: Conceptualiza-
zione; Visualization; Writing – original draft; Writing – review & editing.
FUNDING INFORMATION
DANDRITE, Lundbeckfonden (https://dx.doi.org/10.13039/501100003554), Award ID:
DANDRITE-R248-2016-2518. Gilles Claude Vanwalleghem, Novo Nordisk Fonden (https://
dx.doi.org/10.13039/501100009708). Gilles Claude Vanwalleghem, Aarhus Universitets For-
skningsfond (https://dx.doi.org/10.13039/501100002739). Ethan K. Scott, National Health and
Medical Research Council (https://dx.doi.org/10.13039/501100000925), Award ID:
APP1066887. Ethan K. Scott, Australian Research Council (https://dx.doi.org/10.13039
/501100000923), Award ID: DP140102036 – DP110103612. Ethan K. Scott, Australian
Research Council (https://dx.doi.org/10.13039/501100000923), Award ID: FT110100887.
Dani S. Bassett, Army Research Office (https://dx.doi.org/10.13039/100000183), Award ID:
Bassett-W911NF-14-1-0679 and Grafton-W911NF-16-1-0474.
REFERENCES
Ahissar, E., & Kleinfeld, D. (2003). Closed-loop neuronal computa-
zioni: Focus on vibrissa somatosensation in rat. Cerebral Cortex,
13(1), 53–62. https://doi.org/10.1093/cercor/13.1.53, PubMed:
12466215
Aimon, S., Katsuki, T., Jia, T., Grosenick, L., Broxton, M., Deisseroth,
K . , S e j n o w s k i , T. J . , & G r e e n s p a n , R . J . ( 2 0 1 9 ) . F a s t
near-whole-brain imaging in adult Drosophila during
responses to stimuli and behavior. PLoS Biology, 17(2),
Network Neuroscience
1139
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
T
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
e2006732. https://doi.org/10.1371/journal.pbio.2006732,
PubMed: 30768592
Aittokallio, T., & Schwikowski, B. (2006). Graph-based methods for
analysing networks in cell biology. Briefings in Bioinformatics, 7(3),
243–255. https://doi.org/10.1093/bib/bbl022, PubMed: 16880171
Akil, H., Martone, M. E., & Van Essen, D. C. (2011). Challenges and
opportunities in mining neuroscience data. Scienza, 331(6018),
708–712. https://doi.org/10.1126/science.1199305, PubMed:
21311009
Ambekar, A., Ward, C., Mohammed, J., Male, S., & Skiena, S.
(2009). Name-ethnicity classification from open sources. Nel professionista-
ceedings of the 15th ACM SIGKDD international conference on
knowledge discovery and data mining – KDD ’09. https://doi.org
/10.1145/1557019.1557032
Avena-Koenigsberger, A., Goñi, J., Betzel, R. F., van den Heuvel,
M. P., Griffa, A., Hagmann, P., Thiran, J.-P., & Sporns, O.
(2014). Using Pareto optimality to explore the topology and
dynamics of the human connectome. Philosophical Transactions
of the Royal Society of London B: Biological Sciences, 369(1653),
20130530. https://doi.org/10.1098/rstb.2013.0530, PubMed:
25180308
Avena-Koenigsberger, A., Goñi, J., Solé, R., & Sporns, O. (2015).
Network morphospace. Journal of the Royal Society Interface,
12(103), 20140881. https://doi.org/10.1098/rsif.2014.0881,
PubMed: 25540237
Avitan, L., Pujic, Z., Mölter, J., McCullough, M., Zhu, S., Sun, B.,
Myhre, A.-E., & Goodhill, G. J. (2020). Behavioral signatures of
a developing neural code. Current Biology, 30(17), 3352–3363.
https://doi.org/10.1016/j.cub.2020.06.040, PubMed: 32710821
Avitan, L., Pujic, Z., Mölter, J., van de Poll, M., Sun, B., Teng, H.,
Amor, R., Scott, E. K., & Goodhill, G. J. (2017). Spontaneous
activity in the zebrafish tectum reorganizes over development
and is influenced by visual experience. Current Biology, 27(16),
2407–2419. https://doi.org/10.1016/j.cub.2017.06.056,
PubMed: 28781054
Balaji, R., Bielmeier, C., Harz, H., Bates, J., Stadler, C., Hildebrand,
A., & Classen, A.-K. (2017). Calcium spikes, waves and oscil-
lations in a large, patterned epithelial tissue. Scientific Reports,
7, 42786. https://doi.org/10.1038/srep42786, PubMed:
28218282
Bardin, J.-B., Spreemann, G., & Hess, K. (2019). Topological explo-
ration of artificial neuronal network dynamics. Network Neuro-
science, 3(3), 725–743. https://doi.org/10.1162/netn_a_00080,
PubMed: 31410376
Barlow, H. B. (1972). Single units and sensation: A neuron doctrine
for perceptual psychology? [Review of Single units and sensation:
A neuron doctrine for perceptual psychology?]. Perception, 1(4),
371–394. https://doi.org/10.1068/p010371, PubMed: 4377168
Bassett, D. S., & Bullmore, E. (2006). Small-world brain networks.
The Neuroscientist, 12(6), 512–523. https://doi.org/10.1177
/1073858406293182, PubMed: 17079517
Bassett, D. S., & Bullmore, E. T. (2017). Small-world brain networks
revisited. The Neuroscientist, 23(5), 499–516. https://doi.org/10
.1177/1073858416667720, PubMed: 27655008
Bassett, D. S., & Mattar, M. G. (2017). A network neuroscience of
human learning: Potential to inform quantitative theories of brain
and behavior. Trends in Cognitive Sciences, 21(4), 250–264.
https://doi.org/10.1016/j.tics.2017.01.010, PubMed: 28259554
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844
Bassett, D. S., Zurn, P., & Gold, J. IO. (2018). On the nature and use
of models in network neuroscience. Nature Reviews Neurosci-
ence, 19(9), 566–578. https://doi.org/10.1038/s41583-018-0038
-8, PubMed: 30002509
Basso, E., Arai, M., & Dabaghian, Y. (2016). Gamma synchroniza-
tion influences map formation time in a topological model of
spatial learning. PLoS Computational Biology, 12(9), e1005114.
https://doi.org/10.1371/journal.pcbi.1005114, PubMed:
27636199
Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania,
A., Young, J.-G., & Petri, G. (2020). Networks beyond pairwise
interactions: Structure and dynamics. Physics Reports, 874, 1–92.
https://doi.org/10.1016/j.physrep.2020.05.004
Belilovsky, E., Varoquaux, G., & Blaschko, M. B. (2015). Testing for
differences in Gaussian graphical models: Applications to brain
connectivity. arXiv:1512.08643. https://doi.org/10.48550/arXiv
.1512.08643
Bertolero, M. A., & Bassett, D. S. (2020). On the nature of explana-
tions offered by network science: A perspective from and for
practicing neuroscientists. Topics in Cognitive Science, 12(4),
1272–1293. https://doi.org/10.1111/tops.12504, PubMed:
32441854
Betzel, R. F. (2020). Organizing principles of whole-brain func-
tional connectivity in zebrafish larvae. Network Neuroscience,
4(1), 234–256. https://doi.org/10.1162/netn_a_00121, PubMed:
32166210
Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., Lui, Y., de Reus,
M. A., Griffa, A., Vértes, P. E., Mišic, B., Thiran, J.-P., Hagmann,
P., van den Heuvel, M., Zuo, X.-N., Bullmore, E. T., & Sporns, O.
(2016). Generative models of the human connectome. Neuro-
Image, 124(Pt. UN), 1054–1064. https://doi.org/10.1016/j
.neuroimage.2015.09.041, PubMed: 26427642
Betzel, R. F., & Bassett, D. S. (2017UN). Generative models for net-
work neuroscience: Prospects and promise. Journal of the Royal
Society Interface, 14(136), 20170623. https://doi.org/10.1098/rsif
.2017.0623, PubMed: 29187640
Betzel, R. F., & Bassett, D. S. (2017B). Multi-scale brain networks.
NeuroImage, 160, 73–83. https://doi.org/10.1016/j.neuroimage
.2016.11.006, PubMed: 27845257
Betzel, R. F., & Bassett, D. S. (2018). Specificity and robustness of
long-distance connections in weighted, interareal connectomes.
Proceedings of the National Academy of Sciences, 115(21),
E4880–E4889. https://doi.org/10.1073/pnas.1720186115,
PubMed: 29739890
Bielza, C., & Larrañaga, P. (2014). Bayesian networks in neurosci-
ence: A survey. Frontiers in Computational Neuroscience, 8,
131. https://doi.org/10.3389/fncom.2014.00131, PubMed:
25360109
Blevins, UN. S., & Bassett, D. S. (2020). Topology in biology. In Hand-
book of the Mathematics of the Arts and Sciences (pag. 1–23).
https://doi.org/10.1007/978-3-319-70658-0_87-1
Bobadilla-Suarez, S., Ahlheim, C., Mehrotra, A., Panos, A., & Love,
B. C. (2020). Measures of neural similarity. Computational Brain
and Behavior, 3(4), 369–383. https://doi.org/10.1007/s42113
-019-00068-5, PubMed: 33225218
Network Neuroscience
1140
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
Boccaletti, S., Bianconi, G., Criado, R., Del Genio, C. I., Gómez-
Gardeñes, J., Romance, M., Sendiña-Nadal, I., Wang, Z., &
Zanin, M. (2014). The structure and dynamics of multilayer net-
works. Physics Reports, 544(1), 1–122. https://doi.org/10.1016/j
.physrep.2014.07.001, PubMed: 32834429
Bothorel, C., Cruz, J. D., Magnani, M., & Micenková, B. (2015).
Clustering attributed graphs: Modelli, measures and methods.
Network Science, 3(3), 408–444. https://doi.org/10.1017/nws
.2015.9
BRAINS (Brain Imaging in Normal Subjects) Expert Working Group,
Shenkin, S. D., Pernet, C., Nichols, T. E., Poline, J.-B., Matthews,
P. M., van der Lugt, A., Mackay, C., Lanyon, L., Mazoyer, B.,
Boardman, J. P., Thompson, P. M., Fox, N., Marcus, D. S., Sheikh,
A., Cox, S. R., Anblagan, D., Job, D. E., Dickie, D. A., … Wardlaw,
J. M. (2017). Improving data availability for brain image bio-
banking in healthy subjects: Practice-based suggestions from
an international multidisciplinary working group. NeuroImage,
153, 399–409. https://doi.org/10.1016/j.neuroimage.2017.02
.030, PubMed: 28232121
Branner, A., & Normann, R. UN. (2000). A multielectrode array for
intrafascicular recording and stimulation in sciatic nerve of cats.
Brain Research Bulletin, 51(4), 293–306. https://doi.org/10.1016
/S0361-9230(99)00231-2, PubMed: 10704779
Broido, UN. D., & Clauset, UN. (2019). Scale-free networks are rare.
Nature Communications, 10(1), 1017. https://doi.org/10.1038
/s41467-019-08746-5, PubMed: 30833554
Buldú, J. M., & Porter, M. UN. (2018). Frequency-based brain net-
works: From a multiplex framework to a full multilayer descrip-
zione. Network Neuroscience, 2(4), 418–441. https://doi.org/10
.1162/netn_a_00033, PubMed: 30294706
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038
/nrn2575, PubMed: 19190637
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897
Cámara, P. G. (2017). Topological methods for genomics: Present
and future directions. Current Opinion in Systems Biology, 1,
95–101. https://doi.org/10.1016/j.coisb.2016.12.007, PubMed:
28983521
Caplar, N., Tacchella, S., & Birrer, S. (2017). Quantitative evalua-
tion of gender bias in astronomical publications from citation
conta. Nature Astronomy, 1(6), 0141. https://doi.org/10.1038
/s41550-017-0141
Carrillo-Reid, L., Han, S., O’Neil, D., Taralova, E., Jebara, T., &
Yuste, R. (2021). Identification of pattern completion neurons in
neuronal ensembles using probabilistic graphical models. Jour-
nal of Neuroscience, 41(41), 8577–8588. https://doi.org/10
.1523/JNEUROSCI.0051-21.2021, PubMed: 34413204
Casselberry, G. A., Danylchuk, UN. J., Finn, J. T., DeAngelis, B. M.,
Jordaan, A., Pollock, C. G., Lundgren, I., Hillis-Starr, Z., & Skomal,
G. B. (2020). Network analysis reveals multispecies spatial associ-
ations in the shark community of a Caribbean marine protected
area. Marine Ecology Progress Series, 633, 105–126. https://doi
.org/10.3354/meps13158
Cekic, S., Grandjean, D., & Renaud, O. (2018). Time, frequency,
and time-varying Granger-causality measures in neuroscience.
Statistics in Medicine, 37(11), 1910–1931. https://doi.org/10
.1002/sim.7621, PubMed: 29542141
Chang, A., Yao, T., & Allen, G. IO. (2019). Graphical models and
dynamic latent factors for modeling functional brain connectiv-
ità. 2019 IEEE Data Science Workshop (DSW), 57–63. https://doi
.org/10.1109/DSW.2019.8755783
Chen, T.-W., Wardill, T. J., Sun, Y., Pulver, S. R., Renninger, S. L.,
Baohan, A., Schreiter, E. R., Kerr, R. A., Orger, M. B., Jayaraman,
V., Looger, l. L., Svoboda, K., & Kim, D. S. (2013). Ultrasensitive
fluorescent proteins for imaging neuronal activity. Nature, 499(7458),
295–300. https://doi.org/10.1038/nature12354, PubMed:
23868258
Chen, X., Mu, Y., Eh, Y., Kuan, UN. T., Nikitchenko, M., Randlett, O.,
Chen, UN. B., Gavornik, J. P., Sompolinsky, H., Engert, F., &
Ahrens, M. B. (2018). Brain-wide organization of neuronal activ-
ity and convergent sensorimotor transformations in larval zebra-
pescare. Neuron, 100(4), 876–890. https://doi.org/10.1016/j.neuron
.2018.09.042, PubMed: 30473013
Chiang, A.-S., Lin, C.-Y., Chuang, C.-C., Chang, H.-M., Hsieh, C.-H.,
Yeh, C.-W., Shih, C.-T., Wu, J.-J., Wang, G.-T., Chen, Y.-C., Wu,
C.-C., Chen, G.-Y., Ching, Y.-T., Lee, P.-C., Lin, C.-Y., Lin, H.-H.,
Wu, C.-C., Hsu, H.-W., Huang, Y.-A., … Hwang, J.-K. (2011).
Three-dimensional reconstruction of brain-wide wiring net-
works in Drosophila at single-cell resolution. Current Biology,
21(1), 1–11. https://doi.org/10.1016/j.cub.2010.11.056,
PubMed: 21129968
Cliff, O. M., Lizier, J. T., Tsuchiya, N., & Fulcher, B. D. (2022). Uni-
f y i n g p a i r w i s e i n t e r a c t i o n s i n c o m p l e x d y n a m i c s .
arXiv:2201.11941. https://doi.org/10.48550/arXiv.2201.11941
Constantin, L., Poulsen, R. E., Scholz, l. A., Favre-Bulle, IO. A., Taylor,
M. A., Sun, B., Goodhill, G. J., Vanwalleghem, G. C., & Scott, E. K.
(2020). Altered brain-wide auditory networks in a zebrafish model
of fragile X syndrome. BMC Biology, 18(1), 125. https://doi.org/10
.1186/s12915-020-00857-6, PubMed: 32938458
Crossley, N. A., Mechelli, A., Vértes, P. E., Winton-Brown, T. T.,
Patel, UN. X., Ginestet, C. E., McGuire, P., & Bullmore, E. T.
(2013). Cognitive relevance of the community structure of the
human brain functional coactivation network. Proceedings of
the National Academy of Sciences, 110(28), 11583–11588.
https://doi.org/10.1073/pnas.1220826110, PubMed: 23798414
Curto, C. (2016). What can topology tell us about the neural code?
Bulletin of the American Mathematical Society, 54(1), 63–78.
https://doi.org/10.1090/bull/1554
Curto, C., Degeratu, A., & Itskov, V. (2012). Flexible memory net-
works. Bulletin of Mathematical Biology, 74(3), 590–614. https://
doi.org/10.1007/s11538-011-9678-9, PubMed: 21826564
Cutts, C. S., & Eglen, S. J. (2014). Detecting pairwise correlations in
spike trains: An objective comparison of methods and application
to the study of retinal waves. Journal of Neuroscience, 34(43),
14288–14303. https://doi.org/10.1523/ JNEUROSCI.2767-14
.2014, PubMed: 25339742
da Fontoura Costa, L., Rodrigues, F. A., Travieso, G., & Villas Boas,
P. R. (2007). Characterization of complex networks: A survey of
measurements. Advances in Physics, 56(1), 167–242. https://doi
.org/10.1080/00018730601170527
Dal Maschio, M., Donovan, J. C., Helmbrecht, T. O., & Baier, H.
(2017). Linking neurons to network function and behavior by
two-photon holographic optogenetics and volumetric imaging.
Network Neuroscience
1141
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
/
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
Neuron, 94(4), 774–789. https://doi.org/10.1016/j.neuron.2017
.04.034, PubMed: 28521132
Davison, E. N., Schlesinger, K. J., Bassett, D. S., Lynall, M.-E.,
Mugnaio, M. B., Grafton, S. T., & Carlson, J. M. (2015). Brain net-
work adaptability across task states. PLoS Computational Biology,
11(1), e1004029. https://doi.org/10.1371/journal.pcbi.1004029,
PubMed: 25569227
Davison, E. N., Turner, B. O., Schlesinger, K. J., Mugnaio, M. B., Grafton,
S. T., Bassett, D. S., & Carlson, J. M. (2016). Individual differences
in dynamic functional brain connectivity across the human life-
span. PLoS Computational Biology, 12(11), e1005178. https://
doi.org/10.1371/journal.pcbi.1005178, PubMed: 27880785
Dimitriadis, S. I., Lancaster, T. M., Perry, G., Tansey, K. E., Jones,
D. K., Singh, K. D., Zammit, S., Davey Smith, G., Hall, J.,
O’Donovan, M. C., Owen, M. J., & Linden, D. E. (2021).
Global brain flexibility during working memory is reduced in a
high genetic risk group for schizophrenia. Biological Psychiatry:
Cognitive Neuroscience and Neuroimaging, 6(12), 1176–1184.
https://doi.org/10.1016/j.bpsc.2021.01.007, PubMed: 33524599
Dion, M. L., Sumner, J. L., & Mitchell, S. M. (2018). Gendered cita-
tion patterns across political science and social science method-
ology fields. Political Analysis, 26(3), 312–327. https://doi.org/10
.1017/pan.2018.12
Dunn, T. W., Mu, Y., Narayan, S., Randlett, O., Naumann, E. A.,
Yang, C.-T., Schier, UN. F., Freeman, J., Engert, F., & Ahrens,
M. B. (2016). Brain-wide mapping of neural activity controlling
zebrafish exploratory locomotion. eLife, 5, e12741. https://doi
.org/10.7554/eLife.12741, PubMed: 27003593
Dworkin, J. D., Linn, K. A., Teich, E. G., Zurn, P., Shinohara, R. T., &
Bassett, D. S. (2020). The extent and drivers of gender imbalance
in neuroscience reference lists. Nature Neuroscience, 23(8),
918–926. https://doi.org/10.1038/s41593-020-0658-y, PubMed:
32561883
Eglen, S. J., Marwick, B., Halchenko, Y. O., Hanke, M., Sufi, S.,
Gleeson, P., Silver, R. A., Davison, UN. P., Lanyon, L., Abrams,
M., Wachtler, T., Willshaw, D. J., Pouzat, C., & Poline, J.-B.
(2017). Toward standard practices for sharing computer code
and programs in neuroscience. Nature Neuroscience, 20(6),
770–773. https://doi.org/10.1038/nn.4550, PubMed: 28542156
Fallani, F. D. V., Corazzol, M., Sternberg, J. R., Wyart, C., & Chavez,
M. (2015). Hierarchy of neural organization in the embryonic
spinal cord: Granger-causality graph analysis of in vivo calcium
imaging data. IEEE Transactions on Neural Systems and Rehabil-
itation Engineering, 23(3), 333–341. https://doi.org/10.1109
/TNSRE.2014.2341632, PubMed: 25122836
Favre-Bulle, IO. A., Taylor, M. A., Marquez-Legorreta, E., Vanwalleghem,
G., Poulsen, R. E., Rubinsztein-Dunlop, H., & Scott, E. K. (2020).
Sound generation in zebrafish with Bio-Opto-Acoustics. Nature
Communications, 11(1), 6120. https://doi.org/10.1038/s41467-020
-19982-5, PubMed: 33257652
Favre-Bulle, IO. A., Vanwalleghem, G., Taylor, M. A., Rubinsztein-
Dunlop, H., & Scott, E. K. (2018). Cellular-resolution imaging
of vestibular processing across the larval zebrafish brain. Current
Biology, 28(23), 3711–3722. https://doi.org/10.1016/j.cub.2018
.09.060, PubMed: 30449665
Fernandes, UN. M., Mearns, D. S., Donovan,
J.,
Helmbrecht, T. O., Kölsch, Y., Laurell, E., Kawakami, K.,
(2021). Neural circuitry for
Dal Maschio, M., & Baier, H.
J. C., Larsch,
stimulus selection in the zebrafish visual system. Neuron,
109(5), 805–822. https://doi.org/10.1016/j.neuron.2020.12
.002, PubMed: 33357384
Fornito, A., Zalesky, A., & Bullmore, E. (2016). Fundamentals of
brain network analysis. Academic Press.
Fortunato, S. (2010). Community detection in graphs. Physics Reports,
486(3), 75–174. https://doi.org/10.1016/j.physrep.2009.11.002
Freeman, J., Vladimirov, N., Kawashima, T., Mu, Y., Sofroniew,
N. J., Bennett, D. V., Rosen, J., Yang, C.-T., Looger, l. L., &
Ahrens, M. B. (2014). Mapping brain activity at scale with cluster
computing. Nature Methods, 11(9), 941–950. https://doi.org/10
.1038/nmeth.3041, PubMed: 25068736
Friedrich, R. W., Habermann, C. J., & Laurent, G. (2004). Multiplex-
ing using synchrony in the zebrafish olfactory bulb. Nature Neu-
roscience, 7(8), 862–871. https://doi.org/10.1038/nn1292,
PubMed: 15273692
Gao, J., Buldyrev, S. V., Eugene Stanley, H., & Havlin, S. (2011).
Networks formed from interdependent networks. Nature Physics,
8(1), 40–48. https://doi.org/10.1038/nphys2180
Geniesse, C., Chowdhury, S., & Saggar, M. (2022). NeuMapper: UN
scalable computational framework for multiscale exploration of
the brain’s dynamical organization. Network Neuroscience, 6(2),
467–498. https://doi.org/10.1162/netn_a_00229, PubMed:
35733428
Geniesse, C., Sporns, O., Petri, G., & Saggar, M. (2019). Generating
dynamical neuroimaging spatiotemporal representations
(DyNeuSR) using topological data analysis. Network Neurosci-
ence, 3(3), 763–778. https://doi.org/10.1162/netn_a_00093,
PubMed: 31410378
Ghrist, R. (2007). Barcodes: The persistent topology of data. Bulle-
tin of the American Mathematical Society, 45(1), 61–76. https://
doi.org/10.1090/S0273-0979-07-01191-3
Ghrist, R., & Hiraoka, Y. (2011). Applications of sheaf cohomology
and exact sequences on network codings. Preprint. https://
citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.224.6433
&rep=rep1&type=pdf
Giusti, C., Pastalkova, E., Curto, C., & Itskov, V. (2015). Clique
topology reveals intrinsic geometric structure in neural correlations.
Proceedings of the National Academy of Sciences, 112(44),
13455–13460. https://doi.org/10.1073/pnas.1506407112,
PubMed: 26487684
Gracia-Tabuenca, Z., Díaz-Patiño, J. C., Arelio, I., & Alcauter, S.
(2020). Topological data analysis reveals robust alterations in
the whole-brain and frontal lobe functional connectomes in
attention-deficit/ hyperactivity disorder. bioRxiv. https://doi.org
/10.1101/751008
Granger, C. W. J. (1969). Investigating causal relations by economet-
ric models and cross-spectral methods. Econometrica, 37(3),
424–438. https://doi.org/10.2307/1912791
Haesemeyer, M., Schier, UN. F., & Engert, F. (2019). Convergent tem-
perature representations in artificial and biological neural net-
works. Neuron, 103(6), 1123–1134. https://doi.org/10.1016/j
.neuron.2019.07.003, PubMed: 31376984
Hansen, J., & Ghrist, R. (2020). Opinion dynamics on discourse
sheaves. arXiv:2005.12798. https://doi.org/10.48550/arXiv.2005
.12798
Hastings, J. W., Mitchell, G., Mattingly, P. H., Blinks, J. R., & Van
Leeuwen, M. (1969). Response of aequorin bioluminescence to
Network Neuroscience
1142
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
/
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
rapid changes in calcium concentration. Nature, 222(5198),
1047–1050. https://doi.org/10.1038/2221047a0, PubMed:
4389183
Helmbrecht, T. O., Dal Maschio, M., Donovan, J. C., Koutsouli, S.,
& Baier, H. (2018). Topography of a visuomotor transformation.
Neuron, 100(6), 1429–1445. https://doi.org/10.1016/j.neuron
.2018.10.021, PubMed: 30392799
Hildebrand, D. G. C., Cicconet, M., Torres, R. M., Choi, W., Quan,
T. M., Moon, J., Wetzel, UN. W., Scott Champion, A., Graham,
B. J., Randlett, O., Plummer, G. S., Portugues, R., Bianco, IO. H.,
Saalfeld, S., Baden, UN. D., Lillaney, K., Burns, R., Vogelstein, J. T.,
Schier, UN. F., … Engert, F. (2017). Whole-brain serial-section elec-
tron microscopy in larval zebrafish. Nature, 545(7654), 345–349.
https://doi.org/10.1038/nature22356, PubMed: 28489821
Hilgetag, C. C., & Goulas, UN. (2016). Is the brain really a
small-world network? Brain Structure and Function, 221(4),
2361–2366. https://doi.org/10.1007/s00429-015-1035-6,
PubMed: 25894630
Horvath, S., & Dong, J. (2008). Geometric interpretation of gene
coexpression network analysis. PLoS Computational Biology, 4(8),
e1000117. https://doi.org/10.1371/journal.pcbi.1000117,
PubMed: 18704157
Ince, R. UN. A., Panzeri, S., & Kayser, C. (2013). Neural codes formed
by small and temporally precise populations in auditory cortex.
Journal of Neuroscience, 33(46), 18277–18287. https://doi.org
/10.1523/JNEUROSCI.2631-13.2013, PubMed: 24227737
Javidian, M. A., Wang, Z., Lu, L., & Valtorta, M. (2020). On a hyper-
graph probabilistic graphical model. Annals of Mathematics and
Artificial Intelligence, 88(9), 1003–1033. https://doi.org/10.1007
/s10472-020-09701-7
Kaiser, M., & Varier, S. (2011). Evolution and development of brain
networks: From Caenorhabditis elegans to Homo sapiens. Net-
lavoro, 22(1–4), 143–147. https://doi.org/10.3109/0954898X
.2011.638968, PubMed: 22149674
Kanashiro, T., Ocker, G. K., Cohen, M. R., & Doiron, B. (2017).
Attentional modulation of neuronal variability in circuit models
of cortex. eLife, 6, e23978. https://doi.org/10.7554/eLife.23978,
PubMed: 28590902
Kim, D. H., Kim, J., Marques, J. C., Grama, A., Hildebrand,
D. G. C., Gu, W., Li, J. M., & Robson, D. N. (2017). Pan-neuronal
calcium imaging with cellular resolution in freely swimming zeb-
rafish. Nature Methods, 14(11), 1107–1114. https://doi.org/10
.1038/nmeth.4429, PubMed: 28892088
Knight, B. W. (1972). Dynamics of encoding in a population of neu-
rons. Journal of General Physiology, 59(6), 734–766. https://doi
.org/10.1085/jgp.59.6.734, PubMed: 5025748
Krause, UN. E., Frank, K. A., Mason, D. M., Ulanowicz, R. E., & Taylor,
W. W. (2003). Compartments revealed in food-web structure.
N at u re , 42 6(6 96 4), 2 82 –2 85 . h tt p s : / / d o i . o rg/ 1 0 . 1 0 3 8
/nature02115, PubMed: 14628050
Kunst, M., Laurell, E., Mokayes, N., Kramer, A., Kubo, F., Fernandes,
UN. M., Förster, D., Dal Maschio, M., & Baier, H. (2019). UN
cellular-resolution atlas of the larval zebrafish brain. Neuron,
103(1), 21–38. https://doi.org/10.1016/j.neuron.2019.04.034,
PubMed: 31147152
Lepperød, M. E., Stöber, T., Hafting, T., Fyhn, M., & Kording, K. P.
(2018). Inferring causal connectivity from pairwise recordings
and optogenetics. bioRxiv. https://doi.org/10.1101/463760
Linghu, C., Johnson, S. L., Valdes, P. A., Shemesh, O. A., Park,
W. M., Park, D., Piatkevich, K. D., Wassie, UN. T., Liu, Y., An,
B., Barnes, S. A., Celiker, O. T., Yao, C.-C., Yu, C.-C. J., Wang,
R., Adamala, K. P., Bear, M. F., Keating, UN. E., & Boyden, E. S.
(2020). Spatial multiplexing of fluorescent reporters for imaging
signaling network dynamics. Cell, 183(6), 1682–1698. https://doi
.org/10.1016/j.cell.2020.10.035, PubMed: 33232692
Lisman, J. E., & Grace, UN. UN. (2005). The hippocampal-VTA loop:
Controlling the entry of information into long-term memory. Neu-
ron, 46(5), 703–713. https://doi.org/10.1016/j.neuron.2005.05
.002, PubMed: 15924857
Lovett-Barron, M., Andalman, UN. S., Allen, W. E., Vesuna, S., Kauvar,
I., Burns, V. M., & Deisseroth, K. (2017). Ancestral circuits for the
coordinated modulation of brain state. Cell, 171(6), 1411–1423.
https://doi.org/10.1016/j.cell.2017.10.021, PubMed: 29103613
Luchiari, UN. C., & Chacon, D. M. M. (2013). Physical exercise
improves learning in zebrafish, Danio rerio. Behavioural Pro-
cesses, 100, 44–47. https://doi.org/10.1016/j.beproc.2013.07
.020, PubMed: 23933376
Ma’ayan, A., Cecchi, G. A., Wagner, J., Rao, UN. R., Iyengar, R., &
Stolovitzky, G. (2008). Ordered cyclic motifs contribute to
dynamic stability in biological and engineered networks. Pro-
ceedings of the National Academy of Sciences, 105(49),
19235–19240. https://doi.org/10.1073/pnas.0805344105,
PubMed: 19033453
Maliniak, D., Powers, R., & Walter, B. F. (2013). The gender citation
gap in international relations. International Organization, 67(4),
889–922. https://doi.org/10.1017/S0020818313000209
Marinescu, IO. E., Lawlor, P. N., & Kording, K. P. (2018). Quasi-
experimental causality in neuroscience and behavioural
research. Nature Human Behaviour, 2(12), 891–898. https://doi
.org/10.1038/s41562-018-0466-5, PubMed: 30988445
Marques, J. C., Li, M., Schaak, D., Robson, D. N., & Li, J. M. (2020).
Internal state dynamics shape brainwide activity and foraging
behaviour. Nature, 577(7789), 239–243. https://doi.org/10.1038
/s41586-019-1858-z, PubMed: 31853063
Marshel, J. H., Kim, Y. S., Machado, T. A., Quirin, S., Benson, B.,
Kadmon, J., Raja, C., Chibukhchyan, A., Ramakrishnan, C., Inoue,
M., Shane, J. C., McKnight, D. J., Yoshizawa, S., Kato, H. E.,
Ganguli, S., & Deisseroth, K. (2019). Cortical layer–specific crit-
ical dynamics triggering perception. Scienza, 365(6453),
eaaw5202. https://doi.org/10.1126/science.aaw5202, PubMed:
31320556
Martin, A., Ochagavia, M. E., Rabasa, l. C., Miranda, J., Fernandez-
de-Cossio, J., & Bringas, R. (2010). BisoGenet: A new tool for
gene network building, visualization and analysis. BMC Bioinfor-
matics, 11, 91. https://doi.org/10.1186/1471-2105-11-91,
PubMed: 20163717
Meunier, D., Lambiotte, R., Fornito, A., Ersche, K. D., & Bullmore,
E. T. (2009). Hierarchical modularity in human brain functional
networks. Frontiers in Neuroinformatics, 3, 37. https://doi.org/10
.3389/neuro.11.037.2009, PubMed: 19949480
Migault, G., van der Plas, T. L., Trentesaux, H., Panier, T., Candelier,
R., Proville, R., Englitz, B., Debrégeas, G., & Bormuth, V. (2018).
Whole-brain calcium imaging during physiological vestibular
stimulation in larval zebrafish. Current Biology, 28(23),
3723–3735. https://doi.org/10.1016/j.cub.2018.10.017,
PubMed: 30449666
Network Neuroscience
1143
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
/
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
Miri, A., Daie, K., Burdine, R. D., Aksay, E., & Tank, D. W. (2011).
Regression-based identification of behavior-encoding neurons
during large-scale optical imaging of neural activity at cellular
resolution. Journal of Neurophysiology, 105(2), 964–980.
https://doi.org/10.1152/jn.00702.2010, PubMed: 21084686
Mitchell, S. M., Lange, S., & Brus, H. (2013). Gendered citation pat-
terns in international relations journals. International Studies Per-
spectives, 14(4), 485–492. https://doi.org/10.1111/insp.12026
Miyawaki, A., Llopis, J., Heim, R., McCaffery, J. M., Adams, J. A.,
Ikura, M., & Tsien, R. Y. (1997). Fluorescent indicators for Ca2+
based on green fluorescent proteins and calmodulin. Nature,
388(6645), 882–887. https://doi.org/10.1038/42264, PubMed:
9278050
Mölter, J., Avitan, L., & Goodhill, G. J. (2018). Detecting neural
assemblies in calcium imaging data. BMC Biology, 16(1), 143.
https://doi.org/10. 1186/s12915-018-0606-4, PubMed:
30486809
Mu, Y., Bennett, D. V., Rubinov, M., Narayan, S., Yang, C.-T.,
Tanimoto, M., Mensh, B. D., Looger, l. L., & Ahrens, M. B.
(2019). Glia accumulate evidence that actions are futile and
suppress unsuccessful behavior. Cell, 178(1), 27–43. https://
doi.org/10.1016/j.cell.2019.05.050, PubMed: 31230713
Muldoon, S. F., & Bassett, D. S. (2016). Network and multilayer net-
work approaches to understanding human brain dynamics. Phi-
losophy of Science, 83(5), 710–720. https://doi.org/10.1086
/687857
Muldoon, S. F., Bridgeford, E. W., & Bassett, D. S. (2016). Small-
world propensity and weighted brain networks. Scientific
Reports, 6, 22057. https://doi.org/10.1038/srep22057, PubMed:
26912196
Muller, L., Destexhe, A., & Rudolph-Lilith, M. (2014). Brain net-
works: Small-worlds, after all? New Journal of Physics, 16(10),
105004. https://doi.org/10.1088/1367-2630/16/10/105004
Munch, E. (2017). A user’s guide to topological data analysis. Jour-
nal of Learning Analytics, 4(2), 47–61. https://doi.org/10.18608
/jla.2017.42.6
Murphy, UN. C., Gu, S., Khambhati, UN. N., Wymbs, N. F., Grafton,
S. T., Satterthwaite, T. D., & Bassett, D. S. (2016). Explicitly link-
ing regional activation and function connectivity: Comunità
structure of weighted networks with continuous annotation.
arXiv:1611.07962. https://doi.org/10.48550/arXiv.1611.07962
Murugesan, G. K., Ganesh, C., Nalawade, S., Davenport, E. M.,
Wagner, B., Kim, W. H., & Maldjian, J. UN. (2020). BrainNET:
Inference of brain network topology using machine learning.
Brain Connectivity, 10(8), 422–435. https://doi.org/10.1089
/brain.2020.0745, PubMed: 33030350
Nakai, J., Ohkura, M., & Imoto, K. (2001). A high signal-to-noise
Ca(2+) probe composed of a single green fluorescent protein.
Nature Biotechnology, 19(2), 137–141. https://doi.org/10.1038
/84397, PubMed: 11175727
Naumann, E. A., Fitzgerald, J. E., Dunn, T. W., Rihel, J., Sompolinsky,
H., & Engert, F. (2016). From whole-brain data to functional cir-
cuit models: The zebrafish optomotor response. Cell, 167(4),
947–960. https://doi.org/10.1016/j.cell.2016.10.019, PubMed:
27814522
Nelson, C. J., & Bonner, S. (2021). Neuronal graphs: A graph theory
primer for microscopic, functional networks of neurons recorded
by calcium imaging. Frontiers in Neural Circuits, 15, 662882.
https://doi.org/10.3389/fncir.2021.662882, PubMed: 34177469
Nguyen, J. P., Shipley, F. B., Linder, UN. N., Plummer, G. S., Liu, M.,
Setru, S. U., Shaevitz, J. W., & Leifer, UN. M. (2016). Whole-brain
calcium imaging with cellular resolution in freely behaving Cae-
norhabditis elegans. Proceedings of the National Academy of Sci-
enze, 113(8), E1074–E1081. https://doi.org/10.1073/pnas
.1507110112, PubMed: 26712014
Nicolau, M., Levine, UN. J., & Carlsson, G. (2011). Topology based
data analysis identifies a subgroup of breast cancers with a
unique mutational profile and excellent survival. Proceedings
of the National Academy of Sciences, 108(17), 7265–7270.
https://doi.org/10.1073/pnas.1102826108, PubMed: 21482760
Nicosia, V., Vértes, P. E., Schafer, W. R., Latora, V., & Bullmore, E. T.
(2013). Phase transition in the economically modeled growth of
a cellular nervous system. Proceedings of the National Academy
of Sciences, 110(19), 7880–7885. https://doi.org/10.1073/pnas
.1300753110, PubMed: 23610428
Nielson, J. L., Paquette, J., Liu, UN. W., Guandique, C. F., Tovar,
C. A., Inoue, T., Irvine, K.-A., Gensel, J. C., Kloke, J., Petrossian,
T. C., Lum, P. Y., Carlsson, G. E., Manley, G. T., Young, W., Beattie,
M. S., Bresnahan, J. C., & Ferguson, UN. R. (2015). Topological data
analysis for discovery in preclinical spinal cord injury and trau-
matic brain injury. Nature Communications, 6, 8581. https://doi
.org/10.1038/ncomms9581, PubMed: 26466022
Nienborg, H., & Cumming, B. (2010). Correlations between the
activity of sensory neurons and behavior: How much do they tell
us about a neuron’s causality? Current Opinion in Neurobiology,
20(3), 376–381. https://doi.org/10.1016/j.conb.2010.05.002,
PubMed: 20545019
Oldfield, C. S., Grossrubatscher, I., Chávez, M., Hoagland, A.,
Huth, UN. R., Carroll, E. C., Prendergast, A., Qu, T., Gallant,
J. L., Wyart, C., & Isacoff, E. Y. (2020). Experience, circuit dynam-
ics, and forebrain recruitment in larval zebrafish prey capture.
eLife, 9, e56619. https://doi.org/10.7554/eLife.56619, PubMed:
32985972
Onnela, J.-P., Fenn, D. J., Reid, S., Porter, M. A., Mucha, P. J.,
Fricker, M. D., & Jones, N. S. (2012). Taxonomies of networks
from community structure. Physical Review E, 86(3 Pt. 2),
036104. https://doi.org/10.1103/PhysRevE.86.036104, PubMed:
23030977
Paninski, L., Pillow, J., & Lewi, J. (2007). Statistical models for neu-
ral encoding, decoding, and optimal stimulus design. Progress in
Brain Research, 165, 493–507. https://doi.org/10.1016/S0079
-6123(06)65031-0, PubMed: 17925266
Paulk, UN. C., Kfir, Y., Khanna, UN. R., Mustroph, M. L., Trautmann,
E. M., Soper, D. J., Stavisky, S. D., Welkenhuysen, M., Dutta, B.,
Shenoy, K. V., Hochberg, l. R., Richardson, R. M., Williams,
Z. M., & Cash, S. S. (2022). Large-scale neural recordings with
single neuron resolution using Neuropixels probes in human cor-
tex. Nature Neuroscience, 25(2), 252–263. https://doi.org/10
.1038/s41593-021-00997-0, PubMed: 35102333
Pedersen, M., Zalesky, A., Omidvarnia, A., & Jackson, G. D. (2018).
Multilayer network switching rate predicts brain performance.
Proceedings of the National Academy of Sciences, 115(52),
13376–13381. https://doi.org/10.1073/pnas.1814785115,
PubMed: 30545918
Network Neuroscience
1144
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
Phan-Luong, V. (2008). A framework for integrating information
sources under lattice structure. Information Fusion, 9(2), 278–292.
https://doi.org/10.1016/j.inffus.2007.01.002
Ponce-Alvarez, A., Jouary, A., Privat, M., Deco, G., & Sumbre, G.
(2018). Whole-brain neuronal activity displays crackling noise
dynamics. Neuron, 100(6), 1446–1459. https://doi.org/10.1016
/j.neuron.2018.10.045, PubMed: 30449656
Poulsen, R. E., Scholz, l. A., Constantin, L., Favre-Bulle, I., Vanwalleghem,
G. C., & Scott, E. K. (2021). Broad frequency sensitivity and com-
plex neural coding in the larval zebrafish auditory system. Current
Biology, 31(9), 1977–1987. https://doi.org/10.1016/j.cub.2021
.01.103, PubMed: 33657408
Privat, M., Romano, S. A., Pietri, T., Jouary, A., Boulanger-Weill, J.,
Elbaz, N., Duchemin, A., Soares, D., & Sumbre, G. (2019).
Sensorimotor transformations in the zebrafish auditory system.
Current Biology, 29(23), 4010–4023. https://doi.org/10.1016/j
.cub.2019.10.020, PubMed: 31708392
Quian Quiroga, R., & Panzeri, S. (2009). Extracting information
from neuronal populations: Information theory and decoding
approcci. Nature Reviews Neuroscience, 10(3), 173–185.
https://doi.org/10.1038/nrn2578, PubMed: 19229240
Reimann, M. W., Nolte, M., Scolamiero, M., Turner, K., Perin, R.,
Chindemi, G., Dłotko, P., Levi, R., Hess, K., & Markram, H.
(2017). Cliques of neurons bound into cavities provide a missing
link between structure and function. Frontiers in Computational
Neuroscience, 11, 48. https://doi.org/10.3389/fncom.2017
.00048, PubMed: 28659782
Riquelme, J. L., & Gjorgjieva, J. (2021). Towards readable code in
neuroscience. Nature Reviews Neuroscience, 22(5), 257–258.
https://doi.org/10.1038/s41583-021-00450-y, PubMed:
33707744
Robinson, M. (2013). Understanding networks and their behaviors
using sheaf theory. 2013 IEEE Global Conference on Signal and
Information Processing. https://doi.org/10.1109/GlobalSIP.2013
.6737040
Robinson, M. (2017). Sheaves are the canonical data structure for
sensor integration. Information Fusion, 36, 208–224. https://doi
.org/10.1016/j.inffus.2016.12.002
Rombach, M. P., Porter, M. A., Fowler, J. H., & Mucha, P. J. (2014).
Core-periphery structure in networks. SIAM Journal on Applied
Mathematics, 74(1), 167–190. https://doi.org/10.1137
/120881683
Rubin, A., Sheintuch, L., Brande-Eilat, N., Pinchasof, O., Rechavi,
Y., Geva, N., & Ziv, Y. (2019). Revealing neural correlates of
behavior without behavioral measurements. Nature Communica-
zioni, 10(1), 4745. https://doi.org/10.1038/s41467-019-12724-2,
PubMed: 31628322
Saggar, M., Sporns, O., Gonzalez-Castillo, J., Bandettini, P. A.,
Carlsson, G., Glover, G., & Reiss, UN. l. (2018). Towards a new
approach to reveal dynamical organization of the brain using
topological data analysis. Nature Communications, 9(1), 1399.
https://doi.org/10.1038/s41467-018-03664-4, PubMed:
29643350
Schroeder, M. E., Bassett, D. S., & Meaney, D. F. (2022). A multi-
layer network model of neuron-astrocyte populations in vitro
reveals mGluR5 inhibition is protective following traumatic
injury. Network Neuroscience, 6(2), 499–527. https://doi.org/10
.1162/netn_a_00227, PubMed: 35733423
Shainer, I., Kuehn, E., Laurell, E., Kassar, M. A., Mokayes, N., Sherman,
S., Larsch, J., Kunst, M., & Baier, H. (2022). A single-cell resolu-
tion gene expression atlas of the larval zebrafish brain. bioRxiv.
https://doi.org/10.1101/2022.02.11.479024
Shih, C.-T., Lin, Y.-J., Wang, C.-T., Wang, T.-Y., Chen, C.-C., Su, T.-S.,
Lo, C.-C., & Chiang, A.-S. (2020). Diverse community structures in
the neuronal-level connectome of the Drosophila brain. Neuroin-
formatics, 18(2), 267–281. https://doi.org/10.1007/s12021-019
-09443-w, PubMed: 31797265
Shih, C.-T., Sporns, O., Yuan, S.-L., Su, T.-S., Lin, Y.-J., Chuang, C.-C.,
Wang, T.-Y., Lo, C.-C., Greenspan, R. J., & Chiang, A.-S. (2015).
Connectomics-based analysis of information flow in the Drosoph-
ila brain. Current Biology, 25(10), 1249–1258. https://doi.org/10
.1016/j.cub.2015.03.021, PubMed: 25866397
Singh, G., Mémoli, F., & Carlsson, G. E. (2007). Topological
methods for the analysis of high dimensional data sets and 3D
object recognition. In Eurographics Symposium on Point-Based
Graphics (pag. 91–100).
Sizemore, A., Giusti, C., & Bassett, D. S. (2016). Classification of
weighted networks through mesoscale homological features.
Journal of Complex Networks, 5(2), 245–273. https://doi.org/10
.1093/comnet/cnw013
Sizemore, UN. E., Giusti, C., Kahn, A., Vettel, J. M., Betzel, R. F., &
Bassett, D. S. (2018). Cliques and cavities in the human connec-
tome. Journal of Computational Neuroscience, 44(1), 115–145.
https://doi.org/10.1007/s10827-017-0672-6, PubMed:
29143250
Sizemore, UN. E., Phillips-Cremins, J. E., Ghrist, R., & Bassett, D. S. (2019).
The importance of the whole: Topological data analysis for the
network neuroscientist. Network Neuroscience, 3(3), 656–673.
https://doi.org/10.1162/netn_a_00073, PubMed: 31410372
Sizemore Blevins, A., & Bassett, D. S. (2020). Reorderability of
node-filtered order complexes. Physical Review E, 101(5-1),
052311. https://doi.org/10.1103/ PhysRevE.101.052311,
PubMed: 32575295
Smith, P. F. (2018). On the application of multivariate statistical and
data mining analyses to data in neuroscience. Journal of Under-
graduate Neuroscience Education: JUNE, 16(2), R20–R32.
PubMed: 30057506
Sood, G., & Laohaprapanon, S. (2018). Predicting race and ethnicity
from the sequence of characters in a name. arXiv:1805.02109.
https://doi.org/10.48550/arXiv.1805.02109
Spivak, D. IO. (2009). Higher-dimensional models of networks.
arXiv:0909.4314. https://doi.org/10.48550/arXiv.0909.4314
Sporns, O. (2018). Graph theory methods: Applications in brain
networks. Dialogues in Clinical Neuroscience, 20(2), 111–121.
https://doi.org/10.31887/ DCNS.2018.20.2/osporns, PubMed:
30250388
Steinmetz, N. A., Zatka-Haas, P., Carandini, M., & Harris, K. D.
(2019). Distributed coding of choice, action and engagement
across the mouse brain. Nature, 576(7786), 266–273. https://
doi.org/10.1038/s41586-019-1787-x, PubMed: 31776518
Stevenson, UN. J., Vanwalleghem, G., Stewart, T. A., Condon, N. D.,
Lloyd-Lewis, B., Marino, N., Putney, J. W., Scott, E. K., Ewing,
UN. D., & Davis, F. M. (2020). Multiscale imaging of basal cell
dynamics in the functionally mature mammary gland. Proceedings
of the National Academy of Sciences, 117(43), 26822–26832.
https://doi.org/10.1073/pnas.2016905117, PubMed: 33033227
Network Neuroscience
1145
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
.
T
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
Stevenson, IO. H., & Kording, K. P. (2011). How advances in neural record-
ing affect data analysis. Nature Neuroscience, 14(2), 139–142.
https://doi.org/10.1038/nn.2731, PubMed: 21270781
Stobb, M., Peterson, J. M., Mazzag, B., & Gahtan, E. (2012). Graph
theoretical model of a sensorimotor connectome in zebrafish.
PLoS ONE, 7(5), e37292. https://doi.org/10.1371/journal.pone
.0037292, PubMed: 22624008
Stringer, C., Pachitariu, M., Steinmetz, N., Reddy, C. B., Carandini,
M., & Harris, K. D. (2019). Spontaneous behaviors drive multidi-
mensional, brainwide activity. Scienza, 364(6437), 255. https://
doi.org/10.1126/science.aav7893, PubMed: 31000656
Sugihara, G., May, R., Ye, H., Hsieh, C.-H., Deyle, E., Fogarty, M.,
& Munch, S. (2012). Detecting causality in complex ecosystems.
Scienza, 338(6106), 496–500. https://doi.org/10.1126/science
.1227079, PubMed: 22997134
Tainton-Heap, l. UN. L., Kirszenblat, l. C., Notaras, E. T., Grabowska,
M. J., Jeans, R., Feng, K., Shaw, P. J., & van Swinderen, B. (2021).
A paradoxical kind of sleep in Drosophila melanogaster. Current
Biology, 31(3), 578–590. https://doi.org/10.1016/j.cub.2020.10
.081, PubMed: 33238155
Tajima, S., Mita, T., Bakkum, D. J., Takahashi, H., & Toyoizumi, T.
(2017). Locally embedded presages of global network bursts.
Proceedings of the National Academy of Sciences, 114(36),
9517–9522. https://doi.org/10.1073/pnas.1705981114,
PubMed: 28827362
Tajima, S., Yanagawa, T., Fujii, N., & Toyoizumi, T. (2015). Untan-
gling brain-wide dynamics in consciousness by cross-embedding.
PLoS Computational Biology, 11(11), e1004537. https://doi.org/10
.1371/journal.pcbi.1004537, PubMed: 26584045
Tallon-Baudry, C., Bertrand, O., & Fischer, C. (2001). Oscillatory
synchrony between human extrastriate areas during visual
short-term memory maintenance. Journal of Neuroscience, 21(20),
RC177. https://doi.org/10.1523/JNEUROSCI.21-20-j0008.2001,
PubMed: 11588207
Tang, E., Giusti, C., Baum, G. L., Gu, S., Pollock, E., Kahn, UN. E.,
Roalf, D. R., Moore, T. M., Ruparel, K., Gur, R. C., Gur, R. E.,
Satterthwaite, T. D., & Bassett, D. S. (2017). Developmental
increases in white matter network controllability support a grow-
ing diversity of brain dynamics. Nature Communications, 8(1),
1252. https://doi.org/10.1038/s41467-017-01254-4, PubMed:
29093441
Testa-Silva, G., Loebel, A., Giugliano, M., de Kock, C. P.
J.,
Mansvelder, H. D., & Meredith, R. M. (2012). Hyperconnectivity
and slow synapses during early development of medial prefrontal
cortex in a mouse model for mental retardation and autism. Cere-
bral Cortex, 22(6), 1333–1342. https://doi.org/10.1093/cercor
/bhr224, PubMed: 21856714
Theunissen, F., & Mugnaio, J. P. (1995). Temporal encoding in nervous
systems: A rigorous definition. Journal of Computational Neuro-
science, 2(2), 149–162. https://doi.org/10.1007/ BF00961885,
PubMed: 8521284
Thompson, UN. W., Vanwalleghem, G. C., Heap, l. A., & Scott, E. K.
(2016). Functional profiles of visual-, auditory-, and water
flow-responsive neurons in the zebrafish tectum. Current Biol-
ogy, 26(6), 743–754. https://doi.org/10.1016/j.cub.2016.01.041,
PubMed: 26923787
Thompson, W. H., Brantefors, P., & Fransson, P. (2017). From static
to temporal network theory: Applications to functional brain
connectivity. Network Neuroscience, 1(2), 69–99. https://doi
.org/10.1162/NETN_a_00011, PubMed: 29911669
Tompson, S. H., Kahn, UN. E., Falk, E. B., Vettel, J. M., & Bassett, D. S.
(2020). Functional brain network architecture supporting the
learning of social networks in humans. NeuroImage, 210,
116498. https://doi.org/10.1016/j.neuroimage.2019.116498,
PubMed: 31917325
Torres, L., Blevins, UN. S., Bassett, D. S., & Eliassi-Rad, T. (2020). IL
why, how, and when of representations for complex systems.
arXiv:2006.02870. https://doi.org/10.48550/arXiv.2006.02870
Trinh, M. H., Van Nguyen, C., Lim, Y.-H., & Ahn, H.-S. (2018).
Matrix-weighted consensus and its applications. Automatica,
89, 415–419. https://doi.org/10.1016/j.automatica.2017.12.024
Triplett, M. A., Pujic, Z., Sun, B., Avitan, L., & Goodhill, G. J.
(2020). Model-based decoupling of evoked and spontaneous
neural activity in calcium imaging data. PLoS Computational
Biology, 16(11), e1008330. https://doi.org/10.1371/journal.pcbi
.1008330, PubMed: 33253161
Tsien, R. Y., Pozzan, T., & Rink, T. J. (1982). Calcium homeostasis in
intact lymphocytes: Cytoplasmic free calcium monitored with a
new, intracellularly trapped fluorescent indicator. Journal of Cell
Biology, 94(2), 325–334. https://doi.org/10.1083/jcb.94.2.325,
PubMed: 6980885
Vaiana, M., & Muldoon, S. F. (2020). Multilayer brain networks.
Journal of Nonlinear Science, 30(5), 2147–2169. https://doi.org
/10.1007/s00332-017-9436-8
van Veen, H., Saul, N., Eargle, D., & Mangham, S. (2019). Kepler
Mapper: A flexible Python implementation of the Mapper algo-
rithm. Journal of Open Source Software, 4(42), 1315. https://doi
.org/10.21105/joss.01315
Vanwalleghem, G. C., Ahrens, M. B., & Scott, E. K. (2018). Integra-
tive whole-brain neuroscience in larval zebrafish. Current Opin-
ion in Neurobiology, 50, 136–145. https://doi.org/10.1016/j
.conb.2018.02.004, PubMed: 29486425
Vanwalleghem, G. C., Heap, l. A., & Scott, E. K. (2017). A profile of
auditory-responsive neurons in the larval zebrafish brain. Journal
of Comparative Neurology, 525(14), 3031–3043. https://doi.org
/10.1002/cne.24258, PubMed: 28599354
Vanwalleghem, G. C., Schuster, K., Taylor, M. A., Favre-Bulle, IO. A.,
& Scott, E. K. (2020). Brain-wide mapping of water flow percep-
tion in zebrafish. Journal of Neuroscience, 40(21), 4130–4144.
https://doi.org/10.1523/ JNEUROSCI.0049-20.2020, PubMed:
32277044
Vértes, P. E., Alexander-Bloch, A., & Bullmore, E. T. (2014). Genera-
tive models of rich clubs in Hebbian neuronal networks and
large-scale human brain networks. Philosophical Transactions of
the Royal Society of London B: Biological Sciences, 369(1653),
20130531. https://doi.org/10.1098/rstb.2013.0531, PubMed:
25180309
Vértes, P. E., Alexander-Bloch, UN. F., Gogtay, N., Giedd, J. N., Rapoport,
J. L., & Bullmore, E. T. (2012). Simple models of human brain func-
tional networks. Proceedings of the National Academy of Sci-
enze, 109(15), 5868–5873. https://doi.org/10.1073/pnas
.1111738109, PubMed: 22467830
Vishwanathan, A., Ramirez, UN. D., Wu, J., Sood, A., Yang, R., Kemnitz,
N., Ih, D., Turner, N., Lee, K., Tartavull, I., Silversmith, W. M.,
Jordan, C. S., David, C., Bland, D., Goldman, M. S., Aksay,
E. R. F., Sebastian Seung, H., & the EyeWirers. (2022). Predicting
Network Neuroscience
1146
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
From calcium imaging to graph topology
modular functions and neural coding of behavior from a synaptic
wiring diagram. bioRxiv. https://doi.org/10.1101/2020.10.28
.359620
Vladimirov, N., Wang, C., Höckendorf, B., Pujala, A., Tanimoto,
M., Mu, Y., Yang, C.-T., Wittenbach, J. D., Freeman, J., Preibisch,
S., Koyama, M., Keller, P. J., & Ahrens, M. B. (2018). Brain-wide
circuit interrogation at the cellular level guided by online analy-
sis of neuronal function. Nature Methods, 15(12), 1117–1125.
https://doi.org/10.1038/s41592-018-0221-x, PubMed: 30504888
Warp, E., Agarwal, G., Wyart, C., Friedmann, D., Oldfield, C. S.,
Conner, A., Del Bene, F., Arrenberg, UN. B., Baier, H., & Isacoff,
E. Y. (2012). Emergence of patterned activity in the developing
zebrafish spinal cord. Current Biology, 22(2), 93–102. https://
doi.org/10.1016/j.cub.2011.12.002, PubMed: 22197243
Watanakeesuntorn, W., Takahashi, K., Ichikawa, K., Park, J., Sugihara,
G., Takano, R., Haga, J., & Pao, G. M. (2020). Massively parallel
causal inference of whole brain dynamics at single neuron resolu-
zione. 2020 IEEE 26th International Conference on Parallel and Dis-
tributed Systems (ICPADS), 196–205. https://doi.org/10.1109
/ICPADS51040.2020.00035
Wiener, N. (1956). The theory of prediction: Modern mathematics
for engineers.
Xu, J., Wickramarathne, T. L., & Chawla, N. V. (2016). Representing
higher-order dependencies in networks. Science Advances, 2(5),
e1600028. https://doi.org/10.1126/sciadv.1600028, PubMed:
27386539
Yang, J., McAuley, J., & Leskovec, J. (2013). Community detection in
networks with node attributes. 2013 IEEE 13th International Con-
ference on Data Mining. https://doi.org/10.1109/ICDM.2013.167
Yoo, J., Kim, E. Y., Ahn, Y. M., & Ye, J. C. (2016). Topological per-
sistence vineyard for dynamic functional brain connectivity dur-
ing resting and gaming stages. Journal of Neuroscience Methods,
267, 1–13. https://doi.org/10.1016/j.jneumeth.2016.04.001,
PubMed: 27060383
Yoon, H. R., & Ghrist, R. (2020). Persistence by parts: Multiscale
feature detection via distributed persistent homology.
arXiv:2001.01623. https://doi.org/10.48550/arXiv.2001.01623
Yu, M., Engels, M. M. A., Hillebrand, A., van Straaten, E. C. W.,
Gouw, UN. A., Teunissen, C., van der Flier, W. M., Scheltens, P.,
& Stam, C. J. (2017). Selective impairment of hippocampus and
posterior hub areas in Alzheimer’s disease: An MEG-based mul-
tiplex network study. Brain, 140(5), 1466–1485. https://doi.org
/10.1093/brain/awx050, PubMed: 28334883
Zhang, D. D., Lee, H. F., Wang, C., Li, B., Pei, Q., Zhang, J., & An,
Y. (2011). The causality analysis of climate change and
large-scale human crisis. Proceedings of the National Academy
of Sciences, 108(42), 17296–17301. https://doi.org/10.1073
/pnas.1104268108, PubMed: 21969578
Zhang, X., Braun, U., Harneit, A., Zang, Z., Geiger, l. S., Betzel,
R. F., Chen, J., Schweiger, J. I., Schwarz, K., Reinwald, J. R.,
Fritze, S., Witt, S., Rietschel, M., Nöthen, M. M., Degenhardt,
F., Schwarz, E., Hirjak, D., Meyer-Lindenberg, A., Bassett,
D. S., & Tost, H. (2021). Generative network models of altered
structural brain connectivity in schizophrenia. NeuroImage,
225, 117510. https://doi.org/10.1016/j.neuroimage.2020
.117510, PubMed: 33160087
Zheng, Z., Lauritzen, J. S., Perlman, E., Robinson, C. G., Nichols,
M., Milkie, D., Torrens, O., Price, J., Fisher, C. B., Sharifi, N.,
Calle-Schuler, S. A., Kmecova, L., Ali, IO. J., Karsh, B., Trautman,
E. T., Bogovic, J. A., Hanslovsky, P., Jefferis, G. S. X. E., Kazhdan,
M., … Bock, D. D. (2018). A complete electron microscopy vol-
ume of the brain of adult Drosophila melanogaster. Cell, 174(3),
730–743. https://doi.org/10.1016/j.cell.2018.06.019, PubMed:
30033368
Zhou, D., Cornblath, E. J., Stiso, J., Teich, E. G., Dworkin, J. D., Blevins,
UN. S., & Bassett, D. S. (2020). Gender diversity statement and
code notebook v1.0. Zenodo. https://doi.org/10.5281/ zenodo
.3672110
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
6
4
1
1
2
5
2
0
5
9
7
6
5
N
e
N
_
UN
_
0
0
2
6
2
P
D
T
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Network Neuroscience
1147