RESEARCH PAPER - Ricerca sull'intelligenza artificiale specializzata al MIT

RESEARCH PAPER

Adversarial Neural Collaborative Filtering with
Embedding Dimension Correlations

Yi Gao, Jianxia Chen†, Liang Xiao, Hongyang Wang, Liwei Pan, Xuan Wen, Zhiwei Ye, Xinyun Wu

Hubei University of Technology, School of Computer Science, Wuhan 430068, China

Keywords: Neural Collaborative Filtering; Matrix Factorization; Convolutional Neural Networks; Adversarial

Training; Recommendation systems

Citation: Gao, Y., Chen, J.X., Xiao, L., et al.: Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations.

Data Intelligence. 2022. doi: dint_a_00151

Received: Nov. 10, 2021; Revised: April 15, 2022; Accepted: Giugno 10, 2022

ABSTRACT

Recentemente, convolutional neural networks (CNN) have achieved excellent performance for the
recommendation system by extracting deep features and building collaborative filtering models. Tuttavia,
CNNs have been verified susceptible to adversarial examples. This is because adversarial samples are subtle
non-random disturbances, which indicates that machine learning models produce incorrect outputs.
Therefore, we propose a novel model of Adversarial Neural Collaborative Filtering with Embedding Dimension
Correlations, named ANCF in short, to address the adversarial problem of CNN-based recommendation
system. In particular, the proposed ANCF model adopts the matrix factorization to train the adversarial
personalized ranking in the prediction layer. This is because matrix factorization supposes that the linear
interaction of the latent factors ,which are captured between the user and the item, can describe the
observable feedback, thus the proposed ANCF model can learn more complicated representation of their
latent factors to improve the performance of recommendation. Inoltre, the ANCF model utilizes the outer
product instead of the inner product or concatenation to learn explicitly pairwise embedding dimensional
correlations and obtain the interaction map from which CNNs can utilize its strengths to learn high-order
correlations. As a result, the proposed ANCF model can improve the robustness performance by the
adversarial personalized ranking, and obtain more information by encoding correlations between different
embedding layers. Experimental results carried out on three public datasets demonstrate that the ANCF
model outperforms other existing recommendation models.

† Corresponding author: Jianxia Chen (E-mail: 1607447166@qq.com; ORCID: 0000-0001-6662-1895)

© 2023 Chinese Academy of Sciences. Published under a Creative Commons Attribution 4.0 Internazionale (CC BY 4.0)
licenza.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

1. INTRODUCTION

Since recommendation systems (RS) can alleviate information overload and provide an effective solution
for users’ information search, they are widely adopted in web applications such as E-business, social
software, and so on. Generally, the collaborative filtering (CF) approaches are one of crucial methods among
various recommendation technologies because of their capabilities of both higher efficiency and accuracy.

In particular, matrix factorization (MF) method is one of the most popular CF approaches since the vectors
in the MF can represent latent features of each user and item. Inoltre, the inner products of latent features
vectors can approximate the user-item interaction well, and are powerful for catching the low-rank structure
of sparse data of the interaction between user and item, Tuttavia, its concision and linearity limit the
representation of the predictive function [1, 2]. Recentemente, a growing number of attempts have been made
to address the issues, including two main groups: One improves the model itself to learn user and item
representations via deep neural networks (DNNs); the other enhances the learning strategy, e.g. Bayesian
Personalized Ranking (BPR) [3], learned MF in pairwise ranking perspective [4], eccetera.

Tuttavia, DNNs-based approaches have been verified susceptible to adversarial examples recently. Questo
is because adversarial samples are subtle non-random disturbances, which indicates that machine learning
(ML) models produce incorrect outputs. A large number of studies have reported the failure of ML-based
RS models against adversarial attacks. To improve the robustness, Goodfellow et al. [5] and Moosavi-
Dezfooli et al. [6] developed adversarial training approaches that can correctly classify the dynamically
generated adversarial examples. Inspired by adversarial learning, He et al. [7] designed the Adversarial
Personalized Ranking (APR) to replace the traditional BPR [3], but the effect is neglect, especially in top
recommendation with a small k value.

To highlight the importance of modeling dimensional correlations and improve on the performance of
the robustness for the RS, we present a novel CF-based model with the adversarial training, named
Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations, ANCF in short. In
particular, the proposed ANCF model adopts the matrix factorization to train the adversarial personalized
ranking in the prediction layer. This is because matrix factorization supposes that the linear interaction of
the latent factors,which are captured between the user and the item, can describe the observable feedback,
so the ANCF can learn a much more complicated representation of latent factors to improve the performance
of recommendation. Inoltre, ANCF utilizes the outer product instead of the inner product or concatenation
to learn pairwise embedding dimensional correlations explicitly, and obtain the interaction map from which
CNNs can utilize its strengths to learn high-order correlations. Therefore, the proposed ANCF model can
improve the robustness performance by the adversarial personalized ranking, and obtain more information
by encoding correlations between different embedding layers. Experimental results from three public
datasets demonstrate that the ANCF model outperforms other existing recommendation models.

The contribution of the proposed model is described as follows:

• The proposed model learns high-order correlations from feature map E via CNN.
• The proposed model can solve the adversarial problems via an adversarial matrix factorization.

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

2. RELATED RESEARCH WORK

The paper focuses on the CNN-based CF and adversarial training. Therefore, we introduce their latest

developments and applications in the RS in this section.

2.1 CNN-based Collaborative Filtering

With the development of DNNs in the area of RS, neural collaborative filtering (NCF) has recently
become the most popular framework among the DNN-based CF approaches [8]. This is because NCF
utilizes DNNs to improve either the user and item representation learning or the predictive function much
better [9, 10, 11, 12, 13, 14]. Tuttavia, there is still a problem to be addressed in these NCF models
recently. That is the correlations of the embedding dimensions resulted from the predictive function.
Generally,traditional NCF models often utilize a multi-layer perceptron (MLP) based on the concatenation
or the element-wise product of embedding between the user and the item [8, 14]. Afterward, Du et al.
presented a model named ConvNCF to learn the high-order correlations of the embedding dimensions by
utilizing CNNs-based model via the outer product [15].

Inspired by the ConvNCF model [15], this paper adopts matrix factorization trained with APR (cioè.,

Adversarial Matrix Factorization, AMF) to solve the adversarial problem via a different way.

2.2 Adversarial Recommendation Systems

Adversarial machine learning (AML) focuses on the learning algorithms resisting adversarial attacks and
studying benefits and drawbacks of attackers to support appropriate solutions [16, 17]. In recent years,
many works have pointed out the failure of machine learning recommendation models. Therefore, Lui
et al. [7] proposed an adversarial learning framework for recommendation at first. The proposed adversarial
personalized ranking (APR) model checked both the robustness to adversarial perturbations of users and
embedded items of BPR-MF [3]. Afterward, Anelli et al. [16] researched iterative perturbation technologies
and proved the ineffectiveness of the APR in protecting the RS from attacks.

Generally, adversarial training involves appending adversarial samples, generated by particular attack
models such as FGSM [5] or BIM [17], into the training process. According to reports, both in RS [18, 19]
and ML [20], this kind of training process results in the robustness against adversary samples, and achieves
better performance of generalization against clean samples.

Afterward, AML has been utilized to create fresh generative models, known as generative adversarial
networks (GANs). According to different applications, GAN-based models could improve the negative
sampling for the learning sequencing objective function [21, 22], predict missing scores [23, 24] by using
time [24, 25], and auxiliary information fitting synthesizers, or enhance training datasets [26, 27]. Tuttavia,
we here focus on the Adversarial Matrix Factorization (AMF) instead of GAN due to its computation
consumption [28].

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

3. PROPOSED MODEL

We propose a novel neural network approach named Adversarial Convolutional Neural CF with

Embedding Correlations (ANCF), inspired by the work of [15].

This paper selects CNN as the fundamental neural structure due to three advantages as follows.

• CNN can deal with the feature map well due to its presence as a 2D matrix;
• The sub-region of the feature map has a dimensional relationship represented by CNN;
• CNN can capture the correlations of features both locally and globally.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

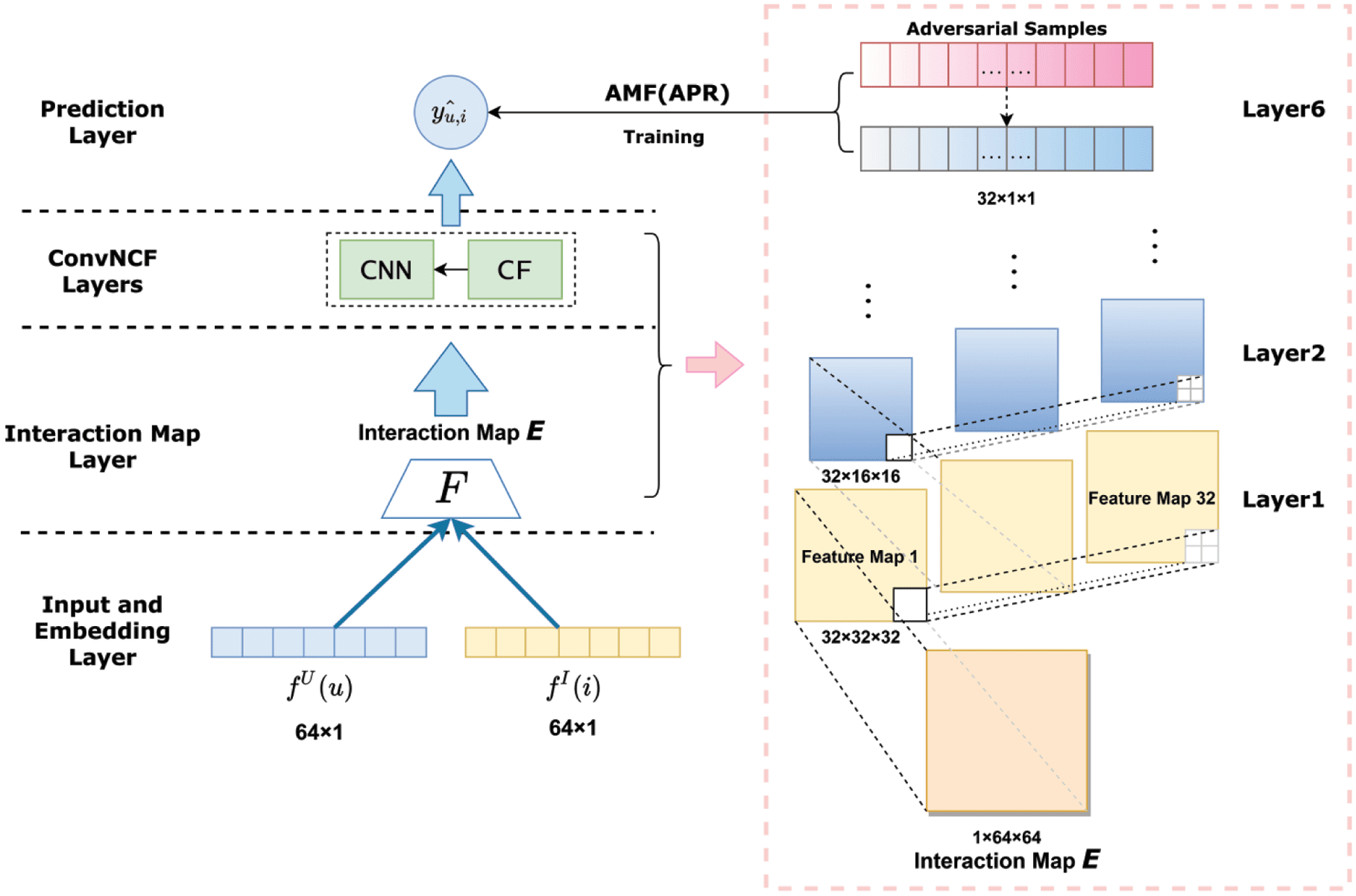
Figura 1. An ov erview of the ANCF Framework.

Come mostrato in figura 1, the ANCF framework consists of four components as follows:

•

The first layer is the embedding and input layer, which contains two embedding functions: f U(tu) E
f I(io). It produces two vectors (of size 64) which represents user u and item i respectively.
The second layer is interaction map layer, which computes the pairwise correlations of the vector
after the embedding and input layer by the Interaction Map E fed to the ConvNCF Layers.

Data Intelligence

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

•

The third layer is ConvNCF Layers including six convolutional layers, following a tower structure with
32 feature maps in each CNN Layer and outputting a tensor in the last CNN layer.

• The last prediction layer obtains prediction ŷ ui trained with the APR to output the final result.

3.1 Layer of Input and Embedding

Given a user u and an item i and their features, we first encode their features by one-hot encoding and

get their embedding f U(tu) and f I(io) via the equation 1:

f U(tu) = PTv U
tu,

f I(io) = QTv I
io

(1)

Dove,

tu: the feature vector of user u;
io: the feature vector for item i;

• v U
• v I
• P ∈RM × K: the embedding matrix for user features;
• Q ∈RN × K: the embedding matrix for item features;
• M: the number of user features;
• K: the embedding size;
• N: the number of item features.

3.2 Layer of the Interaction Map

Although recent works have shown the superiority of inner-product over complex neural networks
(CNN, MLPs), in terms of efficiency and effectiveness, and the applying outer product with CNNs has
more time complexity, we replace the inner product with the outer product, to construct interaction map
of the user and the item embedding. This is because the advantages of outer product are reflected in the
following four aspects:

• It does not have the disadvantage of element product only considering the diagonal elements of the

interaction map;

• It can obtain more information by encoding correlations among various embedding vectors;
• It is more effective than the connection operation merely preserving the original information of the

embedding vector and does not model any other correlation.

The interaction map layer allows the two embedding vectors (f U(tu), f I(io)) to do outer product to get the

interaction map E, shown in the following equation 2:

E = f U(tu) ⊗ f I(io) = f U(tu) ⋅ f I(io)T

(2)

e
where the (k1, k2) – th element in E is:
k k
,
1
embedding dimension are encoded in E.

( )
tu
k
1

⋅

( )
io
k

. Obviously, all correlations of the pairwise

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

3.3 ConvNCF Layer

3.3.1 Neural Collaborative Filtering

Neural collaborative filtering is a set of CF models based on the DNNs, in which side information is

defined as user

and item
È

, the scoring function is shown as the equation 3:

ˆ
R
ui

(
T
user
f U s
tu

⋅

Dove,
•
• h is the parameters of the network.

function f (⋅) is the multi-layer perceptron;

item
V s U V
,
io

⋅

)

(3)

Recentemente, multi-layer perceptron (MLP) has been extensively investigated in the NCF tasks. This is because
many existing RS models are linear methods in essence. Tuttavia, MLP can improve recommendation
performance via adding nonlinear transformations and interpreting them into neural extensions [8].

Despite MLP’s success, there are still some shortcomings. MLP is easy to overfit and needs more computing
resources due to many parameters. For explicit feedback, the whole network can be trained with weighted
square loss. And for the implicit feedback, the whole network can be trained with weighted binary cross-
entropy loss. Equazione 4 is the definition of the cross-entropy loss.
(
log 1

= −

(
1

log

(4)

)

(cid:2)
R

−

)

R
ui

∑
∪
O O

∈

R
ui

−

3.3.2 ConvNCF

(
u i
,

)

Based on the NCF, we designed a ConvNCF layer which sets up 32 kernel for each convolution layer
and generates a feature map c. A 2D matrix Elc represents a feature map c in the convolutional layer l, E
its size is the half of its previous layer l – 1 since the stride is 2. For layer l, a 3D tensor E l represented all
feature maps together. There are 2 × 2 sizes with no padding of convolutional kernels.

Given the interaction map E of the input, we can obtain the feature maps from each layer in the

equation 5 come segue:

l
e
io

+
1
j c
, ,

× ×
s s

Dove

≤ ≤
l

64
+
l
1
2

ReLU b
1

∑∑
e
2
0

+
i a

⋅

1
a b c
,
,

+
j b

(5)

∑∑
l
e
2
0

+
i a

⋅

+
l
1
a b c d
,
,

+
j b

, 1

≤ ≤
l

l
e
io

+
1
j c
, ,

= ⎨

ReLU b
l

• ex, sì, the entry in the interaction map;
• E, a product of f U(tu)x and f I(io)sì;
•
•

[xs:xe], a row range;
[ys:ye], a column range;

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

⎡
⎤
⎣
⎦
⎧
⎛
⎞
⎪
⎜
⎟
⎝
⎠
⎪
⎛
⎞
⎪
⎜
⎟
⎪
⎝
⎠
⎩

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

• Exs:xe, ys:ye, the entries in the adjacent sub-region;
• sub-region,all the basic correlations between f U(tu)xs:xe and f I(io)ys:ye;
• bl + 1, the bias term for layer l + 1, T 1 = [t1
• T l +1 = [t l +1

UN,B,C,D]2×2×32×32, Dove 1 ≤ l ≤ 5.

UN,B,C]2×2×32, where l = 0 is a 3D tensor;

According to the equation 5, this feature e1

X, y is the compound correlation of the four items in the
interaction graph E, presented as [e2x,2sì; e2x,2y+1; e2x+1,2y; e2x+1,2y+1]. T herefore, e1
X, y is a feature of combined
correlation of E2x:2x+1,2y:2y+1, namely second-order correlation. As a result, E1 consists of second-order
correlation. The rest can be done in the sam e manner. E2 consists of 4-order correlation.

We can conclude that only all the entries of the lower feature map can be covered by the entries of
the higher feature map. Così, correlations among all dimensions can be encoded by an entry of the last
hidden layer. Based on the 2D interaction map E, high-order correlations of the embedding dimensions
can be learned by the ConvNCF Layers both locally and globally according to stacking multiple
convolutional layers.

3.4 Prediction Layer

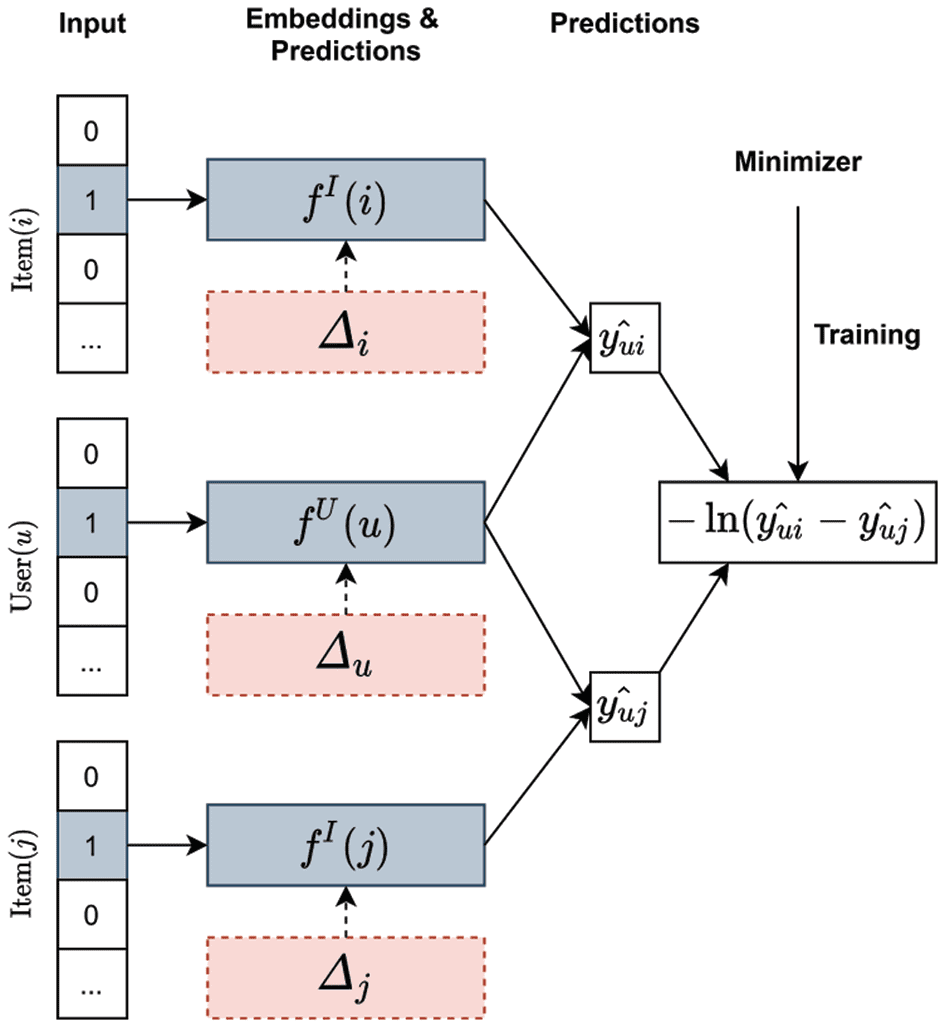
Different from [15], this paper adopts matrix factorization trained with APR (cioè., Adversarial Matrix
Factorization, AMF) in the prediction layer to solve the adversarial problem. The AMF approach is illustrated
in Figure 2.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 2. An Illustration of the AMF.

Data Intelligence

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

3.4.1 Adversarial Personal Ranking

Bayesian Personalized Ranking (BPR) overcomes the challenge that pairwise approaches ca nnot explicitly
model the ranking information among items with stochastic gradient descent (SGD) [3]. Normally, BPR
objective function is denoted in equation 6:

l
BPR

= ∑
)
(
u i
, ,

∈

− lns(ŷ ui(H) − ŷ uj(H)) + lH||H||2

(6)

the s(·) is sigmoid function;

Dove,
•
• lH is the regularization parameter of the model;
• D is the set of pairwise training instances;
+
IO
tu

+
D
IO
\
tu
uI +, the set of items that user u has interacted before;



 I, the whole item set.

∈ ∧ ∈

}
;

u i
, ,

{
(

=
:

)

Tuttavia, BPR model is weak and vulnerable to certain perturbations, when added small perturbations
on its parameters. Così, an adversarial personalized ranking (APR) has been presented to address the
adversarial interference via the objective function optimization [7]. Formalmente, the objective function of the
adversarial personalized ranking defined as equation 7:

(

l
APR
=
adv

)
D
Θ =
|

(

l
BPR

arg max
e
,

≤Δ

l
BPR

)
D
Θ +
|
(

D
Θ + Δ
ˆ
|

l
l
BPR

)

(

D
Θ + Δ
|

)

adv

(7)

Dove,
• ∆adv, the adversarial perturbations aiming to maximize the BPR object function;
• ∆, the disturbance on model parameters;
• e ≥ 0 decides the strength of the disturbance;
• Hˆ , the present parameters of model;
• H, aims to minimize the objective function.

The adversarial term LBPR(D|H + ∆adv) controlled by l is denoted as a regularization for stabilizing the
function in the BPR. -e and l- are two hyper-parameters in BPR. A training instance (tu, io, j) is minimized
by the local objective function as equation 8, and H is updated by the SGD rule in the equation 9:

lAPR ((tu, io, j)|H) = –lns(ŷ ui(H) − ŷ uj(H)) + lH||H||2 − lns(ŷ ui(H + ∆adv) − ŷ uj(H + ∆adv))

Θ = Θ −

∂

APR

)
Θ
|

)

(
(
u i
, ,
∂Θ

(8)

(9)

where g refers to the learning rate.

While models trained with APR are robust to adversarial perturbations, they might not be appropriate

approaches for personalized ranking due to their weak effectiveness.

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Δ
Δ

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

3.4.2 Adversarial Matrix Factorization

Give a pair (tu, io), the predictive function of AMF is defined in equation 10:

(

)
Θ + Δ =

ˆ
sì

(

( )
+ Δ
tu

T
v

)

(

( )
+ Δ
io

)

(10)

Dove,
• v, a trainable weight vector in the prediction layer;
•
•

u ∈ RK, the perturbation vector for user u;
i ∈ RK, the perturbation vector for item i.

We utilize the mini-batch training to get updating rules for parameters in AMF. Firstly, given the mini
batch (of size S) extracts training instances S as D’. Based on the mini batch D’, the parameters are trained.
The APR objective function for AMF is defined in equation 11:

(

)
Θ =
′
|

l
APR

∑
l
)
∈ ′
j D

(
u i
, ,

APR

(
(

u i
, ,

)
Θ
|

)

(11)

where lAPR((tu, io, j)|H) has been defined in the equation 8. Likewise, the updating rule for H is defined in
equation 12:

Θ = Θ −

)

Θ′
|

APRL∂

(
D
∂Θ

Iterate over the above two steps until the AMF converges or performance begins to degrade.

Formalmente, the objective function for ANCF can be defined in equation 13:

l
APR

(

)
Θ +
′
|

l
1

l
2

l
3

ConvNCF

l v
4

(12)

(13)

are the hyper-parameters of the regularization, HU is the parameters in f U(·), Hl is the parameters

where l
in f T(·), HConvNCF is the parameters in ConvNCF and v for the prediction layer.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

4. EXPERIMENTAL RESULTS AND ANALYSIS

4.1 Datasets and Evaluation Protocols

This paper conducts experiments on three datasets including Yelp, Pinterest and Ml-1M.

•

Yelp: a data set of user ratings provided by the Yelp Challenge including 25,677 items, 25,815 utenti,
E 730,791 ratings.
Pinterest: an implicit feedback dataset constructed by He et al. [8] for content-based image
recommendation, including 55,187 utenti, 9,916 items, E 1,500,809 ratings.
Ml-1M: A data set on movie ratings including 3,706 movies, 6,040 MovieLens users, E 1,000,209
anonymous ratings.

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Data Intelligence

Uncorrected Proof

Δ
Δ

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

In the dataset, the latest user interaction is set up as the test set, the training set is set up as the remaining
user interactions. After the model is trained, the next phrase is to obtain a personalized ranking list for the
user via sorting the items in the training set that have no interaction with the user.

To study the performance of Top–k recommendation, this paper truncates the sorted list at position
k ∈ {5, 10, 20}. Evaluation ranking lists in the paper consists of Hit Rate (HR@k), Normalized Discounted
Cumulative Gain (NDCG@k) and Mean Reicprocal Rank (MRR@k). HR@k is a metric based on recalls
measuring whether or not the test item is in the Top–k list. NDCG@k presents the ranking order, the higher
the ranking item, the higher the calculated NDCG value. MRR@k is a statistic measure by producing a list
of possible items to a sample of queries. For these three indicators, the larger the value, the better the
personalized ranking list generated, and the better the recommendation effect. To eliminate the influence
of stochastic oscillations, this paper reports the average score of last 10 epochs on convergence.

4.2 Parameter Settings

Parameters in ConvNCF: (1) the learning rate for embedding parameters is 0.01; (2) the learning rate
for CNN parameters is 0.05; (3) l1, l2, l3, l4 (in equation 13) hyper parameters for regularization are
[0.01, 0.01, 10, 1].

Parameters in AMF: (1) the learning rate for AMF is 0.05; (2) l (in equation 7) hyper parameter for

regularization is 1; (3) e (in equation 7) that controls adversarial perturbation is 0.5.

Data Intelligence

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

4.3 Baselines and Effectiveness Evaluation

All experiments are conducted under tensorflow-1.12 and python-2.7. To justify the proposed approach

effectiveness, this paper compares the proposed approach with other approaches as follows:

• MF-BPR [3]: This approach optimizes MF with BPR, which is a competitive CF-based approach
• AMF [7]: Adversarial training is added to MF-BPR, which is also a part of the proposed approach.
•

FISM [29]: Compared with MF which only embeds the user ID, this model integrates the history of
interaction with the user to represent the user embedding.

• SVD++ [30]: CF model based on the MF and FISM for the user embedding.
•

MLP [8]: an NCF model that concatenates the user embedding and the item embedding without
encoding the embedding dimensional correlations.
JRL [14]: It is an NCF model that improves the performance of GMF [8] by adding hidden layers.
NeuMF [8]: It is an advanced recommendation model that integrates GMF and MLP to learn user-item
interaction information.
ConvNCF-MF, ConvNCF-FISM, and ConvNCF-SVD++ [15]: the dimensional correlation is obtained
through the outer product, based on MF, FISM, and SVD++ respectively.

•
•

•

As shown in Table 1 and Table 2, the proposed approach ANCF achieves the best resu lts based on three
metrics on Yelp. On the datasets of the Pinterest and Ml-1M, ANCF has a remarkable performance. Tuttavia,
on the metric MRR@k, it seems that ANCF is unable to enhance the performance well.

Tavolo 1. Top–k recomm endation performance of different models on Yelp where k ∈ {5, 10, 20}.

Dataset

Model

Yelp

MLP
JRL
NeuMF
ConvNCF-FISM
ConvNCF-SVD++

HR@k

k=10

0.2831
0.2922
0.2958
0.3028
0.3092

k=5

0.1766
0.1858
0.1881
0.1925
0.1991

NDCG@k

k=20

k=5

k=10

k=20

0.4203
0.4343
0.4385
0.4423
0.4457

0.1103
0.1177
0.1189
0.1243
0.1275

0.1446
0.1519
0.1536
0.1598
0.1629

0.1792
0.1877
0.1895
0.1949
0.1973

Tavolo 2. Top–k recommendation performance of different models where k ∈ {5, 10, 20}.

Dataset

Model

HR@k

NDCG@k

MRR@k

k=5

k=10

k=20

k=5

k=10

k=20

k=5

k=10

k=20

Yelp

ConvNCF-MF 0.1978 0.3086 0.4430 0.1243 0.1600 0.1939 0.2264 0.2258 0.2261*
ANCF

0.5308* 0.6649* 0.7859* 0.3821* 0.4246* 0.4535* 0.2321* 0.2275* 0.2250
Pinterest-20 ConvNCF-MF 0.5953 0.7594 0.8800 0.4211 0.4738 0.5032 0.2634* 0.2631 0.2621

Ml-1M

0.5978* 0.7604* 0.8859* 0.4241* 0.4746* 0.5071* 0.2624 0.2639* 0.2631*
ANCF
ConvNCF-MF 0.4688 0.6500 0.8085 0.3272 0.3827 0.4233 0.2229 0.2307* 0.2297*
ANCF

0.4885* 0.6596* 0.8165* 0.3371* 0.3878* 0.4329* 0.2332* 0.2279 0.2287

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

4.4 The Effectiveness of Adversarial Learning

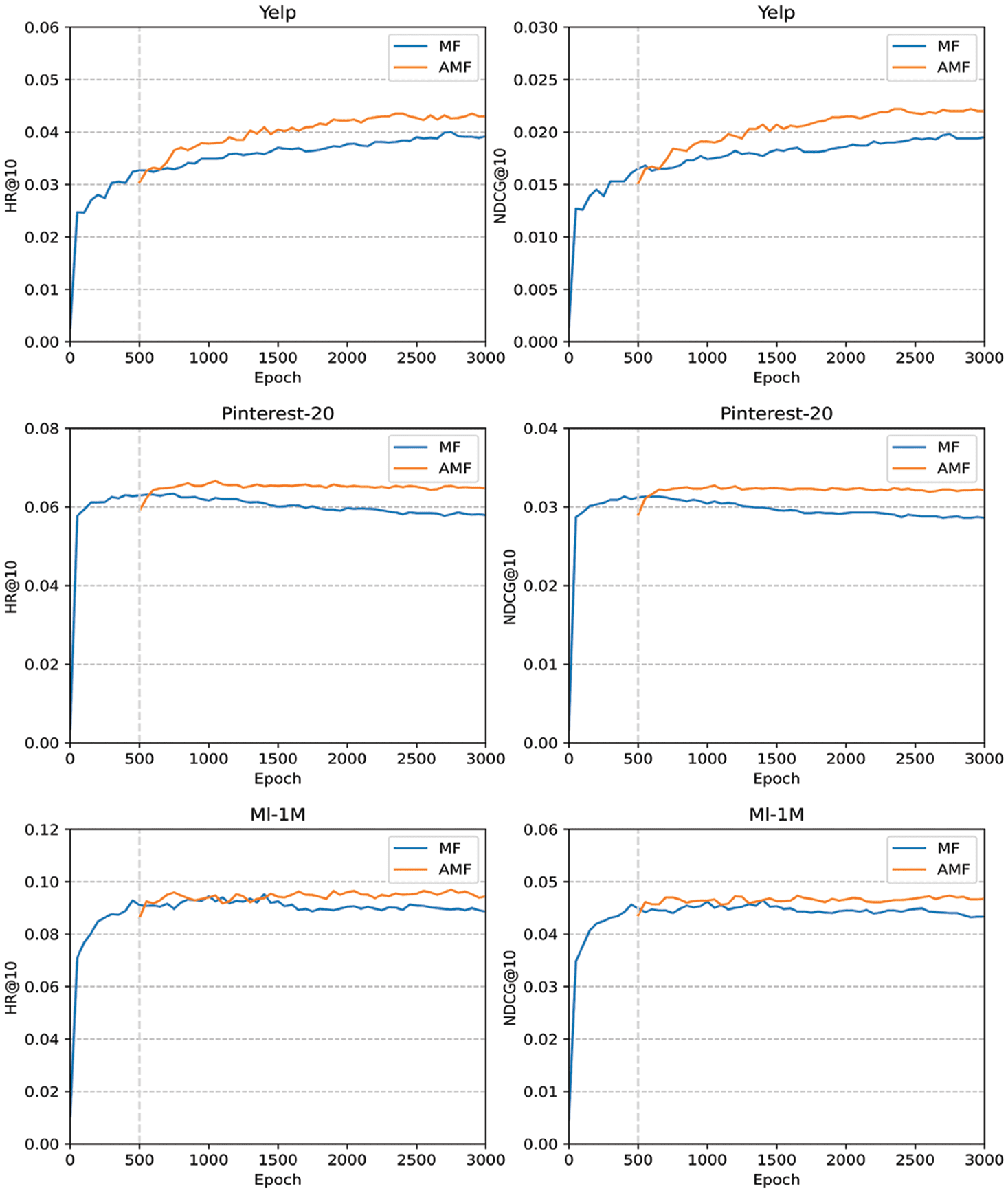
To ensure the good performance during the adversarial training, this paper pre-trained MF-BPR for 500
epochs (close to complete convergence), and then trained MF-APR (AMF); for comparison, this paper
continues to complete the training of MF-BPR, so that the training epoch of the two is the same.

Under the condition of Top-k@10, all the diagrams in Figure 3 reflect that training MF with APR has
achieved good results after 500 training epochs, while using BPR the outcome is not pleasing. It even
declined slightly (in Pinterest and Ml-1M).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 3. MF-BPR and AMF Trainin g curves.

Data Intelligence

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

4.5 The Effectiveness of CNN

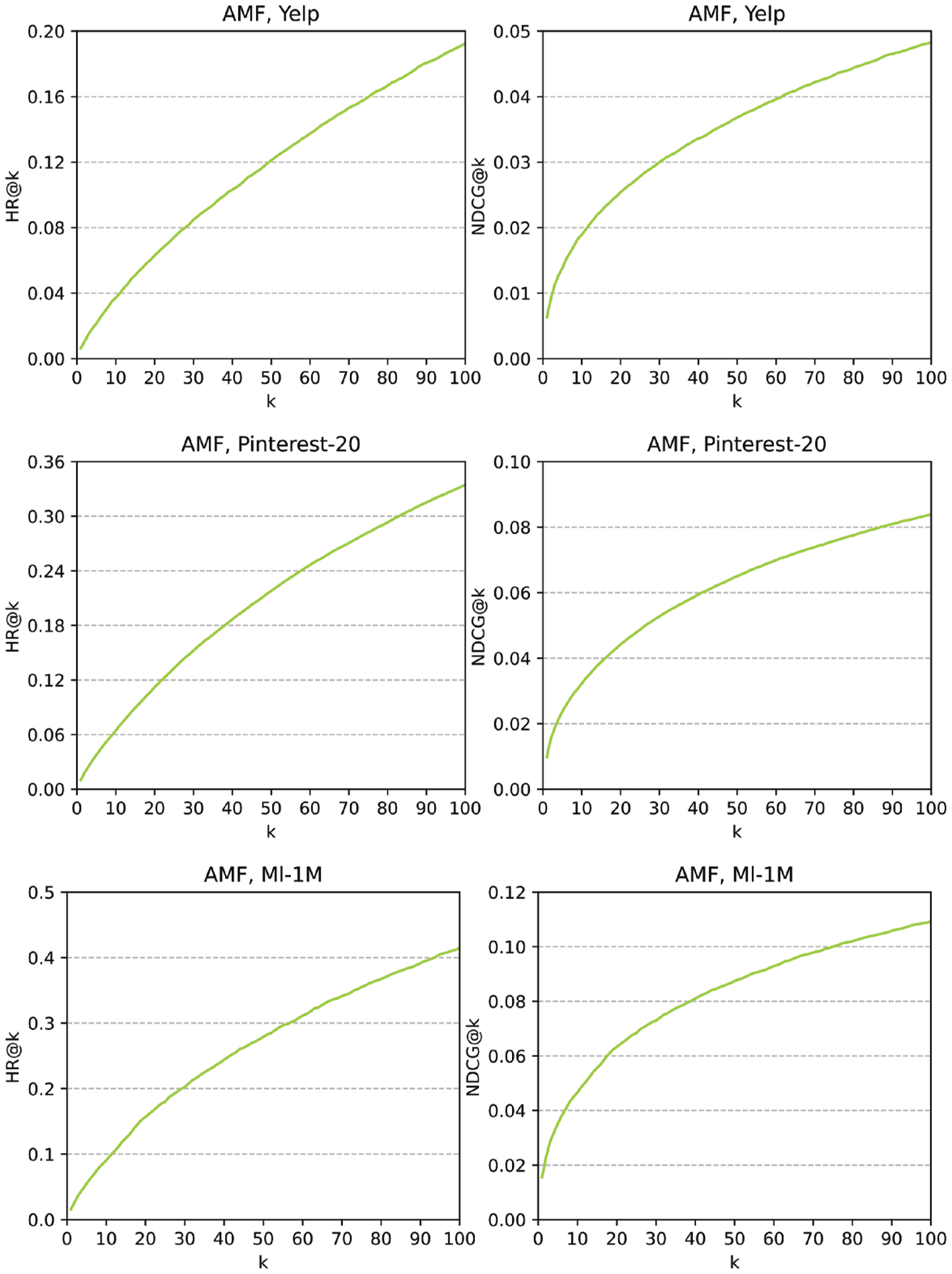
It can be seen from Figure 4 that under the condition of Top–k, k ∈{1, 2, …, 100}, both HR@k [31] E
NDCG@k [32] have been improved, but they are still at a low level, especially the metric NDCG@k; Questo
is because AMF cannot learn enough information.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 4. HR@k and NDCG@k of AMF on Yelp, Pinterest and ML-1M.

Data Intelligence

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

To address this problem, this paper utilized ANCF for training. The outer product layer in ANCF can
explicitly encode the dimensional relationship between embeddings, and CNN can also handle feature
maps well.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 5. ANCF and AMF Training Curves

Data Intelligence

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

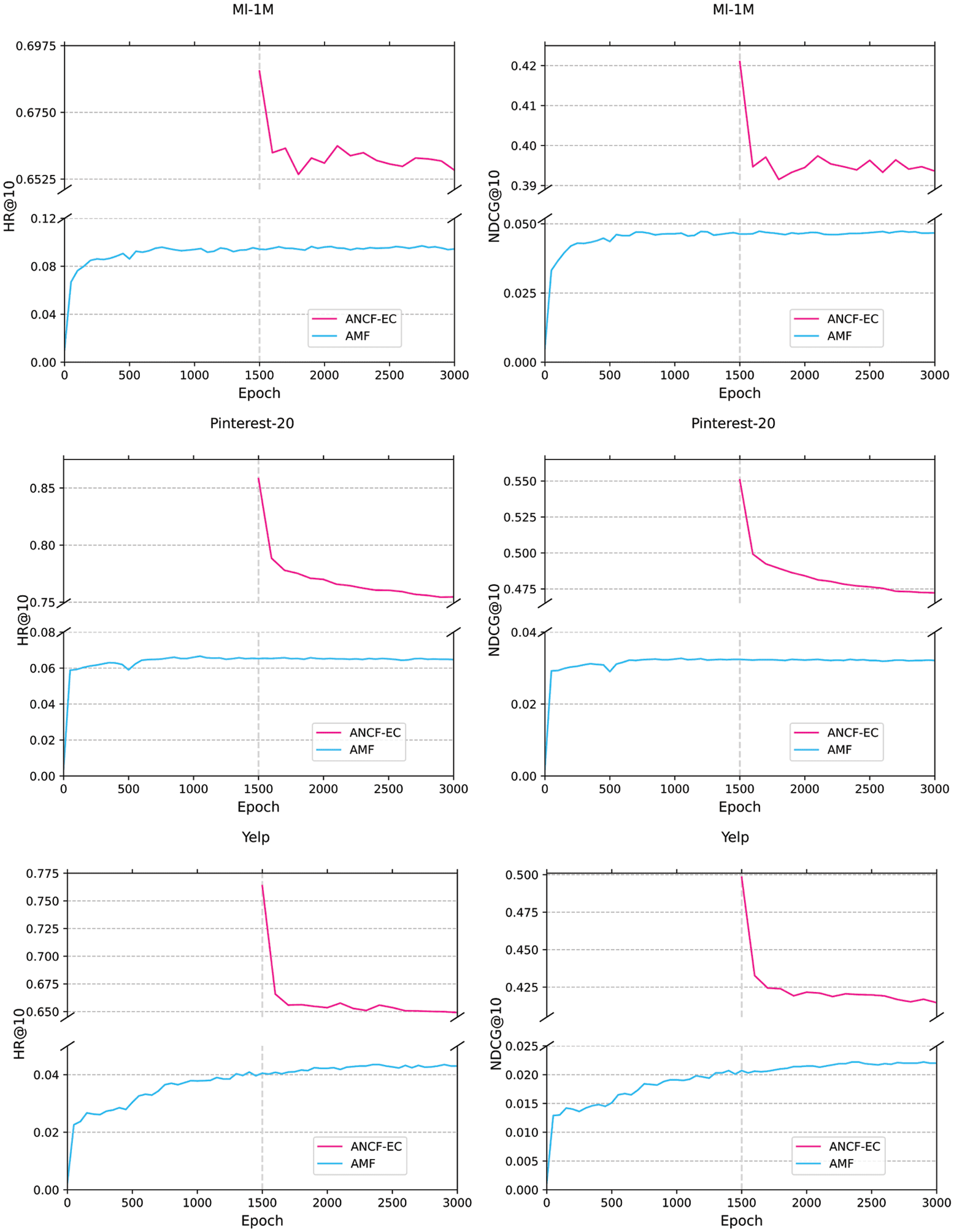
Unde r the condition of Top–k@10, AMF is utilized to be pre-trained 1500 epochs, and then ConvNCF
is utilized to be trained 1500 epochs to learn high-dimensional information. As shown in Figure 5, IL
ANCF proposed in this paper has achieved remarkable results on all datasets. In the Yelp, using ANCF,
HR@10 and NDCG@10 almost increased to 0.6524 E 0.4187 rispettivamente; in the Pinterest, HR@10 and
NDCG@10 are as high as 0.7600 E 0.4764, rispettivamente; in the Ml-1M, HR@10 and NDCG@10 reach
to around 0.6596 E 0.3591, rispettivamente.

5. CONCLUSIONS

We present a novel ANCF model, which can obtain both the potential dimensional information among
embeddings via the outer product and the preference information via multiple convolutional layers.
Particularly, through the proposed adversarial training, ANCF can improve the overall robustness
performance.

Experimental results demonstrated the flexibility and necessity of proposed schemes as follows:

•

it is significant to utilize both adversarial training and calculation of potential dimensional information
in the CF model.
the ANCF performance is much better than the existing advanced models in the context of Top–k item
recommendation.

Our future work will focus on the attention mechanisms via the graph neural networks for the RS. In
aggiunta, we will look at the negative sampling mechanism in BPR and APR; The existing content-based
recommendation model may also be utilized in the design of embedding vectors.

ACKNOWLEDGMENTS

This work is supported by National Natural Science Foundation of China (61902116).

AUTHOR CONTRIBUTION STATEMENT

Yi Gao (E-mail: 2856939182@qq.com, ORCID: 0000-0003-2645-2227): has participated sufficiently in
the work to take public responsibility for the content, including participation in the coding, the experiment
and analysis, writing the manuscript.

Jianxia Chen (E-mail: 1607447166@qq.com, ORCID: 0000-0001-6662-1895): has participated sufficiently
in the work to take public responsibility for the content, including participation in the model design,
problem analysis, writing and revision of the manuscript.

Liang Xiao (E-mail: 48453626@qq.com, ORCID: 0000-0002-1564-2466): has participated sufficiently in
the work to take public responsibility for the content, including participation in the model design and
revision of the manuscript.

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

Hongyang Wang (E-mail: 1586748352@qq.com, ORCID: 0000-0002-8202-6655): has participated
sufficiently in the work to take public responsibility for the content, including participation in the part of
the experiment of recommend system.

Liwei Pan (E-mail: 1547475261@qq.com, ORCID: 0000-0003-2645-2227): has participated sufficiently
in the work to take public responsibility for the content, including participation in the part of the experiment
of deep learning.

Xuan Wen (E-mail: 1595159972@qq.com, ORCID: 0000-0001-9278-2377): has participated sufficiently
in the work to take public responsibility for the content, including participation in the revision of the
experiment in the manuscript.

Zhiwei Ye (E-mail: 27454010@qq.com, ORCID: 0000-0001-6668-4634): has participated sufficiently in
the work to take public responsibility for the content, including participation in the revision of the manuscript.

Xinyun Wu (E-mail: 67144659@qq.com, ORCID: 0000-0002-7525-0114): has participated sufficiently
in the work to take public responsibility for the content, including participation in the revision of the
manuscript.

REFERENCES

[1] Beutel, A., Covington, P., Jain, S., Xu, C., Li, J., Gatto, V., & Chi, E.H.: Latent cross: Making use of context in
recurrent Recommendation systems. In Proceedings of the Eleventh ACM International Conference on Web
Search and Data Mining, pag. 46–54 (2018)

[2] Lui, X., Du, X., Wang, X., Tian, F., Tang, J., & Chua, T.S.: Out er product-based neural collaborative filtering.

In Proceedings of the 27th International Joint Conference on Artificial Intelligence, pag. 2227–2233 (2018)

[3] Rendle, S., Freudenthaler, C., Gantner, Z., & Schmidt-Thieme, l. : BPR: Bayesian personalized ranking from

implicit feedback. arXiv preprint arXiv:1205.2618 (2012)

[4] Han, L., Wu, H., Eh, N., & Qu, B.: Convolutional neural collabor ative filtering with stacked embeddings. In

Asian Conference on Machine Learning, pag. 726–741. PMLR (2019)

[5] Goodfellow, I.J., Shlens, J., & Szegedy, C.: Explaining and har nessing adversarial examples. arXiv preprint

arXiv:1412.6572 (2014)

[6] Moosavi-Dezfooli, S.M., Fawzi, A., Fawzi, O., & Frossard, P.: U niversal adversarial perturbations. In

Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pag. 1765–1773 (2017)

[7] Lui, X., Lui, Z., Du, X., & Chua, T.S.: Adversarial personalized ranking for recommendation. In The 41st
International ACM SIGIR Conference on Research & Development in Information Retrieval, pag. 355–364
(2018)

[8] Lui, X., Liao, L., Zhang, H., Nie, L., Eh, X., & Chua, T.S.: Neu ral collaborative filtering. Negli Atti del

26th International Conference on World Wide Web, pag. 173–182 (2017)

[9] Lui, R., & McAuley, J.: VBPR: visual bayesian personalized rankin g from implicit feedback. Negli Atti di

the AAAI Conference on Artificial Intelligence (Vol. 30, No. 1) (2016)

[10] Wu, Y., DuBois, C., Zheng, A.X., & Ester, M.: Collaborative den oising auto-encoders for top-n
Recommendation systems. In Proceedings of the Ninth ACM International Conference on Web Search and
Data Mining, pag. 153–162 (2016)

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

[11] Xue, H.J., Dai, X., Zhang, J., Huang, S., & Chen, J.: Deep Matr ix Factorization Models for Recommendation

systems. In IJCAI (Vol. 17, pag. 3203–3209) (2017)

[12] Chen, J., Zhang, H., Lui, X., Nie, L., Liu, W., & Chua, T.S.: At tentive collaborative filtering: Multimedia
recommendation with item-and component-level attention. In Proceedings of the 40th International ACM
SIGIR Conference on Research and Development in Information Retrieval, pag. 335–344 (2017)

[13] Yuan, F., Karatzoglou, A., Arapakis, I., Jose, J.M., & Lui, X.: A simple convolutional generative network for
next item recommendation. In Proceedings of the Twelfth ACM International Conference on Web Search
and Data Mining, pag. 582–590 (2019)

[14] Zhang, Y., Ai, Q., Chen, X., & Croft, W.B.: Joint representatio n learning for top-n recommendation with
heterogeneous information sources. Negli Atti del 2017 ACM on Conference on Information and
Knowledge Management pp. 1449–1458 (2017)

[15] Du, X., Lui, X., Yuan, F., Tang, J., Qin, Z., & Chua, T.S.: Mode ling embedding dimension correlations via
convolutional neural collaborative filtering. ACM Transactions on Information Systems (TOIS), 37(4), 1–22
(2019)

[16] Anelli, V.W., Bellogín, A., Deldjoo, Y., Di Noia, T., & Merra, F.A.: Multi-Step Adversarial Perturbations on

Recommendation systems Embeddings. arXiv preprint arXiv:2010.01329 (2020)

[17] Kurakin, A., Goodfellow, I., & Bengio, S.: Adversarial machine le arning at scale. arXiv preprint arXiv:1611.

01236 (2016)

[18] Tang, J., Du, X., Lui, X., Yuan, F., Tian, Q., & Chua, T.S.: Adve rsarial training towards robust multimedia
recommender system. IEEE Transactions on Knowledge and Data Engineering, 32(5), 855–867 (2019)
[19] Fan, W., Derr, T., Mamma, Y., Wang, J., Tang, J., & Li, Q.: Deep adv ersarial social recommendation. arXiv preprint

arXiv:1905.13160 (2019)

[20] Wiyatno, R.R., Xu, A., Dia, O., & de Berker, A.: Adversarial exa mples in modern machine learning: A review.

arXiv preprint arXiv:1911.05268 (2019)

[21] Wang, Q., Yin, H., Eh, Z., Lian, D., Wang, H., & Huang, Z.: Neura l memory streaming recommender
networks with adversarial training. In Proceedings of the 24th ACM SIGKDD International Conference on
Knowledge Discovery & Data Mining, pag. 2467–2475 (2018)

[22] Bharadhwaj, H., Park, H., & Lim, B.Y.: RecGAN: recurrent generat ive adversarial networks for recommendation

systems. In Proceedings of the 12th ACM Conference on Recommendation Systems, pag. 372–376 (2018)

[23] Wang, J., Yu, L., Zhang, W., Gong, Y., Xu, Y., Wang, B., … & Zh ang, D.: Irgan: A minimax game for unifying
generative and discriminative information retrieval models. In Proceedings of the 40th International ACM
SIGIR Conference on Research and Development in Information Retrieval, pag. 515–524 (2017)

[24] Chae, D.K., Kang, J.S., Kim, S.W., & Choi, J.: Rating augmenta tion with generative adversarial networks
towards accurate collaborative filtering. In The World Wide Web Conference, pag. 2616–2622 (2019)
[25] Zhao, W., Wang, B., Ye, J., Gao, Y., Yang, M., & Chen, X.: PLASTI C: Prioritize Long and Short-term Information

in Top-n Recommendation using Adversarial Training. In Ijcai, pag. 3676–3682 (2018)

[26] Du, Y., Fang, M., Yi, J., Xu, C., Cheng, J., & Tao, D.: Enhancing the robustness of neural collaborative filtering

systems under malicious attacks. IEEE Transactions on Multimedia, 21(3), 555–565 (2018)

[27] Dziugaite, G.K., & Roy, D.M.: Neural network matrix factorizati on. arXiv preprint arXiv:1511.06443 (2015)
[28] Chae, D.K., Kang, J.S., Kim, S.W., & Lee, J.T.: Cfgan: A gene ric collaborative filtering framework based on
generative adversarial networks. In Proceedings of the 27th ACM International Conference on Information
and Knowledge Management, pag. 137–146 (2018)

[29] Kabbur, S., Ning, X., & Karypis, G.: Fism: factored item similari ty models for top-n Recommendation systems.
In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data
Mining, pag. 659–667 (2013)

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

[30] Koren, Y.: Factorization meets the neighborhood: a multifaceted c ollaborative filtering model. Negli Atti
of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pag. 426–434
(2008)

[31] Voorhees, E.M.: The TREC-8 question answering track report. In T rec (Vol. 99, pag. 77–82) (1999)
[32] Järvelin, K., & Kekäläinen, J.: Cumulated gain-based evaluation o f IR techniques. ACM Transactions on

Information Systems (TOIS), 20(4), 422–446 (2002)

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Data Intelligence

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

AUTHOR BIOGRAPHY

Yi Gao received the B.S. degree in Data Science and Big Data Technology
from Hubei University of Technology, Wuhan, China, In 2022. He is currently
working toward the M.S. degree in Computer Science and Technology with
the School of Computer Science and Engineering, Nanjing University of
Science and Technology, Nanjing, China. His research interests include
Recommendation Systems, Machine Learning and Data Mining.
ORCID: 0000-0003-2645-2227.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

Jianxia Chen is an associate professor in School of Computer Science at
Hubei University of Technology. She obtained her MS at Huazhong University
of Science & Technology in China. She has worked as a research fellow on
the CCF in China and ACM in USA.Her particular research interests are in
knowledge graph and recommendation systems.
ORCID: 0000-0001-6662-1895

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

Liang Xiao is a professor in School of Computer Science at Hubei University
of Technology. He obtained his BSc at Huazhong University of Science &
Technology in China, his MSc at University of Edinburgh in Scotland and
PhD at Queen’s University, Belfast in Northern Ireland. He has worked as a
research fellow on the EU-funded projects of HealthAgents and OpenKnowledge
in School of Electronics and Computer Science at University of Southampton
in England, and as a post-doctoral research fellow in Health Research Board
(HRB) funded Irish National Research Centre for Primary Care at Royal
College of Surgeons in Ireland (RCSI). His particular research interests are in
Software Adaptivity, Multi-Agent System, and Agent-oriented Clinical Decision
Supporto.
ORCID: 0000-0002-1564-2466

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Data Intelligence

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

Hongyang Wang received the B.S. degree in Software Engineering from
Hubei University of Technology, Wuhan, China in 2022. His research interests
include recommendation systems, machine learning and data mining.
ORCID: 0000-0002-8202-6655.

Liwei Pan is an undergraduate student in Computer Science and Technology
from Hubei University of Technology, Wuhan, China, In 2022. His research
interests include Recommendation System, Machine Learning and Natural
Language Processing.
ORCID: 0000-0003-2645-2227

Xuan Wen received the B.S. degree in Data Science and Big Data
Technology from Hubei University of Technology, Wuhan, China, In 2022.
He is currently working toward the M.S. degree in Computer Science and
Technology with School of Information and Safety Engineering, Zhongnan
University of Economics and Law, Wuhan, China. His research interests
include Recommendation Systems and Nature Language Processing.
ORCID: 0000-0001-9278-2377

Data Intelligence

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
D
N

T
/

UN
R
T
io
C
e
–
P
D

F
/

D
o

io
/

1
0
1
1
6
2
D
N
_
UN
_
0
0
1
5
1
2
0
7
2
3
9
4
D
N
_
UN
_
0
0
1
5
1
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Uncorrected Proof

Adversarial Neural Collaborative Filtering with Embedding Dimension Correlations

Zhiwei Ye is a professor and dean of the school of computer science in
the Hubei University of Technology. He received his doctor degree from the
department of wuhan university in 2006. His main research work is the
machine learning, data mining and intelligent computing.
ORCID: 0000-0001-6668-4634

Xinyun Wu is currently an associate professor at Hubei University of
Tecnologia. He received his BS degree from the Naval University of
Engineering, China, In 2009, and his Ph.D. degree from Huazhong University
of Science and Technology, China, In 2017. He was a Postdoctoral Research
Fellow at Simon Fraser University, Canada, from 2017 A 2018. His research
focuses on implementing meta-heuristics on various NP-hard problems with
graph structures, such as Traffic Grooming, RWA, Network Design, Dominating
Set, eccetera.
ORCID: 0000-0002-7525-0114