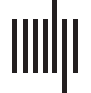RESEARCH ARTICLE - Ricerca sull'intelligenza artificiale specializzata al MIT

RESEARCH ARTICLE

Does the hα-index reinforce the Matthew effect
in science? The introduction of agent-based
simulations into scientometrics

Lutz Bornmann1

, Christian Ganser2

, Alexander Tekles1,2

, and Loet Leydesdorff3

1Division for Science and Innovation Studies, Administrative Headquarters of the Max Planck Society,
Hofgartenstr. 8, 80539 Munich, Germany
2Ludwig-Maximilians-Universität Munich, Department of Sociology, Konradstr. 6, 80801 Munich, Germany
3University of Amsterdam, Amsterdam School of Communication Research (ASCoR), PO Box 15793, 1001 NG Amsterdam,
The Netherlands

Keywords: bibliometrics, h-index, hα-index, Matthew effect, agent-based modeling, bibliometrics-
based heuristics

ABSTRACT

Recentemente, Hirsch (2019UN) proposed a new variant of the h-index called the hα-index.
The hα-index was criticized by Leydesdorff, Bornmann, and Opthof (2019). One of their most
important points is that the index reinforces the Matthew effect in science. The Matthew effect
was defined by Merton (1968) come segue: “the Matthew effect consists in the accruing of
greater increments of recognition for particular scientific contributions to scientists of
considerable repute and the withholding of such recognition from scientists who have not yet
made their mark” (P. 58). We follow up on the point about the Matthew effect in the current
study by using a recently developed Stata command (h_index) and R package (hindex),
which can be used to simulate h-index and hα-index applications in research evaluation. IL
user can investigate under which conditions hα reinforces the Matthew effect. The results of
our study confirm what Leydesdorff et al. (2019) expected: The hα-index reinforces the
Matthew effect. This effect can be intensified if strategic behavior of the publishing scientists
and cumulative advantage effects are additionally considered in the simulation.

INTRODUCTION

The h-index, introduced by Hirsch (2005), is one of the most popular bibliometric indicators
worldwide. The paper by Hirsch (2005) has been cited more than 3,500 times (date of search
in Web of Science (WoS), Clarivate Analytics: Marzo 2019). The h-index has been adopted as
one among other indicators in WoS and Scopus (Elsevier). In the bibliometrics literature, how-
ever, many critical points have been raised about it: Per esempio, Waltman and van Eck (2012)
argued that “for the purpose of measuring the overall scientific impact of a scientist (or some
other unit of analysis), the h-index behaves in a counterintuitive way. In certain cases, the mech-
anism used by the h-index to aggregate publication and citation statistics into a single number
leads to inconsistencies in the way in which scientists are ranked” (P. 406). Inoltre, IL
counting of papers with at least h citations has not been justified by Hirsch (2005); it is equally
possible to count papers with at least h2 citations or h/2 (Egghe, 2006UN,B).

Since the introduction of the h-index, many variants have been proposed, targeting one
or several disadvantages of the h-index. Bornmann, Mutz, Hug, and Daniel (2011)

a n o p e n a c c e s s

j o u r n a l

Citation: Bornmann, L., Ganser, C.,
Tekles, A., & Leydesdorff, l. (2020).
Does the hα-index reinforce the Matthew
effect in science? The introduction of
agent-based simulations into
scientometrics. Quantitative Science
Studi, 1(1), 331–346. https://doi.org/
10.1162/qss_a_00008

DOI:
https://doi.org/10.1162/qss_a_00008

Received: 27 May 2019
Accepted: 28 settembre 2019

Corresponding Author:
Lutz Bornmann
bornmann@gv.mpg.de

Handling Editor:
Ludo Waltman

Copyright: © 2019 Lutz Bornmann,
Christian Ganser, Alexander Tekles,
and Loet Leydesdorff. Published under
a Creative Commons Attribution 4.0
Internazionale (CC BY 4.0) licenza.

The MIT Press

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

concluded, on the basis of a metaevaluation, that most of these variants correlate highly:
“depending on the model, the mean correlation coefficient varies between .8 E .9. This means
that there is redundancy between most of the h index variants and the h index” (P. 346). Recentemente,
Hirsch (2019UN) himself proposed a new variant called the hα-index: “we define the hα index of a
scientist as the number of papers in the h-core of the scientist (i.e. the set of papers that contribute to
the h-index of the scientist) where this scientist is the α-author” (P. 673). The α-author is defined “as
the author of the paper with the highest h-index among all the coauthors” (P. 673). Hirsch (2019UN)
recommended using the new index in combination with the h-index. The author formulated as
follows: “a high h index in conjunction with a high hα ∕h ratio is a hallmark of scientific
leadership” (P. 673).

The hα index was criticized by Leydesdorff et al. (2019). One of their most important points
of criticism is that the index “adds the normative element of reinforcing the Matthew effect in
science” (P. 1163). The Matthew effect was defined by Merton (1968) come segue: “the Matthew
effect consists in the accruing of greater increments of recognition for particular scientific con-
tributions to scientists of considerable repute and the withholding of such recognition from
scientists who have not yet made their mark” (P. 58). Merton (1968) cited a physicist as fol-
lows: “The world is peculiar in this matter of how it gives credit. It tends to give the credit to
(Già) famous people” (P. 57). The Matthew effect is similar to Price’s (1976) “cumulative
advantages,” which he noted as a core mechanism in the sciences explaining, among other
things, the skewed distributions in the indicator values. Barabási (2002) reinvented Price’s
cumulative advantages and Merton’s Matthew effect as “preferential attachment” without
any knowledge of or reference to this bibliometric literature.

In his rejoinder, Hirsch (2019B) partly denied that the hα-index reinforces the Matthew ef-
fect in science: “Strictly speaking at most half of this is true, the higher h-index author in a
collaboration benefits, however the lower h-index author does not get negatively affected,
his/her hα remains the same. More importantly, lower h-index authors have the choice to
not collaborate with high h-index authors but rather pursue their own independent work, O
work with more junior collaborators” (P. 1168).

We agree with Hirsch (2019B) that authors or co-authors with low h-index values cannot be
expected to become “poorer,” because nothing is taken away from them. The first problematic
point in his statement is, Tuttavia, the implicit demand to search strategically for cooperation in
science. According to the norms in the ethos of science (Merton, 1942, 1973), cooperating part-
ners should be selected based on the quality of their research or the fit to the needed expertise
for a certain research project, but not for nonscientific reasons such as the increase of indicator
values. Supervisor–supervised relationships may be another reason for co-authorship.

The second problematic point in Hirsch’s statement above is the remaining uncertainty
about the reinforcement of the Matthew effect by using hα in research evaluations. In this
study, we address this point. We use a recently developed Stata command (h_index) E
R package (hindex) for the simulation of the h-index and hα-index. Based on simulation
results the user can empirically investigate whether hα reinforces the Matthew effect or
non.

2. LITERATURE OVERVIEW AND CONCEPTUAL ROOTS

2.1. The Role of Simulations in Scientometrics

Albeit that simulations are not in the focus of the bibliometric literature, both bibliometrics and
simulation studies have been used as methods in quantitative science and technology studies

Quantitative Science Studies

332

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

(per esempio., Ahrweiler, 2001; Edmonds, Gilbert, Ahrweiler, & Scharnhorst, 2011; Scharnhorst,
Börner, & van den Besselaar, 2012). Gilbert (1997) set the stage with the first simulations of
the structure and dynamics of academic science. He introduced “kenes” as knowledge-
variants of genes; the resulting events showed Lotka-type distributions and were interpretable
using Simon’s (1957) models of social processes. Ahrweiler, Pyka, and Gilbert (2004, 2011)
developed a large innovation model called SKIN: “Simulating Knowledge Dynamics in
Innovation Networks.”

Different from data-oriented studies, simulations enable us to theorize mechanisms and to
specify expectations. Not only observable behavior but also coordination and selection mech-
anisms can be studied. Leydesdorff and van den Besselaar (1998), Per esempio, showed that
the Cobb-Douglas production function can be elaborated into a representation of technolog-
ical trajectories and technological regimes by assuming feedback mechanisms (Leydesdorff &
van den Besselaar, 1994). In a similar vein, one can simulate lock-ins and deadlocks in tech-
nological innovation (Leydesdorff, 2001; Leydesdorff & van den Besselaar, 1998) and synergy
in Triple-Helix models (Ivanova & Leydesdorff, 2014). In the confrontation with data, the in-
sights in mechanisms can be developed into what Bornmann and Marewski (2019) ulteriore
elaborated into bibliometrics-based heuristics (BBH: see section 2.3).

During the early 2000s, this focus on the content of science and technology in more ab-
stract (knowledge-based) terms disappeared because of the popularity of agent-based model-
ing in neighboring disciplines (Edmonds, Hernandez, & Troitzsch, 2007; Tesfatsion, 2002).
Leydesdorff (2015) argued for a focus on (genotypic) mechanisms instead of phenotypical
behavior. From this perspective, the observable dynamics of the sciences can be studied
evolution-theoretically (Campbell, 1991; Distin, 2010; Hodgson & Knudsen, 2011; Ionescu
& Chopard, 2013; Popper, 1972). Meyer, Lorscheid, and Troitzsch (2009) provide a biblio-
metric analysis of the first decade of the Journal of Artificial Societies and Social Simulations
(JASSS). The Matthew effect itself has extensively been simulated (Per esempio, nella fisica) un-
der the heading of preferential attachment (Abbasi, Hossain, & Leydesdorff, 2012; Barabási,
2002; Barabási et al., 2002; Bonitz, Bruckner, & Scharnhorst, 1999; Garavaglia, van der
Hofstad, & Woeginger, 2017; Newman, 2001UN; Petersen et al., 2014).

In a recent study, Backs, Günther, and Stummer (2019) used agent-based modeling as a
decision support system when planning measures to encourage academic patenting within
università. The authors suggest “the application of agent-based modeling and simulation,
an approach that has been successfully used in other, similar, contesti (per esempio., when selecting
useful measures for market introduction and diffusion of new products). We have presented
herein an agent-based model that is suitable for this purpose, and we have demonstrated its
applicability and its potential value for practice [cioè., TTO (technology transfer offices) Uomo-
agement drives increased patenting] and subsequently for society (cioè., more academic patents
lead to an increase in knowledge transfer between universities and industry and/or provide a
basis for spin-off companies) by means of an application example” (P. 454).

You, Han, and Hadzibeganovic (2016) used an agent-based simulation model to assess
how the impact of scientists’ work efficiency and their capability to select important topics
for their research affects the h-index (and other measures). In this simulation model, the agents
(authors or research teams) try to occupy nodes in a citation network (publications). By pro-
viding the citation network a priori, the simulations focus on the process of competing for pos-
sible publications, rather than the collaboration or the citation process. The model proposed
by You et al. (2016) is an example of how the influence of individuals’ actions on macro-level
patterns can be analyzed by means of simulations in scientometrics.

Quantitative Science Studies

333

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

We are aware of only a few simulation studies in scientometrics that focus on the h-index.
These simulations—as a rule—have dealt with the development of single h-index values with-
out considering collaborations between scientists. Lobet (2016) published an h-index evolu-
tion simulator which reveals the development of single h-index values based on various inputs
(per esempio., starting year of publishing, papers per year). The simulator is able to consider certain
behaviors of researchers, Per esempio, to always cite their own papers. Guns and Rousseau
(2009) investigated the h-index’s growth based on computer simulations of publication and
citation processes. They found that “in most simulations the h-index grows linearly in time.
Only occasionally does an S-shape occur, while in our simulations a concave increase is very
rare” (P. 410). Ionescu and Chopard (2013) published two agent-based models which refer to
performance measurements of single scientists and a group of scientists (see also Żogała-
Siudem, Siudem, Cena, & Gagolewski, 2016). They studied, Per esempio, what happens when
low h-index researchers are removed from a community. Their results suggest “a stratified
structure of the scientific community, in which the lower h levels mostly cite papers from
the upper h levels” (P. 426).

2.2. Analytical Sociology

This study follows the approach of analytical sociology, which focuses on the mechanisms
leading to social phenomena (Hedström, 2005; Hedström & Ylikoski, 2010). Epstein (2006)
formulated what he called a “generativist” research program as a manifesto, stating that one
cannot explain a social phenomenon until one has “grown” it by simulating the phenomena
under study as emerging from the bottom up. It is the goal of analytical sociology to work out
the mechanisms (on the micro level) that are the causes of the phenomena (on the macro level;
Bornmann, 2010). In this study, we are interested whether the phenomenon Matthew effect
can be produced by the mechanism “hα-index.” In the simulations, action is an operation at
the micro-level, because action (publishing, being cited, collaborating, and performance mea-
suring) is done by a single agent. The possible outcome is on the macro-level—structures in
the form of certain hα-index distributions. In order to test the relationship between the mech-
anism and the phenomenon in this study, several agent-based simulations have been per-
formed using the Stata h_index command. Most of the model parameters are held constant
across the simulations. Compared to a baseline simulation, only a single parameter is changed
in each of the other three simulations in order to inspect the effect of this parameter. L'interno-
terested reader of this paper can use the command or package to investigate the effects of
further parameter changes.

2.3. Bibliometrics-Based Heuristics

The h_index command and the hindex package can be used to define rules for running
various simulations. Per esempio, we work with certain distributions of h-index values as start-
ing points and define how the agents in the simulation interact. The simulations are used to
obtain an experimental view on the effects of the hα-index use in research evaluation.

Recentemente, Bornmann and Marewski (2019) introduced BBHs. They discussed the use of biblio-
metrics in research evaluations against the backdrop of the fast-and-frugal heuristics research pro-
gram (per esempio., Gigerenzer, Todd, & ABC Research Group, 1999). Heuristics are “models for making
inferences that (UN) rely heavily on core human capacities (such as recognition, recall, or imitation);
(B) do not necessarily use all available information and process the information they use by simple
computations (such as lexicographic rules or aspiration levels); E (C) are easy to understand, ap-
ply, and explain” (Katsikopoulos, 2011, P. 10). In the fast and frugal heuristics framework, “a model

Quantitative Science Studies

334

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

of a heuristic specifies (io) process rules such as search, stopping, and decision rules; (ii) the kinds of
problems the heuristic can solve, questo è, the structures of environments in which it is successful; E
(iii) the capacities that the heuristic exploits” (Marewski, Schooler, & Gigerenzer, 2010, P. 77). IL
application of heuristics in many environments, for instance business, medicine, sports, and crime
(Gigerenzer & Gaissmaier, 2011), has shown that they come to judgments of similar quality com-
pared with more complex decision strategies.

Bornmann and Marewski (2019) defined BBHs as decision strategies in research evaluation
which ignore much data, but use limited information about an entity (cioè., citation and publi-
cation data of a researcher) to assess the entity. By following the fast-and-frugal heuristics re-
search program, Bornmann and Marewski (2019) defined for the use of BBHs some search,
stopping, and decision rules. These rules help to formulate and apply BBHs for a certain re-
search evaluation environment. Per esempio, the rules can be defined as follows: In econom-
ics, publications in top-five journals (American Economic Review, Econometrica, Journal of
Political Economy, Quarterly Journal of Economics, and Review of Economic Studies) decide
about scientific careers (Bornmann, Butz, & Wohlrabe, 2018); reaching a professorship with-
out having published in these journals is frequently not possible. The search, stopping, E
decision rules for filling a professorship can be defined as follows: (UN) search for all publica-
tions of a group of candidates (economists); (B) stop search when all publications have been
identified; (C) select the candidate with the largest number of papers in the top-five journals.

Although this BBH can be expected to exist in economics, it is not clear whether it is a
favorable BBH leading to valid and reliable suggestions for decisions. One objective of the
fast-and-frugal heuristics research program is to identify heuristics used in practice; another—
more important—objective is to develop heuristics leading to reliable and valid decisions.
Further questions in this program are the following: Is the application of bibliometric indicators
in a given environment reasonable? Does the indicator’s use lead to nondesired effects?

in questo documento, we follow therefore the program’s approach by studying the possible advan-
tages and disadvantages of the use of the hα-index in research evaluation. We especially focus
on the assumed sensitivity of the hα-index for the Matthew effect.

IMPLEMENTATION OF OUR SIMULATION MODEL IN STATA AND R

The ado h_index and the hindex package simulate agents who collaborate on publishing
papers. In Stata, type net install h_index, from(https://raw.githubusercon-
tent.com/chrgan/h_index/master/) to install the ado.1 The R package hindex is
available on CRAN and can be installed by typing install.packages(“hindex”).2
The simulation procedure is as follows:

1. As a starting point of the simulation, n agents are generated. The user can specify n, IL
number of agents. The agents have published in the past. The user can choose between
a Poisson or negative binomial distribution for the number of previously published pa-
pers and set parameters of the distribution (the expected value for both distributions,
and an additional dispersion parameter for the negative binomial distribution specifying
a factor by which the variance exceeds the expected value). The choice of these distri-
butions reflects that the number of papers is a discrete variable and allows modeling
different distributional forms. By using a negative binomial function and setting a low

1 The Stata module moremata must be installed in advance ( Jann, 2005).
2 The latest development version is available on https://github.com/atekles/hindex.

Quantitative Science Studies

335

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

expected value together with a high dispersion, one obtains a distribution with many
agents who have published only a few papers and few agents having published many
papers; this may roughly approximate a power law (Newman, 2001B). (Note that our ap-
proach allows for agents who have not yet published.) By specifying a higher expected value
and a lower dispersion, it is possible to approximate a normal distribution as well. It is as-
sumed in the simulation that each paper has been written one to five periods ago (imagine
years, Per esempio). For a share of these papers, the agent is the alpha author. The user can
specify the expected value of this share, which is the same for all agents.
The initial papers have already received citations in the past. The number of citations de-
pends on (UN) the citation distribution and (B) the age of a paper:

(UN) The user can choose between a Poisson and a negative binomial distribution (param-
eters are specifiable as above). He or she can specify the maximum expected number
of citations.

(B) The expected number depends on the papers’ age following a log-logistic function. It
first increases with time (periods), reaches the maximum specified in (UN) after a config-
urable number of periods, and then decreases. The steepness of the log-logistic func-
tion can also be specified.
Così, for each given age of the papers, the number of citations follows the distribution
specified in (UN) with an expected citation number given by its maximum and the age of
the paper.

2. For the initial set of n agents, the h-index and hα-index are calculated.
3. Then, the agents start to collaborate according to the following routine. The user can
specify how many periods the agents collaborate. In each period, the agents form teams
publishing new papers (each agent can publish or co-author at most one paper in each
period). The user can set some properties: the average number of co-authors, the share
of agents who collaborate or publish in each period, and the correlation between the
probability of being active in the current period and the h-index values calculated in
step 23. Così, one can specify that agents with high initial h-index values are more
productive than agents with low initial h index values. By default, the collaborating/
publishing agents are assigned to (co-)authorships at random. Per esempio, if the user
sets the number of agents to 100 and the average number of co-authors to 10, 100/10 =
10 groups of collaborating authors are created by assigning a random integer from the in-
terval [1, 10] to each agent. Agents with the same number are treated as one group.
It is possible to specify that agents with high h-index values avoid co-authorships with
agents who have equal or higher h-index values. In questo caso, the agents with high
h-index values strategically select co-authors to improve their hα. Suppose again there
are 10 groups of agents because the desired average group size is 10 and there are
100 agents. Then, IL 10 agents with the highest h-index values are assigned to groups
1 A 10 before performing the aforementioned random assignment for the rest of the
agents. This assures that the agents with the highest h-index values become members
of groups where all other agents have equal or lower h-index values.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

3 If the user specifies the correlation, an auxiliary variable av is calculated as av ¼ c (cid:2) h0 − μ h0ð
σ h0ð

(cid:2)
rnorm, where c is the desired correlation, μ(h0) is the mean of the initial h-index and σ (h0) its standard
deviation (Perciò, the term h0 − μ h0ð
is the z-standardized distribution of h0), and rnorm is a standard normal
σ h0ð
random variable. Only those agents with the s% highest values on this auxiliary variable engage in publish-
ing, where s is the desired share of publishing agents as specified by the user.

Þ
Þ þ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
1 −c2

Quantitative Science Studies

336

Does the hα-index reinforce the Matthew effect in science?

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1.

Simulation approach.

4. All papers can receive citations each period. The number of citations is determined by
the procedure outlined in step 1. To reflect the possibility of self-citations, the user can
specify an option leading to one additional citation for each paper (published at least
one period ago) where at least one of its authors has an h-index value which exceeds
the number of previous citations of the paper by one or two. This reflects agents stra-
tegically citing their own papers that have citations just below their h-index value. Questo
accelerates the growth of the agents’ h-index values. Finalmente, a “boost” effect can be
specified: Papers of agents with higher h-index values are cited more frequently than
papers of agents with lower h-index values. The citations of a paper are increased by a
user-specified number for every additional h point of the agent with the highest h-index
among the paper’s co-authors, rounded to the next integer. Per esempio, suppose a sin-
gle paper where the highest h-index of its agents is 11. If one specifies the boost effect to
be 0.5, this paper receives additional round (11×0.5) = 6 citations.

5. For each period, the new h-index and hα-index values are calculated. The alpha author
of a paper can be determined at the time of its publication (without changing later on)
or the alpha author of a paper is determined after each period of action based on the
current h-index values of the authors (see Tietze, Galam, & Hofmann, 2019).

6. To ensure the robustness of the results, steps 1 A 5 are repeated r times.

Figura 1 visualizes the single steps of the simulation procedure.

4. RESULTS

The Matthew effect implies that the more reputable scientist receives more credit than the less
reputable scientist for a scientific contribution, although the contribution is of the same scien-
tific quality. Così, the credit is not attributed fairly on the basis of the performed contribution,
Ma (unfairly) on the basis of previous contributions. If we compare this definition of the
Matthew effect with the definition of the hα-index, the similarities are obviously observable.
In case of the hα-index, the credit for a paper is assigned to the co-author with the highest

Quantitative Science Studies

337

Does the hα-index reinforce the Matthew effect in science?

h-index. Although all authors conributed to the co-authored paper in question, only one author
receives the full credit. Inoltre, the credit is assigned to the co-author who is most repu-
table in terms of h-index values. These similarities between the definitions of the Matthew effect
and hα already point out that the simulations that are presented in the following can be ex-
pected to reveal the appearance of the Matthew effect by using the hα-index in performance
measurement.

4.1. First Agent-Based Simulation with 200 Agents (Baseline Simulation)

Similar to the BBHs program with search, stopping, and decision rules (see above), the first
agent-based simulation has three phases: initial setting, acting (collaborating) several periods,
and final data set for further analysis (visualization of the results). Whereas the initial setting
and the final data set are on the macro level (certain distributions are set or analyzed), acting is
on the micro level (see section 2.2). It is the goal of the first agent-based simulation—the base-
line simulation, compared to which one parameter is changed in each of the simulations pre-
sented in the following sections—to compare the mean hα-index values of agents with initial
low or high h-index values after several periods of action (per esempio., collaboration with other
agents). The Stata command for the first agent-based simulation is h_index, R(50)
N(200) per(20) co(3) dp(poisson, mean(10)) dc(poisson, mean(5)) P(3)
sh(.33) clear4.

Initial setting: The first simulation is based on 200 agents [N(200)]. The agents in the
groups have published on different output and impact levels: The distribution of the papers
follows a Poisson distribution and the agents have published 10 papers on average
[dp(poisson, mean(10))]. For 1/3 of all papers published by an agent, the agent itself is
the alpha-author (-agent) [sh(.33)]. h-index and hα-index values are calculated for all agents.

Acting: Agents act (publish, collaborate, receive citations) across 20 periods [per(20)].
Each collaborating group of agents has three agents on average [co(3)]. The citations that
the co-authored papers published by the agent groups receive follow a Poisson distribution
with a specified time-dependent expected value [dc(poisson, mean(5))]. The time-
dependent expected value follows a log-logistic distribution reaching its maximal value of 5
after 3 years (following the general guideline by Glänzel & Schöpflin, 1995) [P(3)]. The agent-
based simulation is repeated 50 times [R(50)] to ensure the robustness of the simulation. Dopo
each simulation, new h-index and hα-index values are calculated for all agents.

Final data set: Two groups of agents are defined with low (<7) and high (>7) initial h-index
values (7 is the median initial h-index value). For each period with actions (20 in total), IL
mean hα-index values are computed (across 50 repetitions of the simulation to have robust
risultati). The results are shown in Figure 2. For each period with actions, the advantage of
the agents with high initial h-index values is clearly visible: They not only start with higher
mean hα-index values (which is as expected), but these values also increase with additional
periods—by considering further cooperation, publications, and additional citations. The mean
hα-index values of the agents with low initial h-index values also increase over time. Tuttavia,
the difference between the two groups becomes larger with onward periods—as the dotted

4 The equivalent function call to produce the simulated data in R is

simulate_hindex(runs = 50, n = 200, periods = 20, coauthors = 3,
distr_initial_papers = ‘poisson’, dpapers_pois_lambda = 10, distr_
citations = ‘poisson’, dcitations_mean = 5, dcitations_peak = 3, alpha_
share = .33)

Quantitative Science Studies

338

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

Figura 2. Results of the first agent-based simulation: mean hα-index values for two groups of agents
with low (<7) and high (>7) initial h-index values (with standard deviations bars).

line in Figure 2 demonstrates. Increasing differences between both groups can be interpreted
as a Matthew effect in operation.

4.2. Second Agent-based Simulation with an Additional Element Leading to More Citations for

Prolific Agents

The second simulation was run using the Stata command h_index, R(50) N(200)
per(20) co(3) dp(poisson, mean(10)) dc(poisson, mean(5)) P(3) sh(.33)
boost(size(.5)).5 It is the same command as in the first agent-based simulation (the baseline
simulation), but we introduce a new element with boost(size(.5)) (which is printed in
boldface). This option means that papers published by agents with higher h-index values are
cited more frequently than papers published by agents with lower h-index values.

The number of citations in the second simulation is increased based on the value specified
con [size(.5)]. Per esempio, suppose agents with a maximal h-index value of 11 Avere
published a certain paper. The value 0.5 as option means that this paper receives round
(11 × 0.5) = 6 additional citations.

Final data set: In the second agent-based simulation, the median of the initial h-index
values (median = 7) is the same as in the first simulation. Così, two groups of agents are
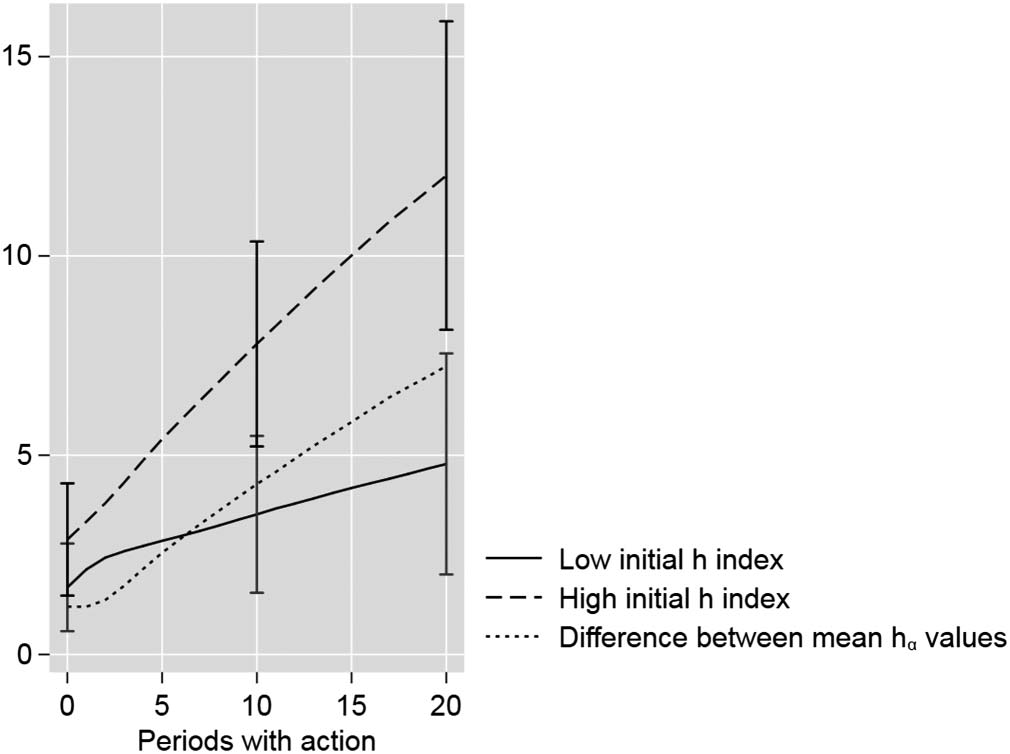
defined with low (<7) and high (>7) initial h-index values. Figura 3 presents the results. IL
results are similar to Figure 2, but the differences between both groups are more pronounced:
Whereas the hα-index values of the group with high initial h-index values increase more
steeply, the hα-index values of the group with low initial h-index values increase similarly
to those in Figure 2. This leads to larger mean hα-index values differences between both groups

5 The equivalent function call to produce the simulated data in R is

simulate_hindex(runs = 50, n = 200, periods = 20, coauthors = 3, distr_
initial_papers = ‘poisson’, dpapers_pois_lambda = 10, distr_citations =
‘poisson’, dcitations_mean = 5, dcitations_peak = 3, alpha_share = .33,
boost = TRUE, boost_size = .5)

Quantitative Science Studies

339

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

Figura 3. Results of the second agent-based simulation: mean hα-index values for two groups of
agents with low (<7) and high (>7) initial h-index values (with standard deviations bars).

(as the dotted line reveals). In other words, the Matthew effect is reinforced by letting the pa-
pers published by agents with higher h-index values be cited more frequently than the agents
with lower h-index values.

4.3. Third Agent-based Simulation Considering the Correlation of New Citations with h-index Values:
Agents with High h-index Values Receive Disproportional Citations

For the third simulation, the following Stata command was used: h_index, R(50)
N(200) per(20) co(3) dp(poisson, mean(10)) dc(poisson, mean(5)) P(3)
sh(.33) dil(correlation(.8) condividere(.6)).6 Similar to the second simulation, only
one option has been changed (which is printed in boldface) in comparison to the first baseline
simulation. The new options [dil(correlation(.8) condividere(.6))] focus on the probability
of publishing new papers depending on initial h-index values. The option [correlation(.8)]
means that agents with high initial h-index values are more productive than agents with low
initial h-index values: the correlation between the probability of publishing new papers and
initial h-index values has been set to 0.8. The option [condividere(.6)] means that 60% del
agents publish. The use of this option can be reasoned, for instance, by the “sacred spark” the-
ory (Cole & Cole, 1973) which claims “that there are substantial, predetermined differences
among scientists in their ability and motivation to do creative scientific research” (Allison &
Stewart, 1974, P. 596).

The third agent-based simulation is intended to check whether the higher productivity of
prolific agents has an effect on the hα-index values development of the groups with high and
low initial h-index values.

6 The equivalent function call to produce the simulated data in R is:

simulate_hindex(runs = 50, n = 200, periods = 20, coauthors = 3, distr_
initial_papers = ‘poisson’, dpapers_pois_lambda = 10, distr_citations =
‘poisson’, dcitations_mean = 5, dcitations_peak = 3, alpha_share = .33,
diligence_corr = .8, diligence_share = .6)

Quantitative Science Studies

340

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

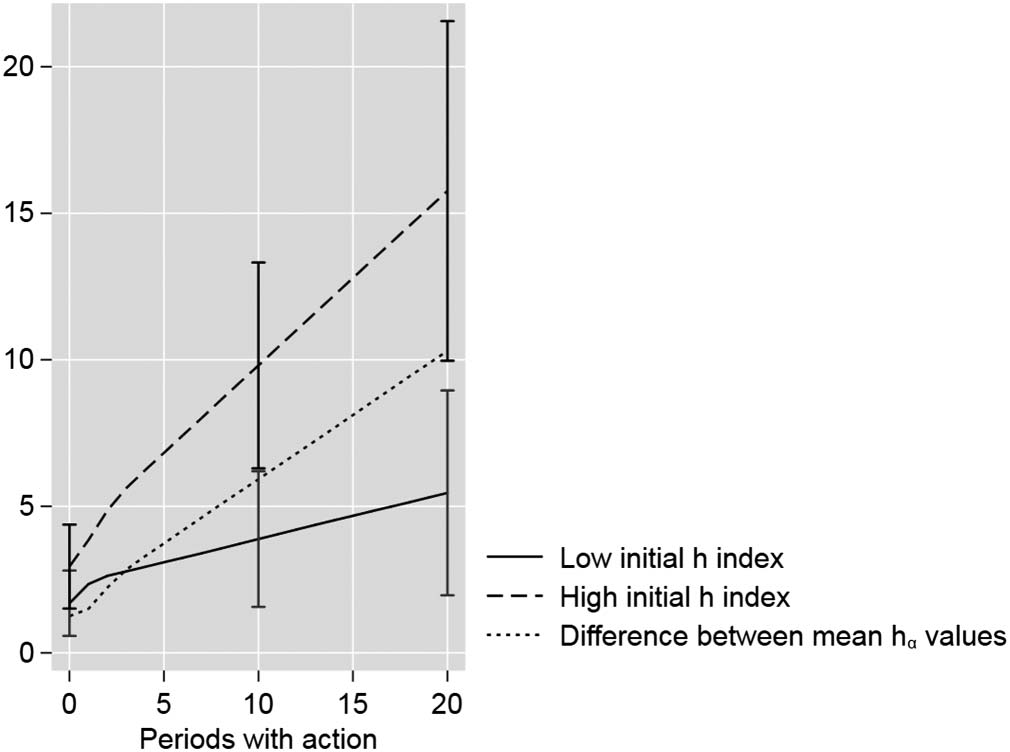
Figura 4. Results of the third agent-based simulation: mean hα-index values for two groups of
agents with low (<7) and high (>7) initial h-index values (with standard deviations bars).

Final data set: The results of the third simulation are presented in Figure 4. Whereas this
third simulation considers a positive correlation between productivity and h-index values, IL
second simulation includes the positive relationship between citations and h-index values (Vedere
Figura 3). The findings in Figure 4 vary (significantly) from the results in Figure 2 and Figure 3.
As the dotted line for the differences between the mean hα-index values reveals, the differences
in Figure 4 increase less strongly over time than in the previous figures.

4.4. Fourth Simulation Considering Strategically Selecting Co-authors

For the fourth simulation, we used the Stata command h_index, R(50) N(200) per(20)
co(3) dp(poisson, mean(10)) dc(poisson, mean(5)) P(3) sh(.33) clear st.7
Compared to the baseline simulation, we considered a strategic element [st], which focuses
on the possible tendency of agents to select other agents as co-authors with lower h-index
values. Such a strategical element (with another focus) has been mentioned by Hirsch
(2019B): “lower h-index authors have the choice to not collaborate with high h-index au-
thors but rather pursue their own independent work, or work with more junior collaborators”
(P. 1168). The strategic option of the h_index command means that first the agents with
the highest h-index values are assigned to the groups of collaborating agents as described in
step 3 of the simulation procedure in section 3. Then, all other agents in the simulation are
randomly allocated to the collaborating groups. Così, the strategic option seizes the idea
of collaborating with lower h-index agents. The strategic option gives much weight to the
effect of strategic collaboration decisions in our simulations, because the agents with the high-
est h-index values never collaborate with each other, so that their hα-index values increase
after every collaboration. The results of this simulation reveal the potential effect of strategic
collaboration decisions on the outcome distribution.

7 The equivalent function call to produce the simulated data in R is:

simulate_hindex(runs = 50, n = 200, periods = 20, coauthors = 3, distr_
initial_papers = ‘poisson’, dpapers_pois_lambda = 10, distr_citations =
‘poisson’, dcitations_mean = 5, dcitations_peak = 3, alpha_share = .33,
strategic_teams = TRUE)

Quantitative Science Studies

341

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

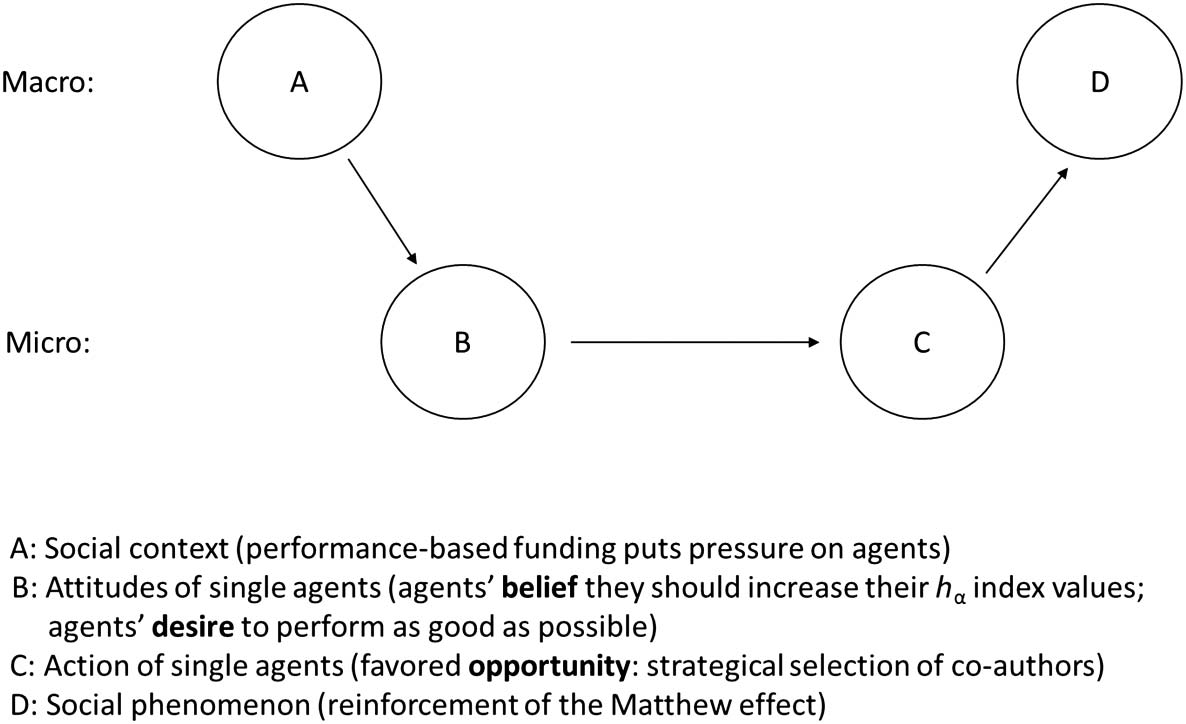
Figura 5. Coleman’s (1990) macro-micro-macro model depicting the relationship between
performance-based funding and reinforcement of the Matthew effect.

The strategic option follows closely Coleman’s (1990) classic macro-micro-macro model
(cioè., “Coleman’s boat”). “The general thrust of this model is that proper explanations of
macro-level change and variation entail showing how macro-states at one point in time in-
fluence the behavior of individual actors, and how these actions add up to new macro-states at a
later time” (Hedström & Swedberg, 1996, P. 296). The model assumes that individual action
results from the social context in a social network. Coleman’s model for the fourth agent-based
simulation (Guarda la figura 5) starts with the possible influence of a social context on the attitudes of
agents (UN). The current situation in science is characterized by performance-based evaluations:
“Especially in universities, government funding of scientific research is increasingly based upon
performance criteria. As research institutions operate more and more in a global market, inter-
national comparisons of institutions are published on a regular basis” (Moed, 2018). This situa-
tion puts pressure on agents doing science in the system.

The second (B) and third (C) steps are characterized by the core components of Hedström’s
(2005) desires, beliefs, and opportunities (DBO) theory. The second step (B) in the macro-micro-
macro model is that the social context (here: increasing focus on performance criteria) influences
the attitudes of single agents: The agents believe (given the pressure in the system) that they should
increase their hα-index values. As acting agents in the system they desire to perform as well as pos-
sible in terms of bibliometric indicators. In step C the agents have several opportunities to act: They
can collaborate with other agents without considering their h-index values or they can consider that
in their reflections (among other alternatives). Because the hα-index can only be improved when
agents publish papers with co-authors having lower h-index values, the strategic option
simulates this possible tendency of agents. In step D the empirical analyses of the development
of hα-index values for agents with low and high initial h-index values across several periods of
action reveal how single actions of agents lead to the social phenomenon on the macro level:
the reinforcement of the Matthew effect.

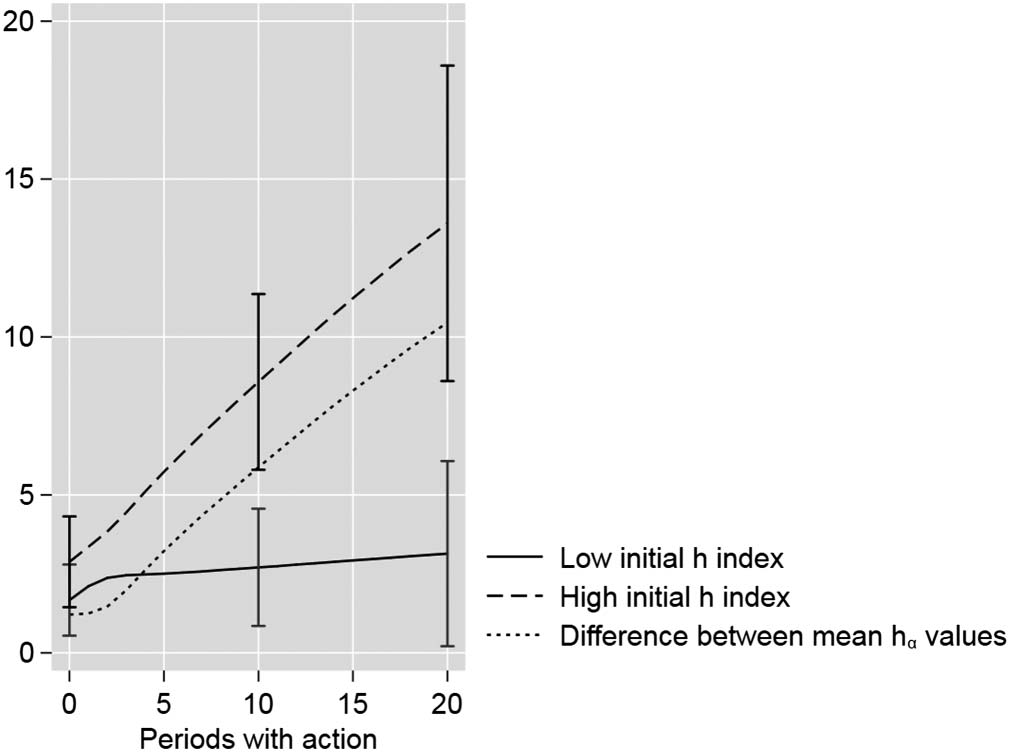
The result of the fourth agent-based simulation is shown in Figure 6. It is clearly visible
that the strategic element significantly reinforces the Matthew effect, which is already vis-
ible in the previous simulations: Agents with low h-index values not only have lower initial
hα-index values than agents with high h-index values, the hα-index values also increase on
a significantly lower level across the periods of evaluation. Across the periods of actions,
the hα index value differences between both h-index groups become larger and larger.

Quantitative Science Studies

342

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

Figura 6. Results of the fourth simulation: mean hα-index values for two groups of agents with low
(<7) and high (>7) initial h-index values (with standard deviations bars).

5. DISCUSSION

The agent-based simulations presented in this paper follow a recent discussion in
Scientometrics about the newly introduced hα-index by Hirsch (2019UN). Leydesdorff et al.
(2019) assumed that the use of the new index reinforces the Matthew effect in research eval-
uations. Scientists with initial high h-index values will profit disproportionally from the use of
the hα-index. Così, the fear is that the use of the index enlarges a problem that is already prev-
alent in the science system. According to Merton (1968) the problem of the Matthew effect in
science is so great that “we are tempted to turn again to the Scriptures to designate the status-
enhancement and status-suppression components of the Matthew effect. We can describe it as
‘the Ecclesiasticus component,’ from the familiar injunction ‘Let us now praise famous men,’
in the non-canonical book of that name” (P. 58).

Based on the definition of the hα-index, Leydesdorff et al. (2019) conjectured that the dispro-
portional attribution of credit by the hα-index—the co-author with the highest h-index receives
the full credit—reflects the operation of the Matthew effect. Così, the hα-index is already the
Matthew effect in operation. One cannot assume that the co-author with the highest h-index
contributes so much to the paper that the other co-authors can be completely discarded in
performance measurement. In this study, we abstained from the single case and tested with
various simulations whether the Matthew effect is visible on the macro level—when reason-
able parameters are set. The results of our study confirm what we expected from the single
case: The hα-index reinforces the Matthew effect. This effect can be intensified if strategic be-
havior of the publishing scientists and accumulative advantage effects are considered in the
simulation.

We situated this study in the tradition of analytical sociology which seeks for mechanism-
based explanations. These explanations try to focus on the crucial elements of a given process
and to abstain from the detailed view (Hedström & Ylikoski, 2010). Agent-based modeling is a
way of connecting the individual to the social level (Hedström, 2005). For studying a phenom-
enon on the macro level, the environment is defined in which the action takes place. Then, IL
action is run following predefined rules (Hanneman, 1988). The result is a data set that includes
the interactions between actions and initial parameters functioning as constraints. This data set
can be used to investigate whether the social phenomenon of interest is observable on the macro

Quantitative Science Studies

343

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

level. By varying the parameters of an agent-based model used as a baseline, the effect of various
situational elements from publishing, being cited, and collaborating on the development of the
distribution of hα-index values can be tested.

This study is rooted not only in analytical sociology but also in Bornmann and Marewski’s
(2019) BBH program. The program demands that indicators are empirically studied to see whether
they can be used in specific evaluation environments (and if so, how they can be used). IL
h_index command and hindex package, which we introduced in this paper, can be used to
simulate the use of the h-index and hα-index in certain predefined environments. Using different
specifications of the command (package functions), the simulation can be adapted to the environ-
ment for investigating where the hα-index is intended to be used. In this study, we used the Stata
command to test whether the Matthew effect becomes apparent when the hα-index is calculated
for a group of agents who collaborate, publish, and receive citations across several periods.

The R package and Stata command allow consideration of some strategic elements in the
agent-based simulations: If the hα-index is used in research evaluation processes, scientists
might try to cooperate strategically with co-authors having lower h-index values. The findings
of our simulations reveal that the consideration of this element leads to a significant reinforce-
ment of the Matthew effect. By using different options of the h_index command or different
parameters for the hindex package functions, the agent-based simulations can consider not
only strategic behavior but also information from the literature on the usual behavior of scien-
tists and distributions of publications and citations in different fields and institutions (per esempio.,
Perianes-Rodrigueza & Ruiz-Castillo, 2014). Per esempio, we considered in our agent-based
simulations that agents with higher h-index values will publish more frequently than agents
with lower h-index values. Many studies have shown that future performance depends on pre-
vious performance (Abramo, D’Angelo, & Soldatenkova, 2017; Allison, Lungo, & Krauze, 1982;
Kwiek, 2015). We also included another element in the simulations that can be derived from
the literature: that authors might tend to cite highly cited papers.

Because the R package and Stata command are freely available, we encourage their use.

We plan to add further functionality to them in the near future.

ACKNOWLEDGMENTS

We thank Jorge Hirsch for encouraging discussions and useful comments to a preliminary
version of this manuscript. We are grateful to Ludo Waltman and two anonymous reviewers
for helpful suggestions to improve the paper.

AUTHOR CONTRIBUTIONS
Lutz Bornmann: conceptualization; data curation; investigation; visualization; writing—original
bozza. Christian Ganser: methodology; software; visualization; writing—review & editing.
Alexander Tekles: data curation; software; writing—review & editing. Loet Leydesdorff: concep-
tualization; writing—review & editing.

COMPETING INTERESTS

We declare that we have no competing interests.

FUNDING INFORMATION

We did not receive specific funding for the research published in this paper.

Quantitative Science Studies

344

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

DATA AVAILABILITY STATEMENT

Not applicable

REFERENCES

Abbasi, A., Hossain, L., & Leydesdorff, l. (2012). Betweenness

Campbell, D. T. (1991). Autopoietic evolutionary epistemology

centrality as a driver of preferential attachment in the evolution
of research collaboration networks. Journal of Informetrics, 6(3),
403–412. https://doi.org/10.1016/j.joi.2012.01.002

Abramo, G., D’Angelo, C. A., & Soldatenkova, UN. (2017). How long
do top scientists maintain their stardom? An analysis by region,
gender and discipline: Evidence from Italy. Scientometrics,
110(2), 867–877. https://doi.org/10.1007/s11192-016-2193-x
Ahrweiler, P. (2001). Informationstechnik und Kommukiationsmanagement:

Netzwerksimulation fuer die Wissenschafts- und
Technikforschung. New York, NY: Campus Verlag.

Ahrweiler, P., Pyka, A., & Gilbert, N. (2004). Simulating knowledge
dynamics in innovation networks (SKIN). In Industry And Labor
Dynamics (Ed.), The Agent-Based Computational Economics
Approach (pag. 284–296): World Scientific Publishing Co. Pte. Ltd.

Ahrweiler, P., Pyka, A., & Gilbert, N. (2011). A new model for

university-industry links in knowledge-based economies. Journal
of Product Innovation Management, 28(2), 218–235. https://doi.
org/10.1111/j.1540-5885.2010.00793.x

Allison, P. D., Lungo, J. S., & Krauze, T. K. (1982). Cumulative
advantage and inequality in science. American Sociological
Review, 47(5), 615–625.

Allison, P. D., & Stewart, J. UN. (1974). Productivity Differences
Among Scientists—Evidence for Accumulative Advantage.
American Sociological Review, 39(4), 596–606. https://doi.org/
10.2307/2094424

Backs, S., Günther, M., & Stummer, C. (2019). Stimulating

academic patenting in a university ecosystem: An agent-based
simulation approach. The Journal of Technology Transfer, 44(2),
434–461. https://doi.org/10.1007/s10961-018-9697-x

Barabási, UN. l. (2002). Linked: The New Science of Networks.

Cambridge, MA: Perseus Publishing.

Barabási, UN. L., Jeong, H., Neda, Z., Ravasz, E., Schubert, A., &
Vicsek, T. (2002). Evolution of the social network of scientific
collaborations. Physica a—Statistical Mechanics and Its
Applications, 311(3–4), 590–614. https://doi.org/10.1016/
S0378-4371(02)00736-7

Bonitz, M., Bruckner, E., & Scharnhorst, UN. (1999). The Matthew
index—Concentration patterns and Matthew core journals.
Scientometrics, 44(3), 361–378. https://doi.org/10.1007/
Bf02458485

Bornmann, l. (2010). Die analytische Soziologie: Soziale

Mechanismen, DBO-Theorie und Agentenbasierte Modelle.
Österreichische Zeitschrift für Soziologie, 35(4), 25–44.
https://doi.org/10.1007/s11614-010-0076-6

Bornmann, L., Butz, A., & Wohlrabe, K. (2018). What are the top

five journals in economics? A new meta-ranking. Applied
Economics, 50(6), 659–675. https://doi.org/10.1080/00036846.
2017.1332753

Bornmann, L., & Marewski, J. N. (2019). Heuristics as conceptual
lens for understanding and studying the usage of bibliometrics in
research evaluation. Scientometrics, 120(2), 419–459.

Bornmann, L., Mutz, R., Hug, S., & Daniel, H. (2011). A multilevel
meta-analysis of studies reporting correlations between the h
index and 37 different h index variants. Journal of Informetrics,
5(3), 346–359. https://doi.org/10.1016/j.joi.2011.01.006

and internal selection. Journal of Social and Biological
Structures, 14(2), 166–173. https://doi.org/10.1016/0140-
1750(91)90137-F

Cole, J. R., & Cole, S. (1973). Social stratification in science.

Chicago, IL: The University of Chicago Press.

Coleman, J. S. (1990). Foundations of social theory. Cambridge,

MA: Belknap Press of Harvard University Press.

Distin, K. (2010). Cultural Evolution. New York, NY: Cambridge

Stampa universitaria.

Edmonds, B., Gilbert, N., Ahrweiler, P., & Scharnhorst, UN. (2011).
Simulating the social processes of science. Journal of Artificial
Societies and Social Simulation, 14(4). https://doi.org/10.18564/
jasss.1842

Edmonds, B., Hernandez, C., & Troitzsch, K. G. (2007). Sociale
Simulation: Technologies, Advances and New Discoveries.
Hershey, PAPÀ: Information Science Reference.

Egghe, l. (2006UN). How to improve the h-index? The Scientist,

20(3), 14.

Egghe, l. (2006B). Theory and practise of the g-index. Scientometrics,

69(1), 131–152. https://doi.org/10.1007/s11192-006-0144-7

Epstein, J. M. (2006). Generative social science: Studies in agent-

based computational modeling. Princeton, NJ: Princeton
Stampa universitaria.

Garavaglia, A., van der Hofstad, R., & Woeginger, G. (2017).

The dynamics of power laws: Fitness and aging in preferential
attachment trees. Journal of Statistical Physics, 168(6),
1137–1179. https://doi.org/10.1007/s10955-017-1841-8
Gigerenzer, G., & Gaissmaier, W. (2011). Heuristic decision
making. Annual Review of Psychology, 62, 451–482.

Gigerenzer, G., Todd, P. M., & ABC Research Group. (1999).
Simple heuristics that make us smart. Oxford, UK: Oxford
Stampa universitaria.

Gilbert, N. (1997). A simulation of the structure of academic

science. Sociological Research Online, 2(2).

Glänzel, W., & Schöpflin, U. (1995). A bibliometric study on aging

and reception processes of scientific literature. Journal of
Information Science, 21(1), 37–53. https://doi.org/10.1177/
016555159502100104

Guns, R., & Rousseau, R. (2009). Simulating growth of the h-index.
Journal of the American Society for Information Science and
Tecnologia, 60(2), 410–417. https://doi.org/10.1002/asi.20973

Hanneman, R. (1988). Computer-Assisted Theory Building:

Modeling Dynamic Social Systems. Newbury Park, CA: Sage.
Hedström, P. (2005). Dissecting the social: On the principles of
analytical sociology. Cambridge, UK: Cambridge University
Press.

Hedström, P., & Swedberg, R. (1996). Social mechanisms. Acta

Sociologica, 39(3), 281–308.

Hedström, P., & Ylikoski, P. (2010). Causal mechanisms in the
social sciences. Annual Review of Sociology, 36, 49–67.
https://doi.org/10.1146/annurev.soc.012809.102632

Hirsch, J. E. (2005). An index to quantify an individual’s scientific

research output. Proceedings of the National Academy of
Sciences of the United States of America, 102(46),
16569–16572. https://doi.org/10.1073/pnas.0507655102

Quantitative Science Studies

345

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
1
3
3
1
1
7
6
0
7
9
1
q
S
S
_
UN
_
0
0
0
0
8
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Does the hα-index reinforce the Matthew effect in science?

Hirsch, J. E. (2019UN). hα: An index to quantify an individual’s
scientific leadership. Scientometrics, 118(2), 673–686.

Hirsch, J. E. (2019B). Response to comment “hα: The scientist as

chimpanzee or bonobo,” by Leydesdorff, Bornmann and Opthof.
Scientometrics, 118(3), 1167–1172. https://doi.org/10.1007/
s11192-019-03019-w

Hodgson, G., & Knudsen, T. (2011). Darwin’s Conjecture: IL

Search for General Principles of Social and Economic Evolution.
Chicago/London: University of Chicago Press.

Ionescu, G., & Chopard, B. (2013). An agent-based model for the
bibliometric h-index. The European Physical Journal B, 86(10),
426. https://doi.org/10.1140/epjb/e2013-40207-0

Ivanova, IO. A., & Leydesdorff, l. (2014). A simulation model of

the Triple Helix of university–industry–government relations and
the decomposition of the redundancy. Scientometrics, 99(3),
927–948. https://doi.org/10.1007/s11192-014-1241-7

Jann, B. (2005). MOREMATA: Stata module (Mata) to provide
various functions, Statistical Software Components S455001:
Boston College Department of Economics, revised 17 May 2019.

Katsikopoulos, K. V. (2011). Psychological heuristics for making
inferences: Definition, performance, and the emerging theory
and practice. Decision Analysis, 8(1), 10–29. https://doi.org/
10.1287/deca.1100.0191

Kwiek, M. (2015). The European research elite: A cross-national study
of highly productive academics in 11 countries. Higher Education,
71(3), 379–397. https://doi.org/10.1007/s10734-015-9910-x

Leydesdorff, l. (2001). Technology and culture: The dissemination
and the potential “lock-in” of new technologies. Journal of
Artificial Societies and Social Simulation, 4(3), U20–U44.

Merton, R. K. (1973). The sociology of science: Theoretical and
empirical investigations. Chicago, IL: University of Chicago
Press.

Meyer, M., Lorscheid, I., & Troitzsch, K. G. (2009). The development
of social simulation as reflected in the first ten years of JASSS: UN
citation and co-citation analysis. Journal of Artificial Societies and
Social Simulation, 12(4), A224–A243.

Moed, H. F. (2018). Assessment and support of emerging research
groups. FEMS Microbiology Letters, 365(17), fny189. https://doi.
org/10.1093/femsle/fny189

Newman, M. E. J. (2001UN). Clustering and preferential attachment
in growing networks. Physical Review E, 64(2). https://doi.org/
10.1103/PhysRevE.64.025102

Newman, M. E. J. (2001B). Scientific collaboration networks. IO.

Network construction and fundamental results. Physical Review
E, 64(1). https://doi.org/10.1103/PhysRevE.64.016131

Perianes-Rodrigueza, A., & Ruiz-Castillo, J. (2014). Within- E
between-department variability in individual productivity. IL
case of economics. In P. Wouters (Ed.), Atti del
Science and Technology Indicators Conference 2014 Leiden
“Context Counts: Pathways to Master Big and Little Data”
(pag. 423–430). Leiden, Netherlands: University of Leiden.

Petersen, UN. M., Fortunato, S., Pan, R. K., Kaski, K., Penner, O.,
Rungi, A., … Pammoli, F. (2014). Reputation and impact in
academic careers. Proceedings of the National Academy of
Scienze, 111(43), 15316–15321. https://doi.org/10.1073/
pnas.1323111111

Popper, K. R. (1972). Objective Knowledge: An Evolutionary

Approach. Oxford, New York: Clarendon Press.

Leydesdorff, l. (2015). Can intellectual processes in the sciences

Price, D. J. D. S. (1976). A general theory of bibliometric and other

also be simulated? The anticipation and visualization of possible
future states. Scientometrics, 105(3), 2197–2214. https://doi.org/
10.1007/s11192-015-1630-6

Leydesdorff, L., Bornmann, L., & Opthof, T. (2019). hα: The scientist as

chimpanzee or bonobo. Scientometrics, 118(3), 1163–1166.

Leydesdorff, L., & den Besselaar, P. (1998). Technological

developments and factor substitution in a complex and dynamic
system. Journal of Social and Evolutionary Systems, 21(2),
173–192. https://doi.org/10.1016/S1061-7361(00)80004-1
Leydesdorff, L., & van den Besselaar, P. (1998). Competing

technologies: Lock-ins and lock-outs. In D. M. Dubois (Ed.),
Computing Anticipatory Systems: CASYS’97 (pag. 309–323).
New York, NY: Woodbury.

Leydesdorff, L., & van den Besselaar, P. (Eds.). (1994). Evolutionary
Economics and Chaos Theory: New Directions in Technology
Studi. London, UK: Pinter.

Lobet, G. (2016). Publish more or publish better? Retrieved April 9,
2019, from http://www.guillaumelobet.be/2016/05/11/publish-
more-publish-better/

Marewski, J. N., Schooler, l. J., & Gigerenzer, G. (2010). Five

principles for studying people’s use of heuristics. Acta
Psychologica Sinica, 42(1), 72−87. https://doi.org/10.3724/SP.
J.1041.2010.00072

Merton, R. K. (1942). Science and technology in a democratic
order. Journal of Legal and Political Sociology, 1, 115–126.
Merton, R. K. (1968). The Matthew effect in science. Scienza,

159(3810), 56–63.

cumulative advantage processes. Journal of the American
Society for Information Science, 27(5–6), 292–306.

Scharnhorst, A., Börner, K., & van den Besselaar, P. (Eds.).

(2012). Models of Science Dynamics: Encounters Between
Complexity Theory and Information Sciences. Heidelberg,
Germany: Springer.

Simone, H. UN. (1957). Models of Man, Social and Rational.

New York, NY: Wiley.

Tesfatsion, l. (2002). Agent-based computational economics:

Growing economies from the bottom up. Artificial Life, 8(1),
55–82. https://doi.org/10.1162/106454602753694765

Tietze, A., Galam, S., & Hofmann, P. (2019). Crediting multi-

authored papers to single authors. Retrieved May 13, 2019,
from https://arxiv.org/pdf/1905.01943.pdf

Waltman, L., & van Eck, N. J. (2012). The inconsistency of the

h-index. Journal of the American Society for Information Science
and Technology, 63(2), 406–415. https://doi.org/10.1002/asi.
21678

You, Z.-Q., Han, X.-P., & Hadzibeganovic, T. (2016). IL
role of research efficiency in the evolution of scientific
productivity and impact: An agent-based model. Physics Letters
UN, 380(7–8), 828–836. https://doi.org/10.1016/j.physleta.
2015.12.022

Żogała-Siudem, B., Siudem, G., Cena, A., & Gagolewski, M. (2016).
Agent-based model for the h-index – exact solution. The European
Physical Journal B, 89(1), 21. https://doi.org/10.1140/epjb/e2015-
60757-1