RESEARCH ARTICLE
Uncited papers are not useless
Michael Golosovsky1
and Vincent Larivière2
1The Racah Institute of Physics, The Hebrew University of Jerusalem, 9190401 Jerusalem, Israel
2École de bibliothéconomie et des sciences de linformation, Université de Montréal, Montréal, Québec, Canada
a n o p e n a c c e s s
j o u r n a l
Keywords: citation analysis, citation dynamics, uncitedness
ABSTRACT
We study the citation dynamics of the papers published in three scientific disciplines (Physics,
Economics, and Mathematics) and four broad scientific categories (Medical, Natural, Sociale
Scienze, and Arts & Humanities). We measure the uncitedness ratio, namely, the fraction of
uncited papers in these data sets and its dependence on the time following publication. These
measurements are compared with a model of citation dynamics that considers acquiring
citations as an inhomogeneous Poisson process. The model captures the fraction of uncited
papers in our collections fairly well, suggesting that uncitedness is an inevitable consequence
of the Poisson statistics.
1.
INTRODUCTION
The problem of uncited papers became prominent on the launch of the Science Citation Index
In 1964. De Solla Price (1965) conjectured that about 10% of all papers remain uncited in the
long term. This early estimate proved to be too optimistic and recent studies by Sugimoto and
Larivière (2018) showed that the fraction of uncited papers is higher and domain specific. In
particular, for the papers published in 1990 and for a citation window of 27 years, the uncit-
edness ratio ranged from 12% for Medical Sciences to 70% for Arts & Humanities.
The proper assessment of uncitedness is important for research policies (Garfield, 1991;
Seglen, 1992; van Noorden, 2017). Information scientists have made a large contribution to
the empirical characterization of the number and composition of uncited papers, studying how
uncitedness depends on the discipline, document kind, country, and year (Dorta-Gonzalez,
Suarez-Vega, & Dorta-Gonzalez, 2020; Hou & Ye, 2020; Thelwall, 2016UN; van Leeuwen &
Moed, 2005; Wallace, Larivière, & Gingras, 2009). The measurements of uncitedness have
been recently reviewed by Nicolaisen and Frandsen (2019) and a summary of the subject
has been presented by van Noorden (2017) and Sugimoto and Larivière (2018). It turns out
that the uncitedness ratio, namely, the fraction of papers in a collection that remain uncited
after a certain period, depends strongly on the length of this period. It is not even clear whether
the uncitedness ratio achieves some limiting value over the long term.
Existing empirical models successfully predict the uncitedness ratio for a collection of pa-
pers during the first couple of years after publication, but fail to account for it over the long
term. In particular, Burrell (2013), Egghe (2013), and Hsu and Huang (2012) analyzed the fac-
tors that determine the uncitedness ratio in a collection of papers and claimed a direct relation
to the mean number of citations for this collection; van Leeuwen and Moed (2005) related the
Citation: Golosovsky, M., & Larivière, V.
(2021). Uncited papers are not useless.
Quantitative Science Studies, 2(3),
899–911. https://doi.org/10.1162/qss_a
_00142
DOI:
https://doi.org/10.1162/qss_a_00142
Peer Review:
https://publons.com/publon/10.1162
/qss_a_00142
Received: 29 Dicembre 2020
Accepted: 17 Giugno 2021
Corresponding Author:
Michael Golosovsky
michael.golosovsky@mail.huji.ac.il
Handling Editor:
Ludo Waltman
Copyright: © 2021 Michael Golosovsky
and Vincent Larivière.
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza.
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
journal uncitedness ratio to the journals’ impact factor, which is determined by the mean number
of citations per paper garnered in the first 1–2 years after publication; whereas Wallace et al.
(2009) demonstrated that the uncitedness ratio is strongly affected by the annual growth in the
number of publications and their reference list length. Yet, a comprehensive study by Thelwall
(2016UN) showed a relation between the uncitedness ratio and the shape of the citation distri-
bution for a given collection. Così, although several factors that affect the uncitedness ratio were
properly identified (the mean number of citations, the growing number of publications, the refer-
ence list length, and the shape of the citation distribution), the existing models of uncitedness
focus only on one or several of these factors and on a short time window comprising a couple of
years after publication. A comprehensive model that includes all these factors and predicts the
uncitedness ratio in the long run has been missing.
Why do we need a better understanding of uncitedness? To answer a burning question:
whether uncited papers are a burden to science or constitute an inherent part of the scientific
enterprise (MacRoberts & MacRoberts, 2010; van Noorden, 2017). In other words, do uncited
papers exert some influence or not? Seglen (1992) argued that uncitedness is the consequence
of the mismatch between the number of publications and the number of references (because
citation distributions are highly skewed, the total number of references is insufficient to pro-
vide citations for all papers); Wallace et al. (2009) and Burrell (2013) suggested that uncited-
ness is related to the Poisson statistics of citations. Both approaches converge on the point that
uncitedness is an inevitable ingredient of the normal citation process. Così, a consistent model
of citation dynamics will account for uncited papers as well. Our objective is to validate this
statement. Infatti, our recently developed model (Golosovsky, 2019, 2021; Golosovsky &
Solomon, 2017) captures many attributes of the citation dynamics of research papers, includ-
ing citation trajectories and citation distributions. In this study, we demonstrate that this model
quantitatively captures the uncitedness ratio for three single disciplines and four broad scien-
tific categories.
2. THE MODEL OF CITATION DYNAMICS AND THE UNCITEDNESS RATIO
We present here a short summary of the model of citation dynamics while focusing on the
phenomenon of uncitedness. Consider a paper j that belongs to some scientific community.
An author of a new publication may cite this paper after finding it in databases, scientific jour-
nals, or following recommendations of colleagues or news portals. We name this a direct
citation of paper j. An author of another new publication can find paper j in the reference lists
of his already selected papers and cite it as well. If paper j was placed into the reference list of
a new publication as a result of the copying strategy, we name it indirect citation.1
The model assumes that the number of citations garnered by a paper follows Poisson
distribution,
λk
j
k! e
j(T) is the papers’ latent citation rate which is postulated to be the sum of the direct
(T) + λindir
(T). The model assumes that the direct
j
where λ
and indirect contributions, namely, λ
citation rate is set at the moment of publication of the paper, and the indirect citation rate is
j(T) = λdir
j
Pj kð Þ ¼
−λj ;
(1)
1 A direct reference is an entry in the reference list of a publication that is not cited by any other reference
there, while an indirect reference is an entry that is cited by one or more references in this list. When the
perspective is shifted to the cited paper, these definitions correspond to direct and indirect citations.
Quantitative Science Studies
900
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
determined by the papers’ citation history. Any paper can be cited directly, but only previously
cited papers can be cited indirectly. For uncited papers, only the direct citation rate matters,
namely, λ
(T).
j(T) = λdir
j
Each publication belongs to some scientific discipline or community and can be cited by
any new publication there. Following Wallace et al. (2009), we assume that
λdir
j
tð Þ ¼ Nreferences t0 þ t
ð
Npapers t0ð Þ
Þ
η
jA tð Þ;
(2)
where t0 is the publication year, t is the number of years after publication, Npapers(t0) is the
number of papers associated with a given discipline that were published in the year t0, E
Nreferences(t0 + T) is the total number of references in the papers belonging to this discipline or
community that were published in the year t0 + T. UN(T) is the aging function for references,
namely, the average fraction of references in the reference lists of papers that belong to this
discipline and which are t years old (we define it in such a way that
j is the
paper’s fitness or intrinsic citation capacity (Milojevic, 2020), which captures its potential for
garnering citations; in other words, it characterizes the appeal that the paper makes to citing
authors after aging and other time-dependent factors have been taken into account. IL
model assumes that each paper is born with some intrinsic fitness that does not change during
the paper’s lifetime.2
R ∞
0 UN(T)dt = 1). η
Così, in the context of uncitedness, our model reduces to the combination of the fitness
model of Caldarelli, Capocci et al. (2002) and the aging model of Wallace et al. (2009).
−Λdir(η,T), where Λdir(T) =
Equazione 1 yields that the probability for a paper with fitness η to remain uncited after t years
T
0 λdir(η , τ)dτ. For a large collection of papers, all published
is P(0) = e
in the same year, the fraction of uncited papers after t years (the uncitedness ratio), È
Z ∞
R
f0 tð Þ ¼
e
0
ð
−Λdir η;T
Þρ ηð Þdη;
where ρ ηð Þ is the fitness distribution for this collection.
We introduce Mdir(T), the mean number of direct citations garnered by the papers in this
collection during t years after publication. Così
ð
Λdir η; T
Þ ¼
η
η0
Mdir tð Þ
(4)
0 =
R ∞
where η
0 ηρ ηð Þdη is the average fitness, namely, the average fraction of direct citations
among all citations of a paper. Although the fitness distribution ρ ηð Þ is determined by the collec-
tion of cited papers for which we calculate the uncitedness ratio (a single discipline, journal,
institution, country, eccetera.), Mdir(T) is determined by the broad collection of papers that can po-
tentially cite the given collection, namely, the whole discipline or community. We introduce
reduced fitness eη =
η
η0
, in such a way that Eqs. 3 E 4 yield
Z ∞
f0 tð Þ ¼
0
−~ηMdir tð Þρ eηð Þdeη;
e
(3)
(5)
where ρ(eη) is the reduced fitness distribution, which only differs from ρ ηð Þ by a constant factor.
2 The factor η
jA(T) corresponds to β
I in Wallace et al. (2009).
Quantitative Science Studies
901
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
Equazione 5 relates the uncitedness ratio to the functions characterizing cited papers, ad esempio
the mean number of direct citations Mdir(T) and the reduced fitness distribution ρ(eη). How can
one measure these functions? The fitness distribution can be determined from the analysis of
citation distributions in different citation windows (Golosovsky, 2021) and Mdir(T) can be
found from the analysis of the direct and indirect citations garnered by the papers in the
collection. D'altra parte, Mdir(T) can be found from an analysis of the reference lists of
R
T
0UN(τ)dτ. We introduce R0(t0 + T),
0
the average reference list length for the papers published in the year t0 + T, in such a way that
Nreferences(t0 + T) = Npapers(t0 + T)R0(t0 + T). Assuming that the number of publications covered by
databases and the average reference list length both grow exponentially (Eh, Leydesdorff, &
βt (Dove
Rousseau, 2020; Sugimoto & Larivière, 2018), namely, N(T + t0) ≈ N(t0)e
R0 stays for R0(t0)), we find
papers. Infatti, Eqs. 2 E 4 yield Mdir(T) =
Nreferences t0þτ
Þ
Npapers t0ð Þ η
≈ R0(t0)e
αt, R0
ð
Mdir tð Þ ≈ R0η0
Z
T
0
ð
αþβ
A τð Þe
Þτ
dτ:
(6)
3. MEASUREMENTS AND COMPARISON WITH MODEL
We measured citation distributions and citation dynamics of papers belonging to several col-
lections, determined the corresponding model parameters, and verified to what extent the
model captures the fraction of uncited papers in these collections.
3.1. Single Disciplines
Mathematics, Economics, and Physics papers published in 1984 were retrieved using the
Clarivate Web of Science ( WoS) database. We considered only articles, letters, and notes writ-
ten in English and excluded non-English and low-circulation journals which contain many
papers whose citations are not covered by the WoS, because, according to our protocol, these
papers would be considered uncited. We also excluded reviews, as their citation careers are
very different from those of ordinary research papers. The publication year 1984 was chosen in
such a way as to provide a long citation window for the cited papers and sufficient coverage
for the citing papers.
We analyzed citation trajectories of papers and the structure of their reference lists. These
were compared to our stochastic model of citation dynamics (Golosovsky, 2019). The corre-
sponding model parameters and functions, such as the average reference list length R0, the sum
of the growth exponents (α + β), the aging function A(T), the average fitness η
0, and the param-
eters that define indirect citations, were estimated for each discipline. We found that the sum
of the growth exponents (α + β) is more or less compatible with the direct measurements of
Sugimoto and Larivière (2018) which report ≈3% annual growth in the reference list length and
≈4% growth in the number of publications. Although we found that the average reference list
length R0 is smaller than the actual reference list length, it should be noted that it counts only
those references that can cite the given paper and that are included in the citation database.
For WoS, these include research papers and exclude books, conference proceedings, eccetera. IL
fraction of these documents in the reference lists of Physics papers is small; hence R0 for
Physics matches our independent measurements. Tuttavia, the fraction of books and confer-
ence proceedings in the reference lists of Economics and Mathematics papers is rather large,
and that is why the effective R0 for these disciplines is so small.
Quantitative Science Studies
902
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
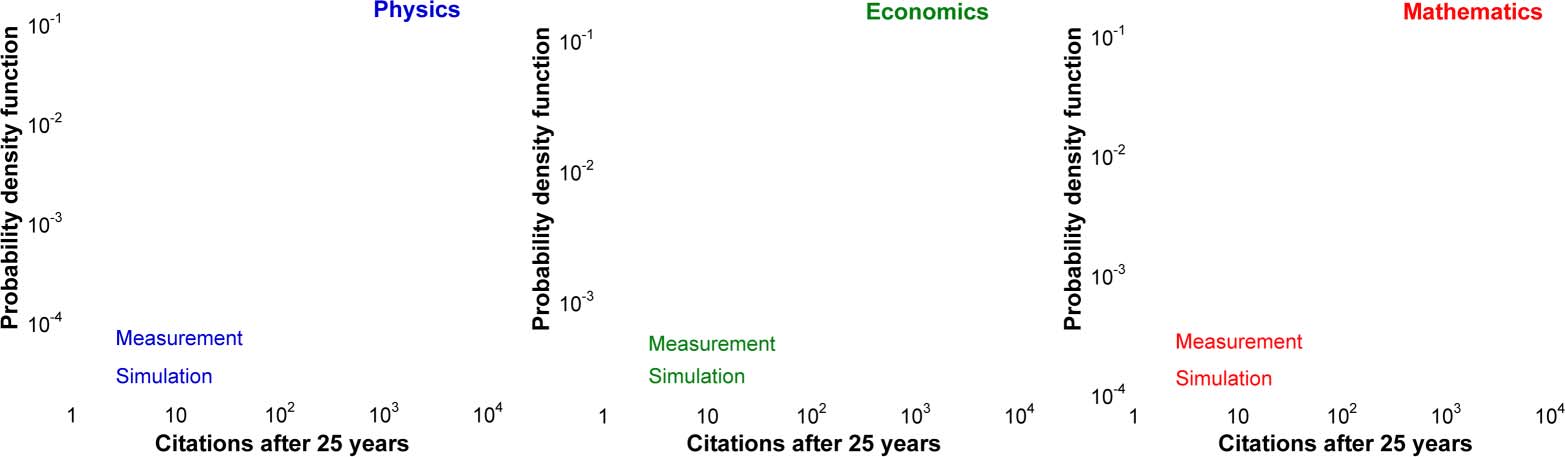
Figura 1. Citation distributions for the papers published in single disciplines in 1984. Citations are counted in 2008. (UN) Physics. Npapers =
40,195. Parameters of the simulation: R0 = 19, (α + β) = 0.090, η
0 =
0.44, σ = 1.13. (C) Mathematics. Npapers = 6,313. R0 = 3.91, (α + β) = 0.092, η
0 = 0.5, σ = 1.13. (B) Economics. Npapers = 3,043. R0 = 8.44, (α + β) = 0.045, η
0 = 0.46, σ = 1.13.
Then we analyzed citation distributions and determined the reduced fitness distribution ρ(eη).
We found that the latter is best modeled by a log-normal distribution
ρ eηð Þ ¼
1
−
p e
ffiffiffiffiffi
2π
eησ
ð
Þ2
ln~ηþσ2
2
2σ2
;
(7)
where σ is the shape factor and
(cid:2)eη = 1, by definition.
Figura 1 shows the measured and numerically simulated citation distributions for three
disciplines. They are virtually indistinguishable.
As the model relates the uncitedness ratio to the mean number of direct citations Mdir(T), we
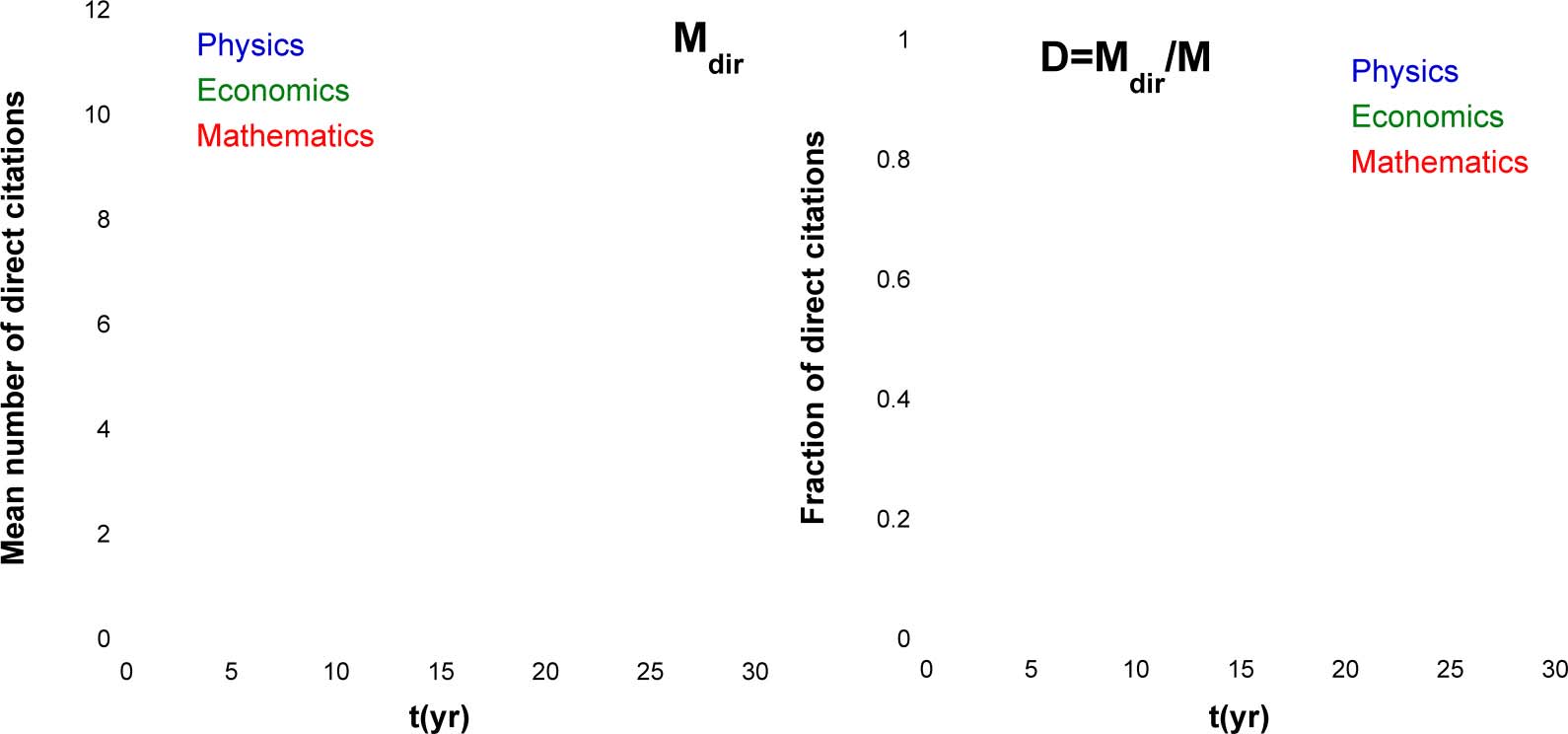
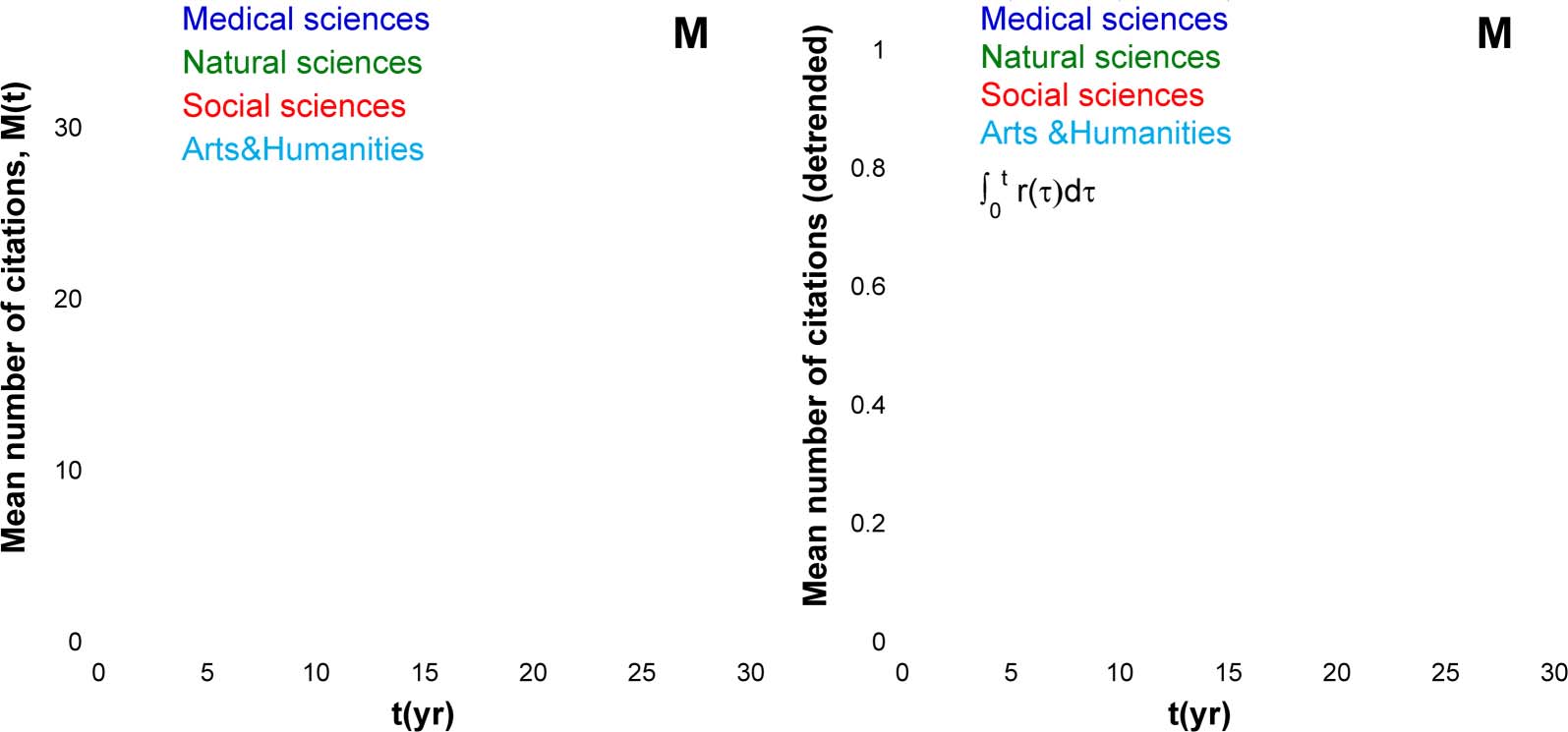
determined the latter basing on Eq. 6. Figura 2(UN) shows that the Mdir(T) dependences do not
come to saturation even after 25 years. It is also instructive to compare Mdir(T) to M(T), the mean
number of all citations for the same collection of papers. A tal fine, we introduced the
Figura 2.
is t = 1.
(UN) Mean number of direct citations. (B) An average fraction of direct citations among all citations of a paper. The publication year
Quantitative Science Studies
903
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
average fraction of direct citations D(T) = Mdir tð Þ
M tð Þ and plotted it on Figure 2(B). Although early after
the publication of a paper its citations are mostly direct (D ≈ 1), after 10–20 years the overall
fraction of direct citations drops to D = 0.3–0.45, depending on the discipline.
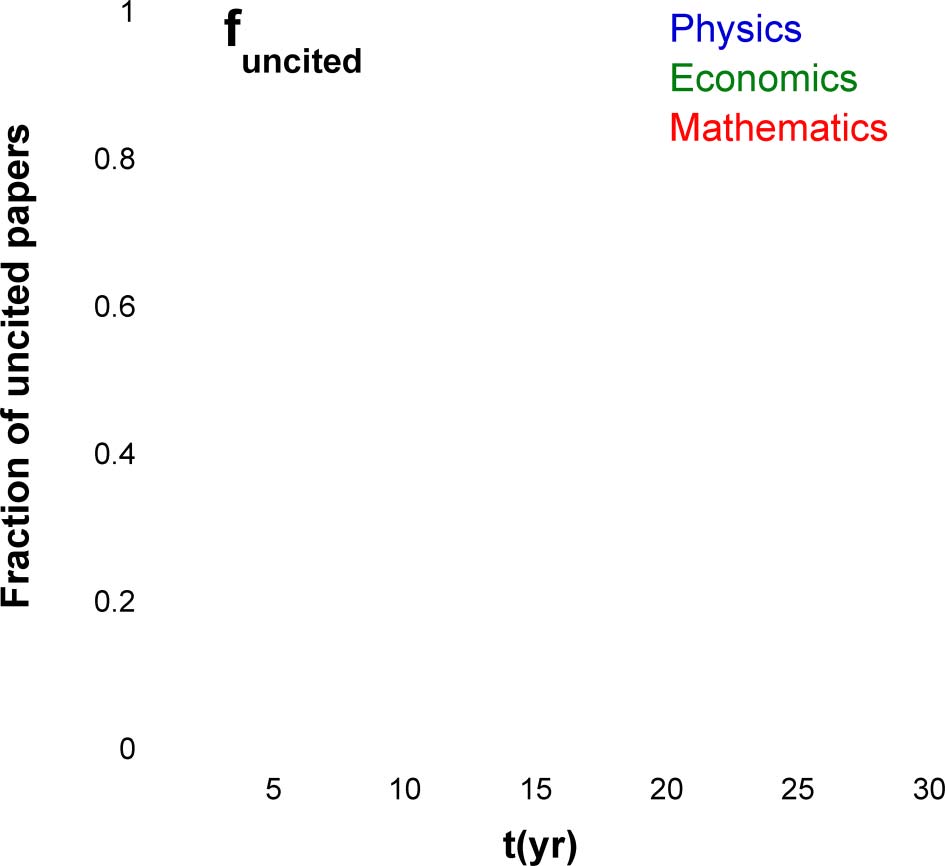
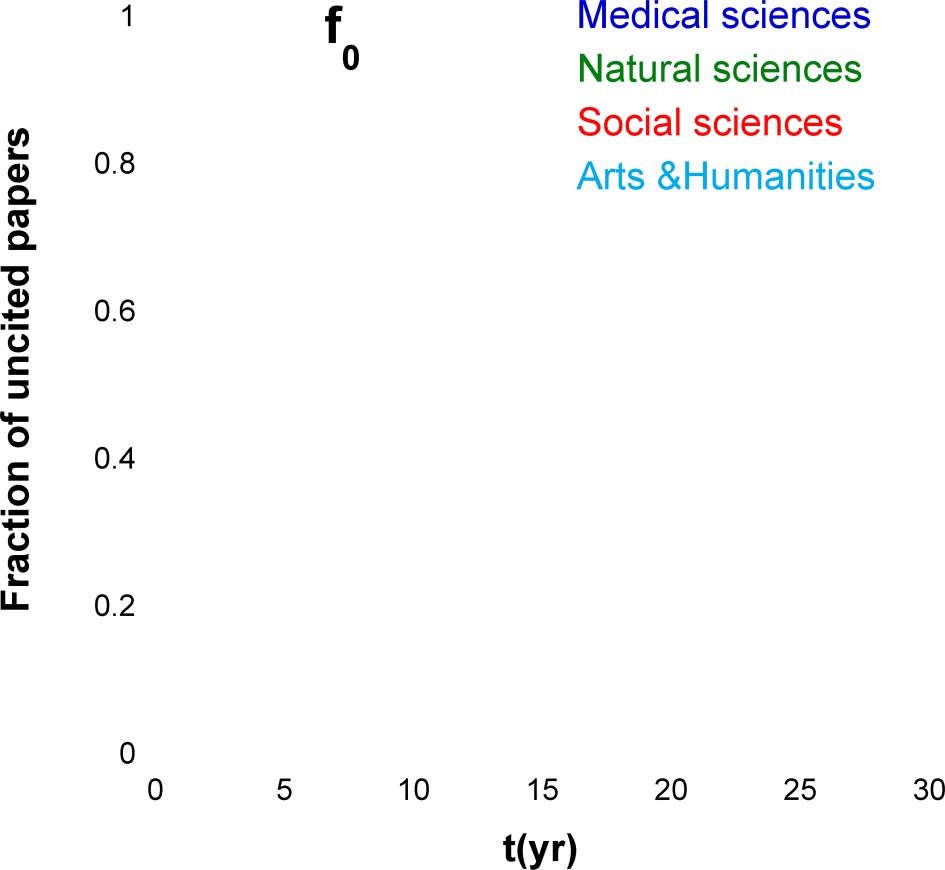
Figura 3 shows the uncitedness ratio f0 and its dependence on the time after publication. For a
citation window of 25 years, the uncitedness ratios for the Physics, Economics, and Mathematics
papers are 7.1%, 14.7%, E 27.3%, correspondingly. Yet, these percentages are not final, because
f0 continuously decreases with time and does not come to saturation even after 25 years. The reason
for the very slow decay of the uncitedness ratio is not only the time after publication, but also the
growth in the number of publications and the average reference list length R0 (see Eqs. 5 E 6).
The continuous lines in Figure 3 show the results of the numerical simulation. As all the
model parameters were found from the analysis of cited papers, the very fact that the same
model captures the fraction of uncited papers is significant and indicates that, at least for these
disciplines, the cited and uncited papers are two sides of the same coin.
3.2. Broad Scientific Categories
We consider here the measurements of uncitedness for the papers published in four broad
scientific categories in 1990 (Sugimoto & Larivière, 2018). To compare these data to Eqs. 5
E 6, we need to find the corresponding model parameters. In principle, this can be done by
measuring the citation trajectories of papers and comparing them to the full stochastic model
of citation dynamics (Golosovsky, 2019; Golosovsky & Solomon, 2017). Here, we did not
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 3. The fraction of uncited papers, f0(T) = Nuncited tð Þ
for the papers belonging to three scientific
disciplines. Npapers is the total number of papers belonging to a certain scientific discipline that
were published in a certain year, Nuncited(T) is the number of uncited papers after t years, and t is
the number of years after publication. The continuous lines show the model prediction obtained by
running the full stochastic model on the synthetic collections containing the same number of papers
as in the measured collection. Note the good correspondence between the model and the
measurements.
Npapers
Quantitative Science Studies
904
Uncited papers are not useless
(UN) The mean number of citations for four broad categories of papers (Sugimoto & Larivière, 2018). Continuous lines show the fit to
Figura 4.
−(α+β)t/R0. All four dependences are remarkably similar
the model (Golosovsky & Solomon, 2017). (B) Reduced mean number of citations, M(T)e
(but not identical) and Eq. 8 suggests that these are nothing else but r(T). Continuous line shows our measurements of r(T) for the Physical
Review B papers published in 1984.
perform this tedious task: For each category, we only measured the annual mean number of
citations M(T) as a function of time and the citation distribution after 27 years. By fitting these
two functions we determined all the model parameters.
Figura 4(UN) shows the M(T) dependences. Their analysis yields the average reference list
length R0 and the sum of the growth exponents (α + β). The basis for this analysis is the
reference-citation duality. Namely, if the number of publications and of the average reference
list length both grow exponentially, then the mean number of citations M(T) is closely related
to R(T), the age distribution of references (synchronous or retrospective citation distribution):
M(T) = R(T)e(α+β)T. This expression can be cast as follows
ð
M tð Þe− αþβ
Þt
R0
¼ r tð Þ;
(8)
where r(T) is the reduced age distribution of references3 and R0 is the average reference list length.
Although M(T) can diverge with time, R(T) converges to R0 in the long run, namely,
R ∞
0 R(T)dt = 1.
Using this constraint, we found R0 and (α + β) from the measured M(T) dependences and Eq. 8.
Figura 4(B) shows the corresponding r(T) dependences. They are remarkably similar, although
not identical. To find the remaining parameters of citation dynamics, we used our full stochas-
tic model and the previously found aging function A(T) (Golosovsky, 2021) and fitted the
citation distributions for each category in the year 2017. We assumed the log-normal reduced
fitness distribution and used its width σ as a fitting parameter. Figura 5 shows that the model
3 The function r(T) is remarkably stable over time and does not vary much from discipline to discipline
(Glanzel, 2004; Golosovsky & Solomon, 2017; Roth, Wu, & Lozano, 2012; Sinatra, Deville et al., 2015).
Quantitative Science Studies
905
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
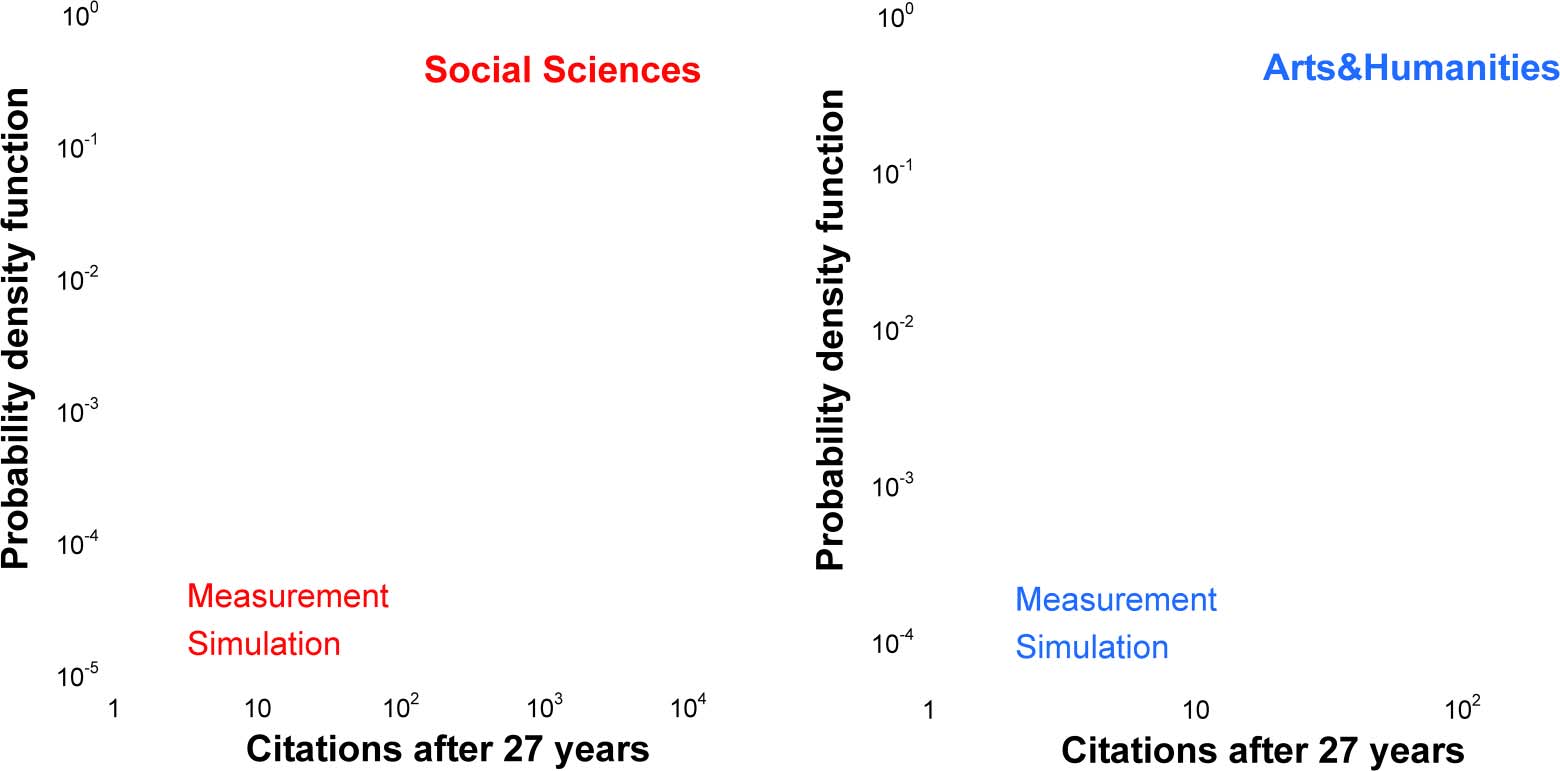
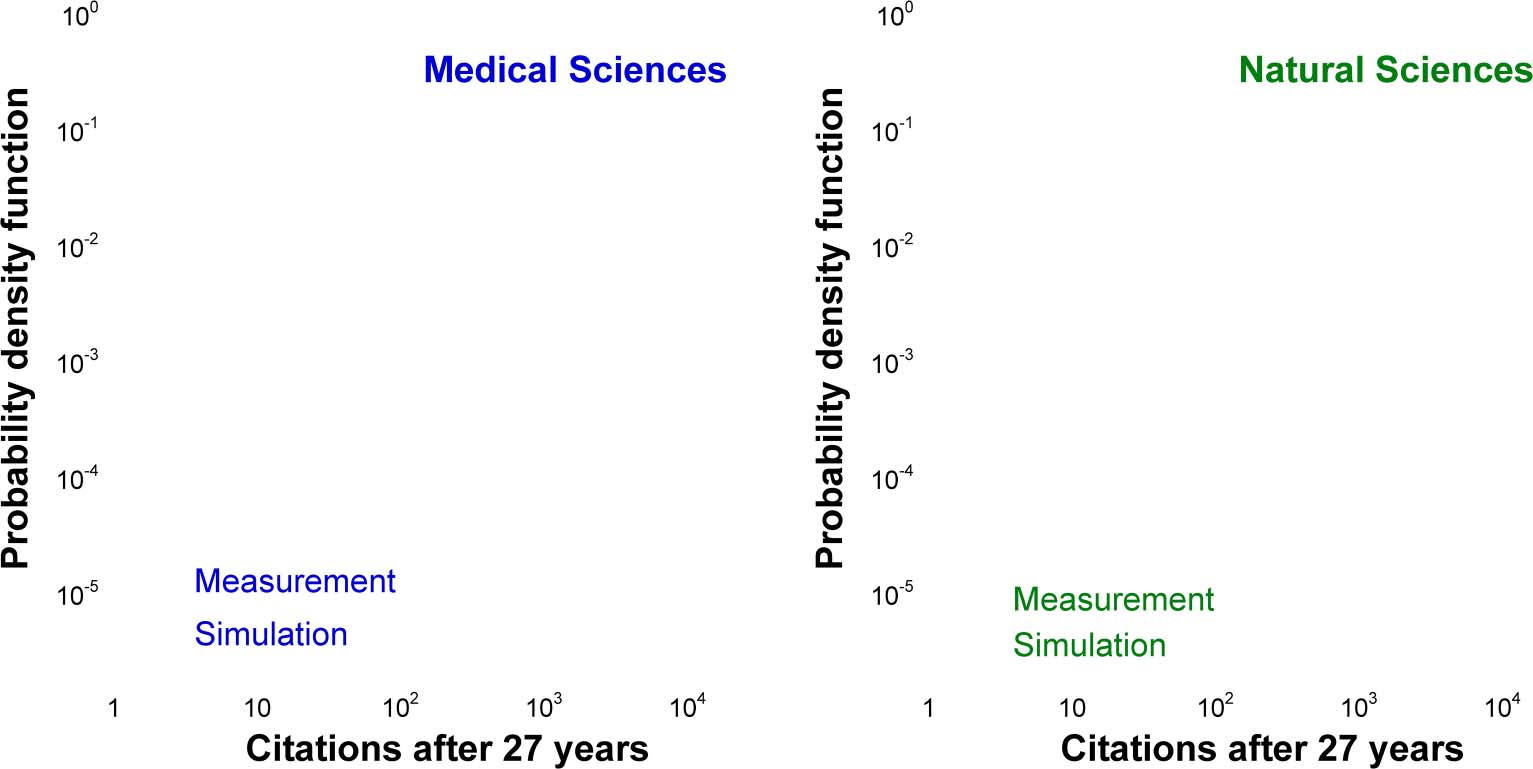
Figura 5. Citation distributions for four broad scientific categories of papers published in 1990. Citations are counted in 2017. (UN) Medical
0 = 0.48, σ = 1.3. (B) Natural Sciences. Npapers =
Scienze. Npapers = 272,192. Parameters of the simulation: R0 = 23.5, (α + β) = 0.050, η
293,030. R0 = 11.27, (α + β) = 0.06, η
0 = 0.42, σ =
1.4. (D) Arts & Humanities. Npapers = 30,069. R0 = 0.587, (α + β) = 0.085, η
0 = 0.47, σ = 1.32. (C) Social Sciences. Npapers = 50,032. R0 = 7.1, (α + β) = 0.095, η
0 = 0.46, σ = 1.1.
accounts for the measured citation distributions4, and Figure 6 demonstrates that the same
model captures the uncitedness ratio as well.
3.3. Fitness Distribution
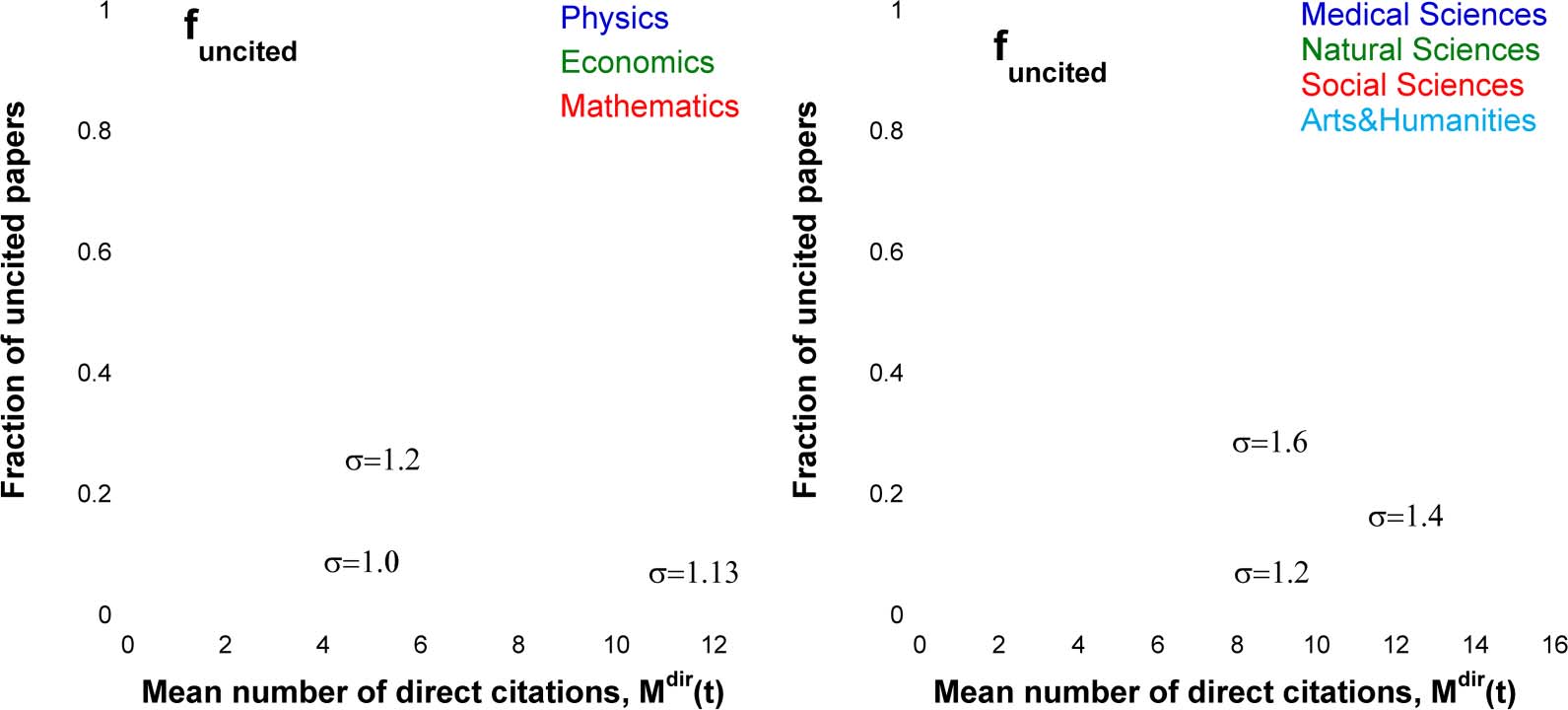
Figura 7 explores the sensitivity of the uncitedness ratio f0(T) to the functional shape of the
fitness distribution. It shows the f0(Mdir) dependences where the time after publication is an
4 A broad scientific category aggregates several disciplines with dissimilar citing habits, namely, those with
0. Because the reduced fitness eη,
different average reference list lengths R0 and different average fitness η
average fitness η
0, and the average reference list length R0 do not appear in Eqs. 5 E 6 separately but
as a product eηη
0R0, our model can still be applied to such aggregated data sets. Tuttavia, the reduced fitness
distribution ρ(eη) will be replaced with the joint distribution ρ(eη, η
0R0). It is no surprise that the latter turns out
to be log-normal. For such a distribution, the variance of the factor η
0R0 among the disciplines belonging to
one category and the variance of eη are added together, in such a way that ρ(eη, η
0R0) is broadened. This is the
reason why the fitness distribution for categories is somehow broadened in comparison with that found in
our analysis of single disciplines.
Quantitative Science Studies
906
Uncited papers are not useless
Figura 6. The fraction of uncited papers f0(T) for the papers published in four broad scientific cat-
egories (Sugimoto & Larivière, 2018). The continuous lines show model predictions obtained by
running the full stochastic model on synthetic collections containing the same number of papers.
implicit parameter and Mdir(T) has been calculated according to Eq. 6. Equazione 5 states that the
function f0(Mdir) is nothing else but the Laplace transform of the reduced fitness distribution ρ(eη).
Figura 7(UN) shows that f0(Mdir) dependences for single disciplines correspond to log-normal dis-
tribution with the shape factor σ ≈ 1.13, and Figure 7(B) shows that the data for the Medical,
Natural, and Social Sciences correspond to log-normal distributions with σ = 1.3–1.4.
Notably, for all disciplines and categories, the fitness distributions derived from the time
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 7. The fraction of uncited papers, f0(T) versus the average number of direct citations Mdir(T), where the latter was calculated using Eq. 6.
The continuous lines show model predictions (Eq. 6) for the log-normal fitness distributions (Eq. 7) with different shape factors σ. (UN) Single
disciplines. All data collapse onto one curve, indicating that the reduced fitness distribution ρ(eη) is almost the same for these three disciplines. It
is best accounted for by the log-normal fitness distribution with the shape factor σ = 1.13. (B) The data for Medical, Natural, and Social
Sciences are best described by the log-normal distribution with σ = 1.3–1.4, while the data for Arts & Humanities can be accounted for
by the log-normal distribution with σ = 1.1.
Quantitative Science Studies
907
Uncited papers are not useless
dependence of the uncitedness ratio are the same as those found in the analysis of citation
distributions (Figures 1 E 5).
4. COMPARISON TO EXISTING MODELS
The models of uncitedness, as summarized by Burrell (2013), assume that when the authors of
a new publication compose the reference list, they choose the target papers basing on some
attribute which we name fitness. When the perspective is shifted to cited papers, this means
that each paper has an individual citation rate determined by its fitness. Statistical distribution
of these rates, for the collection of papers published in one year, has been postulated to be
either exponential or Gamma-distribution (Burrell, 2013), or to result from the preferential
attachment rule (Egghe, 2013; Hsu & Huang, 2012). Assuming that the citation dynamics of
papers is Poissonian, the existing models (Burrell, 2013; Egghe, 2013; Hsu & Huang, 2012)
relate the uncitedness ratio for a collection of papers to the mean number of cumulative cita-
tions for this collection, M(T). In particular, for the exponential fitness distribution, Burrell
(2013) and Egghe (2013) showed theoretically that
f0 tð Þ ¼
1
1 þ M tð Þ
:
(9)
Hsu and Huang (2012) successfully verified this simple relation for the Physics papers pub-
lished in 2007 and for a three-year citation window. Tuttavia, Eq. 9 fails for a long citation
finestra. In particular, given a citation window of 27 years and M(T) from Figure 4, Eq. 9 yields
f0 = 3%, 5.3%, 5.3%, E 46% for the papers in Medical, Natural, Social Sciences, and Arts &
Humanities, correspondingly. Tuttavia, the actual uncitedness ratios, as found from Figure 6,
are much higher: 12%, 20%, 28%, E 70%.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
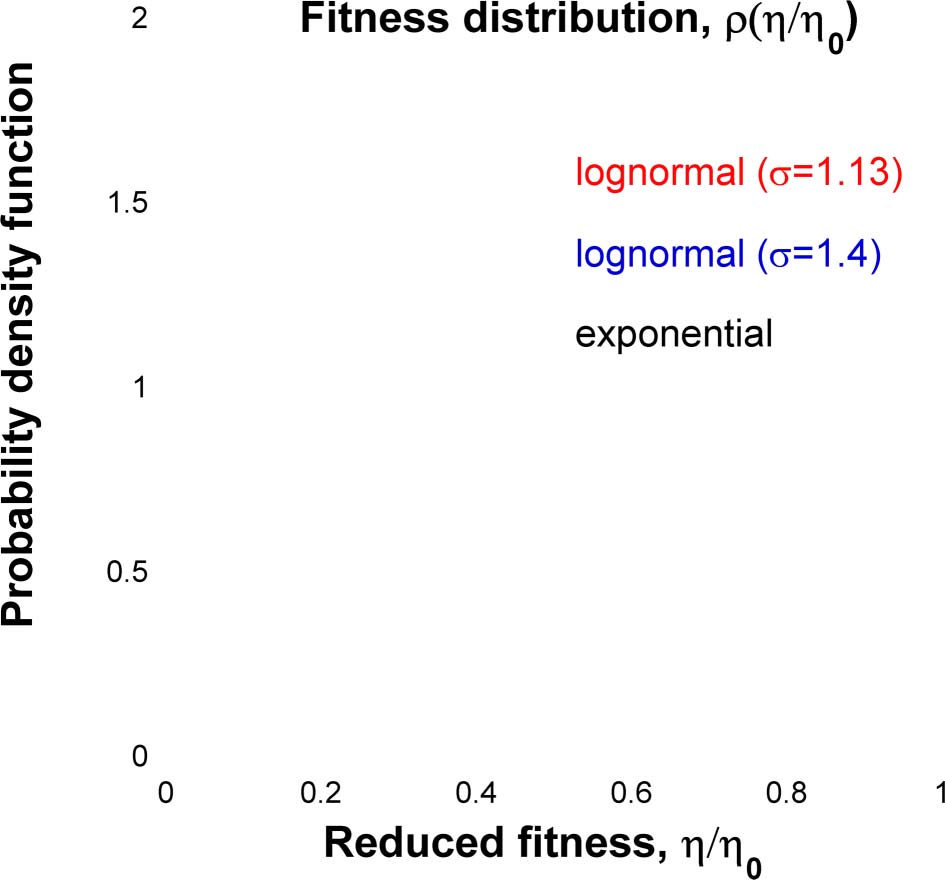
Þ2
Figura 8. The red line shows the log-normal reduced fitness distribution ρ(eη) = 1
2σ2 with
~ησ
σ = 1.13. This distribution characterizes the Physics, Mathematics, and Economics. The blue line
shows the log-normal distribution with σ = 1.4. It characterizes the Medical, Natural, and Social
Scienze. Although the mean of the reduced fitness distribution is unity, by definition, its mode
is much smaller: 0.147 for σ = 1.13 E 0.053 for σ = 1.4. The dashed line shows the exponential
distribution, ρ(eη) = e−~η, for comparison.
−
ffiffiffiffi
p e
2π
ln~ηþσ2
2
ð
Quantitative Science Studies
908
Uncited papers are not useless
In contrast to existing models, we assume a much more realistic scenario of the citation
process which takes into account that, in filling the reference lists of their papers, the authors
combine two strategies: random search (direct references) and “copying” from the reference
lists of the preselected papers (indirect references). When the perspective is shifted to cited
papers, these strategies yield direct and indirect citations, correspondingly. Although Burrell
(2013), Egghe (2013), and Hsu and Huang (2012) related the uncitedness ratio in a collection
of papers published in one year to the mean number of all citations M(T), our model relates it to
Mdir(T), the mean number of direct citations.
In summary, our approach to the problem of uncitedness builds on previous theoretical
speculations but uses a more realistic scenario of the citation process. Primo, we replaced
M(T) by Mdir(T). Secondo, we did not postulate any specific shape of the fitness distribution
but determined it from the measured citation distributions. Figura 8 shows that the actual fit-
ness distributions are very different from the exponential distribution that was postulated in
previous theoretical studies (Burrell, 2013; Egghe, 2013) on an ad hoc basis.
5. DISCUSSION
After achieving a quantitative understanding of the time-dependent uncitedness ratio, we
analyze it. A first question is why, given the same citation window, this ratio is discipline-
specific. To answer this question, we note that Eq. 5 expresses the uncitedness ratio f0 through
the reduced fitness distribution ρ(eη) and the mean number of direct citations Mdir(T). Equazione 6
yields that the latter is determined by the aging function A(T), the sum of the growth exponents
(α + β), and the average reference list length R0. Of these factors and functions, the one that has
the largest variability between the disciplines is R0. In particular, the disciplines with a long
reference list, such as Medical and Natural Sciences, tend to have a relatively low uncitedness
ratio, whereas the disciplines with a short reference list (Mathematics and Arts & Humanities)
have a high uncitedness ratio. Equations 5 E 6 also explain the overall decline of uncited-
ness during the last century, as documented by Wallace et al. (2009). This can be attributed to
the gradual increase of R0 and slower decay of A(T), as has been recently reported by Sinatra
et al. (2015) for Physics.
A second question is: What kind of papers remain uncited? According to our model, some
papers are uncited because they have low fitness. There are also papers with a relatively high
fitness that remain uncited as well—this is an inevitable consequence of the Poissonian cita-
tion process. To estimate the relative weight of these two groups of uncited papers in a col-
lection, we consider the probability that a paper with a certain fitness eη remains uncited after
t years. Equazione 5 yields
P 0ð Þ eη; T
ð
Þ ¼ e
−~ηMdir tð Þ:
(10)
2. Equazione 10 yields that the borderline fitness is eη * =
We define a low-fitness paper as one whose probability of being cited during a citation
window t is less than one-half, P(0) < 1
2. The high-fitness papers are, correspondingly, those
with P(0) ≥ 1
Mdir tð Þ ln2. For a long citation
window of 25 years, this corresponds to 0.13, 0.23, and 0.43 for our collections of the
Physics, Economics, and Mathematics papers, and to 0.074, 0.13, 0.18, and 2.2 for our col-
lections of the Medical, Natural, Social, and Arts & Humanities papers (and the average
(cid:2)eη = 1, by definition). The fraction of the high-fitness papers with eη > eη* that remain
fitness is
uncited after 25 years is 6.6% for Arts & Humanities and 2.5–3.5% for all other collections.
These high-fitness papers make up a small part of all uncited papers for all the disciplines
1
Quantitative Science Studies
909
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
and categories which we studied (possibly excluding Physics). Così, the majority of uncited
papers in our collections are characterized by low fitness.
This brings us to the question of why the fraction of uncited papers for some disciplines is so
high. Our findings suggest that this is the consequence of the highly skewed fitness distribu-
zione, as has been previously conjectured by Seglen (1992). We found that this distribution can
be approximated by a log-normal distribution. This distribution frequently occurs in nature as
the result of a multiplicative random process and is usually associated with some hierarchical
structure. The scientific publication network displays a strong hierarchy: There are break-
through papers that set a new direction of research and initiate a cascade of follow-up papers,
and the latter develop subdirections of this new research and generate new cascades of papers
that deal with specialized topics, close the gaps, and tie up the loose ends. The breakthrough
papers have high citation potential (fitness) because they are of great interest to a broad
audience. The follow-up papers, which deal with more specific research questions, have lower
fitness, not due to their quality but because they address a narrower forum of researchers. Così
it is quite natural that such a hierarchical structure of scientific publications, which results from
the cascades of papers, is characterized by a lognormal fitness distribution. The width of this
distribution hardly varies between the disciplines, because the research style is more or less
uniform (a professor usually spends ~10–15 years pursuing some research direction and this
corresponds to two to three generations of graduate students).
The last question is whether there are papers with eη = 0. To estimate the number of such
uncitable papers, Thelwall (2016B) suggested using a zero-inflated log-normal distribution
instead of a conventional log-normal distribution. We tried to fit our data using the zero-
inflated fitness distribution (this requires an additional fitting parameter—the fraction of
zero-fitness papers) and were unable to improve an already very good fit. We conclude that
the overwhelming majority of uncited papers in our collections are characterized by finite
fitness and have some chance to be cited, provided that there is enough time, and that the
decay of attention to old papers is sufficiently slow. Equazione 4 indicates that this decay is
captured by the factor A(T)e(α+β)T. The aging function A(T) decays very slowly, in such a way
that the exponential factor e(α+β)t can compensate for this decay. Infatti, Figura 3 demonstrates
that although the uncitedness ratio for scientific papers decreases with time, it does not come
to saturation even after 25 years. This lack of saturation implies that, in principle, f0 may
achieve a very small value over an extremely long term. This is the situation with patent cita-
zioni, as the authors of a new patent are required to cite all patents relevant to their invention,
however old they are. Così, the aging function for patent citations decays more slowly than
that for scientific papers. It is no surprise that for many categories of US patents the uncitedness
ratio, in the long run, is only 2–4% (Gandal, Shur-Ofry et al., 2021), which is significantly
lower than the uncitedness ratio for scientific papers.
AUTHOR CONTRIBUTIONS
Michael Golosovsky: Conceptualization, Data Curation, Formal Analysis, Methodology,
Writing. Vincent Larivière: Data Curation, Formal Analysis, Writing.
COMPETING INTERESTS
The authors have no competing interests.
FUNDING INFORMATION
This research was not funded.
Quantitative Science Studies
910
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Uncited papers are not useless
DATA AVAILABILITY
Citation distributions, the mean number of citations, and the fraction of uncited papers and its
time dependence are available at https://doi.org/10.5281/zenodo.5014627.
REFERENCES
Burrell, Q. l. (2013). A stochastic approach to the relation between
the impact factor and the uncitedness factor. Journal of
Informetrics, 7(3), 676–682. https://doi.org/10.1016/j.joi.2013
.03.001
Caldarelli, G., Capocci, A., De Los Rios, P., & Muñoz, M. UN.
(2002). Scale-free networks from varying vertex intrinsic fitness.
Physical Review Letters, 89(25), 258702. https://doi.org/10.1103
/PhysRevLett.89.258702, PubMed: 12484927
de Solla Price, D. J. (1965). Networks of scientific papers. Scienza,
149(3683), 510–515. https://doi.org/10.1126/science.149.3683
.510
Dorta-Gonzalez, P., Suarez-Vega, R., & Dorta-Gonzalez, M. IO. (2020).
Open access effect on uncitedness: A large-scale study controlling
by discipline, source type and visibility. Scientometrics, 124(3),
2619–2644. https://doi.org/10.1007/s11192-020-03557-8
Egghe, l. (2013). The functional relation between the impact factor
and the uncitedness factor revisited. Journal of Informetrics, 7(1),
183–189. https://doi.org/10.1016/j.joi.2012.10.007
Gandal, N., Shur-Ofry, M., Crystal, M., & Shilony, R. (2021). Out of
sight: Patents that have never been cited. Scientometrics. https://
doi.org/10.2139/ssrn.3420061
Garfield, E. (1991). To be an uncited scientist is no cause for shame.
The Scientist, 5(6), 12–13.
Glanzel, W. (2004). Towards a model for diachronous and syn-
chronous citation analyses. Scientometrics, 60(3), 511–522.
https://doi.org/10.1023/B:SCIE.0000034391.06240.2UN
Golosovsky, M. (2019). Citation analysis and dynamics of citation
networks. Springer International Publishing. https://doi.org/10
.1007/978-3-030-28169-4
Golosovsky, M. (2021). Universality of citation distributions—A
new understanding. Quantitative Science Studies, 2(2), 527–543.
https://doi.org/10.1162/qss_a_00127
Golosovsky, M., & Solomon, S. (2017). Growing complex network
of citations of scientific papers: Modeling and measurements.
Physical Review E, 95(1), 012324. https://doi.org/10.1103
/PhysRevE.95.012324, PubMed: 28208427
Hou, J., & Ye, J. (2020). Are uncited papers necessarily all nonim-
pact papers? A quantitative analysis. Scientometrics, 124(2),
1631–1662. https://doi.org/10.1007/s11192-020-03539-w
Hsu, J.-W., & Huang, D.-W. (2012). A scaling between impact
factor and uncitedness. Physica A: Statistical Mechanics and
its Applications, 391(5), 2129–2134. https://doi.org/10.1016/j
.physa.2011.11.028
Eh, X., Leydesdorff, L., & Rousseau, R. (2020). Exponential growth
in the number of items in the WoS. ISSI Newsletter, 16(2), 32–38.
MacRoberts, M., & MacRoberts, B. (2010). Problems of citation
analysis: A study of uncited and seldom-cited influences.
Journal of the American Society for Information Science and
Tecnologia, 61(1), 1–12. https://doi.org/10.1002/asi.21228
Milojevic, S. (2020). Towards a more realistic citation model: IL
key role of research team sizes. Entropy, 22(8), 875. https://doi
.org/10.3390/e22080875, PubMed: 33286646
Nicolaisen, J., & Frandsen, T. F. (2019). Zero impact: A large-scale
study of uncitedness. Scientometrics, 119(2), 1227–1254. https://
doi.org/10.1007/s11192-019-03064-5
Roth, C., Wu, J., & Lozano, S. (2012). Assessing impact and quality
from local dynamics of citation networks. Journal of Informetrics,
6(1), 111–120. https://doi.org/10.1016/j.joi.2011.08.005
Seglen, P. O. (1992). The skewness of science. Journal of the
American Society for Information Science and Technology, 43(9),
628–638. https://doi.org/10.1002/(SICI )1097-4571(199210)
43:9<628::AID-ASI5>3.0.CO;2-0
Sinatra, R., Deville, P., Szell, M., Wang, D., & Barabasi, A.-L.
(2015). A century of physics. Nature Physics, 11, 791–796.
https://doi.org/10.1038/nphys3494
Sugimoto, C. R., & Larivière, V. (2018). Measuring research. Oxford
Stampa universitaria. https://doi.org/10.1093/wentk/9780190640118
.001.0001
Thelwall, M. (2016UN). Are there too many uncited articles? Zero
inflated variants of the discretised lognormal and hooked power
law distributions. Journal of Informetrics, 10(2), 622–633. https://
doi.org/10.1016/j.joi.2016.04.014
Thelwall, M. (2016B). Citation count distributions for large mono-
disciplinary journals. Journal of Informetrics, 10(3), 863–874.
https://doi.org/10.1016/j.joi.2016.07.006
van Leeuwen, T. N., & Moed, H. F. (2005). Characteristics of jour-
nal impact factors: The effects of uncitedness and citation distri-
bution on the understanding of journal impact factors.
Scientometrics, 63(2), 357–371. https://doi.org/10.1007/s11192
-005-0217-z
van Noorden, R. (2017). The science thats never been cited.
Nature, 552, 162–164. https://doi.org/10.1038/d41586-017
-08404-0, PubMed: 29239363
Wallace, M. L., Larivière, V., & Gingras, Y. (2009). Modeling a
century of citation distributions. Journal of Informetrics, 3(4),
296–303. https://doi.org/10.1016/j.joi.2009.03.010
Quantitative Science Studies
911
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
2
3
8
9
9
1
9
7
0
7
8
0
q
S
S
_
UN
_
0
0
1
4
2
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3