RESEARCH ARTICLE - Ricerca sull'intelligenza artificiale specializzata al MIT

RESEARCH ARTICLE

Frequently cocited publications:
Features and kinetics

Sitaram Devarakonda1

, James R. Bradley2

, Dmitriy Korobskiy1

Tandy Warnow3

, and George Chacko1

1Netelabs, NET ESolutions Corporation, McLean, VA, USA
2Raymond A. Mason College of Business, William and Mary, Williamsburg, VA, USA
3Department of Computer Science, University of Illinois Urbana-Champaign, Champaign, USA

Keywords: bibliometrics, cocitation

ABSTRACT

Cocitation measurements can reveal the extent to which a concept representing a novel
combination of existing ideas evolves towards a specialty. The strength of cocitation is
represented by its frequency, which accumulates over time. Of interest is whether underlying
features associated with the strength of cocitation can be identified. We use the proximal citation
network for a given pair of articles (X, sì) to compute (cid:1), an a priori estimate of the probability of
cocitation between x and y, prior to their first cocitation. Così, low values for (cid:1) reflect pairs of
articles for which cocitation is presumed less likely. We observe that cocitation frequencies are a
composite of power-law and lognormal distributions, and that very high cocitation frequencies
are more likely to be composed of pairs with low values of (cid:1), reflecting the impact of a novel
combination of ideas. Inoltre, we note that the occurrence of a direct citation between
two members of a cocited pair increases with cocitation frequency. Finalmente, we identify cases
of frequently cocited publications that accumulate cocitations after an extended period of
dormancy.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

INTRODUCTION

1.
Cocitation, “the frequency with which two documents from the earlier literature are cited together
in the later literature,” was first described in 1973 (Marshakova-Shaikevich, 1973; Small, 1973). As
noted by Small (1973), cocitation patterns differ from bibliographic coupling patterns (Kessler,
1963) but align with patterns of direct citation and frequently cocited publications must have high
individual citations.

Cocitation has been the subject of further study and characterization, Per esempio, compar-
isons to bibliographic coupling and direct citation (Boyack & Klavans, 2010), the study of invis-
ible colleges (Gmür, 2003; Noma, 1984), construction of networks by cocitation (Small &
Sweeney, 1985; Small, Sweeney, & Greenlee, 1985), evaluation of clusters in combination with
textual analysis (Braam, Moed, & van Raan, 1991), textual similarity at the article and other levels
(Colavizza, Boyack, et al., 2018), and the fractal nature of publications aggregated by cocitations
(van Raan, 1990).

Cocitations provide details of the relationship between key (highly cited) ideas, and changes
in cocitation patterns over time may provide insight into the mechanism with which new schools
of thought develop. Implicit in the definition of cocitation are novel combinations of existing
ideas, but only some frequently cocited article pairs reflect surprising combinations. Per esempio,

a n o p e n a c c e s s

j o u r n a l

Citation: Devarakonda, S., Bradley,
J. R., Korobskiy, D.,Warnow, T., &
Chacko, G. (2020). Frequently cocited
publications: Features and kinetics.
Quantitative Science Studies, 1(3),
1223–1241. https://doi.org/10.1162/
qss_a_00075

DOI:
https://doi.org/10.1162/qss_a_00075

Received: 27 Marzo 2020
Accepted: 22 May 2020

Corresponding Author:
George Chacko
george@nete.com

Handling Editor:
Ludo Waltman

Copyright: © 2020 Sitaram
Devarakonda, James R. Bradley,
Dmitriy Korobskiy, Tandy Warnow, E
George Chacko. Published under a
Creative Commons Attribution 4.0
Internazionale (CC BY 4.0) licenza.

The MIT Press

Frequently cocited publications

two publications presenting the leading methods for the same computational problem may be
highly cocited, but this does not reflect a novel combination of ideas. Allo stesso modo, two publications
describing methods that often constitute part of the same workflow may be highly cocited, Ma
these cocitations are also not surprising. D'altra parte, for two articles in different fields,
frequent cocitation is generally unexpected.

Novel, atypical, or otherwise unusual combinations of cocited articles have been explored at
the journal level (Boyack & Klavans, 2014; Bradley, Devarakonda, et al., 2020; Uzzi, Mukherjee,
et al., 2013; Wang, Veugelers, & Stephan, 2017). Tuttavia, journal-level classifications have
limited resolution relative to article-level studies, which may better represent the actual structure
and aggregations of the scientific literature (Gómez, Bordons, et al., 1996; Klavans & Boyack,
2017; Milojevic, 2019; Shu, Julien, et al., 2019; Waltman & van Eck, 2012). Accordingly, we
sought to discover measurable characteristics of frequently cocited publications from an article-
level perspective.

To study frequently cocited articles, we have developed a novel graph-theoretic approach that
reflects the citation neighborhood of a given pair of articles. In seeking to determine the degree to
which a cocited pair of papers represented a surprising combination, we wished to avoid journal-
based field classifications, which present challenges. Invece, we attempted to use citation history
to produce an estimate of the probability that a given pair of publications (X, sì) would be cocited.
As we focus on the activity before they are first cocited, the “probability” of cocitation is zero, by
definition, because there are no cocitations yet. Hence, we approximated cocitation probabilities:
We treat an article that cites one member of a cocited pair and also cites at least one article that
cites the other member as a proxy for cocitation. Specifically, given a pair of publications x, sì, we
construct a directed bipartite graph whose vertex set contains all publications that cite either x or y
previous to their first cocitation. We then compute (cid:1), a normalized count of such proxies, and use it
to predict the probability of cocitation between x and y. This approach enables an evaluation that
is specific to the given pair of articles, and does so without substantial computational cost, while
avoiding definitions of disciplines derived from journals or having to measure disciplinary
distances.

To support our analysis, we constructed a data set of articles from Scopus (Elsevier BV, 2019)
that were published in the 11-year period, 1985–1995, and extracted the cited references in these
articles. Recognizing that frequently cocited publications must derive from highly cited publi-
cations (Small, 1973), we identified those reference pairs (33.6 million pairs) for each article in
the data set that are drawn from the top 1% most cited articles in Scopus and measured their
frequency of cocitation.

To investigate which statistical distributions might best describe the cocitation frequencies in
these 33.6 million cocited pairs, we reviewed prior work on distributions of citation frequency
(Eom & Fortunato, 2011; Newman, 2003; Price, 1965, 1976; Radicchi, Fortunato, & Castellano,
2008; Redner, 2005; Stringer, Sales-Pardo, & Amaral, 2008, 2010; Wang, Song, & Barabási,
2013). This research has fit the frequency distribution of citation strength sometimes to a power
law distribution and other times to a lognormal distribution. A graph of the analogous cocitation
data suggests that power law or lognormal distributions are candidates for describing cocitation
strength as well and so we, accordingly, investigated that conjecture. È interessante notare, Mitzenmacher
(2003) notes that the debate between the appropriateness of power law versus lognormal
distributions is not confined to bibliometrics, but has been at issue in many disciplines and
contesti.

To study how the best-fit distributional function and parameters for cocitation might vary with
(cid:1), we stratified cocitation frequency data. We also measured whether a direct link exists between

Quantitative Science Studies

1224

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

two members of a cocited pair (cioè., whether one member of a pair cites the other) and how this
property is related to cocitation frequencies. We find that the distribution of cocitation frequen-
cies varies with (cid:1) and that a power law distribution fits cocitation frequencies more often when (cid:1) È
piccolo, whereas a lognormal distribution fits more often for large (cid:1).

A pertinent aspect of cocitation is the rate at which frequencies accumulate. While the citation
dynamics of individual publications have been fairly well studied by others, Per esempio, Eom
and Fortunato (2011) and Wallace, Larivière, and Gingras (2009), the dynamics of cocited articles
are less well studied. Our interest was the special case analogous to the Sleeping Beauty phenom-
enon (Ke, Ferrara, et al., 2015; van Raan, 2004), which may reflect delayed recognition of scien-
tific discovery and the causes attributed to it (Barber, 1961; Cole, 1970; Garfield, 1970, 1980;
Glänzel & Garfield, 2004; Merton, 1963). Così, we also identified cocited pairs that featured a
period of dormancy before accumulating cocitations.

2. MATERIALS AND METHODS

2.1. Data

Citation counts were computed for all Scopus articles (88,639,980 records) updated through
Dicembre 2019, as implemented in the ERNIE project (Korobskiy, Davey, et al., 2019).
Records with corrupted or missing publication years or classified as “dummy” by the vendor were
then removed, resulting in a data set of 76,572,284 publications. Hazen percentiles of citation
conta, grouped by year of publication, were calculated for the these data (Bornmann,
Leydesdorff, & Mutz, 2013). The top 1% of highly cited publications from each year were com-
bined into a set of highly cited publications consisting of 768,993 publications.

Publications of type “article,” each containing at least five cited references and published in
the 11-year period from 1985–1995, were subsetted from Scopus to form a data set of 3,394,799
publications and 51,801,106 references (8,397,935 unique). For each of these publications, Tutto
possible reference pairs were generated and then restricted to those pairs where both members
were in the set of highly cited publications (above).

Per esempio, the data for 1985 consisted of 223,485 articles after processing as described
above. Computing all reference pairs (that were also members of the highly cited publication
set of 768,993) from these 223,485 articles gave rise to 2,600,101 reference pairs (Tavolo 1) Quello
ranged in cocitation frequency from 1 A 874 all'interno del 1985 insieme di dati; from 1 A 11,949 across the
11-year period 1985–1995; and from 1 A 35,755 across all of Scopus. Collectively, the publica-
tions in our 1985–1995 data set generated 33,641,395 unique cocitation pairs, for which we
computed cocitation frequencies across all of Scopus (Figura 1).

2.2. Derivation of (cid:1)(cid:1)(cid:1)

We now show how we define our prior on the probability of x and y being cocited, based on the
citation graph restricted to publications that cite either x or y (but not both) up to the year of their
first cocitation. Recall that we defined a proxy cocitation of x and y to be an article that cites one
member of the cocited pair (X, sì) and also cites at least one article that cites the other member. IL
idea behind this definition is that we consider papers that cite x as proxies for x, and papers that
cite y as proxies for y. Così, if a paper a cites both x and y 0 (where y 0 is a proxy for y), then it is a
proxy for a cocitation of x and y. Allo stesso modo, if a paper b cites both y and x 0 (where x 0 is a proxy for x),
it is also a proxy for a cocitation of x and y. This motivates the graph-theoretic formulation, Quale
we now formally present.

Quantitative Science Studies

1225

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

Summary of analyzed data. Publications of type “article” that had at least five cited
Tavolo 1.
references indexed in Scopus were selected from the 11 years 1985–1995. All possible reference
pairs were generated for the cited references of these articles and then restricted to those pairs where
both members were in the set of 768,993 highly cited publications. The fourth column shows the
number of pairs in each year after the restriction was applied

Year
1985

1986

1987

1988

1989

1990

1991

1992

1993

1994

1995

Articles
223,485

238,096

250,575

269,219

285,873

305,010

325,782

343,239

360,916

387,062

405,503

Riferimenti
1,796,502

1,920,225

2,037,654

2,182,571

2,303,481

2,490,909

2,662,005

2,846,607

3,006,374

3,228,240

3,432,228

Cocited pairs
2,600,101

2,840,557

3,180,261

3,406,902

3,793,986

4,546,915

5,039,334

5,622,164

6,121,147

7,022,499

7,626,684

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1. The workflow we used to generate a data set of 33,641,395 cocited publications from references cited by articles in Scopus
published in the years 1985–1995.

Quantitative Science Studies

1226

Frequently cocited publications

We fix the pair x, y and we define N(X) to be the set of all publications that cite x (but do not also
cite y), and are published no later than the year of the first cocitation of x and y. We similarly define
N( sì). We define a directed bipartite graph with vertex set N(X) [ N( sì). Note that if x cites y then
X 2 N( sì), and similarly for the case where y cites x. Note also that because we have restricted N(X) E
N( sì) that N(X) \ N( sì) = =(cid:2). We now describe how the directed edge set E(X, sì) is constructed. For
any pair of articles a, b where a 2 N(X) and b 2 N( sì), if a cites b then we include the directed edge
UN ! b in E(X, sì). Allo stesso modo, we include edge b ! a if b cites a. Finalmente, if a pair of articles both cite
each other, then the graph has parallel edges. By construction, this graph is bipartite, which means
that all the edges go between the two sets N(X) and N( sì) (cioè., no edges exist between two vertices
in N(X), nor between two vertices in N( sì)).

Note that by the definition, every edge in E(X, sì) arises because of a proxy cocitation, so that the
number of proxy cocitations is the number of directed edges in E(X, sì). Consider the situation
where a publication a cites x (so that a 2 N(X)) and also cites b1, b2, b3 in N( sì): this defines three
directed edges from a to nodes of N( sì). We count this as three proxy cocitations, not as one proxy
cocitation. Allo stesso modo, if we have a publication b that cites y and also cites a1, a2, a3, a4 in N(X),
then there are four directed edges that go from b to nodes in N(X) and we will count each of those
directed edges as a different proxy cocitation.

Accordingly, letting |X| denote the cardinality of a set X, we note |E(X, sì)|, (cioè., the number of
directed edges that go between N(X) and N( sì)), is the number of proxy cocitations between x and y.
If no parallel edges are permitted, the maximum number of possible proxy cocitations is |N(X)| × |
N( sì)|. Under the assumption that both N(X) and N( sì) each have at least one article, we define
(cid:1) (X, sì), our prior on the probability of x and y being cocited, come segue:

θ x; yð

Þ ¼

E x; yð
Þ
j
j
j
j (cid:3) N yð Þ
j
N xð Þ

Note that if parallel edges do not occur in the graph, Poi (cid:1)(X, sì) ≤ 1, but that otherwise
the value can be greater than 1. Note also that (cid:1)(X, sì) = 0 if E(X, sì) = =(cid:2) (cioè., if there are no proxy
cocitations) and that (cid:1)(X, sì) = 1 if every possible proxy cocitation occurs.

To efficiently calculate (cid:1), we used the following pipeline. We copied Scopus data from a rela-
tional schema in PostgreSQL into a citation graph from Scopus into the Neo4j 3.5 graph database
using an automated Extract Transform Load (ETL) pipeline that combined Postgres CSV export and
the Neo4j Bulk Import tool. The graph vertex set is all publications, each with a publication year
attribute, and the edge set is all citations between the publications. A Cypher index was created on
the publication year. We developed Cypher queries to calculate (cid:1) and tuned performance by split-
ting input publication pairs into small batches and processing them in parallel, using parallelization
in Bash and GNU Parallel. Batch size, the number of parallel job slots, and other parameters were
tuned for performance, with best results achieved on batch sizes varying from 20 A 100 pairs. IL
results of (cid:1) calculations were cross-checked using SQL calculations. In the small number of cases
Dove (cid:1) computed to >1 (above) it was set to 1 for the purpose of this study.

2.3. Statistical Calculations

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

We denote the observed cocitation frequency data by the multiset

(cid:1)

Xo ¼ xo

1; …; xo
N

(cid:3)

;

where N is the total number of pairs of articles and xo
i is the observed frequency of the ith pair of
papers being cocited. Note that this is in general a multiset, as different pairs of articles can have
the same cocitation frequency. Let n(X) be the number of times that x appears in Xo (equivalently,

Quantitative Science Studies

1227

Frequently cocited publications

Quantitative Science Studies

N(X) is the number of pairs of articles that are cocited x times), and let N (X) =

total number of pairs of articles that are cocited at least x times. Then

f oðx j x ≥

(cid:1)xÞ ¼

n xð Þ
Nð(cid:1)xÞ

for x 2 ½(cid:1)X; ∞Þ;

P∞

y¼x n (sì) denote the

(1)

where x is a parameter we use to analyze the distribution’s right tail starting at varying frequencies.
We describe in this subsection (UN) the statistical computations for fitting log-normal and power law
distributions to right tails of the observed cocitation frequency distributions as defined by Eq. 1 for
various x and (B) how we assessed the quality of those fits. Further, we performed such analyses for
various slices of the data, stratifying by (cid:1) and other parameters, as is described in Section 3.

We used a discrete version of a lognormal distribution to represent integer cocitation frequen-
cies, F(·), following Stringer et al. (2008) and Stringer et al. (2010), while appropriately normalizing
for our conditional assessment of the right tail commencing at x:

fLNðx j μ; P;

(cid:1)xÞ ¼

e
f x j μ; P
ð
Þ
∞ e
f n j μ; P
ð
n¼(cid:1)X

for x ≥

(cid:1)X

e
f x j μ; P
ð

Þ ¼

xþ0:5

x−0:5

dq
ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ
2πσ2

exp −

;

2
Þ

lnq − μ
2σ2

(2)

where μ and (cid:3) are the mean and standard deviation, rispettivamente, of the underlying normal
distribution. These probabilities can be computed with the cumulative normal distribution,

(cid:5)

e
f x j μ; P
ð

Þ ¼ Φ

ln x þ 0:5
Þ
P

(cid:6)

(cid:5)

− Φ

(cid:6)
Þ

;

ln x − 0:5
P

using the well-known error function.

We fit distributions to the cocitation frequency data for various extremities of the right tail,
as parameterized by x, using a maximum (log) likelihood estimator (MLE). We solved for the
best-fit distributional parameters for the lognormal distribution, μ and (cid:3), by modifying a multi-
dimensional interval search algorithm from Press, Teukolsky, et al. (2007) and following
Stringer et al. (2010). A compiled version of this code using the C++ header file amoeba.h
is available on our Github site (Korobskiy et al., 2019).

We fit a discrete power law distribution to the data for various values of x, which was normal-

ized for our conditional observations of the right tail:

fPLðx j α;

(cid:1)xÞ ¼

x−α
ζðα;

(cid:1)xÞ

for x ≥

(cid:1)X;

(3)

where the Hurwitz zeta function,

ζðα;

(cid:1)xÞ ¼

X∞

x¼0

1
ðx þ (cid:1)xÞ

α ;

is a generalization of the Riemann zeta function, (cid:4)((cid:5), 1), as is needed for analysis of the right tail.

We solved first-order conditions for the (log) MLE to find the best-fit distributional exponent (cid:5),

ζ0ðα;
ζðα;

(cid:1)xÞ
(cid:1)xÞ

¼ −

1
Nð(cid:1)xÞ

x2Xoð(cid:1)xÞ

ln x;

(4)

1228

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

as described in Clauset, Shalizi, and Newman (2009) and Goldstein, Morris, and Yen (2004),
where Xo(X) = {X 2 Xo : x ≥ x}, are the observed cocitations with frequencies at least as great
as x and N(X) is the number of such cocitations. We solved Eq. 4 to find (cid:5) using a bisection
algorithm.

We used the (cid:6)2 goodness of fit ((cid:6)2) and the Kolmogorov-Smirnov (K-S) tests to assess the
null hypothesis that the distribution of the observed cocitation frequencies and the best-fit
lognormal distribution are the same, and similarly for the best-fit power law distribution.
We also computed the Kullback-Leibler Divergence (K-L) between the observed data and
the best-fit distributions.

Both the (cid:6)2 and K-S tests employed the null hypothesis that the observed cocitation fre-
quencies, N(X) for x 2 [ X, ∞), were sampled from the best-fit lognormal or power law distribu-
zioni, which we denote by fd(·| X) for d 2 {LN, PL}, while suppressing the parameters specific to
each of the distributions.

The usual (cid:6)2 statistic was computed by, first, grouping each of the observed cocitation

frequencies into k bins, denoted by bi for i 2 {1, …, k}, and then computing

χ2

i¼1

2
Þ

;

Oi − Ei
ð
Ei

where Oi is the observed number of cocitations having frequencies associated with the ith
bin,

Oi ¼

n xð Þ;

x2bi

and Ei is the expected number of observations for frequencies in bin i, if the null hypothesis was
VERO, in a sample with size equal to the number of observed data points, N( X):

Ei ¼

x2bi

fdðx j(cid:1)xÞ Nð(cid:1)xÞ

If the null hypothesis is true, then we would expect Oi and Ei to be approximately equal, con
deviations owing to variability due to sampling.

Constructing the bins bi requires only that Ei

≥ 5 for every i = 1, …, k. Test outcomes are some-
times sensitive to the minimum Ei permitted, which we will denote by E, so we tested with
multiple thresholds, including 10, 20, 50, E 70. Inoltre, statistical tests are stochastic:
These multiple tests permitted a reduction in the probability of erroneously rejecting or accepting
the null hypothesis based on a single test. The distribution of observed cocitation frequencies
≥ E was most critical in
was skewed right with a long tail, so that aggregating bins to satisfy Ei
the right tail. This motivated a bin construction algorithm that aggregated frequencies in reverse
order, starting with the extreme right tail. Algorithm 1 requires a set of the unique observed
^
X o, which includes the elements of the multiset X o without repetition.
≥ E, that criterion was

cocitation frequencies,
While Algorithm 1 does not guarantee in general that all bins satisfy Ei
satisfied for the observed data.

We implemented a K-S test using simulation to generate a sampling distribution to account for
the discrete frequency observations (StackExchange, 2014). We denote the cumulative distribu-
i¼(cid:1)x f o(io | X), and the best-fit cumulative
tion of observed cocitation frequencies by Fo(X | X) =

Quantitative Science Studies

1229

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

Algorithm 1: Frequency bin construction

1: io 1

2: b1 = {}

3: while |

^
Xo| > 0 do

bi bi [ {max (
^
Xo ^

Xo \ max (

^
Xo)}
^
Xo)

if Ei (cid:5) E then

i i + 1

bi {}

end if

10: end while

distribution by Fd(X|X) =

i¼(cid:1)x fd(io|X). The K-S test involves testing the maximum absolute difference

between the observed and theorized cumulative distributions,
(cid:9)
(cid:7) (cid:8)
(cid:9)
− Fd xj(cid:1)X
(cid:9);

(cid:7) (cid:8)
Fo xj(cid:1)X
where n is the number of observations giving rise to Fo(X|X), against the distribution of such differ-
ences between samples from the theorized distribution with the same number of observations, N,
(cid:9)
(cid:7) (cid:8)
(cid:9)
e
(cid:9)
Fd;1 xj(cid:1)X

(cid:9)
(cid:7) (cid:8)
(cid:9)
(cid:9);
Fd;2 xj(cid:1)X

e
Dn ¼ max

Dn ¼ max

− e

(cid:9)
(cid:9)
(cid:9)

Dove

e
Fd,j(X|X) is the empirical distribution of sample j of size n (notation suppressed) drawn from
e
Dn for each test. We reject the null hypothesis if
e
Dn, say all but 5%, for equivalence with a p-value of 0.05.

Fd(X|X). We generated 100 such random variables
Dn is larger than substantially all of the
The number of

e
Dn samples drawn yields a p-value with a resolution of 1%.

We computed the K-L Divergence two ways due to its asymmetry:

DK−L f ojj fd
ð

Þ ¼

DK−L fd jj f o
ð

Þ ¼

(cid:7) (cid:8)
f o xj(cid:1)X

(cid:7) (cid:8)
fd xj(cid:1)X

X
∞

x¼(cid:1)X

X
∞

x¼(cid:1)X

(cid:7) (cid:8)
f o xj(cid:1)X
(cid:7) (cid:8)
fd xj(cid:1)X
(cid:7) (cid:8)
fd xj(cid:1)X
f o xj(cid:1)X

(cid:7) (cid:8) :

Separate from the tests above, we tested whether the distribution of cocitation frequencies was
independent of (cid:1) using a (cid:6)2 test, using the null hypothesis that the cocitation frequency distribu-
tion was independent of (cid:1). We initially created a contingency table on (cid:1) and cocitation frequency
using these bins for (cid:1), {[0.0, 0.2), [0.2, 0.4), [0.4, 0.6), [0.6, 0.8), [0.8, 1.0]}, and logarithmic bins
for frequency to accommodate the skewed distributions:

10; 100
½

Þ; 100; 1000

Þ; 1000; 10000

G:
Þ; 10000; 100000
(cid:4)

We subsequently aggregated these bins to have an expected number of cocitations in each bin
equal to or greater than 5 to account for a decreasing number of observations as (cid:1) and frequency
increased by having just two intervals for frequency: {[10, 100), [100, 100000]}.

Quantitative Science Studies

1230

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

2.4. Kinetics of Cocitation

We extended prior work on delayed recognition and the Sleeping Beauty phenomemon (Glänzel &
Garfield, 2004; Ke et al., 2015; Li & Ye, 2016; van Raan, 2004) towards cocitation. We have
modified the beauty coefficient (B) of Ke et al. (2015) to address cocitations by (UN) counting
citations to a pair of publications (cocitations) rather than citations to individual papers, (B) setting
t0 (age zero) to the first year in which a pair of publications could be cocited (cioè., the publication
year of the more recently published member of a cocited pair), E (C) setting C0 to the number of
cocitations occurring in year t0. Rather than calculate awakening time as in Ke et al. (2015), we
opted to measure the simpler length of time between t0 and the first year in which a cocitation was
recorded; we label this measurement as the time lag tl, so that tl = 0 if a cocitation was recorded
in t0.

3. RESULTS AND DISCUSSION

Our base data set, described in Table 1, consists of the 33,641,395 cocited reference pairs
(33.6 million pairs) and their cocitation frequencies, gathered from Scopus during the 11-year
period from 1985–1995 (Sezione 2). A striking distribution of cocitation frequencies with a long
right tail is observed with a minimum cocitation of 1, a median of 2, and a maximum cocitation
frequency of 51,567 (Figura 2). Approximately 33.3 Di 33.6 million pairs (99% of observations)
have cocitation frequencies ranging from 1–67 and the remaining 1% have cocitation frequen-
cies ranging from 68–51,567. As the focus of our study was cocitations of frequently cited pub-
lications, we further restricted this data set to those pairs with a cocitation frequency of at least 10,
which resulted in a smaller data set of 4,119,324 cocited pairs (4.1 million pairs) with minimum
cocitation frequency of 10, median of 18, and a maximum cocitation frequency of 51,567.
To focus on cocitations derived from highly cited publications, (cid:1) was calculated for all pairs
with a cocitation frequency of at least 10. We also note whether one article in a cocitation pair

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 2. The x-axis shows percentiles for all three plots. Left: Cocitation frequencies of highly cited
publications from Scopus 1985–1995. Cocitation frequencies are plotted against their percentile
values. The upper and lower plots were both generated from 33,641,395 data points. The lower plot
shows the same data with a logarithmic (ln) transformation of the y-axis. The minimum cocitation
frequency is 1, the median is 2, the third quartile is 4, and the maximum is 51,567. Additionally;
15,140,356 pairs (45%) have a cocitation frequency of 1. Frequencies of 12, 22, 67, E 209 corre-
spond to quantile values of 0.9, 0.95, 0.99, E 0.999 rispettivamente. Right: Direct citations between
members of a cocited pair (connectedness) increase with cocitation frequency. The proportion of con-
nected pairs (a direct citation exists between the two members of a pair) within each percentile is
shown. Data are plotted for all pairs with a cocitation frequency of at least 10 (4.1 million pairs).

Quantitative Science Studies

1231

Frequently cocited publications

cites the other (connectedness), reporting a pair as “connected” when such a citation occurs, else
as “not connected.”

Influenced by the use of linked cocitations for clustering (Small & Sweeney, 1985), we also
examined the extent to which members of a cocited pair were also found in other cocited pairs.
We found that 205,543 articles contributed to 4.12 million cocited pairs. The highest frequency
observed in our data set, 51,567 cocitations, was for a pair of articles from the field of physical
chimica: Becke (1993) and Lee, Yang, and Parr (1988). The members of this pair are not con-
nected and are found in 1,504 cocited pairs with frequencies ranging from 10 A 51,567. IL
second highest frequency, 28,407 cocitations, was for another pair of articles from the field of
biochemistry: Bradford (1976) and Laemmli (1970). Members of this pair are not connected
and are found in a staggering 41,909 cocited pairs, 24,558 for the Laemmli gel electrophoresis
article and 17,352 for the Bradford protein estimation article. For the latter pair, both articles de-
scribe methods heavily used in biochemistry and molecular biology, an area with strong referen-
cing activity, so this result is not entirely surprising.

Having developed (cid:1)(X, sì) as a prediction of the probability that articles x and y would be cocited,
we first tested whether the distribution of cocitation frequencies was independent of (cid:1) (Sezione 2).
The null hypothesis that the cocitation frequency distribution was independent of (cid:1) was rejected
with a very small p-value: The statistical software indicated a p-value with no significant nonzero
digits. We next investigated what distribution functions might fit the frequencies of cocitation as
(cid:1) varied.

Based on the long tails of citation frequencies, prior research has assessed the fit of log-normal
and power law distributions (Radicchi et al., 2008; Stringer et al., 2008, 2010). We noted long
right tails in cocitation frequencies, Quale, allo stesso modo, motivated us to assess the fit of lognormal
and power law distributions to cocitation data. Further, we stratified the data according to (UN) IL
minimum frequency for the right tail x, (B) (cid:1), E (C) whether the two members of each cocitation
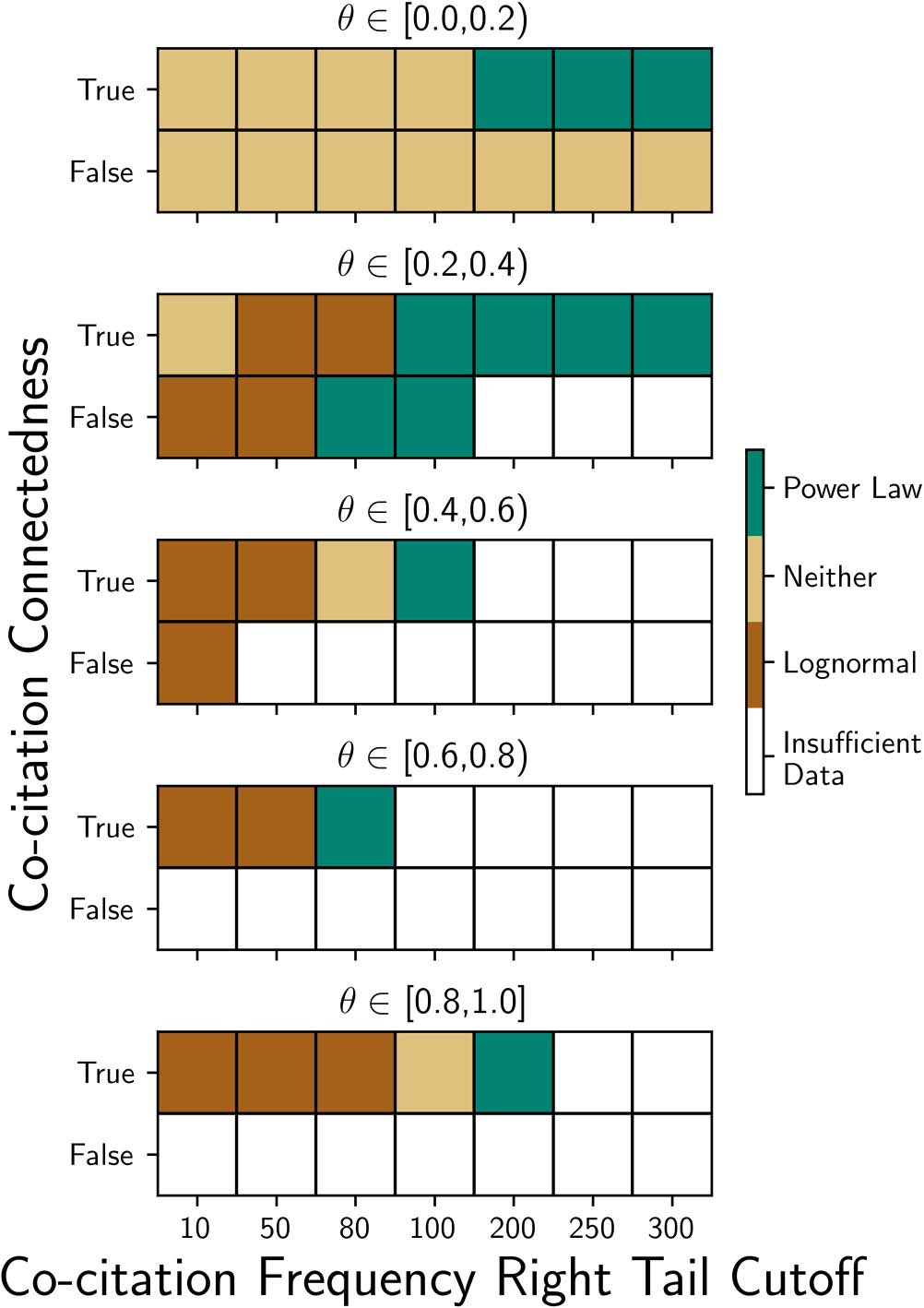
pair were connected. Figura 3 shows which distribution, if either, fits the data in each slice, based
on tests of statistical significance. Note that there were no circumstances where both distributions
fit: If one fit, then the other did not.

Statistical tests were not possible for some slices due to an insufficient number of data points.
This was the case for certain combinations of large x, large (cid:1), and cocitations that were not con-
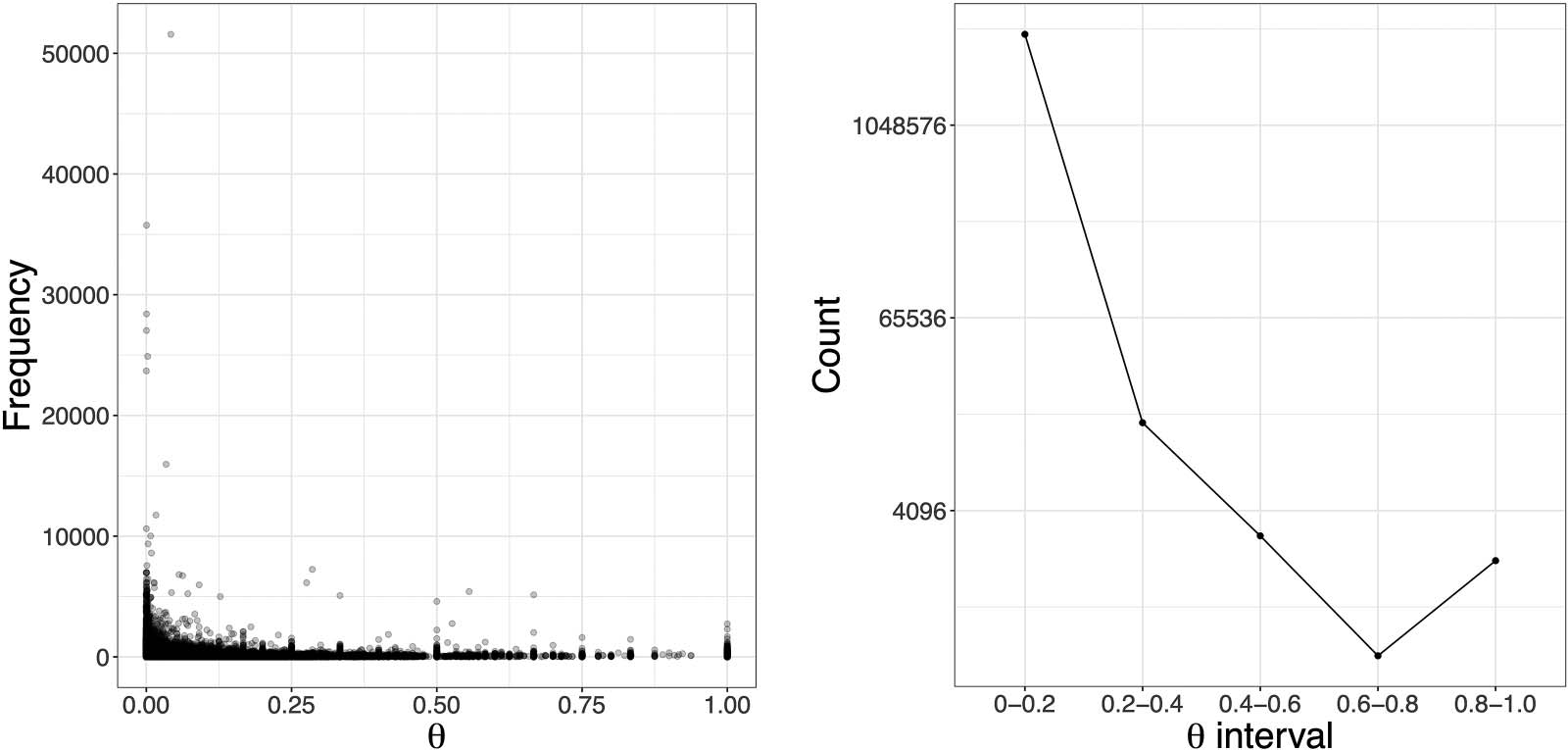
nected. The number of data points obviously decreases as x increases, and we found the decrease
in the number of data points to be more precipitous when (cid:1) was large and cocitations were un-
connected due to the lighter right tails for these parameter combinations. The graph in the right
panel of Figure 4, which has a logarithmic y-axis, shows that the number of data points per (cid:1)
interval analyzed decreases most often by more than an order of magnitude from one interval
to the next as (cid:1) increases. Most pairs of publications that are cocited at least 10 times, Perciò,
have small values of (cid:1).

Figura 3 indicates when the null hypothesis of a best-fit lognormal or power law fitting the
observed data cannot be rejected. We computed two types of statistics for evaluating the null
hypothesis ((cid:6)2 and K-S) E, Inoltre, we computed the (cid:6)2 statistic for four binning strategies.
Figura 3 indicates a distributional fit, specifically, if either the K-S p-value is greater than 0.05 or if
two or more of the (cid:6)2 statistics are greater than 0.05. While we computed the K-L Divergence (Vedere
supplementary material), we did not use these computations for formal statements of distributional
fit because they are neither a norm nor determine statistical significance. These K-L computations
did, Tuttavia, support the findings based on formal tests of statistical significance.

Power law distributions fit most often when cocitations are connected (Figura 3), when more
extreme right tails are considered, and when cocitations have small values of (cid:1). Log-normal

Quantitative Science Studies

1232

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 3. Distributional fits to the observed cocitation frequencies. The graph shows where a
lognormal or power law distribution demonstrated a statistically significant fit with the observed
cocitation frequencies stratified by (cid:1), extent of the right tail tested x, and whether cocitations were
connected. A power law fit more often fore in the intervals [0.0, 0.2) E [0.2, 0.4) when cocitation
constituents were connected. When a lognormal distribution fit, it was for broader portions of the data
set. Data were insufficient for testing as (cid:1) increased due to (UN) fewer observations and (B) less prom-
inent right tails.

distributions fit, conversely, in some circumstances, when a greater portion of the right tail is con-
sidered. These observations support the existence of heavy tails for (cid:1) piccolo, even if a lognormal
distribution fits the observed data more broadly. This observation is consistent with our observa-
tions of the most frequent cocitations having small (cid:1) values, as shown in the scatter plot in the left
panel of Figure 4.

Mitzenmacher (2003) shows a close relationship between the power law and lognormal dis-
tributions vis-à-vis subtle variations in generative mechanisms that determine whether the result-
ing distribution is a power law or lognormal. The stratified layers in Figure 3, where a lognormal
distribution fits for some portion of the right tail and, in the same instance, a power law describes
the more extreme tail, may, Perciò, be due to a generative mechanism whose parameters are
close to those for a power law distribution as well as those for a lognormal distribution.

Tavolo 2 shows the exponents of the best-fit power law distributions when statistical tests indi-
cated that a power law was a good fit and where comparisons were possible among the intervals

Quantitative Science Studies

1233

Frequently cocited publications

Figura 4. Cocitation dynamics relative to (cid:1). (UN) Points represent the Scopus frequency vs. (cid:1) value for each cocited pair. Darker regions
indicate denser plots of the translucent points. cocited pairs with the greater frequency are observed for pairs with smaller (cid:1). (B) The y-axis
employs a log scale and shows the number of cocited pairs per (cid:1) interval. The number of cocited pairs decreases, most often, by more than an
order of magnitude per interval as (cid:1) increases. The dominance of cocited pairs with smaller (cid:1) are also reflected by regions of greater density in
panel (UN).

Di (cid:1): These were possible for (cid:1) intervals of [0.0, 0.2) E [0.2, 0.4), for connected cocitations, E
right tails commencing at x 2 {200, 250, 300}. The power law exponent (cid:5) in these comparisons
was less for (cid:1) 2 [0.0, 0.2) than for (cid:1) 2 [0.2, 0.4), indicating heavier tails for (cid:1) small and, Perciò, UN
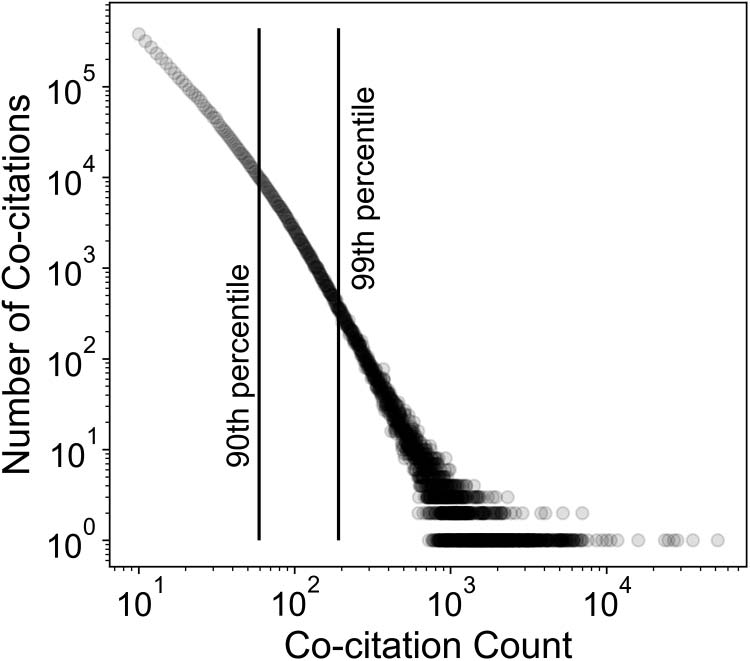
greater chance of extreme cocitation frequency. Figura 5 shows a log-log plot of the number of
cocitations ( y-axis) exhibiting the counts on the x-axis, for (cid:1) in the interval [0.0, 0.2) (note that
both axes employ log scaling). The pattern for points below the 99th percentile clearly indicates
that the number of cocitations referenced at a given frequency decreases greatly as the frequency
increases. Also, the broadening of the scatter where fewer cocitations are cited more frequently is
indicative of a long right tail, as has been observed in other research where lognormal or power
law distributions have been fit to data, as in Montebruno, Bennett, et al. (2019).

Tavolo 2.
Exponents of best-fit power law distributions. These observations are for power law
exponents where comparison across intervals of (cid:1) were possible, and where statistical tests indicated
that a power law was a good fit to the data. The articles of the cocitations were connected for all data
shown

Right tail cutoff (X)
200

200

250

300

(cid:1)

[0.0, 0.2)

[0.2, 0.4)

[0.0, 0.2)

[0.2, 0.4)

[0.0, 0.2)

[0.2, 0.4)

Power law exponent ((cid:5))
3.26

3.37

3.27

3.37

3.22

3.35

Quantitative Science Studies

1234

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

Log-log plot of the number of cocitations versus cocitation count for (cid:1) 2 [0.0, 0.2). IL
Figura 5.
y-axis shows the number of cocited pairs observed having the citation counts plotted along the
x-axis. The tightly clustered plot below the 99th percentile demonstrates a clear pattern of decreasing
number of cocited pairs having an increasing number of citation counts. The scatter plot for the tail
above the 99th percentile broadens, indicating a long tail of relatively few cocited pairs that were
cited with extreme frequency.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perline (2005) warns against fitting a power law function to truncated data. Informally, a portion
of the entire data set can appear linear on a log-log plot, while the entire data set would not. He cites
instances where researchers have mistakenly characterized an entire data set as following a power
law due to an analysis of only a portion of the data, when a lognormal distribution might provide a
better fit to the entire data set. Infatti, the scatter plot in Figure 5 is not linear and so, as Figure 3
shows, a power law does not fit the entire data set. This is what Perline calls a weak power law,
where a power law distribution function fits the tail but not the entire distribution. Our concern,
Tuttavia, is not with characterizing the distributional function for the entire data set, but with char-
acterizing the features of high frequency cocitations, which by definition means we are concerned
with the right tail of the distribution. Inoltre, the results avoid confusion between lognormal and
power law distribution functions because we have shown not only that a power law provides a
statistically significant fit but also that a lognormal distribution function does not fit.

Our analysis found particularly heavy tails that were well fit by power law distributions for
piccolo (cid:1), in the intervals [0.0, 0.2) E [0.2, 0.4), and for cocitations whose constituents are
connected, as shown in Figure 3. The closely related Matthew Effect (Merton, 1968), cumulative
advantage (Price, 1976), and the preferential attachment class of models (Albert & Barabási,
2002) provide possible explanations for citation frequencies following a power law distribution
for some sufficiently extreme portion of the right tail. For greater values of (cid:1), insufficient data in the
right tails precludes a definitive assessment in this regard, although one might argue that the lack
of observations in the tails is counter to the existence of a power law relationship. It is also note-
worthy that the exponents we found for cocitations (Tavolo 2) are close in value to those reported
for citations by Price (1976) and Radicchi et al. (2008).

3.1. Delayed Cocitations

The delayed onset of citations to a well-cited publication, also referred to as Delayed Recognition
and Sleeping Beauty, has been studied by Garfield, van Raan, and others (Bornmann, Ye, & Ye,
2018; Garfield, 1970; Glänzel & Garfield, 2004; Ke et al., 2015; Li & Ye, 2016; van Raan, 2004;
van Raan & Winnink, 2019). We sought to extend this concept to frequently cocited articles

Quantitative Science Studies

1235

Frequently cocited publications

Figura 6. Cocitation frequencies of highly cited publications from Scopus 1985–1995. Upper
panel: Publication 1: Instability of the interface of two gases accelerated by a shock wave (1972)
https://doi.org/10.1007/BF01015969, first cited (1993), total citations (566). Publication 2: Taylor
instability in shock acceleration of compressible fluids (1960) https://doi.org/10.1002/
cpa.3160130207, first cited (1973), total citations (566), first cocited (1993), total cocitations
(541). Lower Panel: Publication 1: Colorimetric assay of catalase (1972) https://doi.org/10.1016/
0003-2697(72)90132-7, first cited (1972), total citations (2,683). Publication 2: Levels of glutathi-
one, glutathione reductase and glutathione S-transferase activities in rat lung and liver (1979) https://
doi.org/10.1016/0304-4165(79)90289-7, first cited (1979), total citations (2,464), first cocited
(1979), total cocitations (470).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

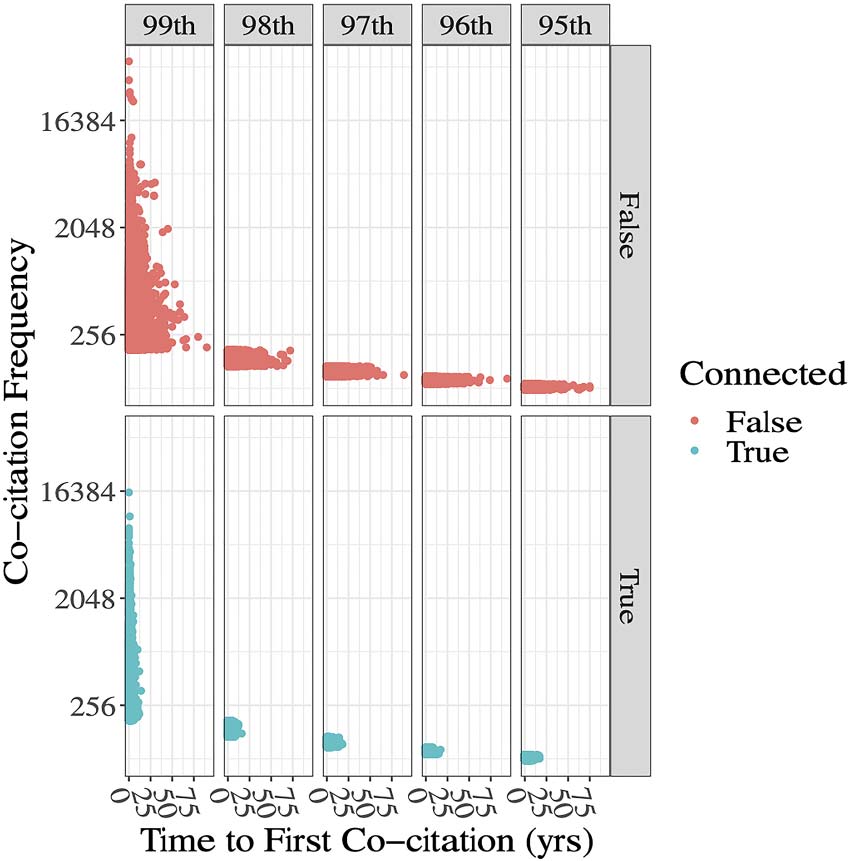
Figura 7. Relationship between time lag (tl) and cocitation frequency. Extended lag times are asso-
ciated with lower cocitation frequencies. Connected pairs have lower tl values. Data are shown for
207,214 pairs consisting of ≥ 95th percentile of cocitation frequencies for the 4.1 million row data
set. The observations are stratified by percentile group (vertical panels) and connectedness (superiore
and lower halves). Cocitation frequency (y-axis) is plotted against tl, the time between first possible
cocitation and first cocitation.

Quantitative Science Studies

1236

Frequently cocited publications

(Figura 6). As an initial step, we calculated two parameters (Sezione 2): (UN) the beauty coefficient
(Ke et al., 2015) modified for cocited articles and (B) timelag tl, the length of time between first
possible year of cocitation and the first year in which a cocitation was recorded. We further focused
our consideration of delayed cocitations to the 95th percentile or greater of cocitation frequencies
in our data set of 4.1 million cocited pairs. Within the bounds of this restriction, 24 cocited pairs
have a beauty coefficient of 1,000 or greater and all 24 are in the 99th percentile of cocitation
frequencies. Così, very high beauty coefficients are associated with high cocitation frequencies.

We also examined the relationship of tl with cocitation frequencies (Figura 7) and observed
that high tl values were associated with lower cocitation frequencies. These data appear to be
consistent with a report from van Raan and Winnink (van Raan & Winnink, 2019), who conclude
that “probability of awakening after a period of deep sleep is becoming rapidly smaller for longer
sleeping periods.” Further, when two articles are connected, they tend to have smaller tl values
compared to pairs that are not connected in the same frequency range.

4. CONCLUSIONS

In questo articolo, we report on our exploration of features that impact the frequency of cocitations. In
particular, we wished to examine article pairs with high cocitation frequencies with respect to
whether they originated from the same school(S) of thought or represented novel combinations
of existing ideas. Tuttavia, defining a discipline is challenging, and determining the discipline(S)
relevant to specific publications remains a challenging problem. Journal-level classifications of
disciplines have known limitations and while article-level approaches offer some advantages,
they are not free from their own limitations (Milojevic, 2019).

Consequently, we designed (cid:1), a statistic that examines the citation neighborhood of a pair of
articles x and y to estimate the probability that they would be cocited. Our approach has advan-
tages compared to alternate approaches: It avoids the challenges of journal-level analyses, it does
not require a definition of “discipline” (or “disciplinary distance”), it does not require assignment
of disciplines to articles, it is computationally feasible, E, most importantly, it enables an eval-
uation that is specific to a given pair of articles.

We note that when x and y are from the same subfield, Poi (cid:1) may be very large, and con-
versely, when x and y are from very different fields, it might be reasonable to expect that (cid:1) will be
piccolo. Così, in a sense, (cid:1) may correlate with disciplinary similarity, with large values for (cid:1) reflect-
ing conditions where the two publications are in the same (or very close) subdisciplines, E
small values for (cid:1) reflecting that the disciplines for the two publications are very distantly related.
We also comment that in this initial study, we have not considered second-degree information,
questo è, publications that cite publications that cite an article of interest.

Our data indicate that the most frequent cocitations occur when cocitations have small
values of (cid:1), as shown in Figure 4. Our study considered the hypothesis that the frequency distri-
bution is independent of (cid:1), but our statistical tests rejected this hypothesis, and showed instead
that the frequency distribution is best characterized by a power law for small values of (cid:1) and con-
nected publications, and in many other regions is best characterized by a lognormal distribution.

The observation that power laws are consistent with small values of (cid:1) and connected
cocitations is consistent with the theory of preferential attachment for these parameter settings.
To the extent that preferential attachment is the mechanism giving rise to a power law, this suggests
that preferential attachment is, almeno, stronger for small (cid:1) values and connected cocitations than
for other parameter combinations, or that preferential attachment is not applicable to other param-
eter values.

Quantitative Science Studies

1237

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

Observing power laws, heavy tails, and pairs with extreme cocitation strength for small values
Di (cid:1) (cioè., pairs that have small a priori probabilities of being cocited) may seem, on its face,
paradoxical. One possible explanation for the pairs in the extreme right tail with both small (cid:1)
and large cocitation strength is that those pairs represent novel combinations of ideas that, Quando
recognized within the research community, catalyze an increased citation rate, consistent with
preferential attachment coupled to time-dependent initial attractiveness (Eom & Fortunato, 2011)
as an underlying generative mechanism. Tuttavia, small values of (cid:1) do not guarantee a high
cocitation count: Infatti, even for small values of (cid:1), cocitations with a power law predom-
inantly have relatively low cocitation strength.

We also note the increasing proportion of connected pairs as the percentile for cocitation
frequency increases (Figura 2); this pair of parameters appears to be associated with a fertile
environment where extremely high cocitation frequencies are possible. This observation raises
the question of whether small values of (cid:1) and connected cocitations are associated with prefer-
ential attachment and, if a causal relationship exists, then how do (cid:1) and cocitation connection
provide an environment supporting preferential attachment? A possibility is that one article in a
cocited pair citing the other makes the potential significance of the combination of their ideas
apparent to researchers. The clear pattern of the highest frequency cocited pairs typically having
low (cid:1) values suggests that these pairs are highly cited and hence impactful because of the novelty
in the ideas or fields that are combined (as reflected in low (cid:1)). Tuttavia, other factors should be
considered, such as the prominence of authors and prestige of a journal (Garfield, 1980) Dove
the first cocitation appears.

We did not apply field normalization techniques when assembling the parent pool of
768,993 highly cited articles consisting of the top 1% of highly cited articles from each year
in the Scopus bibliography. Così, the highly cocited pairs we observe are biased towards
high-referencing areas such as biomedicine and parts of the physical sciences (Small &
Greenlee, 1980). Tuttavia, the data set we analyzed has a lower bound of 10 on cocitation
frequencies and includes pairs from fields other than those that are high referencing. For exam-
ple, the maximum tl we observed in the data set of 4.1 million pairs was 149 years, and is asso-
ciated with a pair of articles independently published in 1840, establishing their eponymous
Staudt-Clausen theorem (Clausen, 1840; von Staudt, 1840); this pair of articles has apparently
been cocited 10 times since their publication. A second pair of articles concerning electron
theory of metals (Drude, 1900UN, 1900B),was first cocited in 1994, 109 times, with tl observed
Di 94 years. Both cases are drawn from mathematics and physics rather than the medical liter-
ature. They are also consistent with the suggestion that the probability of awakening is smaller
after a period of deep sleep (van Raan & Winnink, 2019). As we have defined tl, with its heavy
penalty for early citation, we create additional sensitivity to coverage and data quality especially
for pairs with low citation numbers. Infatti, for the Staudt-Clausen pair, a manual search of other
sources revealed an article (Carlitz, 1961) in which they are cocited. Both these articles were
originally published in German and it is possible that additional cocitations were not captured.
Così, big data approaches that serve to identify trends should be accompanied by more metic-
ulous case studies, where possible. Other approaches for examining depth of sleep and awak-
ening time should certainly be considered (Ke et al., 2015; van Raan, 2004; van Raan &
Winnink, 2019). Lastly, using our approach to revisit invisible colleges (Crane, 1972; Price &
Beaver, 1966; Small & Sweeney, 1985) seems warranted, as it seems likely that the upper bound
of a hundred members predicted by Price and Beaver (1966) is likely to have increased in a
global scientific enterprise with electronic publishing and social media.

Finalmente, we view these results as a first step towards further investigation of cocitation behavior,
and we introduce a new technique based on exploring first-degree neighbors of cocited

Quantitative Science Studies

1238

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

publications; we are hopeful that this graph-theoretic study will stimulate new approaches that will
provide additional insights, and prove complementary to other article-level approaches.

ACKNOWLEDGMENTS

We thank two anonymous reviewers for their helpful and constructive critique. In addition to
support through federal funding, the ERNIE project features a collaboration with Elsevier. Noi
thank our colleagues from Elsevier for their support of the collaboration.

AUTHOR CONTRIBUTIONS
Sitaram Devarakonda: Conceptualization, Methodology, Investigation, Writing—Review &
Editing. James Bradley: Conceptualization, Methodology, Investigation, Writing—Original
Draft; Writing—Review & Editing. Dmitriy Korobskiy: Methodology, Writing—Review &
Editing, Resources. Tandy Warnow: Conceptualization, Methodology, Writing—Original
Draft, Writing—Review & Editing. George Chacko: Conceptualization, Methodology,
Investigation, Writing—Original Draft, Writing—Review & Editing, Funding Acquisition,
Resources, Supervision.

COMPETING INTERESTS

The authors have no competing interests. Scopus data used in this study was available through a
collaborative agreement with Elsevier on the ERNIE project. Elsevier personnel played no role in
conceptualization, experimental design, review of results, or conclusions presented. The content
of this publication is solely the responsibility of the authors and does not necessarily represent the
official views of the National Institutes of Health or Elsevier. Sitaram Devarakonda’s present
affiliation is Randstad USA. His contributions to this article were made while he was a full-time
employee of NET ESolutions Corporation.

SUPPORTING INFORMATION

Supplementary material on K-L calculations is available on our Github site (Korobskiy et al., 2019).

FUNDING INFORMATION

Research and development reported in this publication was partially supported by federal funds
from the National Institute on Drug Abuse (NIDA), National Institutes of Health, NOI. Department
of Health and Human Services, under Contract Nos. HHSN271201700053C (N43DA-17-1216)
and HHSN271201800040C (N44DA-18-1216). Tandy Warnow receives funding from the
Grainger Foundation.

DATA AVAILABILITY

Access to the bibliographic data analyzed in this study requires a license from Elsevier. Code
generated for this study is freely available from our Github site (Korobskiy et al., 2019).

REFERENCES

Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of com-
plex networks. Reviews of Modern Physics, 74(1), 47–97. https://
doi.org/10.1103/RevModPhys.74.47

Barber, B. (1961). Resistance by scientists to scientific discovery. Scienza,

134, 596–602. https://doi.org/10.1126/science.134.3479.596

Becke, UN. D. (1993). Density-functional thermochemistry. III. IL
role of exact exchange. The Journal of Chemical Physics, 98(7),
5648–5652. https://doi.org/10.1063/1.464913

Bornmann, L., Leydesdorff, L., & Mutz, R. (2013). The use of per-
centiles and percentile rank classes in the analysis of bibliometric

Quantitative Science Studies

1239

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Frequently cocited publications

dati: Opportunities and limits. Journal of Informetrics, 7(1), 158–165.
https://doi.org/10.1016/j.joi.2012.10.001

Bornmann, L., Ye, UN. Y., & Ye, F. Y. (2018). Identifying “hot papers”
and papers with “delayed recognition” in large-scale datasets
by using dynamically normalized citation impact scores.
Scientometrics, 116(2), 655–674. https://doi.org/10.1007/s11192-
018-2772-0

Boyack, K., & Klavans, R. (2010). Co-citation analysis, bibliographic
coupling, and direct citation: Which citation approach represents
the research front most accurately? Journal of the American Society
for Information Science and Technology, 61(12), 2389–2404.
https://doi.org/10.1002/asi.21419

Boyack, K., & Klavans, R. (2014). Atypical combinations are
confounded by disciplinary effects. In International Conference
on Science and Technology Indicators (pag. 49–58). Leiden,
Netherlands: CWTS-Leiden University.

Braam, R. R., Moed, H. F., & van Raan, UN. F. J. (1991). Mapping of
science by combined co-citation and word analysis. IO. Structural
aspects. Journal of the American Society for Information Science,
42(4), 233–251. https://doi.org/10.1002/(SICI )1097-4571
(199105)42:4<233::AID-ASI1>3.0.CO;2-IO

Bradford, M. M. (1976). A rapid and sensitive method for the quan-
titation of microgram quantities of protein utilizing the principle
of protein-dye binding. Analytical Biochemistry, 72, 248–254.
https://doi.org/10.1006/abio.1976.9999

Bradley, J., Devarakonda, S., Davey, A., Korobskiy, D., Liu, S., …
Chacko, G. (2020). Co-citations in context: Disciplinary heteroge-
neity is relevant. Quantitative Science Studies, 1(1), 264–276.
https://doi.org/10.1162/qss_a_00007

Carlitz, l. (1961). The Staudt-Clausen Theorem. Mathematics

Magazine, 34, 131–146. https://doi.org/10.2307/2688488

Clausen, T. (1840). Theorem. Astronomische Nachrichten, 17, 351–352.
Clauset, A., Shalizi, C. R., & Newman, M. E. J. (2009). Power-Law
Distributions in Empirical Data. SIAM Review, 51(4), 661–703.
https://doi.org/10.1137/070710111

Colavizza, G., Boyack, K., van Eck, N. J., & Waltman, l. (2018). IL
Closer the Better: Similarity of Publication Pairs at Different
Cocitation Levels. Journal of the Association for Information
Science and Technology, 69(4), 600–609. https://doi.org/10.1002/
asi.23981

Cole, S. (1970). Professional standing and the reception of scientific
discoveries. American Journal of Sociology, 76(2), 286–306.
Retrieved from https://www.jstor.org/stable/2775594

Crane, D. (1972). Invisible colleges: Diffusion of knowledge in scien-

tific communities. Chicago: University of Chicago Press.

Drude, P. (1900UN). Zur Elektronentheorie der Metalle. Annalen der
Physik, 306, 566–613. https://doi.org/10.1002/andp.19003060312
Drude, P. (1900B). Zur Elektronentheorie der Metalle; II. Teil.
Galvanomagnetische und thermomagnetische Effecte. Annalen
der Physik, 308, 369–402. https://doi.org/10.1002/andp.
19003081102

Elsevier BV. (2019). Scopus. Retrieved from https://www.scopus.

com/home.uri (accessed December 2019)

Eom, Y.-H., & Fortunato, S. (2011). Characterizing and modeling
citation dynamics. PLOS ONE, 6(9), 1–7. https://doi.org/10.1371/
journal.pone.0024926

Garfield, E. (1970). Would Mendel’s work have been ignored if the
Science Citation Index was available 100 years ago? Essays of an
Information Scientist, 1, 69–70.

Garfield, E. (1980). Premature Discovery or Delayed Recognition—

Why? Essays of an Information Scientist, 4, 488–493.

Glänzel, W., & Garfield, E. (2004). The myth of delayed recognition.

Scientist, 18(11).

Gmür, M. (2003). Co-citation analysis and the search for invisible
colleges: A methodological evaluation. Scientometrics, 57(1),
27–57. https://doi.org/10.1023/A:1023619503005

Goldstein, M. L., Morris, S. A., & Yen, G. G. (2004). Problems with
fitting to the power-law distribution. The European Physical
Journal B—Condensed Matter and Complex Systems, 41(2), 255–258.
https://doi.org/10.1140/epjb/e2004-00316-5

Gómez, I., Bordons, M., Fernàndez, M., & Méndez, UN. (1996).
Coping with the problem of subject classification diversity.
Scientometrics, 35, 223–235. https://doi.org/10.1007/BF02018480
Ke, Q., Ferrara, E., Radicchi, F., & Flammini, UN. (2015). Defining and
identifying Sleeping Beauties in science. Atti del
National Academy of Sciences, 112(24), 7426–7431. https://doi.
org/10.1073/pnas.1424329112

Kessler, M. M. (1963). Bibliographic coupling between scientific
papers. American Documentation, 14(1), 10–25. (eprint: https://
onlinelibrary.wiley.com/doi/pdf/10.1002/asi.5090140103)
https://doi.org/10.1002/asi.5090140103

Klavans, R., & Boyack, K. (2017). Which type of citation analysis
generates the most accurate taxonomy of scientific and tech-
nical knowledge? Journal of the Association for Information
Science and Technology, 68, 984–998. https://doi.org/10.1002/
asi.23734

Korobskiy, D., Davey, A., Liu, S., Devarakonda, S., & Chacko, G.
(2019). Enhanced Research Network Informatics Environment
(ERNIE) (Github Repository). NET ESolutions Corporation.
Retrieved from https://github.com/NETESOLUTIONS/ERNIE
Laemmli, U. K. (1970). Cleavage of structural proteins during the
assembly of the head of bacteriophage T4. Nature, 227(5259),
680–685. https://doi.org/10.1038/227680a0

Lee, C., Yang, W., & Parr, R. G. (1988). Development of the Colle-
Salvetti correlation-energy formula into a functional of the electron
density. Physical Review B, 37(2), 785–789. https://doi.org/10.1103/
PhysRevB.37.785

Li, J., & Ye, F. Y. (2016). Distinguishing sleeping beauties in science.
Scientometrics, 108(2), 821–828. https://doi.org/10.1007/s11192-
016-1977-3

Marshakova-Shaikevich, IO. (1973). System of document connec-
tions based on references. Scientific and Technical Information
Serial of VINITI, 6(2), 3–8. Retrieved from http://garfield.library.
upenn.edu/marshakova/marshakovanauchtechn1973.pdf

Merton, R. (1963). Resistance to the systematic study of multiple
discoveries in science. European Journal of Sociology, 4(2), 237–282.
Merton, R. (1968). The Matthew effect in science. Scienza, 159(3810),

56–63.

Milojevic, S. (2019). Practical method to reclassify web of science
articles into unique subject categories and broad disciplines.
Quantitative Science Studies, 1(1), 183–206. https://doi.org/10.1162/
qss_a_00014

Mitzenmacher, M. (2003). A brief history of generative models for
power law and lognormal distributions. Internet Mathematics, 1,
226–251.

Montebruno, P., Bennett, R. J., van Lieshout, C., & Smith, H. (2019).
A tale of two tails: Do power law and lognormal models fit firm-
size distributions in the mid-Victorian era? Physica A: Statistical
Mechanics and its Applications, 523, 858–875. https://doi.org/
10.1016/j.physa.2019.02.054

Newman, M. E. J. (2003). The structure and function of complex
networks. SIAM Review, 45(2), 167–256. https://doi.org/
10.1137/S003614450342480

Noma, E. (1984). Co-citation analysis and the invisible college.
Journal of the American Society for Information Science, 35(1),
29–33. https://doi.org/10.1002/asi.4630350105

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D

F
/

1
3
1
2
2
3
1
8
7
0
0
1
2
q
S
S
_
UN
_
0
0
0
7
5
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Quantitative Science Studies

1240

Frequently cocited publications

Perline, R. (2005). Strong, weak and false inverse power laws.

Statistical Science, 20(1), 68–88.

Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. (2007).
Numerical recipes in C: The art of scientific computing (3rd ed.).
New York: Cambridge University Press.

Price, D. de Solla. (1965). Networks of Scientific Papers. Scienza,

149, 510–515.

Price, D. de Solla. (1976). A general theory of bibliometric and other
cumulative advantage processes. Journal of the American Society
for Information Science, 27(5), 292–306. https://doi.org/10.1002/
asi.4630270505

Price, D. de Solla, & Beaver, D. D. (1966). Collaboration in an invis-

ible college. American Psychologist, 21(11), 1011–1018.

Radicchi, F., Fortunato, S., & Castellano, C. (2008). Universality of
citation distributions: Toward an objective measure of scientific
impact. Proceedings of the National Academy of Sciences, 105(45),
17268–17272.

Redner, S. (2005). Citation statistics from 110 years of physical review.

Physics Today, 58(6), 49–54.

Shu, F., Julien, C.-A., Zhang, L., Qiu, J., Zhang, J., & Larivière, V.
(2019). Comparing journal and paper level classifications of science.
Journal of Informetrics, 13(1), 202–225. https://doi.org/10.1016/j.
joi.2018.12.005

Small, H. (1973). Cocitation in the scientific literature: A new mea-
sure of the relationship between two documents. Journal of the
American Society for Information Science, 24(4), 265–269.
https://doi.org/10.1002/asi.4630240406

Small, H., & Greenlee, E. (1980). Citation context analysis of a co-
citation cluster: Recombinant-DNA. Scientometrics, 2(4), 277–301.
https://doi.org/10.1007/BF02016349

Small, H., & Sweeney, E. (1985). Clustering the science citation
index® using cocitations. Scientometrics, 7(3), 391–409. https://
doi.org/10.1007/BF02017157

Small, H., Sweeney, E., & Greenlee, E. (1985). Clustering the science
citation index using co-citations. II. Mapping science. Scientometrics,
8(5), 321–340. https://doi.org/10.1007/BF02018057

StackExchange. (2014). Can I use the Kolmogorov–Smirnov test
on my data? Retrieved from https://stats.stackexchange.

com/questions/112910/can-i-use-kolmogorov-smirnov-test-
on-my-data

Stringer, M. J., Sales-Pardo, M., & Amaral, l. UN. N. (2008).
Effectiveness of journal ranking schemes as a tool for locating
informazione. Journal of the American Society for Information
Science and Technology, 3(2), e1683.

Stringer, M. J., Sales-Pardo, M., & Amaral, l. UN. N. (2010).
Statistical validation of a global model for the distribution of
the ultimate number of citations accrued by papers published
in a scientific journal. PLOS ONE, 61(7), 1377–1385.

Uzzi, B., Mukherjee, S., Stringer, M., & Jones, B. (2013). Atypical
Combinations and Scientific Impact. Scienza, 342(6157), 468–472.
https://doi.org/10.1126/science.1240474

van Raan, UN. F. J. (1990). Fractal dimension of co-citations. Nature,

347(6294), 626. https://doi.org/10.1038/347626a0

van Raan, UN. F. J. (2004). Sleeping Beauties in science. Scientometrics,
59(3), 467–472. https://doi.org/10.1023/ B:SCIE.0000018543.
82441.f1

van Raan, UN. F. J., & Winnink, J. J. (2019). The occurrence of
‘sleeping beauty’ publications in medical research: Their
scientific impact and technological relevance. PLOS ONE, 14(10),
1–34. https://doi.org/10.1371/journal.pone.0223373

von Staudt, K. (1840). Beweis eines Lehrsatzes, die Bernoullischen
Zahlen betreffend. Journal für die reine und angewandte Mathematik,
21, 372–374.

Wallace, M., Larivière, V., & Gingras, Y. (2009). Modeling a century
of citation distributions. Journal of Informetrics, 3(4), 296–303.
Waltman, L., & van Eck, N. J. (2012). A new methodology for con-
structing a publication-level classification system of science.
Journal of the American Society for Information Science and
Tecnologia, 63(12), 2378–2392. https://doi.org/10.1002/asi.22748
Wang, D., Song, C., & Barabási, A.-L. (2013). Quantifying Long-
Term Scientific Impact. Scienza, 342(6154), 127–132. https://
doi.org/10.1126/science.1237825

Wang, J., Veugelers, R., & Stephan, P. (2017). Bias against novelty
in science: A cautionary tale for users of bibliometric indicators.
Research Policy, 46(8), 1416–1436. https://doi.org/10.1016/j.
respol.2017.06.006