RESEARCH ARTICLE
Past as prologue: Approaches to the study
of confirmation in science
Henry Small
SciTech Strategies Inc., Bala Cynwyd, PAPÀ 19004 (USA)
a n o p e n a c c e s s
j o u r n a l
Keywords: Bayesian networks, Bohr’s atom, citation contexts, confirmation in science, constructivism,
explanatory coherence
Citation: Small, H. (2020). Past as
prologue: Approaches to the study of
confirmation in science. Quantitative
Science Studies, 1(3), 1025–1040.
https://doi.org/10.1162/qss_a_00063
DOI:
https://doi.org/10.1162/qss_a_00063
Corresponding Author:
Henry Small
hsmalll@mapofscience.com
Handling Editors:
Loet Leydesdorff, Ismael Rafols, E
Staša Milojević
Copyright: © 2020 Henry Small.
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale (CC BY 4.0)
licenza.
The MIT Press
ABSTRACT
In the 1970s, quantitative science studies were being pursued by sociologists, historians, E
information scientists. Philosophers were part of this discussion, but their role would diminish
as sociology of science asserted itself. An antiscience bias within the sociology of science
became evident in the late 1970s, which split the science studies community, notably causing
the “citationists” to go their own way. The main point of contention was whether science was
a rational, evidence-based activity. To reverse the antiscience trend, it will be necessary to
revive philosophical models of science, such as Bayesian confirmation theory or explanatory
coherence models, where theory-experiment agreement plays a decisive role. A case study
from the history of science is used to illustrate these models, and bibliometric and text-based
methods are proposed as a source of data to test these models.
1. BACKGROUND
I have been fortunate to spend my professional life in the field of what we can now call “quan-
titative science studies” in the company of many inspiring mentors, colleagues, and collabo-
rators. In 1970, the field, broadly conceived, consisted of a motley group of disaffected
historians, sociologists, philosophers, and information scientists searching for new ways of un-
derstanding science as a technical, social, and cultural phenomenon. Some of us had been
trained in the sciences, in my case chemistry, and for one reason or another had abandoned
the lab bench and sought new ways to explore our interest in science. My avenue to quanti-
tative science studies was through the history of science and an internal study of the old quan-
tum theory (Small, 1971). At the time, Thomas Kuhn’s iconic book (Kuhn, 1962) was the
central theoretical text and controversy swirled around it. My case study fit neatly into his
modello. One of my goals in this paper is to reframe that historical project with the benefit of
50 years of hindsight.
In my first job after grad school, I was given the assignment of coming up with an overview
of the field of nuclear physics in the 1930s. As a former chemist, my first instinct was to turn to
the physics literature, and I set about coding articles from the Physical Review and entries from
an early abstracting publication called Science Abstracts. After laboring for many months cod-
ing data on index cards, I had a data set from which I could generate maps of nuclear physics
using the co-occurrence of indexing headings, keywords, cited authors, and cited references.
The paper I wrote describing this work was submitted to the leading history of science journal
but was rejected on the grounds that I had reduced history to its statistical “bare bones.”
Apparently, I had exceeded the limits of what the discipline considered acceptable.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
In those days, historians of science did not generally undertake quantitative studies, con
the exception, Ovviamente, of the pioneering work of Derek J. de Solla Price (Price, 1986).
Initially I had a negative response to his ideas, but this gradually changed as my horizons
broadened. I was impressed with the budding field of sociology of science under the leader-
ship of Robert Merton, and notable exponents such as Harriet Zuckerman, Warren Hagstrom,
Diana Crane, Nick Mullins, Lowell Hargens, Jonathan and Steven Cole, and others. Although
Merton was known mainly for his so-called midrange theoretical writings on the norms and
ethos of science (Merton, 1968), many of his students performed empirical studies, often fo-
cused on the reward system of science and the inequality of recognition (the Matthew effect).
The younger generation of sociologists, on the other hand, gravitated to the study of social
networks and informal communications—what Price had called invisible colleges.
Networks were necessarily at small scale, but nevertheless were treated mathematically by
researchers such as Nick Mullins, Harrison White, and Linton Freeman, Per esempio, to predict
social roles. Mullins thought that citations were the only way to get at the overall social net-
work of science, because the standard survey techniques would only work for small groups.
Information scientists were also quantitative in their approach to scientific information, In-
cluding my early collaborator Belver Griffith and his mentor Bill Garvey in their studies of
scientific communication. Other information scientists were exploring ways of using citations
to do retrieval and automatic classification such as my boss Gene Garfield, Mike Kessler, Sam
Schiminovich, and Gerry Salton. After my work on cocitation, I teamed up with Belver to
work on the mapping science problem.
Although decidedly nonquantitative, I also was exposed to philosophers of science, come
as Thomas Kuhn, Imre Lakatos, Ernan McMullin, Stephen Toulmin, and Larry Laudan. IL
philosophers had retreated from the extreme mathematization of Carnap and the logical pos-
itivists, but philosophical approaches were not purely qualitative and retained a tendency to-
ward symbolic representation. Only later did I become aware of Bayesian philosophy of
science or the explanatory coherence of Paul Thagard, about which more later. One institu-
tional effort at the time was to foster collaboration between historians and philosophers of sci-
ence, which was manifest by naming departments “the history and philosophy of science”
(Feigl, 1970). Allo stesso tempo, sociology of science was moving to affiliate itself with history
of science, and a tug of war ensued. I think it fair to say that sociology won and history and
sociology became the more common moniker. Sociology eventually lost whatever ties it had
with philosophy, which I think led to problems later on.
Around 1975 I learned of a new society called the Society for the Social Study of Science
(4S), which I enthusiastically joined along with many of my new colleagues in the sociology of
science. Their journal was called, appropriately, Science Studies, but was later renamed Social
Studies of Science. I became editor of the 4S Newsletter along with the sociologist Jerry
Gaston. At ISI, where I was working, we had an unexpected visit from a Frenchman named
Bruno Latour, who was looking for citation data on some biochemistry papers published by
the Salk Institute. Pages from the Science Citation Index were dutifully copied for him. Many of
us heard his memorable lecture at the first 4S meeting at Cornell University in 1975, Quale
marked the advent of the anthropology of science.
Thereafter, I became aware of a large contingent of European sociologists of science who
espoused a new approach to science studies called social construction. Among them was
David Edge, who strongly criticized our work on cocitation (Edge, 1977). A subgroup of
the constructivists, the so-called strong program, asserted that the technical substance of sci-
ence is derived from social factors external to science. I got to know many of these scholars,
Quantitative Science Studies
1026
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
including Nigel Gilbert, Mike Mulkay, Steve Woolgar, and Karen Knorr-Cetina. While I did not
agree with them, we had many lively exchanges.
But all was not well with the juxtaposition of quantitative, and especially citation-based,
work and constructivist sociology of science. The tensions became more acute at subsequent
meetings of 4S and eventually erupted in overt hostility. The controversy divided the sociol-
ogists into two camps: the Mertonian normative camp versus the social constructivists.
Constructivists accused the Mertonians of believing that science was objective and evidence
based. They asserted that scientific papers were a kind of propaganda designed to promote
the political or economic interests of their authors, rather than factual presentations constrained
by Mertonian norms. Constructivists emphasized the nonnormative behavior of scientists, E
the various forms of deceptions and biases engaged in by scientists. The so-called citationists
found themselves mainly in the Mertonian camp.
As social construction took hold and became dominant in sociology, Mertonian normative
and quantitative sociology went into decline. Many sociologists of the old school retired or
became less active. My involvement with 4S dwindled, and I turned more to information sci-
ence. While there may be newer, less extreme, versions of the social construction of science
(Giere, 1988), it is not surprising that the approach has given rise to negative attitudes toward
the practice and findings of science both on the part of sociologists and the society at large.
This can be particularly damaging when it comes to existential issues such as climate change.
Has the warming of the climate been socially constructed by climate scientists to further their
interests? The core question is why should we take this science seriously?
2. COUNTERING ANTISCIENCE BIAS
It is interesting to speculate on why such a strong antiscience strain emerged in the sociology
of science. Was it a rebellion against authority advocated by deconstructionists such as
Derrida and Foucault? It is sometimes claimed that social construction represents a “critique”
of science, while others say it debunks the true “interest laden” nature of scientific research.
Any “truth” claims emerging from such an enterprise would of course be suspect. There is also
a long-standing tradition of criticism of science as harmful to humanity on topics such as
nuclear energy, chemical pollution, the abuse of human or animal subjects, or other ethical
issues. Certamente, the general prejudices and faults of society, such as racial and sexual bias,
affect scientists as members of the larger society. But this type of bias, while sometimes man-
ifest in the actions of scientists, does not seem inherent in the nature of science. What the
constructivists’ critique of science was mainly directed at, Tuttavia, was the fundamental ep-
istemic foundations of science itself, and the impossibility of gaining objective knowledge of
the world.
What the constructivists did not anticipate, Tuttavia, was that their antiscience critique
would later find resonance with political and financial groups interested in science denial
in areas such as climate change, smoking and cancer, childhood vaccination, ozone deple-
zione, and biological evolution (Collins, 2014; Oreskes, 2019). Constructivist rhetoric also fil-
tered into political discourse, where social media were exploited to create “truth” or “facts,"
promote conspiracy theories, and label objective reports as “fake” (McIntyre, 2018).
One reason for the success of the social construction was that there was a philosophical
and epistemological vacuum in the sociology of science. Sociologists of science had not paid
attention to questions such as the justification or confirmation of scientific findings and there
was a tendency to leave such questions to philosophers. Robert Merton, Per esempio, while
proposing a comprehensive set of social norms for science, did not offer any epistemic norms
Quantitative Science Studies
1027
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
for the evaluation of scientific findings. An example of such a norm is one of the earliest pre-
cepts that guided Hellenistic philosophy, particularly astronomy, namely “saving the phenom-
ena” or “saving the appearances.” Lloyd gives a fascinating account of this ancient precept as
falling somewhere between 20th-century instrumentalism and philosophical realism (Lloyd,
1978). His interpretation is that the Greek astronomers believed that their models should ac-
cord with the observable evidence, as well as provide physical explanations.
Philosophers and scientists, for their part, were not interested in norms, and tended to dis-
miss or ignore the constructivist claims. Philosophy of science had traditionally been aimed at
supplying a warrant for scientific knowledge, whether through logical deduction, induction, O
abduction. Kuhn’s account of revolutions introduced an element of irrationality into theory
choice when scientists jump to new paradigms, although he denied his theory led to irratio-
nality. Hanson’s notion that observation was theory laden implied that sense evidence was not
necessarily a neutral arbiter, but he also argued that some theories are more plausible than
others (Hanson, 1972). Other philosophers at the time did not lack for theories of confirmation
which included the role of evidence and observation, such as the hypothetico-deductive
method, falsificationism (Popper, 1961), “inference to the best explanation” (Harman,
1965), or “Bayesian confirmation theory” (Salmon, 1967).
Another reason for the neglect of studies of confirmation is our fascination with the context
of discovery, to use Reichenbach’s term, rather than the context of justification. Discovery is
more exciting, delving into creativity and the unknown. Confirmation and corroboration, by
contrasto, seem repetitive and boring. Another excuse is to say that all theories will eventually
be disproved anyway, so why bother looking at the process of confirmation? When a theory
such as Einstein’s general relativity is strikingly confirmed by the observation of a black hole or
gravity waves, or the standard model of particle physics is confirmed by finding a Higgs boson,
we tend to treat these as old news or just things working out as we had expected them to. IL
philosopher Wesley Salmon, Tuttavia, argues that the process of discovery and justification
are intimately intertwined, involving alternating creative leaps and checks against available
evidence (Salmon, 1970).
Clearly the only way to counter the constructivist antiscience bias is to give renewed atten-
tion to studies of confirmation in science: how evidence is used to confirm or disconfirm the-
ories, and how the evidence is generated in the first place. To illustrate one approach to this
problem I will turn the clock back to an episode in the history of science.
3. CONFIRMING AND DISCONFIRMING NIELS BOHR’S THEORY OF THE ATOM
The following is a capsule history of this episode, which is marked by the failure of a theory
(Heilbron & Kuhn, 1969). In 1913 Niels Bohr published his ground-breaking three-part paper
on the constitution of atoms and molecules (Bohr, 1913). The first part dealt primarily with the
hydrogen atom, which was believed to have one orbiting electron, but also touched on the
atoms of other elements. His model of the atom was a mix of assumptions derived from clas-
sical mechanics, quantum theory, electromagnetism, and Rutherford’s recent discovery of the
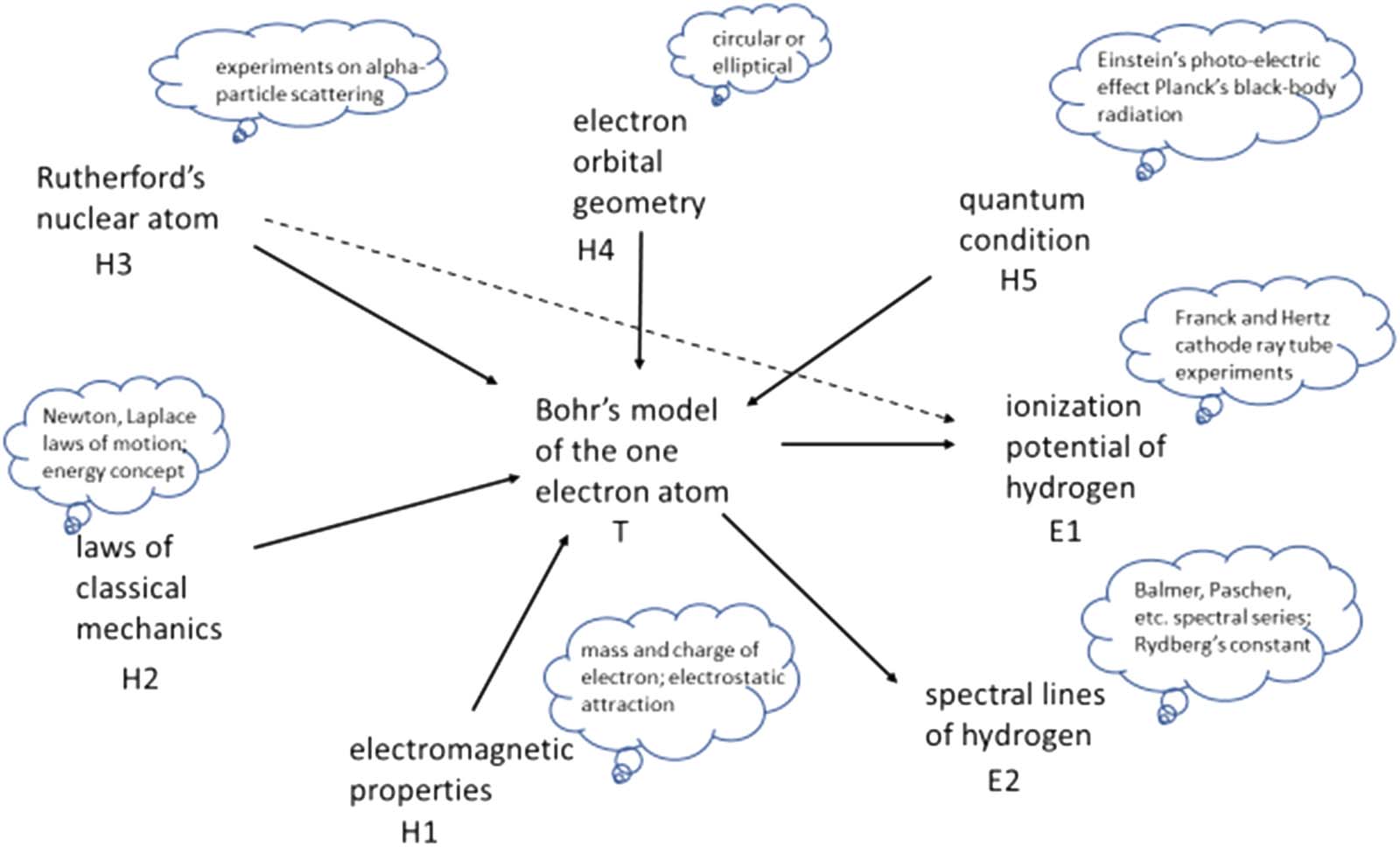
atomic nucleus from experiments on the scattering of alpha particles. Figura 1 is a schematic
representation of this model, showing the component assumptions as incoming links and the
model’s predictions as outgoing links.
As the figure suggests, the theory was successful in predicting the spectral lines of hydrogen
as well as physical properties such as the ionization potential (the energy required to ionize the
atom). Ionization potential measurements were still uncertain, but Bohr believed that agree-
ment would improve when the measurements became more accurate. The dashed link in
Quantitative Science Studies
1028
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 1. Causal model of Bohr’s 1913 model of the hydrogen atom.
Figura 1 connecting Rutherford’s nuclear atom and ionization potential measurements indi-
cates that the interpretation of cathode ray tube experiments was dependent on Rutherford’s
concept of the atom, with its orbiting electron.
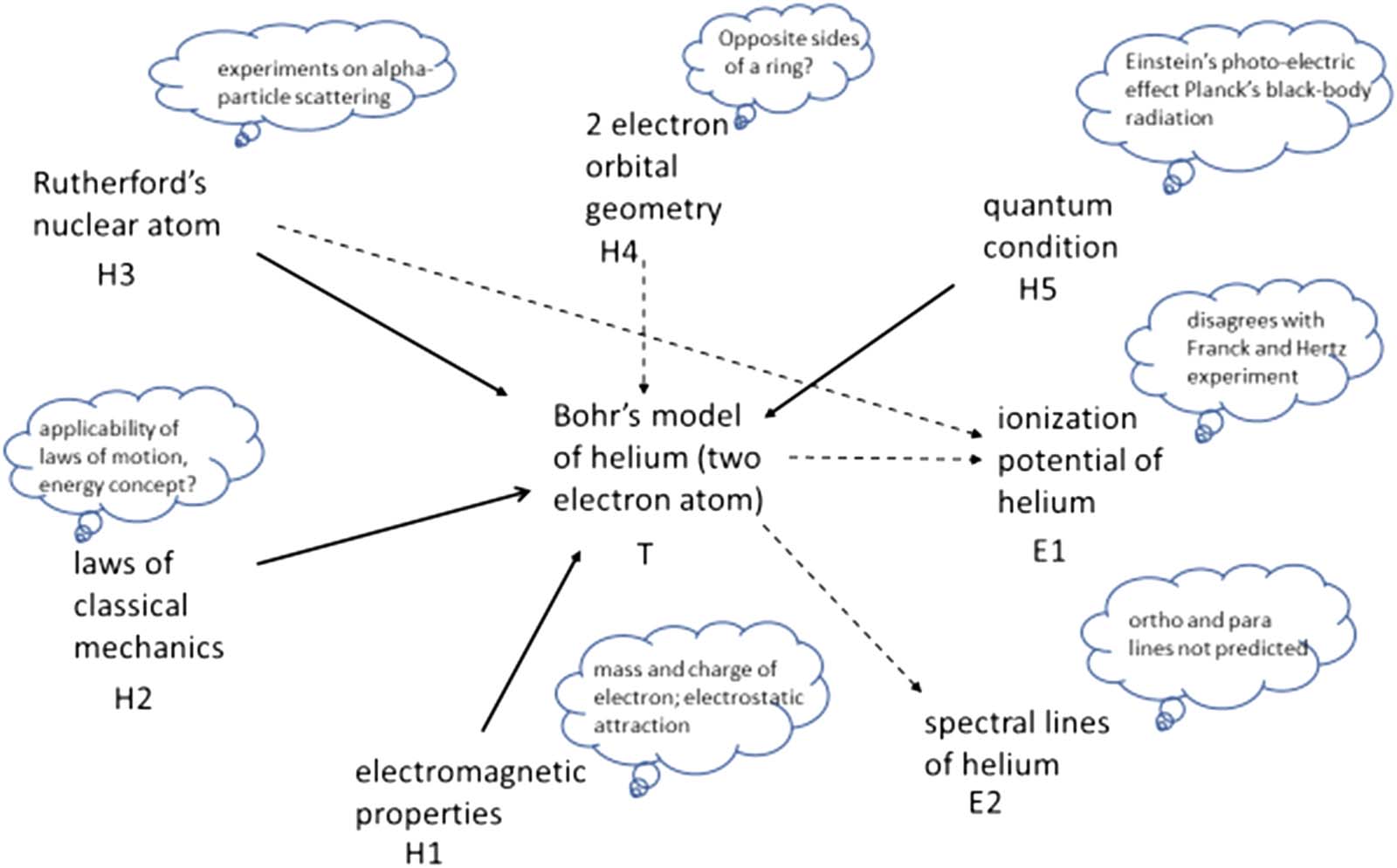
Encouraged by his success with hydrogen, Bohr applied the model to the helium atom,
which contained two orbiting electrons (Small, 1971). Here he needed an additional assump-
tion about the orbital geometry of the second electron, and he opted for a single circular ring
with two electrons on either side. In the case of helium, Tuttavia, success was less certain: IL
ortho and para spectral lines were not predicted, although the model yielded an ionization
potential having the right order of magnitude given existing measurements. Again, Bohr was
optimistic that the model would be vindicated by more accurate measurements.
About 10 years later, Tuttavia, more accurate measurements became available that were
clearly in disagreement with the model. In Figure 2 for the helium atom, the dashed lines to
spectral lines, ionization, and orbital geometry, indicate that these connections were weak.
The response of physicists working on helium was to modify the assumptions used in the
modello. The first assumption to be modified was the orbital geometry of the orbiting elec-
trons, Per esempio, by placing them at an angle to one another or on inner and outer orbits.
When such geometric modifications failed, physicists turned to other perceived weak points,
such as the ad hoc quantum condition, or the electromagnetic force between the electrons
and the nucleus. One researcher even abandoned Rutherford’s nuclear atom altogether, Rif-
verting to Thomson’s plum pudding model, but to no avail. The final bastion was to give up
on the laws of classical mechanics. At that point physicists abandoned the helium problem,
in favor of simpler physical systems such as the single particle oscillator. It was Werner
Heisenberg who finally cracked the problem with his matrix mechanics in 1925, followed
by Erwin Schrodinger’s wave equation in 1926 (Jammer, 1966). As Heisenberg described it,
the two electrons in helium were behaving nonclassically by continuously swapping their
identities. In the late 1920s, a number of physicists, using the matrix mechanics or the wave
Quantitative Science Studies
1029
Approaches to the study of confirmation in science
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
Figura 2. Causal network of Bohr’s 1924 model of the helium atom.
equation, were able to predict the helium ionization potential and the spectral lines to great
accuracy.
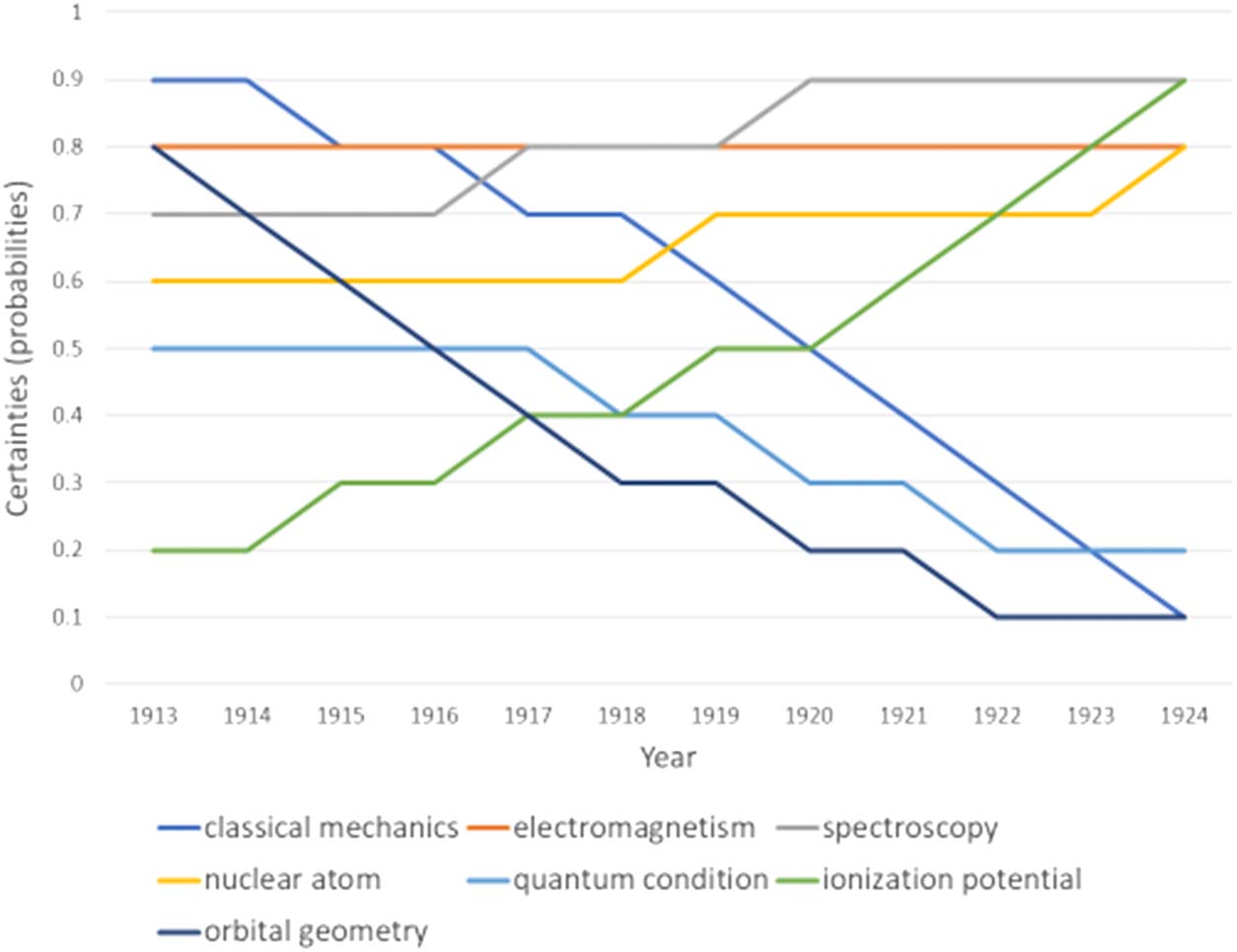
One way of understanding what happened between 1913 E 1924 is to plot the chang-
ing certainty or probability of each assumption in Bohr’s model (Guarda la figura 3) over the
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 3. Estimated certainties (probabilities) of Bohr’s atomic theory assumptions 1913–1924.
Quantitative Science Studies
1030
Approaches to the study of confirmation in science
decade. In particular, the certainty of orbital geometry, classical mechanics, and the quan-
tum condition declined, while the certainty of the measurements of the ionization potential
increased.
In this historical case the probabilities have been approximated based on qualitative histor-
ical evidence, questo è, statements of participants, and the sequence with which hypotheses
were modified over time. Infatti, this case study is a good example of what philosophers call
the Duhem-Quine problem (Howson & Urbach, 2006): Questo è, when a prediction fails, how
do you know which hypothesis is at fault? We can postulate, following Duhem, that the order
in which assumptions were modified was a function of their perceived uncertainty, or improb-
ability (Duhem, 1954). As one hypothesis was modified, others of lesser certainty were then
open to modification too, leading to a proliferation of possible variant models and a loss of
research direction. The most certain of the theoretical assumptions was classical mechanics,
and it was the last one to be modified. In the end, to find a new mechanical basis, the helium
problem had to be abandoned in favor of a simpler atomic system, Heisenberg’s oscillator.
È interessante notare, the two empirical findings, spectral lines and ionization potential, were the most
resilient. They survived the failure of the old theory and were used to test the new theory based
on quantum and wave mechanics. Così, the empirical findings were intrinsically more certain
than the theoretical assumptions, perhaps because they were less encumbered by theory or
were embedded in wider conceptual networks.
This suggests that to assess the certainty or probability of a theoretical or experimental
assumption, we need to look at how embedded they are in existing knowledge networks. UN
comparison of the networks for hydrogen and helium (Figures 1 E 2) shows that the helium
model is less embedded than the hydrogen model due to the weaker links in the helium figure
to spectra, ionization potential, and orbital geometry. Although the hydrogen model had a
higher degree of embeddedness than the helium model, the latter was dependent on and
logically entailed the former, so that neither model survived the quantum mechanical revolu-
tion of the mid-1920s.
Obviously, a complete picture of Bohr’s atomic theory would be extremely complex, be-
cause each of the theoretical or experimental assumptions was embedded in a wider network
of relationships. Per esempio, the “nuclear atom” was embedded in the alpha particle scatter-
ing experiments of Rutherford; the quantum condition was embedded in a quantum theory
network involving earlier work by Planck on blackbody radiation and Einstein’s photoelectric
effect; the spectral lines were embedded in 19th-century spectroscopy of Balmer, Paschen,
and others; the ionization potential from cathode ray tube discharge experiments by Franck;
electromagnetism in the work of Faraday and Maxwell; and classical mechanics in a tradition
going back to Isaac Newton. The only assumption without its own historical network is orbital
geometry, which was the first assumption to be questioned and modified.
4. COMPUTATIONAL APPROACHES TO MODELING CONFIRMATION
Our example from the history of science shows the role that confirmation and disconfirma-
tion can play in directing the development of science through periods of conceptual
change. A set of theoretical assumptions predicted experimental results in one case, Ma
these same assumptions failed to explain experiments in another. Following a period of try-
ing to patch up the theory by modifying its assumptions, a new approach was proposed
which radically altered our view of the atom. It appears the process can be depicted as a
network of connections between theoretical hypothesis and experimental findings, Quale
are in turn imbedded to varying degrees in diverse areas of physics at the time. This suggests
Quantitative Science Studies
1031
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
that a network model of some kind might be a good way to model the processes of confir-
mation and disconfirmation.
The two primary methods available to model such confirmatory networks are Bayesian
causal networks (Pearl & Mackenzie, 2018; Sprenger & Hartmann, 2019), Quale, Per esempio,
have been implemented in the bnlearn package in R (Nagarajan, Scutari, & Lebre, 2013), E
Thagard’s theory of explanatory coherence (TEC) implemented in his ECHO software
(Thagard, 1992). Both models are based on a connectionist view of scientific ideas and operate
by passing or exchanging confirming or disconfirming information to adjacent nodes following
defined paths in the network in the manner of a spreading activation process. In Bayesian
causal networks the links are directional, while in TEC they are undirected and can indicate
agreement or contradiction. Both models require that the networks be defined beforehand,
including all hypotheses and evidence to be explained, and that all parameters be set. TEC
runs until the weights on each node converge to stable values between −1 and +1, while
for the Bayesian network the updated probabilities (between 0 E 1) are obtained by running
queries. The outputs of the Bayesian model are updated probabilities, Per esempio, the prob-
ability of the theory given the evidence, and in TEC, the outputs are updated weights for the
hypotheses and evidence.
In Bayesian networks, confirming or disconfirming information is encoded in conditional
probabilities, and in prior probabilities for hypotheses. These “priors” then increase or de-
crease as new evidence is brought to bear; technically the priors lead to posterior probabil-
ities, which then become the new priors. The posterior probability is the probability of the
theory given the evidence. The Bayesian theory further asserts that, over time, as more ev-
idence comes in, the probability will converge to a stable value. In TEC, the confirming or
disconfirming information is encoded in the structure and type of links and in the starting
weights assigned to hypothesis or evidence nodes. TEC can be rerun when new evidence
comes in.
Rudolf Carnap was one of the first philosophers to advocate a probabilistic approach
to confirmation, although some philosophers, for example Popper, have objected to as-
cribing degrees of belief to hypotheses arguing that only countable events can have prob-
abilities (Popper, 1961, Chapter 10). Others argue that scientists do not behave in a
Bayesian manner (Giere, 1988). Leydesdorff has given an information theoretic interpre-
tation of Bayesian conditionalization without specifying how it might be applied
(Leydesdorff, 1992). Yet a Bayesian probabilistic approach seems well suited to showing
how evidence changes the probability of a theory over time (Salmon, 1967). For exam-
ple, when a theory we are not confident in has an unexpected empirical confirmation,
the prior probability of the evidence P(E ) is small, and the posterior probability increases
following Bayes’ theorem:
P TjEð
Þ ¼ P Tð Þ * P EjTð
½
(cid:2)=P Eð Þ;
Þ
(1)
where P(T|E ) is the posterior probability of the theory given the evidence, P(E|T ) is the
probability of the evidence given the theory, and P(T ) is the prior probability of the the-
ory. The firmness with which the theory necessitates or entails the evidence, P(E|T ), also
increases the posterior probability of the theory, as does a higher prior probability of the
theory P(T ). Conversely,
in a theory and a disconfirming piece of
the posterior probability decreases due to a decrease
evidence unexpectedly appears,
in P(E|T ). Finalmente, the posterior probability increases if there is a low probability of the
evidence given the theory is incorrect, denoted by P(E|~T ), or decreases if, Per esempio,
is high, where the symbol ~ indicates
a rival
theory gives a better fit and P(E|~T )
if we are confident
Quantitative Science Studies
1032
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
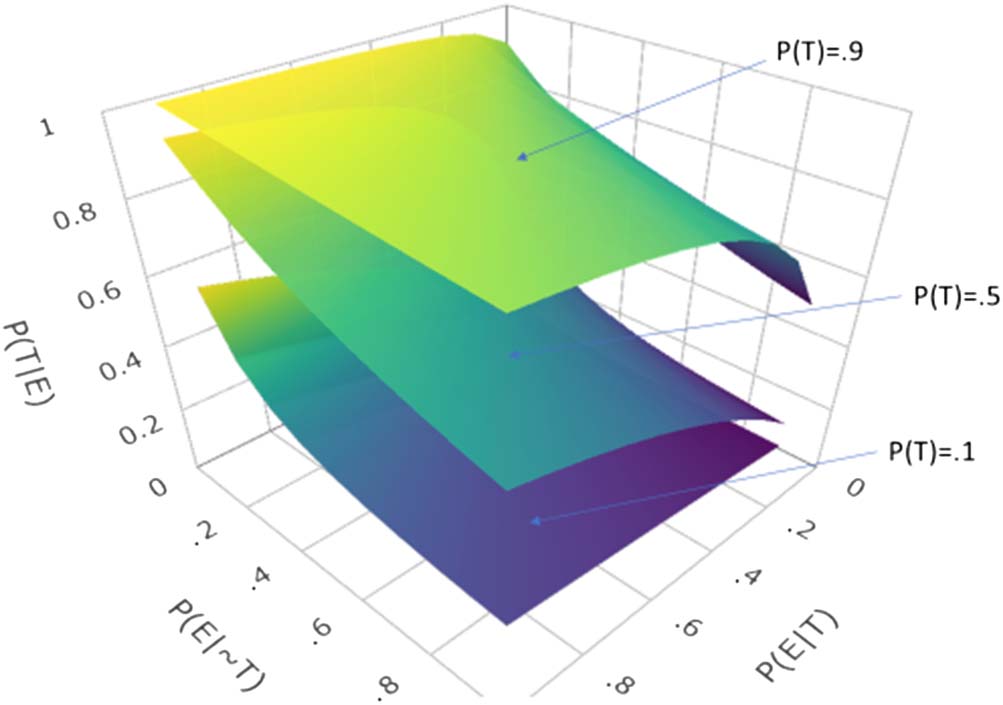
Figura 4. Three-dimensional surface plot of an alternative form of Bayes’ theorem.
negation. This last point is made clear by an alternative form of Bayes’ theorem, namely
Howson and Urbach’s third form of Bayes’ theorem:
(cid:2)= P Tð Þ * P EjTð
Þ
Þ ¼ P Tð Þ * P EjTð
ð
Þ * P Ej∼T
Þ þ P ∼Tð
P TjEð
(2)
(cid:2);
Þ
½
½
where P(~T )
A [1 − P(T )]
is the prior probability the theory is false and is equal
(Howson & Urbach, 2006, P. 21). This form is derived from the standard form of
Bayes’ theorem by applying the theorem of “total probability.”
It is informative to plot this alternative form of Bayes’ theorem as a surface in three-
dimensional space (Figura 4).
The figure shows three surfaces for three different values of the prior probability of the theory
P(T ): 0.1, 0.5, E 0.9. The vertical axis corresponds to P(T|E ), the probability of the theory
given the evidence or posterior probability, while the other two axes plot P(E|T ) and P(E|~T ),
the probabilities of the evidence given the theory is true and false respectively. Note that for
each surface we can trace a diagonal from P(E|T ) = P(E|~T ) = 0 to P(E|T ) = P(E|~T ) = 1, Quale
defines a straight line where the prior equals the posterior probability, P(T ) = P(T|E ), indicating
that neither confirmation nor disconfirmation occurs. Tuttavia, if P(E|T ) is greater than P(E|~T ),
the surface slants upwards from the diagonal and the posterior is greater than the prior proba-
bility, indicating confirmation. Conversely, if P(E|~T ) is greater than P(E|T ), the surface slants
downwards from the diagonal and the posterior is less than the prior probability indicating dis-
confirmation. This sets up a competition between how well the theory entails or predicts the
evidence versus how well another theory might predict it1.
A more recent innovation is the Bayesian causal network, which allow the probabilistic
modeling of complex networks of relationships based on a directed acyclic graph or DAG.
The child and parent nodes in the network iteratively exchange probabilistic information by
a process called belief propagation (Pearl, 2018, P. 112). The simplest such network is T -> E,
where the theory T is considered as causing or leading to the evidence E. This can be modeled
as P(T )*P(E|T ) where P(T ) is the prior probability of the theory and P(E|T ) is the conditional
probability of the evidence given the theory. In this simple case the solution can be computed
exactly using the alternative form of Bayes’ theorem (Eq. 2) as illustrated in Figure 4.
1 In the Bayesian scheme, incorrect or uncertain evidence, denoted as P(~E ), can be accounted for because
P(E|T ) = 1 – P(~E|T ), where P(~E|T ) means the theory predicts incorrect evidence, which decreases P(E|T ).
Quantitative Science Studies
1033
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
Bayesian causal networks simplify the “joint probability distribution,” the product of the
probabilities of all the independent variables, by requiring conditional probabilities be sup-
plied only for the “children” of each “parent node” in the DAG by applying the so-called chain
rule (Pearl, 2000, 14). Per esempio, in the hydrogen atom case with seven true/false variables
for the states of the theoretical assumptions and one experimental finding, without the chain
rule it would be necessary to specify 27 O 128 conditional probabilities. The use of the chain
rule cuts this number in half to 26. The joint probability distribution then can be written as:
P H1ð
Þ * P H2ð
Þ * P H3ð
Þ * P H4ð
Þ * P H5ð
Þ * P TjH1; H2; H3; H4; H5
ð
Þ * P EjTð
Þ;
(3)
where the probabilities of each node follow the labeling in Figure 2 2. Prior probabilities of the
hypotheses H1 through H5 were assigned values in accord with their approximate certainties
circa 1913 (Guarda la figura 3). Historical evidence was, Tuttavia, not available to specify the con-
ditional probabilities of the type P(T|H1,H2,H3,H4,H5) , so a simple rule was used based on
the proportion of “true” hypotheses out of the five that the theory was dependent on. For ex-
ample, P(T|H1,H2,~H3,~H4,~H5) was set to 2/5 = 0.4. This assumes that all hypotheses con-
tribute positively to the theory without creating internal inconsistencies. Finalmente, we set the P(E|
T ) and P(E|~T ) A 0.6 E 0.2, rispettivamente, due to the good fit of the theory to the spectral
lines of hydrogen, and the lack of a rival theory. Based on these settings, we obtain a posterior
probability of the theory, given the evidence, Di 0.87 using the bnlearn package in R
(Nagarajan et al., 2013). This provides a confirmation when compared to the average of prior
probabilities, which was 0.7.
Turning to the helium atom (Figura 2), three changes were made to the input parameters.
Primo, the prior probability of the orbital geometry of the two-electron atom was reduced to 0.1
due to uncertainty regarding this hypothesis circa 1924. Secondly, P(E|T ) was decreased to 0.2
due to the poor fit with the experimental data, and P(E|~T ) was increased to 0.8 on the as-
sumption that an alternative theory would perform better. These changes reduce the posterior
probability to 0.27, which disconfirms the helium model when compared to an average prior
Di 0.6.
Paul Thagard’s TEC model was designed to determine the acceptability of scientific the-
ories and has been the subject of extensive commentary by philosophers, psychologists, E
others (Thagard, 1989). His monograph from 1992 presents numerous case studies from the
history of science which clearly show how his algorithm can be applied to identify the most
coherent theory of those available in a given historical context (Thagard, 1992). Unlike
Bayesian causal networks, the TEC model was designed specifically for assessing theories
given their experimental confirmation or disconfirmation and is much simpler to apply, Rif-
quiring fewer parameters provided you accept his standard system settings. The model is
based on a neural network analogy, where links can be either excitatory in the case of sup-
porting evidence or inhibitory in the case of contradictory evidence. Although TEC does not
have the dynamic nature of the Bayesian approach, where priors are sequentially updated
as new evidence comes in, TEC models can be run at different points in time, as well as
including competing theories in the same network. Rival theories can actively compete with
contradictory assumptions weakening or strengthening each other depending on their rela-
tion to experiment. The weights of the nodes, representing the degrees of confirmation of the
various hypotheses and evidence, change as the spreading activation converges to an equi-
librium. The final weights for each node vary from –1 to +1 and are analogous to the
2 The dependency of the ionization potential on Rutherford’s nuclear atom has not been included, but could
be added with a term P(E|H4) without introducing a cycle in the causal graph.
Quantitative Science Studies
1034
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
posterior probabilities of Bayesian theory. The model has built-in rules, such as a penalty for
multiple supporting hypotheses following the Occam’s razor idea that the fewer hypotheses
the better, and a rule to enhance confirmation by finding analogous explanations and
strengthening them. In this sense, Thagard’s TEC approach takes into consideration a wider
range of modes of confirmation than the Bayesian approach, although this can obscure how
the algorithm works in some cases.
TEC treats the agreement of theory with experiment as a special case, having a constant pre-
set value of one. Treating experimental evidence as a special case can sometimes be problem-
atic because it is difficult to differentiate theory from experiment due to the theory-laden nature
of experiment. Per esempio, in the atomic example, should Rutherford’s nuclear atom be treated
as experimental or theoretical? Clearly it is both. It is perhaps best to treat the initial likelihoods
of experimental evidence or theoretical assumptions in the manner of prior probabilities, E
the software does provide the ability to set prior weights on evidence and hypotheses to values
less than one.
Thagard has implemented TEC in Common Lisp in a program called ECHO. It is easy to run
once the environment is set up and you accept the default settings in the program such as
excitatory and inhibitory weights, decay rate, and so on. Per esempio, to run the hydrogen
atom model all that is necessary is to specify the hypotheses involved in the theory and the
experimental evidence to be explained since there is no competing theory in 1913 and no
contradictory hypotheses are involved:
ð
explain’ H1 H2 H3 H4 H5
ð
Þ’E1
Þ;
(4)
where H1 through H5 are the hypotheses in Figure 1 and E1 stands for the ionization potential.
This single evidence unit gives a final weight for the hypotheses of 0.15 and a weight of 0.52
for the evidence after 140 iterations. To explain both the line spectrum and ionization poten-
tial of hydrogen at the same time we specify
ð
explain’ H1 H2 H3 H4 H5
ð
Þ
Þ’E1
ð
explain’H1 H2 H3 H4 H5
Þ’E2Þ
(5)
(6)
where E2 is the hydrogen spectrum evidence. Using both experimental results gives a much
higher final weight for the hypotheses of 0.41 and a weight of 0.56 for the evidence units after
142 iterations. Because of the multiple hypotheses involved we can assume that the program
has reduced the degree confirmation following the Occam’s razor rule described above.
Tuttavia, in using two experimental confirmations the program will presumably invoke the
“analogy” condition and enhance confirmation.
In the case of the helium model, where experimental agreement was poor for both the ion-
ization potential and spectral lines, we used reduced weights of 0.2 for both the hypotheses
and the evidence as follows:
ð
explain’ H1 H2 H3 H4 H5
ð
Þ’E1:2
Þ
ð
explain’ H1 H2 H3 H4 H5
ð
Þ’E2:2
Þ
ð
data’ E1:2
ð
ð
Þ
Þ E2:2
ð
Þ
Þ
(7)
(8)
(9)
The final weights after 76 iterations were 0.01 for the hypotheses and 0.16 for the evidence
units, a very weak confirmation. Note that in ECHO it is not possible for a hypothesis to
Quantitative Science Studies
1035
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
directly contradict an evidence unit, and thus it is necessary to use low initial weights to rep-
resent this situation.
It is not yet possible to state a clear preference for the TEC or Bayesian network approach,
or whether it might be possible to create an alternative model combining the simplicity of
TEC with the rigor of the probabilistic framework. Cabrera (2017) provides a comparison of
the different approaches. Thagard has expressed reservations concerning the ability of a
Bayesian approach to model historical cases such as Lavoisier’s theory of combustion. Lui
stati: “We would have to take each hypothesis separately and calculate its probability given
the evidence, but it is totally obscure how this could be done… What, Per esempio, is the
conditional probability of burned objects gaining in weight given the hypothesis that oxygen
is combined with them?" (Thagard, 1992, P. 92). It is true that the Bayesian approach in-
volves specifying numerous probabilities that are difficult to tie to historical evidence. On
the other hand, it does not seem difficult to construct a causal network model of Lavoisier’s
oxygen theory of combustion along the lines outlined here for Bohr’s atomic models, taking
each hypothesis as a weighted binary choice. Hypotheses such as “oxygen is a component
of air,” “oxygen has weight,” and “oxygen combines with metals to form calxes” are con-
nected by directed links to a theory node which in turn leads to evidence nodes such as
“calxes show a weight gain after burning” and “burning uses up oxygen from the air.”
Again, the challenge would be to specify all the conditional probabilities based on some
historical rationale.
Mention should also be made of a difficulty with the Bayesian approach, the “problem of
old evidence,” especially as applied to the hydrogen atom and other historical cases (Howson
& Urbach, 2006; Sprenger & Hartmann, 2019). Both the spectral lines of hydrogen and
the ionization potential were known prior to Bohr’s formulation of the theory, which strictly
speaking cannot result in an increase in the posterior probability. Some theorists have argued
that this problem can be overcome by considering such evidence as not being “entailed” by
the new theory until after the theory is formulated. Tuttavia, the prohibition on old evidence
is counterintuitive because our confidence in a theory increases if it can explain any evidence,
whether old or new.
Finalmente, a comment should be made on a new theory that claims that all we need for sci-
entific rationality is a consensus of diverse individuals (Oreskes, 2019). While consensus is
correlated with low hedging and high certainty (Small, 2019), which is measurable using ci-
tation contexts, consensus is not adequate as a theory of rationality or confirmation in science.
If it were, we would have to say that any set of beliefs, if agreed upon by a large enough group,
is justified, including a paradigm such as the old quantum theory regardless of its fit with ex-
periment or the better fit offered by an alternative theory.
Also relevant to this discussion is E. O. Wilson’s concept of consilience (Wilson, 1998) fol-
lowing the 19th-century philosopher William Whewell. In the case of the Bohr atom, we saw
that the theoretical assumptions and empirical confirmations connected work across several
subfields of physics: atomic theory, spectroscopy, cathode ray tube work, particle scattering,
Newtonian mechanics, electromagnetic theory, and quantum theory. Some of these connec-
tions were unexpected or low probability in the Bayesian sense. Per esempio, that Planck’s
constant could be related to spectroscopic data and cathode ray discharge experiments in
the context of an atomic model was striking. The joining of diverse well-established knowl-
edge areas in a network should by itself increase our confidence in the theory (Niiniluoto,
2016). The fact that Bohr’s hydrogen model was superseded in the 1920s did not prevent
Einstein from stating as recently as 1951 that Bohr’s explanation of the spectral lines of
Quantitative Science Studies
1036
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
hydrogen “… appeared to me like a miracle—and appears to me as a miracle even today. Questo
is the highest form of musicality in the sphere of thought.” (ter Haar, 1967, P. 42)
5. FROM HISTORY OF SCIENCE TO BIBLIOMETRICS
There are many similar case studies in the history of science where a Bayesian model fits
the historical narrative (Weinert, 2010), but to generate a wider sample of cases of confirma-
tion or disconfirmation, bibliometric methods seem the most promising. Ideally, the methods
should generate bibliometric networks for specific topics that can be tracked over time so that
changes in the degree of confirmation can be followed. The nodes in the networks should
correspond, to some extent, with theoretical assumptions or empirical findings, and at least
some connections between the nodes should be causal in nature, approximating a DAG.
The existing methods of document clustering and mapping are obvious candidates for such
a wider sampling, including the various citation-based clustering methods (Klavans &
Boyack, 2017).
Inoltre, the method of citation context analysis can be applied for the identification
of causal relationships signaled by words such as cause, predict, explain, suggest, E
demonstrate; questo è, epistemic verbs that appear frequently in scientific texts and especially
citation contexts (Bertin & Atanassova, 2014). Così, if maps are generated by citation data, E
the full texts of papers citing the clustered papers are used to provide citation contexts, then it
might be possible to find causal relationships imbedded in the network. Another way in which
citation contexts can assist is in estimating prior probabilities, questo è, the degrees of certainty
regarding the cited papers representing theories or empirical results. This can be implemented
by counting hedging terms, such as may, might, and could in the citation contexts.
Earlier studies have suggested that such an approach is feasible. In a study of a cocitation
cluster on the topic of leukemia viruses where the contexts of cocitations were analyzed,
about one-third of the links were found to be “causal” (Small, 1986). Per esempio, a cocitation
context for one of the links on the map stated: “In the presence of murine leukemia virus, these
MCF viruses can accelerate the development of tumors.” In other words, a causal relationship
was postulated. Inoltre, the linked documents in the network provided the evidential
basis for the causal assertion.
Allo stesso modo, another case study of a cocitation cluster on water pollution uncovered causal
links among papers showing that the use and subsequent disposal of steroid hormones by hu-
mans could impair the fertility of fish downstream from wastewater treatment plants (Small &
Klavans, 2011). Again, about one-third of the links were causal in nature, representing about
10 distinct causal assertions, such as “These chemicals are probably responsible for elevated
incidence of intersex characteristics in freshwater fish.” As in the previous example, the evi-
dential basis for the assertion was contained in the linked documents, such as water quality
measurements and statistics on fish populations.
Cross-sectional estimates of certainty may also be of interest. Per esempio, a state of high
uncertainty (low prior probability) might be associated with a “causal” link indicating that a
disconfirming event has occurred or that the link is controversial. Using a sample of the top
1,000 highly cited papers from PubMed Central, both the hedging rate and rate of causal
words were computed using citing sentences (Small, 2018). Papers were selected having at
least a 10% rate for both hedging and causality. IL 36 papers selected cover a range of con-
troversial topics, the most prominent of these being inflammation as a cause of disease. As one
citing author states: “Current knowledge on inflammation-induced carcinogenesis is limited
but the widespread implications of this phenomenon on human health warrant further
Quantitative Science Studies
1037
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
studies.” Other topics were the possible toxic effects of nanoparticles and the missing herita-
bility in genetic studies.
Using the same data set, 27 papers were selected having high certainty (≤3% hedging rate)
and high causality (≥10%). About 40% of these were statistical studies on the prevalence of
various diseases in the population, based on epidemiological evidence. This suggests that
strong evidence and high certainty are correlated. In this high certainty sample, it was neces-
sary to restrict papers to nonmethods because method papers have very low hedging rates.
This is consistent with the higher certainty of empirical findings which we saw in the atomic
theory case.
Tuttavia, ideally, we would like to study how the degree of confirmation changes over
time. We can do this with highly cited papers in the following way. Assume we have the citing
papers for each of the highly cited papers and the citing sentences where they are referenced.
Taking the publication years of the citing papers, we find the median citing year for each highly
cited paper and divide the citing sentences into “early” and “late” sets, computing the hedging
rate for the two sets by searching for hedging words. The hedging rate is the percentage of
sentences containing one or more of the hedging words. By comparing the “early” and “late”
hedging rates, we can determine which highly cited papers have increasing or decreasing
hedging rates. Allo stesso modo, we compute the rate of causal words for the two sets. A high causality
rate combined with a decrease or increase in the hedging rate suggests that confirmation or
disconfirmation has occurred.
Such an analysis was performed using the 1,000 highly cited papers from PubMed Central
noted above. We can illustrate the results by considering one of these papers published in
Nature in 1993, entitled “A synaptic model of memory: long-term potentiation in the hippo-
campus.” This paper went from an “early” hedging rate of 12.1% A 5.6% in the “late” period
and had a causal word rate of 8.9%. One citing author stated: “The involvement of NMDA
receptors to the plasticity of synaptic inputs in the CNS has been well demonstrated.” While
we have not constructed a causal network for this research area, a rough Bayesian analysis can
be carried out assuming that the hedging rate is inversely related to the prior probability of the
paper’s findings. Thus taking the “early” prior probability to be 100% – 12%, O 0.88, and the
“late” posterior probability to be 100% – 5.6%, O 0.94, we can apply the alternative form of
Bayes’ theorem (Eq. 2) to compute that posterior probability by setting P(E|T ) and P(E|~T ) at
0.6 E 0.3 rispettivamente. Clearly, the next step is to find a bibliometric justification for these
settings, and this appears to involve quantifying of how well this theory of memory or, its rival
theories, explain the evidence. A crude proxy for this metric might be simply the proportion of
“causal” citations to the paper in the “late” period. Bibliometric methods could also be used to
identify rival theories and assess their hedging and causal rates. Such methods hold promise
for the identifying instances of confirmation, particularly in citation-based clusters.
6. CONCLUSIONS
This paper suggests a new direction for quantitative science studies: Why should we believe
the findings of science? I have argued that it will be important for quantitative science studies
to address confirmation in science and the role of evidence in that process. The neglect of such
studies in the past has fostered the belief that in science “anything goes” and we can invent our
own scientific “facts” and impose our “reality” on others. While this has been a perennial topic
in the philosophy of science, it has been of little concern to sociology, history of science, O
quantitative science studies. This is not about reestablishing some lost authority of science or
asserting its special status as the ultimate arbiter of knowledge, but it is about correcting an
Quantitative Science Studies
1038
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
imbalance in the image of science as an interest-driven and politically motivated activity un-
tethered to evidence.
The field of quantitative science studies has the tools to begin to examine the dynamics of
confirmation in scientific texts. With citation contexts we can assess the collective opinions of
the scientific community, using hedging to measure uncertainty, and epistemic words to locate
causal assertions tied to evidence. One place to begin is to identify causal networks embedded
in our maps of science, tracking them over time to assess the impact of evidence on the cer-
tainty or uncertainty of theoretical assumptions. In approaching confirmation as a bibliometric
problem, we are implicitly moving from the personalist focus of the philosophy of science to a
community or social focus.
Possible theoretical approaches for this effort are Bayesian causal networks and Thagard’s
explanatory coherence. Whether individual scientists really behave to maximize the probabi-
listic “consistency” or “coherence” of their beliefs is not important. What is more important is
whether this can be discerned at the level of a specialty or a community. If what we find is
“mob psychology” as Lakatos feared Kuhn’s theory would lead to (Lakatos, 1970, P. 178), E
not evidence-based rationality, we would have a sound basis for a real critique of science.
The difficulties and limitations of course are substantial. The theoretical models will not be
easy to apply, requiring translating bibliometric and textual data to model variables. A one-to-
one translation of a bibliometric network into a causal network will not, in general, be possi-
ble. The time lags between the appearance of new evidence and its manifestation in the
changing appraisals of the citing community will be difficult to coordinate. On the plus side,
quantitative science studies have the opportunity to address an issue of great importance to
the scientific community generally, namely the integrity of science, and at the same time
rebuild bridges with the philosophy of science that should expand the types of problems
we can address. It is of interest that a recent book on Bayesian philosophy of science has sug-
gested that bibliometric methods might be applicable to the topic (Sprenger & Hartmann,
2019).
A relevant metaphor for the scientific endeavor comes from Lee Smolin (Smolin, 2019, P.
277). To paraphrase, you are walking through a landscape of high peaks of certain knowledge
and deep valleys of uncertainty: “So I have a decision to make: I either keep on the present
sentiero, which will end up on the top of that low hill just past the next village, or head down into
the swamps to stumble along unknown paths in search of undiscovered mountains.”
ACKNOWLEDGMENTS
I would like to thank Paul Thagard for providing his ECHO software and Mike Patek for tech-
nical assistance implementing it. Also, I am grateful to Marco Scutari for comments on the
Bayesian network for Bohr’s theory.
COMPETING INTERESTS
The author has no competing interests.
FUNDING INFORMATION
No funding has been received for this research.
Quantitative Science Studies
1039
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Approaches to the study of confirmation in science
REFERENCES
Bertin, M., & Atanassova, IO. (2014). A study of lexical distribution in
citation contexts through the IMRaD standard. Atti del
First Workshop on Bibliometric-Enhanced Information Retrieval,
36th European Conference on information retrieval, Vol. 1143.
Amsterdam, The Netherlands.
Bohr, N. (1913). On the constitution of atoms and molecules, Part
1. Philosophical Magazine, 26(1), 1–25.
Cabrera, F. (2017). Can there be a Bayesian explanationism?
On the prospects of a productive partnership. Synthese, 194(4),
1245–1272.
Collins, H. (2014). Are we all scientific experts now? Cambridge:
Polity Press.
Niiniluoto, IO. (2016). Unification and confirmation. Theoria-revista
de Teoria Historia y Fundamentos de la Ciencia, 31(1), 107–123.
Oreskes, N. (2019). Why trust science? Princeton, NJ: Princeton
Stampa universitaria.
Pearl, J. (2000). Causality: Modelli, reasoning, and inference.
Cambridge: Cambridge University Press.
Pearl, J. & Mackenzie, D. (2018). The book of why. New York:
Basic Books.
Popper, K. R. (1961). The logic of scientific discovery. New York:
Science Editions.
Price, D. J. de Solla (1986). Little science, big science … and
beyond. New York: Columbia University Press.
Duhem, P. (1954). The aim and structure of physical theory.
Salmon, W. C. (1967). The foundations of scientific inference.
Princeton, NJ: Princeton University Press.
Edge, D. O. (1977). Why I am not a co-citationist. 4S Newsletter,
2(3), 13–19.
Feigl, H. (1970). Beyond peaceful coexistence. In R. H. Stuewer
(Ed.) Historical and philosophical perspectives of science: Vol. V.
(pag. 3–11). Minneapolis: University of Minnesota Press.
Giere, R. N. (1988). Explaining science: A cognitive approach.
Chicago: University of Chicago Press.
Hanson, N. R. (1972). Patterns of discovery: an inquiry into the
conceptual foundations of science. Cambridge: Cambridge
Stampa universitaria.
Harman, G. (1965). The inference to the best explanation.
Philosophical Review, 74, 88–95.
Heilbron, J. L., & Kuhn, T. S. (1969). The genesis of the Bohr atom.
Historical Studies in the Physical Sciences, 1, 211–290.
Howson, C., & Urbach, P. (2006). Scientific reasoning: IL
Bayesian approach. Chicago: Open Court Publishing Co.
Jammer, M. (1966). The conceptual development of quantum
mechanics. New York: McGraw-Hill.
Klavans, R., & Boyack, K. (2017). Which type of citation analysis
generates the most accurate taxonomy of scientific and technical
knowledge? Journal of the Association for Information Science
and Technology, 68(4): 984–998.
Kuhn, T. S. (1962). The structure of scientific revolutions. Chicago:
University of Chicago Press.
Lakatos, IO. (1970). Falsification and the methodology of scientific
research programmes. In I. Lakatos & UN. Musgrave (Eds.), Criticism
and the growth of knowledge (pag. 91–195). Cambridge: Cambridge
Stampa universitaria.
Leydesdorff, l. (1992). Knowledge representations, Bayesian inferences,
and empirical science studies. Social Science Information, 31(2),
213–237.
Lloyd, G. E. R. (1978). Saving the appearances. Classical Quarterly,
28(1), 202–222.
McIntyre, l. (2018). Post-truth. Cambridge, MA: CON Premere.
Merton, R. K. (1968). Social theory and social structure. New York:
Free Press.
Nagarajan, R., Scutari, M., & Lebre, S. (2013). Bayesian networks in
R with applications in systems biology. New York: Springer.
Pittsburgh: University of Pittsburgh Press.
Salmon, W. C. (1970). Bayes’ theorem and the history of science. In
R. H. Stuewer (Ed.). Historical and philosophical perspectives of
science: Vol. V (pag. 68–86). Minneapolis: University of
Minnesota Press.
Small, H. (1971). The helium atom in the old quantum theory
(doctoral dissertation). University of Wisconsin, ProQuest
#7125217.
Small, H. (1986). The synthesis of specialty narratives from co-
citation clusters. Journal of the American Society for Information
Scienza, 37(3), 97–110.
Small, H. (2018). Characterizing highly cited method and non-
method papers using citation contexts: The role of uncertainty.
Journal of Informetrics, 12(2), 461–480.
Small, H. (2019). What makes some scientific findings more certain
than others? A study of citing sentences for low-hedged papers.
Proceedings of the 17th International Conference of the
International Society for Scientometrics and Informetrics, Rome,
Italy.
Small, H., & Klavans, R. (2011). Identifying scientific breakthroughs
by combining co-citation analysis and citation context.
Proceedings of the 13th International Conference of the
International Society for Scientometrics and Informetrics,
Durban, South Africa.
Smolin, l. (2019). Einstein’s unfinished revolution: The search for
what lies beyond the quantum. New York: Penguin Press.
Sprenger, J., & Hartmann, S. (2019). Bayesian philosophy of
science. Oxford: Oxford University Press.
ter Haar, D. (1967). The old quantum theory. Oxford: Pergamon
Press.
Thagard, P. (1989). Explanatory coherence. Brain and Behavioral
Scienze, 12, 435–502.
Thagard, P. (1992). Conceptual revolutions. Princeton, NJ:
Princeton University Press.
Weinert, F. (2010). The role of probability arguments in the history
of science. Studies in History and Philosophy of Sciences, Part A,
41(1), 95–104.
Wilson, E. O. (1998). Consilience: The unity of knowledge. New York:
Alfred A. Knopf.
Quantitative Science Studies
1040
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
q
S
S
/
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
1
3
1
0
2
5
1
8
6
9
9
1
0
q
S
S
_
UN
_
0
0
0
6
3
P
D
/
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3