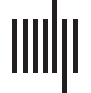RESEARCH - Ricerca sull'intelligenza artificiale specializzata al MIT

RESEARCH

Synergistic information in a dynamical model
implemented on the human structural
connectome reveals spatially distinct
associations with age

Davide Nuzzi1, Mario Pellicoro1, Leonardo Angelini1, Daniele Marinazzo 2,

and Sebastiano Stramaglia

1,3

a n o p e n a c c e s s

j o u r n a l

1Dipartimento Interateneo di Fisica, Universitã degli Studi Aldo Moro, Bari and INFN, Bari, Italy
2Department of Data Analysis, Ghent University, Ghent, Belgium
3Center of Innovative Technologies for Signal Detection and Processing (TIRES), Universitã degli Studi Aldo Moro, Bari, Italy

Keywords: Information theory, Aging, Ising model

ABSTRACT

We implement the dynamical Ising model on the large-scale architecture of white matter
connections of healthy subjects in the age range 4–85 years, and analyze the dynamics in
terms of the synergy, a quantity measuring the extent to which the joint state of pairs of
variables is projected onto the dynamics of a target one. We ﬁnd that the amount of synergy
in explaining the dynamics of the hubs of the structural connectivity (in terms of degree
strength) peaks before the critical temperature, and can thus be considered as a precursor of
a critical transition. Conversely, the greatest amount of synergy goes into explaining the
dynamics of more central nodes. We also ﬁnd that the aging of structural connectivity is
associated with signiﬁcant changes in the simulated dynamics: There are brain regions whose
synergy decreases with age, in particular the frontal pole, the subcallosal area, and the
supplementary motor area; these areas could then be more likely to show a decline in terms
of the capability to perform higher order computation (if structural connectivity was the sole
variable). D'altra parte, several regions in the temporal cortex show a positive
correlation with age in the ﬁrst 30 years of life, questo è, during brain maturation.

AUTHOR SUMMARY

In a previous study implementing the Ising model on a 2D lattice, we showed that the joint
synergistic information shared by two variables on a target one peaks before the transition to
an ordered state (critical point).

Here we implemented the same model on individual structural connectomes, to answer
these questions:

– Does the synergy still peak before the critical point in a nonuniform network?
– Are the hubs of structural connectivity also hubs of synergy?
– Is there association with age?

We found that synergy still peaks before the critical temperature and that hubs of structural
connectivity are not among the nodes towards which synergy is highest. Inoltre, using
robust measures of association we found both positive and negative associations of synergy

Citation: Nuzzi, D., Pellicoro, M.,
Angelini, L., Marinazzo, D., &
Stramaglia, S. (2020). Synergistic
information in a dynamical model
implemented on the human structural
connectome reveals spatially distinct
associations with age. Network
Neuroscience, 4(3), 910–924.
https://doi.org/10.1162/netn_a_00146

DOI:
https://doi.org/10.1162/netn_a_00146

Supporting Information:
https://github.com/
ising_synergy_brain

danielemarinazzo/

Received: 18 Febbraio 2020
Accepted: 08 May 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Authors:
Sebastiano Stramaglia
sebastiano.stramaglia@ba.infn.it
Daniele Marinazzo
daniele.marinazzo@ugent.be

Handling Editor:
Olaf Sporns

Copyright: © 2020
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza

The MIT Press

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

Ising model:
A mathematical model of
ferromagnetism, consisting of
discrete variables called spins that
can be in one of two states
(+1 or − 1) and that are arranged
in a graph allowing each spin to
interact with its neighbors. IL
two-dimensional square-lattice
Ising model is one of the simplest
statistical models to show a phase
transition.

Critical brain hypothesis:
Evidence has been mounting that
biological systems, in particular
neuronal networks, might operate at
the borderline between order and
disorder, questo è, near a critical point.

Brain connectivity network
(connectome):
A network in which the nodes are
brain regions and the links are
anatomical connections
(“anatomical/structural connectivity”)
or statistical dependencies
(“functional connectivity”).

with age, in localized clusters. In some regions this association is continuous with age; In
others it is limited to around the ﬁrst 30 years of age.

INTRODUCTION

Recent advances in diffusion imaging and tractography methods allow noninvasive in vivo
mapping of white matter cortico-cortical projections at relatively high spatial resolution, così
providing a connection matrix of interregional structural connectivity (SC) representing the
geometry of the brain (Sporns, 2010). Dynamical models implemented on the large-scale ar-
chitecture of the human brain may shed light on how function is constrained by the underlying
structure. This is the case of the so-called neural mass or mean-ﬁeld models that describe the
collective activity of cell populations (Deco & Jirsa, 2012), or phase coupling models (Finger
et al., 2016), down to abstract models such as the Ising model (Deco, Senden, & Jirsa, 2012;
Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013; Marinazzo et al., 2014; Stramaglia
et al., 2017). In particular, some studies showed that the resting activity exhibits peculiar scal-
ing properties, resembling the dynamics near the critical point of a second-order phase tran-
sition (Chialvo, 2010). Noise-induced synchronization on the human connectome has been
recently studied in Pang, Gollo, and Roberts (2020). Inoltre, the possible origin and role of
criticality in living adaptive and evolutionary systems has recently been ascribed to adaptive
and evolutionary functional advantages (Hidalgo et al., 2014).

In this paper we implement a dynamical model on the individual large-scale structural con-
nectivity of healthy subjects in the age range 4–85 years, and look for the dynamical properties
of the simulated dynamics that are associated with aging.

Human aging is the set of characteristics that change over time, signifying someone as older
or younger. These changes occur at different hierarchical levels, called metrics of aging: biolog-
ical aging, phenotypic aging, and functional aging (Ferrucci, Levine, Kuo, & Simonsick, 2018).
Connectomics (Bassett & Sporns, 2017) provides a unique resource for examining how brain
organization and connectivity changes across typical aging, both in terms of plasticity and
function, and in terms of how these differences relate to brain disorders. Several studies have
used diffusion imaging to investigate changes in structural connectivity over the healthy hu-
man life span. Generalmente, these studies have observed a nonlinear inverted U-shaped trajectory
association between age and fractional anisotropy (FA), and a U-shaped trajectory (opposite
to FA) for axial, mean, and radial diffusivity (Westlye et al., 2010). A review of age-related dis-
ruption of the brain’s regional integrity and information ﬂow across the brain, as expressed by
age-related differences in functional and structural connectivity, can be found in Damoiseaux
(2017).

Considering the structural connectivity network provided by diffusion imaging as a com-
plex network, some global metrics of the networks have been found to be correlated with age
(Wozniak & Lim, 2006). Age showed signiﬁcant positive correlation to the integrated cost but
signiﬁcant negative correlation to the integrated local efﬁciency, while it showed no signiﬁ-
cant correlation to the integrated global efﬁciency (Sun, Tong, & Yang, 2012). The reorganiza-
tion with age of the whole-brain structural and functional connectivity has been described in
Betzel et al. (2014). The age-related alterations in the topological architecture of the white
matter structural connectome has been also studied in Zhao et al. (2015), where it has been
found that hub integration decreased linearly with age, with loss of frontal hubs and their con-
nections, and that age-related changes in structural connections were predominantly located
within and between the prefrontal and temporal modules. Particularly interesting is also the

Network Neuroscience

911

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

Synergy:
A quantity rooted in information
theory measuring how much the
joint state of pairs of brain regions
is projected onto the dynamics of
a target region.

study of the cognitive performance in healthy older adults, which in Cabral, Vidaurre, E
Marques (2017) has been related to the switching behavior of resting functional connectivity,
and in Hinault, Larcher, Bherer, Courtney, and Dagher (2019) to the preservation of struc-
tural and effective connectivity. The genetic basis of neurocognitive decline and reduced white
matter integrity in normal human brain aging has been studied in Glahn et al. (2013), demon-
strating a heritable component for neurocognitive deterioration with age. Concerning brain
maturation, positive correlation between structural and functional connectivity has been de-
scribed in Hagmann et al. (2010), where in addition it has been observed that this relationship
strengthened with age. A study of structural brain network changes across the adult life span
reported 16 signiﬁcant age-related networks, with weights decreasing with age linearly in all
networks except from the temporal lobe-related network where the decrease was quadratical
(Liu et al., 2017). A recent study (Bonifazi et al., 2018) explored joint functional-structural
network characteristics that are signiﬁcantly correlated with aging.

In order to ﬁnd how a changing structural architecture might inﬂuence information process-
ing of a system whose dynamics are constrained by it, in this paper we implement the Ising
model on the structural geometry of the brain, here estimated from diffusion tensor imaging.
The dynamical properties of the simulated activity that we will consider are derived from the
formalism of information decomposition of target effects from multisource interactions, questo è
the deﬁnition of redundant and synergistic components of the information that a set of source
variables provide about a target (Lizier, 2012). Applying this framework to the two-dimensional
Ising model as a paradigm of a critically transitioning system, and disentangling the compo-
nents of the information both at the static level and at the dynamical one, it has been recently
shown that a key signature of an impending phase transition (approached from the disordered
side) is the evidence that the synergy peaks in the disordered phase, both considering only
instantaneous interactions, and also considering lagged ones: The synergy can thus be consid-
ered a precursor of the transition (Marinazzo, Angelini, Pellicoro, & Stramaglia, 2019).

This study aims to answer three main questions:

Does the synergy still peak before the critical point in the nonuniform structural con-
nectvity network?
Are the hubs of structural connectivity also hubs of incoming synergy?
How does an aging connectome modulate these patterns?

MATERIALS AND METHODS

Data

In this work we analyze data form the NKI-Rockland life span study (Nooner et al., 2012),
in particular the already processed connectome data provided by the USC Multimodal Con-
nectivity Database (Brown, Rudie, Bandrowski, Van Horn, & Bookheimer, 2012), consisting
Di 196 connectomes of healthy subjects based on 3T dMRI acquisition (voxel size, 2 mm3;
64 gradient directions; TR, 10,000 ms; TE, 91 ms; further details are provided in Brown et al.,
2012). The resulting structural connectivity matrices Jij consist of N = 188 regions of interest
(ROIs), obtained using the Craddock atlas (Craddock, James, Holtzheimer, Eh, & Mayberg,
2012), linked together by weighted connections based on the number of streamlines connect-
ing pairs of ROIs. The matrix Jij is symmetric by construction, thus giving rise to a weighted
undirected graph. The age of subjects ranges from 4 A 85 years. We consider the individual
structural connectivity matrices, and the average connectivity matrix Javg
ij obtained averaging
over all subjects.

Network Neuroscience

912

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

Theoretical Framework and Implementation

First we implement the Ising model, with Glauber dynamics, on the average connectome net-
work Javg

, using the following Hamiltonian:

and updating rules given by

H = −

1
2

N
∑
io,j=1

Jijsisj,

P(si → −si) =

1
1 + esp (β∆Ei)

(1)

(2)

where ∆Ei = 2si ∑j Jijsj represents the variation of the total energy of the system following
the ﬂip of the spin si. Varying the inverse temperature β, the susceptibility shows a peak that
identiﬁes the critical state of this ﬁnite-size system, related to a phase transition occurring in
the limit of large networks (Dorogovtsev, Goltsev, & Mendes, 2008). It is worth mentioning that
recently this stretching of criticality (from a single point to a more relaxed regime) observed
in dynamical models deﬁned on brain networks has been described in the frame of Grifﬁth’s
phases (Moretti & Muñoz, 2013). Simulations are initially run for a relaxation time of 105 su-
dates for the ﬁrst value of β, then we start the following procedure: We vary the temperature
adiabatically, discard the ﬁrst 104 updates, and then collect the following 106 updates for statis-
tic. The procedure is repeated for 20 runs at each of the 80 temperature points enclosing the
phase transition. We make sure that the state of each spin is updated exactly one time for each
iteration of the Glauber dynamics; this allows us to collect one time series si(T) for every spin,
where t is a discrete time index running from 0 to the total simulation time. In order to char-
acterize the ﬂow of information between the time series in the context of information theory,
we interpret each si(T) as a single realization of a discrete-time stationary stochastic process
Si(T), but for the sake of simplicity we will use the notation si(T) also to refer to the stochas-
tic process. Joint probabilities used in the calculations of information quantities are obtained
directly from the data samples as the frequency of each conﬁguration.

The ﬂow of information between variables can be measured in the framework of informa-
tion dynamics using the transfer entropy (TE), a quantity introduced in Schreiber (2000) E
based on appropriate conditioning of transition probabilities (Bossomaier, Barnett, Harré, &
Lizier, 2016). Unlike mutual information I(X; Y), a symmetric quantity that measures only the
information that is statistically shared by the variables X and Y, transfer entropy is an inher-
ently asymmetrical quantity and can effectively distinguish between driving and responding
elements. Let si be the stochastic process associated with a given spin, taken as the target vari-
able, and let ˜si be the same process one time step in the future. Let {sj, sk, . . . , sr} be a group
of spins that are assumed to be drivers for the spin si. The transfer entropy from the group of
drivers to the target is deﬁned as

T{jk…R}→i = I(cid:0) ˜si; {sj, . . . , sr}(cid:12)
(cid:12)

si(cid:1).

(3)

The choice of different groups of source variables leads to the deﬁnition of various informa-
tion quantities that are commonly found in the literature. If we choose only one source variable
sj and we average over all possible sources and targets, we get the pairwise transfer entropy; Esso
has been shown that this measure peaks at the critical point both for the Ising model on a regu-
lar 2D lattice and on brain graphs (Barnett, Lizier, Harré, Seth, & Bossomaier, 2013; Marinazzo
et al., 2014). If we choose all the spins but si as sources and then average over all possible

Transfer entropy:
A nonparametric statistic measuring
the amount of directed
(time-asymmetric) transfer of
information between two random
processes.

Network Neuroscience

913

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

targets, we get the global transfer entropy (GTE). Information ﬂow, as quantiﬁed by GTE, peaks
in the paramagnetic phase and is thus able to predict an imminent transition (Barnett et al.,
2013). Unfortunately numerical estimation of this quantity is unfeasible in systems involving
a large number of drivers for each target. As discussed in J. T. Lizier, Prokopenko, and Zomaya
(2010) GTE is a measure of collective information transfer, capturing both pairwise and higher
order (multivariate) correlations to a variable. It follows that explicitly disentangling the com-
ponents of the collective information ﬂow is needed to get a better description of the system in
the proximity of the transition. As it has been demonstrated in Marinazzo et al. (2019) using the
information decomposition frame ﬁrst introduced in Williams and Beer (2010) and Williams
and Beer (2011), considering as few as two sources at the same time is sufﬁcient to construct
a precursor of the transition. Let si be the target spin and sj, sk be two different driver spins;
then the desirable information decomposition is

Tjk→i = Uj→i + Uk→i + Rjk→i + Sjk→i,
Tj→i = Uj→i + Rjk→i,
Tk→i = Uk→i + Rjk→i.

(4)

(5)

(6)

The terms Uj→i and Uk→i quantify the components of the information about the future of
spin si that are unique to the sources sj and sk, rispettivamente. The term Rjk→i describes the re-
dundant information, the component that is shared between the two source variables. Finalmente,
the term Sjk→i quantiﬁes the synergy between the sources, intended as the amount of infor-
mation that can be acquired only considering the sources together, but not considering them
alone. Synergy is the only term in this decomposition that contains higher order correlations
that can’t be captured by pairwise measures ( J. Lizier, Bertschinger, Jost, & Wibral, 2018).

Shannon theory of information does not include a deﬁnition for synergy and redundancy; In
fatto, there are many different conceptual deﬁnitions for those two quantities (Grifﬁth, Chong,
James, Ellison, & Crutchﬁeld, 2014; Harder, Salge, & Polani, 2013; Quax, Har-Shemesh, &
Sloot, 2017). The information decomposition provided in Equation (4) contains only three
equations for the four unknown quantities Uj→i, Uk→i, Rjk→i, Sjk→i, therefore the deﬁnition
of only one of them is needed in order to solve the system. The so-called minimum mutual
informazione (MMI) PID (Barrett, 2015) gives a deﬁnition for the redundancy: It assumes that
the information that is shared between the sources, independently of the correlations between
them, can be identiﬁed with the minimum of the information provided by each individual
source to the target. Speciﬁcally

Rjk→i = min (cid:8)Tj→i, Tk→i(cid:9) .

(7)

Another choice for the information decomposition is given in Bertschinger, Rauh, Olbrich,
Jost, and Ay (2014) and is based on the following idea. Let p(si, sj, sk) be the joint probabil-
ity distribution of the three spins and let p(si, sj), P(si, sk) be the two marginal distributions
that involve the target and only one driver. Then the redundancy and the unique information
should depend on only the marginal distributions but not the particular choice of p(si, sj, sk),
which should only affect the synergy. If we deﬁne ∆p as the set of all the trivariate probability
distributions q that gives rise to the same marginal distributions as p, questo è, q(si, sj) = p(si, sj),
q(si, sk) = p(si, sk), we can deﬁne the synergy as

Sjk→i = Tjk→i − min
q∈∆ p

˜Tjk→i,

(8)

914

Network Neuroscience

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

where ˜T is the transfer entropy evaluated using q as the joint probability distribution. It
has been shown (Barrett, 2015) that in the case of Gaussian stochastic variables those two
approaches are equivalent and provide the same decomposition. We have veriﬁed empirically
that the same holds true for the problem at hand.

The average connectome is a dense network, hence for the dynamics on the average con-
nectome we take into account all the triplets of brain nodes and evaluate the information de-
composition for each triplet: In order to evaluate the typical incoming synergy for each node,
S is averaged over all the triplets having that node as a target.

The individual structural networks, on the other hand, have many nearly zero entries; it is a
sparse network: Therefore we make a selection of relevant triplets of brain nodes {j, k, io}, con
target i, requiring that both Jji and Jki are higher than a threshold Jth. We ﬁx Jth so as the total
number of considered links is 20% of all the possible pairs, and verify that our results are robust
w.r.t. the choice of Jth. For all the selected triplets we evaluate the information decomposition
E, in order to evaluate the typical incoming synergy for each node of an individual network,
we average the synergy over all the triplets, among the selected ones, that have that node as
the target.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

RESULTS

Ising Model on the Average Connectivity Network

Because of the range of strengths of each node, each spin undergoes a dynamical transition
at a different temperature. This phenomenon can be visualized studying the probability for
the spin to ﬂip at each time step, shown in Figure 1. For β = 0 every spin has exactly a 50%

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1. The probability of ﬂip, for each spin at one time step, is depicted as a function of β. IL
nodes are ordered according to increasing strength of the average connectome. At low temperatures
spins freeze, each spin freezing at a different temperature; the ﬁgure shows that the strength of nodes
explains, to a certain extent, the variability of the freezing temperature.

Network Neuroscience

915

Synergistic information on the aging human connectome

chance to ﬂip, while as β gets larger the probability drops to 0 at a different rate, depending
on the strength (for each node, the strength is the sum of the weights of its connections) del
corresponding node; ordering the nodes by their strength shows that stronger nodes tend to
freeze at higher temperatures. As already noted in Marinazzo et al. (2014), as the temperature is
lowered the subnetwork constituted by the hubs (we veriﬁed the average connectivity network
is a rich club) tend to align and to build a cluster of highly correlated spins with slow dynamics.
More and more spins are recruited to join this cluster as the temperature is further lowered,
until all the system is magnetized. As a consequence, this system does not show a critical
temperature, rather it is characterized by a critical range of temperatures, in accordance with
Grifﬁth’s theory (Moretti & Muñoz, 2013).

In Figure 2 we have depicted, as a function of the coupling β, the global quantities re-
lated to the information decomposition, questo è, the trivariate transfer entropy, the average
synergy, and the redundancy, as well as the susceptibility χ, the classical index of critical-
ità. Looking at the ﬁgure, we see that the peak of χ precedes, as β increases, the peaks of
the synergy, the transfer entropy, and the redundancy in order. The peak of χ in this hetero-
geneous system occurs at lower β than the peak of the synergy, different from what happens
in the Ising model on a regular lattice (Marinazzo et al., 2019); Tuttavia, one may consider
the synergy for each target node, averaged over the pairs of driving variables, and realize
that each node experiences its maximum of the synergy at different temperatures. As de-
picted in Figure 3, the hubs show their peak of synergy before the peak of χ, hence their

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Information decomposition for the Ising model on the brain connectome. (UN) Suscepti-
Figura 2.
bility χ versus the inverse temperature β; the temperature where it peaks is considered as the critical
state of the system. (B)(C)(D) Trivariate transfer entropy, redundancy, and synergy averaged over all
spin triplets, depicted against β, peaking in the ferromagnetic state. The dashed line indicates the
critical temperature.

Network Neuroscience

916

Synergistic information on the aging human connectome

Figura 3. The average synergy towards the ﬁve brain nodes with highest strength is depicted versus
β; their plot peaks before the critical temperature, here identiﬁed as the peak of susceptibility.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Incoming and outgoing transfer entropy. The amount of information that a ﬁxed driver
Figura 4.
node transfers to all possible targets (typical outgoing TE) increases steadily with the strength of the
node. D'altra parte, the amount of information received by a target node from all the drivers
(typical incoming TE) behaves similarly for small strength values but decreases above a certain
strength threshold.

synergy can be seen as precursor of the transition to order. A weighted average of the synergy
of each node, with properly ﬁxed weights concentrated on the hubs of the strength, would
also peak before criticality and thus would constitute a global precursor of the transition.
Another interesting remark to be made is that, as noticed for example in Novelli, Atay, Jost
and Lizier (2019), the pairwise transfer entropy from a source to a target node in a network
does not depend solely on the local source-target link weight, but on the wider network struc-
ture that the link is embedded in. Deeply connected is the fact that the information ﬂow
in networks obeys the law of diminishing marginal returns; see Marinazzo, Wu, Pellicoro,
Angelini, and Stramaglia (2012). In Figure 4 we depict the incoming and outgoing transfer

917

The law of diminishing returns:
A fundamental principle of
economics stating that in all
productive processes, adding more of
one factor of production, while
holding all others constant (“ceteris
paribus”), will at some point yield
lower incremental per unit returns. UN
similar scenario is observed in the
information ﬂow pattern of
dynamical networks.

Network Neuroscience

Synergistic information on the aging human connectome

entropy of each node, as a function of the strength of the node, where the temperature is ﬁxed
at the peak of χ. Because of the limited capacity of a spin to encode the incoming informa-
zione, nodes with high strength send more information to the system than it gets; nodes with
low strength send and receive approximately the same amount of information. These ﬁndings
support the picture of a dynamics shaped by the hubs of structural connectivity.

Here we show that a similar behavior holds for the average incoming synergy to each given
node, in other words when we average the synergy of all the triplets with the given node as
the target. In Figure 5 the incoming synergy, at criticality, is depicted versus the topological
character of nodes: strength, betweenness and closeness. We see that the hubs of structural
connectivity, which as described above are the drivers of the dynamics, are not among the
nodes towards which synergy is highest. Measures of centrality, like betweenness and close-
ness, appear to be more associated with synergy than strength: The joint state of brain regions
is more likely to be projected in central regions of the brain.

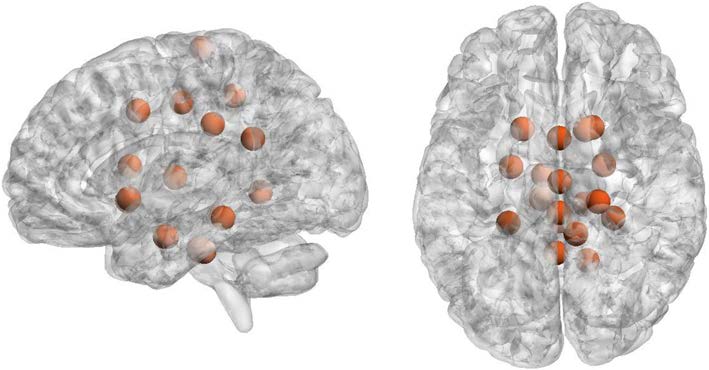
In Figure 6 we have depicted the 10% nodes with highest average incoming synergy. No-
tably these nodes correspond to hippocampus and parahippocampal regions, which are sup-
posed to play important roles in higher order cognitive functions, speciﬁcally learning and

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

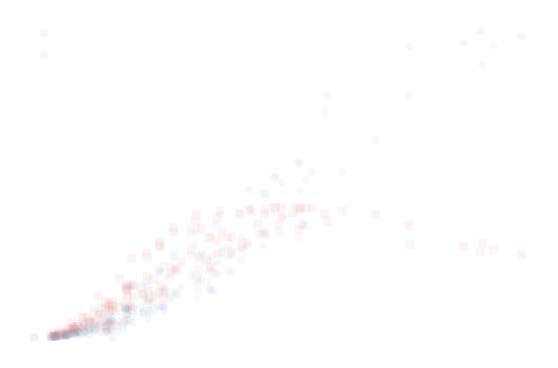
Figura 5. Comparing synergy with topological indices. From the left to the right, for each brain
node the typical incoming synergy at criticality is compared with the strength of nodes, the be-
tweenness, and the closeness.

Figura 6. Hubs of synergy. Top nodes for the value of incoming synergy, radius and color of the
spheres are arbitrary: right hippocampus, brain stem, right parahippocampal posterior left Parahip-
pocampal posterior, right Cingulate posterior, right precentral, left thalamus, left parahippocampal
posterior, left hippocampus, right lingual, right caudate, right cingulate anterior.

Network Neuroscience

918

Synergistic information on the aging human connectome

memory processes (Nemanic, Alvarado, & Bachevalier, 2004); the brain stem, which con-
trols the ﬂow of messages between the brain and the rest of the body, as well as several body
functions; the cingulate cortex, which has been associated with several complex cognitive
functions, such as empathy, impulse control, emotion, and decision-making; and the thala-
mus, whose main function is to relay motor and sensory signals to the cerebral cortex.

These two ﬁgures were plotted with BrainNet Viewer (Xia, Wang, & Lui, 2013).

Ising Model on Individual Connectivity Networks and Correlations with Aging

The implementation of the Ising model on the individual networks of healthy subjects shows
the robustness of the scenario described above. Infatti, qualitatively similar results have been
found on individual networks, each network showing, Tuttavia, its own critical temperature as
evaluated at the peak of the susceptibility. Remarkably, this analysis provides an individual pat-
tern of synergy, evaluated at criticality, so as to evidence those nodes whose synergy covaries
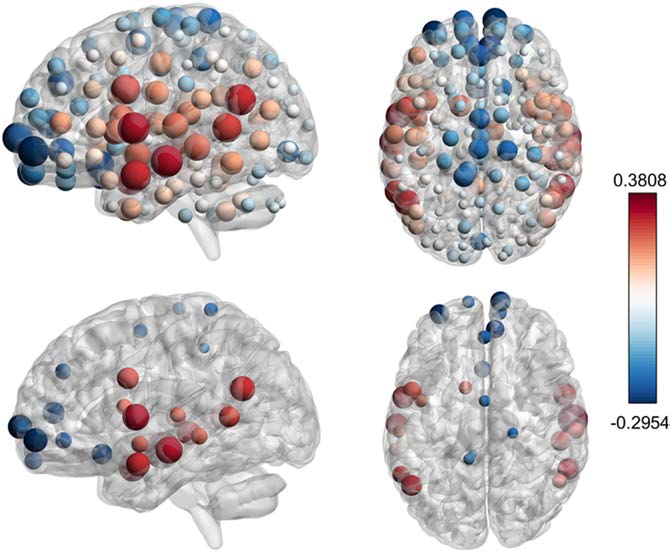
signiﬁcantly with age. In Figure 7 we depict the Spearman correlation coefﬁcient between
incoming synergy and age, for each brain node, showing a symmetric pattern. We choose
measures of association that are robust to the presence of outliers and suitable for multiple

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 7. Correlations between synergy and age. (Top) Spearman correlation coefﬁcient between
the chronological age of the patient and the incoming synergy for each node, questo è, the average of
synergies for all triplets having that node as a target. Both positive (red) and negative (blue) corre-
lations are found. The radius of the spheres is proportional to the absolute value of the correlation.
(Bottom) Only the regions with signiﬁcant correlation are shown, evaluated using Hochberg ad-
justed p values at a signiﬁcance level α = 0.05. Synergy is positively correlated with age in the
following regions: left middle temporal posterior, right middle temporal anterior, left angular, right
superior temporal posterior, left middle temporal temporooccipital, right middle temporal posterior,
left middle temporal temporooccipital, left middle temporal anterior, left central opercular, right su-
perior temporal posterior; and negatively correlated in left frontal pole, left subcallosal, right frontal
pole, paracingulate sulcus, juxtapositional lobule.

Network Neuroscience

919

Synergistic information on the aging human connectome

Figura 8. Scatterplot of synergy and age for two representative brain regions. left: Right superior
temporal posterior, positive correlation. right: Right frontal pole, negative correlation. Local average
and standard deviation are evaluated using the ﬁrst 20 neighbors of each point.

comparisons. We use the implementations contained in the robust statistical toolbox by Rand
Wilcox (Rallfun-v37.txt, update September 2019), using R version 3.5.3 (R Core Team, 2018).
In particular we adopt the skipped Spearman correlation with adjusted p values in conjunc-
tion with Hochberg’s method to control family-wise error. This approach is referred to as L3
in Wilcox, Rousselet, and Pernet (2018), and implemented in the R function scorregciH. Questo
analysis yields 29 regions whose synergy is signiﬁcantly associated with aging at a corrected α
value of 0.05, seventeen regions positively correlated with age, E 12 negatively correlated
with age, depicted in Figure 7.

The nodes whose synergy is signiﬁcantly decreasing with age are frontal poles and subcal-
losal regions, as well as paracingulate sulcus and juxtapositional lobule (formerly supplemen-
tary motor area). It has been suggested that the frontal lobes are the part of the brain most
profoundly affected by the aging process (Tisserand et al., 2002); a review of age-related
changes in MR spectroscopy, functional mri, and diffusion tensor imaging can be found in
Minati, Grisoli, and Bruzzone (2007). Successful cognitive aging and its functional imaging cor-
relates are discussed in Eyler, Sherzai, Kaup, and Jeste (2011). Juxtapositional lobule is among
the cortical motor regions whose dynamic has been shown to be modulated by age in Wang
et al. (2019).

The nodes whose synergy is signiﬁcantly increasing with age are mostly located in the
temporal cortex. In Figure 8 we have depicted, Per esempio, the synergy versus age for two brain
nodes, the right superior temporal posterior (showing a signiﬁcant positive correlation with
age) and the right frontal pole (showing a negative signiﬁcant correlation with age). Figura 8
suggests that some regions show a slow and continuous decrease in synergy. On the other
hand, the brain regions with a signiﬁcant positive correlation actually show an increase in the
synergy in the ﬁrst decades of life, and a plateau later: Hence such an increase of synergy in
the early age could be associated with brain maturation, while the plateau at late age can be
seen as a compensatory effect due to the decline of white matter volume (Westlye et al., 2010)
and of structural connectivity (Liu et al., 2017).

Finalmente, we looked at the correlation with age of the structural strength of the 29 regions
whose synergy is correlated with age. Out of the 17 regions whose synergy signiﬁcantly in-
creases with age, 16 of them also show a signiﬁcantly positive correlation between their

Network Neuroscience

920

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

strength and age; out of the 12 regions whose synergy signiﬁcantly decreases with age, none
of them displays a structural strength signiﬁcantly correlated with age. This indicates that while
the growth of the synergy in the positively age-correlated regions can be simply explained as
a consequence of the increased connectivity of these regions, this does not hold for the syn-
ergy of the regions negatively correlated with age, where the relationship cannot simply be
mapped on terms of some topological metrics and could arise in a more complex way from
the underlying structural network.

DISCUSSION

The analysis of computational models implemented on the realistic brain geometry is nowa-
days considered important to enrich our understanding of the mechanisms contributing to
the formation and dissolution of functional brain networks. Some studies aimed at assessing
to what extent whole-brain computational models reproduce graph-based topological features
of the empirical functional resting-state networks; Per esempio, see Lee, Bullmore, and Frangou
(2017). In Meier et al. (2017), a susceptible-infected-susceptible (SIS) epidemic-spreading model
on the human connectome has been studied to reveal the topological properties of the under-
lying structural network that gives rise to the global pattern of the directional information ﬂow
observed in data.

The Ising model represents the paradigmatic example of phase transitions; here we have
implemented it on the large-scale structural geometry of the brain as measured by difussion
tensor imaging, for individual networks of healthy subjects with different age, as well as on the
average connectome, in order to analyze the simulated neural dynamics in terms of the synergy,
a quantity that has recently been introduced in the ﬁeld of partial information decomposition
of information and that, in the case of the brain, measures to what extent the joint state of pairs
of brain regions is projected onto the dynamics of a target region.

We ﬁnd, as the temperature is lowered, that the synergy can still be considered as a pre-
cursor of transition in an inhomogeneous network and not only in an ordered lattice: IL
synergy towards the most connected brain regions (averaged over pairs of drivers) peaks be-
fore the maximum of the susceptibility, which is conventionally taken as the transition point
in ﬁnite-size systems. The transition to order here is orchestrated by the hubs of the structural
connectivity, and we have shown that the synergy of these hubs peaks at higher temperature
than the critical temperature: Therefore the main ﬁndings of Marinazzo et al. (2019) can be
generalized to heterogeneous networks provided that the synergy of structural hubs is consid-
ered. It is remarkable that the hubs of the synergy are not hubs of the strength; instead they
are central nodes of the network, although neither the betweenness nor the closeness are fully
monotonical with the synergy.

We also ﬁnd that there are brain regions whose incoming synergy decreases continuously
with age, in particular the frontal pole, the subcallosal area, and the supplementary motor
areas: These brain nodes are known to be affected by the aging process (Kievit et al., 2014).
Other brain regions, in the temporal cortex, show a positive correlation with age; Tuttavia,
looking at the scatterplot suggests that the increase stabilizes around the age of 30. As a con-
sequence these results suggest that the temporal cortex experiences a remarkable maturation
in term of the synergy, questo è, on the capability of performing higher order computation. Most
results about brain maturation refer to subcortical regions and prefrontal regions: The analysis
of synergy here seems to suggest a role of the temporal cortex. The pattern of the synergy of the
temporal cortex, described here, seems to correspond in the early age to the increase of the
structural connectivity found in Liu et al. (2017) for the temporal lobe–related network. On

Partial information decomposition:
A recent extension of Shannon
information theory quantifying
the information that several inputs
provide individually (unique
informazione), redundantly (shared
informazione), or only jointly
(synergistic information) Di
the output.

Network Neuroscience

921

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

the other hand, the same quantity showed a decline tendency in the late stage of life (Liu et al.,
2017); the same decline was observed for the white matter volume in the temporal cortex in
Westlye et al. (2010). A possible interpretation would be that the increase of synergy is com-
pensatory for the decline of structural properties of the temporal cortex. Intuitively, synergy is
the information about the target variable that is uniquely obtained by taking the sources to-
gether, but not considering them alone; hence it measures to what extent the activity of a given
target region of the brain is the projection of the joint activity of two other driver regions, In
other words the capability to perform computation of higher level. In this sense, these results
suggest that the function of some regions of the brain may deteriorate with age with a contri-
bution from the changing white matter geometry, while other regions receive more synergistic
information as age increases.

We expect that a similar scenario for the synergy could hold also for models of phases and
other dynamical systems on the connectome. More importantly, most studies so far have stud-
ied aging in terms of statistical dependencies (mainly correlations) between pairs of regions.
Here we focused on higher order effects, which already become evident considering only the
structural geometry of the brain: These higher order effects might be worth investigating also
in empirical brain networks.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

DATA AND CODE AVAILABILITY

The processed connectomes are retrieved from http://umcd.humanconnectomeproject.org
(NKI-Rockland; Brown& Van Horn, 2016). The code to simulate the dynamics of the Ising spins
coupled according to the connectomes, as well as the synergy values for each region and each
subject, is available at https://github.com/danielemarinazzo/ising_synergy_brain (Marinazzo,
2020; Nooner et al., 2012).

AUTHOR CONTRIBUTIONS

Davide Nuzzi: Formal analysis; Software; Visualization; Writing – Original Draft; Writing –
Review & Editing. Mario Pellicoro: Formal analysis; Software. Leonardo Angelini: Conceptual-
ization; Methodology; Project administration. Daniele Marinazzo: Conceptualization; Formal
analysis; Investigation; Methodology; Software; Visualization; Writing – Original Draft; Writing –
Review & Editing. Sebastiano Stramaglia: Conceptualization; Investigation; Methodology; Su-
pervision; Validation; Writing – Original Draft; Writing – Review & Editing.

FUNDING INFORMATION

Sebastiano Stramaglia, Ministero dell’Istruzione, dell’Università e della Ricerca (http://dx.doi.
org/10.13039/501100003407), Award ID: PRIN 2017/WZFTZP.

REFERENCES

Barrett, UN. B. (2015). Exploration of synergistic and redundant infor-
mation sharing in static and dynamical gaussian systems. Physical
Review E, 91(5), 052802.

Barnett, L., Lizier, J. T., Harré, M., Seth, UN. K., & Bossomaier, T.
Information ﬂow in a kinetic ising model peaks in the

(2013).
disordered phase. Physical Review Letters, 111(17), 177203.
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature

Neuroscience, 20(3), 353.

Bertschinger, N., Rauh, J., Olbrich, E., Jost, J., & Ay, N.

(2014).

Quantifying unique information. Entropy, 16(4), 2161–2183.
Betzel, R. F., Byrge, L., Lui, Y., Goñi, J., Zuo, X.-N., & Sporns, O.

(2014). Changes in structural and functional connectivity among
resting-state networks across the human lifespan. NeuroImage,
102, 345–357.

Bonifazi, P., Erramuzpe, A., Diez, I., Gabilondo, I., Boisgontier,
M. P., Pauwels, L., . . . Cortes, J. M. (2018). Structure–function
multi-scale connectomics reveals a major role of the fronto-
striato-thalamic circuit in brain aging. Human Brain Mapping,
39(12), 4663–4677.

Bossomaier, T., Barnett, L., Harré, M., & Lizier, J. T.

(2016). An
introduction to transfer entropy. Cham, Svizzera: Springer
International Publishing.

Network Neuroscience

922

Synergistic information on the aging human connectome

Brown, J. A., Rudie, J. D., Bandrowski, A., Van Horn, J. D., &
Bookheimer, S. Y.
(2012). The UCLA multimodal connectivity
database: A web-based platform for brain connectivity matrix
sharing and analysis. Frontiers in Neuroinformatics, 6, 28.

Brown, J. A., & Van Horn, J. D.

(2016). Connected brains and
minds–The UMCD repository for brain connectivity matrices.
Neuroimage, 124, 1238–1241.

Cabral, J., Vidaurre, D., & Marques, P.

(2017). Cognitive perfor-
mance in healthy older adults relates to spontaneous switching
between states of functional connectivity during rest. Scientiﬁc
Reports, 7, 5135.

Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature

Physics, 6(10), 744–750.

Craddock, R. C., James, G. A., Holtzheimer III, P. E., Eh, X. P., &
Mayberg, H. S. (2012). A whole brain fMRI atlas generated via
spatially constrained spectral clustering. Human Brain Mapping,
33(8), 1914–1928.

Damoiseaux, J. S. (2017). Effects of aging on functional and struc-

tural brain connectivity. NeuroImage, 160, 32–40.

Deco, G., & Jirsa, V. K.

(2012). Ongoing cortical activity at rest:
Criticality, multistability, and ghost attractors. Journal of Neuro-
science, 32(10), 3366–3375.
Deco, G., Senden, M., & Jirsa, V.

(2012). How anatomy shapes
dynamics: A semi-analytical study of the brain at rest by a simple
spin model. Frontiers in Computational Neuroscience, 6, 68.
Dorogovtsev, S. N., Goltsev, UN. V., & Mendes, J. F. (2008). Critical
phenomena in complex networks. Reviews of Modern Physics,
80(4), 1275.

Eyler, l. T., Sherzai, A., Kaup, UN. R., & Jeste, D. V. (2011). A review
of functional brain imaging correlates of successful cognitive ag-
ing. Biological Psychiatry, 70(2), 115–122.

Ferrucci, L., Levine, M. E., Kuo, P.-L., & Simonsick, E. M.

(2018).
Time and the metrics of aging. Circulation Research, 123(7),
740–744.

Finger, H., Bönstrup, M., Cheng, B., Messé, A., Hilgetag, C.,
Thomalla, G., . . . Konig, P.
(2016). Modeling of large-scale
functional brain networks based on structural connectivity from
DTI: Comparison with EEG derived phase coupling networks and
evaluation of alternative methods along the modeling path. PLoS
Computational Biology, 12(8).

Glahn, D. C., Kent, J. W., Sprooten, E., Diego, V. P., Winkler, UN. M.,
Curran, J. E., . . . Blangero J. (2013). Genetic basis of neurocogni-
tive decline and reduced white-matter integrity in normal human
brain aging. Proceedings of the National Academy of Sciences,
110(47), 19006–19011.

Grifﬁth, V., Chong, E. K., James, R. G., Ellison, C. J., & Crutchﬁeld,
J. P. (2014). Intersection information based on common random-
ness. Entropy, 16(4), 1985–2000.

Hagmann, P., Sporns, O., Madan, N., Cammoun, L., Pienaar, R.,
Wedeen, V. J., . . . Grant, P.
(2010). White matter matura-
tion reshapes structural connectivity in the late developing hu-
man brain. Proceedings of the National Academy of Sciences,
107(44), 19067–19072.

Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R.
(2013). Brain organization into resting state networks emerges at
criticality on a model of the human connectome. Physical Review
Letters, 110(17), 178101.

Harder, M., Salge, C., & Polani, D.

(2013). Bivariate measure of

redundant information. Physical Review E, 87(1), 012130.

Hidalgo, J., Grilli, J., Suweis, S., Munoz, M. A., Banavar, J. R., &
Information-based ﬁtness and the emer-
Maritan, UN.
gence of criticality in living systems. Proceedings of the National
Academy of Sciences, 111(28), 10095–10100.

(2014).

Hinault, T., Larcher, K., Bherer, L., Courtney, S. M., & Dagher, UN.
(2019). Age-related differences in the structural and effective
connectivity of cognitive control: A combined fMRI and DTI
study of mental arithmetic. Neurobiology of Aging, 82, 30–39.
Kievit, R. A., Davis, S. W., Mitchell, D. J., Taylor, J. R., Duncan, J., &
Henson, R. N. (2014). Distinct aspects of frontal lobe structure
mediate age-related differences in ﬂuid intelligence and multi-
tasking. Nature Communications, 5(1), 1–10.

Lee, W. H., Bullmore, E., & Frangou, S. (2017). Quantitative evalu-
ation of simulated functional brain networks in graph theoretical
analysis. NeuroImage, 146, 724–733.

Liu, K., Yao, S., Chen, K., Zhang, J., Yao, L., Li, K., . . . Guo, X.
(2017). Structural brain network changes across the adult life-
span. Frontiers in Aging Neuroscience, 9, 275.

Lizier, J. T.

(2012). The local information dynamics of distributed
computation in complex systems. Berlin, Germany: Springer Sci-
ence and Business Media.

Lizier, J., Bertschinger, N., Jost, J., & Wibral, M. (2018). Information
decomposition of target effects from multi-source interactions:
Perspectives on previous, current and future work. Entropy, 20,
307–316.

Lizier, J. T., Prokopenko, M., & Zomaya, UN. Y. (2010). Information
modiﬁcation and particle collisions in distributed computation.
Chaos: An Interdisciplinary Journal of Nonlinear Science, 20(3),
037109.
Marinazzo, D.

Ising model implemented on the indi-
vidual structural connectome, GitHub. https://github.com/
danielemarinazzo/ising_synergy_brain

(2020).

Marinazzo, D., Angelini, L., Pellicoro, M., & Stramaglia, S. (2019).
Synergy as a warning sign of transitions: The case of the two-
dimensional ising model. Physical Review E, 99(4), 040101.
Marinazzo, D., Pellicoro, M., Wu, G., Angelini, L., Cortés, J. M., &
Stramaglia, S. (2014). Information transfer and criticality in the
ising model on the human connectome. PloS ONE, 9(4).

Marinazzo, D., Wu, G., Pellicoro, M., Angelini, L., & Stramaglia, S.
(2012). Information ﬂow in networks and the law of diminishing
marginal returns: Evidence from modeling and human electroen-
cephalographic recordings. PLoS ONE, 7(9).

Meier,

J., Zhou, X., Hillebrand, A., Tewarie, P., Stam, C., &
Van Mieghem, P. (2017). The epidemic spreading model and the
direction of information ﬂow in brain networks. NeuroImage,
152, 639–646.

Minati, L., Grisoli, M., & Bruzzone, M. (2007). MR spectroscopy,
functional MRI, and diffusion-tensor imaging in the aging brain:
A conceptual review. Journal of Geriatric Psychiatry and Neurol-
ogy, 20(1), 3–21.

Moretti, P., & Muñoz, M. UN. (2013). Grifﬁths phases and the stretch-
ing of criticality in brain networks. Nature communications, 4(1),
1–10.

Network Neuroscience

923

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

F
/

4
3
9
1
0
1
8
6
7
3
4
5
N
e
N
_
UN
_
0
0
1
4
6
P
D

B
sì
G
tu
e
S
T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Synergistic information on the aging human connectome

Nemanic, S., Alvarado, M. C., & Bachevalier, J.

(2004). The hip-
pocampal/parahippocampal regions and recognition memory:
Insights from visual paired comparison versus object-delayed
Journal of Neuroscience, 24(8),
nonmatching in monkeys.
2013–2026.

Nooner, K. B., Colcombe, S., Tobe, R., Mennes, M., Benedict, M.,
Moreno, A., . . . Milham, M. P.
(2012). The NKI-Rockland
Sample: model for accelerating the pace of discovery science in
psychiatry. Frontiers in neuroscience, 6, 152.
Novelli, L., Atay, F. M., Jost, J., & Lizier, J. T.

(2019). Deriving
pairwise transfer entropy from network structure and motifs.
arXiv:1911.02931

Pang, J. C., Gollo, l. L., & Roberts, J. UN. (2020). Stochastic synchro-

nization of dynamics on the human connectome. bioRxiv.

Quax, R., Har-Shemesh, O., & Sloot, P.

(2017). Quantifying syn-
ergistic information using intermediate stochastic variables. In-
tropy, 19(2), 85.

Schreiber, T. (2000). Measuring information transfer. Physical Re-

view Letters, 85(2), 461.

Sporns, O. (2010). Networks of the Brain. Cambridge, MA: CON Premere.
Stramaglia, S., Pellicoro, M., Angelini, L., Amico, E., Aerts, H.,
Ising model with con-
Cortés, J., . . . Marinazzo, D.
served magnetization on the human connectome: Implications
on the relation structure-function in wakefulness and anesthesia.
Chaos: An Interdisciplinary Journal of Nonlinear Science, 27(4),
047407.

(2017).

Sun, J., Tong, S., & Yang, G.-Y.

(2012). Reorganization of brain
networks in aging and age-related diseases. Aging and Disease,
3(2), 181.

Tisserand, D. J., Pruessner, J. C., Arigita, E. J. S., van Boxtel, M. P.,
Evans, UN. C., Jolles, J., & Uylings, H. B. (2002). Regional frontal

cortical volumes decrease differentially in aging: An MRI study to
compare volumetric approaches and voxel-based morphometry.
NeuroImage, 17(2), 657–669.

Wang, L., Zhang, Y., Zhang, J., Sang, L., Li, P., Yan, R., . . . Lui, C.
(2019). Aging changes effective connectivity of motor networks
during motor execution and motor imagery. Frontiers in Aging
Neuroscience, 11, 312.

Westlye, l. T., Walhovd, K. B., Dale, UN. M., Bjørnerud, A., Due-
Tønnessen, P., Engvig, A., . . . Fjell, UN. M.
(2010). Life-span
changes of the human brain white matter: Diffusion tensor imag-
ing (DTI) and volumetry. Cerebral Cortex, 20(9), 2055–2068.
Wilcox, R. R., Rousselet, G. A., & Pernet, C. R. (2018). Improved
methods for making inferences about multiple skipped correla-
zioni. Journal of Statistical Computation and Simulation, 88(16),
3116–3131.

Williams, P. L., & Beer, R. D. (2010). Nonnegative decomposition

of multivariate information. arXiv:1004.2515

Williams, P. L., & Beer, R. D.

(2011). Generalized measures of

information transfer. arXiv:1102.1507

Wozniak, J. R., & Lim, K. O.

(2006). Advances in white matter
imaging: A review of in vivo magnetic resonance methodologies
and their applicability to the study of development and aging.
Neuroscience and Biobehavioral Reviews, 30(6), 762–774.

Xia, M., Wang, J., & Lui, Y. (2013). Brainnet viewer: A network vi-
sualization tool for human brain connectomics. PLoS one, 8(7).
Zhao, T., Cao, M., Niu, H., Zuo, X.-N., Evans, A., Lui, Y., . . . Shu,
N. (2015). Age-related changes in the topological organization
of the white matter structural connectome across the human life-
span. Human Brain Mapping, 36(10), 3777–3792.