RESEARCH
Long-range temporal correlations in scale-free
neuromorphic networks
Shota Shirai
Edoardo Galli
1,UN, Susant Kumar Acharya
1,UN, Saurabh Kumar Bose
1, Joshua Brian Mallinson 1,
1, Matteo D. Pike2, Matteo D. Arnold 3, and Simon Anthony Brown 1
1The MacDiarmid Institute for Advanced Materials and Nanotechnology, School of Physical and Chemical Sciences,
Te Kura Mat ¯u, University of Canterbury, Christchurch, New Zealand
2Electrical and Electronics Engineering, University of Canterbury, Christchurch, New Zealand
3School of Mathematical and Physical Sciences, University of Technology Sydney, Australia
aS. S. and S. K. UN. contributed equally to this work.
a n o p e n a c c e s s
j o u r n a l
Keywords: Complex network, Scale-free topology, Scale-free dynamics, Long-range temporal
correlations, Nanoparticle network, Neuromorphic computing
ABSTRACT
Biological neuronal networks are the computing engines of the mammalian brain. These
networks exhibit structural characteristics such as hierarchical architectures, small-world
attributes, and scale-free topologies, providing the basis for the emergence of rich temporal
characteristics such as scale-free dynamics and long-range temporal correlations. Devices
that have both the topological and the temporal features of a neuronal network would be a
significant step toward constructing a neuromorphic system that can emulate the
computational ability and energy efficiency of the human brain. Here we use numerical
simulations to show that percolating networks of nanoparticles exhibit structural properties
that are reminiscent of biological neuronal networks, and then show experimentally that
stimulation of percolating networks by an external voltage stimulus produces temporal
dynamics that are self-similar, follow power-law scaling, and exhibit long-range temporal
correlations. These results are expected to have important implications for the development
of neuromorphic devices, especially for those based on the concept of reservoir computing.
AUTHOR SUMMARY
Biological neuronal networks exhibit well-defined properties such as hierarchical structures
and scale-free topologies, as well as a high degree of local clustering and short path lengths
between nodes. These structural properties are intimately connected to the observed
long-range temporal correlations in the network dynamics. Fabrication of artificial networks
with similar structural properties would facilitate brain-like (“neuromorphic”) computing.
Here we show experimentally that percolating networks of nanoparticles exhibit similar long-
range temporal correlations to those of biological neuronal networks and use simulations to
demonstrate that the dynamics arise from an underlying scale-free network architecture. Noi
discuss similarities between the biological and percolating systems and highlight the
potential for the percolating networks to be used in neuromorphic computing applications.
INTRODUCTION
Next-generation computing concepts like big data, artificial intelligence, and the internet of
things demand high parallelism, error tolerance, and more energy-efficient platforms (Cheng,
Ríos, Pernice, Wright, & Bhaskaran, 2017). Current computing architectures based on digital
Citation: Shirai, S., Acharya, S. K.,
Bose, S. K., Mallinson, J. B., Galli, E.,
Pike, M. D., . . . Brown, S. UN. (2020).
Long-range temporal correlations in
scale-free neuromorphic networks.
Network Neuroscience, 4(2), 432–447.
https://doi.org/10.1162/netn_a_00128
DOI:
https://doi.org/10.1162/netn_a_00128
Supporting Information:
https://doi.org/10.1162/netn_a_00128
Received: 9 agosto 2019
Accepted: 17 Gennaio 2020
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Simon Brown
simon.brown@canterbury.ac.nz
Handling Editor:
Olaf Sporns
Copyright: © 2020
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
N
e
N
_
UN
_
0
0
1
2
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
Neuromorphic computing:
Computation that is inspired by
biological principles, particolarmente
those of the mammalian brain.
Scale-free topology:
A network topology in which the
number of connections per node is
power-law distributed.
Reservoir computing:
A computational framework that
utilizes a nonlinear dynamical system
(a reservoir) to project inputs into a
higher dimensional space, allowing
mapping to desired outputs by
training a single linear readout layer.
Self-similar temporal dynamics:
A temporal structure that has similar
characteristics on multiple
timescales.
Long-range temporal correlations:
Correlations characterized by slowly
power-law-decaying autocorrelation
function in temporal domain.
Network Neuroscience
logic cannot keep up with the demand as they are hampered by the inability to continually
scale complementary metal-oxide-semiconductor technology and by the von Neumann bot-
tleneck (Markov, 2014). Inspired by the human brain, neuromorphic computing is a novel
computing paradigm that seeks to overcome such limitations, and that is attracting attention
for its potential to enable complex computing tasks such as associative memory (Hu et al.,
2015), pattern detection (Wang et al., 2018), and classification (Prezioso et al., 2015). A wide
range of components have been explored for neuromorphic hardware platforms including ar-
tificial silicon-based neurons (Mahowald & Douglas, 1991), cross-bar memristors (Prezioso
et al., 2015; Wang et al., 2018), and novel nanoscale elements that mimic the behavior of
synapses and neurons (Terabe, Hasegawa, Nakayama, & Aono, 2005; Tuma, Pantazi, Le Gallo,
Sebastian, & Eleftheriou, 2016). These approaches aim to emulate the functionality of both neu-
rons and synapses at the individual level, while large-scale neuromorphic computing systems
(Davies et al., 2018; Furber, 2016; Hopkins, Pineda-García, Bogdan, & Furber, 2018; Merolla
et al., 2014) are built by utilizing regular arrays of these elements.
Biological neuronal networks on the other hand are intrinsically complex and operate
through a massive number of nonlinearly interacting neurons (Bullmore & Sporns, 2012).
Biological networks show emergent phenomena (Chialvo, 2010), questo è, the networks ex-
hibit behavior that cannot be produced by the individual elements in isolation. Recent studies
have shown that neuronal networks have small-world properties (Bullmore & Sporns, 2009,
2012; Park & Friston, 2013) and are hierarchically organized (Barabási & Oltvai, 2004; Park &
Friston, 2013) with fractal geometry (Di Ieva, Grizzi, Jelinek, Pellionisz, & Losa, 2014; Werner,
2010), and that the underlying network has a scale-free topology (Bonifazi et al., 2009; Eguíluz,
Chialvo, Cecchi, Baliki, & Apkarian, 2005). These network features bestow the brain with a
number of functional benefits such as the ability to efficiently transport energy, minimal wiring
cost, and maximum local autonomy along with global connectivity (Bullmore & Sporns, 2012;
Park & Friston, 2013).
Inspired by structural characteristics of biological neuronal systems, scale-free, hierarchical
networks are predicted to enable neuromorphic computing approaches such as reservoir com-
puting (RC) (Lukoševiˇcius & Jaeger, 2009; Maass, Natschläger, & Markram, 2002). A reservoir
is a complex network of highly interconnected nonlinear nodes that evolve dynamically in
response to input signals. The reservoir maps input signals onto outputs of higher dimensions,
which are then examined by an external readout function (Lukoševiˇcius & Jaeger, 2009). IL
reservoir computing concept has been discussed extensively in recent literature (see for ex-
ample Du et al., 2017 and Riou et al., 2019, and recent reviews by Dale, Stepney, Mugnaio, &
Trefzer, 2016 and Tanaka et al., 2019) and the concept is further illustrated in the Supporting
Information: Figura 1. While simulations of scale-free reservoirs in software show significant
performance enhancement over conventional random reservoirs (Deng & Zhang, 2007), come
reservoirs are yet to be implemented experimentally.
The information processing in the brain is spatiotemporal in nature (Saha et al., 2013): Esso
relies not only on underlying structure but also on collective neuronal dynamics over time.
Infatti, recent electrophysiological studies show that the fluctuations of collective neuronal
activity exhibit rich temporal properties, including scale-free and self-similar temporal dy-
namics and long-range temporal correlations (LRTC; Linkenkaer-Hansen, Nikouline, Palva,
& Ilmoniemi, 2001; Palva et al., 2013). The presence of LRTC in the dynamics of neuronal
populations indicates that activity at any given time is being influenced by the history of the
system, which is essential for decision-making and working-memory tasks (Meisel, Bailey,
Achermann, & Plenz, 2017). LRTC in neuronal dynamics has also been linked to efficiency
in learning, memory formation, rapid information transfer, and network reorganization
433
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
N
e
N
_
UN
_
0
0
1
2
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
Criticality:
A dynamical state that is poised at a
phase transition, and that exhibits
long-range spatial and temporal
correlations.
(Botcharova, Farmer, & Berthouze, 2014). The link between LRTC and information processing
is further supported by the insight that LRTCs are generic features of a critical point: the posi-
tioning of a dynamical system at a phase transition between two qualitatively different types
of states where both spatial and temporal correlations emerge (Bak & Chen, 1989; Watkins,
Pruessner, Chapman, Crosby, & Jensen, 2016). Numerous computational and experimental
studies have provided support for the hypothesis that the brain also operates at or near a criti-
cal point (Beggs & Plenz, 2003; N. Friedman et al., 2012) and thereby exploits the computa-
tional advantages provided by criticality (Muñoz, 2018). Temporal correlation is an essential
aspect of neuromorphic computing (Stieg et al., 2012; Torrejon et al., 2017) and is a prereq-
uisite for RC approaches such as the echo state network (Lukoševiˇcius & Jaeger, 2009). IL
realization of devices with the topological and dynamical features of biological neuronal net-
works would open new avenues for neuromorphic computing, particularly RC (Muñoz, 2018;
Srinivasa, Stepp, & Cruz-Albrecht, 2015). Note however that
the aim of neuromorphic
computing is to enable new ways of performing computational tasks, such as pattern recogni-
zione, that are performed very efficiently by the brain. The aim is to exploit examples of brain-
like structures, functionality, and/or dynamics, rather than to attempt to replicate the enormous
complexity of the brain in every detail.
In the present study, we focus on self-organised networks of metallic nanoparticles, poised
at the phase transition between an insulating phase and a conducting phase (Bose, Mallinson,
Gazoni, & Brown, 2017; Bose, Shirai, Mallinson, & Brown, 2019; Mallinson et al., 2019; Sattar,
Fostner, & Brown, 2013). Our experiments and numerical simulations show that the underlying
networks have scale-free topology, hierarchical architectures, and small-world attributes such
as a high degree of local clustering and a short average path length. When activated by external
stimuli, this topology ensures that the resulting network dynamics are also self-similar, scala-
free, and show LRTC. We compare the network topology and dynamics to those of biological
neuronal networks, and demonstrate strong similarities. These results take us a step closer to
realizing neuromorphic computing devices with brain-like spatiotemporal properties.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
N
e
N
_
UN
_
0
0
1
2
8
P
D
.
T
Tunnel gaps:
A sub-nanometer gap between two
conducting bodies in which
electronic transport can occur via
quantum tunneling.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
RESULTS
Physical Network Structure
Our percolating networks of nanoparticles are formed through simple deposition techniques:
A substrate with preprepared electrodes is placed in a beam of particles from a magnetron
sputtering source (Bose et al., 2017; Sattar et al., 2013). When deposited on the substrate
(see Materials and Methods), particles come into contact and form interconnected groups that
are separated by tunnel gaps (Supporting Information: Figura 2). The state of the system is
controlled by the surface coverage p (Supporting Information: Figura 3). At the percolation
threshold p ∼ pc (∼ 68%), the system undergoes a second-order phase transition and the
deposition is terminated at this critical point. The resultant devices are self-organized in the
sense that the key structures result from the statistical properties of the randomly deposited
percolating networks and the intrinsic physical processes that take place when the particles
land on the chip (Bose et al., 2017; Sattar et al., 2013), and no manipulation of the deposited
component is required. Figure 1A shows a schematic diagram of our two-electrode device,
comprising groups of conducting nanoparticles deposited at the percolation threshold. IL
postdeposition colorized scanning electron micrograph (SEM) image in Figure 1B shows that
the groups have varying sizes and fractal geometries, consistent with standard percolation
theory (Stauffer & Aharony, 2003; Voss, Laibowitz, & Allessandrini, 1982). The tunnel gaps
between groups can act as switching sites: Upon application of an external voltage stimulus,
Network Neuroscience
434
Long-range temporal correlations in scale-free neuromorphic networks
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
N
e
N
_
UN
_
0
0
1
2
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
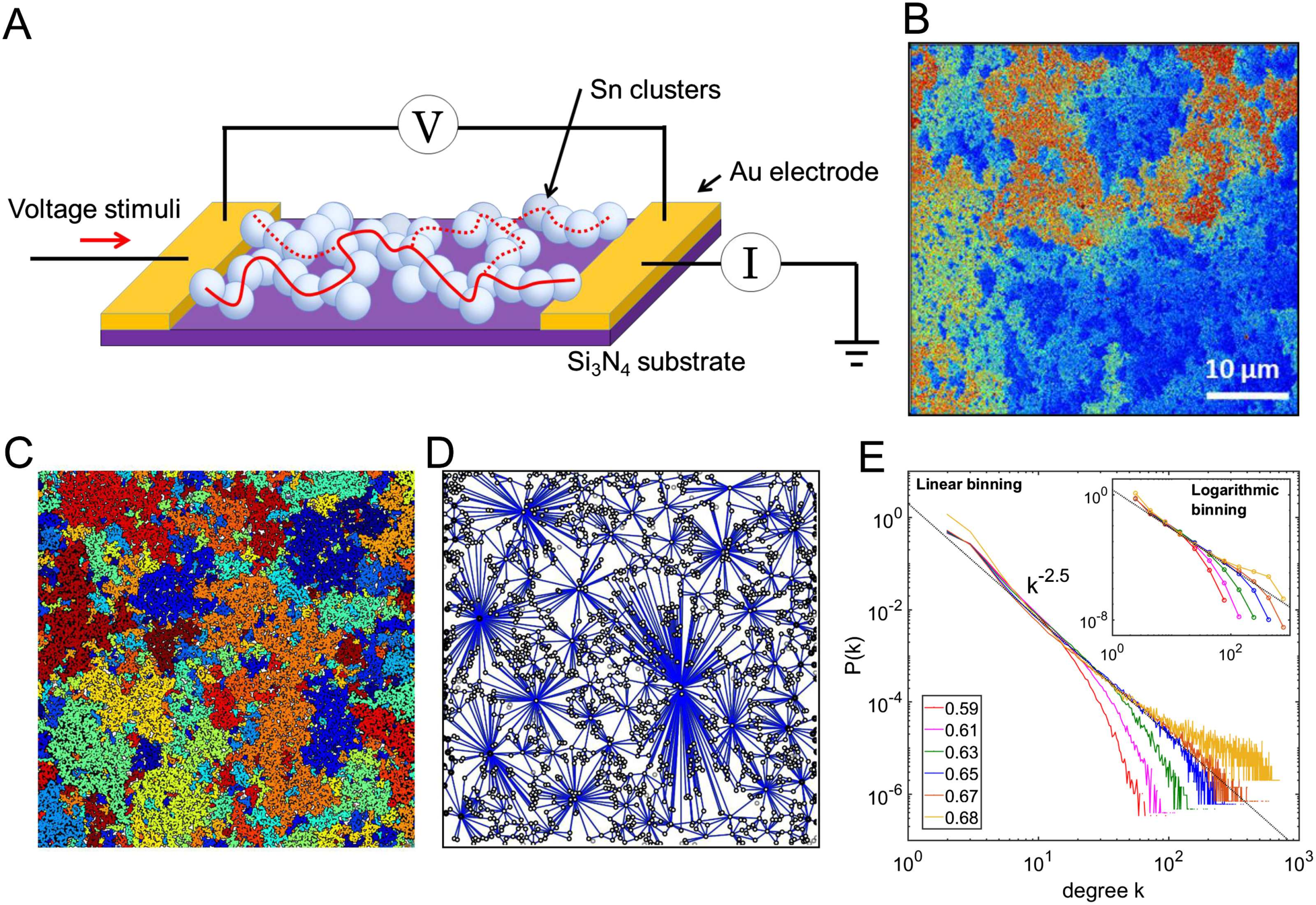
Figura 1. Percolating nanoparticle networks have fractal geometries and scale-free topology. (UN)
Schematic illustration of our two-terminal device geometry comprising a percolating nanoparticle
rete. The solid line represents an Ohmic conduction pathway at p ∼ pc, while the dotted lines
represent tunneling pathways in the network. (B) The postdeposition colorized scanning electron
micrograph of a device indicating that the morphology of the nanoparticle network has fractal ge-
ometry (scale bar = 10 µm). Colorization enhances visualization of connected groups of particles.
(C) Numerical simulation of a system size of 200 × 200 particle diameters near the percolation
threshold showing groups of particles (represented by different colors) that are separated by tunnel
gaps. (D) The map of connections between different groups of particles (nodes) In (C) exhibits a
highly inhomogeneous degree distribution. (E) The probability density function (PDF) of the degree
distribution at different surface coverages. The data are displayed using linear bins, while the in-
sert shows the same distribution with logarithmic bins in order to demonstrate that the heavy-tailed
distribution is independent of the binning method. Each color represents a specific surface cover-
age, while the black dotted line is a guide for the eye corresponding to an exponent of 2.5. IL
degree distribution near percolation threshold (blue and orange lines) is heavy-tailed and is close
to a power-law with exponent 2.5, suggesting that the underlying network has scale-free topology.
atomic-scale filaments can be formed (and subsequently broken) in the tunnel gaps, resulting
in changes in the network conductance (Sattar et al., 2013).
These percolating tunneling networks have been the subject of relatively limited study
(Fostner, Brown, Carr, & Brown, 2014; Fostner & Brown, 2015; Grimaldi, 2014). Their struc-
tural properties are difficult to analyze in the experimental system because of the conflicting re-
quirements to analyze large areas and at the same time to resolve atomic-scale details. Hence,
we begin by simulating the percolating tunneling network for various surface coverage (see the
Supporting Information and refs. Fostner et al., 2014, and Fostner & Brown, 2015, for details of
the simulations). An example of a simulated network near the percolation threshold is shown
in Figure 1C, where connected groups of particles are labeled with a single color. Figure 1D
presents a map of the connections between these groups. Note that the conduction through
the system is dominated by the tunnel gaps that are represented by the blue lines in Figure 1D
Network Neuroscience
435
Long-range temporal correlations in scale-free neuromorphic networks
(and as illustrated schematically in the Supporting Information: Figura 2). It is immediately
apparent that the number of connections k between one group and another is highly inhomo-
geneous, with some groups much more connected than others. This inhomogeneity increases
as the system approaches the percolation threshold, where critical fluctuations become im-
portant (see the Supporting Information: Figura 4; Stauffer & Aharony, 2003). Figure 1E shows
the degree distribution, P(k), which is a fundamental characteristic of the network (Albert &
Barabási, 2002; Strogatz, 2001), for different coverages. At low network coverages (0.59 E
0.61), the tails of the degree distribution have an exponential cutoff (these are not finite size
effects—see the Supporting Information: Figura 5). Near the percolation threshold (coverage
−ϕ
Di 0.65 A 0.67) the degree distribution is heavy-tailed and is close to a power-law P(k) ∼ k
with ϕ ∼ 2.5. For many complex networks, such as biological neuronal networks, ϕ was re-
ported to be between 2.0 A 3.0 (Barabási & Oltvai, 2004). Hence, our percolating networks
have similar connectivity to biological networks and are scale-free (Strogatz, 2001). Impor-
tantly, the power-law degree distribution ensures that there is a small number of heavily con-
nected nodes that promote global connections across the system (Park & Friston, 2013). Noi
emphasize that this scale-free behavior results from the geometry of the tunneling connections
between groups of particles. These tunnel gaps are not considered in standard forms of perco-
lation theory, where for p > pc conduction takes place along a fractal backbone (Voss, 1984)
and where for p < pc there is no conduction between the fractal-shaped groups (Voss et al.,
1982). It is worth noting here that further important quantities such as branching ratios (Beggs
& Plenz, 2003), percolation critical exponents (Stauffer & Aharony, 2003), and precise univer-
sality class (Sethna, Dahmen, & Myers, 2001) are yet to be elucidated for percolating-tunneling
systems.
Further analysis (Supporting Information: Figure 5 B, C) shows that our percolating networks
have a high clustering coefficient and a low average path length, which is indicative of a small-
world topology (Bullmore & Sporns, 2009, 2012; Strogatz, 2001). More detailed analysis in-
dicates that our networks have hierarchical architectures (Supporting Information: Figure 5D)
that seamlessly integrate a scale-free topology with a high degree of local clustering (Barabási
& Oltvai, 2004). These are the same network features that provide the structural basis for
stability and diversity of functional patterns in cortical networks (Kaiser, 2007), and for high
efficiency of information transfer in the brain (Bullmore & Sporns, 2009, 2012). Hierarchical
modularity also plays a major role in regulating the dynamics of neuronal networks that are
more complex in modular networks than corresponding random networks (Sporns, Tononi, &
Kötter, 2005). Hierarchical modular networks assist metastability (Wildie & Shanahan, 2012)
and they are an important structural constituent for enabling the dynamic regime of criticality
(Rubinov & Sporns, 2010), which is characterized by spontaneous and persistent bursts of ac-
tivity. Simulations have also shown that hierarchical network structure and critical dynamics
are mutually reinforcing (E. J. Friedman & Landsberg, 2013). Finally, clustered and hierarchical
topologies are particularly suited to local (segregated) operation and to the global integration
of segregated functions (Park & Friston, 2013), and ensure that the brain has high network
efficiency at low energy and connection cost (Bullmore & Sporns, 2012).
Burstiness and Distributed Switching Activity
Under application of external voltage stimuli, our devices exhibit discrete changes in conduc-
tance (∆G), which are termed switching events. As mentioned above, each switching event is
caused by formation or destruction of an atomic-scale filament in a tunnel gap (Sattar et al.,
2013). The top panel of Figure 2A shows a typical example of temporal evolution of ∆G. The
sequence of switching events can be represented as an event-train (Karsai, Kaski, Barabási,
Network Neuroscience
436
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
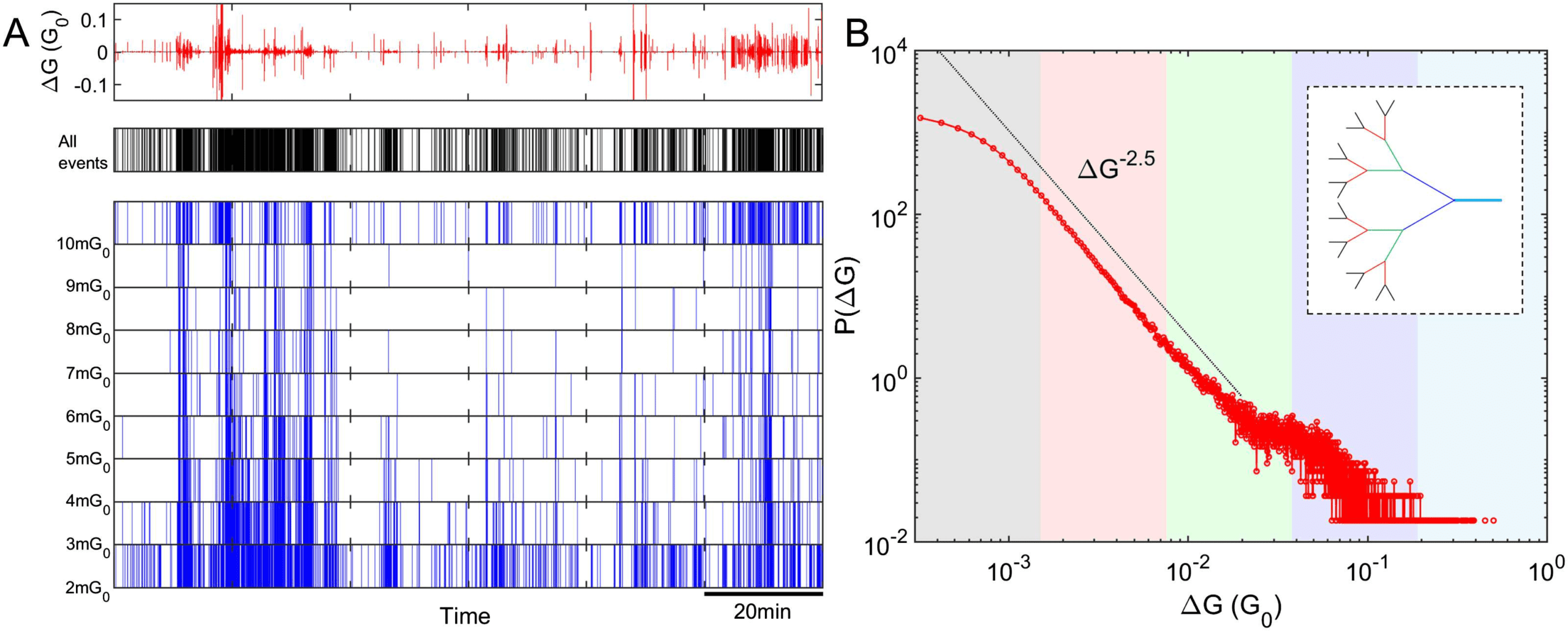
Figure 2. Percolating nanoparticle networks produce complex patterns of switching events that
are bursty in nature and are distributed across the fractal network. (A) (Top panel) The vertical scale
shows change in conductance ∆G (units of G0 = 2e2/h, the quantum of conductance, are used for
convenience; Sattar et al., 2013). (Middle panel) A typical example of a switching activity sequence
(event-train) exhibiting bursty dynamics, that is, significantly enhanced activity levels over short
periods of time followed by periods of inactivity. (Lower panel) The event-train plot from the top
panel is plotted in multiple ranges of ∆G. The bursty subsections contain events with a wide range of
∆G, pointing to a nonlocal origin of events within bursts. (B) The probability density function (PDF)
of changes in total network conductance, P(∆G), resulting from switching activity is heavy-tailed.
The inset shows a schematic illustration of a highly branched fractal network. The P(∆G) distribution
is divided into segments represented by various color shades, where smaller ∆G (e.g., pink-gray
shaded regions) generally originates from higher order branches (e.g., red or black branches in the
inset), while larger ∆G (e.g., blue shaded region) mostly originates from lower order branches (e.g.,
blue branch in the inset). The apparent deviation in the tail of the distribution is most likely due to
insignificant statistical fluctuations.
& Kertész, 2012), that is, a time series with a value of 1 if an event takes place (∆G is above the
detection threshold (Supporting Information: Figure 7), otherwise a value of 0, and is qualita-
tively similar to sequences of action potentials from biological neurons in the brain (Matzner
& Bar-Gad, 2015). A typical event-train is shown in the middle panel of Figure 2A. We observe
highly inhomogeneous bursty switching activity (Karsai et al., 2012), characterized by periods
of intense activity followed by periods of quiescence. Such bursty activity has been reported
in many natural phenomena including earthquakes, solar flares, and neuronal activity (Karsai
et al., 2012). In order to illustrate the burstiness of the data, we generate event-train plots for
multiple ranges of ∆G as shown in the lower part of Figure 2A. The bursty subsections contain
a wide range of ∆G values, indicating that switching is not local behavior on one branch of
the network, but is instead a consequence of correlated activity that is distributed across the
network.
Figure 2B shows the distribution of event sizes, P(∆G), and the inset is a schematic repre-
sentation of a fractal branched conduction pathway. While each atomic filament has the same
conductance (Sattar et al., 2013), their contribution to the change in network conductance
can vary over several orders of magnitude depending on the configuration of the network and
the location of the switching site within the network. Switches on “main branches” (which
have few parallel pathways, e.g., the blue branch in the inset) cause larger changes in network
conductance (blue shaded region in Figure 2B). Conversely, atomic switches on “higher order”
branches (which have many parallel current pathways, e.g., the red or black branches in the
inset) cause a smaller ∆G (pink-gray shaded regions in Figure 2B). Switching events that have
similar ∆G may be the result of either repeated activity at a single site, or activity at different
Network Neuroscience
437
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
sites that sit on different branches of similar order. Note that when an atomic switch changes
state it reconfigures the conduction pathways through the network, and so a switching site
may find itself located on a different branch following the occurrence of a switching event
at another location. P(∆G) spans ∼3.5 orders in ∆G and is heavy-tailed (the guide line on
Figure 2B indicates a power-law exponent of 2.5), supporting the assertion that the switching
activity is highly distributed throughout the different branches of a fractal network. It is worth
noting that the distribution of event sizes in biological neuronal networks is not accessible
for comparison because of relatively low signal-to-noise ratio in those experiments (Gireesh &
Plenz, 2008; Shew et al., 2015).
Scale-Free and Correlated Temporal Dynamics
To visualize the switching patterns on different temporal scales, we generated event-train plots
for multiple timescales; a typical example is shown in Figure 3A. The top panel shows a section
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
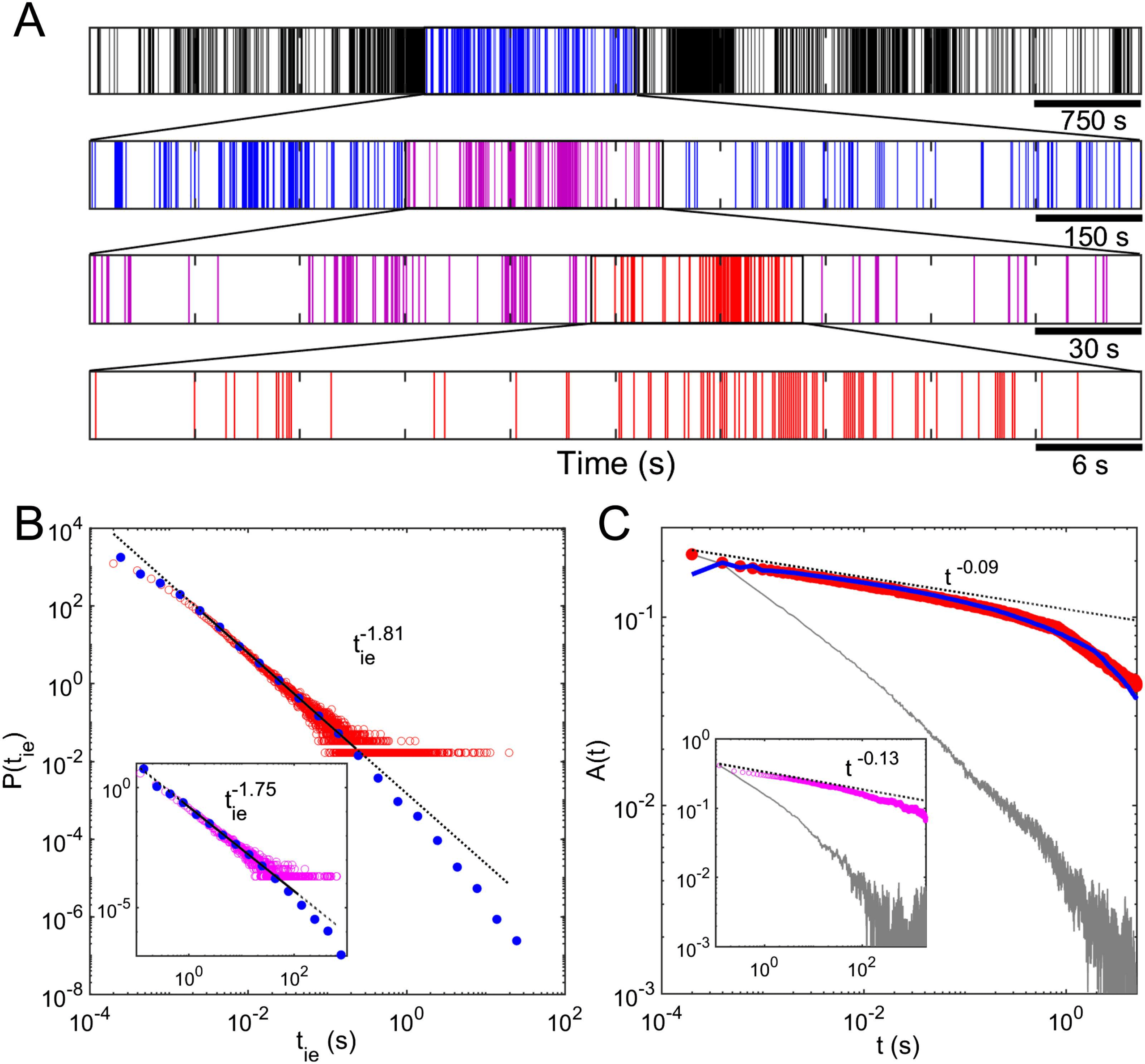
Figure 3. The temporal dynamics of nanoparticle networks are self-similar and exhibit power-law
scaling behavior and long-range temporal correlation (LRTC). (A) The switching activity patterns are
not readily distinguishable at various levels of temporal magnification, which suggests the presence
of self–similar temporal dynamics. (B) The PDF of interevent intervals (IEIs) between successive
switching events follows a power-law distribution, suggesting scale-free dynamics. Red: distribution
presented using standard (linear) bin sizes; blue: distribution presented using logarithmic bin sizes
to allow visualization of the heavy tail; the fitting line is represented by the black line, which is solid
over the fitting range and dashed otherwise. (C) The autocorrelation function (ACF) has slow power-
law decay over several orders (red), suggesting existence of LRTC in switching dynamics. Random
shuffling of the IEI sequence results in significant increase in ACF decay slope (gray), indicating
that the original data are highly correlated. The ACF plot represented by the blue line was obtained
using a model that implements correlation between IEIs drawn from a power-law distribution (see
the Supporting Information). The resulting ACF slope is similar to the experimental ACF slope (red
line), implying that the experimental IEI sequence is highly correlated. The data shown in the insets
of (B) and (C) are obtained for the same device at identical applied voltage but using a different
measurement system with the sampling rate 1,000 times lower. The resulting slopes are almost
identical irrespective of sampling rate, which gives further evidence of temporal self-similarity.
Network Neuroscience
438
Long-range temporal correlations in scale-free neuromorphic networks
Interevent interval (IEI):
Time between two consecutive
events.
of signal comprising 7,500 s of data, while the subsequent panels show sections of the top
panel with the temporal scale magnified 5, 25, and 125 times. The switching activity patterns
in the four panels are not readily distinguishable, which indicates that the switching events on
different timescales are qualitatively self-similar. This self-similarity is independent of sampling
rate (see the Supporting Information: Figure 6 for details), and hence is an intrinsic property of
our devices. Self-similar temporal dynamics are typical in electrophysiological signals from the
cortex (Werner, 2010), and biological physiological measurements such as temporal patterns of
heartbeats (Goldberger et al., 2002) have been interpreted as a consequence of an underlying
fractal physical structure (Di Ieva et al., 2014; Werner, 2010) and are a signature of correlations
on many temporal scales (Linkenkaer-Hansen et al., 2001).
To quantify the temporal structure of switching events, we investigated the interevent in-
terval (IEI) distribution (Segev et al., 2002). The IEIs (tie) are defined as the time between two
−γ
consecutive events. Figure 3B shows that the IEI distribution follows a power-law P(tie) ∼ t
ie
with an exponent γ ∼ 1.8, implying scale-free dynamics. The fit is based on the maximum
likelihood (ML) approach and the Kolmogorov-Smirnov (KS) test (see Materials and Methods).
The inset of Figure 3B shows the IEI distribution of the same device at identical applied volt-
age, but using a different measurement system with 1,000 times slower sampling rate (see
Materials and Methods) than that used in Figure 3B, yet the power-law exponent obtained
is almost identical (γ ∼ 1.75), which gives strong evidence of scale-free temporal dynamics.
These results are consistent with previously reported heavy-tails in the interspike interval dis-
tributions of neuronal populations of in vitro cortical cultures that have been interpreted as a
feature of an excitable system consisting of many nonlinearly interacting subsystems (neurons;
Segev et al., 2002).
A power-law IEI distribution alone does not prove correlation among switching events
(Karsai et al., 2012; Vajna, Tóth, & Kertész, 2013). Therefore, in order to characterize the
correlation between switching events, the autocorrelation function (ACF) was calculated. The
ACF is a measure of the correlation between the observed signal and a delayed version of itself.
The correlation strength can be inferred from the amplitude of the ACF (Meisel et al., 2017;
Scheffer et al., 2009), while persistence of temporal correlation can be inferred from the slope
of the ACF plot (Meisel et al., 2017). Figure 3C presents our experimental ACF for both fast
and slow (inset) sampling rates. Both ACF plots show a power-law decay for more than 3.5
orders of magnitude in time with almost identical decay slope (β ∼ 0.1), which further con-
solidates the evidence for self-similarity in temporal dynamics and suggests the existence of
LRTCs (Linkenkaer-Hansen et al., 2001; Palva et al., 2013). To verify this conclusion, random-
ized time series of switching events were obtained by shuffling the original IEIs. This approach
preserves the total number of switching events and the IEI distribution, but removes temporal
correlations between the switching events. The ACF plot obtained from shuffled IEIs (gray line)
decays much faster than our experimental ACF plots (Vajna et al., 2013), confirming LRTC in
the original switching sequences. These temporal characteristics are invariant across devices
(Supporting Information: Figure 8), showing that they are intrinsic properties of the network.
In neuroscience it is usually difficult to directly measure ACFs and so detrended fluctua-
tion analysis is often the preferred method for quantifying LRTC (see refs. Palva et al., 2013;
Meisel et al., 2017, and citations therein). To facilitate a comparison we use the relationship
β = 2 − 2H (Meisel et al., 2017) to estimate the Hurst exponent (H) and find H ∼ 0.9, con-
firming the strong correlations in percolating tunneling systems.
The power-law decay in P(tie) and ACF show that the distribution of switching events lack a
characteristic time (Papo, 2013). The presence of LRTC suggests that each burst is only a part of
Network Neuroscience
439
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
a series of correlated events, and the fractal temporal structure (as shown in Figure 3A) reflects a
hierarchy of bursts within bursts (Linkenkaer-Hansen et al., 2001). In order to demonstrate that
LRTC in our device is due to a hierarchy of bursts, we have modeled the relationship between
the ACF and the type of burstiness (see the Supporting Information: Figure 9). In this model we
take uncorrelated but power-law-distributed IEIs as input and then we introduce correlation
between successive IEIs by organizing them hierarchically. We then calculate the ACF and
compare with experimental ACF plots. A typical result is presented in Figure 3C, where the
ACF obtained from the model (blue line) has a similar decay slope to the experimental ACF (red
line). As shown in the Supporting Information, neither nonbursty event-trains nor bursty event-
trains that lack a hierarchy exhibit the power-law slope observed experimentally. The essential
point is that hierarchical bursting must be included in the model in order to reproduce the
experimental correlations. This strongly supports the conclusions that our events are highly
correlated and that the correlation stems from their inherent hierarchical organization.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
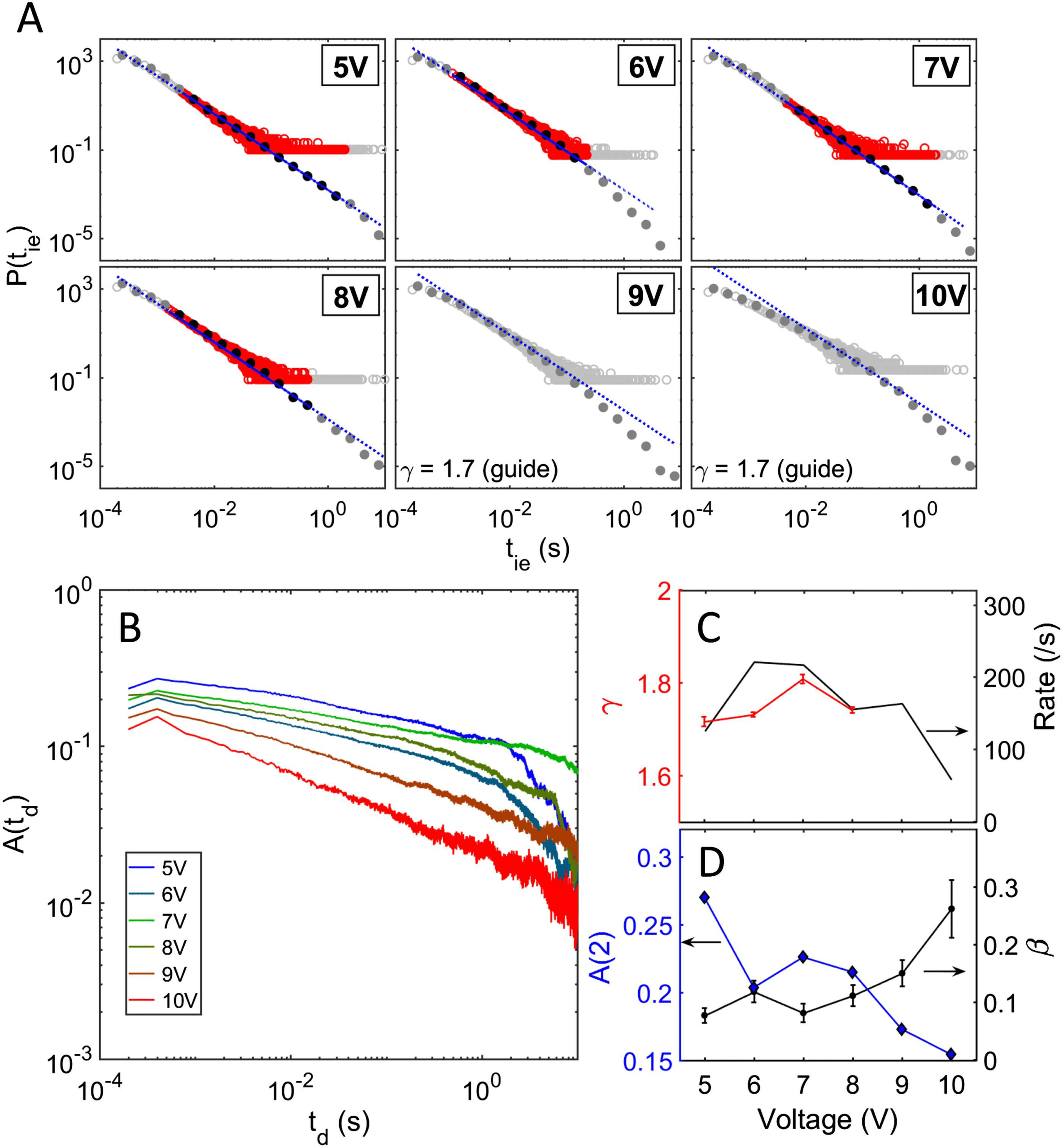
Figure 4. Evolution of switching dynamics and correlation strength with applied voltage. (A) Dis-
tribution of interevent intervals (IEIs) for a range of applied DC voltages between 5 V and 10 V. For
5–8 V the data are consistent with a power-law with slope ∼1.7, but at higher voltages (9 V and
10 V) the data do not follow a strict power-law (see Materials and Methods for details of the fitting
procedure). (B) Corresponding autocorrelation functions (ACFs). (C) Variation of IEI exponent (γ)
and switching rate as a function of applied voltage. (D) Dependence on applied voltage of the ACF
decay exponent (β) and lag-2 autocorrelation amplitude at second time delay, A(2). The maximum
correlation strength is observed at lower operating voltages. At voltages higher than 8 V, the slope
of the ACF increases while A(2) decreases, implying a decrease in correlation. While there is also
a decrease in the switching rate at higher voltages (see C), a decrease in activity is generally asso-
ciated with an increase in the correlation strength (Scheffer et al., 2009). Therefore the decrease in
correlation at higher voltage cannot be attributed to the lower switching rate.
Network Neuroscience
440
Long-range temporal correlations in scale-free neuromorphic networks
Voltage Dependence of the Temporal Switching Activity
In order to investigate the stimulus dependence of the scale-free network activity and temporal
correlation, a range of DC voltages between 5 V (slightly above the switching threshold voltage)
and 10 V were applied to our devices. Figure 4A shows IEI distributions, while Figure 4B shows
ACFs for the range of applied stimuli. The IEI distributions are heavy-tailed, spanning 4 orders
of magnitude in time for all six voltages, while the ACFs for all voltages exhibit LRTC with
decay for over ∼4 orders of magnitude in time. To quantify the voltage dependence of the
ACFs, the correlation strength (the ACF at lag-2; see Materials and Methods) and the slope of
the ACF were calculated and are depicted in Figure 4D. We applied the ML approach and the
KS test to validate the power-law hypothesis in P(tie). For lower voltages (5–8 V) power-law
fits to P(tie) pass the KS test over more than 2 orders of magnitude in time, yielding the slopes
shown in Figure 4C. The lag-2 correlation and the ACF slope also vary only weakly, suggesting
that the correlation strength is independent of the applied voltage up to 8 V. Interestingly, at
higher voltages (9–10 V) P(tie) deviates from a strict power-law (Figure 4A), the correlation
strength at lag-2 is significantly lower than that at 5–8 V, and the ACF slope is much higher.
Hence there is a clear decrease in correlation at voltages higher than 8 V.
In the neuroscience literature, a decline in LRTC has been linked to neurological condi-
tions such as Alzheimer’s disease (Montez et al., 2009) and schizophrenia (Nikulin, Jönsson, &
Brismar, 2012), in addition to a number of cognitive alterations including sustained-wakefulness
(Meisel et al., 2017) and focused attention meditation (Irrmischer et al., 2018). In the case of
Alzheimer’s disease (Montez et al., 2009), the decrease in correlation is attributed to a dis-
connection in large-scale networks, while in the case of sustained-wakefulness, the decrease
in correlation is attributed to fatigue in the brain because of sleep deprivation (Meisel et al.,
2017). In our device, one may speculate that a similar fatiguing process could be responsible
for the decline in LRTC observed at 9–10 V: Higher applied voltage results in larger currents
that may well cause deformation at switching sites because of excessive Joule heating. As such
large currents are distributed across the network, there may be network-wide fatigue, caus-
ing disconnections between different parts of the network. This would disrupt the propagation
of local interaction to global scale (Linkenkaer-Hansen et al., 2001) leading to the observed
decrease in correlation. Nonetheless, the network dynamics of our devices show maximum
correlation at low voltages, which would be the operating point of the devices.
DISCUSSION
Biological neuronal networks generally exhibit small-world properties such as a high degree
of local clustering and a short average path length between all node pairs, as well as hierarchi-
cal network structures and scale-free topologies (Bonifazi et al., 2009; Bullmore & Sporns,
2012; Eguíluz et al., 2005; Park & Friston, 2013). These network properties are important
to the functionality of the brain, including efficient information processing, adaptability, and
divergent functionality within a fixed structure (Park & Friston, 2013), as well as to the ob-
served dynamics (van den Heuvel & Hulshoff Pol, 2010). For example, hierarchical or frac-
tal network topologies confer robustness to dynamics when the connections between nodes
are reconfigured (Robinson, Henderson, Matar, Riley, & Gray, 2009), and lead to the emer-
gence of scale-free temporal dynamics and LRTC (Bullmore & Sporns, 2012; Werner, 2010;
Zhigalov, Arnulfo, Nobili, Palva, & Palva, 2017). Furthermore, hierarchical modular structures
can lead to an extended parameter range for critical behavior known as the Griffiths phase,
which is associated with a generic enhancement of functionality (Moretti & Muñoz, 2013;
Zhigalov et al., 2017).
Network Neuroscience
441
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
The relationships between spatial and temporal correlations, connections to concepts of
self-organized criticality, and the diversity of systems in which they are observed have been
discussed extensively in the literature (see Cavagna, Giardina, & Grigera, 2018 and Watkins
et al., 2016, for reviews) but are still subjects of intense investigation (Chialvo, Cannas, Plenz,
& Grigera, 2019). In systems near criticality, long-range spatial and temporal correlations are
different sides of the same coin, that is, they are interdependent (Bak & Chen, 1989). Long-
range spatial correlations ensure that local changes can propagate throughout the network
on multiple timescales, leading to LRTC (Linkenkaer-Hansen et al., 2001). Long-range spa-
tial correlations are inherent to our system, as a consequence of deposition at the percolation
threshold, where the correlation length diverges (Stauffer & Aharony, 2003). Like the brain,
our devices consist of a network of nonlinearly interacting nodes, and temporal correlations
and fractal dynamics emerge from the underlying fractal structure and local processes that
connect the nodes. It should be noted, however, that in biological systems even single cells
can exhibit fractal dynamics (Johnson, Wright, Xiá, & Wessel, 2019). In the brain, synapses con-
nect/transmit information between neurons. In our networks, switching events occur in tun-
nel gaps by formation and annihilation of atomic-scale wires (Bose et al., 2017, 2019; Sattar
et al., 2013). Under the application of external DC bias, the formation (or annihilation) of an
atomic wire at a tunnel gap redistributes current across the entire network, thereby modify-
ing local electrostatic potentials across other tunnel gaps, and leading to bursts of switching
events, which are similar to neuronal avalanches (Beggs & Plenz, 2003; N. Friedman et al.,
2012; Mallinson et al., 2019). In other words, each switching event influences subsequent
switching events through internal feedforward and feedback networks, giving rise to temporal
correlations.
The observation of LRTC in neuronal networks has several implications for information
processing: (a) LRTCs have been suggested to reflect the degree to which the brain remains
capable of quick reorganization (Linkenkaer-Hansen et al., 2001), providing responsiveness
to different processing demands. (b) Information processing and learning in the human brain
are believed to be carried out by correlated firing patterns of neuronal populations (Franke
et al., 2016). (c) LRTCs are associated with extended timescales and memory effects, which
are thought to provide favorable neuronal substrates for the integration of information across
time and across different cortical areas in order to increase the signal-to-noise ratio during
cognitive tasks (e.g., during decision-making; Meisel et al., 2017). (d) A network consisting
of many subunits (such as neurons) that shows LRTC may provide a distributed network for
memory (Bhattacharya, Edwards, Mamelak, & Schuman, 2005). (e) The presence of LRTC in
cortical dynamics is consistent with the idea that the brain may be operating in a self-organized
critical state (Bhattacharya et al., 2005; Chialvo, 2010; Linkenkaer-Hansen et al., 2001; Palva
et al., 2013), where dynamic range and memory are maximized—both favorable features for
information processing (Palva et al., 2013).
The correlated network dynamics discussed above are consistent with criticality in our per-
colating networks (Mallinson et al., 2019) and might be exploited within the context of a
practically implementable neuromorphic computational framework such as RC (Lukoševiˇcius
& Jaeger, 2009; Stieg et al., 2012). Software simulations of RC have acknowledged the im-
portance of utilizing the rich topological features of biological neuronal networks; for exam-
ple, Deng and Zhang (2007) simulated the use of a scale-free and highly clustered reservoir for
RC, leading to improved performance in a chaotic time series prediction task. Similarly, reser-
voirs with a high degree of clustering have shown better performance in memory capacity
tasks as compared with a random reservoir (Rodriguez, Izquierdo, & Ahn, 2019), while hier-
archical structured reservoirs are particularly suitable to process time series with multiscale
Network Neuroscience
442
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
characteristics such as speech, text, and gestures (Lukoševiˇcius & Jaeger, 2009). To date a re-
liance on lithographic processing for fabrication of neuromorphic hardware has meant that
these network features of the brain have typically been ignored in favor of highly regular ar-
chitectures (Furber, 2016; Merolla et al., 2014; Prezioso et al., 2015; Wang et al., 2018). Our
self-organised devices, which have several topological features of biological neuronal net-
works and exhibit scale-free and self-similar temporal dynamics, and LRTC, therefore provide
an interesting alternative platform for bio-realistic neuromorphic hardware implementation.
To summarize, our networks of nanoparticles operate near a critical point (the percolation
phase transition) and exhibit structural features including scale-free topology and hierarchical
architectures that are similar to those of the brain. These structural features therefore lead to
LRTCs that are similar to those of biological systems. Spatial and temporal correlations are also
key requirements for reservoir computing systems. Given the similarities between the struc-
tural and temporal dynamics of biological neuronal networks, we propose that our percolating
nanoparticle networks provide an ideal physical system for implementation of hardware-based
reservoir computing.
MATERIALS AND METHODS
Device Fabrication
Our percolating devices are fabricated by simple nanoparticle deposition processes (Bose et al.,
2017; Sattar et al., 2013; Schmelzer, Brown, Wurl, Hyslop, & Blaikie, 2002). Sn nanoparticles
of 7 nm are deposited between gold electrodes (spacing 100 µm) on a silicon nitride surface
and coalesce to form particles of 20 nm diameter. Deposition is terminated at the onset of
conduction, which corresponds to the percolation threshold (Schmelzer et al., 2002; Stauffer
& Aharony, 2003). The deposition takes place in a controlled environment with a well-defined
partial pressure of air and humidity, as described in Bose et al. (2017). This process leads to
controlled coalescence and fabrication of robust structures that function for many months, but
that yet allow atomic-scale switching processes to take place unhindered.
Electrical Stimulus and Measurement
Electrical stimuli are applied to the electrode on one side of the percolating device, while the
opposite electrode of the system is held at ground potential. While a variety of types of stimuli
(voltage pulses, ramps) can be applied to the system, constant DC voltages are used in this work
because they facilitate observation of ongoing reconfigurations of the states of the switches in
the devices. Measurements over long time periods are necessary to avoid significant cutoffs
in the power-law distributions (Clauset, Shalizi, & Newman, 2009; Deluca and Corral, 2013).
Here we present data from DC stimulus of four devices (see Figure 3 and Supporting Informa-
tion: Figure 8), but the data presented are consistent with that obtained from DC, pulsed, and
ramped voltage stimulus of a further 10 devices.
Our electrical measurements are performed using two distinct sets of measurement elec-
tronics, to allow measurement of the device conductance on two distinct timescales. The first
method relies on a picoammeter and is limited to a relatively slow sampling rate (0.1 s sampling
interval). The second method utilizes a digital oscilloscope allowing a much higher sampling
rate (200 µs sampling interval for the data presented here). As shown in Figure 3, both methods
resulted in qualitatively and quantitatively similar data, with similar power-law exponents for
each of the main quantities of interest. Our results and conclusions are therefore not influenced
by the sampling rate.
Network Neuroscience
443
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
Data Analysis
The data analysis methods used in this work are substantially the same as those developed in
the neuroscience community to analyze micro-electrode array recordings from biological brain
tissue. Events are defined as changes in the conductance signal that exceed a threshold value
(Supporting Information: Figure 7). We show in Supporting Information Figure 7 that, as in the
neuroscience literature, the choice of threshold in a reasonable range does not significantly
affect the IEI distributions and A(t). Note that, since lag-1 of ACF may be affected by finite
sampling rate, we adopt lag-2 as an indicator of the correlation strength.
Fitting and Goodness-of-Fit
We follow the maximum likelihood (ML) approach of Clauset et al. (2009) and Deluca and
Corral (2013) to estimate power-law exponents in the IEI distributions. The ML estimators are
obtained for both power-law and exponential distributions.
We use the Akaike information criterion (Wagenmakers & Farrell, 2004) to identify which
distribution is more likely and find in all cases that it is the power-law. We then generate
500 random power-law and exponential distributions using the calculated ML estimators, and
iterate the choice of cutoffs (tmin and tmax) for the data range, finding the probability of obtain-
ing a Kolmogorov-Smirnov (KS) distance (Dulce & Corral, 2013) at least as the data from the
device. In all cases, we fail to reject the null hypothesis that IEI distributions are power-law-
distributed (we require p values > 0.2), but we do reject the null hypothesis that the distribu-
tions are exponentially distributed (we find p values < 0.01; Supporting Information: Figure 10).
The KS test is extremely sensitive to small deviations from a mathematical power-law (Deluca
and Corral, 2013; Marshall et al., 2016). The deviation from power-law behavior in our data is
rather small (see Figure 3), but we nevertheless follow Deluca and Corral (2013) and Marshall
et al. (2016) and allow the data to be truncated in order to show definitively that the distribu-
tions are power-law. The IEI distributions are found to be power-law over about 2 orders of
magnitude in time, with both a lower and an upper cutoff (see more details in the Supporting
Information: Figure 11).
The ML methods cannot be applied to data which is not in the form of a probability dis-
tribution, and so the standard linear regression techniques are used to obtain the measured
exponents for A(t).
ACKNOWLEDGMENTS
The authors acknowledge useful discussions with P. Bones, J. Beggs, C. Young, and N.
McNaughton.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00128.
AUTHOR CONTRIBUTIONS
Shota Shirai: Data curation; Formal analysis; Investigation; Software; Writing - Original Draft.
Susant Kumar Acharya: Data curation; Formal analysis; Investigation; Methodology; Writing -
Original Draft; Writing - Review & Editing. Saurabh Kumar Bose: Data curation; Formal analy-
sis; Methodology. Joshua Brian Mallinson: Data curation; Formal analysis; Investigation;
Methodology; Writing - Review & Editing. Edoardo Galli: Data curation; Formal analysis;
Network Neuroscience
444
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
Methodology. Matthew D. Pike: Investigation; Methodology; Software. Matthew D. Arnold:
Formal analysis; Methodology; Software. Simon Brown: Conceptualization; Formal analysis;
Funding acquisition; Investigation; Methodology; Project administration; Resources; Supervi-
sion; Validation; Writing - Original Draft; Writing - Review & Editing.
FUNDING INFORMATION
Simon Brown, MacDiarmid Institute for Advanced Materials and Nanotechnology (http://dx.
doi.org/10.13039/501100013266). Saurabh Kumar Bose, Marsden Fund (http://dx.doi.org/10.
13039/501100009193). Simon Brown, Ministry of Business, Innovation, and Employment
(http://dx.doi.org/10.13039/501100003524), Award ID: UOCX1603.
REFERENCES
Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of com-
plex networks. Reviews of Modern Physics, 74(1), 47–97.
Bak, P., & Chen, K. (1989). The physics of fractals. Physica D: Non-
linear Phenomena, 38(1–3), 5–12.
Barabási, A.-L., & Oltvai, Z. N. (2004). Network biology: Under-
standing the cell’s functional organization. Nature Reviews Ge-
netics, 5(2), 101–113.
Beggs, J. M., & Plenz, D. (2003). Neuronal avalanches in neocorti-
cal circuits. Journal of Neuroscience, 23(35), 11167–11177.
Bhattacharya, J., Edwards, J., Mamelak, A. N., & Schuman, E. M.
(2005). Long-range temporal correlations in the spontaneous
spiking of neurons in the hippocampal-amygdala complex of
humans. Neuroscience, 131(2), 547–555.
Bonifazi, P., Goldin, M., Picardo, M. A., Jorquera, I., Cattani, A.,
Bianconi, G., . . . Cossart, R. (2009). GABAergic hub neurons
orchestrate synchrony in developing hippocampal networks.
Science, 326(5958), 1419–1424.
Bose, S. K., Mallinson, J. B., Gazoni, R. M., & Brown, S. A. (2017).
Stable self-assembled atomic-switch networks for neuromorphic
IEEE Transactions on Electron Devices, 64(12),
applications.
5194–5201.
Bose, S. K., Shirai, S., Mallinson, J. B., & Brown, S. A. (2019). Synap-
tic dynamics in complex self-assembled nanoparticle networks.
Faraday Discussions, 213, 471–485.
Botcharova, M., Farmer, S. F., & Berthouze, L. (2014). Markers of
criticality in phase synchronization. Frontiers in Systems Neuro-
science, 8, 176.
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198.
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
Cavagna, A., Giardina, I., & Grigera, T. S. (2018). The physics of
flocking: Correlation as a compass from experiments to theory.
Physics Reports, 728, 1–62.
Cheng, Z., Ríos, C., Pernice, W. H. P., Wright, C. D., & Bhaskaran,
H. (2017). On-chip photonic synapse. Science Advances, 3(9),
e1700160.
Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature
Physics, 6(10), 744–750.
Chialvo, D. R., Cannas, S. A., Plenz, D., & Grigera, T. S. (2019).
Controlling a complex system near its critical point via temporal
correlations. arXiv:1905.11758.
Clauset, A., Shalizi, C. R., & Newman, M. E. J. (2009). Power-law
distributions in empirical data. SIAM Review, 51(4), 661–703.
Dale, M., Stepney, S., Miller, J. F., & Trefzer, M. (2016). Reservoir
computing in materio: An evaluation of configuration through
evolution. 2016 IEEE Symposium Series on Computational Intel-
ligence (SSCI), 1–8.
Davies, M., Srinivasa, N., Lin, T.-H., Chinya, G., Cao, Y., Choday,
S. H., . . . Wang, H. (2018). Loihi: A neuromorphic manycore
processor with on-chip learning. IEEE Micro, 38(1), 82–99.
Deluca, A., & Corral, Á. (2013). Fitting and goodness-of-fit test of
non-truncated and truncated power-law distributions. Acta Geo-
physica, 61(6), 1351–1394.
Deng, Z., & Zhang, Y. (2007). Collective behavior of a small-world
recurrent neural system with scale-free distribution. IEEE Trans-
actions on Neural Networks, 18(5), 1364–1375.
Di
Ieva, A., Grizzi, F.,
Jelinek, H., Pellionisz, A.
J., & Losa,
G. A. (2014). Fractals in the neurosciences, Part I: General
principles and basic neurosciences. The Neuroscientist, 20(4),
403–417.
Du, C., Cai, F., Zidan, M. A., Ma, W., Lee, S. H., & Lu, W. D. (2017).
Reservoir computing using dynamic memristors for temporal in-
formation processing. Nature Communications, 8(1), 2204.
Eguíluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M., & Apkarian,
A. V. (2005). Scale-free brain functional networks. Physical Re-
view Letters, 94(1), 018102.
Fostner, S., Brown, R., Carr, J., & Brown, S. A. (2014). Continuum
percolation with tunneling. Physical Review B, 89(7), 075402.
Fostner, S., & Brown, S. A. (2015). Neuromorphic behavior in per-
colating nanoparticle films. Physical Review E, 92(5), 052134.
Franke, F., Fiscella, M., Sevelev, M., Roska, B., Hierlemann, A., &
Azeredo da Silveira, R. (2016). Structures of neural correlation
and how they favor coding. Neuron, 89(2), 409–422.
Friedman, E. J., & Landsberg, A. S. (2013). Hierarchical networks,
power laws, and neuronal avalanches. Chaos: An Interdisci-
plinary Journal of Nonlinear Science, 23(1), 013135.
Friedman, N., Ito, S., Brinkman, B. A., Shimono, M., Deville, R. E.,
Dahmen, K. A., . . . Butler, T. C. (2012). Universal critical dynamics
Network Neuroscience
445
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
in high resolution neuronal avalanche data. Physical Review
Letters, 108(20), 208102.
Furber, S. (2016). Large-scale neuromorphic computing systems.
Journal of Neural Engineering, 13(5), 051001.
Gireesh, E. D., & Plenz, D. (2008). Neuronal avalanches organize as
nested theta- and beta/gamma-oscillations during development
of cortical layer 2/3. Proceedings of the National Academy of
Sciences, 105(21), 7576–7581.
Goldberger, A. L., Amaral, L. A. N., Hausdorff, J. M., Ivanov, P. C.,
Peng, C.-K., & Stanley, H. E. (2002). Fractal dynamics in phys-
iology: Alterations with disease and aging. Proceedings of the
National Academy of Sciences, 99(Suppl. 1), 2466–2472.
Grimaldi, C. (2014). Theory of percolation and tunneling regimes
in nanogranular metal films. Physical Review B, 89(21), 214201.
Hopkins, M., Pineda-García, G., Bogdan, P. A., & Furber, S. B.
(2018). Spiking neural networks for computer vision. Interface
Focus, 8(4), 20180007.
Hu, S., Liu, Y., Liu, Z., Chen, T., Wang, J., Yu, Q., . . . Hosaka, S.
(2015). Associative memory realized by a reconfigurable memristive
Hopfield neural network. Nature Communications, 6(1), 7522.
Irrmischer, M., Houtman, S. J., Mansvelder, H. D., Tremmel, M.,
Ott, U., & Linkenkaer-Hansen, K. (2018). Controlling the tempo-
ral structure of brain oscillations by focused attention meditation.
Human Brain Mapping, 39(4), 1825–1838.
Johnson, J. K., Wright, N. C., Xiá, J., & Wessel, R. (2019). Single-cell
membrane potential fluctuations evince network scale-freeness
and quasicriticality. Journal of Neuroscience, 39(24), 4738–4759.
Kaiser, M. (2007). Brain architecture: a design for natural com-
putation. Philosophical Transactions of the Royal Society A:
Mathematical, Physical and Engineering Sciences, 365(1861),
3033–3045.
Karsai, M., Kaski, K., Barabási, A.-L., & Kertész, J. (2012). Univer-
sal features of correlated bursty behaviour. Scientific Reports, 2,
397.
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., & Ilmoniemi,
R. J. (2001). Long-range temporal correlations and scaling behav-
ior in human brain oscillations. Journal of Neuroscience, 21(4),
1370–1377.
Lukoševiˇcius, M., & Jaeger, H. (2009). Reservoir computing ap-
proaches to recurrent neural network training. Computer Science
Review, 3(3), 127–149.
Maass, W., Natschläger, T., & Markram, H. (2002). Real-time com-
puting without stable states: A new framework for neural com-
putation based on perturbations. Neural Computation, 14(11),
2531–2560.
Mahowald, M., & Douglas, R. (1991). A silicon neuron. Nature,
354(6354), 515–518.
Mallinson, J. B., Shirai, S., Acharya, S. K., Bose, S. K., Galli, E., &
Brown, S. A. (2019). Avalanches and criticality in self-organised
nanoscale networks. Science Advances, 5, eaaw8438.
Markov, I. L. (2014). Limits on fundamental limits to computation.
Nature, 512(7513), 147–154.
Marshall, N., Timme, N. M., Bennett, N., Ripp, M., Lautzenhiser, E.,
& Beggs, J. M. (2016). Analysis of power laws, shape collapses,
and neural complexity: New techniques and MATLAB support
via the NCC toolbox. Frontiers in Physiology, 7, 250.
Matzner, A., & Bar-Gad, I. (2015). Quantifying spike train oscil-
lations: Biases, distortions and solutions. PLOS Computational
Biology, 11(4), e1004252.
Meisel, C., Bailey, K., Achermann, P., & Plenz, D. (2017). Decline
of long-range temporal correlations in the human brain during
sustained wakefulness. Scientific Reports, 7(1), 11825.
Merolla, P. A., Arthur, J. V., Alvarez-Icaza, R., Cassidy, A. S.,
Sawada, J., Akopyan, F., . . . Modha, D. S. (2014). A million
spiking-neuron integrated circuit with a scalable communication
network and interface. Science, 345(6197), 668–673.
Montez, T., Poil, S.-S., Jones, B. F., Manshanden, I., Verbunt, J. P. A.,
van Dijk, B. W., . . . Linkenkaer-Hansen, K. (2009). Altered
temporal correlations in parietal alpha and prefrontal theta os-
cillations in early-stage Alzheimer disease. Proceedings of the
National Academy of Sciences, 106(5), 1614–1619.
Moretti, P., & Muñoz, M. A. (2013). Griffiths phases and the stretching
of criticality in brain networks. Nature Communications, 4(1), 2521.
Muñoz, M. A. (2018). Colloquium: Criticality and dynamical scal-
ing in living systems. Reviews of Modern Physics, 90(3), 031001.
Nikulin, V. V., Jönsson, E. G., & Brismar, T. (2012). Attenuation of
long-range temporal correlations in the amplitude dynamics of
alpha and beta neuronal oscillations in patients with schizophre-
nia. NeuroImage, 61(1), 162–169.
Palva, J. M., Zhigalov, A., Hirvonen, J., Korhonen, O., Linkenkaer-
Hansen, K., & Palva, S. (2013). Neuronal long-range temporal
correlations and avalanche dynamics are correlated with behav-
ioral scaling laws. Proceedings of the National Academy of Sci-
ences, 110(9), 3585–3590.
Papo, D. (2013). Time scales in cognitive neuroscience. Frontiers in
Physiology, 4, 86.
Park, H.-J., & Friston, K. (2013). Structural and functional brain net-
works: From connections to cognition. Science, 342(6158), 1238411.
Prezioso, M., Merrikh-Bayat, F., Hoskins, B. D., Adam, G. C.,
Likharev, K. K., & Strukov, D. B. (2015). Training and operation
of an integrated neuromorphic network based on metal-oxide
memristors. Nature, 521(7550), 61–64.
Riou, M., Torrejon, J., Garitaine, B., Abreu Araujo, F., Bortolotti, P.,
Cros, V., . . . Grollier, J. (2019). Temporal pattern recognition with
delayed-feedback spin-torque nano-oscillators. Physical Review
Applied, 12(2), 024049.
Robinson, P. A., Henderson, J. A., Matar, E., Riley, P., & Gray,
R. T. (2009). Dynamical reconnection and stability constraints on
cortical network architecture. Physical Review Letters, 103(10),
108104.
Rodriguez, N., Izquierdo, E., & Ahn, Y.-Y. (2019). Optimal modu-
larity and memory capacity of neural reservoirs. Network Neu-
roscience, 3(2), 551–566.
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069.
Saha, D., Leong, K., Li, C., Peterson, S., Siegel, G., & Raman, B. (2013).
A spatiotemporal coding mechanism for background-invariant
odor recognition. Nature Neuroscience, 16(12), 1830–1839.
Sattar, A., Fostner, S., & Brown, S. A. (2013). Quantized conduc-
tance and switching in percolating nanoparticle films. Physical
Review Letters, 111(13), 136808.
Network Neuroscience
446
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Long-range temporal correlations in scale-free neuromorphic networks
Scheffer, M., Bascompte, J., Brock, W. A., Brovkin, V., Carpenter,
S. R., Dakos, V., . . . Sugihara, G. (2009). Early-warning signals
for critical transitions. Nature, 461(7260), 53–59.
Schmelzer, J., Brown, S. A., Wurl, A., Hyslop, M., & Blaikie, R. J.
(2002). Finite-size effects in the conductivity of cluster assembled
nanostructures. Physical Review Letters, 88(22), 226802.
Segev, R., Benveniste, M., Hulata, E., Cohen, N., Palevski, A.,
Kapon, E., . . . Ben-Jacob, E. (2002). Long term behavior of litho-
graphically prepared in vitro neuronal networks. Physical Review
Letters, 88(11), 118102.
Sethna, J. P., Dahmen, K. A., & Myers, C. R. (2001). Crackling noise.
Nature, 410(6825), 242–250.
Shew, W. L., Clawson, W. P., Pobst, J., Karimipanah, Y., Wright,
N. C., & Wessel, R. (2015). Adaptation to sensory input tunes
visual cortex to criticality. Nature Physics, 11(8), 659–663.
Sporns, O., Tononi, G., & Kötter, R. (2005). The human connectome:
A structural description of the human brain. PLoS Computational
Biology, 1(4), e42.
Srinivasa, N., Stepp, N. D., & Cruz-Albrecht, J. (2015). Criticality
as a set-point for adaptive behavior in neuromorphic hardware.
Frontiers in Neuroscience, 9, 449.
Stauffer, D., & Aharony, A. (2003). Introduction to percolation the-
ory. Taylor & Francis.
Stieg, A. Z., Avizienis, A. V., Sillin, H. O., Martin-Olmos, C., Aono,
M., & Gimzewski, J. K. (2012). Emergent criticality in com-
plex Turing B-type atomic switch networks. Advanced Materials,
24(2), 286–293.
Strogatz, S. H. (2001). Exploring complex networks. Nature, 410,
268–276.
Tanaka, G., Yamane, T., Héroux, J. B., Nakane, R., Kanazawa,
N., Takeda, S., . . . Hirose, A. (2019). Recent advances in
physical reservoir computing: A review. Neural Networks, 115,
100–123.
Terabe, K., Hasegawa, T., Nakayama, T., & Aono, M. (2005). Quan-
tized conductance atomic switch. Nature, 433(7021), 47–50.
Torrejon,
J., Riou, M., Araujo, F. A., Tsunegi, S., Khalsa, G.,
Querlioz, D., . . . Grollier, J. (2017). Neuromorphic computing with
nanoscale spintronic oscillators. Nature, 547(7664), 428–431.
Tuma, T., Pantazi, A., Le Gallo, M., Sebastian, A., & Eleftheriou, E.
(2016). Stochastic phase-change neurons. Nature Nanotechnol-
ogy, 11(8), 693–699.
Vajna, S., Tóth, B., & Kertész, J. (2013). Modelling bursty time series.
New Journal of Physics, 15(10), 103023.
van den Heuvel, M. P., & Hulshoff Pol, H. E. (2010). Exploring the
brain network: A review on resting-state fMRI functional connec-
tivity. European Neuropsychopharmacology, 20(8), 519–534.
Voss, R. F. (1984). The fractal dimension of percolation cluster hulls.
Journal of Physics A, 17(7), L373–L377.
Voss, R. F., Laibowitz, R. B., & Allessandrini, E. I. (1982). Fractal
(scaling) clusters in thin gold films near the percolation thresh-
old. Physical Review Letters, 49(19), 1441–1444.
Wagenmakers, E.-J., & Farrell, S. (2004). AIC model selection using
Akaike weights. Psychonomic Bulletin & Review, 11(1), 192–196.
Wang, Z., Joshi, S., Savel’ev, S., Song, W., Midya, R., Li, Y., . . . Yang,
J. J. (2018). Fully memristive neural networks for pattern classi-
fication with unsupervised learning. Nature Electronics, 1(2),
137–145.
Watkins, N. W., Pruessner, G., Chapman, S. C., Crosby, N. B., &
Jensen, H. J. (2016). 25 years of self-organized criticality: Con-
cepts and controversies. Space Science Reviews, 198(1–4), 3–44.
Werner, G. (2010). Fractals in the nervous system: Conceptual im-
plications for theoretical neuroscience. Frontiers in Physiology,
1, 1–28.
Wildie, M., & Shanahan, M. (2012). Metastability and chimera states
in modular delay and pulse-coupled oscillator networks. Chaos:
An Interdisciplinary Journal of Nonlinear Science, 22(4), 043131.
Zhigalov, A., Arnulfo, G., Nobili, L., Palva, S., & Palva, J. M. (2017).
Modular co-organization of functional connectivity and scale-
free dynamics in the human brain. Network Neuroscience, 1(2),
143–165.
Network Neuroscience
447
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
2
4
3
2
1
8
6
6
6
2
1
n
e
n
_
a
_
0
0
1
2
8
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3