RESEARCH
Impact of higher order network structure
on emergent cortical activity
Max Nolte
1, Eyal Gal
2,3, Henry Markram1,4, and Michael W. Reimann 1
1Blue Brain Project, École Polytechnique Fédérale de Lausanne, Geneva, Svizzera
2Edmond and Lily Safra Center for Brain Sciences, The Hebrew University, Jerusalem, Israel
3Department of Neurobiology, The Hebrew University, Jerusalem, Israel
4Laboratory of Neural Microcircuitry, Brain Mind Institute, École Polytechnique Fédérale de Lausanne, Lausanne, Svizzera
a n o p e n a c c e s s
j o u r n a l
Keywords: Neocortex, Microcircuit, Connectome, Morphology, Topology, Network, Model, Motifs
ABSTRACT
Synaptic connectivity between neocortical neurons is highly structured. The network
structure of synaptic connectivity includes first-order properties that can be described by
pairwise statistics, such as strengths of connections between different neuron types and
distance-dependent connectivity, and higher order properties, such as an abundance of
cliques of all-to-all connected neurons. The relative impact of first- and higher order structure
on emergent cortical network activity is unknown. Here, we compare network structure and
emergent activity in two neocortical microcircuit models with different synaptic connectivity.
Both models have a similar first-order structure, but only one model includes higher order
structure arising from morphological diversity within neuronal types. We find that such
morphological diversity leads to more heterogeneous degree distributions, increases the
number of cliques, and contributes to a small-world topology. The increase in higher order
network structure is accompanied by more nuanced changes in neuronal firing patterns, come
as an increased dependence of pairwise correlations on the positions of neurons in cliques.
Our study shows that circuit models with very similar first-order structure of synaptic
connectivity can have a drastically different higher order network structure, and suggests that
the higher order structure imposed by morphological diversity within neuronal types has an
impact on emergent cortical activity.
AUTHOR SUMMARY
We seek to understand how certain characteristics in the structure of neuron-to-neuron
connectivity shape the activity of local neural circuits. The local connectivity of cortical
networks features a nonrandom higher order structure characterized by the presence of
tightly connected clusters of neurons. We use a biologically detailed model of neocortical
microcircuitry that recreates these features and simplify its complexity algorithmically while
preserving the larger scale connectivity trends. We then simulate spontaneous and evoked
activity in the two models with simplified and complex connectivity and compare the
resulting spiking statistics. The results allow us to characterize the role of the higher level
structure of connectivity in interaction with other biological features shaping neuronal
activity such as synaptic adaptation and noise.
Citation: Nolte, M., Gal, E., Markram, H.,
& Reimann, M. W. (2020). Impact of
higher order network structure on
emergent cortical activity. Network
Neuroscience, 4(1), 292–314.
https://doi.org/10.1162/netn_a_00124
DOI:
https://doi.org/10.1162/netn_a_00124
Supporting Information:
https://doi.org/10.1162/netn_a_00124
Received: 14 ottobre 2019
Accepted: 23 Dicembre 2019
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Michael Wolfgang Reimann
michael.reimann@epfl.ch
Handling Editor:
Olaf Sporns
Copyright: © 2020 Max Nolte, Eyal
Gal, Henry Markram, and Michael W.
Reimann. Published under a Creative
Commons Attribution 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
Synaptic connectivity:
The connections formed between
neurons via chemical synapses.
Motif:
A specific subnetwork of neurons
that can repeatedly be found across
the whole network.
Neocortical microcircuit:
A local collection of highly
interconnected neurons in the
neocortex that stretches across six
layers.
Dendritic and axonal cloud:
The average dendritic and axonal
surface area of neurons of the same
morphological type.
INTRODUCTION
Local synaptic connectivity between neocortical neurons is highly structured (Perin, Berger,
& Markram, 2011; Song, Sjöström, Reigl, Nelson, & Chklovskii, 2005). Details of first-order
structure that can be described by pairwise statistics include distinct mean connection strengths
between different neuron types (Feldmeyer, Lubke, Silver, & Sakmann, 2002; Jiang et al., 2015;
Le Bé, Silberberg, Wang, & Markram, 2007; Silberberg & Markram, 2007), distance-dependent
connectivity that changes between neuron types (Fino & Yuste, 2011; Holmgren, Harkany,
Svennenfors, & Zilberter, 2003; Jiang et al., 2015; Song et al., 2005), and a bias for recipro-
cal connections (Markram et al., 2015; Perin et al., 2011; Song et al., 2005). This first-order
structure is undoubtedly important for emergent electrical activity, for example by constraining
the interlaminar flow of spiking activity (Reyes-Puerta, Sun, Kim, Kilb, & Luhmann, 2014) E
constraining the excitation-inhibition balance (Rosenbaum, Smith, Kohn, Rubin, & Doiron,
2017).
Yet, local synaptic connectivity also contains significant higher order structure that cannot
be described by pairwise statistics (Benson, Gleich, & Leskovec, 2016). Examples are an over-
expression of certain triplet motifs of neurons (Perin et al., 2011; Song et al., 2005) and an abun-
dance of cliques of all-to-all connected neurons (Reimann, Nolte, et al., 2017). Such higher
order structure has been hypothesized to be important for computation (Braitenberg, 1978;
Hebb, 1949; Knoblauch, Palm, & Sommer, 2009; Willshaw, Buneman, & Longuet-Higgins,
1969). In recurrent spiking neural networks, clustering of neurons has been shown to impact
dynamics (Litwin-Kumar & Doiron, 2012), and motifs of neurons have been shown to shape
spike correlations (Bojanek, Zhu, & MacLean, 2019; Eh, Trousdale, Josi, & Shea-Brown, 2013;
Recanatesi, Ocker, Buice, & Shea-Brown, 2019). D'altra parte, modern artificial neural
networks have demonstrated impressive computational capabilities without explicitly mod-
eled, complex higher order microstructures (Simonyan & Zisserman, 2014). Whether compu-
tation in the cortex relies on higher order structure such as multineuron motifs on top of already
complex first-order structure is unknown.
Answering this question in vivo will require simultaneous access to both detailed synaptic
connectivity and electrical activity. While detailed synaptic connectivity of larger areas encom-
passing thousands of neurons might soon become available (Kasthuri et al., 2015; Yin et al.,
2019), it will remain difficult to study the direct impact of the network structure on electrical
activity, and even then it would be difficult to quantify the relative impact of first- and higher
order structure. A modeling approach can help bridge this gap. An algorithmic approach was
developed that uses available data to generate synaptic connectivity in a neocortical micro-
circuit model with diverse morphologies (Reimann, King, Muller, Ramaswamy, & Markram,
2015). When simulated, this neocortical microcircuit model (NMC-model, Figure 1A1) can
reproduce an array of in vivo–like neuronal activity (Markram et al., 2015) and allow us to
compare and manipulate detailed, predicted structure and function.
Here, we utilize a recent finding that first-order connectivity is largely constrained by
morphological diversity between neuronal types, and higher order connectivity by morpholog-
ical diversity within neuronal types (Reimann, Horlemann, Ramaswamy, Muller, & Markram,
2017). Both aspects are captured by the NMC-model, leading to a biologically realistic mi-
crostructure (Gal et al., 2017). By connecting neurons according to average axonal and
dendritic morphologies (axonal and dendritic clouds, Figure 1A2), we create a control cir-
cuit (the cloud-model) that has very similar first–order structure, but reduced higher order
structure. We find that this reduced higher order structure—caused by disregarding morpho-
logical diversity within neuronal types—includes fewer cliques, and decreased small-world
Network Neuroscience
293
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
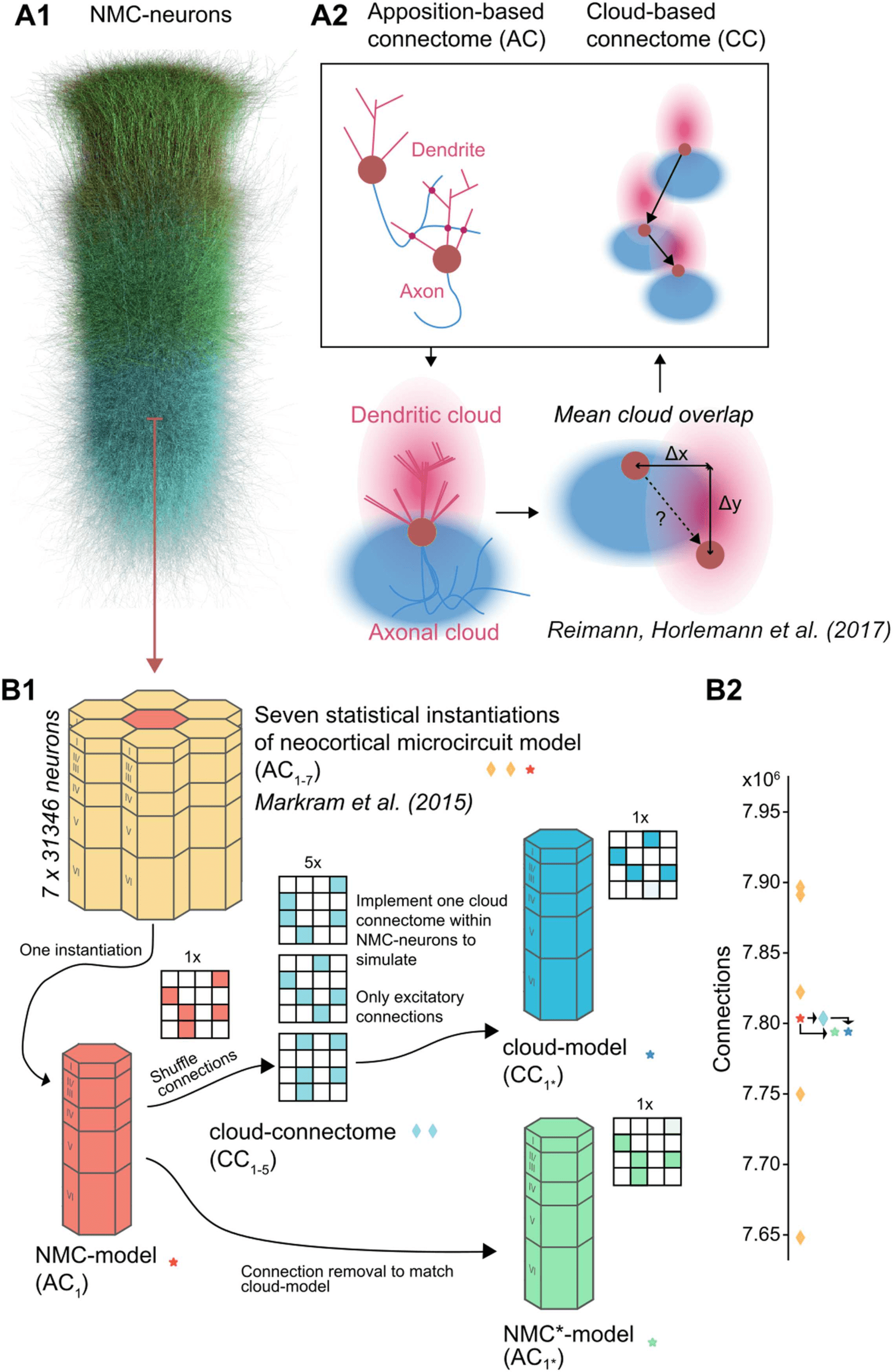
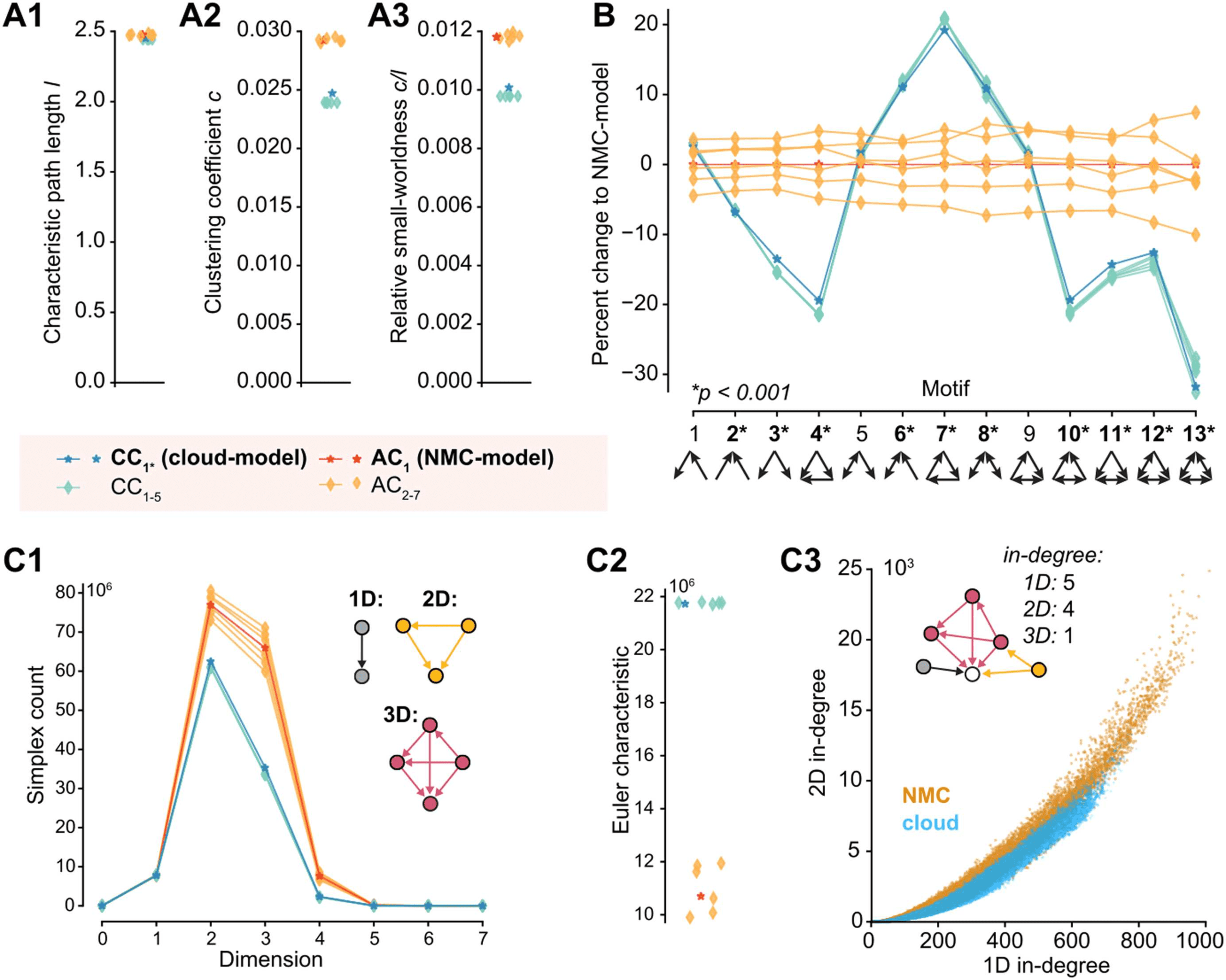
Figura 1. Reducing higher order network structure in a neocortical microcircuit model. (A1)
Neurons in the neocortical microcircuit (NMC-) modello. (A2) Deriving synaptic connectivity be-
tween neocortical neurons: Connectivity in the NMC-model is based on appositions of dendrites and
axons (Reimann et al., 2015). Connectivity in the control cloud-model considers overlap of average
dendritic and axonal clouds (Reimann, Horlemann, et al., 2017). (B1) We computed network prop-
erties for seven statistical instantiations of the microcircuit (apposition-based connectomes AC1–7,
orange diamonds and red star; Markram et al., 2015), and simulated one of them in this study (IL
NMC-model with connectome AC1, red star). Additionally, we studied versions of the model using
the existing NMC-neurons, but synaptic connectivity derived according to the cloud-based
approach (cloud-connectomes CC1–5, blue diamonds). We then implemented one of the alternative
connectomes within the existing synapses of the NMC-neurons, resulting in the cloud-model that
we simulated, with connectome C1* (blue star). The rewiring of the cloud-model was restricted to
excitatory connections. (B2) Number of connections across connectomes. By design, the cloud-
connectomes CC1–5 have the same number of connections as the NMC-model connectome AC1.
Tuttavia, the connectome implemented in the cloud-model CC1* has 0.12% fewer connections
than CC1 because of a mismatch in new connections and available synapses (see Figure 2A). A
control for this loss, we generate a copy of the NMC-model with the same fraction of excitatory
connections randomly removed, the NMC*-model (green star).
Network Neuroscience
294
Impact of higher order network structure on emergent cortical activity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
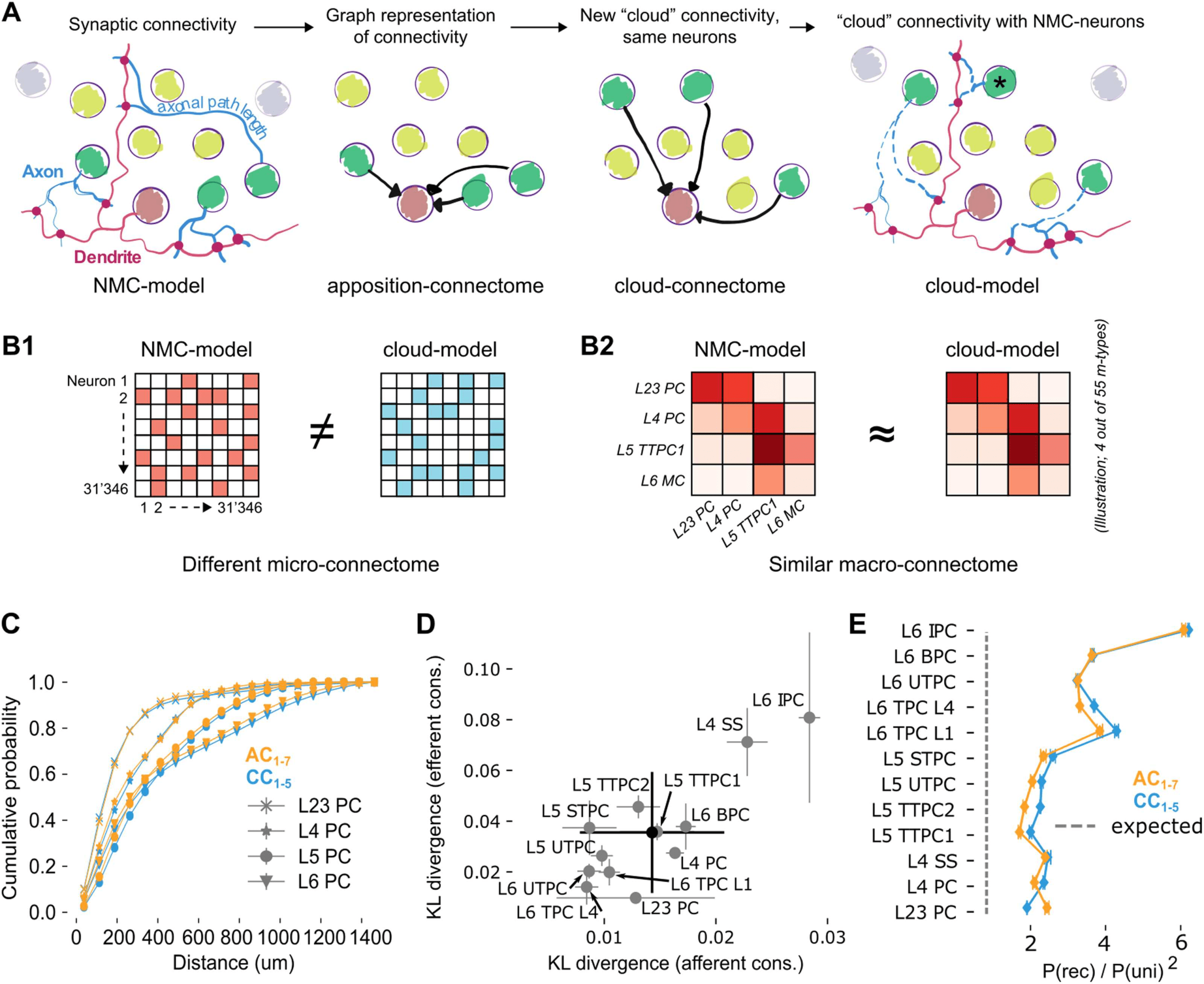
Figura 2. Rewiring synaptic connectivity in a neocortical microcircuit model preserves macro-
connectivity trends. (UN) Left: In the NMC-model, synaptic connections from a given morphological
type (m-type; neurons in light/dark green) are based on axo-dendritic appositions. Synaptic delays
are calculated from axonal path lengths. Center left: The apposition connectome for the m-type can
be represented as a directed graph that excludes neurons from other m-types. Center right: A new,
cloud-based connectome is calculated for the same neuron population. Right: The cloud-based
connectome is implemented by rewiring existing synapses, preserving their dendritic locations and
physiological parameters. The process also preserves their original synaptic delay even for neurons
at a different distance than the original neuron (black asterisk). (B) The NMC- and cloud-models
have a completely different microconnectome in terms of connections between individual neurons
(B1) but a very similar macroconnectome in terms of number of connections between the 55 differ-
ent m-types in the model (B2). (C) Soma-to-soma distance for connected neurons pairs where the
postsynaptic neuron is in the indicated layer (distance of afferent connections) for AC1–7 (orange)
and CC1–5 (blue). (D) Kullback-Leibler divergence of afferent and efferent connection distances
between AC1 and CC1–5. Gray circles and error bars indicate mean and standard deviation over
instances for all excitatory m-types. Black: overall mean and standard deviation over five instances.
(E) Reciprocal overexpression in terms of reciprocal connection probability divided by the square of
the unidirectional connection probabilities for all excitatory m-types. Orange: AC1–7, blue: CC1–5.
Indicated are mean and standard deviation.
topology. Additionally, the cloud-model is characterized by more homogeneous degree distri-
butions with reduced in-degrees at the bottom of layer 6. When we simulate and compare the
electrical activity in the two circuit models, we find that the changes in higher order connectiv-
ity are accompanied by nuanced changes in neuronal firing patterns and reduced topological
ordering of pairwise correlations.
Our study reduces higher order network structure of a neocortical microcircuit model while
leaving first-order structure largely intact, providing an alternative approach to cortical network
Network Neuroscience
295
Impact of higher order network structure on emergent cortical activity
studies that add increasingly complex structure to simple neural network models. Our ap-
proach ensures that the cortical network studied is closer to the biological ground truth than
more simplifying models (albeit less amenable to theoretical analysis). Our comparison of
reduced and nonreduced network structure suggests that higher order network topology of
neocortical microcircuitry shapes cortical function.
RESULTS
Reducing Higher Order Network Structure in a Neocortical Microcircuit Model
The NMC-model consists of 31,346 neurons belonging to 55 different morphological types
(m-types) (Figure 1A1). Synaptic connectivity between the neurons was derived by consid-
ering appositions of dendrites and axons as potential synapse locations (apposition-based
connectome AC1, Figure 1A2, left), which were then filtered according to biological con-
straints (Reimann et al., 2015). While this connectome is merely a null model of connectivity,
it matches a large array of biological measurements, in terms of both its first-order structure and
its higher order structure. We define first-order structure as structure of synaptic connectivity
that can be described by pairwise statistics, such as connection strengths between different
m-types, distance-dependent connectivity, and average degrees, and higher order structure as
structure involving more than two neurons (Benson et al., 2016), such as common-neighbor
bias and overrepresentation of cliques of all-to-all connected neurons. Neuronal and synaptic
physiology in the model are equally well constrained (Markram et al., 2015).
To assess the specific role of the higher order synaptic structure on neuronal activity, we
had to reduce the higher order structure while simultaneously impacting the first-order struc-
ture as little as possible. A tal fine, we used an alternative cloud-based approach to derive
synaptic connectivity, which is based on the overlap of average dendritic and axonal shapes of
the various m-types (Figure 1A2, bottom, right; cloud-model) instead of specific axo-dendritic
appositions of individual neurons as in the NMC-model. This approach (see Methods) has been
shown to yield similar properties of first-order structure, such as distinct connection strengths
between different m-types (and consequently between layers), distance-dependent connectiv-
ità, and a bias for reciprocal connections (Reimann, Horlemann, et al., 2017). Tuttavia, IL
cloud-model cannot reproduce an experimentally observed bias for connected neocortical
neurons to share a common neighbor (Perin et al., 2011; Reimann, Horlemann, et al., 2017),
indicating a reduced complexity of its higher order structure. By comparing electrical activity
between the NMC-model and the cloud-model in simulation experiments, we can study the
relative impact of first- and higher order structure on electrical activity.
To build the cloud-model, we first generated alternative cloud-based connectomes for the
NMC-neurons (Figure 1B1, red to green), using methods introduced by Reimann, Horlemann,
et al. (2017). Briefly, average axon and dendrite shapes were calculated from reconstructions
for all m-types. Prossimo, for each combination of neuron types, their axon and dendrite volumes
were convolved (see Figure 1A2) to yield the expected strength of their overlap for all possible
relative soma locations. Soma locations of neurons were taken from the NMC-model and used
to look up the overlap strengths for all neuron pairs. Selection probabilities for all pairs were
then calculated as proportional to the square of the overlap. For each pair of neuron types, we
randomly picked according to those probabilities a number of connections that were equal
to the number of connections between them in the NMC-model (random picking without
replacement; Figure 1B2, red asterisk and green diamond).
Axo-dendritic apposition:
A spatial location in which axons
and dendrites of two different
neurons are close enough to each
other to form a synapse.
Network Neuroscience
296
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
In- (and out-) degree:
The number of incoming and
outgoing connections of a neuron.
A neuron-to-neuron connection matrix was then instantiated from the probabilities (IL
cloud-connectome, CC1–5) and transplanted into the NMC-neurons, to generate an instance
of the cloud-model that was identical to the NMC-model in terms of neuronal composition,
and morphology and physiology of all individual neurons (Figure 1B1). Allo stesso modo, the physi-
ology of individual synapses (strength, kinetics, and short-term dynamics) and their locations
on dendrites were taken from the NMC-model—we only changed which presynaptic neurons
innervated them when implementing the cloud-based connection matrix (Figure 2A). This re-
assignment of innervation was constrained to select a new innervating neuron only from the
same m-type that innervated it in the NMC-model to preserve the m-type-specific synaptic
physiology. Tuttavia, while synaptic physiology is guaranteed to be conserved in this ap-
proach, the axonal path length, and thus the time it takes for an action potential to propagate
from the soma to the synapse, is potentially biologically implausible. While the average path
lengths per pre-/postsynaptic m-type combination are conserved, an action potential might
potentially arrive earlier or later than is appropriate for the distance between pre- and post-
synaptic neuron (see Figure 2A). To verify that the average distance-dependence of connectiv-
ity is conserved, we considered the probability distribution of distances of connected neurons
for individual layers (Figure 2C). We calculated the Kullback-Leibler divergence of this distribu-
tion between NMC-model and cloud-connectome, both for afferent and efferent connections
(Figure 2D). The divergence for individual m-types ranged from 0.008 A 0.029 with an over-
all mean of 0.014 for afferent connections and from 0.016 A 0.08 with a mean of 0.036 for
efferent connections, much lower than the divergence between the NMC-model and an Erdös-
Rényi (ER) model that preserves in- or out-degrees (1.304 ± 0.661 for afferent connections and
preserving in-degree; 0.749 ± 0.433 efferent, preserving out-degree; not shown). Allo stesso modo, we
validated that the overexpression of reciprocal connectivity is preserved (Figure 2E).
In the cloud-based connection matrix CC1, a small number of neurons receive input from
m-types that do not innervate them in the NMC-model. Consequently, a small fraction of
connections could not be instantiated within the existing synapses of the NMC-neurons and
had to be left out. The loss was minor for excitatory connections (0.12% loss of connections)
but posed a significant problem for inhibitory connections. We therefore implemented the
cloud-connectome only for excitatory connections and kept inhibitory connectivity in the
cloud-model identical to the NMC-model, yielding a hybrid cloud-model connectome CC1*.
Supplementary Figure S1 provides an overview of connection losses in the cloud-model. How-
ever, note that the loss of connections is very small compared with the variability in con-
nections between statistical instantiations of the NMC-model (Figure 1B2, orange diamonds),
which all have very similar dynamical properties (Markram et al., 2015).
To control for the minor loss of excitatory connectivity and the shuffling of axonal path
lengths, we generated an additional control circuit, the NMC*-model (Figure 1B1). A total
Di 0.12% of excitatory connections were randomly removed from the NMC-model to match
the m-type-specific connection losses in the cloud-model (as in Supplementary Figure S1B).
The axonal path length parameter was then shuffled within connections with the same presy-
naptic excitatory m-type to account for a similar scrambling in the cloud-model (see Figure 2A).
All circuit models and connectomes analyzed in this study are summarized in Table 1.
In summary, our approach ensures that for each neuron in the NMC-model, there is a cor-
responding neuron in the cloud-model with identical location, morphology, electrophysiol-
ogy, synaptic physiology, inhibitory innervation, and average excitatory innervation patterns.
On a larger scale, both models consequently have nearly identical macroconnectomes in
terms of the number of connections between morphological types (Figure 2B2), and thus
Network Neuroscience
297
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
Tavolo 1. Overview of circuit models and connectomes analyzed in this study
Nome
Description
NMC-neurons
AC1
NMC-model
AC2–7
CC1–5
Cloud-model
CC1*
NMC*-model
amc2_Column and mc[0, 1, 3-6]_Column respectively at bbp.epfl.ch/nmc-portal/downloads → AVERAGE.
31,346 neuron models of a neocortical microcircuit (Markram et al., 2015).
Apposition-based connectome for NMC-neurons (Markram et al., 2015).UN
Combination of NMC-neurons and AC1 (Markram et al., 2015).
Apposition-based connectomes of statistical variants of NMC-model (Markram et al., 2015).UN
Cloud-based alternatives to AC1 (Reimann, Horlemann, et al., 2017).
Combination of NMC-neurons and CC1 (excitatory connections) and AC1 (inhibitory connections).
Connectome of cloud-model (see above).
NMC-model with axon path length shuffle and 0.12% exc. connection loss as in cloud-model.
(Micro-) connectome:
The complete set of synaptic
connections formed between a
collection of neurons.
also between layers, and between excitatory and inhibitory subpopulations (Supplementary
Figure S1C1–3). Only the microconnectomes defined by connections between individual neu-
rons were changed within tight global constraints (Figure 2B1). An overview of what is con-
served between NMC-model, cloud-model, and NMC*-model can be found in Table 2.
Decreased Heterogeneity of Degree Distributions in the Cloud-Model
By design, the average in- and out-degree of neurons belonging to a specific m-type was pre-
served in the cloud-connectome. Tuttavia, the distribution around the mean was altered.
Degree distributions have been demonstrated to shape cortical network dynamics (Landau,
Egger, Dercksen, Oberlaender, & Sompolinsky, 2016), with long-tailed distributions being
associated with highly structured brain networks (Gal et al., 2017). We can see that both
In- and out-degree distributions are more heterogeneous in the NMC- than in the cloud-model
(Figure 3A1 and 3A2, blue vs. red), which applies to all layers (Supplementary Figure S2), E
is also preserved when connection strength in the form of maximum synaptic conductance
is taken into account (Figure S3). In the NMC-model, the standard deviation of out-degrees
(σout(AC1) = 152, statistical variants: σout(AC2−7) = 150–154 [min – max]) and the standard
deviation of in-degrees (σin(AC1) = 176, σin(AC2–7) = 173–179) are higher than in the cloud-
modello (σout(CC1∗) = 110, cloud-connectomes: σout(CC1–5) = 101.7–101.8; σin(CC1∗) = 158,
Tavolo 2. Overview of control model conservation of NMC-model properties
Microcircuit properties
Specific neuron electrophysiology
& morphology
M-type-specific synaptic physiology
Average (pre-/postsynaptic m-type-
specific) axonal path length
Macroconnectome (between m-types)
Microconnectome (between specific)
neurons
Specific axonal path length
a0.12 excitatory connection loss.
Cloud-model
X
NMC*-model
X
X
X
(X)UN
X
X
X
X
(X)UN
(X)UN
X
By design: neuron models reused;
Figura 1
Synapses reused; connections shuffled
only within m-type; Figure 2A
Reused synapses include path length
parameter; Figure 2A
Figures 1B2, 2CDE
Figures 1B1, 2UN, 2B1, 3
Figure 2A
Network Neuroscience
298
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
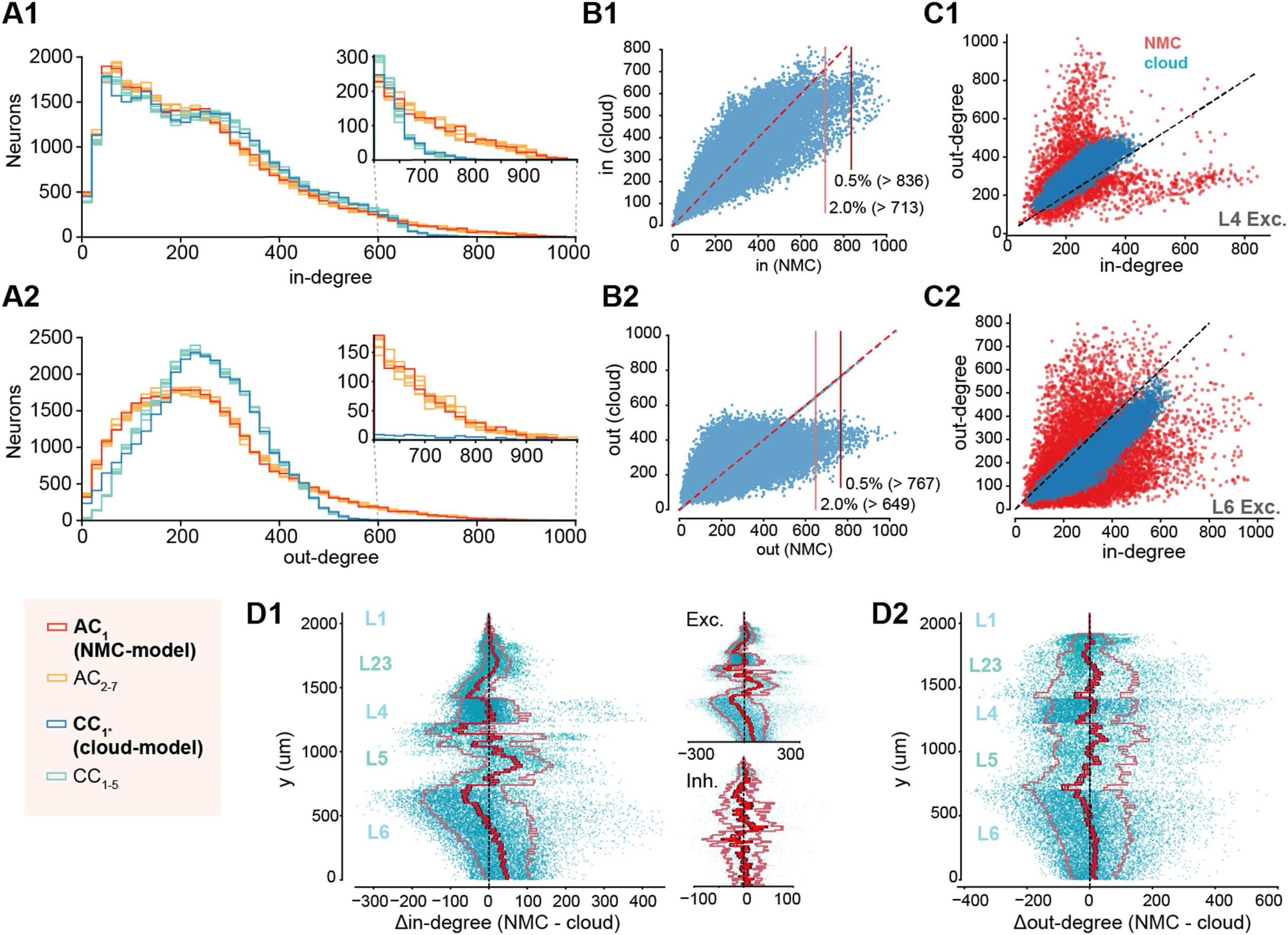
Figura 3. Decreased heterogeneity of degree distributions in cloud-model. (A1) In-degree distri-
butions of neurons in NMC-model (AC1, red), in additional apposition-based connectomes (AC2–7,
orange), the cloud-model (CC1*, blue), and the five cloud-connectomes (CC1–5, light blue). Insets
show the same distributions starting from 600 for easier comparison. (A2) As A1, but for out-degree
distributions. (B) Hub neurons in NMC- and cloud-models. (B1) Scatterplot of in-degree in NMC-
versus cloud-model for the same neurons. Horizontal lines indicate 2.0% E 0.5% percentile in
NMC-model. (B2) As B1 but for out-degree. (C1) In- versus out-degree scatterplot for NMC- E
cloud-model for excitatory neurons in layer 4. (C2) In- versus out-degree scatterplot for NMC- E
cloud-model for excitatory neurons in layer 6. (D1) Difference in in-degree of neurons between
NMC- and cloud-model, across cortical depth. The bright red line indicates the mean across y-bins,
the dark red line the standard error of the mean, and the outer, faded line the standard deviation.
Insets: for excitatory and inhibitory subpopulations. (D2) As D1, but for out-degree.
σin(CC1–5) = 158.2–158.4). The discrepancy in σout and σin of CC1–5 and AC1–7 is significantly
different (σout: p = 3.0 × 10−14, σin: p = 1.6 × 10−8; two-sided t test), although both are almost
one order of magnitude over the value expected in an Erdös-Rényi (ER) network of the same
size and sparseness (P(ER) = 15.7).
The stark difference in connectivity between the NMC- and cloud-models is also reflected
by hub neurons, previously defined as the top 0.5% of neurons in terms of in- or out-degree
(Gal et al., 2017), which vanish in the cloud-model when using the same cutoff value as in
the NMC-model (Figure 3B). We further found a redistribution of connectivity in terms of in-
and out-degree from the bottom to the top of layer 6 (Figure 3D1 and 3D2). Finalmente, differ-
ences in degree distributions extended to higher order properties in the form of correlations
between in- and out-degree (Figure 3C1 and 3C2 for excitatory neurons in layers 4 E 6;
see Supplementary Figure S4 for all neurons), indicating a stronger specialization into input
and output neurons in the NMC-model. In summary, the cloud-model has a strongly reduced
heterogeneity of connectivity in terms of distributions of in- and out-degrees.
Network Neuroscience
299
Impact of higher order network structure on emergent cortical activity
Decreased Small-Worldness and Fewer Directed Simplices in Cloud-Model
The higher order structure of the NMC-model results, Per esempio, in a bias for two con-
nected neurons to share common neighbors (common-neighbor bias), a tendency that has
been demonstrated to be reduced in the cloud-model (Reimann, Horlemann, et al., 2017). It
also manifests itself on a global scale in the form of a small-world network topology (Gal et al.,
2017). A network is considered small-world if its global clustering coefficient is considerably
larger than that of an ER network of the same size and sparseness, while the characteristic path
length is roughly equal to that of the ER network. For networks of the same size and sparseness,
the ratio of the global clustering coefficient c and the characteristic path length l provides a
measure of relative small-worldness. The clustering coefficient describes the probability of neu-
rons that share a common neighbor to be directly connected, a tendency that has previously
been shown to be reduced in the cloud-model (Reimann, Horlemann, et al., 2017). Conse-
quently, we find that the cloud-model has a reduced clustering coefficient (c is around 20%
larger in the NMC-model than in the cloud-model, Figure 4A2). The characteristic path lengths
l of NMC- and cloud-models are, Tuttavia, almost equal to each other (Figure 4A1) and to the
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
4. Decreased small-worldness and fewer directed simplices in cloud-model.
Figura
(A1)
Characteristic path length l of the different connectomes. (A2) Clustering coefficient c of the dif-
ferent connectomes. (A3) Relative small-worldness c/l of the different connectomes. (B) Percentage
change in total number of all triplet motifs from NMC-model (p values: t test between AC1–7 and
CC1–5). (C1) Number of directed cliques (simplices) per dimension in the different connectomes
(for zoom in see Figure S5A). (C2) Euler characteristic (alternating sum of number of simplices). (C3)
Participation at the sink of 1D simplices (standard in-degree) versus 2D simplices (2D in-degree: IL
number of simplices a neuron is part of as the sink of a simplex).
Network Neuroscience
300
Impact of higher order network structure on emergent cortical activity
one of the equivalent ER network (around 2.15). Both models can therefore be considered
small-world networks, although this tendency is significantly stronger in the NMC-model than
in the cloud-model (Figure 4A3).
As an increased clustering coefficient indicates the tendency to form tightly connected
motifs, we next compared the numbers of specific triplet motifs in both models (Figure 4B).
È interessante notare, the cloud-model has a decrease of motifs with forward transitive connectivity
(Figure 4B, motif 4), but an increase in motifs with backwards transitive connectivity, come
as cycles (motif 7). We previously showed that the NMC-model contains an abundance of a
specific class of motifs called directed simplices (Reimann, Nolte, et al., 2017). These sim-
plices generalize the forward transitive connectivity of motif 4 to motifs of any size. The size
of a simplex is then called its dimension, defined as its size minus 1. While simplices of the
same dimension are present in cloud- and NMC-models (Supplementary Figure S5A), the num-
ber of simplices in a given dimension is much higher in the NMC- than in the cloud-model
(Figure 4C1). Allo stesso tempo, the cloud-model is much closer to the NMC-model than sim-
pler control models: In a previously used control that conserves only the distance-dependence
of connectivity, but ignores the shapes of axonal and dendritic clouds, we found a more drastic
decrease from around 80 million to 40 million 2D-simplices (Reimann, Nolte, et al., 2017),
while the cloud-model has more than 60 million 2D-simplices. A distinct Euler characteristic
(Figure 4C2) and distinct Betti numbers (Supplementary Figure S5B) further illustrate the change
in global properties of network topology (see Methods). The increase in simplex numbers in
the NMC-model follows from the more heterogeneous degree distributions, as neurons with
larger degrees are generally part of more simplices (Figure 4C3).
In summary, the cloud-model—with its disregard for morphological diversity within neu-
ronal types—has reduced small-worldness and reduced numbers of high-dimensional, forward
transitive motifs.
Impact of Higher Order Structure on Spontaneous Activity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
To study the impact of the higher order structural differences on emergent activity, we next sim-
ulated spontaneous activity in NMC-, cloud-, and NMC*-models in an in vivo–like state, In
which the NMC-model can reproduce several properties of cortical activity (Markram et al.,
2015). We compared firing rates in this in vivo–like state (Figure 5B, [Ca2+]o = 1.25 mM).
È interessante notare, excitatory firing rates are conserved (Figure 5B2), while inhibitory firing in the
NMC*-model is significantly reduced compared with the cloud-model and NMC-model
(Figure 5B3). Questo è, a small decrease of inhibitory firing rates due to the axonal path length
shuffle and loss of E-to-I synapses in the NMC*-model is reversed by the reduced higher order
structure of the cloud-model, reaching inhibitory firing rates similar to the NMC-model. Questo
implies that the loss of higher order structure in the cloud-model leads to a shift towards more
inhibition (Figure 5C).
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Tuttavia, the functional excitation-inhibition balance also depends on extracellular cal-
cium levels ([Ca2+]o), which differentially modulates the release probability of excitatory and
inhibitory synapses (Markram et al., 2015). In the NMC-model, at low [Ca2+]o, the network
is in an asynchronous state of activity with lower firing rates (Figure 5A1, [Ca2+]o = 1.2 mM,
1.25 mM). At high [Ca2+]o, the circuit is in a nonbiological synchronous state of activity with
spontaneous network bursts and higher firing rates (Figure 5A1, [Ca2+]o = 1.3 mM, 1.35 mM).
A [Ca2+]o = 1.25 mM, just before the transition from the asynchronous to synchronous state,
activity in the microcircuit is in the in vivo–like state described above.
Network Neuroscience
301
Impact of higher order network structure on emergent cortical activity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
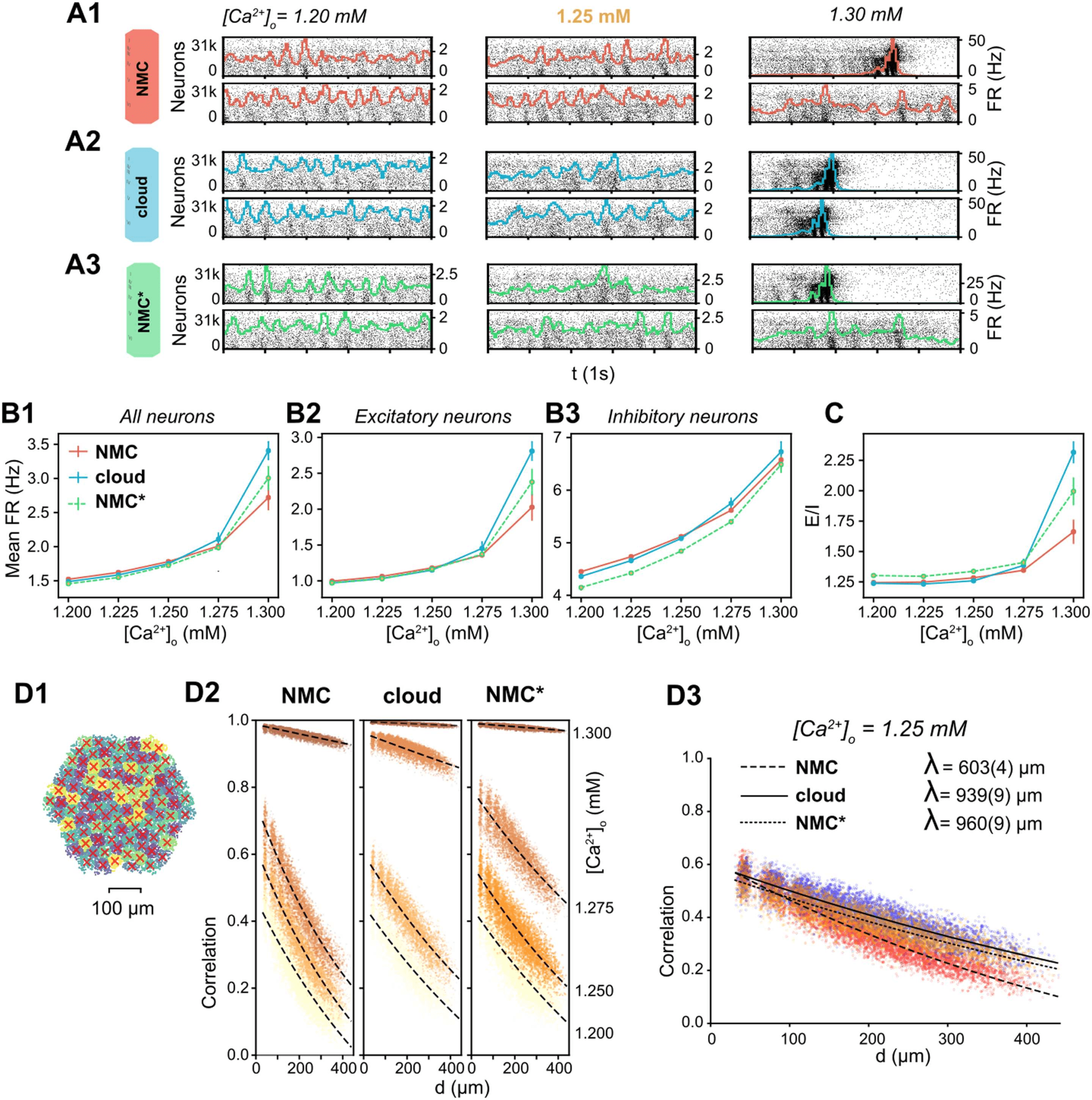
Figura 5. Simulating spontaneous activity in NMC- and cloud-models. (A1) Spontaneous activity of all neurons in the NMC-model for two
trials at different levels of [Ca2+]o. Each spike is represented by a vertical line, whose position on the y-axis is ordered by soma position in the
microcircuit, which was then rasterized. Colored lines depict the population firing rate (∆t = 10 ms). (A2) Spontaneous activity of all neurons
in the cloud-model. (A3) Spontaneous activity of all neurons in the control NMC*-model. (B1) Mean firing rate during spontaneous activity
for all neurons. Mean of 20 trials of 1,000 ms, error bars indicate standard error of the mean. (B2) Mean firing rate during spontaneous activity
for excitatory neurons. Mean of 20 trials of 1,000 ms, error bars indicate standard error of the mean. (B3) Mean firing rate during spontaneous
activity for inhibitory neurons. Mean of 20 trials of 1,000 ms, error bars indicate standard error of the mean. (C) Total spike count of excitatory
neurons divided by the spike count of inhibitory neurons. Mean of 20 trials of 1,000 ms, error bars indicate standard error of the mean. (D1)
All neurons in the microcircuit were divided into 100 interlaminar clusters (k-means clustering). The red cross marks the geographic center
of all neurons for each cluster. (D2) Correlation coefficients between combined firing rate histograms of all neurons of each combination of
clusters versus distance between clusters. From [Ca2+]o = 1.200 mM (bottom fitted curve, bright yellow dots) A [Ca2+]o = 1.300 mM (top
fitted curve, dark brown dots). The fitted line indicates an exponential fit e−d/λ + C. (D3) As in D2, but at [Ca2+]o = 1.25 mM. The fitted line
indicates an exponential fit e−d/λ + C, parentheses indicate the standard error of the fit.
Network Neuroscience
302
Impact of higher order network structure on emergent cortical activity
The cloud-model appears to transition at
inferiore [Ca2+]o than the NMC-model and
NMC*-model, with more rapidly increasing firing rates for higher [Ca2+]o (Figure 5B1–3), an
indication that effective excitation is stronger in the cloud-model than in NMC- and NMC*-
models. [Ca2+]o also regulates distance-dependent correlation coefficients of spiking activity
between neurons (Figure 5D1; Markram et al., 2015). At the transition from asynchronous to
synchronous activity, correlation coefficients rapidly increase (Figure 5D2). We can see that at
[Ca2+]o = 1.25 mM, correlations between NMC- and NMC*-model are very similar, ma il
cloud-model is in fact slightly ahead, with higher correlation coefficients (Figure 5D2). At that
level of [Ca2+]o, correlations also drop slightly faster with distance in the cloud- than in the
NMC-model; Tuttavia, this is fully explained by the nontopological changes controlled for in
the NMC*-model (Figure 5D3).
We thus conclude that the higher order network structure has a superficial impact on emer-
gent population dynamics during spontaneous activity, such as a small increase in inhibitory
firing rates, and paradoxically, a small increase in effective global excitation.
Impact of Higher Order Structure on Evoked Activity
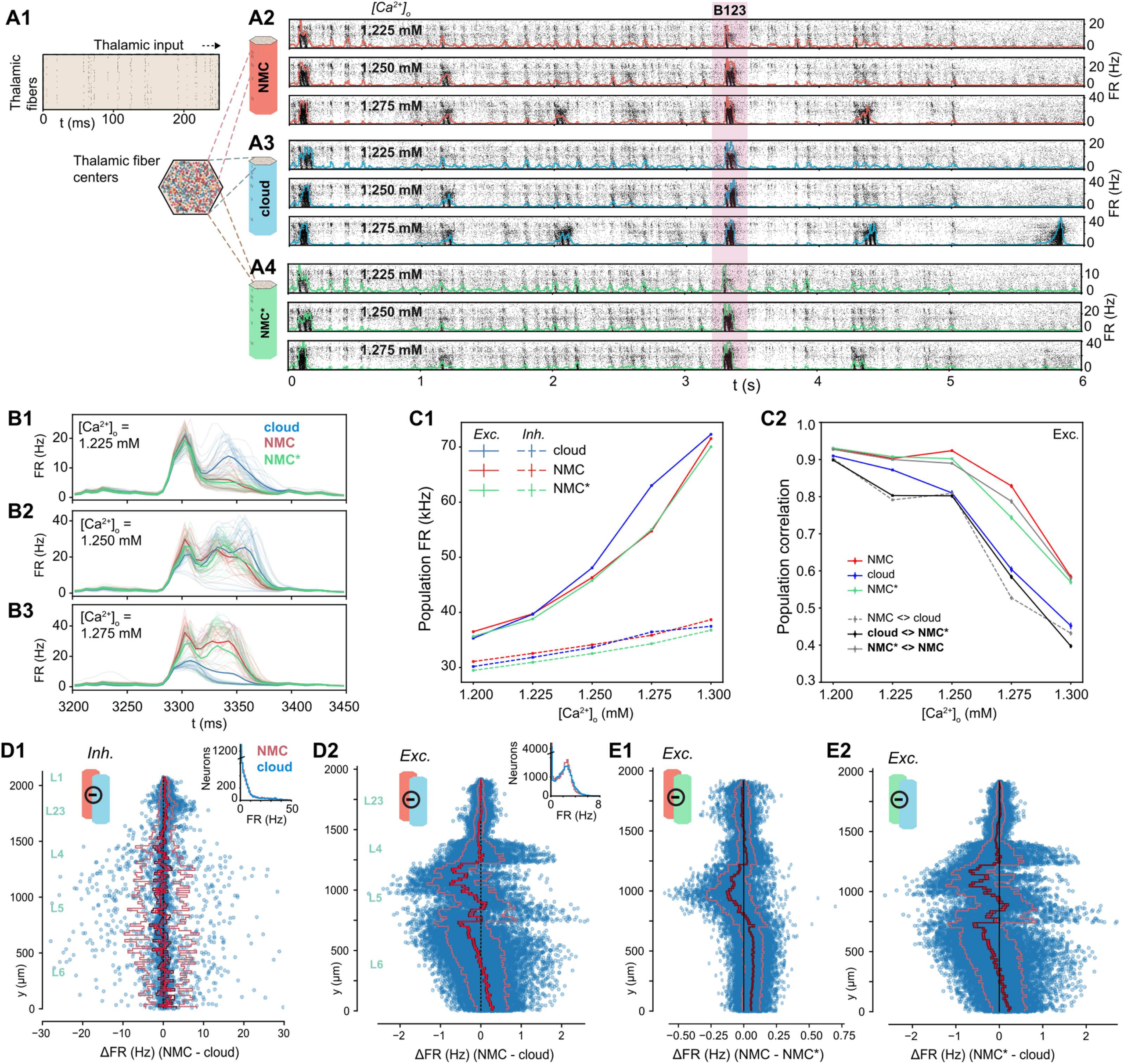
Spontaneous activity in the NMC-model is variable and chaotic, yet thalamic stimuli can
evoke highly reliable responses (Nolte, Reimann, King, Markram, & Muller, 2019). To study
the impact of higher order structure on this evoked activity, we next stimulated the NMC-
and cloud-models with thalamic input (Figure 6A1; see Methods). Similar to spontaneous ac-
attività, the response of the circuits to the input depended on [Ca2+]o (Figure 6A2–4). As we
established that the NMC- and cloud-models have a slightly different transition between dy-
namic states, we compared evoked activity for up to five [Ca2+]o values around the in vivo–
like state. All three models exhibited similar fluctuations of the overall firing rate at various
[Ca2+]o levels, responding robustly with brief increases in firing to periods of correlated tha-
lamic input (Figure 6A2–4). As before, mean firing rates are very similar between the mod-
els, but the cloud-model has increased excitation, especially for larger [Ca2+]o (Figure 6C1,
Supplementary Figure S6A1).
To gain a more detailed understanding of the difference, we next looked at the changes in
firing rates for individual neurons. Excitatory firing rates varied according to the change in in-
degree across cortical depth (Figure 6D2 vs. Figure 3D1). The mean change directly reflects the
change in in-degree shown in Figure 3D1—which is not surprising as any change in in-degree
in the cloud-model is restricted to excitatory connections. While both excitatory and inhibitory
neurons respond to the change in in-degree individually (Supplementary Figure S6B), the sys-
tematic shift in in-degree emerges only for excitatory, but not for inhibitory, neurons (see insets
in Figure 3D1).
Time-dependent response patterns differ between models and [Ca2+]o-levels (Figure 6B1–3),
with distinct patterns and increased trial-by-trial variability in the cloud-model when com-
pared to activity in NMC-models and NMC*-models. To quantify this difference, we calculated
the correlation coefficients of the peristimulus time histograms (PSTHs) between individual
trials of the same model and different models (Figure 6C2, Supplementary Figure S6A2).
The correlation between trials of the same model—that is, the reliability of the popula-
tion response—generally decreased with increasing [Ca2+]o-level, although for the NMC-
and NMC*-models it remained over 0.9 until 1.25 mM and was significantly higher than for
the cloud-model at all levels. Correlations between different models were highest between
Network Neuroscience
303
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 6. Simulating evoked activity in NMC- and cloud-models. (A1) Illustration of the first 250 ms of the thalamic input stimulating
the microcircuit from t = 0 A 5 S. (A2) Evoked activity for all neurons in the NMC-model in response to input from A1 at three different
[Ca2+]o-levels. (A3) Evoked activity for all neurons in the cloud-model at three different [Ca2+]o-levels. (A4) Evoked activity for all neurons
in the NMC*-model at three different [Ca2+]o-levels. (B1) Time-dependent population firing rate for NMC-model (red), cloud-model (blue),
and NMC*-model (green) for a 250-ms time period during the evoked activity (shaded red area in A234) at [Ca2+]o = 1.225 mM. Faint lines:
population means for all 30 trials. Thick line: mean of all 30 trials. Bin size: ∆t = 5 ms. (B2) As B1, but for [Ca2+]o = 1.25 mM. (B3) As
B1 and B2, but for [Ca2+]o = 1.275 mM. (C1) Mean population firing rate of excitatory and inhibitory subpopulations during evoked activity
at different [Ca2+]o-levels. Error bars indicate standard error of the mean over 30 trials. Note that error bars are smaller than linewidth. (C2)
Average correlation coefficient between excitatory population PSTHs (∆t = 5 ms) for 30 trials. Mean of 30 × (30 − 1)/2 = 435 combinazioni
for same model, and mean of 30 × (30 + 1)/2 = 465 combinations between models. (D1) Difference in firing rate of inhibitory neurons during
evoked activity at [Ca2+]o = 1.25 mM. Blue dots indicate values for individual neurons, ordered along their soma positions with respect to
the y-axis (cortical depth). Lines indicate mean (bright red), standard error (dark red), and standard deviation. Inset: Distribution of all mean
firing rates. (D2) As D1, but for excitatory neurons. (E1) As D2, but for NMC-model and NMC*-model. (E2) As D1, but for NMC*-model and
cloud-model.
Network Neuroscience
304
Impact of higher order network structure on emergent cortical activity
Directed simplex:
A specific motif of all-to-all
connected neurons with directed
connectivity between an input and
an output neuron.
NMC- and NMC*-models, further reinforcing that the slight loss of excitatory connections
alone does not explain the observed changes in response patterns of the cloud-model.
We have previously shown that the in-degree also influences the spike-time reliability (rspike)
of individual neurons in response to repeated trials of a thalamic stimulus (Nolte et al., 2019).
While there is overall little change in rspike going from NMC- to cloud-model (Supplementary
Figure S7ABC), we observed a drop in reliability near the top of layer 5, which also displays
a large in-degree reduction in the cloud-model. Further, as neurons with reduced in-degree towards
the bottom of layer 6 spike less, they also become less reliable (Supplementary Figure S7BD).
Similar to the firing rate, the change in spike-time reliability is clearly correlated with the
change in in-degree (Supplementary Figure S7E).
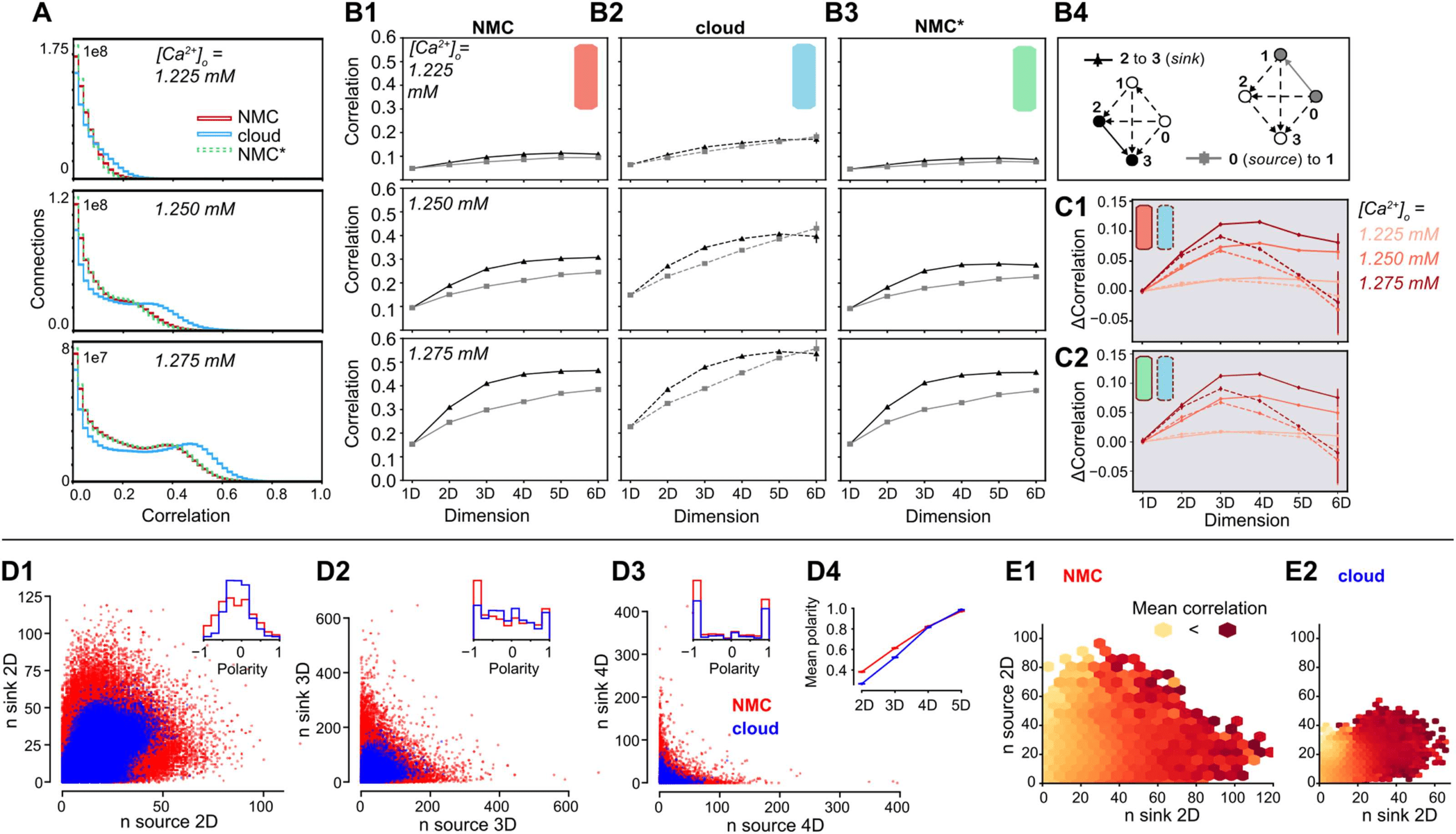
Impact on Ordering of Correlations in Simplices
We have shown that the cloud-model has a reduced bias for forward transitive triplet motifs
(Figure 4B), resulting in a reduced number of directed simplices (Figure 4C1). We have further
demonstrated that this leads to changes in the activity patterns of the circuit, specifically a
reduced reliability of the population response to thalamic input. It has been shown that reliable
responses are linked to increased correlations of synaptic inputs (Nolte et al., 2019; Wang,
Spencer, Fellous, & Sejnowski, 2010), and we previously observed that such input correlations
can be generated by directed simplex motifs with stronger correlations found in larger simplices
(Reimann, Nolte, et al., 2017).
We therefore analyzed the structure of spike-time correlations of pairs of neurons in sim-
plices across models (Figure 7A). As before (see Figure 5D), the overall strengths of correlations
were comparable, though slightly higher in the cloud-model at identical [Ca2+]o-levels. Questo
effect can be explained by the shift along the spectrum from asynchronous to synchronous
activity (see above). Tuttavia, we observed a qualitative difference in the local structure of
correlations within a simplex. As a directed structure, each simplex can be uniquely sorted
from the source neuron, with only outgoing connections to all other neurons in the simplex,
to the sink neuron, with only incoming connections (Figure 7B4). While the correlations in-
creased with simplex size for all three models (Figure 7B1–3), for the NMC- and NMC*-models
they strongly depended on the location of neurons in the simplex, with highest correlations for
the pair at the sink and lowest correlations for the pair at the source. Conversely, in the cloud-
model this difference was reduced and disappeared for the largest simplex sizes (Figure 7C).
In other words, correlations in simplices have a hierarchical organization that leads to a spe-
cialization between input (source) neurons and output (sink) neurons that is diminished in the
cloud-model. This is consistent with the earlier finding that longer-tailed degree distributions
in the NMC-model allow the formation of specialized input- and output-neurons on a struc-
tural level (see Figure 3C). Infatti, this effect extends from the in- and out-degree of individual
neurons to an equivalent measure of simplex participation of connections. For each connec-
zione, we count the number of simplices in which it forms the first connection at the source,
equivalent to the out-degree, and the number of simplices in which it forms the last connection
at the sink, equivalent to the in-degree. As before, we found higher degrees in the NMC-model
(Figure 7D1–3). Two effects led to higher degrees with the same number of connections. Primo,
in the higher order structure of the NMC-model a larger number of simplices were formed
(Figure 4C1); secondly, lower correlations between in- and out-degree in the NMC-model
led to a polarization into connections used predominantly at the sink or source of many sim-
plices. We quantified this polarity of a connection as the relative difference between its in- E
Network Neuroscience
305
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 7. Simplices and correlations in NMC- and cloud-models. (A1) Correlation coefficients of the firing rates (∆t = 20 ms) of all connected
pairs of active neurons in the microcircuit for NMC-model, cloud-model, and NMC*-model, during the 30 trials of the thalamic stimulus
(shown: ≥ 0). (B1) Average correlation coefficient of a connected pair of neurons in a (maximal) simplex of a certain dimension, depending on
the position of the pair in the simplex; for the NMC-model, for three different [Ca2+]o-levels. Black triangles indicate the average correlation
for a pair of neurons at the sink of a simplex, gray squares the average correlation for a pair at the source of a simplex. (B2) As B1, but for
cloud-model. (B3) As B1, but for NMC*-model. (C1) Difference in average correlation coefficient for connections of neurons at the sink and the
source of a (maximal) simplex. Solid lines: NMC-model; dashed lines: cloud-model. (C2) As C1, but for NMC*-model (solid lines) and cloud-
modello (dashed lines). (D1) Participation of connections in the source versus sink of (nonmaximal) 2D-simplices in NMC- and cloud-models
(constrained to connections at the center of layers 4, 5, 6). Inset: Polarity is defined as nsource−nsink
. (D2) As D1, but for 3D-simplices. (D3) As D1,
nsource+nsink
but for 4D-simplices. (D4) Mean polarity for each dimension, defined as mean of |nsource−nsink|
. (E1) Mean correlation given the participation
nsource+nsink
of a connection in (nonmaximal) 2D-simplices at the source and sink, from bright yellow (low correlation) to dark red (high correlation); In
NMC-model, constrained to connections at the center of layers 4, 5, 6. (E2) As D1, but for the cloud-model.
out-degree with respect to simplices of a given dimension. We found that its absolute value
increased with simplex dimension and was overall higher in the NMC-model, indicating a
stronger structural polarization (Figure 7D4).
Taken together, we hypothesize that each simplex provides correlated input to neuron pairs
at its sink, which in turn leads to correlated firing of that pair. While the effect of a single
simplex on a pair may be negligible, strong structural polarization into inputs and outputs
suggests that such pairs are likely to participate as the sink of an unexpectedly high number
of simplices, thus dramatically increasing the size of the effect. The increased number of high-
dimensional simplices and stronger polarization of the NMC-model allows some connections
to participate in even more simplices as the sink. This hypothesis predicts that the correlation
of a neuron pair is determined by the in-degree of its connections and is unaffected by its out-
degree. We therefore quantified how the spike correlations of neuron pairs depend on these
Network Neuroscience
306
Impact of higher order network structure on emergent cortical activity
measures (Figure 7E). Infatti, we found a strong dependence on the in- but not the out-degree
for both models.
DISCUSSION
We introduced a method to reduce the higher order structure of synaptic connectivity in a
neocortical microcircuit model, based on a previously published control connectome with
a reduced common-neighbor bias (Reimann, Horlemann, et al., 2017)—the so-called cloud-
modello. In this cloud-model, excitatory synaptic connectivity between neurons was derived
from average morphologies rather than appositions of axons and dendrites of individual neu-
rons (Figura 1). By design, this approach preserved neuronal and synaptic physiology and loca-
zioni, as well as the aggregate connection strength between m-types. We further demonstrated
that it also preserved macroconnectomic trends, such as distance-dependent and reciprocal
connectivity. We showed that the microconnectome of the cloud-model displayed systematic
changes indicating a reduced higher order structure, such as fewer all-to-all directed cliques
of neurons and reduced small-worldness (Figura 4), but also more homogeneous in- and out-
degree distributions and the disappearance of hub neurons (Figura 3).
Spontaneous and evoked dynamics in the NMC-model and cloud-model are superficially
very similar (Figures 5–6), a result that is not surprising given the conserved first-order struc-
ture, including conserved interlaminar connectivity, structural excitation-inhibition balance,
and distance-dependent connectivity. Tuttavia, some properties of neuronal activity changed.
Spike counts of individual neurons changed according to in-degree, and population responses
were shifted towards more excitation, with less reliable population responses (Figura 6). Most
importantly, a hierarchical dependence of correlation strength on the position of a pair of neu-
rons in directed motifs (simplices) was weaker in the cloud-model than in the NMC-model
(Figura 7). We have demonstrated that this was a result of the more homogeneous in- E
out-degree distributions leading to a reduced polarization into input- and output-neurons, E
consequently reduced participation in simplices.
While the cloud-model has reduced higher order structure, it also has altered degree distri-
butions. The differentiation between conserved first-order structure and reduced higher order
structure is thus not as clean as we might have hoped. Nevertheless, reducing higher order net-
work structure while keeping degree distributions fixed is possible, and such higher order struc-
ture can have an impact on network dynamics (Ritchie, Berthouze, House, & Kiss, 2014). A
better understand the respective impact of changes in in- and out-degrees on one side, E
clustering and high-dimensional motifs on the other side, it will be necessary to create a more
refined control model that conserves degree distributions on top of first-order structure. An al-
ternative derivation of the cloud-connectome could select connections from overlap strengths
such that the in- or out-degree of individual neurons in the NMC-model is preserved, keeping
the degree distributions identical. However this comes at the cost of no longer strictly conserv-
ing the number of connections between pairs of neuron types, thus fundamentally altering the
first-order structure of the circuit.
The comparison between NMC- and cloud-models comes with several caveats. The preser-
vation of distance-dependent connectivity in the cloud-model is better for some m-types than
for others (Figure 2D). Distance-dependance is however much better conserved than in pre-
vious control models that disregarded the average shapes of m-types, resulting in many fewer
simplices (Reimann, Nolte, et al., 2017). The cloud-model further neglects to reduce inhib-
itory higher order structure. Tuttavia, the structural similarity between cloud-connectomes
(changed excitatory and inhibitory connectivity) and the cloud-model (changed excitatory
Network Neuroscience
307
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
connectivity only) suggests that the contribution of inhibitory connections to higher order
network structure in the NMC-model is negligible. This could potentially be due to an un-
derestimation of inhibitory higher order structure in the NMC-model, either because of insuffi-
cient biological data constraining the connectivity, or because inhibitory structure might only
emerge through plasticity (Vogels, Sprekeler, Zenke, Clopath, & Gerstner, 2011).
Infatti, this brings us to the most important caveat: The NMC-model is a statistical recon-
struction of a prototypical microcircuit from sparse data. While it captures a high level of detail
of synaptic connectivity (Gal et al., 2017), with strong constraints on the space of connectivity
that can be explored by structural plasticity (Reimann, Horlemann, et al., 2017), the model
has not learned to respond to specific stimuli or perform certain computations. A compari-
son to numbers of simplices observed in in vitro slice experiments shows that the number of
simplices in the NMC-model is likely underestimated by an order of magnitude (Reimann,
Nolte, et al., 2017). This suggests that a large fraction of biological higher order structure is
not captured by the NMC-model. Allo stesso tempo, learning mechanisms have been shown to
lead to biological structural features, such as overexpression of triplet motifs (Zhang, Zhang, &
Stepanyants, 2018). This leads to at least two interesting questions to be explored in the future:
(UN) What is the functional impact of that additional higher order structure on network dynam-
ics? E (B) Given a biologically plausible model of structural plasticity, could the network
reach similar higher order structure starting from both NMC- and cloud-models?
Our method of separating first-and higher order structure need not only be applied to sta-
tistical connectome models, but might also be useful for the interpretation of future dense re-
constructions of brain tissue using electron microscopy (Kasthuri et al., 2015). Once a volume
large enough to contain several neurons of different m-types can be reconstructed, comparing
the cloud connectivity of average reconstructed neurons to the actual biological connectivity
could serve as a powerful control to interpret the structure of synaptic connectivity. In par-
ticular, it can help quantify how much structure emerges from plasticity mechanisms (Zhang
et al., 2018), and how much is determined by other factors, such as neuronal morphologies
(Gal et al., 2017; Reimann, Horlemann, et al., 2017).
In summary, we investigated the functional impact of higher order network structure of neo-
cortical microcircuitry. Complementing previous investigations of the relation between higher
order structure and activity in simplifying recurrent neural networks (Bojanek et al., 2019; Eh
et al., 2013; Recanatesi et al., 2019), we have quantified the relation in a biologically detailed
model that takes into account important biological properties that shape network dynamics
such as adapting, neuron-type specific synapses, and dendritic filtering. Using tools from alge-
braic topology and classical graph analysis, our analysis demonstrates just how many higher
order structural properties are constrained by neuronal diversity within neuronal types. Nostro
comparison between the two models suggests that the higher order network structure of cortical
synaptic connectivity impacts emergent dynamics and might be a nonnegligible component
of cortical function.
METHODS
Circuit Models
Neocortical microcircuit model (NMC-model). Methods are based on a previously published
model of a neocortical microcircuit of the somatosensory cortex of a two-week-old rat, here
called the NMC-model (Markram et al., 2015). Synaptic connectivity (with apposition-based
connectome/adjacency matrix AC1) between 31,346 neurons belonging to 55 different
Neuronal morphology:
The shape of a neuron, particularly of
its dendrites and axons.
Network Neuroscience
308
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
morphological types (m-types) was derived algorithmically starting from the appositions of den-
drites and axons, and then taking into account further biological constraints such as number of
synapses per connection and bouton densities (Reimann et al., 2015). Neuronal activity in the
NMC-model was then simulated in the NEURON simulation environment (www.neuron.yale.
edu/neuron/). Detailed information about the circuit, NEURON models, and the seven con-
nectomes of the different statistical instantiations of the NMC-model analyzed in this study are
available at www.neuron.yale.edu/neuron/ (Ramaswamy et al., 2015). Simulations and analy-
sis were performed on an HPE SGI 8600 supercomputer (BlueBrain5).
mi
mi
(X, sì) and V axon
Synaptic connectivity based on average morphologies (with cloud-based
Cloud-connectome.
connectome/adjacency matrix CC) was computed with methods previously described by
Reimann, Horlemann, et al. (2017). In brief, for each m-type mi out of the 55 m-types, we
computed Vdendrite
(X, sì), the mean dendrite and axon density of each m-type,
based on 10 reconstructed morphologies per m-type, with a resolution of 2µm × 2µm. Prossimo, we
computed the convolution of axon and dendrite densities Vcloud-overlap
∗
V axon
for all combinations of m-types. This yielded a measure of the expected strength of the
mj
overlap of axon and dendrite for pairs of neurons at all potential relative soma positions. Noi
then looked up this value for all pairs of neurons of a given combination of m-types mi → mj,
based on their locations in the NMC-model and formed a matrix of overlap strengths Ocloud
mi→mj
(stored in a table). We next applied a transfer function ˜O = O2, which was chosen to con-
serve distance-dependent connectivity from the NMC-model for most m-type combinations
(Reimann, Horlemann, et al., 2017). We then normalized the matrix ˜Ocloud
to yield a matrix
mi→mj
of connection probabilities. Finalmente, we turned the matrix into a connectome instance by ran-
domly picking without replacement the same number of connections as in ACmi→mj, questo è
with the following algorithm:
(∆y, ∆x) = Vdendrite
mi→mj
mi
1. Randomly pick an entry according to the connection probabilities in ˜O.
2. Place the connection associated with the picked entry and set its probability to 0 to avoid
picking it again.
3. Renormalize the connection probabilities to compensate.
4. Repeat at Step 1 until the target number of connections has been placed.
The full cloud-based adjacency matrix CC was assembled from individual, randomly gen-
erated matrices for all 55 × 55 mi → mj combinations.
Five example connectomes CC1-5 for each of the seven NMC-connectomes AC1-7 are
available at bbp.epfl.ch/nmc-portal/downloads → AVERAGE (Reimann, Horlemann,
et al., 2017).
Cloud-model. We implemented one of the cloud-model connectomes (CC1) within the ex-
isting neurons of the NMC-model, using preexisting synapses from the NMC-model. To keep
physiological properties such as mean number of synapses per connection conserved, we
rewired connections by changing the source of netCon in NEURON for all synapses in a con-
nection to a new presynaptic neuron according to CC1, and we constrained this rewiring to
connections with the same presynaptic m-type in the cloud- as in the NMC-model. If there
were less connections of a mi → mj combination than required by CC1, we duplicated con-
nections and their synapses. As some neurons receive input in CC1 from neurons that they did
not receive input in in AC1, some connections could not be implemented. This was a particu-
lar problem for inhibitory connections, and we therefore implemented CC1 only for excitatory
Network Neuroscience
309
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
neurons. This resulted in a connectivity matrix CC1* that uses CC1 for excitatory connections
(con un 0.12% loss of connections), and conserved connectivity AC1 for inhibitory connections.
To ensure that any changes in emergent activity were not due to the 0.12%
NMC*-model.
of missing connections, or to a shuffling of path lengths (shuffled delays of action potential
propagation from soma to synapse), we created a control circuit in which we randomly re-
moved exactly the same number of connections per m-type combination (0.12%) from the
NMC-model as could not be implemented in the cloud-model, questo è,
AC1∗,mi→mj = CC1∗,mi→mj
.
(1)
We then shuffled the path length parameter between connections with the same presynaptic
m-type for each postsynaptic neuron (only for excitatory neurons). This recreated the effect of
potentially biologically implausible action potential delays in the cloud-model.
Simulation
Simulation methods are identical to methods described by Markram
Spontaneous activity.
et al. (2015): To simulate spontaneous activity, neurons were injected with a depolarizing so-
matic current, with currents expressed as a percentage of first spike threshold for each neuron
(100% current used). The USE parameter for synaptic transmission of inhibitory and excitatory
synapses was then differentially modulated by changing the extracellular calcium concentra-
zione [Ca2+]o. A [Ca2+]o = 1.25 mM, the circuit was in an in vivo–like state of asynchronous
activity with a global balance of excitation and inhibition. We simulated 20 trials of sponta-
neous activity (2 S) in the NMC-model, cloud-model, and NMC-modelcloud-control at five dif-
ferent [Ca2+]o concentrations around the in vivo–like state at [Ca2+]o = 1.25 mM. We further
added two trials of 2-s duration at other [Ca2+]o concentrations to illustrate the transition from
asynchronous to synchronous activity. The first second of activity was discarded, as the circuit
does not reach a resting state until the second second.
Evoked activity. We simulated spontaneous activity for 7 S, as described above. Dopo 1 S (at
t = 0 ms, as we discard the first second) we apply a thalamic stimulus through synapses of
310 VPM fibers that innervate the microcircuit. The stimulus lasts 5 S (t = 0 A 5 S) and is
identical to a previously described stimulus (Nolte et al., 2019; Reimann, Nolte, et al., 2017)
based on in vivo thalamic recordings to whisker deflection (Bale, Ince, Santagata, & Petersen,
2015). We simulated 30 trials of the same stimulus in the NMC-model, cloud-model, E
NMC-modelcloud-control at five different [Ca2+]o concentrations around the in vivo–like state at
[Ca2+]o = 1.25 mM.
Analysis
In-degree. Number of presynaptic connections a neuron forms with other neurons in the
microcircuit.
Out-degree. Number of postsynaptic connections a neuron forms with other neurons in the
microcircuit.
A simplex is a clique of all-to-all connected neurons. Methods and definitions
Simplices.
were adapted from Reimann, Nolte, et al. (2017). In brief, if G = (V, E) is a directed graph,
Network Neuroscience
310
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
N
e
N
_
UN
_
0
0
1
2
4
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Impact of higher order network structure on emergent cortical activity
where V is a set of vertices (neurons) and E a set of ordered pairs of vertices (directed connec-
tions between neurons), then its directed nD-simplices for n ≥ 1 are (N + 1)-tuples (v0, . . . , vn)
of vertices such that for each 0 ≤ i < j ≤ n, there is an edge in G directed from vi to vj. Neu-
ron 0 (the vertex v0), the source of the simplex (v0, . . . , vn), receives no input from within the
simplex, but innervates all neurons in the simplex (there is an edge directed from v0 to vi for
all 0 < i ≤ n). Neuron 1 (v1), receives input from Neuron 0, and innervates Neurons 2 (v1) to n
(vn), and so forth. Neuron n, the sink, receives input from all neurons in the simplex, but does
not innervate any (there is an edge directed from v0 to vi for all 0 < i ≤ n). See Figure 7B4 for
an illustration. Note that reciprocal connections are counted separately: an n-simplex in G is
defined by the (ordered) sequence (v0, . . . , vn), but not by the underlying set of vertices (neu-
rons). For instance (v1, v2, v3) and (v2, v1, v3) are distinct 2D-simplices with the same neurons.
We computed simplices using flagser (https://github.com/luetge/flagser).
Note that to avoid redundancy, the average correlation in Figures 6ABC is for maximal sim-
plices, simplices that are not part of any higher dimensional simplices (Reimann, Nolte, et al.,
2017), whereas all other figures show all simplices, including ones that are fully contained
within simplices of a higher dimension.
Higher order in-degree. We define the ND-in-degree as the number of ND-simplices a neuron
is the sink of. For 1D-simplices (a pair of connected neurons), this is simply the in-degree.
Simplex participation of pairs of neurons. We define as the ND-participation of connections
at the source or the sink of a simplex how many ND-simplices a connection is part of as the
source (Neurons 0 and 1) or at the sink (neurons N − 1 and N).
In brief, Betti numbers describe the number of cavities or “holes” formed by
Betti numbers.
the simplices in each dimension. Betti numbers were computed using flagser (https://github.
com/luetge/flagser). Detailed methods are as previously described by Reimann, Nolte, et al.
(2017).
Euler characteristic.
of nonzero Betti numbers).
The alternating sum of the number of simplices in each dimension (and
Small-worldness. Methods are as defined by Gal et al. (2017) and were computed using the
Brain Connectivity Toolbox (Rubinov & Sporns, 2010). In brief, we first computed the charac-
teristic path length of the network, defined as the mean shortest directed path length averaged
across all pairs of mutually reachable neurons:
l =
1
N(N − 1)
lij,
∑
i6=j
(2)
where lij denotes the length of the shortest path from neuron i to j.
The clustering coefficient of a node in a directed network, ci, indicating the tendency of the
node’s neighbors to cluster together, was defined as the ratio of the number of existing triangles
among the node and its neighbors to the number of all possible triangles (Fagiolo, 2007):
ci =
(M + MT)3
ii
2(dtot
i (dtot
i − 1) − 2M2
ii)
,
(3)
311
Directed network:
A network of vertices (neurons)
connected by directed edges
(synapses) that transmit information
in a specific direction.
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
n
e
n
_
a
_
0
0
1
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact of higher order network structure on emergent cortical activity
where M is the binary connection matrix and dtot
neuron i. Finally, we defined the network-wide clustering coefficient as
i
the combined in- and out-degree of each
c =
1
N
ci.
∑
i
(4)
Thus, c = 0 indicates that there are no common neighbors, and c = 1 indicates that all
neighbors are mutually connected. The ratio of c/l gives indication about the small-worldness
of the network. We showed previously that the NMC-model has a small-world topology by
comparing it to different control models (Gal et al., 2017). A smaller value of c/l for the cloud
than for the NMC-model thus shows that small-worldness decreases.
Triplet motif counting.
Markram, London, & Segev, 2019) available at https://github.com/gialdetti/netsci.
Triplet motifs were counted using the netsci Python library (Gal, Perin,
Firing rate. We defined the firing rate (FR) as the average number of spikes in a time bin of
size ∆t, divided by ∆t.
Spike-time reliability was quantified with a correlation-based measure
Spike-time reliability.
(Schreiber, Fellous, Whitmer, Tiesinga, & Sejnowski, 2003). The spike times of each neuron n
in each trial k (K = 30 trials) were convolved with a Gaussian kernel of width σS = 5 ms to
result in filtered signals s(n, k; t) for each neuron n and each trial k (∆tS = 0.5 ms). For each
neuron n, the spike-timing reliability is defined as the mean inner product between all pairs
of signals divided by their magnitude:
rspike(n) =
2
K(K − 1)
∑
k6=l
s(n, k; t) · s(n, l; t)
|s(n, k; t)| · |s(n, l; t)|
.
(5)
Note that rspike is thus the mean reliability over all trials and time. Computation of spike-time
reliability is identical to a previous study (Nolte et al., 2019).
Correlation coefficients. We computed peristimulus time histograms (PSTHs) for each neuron
i to the 30 trials of the thalamic stimulus (with a bin size ∆t = 20 ms), and next computed the
normalized covariance matrix of the PSTHs of all neurons:
Rij =
Cij
qCiiCjj
.
(6)
Cij is the covariance of PSTHs of neurons i and j. The analysis is replicating a previous analysis
by Reimann, Nolte, et al. (2017). Population-based correlation coefficients used aggregated
PSTHs of the population of neurons (either subpopulation for spatial correlations, or whole
circuit for correlations between trials and circuits).
ACKNOWLEDGMENTS
We thank the Blue Brain team for developing and maintaining the microcircuit model and
computational infrastructure. We thank Kathryn Hess, Idan Segev, and Eilif Muller for helpful
discussions. We thank Taylor H. Newton for help in editing the manuscript. This study was
supported by funding to the Blue Brain Project, a research center of the École Polytechnique
Network Neuroscience
312
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
n
e
n
_
a
_
0
0
1
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact of higher order network structure on emergent cortical activity
Fédérale de Lausanne, from the Swiss government’s ETH Board of the Swiss Federal Institutes
of Technology. E. G. was supported by the Drahi Family Foundation to Idan Segev, and a grant
from the EU Horizon 2020 program (720270, Human Brain Project).
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00124.
AUTHOR CONTRIBUTIONS
Max Nolte: Conceptualization; Investigation; Methodology; Software; Validation; Visualiza-
tion; Writing - Original Draft; Writing - Review & Editing. Eyal Gal: Investigation. Henry
Markram: Conceptualization; Supervision. Michael Wolfgang Reimann: Conceptualization;
Methodology; Software; Supervision; Validation; Visualization; Writing - Review & Editing.
FUNDING INFORMATION
The Swiss government’s ETH Board of the Swiss Federal Institutes of Technology. Eyal Gal,
Drahi Family Foundation. Eyal Gal, EU Horizon 2020 Programme, Award ID: 720270. École
Polytechnique Fédérale de Lausanne (http://dx.doi.org/10.13039/501100001703).
REFERENCES
Bale, M. R., Ince, R. A. A., Santagata, G., & Petersen, R. S. (2015).
Efficient population coding of naturalistic whisker motion in the
ventro-posterior medial thalamus based on precise spike tim-
ing. Frontiers in Neural Circuits, 9. https://doi.org/10.3389/fncir.
2015.00050
Benson, A. R., Gleich, D. F., & Leskovec, J. (2016). Higher-order or-
ganization of complex networks. Science, 353(6295), 163–166.
https://doi.org/10.1126/science.aad9029
Bojanek, K., Zhu, Y., & MacLean, J. (2019). Cyclic transitions be-
tween higher order motifs underlie sustained activity in asyn-
chronous sparse recurrent networks. bioRxiv: 777219. https://
doi.org/10.1101/777219
Braitenberg, V.
(1978). Cell assemblies in the cerebral cortex.
In Theoretical approaches to complex systems (pp. 171–188).
Berlin, Germany: Springer. https://doi.org/10.1007/978-3-642-
93083-6_9
Fagiolo, G. (2007). Clustering in complex directed networks. Physi-
cal Review E, 76, 026107. https://doi.org/10.1103/PhysRevE.76.
026107
Feldmeyer, D., Lubke, J., Silver, R. A., & Sakmann, B. (2002). Synap-
tic connections between layer 4 spiny neurone-layer 2/3 pyra-
midal cell pairs in juvenile rat barrel cortex: Physiology and
anatomy of interlaminar signalling within a cortical column.
Journal of Physiology, 538(3), 803–822. https://doi.org/10.1113/
jphysiol.2001.012959
Fino, E., & Yuste, R.
(2011). Dense inhibitory connectivity in
neocortex. Neuron, 69(6), 1188–1203. https://doi.org/10.1016/
j.neuron.2011.02.025
Gal, E., London, M., Globerson, A., Ramaswamy, S., Reimann,
M. W., Muller, E., . . . Segev, I. (2017). Rich cell-type-specific
network topology in neocortical microcircuitry. Nature Neuro-
science, 20, 1004–1013. https://doi.org/10.1038/nn.4576
Gal, E., Perin, R., Markram, H., London, M., & Segev, I. (2019). Neu-
ron geometry underlies a universal local architecture in neuronal
networks. bioRxiv: 656058. https://doi.org/10.1101/656058
Hebb, D. (1949). The organization of behaviour. New York, NY:
Wiley & Sons.
Holmgren, C., Harkany, T., Svennenfors, B., & Zilberter, Y. (2003).
Pyramidal cell communication within local networks in layer 2/3
of rat neocortex. Journal of Physiology, 551(1), 139–153. https://
doi.org/10.1113/jphysiol.2003.044784
Hu, Y., Trousdale, J., Josi, K., & Shea-Brown, E. (2013). Motif statis-
tics and spike correlations in neuronal networks. Journal of Sta-
tistical Mechanics: Theory and Experiment, 2013(03), P03012.
https://doi.org/10.1088/1742-5468/2013/03/P03012
Jiang, X., Shen, S., Cadwell, C. R., Berens, P., Sinz, F., Ecker, A. S., . . .
Tolias, A. S. (2015). Principles of connectivity among morpholog-
ically defined cell types in adult neocortex. Science, 350(6264),
aac9462. https://doi.org/10.1126/science.aac9462
Kasthuri, N., Hayworth, K.
J., Berger, D. R., Schalek, R. L.,
Conchello, J. A., Knowles-Barley, S., . . . Lichtman, J. W. (2015).
Saturated reconstruction of a volume of neocortex. Cell, 162(3),
648–661. https://doi.org/10.1016/j.cell.2015.06.054
Landau,
Knoblauch, A., Palm, G., & Sommer, F. T. (2009). Memory capac-
ities for synaptic and structural plasticity. Neural Computation,
22(2), 289–341. https://doi.org/10.1162/neco.2009.08-07-588
J., Oberlaender, M., &
Sompolinsky, H. (2016). The impact of structural heterogene-
ity on excitation-inhibition balance in cortical networks. Neu-
ron, 92(5), 1106–1121. https://doi.org/10.1016/j.neuron.2016.10.
027
I. D., Egger, R., Dercksen, V.
Le Bé, J.-V., Silberberg, G., Wang, Y., & Markram, H. (2007). Mor-
phological, Electrophysiological, and Synaptic Properties of cor-
ticocallosal Pyramidal Cells in the Neonatal Rat Neocortex.
Network Neuroscience
313
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
n
e
n
_
a
_
0
0
1
2
4
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Impact of higher order network structure on emergent cortical activity
Cerebral Cortex, 2204–2213. Retrieved from http://cercor.
oxfordjournals.org/content/17/9/2204
Litwin-Kumar, A., & Doiron, B.
(2012). Slow dynamics and high
variability in balanced cortical networks with clustered connec-
tions. Nature Neuroscience, 15(11), 1498–1505. https://doi.org/
10.1038/nn.3220
Markram, H., Muller, E., Ramaswamy, S., Reimann, M., Abdellah,
M., Sanchez, C., . . . Schrmann, F. (2015). Reconstruction and
simulation of neocortical microcircuitry. Cell, 163(2), 456–492.
https://doi.org/10.1016/j.cell.2015.09.029
Nolte, M., Reimann, M. W., King, J. G., Markram, H., & Muller, E. B.
(2019). Cortical reliability amid noise andchaos. Nature Communi-
cations, 10(1), 1–15. https://doi.org/10.1038/s41467-019-11633-8
Perin, R., Berger, T. K., & Markram, H. (2011). A synaptic orga-
nizing principle for cortical neuronal groups. Proceedings of the
National Academy of Sciences, 108(13), 5419–5424. https://doi.
org/10.1073/pnas.1016051108
Ramaswamy, S., Courcol, J.-D., Abdellah, M., Adaszewski, S. R.,
Antille, N., Arsever, S., . . . Markram, H. (2015). The neocortical
microcircuit collaboration portal: A resource for rat somatosen-
sory cortex. Frontiers in Neural Circuits, 9. https://doi.org/10.
3389/fncir.2015.00044
Recanatesi, S., Ocker, G. K., Buice, M. A., & Shea-Brown, E. (2019).
Dimensionality in recurrent spiki ng networks: Global trends in
activity and local origins in connectivity. PLoS Computational
Biology, 15(7), e1006446. https://doi.org/10.1371/journal.pcbi.
1006446
Reimann, M. W., Horlemann, A.-L., Ramaswamy, S., Muller, E. B.,
& Markram, H. (2017). Morphological diversity strongly con-
strains synaptic connectivity and plasticity. Cerebral Cortex,
27(9), 4570–4585. https://doi.org/10.1093/cercor/bhx150
Reimann, M. W., King, J. G., Muller, E. B., Ramaswamy, S., &
Markram, H. (2015). An algorithm to predict the connectome of
neural microcircuits. Frontiers in Computational Neuroscience,
9. https://doi.org/10.3389/fncom.2015.00120
Reimann, M. W., Nolte, M., Scolamiero, M., Turner, K., Perin, R.,
Chindemi, G., . . . Markram, H. (2017). Cliques of neurons bound
into cavities provide a missing link between structure and func-
tion. Frontiers in Computational Neuroscience, 11. https://doi.
org/10.3389/fncom.2017.00048
Reyes-Puerta, V., Sun, J.-J., Kim, S., Kilb, W., & Luhmann, H. J.
(2014). Laminar and columnar structure of sensory-evoked multi-
neuronal spike sequences in adult rat barrel cortex in vivo. Cere-
bral Cortex, bhu007. https://doi.org/10.1093/cercor/bhu007
Ritchie, M., Berthouze, L., House, T., & Kiss, I. Z. (2014). Higher-
order structure and epidemic dynamics in clustered networks.
Journal of Theoretical Biology, 348, 21–32. https://doi.org/10.
1016/j.jtbi.2014.01.025
Rosenbaum, R., Smith, M. A., Kohn, A., Rubin, J. E., & Doiron, B.
(2017). The spatial structure of correlated neuronal variability.
Nature Neuroscience, 20(1), 107–114. https://doi.org/10.1038/
nn.4433
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003
Schreiber, S., Fellous, J. M., Whitmer, D., Tiesinga, P., & Sejnowski,
T. J. (2003). A new correlation-based measure of spike timing
reliability. Neurocomputing, 5254, 925–931. https://doi.org/10.
1016/S0925-2312(02)00838-X
Silberberg, G., & Markram, H. (2007). Disynaptic inhibition be-
tween neocortical pyramidal cells mediated by martinotti cells.
Neuron, 53(5), 735–746. https://doi.org/10.1016/j.neuron.2007.
02.012
Simonyan, K., & Zisserman, A. (2014). Very deep convolutional net-
works for large-scale image recognition. arXiv:1409.1556 [cs].
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., & Chklovskii, D. B.
(2005). Highly nonrandom features of synaptic connectivity in
local cortical circuits. PLoS Biology, 3(3), e68. https://doi.org/10.
1371/journal.pbio.0030068
Vogels, T. P., Sprekeler, H., Zenke, F., Clopath, C., & Gerstner, W.
(2011). Inhibitory plasticity balances excitation and inhibition in
sensory pathways and memory networks. Science, 334(6062),
1569–1573. https://doi.org/10.1126/science.1211095
Wang, H.-P., Spencer, D., Fellous, J.-M., & Sejnowski, T. J. (2010).
Synchrony of thalamocortical inputs maximizes cortical relia-
bility. Science, 328(5974), 106–109. https://doi.org/10.1126/
science.1183108
Willshaw, D. J., Buneman, O. P., & Longuet-Higgins, H. C. (1969).
Non-holographicassociative memory. Nature,222(5197), 960–962.
Yin, W., Brittain, D., Borseth, J., Scott, M. E., Williams, D., Perkins,
J., . . . da Costa, N. M. (2019). A petascale automated imag-
ing pipeline for mapping neuronal circuits with high-throughput
transmission electron microsopy. bioRxiv:791889. https://doi.
org/10.1101/791889
Zhang, D., Zhang, C., & Stepanyants, A. (2018). Robust associative
learning is sufficient to explain structural and dynamical proper-
ties of local cortical circuits. bioRxiv:320432. https://doi.org/10.
1101/320432
Network Neuroscience
314
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
4
1
2
9
2
1
8
6
6
8
4
7
n
e
n
_
a
_
0
0
1
2
4
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3