Research
The self-organized learning of noisy environmental
stimuli requires distinct phases of plasticity
Steffen Krüppel
1,2
and Christian Tetzlaff
1,2
1Department of Computational Neuroscience, Third Institute of Physics – Biophysics, Georg-August-University,
Göttingen, Germany
2Bernstein Center for Computational Neuroscience, Georg-August-University, Göttingen, Germany
Keywords: Synaptic plasticity, Intrinsic plasticity, Noise-robustness, Apprendimento, Sensory pathways
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
Along sensory pathways, representations of environmental stimuli become increasingly
sparse and expanded. If additionally the feed-forward synaptic weights are structured
according to the inherent organization of stimuli, the increase in sparseness and expansion
leads to a reduction of sensory noise. Tuttavia, it is unknown how the synapses in the brain
form the required structure, especially given the omnipresent noise of environmental stimuli.
Here, we employ a combination of synaptic plasticity and intrinsic plasticity—adapting the
excitability of each neuron individually—and present stimuli with an inherent organization
to a feed-forward network. We observe that intrinsic plasticity maintains the sparseness of the
neural code and thereby allows synaptic plasticity to learn the organization of stimuli in
low-noise environments. Nevertheless, even high levels of noise can be handled after a
subsequent phase of readaptation of the neuronal excitabilities by intrinsic plasticity.
È interessante notare, during this phase the synaptic structure has to be maintained. These results
demonstrate that learning and recalling in the presence of noise requires the coordinated
interplay between plasticity mechanisms adapting different properties of the neuronal circuit.
AUTHOR SUMMARY
Everyday life requires living beings to continuously recognize and categorize perceived
stimuli from the environment. To master this task, the representations of these stimuli become
increasingly sparse and expanded along the sensory pathways of the brain. Inoltre, IL
underlying neuronal network has to be structured according to the inherent organization of
the environmental stimuli. Tuttavia, how the neuronal network learns the required structure
even in the presence of noise remains unknown. In this theoretical study, we show that the
interplay between synaptic plasticity—controlling the synaptic efficacies—and intrinsic
plasticity—adapting the neuronal excitabilities—enables the network to encode the
organization of environmental stimuli. It thereby structures the network to correctly
categorize stimuli even in the presence of noise. After having encoded the stimuli’s
organization, consolidating the synaptic structure while keeping the neuronal excitabilities
dynamic enables the neuronal system to readapt to arbitrary levels of noise resulting in a
near-optimal classification performance for all noise levels. These results provide new insights
into the interplay between different plasticity mechanisms and how this interplay enables
sensory systems to reliably learn and categorize stimuli from the surrounding environment.
Citation: Krüppel, S., & Tetzlaff, C.
(2020). The self-organized learning of
noisy environmental stimuli requires
distinct phases of plasticity. Network
Neuroscience, 4(1), 174–199. https://
doi.org/10.1162/netn_a_00118
DOI:
https://doi.org/10.1162/netn_a_00118
Supporting Information:
https://doi.org/10.1162/netn_a_00118
Received: 31 Luglio 2019
Accepted: 09 Dicembre 2019
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Christian Tetzlaff
tetzlaff@phys.uni-goettingen.de
Handling Editor:
Olaf Sporns
Copyright: © 2019
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
INTRODUCTION
Learning to distinguish between different stimuli despite high levels of noise is an important
ability of living beings to ensure survival. Tuttavia, the underlying neuronal and synaptic
processes of this ability are largely unknown.
The brain is responsible for controlling movements of an agent’s body in response to the
perceived stimulus. For instance, the agent should run away from a predator or run after the
prey. To do so, the agent needs to be able to reliably classify the perceived stimulus despite
its natural variability (per esempio., different individuals of the same predator species) or noise (per esempio.,
impaired vision by obstacles). Generalmente, the sensory processing systems of the brain map the
stimulus representation onto subsequent brain areas yielding successive representations which
are increasingly sparse in activity and expansive in the number of neurons. If the feed-forward
synaptic weights realizing this mapping are structured according to the inherent organization of
the stimuli (per esempio., lion versus pig), the increased sparseness and expansion lead to a significant
reduction of noise and therefore to a reliable classification (Babadi & Sompolinsky, 2014).
Tuttavia, it remains unclear how the synapses form the required structure despite noise during
apprendimento. Inoltre, how can the system reliably adapt to varying levels of noise (per esempio., being
in a silent forest compared with near a loud stream)?
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
In the mouse olfactory system, for instance, 1, 800 glomeruli receiving signals from olfac-
tory sensory neurons project to millions of pyramidal neurons in the piriform cortex yielding
an expansion of the stimulus representation (Franks & Isaacson, 2006; Mombaerts et al., 1996).
Activity of the glomeruli is relatively dense with 10%–30% of glomeruli responding to a given
natural odor (Vincis, Gschwend, Bhaukaurally, Beroud, & Carleton, 2012), while in the piri-
form cortex activity drops to 3%–15% indicating an increase in sparseness (Poo & Isaacson,
2009; Stettler & Axel, 2009). A similar picture can be observed in the Drosophila olfactory sys-
tem. Here, 50 glomeruli project to about 2, 500 Kenyon cells in the mushroom body (Balling,
Technau, & Heisenberg, 1987; Jefferis et al., 2007). While about 59% of projection neurons
respond to a given odor, only 6% of Kenyon cells do (Turner, Bazhenov, & Laurent, 2008).
Similar ratios have been observed in the locust olfactory system (Perez-Orive et al., 2002). In
the cat visual system, the primary visual cortex has 25 times as many outputs than it receives
inputs from the LGN (Olshausen, 2003). Inoltre, V1-responses to natural visual stimuli are
significantly sparser than in the LGN (Dan, Atick, & Reid, 1996; Vinje & Gallant, 2000). Both
principles of increased expansion and sparseness of stimulus representations apply to other
sensory processing systems as well (Brecht & Sakmann, 2002; Chacron, Longtin, & Maler,
2011; Deweese & Zador, 2003).
The functional roles of increased sparseness as well as expansion have already been pro-
posed in the Marr-Albus theory of the cerebellum (Albus, 1971; Marr, 1969). Here, different
representations are thought to evoke different movement responses even though the activity
patterns overlap. The Marr-Albus theory demonstrates that through expansion and the sparse
activity of granule cells, the overlapping patterns are mapped onto nonoverlapping patterns that
can easily be classified. A recent theoretical study has focused on sparse and expansive feed-
forward networks in sensory processing systems (Babadi & Sompolinsky, 2014). Here, piccolo
variations in activity patterns are caused by internal neuronal noise, input noise, or changes in
insignificant properties of the stimuli. For reliable stimulus classification, these slightly varying
activity patterns belonging to the same underlying stimulus should evoke the same response
in a second layer (or brain area) of a sparse and expansive feed-forward network. Surprisingly,
although the network is sparse and expansive, random synaptic weights increase both noise
and overlap of activity patterns in the second layer. D'altra parte, the same network with
Synaptic weights:
The average transmission efficacy of
a synapse quantified as a single
number being adapted by diverse
plasticity processes.
Olfactory system:
The olfactory system includes all
brain areas processing sensory
information related to the sense of
smell.
Piriform cortex:
One brain area in the cerebrum
processing sensory information of the
sense of smell.
Mushroom body:
A brain area in insects that is
important for odor-related learning
and memory.
Cerebellum:
A brain area responsible for the
control of movement-related
functions such as coordination,
timing, or precision.
Network Neuroscience
175
Learning of noisy stimuli requires distinct phases of plasticity
Synaptic plasticity:
General term for different kinds of
biological mechanisms adapting the
weights of synapses depending on
neuronal activities.
Homeostatic synaptic plasticity:
Synaptic plasticity mechanism
adapting the synaptic weights such
that the neuronal dynamics remain in
a desired “healthy” regime.
Intrinsic plasticity:
General term for different kinds of
biological mechanisms adapting the
firing threshold or excitability of a
neuron.
synaptic weights structured according to the organization of stimuli reduces the noise and
overlap of activity patterns, simplifying subsequent classification. How a network is able to
learn the organization of stimuli, shape its synaptic structure according to this organization,
and do so even in the presence of noise is so far unknown.
The generally accepted hypothesis of learning is that it is realized by changes of synap-
tic weights by the process of (long-term) synaptic plasticity (Hebb, 1949; Martin, Grimwood,
& Morris, 2000). Synaptic weights are strengthened or weakened depending on the activity
of the pre- and postsynaptic neurons (Bi & Poo, 1998; Bliss & Lømo, 1973; Markram, Lübke,
Frotscher, & Sakmann, 1997). Hebbian plasticity describes the process of increasing a synaptic
weight if the activity of the two connected neurons is correlated (Hebb, 1949). Several theoret-
ical studies indicate that Hebbian plasticity alone would lead to divergent synaptic and neu-
ronal dynamics, thus requiring homeostatic synaptic plasticity (Triesch, Vo, & Hafner, 2018;
G. G. Turrigiano, Leslie, Desai, Rutherford, & Nelson, 1998) to counterbalance and stabilize
the dynamics (Mugnaio & MacKay, 1994; Tetzlaff, Kolodziejski, Timme, & Wörgötter, 2011; Yger
& Gilson, 2015; Zenke & Gerstner, 2017; Zenke, Hennequin, & Gerstner, 2013). Inoltre,
neurons adapt their excitability by the process of intrinsic plasticity (Triesch, 2007; Zhang &
Linden, 2003). Intrinsic plasticity regulates the excitability of a given neuron so as to main-
tain a desired average activity (Benda & Herz, 2003; Desai, Rutherford, & Turrigiano, 1999;
LeMasson, Marder, & Abbott, 1993; G. Turrigiano, Abbott, & Marder, 1994), which leads to,
for instance, the optimization of the input-output relation of a neuron (Triesch, 2007) or the
encoding of information in firing rates (Stemmler & Koch, 1999). Several theoretical studies in-
dicate that the interplay of intrinsic plasticity with synaptic plasticity allows neuronal systems
to infer the stimulus intensity (Monk, Savin, & Lücke, 2018; Monk, Savin, & Lücke, 2016), A
perform independent component analysis (Savin, Joshi, & Triesch, 2010), or to increase their
computational capacity (Hartmann, Lazar, Nessler, & Triesch, 2015; Lazar, Pipa, & Triesch,
2009). Tuttavia, it remains unclear whether this interplay allows sensory systems, on the one
hand, to learn the organization of stimuli despite noise and, on the other hand, to adapt to
variations of the noise level.
In the present study, we show that in an expansive network intrinsic plasticity regulates the
neuronal activities such that the synaptic weights can learn the organization of stimuli even
in the presence of low levels of noise. È interessante notare, after learning, the system is able to adapt
itself according to changes in the level of noise it is exposed to—even if these levels are high.
To do so, intrinsic plasticity has to readapt the excitability of the neurons while the synaptic
weights have to be maintained, indicating the need of a two-phase learning protocol.
In the following, first, we present the basics of our theoretical model and methods and
demonstrate the ability of a feed-forward network with static random or static structured synap-
tic weights, rispettivamente, to distinguish between noisy versions of 1, 000 different stimuli (similar
to Babadi & Sompolinsky, 2014). Then, we introduce the synaptic and intrinsic plasticity rules
considered in this study. We train the plastic feed-forward network during an encoding phase
without noise and test its performance afterwards by presenting stimuli of different noise lev-
els. Intriguingly, the self-organized dynamics of synaptic and intrinsic plasticity yield a perfor-
mance and network structure similar to the static network initialized with structured synaptic
pesi. Further analyses indicate that the performance of the plastic network to classify noisy
stimuli greatly depends on the neuronal excitability, especially for high levels of noise. Hence,
after learning without noise, we changed the noise level in order to test the performance but
let intrinsic plasticity readapt the excitability of the neurons. This readaptation phase signifi-
cantly increases the performance of the network. Note, Tuttavia, if synaptic plasticity is present
Network Neuroscience
176
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
during this second phase, the increase in performance is impeded by a prolonged and severe
performance decrease. In the next step, we show that in the encoding phase with both intrinsic
and synaptic plasticity the network can also learn from noisy stimuli if the level of noise is low.
Again, high levels of noise impede learning and classification performance. È interessante notare, after
the subsequent readaptation phase the network initially trained with low-noise stimuli per-
forms just as well as a network trained with noise-free stimuli, demonstrating the robustness
of this learning mechanism to noise.
RESULTS
Model Setup and Classification Performance
The main question of this study concerns how sparse and expansive neural systems, come
as sensory processing areas, learn the inherent organization of stimuli enabling a reduction
of noise. To tackle this question, similar to a previous study (Babadi & Sompolinsky, 2014),
we consider a neural network that consists of two layers of rate-based neurons, with the first
layer being linked to the second layer via all-to-all feed-forward synaptic connections. The first
layer, called stimulus layer, is significantly smaller (NS = 1, 000 neurons) than the second one,
called cortical layer (NC = 10, 000 neurons). The activity patterns of the stimulus layer serve
as stimuli or inputs to the cortical layer. These stimulus patterns are constructed of firing rates
Si ∈ {0, 1} of the stimulus neurons i ∈ {1, …, NS} con 0 representing a silent neuron and 1 UN
maximally active one. Neurons belonging to the cortical layer posses a membrane potential
uj (j ∈ {1, …, NC}) modeled by a leaky integrator receiving the inputs from the stimulus layer.
The membrane potential of a cortical neuron is transformed into a firing rate Cj using a sig-
moidal transfer function. Similar to the stimulus neurons, we consider the minimal and max-
imal firing rates F min = 0 and F max = 1. Note that the point of inflection of the sigmoidal
transfer function ε j, also called cortical firing threshold, is neuron-specific.
¯S ν
The different activity patterns of the stimulus layer are organized into P = 1, 000 stimulus
clusters (Figure 1A). Each stimulus cluster ν ∈ {1, …, P} consists of one characteristic activity
pattern, called central stimulus pattern
, which represents the underlying stimulus (per esempio., UN
lion; black dots in the stimulus layer’s phase space in Figure 1A). To construct these central
stimulus patterns, for each cluster ν and each stimulus neuron i we randomly choose a firing
¯S ν
i ∈ {0, 1} with equal probability, thus resulting in random patterns of ones and zeros (Vedere
rate
Figure 1B for schematic examples). Inoltre, a stimulus cluster contains all noisy versions
S ν
of the underlying stimulus (per esempio., a lion behind a tree or a rock; indicated by blue halos in
Figure 1A) generated by randomly flipping firing rates
i of the cluster’s central stimulus pattern
from 1 A 0 or vice versa with probability ΔS/2 (Figure 1B); ΔS thus reflects the average noise
level of all noisy stimulus patterns as well as the stimulus cluster’s size in the stimulus layer’s
phase space. If ΔS = 0, the cluster is only a single point in the stimulus layer’s phase space
(the central stimulus pattern
) and is thus noise-free. The maximum value of the stimulus
cluster size ΔS = 1 represents a cluster that is distributed evenly across the entire phase space.
Here, the noise is so strong that no information remains. The stimulus cluster size ΔS can be
retrieved by the normalized Hamming distance between patterns of the same cluster:
¯S ν
¯S ν
(cid:2)
ΔS =
∑NS
i − ¯S ν
io |
i=1 |S ν
NS · 1/2
(cid:3)
,
S ν,ν
(1)
with the brackets denoting the average over all noisy stimulus patterns S ν
clusters ν.
of all stimulus
Network Neuroscience
177
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
¯S ν
(black dots) and noisy patterns S ν
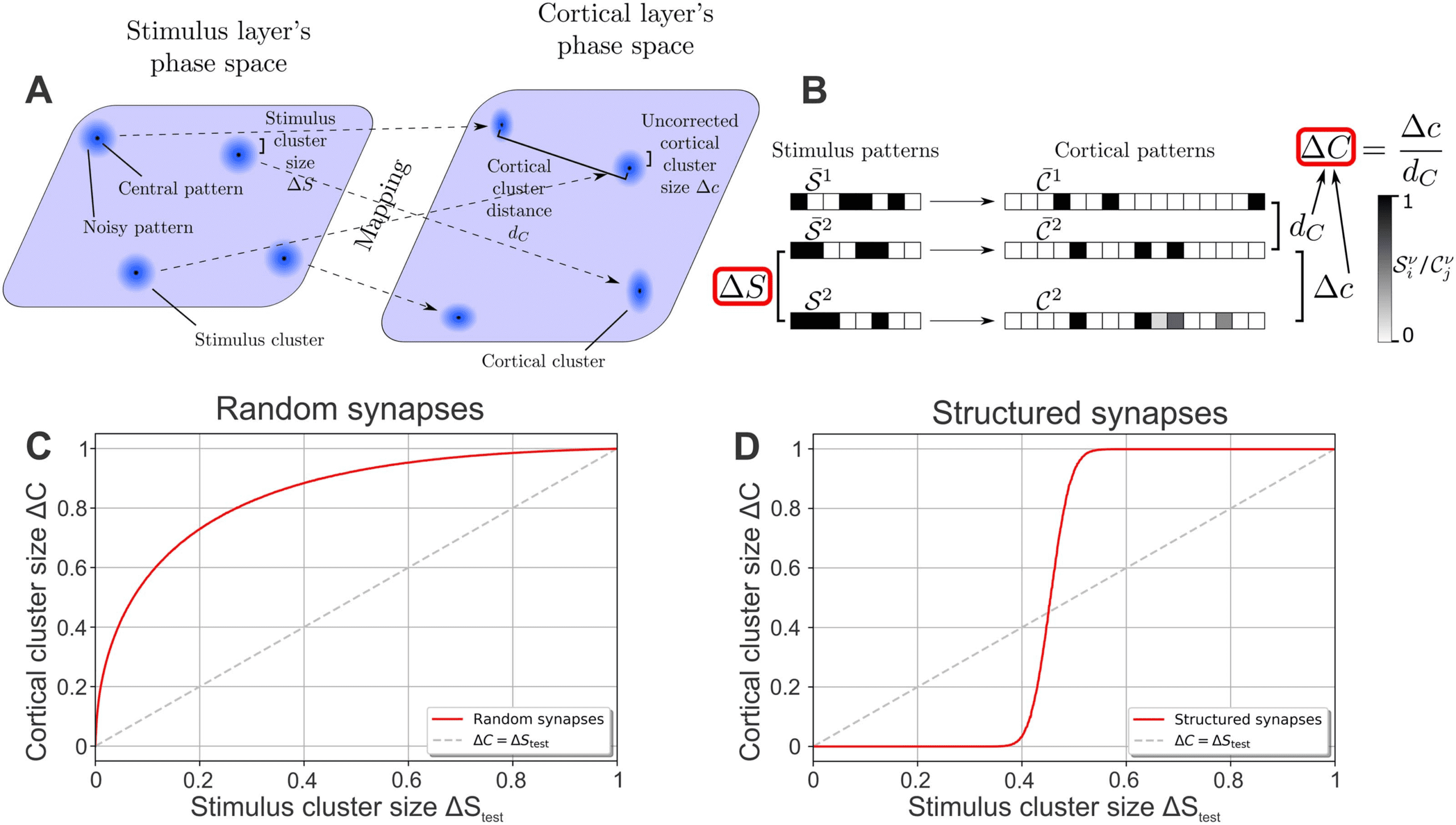
Figura 1. Network model and mathematical approach to quantify the ability of an expansive, sparse network to reduce noise. (UN) The feed-
forward network consists of two layers of rate-based neurons with the stimulus layer projecting stimuli onto the cortical layer via all-to-all
feed-forward synaptic connections. Stimuli are organized in P = 1, 000 clusters, with each cluster ν consisting of a characteristic central
(blue halos around dots). The size of the stimulus clusters ΔS corresponds to the level of noise
pattern
and is indicated schematically by the size of the blue halos. Stimulus clusters are mapped by the synaptic connections to cortical clusters
. (B) Illustration of different patterns and measures used in this study. IL
containing central cortical patterns
of each stimulus
activity of each neuron (box) is indicated by its gray scale (left: stimulus layer; right: cortical layer). The central pattern
in the cortical layer. Noisy versions of a central stimulus pattern (here S 2
)
cluster (underlying stimulus) evokes a specific central pattern
activate different cortical patterns with their average distance Δc from the original pattern depending on the structure of the feed-forward
synaptic weights. (C) Random synaptic weights increase the cluster size for all stimulus cluster sizes, questo è, ΔC > ΔStest; the noise in the
stimuli is thus amplified by the network. (D) Synapses that are structured in relation to the organization of the underlying stimuli (stimulus
) decrease the size of clusters, questo è, the noise, up to a medium noise level (ΔStest ≈ 0.45). (C, D) Dashed line indicates
central patterns
ΔC = ΔStest.
and noisy cortical patterns C ν
¯S ν
¯S ν
¯C ν
¯C ν
Every activity pattern of the stimulus layer elicits an activity pattern in the cortical layer, come
that stimulus clusters are mapped to cortical clusters (dashed arrows in Figure 1A). Similar to
the stimulus cluster, each cortical cluster consists of one central pattern
(evoked by the
noise-free stimulus
). Because of the
complex mapping of the stimulus patterns onto the cortical layer via the feed-forward synaptic
pesi, it is not clear how the level of noise is affected by this mapping. Therefore, we estimate
the noise in the cortical layer in analogy to Equation 1:
¯C ν
(evoked by the noisy stimuli S ν
) and noisy patterns C ν
¯S ν
Δc =
(cid:2)
(cid:3)
j=1 |C ν
∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)
,
C ν,ν
(2)
where Z(C ν, ¯C ν) is a normalization factor (see Methods for more details). As different stim-
ulus clusters are mapped by the same feed-forward weights onto cortical clusters, random
Network Neuroscience
178
Learning of noisy stimuli requires distinct phases of plasticity
correlations between the cortical clusters could be induced. To account for these correlations
we calculate the average distance between clusters by
dC =
(cid:2)
∑NC
j − ¯C λ
j=1 | ¯Cκ
j |
NC · Z( ¯Cκ, ¯C λ)
(cid:3)
,
κ,λ
(3)
and correct Equation 2 using this cortical cluster distance (Equazione 3) analogous to a signal-
to-noise/noise-to-signal ratio to obtain the cortical cluster size
ΔC =
Δc
dC
.
(4)
Therefore, if each pattern S ν
of a stimulus cluster ν is mapped onto a different (random)
pattern C ν
in the cortical layer, ΔC = 1 and the cluster is distributed evenly over the entire
cortical layer’s phase space. If each pattern of a stimulus cluster is mapped onto the same
pattern of the cortical cluster (the central pattern
), ΔC = 0.
¯C ν
In summary, both the stimulus cluster size ΔS as well as the cortical cluster size ΔC are
measures for the amount of random fluctuations of different activity patterns belonging to the
same underlying stimulus. As such, a network tasked with reducing these random fluctuations
should decrease the cluster size, questo è, ΔC < ΔS.
Static Networks
Central to the performance in reducing the cluster size or noise are the feed-forward synaptic
weights ωji between neurons. In the following, we predefine the synaptic weights and test
the performance of the network for different levels of noise ΔStest while keeping the synaptic
weights fixed. For each noise level ΔStest, we create noisy stimulus patterns for all clusters
and use them to evaluate the average noise ΔC in the cortical layer. By doing so, we obtain
a performance curve ΔC(ΔStest) of the network. If the weights are initialized randomly, here
NS), the cortical cluster size ΔC is always larger
drawn from a Gaussian distribution N (0, 2/
than the stimulus cluster size ΔStest, as the performance curve (red line in Figure 1C) is above
the identity line (ΔC = ΔStest; dashed line) for all values of ΔStest. In other words, the noise of
the stimuli (ΔStest) is amplified by the network by increasing the variations between different
cortical patterns of the same underlying stimulus (ΔC > ΔStest). Note that this amplification
of noise is present even though the network is expansive and sparse (Babadi & Sompolinsky,
2014).
√
This picture changes if the weights are structured according to the organization of the en-
vironmental stimuli. To portray such a structure, we initialize the synaptic weights according
to Babadi and Sompolinsky (2014) and Tsodyks and Feigelman (1988):
ωji =
100
NS
P
∑
ν=1
( ¯S ν
i − 1/2)(Rν
j − F T) .
(5)
Note that the factor 100 ensures that the synaptic weights are in the same order of magnitude
as in later analyses. Equazione 5 results in a mapping of the central stimulus patterns
A
(F T = 0.001). È interessante notare, this mapping
randomly generated, F T
yields a reduction of noise for up to medium levels (ΔStest (cid:2) 0.45) such that the cortical
cluster size ΔC is smaller than the stimulus cluster size ΔStest (Figure 1D). In other words, COME
already shown in a previous study (Babadi & Sompolinsky, 2014), a structured network reduces
-sparse cortical patterns Rν
¯S ν
Network Neuroscience
179
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
small fluctuations of representations of the same underlying stimulus. Note that in the random
as well as the structured network each cortical neuron has an individual firing threshold ε j.
Neuron-specific thresholds are required in order to ensure that every cortical neurons’ average
response to the central stimulus patterns equals the target activity; questo è, (cid:5) ¯C ν
for all j.
We chose F T = 0.001 as this results in all cortical neurons of the structured network firing in
response to exactly one central stimulus pattern, and remaining silent in response to all others
(as F T P = 1), which simplifies the qualitative analysis of the results. In the structured network,
the method used for initializing the firing thresholds of each cortical neuron places them at
the center of the strongest and second strongest membrane potentials evoked by the central
stimulus patterns.
j (cid:6)ν = F T
These results show that expansive and sparse networks reduce the noise of stimuli if the
synaptic weights from the stimulus to the cortical layer are structured according to the under-
lying organization of stimuli (here according to the central stimulus patterns
). So far, we
have used Equation 5 to artificially set the synaptic weights to the correct values. The question
remains how a network can learn these values from the environmental stimuli.
¯S ν
Plastic Network
As demonstrated above, a network with random synaptic weights increases the level of noise,
while a structured network decreases it (Figure 1C, D). How can a network develop this
structure in a self-organized manner given only the environmental stimuli? To investigate this
question, we initialized a network with the same random synaptic weights as above, questo è,
Gaussian distributed ωji, and let the system evolve over time using plasticity mechanisms that
adapt the synaptic weights and neuronal excitabilities. These plasticity mechanisms are as-
sumed to depend on local quantities only and thus on the directly accessible neuronal activities
and synaptic weights (Gerstner & Kistler, 2002; Tetzlaff et al., 2011). Given this assumption,
the environmental stimuli influence the dynamics of the plasticity mechanisms as the stimulus
patterns determine the activities of the neurons. We consider two plasticity processes: Synap-
tic weights are controlled by Hebbian correlation learning and an exponential decay term
(for weight stabilization),
˙ωji = μSiCj − ηωji ,
(6)
while a faster intrinsic plasticity mechanism regulates the firing thresholds ε j of the cortical
neurons so as to achieve the target firing rate F T = 0.001:
˙ε j = κ(Cj − F T),
(7)
with the parameters μ, η, κ determining the timescales of the mechanisms. Similar to pre-
vious studies (Lazar et al., 2009; Miner & Triesch, 2016; Triesch, 2007), we consider that the
process of intrinsic plasticity is faster than synaptic plasticity.
¯S ν
Training is carried out in repeated learning steps or trials. In each learning step L, we present
(ν ∈ {1, …, P}) to the network once, ensuring there is no
all central stimulus patterns
chronological information (see Methods for details). This corresponds to a stimulus cluster
= 0 or noise-free learning. At different stages of learning (questo è, after different
size ΔS
numbers of learning steps), we test the performance of the network for different levels of noise
ΔStest as has been done for the static networks.
Imparare
Network Neuroscience
180
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
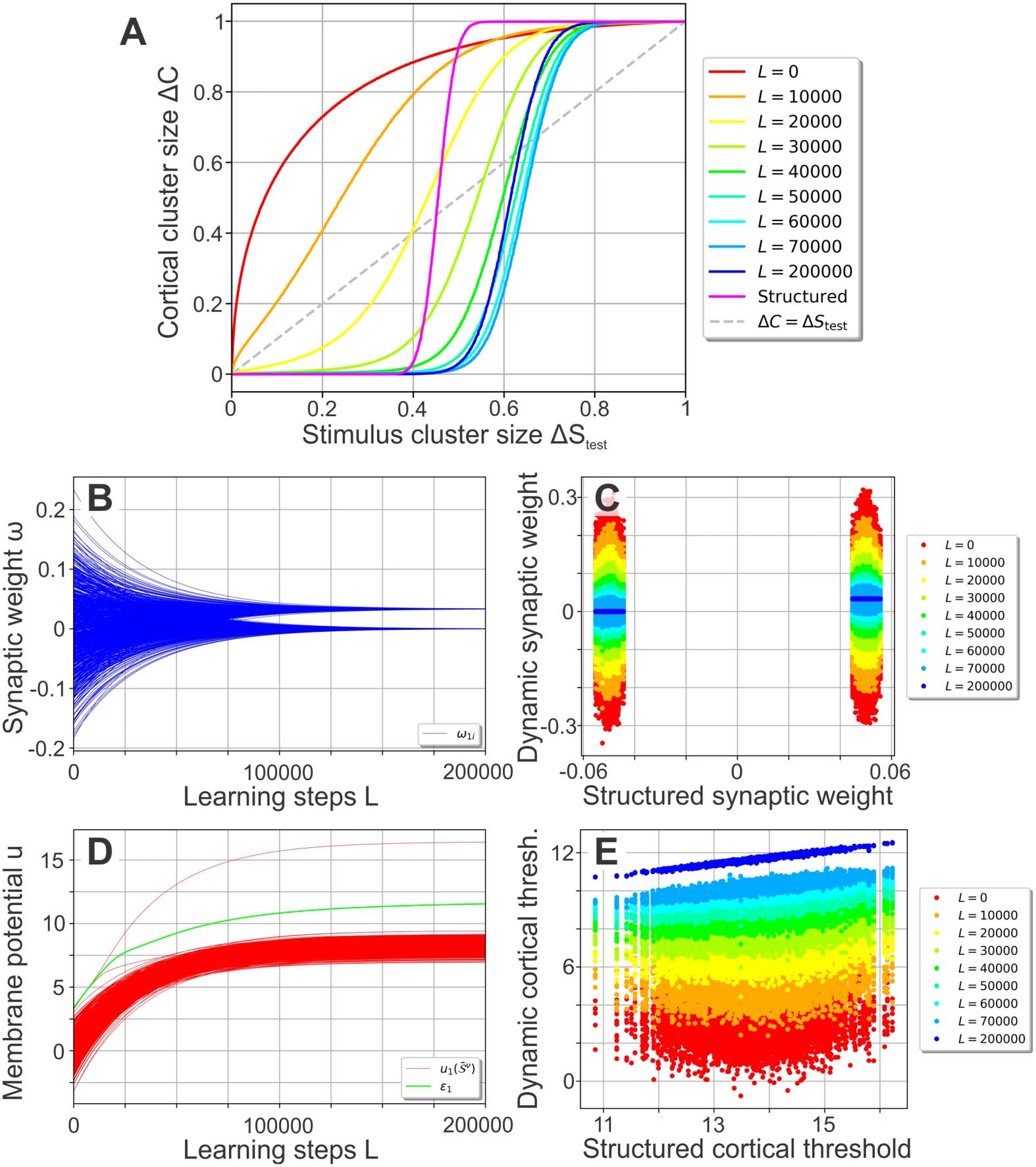
As learning progresses (Figure 2A), the performance curve develops from the random net-
work’s (red line), which amplifies stimulus noise, into one similar to the structured network’s
performance curve (blue compared with magenta line). The plasticity mechanisms (Equations 6
E 7) enable the network to encode the organization of the stimuli (existence of different
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
¯S ν
Figura 2. Self-organization of the synaptic and neuronal structure via synaptic and intrinsic plas-
ticity in a noise-free environment. (UN) By repeatedly presenting one stimulus pattern S ν
per cluster
= 0 (cioè., presenting the central stimulus
per learning step L using a stimulus cluster size ΔS
Imparare
), the network’s performance develops from the noise-amplification of a random network
patterns
(red, equal to Figure 1C) to a performance significantly decreasing the level of noise for ΔStest up to
Di 0.6 (blue). (B, C) During learning, the synaptic weights develop into a bimodal distribution (B;
only the weights connecting to neuron 1 are shown) that is correlated to the distribution of the static,
structured network (C). (D) For each cortical neuron (here shown for neuron 1), the firing threshold
(green) increases such that only one central stimulus pattern can evoke a membrane potential larger
than the threshold (red lines depict membrane potentials). (E) Similar to the synaptic weights (C),
the firing thresholds tend to become correlated to the ones of the static, structured network.
Network Neuroscience
181
Learning of noisy stimuli requires distinct phases of plasticity
clusters) in a self-organized manner, with most of the performance gained in the first L =
60, 000 learning steps: During learning, the synaptic weights evolve from the initial Gaussian
distribution into a bimodal distribution with peaks at about 0.033 E 0 (see Figure 2B for
an example). The emergence of the bimodal weight distribution and its link to the network
performance can be explained as follows: Because of the random initialization of the synap-
tic weights, each central stimulus pattern leads to a different membrane potential in a given
cortical neuron such that all P stimuli together yield a random distribution of evoked mem-
brane potentials (Vedere, per esempio., Figure 2D; red lines depict membrane potentials). As the target
firing rate is chosen such that each neuron ideally responds to only one central stimulus pat-
tern (as F T P = 1), intrinsic plasticity adapts the firing threshold ε j of a neuron such that one of
the evoked membrane potentials leads to a distinctly above-average firing rate. Consequently,
synapses connecting stimulus neurons being active at the corresponding stimulus pattern with
the considered cortical neuron are generally strengthened the most by Hebbian synaptic plas-
ticity. These synapses will likely form the upper peak of the final synaptic weight distribution
(Figure 2B). Nel frattempo, all other synaptic weights are dominated by the synaptic weight decay
(second term in Equation 6) and will later form the lower peak of the distribution at zero. As
the continued differentiation of the synaptic weights increases the evoked membrane potential
of the most influential central stimulus pattern, these two processes of synaptic and neuronal
adaptation drive each other. È interessante notare, the resulting synaptic weights are correlated to the
structured synapses (Figure 2C) initialized using Equation 5 (here the cortical patterns Rν
Di
Equazione 5 were generated using the central cortical patterns C ν
of the plastic network at the
corresponding learning step L; see Methods for further details). Note that the cortical firing
thresholds ε j of the plastic network become correlated to the values of the static, structured
one as well (Figure 2E).
In summary, synaptic and intrinsic plasticity interact and adapt the neuronal network such
Quello, in a noise-free environment, it learns to encode the organization of the stimuli in a way
comparable to a static, prestructured network. The trained network is then able to reduce the
noise of environmental stimuli even for noise levels up to about 0.6.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
The Functional Role of the Cortical Firing Thresholds
While being structurally similar, the performance of the trained, plastic network (Figure 2A,
blue) appears significantly better than the performance of the static, structured network (ma-
genta). This fact is not self-explanatory, since both the synaptic weights as well as the cortical
firing thresholds are strongly correlated between both networks (Figure 2C, E). Tuttavia, UN
closer look at the cortical firing thresholds and their link to the performance of the network
reveals the cause of this difference:
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
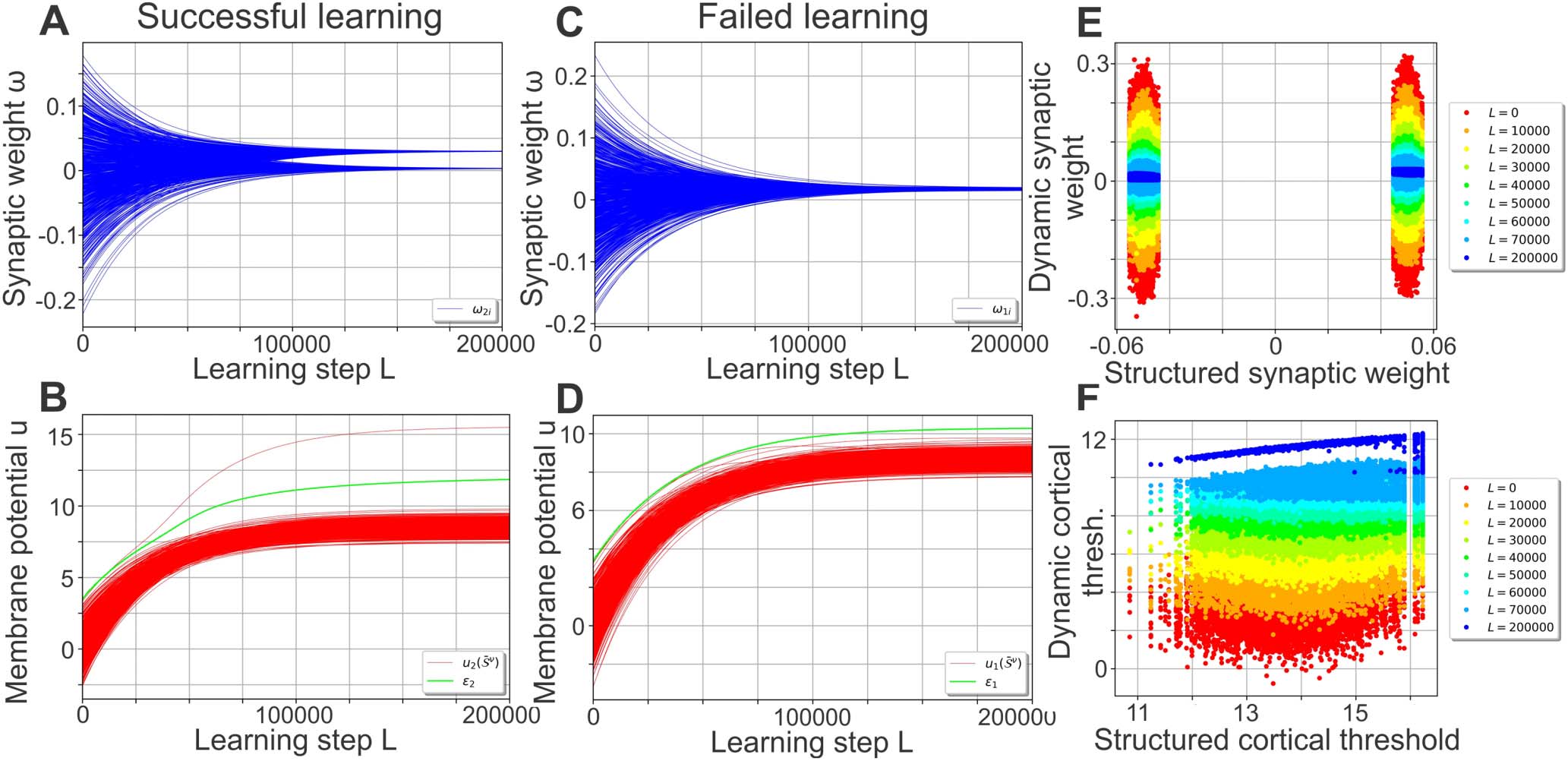
In the trained network (L = 200, 000), as mentioned before, each cortical neuron should fire
in response to the central stimulus pattern
of exactly one cluster and stay silent otherwise.
As an example, we will focus on cortical neuron j = 1, which fires in response to the central
of cluster ν = 842 and remains silent in response to all other central
stimulus pattern
stimulus patterns. Generalmente, two types of errors can occur.
¯S 842
¯S ν
False negatives (a stimulus of cluster 842 is presented and cortical neuron 1 falsely does
not fire): Noisy patterns of cluster 842 elicit a distribution of membrane potentials in corti-
cal neuron 1 (Figure 3A), which depends on the stimulus cluster size ΔStest, questo è, the level
of noise. All noisy stimulus patterns S 842
that evoke a membrane potential in neuron 1 questo è
higher than the neuron’s firing threshold ε1 result in a strong activation of neuron 1. The neuron
Network Neuroscience
182
Learning of noisy stimuli requires distinct phases of plasticity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
Figura 3. The Classification performance of each neuron depends on its firing threshold. In a single cortical neuron (here neuron j = 1),
multiple noisy stimulus patterns of the same stimulus cluster elicit a distribution of membrane potentials. Two distinct distributions can be
identified: (UN) The distribution of membrane potentials evoked by noisy stimulus patterns belonging to the cluster whose central pattern elicits
firing in the given cortical neuron (blue; here cluster ν = 842). For any ΔStest, all stimuli yielding a membrane potential that is below the
neuron’s firing threshold (dashed line; ε1) do not elicit a strong neuronal response representing false negatives. The distribution significantly
depends on the level of noise ΔStest. (B) The membrane potential distribution in response to noisy stimulus patterns of the clusters the neuron
is not tuned to (ν (cid:7)= 842). Here, all stimuli yielding a membrane potential above the firing threshold are false positives. (C) ΔStest = 0: A higher
firing threshold ε leads to more false negatives (orange) but fewer false positives (magenta) and vice versa for a lower threshold. The sum of
errors (dashed red) is negligible in a large regime (blue area: gradient is less than 0.001). (D) ΔStest = 0.7: With higher levels of stimulus noise,
the total error and the classification performance depend critically on the firing threshold. (C, D) ε1,opt: optimal value of the firing threshold
for the given level of noise ΔStest yielding the lowest total error; ε1: value of the firing threshold after learning with noise-free stimuli (ΔStest;
Figura 2); ε1,stat: firing threshold in the static network (Figure 1D).
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
therefore classifies these S 842
correctly as belonging to cluster 842. Tuttavia, noisy patterns
S 842
evoking a lower membrane potential than ε1 do not elicit strong activation of cortical
neuron 1. These noisy patterns are falsely classified as not belonging to cluster 842 and corre-
spond to false negatives.
False positives (a stimulus of a cluster ν (cid:7)= 842 is presented and cortical neuron 1 falsely
fires): Similar to the analysis of false negatives, the analysis of false positives can be done with
Network Neuroscience
183
Learning of noisy stimuli requires distinct phases of plasticity
clusters whose central patterns should not elicit activity in cortical neuron 1. The distribution
of membrane potentials evoked by noisy patterns of these clusters does not significantly de-
pend on the stimulus cluster size ΔStest (Figure 3B). Noisy stimulus patterns S ν
(ν (cid:7)= 842) are
classified correctly as not part of cluster 842 if neuron 1’s membrane potential is lower than
its firing threshold ε1. All noisy patterns evoking a higher membrane potential falsely lead to a
firing of cortical neuron 1. They correspond to false positives.
Both false positives and false negatives depend on the firing threshold ε j of a neuron j.
For all values of ΔStest, a lower firing threshold would generally lead to less false negatives
(e
fn,j; Figure 3A) but simultaneously to more false positives (e
fp,j; Figure 3B) and vice versa for
a higher firing threshold. Consequently, there is a trade-off between false negatives and false
positives with their sum being related to the network’s performance or cortical cluster size
(see Methods for derivation):
ΔC ≈ e
tot,j = e
fn,j + e
fp,j
∀j .
(8)
The performance of the network or the total error e
tot,j thus depends on a cortical neuron’s
firing threshold in a nonlinear manner. Given noise-free stimuli (ΔStest = 0), in a large regime
of different values for the firing threshold cortical neuron 1 makes almost no classification error
(dashed red line in Figure 3C; gradient in shaded blue area is less than 0.001). For a higher noise
level (per esempio., ΔStest = 0.7, Figure 3D), there is no such extended regime of low-error threshold
values. Invece, small variations of the firing threshold can drastically change the classification
performance, since the membrane potential response distributions overlap at these noise levels
(Figure 3A, B).
Imparare
During training without noise (ΔS
= 0), the neuronal firing threshold ε1 rose to the
lower bound of the low-error regime of ΔStest = 0 (blue area; Figure 3C). In the static network,
Tuttavia, firing thresholds ε1,stat were placed at the center of the highest and second highest
membrane potentials in response to central stimulus patterns, leading to much higher values.
Therefore, if the network performance is tested for small stimulus clusters (low noise ΔStest;
Figure 3C), the static and the plastic network have a similar total error and classification per-
formance. For larger stimulus clusters (high noise levels ΔStest; Figure 3D), on the other hand,
the higher firing thresholds of the static network lead to considerably more misclassification
and consequently to a higher cortical cluster size ΔC. Consequently, the fact that the relation
between the threshold and its classification error ej,tot depends on the noise ΔStest provides an
explanation for the large performance differences between the static structured and the plastic
rete (Figure 2A).
This example (Figura 3) demonstrates that the value of the neuron-specific threshold ε j,opt
optimizing a neuron’s classification performance depends on the stimulus cluster size ΔStest or
current level of noise (dotted lines in Figure 4A for neuron 1 in blue and neuron 2 in green). IL
firing thresholds after training (solid lines in Figure 4A), Tuttavia, are independent of ΔStest, COME
= 0). For ΔStest (cid:2) 0.5 these
they are determined by the noise present during training (ΔS
thresholds are within the regime of low total error (shaded areas indicate the low-error regime
for each neuron marked by blue area in Figures 3C and 3D) yielding a high classification
performance of the network. Tuttavia, for ΔStest (cid:3) 0.5 the thresholds ε j resulting from training
= 0) start to deviate significantly from the optimal thresholds ε j,opt,
without noise (ΔS
leading to a decreasing classification performance (Figure 2A and Figure 4C, solid lines for
total error of individual neurons). È interessante notare, the deviation from the optimal threshold is
accompanied by a decrease of the average activity level (solid lines; Figure 4B), while the
Imparare
Imparare
Network Neuroscience
184
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
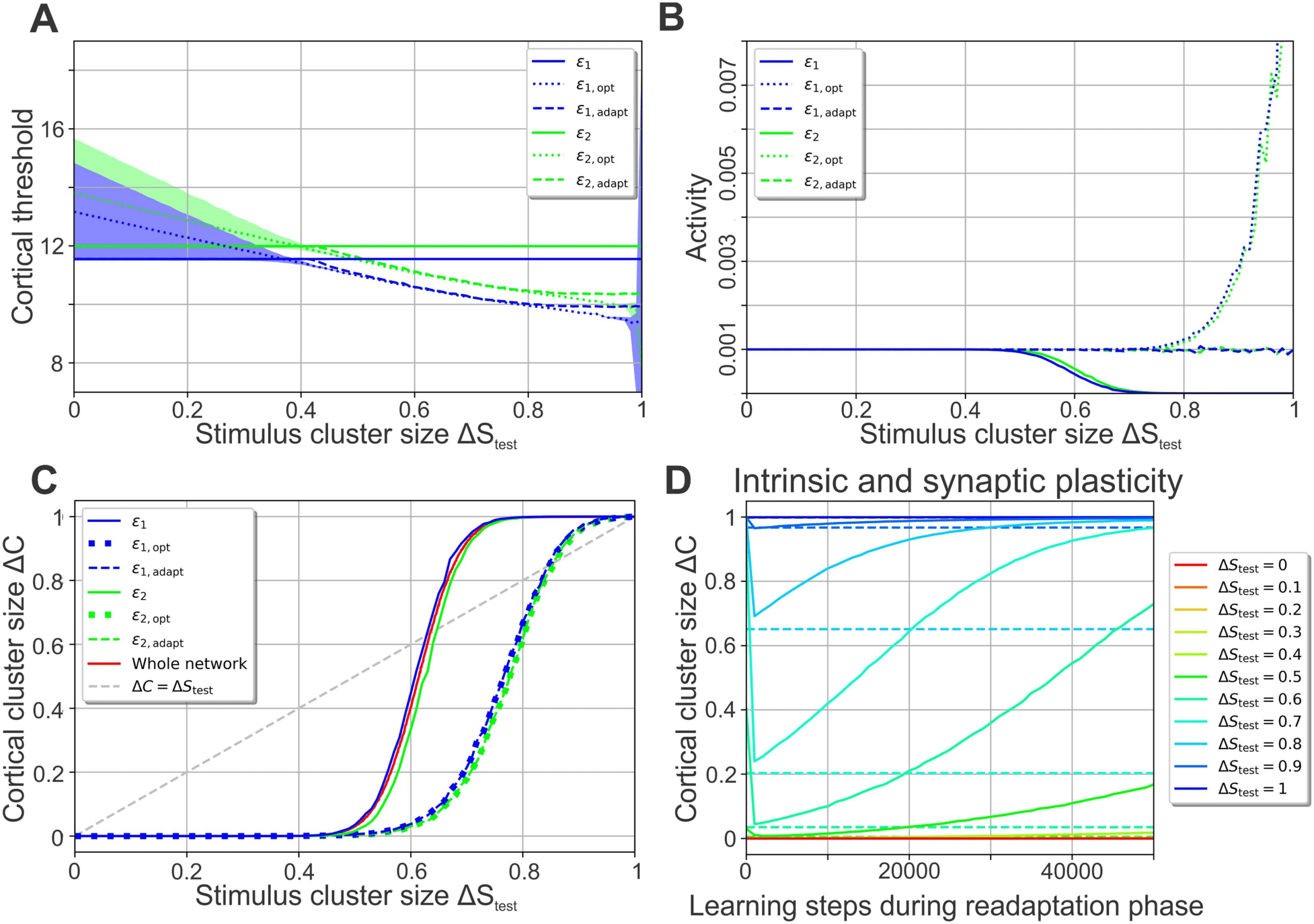
Figura 4. A second learning phase—the readaptation phase—enables the neuronal system to readapt to arbitrary noise levels using intrinsic
plasticity. (A–C) After learning without noise, a second learning phase with the noise level ΔStest and only intrinsic plasticity active enables the
thresholds to readapt from the values after the first learning phase ε j (solid lines) to adapted values ε j,adapt (dashed lines), close to the optimal
threshold values ε j,opt (dotted lines) increasing performance. Blue: neuron 1; green: neuron 2. (UN) ΔStest-dependency of cortical thresholds;
shaded areas indicate regimes of low error gradient (Figure 3C); (B) ΔStest-dependency of average activities; (C) ΔStest-dependency of total
error (dashed lines lie on top of dotted lines). Solid red line shows performance of whole network (from Figure 2A), confirming Equation 8. (D)
If synaptic plasticity is present during the second learning phase as well, ΔC initially drops because of intrinsic plasticity and then increases
with ongoing presentation of noisy stimuli, indicating a disintegration of the synaptic structure (solid lines; different colors represent different
noise levels). Dashed lines indicate ΔC-values for a second learning phase with intrinsic plasticity alone.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
optimal thresholds would keep the cortical activity close to the target activity F T = 0.001
(dotted lines; for ΔStest (cid:3) 0.85 the total error is high and nearly independent of the threshold;
see Supplementary Figure 1). We thus expect that after initial learning, intrinsic plasticity could
readapt the neuronal firing thresholds according to the present level of noise such that the target
activity is maintained and the thresholds ε j,adapt approximate the optimal threshold values ε j,opt.
We therefore considered a second learning phase, the readaptation phase, which is con-
ducted after the initial training or encoding phase is completed. In the readaptation phase,
the stimulus cluster size will be the same that the performance is tested for, questo è, ΔStest. For
now, synaptic plasticity is deactivated as we will only focus on intrinsic plasticity adapting the
Network Neuroscience
185
Learning of noisy stimuli requires distinct phases of plasticity
cortical firing thresholds ε j,adapt. To implement this readaptation phase, after the first learning
phase is completed, we repeatedly presented one noisy pattern S ν
per cluster using a stimulus
cluster size ΔStest. Threshold adaptation was stopped when the mean of all cortical thresholds
changed by less than 0.0001% in one step, which resulted in less than 7, 000 steps for each
ΔStest. As expected, intrinsic plasticity adjusts the firing thresholds during this second phase so
as to achieve the target firing rate F T
for all ΔStest (dashed lines; Figure 4B). Inoltre, IL
adapted thresholds ε j,adapt (dashed lines; Figure 4A) are similar to the optimal thresholds ε j,opt
(dotted lines). This leads to a near-optimal classification performance, which is considerably
better than without a readaptation phase (Figure 4C, dashed lines lie on top of dotted line).
Importantly, if synaptic plasticity is also present during this second learning phase, ΔC in-
creases dramatically with ongoing readaptation (solid lines in Figure 4D; different colors rep-
resent different noise levels). The initial drop of ΔC is due to intrinsic plasticity (dashed lines
show final ΔC-values for intrinsic plasticity alone), while synaptic plasticity leads to a pro-
longed deterioration of the previously learned synaptic structure if stimuli are too noisy. Noi
therefore conclude that the network has to maintain the synaptic weight structure during the
readaptation phase, which we recreate by turning synaptic plasticity off. By doing so, the neu-
ronal system can reliably adjust to stimuli of various noise levels using intrinsic plasticity for
adapting the excitability of neurons.
Plastic Networks in Noisy Environments
Imparare
Up to now, we have shown that a sparse, expansive network can learn the underlying organiza-
= 0) by means of synaptic and intrinsic plasticity. Afterwards,
tion of noise-free stimuli (ΔS
a readaptation phase with intrinsic plasticity alone enables the network to readapt to any ar-
bitrary level of noise ΔStest (Figures 4A–C). Tuttavia, if synaptic plasticity is active during
the readaptation phase, the noise of stimuli leads to a disintegration of the synaptic structure
(Figure 4D). Therefore, it is unclear whether the network can also learn the organization of
stimuli from noisy—instead of noise-free—stimuli by using synaptic plasticity.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
Imparare
Imparare
phase (cioè., ΔS
each learning step L using a stimulus cluster size ΔS
ΔS
To test this, we now investigate the effect of noisy stimuli during training in the encoding
> 0). To do so, we present one noisy stimulus pattern S ν
per cluster in
Imparare. In noisy environments with up to
= 0.2, cortical neurons show neuronal and synaptic dynamics (Figure 5A, B) similar to
noise-free learning (Figure 2B, D). Synaptic weights and firing thresholds become correlated
to the static, structured network (Figure 5E, F) to a comparable degree (Figure 2C, E). Never-
theless, because of the noise of the stimuli, some cortical neurons do not manage to separate
one stimulus cluster from all others (Figure 5D, ∼ 24% of all neurons for ΔS
= 0.2). Contro-
sequently, multiple clusters trigger the Hebbian term of synaptic plasticity (Equazione 6) come
that all synaptic weights approach a medium value (Figure 5C). These synaptic weights dimin-
ish the correlation to the static, structured synaptic weights as the final distribution is slightly
più ampia (Figure 5E) than the one from learning without noise (Figure 2C). Inoltre, IL
cortical neurons without structured incoming synaptic weights (unimodal weight distribution)
on average have a lower final firing threshold (blue outliers in Figure 5F).
Imparare
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Generalmente, low levels of noise (ΔS
(cid:2) 0.25) are tolerated by the network without large
losses in performance (Figure 6A). The failed-learning cortical neurons (Figure 5C, D), Quale
become more with higher noise levels (see Supplementary Figure 3), have a negative effect on
(cid:3) 0.25, the noise is so strong that the system is
the performance of the network. At ΔS
not able to recognize and learn the underlying organization of stimuli (questo è, the existence of
Imparare
Imparare
Network Neuroscience
186
Learning of noisy stimuli requires distinct phases of plasticity
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
Figura 5. Self-organization of the synaptic and neuronal structure in a noisy environment. The dynamics of synaptic and intrinsic plasticity
= 0.2). (UN, B)
enable the sparse, expansive network to learn the underlying organization of stimuli from noisy stimulus patterns (here ΔS
The majority of cortical neurons develop a distribution of incoming synaptic weights (UN, blue lines) and membrane potential responses (B,
red lines) similar to the ones learning without noise (Figure 2B, D). Here shown for neuron 2. Green line in (B) denotes the threshold. (C,
D) Tuttavia, the noise prevents some neurons (∼ 24%) to form a proper synaptic structure (C), yielding a firing threshold (D) that does
not separate the membrane potential evoked by one cluster from the others. Therefore, these neurons are not tuned to one specific cluster.
Here shown for neuron 1. (E, F) Overall, the network trained by noisy stimuli develops synaptic weights (E) and firing thresholds (F) allo stesso modo
correlated to the static, structured network than the network trained without noise (Figure 2C, E). The few neurons that failed learning lead to
a minor broadening of the distributions.
Imparare
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
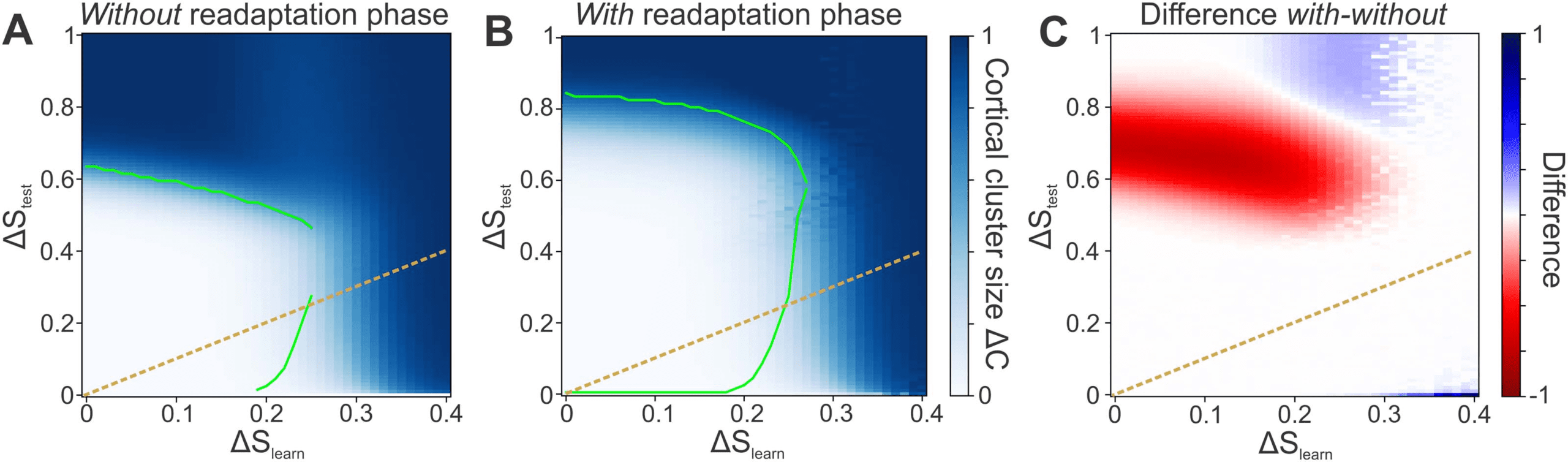
Figura 6. The network can reliably learn from noisy stimuli with and without a readaptation phase. (UN) Despite the presence of noise ΔS
Imparare
during learning, the network can learn the organization of stimuli and, after encoding, classify stimuli of even higher noise levels ΔStest.
learn decrease the performance. Color code depicts ΔC, green line marks ΔC = ΔStest. (B) If the learning phase
Tuttavia, higher levels of ΔS
is followed by a readaptation phase using only intrinsic plasticity and the level of noise ΔStest with which the system is tested, the overall
classification performance increases drastically. Now, stimuli with a noise level of up to ΔStest ≈ 0.8 can be classified. (C) The readaptation
phase leads to a large performance gain for medium and high noise levels ΔStest. Color code depicts the difference between the network
without and with a readaptation phase. Red area represents a benefit by using the readaptation phase. (A–C) Orange dashed line: identity line
ΔS
= ΔStest
Imparare
Network Neuroscience
187
Learning of noisy stimuli requires distinct phases of plasticity
different clusters). Tuttavia, if there is little or even no noise during learning, the network can
subsequently not only classify stimuli of that same level of noise, but also classify significantly
noisier stimuli (white area above orange dashed identity line). This result indicates that the
network does not adapt specifically to only the noise level ΔS
learn it is learning from, but that
the network generalizes across a broad variety of different noise levels ΔStest. For instance,
=
although the network may learn from stimulus patterns with an average noise level of ΔS
0.1, it can reliably classify stimuli of noise levels ΔStest from 0 to about 0.6 afterwards.
Imparare
Inoltre, the performance of a network that was successfully trained in a noisy envi-
ronment can be drastically improved by a subsequent readaptation phase. Using this second
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
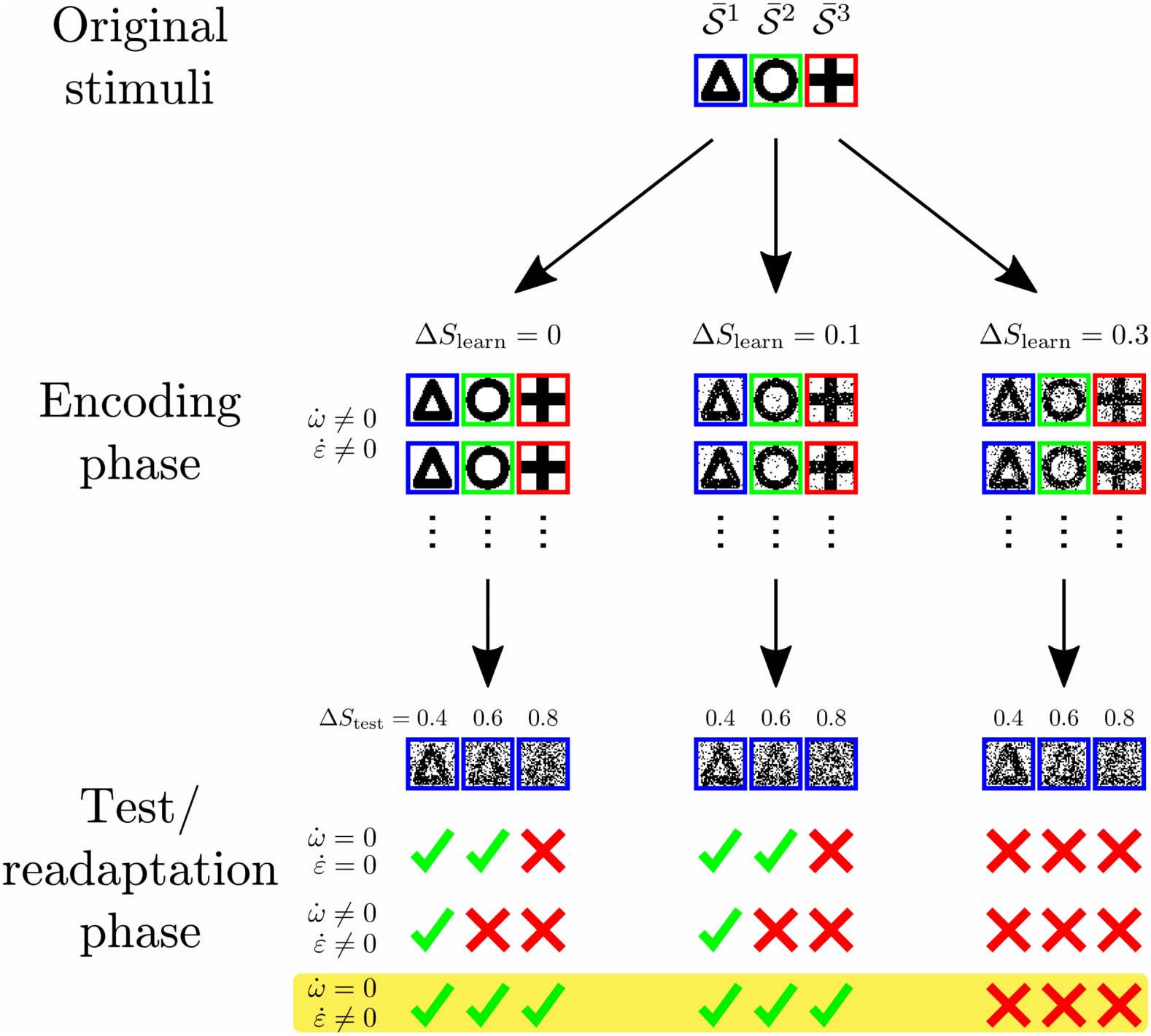
¯S ν
Figura 7. Schematic summary of results. Noisy patterns S ν
are repeatedly generated from original
(per esempio., a triangle, a circle, and a cross) and imprinted on the stimulus layer (encoding
stimuli
phase). If the noise ΔS
learn is sufficiently small, synaptic and intrinsic plasticity lead to the formation
of structure encoding the organization of stimuli (existence of different geometrical forms). Dopo
this initial learning phase, a second learning or readaptation phase enables the network to classify
stimuli even in the presence of very high levels of noise ΔStest. Here, only intrinsic plasticity should
be present ( ˙w = 0; ˙ε (cid:7)= 0). This suggests that learning is carried out in two phases: In the first
phase, the encoding phase, synaptic weights develop to represent the basic organization of the
environmental stimuli. This structuring of synaptic weights is most efficient if the noise ΔS
learn is
low. In the second phase, the readaptation phase, learning is dominated by intrinsic plasticity while
synaptic weights have to be maintained. The cortical firing thresholds are then able to quickly adapt
to the current level of noise ΔStest. Thereby, intrinsic plasticity approximates the optimal thresholds
for a given value of ΔStest maximizing performance.
Network Neuroscience
188
Learning of noisy stimuli requires distinct phases of plasticity
phase in order to (Rif)adapt the neuronal excitabilities to the level of noise ΔStest that will sub-
sequently be tested for enables the network to classify stimuli up to even higher noise levels of
ΔStest ≈ 0.8 (Figure 6B). Consequently, the readaptation phase provides a significant advantage
for a large regime of stimulus cluster sizes (red area in Figure 6C). Even more so, stimulus clus-
ters with sizes ΔStest ∈ (0.6, 0.8) can only be classified by using the readaptation phase. IL
∈ (0.2, 0.3) and ΔStest ∈ (0.8, 1.0)
decrease in performance for noise levels between ΔS
(blue area) is not crucial given the low level of performance (Figure 6A).
Imparare
In summary, sparse, expansive networks can learn the clustered organization of noisy stimuli
(underlying stimuli might be triangle, circle, and cross like in Figure 7) by the interplay of
synaptic and intrinsic plasticity in a self-organized manner. During the initial encoding phase,
low levels of noise ΔS
learn can be tolerated by the system, while higher levels of noise obstruct
the network’s ability to learn the organization of stimuli. After the encoding phase, the network
can reliably classify noisy patterns of up to ΔStest ≈ 0.6 if synaptic weights and neuronal firing
thresholds are fixed ( ˙w = 0; ˙ε = 0). D'altra parte, the performance decreases significantly
if both synaptic and intrinsic plasticity are allowed to modify the network’s structure during
the presentation of these noisy stimuli ( ˙w (cid:7)= 0; ˙ε (cid:7)= 0). È interessante notare, if the synaptic structure is
maintained while the excitability of the cortical neurons can adapt ( ˙w = 0; ˙ε (cid:7)= 0), the network
can successfully classify stimuli even in the presence of very high levels of noise (Guarda la figura 7
bottom for examples). These results suggest that learning in the presence of noise requires
two distinct phases of plasticity: initial learning of the organization of environmental stimuli
via synaptic and intrinsic plasticity in the encoding phase followed by the readaptation phase
using only intrinsic plasticity in order to readapt to the current level of noise.
DISCUSSION
How do neuronal systems learn the underlying organization of the surrounding environment
in realistic, noisy conditions? In this study, we have shown that sparse and expansive networks
can reliably form the required neuronal and synaptic structures via the interplay of synaptic and
intrinsic plasticity. Among others, our results indicate that after learning the classification of
diverse environmental stimuli in the presence of high levels of noise works best if the synaptic
structure is more rigid than the neuronal structure, namely the excitabilities of the neurons.
Thereby, our model predicts that higher levels of noise lead to lower firing thresholds or (SU
average) increased neuronal excitabilities (Figure 4A).
Inoltre, our model predicts that classification performance is highest if the system is
adapted to the perceived level of noise. We propose the following psychophysical experiment
related to pattern recognition in order to test this prediction: Primo, subjects have to learn a set of
previously unknown patterns, such as visual or auditory patterns. Secondo, they have to identify
noisy versions of these patterns. We propose that the classification performance of a given noisy
pattern depends on the history of patterns the subject perceived beforehand. Specifically, our
model predicts that a given noisy pattern is classified most reliably if the previously perceived
patterns had the same level of noise. By transferring this protocol to an animal model, IL
predicted course of the adaptation of the firing thresholds could be verified, pure.
After the successful learning of the inherent organization of stimuli, in this study we changed
the synaptic variability by “turning off” the dynamics of synaptic plasticity (Figura 4). Questo
change of the timescale of synaptic plasticity between the encoding and the readaptation phase
could be related to the dynamics during the development of the visual system (Daw, 2003;
Daw, Fox, Sato, & Czepita, 1992; Hensch, 2004; Hooks & Chen, 2007). During the critical
period, the early visual system is quite susceptible to new sensory experiences and the system
Network Neuroscience
189
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
is very plastic. Inoltre, the visual range during early developmental phases is limited, Quale
could imply lower levels of noise. Così, the encoding phase in our model could be linked to the
critical period. By contrast, the matured visual system is quite rigid, matching the requirements
of the readaptation phase, which predicts that the sensory system should be able to adapt to
different levels of noise by (only) changing the neuronal excitabilities (Figura 6).
One of the major assumptions of this work, similar to a previous study (Babadi & Sompolinsky,
2014), is that environmental stimuli are organized such that they can be grouped into clus-
ters. Each of these clusters has the same Gaussian noise level ΔS. Natural stimuli, Tuttavia,
have much more structured noise statistics. Nevertheless, the mechanisms considered here
that enable the network to compensate for noisy stimuli (cioè., synaptic and intrinsic plastic-
ità) do not specifically rely on the noise being Gaussian. Intrinsic plasticity will still main-
tain the target firing rate independent of precisely how the membrane potential distributions
(Figure 3A, B) are shaped by different types of noise. Given our results (Figura 4), we expect that
the neuronal thresholds resulting in the target firing rate will be close to the optimal threshold.
Inoltre, the exponential synaptic decay may lead to less reliable presynaptic stimulus
neurons having a smaller impact on a cortical neuron’s firing. In addition to clusters not being
Gaussian shaped, in a natural environment each underlying stimulus may also have a different
overall level of noise such that ΔSν
depends on the cluster ν. Tuttavia, if the synaptic structure
has already been learned during the encoding phase, we expect that cluster-specific ΔSν
test do
not have an impact on the classification performance, as each cortical neuron becomes selec-
tive to only one stimulus cluster (Figure 2D). Inoltre, only the noise level of this selected
cluster defines the optimal firing threshold (Figura 3). Therefore, the firing threshold of each
neuron can be tuned to its distinct, optimal threshold value, which is independent of the noise
levels of other clusters. D'altra parte, we expect that different ΔSν
learn during the en-
coding phase will lead to over- and underrepresentations of stimulus clusters in the network.
Since noise attenuates competition between clusters (Figure 5C, D), clusters with high ΔSν
Imparare
are less competitive and will subsequently be underrepresented. Nevertheless, the underrep-
resentation could be an advantage, as stimuli that are too noisy are less informative about the
environment than others; consequently, the neuronal system attributes a smaller amount of
resources (neurons and synapses) to them. Tuttavia, the effect of cluster-specific noise on the
neuronal and synaptic dynamics have to be investigated further.
Additionally, some stimulus clusters might be perceived more often than others. The cor-
responding representations would become larger than average, since their relevant synapses
are strengthened more often by Hebbian synaptic plasticity, leading to a competitive advan-
tage. Larger representations of more frequently perceived stimulus clusters might provide a
behavioral advantage, as these clusters also need to be classified more often. Tuttavia, IL
discrepancy between the frequency of such a cluster and the target firing rate of a cortical neu-
ron responding to it might pose a problem. As intrinsic plasticity tries to maintain the target
activity, the firing threshold would be placed so high that even slight noise could not be toler-
ated. One solution might be that neurons could have different target activities (G. G. Turrigiano,
2008) and clusters are selected such that target activity and presentation frequency match. UN
different mechanism could be global inhibition. A single inhibitory neuron or population of
neurons connected to all relevant cortical neurons could homeostatically regulate the activity
of the cortical layer by providing inhibitory feedback. Such a mechanism has been identified,
for instance, in the Drosophila mushroom body (Eichler et al., 2017; Faghihi, Kolodziejski,
Fiala, Wörgötter, & Tetzlaff, 2013).
In this study, only one combination of three different plasticity rules was investigated. Of
course, many more plasticity mechanisms are conceivable and have been widely studied
Network Neuroscience
190
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
(Dayan & Abbott, 2001; Miner & Triesch, 2016; Tetzlaff, Kolodziejski, Markelic, & Wörgötter,
2012; Zenke, Agnes, & Gerstner, 2015). One mechanism could be synaptic scaling regulating
the synaptic weights instead of the neuronal excitability such that the neurons reach a certain
target firing rate (Desai, Cudmore, Nelson, & Turrigiano, 2002; Hengen, Lambo, Van Hooser,
Katz, & Turrigiano, 2013; Keck et al., 2013; Tetzlaff et al., 2011; G. G. Turrigiano et al., 1998).
Tuttavia, the timescale of synaptic scaling is significantly slower than the timescale of in-
trinsic plasticity, which could increase the duration of the readaptation phase required by the
neuronal system to adapt to new levels of noise. D'altra parte, faster homeostatic mech-
anismo (Zenke & Gerstner, 2017) could result in a shorter duration of readaptation. Tuttavia,
the influence of further plasticity mechanisms on the dynamics of sparse, expansive networks
has to be analyzed in future studies.
It is usually assumed that homeostatic synaptic plasticity is required for competition
(Abbott & Nelson, 2000; Mugnaio, 1996). In the present study, Tuttavia, competition arises from
the interactions of Hebbian synaptic plasticity and homeostatic intrinsic plasticity alone. Home-
ostatic intrinsic plasticity maintains a certain activity of a given cortical neuron. Stimuli com-
pete for this activity. If one stimulus gains an activity advantage, it will see synapses activated
by it strengthened. This leads to less strengthening of other synapses, because the occurrence
of Hebbian synaptic plasticity is limited by homeostatic intrinsic plasticity. Synapses will only
subsequently be weakened due to homeostatic synaptic plasticity (exponential decay term),
which does not interfere in the interaction between Hebbian synaptic and homeostatic intrin-
sic plasticity generating competition (see Supplementary Figure 2). Consequently, the widely
held opinion that homeostatic synaptic plasticity is required for competition might have to be
revised.
Even though expansion is a common feature of sensory processing networks, it is not a
prerequisite for the results presented here. Nonexpansive networks, pure, can learn to distin-
guish different clusters, although they do not reach the performance of an expansive network
(see Supplementary Figure 4). This means that nonexpansive networks as well profit from a
two-phase learning protocol as suggested here.
Overall, this study suggests the following answer to how networks learn to classify stimuli in
noisy environments: Learning takes place in two distinct phases. The first phase is the encoding
phase. Hebbian synaptic and homeostatic intrinsic plasticity structure synaptic weights so as
to represent the organization of stimuli, with each neuron becoming selectively responsive to
a single stimulus cluster. Optimal synaptic structure is achieved if stimuli are noise-free. IL
second learning phase, called readaptation phase, ensues in an arbitrarily noisy environment.
Here, synaptic weights have to be maintained in order to preserve the previously learned
synaptic structure. Nel frattempo, homeostatic intrinsic plasticity regulates the activity of neurons.
The firing thresholds are thereby adapted to their optimal values, maximizing classification
performance in the current environment (Figura 7).
METHODS
Network and Plasticity Mechanisms
In this study, a two-layered feed-forward network of rate-based neurons is investigated
(Figure 1A). The first layer, called stimulus layer, consists of NS = 1, 000 neurons, while the
second layer, called cortical layer, consists of NC = 10, 000 neurons. Feed-forward synaptic
connections exist from all stimulus to all cortical neurons. Their synaptic strengths are given
Network Neuroscience
191
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
by ωji where j ∈ {1, …, NC} denotes the postsynaptic cortical neuron and i ∈ {1, …, NS} IL
presynaptic stimulus neuron. No recurrent connections are present.
The neurons of the stimulus layer will act as input. As such, the firing rate Si of stimulus
neuron i will be set to either 0 O 1. Each input therefore is a pattern of firing rates Si ∈ {0, 1}
on the stimulus layer. These firing rates elicit membrane potentials in the cortical neurons,
which follow the leaky integrator equation ˙uj = −uj + ∑NS
i=1 ωjiSi. We assume that each
input pattern is presented long enough such that the membrane potential mostly resides in the
fixed point for the current input. In order to save computation time, we therefore discard the
leaky integrator dynamics and simplify the membrane potential to the fixed point of the leaky
integrator equation:
uj =
NS
∑
i=1
ωjiSi .
(9)
The membrane potential uj will then be translated into a firing rate Cj of cortical neuron j
via the sigmoidal transfer function
Cj =
F max
1 + esp(β(ε j − uj))
,
(10)
resulting in cortical firing rates between 0 and F max. The steepness of the sigmoidal function
is given by β = 5, the maximum firing rate F max = 1, and the point of inflection ε j is specific
to each cortical neuron j. ε j corresponds to a neuron-specific firing threshold determining the
neuronal excitability.
Intrinsic plasticity regulates this neuron-specific firing threshold ε j. In order for each cortical
neuron j to reach a target firing rate F T = 0.001, the point of inflection of the sigmoidal transfer
curve follows the dynamics
˙ε j = κ(Cj − F T) .
(11)
The parameter κ = 1 · 10−2
firing rate Cj of cortical neuron j is larger than the target firing rate F T
such that Cj decreases (assuming the input stays constant), and vice versa.
determines the adaptation speed of intrinsic plasticity. If the
, the threshold ε j increases
The feed-forward synaptic connections ωji between the postsynaptic cortical neuron j and
the presynaptic stimulus neuron i are controlled by unsupervised synaptic plasticity:
˙ωji = μSiCj − ηωji .
(12)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
and η = 3 · 10−8
The parameters μ = 1 · 10−5
determine the speed of the Hebbian correla-
tion learning term and the exponential decay of synaptic weights, rispettivamente. We assume that
synaptic plasticity acts much slower than the presentation time of a single input pattern such
that the fixed point of the leaky integrator given by Equation 9 does not significantly change
during the presentation of a single input and the simplification thus still holds.
Clustered Stimuli
The structuring of the inputs and the analysis methods are similar to a previous work (Babadi
& Sompolinsky, 2014). Here, sensory stimuli are grouped in P = 1, 000 clusters. Each cluster
Network Neuroscience
192
Learning of noisy stimuli requires distinct phases of plasticity
comprises different sensory impressions of the same environmental stimulus. Its main compo-
nent is a characteristic neuronal firing pattern, called the central stimulus pattern
, Dove
ν ∈ {1, …, P} denotes the cluster (Figure 1A, B). All central patterns are generated by assigning
each stimulus neuron i for each stimulus cluster ν a firing rate
i of either 0 O 1 with equal
probability. In addition to the central pattern, each cluster also contains noisy variants of the
central pattern, called noisy patterns S ν
. Noisy stimulus patterns are generated by randomly
changing the central stimulus pattern’s firing rates from 1 A 0 or vice versa with probability
ΔS/2. ΔS thereby determines the level of noise and consequently the size of the stimulus
clusters, and can range from 0 (no noise) A 1 (no correlation remains). Inoltre, it is the
normalized average Hamming distance of noisy stimulus patterns to their central stimulus pat-
tern:
¯S ν
¯S ν
(cid:2)
ΔS =
∑NS
i − ¯S ν
io |
i=1 |S ν
NS · 1/2
(cid:3)
,
S ν,ν
(13)
with the angular brackets denoting the average over all noisy stimulus patterns S ν
of all
clusters ν.
All central and noisy stimulus patterns elicit central and noisy cortical patterns
and C ν
,
rispettivamente, in the cortical layer of the network. In analogy to Equation (13) IL (uncorrected)
size of the resulting cortical clusters can be defined as Δc via
¯C ν
Δc =
(cid:2)
(cid:3)
∑NC
j − ¯C ν
j=1 |C ν
j |
NC · Z(C ν, ¯C ν)
.
C ν,ν
(14)
As the firing rates C ν
j and
¯C ν
j can take on values between 0 E 1, a more complex normal-
ization Z(Cκ, C λ) for the patterns Cκ
and C λ
is required:
Z(Cκ, C λ) =
1
NC
2
NC
∑
l=1
NC
∑
m=1
|Cκ
l − C λ
M| .
(15)
This normalization quantifies the average overlap two random cortical patterns with the
same firing rates would have.
Being generated randomly, the central stimulus patterns are uncorrelated among each other.
Because of the propagation of these patterns through the synaptic connections, Tuttavia, IL
central cortical patterns might not be uncorrelated. In the context of noise reduction a more
appropriate performance measure compensates for the introduced correlation. The cortical
cluster size ΔC is therefore defined as
ΔC =
Δc
dC
,
(16)
where the cortical cluster distance dC is a measure of the correlation between central cor-
tical patterns:
dC =
(cid:2)
∑NC
j − ¯C λ
j=1 | ¯Cκ
j |
NC · Z( ¯Cκ, ¯C λ)
(cid:3)
.
κ,λ
(17)
193
Network Neuroscience
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
Classification Errors
In the following, the classification errors e
fn,j (false negatives) of single
neurons in a trained network will be set into relation with the cortical cluster size ΔC. To do so,
we will first discuss the cortical cluster distance dC and the ergodicity of the network. We will
then use the results to derive the relation between the cortical cluster size and the classification
errors.
fp,j (false positives) and e
In order to simplify the following derivations for ΔC = Δc
dC , we consider that the cortical
cluster distance dC = 1 in a trained network as discussed in the following. In the ‘Plastic Net-
work’ section (Vedere, per esempio., Figura 2) we have demonstrated that a given cortical neuron becomes
responsive to a single stimulus cluster during training. The stimulus cluster that a neuron be-
comes responsive to is usually the one that initially elicits the strongest membrane potential,
as the related synapses will experience the greatest strengthening by Hebbian plasticity. Questo
cluster is a random one, Anche se, as the initial membrane potential depends only on the initially
random synaptic weights. Consequently, each cortical neuron becomes responsive to a ran-
dom stimulus cluster. This implies that the cortical clusters are uncorrelated since each cortical
neuron’s response to a given cluster is random. By definition, the cortical cluster distance dC
is thus equal to 1. We therefore have
ΔC = Δc =
(cid:2)
(cid:3)
∑NC
j − ¯C ν
j=1 |C ν
j |
NC · Z(C ν, ¯C ν)
.
C ν,ν
(18)
Prossimo, we will assume that a trained network is ergodic, questo è, we can exchange averages
over cortical patterns (“time”) with averages over cortical neurons (“space”). Specifically, we
assume the following relation to hold:
(cid:2)
j=1 |C ν
∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)
(cid:3)
(cid:2)
=
C ν,ν
(cid:3)
j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)
Cj,j
con
Z(C ν, ¯C ν) =
Z(Cj, ¯Cj) =
1
NC
1
P2
2
NC
∑
l=1
P
∑
κ=1
NC
∑
m=1
P
∑
λ=1
|C ν
l − ¯C ν
M| ,
|Cκ
j − ¯C λ
j | .
(19)
(20)
(21)
¯Cj are vectors containing the firing rates of cortical neuron j in response to one noisy/
Cj and
central pattern of each cluster.
In the following, we will divide the assumption about the ergodicity of the network in several
smaller assumptions and discuss whether they are valid. Primo, we assume a large system, questo è,
P, NC → ∞, which approximates the network studied here consisting of P = 1, 000 and NC =
10, 000 adequately. Secondo, we need to assume that the set of cortical clusters is homogeneous,
questo è, ΔC is the same for all clusters. This is a sufficient approximation as ΔS is the same
for all clusters and no cluster is preferred by the cortical neurons in a trained network as
discussed before. Given these two assumptions, we can drop the average over noisy patterns
C ν
in Equation 19, because the average over a single noisy pattern of an infinite number of
clusters is equal to the average over all noisy patterns of an infinite number of clusters as long
as the clusters are homogeneous. Likewise, by assuming that the set of cortical neurons is
Network Neuroscience
194
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
homogeneous, we can drop the average over the sets of noisy firing rates Cj in Equation 19. In
a trained network, where all neurons developed a bimodal weight distribution and have the
same target firing rate, this is a decent approximation. We can thus write the following:
(cid:2)
(cid:2)
P,NC→∞⇐⇒
j=1 |C ν
∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)
j=1 |C ν
∑NC
j − ¯C ν
j |
NC · Z(C ν, ¯C ν)
(cid:3)
C ν,ν
(cid:3)
⇔
⇔
⇐
⇔
ν
∑NC
j − ¯C ν
j=1 |C ν
j |
l=1 ∑NC
∑NC
− ¯C ν
m=1 |C ν
M|
l
j − ¯C ν
|C ν
j |
l=1 ∑NC
m=1 |C ν
l − ¯C ν
M|
1
P
P
∑
ν=1
1
NC
P
∑
ν=1
NC
∑
j=1
1
NC
(cid:2)
2
1
NC
NC
∑
l=1
NC
∑
m=1
1
NC
2 ∑NC
NC
∑
m=1
|C ν
l − ¯C ν
M|
(cid:3)
|C ν
l − ¯C ν
M|
l
=
=
=
=
=
=
(cid:3)
Cj,j
(cid:3)
(cid:2)
(cid:2)
j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)
j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)
j
ν=1 |C ν
∑P
λ=1 ∑P
|C ν
κ=1 ∑P
j − ¯C ν
j |
j − ¯Cκ
κ=1 |C λ
j |
j − ¯C ν
j |
j − ¯C λ
λ=1 |Cκ
j |
P ∑P
1
1
P2 ∑P
1
NC
NC
∑
j=1
P
∑
ν=1
NC
∑
j=1
P
∑
κ=1
P
∑
λ=1
1
P2
(cid:2)
|Cκ
j − ¯C λ
j | ∀j, ν
(cid:3)
1
P
P
∑
λ=1
|Cκ
j − ¯C λ
j |
∀j, ν .
κ
(22)
(23)
(24)
(25)
(26)
(27)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Equazione 26 is a sufficient, but not a necessary, condition for Equation 25. Therefore, if we
can show that Equation 27 is a valid assumption, this suffices (together with the assumptions
mentioned above) for the ergodicity of a trained network.
As demonstrated in the Results section and discussed before, every cortical neuron of the
trained network is responsive to a single, random cluster. We need to further assume that every
central pattern elicits activity in F T NC = 10 of all cortical neurons. This is strictly true only
on average, but if cortical neurons respond to a random cluster, it is a decent approximation.
Consequently, we can do the following transformations:
(cid:2)
(cid:2)
⇔
1
NC
NC
∑
m=1
|C ν
l − ¯C ν
M|
(cid:3)
l
10
NC
|C ν
l − 1| +
NC − 10
NC
|C ν
l − 0|
(cid:3)
l
⇔ (cid:5)C ν
l (cid:6)l
(cid:2)
(cid:2)
1
P
P
∑
λ=1
|Cκ
j − ¯C λ
j |
(cid:3)
κ
1
P
|Cκ
j − 1| +
P − 1
P
|Cκ
j − 0|
(cid:3)
κ
(cid:5)
(cid:4)
Cκ
j
κ
=
=
=
∀j, ν
(28)
∀j, ν
(29)
∀j, ν .
(30)
Questo è, for each ΔS every cortical pattern ν and every cortical neuron j must have the same
average firing rate. This is true given the assumptions we have already discussed: The cortical
neurons are homogeneous, questo è, they all have a bimodal weight distribution and so forth,
and each cortical neuron is responsive to a random cluster.
Network Neuroscience
195
Learning of noisy stimuli requires distinct phases of plasticity
In total, we have divided the assumption of ergodicity (Equazione 19) of a trained network in
simpler assumptions that we were able to validate. Using the ergodicity we now have
ΔC =
(cid:2)
j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)
(cid:3)
.
Cj,j
(31)
Similar to the argument made for Equation 23, in an infinitely large network, averaging
over an infinite set of noisy firing rates Cj of a single cortical neuron j is equal to averaging
over an infinite set of noisy firing rates Cj of all cortical neurons as long as the neurons are
homogeneous. We can thus drop the average over j:
(cid:2)
ΔC =
(cid:3)
j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)
(cid:2)
P,NC→∞
−−−−−→
(cid:3)
Cj,j
j − ¯C ν
∑P
ν=1 |C ν
j |
P · Z(Cj, ¯Cj)
j − ¯C ν
|C ν
Cj
j | + ∑
ν| ¯C ν
j =0
=
=
=
(cid:2)
∑
ν| ¯C ν
j =1
(cid:6)
P ∑P
1
κ=1
1 · |Cκ
|C ν
(cid:2) ∑
ν| ¯C ν
j =1
|C ν
j − ¯C ν
j |
(cid:3)
(cid:7)
Cj
j − 1| + (P − 1) · |Cκ
|C ν
j − ¯C ν
j |
(cid:3)
j − 0|
j − ¯C ν
j | + ∑
ν| ¯C ν
j =0
P ∑P
κ=1 Cκ
j
j − ¯C ν
j |
1 + P−2
(cid:3)
|C ν
(cid:2) ∑
ν| ¯C ν
j =1
1 + P−2
(cid:8)
κ=1 Cκ
j
P ∑P
(cid:9)(cid:10)
false negatives e
fn,j
Cj
j − ¯C ν
j |
|C ν
(cid:2) ∑
ν| ¯C ν
j =0
1 + P−2
+
Cj
(cid:11)
(cid:8)
κ=1 Cκ
j
P ∑P
(cid:9)(cid:10)
false positives e
fp,j
(cid:3)
.
Cj
(cid:11)
(32)
(33)
(34)
(35)
(36)
i − 1
ν=1( ¯S ν
Initialization
When initialized randomly, the synaptic weights ωji are drawn from a Gaussian distribution
2√
with mean 0 and variance
. The synaptic weights can also be initialized in a structured
NS
∑P
manner according to ωji = 100
j − F T) (similar to Babadi & Sompolinsky,
2 )(Rν
NS
2014; Tsodyks & Feigelman, 1988). The factor 100 scales the synaptic weights such that they
are in the same order of magnitude as the synaptic weights in the trained dynamic network
ensuring that they are comparable. Rν
are cortical patterns that are generated using one of the
following methods: For Figure 1 Rν
are random patterns of ones and zeros where each pattern
ν and each cortical neuron j has an activity of F T
are computed via
Rν
j − Tj), where Θ denotes the Heaviside function and the thresholds Tj are chosen
such that each cortical neuron j achieves an activity of F T
. This results in cortical patterns Rν
that are correlated to the central cortical patterns
. For all other results, Rν
of an existing network.
j = Θ( ¯C ν
¯C ν
The cortical membrane thresholds ε j are then initialized such that each cortical neuron j
achieves an average firing rate of the target firing rate F T
at the central cortical patterns. In
order to find the corresponding membrane thresholds ε j, the secant method is used with initial
values of 0 and the mean of the highest and second highest (as F T P = 1) membrane potentials
Network Neuroscience
196
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
of cortical neuron j. If structured synaptic weights are used, this leads to ε j close to the mean
of the highest and second highest membrane potentials of neuron j.
Implementation
Training is done by repeatedly presenting stimulus patterns for one time step Δt = 1 each. IL
high computational demand of simulating a network with 11, 000 neurons for 200, 000 training
steps each containing 1, 000 patterns for just a single parameter set made parallel simulation
of patterns necessary and required the usage of a computer cluster. A tal fine, each training
step consists of parallel simulation of one stimulus pattern per cluster. Stimulus patterns are
generated using a stimulus cluster size ΔS
learn and the current learning step is denoted by L.
The synaptic weights ωji and cortical thresholds ε j are updated at the end of each training
step according to Δωji = ∑P
denotes the cortical
pattern of cluster ν that was simulated in this learning step. This is a reasonable approximation
if a single learning step changes the network’s state only slightly, as is the case in this study.
ν=1 ˙ωji(C ν) and Δε j = ∑P
ν=1 ˙ε j(C ν), where C ν
The cortical cluster size ΔC (cf. Equazione 14 and Equation 16) in response to a stimulus
cluster size ΔStest is approximated using 10 noisy patterns per cluster.
If intrinsic plasticity is active during the testing phase, repeatedly, one noisy pattern per
cluster is simulated using a stimulus cluster size ΔStest. After the mean of all cortical thresholds
changed by less than 0.0001%, the cortical cluster size ΔC is calculated for the given stimulus
¯C ν
cluster size ΔStest. In order to speed up its computation, we used the central cortical patterns
and cortical cluster distance dC from ahead of the adaptation phase and were able to verify that
this does not influence the results. The thresholds are reset to their previous values afterwards.
The entire procedure is performed for all ΔStest, each requiring fewer than 7, 000 learning steps
for the thresholds to converge.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00118.
AUTHOR CONTRIBUTIONS
Steffen Krüppel: Conceptualization; Data curation; Formal analysis; Investigation; Methodol-
ogy; Software; Validation; Visualization; Writing – Original Draft; Writing – Review & Editing.
Christian Tetzlaff: Conceptualization; Funding acquisition; Investigation; Methodology; Project
administration; Resources; Supervision; Writing – Original Draft; Writing – Review & Editing.
FUNDING INFORMATION
Christian Tetzlaff, Horizon 2020 Framework Programme (http://dx.doi.org/10.13039/
100010661), Award ID: 732266. Christian Tetzlaff, Deutsche Forschungsgemeinschaft (http://
dx.doi.org/10.13039/501100001659), Award ID: CRC 1286 (project C1).
REFERENCES
Abbott, l. F., & Nelson, S. B. (2000). Synaptic plasticity: Taming the
beast. Nature Neuroscience, 3(11S), 1178–1183. https://doi.org/
10.1038/81453
Albus, J. S. (1971). A theory of cerebellar function. Mathemat-
ical Biosciences, 10(1), 25–61. https://doi.org/10.1016/0025-
5564(71)90051-4
Babadi, B., & Sompolinsky, H. (2014). Sparseness and expansion in
sensory representations. Neuron, 83(5), 1213–1226. https://doi.
org/10.1016/j.neuron.2014.07.035
Balling, A., Technau, G. M., & Heisenberg, M. (1987). Are
the structural changes in adult Drosophila mushroom bod-
ies memory traces? Studies on biochemical learning mutants.
Network Neuroscience
197
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
Journal of Neurogenetics, 4(1), 65–73. https://doi.org/10.3109/
01677068709102334
Benda, J., & Herz, UN. V. M. (2003). A universal model for spike-
frequency adaptation. Calcolo neurale, 15(11), 2523–2564.
https://doi.org/10.1162/089976603322385063
Bi, G.-q., & Poo, M.-m. (1998). Synaptic modifications in cultured
hippocampal neurons: Dependence on spike timing, synaptic
strength, and postsynaptic cell type. Journal of Neuroscience,
18(24), 10464–10472. https://doi.org/10.1523/JNEUROSCI.18-
24-10464.1998
Bliss, T. V. P., & Lømo, T. (1973). Long-lasting potentiation of synap-
tic transmission in the dentate area of the anaesthetized rabbit
following stimulation of the perforant path. Journal of Physiology,
232(2), 331–356. Retrieved from https://www.ncbi.nlm.nih.gov/
pmc/articles/PMC1350458/
Brecht, M., & Sakmann, B. (2002). Dynamic representation of
whisker deflection by synaptic potentials in spiny stellate and
pyramidal cells in the barrels and septa of layer 4 rat somatosen-
sory cortex. Journal of Physiology, 543(1), 49–70. https://doi.org/
10.1113/jphysiol.2002.018465
Chacron, M. J., Longtin, A., & Maler, l. (2011). Efficient compu-
tation via sparse coding in electrosensory neural networks. Cur-
rent Opinion in Neurobiology, 21(5), 752–760. https://doi.org/
10.1016/j.conb.2011.05.016
Dan, Y., Atick, J. J., & Reid, R. C. (1996). Efficient coding of natural
scenes in the lateral geniculate nucleus: Experimental test of a com-
putational theory. Journal of Neuroscience, 16(10), 3351–3362.
https://doi.org/10.1523/JNEUROSCI.16-10-03351.1996
Daw, N. W. (2003). Critical periods in the visual system. In B.
Hopkins & S. P. Johnson (Eds.), Neurobiology of infant vision.
Westport, CT: Praeger.
Daw, N. W., Fox, K., Sato, H., & Czepita, D. (1992). Critical
period for monocular deprivation in the cat visual cortex. Jour-
nal of Neurophysiology, 67, 197–202. https://doi.org/10.1152/
jn.1992.67.1.197
Dayan, P., & Abbott, l. F.
(2001). Theoretical neuroscience:
Computational and mathematical modeling of neural systems.
Cambridge, MA: CON Premere.
Desai, N. S., Cudmore, R. H., Nelson, S. B., & Turrigiano, G. G.
(2002). Critical periods for experience-dependent synaptic scal-
ing in visual cortex. Nature Neuroscience, 5(8), 783–789. https://
doi.org/10.1038/nn878
Desai, N. S., Rutherford, l. C., & Turrigiano, G. G. (1999). Plasticity
in the intrinsic excitability of cortical pyramidal neurons. Nature
Neuroscience, 2(6), 515–520. https://doi.org/10.1038/9165
Deweese, M. R., & Zador, UN. M. (2003). Binary Coding in audi-
tory cortex. Advances in Neural Information Processing Systems,
117–124.
Eichler, K., Li, F., Litwin-Kumar, A., Park, Y., Andrade, I., Schneider-
Mizell, C. M., . . . Cardona, UN. (2017). The complete connectome
of a learning and memory centre in an insect brain. Nature, 548,
175–182. https://doi.org/10.1038/nature23455
Faghihi, F., Kolodziejski, C., Fiala, A., Wörgötter, F., & Tetzlaff, C.
(2013). An information theoretic model of information process-
ing in the Drosophila olfactory system: The role of inhibitory
neurons for system efficiency. Frontiers in Computational Neu-
roscience, 7, 183.
Franks, K. M., & Isaacson, J. S. (2006). Strong single-fiber sen-
sory inputs to olfactory cortex: Implications for olfactory coding.
Neuron, 49(3), 357–363. https://doi.org/10.1016/j.neuron.2005.
12.026
Gerstner, W., & Kistler, W. M. (2002). Mathematical formulations
of Hebbian learning. Biological Cybernetics, 87, 404–415.
Hartmann, C., Lazar, A., Nessler, B., & Triesch, J. (2015). Where’s
the noise? Key features of spontaneous activity and neural vari-
ability arise through learning in a deterministic network. PLoS
Computational Biology, 11, e1004640. https://doi.org/10.1371/
journal.pcbi.1004640
Hebb, D. O. (1949). The organization of behavior. New York, NY:
Wiley & Sons. Retrieved from http://s-f-walker.org.uk/pubsebooks/
pdfs/The_Organization_of_Behavior-Donald_O._Hebb.pdf
Hengen, K. B., Lambo, M. E., Van Hooser, S. D., Katz, D. B., &
Turrigiano, G. G. (2013). Firing rate homeostasis in visual cortex
of freely behaving rodents. Neuron, 80, 335–342.
Hensch, T. K. (2004). Critical period regulation. Annual Review
of Neuroscience, 27, 549–579. https://doi.org/10.1146/annurev.
neuro.27.070203.144327
Hooks, B. M., & Chen, C. (2007). Critical periods in the visual
system: Changing views for a model of experience-dependent
plasticity. Neuron, 56, 312–326. https://doi.org/10.1016/j.neuron.
2007.10.003
Jefferis, G. S. X. E., Potter, C. J., Chan, UN. M., Marin, E. C., Rohlfing,
T., Maurer, C. R., & Luo, l. (2007). Comprehensive maps of
Drosophila higher olfactory centers: Spatially segregated fruit and
pheromone representation. Cell, 128(6), 1187–1203. https://doi.
org/10.1016/j.cell.2007.01.040
Keck, T., Keller, G. B., Jacobsen, R. I., Eysel, U. T., Bonhoeffer, T., &
Hübener, M. (2013). Synaptic scaling and homeostatic plasticity
in the mouse visual cortex in vivo. Neuron, 80, 327–334.
Lazar, A., Pipa, G., & Triesch, J. (2009). SORN: A self-organizing
recurrent neural network. Frontiers in Computational Neuro-
science, 3, 23.
LeMasson, G., Marder, E., & Abbott, l. F.
(1993). Activity-
dependent regulation of conductances in model neurons. Sci-
ence, 259(5103), 1915–1917. https://doi.org/10.1126/science.
8456317
Markram, H., Lübke, J., Frotscher, M., & Sakmann, B. (1997).
Regulation of synaptic efficacy by coincidence of postsynaptic
APs and EPSPs. Scienza, 275(5297), 213–215. https://doi.org/10.
1126/science.275.5297.213
Marr, D. (1969). A theory of cerebellar cortex. Journal of Physi-
ology, 202(2), 437–470. https://doi.org/10.1113/jphysiol.1969.
sp008820
Martin, S. J., Grimwood, P. D., & Morris, R. G. M. (2000). Synap-
tic plasticity and memory: An evaluation of the hypothesis. An-
nual Review of Neuroscience, 23(1), 649–711. https://doi.org/10.
1146/annurev.neuro.23.1.649
Mugnaio, K. D. (1996). Synaptic economics: Competition and cooper-
ation in synaptic plasticity. Neuron, 17, 371–374.
Mugnaio, K. D., & MacKay, D. J. C. (1994). The role of constraints in
Hebbian learning. Calcolo neurale, 6(1), 100–126. https://
doi.org/10.1162/neco.1994.6.1.100
Miner, D., & Triesch, J. (2016). Plasticity-driven self-organization
under topological constraints account for nonrandom features
Network Neuroscience
198
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Learning of noisy stimuli requires distinct phases of plasticity
of cortical synaptic wiring. PLoS Computational Biology, 12(2),
e1004759.
Mombaerts, P., Wang, F., Dulac, C., Chao, S. K., Nemes, A.,
Mendelsohn, M., . . . Axel, R. (1996). Visualizing an olfac-
tory sensory map. Cell, 87(4), 675–686. https://doi.org/10.1016/
S0092-8674(00)81387-2
Monk, T., Savin, C., & Lücke, J. (2016). Neurons equipped with in-
trinsic plasticity learn stimulus intensity statistics. In Advances in
neural information processing systems (pag. 4278–4286).
Monk, T., Savin, C., & Lücke, J. (2018). Optimal neural inference of
stimulus intensities. Scientific Reports, 8, 10038. https://doi.org/
10.1038/s41598-018-28184-5
Olshausen, B. UN. (2003). Principles of image representation in vi-
sual cortex. The Visual Neurosciences, 2, 1603–1615.
Perez-Orive, J., Mazor, O., Turner, G. C., Cassenaer, S., Wilson, R. I.,
& Laurent, G. (2002). Oscillations and sparsening of odor repre-
sentations in the mushroom body. Scienza, 297(5580), 359–365.
https://doi.org/10.1126/science.1070502
Poo, C., & Isaacson, J. S. (2009). Odor representations in olfac-
tory cortex: “Sparse” coding, global inhibition, and oscillations.
Neuron, 62(6), 850–861. https://doi.org/10.1016/j.neuron.2009.
05.022
Savin, C., Joshi, P., & Triesch, J. (2010). Independent component
analysis in spiking neurons. PLoS Computational Biology, 6(4),
e1000757.
Stemmler, M., & Koch, C. (1999). How voltage-dependent con-
ductances can adapt to maximize the information encoded by
neuronal firing rate. Nature Neuroscience, 2(6), 521–527. https://
doi.org/10.1038/9173
Stettler, D. D., & Axel, R. (2009). Representations of odor in the pir-
iform cortex. Neuron, 63(6), 854–864. https://doi.org/10.1016/j.
neuron.2009.09.005
Tetzlaff, C., Kolodziejski, C., Markelic, I., & Wörgötter, F. (2012).
apprendimento, and plasticity. Biological
Time scales of memory,
Cybernetics, 106(11), 715–726.
Tetzlaff, C., Kolodziejski, C., Timme, M., & Wörgötter, F. (2011).
Synaptic scaling in combination with many generic plasticity
mechanisms stabilizes circuit connectivity. Frontiers in Compu-
tational Neuroscience, 5. https://doi.org/10.3389/fncom.2011.
00047
Triesch, J. (2007). Synergies between intrinsic and synaptic plastic-
ity mechanisms. Calcolo neurale, 19, 885–909.
Triesch, J., Vo, UN. D., & Hafner, A.-S. (2018). Competition for synap-
tic building blocks shapes synaptic plasticity. eLife, 7. https://doi.
org/10.7554/eLife.37836
Tsodyks, M. V., & Feigelman, M. V. (1988). The enhanced storage
capacity in neural networks with low activity level. EPL (Euro-
physics Letters), 6(2), 101. https://doi.org/10.1209/0295-5075/6/
2/002
Turner, G. C., Bazhenov, M., & Laurent, G. (2008). Olfactory rep-
resentations by Drosophila mushroom body neurons. Journal
of Neurophysiology, 99(2), 734–746. https://doi.org/10.1152/jn.
01283.2007
Turrigiano, G., Abbott, L., & Marder, E. (1994). Activity-dependent
changes in the intrinsic properties of cultured neurons. Scienza,
264(5161), 974–977. https://doi.org/10.1126/science.8178157
Turrigiano, G. G. (2008). The self-tuning neuron: Synaptic scaling
of excitatory synapses. Cell, 135, 422–435.
Turrigiano, G. G., Leslie, K. R., Desai, N. S., Rutherford, l. C.,
& Nelson, S. B. (1998). Activity-dependent scaling of quantal
amplitude in neocortical neurons. Nature, 391(6670), 892–896.
https://doi.org/10.1038/36103
Vincis, R., Gschwend, O., Bhaukaurally, K., Beroud, J., & Carleton,
UN. (2012). Dense representation of natural odorants in the mouse
olfactory bulb. Nature Neuroscience, 15(4), 537–539. https://
doi.org/10.1038/nn.3057
Vinje, W. E., & Gallant, J. l. (2000). Sparse coding and decor-
relation in primary visual cortex during natural vision. Sci-
ence, 287(5456), 1273–1276. https://doi.org/10.1126/science.
287.5456.1273
Yger, P., & Gilson, M. (2015). Models of metaplasticity: A review of
concepts. Frontiers in Computational Neuroscience, 9, 138.
Zenke, F., Agnes, E. J., & Gerstner, W. (2015). Diverse synaptic plas-
ticity mechanisms orchestrated to form and retrieve memories in
spiking neural networks. Nature Communications, 6, 6922.
Zenke, F., & Gerstner, W. (2017). Hebbian plasticity requires com-
pensatory processes on multiple timescales. Philosophical Trans-
actions of the Royal Society of London B: Biological Sciences,
372. https://doi.org/10.1098/rstb.2016.0259
Zenke, F., Hennequin, G., & Gerstner, W. (2013). Synaptic plastic-
ity in neural networks needs homeostasis with a fast rate detector.
PLoS Computational Biology, 9(11), e1003330.
Zhang, W., & Linden, D. J. (2003). The other side of the engram:
intrinsic excitability.
Experience-driven changes in neuronal
Nature Reviews Neuroscience, 4, 886–900.
Network Neuroscience
199
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
4
1
1
7
4
1
8
6
6
8
2
2
N
e
N
_
UN
_
0
0
1
1
8
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3