RESEARCH

Cooperative contributions of structural
and functional connectivity to
successful memory in aging

Simon W. Davis

1,2, Amanda Szymanski1,2, Homa Boms1, Thomas Fink1, and Roberto Cabeza

1

1Center for Cognitive Neuroscience, Duke University, Durham, NC, USA
2Department of Neurology, Duke University School of Medicine, Durham, NC, USA

Keywords: Aging, Structural connectivity, Functional connectivity, Episodic memory, Task-related
connectivity, SEM

a n o p e n a c c e s s

j o u r n a l

ABSTRACT

Understanding the precise relation between functional connectivity and structural (white
matter) connectivity and how these relationships account for cognitive changes in older
adults are major challenges for neuroscience. We investigate these issues using an approach
in which structural equation modeling (SEM) is employed to integrate functional and
structural connectivity data from younger and older adults (n = 62), analyzed with a
common framework based on regions connected by canonical tract groups (CTGs). CTGs
(per esempio., uncinate fasciculus) serve as a common currency between functional and structural
connectivity matrices, and ensure equivalent sparsity in connectome information. We used
this approach to investigate the neural mechanisms supporting memory for items and
memory for associations, and how they are affected by healthy aging. We found that
different structural and functional CTGs made independent contributions to source and item
memory performance, suggesting that both forms of connectivity underlie age-related
differences in specific forms of memory. Inoltre, the relationship between functional
and structural connectivity was best explained by a general relationship between latent
constructs—a relationship absent in any specific CTG group. These results provide insights
into the relationship between structural and functional connectivity patterns, and elucidate
their relative contribution to age-related differences in source memory performance.

AUTHOR SUMMARY

Aging is associated with profound changes in how neural systems adapt to perform the
same mental operations in youth. Memory functioning, in particular, demonstrates enormous
neuroplastic changes in the pattern of distributed, connected networks that enable older
adults to perform the same mnemonic operations. Tuttavia, the relationship between the
structural and functional connections supporting these operations is poorly understood.
Here we develop a novel algorithm for comparing structural and functional connectivity,
and use a comprehensive structural equation model (SEM) to show how these network
characteristics contribute to behavioral performance in two forms of episodic memory
retrieval. These results suggest that healthy aging is associated with specific ensembles
of cooperative contributions from both functional and structural tract groups.

Citation: Davis, S. W., Szymanski, A.,
Boms, H., Fink, T., & Cabeza, R. (2019).
Cooperative contributions of structural
and functional connectivity to
successful memory in aging. Network
Neuroscience, 3 (1), 173–194.
https://doi.org/10.1162/netn_a_00064

DOI:
https://doi.org/10.1162/netn_a_00064

Supporting Information:
https://github.com/ElectricDinolab/
Canonical_Tract_Groups

Received: 23 Gennaio 2018
Accepted: 9 Luglio 2018

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Simon W. Davis
simon.davis@duke.edu

Handling Editor:
Edward Bullmore

Copyright: © 2018
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza

The MIT Press

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

INTRODUCTION

One of the most consistent patterns in the literature on episodic memory and aging is that
older adults tend to be more impaired in episodic memory for associations than in episodic
memory for individual items. While this behavioral dissociation has been well known for a long
time (Glisky, Polster, & Routhieaux, 1995; Naveh-Benjamin, 2000), cognitive neuroimaging
provides a complementary method for investigating the underlying neural mechanisms of this
effect (for review, see Old & Naveh-Benjamin, 2008). During the last three decades, cognitive
neuroimaging has gradually moved from an emphasis on individual brain regions to a focus
on the interactions among brain regions, or connectivity, which can be examined at the func-
tional level using functional MRI (fMRI) and at the structural level using diffusion-weighted
imaging (DWI). Given that functional connectivity depends on structural connectivity, a cur-
rent challenge is how to investigate the relationship between these two forms of connectivity
in relation to cognitive function. Here, we propose a new approach for linking structural and
functional connectivity data and apply it to the results of an fMRI-DWI study investigating item
and source memory in younger and older adults.

There are two main challenges in linking structural and functional connectivity. The first
challenge is the problem of translation between structural and functional information. Struc-
tural matrices are considerably more sparse than functional networks (Wang, Dai, Gong, Zhou,
& Lui, 2015), owing to the fact that while disparate regions may demonstrate (potentially spu-
rious) functional correlations in time course activity, structural connectivity based on diffusion
tractography is highly constrained by distance and anatomy (though false positive results are
also a signficant issue here; see Maier-Hein et al., 2017). As such, functional connectivity
distributions are typically Gaussian, while structural connectivity distributions tend to follow
exponential distributions (depending on the metric being used). While the common graph
theoretical practice of thresholding and/or binarizing functional and structural connectomes
to a common upper threshold (per esempio., the top 5% of connections) does help to equalize the
amount of graph information contributing information to structure-function comparisons, IL
underlying sources of information are nonetheless qualitatively distinct in character. Structural
connectivity is also static, while functional connectivity is highly dependent on the active pro-
cess concurrent with data collection (Honey, Kotter, Breakspear, & Sporns, 2007). The second
challenge is the problem of the granularity of mapping; while a large array of techniques have
attempted to delineate structural-functional connectivity relationships at the level of whole-
brain parcellations (Betzel et al., 2014; Zimmermann et al., 2016), between discrete pairs of
regions (Andrews-Hanna et al., 2007; Davis, Kragel, Madden, & Cabeza, 2012; Dennis et al.,
2008), or at the level of voxels (Horn, Ostwald, Reisert, & Blankenburg, 2014), each technique
tends to form a unique claim about how the structure-function relationship changes with age.
Both of these problems preclude any lasting or satisfying conclusions about how these modal-
ities relate to one another, and have issues unique to datasets that include older adults.

Despite this uncertainty, a number of anatomically defined canonical white matter tracts
demonstrate reliable relationships between white matter connectivity and memory, includ-
ing the fornix, uncinate fasciculus, cingulum, and the genu of the corpus callosum. Multiple
measures of connectivity of these tracts have been associated with age-related differences in
scores on verbal source memory (Bendlin et al., 2010; Davis et al., 2009; Kennedy & Raz,
2009; Voineskos et al., 2012), spatial- (Oberlin et al., 2016) or object-based source memory
(Antonenko et al., 2016), and free recall (Metzler-Baddeley et al., 2012). A number of
consistent functional patterns also point to tract-specific relationships in aging and mem-
ory, in particular an increase in hippocampal coupling to the prefrontal cortex (PFC) during

Functional connectivity:
Coherent functional activity between
different cortical regions, over the
course of a certain temporal range.

Structural connectivity:
White matter connectivity between
different cortical regions, typically
assessed with the number of white
matter streamlines.

Source memory:
Memory for the specific context in
which an item is learned, typically
reported with the who/what/when of
the context.

Canonical white matter tract:
A macroanatomical brain feature of
white matter anatomy with a
well-known course and connectivity.

Network Neuroscience

174

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

Item memory:
Memory for the item itself, typically
reported with an old/new decision.

CTG (canonical tract group):
Our derived measure describing the
regions connected by a canonical
fiber (or tract) bundle (per esempio., uncinate
fasciculus, forceps minor).

SEM (structural equation modeling):
A diverse array of statistical methods
used to assess unobservable latent
constructs using observable data.

item memory encoding and retrieval. Così, while young adults demonstrate connectivity from
hippocampus to posterior sensory regions, older adults exhibited greater success-related func-
tional coupling with the dorsolateral PFC and temporal cortex (Dennis et al., 2008; Murty et al.,
2009; St. Jacques, Dolcos, & Cabeza, 2009). The consistency of these tract-specific relation-
ships between (UN) item memory and ventral temporal pathways and (B) source memory and
dorsal frontoparietal pathways suggests a relative specificity of certain connections to specific
forms of memory.

A major goal of connectome research is to discover how structural and functional networks
in the brain are related—an active area with tremendous interest and wide ramifications in
neuroscience. The widespread use of automated connection matrices has led to an explosion
of computational solutions to this problem, typically by directly comparing connectivity matri-
ces (Horn et al., 2014), predicting one modality from the other (Abdelnour, Voss, & Raj, 2014;
Bowman, Zhang, Derado, & Chen, 2012; Messé, Rudrauf, Giron, & Marrelec, 2015), joint anal-
ysis of structural and functional matrices (Honey et al., 2009; Tewarie et al., 2014), or through
the comparison of graph-theoretical properties common to structural and functional networks
(Betzel et al., 2014; Romero-Garcia, Atienza, & Cantero, 2014). These more data-driven ap-
proaches have produced a number of meaningful observations (for an excellent review, Vedere
Zhu et al., 2014), principally that the relationship between functional connectivity and struc-
tural connectivity also appears to strengthen across the life span, and that this relationship is
driven by an increase in the reliance on more long-distance interactions between brain regions
(Betzel et al., 2014; Meunier, Stamatakis, & Tyler, 2014). Nonetheless, these computational ap-
proaches have largely ignored canonical divisions in the structural anatomy of human white
matter pathways. This is problematic in the case of structural models because these models
rarely incorporate known anatomy, leading to spurious connections (Maier-Hein et al., 2017),
and in the case of functional information these computational solutions rarely take into account
the sparsity of structural connection matrices compared with functional data. Così, finding the
adequate basis on which to make the comparison between these modalities is challenging.

The present analysis seeks to address these gaps by using task-based functional connectivity
and whole-brain structural connectivity informed by classical white matter anatomy to ask a
specific question: Do functional and structural connectivity make independent contributions
to memory in older adults? Particularly, we explore the possibility that function-structure re-
lationships are best characterized by either specific linkages between modalities for a given
tract, or instead reflect a general relationship shared by task-relevant tract groups. We test
a model fitting structural and functional connectivity information summarized by canonical
tract groups (CTGs) in order to predict source and item memory in younger and older adults.
Così, the structural equation modeling (SEM) approach used here attempts to provide a rig-
orous statistical framework to examine the complex relationships between age, structural and
task-based functional connectivity, and cognitive performance.

METHODS

Participants

Seventy-six adults—54 older adults (67.68 ± 6.9 y.o., age range 61–87 y.o.) E 22 younger
adults (23.6 ± 3.5 y.o., age range 19–28 y.o.)—participated in the study. All individuals were
screened for contraindications to MRI, and seven individuals were excluded because of scan-
ner issues or poor structural or functional imaging quality (see below). Two individuals did not
complete the memory task, leaving N = 67 with complete data. Written consent was obtained

Network Neuroscience

175

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

for each participant and they received monetary compensation at the end of the study. All ex-
perimental procedures were approved by the Duke University Institutional Review Board.

Memory Task

Materials. We studied item and source memory using a lexical episodic memory task used in
previous studies of our group (Daselaar et al., 2015; Hayes, Buchler, Stokes, Kragel, & Cabeza,
2011). Stimuli consisted of 440 English nouns with normative word frequencies in the lexicon
of 5–15 per million, M = 8.8 (3.1), and a mean length of M = 7.1 (2.3) letters. Unique study
and test lists were randomly generated for each participant and words were assigned to the
following conditions: item (180 parole), source (180), or item lures (80 words—presented only
at retrieval as new words). At retrieval, there were four item test lists, each consisting of
45 targets (old words) E 20 lures (nonstudied words), and four source memory test lists,
each consisting of 45 studied words.

Participants studied the words outside the scanner. Words were presented
Encoding phase.
on a computer monitor in white font on a gray background for 3 s with a 1 s interval using Co-
gent (http://www/vislab.ucl.ac.uk/cogent_2000.php), a stimulus presentation software within
MATLAB (https://www.mathworks.com). For half of the trials, participants made a “pleasant/
unpleasant” judgment, and a “bigger/smaller than a shoebox” judgment for the other half. Half
of the trials were repeated, with the same judgment; Tuttavia, for the purpose of the present
study, we collapsed 1x and 2x encoding trials into one condition for the subsequent fMRI
analysis.

Approximately 15 min after the encoding phase, participants were tested for
Retrieval phase.
their memory of the studied words in the MRI scanner. Words were presented via a mirror in
the scanner head coil and a rear projection system using a PC computer running Cogent. There
were two retrieval conditions: item memory and source memory. In the item memory retrieval
task, participants made new/old responses on a 4-point confidence scale. For the source mem-
ory retrieval task, participants were asked to indicate what type of judgment they made earlier
on a word on a 4-point scale: definitely pleasant/unpleasant, probably pleasant/unpleasant,
probably bigger/smaller, definitely bigger/smaller. Given the current study had no a priori hy-
potheses about the influence of connectivity measures on confidence, we collapsed across
high and low confidence responses. We have clarified this point in the behavioral results.
Nonetheless, for a more explicit analysis of confidence measures using this task, see Hayes
et al. ( 2011). Four item and four source memory runs were presented in consecutive blocks to
minimize the effects of task switching. Retrieval stimuli were presented for 3 S, with a white
crosshair presented for fixation during the intertrial interval (ITI). Stimulus order and ITI jitter
(range: 1–7 s) were determined by a genetic algorithm designed to maximize statistical effi-
ciency and facilitate deconvolution of the hemodynamic response (Wager & Nichols, 2003).

MRI Acquisition and Analysis

The analytical pipeline is summarized in Figure 1. Participants were first scanned on a 3-T
gradient-echo scanner (General Electric 3.0 Tesla Signa Excite HD short bore scanner, equipped
with an 8-channel head coil). Coplanar functional images were acquired using an inverse spi-
ral sequence (64 × 64 matrix, time repetition [TR] = 1,700 ms, time echo [TE] = 31 ms, field
of view [FOV] 240 mm, 37 slices, 3.8-mm slice thickness, 254 images). Following functional
imaging, a high-resolution SPGR series (1-mm sections covering whole brain, interscan

Network Neuroscience

176

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

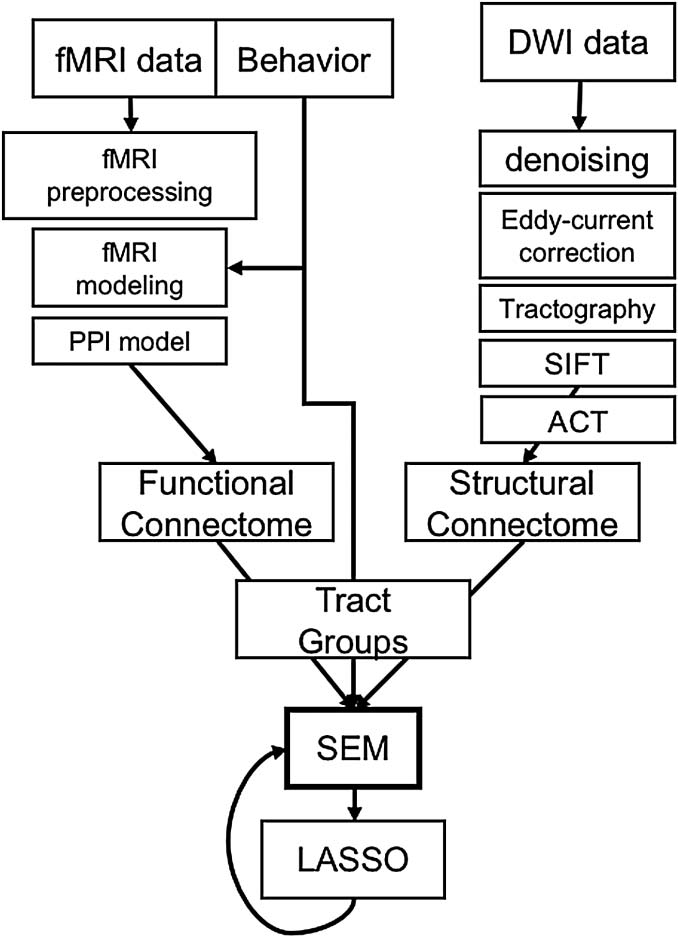
Figura 1. Analytical pipeline. Boxes indicate major steps in the analysis pipeline. Notably, CTGs
act as a common currency, or filter, for structural and functional connectome information.

spacing = 0, matrix = 2562, flip angle = 30, TR = 22 ms, TE = min full, FOV = 19.2 cm) era
collected. Finalmente, DWI data were collected using a single-shot echo-planar imaging sequence
(TR = 1,700 ms, slices = 50, thickness = 2.0 mm, FOV = 256 × 256 mm2, matrix size =
128 × 128, voxel size = 2 mm3, b-value = 1, 000 s/mm2, diffusion-sensitizing directions = 25,
total images = 960, total scan time = 5 min). The anatomical MRI was acquired using a 3-D
T1-weighted echo-planar sequence (matrix = 2,562, TR = 12 ms, TE = 5 ms, FOV = 24 cm,
slices = 68, slice thickness = 1.9 mm, sections = 248). Scanner noise was reduced with ear
plugs, and head motion was minimized with foam pads. Total scan time, including breaks and
structural scans, was approximately 1 hr 40 min. Behavioral responses were recorded with a
four-key fiber-optic response box (Resonance Technology, Inc.), and when necessary, vision
was corrected using MRI-compatible lenses that matched the distance prescription used by
the participant.

Preprocessing of functional scans was performed processed using SPM12 (http://www.fil.
ion.ucl.ac.uk/spm/software/spm12/). Subjects were excluded on the basis of excessive move-
ment during the fMRI session if any scans demonstrated movement in any x/y/z direction
>5 mm, or more than 6% of their total scans with between 3 E 5 mm; based on these
criteria, five subjects were removed (two remaining subjects had poor diffusion scans). In all
remaining datasets, the first four images were discarded to allow for scanner equilibrium. Im-
ages were corrected for asynchronous slice acquisition (slice timing: reference slice = 17,
TA = 1.97) and realigned to the first functional image within the series to correct for head
motion. For normalization, we used a study-specific template created using unified segmenta-
tion and diffeomorphic image registration (DARTEL) in SPM12 (Ashburner, 2007). Primo, each
subject’s image was segmented into gray matter, white matter, and cerebral spinal fluid prob-
abilistic images. The segmented gray matter images were then normalized to MNI space
using the DARTEL procedure integrated in SPM12 (Ashburner, 2007), which uses diffeomor-
phic registration to create a template that is representative of the brain size and shape of all
the participants.

Network Neuroscience

177

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

FA (fractional anisotropy):
A value between zero and one that
describes the degree of anisotropy of
a diffusion process.

Before either structural or functional matrices were con-
Construction of connectivity matrices.
structed, we first sought to establish a consistent parcellation scheme across all subjects and all
modalities (DWI, fMRI) that reflects an accurate summary of full connectome effects. Subjects’
T1-weighted image was segmented using the SPM12, yielding a gray matter (GM) and white
matter (WM) mask in the T1 native space for each subject. The entire GM was then parcellated
into 411 regions of interest (ROIs), each representing a network node by using a version of the
Harvard-Oxford Atlas (Tzourio-Mazoyer et al., 2002), subparcellated to obtain a larger number
of smaller and more equally sized regional nodes (Fornito, Zalesky, & Bullmore, 2010). The T1-
weighted image was then nonlinearly normalized to the ICBM152 template in MNI space using
FMRIB’s Nonlinear Image Registration Tool (FNIRT, FSL, https://www.fmrib.ox.ac.uk/fsl/). IL
inverse transformations were applied to the Harvard-Oxford Atlas in the MNI space, resulting
in native-T1-space GM parcellations for each subject. Then, T1-weigted images were coreg-
istered to native diffusion space using the subjects’ unweighted diffusion image (cioè., the b0
Immagine) as a target; this transformation matrix was then applied to the GM parcellations above,
using FSL’s FLIRT linear registration tool, resulting in a native-diffusion-space parcellation for
each subject.

Structural connection matrices based on DWI data were analyzed utilizing FSL (https://fsl.
fmrib.ox.ac.uk/fsl/fslwiki, v5.0.1) and MRtrix (http://mrtrix.org, v3.0) software packages. Data
were denoised with MRtrix, corrected with eddy current correction from FSL, and brain extrac-
tion was performed with both FSL and MRtrix, whereas bias-field correction was completed
with MRtrix. Primo, fractional anisotropy (FA) maps were created using dwi2tensor followed by
tensor2metric from MRtrix3. Constrained spherical deconvolution (CSD) was utilized in calcu-
lating the fiber orientation distribution (FOD). For CSD map generation, the maximum number
of spherical harmonic terms was set to 6, and a single-fiber response kernel estimated from
white matter voxels with fractional anisotropy FA > 0.3. This FOD was used along with the
brain mask to generate whole-brain tractography, with seeding done at random within the mask
(Tournier, Calamante, & Connelly, 2007; Tournier, Calamante, Gadian, & Connelly, 2004). Rel-
evant parameters regarding track generation are as follows: seed = at random within mask;
step-size = 0.2 mm; 10,000,000 tracts. After tracts were generated, they were filtered using
SIFT (spherical-deconvolution informed filtering of tractograms; Smith, Tournier, Calamante, &
Connelly, 2012). This process utilizes an algorithm that determines whether a streamline should
be removed based on information obtained from the FOD, which improves the selectivity of
structural connectomes by using a cost-function to eliminate false positive tracts (Yeh, Smith,
Liang, Calamante, & Connelly, 2016). Tracts were “SIFTed” until 1 million tracts remained. In
the present analysis we rely on FA (rather than streamlines) as our measure of region-to-region
connectivity. FA is high in areas where there is a dense packing of well-myelinated and co-
herently oriented axonal fibers, and low when axonal structure has been compromised, Quando
fibers are sparse, or when the fibers are organized in a complex geometry that is not adequately
captured by the diffusion model. To obtain the mean FA value along each streamline, the out-
put track files were used to sample values along each track, using the FA image as the image
to be sampled, resulting in an FA scale file. In turn, connectomes were created by using the
original SIFT track files, and the FA scale file from the previous step, with all streamlines in an
edge combined into a single scale value based on the mean of those streamlines. FA values
were then imputed onto all nonzero pathways; in each structural connection matrix (UN), IL
connection strength (Aij) between each pair of cortical regions (io,j) is defined as the average
FA value along the fiber tracts connecting these regions. Lack of connections between a pair
of regions was set to 0. Così, the resulting structural connectomes comprised a summary of
the fractional anisotropy values along all streamlines connecting a given pair of regions (for

Network Neuroscience

178

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

other recent studies using similar methods given equivalent DWI scanning parameters, Vedere
Qi, Meesters, Nicolay, Ter Haar Romeny, & Ossenblok, 2016; Roberts et al., 2016).

Functional connection matrices representing task-related connection strengths were es-
timated using a correlational psychophysical interaction (cPPI) analysis (Fornito, Harrison,
Zalesky, & Simons, 2012). Briefly, the model relies on the calculation of a PPI regressor for
each region, based on the product of that region’s time course and a task regressor of interest,
in order to generate a term reflecting the psychophysical interaction between the seed region’s
activity and the specified experimental manipulation. In the current study the convolved task
regressors for successful (“Hits”) or unsuccessful (“Misses”) retrieval trials were used as the
psychological regressor, which coded subsequently remembered and subsequently forgotten
word pairs with positive and negative weights, rispettivamente, of equal value. This psychological
regressor for successful memory retrieval was based on a linear contrast of Hits > Misses for
both source and item memory blocks; new-items trials during the item memory blocks were
modeled, but not used in the connectivity analysis. This memory success-related regressor was
multiplied with two network time courses for regions i and j. We then computed the partial
correlation ρ
· z, removing the variance z associated with the psychological regressor,
the time courses for regions i and j, and constituent noise regressors. We accounted for the
potential effects of head motion and other confounds by assessing the six motion parameters
and including these parameters in our partial correlation between regions.

PPIi, PPIj

Defining tract groups. We examine only region pairs that are connected by canonical fiber
systems, in other words, canonical tract groups (CTGs). This technique affords three main ben-
efits, namely (UN) integrating structural and functional connectivity information within a com-
mon anatomical framework, (B) constraining the overabundance of functional connections
to known anatomy, E (C) simplifying the number of pairwise comparisons in an informed
maniera. Inoltre, our novel algorithm for summarizing connectivity in canonical, BENE-
characterized fiber systems (and its associated code; see Davis, 2018) is scalable to any of
the numerous cortical parcellations (per esempio., AAL, Craddock, or even voxelwise parcellations)
currently in use. CTG assignment for a given region-to-region connection in the matrix is ac-
complished by assessing the overlap between the ROIs used to define that matrix. Canonical
fiber systems from six tracts defined by the Johns Hopkins University white matter tractog-
raphy atlas (Hua et al., 2008) include the uncinate fasciculus (UF), inferior fronto-occipital
fasciculus (IFOF), forceps minor (FMin), inferior longitudinal fasciculus (ILF), ventral cingu-
late gyrus (CingHipp), and dorsal cingulate gyrus (Cing), as well as the body of the fornix,
based on a novel template (Brown et al., 2017). The corticospinal tract and forceps major were
not included because they were not hypothesized to be involved in item or source memory
functioning.

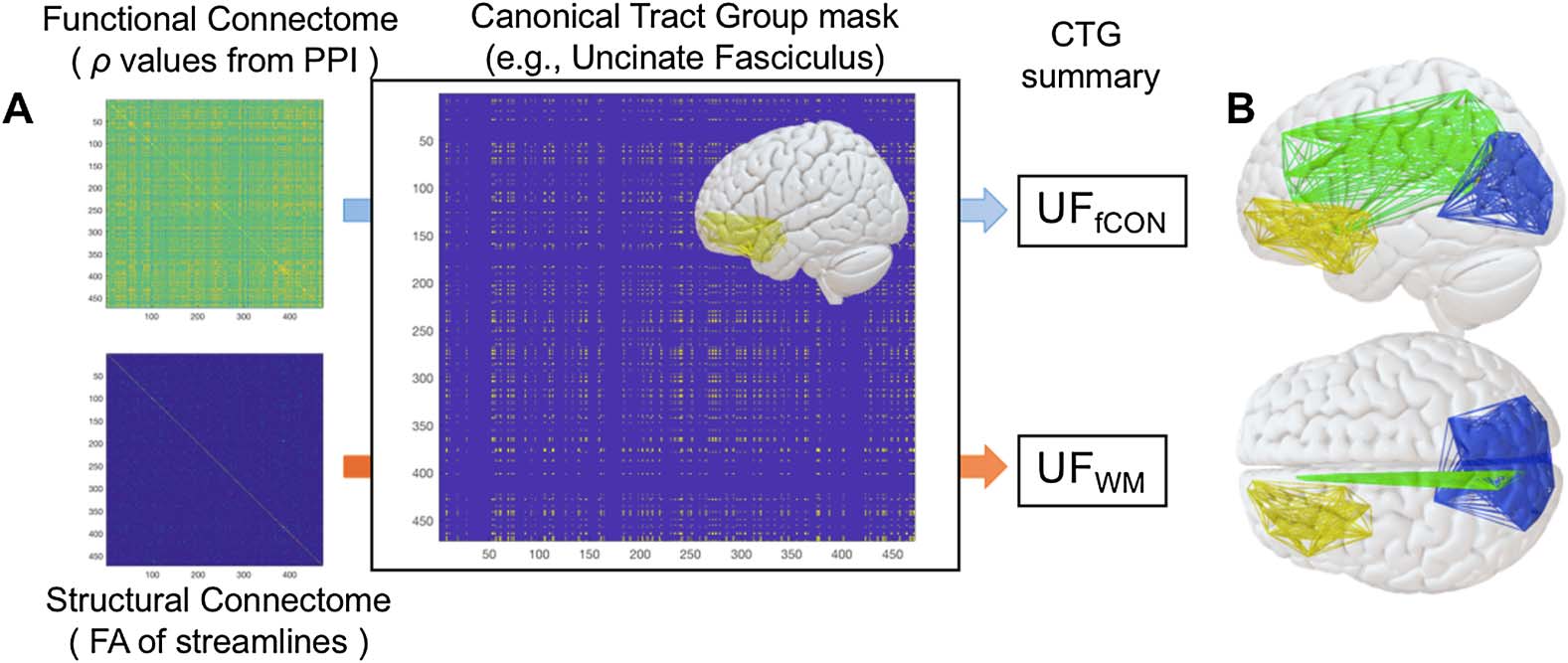
The creation of a CTG (per esempio., the UF) proceeds in two steps. In the first step, we identify the
voxelwise overlap between each tract and each pair of ROIs. If a tract shows overlap with both
ROIA and ROIB, then we consider the connection between those ROIs as a component of a
given CTG (per esempio., CTGUF, Figura 2). Here we define overlap as 10 voxels, though results are
similar with more/less conservative parameters. We refer to this matrix of n x n elements (Dove
n is the number of regions) as the CTG mask. This assignment is then repeated for all seven
tract groups specified above within the JHU Tract Atlas (FSL). In the second step, functional
and structural connectome data for each subject are filtered through these masks, and we
calculate a mean of all surviving connectivity values. These values represent inputs to later
CFA/SEM models described below. Our analysis based on CTGs offers two clear advantages

Network Neuroscience

179

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

Figura 2. Construction of canonical tract groups. After functional and structural connectome con-
struction, a CTG mask for a particular tract is used to filter functional and structural connectivity
informazione. After functional and structural connectome construction, a CTG mask for a particular
tract is used to filter functional and structural connectivity information. All elements in the filtered
matrix are then averaged to create a functional and structural estimate for a given CTG (per esempio., UFfCON
and UFsCON) that is amenable to SEM modeling. Also obvious in these images is the relative sparsity
of structural connection matrices comparted to functional matrices.

to data-driven comparisons between these data types: (UN) CTGs serve as a common currency
between functional and structural connectivity matrices and (B) this method addresses the fact
that structural matrices are much more sparse than functional matrices. Così, by using an
identical set of region pairs from the adjacency matrices in each tract group (see individual
tract groups in Figure 3), we ensure that the same amount of data contributes to structural or
functional connectivity information in the model.

Structural Equation Modeling

After structural and functional (item and source) matrices are filtered by CTGs and summed
across all elements in the matrix, CTG values are averaged across hemisphere for bilateral
tracts, and scaled/mean-centered before inclusion into the SEMs (using the R function scale).
We fit confirmatory SEMs to the mean FA of the seven, bilaterally averaged, WM tract CTGs,
which showed different sensitivities to age. These models were used to test the validity of the
latent variables for structural connectivity (sCON) based on DWI tractography, and functional
connectivity (fCON) associated with successful memory retrieval, based on fMRI collected
from either item or source blocks. The full exploratory models for source and item memory
combine the structural and functional CFAs in our older adult sample with additional model
parameters, including (UN) residual covariance between modalities of connectivity information
within specific tract groups (per esempio., UF f CON —UFsCON ), (B) links between the two latent variables
(sCON—fCON), E (C) mutual inputs from these LVs to a behavioral output (either source or
item memory accuracy). Model syntax and full model output for full SEMs are available in the
GitHub repository mentioned above (Davis, 2018).

LASSO (least absolute shrinkage and
selection operator):
A common method of regularization
used to efficiently estimate a
parsimonious model.

Both CFA and full SEMs were fit using the lavaan package (version 0.5, Rosseel, 2012) In
R version 3.3.3 (R Development Core Team, 2016), and regularized SEM for complex mod-
els using regsem, (version 0.9.2, Jacobucci, Grimm, & McArdle, 2016), which allows the use
of LASSO-based regularization while keeping the SEM model intact, adding penalization di-
rectly into the estimation of the model. LASSO (least absolute shrinkage and selection operator)

Network Neuroscience

180

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

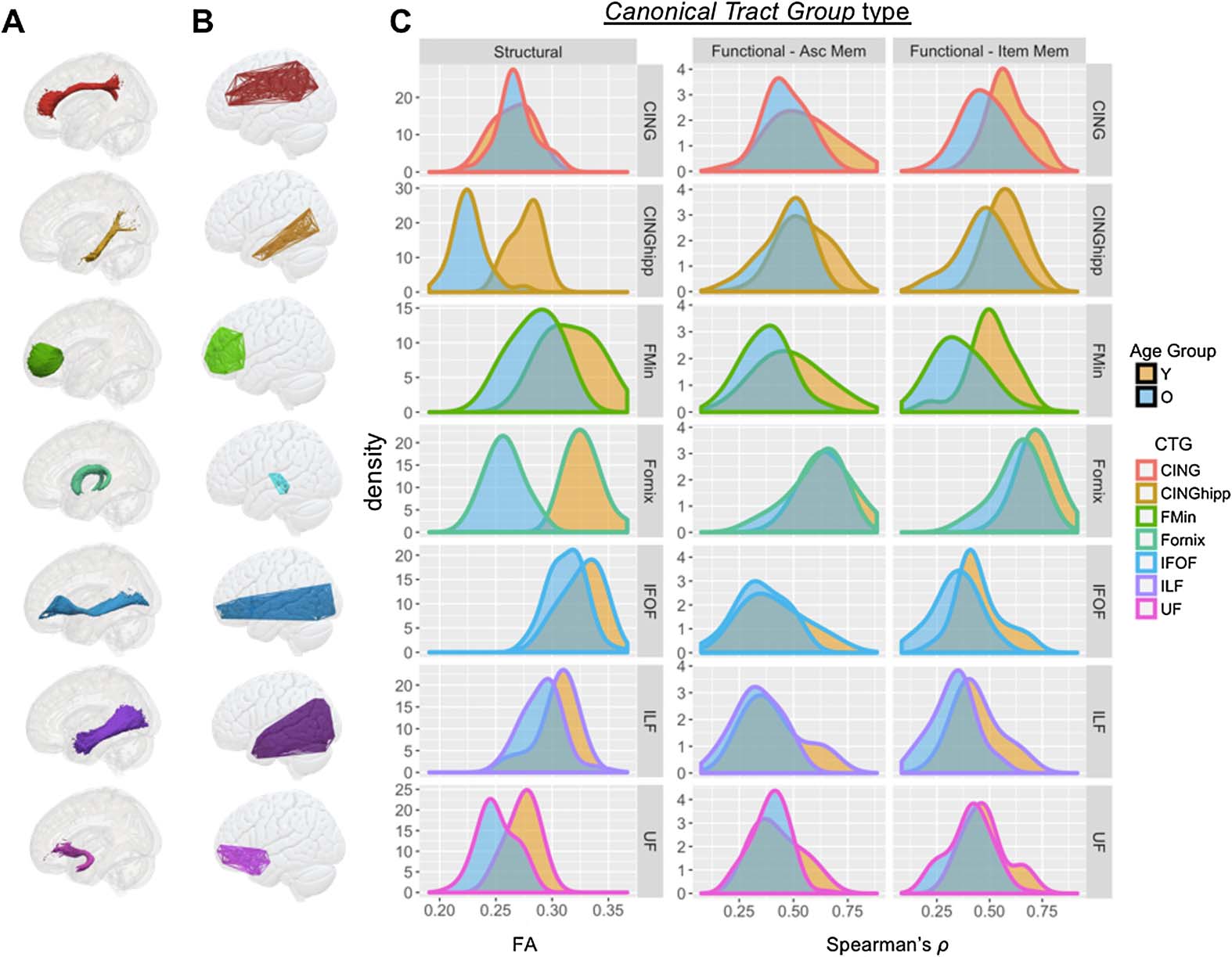
Figura 3.
Illustration and age distributions of canonical tract groups. Column (UN) describes tract
ROIs from the JHU Tract Atlas (see Methods) and column (B) describes the connectome-based
canonical tract groups (CTGs) formed from our algorithm, for each tract. (C) Distribution of CTG
values for structural connectivity (FA) and functional connectivity (Spearman’s rho, as calculated
in PPI) for source and item memory in younger and older adults. CTG values are shown for seven
major CTGs that influence the final SEMs below. Age-related statistics are presented in Table 2.
Cing = cingulum; CingHip = ventral leg of the cingulum; FMin = forceps minor (or genu); IFOF =
inferior fronto-occipital fasciculus; ILF = inferior longitudinal fasciculus; UF = uncinate fasciculus.

imposes a penalty on the regression parameters to ensure that the SEM model remains stable
even when the number of predictors is large. Specifically, it uses the L1 norm to apply a LASSO
(Tibshirani, 1996) penalty, which enforces sparse solutions by shrinking many regression pa-
rameters to 0. We therefore applied LASSO regression to the two full model SEMs in order to
penalize the models and reduce the number of contributing CTGs.

Prior to model fitting, variables were scaled to a standard normal distribution. All models
were fit using maximum likelihood (ML) estimation using robust standard errors and report
overall model fit assessed with the chi-square estimates, root mean squared error of approx-
imation (RMSEA) and its confidence interval, the comparative fit index (CFI). We used the
following guidelines for judging good fit (Bagozzi & Yi, 2012): RMSEA below 0.05 (acceptable:
0.05–0.08) and a CFI above 0.97 (acceptable: 0.95–0.97). Model comparison was estimated
via the χ2 likelihood ratio test. The significance of individual paths was tested with p values
less than 0.05, and the contribution of each predictor was assessed using the R2 value.

Lastly, to test the influence of age (for both func-
Testing age effects using equality constraints.
tional and structural CTGs) in the model, we introduced a younger adult sample into the

Model fit:
The ability of an overidentified
model to reproduce the correlation
or covariance matrix of the variables.

Network Neuroscience

181

Cooperative contributions of structural and functional connectivity

Parameter estimates:
Constants that describe the size of
the relationship between any pair of
observed or unobserved variables in
the model.

modeling framework and performed two separate analyses: (UN) first, model fit in separate
older and younger adult groups using the same likelihood ratio test, fixing parameter estimates
derived from the full models above between the two groups; (B) second, in order to explicitly
address the differences in SEM model fit between our younger and older adult populations,
in order to identify specific parameters in the model affected by age. An equality constraint
constrains an SEM model such that, in reaching its solution, it must provide the identical un-
standardized coefficient for all parameters within a set that has been designated for equality.
Differences in model fit between the constrained and unconstrained model are then assessed
with a chi-square difference, indicating whether the freely estimated estimate of a key path in
the model differs with age.

RESULTS

Behavioral Testing
Source memory accuracy was 0.76 ± 0.016 and RTs were 2.09 s ± 0.49 for successful source
trials, E 2.37 s ± 0.58 for unsuccessful source trials. Source memory was greater for items
encoded with a pleasantness judgment than with a size judgment (T 66 = 5.98, P < 0.00004), consistent with previously observed advantages for personal than perceptual source judgments (Dobbins & Wagner, 2005; Naveh-Benjamin, 2000; Naveh-Benjamin & Craik, 1996). Mean hit rates for item memory were 0.85 ± 0.015 and a mean false alarm rate of 0.22 ± 0.008. RTs during the item memory test were 1.59 ± 0.45 for item Hits, and 2.36 for item Misses. Main effects of age were more pronounced for source memory than item memory (F61,1 = 12.45, p = 0.0008) and overall item memory hit rate (F61,1 = 3.68, p = 0.04), though the interaction between age group and memory type was not significant (F61,2 = 2.18, p = 0.14). Canonical Tract Groups: Descriptive Statistics and Effects of Age Following the method outlined above, we developed a semiautomated pipeline for assigning a given connection between ROIs within a standard atlas to a given canonical tract group. While most CTGs showed significant age differences in the structural domain, success-related functional connectivity differences between younger and older adults were far subtler (Table 1, Figure 3). Two-sample t tests examining age-related differences in structural and functional connectivity found profound differences in structural connectivity (FA; all p < 0.05), and less pronounced age-related difference in functional connectivity (Pearson’s r; p < 0.05 in 2/7 and 7/7 source or item memory CTGs, respectively; see Table 1 for individual tract statistics). Functional CTGs showed consistently moderate relationships with corresponding structural CTGs (e.g., regions structurally connected by the UF tended to be functionally correlated), even after adjusting for the effects of age (all r > 0.21, P < 0.05). SEM Results Confirmatory factor analysis results. We used SEM to test a range of models of how connectivity supports source memory in older adults. 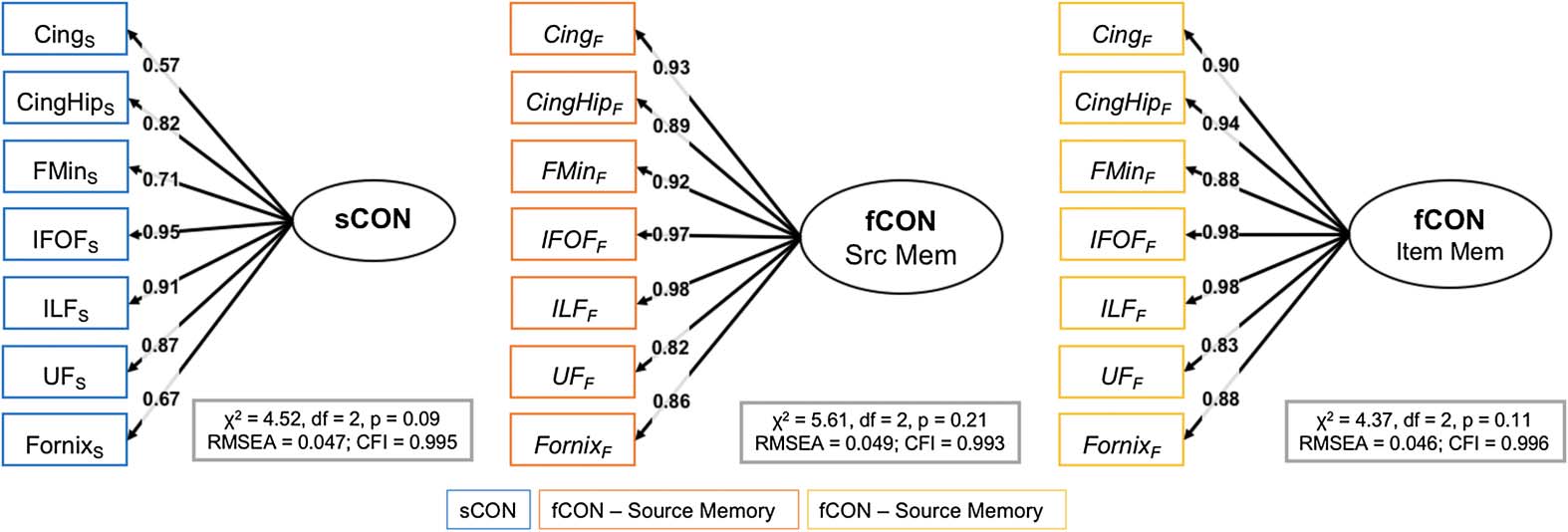We first examined the reliability of the measures to be used in three confirmatory factor analysis (CFA) models, shown in Figure 4, as well as Table 2. In these models, we hypothesize that two latent variables (functional connectivity or fCON and structural connectivity or sCON) capture the covariance between seven connectivity measures estimated from specific CTGs (described above); while the first factor loading is constrained to 1, every other factor loading is estimated freely. Three single-factor CFA models were evaluated: sCON, fCONitem, and fCONsource; these models each fit their respective data well (sCON model: χ2 = 4.52, d f = 2, p = 0.09, RMSEA = 0.047, CFI = 0.995; fCONitem Network Neuroscience 182 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 1 1 7 3 1 0 9 2 3 5 6 n e n _ a _ 0 0 0 6 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Cooperative contributions of structural and functional connectivity Table 1. Effects of age on canonical tract groups Canonical tract group Structural connectivity Cing CingHip FMin IFOF ILF UF Fornix Z 4.190*** 11.959**** 5.616*** 6.746**** 5.328**** 6.026**** 11.889**** Functional connectivity: Source memory Cing CingHip FMin IFOF ILF UF Fornix 1.791 2.372* 1.917* 1.491 1.730 1.368 1.002 Functional connectivity: Item memory Cing CingHip FMin IFOF ILF UF Fornix 3.737*** 3.913*** 4.353*** 3.033** 3.415** 3.043** 2.268* Partial correlation with corresponding sCON tract group† 0.28 0.31 0.24 0.27 0.25 0.26 0.25 0.39 0.34 0.41 0.31 0.24 0.21 0.27 † after adjusting for the effects of age. Cing = cingulum; CingHip = ventral leg of the cingu- lum; FMin = forceps minor (or genu); IFOF = inferior fronto-occipital fasciculus; ILF = inferior longitudinal fasciculus; UF = uncinate fasciculus. Significance: * = p < 0.05; ** = p < 0.01; *** = p < 0.001; **** = p < 0.0001. Figure 4. CFA models. Cing = cingulum; CingHip = ventral leg of the cingulum; FMin = forceps minor (or genu); IFOF = inferior-fronto-occipital fasciculus; ILF = inferior longitudinal fasciculus; UF = uncinate fasciculus. Network Neuroscience 183 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 1 1 7 3 1 0 9 2 3 5 6 n e n _ a _ 0 0 0 6 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Cooperative contributions of structural and functional connectivity Table 2. Model fit parameters for three CFA models CFA model White matter model CTG Parameter estimate Z Source memory model Item memory model Cing CingHip FMin IFOF ILF UF Fornix Cing CingHip FMin IFOF ILF UF Fornix Cing CingHip FMin IFOF ILF UF Fornix 0.57 0.82 0.71 0.95 0.91 0.87 0.67 0.93 0.89 0.92 0.97 0.98 0.82 0.86 0.90 0.94 0.88 0.98 0.98 0.83 0.88 6.24 6.07 6.38 6.35 6.26 5.97 9.70 9.50 9.99 10.03 9.22 9.71 9.71 9.63 9.85 9.86 9.08 9.63 R2 0.32 0.67 0.50 0.90 0.82 0.75 0.44 0.86 0.79 0.87 0.94 0.97 0.68 0.74 0.82 0.88 0.77 0.95 0.96 0.69 0.77 Parameter estimates are fully standardized. Cing = cingulum; CingHip = ventral leg of the cingu- lum; FMin = forceps minor (or genu); IFOF = inferior fronto-occipital fasciculus; ILF = inferior longitudinal fasciculus; UF = uncinate fasciculus. model: χ2 = 4.37, d f = 2, p = 0.11, RMSEA = 0.046, CFI = 0.996; fCONsource model: χ2 = 5.61, d f = 2, p = 0.21, RMSEA = 0.049, CFI = 0.993), suggesting that structural and functional connectivity can be captured by these single (respectively) dimensions. Full model results. Next, using CTGs we fit two full models relating brain connectivity vari- ables to behavioral variables using a standard SEM. These models capture the hypothesis that individual differences in structural and functional connectivity measures make independent contributions to successful memory functioning. These models combine the structural and functional CFAs above by adding (a) residual covariance between modalities for specific tract groups (e.g., U F FU NC—U FST RUCT ), (b) covariance between the two latent variables (sCON— FUNC), and (c) mutual inputs from these LVs to a behavioral output (either source or item memory accuracy). As the number of tracts, and therefore CTGs, should be linearly correlated, we can ask whether a more parsimonious model shows better fit. We fit two models, one focused on source memory, and one focused on item memory. We first estimated the full models with all seven tract groups, and then estimated the regularized model across a range of lambda values, using RMSEA to compare model fit across each Network Neuroscience 184 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 1 1 7 3 1 0 9 2 3 5 6 n e n _ a _ 0 0 0 6 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Cooperative contributions of structural and functional connectivity iteration; the best solution for both models was obtained with the fifth lambda value from regularization, (lambda = 0.24, 0.22 for source and item models, respectively), with four tracts that have nonzero weights in the final model for both source and item models. 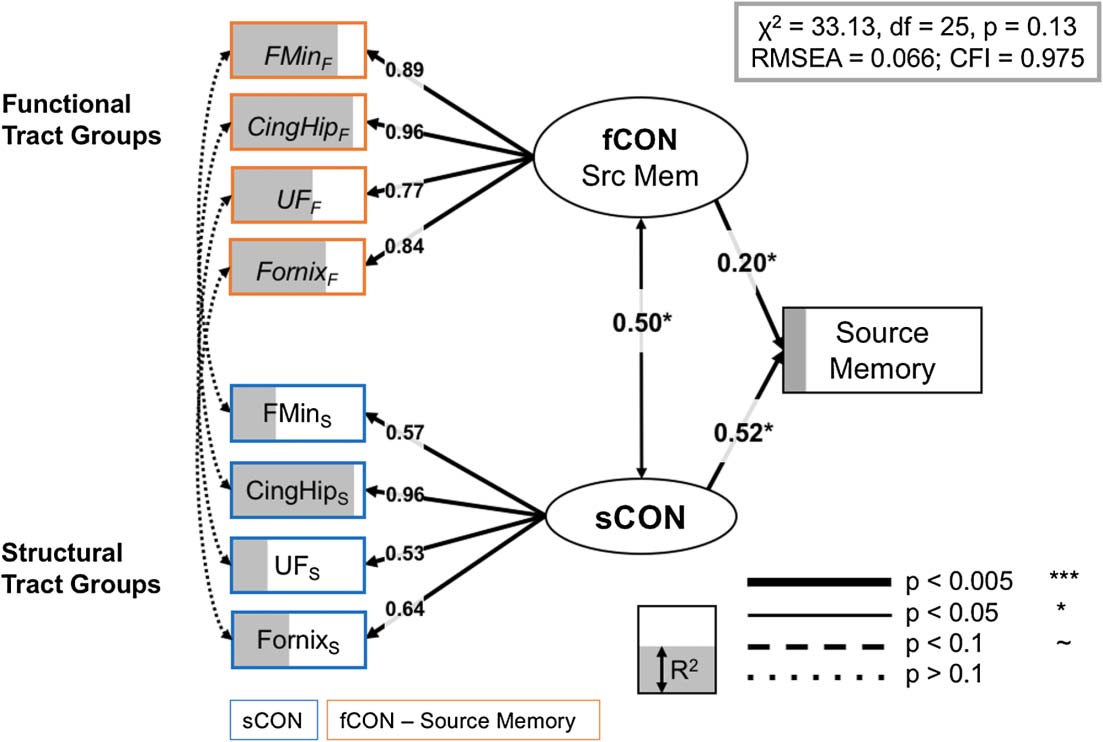The full regularized model for source memory is shown in Figure 5, and it fits the data quite well: χ2 = 30.22, d f = 25, p = 0.35, RMSEA = 0.066, CFI = 0.975. 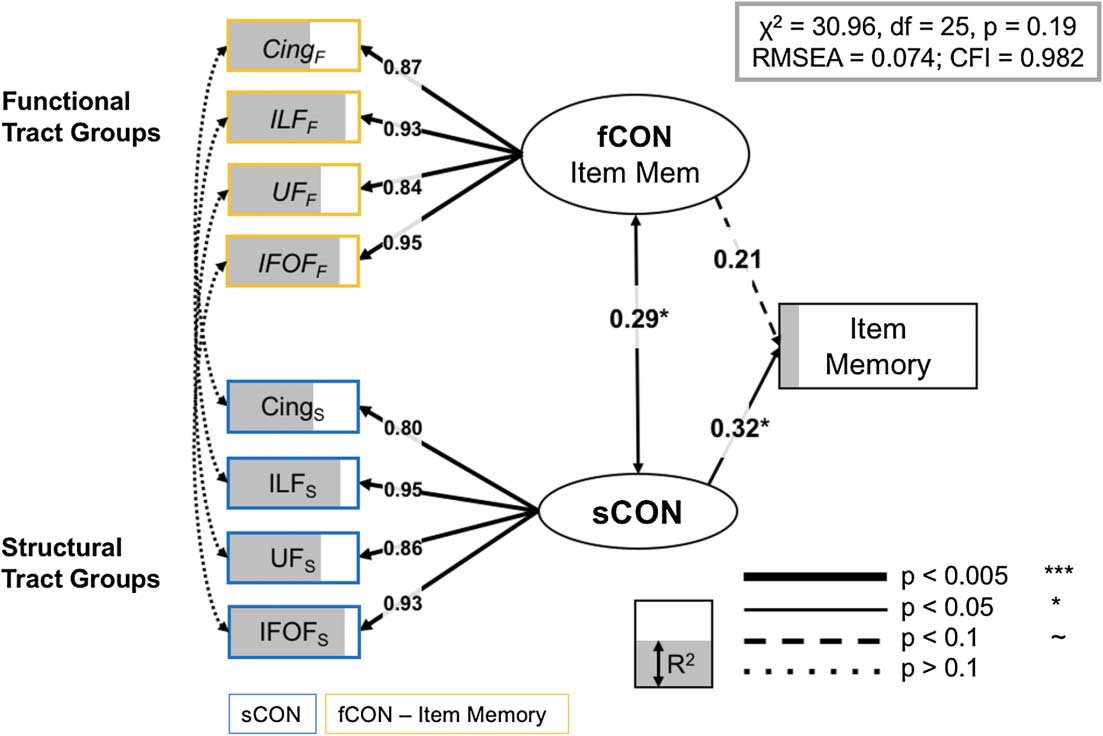The good fit of the full model suggests that the observed covariance pattern in our data is consistent with the statistical con- straints imposed by the model, and allows us to further investigate the relations between the cognitive factors and the neural variables. The full model for item memory (Figure 6) also fits the data well: χ2 = 30.96, d f = 25, p = 0.2, RMSEA = 0.074, CFI = 0.982. While both models share a number of structural and functional inputs, there are a number of unique inputs to each model (discussed below). Tract-specific contributions. We relied on the LASSO regularization to simplify our model and improve model fit; this technique also implicitly provides a means of identifying the specific tract groups that contribute to memory performance. As noted in the Methods section, we constrained model terms to include both structural and functional information pairs for each CTG, such that we could continue to make explicit hypotheses about structural-functional relationships in our final models. In the source memory model, the uncinate fasciculus, fornix, forceps minor, and hippocampal segment of the cingulum each contributed to the overall model (all R2 > 0.61/0.35 for structural/functional information, rispettivamente). Inoltre,
the inclusion of structural and functional information from the forceps minor of the corpus
callosum is in line with previous findings that suggest an important role for prefrontal sCON in
episodic memory functioning in older adult populations (Davis et al., 2009; Kennedy & Raz,
2009).

In contrasto, the final item memory model relied on paired structural and functional informa-
tion from the inferior longitudinal fasciculus, the cingulum, the uncinate fasciculus, and the

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Full model, source memory. Significant paths outlined and R2 (cioè., the amount of vari-
Figura 5.
ance accounted for each term in the model) is represented as the degree of shading of the variables.
Brain measures only have paths to a corresponding CTG in the other modality, or to the appropriate
LV. Notably, no residual covariance modalities for a specific CTG, questo è, between functional and
structural information (left side of SEM), were significant; indeed only latent constructs for sCON
and fCON demonstrated a significant association. CingHip = ventral leg of the cingulum; FMin =
forceps minor; UF = uncinate fasciculus.

Network Neuroscience

185

Cooperative contributions of structural and functional connectivity

Full model, item memory. Significant paths outlined and R2 (cioè., the amount of variance
Figura 6.
accounted for each term in the model) is represented as the degree of shading of the variables. Brain
measures only have paths to a corresponding CTG in the other modality, or to the appropriate LV.
Notably, just as in the source SEM above, we found no residual covariance between functional
and structural information for specific CTGs. Cing = cingulum; IFOF = inferior-fronto-occipital
fasciculus; ILF = inferior longitudinal fasciculus; UF = uncinate fasciculus.

inferior fronto-occipital fasciculus (all R2 > 0.31/0.34 for structural/functional information,
rispettivamente). This result is consistent with the qualitative interpretation that source memory re-
lies on both structural and functional connectivity frontotemporal regions, while item memory
shows a greater dependence on structural systems (structural LV std. param. = 0.32, p = 0.042)
based solely within the temporal lobe (Glisky et al., 1995; Spaniol & Grady, 2012). Lastly, while
the latent variable capturing the variance in overall success-related functional connectivity did
not demonstrate a significant path to behavioral performance on the item memory task (std.
param. = 0.21, p = 0.18), these functional CTGs nonetheless contributed to the overall model
fit; a separate model removing the link from the fCON LV to item memory showed a significant
reduction in model fit (Δχ2 = 34.22, Δd f = 1, P < 0.01) Table 3. Effects of age. Our last question was whether the connectivity measures examined herein captured the effect of age on memory; while Table 2 summarizes the influence of age on independent structural and functional connectivity metrics, a more holistic assessment of the role of age in explaining age-related differences in source and item memory may be more adequately characterized within the full SEMs. However, simply combining younger and older adult groups and then comparing full models either with or without age as a covariate would yield unsurprising benefits to including this covariate. This is in fact what we see—the overall fit was significantly worse in a multigroup model in which ages were included, but paths from age to brain factors were fixed at 0, in both the source memory (Δχ2 = 89.21, Δd f = 2, p < 0.001) and item memory models (Δχ2 = 66.26, Δd f = 2, p < 0.005). This result, again unsurprisingly, demonstrates that chronological age captures a significant proportion of variance in the model and has a strong influence on the latent variables for structural and functional connectivity. However, such a multigroup comparison model for young and older adults is nested, and more appropriate techniques may yield more informative results. An initial assessment of model fit in separate older and younger adult groups (fixing parame- ter estimates derived from the full models above between the two groups) suggested an overall Network Neuroscience 186 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 1 1 7 3 1 0 9 2 3 5 6 n e n _ a _ 0 0 0 6 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Cooperative contributions of structural and functional connectivity Table 3. CTG-specific contributions in both item and source memory SEMs SEM model Source memory model Region Latent variable CingHip FMin UF Fornix Item memory model Latent variable Cing ILF UF IFOF Structural CTG Functional CTG R2 Parameter estimate R2 Parameter estimate 0.82 0.91 0.62 0.61 0.95 0.39 0.44 0.64 0.45 0.31 0.52** 0.96**** 0.56**** 0.53*** 0.64**** 0.32* 0.87**** 0.95**** 0.84**** 0.93**** 0.14 0.76 0.51 0.85 0.36 0.34 0.72 0.67 0.59 0.49 0.20* 0.96**** 0.89**** 0.77**** 0.84**** 0.21 0.80**** 0.95**** 0.86**** 0.93**** Parameter estimates are fully standardized. Cing = cingulum; CingHip = ventral leg of the cingulum; FMin = forceps minor (or genu); IFOF = inferior fronto-occipital fasciculus; ILF = inferior longitu- dinal fasciculus; UF = uncinate fasciculus. Significance: * = p < 0.05; ** = p < 0.01; *** = p < 0.001; **** = p < 0.0001. worse fit in younger than older adults in both source (RMSEAolder = 0.066; RMSEAyounger = 0.227) and item memory SEMs (RMSEAolder = 0.074; RMSEAyounger = 0.209). Consequently, we then used the post hoc approach of equality constraints in order to identify specific param- eters in the model affected by age. An equality constraint simplifies an SEM model such that, in reaching its solution, it must provide the identical unstandardized coefficient for all param- eters within a set that has been designated for equality. In this formulation, the model (i.e., full source and item memory models) is run twice, once without constraints on a particular parameter, and once with the constraint; a significant Δχ2 test (with Δd f ) between these two models therefore suggests that the relevant parameter estimate differs between the groups. Table 4 summarizes the results of this equality constraint analysis, examining both the change in each input parameter, and—critically—a Δχ2 test statistic that characterizes the influence of allowing this parameter to behave unconstrained during model fitting. We found that in our model of source memory, parameters describing structural connectivity in the fornix and functional connectivity in regions connected by the uncinate fasciculus have a stronger influence on model fit in the older adults. In contrast, in our item memory SEM the struc- tural parameters describing sCON in the UF and ILF are generally stronger in the older adult subgroup—a result that is consistent with the fact that the general sCON LV—and not the func- tional connectivity LV—predicted item memory performance in our model above (Figure 6). This approach is therefore diagnostic of which specific parameters (i.e., which sCON or fCON CTGs) contribute to differences in model fit between younger and older adults. These results suggest an age-related change in the reliance on regions connected by the fornix and UF during source memory retrieval, and the UF and ILF during item memory retrieval. DISCUSSION By combining multiple behavioral, demographic, and brain measures from a large sample of younger and older adults, we provide evidence that age-related differences in source and item memory are dissociable by their functional and structural connectivity profiles. In our Network Neuroscience 187 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / / 3 1 1 7 3 1 0 9 2 3 5 6 n e n _ a _ 0 0 0 6 4 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Cooperative contributions of structural and functional connectivity Table 4. Equality constraints analysis results SEM model Source memory model Parameter Δχ2 Δ in parameter estimate Latent variable to: CingHip FMin UF Fornix Item memory model Latent variable to: Cing ILF UF IFOF sCON N/A 1.23 0.03 6.74* sCON N/A 4.73* 7.15** 0.37 fCON N/A 0.08 3.44* 0.01 fCON N/A 0.25 1.33 1.74 sCON 0.034 0.013 0.165 0.094 0.135 0.022 fCON 0.066 0.108 0.075 0.019 0.078 0.049 Parameter estimates are fully standardized. Cing = cingulum; CingHip = ventral leg of the cingulum; FMin = forceps minor fasciculus; ILF = inferior longitudinal fasciculus; UF = uncinate fasciculus. Significance: * = p < 0.05; ** = p < 0.01. IFOF = inferior fronto-occipital (or genu); best-fitting model, individual CTGs based on canonical fiber systems make independent con- tributions to both forms of memory. First, we found that the relationship between structural and functional connectivity information was best characterized by an intermediate level of relationship. Although no specific CTGs demonstrated a significant association between their corresponding fCON and sCON values (i.e., fCON–sCON covariance, as indicated by the curved, dotted lines in Figures 5 and 6), a more general sCON–fCON relationship between latent variables built on these tract-specific measurements was significant in both source and item memory SEMs, suggesting a more general relationship between structural and functional modalities. Second, we found that both sCON and fCON make independent contributions to source memory performance, while only sCON influenced behavior in the item memory SEM. Lastly, age-related influences on our model were much stronger for sCON than for fCON, but age was an essential component of the full model. Our results therefore demonstrate that age-related declines in memory are unlikely to be driven by a single fiber system or a sin- gle data type, but emerge as a confluence of functional and structural differences in multiple anatomically connected systems. Structure-Function Relationships Evidence has shown that brain topology (i.e., structure) supports fluid dynamics (i.e., function), and that brain dynamics in turn reinforce structure via synaptic plasticity. In a very influential work, Honey et al. ( 2007) showed that this relationship is highly dependent on the charac- teristics of the functional data used to test this relationship, including the timescale, local clustering, and brain state. Our use of CTGs integrates structural and functional connectiv- ity information within a common anatomical framework, achieved by constraining functional connections to known anatomy. More specifically, summarizing the structural (FA based on tractography streamlines) and functional (Spearman’s rho based on task-related PPI) relation- ships between pairs of regions connected by canonical tract groups (e.g., the uncinate fasci- culus) helps to link empirical results obtained via adjacency matrices—a now common basis for most graph-theoretical approaches to characterizing aging brain networks—with clinically minded approaches centered on canonical fiber systems. Network Neuroscience 188 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 3 1 1 7 3 1 0 9 2 3 5 6 n e n _ a _ 0 0 0 6 4 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Cooperative contributions of structural and functional connectivity In our best fitting model for source or item memory, no residual covariance between modal- ities (i.e., structural and functional connectivity) for the same CTG reached significance, while latent variables for structural and functional connectivity did show a significant association. When the LV-LV pathway was set to 0, model fit significantly decreased (Δχ2 = 9.78, Δd f = 1, p < 0.016). It is worthwhile to note that, outside the SEM framework, functional and struc- tural CTGs were reliably correlated across subjects (Table 1; all but one CTG r > 0.21, even
after adjusting for age). Taken together, these results suggest that the relationship between
structural and functional connectivity estimates may be best characterized on an intermediate
level. Many of the age-related differences to white matter may appear to manifest as global
changes across different major white matter tracts (Penke et al., 2010), and driven by causal
factors that affect white matter, such as small vessel disease, myelin depletion, or iron accu-
mulation. Nonetheless, a growing model-based literature is emerging that suggests that a more
constrained set of critical white matter fiber systems (forceps minor, cingulum, uncinate fas-
ciculus) provide the best fit for models seeking to explain age-related differences in attention,
memory, and processing speed (Kievit et al., 2016; Lovden et al., 2013; Voineskos et al., 2012).

Tract-Specific Effects on Source and Item Memory

Whether tract-specific relationships or general global declines in white matter health best pre-
dict age-related declines in executive and mnemonic performance is a matter of some ongoing
debate (Kievit et al., 2016, 2014; Lovden et al., 2013; Penke et al., 2010); the value of such de-
bates rests on the anatomical specificity used in creating structural and functional connectivity
values to predict age-related differences in behavior. Our result suggests an intermediate con-
clusion to the general versus specific debate: While the residual covariance between specific
structural-functional modalities for a specific fiber tract does not drive the success of a model
of source or item memory, there are nonetheless a subset of specific tract groups that pro-
vide the best fit to these data. We found that the structural and functional connectivity based
on the fornix had a selective positive influence for source, but not item memory, consistent
with theoretical and empirical results supporting the role of this structure in source retrieval
(Aggleton & Brown, 1999; Antonenko et al., 2016). The fornix is a key white matter tract of the
medial temporal lobe memory system, interconnecting the hippocampal formation with sub-
cortical structures in the basal forebrain and diencephalon. There is evidence of altered white
matter microstructure in the fornix in healthy older adults (Antonenko et al., 2016; Persson
et al., 2006), and measures of fornix microstructure may be useful in detecting early/preclinical
Alzheimer’s disease stages (Nowrangi & Rosenberg, 2015). Allo stesso modo, the finding that the unci-
nate fasciculus—which connects anterior temporal and inferior frontal cortices—is implicated
in both our source and item memory SEMs is consistent with evidence linking this tract to
age-related decline in memory functioning across a wide array of tasks, including visual ob-
ject location (Metzler-Baddeley, Jones, Belaroussi, Aggleton, & O’Sullivan, 2011), color-picture
associations (Lockhart et al., 2012), working memory (Burzynska et al., 2013), and verbal learn-
ing (Lancaster et al., 2016). Allo stesso modo, the item memory–specific role of the IFOF fits well with
electrostimulation-based studies that have shown semantic paraphasias in response to (disrup-
tive) stimulation of this fiber system (Duffau et al., 2005).

È interessante notare, we found that the genu, or forceps minor of the corpus callosum (FMin in our
models), which connects left and right prefrontal cortex, contributed significantly to source
but not to item memory, a finding that is consistent with the assumption that source memory is
more dependent on PFC-mediated functions (Shimamura, 1995), and that bilateral PFC activity
may serve a compensatory role in age-related decline (Cabeza, 2002). We and others have
found that the FA of the genu predicts behavior on a range of episodic memory (Davis et al.,

Network Neuroscience

189

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

2009; Henson et al., 2016) and executive function tasks (Kievit et al., 2016, 2014) in elderly
populations. The dissociation in source versus item memory performance (Glisky et al., 1995) È
consistent with abundant evidence that the PFC is more critical for source than item memory
performance in aging populations (Duarte, Ranganath, Trujillo, & Knight, 2006; Leshikar &
Duarte, 2014; Old & Naveh-Benjamin, 2008; Spaniol & Grady, 2012), and reliance on structural
and functional connectivity in the PFC may be a means of counteracting observed source
deficits (Dennis et al., 2008; Naveh-Benjamin, Hussain, Guez, & Bar-On, 2003).

Effects of Age

Our last findings focused on age-related differences between younger and older adults: Primo,
estimates of model fit (per esempio., RMSEA) were generally better in older than younger adults; second,
modeling equality constraints for all parameters suggested that structural connectivity of the
fornix and functional connectivity mediated by the UF show the strongest differences between
younger and older adults in source memory. Model comparison in aging samples is an unre-
solved issue, and no unanimity exists on how to include chronological age as an operative
term in SEMs examining brain and behavioral factors (Tuttavia, see Bender, Volkle, & Raz,
2016; Henson et al., 2016; Kievit et al., 2016). Nonetheless, consensus opinions are emerging
about the role of cross-sectional and longitudinal datasets in estimating the effects of “age”
versus the effects of “aging.” While our cross-sectional sample is unable to draw inferences
on “aging,” we nonetheless take advantage of the specific qualities of our sample to evaluate
how well our model describes younger and older adult groups separately, in order to draw
inferences on the age-specificity of the observed effects.

Age effects on structural connectivity revealed with DWI are regionally diverse and typically
show an anterior-to-posterior gradient of age-related decline (Davis et al., 2009; Head et al.,
2004; Sullivan, Adalsteinsson, & Pfefferbaum, 2006). Consistent with this evidence, we ob-
served strong declines in FA across nearly all structural connectivity groups, or CTGs (Tavolo 2).
While a number of studies have found single correlation (Kennedy & Raz, 2009) or media-
tion patterns (Madden et al., 2010; Oberlin et al., 2016) that help to explain how these white
matter structures mediated cognitive decline, our analysis advances on these approaches by
considering all of these regions simultaneously, within a statistically rigorous framework. Noi
found that within older adults, successful source memory was associated with structural and
functional connectivity in a set of canonical fiber tracts connecting either within or between
frontal regions: the forceps minor, UF, CingHip, and fornix (Figura 5), even when all brain
measures were adjusted for chronological age. In contrasto, an overlapping but more ventral
set of regions, including the inferior longitudinal fasciculus, helped to predict successful item
memory performance (Figura 6). Inoltre, estimates of the influence of age on our model
are difficult to estimate within this SEM framework, but nonetheless suggest an important role
for (UN) structural integrity of the fornix, and functional information conveyed by regions con-
nected by the UF in predicting source memory differences between older and younger adults,
E (B) structural information in nearly all CTGs in item memory, given the significant Δχ2
after these single parameters were allowed to be freely estimated (holding all other parameters
constant).

With respect to functional connectivity, the finding that CTGs connecting either within (for-
ceps minor) or between the PFC and other regions (UF, IFOF) explain significant variance
in source memory scores is consistent with the general observation that older adults show
higher levels of PFC activity across a range of cognitive tasks (Grady, 2012). Our findings of
age-related increases in task-related frontotemporal functional connectivity during successful

Network Neuroscience

190

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

source memory provide evidence for a compensatory mechanism by demonstrating a reliance
on PFC connectivity from three major inferior temporal white matter fibers: the FMin, UF,
and fornix. Our connectivity measure was based on task-related data, and furthermore used
an explicit contrast between Hits > Misses, in order to isolate connectivity related to suc-
cessful memory functioning. Our result is also consistent with a handful of studies that have
identified an increased reliance on frontotemporal connectivity to maintain source memory
function (Dennis et al., 2008; Spaniol & Grady, 2012), and this finding more generally sup-
ports the idea that frontotemporal interactions support source memory performance (Backus,
Schoffelen, Szebenyi, Hanslmayr, & Doeller, 2016).

Lastly, we must acknowledge some of the relevant limitations of our approach, with re-
spect to modeling the influence of functional and structural connectivity in the aging brain
and its influence on different forms of memory. Clearly a larger, more balanced sample may
have helped to improve some of the inferences concerning the relative influence of connec-
tivity factors in promoting age-related differences in source and item memory, and a more
distributed sample across a range of ages may allow for alternative modeling strategies for this
particular application of SEM. The growth of large population-representative datasets with this
kind of information (per esempio., Cam-CAN.org) is heartening in this respect. Inoltre, in order to
establish a more robust model of the relationship between structural and functional dynamics,
it would be necessary to follow people over time and establish what causal factors (critical
developmental periods, nutrition, cardiovascular fitness, eccetera.) influence this relationship.

CONCLUSIONS

To summarize, we have applied a novel connectome summary algorithm to show that age-
related differences in source and item memory are dependent on distinct combinations of
structural and functional connectivity tract groups. These results help to link graph analyses
of structural and functional data in anatomically informed and theory-driven manner. Usually,
an implicit assumption is that if the structure of the network is observable, an inference of the
underlying structure of the connected system can be based on diffusion tractography structure.
Our results test this assumption explicitly, by using an analytical method that puts structural
and functional connectivity information on equal footing. These results provide further insights
into the interplay between structural and functional connectivity patterns and help to elucidate
their relative contribution to age-related differences in source memory performance.

AUTHOR CONTRIBUTIONS

Simon W. Davis: Conceptualization; Data curation; Formal analysis; Investigation; Method-
ology; Software; Visualization; Writing – original draft; Writing – review & editing. Amanda
Szymanski: Data curation; Formal analysis; Writing – original draft; Writing – review & edit-
ing. Homa Boms: Data curation; Formal analysis. Thomas Fink: Data curation; Formal analysis.
Roberto Cabeza: Conceptualization; Funding acquisition; Resources; Supervision; Writing –
original draft; Writing – review & editing.

FUNDING INFORMATION

Roberto Cabeza, National Institute on Aging (http://dx.doi.org/10.13039/100000049), Award
ID: R01AG19731. Simon W. Davis, National Institute on Aging (http://dx.doi.org/10.13039/
100000049), Award ID: K01AG053539.

Network Neuroscience

191

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

REFERENCES

Abdelnour, F., Voss, H. U., & Raj, UN.

(2014). Network diffu-
sion accurately models the relationship between structural
and functional brain connectivity networks. NeuroImage, 90,
335–347.

Aggleton, J. P., & Brown, M. W. (1999). Episodic memory, amne-
sia, and the hippocampal-anterior thalamic axis. Behavioral and
Brain Sciences, 22, 425–444; discussion 444–489.

Andrews-Hanna, J. R., Snyder, UN. Z., Vincent, J. L., Lustig, C.,
Head, D., Raichle, M. E., & Buckner, R. l.
(2007). Disruption
of large-scale brain systems in advanced aging. Neuron, 56,
924–935.

Antonenko, D., Kulzow, N., Cesarz, M. E., Schindler, K., Grittner,
U., & Floel, UN. (2016). Hippocampal pathway plasticity is asso-
ciated with the ability to form novel memories in older adults.
Frontiers in Aging Neuroscience, 8, 61.

Ashburner, J. (2007). A fast diffeomorphic image registration algo-

rithm. NeuroImage, 38, 95–113.

Backus, UN. R., Schoffelen, J. M., Szebenyi, S., Hanslmayr, S., &
Doeller, C. F. (2016). Hippocampal-prefrontal theta oscillations
support memory integration. Current Biology, 26, 450–457.
Bagozzi, R. P., & Yi, Y. (2012). Specification, evaluation, and inter-
pretation of structural equation models. Journal of the Academy
of Marketing Science, 40, 8–34.

Bender, UN. R., Volkle, M. C., & Raz, N. (2016). Differential aging
of cerebral white matter in middle-aged and older adults: UN
seven-year follow-up. NeuroImage, 125, 74–83.

Bendlin, B. B., Fitzgerald, M. E., Ries, M. L., Xu, G., Kastman, E. K.,
Thiel, B. W., . . . Johnson, S. C.
(2010). White matter in aging
and cognition: A cross-sectional study of microstructure in adults
aged eighteen to eighty-three. Developmental Neuropsychology,
35, 257–277.

Betzel, R. F., Byrge, L., Lui, Y., Goni, J., Zuo, X. N., & Sporns, O.
(2014). Changes in structural and functional connectivity among
resting-state networks across the human lifespan. NeuroImage,
102(Pt. 2), 345–357.

Bowman, F. D., Zhang, L., Derado, G., & Chen, S. (2012). Deter-
mining functional connectivity using fMRI data with diffusion-
based anatomical weighting. NeuroImage, 62, 1769–1779.
Brown, C. A., Johnson, N. F., Anderson-Mooney, UN. J., Jicha, G. A.,
Shaw, l. M., Trojanowski, J. Q., . . . Gold, B. T. (2017). Devel-
opment, validation and application of a new fornix template
for studies of aging and preclinical Alzheimer’s disease. Neuro-
Image: Clinical, 13, 106–115.

Burzynska, UN. Z., Garrett, D. D., Preuschhof, C., Nagel, IO. E., Li,
(2013). A scaffold
S. C., Backman, L., . . . Lindenberger, U.
for efficiency in the human brain. Journal of Neuroscience, 33,
17150–17159.

Cabeza, R. (2002). Hemispheric asymmetry reduction in older
adults: The HAROLD model. Psychology and Aging, 17, 85–100.
Daselaar, S. M., Iyengar, V., Davis, S. W., Eklund, K., Hayes, S. M.,
& Cabeza, R. E. (2015). Less wiring, more firing: Low-performing
older adults compensate for impaired white matter with greater
neural activity. Cerebral Cortex, 25, 983–990.

Davis, S. W. (2018). Electricdinolab, canonical tract groups, Github.
https://github.com/ElectricDinoLab/Canonical_Tract_Groups
Davis, S. W., Dennis, N. A., Buchler, N. G., White, l. E., Madden,
D. J., & Cabeza, R. (2009). Assessing the effects of age on long
white matter tracts using diffusion tensor tractography. Neuro-
Image, 46, 530–541.

Davis, S. W., Kragel, J. E., Madden, D. J., & Cabeza, R. (2012). IL
architecture of cross-hemispheric communication in the aging
brain: Linking behavior to functional and structural connectivity.
Cerebral Cortex, 22, 232–242.

Dennis, N. A., Hayes, S. M., Prince, S. E., Madden, D. J., Huettel,
S. A., & Cabeza, R. (2008). Effects of aging on the neural corre-
lates of successful item and source memory encoding. Journal of
Experimental Psychology: Apprendimento, Memory, and Cognition, 34,
791–808.

Dobbins, IO. G., & Wagner, UN. D.

(2005). Domain-general and
domain-sensitive prefrontal mechanisms for recollecting events
and detecting novelty. Cerebral Cortex, 15, 1768–1778.

Duarte, A., Ranganath, C., Trujillo, C., & Knight, R. T. (2006). Intact
recollection memory in high-performing older adults: ERP and
behavioral evidence. Journal of Cognitive Neuroscience, 18,
33–47.

Duffau, H., Gatignol, P., Mandonnet, E., Peruzzi, P., Tzourio-
(2005). New insights into the
Mazoyer, N., & Capelle, l.
anatomo-functional connectivity of
the semantic system: UN
study using cortico-subcortical electrostimulations. Brain, 128,
797–810.

Fornito, A., Harrison, B. J., Zalesky, A., & Simons, J. S. (2012). Com-
petitive and cooperative dynamics of large-scale brain functional
networks supporting recollection. Proceedings of the National
Acadency of Sciences, 109, 12788–12793.

Fornito, A., Zalesky, A., & Bullmore, E. T. (2010). Network scaling
effects in graph analytic studies of human resting-state fMRI data.
Frontiers in Systems Neuroscience, 4, 22.

Glisky, E. L., Polster, M. R., & Routhieaux, B. C. (1995). Double dis-
sociation between item and source memory. Neuropsychology,
9, 229–235.

Grady, C. (2012). Brain ageing: The cognitive neuroscience of age-

ing. Nature Reviews Neuroscience, 13, 491–505.

Hayes, S. M., Buchler, N., Stokes, J., Kragel, J., & Cabeza, R. (2011).
Neural correlates of confidence during item recognition and
source memory retrieval: Evidence for both dual-process and
strength memory theories. Journal of Cognitive Neuroscience,
23, 3959–3971.

.

Head, D., Buckner, R. L., Shimony, J. S., Williams, l. E., Akbudak,
E., Conturo, T. E.,
(2004). Differential
vulnerability of anterior white matter in nondemented aging
with minimal acceleration in dementia of the Alzheimer type:
Evidence from diffusion tensor imaging. Cerebral Cortex, 14,
410–423.

. Snyder, UN. Z.

.

Henson, R. N., Campbell, K. L., Davis, S. W., Taylor, J. R., Emery, T.,
Erzinclioglu, S., . . . Kievit, R. UN. (2016). Multiple determinants
of lifespan memory differences. Scientific Reports, 6, 32527.

Network Neuroscience

192

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

Honey, C. J., Kotter, R., Breakspear, M., & Sporns, O. (2007). Net-
work structure of cerebral cortex shapes functional connectivity
on multiple time scales. Proceedings of the National Academy
of Sciences, 104, 10240–10245.

Honey, C. J., Sporns, O., Cammoun, L., Gigandet, X., Thiran, J. P.,
Meuli, R., & Hagmann, P. (2009). Predicting human resting-state
functional connectivity from structural connectivity. Proceedings
of the National Academy of Sciences, 106, 2035–2040.

Horn, A., Ostwald, D., Reisert, M., & Blankenburg, F. (2014). IL
structural-functional connectome and the default mode network
of the human brain. NeuroImage, 102(Pt. 1), 142–151.

Hua, K., Zhang, J., Wakana, S., Jiang, H., Li, X., Reich, D. S., . . .
Mori, S. (2008). Tract probability maps in stereotaxic spaces:
Analyses of white matter anatomy and tract-specific quantifica-
zione. NeuroImage, 39, 336–347.

Jacobucci, R., Grimm, K. J., & McArdle, J. J.

(2016). Regularized
structural equation modeling. Structural Equation Modeling, 23,
555–566.

Kennedy, K. M., & Raz, N. (2009). Aging white matter and cog-
nition: Differential effects of regional variations in diffusion
properties on memory, executive functions, and speed. Neuro-
psychologia, 47, 916–927.

Kievit, R. A., Davis, S. W., Griffiths, J., Correia, M. M., Camera, C., &
(2016). A watershed model of individual differ-

Henson, R. N.
ences in fluid intelligence. Neuropsychologia, 91, 186–198.
Kievit, R. A., Davis, S. W., Mitchell, D. J., Taylor, J. R., Duncan, J.,
Cam-CAN Research Team, & Henson, R. N. (2014). Distinct as-
pects of frontal lobe structure mediate age-related differences
in fluid intelligence and multitasking. Nature Communications,
5, 5658.

Lancaster, M. A., Seidenberg, M., Smith, J. C., Nielson, K. A.,
Woodard, J. L., Durgerian, S., & Rao, S. M.
(2016). Diffusion
tensor imaging predictors of episodic memory decline in healthy
elders at genetic risk for alzheimer’s disease. Journal of the Inter-
national Neuropsychological Society, 22, 1005–1015.

Leshikar, E. D., & Duarte, UN. (2014). Medial prefrontal cortex
supports source memory for self-referenced materials in young
and older adults. Cognitive, Affective, and Behavioral Neuro-
science, 14, 236–252.

Lockhart, S. N., Mayda, UN. B., Roach, UN. E., Fletcher, E., Carmichael,
O., Maillard, P., . . . Decarli, C. (2012). Episodic memory-
function is associated with multiple measures of white matter
integrity in cognitive aging. Frontiers in Human Neuroscience,
6, 56.

Lovden, M., Laukka, E. J., Rieckmann, A., Kalpouzos, G., Li, T. Q.,
Jonsson, T., . . . Backman, l. (2013). The dimensionality of
between-person differences in white matter microstructure in
old age. Human Brain Mapping, 34, 1386–1398.

Madden, D. J., Costello, M. C., Dennis, N. A., Davis, S. W., Shepler,
UN. M., Spaniol, J., . . . Cabeza, R. (2010). Adult age differences
in functional connectivity during executive control. NeuroImage,
52, 643–657.

Maier-Hein, K. H., Neher, P. F., Houde,

J. C., Côté, M.-A.,
Garyfallidis, E., Zhong, J., . . . Descoteaux, M. (2017). The chal-
lenge of mapping the human connectome based on diffusion
tractography. Nature Communications, 8, 1349.

Messé, Rudrauf, D., Giron, A., & Marrelec, G. (2015). Predict-
ing functional connectivity from structural connectivity via com-
putational models using MRI: An extensive comparison study.
NeuroImage, 111, 65–75.

Metzler-Baddeley, C., Jones, D. K., Belaroussi, B., Aggleton, J. P., &
O’Sullivan, M. J. (2011). Frontotemporal connections in episodic
memory and aging: A diffusion MRI tractography study. Journal
of Neuroscience, 31, 13236–13245.

Metzler-Baddeley, C., Jones, D. K., Steventon, J., Westacott, L.,
Aggleton, J. P., & O’Sullivan, M. J. (2012). Cingulum microstruc-
ture predicts cognitive control in older age and mild cognitive
impairment. Journal of Neuroscience, 32, 17612–17619.

Meunier, D., Stamatakis, E. A., & Tyler, l. K.

(2014). Age-related
functional reorganization, structural changes, and preserved
cognition. Neurobiology of Aging, 35, 42–54.

Murty, V. P., Sambataro, F., Das, S., Tan, H. Y., Callicott, J. H.,
Goldberg, T. E., . . . Mattay, V. S. (2009). Age-related alterations
in simple declarative memory and the effect of negative stimulus
valence. Journal of Cognitive Neuroscience, 21, 1920–1933.
Naveh-Benjamin, M. (2000). Adult age differences in memory per-
formance: Tests of an associative deficit hypothesis. Journal of
Experimental Psychology: Learning Memory, and Cognition, 26,
1170–1187.

Naveh-Benjamin, M., & Craik, F. IO. (1996). Effects of perceptual and
conceptual processing on memory for words and voice: Differ-
ent patterns for young and old. Quarterly Journal of Experimental
Psychology A, 49, 780–796.

Naveh-Benjamin, M., Hussain, Z., Guez, J., & Bar-On, M. (2003).
Adult age differences in episodic memory: Further support for
an associative-deficit hypothesis. Journal of Experimental Psy-
chology: Apprendimento, Memory, and Cognition, 29, 826–837.

Nowrangi, M. A., & Rosenberg, P. B. (2015). The fornix in mild
cognitive impairment and Alzheimer’s disease. Frontiers in Aging
Neuroscience, 7, 1.

Oberlin, l. E., Verstynen, T. D., Burzynska, UN. Z., Voss, M. W.,
Prakash, R. S., Chaddock-Heyman, L., . . . Erickson, K. IO. (2016).
White matter microstructure mediates the relationship between
cardiorespiratory fitness and spatial working memory in older
adults. NeuroImage, 131, 91–101.

Old, S. R., & Naveh-Benjamin, M. (2008). Differential effects of age
on item and associative measures of memory: A meta-analysis.
Psychology and Aging, 23, 104–118.

Penke, L., Munoz Maniega, S., Murray, C., Gow, UN. J., Hernandez,
M. C., Clayden, J. D., . . . Deary, IO. J. (2010). A general factor
of brain white matter integrity predicts information processing
speed in healthy older people. Journal of Neuroscience, 30,
7569–7574.

Persson, J., Nyberg, L., Lind, J., Larsson, A., Nilsson, l. G., Ingvar,
M., & Buckner, R. l. (2006). Structure-function correlates of cog-
nitive decline in aging. Cerebral Cortex, 16, 907–915.

Qi, S., Meesters, S., Nicolay, K., Ter Haar Romeny, B. M., &
Ossenblok, P. (2016). Structural brain network: What is the
effect of liFE optimization of whole brain tractography? Frontiers
in Computational Neuroscience, 10, 12.

Roberts, J. A., Perry, A., Lord, UN. R., Roberts, G., Mitchell, P. B.,
(2016). The contribution

. Breakspear, M.

Smith, R. E.,

.

.

Network Neuroscience

193

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Cooperative contributions of structural and functional connectivity

of geometry to the human connectome. NeuroImage, 124,
379–393.

Non-negativity constrained super-resolved spherical deconvolu-
zione. NeuroImage, 35, 1459–1472.

Romero-Garcia, R., Atienza, M., & Cantero, J. l. (2014). Predictors
of coupling between structural and functional cortical networks
in normal aging. Human Brain Mapping, 35, 2724–2740.

Rosseel, Y.

(2012).

lavaan: An R package for structural equation

modeling. Journal of Statistical Software, 48, 1–36.

Shimamura, UN. P. (1995). Memory and frontal lobe function. In M. S.
Gazzaniga (Ed.), The cognitive neurosciences (pag. 803–814).
Cambridge, MA: CON Premere.

Smith, R. E., Tournier, J. D., Calamante, F., & Connelly, UN. (2012).
Anatomically constrained tractography: Improved diffusion MRI
streamlines tractography through effective use of anatomical
informazione. NeuroImage, 62, 1924–1938.

Spaniol, J., & Grady, C. (2012). Aging and the neural correlates
of source memory: Over-recruitment and functional reorganiza-
zione. Neurobiology of Aging, 33, 425.e3–425.18.

St. Jacques, P. L., Dolcos, F., & Cabeza, R. (2009). Effects of aging
on functional connectivity of the amygdala during subsequent
memory for negative pictures: A network analysis of fMRI data.
Psychological Science, 20, 74–84.

Sullivan, E. V., Adalsteinsson, E., & Pfefferbaum, UN. (2006). Selective
age-related degradation of anterior callosal fiber bundles quanti-
fied in vivo with fiber tracking. Cerebral Cortex, 16, 1030–1039.
Tewarie, P., Hillebrand, A., van Dellen, E., Schoonheim, M. M.,
Barkhof, F., Polman, C. H., . . . Stam, C. J. (2014). Structural
degree predicts functional network connectivity: A multimodal
resting-state fMRI and MEG study. NeuroImage, 97, 296–307.

Tibshirani, R.

(1996). Regression shrinkage and selection via the
Journal of the Royal Statistical Society: B (Methodologi-

lasso.
cal), 58, 267–288.

Tournier, J. D., Calamante, F., & Connelly, UN.

(2007). Robust de-
termination of the fibre orientation distribution in diffusion MRI:

Tournier, J. D., Calamante, F., Gadian, D. G., & Connelly, UN.
(2004). Direct estimation of the fiber orientation density function
from diffusion-weighted MRI data using spherical deconvolution.
NeuroImage, 23, 1176–1185.

Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., . . . Joliot, M. (2002). Automated
anatomical labeling of activations in SPM using a macroscopic
anatomical parcellation of the MNI MRI single-subject brain.
NeuroImage, 15, 273–289.

Voineskos, UN. N., Rajji, T. K., Lobaugh, N. J., Miranda, D., Shen-
ton, M. E., Kennedy, J. L., . . . Mulsant, B. H. (2012). Age-related
decline in white matter tract integrity and cognitive performance:
A DTI
tractography and structural equation modeling study.
Neurobiology of Aging, 33, 21–34.

Wager, T. D., & Nichols, T. E. (2003). Optimization of experimental
design in fMRI: A general framework using a genetic algorithm.
NeuroImage, 18(2), 293–309.

Wang, Z., Dai, Z., Gong, G., Zhou, C., & Lui, Y.

(2015). Under-
standing structural-functional relationships in the human brain:
A large-scale network perspective. Neuroscientist, 21, 290–305.
Yeh, C. H., Smith, R. E., Liang, X., Calamante, F., & Connelly, UN.
(2016). Correction for diffusion MRI fibre tracking biases: IL
consequences for structural connectomic metrics. NeuroImage,
142, 150–162.

Zhu, D., Zhang, T., Jiang, X., Eh, X., Chen, H., Yang, N., . . . Liu,
T. (2014). Fusing DTI and fMRI data: A survey of methods and
applications. NeuroImage, 102, 184–191.

Zimmermann, J., Ritter, P., Shen, K., Rothmeier, S., Schirner, M., &
(2016). Structural architecture supports func-
McIntosh, UN. R.
tional organization in the human aging brain at a regionwise and
network level. Human Brain Mapping, 37, 2645–2661.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

3
1
1
7
3
1
0
9
2
3
5
6
N
e
N
_
UN
_
0
0
0
6
4
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Network Neuroscience

194

Scarica il pdf