RESEARCH
Variability and stability of large-scale cortical
oscillation patterns
Roy Cox, Anna C. Schapiro, and Robert Stickgold
Department of Psychiatry, Beth Israel Deaconess Medical Center and Harvard Medical School, Boston MA, USA
Keywords: EEG, Oscillations, Networks, Functional connectivity, Individual differences
ABSTRACT
Individual differences in brain organization exist at many spatiotemporal scales and underlie
the diversity of human thought and behavior. Oscillatory neural activity is crucial for these
processes, but how such rhythms are expressed across the cortex within and across
individuals is poorly understood. We conducted a systematic characterization of brain-wide
activity across frequency bands and oscillatory features during rest and task execution. Noi
found that oscillatory profiles exhibit sizable group-level similarities, indicating the presence
of common templates of oscillatory organization. Nonetheless, well-defined subject-specific
network profiles were discernible beyond the structure shared across individuals. These
individualized patterns were sufficiently stable to recognize individuals several months later.
Inoltre, network structure of rhythmic activity varied considerably across distinct
oscillatory frequencies and features, indicating the existence of several parallel information
processing streams embedded in distributed electrophysiological activity. These findings
suggest that network similarity analyses may be useful for understanding the role of
large-scale brain oscillations in physiology and behavior.
AUTHOR SUMMARY
Neural oscillations are critical for the human brain’s ability to optimally respond to complex
environmental input. Tuttavia, relatively little is known about the network properties of
these oscillatory rhythms. We used electroencephalography (EEG) to analyze large-scale
brain wave patterns, focusing on multiple frequency bands and several key features of
oscillatory communication. We show that networks defined in this manner are, Infatti,
distinct, suggesting that EEG activity encompasses multiple, parallel information processing
streams. Remarkably, the same networks can be used to uniquely identify individuals over a
period of approximately half a year, thus serving as neural fingerprints. These findings
indicate that investigating oscillatory dynamics from a network perspective holds
considerable promise as a tool to understand human cognition and behavior.
INTRODUCTION
Although human brains are very similar, every brain is also distinct. Magnetic resonance imag-
ing (MRI) techniques indicate both individual variability in anatomical white matter connec-
attività (Bürgel et al., 2006) and marked differences in interregional functional connectivity
(Gordon, Laumann, Adeyemo, & Petersen, 2015) that relate to cognitive functioning (Finn
et al., 2015; Mueller et al., 2013; Schultz & Cole, 2016). In recent years, MRI network ap-
proaches have yielded powerful insights into the brain’s macroscopic connectivity pattern,
or connectome, and its relation to behavior (Bullmore & Sporns, 2009; van den Heuvel &
a n o p e n a c c e s s
j o u r n a l
Citation: Cox, R., Schapiro, UN. C., &
Stickgold, R. (2018). Variability and
stability of large-scale cortical
oscillation patterns. Network
Neuroscience, 2(4), 481–512.
https://doi.org/10.1162/netn_a_00046
DOI:
https://doi.org/10.1162/netn_a_00046
Supporting Information:
https://doi.org/10.1162/netn_a_00046
Received: 11 ottobre 2017
Accepted: 26 Gennaio 2018
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Roy Cox
roycox.roycox@gmail.com
Handling Editor:
Mark Kramer
Copyright: © 2018
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
N
e
N
_
UN
_
0
0
0
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Large-scale oscillation patterns
Functional connectivity:
Statistical association between
time-varying signals measured at
distinct sites (per esempio., electrodes or
voxels), suggestive of direct or
indirect communication between the
pertaining neural regions.
Connectome:
Comprehensive map of connections
among brain regions, based on
anatomical or functional
connectivity.
Cross-frequency coupling:
Statistical association between
time-varying activity in different
frequency bands, suggestive of
information transfer between neural
processes operating at different
timescales.
Sporns, 2013). Unlike MRI, electroencephalographic (EEG) and magnetoencephalographic
(MEG) techniques are sensitive to rapid, millisecond fluctuations in the electromagnetic fields
generated by neuronal populations, and are therefore more suitable to examine the highly dy-
namic nature of rhythmic brain activity. Inoltre, multichannel EEG combined with spatial
filtering techniques offers a reasonable degree of topographical precision, thereby allowing in-
vestigation of the “oscillatory connectome”—the pattern of distributed oscillatory interactions
across the cortex. Yet, relatively little is known about the detailed properties of such oscillatory
networks, their variability from person to person, or their long-term stability.
Distinct brain oscillations underlie specific cognitive functions (Lopes da Silva, 2013; Siegel,
Donner, & Engel, 2012; Thut, Miniussi, & Gross, 2012), and specific frequencies are expressed
differently across the brain (Congedo, John, De Ridder, & Prichep, 2010; Keitel & Gross, 2016).
Inoltre, different aspects of rhythmic activity are thought to capture distinct aspects of brain
organization and function: whereas oscillatory power reflects the strength of local rhythmic
activity in a particular frequency band, functional connectivity assesses temporally coordinated
activity between brain areas in a similarly band-specific manner. In particular, consistent phase
relations between brain circuits are thought to mediate efficient neural communication on a
cycle-by-cycle basis (Fell & Axmacher, 2011; Fries, 2005), whereas coordinated fluctuations
of signal amplitude capture slower aspects of interregional communication (Bruns, Eckhorn,
Jokeit, & Ebner, 2000) and relate to the correlation structure observed with functional MRI
(Hipp & Siegel, 2015). Importantly, these different measures of activity and connectivity can
be dissociated (Arnulfo, Hirvonen, Nobili, Palva, & Palva, 2015; Bruns et al., 2000; Hillebrand,
Barnes, Bosboom, Berendse, & Stam, 2012), suggesting they reflect distinct facets of neural
dynamics (Bastos & Schoffelen, 2016; Cohen, 2014UN).
This dissociability of oscillatory metrics and frequencies, along with phenomena of cross-
frequency coupling (Aru et al., 2014), has instilled the notion that macroscopic electrophysio-
logical signals reflect multiplexed activity, composed of multiple communication lines
operating in parallel (Ainsworth et al., 2012; Akam & Kullmann, 2014; Panzeri, Macke, Gross,
& Kayser, 2015; Watrous, Fell, Ekstrom, & Axmacher, 2015). Importantly, such concurrently
present signals can serve functionally distinct roles (Gross et al., 2013; Schyns, Thut, & Gross,
2011; Watrous, Tandon, Conner, Pieters, & Ekstrom, 2013) and could constitute a fundamental
computational principle to increase information processing capacity. In light of accumulating
evidence for the fundamental role of distributed oscillatory activity in neuronal communica-
zione (Canolty et al., 2010) and cognition (Honkanen, Rouhinen, Wang, Palva, & Palva, 2015;
J. M. Palva, Monto, Kulashekhar, & Palva, 2010), an intriguing possibility is that multiplexing
can be discerned at the network level. The coexistence of multiple such network configurations
might constitute an important principle of human brain organization, and could offer novel
analysis strategies to elucidate brain functioning. Tuttavia, it is presently unclear whether de-
composition of brain-wide oscillation patterns based on frequency or oscillatory metric yields
separable activity patterns, nor is it known if and how this dissection depends on behavioral
state.
An additional issue regards the variability of oscillatory patterns across individuals. Pre-
vious evidence indicates that network structure differs substantially between individuals (Chu
et al., 2012), but it is unknown how different frequency bands and oscillatory metrics con-
tribute to this variability. Allo stesso modo, spatially organized oscillatory activity remains stable within
an individual over multiple days (Chu et al., 2012), but longer-term stability of frequency- E
metric-specific networks has not been assessed. Given accumulating evidence that individual
differences in rhythmic activity predict cognitive performance (Jiang, van Gerven, & Jensen,
Network Neuroscience
482
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
N
e
N
_
UN
_
0
0
0
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Large-scale oscillation patterns
Multivariate:
Relating to the simultaneous analysis
of more than one outcome variable.
Surface Laplacian:
Spatial filtering approach that, in the
context of EEG, accentuates local
and minimizes global activity,
thereby counteracting volume
conduction.
Volume conduction:
Phenomenon whereby activity from a
single brain source projects to
multiple sensors, potentially resulting
in artificially inflated functional
connectivity.
2015; Klimesch, Schimke, Ladurner, & Pfurtscheller, 1990; Park et al., 2014), fine-grained
characterization of individual oscillatory network differences and stability is critical for a com-
plete understanding of human brain organization.
Prior work on large-scale oscillatory dynamics (per esempio., Brookes et al., 2012, 2014; Chu et al.,
2012; Hillebrand et al., 2012; Hipp, Hawellek, Corbetta, Siegel, & Engel, 2012; Keitel & Gross,
2016; Siems, Pape, Hipp, & Siegel, 2016) has provided valuable insights into various of these
aspects of network organization. Tuttavia, individual studies have focused on only one or a
few of these features, making it difficult to determine how these various sets of findings inter-
relate. We set out to systematically characterize the brain-wide structure of oscillatory net-
works across all of the aforementioned dimensions, comparing EEG network patterns within
and between (1) individuals, (2) behavioral states, (3) frequency bands, (4) distinct metrics
of spectral power, phase synchrony, and amplitude envelope correlation, E (5) time points
hours to months apart. Here, following published approaches to assessing distributed activity
patterns (Haxby, Connolly, & Guntupalli, 2014; Kriegeskorte, 2008), we focus on describing
global multivariate network structure, as opposed to cataloging the (In)variance of individual
network elements across network types. Employing network similarity and classification tech-
Carino, we demonstrate the existence of several highly distinct oscillatory profiles operating
in parallel, both across and within individuals. Nevertheless, we find within-subject patterns
to be sufficiently stable and unique across test sessions spaced hours to months apart to allow
successful long-term identification of individual subjects. This comprehensive examination of
oscillatory network dynamics facilitates the integration of a diverse set of findings into a single,
unified framework of oscillatory human brain organization.
RESULTS
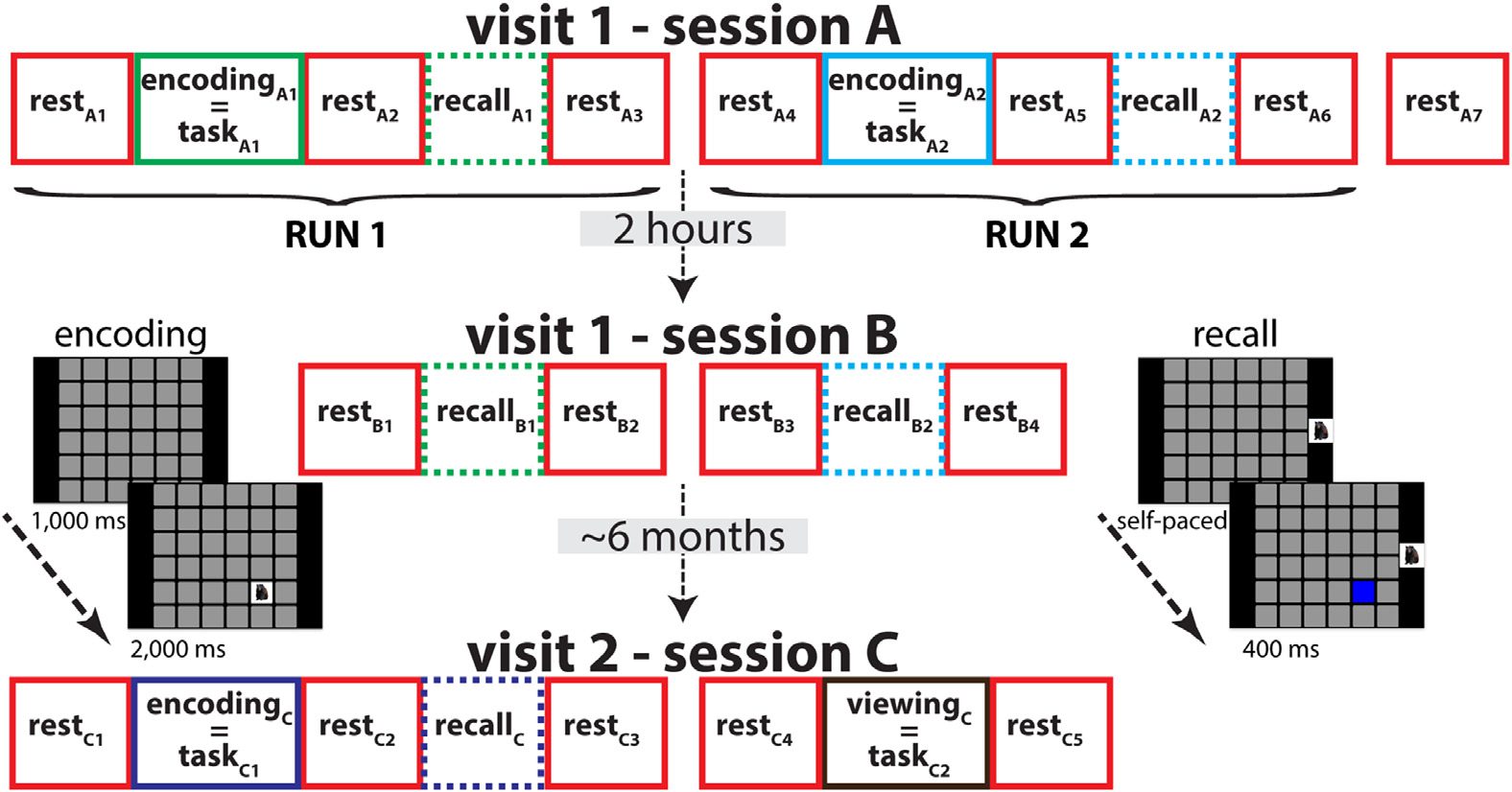
Twenty-one healthy young volunteers completed either one or two visits to the lab (Figura 1).
During the first visit, all subjects underwent 60-channel EEG recording during several eyes-
closed resting-state blocks organized around the encoding and retrieval of visuospatial associ-
ations. The visit included two sessions, separated by 2 hr (Sessions A and B; SA and SB). Three
to eight months later, 14 subjects returned for a second visit (Session C; SC), consisting of sev-
eral additional resting states recordings, another visuospatial memory task, and a nonlearning
control task. in questo documento, we focus on the network structure of rest and task (cioè., encoding
and control) blocks.
Individual blocks are labeled according to their behavioral state, ses-
sion and order, resulting in a total of 20 blocks across three sessions (SA: restA1–restA7 and
taskA1–taskA2; SB: restB1–restB4; SC: restC1–restC5 and taskC1–taskC2). Memory performance is
reported in the Supporting Information (Cox, Schapiro, & Stickgold, 2018).
We collected ∼5-min continuous, surface Laplacian-filtered (Kayser & Tenke, 2006; Perrin,
Pernier, Bertrand, & Echallier, 1989) EEG segments from each block of rest and task activ-
ità. We then determined spectral power at each electrode and calculated phase synchrony
and amplitude envelope correlation for every pair of electrodes (excluding 11% of connec-
tions between neighboring electrodes to restrict undesired volume conduction effects). All os-
cillation metrics (power and both amplitude- and phase-based functional connectivity) were
determined separately for the theta (3–7 Hz), alpha (8–12), beta (13–30), and gamma (32–60)
frequency bands. For our main analyses we used the phase locking value (Lachaux, Rodriguez,
Martinerie, & Varela, 1999) and conventional amplitude correlations (Bruns et al., 2000) COME
measures of functional connectivity. We also performed several control analyses by using al-
ternative functional connectivity metrics (cioè., weighted phase lag index [Vinck, Oostenveld,
Van Wingerden, Battaglia, & Pennartz, 2011] and orthogonalized envelope correlations [Hipp
Network Neuroscience
483
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
N
e
N
_
UN
_
0
0
0
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Large-scale oscillation patterns
Figura 1. Protocol overview. SA and SB wereseparated by2 hr,whereas SC took place after 3–8 months.
In SA, encoding and recall blocks were separated by rest periods. In SB, additional recall blocks
were interspersed with rest. Finalmente, in SC, subjects completed an additional memory task as well
as a viewing control task with no memory component. EEG from rest and task blocks (solid boxes),
but not recall blocks (dashed), was analyzed. During encoding, 36 stimuli were presented, one at
a time, at unique grid locations. During retrieval, subjects were cued by presentation of a learned
stimulus to the right of the grid, and attempted to identify its previous grid location.
et al., 2012]) to confirm that our results cannot be explained by inflated connectivity esti-
mates resulting from volume conduction (Supporting Information, Cox et al., 2018). For the
sake of brevity, we adopt the term “connectivity” as a shorthand for “functional connectivity”
throughout this paper.
Similarity of Large-Scale Oscillatory Networks
We first assessed absolute levels of spectral power and phase- and amplitude-based connectiv-
ity for rest and task segments. In brief, global and topographical measures of oscillatory activity
varied with frequency and were affected differently by task and rest conditions (Supporting In-
formation Results and Supporting Information Figure S1, Cox et al., 2018). To examine the
underlying oscillatory profiles contributing to these group effects, we visualized participants’
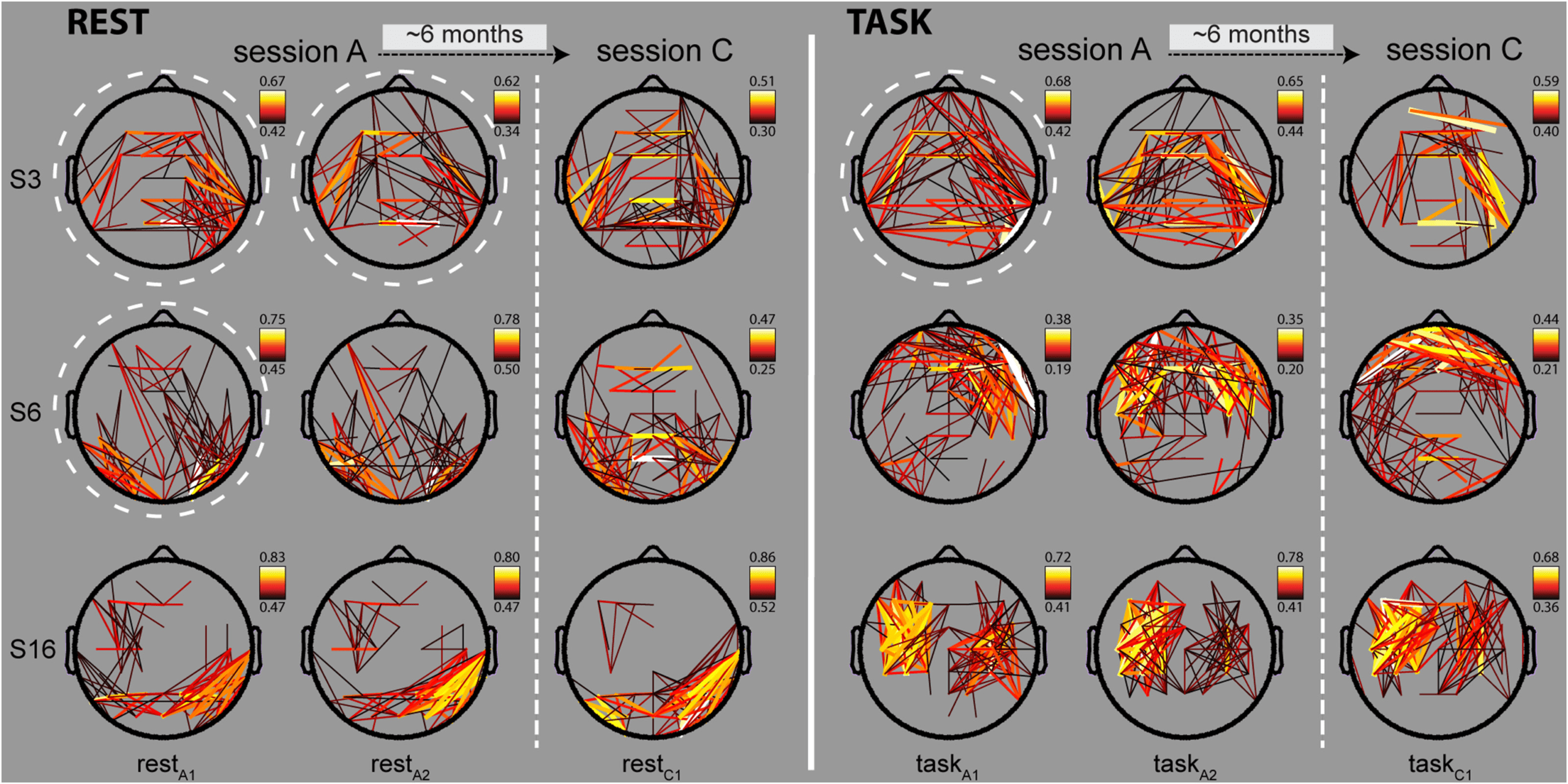
patterns of absolute connectivity across sessions. Figura 2 shows three subjects’ phase-based
alpha profiles during several rest and task segments in both SA and SC. Strikingly, patterns from
the same individual demonstrated a visual resemblance not seen between subjects, in both
rest and task. Inoltre, subject-specific patterns appeared to be stable across the 3–8 month
interval between SA and SC. Different, but similarly consistent patterns were observed in most
subjects, and distinctly discernible individual profiles appeared to exist for different frequen-
cies and connectivity metrics. Topographical power profiles also appeared to be visually stable
within subjects, although these effects were less obvious to the naked eye. Inoltre, whereas
rest and task networks typically demonstrated clearly noticeable differences in oscillatory or-
ganization, some aspects of individuals’ power and connectivity profiles appeared to be stable
across behavioral states. These preliminary visual inspections suggest that distributed patterns
of oscillatory activity exhibit an important degree of constancy within subjects, as well as po-
tential differences between behavioral states, frequencies, and oscillatory metrics, prompting
quantitative evaluation of these qualitative observations.
Network Neuroscience
484
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
N
e
N
_
UN
_
0
0
0
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Large-scale oscillation patterns
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
N
e
N
_
UN
_
0
0
0
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 2. Connectivity maps of phase-based alpha networks. Absolute phase synchrony in the alpha band for three example subjects (rows),
during three rest and three task segments across SA and SC (columns). Strength of connectivity is indicated by both line thickness and color,
with stronger connections in white/yellow, and weaker connections in orange/black. For visualization purposes, only connections between
the median + 2 SD and maximum connection strength are shown for each map (range indicated on color bar). White dashed circles indicate
networks used to illustrate network similarity in Figure 3A–C.
A substantial obstacle regarding such analyses is that measures of absolute activity do not
allow meaningful comparisons of distributed oscillatory patterns as a function of the afore-
mentioned dimensions, since activity levels are often on different scales or even have different
units. These issues can be avoided by comparing the relative distribution of oscillatory activ-
ity across the cortex and its consistency from one condition to another. Così, by focusing on
network similarity, heterogeneous patterns of oscillatory activity are effectively brought into a
common space, enabling direct comparisons across a multitude of dimensions (by individual,
behavioral state, frequency band, oscillation metric, and across time).
Throughout this paper, we use the term “network” to refer to vectors that reflect the brain-
wide pattern of oscillatory activity across all electrodes or connections. For connectivity, we
used vectors of length 1,578 corresponding to every unique channel pair’s connectivity strength
(creating separate vectors for each subject, data segment, and frequency-band combination).
For spectral power, we constructed vectors of length 60 reflecting all electrodes’ power esti-
mates. Inoltre, we constructed “power connectivity” vectors of equal size as the connec-
tivity vectors to enable direct comparisons (see Methods). A specific “network type” reflects
a category of power/connectivity vectors defined by a particular combination of oscillatory
dimensions (per esempio., “amplitude-based beta networks during rest”).
We quantified the degree of similarity between any two networks (cioè., two vectors) as their
Pearson correlation: high similarity between networks indicates a relatively preserved, E
therefore consistent, configuration of connection strengths or local power across the scalp,
Network Neuroscience
485
Large-scale oscillation patterns
Multidimensional scaling:
Technique to project
high-dimensional (or multivariate)
data points onto a lower dimensional
space while optimally preserving the
distances between points.
irrespective of possible differences in absolute connection strength or power. Così,
IL
correlation-based approach critically enables the comparison of heterogeneous network types.
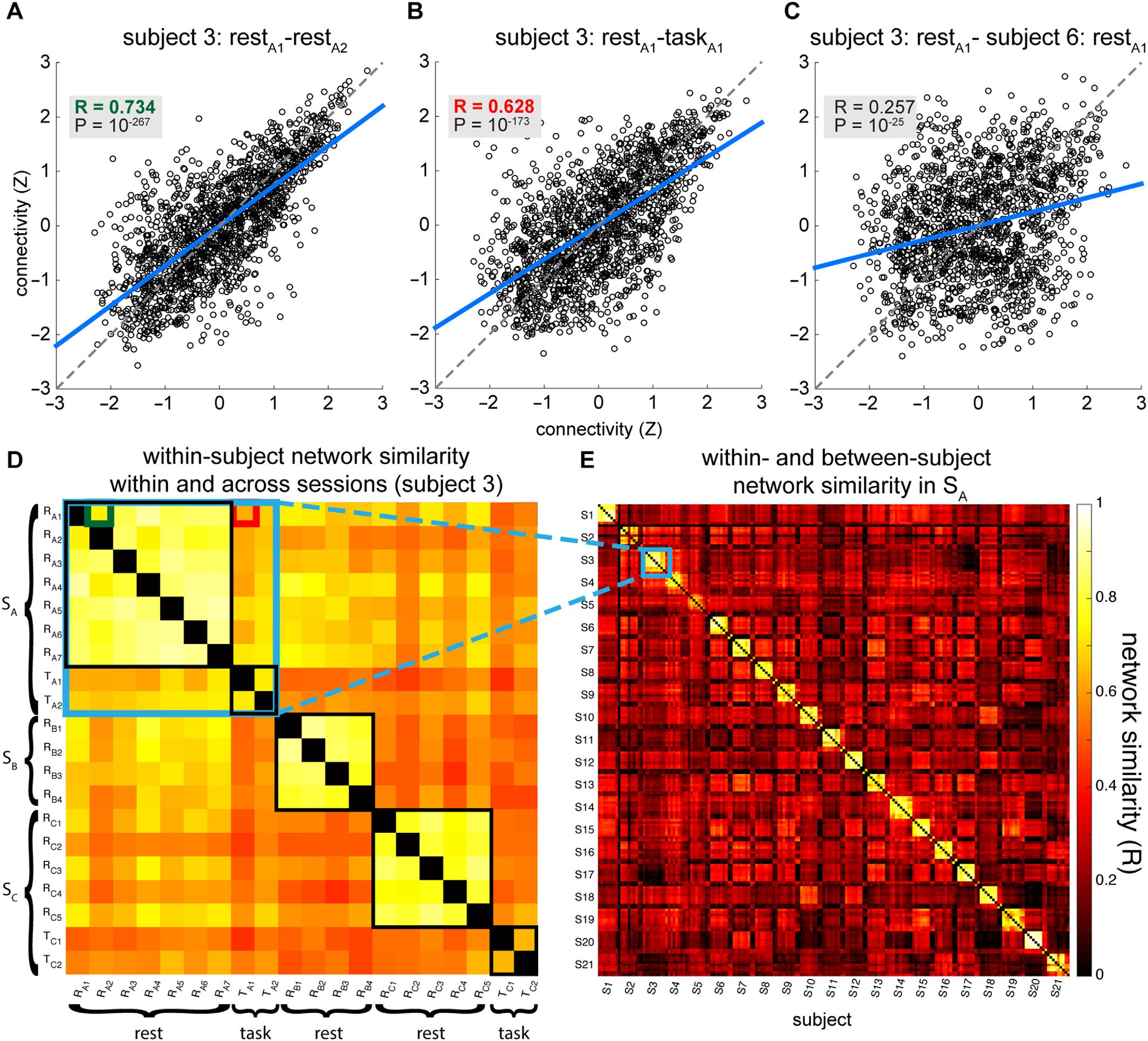
Illustrative scatterplots for alpha phase-based networks from one subject demonstrate the gen-
erally high correspondence of connection weights between segments derived from the same
subject, both within (Figure 3A) and across (Figure 3B) behavioral states. In contrasto, rete
similarity between two different subjects was much lower (Figure 3C).
To examine the notion of within-subject consistency
Network consistency within individuals.
of network configurations, we assessed the similarity among each subject’s data segments
(Kriegeskorte, 2008). This is illustrated for a single subject’s phase-based alpha networks in
Figure 3D. Within SA, we compared task segments by computing the correlation between
taskA1 and taskA2, whereas for resting states we computed all 21 pair-wise correlations be-
tween a subject’s rest segments (restA1-restA7) and averaging the resulting values. We per-
formed this analysis separately for each of 12 network types (4 frequencies × 3 oscillation
metrics). We observed substantial within-subject network similarity, with average Pearson co-
efficients ranging from 0.49 for theta amplitude correlation during task to 0.98 for alpha power
during rest (Supporting Information Table 1A, Cox et al., 2018; due to the large number of net-
work comparisons we performed, here and throughout this report, results are presented at a
summary level, whereas detailed network similarity values and statistics are presented in Sup-
porting Information Tables). We also determined each subject’s network consistency between
rest and task segments. Here, we calculated, for every subject, the average correlation between
each of the 14 unique pairs of rest-task segments (7 rest × 2 task). Compared with the sim-
ilarity of networks from a single behavioral state, correlations were reduced, but still sizable
(range: 0.33 for alpha synchrony to 0.73 for gamma power; Supporting Information Table 1A,
Cox et al., 2018). Overall, within-subject similarity scores indicate that network profiles are
highly correlated, with strong effect sizes within a behavioral state, and moderate to strong
effects between rest and task.
These within-subject correlations reflected network similarities greater than those seen be-
tween subjects, as can be seen qualitatively from the network similarity matrix in Figure 3E.
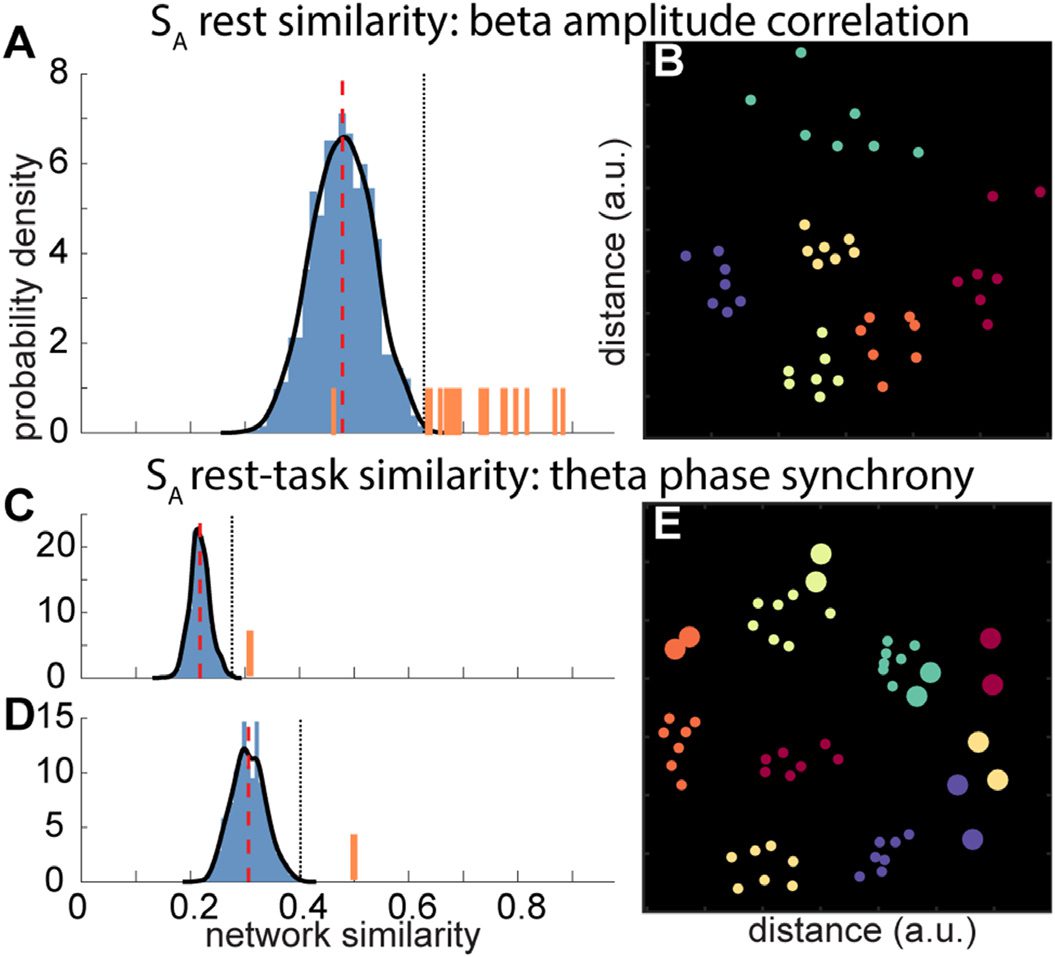
To demonstrate this quantitatively, we adopted a resampling approach in which we randomly
selected networks from the pool of all subjects. Keeping network type constant, we repeat-
edly shuffled subject labels to generate a null distribution of similarity values (see Methods).
Null distributions for rest-rest and rest-task comparisons are shown in Figure 4A, C, and D.
Individual subjects’ values (orange bars) had far higher similarity values than expected by
chance, and were often the most extreme scores. As a complementary tool, we employed multi-
dimensional scaling techniques to visualize the relatedness of these networks (Figure 4B and E).
These plots, with each subject coded in a separate color, demonstrate that oscillatory profiles
for the seven rest and two task segments from one individual are often tightly clustered together
in multivariate space, indicating that network structure is highly stable for a given individual.
This apparent within-subject stability of oscillatory networks was confirmed in two ways.
Primo, at the group level, we performed a series of 12 one-sample t tests (one per network
type) comparing the distribution of observed similarity scores across subjects to a null hypoth-
esis baseline defined as the average similarity across permutations (per esempio., Figure 4A, C, and D:
dashed red lines in the centers of the null distributions). For all network types and data seg-
ment comparisons (rest-rest, task-task, and rest-task) this yielded highly significant results (Tutto
P < 0.002; Supporting Information Table 1A, Cox et al., 2018: group t test), indicating that SA
oscillatory profiles are significantly more similar within than between subjects.
Network Neuroscience
486
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Similarity of phase-based alpha networks. Example scatterplots show network similarity between (A) a single subject’s restA1 and
restA2 segments; (B) the same subject’s restA1 and taskA1 segments; and (C) restA1 from the same subject and the corresponding restA1 of a
second subject (selected networks indicated in Figure 2 with dashed circles). Every dot denotes the connection strength between a pair of
electrodes (1,578 in total) for two separate data segments: the Pearson correlation coefficient (R) constitutes the degree of network similarity.
Axes indicate z-scored connectivity strength, and blue lines reflect least-squares fit. Note that as a result of the large number of network
elements even modest associations have very low p values. (D) Single-subject network similarity matrix of all 20 data segments. Small green
and red squares reflect network comparisons of panels A and B, respectively. Large black squares indicate similarity of within-session rest
or task networks. Large blue square indicates similarity within SA, which is further illustrated in (E), which contains the 7 rest and 2 task SA
segments for all subjects. Clearly visible is the diagonal band showing high within-subject similarity. The off-diagonal pattern demonstrates the
generally much greater between-subject similarity of rest-rest and task-task networks compared with rest-task networks. Specifically, the larger
red/orange squares indicate relatively enhanced between-subject similarity of rest networks, whereas darker bands signify reduced rest-task
similarity. Very small red squares positioned on intersecting dark bands indicate increased task-task similarity. For both D and E, diagonal
elements (indicating self-similarity) were set to zero.
Network Neuroscience
487
Large-scale oscillation patterns
Figure 4. Within-subject similarity of rest and task segments in SA. (Top) Similarity (Pearson’s R)
of rest segment networks based on amplitude correlation in the beta band. (A) Observed within-
subject similarity values (orange bars) are much higher than for the null distribution generated by
resampling across subjects (1,000 permutations; dashed red line: mean of null distribution; dot-
ted black line: maximum value in distribution). (B) Multidimensional scaling plot shows similarity
between networks for same network type as in A as distances between dots, using the correlation
distance (1–R) as the distance metric. Each color represents a single individual. Dots of the same
color are generally clustered together, reflecting high intraindividual network similarity. For visual-
ization purposes only 6 subjects are plotted, although clustering is equally present when including
all 21 subjects. (Bottom) Similarity between task and rest segments for theta phase synchrony net-
works. Each subject’s similarity score across behavioral states was compared with its own null
distribution (created by assessing network similarity between that subject’s task segments and rest
segments randomly selected from the entire population). Distributions for two subjects (C and D)
show much higher within-subject similarity between rest and task structure (orange bars) than ex-
(E) Distance plot for rest-task similarity, as presented in
pected by chance (1,000 permutations).
C and D. Smaller dots indicate rest networks (as above) and larger dots signify task networks. For
several subjects, their two task segments are close to their seven rest segments, indicating a close
correspondence between network structures across behavioral states. At the same time, task net-
works from different subjects tend to cluster together to the right of the plot, suggesting group-level
differences between task and rest networks. Again, only six subjects are plotted for visualization
purposes.
Within-subject network stability was confirmed at the single-subject level as well. To show
this, we z-scored subjects’ network similarity estimates with respect to their own null distribu-
tions and calculated the associated p values. We then used the false discovery rate (Benjamini
& Hochberg, 1995) to correct for multiple tests across individuals (Supporting Information
Table 1A, Cox et al., 2018; individual permutation). Depending on network type, between
90.5% (e.g., gamma phase synchrony) and 100% (e.g., beta power) of individual subjects
displayed significant network similarity (Pcorr < 0.05) within their resting-state recordings.
For task segments, within-subject network stability was significant for 57.1–90.5% of subjects
across network types, except for beta and gamma power profiles (where no subjects showed
significant network stability). Finally, for rest-task similarity 66.7–100% of subjects exhibited
significant network stability across these behavioral states.
Network Neuroscience
488
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
We note that when more lenient uncorrected thresholds were applied to assess significance
of task-task similarity, there was significant network stability in the majority of subjects for all
network types, and in more than 70% of subjects for 10 of the 12 types. Still, subject propor-
tions showing significant within-subject network similarity at this more lenient threshold were
significantly higher for rest-rest than for task-task comparisons across network types (96.4 ±
4.1% vs. 76.6 ± 10.7%; paired t test t[11] = 6.7, p < 10−4
). However, when we repeated
these analyses using only two rest segments (restA2 and restA5), matching the number we had
available for task segments, subject proportions showing significant rest-rest similarity dropped
significantly to 79.0 ± 17.0% (t[11] = –4.2, p = 0.002; Supporting Information Table 1B, Cox
et al., 2018) and no longer differed appreciably from task-task comparisons (t[11] = 0.6, p =
0.56). These findings indicate that the number of available networks is a relevant factor when
assessing significance in a permutation framework, although we note that this did not affect
the observed network similarity values themselves (paired t test across network types based on
seven [0.75 ± 0.12] or two [0.75 ± 0.12] rest segments: t[11] = −1.7, p = 0.11).
Finally, we replicated the results in this section for the second session of the first visit (SB)
and for the second visit (SC) up to 8 months later (Supporting Information Table 1C and D,
Cox et al., 2018), providing independent confirmation of within-subject network consistency
within a single recording session.
Analyses of network patterns showed
Distinct rest and task network profiles across individuals.
striking differences between rest and task behavioral states. This can be seen from the off-
diagonal checkered structure of Figure 3E, indicating that different subjects’ rest segments, and
separately, different subjects’ task segments, were more similar to each other compared with
networks similarity between behavioral states. Similarly, in the distance plot displayed above
(Figure 4E), task segments (larger dots in the lower right of the plot) from different subjects
appeared to cluster together, suggesting group-level differences between task and rest network
structures. To investigate this further, we calculated group-level similarity across all subjects’
rest segments, and separately, across all task segments, and then compared these values with a
baseline distribution of similarity scores obtained through resampling from the combined pool
of rest and task segments across subjects. Calculations were carried out separately for each
network type.
Observed similarity scores during SA varied depending on network type analyzed (Sup-
porting Information Table 2A, Cox et al., 2018), but overall, 10/12 network types exhibited
network configurations that were significantly clustered in multivariate space for rest, task, or
both behavioral states. These findings indicate that network organization across individuals
within a behavioral state (rest, task) is more similar than would be expected by chance, con-
firming the visual impression from Figures 3 and 4. We repeated this procedure for the rest
and task segments from SC and obtained similar results (Supporting Information Table 2B, Cox
et al., 2018). Thus, in addition to individual differences in network organization, both rest and
task networks share common power and connectivity profiles across subjects.
Supervised learning:
Machine learning task of inferring a
mathematical mapping from
(high-dimensional) data points to
their corresponding class labels,
(ideally) allowing correct assignment
of class labels for unseen test data.
We asked whether the observed group-level rest-task differences would allow us to predict
behavioral state from network structure by using a supervised learning strategy. For each net-
work type, we trained a k-nearest neighbors classifier (Cover & Hart, 1967) on SA rest and
In a cross-validated approach, we repeatedly left out each
task networks from all subjects.
subject’s networks from the training procedure and allowed the classifiers to predict their as-
sociated behavioral state. We obtained significantly greater than chance (50%) performance
for all 12 network types (binomial tests: all Pcorr < 0.04). Recognition rates ranged from 59.5%
Network Neuroscience
489
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
K-nearest neighbors classification:
Supervised learning algorithm in
which each unseen test point is
labeled based on the k training
points it is closest to, according to an
arbitrary distance function (e.g.,
correlation or Euclidean distance).
for amplitude- and power-based gamma networks, to 88.1% for phase- and amplitude-based
alpha networks (Supporting Information Table 2A, Cox et al., 2018). Average performance
across the 12 classifiers (i.e., network types) was 77 ± 10%. Rest networks were more accu-
rately classified than task patterns (83 ± 19% vs. 71 ± 12%), although the difference was not
significant (t[11] = 1.85, p = 0.09). Merging evidence from individual classifiers, each based
on a different network type (see Methods), we obtained a classification rate of 92%, indicat-
ing different network types are sensitive to different aspects of rest-task differences. Repeating
these analyses for SC, we again found considerable evidence for distinct task and rest-based
networks (Supporting Information Table 2B, Cox et al., 2018).
We next asked whether rest-task similarity within individuals was greater than the similarity
of each of these behavioral states across individuals. Across network types, we found that rest
and task networks from the same individual were more similar to each other than rest networks
selected across individuals (SA: 0.53 ± 0.13 vs. 0.47 ± 0.15; t[11] = 2.6, p = 0.02; SC: 0.56 ±
0.12 vs. 0.43 ± 0.14; t[11] = 9.4, p < 10−5
). For individual network types, we found consis-
tent significant effects across SA and SC for all phase-based networks, for amplitude networks in
the beta and gamma ranges, and for theta and gamma power profiles (Supporting Information
Table 3A and B, Cox et al., 2018). Repeating these analyses for task networks, we found that
rest and task networks from the same individual were also significantly more similar than task
networks from different individuals for SC (0.56 ± 0.12 vs. 0.39 ± 0.12; t[11] = 8.5, p < 10− 5
),
but less robustly so for SA (0.53 ± 0.13 vs. 0.47 ± 0.11; t[11] = 1.5, p = 0.15). In line with
these weaker effects for SA, we observed that only beta amplitude networks and theta and
alpha power networks showed consistent significant effects across SA and SC.
In sum, these observations, together with those in the previous section, demonstrate, first,
that, within a session, subject-specific networks are similar between periods of rest and task ex-
ecution, second, that the oscillatory profiles of these two behavioral states nonetheless exhibit
global differences discernible at the group level, and third, that state-invariant subject-specific
neural signatures are typically stronger than state-dependent group profiles.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
The analyses presented above demonstrate reliable
Frequency-specific networks for individuals.
within-subject network consistency for all examined frequency bands. However, this leaves
unanswered whether oscillatory profiles are similar across frequencies, which would suggest
that they derive from the same intrinsic network activity, or whether distinct spectral bands
are independently organized, suggesting the existence of multiple parallel modes of neural
processing.
To answer this question, we compared, separately for each individual, the similarity across
networks for one frequency band with the similarity seen when comparing networks selected
randomly from all four bands. For SA resting states, every subject showed significantly en-
hanced network similarity within at least one frequency band relative to cross-band similarity
(Supporting Information Table 4A, Cox et al., 2018), indicating that the involved frequency-
specific networks differed reliably from each other. We found this to be the case for all three
oscillation metrics. In terms of frequency bands, networks in the alpha range were most dis-
tinctly clustered in multivariate space (for all oscillation metrics), and, in terms of oscillatory
feature, networks based on phase synchrony showed most reliable between-frequency dif-
ferences. Overall, across oscillation metrics and frequency bands, 95.2 ± 8.9% of subjects
showed significantly greater than chance within-frequency consistency (Supporting Informa-
tion Table 4A, Cox et al., 2018; individual). We replicated this pattern of results in SB (83.3 ±
15.3%) and SC (79.8 ± 19.5%) (Supporting Information Table 4B and C, Cox et al., 2018). To
Network Neuroscience
490
Large-scale oscillation patterns
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
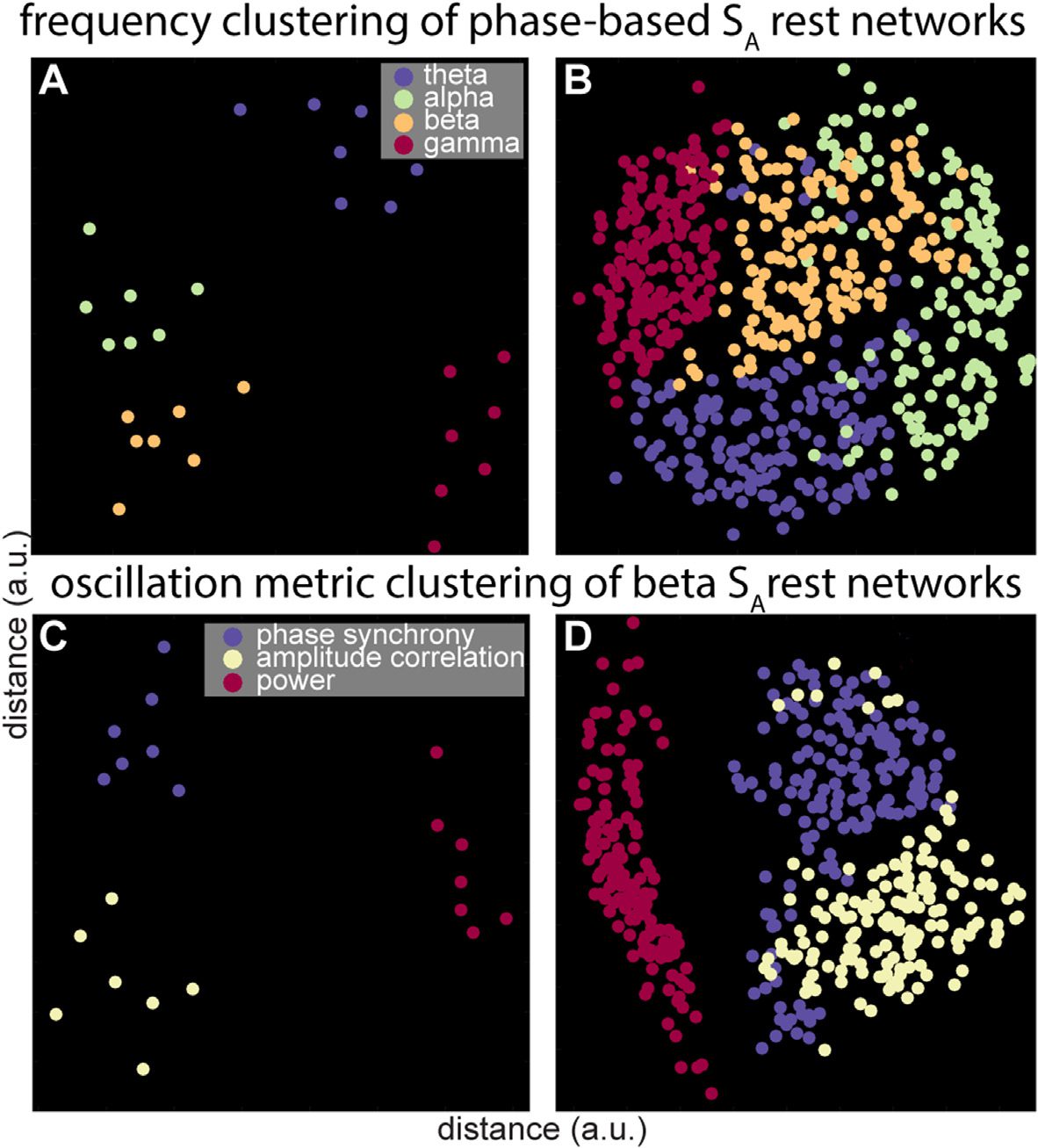
Figure 5. Frequency- and oscillation metric-specific clustering of SA resting-state networks. Single-
subject-level (A) and group-level (B) frequency clustering of phase-based networks indicating greater
similarity of within-frequency than between-frequency oscillatory profiles. Single-subject-level (C)
and group-level (D) oscillation metric clustering in the beta range. Note how power topographies
are distinctly different from both phase- and amplitude-based network profiles.
assist interpretation, Figure 5A employs multidimensional scaling to visualize within-frequency
clustering for a sample subject’s phase-based rest segments, where different colors indicate
different frequencies.
We performed an analogous set of analyses on each individual’s task segments, for both
SA and SC. The observed within-frequency similarity was often the most extreme score of all
possible permutations, although subject proportions reaching significance across all metrics
and frequency bands was reduced relative to rest (SA: 31.3 ± 18.0%; SC: 32.1 ± 22.1%)
(Supporting Information Table 4A and C, Cox et al., 2018). Still, depending on oscillation
metric and session, 65–90% of subjects exhibited frequency-specific task networks for at least
one frequency. All told, these findings strongly indicate that connectivity and power profiles
differ across frequencies within individuals, during both rest and task, suggesting large-scale
oscillatory activity is organized in a frequency-specific manner.
This frequency-band specificity extends to the
Frequency-specific networks across individuals.
group level. Using our permutation approach, we observed significantly enhanced network
similarity across subjects within frequency bands for all oscillation metrics during rest segments
from SA (Supporting Information Table 4A, Cox et al., 2018: group). Correspondingly strong
Network Neuroscience
491
Large-scale oscillation patterns
clustering was visible in multidimensional scaling plots (Figure 5B). Similar group-level corre-
spondences were found for SB and SC rest segments (Supporting Information Table 4B and C,
Cox et al., 2018). Task segments from SA and SC showed comparable levels of group-level
clustering in the beta and gamma bands, but not for theta and alpha connectivity networks
(Supporting Information Table 4A and C, Cox et al., 2018). Thus, these findings indicate not
only the existence of within-subject, frequency-specific networks, but also the presence of
canonical frequency-dependent networks across subjects.
Distinct power-, phase-, and amplitude-based networks for individuals. We also observed impor-
tant distinctions among networks based on the oscillation metric employed. As stated in the
Introduction, estimates of power, amplitude correlation, and phase synchrony are thought to
be sensitive to distinct facets of oscillatory activity and communication (Arnulfo et al., 2015;
Bastos & Schoffelen, 2016; Bruns et al., 2000; Cohen, 2014a; Hillebrand et al., 2012). How-
ever, whether this separation extends to the level of brain-wide EEG patterns is an open ques-
tion. We asked whether network configurations derived from a single oscillatory metric were
reliably more similar than when the networks were randomly selected across oscillatory
measures.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Within individuals, within-metric correlation values for SA rest networks were greater than
the average correlation stemming from permuting across oscillatory metrics (Supporting Infor-
mation Table 5A, Cox et al., 2018). All subjects displayed significant within-metric clustering
for all oscillation metrics for the theta, beta, and gamma bands, and >90% showed significant
clustering for all metrics in the alpha band. Figure 5C displays a corresponding distance plot for
a single subject’s resting beta networks. We replicated this pattern of results for SB and SC (Sup-
porting Information Table 4B and C, Cox et al., 2018) con 92.5 ± 8.2% E 91.7 ± 8.0% Di
subjects, rispettivamente, showing clustering across frequency bands and metrics. (We could not
assess the existence of metric-specific networks within individuals for task networks because
of the low number of possible permutations; see Methods.) Così, these findings demonstrate
that oscillatory profiles based on different oscillatory features are reliably distinct, even when
derived from the same frequency band, for almost all individuals.
Distinct power-, phase-, and amplitude-based networks across individuals. Prossimo, we asked whether,
for a given frequency band, networks based on different oscillation metrics are consistently dis-
tinct across subjects. Permutation testing demonstrated this to be the case for all frequencies
except alpha, for both rest and task segments, for all metrics, and during all sessions. For al-
pha, at least one metric failed to reach significance in each session (Supporting Information
Table 5A–C, Cox et al., 2018). Figure 5D displays the group-level similarity of resting beta
networks across oscillation metrics during SA. In summary, these analyses demonstrate that
power-, phase-, and amplitude-based network patterns are differently organized, not only
within but also across individuals.
As seen in Figure 5C and D, power networks
Distinct phase- and amplitude-based networks.
differed substantially from connectivity networks in general, with phase and amplitude show-
ing less difference. We therefore repeated the preceding subject- and group-level analyses
excluding power networks. Within subjects we found that 59.5 ± 26.1%, 48.8 ± 26.3, E
58.0 ± 26.6% of subjects showed significant within-metric clustering across metrics and fre-
quency bands for SA,SB, andSC, rispettivamente (Supporting Information Table 5D–F, Cox et al.,
2018). Tuttavia, 80–100% of individuals showed significant clustering in at least one of the
Network Neuroscience
492
Large-scale oscillation patterns
two connectivity metrics for the theta, alpha, and beta bands, and 30–60% for gamma. Gen-
erally, phase synchrony networks showed more reliable within-metric network consistency
than amplitude-based networks at the individual level. In contrasto, group-level network con-
sistency was significant mostly for amplitude-based networks. These effects again occurred
for both rest and task networks, and across all sessions and frequency bands. Così, direct
comparisons between functional connectivity networks that are based on mathematically and
theoretically distinct measures of neural communication confirm the distinctiveness of these
networks, both across and within individuals.
Long-Term Stability of Large-Scale Oscillatory Networks
Although the foregoing analyses indicated high within-subject
Network similarity across time.
network consistency within a single 1-h recording session, they do not address the question of
longer-term network stability. Using permutation analyses, we asked whether network similar-
ity across sessions was greater within than across individuals, and found substantial evidence
that this was the case, across all network types and behavioral states (Figura 2, Supporting
Information Table 6A–C, Cox et al., 2018). Infatti, we found very little difference in network
similarity across short- (2 hr: SA−B) and long-term intervals (3–8 months: SAB−C), indicating
remarkable stability in oscillatory network organization across time intervals approaching one
year (Supporting Information Results, Cox et al., 2018).
Based on this striking network stability over time,
Long-term classification of data segments.
we asked whether a supervised learning technique might allow long-term identification of
individuals. To address this question, we trained a set of k-nearest neighbors classifiers, one
for each network type, on the combined SA and SB network configurations. We then used
these trained classifiers to predict subject identities of SC networks. Of note, although data of
only two-thirds of the original volunteers was available to assess classification accuracy, each
classifier was trained on, and allowed to predict, Tutto 21 identities.
After training on all SAB rest or task segments, classifier performance across SC segments
was significantly above the chance rate of 4.8% (1/21) for all network types (binomial: Tutto
P < 10−10
; permutation: all p < 0.001; Table 1). On the whole, the set of rest classifiers
performed similarly to the set of task classifiers (t[11] = 1.7, p = 0.12). A control analysis
Table 1. Classifier performance for all oscillation metrics, frequency bands, and behavioral states. Numbers indicate percentage of data
segments correctly identified. All classifiers performed significantly above chance (4.8%). *Improved classifier performance when combining
frequencies or oscillation metrics. **Further improved performance when combining frequencies and oscillation metrics.
RestAB–restC
Phase synchrony
Amplitude correlation
Power
Combined across oscillation metrics
TaskA–taskC
Phase synchrony
Amplitude correlation
Power
Combined across oscillation metrics
Network Neuroscience
Theta
58.6
32.9
57.1
61.4*
53.6
35.7
50
57.1*
Alpha
72.9
62.9
65.7
81.4*
78.6
71.4
42.9
78.6
Beta
67.1
62.9
54.3
70.0*
57.1
39.3
53.6
75.0*
Gamma
Combined across frequencies
47.1
50
50
62.9*
42.9
57.1
35.7
57.1
75.7*
68.6*
71.4*
81.4
78.6
64.3
53.6
82.1**
493
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
indicated reduced but still highly significant performance with only two data segments per
subject used for training and testing (Supporting Information Results, Supporting Information
Table 7, Cox et al., 2018). In sum, these findings demonstrate that oscillatory network patterns
carry substantial information for classification of individuals across months, for all oscillation
metrics and frequency bands, and for periods of both rest and task.
Our earlier findings highlighted network variability not only across subjects, but also across
network types within an individual. Thus, combining different classifiers sensitive to partly
nonoverlapping information should in theory improve performance. In separate approaches,
we fused classifiers across frequency bands, oscillation metrics, or both, separately for rest
and task. Combining information across frequency bands numerically improved performance
for all oscillation metrics during rest, with each composite classifier showing greater accuracy
than the best-performing individual classifier on which it was based (Table 1), although similar
improvements were not seen for task segment classification. Combining information across
oscillation metrics improved classification accuracy for rest segments in all frequency bands,
and, for task segments, in two out of four bands. Finally, when we combined all classifiers, per-
formance was further boosted to 81 and 82% for rest and task segments, respectively, correctly
identifying the source of 57 out of 70 rest segments and 23 of 28 task segments (binomial: both
p < 10−16
; permutation: both p < 0.001). The improved classifier performance observed after
merging individual classifiers supports the argument that networks based on different metrics
and frequency bands contain unique identifying information.
Successful subject identification does not require correct clas-
Long-term subject recognition.
sification of each individual data segment. Pooling across an individual’s segments, separately
for rest and task segments, classifiers correctly identified 13 of 14 subjects (93%) based on
rest networks, and 11 of 14 (79%) using task networks (binomial: both p < 10−13
; permuta-
tion: both p < 0.001). Task-based classification rates were similar for individual data segments
and for subject identity (82% vs. 79%), but the greater number of rest segments available
for analysis led to numerically improved subject recognition (93%) relative to data segment
classification (81%). In a final step, we also combined rest and task information. Using this
approach, we reached perfect accuracy, correctly identifying all 14 subjects (binomial test:
p < 10−16
; permutation test: p < 0.001).
Contribution of individual network types. We examined the contribution of different network
types to subject recognition performance by repeatedly excluding one or more network types
from the classifier merger procedure (but retaining both rest and task networks). Removing
either all phase- or amplitude-based information (while keeping all frequency bands) did not
In-
affect performance, but excluding power topographies decreased classification to 86%.
cluding only a single oscillation metric, subject recognition was 79% for phase-based net-
works, and 71% for both amplitude-based networks and power topographies.
Including only single frequency bands (but retaining all oscillation metrics), we obtained
classification rates of 64% for theta, 86% for beta, and 79% for gamma. Impressively, including
only the alpha band left accuracy at 100%. Using only single oscillation metrics for alpha
networks, but still combining rest and task information, resulted in recognition rates of 86% for
phase-based, 79% for amplitude-based, and 71% for power-based classifiers. Thus, although
alpha activity affords sufficient discriminatory power on its own, alpha networks based on
different oscillatory metrics capitalize on different sources of discerning information. However,
excluding alpha-based networks altogether still resulted in performance of 86%, indicating that
Network Neuroscience
494
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
alpha activity is not the sole driver of long-term subject recognition. Excluding only theta, beta,
or gamma activity left classifier performance at 93, 100, and 100%, respectively.
Additional analyses revealed that subject recognition was little influenced by parameter
settings or the number of segments used for training or classifying individuals (Supporting In-
formation Results, Cox et al., 2018). These findings provide additional evidence that oscillatory
profiles from distinct behavioral states, frequency bands, and oscillation metrics act as com-
plementary brain-based fingerprints, each carrying unique identifying information.
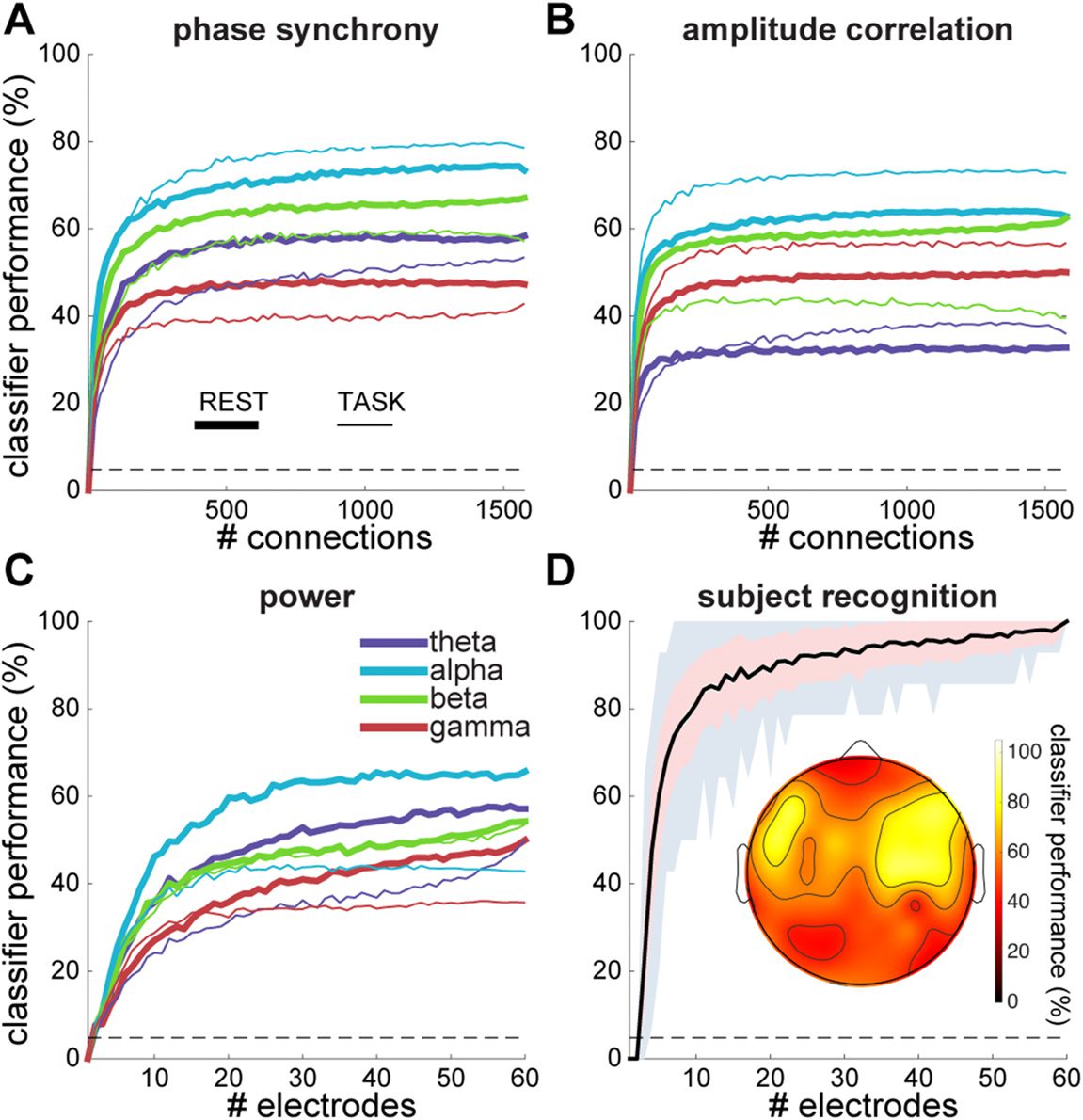
To examine how many network elements are required for accurate
Impact of network size.
classification, we varied the number of included elements in each vector (i.e., electrodes or
connections) used for training and testing classifiers between two and the maximum number
available. Electrodes or connections were selected randomly at each network size, and the
entire process was repeated 10 times. For individual data segments, the percentage of networks
accurately identified by classifiers trained on a single network type reached a plateau quite
early on, when approximately 200 (13%) or 100 (6%) out of 1,578 connections were included
for phase- and amplitude-based networks, respectively (Figure 6A and B). Significantly above-
chance performance (p < 0.05 for one-sample t tests comparing each sample of 10 scores
to 4.8%), was achieved with as few as 4.2 ± 1.3 connections across different network types,
with alpha amplitude correlation showing significant classification using just two connections
(rest: 8.9%, p = 0.001; task: 7.9%, p = 0.03). For power, performance reached stability once
20 (33%) of the 60 electrodes were included (Figure 6C), but significantly higher than chance
performance was observed with only two electrodes for all frequency bands and during both
rest and task execution (mean: 6.8 ± 1.1%).
Next, we asked how subject recognition rates (i.e., when multiple network types and data
segments from the same individual are pooled) depend on these numbers. We randomly se-
lected 2 to 60 electrodes and all pair-wise connections, except neighbors, among them. We
repeated this process 100 times for each montage size, training, testing, and combining the dif-
ferent classifiers to assess subject identity for every montage size. Results indicated improved
performance with larger electrode arrays, with a shape roughly following that of individual
classifiers (Figure 6D). Arrays of 5, 10, and 21 randomly selected electrodes were sufficient to
obtain average subject identification rates of 60, 80, and 90%, respectively.
These analyses provide no information as to whether particular clusters of adjacent sen-
sors contribute more to classifier success than others. We performed a searchlight analysis
in which, for each electrode, we selected all surrounding electrodes and connections, ex-
cluding connections between direct neighbors, within a small radius. We then trained and
tested classifiers on subnetworks containing, on average, eight neighboring electrodes (range:
6–11) around each searchlight center, integrating information across all network types and
behavioral states. Average subject recognition rate across all searchlight centers was 58 ±
14% (range: 36–86%). When we compared searchlight-based recognition rates to recognition
scores from random, and therefore generally more distributed, electrode arrays of similar size
(9 electrodes), we observed far superior performance for these distributed networks (79 ±
11%, t[158] = 10.2, p < 10−16
). Topographically, searchlight-based performance was highest
at 86% in two symmetrically lateralized frontocentral clusters, centered on five electrodes in
total (Figure 6D, inset), suggesting that the largest individual differences manifested in these
regions. This score was significantly elevated compared with randomly distributed networks
of the same size (one-sample t test: t[99] = 6.2, p = 10−8
). However, topographical peaks
Network Neuroscience
495
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Data segment classification and subject recognition accuracy as a function of number of
included connections and electrodes. Percentage of data segments accurately classified as a function
of number of included connections for rest and task segments in different frequency bands, for
phase synchrony (A) and amplitude correlation (B). For visualization purposes, A and B data were
smoothed with a moving average window of size 11 and downsampled by a factor 21. Dashed gray
lines indicate chance level performance. (C) Similar to A and B for power as a function of number
of included electrodes. (D) Subject recognition as a function of electrode array size (electrodes plus
connections among them), including all oscillation metrics, frequency bands, and behavioral states.
Black line indicates average, pink shading standard deviation, and gray shading range of minimum
and maximum values across 100 iterations. Inset: topographical map displaying subject recognition
for searchlight analysis.
for the performance of individual classifiers—based on single network types—were widely
distributed across the cortex.
In sum, although greater numbers of included connections and electrodes improve sub-
ject recognition rates, a remarkable amount of identifying information can be extracted from
networks of much smaller size, especially when electrodes are widely spaced or restricted to
frontocentral regions.
DISCUSSION
The present work offers a systematic analysis of the large-scale network structure of continu-
ous rhythmic brain activity across the scalp. Employing a data-driven approach with internal
replications, we have demonstrated that oscillatory network patterns differ across frequency
bands and oscillation metrics, suggesting that distinct network types, defined by these pa-
rameters, capture separate processing streams operating in parallel. This phenomenon was
present across behavioral states of task and rest, which themselves differed robustly in terms
Network Neuroscience
496
Large-scale oscillation patterns
of network organization. Moreover, despite clear commonalities in oscillatory patterns across
subjects, we also observed prominent individual differences. These individual differences in
network profiles were sufficiently stable to allow successful long-term identification of indi-
viduals across several months, suggesting that individuals exhibit unique and stable oscillatory
fingerprints.
Multiplexing of Oscillatory Networks
The critical role of neural oscillations and their interactions for cognition is widely recognized
(Lopes da Silva, 2013; Siegel et al., 2012; Thut et al., 2012), and is generally thought to result
from oscillations transiently and flexibly routing information flow among behaviorally relevant
neuronal populations. However, precisely how these dynamics are implemented is a topic of
much debate, and numerous schemes have been proposed for how frequency, phase, and
amplitude coordinate spiking activity among cell assemblies (Ainsworth et al., 2012; Akam
& Kullmann, 2014; Canolty et al., 2010; Fries, 2005; Panzeri et al., 2015; Thut et al., 2012;
Watrous et al., 2015). Evidence indicates that multiple coding mechanisms can operate in
parallel, simultaneously encoding multiple stimulus attributes at different frequencies and/or
by orthogonal phase and amplitude features (Gross et al., 2013; Schyns et al., 2011; Watrous
et al., 2013). Our findings advance this notion of multiplexing by decomposing brain-wide
EEG activity into statistically separable power-, phase-, and amplitude-based networks, which,
in turn, are composed of distinct frequency-specific network configurations. These layered
networks can be discerned during periods of both rest and task, and are statistically segregated
even within individuals, emphasizing the robustness of these dynamics.
Several previous MEG and EEG studies have identified frequency-specific networks, most
commonly by parcellating neural regions and connections into spatially restricted subnetworks
(Brookes et al., 2014; Congedo et al., 2010; Hillebrand et al., 2012; Hipp et al., 2012; Keitel
& Gross, 2016; J. M. Palva et al., 2010; Siems et al., 2016). But to the best of our knowl-
edge, direct comparisons of the topology of the resulting networks have not been performed.
Similarly, previous examinations of power-, phase-, and amplitude-based activity have not
addressed these dynamics at the network level. The conclusion that parallel network config-
urations exist in tandem can only be made after bringing these various network types into a
common reference frame and explicitly assessing their similarity, as we have done here.
Our findings of network separability both confirm previous findings and reveal novel in-
sights. Given the well-known posterior distribution of resting alpha activity (Supporting Infor-
mation Figure 1A, Cox et al., 2018), it is perhaps to be expected that alpha power patterns
express high similarity across participants, and that these patterns are distinct from, for exam-
ple, theta profiles. In contrast, it is not immediately evident that connectivity patterns derived
from phase synchrony should differ systematically between, say, the beta and gamma bands.
Although such findings may not be deemed surprising in light of known differences between
beta and gamma power topographies, they should still be demonstrated rather than assumed.
Similarly, given that direct comparisons of power and functional connectivity based on phase
and amplitude have been scarce in prior analyses of human physiological recordings (Arnulfo
et al., 2015; Bruns et al., 2000; Hillebrand et al., 2012), we believe our findings similarly add
important empirical support for the notion that these measures are indeed sensitive to distinct
facets of oscillatory dynamics, and furthermore, that these distinctions hold at the network
level. Perhaps most importantly, all these frequency- and metric-specific networks can be ex-
tracted from the same data in the majority of individuals. We suggest that this organizational
Network Neuroscience
497
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
principle offers novel opportunities to probe the functional and computational processes
underlying cognition from a network perspective.
State-Dependent Network Organization
Group-level network structure differed significantly between rest and task. This observation
is consistent with well-known findings of state-dependent differences in power topographies
(e.g., Pfurtscheller, 1992), which we also observed (Supporting Information Figure 1A, Cox
et al., 2018). More recent examinations have turned to task-induced changes in functional
connectivity (Bassett, Meyer-Lindenberg, Achard, Duke, & Bullmore, 2006; Brookes et al.,
2012; Keitel & Gross, 2016). In line with these observations, we found differential rest-task
network configurations in various frequency bands as measured by phase synchrony and am-
plitude correlation structure. Indeed, the demonstration that classifiers could successfully dif-
ferentiate between an out-of-sample subject’s rest and task states, and, moreover, could do so
for all frequency bands and oscillation metrics, further underscores the similarity of network
patterns across subjects, as well as the differences between these behavioral states. We again
note that although rest-task differences are to be expected for some network types based on
previous findings (e.g., alpha power), the demonstration that this phenomenon holds across
all considered network types, and furthermore, can be discerned within individuals, suggests
that such network reorganization constitutes a fundamental property of large-scale brain or-
ganization. These findings are perhaps even more notable given the marked between-subject
variability we observed, to which we turn next.
Stable Individual Differences of Network Configurations
In addition to the separability of network types based on behavioral state, frequency band,
and oscillation metric, our analyses also revealed substantial individual differences discernible
above and beyond the commonalities shared across subjects, consistent with other findings in
both wakefulness (Chu et al., 2012) and sleep (Cox, Schapiro, Manoach, & Stickgold, 2017;
Finelli, Achermann, & Borbély, 2001).
Indeed, within-subject network similarity across be-
havioral states was generally stronger than between-subject similarities for any single state,
indicating that idiosyncratic patterns of oscillatory activity tend to persist even during ex-
tensive task-induced reorganization. This observation suggests that the same anatomical and
functional individual variability measured by MR-based techniques (Bürgel et al., 2006; Finn
et al., 2015; Gordon et al., 2015; Mueller et al., 2013) is seen in oscillatory profiles. Fur-
thermore, our finding that individual oscillatory profiles persist across months indicates that
these patterns reflect trait rather than state characteristics, similar to our recent findings during
sleep (Cox et al., 2017). More generally, these findings are in line with evidence of strong
genetic control over brain oscillations (Begleiter & Porjesz, 2006; De Gennaro et al., 2008;
Smit, Boomsma, Schnack, Hulshoff Pol, & de Geus, 2012; Smit, Stam, Posthuma, Boomsma,
& De Geus, 2008; Van Beijsterveldt & Van Baal, 2002), and with various other MEG/EEG
features that exhibit stability across days or even years (Chapeton, Inati, & Zaghloul, 2017;
Chu et al., 2012; De Gennaro, Ferrara, Vecchio, Curcio, & Bertini, 2005; Del Pozo-Banos,
Alonso, Ticay-Rivas, & Travieso, 2014; Deuker et al., 2009; Hardmeier et al., 2014; Kondacs
& Szabó, 1999; Maiorana, La Rocca, & Campisi, 2016; Nikulin & Brismar, 2004; Rocca et al.,
2014; Salinsky, Oken, & Morehead, 1991). Given recent links between cognitive functioning
and fMRI network structure (Finn et al., 2015; Mueller et al., 2013; Schultz & Cole, 2016) or
localized oscillatory activity (Jiang et al., 2015; Klimesch et al., 1990; Park et al., 2014), indi-
vidual differences in the brain-wide organization of rhythmic activity may similarly map onto
behavioral and cognitive differences between individuals.
Network Neuroscience
498
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
In further support of the multiplexing hypothesis, classifiers were most successful at iden-
tifying individual subjects when information from multiple network types was combined, in-
dicating that these networks each hold unique information. Although task- and rest-based
classification rates did not differ dramatically, their combined information led to a further per-
formance increase, suggesting that the same network types offer distinct identifying information
during different behavioral states. We also note that not all frequency bands and oscillation
metrics contributed equally to classifier success. Alpha activity was sufficient to correctly
identify all 14 of our test subjects, although this effect may be due to alpha’s high signal-to-
noise ratio, thereby yielding more accurate (and reproducible) oscillatory estimates (Cohen,
2014a).
Importantly, however, long-term classification remained high even after exclusion
of all alpha-based information, indicating oscillatory fingerprints can be found in multiple
frequency bands.
Also noteworthy in this respect is our observation that searchlight-based subject recognition,
employing subnetworks centered on each electrode, was highest in frontocentral regions. This
finding is reminiscent of recent fMRI evidence showing greatest individual variability of net-
work structure in fronto-parietal areas (Finn et al., 2015; Peña-Gómez, Avena-Koenigsberger,
Sepulcre, & Sporns, 2017), raising the possibility that these anatomical areas partly underlie
the topographical effects seen here.
Network Differences and Similarities
The presented findings, derived from a single analytic framework, demonstrate a subtle tension
between network differences and similarities. A key example concerns the combination of (1)
subject-specific patterns within rest and within task, (2) stable subject-specific patterns across
rest and task, and (3) robust group-level rest-task differences. Stated differently, multivariate
patterns may vary systematically along one set of dimensions (i.e., electrodes/connections)
with behavioral state, while varying along other dimensions as a function of subject (and yet
others as a function of frequency and oscillation metric). These manifold dynamics are entirely
compatible, and whether oscillatory organization of different networks is viewed as mostly
similar or mostly different depends on one’s perspective.
In this light, it is worth pointing out that our statistical approach did not directly compare ab-
solute similarity values of different network types. For example, our permutation approach indi-
cated that for both power and phase synchrony, the group-level similarity of alpha rest networks
was significantly higher than the baseline similarity of rest networks from different frequency
bands. However, average similarity among these alpha rest networks was 0.84 for power, but
only 0.28 for phase connectivity (Supporting Information Table 4A, Cox et al., 2018). Thus, for
this particular example, connectivity profiles are much more differentiated between individuals
than are power topographies. Although it was outside the scope of the present report to system-
atically compare networks in this fashion, inspection of the Supporting Information Tables (Cox
et al., 2018) offers some insights into this complementary perspective of network organization.
We also note that the degree of EEG network similarity between cognitive states (range in
SA: 0.33–0.73 depending on frequency band and oscillation metric) is much lower than the
values around 0.90 typically observed with fMRI (Cole, Bassett, Power, Braver, & Petersen,
2014). Thus, networks may express highly similar hemodynamic interaction patterns across
cognitive states while simultaneously showing much more differentiated oscillatory profiles.
This may afford EEG more sensitivity to detect network differences relative to fMRI, although
this claim should be based on direct comparisons between these recording modalities.
Network Neuroscience
499
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
Biometrics:
Metrics of human traits that can be
used to label or identify individuals,
with applications in digital
authentication and access control.
Neuronavigation:
Method for registering electrode
positions in relation to head shape
and/or MRI-based anatomy.
Biometric Applications of EEG Networks
Our long-term classification results suggest interesting biometric applications for EEG net-
work analyses. Although many EEG features have been examined for their biometric potential
(Del Pozo-Banos et al., 2014), large-scale oscillatory patterns, including functional connectiv-
ity profiles, have only recently received attention for subject identification (Garau, Fraschini,
Didaci, & Marcialis, 2016; Maiorana et al., 2016; Rocca et al., 2014). Compared with these
reports, our study examined a substantially longer interval between recordings, demonstrating
the long-term permanence of these oscillatory patterns.
Indeed, we achieved highly accu-
rate recognition rates without the use of neuronavigational tools to ensure similar electrode
cap positioning across visits, thus indicating a remarkable degree of robustness with respect
to precise electrode placement. However, we do not claim that subject identification based
on oscillatory patterns leads to more distinguishable neural fingerprints compared with ap-
proaches employing other EEG features, as we did not perform such comparisons. Likewise,
it was not our objective to fine-tune network-based classification by using more sophisticated
feature selection and supervised learning approaches. Indeed, the fact that high performance
was obtained with relatively straightforward methods underscores the robustness of the ob-
served individual differences.
An open question remains concerning the number of unique individuals our approach could
conceivably recognize before different subjects’ network structures begin to overlap and re-
duce classifier performance. In our sample, networks from different individuals showed high
baseline similarity, suggesting that networks cannot freely occupy arbitrary positions in multi-
dimensional space. Moreover, power and connectivity values between adjacent electrodes
and frequency bands are typically correlated, resulting in substantial levels of baseline simi-
larity between different network types (see Supporting Information Tables, Cox et al., 2018),
further limiting the number of potential network configurations that could be observed. Even
with these constraints, however, the number of possible network states is immense. In fact,
the dimensionality of this space may be arbitrarily increased by estimating network struc-
ture for more fine-grained frequency bands, potentially targeting subject-specific frequencies
(Haegens, Cousijn, Wallis, Harrison, & Nobre, 2014), by including additional oscillation met-
rics (e.g., directional connectivity and cross-frequency coupling measures), or by expanding
the number of cognitive states sampled. Moreover, our results show that substantial reductions
of network size still resulted in quite accurate performance, indicating that sparse montages
already capture a large proportion of between-subject network variability. At the same time,
these findings suggest the possibility that the full networks are able to identify a significantly
greater number of individuals than we tested here.
Limitations and Concerns
Several general caveats should be made. First, by constructing networks from ∼5 min data
segments, our approach assumes relatively stationary network configurations across this time
frame. However, oscillatory network profiles have been shown to fluctuate between different
states at timescales of several hundred milliseconds (Baker et al., 2014; Betzel et al., 2012).
As we did not analyze network dynamics with this degree of temporal granularity, it is an
open question whether each of the multiplexed networks identified here similarly shifts rapidly
among multiple network configurations, and if so, how the time courses of these nested net-
work dynamics relate to each other.
Second, although we have discussed the observed network differences from the perspective
of neuronal oscillations, oscillations may not always have been present in each of the analyzed
Network Neuroscience
500
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
frequency bands and/or on each electrode. Thus, our analyses likely captured an unknown
mixture of true oscillations and arrhythmic noise within each frequency band (He, 2014),
raising the possibility that network differences are related to variability in both types of activity.
Somewhat related, our chosen frequency bands, although conventional, may not always offer
a clean separation of distinct neural phenomena due to individual differences in spectral peak
location (Haegens et al., 2014), harmonics, and/or cross-frequency interactions (Aru et al.,
2014). But these confounds would likely result in reduced network separability, suggesting
that our findings underestimate the true differences in network structure.
Third, extraneous factors, such as idiosyncratic differences in skull shape or residual mus-
cle and eye artifacts, may have contributed to our findings of individual differences and the
long-term stability of EEG characteristics. However, muscle activity is severely attenuated by
the surface Laplacian transform (Fitzgibbon et al., 2013), and skull thickness contributes min-
imally to the scalp EEG (Hagemann, Hewig, Walter, & Naumann, 2008), making it unlikely
these factors underlie the reported between-subject variability. Moreover, ocular artifacts were
virtually absent during eyes-closed rest segments, and remaining eye artifacts were carefully
removed using independent component analysis (ICA). Additional analyses indicated that theta
amplitude fluctuations related to ocular activity were effectively abolished by the combination
of ICA and the Laplacian, whereas fluctuations in the alpha, beta, and gamma bands were not
related to ocular activity at all (Supporting Information Results and Supporting Information
Figure 2, Cox et al., 2018), suggesting our findings are of primarily neural origin. That said,
we cannot fully exclude the possibility that individual differences in the mapping from neu-
ral regions to electrodes, due to variability in head shape, cap size, and/or cap positioning,
contributed to observed network differences.
Fourth, a potential issue affecting our analyses concerns volume conduction, whereby ac-
tivity from a single brain source projects to multiple sensors, giving rise to artificially inflated
connectivity estimates between nearby electrodes (S. Palva & Palva, 2012). Although we used
a surface Laplacian filter to reduce volume conduction (Perrin et al., 1989), and removed con-
tiguous channels from the connectivity matrix, these approaches do not completely eliminate
undesired volume conduction effects. We therefore repeated several key analyses by using
connectivity metrics minimally affected by volume conduction (Hipp et al., 2012; Vinck et al.,
2011). These examinations revealed that although the use of these control metrics tends to
reduce network separability somewhat, our results essentially remained the same, indicat-
ing that they cannot be attributed to spurious connectivity resulting from volume conduction
(Supporting Information Results, Supporting Information Tables 8–12, Cox et al., 2018). This
result likely stems from our unit of analysis being the similarity of distributed patterns of activ-
ity. In such analyses, individual connection strengths are of secondary relevance, analogous to
multivariate fMRI approaches operating on correlated voxels (Tambini & Davachi, 2013). We
also tested whether connectivity estimates could be driven by variations in power, but found
no such relations, either across individuals or across data segments within the same individual
(Supporting Information Results, Cox et al., 2018). On the basis of on these control analyses, as
well as the empirical separability of power-, phase-, and amplitude-based networks, we con-
clude that meaningfully distinct network patterns can be and were derived from sensor-level
EEG activity.
Finally, it may be argued that our approach lacks the anatomical specificity afforded by
source localization approaches, preventing any interpretation of our findings in terms of neu-
ral regions. While this is indeed a limitation, we emphasize that the network similarity ap-
proach taken here deliberately abstracts away from particular cortical regions or connections
Network Neuroscience
501
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
in favor of a more global perspective. Thus, our approach would analyze the same high-level
metric of network similarity for source-level data, disregarding the contributions of individual
anatomical sources. Although source-based network similarity might offer a more accurate de-
scription of true network correspondence, the present sensor-level findings were sufficient to
discern separate network types. Indeed, we adopted the network similarity approach because
of its potentially increased sensitivity to changes in distributed patterns, offering insights into
large-scale brain dynamics not afforded by approaches that rely on mass-univariate statistics
(Haxby et al., 2014; Kriegeskorte, 2008). That said, there would be value in characterizing the
most consistent and most variable network elements between network types, both in sensor
space and anatomically resolved. Such analyses, as well as assessments of graph theoretical
measures (Bullmore & Sporns, 2009; van den Heuvel & Sporns, 2013), are outside the scope
of the present paper.
Conclusion
The examination of large-scale oscillatory networks allows for the analysis of brain dynamics
at a level unavailable to other techniques. Unlike slower imaging techniques like fMRI, it per-
mits viewing of distinct layers of multiplexed network activity occurring simultaneously, but
operating at different oscillatory frequencies and employing distinct modes of neural coordi-
nation. The ability to separate these multiplexed signals may prove critical for the unraveling
of complex cognition and behavioral control. While this study has focused on continuous
oscillatory activity during rest and memory encoding, future studies could investigate network
similarity across multiple tasks, and/or examine its relation to behavior. In addition, network
similarity measures could be applied in an event-related fashion to examine the network dy-
namics of cognitive processes with high temporal precision. Finally, these techniques may be
harnessed to analyze brain dynamics in neurological and psychiatric disorders, where altered
network properties have already been identified (De Vico Fallani et al., 2007; Lynall et al.,
2010; Sanz-Arigita et al., 2010).
In sum, our observations attest to both the human brain’s
incredibly complex oscillatory dynamics, and the wealth of spectral, temporal, and spatial
information that can be extracted from EEG signals. Examining oscillatory activity from a
network similarity perspective will, we believe, contribute useful insights into the principles
of human brain organization.
METHODS
Participants
Twenty-one healthy volunteers from the Boston area (8 men, 13 women, mean age ± SD:
22.0 ± 3.0 years, range: 18–31) completed the first visit of this study. Of these, fourteen (8 men,
6 women, 22.6 ± 3.2 years, range: 19–31) returned for a follow-up visit several months later
(mean: 154 days, range: 109–231). All reported no history of neurological, psychiatric, or
sleep disorders. Participants were instructed to refrain from consuming recreational drugs or
alcohol in the 48 hr prior to the study, and to not consume more than one caffeinated beverage
on the day of the study. Subjects were compensated monetarily for their participation. All
subjects provided written informed consent, and this study was approved by the institutional
review board of Beth Israel Deaconess Medical Center.
Protocol
See Figure 1 for an overview of the protocol. The first visit lasted approximately 5.5 hr. Subjects
reported to the laboratory at 1 p.m., provided informed consent, and were prepared for EEG
Network Neuroscience
502
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
monitoring. Seated approximately 60 cm from a 27-inch computer display, they underwent a
series of rest, memory encoding, and memory retrieval blocks, lasting from 2 to 3 p.m. We refer
to this first series of rest and task activities as Session A (SA). Subjects then remained in the lab
watching a 2-hr documentary. Then, from approximately 5:30 to 6 p.m., subjects underwent a
second series of recordings (SB), during which they engaged in several additional blocks of rest
activity and performed delayed memory tests for the material encoded during SA. After filling
out an exit questionnaire, subjects left the lab around 6:30 p.m. Participants returning for the
follow-up visit (SC) several months later arrived at the lab at variable times (range: 10 a.m. to
6 p.m.). Following a second informed consent procedure and EEG setup, they underwent a
series of rest, encoding, retrieval, and control blocks for about 45 min. Subjects carried out
an additional 30 min protocol unrelated to the current study. Total duration of the second visit
was about 2.5 hr.
We use the term “block” to refer to a demarcated period of time associated with a particular
behavioral state (i.e., rest, encoding, retrieval, and control blocks). Details about the organi-
zation of behavioral blocks are described in Supporting Information Methods and in Figure 1
(Cox et al., 2018). Of note, whereas EEG was recorded during all blocks, retrieval was of
much shorter duration (∼1 min) than the other blocks, and often of poor quality because of
the subjects’ constant movements while operating the mouse. Therefore, we did not analyze
the retrieval EEG. We adopt the term “data segment” (or just “segment”) to refer to the EEG
obtained during a single rest, encoding, or control (but not retrieval) block. Finally, “task”
segments refer to data segments from both encoding and control blocks. Note, however, that
a control block was only included in SC.
All behavioral blocks were presented using custom software written in Java.
Instruction
screens occurred throughout the protocol. Subjects advanced to the next screen by pressing a
keyboard button. During rest segments, subjects were instructed to quietly rest and relax for
5 min with their eyes closed, while remaining awake. An auditory tone at the end of each rest
segment indicated subjects could open their eyes again.
◦
For memory encoding, subjects were instructed to memorize the location of pictures on a
6 × 6 grid. During the task, a square grid of 36 grey squares, subtending approximately 5
of
visual angle per tile, and 31
in total, was continually present on the screen. Thirty-six pictures
were then shown, one at a time on a unique grid tile, for 2,000 ms with an interstimulus interval
of 1,000 ms. This procedure was repeated for a total of three presentations of all 36 pictures.
Picture-location combinations and presentation order were randomized for each subject. An
encoding block lasted 5 min and 20 s. The control task employed in SC used the same basic
design as the encoding protocol, except that the same picture was displayed on each tile,
resulting in a perceptually similar experience but with no memory demands.
◦
During memory retrieval, each picture was presented to the right side of the grid. The par-
ticipant then used the mouse to select the tile on which that picture had been presented, at
which point the selected tile turned blue for 400 ms. Then, the tile returned to its gray color
and the next picture was presented. Subjects did not receive feedback on their performance.
Retrieval was self-paced and lasted 1 to 2 min.
Data Acquisition and Preprocessing
EEG was collected using 62-channel caps with channel positions in accordance with the
10-20 system. Two Ag/AgCl cup electrodes were attached to the mastoid processes, two
around the eyes for electrooculography, and one, as a reference, on the forehead. Channel
Network Neuroscience
503
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
Afz was used as the ground. An AURA-LTM64 amplifier and TWin software were used for data
acquisition (Grass Technologies). Impedances were kept below 25 kΩ, and data were sampled
at 400 Hz with hardware high-pass and low-pass filters at 0.1 and 133 Hz, respectively.
All subsequent data processing and analyses were performed in Matlab (the Mathworks,
Natick, MA) using custom routines in combination with several open source toolboxes, includ-
ing EEGlab (Delorme & Makeig, 2004) and Fieldtrip (Oostenveld, Fries, Maris, & Schoffelen,
2011). EEG recordings were divided into data segments based on triggers derived from the
stimulus software. Following the removal of eye channels, data segments were re-referenced
to average mastoids, high-pass filtered at 0.5 Hz and notch filtered around 60 Hz to sup-
press line noise. Noisy channels were interpolated using a spherical spline algorithm (EEGlab:
pop_interp) and excessively noisy time fragments were removed, resulting in an average seg-
ment length across all 364 segments of all subjects of 291 ± 22 s (typical range: 209–325 s;
one outlier of 48 s). ICA (EEGlab: runica) was performed and components reflecting eye move-
ments, eye blinks, muscle activity, and other obvious artifacts were removed. Next, we applied
a spatial Laplacian filter (Perrin et al., 1989) by using the CSD toolbox (Kayser & Tenke, 2006).
The Laplacian reduces the effects of volume conduction by estimating radial current flow,
thereby highlighting local aspects of neural processing and allowing for superior estimates
of phase coupling and reducing artificial coupling between electrodes (Cohen, 2014b; Tenke
& Kayser, 2015). By decorrelating activity levels across the scalp, this approach “sharpens”
network profiles, thereby improving chances of uncovering subtle network differences.
Power and Functional Connectivity
For each spatially filtered data segment (rest and task) and electrode we estimated power spec-
tral density using Welch’s method with 5-s windows and 50% overlap. Power values were
dB transformed according to dB power = 10 × log10(power) and averaged across frequency
bins corresponding to the theta (3–7 Hz), alpha (8–12 Hz), beta (13–30 Hz), and gamma (32–
60 Hz) bands. This yielded, for every subject, data segment and frequency band, a vector V
of length 60 containing each electrode’s power values. Thus, these vectors reflect the network
organization of oscillatory power across the scalp. The dB transformation yielded vectors con-
taining approximately normally distributed values, which is an important assumption for their
later use in Pearson correlations. Additionally, as a more concise statistic, we defined global
power as the average power across all elements (i.e., electrodes) in a vector: global power =
n ∑n
1
c=1 Vc, where c is the channel number (1, 2, ..., 60).
For connectivity, we band-pass filtered the segments by using the abovementioned cut-off
frequencies (EEGlab: pop_eegfiltnew). We selected these values based on the shape of the
filters’ frequency responses, ensuring that there was minimal overlap between adjacent pass-
bands. Next, we applied the Hilbert transform to each filtered segment and determined the
resulting signals’ instantaneous phase and amplitude. We then subdivided the phase angle and
amplitude time series into 10 equally sized smaller data fragments and calculated connectivity
separately for each fragment. We performed the fragmenting step to reduce the effect of po-
tential outliers on connectivity estimates, and, for phase synchrony, to allow for nonstationary
phase differences within each segment. Fragment length varied across subjects and data seg-
ments because data segments had different amounts of artifact removed. Although the number
of samples affects the signal-to-noise ratio of the resulting connectivity estimates, individual
fragments were sufficiently long (at least 20 s, except for one outlier with fragment lengths of 5 s)
that this variation was unlikely to have had a significant influence on subsequent analyses.
Network Neuroscience
504
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
Amplitude envelope correlations (Bruns et al., 2000), ranging between −1 and 1, were
determined using the Spearman correlation and were assessed between each channel pair’s
Hilbert-amplitudes, yielding a matrix Mamp of 60 × 60 connectivity values for every frag-
ment. We used a nonparametric correlation metric because amplitude envelopes are gener-
ally not normally distributed. Note that because of the monotonic relation between amplitude
and power, amplitude envelope correlations and power envelope correlations are identical in
our approach. Phase synchrony was determined following the phase locking value approach
(Lachaux et al., 1999). We first determined the phase difference for every channel pair (j, k)
at each sample. We then assessed phase synchrony for each channel pair as the length of the
average phase difference vector across samples, expressed in the complex plane as:
PLV jk =
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
1
n
n
∑
t=1
ei∗(ϕj(t)−ϕk(t))
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
where i is the imaginary operator, ϕ indicates phase (in radians), t is the sample, and j and k
index the channels. Phase synchrony values ranged from 0 (random phase relations) to 1 (per-
fect phase consistency). This resulted in another 60 × 60 matrix Mphase, with phase synchrony
values between every channel pair for each data fragment. For both amplitude correlation
and phase synchrony, we then averaged connectivity estimates across the 10 fragments. We
selected the upper triangles of the symmetrical Mamp and Mphase matrices to count each con-
nection only once, resulting in a total of 60 × 59/2 = 1,770 connections.
(See Supporting
Information Methods, Cox et al., 2018, for calculation of orthogonalized amplitude correla-
tions and weighted phase lag index.)
To further limit the effect of spurious coupling on our results, we removed from each con-
nectivity matrix the 192 elements (11%) that reflect pairs of neighboring electrodes (Fieldtrip:
ft_prepare_neighbours with neighbourdist of 0.55). This yielded, for every subject, data seg-
ment, and frequency band, and for both phase synchrony and amplitude correlation, a vector
U of length 1,578 reflecting the degrees of connectivity between all unique nonneighboring
channel pairs. As with power, we also defined a global connectivity metric as the average
c=1 Uc, where c is the connection
across all entries in a vector: global connectivity =
number (1, 2, ..., 1,578). For topographical plots of connectivity, we averaged the 60 ×
60 matrix M (with neighboring and identity connections removed) across one of its dimen-
sions (e.g., row-wise) to obtain the average connectivity between each electrode and all other
electrodes.
n ∑n
1
Connectivity values within each vector U were generally not normally distributed, with
the degree of skewness differing depending on frequency band, connectivity metric, data seg-
ment, and subject. To render the data normally distributed for subsequent Pearson correlation
analyses, we first added a value of 1 to each connectivity vector entry to ensure all values
were positive. We then performed box-cox power transformations to all vectors, in which the
exponent used for transformation was automatically determined for each vector to minimize
the standard deviation of the transformed vector (Box & Cox, 1964). Finally, we z-scored the
resulting vectors to obtain a standardized appearance when visualized in scatter plots. How-
ever, z-scoring does not affect subsequent Pearson correlation statistics. Thus, apart from this
power transformation, which was only performed for connectivity vectors, oscillatory power
and functional connectivity metrics were processed similarly.
We further assessed whether the use of box-cox transformations and the choice of similar-
ity metric could have affected network similarity estimates. To this end, we assessed network
Network Neuroscience
505
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
similarity between every possible pair of connectivity vectors (4,403,028 in total) by using
either transformed vectors and the Pearson correlation (the “canonical” approach: see Net-
work Similarity and Statistics section), or using untransformed vectors in conjunction with
the nonparametric Spearman correlation. The resulting sets of network similarity estimates
were highly similar, although significantly different due to the large number of samples (both
0.24 ± 0.14; paired t(4, 403, 027) = 1, 758, p < 10− 100
). Critically, similarity values were
extremely highly correlated between both approaches (R = 0.996, p < 10−100
), making it
unlikely that downstream analyses were affected by our choice of similarity metric or data
transformation.
To directly compare power and connectivity vectors, which were of different length (V: 60,
U: 1,578), we also constructed “power connectivity” vectors of equal size as the connectivity
vectors. Specifically, we set the weight of each power “connection” to be the average power of
the two involved electrodes. Naturally, this manipulation did not add any novel information,
as each of the newly computed values in the larger vector was a linear combination of the
original power estimates. As a result, this operation did not influence the similarity among
power networks (i.e., power-based network similarity values were identical for vector lengths
of 60 and 1,578), while enabling direct comparisons between power and connectivity metrics.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Similarity and Statistics
Our basic approach for assessing the similarity of networks involved computing the Pearson
correlation coefficient between two vectors (Figure 3). To aggregate network similarities across
more than two networks, we used procedures referred to as representational similarity analy-
sis in the modeling and fMRI literature (Kriegeskorte, 2008). Specifically, we calculated the
Pearson correlation between each unique pair of networks, resulting in a large matrix of
similarity scores. Then, for specific questions of interest, similarity values were averaged across
the relevant entries and compared with a suitable baseline. Thus, we could compare networks
within, between, and across subjects, behavioral states, frequency bands, test sessions, and
oscillation metrics.
In general, we evaluated network similarity statistically on two levels. In “level-1” analyses
we determined how much evidence individual subjects showed for a particular phenomenon.
Then, these results were summarized across subjects and appropriately tested for significance.
In contrast, “level-2” analyses included all subjects’ networks and asked whether there was
reliable support for a particular finding at the group level.
For both level-1 and level-2 analyses, we took a data-driven resampling approach to deter-
mine whether observed similarity scores across networks, selected based on a factor of interest,
were statistically different from what would be expected under the null hypothesis of equal net-
work similarity across levels of this factor. For every comparison of interest we constructed a
null distribution by repeatedly selecting as many random networks as there were included in
the original observation (allowing selection of networks included in the original observation).
At each iteration, similarity scores between each pair of selected networks were averaged,
thereby creating a surrogate distribution of similarity values. The number of resampling itera-
tions we used depended on the number of unique random samples available. If the number of
possible combinations was over 1,000, a truly random sample was selected for each of 1,000
iterations (i.e., Monte Carlo sampling). When the number of combinations was lower, every
unique combination was sampled exactly once (i.e., permutation sampling). Because of the
precise mechanics of shuffling, some level-1 analyses could use the same null distribution for
Network Neuroscience
506
Large-scale oscillation patterns
every individual, whereas others required a different baseline distribution for each individual,
as outlined in detail in Supporting Information Methods (Cox et al., 2018). For every compar-
ison of interest, we defined baseline similarity as the average similarity across permutations
(i.e., the center of the null distribution). In cases where individual subjects had separate null
distributions, baseline similarity was defined as the average of these individual baselines.
We assessed significance in several ways. First, for some analyses we use a one-sample
t test to compare observed level-1 similarity scores to the baseline value. This approach tests
whether single-subject effects, as a group, are different from the permutation-derived base-
line. Second, for both level-1 and level-2 analyses, we used the null distributions to z-score
each observation and calculate the associated p values. We then applied the false discovery
procedure (Benjamini & Hochberg, 1995) to correct for multiple comparisons (i.e., for multi-
ple subjects, frequency bands, oscillation metrics). We used z-based p values, rather than the
“raw” permutation-based p values, because the latter often severely underestimated the size of
the effect. Even with 1,000 iterations the lowest obtainable significance value was p < 0.001,
while z-based p values provide a more accurate estimate of the distance between an obser-
vation and its null distribution. Importantly, for some level-1 analyses the number of possible
permutations was rather low (e.g., 2 task segments × 4 frequency bands = 8 networks; bino-
(cid:3)
(cid:4)
mial coefficient
8
2
= 28). As a consequence, the resulting null distributions were based
on a limited number of samples and were often not Gaussian shaped. In these cases, z-based
p values did not optimally capture the size of the effect. Moreover, even when observed simi-
larity values were more extreme than the entire null distribution, their raw permutation-based
p values were limited by the number of permutations. This state of affairs severely affected
subsequent multiple comparison correction with the false discovery procedure. Therefore,
we additionally present uncorrected, permutation-based p values for these cases, to offer a
complete picture of the pattern of results. Finally, meaningful level-1 permutations could not be
performed for the comparison of task networks based on the three oscillatory metrics (binomial
(cid:4)
(cid:3)
coefficient:
6
2
= 15), and are not reported. A detailed account of the shuffling mechanics
for all different comparisons can be found in Supporting Information Methods (Cox et al.,
2018).
We note that whereas we consistently used the false discovery procedure to control the rate
of false positives, we did so separately for subsets of analyses (as opposed to across larger sets
of analyses or even all possible analyses). For example, for analyses of within-subject network
similarity in SA, we corrected for 21 comparisons, one for each subject, separately for each
network type, rather than correcting for 28 (4 frequencies × 3 metrics × 2 behavioral states)
× 21 = 588 comparisons. Besides that we believe the need to control false positives should
be balanced against the risk of false negatives, we emphasize that we confirmed our effects in
independent sessions SB and SC where possible. Thus, we believe that the nested approach of
permutation testing, false discovery rate correction, and cross-session replication adequately
corrects for the large number of multiple comparisons we performed.
As an additional tool, we employed multidimensional scaling, as implemented in Matlab’s
mdscale function, to visualize the similarity of networks. Multidimensional scaling techniques
project high-dimensional data points onto a space of lower dimension while optimally preserv-
ing the distances between points (Hout, Papesh, & Goldinger, 2013). In our case, each network
can be viewed as a point in 60-dimensional (for power topographies) or 1,578-dimensional
space (for connectivity patterns), and the distance between networks can be expressed as
Network Neuroscience
507
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
(1 – Pearson correlation), such that more similar networks are closer together. By project-
ing these points onto two dimensions, relations between networks of different subjects and
types that are not apparent from inspecting the full-dimensional data can be approximately
visualized. However, all statistics were performed on the full-dimensional data.
Classifiers
We used k-nearest neighbor classifiers (Cover & Hart, 1967) as a supervised learning strat-
egy to distinguish between behavioral states within the same session, and to classify subject
identity across sessions. In both instances, the algorithm (implemented in Matlab as f itcknn)
was trained using the correlation distance (1 - Pearson correlation) between each pair of mul-
tivariate networks, similar to how we assessed network similarity. Different classifiers were
trained for different network types. In the test phase, unseen networks were assigned labels
(e.g., “rest” or “task,” or a subject ID) according to the labels in the training set, such that train-
ing networks closest to each test network (i.e., more similar networks) contributed more to the
final assigned label. This was implemented using an inverse distance-weighting scheme. The
number of nearest training networks allowed to vote (i.e., k) was set to 5, except for the set of
analyses where we investigated classifier performance as a function of k.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
To classify behavioral states within the same session (i.e., rest vs. task), we used a cross-
validated approach in which we repeatedly trained each classifier on the data of all but one
subject, and then tested the classifier on the remaining subject’s networks. For cross-session
subject recognition, we trained classifiers on data from SA and SB and tested them on data
from SC. Classifier performance was calculated as the proportion of test networks that were
assigned the correct label.
To ascertain whether information pooled across network types improves classification rates
of data segments, we combined the information contained by different classifiers. In particular,
every individual classifier Cs (where s is 1, 2, ...., 12 for all network types: 4 frequency bands ×
3 metrics) returns the posterior probabilities that test network Xi belongs to training class Yj,
where j = 1, 2 for behavioral classifiers (rest or task), and j = 1, 2, ..., 21 for subject identity
classifiers. For every test network Xi, we averaged the probabilities across classifiers of interest
to obtain “class weights” indicating how likely it is network Xi belongs to class Yj (note that
resulting values do not necessarily sum to 1 and therefore do not reflect true probabilities).
The test network Xi was then assigned the class label of the class with the highest class weight,
similar to the method used for individual classifiers.
For subject identification, we further averaged these class weights across the multiple data
segments derived from each individual subject. In a final merger step, we combined rest and
task networks by taking, for each training class Yj, the maximum class weight from the com-
posite rest and composite task classifiers, and assigned identity based on this maximum class
weight. Classifier performance was evaluated using both binomial tests and permutation tests
in which we repeatedly shuffled training labels. For various control analyses, we systemati-
cally left out network information from particular frequency bands, oscillation metrics, or data
segments prior to merging them.
For searchlight analysis we used the Fieldtrip function ft_prepare_neighbours with a neigh-
bor distance of 0.65 to determine the neighborhood structure around each electrode. We then
iterated across all electrodes, at each iteration selecting the current electrode, its neighbors,
and all nonneighboring connections among them, and trained and tested classifiers on these
local networks.
Network Neuroscience
508
Large-scale oscillation patterns
Data Availability
Power and functional connectivity estimates of all networks are freely available in Matlab
format from https://doi.org/10.6084/m9.figshare.5755377. Raw data is available upon request
from the lead author.
ACKNOWLEDGEMENTS
We thank Alexandra Morgan for technical assistance, and Mike X. Cohen and Michael Murphy
for valuable comments on earlier versions of this manuscript.
AUTHOR CONTRIBUTIONS
Roy Cox: Conceptualization; Data curation; Formal analysis; Funding acquisition; Investi-
gation; Methodology; Project administration; Software; Visualization; Writing, original draft;
Writing, review & editing. Anna C. Schapiro: Conceptualization; Methodology; Writing, re-
view and editing. Robert Stickgold: Conceptualization; Funding acquisition; Methodology;
Resources; Supervision; Writing, review and editing.
FUNDING INFORMATION
This work was supported by grants from the Netherlands Organization for Scientific Research
(NWO) to R.C. (446-14-009); the National Institutes of Health to A.C.S. (F32-NS093901),
and R.S. (MH048832; MH092638); the Harvard Clinical and Translational Science Center
(TR001102); and the Stanley Center for Psychiatric Research at Broad Institute.
REFERENCES
Ainsworth, M., Lee, S., Cunningham, M. O., Traub, R. D., Kopell,
N. J., & Whittington, M. A. (2012). Rates and rhythms: A synergis-
tic view of frequency and temporal coding in neuronal networks.
Neuron, 75(4), 572–583. https://doi.org/10.1016/j.neuron.2012.
08.004
Akam, T., & Kullmann, D. M.
(2014). Oscillatory multiplexing of
population codes for selective communication in the mammalian
brain. Nature Reviews Neuroscience, 15(2), 111–122. https://
doi.org/10.1038/nrn3668
Arnulfo, G., Hirvonen, J., Nobili, L., Palva, S., & Palva, J. M. (2015).
Phase and amplitude correlations in resting-state activity in hu-
man stereotactical EEG recordings. NeuroImage, 112, 114–127.
https://doi.org/10.1016/j.neuroimage.2015.02.031
Aru, J., Aru, J., Priesemann, V., Wibral, M., Lana, L., Pipa, G., . . .
Vicente, R.
(2014). Untangling cross-frequency coupling in
neuroscience. Current Opinion in Neurobiology, 31, 51–61. https://
doi.org/10.1016/j.conb.2014.08.002
Baker, A. P., Brookes, M. J., Rezek, I. A., Smith, S. M., Behrens, T.,
Smith, P. J. P., & Woolrich, M. (2014). Fast transient networks in
spontaneous human brain activity. eLife, 2014(3), 1–18. https://
doi.org/10.7554/eLife.01867
Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T., &
Bullmore, E.
(2006). Adaptive reconfiguration of fractal small-
world human brain functional networks. Proceedings of the Na-
tional Academy of Sciences of the United States of America,
103(51), 19518–19523.
Bastos, A. M., & Schoffelen, J.-M.
(2016). A tutorial review of
functional connectivity analysis methods and their interpreta-
tional pitfalls. Frontiers in Systems Neuroscience, 9(January), 1–23.
https://doi.org/10.3389/fnsys.2015.00175
Begleiter, H., & Porjesz, B. (2006). Genetics of human brain oscilla-
tions. International Journal of Psychophysiology, 60(2), 162–171.
https://doi.org/10.1016/j.ijpsycho.2005.12.013
Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov-
ery rate: a practical and powerful approach to multiple testing.
Journal of the Royal Statistical Society. https://doi.org/10.2307/
2346101
Betzel, R. F., Erickson, M. a., Abell, M., O’Donnell, B. F., Hetrick,
W. P., & Sporns, O. (2012). Synchronization dynamics and evi-
dence for a repertoire of network states in resting EEG. Frontiers
in Computational Neuroscience, 6(September), 1–13. https://doi.
org/10.3389/fncom.2012.00074
Box, G. E. P., & Cox, D. R. (1964). An analysis of transformations.
Journal of the Royal Statistical Society. Series B (Methodological),
211–252. https://doi.org/10.2307/2287791
Brookes, M. J., Liddle, E. B., Hale, J. R., Woolrich, M. W., Luckhoo,
H., Liddle, P. F., & Morris, P. G.
(2012). Task induced mod-
ulation of neural oscillations in electrophysiological brain net-
works. NeuroImage, 63( 4), 1918–30. https://doi.org/10.1016/
j.neuroimage.2012.08.012
Brookes, M. J., O’Neill, G. C., Hall, E. L., Woolrich, M. W., Baker,
(2014). Measuring
A., Palazzo Corner, S., . . . Barnes, G. R.
Network Neuroscience
509
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
temporal, spectral and spatial changes in electrophysiological
brain network connectivity. NeuroImage, 91, 282–99. https://
doi.org/10.1016/j.neuroimage.2013.12.066
Bruns, A., Eckhorn, R., Jokeit, H., & Ebner, A. (2000). Amplitude
envelope correlation detects coupling among incoherent brain
signals. Neuroreport, 11(7), 1509–14. https://doi.org/10.1097/
00001756-200005150-00028
Bullmore, E., & Sporns, O. (2009). Complex brain networks: graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience, 10(3), 186–198. https://doi.org/10.1038/
nrn2575
Bürgel, U., Amunts, K., Hoemke, L., Mohlberg, H., Gilsbach, J. M.,
& Zilles, K. (2006). White matter fiber tracts of the human brain:
Three-dimensional mapping at microscopic resolution, topogra-
phy and intersubject variability. NeuroImage, 29(4), 1092–1105.
https://doi.org/10.1016/j.neuroimage.2005.08.040
Canolty, R. T., Ganguly, K., Kennerley, S. W., Cadieu, C. F., Koepsell,
K., Wallis, J. D., & Carmena, J. M.
(2010). Oscillatory phase
coupling coordinates anatomically dispersed functional cell as-
semblies. Proceedings of the National Academy of Sciences of
the United States of America, 107(40), 17356–17361. https://
doi.org/10.1073/pnas.1008306107
Chu, C.
Chapeton, J. I., Inati, S. K., & Zaghloul, K. A. (2017). Stable func-
tional networks exhibit consistent timing in the human brain.
Brain, 140(3), 628–640. https://doi.org/10.1093/brain/aww337
J., Bianchi, M. T.,
J., Kramer, M. a., Pathmanathan,
Westover, M. B., Wizon, L., & Cash, S. S.
(2012). Emergence
of stable functional networks in long-term human electroence-
phalography. Journal of Neuroscience, 32(8), 2703–2713. https://
doi.org/10.1523/JNEUROSCI.5669-11.2012
Cohen, M. X. (2014a). Analyzing neural time series data: Theory
and practice. Cambridge, MA: MIT Press.
Cohen, M. X.
(2014b). Comparison of different spatial transfor-
mations applied to EEG data: A case study of error processing.
International Journal of Psychophysiology, 97(3), 245–257. https://
doi.org/10.1016/j.ijpsycho.2014.09.013
Cole, M. W., Bassett, D. S., Power, J. D., Braver, T. S., & Petersen,
S. E.
Intrinsic and task-evoked network architectures
of the human brain. Neuron, 83(1), 238–251. https://doi.org/10.
1016/j.neuron.2014.05.014
(2014).
Congedo, M., John, R. E., De Ridder, D., & Prichep, L.
(2010).
Group independent component analysis of resting state EEG in
large normative samples. International Journal of Psychophysiol-
ogy, 78(2), 89–99. https://doi.org/10.1016/j.ijpsycho.2010.06.
003
Cover, T., & Hart, P. (1967). Nearest neighbor pattern classification.
IEEE Transactions on Information Theory, 13(1), 21–27. https://
doi.org/10.1109/TIT.1967.1053964
Cox, R., Schapiro, A. C., Manoach, D. S., & Stickgold, R. (2017).
Individual differences in frequency and topography of slow and
fast sleep spindles. Frontiers in Human Neuroscience, 11. https://
doi.org/10.3389/fnhum.2017.00433
Cox, R., Schapiro, A. C., & Stickgold, R. (2018). Supporting Infor-
mation for “Variability and stability of large-scale cortical oscil-
lation patterns.” Network Neuroscience, 2(4), 481–512. https://
doi.org/10.1162/netn_a_00046
De Gennaro, L., Ferrara, M., Vecchio, F., Curcio, G., & Bertini,
M.
(2005). An electroencephalographic fingerprint of human
sleep. NeuroImage, 26( 1), 114–122. https://doi.org/10.1016/
j.neuroimage.2005.01.020
De Gennaro, L., Marzano, C., Fratello, F., Moroni, F., Pellicciari,
M. C., Ferlazzo, F., . . . Rossini, P. M.
(2008). The electroen-
cephalographic fingerprint of sleep is genetically determined:
A twin study. Annals of Neurology, 64(4), 455–460. https://doi.
org/10.1002/ana.21434
De Vico Fallani, F., Astolfi, L., Cincotti, F., Mattia, D., Marciani,
M. G., Salinari, S., . . . Babiloni, F. (2007). Cortical functional
connectivity networks in normal and spinal cord injured patients:
Evaluation by graph analysis. Human Brain Mapping, 28(12),
1334–1346. https://doi.org/10.1002/hbm.20353
Del Pozo-Banos, M., Alonso, J. B., Ticay-Rivas, J. R., & Travieso,
C. M.
(2014). Electroencephalogram subject identification: A
review. Expert Systems with Applications, 41(15), 6537–6554.
https://doi.org/10.1016/j.eswa.2014.05.013
Delorme, A., & Makeig, S.
(2004). EEGLAB: An open source
toolbox for analysis of single-trial EEG dynamics including inde-
pendent component analysis. Journal of Neuroscience Methods,
134(1), 9–21. https://doi.org/10.1016/j.jneumeth.2003.10.009
Deuker, L., Bullmore, E. T., Smith, M., Christensen, S., Nathan, P. J.,
Rockstroh, B., & Bassett, D. S. (2009). Reproducibility of graph
metrics of human brain functional networks. NeuroImage, 47(4),
1460–1468. https://doi.org/10.1016/j.neuroimage.2009.05.035
Fell, J., & Axmacher, N. (2011). The role of phase synchronization
in memory processes. Nature Reviews Neuroscience, 12(2), 105–118.
https://doi.org/10.1038/nrn2979
Finelli, L. A., Achermann, P., & Borbély, A. A.
(2001). Individual
“fingerprints” in human sleep EEG topography. Neuropsy-
chopharmacology, 25(5 Suppl), S57–S62. https://doi.org/10.
1016/S0893-133X(01)00320-7
Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J.,
(2015). Functional con-
Chun, M. M., . . . Constable, R. T.
nectome fingerprinting: Identifying individuals using patterns of
brain connectivity. Nature Neuroscience, 18(11), 1664–1671.
https://doi.org/10.1038/nn.4135
Fitzgibbon, S. P., Lewis, T. W., Powers, D. M. W., Whitham, E. W.,
Willoughby, J. O., & Pope, K. J.
(2013). Surface laplacian of
central scalp electrical signals is insensitive to muscle contami-
nation. IEEE Transactions on Biomedical Engineering, 60(1), 4–9.
https://doi.org/10.1109/TBME.2012.2195662
Fries, P.
(2005). A mechanism for cognitive dynamics: Neuronal
communication through neuronal coherence. Trends in Cogni-
tive Sciences, 9(10), 474–480.
Garau, M., Fraschini, M., Didaci, L., & Marcialis, G. L.
(2016).
Experimental results on multi-modal fusion of EEG-based per-
sonal verification algorithms. 2016 International Conference on
Biometrics, ICB 2016. https://doi.org/10.1109/ICB.2016.7550080
Gordon, E. M., Laumann, T. O., Adeyemo, B., & Petersen, S. E.
(2015). Individual variability of the system-level organization of
the human brain. Cerebral Cortex,(October), bhv239. https://doi.
org/10.1093/cercor/bhv239
Gross,
J., Hoogenboom, N., Thut, G., Schyns, P., Panzeri, S.,
Belin, P., & Garrod, S. (2013). Speech rhythms and multiplexed
Network Neuroscience
510
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
n
e
n
_
a
_
0
0
0
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Large-scale oscillation patterns
oscillatory sensory coding in the human brain. PLoS Biology,
11(12). https://doi.org/10.1371/journal.pbio.1001752
Haegens, S., Cousijn, H., Wallis, G., Harrison, P. J., & Nobre,
A. C. (2014). Inter- and intra-individual variability in alpha peak
frequency. NeuroImage, 92, 46–55. https://doi.org/10.1016/
j.neuroimage.2014.01.049
Hagemann, D., Hewig,
J., Walter, C., & Naumann, E. (2008).
Skull thickness and magnitude of EEG alpha activity. Clinical
Neurophysiology, 119(6), 1271–1280. https://doi.org/10.1016/
j.clinph.2008.02.010
Hardmeier, M., Hatz, F., Bousleiman, H., Schindler, C., Stam, C. J.,
& Fuhr, P.
(2014). Reproducibility of functional connectiv-
ity and graph measures based on the phase lag index (PLI) and
weighted phase lag index (wPLI) derived from high resolution
EEG. PloS One, 9(10), e108648. https://doi.org/10.1371/journal.
pone.0108648
Haxby, J. V., Connolly, A. C., & Guntupalli, J. S. (2014). Decoding
neural representational spaces using multivariate pattern analy-
sis. Annual Review of Neuroscience, 37(1), 435–456. https://doi.
org/10.1146/annurev-neuro-062012-170325
He, B. J. (2014). Scale-free brain activity: Past, present, and future.
Trends in Cognitive Sciences, 18(9), 480–487. https://doi.org/10.
1016/j.tics.2014.04.003
Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., &
Stam, C. J.
(2012). Frequency-dependent functional connec-
tivity within resting-state networks: An atlas-based MEG beam-
former solution. NeuroImage, 59(4), 3909–3921. https://doi.org/
10.1016/j.neuroimage.2011.11.005
Hipp, J. F., Hawellek, D. J., Corbetta, M., Siegel, M., & Engel,
A. K. (2012). Large-scale cortical correlation structure of sponta-
neous oscillatory activity. Nature Neuroscience, 15(6), 884–890.
https://doi.org/10.1038/nn.3101
Hipp, J. F., & Siegel, M.
(2015). BOLD fMRI correlation reflects
frequency-specific neuronal correlation. Current Biology, 25(10),
1368–1374. https://doi.org/10.1016/j.cub.2015.03.049
Honkanen, R., Rouhinen, S., Wang, S. H., Palva, J. M., & Palva, S.
(2015). Gamma oscillations underlie the maintenance of feature-
specific information and the contents of visual working memory.
Cerebral Cortex, 25(10), 3788–3801. https://doi.org/10.1093/
cercor/bhu263
Hout, M. C., Papesh, M. H., & Goldinger, S. D.
(2013). Multi-
dimensional scaling. Wiley Interdisciplinary Reviews: Cognitive
Science, 4(1), 93–103. doi: https://doi.org/10.1002/wcs.1203
Jiang, H., van Gerven, M. A. J., & Jensen, O. (2015). Modality-
specific alpha modulations facilitate long-term memory encoding
in the presence of distracters. Journal of Cognitive Neuroscience,
27(3), 583–592. https://doi.org/10.1162/jocn_a_00726
Kayser, J., & Tenke, C. E.
(2006). Principal components analy-
sis of Laplacian waveforms as a generic method for identifying
ERP generator patterns: I. Evaluation with auditory oddball tasks.
Clinical Neurophysiology, 117(2), 348–368. https://doi.org/
10.1016/j.clinph.2005.08.034
(2016).
Keitel, A., & Gross, J.
Individual human brain areas can
be identified from their characteristic spectral activation finger-
prints. PLOS Biology, 14(6), e1002498. https://doi.org/10.1371/
journal.pbio.1002498
Klimesch, W., Schimke, H., Ladurner, G., & Pfurtscheller, G. (1990).
Journal of Psycho-
Alpha frequency and memory performance.
physiology, 4(4), 381–390.
Kondacs, A., & Szabó, M. (1999). Long-term intra-individual vari-
ability of the background EEG in normals. Clinical Neurophysiol-
ogy, 110(10), 1708–1716. https://doi.org/10.1016/S1388-2457
9900122-4
Kriegeskorte, N.
(2008). Representational similarity analysis—
Connecting the branches of systems neuroscience. Frontiers in
Systems Neuroscience, 2(November), 4. https://doi.org/10.3389/
neuro.06.004.2008
Lachaux,
J.-P., Rodriguez, E., Martinerie,
J.
(1999). Measuring phase synchrony in brain signals. Human
Brain Mapping, 8(4), 194–208. https://doi.org/10.1002/(SICI)1097-
0193(1999)8:4<194::AID-HBM4>3.0.CO;2-C
J., & Varela, F.
Lopes da Silva, F. (2013). EEG and MEG: Relevance to neuroscience.
Neuron, 80(5), 1112–1128. https://doi.org/10.1016/j.neuron.2013.
10.017
Lynall, M. E., Bassett, D. S., Kerwin, R., McKenna, P. J., Kitzbichler,
M., Muller, U., & Bullmore, E. (2010). Functional connectivity
and brain networks in schizophrenia. Journal of Neuroscience,
30(28), 9477–87. https://doi.org/10.1523/JNEUROSCI.0333-10.
2010
Maiorana, E., La Rocca, D., & Campisi, P. (2016). On the perma-
nence of EEG signals for biometric recognition. IEEE Transactions
on Information Forensics and Security, 11(1), 163–175. https://
doi.org/10.1109/TIFS.2015.2481870
Mueller, S., Wang, D., Fox, M. D., Sì, B. T. T., Sepulcre, J.,
Sabuncu, M. R., . . . Liu, H.
Individual variability in
functional connectivity architecture of the human brain. Neuron,
77(3), 586–595. doi: https://doi.org/10.1016/j.neuron.2012.12.
028
(2013).
Nikulin, V. V., & Brismar, T. (2004). Long-range temporal correla-
tions in alpha and beta oscillations: Effect of arousal level and
test-retest reliability. Clinical Neurophysiology, 115(8), 1896–1908.
https://doi.org/10.1016/j.clinph.2004.03.019
Oostenveld, R., Fries, P., Maris, E., & Schoffelen, J. M. (2011). Field-
trip: Open source software for advanced analysis of MEG, EEG,
and invasive electrophysiological data. Computational Intelli-
gence and Neuroscience, 2011. https://doi.org/10.1155/2011/
156869
Palva, J. M., Monto, S., Kulashekhar, S., & Palva, S. (2010). Neuronal
synchrony reveals working memory networks and predicts indi-
vidual memory capacity. Proceedings of the National Academy
of Sciences of the United States of America, 107(16), 7580–5.
https://doi.org/10.1073/pnas.0913113107
Palva, S., & Palva, J. M. (2012). Discovering oscillatory interaction
networks with M/EEG: Challenges and breakthroughs. Trends
in Cognitive Sciences, 16(4), 219–229. https://doi.org/10.1016/
j.tics.2012.02.004
Panzeri, S., Macke, J. H., Gross, J., & Kayser, C. (2015). Neural pop-
ulation coding: Combining insights from microscopic and mass
signals. Trends in Cognitive Sciences, 19(3), 162–72. https://doi.
org/10.1016/j.tics.2015.01.002
Park, H., Lee, D. S., Kang, E., Kang, H., Hahm, J., Kim, J. S.,
. . . Jensen, O. (2014). Blocking of irrelevant memories by poste-
rior alpha activity boosts memory encoding. Human Brain Map-
ping, 35(8), 3972–3987. https://doi.org/10.1002/hbm.22452
Network Neuroscience
511
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
N
e
N
_
UN
_
0
0
0
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Large-scale oscillation patterns
Peña-Gómez, C., Avena-Koenigsberger, A., Sepulcre, J., & Sporns,
O.
(2017). Spatiotemporal network markers of individual var-
iability in the human functional connectome. Cerebral Cortex,
(2014), 1–13. https://doi.org/10.1093/cercor/bhx170
Perrin, F., Pernier, J., Bertrand, O., & Echallier, J. F. (1989). Spher-
ical splines for scalp potential and current density mapping.
Electroencephalography and Clinical Neurophysiology, 72(2),
184–187.
Pfurtscheller, G.
(1992). Event-related synchronization (ERS): An
electrophysiological correlate of cortical areas at rest. Electro-
encephalography and Clinical Neurophysiology, 83(1), 62–69.
https://doi.org/10.1016/0013-4694(92)90133-3
Rocca, D. IL, Campisi, P., Vegso, B., Cserti, P., Kozmann, G.,
Babiloni, F., & Fallani, F. D. V. (2014). Human brain distinc-
tiveness based on EEG spectral coherence connectivity. IEEE
Transactions on Biomedical Engineering, 61(9), 2406–2412.
https://doi.org/10.1109/TBME.2014.2317881
Salinsky, M. C., Oken, B. S., & Morehead, l.
(1991). Test-retest
reliability in EEG frequency analysis. Electroencephalography
and Clinical Neurophysiology, 79(5), 382–392. https://doi.org/
10.1016/0013-4694(91)90203-G
Sanz-Arigita, E.
J., Schoonheim, M. M., Damoiseaux,
J. S.,
Rombouts, S. UN. R. B., Maris, E., Barkhof, F., . . . Stam, C. J.
(2010). Loss of “small-world” networks in Alzheimer’s disease:
Graph analysis of fMRI resting-state functional connectivity. PLoS
ONE, 5(11). https://doi.org/10.1371/journal.pone.0013788
Schultz, D. H., & Cole, M. W. (2016). Higher intelligence is associ-
ated with less task-related brain network reconfiguration. Journal
of Neuroscience, 36(33), 8551–8561. https://doi.org/10.1523/
JNEUROSCI.0358-16.2016
Schyns, P. G., Thut, G., & Gross, J.
(2011). Cracking the code of
oscillatory activity. PLoS Biology, 9(5), e1001064. https://doi.
org/10.1371/journal.pbio.1001064
Siegel, M., Donner, T. H., & Engel, UN. K.
(2012). Spectral finger-
prints of large-scale neuronal interactions. Nature Reviews Neuro-
science,13(Febbraio), 20–25. https://doi.org/10.1038/nrn3137
Siems, M., Pape, A.-A., Hipp, J. F., & Siegel, M. (2016). Measuring
the cortical correlation structure of spontaneous oscillatory ac-
tivity with EEG and MEG. NeuroImage, 129, 345–355. https://
doi.org/10.1016/j.neuroimage.2016.01.055
Smit, D. J. A., Boomsma, D. I., Schnack, H. G., Hulshoff Pol, H. E.,
& de Geus, E. J. C. (2012). Individual differences in EEG spectral
power reflect genetic variance in gray and white matter volumes.
Twin Research and Human Genetics, 15(3), 384–392. https://
doi.org/10.1017/thg.2012.6
Smit, D. J. A., Stam, C. J., Posthuma, D., Boomsma, D. I., &
De Geus, E. J. C. (2008). Heritability of “small-world” networks in
the brain: A graph theoretical analysis of resting-state EEG func-
tional connectivity. Human Brain Mapping, 29(12), 1368–1378.
https://doi.org/10.1002/hbm.20468
Tambini, A., & Davachi, l.
(2013). Persistence of hippocampal
multivoxel patterns into postencoding rest is related to memory.
Proceedings of the National Academy of Sciences of the United
States of America, 110(48), 19591–6. https://doi.org/10.1073/
pnas.1308499110
Tenke, C. E., & Kayser, J. (2015). Surface Laplacians (SL) and phase
properties of EEG rhythms: Simulated generators in a volume-
International Journal of Psychophysiology,
conduction model.
97(3), 285–298. https://doi.org/10.1016/j.ijpsycho.2015.05.008
(2012). The functional impor-
tance of rhythmic activity in the brain. Current Biology, 22(16),
R658–R663. https://doi.org/10.1016/j.cub.2012.06.061
Thut, G., Miniussi, C., & Gross, J.
Van Beijsterveldt, C. E. M., & Van Baal, G. C. M.
(2002). Twin
and family studies of the human electroencephalogram: A review
and a meta-analysis. Biological Psychology, 61(1–2), 111–138.
https://doi.org/10.1016/S0301-0511(02)00055-8
van den Heuvel, M. P., & Sporns, O. (2013). Network hubs in the
human brain. Trends in Cognitive Sciences, 17(12), 683–696.
https://doi.org/10.1016/j.tics.2013.09.012
Vinck, M., Oostenveld, R., Van Wingerden, M., Battaglia, F.,
& Pennartz, C. M. UN.
(2011). An improved index of phase-
synchronization for electrophysiological data in the presence of
volume-conduction, noise and sample-size bias. NeuroImage,
55(4), 1548–1565. https://doi.org/10.1016/j.neuroimage.2011.
01.055
Watrous, UN. J., Fell, J., Ekstrom, UN. D., & Axmacher, N.
(2015).
More than spikes: Common oscillatory mechanisms for content
specific neural representations during perception and memory.
Current Opinion in Neurobiology, 31, 33–39. https://doi.org/10.
1016/j.conb.2014.07.024
Watrous, UN. J., Tandon, N., Conner, C. R., Pieters, T., & Ekstrom,
UN. D. (2013). Frequency-specific network connectivity increases
underlie accurate spatiotemporal memory retrieval. Nature Neuro-
science, 16(3), 349– 356. https://doi.org/10.1038/nn.3315
Network Neuroscience
512
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
4
4
8
1
1
0
9
2
2
6
8
N
e
N
_
UN
_
0
0
0
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3