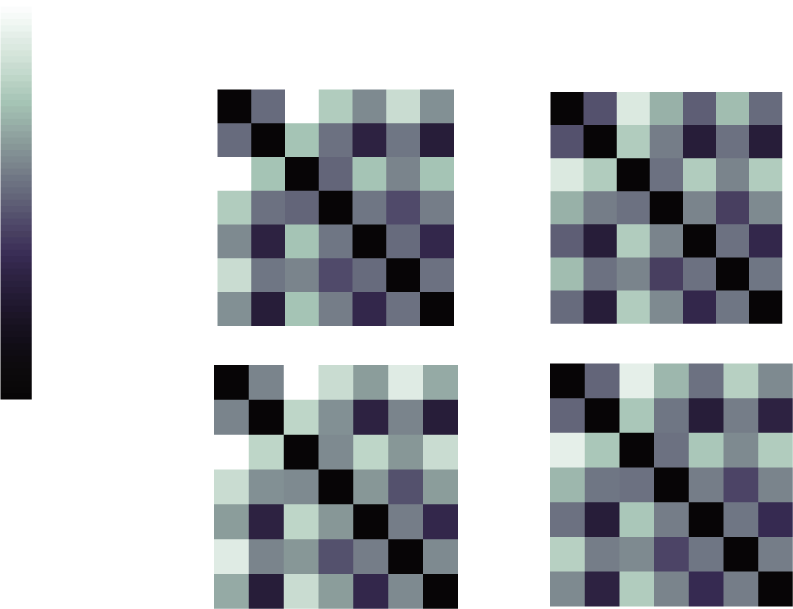RESEARCH
Ensemble stacking mitigates biases in inference
of synaptic connectivity
Brendan Chambers1, Maayan Levy1, Joseph B. Dechery1, and Jason N. MacLean1,2
1Committee on Computational Neuroscience, University of Chicago, Chicago, IL, USA
2Department of Neurobiology, University of Chicago, Chicago, IL, USA
Keywords: Network analysis, Network motifs, Simulation and modeling, Synaptic connectivity,
Information theory, Ensemble learning
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
A promising alternative to directly measuring the anatomical connections in a neuronal
population is inferring the connections from the activity. We employ simulated spiking
neuronal networks to compare and contrast commonly used inference methods that identify
likely excitatory synaptic connections using statistical regularities in spike timing. We find
that simple adjustments to standard algorithms improve inference accuracy: A signing
procedure improves the power of unsigned mutual-information-based approaches and a
correction that accounts for differences in mean and variance of background timing
relationships, such as those expected to be induced by heterogeneous firing rates, increases
the sensitivity of frequency-based methods. We also find that different inference methods
reveal distinct subsets of the synaptic network and each method exhibits different biases in
the accurate detection of reciprocity and local clustering. To correct for errors and biases
specific to single inference algorithms, we combine methods into an ensemble. Ensemble
predictions, generated as a linear combination of multiple inference algorithms, are more
sensitive than the best individual measures alone, and are more faithful to ground-truth
statistics of connectivity, mitigating biases specific to single inference methods. These
weightings generalize across simulated datasets, emphasizing the potential for the broad
utility of ensemble-based approaches.
AUTHOR SUMMARY
Mapping the routing of spikes through local circuitry is crucial for understanding neocortical
computation. Under appropriate experimental conditions, these maps can be used to infer
likely patterns of synaptic recruitment, linking activity to underlying anatomical connections.
Such inferences help to reveal the synaptic implementation of population dynamics and
computation. We compare a number of standard functional measures to infer underlying
connectivity. We find that regularization impacts measures heterogeneously, and that
individual algorithms have unique biases that impact their interpretation. These biases are
nonoverlapping, and thus have the potential to mitigate one another. Combining individual
algorithms into a single ensemble method results in a stronger inference algorithm than the
best individual component measure. Ensemble-based inference can yield higher sensitivity
to underlying connections and an improved estimate of the true statistics of synaptic
recruitment.
Citation: Chambers, B., Levy, M.,
Dechery, J. B., & MacLean, J. N. (2018).
Ensemble stacking mitigates biases in
inference of synaptic connectivity.
Network Neuroscience. 2 (1), 60–85.
https://doi.org/10.1162/netn_a_00032
DOI:
https://doi.org/10.1162/netn_a_00032
Received: 23 May 2017
Accepted: 11 ottobre 2017
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Jason N. MacLean
jmaclean@uchicago.edu
Handling Editor:
Olaf Sporns
Copyright: © 2017
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
INTRODUCTION
Propagation of activity within neuronal networks is largely determined by underlying syn-
aptic connectivity (Gerstein & Perkel, 1969; Kumar, Rotter, & Aertsen, 2010; Lindsey, Morris,
Shannon, & Gerstein, 1997). This link has been demonstrated using recordings from pairs
and small groups of neurons and has provided insights into plasticity processes (Kruskal, Li, &
MacLean, 2013; Lalanne, Abrahamsson, & Sjöström, 2016), circuit structure (Ko et al., 2011;
Perin, Berger, & Markram, 2011; Song, Sjöström, Reigl, Nelson, & Chklovskii, 2005), E
noise correlations (Hofer et al., 2011). While methods such as paired patch clamp recordings
or electron microscopy provide unambiguous indication of a synaptic connection, they are
technically limited to the examination of a small number of connections with unknown func-
tional relationships. Consequently, the statistics of circuit connectivity at the mesoscopic scale
are difficult to conclude because of finite size effect errors (Vegue, Perin, & Roxin, 2017). In
contrasto, measures of dynamics, such as those generated by two-photon imaging of calcium
fluorescence indicators (Sadovsky et al., 2011), allow up to 1,000 neurons to be recorded
but require that synaptic connections be inferred using statistical dependencies in spike tim-
ing. Because neuronal spiking in neocortical networks requires synaptic input, the causal
relationship between connectivity and activity can be exploited to infer network topology in
direct relation to synaptic recruitment (Chambers & MacLean, 2015). In this framework, sta-
tistical dependencies in the spiking activity between pairs of neurons within a population are
summarized as a weighted directed graph, and this weight matrix is informative about the like-
lihood of synaptic connections as well as their functional relationship. Only those synapses
directly contributing to spike-time dependencies can be captured and summarized by these
weight matrices (Chambers & MacLean, 2015). While this lessens the number of synaptic
connections that can be inferred, this subset of connections (which we have referred to as
the “recruitment” network) has particular importance for the propagation of spiking and is a
desirable target for inference (Chambers & MacLean, 2016). Study of the link between struc-
tural and functional connectivity has the promise to reveal mechanistic insights as to how
information flow is directed across networks, and the number of studies employing inference
algorithms has grown rapidly.
In this paper we compare and contrast the performance of a
number of common inference methods, identify biases specific to individual inference meth-
ods, and then combine them in an ensemble to mitigate these biases and consequently improve
inference of synaptic connectivity within large networks of neurons.
The importance of bridging function and structure is highlighted by the increasing diversity
of methods for predicting synaptic connectivity from spiking activity. These efforts encom-
pass methods based on counting lagged firing events (Pajevic & Plenz, 2012), lagged correla-
zione (Sadovsky & MacLean, 2013), mutual information (Endo, Santos, Simpson, Maciel, &
Newland, 2015), and transfer entropy (Ito et al., 2011; Stetter, Battaglia, Soriano, & Geisel,
2012) sometimes also referred to as conditional mutual information (Zhang, Zhao, Hao, Zhao,
& Chen, 2015), as well as other approaches. Crucial to the performance of these methods is
the time resolution of the spike trains, or the bin size in the binning procedure (Chambers &
MacLean, 2015) over relevant timescales relating spiking to synaptic connectivity and inte-
gration. Consequently, we consider a range of bin widths in this work. The majority of these
metrics are formulated in terms of correlations between consecutive time-bins, which implies
causality. Tuttavia, as the number of neurons densely recorded with imaging increases, ac-
quisition time generally increases as well, and the relevant correlations may shift from con-
secutive time-bins towards simultaneous time-bins. We thus propose variations of information
theoretic measures that account for simultaneous and joint time-bin correlations to reflect
common experimental constraints.
Recruitment network:
Contains only synapses that directly
contribute to post-synaptic firing
since these are the only synapses that
can be inferred.
Inference methods/algorithms/
measures:
Capture statistical dependency
between the spike trains of two
neurons. Per esempio, mutual
information and correlation.
Lagged firing:
Two neurons spiking in consecutive
time-bins.
Network Neuroscience
61
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Ensemble method/approach:
A machine-learning-inspired
approach in which multiple
inference methods are pooled.
Because each of the inference algorithms differentially quantifies statistical features of
population dynamics, it is possible that they identify nonidentical sets of connections. There-
fore, it is opportune to turn to progress in machine learning and bioinformatics, which have
shown that combining approaches has the potential to pool over strengths and neutralize
weaknesses of their constituent algorithms (Marbach et al., 2012). Collectively, these strate-
gies are known as ensemble methods. An early formal description of an ensemble method
was introduced to address the difficulty of optimization under conditions of multiple local
minima in neural networks (Hansen & Salamon, 1990). Ensemble learning has been shown to
occur in both the frequentist and Bayesian frameworks of machine learning exemplified respec-
tively by boosting (Freund & Schapire, 1995; Schapire, 1990) and Bayesian optimal classifiers
In diverse settings, combinations of algorithms can be stacked together
(Dietterich, 2000).
to yield an aggregate that outperforms its components (Fast & Jensen, 2008). Tuttavia, it is
unclear whether an ensemble approach can be applied to the problem of synaptic inference.
We investigate this issue using simulated naturalistic spiking networks, where true underlying
connectivity is known in full. Computational models are well suited to investigating synaptic
topology, because they present transparent access to synaptic connectivity and spike timing.
Prior work has demonstrated that random synaptic networks present the greatest challenges
for inferring synaptic connections from activity (Kobayashi & Kitano, 2013). Therefore,
although synaptic networks in the neocortex are known to be nonrandom, random models are
useful for benchmarking success rates in synaptic inference applications. It is also important
to consider naturalistic regimes of population activity, because network state can determine
the success or failure when inferring synaptic connections (Stetter et al., 2012). To compare
diverse inference methods and judge whether they may complement one another, we designed
network simulations to reflect naturalistic dynamics and reflect experimental constraints. Noi
show that an ensemble approach reveals a more extensive subset of the synaptic network, E
one that is more faithful to the true statistics of the synaptic recruitment network measured in
our simulations. A host of weighted combinations improve over the best individual measures,
and these weighting schemes are transferrable from one simulated dataset to another.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
METHODS
Network Simulations
In order to obtain a ground truth for network connectivity, we constructed six networks
of conductance-based leaky-integrate-and-fire (LIF) neurons,
to previous work
(Chambers & MacLean, 2015, 2016). Each simulated dataset was defined as a synaptic con-
nectivity matrix (Figure 1C) con 1,000 excitatory units and 200 inhibitory units, constructed
probabilistically according to a stochastic blocked model with naturalistic connection proba-
bilities. The excitatory subnetwork taken in isolation formed an Erdos-Renyi graph (p = 0.2).
Specifically, we set Pee = 0.2, Pei = 0.35, Pie = 0.25, and Pii = 0.3, with e denoting excitatory
units, i denoting inhibitory neurons, and the first and second letters in the subscript standing
for the pre- and post-synaptic neuron, rispettivamente.
similar
Each neuron’s membrane potential was governed by the following:
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
τm
dV
dt
= ge(Ee − V) + gi(Ei − V) + gl(El − V) + gtonic(Etonic − V),
τe
τi
dge
dt
dgi
dt
= −ge,
= −gi.
(1)
(2)
(3)
62
Network Neuroscience
Ensemble learning for inference of synapses
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 1.
Inferring synaptic connectivity from pairwise spike timing. (UN) Population spike raster
for 50 random excitatory model neurons during 40 s simulated recording. Three representative pairs
matched for firing rates are shown in color: strongly connected (orange), weakly connected (green),
and unconnected (blue). Spikes were binarized at 20 ms time-bins. (B) The same example pairs
as in panel A during another 20 s of simulated recording. (C) Ground-truth synaptic connectivity
for excitatory neurons shown in panel A. Edge width indicates weight. Arrows mark the strongly
connected pair (orange) and weakly connected pair (green). Width was enhanced for visibility
purposes. (D) Schematic of a synaptic network among four active neurons. (E) Synaptic recruitment
is defined as lagged firing between pre- and post-synaptic pairs. Under the conditions of a given
input, network state, and recording duration, not every synaptic connection recruits its post-synaptic
partner to generate an action potential. (F) Inferred synaptic connectivity (solid lines) mirrors the
recruitment network, mapping propagating activity. Errors occur when inference algorithms fail to
detect sites of synaptic recruitment (per esempio., missing edge from neuron 2 to neuron 1), or assign putative
connectivity (dashed lines) where there is none in truth.
A spike occurred every time the membrane potential crossed a threshold, set at −48 mV. Post
spike, membrane potential was then reset to −70 mV, and a 1-ms refractory period imposed.
Conductances and equilibrium potentials were defined for leak (l), excitatory synapses (e),
inhibitory synapses (io), and a tonic input serving to stabilize spiking (tonic) (Tavolo 1).
Tavolo 1. Parameters of the spiking network model
Parameter
Ei
Ee
El
Etonic
Value
−90 mV
0 mV
−65 mV
0 mV
Parameter
gl
gtonic
τm
τe
τi
Value
0.2 mS
0.2 mS
20 mS
10 mS
5 mS
63
Network Neuroscience
Ensemble learning for inference of synapses
Synaptic weights were randomly sampled from a lognormal distribution with location and
scale parameters µ = −0.64 and σ = 0.51. The resulting weights distribution had a mean of
0.6 and variance of 0.11, relative to the scale of the leak conductance. Since an important sub-
set of inhibitory projections onto excitatory cells tend to synapse on the soma and proximal
dendrites (Markram et al., 2004) and are thus more potent, we enhanced I to E weights by
50%. We started each simulation by initializing membrane potentials to values drawn ran-
domly from a normal distribution with a mean of −65 mV and a standard deviation of 5 mV.
A pool of 50 Poisson neurons was used as input to the network. Poisson neurons spiked at
15 Hz and were independently connected to excitatory units with P = 0.1 E 0.6 synap-
tic weight in the units of the leak conductance. The network was driven with the input pool
for 50 ms and activity was allowed to continue for 100 ms, after which the simulation was
terminated. This procedure was repeated over 100 trials with 10 different inputs. All sim-
ulations were carried out using the Brain Simulator (Goodman & Brette, 2009), with Euler’s
method for integration and time steps of 1 ms.
Inference Measures
Spikes were binned in six time resolutions (1, 5, 10, 20, 40, E 80 ms) into time frames con-
taining binary values, resulting in 150,000, 30,000, 15,000, 7,500, 3,750, E 1,875 bins,
rispettivamente. We employed seven pairwise measures of connectivity between neurons: lag
count, abbreviated as count; lag correlation, abbreviated correlation; consecutive mutual in-
formation (cMI); simultaneous MI(sMI); confluent MI(conMI); first-order transfer entropy (TE
[k = 1]); and second-order transfer entropy (TE [k = 2]). We thus consider a wide array of
inference algorithms ranging in sophistication.
For each pair of neurons i, j we defined a binary variable ckl
ij (T), which evaluates to 1 if
io(T) = k and j(T + 1) = l. Per esempio,
c11
ij (T) =
1
0
(
io(T) = 1
and j(T + 1) = 1
otherwise
.
Lag count was then calculated as
countij =
T−1
∑
t=1
c11
ij (T),
where T is the number of time-bins.
Lag correlation between two spike trains was calculated using the phi coefficient:
(4)
(5)
T−1
∑
t=1
c11
ij (T) ·
T−1
∑
t=1
correlationij = (cid:20)
c00
ij (T)
−
T−1
∑
t=1
(cid:21)
(cid:20)
2(T − 1)
c10
ij (T) ·
T−1
∑
t=1
c01
ij (T)
(cid:21)
.
(6)
We use three versions of mutual information; consecutive mutual information (cMI) between
a pair of neurons i, j was calculated as
P
cMIij = ∑
io(T)∈{0,1}
∑
j(t+1)∈{0,1}
P(io(T), j(T + 1)) · log2
P(io(T), j(T + 1))
P(io(T)) · p(j(T + 1))
.
(cid:21)
(cid:20)
(7)
64
Network Neuroscience
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Tuttavia, we note that binning spikes into longer time-bins may result in the pre- and post-
synaptic spikes being binned into the same bin. Così, we also consider simultaneous mutual
informazione (sMI),
sMIij = ∑
io(T)∈{0,1}
∑
j(T)∈{0,1}
P(io(T), j(T)) · log2
P(io(T), j(T))
P(io(T)) · p(j(T))
,
(cid:21)
(cid:20)
and confluent mutual information (conMI),
conMIij = ∑
io(T)∈{0,1}
∑
j(ˆt)∈{0,1}
P(io(T), j(ˆt)) · log2
P(io(T), j(ˆt))
P(io(T)) · p(j(ˆt))
,
(cid:21)
(cid:20)
(8)
(9)
where j(ˆt) =
1
0
(
j(T) = 1 OR j(T + 1) = 1
otherwise
.
As nonsymmetric information theoretical measures we calculated transfer entropies under
first- and second-order Markov models (TE1 and TE2, rispettivamente) between every pair i, j of
neurons:
TE1ij =
∑
j(T),j(t+1),io(T)∈{0,1}
P(io(T), j(T + 1), j(T)) · log2
P(j(T)) · p(io(T), j(T + 1), j(T))
P(io(T), j(T)) · p(j(T + 1), j(T))
(cid:20)
.
(10)
(cid:21)
TE2 is similarly defined, with the information i(T) is providing about j(T + 1) conditioned not
only on j(T) but also on j(t − 1).
Measure Evaluation
In order to evaluate performance of individual measures and the combined ensemble, we
calculated the recruitment network for each model. The recruitment network (Figures 1D–F)
is the intersection between the connectivity matrix and those synapses that directly contribute
to post-synaptic firing, since these are the only synapses that can be inferred using spikes (Vedere
schematic; Chambers & MacLean, 2016). We first defined the active network in a similar
way to countij (Equazione 5), but modified ckl
ij (T) so that both consecutive and simultaneous
time-bins are considered:
ˆc11
ij (T) =
(
1 io(T) = 1 E
0
[j(T) = 1 OR j(T + 1) = 1]
otherwise
,
activeij =
T−1
∑
t=1
ˆc11
ij (T).
The recruitment network was then computed as a binary matrix:
recruitmentij =
1 activeij > 0 AND adjij > 0
otherwise
0
,
(
(11)
(12)
(13)
where adjij is the adjacency matrix used to run the simulation.
The percentage of connections retained in the recruitment network out of the static synaptic
connectivity is described in Table 2. Previously we have reported that it is only possible to
infer connections that are active and temporally proximal to an action potential in the post-
synaptic neuron (Chambers & MacLean, 2015). To reflect this fact we used the recruitment
Network Neuroscience
65
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Tavolo 2. Percentage of connections retained in the recruitment network
Simulated dataset 1
Simulated dataset 2
Simulated dataset 3
Simulated dataset 4
Simulated dataset 5
Simulated dataset 6
Data are shown for six simulated datasets binned at five time resolutions.
20 ms
47.97%
53.18%
52.17%
58.57%
56.08%
54.36%
10 ms
40.82%
46.42%
45.63%
50.85%
49.38%
47.58%
5 ms
34.95%
41.41%
39.81%
45.72%
43.29%
42.32%
40 ms
53.49%
57.75%
56.70%
64.58%
61.04%
59.56%
80 ms
60.89%
65.22%
63.56%
72.32%
68.09%
67.14%
network as ground truth, and defined performance of an algorithm as the number of inferred
connections at 80% true positive rate. This true positive rate was chosen based on survival
curve analysis on three representative measures at all time resolutions (Figura 5). This definition
provides a realistic test of performance, as only those active connections that contribute to
spiking in the post-synaptic neuron can be captured by an inference algorithm of any kind.
A lower threshold and increased coverage under the same true positive rate means that as
the refinement process progresses, inferred adjacency matrices become sparser because false
alarms are being removed from those matrices.
Ensemble Weights and Scores
We employed a simulated annealing strategy with cyclical dynamics to search over weighted
linear combinations of individual measures. Before pooling, individual measures were normal-
ized by their maximum value to provide a uniform scale. The final inputs into the simulated
annealing algorithm were then computed as the following:
S(M)ij =
norm residual(M)ij
max(norm residual(M))
· sgn(norm residual(M)ij),
(14)
S(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
(cid:12)
where norm_residualij is the final transformation of every measure, and defined in the results
(Equazione 20); sgn denotes the sign; and m stands for the measure used, so each measure had
its own Sij.
The random search algorithm was used to train weights independently on each of six sim-
ulated networks using coverage at 80% accuracy as our objective function (Figure 7A). Questo
objective function proved to be pockmarked with many local maxima, motivating the use
of repeated increment and cooling in the annealing process to avoid local maximum traps
(Kirkpatrick, Gelatt, & Vecchi, 1983). As step size decreased, if no further gains were achieved,
the search algorithm would occasionally jump to the last step size that did yield improve-
menti. If these larger jumps still failed to improve the performance, the jump size was further
increased. Weights were learned across five repeats of training for each model and timescale
(Figure 7A, 10 ms).
An ensemble score was then calculated for each pair of neurons as a linear weighted sum
of S(M)ij (Equazione 14):
Ensembleij =
M
∑
m=1
wm · S(M)ij,
(15)
where wm are the weights of the measures found by the annealing algorithm, and M is the
number of measures.
Network Neuroscience
66
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Comparison Between Inference Measures
All comparisons were conducted after completing the regularization steps described in the
Results section, questo è, on the normalized-residual adjacencies. Since summary statistics for
adjacency matrices are impacted by edge density, inferred adjacency matrices were thresh-
olded to match sparseness before conducting any comparisons, isolating just the strongest
relationships for each measure. To match sparseness, thresholding was performed at the 98th
percentile, leaving the top 2% of entries for each measure. Weights exceeding the inclusion
threshold were mapped to 1 and those failing to reach inclusion threshold were mapped to 0.
This pruning procedure allowed us to more clearly identify biases inherent to individual algo-
rithms, and was not used to evaluate performance. Similarity between measures was assessed
by vectorizing adjacency matrices and comparing the Euclidean distances separating each pair
of measures. This comparison was performed independently for each simulated dataset. Reci-
procity was quantified as the probability a randomly selected nonzero edge from neuron i to
neuron j was accompanied by a nonzero edge from j to i. Local clustering for neuron k was
quantified as the counted number of connected triangles including k divided by the number
of possible triangles including k. In this formulation, a triangle must be composed of neuron k
plus two immediate neighbors of k, without constraints on directionality. Così, local clustering
quantifies neighbor-of-neighbor relationships in the immediate neighborhood around k. Reci-
procity and local clustering were aggregated by taking the mean over all edges and neurons,
rispettivamente, in the simulated dataset.
RESULTS
Simulated Neuronal Networks
Randomly connected recurrent networks (Figure 1C) composed of 1,000 excitatory and 200
inhibitory LIF neurons showed persistent naturalistic activity after being driven by a sparse set
of Poisson inputs for 50 ms. Across six randomly connected networks, 99 ± 0.05% (mean ± SD)
of neurons within the excitatory pool spiked at least once, and displayed sparse asynchronous-
irregular firing (Figures 1A and 1B). Firing rates were 1.66 ± 3.30 Hz (mean ± SD) and followed
a lognormal distribution, and single units showed irregular spiking consistent with experimen-
tal measures in cortical neurons (Destexhe, Rudolph, & Paré, 2003; Softky & Koch, 1993), con
inter-spike interval coefficient of variation 1.04 ± 0.20 (mean ± SD). The numbers of spikes
used for inference in the six simulated datasets varied and depended on the size of the time-bin
used (Tavolo 3). Using these simulated networks, which produced naturalistic spiking activity,
we examined whether spiking activity within the network can be used to reveal underlying
synaptic connectivity across the population. We employed sparse recurrent networks with
random connectivity, constructed probabilistically according to naturalistic parameters (Vedere
Tavolo 3. Number of spikes per trial used for inference
Simulated dataset 1
Simulated dataset 2
Simulated dataset 3
20 ms
130.12 ± 224.07
225.82 ± 471.20
251.24 ± 536.08
208.32 ± 339.47
269.80 ± 514.41
216.26 ± 404.11
Simulated dataset 6
Data represent mean ± SD for six simulated networks binned at five time resolutions.
5 ms
135.13 ± 239.70
233.75 ± 513.30
264.25 ± 602.24
212.17 ± 340.30
282.00 ± 557.41
221.79 ± 424.11
10 ms
134.89 ± 238.94
233.34 ± 510.44
263.35 ± 595.56
212.02 ± 339.90
281.34 ± 554.79
221.58 ± 423.26
Simulated dataset 4
Simulated dataset 5
40 ms
118.02 ±189.30
205.27 ± 384.84
222.39 ± 425.01
196.14 ± 295.79
241.43 ± 424.08
200.09 ± 348.86
80 ms
102.41 ± 148.06
178.00 ± 286.54
187.51 ± 311.65
177.62 ± 245.71
205.72 ± 320.39
176.78 ± 274.40
Network Neuroscience
67
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Motif:
A pair or triplet of neurons
connected in a certain pattern. For
esempio, a fan-in triangle.
the Methods section). Under some circumstances, nonrandom connectivity (per esempio., local clus-
tering) can facilitate inference of connections (Kobayashi & Kitano, 2013), so random synaptic
connectivity may provide a more appropriate benchmark for comparing inference methods,
particularly in assessing their propensity towards false-positive errors. Because connectivity
in neocortex is not random (Song et al., 2005), the results presented here can be interpreted
as a proof of concept of what is achievable when applying these inference approaches to
experimental data. While it remains unclear how broadly results generated using randomly
connected networks generalize, we have found that specific motifs of higher order correlations
found in random networks are also found in spiking data collected from neocortex (Chambers
& MacLean, 2016). There have been a number of studies that have examined whether corre-
lation can be informative of causal connections, and it remains unclear how to best utilize the
information provided by different inference approaches to uncover synaptic connectivity. As
can be seen in Figure 1B, synchronous or lagged events occur for both strongly and weakly
connected neuron pairs, as well as by chance for unconnected neurons, rendering the task of
interaction inference difficult. Here we introduce a series of refinements to traditional connec-
tivity measures and demonstrate improvement in our ability to correctly identify monosynaptic
excitatory connections using spiking across a recorded population of neurons.
Signed Information Theoretic Measures: Removing Negative Correlations
There are a number of approaches to inference. Some address the frequency of lagged or si-
multaneous spiking directly, such as the count method and the correlation method. For these
measures, edge e = (io, j) is positive only if there is the possibility that neuron i recruited neu-
ron j to fire—that is, only if j becomes active after i at least once (Figure 2A). In contrasto,
mutual information is related to lagged firing in a more abstract sense. As a practical conse-
quence, the entries of MIij can be large given any type of interaction between the pre- E
post-synaptic neurons. Infatti, we find that many pairs that were ranked highly under mutual
information and transfer entropy had negative correlationij scores (Figures 2B and 2C). E-
surprisingly given the negative scores, the majority of those pairs were not monosynaptically
connected, despite their high information theoretic scores. In order to account for interaction
directionality consistent with causal synaptic interactions, we signed our mutual information
and transfer entropy metrics on the basis of correlationij:
signed(X)ij = Xij · sgn(correlationij),
(16)
where X stands for the information theoretic measure considered (per esempio., signed(conMI)ij is the
signed confluent mutual information between neurons i and j).
The signing procedure yielded gains in accuracy. These improvements are apparent when
comparing the thresholds achieving 80% prediction accuracy for the raw versus signed metrics
(Figures 2B and 2C). We confirmed the intuition that negative interactions can confound the
detection of excitatory connections using information theoretic methods but can be accounted
for. It remains an open question whether negative information theoretic scores are indicative of
inhibitory connections. Inference of inhibitory connectivity is especially challenging, because
of the ambiguity in distinguishing inhibition per se from the absence of excitatory drive. In this
lavoro, we consider only the positive entries of signed(X)ij, and denote those pos(X)ij.
Removing Additional Spurious Correlations
Removing negative correlations allowed us to identify and correct for one source of false pos-
itives. Nevertheless, it remained clear that a significant overlap between our true positive
Network Neuroscience
68
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
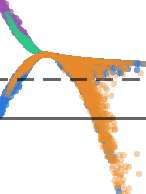
Figura 2. Leveraging anticorrelations to isolate excitatory connections. Data in this figure are from
a randomly chosen representative simulated network binned at 20 ms, and subsampled according
to density for display purposes.
(UN) Unconnected pairs often attained high lagged-count scores,
but tended to exhibit negative-shifted lag correlations compared with connected pairs. Signing
lag count scores on the basis of lag correlation thus improved performance, although signed lag
count still fails to achieve sensitivity at the 80% accuracy threshold. (B) A subset of unconnected
pairs exhibited high consecutive mutual information scores and strong negative lag correlations.
Signing consecutive mutual information entries on the basis of lagged correlations dramatically
improved sensitivity at the 80% accuracy threshold, increasing from 297 putative connections to
1,987 putative connections in the representative model dataset. (C) Transfer entropy is prone to the
same errors, so that signing transfer entropy scores based on lag correlation extends coverage of
putative connections from 176 A 1,611 directed pairs.
signal and false-positive background is still present. We observed that false positives some-
times appeared to span source and target nodes with high weighted out- and in-degrees. In-
deed, functional interactions are known to be heterogeneous with a heavy tail (Nigam et al.,
2016; Sadovsky & MacLean, 2013; Shimono & Beggs, 2015), revealing indiscriminate patterns
of spike-time coordination. Since experimental evidence indicated that synaptic connectivity
is sparse, we reasoned that neurons with extremely high weighted degrees reflected coordi-
nation in activity not arising from monosynaptic connections alone, but rather coordinated
population dynamics. For the purpose of identifying likely synaptic pairs, these are “back-
ground” spurious correlations. We estimated the magnitude of these background correlations,
which depended on pre- and post-synaptic identity, and removed them from inferred weights.
Previous work employing mutual information to infer protein interactions had shown that
removing spurious correlations by linear regression refined inference and preferentially iden-
tified residues known to interact physically (Little & Chen, 2009). Inspired by this work, we
asked whether a similar correlation existed in the neuronal interactions of our networks. Not-
ing that positive values of information theoretic scores have highly skewed distributions, we
reexpressed the measures with the exception of count because of the discrete nature of the
metric. Reexpression was performed by Tukey’s ladder of power (Tukey, 1977), which finds
the exponent that minimizes a distribution skewness:
a =
arg min
UN
skewness(pos(X)UN).
Each measure was reexpressed accordingly:
redist(X) = pos(X)UN.
(17)
(18)
Having reexpressed the scores, we next calculated the background signal for each pair of
neurons. This was achieved by averaging the scores of the pre- and post-synaptic neurons when
Network Neuroscience
69
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
partnered with every other potential post- and pre-synaptic neuron in the network, rispettivamente.
This is equivalent to taking the mean across columns for the pre-synaptic neuron, and across
rows for the post-synaptic neuron, excluding the partner neuron currently examined. Noi
multiplied those mean scores for the pre- and post-synaptic neuron, denoted backgroundij:
backgroundij =
redist(Xi,1:N−{j})
·
redist(X1:N−{io},j)
,
(19)
where h. . .i is the mean.
D
E
D
E
A high average score, while potentially indicative of wide-reaching polysynaptic influence
Infatti, backgroundij
across the network, is unlikely to reveal monosynaptic connections.
was found to be highly correlated with countij (Figure 3A), and only to a lesser extent with
information theoretic measures, although correlations were still significant (Figures 3B and 3C).
In order to remove the influence of this background signal, we calculated the residual of
each measure, residual(X)ij, over background(X)ij by linear regression. We found improved
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
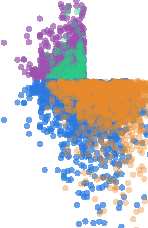
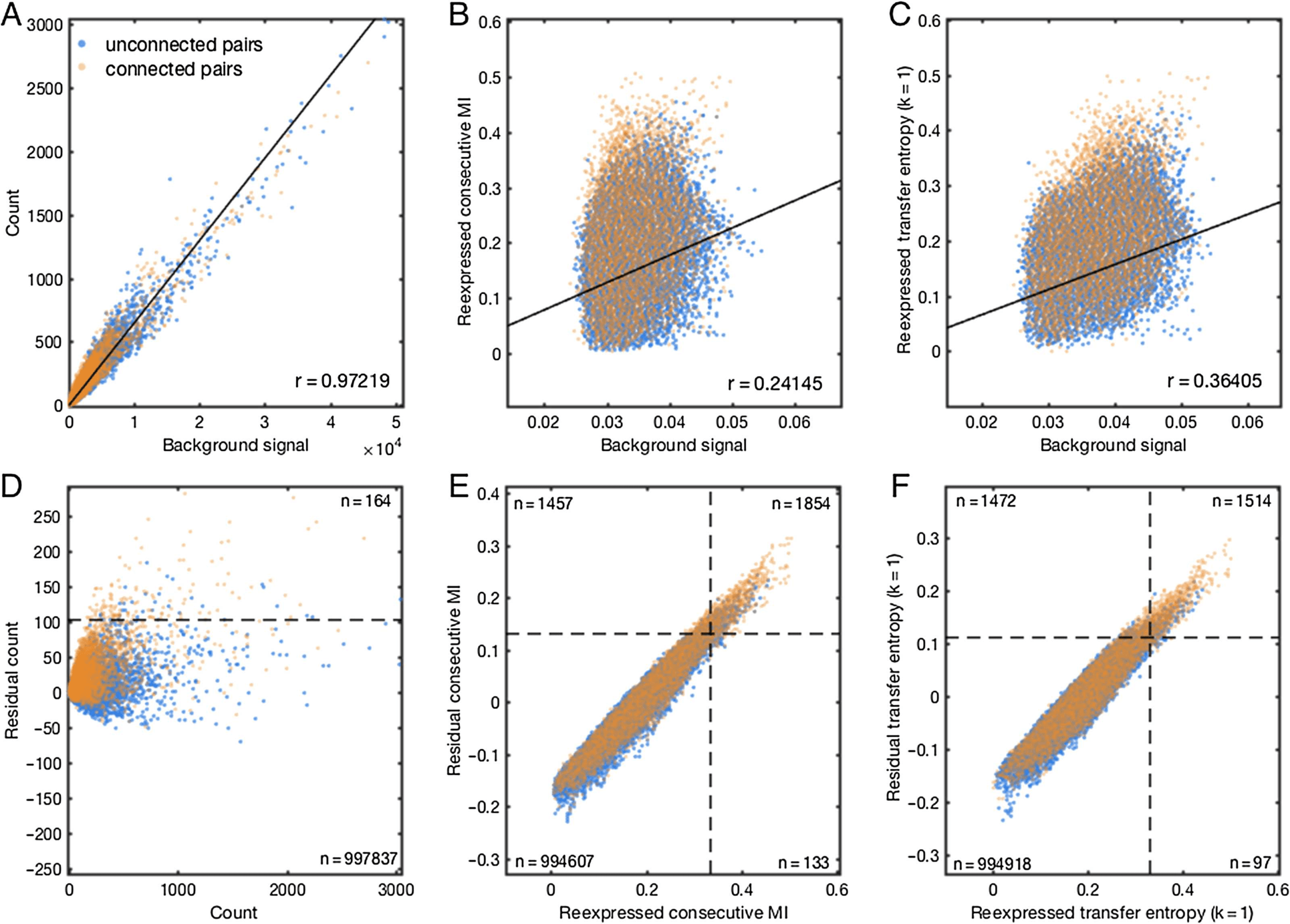
Figura 3. Removal of mean background timing relationships improves detection of synaptic pairs.
Data in this figure are from a randomly chosen representative simulated network binned at 20 ms,
and subsampled according to density for display purposes. (UN) Linear regression revealed a strong
background component in the count measure, reflecting a tendency for strong timing relationships
to appear in tandem at select model neurons, encompassing both connected and unconnected
pairs. (B) After reexpressing global weights for each measure to approximate normality, a weaker
but significant background signal was revealed for the consecutive mutual information measure. (C)
Background signal manifested somewhat more strongly for the transfer entropy (k =1) measure. (D)
Removal of mean neuron-wise background signal improved performance for the count measure, Ma
unconnected pairs with high residual scores remained a serious obstacle to high performance. (E)
For the consecutive mutual information measure, removal of background signal improved coverage
at the 80% accuracy threshold from 1,987 (two right quadrants) A 3,311 (two top quadrants) putative
pairs. (F) For the transfer entropy (k =1) measure, removal of background improved coverage at the
80% accuracy threshold from 1,611 A 2,986 putative pairs.
Network Neuroscience
70
Ensemble learning for inference of synapses
coverage with the residual scores over the reexpressed scores, with up to eightfold increase
(93% increase on average) in connections uncovered with information theoretic measures
corrected in this manner (Figures 3D and 3F).
Scaling Residuals to Account for Heteroskedasticity
Although accounting for the tendency of the neurons to participate in many interactions im-
proved detection, pairs with high background signal were more dispersed around the regres-
sion line, especially for countij. In other words, the variance of residual(X)ij was dependent
on background(X)ij, hence displaying heteroskedasticity. This is evident from examining the
residuals plotted against ranked background(X)ij (Figures 4A–C). These differences in vari-
ance confound detection since pairs with high background signal are more likely to exceed
selection thresholds. We found that heteroskedasticity affected connected as well as uncon-
nected pairs, thus ruling out simple thresholding.
To adjust for heteroskedasticity, we Z-normalized residual(X)ij by the geometric mean of
the pre- and post-synaptic neurons’ standard deviations. To avoid inflating low variances by
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
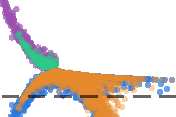
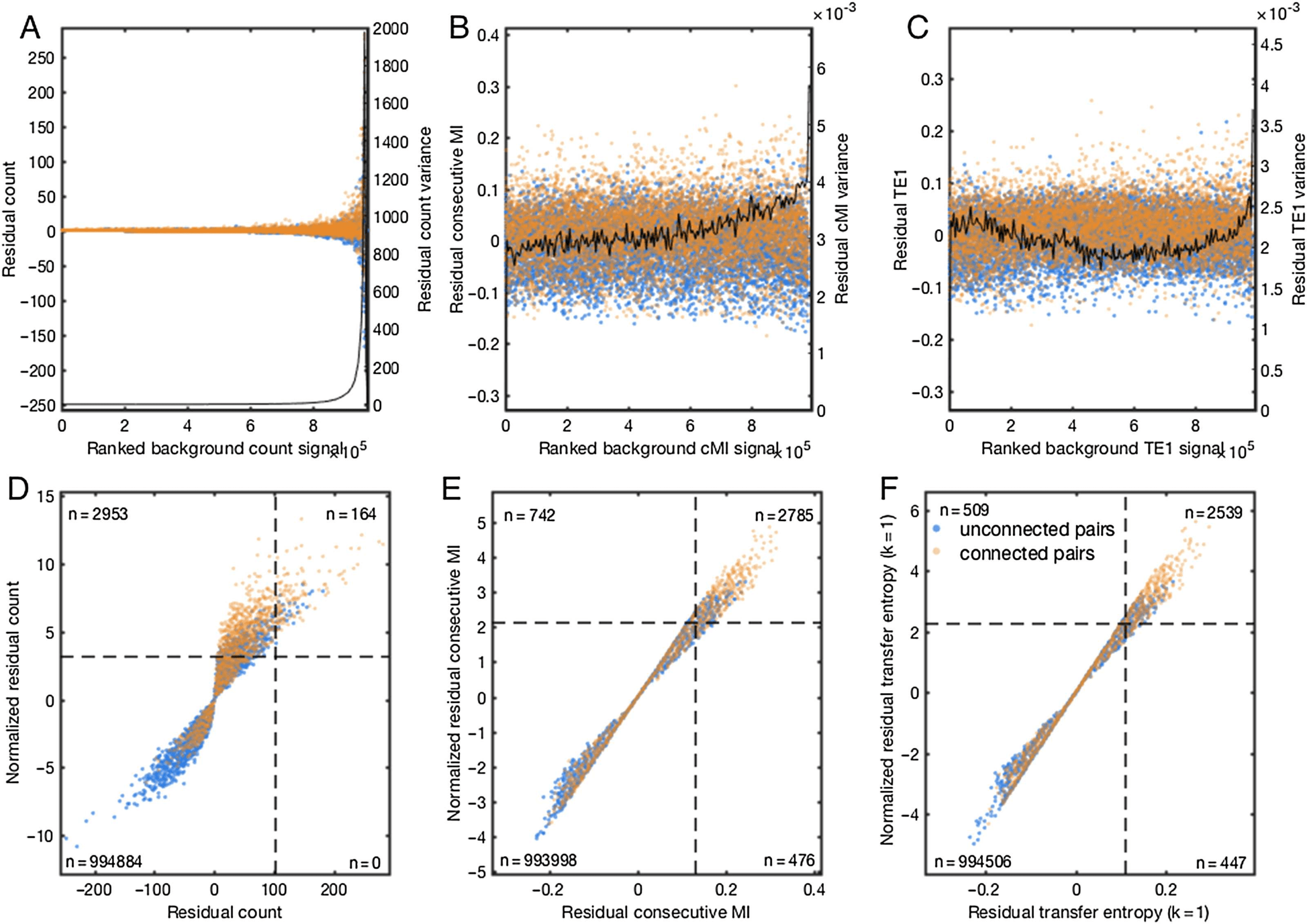
Figura 4. Rescaling neuron-wise residual score variance. Data in this figure are from a randomly
chosen representative simulated network binned at 20 ms, and subsampled according to density
(UN) The count measure exhibited strong scaling of residual variance with
for display purposes.
mean background signal, negatively impacting performance after thresholding.
(B) Consecutive
mutual information exhibited modest heteroskedasticity. (C) Residual variance for transfer entropy
(k = 1) proved to be nonmonotonically associated with mean background signal, with elevated
variance among both the lowest and the highest regularized scores. (D) Z-normalization dramati-
cally improved count performance at the 80% accuracy threshold, increasing coverage of putative
connected pairs from 164 A 3,117. (E) Z-normalization improved consecutive mutual information
coverage from 3,261 A 3,527 putative connected pairs. (F) Transfer entropy (k = 1) was not notably
impacted by Z-normalization, increasing coverage from 2,986 A 3,048 putative pairs.
Network Neuroscience
71
Ensemble learning for inference of synapses
dividing by small values, normalization was limited to a minimum divisor. We denote the
Z-normalized scores by norm_residual(X)ij,
norm residual(X)ij =
residual(X)ij
max(ϕij, ϕcuto f f )
,
q
Dove
ϕij = σ(residual(X)io,1:N−{j}) · σ(residual(X)1:N−{io},j),
and σ denotes the standard deviation.
ϕcuto f f = median(ϕij).
(20)
(21)
Accounting for scaled variance in background timing relationships, this refinement further
improved the coverage of measures (Figures 4D and 4F). The result was particularly dramatic
for the count measure. Its success is particularly surprising since countij was initially a poor
indicator of underlying connection. We suggest that z-scored count estimates provided a
simple and powerful first-pass approach to synaptic inference. The performance of this fi-
nal stage of refinement across timescales and accuracy thresholds is shown in Figures 5A–F).
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 5. Survival curves for norm_residual(count)ij, norm_residual(cMI)ij, and norm_residual
(TE1)ij for multiple time resolutions and accuracy rates. (UN) Count performs best at 5 E 10 ms,
revealing almost 50% of connections in the recruitment network. (B) consecutive MI does similarly
to count, con 5- and 10-ms time resolution achieving the best performance. (C) Same as in A and
B for transfer entropy (k = 1). (D–F) Zoom-in of A–C, rispettivamente, showing true positive rates from
0.6 A 1. Note that inference algorithms calculated with 1-ms time-bins display performance in par
with 20-ms time-bins. Mean and standard deviation across six simulated datasets are illustrated
throughout.
Network Neuroscience
72
Ensemble learning for inference of synapses
As we previously reported (Chambers & MacLean, 2015), a 1-ms lagged relationship between
neurons is less informative compared with inference based on longer time-bins because of the
time constant of synaptic integration. Owing to this finding we used time resolutions varying
between 5 E 80 ms for all subsequent analyses.
Average performance gains at 80% accuracy at each stage of refinement collapsed across
models for countij, cMIij, and TE1ij are shown in Figure 6. The largest improvement to
information theoretic measures resulted from accounting for the interaction sign, whereas
coverage for countij increased mainly because of Z-normalization of the residuals, bringing
norm_residual(count)ij detection in par with norm_residual(cMI)ij and norm_residual(TE1)ij.
We next investigated whether statistical differences in the collections of predicted synaptic
pairs persisted after signing, adjusting for background timing relationships, and selection by
thresholding.
Comparing Similarity and Temporal Preferences Across Measures
We compared the collection of strongest pairwise relationships for each regularized inference
measure. Thresholding was performed independently for each measure to yield sparseness-
matched binary subgraphs. We first compared the similarity of detected synaptic connections
between each pair of measures. Different measures of pairwise timing statistics highlighted
nonidentical, overlapping collections of putative synaptic pairs (Figura 7). Qualitatively, L2
distances between measures were stable across simulated datasets (Figure 7A and 7B). In-
terestingly, count and simultaneous mutual information (sMI) were most dissimilar, reflecting
sensitivity to different temporal structure. Consistent with this interpretation, the most similar
measures were correlation, consecutive MI, and TE1.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 6. Comparing gains in the regularization pipeline. (UN) Inference based on raw count ini-
tially achieved zero coverage at the 80% accuracy threshold. Removal of background signal im-
proved coverage substantially, and the greatest gains resulted from Z-normalization to compensate
for heteroskedasticity. After regularization, count performed as well as the best other individual
inference algorithms. (B) Regularization was also beneficial for the consecutive mutual information
measure, with the greatest gains achieved by signing raw scores to distinguish positive timing rela-
tionships from negative ones. (C) Transfer entropy (k = 1) exhibited similar improvements during
regularization, benefiting from signing and removal of background signal.
Network Neuroscience
73
Ensemble learning for inference of synapses
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 7.
Inference algorithms differ in their statistical preferences. (UN) Comparing the strongest
putative connections inferred by each regularized inference algorithm, after sparseness-matching
and binarization, on the basis of their pairwise Euclidean distances. (B) Stable similarity and dis-
(C) Inference algorithms exhibited
similarity relationships manifested across simulated datasets.
diverse levels of coverage at the 80% accuracy threshold, with all algorithms except simultaneous
mutual information performing better at high temporal resolutions. Regularized count, consecutive
mutual information, and transfer entropy (k = 1) were the best performing measures given high tem-
poral resolution, while confluent mutual information was the best performing measure in conditions
of coarser temporal resolution. Lines and shading represent means and standard errors across six
simulated datasets. (D) The relative contribution of each inference algorithm to the coverage pooled
across all algorithms revealed that measures considering more than one time-bin such as confluent
mutual information and transfer entropy (k = 2) were able to infer more connections at coarser
time resolutions. Lines and shading represent means and standard errors across six models. (E) Dif-
ferent levels of reciprocity were observed across collections of putative connections inferred from
different regularized algorithms. Implausibly high reciprocity characterized simultaneous mutual
informazione, because of its emphasis on bidirectional relationships. (F) Levels of mean local cluster-
ing differed across regularized algorithms to a lesser degree, with simultaneous mutual information
exhibiting highest levels of clustering. (G) Comparison of reciprocity was repeated after excluding
false positives and rematching for sparseness. High levels of reciprocity continued to characterize
simultaneous mutual information, revealing its strong bias for true reciprocally connected pairs.
(H) Comparison of local clustering was repeated after excluding false positives and rematching for
sparseness. Elevated local clustering among simultaneous mutual information was revealed to be
partially an artifact of its insensitivity to directionality. Collections of true inferred connections were
most clustered for the lagged count measure, and least clustered for the lagged correlation measure.
Network Neuroscience
74
Ensemble learning for inference of synapses
To investigate further, we compared the performance of each inference metric across time-
scales. The mean and standard error of coverage and relative coverage are shown in Figures 7C
and 7D. An interesting trend was revealed: At high temporal resolution, the measures focus-
ing on consecutive time-bins, namely count and consecutive MI, performed best. But as time
resolution decreased, optimal performance shifted increasingly towards measures that com-
bine consecutive and simultaneous time-bins, such as confluent MI and TE2. For small bins,
synaptic integration and recruitment often straddle time-bin borders; whereas for large bins,
a given synaptic interaction is more likely to occur entirely within single time-bins. In addi-
tion to choice of statistical measure, performance depends on the correspondence between
relevant timescales of synaptic integration versus the timescale of spike binning (Chambers &
MacLean, 2015).
Of all the measures, simultaneous MI was unique in that it contains only information on the
spikes that occur in the same time-bin (with no consecutive time-bin information). One might
hypothesize that, with large time-bins, sMI would therefore best detect synaptic interactions.
Tuttavia, its inherent symmetry gave rise to frequent errors in directionality. These errors in
assuming bidirectional connectivity prevented it from significantly crossing the 80% accuracy
threshold, and it thus achieved zero coverage at this cutoff. While sMI is fully symmetric in its
raw form, the normalization process removed this symmetry, which explains how the refined
score achieved nonzero coverage at the largest timescale.
Comparing Topological Preferences Across Measures
We hypothesized that the inferred subgraphs of synaptic connections might differ in systematic
ways depending on the algorithm employed and that these differences would be detectable by
comparing the topological organization of the subgraphs. If inferred networks differed in the
lagged relationships that they were sensitive to, it was possible they contained complemen-
tary information about the location of true connections. In previous work we had found that
specific topological motifs found in simulated model activity were also found in experimental
data collected from somatosensory cortex, demonstrating that higher order dynamical organ-
ization has the potential to generalize across network construction (Chambers & MacLean,
2016). We compared estimates of reciprocal connection probability and local clustering to
understand whether different measures made similar estimates of these quantities (Methods).
Inferred topologies were characterized by a diversity of reciprocity and local clustering (Fig-
ure 7E–H). Unsurprisingly, the simultaneous MI measure exceeded all other measures in the
level of reciprocity represented among its strong entries, since through symmetry it tends to
predict bidirectional connectivity. Note that ground-truth reciprocity is 0.2. In contrasto, mea-
sures sensitive to time-lagged statistical relationships tended to be characterized by lower levels
of reciprocity (Figures 7E and 7G). Since pairwise reciprocity sets a lower bound expectation
for local clustering, it is not surprising that measures followed a similar rank ordering for both
estimates, although fractional differences were smaller for estimates of local clustering. Em-
phasizing that the two metrics are related but distinct, we note that count estimates of local
clustering were relatively high in relation to its estimate of reciprocity. Overall, inferred topolo-
gies exhibited nonidentical statistical features depending on the algorithm employed.
We next tested whether these differences were dominated by detection errors, while encom-
passing statistically similar subsets of true synaptic connections. To investigate, we repeated
the analysis above for true positives only. After this step, inferred topologies were matched
in sparseness by thresholding and binarized to prevent any uncontrolled differences in edge
density. These two steps, thresholding and binarization, were conducted solely for these
Network Neuroscience
75
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
comparisons (Methods). After pruning false positives from inferred topologies, estimates of
reciprocity obeyed a qualitatively similar rank ordering (Figure 7G); sMI continued to be domi-
nated by reciprocal edges even after pruning false positives, exhibiting a strong selective prefer-
ence for bidirectional synaptic pairs. Although it does not faithfully represent the ground-truth
statistics of synaptic recruitment (investigated below), this feature could be useful in applied
experimental settings, Per esempio, for targeting multicellular patch clamp recordings to find
reciprocal pairs, potentially generating higher experimental yields. In contrasto, after pruning
false positives, sMI exhibited far lower local clustering (Figure 7H), revealing that false in-
ference of reciprocal connectivity made a misleading impact in quantifying local clustering.
The count subnetwork identified connections related by high local clustering. Correlation and
TE1 measures identified synaptic pairs less likely to be bidirectionally connected or clustered
tightly together. Since different inference measures appeared to prefer distinct subsets of the
synaptic network, we next tested whether their heterogeneous strengths could potentially be
pooled to yield higher sensitivity than was achievable with any measure alone.
Ensemble Approach for Combining Measures
We found that each inference algorithm revealed overlapping but distinct sets of causal con-
nections with different biases. This diversity suggested that an ensemble approach, leveraging
complementary sources of information across measures, could potentially improve upon in-
ferences based on any single measure. We employed a stochastic search strategy (Methods)
to find a weighting scheme for combining measures. The weights we obtained largely paral-
leled the independent performance of the component measures (Tavolo 4), with consecutive
binning being favored at high temporal resolution and confluent or simultaneous binning be-
ing favored at low temporal resolutions. Surprisingly, significant weight was assigned to sMI at
larger exposures despite sMI not being able to achieve any real coverage on its own (see Fig-
ures 7C and 7D). This result emphasized the utility of ensemble approaches in cases in which
low-performing algorithms can still improve the ensemble performance.
Weights were pooled over all models for principal components analysis (PCA), to identify
model-independent features of the score landscape. Weight covariance for 10-ms simulated
temporal resolution is shown in Figure 8B, with entries in the main diagonal masked out for
visualization purposes. The measures count, confluent MI, and TE1 exhibited particularly high
covariance, suggesting that they provide complementary information about synaptic con-
nections. This observation is consistent with their different statistical preferences. TE2 tended
to covary negatively with these measures, suggesting it was being leveraged to disambiguate
pairs without a true connection. The complementary information yielded by TE1 versus TE2
Tavolo 4. Ensemble weights
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Count
Consecutive MI
Simultaneous MI
5 ms
0.1411 ± 0.084
0.2782 ± 0.094
0.0035 ± 0.016
0.2058 ± 0.064
0.1084 ± 0.118
−0.1086 ± 0.036
−0.1302 ± 0.046
10 ms
0.1990 ± 0.125
0.2396 ± 0.116
0.0080 ± 0.015
0.2260 ± 0.080
0.1116 ± 0.124
0.0359 ± 0.066
−0.1052 ± 0.092
20 ms
−0.0029 ± 0.116
0.2098 ± 0.071
0.0591 ± 0.048
0.2487 ± 0.111
0.1484 ± 0.063
0.0984 ± 0.082
−0.1329 ± 0.083
Confluent MI
TE (k = 1)
TE (k = 2)
Correlation
Data reported here as mean ±SD across six simulated datasets; each ran five times through simulated annealing.
40 ms
0.0025 ± 0.051
0.1335 ± 0.129
0.2496 ± 0.125
0.1841 ± 0.120
0.0884 ± 0.062
0.1446 ± 0.081
−0.0555 ± 0.128
80 ms
0.0199 ± 0.037
0.1260 ± 0.121
0.2607 ± 0.112
0.2696 ± 0.117
0.0323 ± 0.057
0.1191 ± 0.092
−0.0527 ± 0.108
Network Neuroscience
76
Ensemble learning for inference of synapses
(UN) Optimal weight-
Figura 8. Pooling individual measures to generate ensemble predictions.
ings were obtained using random-walk search with simulated annealing on step sizes. Independent
searches converged on similar best scores for each simulated dataset, grouped by color. Appro-
priate weights were discovered early, but modest gains persisted throughout the search procedure.
(B) Covariance matrix quantifying common structure in weights throughout the search procedure,
after concatenating all simulated networks and trials. Entries along the main diagonal were masked
out for visualization purposes. (C) Among pooled weights, good scores tended to cluster along one
extreme of the first principle dimension, while robust to differences along the second principle di-
mension. Good solutions also appeared in isolated peaks throughout the solution space. Diverse
weighted combinations yielded good performance in inferring synaptic connectivity. (D) Ensemble-
generated topologies closely reflected the ground-truth reciprocity statistics of synaptic recruitment
in the simulated network. Synaptic recruitment preferentially occurred within a nonrepresentative
subset of the underlying random structural network. (E) Like the ground-truth network of synaptic
recruitment, ensemble-generated topologies were characterized by elevated local clustering. How-
ever, like the best individual measures, ensemble scores somewhat underestimated its true extent.
(F) With respect to reciprocity and local clustering, the two best characterizations of synaptic
recruitment statistics were achieved by count and ensemble inference
reiterated the power of studying functional coupling at multiple time-lags (Ito et al., 2011). IL
search over weight space is illustrated for the first two PCA dimensions with performance indi-
cated by color (Figure 8C). Although score was not factored explicitly into the dimensionality
reduction, effective weightings clustered together as a function of the first principle dimension,
suggesting a large basin of feasible weights. Diverse combinations of weights had the potential
to pool measures productively.
Improved Sensitivity With and Generalization of Ensemble Inference
As we have previously reported, the recruitment network is characterized by elevated cluster-
ing in the local synaptic neighborhood (Chambers & MacLean, 2016). The ensemble method
recapitulates these features better than the best individual measures (Figures 8D–F). The en-
semble also exhibited improved sensitivity at the 80% precision cutoff, with larger relative
improvements as sampling rates decreased. To examine the improvements offered by the
ensemble method, we plotted the coverage for the ensemble score compared with its best
performing component score (Figure 9D). Across all simulated networks, all trials, and all
Network Neuroscience
77
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
exposures, the ensemble method increased coverage, with absolute gains being around 1,000
neuronal pairs over the best measure. Given the low component performance at large expo-
sures, this represented a larger relative gain at these timescales, which is relevant for inferring
connections using common experimental imaging techniques.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Figura 9. Ensemble weightings generalize across simulated datasets and outperform individ-
ual measures.
(UN) Ensemble weightings were optimized for number of connections inferred
using stochastic search (original performance, blue). Weights found for a random dataset with 5-ms
time resolution were used to construct ensemble-generated adjacency matrices for each other data-
set also binned at 5 ms (transfer performance, red). Transfer performance approached the origi-
nal performance based on optimized weighting schemes. (B) Given matched temporal resolution,
transfer performance was nearly as good as original performance for fast temporal resolution. A
slower time-bins, transfer performance was somewhat less effective. (C) Transfer performance was
best when temporal resolution was matched between original and transferred recordings, and mis-
match degradation was worst for weights originally learned from recordings with slow temporal
resolution. Line and shading represent means and standard errors across six simulated datasets.
(D) Ensemble-generated topologies outperformed their best component measures across all bin
sizes and model repetitions. Component measures with the best individual performance varied,
but regularized count, consecutive mutual information, and confluent mutual information were
often the best performing individual measures. Algorithms incorporating information at multiple
timescales fared well, including confluent mutual information and transfer entropy (k = 2).
Network Neuroscience
78
Ensemble learning for inference of synapses
To test whether weights learned for one simulated dataset could transfer to other simu-
lated networks, we computed the ensemble scores for each using weights learned for different
datasets (transferred weights) and compared the performance to the datasets’ performance
with their own weights (original weights). Simulated temporal resolution was matched for the
transferred and original sets of weights. We found weights trained on one simulated network
approached coverage after transfer to another network, con 97.32 ± 0.54% (mean ± SD) Di
pairs inferred with original weights also inferred with transferred weights, at 5-ms time resolu-
zione (Figures 9A and 9B). Generalization of weights across datasets depended on timescales in
a similar manner to overall performance. Nonetheless, retained coverage was still impressive
at 40 ms, with over 85% of inferred connections preserved (Figure 8B), suggesting that simu-
lations of realistic networks may be exploited to train ensemble weights for experimental data,
even in cases in which temporal resolution is limited.
We also explored whether weights can be transferred across both simulated network and
timescales by examining retained performance after transfer from nonmatching time resolu-
zione. Once again, the ensemble method was robust to weights generalization, with trans-
ferred performance remaining above 80% for timescales that are similar yet not identical to
the timescale the measures were originally computed with (Figure 9C). Per esempio, models
binned at 10 ms with weights transferred from 5- and 20-ms models performed at 87.002 ±
3.578% E 86.744 ± 1.890% of their original performance, rispettivamente. Ensemble weights
generalized across simulated datasets, and matching temporal resolution at least coarsely, era
advantageous for transfer performance.
DISCUSSION
Within local cortical circuits, spiking activity propagates through synaptic networks in order
to implement computation and shape behavior. Yet individual connections are weak in isola-
zione, and patterns of coordination are complex and variable. Activity, or functional, mapping
approcci, such as those presented here, infer probable synaptic recruitment patterns from
statistical regularities in spike timing. In this framework, statistical relationships are leveraged
to predict synaptic connections, typically by thresholding to isolate the most reliably coupled
pairs. Importantly, functional graphs, which succinctly summarize circuit dynamics, identify
the synapses that are actively involved in the recruitment of post-synaptic neurons; questo è,
those synapses that drive the post-synaptic neuron to threshold. Explicitly, only those connec-
tions revealed by (UN) the timing of pre-synaptic action potentials, (B) the integrative properties
of the post-synaptic neuron, E (C) the membrane potential of the post-synaptic neuron can
ever be recovered by an inference approach. These are a limiting set of criteria that dramati-
cally lessen the connections that can be recovered using these methods. Consequently, these
approaches are not a realistic means to fully reconstruct a synaptic wiring diagram. Piuttosto, Questo
is an approach that identifies synapses involved in implementing computation, and transmit-
ting information during the specific epoch of dynamics that the graph summarizes, questo è, IL
recruiting network. Di conseguenza, these connections are particularly interesting from a functional
perspective. In this work, we compared methods for inferring excitatory synaptic connections,
in order to understand the strengths and weaknesses of each. For mapping activity propa-
gation through networks, we present two approaches to improve the inference of excitatory
connections: a regularization pipeline to improve the performance of individual inference
algorithms, and an ensemble stacking procedure that combines the best features of diverse
measures.
79
Stacking:
Generating one score from multiple
inference methods by calculating a
weighted sum.
Network Neuroscience
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Refinements of Inference Measures
To improve inference of excitatory connections, we applied a sign to the information theo-
retic measures which disambiguates positive interactions from negative interactions. We note
that negatively signed interactions could potentially provide insight into inhibition within the
rete, a long-standing challenge in connectivity research, but also point out that disam-
In this work we
biguating active inhibition from lack of excitation is a nontrivial endeavor.
focus on the more tractable goal of mapping excitatory connections alone. Assigning valence
to inferred relationships enhanced our recovery of excitatory connections.
Inference algorithms were further strengthened by removing a source of noise, reflecting
background timing coincidences, not reflecting monosynaptic interactions. After reexpressing
measures to conform better to normality, we regressed out the mean component of this back-
ground signal by averaging over pre- and post-synaptic weighted degree. Since connectivity is
sparse even among near neighbors, this averaging procedure was dominated by background
influences specific to each neuron’s firing rate and response profile. This tendency was not
linear in magnitude across degrees, Tuttavia, resulting in heteroskedasticity of residual scores.
We corrected for the variability in standard deviation over the residuals with Z-normalization,
which further increased the accuracy of inferred interactions. This step was particularly effec-
tive for count, transformed by regularization into one of the single most effective indicators of
connectivity. This approach is similar in spirit to the normalized count procedure described in
prior work (Pajevic & Plenz, 2009). These steps can be thought of in terms of informing infer-
ence algorithms not only by regularities within specific connections, but also by the statistics
of the entire network. In this regard the current study differs from previous inference attempts
in neuronal networks and, particularly, improves on previous procedures for thresholding. Noi
suggest similarly inspired next steps would be to incorporate priors about higher order struc-
tures such as motifs and clusters as well as accounting for lognormal distribution of weights
(Song et al., 2005) to further facilitate detection.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble Method
Different inference algorithms capture and summarize subtly different attributes of collective
activity, and it is important to be mindful about these features when interpreting functional
connectivity. Temporal resolution appears to be a particularly key design variable, and bin
sizes of 25–50 ms or smaller are preferable for identifying synaptic connections, likely reflect-
ing synaptic integration times (Chambers & MacLean, 2015). Ovviamente, even at much slower
temporal resolution, the same algorithms can be useful for quantifying average timing relation-
ships among active neurons. For mapping population dynamics, our results suggest that a host
of productive statistical measures exist, which can be leveraged to infer likely patterns of synap-
tic recruitment. These measures are useful in isolation, and they become even more incisive in
combination.
We found that each inference method isolated collections of putative underlying synaptic
connections that are nonidentical. This is an ideal situation for the application of ensemble
metodi. Here we used linear combinations of multiple measures in order to improve pre-
dictions of putative synaptic connections beyond the best single inference method. Nonlinear
combinations of measures have the potential to synergize further, leading to further gains in
performance, but will face increasingly severe difficulties in generalization—a problem typ-
ical of classification in high-dimensional spaces given limited training data (Vapnik, 2013).
Network Neuroscience
80
Ensemble learning for inference of synapses
Ensemble approaches employ a diversity of methods for pooling, and one common method is
majority vote on individual classifiers (Liaw & Wiener, 2002). Tuttavia, ensemble ap-
proaches are also frequently applied to real-valued outputs rather than binary classifier de-
cisions (Mendes-Moreira, Soares, Jorge, & De Sousa, 2012). One of the most common ways to
leverage multiple classifiers in combination is known as bagging, where the ensemble score
is the mean over all real-valued scores of individual measures. We demonstrate that better
performance can be obtained in a weighted combination of the inference approaches. Questo
latter framework for ensemble learning is known as stacking. Generalmente, stacking algorithms
are characterized by a pooling step, known as a combiner algorithm. As an example, high
performers in the Netflix Prize employed linear regression and, Dopo, backpropagation in a
feedforward neural network for their combiner algorithm (Töscher, Jahrer, & Campana, 2009). In
order to optimize stacking weights, we employed an annealing random walk search strategy, UN
common approach in the field of ensemble learning, including evolutionary approaches such
as genetic algorithms and stochastic hill climbing (Ruta & Gabrys, 2005). The question of how
best to pool diverse connectivity inference algorithms remains an area necessitating further
study. In practice, since recording conditions vary from one lab to another, experimenters with
different experimental protocols than the ones studied here in silica should retrain a combiner
algorithm based on their own internal experimental design and selection of available inference
algorithms with the understanding that each algorithm has different biases and the appropriate
ensemble will depend on the expected underlying connectivity and time constant of synaptic
integration.
The measures we studied in this work framed inference of synaptic connectivity as a binary
classification algorithm. Tuttavia, inference has the potential to also be cast as a regression
problem using some continuous-valued measure of pre-synaptic influence (per esempio., induced ex-
citatory post-synaptic potential), which may lead to further gains, particularly in coverage.
Tuttavia, scarcity of ground-truth data and population-level coordination (obstacles facing
any connection-inference approach) will make it challenging to move beyond binary classi-
fication to infer true synaptic connections.
In addition to the algorithms we compared in
this work, a host of other effective approaches have been described in the literature, In-
cluding particle methods (Gerstein & Aertsen, 1985), generalized linear models (GLMs;
Gerhard et al., 2013; Zaytsev, Morrison, & Deger, 2015), and Bayesian methods (Chambers
& MacLean, 2015; Mishchencko, Vogelstein, & Paninski, 2011; Pajevic & Plenz, 2009).
It
may be that ensemble predictions about underlying connectivity could be improved further by
including these approaches in the pooling step.
Inference for Circuit Reconstruction/Insights Into Information Processing
Understanding how connection structure gives rise to synaptic recruitment remains a central
goal for the study of neocortical circuits. Computation and behavior are enacted by propa-
gating activity, so understanding synaptic recruitment mechanistically within active cortical
networks is fundamental to the study of behaving animals. The importance of this issue was
recognized early (Gerstein & Perkel, 1969; Palm, 1982), but technical obstacles limited its
active study.
In the last five years, progress is being made in this area through the study of
functional relationships in active populations. In other words, it is important to consider not
only whether a connection is present, but also which connections are coactive or otherwise
functionally related, and causal to spike propagation in a given context.
A confluence of evidence argues that the function of an individual connection depends
on its arrangement within the local synaptic neighborhood. Per esempio, a given connection
Network Neuroscience
81
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
will make a different impact if it is isolated versus arranged within a local cluster (Pajevic
& Plenz, 2012). In neural cultures, frequent ignition sites were associated with elevated lo-
cal clustering, for which a model of convergent amplification was proposed (Orlandi et al.,
2013). Culture activity maps were characterized by elevated clustering and short mean path
lengths (Pajevic & Plenz, 2009). Intriguingly, clustering motifs, reciprocity, and heavy-tailed
weight distributions may emerge through self-organizing plasticity processes (Miner & Triesch,
2016). These nonrandom features have received high levels of interest and may be consis-
tent with several global topological organization schemas (Vegue et al., 2017). In neocortical
tissue from mouse sensory cortices, spontaneous lagged firing relationships were found to
be characterized by elevated modularity and hierarchical features (Gururangan, Sadovsky, &
MacLean, 2014; Sadovsky & MacLean, 2013). Allo stesso modo, multielectrode array recordings were
marked by rich club structure (Nigam et al., 2016) and broad degree distributions (Timme et al.,
2016). In the latter work, functional hub neurons played a crucial role in supplying inputs to
computationally important neurons downstream. Related theoretical work suggests functional
hubs may take on distinct roles shaped by their assortativity or disassortativity relationships
(Piraveenan, Prokopenko, & Zomaya, 2012). Converging sources of evidence have identified
generalizable nonrandom features within connected neural systems consistent with the idea
that these are key features to consider when describing the flow of activity through the circuit.
Beyond these higher order functional relationships, we have previously shown that inference
is biased towards stronger connections (Chambers & MacLean, 2015). Di conseguenza, inference
methods sometimes pose difficulties in interpretation (James, Barnett, & Crutchfield, 2016),
and they are limited in accuracy as well as sensitivity to weak synaptic connections, which are
crucial for realistic spiking dynamics (Sadovsky & MacLean, 2013; Teramae, Tsubo, & Fukai,
2012). Continued development of tools to understand the large-scale organization of synaptic
networks is an important area for further investigation.
The function of individual connections also depends on recent dynamics of the local circuit.
On short timescales, unexpectedly effective recruitment can arise when inputs to a neuron are
temporally coordinated (Rossant, Leijon, Magnusson, & Brette, 2011), Per esempio, through the
channel dynamics of action-potential generation (Fontaine, Peña, & Brette, 2014) or through
interactions with the dendritic arbor (Major, Larkum, & Schiller, 2013). Higher order connec-
attività, particularly fan-in clustering, may favor coordinated inputs in this way, supporting effec-
tive synaptic integration (Chambers & MacLean, 2016). On moderate timescales, short-term
plasticity imposes additional complexity in predicting the function of individual connections,
where synaptic efficacy depends in part on a hidden state (Buonomano & Maass, 2009). In
aggiunta, diverse sources of neuromodulation can reorganize synaptic efficacy in real time,
in ways that are difficult to understand a priori. Per esempio, circuit-level reorganization can
occur in response to acetylcholine, impacting the salience of extrinsic inputs versus local re-
current drive (Runfeldt, Sadovsky, & MacLean, 2014).
The complexity of structure-function relationships in neocortex is daunting. Isolated struc-
tural features can take on unexpected functional roles in the context of the local active net-
lavoro. Yet out of the extreme diversity of mechanisms shaping cellular communication, stable
statistical relationships in spike timing emerge. Maps of synaptic recruitment are a promis-
ing avenue to summarize the complex effects imparted by these many interlocking subcellular
processes. For progress to continue in understanding large active neural circuits, it is important
that statistics of spike timing among large populations continue to be investigated actively by
the neuroscience community.
Network Neuroscience
82
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
AUTHOR CONTRIBUTIONS
Brendan Chambers and Maayan Levy contributed equally. Brendan Chambers: Conceptu-
alization; Data curation; Formal analysis; Investigation; Methodology; Software; Validation;
Visualization; Writing – original draft; Writing – review & editing. Maayan Levy: Conceptual-
ization; Data curation; Formal analysis; Investigation; Methodology; Software; Validation;
Visualization; Writing – original draft; Writing – review & editing. Joseph B. Dechery: Contro-
Jason N.
ceptualization; Validation; Writing – original draft; Writing – review & editing.
MacLean: Conceptualization; Data curation; Funding acquisition; Investigation; Methodol-
ogy; Project administration; Resources; Software; Supervision; Validation; Writing – original
bozza; Writing – review & editing.
REFERENCES
Buonomano, D. V., & Maass, W. (2009). State-dependent compu-
tations: Spatiotemporal processing in cortical networks. Nature
Reviews Neuroscience, 10(2), 113–125. https://doi.org/10.1038/
nrn2558
Chambers, B., & MacLean, J. N.
(2015). Multineuronal activity
patterns identify selective synaptic connections under realistic
Journal of Neurophysiology, 114(3),
experimental constraints.
1837–1849. https://doi.org/10.1152/jn.00429.2015
Chambers, B., & MacLean, J. N. (2016). Higher-order synaptic inter-
actions coordinate dynamics in recurrent networks. PLoS Com-
putational Biology, 12(8), e1005078. https://doi.org/10.1371/
journal.pcbi.1005078
Destexhe, A., Rudolph, M., & Paré, D. (2003). The high-conductance
state of neocortical neurons in vivo. Nature Reviews Neuro-
science, 4(9), 739–751.
Dietterich, T. G. (2000). Ensemble methods in machine learning. In
International workshop on multiple classifier systems. (pag. 1–15).
Berlin: Springer.
Endo, W., Santos, F. P., Simpson, D., Maciel, C. D., & Newland,
P. l. (2015). Delayed mutual information infers patterns of synap-
Journal of
tic connectivity in a proprioceptive neural network.
Computational Neuroscience, 38(2), 427–438. https://doi.org/
10.1007/s10827-015-0548-6
Fast, A., & Jensen, D. (2008). Why stacked models perform effective
collective classification. In ICDM 2008: Eighth IEEE International
Conference on Data Mining (pag. 785–790). Retrieved from http://
ieeexplore.ieee.org/abstract/document/4781179/
Fontaine, B., Peña, J. L., & Brette, R.
(2014). Spike-threshold
adaptation predicted by membrane potential dynamics in vivo.
PLoS Computational Biology, 10(4), e1003560. https://doi.org/
10.1371/journal.pcbi.1003560
Freund, Y., & Schapire, R. E.
(1995). A desicion-theoretic gene-
ralization of on-line learning and an application to boosting.
In European Conference on Computational Learning Theory
(pag. 23–37). Retrieved from http://link.springer.com/chapter/10.
1007/3-540-59119-2166
Gerhard, F., Kispersky, T., Gutierrez, G. J., Marder, E., Kramer, M.,
& Eden, U.
(2013). Successful reconstruction of a physiologi-
cal circuit with known connectivity from spiking activity alone.
PLoS Computational Biology, 9(7), e1003138. https://doi.org/10.
1371/journal.pcbi.1003138
Gerstein, G. L., & Aertsen, UN. M. (1985). Representation of coop-
erative firing activity among simultaneously recorded neurons.
Journal of Neurophysiology, 54(6), 1513–1528.
Gerstein, G. L., & Perkel, D. H. (1969). Simultaneously recorded
trains of action potentials: Analysis and functional interpretation.
Scienza, 164(3881), 828–830. https://doi.org/10.1126/science.
164.3881.828
Goodman, D. F., & Brette, R. (2009). The brian simulator. Frontiers
in Neuroscience, 3(2), 192.
Gururangan, S. S., Sadovsky, UN. J., & MacLean,
(2014).
Analysis of graph invariants in functional neocortical circuitry
reveals generalized features common to three areas of sensory
cortex. PLoS Computational Biology, 10(7), e1003710. http://
doi.org/10.1371/journal.pcbi.1003710
J. N.
Hansen, l. K., & Salamon, P. (1990). Neural network ensembles.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
12(10), 993–1001. https://doi.org/10.1109/34.58871
Hofer, S. B., Ko, H., Pichler, B., Vogelstein, J., Ros, H., Zeng, H.,
(2011). Differential connectivity and
. . . Mrsic-Flogel, T. D.
response dynamics of excitatory and inhibitory neurons in visual
cortex. Nature Neuroscience, 14(8), 1045–1052. https://doi.org/
10.1038/nn.2876
Ito, S., Hansen, M. E., Heiland, R., Lumsdaine, A., Litke, UN. M.,
(2011). Extending transfer entropy improves
& Beggs, J. M.
identification of effective connectivity in a spiking cortical net-
work model. PLoS ONE, 6(11), e27431. https://doi.org/10.1371/
journal.pone.0027431
James, R. G., Barnett, N., & Crutchfield, J. P. (2016).Information flows?
A critique of transfer entropies. Physical Review Letters, 116(23),
238701. https://doi.org/10.1103/PhysRevLett.116.238701
Kirkpatrick, S., Gelatt, C. D., & Vecchi, M. P. (1983). Optimization
by simulated annealing. Scienza, 220(4598), 671–680. https://
doi.org/10.1126/science.220.4598.671
Ko, H., Hofer, S. B., Pichler, B., Buchanan, K. A., Sjöström, P. J., &
Mrsic-Flogel, T. D. (2011). Functional specificity of local synap-
tic connections in neocortical networks. Nature, 473(7345),
87–91. https://doi.org/10.1038/nature09880
Kobayashi, R., & Kitano, K.
Impact of network topology
on inference of synaptic connectivity from multi-neuronal spike
data simulated by a large-scale cortical network model. Journal
of Computational Neuroscience, 35(1), 109–124.
(2013).
Network Neuroscience
83
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Kruskal, P. B., Li, L., & MacLean, J. N.
(2013). Circuit reactiva-
tion dynamically regulates synaptic plasticity in neocortex. Na-
ture Communications, 4. Retrieved from http://www.nature.com/
ncomms/2013/131010/ncomms3574/full/ncomms3574.html
Kumar, A., Rotter, S., & Aertsen, UN. (2010). Spiking activity propaga-
tion in neuronal networks: Reconciling different perspectives on
neural coding. Nature Reviews Neuroscience, 11(9), 615–627.
https://doi.org/10.1038/nrn2886
Lalanne, T., Abrahamsson, T., & Sjöström, P. J.
(2016). Using
multiple whole-cell recordings to study spike-timing-dependent
plasticity in acute neocortical slices. Cold Spring Harbor Pro-
tocols, 2016(6), pdb.prot091306. https://doi.org/10.1101/pdb.
prot091306
Liaw, A., & Wiener, M.
(2002). Classification and regression by
randomforest. R News, 2(3), 18–22.
Lindsey, B. G., Morris, K. F., Shannon, R., & Gerstein, G. l. (1997).
Repeated patterns of distributed synchrony in neuronal assem-
blies. Journal of Neurophysiology, 78(3), 1714–1719.
Little, D. Y., & Chen, l. (2009). Identification of coevolving residues
and coevolution potentials emphasizing structure, bond forma-
tion and catalytic coordination in protein evolution. PLoS ONE,
4(3), e4762. https://doi.org/10.1371/journal.pone.0004762
Major, G., Larkum, M. E., & Schiller, J.
(2013). Active properties
of neocortical pyramidal neuron dendrites. Annual Review of
Neuroscience, 36, 1–24.
Marbach, D., Costello, J. C., Küffner, R., Vega, N. M., Prill, R. J.,
Camacho, D. M.,
(2012). Wisdom of
crowds for robust gene network inference. Nature Methods, 9(8),
796–804 .
. Stolovitzky, G.
.
.
Markram, H., Toledo-Rodriguez, M., Wang, Y., Gupta, A.,
Interneurons of the neo-
(2004).
Silberberg, G., & Wu, C.
cortical inhibitory system. Nature Reviews Neuroscience, 5(10),
793–807. https://doi.org/10.1038/nrn1519
Mendes-Moreira, J., Soares, C., Jorge, UN. M., & De Sousa, J. F.
(2012). Ensemble approaches for regression: A survey. ACM
Computing Surveys (CSUR), 45(1), 10.
Miner, D., & Triesch, J.
(2016). Plasticity-driven self-organization
under topological constraints accounts for non-random features
of cortical synaptic wiring. PLoS Computational Biology, 12(2),
e1004759. https://doi.org/10.1371/journal.pcbi.1004759
Nigam, S., Shimono, M.,
Mishchencko, Y., Vogelstein, J. T., & Paninski, l. (2011). A Bayesian
approach for inferring neuronal connectivity from calcium fluo-
rescent imaging data. Annals of Applied Statistics, 1229–1261.
Ito, S., Yeh, F.- C., Timme, N.,
Myroshnychenko, M., . . . Beggs, J. M. (2016). Rich-club organ-
Jour-
ization in effective connectivity among cortical neurons.
nal of Neuroscience, 36(3), 670–684. https://doi.org/10.1523/
JNEUROSCI.2177-15.2016
Orlandi,
J. G., Soriano,
J., Alvarez-Lacalle, E., Teller, S., &
Casademunt J. (2013). Noise focusing and the emergence of co-
herent activity in neuronal cultures. Nature Physics, 9(9), 582–590.
(2009). Efficient network reconstruction
from dynamical cascades identifies small-world topology of neu-
ronal avalanches. PLoS Computational Biology, 5(1), e1000271.
Pajevic, S., & Plenz, D. (2012). The organization of strong links in
Pajevic, S., & Plenz, D.
complex networks. Nature Physics, 8(5), 429–436.
Palm, D. G.
(1982). From neural dynamics to cell assemblies.
In D. G. Palm (Ed.), Neural assemblies (pag. 104–116). Berlin:
Springer. https://doi.org/10.1007/978-3-642-81792-212
Perin, R., Berger, T. K., & Markram, H.
(2011). A synaptic orga-
nizing principle for cortical neuronal groups. Atti del
National Academy of Sciences, 108(13), 5419–5424.
Piraveenan, M., Prokopenko, M., & Zomaya, UN.
(2012). Assorta-
tive mixing in directed biological networks. IEEE/ACM Transac-
tions on Computational Biology and Bioinformatics, 9(1), 66–78.
https://doi.org/10.1109/TCBB.2010.80
Rossant, C., Leijon, S., Magnusson, UN. K., & Brette, R. (2011).
Sensitivity of noisy neurons to coincident inputs. Journal of
Neuroscience, 31(47), 17193–17206. https://doi.org/10.1523/
JNEUROSCI.2482-11.2011
Runfeldt, M. J., Sadovsky, UN. J., & MacLean, J. N. (2014). Acetyl-
choline functionally reorganizes neocortical microcircuits. Jour-
nal of Neurophysiology, 112(5), 1205–1216. https://doi.org/10.
1152/jn.00071.2014
Ruta, D., & Gabrys, B. (2005). Classifier selection for majority vot-
ing. Information Fusion, 6(1), 63–81.
Sadovsky, UN.
J., Kruskal, P. B., Kimmel,
J. M., Ostmeyer,
J.,
(2011). Heuristically opti-
Neubauer, F. B., & MacLean, J. N.
mal path scanning for high-speed multiphoton circuit imaging.
Journal of Neurophysiology, 106(3), 1591–1598. https://doi.org/
10.1152/jn.00334.2011
Sadovsky, UN. J., & MacLean, J. N. (2013). Scaling of topologically
similar functional modules defines mouse primary auditory and
somatosensory microcircuitry. Journal of Neuroscience, 33(35),
https://doi.org/10.1523/JNEUROSCI.1977-13.
14048–14060.
2013
Schapire, R. E. (1990). The strength of weak learnability. Machine
Apprendimento, 5(2), 197–227. https://doi.org/10.1007/BF00116037
Shimono, M., & Beggs, J. M. (2015). Functional clusters, hub, E
communities in the cortical microconnectome. Cerebral Cortex,
25(10), 3743–3757.
Softky, W. R., & Koch, C.
(1993). The highly irregular firing of
cortical cells is inconsistent with temporal integration of random
EPSPs. Journal of Neuroscience, 13(1), 334–350.
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., & Chklovskii, D. B.
(2005). Highly nonrandom features of synaptic connectivity in
local cortical circuits. PLoS Biology, 3(3), e68.
Stetter, O., Battaglia, D., Soriano, J., & Geisel, T. (2012). Model-free
reconstruction of excitatory neuronal connectivity from calcium
imaging signals. PLoS Computational Biology, 8(8), e1002653.
https://doi.org/10.1371/journal.pcbi.1002653
Teramae, J., Tsubo, Y., & Fukai, T. (2012). Optimal spike-based
communication in excitable networks with strong-sparse and
weak-dense links. Scientific Reports, 2. Retrieved from http://
www.nature.com/srep/2012/120702/srep00485/full/srep00485.
html
Timme, N. M., Ito, S., Myroshnychenko, M., Nigam, S., Shimono,
M., Yeh, F.-C., . . . Beggs, J. M.
(2016). High-degree neurons
feed cortical computations. PLoS Computational Biology, 12(5),
e1004858. https://doi.org/10.1371/journal.pcbi.1004858
Töscher, A., Jahrer, M., & Campana, R. M. (2009). The BigChaos solution
to the Netflix Grand Prize. Netflix prize documentation, 1–52.
Network Neuroscience
84
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ensemble learning for inference of synapses
Tukey,
J. N.
(1977). Exploratory data analysis. Retrieved from
https://pdfs.semanticscholar.org/2f40/fd06bc9fd00a27437e14ed
171e96e4fd9326.pdf.
Vapnik, V. (2013). The nature of statistical learning theory. New York,
NY: Springer Science & Business Media. Retrieved from https://
books.google.com/books?hl=en&lr=&id=EqgACAAAQBAJ&oi=
fnd&pg=PR7&dq=dimensionality+generalization+learning+
machine&ots=g2M1ew8U23&sig=m0ir4JliLF3FiWM04Fm3MBO9P8
Vegue, M., Perin, R., & Roxin, UN. (2017). On the structure of cortical
micro-circuits inferred from small sample sizes. bioRxiv, 118471.
Zaytsev, Y. V., Morrison, A., & Deger, M. (2015). Reconstruction
of recurrent synaptic connectivity of
thousands of neurons
from simulated spiking activity. Journal of Computational Neu-
roscience, 39(1), 77–103. https://doi.org/10.1007/s10827-015-
0565-5
Zhang, X., Zhao, J., Hao, J.-K., Zhao, X.-M., & Chen, l.
(2015).
Conditional mutual
inclusive information enables accurate
quantification of associations in gene regulatory networks.
Nucleic Acids Research, 43(5), e31. https://doi.org/10.1093/nar/
gku1315
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
2
1
6
0
1
0
9
2
0
0
6
N
e
N
_
UN
_
0
0
0
3
2
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Network Neuroscience
85