RESEARCH
Bisected graph matching improves automated
pairing of bilaterally homologous neurons
from connectomes
Benjamin D. Pedigo1
, Michael Winding2
, Carey E. Priebe2, and Joshua T. Vogelstein1
1Biomedical Engineering, Johns Hopkins University, Baltimore, MD, USA
2Zoology, University of Cambridge, Cambridge, UK
Keywords: Structural connectome, Graph matching, Network alignment, Network analysis,
Homology, Bilateral symmetry
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
Graph matching algorithms attempt to find the best correspondence between the nodes of
two networks. These techniques have been used to match individual neurons in nanoscale
connectomes—in particular, to find pairings of neurons across hemispheres. Tuttavia, since
graph matching techniques deal with two isolated networks, they have only utilized the
ipsilateral (same hemisphere) subgraphs when performing the matching. Here, we present
a modification to a state-of-the-art graph matching algorithm that allows it to solve what
we call the bisected graph matching problem. This modification allows us to leverage the
connections between the brain hemispheres when predicting neuron pairs. Via simulations
and experiments on real connectome datasets, we show that this approach improves matching
accuracy when sufficient edge correlation is present between the contralateral (between
hemisphere) subgraphs. We also show how matching accuracy can be further improved by
combining our approach with previously proposed extensions to graph matching, Quale
utilize edge types and previously known neuron pairings. We expect that our proposed
method will improve future endeavors to accurately match neurons across hemispheres
in connectomes, and be useful in other applications where the bisected graph matching
problem arises.
INTRODUCTION
Graph matching is a widely used optimization technique whereby one can find a matching
between the nodes in one network and those in another. Solving the graph matching problem
yields a matching (cioè., the correspondence between the nodes of the two networks) that min-
imizes edge disagreements between the two networks. The graph matching problem has found
uses in fields as disparate as computer vision (Conte, Foggia, Sansone, & Vento, 2004), bio-
metrics (Conte et al., 2004), social networks (Saad-Eldin, Pedigo, Priebe, & Vogelstein, 2021),
and natural language processing (Marchisio et al., 2021), to name just a few.
Most important for this work is the use of graph matching techniques to find bilaterally
homologous neurons across the two sides of a nervous system (Chung et al., 2021; Sussman,
Park, Priebe, & Lyzinski, 2020). Connectomes—maps of neural connectivity—can naturally be
represented by networks, wherein a node represents a neuron and an edge represents synapses
Citation: Pedigo, B. D., Winding, M.,
Priebe, C. E., & Vogelstein, J. T. (2023).
Bisected graph matching improves
automated pairing of bilaterally
homologous neurons from connectomes.
Network Neuroscience, 7(2), 522–538.
https://doi.org/10.1162/netn_a_00287
DOI:
https://doi.org/10.1162/netn_a_00287
Supporting Information:
https://doi.org/10.1162/netn_a_00287;
https://github.com/neurodata/ bgm;
https://github.com/neurodata/bgm/blob
/main/results/outputs/connectome
_seeded/pair_predictions.csv
Received: 21 Giugno 2022
Accepted: 13 ottobre 2022
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Benjamin D. Pedigo
bpedigo@jhu.edu
Handling Editor:
Olaf Sporns
Copyright: © 2022
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
Schematic describing graph matching (GM) and bisected graph matching (BGM). Both aim to find a matching (which can be
Figura 1.
represented by a permutation, P) of the nodes of one hemisphere with respect to the other. GM does so by minimizing the norm of the edge
differences between ipsilateral (ALL and ARR) subgraphs under some matching. BGM aims to jointly minimize the norm of edge differences
between ipsilateral and contralateral (ALR and ARL) subgraphs under the same matching applied to both. Note that for the contralateral sub-
graphs, a permutation of the right hemisphere nodes amounts to permuting the columns (for ALR) or the rows (for ARL), but not both.
Graph matching:
The process of inferring an alignment
of the nodes of one network with
respect to another, often by trying to
maximize the agreement of edges
between those networks.
Bilaterally homologous neurons:
Neurons which appear to be “mirror
images” of one another across the
two sides of an organism’s nervous
system, often in terms of both
morphology and connectivity.
Ipsilateral:
Relating to the same side of the
body. In this work, this refers to
connections among neurons on the
same side of a nervous system.
Contralateral:
Relating to the opposite side of the
body. In this work, this refers to
connections from neurons on one
side of a nervous system to the other.
from one neuron to another (Bassett & Sporns, 2017; Vogelstein et al., 2019). Previous works
used graph matching techniques to predict neuron pairings between brain hemispheres based
on the observed connectivity (Chung et al., 2021; Sussman et al., 2020). The graph matching
problem by its very formulation is concerned with two separate networks; as such, previous
applications of graph matching to find homologous neuron pairings across hemispheres have
considered one network to be the set of nodes and edges within the left hemisphere, and the
other network to be defined likewise for the right hemisphere (Guarda la figura 1). In other words,
they have only considered the ipsilateral connections which connect within a brain hemi-
sphere, and ignored the contralateral connections which connect one side of the nervous sys-
tem to the other. Contralateral connections are quite common in connectomes studied thus far:
in subset of the larval Drosophila melanogaster (vinegar fly) connectome (Berck et al., 2016;
Burgos et al., 2018; Carreira-Rosario et al., 2018; Eichler et al., 2017; Eschbach et al., 2020,
2021; Fushiki et al., 2016; Gerhard, Andrade, Fetter, Cardona, & Schneider-Mizell, 2017;
Heckscher et al., 2015; Hückesfeld et al., 2021; Jovanic et al., 2016, 2019; Larderet et al.,
2017; Mark et al., 2021; Miroschnikow et al., 2018; Ohyama et al., 2015; Schlegel et al.,
2016; Takagi et al., 2017; Tastekin et al., 2018; Zarin, Segno, Cardona, Litwin-Kumar, &
Doe, 2019; Zwart et al., 2016), an edge picked at random from the network has about a
35% chance of being a contralateral connection. It is natural to wonder, Poi, whether these
connections can be used to improve automated neuron pairing.
Here, we show that rather than ignoring the contralateral connections for the purposes of
predicting neuron pairs, they can be explicitly included in the optimization by generalizing
graph matching to a single network that has been split into two parts. We demonstrate via
simulation that when sufficient edge correlations exist between the contralateral subgraphs,
our proposed method provides an improvement in matching accuracy. We then show that this
methodology indeed improves matching accuracy in our motivating example of a bilateral
nervous system by comparing our algorithm to traditional graph matching on five connectome
datasets. Further, we describe how our method can be combined with previously proposed
generalizations of graph matching to further improve performance.
RESULTS
From Graph Matching to Bisected Graph Matching
Primo, consider the graph matching problem from the perspective of attempting to predict neu-
ron pairs between brain hemispheres (thus adopting the terminology of left/right, eccetera.), Anche se
Network Neuroscience
523
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
the techniques described here could be applied more generally. For now, consider the case
where both hemispheres have exactly n nodes, though methods for matching with an unequal
number of nodes have been described (Fishkind et al., 2019) and are revisited later (see sec-
tion Matching Networks of Differing Sizes and With Seeds). Let ALL be the n × n adjacency
matrix for the subgraph of connections from left hemisphere to left hemisphere neurons, E
let ARR be defined likewise for the right hemisphere. The graph matching problem can then be
written as
(cid:1)
(cid:1)
ALL − PARRP T
(cid:1)
(cid:1)2
F
;
min
P2P
(1)
where the set of permutation matrices on n nodes is denoted by P. This objective function
measures the number of edge disagreements for an unweighted network, or the norm of the
weight disagreements for a weighted network. By trying to minimize this quantity over the set
of permutations, one can search for a matching between the networks under which the
observed edge structure appears similar.
We are interested in some similar measure that also includes the fact that we want the con-
tralateral connections, under some matching, to appear similar. To formalize this, let ALR be
the adjacency matrix for the subgraph of connections from left hemisphere to right hemisphere
neurons, and let ARL be defined likewise for the connections from the right to the left. We add a
term to the graph matching objective function which measures the disagreement between the
contralateral subgraphs under some permutation of the nodes of the right hemisphere:
(cid:1)
(cid:1)
min
P2P
ALL − PARRP T
(cid:1)
(cid:1)2
F
(cid:1)
(cid:1)
þ ALRP T − PARL
(cid:1)
(cid:1)2
F
:
(2)
Bisected graph matching:
The process of inferring the
alignment of the nodes of a split
rete (cioè., the left and right sides
of a connectome) by trying to
maximize the edge agreement of
both ipsilateral and contralateral
connections.
We call the problem in Equation 2 the bisected graph matching problem (illustrated in
Figura 1). With this formulation, the graph matching problem can be seen as a special case
of the bisected graph matching problem, since the objective function in Equation 2 reduces to
that of Equation 1 in the special case where ALR and ARL are both the zero matrix. Note that
this problem is also distinct from the multiplex graph matching problem described in Pantazis
et al. (2022), as the contralateral subgraphs require only a permutation of their rows or their
columns (not both) to maintain the correct structure of the adjacency matrix.
Given this notion of what it means to find a good matching between the hemispheres, our
goal was to develop an algorithm that could efficiently solve this problem (Equazione 2). Unfor-
tunately, graph matching problems in general are known to be NP-hard (Burkard, Dell’Amico,
& Martello, 2009), and as such efficient algorithms for solving these problems are approxima-
zioni. One popular approximation-based algorithm is the Fast Approximate Quadratic (FAQ)
algorithm of Vogelstein et al. (2015). This algorithm first relaxes the (discrete) graph matching
problem to the relaxed graph matching problem, allowing the tools of continuous optimization
to be used (see section Graph Matching Algorithms for discussion of this approximation). FAQ
then uses the Frank-Wolfe method (Frank & Wolfe, 1956) to attempt to minimize Equation 1.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
The Frank-Wolfe method finds a search direction by minimizing a first-order Taylor series of
the objective function, requiring that we compute the objective function’s gradient with
respect to its argument, P. The gradient of Equation 2 with respect to P (see Supporting Infor-
mazione: Derivation of Bisected Graph Matching Gradient) È
(cid:3)
∇f Pð Þ ¼ − ALLPAT
RR
þ AT
LLPARR þ ALRP T AT
RL
þ AT
RLP T ALR
(3)
(cid:4)
:
By substituting this new gradient calculation into the FAQ algorithm and keeping the rest of
the algorithm the same, FAQ can be adapted to solve the bisected graph matching problem.
Network Neuroscience
524
Automated pairing of bilaterally homologous neurons from connectomes
Correlated Erdős-Rényi model:
A generative statistical model of a
pair of networks wherein both
networks come from the Erdős-Rényi
modello (random, independent
edges with the same connection
probability between all nodes), Ma
corresponding potential edges in the
two networks are generated with
some correlation.
We provide a full description of the modified FAQ algorithm in the section Graph Matching
Algorithms. For the remainder of the paper, graph matching (GM) refers to the use of FAQ,
while bisected graph matching (BGM) refers to the use of FAQ as modified above.
Matching Simulated Networks
Here, we demonstrate that this approach improves matching accuracy in simulated datasets
when there is sufficient correlation in the contralateral subgraphs. To understand how this
correlation affects the usefulness of bisected graph matching, we created simulated data using
the correlated Erdős-Rényi model (CorrER). The correlated Erdős-Rényi model is a special
case of the correlated stochastic block model introduced in Lyzinski et al. (2015). Briefly, UN
pair of networks is distributed CorrER(N, P, ρ) if both networks marginally are distributed as
Erdős-Rényi models (Erdős & Rényi, 1960; Gilbert, 1959) with n nodes and global connection
probability p, but the edges of the two networks have Pearson correlation ρ. Note that this
correlation of edges also requires specifying an alignment of one network to the other, Quale
we can use as ground truth for evaluating our algorithm. Here, we use the version of this
model for a directed network to more closely resemble nanoscale connectome data, Quale
has directed edges. We used the correlated Erdő s-Ré nyi model (as implemented in
graspologic; Chung et al., 2019) to construct a simulation of a “bilateral” network as follows:
1. The ipsilateral subgraphs were sampled from a correlated Erdős-Rényi model (CorrER):
ALL; ARR ∼ CorrER 10; 0:3; 0:8
ð
Þ
2.
Independently of the ipsilateral networks, the contralateral subgraphs were sampled
from a correlated Erdős-Rényi model:
ALR; ARL ∼ CorrER 10; 0:2; ρcontra
ð
Þ
3. The full network was defined as
(cid:5)
(cid:6)
A ¼ ALL ALR
ARL ARR
4. To simulate an unknown correspondence between the nodes of the left and right hemi-
spheres, we applied a random permutation (Prand) to the nodes of the “right hemisphere”
in each sampled network:
Ainput ¼
”
In
0
#
”
UN
0
Prand
0
In
0 Prand
#
T
”
¼
ALL
ALRP T
rand
PrandARL PrandARRP T
rand
#
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Ainput is the network that was input to the matching algorithms, obscuring the true matching
from the true alignment in order to evaluate their performance. We varied the value of ρcontra
from zero (ALR and ARL have no correlation, and thus are not helpful for matching) to one (ALR
and ARL are isomorphic, providing extremely helpful information for matching). For each value
of ρcontra, we simulated 1,000 networks. For each network, we ran the graph matching (GM)
and bisected graph matching (BGM) algorithms to attempt to uncover the correct permutation
that would realign the left and right hemispheres. For both algorithms, we used default param-
eters, and one initialization for each algorithm. For each run of each algorithm, we examined
the matching accuracy, which is the proportion of nodes correctly matched.
Figura 2 shows the matching accuracy for both algorithms as a function of ρcontra. For low
values of ρcontra, using bisected graph matching actually degrades performance. When ρcontra =
Network Neuroscience
525
Automated pairing of bilaterally homologous neurons from connectomes
Figura 2. Performance of graph matching (GM) using the FAQ algorithm (Vogelstein et al., 2015)
and bisected graph matching (BGM) (this work) on a simulated dataset constructed such that the
ipsilateral and contralateral connections both come from correlated Erdős-Rényi models (Vedere
section Matching Simulated Networks). Each network had 10 nodes per side, the ipsilateral connec-
tion density was 0.3, the ipsilateral edge correlation was 0.8, and the contralateral connection
density was 0.2. We varied the contralateral edge correlation from 0 A 1, and for each value,
we simulated 1,000 networks and ran both algorithms on the same data with the same initialization.
Lines show the mean matching accuracy, and shaded regions show 95% confidence intervals. As
the correlation in the contralateral connections increases, including them in the optimization
becomes more helpful.
0, the match accuracy drops by ∼29%. This is unsurprising, as in this case the contralateral
subgraphs are effectively noise with respect to the correct matching between the left and right.
For small values of ρcontra, bisected graph matching often found permutations of the contralat-
eral subgraphs which had fewer edge disagreements than the alignment used to generate the
correlated networks (Supporting Information: Understanding Matching for Weakly Correlated
Networks), explaining why including these connections pulls the solution away from the true
matching. Tuttavia, as ρcontra increases, bisected graph matching eventually outperforms
graph matching. For this simulation, when ρcontra is greater than 0.4, the accuracy for bisected
graph matching is higher (by more than ∼20% when ρcontra ≥ 0.9). We also found that this
phenomenon was consistent across a range of network sizes (Supporting Information: Effect of
Network Size in Simulated Experiments).
Whether bisected graph matching improves accuracy is determined by many factors,
including the correlation in contralateral edge structure studied here in this simple simulation.
We next sought to see whether this bisected graph matching would be helpful in our motivat-
ing example of matching neurons between two sides of a nervous system.
Matching Connectomes
We examined the performance of both graph matching algorithms on a set of real connectome
datasets. To ensure we could evaluate the performance of both algorithms, we restricted our
analysis to connectomes for which pairings of individual neurons between sides of the nervous
system were already known. We studied the (chemical) connectomes of both a hermaphrodite
and a male Caenorhabditis elegans worm (Cook et al., 2019), the pharynges of two Pris-
tionchus pacificus worms (Bumbarger, Riebesell, Rödelsperger, & Sommer, 2013), and a subset
of a larval Drosophila melanogaster (Berck et al., 2016; Burgos et al., 2018; Carreira-Rosario
et al., 2018; Eichler et al., 2017; Eschbach et al., 2020, 2021; Fushiki et al., 2016; Gerhard
Network Neuroscience
526
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
et al., 2017; Heckscher et al., 2015; Hückesfeld et al., 2021; Jovanic et al., 2016, 2019;
Larderet et al., 2017; Mark et al., 2021; Miroschnikow et al., 2018; Ohyama et al., 2015;
Schlegel et al., 2016; Takagi et al., 2017; Tastekin et al., 2018; Zarin et al., 2019; Zwart
et al., 2016). For all these datasets, neuron pairings across sides of the nervous system are
not complete—indeed, some neurons appear only on one side of the organism or exactly in
the center (Cook et al., 2019). Così, we restricted our analysis to the subset of neurons that
were present as a bilaterally homologous pair and for which this pairing was known. We then
ensured that the remaining set of nodes was fully (weakly) connected for each dataset, remov-
ing nodes not part of the largest connected component. Tavolo 1 shows summary statistics for
each of the connectome datasets considered here. We treat each network as weighted (by
synapse count) and directed (since the direction of chemical synapses is known). Note that
for each dataset, contralateral edge correlation was high (≥0.7), suggesting that bisected graph
matching could facilitate better matching.
For each connectome, we predicted each neuron’s pair on the other side of the nervous
system by applying either the graph matching or bisected graph matching algorithms. Noi
ran 50 initializations, each from the barycenter, since neither algorithm is deterministic (Vedere
Graph Matching Algorithms section for more explanation on initialization and randomness in
the algorithm). For each initialization, we ran both algorithms with default parameters (Chung
et al., 2019) and measured the matching accuracy with respect to the known pairing of
neurons.
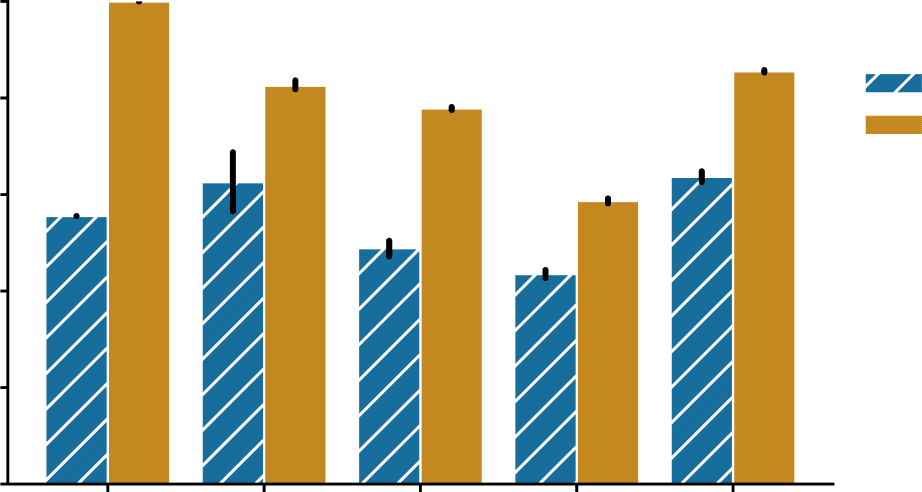
We observed that for all the connectomes studied here, bisected graph matching improves
matching performance (Figura 3), sometimes dramatically so. For all five connectomes, IL
match ratio for the bisected graph matching algorithm was significantly higher (P < 0.0005
for each dataset, two-sided Mann-Whitney U tests). Matching accuracy increased by ∼44%
and ∼20% for the two P. pacificus samples, ∼29% for the hermaphrodite C. elegans, ∼15%
for the male C. elegans, and ∼22% for the Drosophila larva subset, respectively. We also
found that this trend holds when we relaxed the requirement that all nodes in the connectome
have a homologous partner, finding that bisected graph matching always provided increased
matching accuracy even when some neuron pairs in these connectomes were artificially
unmatched (Supporting Information: Matching With Simulated Unpaired Neurons). These
results demonstrate the practical utility of our proposed algorithm for improving bilaterally
homologous pair prediction in connectomes. We next sought to show how our proposed
Barycenter:
The centroid of the doubly stochastic
matrices, i.e., an n × n matrix of all
1
n. For the purposes of initializing a
graph matching algorithm, this can
be thought of as the initialization
wherein all potential permutations
are equally likely.
Table 1.
percentage of contralateral synapses, correlation of ipsilateral subgraphs, and correlation of contralateral subgraphs for each connectome.
Summary of the connectome datasets studied in Matching Connectomes section, showing the number of nodes, number of edges,
Dataset
P. pacificus pharynx 1
P. pacificus pharynx 2
C. elegans hermaphrodite
C. elegans male
D. melanogaster
larva subset
Number
nodes
18
22
286
360
Number
edges
35
33
2,838
2,482
1,240
32,564
% contralateral
synapses
30
Ipsilateral
correlation
0.79
Contralateral
correlation
0.83
32
41
37
31
0.84
0.87
0.81
0.88
0.88
0.86
0.70
0.83
Note. Correlations are Pearson’s correlation coefficient. All metrics are with respect to the datasets after processing to select fully connected networks composed
of neurons who have bilateral pairs, as described in Matching Connectomes section. The number of nodes per hemisphere and (and the number of known pairs)
is always half the total number of nodes, since only paired neurons are considered.
Network Neuroscience
527
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
n
e
n
_
a
_
0
0
2
8
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
Figure 3. Performance of graph matching (GM) and bisected graph matching (BGM) on five bilat-
eral connectome datasets. For each comparison, we performed 50 initializations, and from each
initialization we ran both the graph matching and the bisected graph matching algorithms. The
mean match accuracy is shown for both methods on each dataset. Error bars show 95% confidence
intervals for the mean. For every dataset, bisected graph matching provided a performance improve-
ment over graph matching which ignores contralateral connections; *** indicates a significant
difference where p < 0.0005 (two-sided Mann-Whitney U test).
method can be combined with previously described extensions of graph matching to further
improve performance.
Matching Multiplex Networks
While connectomes are often described as networks, many of these datasets actually lend
themselves to multiplex network representations. For the purposes of this paper, we consider
multiplex networks to have one set of nodes, but potentially multiple types of edges between
these nodes (see Kivelä et al. (2014) for a review of multilayer networks more generally). For
instance, in C. elegans, both chemical (synaptic) and electrical (gap junction) connections
have been mapped (Cook et al., 2019). If we consider these connections to each be of their
own “type,” then we can construct an adjacency matrix for each—these become the “layers”
of our multiplex network. As further examples of edge types in connectomics, Drosophila con-
nectomes are beginning to have neurotransmitter information associated with each synapse
(Eckstein et al., 2020), as well as a differentiation between axo-axonic, axo-dendritic,
dendro-axonic, and dendro-dendritic connections (Buhmann et al., 2021; Schneider-Mizell
et al., 2016).
To match neurons based on connectivity using this multiplex network information, one can
generalize the graph matching problem to a multiplex graph matching problem. Pantazis et al.
(2022) proposed a generalization of the FAQ algorithm to solve this problem. This multiplex
graph matching scheme can easily be combined with the bisected graph matching proposed
in this work, again by simply modifying the graph matching objective function and its gradient
to account for these multiple connection types (see Multilayer Graph Matching section for
more details).
We applied graph matching and bisected graph matching to the connectomes of both
C. elegans sexes, and varied whether the networks used were either chemical, electrical, or
both (multiplex network). Figure 4 displays matching accuracy for both algorithms using each
combination of edge types. We observed a clear advantage to using multilayer graph matching
Network Neuroscience
528
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
n
e
n
_
a
_
0
0
2
8
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
Figure 4. Matching accuracy on the hermaphrodite (left) and male (right) C. elegans connectomes. Accuracy is shown when using various
combinations of network layers (chemical, electrical, or both) and subgraphs (ipsilateral (GM) or ipsilateral and contralateral (BGM)). Labels
denote the mean matching accuracy over 10 initializations. Filled circles below the x-axis indicate the layers/subgraphs used for matching in a
given column. For each combination of layers, BGM always showed an increase in mean matching accuracy over GM ( p values < 0.005 for all
of these comparisons, two-sided Mann-Whitney U test). On both datasets, the best results came from using BGM (this work) in concert with the
multiplex graph matching proposed in Pantazis et al. (2022).
on these datasets: in both connectomes and for both GM and BGM, matching with the mul-
tilayer network outperformed matching for either chemical or electrical connections alone.
We also found that BGM outperforms GM for any combination of network layers for both con-
nectomes. These results highlight the advantages of combining BGM with a previously
described extension of graph matching (Pantazis et al., 2022) when multiple edge types are
available, as the highest accuracy on both datasets came from using both contralateral con-
nections and multiple edge types.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
n
e
n
_
a
_
0
0
2
8
7
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Matching Networks of Differing Sizes and With Seeds
Next, we studied how BGM would work with two further extensions to graph matching based
on the work of Fishkind et al. (2019). Often, the two hemispheres being matched may not have
exactly the same number of neurons, but one still wishes to find a matching between them.
Further, partial matching information is also common—for instance, one could have complete
matching information about a subset of nodes in some brain region, and would like to use this
partial matching to improve matching of the rest of the brain. Fishkind et al. (2019) studied
exactly this setting, proposing “padding” schemes to deal with networks which have different
sizes, as well as a method for incorporating a partial matching or “seed” nodes into the FAQ
algorithm.
We applied the corresponding generalizations of these ideas to the bisected graph matching
case (see Seeded Graph Matching section for details), allowing us to apply our proposed algo-
rithm to a dataset where a partial matching was known ahead of time and the number of neu-
rons in the two hemispheres was not the same. To demonstrate these capabilities, we applied
this method to the Drosophila larva partial connectome (Berck et al., 2016; Burgos et al., 2018;
Carreira-Rosario et al., 2018; Eichler et al., 2017; Eschbach et al., 2020, 2021; Fushiki et al.,
2016; Gerhard et al., 2017; Heckscher et al., 2015; Hückesfeld et al., 2021; Jovanic et al.,
2016, 2019; Larderet et al., 2017; Mark et al., 2021; Miroschnikow et al., 2018; Ohyama
et al., 2015; Schlegel et al., 2016; Takagi et al., 2017; Tastekin et al., 2018; Zarin et al.,
Network Neuroscience
529
Automated pairing of bilaterally homologous neurons from connectomes
2019; Zwart et al., 2016). In the Matching Connectomes section, we restricted our analysis to
the set of nodes for which published pairings existed, such that we could evaluate matching
accuracy. Here, we relaxed this restriction, and used these published pairs as seed nodes. We
also note that the full collection of published neurons has 942 neurons on the left hemisphere
and 938 neurons on the right hemisphere. The padded graph matching of Fishkind et al.
(2019) allowed us to perform a matching on these two networks of differing sizes (resulting
in some neurons on the larger hemisphere not being matched in each run of the algorithm).
To examine the effect of seeds, we performed a cross-validation-like experiment, wherein
some seeds (20%) were reserved for evaluation so that we could compute matching accuracy.
We used some number of the remaining pairings as seeds for either graph matching or bisected
graph matching. Figure 5 shows matching accuracy on these held-out known pairings as a
function of the number of seeds used. We found that for any number of seeds, bisected graph
matching always had a higher mean matching accuracy than graph matching. Conversely,
BGM can be viewed as allowing the user to reach the same accuracy level for a smaller num-
ber of previously known seeds, which can be effortful to obtain for a new dataset.
Given the superiority of BGM over GM across a range of experiments, we finally sought to
examine the matches for neurons where we did not know of a previously presented pairing.
We reran 100 initializations of bisected graph matching on the Drosophila larva subset, using
all known pairings as seeds. Figure 6 shows the morphology of six example-predicted neuron
pairs that were always matched together across all 100 initializations. We found that the
morphology of these frequently matched neurons was generally similar, suggesting that they
may represent true bilaterally homologous pairings. Further investigation will be required to
confirm or reject these candidate matches, but our results demonstrate how bisected graph
matching can be used to easily provide well-informed guesses for these pairings. We also
provide examples of neurons that were very infrequently paired across each initialization
(implying a lower confidence in these matches; Fishkind et al., 2019), suggesting that these
pairs are less likely to be true homologs (Supporting Information Figure S4). We include all
matching results for these previously unpaired neurons in the Supporting Information (see
Code and Data section).
Figure 5. Matching accuracy using seeded matching techniques on the Drosophila larva connec-
tome subset. Here, both GM and BGM leveraged the previously published paired neurons as
“seeds” which can be used to improve the matching of the rest of the network (Fishkind et al.,
2019). Average matching accuracy is shown across 5-folds of cross-validation: 20% of seeds were
used for evaluating accuracy, and some number of the remaining seeds (x-axis) were input to GM
and BGM. Regardless of the number of seeds, BGM always provided an accuracy improvement.
Network Neuroscience
530
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
n
e
n
_
a
_
0
0
2
8
7
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
Figure 6. Morphological comparison of matched neurons in the Drosophila larva connectome subset (Berck et al., 2016; Burgos et al., 2018;
Carreira-Rosario et al., 2018; Eichler et al., 2017; Eschbach et al., 2020, 2021; Fushiki et al., 2016; Gerhard et al., 2017; Heckscher et al.,
2015; Hückesfeld et al., 2021; Jovanic et al., 2016, 2019; Larderet et al., 2017; Mark et al., 2021; Miroschnikow et al., 2018; Ohyama et al.,
2015; Schlegel et al., 2016; Takagi et al., 2017; Tastekin et al., 2018; Zarin et al., 2019; Zwart et al., 2016) using all available seeds and the
BGM algorithm. Each column shows an example neuron match that was always selected by BGM across 100 initializations, indicating high
confidence in that match (Fishkind et al., 2019). Each row shows a different view of a matched pair of neurons (anatomical axes to the left
show: D-dorsal, V-ventral, L-left, R-right, A-anterior, P-posterior). The morphology of these matched neurons appears similar, suggesting that
these are plausible candidates for previously undescribed bilaterally homologous neurons.
DISCUSSION
Summary
We proposed a simple generalization of the graph matching problem, which incorporates any
connections between the two sets of nodes being matched. We then showed how this prob-
lem could be solved by using a new objective function in the framework of a state-of-the-art
graph matching algorithm, FAQ (Vogelstein et al., 2015). In simulations, we saw that as the
strength of the correlation between the contralateral subgraphs increases, these connections
become more useful to include in the matching process. By running both graph matching
and bisected graph matching on five connectome datasets, we provided compelling evi-
dence that for practical purposes in neuroscience, including these contralateral connections
in the optimization is beneficial. We further showed how our algorithm can be applied to
settings involving multiplex networks, networks of differing sizes, and how the algorithm can
leverage a partial, known pairing of neurons to improve matching performance for the
remaining neurons. We have provided a documented, open-source implementation of our
algorithm (Python 3) to enable its easy application to future connectome datasets (see Code
and Data section).
Limitations
As we showed in simulation in Matching Simulated Networks section, bisected graph match-
ing is only likely to improve matching accuracy in connectomes when there is sufficient
correlation between the contralateral subgraphs. For a new organism (or possibly even just
a new sample), this will not be known in practice. Domain knowledge as to the nature of
the contralateral connections in an organism’s brain may be important when choosing
whether to include them in the matching as described in this work, though we note that all
five connectomes studied in this work had a high (>0.7) contralateral correlation (Tavolo 1). In
practice, it may be best to evaluate different matching algorithms (and hyperparameters) on a
subset of the connectome prior to matching a complete dataset.
Network Neuroscience
531
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
Further, other approaches to matching neurons in neuroscience do not use connectivity at
Tutto: Costa, Manton, Ostrovsky, Prohaska, and Jefferis (2016) introduced an algorithm for
matching neurons on the basis of morphology, which has been widely used on connectomic
reconstructions. In practice, it is likely that the best neuron pairings will be achieved by a joint
optimization that considers morphology, multiple edge types, seeds, and the contralateral
connections as proposed in this work. We did not explore this possibility here, but it remains
an intriguing future pursuit.
Outlook
As more connectomes are mapped both from new organisms or for more individuals of the
same species, the tools provided here will accelerate the process of finding correct pairings
of neurons between the two sides of a nervous system, while requiring less human labor to
annotate pairs by hand. These neuron pairings appear to be a fundamental property of the
invertebrate nervous systems studied in connectomics thus far. Finding these neuron pairs is
important for understanding the stereotypy in an organism (cioè., how similar is the connectivity
of the left and the right) (Cook et al., 2019; Randel et al., 2015; Schlegel, Bates, et al., 2021;
Witvliet et al., 2021). Additionally, these neuron pairs can be useful for statistical approaches
which leverage a one-to-one correspondence of nodes across networks (Athreya et al., 2017;
Tang et al., 2017). We also note that the bisected graph matching problem (and the analogous
version of the quadratic assignment problem, which is equivalent to the graph matching prob-
lem up to a sign change (Vogelstein et al., 2015) may arise in other settings where one wishes
to match nodes in a single graph that can be split into two parts and some level of symmetry
exists between them.
METHODS
Graph Matching Algorithms
Since graph matching is an NP-hard problem (Burkard et al., 2009; Conte et al., 2004), NO
efficient algorithm exists that will always yield a perfect matching. Part of the difficulty of
this problem is that the search space of permutations is large (there are n! permutations of n
nodes) and discrete (there is no way to interpolate between two permutations and still have
a permutation). Così, many algorithms relax this constraint, enabling efficient solutions of
the relaxed problem (Fiori, Sprechmann, Vogelstein, Muse, & Sapiro, 2013; Lyzinski et al.,
2016; Vogelstein et al., 2015; Zaslavskiy, Bach, & Vert, 2009). A common approach (used by
FAQ (Vogelstein et al., 2015) and other algorithms (Fiori et al., 2013; Zaslavskiy et al., 2009))
is to relax the (discontinuous) search for a permutation matrix to the convex hull of this set,
the set of doubly stochastic matrices, D (Vogelstein et al., 2015). Note that Lyzinski et al.
(2016) showed that under a model of correlated random Bernoulli graphs, the best solution
to the relaxation used by FAQ almost always yields the correct permutation matrix as the
size of the networks grows (this does not say that FAQ will always find this solution,
Tuttavia).
In this relaxed space of doubly stochastic matrices, FAQ requires an initial position to start
its search. A common default value (which we use in this work) is the barycenter, which is the
centroid of the set of all doubly stochastic matrices, and is simply an n × n matrix where all
elements are 1
N. FAQ then proceeds by using the Frank-Wolfe method to iteratively update its
search for a doubly stochastic matrix that maps one adjacency matrix to another. The algo-
rithm terminates after either a maximum number of iterations or when the search positions
change very little (less than some tolerance parameter) between iterations. After this doubly
Doubly stochastic:
Referring to matrices which are of
shape n × n and have all row and
column sums equal to one.
Network Neuroscience
532
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
stochastic solution has been found, FAQ then projects back onto the set of permutation matri-
ces by solving the linear assignment problem.
Algorithm 1 details the BGM-via-Frank-Wolfe algorithm (referred to simply as BGM in the
testo), which simply adapts this procedure by replacing the objective function and its gradient
to solve the bisected graph matching problem as described in the From Graph Matching to
Bisected Graph Matching section. We refer the interested reader to Vogelstein et al. (2015)
for further details on the original algorithm, and to Fishkind et al. (2019) for many interesting
extensions. We also note that implementations of the FAQ algorithm are available in SciPy
(Virtanen et al., 2020) and graspologic (Chung et al., 2019).
Two nuances of this algorithm for practical usage are worth commenting on. Primo, we note
that FAQ is not guaranteed to find the correct solution to the graph matching problem (E
Ancora, neither is any polynomial-time algorithm (Burkard et al., 2009; Conte et al., 2004)).
Even if the minimizer to the indefinite relaxed graph matching problem is the correct permu-
tazione (as described in Lyzinski et al., 2016), the Frank-Wolfe method may get stuck in a local
minimum, and not find this best solution. Secondo, this algorithm is not deterministic—different
initializations can lead to different solution paths, which may get stuck in local minima. Even
from the same initialization, there may be more than one-step direction (see Algorithm 1 Step
2) at any given position in the solution space, since multiple step directions can be deemed
equally suitable. Our implementation simply chooses one of these at random. Così, even from
the same initialization, it is often beneficial to restart the algorithm multiple times, and choose
the solution with the best objective function value. For this reason, a number of the experi-
ments in the main text specify the number of initializations used.
Multilayer Graph Matching
Multiplex network:
A generalization of a network
wherein there can be multiple edge
types, such as those belonging to
different neurotransmitter types.
In this work, we consider a multiplex network to have multiple edge types. If there are K
different edge types, then a multiplex network (Dire, ALL) can be represented by K different
adjacency matrices,
N
ALL ¼ A
1ð Þ
LL
; UN
2ð Þ
LL
; …; A Kð Þ
LL
o
:
Algorithm 1.
(Vogelstein et al., 2015) (GM), simply set ALR, ARL to the zero matrix.
Bisected Graph Matching (BGM) via Frank-Wolfe. To recover the FAQ algorithm
Require: Adjacency matrices for each of the four subgraphs: ALL, ARR, ALR, ARL 2 ℝn×n.
n1n × 1⊺
Initialize: P(0) 2 D, barycenter (P(0) = 1
N) unless otherwise specified
for i = 1, 2, 3, … while (i ≤ MAXITER) E (∥Pi − Pi−1∥F ≥ TOLERANCE)) do
1. Compute ∇f (P(io )) = −(ALLP(io )AT
RR + AT
LLP(io )ARR + ALRP T
ið ÞARL + AT
RLP T
ið ÞALR)
2. Compute Q(io ) 2 argmin tr(QT∇f (P(io ))) over Q 2 D via linear assignment problem solver,
per esempio., Hungarian algorithm (Kuhn, 1955)
3. Compute step size α(io ) 2 argmin f (αP(io ) + (1 − α)Q(io )), for α 2 [0, 1]
4. Set P(i+1) = αP(io ) + (1 − α)Q(io )
end for
return
^Q 2 argmin tr(QT∇f (P( final ))) over Q 2 P via linear assignment problem solver.
Network Neuroscience
533
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
Matching A to some other multiplex network (which has the same edge types 1, …, K ), ARR,
thus amounts to matching each of their constituent adjacency matrices. Pantazis et al. (2022)
formalized this notion by writing the objective function as
(cid:1)
2
(cid:1)
(cid:1)
F
(cid:1)
(cid:1)
A kð Þ
(cid:1)
− PA kð Þ
f Pð Þ ¼
RR P T
XK
LL
:
k¼1
Note that the same permutation matrix, P, jointly maps each of these adjacency matrices
together. To perform multiplex bisected graph matching, we apply the same generalization
to the bisected graph matching objective function (Equazione 2)
f Pð Þ ¼
XK
(cid:1)
(cid:1)
(cid:1)
k¼1
A kð Þ
LL
− PA kð Þ
RR P T
(cid:1)
(cid:1)
(cid:1)
2
F
(cid:1)
(cid:1)
þ A kð Þ
(cid:1)
LR P T − PA kð Þ
RL
(cid:1)
2
(cid:1)
(cid:1)
F
:
(4)
The gradient of this new objective function is simply the sum of the gradients of each term
∇f Pð Þ ¼
XK
k¼1
(cid:7)
− A kð Þ
LL PA kð ÞT
RR
þ A kð ÞT
LL PA kð Þ
RR
þ A kð Þ
LR P T A kð ÞT
RL
þ A kð ÞT
RL P T A kð Þ
LR
(cid:8)
:
(5)
Using Equations 4 E 5 as the objective and gradient, rispettivamente, in Algorithm 1 yields a
method for solving a multiplex bisected graph matching problem.
Seeded Graph Matching
Fishkind et al. (2019) considered modifying FAQ to solve the so-called seeded graph matching
problem, wherein a subset of the nodes of the two networks are matched ahead of time. IL
goal is to leverage these previously known pairings to improve the pairings of the rest of the
rete. This seeded graph matching problem can be thought of as restricting the search
space of all permutations to only those which respect a particular seed set.
We briefly present the methods for seeded graph matching here, and refer the interested
reader to Fishkind et al. (2019) for more details. Adapting notation to match that of this work,
denote the adjacency matrix of seeded-to-seeded connections in the left-to-left subgraph as
Ass
LL, the matrix of seeded-to-nonseeded connections in the left-to-left subgraph as Asn
LL, E
likewise for the other possible subgraphs. With this definition, Fishkind et al. (2019) showed
that the seeded graph matching objective function has the same minimizer as
!
#
#
”
”
fI Pð Þ ¼ −trace
AssT
LL
AsnT
LL
AnsT
LL
AnnT
LL
(cid:5)
(cid:6)
0
IO
0 P
AssT
RR AnsT
RR AnnT
AsnT
RR
RR
(cid:5)
(cid:6)
0
IO
0 P T
:
(6)
Further, they showed that the gradient of fI(P) with respect to P is
(cid:7)
∇fI Pð Þ ¼ − Ann
LL PAnnT
RR
þ AnnT
LL PAnn
RR
þ Ans
LLAnsT
RR
þ AsnT
LL Asn
RR
(cid:8)
:
(7)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
For the term we added to the graph matching objective for the contralateral adjacency matri-
ces, the minimizer is the same as that of
fC Pð Þ ¼ −trace
”
AssT
LR
AsnT
LR
AnsT
LR
AnnT
LR
#
”
(cid:6)
(cid:5)
0
IO
0 P
RR Asn
Ass
RR
RR Ann
Ans
RR
!
#
(cid:6)
(cid:5)
0
IO
0 P
:
(8)
And similarly to the standard graph matching case, the gradient is
(cid:7)
∇fC Pð Þ ¼ − Ann
LRP T AnnT
RL
þ AnnT
RL P T Ann
LR
þ Ans
LRAnsT
RL
þ AsnT
RL Asn
LR
(cid:8)
:
(9)
For seeded graph matching with ipsilateral and contralateral connections, the full objective
function is fI(P) + fC(P), and its gradient is ∇fI(P) + ∇fC(P). We use this new objective function
Network Neuroscience
534
Automated pairing of bilaterally homologous neurons from connectomes
and gradient in the Frank-Wolfe method (Algorithm 1) to yield a seeded bisected graph match-
ing algorithm.
Padded Graph Matching
Consider the case where ALL has more nodes than ARR (without loss of generality, because we
could swap the left and right sides to yield an equivalent algorithm). Let nL be the number of
nodes on the left, and nR be the number of nodes on the right. Fishkind et al. (2019) proposed a
“padding” scheme, wherein these networks can be made comparable for matching. Their
“naive” padding scheme simply replaces ARR with a new matrix that has added zeros to make
it match the size of ALL:
(cid:5)
Ap
RR
¼
ARR
0 nL−nR
ð
Þ(cid:2)nR
0nR (cid:2) nL−nR
ð
Þ
0 nL−nR
ð
Þ(cid:2) nL−nR
ð
Þ
(cid:6)
where 0m×n is a m × n matrix of all zeros. Ap
RR can now be matched to ALL, though some nodes
on the left would be matched to row/columns of all zeros, and therefore not have a valid
match on the right.
For bisected graph matching, we use the same padding idea adapted to our setting. IL
padded version of ALR is
Ap
LR
(cid:9)
¼ ALR 0nL(cid:2) nL−nR
ð
(cid:10)
Þ
and the padded version of ARL is
(cid:5)
Ap
RL
¼
(cid:6)
:
ARL
0 nL−nR
ð
Þ(cid:2)nL
For padded bisected graph matching, these matrices (Ap
RL) are used in place of the
original subgraphs such that the graph matching algorithms described above (which require
matrices to be of the same size) can be applied. We did not explore the use of the “adopted”
padding scheme, as in our case the two sides of the connectome being matched had
approximately the same number of nodes, and this method was not described for weighted
networks (Fishkind et al., 2019).
RR, Ap
LR, Ap
Code and Data
Analyses relied on graspologic (Chung et al., 2019), NumPy (Harris et al., 2020), SciPy
(Virtanen et al., 2020), Pandas (McKinney, 2010), NetworkX (Hagberg, Swart, & S Chult,
2008), and pymaid (Schlegel, Phelps, & Jefferis, 2021). Plotting was performed using
matplotlib (Hunter, 2007), Seaborn (Waskom, 2021), and NAVis (Schlegel, Barnes,
Jagannathan, Pedigo, & Court, 2021).
All code for this paper (implemented in Python 3) can be found on GitHub at github.com
/neurodata/bgm (Pedigo, 2022UN) and viewed as a Jupyter Book (Executable Books Community,
2020) at docs.neurodata.io/bgm. There are no primary data in the paper (see references in
Matching Connectomes section). All data is included in the GitHub repository, including
the matching results (Pedigo, 2022B) on the Drosophila larva connectome subset. The source
code and data is also archived at doi.org/10.5281/zenodo.6561550.
ACKNOWLEDGMENTS
We thank Thomas Athey for helpful comments.
Network Neuroscience
535
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00287,
https://github.com/neurodata/bgm (Pedigo, 2022UN), and https://github.com/neurodata/bgm
/blob/main/results/outputs/connectome_seeded/pair_predictions.csv (Pedigo, 2022B). IL
algorithm proposed in this work has also been implemented in graspologic at https://github
.com/microsoft/graspologic (Chung et al., 2019).
AUTHOR CONTRIBUTIONS
Benjamin David Pedigo: Conceptualization; Data curation; Formal analysis; Funding acquisi-
zione; Investigation; Methodology; Project administration; Software; Supervision; Validation;
Visualization; Writing – original draft; Writing – review & editing. Michael Winding: Concep-
tualization; Data curation; Investigation; Writing – review & editing. Carey E. Priebe: Concep-
tualization; Funding acquisition; Investigation; Methodology; Supervision; Writing – review &
editing. Joshua T. Vogelstein: Conceptualization; Funding acquisition; Investigation; Method-
ology; Project administration; Resources; Supervision; Writing – review & editing.
FUNDING INFORMATION
Benjamin David Pedigo, National Science Foundation (https://dx.doi.org/10.13039
/100000001), Award ID: DGE1746891. Joshua T. Vogelstein, National Science Foundation
(https://dx.doi.org/10.13039/100000001), Award ID: 1942963. Joshua T. Vogelstein, National
Science Foundation (https://dx.doi.org/10.13039/100000001), Award ID: 2014862. Joshua T.
Vogelstein, Foundation for the National Institutes of Health (https://dx.doi.org/10.13039
/100000009), Award ID: 1RF1MH123233-01. Carey E. Priebe, Foundation for the National
Institutes of Health (https://dx.doi.org/10.13039/100000009), Award ID: 1RF1MH123233-01.
REFERENCES
Athreya, A., Fishkind, D. E., Tang, M., Priebe, C. E., Park, Y.,
Vogelstein, J. T., … Qin, Y. (2017). Statistical inference on random
dot product graphs: A survey. Journal of Machine Learning
Research, 18(1), 8393–8484.
Bassett, D. S., & Sporns, O. (2017). Network neuroscience. Nature
Neuroscience, 20(3), 353–364. https://doi.org/10.1038/nn.4502,
PubMed: 28230844
Berck, M. E., Khandelwal, A., Claus, L., Hernandez-Nunez, L., Si,
G., Tabone, C. J., … Cardona, UN. (2016). The wiring diagram of a
glomerular olfactory system. eLife, 5, e14859. https://doi.org/10
.7554/eLife.14859, PubMed: 27177418
Buhmann, J., Sheridan, A., Malin-Mayor, C., Schlegel, P., Gerhard,
S., Kazimiers, T., … Funke, J. (2021). Automatic detection of syn-
aptic partners in a whole-brain Drosophila electron microscopy
insieme di dati. Nature Methods, 18(7), 771–774. https://doi.org/10
.1038/s41592-021-01183-7, PubMed: 34168373
Bumbarger, D. J., Riebesell, M., Rödelsperger, C., & Sommer, R. J.
(2013). System-wide rewiring underlies behavioral differences
in predatory and bacterial-feeding nematodes. Cell, 152(1),
109–119. https://doi.org/10.1016/j.cell.2012.12.013, PubMed:
23332749
Burgos, A., Honjo, K., Ohyama, T., Qian, C. S., Shin, G. J.-E., Gohl,
D. M., … Grueber, W. B. (2018). Nociceptive interneurons
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
control modular motor pathways to promote escape behavior
in Drosophila. eLife, 7, e26016. https://doi.org/10.7554/eLife
.26016, PubMed: 29528286
Burkard, R. E., Dell’Amico, M., & Martello, S. (2009). Assignment
problems. Philadelphia, PAPÀ: Society for Industrial and Applied
Mathematics (SIAM). https://doi.org/10.1137/1.9780898717754
Carreira-Rosario, A., Zarin, UN. A., Clark, M. Q., Equipaggio, L., Fetter,
R. D., Cardona, A., & Doe, C. Q. (2018). MDN brain descending
neurons coordinately activate backward and inhibit forward
locomotion. eLife, 7, e38554. https://doi.org/10.7554/eLife
.38554, PubMed: 30070205
Chung, J., Bridgeford, E., Arroyo, J., Pedigo, B. D., Saad-Eldin, A.,
Gopalakrishnan, V., … Vogelstein, J. T. (2021). Statistical connec-
tomics. Annual Review of Statistics and Its Application, 8, 463–492.
https://doi.org/10.1146/annurev-statistics-042720-023234
Chung, J., Pedigo, B. D., Bridgeford, E. W., Varjavand, B. K., Helm,
H. S., & Vogelstein, J. T. (2019). GraSPy: Graph statistics in
Python. arXiv:1904.05329. https://doi.org/10.48550/arXiv.1904
.05329
Conte, D., Foggia, P., Sansone, C., & Vento, M. (2004). Thirty years
of graph matching in pattern recognition. International Journal of
Pattern Recognition and Artificial Intelligence, 18(3), 265–298.
https://doi.org/10.1142/S0218001404003228
Network Neuroscience
536
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
T
.
Automated pairing of bilaterally homologous neurons from connectomes
Cook, S. J., Jarrell, T. A., Brittin, C. A., Wang, Y., Bloniarz, UN. E.,
Yakovlev, M. A., … Emmons, S. W. (2019). Whole-animal
connectomes of both Caenorhabditis elegans sexes. Nature,
571(7763), 63–71. https://doi.org/10.1038/s41586-019-1352-7,
PubMed: 31270481
Costa, M., Manton, J. D., Ostrovsky, UN. D., Prohaska, S., & Jefferis,
G. S. X. E. (2016). NBLAST: Rapid, sensitive comparison of neu-
ronal structure and construction of neuron family databases.
Neuron, 91(2), 293–311. https://doi.org/10.1016/j.neuron.2016
.06.012, PubMed: 27373836
Eckstein, N., Bates, UN. S., Du, M., Hartenstein, V., Jefferis,
G. S. X. E., & Funke, J. (2020). Neurotransmitter classification
from electron microscopy images at synaptic sites in Drosophila.
bioRxiv. https://doi.org/10.1101/2020.06.12.148775
Eichler, K., Li, F., Litwin-Kumar, A., Park, Y., Andrade, I., Schneider-
Mizell, C. M., … Cardona, UN. (2017). The complete connectome
of a learning and memory centre in an insect brain. Nature,
548(7666), 175–182. https://doi.org/10.1038/nature23455,
PubMed: 28796202
Erdős, P., & Rényi, UN. (1960). On the evolution of random graphs.
Publication of the Mathematical Institute of the Hungarian Acad-
emy of Sciences, 5(1), 17–60.
Eschbach, C., Fushiki, A., Winding, M., Afonso, B., Andrade, IO. V.,
Cocanougher, B. T., … Zlatic, M. (2021). Circuits for integrating
learned and innate valences in the insect brain. eLife, 10, e62567.
https://doi.org/10.7554/eLife.62567, PubMed: 34755599
Eschbach, C., Fushiki, A., Winding, M., Schneider-Mizell, C. M.,
Shao, M., Arruda, R., … Zlatic, M. (2020). Recurrent architecture
for adaptive regulation of learning in the insect brain. Nature
Neuroscience, 23(4), 544–555. https://doi.org/10.1038/s41593
-020-0607-9, PubMed: 32203499
Executable Books Community. (2020). Jupyter book. Zenodo.
https://doi.org/10.5281/zenodo.4539666
Fiori, M., Sprechmann, P., Vogelstein, J., Muse, P., & Sapiro, G.
(2013). Robust multimodal graph matching: Sparse coding meets
graph matching. In Advances in neural information processing sys-
tems (Vol. 26). Curran Associates, Inc. https://proceedings.neurips
.cc/paper/2013/ hash/1afa34a7f984eeabdbb0a7d494132ee5
-Abstract.html
Fishkind, D. E., Adali, S., Patsolic, H. G., Meng, L., Singh, D.,
Lyzinski, V., & Priebe, C. E. (2019). Seeded graph matching.
Pattern Recognition, 87, 203–215. https://doi.org/10.1016/j
.patcog.2018.09.014
Frank, M., & Wolfe, P. (1956). An algorithm for quadratic program-
ming. Naval Research Logistics Quarterly, 3(1–2), 95–110. https://
doi.org/10.1002/nav.3800030109
Fushiki, A., Zwart, M. F., Kohsaka, H., Fetter, R. D., Cardona, A., &
Nose, UN. (2016). A circuit mechanism for the propagation of
waves of muscle contraction in Drosophila. eLife, 5, e13253.
https://doi.org/10.7554/eLife.13253, PubMed: 26880545
Gerhard, S., Andrade, I., Fetter, R. D., Cardona, A., & Schneider-
Mizell, C. M. (2017). Conserved neural circuit structure across
Drosophila larval development revealed by comparative connec-
tomics. eLife, 6, e29089. https://doi.org/10.7554/eLife.29089,
PubMed: 29058674
Gilbert, E. N. (1959). Random graphs. The Annals of Mathematical
Statistics, 30(4), 1141–1144. https://doi.org/10.1214/aoms
/1177706098
Hagberg, A., Swart, P., & S Chult, D. (2008). Exploring network
structure, dynamics, and function using NetworkX (Tech. Rep.).
Los Alamos, NM: Los Alamos National Laboratory.
Harris, C. R., Millman, K. J., van der Walt, S. J., Gommers, R.,
Virtanen, P., Cournapeau, D., … Oliphant, T. E. (2020). Array pro-
gramming with NumPy. Nature, 585(7825), 357–362. https://doi
.org/10.1038/s41586-020-2649-2, PubMed: 32939066
Heckscher, E. S., Zarin, UN. A., Faumont, S., Clark, M. Q., Equipaggio,
L., Fushiki, A., … Doe, C. Q. (2015). Even-skipped(+) interneu-
rons are core components of a sensorimotor circuit that main-
tains left-right symmetric muscle contraction amplitude. Neuron,
88(2), 314–329. https://doi.org/10.1016/j.neuron.2015.09.009,
PubMed: 26439528
Hückesfeld, S., Schlegel, P., Miroschnikow, A., Schoofs, A., Zinke,
I., Haubrich, UN. N., … Pankratz, M. J. (2021). Unveiling the
sensory and interneuronal pathways of the neuroendocrine con-
nectome in Drosophila. eLife, 10, e65745. https://doi.org/10
.7554/eLife.65745, PubMed: 34085637
Hunter, J. D. (2007). Matplotlib: A 2D graphics environment. Com-
puting in Science & Engineering, 9(3), 90–95. https://doi.org/10
.1109/MCSE.2007.55
Jovanic, T., Schneider-Mizell, C. M., Shao, M., Masson, J.-B.,
Denisov, G., Fetter, R. D., … Zlatic, M. (2016). Competitive
disinhibition mediates behavioral choice and sequences in Dro-
sophila. Cell, 167(3), 858–870. https://doi.org/10.1016/j.cell
.2016.09.009, PubMed: 27720450
Jovanic, T., Winding, M., Cardona, A., Truman, J. W., Gershow, M.,
& Zlatic, M. (2019). Neural substrates of Drosophila larval ane-
motaxis. Current Biology, 29(4), 554–566. https://doi.org/10
.1016/j.cub.2019.01.009, PubMed: 30744969
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., &
Porter, M. UN. (2014). Multilayer networks. Journal of Complex
Networks, 2(3), 203–271. https://doi.org/10.1093/comnet/cnu016
Kuhn, H. W. (1955). The Hungarian method for the assignment
problem. Naval Research Logistics Quarterly, 2(1–2), 83–97.
https://doi.org/10.1002/nav.3800020109
Larderet, I., Fritsch, P. M. J., Gendre, N., Neagu-Maier, G. L., Fetter,
R. D., Schneider-Mizell, C. M., … Sprecher, S. G. (2017). Orga-
nization of the Drosophila larval visual circuit. eLife, 6, e28387.
https://doi.org/10.7554/eLife.28387, PubMed: 30726702
Lyzinski, V., Fishkind, D. E., Fiori, M., Vogelstein, J. T., Priebe, C. E.,
& Sapiro, G. (2016). Graph matching: Relax at your own risk.
IEEE Transactions on Pattern Analysis and Machine Intelligence,
38(1), 60–73. https://doi.org/10.1109/ TPAMI.2015.2424894,
PubMed: 26656578
Lyzinski, V., Sussman, D. L., Fishkind, D. E., Pao, H., Chen, L.,
Vogelstein, J. T., … Priebe, C. E. (2015). Spectral clustering for
divide-and-conquer graph matching. Parallel Computing, 47,
70–87. https://doi.org/10.1016/j.parco.2015.03.004
Marchisio, K., Park, Y., Saad-Eldin, A., Alyakin, A., Duh, K., Priebe,
C., & Koehn, P. (2021). An analysis of Euclidean vs. graph-based
framing for bilingual lexicon induction from word embedding
spazi. In Findings of the Association for Computational Linguis-
tic: EMNLP 2021 (pag. 738–749). Punta Cana, Dominican
Republic: Associazione per la Linguistica Computazionale. https://doi
.org/10.18653/v1/2021.findings-emnlp.64
Segno, B., Lai, S.-L., Zarin, UN. A., Equipaggio, L., Pollington, H. Q.,
Litwin-Kumar, A., … Doe, C. Q. (2021). A developmental
Network Neuroscience
537
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Automated pairing of bilaterally homologous neurons from connectomes
framework linking neurogenesis and circuit formation in the
Drosophila CNS. eLife, 10, e67510. https://doi.org/10.7554
/eLife.67510, PubMed: 33973523
McKinney, W. (2010). Data structures for statistical computing in
Python. In Proceedings of the 9th Python in science conference
(Vol. 445, pag. 51–56). https://doi.org/10.25080/Majora-92bf1922-00a
Miroschnikow, A., Schlegel, P., Schoofs, A., Hueckesfeld, S., Li, F.,
Schneider-Mizell, C. M., … Pankratz, M. J. (2018). Convergence
of monosynaptic and polysynaptic sensory paths onto common
motor outputs in a Drosophila feeding connectome. eLife, 7,
e40247. https://doi.org/10.7554/eLife.40247, PubMed:
30526854
Ohyama, T., Schneider-Mizell, C. M., Fetter, R. D., Aleman, J. V.,
Franconville, R., Rivera-Alba, M., … Zlatic, M. (2015). A multi-
level multimodal circuit enhances action selection in Drosophila.
Nature, 520(7549), 633–639. https://doi.org/10.1038
/nature14297, PubMed: 25896325
Pantazis, K., Sussman, D. L., Park, Y., Li, Z., Priebe, C. E., &
Lyzinski, V. (2022). Multiplex graph matching matched filters.
Applied Network Science, 7(1), 1–35. https://doi.org/10.1007
/s41109-022-00464-0
Pedigo, B. D. (2022UN). neurodata / bgm, GitHub. https://github.com
/neurodata/bgm
Pedigo, B. D. (2022B). neurodata / bgm, GitHub. https://github.com
/neurodata/bgm/blob/main/results/outputs/connectome_seeded
/pair_predictions.csv
Randel, N., Shahidi, R., Verasztó, C., Bezares-Calderón, l. A.,
Schmidt, S., & Jékely, G. (2015). Inter-individual stereotypy of
the Platynereis larval visual connectome. eLife, 4, e08069.
https://doi.org/10.7554/eLife.08069, PubMed: 26061864
Saad-Eldin, A., Pedigo, B. D., Priebe, C. E., & Vogelstein, J. T.
(2021). Graph matching via optimal transport. arXiv:2111.05366.
https://doi.org/10.48550/arXiv.2111.05366
Schlegel, P., Barnes, C., Jagannathan, S., Pedigo, B., & Court, R.
(2021). navis-org/navis: Version 1.1.0. Zenodo. https://doi.org
/10.5281/zenodo.5710143
Schlegel, P., Bates, UN. S., Stürner, T., Jagannathan, S. R.,
Drummond, N., Hsu, J., … Jefferis, G. S. X. E. (2021). Information
flow, cell types and stereotypy in a full olfactory connectome.
eLife, 10, e66018. https://doi.org/10.7554/eLife.66018,
PubMed: 34032214
Schlegel, P., Phelps, J., & Jefferis, G. S. X. E. (2021). schlegelp/
pymaid: Version 2.0.6. Zenodo. https://doi.org/10.5281/zenodo
.5110150
Schlegel, P., Texada, M. J., Miroschnikow, A., Schoofs, A.,
Hückesfeld, S., Peters, M., … Pankratz, M. J. (2016). Synaptic
transmission parallels neuromodulation in a central food-intake
circuit. eLife, 5, e16799. https://doi.org/10.7554/eLife.16799,
PubMed: 27845623
Schneider-Mizell, C. M., Gerhard, S., Longair, M., Kazimiers, T., Li,
F., Zwart, M. F., … Cardona, UN. (2016). Quantitative neuroanat-
omy for connectomics in Drosophila. eLife, 5, e12059. https://doi
.org/10.7554/eLife.12059, PubMed: 26990779
Sussman, D. L., Park, Y., Priebe, C. E., & Lyzinski, V. (2020).
Matched filters for noisy induced subgraph detection. IEEE Trans-
actions on Pattern Analysis and Machine Intelligence, 42(11),
2887–2900. https://doi.org/10.1109/ TPAMI.2019.2914651,
PubMed: 31059426
Takagi, S., Cocanougher, B. T., Niki, S., Miyamoto, D., Kohsaka,
H., Kazama, H., … Nose, UN. (2017). Divergent connectivity of
homologous command-like neurons mediates segment-specific
touch responses in Drosophila. Neuron, 96(6), 1373–1387.
https://doi.org/10.1016/j.neuron.2017.10.030, PubMed:
29198754
Tang, M., Athreya, A., Sussman, D. L., Lyzinski, V., Park, Y., &
Priebe, C. E. (2017). A semiparametric two-sample hypothesis
testing problem for random graphs. Journal of Computational
and Graphical Statistics, 26(2), 344–354. https://doi.org/10
.1080/10618600.2016.1193505
Tastekin, I., Khandelwal, A., Tadres, D., Fessner, N. D., Truman,
J. W., Zlatic, M., … Louis, M. (2018). Sensorimotor pathway con-
trolling stopping behavior during chemotaxis in the Drosophila
melanogaster larva. eLife, 7, e38740. https://doi.org/10.7554
/eLife.38740, PubMed: 30465650
Tripathi, K., & Pedigo, B. D. (2022). Microsoft / graspologic,
GitHub. https://github.com/microsoft/graspologic
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy,
T., Cournapeau, D., … SciPy 1.0 Contributors. (2020). SciPy 1.0:
Fundamental algorithms for scientific computing in Python.
Nature Methods, 17(13), 261–272. https://doi.org/10.1038
/s41592-019-0686-2, PubMed: 32015543
Vogelstein, J. T., Bridgeford, E. W., Pedigo, B. D., Chung, J., Levin,
K., Mensh, B., & Priebe, C. E. (2019). Connectal coding: Discov-
ering the structures linking cognitive phenotypes to individual
histories. Current Opinion in Neurobiology, 55, 199–212.
https://doi.org/10.1016/j.conb.2019.04.005, PubMed: 31102987
Vogelstein, J. T., Conroy, J. M., Lyzinski, V., Podrazik, l. J., Kratzer,
S. G., Harley, E. T., … Priebe, C. E. (2015). Fast approximate
quadratic programming for graph matching. PLoS One, 10(4),
e0121002. https://doi.org/10.1371/journal.pone.0121002,
PubMed: 25886624
Waskom, M. l. (2021). seaborn: Statistical data visualization.
Journal of Open Source Software, 6(60), 3021. https://doi.org/10
.21105/joss.03021
Witvliet, D., Mulcahy, B., Mitchell, J. K., Meirovitch, Y., Berger,
D. R., Wu, Y., … Zhen, M. (2021). Connectomes across develop-
ment reveal principles of brain maturation. Nature, 596(7871),
257–261. https://doi.org/10.1038/s41586-021-03778-8,
PubMed: 34349261
Zarin, UN. A., Segno, B., Cardona, A., Litwin-Kumar, A., & Doe, C. Q.
(2019). A multilayer circuit architecture for the generation of dis-
tinct locomotor behaviors in Drosophila. eLife, 8, e51781. https://
doi.org/10.7554/eLife.51781, PubMed: 31868582
Zaslavskiy, M., Bach, F., & Vert, J.-P. (2009). A path following algo-
rithm for the graph matching problem. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 31(12), 2227–2242.
https://doi.org/10.1109/TPAMI.2008.245, PubMed: 19834143
Zwart, M. F., Pulver, S. R., Truman, J. W., Fushiki, A., Fetter, R. D.,
Cardona, A., & Landgraf, M. (2016). Selective inhibition medi-
ates the sequential recruitment of motor pools. Neuron, 91(3),
615–628. https://doi.org/10.1016/j.neuron.2016.06.031,
PubMed: 27427461
Network Neuroscience
538
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
7
2
5
2
2
2
1
1
8
3
5
7
N
e
N
_
UN
_
0
0
2
8
7
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3