RESEARCH

A perturbative approach to study information
communication in brain networks

Varun Madan Mohan and Arpan Banerjee

National Brain Research Centre, Manesar, India

Keywords: Information flow, Perturbation, Network-dynamical interactions, Computational
modeling, Response asymmetry

a n o p e n a c c e s s

j o u r n a l

ABSTRACT

How communication among neuronal ensembles shapes functional brain dynamics is a
question of fundamental importance to neuroscience. Communication in the brain can be
viewed as a product of the interaction of node activities with the structural network over which
these activities flow. The study of these interactions is, Tuttavia, restricted by the difficulties in
describing the complex dynamics of the brain. There is thus a need to develop methods to
study these network-dynamical interactions and how they impact information flow, without
having to ascertain dynamics a priori or resort to restrictive analytical approaches. Here, we
adapt a recently established network analysis method based on perturbations, it to a
neuroscientific setting to study how information flow in the brain can raise from properties of
underlying structure. For proof-of-concept, we apply the approach on in silico whole-brain
models. We expound on the functional implications of the distributions of metrics that capture
network-dynamical interactions, termed net influence and flow. We also study the network-
dynamical interactions at the level of resting-state networks. An attractive feature of this
method is its simplicity, which allows a direct translation to an experimental or clinical setting,
such as for identifying targets for stimulation studies or therapeutic interventions.

AUTHOR SUMMARY

In this work, we use controlled perturbations in silico to identify regions that influence and mediate
information flow in active brain networks. Conventional approaches of identifying such regions
require the extensive analytical treatment of mathematical models describing node dynamics,
thus restricting its scope only to systems where such models have been defined. The presented
formalism can identify regions of dynamical and functional importance by simply measuring
responses to perturbations, and can thus be applied at any scale where regions can be perturbed,
and without any prerequisite information about node dynamics. Inoltre, the relation of
metrics to interregional communication, functional capabilities, and structure-function mapping
in general affords them considerable practical importance, especially for identifying targets for
therapeutic interventions.

INTRODUCTION

The brain is a complex biological network in which healthy function strongly relies on the efficient
transmission of information between functional entities at multiple scales (Avena-Koenigsberger,

Citation: Madan Mohan, V., & Banerjee,
UN. (2022). A perturbative approach to
study information communication in
brain networks. Network Neuroscience,
6(4), 1275–1295. https://doi.org/10.1162
/netn_a_00260

DOI:
https://doi.org/10.1162/netn_a_00260

Supporting Information:
https://doi.org/10.1162/netn_a_00260;
https:// bitbucket.org/cbdl/netinfluence
-flow/src/master/

Received: 21 Febbraio 2022
Accepted: 15 Giugno 2022

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Arpan Banerjee
arpan@nbrc.ac.in

Handling Editor:
Bratislav Misic

Copyright: © 2022
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza

The MIT Press

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

/

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

Misic, & Sporns, 2018; Battaglia, Benchenane, Sirota, Pennartz, & Wiener, 2011; Goñi et al.,
2014). At the whole-brain scale, it is generally assumed that information flows along channels of
white matter tracts connecting gray matter regions, subsequently leading to the observed brain
dynamics. Tuttavia, determining the precise mapping between the structural connectome (SC),
and the functional connectivity (FC) arising from the observed brain dynamics is an enduring prob-
lem in neuroscience (Honey, Thivierge, & Sporns, 2010; Suárez, Markello, Betzel, & Misic, 2020).
The crucial link to this mapping lies in the particulars of dynamics that evolve over the SC (Forrester,
Crofts, Sotiropoulos, Coombes, & O’Dea, 2020). The dynamical complexity of the brain is well
showcased by the mathematically diverse models used to describe function at multiple spatial
scales (Deco et al., 2013; FitzHugh, 1961; Hodgkin & Huxley, 1952; Naskar, Vattikonda, Deco,
Roy, & Banerjee, 2021; Stefanescu & Jirsa, 2008; Wilson & Cowan, 1972). In aggiunta a
complexity introduced at the node level by these models, an added layer of complexity in brain
function arises from the combination or interaction of such dynamics with the brain’s underlying
structural network. These network-dynamical interactions have previously been implicated in the
rise of emergent phenomena and functional asymmetries that transcend understanding from local
dynamics or structural properties alone (Dayan & Abbott, 2001; Gu et al., 2015; Hansen,
Battaglia, Spiegler, Deco, & Jirsa, 2015; Hens, Harush, Haber, Cohen, & Barzel, 2019; Mišić
et al., 2018; Moon, Lee, Blain-Moraes, & Mashour, 2015; Novelli, Atay, Jost, & Lizier, 2020;
Seguin, Razi, & Zalesky, 2019; Seguin et al., 2019; Sporns, 2014; Strogatz, 2000). Tuttavia,
obtaining insights into how network-dynamical interactions result in patterns of information flow
and other dynamical processes is seldom straightforward, often requiring one to resort to
analytical approaches. Such an approach, Tuttavia, requires that there be a well-defined
mathematical model for the dynamics to begin with, which limits our understanding to a select
few scenarios. Therefore, there is a need for methods that can bypass these conventional
prerequisites to understanding these interactions that underlie interregional communication,
functional capabilities of brain regions, and structure-function mapping in general. Recente
advances in studies of real-world networks (Harush & Barzel, 2017; Hens et al., 2019) Avere
proposed a theoretical framework to tackle problems of this nature.

The fallouts of interactions between the dynamics and the underlying structural network
can be studied by tracing the effects of changes to a node’s activity (akin to the information)
on the rest of the active network—a perturbative approach. Perturbative methods have been
previously used in silico to gather insights into diverse aspects of brain function (Deco et al.,
2018; Gollo, Roberts, & Cocchi, 2017; Sanz Perl et al., 2021; Veit et al., 2021). Here, we
choose to recast the information flow formalism introduced recently in network science
(Harush & Barzel, 2017). The transfer of information can be captured as baseline activity
perturbation that originates in one region and results in a chain of perturbations in subsequent
neighborhoods of intermediary nodes till it reaches the target (Figure 1B). Lo osserviamo
perturbations can be used to unearth asymmetries in the network influencing capabilities of
distinct brain regions, quantified by a metric termed net influence. Inoltre, an extension
of this formalism leads to the definition of a dynamics-dependent communication centrality
measure, termed flow, which quantifies the overall contribution of a region to information
transfer events. This metric can hold considerable insights into possible communication pat-
terns supported by neurodynamical models. The prime advantage of the perturbative
approach is that the method does not alter the structure of the underlying anatomical network.
This preserves structural network properties and helps in singling out dynamical consequences
to the perturbations. Inoltre, the simplicity and mathematical basis of this formalism permits
its easy application onto any experimental framework using perturbations, such as brain stim-
ulation techniques. Most importantly, since the measures developed are at the level of time

Perturbation:
Controlled change in the neural
activity of a region, which results in
changes in activities of other network
nodes.

Net influence:
A metric capturing the difference
between a region’s influence on the
network and the network’s influence
on the region.

Flow:
A metric that captures the role of a
region in mediating the flow of
activities between all possible
sources and targets.

Network Neuroscience

1276

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

/

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

/

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

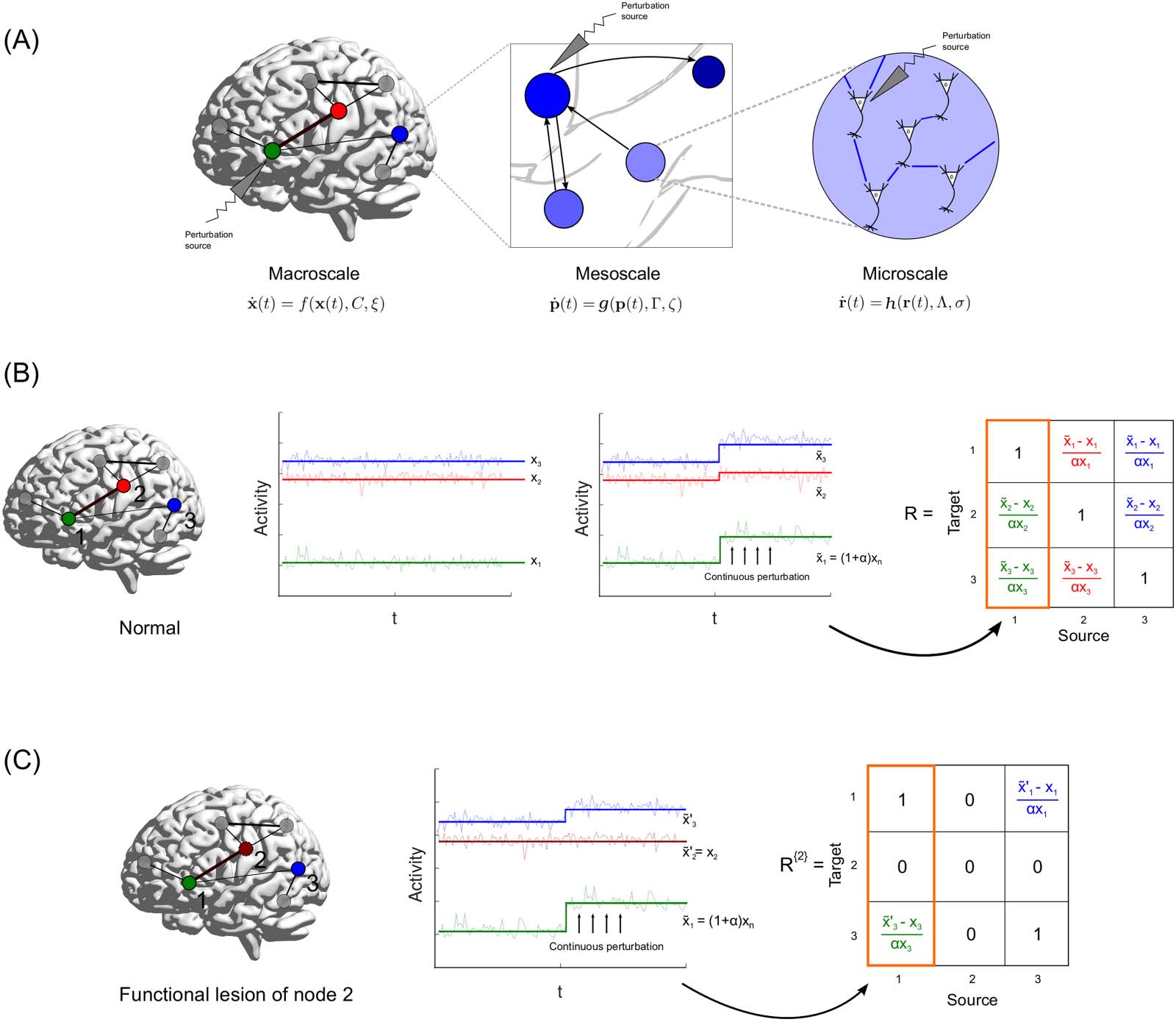
Schematic of perturbation protocol and response matrix before and after freezing node activity. (UN) The multiscale scope of the
Figura 1.
perturbative formalism. Each scale has its own dynamical model evolving over associated networks C, Γ, and Λ. Perturbing the functional units
results in changes in activity across the rest of the connected network, in accordance with the dynamics in that scale. This is then translated to
a region’s influence and role in communication. (B) Nodes 1 (Verde), 2 (Red), E 3 (Blue) are active in a whole-brain network. The steady-
state values at which they stabilize are given by x1, x2, and x3, rispettivamente. A continuous perturbation of node 1, by an amount α results in the
activities of node 2 E 3 to stabilize at new steady-state values, ex2 and ex3, rispettivamente. This is used to populate the first column of the linear
response matrix (highlighted in orange). The colors of the entries of the response matrix R, correspond to the response calculated for a per-
turbation of the node associated with the color. (C) In order to gauge the contribution of node 2 in eliciting the responses of the other nodes, we
perform a functional lesion (freeze the activity of node 2 at its original steady state). The associated columns and rows of node two are thus 0,
indicating that node 2 does not respond to any perturbations. Note that this lesion of 2 leads to a different response of 3 to the perturbation of 1,
with a new steady state at ex 0
3.

series obtained at any voxel or sensor, the approach is suitable for studies of single neurons to
macroscopic brain recordings and is essentially scale-invariant (Figure 1A).

In order to demonstrate the method, we resort to an in silico approach at the whole-brain
scala, using an empirically derived SC that supports established whole-brain node dynamics.
This is done merely as a proof of concept, and the formalism is not restricted to such
approaches alone. Primo, we apply the perturbation protocol on the mean field model (MFM)
(Deco et al., 2013) and look at response asymmetries (net influence distributions) that arise at
the level of single brain regions (Figure 1B). We then implement a functional lesion approach
to compute the metric Flow, which quantifies the centrality of regions in mediating information
flow (Figure 1C). We also show that the distributions of the metrics for MFM dynamics are
qualitatively similar over two largely different datasets. We then compute the average net influ-
ence and flow of nodes classified in terms of their association to resting-state networks (RSNs),

Response asymmetry
(between two regions):
Inequality in the response of a region
upon perturbation of another,
compared to when the source and
target are reversed.

Network Neuroscience

1277

Perturbation based measures of neural information flow

to gauge the typical dynamical influence and information flow mediation capabilities of the
RSNs. We also carry out the perturbation protocol on the linear stochastic model (LSM; Galán,
2008) and compare the results with that of the MFM.

We introduce the perturbation protocols and associated metrics in the Methods section.
Results for the in silico MFM over the multimodal imaging and connectome analysis–
microstructure-informed connectomics (MICA-MICs) dataset is presented in the Results section,
and results from the alternate Cambridge Centre for Ageing and Neuroscience (Cam-CAN)
dataset and LSM is shown in the Supporting Information figures. In the final section, we discuss
the plausibility, functional implications, and limitations of our findings.

METHODS

Net Influence and Flow

We introduce two concepts: (1) net influence of a brain subnetwork and (2) the notion of
“flow,” which help illuminate and quantify network-dynamic interactions. We implement
the method developed in Harush and Barzel (2017) on whole brain neurodynamical models,
whose topological architecture are constrained by empirically derived structural brain net-
works. In an active communicating network, information or activity between two nonneigh-
boring nodes is relayed by intermediary nodes. The original activity or a perturbation of the
source node elicits a perturbation in the activity of its immediate neighbors, which then elicit
responses in their neighbors and so on, till the effect of the source perturbation finally reaches
the target. This perturbation transmission can be easily traced in silico, and the final effect of
perturbing the source can be quantified by computing the change in activity of the target per
unit change of source activity (Figure 1B).

Generalmente, any neurodynamical model can be represented as

_x tð Þ ¼ f x tð Þ; C ; ξ
Þ
ð

(1)

where x(T ) is the vector of time-dependent activities of every region, C represents the network
on which the dynamics evolves, and ξ is the noise function. If the system is stable, permitting it
to evolve for long enough without any external perturbation drives it to its steady state. We can
introduce a continuous perturbation held at a constant strength to a region n, which has the
effect of driving the system to a new steady state. The steady state linear response matrix of a
region m upon a small perturbation of a region n, such that the perturbed state of the source,
~ = (1 + α)xn (where xn denotes the steady state activity of region n), is computed as
xn
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)

fxm − xm
αxm

(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2) ¼

Rmn ¼

(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)

(2)

(cid:2)
(cid:2)
(cid:2)
(cid:2)
(cid:2)

(cid:2)
(cid:2)
(cid:2)
(cid:2)

(cid:2)
(cid:2)
(cid:2)
(cid:2)

¼

dxm
xm
dxn
xn

exm −xm
xm
exn −xn
xn

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

.

/

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Fonte:
The node whose activity is changed,
cioè., the origin of perturbations.

Response:
A resultant change in the neural
activity of a region, brought about by
perturbation of one or more network
constituents.

Target:
The node of interest which responds
(with a change in neural activity) ad a
perturbation of the source.

Linear response matrix:
A matrix populated with the
magnitude of change (difference) in un
region’s activity before and after
perturbation.

where xm is the steady state of node m in the unperturbed system, fxm is the new steady state
of m after perturbation, and α quantifies the amount of perturbation. We implement this com-
putationally by solving the equations of all regions m, while maintaining the activity of region
n at (1 + α)xn. Computing all pairwise responses in this manner generates the linear response
matrix, R. The total response elicited by a region n is then given by

Zn ¼

Rmn

XN

m¼1
m≠n

(3)

1278

Network Neuroscience

Perturbation based measures of neural information flow

We define the net influence of a putative brain region i to be

Ii ¼

XN

XN

Rim:

Rmi −

m¼1

m¼1

(4)

Così, net influence essentially captures the response asymmetry of a node by taking the dif-
ference between magnitude of response elicited on the rest of the network (sum over rows) E
magnitude of response effected by the rest of the network (sum over columns). A region that is
capable of influencing the rest of the network more than being influenced by the network will
have a positive value of net influence—termed “influencers.” On the other hand, regions that
are instead easily influenced by the network but unable to change the dynamics of the rest of
the network to the same extent will have negative net influence—termed “followers.”

Probing the effect of a region i on the response of m elicited by the perturbation of n
requires carrying out the procedure mentioned above, but now with the activity of i fixed at
its unperturbed steady-state value xi (Figure 1C): an effective “functional lesion.” This is tan-
tamount to i remaining at its stable baseline, not being perturbed by n, and thereby removing
its contribution to fxm . Computing the response of all possible target source pairs by freezing
the activity of i generates R{io }. Tuttavia, computing R{io } for all i is a computationally intensive
processi, and so we implement an approximation as used in Harush and Barzel (2017), Quale
holds true only for small perturbations, and only requires R:

R if g
mn

≈ Rmn − RmiRin

(5)

The difference between R{io } and R is captured by the measure flow through region i, com-

puted in two steps, come segue:

F i
n ¼

Zn − Z if g
N
Zn

(6)

where F i
followed by:

n is the flow through node i for a perturbation source at n, to all possible targets,

F i ¼

1

N

XN

n¼1

F i
N

(7)

N

where Z if g
is the total response elicited by perturbing n, when the activity of i is frozen, and Fi
is the flow averaged over all possible sources, resulting in the effective consideration of all
pairwise information transfer scenarios through the node i.

A region with a high value of flow would imply its central role in arbitrary information trans-
fer processes in the brain. Since we consider all possible pairwise information transfer scenar-
ios, of which valid communication pathways will form a subset, regions with high flow can be
viewed as being central to communication in the network.

It must be noted that both the net influence and flow are measured from the response
matrix, whose values are essentially steady-state deviations in response to perturbations.
The response matrix, and any metrics derived from it will thus naturally depend on the form
of underlying dynamics.

To demonstrate the insights gained from the two metrics, we extracted structural brain net-
works from publicly available datasets that incorporated diffusion weighted imaging (DWI)
and functional magnetic resonance imaging (fMRI) modalities. Dynamical models of neural
ensemble activity at macroscopic scales—the mean field model (MFM) and the LSM—can

Network Neuroscience

1279

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

T

/

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

be used to simulate the node dynamics of brain networks (discussed in detail in Neurodyna-
mical Models section). Using an optimization approach of functional connectivity distance
(Naskar et al., 2021; Vattikonda, Surampudi, Banerjee, Deco, & Roy, 2016), we tune
the network parameters to a regime that maximally captures the empirical resting-state
functional connectivity (rs-FC). Using parameter values informed by the optimization pro-
cedure, we carry out the perturbation protocol for a select few models that span the dynamical
landscape. We use the simulated time series to compute the net influence and flow for each
region.

Datasets
The generality of the two measures—net influence and flow—were validated on two separate
human neuroimaging datasets: the Multimodal Imaging and Connectome Analysis–
Microstructure-Informed Connectomics (MICA-MICs) dataset (available in the Canadian
Open Neuroscience Platform Portal) (Royer et al., 2021) and the Cambridge Centre for Ageing
and Neuroscience (Cam-CAN) dataset (Shafto et al., 2014; Taylor et al., 2017). Different
parcellation schemes were used on each of the datasets to further showcase that the outcomes
do not depend on the extent of brain parcellations that govern the size of the network
analyzed.

MICA-MICs. SC matrices derived from DWI data of 50 healthy participants (27 males;
23 females; age: 29.54 ± 5.62 years) were obtained from the publicly available MICA-MICs
dataset (Royer et al., 2021). Of the multiple parcellation schemes available, data parcellated
according to the Schaefer–Yeo seven-network scheme was chosen in order to study network-
level distributions of net influence and flow, and to also eliminate the need for manual assign-
ment of nodes to functional networks, which can be erroneous. Inoltre, to strike a
balance between fine spatial resolution and interpretability of results, we used data parcel-
lated into 300 regions. As elements of the SC denoted number of white matter tracts between
regions, subject-level data was first log transformed to reduce the connectivity strength
variance. Negative connections were then removed, and the SCs were averaged over 50 par-
ticipants and thresholded using a distance-dependent consensus, a method which ensures
that the group SC preserves subject-level network statistics (Betzel, Griffa, Hagmann, & Mišić,
2019).

The group-averaged resting-state functional connectivity (rs-FC) matrix was computed by
Fisher z-transforming subject-level rs-FC matrices, carrying out an average over subjects,
followed by an inverse z-transform back to correlation values. Only positive correlations were
retained. This rs-FC was used as an empirical reference against simulated rs-FCs. We direct the
reader to the original article (Royer et al., 2021) for details of data acquisition.

Cam-CAN. Empirical DWI data of 40 healthy participants (19 males; 21 females; total age
range: 18–38), sampled from the Cam-CAN cohort (Shafto et al., 2014; Taylor et al., 2017)
chosen for an earlier work (Naskar et al., 2021) was used to construct the SC matrix. Cortical
gray matter was parcellated into 150 regions of interest using the Destrieux parcellation
(Destrieux, Fischl, Dale, & Halgren, 2010), and the subject-wise SC matrix was generated
using an automated pipeline by Schirner, Rothmeier, Jirsa, McIntosh, and Ritter (2015), E
was averaged over the 40 subjects to generate the group-averaged SC matrix. A curious reader
may refer to the original article for additional details about the preprocessing steps used
(Naskar et al., 2021).

Network Neuroscience

1280

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

/

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

The rs-FC matrix was required for determination of model parameters that best fit empirical
dati. We use a 150 region Destrieux-parcellated rs-FC matrix that was also used in the earlier
article (Naskar et al., 2021). The rs-FC was generated by computing the pairwise Pearson coef-
ficient between all pairs of z-transformed BOLD timeseries, for 40 subjects, and then averaged
to generate the rs-FC used for empirical model validation.

Neurodynamical Models

A number of neurodynamical models have been formulated to simulate whole brain resting-
state activity from DTI/ DWI-based structural connectomes. Some of the notable models
include the vector auto regressive ( VAR) modello (Messé, Benali, & Marrelec, 2014; Tononi,
Sporns, & Edelman, 1994), LSM (Galán, 2008; Goñi et al., 2014; Hansen et al., 2015),
Wilson-Cowan oscillator (Wilson & Cowan, 1972), Kuramoto oscillator (Abeysuriya et al.,
2018; Cabral, Hugues, Sporns, & Deco, 2011), and MFM (Deco et al., 2013; Hansen et al.,
2015; Naskar et al., 2021; Vattikonda et al., 2016) among others. In order to depict the vari-
ety of network-dynamical interactions supported by an underlying SC, we use two models
that we believe are far apart in terms of their dynamical complexities: the LSM and the
MFM.

Mean field model. The dynamic mean field model (MFM) is obtained by carrying out a mean
field reduction (Deco et al., 2013) of the spiking neuron model (Deco & Jirsa, 2012). The MFM
has also been shown to replicate features of empirical functional state transition dynamics, In
addition to being able to predict time-averaged FC (Hansen et al., 2015). The dynamics of the
MFM nodes are given by the following:

_Si ¼

−Si
τ S

þ 1 − Si
ð

ÞγHi þ ση

i tð Þ

H xið

Þ ¼

axi − b
1 − exp −d axi − b
ð
ð

Þ
Þ

XN

xi ¼ wJSi þ GJ

CijSj þ I0

j¼1

(8)

(9)

(10)

where Si is the NMDA synaptic gating variable of the ith node, H(xi) is the firing rate function
for the input xi, to the node i. Following Deco et al. (2013), the fixed parameters are the local
excitatory recurrence w = 0.9, synaptic coupling J = 0.2609(nA), overall external input I0 =
0.3(nA), kinetic parameters γ = 0.641/1000 and τS = 100(ms), and firing rate function
parameters a = 270(n/C), b = 108(Hz), and d = 0.154(S); σ = 0.001 is the noise amplitude
and ηi(T) is random number sampled from a normal distribution.

In contrast to the LSM, nodes following MFM dynamics can exhibit bistable and nonsym-
metric steady states. We carry out a preliminary exploration of steady states by randomly ini-
tializing the system at both “low” (0 ≤ S(t = 0) ≤ 0.1) and “high” (0.3 ≤ S(t = 0) ≤ 1) initial
conditions (Castro, El-Deredy, Battaglia, & Orio, 2020), and allowing a noiseless evolution of
the system for 40 S, at each value of the global scaling parameter, G, which is a free parameter
in the model. This is done for 10 trials. While the low-activity “spontaneous fluctuations” state
is highly stable for lower values of G, increasing it pushes the system to a bistable regime.
Further increase of G renders the spontaneous state unstable (Supporting Information
Figures S2 and S3).

Network Neuroscience

1281

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

T

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

Linear stochastic model. The LSM (Galán, 2008) is a simple neurodynamical model that can be
obtained by removing the saturation function and inhibitory population of the Wilson–Cowan
modello (Wilson & Cowan, 1972). The dynamics follow:

_x i ¼ −xi þ G

XN

Cijxj tð Þ þ ση

i tð Þ;

j¼1

(11)

where xi(T ) is the activity of region i, G is the global scaling parameter, Cij is an element of
the structural connectivity matrix, σ is the noise amplitude, and ηi(T ) is a random number
from a Gaussian distribution with zero mean and unit variance. All nodes following LSM
dynamics have two possible steady states, depending on the value of G: zero for 0 ≤
G < Gstable and +∞ for G > Gstable. In order to keep noise from pushing the system into
the divergent regime, we first determine Gstable by carrying out a randomly initialized noise-
less simulation by varying G in steps of 0.01 for 20 trials. Once Gstable is determined, we set
the noise amplitude as σ = Gstable − G (Hansen et al., 2015) for the parameter estimation
runs of the model.

Computational Protocol

All neurodynamical models were numerically integrated using the Euler integration algorithm
(Mannella, 2002) with a time step of 1 ms. The initial conditions (Si(t = 0) for the MFM and
xi(t = 0) for the LSM) for all the models were sampled from a uniform distribution in the interval
[0, 1].

Empirical best fit parameter estimation. The first step in the computational protocol was to iden-
tify the critical value of the scaling parameter G for the respective models and datasets. These
simulations were carried out by numerically integrating the respective stochastic neurodyna-
mical differential equations at a certain value of G, for 96 s for the MICA-MICs dataset (315.2 S
for the Cam-CAN dataset). The time series were then passed through a Balloon–Windkessel
hemodynamic filter (Cabral et al., 2011; Friston, Harrison, & Penny, 2003; Friston, Mechelli,
Turner, & Price, 2000) for BOLD signal generation. The parameters for the model were set as
per Friston et al. (2003). We then remove the initial 12 S (39.4 s for Cam-CAN) of BOLD signals
to remove transients, after which the signals are downsampled to the respective TR values of
0.6 s for the MICA-MICs and 1.97 s for the Cam-CAN dataset to match the sampling rate of the
empirical data. The total duration of the simulation and the length of the window to remove
transients were chosen to be long enough to arrive at a good representation of the resting state,
and were also multiples of the respective TR to make the handling of data easier. The synthe-
sized BOLD signals were then z-scored and the pairwise Pearson correlation was computed to
generate the simulated rs-FC. This protocol is repeated for each G value from 0–0.02 in steps
of ΔG = 0.001 (MICA-MICs dataset) and from 0–0.5 in steps of ΔG = 0.01 (Cam-CAN dataset),
with the protocol repeated for 30 trials per G value. The conformity of the simulated rs-FC with
the empirical rs-FC was gauged through the functional connectivity distance between the two
(refer to Parameter Space Identification section). This protocol helped arrive at the critical
parameter value, G*, which was then used along with neighboring values of G, as test cases
of the perturbation protocol.

Perturbation protocol. The perturbation protocol for a neurodynamical model evolving on a
DWI–based structural connectome comprised two major steps: an evolution to steady state,
followed by an evolution to a perturbed steady state. Primo, the model is initialized randomly
and allowed to noiselessly evolve over a period of 60 S, at the end of which the values of the

Network Neuroscience

1282

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

/

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

dynamical variables of the models are stored as the unperturbed steady state. Secondo, each
node is chosen as a source, N, and its value is reset to (1 + α)xn, and the remaining nodes of the
system are initialized at their respective steady-state values. The system is then allowed to
evolve for 5 S, by which it stabilizes at a new “perturbed” steady state, which was then stored.
The value of α was fixed as −0.1 as used in Harush and Barzel (2017). The negative value of
the perturbation was chosen to prevent the system from being pushed to an unstable regime
through the perturbation. The differences between the unperturbed and perturbed steady-state
values are used to compute the linear response matrix, using Equation 2. Simulation times
were ensured to be long enough for steady-state stabilization. We carry out noiseless simula-
tions and forego BOLD generation in the perturbation protocol, as it is sufficient for purposes
of demonstration of the method. For cases where the unperturbed steady state is trivial, we
manually set the steady state to a small positive value (10−60) prior to starting the perturbation
step to avoid division by zero errors in Equation 2. The measurement of net influence through
each node i is then given by Equation 4 and the flow through the node is measured through
Equations 5, 6, E 7.

Parameter Space Identification

Parameter space for the model for each dataset can be tuned using an approach developed by
earlier studies (Naskar et al., 2021; Vattikonda et al., 2016) where the difference between the
model predicted FC and the empirical FC was quantified using the FC distance measure, given
by the following:

v
tu
tu
T

ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
XN
(cid:5)2
Þ

Þ − FCsim i; j

FCemp i; j

XN
(cid:4)

ð

ð

FCD ¼

1

N

i¼1

j¼1

(12)

The value of G at which minimum FCD is observed (Supporting Information Figure S1) È
referred to as the G*.

Net Influence and Flow Through Resting-State Networks

Previously computed node-level net influence and flow values from the MICA-MICs dataset
were used to study how the net influence and flow values are distributed across the nodes
belonging different resting-state networks (RSNs). The Schaefer300 7-Network parcellation
of the MICA-MICs data allows each node from both the hemispheres to be clubbed into
one of the RSNs ( Vis = visual, SMot = somatomotor, DA = dorsal attention, SNVA = salience
network/ventral attention, Lim = limbic, Cont = fronto-parietal control, DMN = default mode
rete). Once the nodes were assigned to their respective networks, they were first sorted in
the descending order in terms of their net influence, after which the RSN distributions of the
top 10% nodes (positive net influence values = Influencers) and bottom 10% nodes (negative
net influence values = Followers) were computed. The RSN distribution of nodes with the top
10% flow values was also similarly computed.

To study whether RSNs have a balanced distribution (zero mean) of net influence and flow
across its constituent nodes, we computed the sums of net influence and flow of every node in
each of the seven RSNs, and averaged them by the number of nodes in the respective RSNs to
arrive at the metrics of net influence and flow per node. Just like the node-level interpretation,
RSNs with a positive value of net influence per node can be viewed as being influential over
network dynamics, whereas those with negative values of net influence per node can be
viewed as being primarily driven by the rest of the networks. Allo stesso modo, RSNs with high flow
per node values can be viewed as centers that mediate information flow.

Network Neuroscience

1283

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

/

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

RESULTS

Net influence and Flow were computed from simulated resting-state time series generated from
the whole-brain connectome where each node can be modeled according to a neurodynami-
cal model—mean field model (MFM) or linear stochastic model (LSM). The structural connec-
attività (SC) matrix for the whole-brain model was generated from the MICA-MICs and
Cam-CAN databases, and resting-state functional connectivity (rs-FC) from empirical data
was used to optimize model parameters (see Methods for details). In this section, we first report
the results of carrying out a perturbation protocol at a node level for the MFM and subse-
quently estimating the net influence for each node in the whole-brain connectome. Secondo,
we present flow distributions for the same network, which implements the functional lesion
step, together with the standard perturbation protocol, and highlights brain regions that are
crucial to the overall transfer of information in the brain. We investigated how this relationship
changed when the free parameter G of MFM was varied, with G* corresponding to the critical
value of G that best fits empirical data. The final result involves the computation of the net
influence and flow per node in each of the seven resting-state networks (RSNs) in the
Schaefer–Yeo parcellation to test whether the RSNs on average have nontrivial network
influencing and information flow mediating capabilities. In the first two analyses, the net influ-
ence and flow are studied as a function of local neighborhood properties (node strength),
whereas the final analysis involves the computation of RSN-level metrics that are then used
to compare the seven RSNs. The computation of net influence and flow for other values of G
(representative of low activity, bistable, and high activity regimes; Supporting Information Fig-
ure S2) further illuminates how the criticality of the nonlinear dynamical system is reflected in
the information transfer properties. The origin of this sensitivity to G lies in the form of the firing
rate of the MFM, which will be further discussed in the Discussion section.

While the main text presents results for the MFM evolving on the SC derived from the
MICA-MICs dataset, as a demonstration of generality, the entire pipeline (except for the RSN-
level analysis) was repeated for the Cam-CAN dataset running both the MFM and the LSM.
These results are presented in the Supporting Information figures.

Perturbation Unearths Asymmetries in Influence Capabilities

Nonzero net influence following a perturbation protocol captures the response asymmetry of a
particular node of the network, and is a function of node strength. We used a group-averaged
SC from the MICA-MICs dataset (Royer et al., 2021), whose elements quantify the number of
white matter tracts between cortical gray matter regions. We observe that the relationship
between net influence and the node strength computed from MFM simulations on the
MICA-MICs SC displays a critical dependence on G (Figura 2). The influencer-follower hier-
archy is most well defined at critical G* = 0.004. As G is increased, we observe that this hier-
archy progressively decreases, with the response of regions to perturbations from the rest of the
network becoming comparable to the response it elicits in the rest of the network through its
own perturbation. The topological profile of the asymmetry, which is captured by its relation to
the node strength, shows that high-strength nodes unequivocally exert a positive influence on
the rest of the network. The influence of the nodes of low strength on the other hand, although
negative, depends on G, with the most negative influence at G* shown by intermediate
strength nodes. For the Cam-CAN dataset, similar dependence with G was observed as well
(Supporting Information Figure S4).

At G*, we find that the top 10% influencers comprise nodes belonging primarily to multi-
modal RSNs, with a small share of unimodal (visual network) regions (7%). The top 10%

Network Neuroscience

1284

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

T

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Perturbation based measures of neural information flow

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

6
4
1
2
7
5
2
0
5
9
7
7
0
N
e
N
_
UN
_
0
0
2
6
0
P
D

.

/

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

N

P

P

m¼1 Rmi −

Figura 2. Node-level response asymmetry. (UN) Response asymmetries, quantified as the net influ-
N
ence of nodes, Ii =
m¼1 Rim, as a function of node strengths (sum of log number of
white matter tracts between regions). The values of the global scaling parameter for which the
asymmetries are computed are shown in Supporting Information Figure S2. Response asymmetry
is maximized at G* = 0.004 and reduces as G is increased. (B) Net influence distribution with node
strength for G*, with nodes displaying the top 10% positive net influence values (green) and top
10% negative net influence values (orange) highlighted (left); the distribution of the top 10%
influencer and follower nodes across the seven resting-state networks (RSNs) (right). Con =
fronto-parietal control network; SNVA = salience/ventral attention network; DMN = default mode
rete; Vis = visual network; Lim = limbic network; SMot = somatomotor network; DA = dorsal
attention network.

Network Neuroscience

1285

Perturbation based measures of neural information flow

followers on the other hand, show a strong unimodal representation (60%), with the highest
number of top followers belonging to the visual network.

We observe a well-defined influencer-follower hierarchy with node strength in the LSM as
BENE (Supporting Information Figure S6). We note that the net influence-node strength relation-
ship bears a faint qualitative resemblance with that of the MFM at its respective G*, with high-
strength influencers and low-strength followers. Tuttavia, the form of the relationship remains
robust throughout G, and unlike the MFM, we see no critical behavior at G* = 0.19. Invece,
the hierarchy progressively increases with G, while maintaining its qualitative form.

Flow is Maximized for Nodes of Intermediate Strength in the MFM

The flow structure (flow-node strength relationship) computed for the MFM shows a clear
dependence on the scaling parameter G (Figura 3). Flow patterns varied from a high-strength
dominated flow structure for G < G* to an increasingly low-strength dominated flow structure for G > G*. At the critical G*, we find that flow is not strictly dominated by low-strength nodes,
and is rather maximized for nodes that have an intermediate strength. We find that as G is
slightly increased, the flow quickly becomes dominated by low-strength nodes.

We also observe that for G ≥ G* the regions displaying high flow also display a net negative
perturbative influence on the network. This relation between the response asymmetry and flow
structure is not observed for G < G*. Identical pipeline run on the Cam-CAN dataset (Support- ing Information Figure S5) yields qualitatively similar patterns, as seen in Figure 3. At G*, we note that the top 10% highest flow nodes comprise members of all seven RSNs, with unequal shares (Figure 3B). The greatest proportion of nodes belong to the visual network, and the least contribution to the high-flow nodes comes from the salience/ventral attention network. We also note that there is an almost 50% split between the unimodal RSNs (visual and somatomotor networks) when compared to the rest of the RSNs combined. We also observe that the RSN distribution of the high-flow nodes is almost identical to the RSN distri- bution of the top 10% followers (Figure 2B). The results of the MFM are in contrast to that of the LSM, which shows a clear low-strength- dominated flow structure throughout G variation (Supporting Information Figure S6). Average Net Influence and Flow of RSNs To investigate whether network-dynamical interactions endow different large-scale RSNs (defined in the Schaefer–Yeo seven network classification; Schaefer et al., 2018; Yeo et al., 2011) with unequal capabilities to influence other functional networks or mediate information flow in the brain, we checked whether the RSNs have a nontrivial net influence and flow per node (see Methods). We find that out of the seven RSNs, only the visual and limbic networks can be classified as followers. The visual network is the strongest follower, and is also the RSN that plays the strongest role in mediating information flow between arbitrary nodes, whereas the somatomotor network has the least amount of flow. The remaining five RSNs are all influ- encers, with the salience/ventral attention network having the strongest net influence per node. Model Dependence of Network-Dynamical Interactions As mentioned in Methods, the response matrix is a construct that captures steady-state devi- ations upon perturbation, thereby being dependent on the form of dynamics of the system. Thus, a change in the dynamical model used should be reflected in the distributions of Network Neuroscience 1286 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. Node-level flow distribution. (A) Flow through a node, quantified as the effect of freezing the activity of node on the magnitude of responses elicited on the rest of the network, as a function of node strengths. The values of the global scaling parameter for which the flow values are com- puted are shown in Supporting Information Figure S2. Flow is maximized for low to intermediate strength nodes when G* = 0.004, but approaches a low-strength flow dominance as G is increased. (B) Flow distribution with node strength for G*, with nodes displaying the top 10% flow values highlighted (left); the distribution of the top 10% nodes with the highest flow across the seven RSNs (right). the net influence and flow of regions, which are derived from the response matrix. Despite both the LSM and the MFM being capable of individually conforming to empirical data (Supporting Information Figure S1), we find that the models are greatly different in terms of their dynamical and information transfer characteristics, as demonstrated by comparing their Network Neuroscience 1287 Perturbation based measures of neural information flow respective net influence and flow distributions (Figures 2 and 3, and Supporting Information Figures S6 and S7). DISCUSSION In this article, we propose a scale-invariant approach, inspired by previous work in network science (Harush & Barzel, 2017), that quantifies the interaction between brain network struc- ture and the dynamics exhibited by constituent nodes. We achieve this by studying the response of individual brain regions and subnetworks to controlled perturbations. We apply this technique on simulated data generated from empirically derived whole-brain connec- tomes where constituent nodes follow mean field model (MFM) and linear stochastic model (LSM) dynamics, for purposes of demonstrating its applicability. We find that the dynamically rich MFM is capable of exhibiting a wide range of qualitatively different network-dynamical interactions that can be captured in the form of response asymmetries and flow structures, as a function of the topological features of the network (node strength) and the model parameters (Figures 2 and 3). We could replicate similar results when a different cohort and parcellation scheme was used to derive the structural connectivity (Supporting Information Figures S4 and S5). We also observe that on using the LSM to simulate resting-state brain dynamics, the computed net influence and flow greatly differ from that of the MFM (Supporting Information Figures S6 and S7). This illuminates the implications of node dynamics on information flow, despite their abilities to synthesize data that conform to empirical observations. Beyond the demonstration on a specific model, the broad objective of this study is to showcase the applicability of this technique on systems of any scale, as long as it is stable and responsive to external perturbations. We focus on the usefulness of the response matrix, which can be easily populated using experimental or clinical stimulation data without a priori knowledge about the dynamics. This matrix can then be used to provide neurodynamical insights through derived metrics that can have considerable use in experiment and interven- tion design. Moreover, the inverse problem of what dynamical form can lead to observed response asymmetries and flow patterns can greatly narrow down the search for candidate models of neural dynamics. In contrast to measures such as Granger–Geweke causality (Dhamala, Liang, Bressler, & Ding, 2018), which use statistical covariations as a proxy for information flow, our proposed approach directly quantifies information as changes in neural activity, which is a direct product of the network architecture and dynamical complexity of the system. Response Asymmetry Along the High-Low Strength Axis The significance of the core-periphery axis has been pointed out by studies on various fronts (Bassett et al., 2013; Battiston, Guillon, Chavez, Latora, & de Vico Fallani, 2018; Castro et al., 2020; Gollo et al., 2017; Gollo, Zalesky, Hutchison, van den Heuvel, & Breakspear, 2015; Harriger, van den Heuvel, & Sporns, 2012; Mišić et al., 2015; van den Heuvel, Kahn, Goñi, & Sporns, 2012). Importantly, studies have also shown that neuropathological conditions are widely associated with changes to the structural core (Crossley et al., 2014; Fornito, Zalesky, & Breakspear, 2015; Stam, 2014; van den Heuvel et al., 2013), as opposed to the periphery. The net influence distributions reported in this work show a clear response asymmetry of nodes along the high-low strength axis, with low-strength follower nodes predominantly exerting a negative influence on the network and high-strength influencer nodes exerting a positive influ- ence on the network. This is observed in both the MFM and the LSM (Figure 2; Supporting Information Figures S4 and S6). A positive net influence translates to the ability of a node, upon Network Neuroscience 1288 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow perturbation, to elicit a greater response on the rest of the network, compared to the network’s effect on it. Thus, any perturbation in the activity of a high-strength region (that can possibly result from a neuropathology, exogenous stimulation, etc.) will have considerable effects on the rest of the network. Our results thus agree with previous studies and suggest that the regions in the core (which by definition will comprise a subnetwork of high-strength nodes) make ideal high impact targets for disruption of network function. Asymmetries in undirected (symmetric) networks have previously been studied in the context of sender-receiver hierar- chies arising from effective connectivity patterns by Seguin et al. (2019). We investigate how response asymmetries as those reported in this work can arise from an otherwise undi- rected network in the Supporting Information Figure S8. Figure 2B additionally shows that the top influencers and followers are primarily associated with multimodal and unimodal RSNs, respectively. Such a functional separation can arise from possibly nonoverlapping strength dis- tributions of the nodes of different RSNs, since the net influence has a well-defined relationship with the node strength. Neurodynamical models have been shown to display critical regimes associated with the onset of dynamical richness and spatiotemporal organization of nodes into RSNs (Deco & Jirsa, 2012; Deco, Jirsa, & McIntosh, 2011; Haimovici, Tagliazucchi, Balenzuela, & Chialvo, 2013). Models that operate at these critical working points are also found to conform to a great degree to empirical resting-state data. Our results show that the criticality of such models are also reflected as stark qualitative changes in information transmission and dynamical influence characteristics, captured through the metrics of net influence and flow (Figures 2 and 3). Flow Hubs Are Mediators of Information Transfer Modeling communication or signaling dynamics in brain networks is an important problem in neuroscience, as communication underlies the healthy function of a functionally heterogeneous entity like the brain (Avena-Koenigsberger et al., 2018; Graham, Avena-Koenigsberger, & Mišić, 2020). Flow is a dynamics-dependent quantity that adds a dimension of complexity to static network–based measures of quantifying roles in communication such as communicability centrality (Estrada, Higham, & Hatano, 2009). The utility of flow lies in its ability to identify nodes through which the maximum amount of information flows, making them ideal targets to study or intervene and modulate the spread of network perturbations. The calculation of flow using Equation 7 condenses the overall effect of the functional lesion of ‘i’ over all possible perturbations in the network, and thus equivalently all possible information transfer scenarios. The lesion of high-flow nodes thus have the greatest impact on information flow in an active network for the given dynamics. This can have particular applications in designing interventions to limit the impact of perturbations to healthy brain function that can be brought about by neuropathologies, which can eventually result in a “new normal” (the disease state), similar to the perturbed steady state in this study. Flow can also find its use in the study of regions facilitating seizure propagation in epilepsy, using whole-brain epileptor models (El Houssaini, Bernard, & Jirsa, 2020; Jirsa et al., 2017; Proix, Bartolomei, Guye, & Jirsa, 2017). Our results show that, for the MFM, flow is maximum for nodes of intermediate strength (Figure 3). Comparing these nodes to the strength distribution (Supporting Information Figure S2B) shows us that these regions are also in much greater abundance than the extreme low/high- strength nodes. Based on Gollo et al. (2015), the abundance of these intermediate strength high-flow nodes suggest that they fall into the “feeder” category, which possibly bridges the low-strength to high-strength nodes and displays fast dynamics. It is also well established that Network Neuroscience 1289 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow the core and peripheral nodes have distinct information processing functions (Bassett et al., 2013; Gollo et al., 2015) and constantly communicate with each other. In line with this, the intermediate strength dominance of flow in the empirical best fit model also suggests a poly- synaptic parallel high-low-strength communication pathway. This can be alternatively viewed as a bidirectional high-intermediate-low pathway, with the intermediate strength nodes playing a central role. The low-strength node dominated flow structure observed in the LSM is in stark contrast to the intermediate strength node dominance of the MFM. Such a flow distribution suggests that the LSM supports a high-low-high information flow pattern, which would suggest that the low-strength nodes are simply relay points in the communication process, instead of being a center of information processing like the high-strength nodes. The MFM thus seems to be a better model in maintaining empirical conformity along with realistically plausible infor- mation flow patterns. It must be noted that, in contrast to the three categories of flow patterns reported in Harush and Barzel (2017), with the MFM, we observe a highly nonlinear flow distribution, which further depends critically on G. The origin of this observation lies in the nonlinear firing rate of the MFM (Equation 9), which prevents the MFM from being written down in the general form of equations used in Harush and Barzel (2017), which is important for not only there being three primary forms of flow structure (degree-averting, degree-driven, homogeneous), but also for the lack of dependence on any scaling of the underlying connectivity matrix. In the case of the LSM, which can easily be recast into the general form, we observe that the qualitative form of the flow distribution is degree-averting and independent of G. By replacing the nonlinear firing rate of the MFM with a linear firing rate function determined using known bounds of the dynamical variable S to arrive at bounds of the function, the MFM equations can be made to conform to the general form used in Harush and Barzel (2017), in which case the linear MFM will also display one of the three primary flow distributions as well as G indepen- dence. This is shown in Supporting Information Figure S9, where the MFM is shown to have a degree-driven flow distribution, similar to the case where G < G* in Figure 3A. The observation that regions with high flow are also likely to show a net negative response asymmetry, that is, response to external stimulations is greater than response elicited, is a fallout of the flow’s dependence on the linear response matrix. The activity of regions with a high negative influence can be altered more by perturbations originating from the rest of the network when compared to that of regions with lesser negative influence. This directly translates to a greater contribution by these negative influence regions to the response of all nodes to arbitrary perturbations. RSN-Level Analysis Offers Network-Dynamical Insights Into Function The RSN-level analysis of net influence and flow (Figure 4) shows that the visual network is a strong follower network, with its nodes having the highest capability of mediating information flow. This result would imply that while regions of the visual network are strongly driven by the other networks (primarily multimodal) the high value of flow would imply that visual informa- tion greatly bolsters the information flow between two arbitrary nodes. This can be visualized as follows: the final response at a target node is the sum of response contributions from all the nodes in the path leading from the perturbation source, and the visual network has the highest contribution to the response compared to all other RSNs. This result could point toward a net- work dynamical perspective to the role of visual information in learning (Lindner, Blosser, & Cunigan, 2009), memory (Grundgeiger et al., 2013), and even its ability to influence multisen- sory processing, as in the McGurk (McGurk & MacDonald, 1976) and ventriloquist effects Network Neuroscience 1290 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow Figure 4. RSN-level response asymmetry and flow. The net influence per node (blue) and flow per node (red) in each of the seven RSNs in the Schaefer–Yeo parcellation. On average, nodes in the visual network have the highest flow and are also strong followers, whereas the nodes in the salience/ventral attention network comprise strong influencers. (Bruns, Liebnau, & Röder, 2011; Radeau & Bertelson, 1974). We also observe that the greatest dynamical influence on the network in this case is exerted by the salience/ventral attention network (SNVA). This result offers a possible network-dynamical take on Menon’s work on the triple network model, which discusses the role of the SNVA in influencing the engagement and disengagement of the default mode network (DMN) and central executive network, the failure of which results in major neuropathologies (Menon, 2011). It is also interesting to note that the DMN, which is located at one extreme of the principal functional gradient (Margulies et al., 2016), neither exerts the greatest influence on the network, nor does it mediate infor- mation flow to the greatest degree. This suggests that the “network-dynamical interaction gra- dient” offers a novel perspective of brain organization in terms of dynamical influence and interregional communication centralities, not previously captured by functional gradients. To summarize, the net influence and flow are attributes of nodes in a network, arising from network-dynamical interactions, that effectively capture their (1) perturbative impact and (2) role in communication, respectively. While perturbation of the influencer (high net influence) nodes exerts the maximum impact on the network, the high-flow nodes are responsible for the transfer of these perturbations to different network targets and contribute the most to the com- munication process. It is thus possible to limit the extent of this network-wide impact from attacks to the influencer nodes by designing interventions that target high-flow nodes instead, which help contain undesirable and possibly harmful perturbations. Methodological Considerations Some points have to be considered regarding this formalism, in order to truly understand its scope, and work on possible limitations. First, while the formalism is general enough to be applied on any scale, the response matrix and derived metrics are dynamics dependent. Second, the analyses here are carried out on noiseless models, as we are interested in the overall change of amplitude (activation) of signals, sufficient for a proof of concept. The formalism can be readily applied to a stable stochastic system as well. Third, the perturbations Network Neuroscience 1291 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow are assumed to be small enough to elicit linear responses. Fourth, although net influence and flow were computed in a dynamical regime in the neighborhood of a stable fixed point, the results are generalizable to any attractor state in node dynamics, as long as they are stable. Fifth, this method cannot be used in a setting where perturbations lead to a qualitative change in the dynamical behavior of the system (such as a Hopf bifurcation). Lastly, the present article does not explicitly showcase the scale-invariance of the method as it deals only with in silico whole-brain models. However, future extension to spike trains, local field potentials and elec- trocorticogram recordings are certainly possible owing to the conceptual simplicity of this technique. Additionally, we have not arrived at an analytical method for identifying the regions of high flow for nonlinear systems like the MFM in the present study. Although a large number of nonlinear models can be arranged in the general form used in Harush and Barzel (2017) for which the flow distributions can be analytically computed, many complex models extensively used in neuroscience like the MFM cannot, making a formal mathematical study into its interaction with the topology an exciting topic for future research. This work presents a simple scale-invariant perturbative formalism that can be used to both probe the distributions of influential nodes in the network, as well as identify nodes that are central to communication processes, both of which have immense experimental and clinical importance in neuroscience. The robust theoretical framework surrounding the formalism additionally opens up possibilities of mathematically studying the communication patterns permitted by established neurodynamical models. Most importantly, the formalism is invariant to the form of the underlying dynamics and instead gathers insights purely based on the response of a perturbed system of neuronal entities, making it ideal for implementation with minimal assumptions about how the system functions. ACKNOWLEDGMENTS We acknowledge the generous support of NBRC Core funds and the Computing facility. For simulations, resources from the Neuroscience Gateway (Sivagnanam et al., 2013) were used. Data collection and sharing for this project was provided by the Cambridge Centre for Ageing and Neuroscience (Cam-CAN). Cam-CAN was supported by the UK Biotechnology and Biological Sciences Research Council (Grant BB/H008217/1), together with support from the UK Medical Research Council and University of Cambridge, UK. In accordance with the data usage agreement for Cam-CAN dataset, the article has been submitted as open access. The preprocessed Multimodal Imaging and Connectome Analysis - Microsturcture-Informed Connectomics (MICA-MICs) dataset was obtained from the publicly accessible Canadian Open Neuroscience Platform Portal (Royer et al., 2021). SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00260. Codes used in this article can be downloaded from https://bitbucket.org/cbdl/netinfluence -flow/src/master/ (Madan Mohan & Banerjee, 2021). AUTHOR CONTRIBUTIONS Varun Madan Mohan: Conceptualization; Formal analysis; Investigation; Methodology; Project administration; Software; Validation; Visualization; Writing – original draft. Arpan Banerjee: Conceptualization; Funding acquisition; Project administration; Resources; Supervi- sion; Writing – review & editing. Network Neuroscience 1292 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow FUNDING INFORMATION Arpan Banerjee, Ministry of Youth Affairs and Sports, Government of India, Award ID: F.NO. K-15015/42/2018/SP-V. Arpan Banerjee, NBRC Flagship program, Department of Biotechnology, Government of India, Award ID: BT/MED-III/NBRC/Flagship/Flagship2019. REFERENCES Abeysuriya, R. G., Hadida, J., Sotiropoulos, S. N., Jbabdi, S., Becker, R., Hunt, B. A., … Woolrich, M. W. (2018). A biophysical model of dynamic balancing of excitation and inhibition in fast oscillatory large-scale networks. PLoS Computational Biology, 14(2), e1006007. https://doi.org/10.1371/journal.pcbi.1006007, PubMed: 29474352 Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu- nication dynamics in complex brain networks. Nature Reviews Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017 .149, PubMed: 29238085 Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha, P. J., & Grafton, S. T. (2013). Task-based core-periphery organi- zation of human brain dynamics. PLoS Computational Biology, 9(9), e1003171. https://doi.org/10.1371/journal.pcbi.1003171, PubMed: 24086116 Battaglia, F. P., Benchenane, K., Sirota, A., Pennartz, C. M., & Wiener, S. I. (2011). The hippocampus: Hub of brain network communication for memory. Trends in Cognitive Sciences, 15(7), 310–318. https://doi.org/10.1016/j.tics.2011.05.008, PubMed: 21696996 Battiston, F., Guillon, J., Chavez, M., Latora, V., & de Vico Fallani, F. (2018). Multiplex core–periphery organization of the human connectome. Journal of the Royal Society Interface, 15(146), 20180514. https://doi.org/10.1098/rsif.2018.0514, PubMed: 30209045 Betzel, R. F., Griffa, A., Hagmann, P., & Mišić, B. (2019). Distance- dependent consensus thresholds for generating group- representative structural brain networks. Network Neuroscience, 3(2), 475–496. https://doi.org/10.1162/netn_a_00075, PubMed: 30984903 Bruns, P., Liebnau, R., & Röder, B. (2011). Cross-modal training induces changes in spatial representations early in the auditory processing pathway. Psychological Science, 22(9), 1120–1126. https://doi.org/10.1177/0956797611416254, PubMed: 21771962 Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of local network oscillations in resting-state functional connectivity. Neu- roImage, 57(1), 130–139. https://doi.org/10.1016/j.neuroimage .2011.04.010, PubMed: 21511044 Castro, S., El-Deredy, W., Battaglia, D., & Orio, P. (2020). Cortical ignition dynamics is tightly linked to the core organisation of the human connectome. PLoS Computational Biology, 16(7), e1007686. https://doi.org/10.1371/journal.pcbi.1007686, PubMed: 32735580 Crossley, N. A., Mechelli, A., Scott, J., Carletti, F., Fox, P. T., McGuire, P., & Bullmore, E. T. (2014). The hubs of the human connectome are generally implicated in the anatomy of brain disorders. Brain, 137(8), 2382–2395. https://doi.org/10.1093 /brain/awu132, PubMed: 25057133 Dayan, P., & Abbott, L. F. (2001). Theoretical neuroscience: Computational and mathematical modeling of neural systems. Cambridge, MA: MIT Press. Deco, G., Cabral, J., Saenger, V. M., Boly, M., Tagliazucchi, E., Laufs, H., … Kringelbach, M. L. (2018). Perturbation of whole-brain dynamics in silico reveals mechanistic differences between brain states. NeuroImage, 169, 46–56. https://doi.org /10.1016/j.neuroimage.2017.12.009, PubMed: 29225066 Deco, G., & Jirsa, V. K. (2012). Ongoing cortical activity at rest: Criticality, multistability, and ghost attractors. Journal of Neurosci- ence, 32(10), 3366–3375. https://doi.org/10.1523/JNEUROSCI .2523-11.2012, PubMed: 22399758 Deco, G., Jirsa, V. K., & McIntosh, A. R. (2011). Emerging concepts for the dynamical organization of resting-state activity in the brain. Nature Reviews Neuroscience, 12(1), 43–56. https://doi .org/10.1038/nrn2961, PubMed: 21170073 Deco, G., Ponce-Alvarez, A., Mantini, D., Romani, G. L., Hagmann, P., & Corbetta, M. (2013). Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. Journal of Neuroscience, 33(27), 11239–11252. https://doi.org/10.1523/ JNEUROSCI.1091-13 .2013, PubMed: 23825427 Destrieux, C., Fischl, B., Dale, A., & Halgren, E. (2010). Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. NeuroImage, 53(1), 1–15. https://doi .org/10.1016/j.neuroimage.2010.06.010, PubMed: 20547229 Dhamala, M., Liang, H., Bressler, S. L., & Ding, M. (2018). Granger- Geweke causality: Estimation and interpretation. NeuroImage, 175, 460–463. https://doi.org/10.1016/j.neuroimage.2018.04 .043, PubMed: 29684646 El Houssaini, K., Bernard, C., & Jirsa, V. K. (2020). The epileptor model: A systematic mathematical analysis linked to the dynam- ics of seizures, refractory status epilepticus, and depolarization block. eNeuro, 7(2). https://doi.org/10.1523/ENEURO.0485-18 .2019, PubMed: 32066612 Estrada, E., Higham, D. J., & Hatano, N. (2009). Communicability betweenness in complex networks. Physica A: Statistical Mechanics and Its Applications, 388(5), 764–774. https://doi .org/10.1016/j.physa.2008.11.011 FitzHugh, R. (1961). Impulses and physiological states in theoret- ical models of nerve membrane. Biophysical Journal, 1(6), 445–466. https://doi.org/10.1016/S0006-3495(61)86902-6, PubMed: 19431309 Fornito, A., Zalesky, A., & Breakspear, M. (2015). The connec- tomics of brain disorders. Nature Reviews Neuroscience, 16(3), 159–172. https://doi.org/10.1038/nrn3901, PubMed: 25697159 Forrester, M., Crofts, J. J., Sotiropoulos, S. N., Coombes, S., & O’Dea, R. D. (2020). The role of node dynamics in shaping emergent functional connectivity patterns in the brain. Network Network Neuroscience 1293 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow Neuroscience, 4(2), 467–483. https://doi.org/10.1162/netn_a _00130, PubMed: 32537537 Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal modelling. NeuroImage, 19(4), 1273–1302. https://doi.org/10 .1016/S1053-8119(03)00202-7, PubMed: 12948688 Friston, K. J., Mechelli, A., Turner, R., & Price, C. J. (2000). Nonlin- ear responses in fMRI: The balloon model, Volterra kernels, and other hemodynamics. NeuroImage, 12(4), 466–477. https://doi .org/10.1006/nimg.2000.0630, PubMed: 10988040 Galán, R. F. (2008). On how network architecture determines the dominant patterns of spontaneous neural activity. PLoS One, 3(5), e2148. https://doi.org/10.1371/journal.pone.0002148, PubMed: 18478091 Gollo, L. L., Roberts, J. A., & Cocchi, L. (2017). Mapping how local perturbations influence systems-level brain dynamics. Neuro- Image, 160, 97–112. https://doi.org/10.1016/j.neuroimage.2017 .01.057, PubMed: 28126550 Gollo, L. L., Zalesky, A., Hutchison, R. M., van den Heuvel, M., & Breakspear, M. (2015). Dwelling quietly in the rich club: Brain network determinants of slow cortical fluctuations. Philosophical Transactions of the Royal Society B: Biological Sciences, 370(1668), 20140165. https://doi.org/10.1098/rstb.2014.0165, PubMed: 25823864 Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., De Mendizabal, N. V., Betzel, R. F., Griffa, A., … Sporns, O. (2014). Resting-brain functional connectivity predicted by ana- lytic measures of network communication. Proceedings of the National Academy of Sciences, 111(2), 833–838. https://doi.org /10.1073/pnas.1315529111, PubMed: 24379387 Graham, D., Avena-Koenigsberger, A., & Mišić, B. (2020). Network communication in the brain. Cambridge, MA: MIT Press. Grundgeiger, T., Sanderson, P., Beltran Orihuela, C., Thompson, A., MacDougall, H., Nunnink, L., & Venkatesh, B. (2013). Prospec- tive memory in the ICU: The effect of visual cues on task execu- tion in a representative simulation. Ergonomics, 56(4), 579–589. https://doi.org/10.1080/00140139.2013.765604, PubMed: 23514201 Gu, S., Pasqualetti, F., Cieslak, M., Telesford, Q. K., Yu, A. B., Kahn, A. E., … Bassett, D. S. (2015). Controllability of structural brain networks. Nature Communications, 6(1), 1–10. https://doi.org /10.1038/ncomms9414, PubMed: 26423222 Haimovici, A., Tagliazucchi, E., Balenzuela, P., & Chialvo, D. R. (2013). Brain organization into resting state networks emerges at criticality on a model of the human connectome. Physical Review Letters, 110, 178101. https://doi.org/10.1103/ PhysRevLett.110 .178101, PubMed: 23679783 Hansen, E. C., Battaglia, D., Spiegler, A., Deco, G., & Jirsa, V. K. (2015). Functional connectivity dynamics: Modeling the switch- ing behavior of the resting state. NeuroImage, 105, 525–535. https://doi.org/10.1016/j.neuroimage.2014.11.001, PubMed: 25462790 Harriger, L., van den Heuvel, M. P., & Sporns, O. (2012). Rich club organization of macaque cerebral cortex and its role in network communication. PLoS One, 7(9), e46497. https://doi.org/10 .1371/journal.pone.0046497, PubMed: 23029538 Harush, U., & Barzel, B. (2017). Dynamic patterns of information flow in complex networks. Nature Communications, 8(1), 1–11. https://doi.org/10.1038/s41467-017-01916-3, PubMed: 29259160 Hens, C., Harush, U., Haber, S., Cohen, R., & Barzel, B. (2019). Spatiotemporal signal propagation in complex networks. Nature Physics, 15(4), 403–412. https://doi.org/10.1038/s41567-018-0409-0 Hodgkin, A. L., & Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excita- tion in nerve. The Journal of Physiology, 117(4), 500–544. https:// doi.org/10.1113/jphysiol.1952.sp004764, PubMed: 12991237 Honey, C. J., Thivierge, J.-P., & Sporns, O. (2010). Can structure predict function in the human brain? NeuroImage, 52(3), 766–776. https://doi.org/10.1016/j.neuroimage.2010.01.071, PubMed: 20116438 Jirsa, V., Proix, T., Perdikis, D., Woodman, M., Wang, H., Gonzalez- Martinez, J., … Bartolomei, F. (2017). The virtual epileptic patient: Individualized whole-brain models of epilepsy spread. Neuro- Image, 145, 377–388. https://doi.org/10.1016/j.neuroimage .2016.04.049, PubMed: 27477535 Lindner, K., Blosser, G., & Cunigan, K. (2009). Visual versus auditory learning and memory recall performance on short-term versus long-term tests. Modern Psychological Studies, 15(1), 39–46. Madan Mohan, V., & Banerjee, A. (2021). Netinfluence&flow. Atlassian. https://bitbucket.org/cbdl/netinfluence-flow/src/master/ Mannella, R. (2002). Integration of stochastic differential equations on a computer. International Journal of Modern Physics C, 13(09), 1177–1194. https://doi.org/10.1142/S0129183102004042 Margulies, D. S., Ghosh, S. S., Goulas, A., Falkiewicz, M., Huntenburg, J. M., Langs, G., … Smallwood, J. (2016). Situating the default-mode network along a principal gradient of macro- scale cortical organization. Proceedings of the National Academy of Sciences, 113(44), 12574–12579. https://doi.org/10.1073/pnas .1608282113, PubMed: 27791099 McGurk, H., & MacDonald, J. (1976). Hearing lips and seeing voices. Nature, 264(5588), 746–748. https://doi.org/10.1038 /264746a0, PubMed: 1012311 Menon, V. (2011). Large-scale brain networks and psychopathology: A unifying triple network model. Trends in Cognitive Sciences, 15(10), 483–506. https://doi.org/10.1016/j.tics.2011.08.003, PubMed: 21908230 Messé, A., Benali, H., & Marrelec, G. (2014). Relating structural and functional connectivity in MRI: A simple model for a com- plex brain. IEEE Transactions on Medical Imaging, 34(1), 27–37. https://doi.org/10.1109/TMI.2014.2341732, PubMed: 25069111 Mišić, B., Betzel, R. F., Griffa, A., De Reus, M. A., He, Y., Zuo, X.-N., … Zatorre, R. J. (2018). Network-based asymmetry of the human auditory system. Cerebral Cortex, 28(7), 2655–2664. https://doi .org/10.1093/cercor/bhy101, PubMed: 29722805 Mišić, B., Betzel, R. F., Nematzadeh, A., Goni, J., Griffa, A., Hagmann, P., … Sporns, O. (2015). Cooperative and competitive spreading dynamics on the human connectome. Neuron, 86(6), 1518–1529. https://doi.org/10.1016/j.neuron.2015.05.035, PubMed: 26087168 Moon, J.-Y., Lee, U., Blain-Moraes, S., & Mashour, G. A. (2015). General relationship of global topology, local dynamics, and directionality in large-scale brain networks. PLoS Computational Biology, 11(4), e1004225. https://doi.org/10.1371/journal.pcbi .1004225, PubMed: 25874700 Naskar, A., Vattikonda, A., Deco, G., Roy, D., & Banerjee, A. (2021). Multiscale dynamic mean field (MDMF) model relates resting-state brain dynamics with local cortical excitatory– Network Neuroscience 1294 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Perturbation based measures of neural information flow inhibitory neurotransmitter homeostasis. Network Neuroscience, 5(3), 757–782. https://doi.org/10.1162/netn_a_00197, PubMed: 34746626 Novelli, L., Atay, F. M., Jost, J., & Lizier, J. T. (2020). Deriving pairwise transfer entropy from network structure and motifs. Proceedings of the Royal Society A, 476(2236), 20190779. https://doi.org/10.1098/rspa.2019.0779, PubMed: 32398937 Proix, T., Bartolomei, F., Guye, M., & Jirsa, V. K. (2017). Individual brain structure and modelling predict seizure propagation. Brain, 140(3), 641–654. https://doi.org/10.1093/ brain/awx004, PubMed: 28364550 Radeau, M., & Bertelson, P. (1974). The after-effects of ventriloquism. The Quarterly Journal of Experimental Psychology, 26(1), 63–71. https://doi.org/10.1080/14640747408400388, PubMed: 4814864 Royer, J., Rodríguez-Cruces, R., Tavakol, S., Larivière, S., Herholz, P., Li, Q., … Bernhardt, B. C. (2021). An open MRI dataset for multiscale neuroscience. bioRxiv. https://doi.org/10.1101/2021 .08.04.454795 Sanz Perl, Y., Pallavicini, C., Pérez Ipiña, I., Demertzi, A., Bonhomme, V., Martial, C., … Tagliazucchi, E. (2021). Perturba- tions in dynamical models of whole-brain activity dissociate between the level and stability of consciousness. PLoS Computa- tional Biology, 17(7), e1009139. https://doi.org/10.1371/journal .pcbi.1009139, PubMed: 34314430 Schaefer, A., Kong, R., Gordon, E. M., Laumann, T. O., Zuo, X.-N., Holmes, A. J., … Yeo, B. T. T. (2018). Local-global parcellation of the human cerebral cortex from intrinsic functional connectivity MRI. Cerebral Cortex, 28(9), 3095–3114. https://doi.org/10.1093 /cercor/bhx179, PubMed: 28981612 Schirner, M., Rothmeier, S., Jirsa, V. K., McIntosh, A. R., & Ritter, P. (2015). An automated pipeline for constructing personalized vir- tual brains from multimodal neuroimaging data. NeuroImage, 117, 343–357. https://doi.org/10.1016/j.neuroimage.2015.03 .055, PubMed: 25837600 Seguin, C., Razi, A., & Zalesky, A. (2019). Inferring neural signalling directionality from undirected structural connectomes. Nature Communications, 10(1), 1–13. https://doi.org/10.1038/s41467 -019-12201-w, PubMed: 31537787 Shafto, M. A., Tyler, L. K., Dixon, M., Taylor, J. R., Rowe, J. B., Cusack, R., … Cam-CAN. (2014). The Cambridge Centre for Ageing and Neuroscience (Cam-CAN ) study protocol: A cross-sectional, lifespan, multidisciplinary examination of healthy cognitive ageing. BMC Neurology, 14(1), 1–25. https:// doi.org/10.1186/s12883-014-0204-1, PubMed: 25412575 Sivagnanam, S., Majumdar, A., Yoshimoto, K., Astakhov, V., Bandrowski, A., Martone, M. E., & Carnevale, N. (2013). Intro- ducing the neuroscience gateway. Proceedings of the 5th Interna- tional Workshop on Science Gateways, 993. Sporns, O. (2014). Network neuroscience. In The future of the brain (pp. 90–99). Princeton, NJ: Princeton University Press. https://doi .org/10.2307/j.ctt9qh0x7.12 Stam, C. J. (2014). Modern network science of neurological disor- ders. Nature Reviews Neuroscience, 15(10), 683–695. https://doi .org/10.1038/nrn3801, PubMed: 25186238 Stefanescu, R. A., & Jirsa, V. K. (2008). A low dimensional descrip- tion of globally coupled heterogeneous neural networks of excit- atory and inhibitory neurons. PLoS Computational Biology, 4(11), e1000219. https://doi.org/10.1371/journal.pcbi.1000219, PubMed: 19008942 Strogatz, S. H. (2000). From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Physica D: Nonlinear Phenomena, 143(1–4), 1–20. https://doi .org/10.1016/S0167-2789(00)00094-4 Suárez, L. E., Markello, R. D., Betzel, R. F., & Misic, B. (2020). Link- ing structure and function in macroscale brain networks. Trends in Cognitive Sciences, 24(4), 302–315. https://doi.org/10.1016/j .tics.2020.01.008, PubMed: 32160567 Taylor, J. R., Williams, N., Cusack, R., Auer, T., Shafto, M. A., Dixon, M., … Henson, R. N. (2017). The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository: Structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. NeuroImage, 144, 262–269. https://doi.org/10.1016/j.neuroimage.2015.09.018, PubMed: 26375206 Tononi, G., Sporns, O., & Edelman, G. M. (1994). A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proceedings of the National Academy of Sciences, 91(11), 5033–5037. https://doi.org/10.1073/pnas.91.11 .5033, PubMed: 8197179 van den Heuvel, M. P., Kahn, R. S., Goñi, J., & Sporns, O. (2012). High-cost, high-capacity backbone for global brain communica- tion. Proceedings of the National Academy of Sciences, 109(28), 11372–11377. https://doi.org/10.1073/pnas.1203593109, PubMed: 22711833 van den Heuvel, M. P., Sporns, O., Collin, G., Scheewe, T., Mandl, R. C., Cahn, W., … Kahn, R. S. (2013). Abnormal rich club orga- nization and functional brain dynamics in schizophrenia. JAMA P s y c h i a t r y, 7 0 ( 8 ) , 7 8 3 – 7 9 2 . h t t p s : / / d o i . o r g / 1 0 . 1 0 0 1 /jamapsychiatry.2013.1328, PubMed: 23739835 Vattikonda, A., Surampudi, B. R., Banerjee, A., Deco, G., & Roy, D. (2016). Does the regulation of local excitation–inhibition bal- ance aid in recovery of functional connectivity? A computational account. NeuroImage, 136, 57–67. https://doi.org/10.1016/j .neuroimage.2016.05.002, PubMed: 27177761 Veit, M. J., Kucyi, A., Hu, W., Zhang, C., Zhao, B., Guo, Z., … Parvizi, J. (2021). Temporal order of signal propagation within and across intrinsic brain networks. Proceedings of the National Academy of Sciences, 118(48), e2105031118. https://doi.org/10.1073/pnas .2105031118, PubMed: 34819365 Wilson, H. R., & Cowan, J. D. (1972). Excitatory and inhibitory interactions in localized populations of model neurons. Biophys- ical Journal, 12(1), 1–24. https://doi.org/10.1016/S0006-3495(72) 86068-5, PubMed: 4332108 Yeo, B. T. T., Krienen, F. M., Sepulcre, J., Sabuncu, M. R., Lashkari, D., Hollinshead, M., … Buckner, R. L. (2011). The organization of the human cerebral cortex estimated by intrinsic functional con- nectivity. Journal of Neurophysiology, 106(3), 1125–1165. https://doi.org/10.1152/jn.00338.2011, PubMed: 21653723 Network Neuroscience 1295 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 6 4 1 2 7 5 2 0 5 9 7 7 0 n e n _ a _ 0 0 2 6 0 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

Scarica il pdf