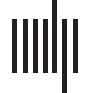RICERCA
Percolation may explain efficiency, robustness,
and economy of the brain
Yang Tian1,2
and Pei Sun1
1Department of Psychology and Tsinghua Laboratory of Brain and Intelligence, Università di Tsinghua, Pechino, Cina
2Laboratory of Advanced Computing and Storage, Central Research Institute, 2012 Laboratories,
Huawei Technologies Co. Ltd., Pechino, Cina
Keywords: Percolation, Brain connectivity, Excitation-inhibition balance, Information transmission
efficiency, Robust flexibility, Brain economy
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
The brain consists of billions of neurons connected by ultra-dense synapses, esibizione
remarkable efficiency, robust flexibility, and economy in information processing. It is generally
believed that these advantageous properties are rooted in brain connectivity; Tuttavia, direct
evidence remains absent owing to technical limitations or theoretical vacancy. This research
explores the origins of these properties in the largest yet brain connectome of the fruit fly. Noi
reveal that functional connectivity formation in the brain can be explained by a percolation
process controlled by synaptic excitation-inhibition (E/I) balance. By increasing the E/I
balance gradually, we discover the emergence of these properties as byproducts of percolation
transition when the E/I balance arrives at 3:7. As the E/I balance keeps increase, an optimal
E/I balance 1:1 is unveiled to ensure these three properties simultaneously, consistent with
previous in vitro experimental predictions. Once the E/I balance reaches over 3:2, an intrinsic
limitation of these properties determined by static (anatomical) brain connectivity can be
observed. Our work demonstrates that percolation, a universal characterization of critical
phenomena and phase transitions, may serve as a window toward understanding the
emergence of various brain properties.
AUTHOR SUMMARY
This research presents a novel framework to study functional connectivity on the largest yet
brain connectome of the fruit fly, revealing that synaptic excitation-inhibition (E/I) balance
characterizes the formation of dynamic brain connectivity as a percolation process. Various
remarkable properties of brain functions, such as information transmission efficiency, robust
flexibility, and economy, emerge as byproducts of percolation transition. These advantages
can be simultaneously ensured at an optimal E/I balance 1:1, consistent with previous in vitro
experimental predictions. Our work demonstrates percolation as a potential way to understand
the emergence of brain function characteristics through connectivity.
INTRODUCTION
To survive through the evolution, our brain should be efficient enough to process external
informazione, robust to accidental damages (per esempio., lesions), and economic in energy using. Over
the last decades, this evolutionary inference has been corroborated by numerous neuroscience
Citation: Tian, Y., & Sun, P. (2022).
Percolation may explain efficiency,
robustness, and economy of the brain.
Network Neuroscience, 6(3), 765–790.
https://doi.org/10.1162/netn_a_00246
DOI:
https://doi.org/10.1162/netn_a_00246
Received: 3 ottobre 2021
Accepted: 11 Marzo 2022
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Authors:
Yang Tian
tiany20@mails.tsinghua.edu.cn
Pei Sun
peisun@tsinghua.edu.cn
Handling Editor:
Alex Fornito
Copyright: © 2022
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
studies. The brain has been discovered to support highly efficient information transmission
between neurons, circuits, and cortices, making it possible to promptly gather and distribute
external
informazione (Amico et al., 2021; Avena-Koenigsberger, Misic, & Sporns, 2018;
Graham, Avena-Koenigsberger, & Misic, 2020; Mišić, Sporns, & McIntosh, 2014). Such infor-
mation transmission efficiency, manifested as the low time cost of communications between
neurons or high broadcasting capacity of information, is demonstrated to vary across different
topological attributes of brain connectivity (Avena-Koenigsberger et al., 2018). Nel frattempo, IL
brain is revealed to feature robust flexibility, a kind of capacity to tolerate the large-scale
destruction of neurons or synaptic connections (per esempio., by lesions) (Aerts, Fias, Caeyenberghs,
& Marinazzo, 2016; Joyce, Hayasaka, & Laurienti, 2013; Kaiser, Martin, Andras, & Young,
2007) while maintaining robust brain functions (Achard, Salvador, Whitcher, Suckling, &
Bullmore, 2006; Aerts et al., 2016; Alstott, Breakspear, Hagmann, Cammoun, & Sporns, 2009;
Avena-Koenigsberger et al., 2017; Crossley et al., 2014; Joyce et al., 2013; Kaiser & Hilgetag,
2004; Kaiser et al., 2007). Although it inevitably requires a vast energy supply and occupies
large space in the animal body due to the ultra-large neuron amounts, the brain is discovered
to be economic in network wiring (low costs for embedding brain network into physics space)
and network running (efficient in energy using) (Bullmore & Sporns, 2012; Friston, 2010; Hahn
et al., 2015; Karbowski, 2007; Kiebel & Friston, 2011; Laughlin, van Steveninck, & Anderson,
1998; Sporns, 2011; Strelnikov, 2010). These economic properties are suggested as the functions
of the brain network size, topology, and synaptic properties (Bullmore & Sporns, 2012).
Till now, it remains unclear where these remarkable properties of brain originate from. IL
close relationships between these properties and the brain network naturally lead to an emer-
gentism hypothesis that argues these properties may originate from specific characteristics of
brain connectivity. In the recent decades, abundant corollaries of this hypothesis have been
verified from different perspectives. For instance, shortest paths in brain connectivity are
inferred as a principal communication substrate in the brain according to the properties of
information transmission efficiency (Avena-Koenigsberger et al., 2018). Although having a
short average path is costly, real brain connectivity still possesses near-minimal path length
(Betzel et al., 2016; Bullmore & Sporns, 2012; Kaiser & Hilgetag, 2006; Rubinov, Ypma, Watson,
& Bullmore, 2015) in functional interactions (Goñi et al., 2014; Hermundstad et al., 2013) A
support efficient information transmission. Inoltre, brain connectivity is inferred as scale-free
according to the robustness of scale-free networks (Albert, Jeong, & Barabási, 2000) and implied
as small-world by the near-minimal path length (Bullmore & Sporns, 2012). While mammalian
brains with scale-free connectivity are robust against random lesions, they are significantly vul-
nerable to hub-targeted attacks (Kaiser & Hilgetag, 2004; Kaiser et al., 2007). Tuttavia, once the
connectivity topology approaches a small-world network while maintaining scale-free property
(per esempio., the macroscopic human brain) (Achard et al., 2006; Alstott et al., 2009; Crossley et al.,
2014; Joyce et al., 2013), the brain becomes more resilient to hub-targeted attacks than a
comparable scale-free network and keeps equally robust to random attacks. Besides these
mentioned corollaries, many other verified corollaries could be found, demonstrating that
brain connectivity pattern critically shapes brain functions.
Tuttavia, these corollaries alone are not sufficient for a complete demonstration of the
emergentism hypothesis. Key supporting evidence remains absent because it is technically
infeasible to capture and control the emergence of these properties in vitro or vivo, almeno
in the near future. One challenge arises from the scarcity of technology to record multi-mode
(including both static and functional connectivity), fine-grained, and high-throughput connec-
tome data (Sporns, Tononi, & Kötter, 2005). Another challenge is lacking experimental
methods to modify the connectivity to control the emergence of these properties. Although
Functional connectivity:
The connectivity formed by dynamic
interactions among neurons.
Network Neuroscience
766
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
Static connectivity:
The anatomic connectivity of the
brain, irrespective of dynamic
interactions among neurons.
Phase transition:
The physical process of transition
between system states defined by
some control parameters.
Percolation transition:
The transition between system
connectivity states (per esempio., from being
fragmentized to being percolate).
the theoretical study may be an alternative choice, current classic models in neuroscience are
either experiment driven and proposed for ex post facto analysis or simulation driven and
designed for imitating phenomena rather than explaining mechanisms. These models are inap-
plicable for an assumption-free analysis when there is no experiment for reference. IL
absence of direct verification due to these challenges makes the validity of the hypothesis
questionable.
Here we discuss the possibility of a feasible and physically fundamental demonstration of
the emergentism hypothesis. These advantageous properties of brain functions are all relevant
to the benefits or costs of forming specific functional connectivity (interactions among neurons)
on the static connectivity (anatomical structure). Perciò, the emergence of these properties
will be detectable if we can formalize the evolution of functional connectivity patterns on static
connectivity. In the present study, we use a fine-grained and high-throughput brain connectome
of the fruit fly, Drosophila melanogaster (Pipkin, 2020; Schlegel et al., 2021; Xu et al., 2020) A
obtain precise information of static connectivity. As for functional connectivity, in real brains, Esso
is subject to both static connectivity and the excitation-inhibition (E/I) properties of synapses; In
our study, it is analyzed under an integrated framework: we begin with a massive neural dynam-
ics computation (Gerstner, Kistler, Naud, & Paninski, 2014) on the whole brain (∼1.2 × 109
times), enabling us to measure the coactivation probability of any pair of connected neurons
and abstract static connectivity as a weight directed graph. Then, we formalize the formation of
functional connectivity on the static connectivity, applying its equivalence relation with the
percolation on random directed graphs, a universal characterization of critical phenomena
and phase transitions (Dorogovtsev, Mendes, & Samukhin, 2001; Li et al., 2021). The motiva-
tion underlying this framework is to regulate the evolution of functional connectivity with a
specific biological factor and verify whether these properties can be established as conse-
quences of these manipulations. Limited by technology issues, the biological factor, the precise
synaptic E/I information that neural dynamics computation requires, can not be recorded in the
electron microscopy (EM) imagery of an insect brain yet (Xu et al., 2020). Tuttavia, the E/I
balance (cioè., the ratio between excitatory and inhibitory synapses) can act as a control param-
eter to randomize the E/I property of each synapse, offering an opportunity to verify if brain
function properties emerge after specific percolation transitions.
RESULTS
Functional Connectivity Formation as Percolation
Topology properties of static connectivity. Let us begin with the static or anatomical connectivity of
the fruit fly brain. The data is acquired from the open source brain connectome lately released by
FlyEM project (Xu et al., 2020). In the present study, neurons and synapses are considered only
when the cell bodies are positioned precisely (assigned with a 10-nm spatial resolution coordi-
nate). The selected data set, including 23,008 neurons, 4,967,364 synaptic connections (synaptic
clefts), E 635,761 pairs of directionally adjacent relations (two neurons are directionally adja-
cent if one synaptic connection comes out of one neuron and leads to another), supports us to
analyze static connectivity on the brain region or macroscopic scale (Figure 1A–B) and the cell
or microscopic scale (Figure 1C–D). Please see the Materials and Methods for data acquisition.
The macroscopic static connectivity is analyzed in terms of the potential input projections
or potential output projections that a brain region can receive from or cast to another brain
region. These projections are treated as potential because static connectivity may not be
equivalent to the functional one. In the analysis, we count these two kinds of projections
between brain regions, based on which the total potential input projections (TPIP, IL
Network Neuroscience
767
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
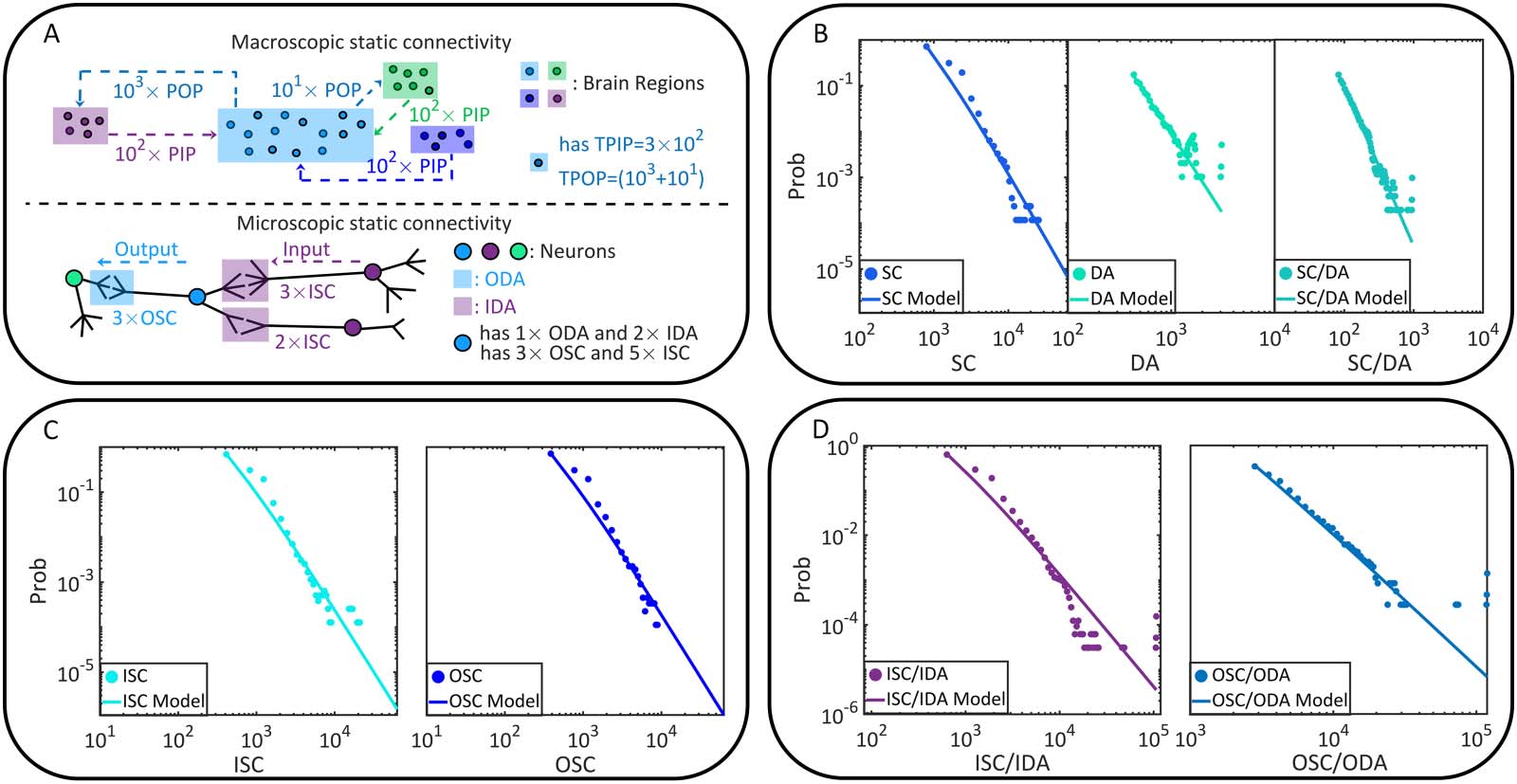
Figura 1. The static brain topology of the fruit fly, Drosophila melanogaster. (UN) The macroscopic static connectivity, where potential
input/output projections are counted between any two brain regions. Note that brain regions are sorted by their names. The heat map and
histogram are shown in a coarse-grained way for a better vision. The heat map can be interpreted like an adjacent matrix, where the number of
potential input/output projections of a brain region can be seen on the corresponding column (or row). (B) Variables of macroscopic static
connectivity are graphically illustrated in this instance. The probability distributions of TPIP and TPOP are shown with corresponding esti-
mated power law models. (C) The microscopic static connectivity, where each node represents a cell body and every directed edge represents
a DA. Neurons are colored according to the number of involved synaptic connections. (D) Variables of microscopic static connectivity are
graphically illustrated. The probability distributions of IDA and ODA are presented with estimated power law models.
macroscopic in-degree) received by each region and the total potential output projections
(TPOP, the macroscopic out-degree) coming from each region can be measured (Figure 1A).
Please see the Materials and Methods and Figure 1B for variable descriptions.
In Figure 1B and Table 1, we analyze the power law distributions of TPIP and TPOP with a
maximum likelihood estimation approach (R. Virkar & Clauset, 2014; Y. Virkar & Clauset,
2014), suggesting that the macroscopic static connectivity is plausibly scale-free (power law
exponent α 2 (2, 3) is estimated with ideal goodness). More details of power law analysis can
be seen in Materials and Methods. Nel frattempo, we verify the symmetry (per esempio., with a balance
between input and output projections) of macroscopic static connectivity using the Pearson
correlations and the average change fractions (Vedi la tabella 2). The connectivity is suggested as
symmetric since (1) there are significant positive correlations between TPIP and TPOP (per esempio.,
larger than 0.9); (2) The average change fraction of TPIP compared with TPOP is sufficiently
piccolo (per esempio., smaller than 1). We also present other corroborative evidence derived from related
Tavolo 1.
Power law analysis results
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Goodness of estimation
0.0074
Scale-free or not
Yes
Type
Macroscopic
Macroscopic
Microscopic
Microscopic
Variable
TPIP
TPOP
IDA
ODA
Probability distribution
P (TPOP = n) ∝ n−2.45
P (TPIP = n) ∝ n−2.17
P (IDA = n) ∝ n−3.69
P (ODA = n) ∝ n−3.22
0.0086
0.0348
0.0623
Nota. Being scale-free requires P ∝ n−α, where α 2 (2, 3). Goodness of estimation is expected as to be less than 0.05.
Network Neuroscience
Yes
No
No
768
Percolation explains efficiency, robustness, and economy of the brain
Tavolo 2.
Symmetry analysis results
Variable
TPIP
IDA
Variable
TPOP
ODA
Pearson correlation
0.9938
P
3.31667 × 10−9
Average change fraction
J
TPIP−TPOP
J
TPOP
= 0.8215
0.8817
< 10−10
IDA−ODA
j
ODA
j
= 0.6443
Symmetric degree
Strictly strong
Less strong
Note. Strong symmetry requires a strong positive correlation (e.g., correlation > 0.9 and p < 10−3). Strong symmetry implies a small average change fraction
(e.g., fraction < 1). The term “strictly strong” means that the strictest criterion of strong symmetry is completely satisfied. The term “less strong” means that the
strictest criterion of strong symmetry is partly satisfied.
variables to support these findings (please see Tables 5–6 and Figure 5 in Materials and
Methods for additional information).
When turn to the cell scale, we characterize microscopic static connectivity depending on
the directionally adjacent relation (DA) between neurons. Two neurons are directionally adja-
cent if there exists at least one synaptic connection coming from one of them to the other (see
Figure 1C). Note that one DA may correspond to multiple synaptic connections because there
can be more than one synaptic cleft. To offer an accurate characterization, we further subdi-
vide variable DA according to input-output relations (e.g., pre- and postsynaptic relations).
Specifically, we count input directionally adjacent relations (IDA) and the output directionally
adjacent relations (ODA) for comparison on each neuron. Details of these variables are
described in the Materials and Methods and Figure 1D.
In Figure 1D and Table 1, we show the power law analysis on the above defined variables.
The same analysis is also conducted on other related variables (please see Table 3 and Figure 5
in Materials and Methods for additional information). Based on these results, the potential
scale-free property of microscopic static connectivity is suggested as uncertain and nonrobust.
Only a few variables (e.g., additional results in Table 5 in Materials and Methods) plausibly
exhibit scale-free properties while others do not (e.g., results in Table 1). Meanwhile, symmetry
analysis is applied to show the approximate symmetry of microscopic static connectivity. In
Table 2, significant positive correlations and small average change fractions are observed
between input-related and output-related variables. Similar properties can be seen on other
variables of microscopic static connectivity (please see Table 6 in Materials and Methods
for additional data). These results principally suggest that microscopic static connectivity is
approximately symmetric, though the symmetric degree is not as strong as macroscopic static
connectivity.
The above analysis conveys three important messages: during the coarse-graining process
from the cell scale to the brain-region scale, potential local asymmetry and diversity gradually
fade away and eventually vanish owing to the loss of information in detailed connectivity. This
finding encourages us to concentrate on fine-grained microscopic static connectivity in the
subsequent analysis to control information loss. Meanwhile, although asymmetric upstream-
Variable
PIP
POP
TPIP
TPOP
Table 3. Macroscopic variable definitions
Meaning
Potential input projections that a brain region can receive from another region
Potential input projections that a brain region can cast to another region
Total potential input projections that a brain region can receive from all other regions (macroscopic in-degree)
Total potential input projections that a brain region can cast to all other regions (macroscopic out-degree)
Network Neuroscience
769
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
downstream relations can be found among brain regions during information processing, these
relations may merely exist in functional connectivity (static connectivity is principally symmet-
ric). This finding reminds us that functional connectivity can not be simply reflected by static
connectivity. Moreover, we speculate that the uncertain scale-free property is relevant with an
existing controversy of whether static brain connectivity is scale-free or not (see pieces of sup-
porting (Kaiser & Hilgetag, 2004; Kaiser et al., 2007)) and opposing evidence (Breskin, Soriano,
Moses, & Tlusty, 2006; Humphries, Gurney, & Prescott, 2006). Scale-free property of the brain
may critically rely on the granularity and the variables used in connectivity characterization.
To this point, the static connectivity of the fruit fly brain has been characterized, below we
turn to formalize the formation of functional connectivity based on the static connectivity.
Neural dynamics computation and coactivation probability graph. As discussed above, the fine-
grained, high-throughput, and simultaneous recording of static connectivity and neural
dynamics remains technically infeasible (Sporns et al., 2005). An alternative is to study the
formation of functional connectivity based on the static connectivity through a theoretical
way, whose first step is to analyze possible coactivation patterns among neurons. While
one prerequisite of neural coactivation analysis, the static connectivity, has been obtained
in the previous section, another prerequisite, the excitation-inhibition (E/I) properties of syn-
apses, can not be recorded in the electron microscopy imagery of the insect brain (Xu et al.,
2020). To avoid this obstacle, previous studies turn to mammalian brain regions (e.g., rat hip-
pocampus) (Amini, 2010; Breskin et al., 2006; Cohen et al., 2010; Eckmann et al., 2007),
where synaptic E/I properties could be easily recorded and controlled, but the connectivity
imaging is much more coarse-grained and low-throughput.
We, however, treat this obstacle as an opportunity to study the role of synaptic E/I balance,
a global factor that reflects the E/I properties of all synapses. Although precise synaptic E/I
properties remain absent, they can be randomly assigned under the restriction of E/I balance
λ 2 (0, 1), the proportion of excitatory synapses in all synapses. After generating the static con-
nection strength of every directionally adjacent relation Ni → Nj (here Ni and Nj are neurons),
we can measure coactivation probability Pij to define the dynamic connection strength. Here
the coactivation probability is estimated by the leaky integrate-and-fire (LIF) model (Gerstner
et al., 2014), a standard approach in neural dynamics computation. Please see the Materials
and Methods for details.
Letting λ vary from 0.05 to 0.95 (Δλ = 0.05), we implement the above computation on
every pair of Ni → Nj to obtain its dynamic connection strength in terms of coactivation prob-
ability Pij under each λ condition. We treat Pij as a variable and sample its probability density
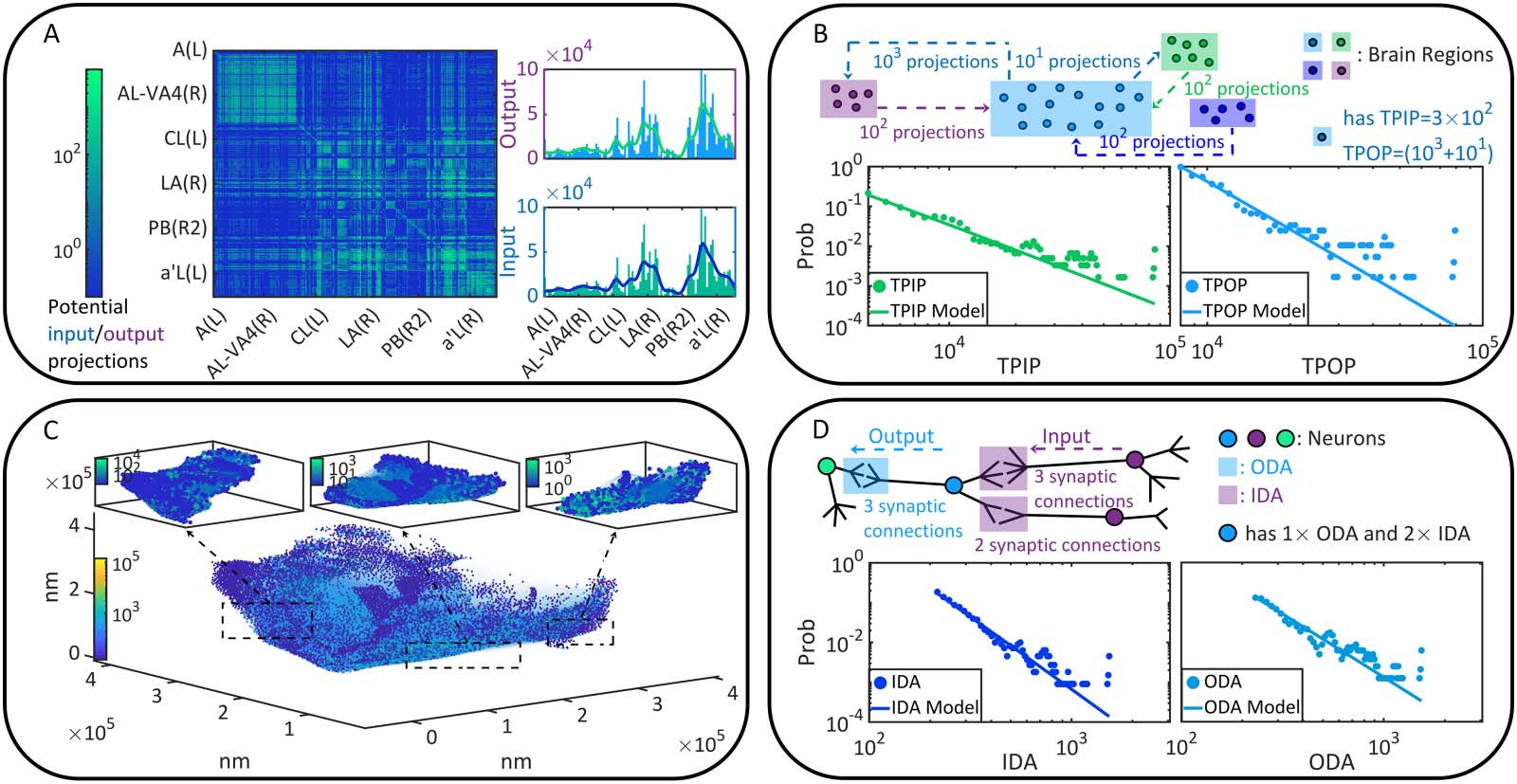
on the whole brain (Figure 2A). According to the density concentration tendency and the first
moment E(Pij), we suggest that Pij increases with λ globally. This phenomenon can be double-
checked if we analyze every binomial distribution Bi(P ij) to find its peak value ^P ij and the
corresponding coordinate ^ξ. The distribution is calculated in terms of a ξ-trial experiment
(ξ = 100) where the success probability for each trial is P ij. Figure 2B illustrates the frequency
distribution of (^ξ, ^Pij) sampled on the whole brain, revealing that ^ξ increases with λ. In Figure 2C,
we show instances of coactivation patterns and their implied functional connectivity situations
under each λ condition, which turn out to be denser when λ increases. Here the existence of
coactivation between Ni and Nj is randomized following Bi(P ij). A directed edge Ni → Nj is
added to functional connectivity when Ni and Nj are coactivated. In Figure 2D–E, we analyze
the properties of the weakly connected cluster ( WCC) and the strongly connected cluster (SCC)
(Bollobás, 2013) on the whole brain. It can be seen that the total numbers of WCCs and SCCs
Weakly connected cluster:
A subgraph of a directed graph,
where each node is an endpoint of at
least one directed edge coming to it
or one directed edge coming out
from it.
Strongly connected cluster:
A subgraph of a directed graph,
where if any two nodes are
connected by a directed path (e.g.,
coming from the first node to the
second one), then there must exist
another antidromic directed path
between them (e.g., coming from the
second node to the first one).
Network Neuroscience
770
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 2. Neural dynamics and coactivation probability graphs. (A) The probability densities of Pij under each λ condition are presented by
colorful areas. Meanwhile, the first moment E(Pij) is shown as a function of λ. (B), The observed occurrence frequency distributions of (^ξ, ^Pij)
(counted on every directionally adjacent relation, DA) and how they vary with λ. (C) Instances of coactivation patterns under each λ condition
are given (upper parallel). The coactivation of neurons Ni and Nj is represented as a point (i, j ). Note that real coactivation patterns are much
sparser than how they are displayed. Moreover, the implied functional connectivity by each coactivation pattern are shown (bottom parallel),
where edges correspond to the DAs through which coactivation happens and neurons are colored based on the number of involved coactiva-
tion relations. (D–E) The cluster number as well as the first and second moments of cluster size are presented as functions of λ. Clusters are
defined in terms of WCC (see D) and SCC (see E), respectively. Although the first moment of cluster size increases with λ, its variation is
sufficiently slower than the second moment and therefore less visible. Missing data points in E are 0 in a logarithmic plot.
decline with λ because specific clusters become larger gradually (the first moment of cluster size
maintains relatively constant while the second moment increases significantly). In sum, the com-
putational costly coactivation analysis (∼1.2 × 109 times of LIF model computation) enables us
to study the E/ I balance λ as a control parameter of functional connectivity formation. As
expected, a higher E/I balance creates stronger functional connectivity because coactivation
occurs more often. More neurons are included in the same cluster rather than maintain isolated,
making it possible for large-scale communication between neurons to emerge.
However, the concordant increase of dynamic connection degree with the increase of E/I
balance λ discussed above is insufficient to give a whole picture of all important information.
A piece of missing information lies in that the observed formation of functional connectivity is
a sigmoid-like process rather than a uniform growth process. While functional connectivity
forms promptly when λ is relatively small, the formation speed becomes stable at a large λ.
The nonuniform speed is not a trivial consequence of λ nor of an artificially manipulation.
Therefore, we conjecture it as an emergence phenomenon triggered by λ and restricted by
specific mechanisms.
Network Neuroscience
771
Percolation explains efficiency, robustness, and economy of the brain
Functional connectivity characterized by percolation. Let us step back from the above analysis
and rethink the nature of functional connectivity. Functional connectivity is rooted in the coac-
tivation probability between neurons and is affected by both static connectivity and the E/I
balance λ. One can interpret functional connectivity as a communication pattern between
neurons, where static connectivity serves as a network of information channels, and λ modifies
the information transmission probability in these channels. Although this idea has been studied
previously in neuroscience computationally (Amico et al., 2021; Graham et al., 2020; Shew,
Yang, Yu, Roy, & Plenz, 2011), we discuss it from a more physically fundamental perspective—
percolation. Percolation is a universal characterization of critical phenomena and phase tran-
sitions in a probabilistic form (Agliari, Cioli, & Guadagnini, 2011; Amini & Fountoulakis, 2014;
Balogh & Pittel, 2007; Baxter, Dorogovtsev, Goltsev, & Mendes, 2010; Ben-Naim & Krapivsky,
2011; Callaway, Newman, Strogatz, & Watts, 2000; Dorogovtsev et al., 2001; Goltsev,
Dorogovtsev, & Mendes, 2008; Li et al., 2021; Panagiotou, Spöhel, Steger, & Thomas, 2011;
Radicchi & Fortunato, 2009). To understand percolation, one can imagine that a porous stone,
where pores or tiny holes are connected randomly, is immersed in water (Figure 3A). Can the
water come into the core or kernel of the stone? This question can be addressed by verifying the
existence of specific paths connected between pores that run through the stone. It is trivial that
the stone will be wetted thoroughly when the connection probability between pores is suffi-
ciently large, as connected pores can form a cluster to penetrate the stone. Replacing the stone
and pores by the brain and neurons, one can see the intriguing similarity between the soaking
process of porous stone and the functional connectivity of neurons (Figure 3A). The only dif-
ference lies in that the space where connections can form changes from the lattice space of the
stone to the random graph characterized by static connectivity. In decades, the equivalence
relation between brain connectivity formation and the percolation on random graphs have
attracted extensive explorations in biology (Bordier, Nicolini, & Bifone, 2017; Carvalho
et al., 2020; Del Ferraro et al., 2018; Kozma & Puljic, 2015; Lucini, Del Ferraro, Sigman, &
Makse, 2019; Zhou, Mowrey, Tang, & Xu, 2015) and physics (Amini, 2010; Breskin et al.,
2006; Cohen et al., 2010; Costa, 2005; da Fontoura Costa & Coelho, 2005; da Fontoura Costa
& Manoel, 2003; Eckmann et al., 2007; Stepanyants & Chklovskii, 2005), serving as a promis-
ing direction to study brain criticality, neural collective dynamics, optimal neural circuitry, and
the relation between brain anatomy and functions.
In the terminology of percolation, neurons are referred to as sites. The dynamic connection
formed between two neurons is called the occupation of the bond between these two sites.
The central question in the following percolation analysis, as suggested above, concerns the
emergence of a cluster of connected sites that penetrates the brain. The brain is referred to as
percolate if such a cluster exists. Mathematically, the criterion of being percolate can be
defined in terms of the giant strongly connected cluster (GSCC), a special SCC whose size
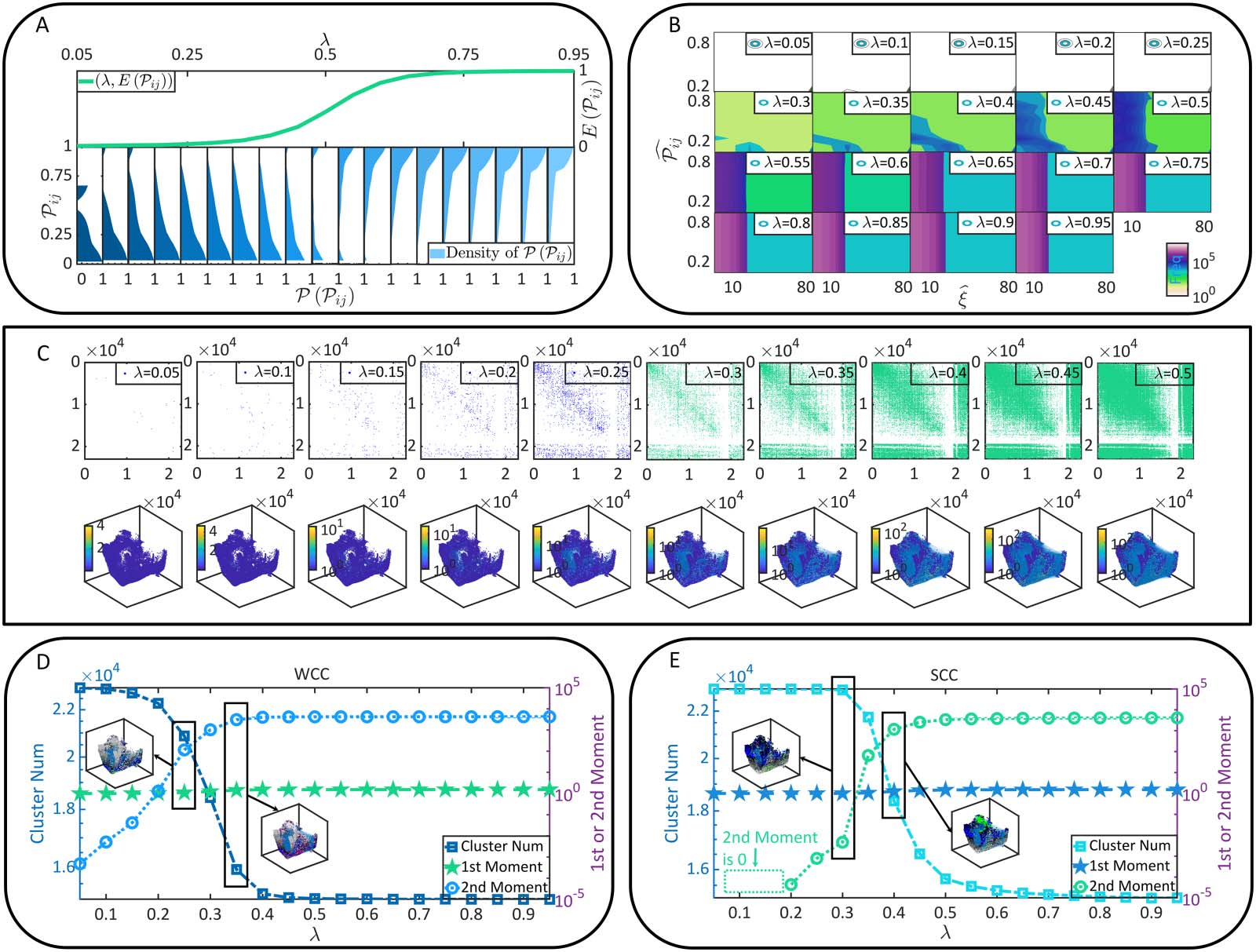
approaches the whole brain size in magnitude order. In Figure 3B, we demonstrate that the
size, the average in-degree, and the average out-degree of the GSCC are sigmoid-like func-
tions of λ. These parameters are closing to 0 when λ is small. Then they increase dramatically
after λ reaches over a specific value and approximate plateau again after λ reaches over
another specific value. This phenomenon is not accidental because it shares similarities with
the observations in Figure 2A and Figure 2E. To explore the underlying mechanism, we
attempt to offer an analytical characterization of the GSCC rather than limit ourselves to com-
putational interpretations. Note that our analysis is implemented under the framework of per-
colation on directed graphs because the connectivity between neurons is unidirectional.
Under each λ condition, we implement the random generation of functional connectivity l
times (l = 5). Note that this setting means that all our subsequent analyses are repeated l times
Percolation on random graphs:
A kind of percolation process defined
on random graphs, concerning the
connectivity states between nodes
(referred to as sites in the terminology
of percolation) or edges (referred to
as bonds in the terminology of
percolation).
Network Neuroscience
772
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Functional connectivity formation as a percolation process. (A) The similarity between the soaking of porous stone and the
Figure 3.
functional connectivity of neurons. (B) The size, the average in-degree, and the average out-degree of the GSCC under different λ conditions.
(C) P in and P out in brain connectome (upper parallel) and their nontrivial solutions (bottom parallel). (D) The probability ϕ predicted by
Equation 7, the experimentally observed probability for a neuron to belong to the GSCC, and the upper bound (UB) of ϕ are presented as
functions of λ. Meanwhile, the error between our theoretical predictions in Equation 7 and experimental observations is measured. (E) The
difference between the nondilution percolation and the diluted one. (F) The percolation threshold ρc, term huvi, and term hki are shown as
functions of λ. The meaningful values of threshold ρc are pointed out. Please note that D and F show l data sets of each variable indepen-
dently derived from l (l = 5) times of functional connectivity generation (e.g., there are l sets of experimental data of ϕ). They highly overlap
with each other to demonstrate that our observations are not accidental and keep consistency across different generated functional
connectivity.
(independently repeated on every generated functional connectivity). Here we do not average
results across l times of analyses to show that our theory is averagely consistent with experi-
ments. On the contrary, we show l sets of analysis results together to suggest that the consis-
tency between our theory and experiments as well as the consistency across the results
obtained on different generated functional connectivity are not accidental (e.g., see the data
points that highly overlap with each other in Figure 3D, Figure 3F, and Figure 4). Given the
benefits of multiple times of functional connectivity generation, let us go back to the details of
generation approach. In each time, the existence of Ni → Nj is randomized following the
binomial distribution Bi(P ij) (this is same as that in Figure 2B). Then we obtain statistics on
functional connectivity, a directed graph, to calculate the probability P(u, v) for a neuron to
have in-degree u and out-degree v. Based on the theory of percolation on directed graphs
(Dorogovtsev et al., 2001; Li et al., 2021), the formation of the GSCC can be analyzed in terms
of the probability Pin that a directed edge leads to the GSCC and the probability Pout that a
directed edge comes from the GSCC. One can easily imagine that Pin and Pout increase with
the size of GSCC. Analytically, P in and P out can be defined by their own self-consistent
Network Neuroscience
773
Percolation explains efficiency, robustness, and economy of the brain
Equations 1 and 2. Here self-consistency means that Pin and Pout can be represented as the
functions of themselves (Dorogovtsev et al., 2001; Li et al., 2021).
Pin ¼ 1−
Pout ¼ 1−
1
kh i
∂
∂x
1
kh i
∂
∂y
ð
G x; y
(cid:1)
(cid:1)
Þ x¼1;y¼1−Pin
;
ð
G x; y
(cid:1)
(cid:1)
Þ x¼1−Pout;y¼1:
(1)
(2)
The normalization term hki in Equations 1 and 2 denotes the average in-degree (or identically,
the average out-degree) in Equation 3.
X
X
kh i ¼
ð
P u; v
Þu ¼
ð
P u; v
Þv:
u;v
u;v
(3)
Equations 1 and 2 are derived based on the probability generating function (Equation 4), a
standard and practical approach to study random graphs, especially in real data sets (Newman,
Strogatz, & Watts, 2001).
X
ð
G x; y
Þ ¼
ð
P u; v
Þx uy v :
(4)
u;v
Merely requiring the knowledge of P(u, v) in Equation 4, Equations 1 and 2 have been pow-
erful enough in studying the formation of the GSCC. In other words, they can predict when the
brain connectivity becomes percolate. Specifically, the sufficient and necessary condition for
the GSCC to emerge is that Equations 1 and 2 have nontrivial solutions in (0, 1] (note that the
trivial solution is Pin = Pout = 0). In practice, it is unnecessary to analytically study the non-
trivial solutions of Equations 1 and 2. Instead, potential solutions can be numerically explored
in a comprehensible way. Specifically, we only need to rewrite Equations 1 and 2 as functions
Win ¼ 1 − Pin −
Wout ¼ 1 − Pout −
1
kh i
∂
∂x
1
kh i
∂
∂y
ð
G x; y
(cid:1)
(cid:1)
Þ x¼1;y¼1−Pin
;
ð
G x; y
(cid:1)
(cid:1)
Þ x¼1−Pout;y¼1;
(5)
(6)
and explore when Win and Wout go through the lines Win = 0 and Wout = 0 (see Figure 3C).
When there exist non-trivial solutions ( ^Pin, ^Pout), the probability ϕ that a neuron belongs to the
GSCC can be calculated in Equation 7. Otherwise, the probability maintains closing to 0.
− G 1; 1 − ^Pin
(cid:3)
ϕ ¼ 1 − G 1 − ^Pout; 1
þ G 1 − ^Pout; 1 − ^Pin
(cid:4)
:
(7)
(cid:3)
(cid:4)
(cid:4)
(cid:3)
In Figure 3D, we compare between ϕ and the real probability that a neuron belongs to the
GSCC in the experiment to quantify the error of our theoretical predictions. High consistency
can be found between the predictions and experiment.
As can be seen in Figure 3B and Figure 3D, a phenomenon referred to as percolation transition
happens at λ = 0.3, where the GSCC emerges suddenly (ϕ = 0 when λ ≤ 0.3 and ϕ ≥ 0.06 when λ >
0.3). This is a transition of the brain from being fragmentized to percolate. In other words, neurons
become extensively coupled with each other to form system-level functional connectivity after λ
reaches over 0.3. Perciò, λ = 0.3 serves as the percolation threshold. Inoltre, probability ϕ in
Equazione 5, as well as the corresponding experimental observations, will eventually approximate
to an upper bound (the growing speed approaches to 0 after λ reaches over 0.6). This phenomenon
hints that the GSCC, reflecting functional connectivity, has a size intrinsically bounded by static
connectivity. Functional connectivity forms through synaptic connections and, Perciò, must
be a subgraph of static connectivity. By recalculating Equations 1–5 in static connectivity, IL
Network Neuroscience
774
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
upper bound of ϕ is obtained in Figure 3D and it is reached by ϕ when λ ≥ 0.6. Note intrinsic
consistency between the observations in Figure 2A, Figure 2D, and Figure 2E and that in
Figure 3D, even quantitative details are different as they concern about different parameters.
Inoltre, the above-observed percolation transition can also be confirmed from the per-
spective of diluted percolation. Under dilution condition, functional connectivity formation is
not only constrained by the coactivation probability between neurons but also by the activa-
tion probability of each neuron itself. In other words, the dilution condition represents a more
realistic situation where neurons are conditionally activated (per esempio., by external stimulus) E
functional connectivity may form only between activable neurons. The nondilution percola-
tion analyzed above serves as a special case of the diluted one (see Figure 3E). Considering the
dilution of neurons (per esempio., each neuron is activated following a probability ρ), another version of
percolation threshold ρc (the control parameter is ρ) can be calculated by Equations 8 E 9
(Dorogovtsev et al., 2001; Li et al., 2021)
ρc ¼ kh i
uvh
X
;
io
uvh
i ¼
ð
P u; v
Þuv:
(8)
(9)
tu;v
In Figure 3F, we can see that a meaningful ρc 2 [0, 1] (the solution of a probability is mean-
ingful if it is in the interval of [0, 1]) emerges only when λ ≥ 0.3. It decreases with λ until
reaching to its lower bound when λ ≥ 0.6. The existence of a meaningful percolation thresh-
old serves as a necessary condition for percolation transition to happen (per esempio., when λ = 0.5,
percolation transition may happen if ρ ≥ ρc = 0.017; when λ = 0.2, percolation transition never
happens since ρc = 6.321 is meaningless). Perciò, the GSCC can form only after λ reaches
Sopra 0.3. These findings are consistent with the above nondilution percolation analysis. In
Figure 3F, we directly show the potential solution of percolation threshold ρc as a function
of λ. Later we will show the benefits of such an illustration.
In summary, our analysis presented above demonstrates that percolation, a universal for-
malism of criticality and phase transitions, can characterize the formation of brain functional
connectivity without other top-down modeling or assumptions. All analytic calculations only
require the knowledge of degree distributions in the brain connectome, which is accessible in
practice. Below, we suggest that the percolation analysis alone is sufficient to explain the
emergence of three key properties of brain functions.
Percolation and Brain Function Properties
In the above section, we have demon-
Percolation explains information transmission efficiency.
strated that functional connectivity formation can be treated as a percolation process. Starting
from this section, we will study how brain function properties emerge as the characteristics of
formed functional connectivity.
Let us begin with information transmission efficiency, which is manifested as the low time
cost of communications between neurons or high broadcasting capacity of neural information.
Such a superiority critically relies on the topological attributes of functional connectivity
(Avena-Koenigsberger et al., 2018) in the real brain.
Here we attempt to quantify information transmission efficiency based on graph-theoretical
metrica. Following the same idea in Figure 2B and Figure 3, we randomize functional connec-
tivity l times (l = 5) under each λ condition. Given each functional connectivity, we calculate
Percolation process:
An evolutionary process of system
connectivity states controlled by
specific parameters, where each
system unit is randomly occupied
and system connectivity states are
characterized by the connections of
occupied system units.
Network Neuroscience
775
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
.
T
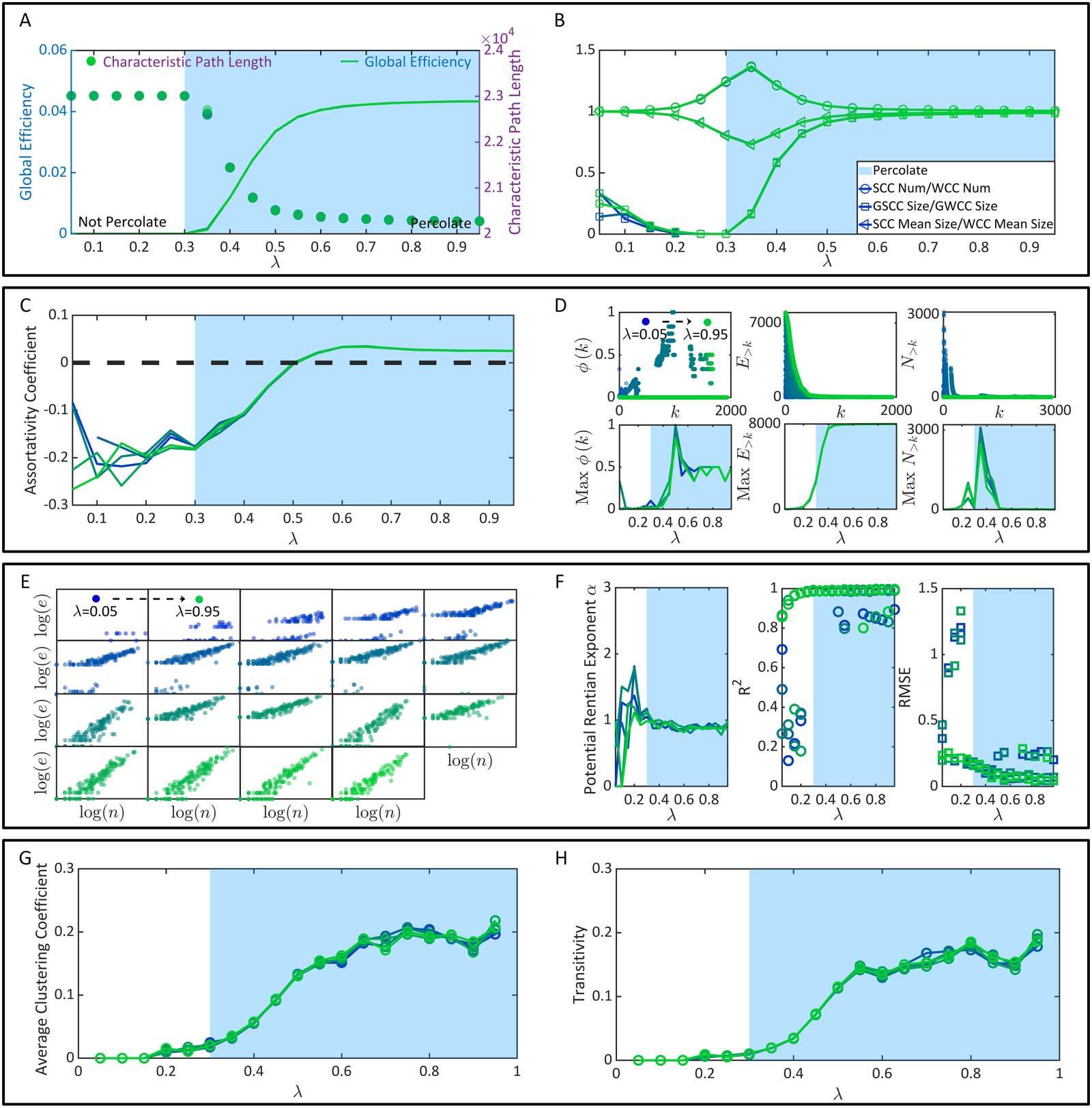
Figura 4. The emergence of brain function superiorities. (UN) The characteristic path length and global efficiency. (B) The properties of con-
nected clusters. (C) The assortativity coefficient. (D) The distributions (upper parallel) and the maximums of ϕ(k), E>k, and N>k (bottom parallel).
(E) Instances of (log(N), log(e)) under each λ condition. (F) The Rentian exponents, the RMSE, and R2. (G) The average clustering coefficient. (H)
The transitivity. Note that all figures show l data sets of each variable independently derived from l (l = 5) times of functional connectivity
generazione.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
its characteristic path length (average shortest path length between all neurons) (Albert &
Barabási, 2002) and global efficiency (average inverse shortest path length between all neu-
rons) (Latora & Marchiori, 2001) (Figura 4). Generalmente, the characteristic path length reflects
the average cost of optimal information transmission (transmission always follows the min-
imal path length principle). The global efficiency is the average optimal information trans-
mission efficiency. In Figure 4A, once λ reaches over the nondilution percolation threshold
0.3, the characteristic path length of functional connectivity drops sharply while the global
efficiency increases significantly. Once λ reaches over 0.6, the variation speeds of these two
metrics approximate 0. High consistency between these variation trends and the percolation
process in Figure 3D can be observed. Nel frattempo, we measure the number ratio and aver-
age size ratio between SCCs and WCCs in functional connectivity, rispettivamente. Anche noi
calculate the size ratio between the GSCC and the GWCC (giant weakly connected cluster).
Network Neuroscience
776
Percolation explains efficiency, robustness, and economy of the brain
These ratios are shown as functions of λ in Figure 4B. They principally reflect the proportion
of the close-knit neural community, where information broadcasting capacity is high, within
all communicable neurons (a neuron is communicable if it may communicate with at least
one other neuron). In Figure 4B, the size ratio between the GSCC and the GWCC has a
similar rising trend with the global efficiency, suggesting that the giant close-knit neural com-
munity will occupy more communicable neurons after percolation transition. Although the
other two ratios (the number ratio and average size ratio between SCCs and WCCs) can not
reflect the improvement of information broadcasting capacity by percolation transition, Essi
fluctuate significantly near the nondilution percolation threshold and may function as
observable markers of percolation transition.
In summary, information transmission efficiency improvement is demonstrated as a bypro-
duct of the percolation process. Percolation transition may be a critical condition for high
transmission efficiency to emerge.
Percolation explains robust flexibility. Then we turn to study the robust flexibility of brain con-
nectivity, which is the capacity of the brain to tolerate the large-scale loss of neurons or syn-
aptic connections (per esempio., by lesions (Aerts et al., 2016; Joyce et al., 2013; Kaiser et al., 2007))
while maintaining robust brain functions.
Generalmente, robust flexibility can be studied directly and indirectly (Rubinov & Sporns,
2010B). Direct analysis of robust flexibility usually compares functional connectivity before
and after presumed attacks (per esempio., removing some neurons) (Aerts et al., 2016; Joyce et al.,
2013; Kaiser et al., 2007). We suggest that these attacks, no matter if they are random or
targeted, are equivalent to the dilution introduced in diluted percolation analysis (Vedere
Figure 3E–F). Those attacked neurons or directionally adjacent relations (DA) are never
included in functional connectivity and, Perciò, can be treated as diluted. From this per-
spective, one can understand the motivation underlying the direct illustration of dilution per-
colation threshold ρc as a function of λ in Figure 3F. It benefits our analysis by showing the
maximum tolerable attack intensity 1 − ρc of the brain while maintaining percolate. Based
on Figure 3F, we discover that the brain can not tolerate attacks until λ reaches over 0.3. IL
robust flexibility increases sharply until λ reaches over 0.6, after which the increasing speed
becomes stable.
As for the indirect analysis of robust flexibility, we implement it in terms of the assortativity
coefficient (Newman, 2002) and the rich-club coefficient (Ball et al., 2014; Colizza, Flammini,
Serrano, & Vespignani, 2006; Van Den Heuvel & Sporns, 2011). The assortativity coefficient is
the Pearson correlation between the degrees of all neurons on two opposite ends of a DA.
Brain connectivity with a positive assortativity coefficient may have a comparatively robust
community of mutually interconnected high-degree hubs, while brain connectivity with a neg-
ative assortativity coefficient may have widely distributed and vulnerable high-degree hubs
(Rubinov & Sporns, 2010B). Allo stesso modo, the rich club coefficient ϕ(k) is the number ratio of
the DAs between neurons of degree > k (denoted by E>k), when all neurons of degree ≤ k have
been removed, to the maximum DAs that such neurons can share (denoted by N>k) (Ball et al.,
2014; Colizza et al., 2006; Van Den Heuvel & Sporns, 2011). The calculations of these two
metrics can be implemented utilizing a toolbox designed by Rubinov and Sporns (2010B). In
Figure 4C, we discover that the assortativity coefficient significantly increases once λ reaches
Sopra 0.3. It becomes positive after λ reaches over 0.5 and becomes relatively changeless after λ
reaches over 0.6. Similar variation trends can also be observed in the maximum ϕ(k) (the max-
imum value is obtained through the comparison across different k). A slight difference lies in
that the maximum ϕ(k) reaches its peak when λ = 0.5 and then drops until λ = 0.6 (Figure 4D).
Network Neuroscience
777
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
In sum, the robust flexibility of functional connectivity, no matter if it is analyzed directly or
indirectly, experiences a sharp increase after percolation transition (λ = 0.3). Inoltre, it is
again intrinsically limited by static connectivity and reaches its bound after λ ≥ 0.6.
Percolation explains brain economy. Finalmente, we analyze brain economy from the perspectives
of network wiring and network running, accordingly.
Measuring the physical embedding efficiency of functional connectivity is a promising
approach to analyze network wiring economy (Bassett et al., 2010). A key organizational prin-
ciple shared by various physical information processing systems is the isometric scaling rela-
tionship between the number of processing units (per esempio., neurons) and the number of connections
(per esempio., directionally adjacent relations), known as the Rentian scaling. Such a property reveals
the relation between the dimensionality of system topology and information processing capac-
ità. Generalmente, the Rentian scaling corresponds to an economic wiring paradigm of embedding
a high-dimensional functional topology in a low-dimensional physical space (Bassett et al.,
2010; Chen, 1999; Ozaktas, 1992). To verify the existence of the Rentian scaling, we need
to partition the physical space into m cubes. Then we count the number n of neurons within
each cube and the number e of directionally adjacent relations (DAs) crossing the cube bound-
aries. The Rentian scaling exists if there is a statistically significant linear regression relation log
(e) = α log(N) + β and α 2 (0, 1). Here α is referred to as the physical Rentian exponent. A smaller
significant exponent corresponds to higher efficiency. We use the coordinate information of
neurons to embed functional connectivity into real size physical space, where the partition
number is set as m = 300. In Figure 4E, we show instances of (log(N), log(e)) distributions gen-
erated from functional connectivity under each λ condition. Qualitatively, we can already find
Quello (log(N), log(e)) may not follow a significant linear regression relation when λ is small.
Quantitatively, we discover that the linear regression performance before the percolation tran-
sition, λ = 0.3, is weak and unstable. This phenomenon is expectable because system-level
functional connectivity has not emerged yet, and the physical space is occupied by isolated
and inefficient neurons (see Figure 4F). Once λ approaches and further reaches over 0.3, IL
linear regression becomes significant with an average physical Rentian exponent α ∼ 0.8999
(the standard error is ∼0.0464). A slight decrease of α can be observed when λ 2 (0.3, 0.6),
suggesting that the physical embedding becomes relatively more efficient. Except being
reported alone, the physical Rentian exponent α calculated through physical space partition
can also be compared to its theoretical minimum to draw the same conclusion from another
perspective (per esempio., see Bassett et al., 2010).
As for the economy of network running, it should be noted that a possible misconception
about the metabolic economy is that the metabolic economy vanishes after system-level func-
tional connectivity emerges. Here we need to emphasize the inequivalence between high
metabolic cost and low metabolic economy. System-level functional connectivity with high
metabolic cost (massive neural dynamics and high E/I balance are metabolically costly; Barta
& Kostal, 2019; Bullmore & Sporns, 2012) is not necessarily inefficient if it can support large
amounts of functions. Low efficiency corresponds to high costs but low functional capacity. In
real brains, high metabolic consumption is inevitable considering billions of neurons and syn-
apses (Bullmore & Sporns, 2012); metabolic economy is mainly determined by the functional
capacity payoff. Such a payoff in real brains is usually shaped by functional segregation and
integration capacities (Rubinov & Sporns, 2010B). Specifically, functional segregation is man-
ifested as specialized and distributed information processing in densely connected groups of
neural clusters, which can be analyzed in terms of modular structure (Rubinov & Sporns,
2010B) and quantified applying the clustering coefficient (Fagiolo, 2007; Watts & Strogatz,
Network Neuroscience
778
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
1998) and the transitivity (Newman, 2003). In Figure 4G–H, these two metrics are shown as
functions of λ, rispettivamente. While they increase sharply after percolation transition, their
increase rates drop once λ reaches over 0.5. In other words, modular structures experience
massive mergers after percolation transition, becoming larger and more close-knit. Tuttavia,
the ever-rising λ > 0.5 can not improve functional segregation without limitation. These mod-
ular structures in functional connectivity are ultimately restricted by static connectivity. Quanto a
functional integration, it refers to the ability to collect and combine specialized information
from distributed neural clusters (Rubinov & Sporns, 2010B). The characteristic path length and
the global efficiency shown in Figure 4A are practical metrics of this property, which have
been demonstrated as explicable by percolation.
Combine the information in Figure 4E–H, we can see that both network wiring economy
and network running economy are optimized after λ ≥ 0.3. Considering that every rise in the
E/I balance causes higher energy consumption (Barta & Kostal, 2019; Bullmore & Sporns,
2012) but may not bring additional payoffs (per esempio., network running economy does not signifi-
cantly increase after λ ≥ 0.5), we suggest that λ ∼ 0.5 may be an optimal choice for the brain
to maintain economy.
DISCUSSION
The Optimal Synaptic E/I Balance for Brain Functions
Let us move forward our analysis by incorporating all above presented findings to solve a crit-
ical question concerned in neuroscience: what is the optimal synaptic E/I balance?
There are several vital values of the E/I balance λ according to our previous analysis: IL
nondilution percolation threshold λ = 0.3 (E/I balance is 3:7) where percolation transition hap-
pens; the approximate value λ = 0.5 (E/I balance is 1:1) which reconciles the actual size of the
GSCC with its increasing rates; the approximate value λ = 0.6 (E/I balance is 3:2), after which
percolation approximates to its bound. The advantageous characteristics of brain functions,
including efficiency (Avena-Koenigsberger et al., 2018), robustness (Aerts et al., 2016; Joyce
et al., 2013; Kaiser et al., 2007), and economy (Bullmore & Sporns, 2012), principally expe-
rience sharp increases after percolation transition at λ = 0.3 and become changeless after λ =
0.6 because they are intrinsically bounded by the characteristics of static or anatomical con-
nectivity. Information transmission efficiency, robust flexibility, and network wiring economy
have relatively large actual quantities and high increasing speeds near λ = 0.5, after which
their increasing speeds gradually approximate 0 and are not sufficient to act as payoffs of
the rising of λ. Perciò, the actual value of network running economy is very likely opti-
mized near λ = 0.5. Above this value a sharp drop is observed. Inoltre, a significantly high
E/I balance may damage information encoding efficiency (Barta & Kostal, 2019; Sprekeler,
2017) and membrane potential stabilizing (Sadeh & Clopath, 2021; Sprekeler, 2017). Taking
all these pieces of evidence together, it is suggested that an optimal E/I balance for the brain to
guarantee advantageous properties simultaneously may be λ ∼ 0.5, consistent with the previ-
ous in vitro experimental finding (Shew et al., 2011). Inoltre, this inferred optimal E/I
balance by percolation theory corroborates the findings of the sufficient condition for neural
dynamics in the brain to be critical (Poil, Hardstone, Mansvelder, & Linkenkaer-Hansen,
2012). In other words, it provides explanations of the origin of cortical criticality, a widespread
phenomenon in multiple species’ brains (Beggs & Timme, 2012; Chialvo, 2004; Fontenele
et al., 2019; Fosque, Williams-García, Beggs, & Ortiz, 2021; Gautam, Hoang, McClanahan,
Grady, & Shew, 2015; Millman, Mihalas, Kirkwood, & Niebur, 2010; Williams-García, Moore,
Beggs, & Ortiz, 2014), from a new perspective. In our research, the E/I balance λ is defined as
Percolation theory:
A physics theory that characterizes
critical phenomena and phase
transitions from a probabilistic and
geometric perspective.
Network Neuroscience
779
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
the fraction of excitatory synapses in all synapses. Because the excitation/inhibition strength
in Equation 10 is uniformly generated, the predicted optimal E/I balance λ ∼ 0.5 implies a
balance between excitation WE and inhibition WI strengths on the whole brain. This result is
consistent with a well-known finding that neural activities with high and robust entropy
occur when WE and WI are balanced (Agrawal et al., 2018). Nel frattempo, we can further
transform the optimal E/I balance λ ∼ 0.5 to parameter ψ, the fraction of excitatory neurons
in all neurons, since WE, WI, and ψ are mathematically related (Agrawal et al., 2018). To guar-
antee high and robust entropy, a large ψ can be derived according to Agrawal et al. (2018). These
results corroborate the abundance of excitatory neurons in mammalian cortices (Hendry,
Schwark, Jones, & Yan, 1987; Meinecke & Peters, 1987; Sahara, Yanagawa, O’Leary, & Stevens,
2012).
A valuable direction of future exploration may be generalizing the quantification of effi-
ciency, robustness, and economy to verify whether the optimal E/I balance that simultaneously
guarantees these advantageous properties still matches percolation theory predictions. IL
generalization is necessary since the measurements of efficiency, robustness, and economy
in brains remains as open challenges. For instance, the graph-theoretical metrics considered
in information transmission efficiency analysis (per esempio., global efficiency) could be nonideal
because neural signal communication may not exhibit near-minimal path length characteristics
(Avena-Koenigsberger et al., 2018; Goñi et al., 2014). Alternative metrics (Avena-Koenigsberger
et al., 2018; Seguin, Tian, & Zalesky, 2020; Seguin, Van Den Heuvel, & Zalesky, 2018) Avere
been recently developed and can be applied to reflect transmission efficiency more
appropriately.
Percolation Theory of the Brain: Opportunities and Challenges
In the present study, we have suggested percolation as a window to understand how brain
function properties emerge during functional connectivity formation. The congruent relation-
ship between brain connectivity and percolation is natural and comprehensible. Just like the
porous stone immersed in a pool of water, the brain is “porous” in terms of neurons and
immersed in a “pool” of information. Through simple analytical calculations, percolation anal-
ysis has shown strong consistency both in theoretical and experimental observations. Forse
because of these advantages, percolation theory has attracted emerging interest in neurosci-
ence. From early explorations that combine limited neural morphology data with computa-
tional simulations to analyze percolation (Costa, 2005; da Fontoura Costa & Coelho, 2005;
da Fontoura Costa & Manoel, 2003; Stepanyants & Chklovskii, 2005) to more recent works
that study percolation directly on the relatively small-scale and coarse-grained brain connec-
tome and electrically stimulated neural dynamics data captured from living neural networks
(per esempio., primary neural cultures in rat hippocampus) (Amini, 2010; Breskin et al., 2006; Cohen
et al., 2010; Eckmann et al., 2007), the efforts from physics have inspired numerous follow-up
explorations in neuroscience (Bordier et al., 2017; Carvalho et al., 2020; Del Ferraro et al.,
2018; Kozma & Puljic, 2015; Lucini et al., 2019; Zhou et al., 2015). These studies capture
an elegant and enlightening view about optimal neural circuitry, neural collective dynamics,
criticality, and the relation between brain connectivity and brain functions. Built on these
works, we present a more systematic and biologically justified framework to formalize func-
tional connectivity formation as percolation on random directed graphs. The merit of our
framework is fourfold. Primo, different from the bootstrap (per esempio., see Eckmann et al., 2007) O
quorum (per esempio., see Cohen et al., 2010) percolation analysis in previous studies, we leave the
criterion of occupation as a work of neural dynamics computation rather than preset the occu-
pation profile of neurons. In the future, this criterion can be optimized by synchronous neural
Network Neuroscience
780
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
dynamics recording when the required technology matures. Secondo, percolation on directed
graphs can capture the directionality of neural dynamics diffusion. Third, the percolation
defined on random graphs is a natural reflection of the inequivalence between static and func-
tional connectivity, consistent with the fact that static connectivity serves as a platform of the
dynamic one. Finalmente, we distinguish between dilution and nondilution conditions, enabling us
to characterize functional connectivity formation in stimulus-driven or attacked situations.
These properties enhance the capacity of our framework to accommodate the real character-
istics of brain connectivity.
Built on the equivalence between functional connectivity formation and the percolation
controlled by synaptic E/I balance, we reveal that brain function properties emerge as bypro-
ducts of percolation transition. Although the present percolation framework is universal, we
hypothesize that the actual quantities of percolation threshold, the optimal E/I balance, E
the E/I balance after which these properties approximate to their bounds determined by static
connectivity, may vary across different species, ages, cortical states, and even be able to serve
as biomarkers of nerve diseases. This speculation is well-founded because the E/I balance
oscillates daily (Bridi et al., 2020; Tao, Li, & Zhang, 2014) and may change owing to dysfunc-
zione (Grent et al., 2018; Ramírez-Toraño et al., 2021). These changes may be consequences of
specific variations of percolation attributes, which remain for future exploration.
Understanding Brain Function Characteristics Through Physics
Rooted in emergentism, the present study attempts to explore the origin mechanisms of brain
function characteristics from a physics perspective and avoid assumption-based modeling.
The underlying mechanisms are suggested to be described by percolation, a universal char-
acterization of critical phenomena and phase transitions (Dorogovtsev et al., 2001; Li et al.,
2021). Our experiments in the largest yet brain connectome of the fruit fly, Drosophila mel-
anogaster (Pipkin, 2020; Schlegel et al., 2021; Xu et al., 2020), have demonstrated the
capacity of percolation to explain the formation of functional connectivity and the emer-
gence of brain function properties without additional assumptions. The strong explanatory
power of percolation theory toward these neuroscience concepts is experimentally observed,
even though they are initially studied in different scientific fields. Such an intriguing connection
reemphasizes the nature of the brain as a physical system. Recentemente, this physics perspec-
tive has seen substantial progress in neuroscience. For instance, the free-energy principle is
demonstrated as a unified foundation of perception, action, and learning (Friston, 2009,
2010, 2012; Friston & Kiebel, 2009; Guevara, 2021). Cortical criticality is discovered to
account for the efficient transformation between cortical states (Beggs & Timme, 2012;
Chialvo, 2004; Fontenele et al., 2019; Fosque et al., 2021; Gautam et al., 2015; Millman
et al., 2010; Williams-García et al., 2014). Inoltre, information thermodynamics is
revealed as a bridge between the physical and the informational brain (Capolupo, Freeman,
& Vitiello, 2013; Collell & Fauquet, 2015; Sartori, Granger, Lee, & Horowitz, 2014; Sengupta,
Stemmler, & Friston, 2013; Street, 2020). In the future, this rising direction may continue con-
tributing to neuroscience as a window to understand the intrinsic bases of brain function
characteristics.
To conclude, the parallels discovered between functional connectivity formation and the
percolation on random directed graphs controlled by synaptic E/I balance serve as a new path-
way toward understanding the emergence of brain function characteristics. The percolation,
an elegant formalism of critical phenomena and phase transitions, may elucidate the emer-
gence of brain function characters from brain connectivity.
Network Neuroscience
781
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
MATERIALS AND METHODS
Brain Connectome Acquisition
The brain connectome data is released as a part of the FlyEM project (Xu et al., 2020). IL
connectome imaging is implemented applying the focused ion beam scanning electron
microscopy (FIB-SEM) technology. Then images are cleaned and enhanced by a series of pipe-
lines (per esempio., automated flood-filling network segmentation), generating the most fine-grained
and high-throughput connectome of the fruit fly central brain (∼2.5 × 105 nm in each dimen-
sion) to date (Xu et al., 2020). There are 21,662 traced (all main branches within the volume
are reconstructed) and uncropped (main arbors are contained in the volume) neurons as well
COME 4,495 traced, cropped, and large (≥1,000 synaptic connections) neurons in the connec-
tome. The complex wiring diagram between neurons consists of ∼6 × 106 traced and
uncropped presynaptic sites as well as ∼1.8 × 107 traced and uncropped post-synaptic den-
sities (Xu et al., 2020).
To efficiently acquire and handle such a large dataset, Google has designed a system
neuPrint to organize brain connectome in an accessible manner. Readers can follow the
instructions in Xu et al. (2020) to download and process the brain connectome data in neu-
Print. Although we acquire the whole brain connectome, we include neurons and synapses
in analyses only when the cell bodies are positioned precisely (assigned with a 10-nm spa-
tial resolution coordinate). The coordinate information is required expressly because it is
necessary in connectivity visualization and the Rentian scaling analysis (Bassett et al.,
2010; Chen, 1999; Ozaktas, 1992). The selected data set contains 23,008 neurons,
4,967,364 synaptic connections (synaptic clefts), E 63,5761 pairs of directionally adjacent
relations (two neurons are directionally adjacent if one synaptic connection comes out of
one neuron and leads to another).
Variables in Brain Connectome Description
To present a systematic characterization of brain connectome, we consider two informative
scales: macroscopic scale (brain regions) and microscopic scales (neurons).
On macroscopic scale, the parcellation of brain regions has been provided by Xu et al.
(2020). According to the upstream and downstream information of each synapse, we can
describe the macroscopic static connectivity with the variables given in Table 3.
One can reasonably treat the macroscopic static connectivity as a directed graph. Nodes
are brain regions and there may be multiple directed edges (PIP and POP) between each pair
of nodes. By summing up all PIPs or POPs of a brain region, we can measure the macroscopic
in-degree (TPIP) and out-degree (TPOP) of it. In our research, variables TPIP and TPOP are
used in our main analyses (please see Tables 1 E 2 and Figure 1 in the main text) Mentre
variables PIP and POP are used to provide additional information (please see Tables 5 E
6 and Figure 5).
Allo stesso modo, we can define the microscopic static connectivity by the variables given in
Tavolo 4.
The microscopic static connectivity corresponds to a directed graph where nodes are neu-
rons. With a fine granularity, we can treat synaptic connections as directed edges. Così, there
may be multiple edges (SCs) between a selected neuron and one of its adjacent neurons. Noi
can further tell whether these edges are coming from (OSCs) or leading to (ISCs) this selected
neuron. With a coarse granularity, we can treat directionally adjacent relations as directed
edges. Under this condition, there is only one edge (DA) between two adjacent neurons
Network Neuroscience
782
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
N
e
N
_
UN
_
0
0
2
4
6
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
Variable
SC
ISC
OSC
DA
IDA
ODA
SC/DA
ISC/IDA
Tavolo 4. Microscopic variable definitions
Meaning
All synaptic connections featured by one neuron
All synaptic connections received by one neuron from other neurons
All synaptic connections coming from one neuron to other neurons
All directionally adjacent relations between one neuron and other neurons
All directionally adjacent relations between one neuron and its presynaptic neurons
All directionally adjacent relations between one neuron and its postsynaptic neurons
Synaptic connections between one neuron and one of its adjacent neuron (the number of SCs per DA)
Synaptic connections between one neuron and one of its presynaptic neuron (the number of ISCs per IDA)
OSC/ODA
Synaptic connections between one neuron and one of its postsynaptic neuron (the number of OSCs per ODA)
and we can similarly distinguish between IDAs and ODAs. The fine-grained information is
necessary in neural dynamics computation while the coarse-grained information in useful in
analyzing microscopic functional connectivity. Perciò, we also calculate SC/DA, ISC/IDA,
and OSC/ODA to reflect how a neuron allocates synaptic connections to each of its neighbors.
These variables offer mappings between fine-grained and coarse-grained information. In our
research, variables relevant with DA are used in our main analyses (please see Tables 1 E 2
and Figure 1 in the main text) while other variables are used to provide auxiliary information
(please see Tables 5 E 6 and Figure 5).
Power Law Analysis and Symmetry Analysis
In our research, power-law analysis in binned empirical data is implemented applying an
open-source toolbox (R. Virkar & Clauset, 2014). Corresponding mathematics derivations
can be seen in Y. Virkar and Clauset (2014). We first do binning on variables of interest, Dove
the number of linearly spaced bins is set as 150. In real cases, the power law may only hold on
specific tails {P(UN)|A ≥ A0} of the empirical distribution of variable A, where A0 denotes a
certain distribution cutoff (Clauset, Shalizi, & Newman, 2009). We apply the Kolmogorov-
Smirnov-statistic-based approach (Y. Virkar & Clauset, 2014) to estimate these distribution
cutoffs. Then we implement a maximum likelihood estimation of power-law exponents (Y. Virkar
& Clauset, 2014) on the distribution tails above cutoffs. Corresponding Kolmogorov–Smirnov
statistics can be calculated between the cumulative probability distributions of estimated power
law models and empirical cumulative probability distributions to reflect the goodness of estima-
zione (Y. Virkar & Clauset, 2014). An ideal estimation is expected to has a sufficiently small
Kolmogorov–Smirnov statistic (<0.05 is suggested as a strict criterion). The authors of Y. Virkar
and Clauset (2014) also propose a statistic significance test based on Kolmogorov–Smirnov
statistics. Although the test measures the statistic significance of rejecting the power law hypoth-
esis, it cannot further imply the correctness of the estimated power law model (Y. Virkar &
Clauset, 2014). Therefore, the test is unnecessary if Kolmogorov–Smirnov statistics have been
sufficiently small.
In Table 5 and Figure 5, we present the auxiliary results of power law analysis. These results
are derived on supplementary variables in static brain connectivity descriptions and provide
corroborative evidence for the main text. In general, macroscopic static connectivity is
Network Neuroscience
783
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
Table 5.
Power law analysis results (supplementary information)
Probability distribution
P (SC = n) ∝ n−2.87
Goodness of estimation
0.0104
Scale-free or not
Yes
Type
Microscopic
Microscopic
Microscopic
Microscopic
Microscopic
Microscopic
Variable
SC
ISC
OSC
DA
SC/DA
ISC/IDA
P (ISC = n) ∝ n−2.78
P (OSC = n) ∝ n−2.81
P (DA = n) ∝ n−3.53
P (SC/DA = n) ∝ n−3.49
P (ISC/IDA = n) ∝ n−2.53
Microscopic
OSC/ODA
P (OSC/ODA = n) ∝ n−2.99
Note. Being scale-free requires P ∝ n−α, where α 2 (2, 3). Goodness of estimation is expected as to be less than 0.05.
0.0177
0.0172
0.0248
0.0244
0.0211
0.0183
Yes
Yes
No
No
Yes
Yes
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
t
.
Supplementary information of static connectivity characterization. (A) Supplementary variables of macroscopic static connectivity
Figure 5.
and microscopic static connectivity are graphically illustrated in an instance. (B) The power law models of synaptic connection number (SC),
directionally adjacent relation number (DA), and the number of synaptic connections per directionally adjacent relation (SC/DA). (C) The
power law models of input synaptic connection number (ISC) and output synaptic connection number (OSC). (D) The power law models
of the number of synaptic connections between one neuron and one of its presynaptic neuron (ISC/IDA) and the number of synaptic connec-
tions between one neuron and one of its postsynaptic neuron (OSC/ODA).
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
suggested as plausibly scale-free. However, the potential scale-free property of microscopic
static connectivity seems to be uncertain and nonrobust.
The symmetry analysis for static connectivity is implemented based on Pearson correlation
and average change fraction between input-related variables and output-related variables.
Pearson correlation reflects if output-related variables have similar variation trends with
input-related variables. Average change fraction of output-related variables compared with
input-related variables reflects if these two kinds of variables are quantitatively similar. The
symmetric static connectivity is expected to have balanced input-related and output-related
variables and, therefore, is required to feature significant positive correlation (e.g., larger than
0.9) and small average change fraction (e.g., smaller than 1). We refer to these two require-
ments as the strictest criterion of strong symmetry. To present a more accurate analysis, we
Network Neuroscience
784
Percolation explains efficiency, robustness, and economy of the brain
Table 6.
Symmetry analysis results (supplementary information)
Variable
PIP
ISC
Variable
POP
OSC
ISC/IDA
OSC/ODA
Pearson correlation
0.9833
0.8977
0.8164
p
< 10−10
< 10−10
< 10−10
Average change fraction
PIP−POP
= 0.6176
POP
j
j
ISC−OSC
j
OSC
j
= 1.7042
Symmetric degree
Strictly strong
Relatively weak
ISC=IDA−OSC=ODA
j
OSC=ODA
j
= 0.8649
Less strong
Note. Strong symmetry requires a strong positive correlation (e.g., correlation > 0.9 and p < 10−3). Strong symmetry implies a small average change fraction
(e.g., fraction < 1). The term “strictly strong” means that the strictest criterion of strong symmetry is completely satisfied. The term “less strong” means that the
strictest criterion of strong symmetry is partly satisfied. The term “relatively weak” means that the strictest criterion of strong symmetry is not satisfied.
suggest that three levels of symmetry can be specified. The symmetry is suggested as strictly
strong if the strictest criterion is completely satisfied. If the criterion is partly satisfied, the sym-
metry is treated as less strong. The symmetry is suggested as relatively weak if both require-
ments are not satisfied (please note that this case does not imply that static connectivity is
purely asymmetric, it only suggests the existence of potential local asymmetry).
In Table 6, we present the symmetry analysis results of supplementary variables in static
brain connectivity descriptions. These results serve as pieces of corroborative evidence to sup-
port our findings in the main text. In general, macroscopic static connectivity is suggested as
robustly symmetric. Although microscopic static connectivity is approximately symmetric, its
symmetric degree is not as strong as the macroscopic one.
Coactivation Probability Calculation
Here we introduce the method of functional connectivity generation. Specifically, every direc-
tionally adjacent relation (DA) Ni → Nj (here Ni and Nj are neurons) has a static connection
strength Sij defined by Equation 10. In the definition, random variable Xi 2 {0, 1} determines
whether Ni is an excitatory or inhibitory neuron. Random variables Yij ∼ U(0,1] and Zij 2∼
U [−1,0] are generated uniformly to measure excitation/inhibition strength (e.g., conductance).
Notion αij denotes the number of synaptic connections (SC) from Ni to Nj (SC/DA, the precise
number of SCs per DA) and h·i denotes the expectation. By calculating
in Equation 10, we
αij
αijh i
i;j
can quantify the effects of SCs on Sij.
Sij ¼
αij
(cid:6)
(cid:5)
αij
i;j
(cid:7)
XiYij þ 1 − Xi
ð
ÞZij
(cid:8)
:
(10)
Under each condition of E/I balance λ, a set of variable {X1, …, Xn} (here n denotes the number of
neurons) is randomly initialized. Then, we update {X1, …, Xn} by the following algorithm: (1)
measure λ^, the fraction of excitatory SCs in all SCs based on the current configuration of {X1,
…, Xn}, and calculate the difference |λ^ − λ|; (2) randomly select a neuron Ni and change the
corresponding Xi (e.g., change Xi from 1 to 0 or from 0 to 1). (the change will not be kept unless
it reduces |λ^ − λ|); (3) repeat steps (1 and 2) until λ^ ∼ λ. Based on this algorithm, the fraction of
excitatory synapses in all synapses is principally controlled by λ with reasonable errors in
practice.
Then, we measure coactivation probability Pij in Equation 11 to define the dynamic con-
nection strength, where δ(·) denotes the Dirac delta function. Probability P ij is quantified in
term of that an activated Ni can activate Nj in m times of experiments (m = 100).
Pij ¼
1
m
Xm
(cid:9)
δ Ik
i
k¼1
(cid:10)
:
− Ik
j
(11)
785
Network Neuroscience
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
Each time all neurons are initialized at the resting potential, −70 mV. Then we continuously
activate Ni (make Ik
i = 1) and several other randomly selected presynaptic neurons of Nj during
an interval of [0, t] (we define t = 50 ms). We ensure that at least 20% of presynaptic neurons of
Nj are activated. Such activation intensity is no longer accidental and should be strong enough
to affect Nj in the real brain. Any activation will be marked by Equation 12, where Ik
j = 1 if Nj is
activated at least one time during [0, t], otherwise Ik
j = 0. The criterion of activation in Equation
12 is to verify if the actual membrane potential Vj(τ) reaches the spiking threshold ^V = −50 mV
based on the unit step function ν(·).
"
¼ ν
Ik
j
(cid:4)
#
:
Xt
(cid:3)
ν Vτ − ^V
τ¼0
(12)
We calculate the actual membrane potential Vj(τ) applying the standard leaky integrate-and-
fire (LIF) model (Gerstner et al., 2014) in Equation 13, where τm is the membrane time constant
(τm = 10 ms), notion Nh searches through all presynaptic neurons of Nj, and τ f
h represents the
arrival time of f-th spike of neuron Nh.
∂Vj τð Þ
∂τ
¼ −
(cid:7)
1
τ m
Vj τð Þ − ^V
(cid:8)
−
X
Shj
(
X
Nh
f
(cid:3)
δ τ − τ f
h
(cid:4)
(cid:7)
(cid:4)
(cid:3)
Vj τ f
h
(cid:3)
− Vh τ f
h
)
(cid:8)
(cid:4)
:
(13)
To make such a computationally costly experiment accessible for readers, we release our
results in Tian and Sun (2021). Readers can freely download the dataset to obtain the co-
activation probability Pij under each λ condition.
Quantification of Efficiency, Robustness, and Economy
In our research, the measurements of the characteristic path length (Albert & Barabási, 2002),
the global efficiency (Latora & Marchiori, 2001), the assortativity coefficient (Newman, 2002),
the rich-club coefficient (Ball et al., 2014; Colizza et al., 2006; Van Den Heuvel & Sporns,
2011), the physical Rentian exponent (Bassett et al., 2010; Chen, 1999; Ozaktas, 1992), the
clustering coefficient (Watts & Strogatz, 1998), and the transitivity (Newman, 2003) are imple-
mented based on the toolbox released by Rubinov and Sporns (2010b). This widely used tool-
box and its instructions can be found in Rubinov and Sporns (2010a). Readers can use the
adjacent matrix of functional connectivity as an input to calculate these properties. One thing
to note is that the original version of the toolbox defines the graph distance between two
unconnected neurons (there is no path between them) as infinity. Although this definition is
mathematically justified, it may bring inconvenience in computational implementations
because inf usually leads to inf or nan in computer programs. Common practices to avoid
the influence of potential infinite values on target results are either excluding these infinite
values during calculations or replacing them with n + 1 (here n denotes the total number of
neurons). To maintain the sample size in analyses, our research chooses the second approach.
ACKNOWLEDGMENTS
Authors are grateful for discussions and assistance of Drs. Ziyang Zhang and Yaoyuan Wang
from the Laboratory of Advanced Computing and Storage, Central Research Institute, 2012
Laboratories, Huawei Technologies Co. Ltd., Beijing, 100084, China.
Network Neuroscience
786
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
AUTHOR CONTRIBUTIONS
Yang Tian: Conceptualization; Data curation; Formal analysis; Investigation; Methodology;
Project administration; Software; Validation; Visualization; Writing – original draft. Pei Sun:
Conceptualization; Funding acquisition; Investigation; Project administration; Resources;
Supervision; Validation; Writing – review & editing.
FUNDING INFORMATION
Pei Sun, Artificial and General Intelligence Research Program of Guo Qiang Research Institute
at Tsinghua University, Award ID: 2020GQG1017.
REFERENCES
Achard, S., Salvador, R., Whitcher, B., Suckling, J., & Bullmore, E.
(2006). A resilient, low-frequency, small-world human brain
functional network with highly connected association cortical
hubs. Journal of Neuroscience, 26(1), 63–72. https://doi.org/10
.1523/JNEUROSCI.3874-05.2006, PubMed: 16399673
Aerts, H., Fias, W., Caeyenberghs, K., & Marinazzo, D. (2016).
Brain networks under attack: Robustness properties and the
impact of lesions. Brain, 139(12), 3063–3083. https://doi.org/10
.1093/brain/aww194, PubMed: 27497487
Agliari, E., Cioli, C., & Guadagnini, E. (2011). Percolation on cor-
related random networks. Physical Review E, 84(3), 031120.
https://doi.org/10.1103/ PhysRevE.84.031120, PubMed:
22060341
Agrawal, V., Cowley, A. B., Alfaori, Q., Larremore, D. B., Restrepo,
J. G., & Shew, W. L. (2018). Robust entropy requires strong and
balanced excitatory and inhibitory synapses. Chaos: An Interdis-
ciplinary Journal of Nonlinear Science, 28(10), 103115. https://
doi.org/10.1063/1.5043429, PubMed: 30384653
Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of com-
plex networks. Reviews of Modern Physics, 74(1), 47. https://doi
.org/10.1103/RevModPhys.74.47
Albert, R., Jeong, H., & Barabási, A.-L. (2000). Error and attack tol-
erance of complex networks. Nature, 406(6794), 378–382.
https://doi.org/10.1038/35019019, PubMed: 10935628
Alstott, J., Breakspear, M., Hagmann, P., Cammoun, L., & Sporns,
O. (2009). Modeling the impact of lesions in the human brain.
PLoS Computational Biology, 5(6), e1000408. https://doi.org/10
.1371/journal.pcbi.1000408, PubMed: 19521503
Amico, E., Abbas, K., Duong-Tran, D. A., Tipnis, U., Rajapandian,
M., Chumin, E., … Goñi, J. (2021). Towards an information the-
oretical description of communication in brain networks. Net-
work Neuroscience, 5(3), 646–665. https://doi.org/10.1162/netn
_a_00185, PubMed: 34746621
Amini, H. (2010). Bootstrap percolation in living neural networks.
Journal of Statistical Physics, 141(3), 459–475. https://doi.org/10
.1007/s10955-010-0056-z
Amini, H., & Fountoulakis, N. (2014). Bootstrap percolation in
power-law random graphs. Journal of Statistical Physics, 155(1),
72–92. https://doi.org/10.1007/s10955-014-0946-6
Avena-Koenigsberger, A., Mišić, B., Hawkins, R. X., Griffa, A., Hagmann,
P., Goñi, J., & Sporns, O. (2017). Path ensembles and a tradeoff
between communication efficiency and resilience in the human
connectome. Brain Structure and Function, 222(1), 603–618.
https://doi.org/10.1007/s00429-016-1238-5, PubMed:
27334341
Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Commu-
nication dynamics in complex brain networks. Nature Reviews
Neuroscience, 19(1), 17–33. https://doi.org/10.1038/nrn.2017
.149, PubMed: 29238085
Ball, G., Aljabar, P., Zebari, S., Tusor, N., Arichi, T., Merchant, N.,
… Counsell, S. J. (2014). Rich-club organization of the newborn
human brain. Proceedings of the National Academy of Sciences,
111(20), 7456–7461. https://doi.org/10.1073/pnas.1324118111,
PubMed: 24799693
Balogh, J., & Pittel, B. G. (2007). Bootstrap percolation on the ran-
dom regular graph. Random Structures & Algorithms, 30(1–2),
257–286. https://doi.org/10.1002/rsa.20158
Barta, T., & Kostal, L. (2019). The effect of inhibition on rate code
efficiency indicators. PLoS Computational Biology, 15(12),
e1007545. https://doi.org/10.1371/journal.pcbi.1007545,
PubMed: 31790384
Bassett, D. S., Greenfield, D. L., Meyer-Lindenberg, A., Weinberger,
D. R., Moore, S. W., & Bullmore, E. T. (2010). Efficient physical
embedding of topologically complex information processing net-
works in brains and computer circuits. PLoS Computational Biol-
ogy, 6(4), e1000748. https://doi.org/10.1371/journal.pcbi
.1000748, PubMed: 20421990
Baxter, G. J., Dorogovtsev, S. N., Goltsev, A. V., & Mendes, J. F.
(2010). Bootstrap percolation on complex networks. Physical
Review E, 82(1), 011103. https://doi.org/10.1103/PhysRevE.82
.011103, PubMed: 20866561
Beggs, J. M., & Timme, N. (2012). Being critical of criticality in the
brain. Frontiers in Physiology, 3, 163. https://doi.org/10.3389
/fphys.2012.00163, PubMed: 22701101
Ben-Naim, E., & Krapivsky, P. (2011). Dynamics of random graphs
with bounded degrees. Journal of Statistical Mechanics: Theory
and Experiment, 2011(11), P11008. https://doi.org/10.1088
/1742-5468/2011/11/P11008
Betzel, R. F., Avena-Koenigsberger, A., Goñi, J., He, Y., De Reus,
M. A., Griffa, A., … Sporns, O. (2016). Generative models of the
human connectome. NeuroImage, 124, 1054–1064. https://doi
.org/10.1016/j.neuroimage.2015.09.041, PubMed: 26427642
Network Neuroscience
787
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
Bollobás, B. (2013). Modern graph theory (Vol. 184). New York, NY:
Springer Science & Business Media.
Bordier, C., Nicolini, C., & Bifone, A. (2017). Graph analysis and
modularity of brain functional connectivity networks: Searching
for the optimal threshold. Frontiers in Neuroscience, 11, 441.
https://doi.org/10.3389/fnins.2017.00441, PubMed: 28824364
Breskin, I., Soriano, J., Moses, E., & Tlusty, T. (2006). Percolation in
living neural networks. Physical Review Letters, 97(18), 188102.
https://doi.org/10.1103/ PhysRevLett.97.188102, PubMed:
17155581
Bridi, M. C., Zong, F.-J., Min, X., Luo, N., Tran, T., Qiu, J., …
Kirkwood, A. (2020). Daily oscillation of the excitation-
inhibition balance in visual cortical circuits. Neuron, 105(4),
621–629. https://doi.org/10.1016/j.neuron.2019.11.011,
PubMed: 31831331
Bullmore, E., & Sporns, O. (2012). The economy of brain network
organization. Nature Reviews Neuroscience, 13(5), 336–349.
https://doi.org/10.1038/nrn3214, PubMed: 22498897
Callaway, D. S., Newman, M. E., Strogatz, S. H., & Watts, D. J.
(2000). Network robustness and fragility: Percolation on random
graphs. Physical Review Letters, 85(25), 5468. https://doi.org/10
.1103/PhysRevLett.85.5468, PubMed: 11136023
Capolupo, A., Freeman, W. J., & Vitiello, G. (2013). Dissipation of
‘dark energy’ by cortex in knowledge retrieval. Physics of Life
Reviews, 10(1), 85–94. https://doi.org/10.1016/j.plrev.2013.01
.001, PubMed: 23333569
Carvalho, T. T., Fontenele, A. J., Girardi-Schappo, M., Feliciano,
T., Aguiar, L. A., Silva, T. P., … Copelli, M. (2020). Subsam-
pled directed-percolation models explain scaling relations
experimentally observed in the brain. Frontiers in Neural Cir-
cuits, 14. https://doi.org/10.3389/fncir.2020.576727, PubMed:
33519388
Chen, W.-K. (1999). The VLSI handbook. Boca Raton, FL: CRC
Press. https://doi.org/10.1201/9781420049671
Chialvo, D. R. (2004). Critical brain networks. Physica A: Statistical
Mechanics and its Applications, 340(4), 756–765. https://doi.org
/10.1016/j.physa.2004.05.064
Clauset, A., Shalizi, C. R., & Newman, M. E. (2009). Power-law dis-
tributions in empirical data. SIAM Review, 51(4), 661–703.
https://doi.org/10.1137/070710111
Cohen, O., Keselman, A., Moses, E., Martínez, M. R., Soriano, J., &
Tlusty, T. (2010). Quorum percolation in living neural networks.
EPL (Europhysics Letters), 89(1), 18008. https://doi.org/10.1209
/0295-5075/89/18008
Colizza, V., Flammini, A., Serrano, M. A., & Vespignani, A. (2006).
Detecting rich-club ordering in complex networks. Nature Phys-
ics, 2(2), 110–115. https://doi.org/10.1038/nphys209
Collell, G., & Fauquet, J. (2015). Brain activity and cognition: A
connection from thermodynamics and information theory. Fron-
tiers in Psychology, 6, 818. https://doi.org/10.3389/fpsyg.2015
.00818, PubMed: 26136709
Costa, L. d. F. (2005). Morphological complex networks: Can indi-
vidual morphology determine the general connectivity and
dynamics of networks? arXiv preprint q-bio/0503041. https://doi
.org/10.48550/arXiv.q-bio/0503041
Crossley, N. A., Mechelli, A., Scott, J., Carletti, F., Fox, P. T.,
McGuire, P., & Bullmore, E. T. (2014). The hubs of the human
connectome are generally implicated in the anatomy of brain
disorders. Brain, 137(8), 2382–2395. https://doi.org/10.1093
/brain/awu132, PubMed: 25057133
da Fontoura Costa, L., & Coelho, R. C. (2005). Growth-driven per-
colations: The dynamics of connectivity in neuronal systems. The
European Physical Journal B-Condensed Matter and Complex
Systems, 47(4), 571–581. https://doi.org/10.1140/epjb/e2005
-00354-5
da Fontoura Costa, L., & Manoel, E. T. M. (2003). A percolation
approach to neural morphometry and connectivity. Neuroinfor-
matics, 1(1), 65–80. https://doi.org/10.1385/ NI:1:1:065,
PubMed: 15055394
Del Ferraro, G., Moreno, A., Min, B., Morone, F., Pérez-Ramírez,
Ú., Pérez-Cervera, L., … Makse, H. A. (2018). Finding influential
nodes for integration in brain networks using optimal percolation
theory. Nature Communications, 9(1), 1–12. https://doi.org/10
.1038/s41467-018-04718-3, PubMed: 29891915
Dorogovtsev, S. N., Mendes, J. F. F., & Samukhin, A. N. (2001).
Giant strongly connected component of directed networks. Phys-
ical Review E, 64(2), 025101. https://doi.org/10.1103/PhysRevE
.64.025101, PubMed: 11497638
Eckmann, J.-P., Feinerman, O., Gruendlinger, L., Moses, E., Soriano,
J., & Tlusty, T. (2007). The physics of living neural networks. Phys-
ics Reports, 449(1–3), 54–76. https://doi.org/10.1016/j.physrep
.2007.02.014
Fagiolo, G. (2007). Clustering in complex directed networks. Phys-
ical Review E, 76(2), 026107. https://doi.org/10.1103/PhysRevE
.76.026107, PubMed: 17930104
Fontenele, A. J., de Vasconcelos, N. A., Feliciano, T., Aguiar, L. A.,
Soares-Cunha, C., Coimbra, B., … Copelli, M. (2019). Criticality
between cortical states. Physical Review Letters, 122(20),
208101. https://doi.org/10.1103/ PhysRevLett.122.208101,
PubMed: 31172737
Fosque, L. J., Williams-García, R. V., Beggs, J. M., & Ortiz, G.
(2021). Evidence for quasicritical brain dynamics. Physical
Review Letters, 126(9), 098101. https://doi.org/10.1103
/PhysRevLett.126.098101, PubMed: 33750159
Friston, K. (2009). The free-energy principle: A rough guide to the
brain? Trends in Cognitive Sciences, 13(7), 293–301. https://doi
.org/10.1016/j.tics.2009.04.005, PubMed: 19559644
Friston, K. (2010). The free-energy principle: A unified brain theory?
Nature Reviews Neuroscience, 11(2), 127–138. https://doi.org/10
.1038/nrn2787, PubMed: 20068583
Friston, K. (2012). The history of the future of the bayesian brain.
NeuroImage, 62(2), 1230–1233. https://doi.org/10.1016/j
.neuroimage.2011.10.004, PubMed: 22023743
Friston, K., & Kiebel, S. (2009). Predictive coding under the
free-energy principle. Philosophical Transactions of the Royal
Society B: Biological Sciences, 364(1521), 1211–1221. https://
doi.org/10.1098/rstb.2008.0300, PubMed: 19528002
Gautam, S. H., Hoang, T. T., McClanahan, K., Grady, S. K., & Shew,
W. L. (2015). Maximizing sensory dynamic range by tuning the
cortical state to criticality. PLoS Computational Biology, 11(12),
e1004576. https://doi.org/10.1371/journal.pcbi.1004576,
PubMed: 26623645
Gerstner, W., Kistler, W. M., Naud, R., & Paninski, L. (2014). Neu-
ronal dynamics: From single neurons to networks and models of
cognition. Cambridge, UK: Cambridge University Press. https://
doi.org/10.1017/CBO9781107447615
Network Neuroscience
788
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
Goltsev, A. V., Dorogovtsev, S. N., & Mendes, J. F. (2008). Percola-
tion on correlated networks. Physical Review E, 78(5), 051105.
https://doi.org/10.1103/PhysRevE.78.051105, PubMed: 19113093
Goñi, J., Van Den Heuvel, M. P., Avena-Koenigsberger, A., De
Mendizabal, N. V., Betzel, R. F., Griffa, A., … Sporns, O.
(2014). Resting-brain functional connectivity predicted by ana-
lytic measures of network communication. Proceedings of the
National Academy of Sciences, 111(2), 833–838. https://doi.org
/10.1073/pnas.1315529111, PubMed: 24379387
Graham, D., Avena-Koenigsberger, A., & Misic, B. (2020). Network com-
munication in the brain. Network Neuroscience, 4(4), 976–979.
https://doi.org/10.1162/netn_e_00167, PubMed: 33195944
Grent, T., Gross, J., Goense, J., Wibral, M., Gajwani, R., Gumley,
A. I., … Uhlhaas, P. J. (2018). Resting-state gamma-band power
alterations in schizophrenia reveal E/ I-balance abnormalities
across illness-stages. Elife, 7, e37799. https://doi.org/10.7554
/eLife.37799, PubMed: 30260771
Guevara, R. (2021). Synchronization, free energy and the embryo-
genesis of the cortex. Physics of Life Reviews, 36, 5–6. https://doi
.org/10.1016/j.plrev.2020.11.006, PubMed: 33348117
Hahn, A., Kranz, G. S., Sladky, R., Ganger, S., Windischberger, C.,
Kasper, S., & Lanzenberger, R. (2015). Individual diversity of
functional brain network economy. Brain Connectivity, 5(3),
156–165. https://doi.org/10.1089/ brain.2014.0306, PubMed:
25411715
Hendry, S. H., Schwark, H., Jones, E., & Yan, J. (1987). Numbers
and proportions of gaba-immunoreactive neurons in different
areas of monkey cerebral cortex. Journal of Neuroscience, 7(5),
1503–1519. https://doi.org/10.1523/JNEUROSCI.07-05-01503
.1987, PubMed: 3033170
Hermundstad, A. M., Bassett, D. S., Brown, K. S., Aminoff, E. M.,
Clewett, D., Freeman, S., … Carlson, J. M. (2013). Structural foun-
dations of resting-state and task-based functional connectivity in
the human brain. Proceedings of the National Academy of Sci-
ences, 110(15), 6169–6174. https://doi.org/10.1073/pnas
.1219562110, PubMed: 23530246
Humphries, M. D., Gurney, K., & Prescott, T. J. (2006). The brain-
stem reticular formation is a small-world, not scale-free, net-
work. Proceedings of the Royal Society B: Biological Sciences,
273(1585), 503–511. https://doi.org/10.1098/rspb.2005.3354,
PubMed: 16615219
Joyce, K. E., Hayasaka, S., & Laurienti, P. J. (2013). The human
functional brain network demonstrates structural and dynamical
resilience to targeted attack. PLoS Computational Biology, 9(1),
e1002885. https://doi.org/10.1371/journal.pcbi.1002885,
PubMed: 23358557
Kaiser, M., & Hilgetag, C. C. (2004). Edge vulnerability in neural and
metabolic networks. Biological Cybernetics, 90(5), 311–317.
https://doi.org/10.1007/s00422-004-0479-1, PubMed: 15221391
Kaiser, M., & Hilgetag, C. C. (2006). Nonoptimal component
placement, but short processing paths, due to long-distance
projections in neural systems. PLoS Computational Biology, 2(7),
e95. https://doi.org/10.1371/journal.pcbi.0020095, PubMed:
16848638
Kaiser, M., Martin, R., Andras, P., & Young, M. P. (2007). Simulation
of robustness against lesions of cortical networks. European Jour-
nal of Neuroscience, 25(10), 3185–3192. https://doi.org/10.1111
/j.1460-9568.2007.05574.x, PubMed: 17561832
Karbowski, J. (2007). Global and regional brain metabolic scaling
and its functional consequences. BMC Biology, 5(1), 1–11.
https://doi.org/10.1186/1741-7007-5-18, PubMed: 17488526
Kiebel, S. J., & Friston, K. J. (2011). Free energy and dendritic
self-organization. Frontiers in Systems Neuroscience, 5, 80.
https://doi.org/10.3389/fnsys.2011.00080, PubMed: 22013413
Kozma, R., & Puljic, M. (2015). Random graph theory and neuro-
percolation for modeling brain oscillations at criticality. Current
Opinion in Neurobiology, 31, 181–188. https://doi.org/10.1016/j
.conb.2014.11.005, PubMed: 25460075
Latora, V., & Marchiori, M. (2001). Efficient behavior of small-world
networks. Physical Review Letters, 87(19), 198701. https://doi
.org/10.1103/PhysRevLett.87.198701, PubMed: 11690461
Laughlin, S. B., van Steveninck, R. R. d. R., & Anderson, J. C. (1998).
The metabolic cost of neural information. Nature Neuroscience,
1(1), 36–41. https://doi.org/10.1038/236, PubMed: 10195106
Li, M., Liu, R.-R., Lü, L., Hu, M.-B., Xu, S., & Zhang, Y.-C. (2021).
Percolation on complex networks: Theory and application.
Physics Reports, 907, 1–68. https://doi.org/10.1016/j.physrep
.2020.12.003
Lucini, F. A., Del Ferraro, G., Sigman, M., & Makse, H. A. (2019).
How the brain transitions from conscious to subliminal percep-
tion. Neuroscience, 411, 280–290. https://doi.org/10.1016/j
.neuroscience.2019.03.047, PubMed: 31051216
Meinecke, D. L., & Peters, A. (1987). GABA immunoreactive neurons in
rat visual cortex. Journal of Comparative Neurology, 261(3), 388–404.
https://doi.org/10.1002/cne.902610305, PubMed: 3301920
Millman, D., Mihalas, S., Kirkwood, A., & Niebur, E. (2010). Self-
organized criticality occurs in non-conservative neuronal net-
works during ‘up’ states. Nature Physics, 6(10), 801–805. https://
doi.org/10.1038/nphys1757, PubMed: 21804861
Mišić, B., Sporns, O., & McIntosh, A. R. (2014). Communication
efficiency and congestion of signal traffic in large-scale brain
networks. PLoS Computational Biology, 10(1), e1003427.
https://doi.org/10.1371/journal.pcbi.1003427, PubMed:
24415931
Newman, M. E. (2002). Assortative mixing in networks. Physical
Review Letters, 89(20), 208701. https://doi.org/10.1103
/PhysRevLett.89.208701, PubMed: 12443515
Newman, M. E. (2003). The structure and function of complex net-
works. SIAM Review, 45(2), 167–256. https://doi.org/10.1137
/S003614450342480
Newman, M. E., Strogatz, S. H., & Watts, D. J. (2001). Random
graphs with arbitrary degree distributions and their applications.
Physical Review E, 64(2), 026118. https://doi.org/10.1103
/PhysRevE.64.026118, PubMed: 11497662
Ozaktas, H. M. (1992). Paradigms of connectivity for computer cir-
cuits and networks. Optical Engineering, 31(7), 1563–1567.
https://doi.org/10.1117/12.57685
Panagiotou, K., Spöhel, R., Steger, A., & Thomas, H. (2011). Explo-
sive percolation in Erdős-Rényi-like random graph processes.
Electronic Notes in Discrete Mathematics, 38, 699–704. https://
doi.org/10.1016/j.endm.2011.10.017
Pipkin, J. (2020). Connectomes: Mapping the mind of a fly. Elife, 9,
e62451. https://doi.org/10.7554/eLife.62451, PubMed:
33030427
Poil, S.-S., Hardstone, R., Mansvelder, H. D., & Linkenkaer-Hansen,
K. (2012). Critical-state dynamics of avalanches and oscillations
Network Neuroscience
789
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Percolation explains efficiency, robustness, and economy of the brain
jointly emerge from balanced excitation/inhibition in neuronal
networks. Journal of Neuroscience, 32(29), 9817–9823. https://doi
.org/10.1523/JNEUROSCI.5990-11.2012, PubMed: 22815496
Radicchi, F., & Fortunato, S. (2009). Explosive percolation in scale-
free networks. Physical Review Letters, 103(16), 168701. https://
doi.org/10.1103/PhysRevLett.103.168701, PubMed: 19905730
Ramírez-Toraño, F., Bruña, R., de Frutos-Lucas, J., Rodŕıguez-Rojo,
I., Marcos de Pedro, S., Delgado-Losada, M., … Maestú, F.
(2021). Functional connectivity hypersynchronization in rela-
tives of alzheimer’s disease patients: An early E/I balance dys-
function? Cerebral Cortex, 31(2), 1201–1210. https://doi.org/10
.1093/cercor/bhaa286, PubMed: 33108468
Rubinov, M., & Sporns, O. (2010a). Brain connectivity toolbox.
https://www.nitrc.org/projects/bct/.
Rubinov, M., & Sporns, O. (2010b). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Rubinov, M., Ypma, R. J., Watson, C., & Bullmore, E. T. (2015).
Wiring cost and topological participation of the mouse brain
connectome. Proceedings of the National Academy of Sciences,
112(32), 10032–10037. https://doi.org/10.1073/pnas.1420315112,
PubMed: 26216962
Sadeh, S., & Clopath, C. (2021). Inhibitory stabilization and cortical
computation. Nature Reviews Neuroscience, 22(1), 21–37. https://
doi.org/10.1038/s41583-020-00390-z, PubMed: 33177630
Sahara, S., Yanagawa, Y., O’Leary, D. D., & Stevens, C. F. (2012).
The fraction of cortical gabaergic neurons is constant from near
the start of cortical neurogenesis to adulthood. Journal of Neuro-
s c i en c e , 3 2 (1 4), 4 75 5 –4 7 6 1. h t t ps : / / d o i . o rg / 1 0. 1 5 2 3
/JNEUROSCI.6412-11.2012, PubMed: 22492031
Sartori, P., Granger, L., Lee, C. F., & Horowitz, J. M. (2014). Ther-
modynamic costs of information processing in sensory adapta-
tion. PLoS Computational Biology, 10(12), e1003974. https://
doi.org/10.1371/journal.pcbi.1003974, PubMed: 25503948
Schlegel, P., Bates, A. S., Stürner, T., Jagannathan, S. R., Drummond,
N., Hsu, J., … Jefferis, G. (2021). Information flow, cell types and
stereotypy in a full olfactory connectome. Elife, 10, e66018.
https://doi.org/10.7554/eLife.66018, PubMed: 34032214
Seguin, C., Tian, Y., & Zalesky, A. (2020). Network communication
models improve the behavioral and functional predictive utility
of the human structural connectome. Network Neuroscience,
4(4), 980–1006. https://doi.org/10.1162/netn_a_00161, PubMed:
33195945
Seguin, C., Van Den Heuvel, M. P., & Zalesky, A. (2018). Naviga-
tion of brain networks. Proceedings of the National Academy of
Sciences, 115(24), 6297–6302. https://doi.org/10.1073/pnas
.1801351115, PubMed: 29848631
Sengupta, B., Stemmler, M. B., & Friston, K. J. (2013). Information
and efficiency in the nervous system—A synthesis. PLoS Compu-
tational Biology, 9(7), e1003157. https://doi.org/10.1371/journal
.pcbi.1003157, PubMed: 23935475
Shew, W. L., Yang, H., Yu, S., Roy, R., & Plenz, D. (2011). Information
capacity and transmission are maximized in balanced cortical net-
works with neuronal avalanches. Journal of Neuroscience, 31(1),
55–63. https://doi.org/10.1523/ JNEUROSCI.4637-10.2011,
PubMed: 21209189
Sporns, O. (2011). The non-random brain: Efficiency, economy, and
complex dynamics. Frontiers in Computational Neuroscience, 5,
5. https://doi.org/10.3389/fncom.2011.00005, PubMed:
21369354
Sporns, O., Tononi, G., & Kötter, R. (2005). The human connec-
tome: A structural description of the human brain. PLoS Compu-
tational Biology, 1(4), e42. https://doi.org/10.1371/journal.pcbi
.0010042, PubMed: 16201007
Sprekeler, H. (2017). Functional consequences of inhibitory plastic-
ity: Homeostasis, the excitation-inhibition balance and beyond.
Current Opinion in Neurobiology, 43, 198–203. https://doi.org
/10.1016/j.conb.2017.03.014, PubMed: 28500933
Stepanyants, A., & Chklovskii, D. B. (2005). Neurogeometry and
potential synaptic connectivity. Trends in Neurosciences, 28(7),
387–394. https://doi.org/10.1016/j.tins.2005.05.006, PubMed:
15935485
Street, S. (2020). Upper limit on the thermodynamic information
content of an action potential. Frontiers in Computational Neuro-
science, 14, 37. https://doi.org/10.3389/fncom.2020.00037,
PubMed: 32477088
Strelnikov, K. (2010). Neuroimaging and neuroenergetics: Brain
activations as information-driven reorganization of energy flows.
Brain and Cognition, 72(3), 449–456. https://doi.org/10.1016/j
.bandc.2009.12.008, PubMed: 20092923
Tao, H. W., Li, Y.-T., & Zhang, L. I. (2014). Formation of
excitation-inhibition balance: Inhibition listens and changes its
tune. Trends in Neurosciences, 37(10), 528–530. https://doi.org
/10.1016/j.tins.2014.09.001, PubMed: 25248294
Tian, Y., & Sun, P. (2021). Co-activation probability between neu-
rons in the largest brain connectome of the fruit fly. Zenodo.
https://doi.org/10.5281/zenodo.5497516
Van Den Heuvel, M. P., & Sporns, O. (2011). Rich-club organiza-
tion of the human connectome. Journal of Neuroscience, 31(44),
15775–15786. https://doi.org/10.1523/ JNEUROSCI.3539-11
.2011, PubMed: 22049421
Virkar, R., & Clauset, A. (2014). Toolbox for power-law distributions
in binned empirical data. https://sites.santafe.edu/~aaronc
/powerlaws/bins/.
Virkar, Y., & Clauset, A. (2014). Power-law distributions in binned
empirical data. The Annals of Applied Statistics, 8(1), 89–119.
https://doi.org/10.1214/13-AOAS710
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of
‘small-world’ networks. Nature, 393(6684), 440–442. https://doi
.org/10.1038/30918, PubMed: 9623998
Williams-García, R. V., Moore, M., Beggs, J. M., & Ortiz, G. (2014).
Quasicritical brain dynamics on a nonequilibrium widom line.
Physical Review E, 90(6), 062714. https://doi.org/10.1103
/PhysRevE.90.062714, PubMed: 25615136
Xu, C. S., Januszewski, M., Lu, Z., Takemura, S.-Y., Hayworth, K. J.,
Huang, G., … Plaza, S. M. (2020). A connectome of the adult
Drosophila central brain. BioRxiv. https://doi.org/10.1101/2020
.01.21.911859
Zhou, D. W., Mowrey, D. D., Tang, P., & Xu, Y. (2015). Percolation
model of sensory transmission and loss of consciousness under
general anesthesia. Physical Review Letters, 115(10), 108103.
https://doi.org/10.1103/ PhysRevLett.115.108103, PubMed:
26382705
Network Neuroscience
790
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
3
7
6
5
2
0
3
5
9
8
5
n
e
n
_
a
_
0
0
2
4
6
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3