PERSPECTIVE

Model-based whole-brain effective connectivity
to study distributed cognition in health
and disease

Matthieu Gilson 1, Gorka Zamora-López1, Vicente Pallarés1, Mohit H. Adhikari1,
Mario Senden2, Adrià Tauste Campo3, Dante Mantini4,5, Maurizio Corbetta6,7,
Gustavo Deco1,8, and Andrea Insabato9

1Center for Brain and Cognition and Department of Information and Communication Technologies, Universitat Pompeu Fabra,
Barcelona, Spain
2Department of Cognitive Neuroscience, University of Maastricht, Maastricht, The Netherlands
3BarcelonaBeta, Barcelona, Spain
4Neuroplasticity and Motor Control Research Group, KU Leuven, Leuven, Belgium
5Brain Imaging and Neural Dynamics Research Group, IRCCS San Camillo Hospital, Venice, Italy
6Department of Neuroscience, Venetian Institute of Molecular Medicine (VIMM) and Padova Neuroscience Center (PNC),
University of Padua, Italy
7Department of Neurology, Radiology, and Neuroscience, Washington University School of Medicine, St. Louis, MO, USA
8Institució Catalana de la Recerca i Estudis Avançats (ICREA), Barcelona, Spain
9Institut de Neurosciences de la Timone, CNRS, Marseille, France

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Keywords: fMRI, Cognition, Whole-brain dynamic model, Effective connectivity, Connectivity esti-
mazione, Machine learning, Classification, Biomarker, Network theory, Recurrent network, Dynamic
communicability and flow, Community analysis

ABSTRACT

Neuroimaging techniques are now widely used to study human cognition. The functional
associations between brain areas have become a standard proxy to describe how cognitive
processes are distributed across the brain network. Among the many analysis tools available,
dynamic models of brain activity have been developed to overcome the limitations of
original connectivity measures such as functional connectivity. This goes in line with the
many efforts devoted to the assessment of directional interactions between brain areas from
the observed neuroimaging activity. This opinion article provides an overview of our
model-based whole-brain effective connectivity to analyze fMRI data, while discussing the
pros and cons of our approach with respect to other established approaches. Our framework
relies on the multivariate Ornstein-Uhlenbeck (MOU) process and is thus referred to as
MOU-EC. Once tuned, the model provides a directed connectivity estimate that reflects the
dynamical state of BOLD activity, which can be used to explore cognition. We illustrate this
approach using two applications on task-evoked fMRI data. Primo, as a connectivity measure,
MOU-EC can be used to extract biomarkers for task-specific brain coordination, understood
as the patterns of areas exchanging information. The multivariate nature of connectivity
measures raises several challenges for whole-brain analysis, for which machine-learning tools
present some advantages over statistical testing. Secondo, we show how to interpret changes
in MOU-EC connections in a collective and model-based manner, bridging with network
analysis. Our framework provides a comprehensive set of tools that open exciting
perspectives to study distributed cognition, as well as neuropathologies.

AUTHOR SUMMARY

Brain connectivity measures have been increasingly used to study cognition and
neuropathologies with neuroimaging data. Many methods have been developed with

a n o p e n a c c e s s

j o u r n a l

Citation: Gilson, M., Zamora-López, G.,
Pallarés, V., Adhikari, M. H., Senden, M.,
Campo, UN. T., . . . Insabato, UN. (2020).
Model-based whole-brain effective
connectivity to study distributed
cognition in health and disease.
Network Neuroscience, 4(2), 338–373.
https://doi.org/10.1162/netn_a_00117

DOI:
https://doi.org/10.1162/netn_a_00117

Supporting Information:
https://doi.org/10.1162/netn_a_00117
https://github.com/mb-BCA/pyMOU
https://github.com/mb-BCA/
NetDynFlow
https://github.com/mb-BCA/
notebooks_review2019

Received: 29 Marzo 2019
Accepted: 02 Dicembre 2019

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Matthieu Gilson
matthieu.gilson@upf.edu

Handling Editor:
Olaf Sporns

Copyright: © 2019
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza

The MIT Press

Modeling whole-brain effective connectivity for cognition and disease

particular objectives, in particular predictability to obtain biomarkers (cioè., which brain
regions exhibit changes in their interactions across conditions) and interpretability (relating
the connectivity measures back to the biology). In this article we present our framework for
whole-brain effective connectivity that aims to find the equilibrium between these two
desired properties, relying on a dynamic model that can be fitted to fMRI time series.
Nel frattempo, we compare it with previous work. Concretely, we show how machine learning
can be used to extract biomarkers and how network-oriented analysis can be used to
interpret the model estimates in terms of brain dynamics.

INTRODUCTION

The study of cognition has flourished in the recent decades because of the abundance of neu-
roimaging data that give access to brain activity in human subjects. Along the years, tools from
various fields like machine learning and network theory have been brought to neuroimaging
applications in order to analyze data. The corresponding tools have their own strengths, like
predictability for machine learning. This article brings together recent studies based on the
same whole-brain dynamic model in a unified pipeline, which is consistent from the model
estimation to its analysis—in particular, the implications of the model assumptions can be
evaluated at each step. This allows us to naturally combine concepts from several fields, In
particular for predictability and interpretability of the data. We stress that our framework can
be transposed to other dynamic models, while preserving the concepts underlying its design.
In the following, we first review previous work on connectivity measures to set our formalism
in context. After presenting the dynamic model (the multivariate Ornstein-Uhlenbeck process,
or MOU), we discuss its optimization procedure to reproduce statistics of the fMRI/BOLD
signals (spatiotemporal covariances), yielding a whole-brain effective connectivity estimate
(MOU-EC). Then two MOU-EC-based applications are examined: machine learning to extract
biomarkers and network analysis to interpret the estimated connectivity weights in a collective
maniera. Nel frattempo, presenting details about our framework, we provide a critical comparison
with previous studies to highlight similarities and differences. We illustrate MOU-EC capabil-
ities in studying cognition in using a dataset where subjects were recorded in two conditions,
watching a movie and a black screen (referred to as rest). We also note that the same tools can
be used to examine cognitive alterations due to neuropathologies.

CONNECTIVITY MEASURES FOR FMRI DATA

Among noninvasive techniques,
functional magnetic resonance imaging (fMRI) has be-
come a tool of choice to investigate how the brain activity is shaped when performing tasks
(Cohen, 2018; Gonzalez-Castillo & Bandettini, 2017; Li, Wang, Yao, Eh, & Friston, 2012;
Naselaris, Kay, Nishimoto, & Gallant, 2011). The blood-oxygen-level-dependent (BOLD) sig-
nals recorded in fMRI measure the energy consumption of brain cells, reflecting modulations in
neural activity (Bartels, Logothetis, & Moutoussis, 2008; Becker, Reinacher, Freyer, Villringer,
& Ritter, 2011; Ekstrom, 2010; Mitra et al., 2018). Since early fMRI analyses, a main focus has
been on identifying with high spatial precision regions of interest (ROIs) in the brain that signif-
icantly activate or deactivate for specific tasks (Cordes et al., 2000; Laird et al., 2013; Walther
et al., 2016). Because the measure of BOLD activity during task requires the quantification
of a baseline, the brain activity for idle subjects became an object of study and developed as
a proper line of research (Biswal, 2012; Snyder & Raichle, 2012). This revealed stereotypical
patterns of correlated activity between brain regions, leading to the definition of the functional
connectivity or FC (Buckner, 2010; Gillebert & Mantini, 2013). Together with studies of the

Network Neuroscience

339

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

anatomical connectivity using structural MRI (Hagmann et al., 2008; Sporns, Tononi, & Kötter,
2005), fMRI studies progressively shifted from focusing on specific ROIs to whole-brain anal-
yses (Deco, Jirsa, & McIntosh, 2011). Per esempio, high-order cognition involves changes in
BOLD activity that are distributed across the whole brain (Chang, Gianaros, Manuck, Krishnan,
& Wager, 2015; Rissman & Wagner, 2012), which cannot be restrained to a small set of pre-
selected ROIs. The typical description of the whole-brain activity in these methods is a ROI-
ROI matrix, which we refer to as connectivity measure.

Glossary

Generative model: Model of (dynamic) equations that generates a signal to be fit to
empirical data. This definition is different from the definition in statistics, where a
generative model describes the joint probability distribution of observed and predicted
variables (here the network activity), as opposed to a discriminative model that de-
scribes the conditional probability of the predicted variables with respect to the ob-
served variables.

Linear Gaussian model (LGM): Generative model of Gaussian variables with linear
relationships. Its output variables have a flat autocovariance (apart from zero time lag)
and is used to model noisy data without temporal structure.

Multivariate autoregressive (MAR) processi: Dynamic generative model in discrete
time with linear relationships. Its output variables have both spatial and temporal
correlations.

Multivariate Ornstein-Uhlenbeck (MOU) processi: Dynamic generative model in con-
tinuous time with linear relationships (referred to as connections). It is the equivalent
of the MAR process in continuous time.

Connections, interactions, and links: In the main text connections refer to a direct and
causal relationship between nodes (ROIs) in a dynamic model, whereas interactions
are used to describe network effects that may be mediated by indirect pathways in
the network (for example with FC or dynamic flow). Links are used in the context of
machine learning as a common term for EC connections or FC interactions.

Lyapunov optimization or natural gradient descent: Tuning procedure for the EC weights
in the MOU network that fits the model FC covariance matrices to their empirical
counterparts.

Classification pipeline: Succession of machine-learning algorithms that aims to learn
the mapping from input vectors of “features” to output “labels” (or categories). Here we
use neuroimaging connectivity measures to predict cognitive conditions (like the task
performed by a subject).

Multinomial logistic regression (MLR): Linear multicategory classifier that assigns a co-
efficient to each input feature to predict the labels. It reduces to logistic regression for
binary classification.

k-nearest neighbor (kNN): Nonlinear classifier that predicts the category of each new
sample based on the most represented category over the k closest samples from the
train set, given a distance metric or similarity measure.

Biomarker: Subset of observed features (here usually EC/FC links) that enable a robust
classification, often paired with weights as in the case of a linear classifier.

Dynamic communicability: Measure of pairwise interactions between nodes (ROIs) In
a network that takes indirect paths into account. In the present article, it corresponds
to interactions over time for the MOU model.

Dynamic flow: Extension of dynamic communicability that incorporates the effect of
input properties in the MOU model.

Network Neuroscience

340

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

Recentemente, fMRI studies for both rest and tasks have also evolved to incorporate the temporal
structure of BOLD signals in their analysis (Cabral et al., 2017; Ciuciu, Abry, & Lui, 2014;
Gilson, Moreno-Bote, Ponce-Alvarez, Ritter, & Deco, 2016; Gonzalez-Castillo & Bandettini,
2017; B. J. Lui, 2011; Hutchison et al., 2013; Mitra, Snyder, Tagliazucchi, Laufs, & Raichle,
2015; Vidaurre et al., 2018), in addition to the spatial structure. Models have also been devel-
oped to formalize the link between the observed BOLD and the neuronal activity (Deco et al.,
2013; Frässle et al., 2018; K. J. Friston, Harrison, & Penny, 2003; Gilson et al., 2016; Li et al.,
2012; Messé, Rudrauf, Benali, & Marrelec, 2014; Vidaurre et al., 2018). This has led to many
definitions for connectivity measures and variations thereof. In this introductory section we
present fundamental concepts about connectivity measures that set our model-based approach
in context (see also the Glossary for definitions).

Model-Based Versus Model-Free Approaches

A recurrent discussion opposes model-free and model-based approaches in neuroscience,
which also applies for connectivity measures. For instance, FC calculated using Pearson corre-
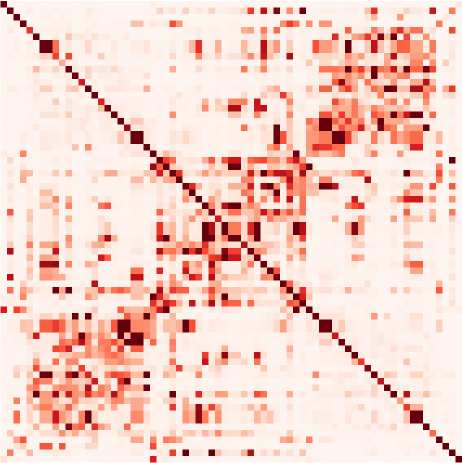
lation between time series (blue matrix in Figure 1A) can be directly calculated from data—see
Equation B.2 in the Supporting Information—and may thus be seen as model-free. Tuttavia,
the interpretation of the FC values for the pairs of ROIs in the matrix is based on the theory of
linear Gaussian models (LGMs), which assumes multivariate normal distributions for the data.
The Pearson correlation is a connectivity measure that can be directly calculated on the gen-
erated activity. The underlying connectivity in the LGM, called the precision matrix, is closely
related to the partial correlations (PC) represented by the green matrix in Figure 1A. The PC
symmetric matrix describes the undirected linear relationships between Gaussian variables
that result in the observed correlations. Our viewpoint is thus that connectivity measures are
always related to a model, so it is crucial to bear in mind their assumptions when interpret-
ing their values. Note that other classifications of methods have been proposed and discussed
in previous work, like directed functional connectivity measures versus effective connectiv-
ity measures (K. Friston, Moran, & Seth, 2013), state-space models versus structural models
for BOLD dynamics (Valdes-Sosa, Roebroeck, Daunizeau, & Friston, 2011) and network-wise
methods versus pairwise inference methods (Bielczyk et al., 2019).

In the literature of whole-brain modeling, three families of connectivity measures have

emerged:

Structural connectivity (SC): It measures the density or probability of anatomical path-
ways that connect two ROIs, mostly via the white matter (Schmahmann & Pandya, 2007).
This led to the definition of the human connectome at the whole-brain level (Hagmann
et al., 2008; Sporns et al., 2005).
Functional connectivity (FC): Pairwise statistical dependencies between the observed
activity of ROIs (Buckner, 2010; Gillebert & Mantini, 2013). Apart from the Pearson
correlation of the BOLD signals (Biswal, 2012; Snyder & Raichle, 2012), other common
FC measures include mutual information (Hlinka, Palus, Vejmelka, Mantini, & Corbetta,
2011) and synchrony of instantaneous phases (Cabral, Hugues, Sporns, & Deco, 2011;
Cabral et al., 2017). Conceptually, FC corresponds to a measure that can be applied to
multiple time series, either the data or the model activity.
Effective connectivity (EC): In this article we define EC as a measure of the directional
relationships in a dynamic model. The original concept arises from electrophysiology
(Aertsen, Gerstein, Habib, & Palm, 1989), where EC determines how the stimulation of
a neuron affects a target neuron (per esempio., combining the source-to-target synaptic weight

Network Neuroscience

341

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

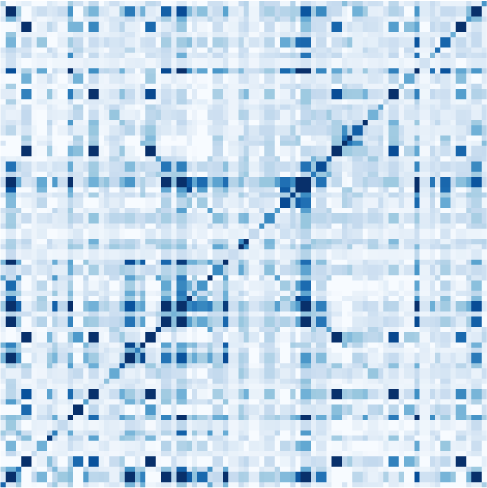
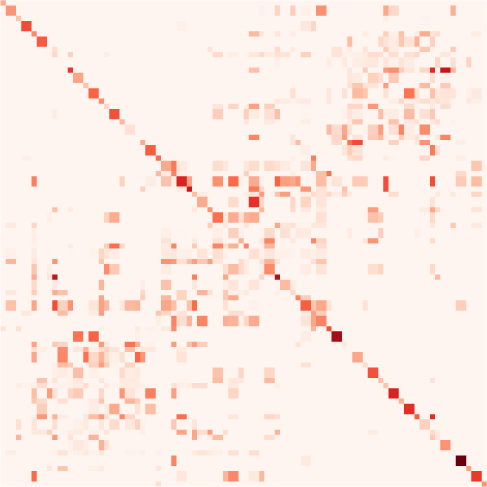
Figura 1. Connectivity measures. (UN) Schematic diagram of six brain regions of interest (ROIs),
whose fMRI activity is captured by several types of connectivity measures. Here the activity is gen-
erated using a directed matrix. The corresponding structural connectivity (SC, black matrix) indicates
the topology of anatomical connections between the six ROIs, which can be estimated using struc-
tural MRI. Functional connectivity (FC, blue matrix), here calculated using the Pearson correlation
of the BOLD signals. The linear Gaussian model (LGM) assumes activity and corresponds to partial
correlations (PC, green matrix). The multivariate autoregressive (MAR, orange matrix) assumes linear
dynamics while taking the temporal structure of the data into account. Effective connectivity (EC,
red matrix), which is the focus of the present article, depends on the choice for dynamic model, COME
well as input properties. Here the dark brown dashed box groups together the connectivity mea-
sures that involve a model inversion for their estimation, as compared with the light brown box
that can be directly computed from the observed data. (B) Autocorrelograms of the data (in light
brown, left plot) for six ROIs and two network models (middle and right plots). The linear Gaussian
model related to the FC and PC (in green) has a flat autocorrelogram away from the central peak.
In contrasto, the profile of the MAR process (in orange) has a decaying exponential profile.

Network Neuroscience

342

Modeling whole-brain effective connectivity for cognition and disease

and the excitability of the target). It was then brought to neuroimaging in the 2000s
when building models of the BOLD response and further developed in the context of the
dynamic causal model (DCM), usually interpreted as neuronal coupling (K. Friston, 2011;
K. J. Friston et al., 2003; Valdes-Sosa et al., 2011). Note that it is also still used close to
its original formulation when measuring stimulation-driven responses in neuroimaging
(Lafleur, Tremblay, Whittingstall, & Lepage, 2016).

To go beyond statistical relationships, the combination of several types of data requires a
modello, as with the SC and FC that are combined in the EC model (see Figure 1A). Therefore
the choice of the model ingredients, especially their dynamics, has important implications that
we detail in the following.

Choice of Model and Interpretability

In our framework we borrow the EC terminology that can be understood in a broad sense as
the directed connectivity in a generative model, here for BOLD activity. When using the LGM
related to Pearson correlations taken as FC, one can take the partial correlation (PC, green
matrix in Figure 1A) as “LGM-EC.” As illustrated by the flat green autocorrelogram for nonzero
time lags in Figure 1B, the generated signals by the linear Gaussian model are independently
and identically distributed (i.i.d.) variables and do not have temporal correlations. In contrasto,
the multivariate autoregressive process (MAR, in orange in Figure 1A–B) has a directed con-
nectivity (asymmetric matrix) and produces temporally correlated signals. When these models
are fitted to data, they do not capture the same part of the data structure. When the MAR
model is considered, the estimation results in directed connectivity that depends on the spa-
tiotemporal correlation structure of the observed activity (or spatiotemporal FC). Tuttavia, IL
linear Gaussian model does not “naturally” give directed connectivity when fitted to the spatial
FC. Note that techniques based on optimization with regularization have been developed to
enforce directionality in the estimated connectivity (Schiefer et al., 2018), Anche se.

EC usually describes causal and directional relationships that interplay with other dynamic
parameters in the model to determine the global network pattern of activity. When optimizing
a model to reproduce BOLD signals, the parameter can be seen as representations or “projec-
tions” of the BOLD signals, in a top-down or data-driven approach (Valdes-Sosa et al., 2011).
Importantly, the estimated EC depends on the choice for the model dynamics. Per esempio, IL
DCM was developed to formalize the link between neural and BOLD activities by explicitly
modeling the hemodynamics (K. Friston, 2011; K. J. Friston et al., 2003; K. Stephan, Harrison,
Penny, & Friston, 2004). The DCM-EC is thus the directed connectivity between the ROIs and
determines their activities, from which the BOLD signals are generated via a hemodynamic
response function (HRF).

We keep in mind that all interpretations of fMRI signals sit on the hypothesis that correlated
BOLD activity between brain areas reflects the activity of their neuronal populations (David et
al., 2008; Goense & Logothetis, 2008; Y. He et al., 2018; Matsui, Murakami, & Ohki, 2018),
which in turn mediates the transmission of neuronal information (Fries, 2005). Tuttavia, many
metabolic mechanisms like breathing (which are usually ignored in whole-brain models) alter
the BOLD signals (Power et al., 2018), and the adequate procedure to minimize the corruption
of data and obtain a satisfactory signal-to-noise ratio is still under debate (Parkes, Fulcher,
Yücel, & Fornito, 2018).

A distinct line of research (Cabral et al., 2011; Deco et al., 2013; Proix et al., 2016; Sanz-
Leon, Knock, Spiegler, & Jirsa, 2015) focuses on the development of whole-brain models in a

Network Neuroscience

343

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

more bottom-up fashion (model-driven), combining various datasets and biologically inspired
mechanisms, such as oscillators to produce rhythms observed in the brain. Such approaches
allow for the study of the influence of specific parameters (as ingredients in the model) In
collectively shaping the global network activity. Compared with connectivity estimation, UN
major distinction of many of those models is that SC is taken as the intracortical connectivity
to focus on the influence of the local dynamics in shaping network activity patterns; see Messé
et al. (2014) for a review.

Consistency of Pipeline From Preprocessed Data to Modeling and Analysis

The incentive for novelty has fostered the development of many methods in computational
neuroscience. This makes results difficult to compare, especially for resting-state fMRI stud-
ies where no ground truth is available. Another caveat concerns network analysis when it is
applied to connectivity estimates from time-varying signals (per esempio., BOLD) with metrics (per esempio., A
detect communities) that do not genuinely relate to the physical values of the data. Our prac-
tical answer to this point is thus to develop for the same dynamic model a set of analysis tools,
covering parameter inference (Gilson et al., 2016) to machine learning and network analysis.
Although the mathematical tractability of the model limits the richness of its dynamic reper-
toire compared with more elaborate bottom-up models (Deco et al., 2013; Sanz-Leon et al.,
2015), it provides an intuitive understanding of the roles of parameters as well as analytical
derivations for the parameter estimation or model interpretation. We believe that such an effort
for formalization and consistency is beneficial to the field, both for didactic purpose and for
designing tailored methodology for complex models.

The present article follows the pipeline displayed in Figure 2A. The second section presents
the dynamic model and our recent optimization procedure (Gilson, Deco, et al., 2018; Gilson
et al., 2016) to estimate MOU-EC for whole-brain fMRI data (Figure 2B). It also discusses tech-
nical aspects in relation with other models used with neuroimaging data. The third section
shows how connectivity measures can be used to predict cognitive states (Figure 2C) and un-
cover their underlying structure. Importantly, the use of datasets with multiple tasks allows for
an in-depth benchmarking of the connectivity measures. It also highlights some advantages
of machine learning over statistical testing in making use of the multivariate nature of con-
nectivity measures, transposing and abstracting concepts presented in a recent study for sub-
ject identification (Pallarés et al., 2018). The fourth section bridges with network analysis
(Gilson et al., 2019; Gilson, Kouvaris, Deco, & Zamora-López, 2018), interpreting changes
in MOU-EC connections in a collective and model-based manner. In particular, it adapts com-
munity detection to our dynamic model (Figure 2D).

CAPTURING THE WHOLE-BRAIN BOLD DYNAMICS WITH MOU-EC

Using a generative model to reproduce the BOLD statistics, the optimized MOU-EC can be
seen as an estimate that extracts spatiotemporal information about the BOLD dynamics. In
fatto, the main innovation of the modeling is the optimization procedure in Figure 2B (Gilson
et al., 2016). This section reviews important points about the underlying multivariate Ornstein-
Uhlenbeck (MOU) dynamic model and its tuning. Further mathematical details can be found in
the Supporting Information (see Figure S1). Our approach aims to combine several key aspects:

Whole-brain connectivity estimates are necessary to properly take into account the ex-
perimentally observed distributed information across distant regions (Chang et al., 2015;
Deco et al., 2011), without a priori selection of ROIs.

Network Neuroscience

344

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

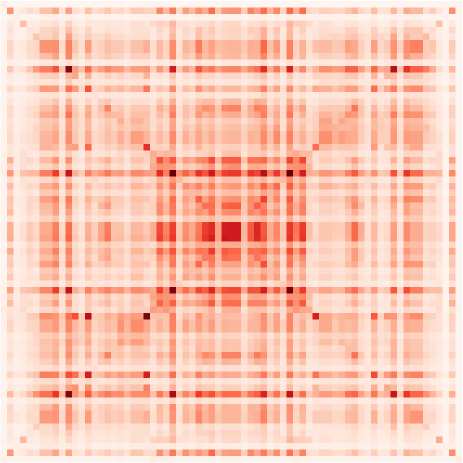
Figura 2. EC-based analysis of empirical BOLD signals. (UN) Pipeline for brain coordination analysis
using MOU-EC. For each fMRI session, the model is optimized by tuning its parameters, especially its
connectivity, to reproduce the statistics of the BOLD signals (depicted in the right side of the brain).
A schematic parcellation is represented on the left hemisphere of brain. The estimated MOU-EC can
then be used to predict cognitive states using classification algorithms. D'altra parte, MOU-
EC can be analyzed as a graph (or network) to uncover collective properties. A contribution of our
approach is to link the network-oriented analysis with machine-learning techniques. (B) From the
BOLD signals, two FC matrices are calculated, FC0 without time lag in blue and FC1 with a time lag
Di 1 TR in green. The model parameters (MOU-EC and Σ) are optimized to reproduce these empirical
FC matrices. Classification focuses on the model connectivity (per esempio., MOU-EC), but the influence of
Σ will be incorporated in the network analysis. See Figure S1 for further details. (C) Schematic
representation of the FC and MOU-EC matrices (one sample per session) in their own spaces for
two cognitive states (R for rest and M for movie). For each connectivity measure, the prediction
of R versus M is robust when the sample distributions represented by the dashed circles do not
sovrapposizione. (D) The left diagram represents community detection in a structural undirected network.
The right diagram represents the MOU-EC networks, from which we want to define dynamics-based
communities.

From the overall spatiotemporal structure of BOLD signals, the dynamic model only
reproduces their covariances (without and with time lag, see Figure 2B). This con-
cerns the same fast timescale as recent studies (Mitra, Snyder, Hacker, & Raichle, 2014;
Mitra et al., 2015), which also demonstrated the influence of behavioral states such as
sleep versus wake. The choice of BOLD covariances to be reproduced by the model
is supported by previous results that showed that most of the information was in the
second-order statistics of BOLD signals (Hlinka et al., 2011).

Network Neuroscience

345

Modeling whole-brain effective connectivity for cognition and disease

Causality is inherent to the concept of EC (K. Friston, 2011; K. J. Friston et al., 2003;
Valdes-Sosa et al., 2011) that is represented by the directed connections in the dynamic
modello (red arrows in Figure 2B). From the estimated MOU-EC that best reproduces the
dati, we interpret strong MOU-EC weights as causal relationships and can examine their
asymmetry to evaluate for a pair of ROIs which one drives the other. The optimization
can deal with common inputs for ROIs, to explain the observed correlated activity by an
interplay between the directed connectivity and correlated inputs (Gilson, Deco, et al.,
2018).
The MOU-EC topology is the interregional infrastructure, namely which connections
exist and which do not in the brain network. When SC is available, its binarization (black
matrix in Figure 1A) can be used to constrain the MOU-EC topology in order to reduce
the number of parameters to estimate. This enforces the model to “explain” changes in
the FC by existing connections only, in contrast to PC and MAR (Figure 1A). It is thus
important to remember that MOU-EC estimates are not related to SC values.
The optimization procedure tunes all MOU-EC weights while taking into account net-
work effects. For each fMRI session, we obtain a multivariate estimate of more than 1,000
parameters that represent the dynamical “state” of the brain activity. This contrasts with
previous models that used the symmetric SC as connectivity matrix in dynamic mod-
els and focused on choosing or tuning the nodal dynamics with a few parameters only
(Deco et al., 2013; Messé et al., 2014; Sanz-Leon et al., 2015).
A limitation of the model estimation procedure up to now is the assumption of stationarity
for the BOLD signals over each fMRI session, which limits our approach to ongoing
nonswitching tasks.
Another limitation of MOU-EC for the interpretation in terms of neuronal coupling is the
absence of explicit hemodynamics in the model. This choice comes from the priority
given so far to the estimation robustness (with simpler dynamics) over the biological
interpretability, as will be discussed later.

Multivariate Ornstein-Uhlenbeck Dynamics as Generative Model for BOLD Signals

Formalmente, our model-based analysis is based on the multivariate Ornstein-Uhlenbeck process
that is described by Equation C.1 in the Supporting Information. It corresponds to a network
with linear feedback that is the equivalent in continuous time of the discrete-time multivariate
autoregressive (MAR) processi. These dynamic systems with linear feedback have been widely
used in neuroscience to model the propagation of fluctuating activity, mixing “noise” and struc-
ture, for example in modeling single neuronal dynamics (Burkitt, 2006), relating the connec-
tivity and activity in a network (Galán, 2008) and defining neural complexity (Barnett, Buckley,
& Bullock, 2009; Tononi, Sporns, & Edelman, 1994). It also corresponds to the linearization
of nonlinear population models like Wilson-Cowan neurons (Wilson & Cowan, 1973).

The choice for the MOU dynamics is motivated by the balance between simplicity, Quale
ensures tractable analytical calculation, and richness of the generated activity when modulat-
ing the parameters (especially the MOU-EC weights). Così, it is well adapted to whole-brain
data with parcellation involving many ROIs (≥ 100). Inoltre, the MOU dynamics implies
exponential decaying autocovariances in the model, which have similar profiles to the empir-
ical data (see the left plot in Figure 1B corresponding to straight lines in log-plot in Figure S1).

Intuitively, it can be understood as a network when fluctuating activity (akin to noise) is gen-
erated at each ROI and propagates via the recurrent EC. In other words, MOU-EC (red matrix in
the bottom box) acts as a “transition matrix” and quantifies the propagation of fluctuating BOLD

Network Neuroscience

346

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

activity across ROIs. The MOU-EC matrix is usually sparse when its topology is constrained by
SC (black matrix) to match anatomical white matter connections between ROIs. The fluctuating
activity for all ROIs is described by their (co)variance matrix Σ, which is diagonal in the present
case (see the purple vector of variances). In a previous study, cross-correlations for Σ also
involve common inputs to homotopic sensory ROIs (Gilson, Deco, et al., 2018).

Parameter Estimation Capturing Network Effects in BOLD Propagation

To capture the BOLD dynamics (cioè., propagation of fluctuating activity), we use the two BOLD
covariance matrices FC0 and FC1 in Figure 2B, without and with time lag, rispettivamente. Questo
also ensures a one-to-one mapping between an FC configuration (a pair FC0 and FC1) E
a MOU-EC configuration. This choice is in line with previous adjustments of DCM to model
the resting state that relied on the cross-spectrum, namely the Fourier transform of covariances
with all possible time lags (K. Friston, 2011). It is richer than fitting only an FC matrix without
time lag (Deco et al., 2013; Messé et al., 2014) and complies with a recent study of the task-
dependent modification of the BOLD temporal structure at short timescales (Mitra et al., 2015).

The MOU-EC estimate is obtained for the minimum model error in reproducing the em-
pirical FC0 and FC1 for each session (see the fit plot between the boxes in Figure S1). IL
optimization is akin to a “natural” gradient descent (Amari, 1998) in that it takes into account
the nonlinearity of the mapping from MOU-EC to the covariances FC0 and FC1. This arises
because of the network feedback (even though linear) and may result in strong correlations (In
FC) for disconnected ROIs (EC = 0) provided strong indirect pathways connect them (via other
ROIs). Appendix D in the Supporting Information provides the mathematical details of the op-
timization, which applies the gradient descent to both MOU-EC and Σ (Gilson, Deco, et al.,
2018), extending the initial formulation with a heuristic optimization for Σ (Gilson et al., 2016).

For illustration purpose, this article uses a whole-brain parcellation consisting with 66 ROIs.
The SC density is 28%, giving 1,180 MOU-EC weights to estimate (see Appendix A in the
Supporting Information). Each fMRI session has 300 time points separated by TR = 2s, so the
number of data points is 66 × 300 ≃ 2.104, Di 16 times larger than the number of model
parameters. EC should be like a summary of the BOLD signals: informative (not too short),
but extracting and compressing relevant information (not too long). Our method was also suc-
cessfully applied to the AAL (Automated Anatomical Labeling) parcellation with 116 ROIs and
sessions of 5 min (Pallarés et al., 2018). Typically, the MOU-EC estimation for a session and
Di 100 ROIs takes less than a minute of computation time on a desktop computer. For
more refined parcellation or shorter sessions, the FC matrices may become quasisingular and
the model estimates are expected to be noisier. The reduction of the number of parameters
to estimate by using SC is crucial to work at the level of individual fMRI session and avoid
overfitting. Here, overfitting would correspond to the situation where many distinct MOU-EC
configurations in the model give very similar pairs of FC0 and FC1 matrices, giving a larger
overlap for MOU-EC than in Figure 2C and the same small overlap for FC. The comparison be-
tween FC and MOU-EC as multivariate representation of cognitive states will be the focus of the
next section. An important conceptual difference between MOU-EC and SC is that MOU-EC
accounts for the dynamical properties of the brain activity, which are modulated when engag-
ing a task. In other words, MOU-EC is hypothesized to account for the concentration of recep-
tors or neurotransmitters, local excitability, and so on not only the density of the synaptic fibers.

Comparison With Other Approaches to Extract Information From BOLD Signals

Other approaches have been proposed to characterize activity “states” based on the tem-
poral structure of BOLD signals. Per esempio, the “dynamic FC” relies on sliding windows

Network Neuroscience

347

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

of several tens of TRs (Gonzalez-Castillo & Bandettini, 2017; Hutchison et al., 2013; Park &
Friston, 2013; Preti, Bolton, & Van De Ville, 2017), thereby focusing on changes in correlation
patterns over minutes. Shorter timescales have been explored using instantaneous phases ob-
tained using the Hilbert transform on the BOLD signals (Cabral et al., 2017) or hidden Markov
models (HMMs; Bolton, Tarun, Sterpenich, Schwartz, & Van De Ville, 2018; Vidaurre et al.,
2018). In contrasto, the MOU-EC describes the BOLD propagation averaged over a session
while assuming stationarity, as calculated in the corresponding statistics (covariances without
lag and with a lag of 1 TR). Note that the “transition matrix” analogy for EC is at the level of the
BOLD activity, not of hidden states as in the case of HMMs. Inoltre, it does not involve a
dynamic modulation of EC as used in the DCM (K. Friston, 2011; Li et al., 2012; Park & Friston,
2013).

A key innovation to tackle whole-brain fMRI data is the optimization constrained by SC
that determines the network topology. This means the model has to explain the spatiotemporal
FC structure using the existing connections only. The “prior” information related to SC avoids
the preselection of ROIs and can be seen as an alternative to model comparison in choosing
the best topology using structural equations (James et al., 2009; McIntosh & Gonzalez-Lima,
1994), Granger causality analysis (Goebel, Roebroeck, Kim, & Formisano, 2003), and early
versions of the DCM (K. J. Friston et al., 2003; Valdes-Sosa et al., 2011)—note that a recent
DCM study incorporates SC for the network topology (Sokolov et al., 2018). Likewise, IL
MOU-EC density usually depends on the threshold applied to SC and the best choice can be
decided using model comparison, although the formulation may not be as natural as in the
Bayesian framework.

Several fundamental properties were discussed a few years ago about the defining concepts
of EC and DCM (Valdes-Sosa et al., 2011). Beyond technical details, three main points are
that DCM-EC corresponds to the connectivity weights in a dynamic model, that the model
incorporates the hemodynamic response function, and that the estimation captures the BOLD
dynamics, including the subsampling related to the low time resolution of BOLD signals. IL
EC terminology was borrowed from the DCM literature (K. Friston, 2011) because of the model-
based aspect. The MOU-EC estimation was developed to solve the trade-off between robust
estimation and application to large brain network (70+ ROIs) by using linear dynamics (Gilson
et al., 2016). Since then, the DCM has been applied to whole-brain fMRI data (Frässle et al.,
2018; Razi et al., 2017).

The FC0 and FC1 matrices in Figure 2B embody the spatiotemporal BOLD structure in
the range of “high” frequencies close to the Nyquist frequency equal to 0.5 Hz. The recent
extension of the DCM to analyze resting-state fMRI data reproduces the BOLD statistics via
the cross-spectrum (Frässle et al., 2018; K. J. Friston, Kahan, Biswal, & Razi, 2014; Razi et al.,
2017), which is in line with our approach. Recall that this contrasts with earlier versions of the
DCM that reproduced the BOLD time series themselves for stimulation protocols (K. J. Friston
et al., 2003; Li et al., 2012). Because it works in continuous time, the MOU model deals with
the BOLD subsampling (Gilson et al., 2016), unlike estimation methods relying on the discrete-
time multivariate autoregressive process that may be sensitive to the subsampling of the BOLD
signals (Seth, Chorley, & Barnett, 2013). Inoltre, the observed lags between ROIs in FC—
similar to cross-correlograms (Mitra et al., 2014, 2015)—are explained by the combination
between the estimated inputs Σ and MOU-EC (Gilson, 2018).

The time constant τx in the MOU model is identical for all ROIs in Equation C.1 in the
Supporting Information, which corresponds to an abstraction of the HRF waveform response

Network Neuroscience

348

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

that was reported with a decay of 5 A 10 S (d’Avossa, Shulman, & Corbetta, 2003). An impor-
tant difference of our model compared with the underlying dynamic model behind DCM
(K. J. Friston et al., 2003; Valdes-Sosa et al., 2011), as well as other bio-inspired network
models (Deco et al., 2013), is the absence of an explicit HRF to link the neural activity to
the measured BOLD signals (Boynton, Engel, Glover, & Heeger, 1996; K. Friston, Mechelli,
Turner, & Price, 2000; K. Stephan et al., 2004). Note that applications of the DCM to resting-
state data involve a linearization of the HRF (Frässle et al., 2018; Razi et al., 2017). Therefore,
a foreseen extension of our approach is that of a state-space model with the MOU process
generating the neuronal activity that is convolved with a linear HRF filtering (Sauvage, Hubert,
Touboul, & Ribot, 2017). The challenge is to keep the gradient-descent optimization tractable,
as was previously done with Granger causality analysis (Barnett & Seth, 2015; Faes, Stramaglia,
& Marinazzo, 2017). Incorporating the HRF may improve the reliability of the estimated EC
(Gitelman, Penny, Ashburner, & Friston, 2003; Olszowy, Aston, Rua, & Williams, 2019). Note
that an alternative consists in performing the deconvolution of the BOLD signals with respect
to a HRF before analyzing the obtained neuronal signals, as was done with Granger causal-
ity analysis (David et al., 2008; Goodyear et al., 2016; Sathian, Deshpande, & Stilla, 2013;
Wheelock et al., 2014) or other connectivity analysis (Ryali, Supekar, Chen, & Menon, 2011).

MACHINE LEARNING FOR EXTRACTING MULTIVARIATE BIOMARKER SPECIFIC
TO COGNITIVE STATES

Beyond their goodness of fit and how many “realistic” biological mechanism they might incor-
porate, models can be used to extract information from data in a top-down approach. Once
tuned, the model parameters can indeed be used to discriminate cognitive conditions, as a
representation of the observed data (BOLD signals here). This conceptually differs from find-
ing the generative model of activity with the best fit. Nonetheless, it is expected that a model
with poor fit hardly extracts any relevant information. Many recent studies have used connec-
tivity measures to predict which tasks are performed by the subjects in the scanner (Gonzalez-
Castillo et al., 2015), the pathological conditions of patients (Kurth, Moyse, Bahri, Salmon,
& Bastin, 2015; Rahim, Thirion, Bzdok, Buvat, & Varoquaux, 2017), and individual iden-
tity (Amico & Goñi, 2018; Calhoun, Lawrie, Mourao-Miranda, & Stephan, 2017; Finn et al.,
2015; Miranda-Dominguez et al., 2014). Machine learning is the standard for identifying bio-
markers of neuropathologies (Varoquaux et al., 2017) and is also widely used in voxel-based
analysis for cognitive tasks (Naselaris et al., 2011; Walther et al., 2016). Tuttavia, it is less
frequently applied for cognition studies using connectivity measures (Varoquaux & Poldrack,
2019). For a given connectivity measure, a biomarker is a subset of connections (or links) Quello
enables the robust identification of a category of fMRI sessions, such as a weighted sum of
the matrix elements that exceeds a threshold for the multinational logistic regression (MLR).
In practice, changes in BOLD activity across cognitive conditions are mixed with individual
traits and session-to-session variability. Disentangling these contributions is the key to obtain
efficient biomarkers (Pallarés et al., 2018).

The present section addresses the following questions:

How to cope with the multivariate nature of connectivity measures (per esempio., > 1, 000
MOU-EC links)? We illustrate some advantages of machine learning compared with sta-
tistical testing, about multiple comparisons and beyond.
What does classification tell about the underlying model? Linear and nonlinear classifiers
apply different metrics on the estimated parameters, revealing the distribution of task-
specific changes across brain regions.

Network Neuroscience

349

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

In a complex environment (per esempio., many tasks), can we uncover a hierarchy in cognitive
stati (subgroups of tasks)?

Adopting the language from machine learning, “samples” refer to fMRI sessions and the
links of the connectivity measures are “features” whose values are used to discriminate “la-
bels”, which are the types of fMRI sessions here. To illustrate our framework, we use data that
were previously analyzed (Demirta¸s et al., 2019; Gilson, Deco, et al., 2018; Hlinka et al.,
2011; Mantini et al., 2012), whose details are summarized in Appendix A in the Supporting
Information. Subjects in the scanner were recorded fixating on a point in a black screen (two
rest sessions R1 and R2) or a movie. The entire movie session was divided in three sessions (M1,
M2, and M3), each corresponding to a different part of the movie. The vectorized MOU-EC
estimates are displayed for all subjects and sessions in Figure 3A. The question is then whether

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

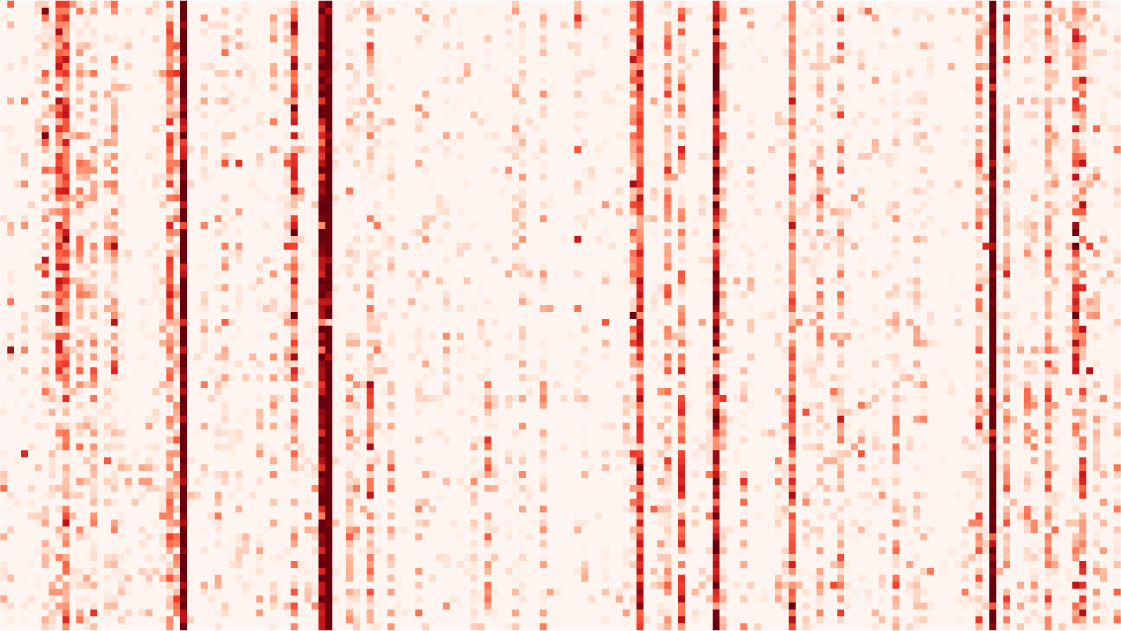
Figura 3. Dimensionality reduction of the connectivity measures. (UN) Connectivity estimates (here
vectorized EC) for five sessions, two for rest and three for movie, for each of the 22 subjects. Each of
the three movie sessions corresponds the three movie sessions each of corresponds to a distinct part
(10 min) of a movie watched and listened to by the subjects. The gray arrow indicates connections
(or links) that strongly differ between rest and movie. (B) Principal component analysis (PCA) applied
to the vectorized EC, FC, and PC (one for each of the 110 sessions) where the same colors as in panel
A correspond to the 4 compiti. For PCA the task labels are not used in the dimensionality reduction
(unsupervised algorithm). (C) Similar plot to panel B with linear discriminant analysis (LDA) for
which the labels are used (supervised learning) to separate the four tasks for the 110 sessions. (D)
The silhouette coefficient measures the quality of the clustering for the four dot clouds when varying
the number of LDA components (see x-axis).

Network Neuroscience

350

Modeling whole-brain effective connectivity for cognition and disease

connectivity measures can capture information to identify the movie sessions individually. For
esempio, the MOU-EC links indicated by the gray arrow exhibit strong changes between rest
and movie (with small and large values, rispettivamente).

Variability of Connectivity Measures With Respect to Cognitive Labels

Before classification, the data structure can be explored to evaluate the similarity or distance
across conditions between the connectivity measures, as representations of the BOLD signals.
For this type of (passive) task, BOLD synchronization patterns during movie viewing between
brain areas (per esempio., visual and auditory) as reflected by intersubject correlations (Hasson, Nir,
Levy, Fuhrmann, & Malach, 2004) are expected to be also captured by the connectivity mea-
sures (Gilson, Deco, et al., 2018). The gray arrow in Figure 3A indicates some MOU-EC links
with strong changes between rest and movie.

A usual technique for multivariate data is dimensionality reduction, for example using prin-
cipal component analysis (PCA; Gonzalez-Castillo et al., 2015) and independent component
analysis (ICA; V. D. Calhoun, Liu, & Adali, 2009). Here we compare two linear transformations,
the unsupervised PCA in Figure 3B with the supervised linear discriminant analysis (LDA) In
Figure 3C. The principal component is the direction in the high-dimension space with largest
variability across the samples, and successive components are ranked in decreasing order for
their corresponding variability. It is called unsupervised because it does not use the task labels
to compute the components, as can be seen for FC where the first component is not related
to the task labels. In comparison, the components for LDA are ranked according to their vari-
ability with respect to task labels. This can be seen for FC where the first component for PCA
does not reflect the separation between movie and rest (the second component does).

The separation of the tasks viewed using the connectivity measures can be evaluated using
silhouette coefficients that measure the clustering quality (Rousseeuw, 1987), ranging from 1
for separated dot clouds to −1 for completely overlapping dot clouds. Applied to the LDA coor-
dinates in Figure 3D, we see a slight increase in silhouette coefficient when incorporating more
components to separate the four clouds. This reflects the difficulty of the four-task discrimina-
zione, as compared with that for the two tasks where a single component is sufficient (Demirta¸s
et al., 2019). The viewpoint here is that of clustering, assuming that the reduced space allows
for isolating the clouds to characterize the cognitive states (Gonzalez-Castillo et al., 2015). In
the following, we rely on various classification techniques for the task discrimination.

Cross-Validation for Assessing the Generalization Capability of Connectivity-Based Classification

Although machine-learning techniques are now increasingly used to analyze neuroimaging
dati, the generalization capabilities are not always properly verified (Varoquaux et al., 2017). For
esempio, clustering algorithms applied on reduced-dimension components (see Figure 3B–C)
give a measure for the separation of the tasks viewed using the connectivity measures (Figure 3D).
Notice that all sessions are used for the dimensionality reduction in Figure 3. This is a problem
since the parameters tuning of the model can be influenced by the specific noise of the data
samples and, in turn, the results will be not generalizable to new samples—a phenomenon
called overfitting. To evaluate the robustness of a classifier, a cross-validation procedure is
the standard for voxel-wise studies for activation maps (Naselaris et al., 2011; Walther et al.,
2016) and for clinical applications (Hohenfeld, Werner, & Reetz, 2018; Rahim et al., 2017).
This procedure consists in splitting the data samples in train and test sets that are respectively
used to fit the classifier and to assess its performance, as described in Figure 4A. Così, one
may have to include preprocessing steps in the cross-validation scheme to properly evaluate

Network Neuroscience

351

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 4. Train-test classification for task or subject identification. (UN) The train-test procedure
consists in splitting the sessions in a train set and a test set. The train set is used to optimize the
classifier (here find the best boundaries between labels; see dashed gray lines), whose accuracy
is then measured on the test set. (B) Accuracy for the classification of test sessions to discriminate
movie versus rest (two labels) for the MLR, 1NN, and LDA classifiers, as indicated by the colors.
The connectivity measures are indicated on the x-axis: The masked FC is the subset of FC features
corresponding to the SC mask used for the MOU-EC model; “heur” corresponds to the symmet-
ric connectivity matrix obtained using the heuristic optimization in Appendix D in the Supporting
Information. The classifiers are trained with 80% of the subjects and tested on the remaining sub-
jects, Sopra 40 repetitions. The dashed line indicates the chance level, which corresponds to predict-
ing always movie (three sessions out of five). The MLR gives perfect classification for all connectivity
measures except for MAR. (C) Same as panel B for the classification of session to identify the four
compiti (three movie sessions and rest). The chance level corresponds to predicting always rest (two
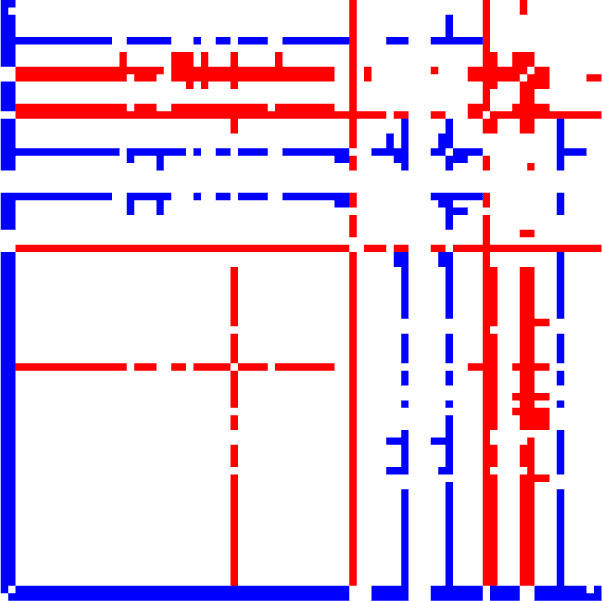
sessions out of five). (D) The left confusion matrix indicates the errors of the MLR classifier trained
with five labels (two labels for rest here), as indicated by the dark green off-diagonal pixels. As
expected from panel B, rest and movie are well separated. The movie sessions (M1 to M3) are dis-
tinguishable to some extent, but not the rest sessions (R1 and R2). The right confusion matrix is the
equivalent for the 1NN classifier. (E–F) Same as panels C–D for the identification of the 22 subjects.
Here 40 splits of the data are considered for two sessions in the train set and three sessions in the test
set, irrespective of rest/movie and individually for each subject. (G) Model error for the MOU-EC
and heuristic optimizations in the two conditions.

Network Neuroscience

352

Modeling whole-brain effective connectivity for cognition and disease

the generalization capability of the classification, for example with functional parcellations
derived from the data that should be calculated on the train set only (Brodersen et al., 2011).
For LDA in Figure 3C, this corresponds to setting a linear boundary using the dimensionality
reduction on the train set and evaluating the performance on the test set. The data splitting
can be repeated several times in order to assess the impact of different samples in the training
and test set on the classification performance. Così, the accuracy distribution provides an
estimate of the generalization capability of the classification scheme to new samples. Different
splitting strategies have been proposed, and here we use the recommended one for neuroimag-
ing applications based on a ratio of 80%:20% for train and test sets, rispettivamente (Varoquaux
et al., 2017). We repeat the classification for 40 random splitting of the data. This is lower than
the recommended 100 times and is justified by the rather low number of 22 subjects in our
dataset, as explained in the box below together with further technical considerations about
choosing a cross-validation scheme.

Remark on cross-validation schemes

The recommended ratio for neuroimaging applications is 80%:20% for train and test sets, Rif-
spectively, chosen by random draws and repeated about 100 times (Varoquaux et al., 2017).
While we agree on this as a good general practice, we highlight that a slightly different scheme
might be better suited when the number of available samples is rather low, as is often the case
in cognitive studies like here with 22 subjects. Another issue concerns the independence or
absence thereof of the measurements used as inputs for classification. For the example of
Figura 3, each subject is scanned in both resting-state and movie conditions, meaning that
fMRI measurements are paired together. There, random resampling based on fMRI sessions
without separating subjects in train and test sets would lead to more similar samples in the train
and test sets than expected by chance. This would likely inflate the evaluated performance for
generalization. A better solution is to apply the cross-validation to “groups” (subjects in this
case) instead of single samples (fMRI sessions). While it is possible to repeat random resam-
pling of the groups several times, the chance of repeating the cross-validation for the exact
same test set becomes nonnegligible when the number of subjects is not sufficiently large. For
our dataset, using four subjects for testing and the remaining 18 for training, there is almost
50% chance of getting the same split twice over 100 repetitions. The consequence would
be an underestimation of performance variability. In such cases, an alternative valid option
is the leave-one-group-out strategy, using a subject for testing and the remaining subjects for
training, yielding a distribution of 22 accuracies. This procedure also has the advantage of
highlighting individual differences in the dataset, showing for example whether some sub-
jects are easier or more difficult to predict. With our data, we find that repeating 80%:20%
shuffle splits 40 times and performing leave-one-out for each of the 22 subjects leads to very
similar accuracy distributions.

We consider task discrimination in two flavors: movie versus rest (two tasks) in Figure 4B and
the movie sessions individually plus rest (4 compiti) in Figure 4C. For each case, the performance
evaluated using the test set should be considered relative to perfect accuracy and chance level
(dashed line). As expected from Figure 3, the four-task discrimination is more difficult that
the two-task one. The relative performance decreases by about a half of perfect accuracy for
the four tasks compared with the two tasks. There are three interesting points coming from the
comparison of the performances between the connectivity measures.

Primo, the MLR and LDA perform much better than the 1NN for the four-task discrimination,
with both MOU-EC and FC; this does not change when using kNN instead of 1NN. This agrees
with previous results on subject identification (Pallarés et al., 2018) that are transposed to the

Network Neuroscience

353

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

T

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

present dataset in Figure 4E. For task identification, the Pearson-correlation similarity for FC
or MOU-EC does not seem the best choice, especially when the environment is complex. UN
technical point here is that LDA takes a long time to be trained for a large number of features or
for many labels (subjects in Figure 4E). Over all these results, the MLR seems the best practical
choice for a classifier, as was found for clinical data (Dadi et al., 2019).

Secondo, and more importantly, the masked FC performs worse than FC for the four tasks in
Figure 4C, demonstrating that the SC mask (con 25% density here) cannot be directly used
to preselect the most informative FC links that contribute to the good performance. In cont-
trast, MOU-EC has the same number of features as the masked FC and performs as well as FC,
even though the silhouette coefficient in Figure 3D is lower for MOU-EC than FC. Inoltre,
the MAR connectivity estimate, which extracts temporal information from BOLD signals as
MOU-EC does, gives very poor accuracy, even for the two-task classification. Partial correla-
tions are somewhat in between. For subject identification, MOU-EC performs better than FC
in Figure 4E, in line with previous results (Pallarés et al., 2018). Taken together, these results
show that the dynamic model used for MOU-EC is a representation of the BOLD signals that
extracts relevant information for both cognitive conditions and individual traits. In terms of
dimensionality, MOU-EC can be seen as a more compressed version of the BOLD information
than FC without loss of information.

Last, we consider the symmetric connectivity obtained by the heuristic optimization in
Appendix D (see the Supporting Information) that tunes the MOU model to reproduce the
zero-lag correlation FC. In Figure 4G the goodness of fit is slightly better for the heuristic
method (smaller model error measure by the matrix distance) compared with EC. It is worth
noting that the heuristic estimate leads to perfect accuracy for the “simple” classification rest
versus movie (Figure 4B). Tuttavia, the accuracy decreases compared with MOU-EC for the
four-task and subject classifications by 5% E 12%, rispettivamente (Figure 4C, E). This shows
that the choice for the connectivity estimation method (with the corresponding measure on
the BOLD activity) is crucial to efficiently extract information from the BOLD signals.

Capturing the Hierarchy of Cognitive States

The high dimensionality of connectivity measures allows for representing complex environ-
menti, such as the four tasks considered here. Beyond their ability to classify, the important
question is whether MOU-EC or FC can capture the structure of the task categories—rest on
one hand and the group of three movie sessions on the other. A similar goal was sought using
clustering on FC to identify subtypes of depression (Drysdale et al., 2017), although concerns
have been raised about the reproducibility of the results (Dinga et al., 2018). Clustering cor-
responds to unsupervised learning (without cognitive labels) and seeks a structure in the data
for a given metric as with the first two components of PCA in Figure 3B.

Invece, we rely on supervised learning and propose labels as an informed guess to a classi-
fier, then assess whether they are meaningful using cross-validation. Beyond the performances
of the two-task and four-task classifications in Figure 4B–C, each classifier thus defines a
similarity metric for the connectivity measures. This is reflected in the confusion matrices in
Figure 4D, where the classification errors (dark off-diagonal green pixels) indicate which cog-
nitive states are difficult to separate. By the naked eye, the structure of the left confusion matrix
for the MLR determines a hierarchy that corresponds to the desired one, similar to the clus-
tering in Figure 3B and C. When asked to discriminate between the two rest sessions, IL
classifier gives a negative answer. The three movie sessions are identifiable even though the

Network Neuroscience

354

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

MLR classifier makes errors between them. In contrasto, the right confusion matrix for the 1NN
does not provide useful information. Similar matrices without a clear hierarchy are obtained
for FC (not shown). This suggests that the Pearson correlation used as a similarity measure in
the 1NN is not well suited to describe the cognitive states with sufficient flexibility. In other
parole, it is less the global EC/FC profile than specific links that significantly vary across tasks
and should be the basis for building the task hierarchy. We do not enter into further details
here, leaving the comparison between unsupervised and supervised learning in estimating la-
bel hierarchies in more depth for future work. As a last comparison, the confusion matrix for
subjects in Figure 4F shows that subjects are well identified and no particular structure in the
errors is observed, indicating an absence of subject groups.

Biomarker Formed of Informative MOU-EC Links: Machine Learning Versus Statistical Testing

The general idea behind a biomarker is the indication of how and where to measure relevant
information in the brain activity for the discrimination of several conditions, here related to
cognition. The biomarkers for the two-task and four-task classifications in Figure 4B–C are
built by identifying the most informative links that contribute to correct classification, also
referred to as support network. Practically, we employ recursive feature elimination (RFE) Quello
efficiently works with the MLR classifier (Guyon, Weston, Barnhill, & Vapnik, 2002). It provides
a ranking of the features in order of importance, and the support network consists of the first
ranked links (with a cutoff when the classification performance based on those selected links
reaches a maximum). A previous study compared these support networks of informative links
for subjects and tasks to see whether the two classifications were biased one by the other
(Pallarés et al., 2018). Here we make another comparison with the two support networks in
Figure 5A, movie versus rest (nine black and two gray links) and for the four tasks (nine black
E 35 red links). The nine common links are also a hallmark of the hierarchy mentioned
in the previous section, in the sense that the more four-task biomarker extends the two-task
biomarker. Inoltre, the two RFE rankings are robustly aligned (Pearson correlation equal
A 0.46 with p value ≪ 10−10), as illustrated in Figure 5C (left plot). If we compare with the
support network for the FC links in Figure 5B, we observe a similar overlap between the two
support networks. Importantly, five FC links out of the 12 for the two-task classification do not
correspond to anatomical connections in SC, E 20 out of 30 for the four-task classification.
This suggests that FC changes reflect network-wise consequences rather than modulations of
anatomical connections between ROIs (in dashed line). Nonetheless, we find that the RFE
rankings for EC and FC are correlated, with a Pearson coefficient of 0.49 (and p value ≪ 10−10);
see the right plot in Figure 5C.

Now we discuss the pros and cons of machine learning compared with statistical testing
in finding correlates (cioè., link changes) of cognitive tasks. Formalmente, these two methods corre-
spond to distinct questions that relate to opposite mappings from measured variables to con-
ditions: changes in the variables across conditions for statistical testing and the prediction of
conditions based on the variables for machine learning. Tuttavia, they can be used to address
the same practical question, especially when interpreting data in two conditions (as here with
rest versus movie). In neuroimaging data a crucial point relates to the high dimensionality of
connectivity measures, which leads to repeated hypothesis testing—are MOU-EC values dif-
ferent across two conditions?—over the 1,180 connections. This calls for correction for mul-
tiple comparisons, which is problematic as the number of connections scales with the square
of the number of ROIs in general. We illustrate this point by calculating the p values for the
nonparametric Mann-Whitney test between rest and movie MOU-EC weights for each connec-
zione (left plot in Figure 5D). To identify links that strongly differ across conditions, we use the

Network Neuroscience

355

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 5. Biomarker for tasks and subjects. (UN) Support network of the 35 most informative
MOU-EC links for the task identification, obtained using recursive feature elimination (RFE). IL
10 black links are common to the easier discrimination between rest and movie, whereas the 29
red links are specific to the four tasks, and the gray link is specific to the two tasks. The ROI colors
indicate anatomical grouping: yellow = occipital, green = parietal, cyan = temporal, gray = central,
orange = frontal, and purple = cingulate. See also Table A.1 for the ROI labels. (B) Same as panel
A for FC links. We obtain eight common black links, three gray links for the two tasks only, E 21
red links for the four tasks only. The links in dashed lines correspond to ROI that are not connected
in SC. (C) Match between EC rankings for the two and four tasks (left plot), as well as between EC
and FC rankings for existing EC links. The Pearson correlation between the matched rankings is
indicated above. (D) Correspondence between p values for Mann-Whitney tests and RFE rankings
for the 1,180 MOU-EC links. For the two tasks, we show two significance thresholds for multiple
comparisons: the Benjamini-Hochberg correction (dashed line) and Bonferroni correction equal to
− log10(0.05/1180) (dashed-dotted line). For the four tasks, the maximum of the p values for the six
pairwise comparisons is plotted, with the same Bonferroni threshold.

significance threshold with Bonferroni correction (dashed-dotted line), here − log10(0.05/1180)
for 1,180 MOU-EC links, or better with Benjamini-Hochberg correction (Benjamini & Hochberg,
1995; dashed line). The same can be done for the four tasks (right plot), which involves
six pairwise tests between the four cognitive states. For each connection we retain the small-
est p value among the six (as it is informative for at least a pairwise discrimination). For the
Bonferroni correction, this gives 98 connections passing the significance threshold for the four-
task, to be compared with 153 for two tasks. Using Benjamini-Hochberg correction, we find
for the two classifications 554 E 498 links, rispettivamente. This does not satisfactorily reflect

Network Neuroscience

356

Modeling whole-brain effective connectivity for cognition and disease

the increase of complexity of the cognitive labels—more labels require more connections in
the biomarker—while the support network obtained using RFE in Figure 5A provides a satis-
factory description. More importantly, the comparison of the mapping between p values and
the RFE ranking in Figure 5D also illustrates that efficient classification may rely on links with
poor p values, and that this phenomenon may be stronger when the number of categories in-
creases (like labels here). This conclusion also holds when using the parametric Welch t test
instead of the nonparametric Mann-Whitney test. Beyond the details of the present example,
machine learning seems better suited than statistical testing to deal with connectivity measures
in a context of multiple labels.

Another conceptual difference between the two approaches is the Gaussian assumption
for the parameter distribution. Per esempio, DCM relies in many cases on a single generative
model with a distribution for each parameters—typically determined by a mean and a variance
for each connection weight—and selects the model that provides the best evidence for all
observed FC matrices. Invece, we estimate a single MOU-EC matrix per session, which builds
a distribution of point samples for each connection. It remains to explore the implications
of the difference in the natures of the estimate distributions and the detection of significant
changes in MOU-EC—using the Bayesian machinery for DCM and standard machine learning
in our case.

NETWORK-ORIENTED ANALYSIS FOR INTERPRETING COLLECTIVE BOLD
DYNAMICS ACROSS CONDITIONS

So far, we have shown how MOU-EC estimates can be used for the classification of cognitive
conditions using machine learning. Now we turn to the collective interpretation of MOU-EC
links as a network. Tools from graph theory have been extensively applied to explore the brain
network and understand how cognitive functions were distributed over subnetworks of ROIs.
The study of both FC and SC has revealed a hierarchical organization of modular networks that
are interconnected by hubs (Hilgetag & Grant, 2010; van den Heuvel & Hulshoff Pol, 2010;
Zamora-López, Zhou, & Kurths, 2011), which can be modulated depending on the subject’s
condition (Bertolero, Sì, & D’Esposito, 2015; Meunier et al., 2012; Senden, Goebel, & Deco,
2012).

A limitation in many SC and FC studies comes from the direct application of graph measures
defined for binary data. In such cases SC or FC matrices are often binarized using an arbitrary
threshold to obtain a graph, discarding the information conveyed by the graded values. For
SC, this gives the skeleton of strong connections. Similar methods have also been used on FC
(de Pasquale et al., 2012; Fair et al., 2007), but the use of a threshold to binarize FC seems
more arbitrary, especially as many pairs of brain regions exhibit strong correlation. Another
important aspect is often overlooked: Brain connectivity measures such as FC are inferred from
signals that have a temporal structure. This means that network analysis should take time into
account. A possibility is to analyze the evolution of snapshot networks over time using dynamic
FC based on sliding windows applied to the observed BOLD signals (Avena-Koenigsberger,
Misic, & Sporns, 2017; Khambhati, Sizemore, Betzel, & Bassett, 2017; Thompson, Brantefors,
& Fransson, 2017).

Going a step further, a particular focus has been on studying the relationship between the SC
and FC (Bettinardi et al., 2017; Sporns, Tononi, & Edelman, 2000), in particular using dynamic
models at the mesoscopic or macroscopic level (Breakspear, 2017; Deco et al., 2011; Frässle
et al., 2018; Galán, 2008; C. J. Honey, Kötter, Breakspear, & Sporns, 2007; Messé et al., 2014;
Park & Friston, 2013; Schmidt, Bakker, Hilgetag, Diesmann, & van Albada, 2018). Following,

Network Neuroscience

357

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

graph analysis can be performed on the modeled BOLD activity (Deco & Kringelbach, 2017;
Fransson, Schiffler, & Thompson, 2018). Nonetheless, it can be argued that such “integration”
measures somehow rely on the observed phenomena (in empirical or model activity) Piuttosto
than their causes. Piuttosto, dynamic models enable the application of graph measures to the
underlying connectivity that generates the dynamics, as was recently proposed (Gilson et al.,
2019; Razi et al., 2017).

Here we follow this novel direction with our adaptation of graph-like measures for the
network dynamics themselves (Gilson et al., 2019; Gilson, Kouvaris, et al., 2018), whose main
details are presented in the following; see also Appendix E in the Supporting Information for
mathematical details. This section illustrates the following aspects of network-oriented analysis
for MOU-EC:

How can we interpret collective changes in MOU-EC in their contribution to shape the
network dynamics? We introduce dynamic communicability with the notion of “integra-
tion time” that discriminates early and late interactions between ROIs in response to a
(local) perturbation in the network via MOU-EC.
Are network measures relevant for discriminating cognitive conditions? By doing so we
want to obtain dynamics-specific biomarkers.
Between the level of individual connections and the global network, are intermediate
scales relevant to interpret the MOU-EC estimates? Can we detect functional communi-
ties of ROIs, and are they task-specific?

Dynamic Flow as Graph-Like Measure for Interactions Between ROIs Across Integration Time

Our definition of dynamic flow takes advantage of the information provided by the dynamic
modello, here applied to the MOU process (Gilson, Kouvaris, et al., 2018). As illustrated in
Figure 6A, MOU-EC quantifies the instantaneous causal interactions between pairs of ROIs,
and the Σ matrix measures the spontaneous or input activity level that each ROI receives (here
represented only for ROI i). Built on those estimates, the dynamic flow measures the influence
of a “perturbation” at a source ROI i onto a target ROI k after a given delay, which we call
integration time. Importantly, it takes into account the network effect (or network response),
meaning the contribution of indirect paths in the network (from ROI i to ROI k via ROI j in the
figure). See Appendix E in the Supporting Information for the mathematical formulation based
on the network impulse response (or Green function), which is analytically tractable for the
MOU process.

The dynamic flow thus aims to capture the dynamic response of the brain to local spon-
taneous activity (or external inputs) as it propagates from region to region in the network. UN
special case of the dynamic flow—termed dynamic communicability—that only depends on
the MOU-EC (and not Σ) can also be defined assuming that all ROIs have independent sponta-
neous activity with the same intensity; it corresponds to a diagonal and homogeneous matrix
Σ. Like the flow, dynamic communicability describes directional interactions, which differs
from the symmetric interactions obtained from the direct application of graph theory to FC or
SC (Gilson et al., 2019). It is worth stressing that the dynamic flow and communicability are
graph-like measures that genuinely capture the properties of weighted networks, similar to the
previously proposed graph communicability (Estrada, 2013; Estrada & Hatano, 2008).

Considering again the fMRI dataset in Appendix A in the Supporting Information, we ex-
amine the dynamic flow at various scales in the brain network for the two conditions, movie
and rest. This complements our previous analysis of the same dataset that showed that the

Network Neuroscience

358

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Modeling whole-brain effective connectivity for cognition and disease

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

/

4
2
3
3
8
1
8
6
6
6
3
9
N
e
N
_
UN
_
0
0
1
1
7
P
D

T

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 6. Network-oriented analysis of MOU-EC using dynamic flow. (UN) Conceptual illustration
of dynamic communicability and flow. The propagation of extra activity resulting from a perturba-
zione (here applied to ROI i in purple) develops over the integration time and then fades away. IL
dashed purple curve represents the corresponding activity increase for ROI k (for legibility purpose,
the equivalent for ROI j is not displayed). This defines interactions between ROIs that are not directly
connected, like here from ROI i to ROI k. The dynamic communicability corresponds to interactions
determined by the connectivity MOU-EC only, while the dynamic flow incorporates the amplitudes
of ongoing perturbations that is quantified by Σ in the model. (B) Two matrices representing the
pairwise interactions as measured by dynamic communicability for all 66 ROIs at two integration
times, in a single subject. Initially similar to MOU-EC values, the communicability becomes homo-
geneous. (C) Total flow for rest and movie, which is the sum of the interactions between all pairs of
ROIs (cioè., sum of all matrix elements in panel B) at each integration time. The error bars indicate the
standard error of the mean over the subjects. The bottom brown horizontal line indicates where the
total flow is larger for movie than for rest with p < 0.01 in a Mann-Whitney test for each integration time step (without correction). (D) Change in input and output flow as a function of integration time, which sum all incoming and outgoing flow interactions for each ROI, respectively. The ROIs are or- dered by anatomical areas and grouped in pairs of left- and right-hemisphere ROIs. The ROIs are anatomically grouped in the same manner as in Figure 5A–B: yellow = occipital, cyan = temporal, green = parietal, gray = central, orange = frontal, and purple = cingulate from bottom to top. modulations of MOU-EC between rest and movie implemented a selection of pathways in the cortex (Gilson, Deco, et al., 2018). In addition, the stimulus load related to sensory inputs in the movie condition corresponded to an increase in Σ in the model for occipital and temporal ROIs. Recall that Σ quantifies the fluctuating BOLD activity intrinsic to each ROI that sub- sequently propagates via MOU-EC in the model. This motivates the use of the dynamic flow that incorporates Σ in order to characterize the whole-brain BOLD propagation, as compared Network Neuroscience 359 Modeling whole-brain effective connectivity for cognition and disease with dynamic communicability. Note that the “effective drive” defined in our previous study (Gilson, Deco, et al., 2018) corresponds to the flow at early integration time. The sum of flow interactions provides insight about how much activity propagates through- out the whole cortical network, which is higher for movie compared with rest in Figure 6C. An- alyzing the interactions at the ROI level, the flow changes in Figure 6D indicate differentiated effects among the ROIs, with increased/decreased listening for input flow and broadcasting for output flow. Here we observe most of the strongest increases in the output flow for oc- cipital and temporal ROIs, which makes sense since the subjects both watch and listen to the movie. A previous analysis based on MOU-EC (Senden et al., 2017) showed task-dependent changes for the outgoing connections from the rich club of ROIs that have dense anatomical connectivity, namely the precuneus (PCUN), superior parietal cortex (SP), and superior frontal cortex (SF), in agreement with previous results about the default mode network also involving the post-cingulate gyrus (PC Vatansever, Menon, Manktelow, Sahakian, & Stamatakis, 2015; Vatansever, Menon, & Stamatakis, 2017). Here we only find a slight increase of input flow for PCUN and SP, which may be explained by the fact that the task is passive viewing and listening. Integration in the Brain network Following experiments on the propagation of stimulus information from sensory areas to “high-level” brain areas in relation to being conscious of the stimuli (Carhart-Harris et al., 2016; Dehaene & Naccache, 2001), the concept of integration was defined in models by quantifying the influence between regions while being in a broader network. Following Figure 6D, we use the dynamic flow to quantify how the BOLD activity propagates from the occipital and tempo- ral ROIs, which exhibit an increased visual and auditory stimulus load in movie, to the rest of the brain. We thus consider the anatomical ROI groups in Figure 7A (same as Figure 5), where the stimulus load is represented by the purple perturbation applied to OCC and TMP (Gilson, Deco, et al., 2018). Figure 7B compares the summed flow between the ROI groups for rest and movie (in black and brown as in Figure 6C). This reveals preferred pathways to the parietal and frontal ROIs (PAR and FRNT) when sensory information is integrated, as represented by the thick arrows in Figure 7A. The machine-learning equivalent of the statistical testing for the summed flow between subnetworks in Figure 7B gives the green violin plots in Figure 7D. Here a good accuracy means that the bidirectional flow summed between all considered ROIs is strongly modulated between rest and movie. The fact that the results are close to chance level indicates strong variability in the overall flow increase across subjects. A different question, more related to biomarkers, is to which extent the detailed pattern of flow (multivariate flow, in orange) vary between movie and rest. This yields robust classification, which strikingly differs from the uni- variate (summed) flow. This indicates that the modification of interactions between ROIs is diverse beyond a simple global increase, hinting at the selection of specific pathways. The flow-based classification even outperforms MOU-EC (in blue) for the same matrix elements when focusing on particular ROI groups; see Figure 7C for details. The discrepancy between the flow and MOU-EC shows the importance of network effects, for all three bidirectional path- ways in Figure 7D. The same classification can be performed with the input and output flows; see Figure 7E. For interpretation purpose, the better performance for incoming than outgoing MOU-EC (pink versus cyan) suggests that ROIs change their pattern of listening/broadcasting communication, especially for PAR and FRNT. However, the overall effect is less pronounced when considering the dynamic flow that incorporates network effects (red versus purple). These Network Neuroscience 360 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. Integration measured by dynamic flow. (A) Example subset of anatomical ROI groups: occipital (OCC), temporal (TMP), parietal (PAR), central (CNT), and frontal (FRNT). (B) Comparison between the flow between the rest (in black) and movie (in brown) conditions. Similar to Figure 6C, the curves are averages over subjects and corresponding sessions with error bars indicating the stan- dard error of the mean. Each row corresponds to the flow summed over all ROIs of the indicated groups (bidirectionally); see also panel A where thick arrows correspond to strong increase in flow for the movie condition. (C) Example of construction of features for the following classification. At the top, the EC matrix corresponds to connections for ROIs in groups and gives multivariate features when vectorized. Below, the flow matrix for the same ROIs equivalently gives multivariate features or can also be summed to obtain a univariate feature. Moreover, the flow matrix can be summed over columns or rows to obtain the input and output flows, here taking all 66 ROIs as sources (y-axis of the matrix) or targets (x-axis). (D) Flow-based classification to discriminate rest versus movie in multivariate (orange violin plots) and univariate (green), compared with EC-based classi- fication (blue). The x-axis indicates the ROI subgroups for which the flow interactions are selected. The dashed black lines indicate chance level, at 60% as in Figure 4B. (E) Same as panel D for the input flow (in red) and output flow (purple), which are compared with the input and output EC strengths (pink and cyan, respectively). Network Neuroscience 361 Modeling whole-brain effective connectivity for cognition and disease results show that dynamics-based biomarkers that describe the propagation of BOLD activity can be built in the same way as connectivity-based biomarkers for the discrimination of cog- nitive tasks. Together with the distributed signature found in Figure 5A, they also highlight the need for a whole-brain approach to understand the cortical reconfiguration (Betti et al., 2013), contrasting with previous studies relying on hypothesis testing for a priori selected ROIs (Ciuciu et al., 2014; Daunizeau, Stephan, & Friston, 2012; Emerson, Short, Lin, Gilmore, & Gao, 2015; Goebel et al., 2003). Detection of Functional Communities Determined by Dynamic Flow In parallel to integration, the concept of complexity has been often used to differentiate brain states (Barnett et al., 2009; Tononi, Edelman, & Sporns, 1998; Tononi et al., 1994; Zamora- López, Chen, Deco, Kringelbach, & Zhou, 2016). Intuitively, complexity measures quantify the diversity of organizational motifs in a network, in the range of interest between the trivial extremes of full disconnectivity and full connectivity. A proxy for complexity is the detection of ROI communities because modular networks are a stereotypical model for complex networks, as was observed with SC (Zamora-López et al., 2011). Here we use the dynamic flow as a basis for the functional ROI communities in a data-driven manner, which contrasts with the anatomical grouping in Figure 7A. Such methods developed initially for graphs with a metric called modularity based on weights (Newman, 2006). Here we consider communities deter- mined by the flow, namely ROIs with strong exchange of activity in the estimated dynamics (Gilson, Kouvaris, et al., 2018). Figure 8A displays the evolution of communities over integration time for rest and movie. Strong coparticipation values indicate the robustness of the community structure across sub- jects. It shows a merging of almost all ROIs that eventually exchange flow in an even man- ner. This agrees with our previous results for resting state only and a different parcellation (Gilson et al., 2019). This speaks to a transition from segregated processing (within each diag- onal block of left matrices) to a global integration. The number of communities can be taken as another proxy for the complexity in the brain network, and our approach provides a dynamical perspective about it. The community merging goes hand in hand with the homogenization of the flow matrix in Figure 8B, as quantified by the diversity of the matrix elements in the flow matrix that decreases and eventually stabilizes (Gilson, Kouvaris, et al., 2018). In our data the diversity is slightly higher for movie compared with rest. Going a step further, we can examine the difference between the community structures of the two conditions; see the bottom row in Figure 8A. This shows that the changes in dynamic flow for specific pairs of ROIs between rest and movie (Figure 7B, D, and E) have an important collective impact. The strongest differences appear when the network effects are very strong at t = 4 TRs. This is confirmed by Figure 8C, where classification shows that the dynamic flow is most different between rest and movie at integration times corresponding to strong network effects (the arrow indicates the start of the plateau for maximum performance). These results speak to an intermediate organization of groups of ROIs between the local and global scales, which can be captured using our network-oriented analysis of MOU-EC. CONCLUSIONS This article illustrates how a model-based approach to whole-brain fMRI analysis combines the desired properties of predictability and interpretability. This goes beyond the goodness of fit for fMRI signals that is commonly used to evaluate and compare generative models. To do so, our framework links tools and concepts from dynamic systems, machine learning, and Network Neuroscience 362 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 8. Community detection. (A) Communities correspond to ROIs that bidirectionally ex- change strong flow. Darker orange pixels indicate stable communities across the subjects for each condition. The top row corresponds to rest and the middle row to movie for three integration times. The bottom row displays the significant increases (in red) and decreases (blue) of the community coparticipation values for movie with respect to rest. Here statistical testing is performed on each coparticipation value by using the Mann-Whitney test with p < 0.01 (without correction). The ROI ordering corresponds to the early community structure for rest. (B) Flow diversity for rest (black curve) and movie (in brown) measuring the heterogeneity within each flow matrix when integra- tion time increases; see Equation E.4. It is a proxy for the “complexity” of interactions between ROIs; for details see Gilson et al. (2019) and Gilson, Kouvaris, et al. (2018). (C) Rest-versus-movie classification based on flow (whole-brain version of multivariate flow in Figure 7C) as a function of integration time and comparison with EC-based classification. Starting t = 4 TRs indicated by the arrow, the performance reaches a maximum plateau. Here the train test consists of 20% of the samples and the test set 80% (the converse compared with before) in order to capture the strongest changes between rest and movie with classification. This exaggerates the evolution over integration time of the performance, which is lower compared with the previous plots. Network Neuroscience 363 Modeling whole-brain effective connectivity for cognition and disease network theory. This results in a consistent pipeline with controlled hypotheses because we use the same whole-brain dynamic model from the estimation to the analysis. General key points for analysis of multivariate neuroimaging data and corresponding results using MOU-EC General key points A dynamic model is a hypothesis on the structure of the data and is useful to com- bine several types of data. Fitting a dynamic network model to time series captures their dynamics and en- ables the characterization of network properties with time involved in the anal- ysis. Adequate machine-learning tools (with cross-validation and feature selection to build biomarkers) are well adapted to re- late multivariate neuroimaging data like fMRI to cognitive states or neuropatholo- gies. Graph-like measures can be applied at multiple scales from the connec- tion/node level to communities and global level in the network. Presented results using MOU-EC The MOU process provides a practically use- ful balance between the richness of the gen- erated BOLD dynamics, the robustness of the model optimization, and intuition for inter- pretability (roles of parameters in the model). The constraint of MOU-EC topology enforces the “explanation” of changes in BOLD sig- nals by modulations of anatomical connec- tions (Figure 5A compared with Figure 5B). MOU-EC describes causal relationships in the network model that collectively explain the observed BOLD covariance structure, involv- ing time lags. The MOU-EC estimates can fur- ther be interpreted in terms of integration in the network using dynamic communicability and flow (Figure 6). Both MOU-EC and dynamic flow can be used for prediction (Figures 4B–C, 5A, and 7D–E), as well as exploring the hierarchy of cognitive states (Figure 4D). The comparison of classification performance for tasks using dynamic flow provides in- sight about the adequate description level of changes in the network; for example, ROI- based measures are sufficient to discriminate the rest and movie conditions (Figure 7D–E). Spatiotemporal BOLD Structure By fitting the dynamic model to the spatiotemporal covariance structure of the BOLD signals, our approach captures the BOLD dynamics averaged over each fMRI session. The estimated MOU-EC can be seen as a “projection” of the BOLD signals on anatomically constrained con- nectivity, thereby characterizing the dynamical state of the brain. In contrast, analyses based on the static FC can be related to a linear Gaussian model, and thus do not take the tem- poral dimension into account (i.e., BOLD values are considered as i.i.d. variables). Dynamic FC methods have been developed to incorporate time in the analysis (Cabral et al., 2017; Gonzalez-Castillo & Bandettini, 2017; Park & Friston, 2013; Preti et al., 2017), but they do not genuinely capture the propagating nature of BOLD signals. Dynamic causal models have just been adapted to deal with whole-brain fMRI data (Frässle et al., 2018; Park, Friston, Pae, Park, & Razi, 2018; Razi et al., 2017), and it will be interesting to compare the estimated connec- tivities. It is also still unclear how short sessions or observation windows can be to robustly characterize dynamical states when calculating EC estimates or MAR-like coupling matrices Network Neuroscience 364 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease in HMMs (Bolton et al., 2018; Vidaurre et al., 2018), in comparison to dynamic FC methods that are typically used with windows of 30 to 60 TRs. Biomarkers for Cognition and Neuropathologies The robust estimation of the (multivariate) parameters allows for a powerful representation of cognitive states by the MOU-EC estimates (Figure 4), as well as the extraction of task-specific biomarkers (Figure 5). An important point considering connectivity measures is that machine learning solves the problem of multiple comparisons: Instead of determining p values and then a threshold for connections with significant changes, we can characterize which MOU-EC links—as features—contribute to the correct classification. It has been recently advocated that machine learning can be used to avoid “excessive reductionism,” namely linking brain ac- tivity in localized regions to narrow experimental protocols in a way that cannot generalize to more complex protocols (Varoquaux & Poldrack, 2019). Although the focus has been on machine-learning techniques, we remind readers that hypothesis testing of significant changes for preselected ROIs or links can be performed in our framework (see Figure 7B with the dy- namic flow). In that case, whole-brain changes can also provide a baseline reference for the considered links or ROIs. On the technical side, it remains to be explored how the classification performance is affected by the resolution of various parcellations (Craddock, James, Holtzheimer, Hu, & Mayberg, 2012; Eickhoff, Thirion, Varoquaux, & Bzdok, 2015; Glasser et al., 2016), as was recently done with FC-like connectivity measures (Dadi et al., 2019). The trade-off to solve is between the richness of the connectivity measure (more links can reproduce richer environ- ments) and their robustness (more parameters may result in noisier estimation). The alignment of distinct datasets with various MRI protocols also remains a difficult question for practical application to large datasets (Varoquaux et al., 2018). In parallel to the study of cognition, the presented framework can be applied to neu- ropathologies with the aim to inform clinical diagnosis (Matthews & Hampshire, 2016). The rationale is that BOLD activity specifically reflects neuropathologies, even in the resting state (Greicius, 2008; Hohenfeld et al., 2018). If SC is increasingly used for strokes or Alzheimer’s disease that strongly impact the brain anatomy, fMRI may provide additional information (Habib et al., 2017; Siegel et al., 2016). Other diseases like depression (Drysdale et al., 2017) or some motor disorders (Rowe & Siebner, 2012) may be better investigated using functional imaging. Importantly, many neural diseases are likely to affect multiple brain regions and thus require adequate tools to capture their distributed nature. Another direction where machine learning is a key tool is the development of personalized medicine, adapting the models to individual patients beyond group analyses (Yahata, Kasai, & Kawato, 2017). Network-Oriented Analysis of Dynamics The network analysis for our dynamic model relies on the dynamic flow, a graph-like con- nectivity measure that describes the integration of propagating activity at multiple scales in the network (Figures 7 and 8). In particular, small changes in EC that are not individually significant can collectively induce large changes in the dynamic flow, especially when feed- back loops are involved. In this sense, the dynamic flow quantitatively captures the interplay between parameters, so the resulting communication cannot always be simply understood at the level of single estimated parameters. As an example, many small changes in EC (below significance level) may collectively result in a strong dynamical effect, as seen for Task A in Figure 9. Strong coordinated changes in EC result in large changes in the dynamics (Task B). Network Neuroscience 365 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease Figure 9. Schematic representation of the extraction of biomarkers for three tasks compared with rest. Connection-wise biomarkers correspond to changes in EC, while the bottom row refers to biomarkers for changes in dynamic flow. Tasks A and B correspond to two modulations of the connectivity, which lead to similar changes in the dynamic flow (stronger for B). For task C, extra inputs are received by two nodes, which increase the dynamic flow towards the corresponding two target nodes. Moreover, changes in input properties may only be captured by the dynamics, in particular when the connectivity does not change (Task C). Building biomarkers that capture network effects is important to make use of the multivariate nature of the fMRI data. This is important when interpreting data in terms of concepts such as integration, segregation, and complexity (Deco, Tononi, Boly, & Kringelbach, 2015; Dehaene & Naccache, 2001; Tononi et al., 1998; Zamora-López et al., 2016). An interesting direction for future work is the study of directional properties of the flow, especially in the characterization of functional communities. Limitations and Future Work As a first warning, we remind readers that any interpretation of BOLD in terms of brain com- munication relies on the assumption that changes in neuronal activity are reliably reflected in the BOLD signals, which is still under debate (Goense & Logothetis, 2008; Y. He et al., 2018; Matsui et al., 2018). In practice, the preprocessing of fMRI signals must strive to increase the signal-to-noise ratio (Parkes et al., 2018; Power et al., 2018). Recall also that causal relationships between brain regions come from the directed connec- tivity in the model, whose “best” parameterization is estimated from the data. The estimation procedure is crucial, in particular for the dynamic flow here since the asymmetry of MOU-EC strongly affects the resulting activity propagation in the model. Moreover, without a proper ex- perimental interaction with the brain activity like using stimulation, the notion of causality is subject to the initial model assumption (Hughes, 1997; Kaplan, 2011). This remark also applies to other methods for directed connectivity, such as Granger causality and DCM (Valdes-Sosa et al., 2011). A key distinction of our approach compared with DCM is that our MOU-EC (or FC) esti- mates are calculated for each fMRI session, so we obtain a sample distribution for connection Network Neuroscience 366 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease weight over all subjects for each condition (e.g., task). In contrast, DCM usually considers a single model per condition that aims to represent the variability over subjects with a parametric distribution (mean and variance) for each connection weight. The limitations and advantages of both approaches in terms of statistical power and generalizability remain to be practically compared, especially for large datasets. Regarding the hemodynamics and explicit HRF modeling discussed at the end of the sec- tion presenting the MOU model, a quantitative comparison between MOU-EC, DCM, and Granger causality analysis to extract biomarkers or interpret fMRI data in terms of neuronal coupling is necessary in the future. A particular point concerns the observed heterogeneity of HRF across different brain regions and how it affects the estimated connectivity and its directionality (Handwerker, Ollinger, & D’Esposito, 2004). Previous works also suggest that the HRF is important for the reliability of connectivity analysis (Gitelman et al., 2003; Olszowy et al., 2019). This may increase the number of parameters in the model, so the robustness of the estimation should be verified using both forward modeling in synthetic whole-brain networks (Smith et al., 2011) and with classification from real data with known categories (e.g., subjects with several sessions each). A first step could be to extend the MOU-EC as a state-space model with a first-order filter for HRF (Sauvage et al., 2017). l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00117. The analysis tools have been organized in a package written in the open-source language Python: https://github.com/mb-BCA/pyMOU (Gilson, Zamora-López, & Insabato, 2019) for the MOU-EC estimation and https://github.com/mb-BCA/NetDynFlow (Zamora-López & Gilson, 2019) for dynamic communicability and flow. The code to reproduce some figures in this paper using data available on https://github.com/mb-BCA/notebooks_review2019. The classification uses the library scikit-learn (Abraham et al., 2014). AUTHOR CONTRIBUTIONS / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t Matthieu Gilson: Conceptualization; Methodology; Software; Writing - Original Draft. Gorka Zamora-López: Conceptualization; Methodology; Software; Writing - Original Draft. Vicente Pallarés: Conceptualization; Methodology; Software; Writing - Original Draft. Mohit H. Adhikari: Conceptualization; Methodology; Software; Writing - Original Draft. Mario Senden: Conceptualization; Methodology; Software; Writing - Original Draft. Adrià Tauste Campo: Conceptualization; Methodology; Software; Writing - Original Draft. Dante Mantini: Resources; Writing - Review & Editing. Maurizio Corbetta: Resources; Writing - Review & Editing. Gustavo Deco: Funding acquisition; Writing - Review & Editing. Andrea Insabato: Conceptualization; Methodology; Software; Writing - Original Draft. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 FUNDING INFORMATION Mario Senden, Horizon 2020 Framework Programme (http://dx.doi.org/10.13039/100010661), Award ID: Human Brain Project SGA2 No. 785907. Gorka Zamora-López, Horizon 2020 Framework Programme (http://dx.doi.org/10.13039/100010661), Award ID: Human Brain Project SGA2 No. 785907. Matthieu Gilson, Horizon 2020 Framework Programme, Award ID: Human Brain Project SGA2 No. 785907. Gustavo Deco, Horizon 2020 Framework Pro- gramme (http://dx.doi.org/10.13039/100010661), Award ID: Human Brain Project SGA2 No. 785907. Andrea Insabato, H2020 Marie Skłodowska-Curie Actions (http://dx.doi.org/10. 13039/100010665), Award ID: MSCA grant agreement No. 841684. Gustavo Deco, Network Neuroscience 367 Modeling whole-brain effective connectivity for cognition and disease Agencia Estatal de Investigación (http://dx.doi.org/10.13039/501100011033), Award ID: PSI2016-75688-P. Gustavo Deco, Consell Català de Recercai Innovació (http://dx.doi.org/10. 13039/501100002810), Award ID: AGAUR Programme 2017 899 SGR 1545. Maurizio Corbetta, Italian Ministry of Research (MIUR), Award ID: Progetto Dipartimenti di Eccellenza Neuro-DiP. Maurizio Corbetta, Horizon 2020 Framework Programme (http://dx.doi.org/10. 13039/100010661), Award ID: FLAG-ERA JTC. REFERENCES Abraham, A., Pedregosa, F., Eickenberg, M., Gervais, P., Mueller, A., Kossaifi, J., . . . Varoquaux, G. (2014). Machine learning for neuroimaging with scikit-learn. Frontiers in Neuroinformatics, 8, 14. https://doi.org/10.3389/fninf.2014.00014 Aertsen, A. M., Gerstein, G. L., Habib, M. K., & Palm, G. (1989). Dynamics of neuronal firing correlation: Modulation of “effective connectivity.” Journal of Neurophysiology, 61, 900–917. Amari, S.-I. (1998). Natural gradient works efficiently in learn- ing. Neural Computation, 10, 251–276. https://doi.org/10.1162/ 089976698300017746 Amico, E., & Goñi, J. (2018). The quest for identifiability in human functional connectomes. Scientific Reports, 8, 8254. https://doi. org/10.1038/s41598-018-25089-1 Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2017). Commu- nication dynamics in complex brain networks. Nature Reviews Neuroscience, 19, 17–33. https://doi.org/10.1038/nrn.2017.149 Barnett, L., Buckley, C. L., & Bullock, S. (2009). Neural complex- ity and structural connectivity. Physical Review E, 79, 051914. https://doi.org/10.1103/PhysRevE.79.051914 Barnett, L., & Seth, A. K. (2015). Granger causality for state-space models. Physical Review E, 91, 040101. https://doi.org/10.1103/ PhysRevE.91.040101 Bartels, A., Logothetis, N. K., & Moutoussis, K. (2008). fMRI and its interpretations: An illustration on directional selectivity in area v5/mt. Trends in Neuroscience,, 31, 444–453. https://doi.org/10. 1016/j.tins.2008.06.004 Becker, R., Reinacher, M., Freyer, F., Villringer, A., & Ritter, P. (2011). How ongoing neuronal oscillations account for evoked fMRI vari- ability. Journal of Neuroscience, 31, 11016–11027. https://doi. org/10.1523/JNEUROSCI.0210-11.2011 Benjamini, Y., & Hochberg, Y. (1995). Controlling the false discov- ery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society, Series B, 57, 289–300. Benzi, M., & Klymko, C. (2013). Total communicability as a central- ity measure. Journal of Complex Networks, 1, 124–149. https:// doi.org/10.1093/comnet/cnt007 Bertolero, M. A., Yeo, B. T. T., & D’Esposito, M. (2015). The modular and integrative functional architecture of the human brain. Pro- ceedings of the National Academy of Sciences, 112, 6798–6807. https://doi.org/10.1073/pnas.1510619112 Betti, V., Della Penna, S., de Pasquale, F., Mantini, D., Marzetti, L., Romani, G. L., & Corbetta, M. (2013). Natural scenes viewing al- ters the dynamics of functional connectivity in the human brain. Neuron, 79, 782–797. Bettinardi, R. G., Deco, G., Karlaftis, V. M., Van Hartevelt, T. J., Fernandes, H. M., Kourtzi, Z., . . . Zamora-López, G. (2017). How structure sculpts function: Unveiling the contribution of anatom- ical connectivity to the brain’s spontaneous correlation structure. Chaos, 27, 047409. https://doi.org/10.1063/1.4980099 Bielczyk, N. Z., Uithol, S., van Mourik, T., Anderson, P., Glennon, J. C., & Buitelaar, J. K. (2019). Disentangling causal webs in the brain using functional magnetic resonance imaging: A review of current approaches. Network Neuroscience, 3, 237–273. https:// doi.org/10.1162/netn_a_00062 Biswal, B. B. (2012). Resting state fMRI: A personal history. Neuro- Image, 62, 938–944. https://doi.org/10.1016/j.neuroimage.2012. 01.090 Bolton, T. A. W., Tarun, A., Sterpenich, V., Schwartz, S., & Van De Ville, D. (2018). Interactions between large-scale functional brain networks are captured by sparse coupled HMMs. IEEE Transactions on Medical Imaging, 37, 230–240. https://doi.org/ 10.1109/TMI.2017.2755369 Boynton, G. M., Engel, S. A., Glover, G. H., & Heeger, D. J. (1996). Linear systems analysis of functional magnetic resonance imag- ing in human V1. Journal of Neuroscience, 16, 4207–4221. Breakspear, M. (2017). Dynamic models of large-scale brain activ- ity. Nature Neuroscience, 20, 340–352. https://doi.org/10.1038/ nn.4497 Brodersen, K. H., Schofield, T. M., Leff, A. P., Ong, C. S., Lomakina, E. I., Buhmann, J. M., & Stephan, K. E. (2011). Generative embed- ding for model-based classification of fMRI data. PLoS Compu- tational Biology, 7, e1002079. https://doi.org/10.1371/journal. pcbi.1002079 Buckner, R. L. (2010). Human functional connectivity: New tools, unresolved questions. Proceedings of the National Academy of Science, 107, 10769–10770. https://doi.org/10.1073/pnas. 1005987107 Burkitt, A. N. (2006). A review of the integrate-and-fire neuron model: I. Homogeneous synaptic input. Biological Cybernetics, 95, 1–19. https://doi.org/10.1007/s00422-006-0068-6 Cabral, J., Hugues, E., Sporns, O., & Deco, G. (2011). Role of lo- cal network oscillations in resting-state functional connectivity. NeuroImage, 57, 130–139. Cabral, J., Vidaurre, D., Marques, P., Magalhães, R., Silva Moreira, P., Miguel Soares, J., . . . Kringelbach, M. L. (2017). Cognitive per- formance in healthy older adults relates to spontaneous switching between states of functional connectivity during rest. Scientific Reports, 7, 5135. https://doi.org/10.1038/s41598-017-05425-7 Calhoun, V. D., Lawrie, S. M., Mourao-Miranda, J., & Stephan, K. E. (2017). Prediction of individual differences from neuroimag- ing data. Neuroimage, 145, 135–136. https://doi.org/10.1016/j. neuroimage.2016.12.012 Calhoun, V. D., Liu, J., & Adali, T. (2009). A review of group ICA for fMRI data and ICA for joint inference of imaging, genetic, and Network Neuroscience 368 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease ERP data. Neuroimage, 45, S163–172. https://doi.org/10.1016/ j.neuroimage.2008.10.057 Carhart-Harris, R. L., Muthukumaraswamy, S., Roseman, L., Kaelen, M., Droog, W., Murphy, K., . . . Nutt, D. J. (2016). Neural correlates of the LSD experience revealed by multimodal neu- roimaging. Proceedings of the National Academy of Sciences, 113, 4853–4858. https://doi.org/10.1073/pnas.1518377113 Chang, L., Gianaros, P., Manuck, S., Krishnan, A., & Wager, T. (2015). A sensitive and specific neural signature for picture- induced negative affect. PLoS Biology, 13, e1002180. Ciuciu, P., Abry, P., & He, B. J. (2014). Interplay between functional connectivity and scale-free dynamics in intrinsic fMRI networks. NeuroImage, 95, 248–263. Cohen, J. R. (2018). The behavioral and cognitive relevance of time- varying, dynamic changes in functional connectivity. NeuroIm- age, 180, 515–525. https://doi.org/10.1016/j.neuroimage.2017. 09.036 Cordes, D., Haughton, V. M., Arfanakis, K., Wendt, G. J., Turski, P. A., Moritz, C. H., . . . Meyerand, M. E. (2000). Mapping func- tionally related regions of brain with functional connectivity MR imaging. American Journal of Neuroradiology, 21, 1636–1644. Craddock, R. C., James, G. A., Holtzheimer, P. E., Hu, X. P., & Mayberg, H. S. (2012). A whole brain fMRI atlas generated via spatially constrained spectral clustering. Human Brain Mapping, 33, 1914–1928. . Dadi, K., Rahim, M., Abraham, A., Chyzhyk, D., Milham, M., Thirion, B., . Alzheimer’s Disease Neuroimaging Initia- tive (2019). Benchmarking functional connectome-based predic- tive models for resting-state fMRI. NeuroImage, 192, 115–134. https://doi.org/10.1016/j.neuroimage.2019.02.062 . Daunizeau, J., Stephan, K., & Friston, K. (2012). Stochastic dynamic causal modelling of fMRI data: Should we care about neural noise? NeuroImage, 62, 464–481. David, O., Guillemain, I., Saillet, S., Reyt, S., Deransart, C., Segebarth, C., & Depaulis, A. (2008). Identifying neural drivers with func- tional MRI: An electrophysiological validation. PLoS Biology, 6, 2683–2697. https://doi.org/10.1371/journal.pbio.0060315 d’Avossa, G., Shulman, G. L., & Corbetta, M. (2003). Identification of cerebral networks by classification of the shape of bold re- sponses. Journal of Neurophysiology, 90, 360–371. https://doi. org/10.1152/jn.01040.2002 Deco, G., Jirsa, V., & McIntosh, A. (2011). Emerging concepts for the dynamical organization of resting-state activity in the brain. Nature Reviews Neuroscience, 12, 43–56. Deco, G., & Kringelbach, M. L. (2017). Hierarchy of informa- tion processing in the brain: A novel “intrinsic ignition” frame- work. Neuron, 94, 961–968. https://doi.org/10.1016/j.neuron. 2017.03.028 Deco, G., Ponce-Alvarez, A., Mantini, D., Romani, G., Hagmann, P., & Corbetta, M. (2013). Resting-state functional connectivity emerges from structurally and dynamically shaped slow linear fluctuations. Journal of Neuroscience, 33, 11239–11252. Deco, G., Tononi, G., Boly, M., & Kringelbach, M. L. (2015). Re- thinking segregation and integration: Contributions of whole- brain modelling. Nature Reviews Neuroscience, 16, 430–439. https://doi.org/10.1038/nrn3963 Dehaene, S., & Naccache, L. (2001). Towards a cognitive neu- roscience of consciousness: Basic evidence and a workspace framework. Cognition, 79, 1–37. Demirta¸s, M., Ponce-Alvarez, A., Gilson, M., Hagmann, P., Mantini, D., Betti, V., . . . Deco, G. (2019). Distinct modes of functional connectivity induced by movie-watching. NeuroImage, 184, 335–348. https://doi.org/10.1016/j.neuroimage.2018.09.042 de Pasquale, F., Della Penna, S., Snyder, A. Z., Marzetti, L., Pizzella, V., Romani, G. L., & Corbetta, M. (2012). A cortical core for dy- namic integration of functional networks in the resting human brain. Neuron, 74, 753–764. Dinga, R., Schmaal, L., Penninx, B., van Tol, M. J., Veltman, D., van Velzen, L., . . . Marquand, A. (2018). Evaluating the evidence for biotypes of depression: Attempted replication of Drysdale et.al. 2017. bioRxiv. https://doi.org/10.1101/416321 Drysdale, A. T., Grosenick, L., Downar, J., Dunlop, K., Mansouri, F., Meng, Y., . . . Liston, C. (2017). Resting-state connectivity biomarkers define neurophysiological subtypes of depression. Nature Medicine, 23, 28–38. https://doi.org/10.1038/nm.4246 Eickhoff, S. B., Thirion, B., Varoquaux, G., & Bzdok, D. (2015). Connectivity-based parcellation: Critique and implications. Hu- man Brain Mapping, 36, 4771–4792. Ekstrom, A. (2010). How and when the fMRI BOLD signal relates to underlying neural activity: The danger in dissociation. Brain Research Reviews, 62, 233–244. Emerson, R. W., Short, S. J., Lin, W., Gilmore, J. H., & Gao, W. (2015). Network-level connectivity dynamics of movie watching in 6-year-old children. Frontiers in Human Neuroscience, 9, 631. Estrada, E. (2013). Communicability in temporal networks. Physi- cal Review E, 88, 042811. https://doi.org/10.1103/PhysRevE.88. 042811 Estrada, E., & Hatano, N. (2008). Communicability in complex net- works. Physical Review E, 77, 036111. https://doi.org/10.1103/ PhysRevE.77.036111 Faes, L., Stramaglia, S., & Marinazzo, D. (2017). On the inter- pretability and computational reliability of frequency-domain granger causality. F1000Research, 6, 1710. https://doi.org/10. 12688/f1000research.12694.1 Fair, D. A., Dosenbach, N. U. F., Church, J. A., Cohen, A. L., Brahmbhatt, S., Miezin, F. M., . . . Schlaggar, B. L. (2007). De- velopment of distinct control networks through segregation and integration. Proceedings of the National Academy of Sciences, 104, 13507–13512. https://doi.org/10.1073/pnas.0705843104 Finn, E. S., Shen, X., Scheinost, D., Rosenberg, M. D., Huang, J., Chun, M. M., . . . Constable, R. T. (2015). Functional connectome fingerprinting: Identifying individuals using patterns of brain con- nectivity. Nature Neuroscience, 18, 1664–1671. https://doi.org/ 10.1038/nn.4135 Fransson, P., Schiffler, B. C., & Thompson, W. H. (2018). Brain network segregation and integration during an epoch-related working memory fMRI experiment. NeuroImage, 178, 147–161. https://doi.org/10.1016/j.neuroimage.2018.05.040 Frässle, S., Lomakina, E. I., Kasper, L., Manjaly, Z. M., Leff, A., Pruessmann, K. P., . . . Stephan, K. E. (2018). A generative model of whole-brain effective connectivity. NeuroImage. https://doi. org/10.1016/j.neuroimage.2018.05.058 Network Neuroscience 369 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease Fries, P. (2005). A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends in Cogni- tive Sciences, 9, 474–480. Friston, K. (2011). Functional and effective connectivity: A review. Brain Connectivity, 1, 8. Friston, K., Mechelli, A., Turner, R., & Price, C. (2000). Nonlinear re- sponses in fMRI: The Balloon Model, Volterra kernels, and other hemodynamics. NeuroImage, 12, 466–477. Friston, K., Moran, R., & Seth, A. K. (2013). Analysing connectivity with granger causality and dynamic causal modelling. Current Opinion in Neurobiology, 23, 172–178. https://doi.org/10.1016/ j.conb.2012.11.010 Friston, K. J., Harrison, L., & Penny, W. (2003). Dynamic causal modelling. Neuroimage, 19, 1273–1302. Friston, K. J., Kahan, J., Biswal, B., & Razi, A. (2014). A DCM for resting state fMRI. NeuroImage, 94, 396–407. https://doi.org/10. 1016/j.neuroimage.2013.12.009 Galán, R. F. (2008). On how network architecture determines the dominant patterns of spontaneous neural activity. PLoS ONE, 3, e2148. https://doi.org/10.1371/journal.pone.0002148 Gillebert, C. R., & Mantini, D. (2013). Functional connectivity in the normal and injured brain. Neuroscientist, 19, 509–522. https:// doi.org/10.1177/1073858412463168 Gilson, M. (2018). Analysis of fMRI data using noise-diffusion net- work models: A new covariance-coding perspective. Biological Cybernetics. https://doi.org/10.1007/s00422-017-0741-y Gilson, M. (2019). PyMOU: Light package for simulation and con- nectivity estimation using the multivariate Ornstein-Uhlenbeck process (MOU). GitHub. https://github.com/mb-BCA/pyMOU Gilson, M., Deco, G., Friston, K., Hagmann, P., Mantini, D., Betti, V., . . . Corbetta, M. (2018). Effective connectivity inferred from fMRI transition dynamics during movie viewing points to a bal- anced reconfiguration of cortical interactions. NeuroImage, 180, 534–546. https://doi.org/10.1016/j.neuroimage.2017.09.061 Gilson, M., Kouvaris, N. E., Deco, G., Mangin, J.-F., Poupon, C., Lefranc, S., & Zamora-López, G. (2019). Network analysis of whole-brain fMRI dynamics: A new framework based on dy- namic communicability. NeuroImage, 201, e116007. https://doi. org/10.1016/j.neuroimage.2019.116007 Gilson, M., Kouvaris, N. E., Deco, G., & Zamora-López, G. (2018). Framework based on communicability and flow to analyze com- plex network dynamics. Physical Review E, 97, 052301. https:// doi.org/10.1103/PhysRevE.97.052301 Gilson, M., Moreno-Bote, R., Ponce-Alvarez, A., Ritter, P., & Deco, G. (2016). Estimation of directed effective connectivity from fMRI functional connectivity hints at asymmetries of cortical connec- tome. PLoS Computational Biology, 12, e1004762. Gilson, M., Zamora-López, G., & Insabato, A. (2019). pyMOU: Light package for simulation and connectivity estimation us- ing the multivariate Ornstein-Uhlenbeck process (MOU). https:// github.com/mb-BCA/pyMOU Gitelman, D. R., Penny, W. D., Ashburner, J., & Friston, K. J. (2003). Modeling regional and psychophysiologic interactions in fMRI: The importance of hemodynamic deconvolution. NeuroImage, 19, 200–207. Glasser, M. F., Coalson, T. S., Robinson, E. C., Hacker, C. D., Harwell, J., Yacoub, E., . . . Van Essen, D. C. (2016). A multi-modal par- cellation of human cerebral cortex. Nature, 536, 171–178. Goebel, R., Roebroeck, A., Kim, D., & Formisano, E. (2003). In- vestigating directed cortical interactions in time-resolved fMRI data using vector autoregressive modeling and Granger causality mapping. Magnetic Resonance Imaging, 21, 1251–1261. Goense, J. B. M., & Logothetis, N. K. (2008). Neurophysiology of the bold fMRI signal in awake monkeys. Current Biology, 18(9), 631–640. https://doi.org/10.1016/j.cub.2008.03.054 Gonzalez-Castillo, J., & Bandettini, P. A. (2017). Task-based dy- namic functional connectivity: Recent findings and open ques- tions. NeuroImage. https://doi.org/10.1016/j.neuroimage.2017. 08.006 Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson, M. E., Buchanan, L. C., Saad, Z. S., & Bandettini, P. A. (2015). Tracking ongoing cognition in individuals using brief, whole- brain functional connectivity patterns. Proceedings of the Na- tional Academy of Sciences, 112, 8762–8767. https://doi.org/10. 1073/pnas.1501242112 Goodyear, K., Parasuraman, R., Chernyak, S., Madhavan, P., Deshpande, G., & Krueger, F. (2016). Advice taking from humans and machines: An fMRI and effective connectivity study. Fron- tiers in Human Neuroscience, 10, 542. https://doi.org/10.3389/ fnhum.2016.00542 Greicius, M. (2008). Resting-state functional connectivity in neuro- psychiatric disorders. Current Opinion in Neurology, 21, 424–430. https://doi.org/10.1097/WCO.0b013e328306f2c5 Guyon, I., Weston, J., Barnhill, S., & Vapnik, V. (2002). Gene se- lection for cancer classification using support vector machines. Machine Learning, 46(1), 389–422. https://doi.org/10.1023/A: 1012487302797 Habib, M., Mak, E., Gabel, S., Su, L., Williams, G., Waldman, A., . . . O’Brien, J. T. (2017). Functional neuroimaging findings in healthy middle-aged adults at risk of Alzheimer’s disease. Age- ing Research Reviews, 36, 88–104. https://doi.org/10.1016/j.arr. 2017.03.004 Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, V. J., & Sporns, O. (2008). Mapping the structural core of human cerebral cortex. PLoS Biology, 6, e159. Handwerker, D. A., Ollinger, J. M., & D’Esposito, M. (2004). Varia- tion of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. NeuroImage, 21, 1639–1651. https://doi.org/10.1016/j.neuroimage.2003.11.029 Hasson, U., Nir, Y., Levy, I., Fuhrmann, G., & Malach, R. (2004). Intersubject synchronization of cortical activity during natural vi- sion. Science, 303, 1634–1640. He, B. J. (2011). Scale-free properties of the functional magnetic resonance imaging signal during rest and task. Journal Neuro- science, 31, 13786–13795. He, Y., Wang, M., Chen, X., Pohmann, R., Polimeni, J. R., Scheffler, K., . . . Yu, X. (2018). Ultra-slow single-vessel BOLD and CBV- based fMRI spatiotemporal dynamics and their correlation with neuronal intracellular calcium signals. Neuron, 97, 925–939. https://doi.org/10.1016/j.neuron.2018.01.025 Network Neuroscience 370 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease Hilgetag, C. C., & Grant, S. (2010). Cytoarchitectural differences are a key determinant of laminar projection origins in the visual cortex. NeuroImage, 51, 1006–1017. https://doi.org/10.1016/j. neuroimage.2010.03.006 Hlinka, J., Palus, M., Vejmelka, M., Mantini, D., & Corbetta, M. (2011). Functional connectivity in resting-state fMRI: Is linear cor- relation sufficient? NeuroImage, 54, 2218–2225. Hohenfeld, C., Werner, C. J., & Reetz, K. (2018). Resting-state con- nectivity in neurodegenerative disorders: Is there potential for an imaging biomarker? NeuroImage: Clinical, 18, 849–870. https:// doi.org/10.1016/j.nicl.2018.03.013 Honey, C. J., Kötter, R., Breakspear, M., & Sporns, O. (2007). Net- work structure of cerebral cortex shapes functional connectivity on multiple time scales. Proceedings of the National Academy of Sciences, 104, 10240–10245. Hughes, R. I. G. (1997). Models and representation. Philosophy of Science, 64, S325–S336. https://doi.org/10.1086/392611 Hutchison, R. M., Womelsdorf, T., Allen, E. A., Bandettini, P. A., Calhoun, V. D., Corbetta, M., (2013). Dy- namic functional connectivity: Promise, issues, and interpreta- tions. Neuroimage, 80, 360–378. . Chang, C. . . Insabato, A., Cunningham, J. P., & Gilson, M. (2018). Bayesian es- timation for large scale multivariate Ornstein-Uhlenbeck model of brain connectivity. arXiv: 1805.10050 James, G., Kelley, M., Craddock, R., Holtzheimer, P., Dunlop, B., Nemeroff, C., . . . Hu, X. (2009). Exploratory structural equation modeling of resting-state fMRI: Applicability of group models to individual subjects. NeuroImage, 45, 778–787. Kaplan, D. M. (2011). Explanation and description in compu- tational neuroscience. Synthese, 183, 339. https://doi.org/10. 1007/s11229-011-9970-0 Khambhati, A. N., Sizemore, A. E., Betzel, R. F., & Bassett, D. S. (2017). Modeling and interpreting mesoscale network dynamics. NeuroImage. https://doi.org/10.1016/j.neuroimage.2017.06.029 Kurth, S., Moyse, E., Bahri, M. A., Salmon, E., & Bastin, C. (2015). Recognition of personally familiar faces and functional connec- tivity in Alzheimer’s disease. Cortex, 67, 59–73. https://doi.org/ 10.1016/j.cortex.2015.03.013 Lafleur, L.-P., Tremblay, S., Whittingstall, K., & Lepage, J.-F. (2016). Assessment of effective connectivity and plasticity with dual-coil transcranial magnetic stimulation. Brain Stimulation, 9, 347–355. https://doi.org/10.1016/j.brs.2016.02.010 Laird, A. R., Eickhoff, S. B., Rottschy, C., Bzdok, D., Ray, K. L., & Fox, P. T. (2013). Networks of task co-activations. NeuroImage, 80, 505–514. Li, B., Wang, X., Yao, S., Hu, D., & Friston, K. (2012). Task- dependent modulation of effective connectivity within the de- fault mode network. Frontiers in Psychology, 3, 206. https://doi. org/10.3389/fpsyg.2012.00206 Mantini, D., Hasson, U., Betti, V., Perrucci, M. G., Romani, G. L., Corbetta, M., . . . Vanduffel, W. (2012). Interspecies activity cor- relations reveal functional correspondence between monkey and human brain areas. Nature Methods, 9, 277–282. Matsui, T., Murakami, T., & Ohki, K. (2018). Neuronal origin of the temporal dynamics of spontaneous BOLD activity correlation. Cerebral Cortex. https://doi.org/10.1093/cercor/bhy045 Matthews, P. M., & Hampshire, A. (2016). Clinical concepts emerg- ing from fMRI functional connectomics. Neuron, 91, 511–528. https://doi.org/10.1016/j.neuron.2016.07.031 McIntosh, A., & Gonzalez-Lima, F. (1994). Structural equation mod- eling and its application to network analysis in functional brain imaging. Human Brain Mapping, 2, 2–22. Messé, A., Rudrauf, D., Benali, H., & Marrelec, G. (2014). Relat- ing structure and function in the human brain: Relative contri- butions of anatomy, stationary dynamics, and non-stationarities. PLoS Computational Biology, 10, e1003530. Meunier, D., Ersche, K. D., Craig, K. J., Fornito, A., Merlo-Pich, E., Fineberg, N. A., . . . Bullmore, E. T. (2012). Brain func- tional connectivity in stimulant drug dependence and obsessive- compulsive disorder. NeuroImage, 59, 1461–1468. https://doi. org/10.1016/j.neuroimage.2011.08.003 Miranda-Dominguez, O., Mills, B. D., Carpenter, S. D., Grant, K. A., Kroenke, C. D., Nigg, J. T., & Fair, D. A. (2014). Connectotyp- ing: Model based fingerprinting of the functional connectome. PLoS ONE, 9, e111048. https://doi.org/10.1371/journal.pone. 0111048 Mitra, A., Kraft, A., Wright, P., Acland, B., Snyder, A. Z., Rosenthal, Z., . . . Raichle, M. E. (2018). Spontaneous infra-slow brain ac- tivity has unique spatiotemporal dynamics and laminar struc- ture. Neuron, 98, 297–305. https://doi.org/10.1016/j.neuron. 2018.03.015 Mitra, A., Snyder, A., Hacker, C., & Raichle, M. (2014). Lag structure in resting-state fMRI. Journal of Neurophysiology, 111, 2374–2391. Mitra, A., Snyder, A. Z., Tagliazucchi, E., Laufs, H., & Raichle, M. (2015). Propagated infra-slow intrinsic brain activity reorganizes across wake and slow wave sleep. eLife, 4. Naselaris, T., Kay, K. N., Nishimoto, S., & Gallant, J. L. (2011). En- coding and decoding in fMRI. NeuroImage, 56, 400–410. https:// doi.org/10.1016/j.neuroimage.2010.07.073 Newman, M. E. J. (2006). Modularity and community structure in net- works. Proceedings of the National Academy of Sciences, 103, 8577–8582. Olszowy, W., Aston, J., Rua, C., & Williams, G. B. (2019). Accurate autocorrelation modeling substantially improves fMRI reliabil- ity. Nature Communications, 10, 1220. https://doi.org/10.1038/ s41467-019-09230-w Pallarés, V., Insabato, A., Sanjuán, A., Kühn, S., Mantini, D., Deco, G., & Gilson, M. (2018). Extracting orthogonal subject- and condition-specific signatures from fMRI data using whole-brain effective connectivity. NeuroImage, 178, 238–254. https://doi. org/10.1016/j.neuroimage.2018.04.070 Park, H.-J., & Friston, K. (2013). Structural and functional brain net- works: From connections to cognition. Science, 342, 1238411. Park, H.-J., Friston, K. J., Pae, C., Park, B., & Razi, A. (2018). Dynamic effective connectivity in resting state fMRI. Neuro- Image, 180, 594–608.https://doi.org/10.1016/j.neuroimage.2017. 11.033 Parkes, L., Fulcher, B., Yücel, M., & Fornito, A. (2018). An evalua- tion of the efficacy, reliability, and sensitivity of motion correc- tion strategies for resting-state functional MRI. NeuroImage, 171, 415–436. https://doi.org/10.1016/j.neuroimage.2017.12.073 Network Neuroscience 371 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease Power, J. D., Plitt, M., Gotts, S. J., Kundu, P., Voon, V., Bandettini, P. A., & Martin, A. (2018). Ridding fMRI data of motion-related influences: Removal of signals with distinct spatial and physical bases in multiecho data. Proceedings of the National Academy of Sciences, 115, E2105–E2114. https://doi.org/10.1073/pnas. 1720985115 Preti, M. G., Bolton, T. A., & Van De Ville, D. (2017). The dy- namic functional connectome: State-of-the-art and perspectives. NeuroImage, 160, 41–54. https://doi.org/10.1016/j.neuroimage. 2016.12.061 Proix, T., Spiegler, A., Schirner, M., Rothmeier, S., Ritter, P., & Jirsa, V. K. (2016). How do parcellation size and short-range connectivity affect dynamics in large-scale brain network models? NeuroImage, 142, 135–149. https://doi.org/10.1016/j. neuroimage.2016.06.016 Rahim, M., Thirion, B., Bzdok, D., Buvat, I., & Varoquaux, G. (2017). Joint prediction of multiple scores captures better individ- ual traits from brain images. NeuroImage, 158, 145–154. https:// doi.org/10.1016/j.neuroimage.2017.06.072 Razi, A., Seghier, M. L., Zhou, Y., McColgan, P., Zeidman, P., Park, H.-J., . . . Friston, K.-J. (2017). Large-scale DCMS for resting- state fMRI. Network Neuroscience, 1, 222–241. https://doi.org/ 10.1162/NETN_a_00015 Rissman, J., & Wagner, A. D. (2012). Distributed representations in memory: Insights from functional brain imaging. Annual Re- view Psychology, 63, 101–128. https://doi.org/10.1146/annurev- psych-120710-100344 Rousseeuw, P. (1987). Silhouettes: A graphical aid to the interpreta- tion and validation of cluster analysis. Journal of Computational and Applied Mathematics, 20, 53–65. https://doi.org/10.1016/ 0377-0427(87)90125-7 Rowe, J. B., & Siebner, H. R. (2012). The motor system and its dis- orders. NeuroImage, 61(2), 464–477. https://doi.org/10.1016/j. neuroimage.2011.12.042 Ryali, S., Supekar, K., Chen, T., & Menon, V. (2011). Multivari- ate dynamical systems models for estimating causal interactions in fMRI. NeuroImage, 54, 807–823. https://doi.org/10.1016/j. neuroimage.2010.09.052 Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Math- ematical framework for large-scale brain network modeling in the virtual brain. NeuroImage, 111, 385–430. https://doi.org/10. 1016/j.neuroimage.2015.01.002 Sathian, K., Deshpande, G., & Stilla, R. (2013). Neural changes with tactile learning reflect decision-level reweighting of perceptual readout. Journal of Neuroscience, 33, 5387–5398. https://doi. org/10.1523/JNEUROSCI.3482-12.2013 Sauvage, A., Hubert, G., Touboul, J., & Ribot, J. (2017). The hemo- dynamic signal as a first-order low-pass temporal filter: Evidence and implications for neuroimaging studies. Neuroimage, 155, 394–405. https://doi.org/10.1016/j.neuroimage.2017.03.053 Schiefer, J., Niederbühl, A., Pernice, V., Lennartz, C., Hennig, J., LeVan, P., & Rotter, S. (2018). From correlation to causation: Estimating effective connectivity from zero-lag covariances of brain signals. PLoS Compututaional Biology, 14, e1006056. https://doi.org/10.1371/journal.pcbi.1006056 Schmahmann, J. D., & Pandya, D. N. (2007). Cerebral white matter– historical evolution of facts and notions concerning the organ- ization of the fiber pathways of the brain. Journal of the His- tory of the Neurosciences, 16, 237–267. https://doi.org/10.1080/ 09647040500495896 Schmidt, M., Bakker, R., Hilgetag, C. C., Diesmann, M., & van Albada, S. J. (2018). Multi-scale account of the network struc- ture of macaque visual cortex. Brain Structure and Function, 223, 1409–1435. https://doi.org/10.1007/s00429-017-1554-4 Senden, M., Goebel, R., & Deco, G. (2012). Structural connectivity allows for multi-threading during test: The structure of the cor- tex leads to efficient alternation between resting state exploratory behavior and default mode processing. NeuroImage, 60, 2274– 2284. https://doi.org/10.1016/j.neuroimage.2012.02.061 Senden, M., Reuter, N., van den Heuvel, M. P., Goebel, R., Deco, G., & Gilson, M. (2017). Task-related effective connectivity re- veals that the cortical rich club gates cortex-wide commu- nication. Human Brain Mapping. https://doi.org/10.1002/hbm. 23913 Seth, A. K., Chorley, P., & Barnett, L. C. (2013). Granger causal- ity analysis of fMRI BOLD signals is invariant to hemodynamic convolution but not downsampling. NeuroImage, 65, 540–555. https://doi.org/10.1016/j.neuroimage.2012.09.049 Siegel, J. S., Ramsey, L. E., Snyder, A. Z., Metcalf, N. V., Chacko, R. V., Weinberger, K., . . . Corbetta, M. (2016). Disruptions in multiple be- of network connectivity predict the National havioral domains after stroke. Proceedings of Academy of Sciences, 113, 4367–4376. https://doi.org/10.1073/ pnas.1521083113 impairment Smith, S., Miller, K., Salimi-Khorshidi, G., Webster, M., Beckmann, C., Nichols, T., . . . Woolrich, M. (2011). Network modelling methods for fMRI. NeuroImage, 54, 875–891. Snyder, A. Z., & Raichle, M. E. (2012). A brief history of the resting state: The washington university perspective. Neuroimage, 62, 902–910. https://doi.org/10.1016/j.neuroimage.2012.01.044 Sokolov, A. A., Zeidman, P., Erb, M., Ryvlin, P., Pavlova, M. A., & Friston, K. J. (2018). Linking structural and effective brain connec- tivity: Structurally Informed Parametric Empirical Bayes (si-PEB). Brain Structure and Function. https://doi.org/10.1007/s00429- 018-1760-8 Sporns, O., Tononi, G., & Edelman, G. M. (2000). Theoretical neu- roanatomy: Relating anatomical and functional connectivity in graphs and cortical connection matrices. Cerebral Cortex, 10, 127–141. Sporns, O., Tononi, G., & Kötter, R. (2005). The human connec- tome: A structural description of the human brain. PLOS Com- putational Biology, 1, 0010042. https://doi.org/10.1371/journal. pcbi.0010042 Stephan, K., Harrison, L., Penny, W., & Friston, K. (2004). Biophys- ical models of fMRI responses. Current Opinion in Neurology, 14, 629–635. Thompson, W. H., Brantefors, P., & Fransson, P. (2017). From static to temporal network theory: Applications to functional brain con- nectivity. Network Neuroscience, 1(2), 69–99. https://doi.org/10. 1162/NETN_a_00011 Tononi, G., Edelman, G. M., & Sporns, O. (1998). Complexity and coherency: Integrating information in the brain. Trends in Cogni- tive Science, 2, 474–484. Network Neuroscience 372 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Modeling whole-brain effective connectivity for cognition and disease Tononi, G., Sporns, O., & Edelman, G. M. (1994). A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proceedings of the National Academy of Sciences, 91, 5033–5037. Valdes-Sosa, P., Roebroeck, A., Daunizeau, J., & Friston, K. (2011). Effective connectivity: Influence, causality and biophysical mod- eling. NeuroImage, 58, 339–361. van den Heuvel, M. P., & Hulshoff Pol, H. E. (2010). Exploring the brain network: A review on resting-state fMRI functional con- nectivity. European Neuropsychopharmacology, 20, 519–534. https://doi.org/10.1016/j.euroneuro.2010.03.008 Varoquaux, G., & Poldrack, R. A. (2019). Predictive models avoid excessive reductionism in cognitive neuroimaging. Cur- rent Opinion in Neurobiology, 55, 1–6. https://doi.org/10.1016/ j.conb.2018.11.002 Varoquaux, G., Raamana, P. R., Engemann, D. A., Hoyos-Idrobo, A., Schwartz, Y., & Thirion, B. (2017). Assessing and tuning brain decoders: Cross-validation, caveats, and guidelines. Neuro- Image, 145, 166–179.https://doi.org/10.1016/j.neuroimage.2016. 10.038 Varoquaux, G., Schwartz, Y., Poldrack, R. A., Gauthier, B., Bzdok, D., Poline, J.-B., & Thirion, B. (2018). Atlases of cognition with large-scale human brain mapping. PLoS Computational Biology, 14, e1006565. https://doi.org/10.1371/journal.pcbi.1006565 Vatansever, D., Menon, D. K., Manktelow, A. E., Sahakian, B. J., & Stamatakis, E. A. (2015). Default mode dynamics for global func- tional integration. Journal of Neuroscience, 35, 15254–15262. https://doi.org/10.1523/JNEUROSCI.2135-15.2015 Vatansever, D., Menon, D. K., & Stamatakis, E. A. (2017). Default mode contributions to automated information processing. Pro- ceedings of the National Academy Sciences, 114, 12821–12826. https://doi.org/10.1073/pnas.1710521114 Vidaurre, D., Abeysuriya, R., Becker, R., Quinn, A. J., Alfaro- Almagro, F., Smith, S. M., & Woolrich, M. W. (2018). Discovering dynamic brain networks from big data in rest and task. Neuro- Image, 180, 646–656.https://doi.org/10.1016/j.neuroimage.2017. 06.077 Walther, A., Nili, H., Ejaz, N., Alink, A., Kriegeskorte, N., & Diedrichsen, J. (2016). Reliability of dissimilarity measures for multi-voxel pattern analysis. NeuroImage, 137, 188–200. https:// doi.org/10.1016/j.neuroimage.2015.12.012 Wheelock, M., Sreenivasan, K., Wood, K., Hoef, L. V., Deshpande, G., & Knight, D. (2014). Threat-related learning relies on distinct dorsal prefrontal cortex network connectivity. NeuroImage, 102, 904–912. https://doi.org/10.1016/j.neuroimage.2014.08.005 Wilson, H., & Cowan, J. (1973). A mathematical theory of the func- tional dynamics of nervous tissue. Kybernetik, 13, 55–80. Yahata, N., Kasai, K., & Kawato, M. (2017). Computational neu- roscience approach to biomarkers and treatments for mental disorders. Psychiatry and Clinical Neurosciences, 71, 215–237. https://doi.org/10.1111/pcn.12502 Zamora-López, G., Chen, Y., Deco, G., Kringelbach, M. L., & Zhou, C. (2016). Functional complexity emerging from anatomical con- straints in the brain: The significance of network modularity and rich-clubs. Science Reports, 6, 38424. https://doi.org/10.1038/ srep38424 Zamora-López, G., & Gilson, M. (2019). NetDynFlow: A package to study complex networks based on the temporal evolution of their Dynamic Communicability and Flow. https://github.com/ mb-BCA/NetDynFlow Zamora-López, G., Zhou, C., & Kurths, J. (2011). Exploring brain function from anatomical connectivity. Frontiers in Neuro- science, 5, 83. https://doi.org/10.3389/fnins.2011.00083 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / / 4 2 3 3 8 1 8 6 6 6 3 9 n e n _ a _ 0 0 1 1 7 p d . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Network Neuroscience 373

Scarica il pdf