Nested Named Entity Recognition via
Second-best Sequence Learning and Decoding
Takashi Shibuya† ∗ Eduard Hovy†
†Carnegie Mellon University, Pittsburgh, PAPÀ 15213, U.S.A.
∗Sony Corporation, Tokyo 141-8610, Japan
shibuyat@jp.sony.com
hovy@cmu.edu
Astratto
When an entity name contains other names
within it, the identification of all combinations
of names can become difficult and expensive.
We propose a new method to recognize not
only outermost named entities but also inner
nested ones. We design an objective function
for training a neural model that treats the tag
sequence for nested entities as the second best
path within the span of their parent entity. In
aggiunta, we provide the decoding method for
inference that extracts entities iteratively from
outermost ones to inner ones in an outside-
to-inside way. Our method has no additional
hyperparameters to the conditional random
field based model widely used for flat named
entity recognition tasks. Experiments demon-
strate that our method performs better than or at
least as well as existing methods capable of
handling nested entities, achieving F1-scores
Di 85.82%, 84.34%, E 77.36% on ACE-
2004, ACE-2005, and GENIA datasets, Rif-
spectively.
1 introduzione
Named entity recognition (NER) is the task of
identifying text spans associated with proper
names and classifying them according to their se-
mantic class such as person or organization.
NER, or in general the task of recognizing entity
mentions, is one of the first stages in deep language
understanding, and its importance has been well
recognized in the NLP community (Nadeau and
Sekine, 2007).
One popular approach to the NER task is to
regard it as a sequence labeling problem. In this
case, it is implicitly assumed that mentions are
not nested in texts. Tuttavia, names often contain
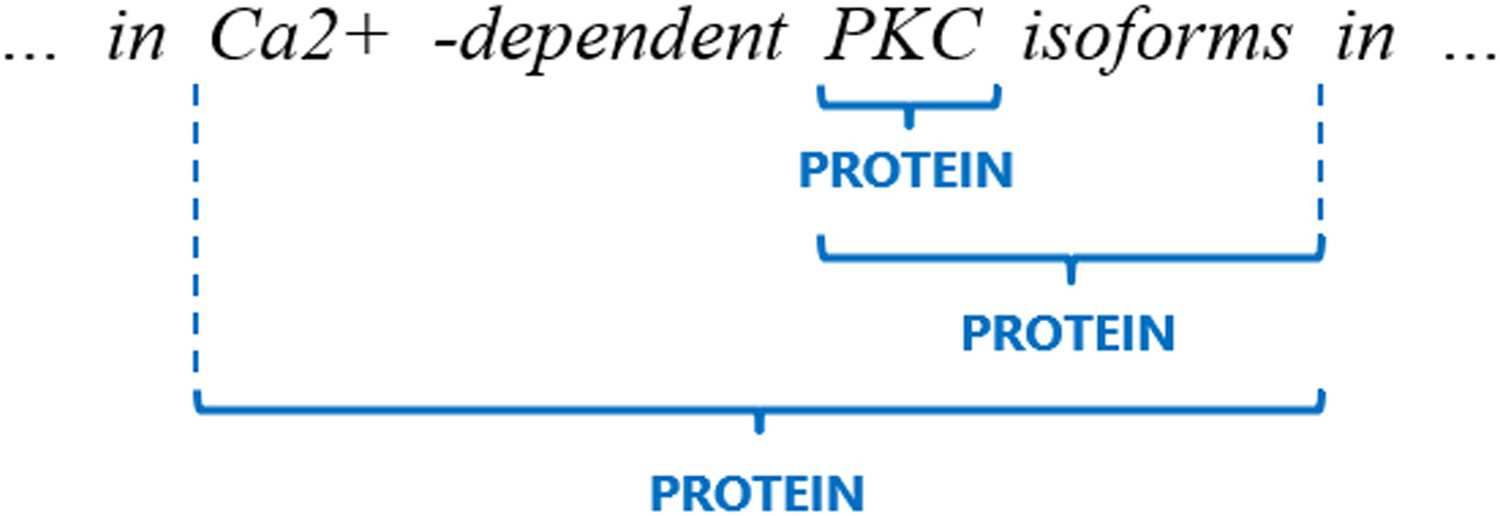
entities nested within themselves, as illustrated
605
in Figure 1, which contains 3 mentions of the
same type (PROTEIN) in the span ‘‘… in Ca2+
-dependent PKC isoforms in …’’, taken from the
GENIA dataset (Kim et al., 2003). Name nest-
ing is common, especially in technical domains
(Alex et al., 2007; Byrne, 2007; Wang, 2009).
The assumption of no nesting leads to loss of
potentially important information and may nega-
tively impact subsequent downstream tasks. For
instance, a downstream entity linking system that
relies on NER may fail to link the correct entity if
the entity mention is nested.
Various approaches to recognizing nested enti-
ties have been proposed. Many of them rely on pro-
ducing and rating all possible (sub)spans, Quale
can be computationally expensive. Wang and Lu
(2018) provided a hypergraph-based approach to
consider all possible spans. Sohrab and Miwa
(2018) proposed a neural exhaustive model that
enumerates and classifies all possible spans. These
metodi, Tuttavia, achieve high performance at
the cost of time complexity. To reduce the running
time, they set a threshold to discard longer entity
mentions. If the hyperparameter is set low, running
time is reduced but longer mentions are missed.
In contrasto, Muis and Lu (2017) proposed a
sequence labeling approach that assigns tags to
gaps between words, which efficiently handles se-
quences using Viterbi decoding. Tuttavia, Questo
approach suffers from structural ambiguity issues
during inference, as explained by Wang and Lu
(2018). Katiyar and Cardie (2018) proposed an-
other hypergraph-based approach that learns the
structure in a greedy manner. Tuttavia, their method
uses an additional hyperparameter as the thresh-
old for selecting multiple mention candidates.
This hyperparameter affects the trade-off between
recall and precision.
in questo documento, we propose new learning and de-
coding methods to extract nested entities without
Operazioni dell'Associazione per la Linguistica Computazionale, vol. 8, pag. 605–620, 2020. https://doi.org/10.1162/tacl a 00334
Redattore di azioni: Mihai Surdeanu. Lotto di invio: 2/2020; Lotto di revisione: 5/2020; Pubblicato 9/2020.
C(cid:13) 2020 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2.1 Usage of CRF
Our decoding and training methods are based on
two key points about our usage of CRF. The first
key point is that we prepare a separate CRF for
each named entity type. This enables our method
to handle the situation where the same mention
span is assigned multiple entity types. The GENIA
dataset indeed has such mention spans. Nel
literature, Muis and Lu (2017) demonstrated that
this approach of multiple CRFs would perform
better on nested NER datasets and even a flat
NER dataset than the standard approach of a single
CRF for all entity types. The second key point is
that each element of the transition matrix of each
CRF has a fixed value according to whether it
corresponds to a legal transition (per esempio., B-X to I-X
in IOBES tagging scheme, where X is the name of
entity type) or an illegal one (per esempio., O to I-X). Questo
is helpful for keeping the scores for tag sequences
including outer entities higher than those of tag
sequences including inner entities.
Formalmente, we use Z = {z1, . . . , zn} to rep-
resent a sequence output from the last hidden
layer of a neural model, where zi is the vector
for the i-th word, and n is the number of tokens.
sì(k) = {sì(k)
N } represents a sequence of
IOBES tags of entity type k for Z. Here, we
define the score function to be
1 , . . . , sì(k)
φk
sì(k)
i−1, sì(k)
(cid:16)
io
, zi
(cid:17)
= P (k)
sì(k)
io
,io
+ UN(k)
i−1,y(k)
sì(k)
io
,
(1)
where P (k)
sì(k)
io
,io
= W (k)
sì(k)
io
· zi + B(k)
sì(k)
io
,
UN(k)
i−1,y(k)
sì(k)
io
=
−∞,
if y(k)
i−1 → y(k)
io
is illegal,
0,
otherwise.
and b(k)
sì(k)
io
denote the weight matrix and the
W (k)
sì(k)
io
bias vector corresponding to y(k)
, rispettivamente.
UN(k) stands for the transition matrix from the
previous token to the current token, e A(k)
i−1,y(k)
sì(k)
is the transition scores from y(k)
. Z is
shared between all of the multiple CRFs as their
input.
i−1 to y(k)
io
io
io
2.2 Decoding
We use three strategies for decoding. Primo, we
consider each entity type separately using multiple
CRFs in decoding, which makes it possible to
Figura 1: Example of nested entities.
any additional hyperparameters. We summarize
our contributions as follows:
• We describe a decoding method that iteratively
recognizes entities from outermost ones to
inner ones without structural ambiguity. It
recursively searches a span of each extracted
entity for inner nested entities using the
Viterbi algorithm. This algorithm does not
require hyperparameters for the maximal
length or number of mentions considered.
• We also provide a novel learning method that
ensures the aforementioned decoding. Modelli
are optimized based on an objective function
designed according to the decoding procedure.
• Empirically, we demonstrate that our method
performs better than or at least as well as the
current state-of-the-art methods with 85.82%,
84.34%, E 77.36% in F1-score on three
standard datasets: ACE-2004,1 ACE-2005,2
and GENIA.
2 Method
We propose applying conditional random fields
(CRFs) (Lafferty et al., 2001), which is commonly
used for flat NER (Lample et al., 2016; Ma and
Blu, 2016; Chiu and Nichols, 2016; Reimers
and Gurevych, 2017; Strubell et al., 2017; Akbik
et al., 2018), to nested NER in this study. We first
explain our usage of CRF, which is the base of
our decoding and training methods. Then, we
introduce our decoding and training methods. Nostro
decoding and training methods focus on the output
layer of neural architectures and therefore can be
combined with any neural model.
1https://catalog.ldc.upenn.edu/LDC2005T09.
2https://catalog.ldc.upenn.edu/LDC2006T06.
606
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Algorithm 1: Nested NER via 2nd-best sequence decoding
K = the set of entity types;
Function main(zi)
M = {}; # the set of detected mentions. Each element of M is a tuple (S, e, k) regarding a mention.
# S, e, and k are the start position, the end position, and the entity type of the mention, rispettivamente.
foreach k ∈ K do
calculate CRF scores Φ for entity type k with the score function φk
, zi
find the best path of the span from position 1 to position n based on the scores Φ;
˜M = the set of the mentions detected in the best path;
M = M ∪ ˜M ;
foreach m ∈ ˜M do
i−1, sì(k)
sì(k)
(cid:16)
io
detectNestedMentions(Φ, m.s, m.e, k, M );
;
(cid:17)
return M ;
Function detectNestedMentions(Φ, S, e, k, M )
if e − s > 1 Poi
find the 2nd best path of the span from position s to position e based on the scores Φ;
˜M = the set of the mentions detected in the 2nd best path;
M = M ∪ ˜M ;
foreach m ∈ ˜M do
detectNestedMentions(Φ, m.s, m.e, k, M );
return;
Figura 2: Overview of our second-best path decoding algorithm to iteratively find nested entities.
handle the situation that the same mention span
is assigned multiple entity types. Secondo, our de-
coder searches nested entities in an outside-to-
inside way,3 which realizes efficient processing
by eliminating the spans of non-entity at an early
stage. More specifically, our method recursively
narrows down the spans to Viterbi-decode. IL
spans to Viterbi-decode are dynamically decided
according to the preceding Viterbi-decoding result.
Only the spans that have just been recognized as
3Our usage of inside/outside is different from the inside-
outside algorithm in dynamic programming.
sì(k)
i−1, sì(k)
(cid:16)
entity mentions are Viterbi-decoded again. Third,
we use the same scores φk
Equazione (1) to extract outermost entities and even
inner entities without re-encoding, which makes
inference more efficient and faster. These three
strategies are deployed and completed only in the
output layer of neural architectures.
, zi
Di
(cid:17)
io
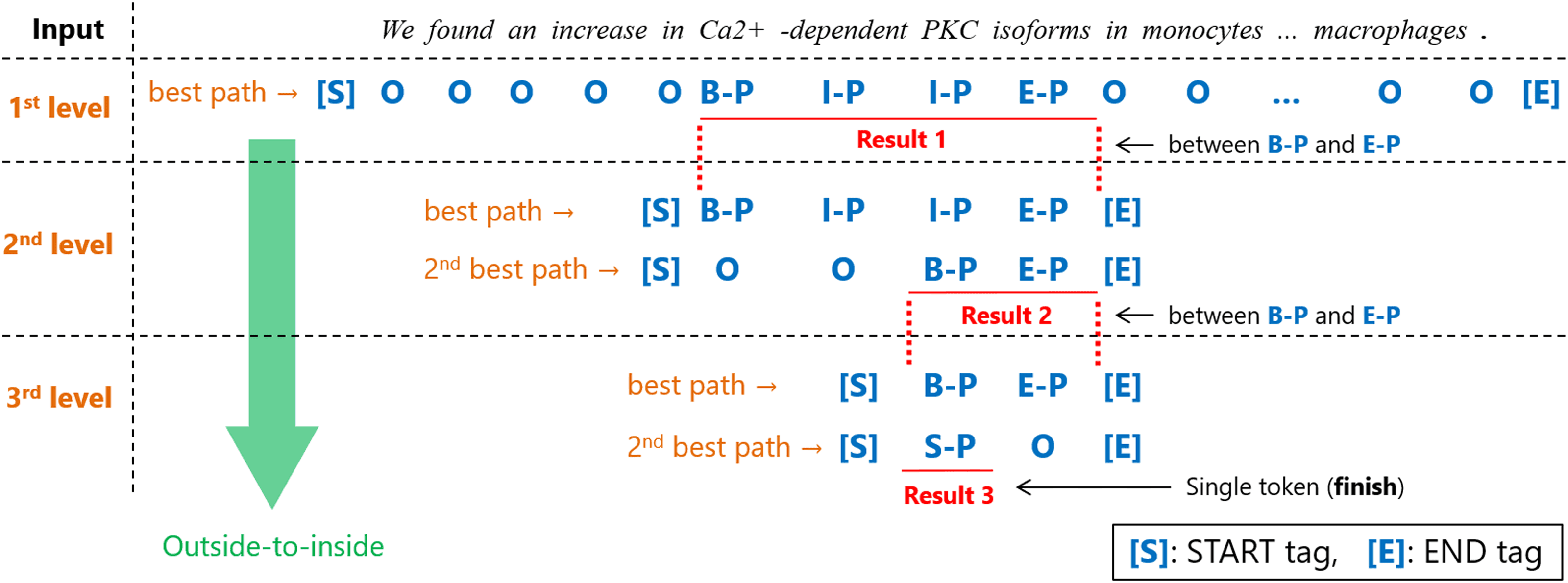
We describe the pseudo-code of our decoding
method in Algorithm 1. Also, we depict the over-
view of our decoding method with an example in
Figura 2. We use the term level in the sense of the
depth of entity nesting. [S] E [E] in Figure 2
607
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
stand for the START and END tags, rispettivamente.
We always attach these tags to both ends of every
sequence of IOBES tags in Viterbi-decoding.
We explain the decoding procedure and mecha-
nism in detail below. We consider each entity type
separately and iterate the same decoding process
regarding distinct entity types as described in
Algorithm 1. In the decoding process for each
entity type k, we first calculate the CRF scores
φk
over the entire sentence. Prossimo,
we decode a sequence with the standard 1-best
Viterbi decoding as with the conventional linear-
chain CRF. ‘‘Ca2+ -dependent PKC isoforms’’
is extracted at the 1st level with regard to the
example of Figure 2.
sì(k)
i−1, sì(k)
, zi
(cid:17)
(cid:16)
io
io
, zi
i−1, sì(k)
sì(k)
(cid:16)
Then, we start our recursive decoding to extract
nested entities within previously extracted entity
spans by finding the 2nd best path. In Figure 2,
the span ‘‘Ca2+ -dependent PKC isoforms’’ is
processed at the 2nd level. Here, if we search
for the best path within each span, the same
tag sequence will be obtained, even though the
processed span is different. This is because we
continue using the same scores φk
(cid:17)
and because all the values of A(k) corresponding
to legal transitions are equal to 0. Regarding the
example of Figure 2, the score of the transition
from [S] to B-P at the 2nd level is equal to the
score of the transition from O to B-P at the 1st
level. This is true for the transition from E-P to
[E] at the 2nd level and the one from E-P to O
at the 1st level. The best path between the [S]
E [E] tags is identical to the best path between
the two O tags under our restriction about the
transition matrix of CRF. Therefore, we search
for the 2nd best path within the span by utilizing
the N -best Viterbi A* algorithm (Seshadri and
Sundberg, 1994; Huang et al., 2012).4 Note that
our situation is different from normal situations
where N -best decoding is needed. We already
know the best path within the span and want to
find only the 2nd best path. Così, we can extract
nested entities by finding the 2nd best path within
each extracted entity. Regarding the example of
4Without our restriction about the transition matrix of
CRF, we would have to watch both the best path and the 2nd
best path. Besides, if a single CRF was used for all entity
types, the decoder could not always narrow down spans with
the 2nd best path. The 2nd best path in a single CRF could
result in the same span tagged a different entity type. Noi
would have to watch lower-ranked paths.
608
Figura 2, ‘‘PKC isoforms’’ is extracted from the
span ‘‘Ca2+ -dependent PKC isoforms’’ at the
2nd level.
We continue this recursive decoding until no
multi-token entities are detected within a span. In
Figura 2, the span ‘‘PKC isoforms’’ is processed
at the 3rd level. At the 3rd or deeper levels, IL
tag sequence of its grandparent level is no longer
either the best path or the 2nd best path because
the start or end position of the current span is
in the middle of the entity mention span at the
grandparent level. As for the example shown in
Figura 2, the word ‘‘PKC’’ is tagged I-P at the
1st level, and the transition from [S] to I-P
is illegal. The scores of the paths that includes
illegal transitions cannot be larger than those of
the paths that consist of only legal transitions
because the elements of the transition matrix A(k)
corresponding to illegal transitions are set to −∞.
That is why at all levels below the 1st level we
only need to find the 2nd best path.
This recursive processing is stopped when no
entities are predicted or when only single-token
entities are detected within a span.5 In Figure 2, IL
span ‘‘PKC’’ is not processed any more because
it is a single-token entity.
Only one nested entity is extracted within
each decoded span in Figure 2, but there can
be cases where multiple multi-token entities are
detected within a decoded span. In such cases,
our algorithm Viterbi-decodes each of their spans
in the way of the depth-first search algorithm.
The aforementioned processing is executed on all
entity types, and all detected entities are returned
as an output result.
2.3 Training
To extract entities from outside to inside success-
fully, a model has to be trained in a way that the
scores for the paths including outer entities will
be higher than those for the paths including inner
entities. We propose a new objective function to
achieve this requirement.
We maximize the log-likelihood of the correct
tag sequence as with the conventional CRF-based
modello. Considering that our model has a separate
5We do not need to recursively decode the span of each
extracted single-token entity because a single-token entity
cannot contain another entity of the same entity type.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
CRF for each entity type, the log-likelihood for
one training data, l (θ), is as follows:
Algorithm 2: LogSumExp of the scores of all
possible paths
l (θ) =
log p
Xk
Y (k)|Z; θ
(cid:16)
(cid:17)
,
(2)
where θ is the set of parameters of a neural
modello, and Y (k) denotes the collection of the
gold IOBES tags for all levels regarding the entity
type k. As we mentioned in Section 2.1, Z is a
sequence output from the last hidden layer of a
neural model and is shared between all of the
multiple CRFs. Therefore, θ is updated through a
backpropagation process so that Z can represent
information about all entity types.
1,1 = 1 and e(k)
In the following, we decompose the log-likelihood
for all levels into the ones for each level. Let
l,j and e(k)
S(k)
l,j denote the start and end positions
of the j-th span at the l-th level. With regard
to the 1st level, S(k)
1,1 = n because
we consider the whole span of a sentence. IL
spans considered at each deeper level, l > 1, are
determined according to the spans of multi-token
entities at its immediate parent level. As for the
example of Figure 2, only the span of ‘‘Ca2+
-dependent PKC isoforms’’ is considered at the
2nd level. Here, the log-likelihood for each entity
type can be expressed as follows:
log p
(cid:16)
+
Y (k)|Z; θ
= L1st
1,1 , . . . , sì(k)
sì(k)
1,N|Z; θ
(cid:17)
sì(k)
L2nd (cid:18)
l,S(k)
l,j
(cid:16)
, . . . , sì(k)
l,e(k)
l,j
|Z; θ
,
(cid:19)
(cid:17)
(3)
Xl>1 Xj
where L1st (. . . ) and L2nd (. . . ) are the log-
likelihoods of the (1st) best and 2nd best paths for
each span, rispettivamente. sì(k)
l,i denotes the correct
IOBES tag of the position i of the l-th level of the
entity type k.
Best path. L1st (. . . ) can be calculated in the
same manner as the conventional linear-chain
CRF:
L1st
ψ(k)
1:N
(cid:16)
1,1 , . . . , sì(k)
sì(k)
sì(k)
1,1 , Z
(cid:16)
(cid:17)
− log
1,N|Z; θ
=
(cid:17)
Xy′∈Y (k)
1:N
exp ψ(k)
1:N (y′, Z) ,
(4)
where ψ(k)
S:e (sì, Z) =
e
φk (yi−1, yi, zi) + UN(k)
ye,ye+1
Xi=s
ys−1 = [S], ye+1 = [E].
,
609
C = {B-X, I-X, E-X, S-X, O};
s = 1; # the start position
e = n; # the end position
foreach c ∈ C do
α(C) = P (k)
C,S + UN(k)
[S],C;
for i = s + 1; i ≤ e; io + + do
foreach c ∈ C do
foreach c′ ∈ C do
αc (c′) = α (c′) + P (k)
C,io + UN(k)
c′,C;
foreach c ∈ C do
α(C) = LogSumExp (αc);
foreach c ∈ C do
α(C)+ = A(k)
C,[E];
return LogSumExp (α);
Y (k)
S:e denotes the set of all possible tag sequences
from position s to position e of the entity type
k. The first term of Equation (4) is the score of
the gold tag sequence, and the second term is the
logarithm of the summation of the exponential
scores of all possible tag sequences. It is well
known that the second term of Equation (4) can
be efficiently calculated by the algorithm shown
in Algorithm 2.
2nd best path. L2nd (. . . ) given the best path
can be calculated by excluding the best path from
all possible paths. This concept is also adopted
by ListNet (Cao et al., 2007), which is used for
ranking tasks such as document retrieval or
recommendation. L2nd (. . . ) can be expressed by
the following equation:
sì(k)
l,S(k)
l,j
, . . . , sì(k)
l,e(k)
l,j
|Z; θ
=
(cid:19)
L2nd (cid:18)
ψ(k)
l,j :e(k)
S(k)
l,j (cid:16)
sì(k)
l,j , Z
− log
Xy′∈ ˜Y (k)
S(k)
l,j :e(k)
l,j
(cid:17)
exp ψ(k)
l,j :e(k)
S(k)
l,j
(y′, Z) ,
(5)
where ˜Y (k)
S:e denotes the set of all possible tag
sequences except the best path within the span
from position s to position e of the entity type k.
Tuttavia, to the best of our knowledge, IL
way of efficiently computing the second term
of Equation (5) has not been proposed yet in
the literature. Simply subtracting the exponential
score of the best path from the summation of the
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
spazi, we can merge them using the calculation
results at time step 3, as shown with the red edges
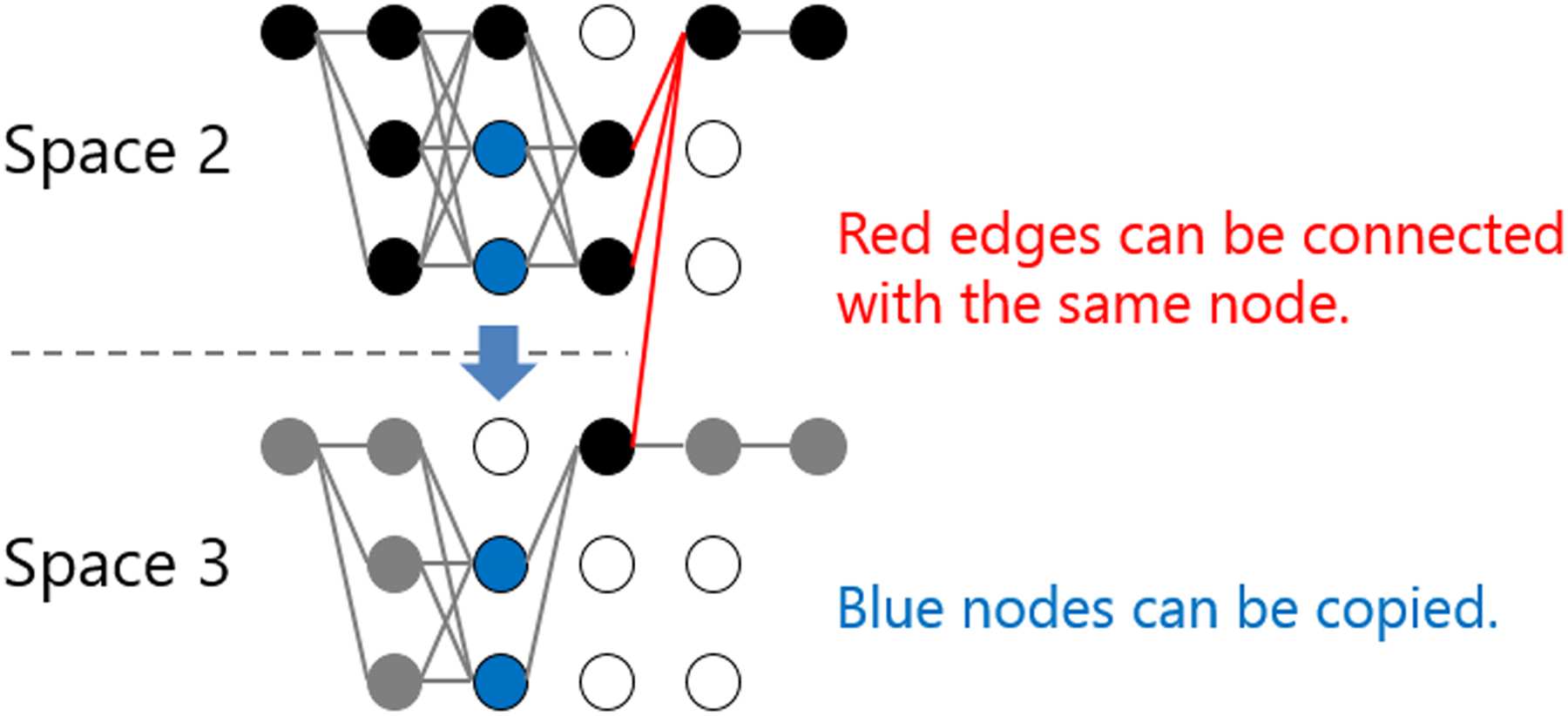
in Figure 5. The second trick is that the blue nodes
in Figure 5 can be copied from Space 2 to Space 3
at time step 2 since the considered paths until that
time step are also the same. These two tricks can
be applied to other pairs of two adjacent spaces,
which relieves the need to separately calculate
the summation of the exponential scores for each
spazio. Therefore, the second term of Equation (5)
can be calculated as shown in Algorithm 3.
Così, we can train a model using the objective
function of Equations 2, 3, 4, E 5.
2.4 Characteristics
(cid:0)
(cid:0)
mn2
Time complexity. Regarding the time complexity
of decoder, the worst case for our method is when
our decoder narrows down the spans one by one,
from n tokens (a whole sentence) A 2 gettoni. IL
time complexity for the worst case is therefore
n2
O (N + · · · + 2) = O
for each entity type,
in total, where m denotes the number
O
of entity types. Tuttavia, this rarely happens.
The ideal average processing time in the case
where our decoding method narrows down spans
successfully according to gold labels is O(dmn),
where d is the average number of gold IOBES
tags of each entity type assigned to a word. IL
average numbers calculated from the gold labels
of ACE-2004, ACE-2005, and GENIA are 1.06,
1.06, E 1.05, rispettivamente.
(cid:1)
(cid:1)
Usability. Some existing methods have hyper-
parameters, such as the maximal length of con-
sidered entities or the threshold that affects the
number of detected entities, beyond those of the
conventional CRF-based model used for flat NER
compiti. These hyperparameters must be tuned de-
pending on datasets. D'altra parte, our
method does not have such hyperparameters and
is easy to use from this viewpoint. Inoltre, our
method focuses on the output layer of neural archi-
tectures; therefore our method can be combined
with any neural model.
We verify the empirical performances of our
methods in the successive sections.
3 Experimental Settings
3.1 Datasets
We perform nested entity extraction experiments
intensively on ACE-2005 (Doddington et al., 2004)
and GENIA (Kim et al., 2003). For ACE-2005, we
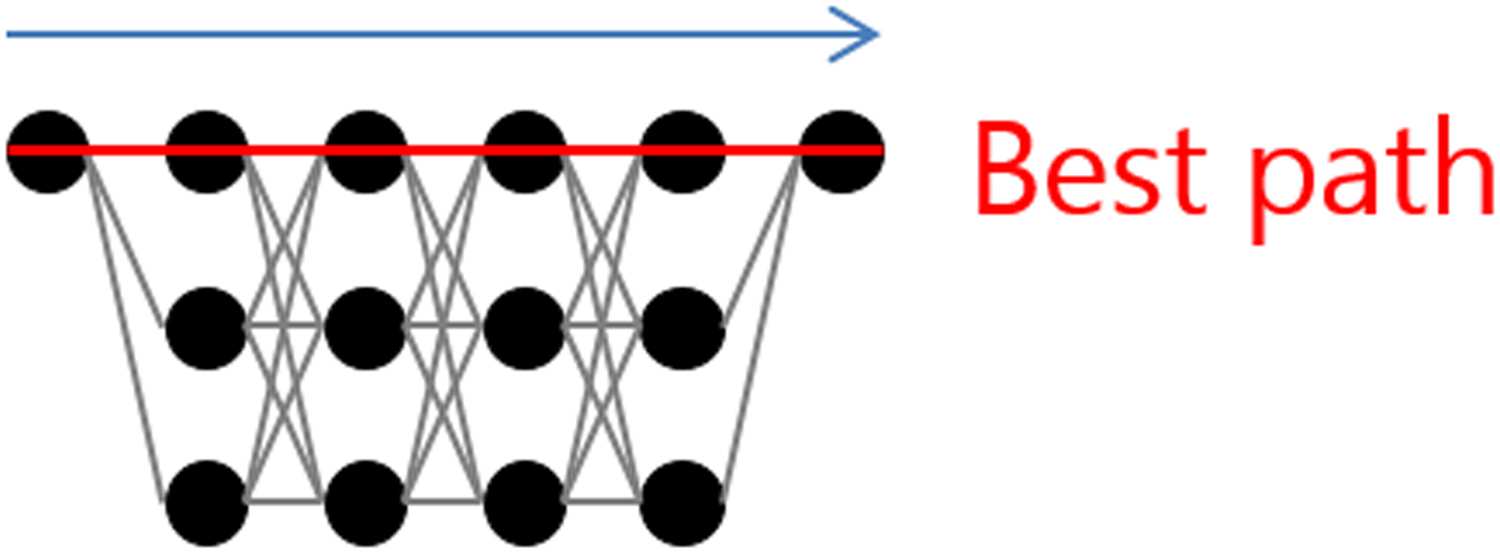
Figura 3: Lattice and best path.
exponential scores of all possible paths causes
underflow, overflow, or loss of significant digits.
We introduce a way of accurately computing it
with the same time complexity as Algorithm 2 for
Equazione (4). For explanation, we use the simpli-
fied example of the lattice depicted in Figure 3,
in which the span length is 4 and the number of
states is 3. The special nodes for start and end states
are attached to the both ends of the span. There are
81(= 34) paths in this lattice. We assume that the
path that consists of top nodes of all time steps are
the best path as shown in Figure 3. No generality
is lost by making this assumption. To calculate the
second term of Equation (5), we have to consider
the exponential scores for all the possible paths
except the best path, 80(= 81 − 1) paths.
We first give a way of thinking, which is not
our algorithm itself but helpful to understand it. In
the example, we can further group these 80 paths
according to the steps where the best path is not
taken. In this way, we have 4 spaces in total as
illustrated in Figure 4. In Space 1, the top node
of time step 4 is excluded from consideration.
54(= 33 × 2) paths are taken into account here.
Since this space covers all paths that do not go
through the top node of time step 4, we only have
to consider the paths that go through this node in
other spaces. In Space 2, this node is always passed
through, and instead the top node of time step 3
is excluded. 18(= 32 × 2) paths are considered
in this space. Allo stesso modo, 6(= 31 × 2) paths and
2(= 30 × 2) paths are taken into consideration
in Space 3 and Space 4, rispettivamente. Così, we
can consider all the possible paths except the best
sentiero, 80(= 54 + 18 + 6 + 2) paths. Tuttavia, Questo
is not our algorithm itself as we mentioned.
We introduce two tricks for making the
calculation more efficient. We explain them with
Figura 5, in which Spaces 2 E 3 are picked up.
The first trick is that the separated two spaces can
be merged at time step 4 because the paths later
than time step 3 are identical. When we reach time
step 4 in the forward iteration in each of the two
610
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 4: Divided search spaces.
Algorithm 3: LogSumExp of the scores of all
possible paths except the best path
C = {B-X, I-X, E-X, S-X, O};
s = s(k)
l,j ; # the start position
e = e(k)
l,j ; # the end position
c1(S) = B-X; # the best path
for i = s + 1; i ≤ e − 1; io + + do
c1(io) = I-X;
Figura 5: Merge of search spaces.
use the same splits of documents as Lu and Roth
(2015), published on their website.6 For GENIA,
we use GENIAcorpus3.02p,7 in which sentences
are already tokenized (Tateisi and Tsujii, 2004).
Following previous work (Finkel and Manning,
2009; Lu and Roth, 2015), we first split the last
10% of sentences as the test set. Prossimo, we use the
first 81% and the subsequent 9% for training and
development sets, rispettivamente. We make the same
modifications as described by Finkel and Manning
(2009) by collapsing all DNA, RNA, and protein
subtypes into DNA, RNA, and protein, keeping
cell line and cell type, and removing other entity
types, resulting in 5 entity types. The statistics of
each dataset are shown in Table 1.
3.2 Model and Training
In this study, we adopt as baseline a BiLSTM-
CRF model, which is widely used for NER tasks
(Lample et al., 2016; Ma and Hovy, 2016;
Chiu and Nichols, 2016; Reimers and Gurevych,
2017). We apply our usage of CRF to this base-
line. We prepare three types of models for fair com-
parisons with existing methods. The first one is the
model to which is fed conventional word embed-
dings and CNN-based character-level representa-
zione (Ma and Hovy, 2016; Chiu and Nichols, 2016;
6http://www.statnlp.org/research/ie.
7http://www.geniaproject.org/genia-corpus/
c1(e) = E-X;
foreach c ∈ C do
α(C) = P (k)
C,S + UN(k)
[S],C;
β = −∞;
for i = s + 1; i ≤ e; io + + do
foreach c ∈ C do
foreach c′ ∈ C do
αc (c′) = α (c′) + P (k)
C,io + UN(k)
c′,C;
if c == c1(io) Poi
foreach c′ ∈ C\{c1(i − 1)} do
βc (c′) = αc (c′);
βc (c1(i − 1)) =
C,io + UN(k)
β + P (k)
c1(i−1),C;
foreach c ∈ C do
α(C) = LogSumExp (αc);
β = LogSumExp (βc);
foreach c ∈ C\{c1(e)} do
α(C)+ = A(k)
C,[E];
α (c1(e)) = β + UN(k)
E-X,[E];
return LogSumExp (α);
Reimers and Gurevych, 2017).8 We initialize
word embeddings with the pretrained embeddings
Guanto (Pennington et al., 2014) of dimension 100
in ACE-2005. For GENIA, we adopt the pretrained
embeddings trained on MEDLINE abstracts (Chiu
et al., 2016) instead. The initialized word embed-
dings are fixed during training. The vectors of the
word embeddings and the character-level repre-
sentation are concatenated and then input into
8https://github.com/yahshibu/nested-ner-
pos-annotation.
tacl2020.
611
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
# documents
# sentences
# mentions
– 1st level
– 2nd level
– 3rd level
– 4th level
# labels per token (D)
Train
370
(7,285)
24,827
21,966
2,635
215
9
1.06
ACE-2005
(%)
(%) Dev
43
(968)
3,234
(88) 2,900 (90)
316 (10)
(11)
(1)
(1)
(0)
(0)
18
0
1.05
GENIA
Test
(%)
(%)
(%)
Train
–
15,022
47,027
(%) Dev
–
1,669
4,469
51
(1,058)
3,041
2,686 (88) 44,611 (95) 4,239 (95) 5,273 (94)
(6)
(0)
(0)
323 (11)
(1)
(0)
(5)
(0)
(0)
(5)
(0)
(0)
Test
–
1,855
5,600
2393
23
0
1.05
230
0
0
1.05
327
0
0
1.05
30
2
1.05
Tavolo 1: Statistics of the datasets used in the experiments. Note that in ACE-2005, sentences are not
originally split. We report the numbers of sentences based on the preprocessing with the Stanford
CoreNLP (Manning et al., 2014).
Hyperparameter
word dropout rate
character embedding dimension
CNN window size
CNN filter number
batch size
LSTM hidden size
LSTM dropout rate
gradient clipping
Value
0.05
128
3
256
32
256
0.2 (w/o BERT)
0.5 (w/ BERT)
5.0
Tavolo 2: Hyperparameters in our experiments.
the BiLSTM layer. The second model
is the
model combined with the pretrained BERT model
(Devlin et al., 2019).9 We use the uncased version
of BERT large model as a contextual word embed-
dings generator without fine-tuning and stack the
BiLSTM layers on top of the BERT model. IL
third model is the BiLSTM-CRF model to which is
fed word embeddings, character-level representa-
zione, BERT embeddings, and FLAIR embeddings
(Akbik et al., 2018) using FLAIR framework
(Akbik et al., 2019).10 All our models have 2
BiLSTM hidden layers, and the dimensionality of
each hidden unit is 256 in all our experiments.
Tavolo 2 lists the hyperparameters used for our
experimental evaluations. We adopt AdaBound
(Luo et al., 2019) as an optimizer. Early stopping
is used based on the performance of development
set. We repeat the experiment 5 times with differ-
ent random seeds and report average and standard
deviation of F1-scores on a test set as the final
performance.
9https://github.com/yahshibu/nested-ner-
tacl2020-transformers.
10https://github.com/yahshibu/nested-ner-
tacl2020-flair.
4 Experimental Results
4.1 Comparison with Existing Methods
Tavolo 3 presents comparisons of our model with
existing methods. Note that some existing methods
use embeddings of POS tags as an additional input
feature whereas our method does not. Our method
outperforms the existing methods with 76.83%
E 77.19% in terms of F1-score when using only
word embeddings and character-level representa-
zione. Especially, our method brings much higher
recall values than the other methods. The recall
scores are improved by 3.1% E 2.4% on ACE-
2005 and GENIA datasets, rispettivamente. These
results demonstrate that our training and decod-
ing algorithms are quite effective for extracting
nested entities. Inoltre, when we use BERT
and FLAIR as contextual word embeddings, we
achieve an F1-score of 83.99% with BERT and
84.34% with BERT and FLAIR on ACE-2005.
D'altra parte, BERT does not perform well
on GENIA. We assume that this is because the
domain of GENIA is quite different from that of
the corpus used for training the BERT model.
Regardless, it is demonstrated that our method
performs better than or at least as well as existing
metodi.
4.2 Ablation Study
We conduct an ablation study to verify the effec-
tiveness of our learning and decoding methods.
We first replace our objective function for training
with the standard objective function of the linear-
chain CRF. The methods for decoding N -best
paths have been well studied because such algo-
rithms have been required in many domains
(Soong and Huang, 1990; Kaji et al., 2010; Huang
et al., 2012). Tuttavia, we hypothesize that our
612
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Method
Katiyar and Cardie (2018)
Ju et al. (2018)11
Wang et al. (2018)† 12
Wang and Lu (2018)†
Sohrab and Miwa (2018)
Zheng et al. (2019)
Fisher and Vlachos (2019)
Lin et al. (2019)†
Strakov´a et al. (2019)†13
This work
Fisher and Vlachos (2019) [BERT]
Strakov´a et al. (2019) [BERT]†
This work [BERT]
Strakov´a et al. (2019) [BERT+FLAIR]†
This work [BERT+FLAIR]
Precision (%)
70.6
74.2
74.5
76.8
–
–
75.1
76.2
76.35
78.27 ± 0.81
82.7
82.58
83.30 ± 0.22
83.48
83.83 ± 0.39
ACE-2005
Recall (%)
70.4
70.3
71.5
72.3
–
–
74.1
73.6
74.39
75.44 ± 0.37
82.1
84.29
84.69 ± 0.37
85.21
84.87 ± 0.09
F1 (%)
70.5
72.2
73.0
74.5
–
–
74.6
74.9
75.36
76.83 ± 0.36
82.4
83.42
83.99 ± 0.27
84.33
84.34 ± 0.20
Precision (%)
79.8
78.5
78.0
77.0
93.2
75.9
–
75.8
79.60
78.70 ± 0.69
−
79.92
77.46 ± 0.65
80.11
77.81 ± 0.69
GENIA
Recall (%)
68.2
71.3
70.2
73.3
64.0
73.6
–
73.9
73.53
75.74 ± 0.64
−
76.55
76.65 ± 0.58
76.60
76.94 ± 1.12
F1 (%)
73.6
74.7
73.9
75.1
77.1
74.7
–
74.8
76.44
77.19 ± 0.10
−
78.20
77.05 ± 0.12
78.31
77.36 ± 0.26
Tavolo 3: Main results. We group methods into three types. The first group consists of the methods that
do not use any contextual word embeddings. The second group consists of the methods that use BERT
but do not use any other contextual word embeddings. The third group consists of the methods that use
both BERT and FLAIR. ‘‘†’’ indicates the methods using POS tags.
ACE-2005
Precision (%) Recall (%)
F1 (%)
This work 78.27 ± 0.81 75.44 ± 0.37 76.83 ± 0.36 78.70 ± 0.69 75.74 ± 0.64 77.19 ± 0.10
60.89 ± 1.30 75.38 ± 1.27 67.34 ± 0.37 70.72 ± 0.39 79.20 ± 1.27 74.71 ± 0.18
– L
77.77 ± 0.31 67.42 ± 0.29 72.22 ± 0.13 79.70 ± 0.56 73.41 ± 0.35 76.43 ± 0.28
– L&D
Precision (%) Recall (%)
F1 (%)
GENIA
Tavolo 4: Results when ablating away the learning (l) and decoding (D) components of our proposed
method.
learning method, as well as our decoding method,
helps to improve performance. That is why we first
remove only our learning method. Then, we also
replace our decoding algorithm with the standard
decoding algorithm of the linear-chain CRF. È
equivalent to preparing the conventional CRF for
each entity type separately.
The results are shown in Table 4. They demon-
strate that introducing only our decoding algorithm
results in high recall scores but hurts precision.
This suggests that our learning method should
be necessary for achieving high precision. Essere-
sides, removing the decoding algorithm results in
lower recall. This is natural because it does not
intend to find any nested entity after extracting
outermost entities. Così, it is demonstrated that
11Note that in ACE-2005, Ju et al. (2018) did their experi-
ments with a different split from Lu and Roth (2015) that we
follow.
12Wang et al. (2018) did not report precision and recall
scores. Instead of Wang et al. (2018), Wang and Lu (2018)
reported the scores for the model of Wang et al. (2018).
13Strakov´a et al. (2019) did not report precision and recall
scores in their paper. We requested this information from the
authors, and they provided their score data.
both our learning and decoding algorithms con-
tribute much to good performance.
4.3 Analysis of Behavior
To further understand how our method handles
nested entities, we investigate the performance for
entities of each level. Tavolo 5 shows the recall
scores for gold entities of each level when using
conventional word embeddings. Among all levels,
our model results in the best performance at the 1st
level that consists of only gold outermost entities.
The deeper a level, the lower recall scores. On the
other hand, Tavolo 6 shows the precision scores
for predicted entities in each level of one trial
on each dataset. Because the number of levels in
the predictions vary between trials, taking macro
average of precision scores over multiple trials is
not representative. Therefore, we show only the
precision scores from one trial in Table 6. IL
precision score for the 5th level on ACE-2005 is
as high as or higher than those of other levels.
Precision scores are less dependent on level. Questo
tendency is also shown in other trials.
Inoltre, we compare the tendency of our
method with that of an existing method. We select
613
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
ACE-2005
GENIA
ACE-2005
GENIA
Level Recall (%) Num. Rcall (%) Num.
76.10 ± 0.50 2,686 77.92 ± 0.72 5,273
1st
71.70 ± 0.70
2nd
327
58.00 ± 5.42
0
3rd
50.00 ± 0.00
4th
0
323 40.61 ± 1.74
30
2
–
–
Level Precision (%) Num. Precision (%) Num.
5,038
2,500
1st
2nd
326
311
3
43
3rd
0
9
4th
0
6
5th
80.29
57.06
66.67
–
–
80.36
72.35
79.07
66.67
83.33
Tavolo 5: Recall scores for gold annotations of each
level.
Tavolo 6: Precision scores for predictions of each
level of one trial.
Wang and Lu (2018) method for comparison.14
We train their model with the ACE-2005 dataset
using their original implementation and repeat
Quello 5 times. The recall scores from the 1st level
to the 4th level are 66.52%, 65.34%, 42.14%,
E 50.00%, rispettivamente. The tendency about
the difference across levels is common to Wang
and Lu (2018) method and our method, and the
scores from our method (Tavolo 5) are entirely
higher than those from their method. It is demon-
strated that our method can extract both outer and
inner entities better. D'altra parte, their
method can extract crossing entities (two entities
overlap but neither is contained in the other),
although our method cannot. Actually, their model
outputs some crossing spans in our experiments. In
this case, we cannot analyze the results regarding
precision scores in the same manner as Table 6.
There are cases where one cannot uniquely decide
the level of an span nested within multiple crossing
spans. Regardless, our method cannot handle cross-
ing entities. Tuttavia, crossing entities are very
rare (Lu and Roth, 2015; Wang et al., 2018).
The test sets of ACE-2005 and GENIA have no
crossing entities. This property of our method
does not have a negative impact on performance,
at least on the ACE-2005 and GENIA datasets.
4.4 Error Analysis
We manually scan the test set predictions on
ACE-2005. We find that many of the errors can
be classified into two types.
The first type is partial prediction error. Given
the following sentence: ‘‘Let me set aside the
hypocrisy of a man who became president
because of a lawsuit trying to eliminate everybody
else’s lawsuits, Ma
instead focus on his own
experience’’. The annotation marks ‘‘a man who
became president because of a lawsuit’’, but our
14We do not use POS tags as one of input features for a
fair comparison with our method.
Maximal depth
1
2
3
4
5
∞ (no restriction)
# tokens per second
6,083
3,761
3,655
3,742
3,723
3,701
Tavolo 7: Decoding speed on ACE-2005.
model extracts a shorter or longer span. È
difficult to extract the proper spans of clauses that
contain numerous modifiers.
The second type is error derived from prono-
minal mention. Consider the following example:
‘‘They roar, they screech.’’. These ‘‘They’’s refer
to ‘‘tanks’’ in another sentence of the same docu-
ment and are indeed annotated as VEH (Vehicle).
Our model fails to detect these pronominal men-
tions or wrongly labels them as PER (Person).
Document context should be taken into considera-
tion to solve this problem.
These types of errors have been reported by
Katiyar and Cardie (2018), Ju et al. (2018), E
Lin et al. (2019) and still remain as challenges.
4.5 Running Time
We investigate how our
recursive decoding
method impacts on the decoding speed in terms of
the number of words processed per second. We use
the model trained with ACE-2005 used for Table 6
and change the maximal depth of decoding to 1, 2,
3, 4, 5, and ∞. When the maximal depth is n, our
decoder Viterbi-decodes only from the 1st level to
the n-th level. Note that, when the maximal depth
È 1, the decoding process is completely the same
as the Viterbi decoding of the standard CRF. Noi
run them on an Intel i7 (2.7 GHz) CPU.
Results are listed in Table 7. The processed
words per second decrease by 38% when the
614
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Method
Katiyar and Cardie (2018)
Wang et al. (2018)†15
Wang and Lu (2018)†
Straková et al. (2019)†16
This work
Straková et al. (2019) [BERT]†
This work [BERT]
Straková et al. (2019) [BERT+FLAIR]†
This work [BERT+FLAIR]
P (%)
72.3
74.9
78.0
78.92
79.93
84.71
85.23
84.51
85.94
R (%)
66.8
71.8
72.4
75.33
75.10
83.96
84.72
84.29
85.69
F1 (%)
69.7
73.3
75.1
77.08
77.44
84.33
84.97
84.40
85.82
Tavolo 8: Comparison on ACE-2004. ‘‘†’’ indicates the methods using POS tags.
maximal depth varies from 1 A 2. There are two
main reasons for this phenomenon. Primo, our de-
coder needs the processing for moving across
different levels. That processing is not necessary
when the maximal depth is 1. Secondo, the number
of the extracted spans at the 2nd level is large
and not negligible (12.5% of that of the extracted
spans at the 1st level as shown in Table 6). IL
numbers of the extracted spans at the 3rd and
lower levels are small, and then the processed
words do not largely decrease when the maximal
depth increases over 2. Regardless, our decoder
does not take twice as long as the standard CRF
on ACE-2005.
4.6 Comparison on ACE-2004
We also compare our method with existing meth-
ods on the ACE-2004 dataset. We use the same
splits as Lu and Roth (2015). The setups are the
same as those of our experiment on ACE-2005.
Tavolo 8 shows the results. As shown, our method
significantly outperforms existing methods. Note
that most of them use POS tags as an additional
input feature whereas our method does not.
4.7 Flat NER
To assess how our model works on flat NER task,
we additionally evaluate our model on CoNLL-
2003 (Tjong Kim Sang and De Meulder, 2003),
which is annotated with outermost entities only.
The setups here are the same as those of our
15Wang et al. (2018) did not report precision and recall
scores. Instead of Wang et al. (2018), Wang and Lu (2018)
reported the scores for the model of Wang et al. (2018).
16Strakov´a et al. (2019) did not report precision and recall
scores in their paper. We requested this information from the
authors, and they provided their score data.
Method
Wang and Lu (2018)†
Strakov´a et al. (2019)†
This work
Lample et al. (2016)‡
Ma and Hovy (2016)‡
Liu et al. (2019)‡
This work − L&D‡
Devlin et al. (2019)‡
Akbik et al. (2018)‡
Liu et al. (2019)‡
Jiang et al. (2019)‡
Baevski et al. (2019)‡
F1 (%)
90.5
90.77
91.14 ± 0.04
90.94
91.21
91.96 ± 0.04
90.84 ± 0.10
92.80
93.09 ± 0.12
93.47 ± 0.03
93.47
93.5
Tavolo 9: Comparison on CoNLL-2003. Noi
group methods into two types. The first
group consists of the methods that do not
use any contextual word embeddings. IL
second one consists of the methods that use
contextual word embeddings such as BERT
and FLAIR. ‘‘†’’ indicates the methods
using POS tags. ‘‘‡’’ indicates the methods
not designed to extract nested entities.
experiment on ACE-2005. We not only prepare
our proposed model but also the ablated model
without our training nor decoding method, as in
Sezione 4.2. The former model can extract spans
nested within other extracted spans regardless of
the property of the dataset, but the latter model
never extracts spans within other extracted spans.
We use the 100-dimensional GloVe embeddings
for both models as in our previous experiments.
The results are in Table 9. We compare our
method with existing methods that do not adopt
any contextual word embeddings (the upside of
Tavolo 9) here, although we also show results from
615
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
T
l
UN
C
_
UN
_
0
0
3
3
4
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
recent work with contextual word embeddings for
reference. Primo, in comparison with the methods
designed for nested NER (Wang and Lu, 2018;
Strakov´a et al., 2019), our method performs better
even on CoNLL-2003. This means that our method
works well on not only nested NER but also flat
NER. Prossimo, we compare with methods that can
handle only flat NER. Tavolo 9 shows that our
method is comparable to the standard BiLSTM-
CRF models (Lample et al., 2016; Ma and Hovy,
2016) on CoNLL-2003. Tuttavia, note that there
are some differences between the experiments of
the previous studies (Lample et al., 2016; Ma and
Blu, 2016) and our experiment. Per esempio,
different word embeddings are used, or the hidden
size of LSTM is not aligned. Nevertheless, we can
compare our proposed model to the ablated model.
As shown in Table 9, there is a significant gap
(P < 0.005 with the permutation test) between the
two scores, 91.14(±0.04)% and 90.84(±0.10)%.
We analyze this gap in detail and find that our
proposed model performs well especially in the
cases where it is difficult to decide which is
suitable, an inner span or an outer span. Given the
following sentence: ‘‘An assessment group made
up of the State Council’s Port Office, the Civil
Aviation Administration of China, the General
Administration of Customs and other authorities
had granted the airport permission to handle
foreign aircraft, Xinhua said .’’. In the CoNLL-
2003 dataset, the four spans ‘‘State Council’’,
‘‘Civil Aviation Administration of China’’, ‘‘Gen-
eral Administration of Customs’’, and ‘‘Xinhua’’
are annotated as ORG (Organization). Both
models correctly detect the latter three entities
in most trials, but the ablated model tends to
extract ‘‘State Council ’s Port Office’’ instead of
‘‘State Council’’. On the other hand, our proposed
model tends to extract both ‘‘State Council ’s Port
Office’’ and ‘‘State Council’’. ‘‘State Council ’s
Port Office’’ is indeed a false-positive, but our
model can detect the correct entity span ‘‘State
Council’’ more steadily than the ablated model.
Thus, our proposed model achieves the higher
F1-score.
Recently, Liu et al. (2019) proposed a new
architecture for sequence labeling, which can
capture global information at the sentence level
better
than BiLSTM, and reported an F1-
score of 91.96% when using conventional word
embeddings (93.47% when using BERT). It is
true that our model based on BiLSTM does not
perform as well as their model, but our decoder
can be combined with their proposed encoder.
We leave it for future work.
5 Related Work
Alex et al. (2007) proposed several ways to
combine multiple CRFs for such tasks. They found
that, when they cascaded separate CRFs of each
entity type by using the output from the previous
CRF as the input features of the current CRF, best
performance was yielded. However, their method
could not handle nested entities of the same entity
type. In contrast, Ju et al. (2018) dynamically
stacked multiple layers that recognize entities
sequentially from innermost ones to outermost
ones. Their method can deal with nested entities
of the same entity type.
Finkel and Manning (2009) proposed a CRF-
based constituency parser for this task such that
each named entity is a node in the parse tree.
However,
its time complexity is the cube of
the length of a given sentence, making it not
scalable to large datasets involving long sentences.
Later on, Wang et al. (2018) proposed a scalable
transition-based approach, a constituency forest
(a collection of constituency trees). Its time
complexity is linear in the sentence length.
Lu and Roth (2015) introduced a mention
hypergraph representation for capturing nested
entities as well as crossing entities (two entities
overlap but neither is contained in the other).
One issue in their approach is the spurious
structures of the representation. Muis and Lu
(2017) incorporated mention separators to address
the spurious structures issue, but it still suffers
from the structural ambiguity issue. Wang and Lu
(2018) proposed a hypergraph representation free
of structural ambiguity. However, they introduced
a hyperparameter,
length of an
to reduce the time complexity. Setting
entity,
the hyperparameter to a small number results in
speeding up but ignoring longer entity segments.
Katiyar and Cardie (2018) proposed another
hypergraph-based approach that learns the struc-
ture using an LSTM network in a greedy manner.
However, their method has a hyperparameter that
sets a threshold for selecting multiple candidate
mentions. It must be carefully tuned for adjusting
the trade-off between recall and precision.
the maximal
616
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
t
l
a
c
_
a
_
0
0
3
3
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Sohrab and Miwa (2018) proposed a neural
exhaustive model that enumerates all possible
spans as potential entity mentions and classifies
them. However, they also use the maximal-length
hyperparameter to reduce time complexity.
Fisher and Vlachos (2019) proposed a novel neu-
ral network architecture that merges tokens or enti-
ties into entities forming nested structures and then
labels each of them. Their architecture, however,
needs the maximal nesting level hyperparameter.
Lin et al. (2019) proposed a sequence-to-nuggets
architecture that first identify anchor words of all
mentions and then recognize the mention bound-
aries for each anchor word. Their method also
use the maximal-length hyperparameter to reduce
time complexity.
Strakov´a et al. (2019) proposed an encoding
algorithm to allow the modeling of multiple named
entity labels in a linearized scheme and proposed
a neural model that predicts sequential labels for
each token. Zheng et al. (2019) proposed a method
that can detect entities boundaries with sequence
labeling models. These two methods do not require
special hyperparameters. They can also deal with
crossing entities as well as nested entities in con-
trast to our method, but our experiments demon-
strate that our method can perform well because
crossing entities are very rare (Lu and Roth, 2015;
Wang et al., 2018).
6 Conclusion
We propose learning and decoding methods for
extracting nested entities. Our decoding method
iteratively recognizes entities from outermost ones
to inner ones in an outside-to-inside way. It recur-
sively searches a span of each extracted entity
for nested entities with second-best sequence de-
coding. We also design an objective function
for training that ensures our decoding algorithm.
Our method has no hyperparameters beyond those
of conventional CRF-based models. Our method
achieves 85.82%, 84.34%, and 77.36% F1-scores
on ACE-2004, ACE-2005, and GENIA datasets,
respectively.
For future work, one interesting direction is
joint modeling of NER with entity linking or
coreference resolution. Previous studies (Durrett
and Klein, 2014; Luo et al., 2015; Nguyen et al.,
2016; Martins et al., 2019) demonstrated that
leveraging mutual dependency of the NER, link-
ing, and coreference tasks could boost each
performance. We would like to address this issue
while taking nested entities into account.
Acknowledgments
We thank Aldrian Obaja Muis for helpful com-
ments, and many anonymous reviewers and the
action editor for helpful feedback on various
drafts of the paper. We are also grateful to Jana
Strakov´a for sharing experimental results. Eduard
Hovy was supported in part by DARPA grant
FA8750-18-2-0018 funded under
the AIDA
program.
References
Alan Akbik, Tanja Bergmann, Duncan Blythe,
Kashif Rasul, Stefan Schweter, and Roland
Vollgraf. 2019. FLAIR: An easy-to-use frame-
work for state-of-the-art NLP. In Proceedings
of the 2019 Conference of the North American
Chapter of the Association for Computational
Linguistics (Demonstrations), pages 54–59,
Minneapolis, Minnesota, Association for Com-
putational Linguistics.
Alan Akbik, Duncan Blythe, and Roland Vollgraf.
2018. Contextual string embeddings for se-
quence labeling. In Proceedings of the 27th
International Conference on Computational
Linguistics, pages 1638–1649, Santa Fe, New
Mexico, USA, Association for Computational
Linguistics.
Beatrice Alex, Barry Haddow, and Claire Grover.
2007. Recognising nested named entities in
biomedical text. In Biological, Translational,
and Clinical Language Processing, pages 65–72,
Prague, Czech Republic. Association for Com-
putational Linguistics.
Alexei Baevski, Sergey Edunov, Yinhan Liu, Luke
Zettlemoyer, and Michael Auli. 2019. Cloze-
driven pretraining of self-attention networks.
In Proceedings of the 2019 Conference on Em-
pirical Methods in Natural Language Processing
and the 9th International Joint Conference on
Natural Language Processing (EMNLP-IJCNLP),
pages 5360–5369, Hong Kong, China. Associ-
ation for Computational Linguistics.
Kate Byrne. 2007. Nested named entity recogni-
tion in historical archive text. In International
617
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
t
l
a
c
_
a
_
0
0
3
3
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Conference on Semantic Computing (ICSC
2007), pages 589–596.
Zhe Cao, Tao Qin, Tie-Yan Liu, Ming-Feng
Tsai, and Hang Li. 2007. Learning to rank:
From pairwise approach to listwise approach.
In Proceedings of the 24th International Con-
ference on Machine Learning, pages 129–136.
Billy Chiu, Gamal Crichton, Anna Korhonen, and
Sampo Pyysalo. 2016. How to train good word
embeddings for biomedical NLP. In Proceed-
ings of
the 15th Workshop on Biomedical
Natural Language Processing, pages 166–174,
Berlin, Germany. Association for Computa-
tional Linguistics.
Jason P. C. Chiu and Eric Nichols. 2016. Named
entity recognition with bidirectional LSTM-
CNNs. Transactions of
the Association for
Computational Linguistics, 4:357–370.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In Proceedings of
the 2019
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, Volume 1
(Long and Short Papers), pages 4171–4186,
Minneapolis, Minnesota. Association for Com-
putational Linguistics.
George Doddington, Alexis Mitchell, Mark
Przybocki, Lance Ramshaw, Stephanie Strassel,
and Ralph Weischedel. 2004. The automatic
content extraction (ACE) program – tasks,
In Proceedings of
data, and evaluation.
the Fourth International Conference on Lan-
guage Resources and Evaluation (LREC’04),
Lisbon, Portugal. European Language Re-
sources Association (ELRA).
Greg Durrett and Dan Klein. 2014. A joint model
for entity analysis: Coreference, typing, and
linking. Transactions of the Association for
Computational Linguistics, 2:477–490.
Jenny Rose Finkel and Christopher D. Manning.
2009. Nested named entity recognition. In Pro-
ceedings of the 2009 Conference on Empirical
Methods in Natural Language Processing,
pages 141–150, Singapore. Association for
Computational Linguistics.
Joseph Fisher and Andreas Vlachos. 2019.
Merge and label: A novel neural network
architecture for nested NER. In Proceedings of
the 57th Annual Meeting of the Association for
Computational Linguistics, pages 5840–5850,
Florence, Italy. Association for Computational
Linguistics.
Zhiheng Huang, Yi Chang, Bo Long, Jean-
Francois Crespo, Anlei Dong, Sathiya Keerthi,
and Su-Lin Wu. 2012. Iterative Viterbi A*
algorithm for k-best sequential decoding. In
Proceedings of the 50th Annual Meeting of
the Association for Computational Linguistics
(Volume 1: Long Papers), pages 611–619, Jeju
Island, Korea. Association for Computational
Linguistics.
Yufan Jiang, Chi Hu, Tong Xiao, Chunliang
Zhang, and Jingbo Zhu. 2019.
Improved
differentiable architecture search for language
modeling and named entity recognition. In
the 2019 Conference on
Proceedings of
Empirical Methods
in Natural Language
Processing and the 9th International Joint
Conference on Natural Language Processing
(EMNLP-IJCNLP), pages 3585–3590, Hong
Kong, China. Association for Computational
Linguistics.
layered model
Meizhi Ju, Makoto Miwa, and Sophia Ananiadou.
for nested
2018. A neural
named entity recognition. In Proceedings of
the 2018 Conference of the North American
Chapter of the Association for Computational
Linguistics: Human Language Technologies,
Volume 1 (Long Papers), pages 1446–1459,
New Orleans, Louisiana. Association for Com-
putational Linguistics.
Nobuhiro Kaji, Yasuhiro Fujiwara, Naoki
Yoshinaga, and Masaru Kitsuregawa. 2010.
Efficient staggered decoding for sequence
labeling. In Proceedings of the 48th Annual
Meeting of the Association for Computational
Linguistics, pages 485–494, Uppsala, Sweden,
Association for Computational Linguistics.
Arzoo Katiyar and Claire Cardie. 2018. Nested
named entity recognition revisited. In Pro-
ceedings of the 2018 Conference of the North
American Chapter of
the Association for
Computational Linguistics: Human Language
618
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
t
l
a
c
_
a
_
0
0
3
3
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Technologies, Volume 1 (Long Papers),
pages 861–871, New Orleans, Louisiana,
Association for Computational Linguistics.
J.-D. Kim, T. Ohta, Y. Tateisi, and J. Tsujii. 2003.
GENIA corpus—a semantically annotated
for bio-textmining. Bioinformatics,
corpus
19(Suppl 1):i180–i182.
John D. Lafferty, Andrew McCallum, and
Fernando C. N. Pereira. 2001. Conditional ran-
dom fields: Probabilistic models for segmenting
and labeling sequence data. In Proceedings
of the Eighteenth International Conference on
Machine Learning, pages 282–289.
Guillaume Lample, Miguel Ballesteros, Sandeep
Subramanian, Kazuya Kawakami, and Chris
Dyer. 2016. Neural architectures for named
entity recognition. In Proceedings of the 2016
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, pages 260–270,
San Diego, California. Association for Com-
putational Linguistics.
Hongyu Lin, Yaojie Lu, Xianpei Han, and Le
Sun. 2019. Sequence-to-nuggets: Nested entity
mention detection via anchor-region networks.
In Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics,
pages 5182–5192, Florence, Italy. Association
for Computational Linguistics.
Yijin Liu, Fandong Meng, Jinchao Zhang, Jinan
Xu, Yufeng Chen, and Jie Zhou. 2019. GCDT:
A global context enhanced deep transition
architecture for sequence labeling. In Pro-
ceedings of the 57th Annual Meeting of the
Association for Computational Linguistics,
pages 2431–2441, Florence, Italy. Association
for Computational Linguistics.
In Proceedings of
Wei Lu and Dan Roth. 2015. Joint mention
extraction and classification with mention
the 2015
hypergraphs.
Conference on Empirical Methods in Natural
Language Processing, pages 857–867, Lisbon,
Portugal. Association
for Computational
Linguistics.
Gang Luo, Xiaojiang Huang, Chin-Yew Lin, and
Zaiqing Nie. 2015. Joint entity recognition and
disambiguation. In Proceedings of the 2015
Conference on Empirical Methods in Natural
Language Processing, pages 879–888, Lisbon,
Portugal. Association
for Computational
Linguistics.
Liangchen Luo, Yuanhao Xiong, Yan Liu, and
Xu Sun. 2019. Adaptive gradient methods with
dynamic bound of learning rate. CoRR, abs/
1902.09843. Version 1.
Xuezhe Ma and Eduard Hovy. 2016. End-
to-end sequence labeling via bi-directional
the
LSTM-CNNs-CRF.
54th Annual Meeting of the Association for
Computational Linguistics (Volume 1: Long
Papers), pages 1064–1074, Berlin, Germany.
Association for Computational Linguistics.
In Proceedings of
Christopher Manning, Mihai Surdeanu, John
Bauer, Jenny Finkel, Steven Bethard, and David
McClosky. 2014. The Stanford CoreNLP natu-
ral language processing toolkit. In Proceedings
of 52nd Annual Meeting of the Association
for Computational Linguistics: System Demon-
strations, pages 55–60, Baltimore, Maryland.
Association for Computational Linguistics.
Pedro Henrique Martins, Zita Marinho, and
Andr´e F. T. Martins. 2019. Joint learning of
named entity recognition and entity linking.
In Proceedings of the 57th Annual Meeting of
the Association for Computational Linguistics:
Student Research Workshop, pages 190–196,
Florence, Italy. Association for Computational
Linguistics.
Aldrian Obaja Muis and Wei Lu. 2017. Label-
ing gaps between words: Recognizing overlap-
ping mentions with mention separators. In
Proceedings of the 2017 Conference on Empiri-
cal Methods in Natural Language Processing,
pages 2608–2618, Copenhagen, Denmark.
Association for Computational Linguistics.
David Nadeau and Satoshi Sekine. 2007. A survey
of named entity recognition and classification.
Lingvisticæ Investigationes, 30(1):3–26.
Dat Ba Nguyen, Martin Theobald, and Gerhard
Weikum. 2016. J-NERD: Joint named entity
recognition and disambiguation with rich
linguistic features. Transactions of the Associa-
tion for Computational Linguistics, 4:215–229.
619
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
t
l
a
c
_
a
_
0
0
3
3
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Jeffrey
and
Pennington, Richard Ocher,
Christopher Manning. 2014. GloVe: Global
vectors for word representation. In Proceedings
of the 2014 Conference on Empirical Methods
in Natural Language Processing (EMNLP),
pages 1532–1543, Doha, Qatar. Association for
Computational Linguistics.
Nils Reimers
and Iryna Gurevych. 2017.
Reporting score distributions makes a differ-
ence: Performance study of LSTM-networks
for sequence tagging. In Proceedings of the
2017 Conference on Empirical Methods in
Natural Language Processing, pages 338–348,
Copenhagen, Denmark. Association for Com-
putational Linguistics.
Nambirajan Seshadri and Carl-Erik W. Sundberg.
1994. List Viterbi decoding algorithms with
applications. IEEE Transactions on Communi-
cations, 42(234):313–323.
Mohammad Golam Sohrab and Makoto Miwa.
2018. Deep exhaustive model for nested named
entity recognition. In Proceedings of the 2018
Conference on Empirical Methods in Natural
Language Processing, pages 2843–2849, Brus-
sels, Belgium. Association for Computational
Linguistics.
Frank K. Soong and Eng-Fong Huang. 1990. A
Tree.Trellis based fast search for finding the n
best sentence hypotheses in continuous speech
recognition. In Speech and Natural Language:
Proceedings of a Workshop Held at Hidden
Valley, Pennsylvania, June 24-27,1990.
Jana Strakov´a, Milan Straka, and Jan Hajic.
2019, Jul. Neural architectures for nested NER
through linearization. In Proceedings of the
57th Annual Meeting of the Association for
Computational Linguistics, pages 5326–5331,
Florence, Italy. Association for Computational
Linguistics.
Emma Strubell, Patrick Verga, David Belanger,
and Andrew McCallum. 2017. Fast and
accurate entity recognition with iterated dilated
the 2017
convolutions.
In Proceedings of
Conference on Empirical Methods in Natural
Language Processing,
2670–2680,
Copenhagen, Denmark. Association for Com-
putational Linguistics.
pages
Yuka Tateisi and Jun-ichi Tsujii. 2004. Part-of-
speech annotation of biology research abstracts.
In Proceedings of the Fourth International Con-
ference on Language Resources and Evalua-
tion (LREC’04), Lisbon, Portugal. European
Language Resources Association (ELRA).
Erik F. Tjong Kim Sang and Fien De Meulder.
2003. Introduction to the CoNLL-2003 shared
task: Language-independent named entity re-
cognition. In Proceedings of the Seventh Con-
ference on Natural Language Learning at
HLT-NAACL 2003, pages 142–147.
Bailin Wang and Wei Lu. 2018. Neural segmental
hypergraphs for overlapping mention recogni-
tion. In Proceedings of the 2018 Conference
on Empirical Methods in Natural Language
Processing, pages 204–214, Brussels, Belgium.
Association for Computational Linguistics.
Bailin Wang, Wei Lu, Yu Wang, and Hongxia
Jin. 2018. A neural transition-based model for
nested mention recognition. In Proceedings of
the 2018 Conference on Empirical Methods in
Natural Language Processing, pages 1011–1017,
Brussels, Belgium. Association for Computa-
tional Linguistics.
Yefeng Wang. 2009. Annotating and recognising
named entities in clinical notes. In Proceedings
of the ACL-IJCNLP 2009 Student Research
Workshop, pages 18–26, Suntec, Singapore.
Association for Computational Linguistics.
Changmeng Zheng, Yi Cai, Jingyun Xu, Ho-fung
Leung, and Guandong Xu. 2019. A boundary-
aware neural model for nested named entity
recognition. In Proceedings of the 2019 Confer-
ence on Empirical Methods in Natural Lan-
guage Processing and the 9th International
Joint Conference on Natural Language Pro-
cessing (EMNLP-IJCNLP), pages 357–366,
Hong Kong, China. Association for Compu-
tational Linguistics.
620
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
3
4
1
9
2
3
7
9
5
/
/
t
l
a
c
_
a
_
0
0
3
3
4
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3