METHODS
NeuMapper: A scalable computational framework
for multiscale exploration of the brain’s
dynamical organization
Caleb Geniesse1,2*, Samir Chowdhury2*, and Manish Saggar2
1Biophysics Program, Stanford University, Stanford, CA, USA
2Department of Psychiatry and Behavioral Sciences, Stanford University, Stanford, CA, USA
*Equal contribution.
Keywords: TDA, Mapper, Optimal transport, Multitask fMRI, Ongoing cognition, NeuroSynth
a n o p e n a c c e s s
j o u r n a l
ABSTRACT
For better translational outcomes, researchers and clinicians alike demand novel tools to distill
complex neuroimaging data into simple yet behaviorally relevant representations at the single-
participant level. Recentemente, the Mapper approach from topological data analysis (TDA) ha
been successfully applied on noninvasive human neuroimaging data to characterize the entire
dynamical landscape of whole-brain configurations at the individual level without requiring
any spatiotemporal averaging at the outset. Despite promising results, initial applications of
Mapper to neuroimaging data were constrained by (1) the need for dimensionality reduction
E (2) lack of a biologically grounded heuristic for efficiently exploring the vast parameter
spazio. Here, we present a novel computational framework for Mapper—designed specifically
for neuroimaging data—that removes limitations and reduces computational costs associated
with dimensionality reduction and parameter exploration. We also introduce new meta-analytic
approaches to better anchor Mapper-generated representations to neuroanatomy and behavior.
Our new NeuMapper framework was developed and validated using multiple fMRI datasets
where participants engaged in continuous multitask experiments that mimic “ongoing”
cognition. Looking forward, we hope our framework will help researchers push the boundaries
of psychiatric neuroimaging toward generating insights at the single-participant level across
consortium-size datasets.
Citation: Geniesse, C., Chowdhury, S.,
& Saggar, M. (2022). NeuMapper: UN
scalable computational framework for
multiscale exploration of the brain’s
dynamical organization. Network
Neuroscience, 6(2), 467–498. https://doi
.org/10.1162/netn_a_00229
DOI:
https://doi.org/10.1162/netn_a_00229
Supporting Information:
https://doi.org/10.1162/netn_a_00229
Received: 3 Luglio 2021
Accepted: 4 Gennaio 2022
AUTHOR SUMMARY
Modern neuroimaging promises to transform how we understand human brain function, COME
well as how we diagnose and treat mental disorders. Tuttavia, this promise hinges on the
development of computational tools for distilling complex, high-dimensional neuroimaging
data into simple representations that can be explored in research or clinical settings. IL
Mapper approach from topological data analysis (TDA) can be used to generate such
representations. Here, we introduce several improvements to the underlying algorithm to aid
scalability and parameter selection for high-dimensional neuroimaging data. We also provide
new analytical tools for annotating and extracting neurobiological and behavioral insights
from the generated representations. We hope this new framework will help facilitate
translational applications of precision neuroimaging in clinical settings.
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Manish Saggar
saggar@stanford.edu
Handling Editor:
Michael Breakspear
Copyright: © 2022
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Mapper:
TDA-based technique for generating
graph representations that identify
meaningful subgroups of high-
dimensional data.
Topological data analysis (TDA):
Applied mathematical approaches
for analyzing datasets—using
techniques from algebraic topology—
that learn and leverage information
about the shape of complex data.
Shape graph:
Compressed network representation
generated by Mapper; nodes
correspond to local clusters and
edges connect clusters that share
data points.
Dimensionality reduction:
Process of selecting and extracting
features from data to reduce the
number of variables under
consideration.
INTRODUCTION
Modern noninvasive brain imaging technologies such as structural and functional magnetic
resonance imaging promise to not only provide a better understanding of the neural basis
of behavior but also to fundamentally transform how we diagnose and treat mental health
disorders (Saggar & Uddin, 2019). Tuttavia, unlike structural imaging, which has become stan-
dard in clinical practice, the clinical use of functional imaging (per esempio., fMRI) has been limited to
presurgical planning and functional mapping (Mitchell et al., 2013; Tie et al., 2014). One of the
main reasons for the lack of fMRI-based clinical translation is that the traditional neuroimaging
analyses (per esempio., GLM or functional connectivity) tend to measure group-averaged (or central) ten-
dencies, largely due to the low signal-to-noise ratio of the blood oxygenation level–dependent
(BOLD) signal (Welvaert & Rosseel, 2013, 2014). Relatively newer functional connectome-based
predictive modeling approaches have made some progress in generating insights at the single indi-
vidual level (Bzdok et al., 2020; Shen et al., 2017), but several methodological issues need to be
resolved before their clinical application becomes a reality (Dadi et al., 2019).
Recentemente, an approach called Mapper from the field of topological data analysis (TDA) ha
shown promise in generating data-driven insights from fMRI data at the single-participant level
(Geniesse et al., 2019; Saggar et al., 2018). TDA is a recently developed field of mathematics
that combines ideas from algebraic topology and network science (Carlsson, 2014), and TDA-
based algorithms have gained recognition for their ability to generate robust, interpretable, E
multiscale models of high-dimensional data (Giusti et al., 2016; Munch, 2017; Petri et al.,
2014). Among these techniques, Mapper is a particularly successful method that produces a
shape graph—a graphical representation of the underlying structure or shape of the
high-dimensional data (Lum et al., 2013; Singh et al., 2007). Although Mapper bears some
similarity to established dimensionality reduction methods (Belkin & Niyogi, 2003; Coifman
& Lafon, 2006; Tenenbaum et al., 2000; Van Der Maaten & Hinton, 2008), it extends and
improves upon such methods by (1) reincorporating high-dimensional information in the
low-dimensional projection and thereby putatively reducing information loss due to projec-
zione, E (2) producing a compressed (and putatively robust) graphical representation of the
underlying structure that can be analyzed using network science tools. The revealed graphical
representation can also be annotated using meta-information to extract further insights about
the underlying structure of the data. Analogous to how a geographical map encodes large-
scale topographical features such as mountains, valleys, and plains, a shape graph produced
by Mapper encodes essential topological features such as connectivity, adjacency, and enclo-
sure. In the context of functional neuroimaging data, the shape graph encodes the higher order
spatiotemporal features of brain activity that underlie cognition.
Mapper has been previously applied to generate insights from the underlying shape of data in
oncology (Nicolau et al., 2011), transcriptomics (Rizvi et al., 2017), spinal cord and brain injury
(Nielson et al., 2015), fragile X syndrome (Bruno et al., 2017; Romano et al., 2014), gene expres-
sion (Jeitziner et al., 2019), protein interaction (Sardiu et al., 2019), and materials science (Lee
et al., 2017). In the field of neuroimaging, Mapper has been recently used to explore the
whole-brain dynamics associated with different cognitive tasks and transitions during simulated
“ongoing” cognition (Saggar et al., 2018); visualize the distributed and overlapping patterns of
neural activity associated with different categories of visual stimuli via the DyNeuSR platform
(Geniesse et al., 2019); and relate gene co-expression to brain function (Patania et al., 2019).
While initial neuroimaging applications of Mapper have been promising, several key meth-
odological improvements to the processing pipeline are still needed, especially before the
approach can be scaled up to larger consortium-style datasets. Primo, Mapper requires
Network Neuroscience
468
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Partial clustering:
Applying a clustering algorithm to a
subset of data points. Used to obtain
cluster bins from cover bins.
Optimal transport (OT) metric:
A measure of similarity (O
dissimilarity) between two
probability distributions (per esempio.,
1-Wasserstein distance). When
comparing distributions on a graph,
these metrics consider both global
and local properties.
NeuroSynth:
A meta-analytic database of
probabilistic mappings between
cognitive (per esempio., terms, topics) E
neural states (cioè., activations) Quello
can be used for a broad range of
neuroimaging applications.
Mesoscale structure:
A description of network structure in
terms of node density and within-
group connectivity, Per esempio, IL
clustering of nodes into different
groups (cioè., modularity) or the
partitioning of nodes into dense core
and sparse peripheral regions (cioè.,
core-periphery).
embedding the data into a low-dimensional space via a user-chosen target dimension d and filter
function f : ℝp → ℝd. Although the Mapper pipeline includes a partial clustering step to reincorporate
some of the information loss due to initial projection (Singh et al., 2007), low-dimensional embedding
is by definition an inefficient step due to an invariable loss of information by going down 2–3 orders of
magnitude in dimensions. Secondo, the Mapper approach traditionally rescales the low-dimensional
embedding to be inside a grid with overlapping cells. The size of the grid and the level of overlap are
controlled by the resolution (R) and gain (G) parameters, rispettivamente. A caveat with this construction is
that the number of cells in a grid with fixed r, g grows exponentially in dimension d, leading to
inefficient computations. Given recent evidence (and growing consensus) that large-scale
consortium-level sample sizes are essential for accurately and reproducibly linking brain
function and behavior (Marek et al., 2020), computational costs and scalability have thus
become critical issues. Third, although Mapper results are stable over parameter perturbations,
initial fine tuning of Mapper parameters is required due to their dependence on the data
acquisition parameters (Saggar et al., 2018). Altogether, we argue that a systematic approach is
required for exploring Mapper parameters, including f, D, R, and g, in order to select those that
best capture the multiscale information putatively available in the neuroimaging data.
In this work, we provide significant methodological advances for each step of the Mapper pro-
cessing pipeline and introduce novel approaches to generate neurobiological insights from the
shape graphs. Hereinafter, we refer to our neuroimaging-focused Mapper pipeline as NeuMapper.
Our framework moves away from dimensionality reduction altogether in favor of working directly
with distance metrics in the original acquisition space, leading to a significantly faster pipeline
that simultaneously avoids information loss due to low-dimensional projection. Toward optimiz-
ing parameter space exploration, we provide a semiautomatic parameter selection scheme using
neuroimaging-specific objectives to remove all but a few parameter choices. Apart from the meth-
odological advancements, we also introduce methods to generate novel neurobiological insights.
Per esempio, we introduce quantitative tools from computational optimal transport (OT) (Peyré &
Cuturi, 2019) for better handling of overlapping graphical annotations as they take into account
both global and local properties of the graph. Further, to better anchor the Mapper representations
into cognitive neuroscience, we present a novel approach for annotating shape graph nodes using
the NeuroSynth meta-analytic cognitive decoding framework (Yarkoni et al., 2011).
Using NeuMapper, we not only reproduce and independently validate the results obtained
by the traditional Mapper approach (Saggar et al., 2018) but also reveal several new neuro-
behavioral insights. We show that individual differences in the mesoscale structure (per esempio., mod-
ularity) of the NeuMapper-generated shape graphs could reveal important neurobehavioral
insights. Per esempio, in line with the previous work, we found that recruiting task-specific
brain circuits led to better performance on the task. Further, applying tools from OT on shape
graphs, we provide an avenue to study relations and dependencies between cognitive tasks.
Per esempio, we found that higher degree of overlap between brain circuits engaged during
working memory and math is required for better performance on the math task. Lastly, by link-
ing the NeuroSynth meta-analytic database with NeuMapper-generated shape graphs, noi professionisti-
vide a new avenue to study and decode cognitively anchored changes in mental states at the
highest temporal resolution. Here, we showed that such decoding could be helpful in reveal-
ing the negative impact of overreflection or attention lapses on task performance.
RESULTS
Our results are grouped into three parts. In the first part (see section Methodological Advances
in the NeuMapper Framework), we start by presenting the standard Mapper approach and the
Network Neuroscience
469
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
methodological advances in NeuMapper. In the next part (section Mesoscale Structure of
Shape Graphs Informs Behavior), we show the relevance of mesoscale network statistics for
deriving brain-behavior insights from shape graphs. In the final part (section Anchoring Shape
Graphs Into Known Cognitive Constructs), we anchor shape graphs into cognitive topic terms
using the meta-analysis framework of NeuroSynth (Yarkoni et al., 2011).
To test the efficacy of our NeuMapper approach, we used two independent fMRI datasets,
of which the first was used for method development and the second was used as held-out data
to be used only for final quantitative evaluation. In both datasets, participants performed a
continuous multitask experiment with known ground truth about the timing of transitions
between mental states as dictated by the task blocks. These datasets also contained task per-
formance scores for each participant and hence could be used to ground Mapper-generated
insights into behavior. Dataset 1 (n = 18) was previously collected by Gonzalez-Castillo et al.
(2015) and comprised four task blocks (180 s each; repeated twice) consisting of resting state
(R), working memory (M), math/arithmetic (UN), and visual attention ( V) compiti. We indepen-
dently acquired Dataset 2 (n = 32) using the same paradigm as Dataset 1, but at a faster tem-
poral resolution and shorter duration for task blocks (90 S; repeated twice). After discarding
subjects due to excessive head motion and compliance issues resulting in very low behavioral
scores, we retained 25 subjects in Dataset 2 (see Methods for details). We used Dataset 1 for
methods development, leaving Dataset 2 aside for use only in the final quantitative analysis.
Further, to demonstrate the robustness of our framework, we additionally performed reliability
and validation checks via (1) extensive perturbation of Mapper parameters; E (2) compari-
son of results from real data with data generated from the phase-randomized null models.
Methodological Advances in the NeuMapper Framework
We first begin by describing the traditional Mapper algorithm for generating a shape graph,
followed by introducing two main improvements. Briefly, a shape graph is constructed from a
dataset X 2 ℝp via a four-step recipe: filtering, binning, partial clustering, and graph generation.
In detail: (1) a dimension-reducing filter function f : ℝp → ℝd computes a low-dimensional
embedding of X, (2) the embedding is covered by overlapping d-dimensional hypercubes; points
in X are said to be in the same cover bin if their projections land in the same hypercube, (3)
points in the same cover bin are further clustered into smaller cluster bins to account for faraway
points (in p-dimensional space) erroneously landing in the same cover bin during projection,
E (4) a graph is constructed with cluster bins as nodes, and edges between cluster bins that
share points. Naively, the number of bins grows exponentially in dimension and becomes pro-
hibitively expensive (Hinneburg & Keim, 1999; Sheikholeslami et al., 1998) to compute for d ≫
2, thus putatively requiring conventional Mapper applications to rely on an initial embedding
into no more than one or two dimensions. This poses a problem for neuroimaging data, Dove
meaningful dimension reduction requires embedding dimensions ranging from five (Shine et al.,
2019UN) A 25 (Stevner et al., 2019) A 50 (Vidaurre et al., 2017). Additionally, exploring the large
parameter space of Mapper is prohibitively expensive. While this issue could be mitigated by
restricting the search space to fit within a preestablished computational budget, currently there
are no neuroimaging-specific guidelines for obtaining this restricted search space.
Our first methodological contribution (Figure 1A) is to modify the core Mapper algorithm to
avoid relying on an explicit low-dimensional embedding. Invece, we start with a matrix D of
distances (between whole or parcellated brain volumes) in the native high-dimensional space
and produce a transformed matrix D 0 that approximates the geometry of temporal trajectories
through brain activity space. Specifically, we obtain D 0 as geodesic distances on a reciprocal
470
Binning:
A step of Mapper-type algorithms
that partitions a dataset. Neighboring
partition blocks are encouraged to
have overlaps.
Cover bins:
A collection of overlapping sets
returned by the binning procedure.
Cluster bins:
A refined collection of overlapping
sets produced by clustering each set
in the collection of cover bins
independently.
Geodesic distance matrix:
A distance matrix describing the
pairwise shortest path lengths
between nodes in a graph.
Network Neuroscience
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
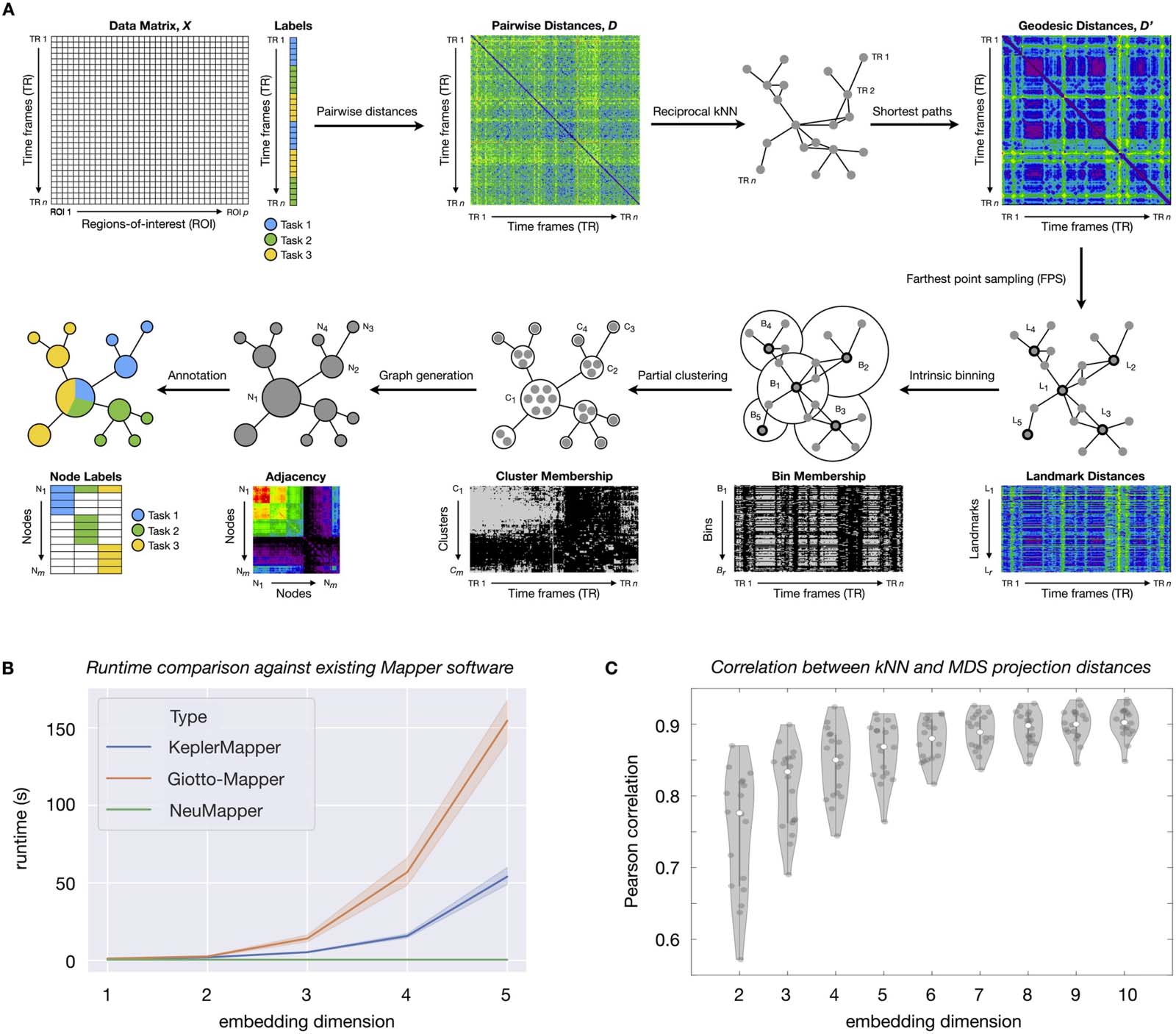
Figura 1. Methodological advances in the NeuMapper framework. (UN) Given, a data matrix X, we first compute an initial distance matrix D
and subsequently a reciprocal kNN graph. Prossimo, we compute geodesic distances on this graph to obtain a transformed matrix D 0 that captures
nonlinear structure in the data. To access the hierarchical structure of this graph, we select landmarks L1, …, Lr on the data for a resolution
parameter r and produce an overlapping partition with bins B1, …, Br centered at these landmarks. Each bin is refined by a clustering step that
uses the initial distances D, thus yielding a set of refined bins C1, …, Cm where m is possibly larger than r. Note that this step injects information
from the native space of the data. Finalmente, a graph is constructed with nodes N1, …, Nm indexed by the refined bins and edges for overlapping
bins. The nodes are further annotated by the labels of the data points, which may be user provided (per esempio., different tasks in a blocked design, COME
shown here by Tasks 1–3) or generated by meta-analytic or otherwise data-driven approaches. (B) Open-source Mapper approaches (Kepler-
Mapper 1.2.0 and Giotto-tda 0.2.2) explicitly construct a low-dimensional embedding and create hypercubes in the low-dimensional space.
The complexity of this operation increases exponentially in dimension. NeuMapper avoids this step by performing implicit changes to the
underlying distance matrix and can be much faster in practice. Here we standardized NeuMapper parameters to have the same y-intercept as
KeplerMapper and Giotto-Mapper. Note also that KeplerMapper and Giotto-Mapper are written in Python and may obtain other benefits from
interfacing with libraries such as scikit-learn. NeuMapper results reported here are from a version written in Matlab and meant to show only
that the intrinsic binning method scales well with embedding dimension in practice. These results suggest that incorporating the NeuMapper
methodology into KeplerMapper will allow the best of both pipelines. Differences in KeplerMapper and Giotto-Mapper runtimes are likely due
to implementation differences, although we do not investigate these differences further. (C) Geodesic distances on the kNN graph can be
embedded in Euclidean space using multidimensional scaling (MDS), but this projection step causes distortion. The amount of distortion goes
down with increasing embedding dimension. Tuttavia, using a high embedding dimension leads to costly computations in the standard Map-
per approach. In contrasto, our approach can work directly with the kNN distances and avoid this projection loss.
k-nearest neighbor (kNN) graph:
A graph built on point cloud data where
nodes correspond to data points, E
edges connect a node to its k (a positive
integer) closest data points.
k-nearest neighbor (kNN) graph. This construction is reminiscent of a standard kNN graph,
where data points are nodes and each point is connected to its k-closest neighbors, ma il
reciprocal variant adds an extra pruning step that reduces the effect of outliers (Qin et al.,
2011). Supporting Information Figure S6 contains a toy example motivating our use of the
Network Neuroscience
471
NeuMapper: A computational framework for exploration of brain dynamics
Reciprocal kNN:
A k-nearest neighbors graph created
by dropping nonsymmetric neighbors
(cioè., two points are only considered
neighbors if each is a k-closest
neighbor of the other). Found to better
respect local density when connecting
neighbors than standard kNN.
Intrinsic binning:
A binning method that uses
landmarks and distances from these
landmarks to partition data points.
reciprocal kNN. Prossimo, we perform an intrinsic binning step that produces overlapping parti-
tions of the data, but using only D 0 and not any ambient space (for another application of this
method, see Dłotko, 2019). Note that this intrinsic binning is a general way of scaling up
computations and does not rely on a particular method of generating D 0, so one could just
as easily apply a moderate- to high-dimensional projection and calculate distances (per esempio.,
Euclidean distances) to obtain D 0. Our use of geodesic distances as above is not necessary
for the framework, but effective for producing useful neurobiological insights. Overall, intrinsic
binning simultaneously avoids high runtimes (Figure 1B) and projection-related information
loss (Figure 1C) as compared to existing Mapper implementations that perform binning by
constructing grids in the d-dimensional embedding space. Supporting Information Figure S1
provides a visual summary of the standard Mapper algorithm and adaptations for NeuMapper.
Our second methodological contribution is a semiautomated parameter selection frame-
work that we developed to guide parameter exploration and selection. Specifically, noi professionisti-
vide a heuristic algorithm that leverages the autocorrelation structure naturally present in fMRI
dati (due to the slow hemodynamic response) and returns a parameter choice that presents a
mesoscale view—that is, between views that are “too local” or “too global”—of the data. Vedere
Methods for more details of our methodological contributions.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Mesoscale Structure of Shape Graphs Informs Behavior
To ensure that our methodological advancements, Per esempio, doing away with dimensionality
reduction and utilizing an intrinsic binning strategy, can still recover previously reported neuro-
behavioral insights obtained using the traditional Mapper approach (Saggar et al., 2018), we first
replicated initial results pertaining to the mesoscale properties of the shape graphs. Using our
NeuMapper approach we not only replicated results based on the original dataset used by
Saggar et al. (2018) (cioè., Dataset 1), but also reproduced the findings using an independent
dataset (Dataset 2). In addition to replicating the mesoscale properties of the shape graphs,
our NeuMapper approach can also capture temporal transitions in the brain activity patterns
at the level of single time frames. In this section, we also show how our NeuMapper approach
extends previous work using tools from OT theory to reveal pairwise mesoscale statistics.
Complex networks are often characterized by their hierarchical structure (Lancichinetti
et al., 2009; Ravasz & Barabási, 2003), ranging from local descriptors at the node or edge level
to global descriptors at the whole-graph level. At the mesoscale range are cohesive groups or
clusters of nodes that are more densely connected to each other than to other nodes. Nel
most well-known model of these mesoscales, community structure, a group of nodes have
higher density of within-group connections than a null model graph (Newman, 2006). A sec-
ond, increasingly popular model is the core-periphery structure, where the network contains a
dense core with high within-group connectivity that also occupy central positions in the net-
lavoro, and a periphery of nodes that are sparsely connected to each other (Borgatti & Everett,
2000; Rombach et al., 2014). Community and core-periphery structures have both been used
extensively to gain insights into predictive components of functional brain networks, and new
approaches into studying such mesoscale structures promise to deliver fundamentally new
insights (Bassett et al., 2013; Sporns, 2013).
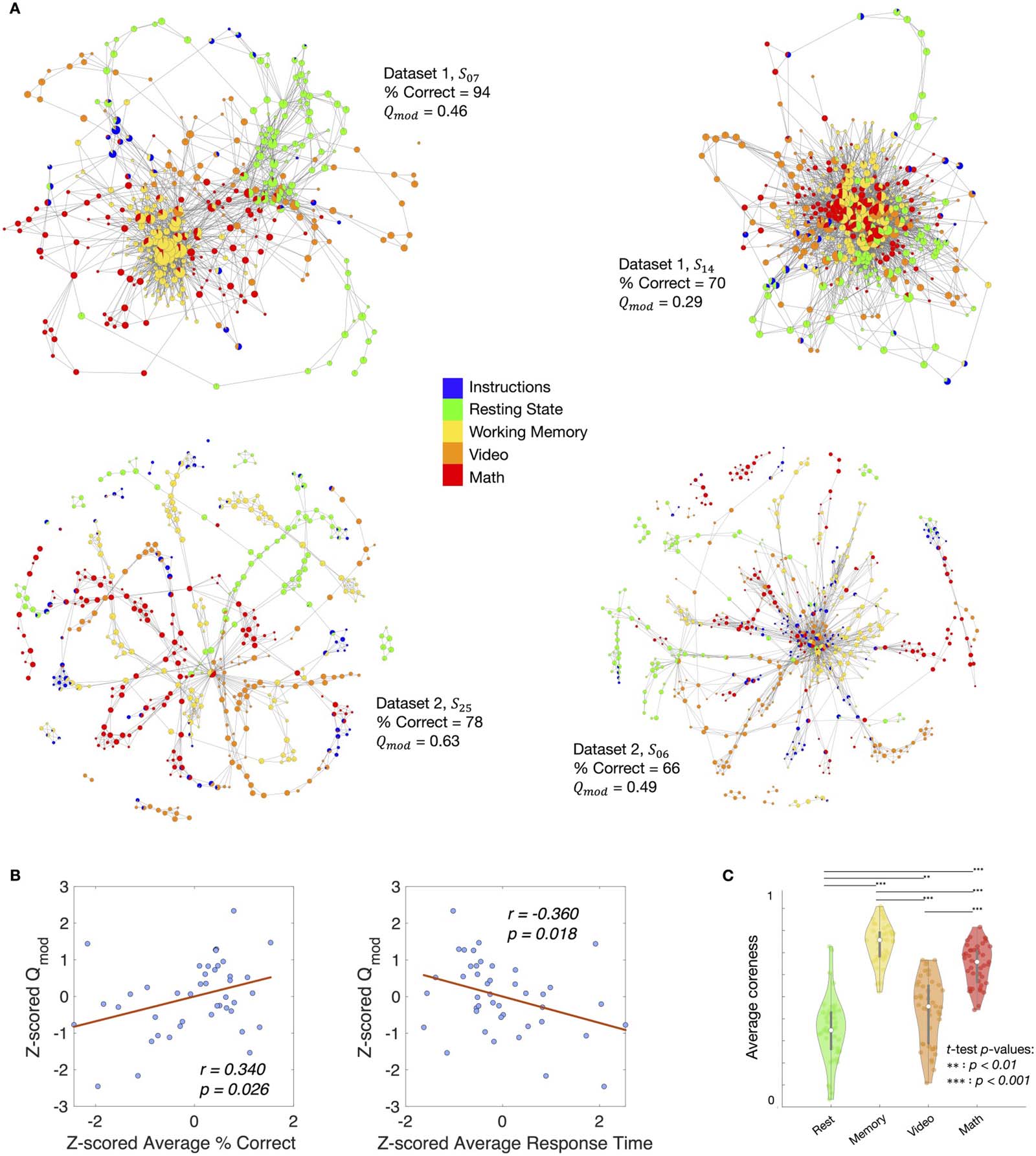
Given a graph partition that yields communities, the modularity Q-score (Qmod) measures
the quality of modularity or community structure (Newman, 2006). A higher Qmod score
implies better community structure. Previously, Saggar et al. (2018) annotated the shape
graphs based on task blocks and computed the modularity using node-level task-based anno-
tation as community assignment. Using Dataset 1, they found that participants whose shape
Network Neuroscience
472
NeuMapper: A computational framework for exploration of brain dynamics
graph had higher task-based modularity performed better across the tasks in the continuous
multitask paradigm (CMP) (in terms of both accuracy and response time). This suggested that
participants with task-specific functional activations performed better on average across differ-
ent tasks. We first replicated this finding on Dataset 1 using our NeuMapper framework to ensure
that our strategy of moving away from dimension reduction still recovers previously reported
brain-behavior relations. Specifically, we observed a significant correlation between the average
task performance (accuracy) and the task-based modularity of the shape graphs (r = 0.561, p =
0.015). Additionally, we observed a significant correlation between response time and modu-
larity (r = −0.488, p = 0.040). We further validated the task accuracy (r = 0.340, p = 0.026) E
response time (r = −0.360, p = 0.018) findings in a larger dataset, n = 43, combining participants
from Datasets 1 E 2 (Figure 2B). Supporting Information Figure S2 shows the modularity-
behavior correlations for the individual datasets. Further, to verify that these results cannot be
reproduced via null models that preserve linear properties of the data, we carried out the analysis
pipeline on phase-randomized null surrogates and observed that these correlations disappeared
(Supporting Information Figure S3). Finalmente, to show that the modularity-behavior correlations
described above are largely stable to parameter perturbation, we performed a grid search over
a moderate region of parameter space surrounding the optimal parameter values for each
dataset, and then computed modularity-behavior correlations across Datasets 1 E 2. Noi
report heat maps of these correlations and their significance ( p values) in Supporting Informa-
tion Figure S4.
Prossimo, we examined the core-periphery mesoscale structure of shape graphs. In the context
of neural processes engaged during the CMP, core nodes could represent whole-brain config-
urations that consistently appear across a scan session, Per esempio, due to task-switching in a
CMP or due to high cognitive demands (Saggar et al., 2018; Shine et al., 2019UN). To replicate
previous finding that configurations from resting state are better represented by peripheral
excursions, whereas those from high cognitive load are better represented by the core nodes,
we estimated coreness scores for nodes in the shape graphs. We recover the core-periphery
structure observed by Saggar et al. (2018), questo è, one-way ANOVA revealed a significant
effect of task in Dataset 1 (F(3, 68) = 67.0, p = 2.9 · 10−20) such that tasks with high cognitive
load such as working memory or math were associated with nodes found relatively deep
inside the core of the shape graphs, whereas resting-state nodes were relatively more periph-
eral. We additionally carried out the nonparametric Kruskal–Wallis test and observed a signif-
icant effect of task (H(3) = 55.8, p = 4.8 · 10−12). We further validated these findings on Dataset
2 using both one-way ANOVA (F(3, 96) = 35.6, p = 1.5 · 10−15) and the Kruskal–Wallis test
(H(3) = 54.2, p = 1.0 · 10−11) with the same observation regarding working memory nodes
being in the core and resting-state nodes being in the periphery. The results obtained by com-
bining participants from Datasets 1 E 2 are shown in Figure 2C. Supporting Information
Figure S2 shows the core-periphery structure for the individual datasets. Additionally, we
observed that this core-periphery structure disappeared in the phase-randomized null surro-
gates (Supporting Information Figure S3).
As a final replication step, we also examined whether our NeuMapper approach can reveal
transitions in task-evoked brain activity at the level of individual time frames. Given a shape
graph, we follow Saggar et al. (2018) in constructing a (#time frames × #time frames) temporal
connectivity matrix (TCM) that shows how each time frame is connected (or similar) to all
other time frames in the graph. Using the traditional Mapper approach on Dataset 1, Saggar
et al. (2018) found that time frames associated with tasks (per esempio., working memory, video, math)
typically had a higher degree of connectivity in the TCM, while those occurring between task
blocks or during rest typically displayed a lower degree of connectivity. Further, they found
Network Neuroscience
473
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 2. Mesoscale structure of shape graphs. (UN) Shape graphs from two representative participants from Dataset 1 (S07 and S14) e due
representative participants from Datset 2 (S25 and S06) colored by experimental task annotations. On the one hand, S07 from Dataset 1 is an
example of a good performer (cioè., high average percent correct) and their shape graph had a highly modular structure (cioè., nodes are pref-
erentially connected to other nodes associated with the same task). D'altra parte, S14 from Dataset 1 is an example of a relatively worse
performer (cioè., lower average percent correct) and their shape graph had a much less modular structure (cioè., nodes associated with different
tasks are connected to each other without any preference for those associated with the same task). (B) Significant correlations between the
modularity score (Qmod) and average task performance (per esempio., percent correct, response time) were observed across both datasets (after z-scoring
within each dataset, separately). These results replicate and strengthen the findings by Saggar et al. (2018) that higher modularity in the shape
graph was associated with better task performance. (C) Separation between tasks as measured by core-periphery scores was observed across
both datasets. These results further reproduce and strenghten the finding by Saggar et al. (2018) that nodes containing resting time frames
mainly resided in the periphery (cioè., lower coreness scores), while nodes associated with the more cognitively demanding tasks (per esempio., memory,
math) tended to localize relatively deeper inside the shape graph (cioè., higher coreness scores).
that the temporal evolution of the degree connectivity (cioè., of each time frame, across the
entire scan) recovered the task block structure (cioè., higher degrees evoked by and maintained
during non-rest task blocks) and between-task transitions (cioè., lower degrees spanning the
between-task instructional periods) of the CMP. We reproduced these previous findings on
Network Neuroscience
474
NeuMapper: A computational framework for exploration of brain dynamics
the same Dataset 1 using NeuMapper (Supporting Information Figure S5). Further validating
our new framework, these results suggest that shape graphs produced by NeuMapper can cap-
ture similar temporal properties of the data compared to those produced by the traditional
Mapper approach.
While the two mesoscale properties of shape graphs present critical insights about neuro-
behavior, they can still be thought of as first-order insights. Così, even though these mesoscale
properties inform about how individual task blocks are represented on the graph, they miss
any putative second-order structure, Per esempio, how well individual task blocks are sepa-
rated from each other on the shape graphs. To better account for such second-order structures,
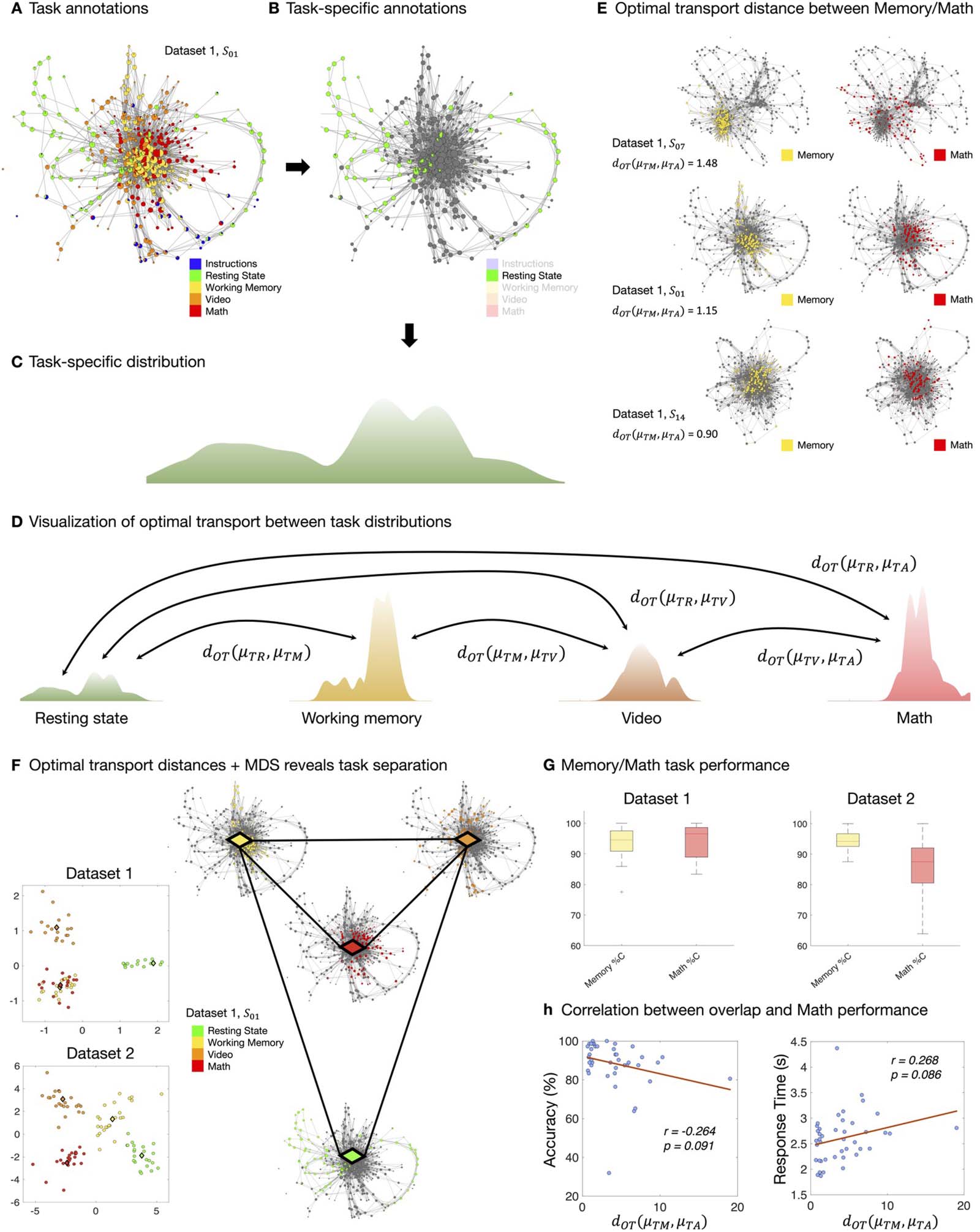
we use tools from optimal transport theory (Peyré & Cuturi, 2019). The pie chart–based pro-
portional annotation of a shape graph node means that each task block contributes a fraction
(possibly zero) of the time points making up the node. After normalizing, each task block thus
yields a probability distribution over the nodes of the graph. We compare the dissimilarities
between these distributions using an OT distance dOT. Intuitively, task annotations correspond
to different landforms making up the global landscape on which whole-brain dynamics occur
during the CMP, and knowledge of pairwise distances between these landforms encodes the
knowledge of the global structure of the landscape. Figura 3 further illustrates this construction
on Datasets 1 E 2, where we additionally visualize interpolations between the shapes of the
task landforms (Figure 3D).
The OT distances between tasks in the shape graphs possess nontrivial structure (Figura 3).
For both Datasets 1 E 2, one-way ANOVA (Dataset 1: F(5,102) = 11.1, p = 1.4 · 10−8; Data-
set 2: F(5,138) = 3.09, p = 0.011) and the Kruskal–Wallis test (Dataset 1: H(5) = 51.6, p = 6.5 ·
10−10; Dataset 2: H(5) = 24.0, P < 0.001) revealed significant effects of task such that the
whole-graph distributions of different task blocks were separated from each other.
To visualize between-task distances derived from OT, we used multidimensional scaling
(Figure 3F). Across both datasets, tasks with low cognitive load (e.g., resting state and video
watching) were well separated from those with putatively higher cognitive load (e.g., working
memory and math). However, only in Dataset 2, math and working memory task blocks were
also separated. Given the previous work that suggests a significant role of working memory
during arithmetic, higher overlap between the two tasks was expected (Cragg & Gilmore,
2014; Raghubar et al., 2010). Lack of such overlap between working memory and math could
indicate poor performance during arithmetic task. We verified this OT-generated observation
by examining differences in behavioral performance during working memory and math tasks
in both datasets. Although the performance during working memory was not different between
datasets (t = −0.718, p = 0.477), there was a significant difference in math performance
between datasets (t = 2.69, p = 0.010). Participants in Dataset 2 performed significantly worse
in math than those in Dataset 1 (Figure 3G). Further, within Dataset 2, we observed a negative
relation trending toward significance (Figure 3H) between OT-derived distance between mem-
ory and math and behavioral performance during math task as measured by accuracy (r =
−0.264, p = 0.091) and response time (r = 0.269, p = 0.086). Thus, providing preliminary evi-
dence in capturing behaviorally relevant interplay between working memory and arithmetic
tasks using our NeuMapper framework.
Anchoring Shape Graphs Into Known Cognitive Constructs
To anchor NeuMapper-generated shape graphs into known cognitive constructs and to poten-
tially decode mental states revealed by the shape graphs, we annotated nodes using the Neu-
roSynth decoding database (Yarkoni et al., 2011). Each node of the shape graph was annotated
Network Neuroscience
475
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
Figure 3. Quantifying pairwise similarity between annotations via optimal transport (OT). (A–C) Individual annotations can be isolated and
normalized into probability distributions, which we can visualize as landscapes. (D) Annotations collapse data across time. Transitions in their
spatial distribution can be quantified via OT distances. (E) These OT distances can be interpreted as follows: S14 has small dOT because their
memory and math annotations are close in the graph, whereas S07 has large dOT because their memory and math annotations occupy different
portions of the graph. We write μTM, μTA for the task annotations corresponding to memory and arithmetic/math, respectively. (F) Because dOT
provides distances, the separation between annotations can be visualized via MDS projection. MDS plots of separation between task anno-
tations across the two datasets are shown in the two panels. For the task annotations, the projection reveals a subtle difference in the shape
graphs from Dataset 1 and 2, showing higher separation between math and memory annotations for Dataset 2 than for Dataset 1. This lack of
overlap is unexpected, due to the recruitment of working memory during arithmetic tasks and may suggest poorer performance in the math
task. (G) Separation between task annotations may be related to the higher separation between memory and math performance in Dataset 2
than in Dataset 1, as reported in the boxplots. (H) We further compute and report Pearson correlations between two quantities: (1) dOT ( μTM,
μTA) between memory task and math/arithmetic task annotations, and (2) math performance in terms of accuracy and response time. These
plots show that lower overlap between memory task and math task annotations is related to poorer math performance.
Network Neuroscience
476
NeuMapper: A computational framework for exploration of brain dynamics
by the strength of spatial cross-correlation between the brain configuration represented by that
node and configurations for related cognitive topics from the NeuroSynth decoding database
(Yarkoni et al., 2011). A similar decoding analysis using NeuroSynth topic terms has been pre-
viously performed for time-varying functional connectivity matrices (Gonzalez-Castillo et al.,
2019).
Here, we first selected two topic terms from the NeuroSynth v4-topics-50 database—task-
positive (Topic 002) and task-negative (Topic 010)—to annotate shape graphs. We then
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
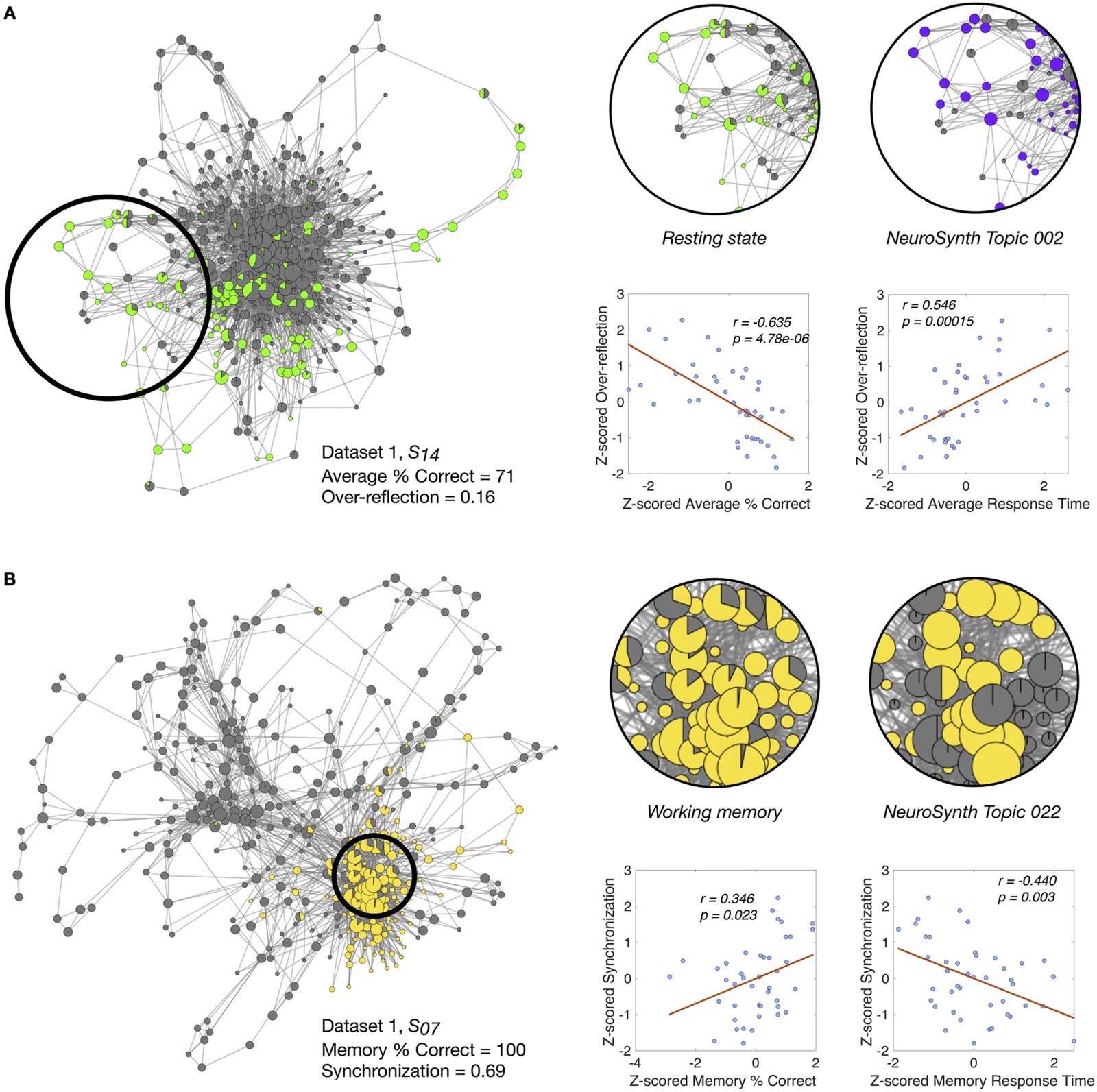
Figure 4. Novel insights from NeuroSynth-generated annotations. (A) We first computed an overreflection score to quantify how often whole-
brain configurations visited during the resting state were more similar to meta-analytic brain configurations generally associated with task-
related cognition (i.e., Topic 002). Here we show the shape graph for a poor performer from Dataset 1, highlighting an example where the
participant may have been thinking excessively of a task when the experimental instruction was to remain at rest. The nodes are colored by the
experimental rest condition and the NeuroSynth-decoded task-positive topic annotations. The corresponding plots show the Pearson corre-
lation between the (z-scored) overreflection score and average task accuracy/response time. (B) We then computed a “synchronization” score
to quantify how often brain configurations visited during the working memory task were more similar to the meta-analytic brain configuration
generally associated with working memory. Here we show the shape graph for a good performer from Dataset 1, highlighting the annotation
overlap captured by the synchronization score. The nodes are colored by the experimental working memory task structure and NeuroSynth-
decoded working memory topic annotations (i.e., Topic 022). The corresponding plots show the Pearson correlation between the (z-scored)
synchronization score and accuracy/response time for the working memory task.
Network Neuroscience
477
NeuMapper: A computational framework for exploration of brain dynamics
compared “empirical” annotations of shape graph nodes based on NeuroSynth topic maps
with annotations based on the expected task structure. We hypothesized that participants’ task
performance would be higher whenever the empirical and expected annotations would match
and that performance would be lower in case of a mismatch.
Interestingly, we observed that eliciting brain configurations that are more similar to the
task-positive topic model during the expected resting-state blocks (i.e., a mismatch) was sig-
nificantly negatively correlated with the percentage of correct responses (averaged across
tasks; r = −0.635, p = 4.78 · 10−6) and significantly positively correlated with average response
time (averaged across tasks; r = 0.546, p = 0.00015) (Figure 4A). These findings suggest that
perhaps this negative relation is associated with putative overreflection about tasks during
periods of rest (i.e., when the participants are instructed to let their minds wander). Note that
we did not find any significant correlations in the reverse case, that is, eliciting brain config-
urations akin to task-negative topic model during nonresting-state task blocks.
Next, we computed a synchronization score by counting the proportion of nodes where the
empirical task-positive annotation coincided with the expected task (M, V, A) blocks and the
task-negative annotation coincided with the expected rest (R) block. As hypothesized, we
observed a significant correlation between the synchronization score and the average accuracy
(r = 0.422, p = 0.005) and response time (r = 0.474, p = 0.001). To go further beyond the
task-positive topic model, we then asked ourselves if specific topic models corresponding to
the tasks (M, V, A) could be related to performance in each individual task. Because the
n-back working memory paradigm has been widely used in the literature and has been highly
sampled in the NeuroSynth database (i.e., Topic 022 is associated with 933 studies), we limited
ourselves to the working memory task block. Specifically, using a specific topic model for the
working memory task (Topic 022), we examined whether performance in the working memory
blocks is associated with eliciting brain configurations that are more similar to the meta-analytic
brain configurations generally related with working memory. Here, we again found that having a
higher match between empirical and expected task annotations—that is, memory (Topic 022)
annotations predicted by NeuroSynth in nodes that were also annotated with the memory exper-
imental task label—was significantly positively correlated with the percentage of correct
responses for the memory task (r = 0.346, p = 0.023) and significantly negatively correlated with
response time for the memory task (r = −0.440, p = 0.003) (Figure 4B). In other words, this finding
suggests that an individual’s performance tends to increase when the participants duly engage
the task-specific brain circuits while performing the task. This results also amplifies the putative
role that NeuMapper can play in decoding mental states.
DISCUSSION
We present a fast, end-to-end computational framework that incorporates and extends the
Mapper algorithm—a powerful manifold learning technique within the suite of methods pro-
vided by the field of TDA (Lum et al., 2013; Rabadán & Blumberg, 2019; Singh et al., 2007)—
by integrating novel algorithmic contributions as well as downstream processing techniques
for capturing second-order mesoscale structure and meta-analysis guided inference. We used
our NeuMapper framework to study multiple functional neuroimaging datasets where partic-
ipants engaged in a CMP simulating ongoing cognition. Our adaptations of methods for
approximating nonlinear geometry revealed interesting topological structure in our datasets
from the outset and our heuristics for parameter selection enabled efficient discovery of mean-
ingful scales at which to observe various types of community structure in the data. We intro-
duced tools from OT theory (Peyré & Cuturi, 2019) to further understand the second-order
Network Neuroscience
478
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
structure of groupings of data points as delineated by experiment design, and also introduced
the use of NeuroSynth-based meta-analyses (Yarkoni et al., 2011) to enrich our shape graphs
with additional semantic meaning. Finally, we translated these computational methods into
markers of individual differences in how the brain adapts to stimuli during ongoing cognition.
In summary, we provide a validated computational pipeline for neuroimaging data that can be
easily used by researchers and clinicians for interactive data representation with simultaneous
access to quantitative insights.
The success of approaches based on dynamic methods for translating patterns of ongoing
cognition into meaningful cognitive states has led to a burgeoning landscape of computational
methodologies for functional neuroimaging data (Bassett et al., 2011; Bullmore & Sporns,
2009; Calhoun et al., 2014; Lurie et al., 2020; Preti et al., 2017; Sporns, 2011; Tagliazucchi
et al., 2012; Turk-Browne, 2013; van der Meer et al., n.d.; Vidaurre et al., 2017). In contrast to
the dynamic functional connectivity approaches that estimate interregional coactivity over
time, topology/geometry processing techniques such as Mapper instead use whole-brain acti-
vation patterns to infer the shape of an underlying landscape of brain activity (Geniesse et al.,
2019; Saggar et al., 2018). By enriching this inferred landscape with annotations coming from
experimental task block labels or meta-analysis based decoding (Yarkoni et al., 2011) and sub-
sequently capturing second-order interactions across groups of annotations—both experimen-
tally based and decoded—we show that it is possible to use TDA methods to both infer
dynamics and obtain a semantic segmentation of the underlying state space. This exploration
of second-order interactions is concurrent with the development of related strategies for higher
order dynamic connectivity (Faskowitz et al., 2020; Owen et al., 2019). Overall, we corrob-
orate and extend prior findings (Saggar et al., 2018) on the relation between task performance
and quantitative measures of shape graphs, and further contribute to the computational meth-
odologies for understanding the brain’s dynamic adaptations to external stimuli.
Our framework extends the traditional Mapper approach without discarding any of its key
properties, and the modular organization of our pipeline suggests replacements based on user
preference. For example, numerous works (Cunningham & Yu, 2014; Nichols et al., 2017)
have found evidence to suggest that brain activity is fundamentally low dimensional, and that
a linear technique such as principal component analysis (PCA) potentially captures this activ-
ity along interpretable axes (Shine et al., 2019a; Shine et al., 2019b). Our framework could be
freely used to this end, by simply replacing the kNN graph construction with a PCA projection.
At the same time, depending on the amount of variance to be explained, one may need a
moderate to high number of projection dimensions when carrying out PCA. More generally,
dimension reduction techniques tend to preserve more information as the embedding dimen-
sion increases (see Figure 1C, for an example). Runtime comparisons showed that our intrinsic
binning approach tended to be much faster than existing open-source Mapper implementa-
tions such as Giotto-Mapper and KeplerMapper when higher embedding dimensions were
used, suggesting that our methods could be incorporated as modules within such frameworks
(Tauzin et al., 2021; van Veen et al., 2019). We note also that techniques for high-dimensional
information retrieval and clustering (Agrawal et al., 2005; Beyer et al., 1998; Hinneburg &
Keim, 1999; Indyk & Motwani, 1998; Radovanović et al., 2010) could potentially be used
to develop a unified computational framework for the binning stage of the Mapper algorithm
that scales well with dimension, and use this work to invite future progress in developing Map-
per applications that do not use low-dimensional embeddings at the outset. Recent works have
fused graph neural network techniques with Mapper to consume graph-structured data as
input and return meaningful embeddings (Bodnar et al., 2020), and such a module could
be easily inserted between the reciprocal kNN and intrinsic binning steps in our framework
Network Neuroscience
479
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
to take advantage of the representational power of neural networks. Along the lines of
hardware-driven scalability, Mapper Interactive (Zhou et al., n.d.) provides state-of-the-art
GPU implementations of the Mapper algorithm for embedding dimensions 1 and 2, and our
method could be adapted to fit into such a pipeline. In addition to such scalability improve-
ments, semiautomated mesoscale network structure analysis is a fundamental aspect of our
pipeline, and we have demonstrated multiple ways in which a user can supply annotations
(i.e., based on task structure or NeuroSynth meta-analyses) to yield quantitative results from
data. Combining these modules with the functionality of existing open-source Mapper imple-
mentations may be crucial in obtaining new insights via geometric and TDA on consortium-
sized data (Marek et al., 2020).
Toward moving Mapper analysis from exploratory to quantitative, we introduced OT tech-
niques that naturally delineate the overlapping categorical labels of shape graph nodes and
quantify the dissimilarity between categories from the perspective of the shape graph. From
an interesting dual perspective, the shape graphs themselves may thus be viewed as filters
through which to quantify the overall landscape of different cognitive constructs, hence lend-
ing a Mapper of Mappers theme to our contributions. Our use of NeuroSynth-based decoding
provided a new angle on obtaining learned categorical labels and introduced a novel study of
semantically-aware TDA in analogy with the semantic segmentation approaches in modern
deep-learning based computer vision (Qi et al., 2017). Our developments suggest that it
may be helpful to view Mapper as less of a fixed, immutable algorithm, and more of a philos-
ophy that may be woven into alternative and diverse computational pipelines.
With regards to neuroimaging studies, an important issue that is not directly addressed in
this work and requires future effort is to estimate the minimum amount of data required per
individual for stable estimation of Mapper-generated shape graphs. In this and previous works
using Mapper, we used 20–30 min of task fMRI data per individual. While access to large
quantities of artifact-free data (Gordon et al., 2017) would be ideal for any computational
method, for clinical populations it is often more practical to aggregate data across sites and
studies (Saggar & Uddin, 2019). In the current work, we carried out two forms of aggregation:
(1) Dataset 2 comprised two runs for each subject that we aggregated before computing shape
graphs, and (2) shape graph properties such as modularity were aggregated across both data-
sets when reporting relations to behavior. Note that Datasets 1 and 2 were obtained at different
sites and under different acquisition parameters, including scanner strengths and repetition
times. Because our framework provided successful inference on the aggregated shape graph
properties, we suggest that future work could consider further aggregations of shape graph
properties for data collected under more variable acquisition parameters to fully test any lim-
itations of our method. We also note that in related work, Saggar et al. (2021) applied the
traditional Mapper approach to data from 100 unrelated subjects in the Human Connectome
Project combined over four 15-min runs. Altogether, these observations suggest that Mapper-
based frameworks may be well suited for data aggregation across runs and that shape graph
properties may be aggregated across datasets acquired under different scanning parameters.
While we focused on some of the most salient aspects of neuroimaging-specific Mapper
design, there were certain choices that we left for future work. In our NeuMapper filter design,
the landmarks obtained via farthest point sampling do not have any particular biological rele-
vance. However, it is possible to augment this step by choosing landmarks using some additional
criterion, for example, by averaging over a proportion of frames to define a “baseline” state for
each task (Duman et al., 2019; Khambhati et al., 2018). In particular, for resting-state studies,
an interesting possibility in our NeuMapper design could be to choose a single base point in
the kNN graph representing a baseline state, and then filter the remaining graph vertices by a
Farthest point sampling (FPS):
An algorithm for selecting a well-
separated set of landmark points from
a dataset.
Network Neuroscience
480
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
one-dimensional number: the distance to the base point (Chowdhury et al., 2020). This one-
dimensional filter setting allows the import of the statistical guarantees provided by the seminal
work of Carriere et al. (2018) and should be carried out in future work. Further down the Mapper
pipeline, the partial clustering step is itself a specialized clustering problem for which Belchi et al.
(2020) have provided theoretical guarantees as well as practical frameworks utilizing k-fold cross-
validation. For expediency, we performed quick initial checks using hierarchical and nonhierar-
chical clustering techniques (James et al., 2000) such as average linkage, complete linkage,
DBSCAN, and HDBSCAN before settling on a simplistic choice of single linkage with a fixed cutoff
parameter. Future work could look into invoking neurobiologically motivated clustering tech-
niques along with additional cross-validation (Belchi et al., 2020).
As shown with CMP datasets, the shape graph representation of functional brain activity
converts high-dimensional neural activity recordings into a landscape on which we can study
whole-brain dynamics driven by the processes underlying cognitive states, and ultimately
relate these analyses to multidimensional behavioral measures and clinical outcomes. A crit-
ical next step will be to demonstrate how our NeuMapper framework can be applied in
unconstrained resting-state paradigms, where there is no known ground truth of the internal
cognitive state of each participant. Our demonstration of NeuroSynth-based decoding of
underlying cognitive states, following Gonzalez-Castillo et al. (2019), provided strong quanti-
tative suggestion that such an approach could be viable and successful. While we did not test
our approach on resting-state or naturalistic fMRI data, we note that the standard Mapper
approach (extrinsic 2-D binning) has recently been applied (Saggar et al., 2021) to 5 hours
of resting-state fMRI data from the Midnight Scan Club dataset (Gordon et al., 2017). There
the authors observed highly subject-specific shape graphs with a central “basin of attraction”
surrounded by peripheral areas having distinct network configurations. Based on these results,
we expect that our approach will extend nicely to resting-state and naturalistic paradigms.
Moreover, the scalability of our approach will allow us to explore some of the consortium-
level naturalistic datasets that are increasingly becoming available.
While designing our NeuMapper framework, we paid particular attention to potential scal-
ability issues when working with the consortium-size datasets needed to reduce statistical error
in brain-behavior association studies (Marek et al., 2020). Given a fixed set of parameters and
assuming the use of the nonlinear reciprocal kNN graph construction, the most expensive com-
putation in our framework comprises a fixed number of calls to the O((|V | + |E |) log(|V |)) Dijkstra
algorithm. For standard fMRI datasets of individual participants with up to several thousand
frames, this computation can be carried out within seconds on standard hardware. For
group-level analysis where datasets may be concatenated to contain up to several million frames
(e.g., for datasets such as the Human Connectome Project), we may utilize GPU libraries such as
cuGraph or nvGRAPH to carry out such computations in a few hours. The remaining steps of the
NeuMapper pipeline—namely parameter selection and post hoc computations—are easily par-
allelized, for example, via the implementation that we used in this work. Future work should
investigate large-scale application of NeuMapper to consortium-size datasets in order to
generate a population-level “template” landscape on which we can map and study the
dynamics of whole-brain activation during cognition. Because shape graphs may be of different
sizes, this requires solving a node-correspondence problem. This can potentially be resolved
using our recently developed extensions of OT theory for scalable generation of correspon-
dences (Chowdhury & Mémoli, 2019; Chowdhury & Needham, 2020, 2021). Looking forward,
our OT based approach could allow researchers to carefully parse population-level heteroge-
neity in the data, for example, by applying PCA on the space of shape graphs (Chowdhury &
Needham, 2020).
Network Neuroscience
481
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Lastly, we expect that a powerful use case of our NeuMapper framework will be in the setting of
multimodal neuroimaging data analysis, where different types and scales of information that are
uniquely captured by different neuroimaging modalities are combined into an overall representa-
tion that conveys more information than any individual modality. For example, analyses of the
inherent temporal structure and dynamical properties measured by fMRI data could be augmented
by high-resolution anatomical information provided by diffusion tract imaging. Combining these
different information-rich sources of data into unified and individual-specific descriptions and
signatures of brain activity could better capture individual differences in behaviorally relevant
dynamics and in turn could improve the prospects of precision medicine.
In summary, we provide a computationally scalable, biologically anchored, and down-
stream analysis-friendly Mapper framework for application in the empirical sciences in general
and neurosciences in particular.
METHODS
Data Acquisition
In this study, we utilized a previously collected con-
Dataset 1: Continuous multitask paradigm.
tinuous multitask fMRI dataset to develop our framework, and we acquired a second dataset
using a similar paradigm but at a faster temporal resolution to validate our approach. The first
dataset was originally collected by Gonzalez-Castillo et al. (2015), using a CMP. We retrieved
the data from the XNAT Central public repository (https://central.xnat.org; Project ID: FCState-
Classif ). The dataset contained de-identified fMRI and behavioral data from 18 participants
who completed the CMP experiments as part of the original study (Gonzalez-Castillo et al.,
2015). Informed consent was obtained from all participants, and the local Institutional Review
Board of the National Institute of Mental Health in Bethesda, MD, reviewed and approved the
CMP data collection.
Details about the experimental paradigm are described elsewhere (Gonzalez-Castillo et al.,
2015). Briefly, participants were scanned continuously for ∼25 min while performing four dif-
ferent cognitive tasks. Each task was presented for two separate 180-s blocks, with each task
block being preceded by a 12-s instruction period. The order of task blocks was randomized
such that each task was always preceded and followed by a different task. The same random
ordering of tasks was used for all participants. The four cognitive tasks were (1) Rest (R), where
participants were instructed to fixate on a crosshair in the center of the screen and let their
mind wander; (2) Working Memory (M), where participants were presented with a continuous
sequence of individual geometric shapes and were instructed to press a button when the cur-
rent shape had also appeared two shapes prior (2-back design); (3) Math/Arithmetic (A), where
participants were presented with simple arithmetic operations, involving three numbers
between 1 and 10 and two operands (either addition or subtraction)—operations remained
on the screen for 4 s, and successive trials were separated by a blank screen that appeared
for 1 s, yielding a total of 36 operations per each 180-s block—and (4) Video ( V), where par-
ticipants watched a video of a fish tank from a single point of view with different types of fish
swimming into an out of the frame. Participants were instructed to press a button when a red
crosshair appeared on a clown fish and another when it appeared on any other type of fish.
These targets appeared for 200 ms with a total of 16 targets during each of the 180-s blocks.
The fMRI data were acquired on a Siemens 7 Tesla MRI scanner equipped with a
32-channel head coil using a whole-brain echo planar imaging (EPI) sequence (repetition time
[TR] = 1.5 s, echo time [TE] = 25 ms, and voxel size = 2 mm isotropic). A total of 1,017
volumes were acquired while participants performed the CMP.
Network Neuroscience
482
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Functional and anatomical MR images were preprocessed using the Configurable Pipeline
for the Analysis of Connectomes (C-PAC version 0.3.4; https://fcp-indi.github.io/docs/user
/index.html). Details about this processing are provided elsewhere (Saggar et al., 2018). Briefly,
the fMRI data preprocessing steps included ANTS registration into MNI152 space, slice timing
correction, motion correction, skull stripping, grand mean scaling, spatial smoothing (FWHM
of 4 mm), and temporal band-pass filtering (0.009 Hz < f < 0.08 Hz). For each voxel, nuisance
signal correction was performed by regressing out linear and quadratic trends, physiological
noise (white matter and cerebrospinal fluid), motion-related noise (three translational and three
rotational head-motion parameters) using the Volterra expansion (Friston et al., 1996) (i.e., six
parameters, their temporal derivatives, and each of these values squared), and residual signal
unrelated to neural activity extracted using the CompCor algorithm (Behzadi et al., 2007) (i.e.,
five principal components derived from noise regions in which the time series data were
unlikely to be modulated by neural activity). The resulting data were brought to 3-mm MNI
space, and the mean time series was extracted from 375 predefined regions of interest (ROIs)
using the Shine et al. (2016) atlas. The atlas includes 333 cortical regions from the Gordon
et al. (2016) atlas, 14 subcortical regions from the Harvard-Oxford subcortical atlas, and 28
cerebellar regions from the SUIT atlas (Diedrichsen et al., 2009). Before running Mapper, the
preprocessed ROI time series data were converted to z-scores, and individual ROIs with zero
variance were excluded.
The behavioral data included both responses and reaction times for working memory, math,
and video tasks. Participants were instructed to respond as quickly and accurately as possible
with only one response per question. Behavior scores including the percent correct, percent
missed, and response times for Working Memory (M), Math/Arithmetic (A), and Video ( V) tasks
were computed for each participant.
Dataset 2: Continuous multitask experiment. We collected the second fMRI dataset at a faster
temporal resolution using a modified CMP (Gonzalez-Castillo et al., 2015) as part of a simul-
taneous EEG and MRI functional neuroimaging (SEMFNI) study. The raw data includes fMRI
scans and behavioral scores collected for 32 participants who completed two separate con-
tinuous multitask runs within a single scanning session, as part of the SEMFNI study. Informed
consent was obtained from all participants, and the Stanford University Institutional Review
Board reviewed and approved the SEMFNI data collection.
Briefly, the paradigm used by the continuous multitask experiment was adapted from the
original CMP (Gonzalez-Castillo et al., 2015) so that data could be collected for two separate
runs over the course of a single ∼30-min session. For each run, participants were scanned
continuously for ∼15 min while performing four different cognitive tasks. Each task was pre-
sented for two separate 90-s blocks, with each task block being preceded by a 12-s instruction
period. The order of task blocks presented during each run was randomized such that each
task was always preceded and followed by a different task. The same random ordering of tasks
was used for all participants and for both runs. The randomized order of trials presented during
each task block was modified from the original paradigm (Gonzalez-Castillo et al., 2015) such
that the trials presented during the first run were different than the trials presented during the
second run (i.e., trials from the first 90 s of each 180-s task block in the original paradigm were
used for the first run of the modified paradigm, trials from the second half of each 180-s task
block in the original paradigm were used for the second run of the modified paradigm).
The fMRI data were acquired on a modified Siemens Skyra 3 Tesla MRI scanner equipped
with a 32-channel head coil using a whole-brain EPI sequence (repetition time [TR] = 750 ms,
echo time [TE] = 30 ms, and voxel size = 2 mm isotropic). A multiband acceleration factor of 8
Network Neuroscience
483
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
was used to increase temporal resolution. A total of 2,160 volumes were acquired over two
separate runs. The 1,080 volumes acquired during each run were preprocessed separately.
Functional and anatomical MR images were preprocessed using fMRIPrep (version 1.5.4;
https://fmriprep.readthedocs.io) (Esteban et al., 2018a, 2018b). Before running fMRIPrep, bias
correction was performed on individual anatomical MR images using FMRIB’s Automated
Segmentation Tool. Individual functional MR images and the bias-corrected anatomical MR
images were transformed into MNI152 space using FSL’s MNI ICBM 152 nonlinear 6th
Generation Asymmetric Average Brain Stereotaxic Registration Model (Evans et al., 2012).
The fMRI data preprocessing steps included skull stripping, head motion and susceptibility
distortion correction, boundary-based registration, and confound collection. After running
fMRIPrep, motion censoring, demeaning, detrending, nuisance signal correction, and tempo-
ral filtering were performed in Matlab. Here, we only considered voxels within the gray matter.
The brain masks provided by fMRIPrep were brought to 2-mm MNI space (in version 1.5.4 the
provided brain masks retain the original 1-mm pixel dimensions), and these 3-D spatial masks
were then used to extract the gray-matter voxel time series from the preprocessed 4-D fMRI
data. The resulting 4-D fMRI signals were then transformed into a 2-D matrix. The first 10
frames (i.e., nonsteady state) of data were discarded, and individual time frames with high
framewise displacement (FD >0.5 mm) were annotated as motion outliers. The data corre-
sponding to these frames were replaced with NaN values, such that these frames were ignored
during subsequent processing steps. After motion censoring, the voxel-wise data were
demeaned, and linear trends were removed. For each voxel, nuisance signal correction was
then performed by regressing out physiological noise (white matter and cerebrospinal fluid)
and motion-related noise (three translational and three rotational head-motion parameters)
using the Volterra expansion (Friston et al., 1996) of the two physiological signals and six
motion parameters (cioè., eight parameters, their temporal derivatives, and each of these
values squared). Linear interpolation was applied to the residual voxel signals to smooth
over any missing data corresponding to high-motion frames, and temporal band-pass filtering
(0.009 Hz < f < 0.08 Hz) was performed. The mean time series was extracted from 375 pre-
defined ROIs using the Shine et al. (2016) atlas. The atlas includes 333 cortical regions from the
Gordon et al. (2016) atlas, 14 subcortical regions from the Harvard-Oxford subcortical atlas,
and 28 cerebellar regions from the SUIT atlas (Diedrichsen et al., 2009). Before running
Mapper, individual runs were concatenated together, and individual ROIs with zero variance
were excluded.
Behavioral data was collected during each run, including responses and reaction times for
the different tasks. Participants were instructed to respond as quickly and accurately as possi-
ble with only one response per question. Behavior scores including the percent correct (%C),
percent missed, and reaction times for Working Memory (M), Math/Arithmetic (A), and Video
( V) tasks were computed (and averaged across runs) for each participant.
Note that one participant’s data were excluded from preprocessing altogether due to incon-
sistent data acquisition (i.e., too many volumes were collected during the second run due to a
technical issue), one participant was excluded from our final analysis due to excessive in-
scanner head motion (i.e., more than 10% of the acquired datapoints had framewise displace-
ment above 0.5 mm), and five participants were excluded from the final analysis because their
average %Correct scores were substantially lower than those of the other participants. Specif-
ically, after plotting all average %Correct scores on a histogram with bins of width 10, the
scores of these five participants comprised a left tail (i.e., very poor performance) that was
clearly separated from the scores of all other participants. At the final stage, Dataset 2 included
25 participants. Overall, this yielded n = 43 participants across both datasets.
Network Neuroscience
484
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
.
t
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
The NeuMapper Framework
Geometric and TDA for neuroimaging data. Consider an n × p data matrix X where the columns
correspond to voxels or brain ROIs and the rows correspond to acquisitions of whole-brain
activation patterns. Standard neuroimaging techniques such as functional connectivity (FC)
or dynamic functional connectivity (dFC) work on the columns of the data matrix to produce
one or more p × p correlation matrices. While such techniques capture the coactivation of
brain regions in response to external stimuli, an alternative approach is to study n × n matrices
of distances between acquisitions to understand the overall geometry of the states traversed by
the brain during the experiment. Examples such as Anscombe’s quartet (Anscombe, 1973) and
related generalizations (Matejka & Fitzmaurice, 2017) show that studying this underlying
geometry may provide strictly complementary insights, and in our work we emphasize the
importance of studying this geometry of brain states.
Each of our data matrices had rows labeled by the tasks in the experiment design (Rest, R;
Memory, M; Video, V; and Math/Arithmetic, A). To obtain a coarse understanding of the high-
dimensional geometry of the data, we first applied a variety of linear and nonlinear dimension
reduction methods (Van Der Maaten et al., 2009) to data from a single subject (S01 from
Dataset 1) and visualized the results in simple 3-D plots. The full list of methods and plots
is provided in Supporting Information Figure S8. Of these methods, the linear approaches,
for example, PCA, attempt to find linear combinations of features that best explain the data.
Such approaches, while useful, do not consider the intrinsic geometry of data. In contrast,
nonlinear approaches attempt to capture intrinsic geometry by considering the local neighbor-
hood of each data point, as determined by a k-nearest neighbor (kNN) graph built on the data.
While promising for capturing the geometry of brain states, such approaches work best when
the data is sampled both uniformly and without noise from its underlying distribution, and are
otherwise prone to a type of error called topological instability (Balasubramanian & Schwartz,
2002). Because fMRI data are inherently noisy and suffer from sampling variability, we expect
that this error would be unavoidable for standard methods and thus resort to specialized
techniques that capture intrinsic geometry while mitigating such errors due to noise.
One plausible solution to the topological instability problem is to use techniques from
TDA, namely, the Mapper algorithm. The standard Mapper approach initially applies a
d-dimensional projection to the data matrix (filtering), and then constructs a d-dimensional
grid with overlapping cells to cover the projected data points (binning). A clustering scheme
is then applied to refine each cell (partial clustering), and finally a graph is constructed with the
refined cells as nodes, and edges between nodes if the corresponding cells share one or more
data points. Notably, the partial clustering scheme operates on the native high-dimensional
embedding of the points in each cell, and thus avoids some of the information loss due to
projection. Specifically, low-dimensional projection tends to erroneously collapse points close
together, and partial clustering attempts to reverse this collapse. Thus, a way to address the
topological instability of kNN-based approaches is to fuse together the partial clustering step
from the Mapper algorithm.
However, there is still a caveat that information loss is inevitable when representing data
that is natively on the order of several hundred to thousands of dimensions in just two or three
dimensions. Given that the final output of Mapper is a combinatorial graph, there is a surpris-
ing lack of methods in the existing literature that implicitly map the data matrix X into the
output graph without incurring the information loss from low-dimensional projection. Here,
we propose such an implicit method that moves away from low-dimensional projection and
operates directly at the level of distance matrices. The key insight is that we can obtain the
Network Neuroscience
485
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
n
e
n
_
a
_
0
0
2
2
9
p
d
t
.
f
b
y
g
u
e
s
t
t
o
n
0
8
S
e
p
e
m
b
e
r
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
topological stabilization properties of Mapper by operating directly on the native high-
dimensional metric D and any transformation D0 thereof without explicitly constructing a
low-dimensional embedding.
Reciprocal kNN. To gain access to the intrinsic geometry of the high-dimensional data, our
constructions leverage a particular type of kNN graph and the matrix of geodesic distances
on this graph. First, we fix a choice of metric for our dataset X (in our case, the L1 metric, also
known as the Manhattan distance) and use this to build an n × n matrix D of pairwise distances
between the rows of X. We choose L1 over the more standard L2 (Euclidean) metric due to
higher effectiveness for nearest neighbor searches in high dimensions (Aggarwal et al.,
2001). Next, for each row x, we select the top-k nearest neighbors and call this set NNk(x).
Then we build a graph G where the node set is indexed by X, and an edge (xi, xj) is added
whenever xi 2 NNk(xj) and xj 2 NNk(xi). This final condition of creating edges by a symmetric
criterion is referred to as reciprocal kNN. Notice that these operations can be easily imple-
mented using sort operations. We finally define a new metric matrix D 0 by taking the shortest
path distances (i.e., geodesic distances) on G. Note that this can be implemented in O(|V |3)
time using a Floyd–Warshall algorithm, although the next section shows that we can alterna-
tively utilize a small number of calls to the O((|V | + |E |) log(|V |)) Dijkstra algorithm.
The choice of reciprocal kNN is a crucial aspect of our method, as it helps stabilize the
noise levels of fMRI data by pruning connections across areas with different local data density
(Qin et al., 2011). Supporting Information Figure S6 contains a toy example illustrating how
reciprocal kNN reduces “false” connections compared to standard kNN. Additionally, in Sup-
porting Information Figure S8 we show for an exemplar subject in Dataset 1 that replacing the
kNN construction in a standard nonlinear dimension reduction method with a reciprocal kNN
construction yields a low-dimensional embedding where data points associated to different
tasks form distinctive topological structures. We also note that kNN constructions have been
used before in Mapper applications (Duponchel, 2018), although in such applications the
kNN graph construction has been followed by a low-dimensional projection via a graph
drawing algorithm. In contrast, we use a tall, skinny submatrix of the matrix D0 with columns
corresponding to landmarks chosen via the procedure described next.
Finally, we note that the dimensionality of the data has an important effect on the compu-
tation of nearest neighbors. While techniques such as kd-trees can be very effective for nearest
neighbor queries in dimensions below 10, for dimensions p > 10 it may be preferable to com-
pute nearest neighbors via a linear scan which runs in in O(np) time (Weber et al., 1998). A
obtain sublinear dependence on n, it is possible to use techniques such as locality sensitive
hashing (Indyk & Motwani, 1998), although this approach is not addressed in the current work.
In Supporting Information Figure S7 we show that the runtime of our method initially scales
linearly with data dimension before flattening and showing logarithmic dependence. We also
note that when applying our method to voxel-level fMRI data, where p is in the order of
hundreds of thousands, one may use scalable approximate nearest neighbor methods (Dong
et al., 2011).
Thus far, we have replaced the filtering step, questo è, the low-dimensional projection, del
standard Mapper algorithm by a technique for obtaining a pairwise distance matrix D 0 Quello
encodes the intrinsic geometry of the data. Prossimo, we carry out a sampling procedure that
obtains landmarks on the data for use in a binning step while assuming access only to D 0.
Farthest point sampling (FPS). FPS is a greedy algorithm for landmarking data (Gonzalez, 1985).
In this algorithm, one starts with a seed point x0 2 X. Then one chooses x1 to be a point that
Distance matrix:
A square matrix describing the
pairwise distances (per esempio., Euclidean)
between points in a dataset.
Network Neuroscience
486
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
maximizes the D 0 distance to x0, possibly with some arbitrary tie breaking between equidistant
points. Next one chooses x2 to be a point that maximizes the distance to {x0, x1}, where the latter
is defined as min(D 0(x2, x0), D 0(x2, x1)). The algorithm proceeds in this manner until xr −1 has been
chosen, where r is a user-specified resolution parameter. We utilized the Matlab implementation
provided in (De Silva & Perry, 2003). Note also that each step requires only a call to Dijkstra’s
algorithm for a total of r calls, as well as some max and min operations. The final output of this
step is a set of landmark points {x0, x1, …, xr −1} and a real number (cid:1) corresponding to the maximal
distance from any point in X to its closest landmark point according to D 0.
Toward reproducibility, we attempted to minimize randomness during landmark selection
in due modi. Primo, while FPS typically begins with the random selection of an initial seed point,
we instead define the seed point to always be the first row of X. This ensures that landmark
selection is at least reproducible given the same input matrix X. Secondo, while the sequence of
landmarks visited during FPS depends heavily on the choice of initial seed point, the following
argument shows that the output of applying FPS to D 0 is minimally affected by randomness in
the seed point. Primo, FPS achieves a 2-approximation of the optimal locations for placing land-
marks (also known in the literature as the metric k-center problem) (Gonzalez, 1985). Prossimo,
by appealing to this result and additional results from metric geometry (Burago et al., 2001,
Esempio 7.3.11 and Corollary 7.3.28), any two sets of samples obtained by FPS yield distance
matrices that are guaranteed to approximate the input distance matrix D 0 up to a small
multiplicative factor. This approximation guarantee in turn ensures that landmark selection
is minimally affected by randomness, and the approximated distance matrix converges to
D 0 as the number of landmarks approaches the number of data points.
Intrinsic binning. Having constructed landmarks, we now partition the data into r overlapping
bins as follows: for each landmark xi, define
N
Bi ≔ x : D 0 xi; X
ð
Þ ≤ 4(cid:1) : G
100
o
;
Extrinsic binning:
A binning method that uses a grid to
partition data points. Good for cases
where the ambient space is low
dimensional.
where g is a gain parameter that controls the level of overlap. The choice of (cid:1)g/25 is set up for
the following scenario: suppose xi, xj are two landmarks satisfying D 0(xi, xj) = 2(cid:1) and p is a
point such that D 0(xi, P) = (cid:1) = D 0( P, xj). Then a gain of 50 (interpreted as 50%) allows the
inclusion xj 2 Bi. We set the minimum value of g to 25, which ensures that the collection
of bins Bi fully covers X. We refer to this procedure of binning points using landmarks and
the intrinsic metric D0 as intrinsic binning. In contrasto, the standard Mapper algorithm uses
a d-dimensional grid with overlapping cells that fully covers a d-dimensional projection of
X, and we refer to this approach as extrinsic binning due to its use of the ambient space
ℝd. Note that d-dimensional cubes tend to be mostly empty when d is large, and hence the
extrinsic binning approach becomes increasingly wasteful and computationally expensive as d
increases. Further analysis of this extrinsic binning procedure is carried out in Dłotko (2019),
where additionally a linear variant of intrinsic binning was utilized.
A property of this intrinsic binning procedure over binning using d-dimensional cubes is
that it is data driven, and is grounded in techniques commonly used in TDA methods (Giusti
et al., 2016). The resolution and gain parameters used above are analogous to those used in
the conventional Mapper algorithm. We note that controlling gain via a single parameter is not
necessarily optimal, as our data is unlikely to be uniformly sampled. Techniques such as
UMAP (McInnes et al., 2018) suggest that one may instead carry out local computations
around each landmark to set adaptive gain values gi for each Bi that better reflect the data
distribution. Tuttavia, invoking such a method requires much more additional mathematical
machinery, and we leave such extensions to future work.
Network Neuroscience
487
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
To complete the description of the intrinsic binning procedure, we consider the case where
G is not connected. In some techniques utilizing kNN graphs, one often proceeds by dropping
all but the largest connected component (Van Der Maaten et al., 2009), which directly causes
information loss. In our setting, Tuttavia, we simply reallocate the number of landmark points
to use for each connected component. Specifically, we allocate
(cid:3)
(cid:2)
ceiling r : # nodes in component
total # nodes
landmark points to each connected component and perform binning for each component indi-
vidually as above.
A different strategy that we also tried was to form a connected graph by augmenting edges
with exponentially penalized weights, as described in (Bayá & Granitto, 2011). Tuttavia, IL
binning strategy used above yielded greater signal and statistical power in downstream
analysis.
Toward scalability, we next consider computation times of intrinsic versus extrinsic binning.
In our tests, standard open-source Mapper implementations (KeplerMapper; van Veen et al.,
2019; and Giotto-Mapper; Tauzin et al., 2021) suffered from significant slowdowns (Figure 1B)
when carrying out the extrinsic binning procedure of the traditional Mapper approach after
projecting data to spaces of four or more dimensions. A natural question then becomes:
how many dimensions are needed to represent data? Intuitively, more dimensions are better
for preserving information. In our case, to use existing open-source Mapper implementations
after constructing a reciprocal kNN graph and computing graph geodesic distances, the easiest
approach would be to apply an MDS projection in analogy with the Isomap algorithm for
dimension reduction (Tenenbaum et al., 2000). We observed (Figure 1C) that the Pearson cor-
relation between graph geodesic distances and distances after MDS projection increased with
the dimension of the target space. Specifically, we needed 4- and 8-dimensional projections,
rispettivamente, to achieve correlation values exceeding 0.85 E 0.9. This suggests that informa-
tion loss would be reduced by using a larger projection dimension, which unfortunately runs
into the issue of slow runtime (Figure 1B). In contrasto, once a matrix of distances D 0 has been
provided, our projection-free intrinsic binning approach can be naively implemented in O(nr)
operations, where n is the number of data points and r is the number of landmarks. In partic-
ular, there is no dependence on projection dimension, whereas the extrinsic binning approach
requires computing a d-dimensional grid comprising a number of cells in the order O(r d ), Quello
È, exponential dependence on dimension (Figure 1B). Così, in cases where we expect to need
a moderate number of dimensions (>10) to represent our data, intrinsic binning should be pref-
erable to using extrinsic binning. Note that in standard neuroimaging literature where PCA is
used for dimension reduction, standard choices for the embedding dimension range from 5–10
(Shine et al., 2019UN) A 50 (Vidaurre et al., 2017).
Finalmente, we remark that the procedure of computing a transformed metric D 0, Per esempio,
via the reciprocal kNN construction, and subsequently an overlapping cover of X via intrinsic
binning, has the same inputs and outputs as the filtering and extrinsic binning approach of
the standard Mapper pipeline. Therefore, these aspects of our overall pipeline comprise a
self-contained module that can be incorporated into existing Mapper packages such as Kepler-
Mapper or Giotto-Mapper, thus enriching their diverse functionality with scalability improve-
ments toward qualitative and quantitative exploration of consortium-sized datasets.
Partial clustering and graph generation. For partial clustering, we use the method described in
the original Mapper literature (Singh et al., 2007). For each bin Bi, we apply single linkage
Network Neuroscience
488
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
clustering using the native, high-dimensional metric D. Then we investigate the histogram of
linkage values and set a cutoff threshold to be the first histogram bin edge at which the histo-
gram bin count becomes zero. This threshold is then used to partition Bi into clusters.
Intuitively, if Bi contains two well-separated clusters, then this cutoff value would sep-
arate the clusters. As noted in Singh et al. (2007), this method has its limitations, namely,
that if a bin contains clusters of differing densities, it tends to recover only the high-density
cluster. Tuttavia, this simple histogram-based method has worked sufficiently well for our
purposes.
The output of the partial clustering step is an overlapping collection of bins C0, C1, …, CN.
The final NeuMapper shape graph is generated by taking the Ci as nodes and inserting edges
(Ci, Cj) whenever Ci and Cj share one or more data points.
Annotations. Labels on data points are conveniently aggregated into annotations for each
node of the shape graph. Specifically, given a shape graph on N nodes and T categorical
labels, we construct an N × T annotation matrix where entry (v, T ) counts the number of data
points labeled t that belong to node v. The row vector (v, ·) comprises an annotation for node v.
These annotations can be displayed as pie charts (Geniesse et al., 2019; Saggar et al., 2018) O
used downstream in further analysis (see Results). While the labels themselves are typically
supplied by the experiment design, we show below how these labels may be derived from
meta-analysis to derive further insights into the data.
Parameter optimization. As is standard in machine learning pipelines, parameter optimization
for NeuMapper may be carried out via cross-validation. Tuttavia, it is always appealing to
obtain heuristics for good parameter initializations, and here we outline one such heuristic
for optimizing parameters (R, k, G) that uses the autocorrelation structure of fMRI data. Specif-
ically, given a data matrix X, we plot the autocorrelation function for each column of X and
visually determine the “elbow,” that is, the number of lags at which the autocorrelation func-
tion becomes level. We multiply this number by the sampling period of the dataset to obtain a
critical lag τ in units of seconds. In the fMRI context, autocorrelation is naturally present due to
the hemodynamic response function (HRF), and it is desirable to view data at a scale which
incorporates signal that is not just driven by HRF. Toward this goal, we specify a percentage
value α and set the criteria—denoted AutoCorrCrit—that an output shape graph should have at
least α% nodes containing data points that were acquired at least τ seconds apart, questo è, are
less susceptible to the HRF. We set τ = 11s (corresponding to the HRF peak; Lindquist et al.,
2009) and α = 25% for both datasets.
The procedure outlined above heuristically attempts to mitigate the dependency of Neu-
Mapper shape graph nodes on autocorrelated samples. Tuttavia, thus far we do not have
any conditions guaranteeing that the output shape graphs will be sufficiently connected for
carrying out downstream analysis by using network science tools. A tal fine, we introduce
an additional percentage value β and require that for group-level analysis, each shape graph
contains at least β% of its nodes in its largest connected component. We set β = 50% for both
datasets. To ensure consistency in group-level analysis, we require a consensus (R, k, G) triplet
that can be used to generate shape graphs for each dataset, questo è, for data acquired under the
same scanning parameters. In summary, we first obtain parameters for each shape graph in the
dataset according to α, obtain a consensus (R, k, G) triplet for the full dataset, and finally perturb
the consensus triple (if necessary) to satisfy the connectivity constraint β. While other strategies
may also be invoked to satisfy our criteria, we found that this order of operations worked suf-
ficiently well.
Network Neuroscience
489
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
In detail, the optimization at the level of a single subject is carried out as follows. We first
specify a broad range of values for the r parameter, and choices of small initial k and g param-
eters. For each value of r, we carry out the following procedure:
(cid:129) Compute a shape graph with the initial values for k and g.
(cid:129) Verify that AutoCorrCrit is satisfied. If not, increment k ← k + 1 and g ← g + 3.
(cid:129) Iterate until AutoCorrCrit is satisfied.
More specifically, for the r parameter, we explored 10 different values evenly spaced along
the interval [pavimento(0.1 · n), pavimento(0.3 · n)], where n is the number of time points in the dataset.
For the k and g parameters, we used small initial values of k = 3 and g = 25, rispettivamente. IL
step sizes for incrementing k, g were chosen to be the smallest integers such that perturbing the
corresponding parameters produced observable changes to the shape graphs.
Multiple r values may have the same optimal (k, G) parameters. To reduce these choices
down to a manageable number, we cluster the different optimal k values (equivalently g
values, as we increment k, g together) using the classical DBSCAN density-based clustering
algorithm. We then discard all but the top three largest clusters of optimal k values. Typically,
each cluster will have a unique k value, but to ensure this programmatically, we select the
minimum k value for each cluster. Finalmente, for each cluster we record the most frequently
occurring r value. This yields a total of three optimal (R, k, G) triplets for a data matrix X.
We repeat this procedure for the data matrix for each subject. To obtain consensus, noi usiamo
a simple voting procedure to select three (R, k, G) triplets that occur most frequently among the
optimal triples for each subject. This procedure returns three consensus (R, k, G) triplets at the
group level. We observed that these three optimal parameter triples correspond to three dif-
ferent scales of shape graphs, and the triplet with intermediate values of (R, k, G) best corre-
sponds to a mesoscale view with interesting structure.
Having chosen a consensus (R, k, G) triplet, we then verified for each dataset that each of the
shape graphs had over β% of the nodes in the largest connected component. If not, we
increased k and decreased r (both steps incorporate more global information) in small steps
Di 3 E 5, rispettivamente, until all graphs had a sufficient fraction of nodes in the largest con-
nected component. Note that we could not perform this step before choosing the consensus
triplet, as the procedure for obtaining consensus could result in some graphs no longer satisfy-
ing the connectivity criterion. For Dataset 1, the consensus triplet yielded r = 192, k = 8, g = 40.
For these parameters, each of the shape graphs satisfied the connectivity criterion, and no
further parameter tuning was needed. and we directly used these parameters for generating
graphs via NeuMapper. For Dataset 2, the mesoscale triple yielded r = 260, k = 6, g = 34. How-
ever, visual inspection of the graphs generated using these parameters revealed highly discon-
nected graphs for multiple participants, suggesting that the data for these participants had
different spatial characteristics from that of the rest of the group. After carrying out parameter
tuning as described above, the final (R, k, G) triple that we used for Dataset 2 era (240, 18, 34).
Methods for Analyzing Shape Graph Annotations
Toward qualitative and interactive exploration, we created visualizations of the shape graphs
obtained by NeuMapper using the DyNeuSR platform (Geniesse et al., 2019) and used its
node annotation features to demonstrate insights into behavior (Figura 2). On the quantitative
side, we show that shape graphs are compressed graph representations of the data on which
post hoc analysis via network science tools can be carried out efficiently.
Network Neuroscience
490
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Community detection tools. We used two standard community detection methods in our analysis:
modularity (Newman, 2006), which tracks the appearance of densely connected groups of ver-
tices with sparse connections across groups, and core-periphery (Borgatti & Everett, 2000), Quale
tracks the appearance of a centrally located group of vertices with dense connections to the whole
graph that is surrounded by a periphery with sparse connections. Modularity of each Mapper-
generated graph was computed as follows. Using the ground-truth labels, each node was
assigned to a community (one of the four tasks) via winner-take-all voting. The modularity of this
community assignment was then computed using the standard Q-score (Newman, 2006). For
core-periphery, we used the score derived in Everett and Borgatti (2000), Newman (2006), E
Rubinov et al. (2015) and validated in Saggar et al. (2018). Specifically we used the implemen-
tation core_periphery_dir provided in the Brain Connectivity Toolbox (Rubinov & Sporns, 2010).
In this implementation, each node is given a binary core-periphery assignment. The coreness of
each task was defined to be the fraction of time points for each task that belonged to core nodes.
Optimal transport. The main tool from OT that we use is the 1-Wasserstein distance, also
known as the Earth Mover’s Distance (Rubner et al., 2000). The origin of OT is attributed to
the work of Monge in the late 1700s and that of Kantorovich in the 1940s.
The 1-Wasserstein distance is defined in our setting as follows. We start with a connected
shape graph G = (X, E ) (restricting to the largest connected component as necessary), matrix of
graph geodesic distances D 0, and probability distributions p, q defined on the vertices of G. For
shape graphs, probability distributions arise naturally from task or NeuroSynth-derived anno-
tations: for a given annotation S and any shape graph vertex v, we first compute the proportion
of data points in v that are annotated by S, and then normalize these proportions over all of G
to get a vector of length n × 1 (where n = jXj) with nonnegative numbers that sum to 1. Fol-
lowing this procedure for two separate annotations yields two annotation-derived probability
distributions p and q. Intuitively p, q correspond to distributions of “mass” on the points of G.
Next we consider the set of all joint probability distributions with marginals p, q, denoted
Π( P, q). Each μ 2 Π( P, q) is an n × n matrix with nonnegative entries summing to 1 and row
and column sums equal to p and q, rispettivamente. Finalmente, the 1-Wasserstein distance is defined as:
dOT p; qð
Þ ≔ min
μ2Π p;qð
Þ
Xn
io;j¼1
Dij μ
ij
:
This is a linear program that can be solved using standard techniques in linear programming.
We use the Matlab wrapper written by Antoine Rolet for the C++ implementation provided in
Bonneel et al. (2011).
This OT distance is a bona fide metric between probability distributions that calculates the
cost of transforming one distribution into another while taking into account the ground dis-
tances between the points supporting the two distributions. In the language of network flows
(Ahuja et al., 1989), computing this metric amounts to solving a minimum cost flow from one
distribution to another. For the NeuMapper setting, dOT is a principled method for computing
second-order information from different annotations. Figura 3 shows the use of pairwise dOT
followed by an MDS projection to get a 2-D summary of the separation between task anno-
tations on shape graphs across our two datasets.
Generating annotations via meta-analysis. To better anchor the NeuMapper-generated graphs
into neurobiology, we generated a second set of node-level annotations using topic associa-
tion maps based on the NeuroSynth decoding framework (Yarkoni et al., 2011). Topic associ-
ation maps were downloaded from neurosynth.org using the NeuroSynth v4-topics-50
Network Neuroscience
491
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
database—a set of 50 topics extracted from all abstracts in the NeuroSynth database as of July
2015. For the purpose of this study, we limited our analysis to the topic association maps (cioè.,
Topics 010, 022, 011, 042) most relevant to the four tasks used in the CMP experiment (cioè.,
resting state, working memory, video, math), and a fifth topic association map corresponding
to “task-positive” cognition (cioè., Topic 002).
For each topic association map, we extracted the mean values from 333 predefined cortical
ROIs based on the Gordon et al. (2016) atlas, and transformed the resulting 3-D NIFTI image
into a 2-D topic association matrix. These two steps were performed simultaneously, using the
“NiftiLabelsMasker” object from the Nilearn software package (Abraham et al., 2014). Note,
the atlas used to prepare the fMRI data for input into NeuMapper was processed using the
Shine 375 atlas (as described in Data Acquisition section), which includes the same 333 cor-
tical regions from the Gordon et al. (2016) atlas used here to process the topic association
maps. Così, before computing any correlations between the fMRI data and the NeuroSynth
topic association maps, we extracted data corresponding to the same 333 cortical regions from
each of the preprocessed fMRI data matrices. Further, the resulting data matrices were con-
verted to z-scores (computed for each subject, separately), and individual ROIs with zero var-
iance were excluded from further analysis.
Prossimo, for each subject, we computed “framewise” correlations between each topic associ-
ation map and every time frame in the data matrix. This yielded a frame-by-topic correlation
matrix that was then used to aggregate node-level annotations. For each node, the topic cor-
relation scores corresponding to time frames associated with the node were extracted from the
precomputed frame-by-topic correlation matrix, and then further restricted to include only
those within the top 99th-percentile of strongest positive correlations associated with the node.
Finalmente, to generate the node-level annotations, we counted the number of retained positive
frame-by-topic correlations associated with each node, and then used these node-by-topic
association counts as the annotations for each node. This yielded a final node-by-topic anno-
tation matrix that could then be used to color the NeuMapper-generated graphs and perform
further analysis (as described in Anchoring Shape Graphs Into Known Cognitive Constructs
section).
Overreflection and synchronization measures. To better understand how the “decoded” cogni-
tive topic annotations relate to “expected” task structure and experimental task performance,
we developed two new measures to quantify the amount of overlap between NeuroSynth
topic annotations and experimental task labels.
Overreflection/mismatch was computed as follows. For each subject, the experimental task
labels (R, M, V, UN) were used to compute a node-by-task annotation matrix ^Θ, from which we
obtained a condensed two-column node-by-task annotation matrix Θ by summing the M, V,
and A task columns. We also used NeuroSynth task-positive and task-negative topic annota-
zioni (Topic 002 and Topic 010) to compute a two-column node-by-topic association matrix
Φ. We then computed the matrix product ΦTΘ and normalized this 2 × 2 matrix by its sum,
formally written as ΦTΘ/hΦTΘ, 1iF where h·iF denotes the matrix Frobenius product. Each entry
of this matrix corresponds to the overlap between an empirical (NeuroSynth-decoded) anno-
tation and an expected (experimental task-derived) annotazione. The overreflection score was
then defined to be the off-diagonal entry corresponding to the NeuroSynth-decoded task-
positive annotation and the experimental rest annotation.
Synchronization/match between the empirical and expected rest annotations and the
empirical/expected task annotations was computed in two stages: once for aggregated tasks,
Network Neuroscience
492
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
and once for the individual memory task. Primo, synchronization at the task-aggregated level
was taken to be the trace (cioè., the sum of the diagonal) of ΦTΘ/hΦTΘ, 1iF. Secondo, for
synchronization of the individual memory task, we used NeuroSynth rest and working memory
topic annotations (Topic 010 and Topic 022) to compute a two-column node-by-topic annotation
matrix (cid:2)Φ. We also extracted the R, M columns from ^Θ to obtain a corresponding two-column
node-by-task annotation matrix (cid:2)Θ. We then computed a synchronization score by taking
the trace of the normalized matrix product (cid:2)ΦT (cid:2)Θ=h (cid:2)ΦT (cid:2)Θ; 1i as before.
Validation and Replicability Analysis
Phase-randomized surrogates. To ground NeuMapper in a randomization framework, we vali-
dated our pipeline against null datasets produced via Fourier phase randomization (Theiler
et al., 1992). Phase randomization takes a collection of time series data, applies a discrete
Fourier transform to each time course, adds a uniformly distributed random phase to each
frequency, and then inverts the discrete Fourier transform. Phase randomization produces
stationary, linear, Gaussian null data that—by the Wiener-Khintchine theorem—preserves
the autocorrelation structure of the original data (Khintchine, 1934; Prichard & Theiler,
1994; Wiener, 1930). Thus by testing against phase-randomized surrogates, we test against
the possibility that our results are driven by stationarity, linearity, Gaussianity, or any combi-
nation of these properties (Liégeois et al., 2017). We validated our framework on phase-
randomized surrogates from both Datasets 1 E 2 (Supporting Information Figure S3), using
10 random surrogates for the data coming from each participant. Surrogate data were gener-
ated using the code accompanying (Liégeois et al., 2017).
Parameter perturbation. To ensure that our results are stable to parameter perturbation, we
repeated several of our analysis pipelines on a grid of (R, k, G) parameters surrounding the cho-
sen parameters for Datasets 1 E 2. Results for the correlations between modularity and task
performance as well as the core-periphery structure are presented in Supporting Information
Figure S4. Overall, we find that our results are stable to nearby parameter perturbations, con
the gain parameter showing the most discrete changes. Future work should clarify the role of
the gain parameter; some of our tests indicated that at least for methods based on kNN con-
structions, the gain parameter could be removed altogether, leaving only the (R, k) parameter
pair to be tuned.
ACKNOWLEDGMENTS
The authors thank the reviewers for their helpful comments. We also thank the research staff
and students for their support in data collection, particolarmente, Javier Gonzalez-Castillo for
Dataset 1 and Amber Howell, Sahar Jahanikia, Rafi Ayub, and Hua Xie for Dataset 2.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00229.
Dataset 1 was originally collected by Gonzalez-Castillo et al. (2015) and is available for down-
load from the XNAT Central public repository (https://central.xnat.org; Project ID: FCStateClassif ).
The preprocessed data used for Dataset 2 is available upon reasonable request.
Custom Matlab scripts used to generate and analyze the shape graphs can be found at
https://github.com/braindynamicslab/neumapper. The DyNeuSR Python package used to visu-
alize the shape graphs can be found at https://github.com/braindynamicslab/dyneusr.
Network Neuroscience
493
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
AUTHOR CONTRIBUTIONS
Caleb Geniesse: Conceptualization; Investigation; Methodology; Software; Validation; Visual-
ization; Writing – original draft; Writing – review & editing. Samir Chowdhury: Conceptuali-
zation; Investigation; Methodology; Software; Validation; Visualization; Writing – original
bozza; Writing – review & editing. Manish Saggar: Conceptualization; Data curation; Formal
analysis; Funding acquisition; Investigation; Methodology; Project administration; Resources;
Software; Supervision; Validation; Visualization; Writing – review & editing.
FUNDING INFORMATION
Manish Saggar, National Institute of Mental Health (https://dx.doi.org/10.13039/100000025),
Award ID: MH-119735. Manish Saggar, National Institute of Mental Health (https://dx.doi.org
/10.13039/100000025), Award ID: MH-104605. Manish Saggar, Stanford University MCHRI
Faculty Scholar.
REFERENCES
Abraham, A., Pedregosa, F., Eickenberg, M., Gervais, P., Mueller, A.,
Kossaifi, J., Gramfort, A., Thirion, B., & Varoquaux, G. (2014).
Machine learning for neuroimaging with scikit-learn. Frontiers in
Neuroinformatics, 8. https://doi.org/10.3389/fninf.2014.00014,
PubMed: 24600388
Aggarwal, C. C., Hinneburg, A., & Keim, D. UN. (2001). On the sur-
prising behavior of distance metrics in high dimensional space.
In J. Van den Bussche & V. Vianu (Eds.), Database theory — ICDT
2001. Lecture notes in computer science: Vol. 1973. Berlin:
Springer. https://doi.org/10.1007/3-540-44503-X_27
Agrawal, R., Gehrke, J., Gunopulos, D., & Raghavan, P. (2005).
Automatic subspace clustering of high dimensional data. Data
Mining and Knowledge Discovery. https://doi.org/10.1007
/s10618-005-1396-1
Ahuja, R. K., Magnanti, T. L., & Orlin, J. B. (1989). Network flows.
In Handbooks in operations research and management science.
Elsevier. https://doi.org/10.1016/S0927-0507(89)01005-4
Anscombe, F. J. (1973). Graphs in statistical analysis. American
Statistician. https://doi.org/10.1080/00031305.1973.10478966
Balasubramanian, M., & Schwartz, E. l. (2002). The isomap algo-
rithm and topological stability. Scienza. https://doi.org/10.1126
/science.295.5552.7a, PubMed: 11778013
Bassett, D. S., Wymbs, N. F., Porter, M. A., Mucha, P. J., Carlson,
J. M., & Grafton, S. T. (2011). Dynamic reconfiguration of human
brain networks during learning. Proceedings of the National
Academy of Sciences of the United States of America. https://
doi.org/10.1073/pnas.1018985108, PubMed: 21502525
Bassett, D. S., Wymbs, N. F., Rombach, M. P., Porter, M. A., Mucha,
P. J., & Grafton, S. T. (2013). Task-based core-periphery organi-
zation of human brain dynamics. PLoS Computational Biology,
9(9), 1–16. https://doi.org/10.1371/journal.pcbi.1003171,
PubMed: 24086116
Bayá, UN. E., & Granitto, P. M. (2011). Clustering gene expression
data with a penalized graph-based metric. BMC Bioinformatics,
12(1), 2. https://doi.org/10.1186/1471-2105-12-2, PubMed:
21205299
Behzadi, Y., Restom, K., Liau, J., & Liu, T. T. (2007). A component
based noise correction method (CompCor) for BOLD and
perfusion based fMRI. NeuroImage, 37(1), 90–101. https://doi
.org/10.1016/j.neuroimage.2007.04.042, PubMed: 17560126
Belchi, F., Brodzki, J., Burfitt, M., & Niranjan, M. (2020). A numer-
ical measure of the instability of mapper-type algorithms. Journal
of Machine Learning Research, 21, 1–45.
Belkin, M., & Niyogi, P. (2003). Laplacian eigenmaps for dimen-
sionality reduction and data representation. Calcolo neurale.
https://doi.org/10.1162/089976603321780317
Beyer, K., Goldstein, J., Ramakrishnan, R., & Shaft, U. (1998).
When is “nearest neighbor” meaningful? Lecture notes in
computer science (Including subseries lecture notes in artificial
intelligence and lecture notes in bioinformatics). https://doi.org
/10.1007/3-540-49257-7_15
Bodnar, C., Cangea, C., & Liò, P. (2020). Deep Graph Mapper:
Seeing graphs through the neural
lens. arXiv Preprint
arXiv:2002.03864. https://doi.org/10.3389/fdata.2021.680535,
PubMed: 34282408
Bonneel, N., Van De Panne, M., Paris, S., & Heidrich, W. (2011).
Displacement interpolation using Lagrangian mass transport.
ACM Transactions on Graphics. https://doi.org/10.1145
/2024156.2024192
Borgatti, S. P., & Everett, M. G. (2000). Models of core/periphery
structures. Social Networks, 21(4), 375–395. https://doi.org/10
.1016/S0378-8733(99)00019-2
Bruno, J. L., Romano, D., Mazaika, P., Lightbody, UN. A., Hazlett,
H. C., Piven, J., & Reiss, UN. l. (2017). Longitudinal identification
of clinically distinct neurophenotypes in young children with
fragile X syndrome. Proceedings of the National Academy of Sci-
ences of the United States of America. https://doi.org/10.1073
/pnas.1620994114, PubMed: 28923933
Bullmore, E., & Sporns, O. (2009). Complex brain networks: Graph
theoretical analysis of structural and functional systems. Nature
Reviews Neuroscience. https://doi.org/10.1038/nrn2575,
PubMed: 19190637
Burago, D., Burago, Y., & Ivanov, S. (2001). Graduate studies in
mathematics: Vol. 33. A course in metric geometry. Providence,
RI: American Mathematical Society. https://doi.org/10.1090
/gsm/033
Network Neuroscience
494
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Bzdok, D., Varoquaux, G., & Steyerberg, E. W. (2020). Prediction,
not association, paves the road to precision medicine. JAMA Psy-
chiatry. https://doi.org/10.1001/jamapsychiatry.2020.2549,
PubMed: 32804995
Calhoun, V. D., Mugnaio, R., Pearlson, G., & Adali, T. (2014). IL
chronnectome: Time-varying connectivity networks as the next
frontier in fMRI data discovery. Neuron, 84(2), 262–274.
https://doi.org/10.1016/j.neuron.2014.10.015, PubMed:
25374354
Carlsson, G. (2014). Topological pattern recognition for point cloud
dati. Acta Numerica, 23, 289–368. https://doi.org/10.1017
/S0962492914000051
Carriere, M., Michel, B., & Oudot, S. (2018). Statistical analysis and
parameter selection for Mapper. The Journal of Machine Learning
Research, 19(1), 478–516.
Chowdhury, S., Clause, N., Mémoli, F., Sánchez, J. Á., & Wellner,
Z. (2020). New families of stable simplicial filtration functors.
Topology and Its Applications. https://doi.org/10.1016/j.topol
.2020.107254
Chowdhury, S., & Mémoli, F. (2019). The Gromov–Wasserstein dis-
tance between networks and stable network invariants. Informa-
tion and Inference: A Journal of the IMA, 8(4), 757–787. https://
doi.org/10.1093/imaiai/iaz026
Chowdhury, S., & Needham, T. (2020). Gromov-Wasserstein aver-
aging in a Riemannian framework. In 2020 IEEE/CVF conference
on computer vision and pattern recognition workshops
(CVPRW), Seattle, WA, USA, 2020 (pag. 3676–3684). https://doi
.org/10.1109/CVPRW50498.2020.00429
Chowdhury, S., & Needham, T. (2021). Generalized spectral
clustering via Gromov-Wasserstein learning. AISTATS.
arXiv:2006.04163
Coifman, R. R., & Lafon, S. (2006). Diffusion maps. Applied and
Computational Harmonic Analysis. https://doi.org/10.1016/j
.acha.2006.04.006
Cragg, L., & Gilmore, C. (2014). Skills underlying mathematics: IL
role of executive function in the development of mathematics
proficiency. Trends in Neuroscience and Education. https://doi
.org/10.1016/j.tine.2013.12.001
Cunningham, J. P., & Yu, B. M. (2014). Dimensionality reduction for
large-scale neural recordings. Nature Neuroscience. https://doi
.org/10.1038/nn.3776, PubMed: 25151264
Dadi, K., Rahim, M., Abraham, A., Chyzhyk, D., Milham, M.,
Thirion, B., & Varoquaux, G. (2019). Benchmarking functional
connectome-based predictive models for resting-state fMRI.
NeuroImage, 192. https://doi.org/10.1016/j.neuroimage.2019
.02.062, PubMed: 30836146
De Silva, V., & Perry, P. (2003). Plex: A MATLAB library for studying
simplicial homology. TMSCSCS: Plex, 24.
Diedrichsen, J., Balsters, J. H., Flavell, J., Cussans, E., & Ramnani,
N. (2009). A probabilistic MR atlas of the human cerebellum.
N e u ro I m a g e , 4 6 ( 1 ) , 3 9 – 4 6 . h t t p s : / / d o i . o rg / 1 0 . 1 0 1 6 / j
.neuroimage.2009.01.045, PubMed: 19457380
Dłotko, P. (2019). Ball mapper: A shape summary for topological
data analysis. arXiv Preprint arXiv:1901.07410.
Dong, W., Charikar, M., & Li, K. (2011). Efficient K-nearest neighbor
graph construction for generic similarity measures. Proceedings
of the 20th International Conference on World Wide Web,
WWW 2011. https://doi.org/10.1145/1963405.1963487
Duman, UN. N., Tatar, UN. E., & Pirim, H. (2019). Uncovering dynamic
brain reconfiguration in MEG working memory n-back task using
topological data analysis. Brain Sciences. https://doi.org/10.3390
/brainsci9060144, PubMed: 31248185
Duponchel, l. (2018). Exploring hyperspectral imaging data sets with
topological data analysis. Analytica Chimica Acta, 1000, 123–131.
https://doi.org/10.1016/j.aca.2017.11.029, PubMed: 29289301
Esteban, O., Blair, R., Markiewicz, C. J., Berleant, S. L., Moodie, C.,
Mamma, F., … Gorgolewski, K. J. (2018UN). fMRIPrep. Software. https://
doi.org/10.5281/zenodo.852659
Esteban, O., Markiewicz, C., Blair, R. W., Moodie, C., Isik, UN. I.,
Erramuzpe Aliaga, A., … Gorgolewski, K. J. (2018B). fMRIPrep:
A robust preprocessing pipeline for functional MRI. Nature
Methods. https://doi.org/10.1038/s41592-018-0235-4, PubMed:
30532080
Evans, UN. C., Janke, UN. L., Collins, D. L., & Baillet, S. (2012). Brain
templates and atlases. NeuroImage, 62(2), 911–922. https://doi
.org/10.1016/j.neuroimage.2012.01.024, PubMed: 22248580
Everett, M. G., & Borgatti, S. P. (2000). Peripheries of cohesive sub-
sets. Social Networks, 21(4), 397–407. https://doi.org/10.1016
/S0378-8733(99)00020-9
Faskowitz, J., Esfahlani, F. Z., Jo, Y., Sporns, O., & Betzel, R. F.
(2020). Edge-centric functional network representations of
human cerebral cortex reveal overlapping system-level architec-
ture. Nature Neuroscience. https://doi.org/10.1038/s41593-020
-00719-sì, PubMed: 33077948
Friston, K. J., Williams, S., Howard, R., Frackowiak, R. S. J., &
Turner, R. (1996). Movement-related effects in fMRI time-series.
Magnetic Resonance in Medicine, 35(3), 346–355. https://doi.org
/10.1002/mrm.1910350312, PubMed: 8699946
Geniesse, C., Sporns, O., Petri, G., & Saggar, M. (2019). Generating
dynamical neuroimaging spatiotemporal representations
(DyNeuSR) using topological data analysis. Network Neuroscience,
3(3). https://doi.org/10.1162/netn_a_00093, PubMed: 31410378
Giusti, C., Ghrist, R., & Bassett, D. S. (2016). Two’s company, three
(or more) is a simplex: Algebraic-topological tools for under-
standing higher-order structure in neural data. Journal of Compu-
tational Neuroscience, 41(1), 1–14. https://doi.org/10.1007
/s10827-016-0608-6, PubMed: 27287487
Gonzalez-Castillo, J., Caballero-Gaudes, C., Topolski, N., Handwerker,
D. A., Pereira, F., & Bandettini, P. UN. (2019). Imaging the sponta-
neous flow of thought: Distinct periods of cognition contribute to
dynamic functional connectivity during rest. NeuroImage, 202,
116129. https://doi.org/10.1016/j.neuroimage.2019.116129,
PubMed: 31461679
Gonzalez-Castillo, J., Hoy, C. W., Handwerker, D. A., Robinson,
M. E., Buchanan, l. C., Saad, Z. S., & Bandettini, P. UN. (2015).
Tracking ongoing cognition in individuals using brief, whole-
brain functional connectivity patterns. Proceedings of the National
Academy of Sciences of the United States of America, 112(28),
8762–8767. https://doi.org/10.1073/pnas.1501242112,
PubMed: 26124112
Gonzalez, T. F. (1985). Clustering to minimize the maximum inter-
cluster distance. Theoretical Computer Science. https://doi.org/10
.1016/0304-3975(85)90224-5
Gordon, E. M., Laumann, T. O., Adeyemo, B., Huckins, J. F., Kelley,
W. M., & Petersen, S. E. (2016). Generation and evaluation of a
cortical area parcellation from resting-state correlations. Cerebral
Network Neuroscience
495
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Cortex, 26(1), 288–303. https://doi.org/10.1093/cercor/bhu239,
PubMed: 25316338
Gordon, E. M., Laumann, T. O., Gilmore, UN. W., Newbold, D. J.,
Greene, D. J., Berg, J. J., … Dosenbach, N. U. F. (2017). Precision
functional mapping of individual human brains. Neuron. https://
doi.org/10.1016/j.neuron.2017.07.011, PubMed: 28757305
Hinneburg, A., & Keim, D. UN. (1999). Optimal grid-clustering:
Towards breaking the curse of dimensionality in high-dimensional
clustering. In Proceedings of the 25th international conference on
very large data bases ( VLDB ʼ99) (pag. 506–517). San Francisco,
CA: Morgan Kaufmann.
Indyk, P., & Motwani, R. (1998). Approximate nearest neighbors:
Towards removing the curse of dimensionality. Conferenza
Proceedings of the Annual ACM Symposium on Theory of Com-
puting. https://doi.org/10.4086/toc.2012.v008a014
James, G., Witten, D., Hastie, T., & Tibshirani, R. (2000). An intro-
duction to statistical learning. Current Medicinal Chemistry.
https://doi.org/10.1007/978-1-4614-7138-7
Jeitziner, R., Carrière, M., Rougemont, J., Oudot, S., Hess, K., &
Brisken, C. (2019). Two-Tier Mapper, an unbiased topology-
based clustering method for enhanced global gene expression
analysis. Bioinformatics, 35(18), 3339–3347. https://doi.org/10
.1093/bioinformatics/btz052, PubMed: 30753284
Khambhati, UN. N., Sizemore, UN. E., Betzel, R. F., & Bassett, D. S.
(2018). Modeling and interpreting mesoscale network dynamics.
NeuroImage. https://doi.org/10.1016/j.neuroimage.2017.06.029,
PubMed: 28645844
Khintchine, UN. (1934). Korrelationstheorie der stationären stochas-
tischen Prozesse. Mathematische Annalen. https://doi.org/10
.1007/BF01449156
Lancichinetti, A., Fortunato, S., & Kertész, J. (2009). Detecting the
overlapping and hierarchical community structure in complex
networks. New Journal of Physics. https://doi.org/10.1088/1367
-2630/11/3/033015
Lee, Y., Barthel, S. D., Dłotko, P., Moosavi, S. M., Hess, K., & Smit,
B. (2017). Quantifying similarity of pore-geometry in nanoporous
materiali. Nature Communications. https://doi.org/10.1038
/ncomms15396, PubMed: 28534490
Liégeois, R., Laumann, T. O., Snyder, UN. Z., Zhou, J., & Sì, B. T. T.
(2017). Interpreting temporal fluctuations in resting-state func-
tional connectivity MRI. NeuroImage. https://doi.org/10.1016/j
.neuroimage.2017.09.012, PubMed: 28916180
Lindquist, M. A., Meng Loh, J., Atlas, l. Y., & Wager, T. D. (2009).
Modeling the hemodynamic response function in fMRI: Effi-
ciency, bias and mis-modeling. NeuroImage. https://doi.org/10
.1016/j.neuroimage.2008.10.065, PubMed: 19084070
Lum, P. Y., Singh, G., Lehman, A., Ishkanov, T., Vejdemo-Johansson,
M., Alagappan, M., Carlsson, J., & Carlsson, G. (2013). Extracting
insights from the shape of complex data using topology. Scientific
Reports, 3, 1–8. https://doi.org/10.1038/srep01236, PubMed:
23393618
Lurie, D. J., Kessler, D., Bassett, D. S., Betzel, R. F., Breakspear, M.,
Kheilholz, S., … Calhoun, V. D. (2020). Questions and controver-
sies in the study of time-varying functional connectivity in resting
fMRI. Network Neuroscience, 4(1), 30–69. https://doi.org/10
.1162/netn_a_00116, PubMed: 32043043
Marek, S., Tervo-Clemmens, B., Calabro, F. J., Montez, D. F., Kay,
B. P., Hatoum, UN. S., … Dosenbach, N. (2020). Towards
reproducible brain-wide association studies. bioRxiv. https://doi
.org/10.1101/2020.08.21.257758
Matejka, J., & Fitzmaurice, G. (2017). Same stats, different graphs:
Generating datasets with varied appearance and identical statis-
tics through simulated annealing. Conference on Human Factors
in Computing Systems – Proceedings. https://doi.org/10.1145
/3025453.3025912
McInnes, L., Healy, J., & Melville, J. (2018). UMAP: Uniform man-
ifold approximation and projection for dimension reduction.
arXiv:1802.03426
Mitchell, T. J., Hacker, C. D., Breshears, J. D., Szrama, N. P.,
Sharma, M., Bundy, D. T., … Leuthardt, E. C. (2013). A novel
data-driven approach to preoperative mapping of functional cor-
tex using resting-state functional magnetic resonance imaging.
Neurosurgery, 73(6), 963–969. https://doi.org/10.1227/ NEU
.0000000000000141, PubMed: 24264234
Munch, E. (2017). A user’s guide to topological data analysis. Jour-
nal of Learning Analytics. https://doi.org/10.18608/jla.2017.42.6
Newman, M. E. J. (2006). Modularity and community structure in
networks. Proceedings of the National Academy of Sciences of
the United States of America, 103(23), 8577–8582. https://doi
.org/10.1073/pnas.0601602103, PubMed: 16723398
Nichols, UN. l. A., Eichler, T., Latham, R., & Zimmer, M. (2017). UN
global brain state underlies C. Elegans sleep behavior. Scienza.
https://doi.org/10.1126/science.aam6851, PubMed: 28642382
Nicolau, M., Levine, UN. J., & Carlsson, G. (2011). Topology based
data analysis identifies a subgroup of breast cancers with a
unique mutational profile and excellent survival. Proceedings
of the National Academy of Sciences of the United States of
America, 108(17), 7265–7270. https://doi.org/10.1073/pnas
.1102826108, PubMed: 21482760
Nielson, J. L., Paquette, J., Liu, UN. W., Guandique, C. F., Tovar,
C. A., Inoue, T., … Ferguson, UN. R. (2015). Topological data anal-
ysis for discovery in preclinical spinal cord injury and traumatic
brain injury. Nature Communications, 6, 8581. https://doi.org/10
.1038/ncomms9581, PubMed: 26466022
Owen, l. l. W., Chang, T. H., & Equipaggio, J. R. (2019). High-level
cognition during story listening is reflected in high-order dynamic
correlations in neural activity patterns. bioRxiv. https://doi.org/10
.1101/763821
Patania, A., Selvaggi, P., Veronese, M., Dipasquale, O., Expert, P., &
Petri, G. (2019). Topological gene expression networks recapitu-
late brain anatomy and function. Network Neuroscience. https://
doi.org/10.1162/netn_a_00094, PubMed: 31410377
Petri, G., Expert, P., Turkheimer, F., Carhart-Harris, R., Nutt, D.,
Hellyer, P., & Vaccarino, F. (2014). Homological scaffolds of
brain functional networks. Journal of The Royal Society Interface,
11(101), 20140873. https://doi.org/10.1098/rsif.2014.0873,
PubMed: 25401177
Peyré, G., & Cuturi, M. (2019). Computational optimal transport.
Foundations and Trends in Machine Learning. https://doi.org/10
.1561/2200000073
Preti, M. G., Bolton, T. A., & Van De Ville, D. (2017). The dynamic
functional connectome: State-of-the-art and perspectives. Neuro-
Image, 160, 41–54. https://doi.org/10.1016/j.neuroimage.2016
.12.061, PubMed: 28034766
Prichard, D., & Theiler, J. (1994). Generating surrogate data for time
series with several simultaneously measured variables. Physical
Network Neuroscience
496
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
Review Letters. https://doi.org/10.1103/ PhysRevLett.73.951,
PubMed: 10057582
Qi, C. R., Su, H., Mo, K., & Guibas, l. J. (2017). PointNet: Deep
learning on point sets for 3D classification and segmentation.
In 2017 IEEE conference on computer vision and pattern recogni-
zione (CVPR) (pag. 77–85). https://doi.org/10.1109/CVPR.2017.16
Qin, D., Gammeter, S., Bossard, L., Quack, T., & Van Gool, l.
(2011). Hello neighbor: Accurate object retrieval with k-reciprocal
nearest neighbors. Proceedings of the IEEE Computer Society
Conference on Computer Vision and Pattern Recognition.
https://doi.org/10.1109/CVPR.2011.5995373
Rabadán, R., & Blumberg, UN. J. (2019). Topological data analysis for
genomics and evolution: Topology in biology. https://doi.org/10
.1017/9781316671665
Radovanović, M., Nanopoulos, A., & Ivanović, M. (2010). Hubs in
spazio: Popular nearest neighbors in high-dimensional data. Jour-
nal of Machine Learning Research, 11(2010), 2487–2531.
Raghubar, K. P., Barnes, M. A., & Hecht, S. UN. (2010). Working
memory and mathematics: A review of developmental, individ-
ual difference, and cognitive approaches. Learning and Individ-
ual Differences. https://doi.org/10.1016/j.lindif.2009.10.005
Ravasz, E., & Barabási, UN. l. (2003). Hierarchical organization in
complex networks. Physical Review E – Statistical Physics,
Plasmas, Fluids, and Related Interdisciplinary Topics. https://doi
.org/10.1103/PhysRevE.67.026112, PubMed: 12636753
Rizvi, UN. H., Camara, P. G., Kandror, E. K., Roberts, T. J., Schieren,
I., Maniatis, T., & Rabadan, R. (2017). Single-cell topological
RNA-seq analysis reveals insights into cellular differentiation
and development. Nature Biotechnology. https://doi.org/10
.1038/nbt.3854, PubMed: 28459448
Romano, D., Nicolau, M., Quintin, E. M., Mazaika, P. K., Lightbody,
UN. A., Cody Hazlett, H., Piven, J., Carlsson, G., & Reiss, UN. l.
(2014). Topological methods reveal high and low functioning
neuro-phenotypes within fragile X syndrome. Human Brain Map-
ping. https://doi.org/10.1002/hbm.22521, PubMed: 24737721
Rombach, M. P., Porter, M. A., Fowler, J. H., & Mucha, P. J. (2014).
Core-periphery structure in networks. SIAM Journal on Applied
Mathematics. https://doi.org/10.1137/120881683
Rubinov, M., & Sporns, O. (2010). Complex network measures of
brain connectivity: Uses and interpretations. NeuroImage, 52(3),
1059–1069. https://doi.org/10.1016/j.neuroimage.2009.10.003,
PubMed: 19819337
Rubinov, M., Ypma, R. J. F, Watson, C., & Bullmore, E. T. (2015).
Wiring cost and topological participation of the mouse brain
connectome. Proceedings of the National Academy of Sciences
of the United States of America, 112(32), 10032–10037. https://
doi.org/10.1073/pnas.1420315112, PubMed: 26216962
Rubner, Y., Tomasi, C., & Guibas, l. J. (2000). The earth mover’s
distance as a metric for image retrieval. International Journal of
Computer Vision, 40(2), 99–121. https://doi.org/10.1023
/UN:1026543900054
Saggar, M., Shine, J. M., Liégeois, R., Dosenbach, N. U. F., & Fair, D.
(2021). Precision dynamical mapping using topological data
analysis reveals a unique hub-like transition state at rest. BioRxiv.
https://doi.org/10.1101/2021.08.05.455149
Saggar, M., Sporns, O., Gonzalez-Castillo, J., Bandettini, P. UN. P. A.,
Carlsson, G., Glover, G., & Reiss, UN. l. (2018). Towards a new
approach to reveal dynamical organization of the brain using
topological data analysis. Nature Communications, 9(1). https://
doi.org/10.1038/s41467-018-03664-4, PubMed: 29643350
Saggar, M., & Uddin, l. Q. (2019). Pushing the boundaries of psy-
chiatric neuroimaging to ground diagnosis in biology. ENeuro.
https://doi.org/10.1523/ ENEURO.0384-19.2019, PubMed:
31685674
Sardiu, M. E., Gilmore, J. M., Groppe, B. D., Dutta, A., Florens, L.,
& Washburn, M. P. (2019). Topological scoring of protein inter-
action networks. Nature Communications. https://doi.org/10
.1038/s41467-019-09123-y, PubMed: 30850613
Sheikholeslami, G., Chatterjee, S., & Zhang, UN. (1998). Waveclus-
ter: A multi-resolution clustering approach for very large spatial
databases. In Proceedings of the 24rd international conference on
very large data bases ( VLDB ʼ98) (pag. 428–439). San Francisco,
CA: Morgan Kaufmann.
Shen, X., Finn, E. S., Scheinost, D., Rosenberg, M. D., Chun, M. M.,
P a p a d e m e t r i s , X . , & C o n s t a b l e , R . T.
( 2 0 1 7 ) . U s i n g
connectome-based predictive modeling to predict individual
behavior from brain connectivity. Nature Protocols, 12(3).
https://doi.org/10.1038/nprot.2016.178, PubMed: 28182017
Shine, J. M., Bissett, P. G., Campana, P. T., Koyejo, O., Balsters, J. H.,
Gorgolewski, K. J., Moodie, C. A., & Poldrack, R. UN. (2016).
The dynamics of functional brain networks: Integrated network
states during cognitive task performance. Neuron. https://doi
.org/10.1016/j.neuron.2016.09.018, PubMed: 27693256
Shine, J. M., Breakspear, M., Campana, P. T., Martens, K. UN. E., Shine, R.,
Koyejo, O., Sporns, O., & Poldrack, R. UN. (2019UN). Human cog-
nition involves the dynamic integration of neural activity and
neuromodulatory systems. Nature Neuroscience, 22(2), 289.
https://doi.org/10.1038/s41593-018-0312-0, PubMed:
30664771
Shine, J. M., Hearne, l. J., Breakspear, M., Hwang, K., Müller, E. J.,
Sporns, O., Poldrack, R. A., Mattingley, J. B., & Cocchi, l.
(2019B). The low-dimensional neural architecture of cognitive
complexity is related to activity in medial thalamic nuclei. Neu-
ron. https://doi.org/10.1016/j.neuron.2019.09.002, PubMed:
31653463
Singh, G., Mémoli, F., & Carlsson, G. (2007). Topological methods
for the analysis of high dimensional data sets and 3D object rec-
ognition. Symposium on point-based graphics (pag. 91–100).
Geneva, Svizzera: Eurographics Association. https://doi.org
/10.2312/SPBG/SPBG07/091-100
Sporns, O. (2011). Networks of the brain. Cambridge, MA: MIT
Press. https://doi.org/10.7551/mitpress/8476.001.0001
Sporns, O. (2013). Making sense of brain network data. Nature
Methods. https://doi.org/10.1038/nmeth.2485, PubMed:
23722207
Stevner, UN. B. A., Vidaurre, D., Cabral, J., Rapuano, K., Nielsen, S. F. V.,
Tagliazucchi, E., … Kringelbach, M. l. (2019). Discovery of key
whole-brain transitions and dynamics during human wakefulness
and non-REM sleep. Nature Communications. https://doi.org/10
.1038/s41467-019-08934-3, PubMed: 30833560
Tagliazucchi, E., Balenzuela, P., Fraiman, D., & Chialvo, D. R.
(2012). Criticality in large-scale brain fMRI dynamics unveiled
by a novel point process analysis. Frontiers in Physiology.
https://doi.org/10.3389/fphys.2012.00015, PubMed: 22347863
Tauzin, G., Lupo, U., Tunstall, L., Prez, J. B., Caorsi, M., Medina-
Mardones, A., Dassatti, A., & Hess, K. (2021). giotto-tda: UN
Network Neuroscience
497
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
NeuMapper: A computational framework for exploration of brain dynamics
topological data analysis toolkit for machine learning and data
exploration. Journal of Machine Learning Research, 22(2021),
1–6.
Tenenbaum, J. B., De Silva, V., & Langford, J. C. (2000). A global
geometric framework for nonlinear dimensionality reduction.
Scienza, 290(5500), 2319–2323. https://doi.org/10.1126
/science.290.5500.2319, PubMed: 11125149
Theiler, J., Eubank, S., Longtin, A., Galdrikian, B., & Doyne Farmer,
J. (1992). Testing for nonlinearity in time series: The method of
surrogate data. Physica D: Nonlinear Phenomena. https://doi
.org/10.1016/0167-2789(92)90102-S
Tie, Y., Rigolo, L., Norton, IO. H., Huang, R. Y., Wu, W., Orringer, D.,
Mukundan, S., & Golby, UN. J. (2014). Defining language net-
works from resting-state fMRI for surgical planning—A feasibility
study. Human Brain Mapping, 35(3), 1018–1030. https://doi.org
/10.1002/hbm.22231, PubMed: 23288627
Turk-Browne, N. B. (2013). Functional interactions as big data in
the human brain. Scienza. https://doi.org/10.1126/science
.1238409, PubMed: 24179218
Van Der Maaten, L., & Hinton, G. (2008). Visualizing data using
t-SNE. Journal of Machine Learning Research, 9(2008), 2579–2605.
Van Der Maaten, L., Postma, E., & den Herik, J. (2009). Dimension-
ality reduction: A comparative review. Journal of Machine Learn-
ing Research, 10(66–71), 13.
van der Meer, J. N., Breakspear, M., Chang, l. J., Sonkusare, S., &
Cocchi, l. (n.d.). Movie viewing elicits rich and reliable brain
state dynamics. https://doi.org/10.1038/s41467-020-18717-w,
PubMed: 33020473
van Veen, H., Saul, N., Eargle, D., & Mangham, S. (2019). Kepler
Mapper: A flexible Python implementation of the Mapper
algorithm. Journal of Open Source Software. https://doi.org/10
.21105/joss.01315
Vidaurre, D., Smith, S. M., & Woolrich, M. W. (2017). Brain net-
work dynamics are hierarchically organized in time. Proceedings
of the National Academy of Sciences of the United States of
America, 114(48), 12827–12832. https://doi.org/10.1073/pnas
.1705120114, PubMed: 29087305
Weber, R., Schek, H. J., & Blott, S. (1998). A quantitative analysis
and performance study for similarity-search methods in high-
dimensional spaces. In Proceedings of the 24th international
conference on very large data bases (pag. 194–205). San Francisco,
CA: Morgan Kaufmann.
Welvaert, M., & Rosseel, Y. (2013). On the definition of signal-to-
noise ratio and contrast-to-noise ratio for fMRI data. PLoS One,
8(11). https://doi.org/10.1371/journal.pone.0077089, PubMed:
24223118
Welvaert, M., & Rosseel, Y. (2014). A review of fMRI simulation
studies. PLoS One, 9(7), e101953. https://doi.org/10.1371
/journal.pone.0101953, PubMed: 25048024
Wiener, N. (1930). Generalized harmonic analysis. Acta Mathema-
tica. https://doi.org/10.1007/BF02546511
Yarkoni, T., Poldrack, R. A., Nichols, T. E., Van Essen, D. C., &
Wager, T. D. (2011). Large-scale automated synthesis of human
functional neuroimaging data. Nature Methods, 8(8), 665–670.
https://doi.org/10.1038/nmeth.1635, PubMed: 21706013
Zhou, Y., Chalapathi, N., Rathore, A., Zhao, Y., & Wang, B. (n.d.).
Mapper Interactive: A scalable, extendable, and interactive
toolbox for the visual exploration of high-dimensional data. IEEE
Pacific Visualization (PacificVis). https://mapperinteractive
.github.io/
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
T
/
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
/
6
2
4
6
7
2
0
2
8
1
4
9
N
e
N
_
UN
_
0
0
2
2
9
P
D
.
T
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Network Neuroscience
498