METHODS
Increasing robustness of pairwise methods for
effective connectivity in magnetic resonance
imaging by using fractional moment series
of BOLD signal distributions
Natalia Z. Bielczyk
1,3, Jan K. Buitelaar
Jeffrey C. Glennon1,2, and Christian F. Beckmann 1,2,3,4
1,2, Alberto Llera
1,2,
a n o p e n a c c e s s
j o u r n a l
1Donders Institute for Brain, Cognition and Behavior, Nijmegen, the Netherlands
2Department of Cognitive Neuroscience, Radboud University Nijmegen Medical Centre, Nijmegen, the Netherlands
3Radboud University Nijmegen, Nijmegen, the Netherlands
4Oxford Centre for Functional MRI of the Brain, University of Oxford, Oxford, UK
Keywords: Causal
Pairwise causal inference
inference, Effective connectivity, Functional magnetic resonance imaging,
ABSTRACT
Estimating causal interactions in the brain from functional magnetic resonance imaging
(fMRI) data remains a challenging task. Multiple studies have demonstrated that all current
approaches to determine direction of connectivity perform poorly when applied to synthetic
fMRI datasets. Recent advances in this field include methods for pairwise inference, Quale
involve creating a sparse connectome in the first step, and then using a classifier in order to
determine the directionality of connection between every pair of nodes in the second step. In
this work, we introduce an advance to the second step of this procedure, by building a
classifier based on fractional moments of the BOLD distribution combined into cumulants.
The classifier is trained on datasets generated under the dynamic causal modeling (DCM)
generative model. The directionality is inferred based on statistical dependencies between
the two-node time series, Per esempio, by assigning a causal link from time series of low
variance to time series of high variance. Our approach outperforms or performs as well as
other methods for effective connectivity when applied to the benchmark datasets. Crucially, Esso
is also more resilient to confounding effects such as differential noise level across different
areas of the connectome.
AUTHOR SUMMARY
Estimating causal interactions from functional magnetic resonance imaging (fMRI) data is a
formidable task. Recent advances in this field include methods for pairwise inference. Nel
first step of this procedure, connections are revealed by means of functional connectivity. In
the second step, every detected connection is analyzed separately to reveal the direction of
the causal links. We introduce an advance to the second step of this procedure by building a
classifier based on the novel concept of fractional moments of the BOLD distribution
combined into cumulants. The classifier is trained on datasets generated under the dynamic
causal modeling (DCM) generative model. Using fractional cumulants gives a measure
resilient to confounding effects such as differential noise levels across different areas of the
connectome.
Citation: Bielczyk, N. Z., Llera, A.,
Buitelaar, J. K., Glennon, J. C., &
Beckmann, C. F. (2019). Increasing
robustness of pairwise methods for
effective connectivity in magnetic
resonance imaging by using fractional
moment series of BOLD signal
distributions. Network Neuroscience,
3(4), 1009–1037. https://doi.org/
10.1162/netn_a_00099
DOI:
https://doi.org/10.1162/netn_a_00099
Supporting Information:
https://doi.org/10.1162/netn_a_00099
Received: 11 May 2018
Accepted: 3 Giugno 2019
Competing Interests: The authors have
declared that no competing interests
exist.
Corresponding Author:
Natalia Bielczyk
natalia.bielczyk@gmail.com
Handling Editor:
Shella Keilholz
Copyright: © 2019
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza
The MIT Press
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
T
/
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
N
e
N
_
UN
_
0
0
0
9
9
P
D
/
T
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
Effective connectivity:
Causal relations between nodes of
the investigated network. In fMRI,
effective connectivity (as opposed to
directed functional connectivity) È
typically derived from a model that
additionally considers the underlying
neuronal processes (Vedere: dynamic
causal modeling).
Dynamic Causal Modeling:
The most popular generative model
in the fMRI connectivity research. It
assumes that the observable BOLD
fMRI signal is a product of an
underlying neuronal communication
smoothed with a slow hemodynamic
risposta.
Functional connectivity:
Statistical associations between
activity in nodes of the investigated
rete. In fMRI, functional
connectivity is most often evaluated
by means of Pearson/partial
correlation or mutual information.
Pairwise inference:
A two-step causal inference
procedure that reduces causal
inference in a large graph to studying
two-node interactions.
INTRODUCTION
In the context of functional magnetic resonance research, effective connectivity refers to the
process of estimating causal interactions between distinct regions within the brain. Several
characteristics of fMRI data impose severe restrictions on the possibility of estimating such
effective connectivity (Valdes-Sosa, Roebroeck, Daunizeau, & Friston, 2011; Friston, 2011;
Bielczyk et al., 2019). Primo, the temporal resolution of the image acquisition is low (sampling
rate typically <1 Hz). Furthermore, blood oxygen level–dependent (BOLD) activity is delayed
with respect to neuronal firing, with a delay of 3–6 s in the adult human brain (Arichi et al.,
2012). The delayed hemodynamic response can also induce spurious cross-correlations between
two BOLD time series (Ramsey al., 2010; Bielczyk, Llera, Buitelaar, Glennon, & Beckmann,
2017). Both subject-to-subject and region-to-region variability shape hemodynamic
response (Devonshire 2012) provide general limitation methods for effective
connectivity research fMRI: when one region faster than
in another, temporal precedence peak easily
be mistaken causation. Secondly, fMRI data characterized by relatively low signal-to-
noise ratio. Within gray matter at field strengths 3 T, task-induced signal changes
range within 2–3% mean depending on task (Kruger, 2018). Furthermore,
the stochastic noise has been shown have scale-free spectral characteristic
(He, 2014; Bédard, Kröger, Destexhe, 2006; Dehghani, Cash, Halgren, Destexhe,
2010), which additionally hinders identifiability causal structures derived from data
(Bielczyk, Beckmann, 2017). Moreover, typical protocols in-
volve short (a few hundred samples), estimation conditional
probabilities between variables, higher order statistic becomes difficult.
Multiple were proposed estimate effective connectivities (Friston,
2011). In computational study Smith al. (2011), range con-
nectivity tested synthetic datasets dynamic modeling forward
model (DCM; Friston, Harrison, Penny, 2003). this study, most estimating
causal interactions remained chance level. One method highlighted as successful
at identifying links based Patel’s tau measure (PT; Patel, Bowman, Rilling, 2006;
Smith 2011). PT entails two-step approach first step involves identifying
the (undirected) connections means functional connectivity. This achieved basis
of correlations different regions, referred Patel’s
kappa (Patel 2011).
One note make that, other pairwise inference procedures assume that causation
implies correlation. assumption necessary perform infer-
ence procedure, is, select reliable further classification into upstream
and downstream regions. However, although often true, not always
the case under certain circumstances (e.g., control systems) causation might be as-
sociated correlation (Kennaway, 2015). recent Di Biswal (2019), the
authors investigated task-modulated whole-brain connectivity six block-design
and event-related cognitive task. By using psychophysiological pairs
of regions interest (ROIs) whole brain, authors identified statistically significant
task modulations connectivity, reported, “task modulated was
found only activated during but were
not or deactivated.” suggests considering pairs which
activity correlated neglect some underlying connections.
There are multiple strategies implementing thresholding connectivity
estimates (Varoquaux Craddock, 2013). Since Pearson typically returns dense
Network Neuroscience
1010
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
> 0).
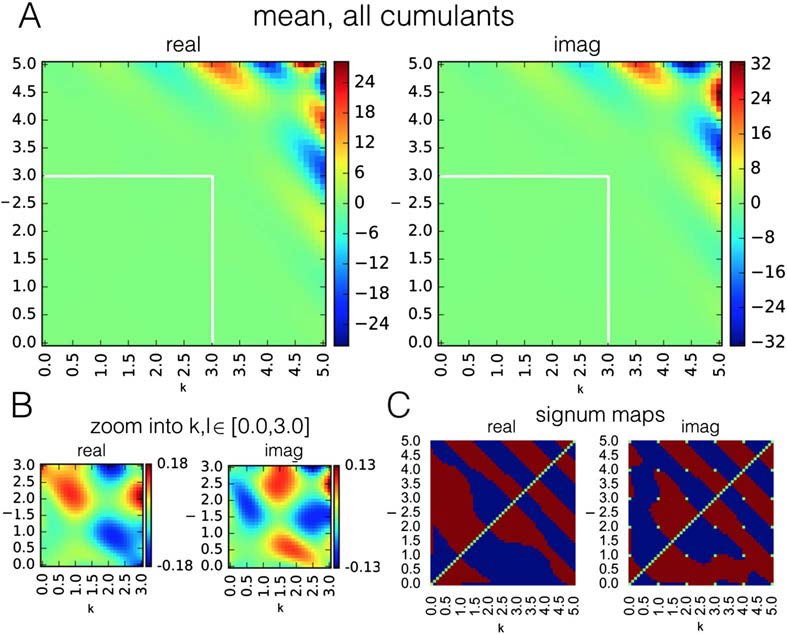
È interessante notare, the range of high discriminability is different for real and imaginary compo-
nents. Maximal discriminability in both real and imaginary cumulants exists in the range of k
+ l > 5.0. Additionally, in real cumulants there is a region of high discriminability in the range
k + l < 2.0, and in imaginary cumulants there is such region in the range 2.0 < k + l < 5.0
(Figure 3, both boundary lines marked with a white line). This different characteristic along the
imaginary axis illustrates that moving from integer to fractional moments of the distribution
provides additional predictive power. Note also that as we are deriving the discriminability
maps from the DCM generative model. These maps are fingerprints of the particular problem
of effective connectivity in fMRI; when derived from another generative model simulating
another dataset, the maps would be different.
Network Neuroscience
1016
Improving pairwise inference in fMRI using fractional moments of BOLD
Figure 3. Discriminative power for all cumulants in range k, l in [0.0, 5.0], in the ideal case of a
very long BOLD time series and no background neuronal noise. Maximal discriminability in both
real and imaginary cumulants exists in the range of k + l > 5.0. Additionally, in real cumulants
there is a region of high discriminability in the range k + l < 2.0, and in imaginary cumulants there
is such region in the range 2.0 < k + l < 5.0 (both boundary lines marked with a white line).
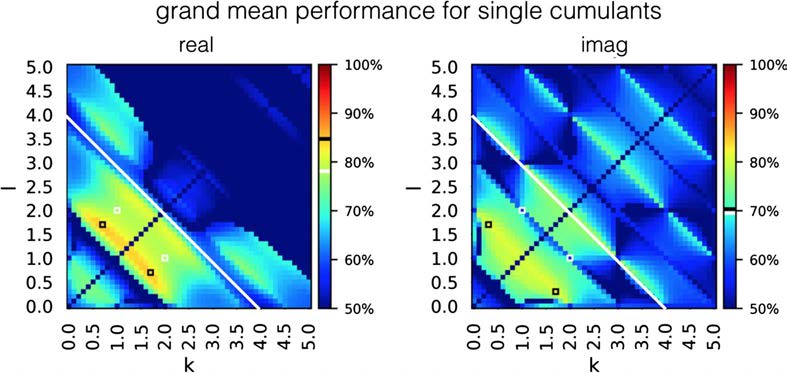
In order to investigate how the performance of classification based on single cumulants
changes when a single connection is embed in a bigger network, we evaluated their success
rate in estimating connectivity for benchmark synthetic datasets (Smith et al., 2011). Figure 4
presents the grand mean success rate achieved by every cumulant separately, across all 28
benchmark synthetic datasets (Smith et al., 2011).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Success rate for all the individual cumulants, averaged over 28 simulations from the
Figure 4.
synthetic benchmark datasets (Smith et al., 2011). White-edged square denotes a single cumulant
used by Hyvärinen and Smith (2013). The performance of this cumulant is shown in the color
bar, white band. Black-edged squares denote cumulants that give the highest performance on this
dataset. Their performance is presented in the color bar, black band. For the cumulants of high
indexes k + l > 4.0 (white line), the success rate is not as high as the discriminability presented
in Figure 3 would suggest. The high success rate is not preserved for high-indexed cumulants that
achieved high discriminability on two-node simulations. The maximal grand mean performance
equals 0.847 for the real components and 0.814 for imaginary components.
Network Neuroscience
1017
Improving pairwise inference in fMRI using fractional moments of BOLD
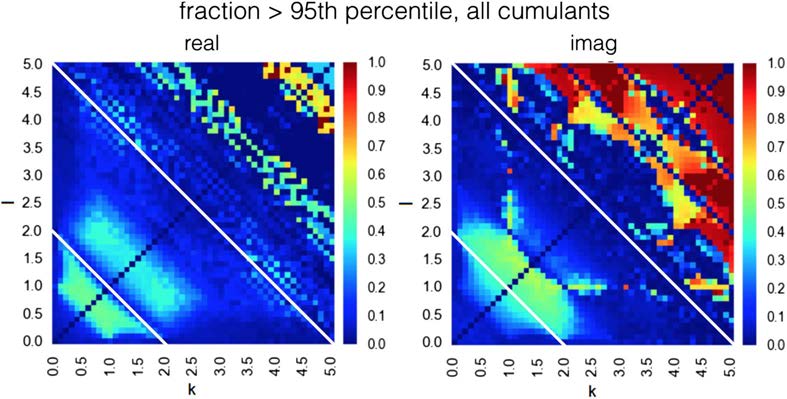
The success rate for each of the 28 separate synthetic datasets (Smith et al., 2011) is pre-
sented in Supporting Information 4. The maps of simulation-dependent success rate relate to
the maps of discriminative power (Figura 3), but they are not identical and differ between sim-
ulazioni. One difference is that for the cumulants of high indexes k + l > 4.0, the success
rate is not as high as the discriminability presented in Figure 3 would suggest. This is because
Figura 3 represents the limit of a system of two isolated nodes with infinite SNR, and a very
long BOLD time series, whereas benchmark synthetic datasets refer to a more realistic case
when for each pair of nodes, the time series is short, there are confounding signals from
other nodes in the network, and there is a certain degree of noise in the communication (Vedere
Supporting Information 2). Altogether, these factors make the high moments hard to estimate
in practice.
Combining Fractional Cumulants into a Classifier
We propose to combine information contained in multiple cumulants by building the classifier
based on a “voting” scheme between the cumulants. This classifier determines whether the
map of cumulants obtained for a pair of time series X(T), Y(T) is closer to the benchmark maps
presented in Figure 2A (which is an evidence for a connection X → Y), or their inverse (Quale
is an evidence for a flipped connection Y → X). Each of the cumulants Ckl votes due to sign
Srk,l, Sik,l (Figure 2C). If the sign of the cumulant is the same as in Figure 2C, it adds to the
evidence for a connection X → Y, and against this connection otherwise.
Since in realistic conditions (short datasets, large TRs), high index cumulants, k + l > 3.0,
yield the aforementioned estimation problem, we discount their contribution in the voting by
using a nonlinearity of a form (further referred to as weighting throughout the manuscript):
F (X) = log(cosh(max(X, 0)))
(3)
A similar function was proposed to discount the outliers present in the BOLD time series in
the work by Hyvärinen and Smith (2013). The final classifier yields:
{ X → Y i f ∑k,l[Srk,l f (Crk,l) + Sik,l f (Cik,l)] ≥ 0
Y → X
otherwise
in the weighted case, E
{ X → Y i f ∑k,l[Srk,lCrk,l + Sik,lCik,l] ≥ 0
Y → X
otherwise
(4)
(5)
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
/
T
e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D
l
F
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
N
e
N
_
UN
_
0
0
0
9
9
P
D
T
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
in the unweighted case.
Supervised Learning Using Synthetic Benchmark Datasets
In this work, we derive the classifier by using sign maps Srk,l, Sik,l (Figure 2C) developed using
multiple realizations of a two-node simulation under the DCM generative model, which is a
form of supervised learning. In a different application and under a different generative model,
these maps would look differently.
Network Neuroscience
1018
Improving pairwise inference in fMRI using fractional moments of BOLD
We know that cumulants differ with respect to discriminability (Figura 3), and that the suc-
cess rate of cumulants differs depending on the range k + l <= Indmax (Figure 4). Therefore,
we optimize the performance of the classifier with respect to these two dimensions by finding
a combination that gives the best grand mean performance across the 28 simulations from
the synthetic benchmark datasets, as they represent the variety of experimental conditions en-
countered in real-life fMRI setups.
First, we fix Indmax = max(k, l) = 3.1, and consider cumulants on a triangle k; l >= 0.1, k +
l < Indmax. We then choose only cumulants of discriminability exceeding a particular value to
be fed into the classifier. For instance, a cutoff value of 0.1 means that we include the vote from
all cumulants for which the discriminative value is not less than 0.1. We can then evaluate the
grand mean success rate (as the mean success rate over all 28 benchmark synthetic datasets) in
the function of the thresholding discriminability value. Figure 5A, demonstrates that including
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
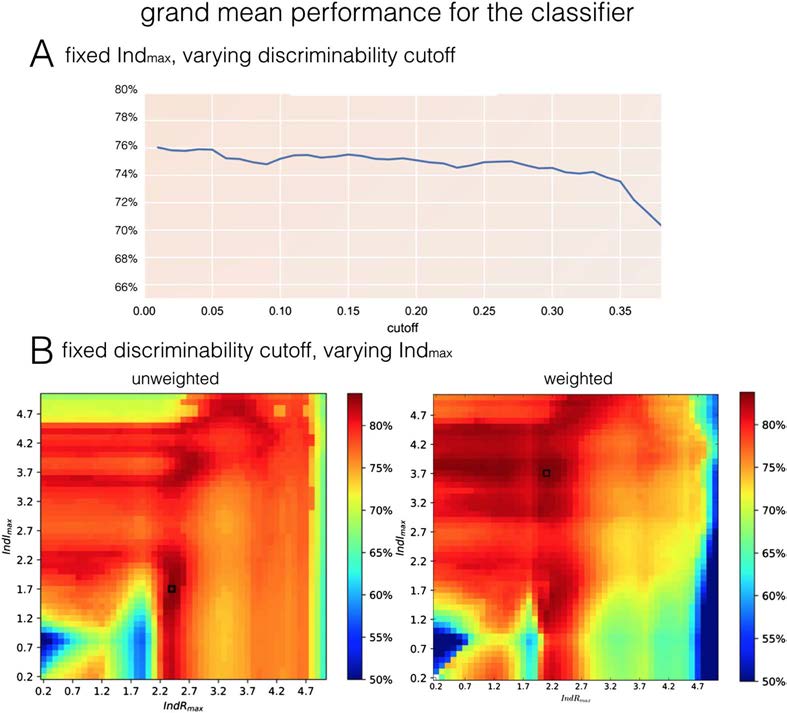
Figure 5. Dependence of the grand mean performance on synthetic datasets on the choice of
cumulants. (A) Grand mean performance for unweighted cumulants in range k + l <= 3.1, in
the function of the cutoff discriminative value. The higher cutoff, the less cumulants we take into
account while voting for the directionality of the link. The results clearly show that in order to
maximize the success rate in estimating effective connectivity, all the cumulants should be taken
into account, except for the diagonal of k = l. (B) The grand mean performance based on cumulants
of indexes k, l between 0.1 and k + l <= Indmax, in the function of that maximal index. The optimal
performance in unweighted case equals 0.835 for [IndRmax; IndImax] = (2.4, 1.7), and 0.886 for
[IndRmax; IndImax] = (2.1, 3.7) in weighted case.
Network Neuroscience
1019
Improving pairwise inference in fMRI using fractional moments of BOLD
all the cumulants with a positive discriminative value (all cumulants except for k = l, for which
discriminability is always zero) gives the best classification performance.
Second, we optimize the window Indmax for indexes k, l and compare between classifier
with and without weighting with the discount function introduced in Equation 3. Since dis-
criminability is generally higher for low indexes k, l (Figure 3), we will evaluate the grand
mean performance based on cumulants of indexes between 0 and a maximum Indmax in the
function of that maximum. We consider the maximal indexes along real and imaginary di-
mension separately. The results are presented in Figure 5B. The optimal performance in an
unweighted case equals 0.835 for [IndRmax, IndImax] = (2.4, 1.7), and 0.886 for [IndRmax,
IndImax] = (2.1, 3.7) in a weighted case, which exceeds both the grand mean performance of
the “PW-LR skew r” method by Hyvärinen (0.845) and the maximal grand mean performance
of any single cumulant in our study (Figure 4, the maximum of 0.847).
Selection of Other Approaches for Effective Connectivity Research in fMRI
In order to benchmark our classifier, we compare the performance against other methods. As
mentioned in the Introduction, the field of effective connectivity in fMRI is very wide (Smith
et al., 2011); therefore, we restricted ourselves to the most popular approaches (other than
DCM itself; Friston et al., 2003):
1. State-space implementation of Granger causality (GC; Granger, 1969; Seth, Barrett, &
Barnett, 2015) is a multivariate method inferring effective connectivity between a pair of
time series under the assumption that both of them can be expressed as autoregressive
processes. We used a simple version of GC featuring ordinary least square regression
with lag of 1, implemented in Multivariate Granger Causality Toolbox (Barnett & Seth,
2014), obtained from http://www.sussex.ac.uk/sackler/mvgc. For GC based on VAR pro-
cess, as in our study, the state-space implementation is more robust than spectral GC
(Geweke, 1982, 1984), because the frequency-domain version has a bias-variance trade-
off (a function of the VAR model order that can induce spurious conditional GG causality
estimates, such as erroneous peaks in the frequency domain, as indicated in the recent
work by Stokes and Purdon, 2017). Furthermore, the state-space formulation of GC is the
most robust, mitigating effects of bias and variance due to the fact that the reduced model
is VAR rather than VARMA (Barnett & Seth, 2015). In order to compare performance with
the methods for pairwise inference, we used GC in a bivariate rather than multivariate
fashion: by applying GC to each of the previously found connections separately
2. Partial Directed Coherence (PDC; Baccalá & Sameshima, 2001) is known as a method
conceptually close to Directed Transfer Function (Kami ´nski & Blinowska, 1991; Baccalá
& Sameshima, 2001). Both these methods are derivatives from Geweke spectral measures
of GC (Geweke, 1982, 1984), and all three methods have similar limitations (Chicharro,
2011). However, PDC is used substantially more often in fMRI studies than the other
two methods, especially when compared with spectral GC. For this reason, we chose
PDC as a method representing this class of approaches. We used PDC implementation
from the Extended Multivariate Autoregressive Modelling Toolbox (Faes, Erla, Porta, &
Nollo, 2013; http://www.lucafaes.net/emvar.html). As in case of GC, we applied PDC in
a bivariate fashion
3. Patel’s tau (PT; Patel et al., 2006), as described in the Introduction, is implemented sim-
ilarly as in Smith et al. (2011) by recalculating each time series into the range [0, 1],
setting samples under the 10th percentile to 0, over the 90th percentile to 1, and linearly
Network Neuroscience
1020
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
mapping the remaining samples to the range [0, 1]. Then, we infer the directionality of
connection from the difference between P (X|Y) and P (Y|X). In addition to the previous
implementation, however, we also integrate the results over all the possible thresholds
in order to eliminate the thresholding problem while calculating the conditional proba-
bilities P (X|Y), P (Y|X).
4. Pairwise likelihood ratios methods (PW-LR; Hyvärinen & Smith, 2013) are represented
by “PW-LR r skew,” as it gives the highest performance among all the PW-LR methods
when applied to synthetic fMRI data. We obtained the codes for the PW-LR methods from
https://www.cs.helsinki.fi/u/ahyvarin/code/pwcausal/ (Hyvärinen used the cumulant k;
l = (2; 1) weighted with covariance for synthetic benchmark datasets). Therefore, for this
comparison, we use the classifier based on fractional cumulants weighted with covari-
ance. For our study, we chose a PW-LR r skew version of the method, which involves
an inference based on a third cumulant with a discount for outliers (Hyvärinen & Smith,
2013)
As in Hyvärinen & Smith (2013), we performed the first step of the inference as inverse co-
variance thresholded with permutation testing. All the methods, including multivariate meth-
ods such as GC and PDC, were then applied in a pairwise fashion (i.e., separately for each
two-node network representing a single connection found in the previous step).
Furthermore, we did not include the DCM procedure in this comparison, for the same
reasons as Smith et al. (2011): DCM is not an exploratory method and using it in this context,
namely for exploratory causal research on the set of benchmark synthetic datasets (where
the smallest network consists of five nodes) is not computationally feasible. Furthermore, the
characteristics of this synthetic benchmark dataset is that input signals (Figure 1A) represent
random events and can therefore emulate all types of fMRI experiments: classic task-fMRI
studies, event-related responses or resting-state BOLD time series. In DCM, however, the inputs
must be strictly specified in the block design, otherwise DCM inference cannot be initiated.
Therefore, assumptions of DCM do not fit a research problem formulated in this particular way.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Testing Robustness of the Methods Against Confounds
In addition to evaluating our approach against the existing simulations from Smith et al. (2011),
we further evaluate the performance under additional yet typical modes of variation in the data.
Specifically we are interested in characterizing the discriminative performance relative to (i)
more complex forms of stochastic noise in the data and (ii) unequal levels of SNR per node.
The benchmark synthetic datasets involve temporally uncorrelated, white background noise
of a low magnitude on the neuronal level (Smith et al., 2011). This type of noise is not physio-
logically plausible, as it is known from physiological studies that in the neuronal net-
works, the background noise has a scale-free power spectrum (He, 2014; Bédard et al., 2006;
Dehghani et al., 2010; Bielczyk et al., 2017). Therefore, we simulated a two-node system and
introduced scale-free (pink) noise to the system. Then, we varied the variance of the noise in
the range of [0.2, 5.0] while keeping the amplitude of the inputs si(t) fixed to 1.0. We per-
formed 500 realizations of 10 min simulation at high temporal resolution of Fs = 200 Hz, for
each configuration of the noise variances.
Furthermore, in the original version of the DCM procedure (Friston et al., 2003), as well
as in most computational studies (Smith et al., 2011), equal stimulus strengths to both nodes
si(t) are assumed. This assumption might not hold true in the real fMRI datasets. Therefore,
we performed another, noiseless simulation, in which we varied signal strengths between the
Network Neuroscience
1021
Improving pairwise inference in fMRI using fractional moments of BOLD
upstream and downstream region. We performed 500 realizations of 10-min simulation at high
temporal resolution of Fs = 200 Hz for each configuration of input strengths in the range of
[0.2, 5.0].
RESULTS
Supervised Learning Using Synthetic Benchmark Datasets
The best version of the classifier was obtained for voting between cumulants in the range
[IndRmax; IndImax] = (2.1; 3.7), and with the discount for high moment indexes (Equation 3).
The comparison of this classifier against four other methods, GC, PDC, PT, and PW-LR r skew,
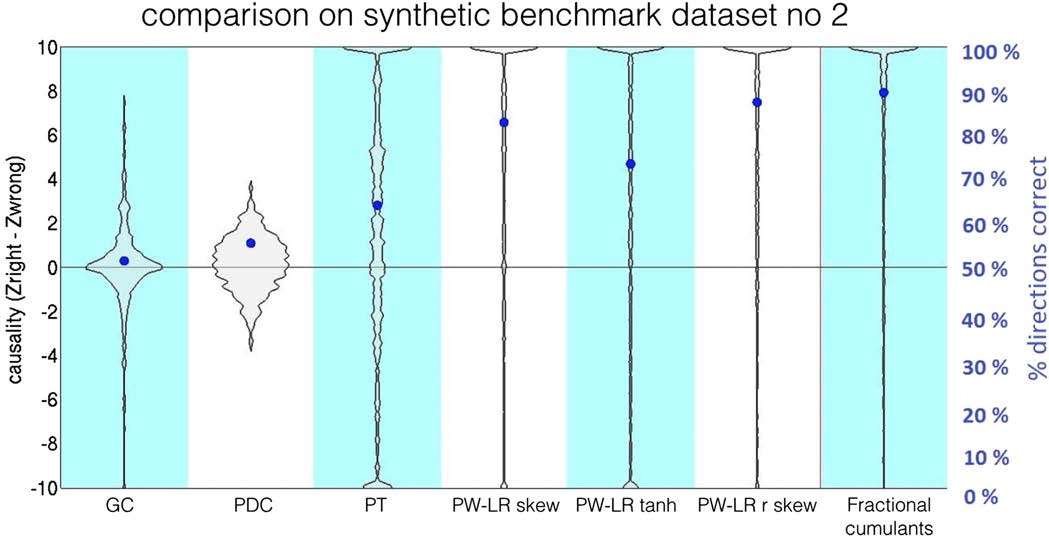
on the benchmark simulation no. 2 is presented in Figure 6. The violin plots denote the distri-
bution of the z-scores for connections as compared to the null distribution. Blue dots denote
the percentage of correct assignments for the true connections, as in Smith et al. (2011). In most
of the other 27 benchmark datasets, our classifier outperforms all the other methods (Support-
ing Information 5. As in the original study by Smith et al. (2011), lagged methods, GC, and
PDC perform worse than the structural methods. PW-LR r skew and fractional cumulants both
outperform PT, most probably because PT is based on the thresholded signal and therefore
contains a free parameter.
In general, in the benchmark synthetic datasets, fractional cumulants outperform all other
techniques in almost all cases, although the difference between performance of the fractional
cumulants and PW-LR methods is small.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 6. Comparison between the classifier based on the fractional cumulants and several other methods on benchmark simulation no. 2.
The violin plots denote the distribution of the z-scores for connections as compared with the null distribution. Blue dots denote the percentage
of correct assignments for the true connections (Smith et al., 2011). The difference in performance between the classifier based on fractional
cumulants and PW-LR r skew (Hyvärinen & Smith, 2013) is small.
Network Neuroscience
1022
Improving pairwise inference in fMRI using fractional moments of BOLD
Robustness of the Methods with Respect to Confounds
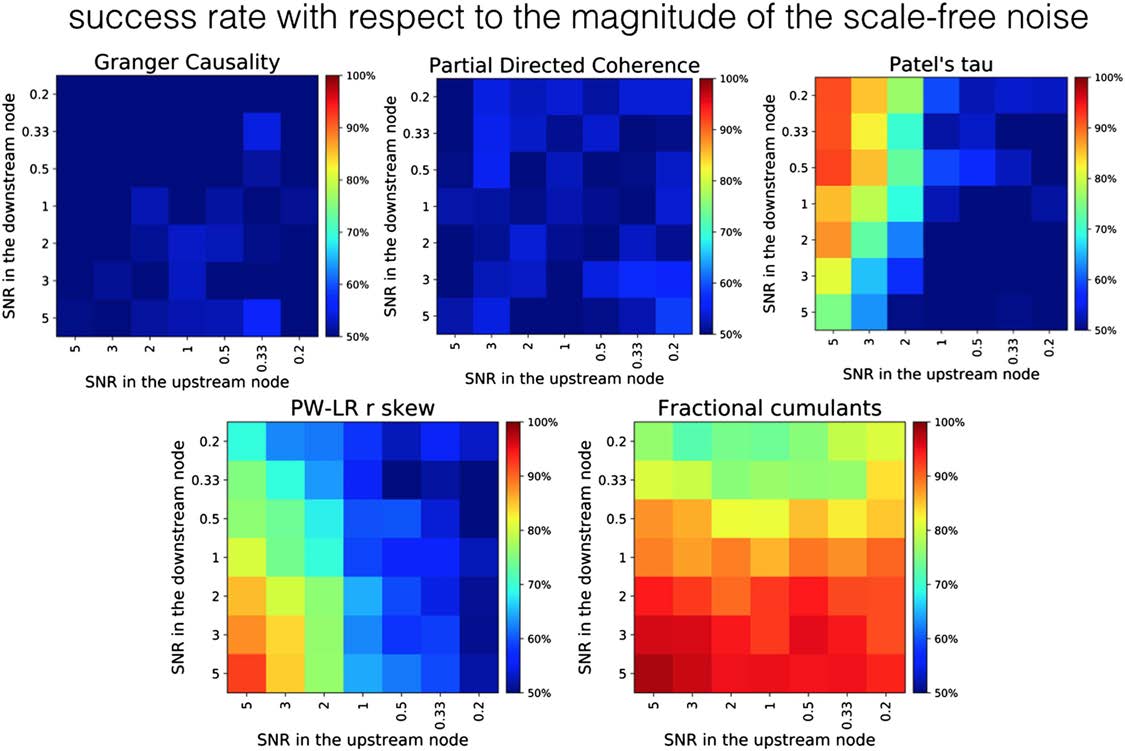
Figure 7 presents the comparison between the fractional cumulant classifier and various other
methods on a two-node simulation under the addition of varying levels of physiologically
plausible, scale-free neuronal noise across various levels of SNR for the upstream and down-
stream regions. The results suggest that all previously tested methods show low levels of ro-
bustness toward such additional sources of variability in the data. GC as well as PDC are at the
lowest performance, and give results on a chance level across the whole parameter space. In
PT, the success rate in proper classification between upstream and downstream node rapidly
drops toward 50% along with a decrease in SNR in the upstream node. However, in case SNR
in the upstream node is higher than 1 (left half of the Patel’s tau panel, Figure 7), PT is resilient
to the variance of SNR in the downstream node. The performance of PW-LR r skew drops
down to the chance level with respect to both the noise level in the upstream and downstream
region, whereas GC and PDC are performing almost equally poorly under any combination
of noise variances (probably because the variance of the noise from the fitted autoregressive
model is used to establish the directionality of the causal influence in GC).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 7. Robustness of the methods against the background scale-free neuronal noise. The variance of the background noise s(t) differs
between upstream and downstream region in the range of [0:2; 5:0]. As signal magnitude is constant and equal to 1 in these simulations, the
signal-to-noise ratio (SNR) was calculated as 1/var(σ).
Network Neuroscience
1023
Improving pairwise inference in fMRI using fractional moments of BOLD
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
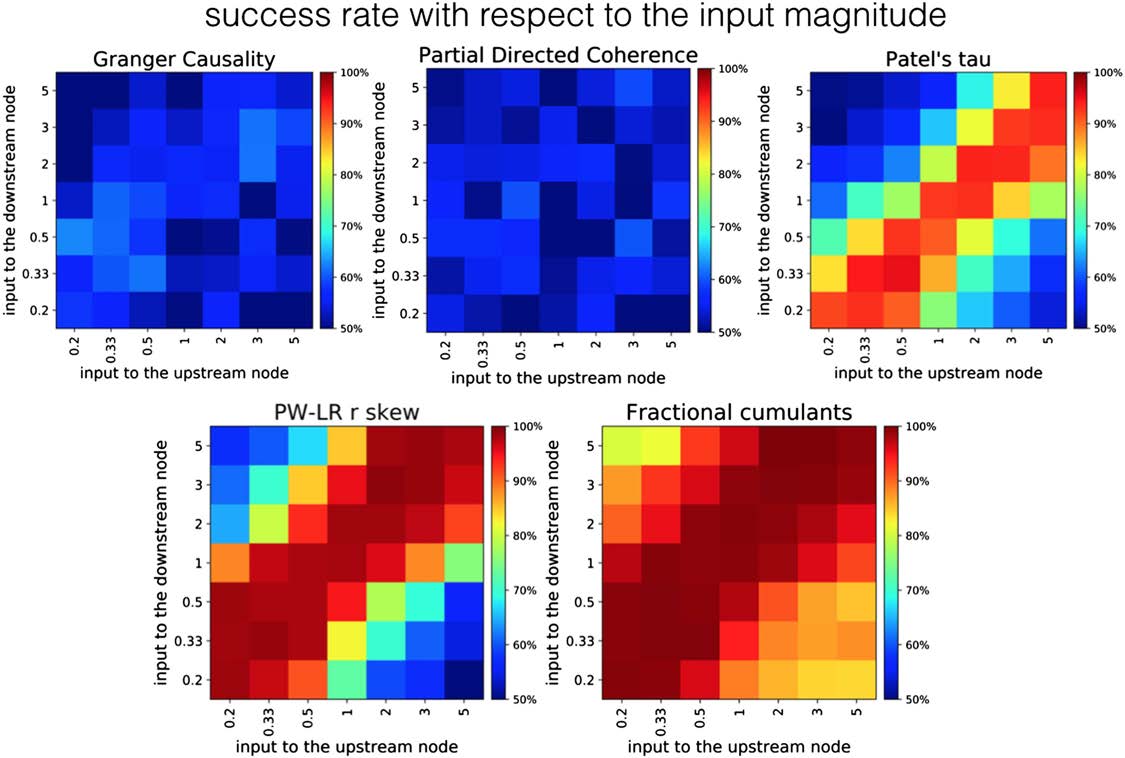
Figure 8. Robustness of different methods to the change in signal strengths. The variance of the signal differs between upstream and down-
stream region, both in the range of [0:2, 5:0]. GC and PDC give performance around the chance level across the whole parameter space,
whereas PW-LR r skew and PT exhibit certain resilience toward this variability in the inputs. However, the classifier based on fractional
cumulants is the only method whose performance does not fall toward the chance level within the parameter space.
Figure 8 presents the comparison between the classifier based on fractional cumulants and
other methods, given noiseless simulation and varying signal magnitudes. The classifier based
on fractional cumulants is the only method where the performance does not decrease down to
a chance level within the chosen parameter space. GC and PDC give performance around the
chance level across the whole parameter space, whereas PW-LR r skew and PT exhibit certain
resilience toward this variability in the inputs. However, the performance breaks down to the
chance level in cases when signal magnitudes between the upstream and downstream node
becomes highly disproportionate (higher than 3.0).
DISCUSSION
Summary
This work provides an advance to the effective connectivity research in fMRI, by utilizing the
additional information contained in the BOLD time series with use of fractional moments of the
BOLD distribution combined into cumulants. Usage of this additional information (embedded
within a classifier) significantly increases the robustness toward plausible sources of variability
Network Neuroscience
1024
Improving pairwise inference in fMRI using fractional moments of BOLD
in fMRI, namely presence of physiologically realistic (scale-free) background noise as well
as disproportion in the inputs strength, either due to differences in the amount of neuronal
activity locally induced and/or due to effective differences induced by, for example, regional
variations in the coil sensitivity profiles. This is where the value of added information coming
from fractional cumulants becomes apparent: among the methods tested in this work, only the
classifier based on the fractional cumulants gives a performance better than chance across the
whole parameter space in these experimentally realistic conditions.
Effective connectivity is a research problem directly related to the notion of causality. Causal-
ity is, in general, difficult both to define (Pearl, 2000) and to measure. In the most basic for-
mulation, in X causes Y, it means that without X, Y would not occur. The picture is far less
clear in complex dynamic systems such as brain networks: for any event, a high number of
potential causes can be defined, and these causes most often interfere with each other. This
research problem was recently discussed by Albantakis, Marshall, Hoel, and Tononi (2017)
who decomposed causality into independent dimensions: realization, composition, informa-
tion, integration, and exclusion. Also, interpretation of a causal component in a given process
depends on the context. For example, respiratory movement is typically considered a con-
found in fMRI experiments, unless we are interested in the influence of respiration speed on
the activity of neuronal populations. Furthermore, in brain networks, temporal ordering of the
cause of cause and effect is hard to maintain, as information is circulating in recurrent rather
than feed forward networks (Schurger & Uithol, 2015).
Furthermore, If we have an interventional study at disposal, establishing causality becomes
straightforward, but this is rarely the case in human brain research. In human fMRI, all the
studies are observational rather than interventional. In such cases, causation can never be
observed directly, just correlation (Hume, 1772). When a correlation is highly stable, we are
inclined to infer a causal link. Additional information is then needed to assess the direction of
the assumed causal link, as correlation indicates for association and not for causation (Altman
& Krzywinski, 2015).
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
.
t
/
In the simulations, we used multiple realizations of the dynamics for every network pattern.
We needed to run multiple instantiations of a noisy system in order to evaluate the mean
success rate of the methods under noisy circumstances. We also simulated long runs of the
dynamics aiming to find an upper bound on the methods’ performance in a function of the SNR
disproportion and background noise levels. We did not investigate the effects of the sample
length on the results. This is because in our study, we focused on the confounding factors
which—unlike the duration of the study—cannot be influenced by the researcher.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Although fractional moments of a distribution, as a mathematical concept, were studied
before (Dremlin, 1994; Matsui& Pawlas, 2013), this concept was not applied to biomedical
sciences to date. One reason for this lack of applications might be that the fractional moments
become complex numbers for the normalized time series, and that subsequently, the features
characterized by these moments cannot be conceptualized as easily as the features character-
ized by the integer moments (e.g., skewness can be interpreted as a measure of “asymmetry”
of the distribution, and kurtosis can be interpreted as its “flatness”). However, although the
fractional moments of a distribution are a mathematical concept with limited practical in-
terpretation, nevertheless they could still contain valuable, in our case causal, information.
In this work, we demonstrate that fractional moments provide important additional informa-
tion about the distribution of BOLD values. We first perform supervised learning of the clas-
sifier on the set of benchmark synthetic datasets, and then validate the classifier on two-node
Network Neuroscience
1025
Improving pairwise inference in fMRI using fractional moments of BOLD
simulations with biologically realistic confounds. We believe that confounding factors such
as a physiological background noise of a magnitude varying between the nodes is important
to overcome for any method for causal inference in fMRI. This is because every network in
the brain is embedded in larger networks, and therefore the background activity of other inter-
connected networks can be interpreted as “noise” (Deco, Jirsa, & McIntosh, 2011). We demon-
strate that our approach can increase the robustness of the methods for pairwise inference in
fMRI to the main sources of variability in BOLD fMRI.
therefore it
Unlike the previous methods for pairwise inference in fMRI (Hyvärinen & Smith, 2013),
the classifier defined in this study is informed by the dynamic causal modeling generative
incorporates the priors derived from the neurophysiological studies
model,
(Buxton, Wong, & Frank, 1998). Deriving benchmark signum maps for the classifier from the
multiple instantiations of the DCM generative model allows for marginalizing out all the param-
eters unimportant for the effective connectivity research: the classification procedure focuses
only on classifying a pair of regions into upstream and downstream instead of fitting all the
hyperparameters as is done in the classic DCM inference procedure. Therefore, this approach
is a reduction of the problem of effective connectivity in a large network to a two-node classi-
fication problem on one hand, and an extension of the feature space from integer to fractional
moments on the other hand.
The signum maps derived in the training process are dependent on the generative model.
In this study, we chose the canonical, original formulation of the DCM (Friston et al., 2003).
There are also newer formulations of the DCM, for example, the canonical microcircuit ap-
proach (Pinotsis et al., 2017; Friston et al., 2017), in which layer-specific neuronal populations
in the cortex are modeled with use of a neural mass model. In this case, we assume that the
inference is performed on mesoscale level, in which ROIs represent brain regions (cortex re-
gions or subcortical nuclei) rather than cortex components. Furthermore, although versions of
DCM containing higher order, nonlinear effects (Stephan et al., 2008) are also developed, we
believe that a (bi)-linear model is a good simplification to describe the underlying neuronal
dynamics, as it refers to the linear part of the sigmoidal transfer functions between neuronal
populations in the brain (Silver, 2010; Bielczyk, Buitelaar, Glennon, & Tiesinga, 2015). Mod-
eling communication between nodes in the network with use of linear transfer functions is
a common practice in modeling effective connectivity in fMRI (see, e.g., structural equation
models (Mclntosh & Gonzalez-Lima, 1994) or LiNGAM-ICA (Shimizu et al., 2006; Smith et al.,
2011). The bilinear version of DCM, often referred to as the general linear model approach, is
still a very popular tool for finding effective connectivity patterns from fMRI in clinical practice
(see, e.g., recent work by Zhang et al., 2018; Nackaerts et al., 2018; Arioli et al., 2018; Pool
et al., 2018).
We reproduced the DCM generative model after Smith et al. (2011). This implementation is
acknowledged in the field as a benchmark setting for testing new methods for functional and
effective connectivity in fMRI (see, e.g., Hyvärinen & Smith, 2013; Hinne et al., 2015; Bielczyk
et al., 2019). In this implementation, bilinear effects (namely, modulation of connections by
experimental inputs) are not modeled. In pairwise inference this omission is justified, as mod-
ulation of connection only affects the strength of connection weight A12, which will influence
cumulant values quantitatively and not qualitatively, which does not influence the outcome
signum maps.
Evaluating methods with the use of synthetic datasets as the ground truth is typically the first
step in the validation of any new data analytic framework. Validating new methods with use of
Network Neuroscience
1026
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
.
/
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
synthetic datasets is a state of the art technique across the whole field of neuroimaging, from
single cell imaging to whole-brain imaging with fMRI or EEG/MEG. This tradition has a long
history, starting from the Nobel-winning Hodgkin and Huxley model for initiation and propa-
gation of action potential (Hodgkin & Huxley, 1952). Today, methods for effective connectivity
between neuronal assemblies measured with multielectrode arrays are still validated on syn-
thetic datasets generated from this classical model, including recent approaches: nonlinear
data assimilation (Hamilton, Berry, Peixoto, & Sauer, 2013) and differential covariance (Lin,
Das, Krishnan, Bazhenov, & Sejnowski, 2017). In cognitive neuroimaging, testing methods
on synthetic datasets from generative models is also a standard. In EEG/MEG research, there
are multiple classes of generative models generating different type of dynamics, depending
on the purpose of the modeling study, for example, the nonlinear lumped-parameter model
for generating alpha rhythms and its neural mass extension by (David & Friston, 2003), the
Wong-Wang model for winner-take-all dynamics (Wong & Wang, 2006), the Hindmarsh-Rose
model for epileptor dynamics (Hindmarsh & Rose, 1984), and DCM for EEG/MEG (Kiebel,
Garrido, Moran, Chen, & Friston, 2009; Steen, Almgren, Razi, Friston, & Marinazzo, 2018;
Moran, Pinotsis, & Friston, 2013). Furthermore, the Human Neocortical Neurosolver simula-
tor developed at Brown University (HNN, https://hnn.brown.edu) is a complex tool simulating
local field potentials measured with EEG/MEG by bottom-up modeling of clusters of neurons.
All these tools can serve to validate new methods for functional and effective connectivity in
EEG/MEG (Valdes-Sosa et al., 2011; Wang et al., 2014).
In fMRI, the selection of generative models is narrower than in EEG/MEG: DCM (Friston,
Moran, & Seth, 2013; Smith et al., 2011) achieved a status of the standard generative model.
With use of this synthetic data generated from this model, new methods for effective connectiv-
ity in fMRI are validated, for example, the third- and fourth-cumulant method by Hyvärinen and
Smith (2013) and artificial immune algorithm combined with the Bayes net method (AIAEC; Ji,
Liu, Liang, & Zhang, 2016).
To date, DCM is the most biologically relevant generative model proposed in the field of
functional magnetic resonance imaging. The implementation of benchmark synthetic datasets
based on DCM by Smith et al. (2011) has gained a lot of attention and following in the field,
but it has also gained its critics. For instance, according to Smith’s results, PT (Patel, Bowman,
& Rilling, 2006) is one of the methods giving best performance in retrieving directed con-
nectivity patterns from synthetic benchmark datasets. In a recent work, Wang, David, Hu, and
Deshpande (2017) performed a modeling study on datasets derived from an experiment by
David et al. (2008) in which fMRI activity was measured in genetically modified rats suffering
from epilepsy. Activity from the same set of regions was recorded in an associated intracere-
bral EEG study in order to provide ground truth information flow. The authors chose primary
somatosensory cortex barrel field (S1BF), thalamus, and striatum (caudate-putamen; CPu) as
ROIs and demonstrated that Patel’s tau is no better than chance in recovering directional con-
nectivity patterns from this data in both raw and deconvolved fMRI datasets. On the contrary,
DCM and Granger causality proved to correctly estimate the directionality of the information
flow on the group level and on the deconvolved data.
There are more caveats to be noted with respect to the benchmark DCM simulations by
Smith et al. (2011). First, the synthetic datasets derived by the authors of the study involve
a low noise condition, in which the background noise in the networks in as low as 5% of
the signal magnitude. Given that the background activity in the brain networks includes not
only noise but also echo of cognitive processes unrelated to the experiment, 5% of back-
ground activity seems to be on the lower end of the spectrum of possibilities. Second, networks
Network Neuroscience
1027
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
investigated by Smith et al. are sparse (a number of connections in a network of size N is of
order of N) and almost acyclic, which also seems to be a very optimistic scenario. Third, Smith
et al. used a TR of 3 s and time series of 200 data points. This TR is too long, and the time series
length too short for generalizing the empirical datasets used today. Today, shorter TRs (1 s or
less, e.g., 0.72 s as in Human Connectome Project datasets; Van Essen et al., 2013), and longer
time series have become the norm (e.g., 4,800 samples in resting-state datasets from Human
Connectome Project datasets; Van Essen et al., 2013). Last, Smith et al. used a fixed delays of
50 ms in the first layer of the DCM model, representing the underlying neuronal commu-
nication. This delay represents synaptic transmission delays and axonal transmission delays
between nodes of the network. The constant value of delay is a crude estimation, especially
given that pairs of brain regions positioned at different distances from each other should have
different axonal transmission delays. Also, given polysynaptic connections, effective delays
between neuronal populations might be much higher than the aforementioned 50 ms. For ex-
ample, P300 potential appears after 300 ms (Polich, 2007), and some other cortical potentials
have even slower latencies. This lack of attention toward modeling neuronal delays might fa-
vor nonlagged methods (i.e., PT or LiNGAM) and might be preferred in this analysis over the
lagged methods. Altogether, there are reasons to believe that benchmark datasets derived by
Smith et al. are, to some extent, not representative of the real fMRI datasets. For these reasons,
results of validation on the benchmark datasets should be interpreted with care.
There are also other, competitive generative models in the field, for example, the model
proposed by Seth et al. (2013). In this model, the authors used a simple VAR generative model
in order to simulate neuronal dynamics in the testing network of five regions, based on work
by Baccalá and Sameshima (2001). Subsequently, the VAR model output is convolved with
five different HRF kernels generated with use of the difference-of-gamma approach as imple-
mented in SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/). Another possibility, would
be to use local field potentials (LFPs) instead of neuronal dynamics simulated as a system of
differential equations with delay, and convolve LFPs with HRF (Deshpande, Sathian, & Hu,
2010). However, to date, Smith’s synthetic datasets derived from the DCM generative model
remains the benchmark datasets.
Furthermore, in this work, we performed the inference on the full BOLD response, without
deconvolving the BOLD time series into the neuronal time series. It has been shown in synthetic
and empirical data that incorporating a physiologically based model of spatiotemporal hemo-
dynamic response function into the preprocessing pipeline leads to an improvement in the esti-
mated neuronal activation (Aquino, Robinson, Schira, & Breakspear, 2014). It was also shown
that it is generally difficult to accurately recover true task-evoked changes in BOLD fMRI time
series irrespectively of the method chosen for modeling HRF response (Lindquist et al., 2009).
Hence, there is a long-lasting debate in the field of connectomics on whether or not a (blind)
hemodynamic deconvolution is necessary to perform the (effective) connectivity research in
fMRI (Wu et al., 2013). For instance, structural equation models (Mclntosh & Gonzalez-Lima,
1994) are often applied without deconvolution to fMRI datasets (Schlösser et al., 2003; Zhuang,
LaConte, Peltier, Zhang, & Hu, 2005). Our previous theoretical research in synthetic datasets
generated from the DCM model suggests that deconvolution is not necessary in effective
connectivity research in fMRI if the method used in the study is not lag dependent (Bielczyk
et al., 2017). This is because under the assumption that the underlying signal on the neuronal
level is in the low-frequency range, the hemodynamic response—as a low-pass filter—does
not affect the signatures of different connectivity patterns present in the outcome BOLD re-
sponse. Therefore, in this work, we did not perform the deconvolution step before assessing
effective connectivity with any of the tested methods, including Granger causality. In fMRI
Network Neuroscience
1028
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
/
t
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
literature, GC is applied both with (David et al., 2008; Ryali, Supekar, Chen, & Menon, 2011;
Ryali et al., 2016; Hutcheson et al., 2015; Wheelock et al., 2014; Sathian, Deshpande, & Stilla,
2013; Goodyear et al., 2016) and without (Zhao et al., 2016; Regner et al., 2016; Chen et al.,
2017) use of deconvolution. Recent research suggests that all connectivity methods (includ-
ing functional connectivity) will improve their estimation accuracy post-HRF deconvolution
(Rangaprakash, Wu, Marinazzo, Hu, & Deshpande, 2018). However, in this work, we chose
for implementation without deconvolution, to be consistent with (Smith et al., 2011).
Here, we would like to mention that in recent years a lot of progress has been made in the
area of modeling local hemodynamics from fMRI datasets. For example, Havlicek et al. (2011)
proposed a new approach to modeling hemodynamic response functions based on cubature
Kalman filtering. Furthermore, Bush et al. (2015) proposed and validated a meta-algorithm for
performing semiblind deconvolution of the BOLD fMRI by using bootstrapping. This method
allows for estimating the timing of the underlying neural events stimulating BOLD responses,
together with confidence levels. Sreenivasan et al. (2015) proposed a nonparametric blind
BOLD deconvolution method based on homomorphic filtering.
Last, in our simulations we have set the connection strength to a fixed value of a = 0.9.
On this stage, the output of the classifier (Equation 4 and Equation 5) is a binary response,
that is, an indication for a connection, either X → Y or Y → X. This indication is based on a
linear combination the binary signum maps Sr, Si (Figure 2C) with the values of the cumulants
Cr, Ci computed for the given dataset X(t), Y(t), in either weighted or unweighted form. If the
connection strength varies, the strength of the coupling between fractional moments in X(t) and
Y(t) varies accordingly. Therefore, the absolute values of the associated fractional cumulants
will also adjust. If cumulant values scale, then the RHS sum in Equations 4 and 5 will scale
accordingly, but the signum of this sum should stay the same. Therefore, in a noiseless case,
this classifier should give the same response regardless of the connection strength a.
Limitations of the Method
It is also important to remember that there are always two independent aspects to a method for
causal inference. First, the method should have assumptions grounded in a biologically plau-
sible framework relevant for the given research problem. For instance, a method for causal
inference in fMRI should respect (1) the confounding, region-, and subject-specific BOLD dy-
namics (Handwerker, Ollinger, & D’Esposito, 2004) and (2) co-occurrence of cause and effect
(since the time resolution of the data is low compared with the underlying neuronal dynamics;
the causes and their effects most likely happen within the same frame in the fMRI data). The
new methods for pairwise inference such as classifying on the basis of fractional cumulants ad-
dress this issue by (1) breaking the time order, and performing causal inference on the basis of
statistical properties of the distribution of the BOLD samples, and not from the timing of events;
and (2) using correlation in order to detect connections. A good counterexample here is GC,
which has been proven useful in multiple disciplines. However, there is an ongoing discus-
sion on whether or not GC is suited for causal interpretations of fMRI data. On the one hand,
theoretical work by Seth, Chorley, and Barnett (2013) and Roebroeck, Formisano, & Goebel
(2005) suggest that despite the slow hemodynamics, GC can still be informative about the
directionality of causal links in the brain. Second, an estimation procedure needs to be com-
putationally stable. Even if the generative model faithfully describes the data, it still depends
on the estimation algorithm as to whether the method will return correct results. However, the
face validity of the algorithms can only be tested in particular paradigms, in which the ground
truth is known. If in the given paradigm the ground truth is unknown, which is most often the
case in fMRI experiments, only reliability can be tested.
Network Neuroscience
1029
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
Our approach requires certain assumptions. For instance, we assume that on the neuronal
level, effects of directed connectivity are linear. This is also an assumption underlying the orig-
inal DCM model used in this study. However, it is known that this is not always the case in the
neuronal dynamics. For instance, shunting inhibition (Alger & Nicoll, 1979) is a phenomenon
in which excitatory potential is reduced by division rather than by subtraction. However, effects
such as shunting inhibition typically happen in microscale and should not affect large-scale
neuronal dynamics as measured by BOLD fMRI. Therefore, we do not consider effects such as
shunting inhibition as plausible confounds to our approach.
One crucial limitation of our approach (as well as previous methods such as pairwise like-
lihood ratios) is that these techniques only retrieve the net connectivity. Namely, what these
methods effectively pick up on is the difference between connectivity strengths, and in a sce-
nario where the connectivity strengths X → Y and Y → X are equal, the outcome cumulant
map for the system will have lower amplitudes than in case of a unidirectional connection
X → Y with the same connection strength. The significance of the cumulant values (whether
or not the values are significantly different from zero) can be established with use of permuta-
tion testing. For more details, see Supporting Information 6, Figure 12B. However, since in the
first step of the inference we select only strong functional links for further classification, we can
interpret ambiguous output from the classifier as a bidirectional connection. Since the quality
of the classifier depends on the ability to determine the directionality of a unidirectional con-
nection, we used only unidirectional connections in the validation stage. One point to make
here is that bidirectional connections are hard to disambiguate for many methods for effec-
tive connectivity, as they represent cyclic nets. This is an issue, for example, in applications
of Bayesian nets (Pearl, 2000), in which joint probability for a certain graph is not tractable
when propagation of information in the network is cyclic. Also, the third- and fourth-cumulant
method by Hyvärinen and Smith (2013) falls into this category, as the asymmetry between third
cumulants in the case of bidirectional connections will be equal to zero.
One interesting direction for the method development would be also classification between
excitatory and inhibitory connectivity. This aspect is missing in our study, as we focus on the
connections of a positive sign only deriving a classifier able to distinguish between excitatory
and inhibitory connections would require deriving an additional set of benchmark Sr and Si
maps built on the basis of repetitive simulations of an inhibitory connection, and creating a
new set of benchmark synthetic datasets, as the original datasets by Smith et al. (2011) involve
excitatory links only. The reason why inhibition is not implemented yet, is because the cu-
mulant patterns for inhibitory connection are different from patterns given in Figure 2 (we did
not include the pictures in this manuscript though). The classifier in its current form gives a
binary decision on whether the connection is going in the direction of X → Y or Y → X. The
decision is based on whether the cumulant pattern obtained from the given dataset X(t), Y(t) is
more similar to the signum maps derived from DCM for connection X → Y (Figure 2C) or to
the inverse of these signum maps. In order to add inhibition to the picture, one would need to
extend the number of possible classes by adding signum maps derived from DCM for inhibitory
connection X → Y and introducing some metrics of distance to excitatory/inhibitory signum
maps. This is the next step to take. One thing to note in addition is whether or not inhibitory
effective connectivity is expected in large-scale networks investigated with fMRI; this is a mat-
ter for debate. On one hand, it is known that long-distance projections in the brain are mostly
excitatory as inhibition is typically local, presented by groups of tightly connected interneu-
rons within single brain regions (Markram et al., 2004), which is also modeled in the DCM
generative model with use of the self-inhibition term (Friston et al., 2003). On the other hand,
several anatomical and physiological studies indicate that there are also long-range inhibitory
Network Neuroscience
1030
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
Confounder:
A factor latent in the experiment
that can influence the causal
inference. It can be a node that
projects information to two other
nodes in the network, causing a
spurious causal association between
them, or a background neuronal
noise of magnitude varying across
the brain.
connections, for example, between hippocampus and entorhinal cortex in rats (Melzer et al.,
2012).
Furthermore, we consider local variability in brain physiology by varying hemodynamic
responses between realizations of the simulation and by studying the effects of the scale-free
background noise on the resulting effective connectivity measures. The DCM generative model
summarizes the current state of knowledge about the mechanisms underlying generation of
the BOLD response (Friston et al., 2017; Havlicek et al., 2015; Havlicek, Ivanov, Roebroeck,
& Uluda˘g, 2017). Therefore, we do not have efficient ways of incorporating human brain phys-
iology into our consideration in any more depth than this model allows for.
However, at the same time, we do not consider the influence of artifacts from the data ac-
quisition, such as the effects of movement in the scanner. We believe that the influence of such
confounders should be limited by a proper data preprocessing. For instance, motion artifacts
can be reduced with use of new, data-driven protocols for motion artifacts removal such as
ICA-AROMA (Pruim et al., 2015) or a censoring-based artifact removal strategy based on vol-
ume censoring (Power et al., 2014). Therefore, developing efficient strategies for controlling
such confounders is beyond the scope of this paper.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
t
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Future Research
In the context of fMRI research, increasing the granularity of moments in order to better char-
acterize the distribution is an especially useful application because the experimental fMRI
datasets are short (a few thousand samples at most); therefore, the estimation error for the
high-order integer moments of the distribution becomes high. However, the subsequent cu-
mulants contain information redundant to a certain extent, as they are correlated for any
given time series x(t). We chose the granularity that gives smooth patterns of discriminability
(Figure 3), which is Δ
k = 0.1. Choosing the optimal moment resolution is a subject to future
research; although, we believe that increasing index resolution to substantially less than 0.1
would not be beneficial, yet it would substantially increase the computational cost for the
method.
In this work, we validated our approach by using synthetic benchmark datasets derived from
the DCM generative model. Using generative models is valuable in neuroimaging, in terms of
validating new methods as mentioned in point 2, but also in applied research. Especially in
the fields of applied computational psychiatry (Frässle et al., 2018) and network neuroscience
in general (Betzel & Bassett, 2017), using generative models is valuable because these models
enable inference on model parameters, which afford for some degree of mechanistic inter-
pretability on the putative processes underlying the studied phenomena. Generative models,
especially DCM, are acknowledged in multiple contexts in the field of cognitive neuroimaging,
from method validation to application in clinical datasets. However, a valuable method should
also give predictions testable in clinics (e.g., lead to more reliable estimation of directed causal
influences during cognitive tasks, lead to better stratification of clinical populations in resting
state, etc.), which we will also further investigate.
In this work, we faithfully reproduced the pipeline after Smith et al. (2011). However, since
the original version of DCM (Friston, Harrison, & Penny, 2003) based on the original Balloon-
Windkessel model (Buxton, Wong, & Frank, 1998) was published, substantial advancements
to the hemodynamic model have been proposed. First, Obata et al. (2004) reported an error in
the expression for the outcome BOLD response (Equation 8, Supporting Information 1: DCM
forward model). Stephan, Weiskopf, Drysdale, Robinson, & Friston (2007) proposed a more
Network Neuroscience
1031
Improving pairwise inference in fMRI using fractional moments of BOLD
accurate expression for one of the terms in this formula. Second, Heinzle, Koopmans, den
Ouden, Raman, & Stephan (2016) proposed an updated formula for field strengths higher than
1.5 T. In the following work, we will take these improvements into account.
Furthermore, the approach needs to further be tested and compared against other methods
with use of experimental fMRI datasets, such as, for example, the Human Connectome Project
data (Van Essen et al., 2013; Barch et al., 2013). Since little is known about causal connections
in large-scale brain networks, especially in the resting state, such a validation might be quan-
titative (i.e., by means of reliability) rather than qualitative. Alternatively, one could perform
such a validation in particular pathways in which one can make assumptions about the direc-
tionality of information flow, such as the dorsal and the ventral stream in the visual cortex.
One possibility is testing using datasets coming from an interventional study in which neural
activity was evoked and, therefore, the ground truth is known: a fused fMRI-optogenetic ex-
periment (Ryali et al., 2016), in which intervention with use of optogenetics guarantees causal
link between investigated neuronal populations.
CONCLUSIONS
The field of effective connectivity research in fMRI is still growing. For instance, in recent years,
multiple algorithms for the graph network search have been developed and applied to fMRI
datasets, including independent multiple-sample greedy equivalence search (IMaGES; Ramsey
et al., 2010), group iterative multiple model estimation (GIMME; Gates & Molenaar, 2012), or
fast greedy equivalence search (FGES; Ramsey et al., 2016). It is material for debate whether or
not bivariate or multivariate inference serves a better purpose for effective connectivity research
in fMRI. In our work, we focused on the pairwise inference, and we achieved a significant im-
provement over previous approaches for pairwise estimation of functional causal interactions.
Most importantly, the robustness against known sources of variability (possible differences be-
tween up- and downstream noise magnitude and possible presence of non-Gaussian scale-free
noise) significantly increases due to the simultaneous incorporation of multiple aspects of the
associated BOLD distributions. We believe that, as this approach based on fractional moments
of a distribution increases resilience of the methods for pairwise connectivity to potential con-
founds in the experimental data, it can become a generic method to increase the power of
causal discovery studies, both in cognitive neuroimaging and beyond.
SUPPORTING INFORMATION
Supporting information for this article is available at https://doi.org/10.1162/netn_a_00099.
ACKNOWLEDGMENTS
We thank the whole SIN group at the Donders Institute for Brain, Cognition and Behavior for
advice and engagement in the project.
AUTHOR CONTRIBUTIONS
Natalia Bielczyk: Conceptualization; Formal analysis; Methodology; Validation; Visualization;
Writing – Original Draft; Writing – Review & Editing. Alberto Llera: Conceptualization; Formal
analysis; Supervision; Writing – Review & Editing. Jeffrey Glennon: Funding acquisition. Jan
Buitelaar: Supervision; Writing – Review & Editing. Christian Beckmann: Conceptualization;
Formal analysis; Methodology; Supervision; Writing – Review & Editing; Funding acquisition.
Network Neuroscience
1032
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
t
/
/
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
t
.
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
FUNDING INFORMATION
Jeffrey Glennon, FP7 Ideas: European Research Council, Award ID: 305697 (OPTIMISTIC).
Jeffrey Glennon, European Community’s Seventh Framework Programme (FP7/2007-2013),
Award ID: 278948 (TACTICS). Jeffrey Glennon, European Union’s Seventh Framework Pro-
gramme, Award ID: 603016 (MATRICS). Christian Beckmann, Wellcome Trust UK Strategic
Award, Award ID: 098369/Z/12/Z. Christian Beckmann, Netherlands Organization for Interna-
tional Cooperation in Higher Education (NL) Netherlands Organisation for Scientific Research
(NWO-Vidi, Award ID: 864-12-003.
REFERENCES
Albantakis, L., Marshall, W., Hoel, E., & Tononi, G. (2017). What
caused what? A quantitative account of actual causation using
dynamical causal networks. ArXiv:1708.06716 [Cs, Math, Stat].
Retrieved from http://arxiv.org/abs/1708.06716
Aldrich, J.
(1995). Correlations genuine and spurious in Pearson
and Yule. Statistical Science, 10(4), 364–376. https://doi.org/10.
1214/ss/1177009870
Alger, B. E., & Nicoll, R. A. (1979). GABA-mediated biphasic
inhibitory responses in hippocampus. Nature, 281, 315–317.
https://doi.org/10.1038/281315a0
Altman, N., & Krzywinski, M. (2015). Points of significance: Associ-
ation, correlation and causation. Nature Methods, 12, 899–900.
https://doi.org/10.1038/nmeth.3587
Aquino, K. M., Robinson, P. A., Schira, M. M., & Breakspear,
M.
(2014). Deconvolution of neural dynamics from fMRI
data using a spatiotemporal hemodynamic response function.
NeuroImage, 94, 203–215. https://doi.org/10.1016/j.neuroimage.
2014.03.001
Arichi, T., Fagiolo, G., Varela, M., Melendez-Calderon, A.,
Allievi, A., Merchant, N., . . . Edwards, A. D. (2012). Devel-
opment of BOLD signal hemodynamic responses in the hu-
man brain. NeuroImage, 63(2), 663–673. https://doi.org/10.1016/
j.neuroimage.2012.06.054
Arioli, M., Perani, D., Cappa, S., Proverbio, A. M., Zani, A., Falini, A.,
& Canessa, N.
(2018). Affective and cooperative social inter-
actions modulate effective connectivity within and between the
mirror and mentalizing systems. Human Brain Mapping, 39(3),
1412–1427. https://doi.org/10.1002/hbm.23930
Baccalá, L. A., & Sameshima, K. (2001). Partial directed coherence:
a new concept in neural structure determination. Biological Cy-
bernetics, 84(6), 463–474. https://doi.org/10.1007/PL00007990
Barch, D. M., Burgess, G. C., Harms, M. P., Petersen, S. E.,
Schlaggar, B. L., Corbetta, M., . . . WU-Minn HCP Consor-
tium. (2013). Function in the human connectome: Task-fMRI and
individual differences in behavior. NeuroImage, 80, 169–189.
https://doi.org/10.1016/j.neuroimage.2013.05.033
Barnett, L., & Seth, A. K. (2014). The MVGC multivariate Granger
causality toolbox: A new approach to Granger-causal inference.
Journal of Neuroscience Methods, 223, 50–68. https://doi.org/
10.1016/j.jneumeth.2013.10.018
Barnett, L., & Seth, A. K. (2015). Granger causality for state-space
models. Physical Review E, 91(4), 040101. https://doi.org/10.
1103/PhysRevE.91.040101
Bédard, C., Kröger, H., & Destexhe, A. (2006). Does the 1/f fre-
quency scaling of brain signals reflect self-organized critical
states? Physical Review Letters, 97(11), 118102. https://doi.org/
10.1103/PhysRevLett.97.118102
Berkson, J. (1946). Limitations of the application of fourfold table
analysis to hospital data. Biometrics Bulletin, 2(3), 47–53. https://
doi.org/10.2307/3002000
Betzel, R. F., & Bassett, D. S. (2017). Generative models for network
neuroscience: Prospects and promise. Journal of The Royal So-
ciety Interface, 14(136), 20170623. https://doi.org/10.1098/rsif.
2017.0623
Bielczyk, N. Z., Buitelaar, J. K., Glennon, J. C., & Tiesinga, P. H. E.
(2015). Circuit to construct mapping: A mathematical tool for
assisting the diagnosis and treatment in major depressive dis-
order. Frontiers in Psychiatry, 6. https://doi.org/10.3389/fpsyt.
2015.00029
Bielczyk, N. Z., Llera, A., Buitelaar,
J. C., &
Beckmann, C. F. (2017). The impact of hemodynamic variability
and signal mixing on the identifiability of effective connectivity
structures in BOLD fMRI. Brain and Behavior, 7(8). https://doi.
org/10.1002/brb3.777
J. K., Glennon,
Bielczyk, N. Z., Walocha, F., Ebel, P. W., Haak, K. V., Llera,
A., Buitelaar, J. K., . . . Beckmann, C. F.(2018). Thresholding
functional connectomes by means of mixture modeling. Neuro-
Image,171, 402–414. https://doi.org/10.1016/j.neuroimage.2018.
01.003
Bielczyk, N. Z., Uithol, S., van Mourik, T., Anderson, P., Glennon,
J. C., & Buitelaar, J. K. (2019). Disentangling casaul webs in the
brain using functional magnetic resonance imaging: A review of
current approaches. Network Neuroscience, 237–273. https://
doi.org/10.1162/netn_a_00062
Bush, K., Cisler, J., Bian, J., Hazaroglu, G., Hazaroglu, O., & Kilts, C.
(2015). Improving the precision of fMRI BOLD signal decon-
volution with implications for connectivity analysis. Magnetic
Resonance Imaging, 33(10), 1314–1323. https://doi.org/10.1016/
j.mri.2015.07.007
Buxton, R. B., Wong, E. C., & Frank, L. R., (1998). Dynamics of blood
flow and oxygenation changes during brain activation: the bal-
loon model. Magnetic Resonance in Medicine, 39(6), 855–864.
https://doi.org/10.1002/mrm.1910390602
Chen, Y. -C., Xia, W., Chen, H., Feng, Y., Xu, J.-J., Gu, J.-P., . . . Yin, X.
(2017). Tinnitus distress is linked to enhanced resting-state func-
tional connectivity from the limbic system to the auditory cor-
tex. Human Brain Mapping, 38(5), 2384–2397. https://doi.org/
10.1002/hbm.23525
Network Neuroscience
1033
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
Chicharro, D.
(2011). On the spectral
formulation of Granger
causality. Biological Cybernetics, 105(5–6), 331–347. https://doi.
org/10.1007/s00422-011-0469-z
David, O., & Friston, K.
for
MEG/EEG: NeuroImage, 20(3), 1743–1755. https://doi.org/10.
1016/j.neuroimage.2003.07.015
(2003). A neural mass model
J.
David, O., Guillemain,
I., Saillet, S., Reyt, S., Deransart, C.,
Segebarth, C., & Depaulis, A. (2008). Identifying neural drivers
with functional MRI: An electrophysiological validation. PLoS
Biology, 6(12). https://doi.org/10.1371/journal.pbio.0060315
Deco, G., Jirsa, V. K., & McIntosh, A. R. (2011). Emerging con-
cepts for the dynamical organization of resting-state activity in
the brain. Nature Reviews Neuroscience, 12(1), 43–56. https://
doi.org/10.1038/nrn2961
Dehghani, N., Bédard, C., Cash, S. S., Halgren, E., & Destexhe, A.
(2010). Comparative power spectral analysis of simultaneous ele-
croencephalographic and magnetoencephalographic recordings
in humans suggests non-resistive extracellular media. Journal
of Computational Neuroscience, 29(3), 405–421. https://doi.org/
10.1007/s10827-010-0263-2
Deshpande, G., Sathian, K., & Hu, X. (2010). Effect of hemody-
namic variability on Granger causality analysis of fMRI. Neuro-
Image, 52(3), 884–896. https://doi.org/10.1016/j.neuroimage.
2009.11.060
Di, X., & Biswal, B. B. (2019). Toward task connectomics: Exam-
ining whole-brain task modulated connectivity in different task
domains. Cerebral Cortex, 29(4), 1572–1583. https://doi.org/10.
1093/cercor/bhy055
Devonshire, I. M., Papadakis, N. G., Port, M., Berwick, J., Kennerley,
A. J., Mayhew, J. E. W., & Overton, P. G. (2012). Neurovascular cou-
pling is brain region-dependent. NeuroImage, 59(3), 1997–2006.
https://doi.org/10.1016/j.neuroimage.2011.09.050
Dremlin, I. M. (1994). Fractional moments of distributions. Journal
of Experimental and Theoretical Physics Letters, 59(9), 585–588.
Van Essen, D. C., Smith, S. M., Barch, D. M., Behrens, T. E. J.,
Yacoub, E., Ugurbil, K.,
. WU-Minn HCP Consortium.
.
(2013). The WU-minn Human Connectome Project: an overview.
NeuroImage, 80, 62–79. https://doi.org/10.1016/j.neuroimage.
2013.05.041
.
Faes, L., Erla, S., Porta, A., & Nollo, G. (2013). A framework for
assessing frequency domain causality in physiological time se-
ries with instantaneous effects. Philosophical, Transactions. Series
A, Mathematical, Physical, and Engineering Sciences, 371(1997),
20110618. https://doi.org/10.1098/rsta.2011.0618
Frässle, S., Yao, Y., Schöbi, D., Aponte, E. A., Heinzle, J., & Stephan,
K. E. (2018). Generative models for clinical applications in com-
putational psychiatry. Wiley Interdisciplinary Reviews. Cognitive
Science, 9(3), e1460. https://doi.org/10.1002/wcs.1460
Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse
lasso. Biostatis-
covariance estimation with the graphical
tics (Oxford, England), 9(3), 432–441. https://doi.org/10.1093/
biostatistics/kxm045
Friston, K., Moran, R., & Seth, A. K., (2013). Analysing connectiv-
ity with Granger causality and dynamic causal modelling. Cur-
rent Opinion in Neurobiology, 23(2), 172–178. https://doi.org/
10.1016/j.conb.2012.11.010
Friston, K. J., Harrison, L., & Penny, W.
(2003). Dynamic causal
modelling. NeuroImage, 19(4), 1273–1302.
Friston, K. J. (2011). Functional and effective connectivity: A re-
view. Brain Connectivity, 1(1), 13–36. https://doi.org/10.1089/
brain.2011.0008
Friston, K. J., Preller, K. H., Mathys, C., Cagnan, H., Heinzle, J.,
Razi, A., & Zeidman, P. (2017). Dynamic causal modelling re-
visited. NeuroImage. https://doi.org/10.1016/j.neuroimage.2017.
02.045
Gates, K. M., & Molenaar, P. C. M. (2012). Group search algo-
rithm recovers effective connectivity maps for individuals in
homogeneous and heterogeneous samples. NeuroImage, 63(1),
310–319. https://doi.org/10.1016/j.neuroimage.2012.06.026
Geweke, J. (1982). Measurement of linear dependence and feed-
back between multiple time series. Journal of the American
Statistical Association, 77(378), 304–313. https://doi.org/10.1080/
01621459.1982.10477803
Geweke, J. F. (1984). Measures of conditional linear dependence
and feedback between time series. Journal of the American Sta-
tistical Association, 79(388), 907–915. https://doi.org/10.1080/
01621459.1984.10477110
Goodyear, K., Parasuraman, R., Chernyak, S., Madhavan, P.,
Deshpande, G., & Krueger, F. (2016). Advice taking from humans
and machines: An fMRI and effective connectivity study. Fron-
tiers in Human Neuroscience, 10, 542. https://doi.org/10.3389/
fnhum.2016.00542
Granger, C. W. J. (1969). Investigating causal relations by econo-
metric models and cross-spectral methods. Econometrica, 37(3),
424–438. https://doi.org/10.2307/1912791
Hamilton, F., Berry, T., Peixoto, N., & Sauer, T. (2013). Real-time
tracking of neuronal network structure using data assimilation.
Physical Review E, 88(5). https://doi.org/10.1103/PhysRevE.88.
052715
Handwerker, D. A., Ollinger, J. M., & D’Esposito, M. (2004). Varia-
tion of BOLD hemodynamic responses across subjects and brain
regions and their effects on statistical analyses. NeuroImage,
21(4), 1639–1651. https://doi.org/10.1016/j.neuroimage.2003.
11.029
Havlicek, M., Friston, K. J., Jan, J., Brazdil, M., & Calhoun, V. D.
(2011). Dynamic modeling of neuronal responses in fMRI us-
ing Cubature Kalman filtering. NeuroImage, 56(4), 2109–2128.
https://doi.org/10.1016/j.neuroimage.2011.03.005
Havlicek, M., Roebroeck, A., Friston, K., Gardumi, A., Ivanov, D.,
& Uludag, K. (2015). Physiologically informed dynamic causal
modeling of fMRI data. NeuroImage, 122, 355–372. https://doi.
org/10.1016/j.neuroimage.2015.07.078
Havlicek, M., Ivanov, D., Roebroeck, A., & Uluda˘g, K. (2017).
Determining excitatory and inhibitory neuronal activity from
multimodal fMRI data using a generative hemodynamic model.
Frontiers in Neuroscience, 11, 616. https://doi.org/10.3389/
fnins.2017.00616
He, B. J. (2014). Scale-free brain activity: Past, present, and future.
Trends in Cognitive Sciences, 18(9), 480–487. https://doi.org/10.
1016/j.tics.2014.04.003
Heinzle, J., Koopmans, P. J., den Ouden, H. E. M., Raman, S., &
Stephan, K. E. (2016). A hemodynamic model for layered BOLD
Network Neuroscience
1034
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
signals. NeuroImage, 125, 556–570. https://doi.org/10.1016/j.
neuroimage.2015.10.025
van den Heuvel, M. P., de Lange, S. C., Zalesky, A., Seguin, C.,
Yeo, B. T. T., & Schmidt, R. (2017). Proportional thresholding in
resting-state fMRI functional connectivity networks and conse-
quences for patient-control connectome studies: Issues and rec-
ommendations. NeuroImage, 152, 437–449. https://doi.org/10.
1016/j.neuroimage.2017.02.005
Hindmarsh, J. L., & Rose, R. M. (1984). A model of neuronal
bursting using three coupled first order differential equations.
Proceedings, of the Royal Society of London. Series B, Biolog-
ical Sciences, 221(1222), 87–102. https://doi.org/10.1098/rspb.
1984.0024
Hinne, M., Janssen, R. J., Heskes, T., & van Gerven, M. A. J. (2015).
Bayesian estimation of conditional independence graphs im-
proves functional connectivity estimates. PLoS Computational Bi-
ology, 11(11), e1004534. https://doi.org/10.1371/journal.pcbi.
1004534
Hodgkin, A. L., & Huxley, A. F. (1952). A quantitative description
of membrane current and its application to conduction and ex-
citation in nerve. The Journal of Physiology, 117(4), 500–544.
Hume, D. (1772). Cause and effect. In An Enquiry Concerning Hu-
man Understanding.
Hutcheson, N. L., Sreenivasan, K. R., Deshpande, G., Reid, M. A.,
Hadley, J., White, D. M., . . . Lahti, A. C. (2015). Effective
connectivity during episodic memory retrieval in schizophrenia
participants before and after antipsychotic medication. Human
Brain Mapping, 36(4), 1442–1457. https://doi.org/10.1002/hbm.
22714
Hyvärinen, A., Zhang, K., Shimizu, S., & Hoyer, P. O. (2010). Esti-
mation of a structural vector autoregression model using non-
Gaussianity. Journal of Machine Learning Research, 11(May),
1709–1731.
Hyvärinen, A., & Smith, S. M. (2013). Pairwise likelihood ratios for
estimation of non-Gaussian structural equation models. Journal
of Machine Learning Research, 14(Jan), 111–152.
J., Zscheischler,
Janzing, D., Mooij,
J.,
J., Zhang, K., Lemeire,
Daniušis, P., . . . Schölkopf, B. (2012). Information-geometric
approach to inferring causal directions. Artificial Intelligence,
182–183, 1–31. https://doi.org/10.1016/j.artint.2012.01.002
Ji, J., Liu, J., Liang, P., & Zhang, A. (2016). Learning effective con-
nectivity network structure from fMRI data based on artificial im-
mune algorithm. PloS One, 11(4), e0152600. https://doi.org/10.
1371/journal.pone.0152600
Kami ´nski, M. J., & Blinowska, K. J. (1991). A new method of the
description of the information flow in the brain structures. Bio-
logical Cybernetics, 65(3), 203–210.
Kennaway, R. (2015). When causation does not imply correlation:
Robust violations of the faithfulness axiom. ArXiv:1505.03118
[Math, Stat]. Retrieved from http://arxiv.org/abs/1505.03118
Kiebel, S. J., Garrido, M. I., Moran, R., Chen, C.-C., & Friston, K. J.
(2009). Dynamic causal modeling for EEG and MEG. Human
Brain Mapping, 30(6), 1866–1876. https://doi.org/10.1002/hbm.
20775
Kötter, R., & Stephan, K. E. (2003). Network participation indices:
Characterizing component roles for information processing in
neural networks. Neural Networks, 16(9), 1261–1275. https://
doi.org/10.1016/j.neunet.2003.06.002
Kruger, P. (2018). Why it is not a ‘failure’ to leave academia. Nature,
560, 7716. https://doi.org/10.1038/d41586-018-05838-y
Ledoit, O., & Wolf, M. (2004). A well-conditioned estimator for
large-dimensional covariance matrices. J. Multivar. Anal., 88(2),
365–411. https://doi.org/10.1016/S0047-259X(03)00096-4
Lin, T. W., Das, A., Krishnan, G. P., Bazhenov, M., & Sejnowski, T. J.
(2017). Differential covariance: A new class of methods to esti-
mate sparse connectivity from neural recordings. Neural Com-
putation, 29(10), 2581–2632. https://doi.org/10.1162/neco_a_
01008
Lindquist, M. A., Loh, J. M., Atlas, L. Y., & Wager, T. D. (2009). Mod-
eling the hemodynamic response function in fMRI: efficiency,
bias and mis-modeling. Neuroimage, 45(1 Suppl), S187–S198.
https://doi.org/10.1016/j.neuroimage.2008.10.065
Markram, H., Toledo-Rodriguez, M., Wang, Y., Gupta, A.,
Silberberg, G., & Wu, C.
the neo-
(2004).
cortical inhibitory system. Nature Reviews Neuroscience, 5(10),
793–807. https://doi.org/10.1038/nrn1519
Interneurons of
Marrelec, G., Krainik, A., Duffau, H., Pélégrini-Issac, M., Lehéricy,
S., Doyon, J., & Benali, H. (2006). Partial correlation for func-
tional brain interactivity investigation in functional MRI. Neuro-
Image,32(1), 228–237.https://doi.org/10.1016/j.neuroimage.2005.
12.057
Matsui, M., & Pawlas, Z. (2013). Fractional absolute moments of
heavy tailed distributions. ArXiv:1301.4804 [Math, Stat]. Re-
trieved from http://arxiv.org/abs/1301.4804
Mclntosh, A. R., & Gonzalez-Lima, F. (1994). Structural equation
modeling and its application to network analysis in functional
brain imaging. Human Brain Mapping, 2(1–2), 2–22. https://doi.
org/10.1002/hbm.460020104
Melzer, S., Michael, M., Caputi, A., Eliava, M., Fuchs, E. C.,
Whittington, M. A., & Monyer, H. (2012). Long-range–projecting
GABAergic neurons modulate inhibition in hippocampus and
entorhinal cortex. Science, 335(6075), 1506–1510. https://doi.
org/10.1126/science.1217139
Moran, R. J., Pinotsis, D. A., & Friston, K. J. (2013). Neural masses
and fields in dynamic causal modeling. Frontiers in Compu-
tational Neuroscience, 7. https://doi.org/10.3389/fncom.2013.
00057
Nackaerts, E., Michely, J., Heremans, E., Swinnen, S. P., Smits-
Engelsman, B. C. M., Vandenberghe, W., . . . Nieuwboer, A.
(2018). Training for micrographia alters neural connectivity in
Parkinson’s disease. Frontiers in Neuroscience, 12, 3. https://doi.
org/10.3389/fnins.2018.00003
Nie, L., Yang, X., Matthews, P. M., Xu, Z., & Guo, Y. (2015). Minimum
partial correlation: An accurate and parameter-free measure of
functional connectivity in fMRI. In Y. Guo, K. Friston, F. Aldo,
S. Hill, & H. Peng (Eds.), Brain Informatics and Health (Vol. 9250,
125–135). Cham: Springer International Publishing.
Obata, T., Liu, T. T., Miller, K. L., Luh, W.-M., Wong, E. C., Frank,
L. R., & Buxton, R. B. (2004). Discrepancies between BOLD and
flow dynamics in primary and supplementary motor areas: Appli-
cation of the balloon model to the interpretation of BOLD tran-
sients. NeuroImage, 21(1), 144–153. https://doi.org/10.1016/j.
neuroimage.2003.08.040
Patel, R. S., Bowman, F. D., & Rilling, J. K. (2006). A Bayesian
the human brain.
approach to determining connectivity of
Network Neuroscience
1035
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
/
.
t
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
Human Brain Mapping, 27(3), 267–276. https://doi.org/10.1002/
hbm.20182
J.
(2000). Causality: Models, Reasoning, and Inference
Pearl,
Cambridge, UK: Cambridge University Press.
Pinotsis, D. A., Geerts, J. P., Pinto, L., FitzGerald, T. H. B., Litvak,
V., Auksztulewicz, R., & Friston, K. J. (2017). Linking canonical
microcircuits and neuronal activity: Dynamic causal modelling of
laminar recordings. NeuroImage, 146, 355–366. https://doi.org/
10.1016/j.neuroimage.2016.11.041
Polich, J. (2007). Updating P300: An integrative theory of P3a and
P3b. Clinical Neurophysiology, 118(10), 2128–2148. https://doi.
org/10.1016/j.clinph.2007.04.019
Pool, E.-M., Leimbach, M., Binder, E., Nettekoven, C., Eickhoff,
S. B., Fink, G. R., & Grefkes, C. (2018). Network dynamics en-
gaged in the modulation of motor behavior in stroke patients.
Human Brain Mapping, 39(3), 1078–1092.https://doi.org/10.1002/
hbm.23872
Power, J. D., Mitra, A., Laumann, T. O., Snyder, A. Z., Schlaggar,
B. L., & Petersen, S. E. (2014). Methods to detect, characterize,
and remove motion artifact in resting state fMRI. NeuroImage,
84. https://doi.org/10.1016/j.neuroimage.2013.08.048
Pruim, R. H. R., Mennes, M., van Rooij, D., Llera, A., Buitelaar,
J. K., & Beckmann, C. F. (2015). ICA-AROMA: A robust ICA-based
strategy for removing motion artifacts from fMRI data. Neuro-
Image,112,267–277. https://doi.org/10.1016/j.neuroimage.2015.
02.064
Ramsey,
J. D., Hanson, S.
J., Hanson, C., Halchenko, Y. O.,
Poldrack, R. A., & Glymour, C. (2010). Six problems for causal
inference from fMRI. NeuroImage, 49(2), 1545–1558. https://doi.
org/10.1016/j.neuroimage.2009.08.065
Rangaprakash, D., Wu, G.-R., Marinazzo, D., Hu, X., &
Deshpande, G. (2018). Hemodynamic response function (HRF)
variability confounds resting-state fMRI functional connectivity.
Magnetic Resonance in Medicine, 80(4), 1697–1713. https://doi.
org/10.1002/mrm.27146
Regner, M. F., Saenz, N., Maharajh, K., Yamamoto, D. J., Mohl,
B., Wylie, K., . . . Tanabe, J. (2016). Top-down network effec-
tive connectivity in abstinent substance dependent individuals.
PLoS One, 11(10), e0164818. https://doi.org/10.1371/journal.
pone.0164818
Roebroeck, A., Formisano, E., & Goebel, R. (2005). Mapping di-
rected influence over the brain using Granger causality and
fMRI. NeuroImage, 25(1), 230–242. https://doi.org/10.1016/j.
neuroimage.2004.11.017
Ryali, S., Supekar, K., Chen, T., & Menon, V. (2011). Multivari-
ate dynamical systems models for estimating causal interactions
in fMRI. NeuroImage, 54(2), 807–823. https://doi.org/10.1016/j.
neuroimage.2010.09.052
Ryali, S., Shih, Y.-Y. I., Chen, T., Kochalka, J., Albaugh, D., Fang,
Z., . . . Menon, V. (2016). Combining optogenetic stimulation
and fMRI to validate a multivariate dynamical systems model for
estimating causal brain interactions. NeuroImage, 132, 398–405.
https://doi.org/10.1016/j.neuroimage.2016.02.067
Sathian, K., Deshpande, G., & Stilla, R. (2013). Neural changes with
tactile learning reflect decision-level reweighting of perceptual
readout. Journal of Neuroscience, 33(12), 5387–5398. https://
doi.org/10.1523/JNEUROSCI.3482-12.2013
Schlösser, R., Gesierich, T., Kaufmann, B., Vucurevic, G., Hunsche,
S., Gawehn, J., & Stoeter, P. (2003). Altered effective connectivity
during working memory performance in schizophrenia: A study
with fMRI and structural equation modeling. NeuroImage, 19(3),
751–763.
Schurger, A., & Uithol, S. (2015). Nowhere and everywhere: The
causal origin of voluntary action. Review of Philosophy and Psy-
chology, 6(4), 761–778.
Seth, A. K., Chorley, P., & Barnett, L. C. (2013). Granger causal-
ity analysis of fMRI BOLD signals is invariant to hemodynamic
convolution but not downsampling. NeuroImage, 65, 540–555.
https://doi.org/10.1016/j.neuroimage.2012.09.049
Seth, A. K., Barrett, A. B., & Barnett, L. (2015). Granger causal-
ity analysis in neuroscience and neuroimaging. The Journal
of Neuroscience, 35(8), 3293–3297. https://doi.org/10.1523/
JNEUROSCI.4399-14.2015
Sgouritsa, E., Janzing, D., Hennig, P., & Schölkopf, B. (2015). In-
ference of cause and effect with unsupervised inverse regres-
sion. In Proceedings of the UAI 2015 Conference on Advances in
Causal Inference - Volume 1504. (pp. 89–89) Aachen, Germany,
Germany: CEUR-WS.org. Retrieved from http://dl.acm.org/
citation.cfm?id=3020267.3020280
Shimizu, S., Hoyer, P. O., Hyvärinen, A., & Kerminen, A. (2006). A
linear non-Gaussian acyclic model for causal discovery. Journal
of Machine Learning Research, 7, 2003–2030.
Silver, R. A. (2010). Neuronal arithmetic. Nature Reviews Neuro-
science, 11(7), 474–489. https://doi.org/10.1038/nrn2864
Smith, S. M., Miller, K. L., Salimi-Khorshidi, G., Webster, M.,
Beckmann, C. F., Nichols, T. E., . . . Woolrich, M. W. (2011).
Network modelling methods for FMRI. NeuroImage, 54(2),
875–891. https://doi.org/10.1016/j.neuroimage.2010.08.063
Sreenivasan, K. R., Havlicek, M., & Deshpande, G., (2015). Non-
parametric hemodynamic deconvolution of FMRI using homo-
morphic filtering. IEEE Transactions on Medical Imaging, 34(5),
1155–1163. https://doi.org/10.1109/TMI.2014.2379914
Steen, F. V., Almgren, H. B. J., Razi, A., Friston, K. J., & Marinazzo,
D. (2018). Dynamic causal modelling of fluctuating connectivity
in resting-state EEG. BioRxiv, 303933. https://doi.org/10.1101/
303933
Stephan, K. E., Weiskopf, N., Drysdale, P. M., Robinson, P. A.,
& Friston, K. J. (2007). Comparing hemodynamic models with
DCM. NeuroImage, 38(3), 387–401. https://doi.org/10.1016/j.
neuroimage.2007.07.040
Stephan, K. E., Kasper, L., Harrison, L. M., Daunizeau,
J.,
den Ouden, H. E. M., Breakspear, M., & Friston, K. J. (2008).
Nonlinear dynamic causal models for fMRI. NeuroImage, 42(2),
649–662. https://doi.org/10.1016/j.neuroimage.2008.04.262
Stokes, P. A., & Purdon, P. L. (2017). A study of problems encoun-
tered in Granger causality analysis from a neuroscience perspec-
tive. Proceedings of the National Academy of Sciences of the
United States of America, 114(34), E7063–E7072. https://doi.org/
10.1073/pnas.1704663114
Valdes-Sosa, P. A., Roebroeck, A., Daunizeau, J., & Friston, K.
(2011). Effective connectivity: Influence, causality and biophys-
ical modeling. NeuroImage, 58(2), 339–361. https://doi.org/10.
1016/j.neuroimage.2011.03.058
Network Neuroscience
1036
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
.
t
/
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Improving pairwise inference in fMRI using fractional moments of BOLD
Varoquaux, G., & Craddock, R. C. (2013). Learning and compar-
ing functional connectomes across subjects. NeuroImage, 80,
405–415. https://doi.org/10.1016/j.neuroimage.2013.04.007
Wang, H. E., Bénar, C. G., Quilichini, P. P., Friston, K. J., Jirsa, V. K.,
& Bernard, C. (2014). A systematic framework for functional con-
nectivity measures. Frontiers in Neuroscience, 8. https://doi.org/
10.3389/fnins.2014.00405
Wang, Y., David, O., Hu, X., & Deshpande, G.
(2017). Can
Patel’s τ accurately estimate directionality of connections in brain
networks from fMRI? Magnetic Resonance in Medicine, 78(5),
2003–2010. https://doi.org/10.1002/mrm.26583
Wheelock, M. D., Sreenivasan, K. R., Wood, K. H., Ver Hoef,
L. W., Deshpande, G., & Knight, D. C. (2014). Threat-related
learning relies on distinct dorsal prefrontal cortex network
connectivity. NeuroImage, 102 Pt 2, 904–912. https://doi.org/10.
1016/j.neuroimage.2014.08.005
Wong, K.-F., & Wang, X.-W. (2006). A recurrent network mech-
Journal
anism of
of Neuroscience, 26(4), 1314–1328. https://doi.org/10.1523/
JNEUROSCI.3733-05.2006
time integration in perceptual decisions.
Wu, G.-R., Liao, W., Stramaglia, S., Ding,
J.-R., Chen, H., &
Marinazzo, D. (2013). A blind deconvolution approach to re-
cover effective connectivity brain networks from resting state
fMRI data. Medical Image Analysis, 17(3), 365–374. https://doi.
org/10.1016/j.media.2013.01.003
Zhang, L., Opmeer, E. M., van der Meer, L., Aleman, A., ´Curˇci´c-
Blake, B., & Ruhé, H. G. (2018). Altered frontal-amygdala effec-
tive connectivity during effortful emotion regulation in bipolar
disorder. Bipolar Disorders, 20(4), 349–358. https://doi.org/10.
1111/bdi.12611
Zhao, Z., Wang, X., Fan, M., Yin, D., Sun, L., Jia, J., . . . Gong, J.
(2016). Altered effective connectivity of the primary motor cor-
tex in stroke: A resting-state fMRI study with Granger Causality
analysis. PloS One, 11(11), e0166210. https://doi.org/10.1371/
journal.pone.0166210
Zhuang, J., LaConte, S., Peltier, S., Zhang, K., & Hu, X. (2005).
Connectivity exploration with structural equation modeling:
An fMRI study of bimanual motor coordination. NeuroImage,
25(2), 462–470. https://doi.org/10.1016/j.neuroimage.2004.11.
007
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
/
t
e
d
u
n
e
n
a
r
t
i
c
e
-
p
d
l
f
/
/
/
/
3
4
1
0
0
9
1
8
6
6
8
0
3
n
e
n
_
a
_
0
0
0
9
9
p
d
t
/
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Network Neuroscience
1037