LINKING TEACHER QUALITY, STUDENT - Ricerca sull'intelligenza artificiale specializzata al MIT

LINKING TEACHER QUALITY, STUDENT

ATTENDANCE, AND STUDENT ACHIEVEMENT

Seth Gershenson

School of Public Affairs

American University
Washington, DC 20016-8070

gershens@american.edu

Astratto
Research on the effectiveness of educational inputs, particularly
research on teacher effectiveness, typically overlooks teachers’
potential impact on behavioral outcomes, such as student atten-
dance. Using longitudinal data on teachers and students in North
Carolina I estimate teacher effects on primary school student
absences in a value-added framework. The analysis yields two
main ﬁndings: Primo, teachers have arguably causal, statistically
signiﬁcant effects on student absences that persist over time. Sez-
ond, teachers who improve test scores do not necessarily improve
student attendance, suggesting that effective teaching is multidi-
mensional and teachers who are effective in one domain are not
necessarily effective in others.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

125

doi:10.1162/EDFP_a_00180
C(cid:2) 2016 Association for Education Finance and Policy

Teachers’ Effects on Student Absences

I N T R O D U C T I O N

1 .
Research on the technology of skill formation routinely ﬁnds evidence of a direct
causal relationship between character skills and long-run socioeconomic outcomes
(Heckman, Stixrud, and Urzua 2006; Cunha, Heckman, and Schennach 2010).1 For
esempio, character skills such as conscientiousness, motivation, and self discipline pre-
dict important socioeconomic outcomes such as educational attainment, employment,
earnings, marriage, and crime (per esempio., Jacob 2002; Borghans et al. 2008; Almlund et al.
2011; Lundberg 2012, 2013; Heckman and Kautz 2013; Jackson 2013). Attendance is an
objectively measurable behavior that is correlated with at least three of the “Big Five”
character skills identiﬁed by psychologists: Attendance is positively associated with con-
scientiousness (Duckworth et al. 2007) and negatively associated with neuroticism and
low levels of agreeableness (Lounsbury et al. 2004).2 Conscientiousness is a character
skill that is valued in the labor market (Heckman and Kautz 2013) and regular atten-
dance is highly valued by employers (Morrison et al. 2011; Lerman 2013; Pritchard 2013).
Allo stesso modo, regular school attendance is positively associated with academic achievement
(Gottfried 2009; Aucejo and Romano 2013; Gershenson, Jacknowitz, and Brannegan
2015) and negatively associated with grade retention (Nield and Balfanz 2006), drug
use (Hallfors et al. 2002), and dropping out of school (Rumberger and Thomas 2000).
Di conseguenza, identifying the educational inputs and interventions that improve stu-
dents’ attendance is likely of interest to both educators and policy makers. Most inter-
ventions, Tuttavia, are designed to increase cognitive skills, as measured by standard-
ized tests, and evaluated accordingly (Heckman 2000). This is despite the facts that
character skills are more malleable than cognitive skills (Cunha and Heckman 2008;
Heckman 2000) and such a focus on testing may cause teachers and schools to divert
resources away from nontested skills (Baker et al. 2010; Harris 2011). A similar critique
applies to the large literature on teacher effectiveness, despite widespread agreement
that teachers are the most important school-provided educational input (per esempio., Rivkin,
Hanushek, and Kain 2005; Clotfelter, Ladd, and Vigdor 2007; Goldhaber 2007; Harris
2011) and the fact that teachers likely affect students’ development in numerous areas
outside the reading and math skills measured by standardized tests (Ladd and Sorensen
2014).

The current study contributes to this gap in the literature by estimating teacher
effects on primary school students’ absences in a value-added (VA) framework. Questo
work complements research by Jackson (2013) on ninth-grade teachers’ effects on an
index of noncognitive skills, as at least some of the mechanisms through which teachers
affect primary school attendance likely differ from the ways that teachers affect sec-
ondary school attendance.3 Moreover, identifying the educational inputs that improve
the attendance of younger students is particularly important given that character skills
are shaped by children’s early environments (Heckman, Stixrod, and Urzua 2006),

1. Character skills encompass a variety of skills and behaviors that have previously been referred to as noncognitive
skills, noncognitive ability, soft skills, character traits, personality traits, and sociobehavioral skills, among other
names (Heckman and Kautz 2013).

2. The Big Five character skills are Openness, Conscientiousness, Extraversion, Agreeableness, and Neuroticism

(OCEAN) (Heckman and Kautz 2013, pag. 10–12).

3. Student absences, suspensions, grade promotion, and grade point average comprise the noncognitive index

used in Jackson (2013).

126

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Seth Gershenson

problems of chronic absence and school disengagement manifest as early as ﬁrst grade
(Alexander, Entwisle, and Kabbani 2001), and socioeconomic gaps in character skills
exist prior to kindergarten and grow over time (Duncan and Magnuson 2011). Improv-
ing the character skills and attendance habits of disadvantaged children will likely foster
socioeconomic mobility and social inclusion, and increase the returns to subsequent
educational attainment (Heckman and Kautz 2013). The mechanisms through which
teachers might affect primary school students’ attendance are discussed in section 2.

In addition to identifying what effect, if any, primary-school teachers have on stu-
dent absences, the current study also contributes to the literature on the validity of VA
estimates of teacher effectiveness more generally by addressing one of the central ques-
tions regarding VA articulated by Chetty, Friedman, and Rockoff (2014): Do high-VA
teachers improve student outcomes other than test scores? Estimating teachers’ effects
on an objective outcome such as student absences addresses the common criticism that
VA measures of teacher effectiveness focus too narrowly on students’ performance on
standardized tests. The focus on standardized tests is potentially problematic for several
reasons: It may cause teachers and schools to divert resources away from nontested
topics and skills (Baker et al. 2010; Harris 2011), it disregards Fenstermacher and
Richardson’s (2005) broad deﬁnition of quality teaching, and it potentially biases es-
timates of teacher quality by ignoring teachers’ effects on students’ character skills
and related behaviors (attendance, study habits, eccetera.) (Heckman 2000). Accordingly, IO
assess the importance of objectively evaluating teachers along multiple dimensions by
comparing rankings of teacher effectiveness based on teachers’ effects on test scores
to similar rankings based on teachers’ effects on student attendance. Signiﬁcant dif-
ferences between the two rankings would suggest that teacher evaluations based solely
on teachers’ abilities to improve student test scores miss an important dimension
of teacher quality, systematically misclassifying effective teachers as ineffective, E
vice versa. Estimates of teachers’ effects on student absences also provide objective
measures of effectiveness for teachers who do not teach in tested grades or subjects.

Speciﬁcally, I address two research aims. Primo, I estimate teachers’ effects on
student attendance by estimating VA models that consider student attendance as an
output of the education production function. Secondo, I estimate corresponding teacher
effects on academic achievement (cioè., test scores) and compare the resulting rankings
of teacher effectiveness to rankings based on teachers’ effects on student attendance.
Both sets of VA models are estimated using rich longitudinal administrative data on
both teachers and students from North Carolina. The main results generally suggest
that teachers signiﬁcantly affect student absences and that this relationship is arguably
causal. È interessante notare, teacher effectiveness is not stable across domains, as rank correla-
tions between teachers’ effects on test scores and teachers’ effects on student absences
are generally close to zero. Additional analyses show that these results are not speciﬁc
to North Carolina, teachers’ effects on student absences persist over time, and teachers’
effectiveness in reducing absences is positively correlated over time and with teaching
experience.

The paper proceeds as follows: Sezione 2 describes the mechanisms through which
teachers might affect student attendance and brieﬂy reviews the relevant literature on
teacher effectiveness. Sezione 3 describes the data and section 4 describes the identi-
ﬁcation strategy. Sezione 5 presents the main results and section 6 presents further

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

127

Teachers’ Effects on Student Absences

analyses of the intertemporal stability, persistence, and relationship with teaching ex-
perience of teachers’ effects on student absences. Sezione 7 examines the cross-domain
stability of teacher effectiveness by comparing rankings based on teachers’ effects on
student absences to rankings based on their effects on student achievement. Sezione 8
concludes.

2 . C O N C E P T U A L B A C K G R O U N D A N D P R E V I O U S L I T E R A T U R E
Chetty et al. (2011) found small transitory effects of kindergarten classrooms on cogni-
tive development (cioè., test scores) but signiﬁcant effects on long-run outcomes such
as earnings. One interpretation of these seemingly contradictory results is that teach-
ers affect long-run outcomes by building students’ noncognitive skills (Jackson 2013).
Infatti, Jackson (2013) develops a formal latent factor model in which both student
and teacher ability are two-dimensional (cioè., cognitive and noncognitive), and shows
that teachers who affect students’ noncognitive development but not cognitive develop-
ment can substantively affect students’ long-run outcomes. It is generally believed that
instruction can improve character skills and there is a long history of using observed
behaviors as proxies for character skills (Almlund et al. 2011; Heckman and Kautz
2013). Attendance is one such proxy, which is both objective and easily observable, Quello
previous researchers have utilized (per esempio., Jacob 2002; Jackson 2013).

Teachers potentially increase student attendance through some combination of fos-
tering a passion for learning, increasing student engagement, creating a strong sense
of community in the classroom, and stressing the importance of regular attendance
(Monk and Ibrahim 1984; Baker et al. 2010; Kelly 2012; Ladd and Sorensen 2014). Of
course, some of these mechanisms might be more relevant to older students whose
attendance is arguably less inﬂuenced by their parents. Another way that elementary
school teachers might affect young children’s attendance is by inﬂuencing parents’ and
other household adults’ attitudes toward children’s school attendance and punctuality,
as parental involvement is thought to be malleable.4 Teachers might do so early in the
school year at “back to school” nights or during parent–teacher conferences throughout
the year. Inoltre, anecdotal evidence from private conversations with primary school
teachers suggests that some teachers initiate contact with students’ parents in response
to frequent absences. Some schools even have formal policies regarding parental out-
reach in response to student absences. Per esempio, section 4400.4 of North Carolina’s
Newlin Elementary School’s 2013–14 Parent/Student Handbook states that the school
will initiate a student–parent conference after a student accumulates six unexcused
absences.5

Teachers likely vary in their inﬂuence on noncognitive behaviors, such as atten-
dance, for at least three reasons. Primo, some teachers may simply be better than others
at inﬂuencing students’ character skills and/or parental involvement. Secondo, teach-
ers’ attitudes toward the importance of teaching character skills relative to academic
skills may vary (Dombkowski 2001), resulting in differences across classrooms in time

4. Per esempio, 6 percent of respondents in a 2004 Gallup Poll listed “increasing parental involvement” as the

“best way to improve K–12 education in the United States (U.S.)" (Gallup 2004).

5. See www.abss.k12.nc.us/cms/lib02/NC01001905/Centricity/Domain/166/Newlin%20ElementaryHandbook

%2013–14.pdf (P. 17).

128

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Seth Gershenson

and effort allocations. Third, teachers may allocate effort based on their perceived
ability to inﬂuence students’ character skills, regardless of the importance they attach
to inﬂuencing such skills (Jennings and DiPrete 2010).

To date, Tuttavia, only four studies have empirically investigated the impact of
teachers on students’ character skills.6 First, Dobbie (2011) found that some of the
criteria used to determine admission into the Teach For America program are as-
sociated with improved classroom behavior but little evidence of an effect of the
Teach For America criteria on student absences. Secondo, Jennings and DiPrete (2010)
found that kindergarten and ﬁrst-grade teachers in the Early Childhood Longitudinal
Study—Kindergarten Cohort (ECLS-K) have sizable effects on a “social-behavioral in-
dex” that measures children’s approaches to learning, self-control, and interpersonal
skills. È interessante notare, the authors found that the teachers who had the largest effects
on children’s behavior did not always have large effects on children’s test scores, sug-
gesting that by focusing only on teachers’ effects on test scores, effective teachers may
be misclassiﬁed as ineffective, and vice versa. Third, Ladd and Sorensen (2014) inves-
tigated the relationship between North Carolina middle school teachers’ experience
and student absences, time spent reading for pleasure, time spent on homework, E
disruptive behavior in the classroom. The authors found signiﬁcant effects of teacher ex-
perience on student absences. Finalmente, using administrative data from North Carolina,
Jackson (2013) found that ninth-grade teachers have signiﬁcant effects on students’
noncognitive skills, as measured by an index of student absences, suspensions, grade
promotion, and grade point averages. Like Jennings and DiPrete, Jackson ﬁnds that
many of the teachers who most effectively develop students’ noncognitive skills have
only average effects on test scores, suggesting that focusing on test scores alone will fail
to identify some effective teachers. These ﬁndings are consistent with the robust result
in the VA literature that rankings of teacher effectiveness are not perfectly correlated
across academic subjects (per esempio., Koedel and Betts 2007; Lockwood et al. 2007; Loeb and
Candelaria 2012; Loeb, Kalogrides, and B´eteille 2012; Goldhaber, Cowan, and Walch
2013), though cross-subject rank correlations tend to be signiﬁcantly more stable than
the cross-domain rank correlations identiﬁed in the current study.

The general lack of attention paid to teachers’ impacts on students’ character skills
is therefore surprising, as identifying effective teachers is hugely important and there
is a growing consensus that providing high-quality teachers to all students must play
a prominent role in closing achievement gaps between students of different demo-
graphic and socioeconomic backgrounds (Rivkin, Hanushek, and Kain 2005; Har-
ris 2011). VA models that attempt to identify individual teachers’ contributions to
gains in student achievement are gaining popularity and acceptance as useful mea-
sures of teacher effectiveness, though such measures remain controversial (Baker
et al. 2010; Harris 2011; Chetty, Friedman, and Rockoff 2014). Speciﬁcally, critics
of VA measures of teacher effectiveness question whether policies that incentivize
schools and teachers to increase test scores displace beneﬁcial classroom activities

6. The Talent Development high school program is a notable intervention designed to improve student atten-
dance. Initially launched in ﬁve Philadelphia public high schools, the program increased student attendance
by 3 A 7 percent in the ﬁrst three treated cohorts (Kemple, Herlihy, and Smith 2005). The program provided
students with individualized support that, among other things, prioritized high attendance.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

129

Teachers’ Effects on Student Absences

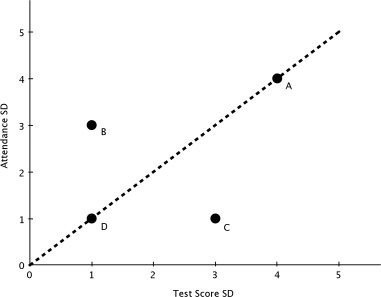
Figura 1. Two-Dimensional Model of Teacher Effectiveness.

that develop character skills and learning in nontested academic subjects. Inoltre
to identifying primary-school teachers’ effects on student attendance, the current study
also contributes to the general VA literature by speaking to the practical signiﬁcance of
this criticism.

I assess the practical importance of the criticism that VA models focus too narrowly
on students’ performance on standardized tests by comparing the stability of teacher
rankings of their effects on achievement gains to corresponding rankings based on
teachers’ effects on absences. If some teachers who excel at increasing test scores are
less able to promote attendance, and vice versa, policies that evaluate teachers on only
one dimension will necessarily misclassify a nontrivial subset of teachers. This idea
is formalized in ﬁgure 1, which assumes teacher quality is two-dimensional. Teacher
A is unambiguously the most effective teacher in ﬁgure 1, as teacher A exerts the
largest impact on students’ attendance and academic achievement. Note that if all two-
dimensional measures of teachers’ effectiveness were to fall on the dashed 45-degree
line then the dimension along which teachers are evaluated would not matter. Previous
research suggests this is not the case (Jennings and DiPrete 2010; Jackson 2013).

Now consider the effectiveness of teachers B, C, and D in ﬁgure 1. In the two-
dimensional setting, teacher D is unambiguously the least effective and has the small-
est impacts on both attendance and achievement. Nel frattempo, teacher B excels at
improving students’ attendance and teacher C excels at improving students’ academic
achievement. An accountability system that evaluated teachers solely based on their
ability to improve student test scores, Tuttavia, would mistakenly conclude that teacher
C is more effective than teachers B and D, who appear equally effective. By estimat-
ing teachers’ effects on both student absences and academic achievement, the current
study identiﬁes the ability of an important educational input (teachers) to affect an
important noncognitive behavior (attendance). More generally, the current study pro-
vides evidence on the extent to which teachers excel along multiple dimensions and
the general importance of evaluating teachers along multiple objective dimensions.

3 . D A T A
I estimate teachers’ effects on student absences using longitudinal administrative data
on the population of third through ﬁfth graders who attended North Carolina’s public

130

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Seth Gershenson

schools between the 2005–06 and 2009–10 school years. These student-level data
are maintained and provided by the North Carolina Education Research Data Center
(NCERDC).7 The NCERDC data contain administrative records on students’ race, gen-
der, poverty status, limited English proﬁciency status, whether the student had adminis-
tratively classiﬁed math or reading learning disabilities, total absences, student–teacher
links, and end-of-grade math and reading test scores.8 North Carolina’s end-of-grade
tests are state-mandated, criterion-referenced, vertically aligned, and are given to all
students in the spring of third, fourth, and ﬁfth grades. Third-grade and 2006 dati
are used as lags in value-added models and thus the analytic sample comprises fourth
and ﬁfth graders between 2007 E 2010. Students who either experienced a mid-year
classroom change; repeated third, fourth, or ﬁfth grade; or are missing achievement,
absence, or demographic data are excluded from the analysis. These exclusions result
in an analytic sample of 446,244 student-year observations, 27,943 unique classrooms,
E 13,391 unique teachers.

Tavolo 1 summarizes the variation in student absences and the composition of the
analytic sample. The average student was absent about six times per year and the
standard deviation (SD) of about 5.5 indicates that there is substantial variation across
student-years in the sample. I decompose the variation in student absences between
schools, school years, teachers, classrooms, and students by estimating corresponding
“within-unit” SD in absences by computing the SDs of the residuals of regressions of
student absences on sets of school, school-by-year, teacher, classroom, or student ﬁxed
effects. The within-school and within–school year SDs are quite similar to the overall
SD, indicating that most of the variation in student absences exists within, as opposed
to between, schools. The within-teacher and within-classroom SDs are slightly smaller,
though still constitute 95 A 97 percent of the variation in student absences. Again,
this indicates that within schools, most variation in student absences exists within, COME
opposed to between, classrooms. È interessante notare, the within-student SD is substantially
smaller, indicating about one third of the variation in student absences is due to
within-student changes in absence rates over time. Although this suggests absences
are somewhat “sticky,” there is signiﬁcant within-student variation in absences over
time that might be partially attributable to teachers.

I D E N T I F I C A T I O N S T R A T E G Y

4 .
Teacher effects on student absences are identiﬁed by estimating VA models of the
form:

Ai j g s t = α Ai,t−1 + βxit + γ c−i, j g s t + θ j + πg + ωs t + ui j g s t ,

(1)

where i, j, G, S, and t index students, teachers, grades, schools, and years, rispettivamente;
A is annual student absences, standardized by grade and year to facilitate comparisons
with the achievement results; x is a vector of observed student characteristics including

7. See www.childandfamilypolicy.duke.edu/research/nc-education-data-center for additional information. Vedere
Goldhaber (2007), Rothstein (2010), and Jackson (2013) for examples of other studies that have ﬁt VA models
to the NCERDC data.

8. Students were matched to teachers using administrative roster data (Course Membership ﬁle) that accurately
link students and teachers to courses. Such records exist for over 80 percent of students. Because absences
can be affected by multiple teachers, the sample is restricted to self-contained teachers who taught the student
both math and reading.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

131

Teachers’ Effects on Student Absences

Tavolo 1.

North Carolina Analytic Sample Summary Statistics

Variable

Absences

(within school)

(within school-year)

(within teacher)

(within classroom)

(within student)

Standardized (Mean 0, SD 1)

Absences

Math score

Reading score

Lagged standardized

Absences

Math score

Reading score

Fourth grade

Fifth grade

Child race/ethnicity

Non-Hispanic white

Non-Hispanic black

Hispanic

Other

Female

Below poverty level

Limited English proﬁciency

Math disability

Reading disability

School year

2006–07

2007–08

2008–09

2009–10

N (Teachers)

N (Classrooms)

N (Student years)

(5.52)
(5.44)
(5.40)
(5.34)
(5.22)
(1.75)

(0.96)
(0.97)
(0.97)

(0.96)
(0.96)
(0.95)

Mean

6.10

−0.02
0.09
0.07

−0.04
0.10
0.09
0.56
0.44

0.56
0.26
0.11
0.07
0.51
0.46
0.01
0.01
0.03

0.25
0.25
0.24
0.26

13,391

27,943

446,244

Notes: SD: standard deviation. Standardized absence and test score means
and SD are not precisely 0 E 1 because the standardization was per-
formed using all available absence and test score data.

race, genere, poverty status, special education, and English language proﬁciency; c is
a vector of classroom characteristics including class size, class composition, and the
average of student i’s classmates’ lagged absences and lagged achievement; θ , π , E
ω, are teacher, grade, and school-by-year ﬁxed effects (FE), rispettivamente; and u is an
idiosyncratic error term.9

9. Appendix table A.1 (available in a separate online appendix that can be accessed on Education Finance and
Policy’s Web site at www.mitpressjournals.org/efp) investigates the sensitivity of the main results to using
three alternative deﬁnitions of student absences: levels (unstandardized), natural logs, and indicators for
“chronically absent.” These results are consistent with the main results reported in table 2.

132

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Seth Gershenson

The school-by-year FE are central to the identiﬁcation strategy and imply that the
teacher effects in equation 1 are identiﬁed by comparing teachers who were in the same
school during the same academic year.10 Importantly, this controls for the sorting of
teachers across schools, nonparametric school time trends, and variation across both
schools and time in the length of academic calendars. The latter is important in the
current context because longer school calendars provide more opportunities to be ab-
sent. Inoltre, school-by-year FE control for school-level leadership and policy changes
that either directly inﬂuence student attendance or the way that student absences are
administratively recorded.

Ordinary least squares (OLS) is taken as the preferred estimator of equation 1 for
two reasons. Primo, Guarino, Reckase, and Wooldridge (2015) ﬁnd OLS to be the most
robust estimator to a variety of potential student–teacher assignment scenarios. Questo
is potentially important, as Rothstein (2010) ﬁnds evidence of nonrandom sorting in
North Carolina. Secondo, Chetty, Friedman, and Rockoff (2014) ﬁnd that most sorting
of students to teachers is based on lagged test scores and that conditioning on lagged
test scores alone yields estimated teacher effects with near-zero bias. Allo stesso modo, Kane
and Staiger (2008) ﬁnd that controlling for lagged test scores yields unbiased estimates
of teacher effects and controlling for average classroom characteristics (cioè., the vector
C) improves the precision of estimated teacher effects. I also consider an extension of
equation 1 that conditions on lagged test scores and lagged absences, which produces
qualitatively similar estimates.

Ancora, even after conditioning on observed student and classroom characteristics,
within school-year endogenous sorting of students to teachers remains a threat to
identiﬁcation. Accordingly, in testing for endogenous sorting based on observable
student characteristics, I follow Jackson (2013) and Chetty, Friedman, and Rockoff
(2014) by regressing predicted outcomes on estimated out-of-sample teacher effects
and school-by-year FE in the following linear regression model:

ˆyi j g s t = δ ˆθ j t + ωs t + ui j g s t .

(2)

The ˆθ in equation 2 are year-speciﬁc out-of-sample teacher effects estimated by
equation 1 using all non-t years of data. The ˆy in equation 2 are ﬁtted values from
OLS regressions of actual student absences, math scores, and reading scores on their
lagged values and observed student characteristics. Intuitively, a signiﬁcant correlation
between teacher effectiveness and predicted student outcomes is suggestive of endoge-
nous sorting. The estimated sign of δ speaks to the type of sorting (per esempio., a positive δ
means that on average high-performing students are assigned to more effective teach-
ers). The results of these tests, presented in section 5, provide no evidence that OLS
estimates of equation 1 are biased by endogenous sorting based on observables.

10. Some policy makers may wish to compare teachers within or between schools, Tuttavia, and different spec-
iﬁcations can produce different rankings (per esempio., Goldhaber and Theobald 2012). Table A.2 (available on the
Education Finance and Policy Web site) examines the sensitivity of the main results reported in table 2 by
replacing the school-by-year FE with school FE or removing them altogether. Identiﬁcation in the former is
driven by teachers who changed schools during the sample time period. The latter provide state-wide teacher
comparisons. Both sets of estimates show qualitatively similar patterns to those generated by the preferred
baseline speciﬁcation of equation 1.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

133

Teachers’ Effects on Student Absences

Prossimo, I quantify the magnitude and variation in estimated teacher effects by test-
ing their joint signiﬁcance, estimating the SD of the teacher effect estimates, e da
comparing estimated teacher effects at different points in the distribution (per esempio., 25th
versus 75th percentiles). I estimate SD of the estimated teacher effects by following
the two-step procedure outlined in Jackson (2013, P. 14), which follows from Kane and
Staiger (2008). Primo, I compute classroom-level average residuals from estimates of
equation 1 that leave the teacher effects in the model’s error term. Secondo, I compute
the covariance between each classroom’s average residual and that from a randomly-
chosen classroom taught by the same teacher in a different year. To avoid potentially
compromising effects of outliers, I repeat step two 50 times and report the median esti-
mated SD (Jackson 2013). This approach is preferred to estimating the SD of estimated
teacher FE because it eliminates variation due to both sampling error and unobserved
classroom shocks that are not associated with teacher effectiveness.

To facilitate comparisons of the magnitude and distribution of estimated teacher
effects on student absences to those on academic achievement, I estimate traditional
VA model analogs to equation 1 that replace A with math and reading test scores. Tutto
test scores are standardized by grade, year, and subject to have mean zero and SD
of one (Ballou 2009). The achievement VA models also condition on current student
absences, which raises a potentially interesting modeling question, though in practice
models that do and do not control for current student absences produce nearly identical
results.11 In section 7, these estimates are used to examine the cross-domain stability
of VA measures of teacher effectiveness by comparing VA-based rankings of teachers’
effects on student absences to analogous rankings of teachers’ effects on academic
achievement.

5 . M A I N R E S U L T S
Teacher Effects on Student Absences
Tavolo 2 summarizes estimates of equation 1 for fourth and ﬁfth graders’ absences, math
achievement, and reading achievement. The baseline estimates of teachers’ effects on
student absences reported in column 1 are strongly jointly signiﬁcant and exhibit
signiﬁcant variation across teachers: the Kane and Staiger (2008) consistent estimate
of the SD of teacher effects on absences is 0.07 of an absence SD. The difference
between the effect of a 90th percentile teacher and a 10th percentile teacher is about
90 percent of an absence SD, and the difference between teachers at the ﬁrst and third
quartiles is about 40 percent of an absence SD. Column 2 shows that the preferred
baseline results reported in column 1 are robust to controlling for lagged test scores.

11. Speciﬁcally, because absences are at least partly outside of teachers’ control, it is unclear whether absences
should be controlled for in VA models designed to identify teachers’ effects on academic achievement (Noell
et al. 2008; Harris 2011). On the one hand, at least some student absences are completely outside teachers’
control and these absences should unambiguously be controlled for (Harris 2011). D'altra parte, absences
caused by teachers are outcomes of the education production function and are thus “bad controls” (per esempio., Angrist
and Pischke 2009, P. 64). In practice, the precise number of absences caused by teachers is unknown and
analysts are left with two suboptimal options: either omit student absences from the VA model and suffer
from potential omitted variables bias or control for student absences at the risk of “over controlling” and
penalizing teachers who improve test scores via improving student attendance. Appendix table A.3 (available
on the Education Finance and Policy Web site) shows that this is a practically unimportant modeling decision,
as rankings of teacher effectiveness generated by VA models that do condition on student absences are nearly
identical to rankings generated by VA models that do not condition on student absences.

134

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
e
D
P
UN
R
T
io
C
e
–
P
D

F
/

1
1
2
1
2
5
1
6
9
0
1
9
0
e
D
P
_
UN
_
0
0
1
8
0
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Seth Gershenson

Tavolo 2.

Baseline Teacher Effect Estimates

Outcome

Lagged absences

Lagged math

Lagged reading

Current absences

Controls

Teacher FE

Sch-by-yr FE
Adj. R2

Teacher FE

Joint sig. (F statistic)

Mean

SD of FE

SD (K-S)
90th – 10th percentile
75th – 25th percentile

Absences

Math

Reading

0.580
(0.003)∗∗∗

Yes

Yes
0.38

1.33∗∗∗
0.01
0.48
0.07
−0.91∗∗∗
−0.39∗∗∗

0.577
(0.003)∗∗∗
−0.041
(0.002)∗∗∗
0.011
(0.002)∗∗∗

Yes

Yes
0.38

1.33∗∗∗
0.01
0.48
0.07
−0.91∗∗∗
−0.40∗∗∗

0.780
(0.001)∗∗∗

−0.007
(0.000)∗∗∗
Yes

Yes

Yes
0.73

4.04∗∗∗

−0.02
0.41
0.13
0.90∗∗∗
0.43∗∗∗

0.758
(0.002)∗∗∗
−0.004
(0.000)∗∗∗
Yes

Yes

Yes
0.68

1.78∗∗∗

−0.01
0.41
0.07
0.84∗∗∗
0.38∗∗∗

Sorting test (N = 380,670)

Predicted Absences

Predicted Math

Predicted Reading

ˆθ (Eq. 2)

0.002
(0.002)

0.002
(0.005)

Notes: N = 446,244 student-year observations taught by 13,391 unique teachers. Standard errors are
clustered by school. Controls include indicators of child’s race/ethnicity, poverty status, limited English
proﬁciency, administratively classiﬁed learning disability, year indicators, and classroom characteristics
including class size, lagged peer achievement and absences, percent of classroom eligible for free or
reduced price lunch, and classroom racial composition. Absences and test scores are standardized by
subject, grade, and year to have mean zero and standard deviation (SD) one. K-S refers to Kane and
Staiger’s (2008) method for computing consistent estimates of the SD of estimated teacher effects.
The sorting test is described by equation 2 in the text.
∗∗∗p < 0.01. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d / f . Columns 3 and 4 of table 2 report estimates for math and reading achievement, respectively. The estimated coefﬁcients on student absences are negative, statistically signiﬁcant, and similar in magnitude to estimates reported in the existing literature (e.g., Gottfried 2009; Aucejo and Romano 2013; Gershenson, Jacknowitz, and Bran- negan 2015). Consistent with prior research on teacher effectiveness, the results re- ported in columns 3 and 4 of table 2 suggest that teachers have greater inﬂuence on students’ math achievement than on reading achievement (e.g., Rockoff 2004; Kane and Staiger 2008; Hanushek and Rivkin 2010; Jackson 2013). Moreover, the estimated SD of teacher effects on math and reading are similar in magnitude to those found in previous studies of primary school teachers in North Carolina (e.g., Rothstein 2010) and across the United States (Hanushek and Rivkin 2010). Interestingly, the estimated SD of teacher effects on student absences reported in columns 1 and 2 of table 2 are similar in magnitude to those of teacher effects on both math and reading achievement. Indeed, they are identical to those for reading. Taken together, the results reported in table 2 suggest that the total variation in teachers’ effects on student absences is similar to that in teachers’ effects on academic achievement. f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 135 Teachers’ Effects on Student Absences The bottom panel of table 2 provides evidence that the estimated teacher effects are not biased by endogenous sorting of students to teachers based on observable characteristics. Speciﬁcally, none of the estimated coefﬁcients on the out-of-sample estimates of teacher quality (δ in equation 2) are signiﬁcantly different from zero at traditional conﬁdence levels. Moreover, the estimated coefﬁcients and corresponding standard errors are relatively small in magnitude. This is reassuring and suggests that the teacher effect estimates from equation 1 are causal. External Validity of Main Results The generalizability of any state-level analysis is a concern, even in as diverse a state as North Carolina. Accordingly, I augment the main results presented above with similar analyses of the nationally representative ECLS-K. The ECLS-K is a longitudinal data set collected by the National Center for Education Statistics (NCES). The original sample of approximately 22,000 children from about 1,000 kindergarten programs was designed to be nationally representative of kindergartners during the 1998–99 academic year. Subsequent analyses of the ECLS-K data are conducted using sampling weights provided by NCES that adjust for the oversampling of certain demographic groups.12 Importantly, the ECLS-K administered age-appropriate math and reading assessments each spring and asked school administrators to report each student’s total annual absences. The ECLS-K surveyed children, parents, teachers, and school administrators during the fall and spring of kindergarten and the spring of ﬁrst, third, and ﬁfth grades. As a result, VA models similar to equation 1 can only be estimated for ﬁrst-grade students conditional on kindergarten absences. Like in the North Carolina analysis, students who experienced a mid-year classroom change, repeated kindergarten or ﬁrst grade, or are missing test-score or demographic data, are excluded from the analysis. The analytic sample is also restricted to classrooms in which at least ﬁve students were sampled by the ECLS-K, so that there are a reasonable number of data points with which to estimate classroom effects. These exclusions yield an analytic sample of 2,350 student- year observations.13 The reference to classrooms and not teachers is intentional, as the ECLS-K followed one cohort of students and observes each teacher in only one year. Speciﬁcally, the ECLS-K analog to equation 1 is Ai j g s t = α Ai,t−1 + βxit + λ j g s t + ui j g s t , (3) where λ is a classroom FE. Importantly, the classroom effects in equation 3 can neither be interpreted as, nor decomposed into, teacher effects. For example, the classroom FE speciﬁcation of equation 3 cannot distinguish teacher effects from class size effects, as the classroom effects are treated as ﬁxed rather than random and classrooms are nested within teachers. As a result, the ECLS-K results cannot be directly compared to the analyses of North Carolina teacher effects discussed earlier. Given that the ECLS-K follows one cohort of students over time, a teacher FE speciﬁcation equivalent to equa- tion 1 cannot be estimated using the ECLS-K data because each teacher is only observed 12. Speciﬁcally, I use the C#CW0 longitudinal weight, where # is wave number. 13. Reported ECLS-K sample sizes are rounded to the nearest 50. See Gershenson, Jacknowitz, and Brannegan (2015) for further discussion of the ECLS-K’s student assessments and absence data. 136 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d . / f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Seth Gershenson Table 3. Classroom Effect Estimates in North Carolina and the ECLS-K Outcome Absences Math Reading Lagged absences Lagged math Lagged reading Current absences Controls Classroom FE North Carolina Joint sig. (F stat) Mean SD of FE 90th – 10th percentile 75th – 25th percentile ECLS-K Joint sig. (F) Mean SD of FE 90th – 10th percentile 75th – 25th percentile 1 Yes No No No Yes Yes 1.68∗∗∗ 0.01 0.33 −0.62∗∗∗ −0.31∗∗∗ 76.6∗∗∗ 0.0003 0.39 −0.53∗∗∗ −0.27∗∗∗ 2 Yes Yes Yes No Yes Yes 1.68∗∗∗ 0.01 0.33 −0.62∗∗∗ −0.31∗∗∗ 97.5∗∗∗ 0.001 0.39 −0.53∗∗∗ −0.27∗∗∗ 3 No Yes No Yes Yes Yes 4.16∗∗∗ −0.01 0.28 0.68∗∗∗ 0.35∗∗∗ 80.9∗∗∗ 0.22 0.28 0.69∗∗∗ 0.38∗∗∗ 4 No No Yes Yes Yes Yes 1.98∗∗∗ −0.01 0.23 0.52∗∗∗ 0.27∗∗∗ 209.8∗∗∗ 0.08 0.27 0.66∗∗∗ 0.34∗∗∗ Notes: The North Carolina sample contains 446,244 student-year observations and 27,943 classrooms. The ECLS-K sample contains 2,350 ﬁrst grade students and 300 classrooms (sample sizes rounded to nearest 50). Standard errors are clustered by school. Student con- trols include indicators of mother’s educational attainment, child’s race/ethnicity, poverty status, English spoken at home, and special education designation. Absences and test scores are standardized by subject, grade, and year to have mean zero and standard deviation (SD) one. The four classroom-FE speciﬁcations reported here correspond to the four teacher-FE speciﬁcations reported in table 2. ∗∗∗p < 0.01. in one academic year. Similarly, the school, grade, and year FE commonly included in VA models (e.g., equation 1) are subsumed by the classroom FE in equation 3. Nonetheless, equation 3 can be estimated using both the North Carolina and ECLS-K data. The generalizability of the main results can then be inferred by comparing esti- mates of equation 3 using the North Carolina data to estimates of equation 3 using the ECLS-K data. Table 3 summarizes the variation in estimated classroom effects in both data sets. The similarities across data sets are striking. For example, the differences between classroom effects at the 25th and 75th percentiles are about one third of a standard deviation for each outcome in each data set. Together, the results reported in table 3 suggest that the analysis of North Carolina teachers is at least somewhat representative of public primary school teachers in the United States. 6 . F U R T H E R A N A L Y S E S O F T E A C H E R S ’ E F F E C T S O N S T U D E N T A B S E N C E S Having shown that the main results are arguably internally and externally valid, this section provides three additional pieces of evidence regarding the internal validity of the ﬁnding that teachers affect student absences. Speciﬁcally, this section investigates l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d . f / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 137 Teachers’ Effects on Student Absences Table 4. Intertemporal Stability of Teacher Effect Estimates Outcome Absences Math Reading N (teachers) Two-year teacher effects 2007–08 to 2009–10 0.13∗∗∗ 0.45∗∗∗ 0.23∗∗∗ 2,250 Classroom effects 2007 to 2008 2008 to 2009 2009 to 2010 Weighted average 0.05∗∗∗ 0.09∗∗∗ 0.10∗∗∗ 0.08∗∗∗ 0.43∗∗∗ 0.39∗∗∗ 0.39∗∗∗ 0.40∗∗∗ 0.23∗∗∗ 0.24∗∗∗ 0.22∗∗∗ 0.23∗∗∗ 4,557 4,439 4,571 . Notes: Spearman rank correlations are reported. Two-year teacher effects are estimated by splitting the data in two two-year samples and estimating equation 1 twice: once using 2006–07 and 2007–08 data and once using 2008–09 and 2009–10 data. Year-speciﬁc classroom effects come from estimating equation 3 separately for each school year between 2006 and 07 and 2009–10. The absence, math, and reading estimates are based on the preferred speciﬁcations reported in columns 1, 3, and 4 of tables 2 and 3. ∗∗∗p < 0.01. the extent to which individual teachers’ effects on student absences are stable over time, the persistence of grade g teachers’ effects on student absences in grade g+1, and whether the ability to improve student attendance evolves over teachers’ careers. In doing so, the results presented in this section shed some light on the mechanisms through which teachers affect students’ attendance. Taken as a whole, these results lend additional empirical support to the general ﬁnding that teachers modestly affect student attendance. Intertemporal Stability of Estimated Teacher Effects on Student Absences If the teacher effects discussed in section 5 merely reﬂect noise or the composition of teachers’ classrooms in speciﬁc years, then the intertemporal stability of teachers’ contemporaneous effects on student absences would be indistinguishable from zero. Alternatively, if there is a stable component in teachers’ ability to inﬂuence student absences, teacher rankings should be positively correlated across years. Accordingly, table 4 reports two types of intertemporal Spearman rank correlations of teachers’ effects on student absences, math achievement, and reading achievement. The top panel of table 4 compares teacher rankings generated by data from the 2006–07 and 2007–08 school years to teacher rankings generated by data from the 2008–09 and 2009–10 school years. These teacher effects were generated by estimating equation 1 separately for each of the two two-year time periods for teachers for whom data are avail- able for all four years. The bottom panel of table 4 compares classroom rankings across each pair of contiguous years and the weighted average of these three correlations. These classroom effects were generated by estimating equation 3 separately for each year and comparing the resulting rankings for teachers who taught in two consecutive years. Both panels of table 4 provide evidence that is consistent with signiﬁcant teacher effects on student absences, as the intertemporal rank correlations are about one tenth of a SD and are strongly statistically signiﬁcant. Nonetheless, the intertemporal rank correlations in teachers’ effects on student absences are only about one fourth to one half the size of the intertemporal rank correlations in teachers’ effects on test scores. 138 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d . f / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Seth Gershenson Table 5. One-Year Persistence of Fourth-Grade Teacher Effects Outcome OLS Long Run (LR) Persistence (P) Classroom FE Controls Absences 1 0.59 (0.005)∗∗∗ 0.88 (0.005)∗∗∗ 0.51 (0.25)∗∗ Yes Yes Math 2 0.78 (0.002)∗∗∗ 0.98 (0.003)∗∗∗ 0.35 (0.06)∗∗∗ Yes Yes Reading 3 0.75 (0.002)∗∗∗ 0.98 (0.003)∗∗∗ 0.48 (0.09)∗∗∗ Yes Yes Notes: N = 101,679 ﬁfth-grade students for whom twice-lagged test scores and absences and once-lagged out-of-sample estimated teacher quality are observed. Each cell represents the estimated coefﬁcient on the lagged dependent variable in equation 3 from a separate regression, as described in Jacob et al. (2010). Standard errors are clustered by classroom (Jacob et al. 2010). Controls include indicators of child’s race/ethnicity, poverty status, limited English proﬁciency, and administratively classiﬁed learning disabilities. Absences and test scores are standardized by subject, grade, and year to have mean zero and standard deviation one. ∗∗p < 0.05; ∗∗∗p < 0.01. This could be because estimated effects on student absences are noisier or because teachers’ abilities to affect student absences are more limited and context-dependent than their abilities to affect test scores. Finally, estimates of the intertemporal stability of teachers’ effects on test scores are consistent with those in the existing literature (e.g., McCaffrey et al. 2009; Loeb and Candelaria 2012; Goldhaber and Hansen 2013). Persistence of Teachers’ Effects on Student Absences The mechanisms through which teachers can affect student absences, discussed in section 2, suggest that teachers’ effects on student attendance should persist in subse- quent school years. For example, a teacher who instills a love of learning in students or who successfully motivates parents to facilitate regular attendance will likely affect students’ current and future attendance. To test whether this is the case, I use the method proposed by Jacob, Lefgren, and Sims (2010) to estimate the average persis- tence of fourth grade teachers’ effects on students’ ﬁfth-grade outcomes. Speciﬁcally, Jacob, Lefgren, and Sims (2010) show that the OLS estimate of α in equation 3 can be interpreted as the persistence of observed outcome y (αOLS), and the instrumental variables (IV) estimate of α that instruments for yi,t−1 with yi,t−2 can be interpreted as the persistence of the long-run (LR) component of y (αLR). Finally, the authors show that the IV estimate of α that instead instruments for yi,t−1 with ˆθi,t−1, as deﬁned in equation 2, can be interpreted as the fraction of variation in the LR component of y attributable to teachers. Accordingly, the third estimate of α represents the average persistence of teacher effects (αP). Table 5 reports each of these three estimates of α for absences, math achievement, and reading achievement. Estimates of αOLS and αLR are slightly smaller for absences than for math and reading achievement, suggesting that absences are less persistent over time than academic skills. This is consistent with the general result that noncog- nitive skills are more malleable than cognitive skills (e.g., Heckman 2000; Cunha and l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d . / f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 139 Teachers’ Effects on Student Absences Heckman 2008). It is also reassuring that the estimates of αOLS and αLR for math and reading reported in table 5 are similar to the corresponding estimates reported by Jacob, Lefgren, and Sims (2010). Interestingly, the estimate of αP for absences is larger than the corresponding estimates for math and reading achievement, though the absence estimate is less precisely estimated. Still, the null hypothesis of zero persistence in teachers’ effects on absences can be rejected with 5 percent conﬁdence. This suggests that teachers’ effects on student absences are at least as persistent as teachers’ effects on academic achievement, despite less intertemporal persistence in the LR compo- nent of students’ absences than in the LR components of math and reading ability. Speciﬁcally, the point estimate of 0.51 reported in column 1 of table 5 suggests that about half the variation in fourth-grade student absences attributable to fourth-grade teachers persists in ﬁfth grade. Again, this result is consistent with the general ﬁnding that teachers affect student attendance. Does Teaching Experience Affect Student Absences? Finally, if teachers do affect student attendance, it stands to reason that their ability to do so improves with teaching experience (Ladd and Sorensen 2014). For example, more experienced teachers might converse with parents and teach character skills more effectively than their less-experienced counterparts. Evidence of an “experience gradient” in teachers’ effects on student attendance would lend additional empirical support to the claim that teachers affect student attendance. Accordingly, I estimate the effect of teachers’ experience on student absences using the nonparametric speciﬁ- cation and estimation framework advocated by Wiswall (2013). Speciﬁcally, the returns to teaching experience are estimated in a two-step procedure. First, the classroom ﬁxed effects in equation 3 are estimated (ˆλ) and saved for use in step 2. Second, the (ˆλ) are regressed on teacher experience (exper); teacher, grade, and year FE; and the vector of classroom characteristics from equation 1. Following Wiswall (2013), I model teach- ers’ experience as a set of K = 36 binary indicators for each experience level from 1 to 35 plus a category for 36+ years of experience, where new teachers with zero experience constitute the omitted reference category. Formally, ˆλi j g s t = K(cid:2) k=1 ϕk1{exper j t = k} + γ c−i, j g s t + θ j + πg + δt + ui j g s t , (4) where 1{·} is the indicator function.14 The thirty-six estimated ϕ parameters for each outcome (i.e., absences, math achievement, and reading achievement) are plotted in ﬁgure 2. For math, the non- parametric estimates suggest that returns to experience continue to accrue over the ﬁrst twenty years of teaching, which are consistent with the ﬁndings of Wiswall (2013). The relationship between teaching experience and students’ reading achievement fol- lows a similar pattern but the effects are only about half as large as those for math achievement. Again, this is consistent with previous research on the returns to teach- ing experience (e.g., Clotfelter, Ladd, and Vigdor 2007; Kane, Rockoff, and Staiger 2008; Ladd and Sorensen 2014) and with results presented earlier in this article that 14. School FE are omitted from equation 4 because relatively few teachers in the analytic sample changed schools. 140 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d f / . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Seth Gershenson Notes: This ﬁgure reports nonparametric estimates of the effect of teaching experience on three outcomes: student absences, math achievement, and reading achievement. Each outcome is standardized to have mean zero and standard deviation one. New teachers with zero years of experience constitute the omitted category, so each coefﬁcient compares the returns to a given level of experience to a new teacher. Teachers with more than 35 years of experience are grouped together in the ﬁnal category. Estimates were generated by the two-stage estimation strategy described in the text and follow from Wiswall (2013). All models control for lagged student outcomes, student characteristics, classroom characteristics, and teacher, grade, and year ﬁxed effects. Models were estimated using the subset of NCERDC data for which teacher experience data were available. N = 295,305 student years and 9,064 unique teachers. Figure 2. Nonparametric Estimates of Returns to Teaching Experience. suggest that teacher effects on reading achievement are about half as large as those on math achievement (e.g., table 2). The estimated relationship between teaching experience and student absences mir- rors that between teaching experience and reading achievement, suggesting that more experienced teachers are modestly more effective at reducing student absences. For example, on average, students assigned to teachers who have twenty years of teach- ing experience have about 20 percent of a SD fewer absences than similar students assigned to new teachers. Generally, these effects are smaller in magnitude than the effects of middle school math and English teachers on middle school student absences in North Carolina found by Ladd and Sorensen (2014). For example, the authors ﬁnd that teachers who have twenty years of experience decrease student absences by about 60 percent of a student-absence SD. This difference could result from middle school students having relatively more agency over their absences than primary school stu- dents. Still, that the effects of primary school teachers’ teaching experience on student absences shown in ﬁgure 2 are similar in magnitude to those on reading achievement is again consistent with the main results presented in table 2 and suggestive of a causal relationship between teacher effectiveness and student attendance. 7 . C R O S S - D O M A I N S T A B I L I T Y O F E S T I M A T E D T E A C H E R E F F E C T S I now compare the estimated teacher effects on student absences to those on aca- demic achievement to examine the stability of teacher effectiveness across cognitive and noncognitive domains. I do so by comparing rankings of teacher and classroom effectiveness based on the teacher and classroom effects generated by equations 1 and 3. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d / f . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 141 Teachers’ Effects on Student Absences Table 6. Cross-Domain Stability of Estimated Teacher and Classroom Rankings Spearman Corr. Coeff. Both Above 90th Percentile Both Above 75th Percentile North Carolina Teacher Rankings Absence-Math Absence-Reading −0.04∗∗∗ −0.02∗ Math-Reading 0.34∗∗∗ North Carolina Classroom Rankings 0.06∗∗∗ 0.05∗∗∗ 0.46∗∗∗ Absence-Reading Absence-Math Math-Reading ECLS-K Classroom Rankings Absence-Math Absence-Reading Math-Reading −0.07 0.10∗ 0.37∗∗∗ 1.7% 1.8% 3.5% 1.3% 1.3% 3.1% 1.0% 2.0% 2.6% 6.5% 7.2% 11.3% 6.7% 6.7% 11.8% 5.6% 8.5% 11.8% Both Above Mean 25.5% 24.7% 30.4% 27.9% 28.0% 33.9% 24.8% 28.1% 31.7% Both Above Median Both Below 25th Percentile Both Below 10th Percentile 24.9% 25.1% 31.0% 26.1% 25.9% 33.2% 22.9% 27.5% 30.1% 6.6% 7.1% 10.9% 7.1% 7.3% 12.0% 4.6% 5.9% 9.8% 1.1% 1.6% 2.9% 1.4% 1.7% 3.4% 0.7% 1.3% 2.6% Notes: The North Carolina sample contains 446,244 student-year observations and 27,943 classrooms. The ECLS-K sample contains 2,350 ﬁrst grade students and 300 classrooms (sample sizes rounded to nearest 50). Teacher rankings are based on the teacher effects estimated in columns 1, 3, and 4 of table 2. Classroom rankings are based on the classroom effects reported in columns 1, 3, and 4 of table 3. Absence-subject and math-reading refer to cross-domain and cross-subject stability, respectively. ∗p < 0.1; ∗∗∗p < 0.01. Comparisons are made between rankings rather than between point estimates because VA models frequently produce reliable rankings of teacher effectiveness even when the point estimates are inconsistent (Guarino et al. 2014) and rankings are arguably more policy relevant than point estimates. Speciﬁcally, rankings are compared across domains in three ways. First, I compute Spearman rank correlations. Second, I com- pute the percentage of teachers who are above average in both rankings, and similarly for various quantiles of interest. Finally, more nuanced transition matrixes are reported in Appendix table A.4 (available on the Education Finance and Policy Web site). The ﬁrst panel of table 6 summarizes these relationships for teachers. Spearman rank correlations between the absence and academic achievement rankings are close to zero and actually negative, suggesting that teachers who excel in one domain do not necessarily excel along others. This is further evidenced by the fact that relatively few teachers are above or below speciﬁc thresholds in both rankings. For example, only about 1 to 2 percent of teachers are in the top (bottom) decile, 7 percent are in the top (bottom) quartile, and 25 percent are in the top (bottom) half of both the absence and academic rankings.15 There is noticeably more stability between the math and reading 15. These numbers can be converted into the percentage of eligible teachers by dividing by the quantile’s range. For example, 17 percent (1.7/10) of teachers in the top decile of the absence ranking are in the top decile of the math ranking. It is also worth noting that table A.4 in the online appendix (available on the Education Finance and Policy Web site) reports transition matrixes that provide a more nuanced view of the cross-domain and cross-subject stability of teacher rankings, as correlations can mask large swings in rankings (Goldhaber and Theobald 2012). Again, rankings are less stable across domains than across subjects. For example, only about 22 percent of teachers in the top (bottom) ﬁfth of the math rankings are also in the top (bottom) ﬁfth of the absence rankings. The cross-subject transition matrixes are consistent with previous research that ﬁnds about 40 percent of the lowest (highest) performing teachers in math are similarly low (high) performing in reading (e.g., Loeb, Kalogrides, and B´eteille 2012). 142 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d f . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Seth Gershenson rankings. It is reassuring that the cross-subject correlation of 0.34 ﬁts comfortably within the range of previous estimates (e.g., Loeb and Candelaria 2012; Goldhaber, Cowan, and Walch 2013). The second and third panels of table 6 compare the cross-domain and cross-subject stability of estimated classroom effects using the NCERDC and ECLS-K data sets, respectively. Once again, the North Carolina and ECLS-K analyses yield remarkably similar results, suggesting that the North Carolina results generalize to the U.S. pop- ulation. The cross-domain rank correlations are close to zero in both data sets and the cross-subject rank correlations are about 0.4. Taken together, the results presented in table 6 suggest that teachers who are (in)effective in one domain are not necessarily (in)effective in others. This result is consistent with research by Jackson (2013) and Jennings and DiPrete (2010) and suggests that narrowly focusing on test scores will potentially misclassify teachers who improve students’ character skills, such as regular attendance, as ineffective. 8 . D I S C U S S I O N This paper uses longitudinal administrative data on teachers and students in North Carolina to estimate teacher effects on both student absences and academic achieve- ment. The analyses yield two novel ﬁndings, which are generally consistent with similar analyses of the nationally representative ECLS-K and robust to a variety of VA model speciﬁcations. First, teachers have statistically signiﬁcant effects on student absences, which are not biased by endogenous sorting of students to teachers based on observable student characteristics, and are similar in magnitude to teachers’ effects on reading test scores. Second, there is essentially zero correlation between rankings of teacher effects on absences and rankings of teacher effects on academic achievement, which suggests that there are multiple dimensions of effective teaching, and teachers who excel along one dimension do not necessarily excel along others. These ﬁndings are generally consistent with previous studies of teachers’ ability to affect noncognitive and sociobehavioral skills in other contexts (Jennings and DiPrete 2010; Jackson 2013). Three additional results lend additional support to the ﬁnding that teachers affect student absences. First, teachers’ contemporaneous effects on student absences are positively correlated over time, suggesting that there is a permanent component to teachers’ effects on student absences over and above transitory components associ- ated with a particular classroom. Second, teachers’ effects on student absences persist into the following academic year, suggesting that teachers affect students’ (or par- ents’) attitudes and preferences, rather than simply providing short-run incentives to attend class. Third, more experienced teachers tend to have larger effects on student attendance. This could either be because learning to alter student behaviors, such as attendance, takes time or because new teachers initially choose to focus on improving their academic instructional skills. It would be useful for future research to investigate the underlying sources of the experience gradient in teachers’ effects on character skills. Similarly, future research might extend the analyses conducted in section 6 to other contexts and investigate how teachers affect other types of character skills and related student outcomes. The results presented in this article contribute to two distinct literatures in the eco- nomics of education, as well as to our understanding of the educational process more l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d f / . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 143 Teachers’ Effects on Student Absences generally. First, the ﬁnding that teachers affect primary school students’ attendance furthers our understanding of the education production function and the educational inputs that develop character skills. Based on existing estimates of student absences’ effects on test scores (e.g., Aucejo and Romano 2013; Gershenson, Jacknowitz, and Brannegan 2015), the decrease in student absences attributable to a one SD improve- ment in teacher effectiveness (i.e., 0.07 absence SD, or about 0.4 student absences) translates into relatively small achievement gains comparable to about 3 percent of the test-score gains attributable to a one SD improvement in teacher effectiveness (as measured by effects on test scores). Nonetheless, student absences, particularly in primary school, are important over and above their direct impact on test scores for several reasons. Children form habits and undergo substantial developmental changes during these formative years, which is important given that high school absences predict negative long-run outcomes such as grade retention (Nield and Balfanz 2006), drug use (Hallfors et al. 2002), and dropping out of school (Rumberger and Thomas 2000) and the longer-term importance of regular attendance in the labor market (Heckman and Kautz 2013). Indeed, improving attendance habits could be one mechanism through which primary school teachers affect long-run socioeconomic outcomes. Moreover, there are positive externalities, or peer effects, of individual students’ attendance and school engagement on the academic achievement of their classmates (Gottfried 2011). It could also be the case that student absences inﬂuence peers’ attendance habits. Finally, from a practical standpoint, the ﬁnding that teachers affect student attendance is likely to be of direct interest to school principals and administrators seeking to improve the academic performance and school engagement of disadvantaged and chronically absent students. Information on the teachers who most effectively improve student attendance might be used either to identify the classroom characteristics and teaching strategies that contribute to improvements in student attendance or to strategically assign students to teachers. Similarly, the ﬁnding that teachers can and do affect student attendance might be used in pre-service and professional-development training to motivate the importance and ability of teachers to inﬂuence students’ socioemotional behaviors. Second, the current study also contributes to the general literature on the use and estimation of VA models of teacher effectiveness. The small and sometimes negative correlation between rankings of teacher effectiveness across domains (absences versus academic achievement) suggests the importance of evaluating teachers along multiple objective dimensions. The lack of a strong positive relationship between these rankings could result from some teachers eliciting test score gains by running a strict, drill-based classroom at the expense of maintaining a stimulating learning environment. Alterna- tively, if teachers who improve attendance have larger average class sizes as a result, a “bad apple” model of peer effects (Lazear 2001) might undermine the classroom’s average test performance. It would be useful for future research to further investigate the within-teacher relationships between different types of teaching skills. Similarly, future research might probe the exact mechanisms through which teachers affect at- tendance and related character skills, as the current study is unable to disentangle effects on parental involvement from effects on students’ dispositions and behaviors. In the meantime, however, current teacher evaluation systems that prioritize teachers’ 144 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / f / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d . / f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Seth Gershenson effects on student test scores are potentially failing to recognize the effectiveness of teachers who facilitate students’ development in other domains and potentially divert teachers’ time and energy away from lessons and activities that develop character skills. It is therefore important that teacher evaluation systems include multiple measures of teacher effectiveness, perhaps including measures of teachers’ ability to improve students’ attendance and related character skills. Indeed, if teachers were incentivized and encouraged to improve student attendance and related character skills, their effects on such behaviors would likely be even larger than those found here. ACKNOWLEDGMENTS The author is grateful for ﬁnancial support from the Spencer Foundation and the American Educational Research Association (AERA). AERA receives funds for its AERA Grants Program from the National Science Foundation under NSF grant DRL-0941014. Opinions reﬂect those of the author and not necessarily those of the funding agencies. The author thanks the North Carolina Education Research Data Center for providing access to the restricted-use North Car- olina data. The author thanks Nora Gordon, Cassie Guarino, Mike Hansen, two anonymous referees, seminar participants at American University, Johns Hopkins University, Oregon State University, The College Board, and The University of Oregon, and conference participants at the 2014 meetings of the Association for Education Finance and Policy and Society for Research on Educational Effectiveness for providing helpful comments. Andrew Brannegan and Michael S. Hayes provided excellent research assistance. Any remaining errors are my own. REFERENCES Alexander, Karl, Doris Entwisle, and Nader Kabbani. 2001. The dropout process in life course perspective: Early risk factors at home and school. Teachers College Record 103(5):760–822. Almlund, Mathilde, Angela Lee Duckworth, James J. Heckman, and Tim D. Kautz. 2011. Per- sonality psychology and economics. In Handbook of economics of education, vol. 4, edited by Eric A. Hanushek, Stephen Machin, and Ludger Woessmann, pp. 1–181. Amsterdam: North Holland. doi:10.1016/B978-0-444-53444-6.00001-8 Angrist, Joshua, and J¨orn-Steffen Pischke. 2009. Mostly harmless econometrics: An empiricists’ companion. Princeton, NJ: Princeton University Press. Aucejo, Esteban M., and Teresa Foy Romano. 2013. Assessing the effect of school days and ab- sences on test score performance. CFP Discussion Paper No. 1302, London School of Economics. Baker, Eva L., Paul E. Barton, Linda Darling-Hammond, Edward Haertel, Helen F. Ladd, Robert L. Linn, Diance Ravitch, Richard Rothstein, Richard J. Shavelson, and Lorrie A. Shepard. 2010. Problems with the use of student test scores to evaluate teachers. EPI Brieﬁng Paper No. 278. Washing- ton, DC: Economic Policy Institute. Ballou, Dale. 2009. Test scaling and value-added measurement. Education Finance and Policy 4(4):351–383. doi:10.1162/edfp.2009.4.4.351 Borghans, Lex, Angela Lee Duckworth, James J. Heckman, and Bas ter Weel. 2008. The eco- nomics and psychology of personality traits. Journal of Human Resources 43(4):972–1059. Chetty, Raj, John N. Friedman, Nathaniel Hilger, Emmanuel Saez, Diane Whitmore Schanzen- bach, and Danny Yagan. 2011. How does your kindergarten classroom affect your earnings? Evi- dence from Project Star. Quarterly Journal of Economics 126(4):1593–1660. doi:10.1093/qje/qjr041 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d . f / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 145 Teachers’ Effects on Student Absences Chetty, Raj, John N. Friedman, and Jonah E. Rockoff. 2014. Measuring the impacts of teachers I: Evaluating bias in teacher value-added estimates. American Economic Review 104(9):2593–2632. doi:10.1257/aer.104.9.2593 Clotfelter, Charles T., Helen F. Ladd, and Jacob L. Vigdor. 2007. Teacher credentials and student achievement: Longitudinal analysis with student ﬁxed effects. Economics of Education Review 26(6):673–682. doi:10.1016/j.econedurev.2007.10.002 Cunha, Flavio, and James J. Heckman. 2008. Formulating, identifying and estimating the tech- nology of cognitive and noncognitive skill formation. Journal of Human Resources 43(4):738–782. Cunha, Flavio, James J. Heckman, and Susanne M. Schennach. 2010. Estimating the tech- nology of cognitive and noncognitive skill formation. Econometrica 78(3):883–931. doi:10.3982 /ECTA6551 Dobbie, Will. 2011. Teacher characteristics and student achievement: Evidence from Teach for America. Unpublished paper, Princeton University. Dombkowski, Kristen. 2001. Will the real kindergarten please stand up? Deﬁning and re- deﬁning the 20th century U.S. kindergarten. History of Education 30(6):527–545. doi:10.1080 /00467600110064762 Duckworth, Angela L., Christopher Peterson, Michael D. Matthews, and Dennis R. Kelly. 2007. Grit: Perseverance and passion for long-term goals. Journal of Personality and Social Psychology 92(6):1087–1101. doi:10.1037/0022-3514.92.6.1087 Duncan, Greg J., and Katherine Magnuson. 2011. The nature and impact of early achievement skills, attention skills, and behavior problems. In Whither opportunity, edited by G. Duncan and R. Murnane, pp. 47–69. New York: Russel Sage Foundation. Fenstermacher, Gary D., and Virginia Richardson. 2005. On making determinants of quality in teaching. Teachers College Record 107(1):186–213. Gallup. 2004. Education polls. Available www.gallup.com/poll/1612/education.aspx. Accessed 15 April 2014. Gershenson, Seth, Alison Jacknowitz, and Andrew Brannegan. 2015. Are student absences worth the worry in U.S. primary schools? IZA Discussion Paper No. 9558. Goldhaber, Dan. 2007. Everyone’s doing it, but what does teacher testing tell us about teacher effectiveness? Journal of Human Resources 42(4):765–794. Goldhaber, Dan, James Cowan, and Joe Walch. 2013. Is a good elementary teacher always good? Assessing teacher performance estimates across subjects. Economics of Education Review 36:216–228. doi:10.1016/j.econedurev.2013.06.010 Goldhaber, Dan, and Michael Hansen. 2013. Is it just a bad class? Assessing the long-term stability of estimated teacher performance. Economica 80(319):589–612. doi:10.1111/ecca.12002 Goldhaber, Dan, and Roddy Theobald. 2012. Do different value-added models tell us the same things? Available www.carnegieknowledgenetwork.org/briefs/value-added/different-growth-models/. Accessed 11 November 2014. Gottfried, Michael A. 2009. Excused versus unexcused: How student absences in elementary school affect academic achievement. Educational Evaluation and Policy Analysis 31(4):392–419. Gottfried, Michael A. 2011. Absent peers in elementary years: The negative classroom effects of unexcused absences on standardized testing outcomes. Teachers College Record 113(8):1597–1632. 146 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d f / . f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Seth Gershenson Guarino, Cassandra M., Mark D. Reckase, and Jeffrey M. Wooldridge. 2015. Can value- added measures of teacher performance be trusted? Education Finance and Policy 10(1):117–156. doi:10.1162/EDFP_a_00153 Guarino, Cassandra M., Mark D. Reckase, Brian W. Stacy, and Jeffrey M. Wooldridge. 2014. Evaluating speciﬁcation tests in the context of value-added estimation. Journal of Research on Educational Effectiveness 8(1):35–59. doi:10.1080/19345747.2014.981905 Hallfors, Denise, Jack L. Vevea, Bonita Iritani, Hyun San Cho, Shereen Khatapoush, and Leonard Saxe. 2002. Truancy, grade point average, and sexual activity: A meta-analysis of risk indica- tors for youth substance use. Journal of School Health 72(5):205–211. doi:10.1111/j.1746-1561.2002 .tb06548.x Hanushek, Eric A., and Steven G. Rivkin. 2010. Generalizations about using value-added mea- sures of teacher quality. American Economic Review 100(2):267–271. doi:10.1257/aer.100.2.267 Harris, Douglas N. 2011. Value-added measures in education. Cambridge, MA: Harvard Education Press. Heckman, James J. 2000. Policies to foster human capital. Research in Economics 54(1):3–56. doi:10.1006/reec.1999.0225 Heckman, James J., and Tim Kautz. 2013. Fostering and measuring skills: Interventions that improve character and cognition. NBER Working Paper No. 19656. Heckman, James J., Jora Stixrud, and Sergio Urzua. 2006. The effects of cognitive and noncog- nitive abilities on labor market outcomes and social behavior. Journal of Labor Economics 24(3):411–482. doi:10.1086/504455 Jackson, C. Kirabo. 2013. Non-cognitive ability, test scores, and teacher quality: Evidence from 9th grade teachers in North Carolina. NBER Working Paper No. 18624. Jacob, Brian A. 2002. Where the boys aren’t: Non-cognitive skills, returns to school and the gender gap in higher education. Economics of Education Review 21(6):589–598. doi:10.1016/S0272 -7757(01)00051-6 Jacob, Brian A., Lars Lefgren, and David P. Sims. 2010. The persistence of teacher-induced learning. Journal of Human Resources 45(4):915–943. doi:10.1353/jhr.2010.0029 Jennings, Jennifer L., and Thomas A. DiPrete. 2010. Teacher effects on social and behavioral skills in early elementary school. Sociology of Education 83(2):135–159. doi:10.1177/0038040710368011 Kane, Thomas J., and Douglas O. Staiger. 2008. Estimating teacher impacts on student achieve- ment: An experimental evaluation. NBER Working Paper No. 14607. Kane, Thomas J., Jonah E. Rockoff, and Douglas O. Staiger. 2008. What does certiﬁcation tell us about teacher effectiveness? Evidence from New York City. Economics of Education Review 27(6):615–631. doi:10.1016/j.econedurev.2007.05.005 Kelly, Sean. 2012. Understanding teacher effects: Market versus process models of educational improvement. In Assessing teacher quality: Understanding teacher effects on instruction and achieve- ment, edited by Sean Kelly, pp. 7–32. New York: Teachers College Press. Kemple, James J., Corinne M. Herlihy, and Thomas J. Smith. 2005. Making progress toward graduation: Evidence from the talent development high school model. New York: MDRC. Koedel, Cory, and Julian R. Betts. 2007. Re-examining the role of teacher quality in the educa- tional production function. Working Paper No. 2007–03, Vanderbilt University. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / f e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d f . / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 147 Teachers’ Effects on Student Absences Ladd, Helen F., and Lucy C. Sorensen. 2014. Returns to teacher experience: Student achieve- ment and motivation in middle school. Calder Working Paper No. 112, American Institutes for Research. Lazear, Edward P. 2001. Educational production. Quarterly Journal of Economics 116(3):777–803. doi:10.1162/00335530152466232 Lerman, Robert I. 2013. Are employability skills learned in US youth education and training programs? IZA Journal of Labor Policy 2: Article 6. doi:10.1186/2193-9004-2-6 Lockwood, J. R., Daniel F. McCaffrey, Laura S. Hamilton, Brian M. Stecher, Vi-Nhuan Le, and Jose Felipe Martinez. 2007. The sensitivity of value added teacher effect estimates to dif- ferent mathematics achievement measures. Journal of Educational Measurement 44(1):47–67. doi:10.1111/j.1745-3984.2007.00026.x Loeb, Susanna, and Christopher A. Candelaria. 2012. How stable are value-added esti- mates across years, subjects, and student groups? Available www.carnegieknowledgenetwork.org /briefs/value-added/value-added-stability/. Accessed 11 November 2014. Loeb, Susanna, Demetra Kalogrides, and Tara B´eteille. 2012. Effective schools: Teacher hiring, assignment, development, and retention. Education Finance and Policy 7(3):269–304. doi:10.1162 /EDFP_a_00068 Lounsbury, John W., Robert P. Steel, James M. Loveland, and Lucy W. Gibson. 2004. An investigation of personality traits in relation to adolescent school absenteeism. Journal of Youth and Adolescence 33(5):457–466. doi:10.1023/B:JOYO.0000037637.20329.97 Lundberg, Shelly. 2012. Personality and marital surplus. IZA Journal of Labor Economics 1: Article 3. doi:10.1186/2193-8997-1-3 Lundberg, Shelly. 2013. The college type: Personality and educational inequality. Journal of Labor Economics 31(3):421–441. doi:10.1086/671056 McCaffrey, Daniel F., Tim R. Sass, J. R. Lockwood, and Kata Mihaly. 2009. The intertemporal variability of teacher effect estimates. Education Finance and Policy 4(4):572–606. doi:10.1162/edfp .2009.4.4.572 Monk, David H., and Mohd Arifﬁn Ibrahim. 1984. Patterns of absence and pupil achievement. American Educational Research Journal 21(2):295–310. doi:10.3102/00028312021002295 Morrison, Toni, Bob Maciejewski, Craig Gifﬁ, Emily Stover DeRocco, Jennifer McNelly, and Gardner Carrick. 2011. Boiling point? The skills gap in U.S. manufacturing. Washington, DC: The Manufacturing Institute. Nield, Ruth C., and Robert Balfanz. 2006. An extreme degree of difﬁculty: The educational demographics of urban neighborhood high schools. Journal of Education for Students Placed at Risk 11(2):123–141. doi:10.1207/s15327671espr1102_1 Noell, George H., Bethany A. Porter, R. Maria Patt, and Amanda Dahir. 2008. Value added assessment of teacher preparation in Louisiana: 2004–2005 to 2006–2007. Unpublished paper, Louisiana State University. Pritchard, Jennifer. 2013. The importance of soft skills in entry-level employment and postsecondary success: Perspectives from employers and community colleges. Seattle, WA: Seattle Jobs Initiative. Rivkin, Steven G., Eric A. Hanushek, and John F. Kain. 2005. Teachers, schools, and academic achievement. Econometrica 73(2):417–458. doi:10.1111/j.1468-0262.2005.00584.x 148 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d . f / f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 Seth Gershenson Rockoff, Jonah E. 2004. The impact of individual teachers on student achievement: Evidence from panel data. American Economic Review 94(2):247–252. doi:10.1257/0002828041302244 Rothstein, Jesse. 2010. Teacher quality in educational production: Tracking, decay, and student achievement. Quarterly Journal of Economics 125(1):175–214. doi:10.1162/qjec.2010.125.1.175 Rumberger, Russell W., and Scott L. Thomas. 2000. The distribution of dropout and turnover rates among urban and suburban high schools. Sociology of Education 73(1):39–67. doi:10.2307 /2673198 Wiswall, Matthew. 2013. The dynamics of teacher quality. Journal of Public Economics 100:61–78. doi:10.1016/j.jpubeco.2013.01.006 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . f / / e d u e d p a r t i c e - p d l f / / / / 1 1 2 1 2 5 1 6 9 0 1 9 0 e d p _ a _ 0 0 1 8 0 p d / . f f b y g u e s t t o n 0 8 S e p e m b e r 2 0 2 3 149 LINKING TEACHER QUALITY, STUDENT image

Scarica il pdf