LETTER
Communicated by Mark Van Rossum
CosMIC: A Consistent Metric for Spike Inference
from Calcium Imaging
Stephanie Reynolds
stephanie.reynolds09@imperial.ac.uk
Department of Electrical and Electronic Engineering and Centre for Neurotechnology,
Imperial College London, London SW7 2AZ, U.K.
Therese Abrahamsson
therese.abrahamsson@gmail.com
Per Jesper Sjöström
jesper.sjostrom@mcgill.ca
Centre for Research in Neuroscience, Brain Repair and Integrative Neuroscience
Programma, Department of Neurology and Neurosurgery, Research Institute of the
McGill University Health Centre, Montréal General Hospital, Montréal,
Quebec H3G 1A4, Canada
Simon R. Schultz
s.schultz@imperial.ac.uk
Centre for Neurotechnology and Department of Bioengineering, Imperial College
London, London SW7 2AZ, U.K.
Pier Luigi Dragotti
p.dragotti@imperial.ac.uk
Department of Electrical and Electronic Engineering, Imperial College London,
London SW7 2AZ, U.K.
In recent years, the development of algorithms to detect neuronal spiking
activity from two-photon calcium imaging data has received much atten-
zione, yet few researchers have examined the metrics used to assess the
similarity of detected spike trains with the ground truth. We highlight
the limitations of the two most commonly used metrics, the spike train
correlation and success rate, and propose an alternative, which we refer to
as CosMIC. Rather than operating on the true and estimated spike trains
directly, the proposed metric assesses the similarity of the pulse trains ob-
tained from convolution of the spike trains with a smoothing pulse. IL
pulse width, which is derived from the statistics of the imaging data, Rif-
flects the temporal tolerance of the metric. The final metric score is the size
of the commonalities of the pulse trains as a fraction of their average size.
Viewed through the lens of set theory, CosMIC resembles a continuous
Sørensen-Dice coefficient—an index commonly used to assess the
Calcolo neurale 30, 2726–2756 (2018) © 2018 Istituto di Tecnologia del Massachussetts.
doi:10.1162/neco_a_01114
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale (CC BY 4.0) licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2727
similarity of discrete, presence/absence data. We demonstrate the ability
of the proposed metric to discriminate the precision and recall of spike
train estimates. Unlike the spike train correlation, which appears to re-
ward overestimation, the proposed metric score is maximized when the
correct number of spikes have been detected. Inoltre, we show that
CosMIC is more sensitive to the temporal precision of estimates than the
success rate.
1 introduzione
Two-photon calcium imaging has enabled neuronal population activity to
be monitored in vivo in behaving animals (Dombeck, Harvey, Tian, Looger,
& Tank, 2010; Peron, Freeman, Iyer, Guo, & Svoboda, 2015). Modern mi-
croscope design allows neurons to be imaged at subcellular resolution in
volumes spanning multiple brain areas (Sofroniew, Flickinger, King, & Svo-
boda, 2016). Coupled with the current generation of fluorescent indicators
(Chen et al., 2013), which have sufficient sensitivity to read out single spikes,
this imaging technology has great potential to further our understanding of
information processing in the brain.
The fluorescent probe, Tuttavia, does not directly report spiking activ-
ità. Piuttosto, it reads out a relatively reliable indicator of spiking activity—a
cell’s intracellular calcium concentration—from which spike times must be
inferred. A diverse array of techniques have been proposed for this task, In-
cluding deconvolution approaches (Vogelstein et al., 2010; Friedrich, Zhou,
& Paninski, 2017; Pachitariu, Stringer, & Harris, 2017), methods that iden-
tify the most likely spike train given a signal model (Vogelstein et al., 2009;
Deneux et al., 2016), and approaches that exploit the sparsity of the under-
lying spike train (Oñativia, Schultz, & Dragotti, 2013). To enable the inves-
tigation of neural coding hypotheses, reconstructed spike trains must have
sufficient temporal precision for analysis of synchrony between neurons
and behavioral variables (Huber et al., 2012) while accurately inferring the
rate of spiking activity.
Although the development of spike detection algorithms has received
a lot of recent attention, few researchers have examined the metrics used
to assess an algorithm’s performance. At present, there is no consensus on
the best choice of metric. Infatti, from our survey, 44% of papers presenting
a new method assess its performance using a metric unique to that paper.
This inconsistency impedes progress in the field: algorithms are not directly
comparable, E, consequently, data collectors cannot easily select the op-
timal algorithm for a new data set.
The two most commonly used metrics, the spike train correlation (STC)
and the success rate, are not well suited to the task. The STC, which is invari-
ant under linear transformations of the inputs, is not able to discriminate
the similarity of the rates of two spike trains (Paiva, Park, & Príncipe, 2010).
Inoltre, the temporal binning that occurs prior to spike train comparison
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2728
S. Reynolds et al.
impairs the STC’s ability to compare spike train synchrony (Paiva et al.,
2010). These limitations suggest that although the STC is a quick and intu-
itive method, it is not appropriate for assessing an algorithm’s spike de-
tection performance. The success rate, which accurately compares spike
rates, does not reward increasing temporal precision above a given thresh-
old. Consequently, it is not an appropriate metric for evaluating an algo-
rithm’s performance when the end goal is, Per esempio, to investigate the
synchrony of activations within a network.
In this letter, we present a metric that can discriminate both the temporal
and rate precision of an estimated spike train with respect to the ground-
truth spike train. Unlike the STC, we do not bin the spike trains. Piuttosto,
spike trains are convolved with a smoothing pulse that allows compari-
son of spike timing with an implicit tolerance. The similarity between the
resulting pulse trains is subsequently assessed. This type of continuous ap-
proach is also preferred by metrics assessing the relationship between spike
trains from different neurons (van Rossum, 2001; Schreiber, Fellous, Whit-
mer, Tiesinga, & Sejnowski, 2003). We set the pulse width to reflect the tem-
poral precision that an estimate is able to achieve given the statistics of the
insieme di dati. As such, the metric is straightforward to implement since there are
no parameters to tune. For convenience, we refer to the proposed metric
as CosMIC (consistent metric for spike inference from calcium imaging). In
the following, we demonstrate CosMIC’s ability to discriminate spike train
similarity on real and simulated data. We include comparisons against the
two most commonly used metrics, the spike train correlation and the suc-
cess rate, and against two metrics designed to assess similarity between
spike trains from different neurons (Victor & Purpura, 1997; van Rossum,
2001).
2 Constructing the Metric
In this letter, we present a metric for comparing the similarity of two sets
} ˆK
k=1, and a set of estimates, ˆS = {ˆtk
}K
of spikes: a ground-truth set, S = {tk
k=1.
Due to limiting factors, such as noise and model mismatch, it is improbable
that an estimate will match a true spike with infinite temporal precision. As
= tk for any j or k. Piuttosto, we wish to reward
come, we do not expect that ˆt j
estimates within a reasonable range of accuracy given the limitations of the
dati. We achieve this by leveraging results from fuzzy set theory (Zimmer-
mann, 2010).
In contrast to classical sets, to which an element either belongs or does
not belong, fuzzy sets contain elements with a level of certainty represented
by a membership function: the higher the value of the membership func-
zione, the more certain the membership. In the following, we define two
fuzzy sets, S(cid:2) and ˆS(cid:2), that represent the original sets of spikes, S and ˆS, con
a level of temporal tolerance defined by a parameter (cid:2). We set (cid:2) to reflect
the temporal precision that an estimate is able to achieve given the statistics
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2729
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
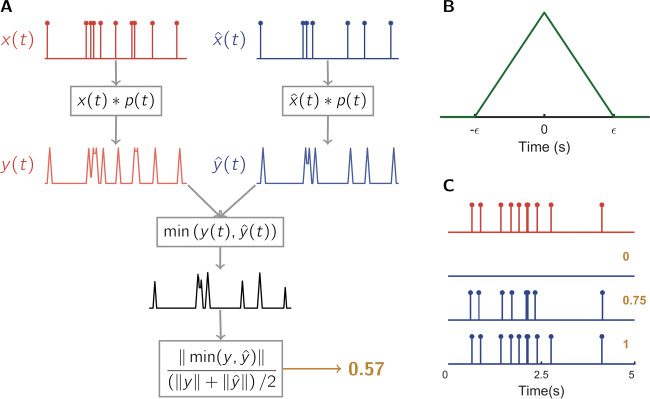
Figura 1: A flow diagram of the proposed metric. The ground-truth spike train
and estimated spike train are convolved with a triangular pulse (B), whose
width is determined by the statistics of the data. The metric compares the differ-
ence between the resulting pulse trains (UN). Metric scores are in the range [0,1];
a perfect estimate achieves score 1, and an empty spike train is scored 0 (C).
of a data set (see section 3). The corresponding membership functions y(T)
and ˆy(T), which are defined for t ∈ R, are calculated through convolution of
the spike trains,
X(T) =
K(cid:2)
k=1
δ(t − tk)
and ˆx(T) =
ˆK(cid:2)
k=1
δ(t − ˆtk),
(2.1)
with a triangular pulse, P(cid:2) (T), such that y(T) = x(T) ∗ p(cid:2) (T) and ˆy(T) = ˆx(T) ∗
P(cid:2) (T). The resulting functions have local maxima at the locations of the re-
spective sets of spikes (see Figure 1A). As x(T) and ˆx(T) are analogous to
the membership functions of the classical sets of spikes, we can think of the
convolution as a temporal smoothing of the membership. The pulse that we
employ is a triangular B-spline (see Figure 1B):
(cid:3)
P(cid:2) (T) =
(cid:2)−|T|
(cid:2)
0
|T| ≤ (cid:2),
otherwise.
(2.2)
Using this triangular pulse means that the farther a time point, T, is from a
spike, the less weight the membership function receives at that point. Past
2730
S. Reynolds et al.
Figura 2: The proposed metric quantifies the commonalities of the sets of true
and estimated spikes as a proportion of the average size of those sets. Com-
monalities are found by taking the minimum of the pulse trains; as such, spikes
that appear in only one pulse train are excluded (UN) and estimates with lower
temporal precision receive a lower score (B and C).
a certain distance, (cid:2), the membership function receives no weight. Many
pulse shapes could be chosen to introduce this grading of temporal preci-
sion; we select a triangular pulse as it is straightforward to examine analyt-
ically and implement computationally.
We design the proposed metric to quantify the size of the intersection of
the fuzzy sets of true and estimated spikes with respect to the average size
of the sets such that
(cid:4)
(cid:5)
S, ˆS
M
=
μ(S(cid:2) ∩ ˆS(cid:2) )
(cid:4)
(cid:5)
μ (S(cid:2) ) + μ( ˆS(cid:2) )
,
/2
(2.3)
(cid:6)
where μ is the L1-norm: μ(S(cid:2) ) = (cid:6)sì(cid:6) =
R |sì(T)| dt. An analogous formula
was presented for discrete fuzzy sets by Pappis and Karacapilidis (1993).
Our formula can be interpreted as the continuous version of the Sørensen-
Dice coefficient (Dice, 1945; Sørensen, 1948), a score commonly used to as-
sess the similarity of discrete, presence/absence data. Also known as the
F1-score, in the context of spike detection, the Sørensen-Dice coefficient is
referred to as the success rate (see section 4.1).
The membership function of an intersection of sets is the minimum of
their respective membership functions. It follows that
μ(S(cid:2) ∩ ˆS(cid:2) ) = (cid:6) min(sì, ˆy)(cid:6) =
(cid:7)
R
| min(sì(T), ˆy(T))| dt.
(2.4)
Taking the minimum of the membership functions produces a conservative
representation of the intersection of two sets; in our context, spikes that ap-
pear in one spike train and not in the other are removed (see Figure 2A),
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2731
and spikes that are detected with poor temporal precision are assigned less
weight (see Figures 2B and 2C).
The metric can also be written in an alternative form,
(cid:4)
(cid:5)
S, ˆS
M
= 1 −
(cid:6)y − ˆy(cid:6)
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
,
(2.5)
the derivation of which is shown in appendix A.1. From equation 2.5, it is
clear that the maximal score of 1 is achieved when the membership func-
zioni, and therefore the sets of true and estimated spikes are equivalent.
The minimal score of 0 is achieved when the supports of the membership
functions do not overlap, questo è, no estimates are within the tolerance of
the metric (see Figure 1C).
2.1 Ancestor Metrics. Like the success rate, CosMIC can alternatively
be derived from a pair of metrics, which we refer to as ancestor metrics. IL
first of these metrics measures the proportion of ground-truth spikes that
were detected within the precision of the pulse width, such that
RCosMIC
=
μ(S(cid:2) ∩ ˆS(cid:2) )
μ(S(cid:2) )
=
(cid:6) min(sì, ˆy)(cid:6)
(cid:6)sì(cid:6)
.
(2.6)
This score is analogous to the recall of a spike train estimate, one of the
ancestor metrics from which the success rate is formed. The second of Cos-
MIC’s ancestor metrics measures the proportion of estimated spikes that
detect a ground-truth spike within the precision of the pulse width, come
Quello
PCosMIC
=
μ(S(cid:2) ∩ ˆS(cid:2) )
μ( ˆS(cid:2) )
=
(cid:6) min(sì, ˆy)(cid:6)
(cid:6) ˆy(cid:6)
.
(2.7)
This is analogous to the precision, the second metric used to compute the
success rate. Finalmente, computing the harmonic mean of the two ancestor met-
rics and rearranging, we obtain CosMIC:
2
RCosMIC
RCosMIC
∗ PCosMIC
+ PCosMIC
= 2
μ(S(cid:2) ∩ˆS(cid:2) )
μ(S(cid:2) )
μ(S(cid:2) ∩ˆS(cid:2) )
μ(S(cid:2) )
μ(S(cid:2) ∩ˆS(cid:2) )
μ( ˆS(cid:2) )
+ μ(S(cid:2) ∩ˆS(cid:2) )
μ( ˆS(cid:2) )
= 2
μ(S(cid:2) ∩ ˆS(cid:2) )
μ (S(cid:2) ) + μ( ˆS(cid:2) )
= M(S, ˆS).
(2.8)
The analogy to the success rate can be seen clearly from the presentation of
that metric in section 4.1.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2732
S. Reynolds et al.
3 Temporal Error Tolerance
The width of the triangular pulse with which the spike trains are convolved
reflects the accepted tolerance of an estimated spike’s position with respect
to the ground truth. To set this width, we calculate a lower bound on the
temporal precision of the estimate of one spike, the Cramér-Rao bound
(CRB), from the statistics of the data. The CRB reports the lower bound on
the mean square error of any unbiased estimator (Kay, 1993). It is there-
fore useful as a benchmark; an estimator that achieves the CRB should be
awarded a relatively high metric score. In section 3.1, we detail the calcula-
tion of the CRB. In section 3.2, we outline how we use this bound to deter-
mine the pulse width. Then, in section 3.3, we provide practical advice on
the calculation of the bound.
3.1 Cramér-Rao Bound for Spike Detection. We consider the problem
of estimating the location of one spike, t0, from noisy calcium imaging data.
The fluorescence signal is modeled as
(cid:8)
F (T) = A
−α(t−t0 ) − e
e
−γ (t−t0 )
(cid:9)
,
1t>t0
(3.1)
where α, γ , and A are parameters that determine the shape and amplitude
of the calcium transient. We assume that we have access to N noisy samples
such that
sì[N] = f [N] + ξ [N],
n ∈ {0, 1, . . . , N − 1},
(3.2)
where ξ [N] are independent samples of a zero-mean gaussian process with
standard deviation σ and f [N] = f (nT ) are samples of the fluorescence sig-
nal with time resolution T. The CRB on the uncertainty in the estimated
position of t0 is
CRB(t0) =
(cid:10)
A2
P 2
N−1(cid:2)
n=0
(cid:8)
αe
−α(nT−t0 ) − γ e
−γ (nT−t0 )
(cid:9)
2
1nT>t0
(cid:11)−1
.
(3.3)
This bound was first presented by Schuck et al. (2018). The bound is derived
by calculating the inverse of the Fisher information, Quale, in the case of
samples corrupted by independent, zero-mean gaussian noise, È
IO(t0) = 1
P 2
(cid:12)
N−1(cid:2)
n=0
∂ f
∂t0
(cid:13)
2
(nT )
,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2733
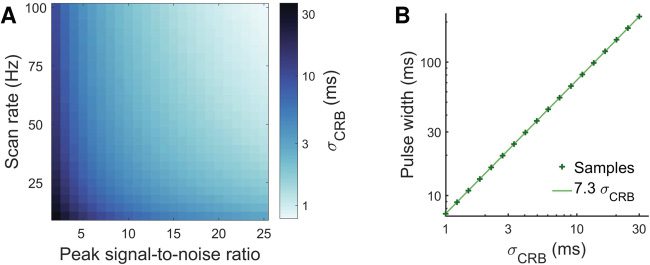
Figura 3: The pulse width is set to reflect the temporal precision achievable
given the statistics of the dataset. We calculate the Cramér-Rao bound (CRB),
P 2
CRB, a lower bound on the mean square error of the estimated location of one
spike from calcium imaging data (UN). This bound decreases as the scan rate (Hz)
and peak signal-to-noise ratio (squared calcium transient peak amplitude/noise
variance) increase. We set the pulse width to ensure that an estimate of one spike
at the temporal precision of the CRB achieves, on average, a score of 0.8. Questo
results in a pulse width of approximately 7.3 P
CRB (B).
where ∂ f /∂t0 is the derivative of the fluorescence signal with respect to the
spike time, t0:
(cid:8)
(nT ) = A
αe
∂ f
∂t0
−α(nT−t0 ) − γ e
−γ (nT−t0 )
(cid:9)
1nT>t0
.
CRB
(cid:14)
= 1
M
M
m=1 CRB(tm
In this work, we use the CRB to set the temporal tolerance of the metric.
In order that the CRB holds for an arbitrarily placed spike, we remove the
dependency on the true spike time by averaging the result over several val-
ues of t0. We compute σ 2
0 are evenly placed
in the interval (nT, (N + 1)T ) for a fixed n. In Figure 3, we plot σ
CRB as the
sampling rate, and peak signal-to-noise ratio (PSNR) of the data vary. IL
/P 2, where σ is the standard deviation of the
PSNR is computed as A2
noise and Apeak is the peak amplitude (maximum) of the fluorescence sig-
−1,
nal in equation 3.1. For this example, we use α = 3.18 S
the parameters for a Cal-520 AM pulse (Tada, Takeuchi, Hashizume, Kita-
mura, & Kano, 2014). We see that the CRB decreases as either the scan rate
or the PSNR of the data increases.
−1 and γ = 34.49 S
0 ), where tm
peak
3.2 Pulse Width. The CRB can be used as a benchmark for temporal pre-
cision of any unbiased estimator. As such, we set the pulse width to ensure
that on average, an estimate at the precision of the CRB achieves a relatively
high score. We set the benchmark metric score at 0.8, as this represents a
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2734
S. Reynolds et al.
relatively high value in the range of the metric, which is between 0 E
1. The importance of this score is not the particular benchmark value—
a range of values give similar performance—but rather that it is a repro-
ducible number with a clear interpretation. In this letter, we characterize
the discrimination performance of CosMIC with a benchmark value of 0.8,
so that its scores can be interpreted when applied to spike inference algo-
rithms on real data. The benchmark value was set lower than the metric’s
maximum value, 1, so that the score does not saturate when the model as-
sumptions are not ideally satisfied. On real data, the noise may not be sta-
tionary (σ may vary in time), and so algorithms may appear to outperform
the CRB. A benchmark score of 0.8 means that the metric score does not
saturate in this scenario.
We consider a true spike at t0 and an estimate, U, normally distributed
, P 2
CRB). Then we
, U )] = 0.8. In appendix A.3,
around it at the precision of the CRB, such that U ∼ N (t0
fix the pulse width so that on average, E [M(t0
we show that this condition is satisfied when
0.4 = ((cid:9)(1/β ) − 0.5)
(cid:4)
(cid:5)
+
β 2 + 1
β
√
2π
(cid:4)
esp(−1/2β 2) − 2
(cid:5)
,
(3.4)
CRB
where β = σ
/w, w is the pulse width, E (cid:9) denotes the cumulative dis-
tribution function of the standard normal distribution. We observe that the
pulse width that solves this equation is approximately equal to 7σ
CRB (Vedere
Figure 3B).
3.3 Implementation. Code to implement the metric can be found at
github.com/stephanierey/metric along with a demonstration. In order to
use the metric, one must have estimates of the fluorescence signal parame-
ters, {α, γ , UN, P } (see equation 3.1). In the following, we provide some guid-
ance on the estimation of these parameters. Alternative strategies have been
suggested by numerous model-based algorithms, whose spike detection
procedures use a subset of the above parameters (Vogelstein et al., 2009;
Pnevmatikakis, Merel, Pakman, & Paninski, 2013; Pnevmatikakis et al.,
2016; Deneux et al., 2016).
The standard deviation of the noise, P , can be computed as the sample
standard deviation of a portion of the data in which there were no calcium
transients. The parameters that determine the speed of the rise and decay of
the pulse, α and γ , are predominantly defined by characteristics of the fluo-
rescent indicator that was used to generate the imaging data. In Table 1, we
provide documented values of α and γ for four commonly used fluorescent
indicators, extracted from the corresponding references: Cal-520 AM (Tada
et al., 2014), OGB-1 AM (Lütcke, Gerhard, Zenke, Gerstner, & Helmchen,
2013), and GCaMP6f and GCaMP6s (Chen et al., 2013). These values can be
used as a guideline; in practice, they will vary with the indicator expres-
sion level, as well as the cell type. We note that the time taken for a calcium
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2735
Tavolo 1: Calcium Indicator Rise and Decay Parameters.
Fluorescent Indicator
GCaMP6f
GCaMP6s
OGB-1 AM
Cal-520 AM
α (S
−1 )
4.88
1.26
1.5
3.18
γ (S
−1 )
60.97
15.16
101.5
34.39
Notes: To calculate CosMIC’s pulse width, the parame-
ters that define the speed of rise and decay of the calcium
transient, α and γ , are required. Here, we provide doc-
umented values of these parameters for four commonly
used fluorescent indicators.
transient to rise to its peak and the decay time are functions of both α and
γ ; the values presented in Table 1 are thus not easily interpretable in terms
of the shape of a calcium transient pulse.
It is typically necessary for a spike detection algorithm to estimate the
value of the amplitude parameter, UN, in order to detect spikes. Infatti, Vo-
gelstein et al. (2009) integrate this step into the spike detection procedure,
iteratively estimating the spike locations and the amplitude, among other
parameters. If, Tuttavia, A is not known, we recommend that the parameter
is fit from the data samples and the signal model, such that
G(T) = b(T) + UN
(cid:8)
−α(t−tk ) − e
e
−γ (t−tk )
(cid:9)
,
1t>tk
K(cid:2)
k=1
(3.5)
where b(T) is a baseline component and α, γ are the estimated pulse shape
parameters. When the baseline component is constant and there is no indi-
cator saturation, this is a linear problem. In practice, a neuron’s spike am-
plitude is not constant over time. Infatti, depending on the fluorescent in-
dicator, the amplitude may increase (Chen et al., 2013) or saturate (Lütcke
et al., 2013) at high spike rates. We recommend that the amplitude parame-
ter is fit from a subset of the data in which neither saturation nor supralinear
amplitudes are present.
4 Numerical Experiments
To assess the discriminative ability of CosMIC, we simulate true and esti-
mated spike trains in various informative scenarios. We compare CosMIC
with the two most commonly used metrics in the spike inference literature,
which we define in sections 4.1 E 4.2 for completeness. We also compare
against two metrics designed to assess the similarity of spike trains from
different neurons. We define the metrics of Victor and Purpura (1997) E
van Rossum (2001) in sections 4.3 E 4.4, rispettivamente.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2736
S. Reynolds et al.
4.1 Success Rate. The success rate, which is defined as a function of
the true- and false-positive rates or, alternatively, as a function of precision
and recall, appears in various forms in the literature. Spike inference per-
formance has been assessed using true- and false-positive rates (Rahmati,
Kirmse, Markovi´c, Holthoff, & Kiebel, 2016), precision and recall analysis
(Reynolds et al., 2017), and using the complement of the success rate, IL
error rate (Deneux et al., 2016). We study this class of metrics under the
umbrella of the success rate, which we define here.
/2 (S) of that spike, where δ
A ground-truth spike is deemed to have been detected if there is an es-
timate within δ
1 is a free parameter. Only one
1
estimate can be deemed to detect one ground-truth spike. The recall is the
percentage of ground-truth spikes that were detected. The precision is the
percentage of estimates that detect a ground-truth spike. Then the success
rate is the harmonic mean of the precision and recall, such that
Success rate = 2
precision ∗ recall
precision + recall
.
(4.1)
A binary true detection region centered around each ground-truth spike is
analogous to an implementation of CosMIC with a box function pulse. A
ensure that the success rate “pulse” has the same width as CosMIC’s pulse,
we set δ
1
= 2(cid:2), Dove (cid:2) is half the pulse width (Guarda la figura 4).
4.2 Spike Train Correlation. The first step in the calculation of the spike
train correlation (STC) is the discretization of the temporal interval into bins
of width δ
2. Two vectors of spike counts, c and ˆc, are subsequently pro-
duced, whose ith elements equal the number of spikes in the ith time bin
for the true and estimated spike trains, rispettivamente. The STC is the Pearson
product-moment correlation coefficient of the resulting vectors,
STC =
(cid:9)c − m(C), ˆc − m(ˆc)(cid:10)
(cid:15)
(cid:15)
v (C)
v (ˆc)
,
(4.2)
= δ
1
= 2(cid:2).
Dove (cid:9)·, ·(cid:10), M(·), and v (·) represent the inner product, sample mean, E
sample variance, rispettivamente. To remain consistent with the success rate in
all numerical experiments, we define δ
2
The STC takes values in the range [−1, 1]. In practice, Tuttavia, it is rare
for a spike detection algorithm to produce an estimate that is negatively cor-
related with the ground truth (Berens et al., 2017). Inoltre, an estimate
with maximal negative correlation is equally as informative as one with
maximal positive correlation. In this letter, we use the normalized spike
train correlation, the absolute value of the STC. This ensures that the range
of each metric that we analyze is equivalent (and equal to [0,1]) and that, COME
a consequence, the distribution of metric values are comparable.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2737
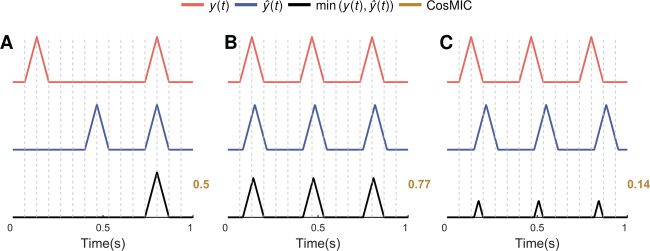
Figura 4: We compare the scores of three metrics: CosMIC, the spike train cor-
relation (STC), and the success rate (SR). None of the metrics compute scores
directly from the true and estimated spike trains (UN). Piuttosto, CosMIC initially
convolves the spike trains with a triangular pulse (B). The STC first discretizes
the temporal interval and uses the counts of spikes in each time bin; the bin
edges and counts are plotted in panel C. The SR uses a bin centered around
each true spike; an estimate in that bin is deemed a true detection (D). In order
that the metric scores are comparable, we fix the STC and SR bin widths to be
equal to CosMIC’s pulse width.
= {t1
k
4.3 Victor-Purpura Dissimilarity. Victor and Purpura (1997) intro-
duced a distance metric to compare the dissimilarity between sets of spikes
}K2
from different neurons: S1
k=1. The distance is the
minimum cost of transforming one set of spikes into the other using a set of
three operations: insertion, deletion, and temporal shifts of spikes. A cost is
associated with each operation; both insertion and deletion carry a cost of
one, whereas the cost of a temporal shift depends on the extent of the shift
and the value of a parameter, q. In particular, the cost of transforming one
spike into another is
}K1
k=1 and S2
= {t2
k
(cid:3)
Kq(t1
k
, t2
j ) =
− t2
j
(cid:6)
q(cid:6)t1
k
2
− t2
(cid:6)t1
if
j
k
otherwise.
(cid:6) < 2/q,
(4.3)
If the spikes are within the precision prescribed by the shift parameter, 2/q,
the cost relates to a temporal shift. Otherwise, the cost invoked is the sum
of the costs of deleting one spike and inserting another at the correct loca-
tion. In all experiments, we set 2/q to be equal to CosMIC’s pulse width, so
that the minimum tolerated precision of CosMIC and this metric are equiv-
, S2), is the
alent. Finally, the distance between two sets of spikes, DVP(S1
minimum total cost of the operations transforming one spike train to the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
2738
S. Reynolds et al.
other. A larger score indicates less similar spike trains, whereas the mini-
mum score, zero, is awarded to identical spike trains.
4.4 van Rossum Dissimilarity. A distance metric introduced by van
Rossum (2001) was also designed to quantify the dissimilarity between sets
of spikes from different neurons. The respective spike trains are first con-
volved with a biologically motivated pulse, q(t) = exp (−t/τ ) 1t>0, where τ
is a tunable parameter and 1 is the indicator function. The metric score is
the Euclidean distance between the resulting pulse trains, f1,τ and f2,τ , come
Quello
DvR(S1
, S2) = 1
τ
(cid:7) ∞
0
( f1,τ (T) − f2,τ (T))2 dt.
(4.4)
Following Kreuz, Haas, Morelli, Abarbanel, and Politi (2007), when com-
puting the score of the van Rossum dissimilarity, we set τ with respect to
the Victor-Purpura metric parameter: τ = 1/q.
5 Results
To investigate metric properties, we simulated estimated and ground-truth
spike trains and analyzed the metric scores. To mimic the temporal error
in spike time estimation, unless otherwise stated, estimates were normally
distributed about the true spike times. In the following, we refer to the stan-
dard deviation of the normal distribution as the jitter of the estimates.
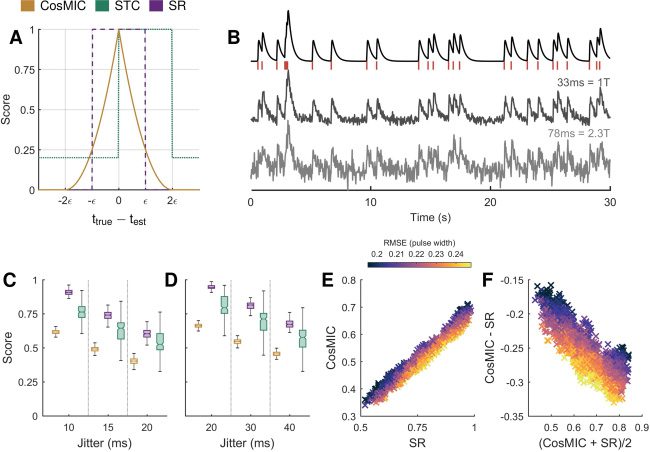
5.1 CosMIC Rewards High Temporal Precision. CosMIC was more
sensitive to temporal precision than the STC or success rate (Guarda la figura 5).
Primo, we investigated this characteristic at the level of estimates of a single
spike, ttrue. CosMIC depends only on the absolute difference between the es-
timate, test, and the true spike: the farther the distance, the smaller the score.
The relationship between CosMIC and the temporal error, δ = ttrue
− test, È
M(ttrue
, test) =
(cid:9)
2
|δ|
w
− 1
⎧
⎨
⎩
(cid:8)
0
|δ| < w
if
otherwise,
(5.1)
where w is the width of the pulse. The derivation of this result is given in
appendix A.2. The success rate, however, does not reward increasing tem-
poral precision above the bin width; an estimate is assigned a score of 1 or
0 when its precision is above or below the bin width, respectively. More-
over, the STC is asymmetric in the temporal error; estimates the same dis-
tance from the true spike are not guaranteed to be awarded the same score
(see Figure 5A). This asymmetry stems from this metric’s temporal dis-
cretization. The temporal interval is first discretized into time bins, and the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2739
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
Figure 5: CosMIC was more sensitive to the temporal precision of estimates
than the spike train correlation (STC) or success rate (SR). Unlike the STC, Cos-
MIC awards estimated spikes (test) with the same proximity to the true spike
(ttrue) the same score (A). In contrast to both the STC and SR, CosMIC rewards
increasing precision above the pulse width (2(cid:2)) with strictly increasing scores.
In panels C and D, we plot the distribution of scores awarded to estimates that
detect the correct number of spikes at varying temporal precision, in a low- and
high-noise setting, respectively. In panel B, a sample of each of the following sig-
nals is plotted: the ground-truth spike train, simulated as a Poisson process at
rate 1 Hz over 200 s; the corresponding calcium transient signal, sampled with
interval T = 1/30 s; the low- and high-noise fluorescence signal and the corre-
sponding pulse widths. At each noise and jitter level, 100 realizations of spike
train estimates normally distributed about the true spike times were generated.
In both the low- (C) and high-noise (D) settings, the STC exhibited a relatively
large variation in the scores awarded to estimates of the same jitter. CosMIC and
the SR were roughly linearly related (E). CosMIC was boosted with respect to
the success rate when temporal error, represented by the root mean square error
(RMSE) of estimates as a fraction of the pulse width, was low (F). Conversely,
CosMIC was relatively low with respect to the SR when temporal error was rel-
atively high. The color map in panels E and F is thresholded at the 1st and 99th
percentiles of the RMSE for visual clarity.
spikes in each bin are counted (see Figure 4). It follows that estimated spikes
that are the same absolute distance from a true spike can fall into different
time bins, thus achieving a different score. We note that the STC is always
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
2740
S. Reynolds et al.
positive in Figure 5A as, in this letter, we use the absolute value of the cor-
relation (see section 4.2).
On simulated data, we investigated the effect of these properties when
spike train estimates, rather than single spikes, were evaluated. In partic-
ular, we analyzed the metric scores when spike train estimates contained
the correct number of spikes but their temporal precision varied. We simu-
lated the ground-truth spike train as a Poisson process with rate 1 Hz over
200 s. The corresponding calcium transient signal was generated assuming
a Cal-520 pulse shape (see Table 1) and a sampling rate of 30 Hz. White
gaussian noise was added to the calcium transient signal to generate two
fluorescence signals, one with low and the other with relatively high noise
(see Figure 5B). The corresponding metric pulse widths, as calculated from
the CRB, were 33 ms and 78 ms, or 1 and 2.3 sample widths, respectively.
Spike train estimates were normally distributed about the true spikes with
varying jitter. The metric scores were then calculated for 100 realizations
of spike train estimates at each jitter level in both the low- and high-noise
settings (see Figures 5C and 5D, respectively).
As the correct number of spikes was always estimated, the level of jitter
represented the quality of a spike train estimate in this setting. Ideally, a
metric would reliably reward spike train estimates of the same quality with
the same score. The STC, however, took a relatively large range of values for
estimates of the same jitter (see Figures 5C and 5D), despite having the same
range as CosMIC and the success rate. This inconsistency is a consequence
of the edge effects introduced by binning. Here, we use the term consistency
in line with its semantic rather than mathematical definition.
We observed a roughly linear trend in the scores of CosMIC and the suc-
cess rate (see Figure 5E). As expected, CosMIC was boosted with respect to
the success rate when the root mean square error (RMSE) of detected spikes
was relatively low when measured as a fraction of the pulse width. In each
case, the RMSE was computed empirically from the estimated spikes within
the precision of CosMIC and the success rate’s pulse width. Conversely,
CosMIC was relatively low with respect to the success rate when the RMSE
was relatively high. This trend is visible in the Bland-Altman plot (Altman
& Bland, 1983; Giavarina, 2015), in which the mean of the two methods is
plotted against the difference. We conclude that CosMIC is more sensitive
to the temporal precision of detected spikes, as, unlike the success rate, it
discriminates precision above the bin width.
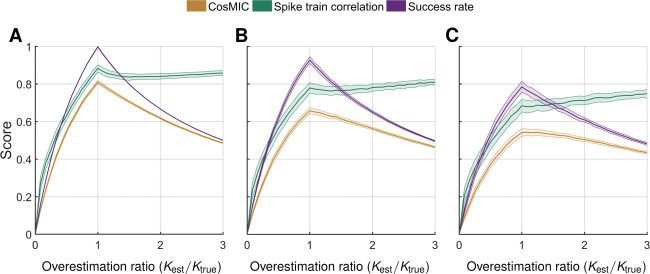
5.2 CosMIC Penalizes Overestimation. As opposed to the STC, Cos-
MIC and the success rate penalized overestimation of spikes (see Figure 6).
We simulated spike train estimates that were normally distributed about
the true spike times. When there were fewer detected spikes (Kest) than the
number of true spikes (Ktrue), the locations about which the estimates were
> Ktrue, the set of
distributed were chosen without replacement. When Kest
locations included all the true spikes plus a subset of extras chosen with
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2741
Figura 6: In contrast to the spike train correlation, CosMIC and the success rate
were maximized when the correct number of spikes was detected. We display
the distribution of metric scores as the number of estimated spikes (Kest) varies
with respect to the number of true spikes (Ktrue). The true spike train, which was
identical throughout, consisted of 200 spikes simulated from a Poisson process
with spike rate 1 Hz. Estimated spikes were normally distributed about the true
CRB (B), E 3 P
spikes, with jitter σ
CRB
= 20 ms. When the number of estimated spikes was greater than the number
of true spikes, estimates were distributed around a set of locations, including
all true spikes plus an extra subset chosen with replacement. For each metric,
we plot the mean (darker central line) and standard deviation (edges of shaded
region) of metric scores on a set of 100 spike train estimates generated at each
overestimation and jitter combination.
CRB (C), rispettivamente, where σ
CRB (UN), 2 P
/Ktrue) reflects the degree of ac-
replacement. The overestimation ratio (Kest
curacy to which an estimate matches the rate of a ground-truth spike train.
We observed that rather than penalizing overestimation, the STC increased
with the overestimation ratio. In contrasto, CosMIC and the success rate were
maximized when the correct number of spikes was detected. This behavior
was consistent as the jitter of the estimated spikes varied; in this example,
the jitter was σ
CRB (Vedere
Figure 6C), respectively.
CRB (see Figure 6B), E 3 P
CRB (see Figure 6A), 2 P
It is the type of normalization used by the STC that caused it to be insen-
sitive to overestimation. Scaling factors present in the spike count vectors
cancel out in the numerator and denominator (see equation 4.2), rendering
the STC invariant under scalar transformations of the inputs. When the STC
was adapted to the continuous-time assessment of spike train similarity, by
first convolving spike trains with a smoothing pulse, this flaw persisted
(Paiva et al., 2010).
When the spike train estimates have jitter σ
CRB and their rate increases
from perfect rate estimation to an overestimation ratio of 3, the success rate
and CosMIC scores are reduced by 49% E 40%, rispettivamente. Both metrics
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2742
S. Reynolds et al.
are thus penalizing overestimation, with the former metric doing so more
harshly. When the jitter is larger than the CRB, the reduction in CosMIC
from perfect rate estimation to overestimation is relatively smaller, as Cos-
MIC is already substantially penalizing the temporal discrepancy.
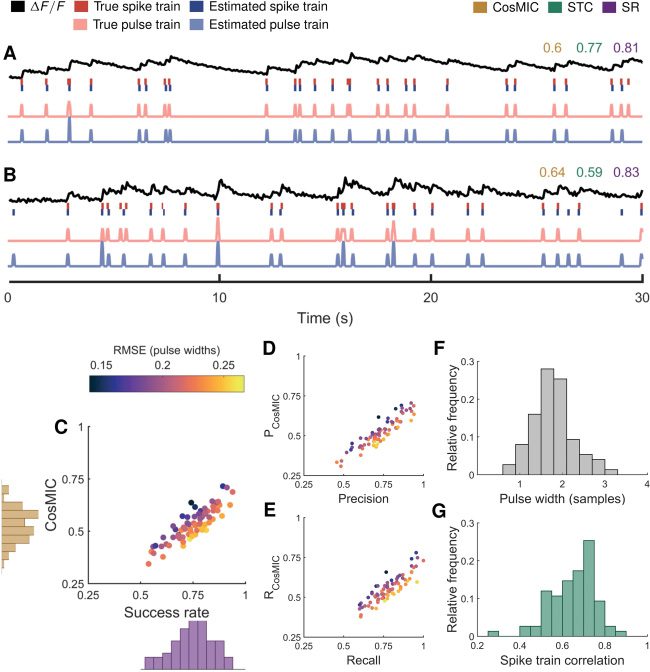
5.3 Application to Real Imaging Data. On imaging data of the mouse
visual cortex at a frame rate of 13 Hz, CosMIC was more sensitive than the
success rate to the temporal precision of detected spikes (Guarda la figura 7). (For
a detailed description of the imaging data, see Reynolds, Abrahamsson,
Schuck, Sjöström, Schultz, & Dragotti, 2017.) Briefly, four neocortical layer-5
pyramidal cells were simultaneously recorded in whole-cell configuration,
different Poisson spiking patterns were evoked by brief current pulses, E
calcium transients were imaged with a two-photon laser-scanning micro-
scope (see Abrahamsson et al., 2017), thus establishing a realistic imaging
data set with electrophysiological ground truth. An existing algorithm was
used to detect spikes from each of 83 traces (Oñativia et al., 2013; Reynolds,
Copeland, Schultz, & Dragotti, 2016). Detected spike trains were subse-
quently compared to the electrophysiological ground truth using CosMIC,
the success rate and the STC.
As detailed in section 3, the metric’s pulse width was set with respect to
the CRB. On this data set, the pulse widths were concentrated between 1
E 3 sample widths; this range encompassed 92% of the data (Guarda la figura
7F). As the noise level of the data increases, so does the pulse width. Con-
sequently, the tolerance of the metric with regard to the temporal precision
of estimates also increases. Di conseguenza, estimates on noisier data (see Fig-
ure 7B) were scored with more lenience than those on less noisy data (Vedere
Figure 7A).
As was found on simulated data in section 5.1, there was a linear trend
between the scores of CosMIC and the success rate (see Figure 7C). Cos-
MIC was relatively high with respect to the success rate when the temporal
precision, represented by RMSE as a fraction of the pulse width, was rel-
atively high. Conversely, CosMIC was low with respect to the success rate
when the temporal precision was relatively low. This pattern was conserved
when CosMIC’s ancestor metrics, PCosMIC and RCosMIC (see section 2.1), were
compared to the precision and recall (see Figures 7D and 7E). The average
RMSE over all traces was 27 ms, O 0.37 sample widths. As CosMIC is able
to discriminate precision above the pulse width, it is better able to reward
this superresolution performance than the success rate or STC.
5.4 CosMIC Discriminates Precision and Recall of Spike Trains. By
construction, CosMIC bears a strong resemblance to the Sørensen-Dice co-
efficiente, Quale, in the context of spike detection, is referred to as the suc-
cess rate. The success rate is the harmonic mean of the precision and recall,
two intuitive metrics that represent the proportion of estimates that detect a
ground-truth spike and the proportion of true spikes detected, respectively.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2743
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
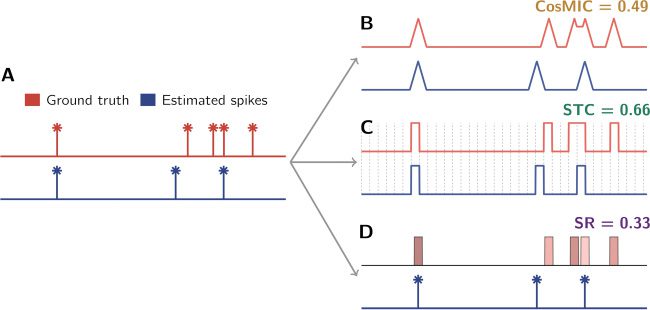
Figura 7: On mouse in vitro imaging data, CosMIC was more sensitive than the
success rate (SR) to the temporal precision of detected spikes. Spikes were de-
tected using an existing algorithm (Onativia et al., 2013; Reynolds et al., 2016)
from 83 traces sampled from visual cortex slices at 13 Hz. (UN, B) We display
from top to bottom an example fluorescence trace ((cid:13)F/F), ground-truth and
detected spike trains, and the corresponding pulse trains. (C) There was an ap-
proximately linear relationship between CosMIC and the SR. CosMIC was rel-
atively high with respect to the SR when temporal error, represented by root
mean square error (RMSE) as a fraction of the pulse width, was relatively low.
Conversely, CosMIC was low with respect to the SR when temporal error was
relatively high. This pattern was conserved in the relationship between the pre-
cision and CosMIC’s analogous ancestor metric, PCosMIC, (D) and between the
recall and RCosMIC (E). The range of pulse widths as computed from the Cramér-
Rao bound (F) and the range of spike train correlation (STC) scores (G) are also
shown.
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2744
S. Reynolds et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
Figura 8: CosMIC scored estimated spike trains of the same recall and fallout
rate consistently, unlike the spike train correlation (STC). When a spike train
estimate detected precisely the location of a subset of spikes from a true spike
train, the scores of CosMIC and the success rate depended only on the percent-
age of spikes detected (the recall), not the location of the detected spikes (UN, D).
In contrasto, the STC varied with the subset of spikes detected. When a spike train
estimate detected all the true spikes precisely plus a number of surplus spikes,
the STC varied with the placement of the surplus spikes (B, E). In contrasto, IL
success rate and CosMIC depended only on the percentage of estimated spikes
that did not correspond to ground-truth spikes (the fallout rate, also known as
the false-positive rate). The distribution of correlation scores plotted in panels
D and E stems from 100 realizations of estimated spike trains at each recall and
fallout rate. In panel C, we plot an example of a true spike train. In panels D
and E, we plot estimated spike trains, with a recall and fallout rate of 50% E
33%, rispettivamente, along with the corresponding metric scores. The spikes with
a black x marker in E indicate the surplus spikes.
In this section, we demonstrate that CosMIC can accurately discriminate
both the precision and recall of spike train estimates.
When a spike train estimate detects exactly a subset of the true spikes,
plus no remainders, CosMIC and the success rate depend only on the per-
centage of true spikes detected (the recall), not the location of that subset
(see Figures 8A and 8D). Denoting the size of the subset of true detections
as K − R, with K the number of true spikes and 0 ≤ R ≤ K, we have
(cid:4)
(cid:5)
S, ˆS
M
= 1 −
1
2K/R − 1
(5.2)
CosMIC: A Consistent Spike Inference Metric
2745
(see appendix A.4 for a proof). Così, CosMIC depends only on the pro-
portion of “missing” spikes, R/K, not their location. In contrasto, the STC
exhibited significant variation at each level of recall. This is illustrated in
Figure 8A, in which we plot the distribution of CosMIC, success rate, E
correlation scores over 100 realizations of spike train estimates at each level
of recall. It can be seen that in this setting, CosMIC and the success rate are
fixed with the recall of the spike train estimates.
When all the true spikes were exactly detected plus R ≥ 0 surplus spikes,
CosMIC and the success rate depend only on the level of precision, not the
location of the surplus spikes (see Figures 8B and 8E). We have
M(S, ˆS) =
1
1 + R/2K
,
(5.3)
where K is the number of true spikes (see appendix A.5 for a proof). IL
fallout rate, which is the complement of the precision, is the proportion of
estimates that were not deemed to have detected a ground-truth spike. It
is apparent from equation 5.3 that in this setting, CosMIC depends only on
the fallout rate, R/K. The correlation, on the other hand, varied with the
location of the surplus spikes. In Figure 8B, we plot the distribution of the
correlation scores for 100 realizations of spike train estimates at each level of
precision. CosMIC and the success rate, which were constant (and identical)
at a given precision in this scenario, are also shown.
5.5 Comparison with Victor-Purpura and van Rossum Distances. IL
Victor-Purpura (VP) and van Rossum (vR) spike distances were originally
designed to quantify the dissimilarity between spike trains from different
neurons (Victor & Purpura, 1997; van Rossum, 2001). Due to the obvious
parallels between that scenario and ours, we investigated the applicability
of the VP and vR metrics to scoring spike inference.
The vR metric initially convolves the respective spike trains with a causal
exponential pulse and computes the Euclidean distance between the result-
ing pulse trains (see section 4.4). Despite the causality of the pulse, the met-
ric score is symmetric in the error of a single estimate about a true spike (Vedere
Figure 9A). The VP distance implicitly evokes a box function pulse, result-
ing in a piecewise linear relationship between the error of an estimate and
the metric score (see Figure 9A). Although the VP distance is not defined
with respect to a smoothing pulse, this interpretation follows from an anal-
ogous argument to that presented in appendix A.2. It is known that as the
pulse width increases from small to large with respect to the interspike in-
terval, both metrics vary between coincidence detectors and rate detectors.
To the best of our knowledge, the optimal pulse width for a compromise
between rate and timing detection is not known, so we set the widths of vR
and VP with respect to CosMIC’s pulse width.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2746
S. Reynolds et al.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
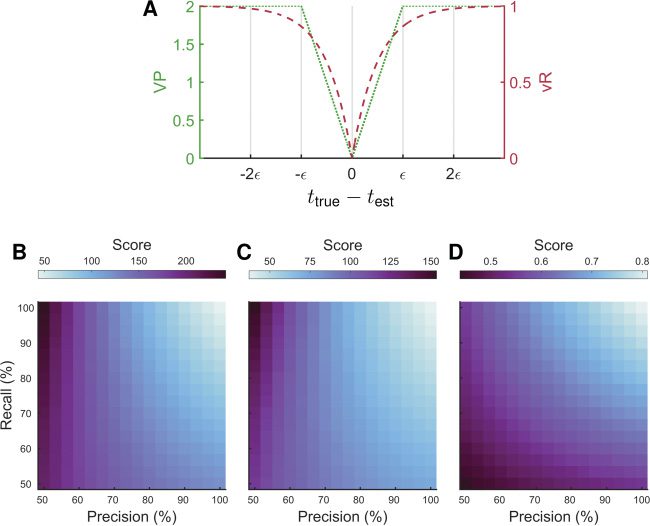
Figura 9: CosMIC was more sensitive to the precision and recall of spike train
estimates than the Victor-Purpura (VP) or van Rossum (vR) spike distances.
Both VP and vR are dissimilarity metrics, reaching a minimum of zero when
a true spike train and estimated spike train are equivalent. (UN) This is demon-
strated for one estimate (test) of one spike (ttrue). The parameters of VP and vR
were set with respect to CosMIC’s pulse width, 2(cid:2), Quale, in this example, era
computed from a CRB of 20 ms. The VP and vR distances were less sensitive
to the recall than the precision of spike train estimates (B, C, rispettivamente). Cos-
MIC, Tuttavia, attained a relatively high score only when both the precision and
recall were high (D). At each level of precision and recall, the metric scores were
averaged over 100 realizations of spike train estimates. The ground-truth spike
train contained 200 Poisson distributed spikes at rate 1 Hz. False positives were
uniformly distributed about the temporal interval, whereas true positives were
normally distributed about true spikes with jitter 20 ms.
Although it is already clear that when the width is set correctly, VP and
vR can discriminate the rate and temporal precision of spike trains with re-
spect to one another (Paiva et al., 2010), it is not clear whether they are suit-
able for scoring spike train estimates. In Figures 9B to 9D, we plot the scores
of VP, vR, and CosMIC, rispettivamente, as the precision and recall of spike
train estimates vary. We observed that vR and VP were less sensitive to the
CosMIC: A Consistent Spike Inference Metric
2747
recall than the precision of spike train estimates; relatively low distances
were obtained when only 50% of true spikes were detected. In contrasto,
CosMIC attained a relatively high score only when both the precision and
recall were high (see Figure 9D). As it is crucial that a spike inference metric
penalizes both undetected and falsely detected spikes, this result suggests
Quello, without modification, VP and vR are not ideal for scoring spike train
estimates.
The results correspond to a ground-truth spike train consisting of 200
spikes generated from a Poisson process with rate 1 Hz. False positives were
uniformly distributed about the temporal interval, whereas true positives
were normally distributed about true spikes with jitter 20 ms. The pulse
width was set assuming a CRB of 20 ms. At each level of precision and
recall, results were averaged over 100 realizations of spike train estimates.
6 Discussion
Much recent attention has been focused on the development of algorithms
to detect spikes from calcium imaging data, while the suitability of the met-
rics that assess those algorithms has been predominantly overlooked. In this
letter, we presented a novel metric, CosMIC, to assess the similarity of spike
train estimates compared to the ground truth. Our results demonstrate that
CosMIC accurately discriminates both the temporal and rate precision of
estimates with respect to the ground truth.
Using two-photon calcium imaging, the activity of neuronal populations
can be monitored in vivo in behaving animals. Inferred spike trains can be
used to investigate neural coding hypotheses by analyzing the rate and syn-
chrony of neuronal activity with respect to behavioral variables. To justify
such analysis, the ability of spike detection algorithms to generate accurate
spike train estimates must be verified. When spike frequency is to be in-
vestigated, it is crucial that an estimate accurately matches the rate of the
ground-truth spike train. We have shown that the STC is not fit for this pur-
pose; rather than penalizing overestimation of the number of spikes, it is
rewarded (Guarda la figura 6). In contrasto, CosMIC and the success rate are max-
imized when the correct number of spikes is detected. When the ultimate
goal is to analyze spike timing with respect to other variables, it is critical
that spikes can be detected with high temporal precision. We have shown
that CosMIC has superior discriminative ability in this regard, compared to
the success rate and STC (Guarda la figura 5).
The current inconsistency in the metrics used to assess spike detection
algorithms hinders both experimentalists, aiming to select an algorithm for
data analysis, and developers. In light of this problem, a recent benchmark-
ing study tested a range of algorithms on a wide array of imaging data
(Berens et al., 2017). Although informative, the study, which relied heav-
ily on the STC to assess algorithm performance, may not provide the full
picture. By introducing a new metric, we hope to complement such efforts
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2748
S. Reynolds et al.
in the pursuit of a thorough, quantitative evaluation of spike inference al-
gorithms.
By construction, CosMIC bears a resemblance to the Sørensen-Dice co-
efficiente, which is commonly used to compare discrete, presence/absence
dati (Dice, 1945; Sørensen, 1948). This metric, which is also known as the
F1-score, is widely used in many fields, including ecology (Bray & Curtis,
1957) and image segmentation (Zou et al., 2004). When applied to spike in-
ference, this coefficient is referred to as the success rate and is one of the two
most commonly used metrics. We have demonstrated that this construction
confers some of the advantages of the success rate to CosMIC. In particu-
lar, CosMIC is able to accurately discriminate the precision and recall of
estimated spike trains (Guarda la figura 8). We have also shown the advantages
of CosMIC over the success rate; most important, it is more sensitive to a
spike train estimate’s temporal precision than the success rate (Guarda la figura
5). Inoltre, CosMIC’s parameter is defined with respect to the statis-
tics of the data set and, unlike the success rate’s bin size, it does not need to
be selected by a user.
We demonstrated that CosMIC is boosted with respect to the success rate
when temporal precision is relatively high. In particular, as temporal preci-
sion approaches the CRB, CosMIC increases to a maximum. It is not clear
how close existing algorithms are to this theoretical bound. Nevertheless, Esso
is important to discriminate between the temporal precision of algorithms
even if the performance is not yet optimal. Per esempio, if all algorithms
produce estimates with error on the order of a sample width, it is still of in-
terest to know which algorithm produces the lowest error. With its graded
pulse shape, CosMIC is able to penalize decreasing error in this way.
The width of the pulse is computed from a lower bound on temporal pre-
cision (see section 3), which in turn is derived from the statistics of the data
set. Di conseguenza, the metric will be more lenient for spike inference algorithms
on noisier or lower sampling rate data. This is due to our assumption that
a metric score should reflect the difficulty of the spike inference problem.
To calculate the bound, knowledge of the calcium transient pulse parame-
ters and the standard deviation of the noise is required. These parameters
are typically used by algorithms in the spike detection process (Vogelstein
et al., 2010; Deneux et al., 2016). Using only one pulse amplitude parameter,
which relates to the amplitude of a single spike, is a simplification. Depend-
ing on the fluorescent indicator, amplitudes do in fact decrease (Lütcke, Ger-
hard, Zenke, Gerstner, & Helmchen, 2013) or increase (Chen et al., 2013) at
high firing rates. Consequently, CosMIC may be slightly more punitive in
the former case than the latter.
The problem of comparing a ground-truth and estimated spike train is
analogous to that of comparing spike trains from different neurons. Nel
spike train metric literature, binless measures have been found to outper-
form their discrete counterparts (Paiva et al., 2010). It is also common to con-
volve spike trains with a smoothing pulse prior to analysis (van Rossum,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2749
2001; Schreiber et al., 2003). In that context, the width and shape of the pulse
reflect hypotheses about the relationship between neuronal spike trains. UN
width that is large with respect to the average interspike interval results
in a metric tuned to the comparison of neuronal firing rates. Conversely, UN
relatively small width produces a metric that acts as a coincidence detec-
tor. To apply CosMIC to the problem of spike train comparison, one could
similarly vary the pulse width to tailor its performance to the neural cod-
ing scheme. In the context of spike detection, which we view as a param-
eter estimation problem, the pulse width is fixed with respect to a lower
bound on the precision with which a spike time can be estimated. Setting
the width via this bound, which is tailored to calcium imaging data, risultati
in a metric that assesses how accurately parameters have been estimated
given the constraints of the data. This approach would need to be altered
to extend CosMIC to other applications. We note that in the absence of this
pulse width, CosMIC is sufficiently universal to be applied to the compar-
ison of any point processes.
Finalmente, we note that the developed metric is able to accurately assess an
estimate’s temporal and rate precision. This information is unified in a sin-
gle score that summarizes the overall performance of an algorithm. We con-
sider a single summary score to be practical for users who do not have the
time or desire to analyze multidimensional trade-offs. Alternatively, Cos-
MIC’s ancestor metrics, RCosMIC and PCosMIC, can be used to determine the
extent to which errors stem from undetected or falsely-detected spikes.
Appendix: Further Analytical Results
In the appendix, we provide derivations of some results presented in the
main text. The following notation is consistent throughout. We denote with
X(T) and ˆx(T) the true and estimated spike trains (see equation 2.1). Noi
denote the triangular smoothing pulse with p(cid:2) (T) (see equation 2.2). IL
true and estimated pulse trains are denoted y(T) = x(T) ∗ p(cid:2) (T) and ˆy(T) =
ˆx(T) ∗ p(cid:2) (T), rispettivamente. The proposed metric score, when comparing the
similarity between a ground-truth set of spikes, S = {tk
}K
k=1, with a set of
estimates, ˆS = {ˆtk
} ˆK
k=1, È
M(S, ˆS) = 2
(cid:6) min(sì, ˆy)(cid:6)
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
,
Dove (cid:6) · (cid:6) is the L1-norm.
(A.1)
A.1 Alternative Metric Form. In the following, we derive an alternative
equation for CosMIC. We show that
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
N
e
C
o
_
UN
_
0
1
1
1
4
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
9
S
e
P
e
M
B
e
R
2
0
2
3
2750
S. Reynolds et al.
M(S, ˆS) = 1 −
(cid:6)y − ˆy(cid:6)
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
.
(A.2)
We have
1 −
(cid:6)y − ˆy(cid:6)
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
=
=
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6) − (cid:6)y − ˆy(cid:6)
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
(cid:6)
R y(T) + ˆy(T) dt −
(cid:6)
R |sì(T) − ˆy(T)| dt
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
,
where we have used the fact that y(T) and ˆy(T) are nonnegative for all t ∈ R.
Decomposing both integrals over R into their counterparts over the disjoint
sets {t ∈ R : sì(T) > ˆy(T)} E {t ∈ R : sì(T) ≤ ˆy(T)} and subsequently combin-
ing them, we have
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
1 −
(cid:6)y − ˆy(cid:6)
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
=
(cid:6)
y> ˆy ˆy(T)dt + 2
(cid:6)
2
y≤ ˆy y(T)dt
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
= 2(cid:6) min (sì, ˆy) (cid:6)
(cid:6)sì(cid:6) + (cid:6) ˆy(cid:6)
= M(S, ˆS).
Equation A.2 then follows.
A.2 Score for Estimate of One Spike. We now derive an expression
for the metric score of the estimate of the location of one spike in terms of
the temporal error of the estimate, |tu|. We see that as the temporal preci-
sion increases above the threshold precision (2(cid:2)), the metric score increases
monotonically.
Proposition 1. The score given to an estimate of the location of a single spike, t0,
with temporal error u ∈ R is
M(t0
, t0
+ tu) =
(cid:9)
2
|tu|
2(cid:2)
− 1
(cid:3) (cid:8)
0
|tu| < 2(cid:2)
if
otherwise,
(A.3)
where (cid:2) is half the width of the pulse, p(cid:2) (t), as in equation 2.2.
= 0,
Proof. Without loss of generality, we let the true spike location be at t0
as the metric score depends on the relative rather than absolute locations of
the estimated and ground truth spikes. From equation A.1, we have
M(0, u) = 2
(cid:6) min(p(cid:2) (t), p(cid:2) (t − u))(cid:6)
(cid:6)p(cid:2) (t)(cid:6) + (cid:6)p(cid:2) (t − u)(cid:6)
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2751
When |u| > 2(cid:2), the pulses do not overlap and, consequently, the numerator
is equal to zero. Therefore, the metric score is zero for all |tu| > 2(cid:2). For |tu| ≤
2(cid:2), we write
M(0, tu) = 1
(cid:2)
(cid:12)(cid:7)
(cid:7)
(cid:13)
P(cid:2) (T) dt +
P(cid:2) (t − u) dt
,
UN
B
(A.4)
which follows from (cid:6)P(cid:2)(cid:6) = (cid:2), A = {t ∈ R : P(cid:2) (T) < p(cid:2) (t − u)}, and B = {t ∈
R : p(cid:2) (t) ≥ p(cid:2) (t − u)}. From the change of variables v = t + u, we see that
M(0, u) = M(0, −u). As M is even in the second argument, we must only
calculate M(0, u) for 0 < u < 2(cid:2). To identify the support of A and B, we must
identify the point at which p(cid:2) (t) = p(cid:2) (t − u). We have
p(cid:2) (t) = p(cid:2) (t − u) ⇔ 1 −
|t|
(cid:2)
= 1 −
|t − u|
(cid:2)
⇔ |t| = |t − u|.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
For 0 < u < 2(cid:2), the intersection point occurs in the right half of p(cid:2) (t) and
the left half of p(cid:2) (t − u); it follows that t = u/2. equation A.4 becomes
(cid:7)
(cid:13)
(cid:12)(cid:7) (cid:2)
M(0, u) = 1
(cid:2)
p(cid:2) (t) dt +
p(cid:2) (t) dt +
u/2
(cid:12)(cid:7) (cid:2)
u/2
(cid:7) (cid:2)
p(cid:2) (t) dt,
u/2
= 1
(cid:2)
= 2
(cid:2)
u/2
u−(cid:2)
(cid:7) −u/2
−(cid:2)
p(cid:2) (t − u) dt
(cid:13)
p(cid:2) (v ) dv
which follows from the change of variables v = t + u and the symmetry of
p(cid:2) (t) about 0. Evaluating the integral, we obtain M(0, u) = (|u|/2(cid:2) − 1)2 , for
(cid:2)
|u| < 2(cid:2).
A.3 Metric Score at Precision of CRB. The CRB is commonly used as a
benchmark for algorithm performance in parameter estimation problems.
In the context of calcium imaging, it has been previously used to evaluate
detectability of spikes under different imaging modalities (Reynolds, Oña-
tivia, Copeland, Schultz, & Dragotti, 2015; Schuck et al., 2018). In this case,
the CRB reports the minimum uncertainty achievable by any unbiased es-
timator when estimating the location of one spike. We thus set the width of
the pulse to ensure that, on average, an estimate of the location of one spike
at the precision of the CRB achieves a metric score of 0.8. This benchmark
score is relatively high in the range of the metric, which is between 0 and 1,
while allowing leeway to be exceeded.
Proposition 2. Let t0 denote the location of the true spike. The estimate is normally
distributed about the true spike at the precision of the CRB; it is modeled with the
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
2752
S. Reynolds et al.
(cid:4)
random variable U ∼ N
t0
width. Then we have E [M(t0
(cid:5)
. We denote β = σ
, σ 2
CRB
, U )] = 0.8 if β satisfies the following equation,
/w, where w is the pulse
CRB
0.4 = ((cid:9)(1/β ) − 0.5)
(cid:4)
(cid:5)
+
β 2 + 1
β
√
2π
(cid:4)
exp(−1/2β 2) − 2
(cid:5)
,
(A.5)
where (cid:9) denotes the cumulative distribution function of the standard normal dis-
tribution.
Proof. We want to identify the pulse width at which 0.8 = E [M(t0
Without loss of generality, we consider the case where t0
fact that M(0, ·) is even and the results of section A.2, we have
, U )] .
= 0. Due to the
(cid:7)
E [M(0, U )] =
M(0, u) f (u)du
R
(cid:7) w
(cid:8)
(cid:9)
2
u
w
− 1
f (u)du
= 2
0
= 2
w2
(cid:7) w
0
u2 f (u)du − 4
w
(cid:7) w
0
u f (u)du + 2
(cid:7) w
0
f (u)du
= 2
w2 I1
− 4
w I2
+ 2I3
,
where f (·) is the probability density function of U. Applying integration by
parts to I1, we obtain
I1
= σ 2
CRB Pr (U ∈ [0, w)) − σ 2
CRB f (w)w.
The remaining integrals are I2
[0, w)), respectively. Putting the integrals together,
(cid:20)
(cid:19)
(cid:10)
= −σ 2
CRB( f (w) − f (0)) and I3
= Pr(U ∈
σ 2
CRB
w2
+ 1
+
(cid:11)
σ 2
w ( f (w) − 2 f (0))
CRB
.
E [M(0, U )] = 2
Pr (U ∈ [0, w))
Writing β = σ
CRB
/w, we have
(cid:12)
E [M(0, U )] = 2
((cid:9)(1/β ) − 0.5)
(cid:4)
(cid:5)
+
β 2 + 1
(cid:4)
β
√
2π
exp(−1/2β 2) − 2
(cid:13)
(cid:5)
.
(cid:2)
A.4 Exact Detection of Subset of True Spikes. We have a set of K true
spikes, S, and ˆK estimates, ˆS. The set of estimates contains a subset of the
ground-truth spike times with the exception of R missing spikes and no
extras, such that ˆK = K − R with 0 ≤ R ≤ K. Due to the distributivity of the
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2753
convolution operation,
ˆy(t) = ˆx(t) ∗ p(cid:2) (t) = (x(t) − xr(t)) ∗ p(cid:2) (t) = y(t) − r(t),
where xr(t) and r(t) are the spike train and pulse train, respectively, of the
spikes missing from ˆS. From the form in equation A.2, the metric score be-
comes
M(y, ˆy) = 1 −
= 1 −
= 1 −
(cid:6)y − ˆy(cid:6)
(cid:6)y(cid:6) + (cid:6) ˆy(cid:6)
(cid:6)y − (y − r)(cid:6)
(cid:6)y(cid:6) + (cid:6)y − r(cid:6)
R(cid:6)p(cid:2)(cid:6)
K(cid:6)p(cid:2)(cid:6) + (K − R) (cid:6)p(cid:2)(cid:6)
= 1 −
1
2K/R − 1
.
A.5 Exact Detection of All True Spikes with Overestimation. We have
a set of K true spikes, S, and ˆK estimates, ˆS. The set of estimates contains all
the ground-truth spike times plus R ≥ 0 extra spikes, such that ˆK = K + R.
Due to the distributivity of the convolution operator, the estimated pulse
train can be written as
ˆy(t) = ˆx(t) ∗ p(cid:2) (t) = (x(t) + xr(t)) ∗ p(cid:2) (t) = y(t) + r(t),
where xr(t) and r(t) are the spike train and pulse train, respectively, of the
surplus spikes. From the form in equation A.2, the metric score becomes
M(S, ˆS) = 2(cid:6) min(y, ˆy)(cid:6)
(cid:6)y(cid:6) + (cid:6) ˆy(cid:6)
= 2(cid:6) min(y, y + r)(cid:6)
(cid:6)y(cid:6) + (cid:6)y + r(cid:6)
2(cid:6)y(cid:6)
2(cid:6)y(cid:6) + (cid:6)r(cid:6)
=
=
1
1 + (cid:6)r(cid:6)/(2(cid:6)y(cid:6))
,
where the penultimate line follows from the nonnegativity of y and r. As
(cid:6)y(cid:6) = K(cid:6)p(cid:2)(cid:6) and (cid:6)r(cid:6) = R(cid:6)p(cid:2)(cid:6), it follows that
M(S, ˆS) =
1
1 + R/2K
.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
2754
S. Reynolds et al.
Acknowledgments
This work was supported by European Research Council starting investi-
gator award, grant 277800, to P. L. D.; Biotechnology and Biological Sci-
ences Research Council, grant BB/K001817/1, to S. R. S.; EU Marie Curie
FP7 Initial Training Network, grant 289146, to S. R. S.; CIHR New Investi-
gator Award, grant 288936, to P. J. S.; CFI Leaders Opportunity Fund, grant
28331, to P. J. S.; CIHR Operating Grant, grant 126137, to P. J. S.; and NSERC
Discovery Grant, grant 418546-2, to P. J. S.
References
Abrahamsson, T., Chou, C., Li, S., Mancino, A., Costa, R. P., Brock, A., . . . Sjöström,
P. J., (2017). Differential regulation of evoked and spontaneous release by pre-
synaptic NMDA receptors. Neuron, 96(4), 839–855.
Altman, D. G., & Bland, J. M. (1983). Measurement in medicine: The analysis of
method comparison studies. Journal of the Royal Statistical Society. Series D, 32(3),
307–317.
Berens, P., Freeman, J., Deneux, T., Chenkov, N., McColgan, T., Speiser, A., . . . Bethge,
M. (2017). Community-based benchmarking improves spike inference from two-photon
calcium imaging data. bioRxiv.
Bray, J. R., & Curtis, J. T. (1957). An ordination of the upland forest communities of
southern Wisconsin. Ecological Monographs, 27(4), 325–349.
Chen, T.-W., Wardill, T. J., Sun, Y., Pulver, S. R., Renninger, S. L., Baohan, A., . . . Kim,
D. S. (2013). Ultrasensitive fluorescent proteins for imaging neuronal activity. Na-
ture, 499(7458), 295–300.
Deneux, T., Kaszas, A., Szalay, G., Katona, K., Lakner, T., Grinvald, A., . . . Vanzetta,
I. (2016). Accurate spike estimation from noisy calcium signals for ultrafast three-
dimensional imaging of large neuronal populations in vivo. Nature Communica-
tions, 7, 12190.
Dice, L. R. (1945). Measures of the amount of ecologic association between species.
Ecology, 26(3), 297–302.
Dombeck, D. A., Harvey, C. D., Tian, L., Looger, L. L., & Tank, D. W. (2010). Func-
tional imaging of hippocampal place cells at cellular resolution during virtual
navigation. Nature Neuroscience, 13, 1433–1440.
Friedrich, J., Zhou, P., & Paninski, L. (2017). Fast online deconvolution of calcium
imaging data. PLoS Computational Biology, 13(3), 1–26.
Giavarina, D. (2015). Understanding Bland Altman analysis. Biochemia Medica, 25(2),
141–151.
Huber, D., Gutnisky, D. A., Peron, S., O’Connor, D. H., Wiegert, J. S., Tian, L., . . .
Svoboda, K. (2012). Multiple dynamic representations in the motor cortex during
sensorimotor learning. Nature, 484, 473–478.
Kay, S. M. (1993). Fundamentals of statistical signal processing. Upper Saddle River, NJ:
Prentice Hall.
Kreuz, T., Haas, J. S., Morelli, A., Abarbanel, H. D., & Politi, A. (2007). Measuring
spike train synchrony. Journal of Neuroscience Methods, 165(1), 151–161.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
CosMIC: A Consistent Spike Inference Metric
2755
Lütcke, H., Gerhard, F., Zenke, F., Gerstner, W., & Helmchen, F. (2013). Inference
of neuronal network spike dynamics and topology from calcium imaging data.
Frontiers in Neural Circuits, 7, 201.
Oñativia, J., Schultz, S. R., & Dragotti, P. L. (2013). A finite rate of innovation algo-
rithm for fast and accurate spike detection from two-photon calcium imaging.
Journal of Neural Engineering, 10(4), 046017.
Pachitariu, M., Stringer, C., & Harris, K. D. (2017). Robustness of spike deconvolution
for calcium imaging of neural spiking. bioRxiv.
Paiva, A. R. C., Park, I., & Príncipe, J. C. (2010). A comparison of binless spike train
measures. Neural Computing and Applications, 19(3), 405–419.
Pappis, C. P., & Karacapilidis, N. I. (1993). A comparative assessment of measures of
similarity of fuzzy values. Fuzzy Sets and Systems, 56(2), 171–174.
Peron, S. P., Freeman, J., Iyer, V., Guo, C., & Svoboda, K. (2015). A cellular reso-
lution map of barrel cortex activity during tactile behavior. Neuron, 86(3), 783–
799.
Pnevmatikakis, E. A., Merel, J., Pakman, A., & Paninski, L. (2013). Bayesian spike
inference from calcium imaging data. In Proceedings of the 2013 Asilomar Conference
on Signals, Systems and Computers (pp. 349–353). Piscataway, NJ: IEEE.
Pnevmatikakis, E. A., Soudry, D., Gao, Y., Machado, T. A., Merel, J., Pfau, D., . . .
Paninski, L. (2016). Simultaneous denoising, deconvolution, and demixing of cal-
cium imaging data. Neuron, 89(2), 285–299.
Rahmati, V., Kirmse, K., Markovi´c, D., Holthoff, K., & Kiebel, S. J. (2016). Inferring
neuronal dynamics from calcium imaging data using biophysical models and
bayesian inference. PLoS Computational Biology, 12(2), 1–42.
Reynolds, S., Abrahamsson, T., Schuck, R., Sjöström, P. J., Schultz, S. R., & Dragotti,
P. L. (2017). ABLE: An activity-based level set segmentation algorithm for two-
photon calcium imaging data. eNeuro, 4(5).
Reynolds, S., Copeland, C. S., Schultz, S. R., & Dragotti, P. L. (2016). An extension of
the FRI framework for calcium transient detection. In Proceedings of the 2016 IEEE
13th International Symposium on Biomedical Imaging (pp. 676–679). Piscataway, NJ:
IEEE.
Reynolds, S., Oñativia, J., Copeland, C. S., Schultz, S. R., & Dragotti, P. L. (2015). Spike
detection using FRI methods and protein calcium sensors: Performance analysis
and comparisons. In Proceedings of the 11th International Conference on Sampling
Theory and Applications. Piscataway, NJ: IEEE.
Schreiber, S., Fellous, J., Whitmer, D., Tiesinga, P., & Sejnowski, T. (2003). A
new correlation-based measure of spike timing reliability. Neurocomputing, 52–
54(Suppl. C), 925–931.
Schuck, R., Go, M. A., Garasto, S., Reynolds, S., Dragotti, P. L., & Schultz, S. R. (2018).
Multiphoton minimal inertia scanning for fast acquisition of neural activity sig-
nals. Journal of Neural Engineering, 15(2), 025003.
Sofroniew, N. J., Flickinger, D., King, J., & Svoboda, K. (2016). A large field of view
two-photon mesoscope with subcellular resolution for in vivo imaging. eLife, 5,
e14472.
Sørensen, T. J. (1948). A method of establishing groups of equal amplitude in plant sociology
based on similarity of species content and its application to analyses of the vegetation on
Danish commons. København: I kommission hos E. Munksgaard.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3
2756
S. Reynolds et al.
Tada, M., Takeuchi, A., Hashizume, M., Kitamura, K., & Kano, M. (2014). A highly
sensitive fluorescent indicator dye for calcium imaging of neural activity in vitro
and in vivo. European Journal of Neuroscience, 39(11), 1720–1728.
van Rossum, M. C. W. (2001). A novel spike distance. Neural Computation, 13(4), 751–
763.
Victor, J. D., & Purpura, K. P. (1997). Metric-space analysis of spike trains: Theory,
algorithms and application. Network: Computation in Neural Systems, 8(2), 127–164.
Vogelstein, J. T., Packer, A. M., Machado, T. A., Sippy, T., Babadi, B., Yuste, R., &
Paninski, L. (2010). Fast nonnegative deconvolution for spike train inference from
population calcium imaging. Journal of Neurophysiology, 104(6), 3691–3704.
Vogelstein, J. T., Watson, B. O., Packer, A. M., Yuste, R., Jedynak, B., & Paninski,
L. (2009). Spike inference from calcium imaging using sequential Monte Carlo
methods. Biophysical Journal, 97(2), 636–655.
Zimmermann, H.-J. (2010). Fuzzy set theory. Wiley Interdisciplinary Reviews: Compu-
tational Statistics, 2(3), 317–332.
Zou, K. H., Warfield, S. K., Bharatha, A., Tempany, C. M., Kaus, M. R., Haker, S. J.,
. . . Kikinis, R. (2004). Statistical validation of image segmentation quality based
on a spatial overlap index: Scientific reports. Academic Radiology, 11(2), 178–189.
Received December 21, 2017; accepted April 26, 2018.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
/
e
d
u
n
e
c
o
a
r
t
i
c
e
-
p
d
/
l
f
/
/
/
/
3
0
1
0
2
7
2
6
2
0
1
5
0
6
6
n
e
c
o
_
a
_
0
1
1
1
4
p
d
.
/
f
b
y
g
u
e
s
t
t
o
n
0
9
S
e
p
e
m
b
e
r
2
0
2
3