LETTER

Communicated by Yoshua Bengio

An Approximation of the Error Backpropagation
Algorithm in a Predictive Coding Network
with Local Hebbian Synaptic Plasticity

James C. R. Whittington
james.whittington@ndcn.ox.ac.uk
MRC Brain Network Dynamics Unit, University of Oxford, Oxford, OX1 3TH, U.K.,
and FMRIB Centre, Nuffield Department of Clinical Neurosciences, Università
of Oxford, John Radcliffe Hospital, Oxford, OX3 9DU, U.K.

Rafal Bogacz
rafal.bogacz@ndcn.ox.ac.uk
MRC Brain Network Dynamics Unit, University of Oxford, Oxford OX1 3TH, U.K.,
and Nuffield Department of Clinical Neurosciences, University of Oxford,
John Radcliffe Hospital, Oxford OX3 9DU, U.K.

To efficiently learn from feedback, cortical networks need to update
synaptic weights on multiple levels of cortical hierarchy. An effective and
well-known algorithm for computing such changes in synaptic weights
is the error backpropagation algorithm. Tuttavia, in this algorithm, IL
change in synaptic weights is a complex function of weights and activi-
ties of neurons not directly connected with the synapse being modified,
whereas the changes in biological synapses are determined only by the
activity of presynaptic and postsynaptic neurons. Several models have
been proposed that approximate the backpropagation algorithm with lo-
cal synaptic plasticity, but these models require complex external control
over the network or relatively complex plasticity rules. Here we show that
a network developed in the predictive coding framework can efficiently
perform supervised learning fully autonomously, employing only simple
local Hebbian plasticity. Inoltre, for certain parameters, the weight
change in the predictive coding model converges to that of the backprop-
agation algorithm. This suggests that it is possible for cortical networks
with simple Hebbian synaptic plasticity to implement efficient learning
algorithms in which synapses in areas on multiple levels of hierarchy are
modified to minimize the error on the output.

1 introduzione

Efficiently learning from feedback often requires changes in synaptic
weights in many cortical areas. Per esempio, when a child learns sounds
associated with letters, after receiving feedback from a parent, the synaptic

Calcolo neurale 29, 1229–1262 (2017)
doi:10.1162/NECO_a_00949

C(cid:2) 2017 Istituto di Tecnologia del Massachussetts.
Pubblicato sotto Creative Commons
Attribuzione 3.0 Unported (CC BY 3.0) licenza.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1230

J. Whittington and R. Bogacz

weights need to be modified not only in auditory areas but also in asso-
ciative and visual areas. An effective algorithm for supervised learning of
desired associations between inputs and outputs in networks with hier-
archical organization is the error backpropagation algorithm (Rumelhart,
Hinton, & Williams, 1986). Artificial neural networks (ANNs) employing
backpropagation have been used extensively in machine learning (LeCun
et al., 1989; Chauvin & Rumelhart, 1995; Bogacz, Markowska-Kaczmar,
& Kozik, 1999) and have become particularly popular recently, with the
newer deep networks having some spectacular results, now able to equal
and outperform humans in many tasks (Krizhevsky, Sutskever, & Hinton,
2012; Hinton et al., 2012). Inoltre, models employing the backprop-
agation algorithm have been successfully used to describe learning in the
real brain during various cognitive tasks (Seidenberg & McClelland, 1989;
McClelland, McNaughton, & O’Reilly, 1995; Plaut, McClelland, Seidenberg,
& Patterson, 1996).

Tuttavia, it has not been known if natural neural networks could em-
ploy an algorithm analogous to the backpropagation used in ANNs. In
ANNs, the change in each synaptic weight during learning is calculated
by a computer as a complex, global function of activities and weights of
many neurons (often not connected with the synapse being modified). Nel
brain, Tuttavia, the network must perform its learning algorithm locally,
on its own without external influence, and the change in each synaptic
weight must depend on just the activity of presynaptic and postsynaptic
neurons. This led to a common view of the biological implausibility of this
algorithm (Crick, 1989)—for example: “Despite the apparent simplicity and
elegance of the back-propagation learning rule, it seems quite implausible
that something like equations [. . .] are computed in the cortex” (O’Reilly &
Munakata, 2000, P. 162).

Several researchers aimed at developing biologically plausible algo-
rithms for supervised learning in multilayer neural networks. Tuttavia,
the biological plausibility was understood in different ways by different re-
searchers. Così, to help evaluate the existing models, we define the criteria
we wish a learning model to satisfy, and we consider the existing models
within these criteria:

1. Local computation. A neuron performs computation only on the basis
of the inputs it receives from other neurons weighted by the strengths
of its synaptic connections.

2. Local plasticity. The amount of synaptic weight modification is depen-
dent on only the activity of the two neurons the synapse connects (E
possibly a neuromodulator).

3. Minimal external control. The neurons perform the computation au-
tonomously with as little external control routing information in dif-
ferent ways at different times as possible.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1231

4. Plausible architecture. The connectivity patterns in the model should
be consistent with basic constraints of connectivity in neocortex.

The models proposed for supervised learning in biological multilayer
neural networks can be divided in two classes. Models in the first class
assume that neurons (Barto & Jordan, 1987; Mazzoni, Andersen, & Jordan,
1991; Williams, 1992) or synapses (Unnikrishnan & Venugopal, 1994; Se-
ung, 2003) behave stochastically and receive a global signal describing the
error on the output (per esempio., via a neuromodulator). If the error is reduced,
the weights are modified to make the produced activity more likely. Many
of these models satisfy the above criteria, but they do not directly approxi-
mate the backpropagation algorithm, and it has been pointed out that under
certain conditions, their learning is slow and scales poorly with network
size (Werfel, Xiew, & Seung, 2005). The models in the second class explic-
itly approximate the backpropagation algorithm (O’Reilly, 1998; Lillicrap,
Cownden, Tweed, & Akerman, 2016; Balduzzi, Vanchinathan, & Buhmann,
2014; Bengio, 2014; Bengio, Lee, Bornschein, & Lin, 2015; Scellier & Bengio,
2016), and we will compare them in detail in section 4.

Here we show how the backpropagation algorithm can be closely ap-
proximated in a model that uses a simple local Hebbian plasticity rule. IL
model we propose is inspired by the predictive coding framework (Rao &
Ballard, 1999; Friston, 2003, 2005). This framework is related to the autoen-
coder framework (Ackley, Hinton, & Sejnowski, 1985; Hinton & McClelland,
1988; Dayan, Hinton, Neal, & Zemel, 1995) in which the GeneRec model
(O’Reilly, 1998) and another approximation of backpropagation (Bengio,
2014; Bengio et al., 2015) were developed. In both frameworks, the networks
include feedforward and feedback connections between nodes on different
levels of hierarchy and learn to predict activity on lower levels from the
representation on the higher levels. The predictive coding framework de-
scribes a network architecture in which such learning has a particularly
simple neural implementation. The distinguishing feature of the predictive
coding models is that they include additional nodes encoding the differ-
ence between the activity on a given level and that predicted by the higher
level, and that these prediction errors are propagated through the network
(Rao & Ballard, 1999; Friston, 2005). Patterns of neural activity similar to
such prediction errors have been observed during perceptual decision tasks
(Summerfield et al., 2006; Summerfield, Trittschuh, Monti, Mesulam, & Eg-
ner, 2008). In this letter, we show that when the predictive coding model
is used for supervised learning, the prediction error nodes have activity
very similar to the error terms in the backpropagation algorithm. There-
fore, the weight changes required by the backpropagation algorithm can be
closely approximated with simple Hebbian plasticity of connections in the
predictive coding networks.

In the next section, we review backpropagation in ANNs. Then we de-
scribe a network inspired by the predictive coding model in which the

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1232

J. Whittington and R. Bogacz

Tavolo 1: Corresponding and Common Symbols Used in Describing ANNs and
Predictive Coding Models.

Backpropagation Predictive Coding

Activity of a node (before nonlinearity)
Synaptic weight
Objective function
Prediction error
Activation function
Number of neurons in a layer
Highest index of a layer
Input from the training set
Output from the training set

(l)
sì
io
w(l)
io, j
E
δ(l)
io

(l)
X
io
θ (l)
io, j
F
ε(l)
io

F
(l)

N
lmax
sin
io
sout
io

weight update rules approximate those of conventional backpropagation.
We point out that for certain architectures and parameters, learning in the
proposed model converges to the backpropagation algorithm. We compare
the performance of the proposed model and the ANN. Inoltre, we
characterize the performance of the predictive coding model in supervised
learning for other architectures and parameters and highlight that it allows
learning bidirectional associations between inputs and outputs. Finalmente, we
discuss the relationship of this model to previous work.

2 Modelli

While we introduce ANNs and predictive coding below, we use a slightly
different notation than in their original description to highlight the cor-
respondence between the variables in the two models. The notation will
be introduced in detail as the models are described, but for reference it is
summarized in Table 1. To make dimensionality of variables explicit, we
denote vectors with a bar (per esempio., X). Matlab codes simulating an ANN and the
predictive coding network are freely available at the ModelDB repository
with access code 218084.

2.1 Review of Error Backpropagation. ANNs (Rumelhart et al., 1986)
are configured in layers, with multiple neuron-like nodes in each layer
as illustrated in Figure 1A. Each node gets input from a previous layer
weighted by the strengths of synaptic connection and performs a nonlinear
transformation of this input. To make the link with predictive coding more
visible, we change the direction in which layers are numbered and index
the output layer by 0 and the input layer by lmax. We denote by y
IL
input to the ith node in the lth layer, while the transformation of this by an
(l)
activation function is the output, F (sì
io

). Così:

(l)
io

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1233

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1: Backpropagation algorithm. (UN) Architecture of an ANN. Circles de-
note nodes, and arrows denote connections. (B) An example of activity and
weight changes in an ANN. Thick black arrows between the nodes denote con-
nections with high weights, and thin gray arrows denote the connections with
low weights. Filled and open circles denote nodes with higher and lower activ-
ità, rispettivamente. Rightward-pointing arrows labeled δ(l)
i denote error terms, E
their darkness indicates how large the errors are. Upward-pointing red arrows
indicate the weights that would most increase according to the backpropagation
algorithm.

(l)
io

sì

=

N(l+1)(cid:2)

j=1

w(l+1)
io, j

F

(cid:4)

(cid:3)

(l+1)
j

sì

(2.1)

where w(l)
io, j is the weight from the jth node in the lth layer to the ith node
in the (l − 1)th layer, and n(l) is the number of nodes in layer l. For brevity,
we refer to variable y

(l)
i as the activity of a node.

The output the network produces for a given input depends on the
values of the weight parameters. This can be illustrated in an example of
(0)
an ANN shown in Figure 1B. The output node y
1 has a high activity as it
(2)
receives an input from the active input node y
1 via strong connections. By

1234

J. Whittington and R. Bogacz

contrasto, for the other output node y
the active input node via strong connections, so its activity is low.

(0)
2 , there is no path leading to it from

The weight values are found during the following training procedure.

(lmax
At the start of each iteration, the activities in the input layer y
are set
io
to values from input training sample, which we denote by sin
io . The network
first makes a prediction: the activities of nodes are updated layer by layer
(0)
according to equation 2.1. The predicted output in the last layer y
È
io
then compared to the output training sample sout
. We wish to minimize the
difference between the actual and desired output, so we define the following
objective function:1

)

io

E = − 1
2

N(0)(cid:2)

(cid:3)

i=1

sout
io

− y

(0)
io

(cid:4)

2.

(2.2)

The training set contains many pairs of training vectors (sin, sout ), Quale
are iteratively presented to the network, but for simplicity of notation, we
consider just changes in weights after the presentation of a single training
pair. We wish to modify the weights to maximize the objective function,
so we update the weights proportionally to the gradient of the objective
function,

(cid:5)w(UN)
B,C

= α

∂E
∂w(UN)
B,C

,

(2.3)

where α is a parameter describing the learning rate.

Since weight w(UN)

B,c determines activity y

(a−1)
B

, the derivative of the objective

function over the weight can be found by applying the chain rule:

∂E
∂w(UN)
B,C

=

∂E
(a−1)
B

∂y

(a−1)
∂y
B
∂w(UN)
B,C

.

(2.4)

The first partial derivative on the right-hand side of equation 2.4 ex-
presses by how much the objective function can be increased by increasing
the activity of node b in layer a − 1, which we denote by

(0)
io

1As in previous work linking the backpropagation algorithm to probabilistic inference
(Rumelhart, Durbin, Golden, & Chauvin, 1995), we consider the output from the network
), as it simplifies the notation of the equivalent probabilistic
to be y
modello. This corresponds to an architecture in which the nodes in the output layer are
linear. A predictive coding network approximating an ANN with nonlinear nodes in all
layers was derived in a previous version of this letter (Whittington & Bogacz, 2015).

rather than f (sì

(0)
io

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

δ(a−1)
B

=

∂E
(a−1)
B

∂y

.

1235

(2.5)

io

2

. The error term δ(0)

The values of these error terms for the sample network in Figure 1B are
indicated by the darkness of the arrows labeled δ(l)
È
high because there is a mismatch between the actual and desired network
(0)
produzione, so by increasing the activity in the corresponding node y
2 , IL
objective function can be increased. By contrast, the error term δ(0)
is low
(0)
because the corresponding node y
1 already produces the desired output,
so changing its activity will not increase the objective function. The error
term δ(1)
(1)
is high because the corresponding node y
2 projects strongly to
(1)
(0)
2 producing output that is too low, so increasing the value of y
the node y
2
can increase the objective function. For analogous reasons, the error term
δ(1)
1

is low.
Now let us calculate the error terms δ(a−1)

2

1

B

. It is straightforward to eval-

(2.6)

uate them for the output layer:

∂E
(0)
∂y
B

= sout
B

− y

.

(0)
B

If we consider a node in an inner layer of the network, then we must
consider all possible routes through which the objective function is modified
when the activity of the node changes, questo è, we must consider the total
derivative:

∂E
(a−1)
B

∂y

N(a−2)(cid:2)

=

i=1

∂E
(a−2)
io

∂y

∂y
∂y

(a−2)
io
(a−1)
B

.

(2.7)

Using the definition of equation 2.5 and evaluating the last derivative of
equation 2.7 using the chain rule, we obtain the recursive formula for the
error terms:

⎧
⎪⎪⎪⎨
⎪⎪⎪⎩

δ(a−1)
B

=

sout
B

− y

(a−1)
B

if a − 1 = 0

N(a−2)(cid:2)

i=1

δ(a−2)
io

w(a−1)
io,B

(cid:3)(sì

F

(a−1)
B

)

if a − 1 > 0

.

(2.8)

The fact that the error terms in layer l > 0 can be computed on the basis
of the error terms in the next layer l − 1 gave the name “error backpropa-
gation” to the algorithm.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1236

J. Whittington and R. Bogacz

Substituting the definition of error terms from equation 2.5 into equation
2.4 and evaluating the second partial derivative on the right-hand side of
equation 2.4, we obtain

= δ(a−1)
B

F

(cid:3)

(cid:4)

.

(UN)
C

sì

∂E
∂w(UN)
B,C

(2.9)

According to equation 2.9, the change in weight w(UN)
B,c is proportional to
the product of the output from the presynaptic node f (sì(UN)
) and the error
C
term δ(a−1)
associated with the postsynaptic node. Red upward-pointing
arrows in Figure 1B indicate which weights would be increased the most in
this example, and it is evident that the increase in these weights will indeed
increase the objective function.

B

In summary, after presenting to the network a training sample, each
weight is modified proportionally to the gradient given in equation 2.9 con
the error term given by equation 2.8. The expression for weight change (Vedere
equations 2.9 E 2.8) is a complex global function of activities and weights
of neurons not connected to the synapse being modified. In order for real
neurons to compute it, the architecture of the model could be extended to
include nodes computing the error terms, which could affect the weight
i cambiamenti. As we will see, analogous nodes are present in the predictive
coding model.

2.2 Predictive Coding for Supervised Learning. Due to the generality
of the predictive coding framework, multiple network architectures within
this framework can perform supervised learning. In this section, we de-
scribe the simplest model that can closely approximate the backpropaga-
zione; we consider other architectures later. The description in this section
closely follows that of unsupervised predictive coding networks (Rao & Bal-
lard, 1999; Friston, 2005) but is adapted for the supervised setting. Also, we
provide a succinct description of the model. For readers interested in a grad-
ual and more detailed introduction to the predictive coding framework, we
recommend reading sections 1 E 2 of a tutorial on this framework (Bo-
gacz, 2017) before reading this section.

We first propose a probabilistic model for supervised learning. Then we
describe the inference in the model, its neural implementation, and finally
learning of model parameters.

2.2.1 Probabilistic Model. Figure 2A shows a structure of a probabilistic
model that parallels the architecture of the ANN shown in Figure 1A. It
consists of lmax layers of variables, such that the variables on level l depend
on the variables on level l + 1. It is important to emphasize that Figure 2A
does not show the architecture of the predictive coding network, only the
structure of the underlying probabilistic model. As we will see, the inference

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1237

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 2: Predictive coding model. (UN) Structure of the probabilistic model.
Circles denote random variables, and arrows denote dependencies between
them. (B) Architecture of the network. Arrows and lines ending with circles
denote excitatory and inhibitory connections, rispettivamente. Connections without
labels have weights fixed to 1.

in this model can be implemented by a network with the architecture shown
in Figure 2B.

)

are fixed to the input sample sin

By analogy to ANNs, we assume that variables on the highest level
(lmax
X
io , and the inferred values of variables
io
on level 0 are the output from the network. Readers familiar with predictive
coding models for sensory processing may be surprised that the sensory
input is provided to the highest level; traditionally in these models, IL
input is provided to level 0. Infatti, when biological neural networks learn
in a supervised manner, both input and output are provided to sensory
cortices. Per esempio, when a child learns the sounds of the letters, IL
input (cioè., the shape of a letter) is provided to visual cortex, the output (cioè.,
the sound) is provided to the auditory cortex, and both of these sensory
cortices communicate with associative cortex. The model we consider in this
section corresponds to a part of this network: from associative areas to the
sensory modality to which the output is provided. So in the example, level

1238

J. Whittington and R. Bogacz

0 corresponds to the auditory cortex, while the highest levels correspond to
associative areas. Così, the input sin
i presented to this network corresponds
not to the raw sensory input but, Piuttosto, to its representation preprocessed
by visual networks. We discuss how the sensory networks processing the
input modality can be introduced to the model in section 3.

¯X (l) be a vector of random variables on level l, and let us denote
¯X (l) by ¯x(l). Let us assume the following
a sample from random variable
relationship between the random variables on adjacent levels (for brevity
of notation, we write P( ¯x(l)) instead of P( ¯X (l) = ¯x(l))):

Let

(cid:3)
X

P

(l)
io

| ¯x

(l+1)

(cid:4)

= N

(cid:3)
X

(l)
io

; μ(l)
io

, (cid:8)(l)
io

(cid:4)

.

(2.10)

In equation 2.10, N (X; μ, (cid:8)) is the probability density of a normal dis-
tribution with mean μ and variance (cid:8). The mean of probability density on
level l is a function of the values on the higher-level analogous to the input
to a node in ANN (see equation 2.1):

μ(l)
io

=

N(l+1)(cid:2)

j=1

θ (l+1)
io, j

F

(cid:3)

(cid:4)

.

(l+1)
j

X

(2.11)

In equation 2.11, N(l) denotes the number of random variables on level
are the parameters describing the dependence of random vari-
i are learned

l, and θ (l+1)
ables. For simplicity in this letter, we do not consider how (cid:8)(l)
(Friston, 2005; Bogacz, 2017), but treat them as fixed parameters.

io, j

(lmax

−1) | ¯x

2.2.2 Inference. We now move to describing the inference in the model:
finding the most likely values of model variables, which will determine
the activity of nodes in the predictive coding network. We wish to find the
most likely values of all unconstrained random variables in the model that
)) (see Friston, 2005, E
maximize the probability P( ¯x(0), . . . , ¯x
Bogacz, 2017, for the technical details, however we are only considering the
first moment of an approximate distribution for each random variable and
(l)
from now onwards we will use the same notation x
to describe the first
io
(lmax
= sin
moments). Since the nodes on the highest levels are fixed to x
io ,
io
their values are not being changed but, Piuttosto, provide a condition on other
variables. To simplify calculations, we define the objective function equal
to the logarithm of the joint distribution (since the logarithm is a monotonic
operator, a logarithm of a function has the same maximum as the function
itself):

(lmax

)

(cid:3)

F = ln

P( ¯x

(0), . . . , ¯x

(lmax

−1) | ¯x

(lmax

(cid:4)
))

.

(2.12)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1239

Since we assumed that the variables on one level depend on variables of

the level above, we can write the objective function as

F =

−1(cid:2)
lmax

l=0

(cid:3)

ln

P( ¯x

(l) | ¯x

(cid:4)
(l+1))

.

(2.13)

Substituting equation 2.10 and the expression for a normal distribution

into the above equation, we obtain:

F =

(cid:9)

−1(cid:2)
lmax

N(l)(cid:2)

ln

l=0

i=1

1√

2π(cid:8)(l)

io

(cid:3)

X

−

(l)
io

− μ(l)
io
2(cid:8)(l)

io

(cid:10)

(cid:4)

2

.

(2.14)

Then, ignoring constant terms, we can write the objective function as

F = − 1
2

−1(cid:2)
lmax

N(l)(cid:2)

l=0

i=1

(cid:3)
X

(l)
io

(cid:4)
2

.

− μ(l)
io
(cid:8)(l)
io

(2.15)

(l)
Recall that we wish to find the values x
io

that maximize the above
(l)
objective function. This can be achieved by modifying x
i proportionally to
the gradient of the objective function. To calculate the derivative of F over
(l)
(l)
X
influences F in two ways: it occurs in equation 2.15
i we note that each x
io
explicitly, but it also determines the values of μ(l−1)
. Così, the derivative
contains two terms:

j

∂F
(UN)
∂x
B

= −

X

(UN)
B

− μ(UN)
B
(cid:8)(UN)
B

N(a−1)(cid:2)

+

i=1

X

(a−1)
io

− μ(a−1)
io
(cid:8)(a−1)
io

θ (UN)
io,b f

(cid:3)

(cid:3)

(cid:4)

.

(UN)
B

X

(2.16)

In equation 2.16, there are terms that repeat, so we denote them by

= x

ε(l)
io

(l)
io

− μ(l)
io
(cid:8)(l)
io

.

(2.17)

These terms describe by how much the value of a random variable on a
given level differs from the mean predicted by a higher level, so we refer
to them as prediction errors. Substituting the definition of prediction errors
(UN)
into equation 2.16, we obtain the following rule describing changes in x
B
over time:

˙x

(UN)
B

= −ε(UN)

B

+

ε(a−1)
io

θ (UN)
io,b f

(cid:3)

(cid:3)

(cid:4)

.

X

(UN)
B

N(a−1)(cid:2)

i=1

(2.18)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1240

J. Whittington and R. Bogacz

Figura 3: Possible implementation of nonlinearities in the predictive coding
modello (magnification of a part of the network in Figure 2B). Filled arrows
and lines ending with circles denote excitatory and inhibitory connections,
rispettivamente. Open arrow denotes a modulatory connection with multiplicative
effect. Circles and hexagons denote nodes performing linear and nonlinear
computations, rispettivamente.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

io

io, j

(l)
io

. The prediction errors ε(l)

2.2.3 Neural Implementation. The computations described by equations
2.17 E 2.18 could be performed by a simple network illustrated in Figure
2B with nodes corresponding to prediction errors ε(l)
and values of ran-
dom variables x
i are computed on the basis of
(l)
excitation from corresponding variable nodes x
i and inhibition from the
nodes on the higher level x
weighted by strength of synaptic connec-
(l)
tions θ (l+1)
i make computations on the basis of
the prediction error from the corresponding level and the prediction errors
from the lower level weighted by synaptic weights.

. Conversely, the nodes x

(l+1)
j

It is important to emphasize that for a linear function f (X) = x, the non-
linear terms in equations 2.17 E 2.18 would disappear, and these equa-
tions could be fully implemented in the simple network shown in Figure 2B.
To implement equation 2.17, a prediction error node would get excitation
from the corresponding variable node and inhibition equal to synaptic in-
put from higher-level nodes; così, it could compute the difference between
them. Scaling the activity of nodes encoding prediction error by a constant
(cid:8)(l)
could be implemented by self-inhibitory connections with weight (cid:8)(l)
io
(we do not consider them here for simplicity: for details see Friston, 2005,
and Bogacz, 2017). Analogous to implementing equation 2.18, a variable
node would need to change its activity proportionally to its inputs.

io

One can imagine several ways that the nonlinear terms can be imple-
mented, and Figure 3 shows one of them (Bogacz, 2017). The prediction
error nodes need to receive the input from the higher-level nodes trans-
formed through a nonlinear function, and this transformation could be
(1)
implemented by additional nodes (indicated by a hexagon labeled f (X
)
1
in Figure 3). Introducing additional nodes is also necessary to make the
pattern of connectivity in the model more consistent with that observed in
the cortex. In particular, in the original predictive coding architecture (Vedere

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1241

Figure 2B), the projections from the higher levels are inhibitory, whereas
connections between cortical areas are excitatory. Così, to make the pre-
dictive coding network in accordance with this, the sign of the top-down
input needs to be inverted by local inhibitory neurons (Spratling, 2008).
Here we propose that these local inhibitory neurons could additionally
perform a nonlinear transformation. With this arrangement, there are indi-
), and each node sends only the value
vidual nodes encoding x
it encodes. According to equation 2.18, the input from the lower level to a
variable node needs to be scaled by a nonlinear function of the activity of
variable node itself. Such scaling could be implemented by either a sepa-
rate node (indicated by a hexagon labeled f (cid:3)(X
) in Figure 3) or intrinsic
mechanisms within the variable node that would make it react to excitatory
inputs differentially depending on its own activity level.

(UN)
b and f (X

(1)
1

(UN)
B

In the predictive coding model, after the input is provided, all nodes are
updated according to equations 2.17 E 2.18, until the network converges
to a steady state. We label variables in the steady state with an asterisk (per esempio.,
X

or F∗).

∗(l)
io

(2)
1

Figure 4A illustrates values to which a sample model converges when
presented with a sample pattern. The activity in this case propagates from
node x
through the connections with high weights, resulting in activation
(1)
of nodes x
1 and x
(note that the double inhibitory connection from higher
to lower levels has overall excitatory effect). Initially the prediction error
nodes would change their activity, but eventually their activity converges
A 0 as their excitatory input becomes exactly balanced by inhibition.

(0)
1

2.2.4 Learning Parameters. During learning, the values of the nodes on
the lowest level are set to the output sample, ¯x(0) = ¯sout, as illustrated in
Figure 4B. Then the values of all nodes on levels l ∈ {1, . . . , lmax
− 1} are
modified in the same way as described before (see equation 2.18).

Figure 4B illustrates an example of operation of the model. The model is
(0)
presented with the desired output in which both nodes x
2 are ac-
(1)
tive. Node x
1 becomes active as it receives both top-down and bottom-up
input. There is no mismatch between these inputs, so the corresponding pre-
diction error nodes (ε(0)
(1)
2 gets
bottom-up but no top-down input, so its activity has intermediate value,
and the prediction error nodes connected with it (ε(0)

1 ) are not active. By contrast, the node x

1 and ε(1)

(0)
1 and x

2 and ε(1)

2 ) are active.

Once the network has reached its steady state, the parameters of the
model θ (l)
io, j are updated, so the model better predicts the desired output.
This is achieved by modifying θ (l)
io, j proportionally to the gradient of the
objective function over the parameters. To compute the derivative of the
objective function over θ (l)
io, j affects the value of function F
of equation 2.15 by influencing μ(l−1)

io, j , we note that θ (l)
, hence

io

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1242

J. Whittington and R. Bogacz

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 4: Example of a predictive coding network for supervised learning.
(UN) Prediction mode. (B) Learning mode. (C) Learning mode for a network with
high value of parameter describing sensory noise. Notation as in Figure 2B.

= ε∗(a−1)
B

F

(cid:3)

(cid:4)

.

∗(UN)
C

X

∂F∗
∂θ (UN)
B,C

(2.19)

According to equation 2.19, the change in a synaptic weight θ (UN)

B,c of con-
nection between levels a and a − 1 is proportional to the product of quanti-
ties encoded on these levels. For a linear function f (X) = x, the nonlinearity

Error Backpropagation in Cortical Networks

1243

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

in equation 2.19 would disappear, and the weight change would simply
be equal to the product of the activities of presynaptic and postsynaptic
nodes (see Figure 2B). Even if the nonlinearity is considered, as in Figure 3,
the weight change is fully determined by the activity of presynaptic and
postsynaptic nodes. The learning rules of the top and bottom weights must
be slightly different. For the bottom connection labeled θ (1)
1,1 in Figure 3, IL
change in a synaptic weight is simply equal to the product of the activity of
nodes it connects (round node ε(0)
)). For the top
connection, the change in weights is equal to the product of activity of the
presynaptic node (ε(0)
1 ) and function f of activity of the postsynaptic node
(1)
(round node x
1 ). This then maintains the symmetry of the connections: IL
bottom and the top connections are modified by the same amount. We refer
to these changes as Hebbian in a sense that in both cases, the weight change
is a product of monotonically increasing functions of activity of presynaptic
and postsynaptic neurons.

1 and hexagonal node f (X

(1)
1

Figure 4B illustrates the resulting changes in the weights. In the example
in Figure 4B, the weights that increase the most are indicated by long red
upward arrows. There would also be an increase in the weight between
(1)
ε(0)
2 and x
2 , indicated by a shorter arrow, but it would be not as large as
(1)
node x
2 has lower activity. It is evident that after these weight changes,
the activity of prediction error nodes would be reduced indicating that
the desired output is better predicted by the network. In algorithm 1, we
include pseudocode to clarify how the network operates in training mode.

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1244

3 Results

J. Whittington and R. Bogacz

3.1 Relationship between the Models. An ANN has two modes of
operation: during prediction, it computes its output on the basis of ¯sin,
while during learning, it updates its weights on the basis of ¯sin and ¯sout. IL
predictive coding network can also operate in these modes. We next discuss
the relationship between computations of an ANN and a predictive coding
network in these two modes.

3.1.1 Prediction. We show that the predictive coding network has a stable
fixed point at the state where all nodes have the same values as the corre-
sponding nodes in the ANN receiving the same input ¯sin. Since all nodes
change proportionally to the gradient of F, the value of function F always
increases. Since the network is constrained only by the input, the maximum
value that F can reach is 0; because F is a negative of sum of squares, Questo
maximum is achieved if all terms in the summation of equation 2.15 are
equal to 0, questo è, Quando

∗(l)
io

X

= μ∗(l)
io

(3.1)

io

Since μ(l)

(l)
is defined in analogous way as y
io

(cf. equations 2.1 E 2.11),
the nodes in the prediction mode have the same values at the fixed point as
∗(l)
the corresponding nodes in the ANN: X
io
The above property is illustrated in Figure 4A, in which weights are set
to the same value as for the ANN in Figure 1B, and the network is presented
with the same input sample. The network converges to the same pattern of
activity on level l = 0 as for the ANN in Figure 1B.

= y

(l)
io

.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

3.1.2 Apprendimento. The pattern of weight change in the predictive coding
network shown in Figure 4B is similar as in the backpropagation algorithm
(see Figure 1B). We now analyze under what conditions weight changes
in the predictive coding model converge to that in the backpropagation
algorithm.

The weight update rules in the two models (see equations 2.9 E 2.19)
have the same form; Tuttavia, the prediction error terms δ(l)
i were
defined differently. To see the relationship between these terms, we now
derive the recursive formula for prediction errors ε(l)
i analogous to that for
δ(l)
in equation 2.8. We note that once the network reaches the steady state
io
in the learning mode, the change in activity of each node must be equal to
zero. Setting the left-hand side of equation 2.18 A 0, we obtain

i and ε(l)

ε∗(UN)
B

=

N(a−1)(cid:2)

i=1

ε∗(a−1)
io

θ (UN)
io,b f

(cid:3)

(cid:3)

(cid:4)

.

X

∗(UN)
B

(3.2)

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1245

We can now write a recursive formula for the prediction errors:

⎧
⎪⎪⎪⎨
⎪⎪⎪⎩

ε∗(a−1)
B

=

(cid:3)

sout
B

− μ∗(a−1)
B

(cid:4)

/(cid:8)(0)
B

if a − 1 = 0

ε∗(a−2)
io

θ (a−1)
io,B

F

(cid:4)

(cid:3)

(cid:3)

∗(a−1)
B

X

if a − 1 > 0

N(a−2)(cid:2)

i=1

.

(3.3)

io

(l)
io

(l)
io

∗(l)
io

∗(l)
io

= y

∗(0)
io

We first consider the case when all variance parameters are set to (cid:8)(l)
= 1
(this corresponds to the original model of Rao & Ballard, 1999, dove il
prediction errors were not normalized). Then the formula has exactly the
same form as for the backpropagation algorithm, equation 2.8. Therefore, Esso
may seem that the weight change in the two models is identical. Tuttavia,
for the weight change to be identical, the values of the corresponding nodes
(it is sufficient for this condition to hold for l > 0,
must be equal: X
because x
do not directly influence weight changes). Although we have
= y
shown in that x
in the prediction mode, it may not be the case
(0)
in the learning mode, because the nodes x
), and thus
io
function F may not reach the maximum of 0, so equation 3.1 may not be
satisfied.

are fixed (to sout

(l)
is equal or close to y
io

∗(l)
We now consider under what conditions x
io

.
Primo, when the networks are trained such that they correctly predict the
output training samples, then objective function F can reach 0 during the
∗(l)
relaxation and hence x
, and the two models have exactly the same
io
weight changes. In particular, the change in weights is then equal to 0; così,
the weights resulting in perfect prediction are a fixed point for both models.
Secondo, when the networks are trained such that their predictions are
(0)
close to the output training samples, then fixing x
i will only slightly change
the activity of other nodes in the predictive coding model, so the weight
change will be similar.

= y

(l)
io

io

1,1 and w(2)

To illustrate this property, we compare the weight changes in predictive
coding models and ANN with the very simple architecture shown in Fig-
= 2) and one node in
ure 5A. This network consists of just three layers (lmax
each layer (N(0) = n(1) = n(2) = 1). Such a network has only two weight pa-
rameters (w(1)
1,1), so the objective function of the ANN can be easily
visualized. The network was trained on a set in which input training sam-
∈ [−5, 5], E
ples were generated randomly from uniform distribution sin
1
= W (1) di pesce(W (2) di pesce(sin
)),
output training samples were generated as sout
io
1
where W (1) = W (2) = 1 (see Figure 5B). Figure 5C shows the objective func-
tion of the ANN for this training set. Così, an ANN with weights equal to
w(l)
= W (l) perfectly predicts all samples in the training set, so the objective
1,1
function is equal to 0. There are also other combinations of weights resulting
in good prediction, which create a ridge of the objective function.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1246

J. Whittington and R. Bogacz

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 5: Comparison of weight changes in backpropagation and predictive
coding models. (UN) The structure of the network used. (B) The data that the
models were trained on—here, sout = tanh(di pesce(sin)). (C) The objective func-
tion of an ANN for a training set with 300 samples generated as described. IL
objective function is equal to the sum of 300 terms given by equation 2.2 cor-
responding to individual training samples. The red dot indicates weights that
maximize the objective function. (D) The objective function of the predictive
coding model at the fixed point. For each set of weights and training sample, A
find the state of predictive coding network at the fixed point, the nodes in lay-
ers 0 E 2 were set to training examples, and the node in layer 1 was updated
according to equation 2.18. This equation was solved using the Euler method. UN
dynamic form of the Euler integration step was used where its size was allowed
to reduce by a factor should the system not be converging (cioè., the maximum
change in node activity increases from the previous step). The initial step size
era 0.2. The relaxation was performed until the maximum value of ∂F/∂x(l)
i was
lower than 10−6/(cid:8) (0)
O 1 million iterations had been performed. (E–G) Angle
difference between the gradient for the ANN and the gradient for the predictive
coding model found from equation 2.19. Different panels correspond to differ-
ent values of parameter describing sensory noise. (E) (cid:8)(0)
= 8.
(G) (cid:8) (0)

= 1. (F) (cid:8) (0)

= 256.

1

1

io

1

Figure 5E shows the angle between the direction of weight change in
backpropagation and the predictive coding model. The directions of the
gradient for the two models are very similar except for the regions where
the objective functions E and F∗ are misaligned (see Figures 5C and 5D).

Error Backpropagation in Cortical Networks

1247

Nevertheless, close to the maximum of the objective function (indicated by
a red dot), the directions of weight change become similar and the angle
decreases toward 0.

io

io

(l)
io

(l)
io

= y

is increased relative to other (cid:8)(l)

There is also a third condition under which the predictive coding network
approximates the backpropagation algorithm. When the value of parame-
(0)
ters (cid:8)(0)
i on the
activity of other nodes is reduced, because ε(0)
i becomes smaller (see equa-
∗(l)
zione 2.17) and its influence on activity of other nodes is reduced. Thus x
io
(for l > 0), and the weight change in the predictive coding
is closer to y
model becomes closer to that in the backpropagation algorithm (recall that
∗(l)
the weight changes are the same when x
io

, the impact of fixing x

Multiplying (cid:8)(0)

i by a constant will also reduce all ε(l)
i by the same con-
stant (see equation 3.3); consequently, all weight changes will be reduced
by this constant. This can be compensated by multiplying the learning rate
α by the same constant, so the magnitude of the weight change remains
constant. In questo caso, the weight updates of the predictive coding network
will become asymptotically similar to the ANN, regardless of prediction
accuracy.

for l > 0).

Figures 5F and 5G show that as (cid:8)(0)

increases, the angle between weight
changes in the two models decreases toward 0. Così, as the parameters (cid:8)(0)
are increased, the weight changes in the predictive coding model converge
to those in the backpropagation algorithm.

. It reduces ε(0)

Figure 4C illustrates the impact of increasing (cid:8)(0)

2 , Quale
io
2 and ε(1)
(1)
in turn reduces x
2 . This decreases all weight changes, particularly
the change of the weight between nodes ε(0)
(indicated by a short
red arrow) because both of these nodes have reduced activity. After com-
pensating for the learning rate, these weight changes become more similar
to those in the backpropagation algorithm (compare Figures 4B, 4C, E
1B). Tuttavia, we note that learning driven by very small values of the
error nodes is less biologically plausible. In Figure 6, we will show that a
high value of (cid:8)(0)

is not required for good learning with these networks.

2 and x

(1)
2

io

io

io

3.2 Performance on More Complex Learning Tasks. To efficiently learn
in more complex tasks, ANNs include a “bias term,” or an additional node
in each layer that does not receive any input but has activity equal to 1. Noi
(l)
define this node as the node with index 0 in each layer, so f (sì
) = 1. Con
0
such a node, the definition of synaptic input (see equation 2.1) is extended to
include one additional term w(l+1)
, which is referred to as the bias term. IL
weight corresponding to the bias term is updated during learning according
to the same rule as all other weights (see equation 2.9).

io,0

An equivalent bias term can be easily introduced to the predictive coding
(l)
models. This would be just a node with a constant output of f (X
) = 1,
0
which projects to the next layer but does have an associated error node.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1248

J. Whittington and R. Bogacz

The activity of such a node would not change after the training inputs
are provided, and corresponding weights θ (l+1)
io,0 would be modified like all
other weights (see equation 2.19).

To assess the performance of the predictive coding model on more com-
plex learning tasks, we tested it on the MNIST data set. This is a data set
Di 28 by 28 images of handwritten digits, each associated with one of the
10 corresponding classes of digits. We performed the analysis for an ANN
= 3), with predictive coding networks of the
of size 784-600-600-10 (lmax
corresponding size. We use the logistic sigmoid as the activation function.
We ran the simulations for both the (cid:8)(0)
= 100 case.
Figura 6 shows the learning curves for these different models. Each curve is
the mean from 10 simulations, with the standard error shown as the shaded
regions.

= 1 case and the (cid:8)(0)

io

io

io

We see that the predictive coding models perform similarly to the ANN.
For a large value of parameter (cid:8)(0)
, the performance of the predictive coding
model was very similar to the backpropagation algorithm, in agreement
with an earlier analysis showing that the weight changes in the predictive
coding model then converge to those in the backpropagation algorithm.
Should we have had more than 20 steps in each inference stage (cioè., allowed
the network to converge in inference), the ANN and the predictive coding
network with (cid:8)(0)
= 100 would have had an even more similar trajectory.
We see that all the networks eventually obtain a training error of 0.00%
and a validation error of 1.7% A 1.8%. We did not optimize the learning
rate for validation error as we are solely highlighting the similarity between
ANNs and predictive coding.

io

3.3 Effects of the Architecture of the Predictive Coding Model. Since
the networks we have considered so far corresponded to the associative
areas and sensory area to which the output sample was provided, the input
samples sin
i were provided to the nodes at the highest level of hierarchy,
so we assumed that sensory inputs are already preprocessed by sensory
areas. The sensory areas can be added to the model by considering an
architecture in which there are two separate lower-level areas receiving
sin
i and sout
, which are both connected with higher areas (de Sa & Ballard,
1998; Hyvarinen, 1999; O’Reilly & Munakata, 2000; Larochelle & Bengio,
2008; Bengio, 2014; Srivastava & Salakhutdinov, 2012; Hinton, Osindero,
& Teh, 2006). Per esempio, in case of learning associations between visual
stimuli (per esempio., shapes of letters) and auditory stimuli (per esempio., their sounds), sin
io
and sout
could be provided to primary visual and primary auditory cortices,
rispettivamente. Both of these primary areas project through a hierarchy of
sensory areas to a common higher associative cortex.

io

io

To understand the potential benefit of such an architecture over the
standard backpropagation, we analyze a simple example of learning the
association between one-dimensional samples shown in Figure 7A. Since

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1249

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

(cid:11)

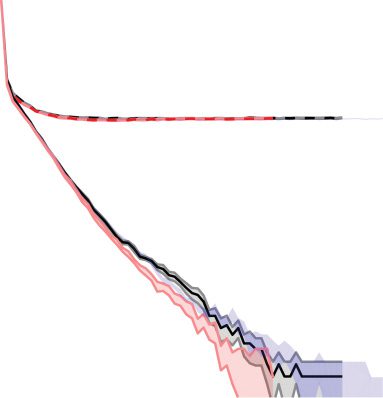
Figura 6: Comparison of prediction accuracy (%) for different models (indicated
by colors; see the key) on the MNIST dataset. Training errors are shown with
solid lines and validation errors with dashed lines. The dotted gray line denotes
2% error. The models were run 10 times each, initialized with different weights.
When the training error lines stop, this is when the mean error of the 10 runs
was equal to zero. The weights were drawn from a uniform distribution with
maximum and minimum values of ±4
6
N , where N is the total number of
neurons in the two layers on either side of the weight. The input data were first
transformed through an inverse logistic function as preprocessing before being
given to the network. When the network was trained with an image of class
C, the nodes in layer 0 were set to x(0)
= 0.03. After inference
C
and before the weight update, the error node values were scaled by (cid:8)(0)
so as
to be able to compare between the models. We used a batch size of 20, con un
learning rate of 0.001 and the stochastic optimizer Adam (Kingma & Ba, 2014)
to accelerate learning; this is essentially a per parameter learning rate, Dove
weights that are infrequently updated are updated more and vice versa. Noi
chose the number of steps in the inference phase to be 20; at this point, IL
network will not necessarily have converged, but we did so to aid speed of
training. This is not the minimum number of inference iterations that allows
for good learning, a notion that we will explore in a future paper. Otherwise
simulations are according to Figure 5. The shaded regions in the fainter color
describe the standard error of the mean. The figure is shown on a logarithmic
plot.

= 0.97 and x

(0)
j(cid:7)=c

io

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1250

J. Whittington and R. Bogacz

= a + b and sout
1

Figura 7: The effect of variance associated with different inputs on network pre-
dictions. (UN) Sample training set composed of 2000 randomly generated sam-
= a − b where a ∼ N (0, 1) and b ∼ N (0, 1/9).
ples, such that sin
1
Lines compare the predictions made by the model with different parameters
with predictions of standard algorithms (see the key). (B) Structure of the prob-
abilistic model. (C) Architecture of the simulated predictive coding network.
Notation as in Figure 2. Connections shown in gray are used if the network
predicts the value of the corresponding sample. (D) Root mean squared error
(RMSE) of the models with different parameters (see the key in panel A) trained
on data as in panel A and tested on a further 100 samples generated from the
same distribution. During the training, for each sample the network was al-
lowed to converge to the fixed point as described in the caption of Figure 5 E
the weights were modified with learning rate α = 1. The entire training and
testing procedure was repeated 50 times, and the error bars show the standard
error.

there is a simple linear relationship (with noise) between the samples in
Figure 7A, we will consider predictions generated by a very simple network
derived from a probabilistic model shown in Figure 7B. During the training
of this network, the samples are provided to the nodes on the lowest level
(X

= sout

(0)
2

= sin
1 ).

1 and x

(0)
1

For simplicity, we assume a linear dependence of variables on the higher

level:

(cid:3)
X

P

(0)
io

| X

(1)
1

(cid:4)

= N

(cid:3)
X

(0)
io

; θ (1)
io,1 X

(1)
1

, (cid:8)(0)
io

(cid:4)
.

(3.4)

Since the node on the highest level is no longer constrained, we need to
specify its prior probability, but for simplicity, we assume an uninformative

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1251

(1)
1

flat prior P(X
) = c, where c is a constant. Since the node on the highest
level is unconstrained, the objective function we wish to maximize is the
logarithm of the joint probability of all nodes:

F = ln

(cid:3)

P( ¯x

(0), X

(cid:4)
(1))

.

(3.5)

Ignoring constant terms, this function has an analogous form as in equa-

zione 2.15:

F = − 1
2

N(0)(cid:2)

(cid:3)
X

(0)
io

i=1

(cid:4)

2

(1)
1

.

− θ (1)
io,1 X
(cid:8)(0)
io

(3.6)

During training, the nodes on the lowest level are fixed, and the node on
the top level is updated proportionally to the derivative of F, analogous to
the models discussed previously:

˙x

(1)
1

=

N(0)(cid:2)

i=1

ε(0)
io

θ (1)
io,1

.

(3.7)

As before, such computation can be implemented in the simple network
shown in Figure 7C. After the nodes converge, the weights are modified to
maximize F, which here is simply (cid:5)θ (1)
(1)
1 .
io,1
= sin
1 and let both nodes x
A
be updated to maximize F—the node on the top level evolves according to
equation 3.7, while at the bottom level, ˙x

(0)
During testing, we only set x
2

(1)
1 and x

∼ ε(0)
i x

(0)
1

= ε(0)
io

(0)
io

.

This simple linear dependence could be captured by using a predictive
coding network without a hidden layer and just by learning the means
= N
, where ¯μ is the mean and
and covariance matrix, questo è, P
(cid:2) the covariance matrix. Tuttavia, we use a hidden layer to show the
more general network that could learn more complicated relationships if
nonlinear activation functions are used.

(cid:3)
(cid:4)
¯x; ¯μ, (cid:2)

(cid:3)
¯x

(cid:4)

∗(0)
1

= sin

(0)
) after providing different inputs (cioè., X
2

The solid lines in Figure 7A show the values predicted by the model (cioè.,
X
1 ), and different colors
correspond to different noise parameters. When equal noise is assumed in
input and output (red line), the network learns the probabilistic model that
explains the most variance in the data, so the model learns the direction in
which the data are most spread out. This direction is the same as the first
principal component shown in the dashed red line (any difference between
the two lines is due to the iterative nature of learning in the predictive
coding model).

When the noise parameter at the node receiving output samples is large
(the blue line in Figure 7A), the dynamics of the network will lead to the

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1252

J. Whittington and R. Bogacz

∗(1)
). Given
node at the top level converging to the input sample (cioè., X
1
the analysis presented earlier, the model converges then to the backprop-
agation algorithm, which in the case of linear f (X) simply corresponds to
linear regression, shown by the dashed blue line.

≈ sin
1

Conversely, when the noise at the node receiving input samples is large
(the green line in Figure 7A), the dynamics of the network will lead to the
∗(1)
).
node at the top level converging to the output sample (cioè., X
1
The network in this case will learn to predict the input sample on the basis
of the output sample. Hence, its predictions correspond to that obtained
by finding linear regression in inverse direction (cioè., the linear regression
predicting sin on the basis of sout), shown by the dashed green line.

≈ sout
1

Different predictions of the models with different noise parameters will
lead to different amounts of error when tested, which are shown in the left
part of Figure 7D (labeled “sin predicts sout”). The network approximating
the backpropagation algorithm is the most accurate, as the backpropagation
algorithm explicitly minimizes the error in predicting output samples. Prossimo
in accuracy is the network with equal noise on both input and output,
followed by the model approximating inverse regression.

Due to the flexible structure of the predictive coding network, we can
also test how well it is able to infer the likely value of input sample sin on
the basis of the output sample sout. In order to test it, we provide the trained
(1)
(0)
1 ) and let both nodes x
network with the output sample (X
1 E
1
(0)
2 be updated. The value x
X
to which the node corresponding to the
input converged is the network’s inferred value of the input. We compared
these values with actual sin in the testing examples, and the resulting root
mean squared errors are shown in the right part of Figure 7D (labeled “sout
predicts sin”). This time, the model approximating the inverse regression is
most accurate.

= sout

∗(0)
2

Figure 7D illustrates that when noise is present in the data, there is a
trade-off between the accuracy of inference in the two directions. Nev-
ertheless, the predictive coding network with equal noise parameters for
inputs and outputs is predicting relatively well in both directions, being just
slightly less accurate than the optimal algorithm for the given direction.

It is also important to emphasize that the models we analyzed in this
section generate different predictions only because the training samples are
noisy. If the amount of noise were reduced, the models’ predictions would
become more and more similar (and their accuracy would increase). Questo
parallels the property discussed earlier that the closer the predictive coding
models predict all samples in the training set, the closer their computation
to ANNs with backpropagation algorithm.

The networks in the cortex are likely to be nonlinear and include multiple
layers, but predictive coding models with corresponding architectures are
still likely to retain the key properties outlined above. Namely, they would
allow learning bidirectional associations between inputs and outputs, and if

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1253

the mapping between the inputs and outputs could be perfectly represented
by the model, the networks could be able to learn them and make accurate
predictions.

4 Discussion

In this letter, we have proposed how the predictive coding models can be
used for supervised learning. We showed that they perform the same com-
putation as ANNs in the prediction mode, and weight modification in the
learning mode has a similar form as for the backpropagation algorithm. Fur-
thermore, in the limit of parameters describing the noise in the layer where
output training samples are provided, the learning rule in the predictive
coding model converges to that for the backpropagation algorithm.

4.1 Biological Plausibility of the Predictive Coding Model. In this sec-
tion we discuss various aspects of the predictive coding model that require
consideration or future work to demonstrate the biological plausibility of
the model.

In the first model we presented (see section 2.2) and in the simulations
of handwritten digit recognition, the inputs and outputs corresponded to
layers different from the traditional predictive coding model (Rao & Bal-
lard, 1999), where the sensory inputs are presented to layer l = 0 while the
higher layers extract underlying features. Tuttavia, supervised learning in
a biological context would often involve presenting the stimuli to be asso-
ciated (per esempio., image of a letter, and a sound) to sensory neurons in different
modalities and thus would involve the network from “input modality” via
the higher associative cortex to the “output modality.” We focused in this
letter on analyzing a part of this network from the higher associative cortex
to the output modality, and thus we presented sout to nodes at layer l = 0.
We did this only for this case because it is easy to show analytically the re-
lationship between predictive coding and ANNs. Nevertheless, we would
expect the predictive coding network to also perform supervised learning
when sin is presented to layer 0, while sout to layer lmax, because the model
minimizes the errors between predictions of adjacent levels so it learns
the relationships between the variables on adjacent levels. It would be an
interesting direction for future work to compare the performance of the
predictive coding networks with input and outputs presented to different
layers.

In section 3.3, we briefly considered a more realistic architecture in-
volving both modalities represented on the lowest-level layers. Such an
architecture would allow for a combination of supervised and unsuper-
vised learning. If one no longer has a flat prior on the hidden node but a
gaussian prior (so as to specify a generative model), then each arm could
be trained separately in an unsupervised manner, while the whole network
could also be trained together. Consider now that the input to one of the

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1254

J. Whittington and R. Bogacz

arms is an image and the input at the other arm is the classification. It would
be interesting to investigate if the image arm could be pretrained separately
in an unsupervised manner alone and if this would speed up learning of
the classification.

We now consider the model in the context of the plausibility criteria
stated in section 1. The first two criteria of local computation and plasticity
are naturally satisfied in a linear version of the model (with f (X) = x),
and we discussed possible neural implementation of nonlinearities in the
modello (Guarda la figura 3). In that implementation, some of the neurons have a
(2)
linear activation curve (like the value node x
in Figure 3) and others are
1
)), which is consistent with the variability of
nonlinear (like the node f (X
the firing-input relationship (or f-I curve) observed in biological neurons
(Bogacz, Moraud, Abdi, Magill, & Baufreton, 2016).

(2)
1

The third criterion of minimal external control is also satisfied by the
modello, as it performs computations autonomously given input and outputs.
The model can also autonomously “recognize” when the weights should
be updated, because this should happen once the nodes converged to an
equilibrium and have stable activity. This simple rule would result in weight
update in the learning mode, but no weight change in the prediction mode,
because then the prediction error nodes have activity equal to 0, so the
weight change (see equation 2.19) is also 0. Nevertheless, without a global
control signal, each synapse could detect only if the two neurons it connects
have converged. It will be important to investigate if such a local decision
of convergence is sufficient for good learning.

io

The fourth criterion of plausible architecture is more challenging for the
predictive coding model. Primo, the model includes special one-to-one con-
(l)
nections between variable nodes (X
io ) and the corresponding prediction
error nodes (ε(l)
), while there is no evidence for such special pairing of
neurons in the cortex. It would be interesting to investigate if the predic-
tive coding model would still work if these one-to-one connections were
replaced by distributed ones. Secondo, the mathematical formulation of the
predictive coding model requires symmetric weights in the recurrent net-
lavoro, while there is no evidence for such a strong symmetry in cortex.
Tuttavia, our preliminary simulations suggest that symmetric weights are
not necessary for good performance of predictive coding network (as we
will discuss in a forthcoming paper). Third, the error nodes can be either
positive or negative, while biological neurons cannot have negative activ-
ità. Since the error neurons are linear neurons and we know that rectified
linear neurons exist in biology (Bogacz et al., 2016), a possible way we can
approximate a purely linear neuron in the model with a biological rectified
linear neuron is if we associate zero activity in the model with the base-
line firing rate of a biological neuron. Nevertheless, such an approximation
would require the neurons to have a high average firing rate, so that they
rarely produce a firing rate close to 0, and thus rarely become nonlinear.
Although the interneurons in the cortex often have higher average firing

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1255

rates, the pyramidal neurons typically do not (Mizuseki & Buzs´aki, 2013).
It will be important to map the nodes in the model on specific populations
in the cortex and test if the model can perform efficient computation with
realistic assumptions about the mean firing rates of biological neurons.

Nevertheless, predictive coding is an appealing framework for modeling
cortical networks, as it naturally describes a hierarchical organization con-
sistent with those of cortical areas (Friston, 2003). Inoltre, responses
of some cortical neurons resemble those of prediction error nodes, as they
show a decrease in response to repeated stimuli (Brown & Aggleton, 2001;
Mugnaio & Desimone, 1993) and an increase in activity to unlikely stimuli
(Campana, Summerfield, Morin, Malecek, & Ungerleider, 2016). Additionally,
neurons recently reported in the primary visual cortex respond to a mis-
match between actual and predicted visual input (Fiser et al., 2016; Zmarz
& Keller, 2016).

4.2 Does the Brain Implement Backprop? This letter shows that a pre-
dictive coding network converges to backpropagation in a certain limit of
parameters. Tuttavia, it is important to add that this convergence is more
of a theoretical result, as it occurs in a limit where the activity of error nodes
becomes close to 0. Così, it is unclear if real neurons encoding informa-
tion in spikes could reliably encode the prediction error. Nevertheless, IL
conditions under which the predictive coding model converges to the back-
propagation algorithm are theoretically useful, as they provide alternate
probabilistic interpretations of the backpropagation algorithm. This allows
a comparison of the assumptions made by the backpropagation algorithm
with the probabilistic structure of learning tasks and questions whether
setting the parameters of the predictive coding models to those approxi-
mating backpropagation is the most suitable choice for solving real-world
problems that animals face.

Primo, the predictive coding model corresponding to backpropagation as-
sumes that output samples are generated from a probabilistic model with
multiple layers of random variables, but most of the noise is added only
at the level of output samples (cioè., (cid:8)(0)
). By contrast, probabilis-
io
tic models corresponding to most of real-world data sets have variability
entering on multiple levels. Per esempio, if we consider classification of
images of letters, the variability is present in both high-level features like
length or angle of individual strokes and low-level features like the colors
of pixels.

>> (cid:8)(l>0)
io

Secondo, the predictive coding model corresponding to backpropagation
assumes a layered structure of the probabilistic model. By contrast, proba-
bilistic models corresponding to many problems may have other structures.
Per esempio, in the task from section 1 of a child learning the sounds of
the letters, the noise or variability is present in both the visual and audi-
tory stimuli. Così, this task could be described by a probabilistic model

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1256

J. Whittington and R. Bogacz

including a higher-level variable corresponding to a letter, which deter-
mines both the mean visual input perceived by a child and the sound made
by the parent. Così, the predictive coding networks with parameters that do
not implement the backpropagation algorithm exactly may be more suited
for solving the learning tasks that animals and humans face.

In summary, the analysis suggests that it is unlikely that brain networks
implement the backpropagation algorithm exactly. Invece, it seems more
probable that cortical networks perform computations similar to those of
a predictive coding network without any variance parameters dominating
any others. These networks would be able to learn relationships between
modalities in both directions and flexibly learn probabilistic models well
describing observed stimuli and the associations between them.

4.3 Previous Work on Approximation of the Backpropagation Algo-
rithm. As we mentioned in section 1, other models have been developed
describing how the backpropagation algorithm could be approximated in
a biological neural network. We now review these models, relate them to
the four criteria stated in section 1, and compare them with the predictive
coding model.

O’Reilly (1998) considered a modified ANN that also includes feedback
weights between layers that are equal to feedforward weights. In this mod-
ified ANN, the output of hidden nodes in the equilibrium is given by

(l)
o
io

= f

⎛

⎝

N(l+1)(cid:2)

j=1

w(l+1)
io, j

(l+1)
o
j

+

⎞

w(l)
j,i o

(l−1)
j

⎠ ,

N(l−1)(cid:2)

j=1

(4.1)

and the output of the output nodes satisfies in equilibrium the same condi-
tion as for the standard ANN (an equation similar to the one above but in-
cluding just the first summation). It has been demonstrated that the weight
change minimizing the error of this network can be well approximated by
the following update (O’Reilly, 1998):

(cid:5)w(l)
io, j

∼ o

(l−1),train
io

(l),train
o
j

− o

(l−1),pred
io

(l),pred
o
j

.

(4.2)

(l),pred
j

et al., 1985). In equation 4.2, o

prediction phase, when the input nodes are set to o

This is the contrastive Hebbian learning weight update rule (Ackley
denotes the output of the nodes in the
= sin
j and all the other
nodes are updated as described above, while o
denotes the output in
= sout
the training phase when, in addition, the output nodes are set to y
j
and the hidden nodes satisfy equation 4.1. Così, according to the plasticity
rule, each synapse needs to be updated twice—once after the network
settles to equilibrium during prediction and once after the network settles

(lmax
j
(l),train
j

(0)
j

)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1257

following the presentation of the desired output sample. Each of these two
updates relies just on local plasticity, but they have the opposite sign. Così,
the synapses on all levels of hierarchy need “to be aware” of the presence of
sout on the output and use Hebbian or anti-Hebbian plasticity accordingly.
Although it has been proposed how such plasticity could be implemented
(O’Reilly, 1998), it is not known if cortical synapses can perform such form
of plasticity.

In the above GeneRec model, the error terms δ are not explicitly repre-
sented in neural activity, and instead the weight change based on errors is
decomposed into a difference of two weight modifications: one based on
target value and one based on predicted value. By contrast, the predictive
coding model includes additional nodes explicitly representing error and,
thanks to them, has a simpler plasticity rule involving just a single Hebbian
modification. A potential advantage of such a single modification is robust-
ness to uncertainty about the presence of sout because no mistaken weight
updates can be made when sout is not present.

Bengio and colleagues (Bengio, 2014; Bengio et al., 2015) considered
how the backpropagation algorithm can be approximated in a hierarchical
network of autoencoders that learn to predict their own inputs. The general
frameworks of autoencoders and predictive coding are closely related, COME
both of the networks, which include feedforward and feedback connections,
learn to predict activity on lower levels from the representation on the
higher levels. This work (Bengio, 2014; Bengio et al., 2015) includes many
interesting results, such as improvement of learning due to the addition
of noise to the system. Tuttavia, it was not described how it is mapped
on a network of simple nodes performing local computation. There is a
discussion of a possible plasticity rule at the end of Bengio (2014) that has
a similar form as equation 4.2 of the GeneRec model.

Bengio and colleagues (Scellier & Bengio, 2016; Bengio & Fischer, 2015)
introduce another interesting approximation to implement backpropaga-
tion in biological neural networks. It has some similarities to the model
presented here in that it minimizes an energy function. Tuttavia, like con-
trastive Hebbian learning, it operates in two phases, a positive and a neg-
ative phase, where weights are updated from information obtained from
each phase. The weights are changed following a differential equation up-
date starting at the end of the negative phase and until convergence of
the positive phase. Learning must be inhibited during the negative phase,
which would require a global signal. This model also achieves good results
on the MNIST data set.

Lillicrap et al. (2016) focused on addressing the requirement of the
backpropagation algorithm that the error terms need to be transmitted
backward through exactly the same weights that are used to transmit in-
formation feedforward. Remarkably, they have shown that even if ran-
dom weights are used to transmit the errors backward, the model can still
learn efficiently. Their model requires external control over nodes to route

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1258

J. Whittington and R. Bogacz

information differentially during training and testing. Inoltre, we note
that the requirement of symmetric weights between the layers can be en-
forced by using symmetric learning rules like those proposed in GeneRec
and predictive coding models. Equally, we will show in a future paper
that the symmetric requirement is not actually necessary in the predictive
coding model.

Balduzzi et al. (2014) showed that efficient learning may be achieved by
a network that receives a global error signal and in which synaptic weight
modification depends jointly on the error and the terms describing the
influence of each neuron of final error. Tuttavia, it is not specified in this
work how these influence terms could be computed in a way satisfying the
criteria stated in section 1.

Finalmente, it is worth pointing out that previous papers have shown that
certain models perform similar computations as ANNs or that they approx-
imate the backpropagation algorithm, while in this letter, we show, for the
first time, that a biologically plausible algorithm may actually converge to
backpropagation. Although this convergence in the limit is more of a the-
oretical result, it provides a mean to clarify the computational relationship
between the proposed model and backpropagation, as described above.

4.4 Relationship to Experimental Data. We hope that the proposed
extension of the predictive coding framework to supervised learning will
make it easier to test this framework experimentally. The model predicts
that in a supervised learning task, like learning sounds associated with
shapes, the activity after feedback, proportional to the error made by a
participant, should be seen not only in auditory areas but also visual and
associative areas. In such experiments, the model can be used to estimate
prediction errors, and one could analyze precisely which cortical regions
or layers have activity correlated with model variables. Inspection of the
neural activity could in turn refine the predictive coding models, so they
better reflect information processing in cortical circuits.

The proposed predictive coding models are still quite abstract, and it is
important to investigate if different linear or nonlinear nodes can be mapped
on particular anatomically defined neurons within a cortical microcircuit
(Bastos et al., 2012). Iterative refinements of such mapping on the basis of
experimental data (such as f-I curves of these neurons, their connectivity,
and activity during learning tasks) may help understand how supervised
and unsupervised learning is implemented in the cortex.

Predictive coding has been proposed as a general framework for de-
scribing computations in the neocortex (Friston, 2010). It has been shown
in the past how networks in the predictive coding framework can perform
unsupervised learning, attentional modulations, and action selection (Rao
& Ballard, 1999; Feldman & Friston, 2010; Friston, Daunizeau, Kilner, &
Kiebel, 2010). Here we add to this list supervised learning, and associative
memory (as the networks presented here are able to associate patterns of

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Error Backpropagation in Cortical Networks

1259

neural activity with each other). It is remarkable that the same basic net-
work structure can perform this variety of the computational tasks, also
performed by the neocortex. Inoltre, this network structure can be
optimized for different tasks by modifying proportions of synapses among
different neurons. Per esempio, the networks considered here for super-
vised learning did not include connections encoding covariance of random
variables, which are useful for certain unsupervised learning tasks (Bogacz,
2017). These properties of the predictive coding networks parallel the orga-
nization of the neocortex, where the same cortical structure is present in all
cortical areas, differing only in proportions and properties of neurons and
synapses in different layers.

Ringraziamenti

This work was supported by Medical Research Council grant MC UU
12024/5 and the EPSRC. We thank Tim Vogels, Chris Summerfield, E
Eduardo Martin Moraud for reading the previous version of this letter and
providing very useful comments.

Riferimenti

Ackley, D. H., Hinton, G. E., & Sejnowski, T. J. (1985). A learning algorithm for

Boltzmann machines. Cognitive Science, 9, 147–169.

Balduzzi, D., Vanchinathan, H., & Buhmann, J. (2014). Kickback cuts backprop’s red-tape:

Biologically plausible credit assignment in neural networks. arXiv:1411.6191v1.

Barto, A., & Jordan, M. (1987). Gradient following without back-propagation in
layered networks. In Proceedings of the 1st Annual International Conference on Neural
Networks (vol. 2, pag. 629–636). Piscataway, NJ.

Bastos, UN. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries, P., & Friston,
K. J. (2012). Canonical microcircuits for predictive coding. Neuron, 76, 695–
711.

Campana, UN. H., Summerfield, C., Morin, E. L., Malecek, N. J., & Ungerleider, l. G. (2016).
Encoding of stimulus probability in macaque inferior temporal cortex. Current
Biology, 26(17), 2280.

Bengio, Y. (2014). How auto-encoders could provide credit assignment in deep networks via

target propagation. arXiv:1407.7906.

Bengio, Y., & Fischer, UN. (2015). Early inference in energy-based models approximates

back-propagation. arXiv:1510.02777.

Bengio, Y., Lee, D.-H., Bornschein, J., & Lin, Z. (2015). Towards biologically plausible

deep learning. arXiv:1502.04156.

Bogacz, R. (2017). A tutorial on the free-energy framework for modelling perception

and learning. Journal of Mathematical Psychology, 76, 198–211.

Bogacz, R., Markowska-Kaczmar, U., & Kozik, UN. (1999). Blinking artefact recog-
nition in EEG signal using artificial neural network. In Proceedings of 4th Con-
ference on Neural Networks and Their Applications (pag. 502–507). Politechnika
Czestochowska.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

2
9
5
1
2
2
9
2
0
1
5
0
8
0
N
e
C
o
_
UN
_
0
0
9
4
9
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

1260

J. Whittington and R. Bogacz

Bogacz, R., Moraud, E. M., Abdi, A., Magill, P. J., & Baufreton, J. (2016). Properties
of neurons in external globus pallidus can support optimal action selection. PLoS
Comput. Biol., 12(7), e1005004.

Brown, M. W., & Aggleton, J. P. (2001). Recognition memory: What are the roles of
the perirhinal cortex and hippocampus? Nature Reviews Neuroscience, 2(1), 51–61.
Chauvin, Y., & Rumelhart, D. E. (1995). Backpropagation: Theory, architectures, E

applications. Mahwah, NJ: Erlbaum.

Crick, F. (1989). The recent excitement about neural networks. Nature, 337, 129–132.
Dayan, P., Hinton, G. E., Neal, R. M., & Zemel, R. S. (1995). The Helmholtz machine.