LETTER
Communicated by Jurgen Schmidhuber
Continuous Online Sequence Learning with an Unsupervised
Neural Network Model
Yuwei Cui
ycui@numenta.com
Subutai Ahmad
sahmad@numenta.com
Jeff Hawkins
jhawkins@numenta.com
Numenta, Inc. Redwood City, CA 94063, U.S.A.
The ability to recognize and predict temporal sequences of sensory in-
puts is vital for survival in natural environments. Based on many known
properties of cortical neurons, hierarchical temporal memory (HTM) se-
quence memory recently has been proposed as a theoretical framework
for sequence learning in the cortex. In this letter, we analyze properties of
HTM sequence memory and apply it to sequence learning and prediction
problems with streaming data. We show the model is able to continuously
learn a large number of variable order temporal sequences using an unsu-
pervised Hebbian-like learning rule. The sparse temporal codes formed
by the model can robustly handle branching temporal sequences by main-
taining multiple predictions until there is sufficient disambiguating ev-
idence. We compare the HTM sequence memory with other sequence
learning algorithms, including statistical methods—autoregressive inte-
grated moving average; feedforward neural networks—time delay neural
network and online sequential extreme learning machine; and recurrent
neural networks—long short-term memory and echo-state networks on
sequence prediction problems with both artificial and real-world data.
The HTM model achieves comparable accuracy to other state-of-the-art
algorithms. The model also exhibits properties that are critical for se-
quence learning, including continuous online learning, the ability to
handle multiple predictions and branching sequences with high-order
statistics, robustness to sensor noise and fault tolerance, and good per-
formance without task-specific hyperparameter tuning. Therefore, IL
HTM sequence memory not only advances our understanding of how
the brain may solve the sequence learning problem but is also applicable
to real-world sequence learning problems from continuous data streams.
Calcolo neurale 28, 2474–2504 (2016)
doi:10.1162/NECO_a_00893
C(cid:2) 2016 Istituto di Tecnologia del Massachussetts.
Pubblicato sotto Creative Commons
Attribuzione 3.0 Unported (CC BY 3.0) licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2475
1 introduzione
In natural environments, the cortex continuously processes streams of sen-
sory information and builds a rich spatio temporal model of the world.
The ability to recognize and predict ordered temporal sequences is critical
to almost every function of the brain, including speech recognition, active
tactile perception, and natural vision. Neuroimaging studies have demon-
strated that multiple cortical regions are involved in temporal sequence
processing (Clegg, Digirolamo, & Keele, 1998; Mauk & Buonomano, 2004).
Recent neurophysiology studies have shown that even neurons in primary
visual cortex can learn to recognize and predict spatiotemporal sequences
(Gavornik & Bear, 2014; Xu, Jiang, Poo, & Dan, 2012) and that neurons in
primary visual and auditory cortex exhibit sequence sensitivity (Brosch &
Schreiner, 2000; Nikoli´c, H¨ausler, Singer, & Maass, 2009). These studies sug-
gest that sequence learning is an important problem that is solved by many
cortical regions.
Machine learning researchers have also extensively studied sequence
learning independent of neuroscience. Statistical models, such as hidden
Markov models (HMM; Fine, Singer, & Tishby, 1998; Rabiner & Juang,
1986) and autoregressive integrated moving average (ARIMA; Durbin &
Koopman, 2012), have been developed for temporal pattern recognition
and time-series prediction, rispettivamente. A variety of neural network mod-
els have been proposed to model sequential data. Feedforward networks
such as time-delay neural networks (TDNN) have been used to model se-
quential data by adding a set of delays to the input (Waibel, Hanazawa,
Hinton, Shikano, & Lang, 1989). Recurrent neural networks can model se-
quence structure with recurrent lateral connections and process the data
sequentially one record at a time. Per esempio, long short-term memory
(LSTM) has the ability to selectively pass information across time and can
model very long-term dependencies using gating mechanisms (Hochreiter
& Schmidhuber, 1997) and gives impressive performance on a wide va-
riety of real-world problems (Greff, Srivastava, Koutnik, Steunebrink, &
Schmidhuber, 2015; Lipton, Berkowitz, & Elkan, 2015; Sutskever, Vinyals,
& Le, 2014). Echo state network (ESN) uses a randomly connected recur-
rent network as a dynamics reservoir and models a sequence as a trainable
linear combination of these response signals (Jaeger & Haas, 2004).
Can machine learning algorithms gain any insight from cortical algo-
rithms? The current state-of-the-art statistical and machine learning algo-
rithms achieve impressive prediction accuracy on benchmark problems
Tuttavia, most time-series prediction benchmarks do not focus on model
performance in dynamic, nonstationary scenarios. Benchmarks typically
have separate training and testing data sets, where the underlying assump-
tion is that the test data share similar statistics as the training data (Ben Taieb,
Bontempi, Atiya, & Sorjamaa, 2012; Crone, Hibon, & Nikolopoulos, 2011).
In contrasto, sequence learning in the brain has to occur continuously to deal
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2476
Y. Cui, S. Ahmad, and J. Hawkins
with the noisy, constantly changing streams of sensory inputs. Notably,
with the increasing availability of streaming data, there is also an increas-
ing demand for online sequence algorithms that can handle complex, noisy
data streams. Therefore, reverse-engineering the computational principles
used in the brain could offer additional insights into the sequence learning
problem that lies at the heart of many machine learning applications.
The exact neural mechanisms underlying sequence memory in the brain
remain unknown, but biologically plausible models based on spiking neu-
rons have been studied. Per esempio, Rao and Sejnowski (2001) showed
that spike-time-dependent plasticity rules can lead to predictive sequence
learning in recurrent neocortical circuits. Spiking recurrent network mod-
els have been shown to recognize and recall precisely timed sequences of
inputs using supervised learning rules (Brea, Senn, & Pfister, 2013; Ponulak
& Kasi ´nski, 2010). These studies demonstrate that certain limited types of
sequence learning can be solved with biologically plausible mechanisms.
Tuttavia, only a few practical sequence learning applications use spiking
network models as these models recognize only relatively simple and lim-
ited types of sequences. These models also do not match the performance
of nonbiological statistical and machine learning approaches on real-world
problems.
In this letter, we present a comparative study of HTM sequence mem-
ory, a detailed model of sequence learning in the cortex (Hawkins & Ah-
mad, 2016). The HTM neuron model incorporates many recently discovered
properties of pyramidal cells and active dendrites (Antic, Zhou, Moore,
Corto, & Ikonomu, 2010; Major, Larkum, & Schiller, 2013). Complex se-
quences are represented using sparse distributed temporal codes (Ahmad
& Hawkins, 2016; Kanerva, 1988), and the network is trained using an on-
line unsupervised Hebbian-style learning rule. The algorithms have been
applied to many practical problems, including discrete and continuous se-
quence prediction, anomaly detection (Lavin & Ahmad, 2015), and sequence
recognition and classification.
We compare HTM sequence memory with four popular statistical and
machine learning techniques: ARIMA, a statistical method for time-series
forecasting (Durbin & Koopman 2012); extreme learning machine (ELM),
a feedforward network with sequential online learning (Huang, Zhu, &
Siew, 2006; Liang, Huang, Saratchandran, & Sundararajan, 2006); e due
recurrent networks, LSTM and ESN. We show that HTM sequence mem-
ory achieves comparable prediction accuracy to these other techniques. In
aggiunta, it exhibits a set of features that is desirable for real-world se-
quence learning from streaming data. We demonstrate that HTM networks
learn complex high-order sequences from data streams, rapidly adapt to
changing statistics in the data, naturally handle multiple predictions and
branching sequences, and exhibit high tolerance to system faults.
The letter is organized as follows. In section 2, we discuss a list of desired
properties of sequence learning algorithms for real-time streaming data
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2477
analysis. In section 3, we introduce the HTM temporal memory model. In
sections 4 E 5, we apply the HTM temporal memory and other sequence
learning algorithms to discrete artificial data and continuous real-world
dati, rispettivamente. Discussion and conclusions are given in section 6.
2 Challenges of Real-Time Streaming Data Analysis
With the increasing availability of streaming data, the demand for online
sequence learning algorithms is increasing. Here, a data stream is an or-
dered sequence of data records that must be processed in real time using
limited computing and storage capabilities. In the field of data stream min-
ing, the goal is to extract knowledge from continuous data streams such as
computer network traffic, sensor data, and financial transactions (Domin-
gos & Hulten, 2000; Gaber, Zaslavsky, & Krishnaswamy, 2005; Gama, 2010),
which often have changing statistics (nonstationary) (Sayed-Mouchaweh &
Lughofer, 2012). Real-world sequence learning from such complex, noisy
data streams requires many other properties in addition to prediction accu-
racy. This stands in contrast to many machine learning algorithms, Quale
are developed to optimize performance on static data sets and lack the
flexibility to solve real-time streaming data analysis tasks.
In contrast to these algorithms, the cortex solves the sequence learn-
ing problem in a drastically different way. Rather than achieving optimal
performance for a specific problem (per esempio., through gradient-based optimiza-
zione), the cortex learns continuously from noisy sensory input streams and
quickly adapts to the changing statistics of the data. When information is in-
sufficient or ambiguous, the cortex can make multiple plausible predictions
given the available sensory information.
Real-time sequence learning from data streams presents unique chal-
lenges for machine learning algorithms. In addition to prediction accuracy,
we list a set of criteria that apply to both biological systems and real-world
streaming applications.
2.1 Continuous Learning. Continuous data streams often have chang-
ing statistics. Di conseguenza, the algorithm needs to continuously learn from
the data streams and rapidly adapt to changes. This property is impor-
tant for processing continuous real-time sensory streams but has not been
well studied in machine learning. For real-time data stream analysis, it is
valuable if the algorithm can recognize and learn new patterns rapidly.
Machine learning algorithms can be classified into batch or online learn-
ing algorithms. Both types of algorithms can be adopted for continuous
learning applications. To apply a batch-learning algorithm to continuous
data stream analysis, one needs to keep a buffered data set of past data
records. The model is retrained at regular intervals because the statistics
of the data can change over time. The batch-training paradigm poten-
tially requires significant computing and storage resources, particularly in
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2478
Y. Cui, S. Ahmad, and J. Hawkins
situations where the data velocity is high. In contrasto, online sequential al-
gorithms can learn sequences in a single pass and do not require a buffered
insieme di dati.
2.2 High-Order Predictions. Real-world sequences contain contextual
dependencies that span multiple time steps (cioè., the ability to make high-
order predictions). The term order refers to Markov order, specifically the
minimum number of previous time steps the algorithm needs to consider
in order to make accurate predictions. An ideal algorithm should learn the
order automatically and efficiently.
2.3 Multiple Simultaneous Predictions. For a given temporal context,
there could be multiple possible future outcomes. With real-world data, Esso
is often insufficient to consider only the single best prediction when infor-
mation is ambiguous. A good sequence learning algorithm should be able
to make multiple predictions simultaneously and evaluate the likelihood of
each prediction online. This requires the algorithm to output a distribution
of possible future outcomes. This property is present in HMMs (Rabiner &
Juang, 1986) and generative recurrent neural network models (Hochreiter
& Schmidhuber, 1997), but not in other approaches like ARIMA, which are
limited to maximum likelihood prediction.
2.4 Noise Robustness and Fault Tolerance. Real-world sequence learn-
ing deals with noisy data sources where sensor noise, data transmission
errors, and inherent device limitations frequently result in inaccurate or
missing data. A good sequence learning algorithm should exhibit robust-
ness to noise in the inputs.
The algorithm should also be able to learn properly in the event of sys-
tem faults such as loss of synapses and neurons in a neural network. IL
property of fault tolerance and robustness to failure, present in the brain,
is important for the development of next-generation neuromorphic proces-
sors (Tran, Yanushkevich, Lyshevski, & Shmerko, 2011). Noise robustness
and fault tolerance ensure flexibility and wide applicability of the algorithm
to a wide variety of problems.
2.5 No Hyperparameter Tuning. Learning in the cortex is extremely
robust for a wide range of problems. In contrasto, most machine learning
algorithms require optimizing a set of hyperparameters for each task. It
typically involves searching through a manually specified subset of the hy-
perparameter space, guided by performance metrics on a cross-validation
insieme di dati. Hyperparameter tuning presents a major challenge for applica-
tions that require a high degree of automation, like data stream mining. An
ideal algorithm should have acceptable performance on a wide range of
problems without any task-specific hyperparameter tuning.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2479
Many of the existing machine learning techniques demonstrate these
properties to various degrees. A truly flexible and powerful system for
streaming analytics would meet all of them. In the rest of the letter, we
compare HTM sequence memory with other common sequence learning
algorithms (ARIMA, ELM, ESN, TDNN, and LSTM) on various tasks using
the above criteria.
3 HTM Sequence Memory
In this section we describe the computational details of HTM sequence
memory. We first describe our neuron model. We then describe the repre-
sentation of high-order sequences, followed by a formal description of our
learning rules. We point out some of the relevant neuroscience experimen-
tal evidence in our description. A detailed mapping to the biology can be
found in Hawkins and Ahmad (2016).
3.1 HTM Neuron Model. The HTM neuron (see Figure 1B) implements
nonlinear synaptic integration inspired by recent neuroscience findings re-
garding the function of cortical neurons and dendrites (Major et al., 2013;
Spruston, 2008). Each neuron in the network contains two separate zones:
a proximal zone containing a single dendritic segment and a distal zone
containing a set of independent dendritic segments. Each segment main-
tains a set of synapses. The source of the synapses is different depending on
the zone (see Figure 1B). Proximal synapses represent feedforward inputs
into the layer, whereas distal synapses represent lateral connections within
a layer and feedback connections from a higher region. In this letter, we
consider only a single layer and ignore feedback connections.
Each distal dendritic segment contains a set of lateral synaptic connec-
tions from other neurons within the layer. A segment becomes active if
the number of simultaneously active connections exceeds a threshold. An
active segment does not cause the cell to fire but instead causes the cell to
enter a depolarized state, which we call the predictive state. In this way,
each segment detects a particular temporal context and makes predictions
based on that context. Each neuron can be in one of three internal states:
an active state, a predictive state, or a nonactive state. The output of the
neuron is always binary: it is active or not.
This neuron model is inspired by a large number of recent experimental
findings that suggest neurons do not perform a simple weighted sum of
their inputs and fire based on that sum (Polsky, Mel, & Schiller, 2004; Smith,
Smith, Branco, & H¨ausser, 2013) as in most neural network models (LeCun,
Bengio, & Hinton, 2015; McFarland, Cui, & Butts, 2013; Schmidhuber, 2014).
Invece, dendritic branches are active processing elements. The activation of
several synapses within close spatial and temporal proximity on a dendritic
branch can initiate a local NMDA spike, which then causes a significant and
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2480
Y. Cui, S. Ahmad, and J. Hawkins
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
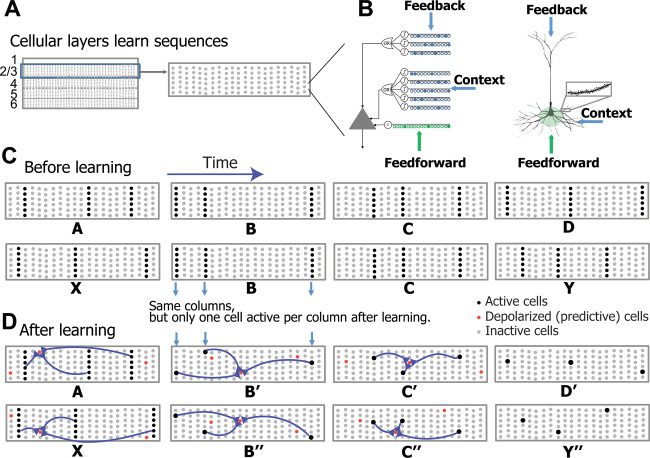
Figura 1: The HTM sequence memory model. (UN) The cortex is organized into
six cellular layers. Each cellular layer consists of a set of minicolumns, con
each minicolumn containing multiple cells. (B) An HTM neuron (left) has three
distinct dendritic integration zones, corresponding to different parts of the den-
dritic tree of pyramidal neurons (right). An HTM neuron models dendrites and
NMDA spikes as an array of coincident detectors each with a set of synapses. IL
coactivation of a set of synapses on a distal dendrite will cause an NMDA spike
and depolarize the soma (predicted state). (C, D) Learning high-order Markov
sequences with shared sub-sequences (ABCD versus XBCY). Each sequence el-
ement invokes a sparse set of minicolumns due to intercolumn inhibition. (C)
Prior to learning the sequences all the cells in a minicolumn become active. (D)
After learning, cells that are depolarized through lateral connections become
active faster and prevent other cells in the same column from firing through in-
tracolumn inhibition. The model maintains two simultaneous representations:
one at the minicolumn level representing the current feedforward input and the
other at the individual cell level representing the context of the input. Because
different cells respond to C in the two sequences (C’ and C”), they can invoke
the correct high-order prediction of either D or Y.
sustained depolarization of the cell body (Antic et al., 2010; Major et al.,
2013).
3.2 Two Separate Sparse Representations. The HTM network consists
of a layer of HTM neurons organized into a set of columns (see Figure 1A).
The network represents high-order sequences using a composition of two
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2481
separate sparse representations. At any time, both the current feedforward
input and the previous sequence context are simultaneously represented
using sparse distributed representations.
The first representation is at the column level. We assume that all neu-
rons within a column detect identical feedforward input patterns on their
proximal dendrites (Buxhoeveden, 2002; Mountcastle, 1997). Through an
intercolumnar inhibition mechanism, each input element is encoded as a
sparse distributed activation of columns at any point in time. At any time,
the top 2% columns that receive the most active feedforward inputs are
activated.
The second representation is at the level of individual cells within these
columns. At any given time point, a subset of cells in the active columns
will represent information regarding the learned temporal context of the
current pattern. These cells in turn lead to predictions of the upcoming
input through lateral projections to other cells within the same network. IL
predictive state of a cell controls inhibition within a column. If a column
contains predicted cells and later receives sufficient feedforward input,
these predicted cells become active and inhibit others within that column.
If there were no cells in the predicted state, all cells within the column
become active.
To illustrate the intuition behind these representations consider two ab-
stract sequences A-B-C-D and X-B-C-Y (see Figures 1C and 1D). In this
example remembering that the sequence started with A or X is required to
make the correct prediction following C. The current inputs are represented
by the subset of columns that contains active cells (black dots in Figures 1C
and 1D). This set of active columns does not depend on temporal con-
testo, just on the current input. After learning, different cells in this subset of
columns will be active depending on predications based on the past context
(B’ versus B”, C’ versus C”, Figure 1D). These cells then lead to predictions
of the element following C (D or Y) based on the set of cells containing
lateral connections to columns representing C.
This dual representation paradigm leads to a number of interesting prop-
erties. Primo, the use of sparse representations allows the model to make
multiple predictions simultaneously. Per esempio, if we present input B to
the network without any context, all cells in columns representing the B
input will fire, which leads to a prediction of both C’ and C”. Secondo, be-
cause information is stored by coactivation of multiple cells in a distributed
maniera, the model is naturally robust to both noise in the input and system
faults such as loss of neurons and synapses. (A detailed discussion on this
topic can be found in Hawkins & Ahmad, 2016.)
3.3 HTM Activation and Learning Rules. The previous sections pro-
vided an intuitive description of network behavior. In this section we de-
scribe the formal activation and learning rules for the HTM network. Contro-
sider a network with N columns and M neurons per column; we denote the
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2482
Y. Cui, S. Ahmad, and J. Hawkins
activation state at time step t with an M × N binary matrix At, where at
i j
is the activation state of the ith cell in the jth column. Allo stesso modo, an M × N
binary matrix (cid:2)t denotes cells in a predictive state at time t, where π t
i j is
the predictive state of the ith cell in the jth column. We model each synapse
with a scalar permanence value and consider a synapse connected if its
permanence value is above a connection threshold. We use an M × N ma-
trix Dd
i j to denote the permanence of the dth segment of the ith cell in the
jth column. The synaptic permanence matrix is bounded between 0 E 1.
We use a binary matrix
i j to denote only the connected synapses. IL
network can be initialized such that each segment contains a set of poten-
tial synapses (cioè., with nonzero permanence value) to a randomly chosen
subset of cells in the layer. To speed up simulation, instead of explicitly
initializing a complete set of synapses across every segment and every cell,
we greedily create segments at run time (see the appendix).
˜Dd
The predictive state of the neuron is handled as follows: if a dendritic
segment receives enough input, it becomes active and subsequently depo-
larizes the cell body without causing an immediate spike. Mathematically,
the predictive state at time step t is calculated as follows:
(cid:2)
π t
i j
=
(cid:4) ˜Dd
1 if ∃
D
0 otherwise
i j
◦ AT (cid:4)
> θ
1
.
(3.1)
Threshold θ represents the segment activation threshold, and ◦ represents
element-wise multiplication. Since the distal synapses receive inputs from
previously active cells in the same layer, it contains contextual information
of past inputs, which can be used to accurately predict future inputs (Vedere
Figure 1B).
At any time, an intercolumnar inhibitory process selects a sparse set of
columns that best match the current feedforward input pattern. We calculate
the number of active proximal synapses for each column and activate the
top 2% of the columns that receive the most synaptic inputs. We denote this
set as Wt. The proximal synapses were initialized such that each column
is randomly connected to 50% of the inputs. Since we focus on sequence
learning in this letter, the proximal synapses were fixed during learning.
In principle, the proximal synapses can also adapt continuously during
learning according to a spatial competitive learning rule (Hawkins, Ahmad,
& Dubinsky, 2011; Mnatzaganian, Fokou´e, & Kudithipudi, 2016).
Neurons in the predictive state (cioè., depolarized) will have competi-
tive advantage over other neurons receiving the same feedforward inputs.
Specifically, a depolarized cell fires faster than other nondepolarized cells
if it subsequently receives sufficient feedforward input. By firing faster, Esso
prevents neighboring cells in the same column from activating with intra-
column inhibition. The active state for each cell is calculated as follows:
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
⎧
⎪⎨
⎪⎩
=
at
i j
1 if j ∈ Wt and π t−1
(cid:7)
i j
1 if j ∈ Wt and
= 1
π t−1
i j
0 otherwise
io
= 0
.
2483
(3.2)
The first conditional expression of equation 3.2 represents a cell in a winning
column becoming active if it was in a predictive state during the preceding
time step. If none of the cells in a winning column are in a predictive
state, all cells in that column become active, as in the second conditional of
equation 3.2.
The lateral connections in the sequence memory model are learned using
a Hebbian-like rule. Specifically, if a cell is depolarized and subsequently
becomes active, we reinforce the dendritic segment that caused the depolar-
ization. If no cell in an active column is predicted, we select the cell with the
most activated segment and reinforce that segment. Reinforcement of a den-
dritic segment involves decreasing permanence values of inactive synapses
by a small value p− and increasing the permanence for active synapses by
a larger value p+:
(cid:5)Dd
i j
= p
+ ˙Dd
i j
◦ At−1 − p
− ˙Dd
i j
◦ (1 − At−1).
(3.3)
i j denotes a binary matrix containing only the positive entries in Dd
i j, Quello
˙Dd
È,
(cid:8)
˙Dd
i j
=
> 0
1 if Dd
i j
0 otherwise
.
(3.4)
We also apply a very small decay to active segments of cells that did
not become active, mimicking the effect of long-term depression (Massey
& Bashir, 2007):
(cid:5)Dd
i j
= p
−− ˙Dd
i j where at
i j
= 0 E (cid:4) ˜Dd
i j
◦ At−1(cid:4)
1
> θ ,
(3.5)
where p−− (cid:7) p−.
The learning rule is inspired by neuroscience studies of activity-
dependent synaptogenesis (Zito & Svoboda, 2002), which showed that the
adult cortex generates new synapses in response to sensory activity rapidly.
The mathematical formula we chose captured this Hebbian synaptogenesis
learning rule. We did not derive the rule by implementing gradient descent
on a cost function. There could be other mathematical formulations that
give similar or better results.
A complete set of parameters and further implementation details can be
found in the appendix. These parameters were set based on properties of
sparse distributed representations (Ahmad & Hawkins, 2016). Notably, we
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2484
Y. Cui, S. Ahmad, and J. Hawkins
Figura 2: Functional steps for using HTM on real-world sequence learning
compiti.
used the same set of parameters for all of the different types of sequence
learning tasks in this letter.
3.4 SDR Encoder and Classifier. The HTM sequence memory operates
with sparse distributed representations (SDRs) internally. To apply HTM to
real-world sequence learning problems, we need to first convert the original
data to SDRs using an encoder (Guarda la figura 2). We have created a variety of
encoders to deal with different data types (Purdy, 2016). In this letter, we
used a random SDR encoder for categorical data and scalar and date-time
encoders for the taxi passenger prediction experiment.
To decode prediction values from the output SDRs of HTM, we con-
sidered two classifiers: a simple classifier based on SDR overlaps and a
maximum-likelihood classifier. For the single-step discrete sequence pre-
diction task, we computed the overlap of the predicted cells with the SDRs
of all observed elements and selected the one with the highest overlap. For
the continuous scalar value prediction task, we divided the whole range of
scalar value into 22 disjoint buckets and used a single-layer feedforward
classification network. Given a large array of cell activation pattern x, IL
classification network computes a probability distribution over all possible
classes using a softmax activation function (Bridle, 1989). There are as many
output units as the number of possible classes. The jth output unit receives
a weighted summation of all the inputs,
=
a j
N(cid:9)
i=1
w
.
i jxi
(3.6)
w
i j is the connection weight from the ith input neuron to the jth output
neuron. The estimated class probability is given by the activation level of
the output units:
= P
yk
(cid:11)
(cid:10)
Ck
|X
=
(cid:7)
eak
K
i=1 eak
.
(3.7)
Using a maximum likelihood optimization, we derived the learning rule
for the weight matrix w:
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
(cid:5)w
= −λ(y j
− z j
)xi
.
i j
2485
(3.8)
z j is the observed (target) distribution and λ is the learning rate. Note that
since x is highly sparse, we only need to update a very small fraction of
the weight matrix at any time. Therefore, the learning algorithm for the
classifier is fast despite the high dimensionality of the weight matrix.
4 High-Order Sequence Prediction with Artificial Data
We conducted experiments to test whether the HTM sequence mem-
ory model, online sequential extreme learning machine (OS-ELM), time-
delayed neural network (TDNN), and LSTM network are able to learn
high-order sequences in an online manner, recover after modification to
the sequences, and make multiple predictions simultaneously. LSTM rep-
resents the state-of-the-art recurrent neural network model for sequence
learning tasks (Graves 2012; Hochreiter & Schmidhuber, 1997). OS-ELM is
a feedforward neural network model that is widely used for time-series
predictions (Huang, Wang, & Lan, 2011; Wang & Han, 2014). TDNN is a
classical feedforward neural network designed to work with sequential data
(Waibel et al., 1989). LSTM and HTM use the current pattern only as input
and are able to learn the high-order structure. ELM and TDNN require the
user to determine the number of steps to use as temporal context.
4.1 Continuous Online Learning from Streaming Data. We created
a discrete high-order temporal sequence data set. Sequences are designed
such that any learning algorithm would have to maintain context of at least
the first two elements of each sequence in order to correctly predict the last
element of the sequence (Guarda la figura 3). We used the sequence data set in a
continuous streaming scenario (see Figure 3C). At the beginning of a trial,
we randomly chose a sequence from the data set and sequentially presented
each of its elements. At the end of each sequence, we presented a single noise
element to the model. The noise element is randomly chosen from a large
set of 50,000 noise symbols (not used among the set of sequences). This is a
difficult learning problem, since sequences are embedded in random noise;
the start and end points are not marked. The set of noise symbols is large
so the algorithm cannot learn every possible noise transition. We tested the
algorithms for predicting the last element of each sequence continuously as
the algorithm observed a stream of sequences and reported the percentage
of correct predictions over time.
We encoded each symbol in the sequence as a random SDR for HTM
sequence memory, con 40 randomly chosen active bits in a vector of 2048
bits. This SDR representation matches the internal representation used in
HTM, which has 2048 columns with 40 active at any time (see the ap-
pendix). We initially tried to use the same SDR encoding for TDNN, ELM,
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2486
Y. Cui, S. Ahmad, and J. Hawkins
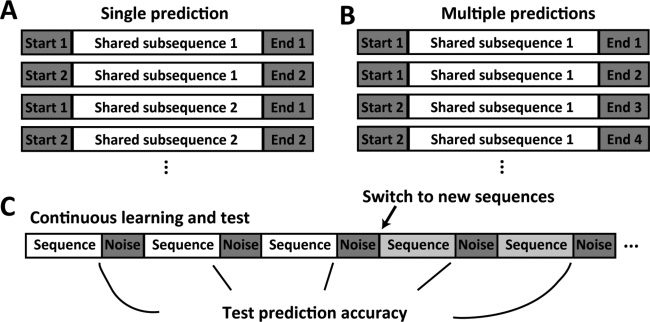
Figura 3: Design of the high-order sequence prediction task. (UN). Structure
of high-order sequences with shared sub-sequences. (B). High-order sequences
with multiple possible endings. (C). Stream of sequences with noise between se-
quences. Both learning and testing occur continuously. After the model learned
one set of sequences, we switched to a new set of sequences with contradictory
endings to test the adaptation to changes in the data stream.
and LSTM. This high-dimensional representation does not work well due
to the large number of parameters required. Invece, we used a random
real-valued dense distributed representation for TDNN, ELM, and LSTM.
Each symbol is encoded as a 25-dimensional vector with each dimension’s
value randomly chosen from [−1, 1].1 We chose this encoding format be-
cause it both gives better accuracy and has large representational capacity
which is required for streaming data analysis. Similar dense distributed
representations are commonly used for LSTM in natural language process-
ing applications (Mikolov, Chen, Corrado, & Dean, 2013). We could not use
one-hot vector encoding because its limited capacity prevents representing
the noise elements between sequences, which are drawn from a very large
dictionary.
Since the sequences are presented in a streaming fashion and predictions
are required continuously, this task represents a continuous online learn-
ing problem. The HTM sequence memory is naturally suitable for online
learning as it learns from every new data point and does not require the
data stream to be broken up into predefined chunks. ELM also has a well-
established online sequential learning model (Liang et al., 2006). An online
sequential algorithm, such as real-time recurrent learning (RTRL), has been
1We manually tuned the number of dimensions and found that 25 dimensions gave
the best performance on our tasks.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2487
proposed for LSTM in the past (Hochreiter & Schmidhuber, 1997; Williams
& Zipser, 1989). Tuttavia, most LSTM applications used batch learning due
to the high computational cost of RTRL (Jaeger, 2002). We use two variants
of LSTM networks for this task. Primo, we retrained an LSTM network at
regular intervals on a buffered data set of the previous time steps using a
variant of the resilient backpropagation algorithm until convergence (Igel &
H ¨usken, 2003). The experiments include several LSTM models with varying
buffer sizes. Secondo, we trained an LSTM network with online truncated
backpropagation through time (BPTT) (Williams & Peng, 1990). At each time
point, we calculated the gradient using BPTT over the last 100 elements and
adjusted the parameters along the gradient by a small amount.
We tested sequences with either single or multiple possible endings (Vedere
Figures 3A and 3B). To quantify model performance, we classified the state
of the model before presenting the last element of each sequence to retrieve
the top K predictions, where K = 1 for the single prediction case and K = 2
O 4 for the multiple predictions case. We considered the prediction correct
if the actual last element was among the top K predictions of the model.
Since these are online learning tasks, there are no separate training and test
phases. Invece, we continuously report the prediction accuracy of the end
of each sequence before the model has seen it.
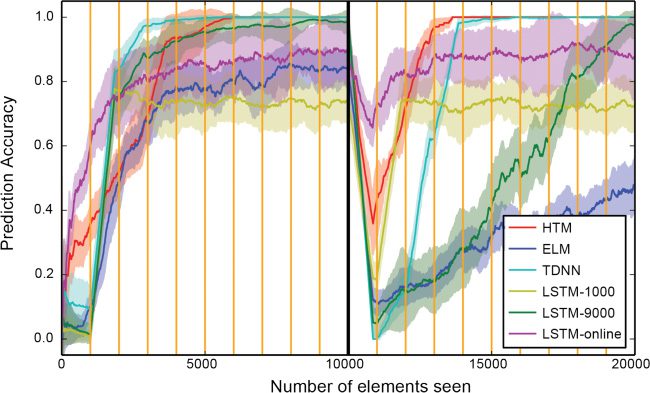
In the single prediction experiment (Guarda la figura 4, left of the black solid
line), each sequence in the data set has only one possible ending given its
high-order context (see Figure 3A). The HTM sequence memory quickly
achieves perfect prediction accuracy on this task (Guarda la figura 4, red). Given a
large enough learning window, LSTM also learns to predict the high-order
sequences (Guarda la figura 4, green). Despite comparable model performance,
HTM and LSTM use the data in different ways: LSTM requires many passes
over the learning window—each time it is retrained to perform gradient-
descent optimization, whereas HTM needs to see each element only once
(one-pass learning). LSTM also takes longer than HTM to achieve perfect
accuracy; we speculate that since LSTM optimizes over all transitions in the
data stream, including the random ones between sequences, it is initially
overfitting on the training data. Online LSTM and ELM are also trained in
an online, sequential fashion similar to HTM. But both algorithms require
keeping a short history buffer of the past elements. ELM learned the se-
quences more slowly than HTM and never achieved perfect performance
(Guarda la figura 4, blue). Online LSTM has the best performance initially, Ma
does not achieve perfect performance in the end. HTM, LSTM, and TDNN
are able to achieve perfect prediction accuracy on this task.2
2For TDNN, the user has to know the length of temporal context ahead of time in
order to obtain perfect performance. The results in Figure 3 used a lag of 10 steps. Noi
could not obtain perfect performance with a lag of 5 O 20 steps.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2488
Y. Cui, S. Ahmad, and J. Hawkins
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 4: Prediction accuracy of HTM (red), LSTM (yellow, green, purple), ELM
(blue), and TDNN (cyan) on an artificial data set. The data set contains four
sixth order sequences and four seventh order sequences. Prediction accuracy
is calculated as a moving average over the last 100 sequences. The sequences
are changed after 10,000 elements have been seen (black dashed line). HTM
sees each element once and learns continuously. ELM is trained continuously
using a time lag of 10 steps. TDNN is retrained every 1000 elements (orange
vertical lines) on the last 1000 elements (cyan). LSTM is either retrained every
1000 elements on the last 1000 elements (yellow) O 9000 elements (green), O
continuously adapted using truncated BPTT (purple).
4.2 Adaptation to Changes in the Data Stream. Once the models have
achieved stable performance, we altered the data set by swapping the last
elements of pairs of high-order sequences (Guarda la figura 4, black dashed line).
This forces the model to forget the old sequences and subsequently learn
the new ones. HTM sequence memory and online LSTM quickly recover
from the modification. In contrasto, it takes a long time for batch LSTM,
TDNN, and ELM to recover from the modification as its buffered data
set contains contradictory information before and after the modification.
Although using a smaller learning window can speed up the recovery (Vedere
Figura 4, blue purple), it also causes worse prediction performance due to
the limited number of training samples.
A summary of the model performance on the high-order sequence pre-
diction task is shown in Figure 5. Generalmente, there is a trade-off between
prediction accuracy and flexibility. For batch learning algorithms, a shorter
learning window is required for fast adaptation to changes in the data, but a
longer learning window is required to perfectly learn high-order sequences
Online Learning with HTM Sequence Memory
2489
Figura 5: Final prediction accuracy as a function of the number of samples
required to achieve final accuracy before (left) and after (right) modification of
the sequences. Error bars represent standard deviations.
(Guarda la figura 5, green versus yellow). Although online LSTM and ELM do
not require batch learning, the user is required to specify the maximal lag,
which limits the maximum sequence order it can learn. The HTM sequence
memory model dynamically learns high-order sequences without requir-
ing a learning window or a maximum sequence length. It achieved the best
final prediction accuracy with a small number of data samples. After the
modification to the sequences, HTM’s recovery is much faster than ELM
and LSTM trained with batch learning, demonstrating its ability to adapt
quickly to changes in data streams.
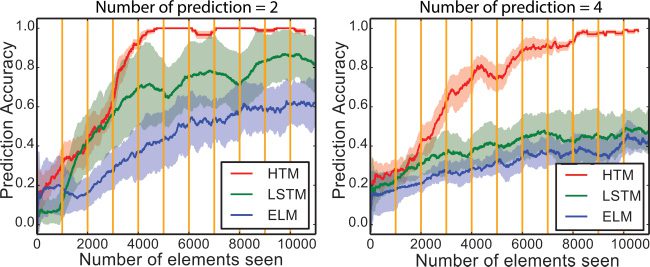
4.3 Simultaneous Multiple Predictions. In the experiment with mul-
tiple predictions (see Figure 3B), each sequence in the data set has two
or four possible endings, given its high-order context. The HTM sequence
memory model rapidly achieves perfect prediction accuracy for both the 2-
predictions and the 4-predictions cases (Guarda la figura 6). While only these two
cases are shown, in reality HTM is able to make many multiple predictions
correctly if the data set requires it. Given a large learning window, LSTM
is able to achieve good prediction accuracy for the 2-predictions case, Ma
when the number of predictions is increased to 4 or greater, it is not able to
make accurate predictions.
HTM sequence memory is able to simultaneously make multiple pre-
dictions due to its use of SDRs. Because there is little overlap between two
random SDRs, it is possible to predict a union of many SDRs and clas-
sify a particular SDR as being a member of the union with low chance of a
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2490
Y. Cui, S. Ahmad, and J. Hawkins
Figura 6: Performance on high-order sequence prediction tasks that require
two (left) or four (right) simultaneous predictions. Shaded regions represent
standard deviations (calculated with different sets of sequences). The data set
contains four sets of sixth order sequences and four sets of seventh-order se-
quences.
false positive (Ahmad & Hawkins, 2016). D'altra parte, the real-valued
dense distributed encoding used in LSTM is not suitable for multiple predic-
tions because the average of multiple dense representations in the encoding
space is not necessarily close to any of the component encodings, particolarmente
when the number of predictions being made is large. The problem can be
solved by using local one-hot representations to code target inputs, but such
representations have very limited capacity and do not work well when the
number of possible inputs is large or unknown upfront. This suggests that
modifying LSTMs to use SDRs might enable better performance on this
task.
4.4 Learning Long Term Dependencies from High-Order Sequences.
For feedforward networks like ELM, the number of time lags that can
be included in the input layer significantly limits the maximum sequence
order a network can learn. The conventional recurrent neural networks can-
not handle sequences with long-term dependencies because error signals
“flowing backward in time” tend to either blow up or vanish with the clas-
sical backpropagation-through-time (BPTT) algorithm. LSTM is capable of
learning very long-term dependencies using gating mechanisms (Henaff,
Szlam, & Lecun, 2016). Here we tested whether HTM sequence memory
can learn long-term dependencies by varying the Markov order of the se-
quences, which is determined by the length of shared sub-sequences (Vedere
Figure 3A).
We examined the prediction accuracy over training while HTM sequence
memory learns variable-order sequences. The model is able to achieve per-
fect prediction performance up to 100-order sequences (see Figure 7A).
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2491
Figura 7: (UN) Prediction accuracy over learning with sequences of different
orders. (B) Number of sequences required to achieve perfect prediction as a
function of sequence order. The sequence data set contains four high-order
sequences with the structure shown in Figure 3A.
The number of sequences that are required to achieve perfect prediction
performance increase linearly as a function of the order of sequences (Vedere
Figure 7B). Note that the model quickly achieves 50% accuracy much faster
because it requires only first-order knowledge, yet it requires high-order
knowledge to make a perfect prediction (see Figure 3A).
4.5 Disruption of High-Order Context with Temporal Noise. Nel
previous experiments, noise was presented between sequences. In this ex-
periment, we tested the effect of noise within sequences. At run time, we ran-
domly replaced either the second, third, or fourth element in each sequence
with a random symbol. Such temporal noise could disrupt the high-order
sequence context and make it much harder to predict the sequence endings.
We considered two scenarios: (1) temporal noise throughout training and
(2) noise introduced only after the models achieved perfect performance.
The performances of HTM and LSTM are shown in Figure 8. If temporal
noise is present throughout training, neither HTM nor LSTM can make
perfect predictions (see Figure 8A). LSTM has slightly better performance
than HTM in this scenario, presumably because the gating mechanisms in
LSTM can maintain some of the high-order sequence context. HTM behaves
like a first-order model and has an accuracy of about 0.5. This experiment
demonstrates the sensitivity of the HTM model to temporal noise.
If we inject temporal noise after the models achieve perfect performance
on the noise-free sequences, the performance of both models drops rapidly
(see Figure 8B). The performance of HTM drops to 0.5 (performance of
the first-order model), whereas LSTM has worse performance. This result
demonstrates that if the high-order sequence context is disrupted, HTM
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2492
Y. Cui, S. Ahmad, and J. Hawkins
Figura 8: (UN) Prediction accuracy over learning with the presence of temporal
noise for LSTM (gray) and HTM (black). (B) HTM and LSTM are trained with
clean sequences. Temporal noise was added after 12,000 elements. The sequence
data set is same as in Figure 4.
would robustly behave as a low-order model, whereas the performance of
LSTM is dependent on the training history.
4.6 Robustness of the Network to Damage. We tested the robustness of
the ELM, LSTM, and HTM networks with respect to the removal of neurons.
This fault tolerance property is important for hardware implementations
of neural network models. After the models achieved stable performance
on the high-order sequence prediction task (at the black dashed line, In
Figura 2), we eliminated a fraction of the cells and their associated synaptic
connections from the network. We then measured the prediction accuracy
of both networks on the same data streams for an additional 5000 steps
without further learning. There is no impact on the HTM sequence memory
model performance at up to 30% cell death, whereas the performance of
the ELM and LSTM networks declined rapidly with a small fraction of cell
death (Guarda la figura 9).
Fault tolerance of traditional artificial neural networks depends on many
factors, such as the network size and training methods (Lee, Hwang, &
Sung, 2014). The experiments here applied commonly used training meth-
ods for ELM and LSTM (see the appendix). It is possible that the fault
tolerance of LSTM or any other artificial neural network may be improved
by introducing redundancy (replicating trained network) (Tchernev, Mul-
vaney, & Phatak, 2005) or by a special training method such as dropout
(Hinton, Krizhevsky, Sutskever, & Salakhutdinov, 2012). In contrasto, IL
fault tolerance of HTM is naturally derived from properties of sparse
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2493
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 9: Robustness of the network to damage. The prediction accuracy after
cell death is shown as a function of the fraction of cells that were removed from
the network.
distributed representations (Ahmad & Hawkins, 2016), in analogy to bi-
ological neural networks.
5 Prediction of New York City Taxi Passenger Demand
In order to compare the performance of HTM sequence memory with other
sequence learning techniques in real-world scenarios, we consider the prob-
lem of predicting taxi passenger demand. Specifically, we aggregated the
passenger counts in New York City taxi rides at 30 minute intervals us-
ing a public data stream provided by the New York City Transportation
Authority.3 This leads to sequences exhibiting rich patterns at different
timescales (see Figure 10A). The task is to predict taxi passenger demand
five steps (2.5 hours) in advance. This problem is an example of a large class
of sequence learning problems that require rapid processing of streaming
data to deliver information for real-time decision making (Moreira-Matias,
Gama, Ferreira, Mendes-Moreira, & Damas, 2013).
We applied HTM sequence memory and other sequence prediction al-
gorithms to this problem. The ARIMA model is a widely used statistical
approach for time series analysis (Hyndman & Athanasopoulos, 2013). As
before, we converted ARIMA, TDNN, and LSTM to an online learning al-
gorithm by retraining the models on every week of data with a buffered
3http://www.nyc.gov/html/tlc/html/about/trip_record_data.shtml.
2494
Y. Cui, S. Ahmad, and J. Hawkins
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Figura 10: Prediction of the New York City taxi passenger data. (UN) Esempio
portion of taxi passenger data (aggregated at 30 min intervals). The data have
rich temporal patterns at both daily and weekly timescales. (B, C) Prediction
error of different sequence prediction algorithms using two metrics: mean ab-
solute percentage error (B), and negative log likelihood (C).
data set of the previous 1000, 3000 O 6000 samples (see the appendix). ELM
and ESN were adapted at every time step using sequential online learn-
ing methods. The parameters of the ESN, ELM, and LSTM network were
extensively hand-tuned to provide the best possible accuracy on this data
set The ARIMA model was optimized using R’s “auto ARIMA” package
(Hyndman & Khandakar, 2008). The HTM model did not undergo any pa-
rameter tuning; it uses the same parameters that were used for the previous
artificial sequence task.
Online Learning with HTM Sequence Memory
2495
Figura 11: Prediction accuracy of LSTM and HTM after the introduction of
new patterns. (UN). The mean absolute percent error of HTM sequence memory
(red) and LSTM networks (green, blue) after artificial manipulation of the data
(black dashed line). The LSTM networks are retrained every week at the yellow
vertical lines (B, C). Prediction error after the manipulation. HTM sequence
memory has better accuracy on both the MAPE and the negative log-likelihood
metrics.
We used two error metrics to evaluate model performance: mean abso-
lute percentage error (MAPE) and negative log likelihood. The MAPE met-
rics focus on the single best point estimation, while negative log likelihood
evaluates the models’ predicted probability distributions of future inputs
(see appendix for details). We found that the HTM sequence memory had
comparable performance to LSTM on both error metrics. Both techniques
had a much lower error than ELM, ESN, and ARIMA (see Figure 10B). Note
that HTM sequence memory achieves this performance with a single-pass
training paradigm, whereas LSTM requires multiple passes on a buffered
insieme di dati.
We then tested how fast different sequence learning algorithms can adapt
to changes in the data (Guarda la figura 11). We artificially modified the data by
decreasing weekday morning traffic (7 a.m.–11 a.m.) by 20% and increasing
weekday night traffic (9 p.m.–11 p.m.) by 20% starting from April 1, 2015.
These changes in the data caused an immediate increase in prediction error
for both HTM and LSTM (see Figure 11A). The prediction error of HTM
sequence memory quickly dropped back in about two weeks, whereas the
LSTM prediction error stayed high much longer. Di conseguenza, HTM sequence
memory had better prediction accuracy than LSTM and other models after
the data modification (see Figures 11B and 11C).
6 Discussion and Conclusions
In this letter, we have applied HTM sequence memory, a recently devel-
oped neural network model, to real-time sequence learning problems with
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2496
Y. Cui, S. Ahmad, and J. Hawkins
time-varying input streams. The sequence memory model is derived from
computational principles of cortical pyramidal neurons (Hawkins & Ah-
mad, 2016). We discussed model performance on both artificially generated
and real-world data sets. The model satisfies a set of properties that are
important for online sequence learning from noisy data streams with con-
tinuously changing statistics, a problem the cortex has to solve in natural
environments. These properties govern the overall flexibility of an algo-
rithm and its ability to be used in an automated fashion. Although HTM is
still at a very early stage compared to other traditional neural network mod-
els, it satisfies these properties and shows promising results on real-time
sequence learning problems.
6.1 Continuous Learning with Streaming Data. Most supervised se-
quence learning algorithms use a batch-training paradigm, where a cost
function, such as prediction error, is minimized on a batch training data
set (Bishop, 2006; Dietterich, 2002). Although we can train these algorithms
continuously using a sliding window (Sejnowski & Rosenberg, 1987), Questo
batch-training paradigm is not a good match for time-series prediction
on continuous streaming data. A small window may not contain enough
training samples for learning complex sequences, while a large window in-
troduces a limit on how fast the algorithm can adapt to changing statistics
in the data. In either case, a buffer must be maintained, and the algorithm
must make multiple passes for every retraining step. It may be possible to
use a smooth forgetting mechanism instead of hard retraining (Lughofer &
Angelov, 2011; Williams & Zipser, 1989), but this requires the user to tune
parameters governing the forgetting speed to achieve good performance.
In contrasto, HTM sequence memory adopts a continuous learning
paradigm. The model does not need to store a batch of data as the “train-
ing dataset.” Instead, it learns from each data point using unsupervised
Hebbian-like associative learning mechanisms (Hebb, 1949). Di conseguenza,
the model rapidly adapts to changing statistics in the data.
6.2 Using Sparse Distributed Representations for Sequence Learning.
A key difference between HTM sequence memory and previous biologically
inspired sequence learning models (Abeles, 1982; Brea et al., 2013; Ponulak
& Kasi ´nski, 2010; Rao & Sejnowski, 2001) is the use of sparse distributed
representations (SDRs). In the cortex, information is primarily represented
by strong activation of a small set of neurons at any time, known as sparse
coding (F ¨oldi´ak 2002, Olshausen & Field, 2004). HTM sequence memory
uses SDRs to represent temporal sequences. Based on mathematical prop-
erties of SDRs (Ahmad & Hawkins, 2016; Kanerva, 1988), each neuron in
the HTM sequence memory model can robustly learn and classify a large
number of patterns under noisy conditions (Hawkins & Ahmad, 2016).
A rich distributed neural representation for temporal sequences emerges
from computation in HTM sequence memory. Although we focus on se-
quence prediction in this letter, this representation is valuable for a number
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2497
of tasks, such as anomaly detection (Lavin & Ahmad, 2015) and sequence
classification.
The use of a flexible coding scheme is particularly important for online
streaming data analysis, where the number of unique symbols is often not
known upfront. It is desirable to be able to change the range of the coding
scheme at run time without affecting previous learning. This requires the
algorithm to use a flexible coding scheme that can represent a large number
of unique symbols or a wide range of data. The SDRs used in HTM have
a very large coding capacity and allow simultaneous representations of
multiple predictions with minimal collisions These properties make SDR
an ideal coding format for the next generation of neural network models.
6.3 Robustness and Generalization. An intelligent learning algorithm
should be able to automatically deal with a large variety of problems with-
out parameter tuning, yet most machine learning algorithms require a task-
specific parameter search when applied to a novel problem. Learning in the
cortex does not require an external tuning mechanism, and the same corti-
cal region can be used for different functional purposes if the sensory input
i cambiamenti (Sadato et al., 1996; Sharma, Angelucci, & Sur, 2000). Using com-
putational principles derived from the cortex, we show that HTM sequence
memory achieves performance comparable to LSTM networks on very dif-
ferent problems using the same set of parameters. These parameters were
chosen according to known properties of real cortical neurons (Hawkins
& Ahmad, 2016) and basic properties of sparse distributed representations
(Ahmad & Hawkins, 2016).
6.4 Limitations of HTM and Future Directions. We have identified a
few limitations of HTM. Primo, as a strict one-pass algorithm with access
to only the current input, it may take longer for HTM to learn sequences
with very long-term dependencies (Guarda la figura 7) than algorithms that have
access to a longer history buffer. Learning of sequences with long-term
dependencies can be sped up if we maintain a history buffer and run HTM
on it multiple times. Infatti, it has been argued that an intelligent agent
should store the entire raw history of sensory inputs and motor actions
during interaction with the world (Schmidhuber, 2009). Although it may
be computationally challenging to store the entire history, doing so may
improve performance given the same amount of sensory experience.
Secondo, although HTM is robust to spatial noise due to the use of sparse
distributed representations, the current HTM sequence memory model is
sensitive to temporal noise. It can lose high-order sequence context if el-
ements in the sequence are replaced by a random symbol (Guarda la figura 8).
In contrasto, the gating mechanisms of LSTM networks appear to be more
robust to temporal noise. The noise robustness of HTM can be improved
by using a hierarchy of sequence memory models that operate on different
timescales. A sequence memory model that operates over longer timescales
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2498
Y. Cui, S. Ahmad, and J. Hawkins
would be less sensitive to temporal noise. A lower region in the hierarchy
may inherit the robustness to temporal noise through feedback connections
to a higher region.
Third, the HTM model as discussed does not perform as well as LSTM
on grammar learning tasks. We found that on the Reber grammar task
(Hochreiter & Schmidhuber, 1997), HTM achieves an accuracy of 98.4% E
ELM an accuracy of 86.7% (online training after observing 500 sequences),
whereas LSTM achieves an accuracy of 100%. HTM can approximately
learn artificial grammars by memorizing example sentences. This strategy
could require more training samples to fully learn recursive grammars with
arbitrary sequence lengths. In contrasto, LSTM learns grammars much faster
using the gating mechanisms. Unlike the HTM model, LSTMs can also
model some Boolean algebra problems like the parity problem.
Finalmente, we have tested HTM only on low-dimensional categorical or
scalar data streams in this letter. It remains to be determined whether HTM
can handle high-dimensional data such as speech and video streams. IL
high capacity of the sparse distributed representations in HTM should be
able to represent high-dimensional data. Tuttavia, it is more challenging to
learn sequence structure in high-dimensional space, as the raw data could
be much less repeatable. It may require additional preprocessing, ad esempio
dimensionality reduction and feature extractions, before HTM can learn
meaningful sequences with high-dimensional data. It would be an interest-
ing future direction to explore how to combine HTM with other machine
learning methods, such as deep networks, to solve high-dimensional se-
quence learning problems.
Appendix: Implementation Details
A.1 HTM Sequence Model Implementation Details. In our software
implementation, we made a few simplifying assumptions to speed up sim-
ulation for large networks. We did not explicitly initialize a complete set of
synapses across every segment and every cell. Invece, we greedily created
segments on the least-used cells in an unpredicted column and initialized
potential synapses on that segment by sampling from previously active
cells. This happened only when there is no match to any existing segment.
The initial synaptic permanence for newly created synapses is set as 0.21
(Vedi la tabella 1), which is below the connection threshold (0.5).
The HTM sequence model operates with sparse distributed representa-
zioni (SDRs). Specialized encoders are required to encode real-world data
into SDRs. For the artificial data sets with categorical elements, we simply
encoded each symbol in the sequence as a random SDR, con 40 randomly
chosen active bits in a vector of 2048 bits.
For the New York City taxi data set, three pieces of information were fed
into the HTM model: raw passenger count, the time of day, and the day
of week (LSTM received the same information as input). We used NuPIC’s
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2499
Tavolo 1: Model Parameters for HTM.
Parameter Name
Number of columns N
Number of cells per column M
Dendritic segment activation threshold θ
Initial synaptic permanence
Connection threshold for synaptic permanence
Synaptic permanence increment p
Synaptic permanence decrement p
Synaptic permanence decrement for predicted inactive segments p
Maximum number of segments per cell
Maximum number of synapses per segments
Maximum number new synapses added at each step
−
+
−
Value
2048
32
15
0.21
0.5
0.1
0.1
0.01
128
128
32
standard scalar encoder to convert each piece of information into an SDR.
The encoder converts a scalar value into a large binary vector with a small
number of ON bits clustered within a sliding window, where the center
position of the window corresponds to the data value. We subsequently
combined three SDRs via a competitive sparse spatial pooling process,
which also resulted in 40 active bits in a vector of 2048 bits as in the artificial
insieme di dati. The spatial pooling process is described in detail in Hawkins et al.
(2011).
The HTM sequence memory model used an identical set of model param-
eters for all the experiments described in the letter. A complete list of model
parameters is shown below. The full source code for the implementation is
available on Github at https://github.com/numenta/nupic.research.
A.2 Implementation Details of Other Sequence Learning Algorithms.
A.2.1 ELM. We used the online sequential learning algorithm for ELM
(Liang et al., 2006). The network used 50 hidden neurons and a time lag of
100 for the taxi data and 200 hidden neurons and a time lag of 10 for the
artificial data set.
A.2.2 ESN. We used the Matlab toolbox for echo state network devel-
oped by Jaeger’s group (http://reservoir-computing.org/node/129). IL
ESN network has 100 internal units, a spectral radius of 0.1, a teacher scal-
ing of 0.01, and a learning rate of 0.1 for the ESN model. The parameters were
hand-tuned to achieve the best performance. We used the online learning
mode and adapted the weight at every time step.
A.2.3 LSTM. We used the PyBrain implementation of LSTM (Schaul
et al., 2010). For the artificial sequence learning task, the network contains
25 input units, 20 internal LSTM neurons, E 25 output units. For the NYC
taxi task, the network contains 3 input units, 20 LSTM cells, 1 output unit
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2500
Y. Cui, S. Ahmad, and J. Hawkins
for calculation of the MAPE metric, E 22 output units for calculation of
the sequence likelihood metric. The LSTM cells have forget gates but not
peephole connections. The output units have a biased term. The maximum
time lag is the same as the buffer size for the batch-learning LSTMs. We used
two training paradigms. For the batch-learning paradigm, the networks
were retrained every 1000 iterations with a popular version of the resilient
backpropagation method (Igel & H ¨usken 2003). For the online learning
paradigm, we calculated the gradient at every time step using truncated
backpropgation through time over the last 100 elements (Williams & Peng,
1990), and adjusted the parameters along the gradient with a learning rate
Di 0.01.
A.2.4 TDNN. Time-delayed neural network was implemented as a sin-
gle hidden layer feedforward neural network with time-delayed inputs
with PyBrain. For the artificial data set, the network contains 250 input
units (10 time lags × 25 dimensional input per time step), 200 hidden units,
E 25 output units. For the taxi data, the network contains 100 input units
(100 time labs), 200 hidden units, E 1 output unit. We included bias for
both input and output units in both cases. The networks were retrained
every 1000 iterations (artificial data set) or every 336 iterations (taxi data)
on the past 3000 data records using standard backpropagation.
A.3 Evaluation of Model Performance in the Continuous Sequence
Learning Task. Two error metrics were used to evaluate the prediction
accuracy of the model. Primo, we considered the mean absolute percentage
error (MAPE) metric, an error metric that is less sensitive to outliers than
root mean squared error:
MAPE =
(cid:7)
|yt
N
t=1
(cid:7)
N
t=1
|
.
− ˆyt
|
|yt
(A.1)
In equation A.1, yt is the observed data at time t, ˆyt is the model prediction
for the data observed at time t, and N is the length of the data set.
A good prediction algorithm should output a probability distribution of
future elements of the sequence. Tuttavia, MAPE, consider only the single
best prediction from the model and thus does not incorporate other possible
predictions from the model. We used negative log likelihood as a comple-
mentary error metric to address this problem. The sequence probability can
be decomposed into
P(y1
, y2
, . . . , yt
) = p(y1
)P(y2
|y1
)P(y3
|y1
, y2
)P(yt
|y1
, . . . , yt−1
).
(A.2)
The conditional probability distribution is modeled by HTM or LSTM
based on network state at the previous time step:
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
P(yt
|y1
, . . . , yt−1
) = P(yt
|network statet−1
).
The negative log likelihood of the sequence is then given by
NLL = 1
N
N(cid:9)
t=1
log P(yt
|modello).
Ringraziamenti
2501
(A.3)
(A.4)
We thank the NuPIC open source community (numenta.org) for continuous
support and enthusiasm about HTM. We thank the reviewers for numerous
suggestions that significantly improved the overall letter. We also thank
Chetan Surpur for helping to run some of the simulations and our Numenta
colleagues for many helpful discussions.
Riferimenti
Abeles, M. (1982). Local cortical circuits: An electrophysiological study. Berlin: Springer.
Ahmad, S., & Hawkins, J. (2016). How do neurons operate on sparse distributed representa-
zioni? A mathematical theory of sparsity, neurons and active dendrites. arXiv.1601.00720
Antic, S. D., Zhou, W. L., Moore, UN. R., Corto, S. M., & Ikonomu, K. D. (2010). IL
decade of the dendritic NMDA spike. J. Neurosci. Res., 88, 2991–3001.
Ben Taieb, S., Bontempi, G., Atiya, UN. F., & Sorjamaa, UN. (2012). A review and com-
parison of strategies for multi-step ahead time series forecasting based on the
NN5 forecasting competition. Expert Syst. Appl., 39(8), 7067–7083.
Bishop, C. (2006). Pattern recognition and machine learning. Singapore: Springer.
Brea, J., Senn, W., & Pfister, J.-P. (2013). Matching recall and storage in sequence
learning with spiking neural networks. J. Neurosci., 33(23), 9565–9575.
Bridle, J. (1989). Probabilistic interpretation of feedforward classification network
outputs, with relationships to statistical pattern recognition. In F. Fogelman Souli´e
& J. H´eravlt (Eds.), Neurocomputing: Algorithms, architectures and applications (pag.
227–236). Berlin: Springer-Verlag.
Brosch, M., & Schreiner, C. E. (2000). Sequence sensitivity of neurons in cat primary
auditory cortex. Cereb. Cortex., 10(12), 1155–1167.
Buxhoeveden, D. P. (2002). The minicolumn hypothesis in neuroscience. Brain, 125(5),
935–951.
Clegg, B. A., Digirolamo, G. J., & Keele, S. W. (1998). Sequence learning. Trends Cogn.
Sci. 2(8), 275–281.
Crone, S. F., Hibon, M., & Nikolopoulos, K. (2011). Advances in forecasting with
neural networks? Empirical evidence from the NN3 competition on time series
prediction. Int. J. Forecast., 27(3), 635–660.
Dietterich, T. G. (2002). Machine learning for sequential data: A review. Negli Atti
of the Jt. IAPR Int. Work. Struct. Syntactic, Stat. Pattern Recognition (pag. 15–30).
Berlin: Springer-Verlag.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2502
Y. Cui, S. Ahmad, and J. Hawkins
Domingos, P., & Hulten, G. (2000). Mining high-speed data streams. Proceedings of
the Sixth ACM SIGKDD Int. Conf. Knowl. Discov. Data Mining (pag. 71–80). Nuovo
York: ACM Press.
Durbin, J., & Koopman, S. J. (2012). Time series analysis by state space methods (2nd
ed.). New York: Oxford University Press.
Fine, S., Singer, Y., & Tishby, N. (1998). The hierarchical hidden markov model:
Analysis and applications. Mach. Learn., 32(1), 41–62.
F ¨oldi´ak, P. (2002). Sparse coding in the primate cortex. In M. UN. Arbib (Ed.), IL
handbook of brain theory and neural networks ( 2nd ed.), (pag. 1064–1068). Cambridge,
MA: CON Premere.
Gaber, M. M., Zaslavsky, A., & Krishnaswamy, S. (2005). Mining data streams. ACM
SIGMOD Rec., 34(2), 18.
Gama, J. (2010). Knowledge discovery from data streams. Boca Raton, FL: Chapman and
Hall/CRC.
Gavornik, J. P., & Bear M. F. (2014). Learned spatiotemporal sequence recognition
and prediction in primary visual cortex. Nat. Neurosci., 17, 732–737.
Graves, UN. (2012). Supervised sequence labelling with recurrent neural networks. Nuovo
York: Springer.
Greff, K., Srivastava, R., Koutnik, J., Steunebrink, B. R., & Schmidhuber, J. (2015).
LSTM: A search space Odyssey. arXiv.1503.04069
Hawkins, J., & Ahmad, S. (2016). Why neurons have thousands of synapses: A theory
of sequence memory in neocortex. Front. Neural Circuits, 10.
Hawkins, J., Ahmad, S., & Dubinsky, D. (2011). Cortical learning algorithm and hier-
archical temporal memory. Numenta white paper. http://numenta.org/resources/
HTM_CorticalLearningAlgorithms.pdf
Hebb, D. (1949). The organization of behavior: A neuropsychological theory. Sci.
Educ., 44(1), 335.
Henaff, M., Szlam, A., & Lecun, Y. (2016). Orthogonal RNNs and long-memory tasks.
arXiv.1602.06662
Hinton, G., Srivastava, N., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R.
(2012). Improving neural networks by preventing co-adaptation of feature detectors.
arXiv.1207.0580
Hochreiter, S., & Schmidhuber, J. (1997). Memoria a lungo termine. Neural Comput.,
9(8), 1735–1780.
Huang, G.-B., Wang, D. H., & Lan, Y. (2011). Extreme learning machines: A survey.
Int. J. Mach. Learn. Cybern., 2(2), 107–122.
Huang, G.-B., Zhu, Q.-Y., & Siew, C.-K. (2006). Extreme learning machine: Theory
e applicazioni. Neurocomputing, 70, 489–501.
Hyndman, R. J., & Athanasopoulos, G. (2013). Forecasting: Principles and practice.
OTexts, https://www.otexts.org/fpp.
Hyndman, R. J., & Khandakar, Y. (2008). Automatic time series forecasting: IL
forecast package for R. J. Stat. Softw., 26(3).
Igel, C., & H ¨usken, M. (2003). Empirical evaluation of the improved Rprop learning
algorithms. Neurocomputing, 50, 105–123.
Jaeger, H. (2002). Tutorial on training recurrent neural networks, covering BPPT, RTRL,
EKF and the “echo state network” approach (GMD Rep. 159. 48). Hanover: German
National Research Center for Information Technology.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
Online Learning with HTM Sequence Memory
2503
Jaeger, H., & Haas, H. (2004). Harnessing nonlinearity: Predicting chaotic systems
and saving energy in wireless communication. Scienza, 304(5667), 78–80.
Kanerva, P. (1988). Sparse distributed memory. Cambrige, MA: CON Premere.
Lavin, A., & Ahmad, S. (2015). Evaluating real-time anomaly detection algorithms:
The Numenta anomaly benchmark. In Proceedings of the 14th Int. Conf. Mach. Learn.
Appl. Piscataway, NJ: IEEE.
LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–
444.
Lee, M., Hwang, K., & Sung, W. (2014). Fault tolerance analysis of digital feedforward
deep neural networks. Negli Atti del 2014 IEEE Int. Conf. Acoust. Speech
Signal Processing, (pag. 5031–5035). Piscataway, NJ: IEEE.
Liang, N.-Y., Huang, G.-B., Saratchandran, P., & Sundararajan, N. (2006). A fast and
accurate online sequential learning algorithm for feedforward networks. IEEE
Trans. Neural Netw., 17(6), 1411–1423.
Lipton, Z. C., Berkowitz, J., & Elkan, C. (2015). A critical review of recurrent neural
networks for sequence learning. arXiv.1506.00019[cs.LG]
Lughofer, E., & Angelov, P. (2011). Handling drifts and shifts in on-line data streams
with evolving fuzzy systems. Appl. Soft Comput., 11(2), 2057–2068.
Major, G., Larkum, M. E., & Schiller, J. (2013). Active properties of neocortical pyra-
midal neuron dendrites. Annu. Rev. Neurosci., 36 1–24.
Massey, P. V., & Bashir, Z. IO. (2007). Long-term depression: Multiple forms and
implications for brain function. Trends Neurosci., 30(4), 176–184.
Mauk, M. D., & Buonomano, D. V. (2004). The neural basis of temporal processing.
Annu. Rev. Neurosci., 27, 307–340.
McFarland, J. M., Cui, Y., & Butts, D. UN. (2013). Inferring nonlinear neuronal computa-
tion based on physiologically plausible inputs. PLoS Comput. Biol., 9(7), e1003143.
Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient estimation of word
representations in vector space. arXiv.1301.3781
Mnatzaganian, J., Fokou´e, E., & Kudithipudi, D. (2016). A mathematical formalization
of hierarchical temporal memory’s spatial pooler. arXiv.1601.06116.
Moreira-Matias, L., Gama, J., Ferreira, M., Mendes-Moreira, J., & Damas, l. (2013).
Predicting taxi–passenger demand using streaming data. IEEE Trans. Intell.
Transp. Syst., 14(3), 1393–1402.
Mountcastle, V. B. (1997). The columnar organization of the neocortex. Brain, 120 (Pt.
4), 701–722.
Nikoli´c, D., H¨ausler, S., Singer, W., & Maass, W. (2009). Distributed fading memory
for stimulus properties in the primary visual cortex. PLoS Biol., 7(12), e1000260.
Olshausen, B. A., & Field, D. J. (2004). Sparse coding of sensory inputs. Curr. Opin.
Neurobiol., 14, 481–487.
Polsky, A., Mel, B. W., & Schiller, J. (2004). Computational subunits in thin dendrites
of pyramidal cells. Nat. Neurosci., 7(6), 621–627.
Ponulak, F., & Kasi ´nski, UN. (2010). Supervised learning in spiking neural networks
with ReSuMe: Sequence learning, classification, and spike shifting. Neural Com-
put., 22(2), 467–510.
Purdy, S. (2016). Encoding data for HTM systems. arXiv.1602.05925
Rabiner, L., & Juang, B. (1986). An introduction to hidden Markov models. IEEE
ASSP Mag., 3(1), 4–16.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3
2504
Y. Cui, S. Ahmad, and J. Hawkins
Rao, R. P., & Sejnowski, T. J. (2001). Predictive learning of temporal sequences in
recurrent neocortical circuits. In Proceedings of the Novartis Found. Symp., 239, (pag.
208–229; discussion 229–240).
Sadato, N., Pascual-Leone, A., Grafman, J., Iba ˜nez, V., Deiber, M. P., & Hallett, M.
(1996). Activation of the primary visual cortex by Braille reading in blind subjects.
Nature, 380(6574), 526–528.
Sayed-Mouchaweh, M., & Lughofer, E. (2012). Learning in non-stationary environ-
menti: Methods and applications. New York: Springer.
Schaul, T., Bayer, J., Wierstra, D., Sun, Y., Felder, M., Sehnke, F., . . . Schmidhuber, J.
(2010). PyBrain. J. Mach. Learn. Res. 11, 743–746.
Schmidhuber, J. (2009). Simple algorithmic theory of subjective beauty, novelty,
sorpresa, interestingness, Attenzione, curiosity, creativity, art, science, music, jokes.
Journal of the Society of Instrument and Control Engineers, 48(1), 21–32.
Schmidhuber, J. (2014). Deep learning in neural networks: An overview. Neural
Networks, 61, 85–117.
Sejnowski, T., & Rosenberg, C. (1987). Parallel networks that learn to pronounce
English text. J. Complex Syst., 1(1), 145–168.
Sharma, J., Angelucci, A., & Sur, M. (2000). Induction of visual orientation modules
in auditory cortex. Nature, 404(6780), 841–847.
Smith, S. L., Smith, IO. T, Branco, T., & H¨ausser, M. (2013). Dendritic spikes enhance
stimulus selectivity in cortical neurons in vivo. Nature, 503(7474), 115–120.
Spruston, N. (2008). Pyramidal neurons: Dendritic structure and synaptic integra-
zione. Nat. Rev. Neurosci., 9(3), 206–221.
Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to sequence learning with
neural networks. In Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, &
K. Q. Weinberger (Eds.), Advances in neural information processing systems, 27 (pag.
3104–3112). Red Hook, NY: Curran.
Tchernev, E. B., Mulvaney, R. G., & Phatak, D. S. (2005). Investigating the fault
tolerance of neural networks. Neural Comput., 17(7), 1646–1664.
Tran, UN. H., Yanushkevich, S. N., Lyshevski, S. E., & Shmerko, V. P. (2011). Design of
neuromorphic logic networks and fault-tolerant computing. Negli Atti del
2011 11th IEEE Int. Conf. Nanotechnology, (pag. 457–462). Piscataway, NJ: IEEE.
Waibel, A., Hanazawa, T., Hinton, G., Shikano, K., & Lang, K. J. (1989). Phoneme
recognition using time-delay neural networks. IEEE Trans. Acoust., 37(3), 328–339.
Wang, X., & Han, M. (2014). Online sequential extreme learning machine with kernels
for nonstationary time series prediction. Neurocomputing, 145, 90–97.
Williams, R. J., & Peng, J. (1990). An efficient gradient-based algorithm for on-line
training of recurrent network trajectories. Neural Comput., 2(4), 490–501.
Williams, R. J., & Zipser, D. (1989). A learning algorithm for continually running
fully recurrent neural networks. Neural Comput., 1(2), 270–280.
Xu, S., Jiang, W., Poo, M.-M., & Dan, Y. (2012). Activity recall in a visual cortical
ensemble. Nat. Neurosci., 15(3), 449–455, S1–S2.
Zito, K., & Svoboda, K. (2002). Activity-dependent synaptogenesis in the adult Mam-
malian cortex. Neuron, 35(6), 1015–1017.
Received December 10, 2015; accepted July 11, 2016.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
/
e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D
/
l
F
/
/
/
/
2
8
1
1
2
4
7
4
2
0
1
5
8
2
9
N
e
C
o
_
UN
_
0
0
8
9
3
P
D
.
/
F
B
sì
G
tu
e
S
T
T
o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3