LETTER

Communicated by Justin Dauwels

Reverse-Engineering Neural Networks to Characterize
Their Cost Functions

Takuya Isomura
takuya.isomura@riken.jp
Brain Intelligence Theory Unit, RIKEN Center for Brain Science,
Wako, Saitama 351-0198, Japan

Karl Friston
k.friston@ucl.ac.uk
Wellcome Centre for Human Neuroimaging, Institute of Neurology,
University College London, London, WC1N 3AR, U.K.

This letter considers a class of biologically plausible cost functions for
neural networks, where the same cost function is minimized by both neu-
ral activity and plasticity. We show that such cost functions can be cast
as a variational bound on model evidence under an implicit generative
modello. Using generative models based on partially observed Markov de-
cision processes (POMDP), we show that neural activity and plasticity
perform Bayesian inference and learning, rispettivamente, by maximizing
model evidence. Using mathematical and numerical analyses, we estab-
lish the formal equivalence between neural network cost functions and
variational free energy under some prior beliefs about latent states that
generate inputs. These prior beliefs are determined by particular con-
stants (per esempio., thresholds) that define the cost function. This means that the
Bayes optimal encoding of latent or hidden states is achieved when the
network’s implicit priors match the process that generates its inputs. Questo
equivalence is potentially important because it suggests that any hyper-
parameter of a neural network can itself be optimized—by minimization
with respect to variational free energy. Inoltre, it enables one to
characterize a neural network formally, in terms of its prior beliefs.

1 introduzione

Cost functions are ubiquitous in scientific fields that entail optimization—
including physics, chimica, biologia, engineering, and machine learning.
Inoltre, any optimization problem that can be specified using a cost
function can be formulated as a gradient descent. In the neurosciences, Questo
enables one to treat neuronal dynamics and plasticity as an optimization
processi (Marr, 1969; Albus, 1971; Schultz, Dayan, & Montague, 1997; Sut-
ton & Barto, 1998; Linsker, 1988; Brown, Yamada, & Sejnowski, 2001). These

Calcolo neurale 32, 2085–2121 (2020) © 2020 Istituto di Tecnologia del Massachussetts.
https://doi.org/10.1162/neco_a_01315
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale (CC BY 4.0) licenza.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2086

T. Isomura and K. Friston

examples highlight the importance of specifying a problem in terms of cost
functions, from which neural and synaptic dynamics can be derived. In
other words, cost functions provide a formal (cioè., normative) expression of
the purpose of a neural network and prescribe the dynamics of that neural
rete. Crucially, once the cost function has been established and an initial
condition has been selected, it is no longer necessary to solve the dynam-
ics. Invece, one can characterize the neural network’s behavior in terms
of fixed points, basin of attraction and structural stability—based only on
the cost function. In short, it is important to identify the cost function to
understand the dynamics, plasticity, and function of a neural network.

A ubiquitous cost function in neurobiology, theoretical biology, and ma-
chine learning is model evidence or equivalently, marginal likelihood or
surprise—namely, the probability of some inputs or data under a model of
how those inputs were generated by unknown or hidden causes (Bishop,
2006; Dayan & Abbott, 2001). Generally, the evaluation of surprise is in-
tractable (especially for neural networks) as it entails a logarithm of an in-
tractable marginal (cioè., integral). Tuttavia, this evaluation can be converted
into an optimization problem by inducing a variational bound on surprise.
In machine learning, this is known as an evidence lower bound (ELBO; Blei,
Kucukelbir, & McAuliffe, 2017), while the same quantity is known as vari-
ational free energy in statistical physics and theoretical neurobiology.

Variational free energy minimization is a candidate principle that gov-
erns neuronal activity and synaptic plasticity (Friston, Kilner, & Harrison,
2006; Friston, 2010). Here, surprise reflects the improbability of sensory in-
puts given a model of how those inputs were caused. In turn, minimizing
variational free energy, as a proxy for surprise, corresponds to inferring the
(unobservable) causes of (observable) consequences. To the extent that bi-
ological systems minimize variational free energy, it is possible to say that
they infer and learn the hidden states and parameters that generate their
sensory inputs (von Helmholtz, 1925; Knill & Pouget, 2004; DiCarlo, Zoc-
colan, & Rust, 2012) and consequently predict those inputs (Rao & Ballard,
1999; Friston, 2005). This is generally referred to as perceptual inference
based on an internal generative model about the external world (Dayan,
Hinton, Neal, & Zemel, 1995; George & Hawkins, 2009; Bastos et al., 2012).
Variational free energy minimization provides a unified mathematical
formulation of these inference and learning processes in terms of self-
organizing neural networks that function as Bayes optimal encoders. More-
Sopra, organisms can use the same cost function to control their surrounding
environment by sampling predicted (cioè., preferred) inputs. This is known
as active inference (Friston, Mattout, & Kilner, 2011). The ensuing free-
energy principle suggests that active inference and learning are mediated
by changes in neural activity, synaptic strengths, and the behavior of an or-
ganism to minimize variational free energy as a proxy for surprise. Cru-
cially, variational free energy and model evidence rest on a generative
model of continuous or discrete hidden states. A number of recent studies

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2087

have used Markov decision process (MDP) generative models to elaborate
schemes that minimize variational free energy (Friston, FitzGerald, Rigoli,
Schwartenbeck, & Pezzulo, 2016, 2017; Friston, Parr, & de Vries, 2017; Fris-
ton, Lin et al., 2017). This minimization reproduces various interesting dy-
namics and behaviors of real neuronal networks and biological organisms.
Tuttavia, it remains to be established whether variational free energy min-
imization is an apt explanation for any given neural network, as opposed
to the optimization of alternative cost functions.

In principle, any neural network that produces an output or a decision
can be cast as performing some form of inference in terms of Bayesian deci-
sion theory. On this reading, the complete class theorem suggests that any
neural network can be regarded as performing Bayesian inference under
some prior beliefs; Perciò, it can be regarded as minimizing variational
free energy. The complete class theorem (Wald, 1947; Brown, 1981) stati
that for any pair of decisions and cost functions, there are some prior beliefs
(implicit in the generative model) that render the decisions Bayes optimal.
This suggests that it should be theoretically possible to identify an implicit
generative model within any neural network architecture, which renders
its cost function a variational free energy or ELBO. Tuttavia, although the
complete class theorem guarantees the existence of a generative model, Esso
does not specify its form. In what follows, we show that a ubiquitous class
of neural networks implements approximates Bayesian inference under a
generic discrete state space model with a known form.

In brief, we adopt a reverse-engineering approach to identify a plausible
cost function for neural networks and show that the resulting cost function
is formally equivalent to variational free energy. Here, we define a cost func-
tion as a function of sensory input, neural activity, and synaptic strengths
and suppose that neural activity and synaptic plasticity follow a gradient
descent on the cost function (assumption 1). For simplicity, we consider
single-layer feedforward neural networks comprising firing-rate neuron
models—receiving sensory inputs weighted by synaptic strengths—whose
firing intensity is determined by the sigmoid activation function (assump-
zione 2). We focus on blind source separation (BSS), namely the problem
of separating sensory inputs into multiple hidden sources or causes (Essere-
louchrani, Abed-Meraim, Cardoso, & Moulines, 1997; Cichocki, Zdunek,
Phan, & Amari, 2009; Comon & Jutten, 2010), which provides the minimum
setup for modeling causal inference. A famous example of BSS is the cocktail
party effect: the ability of a partygoer to disambiguate an individual’s voice
from the noise of a crowd (Brown et al., 2001; Mesgarani & Chang, 2012).
Previously, we observed BSS performed by in vitro neural networks (Iso-
mura, Kotani, & Jimbo, 2015) and reproduced this self-supervised process
using an MDP and variational free energy minimization (Isomura & Fris-
ton, 2018). These works suggest that variational free energy minimization
offers a plausible account of the empirical behavior of in vitro networks.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2088

T. Isomura and K. Friston

In this work, we ask whether variational free energy minimization can
account for the normative behavior of a canonical neural network that min-
imizes its cost function, by considering all possible cost functions, within
a generic class. Using mathematical analysis, we identify a class of cost
functions—from which update rules for both neural activity and synaptic
plasticity can be derived. The gradient descent on the ensuing cost func-
tion naturally leads to Hebbian plasticity (Hebb, 1949; Bliss & Lømo, 1973;
Malenka & Bear, 2004) with an activity-dependent homeostatic term. Noi
show that these cost functions are formally homologous to variational free
energy under an MDP. Crucially, this means the hyperparameters (cioè., any
variables or constants) of the neural network can be associated with prior
beliefs of the generative model. In principle, this allows one to optimize the
neural network hyperparameters (per esempio., thresholds and learning rates), given
some priors over the causes (cioè., latent states) of inputs to the neural net-
lavoro. Inoltre, estimating hyperparameters from the dynamics of (In
silico or in vitro) neural networks allows one to quantify the network’s im-
plicit prior beliefs. In this letter, we focus on the mathematical foundations
for applications to in vitro and in vivo neuronal networks in subsequent
lavoro.

2 Methods

In this section, we formulate the same computation in terms of variational
Bayesian inference and neural networks to demonstrate their correspon-
dence. We first derive the form of a variational free energy cost function un-
der a specific generative model, a Markov decision process.1 We present the
derivations carefully, with a focus on the form of the ensuing Bayesian be-
lief updating. The functional form of this update will reemerge later, Quando
reverse engineering the cost functions implicit in neural networks. These
correspondences are depicted in Figure 1 and Table 1. This section starts
with a description of Markov decision processes as a general kind of gener-
ative model and then considers the minimization of variational free energy
under these models.

2.1 Generative Models. Under an MDP model (see Figure 1A), a mini-
mal BSS setup (in a discrete space) reduces to the likelihood mapping from
Ns hidden sources or states st ≡
to No observations ot ≡
S(1)
(cid:2)
T
T
o(1)
. Each source and observation takes a value of one (ON state)
T

, . . . , o(No)

, . . . , S(Ns )

(cid:3)

(cid:3)

(cid:2)

T

T

T

1

Strictly speaking, the generative model we use in this letter is a hidden Markov model
(HMM) because we do not consider probabilistic transitions between hidden states that
depend on control variables. Tuttavia, for consistency with the literature on variational
treatments of discrete statespace models, we retain the MDP formalism noting that we are
using a special case (with unstructured state transitions).

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2089

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

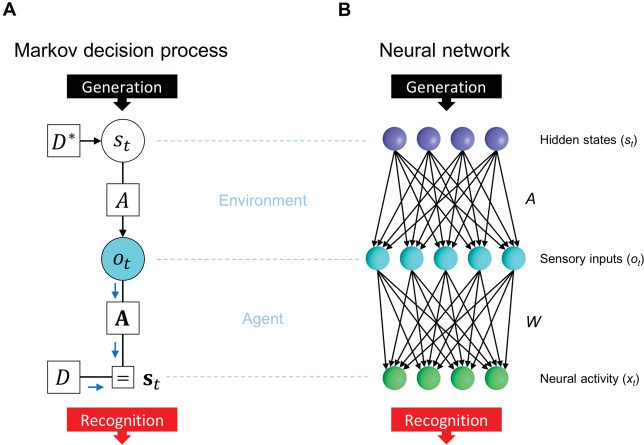
Figura 1: Comparison between an MDP scheme and a neural network. (UN) MDP
scheme expressed as a Forney factor graph (Forney, 2001; Dauwels, 2007) based
on the formulation in Friston, Parr et al. (2017). In this BSS setup, the prior
D determines hidden states st, while st determines observation ot through the
likelihood mapping A. Inference corresponds to the inversion of this gener-
ative process. Here, D∗ indicates the true prior, while D indicates the prior
under which the network operates. If D = D∗, the inference is optimal; other-
wise, it is biased. (B) Neural network comprising a singlelayer feedforward net-
work with a sigmoid activation function. The network receives sensory inputs
)T
)T that are generated from hidden states st
ot
T
, . . . , xtNx )T . Here, xt j should encode the
and outputs neural activities xt
posterior expectation about a binary state s( j)
. In an analogy with the cocktail
T
party effect, st and ot correspond to individual speakers and auditory inputs,
rispettivamente.

, . . . , o(No)

, . . . , S(Ns )

= (o(1)
T

= (S(1)
T

= (xt1

T

(cid:2)

or zero (OFF state) at each time step, questo è, S( j)
∈ {1, 0}. Throughout this
T
letter, j denotes the jth hidden state, while i denotes the ith observation.
(cid:3)
(cid:3)
The probability of s( j)
,
T
, D( j)
where D( j) ≡
0

(cid:2)
S( j)
T
= 1 (see Figure 1A, top).

follows a categorical distribution P

∈ R2 with D( j)
1

+ D( j)
0

= Cat

D( j)
1

, o(io)
T

D( j)

The probability of an outcome is determined by the likelihood mapping
from all hidden states to each kind of observation in terms of a categor-
= Cat(UN(io)) (see Figure 1A, middle). Here,
ical distribution, P
each element of the tensor A(io) ∈ R2×2Ns parameterizes the probability that

|st, UN(io)

o(io)
T

(cid:3)

(cid:3)

(cid:2)

(cid:2)

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2090

T. Isomura and K. Friston

Tavolo 1: Correspondence of Variables and Functions.

Neural Network Formation

Neural activity

Sensory inputs

Synaptic strengths

Perturbation term

Threshold

h j1

Initial synaptic strengths

Variational
Bayes Formation

State posterior

Observations

Parameter posterior

State prior

⇐⇒ s( j)
xt j
t1
ot ⇐⇒ ot
(cid:4)
−1

(cid:5)

Wj1

ˆWj1

UN(·, j)

11

⇐⇒ sig
≡ sig(Wj1 ) ⇐⇒ A(·, j)
⇐⇒ ln D( j)
φ
j1
(cid:4)
1
(cid:2)1 − A(·, j)
· (cid:2)1 + ln D( j)
1

(cid:5)

11

11

⇐⇒ ln

λ

j1

(cid:7) ˆW init
j1

⇐⇒ a(·, j)

11

Parameter prior

(cid:3)

(cid:2)

(cid:2)

(cid:3)

(cid:2)

o(io)
T

UN(io)
·(cid:2)l

= k|st = (cid:2)l

(cid:3)
, where k ∈ {1, 0} are possible observations and (cid:2)l ∈ {1, 0}Ns
P
encodes a particular combination of hidden states. The prior distribution of
each column of A(io), denoted by A(io)
=
·(cid:2)l
∈ R2. We use Dirichlet distribu-
Dir
zioni, as they are tractable and widely used for random variables that take
a continuous value between zero and one. Inoltre, learning the likeli-
hood mapping leads to biologically plausible update rules, which have the
form of associative or Hebbian plasticity (see below and Friston et al., 2016,
for details).

with concentration parameter a(io)
·(cid:2)l

, has a Dirichlet distribution P

We use ˜o ≡ (o1

, . . . , ot ) and ˜s ≡ (s1

, . . . , st ) to denote sequences of obser-
vations and hidden states, rispettivamente. With this notation in place, the gen-
erative model (cioè., the joint distribution over outcomes, hidden states and
the parameters of their likelihood mapping) can be expressed as

UN(io)
·(cid:2)l

P ( ˜o, ˜s, UN) = P (UN)

T(cid:6)

τ =1

P (oτ |sτ , UN) P (sτ )

=

No(cid:6)

i=1

P(UN(io)) ·

⎧
⎨

No(cid:6)

⎩

i=1

T(cid:6)

τ =1

(cid:4)
τ |sτ , UN(io)
o(io)

P

(cid:5) Ns(cid:6)

(cid:4)
S( j)
τ

P

j=1

⎫
⎬

(cid:5)

.

⎭

(2.1)

Throughout this letter, t denotes the current time, and τ denotes an arbitrary
time from the past to the present, 1 ≤ τ ≤ t.

2.2 Minimization of Variational Free Energy. In this MDP scheme, IL
aim is to minimize surprise by minimizing variational free energy as a

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2091

proxy, questo è, performing approximate or variational Bayesian inference.
From the generative model, we can motivate a mean-field approximation
to the posterior (cioè., recognition) density as follows,

Q ( ˜s, UN) = Q (UN) Q ( ˜s) =

No(cid:6)

i=1

Q(UN(io)) ·

(cid:4)

Q

S( j)
τ

(cid:5)
,

T(cid:6)

Ns(cid:6)

τ =1

j=1

(2.2)

(cid:3)

(cid:2)

(cid:3)

(cid:3)

UN(io)

= Dir

where A(io) is the likelihood mapping (cioè., tensor), and the marginal poste-
(cid:2)
rior distributions of s( j)
τ and A(io) have a categorical Q
E
(cid:2)
UN(io)
Dirichlet distribution Q
, rispettivamente. For simplicity, we
assume that A(io) factorizes into the product of the likelihood mappings from
the jth hidden state to the ith observation: UN(io)
(Dove
⊗ denotes the outer product and A(io, j) ∈ R2×2). Questo (mean-field) approxi-
mation simplifies the computation of state posteriors and serves to specify a
particular form of Bayesian model which corresponds to a class of canonical
neural networks (see below).

k· ⊗ · · · ⊗ A(io,Ns )

k· ≈ A(io,1)

(cid:2)
= Cat

S( j)
τ

S( j)
τ

(cid:3)

k

In what follows, a case variable in bold indicates the posterior expecta-
tion of the corresponding variable in italics. Per esempio, S( j)
takes the value
τ
0 O 1, while the posterior expectation s( j)
τ ∈ R2 is the expected value of s( j)
τ
that lies between zero and one. Inoltre, UN(io, j) ∈ R2×2 denotes positive con-
centration parameters. Below, we use the posterior expectation of ln A(io, j) A
encode posterior beliefs about the likelihood, which is given by

ln A(io, j)
· j

≡ EQ(UN(io, j))

= ln a(io, j)

·l

(cid:14)

(cid:13)
ln A(io, j)
· j
(cid:4)
UN(io, j)

− ln

1l

(cid:4)

= ψ

(cid:5)

UN(io, j)
·l
(cid:5)

− ψ
(cid:15)(cid:4)

(cid:4)
UN(io, j)
(cid:5)−1

1l

+ UN(io, j)
(cid:16)

0l

(cid:5)

+ UN(io, j)

0l

+ O

UN(io, j)
·l

,

(2.3)

where l ∈ {1, 0}. Here, ψ (·) ≡ (cid:6)(cid:11)
(·) /(cid:6) (·) denotes the digamma function,
which arises naturally from the definition of the Dirichlet distribution. (Vedere
Friston et al., 2016, for details.) EQ(UN(io, j)) [·] denotes the expectation over the
posterior of A(io, j).

The ensuing variational free energy of this generative model is then

given by

F ( ˜o, Q ( ˜s) , Q (UN)) ≡

T(cid:17)

(cid:18)

EQ(sτ )Q(UN) [− ln P (oτ |sτ , UN)] + D

(cid:19)
KL [Q (sτ ) ||P (sτ )]

τ =1
+ D

KL [Q (UN) ||P (UN)]

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2092

T. Isomura and K. Friston

Ns(cid:17)

T(cid:17)

=

S( j)
τ

·

j=1
(cid:22)

τ =1

(cid:20)

No(cid:17)

−

ln A(io, j) · o(io)
(cid:23)(cid:24)
accuracy+state complexity

i=1

τ + ln s( j)

τ − ln D( j)

Ns(cid:17)

No(cid:17)

+

i=1
(cid:22)

j=1

{(UN(io, j) − a(io, j)) · ln A(io, j) − ln B(UN(io, j))}
,
(cid:25)

(cid:23)(cid:24)

(cid:21)

(cid:25)

(2.4)

parameter complexity

τ

·

1l

0l

1l

0l

(cid:3)

(cid:2)

(cid:3)

(cid:3)

(cid:3)

(cid:2)

(cid:2)

(cid:2)

(cid:2)

(cid:2)

(cid:2)

(cid:3)

(cid:2)

No

B

(cid:3)(cid:3)

/(cid:6)

S( j)
τ

(cid:3)
(cid:6)

UN(io, j)

UN(io, j)

UN(io, j)

ln s( j)

UN(io, j)
·1

UN(io, j)
·l

with B

+ UN(io, j)

(cid:2)
UN(io, j)
·0

τ − ln D( j)

τ , D
(cid:3)

E (state) complexity

i=1 ln A(io, j) · o(io)

function. The first term in the final equality comprises the accuracy
(cid:26)

where ln A(io, j) · o(io)
hot encoded vector of o(io)
Kullback–Leibler divergence (Kullback & Leibler, 1951) and B
(cid:2)
(cid:3)
B
≡ (cid:6)

τ denotes the inner product of ln A(io, j) and a one-
KL [·(cid:12)·] is the complexity as scored by the
≡

UN(io, j)
is the beta
− s( j)
·
τ
. The accu-
racy term is simply the expected log likelihood of an observation, while
complexity scores the divergence between prior and posterior beliefs. In
other words, complexity reflects the degree of belief updating or degrees
of freedom required to provide an accurate account of observations. Both
belief updates to states and parameters incur a complexity cost: the state
complexity increases with time t, while parameter complexity increases on
the order of ln t—and is thus negligible when t is large (see section A.1 for
details). This means that we can ignore parameter complexity when the
scheme has experienced a sufficient number of outcomes. We drop the pa-
rameter complexity in subsequent sections. In the remainder of this section,
we show how the minimization of variational free energy transforms (cioè.,
updates) priors into posteriors when the parameter complexity is evaluated
explicitly.

Inference optimizes posterior expectations about the hidden states by
minimizing variational free energy. The optimal posterior expectations are
obtained by solving the variation of F to give

S( j)
T

= σ

(cid:27)

No(cid:17)

i=1

(cid:28)

ln A(io, j) · o(io)
T

+ ln D( j)

= σ

(cid:4)
ln A(·, j) · ot + ln D( j)

(cid:5)

,

(2.5)

where σ (·) is the softmax function (see Figure 1A, bottom). As s( j)
is a binary
T
value in this work, the posterior expectation of s( j)
taking a value of one (ON
T
state) can be expressed as

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2093

S( j)
t1

=

(cid:4)
ln A(·, j)
·1

esp
(cid:4)
ln A(·, j)
·1

= sig

esp

(cid:4)
ln A(·, j)
·1
(cid:5)
· ot + ln D( j)
1

(cid:5)

· ot + ln D( j)
1
(cid:4)
ln A(·, j)
·0

+ esp

(cid:5)

· ot + ln D( j)
0
(cid:5)

· ot − ln A(·, j)
·0

· ot + ln D( j)
1

− ln D( j)
0

(2.6)

= 1 − s( j)

= 0.5 in this BSS setup.

using the sigmoid function sig (z) ≡ 1/(1 + esp (−z)). Così, the posterior
expectation of s( j)
t1 . Here, D( j)
taking a value zero (OFF state) is s( j)
T
t0
1
and D( j)
0 are constants denoting the prior beliefs about hidden states. Bayes
optimal encoding is obtained when and only when the prior beliefs match
the genuine prior distribution: D( j)
= D( j)
1
0
This concludes our treatment of inference about hidden states under
this minimal scheme. Note that the updates in equation 2.5 have a bi-
ological plausibility in the sense that the posterior expectations can be
associated with nonnegative sigmoid-shape firing rates (also known as neu-
rometric functions; Tolhurst, Movshon, & Dean, 1983; Newsome, Britten, &
Movshon, 1989), while the arguments of the sigmoid (softmax) function can
be associated with neuronal depolarization, rendering the softmax function
a voltage-firing rate activation function. (See Friston, FitzGerald et al., 2017,
for a more comprehensive discussion and simulations using this kind of
variational message passing to reproduce empirical phenomena, ad esempio
place fields, mismatch negativity responses, phase-precession, and preplay
activity in systems neuroscience.)

In terms of learning, by solving the variation of F with respect to a(io, j),

the optimal posterior expectations about the parameters are given by

UN(io, j) = a(io, j) +

T(cid:17)

τ =1

τ ⊗ s( j)
o(io)

τ = a(io, j) + A(io)
T

⊗ s( j)
T

,

(2.7)

where a(io, j) is the prior, o(io)
⊗ s( j)
encoded vector of o(io)
T
optimal posterior expectation of matrix A is

τ , and o(io)
T

τ and s( j)

τ ⊗ s( j)

τ expresses the outer product of a one-hot
(cid:26)
T

τ =1 o(io)

τ ⊗ s( j)

τ . Così, IL

≡ 1
T

⎧

⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎩

UN(io, j)

11

=

UN(io, j)

10

=

11

UN(io, j)
+ UN(io, j)

01

UN(io, j)

11

10

UN(io, j)
+ UN(io, j)

00

UN(io, j)

10

= to(io)
ts( j)
t1

t s( j)
+ UN(io, j)

11

t1

+ UN(io, j)

11

+ UN(io, j)

01

= to(io)
ts( j)
t0

t s( j)
+ UN(io, j)

10

t0

+ UN(io, j)

10

+ UN(io, j)

00

(cid:16)

,

(cid:16)

(cid:15)

(cid:15)

1
T

1
T

+ O

+ O

t s( j)
= o(io)
t1
S( j)
t1

t s( j)
= o(io)
t0
S( j)
t0

(2.8)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2094

T. Isomura and K. Friston

(cid:26)
T

(cid:26)
T

(cid:26)
T

t0

t1

01

00

= 1
T

τ s( j)

τ s( j)

= 1
T
= 1 − A(io, j)

t s( j)
τ =1 s( j)
τ 1 , o(io)
11 e A(io, j)

τ 1 , S( j)
τ =1 o(io)
= 1
T
τ 0 . Further, UN(io, j)
τ =1 s( j)

t s( j)
τ =1 o(io)
where o(io)
τ 0 , E
t1
(cid:26)
= 1 − A(io, j)
S( j)
= 1
T
10 . The prior
t0
T
of parameters a(io, j) is on the order of one and is thus negligible when t is
large. The matrix A(io, j) expresses the optimal posterior expectations of o(io)
T
is ON (UN(io, j)
taking the ON state when s( j)
10 ), or o(io)
taking the
T
01 ) or OFF (UN(io, j)
OFF state when s( j)
00 ). Although this expression
T
may seem complicated, it is fairly straightforward. The posterior expecta-
tions of the likelihood simply accumulate posterior expectations about the
co-occurrence of states and their outcomes. These accumulated (Dirichlet)
parameters are then normalized to give a likelihood or probability. Cru-
cially, one can observe the associative or Hebbian aspect of this belief up-
date, expressed here in terms of the outer products between outcomes and
posteriors about states in equation 2.7. We now turn to the equivalent up-
date for neural activities and synaptic weights of a neural network.

11 ) or OFF (UN(io, j)

is ON (UN(io, j)

T

2.3 Neural Activity and Hebbian Plasticity Models. Prossimo, we consider
the neural activity and synaptic plasticity in the neural network (Guarda la figura
1B). The generation of observations ot is exactly the same as in the MDP
model introduced in section 2.1 (see Figure 1B, top to middle). We assume
that the jth neuron’s activity xt j (see Figure 1B, bottom) is given by

˙xt j

∝ − f

(cid:11)

(xt j )
(cid:22) (cid:23)(cid:24) (cid:25)

leakage

(cid:22)

+ Wj1ot − Wj0ot
(cid:25)
(cid:23)(cid:24)
synaptic input

+ h j1
(cid:22)

− h j0
(cid:25)
(cid:23)(cid:24)

.

threshold

(2.9)

∈ RNo and Wj0
∈ RNo comprise row vectors of synapses
We suppose that Wj1
∈ R are adaptive thresholds that depend on the val-
∈ R and h j0
and h j1
ues of Wj1 and Wj0, rispettivamente. One may regard Wj1 and Wj0 as excitatory
and inhibitory synapses, rispettivamente. We further assume that the nonlinear
leakage f (cid:11)
(·) (cioè., the leak current) is the inverse of the sigmoid function
(cioè., the logit function) so that the fixed point of xt j (cioè., the state of xt j that
gives ˙xt j

= 0) is given in the form of the sigmoid function:

xt j

= sig

=

esp

(cid:3)

(cid:2)
Wj1ot − Wj0ot + h j1
(cid:2)
Wj1ot + h j1
(cid:2)
(cid:3)
Wj0ot + h j0
+ esp

esp
(cid:2)
Wj1ot + h j1

− h j0
(cid:3)

(cid:3) .

(2.10)

Equations 2.9 E 2.10 are a mathematical expression of assumption 2. Fur-
ther, we consider a class of synaptic plasticity rules that comprise Hebbian

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2095

plasticity with an activity-dependent homeostatic term as follows:

(cid:20)

(cid:8)Wj1 (T) ≡ Wj1 (T + 1) − Wj1 (T) ∝ Hebb1

(cid:8)Wj0 (T) ≡ Wj0 (T + 1) − Wj0 (T) ∝ Hebb0

(cid:2)

(cid:2)

xt j

, ot, Wj1

xt j

, ot, Wj0

(cid:3)

(cid:3)

+ Home1

+ Home0

(cid:2)

(cid:2)

xt j

, Wj1

xt j

, Wj0

(cid:3)

(cid:3) ,

(2.11)

where Hebb1 and Hebb0 denote Hebbian plasticity as determined by the
product of sensory inputs and neural outputs and Home1 and Home0 de-
note homeostatic plasticity determined by output neural activity. Equazione
2.11 can be read as an ansatz: we will see below that a synaptic update rule
with the functional form of equation 2.11 emerges as a natural consequence
of assumption 1.

(cid:2)

(cid:3)

(cid:3)

(cid:3)

(cid:2)

11

10

10

−1

= sig

= sig

UN(·, j)

and ln A(·, j)

(cid:2)
(cid:2)1 − A(·, j)

In the MDP scheme, posterior expectations about hidden states and pa-
rameters are usually associated with neural activity and synaptic strengths.
Here, we can observe a formal similarity between the solutions for the state
posterior (see equation 2.6) and the activity in the neural network (see equa-
zione 2.10; see also Table 1). By this analogy, xt j can be regarded as encod-
ing the posterior expectation of the ON state s( j)
t1 . Inoltre, Wj1 and Wj0
(cid:2)
correspond to ln A(·, j)
UN(·, j)
(cid:2)1 −
− ln
(cid:3)
11
UN(·, j)
−1
, rispettivamente, in the sense that they express the ampli-
tude of ot influencing xt j or s( j)
t1 . Here, (cid:2)1 = (1, . . . , 1) ∈ RNo is a vector of ones.
In particular, the optimal posterior of a hidden state taking a value of one
(see equation 2.6) is given by the ratio of the beliefs about ON and OFF
stati, expressed as a sigmoid function. Così, to be a Bayes optimal en-
coder, the fixed point of neural activity needs to be a sigmoid function. Questo
requirement is straightforwardly ensured when f (cid:11)
is the inverse of the
sigmoid function (see equation 2.13). Under this condition the fixed point
or solution for xtk (see equation 2.10) compares inputs from ON and OFF
pathways, and thus xt j straightforwardly encodes the posterior of the jth
hidden state being ON (cioè., xt j
t1 ). In short, the above neural network
is effectively inferring the hidden state.

→ s( j)

− ln

xt j

10

11

(cid:2)

(cid:3)

If the activity of the neural network is performing inference, does the
Hebbian plasticity correspond to Bayes optimal learning? In other words,
does the synaptic update rule in equation 2.11 ensure that the neural activity
and synaptic strengths asymptotically encode Bayes optimal posterior be-
(cid:3)(cid:3)
liefs about hidden states
,
rispettivamente? A tal fine, we will identify a class of cost functions from
which the neural activity and synaptic plasticity can be derived and con-
sider the conditions under which the cost function becomes consistent with
variational free energy.

and parameters

→ s( j)
t1

(cid:2)
Wj1

→ sig

UN(·, j)

xt j

−1

11

(cid:3)

(cid:2)

(cid:2)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2096

T. Isomura and K. Friston

2.4 Neural Network Cost Functions. Here, we consider a class of func-
tions that constitute a cost function for both neural activity and synaptic
plasticity. We start by assuming that the update of the jth neuron’s ac-
attività (see equation 2.9) is determined by the gradient of cost function L j:
/∂xt j. By integrating the right-hand side of equation 2.9, we ob-
˙xt j
tain a class of cost functions as

∝ −∂L j

T(cid:17)
(cid:2)

(cid:2)

(cid:3)

F

xτ j

=

L j

− xτ jWj1oτ −

(cid:3)

(cid:2)

1 − xτ j

Wj0oτ − xτ jh j1

−

(cid:2)

1 − xτ j

(cid:3)

(cid:3)

h j0

+ O (1)

τ =1

T(cid:17)

τ =1

⎛

⎝ f

=

(cid:28)

T

(cid:27)(cid:27)

(cid:27)

(cid:2)

(cid:3)

xτ j

−

xτ j
1 − xτ j

(cid:28)

(cid:27)

(cid:28)(cid:28)⎞

Wj1

Wj0

oτ +

h j1

h j0

⎠+ O(1),

(2.12)

(2.13)

where the O(1) term, which depends on Wj1 and Wj0, is of a lower order
than the other terms (as they are O (T)) and is thus negligible when t is large
(See section A.2 for the case where we explicitly evaluate the O(1) term to
demonstrate the formal correspondence between the initial values of synap-
tic strengths and the parameter prior p (UN). The cost function of the entire
j=1 L j. When f (cid:11)
network is defined by L ≡
is the inverse of the sig-
moid function, we have
(cid:3)

xτ j

(cid:26)

Nx

(cid:2)

(cid:2)

(cid:3)

(cid:2)

(cid:3)

(cid:3)

(cid:2)

F

xτ j

= xτ j ln xτ j

+

1 − xτ j
(cid:2)

ln

(cid:3)

1 − xτ j
(cid:2)

−1

(cid:3)

up to a constant term (ensure f (cid:11)
). We further assume that
the synaptic weight update rule is given as the gradient descent on the same
cost function L j (see assumption 1). Così, the synaptic plasticity is derived
come segue:

= sig

xτ j

xτ j

⎧

⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩

˙Wj1

∝ − 1
T

˙Wj0

∝ − 1
T

∂L j
∂Wj1
∂L j
∂Wj0

= xt joT
T

+ xt jh

(cid:11)
j1

(cid:2)

=

1 − xt j

(cid:3)

oT
T

+ 1 − xt jh

(cid:11)
j0

,

(2.14)

(cid:2)

(cid:3)

(cid:26)
T

(cid:26)
T
τ =1 xτ j,
≡ ∂h j1

(cid:26)
T
τ =1 xτ joT
(cid:2)
(cid:26)
T
τ =1

≡ 1
T
≡ 1
T

xt joT
T
τ , 1 − xt j

1 − xt j
oT
T
/∂Wj1, and h(cid:11)

τ =1(1 −
≡ 1
τ , xt j
Dove
(cid:3)
T
, H(cid:11)
/∂Wj0.
1 − xτ j
xτ j )oT
j1
Note that the update of Wj1 is not directly influenced by Wj0, and vice versa
because they encode parameters in physically distinct pathways (cioè., IL
updates are local learning rules; Lee, Girolami, Campana, & Sejnowski, 2000;
Kusmierz, Isomura, & Toyoizumi, 2017). The update rule for Wj1 can be
viewed as Hebbian plasticity mediated by an additional activity-dependent
term expressing homeostatic plasticity. Inoltre, the update of Wj0 can
be viewed as anti-Hebbian plasticity with a homeostatic term, in the sense

≡ 1
T
≡ ∂h j0

j0

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2097

that Wj0 is reduced when input (ot ) and output (xt j ) fire together. The fixed
points of Wj1 and Wj0 are given by

⎧

⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩

Wj1

= h

(cid:11)−1
1

(cid:27)

(cid:28)

− xt joT
xt j

T

(cid:27)

(cid:2)

Wj0

= h

(cid:11)−1
0

−

(cid:3)

1 − xt j
1 − xt j

oT
T

(cid:28) .

(2.15)

Crucially, these synaptic strength updates are a subclass of the general
synaptic plasticity rule in equation 2.11 (see also section A.3 for the mathe-
matical explanation). Therefore, if the synaptic update rule is derived from
the cost function underlying neural activity, the synaptic update rule has
a biologically plausible form comprising Hebbian plasticity and activity-
dependent homeostatic plasticity. The updates of neural activity and
synaptic strengths—via gradient descent on the cost function—enable us
to associate neural and synaptic dynamics with optimization. Although the
steepest descent method gives the simplest implementation, other gradient
descent schemes, such as adaptive moment estimation (Adam; Kingma &
Ba, 2015), can be considered, while retaining the local learning property.

2.5 Comparison with Variational Free Energy. Here, we establish a
formal relationship between the cost function L and variational free en-
ergy. We define ˆWj1
as the sigmoid func-
tions of synaptic strengths. We consider the case in which neural activity
=
is expressed as a sigmoid function and thus equation 2.13 holds. As Wj1
ln ˆWj1

≡ sig(Wj1) and ˆWj0

, equation 2.12 becomes

(cid:2)
(cid:2)1 − ˆWj1

(cid:2)
Wj0

≡ sig

− ln

(cid:3)

(cid:3)

(cid:27)

Nx(cid:17)

T(cid:17)

j=1

τ =1

xτ j
1 − xτ j

(cid:28)

T

⎧
⎨

(cid:27)

⎩

L =

(cid:27)

(cid:28)

(cid:27)

(cid:28)

×

oτ
(cid:2)1 − oτ

−

h j1

h j0

(cid:28)

ln
⎛

⎜
⎝

+

−

(cid:3)

ln xτ j
(cid:2)
1 − xτ j
(cid:4)
(cid:2)1 − ˆWj1
(cid:4)
(cid:2)1 − ˆWj0

ln

ln

⎛

⎝

ln ˆWj1

ln ˆWj0
⎫
⎪⎬

(cid:5)

(cid:5)

⎞

⎟
⎠(cid:2)1

(cid:4)
(cid:2)1 − ˆWj1
(cid:4)
(cid:2)1 − ˆWj0

ln

ln

(cid:5)

⎞

⎠

(cid:5)

+ O(1),

⎪⎭

(2.16)

Dove (cid:2)1 = (1, . . . , 1) ∈ RNo. One can immediately see a formal correspon-
dence between this cost function and variational free energy (see equation
(cid:2)
11 , E
2.4). Questo è, when we assume that
ˆWj0
10 , equation 2.16 has exactly the same form as the sum of the ac-
curacy and state complexity, which is the leading-order term of variational
free energy (see the first term in the last equality of equation 2.4).

T = s( j)
T

= A(·, j)

= A(·, j)

, 1 − xt j

ˆWj1

xt j

(cid:3)

,

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2098

T. Isomura and K. Friston

(cid:2)
(cid:2)1 − ˆWj1

(cid:3)

(cid:3)

− ln

− ln

· (cid:2)1 = ln D( j)

(cid:2)
(cid:2)1 − ˆWj0

Specifically, when the thresholds satisfy h j1

· (cid:2)1 = ln D( j)
1
and h j0
0 , equation 2.16 becomes equivalent to
equation 2.4 up to the ln t order term (that disappears when t is large).
Therefore, in this case, the fixed points of neural activity and synaptic
strengths become the posteriors; così, xt j asymptotically becomes the Bayes
optimal encoder for a large t limit (provided with D that matches the gen-
uine prior D∗

In other words, we can define perturbation terms φ
(cid:3)
(cid:2)
(cid:2)1 − ˆWj0

(cid:2)
(cid:2)1 −
· (cid:2)1 as functions of Wj1 and Wj0, respec-

ˆWj1
tively, and can express the cost function as

· (cid:2)1 and φ

≡ h j0

≡ h j1

− ln

− ln

).

(cid:3)

j1

j0

L =

(cid:27)

Nx(cid:17)

T(cid:17)

τ =1

j=1
(cid:27)

xτ j
1 − xτ j
(cid:27)
(cid:28)

×

oτ
(cid:2)1 − oτ

−

(cid:28)

(cid:20) (cid:27)

T

ln xτ j
(cid:2)
1 − xτ j

(cid:3)

ln

(cid:28)

⎛

⎜
⎝

−

ln ˆWj1

ln ˆWj0

(cid:4)
(cid:2)1 − ˆWj1
(cid:4)
(cid:2)1 − ˆWj0

ln

ln

(cid:5)

⎞

⎟
⎠

(cid:5)

(cid:28) (cid:21)

φ

φ

j1

j0

+ O(1).

(2.17)

Here, without loss of generality, we can suppose that the constant terms
= 1. Under
+ esp
j1 and φ
in φ
this condition,
can be viewed as the prior belief about
hidden states

j0 are selected to ensure that exp

, esp

(cid:2)
φ

(cid:2)
φ

esp

(cid:3)(cid:3)

φ

φ

(cid:2)

(cid:3)

(cid:2)

(cid:3)

(cid:3)

(cid:2)

j0

j0

j1

j1

⎧
⎨

⎩

φ

φ

j1

j0

= ln D( j)
1
= ln D( j)
0

(2.18)

(cid:2)

(cid:3)

D( j)

and thus equation 2.17 is formally equivalent to the accuracy and state com-
plexity terms of variational free energy.

This means that when the prior belief about states

is a function
of the parameter posteriors (UN(·, j)), the general cost function under consid-
eration can be expressed in the form of variational free energy, up to the
O (ln t) term. A generic cost function L is suboptimal from the perspective
of Bayesian inference unless φ
j0 are tuned appropriately to express
the unbiased (cioè., optimal) prior belief. In this BSS setup, φ
= const
is optimal; così, a generic L would asymptotically give an upper bound of
variational free energy with the optimal prior belief about states when t is
large.

j1 and φ

= φ

j1

j0

2.6 Analysis on Synaptic Update Rules. To explicitly solve the fixed
points of Wj1 and Wj0 that provide the global minimum of L, we suppose
φ

j0 as linear functions of Wj1 and Wj0, rispettivamente, given by

j1 and φ

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

(cid:20)

φ

φ

j1

j0

= α

= α

+ Wj1
+ Wj0

β

β

j1

j0

j1

j0

,

2099

(2.19)

j1

, α

∈ R, and β

∈ RNo are constants. By solving the variation
where α
of L with respect to Wj1 and Wj0, we find the fixed point of synaptic strengths
COME

, β

j0

j1

j0

⎧

⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩

Wj1

= sig

−1

Wj0

= sig

−1

(cid:27)

(cid:28)

xt joT
T
xt j

+ β T
j1

(cid:27) (cid:2)

(cid:3)

1 − xt j
1 − xt j

oT
T

+ β T
j0

(cid:28) .

(2.20)

(cid:3)

(cid:7)

Since the update from t to t + 1 is expressed as sig
(cid:2) $ $(cid:8)Wj1
= ˆWj1
(cid:7) (cid:8)Wj1
and sig
≈ x(t+1) joT
/xt j
2 = x(t+1) joT
− x(t+1) jxt joT
T
we recover the following synaptic plasticity:

(cid:2)
(cid:2)1 − ˆWj1
/xt j

/xt j

+ O

$ $2

t+1

t+1

(cid:3)

(cid:3)

(cid:2)
Wj1
(cid:2)
Wj1
(cid:2)
−
ˆWj1

+ (cid:8)Wj1
+ (cid:8)Wj1
− β T
j1

(cid:3)

(cid:2)
− sig
Wj1
(cid:3)
− sig(Wj1)
/xt j,
X(t+1) j

(cid:3)

⎧
⎪⎪⎨

⎪⎪⎩

(cid:7)

⎫
⎪⎪⎬

X(t+1) joT
(cid:23)(cid:24)
(cid:22)

t+1
(cid:25)

− ( ˆWj1
(cid:22)

− β T
(cid:23)(cid:24)

j1)X(t+1) j
⎪⎪⎭
(cid:25)

Hebbian plasticity

homeostatic plasticity

(cid:8)Wj1

=

{ ˆWj1

(cid:7) ((cid:2)1 − ˆWj1)}(cid:7)−1

(cid:22)

xt j
(cid:23)(cid:24)

(cid:25)

adaptive learning rate

(cid:8)Wj0

=

{ ˆWj0

(cid:7) ((cid:2)1 − ˆWj0)}(cid:7)−1

(cid:22)

1 − xt j
(cid:23)(cid:24)

(cid:25)

adaptive learning rate
⎧
⎪⎪⎨

⎧

⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩

(cid:7)

⎪⎪⎩

(1 − x(t+1) j )oT
(cid:23)(cid:24)
(cid:22)

t+1
(cid:25)

− ( ˆWj0
(cid:22)

− β T

j0)(1 − x(t+1) j )
(cid:25)
(cid:23)(cid:24)

anti-Hebbian plasticity

homeostatic plasticity

(2.21)
(cid:2)
(cid:2)1 −
Dove (cid:7) denotes the elementwise (Hadamard) product and
(cid:2)
(cid:3)
(cid:2)1 − ˆWj1
ˆWj1
denotes the element-wise inverse of ˆWj1
. This synap-
tic plasticity rule is a subclass of the general synaptic plasticity rule in
equation 2.11.

(cid:18)
ˆWj1

(cid:3)(cid:19)(cid:7)−1

(cid:7)

(cid:7)

In summary, we demonstrated that under a few minimal assumptions
and ignoring small contributions to weight updates, the neural network
under consideration can be regarded as minimizing an approximation to
model evidence because the cost function can be formulated in terms of

,

⎫
⎪⎪⎬

⎪⎪⎭

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2100

T. Isomura and K. Friston

variational free energy. In what follows, we will rehearse our analytic results
and then use numerical analyses to illustrate Bayes optimal inference (E
apprendimento) in a neural network when, and only when, it has the right priors.

3 Results

3.1 Analytical Form of Neural Network Cost Functions. The analysis

in the preceding section rests on the following assumptions:

1. Updates of neural activity and synaptic weights are determined by a

gradient descent on a cost function L.

2. Neural activity is updated by the weighted sum of sensory inputs

and its fixed point is expressed as the sigmoid function.

Under these assumptions, we can express the cost function for a neural net-
work as follows (see equation 2.17):

(cid:28)

(cid:20) (cid:27)

T

ln xτ j
(cid:2)
1 − xτ j

(cid:3)

ln

(cid:28)

⎛

⎝

−

ln ˆWj1

ln ˆWj0

(cid:4)
(cid:2)1 − ˆWj1
(cid:4)
(cid:2)1 − ˆWj0

ln

ln

(cid:5)

⎞

⎠

(cid:5)

L =

(cid:27)

Nx(cid:17)

T(cid:17)

τ =1

j=1
(cid:27)

xτ j
1 − xτ j
(cid:27)
(cid:28)

×

oτ
(cid:2)1 − oτ

−

(cid:28) (cid:21)

φ

φ

j1

j0

+ O(1),

(cid:3)

= sig

j1 and φ

hold and φ

= sig(Wj1) and ˆWj0

(cid:2)
where ˆWj1
Wj0
j0 are functions
of Wj1 and Wj0, rispettivamente. The log-likelihood function (accuracy term)
and divergence of hidden states (complexity term) of variational free energy
emerge naturally under the assumption of a sigmoid activation function
(assumption 2). Additional terms denoted by φ
j1 and φ
j0 express the state
prior, indicating that a generic cost function L is variational free energy un-
(cid:2)
S( j)
= ln D( j) = φ
der a suboptimal prior belief about hidden states: ln P
j,
T
where φ
. This prior alters the landscape of the cost function in a
suboptimal manner and thus provides a biased solution for neural activities
and synaptic strengths, which differ from the Bayes optimal encoders.

(cid:2)
φ

, φ

≡

(cid:3)

(cid:3)

j1

j0

j

For analytical tractability, we further assume the following:

3. The perturbation terms (φ

j0) that constitute the difference
between the cost function and variational free energy with optimal
prior beliefs can be expressed as linear equations of Wj1 and Wj0.

j1 and φ

From assumption 3, equation 2.17 becomes

Nx(cid:17)

(cid:27)

T(cid:17)

⎡

⎣

j=1

τ =1

xτ j
1 − xτ j

(cid:28)

T

⎧
⎨

(cid:27)

⎩

L =

ln xτ j
(cid:2)
1 − xτ j

(cid:3)

ln

(cid:28)

⎛

⎝

−

ln ˆWj1

ln ˆWj0

(cid:4)
(cid:2)1 − ˆWj1
(cid:4)
(cid:2)1 − ˆWj0

ln

ln

(cid:5)

⎞

⎠

(cid:5)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

−

(cid:19)

Reverse-Engineering Neural Networks

(cid:27)

(cid:28)

(cid:27)

×

oτ
(cid:2)1 − oτ

α

α

j1

j0

+ Wj1
+ Wj0

β

β

j1

j0

(cid:28)(cid:21)’

+ O(1),

2101

(3.1)

(cid:18)

α

, α

, β

, β

j1

j0

j1

are constants. The cost function has degrees of free-
Dove
j0
, α
dom with respect to the choice of constants
, which corre-
spond to the prior belief about states D( j). The neural activity and synaptic
strengths that give the minimum of a generic physiological cost function
L are biased by these constants, which may be analogous to physiological
constraints (see section 4 for details).

(cid:18)
α

, β

, β

(cid:19)

j1

j0

j0

j1

j. Così, after fixing φ

The cost function of the neural networks considered is characterized only
(cid:3)
by φ
,
j by fixing constraints
the remaining degrees of freedom are the initial synaptic weights. These
correspond to the prior distribution of parameters P (UN) in the variational
Bayesian formulation (see section A2).

E

, α

, β

α

β

(cid:3)

(cid:2)

(cid:2)

j1

j0

j0

j1

(cid:2)

(cid:3)

β

, β

The fixed point of synaptic strengths that give the minimum of L is given
analytically as equation 2.20, expressing that
deviates the center
of the nonlinear mapping—from Hebbian products to synaptic strengths—
from the optimal position (shown in equation 2.8). As shown in equation
2.14, the derivative of L with respect to Wj1 and Wj0 recovers the synaptic
update rules that comprise Hebbian and activity-dependent homeostatic
terms. Although equation 2.14 expresses the dynamics of synaptic strengths
that converge to the fixed point, it is consistent with a plasticity rule that
gives the synaptic change from t to t + 1 (see equation 2.21).

j1

j0

Hence, based on assumptions 1 E 2 (irrespective of assumption
3), we find that the cost function approximates variational free energy.
Tavolo 1 summarizes this correspondence. Under this condition, neural ac-
=
tivity encodes the posterior expectation about hidden states, xτ j
(cid:2)
Q

(cid:3)
S( j)
τ = 1
, and synaptic strengths encode the posterior expectation of the
10 . In addi-
parameters,
zione, based on assumption 3, the threshold is characterized by constants
(cid:18)
α
. From a Bayesian perspective, these constants can be
j0
(cid:3)
viewed as prior beliefs, ln P
.
j0
, IL
When and only when
cost function becomes variational free energy with optimal prior beliefs (for
BSS) whose global minimum ensures Bayes optimal encoding.

(cid:2)
S( j)
(cid:3)
T
= (− ln 2, − ln 2) E

= sig
ˆWj1
(cid:19)

+ Wj0
β
(cid:3)
(cid:2)
(cid:2)0,(cid:2)0

= ln D( j) =

+ Wj1
(cid:2)
β

and ˆWj0

= A(·, j)

= A(·, j)

(cid:2)
Wj1

(cid:2)
Wj0

= s( j)
τ 1

= sig

β
j1
, β

(cid:2)
α

, α
(cid:3)

j0
=

, α

, α

, β

, β

α

11

(cid:3)

(cid:2)

(cid:3)

(cid:3)

j0

j1

j0

j1

j0

j1

j1

j1

In short, we identify a class of biologically plausible cost functions from
which the update rules for both neural activity and synaptic plasticity can
be derived. When the activation function for neural activity is a sigmoid
function, a cost function in this class is expressed straightforwardly as vari-
ational free energy. With respect to the choice of constants expressing phys-
iological constraints in the neural network, the cost function has degrees
of freedom that may be viewed as (potentially suboptimal) prior beliefs

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2102

T. Isomura and K. Friston

from the Bayesian perspective. Now, we illustrate the implicit inference and
learning in neural networks through simulations of BSS.

3.2 Numerical Simulations. Here, we simulated the dynamics of neu-
ral activity and synaptic strengths when they followed a gradient descent
on the cost function in equation 3.1. We considered a BSS comprising two
hidden sources (or states) E 32 observations (or sensory inputs), formu-
lated as an MDP. The two hidden sources show four patterns: st = s(1)
⊗
T
S(2)
T
likelihood mapping A(io), defined as

= (0, 0) (1, 0) (0, 1) (1, 1). An observation o(io)

t was generated through the

⎧
⎪⎨

⎪⎩

(cid:4)
o(io)
T

P
(cid:4)
o(io)
T

P

(cid:5)

= 1|st, UN(io)
(cid:5)

= 1|st, UN(io)

= A(io)

1· =

(cid:2)
0, 3
4

, 1
4

= A(io)

1· =

(cid:2)
0, 1
4

, 3
4

(cid:3)

, 1
(cid:3)

, 1

for 1 ≤ i ≤ 16

for 17 ≤ i ≤ 32

.

(3.2)

T

(cid:3)

1· = 3/4 for 1 ≤ i ≤ 16 is the probability of o(io)

Here, Per esempio, UN(io)
taking
0· = (cid:2)1 − A(io)
one when st = (1, 0). The remaining elements were given by A(io)
1· .
The implicit state priors employed by a neural network were varied be-
tween zero and one in keeping with D( j)
= 1; whereas, the true state
(cid:2)
1
= (0.5, 0.5). Synaptic strengths were ini-
priors were fixed as
tialized as values close to zero. The simulations preceded over T = 104 time
steps. The simulations and analyses were conducted using Matlab. Notably,
this simulation setup is exactly the same experimental setup as that we
used for in vitro neural networks (Isomura et al., 2015; Isomura & Friston,
2018). We leverage this setup to clarify the relationship among our empir-
ical work, a feedforward neural network model, and variational Bayesian
formulations.

∗( j)
, D
0

+ D( j)
0

∗( j)
D
1

j0

j1

j1

j0

(cid:2)

(cid:3)

(cid:2)

(cid:3)

β

α

=

=

(cid:3)(cid:3)

(cid:2)(cid:2)

, β

, α

(cid:2)
(cid:2)0,(cid:2)0

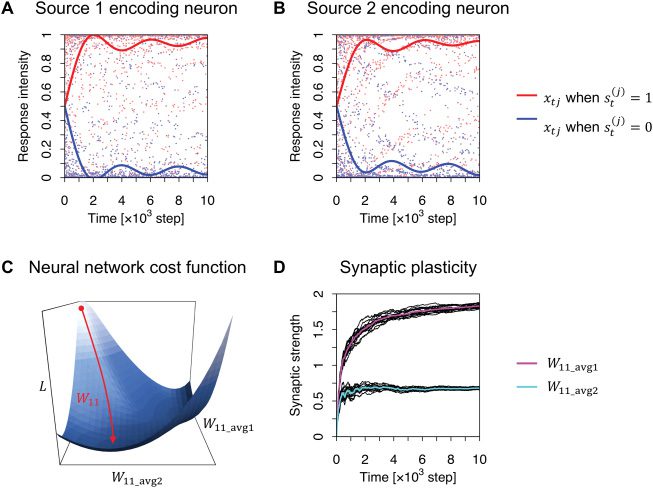
Primo, as in Isomura and Friston (2018), we demonstrated that a network
(cid:3)
− ln 2, − ln 2
with a cost function with optimized constants
E
can perform BSS successfully (Guarda la figura 2). The re-
sponses of neuron 1 came to recognize source 1 after training, indicating
that neuron 1 learned to encode source 1 (see Figure 2A). Nel frattempo, neu-
ron 2 learned to infer source 2 (see Figure 2B). During training, synaptic
plasticity followed gradient descent on the cost function (see Figures 2C and
2D). This demonstrates that minimization of the cost function, with optimal
constants, is equivalent to variational free energy minimization and hence
is sufficient to emulate BSS. This process establishes a concise representa-
tion of the hidden causes and allows maximizing information retained in
the neural network (Linsker, 1988; Isomura, 2018).

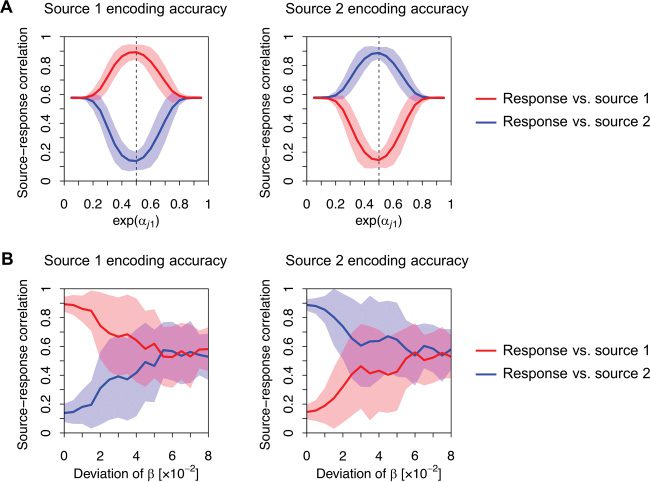
Prossimo, we quantified the dependency of BSS performance on the form
of the cost function, by varying the above-mentioned constants (see Fig-
≤ 0.95, while
ure 3). We varied

in a range of 0.05 ≤ exp

, α

α

α

(cid:2)

(cid:3)

(cid:2)

(cid:3)

j1

j0

j1

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2103

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Figura 2: Emergence of response selectivity for a source. (UN) Evolution of neu-
ron 1’s responses that learn to encode source 1, in the sense that the response is
high when source 1 takes a value of one (red dots), and it is low when source
1 takes a value of zero (blue dots). Lines correspond to smoothed trajectories
obtained using a discrete cosine transform. (B) Emergence of neuron 2’s re-
sponse that learns to encode source 2. These results indicate that the neural net-
work succeeded in separating two independent sources. (C) Neural network
cost function L. It is computed based on equation 3.1 and plotted against the
averaged synaptic strengths, where W11_avg1 (z-axis) is the average of 1 A 16 el-
ements of W11, while W11_avg2 (x-axis) is the average of 17 A 32 elements of W11.
The red line depicts a trajectory of averaged synaptic strengths. (D) Trajectory
of synaptic strengths. Black lines show elements of W11, and magenta and cyan
lines indicate W11_avg1 and W11_avg2, rispettivamente.

(cid:2)
α

(cid:3)

(cid:2)

(cid:3)

(cid:2)

(cid:3)

j1

j0

α

α

+ esp

= 1 and found that changing

maintaining exp
j0
from (− ln 2, − ln 2) led to a failure of BSS. Because neuron 1 encodes source
1 with optimal α, the correlation between source 1 and the response of neu-
ron 1 is close to one, while the correlation between source 2 and the response
of neuron 1 is nearly zero. In the case of suboptimal α, these correlations fall
to around 0.5, indicating that the response of neuron 1 encodes a mixture
of sources 1 E 2 (Figure 3A). Inoltre, a failure of BSS can be induced
when the elements of β take values far from zero (see Figure 3B). When
the elements of β are generated from a zeromean gaussian distribution,

, α

j1

2104

T. Isomura and K. Friston

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

T

, xt1)| E |corr(S(2)

Figura 3: Dependence of source encoding accuracy on constants. Left panels
show the magnitudes of the correlations between sources and responses of a
, xt1)|. The right
neuron expected to encode source 1: |corr(S(1)
T
panels show the magnitudes of the correlations between sources and responses
, xt2)|.
of a neuron expected to encode source 2: |corr(S(1)
T
(UN) Dependence on the constant α that controls the excitability of a neuron when
(cid:3)
(cid:2)
β is fixed to zero. The dashed line (0.5) indicates the optimal value of exp
.
= (− ln 2, − ln 2). El-
(B) Dependence on constant β when α is fixed as
ements of β were randomly generated from a gaussian distribution with zero
mean. The standard deviation of β was varied (horizontal axis), where zero
deviation was optimal. Lines and shaded areas indicate the mean and stan-
dard deviation of the source-response correlation, evaluated with 50 different
sequences.

, xt2)| E |corr(S(2)

(cid:2)
α

, α

α

(cid:3)

j1

j0

j1

T

the accuracy of BSS—measured using the correlation between sources and
responses—decreases as the standard deviation increases.

Our numerical analysis, under assumptions 1 A 3, shows that a network
needs to employ a cost function that entails optimal prior beliefs to perform
BSS or, equivalently, causal inference. Such a cost function is obtained when
its constants, which do not appear in the variational free energy with the op-
timal generative model for BSS, become negligible. The important message
here is that in this setup, a cost function equivalent to variational free en-
ergy is necessary for Bayes optimal inference (Friston et al., 2006; Friston,
2010).

Reverse-Engineering Neural Networks

2105

j

3.3 Phenotyping Networks. We have shown that variational free en-
ergy (under the MDP scheme) is formally homologous to the class of bi-
ologically plausible cost functions found in neural networks. The neural
network’s parameters φ
= ln D( j) determine how the synaptic strengths
change depending on the history of sensory inputs and neural outputs;
così, the choice of φ
j provides degrees of freedom in the shape of the neural
network cost functions under consideration that determine the purpose or
function of the neural network. Among various φ
= (− ln 2, − ln 2)
can make the cost function variational free energy with optimal prior beliefs
for BSS. Hence, one could regard neural networks (of the sort considered
in this letter: single-layer feedforward networks that minimize their cost
function) as performing approximate Bayesian inference under priors that
may or may not be optimal. This result is as predicted by the complete class
theorem (Brown, 1981; Wald, 1947) as it implies that any response of a neu-
ral network is Bayes optimal under some prior beliefs (and cost function).
Therefore, in principle, under the theorem, any neural network of this kind
is optimal when its prior beliefs are consistent with the process that gener-
ates outcomes. This perspective indicates the possibility of characterizing a
neural network model—and indeed a real neuronal network—in terms of
its implicit prior beliefs.

j, only φ

j

One can pursue this analysis further and model the responses or de-
cisions of a neural network using the Bayes optimal MDP scheme under
different priors. Così, the priors in the MDP scheme can be adjusted to max-
imize the likelihood of empirical responses. This sort of approach has been
used in system neuroscience to characterize the choice behavior in terms
of subject-specific priors. (See Schwartenbeck & Friston, 2016, for further
details.)

From a practical perspective for optimizing neural networks, under-
standing the formal relationship between cost functions and variational free
energy enables us to specify the optimum value of any free parameter to
realize some functions. In the present setting, we can effectively optimize
the constants by updating the priors themselves such that they minimize
the variational free energy for BSS. Under the Dirichlet form for the priors,
the implicit threshold constants of the objective function can then be opti-
mized using the following updates:

φ

j

= ln D( j) = ψ

(cid:3)

(cid:2)

D( j)

(cid:2)

− ψ

(cid:3)

D( j)
1

+ D( j)
0

D( j) = d( j) +

T(cid:17)

τ =1

S( j)
τ .

(3.3)

(See Schwartenbeck & Friston, 2016, for further details.) In effect, Questo
update will simply add the Dirichlet concentration parameters, D( j) =
(cid:2)
D( j)
, to the priors in proportion to the temporal summation of the
1

, D( j)
0

(cid:3)

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2106

T. Isomura and K. Friston

posterior expectations about the hidden states. Therefore, by committing
to cost functions that underlie variational inference and learning, any free
parameter can be updated in a Bayes optimal fashion when a suitable gen-
erative model is available.

3.4 Reverse-Engineering Implicit Prior Beliefs. Another situation im-
portant from a neuroscience perspective is when belief updating in a neural
network is slow in relation to experimental observations. In questo caso, IL
implicit prior beliefs can be viewed as being fixed over a short period of
time. This is likely when such a firing threshold is determined by a homeo-
static plasticity over longer timescales (Turrigiano & Nelson, 2004).

(cid:3)

, α

The considerations in the previous section speak to the possibility of us-
ing empirically observed neuronal responses to infer implicit prior beliefs.
, Wj0) can be estimated statistically from response
The synaptic weights (Wj1
dati, through equation 2.20. By plotting their trajectory over the training pe-
riod as a function of the history of a Hebbian product, one can estimate the
cost function constants. If these constants express a near-optimal φ
j, it can
be concluded that the network has, effettivamente, the right sort of priors for
BSS. As we have shown analytically and numerically, a cost function with
(cid:2)
α
fails as a
Bayes optimal encoder for BSS. Since actual neuronal networks can perform
BSS (Isomura et al., 2015; Isomura & Friston, 2018), one would envisage that
the implicit cost function will exhibit a near-optimal φ
j.
(cid:2)
cioè., φ
j can be viewed as a constant
during a period of experimental observation, the characterization of thresh-
olds is fairly straightforward: using empirically observed neuronal re-
sponsorizzato, through variational free energy minimization, under the constraint
of eφ

far from (− ln 2, − ln 2) or a large deviation of

j0 = 1, the estimator of φ

In particular, when φ

j is obtained as follows:

j1 + eφ

(cid:2)
α

, α

, β

=

β

(cid:3)

(cid:3)

(cid:3)

(cid:2)

j0

j1

j1

j0

j1

j0

T

j

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

φφj

= ln

(cid:27)

1
T

(cid:27)

T(cid:17)

τ =1

xt j
1 − xt j

(cid:28)(cid:28)

.

(3.4)

Crucially, equation 3.4 is exactly the same as equation 3.3 up to a negligi-
ble term d( j). Tuttavia, equation 3.3 represents the adaptation of a neural
rete, while equation 3.4 expresses Bayesian inference about φ
j based
on empirical data. We applied equation 3.4 to sequences of neural activ-
ity generated from the synthetic neural networks used in the simulations
reported in Figures 2 E 3, and confirmed that the estimator was a good
approximation to the true φ
j (see Figure 4A). This characterization enables
the identification of implicit prior beliefs (D) and consequently, the recon-
struction of the neural network cost function, questo è, variational free energy
(see Figure 4B). Inoltre, because a canonical neural network is sup-
posed to use the same prior beliefs for the same sort of tasks, one can use the

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Reverse-Engineering Neural Networks

2107

Figura 4: Estimation of prior beliefs enables the prediction of subsequent learn-
ing. (UN) Estimation of constants (α
11) that characterize thresholds (cioè., prior be-
liefs) based on sequences of neural activity. Lines and shaded areas indicate the
mean and standard deviation. (B) Reconstruction of cost function L using the
obtained threshold estimator through equation 3.1. The estimated L well ap-
proximates the true L shown in Figure 2C. (C) Prediction of learning process
with new sensory input data generated through different likelihood mapping
characterized by a random matrix A. Supplying the sensory (cioè., input) dati
to the ensuing cost function provides a synaptic trajectory (red line), which pre-
dicts the true trajectory (black line) in the absence of observed neural responses.
Inset panel depicts a comparison between elements of the true and predicted
W11 at t = 104.

reconstructed cost functions to predict subsequent inference and learning
without observing neural activity (see Figure 4C). These results highlight
the utility of reverse-engineering neural networks to predict their activity,
plasticity, and assimilation of input data.

4 Discussion

In this work, we investigated a class of biologically plausible cost functions
for neural networks. A single-layer feedforward neural network with a sig-
moid activation function that receives sensory inputs generated by hidden
stati (cioè., BSS setup) was considered. We identified a class of cost functions
by assuming that neural activity and synaptic plasticity minimize a com-
mon function L. The derivative of L with respect to synaptic strengths fur-
nishes a synaptic update rule following Hebbian plasticity, equipped with
activity-dependent homeostatic terms. We have shown that the dynamics of
a single-layer feedforward neural network, which minimizes its cost func-
zione, is asymptotically equivalent to that of variational Bayesian inference
under a particular but generic (latent variable) generative model. Hence,
the cost function of the neural network can be viewed as variational free
energy, and biological constraints that characterize the neural network—
in the form of thresholds and neuronal excitability—become prior beliefs

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

2108

T. Isomura and K. Friston

about hidden states. This relationship holds regardless of the true gener-
ative process of the external world. In short, this equivalence provides an
insight that any neural and synaptic dynamics (in the class considered) Avere
functional meaning and any neural network variables and constants can be
formally associated with quantities in the variational Bayesian formation,
implying that Bayesian inference is universal characterisation of canonical
neural networks.

According to the complete class theorem, any dynamics that minimizes a
cost function can be viewed as performing Bayesian inference under some
prior beliefs (Wald, 1947; Brown, 1981). This implies that any neural net-
work whose activity and plasticity minimize the same cost function can
be cast as performing Bayesian inference. Inoltre, when a system has
reached a (possibly nonequilibrium) steady state, the conditional expecta-
tion of internal states of an autonomous system can be shown to parameter-
ize a posterior belief over the hidden states of the external milieu (Friston,
2013, 2019; Parr, Da Costa, & Friston, 2020). Again, this suggests that any
(nonequilibrium) steady state can be interpreted as realising some elemen-
tal Bayesian inference.

Having said this, we note that the implicit generative model that under-
writes any (per esempio., neural network) cost function is a more delicate problem—
one that we have addressed in this work. In other words, it is a mathemat-
ical truism that certain systems can always be interpreted as minimizing
a variational free energy under some prior beliefs (cioè., generative model).
Tuttavia, this does not mean it is possible to identify the generative model
by simply looking at systemic dynamics. To do this, one has to commit to
a particular form of the model, so that the sufficient statistics of posterior
beliefs are well defined. We have focused on discrete latent variable mod-
els that can be regarded as special (reduced) cases of partially observable
Markov decision processes (POMDP).

Note that because our treatment is predicated on the complete class the-
orem (Brown, 1981; Wald, 1947), the same conclusions should, in principle,
be reached when using continuous state-space models, such as hierarchi-
cal predictive coding models (Friston, 2008; Whittington & Bogacz, 2017;
Ahmadi & Tani, 2019). Within the class of discrete state-space models, Esso
is fairly straightforward to generate continuous outcomes from discrete la-
tent states, as exemplified by discrete variational autoencoders (Rolfe, 2016)
or mixed models, as described in Friston, Parr et al. (2017). We have de-
scribed the generative model in terms of an MDP; Tuttavia, we ignored
state transitions. This means the generative model in this letter reduces to
a simple latent variable model, with categorical states and outcomes. Noi
have considered MDP models because they predominate in descriptions of
variational (Bayesian) belief updating, (per esempio., Friston, FitzGerald et al., 2017).
Clearly, many generative processes entail state transitions, leading to hid-
den Markov models (HMM). When state transitions depend on control vari-
ables, we have an MDP, and when states are only partially observed, we

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

e
D
tu
N
e
C
o
UN
R
T
io
C
e
–
P
D

/

l

F
/

/

/

/

3
2
1
1
2
0
8
5
1
8
6
5
4
2
3
N
e
C
o
_
UN
_
0
1
3
1
5
P
D

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3