Latent Compositional Representations Improve Systematic
Generalization in Grounded Question Answering
Ben Bogin1 Sanjay Subramanian2 Matt Gardner2
Jonathan Berant1,2
1Tel-Aviv University 2Allen Institute for AI
{ben.bogin,joberant}@cs.tau.ac.il, {sanjays,mattg}@allenai.org
Astratto
Answering questions that involve multi-step
reasoning requires decomposing them and
using the answers of intermediate steps to
reach the final answer. Tuttavia, state-of-the-
art models in grounded question answering
often do not explicitly perform decomposition,
leading to difficulties in generalization to out-
of-distribution examples. In this work, we
propose a model that computes a representa-
tion and denotation for all question spans in
a bottom-up, compositional manner using a
CKY-style parser. Our model induces latent
trees, driven by end-to-end (the answer)
supervision only. We show that this induc-
tive bias towards tree structures dramatically
improves systematic generalization to out-of-
distribution examples, compared to strong
baselines on an arithmetic expressions bench-
mark as well as on CLOSURE, a dataset that focuses
on systematic generalization for grounded ques-
tion answering. On this challenging dataset,
our model reaches an accuracy of 96.1%,
significantly higher than prior models that
almost perfectly solve the task on a random,
in-distribution split.
1
introduzione
Humans can effortlessly interpret new language
utterances, if they are composed of previously
observed primitives and structure (Fodor and
Pylyshyn, 1988). Neural networks, conversely,
do not exhibit this systematicity: Although they
generalize well to examples sampled from the dis-
tribution of the training set, they have been shown
to struggle in generalizing to out-of-distribution
(OOD) examples that contain new compositions
in grounded question answering (Bahdanau et al.,
2019UN,B) and semantic parsing (Finegan-Dollak
et al., 2018; Keysers et al., 2020). Consider the
195
question in Figure 1. This question requires query-
ing object sizes, comparing colors, identifying spa-
tial relations, and computing intersections between
sets of objects. Neural models succeed when these
concepts are combined in ways that were seen at
training time. Tuttavia, they commonly fail when
concepts are combined in new ways at test time.
A possible reason for this phenomenon is
the expressivity of architectures such as LSTMs
(Hochreiter e Schmidhuber, 1997) and Trans-
formers (Vaswani et al., 2017), where ‘‘global’’
representations that depend on the entire input
are computed. Contextualizing token representa-
tions using the entire utterance potentially lets the
model avoid step-by-step reasoning, ‘‘collapse’’
reasoning steps, and rely on shortcuts (Jiang and
Bansal, 2019; Subramanian et al., 2019, 2020).
Such failures are revealed when evaluating models
for systematic generalization on OOD examples.
This stands in contrast to pre-neural log-linear
models, where hierarchical representations were
explicitly constructed over the input (Zettlemoyer
and Collins, 2005; Liang et al., 2013).
In this work, we propose a model for visual
question answering (QA) Quello, analogous to these
classical pre-neural models, computes for every
span in the input question a representation and a
denotation, questo è, the set of objects in the image
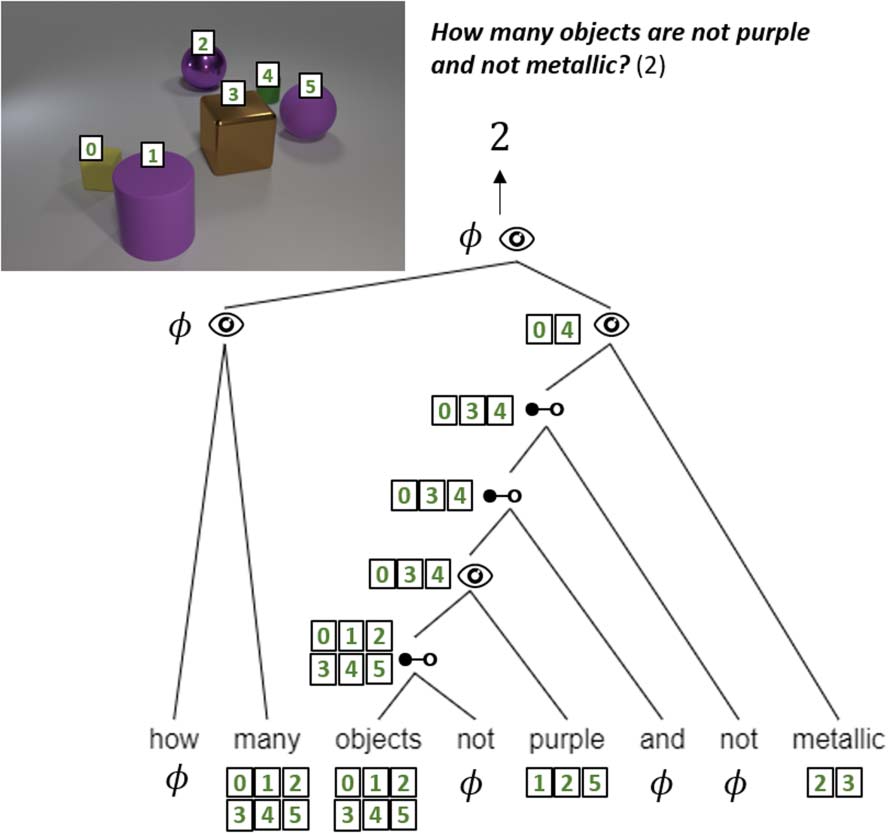
that the span refers to (Guarda la figura 1). Denotations
for long spans are recursively computed from
shorter spans using a bottom–up CKY-style parser
without access to the entire input, leading to an
inductive bias that encourages compositional com-
putation. Because training is done from the final
answer only, the model must effectively learn to
induce latent trees that describe the compositional
structure of the problem. We hypothesize that this
explicit grounding of the meaning of sub-spans
through hierarchical computation should result in
better generalization to new compositions.
We evaluate our approach in two setups: (UN)
a synthetic arithmetic expressions dataset, E
Operazioni dell'Associazione per la Linguistica Computazionale, vol. 9, pag. 195–210, 2021. https://doi.org/10.1162/tacl a 00361
Redattore di azioni: Jing Jiang. Lotto di invio: 7/2020; Lotto di revisione: 10/2020; Pubblicato 3/2021.
C(cid:2) 2021 Associazione per la Linguistica Computazionale. Distribuito sotto CC-BY 4.0 licenza.
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
T
l
UN
C
_
UN
_
0
0
3
6
1
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
T
l
UN
C
_
UN
_
0
0
3
6
1
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
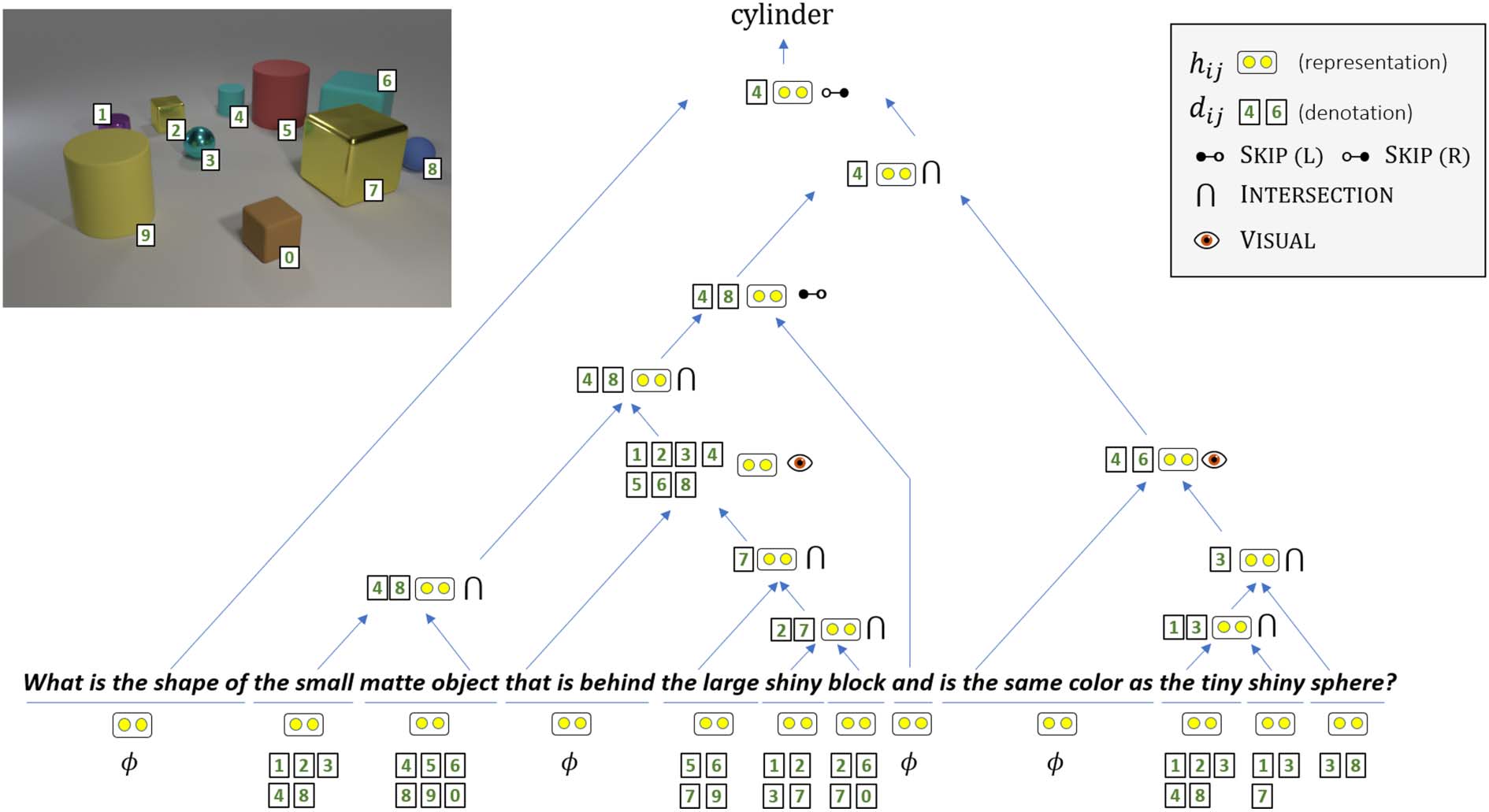
Figura 1: An example from CLOSURE illustrating how our model learns a latent structure over the input,
where a representation and denotation is computed for every span (for denotation we show the set of
objects with probability > 0.5). For brevity, some phrases were merged to a single node of the tree. For
each phrase, we show the split point and module with the highest probability, although all possible split
points and module outputs are softly computed. SKIP(l) and SKIP(R) refer to taking the denotation of the
left or right sub-span, rispettivamente.
(B) CLOSURE (Bahdanau et al., 2019B), a visual
QA dataset focusing on systematic generalization.
On a random train/test split (i.i.d split), both our
model and prior baselines obtain near perfect per-
formance. Tuttavia, on splits that require general-
ization to new compositions (compositional split)
our model dramatically improves performance:
On the arithmetic dataset, a Transformer-based
model fails to generalize and obtains 2.9% accu-
racy, whereas our model, Grounded Latent Trees
(GLT), gets 98.4%. On CLOSURE, our model’s
accuracy is 96.1%, 24 absolute points higher than
strong baselines and even 19 points higher than
models that use gold structures at training time or
depend on domain-knowledge.
To conclude, we propose a model with an inher-
ent inductive bias for compositional computation,
which leads to gains in systematic generaliza-
zione, and induces latent structures that are useful
for understanding its inner workings. This sug-
gests that despite the success of general-purpose
architectures built on top of contextualized repre-
sentations, restricting information flow inside
the network can benefit compositional gen-
eralization. Our code and data can be found
at https://github.com/benbogin/glt
-grounded-latent-trees-qa.
2 Compositional Generalization
Language is mostly compositional; humans can
understand and produce a potentially infinite
number of novel combinations from a finite
set of components (Chomsky, 1957; Montague,
1970). Per esempio, a person would know what a
‘‘winged giraffe’’ is even if she’s never seen one,
assuming she knows the meaning of ‘‘winged’’
and ‘‘giraffe’’. This ability, termed compositional
generalization, is fundamental for building robust
models that learn from limited data (Lake et al.,
2018).
Neural networks have been shown to gen-
eralize well
in many language understanding
tasks in i.i.d splits (Devlin et al., 2019; Linzen,
2020). Tuttavia, when evaluated on splits that
require compositional generalization, a significant
drop in performance is observed. Per esempio, In
SCAN (Lake and Baroni, 2018) and gSCAN (Ruis
et al., 2020), synthetically generated commands
are mapped into a sequence of actions. When
196
tested on unseen command combinations, models
perform poorly. A similar trend was shown in
text-to-SQL parsing Finegan-Dollak et al. (2018),
where splitting examples by the template of the tar-
get SQL query resulted in a dramatic performance
drop. SQOOP (Bahdanau et al., 2019UN) shows the
same phenomena on a synthetic visual task, Quale
tests for generalization over unseen combinations
of object properties and relations. This also led
to methods that construct compositional splits
automatically (Keysers et al., 2020).
In this work, we focus on answering com-
plex grounded questions over images. The CLEVR
benchmark (Johnson et al., 2017UN) contains syn-
thetic images and questions that require multi-step
reasoning, Per esempio, ‘‘Are there any cyan
spheres made of the same material as the green
sphere?’’. While performance on this task is
high, with an accuracy of 97%–99% (Perez et al.,
2018; Hudson and Manning, 2018), recent work
(Bahdanau et al., 2019B) introduced CLOSURE: UN
new set of questions with identical vocabulary but
different structure than CLEVR, asked on the same
set of images. They evaluated generalization of
different models and showed that all fail on a
large fraction.
The most common approach for grounded QA
is based on end-to-end differentiable models such
as FiLM (Perez et al., 2018), MAC (Hudson
and Manning, 2018), LXMERT (Tan and Bansal,
2019), and UNITER (Chen et al., 2020). These
models do not explicitly decompose the prob-
lem into smaller sub-tasks, and are thus prone
to fail on compositional generalization. A differ-
ent approach (Yi et al., 2018; Mao et al., 2019)
is to parse the image into a symbolic or dis-
tributed knowledge graph with objects, attributes,
and relations, and then parse the question into an
executable logical form, which is deterministically
executed. Last, Neural Module Networks (NMNs;
Andreas et al. 2016) parse the question into an exe-
cutable program, where execution is learned: Each
program module is a neural network designed to
perform an atomic task, and modules are com-
posed to perform complex reasoning. The latter
two model families construct compositional pro-
grams and have been shown to generalize better
on compositional splits (Bahdanau et al., 2019UN,B)
compared with end-to-end models. Tuttavia, pro-
grams are not explicitly tied to question spans,
and search over the space of programs is not
differentiable, leading to difficulties in training.
In this work, we learn a latent structure for
the question and tie each question span to an
executable module in a differentiable manner.
Our model balances distributed and symbolic
approcci: We learn from downstream supervi-
sion only and output an inferred tree, describing
how the answer was computed. We base our
work on latent tree parsers (Le and Zuidema,
2015; Liu et al., 2018; Maillard et al., 2019;
Drozdov et al., 2019) that produce representations
for all spans, and softly weight all possible trees.
We extend these parsers to answer grounded
questions, grounding sub-trees in image objects.
Closest to our work is Gupta and Lewis (2018)
(GL), who have proposed to compute denotations
for each span by constructing a CKY chart. Nostro
model differs in several important aspects: Primo,
while both models compute the denotations of all
spans, we additionally compute dense representa-
tions for each span using a learned composition
increasing the expressiveness of our
function,
modello. Secondo, we compute the denotations using
simpler and more generic composition operators,
while in GL the operators are fine-grained and
type-driven. Last, we work with images rather
than a knowledge graph, and propose several mod-
ifications to the chart construction mechanism to
overcome scalability challenges.
3 Model
We first give a high-level overview of our
proposed GLT model (§3.1), and then explain
our model in detail.
3.1 High-level Overview
Problem Setup Our task is visual QA, Dove
given a question q = (q0, . . . , qn−1) and an image
IO, we aim to output an answer a ∈ A from a fixed
set of natural language phrases. We train a model
from a training set {(qi, I i, ai)}N
i=1. We assume
we can extract from the image up to nobj features
vectors of objects, and represent them as a matrix
V ∈ Rnobj×hdim (details on object detection and
representation are in §3.4).
Our goal is to compute for every question span
qij = (qi, . . . , qj−1) a representation hij ∈ Rhdim
and a denotation dij ∈ [0, 1]nobj, interpreted as the
probability that the question span refers to each
object. We compute hij and dij in a bottom–up
fashion, using CKY (Cocke, 1969; Kasami, 1965;
Younger, 1967). Algorithm 1 provides a high-
level description of the procedure. We compute
197
l
D
o
w
N
o
UN
D
e
D
F
R
o
M
H
T
T
P
:
/
/
D
io
R
e
C
T
.
M
io
T
.
e
D
tu
/
T
UN
C
l
/
l
UN
R
T
io
C
e
–
P
D
F
/
D
o
io
/
.
1
0
1
1
6
2
/
T
l
UN
C
_
UN
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
T
l
UN
C
_
UN
_
0
0
3
6
1
P
D
.
F
B
sì
G
tu
e
S
T
T
o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3
Algorithm 1
Require: question q, image I, word embedding matrix E,
visual representations matrix V
1: H: tensor holding representations hij, ∀i, j s.t. io < j
2: D: tensor holding denotations dij, ∀i, j s.t. i < j
3: for i = 1 . . . n do
4:
hi ← Eqi , di ← fground(Eqi , V ) (see §3.4)
//Handle single-token spans
compute hij, dij for all entries s.t j − i = l
5: for l = 1 . . . n do
6:
7: p(a | q, I) ← softmax(W [h0n; d0nV ])
8: return arg maxa p(a | q, I)
//Handle spans of length l
representations and denotations for length-1 spans
(we use hi = hi(i+1), di = di(i+1) for brevity)
by setting the representation hi = Eqi
to be
the corresponding word representation in an
embedding matrix E, and grounding each word in
the image objects: di = fground(Eqi, V ) (lines 3–4;
fground is described in §3.4). Then, we recursively
compute representations and denotations of larger
spans (lines 5–6). Last, we pass the question
representation, h0n, and the weighted sum of the
visual representations (d0nV ) through a softmax
to produce a final answer distribution
layer
(line 1), using a learned classification matrix
W ∈ RA×2hdim.
Computing hij, dij for all spans requires over-
coming some challenges. Each span representation
hij should be a function of two sub-spans hik, hkj.
We use the term sub-spans to refer to all adjacent
pairs of spans that cover qij: {(qik, qkj)}j−1
k=i+1.
However, we have no supervision for the ‘‘cor-
rect’’ split point k. Our model considers all
possible split points and learns to induce a latent
tree structure from the final answer only (§3.2).
We show that this leads to an interpretable com-
positional structure and denotations that can be
inspected at test time.
In §3.3 we describe the form of the composition
functions, which compute both span representa-
tions and denotations from two sub-spans. These
functions must be expressive enough to accom-
modate a wide range of interactions between
sub-spans, while avoiding reasoning shortcuts
that might hinder compositional generalization.
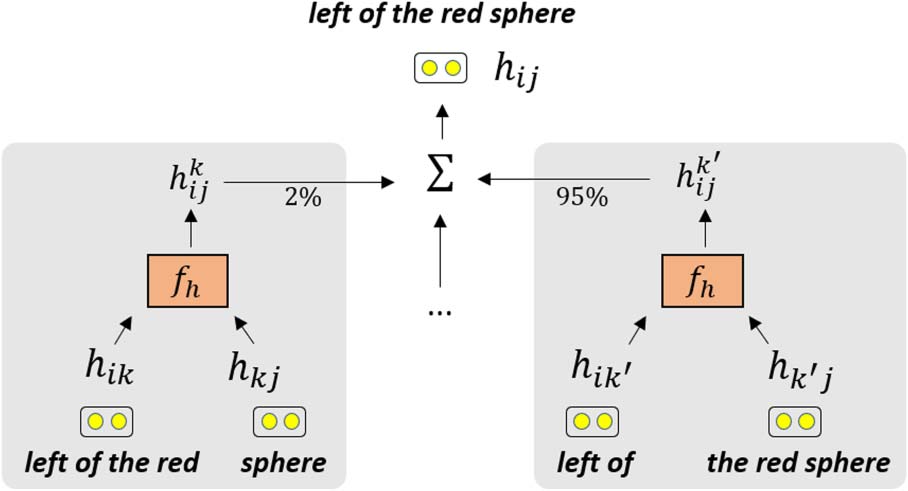
Figure 2: Computing hij: we consider all split
points and compose pairs of sub-spans using
fh. The output
is a weighted sum of these
representations.
sub-spans qik, qkj that meet at a split point k. Sim-
ilarly, we define a representation hk
ij conditioned
on the split point and constructed from previously
computed representations of two sub-spans:
hk
ij = fh(hik, hkj),
(1)
where fh(·) is a composition function (§3.3).
Because we want the loss to be differentiable,
we do not pick a particular value k, but instead use
a continuous relaxation. Specifically, we compute
αk
that represents the probability of k being
ij
the split point for the span qij, given the tensor
H of computed representations of shorter spans.
We then define the representation hij to be the
expected representation over all possible split
points:
(cid:2)
hij =
k
αk
ij
· hk
ij = E
[hk
ij].
αk
ij
(2)
∝ exp(sT hk
The
split point distribution is defined as
ij), where s ∈ Rhdim is a parameter
αk
ij
vector that determines what split points are likely.
Figure 2 illustrates computing hij.
Next, we compute the denotation dij of
each span. Conceptually, computing dij can be
analogous to hij; that is, a function fd will compute
ij for every split point k, and dij = E
dk
ij].
However, the function fd (see §3.3) interacts with
the visual representations of all objects and is thus
computationally costly. Therefore, we propose a
less expressive but more efficient approach, where
fd(·) is applied only once for each span qij.
[dk
αk
ij
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
3.2 Grounded Chart Parsing
Specifically, we compute the expected deno-
We now describe how to compute hij, dij from
previously computed representations and deno-
tations. In standard CKY, each constituent over
a span qij
is constructed by combining two
198
tation of the left and right sub-spans of qij:
∈ Rnobj,
[dik]
¯dijL = E
¯dijR = E
αk
ij
[dkj]
αk
ij
∈ Rnobj.
(3)
(4)
If αk
ij puts most probability mass on a single split
point k(cid:7), then the expected denotation will be
similar to picking that particular split point.
Now we can compute dij given the expected
sub-span denotations and representations with a
single application of fd(·):
dij = fd(¯dijL, ¯dijR, hij),
(5)
αk
ij
which is more efficient
E
than the alternative
[fd(dik, dkj, hij)]: fd is applied O(n2) times
compared to O(n3) with the simpler solution. This
makes training tractable in practice.
3.3 Composition Functions
We now describe the exact form of the com-
position functions fh and fd.
Composing Representations We describe the
function fh(hik, hkj), used to compose the
representations of two sub-spans (Equation 1).
The goal of this function is to compose the
‘‘meanings’’ of two adjacent spans, without access
to the rest of the question or the denotations
of the sub-spans. For example, composing the
representations of
to a
representation for ‘‘same size’’. At a high-level,
composition is based on an attention mechanism.
Specifically, we use attention to form a convex
combination of the representations of the two sub-
spans (Equations 6, 7), and apply a non-linearity
with a residual connection (Equation 8).
‘‘same’’ and ‘‘size’’
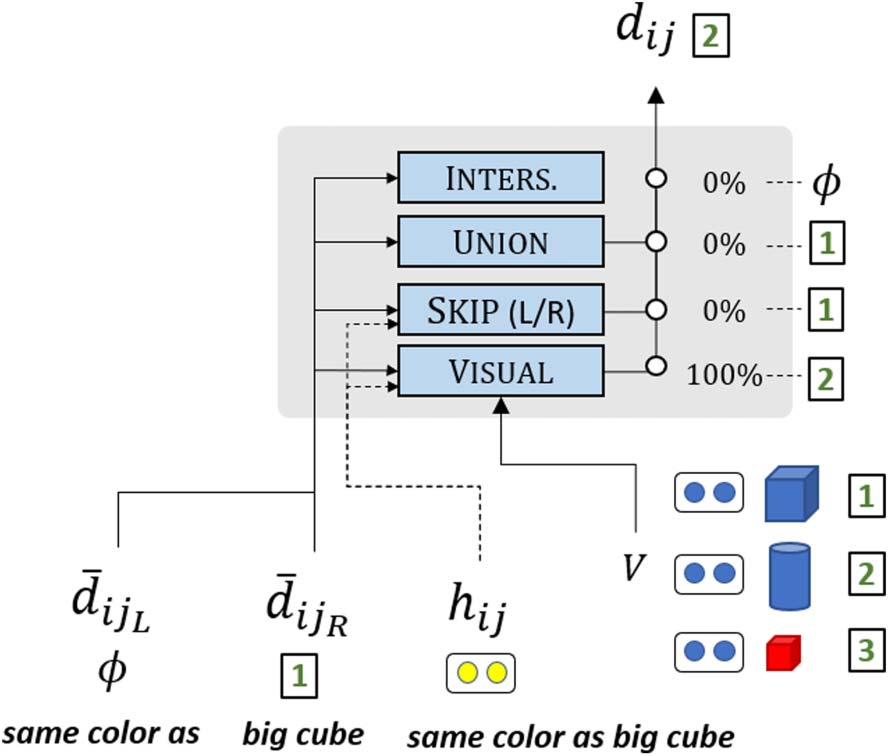
Figure 3: Illustration of how dij is computed. We
compute the denotations of all modules, and a
weight for each one of the modules. The span
denotation is then the weighted sum of the module
outputs.
functions that consider the visual representations
of different objects (spatial relations, colors, etc.).
We define four modules in fd(·) for computing
denotations and let the model learn when to use
each module. The modules are: SKIP, INTERSECTION,
UNION, and a general-purpose VISUAL function,
where only VISUAL uses the visual representations
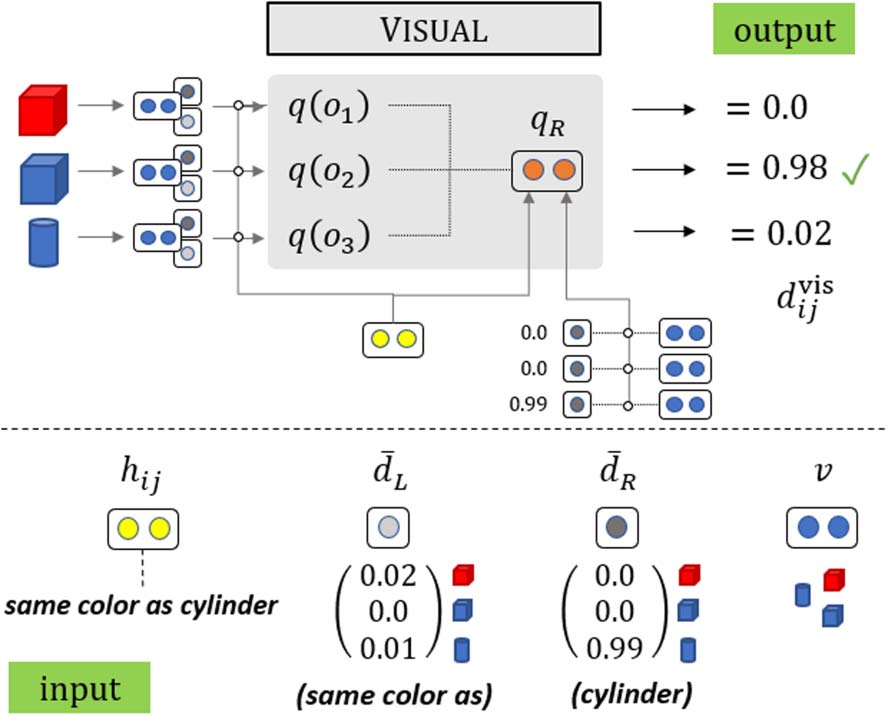
V . As illustrated in Figure 3, each module m
∈ [0, 1]nobj, and
outputs a denotation vector dm
ij
the denotation dij is a weighted average of the
four modules:
βk
ij = softmax ([aLhik, aRhkj])
k
ˆh
WLhik + βk
ij = βk
(cid:3)
ij(1)
WRhkj
(cid:4)
k
ij
+ ˆh
ij(2)
k
ˆh
ij
fh(hik, hkj) = FFrep
∈R2
∈Rhdim
∈Rhdim
(6)
(7)
(8)
p(m|i, j) ∝ exp(Wmodhij)
(cid:2)
dij =
m
p(m|i, j) · dm
ij
∈ R4
∈ Rnobj,
(9)
(10)
where aL, aR ∈ Rhdim, WL, WR ∈ Rhdim×hdim,
and FFrep(·) is a linear layer of size hdim × hdim
followed by a non-linear activation.1
where Wmod ∈ Rhdim×4. Next, we define the four
modules (see Figure 4).
Composing Denotations Next, we describe the
function fd(¯dijL, ¯dijR, hij), used to compute the
span denotation dij (Equation 5). This function
has access only to words in the span qij and not to
the entire input utterance. We want fd(·) to support
both simple compositions that depend only on the
denotations of sub-spans, as well as more complex
1We also use Dropout and Layer-Norm (Ba et al., 2016)
throughout the paper, omitted for simplicity.
199
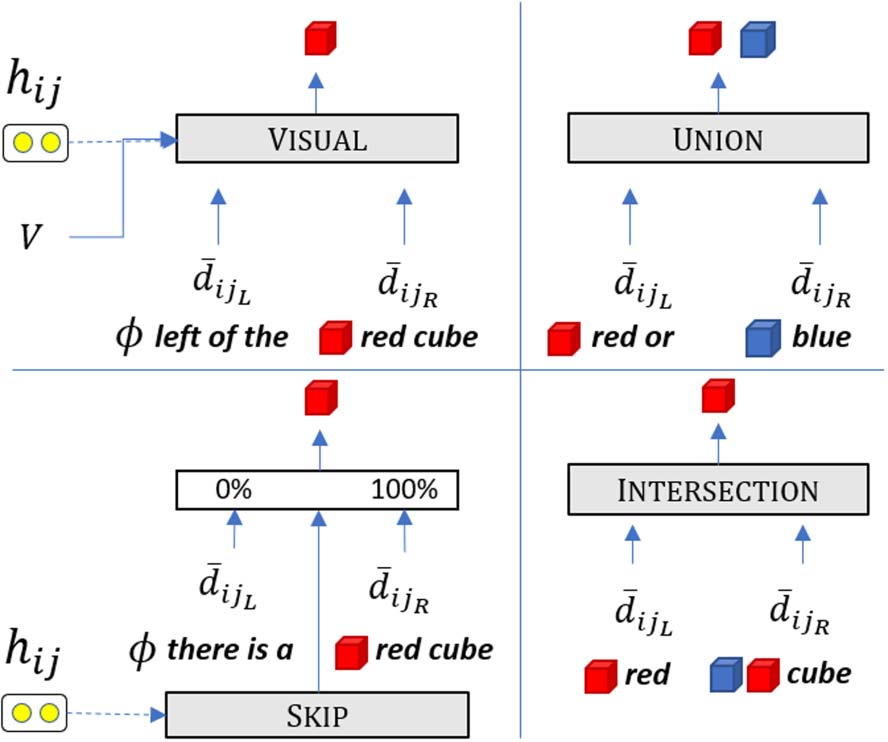
SKIP
In many cases, only one of the left or
right sub-spans have a meaningful denotation: for
example, for ‘‘there is a’’ and ‘‘red cube’’, we
should only keep the denotation of the right sub-
span. To that end, the SKIP module weighs the two
denotations and sums them (Wsk ∈ Rhdim×2):
(cij(1), cij(2)) = softmax (Wskhij) ∈R2
· dijL + cij(2)
dsk
ij = cij(1)
· dijR
∈Rnobj.
(11)
(12)
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 4: The different modules used with their
inputs and expected output.
INTERSECTION and UNION We
two
modules that only use the denotations ¯dijL and
¯dijR. The first corresponds to intersection of two
sets, and the second to union:
define
(cid:5)
dint
ij = min
duni
ij = max
¯dijL, ¯dijR
(cid:5)
¯dijL, ¯dijR
(cid:6)
(cid:6)
∈ Rnobj
∈ Rnobj,
(13)
(14)
where min(·) and max(·) are computed element-
wise.
VISUAL This module is responsible for visual
computations, such as computing spatial rela-
tions (‘‘left of the red sphere’’) and comparing
attributes of objects (‘‘has the same size as
the red sphere’’). Unlike other modules, it also
uses the visual representations of the objects,
V ∈ Rnobj×hdim. For example, for the sub-spans
‘‘left of’’ and ‘‘the red object’’, we expect the
function to ignore ¯dijL (since the denotation of
‘‘left to’’ is irrelevant), and return a denotation
with high probability for objects that are left to
objects with high probability in ¯dijR.
To determine if an object with index o should
have high probability, we need to consider its rela-
tion to all other objects. A simple scoring function
between object o and another arbitrary object oz
might be (hij +vo)T (hij +voz ), which will capture
the relation between the objects conditioned on
the span representation. However, computing this
for all pairs is quadratic in nobj. Instead, we pro-
pose a linear alternative that leverages expected
denotations of sub-spans. Specifically, we com-
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Figure 5: Overview of
the VISUAL module.
We compute a representation for each object,
q(o), augmented with the span denotation,
representation, and visual embeddings, and then
compute its dot-product with qR, a representation
conditioned on the weighted sum of the right
sub-span objects and representations.
pute the expected visual representation of the right
sub-span and pass it through a feed-forward layer:
¯vR = ¯dRV ∈ Rhdim
qR = FFR (Whhij + ¯vR) ∈ Rhdim.
(15)
(16)
We use the right sub-span because the syntax in
CLEVR is mostly right-branching.2 Then, we gen-
erate a representation q(o) for every object con-
ditioned on the span representation hij, the object
probability under the sub-span denotations, and its
visual representation. The final object probability
is based on the interaction of q(o) and qR:
(cid:5)
q(o) = FFvis
(cid:3)
dvis
ij (o) = σ
Whhij + vo + ¯dL(o)sL + ¯dR(o)sR
q(o)T qR
(cid:4)
,
(cid:6)
where Wh ∈ Rhdim×hdim, sL, sR ∈ Rhdim are learned
is a feed-forward layer
embeddings and FFvis
of size hdim × hdim with a non-linear activation.
This is the most expressive module we propose.
A visual overview is shown in Figure 5.
3.4 Grounding
In lines 3–4 of Algorithm 1, we handle length-1
spans. The span representation hi is initialized as
the corresponding word embedding Eqi, and the
2Using the left sub-span instead substantially reduces
performance on CLEVR and CLOSURE.
200
denotation is computed with a grounding function.
A simple implementation for fground would use the
dot product between the word representation and
the visual representations of all objects: σ(h(cid:8)
i V ).3
But, in the case of co-reference (‘‘it’’), we should
ground the co-referring pronoun in the denotation
of a previous span. We now describe this case.
Co-reference Sentences such as ‘‘there is a red
sphere; what is its material?’’ are challenging
given a CKY parser, because the denotation of
‘‘its’’ depends on a distant span. We propose a
simple heuristic that addresses the case where the
referenced object is the denotation of a previous
sentence. This could be expanded in future work,
to a wider array of coreference phenomena.
In every example that comprises two sentences:
(a) We compute the denotation dfirst for the
entire first sentence as previously described; (b)
We ground each word in the second sentence
second
as proposed above: ˆd
V ); (c)
i
For each word in the second sentence, we
predict whether it co-refers to dfirst using a
(cid:6)
FFcoref(hsecond
learned gate (r1, r2) = softmax
)
,
where FFcoref ∈ Rhdim×2. (d) We define dsecond
=
r1 · dfirst + r2 · ˆd
.
= σ(hsecond
i
second
i
(cid:5)
(cid:8)
i
i
Visual Representations Next, we describe how
we compute the visual embedding matrix V . Two
common approaches to obtain visual features
are (1) computing a feature map for the entire
image and letting the model learn to attend to the
correct feature position (Hudson and Manning,
2018; Perez et al., 2018); and (2) predicting the
locations of objects in the image, and extracting
features just for these objects (Anderson et al.,
2018; Tan and Bansal, 2019; Chen et al., 2020).
We use the latter approach, because it simplifies
learning over discrete sets, and has better memory
efficiency – the model only attends to a small set
of objects rather then the entire image feature map.
We train an object detector, Faster R-CNN
(Ren et al., 2015), to predict the location bbpred ∈
Rnobj×4 of all objects, in the format of bounding
boxes (horizontal and vertical positions).
We use gold scene data of 5,000 images from
CLEVR for training (and 1,000 images for valida-
tion). In order to extract features for each predicted
bounding box, we use the bottom–up top-down
3To improve runtime efficiency in the case of a large
knowledge-graph, one could introduce a fast filtering function
to reduce the number of proposed objects.
201
attention method of Anderson et al. (2018),4 which
produces the features matrix Vpred ∈ Rnobj×D,
where D = 2048. Bounding boxes and features
are extracted and fixed as a pre-processing step.
Finally, to compute V , similar to LXMERT
and UNITER we augment object representations
in Vpred with their position embeddings, and
pass them through a single Transformer self-
attention layer to add context about other objects:
V = TransformerLayer(VpredWfeat + bbpredWpos),
where Wfeat ∈ RD×hdim and Wpos ∈ R4×hdim.
Complexity Similar to CKY, we go over all
O(n2) spans in a sentence, and for each span com-
pute hk
ij for each of the possible O(n) splits (there
is no grammar constant since the grammar has
effectively one rule). To compute denotations dij,
for all O(n2) spans, we perform a linear computa-
tion over all nobj objects. Thus, the algorithm runs
in time O(n3 + n2nobj), with similar memory con-
sumption. This is higher than end-to-end models
that do not compute explicit span representations.
3.5 Training
The model is fully differentiable, and we simply
maximize the log probability log p(a∗ | q, I) of
the correct answer a∗ (see Algorithm 1).
4 Experiments
In this section, we evaluate our model on both
in-distribution and OOD splits.
4.1 Arithmetic Expressions
It has been shown that neural networks can be
trained to perform numerical reasoning (Zaremba
and Sutskever, 2014; Kaiser and Sutskever, 2016;
Trask et al., 2018; Geva et al., 2020). However,
models are often evaluated on expressions that are
similar to the ones they were trained on, where
only the numbers change. To test generalization,
we create a simple dataset and evaluate on two
splits that require learning the correct operator
precedence. In the first split, sequences of opera-
tors that appear at test time do not appear at train-
ing time. In the second split, the test set contains
longer sequences compared to the training set.
4Specifically, we use this version: https://github
.com/airsplay/py-bottom-up-attention.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Easy split
Op. split
Len. split
Transformer
GLT
100.0 ± 0.0
99.9 ± 0.2
2.9 ± 1.1
98.4 ± 0.7
10.4 ± 2.4
94.9 ± 1.1
Table 1: Arithmetic expressions results for easy
split, operation split, and length split.
which are not shared across layers. Thus, at
test time when processing an expression longer
than observed at
training time, we use the
layer-normalization parameters (total of 2 · hdim
parameters per layer) from the longest span seen
at training time.5
Results Results are reported in Table 1. We
see that both models almost completely solve
the in-distribution setup, but on OOD splits the
Transformer performs poorly, while GLT shows
only a small drop in accuracy.
4.2 CLEVR and CLOSURE
We evaluate performance on grounded QA using
CLEVR (Johnson et al., 2017a), consisting of
100,000 synthetic images with multiple objects
of different shapes, colors, materials and sizes.
864,968 questions were generated using 80 differ-
ent templates, including simple questions (‘‘what
is the size of red cube?’’) and questions requiring
multi-step reasoning (Figure 1). The split in this
dataset is i.i.d: The same templates are used for
the training, validation, and test sets.
To test compositional generalization when
training on CLEVR, we use the CLOSURE dataset
(Bahdanau et al., 2019b), which includes seven
new question templates, with a total of 25,200
questions, asked on the CLEVR validation set
images. The templates are created by taking refer-
ring expressions of various types from CLEVR and
combining them in novel ways.
A problem found in CLOSURE is that sentences
from the template embed mat spa are ambigu-
ous. For example, in the question ‘‘Is there a
sphere on the left side of the cyan object that is
the same size as purple cube?’’, the phrase ‘‘that
is the same size as purple cube’’ can modify
either ‘‘the sphere’’ or ‘‘the cyan object’’, but the
answer in CLOSURE is always the latter. Therefore,
we deterministically compute both of the two
5Removing layer normalization leads
to improved
accuracy of 99% on the arithmetic expressions length split,
but training convergence on CLEVR becomes too slow.
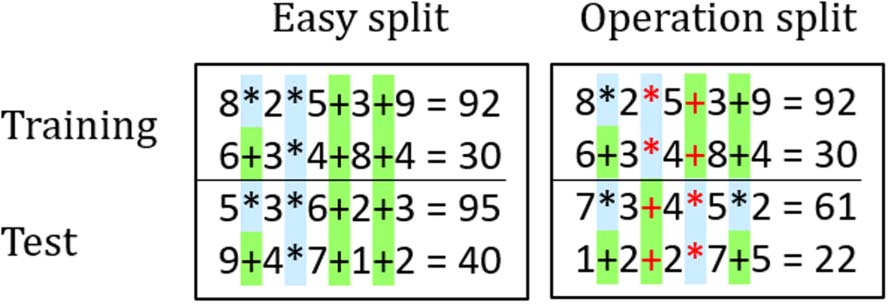
Figure 6: Arithmetic expressions: Unlike the easy
setup, we evaluate models on expressions with
operations ordered in ways unobserved at training
time. Flipped operator positions are in red.
We define an arithmetic expression as a se-
quence containing n numbers with n − 1 arith-
metic operators between each pair. The answer a
is the result of evaluating the expression.
Evaluation Setups The sampled operators are
addition and multiplication, and we use only
expressions where a ∈ {0, 1, . . . , 100} to train as
a multi-class problem. At training, we randomly
pick the length n to be up to ntrain, and at test
time we choose a fixed length ntest. We eval-
uate on three setups, (a) Easy split: we choose
ntrain = ntest = 8, and randomly sample operators
from a uniform distribution for both training and
test examples. In this setup, we only check that
the exact same expression is not shared between
the training and test set. (b) Operation split: We
randomly pick 3 positions, and for each one ran-
domly assign exactly one operator that will appear
at training time. On the test set, the operators in
all three positions are flipped, so that they contain
the unseen operator (Figure 6). The same lengths
are used as in the easy split. (c) Length split: we
train with ntrain = 8 and test with ntest = 10.
Examples for all setups are generated on-the-fly
for 3 million steps (batch size is 100).
Models We compare GLT to a standard Trans-
former, where the input is the expression, and
the output is predicted using a classification layer
over the [CLS] token. All models are trained
with cross-entropy loss given the correct answer.
For both models, we use an in-distribution
validation set for hyper-parameter tuning. Since
here we do not have an image, we only compute
for all spans, and define p(a | q) =
hij
softmax(W h0n).
GLT layers are almost entirely recurrent, that
the same parameters are used to compute
is,
representations for spans of all lengths. The only
exception are layer-normalization parameters,
202
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
possible answers and keep two sets of question-
answer pairs of this template for the entire dataset.
We evaluate models6 on this template by taking
the maximum score over these two sets (such that
models must be consistent and choose a single
interpretation for the template to get a perfect
score).
Baselines We evaluate against
the baselines
from Bahdanau et al. (2019b). The most compa-
rable baselines are MAC (Hudson and Manning,
2018) and FiLM (Perez et al., 2018), which are
differentiable and do not use program annotations.
We also compare to NMNs that require a few
hundred program examples for training. We show
results for PG+EE (Johnson et al., 2017b) and an
improved version, PG-Vector-NMN (Bahdanau
et al., 2019b). Last, we compare to NS-VQA,
which in addition to parsing the question, also
parses the scene into a knowledge graph. NS-VQA
requires additional gold data to parse the image
into a knowledge graph based on data from CLEVR
(colors, shapes, locations, etc.).
Setup Baseline results are taken from previous
papers (Bahdanau et al., 2019b; Hudson and
Manning, 2018; Yi et al., 2018; Johnson et al.,
2017b), except for MAC and FiLM on CLOSURE,
which we re-executed due to the aforementioned
evaluation change. For GLT, we use CLEVR’s
validation set for hyper-parameter tuning and
early-stopping, for a maximum of 40 epochs. We
run 4 experiments to compute mean and standard
deviation on CLOSURE test set.
Because of our model’s run-time and memory
demands (see §3.4), we found that running on
CLEVR and CLOSURE, where question length goes up
to 43 tokens, can be slow. Thus, we delete function
words that typically have empty denotations and
can be safely skipped,7 reducing the maximum
length to 25. We run a single experiment where
stop words were not removed and report results
in Table 3 (with stop-words), showing that per-
formance only mildly change.
CLEVR and CLOSURE
In this experiment we
compare results on i.i.d and compositional splits.
Results are in Table 2. We see that GLT performs
6We update the scores on CLOSURE for MAC, FiLM, and
GLT due to this change in evaluation. The scores for the rest
of the models were not affected.
7The removed tokens are punctuations, ‘the’, ‘there’, ‘is’,
‘a’, ‘as’, ‘of’, ‘are’, ‘other’, ‘on’, ‘that’.
CLEVR
CLOSURE
MAC
FiLM
GLT (our model)
NS-VQA † ∓
PG+EE (18K prog.) †
PG-Vector-NMN †
GT-Vector-NMN † ‡
98.5
97.0
99.1
100
95.4
98.0
98.0
72.4
60.1
96.1 ± 2.5
77.2
–
71.3
94.4
Table 2: Test results for all models on CLEVR and
CLOSURE. † stands for models trained with gold
programs, ‡ for oracle models evaluated using gold
programs, and ∓ for deterministically executed
models that depend on domain-knowledge for
execution (execution is not learned).
CLEVR
CLOSURE
C.Humans
GLT
99.1 ± 0.0 96.1 ± 2.7
75.8 ± 0.7
98.9 ± 0.1 91.8 ± 10.1 76.3 ± 0.6
72.0 ± 1.6
99.0 ± 0.1 83.8 ± 1.8
75.4
99.3
{VISUAL, SKIP}
{VISUAL}
with stop-words
contextualized input 98.9 ± 0.1 87.5 ± 12.1 76.1 ± 0.9
75.8 ± 2.3
non-compositional
97.7 ± 2.0 83.5 ± 0.5
93.2
Table 3: Ablations on the development sets of
CLEVR, CLOSURE, and CLEVR-Humans.
well on CLEVR and gets the highest score on
CLOSURE, improving by almost 24 points over
comparable models, and by 19 points over NS-
VQA, outperforming even the oracle GT-Vector-
NMN which uses gold programs at test time.
Removing Modules We defined (§3.3) two
modules specifically for CLEVR, INTERSECTION and
UNION. We evaluate performance without them,
keeping only VISUAL and SKIP, and show results in
Table 3, observing only a moderate loss in accu-
racy and generalization. Removing these modules
leads to more cases where the VISUAL function
is used, effectively performing intersection and
union as well. While the drop in accuracy is small,
this model is harder to interpret since VISUAL now
performs multiple functions.
Next, we evaluate performance when training
only with the VISUAL module. Results show that
even a single high-capacity module is enough for
in-distribution performance, but generalization to
CLOSURE now substantially drops to 83.8.
Contextualizing Question Tokens We hypoth-
esized that the fact that question spans do not
203
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
CLOSURE FS C.Humans
MAC
FiLM
GLT (our model)
90.2
–
97.4 ± 0.3
NS-VQA
PG-Vector-NMN
PG+EE (18K prog.)
92.9
88.0
–
81.5
75.9
76.2
67.0
–
66.6
were unseen in CLEVR. We train on CLEVR and fine-
tune on CLEVR-Human, similar to prior work.
We use GloVe embeddings (Pennington et al.,
2014) for words unseen in CLEVR. Table 4 shows
that GLT gets better results than models that use
programs, showing its flexibility to learn new
concepts and phrasings. It is also comparable to
FILM, but gets lower results than MAC (see error
analysis below).
Table 4: Test results in the few-shot setup and for
CLEVR-Humans.
4.3 Error analysis
observe the entire input might aid composition
generalization. To check this, we pass the ques-
tion tokens q through a Transformer self-attention
layer, to get contextualized tokens embeddings
Eqi. We show in Table 3 that performance on
CLEVR remains the same, but on CLOSURE it drops
to 87.5.
Non-compositional Representations To assess
the importance of compositional representations,
we replace hij (Equation 2) with a sequential
encoder. Concretely, we set the representation of
the span qij to be hij = BiLSTM(qij), the output
of a single layer bi-directional LSTM which is
given the tokens of the span as input. We see a
drop in both CLEVR and CLOSURE (experiments
were more prone to overfitting), showing the
importance of compositional representations.
Few-shot
In the few-shot (FS) setup, we train
with additional 252 OOD examples: 36 questions
for each CLOSURE template. Similar to Bahdanau
et al. (2019b), we take a model that was trained
on CLEVR and fine-tune adding oversampled CLO-
SURE examples (300x) to the original training set.
To make results comparable to Bahdanau et al.
(2019b), we perform model selection based on
CLOSURE validation set, and evaluate on the test
set. As we see in Table 4, GLT gets the best
accuracy. If we perform model selection based
on CLEVR (the preferred way to evaluate in the
OOD setup, Teney et al. 2020), accuracy remains
similar at 97.0 ± 2.0 (and is still highest).
CLEVR-Humans To test performance on real
language, we use CLEVR-Humans (Johnson et al.,
2017b), which includes 32,164 questions over
images from CLEVR. These questions, asked by
humans, contain words and reasoning steps that
We sampled 25 errors from each dataset (CLEVR,
CLOSURE, and CLEVR-Humans) for analysis. On
CLEVR, most errors (84%) are due to problems
in visual processing such as grounding the
word ‘‘rubber’’ to a metal object, problems in
bounding box prediction or questions that require
subtle spatial reasoning, such as identifying if an
object is left to another object of different size,
when they are at an almost identical x-position.
The remaining errors (16%) are due to failed
comparisons of numbers or attributes (‘‘does the
red object have the same material as the cube’’).
On CLOSURE, 60% of the errors were similar to
CLEVR, for example, problematic visual process-
ing or failed comparisons. In 4% of cases, the
execution of the VISUAL module was wrong, for
example, it collapsed two reasoning steps (both
intersection and finding objects of same shape),
but did not output the correct denotation. Other
errors (36%) are in the predicted latent tree, where
the model was uncertain about the split point and
softly predicted more than one tree, resulting in
a wrong answer. In some cases (16%) this was
due to question ambiguity (see §4.2), and in others
cases the cause was unclear (e.g., for the phrase
‘‘same color as the cube’’ the model gave a
similar probability for the split after ‘‘same’’ and
after ‘‘color’’, leading to a wrong denotation of
that span).
On CLEVR-Humans, the model successfully
learned certain new ‘‘concepts’’ such as colors
(‘‘gold’’), superlatives (‘‘smallest’’, ‘‘furthest’’),
relations (‘‘next to’’, ‘‘between’’), negation (see
Figure 7), and the ‘‘all‘‘ quantifier.
It also
answered correctly questions that had different
style from CLEVR (‘‘Are there more blocks or
balls?’’). However, the model is not always robust
to these new concepts, and fails in other cases that
require counting of abstract concepts (such as
colors or shapes) or that use CLEVR’s operators
204
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
even when denotations do not accurately repre-
sent reasoning, the model can still ‘‘fall back’’ to
the flexible answer function, which can take the
question and image representations and, in theory,
perform anyf needed computation. In such cases,
the model will not be interpretable, similar to other
high-capacity models such as Transformers. In
future work, we will explore combining the com-
positional generalization abilities of GLT with the
advantages of high-capacity architectures.
4.5 Interpretability
of
trees
latent
advantage
A key
is
interpretability—one can analyze the structure of
a given question. Next, we quantitatively inspect
the quality of the intermediate outputs produced
by the model by (a) comparing these outputs to
ground truth and (b) assessing how helpful they
are for humans.
Evaluating Intermediate Outputs We assess
how accurate our intermediate outputs are com-
pared to ground truth trees. Evaluating against
ground truth trees is not
trivial, since for a
given question, there could be many ‘‘correct’’
trees—that is, trees that represent a valid way to
answer the question. For example, the two possible
ways to split the phrase ‘‘large shiny block’’ are
both potentially valid. Thus, even if we had one
ground-truth tree for each question, comparing
predicted trees to ground-truth trees might not be
reliable.
Instead, we exploit the fact that for the synthetic
questions in CLEVR, it is possible to define a set of
certain constituents that must appear in any valid
tree. For example, phrases starting with ‘‘the’’,
followed by adjectives and then a noun (‘‘the
shiny tiny sphere’’), should always be considered
a constituent. We use such manually defined rules
to extract the set cq of obligatory constituents for
any question q in CLEVR and CLOSURE validation
sets.
We compute a recall score for each question q,
by producing predicted trees (we greedily take
the maximum probability split in each node),
extracting a set ˆcq of all constituents, and then
computing the proportion of constituents in cq that
are also in ˆcq. We show results in Table 6 for both
CLEVR and CLOSURE. We see that 81.6%–83.1% of
the expected constituents are correctly output by
205
Figure 7: An example from CLEVR-Humans. The
model learned to negate (‘‘not’’) using the VISUAL
module (negation is not part of CLEVR).
differently than the original uses. See Table 5 for
our manually performed analysis and examples
over 150 CLEVR-Humans validation questions.
4.4 Limitations
While some of the errors shown in Table 5 can be
improved with careful design of modules archi-
tectures, improvement of the image features, or
by introducing a pre-training mechanism, some
question structures are inherently more difficult
to correctly answer using our model. We describe
two main limitations.
One key issue is discrepancy between the text
of the question and the actual reasoning steps that
are required to correctly answer it. For example, in
the question ‘‘What is the most common shape?’’,
the phrase ‘‘most common’’ entails grouping and
counting shapes, and then taking an argmax as
an answer. This complex reasoning cannot be
constructed compositionally from question spans.
The second issue is the supported types of
phrase denotations. GLT only grounds objects in
the image to a phrase, however, in some cases
denotations should be a number or an attribute. For
example, in comparison questions (‘‘is the number
of cubes higher than the number of spheres?’’) a
model would ideally have a numerical denotation
for each group of objects.
Importantly, these limitations do not prevent the
model from answering questions correctly, since
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Category
Negation
Spelling mistakes
Superlatives
Examples
– How many objects are not shiny? ✓
– What color is the cylinder that is not the same (cid:2)(cid:2)colr as the sphere? ✗
cumes? ✓
– Are there two green(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)
– How many rubber (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)
– What color is the object furthest to the right? ✓
– What shape is the smallest matte object? ✓
spehres are there here? ✗
Visual Concepts: obscuring, between
– Is the sphere the same color as the object that is obscuring it? ✓
– What color is the object in between the two large cubes? ✓
Visual Concepts: reflection, shadow
Visual Concepts: relations
All quantifier
Counting abstract concepts
Complex logic
Different question structure
Uniqueness
Long-tail concepts
Operators used differently than CLEVR
– Which shape shows the largest reflection ✗
– Are all of the objects casting a shadow? ✗
– What color is the small ball near the brown cube? ✓
– What is behind and right of the cyan cylinder? ✗
– Are all the spheres the same size? ✓
– Are all the cylinders brown? ✗
– How many different shapes are there? ✓
– How many differently colored cubes are there? ✗
– if these objects were lined up biggest to smallest, what would be in the middle? ✓
– if most of the items shown are shiny and most of the items shown are blue, would
it be fair to say most of the items are shiny and blue? ✗
– Are more objects metallic or matte? ✓
– Each shape is present 3 times except for the ✗
– What color object is a different material from the rest? ✓
– What color is the object that does not match the others? ✗
– Can you roll all the purple objects? ✓
– How many of these things could be stacked on top of each other? ✗
– Are the large cylinders the same color? ✓
– Are there more rubber objects than matte cylinders and green cubes? ✗
Same operators as CLEVR,
possibly different phrasing
– What color is the cube directly in front of the blue cylinder? ✓
– What color is the little cylinder? ✗
Correct
1/2 (50%)
1/5 (20%)
8/10 (80%)
5/7 (71%)
0/2 (0%)
3/8 (38%)
10/12 (83%)
1/4 (25%)
3/4 (75%)
1/2 (50%)
1/2 (50%)
2/5 (40%)
2/5 (40%)
1/80 (89%)
Table 5: Categorization of 150 CLEVR-Humans examples, together with the accuracy of the GLT
model (for many categories, sample is too small to make generalizations on model performance).
underlined. Some examples were labeled with multiple categories. Six examples
Spelling mistakes are (cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)(cid:2)
with gold-label mistakes were ignored.
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
GLT, for CLEVR and CLOSURE respectively. Next,
we sample and analyze 25 cases from each dataset
where the expected constituents were not output.
We observe that almost all missed constituents
actually were output as a constituent by the
model, but with an additional prefix that caused a
wrong split. For example, instead of the expected
constituent ‘‘tiny green objects‘‘ we found the
constituent ‘‘any tiny green objects’’ (split after
‘‘tiny’’). These mistakes did not cause any error in
module execution, except for one case in CLOSURE.
Additionally, we obtain the gold set of objects
for each constituent in cq by deterministically
mapping each constituent to a program that we
execute on the scene. For each constituent in
cq ∩ ˆcq, we compare the predicted set of objects
(objects with probability above 50%) with the
gold set of objects, and report the average F1. As
CLEVR
CLOSURE
Constituents (%)
Denotations (F1)
83.1
95.9
81.6
94.7
Table 6: Evaluation of the intermediate outputs,
showing both the recall of expected constituents
(%) and average F1 of predicted objects.
can be seen in Table 6, reported score for CLEVR
is 95.9% and for CLOSURE it is 94.7%.
Human Interpretability Next, we want
to
assess how useful are the intermediate outputs
produced by the model for humans. We perform
the ‘‘forward prediction’’ test (Hu et al., 2018)
that evaluates interpretability by showing humans
questions accompanied with intermediate outputs,
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
206
CLEVR
CLOSURE
C.Humans
A - w/o tree
B - w/ tree
61.4%
62.5%
58.1%
82.5%
52.3%
77.5%
Table 7: Results for the ‘‘forward prediction’’ test.
Group A sees only the question, image and gold
answer, group B additionally sees the denotation
tree.
and asking them to predict if the model will be
correct. This test is based on the assumption that
humans can more easily predict the accuracy of
an interpretable model versus a non-interpretable
one. Thus, we also ask a separate group of
the accuracy without
participants to predict
for
showing them the intermediate outputs
comparison.
We show each of
the 20 participants 12
questions evenly split into CLEVR, CLOSURE, and
CLEVR-Humans, where for each dataset we show
two correct and two incorrect examples per person.
We assign 11 participants to the baseline group
(group A) that sees only the question, image,
and gold answer, and 9 participants to the tested
group (group B) which are also given the predicted
denotation tree of our model, similar to Figure 1.
Both groups are given the same 8 ‘‘training’’
examples of questions, with the predicted answer
of the model along with the gold answer, to
improve their understanding of the task. In these
training examples, group B participants also see
example denotation trees, along with a basic
explanation of how to read those.
We show results in Table 7. We see that for
CLOSURE and CLEVR-Humans, accuracy for group
B is significantly higher (p < 0.05), but for CLEVR
results are similar. We observe that in CLEVR,
where accuracy is 99.1%, wrong predictions are
mostly due to errors in the less interpretable VISUAL
module, while for CLOSURE and CLEVR-Humans
errors are more often due to wrong selection of
constituents and modules, which can be spotted
by humans.
5 Conclusion
Developing models that generalize to composi-
tions that are unobserved at training time has
recently sparked substantial research interest. In
this work we propose a model with a strong
inductive bias towards compositional computa-
tion, which leads to large gains in systematic
generalization and provides an interpretable struc-
ture that can be inspected by humans. Moreover,
our model also obtains high performance on real
language questions (CLEVR-humans). In future
work, we will investigate the structures revealed
by our model in other grounded QA setups, and
will allow the model freedom to incorporate non-
compositional signals, which go hand in hand with
compositional computation in natural language.
Acknowledgments
This research was partially supported by The
Yandex Initiative for Machine Learning, and
the European Research Council (ERC) under
the European Union Horizons 2020 research
and innovation programme (grant ERC DELPHI
802800). We thank Jonathan Herzig and the
anonymous reviewers for their useful comments.
This work was completed in partial fulfillment for
the Ph.D. degree of Ben Bogin.
References
Peter Anderson, Xiaodong He, Chris Buehler,
Damien Teney, Mark Johnson, Stephen Gould,
and Lei Zhang. 2018. Bottom-up and top-down
attention for image captioning and visual ques-
tion answering. In 2018 IEEE/CVF Conference
on Computer Vision and Pattern Recogni-
tion, pages 6077–6086. DOI: https://doi
.org/10.1109/CVPR.2018.00636
Jacob Andreas, Marcus Rohrbach, Trevor Darrell,
and Dan Klein. 2016. Neural module networks.
In 2016 IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 39–48.
DOI: https://doi.org/10.1109/CVPR
.2016.12
Lei Jimmy Ba, Jamie Ryan Kiros, and Geoffrey E.
Hinton. 2016. Layer normalization. CoRR,
abs/1607.06450.
Dzmitry Bahdanau, Shikhar Murty, Michael
Noukhovitch, Thien Huu Nguyen, Harm de
Vries, and Aaron Courville. 2019a. Systematic
is required and can it
generalization: What
be learned? In International Conference on
Learning Representations.
207
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Dzmitry Bahdanau, Harm de Vries, Timothy J.
O’Donnell, Shikhar Murty, Philippe Beaudoin,
Yoshua Bengio, and Aaron C. Courville.
2019b. CLOSURE: Assessing
systematic
generalization of CLEVR models. CoRR,
abs/1912.05783.
Yen-Chun Chen, Linjie Li, Licheng Yu, A. E.
Kholy, Faisal Ahmed, Zhe Gan, Y. Cheng,
and Jing jing Liu. 2020. UNITER: Universal
image-text representation learning. In ECCV.
DOI: https://doi.org/10.1007/978
-3-030-58577-8 7
Noam Chomsky. 1957. Syntactic Structures,
Mouton. DOI: https://doi.org/10
.1515/9783112316009
John Cocke. 1969. Programming Languages and
Their Compilers: Preliminary Notes, New York
University.
Jacob Devlin, Ming-Wei Chang, Kenton Lee, and
Kristina Toutanova. 2019. BERT: Pre-training
of deep bidirectional transformers for language
understanding. In Proceedings of
the 2019
Conference of the North American Chapter of
the Association for Computational Linguistics:
Human Language Technologies, Volume 1
(Long and Short Papers), pages 4171–4186,
Minneapolis, Minnesota. Association
for
Computational Linguistics.
Andrew Drozdov, Patrick Verga, Mohit Yadav,
Mohit Iyyer, and Andrew McCallum. 2019.
Unsupervised latent tree induction with deep
inside-outside recursive auto-encoders. In Pro-
ceedings of the 2019 Conference of the North
American Chapter of the Association for Com-
putational Linguistics: Human Language Tech-
nologies, Volume 1 (Long and Short Papers),
pages 1129–1141, Minneapolis, Minnesota.
Association for Computational Linguistics.
DOI: https://doi.org/10.18653/v1
/N19-1116
Catherine
Jonathan
Finegan-Dollak,
K.
Kummerfeld, Li Zhang, Karthik Ramanathan,
Sesh Sadasivam, Rui Zhang, and Dragomir
Radev. 2018. Improving text-to-SQL evalua-
tion methodology. In Proceedings of the 56th
Annual Meeting of the Association for Compu-
tational Linguistics (Volume 1: Long Papers),
pages 351–360, Melbourne, Australia. Asso-
ciation for Computational Linguistics. DOI:
https://doi.org/10.18653/v1/P18
-1033
Jerry A. Fodor and Zenon W. Pylyshyn. 1988.
Connectionism and Cognitive Architecture:
A Critical Analysis. MIT Press, Cambridge,
MA, USA. ISBN 0262660644, pp. 3–71. DOI:
https://doi.org/10.1016/0010
-0277(88)90031-5
Mor Geva, Ankit Gupta, and Jonathan Berant.
2020. Injecting numerical reasoning skills into
language models. In Proceedings of the 58th
Annual Meeting of the Association for Com-
putational Linguistics, pages 946–958, Online.
Association for Computational Linguistics.
DOI: https://doi.org/10.18653/v1
/2020.acl-main.89
Nitish Gupta and Mike Lewis. 2018. Neural
compositional denotational semantics for ques-
tion answering. In Proceedings of the 2018
Conference on Empirical Methods in Natu-
ral Language Processing, pages 2152–2161,
Brussels, Belgium. Association for Compu-
tational Linguistics. DOI: https://doi
.org/10.18653/v1/D18-1239, PMID:
30485774
Sepp Hochreiter and J¨urgen Schmidhuber. 1997.
Long short-term memory. Neural Compu-
tation, 9:1735–1780. DOI: https://doi
.org/10.1162/neco.1997.9.8.1735,
PMID: 9377276
Ronghang Hu, Jacob Andreas, Trevor Darrell,
and Kate Saenko. 2018. Explainable neural
computation via stack neural module networks.
In Proceedings of the European Conference on
Computer Vision (ECCV).
Drew Arad Hudson and Christopher D. Manning.
2018. Compositional attention networks for
machine reasoning. In International Conference
on Learning Representations.
Yichen Jiang and Mohit Bansal. 2019. Avoiding
reasoning shortcuts: Adversarial evaluation,
training, and model development for multi-
hop QA. In Proceedings of the 57th Annual
Meeting of the Association for Computational
Linguistics, pages 2726–2736, Florence, Italy.
208
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
Association for Computational Linguistics.
DOI: https://doi.org/10.18653/v1
/P19-1262, PMID: 31353678
Justin Johnson, Bharath Hariharan, Laurens
van der Maaten, Li Fei-Fei, C. Lawrence
Zitnick, and Ross Girshick. 2017a. CLEVR: A
diagnostic dataset for compositional language
and elementary visual reasoning. In 2017 IEEE
Conference on Computer Vision and Pattern
Recognition (CVPR), pages 1988–1997. DOI:
https://doi.org/10.1109/CVPR.2017
.215
Justin Johnson, Bharath Hariharan, Laurens
van der Maaten, Judy Hoffman, Li Fei-Fei,
C. Lawrence Zitnick, and Ross Girshick. 2017b.
Inferring and executing programs for visual rea-
soning. In 2017 IEEE International Conference
on Computer Vision (ICCV), pages 3008–3017.
DOI: https://doi.org/10.1109/ICCV
.2017.325, PMID: 28556096
Lukasz Kaiser
and Ilya Sutskever. 2016.
Neural GPUs learn algorithms. International
Conference on Learning Representations.
Tadao Kasami. 1965, An efficient recognition
and syntax analysis algorithm for context-
free languages, Air Force Cambridge Research
Laboratory, Bedford, MA.
Daniel Keysers, Nathanael Sch¨arli, Nathan
Scales, Hylke Buisman, Daniel Furrer,
Sergii Kashubin, Nikola Momchev, Danila
Sinopalnikov, Lukasz Stafiniak, Tibor Tihon,
Dmitry Tsarkov, Xiao Wang, Marc van Zee,
and Olivier Bousquet. 2020. Measuring com-
positional generalization: A comprehensive
In International
method on realistic data.
Conference on Learning Representations.
Brenden M. Lake and Marco Baroni. 2018.
Generalization without systematicity: On the
compositional skills of sequence-to-sequence
recurrent networks. In ICML.
Brenden M. Lake, Tomer D. Ullman, Joshua B.
Tenenbaum, and Samuel Gershman. 2018.
learn and think
that
Building machines
like people. Behavioral and Brain Sciences,
40:e253.
209
Phong Le and Willem Zuidema. 2015. The forest
convolutional network: Compositional distri-
butional semantics with a neural chart and
without binarization. In Proceedings of the 2015
Conference on Empirical Methods in Natural
Language Processing, pages 1155–1164, Lis-
bon, Portugal. Association for Computational
Linguistics.
I.
Percy Liang, Michael
Jordan, and Dan
Klein. 2013. Learning dependency-based com-
positional semantics. Computational Linguis-
tics, 39(2):389–446. DOI: https://doi
.org/10.1162/COLI a 00127
Tal Linzen. 2020. How can we
acceler-
ate progress towards human-like linguistic
generalization? In Proceedings of
the 58th
Annual Meeting of
the Association for
Computational Linguistics, pages 5210–5217,
Online. Association for Computational Linguis-
tics. DOI: https://doi.org/10.18653
/v1/2020.acl-main.465
Yang Liu, Matt Gardner, and Mirella Lapata.
2018. Structured alignment networks
for
matching sentences. In Proceedings of the 2018
Conference on Empirical Methods in Natural
Language Processing,
1554–1564,
Brussels, Belgium. Association for Compu-
tational Linguistics. DOI: https://doi
.org/10.18653/v1/D18-1184
pages
Jean Maillard, Stephen Clark,
and Dani
Yogatama. 2019. Jointly learning sentence
embeddings and syntax with unsupervised
tree-LSTMs. Natural Language Engineering,
25(4):433–449. DOI: https://doi.org
/10.1017/S1351324919000184
Jiayuan Mao, Chuang Gan, Pushmeet Kohli,
and Jiajun Wu.
Joshua B. Tenenbaum,
2019. The neuro-symbolic concept
learner:
Interpreting scenes, words, and sentences
In International
from natural
supervision.
Conference on Learning Representations.
Richard Montague. 1970. Universal grammar.
Theoria, 36(3):373–398. DOI: https://
doi.org/10.1111/j.1755-2567.1970
.tb00434.x
Jeffrey
Pennington, Richard
and
Christopher Manning. 2014. GloVe: Global
Socher,
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3
vectors for word representation. In Proceedings
of the 2014 Conference on Empirical Methods
in Natural Language Processing (EMNLP),
pages 1532–1543, Doha, Qatar. Association for
Computational Linguistics. DOI: https://
.org/10.3115/v1/D14-1162
Ethan Perez, Florian Strub, Harm de Vries,
Vincent Dumoulin, and Aaron Courville.
2018. FiLM: Visual reasoning with a general
conditioning layer. In AAAI Conference on
Artificial Intelligence.
Shaoqing Ren, Kaiming He, Ross Girshick, and
Jian Sun. 2015. Faster R-CNN: Towards real-
time object detection with region proposal net-
works. In Proceedings of the 28th International
Conference on Neural Information Processing
Systems - Volume 1. NIPS’15, pages 91–99,
Cambridge, MA, USA. MIT Press.
Laura Ruis, Jacob Andreas, Marco Baroni, Diane
Bouchacourt, and Brenden M. Lake. 2020.
A benchmark for systematic generalization
in grounded language understanding. CoRR,
abs/2003.05161.
Sanjay Subramanian, Ben Bogin, Nitish Gupta,
Tomer Wolfson, Sameer Singh,
Jonathan
Berant, and Matt Gardner. 2020. Obtaining
faithful interpretations from compositional neu-
ral networks. In Proceedings of the 58th Annual
Meeting of the Association for Computational
Linguistics, pages 5594–5608, Online. Asso-
ciation for Computational Linguistics. DOI:
https://doi.org/10.18653/v1/2020
.acl-main.495
Sanjay Subramanian, Sameer Singh, and Matt
Gardner. 2019. Analyzing compositionality
In NeurIPS
in visual question answering.
Workshop on Visually Grounded Interaction
and Language.
Hao Tan and Mohit Bansal. 2019. LXMERT:
Learning cross-modality encoder representa-
tions from transformers. In Proceedings of
the 2019 Conference on Empirical Meth-
ods in Natural Language Processing and the
9th International Joint Conference on Natu-
ral Language Processing (EMNLP-IJCNLP),
pages
5100–5111, Hong Kong, China.
Association for Computational Linguistics.
DOI: https://doi.org/10.18653/v1
/D19-1514
Damien Teney, Kushal Kafle, Robik Shrestha,
Ehsan Abbasnejad, Christopher Kanan, and
Anton van den Hengel. 2020. On the value
of out-of-distribution testing: An example of
goodhart’s law. CoRR, abs/2005.09241.
Andrew Trask, Felix Hill, Scott E. Reed, Jack
Rae, Chris Dyer, and Phil Blunsom. 2018.
Neural arithmetic logic units. In Advances
in Neural Information Processing Systems,
pages 8035–8044.
Ashish Vaswani, Noam Shazeer, Niki Parmar,
Jakob Uszkoreit, Llion Jones, Aidan N.
Gomez, Łukasz Kaiser, and Illia Polosukhin.
2017. Attention is all you need. Advances in
Neural Information Processing Systems 30,
pages 5998–6008. Curran Associates, Inc.
Kexin Yi, Jiajun Wu, Chuang Gan, Antonio
Torralba,
Josh
Pushmeet Kohli,
Tenenbaum. 2018. Neural-symbolic VQA:
Disentangling reasoning from vision and lan-
guage understanding. In Advances in Neural
Information Processing Systems, volume 31,
pages 1031–1042. Curran Associates, Inc.
and
Daniel H. Younger. 1967. Recognition and
parsing of context-free languages in time n3.
Information and Control, 10(2):189–208. DOI:
https://doi.org/10.1016/S0019
-9958(67)80007-X
Wojciech Zaremba and Ilya Sutskever. 2014.
Learning to execute. CoRR, abs/1410.4615.
Luke Zettlemoyer and Michael Collins. 2005.
Learning to map sentences to logical form:
Structured classification with probabilistic
categorial grammars. In UAI.
210
l
D
o
w
n
o
a
d
e
d
f
r
o
m
h
t
t
p
:
/
/
d
i
r
e
c
t
.
m
i
t
.
e
d
u
/
t
a
c
l
/
l
a
r
t
i
c
e
-
p
d
f
/
d
o
i
/
.
1
0
1
1
6
2
/
t
l
a
c
_
a
_
0
0
3
6
1
1
9
2
4
2
2
5
/
/
t
l
a
c
_
a
_
0
0
3
6
1
p
d
.
f
b
y
g
u
e
s
t
t
o
n
0
7
S
e
p
e
m
b
e
r
2
0
2
3