Kleban, E., Jones, D. K., & Tax, C. M. W. (2023). The Impact of Head Orientation with Respect
to B0 on diffusion tensor MRI Measures. Imaging Neuroscience, Advance Publication.
https://doi.org/10.1162/imag_a_00012
The Impact of Head Orientation with Respect to B0 on
diffusion tensor MRI measures
Elena Kleban1,2, Derek K Jones1,3, Chantal MW Tax4,5
1CUBRIC, School of Psychology, Cardiff University, Cardiff, UK
2Inselspital, University of Bern, Bern, Svizzera
3MMIHR, Faculty of Health Sciences, Australian Catholic University, Melbourne,
Australia
4CUBRIC, School of Physics and Astronomy, Cardiff University, Cardiff, UK
5UMC Utrecht, Utrecht University, Utrecht, The Netherlands
Astratto
Diffusion tensor MRI (DT-MRI) remains the most commonly used approach
to characterise white matter (WM) anisotropy. Tuttavia, DT estimates may be
affected by tissue orientation w.r.t. due to local gradients and intrinsic
orientation dependence induced by the microstructure. This work aimed to
investigate whether and how diffusion tensor MRI-derived measures depend on the
orientation of the head with respect to the static magnetic field, . By simulating
© 2023 Istituto di Tecnologia del Massachussetts. Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale (CC BY 4.0) licenza. 1
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
WM as two compartments, we demonstrated that compartmental anisotropy can
induce the dependence of diffusion tensor measures on the angle between WM
fibres and the magnetic field. In in vivo experiments, reduced radial diffusivity and
increased axial diffusivity were observed in white matter fibres perpendicular to
compared to those parallel to . Fractional anisotropy varied by up to as a
function of the angle between WM fibres and the orientation of the main magnetic
field. To conclude, fibre orientation w.r.t. is responsible for up to variance
in diffusion tensor measures across the whole brain white matter from all subjects
and head orientations. Fibre orientation w.r.t. may introduce additional variance
in clinical research studies using diffusion tensor imaging, particularly when it is
difficult to control for (e.g. fetal or neonatal imaging, or when the trajectories of
fibres change due to e.g. space occupying lesions).
Keywords: Diffusion Tensor Imaging, Magnetic Resonance Imaging,
Transverse relaxation, orientation anisotropy, fibre direction
1. introduzione
MRI can provide invaluable information on tissue composition and structure
in vivo through the manipulation of spins with magnetic fields. Several MRI
2
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
contrasts have shown a dependence on tissue orientation w.r.t. the main magnetic
field direction ( ), including
, , and magnetisation transfer [1–19].
Orientation-dependence of the apparent
in adult white matter (WM) ha
primarily been attributed to local magnetic susceptibility-induced gradients from the
myelin sheath, and as such can provide valuable information on its condition in
health and disease [10, 19]. Inoltre, recent work [20] found that orientational
anisotropy of transverse relaxation rates in newborn WM, with a much lower degree
of myelination, followed the pattern of residual dipolar coupling. Recent works have
demonstrated different orientational behaviours of -estimates in intra- E
extra-axonal microstructural WM compartments [21, 22], see also Appendix A.
In diffusion MRI (dMRI) typically only the orientation-dependence on
externally applied spatial gradients is considered: it sensitises the signal to the
diffusion of water molecules in one or multiple directions by deliberately applying
magnetic field gradients, and as such can infer information on the directional
organisation of tissue. At low to moderate diffusion weightings, the diffusion tensor
MRI (DT-MRI) representation [23] remains the most commonly used approach to
characterise the diffusion process, and DT-MRI-derived measures such as mean
diffusivity (MD) and fractional anisotropy (FA) reflect both intra-and extra-axonal
signal contributions.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
3
Theoretically, dMRI signals and derived measures can also exhibit
-orientation dependence when magnetic susceptibility variation is combined with
anisotropic geometry at a subvoxel level. Several mechanisms may contribute to
dMRI-signal-anisotropy in this case. Firstly, several works have considered the
interaction (or cross-term) of susceptibility-induced gradients with the externally
applied diffusion encoding gradients, and their effect on estimates of the apparent
diffusion coefficient (ADC) [15, 24–29]. Specifically, local gradients in the
direction of the diffusion encoding gradient can lead to an under- or overestimation
of ADC from individual isochromats, leading to a reduction of the overall ADC
because isochromats with reduced ADC contribute a higher weighting [24]. By
employing sequences sensitive and insensitive to local susceptibility-induced
gradients, early ex vivo experiments in WM [26, 30] concluded that the effects from
local gradients on diffusivity values did not have a measurable role in nerve samples
at 4.7T and 2.35T, rispettivamente, which was later corroborated in vivo at 1.5T [27].
È interessante notare, [26] did observe that diffusivity values along the axon varied by about
15% due to reorientation w.r.t. . In silico works provided theoretical background
on the effect of mesoscopic susceptibility on ADC and DT-derived measures under
variable diffusion times [29] and sample orientation [15], rispettivamente. Inoltre,
the recent observation of differences in compartmental -anisotropy suggests
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
4
another mechanism of -orientation dependence in DT-measures. The intrinsic
-weighting of
the diffusion-weighted spin-echo sequence affects
IL
-weighting of intra- and extra-axonal signal fractions. Di conseguenza, differences in
compartmental
-orientation
dependence w.r.t.
can
Guida
A
orientation-dependent variation
in compartmental
signal
fractions and,
consequently, affect DT-measures.
This motivates further investigation of the potential orientational dependence
of DT measure w.r.t. . The additional dMRI dependence on tissue-orientation
w.r.t. may introduce variability in the results when not taken into account,
potentially reducing statistical power to detect true effects, and could even provide
important additional information on tissue microstructure (e.g. myelin). The aim of
this work is to determine the variation of DT-MRI-derived measures as a function of
fibre orientation w.r.t. . A tal fine, we investigate the effect of head-orientation
dependence of compartmental [21] E
the consequent variation of
compartmental signal fractions on DT-MRI measures in silico, and characterise the
-orientation dependence in in vivo human brain data at 3 T using a tiltable RF coil.
2. Methods
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
5
2.1. Simulations
The following simple simulations investigate the effect of -orientation
dependence of compartmental [21] on estimated DT-MRI measures, thereby not
considering cross terms between the diffusion and background gradient. IL
simulations are based on a ‘standard model’ of diffusion for white matter in the
long-time limit, which models the intra-axonal space as a ‘stick’ with zero
perpendicular apparent diffusivity and the extra-axonal space as axially symmetric
tensor [31–34]. Different levels of complexity are investigated: Primo, in the case of
no fibre dispersion and no noise, one can derive analytical equations for the ADC as
a function of compartmental diffusivities, signal fractions, and compartmental
(which can be -orientation dependent). Secondo, still in the case of no dispersion,
the signal can be generated from analytical equations, noise added, and the DT
fitted. Finalmente, this can be repeated for signals generated in the case of fibre
dispersion.
For all simulations, scenarios for a range of (cioè., orientation w.r.t. )
were generated corresponding to the distribution of observed in the in vivo data of
all subjects and head orientations (see section 2.2).
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
6
Analytical case: no dispersion and no noise. Consider a simplified
two-compartment model of the diffusion- and relaxation-weighted signal in WM
(no fibre dispersion) as a function of the echo time, , and -value:
(1)
where subscripts i/e denote intra-/extra-axonal compartments, rispettivamente,
are the relaxation rates, are positive semi-definite diffusion tensors,
and is intra-axonal signal fraction. Suppose and have equal principal
eigenvectors (denoted by ) and parallel and perpendicular eigenvalues
(Dove ) and respectively, then the signal can be simplified as
(2)
Dove .
Considering DTI as a signal representation at sufficiently low -values, i.e.
capturing the first order -term in the Cumulant expansion [35], one can derive
7
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
expressions for the ADC, e.g. by expanding in powers of the analytic expression
for (Eq. 2). For non-interacting compartments, the diffusion coefficient is a
weighted sum of the diffusivities in the individual compartments where the signal
fractions are -weighted. Specifically, the ADC is the first order term of the
Maclaurin series expansion of in :
(3)
Eq. 3 was used to compute apparent axial diffusivity (AD, ), radial diffusivity
(RD, ), MD, and FA. Recent work suggests that the effect of WM fibre
orientation to the magnetic field can most prominently be observed in the
extra-axonal apparent transversal relaxation rate [21]. IL
dependence could be described as
(4)
This orientational dependence of will result in orientational dependence of
the ADC in addition to a straightforward TE dependence.
Analytical noiseless scenarios were simulated using Eq. 3 E 4. TEs were
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
8
selected to match the in vivo acquisition (cf., section 2.2.1). The axonal fraction was
varied and diffusivities and relaxation rates were
set to the following values: , E
, , rispettivamente.
Noise simulations without dispersion. Eq. 2 was used to simulate signals
with and matching the in vivo data section 2.2. Signals were simulated
using the same fractions, intra- and extra-axonal diffusivities and relaxation rates as
for the analytical simulations. Rician noise was added to the signal with an SNR of
100 on the , signal, similar to the in vivo acquisitions [21]. DT were
estimated for each on data using iterative weighted linear
least squares, and AD, RD, MD, and FA were computed.
Noise simulations with dispersion. Finalmente, the effect of fibre orientation
dispersion was studied by forward simulating a distribution of orientation-dispersed
compartments according to a Watson distribution, where each sub-compartment (i.e.
each distinctly oriented extra-axonal compartment) can separately exhibit
-orientation dependence [21, Appendix A]. Tissue properties, noise, E
estimation were as described in the simulations without dispersion.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
9
Data analysis. To quantify the magnitude of orientation dependence, , IL
simulated values of each DTI-derived measure at each TE were directly represented
by a function of :
(5)
We note that this representation does not exactly describe the orientation
dependence even in the simplest analytical case (Eq. 3), but nevertheless provides a
close approximation (see an example of a -fitting in supporting Figure S1) E
allows for the quantification of anisotropy through the estimation of . IL
performance of the anisotropic representation relative to the isotropic case,
, was estimated using the rescaled Akaike’s Information Criterion (AIC)
[36, 37]: . Here, is the minimal AIC value in the set.
Per [37], values allow comparison of the relative merits of representations in
the set as follows: representations having are considered to have similar
substantial support as the representation with , those with
have considerably less evidence, and those with have no support.
Additionally, the isotropic model is selected over the anisotropic, if the
confidence interval of the magnitude of anisotropy included zero [38].
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
10
2.2. In vivo data
In this work we used a subset of the multi-dimensional diffusion- dati
presented in previous work [21], relevant data acquisition and pre-processing steps
are re-iterated below. The study was approved by the Cardiff University School of
Psychology Ethics Committee and written informed consent was obtained from all
participants in the study.
2.2.1. Data acquisition.
Multi-dimensional diffusion- -weighted data were acquired from five
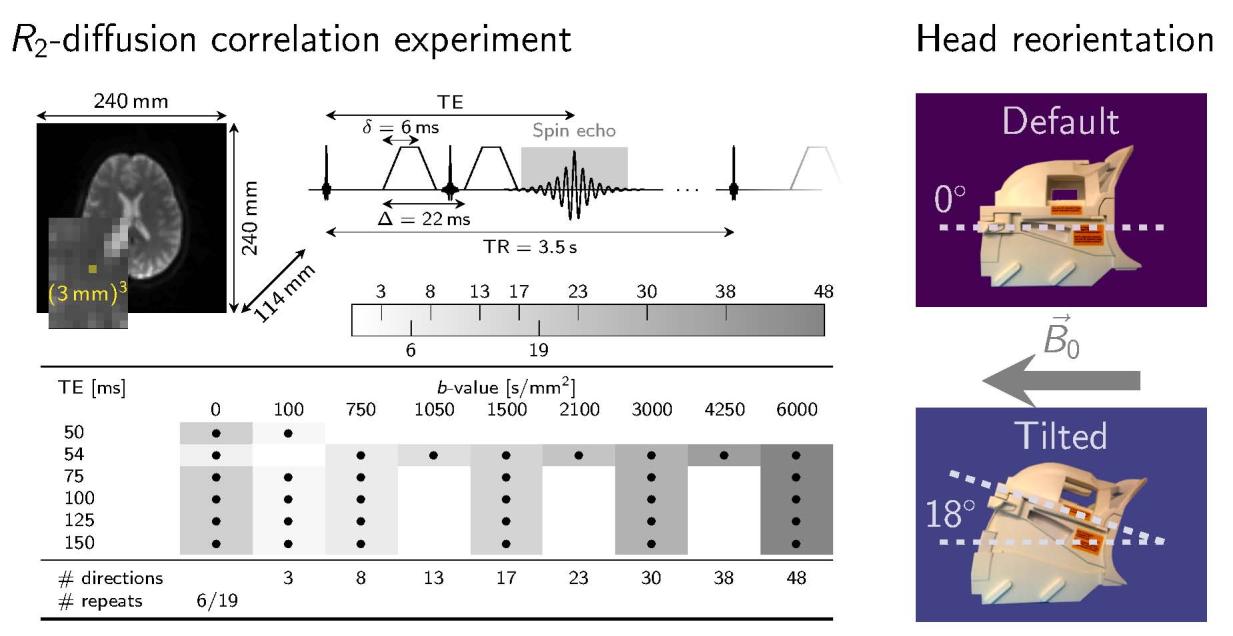
healthy participants (3 female, 25-31 y.o.) on a 3 T MRI scanner equipped with a
300 mT/m gradient system and a 20ch head/neck receive coil that can tilt about the
L-R axis (Siemens Healthineers, Erlangen, Germany). The acquisition was repeated
in default ( ) and tilted ( ) coil-orientation to introduce variable anatomical
orientation w.r.t. . Acquisition parameters are summarised in Figure 1A.
2.2.2. Data processing.
The data were checked for slice-wise outliers [39] and signal drift, corrected
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
11
for Gibbs ringing [40], subject motion, geometrical distortions [41–43] and noise
bias [44–47].
From the pre-processed data a subset with diffusion weightings matching
across echo times was selected (Figure 1B), and for each echo time diffusion tensors,
fibre orientation w.r.t. and single fibre population masks were obtained as
described below. DT were estimated for each on the nominal
dati, using iterative weighted linear least squares. Gradient
non-linearities were considered and -values/-vectors were corrected
correspondingly prior to fitting [48]. Fibre orientations w.r.t. were computed
from the first eigenvector of the estimated DT. Note that has to be in image
coordinates of each subject/head orientation.
Fibre orientation distribution functions (fODF) [49, 50] were estimated per
using multi-shell multi-tissue constrained spherical deconvolution [51] from the
data acquired at . From the fODFs single-fibre population (SFP) voxels
with low dispersion ( ) were identified [52]. Dispersion was quantified by
, where are spherical harmonics coefficients [21, 53,
54].
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
12
We used WM tract segments extracted in previous work [21]. Briefly, 18
major WM tracts and, where applicable, their bilateral counterparts were extracted
and segmented using TractSeg [55].
2.2.3. Data analysis.
-dependence of DT measures: pooling all SFP voxels. General trends in
orientational anisotropy of DTI measures were investigated by subdividing the
range of angles into bins, averaging the estimates within each bin, and smoothing.
Specifically, the data were binned in -subsets and the corresponding DT-measure
estimates and -values were averaged across each bin, denoted as and
. Then, a smoothing spline as a function of and weighted by the number
of data points in each bin was fitted to . An example of this
procedure is shown in supporting Figure S2 for the lowest TE.
The magnitude of anisotropy was defined as the difference between the
minimal and the maximal values of the fitted curves. Their signs were set negative if
the minimal values were below those at . The contribution of orientational
anisotropy to overall variance was calculated as: . Here,
and are the standard deviations across all SFP voxels with and
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
13
without orientational anisotropy being considered, rispettivamente. Additionally, mean
values across all SFP voxels were obtained for each measure and TE.
In addition to the spline-analysis, to assess whether DT measures as a function
of showed significant orientation-dependence, we assessed whether an
anisotropic representation described the data better than isotropic (cf., Supporting
Information), using the approach similar to the in silico analysis described in section
2.1.
-dependence of DT measures: tractometry analysis to achieve spatial
correspondence. By comparing the measures estimated within the same anatomical
region at default or tilted coil orientation, we aimed to reduce the effects of the
potential microstructural variability across the WM in the approach described above.
The anatomical correspondence between the coil-orientations was established using
the segments derived from the tractometry approach. The outer-most 20% of tract
segments and the segments with 3 or fewer voxels were excluded to minimise the
effects of fanning and noise, rispettivamente. To obtain the effect of the re-orientation
we evaluated as a function of
. Here, denotes the average of corresponding values from SFP voxels
over each segment, and the subscripts and correspond to default and tilted
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
14
head-orientations, rispettivamente.
3. Results
3.1. Simulations
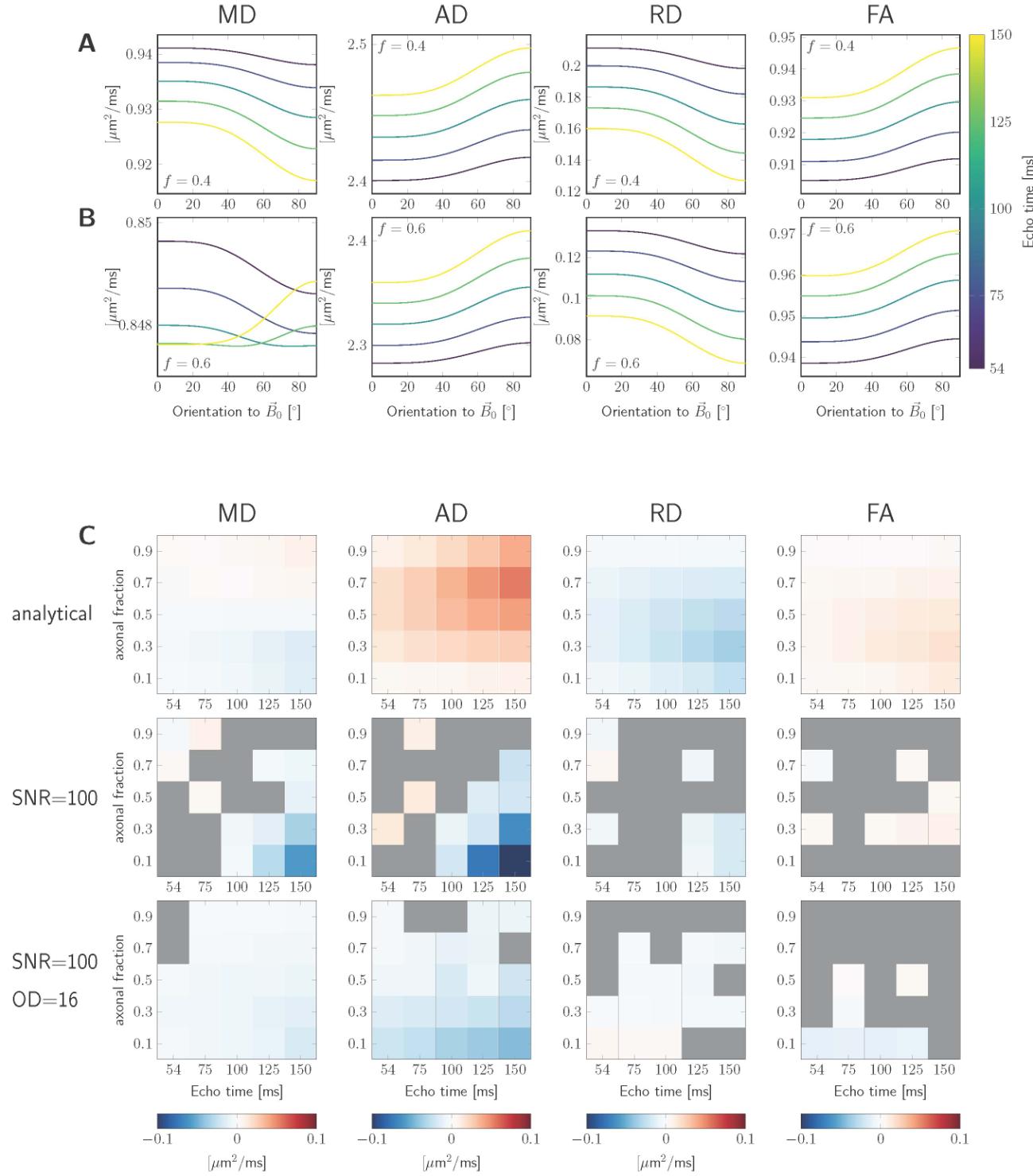
Figure 2AB shows examples of MD, AD, RD, and FA as a function of fibre
orientation to for the noiseless analytical simulations without fibre
dispersion. For the parameter settings investigated, AD and FA increase with (IL
magnitude of anisotropy, ), while RD decreases ( ). The absolute value
of the magnitude of anisotropy, , generally increases with . The resulting
behaviour of MD is non-trivial and sensitive to simulation parameters (per esempio., axonal
signal fraction ), with possible sign flips of for increasing .
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
15
UN. Multi-dimensional -diffusion data were acquired under simultaneous
modulation of echo times and diffusion-gradient amplitudes in a pulsed-gradient
spin-echo sequence with EPI readout. Time between diffusion gradients,
ms, and diffusion gradient duration, ms, were kept fixed for all echo
times. The gradient orientations were defined in scanner coordinates and thus were
not rotated with the head re-orientation. Additional modulation of fibre orientation
was achieved by head re-orientations relative to .
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
16
B. A subset of the pre-processed multi-dimensional diffusion- -weighted dataset
from previous work[21] was used to calculate echo-time-dependent diffusion
tensors and fibre orientation to (denoted by ) (blue, bottom left), E
single-fibre-population (SFP) voxels (green, top left).
Figura 1: Methods
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
17
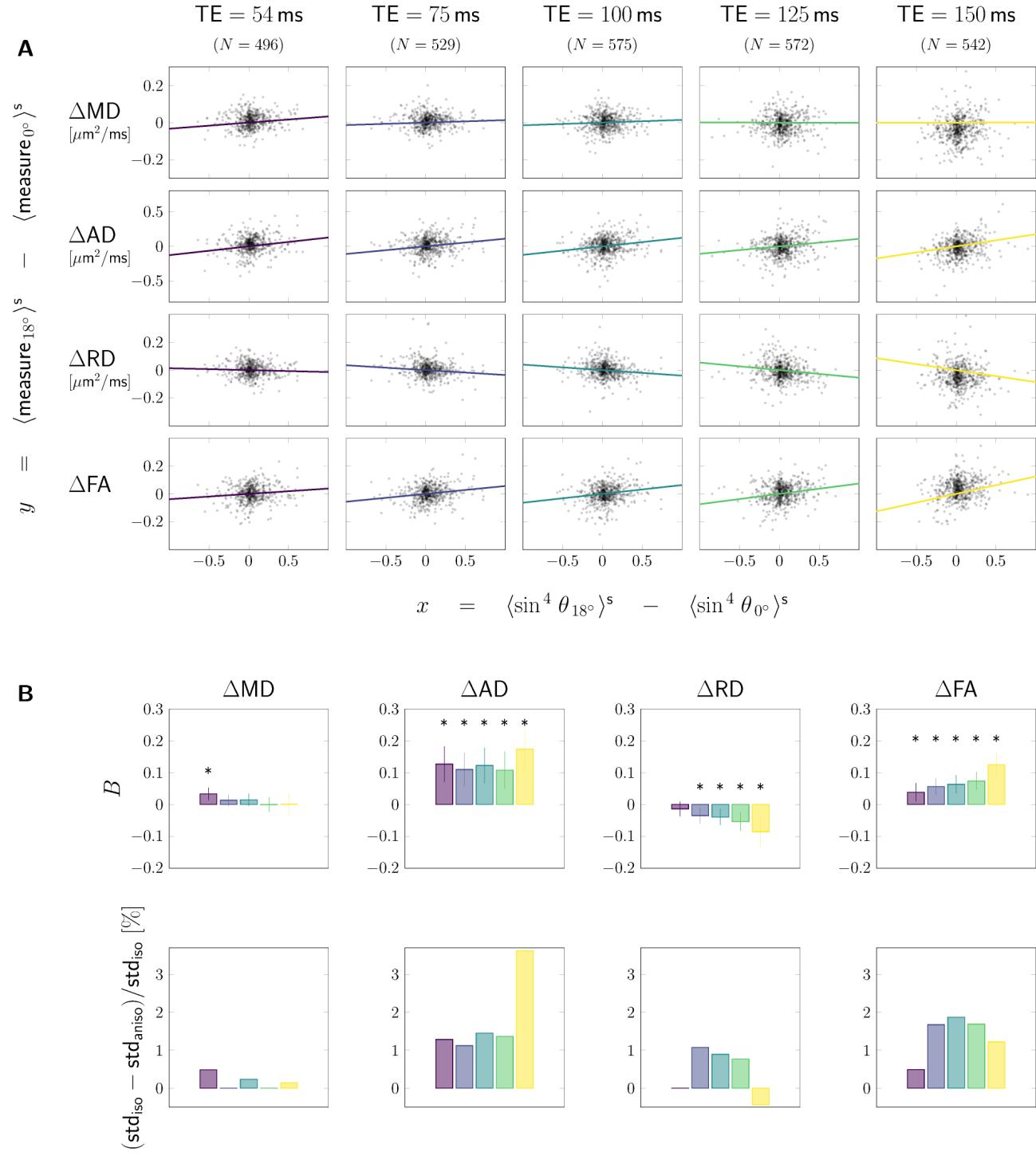
Figura 2: Simulation results. The signals were estimated for variable echo times
and axonal fractions, , and fixed diffusivities
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
18
, and relaxation rates , . Figures in A. and B.
were estimated analytically (Equations 3 E 4) and show MD, AD, RD, and FA as
functions of fibre orientation w.r.t. for , E , rispettivamente. In
C. the magnitude of anisotropy, , (colors) is shown as a bi-modal function of the
echo time (horizontal axis) and the axonal fraction (vertical axis,
). Columns left-to-right are different DTI measures: MD, AD,
RD, FA; rows top-to-bottom are different simulation conditions: using the analytical
expression, assuming noisy signal with , and adding fibre dispersion
( ) in addition to noise, rispettivamente.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
19
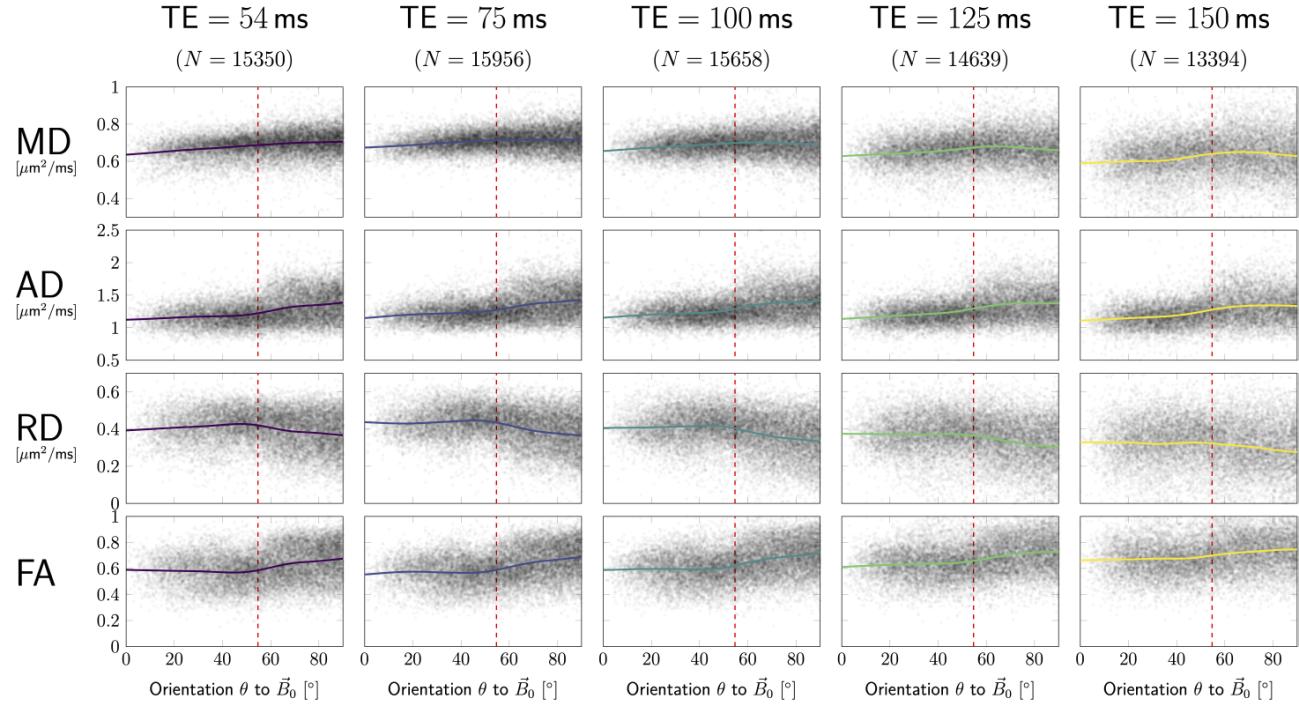
UN. Each DTI measure (rows) from SFP voxels was plotted against the fibre
orientation, , to the magnetic field. Each column/colour corresponds to a different
TE. Solid lines represent best fitting smoothing spline curves. Dashed red lines
indicate the magic angle of .
B. The estimated mean value, , and the magnitude of anisotropy, , over all SFP
voxels are shown in the first and the second column, rispettivamente. Third column
shows the amount of decrease in variation of values when orientation w.r.t. È
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
20
taken into account. Colours represent the corresponding echo times, for which
anisotropy of the measures was investigated.
Figura 3: Pooled SFP data results.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
21
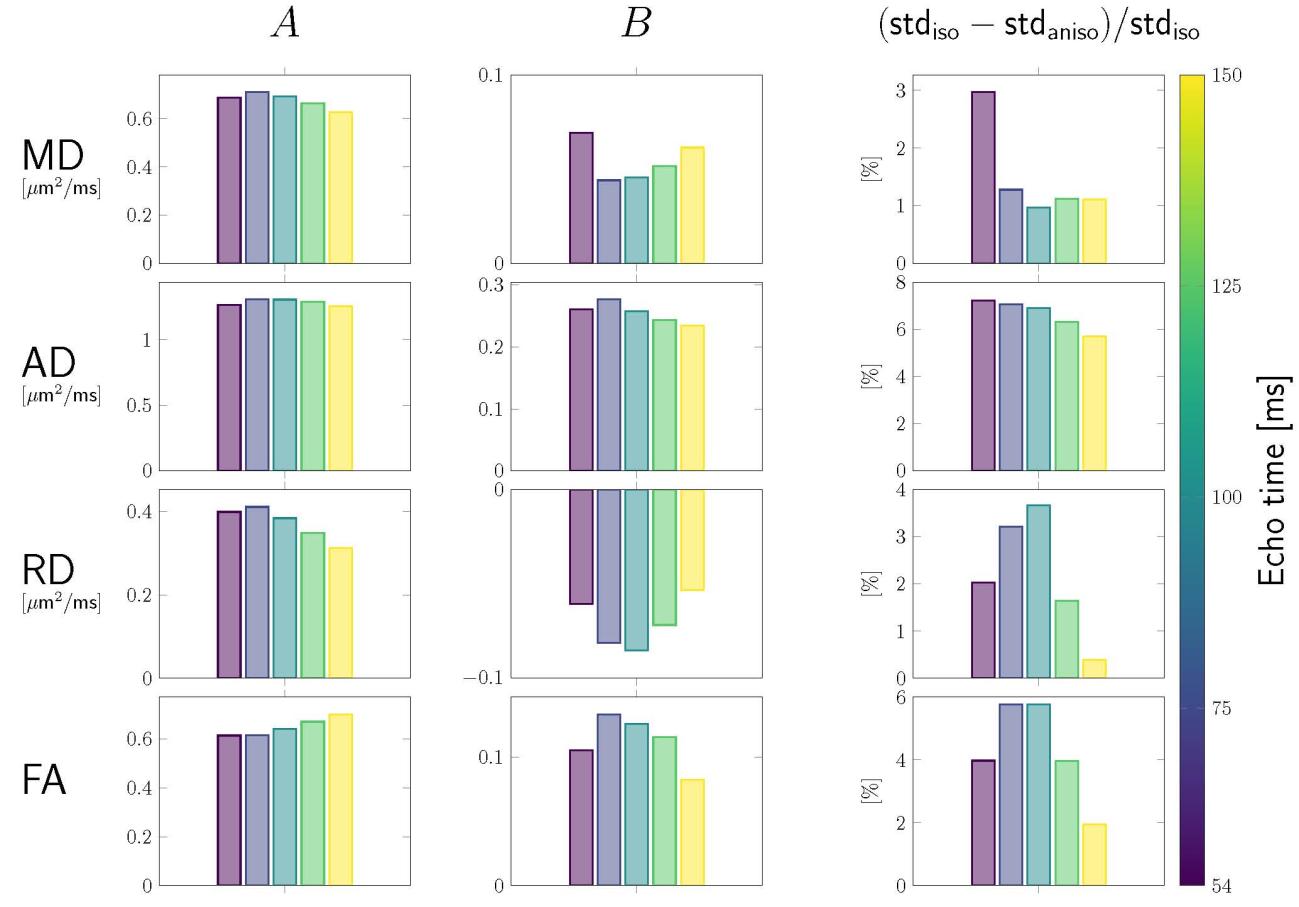
Figura 4: Tractometry results. Tractometry was used to achieve anatomical
correspondence between tilted and default head orientation, by comparing values of
DTI-measures in default vs tilted head orientations tract- and segment-wise. UN. In
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
22
scatterplots, changes in value of the respective DTI measure with re-orientation
(rows) are plotted as a function of the corresponding change in . B. Barplots
show: the magnitude of anisotropy estimated for each DTI measure and each echo
time (top row); and the change in standard deviation (std) when fibre anisotropy is
taken into account (bottom row). Data in which anisotropic representation (
) described the data better ( ) than isotropic assumption
( ) were indicated by a *-symbol.
Figure 2C shows results for the analytical simulations following Eq. 3 E 4
(prima riga), and the noisy simulations without (fila centrale) and with (third row) fibre
dispersion. The plots show the estimated anisotropy (colormap) for the scenario
i m ms, e m ms, and e m ms, echo times matching
the acquisition parameters (horizontal axis) and a range of (vertical axis). IL
columns show results for different DT measures. A grey colour indicates scenarios
for which an isotropic representation was favoured (section 2.2.3). It becomes
immediately apparent that the effect on DT measures can be vastly different
depending on the scenario: in the simple analytical simulations for MD can either
be positive (high ) or negative (low ) depending on the intra-axonal signal
fraction and its absolute value becomes larger for increasing . For the simulation
with noise and no dispersion can be positive or negative, and in the case of
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
23
dispersion is lower and negative in the cases investigated. For AD, È
predominantly positive in non-dispersion analytical scenario and has the largest
value for high , but in the noisy simulations could be negative. The behaviour
of is more consistent across simulation scenarios. Whereas is mostly
positive and largest for high and low in the no-dispersion noiseless and noisy
cases, can be positive or negative in the noisy scenarios but is overall low or
non-significant.
3.2. In vivo data
Pooled data. In Figure 3A DT measures are plotted as functions of fibre
orientation w.r.t. (horizontal axes), and echo time (columns), along with
the corresponding smoothing spline curves highlighting anisotropic effects. IL
data were pooled from all subjects and both head orientations, each data point
represents one SFP voxel. RD and FA show global maxima and minima,
rispettivamente, closed to the magic angle (dashed red lines), most prominently for low
TE.
The barplots in Figure 3B show the average value ( , first column) or the
magnitude of anisotropy ( , second column) obtained from all SFP voxels for a
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
24
given measure (rows). MD, AD and FA increase as a function of ( ), while
RD decreases ( ). The anisotropic component is least dependent on the echo
time for axial diffusivity. For other measures is non-monotonic (for
evaluated TE-s) with its absolute value being minimal (for MD) or maximal (RD,
FA) at around 75-100 ms. The fibre-orientation-independent component (first
column, Figure 3B) evolves non-monotonically as a function of TE. The relative
range of change of DT-measures across angles (computed as , results not
shown) can reach values up to 20%. Finalmente, column three of Figure 3B shows the
fraction by which anisotropy effects contribute to overall variance, showing the
largest contribution for AD (around at ms). For MD, RD, and FA the
variance contribution was , , E , rispettivamente, at the same shortest echo
time
We also observed an overall similar behaviour in magnitude of anisotropy
when the pooled data were evaluated using sin -representation instead of the
spline-fit (cf., supporting Figure S3).
Segment-wise comparison. The scatterplots
in Figure 4A show
segment-wise differences between the values in tilted and default head orientation of
each measure (rows) against the sin of fibre orientations w.r.t. . Each column
25
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
and the corresponding colour of the linear fit represent different echo
times. The fitting results are summarised in the top row of Figure 4B, and the
fraction of variance contributed by the anisotropy effects is in the barplots of the
bottom row.
Compared to the pooled analysis, the sign of anisotropy was the same
(positive for MD, AD, and FA and negative for RD), but the trend as a function of
TE was different for the segment-wise analysis (e.g. the magnitude of anisotropy
in RD increased with echo time whereas the pooled analysis showed a decrease
for the largest echo times).
4. Discussion
We used diffusion- -correlation data acquired in two head-orientations using
a tiltable coil [21] to achieve a larger range of orientations and investigate the effect
of head-orientation on diffusion tensor measures: mean, axial and radial
diffusivities, and fractional anisotropy. We observed that fibre orientation w.r.t.
may be responsible for up to three, seven, and two percent of variance in MD, AD,
and RD, rispettivamente, at ms and about four percent of variance in FA at
the same TE. We also utilised tractometry to achieve anatomical correspondence
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
26
and used the sin -representation to estimate the effect of head-reorientation.
4.1. TE-dependence of DTI-measures.
Echo-time-dependence of diffusion coefficients and DT-derived measures
has long been recognised. [56] have reported an increase/decrease of ADC with
longer when diffusion weighting was applied parallel/perpendicular to the rat’s
trigeminal nerve. These are in correspondence with analytical observations
visualised in e.g. Figure 2A: axial diffusivity, AD, increases, while radial diffusivity,
RD, decreases with longer echo times. Assaf and Cohen [57] performed diffusion
experiments with variable echo time to demonstrate the presence of two distinct
diffusing compartments, they also found that the signal of the slow diffusing
component has a lower relaxation rate. Questo, Ancora, would correspond to the
decrease in radial diffusivity with longer TE. Finalmente, Qin et al. [58] have explored
DTI measures as functions of echo time in rhesus monkey internal capsule. They
similarly reported a decrease in the radial and increase in axial diffusivities with
longer TEs, but also an increase in fractional anisotropy and no significant changes
to the mean diffusivity. Lin et al. [59] made similar observations for the human
corpus callosum and internal capsule, in addition they observed no TE-dependence
of AD in the corpus callosum.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
27
In our data, which were pooled from WM SFP voxels, we did not observe any
linear trends (cf. isotropic representation, , Figure 3B), the non-monotonic
variations of the DTI-measures could be due to the variability of each measure as a
function of TE between SFP voxels. Additionally, the much noisier data at longer
TEs could also have contributed to these differences. Yet, for echo times ms
we observed a decrease in RD and an increase in FA, which agree with observations
made by Qin et al. [58] and Lin et al. [59], and similar to the latter we saw no
significant changes in AD.
From the same data compartmental transverse relaxation rates were
previously estimated [21], and faster extra-axonal signal decay was observed, Quale
is in correspondence with previous findings [56, 57, 60, 61].
4.2. Head-orientation dependence of DT measures
Orientational anisotropy of DT measures observed in vivo and in silico.
We estimated non-zero magnitude of orientation anisotropy in all DTI measures
with both methods: pooled SFP voxels, and tract-segment-wise comparison between
default and tilted head orientations. Under the assumption of sin -behaviour, IL
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
28
correspondence in estimated magnitude of anisotropy between the two methods was
higher at shorter echo times of ms and ms, the accuracy at longer echo times
was potentially compromised by decreased SNR. Allo stesso modo, the contribution of
anisotropy effects to the variance of DTI measures decreased with increasing echo
time. Comparing the spline with the sin -representation in the pooled results, IL
absolute values of obtained using spline fitting were subtly higher than those
estimated using the sin -approximation, but overall followed the same trend as a
function of TE.
The in vivo RD and MD estimates as a function of followed trends also
seen in the analytical simulations, i.e. positive for AD and FA and negative for
RD. Tuttavia, also opposite signs for were observed in the noisy simulations,
e.g. in AD. This could not merely be caused by e i (the opposite was
simulated), but it is hypothesised that this could be attributed to the complexity of
tissue (e.g. dispersion, a distribution of diffusivities and within and across voxels
in the in vivo results, and other origins of orientation dependence) and different
levels of noise, amongst others. One can also observe that the estimated of AD
decreased as function of in vivo in contrast to the increase in the toy-example.
Origin of anisotropic effects of DTI in WM. The simulations considered the
29
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
effect of -weighting and different -anisotropy behaviour in the intra- E
extra-axonal space on DT measures, assuming a dominant role for myelin
susceptibility effects in the extra-axonal space. Tuttavia, the origin of the
orientation dependence may be more complex. In in vivo data both the sin
behaviour and a more general spline representation were used to investigate the
-dependence,
indeed resulting
in a similar estimated contribution of
orientation-dependence to the variance of DT measures in the pooled analysis and
similar magnitudes of anisotropy. This similarity partially supported the assumption
made in simulations, cioè., that the difference in -dependence between the
intra- and extra-axonal signals (i.e. sin -dependence in the extra-axonal space) is a
major contributor to the orientational anisotropy. Yet the behaviour of the spline
curves deviates from the typical sin -shape which indeed suggests that the nature
of anisotropy must be more complex.
The hypothesis that self-induced gradients arising from local variations in
magnetic susceptibility could be an additional source of variation in apparent
diffusion coefficients has been proposed by several works [26, 30]. Trudeau et al.
[30] measured diffusivity values at 4.7T in excised porcine spinal cords at room
temperature, with diffusion gradients applied parallel and perpendicular to the
primary fibre orientation. By reorienting the sample relative to the main magnetic
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
30
field direction, they were able to manipulate the distribution of local magnetic
susceptibility. Beaulieu and Allen [26] performed similar experiments at 2.35T on
excised nerve fibres from garfish and frog. Both studies reported no detectable
impact of local gradients on diffusivity values in these samples, and neither
attributed the observed [26] orientation dependence w.r.t. to the effects of local
gradients. Upon closer inspection of [30, FIG. 3], a trend may be apparent with
regards to fibre orientation w.r.t. . Although the distributions of – or -values
overlap when measured at either sample orientation, the average values for seem
lower and the average values for seem higher when the primary fibre orientation
is along . Beaulieu and Allen [26] solidified the apparent trend for the
dependence of -values on primary fibre orientation w.r.t. , by reporting
lower values measured when fibres were along the magnetic field. Allo stesso modo, in our
in vivo data axial diffusivities were higher for fibres across compared to fibres
along , while radial diffusivities followed the opposite trend. Knight et al. [15]
have previously simulated the effects of mesoscopic magnetic field inhomogeneities
near a hollow cylinder on and also reported head-orientation dependence of MD
and FA values. They considered cross-terms between local gradients and encoding
gradients to be negligible. Wang et al.[62] have rotated an extracted mouse brain
w.r.t. the main magnetic field and evaluated MD and FA for seven major brain
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
31
regions, one of which was white matter. They did not observe any significant
variations across orientations of MD/FA in WM, however they did not break down
WM into sub-ROIs of similar fibre orientation, potentially averaging away effects
due to re-orientation. Bartels et al. [63] have recently studied MD, AD and RD as
function of fibre orientation w.r.t. . They reported MD to behave in
correspondence with simulations by Knight et al. [15], but AD/RD obtained from
their data are respectively minimal/maximal around the magic angle, suggesting a
different origin of anisotropy. È interessante notare, our data showed similar trends (cf.,
spline curves or piecewise average in SI). RD also showed a local maximum near the
magic angle. The AD-curves appeared monotonous but still an increase in gradient
around the same angle was evident. Additionally, a local minimum was apparent in
the FA-curves. Pang [64, 65] also suggests an important role for magic angle effects.
Studies which investigate the -related anisotropic effects in DTI are limited
in number. Yet, the anisotropic effects in DTI measures from WM observed here are
coherent with those seen in previous works investigating
-anisotropy, Anche se
comparatively less pronounced. The majority of studies cover anisotropic effects of
the WM signal evolution from the multi-echo gradient-recalled-echo (mGRE)
sequence [1–12]: thanks to its sensitivity to -inhomogeneities it provides strong
contrast in regions composed of tissues with different magnetic susceptibilities
32
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
(myelinated WM fibres, in this particular case). Although most dMRI sequences are
spin-echo-based,
in which
the -effects are refocused, some magnetic
susceptibility effects may shine through. On one hand, incoherent molecular motion
happening between the excitation pulse and the spin-echo combined with local
-inhomogeneities induced by the myelin sheath may lead to residual
non-fully-refocused phases, on the other hand, echo-planar readout has some
unavoidable
-weighting during the acquisition window. That said, the centre of
the -space is closer to the centre spin-echo, and is therefore less affected;
additionally, lower-resolution data are expected to suffer less from this effect.
Infatti, Gil et al. [14] reported sin -dependence of macroscopic -values on
fibre orientation to .
Another candidate for
the orientational dependence of is
IL
aforementioned magic angle effect (or dipole-dipole interactions) with the
characteristic cos -behaviour. So far those were not considered the
primary source of WM -anisotropy in adults in vivo and postmortem brain, Ma
also not excluded as a potential contributor [6, 11, 66]. È interessante notare, Bartels et al.
[20] studied orientation dependence in the newborn brain having low
myelination and observed very different behaviour from the adult brain, suggesting
a primary role for residual dipolar coupling. In the absence of myelin,
33
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
neurofilaments and microtubules of the axonal cytoskeleton are aligned with the
axon were hypothesised
to contribute
to orientation-dependence. Similar
observations were made on our data separating the intra- and extra-axonal relaxation
rates [21]: cos fitted the intra-axonal data best.
Summarising, compartmental
-values have been reported to depend on
orientation differentially [7, 9, 21, 67], which could intrinsically lead to
DT-dependence on fibre orientation w.r.t. , regardless of the underlying
microscopic mechanisms.
4.3. Limitations and future work
Anatomical correspondence. The pooled analysis considers all single fibre
population voxels throughout the WM together to estimate a single magnitude of
orientation dependence, however the simulations reveal that micro-anatomical
differences (per esempio., signal fractions, myelin sheath thickness, fibre density and other
potential contributors to compartmental -differences) can lead to different
orientation dependence. The tractometry analysis aims to address this to a certain
extent by pooling voxels more locally, but with two head orientations as used in this
study it remains challenging to estimate local differences in orientation dependence.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
34
More head orientations and a boost in SNR could help to further investigate this.
Here, more efficient acquisition-schemes, such as ZEBRA [68], would be beneficial
to enable reasonable acquisition times. Inoltre, anatomical correspondence could
be further achieved by co-registering the data from the two head orientations in
future work. To accomplish this, it is essential to employ a reliable registration
method that can effectively handle the residual nonlinear effects. Inoltre, by
pooling the data from all subjects’ S P WM voxels we were able to compensate for
low number of subjects. With more subjects one could investigate the anisotropy
w.r.t. of individual tracts and consequently provide additional anatomical
informazione.
Gradient nonlinearities. Another
limitation potentially arises from
nonlinearities of gradient fields. With the rotation of the tiltable coil the head is
positioned further from the iso-centre, where gradient nonlinearities have a larger
effect. This in turn influences the effective -matrix, and could introduce additional
variability between the non-tilted and tilted orientation. In addition to effects
reported as a result of the effective -matrix not being taken into account [69–71], if
gradient nonlinearities cause the effective -value to be higher than the imposed
value, kurtosis effects may start to play a more prominent role and bias DT
estimates. In the current work we take into account the effective -matrices, and to
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
35
further minimise this potential confound we analysed a subset of the data at
ms for which a lower -value of s mm was available (Figure 1A).
Supplementary Figure S4
shows a comparison of
the pooled- E
tractometry-analyses with maximum -value of s mm and s mm .
The observation of orientation dependence remained unchanged, with larger
estimated absolute magnitude of anisotropy at the lower -value for AD, RD, E
FA in both analyses and also MD in the tractometry analysis.
We also considered the effect of gradient non-linearities in the estimation of
the fibre direction. In this work, the first eigenvector of the DT was used, but this can
be done in alternative ways and with different estimation techniques, e.g. spherical
deconvolution to obtain the fODF. The reason this work opted for the current
approach is that spherical deconvolution approaches typically do not take into
account gradient nonlinearities [70]. The DT estimation used in this manuscript does
take this into account and the estimates of the maps and fibre direction come from
the same DT estimate.
Crossing fibres. This scope of this work is limited to single fibre population
voxels. Previous work has characterised per fibre population in crossing fibre
voxels, Per esempio [72]. In the current work, based on [21], we have simulated a
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
36
distribution of orientation-dispersed compartments according to a Watson
distribution, where each sub-compartment (e.g. each extra-axonal zeppelin) can
separately exhibit -orientation dependence. This could be straightforwardly
adapted to model crossing fibres, but the bundles will have to have the same
relaxation properties. A recently presented abstract described estimation of such a
model for multi-echo gradient-echo sequences [73].
SNR. Finalmente,
the SNR distribution
in WM can change with
head-reorientation. While the tiltable coil minimises differences in the coil-to-brain
distance across different head orientations, SNR may still be affected due to e.g.
change in the reception efficiency of the tiltable coil as the axis of the coil is rotated
away from , gradient non-uniformities, or shim. Previous work [21] showed
that the temporal SNR (tSNR) distribution in WM globally overlapped between
tilted and default orientation, and Supplementary Figure S5 further investigates this
per tract-segment from the tractometry pipeline. Overall the estimated tSNR of the
same location in tilted vs default orientation is distributed along the line , but a
global fit through tSNR measurements from all locations implies that tSNR values in
the tilted position could be up to lower than in the default orientation.
Preliminary experiments in a phantom with the body coils for signal reception
suggest that the impact of shim and gradient non-uniformities may be greater
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
37
than the impact of receive coil efficiency (results not shown). While we have
attempted to correct for noise bias – which can significantly impact DTI estimates
[74] – denoising strategies could further reduce the impact of noise-differences
especially at longer TE.
5. Conclusione
DT measures may vary up to as a function of WM fibre orientation
w.r.t. in the scenarios investigated. Fibre orientation can be responsible for up to
variance in diffusion tensor measures across single fibre populations of the
whole brain white matter. While potentially containing useful information on e.g.
myelination, the orientation dependence of DTI w.r.t. can be an additional
source of variance camouflaging the effect-of-interest in clinical research studies,
particularly when the effect size is small and it is difficult to control for fibre
orientation w.r.t. (e.g. fetal or neonatal imaging, or when the trajectories of
fibres change due to e.g. space occupying lesions).
Acknowledgements
For the purpose of open access, the author has applied a CC BY public
38
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
copyright licence to any Author Accepted Manuscript version arising from this
submission. CMWT is supported by the Wellcome Trust [215944/Z/19/Z] and a
Veni grant (17331) from the Dutch Research Council (NWO). DKJ, CMWT, E
EK were all supported by a Wellcome Trust Investigator Award (096646/Z/11/Z)
and DKJ and EK were supported by a Wellcome Strategic Award (104943/Z/14/Z).
The data were acquired at the UK National Facility for In Vivo MR Imaging
of Human Tissue Microstructure funded by the EPSRC (grant EP/M029778/1), E
The Wolfson Foundation.
We would like to thank Siemens Healthineers, and particularly Fabrizio
Fasano, Peter Gall, and Matschl Volker, for the provision of the tiltable RF-coil used
in this work. We would also like to thank John Evans, Greg Parker and Umesh
Rudrapatna for technical support, Maxime Chamberland for the tractometry analysis
in the original publication on compartmental -anisotropy, and Stefano Zappalà for
helpful discussions.
Data Availability Statement
Data available on request due to privacy/ethical restrictions.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
39
Author Contributions
EK: Conceptualization; Formal analysis; Investigation; Methodology;
Software; Validation; Visualization; Writing – original draft; Writing – review &
editing.
DK: Funding acquisition; Resources; Writing – review & editing.
CMWT: Conceptualization; Formal analysis; Investigation; Methodology;
Project administration; Software; Supervision; Validation; Writing – original draft;
Writing – review & editing
Declaration of Competing Interests
No conflict of interest to disclose.
Riferimenti
[1] B. Bender and U. Klose. The in vivo influence of white matter fiber
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
40
orientation towards on
in the human brain. NMR in Biomedicine,
23(9):1071–1076, nov 2010. ISSN 09523480. doi: 10.1002/nbm.1534.
[2] Andrea Cherubini, Patrice Péran, Gisela Elisabeth Hagberg, Ambra Erika
Varsi, Giacomo Luccichenti, Carlo Caltagirone, Umberto Sabatini, and Gianfranco
Spalletta. Characterization of white matter fiber bundles with
relaxometry and
diffusion tensor imaging. Magnetic Resonance in Medicine, 61(5):1066–1072,
2009. doi: 10.1002/mrm.21978. URL
https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.219
78.
[3] Christian Denk, Enedino Hernandez Torres, Alex MacKay, and Alexander
Rauscher. The influence of white matter fibre orientation on MR signal phase and
decay. NMR in Biomedicine, 24(3):246–252, 2011. doi: 10.1002/nbm.1581.
[4] C Wiggins, V Gudmundsdottir, D Le Bihan, V Lebon, and M Chaumeil.
Orientation Dependence of White Matter
Contrast at T : A Direct
Demonstration. In Proceedings 16th Scientific Meeting, International Society for
Magnetic Resonance in Medicine, Toronto, 2008.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
41
[5] Jongho Lee, Karin Shmueli, Masaki Fukunaga, Peter van Gelderen,
Hellmut Merkle, Afonso C Silva, and Jeff H Duyn. Sensitivity of MRI resonance
frequency to the orientation of brain tissue microstructure. Atti del
National Academy of Sciences, 107(11):5130–5135, mar 2010. ISSN 0027-8424.
doi: 10.1073/pnas.0910222107.
[6] Jongho Lee, Peter van Gelderen, Li-Wei Kuo, Hellmut Merkle, Afonso C.
Silva, and Jeff H. Duyn.
-based fiber orientation mapping. NeuroImage,
57(1):225 – 234, 2011. ISSN 1053-8119. doi: 10.1016/j.neuroimage.2011.04.026.
[7] Samuel Wharton and Richard Bowtell. Fiber orientation-dependent white
matter contrast in gradient echo MRI. Proceedings of the National Academy of
Sciences of the United States of America, 109(45):18559–18564, nov 2012. ISSN
00278424. doi: 10.1073/pnas.1211075109.
[8] Pascal Sati, Afonso C. Silva, Peter van Gelderen, Maria I. Gaitan, Jillian
E. Wohler, Steven Jacobson, Jeff H. Duyn, and Daniel S. Reich. In vivo
quantification of
anisotropy in white matter fibers in marmoset monkeys.
NeuroImage, 59(2):979 – 985, 2012. ISSN 1053-8119. doi:
10.1016/j.neuroimage.2011.08.064. URL
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
42
http://www.sciencedirect.com/science/article/pii/S1053811
911009815.
[9] Pascal Sati, Peter van Gelderen, Afonso C. Silva, Daniel S. Reich, Hellmut
Merkle, Jacco A. De Zwart, and Jeff H. Duyn. Micro-compartment specific
relaxation in the brain. NeuroImage, 77:268–278, aug 2013. ISSN 10538119. doi:
10.1016/j.neuroimage.2013.03.005.
[10] Samuel Wharton and Richard Bowtell. Gradient echo based fiber
orientation mapping using
and frequency difference measurements.
NeuroImage, 83:1011 – 1023, 2013. ISSN 1053-8119. doi:
10.1016/j.neuroimage.2013.07.054.
[11] Se-Hong Oh, Young-Bo Kim, Zang-Hee Cho, and Jongho Lee. Origin of
orientation dependent
in white matter. NeuroImage, 73:71 – 79,
2013. ISSN 1053-8119. doi: doi.org/10.1016/j.neuroimage.2013.01.051. URL
http://www.sciencedirect.com/science/article/pii/S10538
11913000980.
[12] David A. Rudko, l. Martyn Klassen, Sonali N. De Chickera, Joseph S.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
43
Gati, Gregory A. Dekaban, and Ravi S. Menon. Origins of
orientation
dependence in gray and white matter. Proceedings of the National Academy of
Sciences of the United States of America, 111(1), 2014. ISSN 00278424. doi:
10.1073/pnas.1306516111.
[13] Michael J. Knight, Bryony Wood, Elizabeth Couthard, and Risto
Kauppinen. Anisotropy of spin-echo relaxation by magnetic resonance imaging
in the human brain in vivo. Biomedical Spectroscopy and Imaging, 4(3):299–310,
jun 2015. ISSN 22128808. doi: 10.3233/BSI-150114. URL
http://www.medra.org/servlet/aliasResolver?alias=iospre
ss&doi=10.3233/BSI-150114.
[14] Rita Gil, Diana Khabipova, Marcel Zwiers, Tom Hilbert, Tobias Kober,
and José P. Marques. An in vivo study of the orientation-dependent and independent
components of transverse relaxation rates in white matter. NMR in Biomedicine,
29(12):1780–1790, dec 2016. ISSN 10991492. doi: 10.1002/nbm.3616.
[15] Michael J. Knight, Serena Dillon, Lina Jarutyte, and Risto A. Kauppinen.
Magnetic Resonance Relaxation Anisotropy: Physical Principles and Uses in
Microstructure Imaging. Biophysical Journal, 112(7):1517–1528, apr 2017. ISSN
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
44
15420086. doi: 10.1016/j.bpj.2017.02.026.
[16] André Pampel, Dirk K. Müller, Alfred Anwander, Henrik Marschner,
and Harald E. Möller. Orientation dependence of magnetization transfer parameters
in human white matter. NeuroImage, 114:136 – 146, 2015. ISSN 1053-8119. doi:
https://doi.org/10.1016/j.neuroimage.2015.03.068. URL
http://www.sciencedirect.com/science/article/pii/S10538
11915002645.
[17] Felix Schyboll, Uwe Jaekel, Bernd Weber, and Heiko Neeb. The impact
of fibre orientation on -relaxation and apparent tissue water content in white
matter. Magnetic Resonance Materials in Physics, Biology and Medicine, 2018.
ISSN 13528661. doi: 10.1007/s10334-018-0678-8.
[18] Felix Schyboll, Uwe Jaekel, Francesco Petruccione, and Heiko Neeb.
Fibre-orientation dependent relaxation in the brain: The role of
susceptibility induced spin-lattice relaxation in the myelin water compartment.
Journal of Magnetic Resonance, 300:135 – 141, 2019. ISSN 1090-7807. doi:
https://doi.org/10.1016/j.jmr.2019.01.013. URL
http://www.sciencedirect.com/science/article/pii/S10907
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
45
80719300138.
[19] Michael J. Knight, Robin A. Damion, and Risto A. Kauppinen.
Observation of angular dependence of in the human white matter at 3T.
Biomedical Spectroscopy and Imaging, 2018. ISSN 22128794. doi:
10.3233/bsi-180183.
[20] Lara M. Bartels, Jonathan Doucette, Christoph Birkl, Yuting Zhang,
Alexander M. Weber, and Alexander Rauscher. Orientation dependence of r2
relaxation in the newborn brain. NeuroImage, 264:119702, 2022. ISSN 1053-8119.
doi: 10.1016/j.neuroimage.2022.119702. URL
https://doi.org/10.1016/j.neuroimage.2022.119702.
[21] Chantal M.W. Tax, Elena Kleban, Maxime Chamberland, Muhamed
Barakovć, Umesh udrapatna, and erek K. Jones. Measuring compartmental
-orientational dependence in human brain white matter using a tiltable RF coil and
diffusion- correlation MRI. NeuroImage, 236:117967, 2021. ISSN 1053-8119.
doi: 10.1016/j.neuroimage.2021.117967.
[22] Emilie T. McKinnon and Jens H. Jensen. Measuring intra-axonal in
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
46
white matter with direction-averaged diffusion MRI. Magnetic Resonance in
Medicine, 81(5):2985–2994, 2019. ISSN 07403194. doi: 10.1002/mrm.27617.
[23] P.J. Basser, J. Mattiello, and D. Lebihan. Estimation of the Effective
Self-Diffusion Tensor from the NMR Spin Echo, 1994. ISSN 10641866. URL
https://doi.org/10.1006/jmrb.1994.1037.
[24] Jianhui Zhong, Richard P Kennan, and John C Gore. Effects of
susceptibility variations on NMR measurements of diffusion. Journal of Magnetic
Resonance (1969), 95(2):267–280, novembre 1991. ISSN 0022-2364. URL
https://doi.org/10.1006/jmre.1999.1872.
[25] Jianhui Zhong and John C. Gore. Studies of restricted diffusion in
heterogeneous media containing variations in susceptibility. Magnetic Resonance in
Medicine, 19(2):276–284, 1991. ISSN 1522-2594. URL
https://doi.org/10.1002/mrm.1910190215.
[26] Christian Beaulieu and Peter S. Allen. An in vitro evaluation of the
effects of local magnetic-susceptibility-induced gradients on anisotropic water
diffusion in nerve. Magnetic Resonance in Medicine, 36(1):39–44, 1996. URL
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
47
https://doi.org/10.1002/mrm.1910360108.
[27] C. UN. Clark, G. J. Barker, and P. S. Tofts. An in Vivo Evaluation of the
Effects of Local Magnetic Susceptibility-Induced Gradients on Water Diffusion
Measurements in Human Brain. Journal of Magnetic Resonance, 141(1):52–61,
novembre 1999. ISSN 1090-7807. URL
https://doi.org/10.1006/jmre.1999.1872.
[28] Mark D. Fa, Jianhui Zhong, and John C. Gore. In vivo measurement of
ADC change due to intravascular susceptibility variation. Magnetic Resonance in
Medicine, 41(2):236–240, 1999. ISSN 1522-2594. URL
https://doi.org/10.1002/(SICI)1522-2594(199902)41:2<236 ::AID-MRM4>3.0.CO;2-3.
[29] Dmitry S. Novikov, Marco Reisert, and Valerij G. Kiselev. Effects of
mesoscopic susceptibility and transverse relaxation on diffusion nmr. Journal of
Magnetic Resonance, 293:134–144, 2018. ISSN 1090-7807. URL
https://doi.org/10.1016/j.jmr.2018.06.007.
[30] J.D. Trudeau, W.T. Dixon, and J. Hawkins. The effect of inhomogeneous
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
48
sample susceptibility on measured diffusion anisotropy using nmr imaging. Journal
of Magnetic Resonance, Series B, 108(1):22–30, 1995. ISSN 1064-1866. doi:
https://doi.org/10.1006/jmrb.1995.1098. URL
https://doi.org/10.1006/jmrb.1995.1098.
[31] Dmitry S. Novikov, Els Fieremans, Sune N. Jespersen, and Valerij G.
Kiselev. Quantifying brain microstructure with diffusion MRI: Theory and
parameter estimation. NMR in Biomedicine, 32(4):e3998, 2019. URL
https://doi.org/10.1002/nbm.3998.
[32] Yaniv Assaf and Peter J. Basser. Composite hindered and restricted
model of diffusion (charmed) mr imaging of the human brain. NeuroImage,
27(1):48–58, 2005. ISSN 1053-8119. URL
https://doi.org/10.1016/j.neuroimage.2005.03.042.
[33] Christopher D. Kroenke, Joseph J.H. Ackerman, and Dmitriy A.
Yablonskiy. On the nature of the NAA diffusion attenuated MR signal in the central
nervous system. Magnetic Resonance in Medicine, 52(5):1052–1059, nov 2004.
ISSN 0740-3194. doi: 10.1002/mrm.20260. URL
http://doi.wiley.com/10.1002/mrm.20260.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
49
[34] Sune N. Jespersen, Christopher D. Kroenke, Leif Østergaard, Joseph J.H.
Ackerman, and Dmitriy A. Yablonskiy. Modeling dendrite density from magnetic
resonance diffusion measurements. NeuroImage, 34(4):1473–1486, feb 2007. ISSN
1053-8119. URL
https://doi.org/10.1016/J.NEUROIMAGE.2006.10.037.
[35] Jens H. Jensen, Joseph A. Helpern, Anita Ramani, Hanzhang Lu, E
Kyle Kaczynski. Diffusional kurtosis imaging: The quantification of non-gaussian
water diffusion by means of magnetic resonance imaging. Magnetic Resonance in
Medicine, 53(6):1432–1440, 2005. URL
https://doi.org/10.1002/mrm.20508.
[36] H. Akaike. A new look at the statistical model identification. IEEE
Transactions on Automatic Control, 19(6):716–723, 1974. doi:
10.1109/TAC.1974.1100705.
[37] Kenneth P. Burnham and David R. Anderson. Multimodel inference:
Understanding aic and bic in model selection. Sociological Methods & Research,
33(2):261–304, 2004. doi: 10.1177/0049124104268644. URL
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
50
https://doi.org/10.1177/0049124104268644.
[38] Todd W. Arnold. Uninformative parameters and model selection using
akaike’s information criterion. The Journal of Wildlife Management,
74(6):1175–1178, 2010. doi: 10.1111/j.1937-2817.2010.tb01236.x . URL
https://wildlife.onlinelibrary.wiley.com/doi/abs/10.111
1/j.1937-2817.2010.tb01236.x.
[39] Viljami Sairanen, Alexander Leemans, and Chantal MW Tax. Fast and
accurate Slicewise OutLIer Detection (SOLID) with informed model estimation for
diffusion MRI data. NeuroImage, 181:331–346, 2018. doi:
10.1016/J.NEUROIMAGE.2018.07.003.
[40] Elias Kellner, Bibek Dhital, Valerij G. Kiselev, and Marco Reisert.
Gibbs-ringing artifact removal based on local subvoxel-shifts. Magnetic Resonance
in Medicine, 76(5):1574–1581, 2016. doi: 10.1002/mrm.26054.
[41] Jesper L.R. Andersson, Stefan Skare, and John Ashburner. How to
correct susceptibility distortions in spin-echo echo-planar images: application to
diffusion tensor imaging. NeuroImage, 20(2):870–888, 2003. doi:
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
51
10.1016/S1053-8119(03)00336-7.
[42] Jesper L.R. Andersson and Stamatios N. Sotiropoulos. An integrated
approach to correction for off-resonance effects and subject movement in diffusion
MR imaging. NeuroImage, 125:1063–1078, 2016. doi:
10.1016/j.neuroimage.2015.10.019.
[43] Matthew F. Glasser, Stamatios N. Sotiropoulos, J. Anthony Wilson,
Timothy S. Coalson, Bruce Fischl, Jesper L. Andersson, Junqian Xu, Saad Jbabdi,
Matthew Webster, Jonathan R. Polimeni, David C. Van Essen, and Mark Jenkinson.
The minimal preprocessing pipelines for the Human Connectome Project.
NeuroImage, 80:105–124, 2013. doi: 10.1016/J.NEUROIMAGE.2013.04.127.
[44] Cheng Guan Koay, Evren Özarslan, and Carlo Pierpaoli. Probabilistic
Identification and Estimation of Noise (PIESNO): A self-consistent approach and its
applications in MRI. Journal of Magnetic Resonance, 199(1):94–103, 2009. doi:
10.1016/J.JMR.2009.03.005.
[45] Cheng Guan Koay, Evren Ozarslan, and Peter J Basser. A signal
transformational framework for breaking the noise floor and its applications in MRI.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
52
Journal of magnetic resonance (San Diego, Calif. : 1997), 197(2):108–19, 2009.
doi: 10.1016/j.jmr.2008.11.015.
[46] Samuel St-Jean, Pierrick Coupé, and Maxime Descoteaux. Non Local
Spatial and Angular Matching: Enabling higher spatial resolution diffusion MRI
datasets through adaptive denoising. Medical Image Analysis, 32:115–130, 2016.
doi: 10.1016/J.MEDIA.2016.02.010.
[47] Samuel St-Jean, Alberto De Luca, Chantal M.W. Tax, Max A. Viergever,
and Alexander Leemans. Automated characterization of noise distributions in
diffusion MRI data. Medical Image Analysis, page 101758, 2020. doi:
10.1016/j.media.2020.101758.
[48] Umesh Rudrapatna, Greg D. Parker, Jamie Roberts, and Derek K. Jones.
A comparative study of gradient nonlinearity correction strategies for processing
diffusion data obtained with ultra-strong gradient MRI scanners. Magnetic
Resonance in Medicine, 85(2):1104–1113, 2021. doi:
https://doi.org/10.1002/mrm.28464. URL
https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.284
64.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
53
[49] J-Donald Tournier, Fernando Calamante, and Alan Connelly. Robust
determination of the fibre orientation distribution in diffusion MRI: Non-negativity
constrained super-resolved spherical deconvolution. NeuroImage,
35(4):1459–1472, 2007. doi: 10.1016/j.neuroimage.2007.02.016.
[50] Maxime Descoteaux, Rachid Deriche, Thomas R Knosche, and Alfred
Anwander. Deterministic and probabilistic tractography based on complex fibre
orientation distributions. IEEE transactions on medical imaging, 28(2):269–286,
2008.
[51] Ben Jeurissen, Jacques Donald Tournier, Thijs Dhollander, Alan
Connelly, and Jan Sijbers. Multi-tissue constrained spherical deconvolution for
improved analysis of multi-shell diffusion MRI data. NeuroImage, 103:411–426,
2014. doi: 10.1016/j.neuroimage.2014.07.061.
[52] Chantal MW Tax, Ben Jeurissen, S.B. Vos, M.A. Viergever, e A.
Leemans. Recursive calibration of the fiber response function for spherical
deconvolution of diffusion MRI data. NeuroImage, 86, 2014. doi:
10.1016/j.neuroimage.2013.07.067.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
54
[53] Marco Reisert, Elias Kellner, Bibek Dhital, Jürgen Hennig, and Valerij
G. Kiselev. Disentangling micro from mesostructure by diffusion MRI: A Bayesian
approach. NeuroImage, 147:964–975, feb 2017. ISSN 1053-8119. doi:
10.1016/J.NEUROIMAGE.2016.09.058. URL
https://www.sciencedirect.com/science/article/pii/S1053
811916305353?via%3Dihub.
[54] Dmitry S. Novikov, Jelle Veraart, Ileana O. Jelescu, and Els Fieremans.
Rotationally-invariant mapping of scalar and orientational metrics of neuronal
microstructure with diffusion MRI. NeuroImage, 174:518–538, jul 2018. ISSN
1053-8119. doi: 10.1016/J.NEUROIMAGE.2018.03.006. URL
https://www.sciencedirect.com/science/article/pii/S1053
811918301915?via%3Dihub.
[55] Jakob Wasserthal, Peter Neher, and Klaus H. Maier-Hein. TractSeg –
Fast and accurate white matter tract segmentation. NeuroImage, 183:239–253, 2018.
ISSN 10959572. doi: 10.1016/j.neuroimage.2018.07.070.
[56] Mark D. Does and John C. Gore. Compartmental study of diffusion and
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
55
relaxation measured in vivo in normal and ischemic rat brain and trigeminal nerve.
Magnetic Resonance in Medicine, 43(6):837–844, 2000. doi:
10.1002/1522-2594(200006)43:6<837::AID-MRM9>3.0.CO;2-O.
[57] Yaniv Assaf and Yoram Cohen. Assignment of the water slow-diffusing
component in the central nervous system using -space diffusion MRS:
Implications for fiber tract imaging. Magnetic Resonance in Medicine,
43(2):191–199, 2000. doi:
10.1002/(SICI)1522-2594(200002)43:2<191::AID-MRM5>3.0.CO;2-B.
[58] Wen Qin, Chun Shui Yu, Fan Zhang, Xiang Ying Du, Heng Jiang, Yu
Xia Yan, and Kun Cheng Li. Effects of echo time on diffusion quantification of
brain white matter at 1.5t and 3.0t. Magnetic Resonance in Medicine,
61(4):755–760, 2009. doi: 10.1002/mrm.21920. URL
https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.219
20.
[59] Mu Lin, Hongjian He, Qiqi Tong, Qiuping Ding, Xu Yan, Thorsten
Feiweier, and Jianhui Zhong. Effect of myelin water exchange on DTI-derived
parameters in diffusion MRI: Elucidation of TE dependence. Magnetic Resonance
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
56
in Medicine, 79(3):1650–1660, 2018. doi: 10.1002/mrm.26812.
[60] Sharon Peled, David G. Cory, Stephen A. Raymond, Daniel A.
Kirschner, and Ferenc A. Jolesz. Water diffusion, , and compartmentation in frog
sciatic nerve. Magnetic Resonance in Medicine, 42(5):911–918, nov 1999. ISSN
0740-3194. doi:
10.1002/(SICI)1522-2594(199911)42:5<911::AID-MRM11>3.0.CO;2-J. URL
http://doi.wiley.com/10.1002/%28SICI%291522-2594%281999
11%2942%3A5%3C911%3A%3AAID-MRM11%3E3.0.CO%3B2-J.
[61] Jelle Veraart, Dmitry S. Novikov, and Els Fieremans. TE dependent
Diffusion Imaging (TEdDI) distinguishes between compartmental relaxation
times. NeuroImage, 182:360–369, nov 2018. ISSN 1053-8119. doi:
10.1016/J.NEUROIMAGE.2017.09.030. URL
https://www.sciencedirect.com/science/article/pii/S1053
811917307784?via%3Dihub.
[62] Nian Wang, Qiuting Wen, Surendra Maharjan, Anthony J. Mirando, Yi
Qi, Matthew J. Hilton, and Charles E. Spritzer. Magic angle effect on diffusion
tensor imaging in ligament and brain. Magnetic Resonance Imaging, 92:243–250,
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
57
2022. ISSN 0730-725X. doi: 10.1016/j.mri.2022.06.008. URL
https://doi.org/10.1016/j.mri.2022.06.008.
[63] Lara Bartels, Jonathan Doucette, Christoph Birkl, Alexander M. Weber,
and Alexander Rauscher. Diffusion metrics in human white matter depend on fibre
orientation. In ISMRM, page 2456, 2022. URL
https://cds.ismrm.org/protected/22MPresentations/abstra
cts/2456.html.
[64] Yuxi Pang. Is diffusion tensor principal diffusivity aligned with axon
fibre in the human brain white matter? In ISMRM, page 0648, 2022. URL
https://cds.ismrm.org/protected/22MPresentations/abstra
cts/0648.html.
[65] Yuxi Pang. Orientation dependent proton transverse relaxation in the
human brain white matter: The magic angle effect on a cylindrical helix. Magnetic
Resonance Imaging, 100:73–83, 2023. URL
https://doi.org/10.1016/j.mri.2023.03.010.
[60] Christoph Birkl, Jonathan Doucette, Michael Fan, Enedino
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
58
Hernández-Torres, and Alexander Rauscher. Myelin water imaging depends on
white matter fiber orientation in the human brain. Magnetic Resonance in Medicine,
n/a(n/a), 2020. doi: 10.1002/mrm.28543. URL
https://onlinelibrary.wiley.com/doi/abs/10.1002/mrm.285
43.
[67] Elena Kleban, Chantal M.W. Tax, Umesh S. Rudrapatna, Derek K.
Jones, and Richard Bowtell. Strong diffusion gradients allow the separation of intra-
and extra-axonal gradient-echo signals in the human brain. NeuroImage,
217:116793, 2020. ISSN 1053-8119. doi:
https://doi.org/10.1016/j.neuroimage.2020.116793. URL
http://www.sciencedirect.com/science/article/pii/S10538
11920302809.
[68] Jana Hutter, Paddy J. Slator, Daan Christiaens, Rui Pedro A. G. Teixeira,
Thomas Roberts, Laurence Jackson, Anthony N. Price, Shaihan Malik, and Joseph
V. Hajnal. Integrated and efficient diffusion-relaxometry using ZEBRA. Scientific
Reports, 8(1):15138, dec 2018. ISSN 2045-2322. doi:
10.1038/s41598-018-33463-2. URL
http://www.nature.com/articles/s41598-018-33463-2.
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
59
[69] R. Bammer, M. Markl, UN. Barnett, B. Acar, M.T. Alley, N.J. Pelc, G.H.
Glover, and M.E. Moseley. Analysis and generalized correction of the effect of
spatial gradient field distortions in diffusion-weighted imaging. Magnetic
Resonance in Medicine, 50(3):560–569, sep 2003. ISSN 0740-3194. doi:
10.1002/mrm.10545. URL
http://doi.wiley.com/10.1002/mrm.10545.
[70] Fenghua Guo, Alberto De Luca, Greg Parker, Derek K Jones, Max A
Viergever, Alexander Leemans, and Chantal MW Tax. The effect of gradient
nonlinearities on fiber orientation estimates from spherical deconvolution of
diffusion magnetic resonance imaging data. Human Brain Mapping, 42(2):367–383,
2020. doi: 10.1002/hbm.25228. URL
https://onlinelibrary.wiley.com/doi/abs/10.1002/hbm.252
28.
[71] Hamed Y. Mesri, Szabolcs David, Max A. Viergever, and Alexander
Leemans. The adverse effect of gradient nonlinearities on diffusion mri: From
voxels to group studies. NeuroImage, 205:116127, 2020. ISSN 1053-8119. doi:
10.1016/j.neuroimage.2019.116127. URL
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
60
https://doi.org/10.1016/j.neuroimage.2019.116127.
[72] UN. Reymbaut, J. P. de Almeida Martins, C. M. W. Tax, F.
Szczepankiewicz, D. K. Jones, and D. Topgaard. Resolving orientation-specific
diffusion-relaxation features via monte-carlo density-peak clustering in
heterogeneous brain tissue, 2020.
[73] Anders Dyhr Sandgaard, Valerij G. Kiselev, Noam Shemesh, and Sune
Nørhøj Jespersen. Orientation-Dependent Susceptibility Effects in the Standard
Model of Diffusion in White Matter. In ISMRM Workshop on Diffusion MRI: From
Research to Clinic, page 66, 2022.
[ ] “Squashing peanuts and smashing pumpkins” ’: How noise distorts
diffusion-weighted MR data. Magnetic Resonance in Medicine, 52(5):979-993,
2004. doi: 10.1002/mrm.20283. URL
https://doi.org/10.1002/mrm.20283.
UN. Appendix: Key findings from Tax et al. [21]
In our previous work, we estimated the apparent -values for intra- E
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
61
extra-axonal compartments from the WM SFP data acquired by varying nominal
-values and TEs simultaneously. The acquisition parameters are reproduced in this
work in Figure 1A. The compartmental spin-echo signals with associated apparent
-values were included in the compartmental model of diffusion in WM. The latter
describes the signal as a convolution of the signal associated with a population of
perfectly parallel fibres with a fibre orientation distribution function. The diffusion
in the intra- and extra-axonal spaces was described by ‘stick’ and ‘zeppelin’ tensors,
rispettivamente.
We then characterised the dependence of the compartmental -values on
WM fibre orientation angle w.r.t. :
iso
aniso sin aniso sin
(A1)
(A2)
iso is a -independent isotropic component of , whereas describes
the orientation-dependent component. We allowed the corresponding anisotropic
coefficients aniso to be independent, linked, or set to zero, to achieve different
variations of this generalised representation. This resulted in a set of the following
five representations:
62
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
iso
iso aniso sin
iso aniso sin
iso aniso
cos
iso aniso sin aniso sin
(A3)
(A4)
(A5)
(A6)
(A7)
All of them were used to analyse the data pooled from all SFP voxels and head
orientations, while only the first three were applied to analyse data, which were
anatomically matched between head orientations using tractometry. We also
analysed the -values estimated by fitting a mono-exponential function to the data
obtained at to compare them to previous studies.
Main results from the pooled data. Intra-axonal -values were best
described by the Eq. A6 with the isotropic component of s and the
magnitude of anisotropy of s . The AIC of the isotropic representation (Eq.
A3) was larger than that of the anisotropic representation with and
iso s . Extra-axonal -values were best represented by the Eq. A5 with
the isotropic component of s and the magnitude of anisotropy of s .
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
63
The corresponding isotropic representation was not supported with
and iso s .
Main results from the tractometry analysis. Intra-axonal values were best
supported by the isotropic representation, while extra-axonal values were best
supported by sin -representation with the magnitude of anisotropy of
S .
Scaricato da http://direct.mit.edu/imag/article-pdf/doi/10.1162/imag_a_00012/2154900/imag_a_00012.pdf by guest on 07 settembre 2023
64