Imaginative Reinforcement Learning: Computational
Principles and Neural Mechanisms
Samuel J. Gershman, Jimmy Zhou, and Cody Kommers
Astratto
■ Imagination enables us not only to transcend reality but also to
learn about it. In the context of reinforcement learning, an agent
can rationally update its value estimates by simulating an internal
model of the environment, provided that the model is accurate. In
a series of sequential decision-making experiments, we investi-
gated the impact of imaginative simulation on subsequent deci-
sions. We found that imagination can cause people to pursue
imagined paths, even when these paths are suboptimal. This bias
is systematically related to participants’ optimism about how much
reward they expect to receive along imagined paths; providing feed-
back strongly attenuates the effect. The imagination effect can be
captured by a reinforcement learning model that includes a bonus
added onto imagined rewards. Using fMRI, we show that a network
of regions associated with valuation is predictive of the imagination
effect. These results suggest that imagination, although a powerful
tool for learning, is also susceptible to motivational biases. ■
INTRODUCTION
Imagination is a fertile source of knowledge. Philoso-
phers and scientists routinely use thought experiments
to explore their mental models of the world and thereby
make “discoveries” in the absence of new experience.
Lucretius inferred the infinitude of space by picturing
himself throwing spears at the boundary of the universe,
and Einstein discovered relativity by picturing himself
riding on a beam of light.
Imagination has also been put to practical use in com-
puter science. Niyogi, Girosi, and Poggio (1998) Di-
scribed how an image classifier could be fed training
examples synthesized by applying mental transforma-
tions to a set of objects. Per esempio, suppose you were
training a classifier to recognize faces. You might only
have a single image for a given face, but in the real world,
faces appear in many orientations and positions. If you
have access to a 3-D model of the face, then you can
mentally apply transformations that preserve identity
(per esempio., rotating the face). Each transformation yields a
new image with the same label and more training data
for the classifier.
A similar idea was applied to reinforcement learning by
Sutton (1990): A model of the environment can be used
to simulate training data (transitions and rewards) for a
computationally cheap “model-free” learning algorithm
that updates a set of cached value estimates (future re-
ward expectations). In this architecture, the same learn-
ing algorithm operates on both real and simulated
experiences. The key advantage is that a model-based
Harvard University
© 2017 Istituto di Tecnologia del Massachussetts
action policy can be approximated without computation-
ally expensive model-based algorithms like tree search or
dynamic programming; the model-free cached values
map directly to a policy without additional computation.
These examples illustrate how learning systems can be
integrated with imaginative simulation to acquire knowl-
edge in the absence of new experience. Tuttavia, there
is relatively little direct evidence that the brain uses imag-
ination in this way.
Indirect evidence for the role of imaginative simulation
in reinforcement learning comes from a series of retro-
spective revaluation experiments (Gershman, Markman,
& Otto, 2014). In these experiments, human participants
learned conflicting policies at different stages of a se-
quential decision task and were then tested for revalua-
tion of the policy learned earlier in the task. A period of
quiet rest before the test phase enhanced retrospective
revaluation, consistent with the idea that model-free
cached values can be updated via offline simulation. Questo
finding cannot be explained by pure model-based or
model-free accounts of learning or even by stochastic
mixtures of the two (Daw, Gershman, Seymour, Dayan,
& Dolan, 2011); it appears to require a particular kind
of cooperative interaction between the systems.
In questo articolo, we take a closer look at the role of imag-
inative simulation in reinforcement learning. We asked
human participants to perform a sequential decision task
with dynamic rewards, while intermittently having them
imagine particular paths through the state space.
Although participants do not gain any information from
these imagination trials, it has a potent effect on their
subsequent decision behavior, influencing them to
pursue imagined paths that are in fact suboptimal. Noi
Journal of Cognitive Neuroscience 29:12, pag. 2103–2113
doi:10.1162/jocn_a_01170
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
F
/
T
T
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
C
7
N
7
_
7
UN
/
_
j
0
o
1
C
1
N
7
0
_
UN
P
_
D
0
1
B
1
sì
7
G
0
tu
.
e
P
S
T
D
o
F
N
B
0
sì
7
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
/
F
T
.
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
show that this bias arises in part because participants are
optimistic about the amount of reward they will receive
in imagined states; the bias is reduced when participants
are given feedback about the true reward. A simple rein-
forcement learning model with an “imagination bonus”
can capture the bias. Using fMRI, we find that the bias
is associated with activation in medial pFC and OFC, con-
sistent with the role of those regions in reward expecta-
zione. Taken together, these findings suggest that
imagination can drive reinforcement learning, although
it can fall prey to miscalibrated reward expectations.
ity for participation in the scanning portion. Participants
gave informed consent before both sessions. The study
was approved by the ethics committee of Harvard Univer-
sity. Participants earned $35 for the scanning session and $10 for the behavioral session, plus a performance-based
bonus in both.
Inoltre, we recruited 230 human participants using
the Amazon Mechanical Turk Web service. All partici-
pants were given informed consent and paid for their
participation. This study was also approved by the ethics
committee of Harvard University.
METHODS
Participants
Twenty healthy volunteers (10 women; mean age =
25.45 years, SD = 4.5 years) participated in the scanning
portion of this study. These same 20 individuals also par-
ticipated in a behavioral session to determine their eligibil-
Design and Procedure: fMRI Experiment
The following describes the task that participants per-
formed in the scanning experiment. There were two
kinds of trials: “decision” trials and “imagination” trials
(Figura 1). A block consisted of five decision trials followed
by one imagination trial with the addition of a single
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
T
T
F
/
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
C
7
N
7
_
7
UN
/
_
j
0
o
1
C
1
N
7
0
_
UN
P
_
D
0
1
B
1
sì
7
G
0
tu
.
e
P
S
T
D
o
F
N
B
0
sì
7
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
.
T
/
F
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
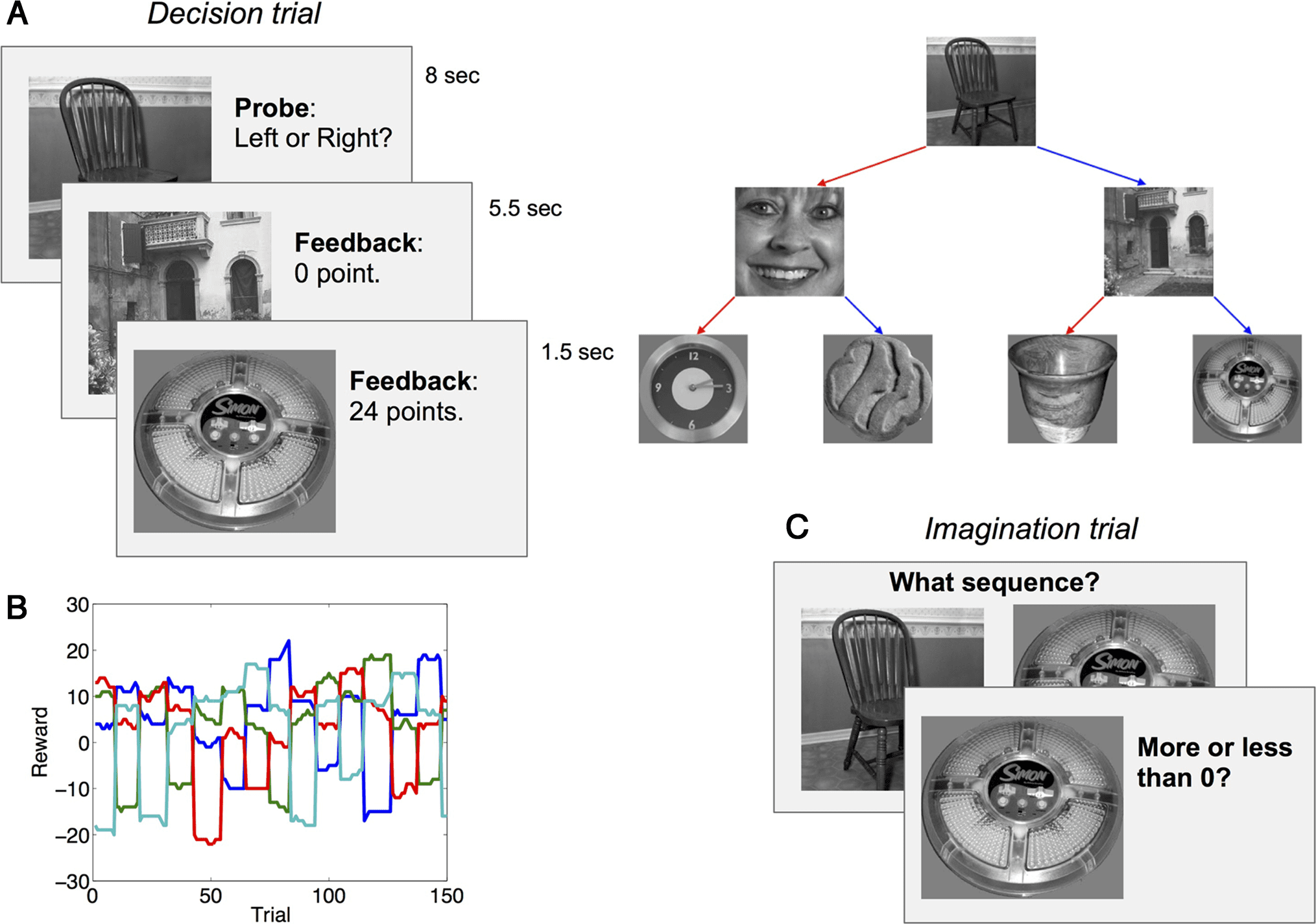
Figura 1. Experimental design. The design of the fMRI study is shown here, which is identical to the design of the behavioral studies except that the
timing was faster in the behavioral studies (see Methods) and they used a continuous reward prediction rather than a binary judgment. (UN) On
decision trials, participants traversed the state space by making a sequence of two decisions, followed by a reward in the terminal state. State
transition diagram is shown on the right; colored arrows correspond to available actions in each state. (B) Example reward sequence. Each line
corresponds to a terminal state. (C) On imagination trials, participants performed the sequence of actions necessary to arrive at a particular terminal
state (shown on the right) and then predicted whether the reward would be greater or less than 0 in that terminal state. In the behavioral studies,
participants made a continuous numerical reward prediction.
2104
Journal of Cognitive Neuroscience
Volume 29, Numero 12
decision trial at the end, because we were particularly in-
terested in the decision trials immediately after an imagi-
nation trial. A run consisted of eight blocks. Participants
performed five runs in the scanner. Most participants per-
formed all five runs, but some participants had exceptions
in the number of runs, with some participants completing
fewer runs because of experimental glitches (two partici-
pants: two runs, one participant: three runs, two partici-
pant: four runs) and some initial participants completing
more runs when we were first piloting the experiment
(three participants: six runs, one participant: eight runs).
In decision trials, participants made two consecutive
decisions of left or right and received feedback after each
decision. These left or right decisions allowed the partic-
ipant to navigate different states. Each trial began with
the same start state. There were two intermediate states
(one for left, one for right) and four terminal states (left
or right from either of the second-level states). These
states were represented by black and white pictures of
objects or scenes. The transitions between states were de-
terministic. We showed participants the transition struc-
ture of these states before the start of the experiment.
The decision trials began with the participant seeing
the first state and receiving a prompt for a forced-choice,
two-alternative (left or right) decision. Participants had
1.5 sec to make this decision. If participants failed to
make a decision, then they were shown a fixation cross
during the remaining time allotted for the trial (8 sec
from onset of the first picture to the end of final feed-
back). After the first decision, participants were given re-
ward feedback and shown the picture associated with the
intermediate state (one of two possible states depending
on whether they chose left or right). The reward feed-
back after the first decision was always 0 and was shown
for 1.5 sec. Participants were then prompted to make
another forced-choice left/right decision. They had
1.5 sec to make this decision. Again, if they failed to make
a decision, they were shown a fixation cross during the
remaining time allotted for the trial. After they made their
second decision, participants were given reward feedback
and shown the picture associated with the terminal state
they had selected. The feedback lingered for 1.5 sec before
participants were shown a fixation cross for 2–4 sec of
jitter, after which the next trial would begin.
The underlying rewards were predetermined for each
trial, independent of the path chosen by the participant.
The underlying reward structure defines the ground-
truth optimal path. Rewards were randomly generated
at the time of each new block. Rewards were symmetri-
cally distributed, such that the highest and lowest re-
wards were on the same branch of the path structure
(per esempio., the highest and lowest could be associated with
the two terminal states reachable from the left intermedi-
ate state) and the average expected reward was the same
at both intermediate states. The highest reward was sam-
pled from a uniform distribution between 15 E 25. IL
two intermediate rewards were sampled from a uniform
distribution between 0 E 10. The lowest reward was
sampled from a uniform distribution between −15 and
−5. Rewards reset, on average, every 10 trials (chosen
uniformly from 8 A 12). These rewards drifted according
to a Gaussian random walk (SD = 0.5) until the next reset
occurred. We chose this distribution, which was biased to
yield positive rewards on average, so that participants
would not get frustrated by experiencing a large number
of losses. For some participants (n = 39), the mean re-
wards of the left and right branches of the tree were
matched (cioè., the sum of the highest and lowest rewards
was about equal to the sum of the two middle rewards).
For the rest of the participants, the rewards were un-
matched. These reward sequences were qualitatively sim-
ilar, so we collapsed across the different sequence types.
In imagination trials, participants were shown the pic-
ture representing the start state and the picture rep-
resenting one of the terminal states, with an arrow
pointing from the start state to the terminal state. IL
terminal state was selected at random from one of the
three states that did not offer the highest reward. Partic-
ipants were asked to imagine the sequence of actions
that would take them from the start state to the indicated
terminal state and then to indicate the appropriate se-
quence of left or right decisions (per esempio., press left and right
or left and left). Participants had 4 sec to indicate the cor-
rect path, and 2–4 sec of jitter followed after indicating
the imagined path. There was no fixation cross if the par-
ticipants failed to make the decisions. Participants were
then asked to predict whether the imagined path would
yield a reward that was more or less than zero. They had
2.5 sec to respond and then were given 2–4 sec of jitter
before the onset of the next decision trial.
We first recruited participants to participate in the be-
havioral portion of the experiment outside the scanner.
In this behavioral session, a run consisted of eight blocks
with the addition of a single decision trial at the end.
Each participant performed four runs. Participants prac-
ticed the task for one run before beginning the actual
experiment. After the participant had completed the
behavioral session, we invited them to return for the
scanning portion if their data showed an increased prob-
ability of selecting the imagined path on the decision tri-
als immediately after the imagined trials (the basis for the
effect in Experiment 1). We had 35 participants partici-
pate in this behavioral portion of the task, 15 of which
were excluded from scanning because either they did
not show the effect or they declined our invitation to re-
turn for the scanning session (8 Di 35 participants did not
show effect and were excluded from scanning accord-
ingly; 7 Di 35 participants declined invitation to return
for scanning session). Although we selected participants
for scanning on the basis of the imagination effect, we still
found a significant effect on average when analyzing all
35 participants. More generally, the choice behavior re-
ported in the Results section was quantitatively and qual-
itatively unchanged when including all 35 participants.
Gershman, Zhou, and Kommers
2105
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
F
/
T
T
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
C
7
N
7
_
7
UN
/
_
j
0
o
1
C
1
N
7
0
_
UN
P
_
D
0
1
B
1
sì
7
G
0
tu
.
e
P
S
T
D
o
F
N
B
0
sì
7
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
/
F
T
.
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
Individual trials were excluded from the behavioral and
model analyses if participants failed to reach a terminal
state (cioè., they did not make two decisions).
Design and Procedure: Behavioral Experiments
Experiment 1 featured the same experimental paradigm
as the scanning experiment described above, except that
participants made continuous (numerical) predictions in
the imagination trial. Individual trials were excluded if
participants made a prediction with an absolute value
greater than or equal to 25. Inoltre, participants were
required to indicate the correct imagined path before
moving onto the next trial. Per esempio, if the correct
decision sequence was left and then right, they were
prompted to repeat the decision sequence until they se-
lected the correct one. The time constraints described in
the scanning experiment were relaxed in these experi-
menti. A block consisted of five decision trials and one
imagination trial with the addition of a single decision
trial at the end. Each participant performed 31 blocks.
Experiment 2 was the same as Experiment 1 described
above, except that, after participants had made their
predictions, they received veridical feedback about the
reward associated with the imagined path.
Experiment 3 was the same as Experiment 1 described
above, except that participants were asked neither to
imagine the path nor to indicate the sequence of deci-
sions to get there. They only made a prediction about
the value of a given terminal state.
Computational Model Fitting and Comparison
We fit the four computational models described in the
Results section to the choice data from the decision trials.
Maximum likelihood estimates of each parameter were
obtained for each participant individually using nonlinear
optimization (MATLAB’s fmincon function) with five ran-
dom initializations to avoid local optima; the parameter
estimates achieving the highest likelihood across the ran-
dom initializations were used in subsequent analyses. Noi
placed the following bounds on the parameters: inverse
temperature [0,10], learning rate [0,1], eligibility trace
[0,1], imagination bonus [0,20], and forgetting decay
[1,3]. No transformations were applied to the parameters
during model fitting.
Models were compared using random effects Bayesian
model comparison (Rigoux, Stephan, Friston, & Daunizeau,
2014), which estimates the frequency of each model class
in the population. The input to this procedure is the log
model evidence for each participant, which we approx-
imated using −0.5 × BIC, where BIC is the Bayesian Infor-
mation Criterion. We used the exceedance probability (IL
posterior probability that a particular model is more
frequent in the population than the other models under
consideration) as a model comparison metric.
fMRI Data Acquisition
Neuroimaging data were collected using a 3-T Siemens
Magnetom Prisma MRI scanner (Siemens Healthcare,
Erlangen, Germany) with the vendor’s 32-channel head
coil. Anatomical images were collected with a T1-weighted
multiecho MPRAGE sequence (176 sagittal slices; repe-
tition time = 2530 msec; echo times = 1.64, 3.50, 5.36,
E 7.22 msec; flip angle = 7°; 1-mm3 voxels; field of
view = 256 mm). All BOLD data were collected via a
T2*-weighted EPI pulse sequence that employed multi-
band RF pulses and Simultaneous Multi-Slice (SMS) ac-
quisition (Xu et al., 2013; Feinberg et al., 2010; Moeller
et al., 2010). For the six task runs, the EPI parameters
were as follows: 69 interleaved axial–oblique slices
(25° toward coronal from AC–PC alignment), repetition
time = 2000 msec, echo time = 35 msec, flip angle = 80°,
2.2-mm3 voxels, field of view = 207 mm, and SMS = 3.
The SMS-EPI acquisitions used the CMRR-MB pulse
sequence from the University of Minnesota.
fMRI Data Preprocessing and Analysis
Data preprocessing and statistical analyses were per-
formed using SPM12 (Wellcome Department of Imaging
Neuroscience, London, UK). Functional (EPI) image vol-
umes were realigned to correct for small movements oc-
curring between scans. This process generated an aligned
set of images and a mean image per participant. Each
participant’s T1-weighted structural MRI was then co-
registered to the mean of the realigned images and seg-
mented to separate out the gray matter, which was
normalized to the gray matter in a template image based
on the Montreal Neurological Institute reference brain.
Using the parameters from this normalization process,
the functional images were normalized to the Montreal
Neurological Institute template (resampled voxel size =
2 mm isotropic) and smoothed with an 8-mm FWHM
Gaussian kernel. A high-pass filter of 1/128 Hz was used
to remove low-frequency noise, and a first-order auto-
regressive model was used to correct for temporal
autocorrelations.
We defined two general linear models (GLMs) to ana-
lyze the fMRI data. Both GLMs included stimulus events
(cues and outcomes) as impulse regressors convolved
with the canonical hemodynamic response function
(HRF). In GLM1, a boxcar regressor was defined over
the entire imagination trial epoch and then convolved
with the canonical HRF. Separate regression coefficients
were estimated for imagination trials, which were fol-
lowed by a choice of the imagined path, and trials, Quale
were followed by a choice of the optimal path. In GLM2,
the temporal difference prediction error from the imagi-
nation + forgetting model was entered as a parametric
modulator of the outcome events on decision trials and
orthogonalized with respect to the outcome event re-
gressor and convolved with the canonical HRF.
2106
Journal of Cognitive Neuroscience
Volume 29, Numero 12
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
F
/
T
T
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
C
7
N
7
_
7
UN
/
_
j
0
o
1
C
1
N
7
0
_
UN
P
_
D
0
1
B
1
sì
7
G
0
tu
.
e
P
S
T
D
o
F
N
B
0
sì
7
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
.
T
F
/
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
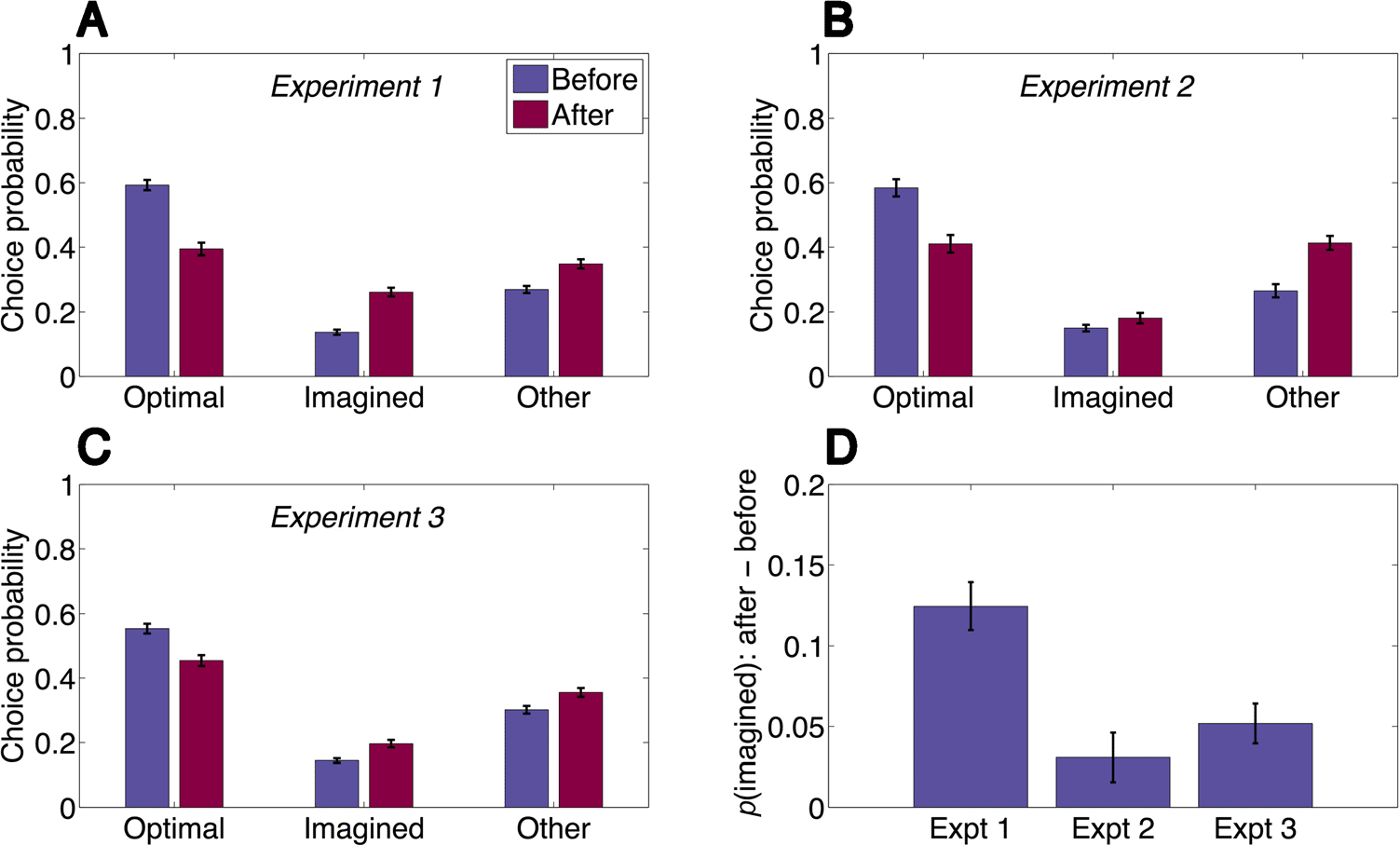
Figura 2. Imagination trials
affect subsequent decisions.
(UN) Participants are more likely
to take the imagined path
after an imagination trial than
before an imagination trial and
correspondingly less likely to
take the optimal path. They are
also slightly more likely to take a
path that is neither optimal nor
imagined. (B) Providing reward
feedback on imagination
trials strongly attenuates the
imagination effect. (C) Asking
participants to make reward
predictions without imagining
the action sequence also strongly
attenuates the imagination
effect. (D) Comparison of effects
across experiments. The y axis
shows the difference in
probability of choosing the
imagined path after and before
an imagination trial. Error bars
denote SEM. Expt = experiment.
Group-level results were analyzed using t contrasts
with cluster-based FWE thresholding at the whole-brain
level ( P < .05) using a cluster-forming threshold of
p < .001.
For the ventral striatum analysis, we used a bilateral
anatomical mask taken from the automated anatomical
labeling atlas (Tzourio-Mazoyer et al., 2002).
RESULTS
Behavioral Results
Human participants (N = 87) performed a reinforcement
learning task in which they navigated through a sequence
of states to maximize rewards (Figure 1A). Rewards were
only delivered in the terminal states, and the reward mag-
nitudes changed dynamically (Figure 1B), such that par-
ticipants had to be continually updating their policy and
exploring the decision tree. In addition to these “deci-
sion” trials, participants intermittently performed “imagi-
nation” trials in which they were asked to first enter the
sequence of actions that would take them to a particular
terminal state and then to make a prediction about how
much reward they would obtain in that state (Figure 1C).
The key question we asked was how imagination trials
affected behavior on subsequent decision trials. A partic-
ipant’s choice of path on a decision trial can be broken
down into three categories: the objectively optimal path,
the previously imagined path, and the two other possible
paths, which are neither optimal nor imagined. Critically,
we asked participants to imagine paths that were always
suboptimal, setting up a conflict between optimal and
imagined paths. We found that participants were more
likely to choose the imagined path after an imagination
trial compared with before an imagination trial (t(86) =
8.46, p < .0001; Figure 2A) and correspondingly less likely
to choose the optimal path (t(86) = 11.5, p < .0001).
Participants were also more likely to choose an “other”
path (t(86) = 5.28, p < .0001), suggesting the possibility
that participants simply forgot the optimal path because
of memory interference from the imagination trial, as op-
posed to being systematically biased toward the imagined
path. However, the shift toward the imagined path was
marginally stronger than the shift toward the other paths
(t(86) = 1.88, p = .06). We will address the question of
forgetting further using computational modeling in the
next section.
We next explored several variations of our paradigm. In
Experiment 2 (n = 46), participants received feedback
about the true rewards after their predictions on imagina-
tion trials. This attenuated the imagination effect (change
in probability of choosing the imagined path after an
imagination trial) relative to Experiment 1 (t(131) =
4.05, p < .0001; Figure 2D), but the effect was still mar-
ginally significant (t(45) = 2.02, p = .05; Figure 2B). The
imagination effect was significantly smaller than the
change in probability of choosing one of the “other”
paths (t(45) = 4.03, p < .001), and the magnitude of this
“other” effect was comparable with Experiment 1, indicat-
ing that reward feedback selectively reduced the imagina-
tion effect without affecting the “other” effect.
In Experiment 3 (n = 97), participants made reward
predictions (without feedback) but did not enter the
path that would take them to the specified terminal state.
We hypothesized that this experiment would reduce the
demands on imaginative simulation. The imagination
effect was again attenuated relative to Experiment 1
(t(182) = 3.81, p < .001; Figure 2D) but significantly
Gershman, Zhou, and Kommers
2107
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
c
7
n
7
_
7
a
/
_
j
0
o
1
c
1
n
7
0
_
a
p
_
d
0
1
b
1
y
7
g
0
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
t
.
f
/
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
greater than 0 (t(96) = 4.2, p < .0001; Figure 2C). There
was no significant difference in the size of the imagina-
tion effect between Experiments 2 and 3 ( p = .31).
One clue about the nature of the underlying mecha-
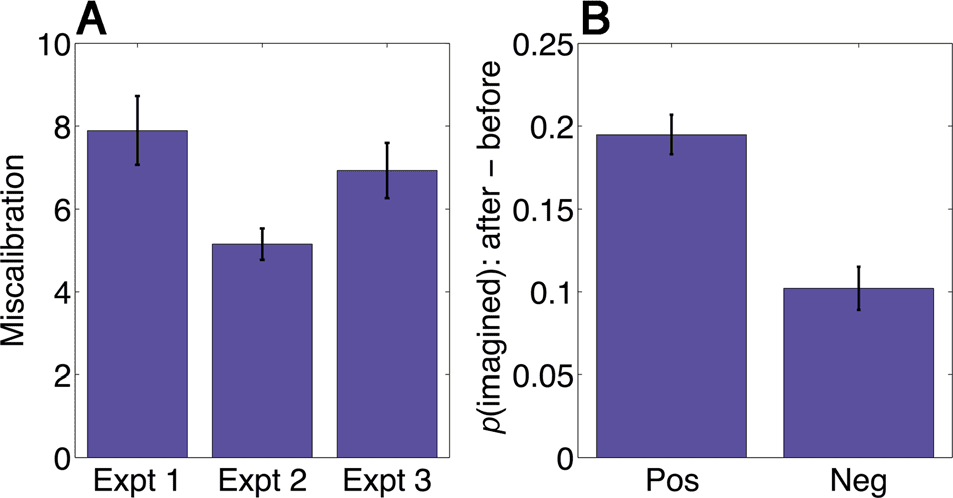
nisms comes from inspection of the reward predictions
themselves (Figure 3A): Participants are systematically
miscalibrated across all three experiments ( p < .0001),
estimating the rewards to be greater than they actually
are. In other words, reward predictions are optimistic,
even when reward feedback is provided in Experiment
2 (although the miscalibration is significantly reduced
relative to Experiment 1; t(131) = 2.35, p < .05). This
miscalibration is predictive of behavior on subsequent
decision trials in Experiment 1: The imagination effect
is significantly greater after positively miscalibrated (opti-
mistic) imagination trials compared with negatively mis-
calibrated (pessimistic) trials (t(77) = 3.91, p < .001;
Figure 3B), although it is still significantly greater than
0 after negatively miscalibrated trials (t(77) = 5.00, p <
.0001).
To summarize so far, the imagination effect depends
on both reward feedback and imaginative simulation.
An important (but not exclusive) contributing factor is
the prevalence of miscalibrated reward predictions, such
that imaginative simulation combined with optimistic
reward predictions increase the probability of choosing
the imagined path.
Computational Modeling
To disentangle the different possible mechanisms driving
the imagination effect, we fit a family of reinforcement
learning models to choice behavior. All of these models
have in common the well-accepted idea that cached
values are updated using temporal difference learning
(Daw et al., 2011; Gläscher, Daw, Dayan, & O’Doherty,
2010; Seymour et al., 2004; Schultz, Dayan, & Montague,
Figure 3. Miscalibration of reward predictions. (A) Participants are
optimistic (positively miscalibrated) about expected reward in imagined
states. This optimism is reduced, but not eliminated, by reward
feedback. (B) Participants are more likely to switch to the imagined
path when they are positively miscalibrated compared with when they
are negatively miscalibrated. Error bars denote SEM. Neg = negative;
Pos = positive.
1997). In addition, the models assume that the same
learning algorithm applies to imagined paths and rewards.
The critical differences between the models lie in how
imagined rewards are distorted and whether cached
values can be forgotten.
Cached values encode estimates of expected dis-
counted future return in a lookup table. Specifically, we
define the Q value of taking action a in state s as
Q s; að
Þ ¼ E½
X∞
t¼0
γtrt s0 ¼ s; a0 ¼ a
j
(cid:2)
where rt is the reward received at time t and γ is a
discount factor that down-weights distal rewards. The
temporal difference learning algorithm (specifically the
SARSA algorithm; see Sutton & Barto, 1998) updates a
cached value estimate ^Qt s; að
Þ according to the prediction
error
δt ¼ rt þ γ ^Qt stþ1; atþ1
ð
Þ − ^Qt st; at
ð
Þ:
This same update can apply to both experienced and
imagined state–action pairs, a key insight of Sutton’s (1990)
Dyna architecture. We refer to this as the “standard”
model. Note that, although we focus on model-free
learning algorithms in this article, our data can also be
accounted for by model-based variants. We do not explore
these here because they make essentially the same
predictions.
We consider two modifications of the standard model.
In the “forgetting” model, all the Q values are decayed
toward 0 by a factor ω. This captures the idea that the
imagination trial can lead to forgetting of the Q values,
independent of any effect of imagination per se. In the
“imagination bonus” model (“imagination” model for
short), reward predictions are distorted by a fixed addi-
tive bias, ε. This captures the idea that imagination can
be contaminated by optimistic or pessimistic beliefs
about unknown rewards. Finally, we considered a hybrid
of these two extended models (the “imagination +
forgetting” model), which includes both parameters.
Parameters were estimated by fitting the model to the
choice data from the decision trials (see Methods for de-
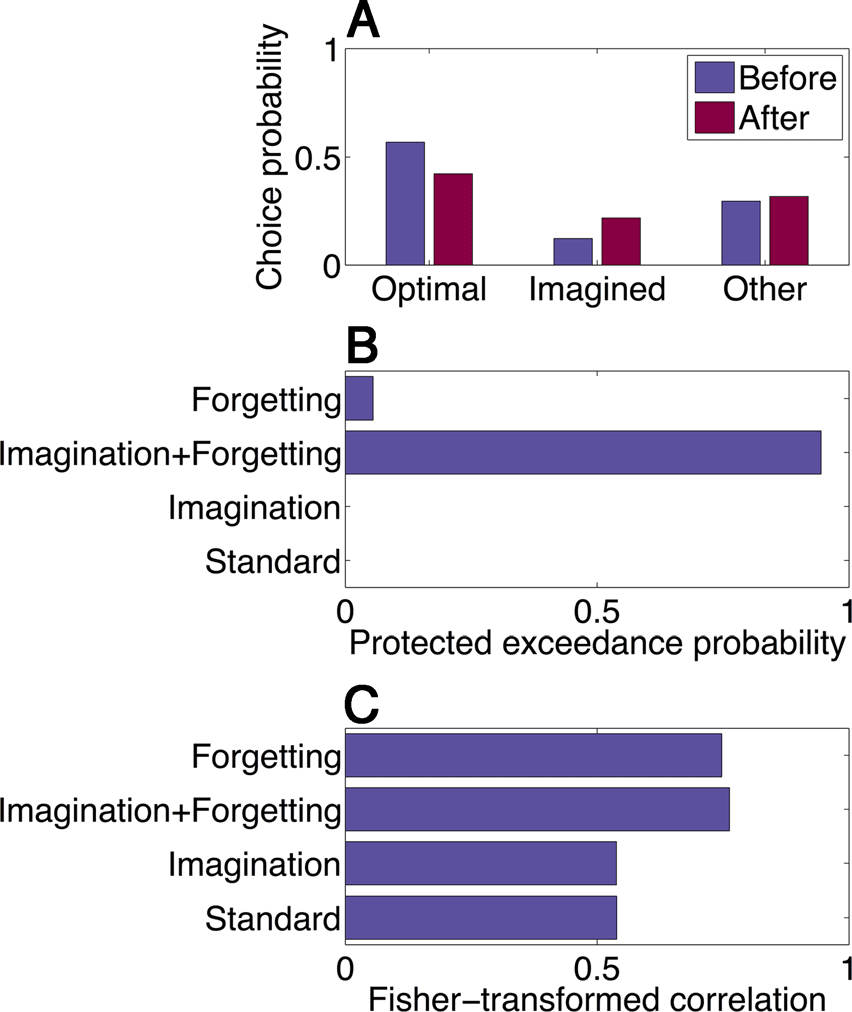
tails). We found that the imagination + forgetting model
could qualitatively capture the pattern of experimental
results (Figure 4A), and random effects Bayesian model
comparison favored this model over the other variants
(protected exceedance probability of .94; Figure 4B).
As an additional test of the models, we matched their
reward predictions on the imagination trials to the empir-
ical data (note that the models were not fit to these data).
The average correlation between model and empirical re-
ward predictions for the imagination + forgetting model
was .57 ± .03 SEM (Figure 4C). After Fisher z transform-
ing to approximate a normally distributed random vari-
able, this correlation was significantly larger than the
correlation for the forgetting model (t(86) = 3.18, p <
.005). Thus, the reward prediction analysis recapitulates
2108
Journal of Cognitive Neuroscience
Volume 29, Number 12
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
c
7
n
7
_
7
a
/
_
j
0
o
1
c
1
n
7
0
_
a
p
_
d
0
1
b
1
y
7
g
0
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
f
.
/
t
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Neuroimaging Results
A separate group of participants (n = 20) completed our
task while their brains were scanned with fMRI. We first
asked whether neural activity during imagination trials
could predict whether imagined or optimal paths would
be taken on the subsequent decision trial. The contrast
between subsequently imagined versus subsequently
optimal paths revealed a striking dissociation between
several brain regions (Figure 5A). Medial pFC, OFC, and
lateral temporal cortex showed greater activity during
imagination trials that lead to choosing the imagined
path on the next decision trial, compared with trials that
lead to choosing the optimal path. The reverse contrast
showed greater activity in regions of the parietal cortex as
well as precuneus, fusiform gyrus, and calcarine sulcus.
Motivated by data indicating involvement of the hippo-
campus in imaginative simulation (Buckner, 2010), we
tested the a priori hypothesis that the hippocampus
would show greater activity for the imagined versus opti-
mal contrast. The hippocampus showed weak bilateral
activation for imagined > optimal (Figure 5B), although
this effect did not survive small-volume correction within
an anatomically defined ROI.
Reward prediction errors derived from temporal differ-
ence models reliably correlate with BOLD signal in the
ventral striatum (Daw et al., 2011; Gläscher et al., 2010;
Seymour et al., 2004). This is the case in our study as well
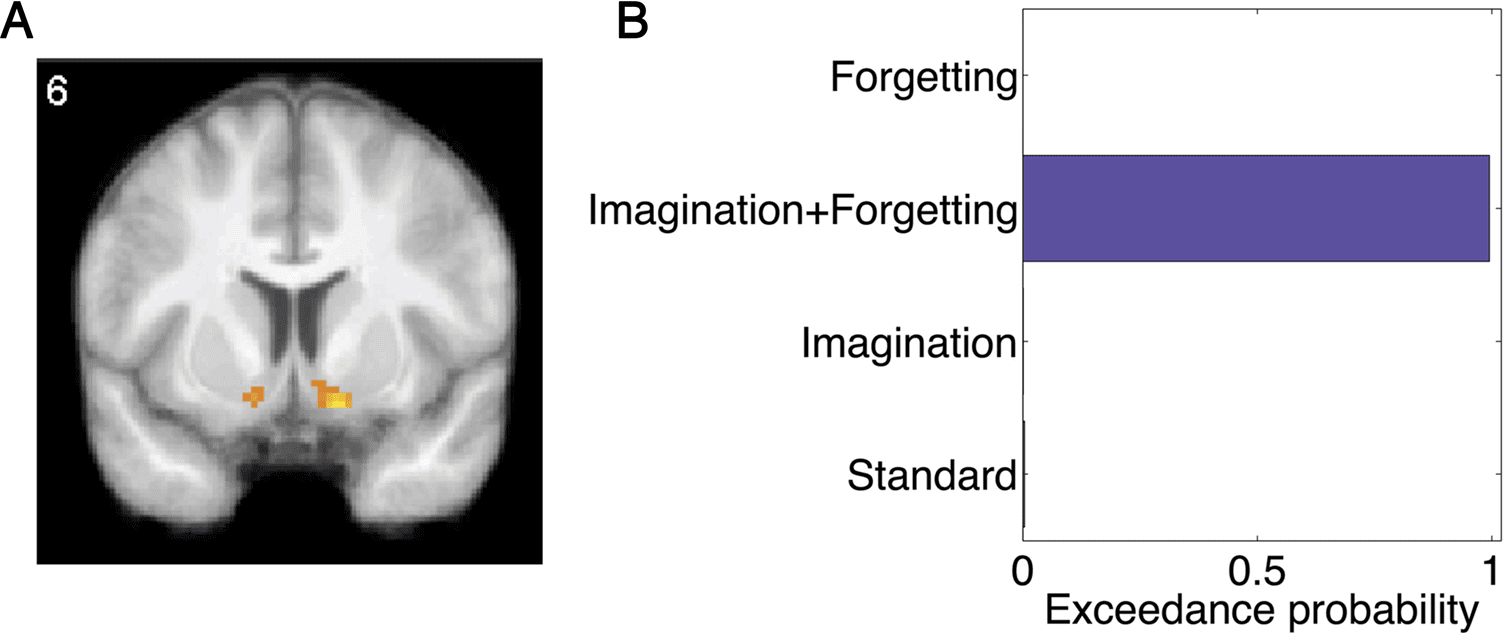
(Figure 6A). Crucially, Bayesian model comparison applied
to the ventral striatum strongly favored the imagination +
forgetting model (exceedance probability of .99; Figure 6B).
Così, the neural and behavioral model comparisons pro-
vide converging evidence for a model in which imagina-
tion both decays and distorts cached values.
Figura 4. Computational modeling. (UN) A reinforcement learning
model that includes both an imagination bonus and a forgetting
parameter can reproduce the pattern of choice behavior in Experiment 1
(compare with Figure 2A). (B) Bayesian model comparison favors
the imagination + forgetting model over models with forgetting only,
imagination only, or a standard model (neither imagination nor
forgetting). The x axis represents the protected exceedance probability
(Rigoux et al., 2014)—the probability that a particular model is more
frequent in the population compared with all other models under
consideration. (C) Models fit to decision trial data correlate with reward
predictions on imagination trials in Experiment 1. The imagination +
forgetting model has a significantly higher correlation compared with
the next best model (forgetting only).
the results of the Bayesian model comparison, support-
ing the imagination + forgetting model as the best quan-
titative account of our behavioral data among the
alternatives we considered.
DISCUSSION
Whereas learning from experience has figured prom-
inently in computational theories of reinforcement
D
o
w
N
l
o
UN
D
e
D
F
R
o
M
l
l
/
/
/
/
j
F
/
T
T
io
T
.
:
/
/
H
T
T
P
:
/
D
/
o
M
w
io
N
T
o
P
UN
R
D
C
e
.
D
S
F
io
R
o
l
M
v
e
H
R
C
P
H
UN
D
io
io
R
R
e
.
C
C
T
.
o
M
M
/
j
e
o
D
tu
C
N
o
/
C
UN
N
R
UN
T
R
io
T
io
C
C
l
e
e
–
P
–
D
P
D
2
F
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
C
7
N
7
_
7
UN
/
_
j
0
o
1
C
1
N
7
0
_
UN
P
_
D
0
1
B
1
sì
7
G
0
tu
.
e
P
S
T
D
o
F
N
B
0
sì
7
S
M
e
IO
P
T
e
M
l
io
B
B
e
R
R
UN
2
R
0
2
io
3
e
S
/
j
.
T
F
/
tu
S
e
R
o
N
1
7
M
UN
sì
2
0
2
1
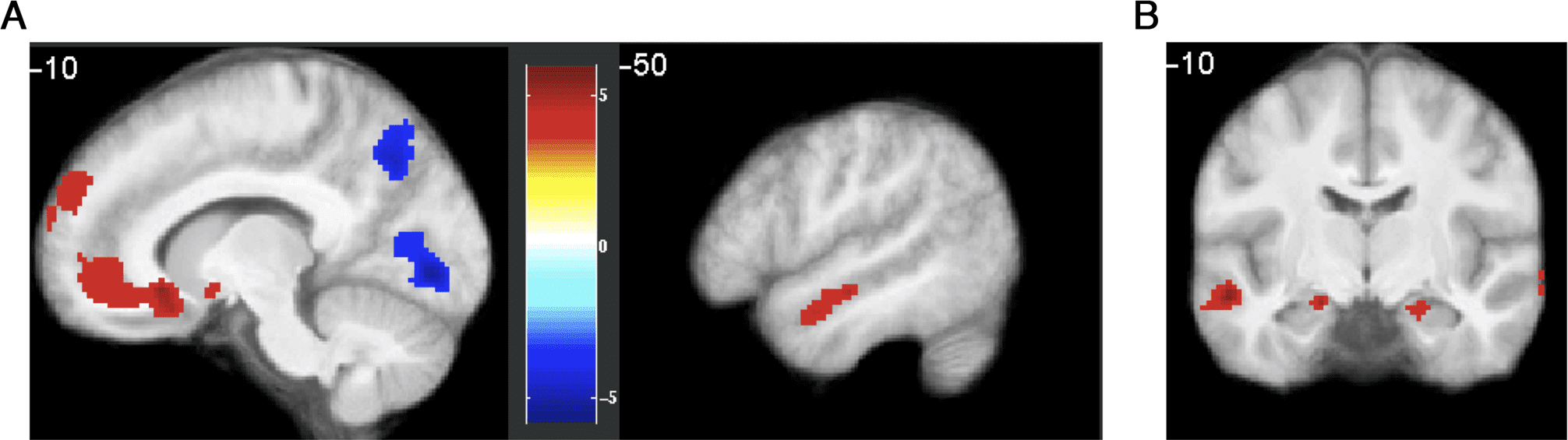
Figura 5. Brain regions showing greater BOLD activity during imagination trials before choosing the imagined path, compared with trials before
choosing the optimal path. (UN) Medial pFC, OFC, and lateral temporal cortex were activated more strongly for imagined > optimal, whereas
inferior parietal, occipital, precuneus, and fusiform regions were activated more strongly for optimal > imagined. Results are thresholded at p < .05,
cluster FWE. (B) Bilateral activation in anatomical hippocampus ROI for optimal > imagined, P < .001, uncorrected. Note that this activation
did not survive small-volume correction.
Gershman, Zhou, and Kommers
2109
Figure 6. Neural model
comparison in the ventral
striatum. (A) Temporal
difference prediction errors
correlated with BOLD activity in
the ventral striatum, p < .001,
uncorrected. The prediction
error regressor was derived
from the imagination +
forgetting model. (B) Bayesian
model comparison within an
anatomically defined ventral
striatum ROI favored the
imagination + forgetting
model.
learning, learning from imagination remains poorly under-
stood. Our experiments provide novel insights into the
contribution of imagination, demonstrating that people
will shift their policies toward imagined paths, even
when these are objectively suboptimal. A key factor in
this “imagination effect” is the miscalibration of reward
predictions: People are consistently optimistic about
how much reward they expect to receive in imagined
states and are more likely to take imagined paths when
they are more optimistic. This optimism can be captured
in reinforcement learning models that learn from both
experience and imagination (Gershman et al., 2014;
Sutton, 1990). Our fMRI data provide converging evidence
for such models, showing that classical value-coding regions,
such as ventromedial cortex and OFC, are more active dur-
ing imagination trials that lead to subsequently choosing the
imagined path.
Two main conclusions can be drawn from our findings.
First, they argue against a plausible alternative hypoth
esis that imagination is cognitively encapsulated from
learning—a kind of “transcendent” use of the imagina-
tion (cf. Kind & Kung, 2016). This hypothesis would pre-
dict that the imagination trials should have no influence
on subsequent decision-making, contrary to our findings.
Instead, they support the “instructive” use of imagina-
tion, whereby an agent can learn new things about the
world purely through acts of imagination. Philosophers
have long debated the epistemic status of such acts, in
particular, whether imagination can produce genuinely
new knowledge (Sorensen, 1992), but regardless of the
answer to this question, our findings demonstrate empir-
ically that imagination can guide reinforcement learning.
The second conclusion is that imaginative simulation is
susceptible to optimism bias (Sharot, 2011). This sug-
gests that, although learning from the imagination is a
powerful tool for going beyond limited experience, it is
susceptible to, and may even amplify, certain cognitive
biases.
One limitation of our study is that we cannot entirely
rule out a demand effect where the participant assumes
that the experimenter is implicitly recommending a
destination in the imagination trials. However, this possi-
bility does not explain why participants are sometimes
negatively miscalibrated (i.e., pessimistic) and why this
miscalibration predicts the imagination effect. Moreover,
it does not explain why participants sometimes chose the
nonimagined/nonoptimal path. Nonetheless, these
observations do not exclude the possibility that demand
effects are exerting an influence on behavior in our task;
further control experiments will be necessary to deci-
sively rule out demand effects.
Acquiring Knowledge through Imagination
Our findings dovetail with several other lines of research
on the role of imagination in learning. Motor skills can
improve after a rest period without additional training
(Korman, Raz, Flash, & Karni, 2003; Walker, Brakefield,
Morgan, Hobson, & Stickgold, 2002), and reactivating
memories during sleep can enhance subsequent task
performance (Oudiette & Paller, 2013). Explicit mental
practice tasks have yielded similar results (Tartaglia,
Bamert, Mast, & Herzog, 2009; Wohldmann, Healy, &
Bourne, 2007; Driskell, Copper, & Moran, 1994).
Mast and Kosslyn (2002) provide a striking example of
learning from imagination in the domain of visual percep-
tion. They presented participants with an ambiguous im-
age whose alternative interpretation was only revealed
after rotating it. Critically, participants could discover this
alternative interpretation by mentally rotating the image,
indicating that imagery is sufficient for discovering new
information about the world.
Similar processes may underlie ubiquitous (yet still
mysterious) animal learning phenomena such as sponta-
neous recovery and latent inhibition (Ludvig, Mirian,
Kehoe, & Sutton, 2017). Another animal learning phe-
nomenon that may lend itself to this analysis is “paradox-
ical enhancement of fear” (Rohrbaugh & Riccio, 1970):
Animals conditioned to associate a tone and a shock will
increase their fear after being presented with a single iso-
lated tone, despite the fact that this presentation is oper-
ationally an extinction trial and would be expected to
2110
Journal of Cognitive Neuroscience
Volume 29, Number 12
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
c
7
n
7
_
7
a
/
_
j
0
o
1
c
1
n
7
0
_
a
p
_
d
0
1
b
1
y
7
g
0
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
t
.
/
f
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
decrease fear. This finding might be accommodated by
positing that the animal is learning from the reinforcing
effects of an imagined shock.
Interactions between Model-based and Model-free
Reinforcement Learning
The current standard theory of reinforcement learning in
the brain depicts two systems (one model-based and one
model-free) locked in competition for control of behav-
ior (Kool, Cushman, & Gershman, 2016; Dolan & Dayan,
2013; Daw et al., 2011; Daw, Niv, & Dayan, 2005). Con-
siderable evidence supports this theory, including the
fact that the systems can be independently manipulated
both neurally (Smittenaar, FitzGerald, Romei, Wright, &
Dolan, 2013; Wunderlich, Smittenaar, & Dolan, 2012;
Balleine & Dickinson, 1998) and behaviorally (Otto,
Gershman, Markman, & Daw, 2013).
Despite its success, the competitive theory is incom-
plete; other lines of research indicate that several forms
of cooperation between the systems also occur (see
Kool, Cushman, & Gershman, in press, for a review).
The model-free system may select goals for the model-
based system to pursue (Cushman & Morris, 2015) or
provide value estimates for approximate model-based
planning (Keramati, Smittenaar, Dolan, & Dayan, 2016).
Imaginative reinforcement learning is based on the idea
that influence can flow in the opposite direction, with the
model-based system supplying simulations for training
the model-free system (Gershman et al., 2014; Pezzulo,
Rigoli, & Chersi, 2013; Sutton, 1990).
Neural Substrates of Imaginative
Reinforcement Learning
Several previous studies have examined the neural corre-
lates of imagination during reward-based tasks. Bray,
Shimojo, and O’Doherty (2010) asked participants to
either experience or imagine rewards in the scanner,
finding that medial OFC was active for both experienced
and imagined rewards. This same region was sensitive to
hypothetical rewards in a Pavlovian conditioning task,
along with the midbrain, which parametrically tracked
expectations about the amount of hypothetical reward
(Miyapuram, Tobler, Gregorios-Pippas, & Schultz,
2012). Finally, Bulganin and Wittmann (2015) found that
imagination of rewarding personal events activated the
striatum, midbrain, and hippocampus as well as increased
functional connectivity between these regions.
Johnson and Redish (2005) have suggested that place
cells in the hippocampus may act as the neural substrate
for a simulation engine. The key evidence for this hy-
pothesis comes from studies showing that place cells
replay sequences visited locations during rest and sleep
(see Carr, Jadhav, & Frank, 2011, for a review). Many
human brain imaging studies have also implicated the
hippocampus in imaginative simulation (Buckner,
2010). Consistent with these prior results, we found weak
evidence that hippocampal activity predicted whether
imagined paths would be subsequently taken, with the
caveat that this effect did not survive correction for
multiple comparisons.
In addition to the hippocampus, our analyses revealed
a collection of regions involved in imaginative effects on
decision-making. Broadly speaking, relatively anterior
regions (medial pFC, OFC, and lateral temporal cortex)
predicted the choice of the imagined path, whereas rel-
atively posterior regions (parietal and occipital cortex,
precuneus, fusiform gyrus, and calcarine sulcus) pre-
dicted the choice of the optimal path. A perhaps overly
simplistic functional division would be into anterior
regions dedicated to evaluating the motivational conse-
quences of decisions and posterior regions dedicated
to simulating the perceptual consequences of decisions.
Some of these same regions have been implicated in
several different forms of prospection (Spreng, Mar, &
Kim, 2009).
Prior studies have found that inferior parietal cortex and
precuneus predict correct rejection of imagined informa-
tion during memory retrieval (Kensinger & Schacter,
2006; Gonsalves et al., 2004). In some cases, false memo-
ries are associated with activity in ventromedial pFC
(Kensinger & Schacter, 2006), consistent with our neuro-
imaging results. However, no prior studies have directly ex-
amined the neural processes involved in imagination
during reinforcement learning.
Bug or Feature?
Is imagination useful or hurtful? Clearly, the ability to
imagine certain scenarios without actually experiencing
them can be useful, perhaps even indispensable in the
real world. Most of us do not need to experience killing
someone to know that it has undesirable consequences.
Moreover, simulating such scenarios can exert a powerful
effect on psychophysiological measures of aversion
(Cushman, Gray, Gaffey, & Mendes, 2012), suggesting
that acts of imagination approach the potency of real
experience.
On the other hand, we have demonstrated that imag-
ination falls prey to the well-known optimism bias
(Sharot, 2011), and this in turn influences subsequent
decisions. Our findings are also closely related to another
bias: imagination inflation, the observation that simply
imagining an event can increase one’s judgment of its
likelihood. For example, participants asked to imagine
either Gerald Ford or Jimmy Carter winning the 1976
presidential race subsequently rated the imagined event
as more likely (Carroll, 1978). In essence, our main find-
ing is a reinforcement learning version of imagination
inflation, whereby imagining an event increases one’s
judgment of its value.
Thus, overzealous use of the imagination could easily
go awry. As philosophers have recognized (Kind & Kung,
Gershman, Zhou, and Kommers
2111
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
f
/
t
t
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
c
7
n
7
_
7
a
/
_
j
0
o
1
c
1
n
7
0
_
a
p
_
d
0
1
b
1
y
7
g
0
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
f
/
t
.
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
2016; Sorensen, 1992), the instructive use of the imagina-
tion is critically dependent on its obedience to con-
straints imposed by the real world. If imagination can
be untethered from these constraints, then we may find
ourselves mistakenly using it to transcend reality rather
than to learn about it.
Acknowledgments
This project was made possible through grant support from the
National Institutes of Health (CRCNS R01-1207833). This work
involved the use of instrumentation supported by the NIH
Shared Instrumentation Grant Program, grant number
S10OD020039. We acknowledge the University of Minnesota
Center for Magnetic Resonance Research for use of the multi-
band-EPI pulse sequences. We are grateful to Bradley Doll for
sharing his stimuli, to Florian Froehlich for helping to collect
data, and to Adam Morris for comments on a previous draft
of the article.
Reprint requests should be sent to Samuel J. Gershman,
Department of Psychology, Harvard University, Room 295.05,
52 Oxford St., Cambridge, MA 02138, or via e-mail: gershman@
fas.harvard.edu.
REFERENCES
Balleine, B. W., & Dickinson, A. (1998). Goal-directed
instrumental action: Contingency and incentive learning and
their cortical substrates. Neuropharmacology, 37, 407–419.
Bray, S., Shimojo, S., & O’Doherty, J. P. (2010). Human medial
orbitofrontal cortex is recruited during experience of
imagined and real rewards. Journal of Neurophysiology, 103,
2506–2512.
Buckner, R. L. (2010). The role of the hippocampus in
prediction and imagination. Annual Review of Psychology,
61, 27–48.
Bulganin, L., & Wittmann, B. C. (2015). Reward and novelty
enhance imagination of future events in a motivational-
episodic network. PLoS One, 10, e0143477.
Carr, M. F., Jadhav, S. P., & Frank, L. M. (2011). Hippocampal
replay in the awake state: A potential physiological substrate
of memory consolidation and retrieval. Nature
Neuroscience, 14, 147–153.
Carroll, J. S. (1978). The effect of imagining an event on
expectations for the event: An interpretation in terms of the
availability heuristic. Journal of Experimental Social
Psychology, 14, 88–96.
Cushman, F., & Morris, A. (2015). Habitual control of goal
selection in humans. Proceedings of the National Academy
of Sciences, U.S.A., 112, 13817–13822.
Cushman, F. A., Gray, K., Gaffey, A., & Mendes, W. (2012).
Simulating murder: The aversion to harmful action. Emotion,
12, 2–7.
Daw, N. D., Gershman, S. J., Seymour, B., Dayan, P., & Dolan,
R. J. (2011). Model-based influences on humans’ choices
and striatal prediction errors. Neuron, 69, 1204–1215.
Daw, N. D., Niv, Y., & Dayan, P. (2005). Uncertainty-based
competition between prefrontal and dorsolateral striatal
systems for behavioral control. Nature Neuroscience, 8,
1704–1711.
Dolan, R. J., & Dayan, P. (2013). Goals and habits in the brain.
Neuron, 80, 312–325.
Driskell, J. E., Copper, C., & Moran, A. (1994). Does mental
practice enhance performance? Journal of Applied
Psychology, 79, 481–492.
Feinberg, D. A., Moeller, S., Smith, S. M., Auerbach, E.,
Ramanna, S., Gunther, M., et al. (2010). Multiplexed echo
planar imaging for subsecond whole brain FMRI and fast
diffusion imaging. PLoS One, 5, e15710.
Gershman, S. J., Markman, A. B., & Otto, A. R. (2014).
Retrospective revaluation in sequential decision making: A
tale of two systems. Journal of Experimental Psychology:
General, 143, 182–194.
Gläscher, J., Daw, N., Dayan, P., & O’Doherty, J. P. (2010).
States versus rewards: Dissociable neural prediction error
signals underlying model-based and model-free reinforcement
learning. Neuron, 66, 585–595.
Gonsalves, B. D., Reber, P. J., Gitelman, D. R., Parrish, T. B.,
Mesulam, M. M., & Paller, K. A. (2004). Neural evidence that
vivid imagining can lead to false remembering. Psychological
Science, 15, 655–660.
Johnson, A., & Redish, A. D. (2005). Hippocampal replay
contributes to within session learning in a temporal
difference reinforcement learning model. Neural Networks,
18, 1163–1171.
Kensinger, E. A., & Schacter, D. L. (2006). Neural processes
underlying memory attribution on a reality-monitoring task.
Cerebral Cortex, 16, 1126–1133.
Keramati, M., Smittenaar, P., Dolan, R. J., & Dayan, P.
(2016). Adaptive integration of habits into depth-limited
planning defines a habitual-goal-directed spectrum.
Proceedings of the National Academy of Sciences, U.S.A.,
113, 12868–12873.
Kind, A., & Kung, P. (2016). Knowledge through imagination.
New York: Oxford University Press.
Kool, W., Cushman, F. A., & Gershman, S. J. (2016). When does
model-based control pay off? PLoS Computational Biology,
12, e1005090.
Kool, W., Cushman, F. A., & Gershman, S. J. (in press).
Competition and cooperation between multiple
reinforcement learning systems. In R. W. Morris, A. Bornstein,
& A. Shenhav (Eds.), Goal-directed decision making:
Computations and neural circuits. New York: Elsevier.
Korman, M., Raz, N., Flash, T., & Karni, A. (2003). Multiple shifts
in the representation of a motor sequence during the
acquisition of skilled performance. Proceedings of the
National Academy of Sciences, U.S.A., 100, 12492–12497.
Ludvig, E. A., Mirian, M. S., Kehoe, E. J., & Sutton, R. S. (2017).
Associative learning from replayed experience. http://www.
biorxiv.org/content/early/2017/01/16/100800.
Mast, F. W., & Kosslyn, S. M. (2002). Visual mental images can
be ambiguous: Insights from individual differences in spatial
transformation abilities. Cognition, 86, 57–70.
Miyapuram, K. P., Tobler, P. N., Gregorios-Pippas, L., & Schultz,
W. (2012). BOLD responses in reward regions to hypothetical
and imaginary rewards. Neuroimage, 59, 1692–1699.
Moeller, S., Yacoub, E., Olman, C. A., Auerbach, E., Strupp, J.,
Harel, N., et al. (2010). Multiband multislice GE-EPI at 7 tesla,
with 16-fold acceleration using partial parallel imaging with
application to high spatial and temporal whole-brain fMRI.
Magnetic Resonance Medicince, 63, 1144–1153.
Niyogi, P., Girosi, F., & Poggio, T. (1998). Incorporating prior
information in machine learning by creating virtual examples.
Proceedings of the IEEE, 86, 2196–2209.
Otto, A. R., Gershman, S. J., Markman, A. B., & Daw, N. D.
(2013). The curse of planning: Dissecting multiple
reinforcement-learning systems by taxing the central
executive. Psychological Science, 24, 751–761.
Oudiette, D., & Paller, K. A. (2013). Upgrading the sleeping
brain with targeted memory reactivation. Trends in Cognitive
Sciences, 17, 142–149.
Pezzulo, G., Rigoli, F., & Chersi, F. (2013). The mixed
instrumental controller: Using value of information to
2112
Journal of Cognitive Neuroscience
Volume 29, Number 12
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
c
7
n
7
_
7
a
/
_
j
0
o
1
c
1
n
7
0
_
a
p
_
d
0
1
b
1
y
7
g
0
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
.
f
/
t
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
combine habitual choice and mental simulation. Frontiers in
Psychology, 4, 92.
Rigoux, L., Stephan, K. E., Friston, K. J., & Daunizeau, J. (2014).
Bayesian model selection for group studies—Revisited.
Neuroimage, 84C, 971–985.
Rohrbaugh, M., & Riccio, D. (1970). Paradoxical enhancement
of learned fear. Journal of Abnormal Psychology, 75, 210–216.
Schultz, W., Dayan, P., & Montague, P. R. (1997). A neural
substrate of prediction and reward. Science, 275, 1593–1599.
Seymour, B., O’Doherty, J. P., Dayan, P., Koltzenburg, M., Jones,
A. K., Dolan, R. J., et al. (2004). Temporal difference models
describe higher-order learning in humans. Nature, 429,
664–667.
Sharot, T. (2011). The optimism bias. New York: Pantheon.
Smittenaar, P., FitzGerald, T. H. B., Romei, V., Wright, N. D., &
Dolan, R. J. (2013). Disruption of dorsolateral prefrontal
cortex decreases model-based in favor of model-free control
in humans. Neuron, 80, 914–919.
Sorensen, R. E. (1992). Thought experiments. Oxford: Oxford
University Press.
Spreng, R. N., Mar, R. A., & Kim, A. S. N. (2009). The common
neural basis of autobiographical memory, prospection,
navigation, theory of mind, and the default mode: A quantitative
meta-analysis. Journal of Cognitive Neuroscience, 21, 489–510.
Sutton, R. S. (1990). Integrated architectures for learning,
planning, and reacting based on approximating dynamic
programming. In M. Morgan (Ed.), Proceedings of the
Seventh International Conference on Machine Learning
(pp. 216–224). San Francisco: Morgan Kaufmann.
Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An
introduction. Cambridge, MA: MIT Press.
Tartaglia, E. M., Bamert, L., Mast, F. W., & Herzog, M. H. (2009).
Human perceptual learning by mental imagery. Current
Biology, 19, 2081–2085.
Tzourio-Mazoyer, N., Landeau, B., Papathanassiou, D., Crivello,
F., Etard, O., Delcroix, N., et al. (2002). Automated
anatomical labeling of activations in SPM using a macroscopic
anatomical parcellation of the MNI MRI single-subject brain.
Neuroimage, 15, 273–289.
Walker, M. P., Brakefield, T., Morgan, A., Hobson, J. A., &
Stickgold, R. (2002). Practice with sleep makes perfect:
Sleep-dependent motor skill learning. Neuron, 35,
205–211.
Wohldmann, E. L., Healy, A. F., & Bourne, L. E., Jr. (2007).
Pushing the limits of imagination: Mental practice for learning
sequences. Journal of Experimental Psychology: Learning,
Memory, and Cognition, 33, 254–261.
Wunderlich, K., Smittenaar, P., & Dolan, R. (2012). Dopamine
enhances model-based over model-free choice behavior.
Neuron, 75, 418–424.
Xu, J., Moeller, S., Auerbach, E. J., Strupp, J., Smith, S. M.,
Feinberg, D. A., et al. (2013). Evaluation of slice accelerations
using multiband echo planar imaging at 3T. Neuroimage, 83,
991–1001.
D
o
w
n
l
o
a
d
e
d
f
r
o
m
l
l
/
/
/
/
j
t
t
f
/
i
t
.
:
/
/
h
t
t
p
:
/
D
/
o
m
w
i
n
t
o
p
a
r
d
c
e
.
d
s
f
i
r
o
l
m
v
e
h
r
c
p
h
a
d
i
i
r
r
e
.
c
c
t
.
o
m
m
/
j
e
o
d
u
c
n
o
/
c
a
n
r
a
t
r
i
t
i
c
c
l
e
e
-
p
-
d
p
d
2
f
9
/
1
2
2
9
/
2
1
1
2
0
/
3
2
1
1
9
0
5
3
3
/
2
1
6
6
7
8
o
6
c
7
n
7
_
7
a
/
_
j
0
o
1
c
1
n
7
0
_
a
p
_
d
0
1
b
1
y
7
g
0
u
.
e
p
s
t
d
o
f
n
b
0
y
7
S
M
e
I
p
T
e
m
L
i
b
b
e
r
r
a
2
r
0
2
i
3
e
s
/
j
f
t
/
.
u
s
e
r
o
n
1
7
M
a
y
2
0
2
1
Gershman, Zhou, and Kommers
2113