How Do Feynman - Ricerca sull'intelligenza artificiale specializzata al MIT

How Do Feynman
Diagrams Work?

James Robert Brown
University of Toronto

introduzione

1.
Feynman diagrams (hereafter FDs) are now iconic. Like pictures of the Bohr
atom, everyone knows they have something important to do with physics.
Those who work in quantum ﬁeld theory, string theory, and other esoteric
ﬁelds of physics use them extensively. In spite of this, it is far from clear what
they are or how they work. Are they mere calculating tools? Are they some-
how pictures of physical reality? Are they models in any interesting sense?
Or do they play some other kind of role?

It is safe to say they are linked to some sort of calculation tool, but after
that it is far from clear. If you ask me how to get from Toronto to Montreal,
I could respond two ways: (1) I could tell you to drive north until you reach
the main highway, then turn right and continue on for about ﬁve hours, O
(2) I could give you a map and tell you where you presently are on it. Both
ways provide the information to get you successfully to Montreal. The map in
the second method is clearly a model; the instruction in the ﬁrst method is
clearly not. What I’m going to argue is that Feynman diagrams are a lot like
(1) in spite of appearing a lot like (2). In other words, they are not pictures or
descriptions of reality, nor are they models in any reasonable sense. They play
a different kind of role in physics.

I had many pleasant and productive conversations on FDs with Michael Stöltzner and Mauro
Dorato while we passed the summer of 2012 in Bielefeld. Michael’s student, Jim Talbert wrote
a ﬁne thesis that got us started. Thanks also to Letitia Meynell for several helpful conversations
and especially for bringing serious aesthetic considerations to the issue, and to Adrian
Wüthrich for his excellent recent book, The Genesis of Feynman Diagrams, from which I
learned much and pinched a lot. Adrian, Letitia, Mauro, Michael, and I had a ﬁrst go on
this topic at a joint session at the European Philosophy of Science Association meeting
in Helsinki, agosto 2013. I’m grateful to the audience there for a valuable discussion.

Perspectives on Science 2018, vol. 26, NO. 4
© 2018 by The Massachusetts Institute of Technology

doi:10.1162/posc_a_00281

423

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

424

How Do Feynman Diagrams Work?

It is a truth universally acknowledged, as Jane Austen might say, Quello
anything can stand for anything else. In Pride and Prejudice Elizabeth Bennet
and Mr. Darcy represent gender relations and class tensions in Regency
England. At dinner, someone says a salt shaker stands for Napoleon while
the potato salad represents La Grande Armée. That same salt and salad is
used by another person to model a hydrogen atom; they play the respective
roles of electron and nucleus. Add the pepper as a second electron in orbit
around the salad and we have a model of helium. If we take a sufﬁciently
liberal view, then there could hardly be a question about Feynman diagrams
representing or modeling physical reality. For instance, I could stipulate that
Feynman’s ﬁrst diagram stands for Napoleon and his second for Kutuzov.
Ovviamente, this is silly and nothing useful is likely to come of it—but it could
be done, which is the point. The question is much more interesting when
we put a reasonable constraint on it and require some appropriate sort of
similarity. I can’t say what that similarity is, since there is no consensus on
the nature of similarities in models at all. But I will assume that there is a
clear difference between the two possibilities that I will eventually discuss:
Feynman diagrams might be typical models or representations, on the one
hand, or they might be something very different from that, on the other.

I will begin by mentioning a few background assumptions. Primo, I will
somewhat dogmatically adopt a broadly realist outlook. At times I might be
forced to be speciﬁc about the details of realism, but for the most part my
default position is a fairly common view of the matter. Secondo, let’s assume
standard quantum theory, as normally understood. Consequently, some of my
claims might be incompatible with, Dire, Bohmian mechanics. The aim is to
make sense of FDs in a broad framework that would be generally accepted,
a framework that does not stretch normal credence.

There are a number of questions involved in understanding FDs. How
did they ﬁrst arise? How did they evolve so that they were practically useful
in QED? How were they extended to quantum chromodynamics and other
ﬁelds? These are historical questions and have been well discussed in the
excellent books by Kaiser (2005), Schweber (1994), and Wüthrich (2010).
I am more interested in philosophical issues concerning how FDs are cur-
rently used and why they are successful.

When I say “currently used,” however, I should note that FDs might be
on their way out. New techniques have appeared on the scene that seem
more powerful and could replace FDs as the standard method of calculating
in the near future.1 In that case, I would then be discussing something that

1. A good place to start is Bern et al (2012). See also Brito (http://arxiv.org/abs/1012.4493v2)
for a review, Brito et al (http://arxiv.org/abs/hep-th/0501052v2) for an important preliminary
result, and Arkani-Hamid (arXiv:1012.6030v1 [hep-th]) for important applications.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

425

Figura 1. Simple Feynman diagram: electron-positron interaction. (Time runs
from left to right.)

after 70 years of fruitful service is about to become passé. No matter; IL
nature of FDs remains philosophically interesting even if we are only trying
to make sense of old techniques.2

2. Basic Properties
There are a number of rules for constructing FDs. For the most part I will
stick to QED, where the relevant particles are fermions (electrons e−,
positrons e+) and bosons (photons γ) that can interact with one another.
Diagrams represent the different ways interactions could happen. For ex-
ample, an electron and a positron annihilate each other and in so doing
they create a photon, which in turn creates another electron and positron
(Figura 1).

The phrase “Feynman diagram” is somewhat generic. It often covers
both the diagrams and the process of constructing the mathematical ex-
pression associated with the diagrams. There are, Tuttavia, distinct rules
for each. The process of constructing the mathematical expression to go
with a diagram is, unsurprisingly, known as “the Feynman rules.” I will
brieﬂy explain both, starting with the diagrams.

Three symbols are used to depict QED processes: solid straight lines for
the fermions, wavy lines for photons, and dots or vertices for the interaction.
An electron in the initial state is represented by a solid line with an arrow
, but in the ﬁnal state it is represented by
pointing toward the vertex,
a line with an arrow pointing away from the vertex,
. A positron in
the initial (ﬁnal) state reverses the direction of the arrows. A photon in the
initial or ﬁnal states is represented, rispettivamente, by a wavy line meeting a
. A vertex always has three lines attached to
vertex,

2. I should mention that I had a brief go at this topic several years ago as part of a more
general account of diagrams in science (Brown 1996). My account of FDs in that article was
criticized by Meynell (2008) and Wüthrich (2010). The present paper is an attempt to go
deeper into the issue. My beliefs about how FDs work remains largely intact, somewhat to
my surprise, though I hope they have become a bit more sophisticated and better defended.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

426

How Do Feynman Diagrams Work?

Figura 2. Two second order diagrams of the Compton effect. (Time runs from left
to right.)

Figura 3. Some 4th-order diagrams of the Compton effect.

Esso: one boson, one fermion pointing in, and another fermion pointing out.
The order of a FD is the number of vertices in it. Figura 1 above, for instance,
is second order. The higher the order, the greater the complexity and the more
terms in the corresponding series.3 For a given process draw an FD of lowest
order. There might be more than one at lowest order, so it is important to draw
all possible. The reason for this is Feynman’s particular way of doing quan-
tum mechanics, which is to sum over all possible processes. Così, for in-
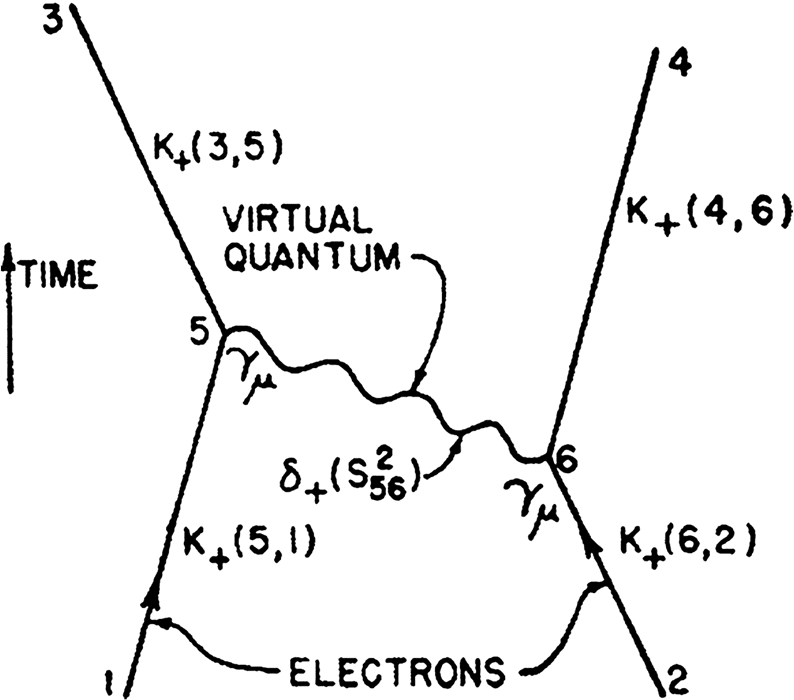
stance, there are two second order diagrams for the Compton effect (Figura 2).
Both of these have the same input (a photon and an electron) and the
same output (a photon and an electron). The electron between the two ver-
tices is a virtual electron. Its existence is very short-lived, so it does not
violate the energy-time uncertainty principle. On the left, a photon and
electron are annihilated; a virtual electron is created; it in turn is annihi-
lated in favor of an electron and photon. On the right, a photon and elec-
tron exchange a virtual electron and create an electron and a photon.

The next step is to draw higher-order diagrams, starting with all possible
4th-order diagrams (four interaction vertices). An electron, for instance,
could emit and absorb a virtual photon. The next ﬁgure (Figura 3) shows
some of the possibilities. In principle we continue drawing higher-order
diagrams; there is no limit. In practice, Ovviamente, we stop after a while, since
there will be no measurable consequences of going beyond a certain point.

3. The terminology is not uniform. Some authors use “1st-order” for diagrams with two
vertices, “2nd-order” for diagrams with four vertices, and so on. Consequently, some cau-
tion is called for when encountering phrases such as “2nd-order effect.”

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

427

Figura 4. Diagram elements corresponding to Feynman rules.

The next step is to construct the series of mathematical terms that are
associated with the elements of each of the diagrams. Freeman Dyson
played a huge role in the development of QED and FDs in particular. Dyson
(1949) proved a crucial result that links the diagrams and the mathematical
terms: There is a one-to-one correspondence between them. Here are some
of the explicit rules for setting up the mathematical expressions.

1.
2.

For each vertex (as in Figure 4(UN)) write ie γα
For each internal photon with momentum k (as in Figure 4(B)) write
i − gαβ/k2+iε
For each internal electron with momentum p (as in Figure 4(C))
write i/p/ − m + iε (where p/ is an instance of the slash notation,
an abbreviation for a long formula that I won’t include here)
For each external electron (as in Figure 4(D)) write ur(P)

Add the terms together. Do this for each diagram. Finalmente, we add all the
terms from all the diagrams and calculate the end result, M, Quale (Quando
squared) gives us the probability of the event.

These are just a few of the many rules. Some of the ones I am skipping
are quite important; for instance, they involve considerations of symmetry
and the requirement that momentum be conserved at each vertex. What I
have included, Tuttavia, should be sufﬁcient for my purposes, which is to
provide an account of three things: an FD, the perturbation series associ-
ated with the FD, and the physical process associated with the perturba-
tion series and hence to the FD. This process of drawing diagrams and
assigning mathematical terms is terminated at some stage. The contribu-
tion coming from higher-order diagrams is rapidly diminishing, so typi-
cally the series is cut off rather soon.

3. Feynman’s Understanding
What did Feynman think of FDs? Did he take them to be pictures of
physical process or were they devices for keeping track of computations,
or perhaps a combination of the two? It is far from clear.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

428

How Do Feynman Diagrams Work?

Figura 5. Feynman’s ﬁrst published diagram (Feynman, 1949UN, 1949B).

Freeman Dyson knew Feynman well and spent many hours with him in
the late 1940s discussing his approach to QED. Ovviamente, this does not
guarantee that he understood Feynman properly, but he was in a good
position to get this right. It seemed to Dyson at this time that Feynman
took his diagrams to provide a picture of physical processes.

In Feynman’s theory the graph corresponding to a particular matrix
element is regarded, not merely as an aid to calculation, but as a
picture of the physical process which gives rise to that matrix
element. Per esempio, an electron line joining x1 to x2 represents the
possible creation of an electron at x1 and its annihilation at x2,
together with the possible creation of a positron at x2 and its
annihilation at x1. (Dyson 1949, P. 496)

Negli anni '60, Tuttavia, Feynman seemed to take a different view. In an
interview with Charles Weiner, Feynman seems to deny that FDs are in
any way a picture or model of reality but are instead an aid to calculation
and nothing more.

Feynman: I can’t tell you when I ﬁrst wrote them. [ … ] I probably
made diagrams to help me think about [perturbation expressions].
[ … ] It was probably not any speciﬁc invention but just a sort of
a shorthand with which I was helping myself think, which gradually
developed into speciﬁc rules for some diagrams. [ … ]

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

429

Weiner: For helping you think physically? In other words, you were
seeing in physical—
Feynman: No, mathematical expressions. Mathematical expressions.
A diagram to help write down the mathematical expressions. (Quoted
in Wüthrich 2010, P. 6)

These are very different accounts of FDs coming from Feynman himself.
Did he change his mind? Was he aware of the tension between these two
views? It is not crucial that we know what he thought about the issue. Ma
it does mean we can’t turn to the creator of FDs as an unimpeachable
authority who might pronounce infallibly on how these things were then
intended to work or how they are intended to work today.

The Issues

4.
FDs are useful for calculating, but do they do anything beyond this?
The principle philosophical issues involving Feynman diagrams are these:

1. Are FDs pictures of physical reality?
2. Do FDs represent (in any sense) physical processes?
3.

If FDs do not represent physical objects or processes, what do they
do and why are they successful at it?

Of the more sophisticated views that I consider wrong are Adrian Wüthrich’s
and Letitia Meynell. Wüthrich contends that FDs “can function simulta-
neously as idealized representation of the phenomena under study and as a
tool for deriving statements about these phenomena” ( Wüthrich 2010,
P. 13). Letitia Meynell (2008) makes a similar claim that FDs can be both
computationally useful and in some important sense representational. My
reply is the same to both: Tool? — yes. Ideal representation? — no.

5. Pictures of Physical Reality
I won’t try to deﬁne “picture,” but take it as understood. Photos and
drawings that closely resemble their targets are obvious examples. They
can be more abstract and still be pictures (think of a Picasso painting),
but there is not likely to be a sharp boundary between pictures and other
forms of representation. With this rough characterization of picture in mind,
we can ask: Are FDs pictures of physical reality, speciﬁcally of quantum
systems?

At ﬁrst glance it might seem so. Freeman Dyson (as I quoted above), In
his famous paper that uniﬁed the theories of Tomonaga, Schwinger, E
Feynman, wrote, “In Feynman’s theory the graph corresponding to a
particular matrix element is regarded, not merely as an aid to calculation,

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

430

How Do Feynman Diagrams Work?

but as a picture of the physical process…” (Dyson 1949, P. 496). FDs
are depicted as processes in space and time; Infatti, they ﬁrst appeared
in Feynman’s article titled “A Space-time Approach…” and they look like
cloud chamber tracks. There is even an interesting similarity with knot
diagrams and the notations used to represent them. Eventually the anal-
ogy breaks down, but it is instructive to compare them, which I will do
momentarily.

A number of people have objected to the idea that FDs are pictures of
physical objects or processes. One of these objections is based on a familiar
feature of quantum mechanics, namely, the non-existence of trajectories. In
an earlier article on this theme I wrote,

Feynman diagrams look like cloud chamber pictures, and they are
often called space-time diagrams. This leads to the confusion. Infatti,
the diagrams do not picture physical processes at all. Invece, Essi
represent probabilities (actually, probability amplitudes). IL
argument for this is very simple. In quantum mechanics (as normally
understood) the Heisenberg uncertainty relations imply that no
particle could have a position and a momentum simultaneously,
which means there are no such things as trajectories, paths, through
space-time. So the lines in a Feynman diagram cannot be representations
of particles and their actual paths through space-time. (Brown 1996,
pag. 265–67)

This point is certainly not new; Bohr made it at Feynman’s first
presentation in 1948 of his account of QED. Feynman, it seems, era
perfectly aware; he was not claiming otherwise. This rejection of FDs as
pictures of motion in space and time seems right as far as it goes, ma il
conclusion that FDs are merely calculation tools is not yet warranted and
has been rightly criticized (Meynell 2008; Wüthrich 2010). There are
other representational possibilities to consider (most recently by Stöltzner
2017).

Before looking in very different places, it is worth considering the
similarity or lack of it in a speciﬁc physics example. The Compton
effect, concerning the interaction of light with electrons, was one of the
most important discoveries in the development of quantum mechanics
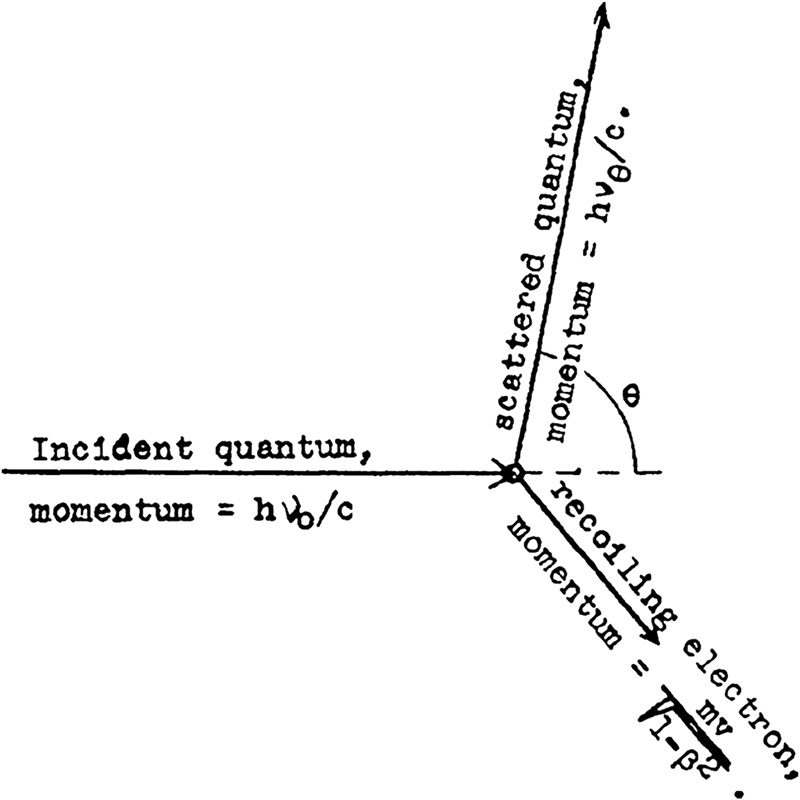
(Compton 1923). Figura 6 is the diagram that appeared in Compton’s
original article.

When this diagram was published in 1923, Heisenberg’s Principle had
not yet arrived on the scene. At that time it would have been taken as a
schematic picture of the actual physical process as it happened in space.
Other diagrams from that period are pretty much the same. It is interesting
to compare them with contemporary FDs of the Compton effect (Figura 7).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

431

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

Figura 6. Compton’s original diagram (Compton 1923).

As representations, they look similar, and so they should both be thought
of as pictures of physical processes or neither should be. As a matter of fact,
neither should for the reason already given — quantum mechanics is in-
compatible with trajectories through spacetime. In the case of the Compton
effect diagram (Figures 6 E 7 [left]) we do take it to be a picture of the
physical process, but the mistake of assuming trajectories is harmless, since
the picture does no serious work. We should not make the same mistake in
the FD version (Figura 7 [right]), since the diagram is instrumental only in
making the relevant calculations.

A second objection to FDs being pictures of the physical realm is based
on their use of virtual particles. In may FDs, a process is depicted that
could not be observed in any sense, because, for instance, it violates the

Figura 7. Two contemporary diagrams of the Compton effect: A standard diagram
(left), and a Feynman diagram (right). (Time runs from left to right.)

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

432

How Do Feynman Diagrams Work?

conservation of energy. Tuttavia, if this process lasts less than a given small
time (cioè., does not violate the time-energy uncertainty relation), then its
existence is not logically ruled out. A number of critics argue that such
virtual entities do not exist. Two attitudes are possible in light of this
objection. One is that physics should reject the use of virtual particles.
The other is that they may be used but we should recognize their merely
instrumental or ﬁctional nature. In either case, diagrams with virtual
entities do not picture reality. Ovviamente, this objection to FDs being pic-
tures is only as good as the objection to virtual particles, but the case
against them is strong. We will not repeat these arguments, but instead
refer readers to a sample from the literature. Vedere, for instance, Bunge
(1970) or Teller (1995).

There is a third objection, weaker than the others but worth mention-
ing. FDs assume a particle interpretation of QED. Such an interpretation
is far from obviously correct and many would dispute it. The point, how-
ever, is that FDs would work perfectly well, even if such a particle inter-
pretation is wrong. So, if FDs were pictures, they would be pictures of
point particles, but if point particles don’t exist, then FDs would still be
successful. Ancora, their success would be a mystery.

6. Free Body Diagrams
There is an interesting analogy with so called free body diagrams (also
known as force diagrams).4 We start with the actual physical situation,
which might be visible, or a fairly realistic diagram or photo. Then we
draw a free body diagram. Usually this is a separate diagram, but it might
be superimposed on the realistic picture. Finalmente, guided by the diagram,
we attach numbers and use them in the appropriate equations to solve
some problem of interest.

Start with a child on a slide. Let’s suppose that the slide is frictionless,
the angle of the slide with the ground is 45°, and the mass of the child is
25 Kg. We want to know the acceleration a of the child. (Figura 8)

There is a straightforward way to do this. The free body diagram shows
all the forces. The force due to gravity Fgravity is resolved into a force that is
normal Fnormal to the slide and a force along the slide Fslide. The last of
these is Fslide = Fgravity × sin 45. Since F = ma, the force Fgravity = mg =
25 × 9.8 Newtons. Così, the force on the child is Fslide = 25 × 9.8 × sin
45 = 173 Newtons. Consequently, the acceleration of the child down the slide
is a = F/m = 173/25 = 6.9 m/s2.

4. Wüthrich (2010, P. 14) uses a similar example, but draws the opposite conclusion,

claiming it is similar to an FD.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

433

Figura 8. Child on slide and free body diagram representing the forces.

The reasoning pattern is simple:

physical system (or realistic picture)
↓
free body diagram
↓
Mathematics

If FDs were analogous to free body diagrams, then the pattern would
be similar:

physical system (or realistic picture)
↓
Feynman diagram
↓
Mathematics

Ovviamente, there is one obvious dis-analogy. In the typical example
drawn from classical physics we have a clear understanding of the phys-
ical system in the sense that we know how to draw a free body diagram
after looking at it (or at a realistic picture) and we know from seeing
the actual system how to attach numbers to the elements of the free
body diagram. This we cannot do in the quantum case. Invece, we
are presented with something of a mystery. Instead of an independently
accessible physical system, we really have little or no idea of how these
processes work. We have little or no idea what the system could be or
how the FDs might be linked to it. Instead of the diagram above, IL
situation seems more like this:

Inaccessible physical system
↓
Feynman diagram ↔ mathematics

The Feynman rules tell us how to link FDs to mathematics, but there
is no guidance from the physical system. Infatti, a significant problem
becomes apparent. What link, if any, is there between the world and
FDs? Why should we think any FD has any relation to reality at all that

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

434

How Do Feynman Diagrams Work?

we could think of as a realistic representation or picture? It seems that FDs
are just a way of helping with calculations. The Feynman rules keep track
of the mathematics by utilizing the FDs. This neatly answered the ques-
zione, how do FDs work? Still it leaves us with a major puzzle that we can
express as a dilemma.

A free body diagram mediates between reality (or realistic picture of
reality) and the mathematical realm with which we calculate measurable
quantities. There are three independently accessible entities involved: IL
physical system, the diagram, and the mathematics. With a FD there are
only two, the diagram and the mathematics. We could get a third element
by having the FD do double duty: we assume it is a realistic picture of
reality and that it is akin to a free body diagram. Or we could be content
with there just being two components, the diagram and the mathematics.
If we take the ﬁrst route, we run into the acknowledged problem of vio-
lating the uncertainty principle, since electrons, and other elementary par-
ticles do not have trajectories. If we take the second route, then we have no
connection between the FD and reality. It would be similar to having a free
body diagram with no idea of what it represents, questo è, no connection to
the world at all. This is our dilemma.

7. Representations
Pictures of physical reality are not the only way to represent. Could FDs
be representations of the physical realm in some more abstract way?
Pictures, Ovviamente, form a range; they can be very similar to their targets
or they can be rather schematic. But there are forms of representation that
are not pictures in any sense. For instance, some periodic process might be
represented by a sine curve (Figura 9), which in turn might be represented
by a Taylor series:

sinx ¼ x − x3=3! þ x5=5! − x7=7! …

Perhaps FDs represent physical processes in this more abstract way, like a
Taylor series. Questo, I think, is Wüthrich’s view.

…it needs to be made clear that Feynman diagrams (certainly by
the time that Dyson systematized the diagrams) are not classical
representations of scattering events. They represent the latter’s
relevant aspects in a more abstract way: they show the connections
between the creation and annihilation events, and these connections
are understood to be the vacuum expectation values of ﬁeld
operators. ( Wüthrich 2010, P. 31)

Letitia Meynell has argued at length for such an account (Meynell 2008).
She acknowledges the argument that says FDs cannot in any ordinary sense

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

435

Figura 9. Sine curve.

be pictures of physical processes but claims that they might be representa-
tions nevertheless at some more abstract level. To this end she develops
and applies the aesthetic views of Kendall Walton on ﬁctions and make-
believe. The crucial distinction she employs is that between “denotation”
and “representation.” The former refers to something but the latter need
non. She concludes that FDs are indeed calculation devices, but that they
are also representations of physical processes. “…we play a kind of make-
believe with the diagrams that allows one to imagine the subatomic
realm” (Meynell 2008, P. 55). Could it be that FDs are calculation tools
and represent physical processes in some highly abstract sense? I will con-
sider some proposals, but ﬁrst, a brief discussion of the nature of applied
mathematics.

8. How Does Mathematics Hook onto the World?5
Let us assume two distinct realms: one is a mathematical realm, che è
rich enough to represent the second, a physical realm. We pick out an
aspect of the physical world and ﬁnd a similar mathematical structure to
represent it. Per esempio, weight is represented on a numerical scale. IL
main physical relations among objects that have weight determined, Dire,
by a balance beam, are that some have more weight than others and that
when objects are combined, their joint weight is greater than either of
their individual weights. Weight can then be represented by any mathe-
matical structure, such as the positive real numbers in which there is a
greater-than relation matching the physical greater-than relation, and an
addition relation matching the physical combination relation.

More generally, a mathematical representation of a non-mathematical
realm occurs when there is a homomorphism between a relational system

5. This section is adapted from Brown (2008).

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

436

How Do Feynman Diagrams Work?

P and a mathematical system M. P will consist of a domain D and rela-
tions R1, R2, … deﬁned on that domain; M similarly consists of a domain
D* and relations R*1, R*2, … on that domain. A homomorphism is a
mapping φ from D to D* that preserves the structure in an appropriate
modo. Consider a simpliﬁed example. Let D be a set of bodies with weight,
let D* = R, the set of real numbers; furthermore, let ≼ and ⊕ be the
relations of physically weighs the same or less than and physical composition.
The relations ≤ and + are the usual relations on real numbers of equal or
less than and addition, rispettivamente. The two systems, Poi, are P = hD,
≼, ⊕i and M = hR, ≤, +io. Numbers are then associated with the bodies
(UN, B, … 2 D) by the homomorphism φ: D → R which satisﬁes the two
conditions:

(1)

(2)

a ≼ b → φ að Þ ≤ φ bð Þ

φ a ⊕ b

Þ ¼ φ að Þ þ φ bð Þ:

In plain English, (1) says that if a weighs the same or less than b, then the
real number associated with a is equal to or less than the number asso-
ciated with b, E (2) says that the number associated with the weight
of the combined object a ⊕ b is equal to the sum of the numbers associ-
ated with the objects separately. In other words, the relations that hold
among physical bodies get encoded into the mathematical realm and
are there represented by relations among real numbers. One of the objects
can be singled out arbitrarily (but usually with an eye to convenience) A
serve as the unit weight, tu, so that φ(tu) = 1.

The crucial point is that mathematics applies to the physical world by
providing models or analogies, not by directly describing things. Strictly
speaking, mass is not a number and force is not a vector, but they are
represented by real numbers and vectors, rispettivamente. The common
phrase “a mathematical description of reality” is misleading if it means
anything more than mathematics being used by a theory in this analog-
ical way.

The physical combination of two bodies with weight, as noted above,
is represented by the addition of two real numbers. But the embedding
homomorphism is not always as simple as in this case. The relativistic
addition of two velocities, Per esempio, is constrained by an upper limit
on their joint velocity. It is instructive to consider the difference.

Imagine a ball thrown forward with speed W inside an airplane that is
ﬂying at speed V with respect to the ground. Take W and V to be speeds,
not the numbers representing them, just as we distinguished weight from
their representing numbers. As outlined above, we associate real numbers

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

437

with these speeds: φ (W ) = w and φ (V ) = v. In Newtonian physics the
composition of speeds takes a simple and familiar form: φ(W ⊕ V ) =
φ(W ) + φ (V ) = w + v. Tuttavia, in relativistic physics the composition
of speeds is more complicated:6

φ W⊕V

Þ ¼

φ Wð

Þ þ φ Vð Þ

φ Wð

1 þ

Þ (cid:2) φ Vð Þ
c2

¼ w þ v
1 þ wv
c2

The shift from Galilean to relativistic addition of speed should be easy to
follow, even though the latter is a departure from common sense. This is
not always the case. Often, after an initial association between the physical
realm and the mathematical, there is still much that is left open. We have
yet to discover the full range of consequences of the initial association.
Major mathematical innovations may be required. But we have said enough
about the application of mathematics to the physical realm to pose our
problem clearly.

With this account of mathematics behind us, we can now more clearly
state the problem of FDs as follows: Do FDs represent the physical system
P or the mathematical system M? Questo è, if FDs represent something,
then what? Do they represent the physical, or the mathematical, both,
or neither? I am going to argue that the correct answer is neither. Before
getting to that, a brief digression to help set the stage.

9. Divergent Series
The perturbation series used by QED does not converge. This was proven
long ago by Dyson (1952). È, Tuttavia, an asymptotic series, so it will
work in the sense of giving useful answers for low order approximations,
but it will eventually diverge as more terms are included. Così, the math-
ematical representation of QED is in an important sense not consistent.
This means that FDs cannot be a consistent representation of anything
in the physical world. They could still be a representation that, perhaps,
is pragmatically useful but not “intelligible.”

A word of explanation about divergent series might be useful. A simple ex-
8 þ …=
,
ample of a convergent series is the series
since it equals 1, a ﬁnite number. The series 1+ 2+ 3+ 4+ … is divergent;
it obviously sums to inﬁnity, as does the series
3 þ …=
.

n ¼ 1 þ 1
=

2n ¼ 1
=

4 þ 1
=

2 þ 1
=

2 þ 1

P∞
1

6. Note that the range of φ is different in the two cases. Letting N be the set of all
possible speeds in the Newtonian case, we have φ : N → R, while in the Einsteinian case,
with E the set of possible speeds, we have φ : E → (−c, C), since c is a bound for any frame of
reference.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

438

How Do Feynman Diagrams Work?

The perturbation series of QED is divergent, but asymptotic, Quale
means that we can truncate it after a few terms and get a useful, ﬁnite
answer. Divergent series are, to say the least, dodgy. The great mathe-
matician Abel called them the Devil’s work and said they should shunned.
Since his day, Tuttavia, mathematicians have grown comfortable with
their use, a use that has become quite fruitful.

In spite of their utility, the divergence of the perturbation series makes
even the following modest attempt at a representational account impossible.

Please understand: these Feynman diagrams are purely symbolic;
they do not represent particle trajectories (as you might see them in, Dire,
a bubble chamber photograph). The vertical dimension is time, E
horizontal spacings do not correspond to physical separations. … All the
diagram says is: “Once there was an electron and a positron; Essi
exchanged a photon; then there was an electron and a positron
again.” (Grifﬁths 1987, P. 59. Cited in Wüthrich 2010, P. 3)

The author wants (quite rightly) to warn readers not to be naïve about
FDs; they do not represent processes in space and time. Tuttavia, he does
Dire, “Once there was an electron and a positron; they exchanged a photon;
then there was an electron and a positron again.” Even this might be
saying too much, as the following considerations suggests.

I now want to put two things together that were mentioned earlier:
ﬁrst, Dyson’s argument for the one-one correspondence between diagrams
and series terms, and second, Dyson’s proof that the series is divergent. To be
precise,

1. There is a one-one correspondence between diagrams and series

terms.

2. The series diverges.
3. Così, the series cannot coherently and correctly represent any phys-

ical process.

4. Therefore, diagrams cannot represent any physical process (ie, cannot

represent in any reasonable sense of the term).

10. Flowcharts
We need a different way of thinking about FDs. I suggest that they are
ﬂow charts. To spell this out, I ﬁrst need to distinguish two kinds of ﬂow
charts: descriptive and prescriptive. A prescriptive ﬂow chart is not a
model of a physical system or process. Instead it is a set of rules, instruc-
zioni, or commands. By contrast, a descriptive ﬂow chart is (at least typ-
ically) a model or representation of some process. Here are two simple
illustrations.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Prescriptive ﬂowchart: A recipe

Descriptive ﬂowchart: Digestion

Perspectives on Science

439

Preheat oven and grease two pans

↓

Stir sugar, ﬂour, eggs, milk,
and coco in large bowl

↓

Pour into the greased pans
↓

Bake for 35 mins at 190 C
↓

Let cool
↓

Stack the two layers and cover
with chocolate frosting

Mouth
↓

Pharynx
↓

Esophagus
↓

Stomach
↓

Small intestine
↓

Large intestine
↓

Rectum (excretion)

It only takes a moment’s reﬂection to see a huge difference. The descriptive
ﬂowchart is a description of reality (a purported description, Ovviamente; it is
fallible). As representations go, it is perfectly straightforward. By contrast,
the recipe does not even try to represent or model reality; it tells us how to
achieve something.

With the descriptive-prescriptive distinction in mind, a FD is, I would
suggest, a prescriptive ﬂowchart. It is a set of commands. È (implicitly)
a set of instructions for assigning equations to physical processes. Wüthrich
suggests something similar, calling them “algorithms.”

That the mathematical expressions M can be reduced to a diagram,
described by Dyson as the “graphical representation of matrix
elements,” might do away with the need to write down a long
integral expression in some cases, but this is not at all the main
function of the diagrams. This visualization of the mathematical
expressions is secondary. Piuttosto, the most important function of the
diagrams is that the graphical rules of connecting vertices and the
subsequent translation into a mathematical expression form an
algorithm to ﬁnd all the non-zero matrix elements, and these alone.
(Wüthrich 2010, P. 155)

There may be a sense in which even a recipe could be said to be represen-
tational: Reality is such that the recipe (above) for a chocolate cake will indeed

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

440

How Do Feynman Diagrams Work?

result in a chocolate cake. Not all recipes do. Particularly unpromising is this
recipe from Macbeth: “Eye of newt, and toe of frog / Wool of bat, and tongue of
dog, / Adder’s fork, and blind-worm’s sting, / Lizard’s leg, and howlet’s wing,
/ For a charm of powerful trouble, / Like a hell-broth boil and bubble.” As
charms go, it has no power. As for making soup for lunch—don’t even ask.

11. Osservazioni conclusive
We have three things to think about: the physical world, the mathematical
realm that represents or models the physical world, and FDs, which seem to
exist independently from the other two. The key question concerns the status
of those diagrams. Are they models of the physical realm? If so, how do they
modello? If they are not representational, then what is their relation to both
the physical realm and the mathematical realm? My answer has been that
FDs are not descriptive or representational in any signiﬁcant sense. Invece,
they are prescriptions, instructions for how to write down the perturbation
series that is a mathematical model of reality. The distinction between de-
scriptive and prescriptive ﬂow charts seems to capture this well.

So, what then is being visualized? I think the answer is simply this: FDs
are geometric representations of probability functions. They are not pictures
of phenomena. We should not confuse the visualization of the technique
for constructing the perturbation series with a visualization of the physical
process modelled by the perturbation series.

Understanding is a nebulous and subjective concept. A spacetime diagram
of a physical process often provides considerable understanding of what is
going on. FDs seem to provide that sort of understanding. But it is an illu-
sion. They are wonderful at what they do, but they explain nothing and they
provide nothing in the way of understanding the workings of nature.

FDs are excellent tools to help with calculations. They are no more than
Quello. They are not pictures, they do not represent anything, and they do not
provide some sort of insight into the quantum realm. Josef Jauch was right
when he complained long ago:

The pragmatic tendency of modern research has often obscured the
difference between knowing the usage of a language and understanding
the meaning of its concepts. There are many students everywhere who
passed their examinations in quantum mechanics with top grades
without really understanding what it all means. Often it is even
worse than that. Instead of learning quantum mechanics in parrot-like
fashion, they may learn in this fashion only particular approximation
techniques (such as perturbation theory, Feynman diagrams or dispersion
relations), which then lead them to believe that these useful techniques
are identical with the conceptual basis of the theory. ( Jauch 1968, P. v)

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

Perspectives on Science

441

Riferimenti
Arkani-Hamid, N., J. Bourjaily, F. Cachazoc, UN. Hodgesd and J. Trnka.
2010. “A Note on Polytopes for Scattering Amplitudes,” arXiv:1012.6030v1
[hep-th] 29 Dicembre.

Brown, James Robert. 1996. “Illustration and Inference.” Pp. 250–268
in Picturing Knowledge: Historical and Philosophical Problems Concerning
the Use of Art in Science. Edited by B. Baigrie. Toronto: University of
Toronto Press.

Brown, James Robert. 2008. Philosophy of Mathematics: A Contemporary
Introduction to the World of Proofs and Pictures. London and New York:
Routledge.

Bunge, Mario. 1970. “Virtual Processes and Virtual Particles: Real
for Theoretical Physics, 3(6):

or Fictitious?” International Journal
507–508.

Bern, Z., Lance J. Dixon and David A. Kosower. 2012. “Loops, Trees, E

the Search for New Physics.” Scientiﬁc American, 306(5): 34–41.

Compton, UN. H. 1923. “A Quantum Theory of the Scattering of X-Rays

by Light elements,” Physical Review, 21(5): 483–502.

Dyson, F. J. 1949. “The Radiation Theories of Tomonaga, Schwinger, E

Feynman.” Physical Review, 75(3): 486–502.

Dyson, F. J. 1952. “Divergence of Perturbation Theory in Quantum Electro-

dynamics,” Physical Review, 85(4): 631–632.

Feynman, R. P. 1949UN. “Space-Time Approach to Quantum Electro-

dynamics.” Physical Review, 76(6): 769–789.

Feynman, R. P. 1949B. “The Theory of Positrons,” Physical Review, 76(6):

749–759.

Grifﬁths, David. 1987. Introduction to Elementary Particles. New York:

Wiley.

Jauch, J. 1968. Foundations of Quantum Mechanics. New York: Addison

Wesley.

Kaiser, D. 2005. Drawing Theories Apart: The Dispersion of Feynman Diagrams

in Postwar Physics. Chicago: The University of Chicago Press.

Meynell, Letitia. 2008. “Why Feynman Diagrams Represent.” International

Studies in the Philosophy of Science, 22(1): 39–59.

Schweber, S. S. 1994. QED and the Men Who Made It: Dyson, Feynman,

Schwinger, and Tomonaga. Princeton: Princeton University Press.

Stöltzner, M. 2017. “Feynman Diagrams as Models.” The Mathematical

Intelligencer, 46–54, DOI 10.1007/s00283-017-9716-z.

Teller, Paul. 1995. An Interpretive Introduction to Quantum Field Theory.

Princeton: Princeton University Press.

Wüthrich, Adrian. 2010. The Genesis of Feynman Diagrams. Dordrecht,

London: Springer.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D

F
/

2
6
4
4
2
3
1
7
9
0
6
4
8
P
o
S
C
_
UN
_
0
0
2
8
1
P
D

B
sì
G
tu
e
S
T

o
N
0
8
S
e
P
e
M
B
e
R
2
0
2
3

442

How Do Feynman Diagrams Work?

Additional Resources
Britto, Ruth. 2010. “Loop Amplitudes in Gauge Theories: Modern Analytic

Approaches.” http://arxiv.org/abs/1012.4493v2

Britto, Ruth, Freddy Cachazo, Bo Feng, and Edward Witten. 2005. “Direct
Proof of Tree-Level Recursion Relation in Yang-Mills Theory.” http://
arxiv.org/abs/hep-th/0501052v2

de Regt, Henk. 2014. “Visualization as a Tool for Understanding.” Perspectives

on Science, 22(3): 377–396.

Harré, R. 1988. Parsing the Amplitudes. Pp. 59–71 in Philosophical Foun-
dations of Quantum Field Theory. Edited by H. R. Brown and R. Harré.
Oxford: Clarendon Press.

Gross, Ari. 2012. “Pictures and Pedagogy: The Role of Diagrams in
Feynman’s Early Lectures,” Studies in History and Philosophy of Modern
Physics, 43: 184–194.

Laudan, l. 1981. “A Confutation of Convergent Realism.” Philosophy of Science,

48(1): 19–49.

Mattuck, Richard. 2012. A Guide to Feynman Diagrams in the Many-Body

Problema, 2nd ed., New York: Dover.

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

:
/
/

D
io
R
e
C
T
.

io
T
.

e
D
tu
P
o
S
C
/
UN
R
T
io
C
e
–
P
D