G e n e rAl A r t i c l e
Inverting the paradigm
From Art to Granular Science
b En jAmIn l E I Gh t o n , FR An ç oI S G uIl lA Rd ,
k A R In EInA v p E R Ez , An d I t A I EInA v
T
C
UN
R
T
S
B
UN
The interface between art and science is an increasingly recognized
source of innovation, yet explorations tend to skew toward art reaping
the benefits of scientific developments. While, today, art is often freely
embraced within scientific fields, it is rarely afforded the freedom to
transform scientific research. The authors explore a new paradigm of
“art-inspired science” by reimagining and computationally simulating an
existing artwork as a dynamic body of cohesive particles. In the process,
hanging forms of “granular stalactites” are identified and subsequently
reproduced in an idealized simulated system. A theoretical “stickiness”
model was then developed to predict their maximum height, which could
have wide technological application. Artworks may therefore serve as
catalysts for distinctive scientific research, allowing a mutually productive
relationship between the disciplines.
The connection between art and science has been extensively
analyzed [1–5], with numerous sources acknowledging that,
historically, both disciplines have frequently been concerned
with the same fundamental concepts [6,7]. While their ap-
proaches are vastly different, both art and science seek to
interpret the world around us. This has famously been seen
through shared interest in the Fibonacci sequence, with art-
ists recognizing the Fibonacci spiral as a guide to balancing
composition and scientists such as Arthur Church explor-
ing Fibonacci geometry in the natural world [8]. As well as
acknowledging this shared motivation, the literature has
increasingly sought to explore the recent upsurge in cross-
pollination between art and science, which has been particu-
larly productive through the adoption of scientific concepts
into artistic endeavors [9–11].
Benjamin Leighton (engineer), School of Civil Engineering, University of Sydney,
NSW 2006, Australia. E-mail: benjaminleighton@me.com.
François Guillard (lecturer, researcher), School of Civil Engineering, University of
Sydney, NSW 2006, Australia. E-mail: francois.guillard@sydney.edu.au. ORCID:
0000-0003-3820-2348.
Karin Einav Perez (brand designer, artist), Brown Hotels, Tel Aviv 6380115, Israel.
E-mail: putchnik@yahoo.com.
Itai Einav (professor, research director), School of Civil Engineering, University of
Sydney, NSW 2006, Australia. E-mail: itai.einav@sydney.edu.au. ORCID: 0000-
0003-2352-1354.
See https://direct.mit.edu/leon/issue/55/5 for supplemental files associated with
this issue.
Figura 1 highlights several examples in which artists have
used modern technologies and scientific understanding at
varying levels of complexity to create innovative works of
art. Figure 1a presents a work from Susan Aldworth’s Brain-
scapes series, in which the artist created etchings of a patient’s
brain scans to provide a unique “portrait” of the person and
an exploration into the question of self. Figure 1b, a “nano
sculpture” by artist Jonty Hurwitz, displays an example of an
artwork relying on cutting-edge technological developments.
The artist has successfully adopted an innovative lithography
process whereby the photons in a high-intensity laser beam
are able to polymerize a photosensitive material and create
three-dimensional forms at the same scale as a human hair.
Figure 1c, akin to the scientific work that is explored below in
this paper, shows an artistic exploration into the dynamics of
granular patterns. The figure shows a small-scale recreation
of Marinus Boezem’s 1964 Sand Fountain. The original work,
an example of land art, saw Boezem install machines in the
sandy Camargue landscape of southern France to create a
fountain of sand that spewed forth from a crater at varying
wind speeds. Examples such as these highlight an evolution
in art that has only been possible through the incorporation
of modern scientific knowledge and tools, an increasingly
common trend [12–14]. On the contrary, while the use of art
within science has become more prevalent [15–17], it has not
been adopted to the same extent [18]. To critique this bias we
explore an example of art-inspired science. In doing so, we
promote an inversion of the existing paradigm and support
a more balanced interaction between art and science.
The catalyst for our art-science exploration began with the
artwork Like a Rock (Fig. 2, top left), by Karin Einav Perez
(2014). The work consists of a geometric web of oil marker
lines set against a background of dark India ink and blank
canvas. It is one piece in the larger series Everything Con-
nects, which Einav Perez developed as an exploration of un-
conscious connection. The artist describes the works in the
series (Fig. 2) as “obsessive art” that bears similarity to the
meditative sketches that many people find themselves draw-
482 LEONARDO, Vol. 55, No. 5, pag. 482–488, 2022
https://doi.org/10.1162/leon_a_02252 ©2022 ISAST
Published under a Creative Commons Attribution 4.0 Internazionale (CC BY 4.0) licenza.
Scaricato da http://direct.mit.edu/leon/article-pdf/55/5/482/2045724/leon_a_02252.pdf by guest on 07 settembre 2023
UN
B
C
Fig. 1. Artists inspired by science: (UN) one of Susan Aldworth’s Brainscapes, aquatint and etching, 30 × 25 cm, 2005 (© Susan Aldworth, image courtesy of the
artist); (B) Jonty Hurwitz’s Trust, polymer nano sculpture, 80 × 100 × 20 microns, 2014 (© Jonty Hurwitz); (C) A modern, small-scale recreation (2021) of Marinus
Boezem’s Sand Fountain (1964) for the exhibition Marinus Boezem. All Shows. (© Marinus Boezem)
ing to keep their hands busy as they speak on the phone.
Each artwork was begun with no clear final image in mind,
and the artist allowed the obsessive geometric patterns to
grow and take on their own forms. In doing so, Einav Perez
found the shapes that naturally emerged could often be re-
lated back to memories or images that resonated with her.
Per esempio, upon reflection, the artist realized that the form
seen in Like a Rock bore similarity to the Devils Tower rock
formation featured in Steven Spielberg’s Close Encounters of
the Third Kind, one of the first films she recalls watching as
a child. Despite not being grounded in any scientific theory,
the artist’s portrayal of geometric patterns prompted the co-
authors to imagine a variety of granular phenomena. Così,
the work was seen to offer an interesting bridge between the
disciplines and a launching point for art-inspired science.
From a granular physics perspective, Like a Rock can be
imagined to reflect patterns such as sandpiles [19], angles
of repose [20], and cohesive granular behavior [21–23]. IL
structure of the artwork itself is also reminiscent of the
Delaunay contact network of a granular system [24]. Con
these similarities as a foundation, we started by imagining
a physical, granular process from which a similar structure
could emerge. In this process, a finite amount of cohesive
(or “sticky”) particles are poured over an intermediate sieve
and discharged through regularly spaced outlets. As they exit
these outlets, some particles stick to the underside of the
intermediate sieve through cohesive bonding and produce
hanging formations of granular stalactites. The remainder of
the particles discharge through to the floor. Eventually, clog-
ging of the outlets allows the formation of a stable pile above.
Scaricato da http://direct.mit.edu/leon/article-pdf/55/5/482/2045724/leon_a_02252.pdf by guest on 07 settembre 2023
Fig. 2. A selection of works
from Karin Einav Perez’s
Everything Connects series,
which explores the concept of
“obsessive art.” The top left
Immagine, Like a Rock (2014),
inspired the granular science of
this paper. (© Karin Einav Perez)
Leighton et al., Inverting the Paradigm 483
UN
B
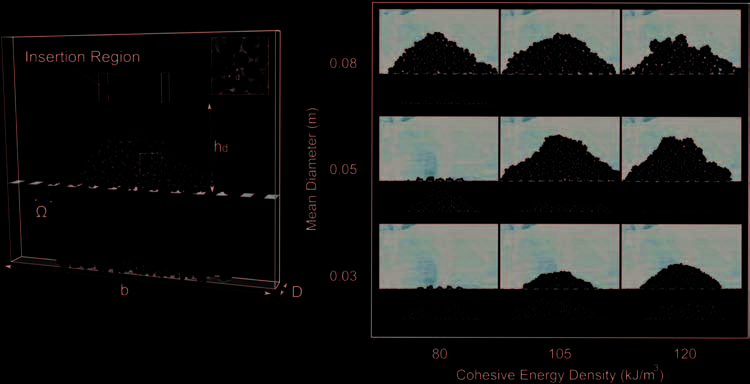
Fig. 3. Discrete Element
Method simulations:
(UN) setup for the recreation
of Like a Rock; (B) phase
diagram illustrating qualitative
observations of system behavior
with changing diameter and
cohesion.
Once at a final state of rest, a snapshot of the system’s contact
network would resemble the image portrayed in Like a Rock.
This imagined system then served as a foundation to explore
a scientific process. To make the leap from art to science, we
performed an investigation in two phases. Initially, we car-
ried out a trial-and-error phase in order to recreate the art-
work by simulating our imagined particulate system using a
physics-based computational model of granular systems. Questo
produced a qualitative understanding of the artwork’s “scien-
tific form” and identified the existence of cohesive hanging
structures. The second phase involved additional simplified
computational simulations that made it possible to quantita-
tively analyze these structures. While essential to the para-
digm proposed, we keep the following technical description
as brief as possible while leaving most of the mathematics to
the Methods section in the Appendix. Those not interested in
the technical process underpinning the scientific result may
wish to skip to the two concluding paragraphs.
The initial qualitative understanding phase was performed
by employing the Discrete Element Method (DEM) [25] A
model the imagined cohesive granular system and recreate
the image seen in Like a Rock (for further details, see Meth-
ods in the Appendix). A simulation domain (Fig. 3UN) era
created containing a simple mesh layer with regularly spaced,
rectangular orifices. Particles of different sizes were inserted
at a fixed mass rate and allowed to cascade over the mesh
and filter through, until clogging occurred. For a fixed outlet
width Ω, we iteratively altered the cohesive energy density
κ (a property that represents the ability of particles to stick),
and mean particle diameter d until a system with an appear-
ance similar to Like a Rock was successfully created.
It was possible to produce a number of qualitative observa-
tions about the behavior of cohesive particulate flow during
this trial and error phase. In particular, we observed that
the grain diameter and cohesive energy density were critical
parameters in shaping the system. Figure 3b graphically sum-
marizes the observed qualitative trends. It can be seen that
both a high κ and large d led to early clogging that prevented
sufficient material from passing through to the lower section.
Conversely, small particle diameters resulted in no visible
clogging and consequently prevented formation of a stable
granular pile above the mesh. This observation aligns with
existing literature regarding the clogging of silos [26,27]. Basso
cohesion was also unsuitable due to the inability of grains to
bond to the underside of the mesh.
Through a balance of these parameters, we identified a
suitable range in which simulations led to a system that had
high visual similarity to Like a Rock. Post-processing was
then used to enhance the visual link, with three-dimensional
high-resolution rendering performed in Blender [28] to aes-
thetically improve each frame individually. An animation
was then created to illustrate the formation of the imagined
system over time. Figures 4a–c display snapshots of this ani-
mation at various time steps. Once a steady state was reached,
all particles were removed to show their centers (Fig. 4D),
and the Delaunay tessellation of these particles was projected
onto a 2D plane (Fig. 4e). A video of this animated process is
available in supplementary materials.
During this trial-and-error recreation, we placed a large
amount of focus on recreating the granular stalactites that
cling from the underside of the intermediate layer. Questo
proved the most subtle phenomenon to capture computa-
tionally but critical to understand in order to successfully
recreate the artwork. Most notably, thanks to the art-driven
computational exploration of these stalactites, we have iden-
tified a current gap in scientific literature surrounding the
micromechanics controlling the thickness of such cohesive
formations. Understanding these physics has the potential
to benefit industrial granular processes where “stickiness” is
a defining factor [29–31]. From our qualitative observations
(Fig. 3B) it became clear that the main factors controlling
these structures are grain properties.
Così, in order to gain a more universal understanding
of hanging formations beneath solid surfaces, we removed
geometrical complexities and performed a second phase of
simulations. In these simulations, the outlets along the hori-
zontal plane are removed. A layer of cohesive grains of thick-
ness h0 is first deposited against the horizontal plane (Fig. 5UN).
The gravity is then progressively increased from 0 to a certain
gc, at which point most of the grains detach as a block from
the plane (Fig. 5B), leaving behind a limited number of grains
that form hanging structures (Fig. 5C).
484 Leighton et al., Inverting the Paradigm
Scaricato da http://direct.mit.edu/leon/article-pdf/55/5/482/2045724/leon_a_02252.pdf by guest on 07 settembre 2023
UN
D
B
e
C
F
Fig. 4. Simulating an
artwork: snapshots of the DEM
simulation at (UN) 0.2 seconds,
(B) 2 seconds, E (C) 5
seconds; (D) particle centers
projected onto a 2D plane;
(e) Delaunay tessellation
projected onto a 2D plane;
(F) the original artwork, Like
a Rock. For further details,
see the video animation in
supplementary materials.
Note that the process always involves a catastrophic de-
tachment of a large block of grains of thickness hc ~ h0, as the
tensile pull from the weight of the grains is maximal near the
plane. As detailed in Methods in the Appendix, one can relate
the maximum tension force that an individual contact could
carry to the mass of the detaching layer. This defines a di-
mensionless proportionality coefficient α (Eq. (9) in the Ap-
pendix), which is a measure of the efficiency of the random
contact force network to hold the grains under gravitational
pulling. Quantitatively, a regular square lattice of grains
where all the contacts are the same on a given horizontal
plane would lead to detachment for α = 1. Tuttavia, natural
grain assemblies do not follow such a regular organization.
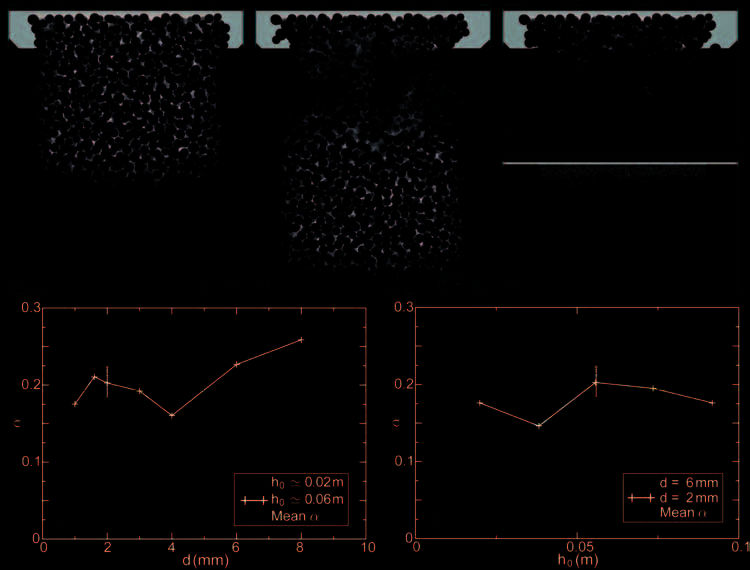
Therefore, to examine the actual value of α, we assembled on
Figs 5e and 5f the results of various simulations with different
initial layer thicknesses and grain sizes. Figure 5e plots the
measured α coefficient for various grain diameters d (using
two different initial layer thicknesses h0). Figure 5f plots the
observed α for various h0 (using two different ds). Note the
10 experimental points under the h0 = 0.06 m and d = 2 mm
cases, which were obtained using repeated experiments for
different randomized initial grain locations, to examine the
Fig. 5. Granular science
from art: three snapshots of
granular layer detachment
under gravitational pulling for
h0 = 0.04 m and d = 2 mm.
(UN) initial granular layer,
(B) during rupture, (C) final
“stalactite” state, E
(D) Delaunay tessellation of
(C) using the same algorithm
adopted for Fig. 4e, IL
measured α coefficient for
various grain diameters d
(using two different initial layer
thicknesses h0) and 4f for
various h0 (for two different ds),
rispettivamente.
Leighton et al., Inverting the Paradigm 485
Scaricato da http://direct.mit.edu/leon/article-pdf/55/5/482/2045724/leon_a_02252.pdf by guest on 07 settembre 2023
uncertainty in the α measurement across the simulations.
From all those simulations a representative α ≈ 0.19 was re-
trieved. This low average α points to the fact that the contact
network is actually quite dispersed and thus ineffective at
holding the suspended grain layer.
D'altra parte, the absence of systematic variation of
with either h0 or d shows that the physical mechanism identi-
fied to derive Eq. (9) in the Appendix is indeed at the origin
of the observed dynamics. Therefore, we may rearrange that
equation with the average value of α . 0.19 from the simula-
tions to define a scaling law for the maximum thickness of
granular material that could be stuck vertically under a plane
for a given gravity constant g:
hc =
2απ3
27
κ3
k2
nϕρg
, α . 0.19, (1)
where ϕ . 0.62 is the volume fraction of grains for dense ran-
dom packings, ρ is the particle density, and κ and kn are the
cohesive energy and normal stiffness at contacts respectively.
Qualitatively, the finding α < 1 highlights the relative weak-
ness of a dense random packing to hold itself from cohe-
sive forces when compared with a regular square lattice of
sticky grains. This could be attributed to at least three ef-
fects, namely (i) that the density of contacts on the fracture
plane is not the same in random and square packings, (ii) that
contact orientations are misaligned from the vertical direc-
tion and thus only partially mobilize the contact adhesion to
act against the gravitational pulling force, and (iii) that only
some contacts are being fully loaded due to the heterogene-
ity of the contact network. Considering these art-inspired
realizations opens the door to future scientific research de-
veloping an analytic mathematical model that would quan-
titatively explain the numerically observed value of α . 0.19
for sticky granular stalactites.
This paper successfully demonstrates that consideration
of artworks provokes unconventional thinking that can be
adapted to produce “art-inspired science.” Through this art-
inspired science, we have shown that it is possible to explore
concepts that may not have been otherwise considered. If
not for our curiosity regarding the artwork Like a Rock and
subsequent desire to model a system that resembled it, it
is unlikely that the authors of this paper would ever have
considered hanging grain stalactites or thought to explore
the mechanics of them. In developing a “stickiness model”
for these stalactites, we have demonstrated that there is a
tangible scientific benefit to exploring the thoughts that de-
velop from an artistic foundation. From this one particular
instance of granular stalactites, it is clear that there is poten-
tial for an inversion of the existing art-science paradigm. Just
as art benefits from the technical innovations of scientific
disciplines, those in the scientific community should look to
draw more frequently on the creative and unorthodox think-
ing that is inherent to art.
Art, by its very nature, prompts each viewer to explore
the artwork and find their own subjective interpretation. In
fact, in discussion with a colleague, we discovered that seeing
Like a Rock caused them immediately to think of their own
work on traffic networks. Similarly, one of the reviewers of
this paper was drawn to thoughts of capillary adhesion and
the Rayleigh-Plateau instability of a falling jet. While this
paper has shown the success of art-inspired science specifi-
cally within the realm of granular mechanics, such alterna-
tive interpretations hint at the possibility of exploring this
across a variety of disciplines. While this exploration has
been seen to some extent [32,33], the attainment of a more
balanced reciprocity between art and science will require it
to be explored on a much larger scale.
AppEndIx
Methods
DeM description. The Discrete Element Method (DEM)
simulations were performed using Liggghts [34]. In the
models, spherical particles interacted elastically using a
Hertz contact model superposed by damping dissipation in
both normal and tangential directions and cohesive force in
the normal direction, while the overall tangential force was
truncated by a frictional threshold. This was calculated for
the normal and tangential forces, respectively, using:
–1
–1
–1
–3
– γn(r*δn)4
2
2
2
νn – Fcohe, (2)
m*
δn
Fn = knr*
–1
–1
–1
νt, µFn4, (3)
Ft = min3kt(r*δn)2
δt – γt(r*δn)4
2
m*
where r* = (1/ri + 1/rj)–1 is the weighted radius and m* =
(1/mi + 1/mj)–1 is the weighted mass of a pair of contacting
i and j particles with radii ri and rj and masses mi and mj,
respectively. Furthermore, δn and δt denote the normal and
tangential interpenetrations between those particles, while
νn and νt are their relative normal and tangential velocities.
For all simulations, the following interparticle model param-
eters were kept constant: normal stiffness kn = 3.7 × 106 Pa,
tangential stiffness kt = 4.5 × 106 Pa, normal damping coef-
ficient γn = 2 × 103 Pa1/2, tangential damping coefficient γt =
1.8 × 103 Pa1/2, and friction coefficient µ = 0.5. Particle masses
were calculated given a constant particle density of ρ = 850
kg. m–3. Further details on the physics behind the two laws
above could be found in [35].
To model cohesive interactions between particles, the
cohesive force Fcohe was calculated using the simple SJKR
(Simple Johnson Kendall Robertson) [36] model of cohe-
sion. This model is computationally efficient as it relates the
cohesive force only to a simplified cohesive energy density
and to the contact area Acontact:
Fcohe = κAcontact. (4)
The equations of motion were solved for all particles by
accounting for their contact forces above using a Verlet al-
gorithm with timestep dt = 10–6 s. Although the simulations
are performed dimensionally for easier physical interpreta-
tions, all the values can be nondimensionalized using the
particle diameter d as unit length, ρπd3/6 as unit mass, and
dt as unit time.
Two separate geometries were established for the two dif-
ferent DEM calculation phases of this paper. The simulation
486 Leighton et al., Inverting the Paradigm
Downloaded from http://direct.mit.edu/leon/article-pdf/55/5/482/2045724/leon_a_02252.pdf by guest on 07 September 2023
domains were created as 3D environments with rectangular
cross sections and narrow nominal depths, to save on com-
putation time.
Substituting δc back into Eq. (5) gives the maximum
tensile force a contact can take in terms of the known
parameters:
DeM model for recreating like a rock . The setup used to
recreate Like a Rock (seen in Fig. 2, top left) was a rectangular
box of width b = 0.3 m and depth D = 0.02 m, with periodic
boundaries in those two directions to prevent unwanted
friction with walls and preserve the dynamics of the falling
mass. Particles were randomly generated at the top using
a mass rate of 0.075 kg.s–1, using a ±20% polydispersity
(variation in grain size).
Particles fell from a “drop height” hd = 0.1 m under the in-
fluence of gravity until they interacted with the intermediate
mesh or particles retained by the mesh. That mesh consisted
of a plane with regularly spaced orifices of width Ω = 13 mm
and thickness 0.5 mm. The cohesive strength κ and particle
diameter d = 2r were systematically altered. Through trial
and error and the phase diagram illustrated in Fig. 3b, these
were identified as the critical parameters in controlling the
system to the desired form.
DeM model of hanging cohesive layers. A simplified setup
was employed to parametrically explore the height of hanging
cohesive formations, where the cohesive energy is fixed to
κ = 100 kJ.m3. The horizontal dimensions were made equal
(b = D = 20d), and particles with ±15% polydispersity in size
were poured over the entire width of the simulation domain
onto a solid plane with no outlets and left to settle until a final
rest state was achieved (Fig. 5a). Following this, the gravity
direction was very slowly reversed and its intensity gradually
increased to eventually induce a catastrophic event where a
layer of particles detached and fell away from the solid plane
(Fig. 5b). This process left only granular stalactites attached
to the plane as shown in Fig. 5c.
Theoretical model. To better understand the governing
mechanism behind the detachment of the cohesive granular
layer under gravity, we develop a simple theoretical model
for the maximum cohesive layer thickness that can support
its own weight under the assumption of a square lattice of
contacts, which are susceptible to break on an assumed
horizontal failure plane (Fig. 6).
At equilibrium, with νn = 0, Eq. (2) can be rewritten to
obtain the attractive normal force on a single contact:
d
2 δn –
Fatt = κn
kn
2
–3
2
Ï·dδn
, (5)
The maximum of Fatt represents the highest cohesive
strength that can be achieved given the grain parameters.
Equation (5) was then differentiated with respect to δn and
equated to zero to determine the critical delta δc, representing
the overlap at which the interparticle attractive force reaches
its maximum:
δc =
4
9
κπ
1
k 22
d, (6)
max ≡ ma
Fatt
δ
x(Fatt) =
2π3
27
κ3
k2
n
d2, (7)
In the simulations we observe a layer of thickness hc de-
taching on an essentially horizontal plane. Dimensionally,
the number of breaking contacts on that plane should scale
with D2/d2. However, in reality the actual maximum force
potentially transmitted vertically through breaking contact
max due to the various contact ori-
can only be a fraction of Fatt
entations and the heterogeneity of the actual force network,
which may be represented by introducing a proportionality
constant α. Considering force equilibrium prior to detach-
ment for a layer of sticky grains of thickness h under gravity
g, we have
αFatt
max
D2
d2 = D2hϕg, (8)
where ϕ . 0.62 is the volume fraction of grains for a dense
random packing. Therefore, using Eq. (7) it is possible to
compute α directly from the simulations for the observed
grain layer thickness at the point of rupture hc under the
critical gravity gc:
α =
k2
nϕρ
27
κ3 = gchc, (9)
2π3
This relation was used to extract numerically observed
values of α at critical rupture points for various simulation
scenarios, as shown in Fig. 5. From that figure, we find a rep-
resentative α . 0.19, which to a leading order is insensitive
to the chosen grain parameters. Therefore, this numerical
proportionality constant could then be used to express the
practical scaling law for critical sticky layer thickness hc un-
der constant gravity g as given by Eq. (1).
Fig. 6. Idealized lattice with a horizontal failure plane passing through
breaking contacts at the point of rupture.
Leighton et al., Inverting the Paradigm 487
Downloaded from http://direct.mit.edu/leon/article-pdf/55/5/482/2045724/leon_a_02252.pdf by guest on 07 September 2023
references and notes
1 R. Taylor, “From Science to Art and Back Again,” Science: Next Wave
27 (2001).
2 M. Kemp, “From Science in Art to the Art of Science,” Nature 434
(2005) pp. 308–309.
3 K. McMullen, “Experimental Physics, Experimental Art,” Nature 434
(2005) pp. 310–311.
4 R. Lupacchini and A. Angelini, eds., The Art of Science: From Per-
spective Drawing to Quantum Randomness (Springer International
Publishing, 2014).
5 C. Sleigh and S. Craske, “Art and Science in the UK: A Brief History
and Critical Reflection,” Interdisciplinary Science Reviews 42, No. 4,
313–330 (2017).
6 M. Kemp, Structural Intuitions: Seeing Shapes in Art and Science
(Charlottesville, VA: University of Virginia Press, 2016).
7 N. Zabusky, “Fluids in Motion: Inspiration and Realization for Art-
ists and STEMists,” Leonardo 48, No. 2, 138–146 (2015).
8 T. Cook, Spirals in Nature and Art: A Study of Spiral Formations
Based on the Manuscripts of Leonardo da Vinci, with Special Reference
to the Architecture of the Open Staircase at Blois, in Touraine, Now
for the First Time Shown to Be from His Designs (London: J. Murray,
1903).
9 Kemp [2].
10 McMullen [3].
11 E. Fratzeskou, “YLEM Journal: Artists Using Science Technology,”
Leonardo 42, No. 1 (2009) p. 78.
12 M. Kemp, “Science in Culture,” Nature 424 (2003) p. 18.
23 S. Luding, “Cohesive, Frictional Powders: Contact Models for Ten-
sion,” Granular Matter 10 (2008) p. 235.
24 B. Delaunay, “Sur la sphere vide : A la mémoire de Georges Voronoï,”
Bulletin de l’Académie des Sciences de L’URSS, Classe des sciences
mathématiques et naturelles 6 (1934) pp. 793–800.
25 P. Cundall and O. Strack, “A Discrete Numerical Model for Granular
Assemblies,” Géotechnique 29, No. 1, 47–65 (1979).
26 K. To, P. Lai, and H. Pak, “Jamming of Granular Flow in a Two-
Dimensional Hopper,” Physical Review Letters 86, No. 1, 71–74 (2001).
27 K. To and P. Lai, “Jamming Pattern in a Two-Dimensional Hopper,”
Physical Review E 66 (2002).
28 T. Roosendaal, “Blender—A 3D Modelling and Rendering Package”:
www.blender.org.
29 B. Adhikari et al., “Stickiness in Foods: A Review of Mechanisms and
Test Methods,” International Journal of Food Properties 4, No. 1, 1–33
(2001).
30 R. Zumsteg and A. Puzrin, “Stickiness and Adhesion of Conditioned
Clay Pastes,” Tunnelling and Underground Space Technology 31 (2012)
pp. 86–96.
31 U. Zafar et al., “A Review of Bulk Powder Caking,” Powder Technology
313 (2017) pp. 389–401.
32 R. Taylor, “Order in Pollock’s Chaos,” Scientific American 287 (2002)
pp. 116–121.
33 E. Gates-Stuart et al., “Art and Science as Creative Catalysts,” Leo-
nardo 49, No. 5, 452–453 (2016).
34 C. Kloss et al., “Models, Algorithms and Validation for Opensource
DEM and CFD-DEM,” Progress in Computational Fluid Dynamics
12, Nos. 2/3, 140–152 (2012).
13 T. Reagan, “Ylem: Serving Artists Using Science and Technology,
1981–2009,” Leonardo 51, No. 1, 48–52 (2018).
35 B. Andreotti, Y. Forterre, and O. Pouliquen, Granular Media: Between
Fluid and Solid (Cambridge Univ. Press, 2013).
14 I. Hediger and J. Scott, eds., Recomposing Art and Science: Artists-in-
Labs (Berlin: De Gruyter, 2016).
15 E. Landhuis, “Cancer Researcher Looks to Artists for Inspiration,”
Proceedings of the National Academy of Sciences 115, No. 5, 826–827
(2018).
16 R. Zattore, “Music, the Food of Neuroscience?” Nature 434 (2005)
pp. 312–315.
17 J. Martin, “A Brief History of Experiments in Art and Technology,”
IEEE Potentials 34, No. 6, 13–19 (2015).
18 I. Plonczak and S. Zwirn, “Understanding the Art in Science and
the Science in Art Through Crosscutting Concepts,” Science Scope
38 (2015) pp. 57–63.
19 H.M. Jaeger, S.R. Nagel, and R.P. Behringer, “Granular Solids, Liq-
uids, and Gases,” Reviews of Modern Physics 68 (1996) pp. 1259–1273.
20 H.M. Jaeger, C.-h. Liu, and S.R. Nagel, “Relaxation at the Angle of
Repose,” Physical Review Letters 62 (1989) p. 40.
21 P.G. Rognon et al., “Dense Flows of Cohesive Granular Materials,”
Journal of Fluid Mechanics 596 (2008) pp. 21–47.
22 P.G. Rognon et al., “Rheophysics of Cohesive Granular Materials,”
Europhysics Letters 74, No. 4, 644–650 (2006).
36 K.L. Johnson, K. Kendall, and A. Roberts, “Surface Energy and the
Contact of Elastic Solids,” Proceedings of the Royal Society A 324, No.
1558, 301–313 (1971).
Manuscript received 27 September 2021.
BenjaMIn leIGhton is a graduate of the civil engineering
faculty of the University of Sydney. He now works in the private
sector and is currently engaged in the construction industry in
Tokyo, Japan.
françoIs GuIllard is a lecturer at the University of Syd-
ney. His research uses numerical and experimental tools to
understand granular flows and brittle porous media.
KarIn eInaV Perez is a brand designer at Brown Hotels
and an established artist who is inspired both by her inner
imaginative soul and by the outside world.
ItaI eInaV is a professor of geomechanics at the University of
Sydney. His research encompasses both theoretical and applied
problems related to granular and porous materials.
488 Leighton et al., Inverting the Paradigm
Downloaded from http://direct.mit.edu/leon/article-pdf/55/5/482/2045724/leon_a_02252.pdf by guest on 07 September 2023