FOCUS FEATURE:
Network Communication in the Brain

Multisensory integration in the mouse cortical
connectome using a network diffusion model

Kamal Shadi

1, Eva Dyer

2, and Constantine Dovrolis

1

1School of Computer Science, Georgia Institute of Technology, Atlanta, GA, USA

2Department of Biomedical Engineering, Georgia Institute of Technology, Atlanta, GA, USA

a n o p e n a c c e s s

j o u r n a l

Keywords: Mouse connectome, Claustrum, Parietal temporal cortex, Network diffusion cascade,
Asynchronous linear threshold model, Hourglass effect

ABSTRACT

Having a structural network representation of connectivity in the brain is instrumental in
analyzing communication dynamics and neural information processing. In this work, we
make steps towards understanding multisensory information flow and integration using a
network diffusion approach. In particular, we model the flow of evoked activity, initiated by
stimuli at primary sensory regions, using the asynchronous linear threshold (ALT) diffusion
modello. The ALT model captures how evoked activity that originates at a given region of the
cortex “ripples through” other brain regions (referred to as an activation cascade). We find
that a small number of brain regions–the claustrum and the parietal temporal cortex being at
the top of the list–are involved in almost all cortical sensory streams. This suggests that the
cortex relies on an hourglass architecture to first integrate and compress multisensory
information from multiple sensory regions, before utilizing that lower dimensionality
representation in higher level association regions and more complex cognitive tasks.

AUTHOR SUMMARY

Having a structural network representation of connectivity in the brain is instrumental in
analyzing communication dynamics and neural information processing. In this work, we
make steps towards understanding multisensory information flow and integration using a
network diffusion approach. In particular, we model the flow of evoked activity, initiated by
stimuli at primary sensory regions, using the asynchronous linear threshold (ALT) diffusion
modello. The ALT model captures how evoked activity that originates at a given region of the
cortex “ripples through” other brain regions (referred to as an activation cascade). We apply
the ALT model to the mouse connectome provided by the Allen Institute for Brain Science. UN
first result, using functional datasets based on voltage-sensitive dye (VSD) imaging, is that the
ALT model, despite its simplicity, predicts the temporal ordering of each sensory activation
cascade quite accurately. We further apply this model to study multisensory integration and
find that a small number of brain regions—the claustrum and the parietal temporal cortex
being at the top of the list—are involved in almost all cortical sensory streams. This suggests
that the cortex relies on an hourglass architecture to first integrate and compress multisensory
information from multiple sensory regions, before utilizing that lower dimensionality
representation in higher level association regions and more complex cognitive tasks.

Citation: Shadi, K., Dyer, E., & Dovrolis,
C. (2020). Multisensory integration in
the mouse cortical connectome using
a network diffusion model. Network
Neuroscience, 4(4), 1030–1054.
https://doi.org/10.1162/netn_a_00164

DOI:
https://doi.org/10.1162/netn_a_00164

Supporting Information:
https://doi.org/10.1162/netn_a_00164

Received: 18 novembre 2019
Accepted: 3 agosto 2020

Competing Interests: The authors have
declared that no competing interests
exist.

Corresponding Author:
Constantine Dovrolis
constantine@gatech.edu

Handling Editor:
Bratislav Misic

Copyright: © 2020
Istituto di Tecnologia del Massachussetts
Pubblicato sotto Creative Commons
Attribuzione 4.0 Internazionale
(CC BY 4.0) licenza

The MIT Press

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

4
4
1
0
3
0
1
8
6
7
1
4
0
N
e
N
_
UN
_
0
0
1
6
4
P
D

.

/

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Multisensory integration in the mouse cortical connectome

INTRODUCTION

Perception requires the integration of multiple sensory inputs across distributed areas through-
out the brain (Stein & Meredith, 1993). While sensory integration at the behavioral level has
been extensively studied (Seilheimer, Rosenberg, & Angelaki, 2014), the network and system-
level mechanisms underlying multisensory integration (MSI) are still not well understood, es-
pecially in terms of the role that cortex plays. The traditional view of primary cortical sensory
areas as processing a single modality is rapidly shifting towards a view of the cortex as highly
integrated and multisensory (Meredith, 2002). The somatosensory, visual, auditory, gustatory,
and other sensory streams come together (integrate) and separate (diverge) to be processed in
different parts of the cortex. The neural basis of how these sensory streams are processed and
how they generate a coherent perceptual state remains elusive (Shine et al., 2019). It is likely
that this state is created and regulated by multiple structures distributed throughout the cortex
working together in concert (Ghazanfar & Schroeder, 2006).

To understand the architectural principles that enable MSI, we need data and models that
span the entire brain—focusing not on individual neurons, regions, or even circuits, but on
distributed networks. The connectome is thus a potentially powerful tool for studying MSI.
Tuttavia, it would not be enough to just know how different brain regions are connected
anatomically. Piuttosto, we need models that combine structure (connectomics) with function
(Barrat, Barthelemy, & Vespignani, 2008) to address the question of which connections and
paths are “activated” by different sensory modalities (Abdelnour, Dayan, Devinsky, Thesen, &
Raj, 2018; Abdelnour, Voss, & Raj, 2014; Park & Friston, 2013; Sporns, 2013; Zhang et al.,
2017). Having both a structural network and a functional model in hand, we can begin to
tackle the problem of discovering the networks that support and constrain MSI.

Here, we adopt a variation of the asynchronous linear threshold (ALT) network diffusion
modello (Worrell, Rumschlag, Betzel, Sporns, & Miši´c, 2017) to capture the communication
dynamics of networks that contribute to MSI. In particular, we focus on how information prop-
agates throughout the brain, starting from different primary sensory regions (per esempio., primary visual
cortex, auditory cortex, and different somatosensory regions). The ALT model assumes that a
“node” (brain region)1 becomes active when more than a fraction of the neighboring nodes it
receives afferent projections from are active. We use a variation of this model with weighted
connections, where the weights are based on the connection density of the projections (Worrell
et al., 2017). The ALT model is simple, yet it incorporates information about distances between
areas (to model connection delays) and uses local information (a thresholding nonlinearity) A
potentially gate the flow of information. With such a model, it is possible to understand how
activation cascades propagate in the brain, and then combine them to study the global archi-
tecture of MSI.

We apply this model to the Mouse Connectivity Atlas provided by the Allen Institute for
Brain Science (Oh et al., 2014). This connectome has been available since 2014, and consists
of estimates of the connection density between cortical as well as subcortical regions, provid-
ing access to information about whole-brain connectivity across functionally and structurally
distinct regions. By coupling the ALT network diffusion model with this representation of the
connectome, we can ask questions such as the following: What is the relative order in which
different regions get activated after, Dire, a visual or auditory stimulation? Which are the most
central regions for each activation cascade? Are these cascades largely independent of each

1 We use the terms node, region, and ROI (region of interest) interchangeably.

Asynchronous linear threshold
(ALT) modello:
A network diffusion model in which
a node becomes active if the
cumulative weight of incoming
connections from active neighbors is
more than a given threshold. Each
connection can also have a distinct
propagation delay.

Network diffusion:
A dynamic process through which
the exogenous activity at one or
more seed nodes spreads, almeno
partially, to the rest of the network
through neighboring nodes.

Activation cascade:
A directed acyclic graph that shows
the network diffusion process from a
given source node that corresponds
to a primary sensory brain region.

Network Neuroscience

1031

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

4
4
1
0
3
0
1
8
6
7
1
4
0
N
e
N
_
UN
_
0
0
1
6
4
P
D

T

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Multisensory integration in the mouse cortical connectome

other, or are there a few “bottleneck” regions through which almost all cascades go through?
If so, which are these regions and what is their topological role in each cascade?

To examine the accuracy of the ALT model, we use voltage-sensitive dye (VSD) imaging to
capture how activity that is triggered from unisensory stimulation in a specific primary sensory
area (per esempio., primary visual cortex, VisP; primary auditory cortex, AudP) propagates throughout
the cortex (Mohajerani et al., 2013). Such comparisons reveal that the ALT model correctly
predicts the temporal ordering of node activations in a cascade when the VSD data provide
sufficient temporal resolution to permit activation time comparisons. This suggests that despite
the simplicity of linear threshold models, they can provide a useful approach for studying
communication dynamics in brain networks.

We then aggregate the unisensory activation cascades predicted by the ALT model to in-
vestigate the architecture of MSI. To do so, we consider the number of activation paths that
traverse each node across all of the different unisensory cascades inferred by the ALT model.
We find that a small set of brain regions (around ten) form a “bottleneck” through which almost
all such activation paths traverse. The claustrum (CLA), despite its small size, is the most cen-
tral bottleneck region in the flow of sensory information from primary sources towards higher
level brain regions (Mathur, 2014). The posterior parietal (PTLp) cortex is the second bottleneck
node, covering almost as many activation paths as CLA.

METHODS AND DATA

The ALT model focuses on how stimulation of one cortical region propagates to the rest of the
brain when constrained by the underlying connectome. In the rest of this section, we describe
the main components of our approach: the mouse connectome, the ALT diffusion model, IL
hourglass network analysis framework, and the VSD-based model validation.

Structural Network

The structural (cioè., anatomical) network we analyze is the Allen Mouse Brain Connectivity
Atlas (Oh et al., 2014), which is based on tracking axonal projections labeled by viral trac-
ers. It consists of 213 regoins of interest (ROIs) that cover the entire brain—all tracer injec-
zioni, Tuttavia, were performed at the right hemisphere (Oh et al., 2014). This means that
the contralateral connections from the left hemisphere to the right and the ipsilateral connec-
tions at the left hemisphere are not mapped. For this reason we analyze only right hemisphere
connections.

The strength of the connection from a source ROI to a target ROI is quantified by a metric
that Oh et al. (2014) refer to as connection density. This metric can be thought of as the total
number of axons from the source ROI to the target ROI, normalized by the size of the target
ROI.

Each connection is associated with a p value that quantifies the statistical confidence that
that connection exists (Oh et al., 2014). We filter out connections with p value higher than
0.05.2 The reason that we do not filter connections based on their weight is because there are
many weak but statistically significant connections, as shown in Figure SI-1. It is well known
that weak connections can play an important role in network diffusion phenomena as long as
there are many of them (Gallos, Makse, & Sigman, 2012).

2 We have repeated the analysis for other p values in the range 0.01-0.1 – see SI Section “Connectome filtering”.

Network Neuroscience

1032

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

4
4
1
0
3
0
1
8
6
7
1
4
0
N
e
N
_
UN
_
0
0
1
6
4
P
D

/

.

T

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Multisensory integration in the mouse cortical connectome

The physical length of the connections is approximated based on the Euclidean distance be-
tween the two corresponding ROIs’ centroids. This is only an approximation but it is probably
accurate because the mouse cortical surface is small and smooth with little folding
(Mota & Herculano-Houzel, 2012; Sun & Hevner, 2014). Additionally, as shown in Section
“Robustness of tau-core nodes,” the results are robust to the selection of the connection weights
or physical lengths.

In most of the analysis, we consider a portion of the mouse connectome that consists of
IL 67 ROIs that cover the four right hemisphere components of the cerebral cortex: isocor-
tex, olfactory areas, hippocampal formation, and cortical subplate. The complete list of these
ROIs is given in Table SI-1. We exclude subcortical ROIs that reside in the cerebellar cortex,
cerebellar nuclei, striatum, medulla, pallidum, midbrain, pons, thalamus, and hypothalamus
for the following reasons.

The cortical network, denoted as Nc, consists of 617 directed edges between 67 nodes;
each node corresponds to one of the ROIs in our model. The density of Nc is 13.9%. IL
distribution of edge weights is skewed, con 80% of the edges having a weight of less than 5
and few edges having a weight of up to 40. The distribution of edge lengths is almost uniform
in the 1–7 mm range. The diameter of the network (maximum shortest path length between
any two nodes) È 7 hops, while a node is on the average about 4 hops away from any other
node. The average in-degree of each node is 9.2 connections (σ = 3.1), while the out-degree
distribution has the same mean but larger variability (σ = 8.3). Additionally, the network Nc is
strongly clustered, with an average clustering coefficient of 60% (Fagiolo, 2007).

IL 10 primary sensory regions associated with the visual, auditory, gustatory, and olfactory
systems, as well as 6 somatosensory regions for different body parts, have a special role in our
analysis: They are viewed as sources of sensory information in the cortex (Bota, Sporns, &
Swanson, 2015; Taylor, Hobbs, Burroni, & Siegelmann, 2015). The complete list and location
of these ten ROIs in the Allen Mouse Brain Atlas are shown at Table SI-2.

The ALT Model and Activation Cascades

The connectome is a structural network and so it constraints, but it does not determine by itself,
the paths through which information flows in the brain. To study that flow, we also need to
model how dynamic brain activity propagates on the connectome.

We choose a simple network diffusion linear threshold model (Granovetter, 1978), mostly
because it involves a single parameter—more realistic neural mass models, such as Wilson-
Cowan, depend on several parameters (Sanz-Leon, Knock, Spiegler, & Jirsa, 2015). The model
assumes that nodes are either inactive (state = 0) or active (state = 1). In the model’s simplest
form, a node i becomes active when more than a fraction θ of its neighbors become active.
Here, we deploy a variation for directed and weighted networks in which each edge is associ-
ated with a communication delay and a weight, referred to as asynchronous linear thereshold
(ALT) modello.

Specifically, the state of node ni is represented by si(T), the neighbors of ni with an incoming
edge to ni are denoted by Nin(ni), the communication delay from node nj ∈ Nin(ni) is tji,
while the weight of that connection is wji. Initially, the state of every node is set to 0, except
the source node of the activation cascade, which is set to active at time t = 0. The state of
each node ni is then updated asynchronously based on the state of its neighbors as follows:

si(T) = 1 if ∑

wji sj(t − tji) > θ,

j∈Nin(io)

where θ represents the activation threshold.

(1)

1033

Network Neuroscience

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

/

/

T

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

4
4
1
0
3
0
1
8
6
7
1
4
0
N
e
N
_
UN
_
0
0
1
6
4
P
D

T

.

/

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Multisensory integration in the mouse cortical connectome

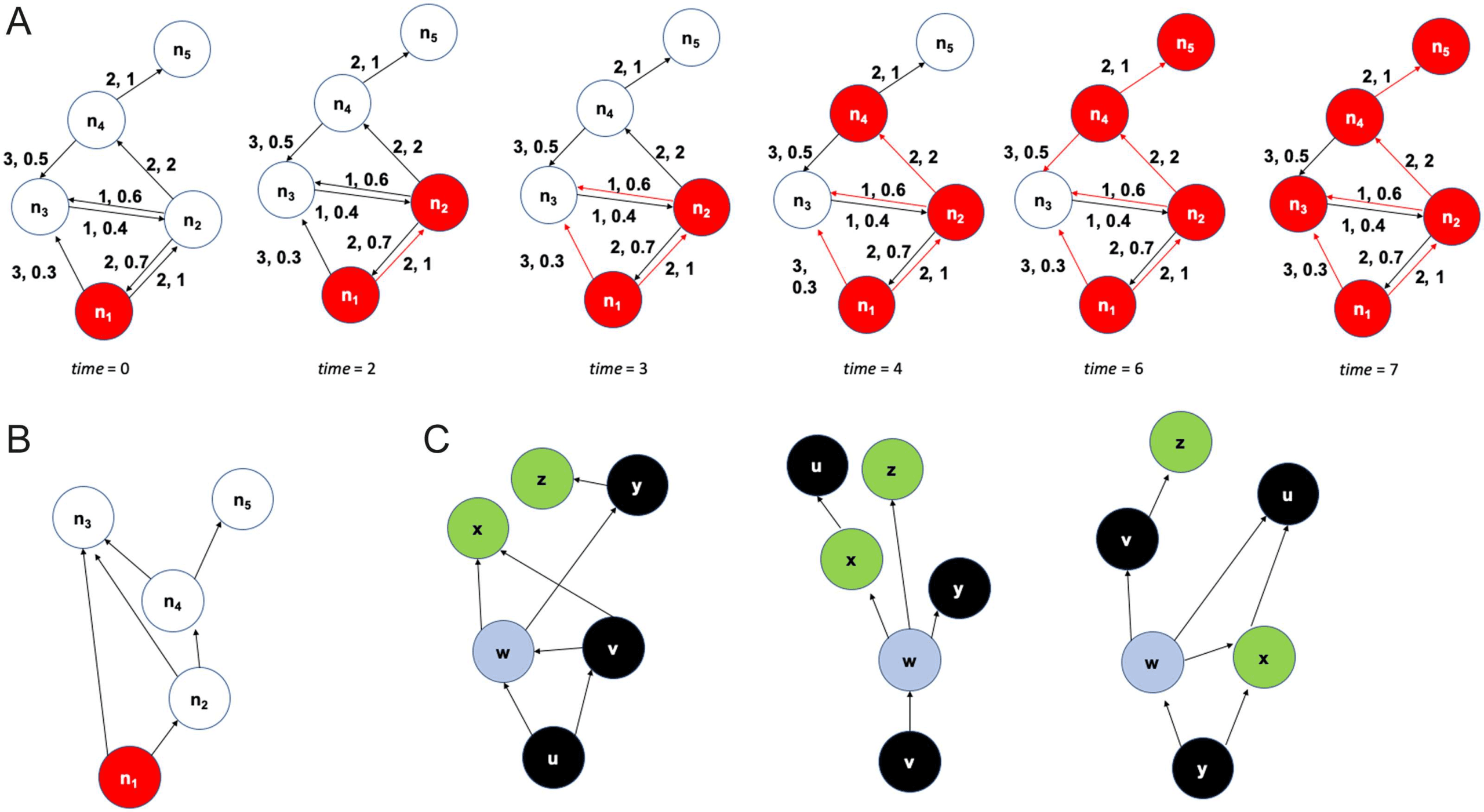
Figure 1A illustrates the ALT model with a toy example, where we can think of each node
as a brain region. IL (directed) edges between nodes represent the structural connections
between the corresponding regions. In this example, the activation threshold θ is set to 1. For
this value, the cascade covers the entire network node within 7 time steps. If θ was larger than
1, the cascade would not take place—the only active node would be n1. As we will see in the
next section, this sharp transition between not having a cascade and a complete cascade as θ
decreases also occurs in the mouse connectome.

An activation cascade also reveals the node(S) that contribute in a causal manner in the
activation of a node. Per esempio, the activation of n1 and of n2 in the previous example is not
sufficient to activate n3; the latter is activated only when n1, n2, and n4 are all active. Suppose
that ta
i denotes the time at which ni becomes active according to the ALT model. We say that
node nj contributes in the activation of ni (denoted by nj → ni) if nj ∈ Nin(ni) and ta
j + tji.
io
In other words, the nodes j that contribute to the activation of ni have a connection to ni and
they should be active at least tji time units before the activation of ni. The set of relations
nj → ni form a directed acyclic graph (DAG) with a single source node that covers all nodes
that participate in the cascade. The DAG edges are a subset of the connections in the underlying
structural network. The cascade for the previous example is shown in Figure 1B.

≥ ta

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

Directed acyclic graph (DAG):
A directed network without cycles.
A DAG always includes one or more
source nodes (no incoming edges)
and one or more terminal nodes
(no outgoing edges).

T

/

/

e
D
tu
N
e
N
UN
R
T
io
C
e
–
P
D

l

F
/

/

/

/

4
4
1
0
3
0
1
8
6
7
1
4
0
N
e
N
_
UN
_
0
0
1
6
4
P
D

T

/

.

F

B
sì
G
tu
e
S
T

T

o
N
0
7
S
e
P
e
M
B
e
R
2
0
2
3

Figura 1.
Illustration of ALT model and τ-core analysis. (UN) A toy example of a five-node network on which we run the ALT model. Each
edge is marked with a communication delay, followed by a weight. The activation threshold is θ = 1. The black edges represent the underlying
structural network, while the red unidirectional edges represent the activation cascade as it unfolds over time. (B) The activation cascade (UN
directed acyclic graph) for the previous toy example. The source of the cascade is n1. (C) A different toy example with three activation cascades
(the sources are nodes u, v, and y). The total number of source-target paths is 12 (5 at the left, 3 at the middle, E 4 at the right). Node w has
the highest path centrality (P(w) = 10/12). If τ ≤ 10/12, the τ-core consists of only that node.

Network Neuroscience

1034

Multisensory integration in the mouse cortical connectome

Analysis of Activation Cascades

An activation cascade consists of a collection of source-target paths, with each such path origi-
nating at the source of the cascade and terminating at a node without any outgoing edges in the
cascade. A source-target path is a sequence of ROI activations that propagate in a causal man-
ner from the source node to a target node. For instance, the cascade of Figure 1B includes three
source-target paths from n1 to n3 because the activation of the latter requires the activation of
n1, n2, and n4.

After constructing a cascade for each source, we use network analysis to identify the nodes
that play a more central role in the collection of all cascades. The centrality metric we use
has the following graph theoretic interpretation: For each node v, the path centrality P(v) Di
node v is the fraction of all source-target paths, across all cascades, that traverse v (following
the terminology of Sabrin & Dovrolis, 2017). Figure 1C illustrates this metric with three small
cascades. Nodes with higher path centrality (PC) are expected to be more important because
the activation cascades depend more heavily on them. Note that a source node is traversed by
all source-target paths in its own cascade but it may have low path centrality when we consider
the collection of all cascades.

l

D
o
w
N
o
UN
D
e
D

F
R
o
M
H

T
T

P

:
/
/

D
io
R
e
C
T
.

M

io
T
.

The PC metric quantifies the importance of each node in isolation. We are interested, on the
other hand, in the smallest set of nodes that can jointly cover almost all source-target paths in
the given set of cascades. To answer this question, we adopt the τ-core definition of Sabrin and
Dovrolis (2017): The τ-core is the minimal set of nodes such that the fraction of source-target
paths that traverse any node in the set is at least τ. The τ-core problem is NP-Hard for τ < 1 (Sabrin & Dovrolis, 2017). It can be approximated with a greedy heuristic in which the node with the highest PC joins the set in each iteration. That node is then removed from all cascades it appears in. The PC of the remaining nodes is recomputed after each iteration. If the τ-core is a small set, relative to the total number of nodes in the network, the nodes of that set can be thought of as the bottleneck of the activation cascades (see Figure 1C for an example). / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d . / t Path centrality: Given a set of activation cascades (one for each sensory source), the path centrality of a node is the total number of source-to-target paths, across all activation cascades, that traverse that node. τ-core: Given a set of activation cascades, the τ-core is a set of nodes (brain regions) that collectively cover at least a fraction τ of all source-to-target paths. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Comparison of Modeling Results With Functional Data To examine whether the ALT model can accurately predict the propagation of sensory stimula- tion in the cortex, we need an experimental setup in which we can stimulate different sensory modalities of a living animal, and monitor at the same time and in a fine temporal resolution (in the order of a millisecond) the activity of different cortical neural populations (in a spatial resolution of few µm). Such experiments are possible today, relying on technologies such as calcium imaging or voltage-sensitive dies (VSD) in conjuction with fluorescence microscopy. Here, we leverage the experimental results of an earlier study to examine the accuracy of the ALT model in the context of whole-cortex imaging in mice under single sensory stimulation (Mohajerani et al., 2013). In brief, the experiments include five types of sensory stimulation: visual (flash), auditory (tone), whisker touch, forelimb touch, and hindlimb touch. Each stimulation experiment is repeated 10 times and on several different animals (we analyze data for five animals). The recorded images cover almost the entire cortical surface, have a temporal resolution of 6.67 ms, and a size of 128 × 128 pixels at a spatial resolution of 50µm/pixel. As it will become clear in Section “Model validation,” the experimental spatial resolution is sufficient for our purposes, given that each network node in the ALT model refers to an entire cortical ROI of the Allen mouse brain atlas. The temporal resolution, however, is marginally sufficient because for about 20–30% of Network Neuroscience 1035 Multisensory integration in the mouse cortical connectome all ROI pairs we cannot tell which ROI gets activated first as they appear to be activated during the same frame. 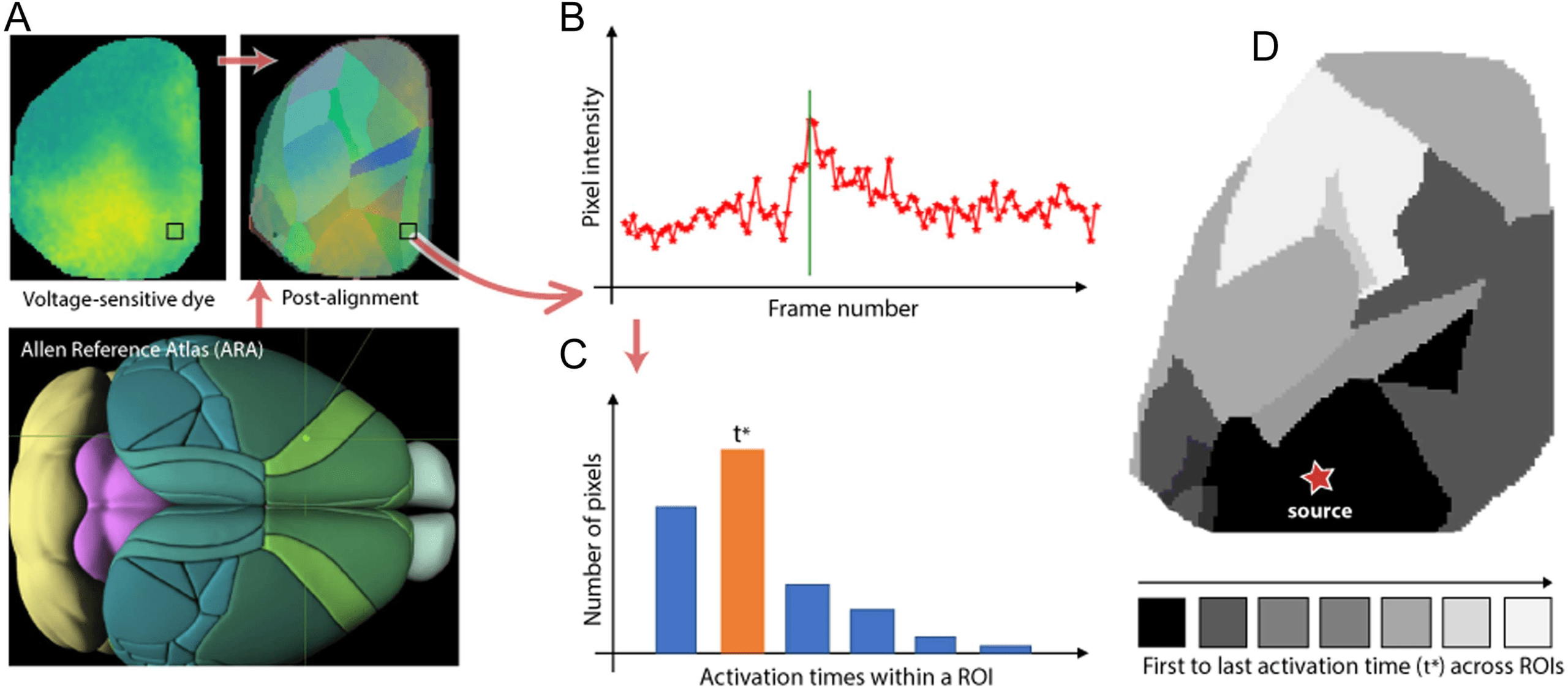To compare the VSD-based results with our modeling results, we perform the following steps: Step 1. Register: Register the native cortical surface of each animal to the Allen Mouse Brain Atlas. This step is performed using an affine transformation that minimizes the least-squares error between the coordinates of the centroid of a primary sensory ROI (e.g., VISp) in the Allen atlas, and the coordinates of the pixel that first gets activated after the corresponding sensory stimulation (visual in this example). We use five primary sensory ROIs to construct this transformation: VISp, SSp-bfd, SSp-ll, SSp-ul, and AUD-p. Step 2. Parcellate into ROIs: Parcellate the native cortical surface into ROIs using the Allen Mouse Brain Atlas and the previous affine transformation. Some cortical ROIs are not visible in the VSD images: FRP, PL, ACAd, VISpl, and VISpor. Also, the MOs region is only partially captured in the VSD images. Step 3. Estimate activation time: Estimate an activation time for each ROI in the experi- mental data. To perform this step, we first identify the maximum poststimulus activity for each pixel in that ROI—this is defined as the activation time of that pixel. The image frame that corresponds to the activation time for most pixels of that ROI is defined as the activation time of the ROI. This processing pipeline is summarized in Figure 2. The ALT model, on the other hand, models each cortical ROI as a single node, and it assumes that the transition of each node from inactive to active occurs instantaneously. We l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 2. VSD data-processing pipeline. (A) Lower: The Allen Reference Atlas (ARA). Upper left: A sample VSD image covering most of the left cortical surface five frames after visual stimulation. Upper right: The ROIs at the left ARA cortical surface mapped to the native cortical surface of an animal. (B) The activation time of a pixel is defined as the frame of maximum poststimulus VSD signal at that pixel. (C) The activation time of an ROI is defined as the activation time of most pixels in that ROI. (D) The output of this pipeline is an activation time for each ROI, depicted here with a gray scale map (black for the first ROI activation and white for the last). Network Neuroscience 1036 Multisensory integration in the mouse cortical connectome examine the consistency of the temporal ordering of activations in the ALT model and in the VSD experiments using both Kendall’s rank correlation coefficient as well as using the follow- ing approach: If X and Y are two ROIs, and X is activated before Y in the modeling results, is it also the case that X is activated before Y in the VSD data? If so, we count that ROI pair as a temporal agreement. If X and Y are activated in the same VSD frame, we count that pair as a case of insufficient temporal resolution. Finally, if X is activated after Y in the VSD data, we count that ROI pair as temporal disagreement. RESULTS Sensory-Specific Activation Cascades in the Mouse Cortex The ALT model requires the selection of a single parameter, the activation threshold θ. This threshold controls the size of the cascade, that is, the fraction of network nodes that become active after the activation of a source node. 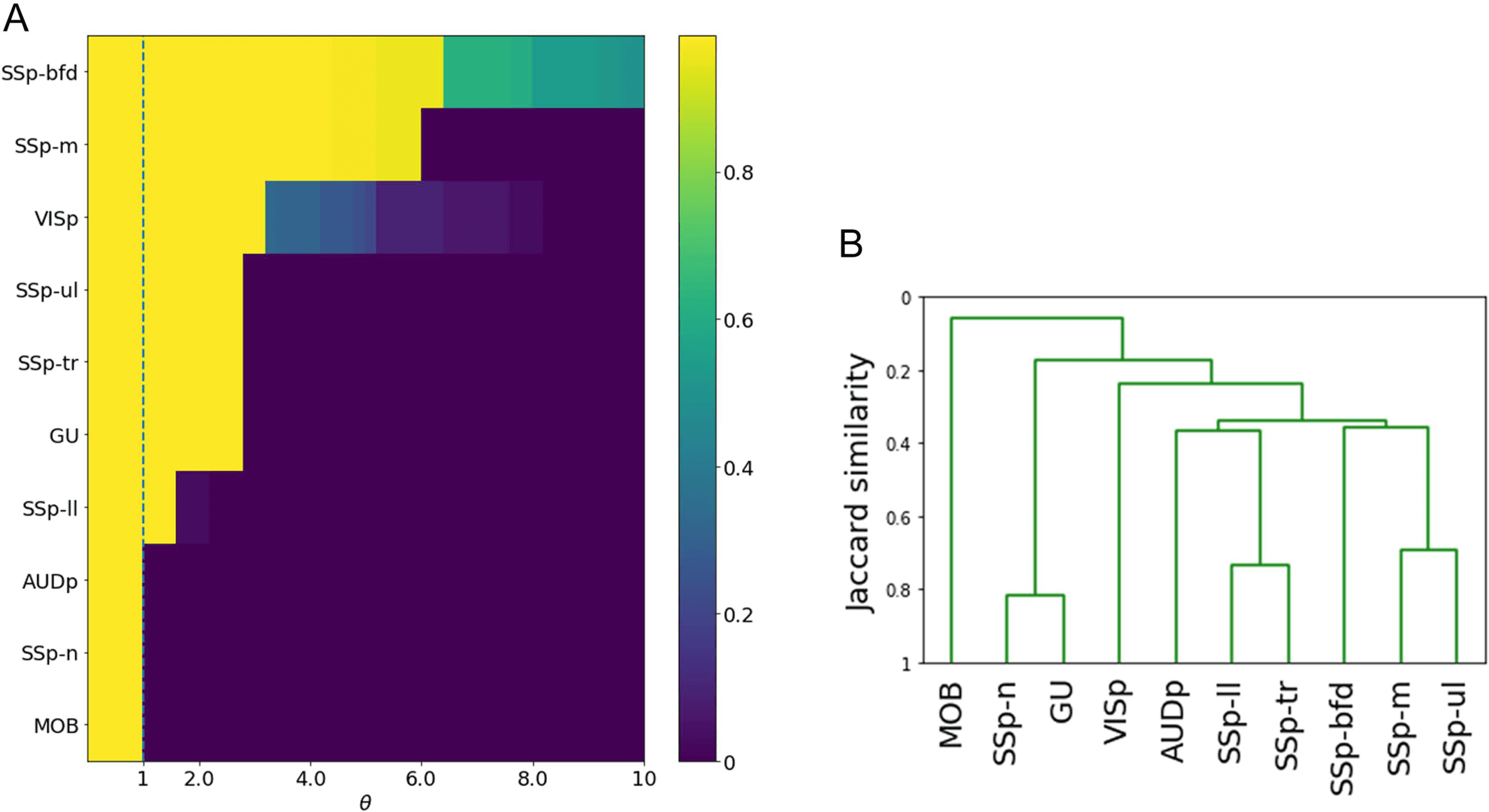One may expect that as θ decreases towards zero, the size of the cascade becomes gradually larger. This is not the case, however. Figure 3A shows that as θ decreases we observe a rapid transition from the absence of a cascade (where only the source node is active) to a complete cascade, in which all nodes become active. This is true for all source nodes listed in Table SI-2. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . The reason behind this rapid transition is the highly clustered topology of the mouse con- nectome. This property is often quantified by the clustering coefficient (Newman, 2018), which has an average value of 0.60 in the mouse connectome. This means that if a node v connects / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 3. Effect of parameter θ on cascade size, and similarity between the 10 cascades. (A) Each row of the heat map shows the fraction of activated nodes after the stimulation of a single source, for different values of the threshold θ. The selected threshold is marked with the dashed vertical line. (B) Similarity between the 10 sensory cascades using the average-linkage hierarchical clustering method. Network Neuroscience 1037 Multisensory integration in the mouse cortical connectome to two nodes u and w, there is a probability of 60% that there is an edge from u to w or in the opposite direction, “closing the triangle” formed by the three nodes u, v, w. So, if v is the source of the activation and θ is low enough so that v activates at least one of its neighbors, say u, it is highly likely that other neighbors of v receive input from u as well, increasing the chances that they will also get activated. The same argument applies to all other pairs of activated nodes—not only the source and its direct neighbors. We choose θ so that the ALT model produces a complete cascade, for every source we con- sider (Beggs & Timme, 2012). This choice is motivated by experimental results (Mohajerani et al., 2013): At least some activity is detected in all cortical regions after sensory stimulation (visual, auditory, touch) in anesthetized mice. It may appear counterintuitive that visual stimu- lation, for example, can impact activity in regions associated with different sensory modalities (e.g., gustatory), but such interactions are possible through the many feedback connections in the connectome, and they are consistent with several prior studies that argue that there are no strictly unisensory regions, and that to some extent the entire cortex is a multisensory organ (Cappe & Barone, 2005; Falchier, Clavagnier, Barone, & Kennedy, 2002; Ghazanfar & Schroeder, 2006; Morrill & Hasenstaub, 2018). Lower values of θ would also result in complete cascades. However, as θ decreases, the dynamics of the underlying cortical networks would move away from the critical boundary between sensitivity to internal or external stimulation and stability (Chialvo, 2010; Plenz & Thiagarajan, 2007). Based on the previous considerations, we select θ = 0.98 asthe lowest value that results in a complete cascade across all sensory modalities. We have repeated the analysis for two more values of θ (0.90 and 0.95) without any significant changes in the results (see SI Section “Sensitivity to activation threshold θ”). Similarity of Sensory Cascades. How similar are the 10 sensory cascades predicted by the ALT model? The similarity between two cascades can be quantified using the Jaccard similarity metric. It is defined as the ratio of the common connections in two cascades over the total number of connections in those cascades. After calculating the Jaccard similarity between every pair of cascades, we use an agglom- erative hierarchical clustering algorithm to construct a dendrogram of the 10 cortical sensory cascades. This dendrogram was computed for three linkage methods: average linkage (the sim- ilarity between two clusters is based on the average similarity across all pairs of cascades in the two clusters), single linkage (based on maximum similarity), and complete linkage (based on minimum similarity). The resulting dendrograms are quite similar across the three linkage methods. Figure 3B shows the dendrogram with average linking—the two others are shown in Figure SI-3. A first observation is that the olfactory cascade (originating at the main olfactory bulb [MOB]) is very different than all other sensory cascades—its similarity is less than 10% with the cluster of all other cascades. This is expected given that olfaction is quite different from all other sensory processes, it bypasses the thalamus, and MOB is the only primary sensory ROI in the mouse connectome that is not located in the isocortex (Johnson, Illig, Behan, & Haberly, 2000; Srinivasan & Stevens, 2017). Interestingly, the two most similar cascades are the gustatory (GU) and the somatosensory cascade of the nose (SSp-n). Further, these two cascades are quite different from all others, in- cluding the rest of the somatosensory cascades. The somatosensory cascades are quite similar Network Neuroscience 1038 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d . t / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome to each other and they tend to cluster as follows: trunk and lower limb (similarity of about 75%), mouth and upper limb (about 70%), while the whiskers produce a significantly differ- ent cascade than the previous four (similarity of about 40%). This organization mirrors the anatomical layout of the somatosensory regions. The auditory and visual cascades are also quite distinct from all other cascades—but not as dramatically different as olfaction. 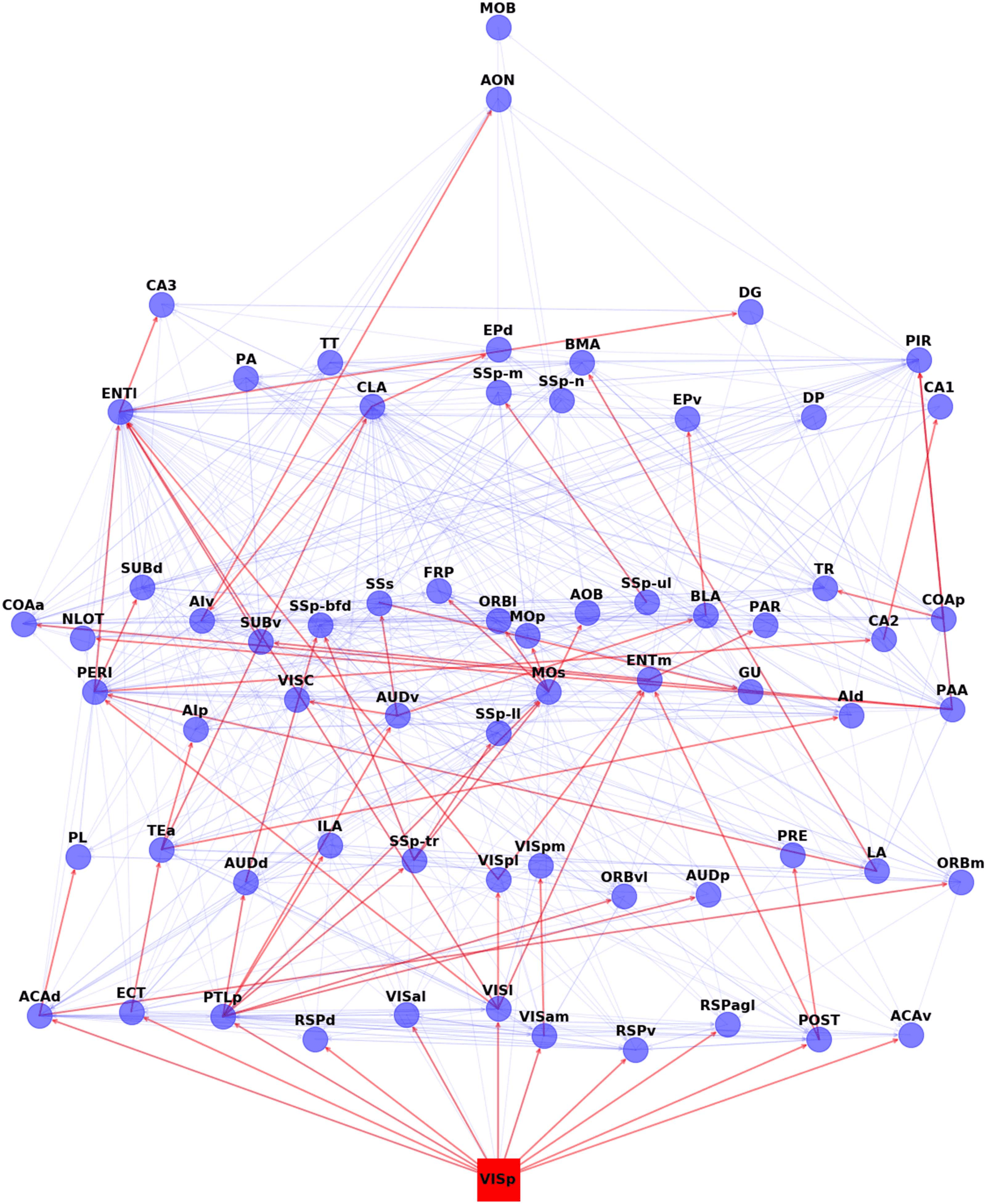Visual Cascade. Figure 4 shows the complete activation cascade when the source of the stim- ulation is the primary visual cortex (VISp)—the corresponding cascades for the other sensory l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 4. The visual activation cascade, according to ALT (θ = 0.98). The source for this cascade is the primary visual cortex (VISp). The red edges form the activation cascade, while the underlying blue edges show anatomical connections that do not participate in this cascade, those connections may be present in other sensory cascades or they may play a role in feedback (or second-order) interactions that are not captured by the “first ripple” scope of the ALT model. To help with the visualization, we place the nodes in eight layers, so that cascade edges only point from a layer to a higher layer (never to the same or lower layer). The vertical position of each node is slightly “jittered” to avoid cluttering due to anatomical connections between nodes of the same layer. Network Neuroscience 1039 Multisensory integration in the mouse cortical connectome modalities are included in the Supporting Information (see SI Section “The ALT cascade of each sensory source”). Note that the activation of the source triggers the activation of 11 other ROIs. Only a few of them, however, play a major role in extending the cascade to the rest of the network: ECT (ectorhinal), PTLp (posterior parietal association), VISl (lateral visual), and POST (postsubiculum). PTLp in particular causes the activation of seven more ROIs at the next step of the cascade. The activation of the claustrum (CLA), in this cascade, takes place through the sequence of ECT, followed by TEa (temporal association). We emphasize that the hierarchical layout shown in Figure 4 is specific to each sensory modality and it represents the activation cascade from the corresponding source to the rest of the cortex. This notion of hierarchy should not be confused with the hierarchical organization of the cortex (Markov et al., 2013) that results from anatomical distinctions of intracortical connections (feedforward versus feedback, based on laminar markers; Harris et al., 2018). The latter is an anatomical hierarchical structure, it is not specific to any particular sensory modality, and it does not convey any functional information about how one ROI may be affecting another in the presence of a specific external or internal stimulation. An activation cascade, on the other hand, reveals the putative sequence and causal dependencies through which ROIs get activated after an initial activation at the source ROI. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 The reader can find the activation cascade of each sensory source in SI Section “The ALT cascade of each sensory source.” It turns out that only about half the connections of the anatom- ical connectome appear in sensory activation cascades, and a quarter of the former appear in only one sensory cascade. In Section Figure SI-4 we examine: which anatomical connections are more important in terms of MSI? The results of that analysis suggest that sensory cascades spread through short connections connecting physically adjacent regions, rather than through the (relatively few) long connections that connect remote regions. Model Validation We examine the validity of the ALT model predictions using functional imaging data dur- ing sensory stimulation experiments, as discussed in “Comparison of Modeling Results With Functional Dat” section. The question we focus on is the following: After stimulating a specific sensory modality (e.g., visual), if the ALT model predicts that an ROI X should be activated before an ROI Y, is it true that X gets activated before Y in the functional imaging data? When this is the case, we count the pair (X, Y) as a temporal agreement. If X gets activated before Y in the ALT model but the opposite is true for the experimental data, we count (X, Y) as a temporal disagreement. Because of the finite temporal resolution in the experimental results (each frame is sampled every 7 ms roughly), there are also cases where X and Y appear to be activated during the same frame, while the model always predicts a temporal difference be- tween two activations. When that is the case, we count (X, Y) as a case of insufficient temporal resolution. 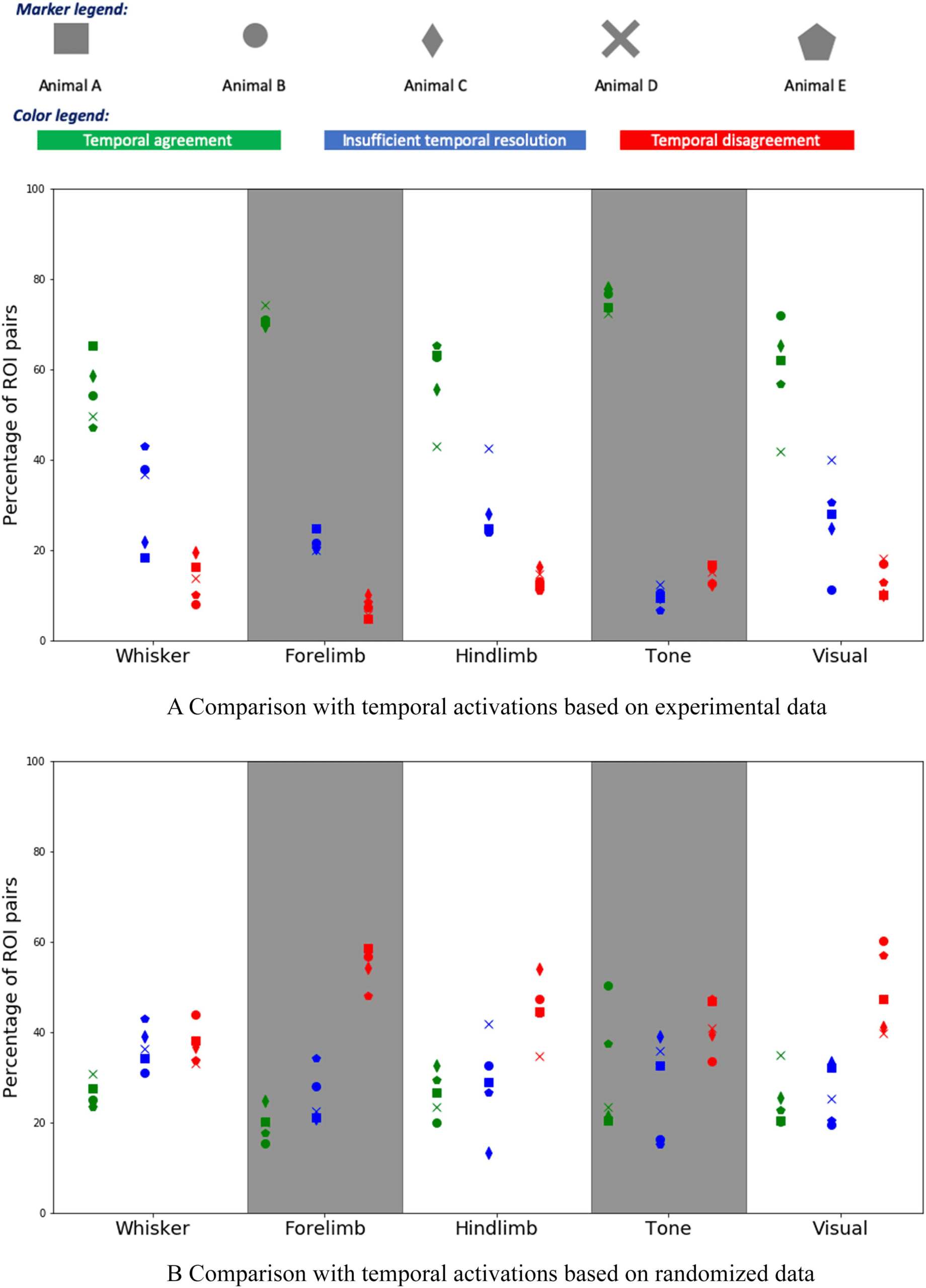Figure 5A shows the percentage of (X, Y) ROI pairs that show temporal agreement, temporal disagreement, and insufficient temporal resolution between the activation order of X and Y in the modeling results and the mouse experiments. The plot shows results for five animals and for five sensory stimulations. Even though the variability across animals is considerable, we observe that the percentage of temporal agreement pairs, averaged across the five animals, is higher than 50% and it varies between 55% to 80% depending on the sensory modality. On the other hand, the corresponding percentage of temporal disagreement is less than 10%–20%, depending on the stimulation. In the rest of the cases, the temporal resolution is not sufficient. Network Neuroscience 1040 Multisensory integration in the mouse cortical connectome l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 5. Comparison between model-based and experimental temporal ordering of ROI activa- tions. (A) The y-axis shows the percentage of (X, Y) ROI pairs that show temporal agreement (green), temporal disagreement (red), and insufficient temporal resolution (blue) between the activation or- der of X and Y in the modeling results and the mouse experiments. The plot shows results for five animals and for five sensory stimulations (a touch at the whiskers, forelimb, and hindlimb, as well as an auditory and a visual stimulation). (B) The same comparison, but here we have randomized the ROIs that are active during each frame, preserving the number of ROI activations in each frame. Note that the VSD experiments were repeated 10 times (for each animal, and for each sensory stimulation), as described in (Mohajerani et al., 2013). In our analysis however, we only have access to the aggregated results of those 10 experiments, and so we have a single sample for each animal and for each sensory stimulation. This is a limitation of the current Network Neuroscience 1041 Multisensory integration in the mouse cortical connectome Hourglass architecture: Given a set of activation cascades, the corresponding network has an hourglass architecture if almost all source-to-target paths go through a small number of intermediate nodes (the waist of the hourglass). analysis. To quantify the variability of these results, we show five point estimates, one for each animal. We also compare the ALT modeling results with a randomized sequence of experimental activations in which we preserve the number of ROIs that are activated in each frame but assign random ROI activations during each frame. This comparison shows that the ALT model has significant prediction power on the temporal sequence of ROI activations, relative to a randomized baseline. Finally, we analyzed the temporal disagreement cases between VSD experiments and mod- eling results to examine whether certain brain regions, or pairs of regions, are overrepresented in those disagreements (see SI Section “Analysis of disagreement cases between VSD data and ALT modeling results”). The main result of that analysis is that the ROIs with highest disagree- ment cases appear at the boundary of the cortical surface at the VSD datasets and they are only partially visible. So, it is likely that the VSD data may not accurately capture the time at which those boundary regions are activated after each stimulation. 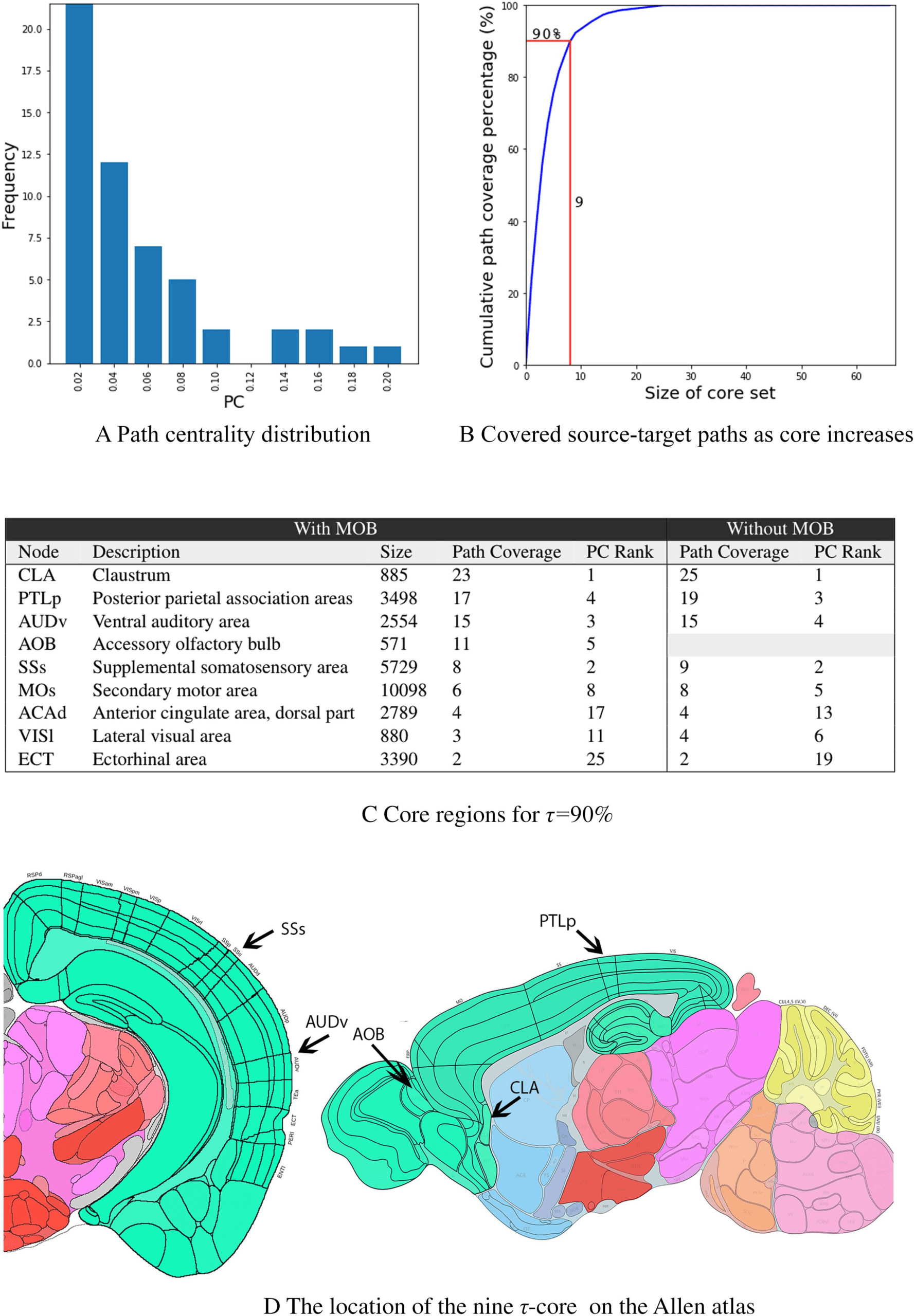Core ROIs and Hourglass Architecture In this section, we analyze the collection of 10 activation cascades (one cascade for each source) using the network analysis approach described in Section “Analysis of Activation Cascades.” The total number of source-target paths in the 10 cascades is 560. The path cen- trality distribution, which captures how many activation paths traverse each node, is shown in Figure 6A. Almost half of the nodes have very low path centrality (2% or less). On the other hand, there are four nodes with much larger path centrality—each of them covering about 20% of the source-target paths in the collection of activation cascades. These ROIs are the CLA (claustrum), SSs (supplemental somatosensory), PTLp (posterior parietal association), and AUDv (ventral auditory) areas. Some activation paths can traverse more than one of these highly central regions. For this reason, we compute the minimal set of nodes that cover a given fraction τ of all source- target paths, that is, what is referred to as τ-core (Sabrin & Dovrolis, 2017). Figure 6B shows the fraction of covered source-target paths as we increase the size of the τ-core. The “knee- shaped” shape of this curve suggests that a small set of nodes is sufficient to cover almost all source-target paths in the activation cascades, forming a bottleneck in the MSI process. For instance, a set of nine nodes is sufficient to cover more than 90% of all source-target paths. These nine ROIs account for 14.7% of the brain volume of the ROIs we consider in the network Nc. The small size of the τ-core, relative to the size of the network, suggests that the cortex follows an hourglass architecture, in which the sensory information from different modalities is first integrated (other terms could be “encoded” or “compressed”) by a small set of τ-core ROIs that form the “waist” (or bottleneck) of the hourglass. Those τ-core ROIs then drive a large number of downstream ROIs that presumably operate on multisensory information and contribute in higher level cognitive processes. The benefit of an hourglass architecture is that it reduces the dimensionality of the input, computing a more compact intermediate-level sensory representation at the waist of the hourglass. The τ-core nodes for τ = 90% are listed in Figure 6. Together with the percentage of addi- tional source-target paths that each node contributes to the τ-core (path coverage), the figure also shows the path centrality (PC) rank of that node. As expected, the node with the highest PC is the first node in the τ-core. After that point, the order in which nodes join the τ-core does not follow their PC ranking. The top three nodes (CLA, PTLp, AUDv) are sufficient to col- lectively cover about 60% of the activation paths. Note that none of these τ-core ROIs are a Network Neuroscience 1042 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 6. Path centrality and τ-core analysis. (A) Path Centrality (PC) histogram for the 67 regions in Nc, considering all source-target paths across the 10 activation cascades. (B) Cumulative path coverage by the top X core nodes for X = 1, · · · , 67. Nine regions are sufficient to cover τ = 90% of all paths. (C) Core regions for τ = 90% also showing the path coverage contributed by each of them and its path centrality rank. (D) The location of the top five core regions. Network Neuroscience 1043 Multisensory integration in the mouse cortical connectome primary sensory region (i.e., a source node). Instead, they are either ROIs that are not typically associated with a single sensory modality (CLA, PTLp, ACAd, ECT) or they are ROIs that are often thought of as secondary or supplemental to a certain sensory modality (AOB, AUDv, SSs, MOs, or VISl). If we exclude the MOB cascade, the only difference is that the τ-core will not include the AOB region. The previous analysis is based on the path centrality metric and the τ-core notion. In SI Section “Comparison with other centrality metrics and other network core notions,” we examine the correlation between the path centrality metric and other, more commonly used centrality metrics. That section also compares the nodes in the τ-core with other core node sets (rich-club and Rombach core-periphery). Further, in SI Section “Activation cascades when two sensory sources are activated simul- taneously,” we extend the previous analysis in the case that two source nodes become simul- taneously active. It turns out that the core nodes are the same with the single-source case, except that the anterior cingulate area—dorsal part (ACAd) and the ectorhinal area (ECT)—are replaced by the perirhinal area (PERI). Location of τ-Core Nodes in Activation Cascades In this section, we first investigate the topological location (rather Location Relative to Sources. than anatomical location) of the τ-core nodes relative to the source of each activation cascade. Are the τ-core nodes, which form the waist of the hourglass architecture, closer to the sources or targets of the activation cascades? And how does their location compare with the location of the sources and of other cortical ROIs? These questions are related to recent experimental work suggesting that cross-modal representations are constructed at early stages of the sensory information flow (Cayco-Gajic & Sweeney, 2018). 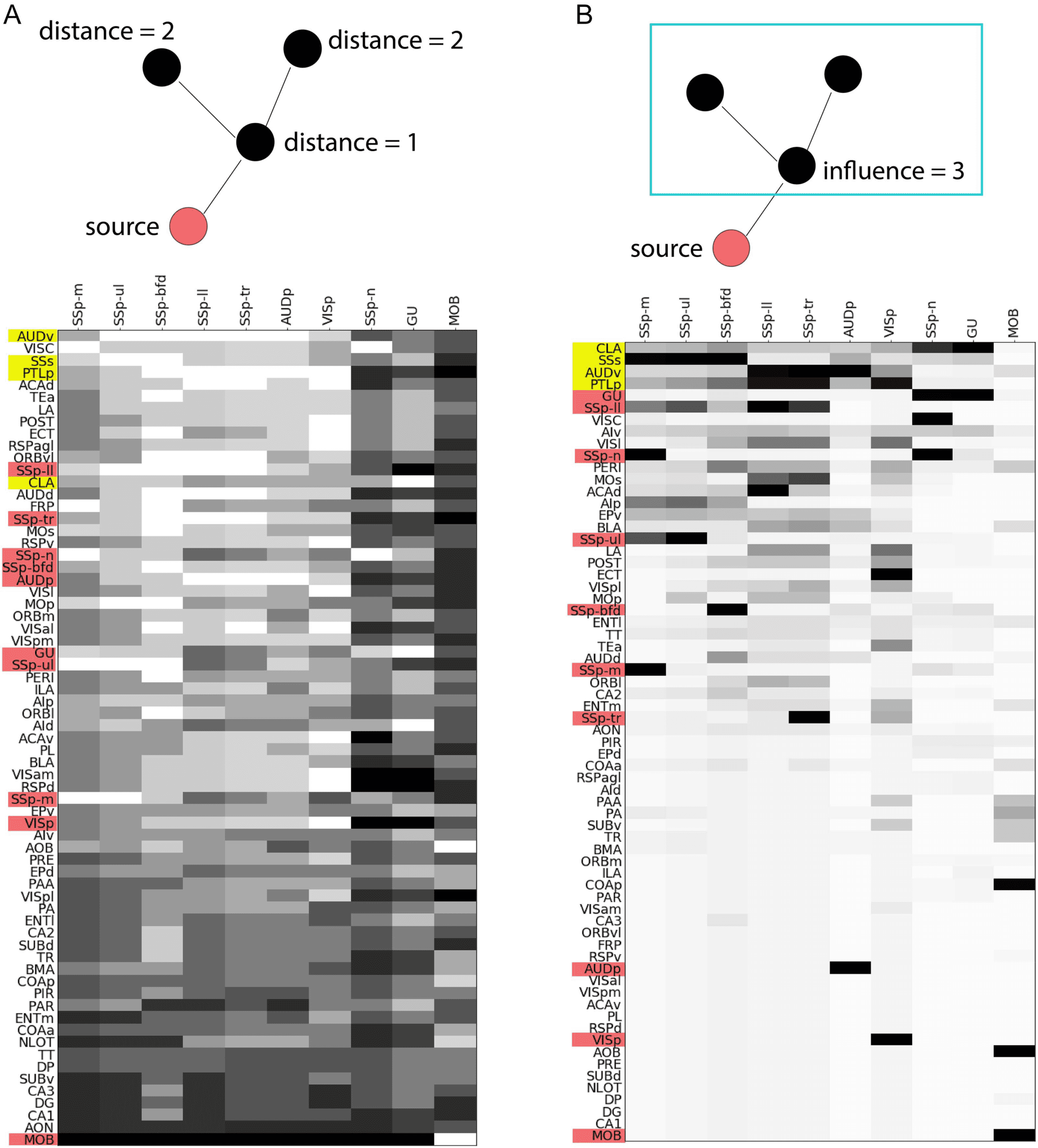We focus on the top four τ-core nodes (CLA, PTLp, AUDv, SSs), which collectively cover about τ = 70% of all source-target paths (see Figure 6). Figure 7A visualizes in gray scale the location of each node (matrix row) in each activation cascade (matrix column). Each source node (represented with red) is obviously at a distance of 0 in its own activation cascade. Note however that source nodes can be at a much larger distance from sources of other activation cascades. For instance, the primary visual cortex (VISp) appears at the maximum distance in the nose (SSp-n) and gustatory (GU) cascades. The four τ-core nodes we consider (represented with yellow rows) are relatively close to all source nodes: AUDv has the lowest average distance to all of the primary source areas, while SSs and PTLp are ranked as third and fourth. The claustrum (CLA) is slightly farther away from the sources, ranked 13th (out of 67) in the previous ranking. If we consider a higher value of τ = 90%, the additional τ-core nodes (MOs, ACAd, VISl, and ECT) are ranked as 17th, 5th, 22nd, and 9th in terms of their average distance from sources. In summary, all τ-core nodes appear in the top one third of the distance ranking, and so they are closer to the sources of the hourglass architecture than to its targets. Another way to examine the location of a node v in the Location Relative to Targets—Influence. hourglass architecture is in terms of how many nodes appear in activation paths downstream of v—a metric that we refer to as the influence of v. Figure 7B visualizes in gray scale the influence of each node (matrix row) in each activation cascade (matrix column). The source of a specific cascade has, by definition, maximal influence (i.e., all network nodes) in its own cascade—but it may have a much lower influence in other cascades. Indeed, the influence of source ROIs (shown in red) does not seem to follow a coherent pattern: The gustatory (GU) and somatosensory area of the lower limb (SSp-ll) are sources with high influence but the primary Network Neuroscience 1044 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d / . t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d . / t f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 7. Location-related metrics. In both matrices, a column represents one of the 10 activation cascades, originating at the node shown at the top of the column. (A) Each row represents the source-distance of the corresponding node from the source of that column’s cascade. White denotes a distance of one hop, while black denotes the maximum distance for that cascade. Rows are ordered in terms of the average distance (in number of hops) of the corresponding node from the sources of all activation cascades (excluding the MOB cascade, which is very different). (B) Each row represents the influence of the corresponding node, that is, the number of nodes that are reachable from that node in the activation cascade that the column represents. White denotes an influence of one (only that node), while black denotes an influence that covers all network nodes. Rows are ordered in terms of the average influence of the corresponding node across all activation cascades (excluding the MOB cascade). Network Neuroscience 1045 Multisensory integration in the mouse cortical connectome visual cortex (VISp), the primary auditory cortex (AUDp), and the main olfactory bulb (MOB) are sources with low influence in other cascades. On the other hand, the four most important τ-core nodes (CLA, PTLp, AUDv, and SSs) also occupy the top four positions in terms of influence. The next four τ-core nodes (MOs, ACAd, VISl, and ECT) have high influence as well, ranked as 12th, 13th, 9th, and 20th, respectively. Combining the previous observations about the influence of τ-core nodes as well as their distance from sources, we can summarize our findings as follows: τ-core nodes are close to most sensory sources and they also influence the activation of many downstream nodes. These two features place τ-core nodes at a location that allows them to both integrate sensory information from different sources as well as to use that integrated information in driving many downstream ROIs. Robustness of τ-Core Nodes In this section, we examine the robustness of the previous results regarding the τ-core when we randomize the edges and weights of the underlying connectome. We also examine whether the length and/or weights of these connections are responsible for the hourglass effect and for the specific regions that form the τ-core. We create ensembles of random connectomes, derived from the mouse connectome in four different ways: 1. Randomize the weight assigned to each edge, reallocating the weights of the original connectome across randomly selected connections but maintaining the topology. 2. Randomize the physical length of each edge (and thus its communication delay in the ALT model), again reallocating randomly the lengths of the original connections but maintaining the topology. 3. Randomize both the weights and the lengths assigned to each edge, as previously men- tioned. We do not maintain any correlation between weights and lengths. 4. Randomize the connectome’s topology by swapping connections between randomly se- lected pairs of nodes. This randomization method preserves the in-degree and out-degree of each node. 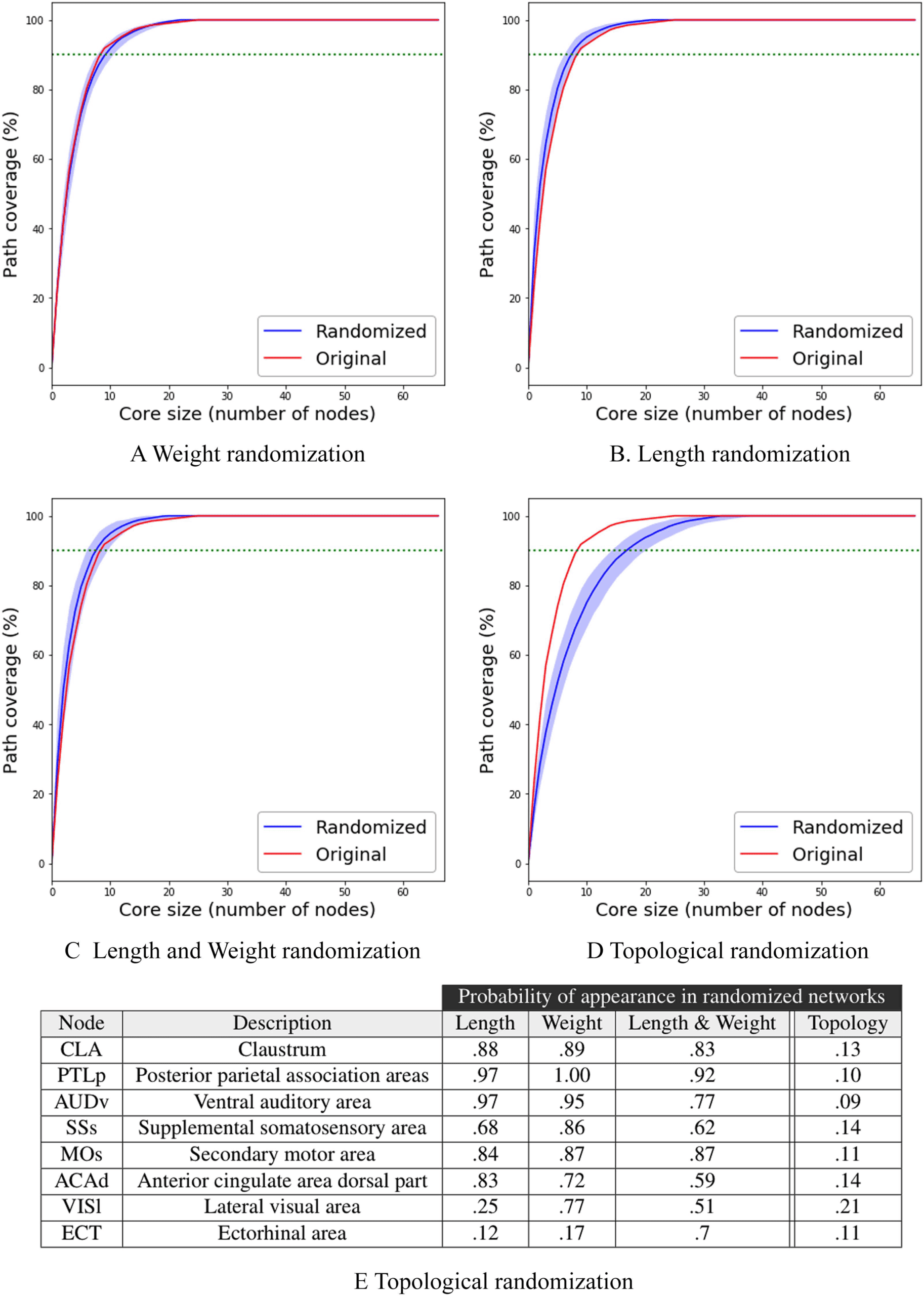Figures 8A–8D focus on the first three randomization methods: weights, lengths, and their combination. In all cases, the τ-core size of the original network is contained in the 5% confi- dence interval of 100 randomized networks. In other words, the weights and physical lengths of the connectome’s connections do not play a significant role in the number of τ-core nodes, for any value of τ On the other hand, when we randomize the topology of the connectome, the τ-core size doubles in size when τ = 90%: from 9 nodes in the original network to 18. Additionally, it takes about half of the entire network to cover all activation paths in the collection of 10 A-DAGs. So, it is the graph structure of the connectome (i.e., its topology) that leads to a small τ-core size, not the weight and/or length of the connections. Even though the weight and length of the connections do not have a strong effect on the τ-core size, do they affect the identity of the ROIs that participate in that τ-core? To answer this question, Figure 8E shows the fraction of random networks that include each of the nine τ-core nodes in Figure 6C. The claustrum (CLA), for instance, appears in the MSI τ-core of 88% of the networks that have randomized connection lengths (89% for randomized weights) Network Neuroscience 1046 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d / t . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Figure 8. Robustness results. The effect of different connectome randomization methods on the core size. Light blue shade marks the 5% to 95% values among 100 randomization runs, while the solid blue line is the median of these runs. The red line represents the τ-core size for the original connectome. The dotted green line marks the τ-core size for τ = 90%. The table at the bottom shows the fraction of random networks that include each of the eight τ-core nodes. but in only 13% of the networks that have randomized topology. The results are similar for the top six MSI τ-core nodes: They appear in the MSI τ-core of most randomized networks when we randomize connections weights and/or lengths, but they rarely appear in the MSI τ- core when we randomize the topology. For the last two MSI τ-core nodes (VISl and ECT) their Network Neuroscience 1047 Multisensory integration in the mouse cortical connectome membership in the MSI τ-core is not as robust: Randomizing connection lengths has a major effect in the appearance of VISl in the τ-core, and randomizing any aspect of the network has a major effect in the appearance of ECT in the τ-core. Finally, we have applied the ALT model on the four types of randomized connectomes (ran- domized weights, lengths, weights and lengths, and topology) and compared the resulting cas- cades with the corresponding VSD-based visual cascade. The results of this comparison (see SI Section “Modeling versus experimental results on randomized connectomes”) confirm that the randomization of lengths and/or weights has a minimal effect, while topological randomiza- tion causes a major reduction in the percentage of ROI pairs that show “temporal agreement” between modeling and experimental results. Effect of Subcortical Regions on Cortical Cascades In this section, we examine the effect of subcortical regions on cortical sensory cascades. The cascade sources remain the same 10 cortical primary sensory regions. The network on which we apply the ALT model, however, now covers the entire mouse connectome. So, the activation paths that originate from a source can now also traverse both cortical and subcortical regions One first observation is that using the same activation threshold value (θ = 0.98) as in the cortical network, the cascade from every source covers the entire brain, including all subcorti- cal regions. In other words, the activation threshold is sufficiently low to include all subcortical regions in the sensory cascades. When we consider the whole connectome, the activation paths that originate from a cer- tain source node can be classified in three major groups: C-paths (traversing only cortical regions), CS-paths (crossing the cortical-subcortical boundary once and terminating at subcor- tical regions), and CSC+-paths (crossing the cortical-subcortical boundary twice or more but terminating at cortical regions.3 Across all 10 sources, C-paths account for 25%, CS-paths for 65%, and CSC+-paths for about 10% of all paths. In the rest of this section, we focus on the union of C-paths and CSC+- paths because, first, the validation of the ALT-based cascades with VSD data is only applicable to cortical regions, and second, we are primarily interested in multisensory integration in the cortex. To examine whether the inclusion of subcortical regions affects the sensory cascades in the cortex, we examine, for a given source (e.g., visual stimulation), how similar the ALT-based cascades that terminate at cortical nodes are, with and without the CSC+-paths. Note that we do include CS-paths because they do not participate in that portion of the cascades. At the visual cascade, for instance, the Kendall τ coefficient between the two activation sequences is 92% (p value < 10−27). The correlations are similarly high for the other sources. This suggests that the inclusion of subcortical regions does not significantly affect the timing sequence at which cortical regions get activated after a sensory stimulus. We also compute the τ-core for the union of C-paths and CSC+-paths. The results are shown in Table 1 for τ = 90%. The core is now slightly larger (14 nodes instead of the 9 nodes in Figure 6C). The top six nodes are the same as in Figure 6C but in different order. The core 3 The fraction of paths that cross the cortical-subcortical paths twice or more and terminate at the subcortex is negligible. Network Neuroscience 1048 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t . / f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome Table 1. Core nodes for τ = 90% when we include the subcortical regions in the cortical sensory cascades. Description Region Size Path Coverage PC Rank Node SSs PTLp AOB CLA Supplemental somatosensory area Isocortex Posterior parietal association areas Isocortex Accessory olfactory bulb Claustrum AUDv Ventral auditory area MOs Secondary motor area Olfactory areas Cortical subplate Isocortex Isocortex RT Reticular nucleus of the thalamus Thalamus ACAd Anterior cingulate area, dorsal part Isocortex VISl PP PERI MOp MA Lateral visual area Peripeduncular nucleus Perirhinal area Primary motor area Magnocellular nucleus Isocortex Thalamus Isocortex Isocortex Pallidum ENTm Entorhinal area, medial part, Hippocampal dorsal zone formation 5,729 3,498 571 885 2,554 10,098 1,395 2,789 880 111 1,412 11,760 376 3,106 18 16 15 10 9 4 4 3 3 2 2 2 2 1 1 4 3 2 5 10 25 18 12 53 8 19 59 13 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l now also includes three subcortical regions: The reticular nucleus (RT) and the peripeduncular nucleus (PP) in the thalamus, and the magnocellular nucleus in the pallidum. The appearance of RT in this list is not surprising: This region is known to be highly inter- connected with many cortical areas, and it provides a strong modulatory input to cortex that drives the brain into different attentional states (Halassa et al., 2014) and gates the flow of many different sensory streams to cortex (Zikopoulos & Barbas, 2007). f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d . t / Mesoscale network: A graph that models the structural connectivity between brain regions, typically at the spatial resolution of few hundreds of micrometers. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 DISCUSSION This work built a suite of modeling and analysis tools to study multisensory integration from the perspective of communication dynamics. We chose to analyze the mouse connectome because of the availability of a detailed mesoscale anatomical map and because the prob- lem of multisensory integration is relatively well studied in rodents (Meijer, Mertens, Pennartz, Olcese, & Lansink, 2019). In particular, we analyzed the cortical brain network from the Allen Mouse Brain Connectivity Atlas (Oh et al., 2014) and focused on “early" dynamics of sen- sory integration. By early we specifically mean the first wave of cortical activity, starting from primary sensory areas and propagating to the whole hemisphere. This point differentiates our work from earlier models of multisensory integration (Ripp et al., 2018; Zamora-López, Zhou, & Kurths, 2010). The underlying anatomical pathways recruited by diverse sensory modalities (e.g., visual, auditory, somatosensory) branch out rapidly and become increasingly complex as they reach the higher associative cortical areas (Mohajerani et al., 2013). To capture the nonlinear and asynchronous nature of these dynamics, we used a diffusion model that can capture both nonlinearity and communication delays, called asynchronus linear thresholding (ALT). While this model is surprisingly simple, we found that ALT can closely recapitulate sensory cascades when compared with VSD datasets from sensory stimulation experiments on mice (Mohajerani et al., 2013). Network Neuroscience 1049 Multisensory integration in the mouse cortical connectome ALT is a phenomenological model that aims to describe (but not explain mechanistically) the diffusion of information at the ROI level. As such, it does not model the underlying mech- anisms of neuronal communication through chemical or electrical synapses, and it cannot capture more complex dynamics such as sustained oscillations at certain frequencies or feed- back from a newly activated region back to regions that were activated earlier. Modeling such dynamics would require more elaborate neural mass models (Destexhe & Sejnowski, 2009). The validation of such models, however, would require whole-brain neuroimaging data of fine spatial and temporal resolution (higher temporal resolution than fMRI and higher spa- tial resolution that EEG). Additionally, those more complex models may not be necessary when the goal is to map the feedforward initial propagation of brain activity after a sensory stimulation. Similar to neuroimaging modalities of similar spatial resolution (such as task-based fMRI), ALT aims to capture how a certain activity, namely the stimulation of a primary sensory region, causes the activation of other brain regions. A difference with fMRI or MEG, however, is that the resulting activation cascades can be analyzed to infer interactions between ROIs that par- ticipate in the cascade. Additionally, ALT depends on the communication delays and weights of the connections between brain regions. Thus, it produces a timeline of activation events, one for each ROI that participates in the cascade. The length of the time interval between activation events, at least in relative terms, can be compared with experimental results from neuroimaging modalities such as VSD (used in this study) or calcium imaging. We emphasize that ALT is not the only plausible modeling approach to study the diffusion of sensory information in the brain. There are several other models in the literature that attempt to capture communication dynamics in the brain based on shortest path lengths, search infor- mation (Goñi et al., 2014), navigation (Seguin, van den Heuvel, & Zalesky, 2018), diffusion efficiency (Goñi et al., 2013), and others (Avena-Koenigsberger, Misic, & Sporns, 2018). Which of these models produces the most accurate results, compared with experimentally observed activation cascades, is an open question that deserves further investigation. l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d / t . A major result of this study is that relatively few cortical regions are responsible for integrat- ing almost all sensory information. This finding supports the idea that multisensory integration is performed through an hourglass architecture. The benefit of an hourglass architecture is that first it reduces the input dimensionality of the sensory stimulus at few intermediate-level modules that reside at the hourglass waist. Second, it reuses those compressed intermediate- level representations across higher level tasks, reducing redundancy between the latter. The hourglass analysis framework was first developed in Sabrin & Dovrolis (2017), and it has been recently applied in the connectome of C. elegans (Sabrin, Wei, van den Heuvel, & Dovrolis, 2020). There are two fundamental differences in our study: (a) We rely on communication dynamics, while Sabrin et al. (2020) uses a predefined set of “routing mechanisms” to con- struct ensembles of sensory pathways. (b) The sources and targets of the C. elegans cascade are the sensory and motor neurons, respectively. Nonetheless, it is interesting that the hour- glass architecture emerges in both studies. One possibility is that this architecture is selected by evolution because it drives a network towards reusing a small set of intermediate functions in constructing a range of redundant output functions. f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Rather than studying each sensory cascade in isolation, our analysis framework is based on the combination of all sensory cascades. Comparative and competitive cascades have been studied in Miši´c et al. (2015) to quantify the combined effect of multiple cascades, using si- multaneously activated source nodes. Sensory stimuli of different modalities, however, do not Network Neuroscience 1050 Multisensory integration in the mouse cortical connectome need to arrive at the cortex simultaneously in order to be integrated (Noel, Łukowska, Wallace, & Serino, 2016). Different sensory stimuli travel at different speeds through body receptors (Zhou et al., 2019). The analysis framework that we followed constructs unisensory cascades and merges their activation paths. We have also experimented with cascades originating from two simultaneously activated sources (see SI Section “Activation cascades when two sensory sources are activated simultaneously”). The hourglass architecture is still observed in that case, and the core nodes are mostly the same. The claustrum is known for its anatomical uniqueness (Baizer, Sherwood, Noonan, & Hof, 2014) and its precise function has been enigmatic (Mathur, 2014; Van Horn, 2019). The late F. Crick has hypothesized that the claustrum may be a potential gateway to consciousness (Crick & Koch, 2005). More recent results have demonstrated that the claustrum is important in gating sensory information, and in attention mechanisms in visual perception (Van Horn, 2019). These and other studies provide strong evidence that the claustrum is a crucial node for multisensory integration. Our findings are in agreement with this growing body of work. The posterior parietal cortex is the second most important region for MSI, according to our analysis. This stems from its strong and immediate connectivity to primary sensory regions and its projections to motor areas. PTLp’s connectivity points to its role in integrating sensory infor- mation to direct immediate motor commands (Whitlock, 2017). The experiments of Nikbakht, Tafreshiha, Zoccolan, and Diamond (2018) provide direct evidence that PTLp is multisensory at both the behavioural and the neurophysiological levels, and it provides sensory-independent information about the orientation and categorization of objects in the environment. We refer the reader to Mohan, de Haan, Mansvelder, & de Kock (2018) for further discussion. Three additional core nodes have been associated with specific sensory modalities in the past: ventral auditory area (AUDv), supplemental somatosensory area (SSs), and lateral visual area (VISl). However, all of them have also been implicated to some extent with multisensory processing. For instance, Hishida, Kudoh, and Shibuki (2014) found that activity propagating to the parietal association area passes through the ventral auditory region, irrespective of the sensory stream source (visual, auditory, or somatosensory). Similarly, Menzel and Barth (2005) suggest that SSs has a major role in bringing context to the sensory pathways (Romo, Hernández, Zainos, Lemus, & Brody, 2002). VISl is on the dorsal visual stream is associated mostly with spatial location action guidance (Marshel, Garrett, Nauhaus, & Callaway, 2011), while the other secondary visual areas participate in the ventral stream (Hebart & Hesselmann, 2012). Various nuclei in the thalamus or the superior colliculus are known to be crucial in MSI (Stein, Stanford, & Rowland, 2014). An integrated model of both cortical and subcortical activ- ity, in the context of sensory integration, may help in the future to explain the complex cortico- thalamic feedback mechanisms (Jiang, Wallace, Jiang, Vaughan, & Stein, 2001; Tyll, Budinger, & Noesselt, 2011). Disentangling such communication dynamics requires working at finer spatial resolutions, and including distinct cortical layers (laminar divisions) (Goulas, Zilles, & Hilgetag, 2018). Incorporating high-resolution (Knox et al., 2018) and cell-type-specific (Harris et al., 2018) information about connectivity in our pipeline is an interesting direction that can allow segregation of different communication channels. By increasing the spatial res- olution and the complexity of the model dynamics, we may be able to capture more complex population-level activity patterns (e.g., Wilson-Cowan [Destexhe & Sejnowski, 2009]) and bet- ter understand the role of mesoscale network topology in constructing a coherent perceptual state from raw sensory streams. Network Neuroscience 1051 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome ACKNOWLEDGMENTS The authors are deeply grateful to Professor Majid Mohajerani for providing the VSD data used in this study, and his student Zahra Rezaei for her help with that dataset. SUPPORTING INFORMATION Supporting information for this article is available at https://doi.org/10.1162/netn_a_00164. AUTHOR CONTRIBUTIONS Kamal Shadi: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Software; Visualization. Eva Dyer: Conceptualization; Supervision; Visualization; Writing - Review & Editing. Constantine Dovrolis: Conceptualization; Data curation; Formal analysis; Funding acquisition; Investigation; Methodology; Project administration; Resources; Supervi- sion; Validation; Visualization; Writing - Original Draft; Writing - Review & Editing. FUNDING INFORMATION Constantine Dovrolis, Defense Sciences Office, DARPA (http://dx.doi.org/10.13039/100006502), Award ID: HR0011-18-2-0019. Eva Dyer, National Science Foundation (http://dx.doi.org/10 .13039/100000001), Award ID: IIS-175587. REFERENCES Abdelnour, F., Dayan, M., Devinsky, O., Thesen, T., & Raj, A. (2018). Functional brain connectivity is predictable from anatomic net- work’s Laplacian eigen-structure. NeuroImage, 172, 728–739. DOI: https://doi.org/10.1016/j.neuroimage.2018.02.016, PMID: 29454104, PMCID: PMC6170160 Abdelnour, F., Voss, H. U., & Raj, A. (2014). Network diffusion accurately models the relationship between structural and func- tional brain connectivity networks. NeuroImage, 90, 335–347. DOI: https://doi.org/10.1016/j.neuroimage.2013.12.039, PMID: 24384152, PMCID: PMC3951650 Avena-Koenigsberger, A., Misic, B., & Sporns, O. (2018). Communi- cation dynamics in complex brain networks. Nature Reviews Neuroscience, 19(1), 17. DOI: https://doi.org/10.1038/nrn.2017 .149, PMID: 29238085 Baizer, J. S., Sherwood, C. C., Noonan, M., & Hof, P. R. (2014). Comparative organization of the claustrum: What does struc- ture tell us about function? Frontiers in Systems Neuroscience, 8, 117. DOI: https://doi.org/10.3389/fnsys.2014.00117, PMID: 25071474, PMCID: PMC4079070 Barrat, A., Barthelemy, M., & Vespignani, A. (2008). Dynamical pro- cesses on complex networks. Cambridge University Press. DOI: https://doi.org/10.1017/CBO9780511791383 Beggs, J. M., & Timme, N. (2012). Being critical of criticality in the brain. Frontiers in Physiology, 3, 163. DOI: https://doi.org/10.3389 /fphys.2012.00163, PMID: 22701101, PMCID: PMC3369250 Bota, M., Sporns, O., & Swanson, L. W. (2015). Architecture of the cerebral cortical association connectome underlying cognition. Proceedings of the National Academy of Sciences, 112(16), E2093–E2101. DOI: https://doi.org/10.1073/pnas.1504394112, PMID: 25848037, PMCID: PMC4413280 Cappe, C., & Barone, P. (2005). Heteromodal connections support- ing multisensory integration at low levels of cortical processing in the monkey. European Journal of Neuroscience, 22(11), 2886– 2902. DOI: https://doi.org/10.1111/j.1460-9568.2005.04462.x, PMID: 16324124 Cayco-Gajic, N., & Sweeney, Y. (2018). Delving deep into cross- modal integration. Journal of Neuroscience, 38(29), 6442–6444. DOI: https://doi.org/10.1523/JNEUROSCI.0988-18.2018, PMID: 30021764, PMCID: PMC6052241 Chialvo, D. R. (2010). Emergent complex neural dynamics. Nature Physics, 6(10), 744. DOI: https://doi.org/10.1038/nphys1803 Crick, F. C., & Koch, C. (2005). What is the function of the claus- trum? Philosophical Transactions of the Royal Society B: Biologi- cal Sciences, 360(1458), 1271–1279. DOI: https://doi.org/10 .1098/rstb.2005.1661, PMID: 16147522, PMCID: PMC1569501 Destexhe, A., & Sejnowski, T. J. (2009). The Wilson–Cowan model, 36 years later. Biological Cybernetics, 101(1), 1–2. DOI: https:// doi.org/10.1007/s00422-009-0328-3, PMID: 19662434, PMCID: PMC2866289 Fagiolo, G. (2007). Clustering in complex directed networks. Physical Review E, 76(2), 026107. DOI: https://doi.org/10.1103 /PhysRevE.76.026107, PMID: 17930104 Falchier, A., Clavagnier, S., Barone, P., & Kennedy, H. (2002). Anato- mical evidence of multimodal integration in primate striate cor- tex. Journal of Neuroscience, 22(13), 5749–5759. DOI: https:// doi.org/10.1523/JNEUROSCI.22-13-05749.2002, PMID: 12097528, PMCID: PMC6758216 Gallos, L. K., Makse, H. A., & Sigman, M. (2012). A small world of weak ties provides optimal global integration of self-similar mod- ules in functional brain networks. Proceedings of the National Network Neuroscience 1052 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . t / / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome Academy of Sciences, 109(8), 2825–2830. DOI: https://doi .org/10.1073/pnas.1106612109, PMID: 22308319, PMCID: PMC3286928 Ghazanfar, A. A., & Schroeder, C. E. (2006). Is neocortex essentially multisensory? Trends in Cognitive Sciences, 10(6), 278–285. DOI: https://doi.org/10.1016/j.tics.2006.04.008, PMID: 16713325 Goñi, J., Avena-Koenigsberger, A., Velez de Mendizabal, N., van den Heuvel, M. P., Betzel, R. F., & Sporns, O. (2013). Explor- ing the morphospace of communication efficiency in complex networks. PLoS ONE, 8(3), e58070. DOI: https://doi.org/10.1371 /journal.pone.0058070, PMID: 23505455, PMCID: PMC3591454 Goñi, J., van den Heuvel, M. P., Avena-Koenigsberger, A., De Mendizabal, N. V., Betzel, R. F., Griffa, A., . . . Sporns, O. (2014). Resting-brain functional connectivity predicted by analytic mea- sures of network communication. Proceedings of the National Academy of Sciences, 111(2), 833–838. DOI: https://doi.org/10 .1073/pnas.1315529111,PMID: 24379387, PMCID: PMC3896172 Goulas, A., Zilles, K., & Hilgetag, C. C. (2018). Cortical gradients and laminar projections in mammals. Trends in Neurosciences, 41(11), 775–788. DOI: https://doi.org/10.1016/j.tins.2018.06 .003, PMID: 29980393 Granovetter, M. (1978). Threshold models of collective behavior. American Journal of Sociology, 83(6), 1420–1443. DOI: https:// doi.org/10.1086/226707 Halassa, M. M., Chen, Z., Wimmer, R. D., Brunetti, P. M., Zhao, S., Zikopoulos, B., . . . Wilson, M. A. (2014). State-dependent archi- tecture of thalamic reticular subnetworks. Cell, 158(4), 808–821. DOI: https://doi.org/10.1016/j.cell.2014.06.025, PMID: 25126786, PMCID: PMC4205482 Harris, J. A., Mihalas, S., Hirokawa, K. E., Whitesell, J. D., Knox, J., Bernard, A., . . . Zeng, H. (2018). The organization of intracortical connections by layer and cell class in the mouse brain. bioRxiv: 202061. DOI: https://doi.org/10.1101/292961 Hebart, M. N., & Hesselmann, G. (2012). What visual information is processed in the human dorsal stream? Journal of Neuroscience, 32(24), 8107–8109. DOI: https://doi.org/10.1523/JNEUROSCI .1462-12.2012, PMID: 22699890, PMCID: PMC6703654 Hishida, R., Kudoh, M., & Shibuki, K. (2014). Multimodal cortical sensory pathways revealed by sequential transcranial electrical stimulation in mice. Neuroscience Research, 87, 49–55. DOI: https://doi.org/10.1016/j.neures.2014.07.004, PMID: 25066521 Jiang, W., Wallace, M. T., Jiang, H., Vaughan, J. W., & Stein, B. E. (2001). Two cortical areas mediate multisensory integration in superior colliculus neurons. Journal of Neurophysiology, 85(2), 506–522. DOI: https://doi.org/10.1152/jn.2001.85.2.506, PMID: 11160489 Johnson, D. M., Illig, K. R., Behan, M., & Haberly, L. B. (2000). New features of connectivity in piriform cortex visualized by intracellular injection of pyramidal cells suggest that “primary” olfactory cortex functions like “association” cortex in other sen- sory systems. Journal of Neuroscience, 20(18), 6974–6982. DOI: https://doi.org/10.1523/JNEUROSCI.20-18-06974.2000, PMID: 10995842, PMCID: PMC6772836 Knox, J. E., Harris, K. D., Graddis, N., Whitesell, J. D., Zeng, H., Harris, J. A., . . . Mihalas, S. (2018). High-resolution data-driven model of the mouse connectome. Network Neuroscience, 3(1), 217–236. DOI: https://doi.org/10.1162/netn_a_00066, PMID: 30793081, PMCID: PMC6372022 Markov, N. T., Ercsey-Ravasz, M., Van Essen, D. C., Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). Cortical high-density coun- Science, 342(6158), 1238406. DOI: terstream architectures. https://doi.org/10.1126/science.1238406, PMID: 24179228, PMCID: PMC3905047 Marshel, J. H., Garrett, M. E., Nauhaus, I., & Callaway, E. M. (2011). Functional specialization of seven mouse visual cortical areas. Neuron, 72(6), 1040–1054. DOI: https://doi.org/10.1016/j.neuron .2011.12.004, PMID: 22196338, PMCID: PMC3248795 Mathur, B. N. (2014). The claustrum in review. Frontiers in Systems Neuroscience, 8, 48. DOI: https://doi.org/10.3389/fnsys.2014.00048, PMID: 24772070, PMCID: PMC3983483 Meijer, G. T., Mertens, P. E., Pennartz, C. M., Olcese, U., & Lansink, C. S. (2019). The circuit architecture of cortical multisensory pro- cessing: Distinct functions jointly operating within a common anatomical network. Progress in neurobiology, 174, 1–15. DOI: https://doi.org/10.1016/j.pneurobio.2019.01.004, PMID: 30677428 Menzel, R. R., & Barth, D. S. (2005). Multisensory and secondary somatosensory cortex in the rat. Cerebral Cortex, 15(11), 1690–1696. DOI: https://doi.org/10.1093/cercor/bhi045, PMID: 15703251 Meredith, M. A. (2002). On the neuronal basis for multisensory convergence: A brief overview. Cognitive Brain Research, 14(1), 31–40. DOI: https://doi.org/10.1016/S0926-6410(02)00059-9 Miši´c, B., Betzel, R. F., Nematzadeh, A., Goni, J., Griffa, A., Hagmann, P., . . . Sporns, O. (2015). Cooperative and competitive spreading dynamics on the human connectome. Neuron, 86(6), 1518–1529. DOI: https://doi.org/10.1016/j.neuron.2015.05.035, PMID: 26087168 Mohajerani, M. H., Chan, A. W., Mohsenvand, M., LeDue, J., Liu, R., McVea, D. A., . . . Murphy, T. H. (2013). Spontaneous cortical activity alternates between motifs defined by regional axonal projections. Nature Neuroscience, 16(10), 1426. DOI: https://doi.org/10.1038/nn.3499, PMID: 23974708, PMCID: PMC3928052 Mohan, H., de Haan, R., Mansvelder, H. D., & de Kock, C. P. (2018). The posterior parietal cortex as integrative hub for whisker sensori- motor information. Neuroscience, 368, 240–245. DOI: https:// doi.org/10.1016/j.neuroscience.2017.06.020, PMID: 28642168 Morrill, R. J., & Hasenstaub, A. R. (2018). Visual information present in infragranular layers of mouse auditory cortex. Journal of Neuro- science, 3102–3117. DOI: https://doi.org/10.1523/JNEUROSCI .3102-17.2018, PMID: 29440554, PMCID: PMC5852663 Mota, B., & Herculano-Houzel, S. (2012). How the cortex gets its folds: An inside-out, connectivity-driven model for the scal- ing of mammalian cortical folding. Frontiers in neuroanatomy, 6, 3. DOI: https://doi.org/10.3389/fnana.2012.00003, PMID: 22347170, PMCID: PMC3270328 Newman, M. (2018). Networks. New York, NY: Oxford University Press. DOI: https://doi.org/10.1093/oso/9780198805090.001 .0001 Nikbakht, N., Tafreshiha, A., Zoccolan, D., & Diamond, M. E. (2018). Supralinear and supramodal integration of visual and tactile signals in rats: psychophysics and neuronal mechanisms. Network Neuroscience 1053 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / / t e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3 Multisensory integration in the mouse cortical connectome Neuron, 97(3), 626–639. DOI: https://doi.org/10.1016/j.neuron .2018.01.003, PMID: 29395913, PMCID: PMC5814688 Sporns, O. (2013). Structure and function of complex brain net- works. Dialogues in Clinical Neuroscience, 15(3), 247. Noel, J.-P., Łukowska, M., Wallace, M., & Serino, A. (2016). Multi- sensory simultaneity judgment and proximity to the body. Journal of Vision, 16(3), 21–21. DOI: https://doi.org/10.1167/16.3.21, PMID: 26891828, PMCID: PMC4777235 Oh, S. W., Harris, J. A., Ng, L., Winslow, B., Cain, N., Mihalas, S., . . . Zeng, H. (2014). A mesoscale connectome of the mouse brain. Nature, 508(7495), 207–214. DOI: https://doi.org/10.1038 /nature13186, PMID: 24695228, PMCID: PMC5102064 Park, H.-J., & Friston, K. (2013). Structural and functional brain networks: From connections to cognition. Science, 342(6158), 1238411. DOI: https://doi.org/10.1126/science.1238411, PMID: 24179229 Plenz, D., & Thiagarajan, T. C. (2007). The organizing principles of neuronal avalanches: cell assemblies in the cortex? Trends in Neurosciences, 30(3), 101–110. DOI: https://doi.org/10.1016/j .tins.2007.01.005, PMID: 17275102 Ripp, I., zur Nieden, A.-N., Blankenagel, S., Franzmeier, N., Lundström, J. N., & Freiherr, J. (2018). Multisensory integration processing during olfactory-visual stimulation—An fMRI graph theoretical network analysis. Human Brain Mapping, 39(9), 3713–3727. DOI: https://doi.org/10.1002/hbm.24206, PMID: 29736907, PMCID: PMC6866557 Romo, R., Hernández, A., Zainos, A., Lemus, L., & Brody, C. D. (2002). Neuronal correlates of decision-making in secondary so- matosensory cortex. Nature Neuroscience, 5(11), 1217. DOI: https://doi.org/10.1038/nn950, PMID: 12368806 Sabrin, K. M., & Dovrolis, C. (2017). The hourglass effect in hierar- chical dependency networks. Network Science, 5(4), 490–528. DOI: https://doi.org/10.1017/nws.2017.22 Sabrin, K. M., Wei, Y., van den Heuvel, M., & Dovrolis, C. (2020). The hourglass organization of the Caenorhabditis elegans connectome. PLoS Computational Biology, 16(2), e1007526. DOI: PMID: https://doi.org/10.1371/journal.pcbi.1007526, 32027645, PMCID: PMC7029875 Sanz-Leon, P., Knock, S. A., Spiegler, A., & Jirsa, V. K. (2015). Math- ematical framework for large-scale brain network modeling in the virtual brain. NeuroImage, 111, 385–430. DOI: https://doi.org /10.1016/j.neuroimage.2015.01.002, PMID: 25592995 Seguin, C., van den Heuvel, M. P., & Zalesky, A. (2018). Naviga- tion of brain networks. Proceedings of the National Academy of Sciences, 115(24), 6297–6302. DOI: https://doi.org/10.1073 /pnas.1801351115, PMID: 29848631, PMCID: PMC6004443 Seilheimer, R. L., Rosenberg, A., & Angelaki, D. E. (2014). Models and processes of multisensory cue combination. Current Opinion in Neurobiology, 25, 38–46. DOI: https://doi.org/10.1016/j.conb .2013.11.008, PMID: 24709599, PMCID: PMC3980502 Shine, J. M., Breakspear, M., Bell, P. T., Martens, K. A. E., Shine, R., Koyejo, O., . . . Poldrack, R. A. (2019). Human cognition involves the dynamic integration of neural activity and neuromodulatory systems. Nature Neuroscience, 22(2), 289. DOI: https://doi.org /10.1038/s41593-018-0312-0, PMID: 30664771 Srinivasan, S., & Stevens, C. F. (2017). A quantitative description of the mouse piriform cortex. bioRxiv:099002. DOI: https://doi.org /10.1101/099002 Stein, B. E., & Meredith, M. A. (1993). The merging of the senses. MIT Press. Stein, B. E., Stanford, T. R., & Rowland, B. A. (2014). Development of multisensory integration from the perspective of the individual neuron. Nature Reviews Neuroscience, 15(8), 520. DOI: https://doi .org/10.1016/j.conb.2013.11.008, PMID: 24709599, PMCID: PMC3980502 Sun, T., & Hevner, R. F. (2014). Growth and folding of the mam- malian cerebral cortex: From molecules to malformations. Na- ture Reviews Neuroscience, 15(4), 217. Taylor, P., Hobbs, J., Burroni, J., & Siegelmann, H. (2015). The global landscape of cognition: Hierarchical aggregation as an organi- zational principle of human cortical networks and functions. Sci- entific Reports, 5, 18112. Tyll, S., Budinger, E., & Noesselt, T. (2011). Thalamic influences on multisensory integration. Communicative & Integrative Biology, 4(4), 378–381. DOI: https://doi.org/10.4161/cib.15222 Van Horn, J. D. (2019). What is old is new again: Investigating and analyzing the mysteries of the claustrum. Springer. DOI: https://doi.org/10.1007/s12021-018-9411-z, PMID: 30617757 Whitlock, J. R. (2017). Posterior parietal cortex. Current Biology, 27(14), R691–R695. DOI: https://doi.org/10.1016/j.cub.2017.06 .007, PMID: 28743011 Worrell, J. C., Rumschlag, J., Betzel, R. F., Sporns, O., & Miši´c, B. (2017). Optimized connectome architecture for sensory-motor inte- gration. Network Neuroscience, 1(4), 415–430. DOI: https://doi .org/10.1162/NETN_a_00022, PMID: 30090872, PMCID: PMC6063718 Zamora-López, G., Zhou, C., & Kurths, J. (2010). Cortical hubs form a module for multisensory integration on top of the hi- Frontiers in Neuroinformatics, erarchy of cortical networks. 4, 1. DOI: https://doi.org/10.3389/neuro.11.001.2010, PMID: 20428515, PMCID: PMC2859882 Zhang, J., Zhang, Y., Wang, L., Sang, L., Yang, J., Yan, R., . . . Qui, M. (2017). Disrupted structural and functional connectivity net- works in ischemic stroke patients. Neuroscience, 364, 212–225. DOI: https://doi.org/10.1016/j.neuroscience.2017.09.009, PMID: 28918259 Zikopoulos, B., & Barbas, H. Zhou, G., Lane, G., Noto, T., Arabkheradmand, G., Gottfried, J. A., Schuele, S. U., . . . Zelano, C. (2019). Human olfactory-auditory integration requires phase synchrony between sensory cortices. Nature Communications, 10(1), 1168. DOI: https://doi.org1038 /s41467-019-09091-3, PMID: 30858379, PMCID: PMC6411726 (2007). Circuits for multisensory integration and attentional modulation through the prefrontal cortex and the thalamic reticular nucleus in primates. Reviews in the Neurosciences, 18(6), 417–438. DOI: https://doi.org/10 .1515/REVNEURO.2007.18.6.417, PMID: 18330211, PMCID: PMC2855189 Network Neuroscience 1054 l D o w n o a d e d f r o m h t t p : / / d i r e c t . m i t . / t / e d u n e n a r t i c e - p d l f / / / / 4 4 1 0 3 0 1 8 6 7 1 4 0 n e n _ a _ 0 0 1 6 4 p d t / . f b y g u e s t t o n 0 7 S e p e m b e r 2 0 2 3

Scarica il pdf